Lectiones Opticae
[1][2][3]Inventio Telescopiorum nupera plerosque Geometras ita exercuit, ut nihil in Optica non tritum, nullum inventioni præterea locum alijs reliquisse videantur. Et insuper cùm dissertationes quas hic non ita pridem audivistis, tantâ rerum Opticarum varietate, novorum copiâ, et accuratissimis eorundem demonstrationibus fuerint compositæ; frustranei fortè videantur conatus et labor inutilis, si ego scientiam hanc iterum tractandam suscepero. Verùm cùm Geometras in quadam lucis proprietate, quæ ad Refractiones spectat hucusque hallucinatos videam, dum demonstrationibus suis Hypothesin quandam Physicam haud benè stabilitam tacitè supponunt: non ingratum me facturum judico, si principia Scientiæ hujus examini severiori subjiciam, et quæ ego de ijs simul excogitavi, et experientia multiplici habeo comperta, subnectam ijs, quæ Reverendus meus Antecessor hic loci postrema dixit.
Imaginantur sibi Dioptrices studiosi, quòd Perspicilla ad quemlibet perfectionis gradum perduci possent, si modò vitris dum perpoliuntur, geometricam, quam vellent, figuram communicare concederetur. Et in eum finem instrumenta varia fuerunt excogitata, quibus vitra in figuras Hyperbolicas vel etiam Parabolicas contererentur; Sed exacta figurarum istarum fabricatio nemini hucusq́ue successit. Scilicet aratur littus; et nè labores suos in negotio desperato diutiùs insumant, ijs audeo spondere, quòd licet omnia fierent perquam felicitèr, nihil minùs tamen quàm votis suis responderent: Etenim vitra licèt efformentur secundum figuras in istum finem optimas, quæ possunt excogitari, tamen non duplo plus præstabunt quam sphærica, æquali politurâ perfecta. Hæc autem non ideò loquor, quasi peccatum esse a scriptoribus Optices contenderem; illi enim omnia pro intentione demonstrationum suarum accuratè quidem et verissimè dixerunt, sed aliquid tamen idq́ue maximi momenti reliquerunt posteris inveniendum. Scilicet in refractionibus irregularitatem quandam reperio, quæ omnia perturbat, et non solum efficit, ut figuræ Conicarum Sphæricas non multùm superent, sed etiam ut sphæricæ multò minus præstent quàm præstarent, si dicta refractio esset uniformis.
Itaque in Dioptricâ pedem fixi non ut pertractarem de integro, sed tantùm, ut hanc de natura lucis proprietatem rimarer primò, deinde ut ostenderem quantum ex hac proprietate perfectio Dioptrices impeditur, & quo pacto incommodum istud, quatenus natura rei sinit, devitetur. Ubi nonnulla proferam quæ ad Telescopiorum, juxta et Microscopiorum, tum Theoriam tum Praxin spectant; ostendens quod Optices summa perfectio (præter opinionem receptam) ex Dioptrica et Catoptrica mixtis petenda est. Ac interea discrimen colorum et eorum genesin a Prismatibus, et corporibus etiam coloratis fusè explicabo.
[4]De luce itaque compertum habeo, quòd radij ejus quoad quantitatem refractionis ab invicem differunt: Ex ijs qui omnes habent eundem angulum incidentiæ, alij angulum refractionis aliquantò majorem alijs habebunt. Plenioris illustrationis gratiâ, sit EFG superficies quælibet refringens puta vitrea; Et ducàtur quævis OF 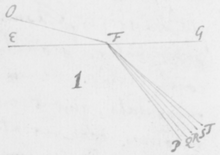 huic occurrens in F, et cum ea efficiens angulum OFE acutum: Concipe etiam radios solares per istam lineam OF sibi continuò successivos fluere, ita ut alij post alios in punctum F impingant, ibidemque in medium densius refringantur. Iam ex opinione receptâ hi radij eandem habentes incidentiam, eandem quoque omnes refractionem habere debent, puta in lineam FR. At contrarium compertum habeo; scilicet quòd postquam refringuntur, divergent ab invicem; quasi quidam refringerentur in lineam FP, alij in lineam FQ, & alij in lineas FR, FS, & FT; ac alij etiam innumeri per spatia istis intermedia, ut et ultra citraque nonnulli pervagantes; prout radius quilibet ad refractionem majorem minoremve patiendam sit aptus. Invenio præterea, quòd radij FP maximè refracti colores purpureos producunt et illi FT minimè refracti rubros, qui autem hisce intermedij pergunt FQ, FR, FS, ij colores intermedios nempe cæruleos , virides et flavos generant. Et sic radij prout apti sunt ut alij alijs magis atque magis refringantur, hos ordine colores, rubrum, flavum, viridem, cæruleum, et purpureum generant, unà cum omnibus intermedijs quos in Iride liceat conspicere. Unde productio colorum Prismatis et Iridis patebit facilè: sed his jam perfunctoriè notatis, quæ de coloribus dicenda sunt, in posterum differo.
huic occurrens in F, et cum ea efficiens angulum OFE acutum: Concipe etiam radios solares per istam lineam OF sibi continuò successivos fluere, ita ut alij post alios in punctum F impingant, ibidemque in medium densius refringantur. Iam ex opinione receptâ hi radij eandem habentes incidentiam, eandem quoque omnes refractionem habere debent, puta in lineam FR. At contrarium compertum habeo; scilicet quòd postquam refringuntur, divergent ab invicem; quasi quidam refringerentur in lineam FP, alij in lineam FQ, & alij in lineas FR, FS, & FT; ac alij etiam innumeri per spatia istis intermedia, ut et ultra citraque nonnulli pervagantes; prout radius quilibet ad refractionem majorem minoremve patiendam sit aptus. Invenio præterea, quòd radij FP maximè refracti colores purpureos producunt et illi FT minimè refracti rubros, qui autem hisce intermedij pergunt FQ, FR, FS, ij colores intermedios nempe cæruleos , virides et flavos generant. Et sic radij prout apti sunt ut alij alijs magis atque magis refringantur, hos ordine colores, rubrum, flavum, viridem, cæruleum, et purpureum generant, unà cum omnibus intermedijs quos in Iride liceat conspicere. Unde productio colorum Prismatis et Iridis patebit facilè: sed his jam perfunctoriè notatis, quæ de coloribus dicenda sunt, in posterum differo.
[5] Sententia nostra de hac re in genere sic explicatâ, ne putetis fabulas pro veris enarratas esse, rationes et experimenta, quibus isthæc innituntur, continuò proferam. Et quoniam experimentum quoddam Prismatis valde obvium mihi primò dedit occasionem excogitandi reliqua, istud primum explicabo. Sit  F foramen aliquod in pariete vel fenestrâ Cubiculi, per quod radij solares OF trajiciantur, reliquis ubique foraminibus diligenter obturatis, nè lux alibi ingrediatur. Ista autem obscuratio Cubiculi non est omninò necessaria, sed efficit tantùm ut Experimentum evadat aliquantò evidentius. Deinde Prisma triangulare vitreum AαBβCκ ad foramen istud applicetur, quod radios OF per se trajectos refringat versus PYTZ, quos radios opposito pariete vel papyro aliquâ ad distantiam a Prismate satis magnam objectâ terminatos, videbis in figuram PYTZ valdè oblongam efformari: cujus nempe longitudo PT sit quadruplex latitudinis YZ, et amplius. Et hinc evinci certò videtur quòd radiorum æqualitèr incidentium alij majorem alijs refractionem patiuntur. Nam si contrarium esset verum, prædicta Solis imago appareret ferè orbicularis, & in quadam positione Prismatis omninò ad sensum orbicularis conspiceretur; Id quod contra omnem experientiam est; Quocunque enim situ Prisma disposui, nunquam tamen potui efficere, quin longitudo imaginis esset latitudinis plusquam quadrupla: angulo scilicet Prismatis ACB vel ακβ existente graduum plus minus sexaginta.
F foramen aliquod in pariete vel fenestrâ Cubiculi, per quod radij solares OF trajiciantur, reliquis ubique foraminibus diligenter obturatis, nè lux alibi ingrediatur. Ista autem obscuratio Cubiculi non est omninò necessaria, sed efficit tantùm ut Experimentum evadat aliquantò evidentius. Deinde Prisma triangulare vitreum AαBβCκ ad foramen istud applicetur, quod radios OF per se trajectos refringat versus PYTZ, quos radios opposito pariete vel papyro aliquâ ad distantiam a Prismate satis magnam objectâ terminatos, videbis in figuram PYTZ valdè oblongam efformari: cujus nempe longitudo PT sit quadruplex latitudinis YZ, et amplius. Et hinc evinci certò videtur quòd radiorum æqualitèr incidentium alij majorem alijs refractionem patiuntur. Nam si contrarium esset verum, prædicta Solis imago appareret ferè orbicularis, & in quadam positione Prismatis omninò ad sensum orbicularis conspiceretur; Id quod contra omnem experientiam est; Quocunque enim situ Prisma disposui, nunquam tamen potui efficere, quin longitudo imaginis esset latitudinis plusquam quadrupla: angulo scilicet Prismatis ACB vel ακβ existente graduum plus minus sexaginta.
[6]Quod autem quædam datur positio Prismatis in quâ Imago Solis, ex opinione de refractionibus receptâ, appareret orbicularis, sic ostendo. Iuxta foramen in Fenestra cubiculi factum, Prisma collocetur foras; vel, quod eodem recidit, sit EG corpus aliquod opacum citra 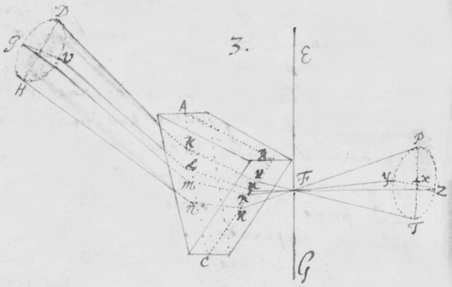 Prisma locatum in quo sit F foramen indefinitè parvum et orbiculare, per quod radij refracti in parietem directè oppositum ad imaginem PYTZ ibi depingendam trajiciantur. Et ponatur ABC esse planum secans AC & BC plana refringentia perpendiculariter, atque etiam transiens per foramen F, ut et per centrum solis DIHV, quem bisecet secundum diametrum ejus DH, a cujus extremitatibus duo radij DK et HN in eodem plano jacentes adveniant, qui postquam refringuntur DK in Kν et νT, atque HN in Nκ et κP, utrique pergant per centrum foraminis F. Et præterea sit talis inclinatio Prismatis ad istos radios ut anguli AKD & BκF fiant æquales. Deinde sit IV alia Solis diameter prædicto plano ABC perpendicularis a cujus extremitatibus alij duo radij VL et IM adveniant, alter IM eis planum ABC, qui refringatur in Mλ & λY, alter verò VL ultra planum istud qui refringatur in Lμ & μZ. Et prædicti quatuor radij sese omnes decussent in medio foramine F. Denique ponatur quòd imago lucida PYTZ foramen F directè respiciat, ita scilicet ut FP et FT, item FY et FZ æquales fiant. Dico jam quòd in illâ positione Prismatis, anguli PFT ac YFZ æquales essent, supposito quòd radij omnes æque refringuntur qui eundem habent angulum incidentiæ: Et proinde quòd imago ista, sensui saltem, debet esse orbicularis, utpote cujus diametri PT ac YZ sese decussant perpendicularitèr, et æquales istos angulos subtendunt.
Prisma locatum in quo sit F foramen indefinitè parvum et orbiculare, per quod radij refracti in parietem directè oppositum ad imaginem PYTZ ibi depingendam trajiciantur. Et ponatur ABC esse planum secans AC & BC plana refringentia perpendiculariter, atque etiam transiens per foramen F, ut et per centrum solis DIHV, quem bisecet secundum diametrum ejus DH, a cujus extremitatibus duo radij DK et HN in eodem plano jacentes adveniant, qui postquam refringuntur DK in Kν et νT, atque HN in Nκ et κP, utrique pergant per centrum foraminis F. Et præterea sit talis inclinatio Prismatis ad istos radios ut anguli AKD & BκF fiant æquales. Deinde sit IV alia Solis diameter prædicto plano ABC perpendicularis a cujus extremitatibus alij duo radij VL et IM adveniant, alter IM eis planum ABC, qui refringatur in Mλ & λY, alter verò VL ultra planum istud qui refringatur in Lμ & μZ. Et prædicti quatuor radij sese omnes decussent in medio foramine F. Denique ponatur quòd imago lucida PYTZ foramen F directè respiciat, ita scilicet ut FP et FT, item FY et FZ æquales fiant. Dico jam quòd in illâ positione Prismatis, anguli PFT ac YFZ æquales essent, supposito quòd radij omnes æque refringuntur qui eundem habent angulum incidentiæ: Et proinde quòd imago ista, sensui saltem, debet esse orbicularis, utpote cujus diametri PT ac YZ sese decussant perpendicularitèr, et æquales istos angulos subtendunt.
[7]Angulos autem istos PFT et YFZ æquales esse sic demonstro. Concipe radium aliquem a P per κ et N retrocedere, dum alius radius pergit a D per K et ν: Itaque cùm anguli AKD, & BκF supponuntur æquales, erunt etiam anguli per primas refractiones facti AKν et BκN æquales. Unde triangula CKν & CκN erunt similia et eorum anguli externi κNA, KνB æquales; et proinde anguli per secundas refractiones facti ANH & BνF etiam æquales{.} Quare cùm anguli AKD & BκF, item ANH et BνF sint æquales, eorum differentiæ erunt etiam æquales, hoc est angulus νFκ sive PFT æqualis angulo quem radij DK et HN comprehendunt, sive diametro solari. Est itaque angulus PFT æqualis diametro solari: Quare cùm præterea demonstratum fuerit, quod angulus YFZ æquatur eidem diametro, liquebit propositum. Istud autem ut fiat, Theorema quoddam more Lemmatis præsternendum est quod cùm postea nobis forsam erit ex usu, jam facere non pigebit.
[8]Sunto duo plana ABCD et EFGH sibimet perpendicularia quorum communis intersectio sit KL. Et sit IP radius quilibet qui 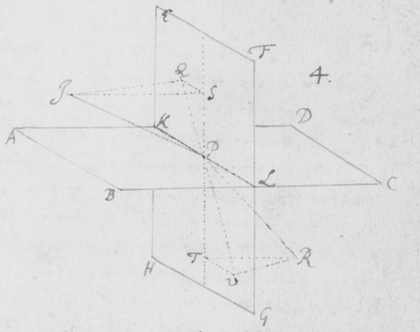 in planum ABCD incidens ad punctum P ab eo refringitur in PR. Dico quòd sinus anguli quem radius incidens IP efficit cum plano perpendiculari FH, est ad sinum anguli quem radius refractus PR efficit cum eodem plano, sicut sinus incidentiæ ad sinum refractionis; et proinde in ratione datâ. Sumptis enim radijs IP et PR æqualibus et demissis IQ et RV ad planum FH perpendicularibus et præterea ad punctum incidentiæ P erectâ SPT perpendiculari ad planum refringens BD (quæ ideò cum altero plano FH coincidet,) et ad istam demissis IS et RT iterum perpendicularibus: Erit IPQ angulus quem radius incidens IP efficit cum plano perpendiculari FH, et RPV angulus quem radius refractus PR efficit cum eodem plano: Item IPS angulus incidentiæ et RPT angulus refractionis. Quare si IP vel PR supponatur radius circuli, erunt IQ, RV, IS, et RT dictorum angulorum sinus. Sed IQ et RV sunt paralleli a[9] propterea quod eidem plano FH sunt perpendiculares. Item IS et RT sunt paralleli b[10], quia jacentes in eodem plano ISPTR eidem rectæ ST perpendicularitèr insistunt. Hoc est rectæ IQ, IS quæ angulum QIS comprehendunt sunt parallelæ rectis RV, RT comprehendentibus angulum VRT. Quare isti anguli QIS & VRT sunt æquales c[11]. Ductis autem QS & VT fient anguli IQS et RVT recti d[12], quia rectæ IQ et RV plano FH perpendiculariter insistunt. Ergo triangula IQS et RVT sunt similia e[13]: Et . Hoc est sinus angulorum quos radius incidens & refractus efficiunt cum plano aliquo FH ad refringens planum BD perpendiculari, sunt ut sinus incidentiæ et refractionis; & proinde in ratione datâ. Quippe sinuum istorum rationem esse datam Cartesius edocuit, & alij deinde fuêrunt experti.
in planum ABCD incidens ad punctum P ab eo refringitur in PR. Dico quòd sinus anguli quem radius incidens IP efficit cum plano perpendiculari FH, est ad sinum anguli quem radius refractus PR efficit cum eodem plano, sicut sinus incidentiæ ad sinum refractionis; et proinde in ratione datâ. Sumptis enim radijs IP et PR æqualibus et demissis IQ et RV ad planum FH perpendicularibus et præterea ad punctum incidentiæ P erectâ SPT perpendiculari ad planum refringens BD (quæ ideò cum altero plano FH coincidet,) et ad istam demissis IS et RT iterum perpendicularibus: Erit IPQ angulus quem radius incidens IP efficit cum plano perpendiculari FH, et RPV angulus quem radius refractus PR efficit cum eodem plano: Item IPS angulus incidentiæ et RPT angulus refractionis. Quare si IP vel PR supponatur radius circuli, erunt IQ, RV, IS, et RT dictorum angulorum sinus. Sed IQ et RV sunt paralleli a[9] propterea quod eidem plano FH sunt perpendiculares. Item IS et RT sunt paralleli b[10], quia jacentes in eodem plano ISPTR eidem rectæ ST perpendicularitèr insistunt. Hoc est rectæ IQ, IS quæ angulum QIS comprehendunt sunt parallelæ rectis RV, RT comprehendentibus angulum VRT. Quare isti anguli QIS & VRT sunt æquales c[11]. Ductis autem QS & VT fient anguli IQS et RVT recti d[12], quia rectæ IQ et RV plano FH perpendiculariter insistunt. Ergo triangula IQS et RVT sunt similia e[13]: Et . Hoc est sinus angulorum quos radius incidens & refractus efficiunt cum plano aliquo FH ad refringens planum BD perpendiculari, sunt ut sinus incidentiæ et refractionis; & proinde in ratione datâ. Quippe sinuum istorum rationem esse datam Cartesius edocuit, & alij deinde fuêrunt experti.
Quinetiam Theorematis jam demonstrati veritas manebit salva, licèt planum EF plano refringenti BD alibi perpendicularitèr insistat, quàm ad punctum refringens P. Exinde enim neque anguli cum radijs et plano FH effecti, neque ideò sinus istorum angulorum immutabuntur.
[14]Hisce ita præmonstratis ad propositum jam revertor, demonstraturus scilicet angulum YFZ (in Figura 3) diametro Solis ac proin angulo PFT æquari. Ex supra positis liquet quod planum KDHNκFν bisecat angulum radijs IM et VL utrinque jacentibus contentum. Itaque cùm iste angulus æqu{e}tur diametro Solari, angulus quem radiorum alter puta IM cum dicto plano facit æquabitur semidiametro Solari, cujus esto sinus α, et β sinus anguli quem radius ille refractus Mλ facit cum eodem plano. Iam cùm planum istud supponatur perpendiculare ad refringens planum prismatis AC, erit ex præcedenti Lemmate sinus α, ad sinum β, sicut sinus incidentiæ, ad sinum refractionis e rariori medio in medium densius. Vel e contra sicut sinus incidentiæ ad sinum refractionis e medio densiori in rarius, ita erit β ad α. Quare cùm dictum planum DHF etiam perpendiculare sit ad alterum planum Prismatis BC quod radios e medio densiori in rarius refringit; et insuper cum β supponatur sinus anguli quem radius incidens Mλ facit cum plano isto perpendiculari DHF: erit (per Lemma præcedens) α sinus anguli quem radius refractus λF facit cum eodem plano DHF. Sed α ponitur sinus semidiametri solaris; ergo ille angulus quem refractus radius λF facit cum plano DHF æquatur semidiametro solari: Et ejus duplus λFμ sive YFZ toti diametro. Et cùm supra fuerit ostensum, quòd angulus PFT sit eidem diametro æqualis, isti duo anguli YFZ et PFT erunt æquales. Q.E.D.
Iam si planum YFZ esset perpendiculare plano imaginis PYTZ æque ac planum PFT, istæ quatuor lineæ FP, FT, FY, & FZ quæ angulos æquales comprehendunt essent omnes inter se æquales, & proin subtensæ PT & YZ etiam æquarentur. Sed qui rem seriò perpendet, inveniet radios collaterales VLμFZ, & IMλFY duobus reliquis DKνFT & HNκFP paulò minùs refringi; et idcircò planum YFZ paulò magis declinabit a radio FP quàm ab FT, secans lineam PT infra medium ejus punctum X. Et sic divaricans a perpendiculari FX (quam concipe ductam,) erit aliquantulùm obliquum ad planum imaginis PYTZ. Et ea de causa lineæ FY & FZ erunt paulò majores quàm FP et FT, et subtensa YZ paulò major quàm subtensa PT. Sed hujus rei demonstrationem utpote longiusculam et proposito meo non omninò necessariam prætermitto: Etenim non multùm refert utrùm planum YFZ sit rectum ad planum imaginis PYTZ, vel nonnihil obliquum, hoc est, utrum YZ sit æqualis vel major quàm PT; sufficit quod nequit esse minor. Imò cùm propter ἰσοςκελέα PFT et YFZ, sit , atque FP & FY sint quàm proximè æquales; tantilla erit inter PT et YZ differentia ut quoad sensum pro æqualibus habeantur.
[15]Ostensus itaque casus est in quo longitudo solaris imaginis per Prisma trajectæ conspiceretur æqualis ejusdem latitudini; Et proinde in quo imago ista quasi orbicularis appareret, modò vera esset opinio vulgaris. Quinimò licèt positio Prismatis alia sit atque descripsi, modò radij refractionem utrinque non valde inæqualem patiantur figura tamen imaginis ea propter vix immutabitur. Nec multùm interest an corpus opacum EG, foramine F ad radios transmittendos terebratum, citra Prisma collocetur vel ultra: neque figura foraminis multùm curanda est modò sit exigua. Etenim tam parvæ variationes haud plus mutabunt imaginem quàm decimâ fortè vel quintâ parte diametri suæ, sicut cogitanti patebit. Atque ita ut paucis tandem comprehendam omnia, liquet quod imago solis refracta utplurimùm deberet esse sensui quasi orbicularis; si modò ejusdem incidentiæ in idem medium refractio semper foret eadem. Sed prius repugnat experientiæ, longitudine scilicet ejus latitudinem plusquam quatuor vicibus, ut dictum fuit, excedente. Ergo posterius repugnat veritati; & ejusdem incidentiæ refractio est varia.
[16]Ex eodem experimento potui propositum sic breviùs indicasse. Nempe cùm ita disposuissem Prisma ut refractio radiorum tum ingredientium tum egredientium foret quasi æqualis; angulos PFT & YFZ (figuræ 2 vel 3) dimensus sum et inveni quidem angulum YFZ semissi gradûs sive diametro solis æqualem, at angulus RFS eandem diametrum quatèr et ampliùs superavit, cui tamen æqualis esse debuisset ex parte priori demonstrationis præcedentis: Et inde planissimè liquet propositum. Verùm in eorum gratiam quæ mox sequentur, oporteret demonstrasse quod illi radij quorum refrangibilitas non est dispar, efformabunt imaginem penè orbicularem. Et eâ de re mihi visum fuit demonstrationem istam etiamsi longiusculam in illustrationem hujus experimenti hic adduxisse.
[17]Verùm cùm in experiendis prædictis, eam esse positionem Prismatis supposuerim ut radij ad utramque faciem Prismatis æqualiter refringantur: Conclusionis loco, dicam quâ ratione istud citò fiat, et facilè. Si Prisma teneatur in luce solari & motu lento circa suum axin convertatur, videbis colores quòs efficit, de loco in locum continuo motu translatos esse, ita quidem ut aliquando progredi, deinde verò regredi videantur. Observabis itáque medietatem inter istos contrarios motus, quando colores modò progressi et statim regressuri, videntur sistere. Quod ubi vides siste Prisma, et in eo situ fige. Dico factum. Scilicet in eo citu summa refractionum utrobique factarum, sive radij emergentis ad incidentem inclinatio evadit omnium minima; quod cum accidit, refractiones utrobique sunt æquales, uti posthac demonstrabitur.
[18]
[19]Et primo notandum venit quòd imaginis istius figura secundum longitudinem suam lineis rectis terminata fuit, et secundum latitudinem duobus (ut ex visu potui judicare) semicirculis. In figura 5 sit PT 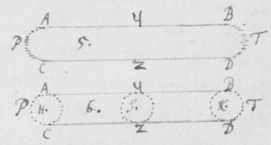 imago solis prismate refracta: Hanc observabam ad latera duabus lineis AB et CD sensui rectis et sibi parallelis terminari, ad extremitates autem duobus semicirculis APC et BTD. Cujus quidem eventus causa ex præmonstratis sic determinatur.
imago solis prismate refracta: Hanc observabam ad latera duabus lineis AB et CD sensui rectis et sibi parallelis terminari, ad extremitates autem duobus semicirculis APC et BTD. Cujus quidem eventus causa ex præmonstratis sic determinatur.
[20]Semicirculi illi terminales in circulos compleantur ut vides in figura 6. Et alius inscribatur circulus YZ istis intermedius. Iam concipe radios quosdam a Sole provenientes qui apti sunt ut incidentes æquè, etiam æquè refringantur: Illi per Prisma trajecti, ex supra demonstratis, imaginem quoad sensum (si sola posset videri) circularem depingent, puta BD. Deinde concipe alios ejusdem solis radios sibi etiam conformes, qui apti sunt ut prioribus paulò magis refringantur, illi itaq́ue aliam imaginem depingent circularem puta YZ: Et alios etiam radios adhuc magis refrangibiles concipe, qui tertiam circularem imaginem AC efficiant. Denique alios innumeros cogita prædictis plus et minus refrangibiles, et illi alias etiam innumeras circulares imagines prioribus tum intermedias tum extremas efformabunt, illuminantes oblongum spatium PYTZ lineis AB & CD, duobusque semicirculis contentum. Verùm cùm imagines illæ sunt omnes ejusdem penè magnitudinis et inter lineas AB et CD in directum dispositæ, istæ lineæ AB et CD pro rectis sibi parallelis possunt haberi et ad sensum tales videbuntur. Et sic totum spatium PYTZ radijs ex eâdem incidentiâ variè refractis illuminatum, partim parallelis rectis & partim semicirculis oppositis terminabitur: sicut experientiâ compertum est.
[21]Hanc autem conjecturam ut penitùs probarem, cogitabam de imagine Solis per foramen aliquod sine ullâ refractione ad distantiam magnam trajectâ, scilicet quòd malè definitur, termino existente inter lucem et tenebras minimè distincto: at si radij isti per lentem convexam transeant, cujus focus ad imaginem est, imago terminabitur distinctissimè. Simili modo de radijs æquè refrangibilibus intellexi quod si per Prisma trajicerentur ad distantiam magnam, depingerent imaginem circularem malè definitam, cujus tamen terminus, mediante lente convexâ, distinctissimus evaderet. Itáque cùm vidissem terminos imaginis refractæ PYTZ non admodum distinctos, de imaginibus BD, YZ, AC & reliquis circularibus oblongam istam formantibus conjiciebam quòd multò distinctiùs terminarentur per lentem convexam trajectæ quàm alitèr. Et experienti res patuit: Nam rectas AB et CD, in quas imagines omnes istæ circulares utrinque terminantur, vidi admodùm distinctas, quas antea confusas videram.
[22]Sed quod notatu valdè dignum videtur, termini circulares APC ac BTD imaginis istius semper apparuêre maximè confusi, luce paulatim deficiente donec tandem in tenebras desijt. Scilicet intermedij circuli, ut YZ, miscentur alijs circulis utrinque cadentibus, quibuscum, ex aliquâ sui parte, coincidunt: at extremi quidem circuli AC et BD, ex unâ tantùm parte cum alijs concurrunt, et eorum concursus continuò fit rarior, et exinde lux usque remissior dum ad extremitates P ac T deventum est. Sed et alia prodit istius rei causa, scilicet quòd radiorum maxima copia apta sit ut mediocrem refractionem patiatur; Et sic in medium imaginis incidat.
[23]Cæterum ad isthæc experienda Lentes adhiberi vellem quarum foci sunt longinqui, sex fortè vel duodecim pedibus a lentibus distantes, modò tales præsto sunt: Saltem non sint minùs distantes quàm duobus{.} Atque etiam latera Prismatis debent esse accuratè plana. Sin latera ejus sint aliquatenus convexa tum præstat adhibere lentem cujus focus ad pedes tantùm duos tresve a se remotus est. Quibus paratis Lentem Prismati ex utravis parte vicinam colloca: ita scilicet ut radios per se trajectos directè respiciat. Deinde radij in papyrum aliquam excipiantur, quam ultrò citróque transfer, donec imaginem coloratam utrinque rectis parallelis distinctissimè terminatam videas.
[24]Sed observandum est quòd cùm Prisma collocetur ultra foramen F, ut in figura 3, vel ipsi quàm proximè citra; et lens magis distet ab isto foramine quàm focus lentis, quem radij in eam parallelos incidentes efficerent, distat a lente: duplicem invenies casum in quo imago in papyrum projecta evadet distincta; alter quando radij omnes homogenei qui in Lentem paralleli incidunt ita refringantur ut ad papyrum istam in eodem puncto concurrant, quod fit cùm vides imaginem coloratam, oblongam, et parallelis rectis distinctè terminatam. Alter casus est quando radij omnes homogenei ab uno puncto foraminis F divergentes, postquam a lente refringuntur, ad unum iterum punctum dictæ papyri convergunt. Id autem accidit cùm imaginem albam, orbicularem, et undique benè definitam vides: De quo fusè dicetur alibi; sufficiat hoc monitum hic dedisse, nequis hæc proprijs experturus oculis, per ambiguitatem effectus incautè decipiatur, et exinde prædicta in dubium revocet.
[25]Ut dictas proprietates lucis quâ potui diligentiâ perscrutarer sequentem præterea modum excogitavi quo illas examini subjicerem. Nempe, in figura 6, cùm magnitudo circulorum AC, YZ, BD, dependeat a magnitudine solari: si diameter solis fieret aliquantò minor quàm nunc reverà existit, tum illi etiam circuli fierent minores, distantiâ centrorum H, I, K non omninò mutatâ: ut videre est in figura 8. Et sic 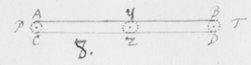 latitudo imaginis ad ejusdem longitudinem comparata multò minor evaderet quàm antea, utrâque scilicet per eandem quantitatem diminutâ. Hæc probaturus effeci ut radij Solis per duo parva foramina ab invicem longè distantia transirent antequam inciderent Prismati, quo pacto radij ab extremis partibus solis venientes excludebantur, et res perinde successit quasi diameter Solis reverà fuisset diminuta. Illustrationis
latitudo imaginis ad ejusdem longitudinem comparata multò minor evaderet quàm antea, utrâque scilicet per eandem quantitatem diminutâ. Hæc probaturus effeci ut radij Solis per duo parva foramina ab invicem longè distantia transirent antequam inciderent Prismati, quo pacto radij ab extremis partibus solis venientes excludebantur, et res perinde successit quasi diameter Solis reverà fuisset diminuta. Illustrationis 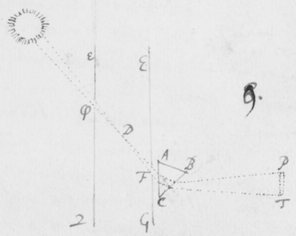 gratiâ sit (in figura 9{)} εφγ fenestra parvo foramine φ penetrata, per quod radij solares cubiculum alias obscuratum ingrediantur. Deinde sit EFG corpus aliquod opacum perforatum ad F, et in medio cubiculo ita locatum ut radij iterum permeent foramen istud antequam Prisma ABC ponè locatum attingant. Iam foraminum istorum diametro existente digiti, et eorundem distantiâ φF 12 pedibus, (ita scilicet ut maxima radiorum utrumque foramen permeantium inclinatio foret angulus sex minutorum ferè, hoc est quasi quinta pars diametri solaris;) atque etiam imagine RS projectâ in papyrum decem pedes a Prismate distantem, prout angustia cubiculi tulit: inveni longitudinem imaginis esse plusquam quatuor digitorum cum semisse et latitudinem trientis digiti, hoc est longitudinem plusquam quatuordecim vicibus majorem latitudine, sicut ex prædictis oportuit evenisse. Etenim cùm isti tantùm radij mittuntur intrò qui minùs quàm quintâ parte solaris diametri ad se invicem inclinantur, diametri AC, YZ, & BD diminutæ diametro foraminis F debent esse quintuplo minores quàm secundum priora contingeret; ut videre est in figuris 6 & 7. Quasi a Sole essent effectæ cujus diameter sit quinquies minor diametro solis nostri. Verùm si corpus opacum φγ (figura 8) tolleretur ut radij per unum solummodò foramen F ad Prisma transirent, sicut in prioribus factum est: latitudo imaginis evaderet et longitudo plusquam : angulo nempe Prismatis existente , vel paulo magis eò. Itaque diameter circulorum AC, YZ, & BD, qui eo quo dictum est modo imaginem constituunt, esset . A quâ subducatur diameter foraminis nempe , & manebit cujus quintæ parti rursus adjungatur eadem foraminis diameter sive et prodibit , diameter circulorum AC, YZ & BD in Figura 8: quæ minor est quàm diameter circulorum istorum in figura 6, quantitate . Quamobrem figura septima quaquaversum minor est quàm sexta, quantitate . Atque ideò longitudo ejus fit plusquam , latitudo autem digiti triens. Id quod cum experientia mox recensitâ quadrat. Ad eundem modum si foramina φ et F adhuc minora forent, vel si distantia φF foret major, imago RS oblongior evaderet. Quod idem quoque quadantenus contingeret, ex imagine RS a Prismate longiùs dissitâ. Cæterùm notandum est quod foramina φ et F ad radios directè respicientia suppono, licèt non multùm refert an situs eorum sit parùm obliquus ut in appositâ figurâ nonâ factum est.
gratiâ sit (in figura 9{)} εφγ fenestra parvo foramine φ penetrata, per quod radij solares cubiculum alias obscuratum ingrediantur. Deinde sit EFG corpus aliquod opacum perforatum ad F, et in medio cubiculo ita locatum ut radij iterum permeent foramen istud antequam Prisma ABC ponè locatum attingant. Iam foraminum istorum diametro existente digiti, et eorundem distantiâ φF 12 pedibus, (ita scilicet ut maxima radiorum utrumque foramen permeantium inclinatio foret angulus sex minutorum ferè, hoc est quasi quinta pars diametri solaris;) atque etiam imagine RS projectâ in papyrum decem pedes a Prismate distantem, prout angustia cubiculi tulit: inveni longitudinem imaginis esse plusquam quatuor digitorum cum semisse et latitudinem trientis digiti, hoc est longitudinem plusquam quatuordecim vicibus majorem latitudine, sicut ex prædictis oportuit evenisse. Etenim cùm isti tantùm radij mittuntur intrò qui minùs quàm quintâ parte solaris diametri ad se invicem inclinantur, diametri AC, YZ, & BD diminutæ diametro foraminis F debent esse quintuplo minores quàm secundum priora contingeret; ut videre est in figuris 6 & 7. Quasi a Sole essent effectæ cujus diameter sit quinquies minor diametro solis nostri. Verùm si corpus opacum φγ (figura 8) tolleretur ut radij per unum solummodò foramen F ad Prisma transirent, sicut in prioribus factum est: latitudo imaginis evaderet et longitudo plusquam : angulo nempe Prismatis existente , vel paulo magis eò. Itaque diameter circulorum AC, YZ, & BD, qui eo quo dictum est modo imaginem constituunt, esset . A quâ subducatur diameter foraminis nempe , & manebit cujus quintæ parti rursus adjungatur eadem foraminis diameter sive et prodibit , diameter circulorum AC, YZ & BD in Figura 8: quæ minor est quàm diameter circulorum istorum in figura 6, quantitate . Quamobrem figura septima quaquaversum minor est quàm sexta, quantitate . Atque ideò longitudo ejus fit plusquam , latitudo autem digiti triens. Id quod cum experientia mox recensitâ quadrat. Ad eundem modum si foramina φ et F adhuc minora forent, vel si distantia φF foret major, imago RS oblongior evaderet. Quod idem quoque quadantenus contingeret, ex imagine RS a Prismate longiùs dissitâ. Cæterùm notandum est quod foramina φ et F ad radios directè respicientia suppono, licèt non multùm refert an situs eorum sit parùm obliquus ut in appositâ figurâ nonâ factum est.
[26]Porrò si in hoc experimento convexam Lentem ut priùs adhibueris, cujus focus ad imaginem cadit, foramine F si placet dilatato vel opaco corpore EG prorsus ablato, ut radij per longinquum foramen φ solummodò transeant et si foramen istud φ effeceris angustius quàm antea, cæteris ut priùs stantibus, imaginem valdè oblongam & pro longitudine lucidiorem videbis quàm in casu priori. Exempli gratia si diameter foraminis sit pars digiti vigesima, & si pedibus abinde duodecim Prisma cum Lente disposueris, videbis longitudinem imaginis plusquam 80 vel 100 vicibus latitudine majorem. Sed in his experiendis oportet cubiculum quaquaversus benè obturatum esse, ne lux alibi quàm per foramen φ ingressa perturbet imaginem et juxta circulares ejus extremitates obscuram reddat. Et præterea si superficies Prismatis sint accuratè planæ, præstat adhibere lentem, quæ focum ad distantiam magnam projicit, puta ad 12 aut 20 pedes, modò loci amplitudo sinat; quo pacto de proportionibus imaginis satiùs judicium proferas. Quod si latera Prismatis sint aliquantulùm convexa, ut ijs nonnunquam contingit quæ vulgò venduntur: licebit istud absque ullâ lente solum adhibere, et ejus convexitas radios vice lentis ad magnam distantiam congregabit. Quinimò si cum Prismate quolibet lentem parvam adhibeas cujus focus non sit duobus tribúsve pedibus longinquior, imaginem conspicies satis longam quidem, sed cujus latitudo tamen haud sensibilis existit: Id quod proposito nostro non minùs inservit quàm si posses de proportione longitudinis ad latitudinem ejus accuratè judicare. In istis etiam experiendis notetur præterea quòd lens non debet ita longè post Prisma locari, quin ut possit ad omnes radios simul transmittendos extendi: nè imaginem successivè per partes tantùm observare sis coactus. Et notetur denique quòd si foramen F citra Prisma locaveris & lentem deinceps citra foramen istud, ad distantiam ab eo majorem quàm focus radiorum a foramine φ longinquiori manantium abest a lente; duplex erit casus in quo imago in papyrum projecta conspicietur distincta, prout radij venientes a singulis punctis foraminis F aut a singulis punctis foraminis φ, in totidem iterum punctis papyri colliguntur. In uno casu imago erit alba et orbicularis, uti priùs commonui a[27]; in altero autem oblonga et colorata, sicut præsens experimentum exigit.
[28]Iam liquet ex præfatis quod imaginis PT latitudo semper evadit eo minor quo foramen φ longinquum factum est angustius: ut nihil dubitandum sit quin dicta latitudo prorsus evanesceret si vice foraminis istius translucidi unum duntaxat punctum ibi lucidissimum existeret. Atque istud sic futurum esse confirmatur ex observatione non dissimili quam habui quondam de stellâ Veneris. Cubiculo nempe quaquaversus obturato, excepto foramine paulo plusquam duos digitos lato, ut tenebrosissimum efficeretur. In isto foramine vitrum objectivum Perspicilli septempedalis collocavi; latitudine ejus, ad sufficientem radiorum copiam transmittendam, duos digitos et ampliùs apertâ. Deinde ad distantiam septem pedum papyro transversè positâ, in eam vidi sideris imaginem ad instar puncti lucidi projectam. Et interposito Prismate ad distantiam pedis unius duorúmve ab istâ papyro, per quod radij trajecti aliò refringerentur: pro puncto illo lucido ad distantiam indè plusquam pedalem, vidi lineolam licèt non valdè lucidam facilè conspicuam tamen; et cujus longitudo semissem digiti superavit; latitudo autem fuit quoad sensum nulla, saltem haud major quàm ut sentiretur. Atque idem credo de Stellis primæ magnitudinis, uti de Sirio, liceat observare: præsertim si lens adhibeatur quatuor vel sex digitos lata, ut plures radios transmittat.
[29]Hoc experimentum quàm benè convenit cum explicatione nostrâ quam de refractione radiorum ad eundem angulum incidentium variâ, sub initio dedi, operæ pretium videatur adnotare. In figurâ primâ, supposui complures radios per eandem rectam in superficiem aliquam refringentem successivè delatos esse, ibidemq́ue alios alijs paulò magis, gradatim, refringi. Quod si fieri concipiatur, abinde sequeretur quod radij sic refracti, si corpore deinceps opaco quovis, ut papyro, interciperentur, lineolam ibi lucidam expingerent. Iam licet radij a Stellâ aliquâ venientes, non omnes in eâdem rectâ pergant; tamen, quod tantundem est, pro parallelis possunt haberi. Et quòd a lente convexâ effecti sunt convergentes antequam attingant Prisma, hoc adeò non destruit Analogiam ut eam maximè confirmet. Etenim pro singulis radijs in eâdem rectâ pergentibus, debes tantùm concipere tot radiorum penicillos, qui omnes habent eundem axem et idem punctum concursûs: Et quòd istorum penicillorum alij magis alijs a Prismate refringuntur, ita ut eorum puncta concursus sive foci qui priùs concidêre, jam singuli cadant seorsim, lineam rectam conficientes. Ac proinde quod axes penicillorum qui, radijs puta successivis, eousque coincidebant donec attigêre Prisma, ibi per variam refractionem sint effecti divergentes, ut ad focos penicillorum in lineâ rectâ jacentes pergant.
[30]Si Prisma Stellæ Veneris vicinius quàm Lentem collocaveris, ut radij per illud primò trajiciantur, et a lente deinde convergentes fiant: eandem lineolam ut priùs videbis, licèt minùs conspicuam et inventu difficilliorem. Iam in hoc specimine cùm radij omnes adveniant paralleli, si æqualiter refringerentur transientes Prisma, manerent postea paralleli usque dum Lenti inciderent. Et in eâ proinde sic refringerentur ut omnes deinceps ad idem punctum pergerent. Et sic punctum lucidum, conspiceretur. Quare cùm vice puncti istius apparet linea, concludendum est quod omnes radij non æqualiter refringuuntur.
[31] Si jam objiciat aliquis quòd in refractionibus detur quidem irregularitas sed eam esse contingentem et non ex prævia radiorum dispositione vel ullis certis legibus ortam. Respondeo quod imago solis praefata si radijs nullâ certâ lege refractis fieret oblonga, non posset in lineas rectas secundum longitudinem suam distinctè terminari: sicut ad figuram quintam ostensum est. Quinetiam non omninò deberet esse oblonga, sed parte ejus mediâ et magis splendidâ in morem orbis effingi, sensibilique termino distingui ab erraticâ luce debiliori quaquaversum dispersâ: Perinde ut Sol apparet cum nubibus penè obscuratur; Vel ut ejus imago cernitur cum trajicitur per laminam vitream parallelis planis terminatam et halitu vel fumo levitèr obductam, ut lux inter refringendum paululum conturbetur. Adhæc si duo Prismata similia ABC et αβκ juxtaponantur, secundum longitudinem suam parallela, cum lateribus planis AC & ακ, item BC & βκ etiam parallelis; Et si Sol transluceat utrumque in locum Z, ubi corpus opacum luci directè objicitur; radijs tamen ejus 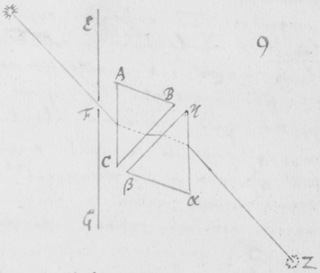 per orbiculare foramen F prius trajectis: Lux incidens in dictum Z apparebit distinctè orbicularis, non secùs quàm si directè tenderet ab F, Prismatibus non omninò interpositis. Fatendum est itaque quod utriusque Prismatis conjunctim refractiones sunt regulares, et proinde etiam refractiones alterutrius. Scilicet radij illi similiter incidentes non omnes æquè refringuntur in primo Prismate ABC, ut neque in secundo αβκ: tamen cùm ea refractionis inæqualitas non contingens est sed oritur ex prævia radiorum dispositione: ideò licèt varij radij variè refringantur tamen ejusdem radij eadem erit refractionis quantitas in utroque Prismate, et quantum incurvatur a priori ABC, tantum recurvabitur a posteriori αβκ. Unde radius quilibet utcunque sit refringibilis, postquam ex utroque Prismate emerserit, sibimet ipsi cùm nondum ijs inciderat fiet parallelus. Atque adeò cùm omnes ad easdem plagas tendunt ad quas liberè tenderent si Prismatibus non interciperentur: necesse est ut eandem orbicularem imaginem ad Z exhibeant quas illuc liberè tendentes exhiberent. Quod si imago oblonga per refractionem unici Prismatis (ut dictum est) effecta, figuram suam a radijs nullâ certâ lege divaricantibus sed forte fortuna huc illuc vage refractis acquireret: cùm refractiones binis Prismatibus geminentur, errores etiam radiorum duplo plures evaderent, ut et duplo majores. Et exinde imago ad Z fieret multò oblongior, quæ tamen, experientia teste, in orbem contrahitur{.}
per orbiculare foramen F prius trajectis: Lux incidens in dictum Z apparebit distinctè orbicularis, non secùs quàm si directè tenderet ab F, Prismatibus non omninò interpositis. Fatendum est itaque quod utriusque Prismatis conjunctim refractiones sunt regulares, et proinde etiam refractiones alterutrius. Scilicet radij illi similiter incidentes non omnes æquè refringuntur in primo Prismate ABC, ut neque in secundo αβκ: tamen cùm ea refractionis inæqualitas non contingens est sed oritur ex prævia radiorum dispositione: ideò licèt varij radij variè refringantur tamen ejusdem radij eadem erit refractionis quantitas in utroque Prismate, et quantum incurvatur a priori ABC, tantum recurvabitur a posteriori αβκ. Unde radius quilibet utcunque sit refringibilis, postquam ex utroque Prismate emerserit, sibimet ipsi cùm nondum ijs inciderat fiet parallelus. Atque adeò cùm omnes ad easdem plagas tendunt ad quas liberè tenderent si Prismatibus non interciperentur: necesse est ut eandem orbicularem imaginem ad Z exhibeant quas illuc liberè tendentes exhiberent. Quod si imago oblonga per refractionem unici Prismatis (ut dictum est) effecta, figuram suam a radijs nullâ certâ lege divaricantibus sed forte fortuna huc illuc vage refractis acquireret: cùm refractiones binis Prismatibus geminentur, errores etiam radiorum duplo plures evaderent, ut et duplo majores. Et exinde imago ad Z fieret multò oblongior, quæ tamen, experientia teste, in orbem contrahitur{.}
Ex dictis opinor satis supeŕque constat id quod initio proposui commonstrandum: quoniam verò jucunditatem intellectui et assensum plerumque firmiorem harmonia rerum plurium affert quàm unici licèt maximè scientifici argumenti testimonium: non erit abs re si in aliud experimentorum genus præcedentibus affinium experturos breviter introducam.
[32]In figura 12 Sit F foramen valde exiguum per quod lumen Solis trajiciatur: deinde ad distantiam pro lubitu magnam statuatur Prisma ABC, per quod radij transeant 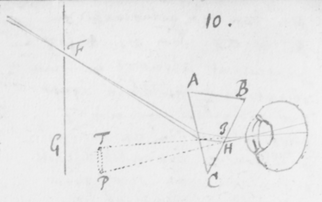 refracti; pro eo ut in prioribus explicui. Tum oculo pone admoto circularis foraminis F videbis imaginem TP oblongam; cujus longitudo ad latitudinem collata tanto major erit quanto foramen F fiat angustius. Et exinde pateat quod radiorum alij tendentes ad oculum per H quasi manavissent ab P, sunt magis refracti quàm alij tendentes per I, quasi a T venissent. Et radijs sic in oculum non secus ingressis quàm si profluxissent ab oblongo spatio PT; necesse est ut spatium istud longum appareat luminosum.
refracti; pro eo ut in prioribus explicui. Tum oculo pone admoto circularis foraminis F videbis imaginem TP oblongam; cujus longitudo ad latitudinem collata tanto major erit quanto foramen F fiat angustius. Et exinde pateat quod radiorum alij tendentes ad oculum per H quasi manavissent ab P, sunt magis refracti quàm alij tendentes per I, quasi a T venissent. Et radijs sic in oculum non secus ingressis quàm si profluxissent ab oblongo spatio PT; necesse est ut spatium istud longum appareat luminosum.
Sed cavendum est ne foraminis F tanta sit apertura ut nimiæ lucis introitu lædatur oculus: imò ne tanta sit quin ut possis nudo oculo particulam solis per foramen istud quasi punctum lucidum distinctè et absque ullâ circumradiatione transpicere. Verum si lumen solis censeatur nimium, huic experiendo lumen a nubibus transmissum sufficiat; modo talis sit oculi tui dispositio ut foramen sine radijs circumcirca superfluis distinctum cernas antequam interponas Prisma: alias imaginem ejus non cernes distinctam neque debita longitudine diductam. Adhæc liceat tantundem observare si filum albens interposito Prismate aspicias, etenim filum multò latius apparebit cum in situ ad longitudinem Prismatis parallelo quàm cùm in transverso statuitur. Cæterum ut in uno comprehendam omnia, si stellam fixam primæ magnitudinis mediante Prismate intuearis, ejus etiam imago conspicietur longa: At cùm radij stellarum pro parallelis habeantur, si omnes æquè refringerentur manerent etiam paralleli postquam egrediuntur Prismate, & oculum sic ingressi efficerent imaginem omnino similem Stellæ vel puncto lucido, & nullatenus oblongam: perinde ut fit cùm Stella parallelos radios in oculum directè mittit. Videtis itaque quòd radij paralleli superficiebus planis refracti, fiunt inclinati, unde necesse est ut inæqualem refractionem patiantur. In transitu autem notetur quòd Telescopio si placeat primùm adhibito, tum ut copia lucis ad oculum transmittatur, tum ut scintillatio quâ fixæ quasi coronâ solent cingi, minuatur: et Prismate deinceps interposito, videbis albicantem lineam distinctiorem quàm priùs, cum latitudine vix aut ne vix quidem conspicuâ{.}
Atque hæc in præsentiâ sufficiant ad propositum nostrum stabiliendum adducta. Verùm ut innotescat quis sit harum rerum sensus plenior, et in quem finem tendunt; naturam colorum quatenus ex hisce dependent in proximo tractandam aggrediar.
[33][34]Qui in fabricandis Telescopijs occupati sunt, de coloribus conqueruntur quibus objecta dum vitris istis mediantibus aspiciuntur tingi solent; quique eo magis augentur et apparent quo vitrum oculare ex sphæris minoribus efformatur, vel etiam quo vitrum objectivum majori latitudine radijs intrantibus patet. Unde duplici incommodo implicati, impediuntur ne perspicilla ad optatum perfectionis gradum perducant: tum quod oculare vitrum ultra certos gradus parvum ad objecta magis amplianda nequeant adhibere, tum quod vitrum objectivum ultra certos limites aperire nequeant ad objecta magis lucida et perspicua reddenda. Qui gradus vel limites si non probè observentur, objecta coloribus involuta reddentur & multò minùs distincta quàm si vel minora cernerentur, ope vitri ocularis minùs convexi; vel minùs lucida, diminutâ perspicilli aperturâ. Iam cùm istæ perfectiones præcipuæ sint, quæ in Perspicillis desiderantur, nempe ut objecta magis amplient & reddant lucidiora: operæ pretium videtur in naturam colorum inquirere, ut investigemus tandem quid in causa sit quod ita appareant et objecta reddant indistincta. Hujus enim ignorantia quamplurimos labore non exiguo sed inani tamen exercuit dum imperfectionem Telescopiorum a vitiosis vitrorum figuris ortam credentes, in istis meliori figurâ perpoliendis navârunt operam. Quod si nossent hasce colorum productiones ab alio fonte derivari, et quod in vitris quantumvis perfectis illi non secus sint apparituri: certè conatus suos mutassent; et laboribus istis secundum aliam methodum dispositis, Opticam in gradum multò perfectiorem jam promotam haberemus.
[35]Qui de coloribus hucusque disseruêre, vel id nomine tenus fecerunt ut Peripatetici, vel in eorum naturam et causas inquirere conabantur ut Epicurei et alij recentiores. Quæ Peripatetici de hisce tradidêre, etsi vera forent, ad nostrum tamen propositum nihil valerent: quippe dum modum quo generantur et causas unde fiunt tam varij, non omninò attingunt. Etenim illi de originibus & varijs rerum speciebus disputantes, pro causis ex quibus ipsarum existentiam et discrimen mutuantur varias quasdam formas assignarunt; verùm de particulari cujusvis formæ causâ, et ratione ob quam differt ab alijs haud unquam quicquam disseruêre. Et sic ea fecerunt missa, quorum explicatio videtur summum Philosophorum officium, imò quæ sola mentem scientiæ naturalis avidam explere possint{.}
Attamen nè mancam tradidisse Philosophiam viderentur, effecerunt ut ejusmodi disquisitiones pro maximè absurdis & ridendis habeantur, utpote quæ supponunt formarum esse alias formas, et qualitates qualitatum. Itáque cùm lux definiatur esse qualitas vel forma quæ dat esse lucidum, non expectandum est ut aliquid de ejus causis audiamus, vel quâ ratione ad varios colores producendos fit varia. Dicunt equidem quod plus luminis quibusdam coloribus immiscetur quam alijs: at hoc non sufficit ad eorum productionem tum quòd nullus omninò color ex albedine et nigredine solummodo mixtis præter fuscos intermedios generatur: tum quòd quantitas lucis non mutat speciem coloris. Corpus enim rubrum, verbi gratiâ, semper apparet rubrum sive aspiciatur in crepusculo sive in meridie lucidissimâ. Porro autem ipsa definitio quam attribuunt coloribus adeò non pandit eorum naturam, ut eos nè nomine tenus exprimat. Ait Aristoteles χρῶμα δέ ἐςτι τ;ȣ̃ διαφανȣ̃ς ἐν σὼματι ὡρισμένω πέρας. Quæ superficiei coloratæ potiùs quàm coloris descriptio est. Illa enim dici potest extremitas perspicui in corpore terminato: at color plerumque videtur ubi nulla talis datur extremitas: ut in Iride; in Prismate; in vitris vel liquoribus perspicuis et aliquo colore leviter tinctis; in aquâ marinâ quæ viridis ut plurimum apparet, qui tamen color non in extremitate aquæ sed per totam ejus crassitiem generatur; in aere qui licèt maximè perspicuus et nullo corpore denso terminatus serenâ tamen nocte cæruleus apparet; & in flammâ, quæ non minùs perspicua est, et luci pervia quàm ipse aer. Sic cùm humores oculi colore aliquo tinguntur, omnia videntur eodem colore tincta, licèt extremitas perspicui sit alijs coloribus prædita. Et cùm Solem nudis oculis aspexeris modò, luminosa omnia deinceps videntur rubra, et nigra plerumque apparent cærulea; qui color erit magis conspicuus, si clausis oculis te in locum aliquem tenebrosissimum statim conferas. Imò premendo oculum colores in tenebris excitare liceat; quis autem vocabit illos extremitatem perspicui? Cæterùm non opus est ut has opiniones enixè refutem quæ nòn videntur tanti, neque proposito meo adversantur. Esto lux qualitas corporis lucidi, esto lumen actus perspicui, et color ejus extremitas, et quicquid de istis dixerunt, esto; abinde tamen haud concipi poterit quo pacto lux refringatur, unde colores sint varij, quid in causâ sit quod in Perspicillis apparent, et quâ ratione incommodum istud devitari possit.
[36]Ad opiniones aliorum Philosophorum quod attinet, dixêrunt colores vel ex umbrâ lucèque variè mixtis; vel ex contortione globulorum aut eorum varijs pressionibus generari; vel denique ex varijs modis quibus Medium quoddam æthereum vibratur, statuentes scilicet lucem productam esse ex impulsu vibrantis ætheris in retiformem tunicam delato. Extra oleas nimis evagarer, si has opiniones sigillatim confutandas adortus fuerim; nec opus est ut faciam cùm omnes in communi quodam errore consentiant: Scilicet quod modificatio lucis, quâ singulos colores exhibet, ei non sit insita ab origine suâ, sed inter reflectendum vel refringendum acquiritur. Inter radios lucis nullum contemplantur discrimen priusquam incidant in corpus aliquod colorificum; opinati tantùm quòd pro variâ dispositione corporis istius, varijs modis reflectuntur vel refringuntur et pro specie modificationis quam sic acquirunt, varia deinde colorum phantasmata spectantibus exhibent. Mixtura lucis et umbræ, gyratio globulorum, vel varia vibratio Medij non supponitur inesse radijs antecedentèr ad eorum reflexiones vel refractiones, sed per istas actiones generari creditur. Quemadmodum et Peripatetici statuunt colores a corporibus originem sumere quorum dicunt esse qualitates. Attamen contrarium esse verum ex sequentibus abunde patebit. [37]Invenio scilicet quòd modificatio lucis unde colores originem sumunt, luci connata sit, et non oritur a reflexione neque a refractione neque a qualitatibus corporum aut modis quibuslibet, nec ab ijs vel destrui potest vel ullo modo mutari.
[38]Verùm ut sententiam meam distinctius proferam: Invenio primò quod radij, qui ex incidentiâ pari maximè omnium refringuntur, colores efficiunt purpureos sive violaceos; illi autem rubros qui minimè omnium refringuntur; ac illi cæruleos, virides, et flavos, qui refringuntur mediocritèr.
Secundò e contra invenio quòd radij qui purpureos colores efficiunt, ex incidentiâ pari maximè omnium refringuntur; et illi minimè omnium qui rubeos efficiunt; illi autem mediocriter qui generant cæruleos, virides, ac flavos. Hoc est invenio quòd radij pariter incidentes refractionem continuò majorem patiuntur atque adhuc majorem deinceps, prout apti sunt ad hos ordine colores rubrum, flavum, viridem, cæruleum, & violaceum generandos, unà cum omnibus eorum successivis gradibus & coloribus intermedijs.
Tertiò invenio quòd ex varijs horum radiorum mixturis cæteri omnes colores producuntur: Et quod color albus fuscus et niger fit ex radijs cujusque speciei confusè mixtis.
Quarto invenio quòd omnes omnium corporum colores non aliunde generantur quàm e dispositione quâdam quâ apta sunt ut alios radios reflectant et intromittant alios. Sic corpus rubrum est quod radios ad rubedinem aptos reflectit maximè, et plerosque cæteros intromittit: purpureum quod radios isti colori generando proprios reflectit, et intromittit alios: album verò quod ferè omnes reflectit, & nigrum quod omnes intromittit, paucissimis, sed omnium tamen specierum radijs repercussis.
[39]Verùm ne videar officij limites excessisse dum naturam colorum pertrectare aggredior, qui nihil ad Mathesin attinere censeantur: non abs re erit si de ratione incepti hujus iterum commonefaciam. Nimirum tanta est inter proprietates refractionum et colorum affinitas, ut seorsim explicari nequeant. Qui alterutras ritè velit cognoscere, ut alteras cognoscat necesse est. Et præterea si de refractionibus non agerem, et earum disquisitio non esset in causâ quòd negotium de coloribus simul explicandis inceptarem: tamen generatio colorum tantam Geometriam complectitur et eorum cognitio tantâ firmatur evidentiâ, ut vel ipsorum gratiâ possem aggredi, sic limites Mathesis nonnihil ampliaturus. Quemadmodum enim Astronomia, Geographia, Navigatio, Optica, et Mechanica pro scientijs mathematicis habentur, licèt in ijs agatur de rebus Physicis, Cælo, Terra, Navibus, luce et motu locali: Sic etiamsi colores ad Physicam pertineant, eorum tamen scientia pro Mathematicâ habenda est, quatenus ratione mathematicâ tractantur. Imò verò cùm horum accurata scientia videatur ex difficillimis esse quæ Philosophus desideret; spero me quasi exemplo monstraturum quantùm Mathesis in Philosophiâ naturali valeat; et exinde ut homines Geometras ad examen Naturæ strictiùs aggrediendum, & avidos scientiæ naturalis ad Geometriam priùs addiscendam horter: ut nè priores suum omninò tempus in speculationibus humanæ vitæ nequaquam pro futuris absumant, neque posteriores operam præposterâ methodo usque navantes, a spe suâ perpetuò decidant: Verùm ut Geometris philosophantibus & Philosophis exercentibus Geometriam, pro conjecturis et probabilibus quæ venditantur ubique, scientiam Naturæ summis tandem evidentijs firmatam nanciscamur.
[40]Itáque ad institutum redeo de coloribus secundum præcedentes quatuor propositiones explicatis disceptaturus. Et ad propositionem primam quod attinet, utpote quòd ex radijs similitèr incidentibus maximè refracti purpuram efficiant, minimè refracti ruborem, et refracti mediocriter colores mediocres, ea pateant ex antedictis. [41]Quippe notissimum est quòd colores Prismatis purpureus, cæruleus, viridis, flavus, & rubeus ita sese ab P versus T in ordine nominato subsequuntur, ut purpureus color ad P semper jaceat in angulo TFO radijs incidentibus OF ijsque FT ad colorem rubeum T refractis contento: atque adeò ut radij ad purpuram tendentes magis deflectant a directo cursu, sive magis refringantur quàm illi qui tendunt ad rubedinem.
[42]Non opus est ut hanc primam propositionem de industriâ porrò illustrandam prosequar, cùm scopus ejus et veritas in sequentibus manifestior evadet. Itaque ad secundam pergo monstraturus e contra quòd radij ex eâdem incidentiâ refractiones varias patiuntur qui varios colores producunt, scilicet quòd magis atque magis refringuntur prout colores hoc ordine rubeum, flavum, viridem, cæruleum et purpureum successivos cum omnibus eorum gradibus intermedijs generant.
[43]Hoc autem ut pateat, iterum repetatur experimentum Prismatis quod in prioribus adduxeram. Nempe ponatur quod radij solares ad foramen F ingressi cubiculum obtenebratum, a Prismate ABC quàm proximè foramen intus disposito refringantur, tendentes deinde versus oppositum parietem HI ad imaginem PT ibi depingendam. Et Imago illa ut vulgò notum est coloribus tingetur, rubeo ad T, purpureo ad P, cæruleo viridique et flavo ad Q R et S. Explorandum est itáque an radij tendentes versus P magis refringantur quàm isti qui tendunt versus T. Id quod varijs modis tentare liceat, quorum facillimum et maximè perspicuum sequentem existimo. Sume aliud Prisma αβκ (figura ) et illud alicubi inter Prisma primum ABC et imaginem PT ita colloca, ut sit illi Prismati ABC transversum sive parallelum imagini , radiosque versus PT tendentes intercipiat et alioversum refringat, puta versus πτ. 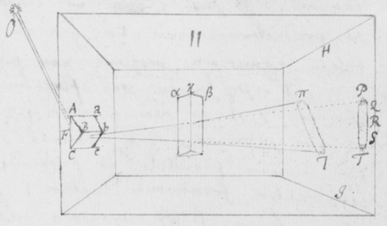 Quo facto, imaginem πτ refractionibus utriusque Prismatis sic effectam, videbis ut priùs coloratam, sed in alio tamen situ dispositam: Non parallelam imagini PT sed secundum extremitates rubras manifestò convergentem. Iam cùm radij ad utrosque colores rubeum T et purpureum P pertinentes similiter incidant in Prisma secundum αβκ, si eandem præterea refractionem paterentur, imagines PT ac πτ deberent esse parallelæ. Et ideò cùm non existant parallelæ, sed imaginis πτ extremitas purpurea π longiùs ab alterâ imagine PT transferatur quàm extremitas rubea τ: necessariò concedendum est quòd radij ad extremitatem purpuream P tendentes magis refringantur quàm qui tendunt ad extremitatem rubeam T. Hoc est, quòd radij generantes purpuram apti sint ut magis refringantur quàm ruborem efficientes. Atque idem quoque de coloribus intermedijs eâdem ratione constabit, sicut ostendendum proposui.
Quo facto, imaginem πτ refractionibus utriusque Prismatis sic effectam, videbis ut priùs coloratam, sed in alio tamen situ dispositam: Non parallelam imagini PT sed secundum extremitates rubras manifestò convergentem. Iam cùm radij ad utrosque colores rubeum T et purpureum P pertinentes similiter incidant in Prisma secundum αβκ, si eandem præterea refractionem paterentur, imagines PT ac πτ deberent esse parallelæ. Et ideò cùm non existant parallelæ, sed imaginis πτ extremitas purpurea π longiùs ab alterâ imagine PT transferatur quàm extremitas rubea τ: necessariò concedendum est quòd radij ad extremitatem purpuream P tendentes magis refringantur quàm qui tendunt ad extremitatem rubeam T. Hoc est, quòd radij generantes purpuram apti sint ut magis refringantur quàm ruborem efficientes. Atque idem quoque de coloribus intermedijs eâdem ratione constabit, sicut ostendendum proposui.
[44]In experiendis hisce notari poterit quòd quo vicinius anteriori Prismati ABC sive quò remotiùs à pariete HI collocetur Prisma posterius αβκ imagines PT ac πτ co magis ab invicem distantes, etiam ad se magis inclinabuntur. Adeò ut angulum semirectum vel paulo minorem eo contineant cùm prismata collocantur ad invicem vicinissima. Cujus rei ratio facillima est consideranti quòd distantiæ Pπ ac Tτ sunt in datâ quâdam ratione. Sic in Figura 12 si parallelæ Pπ ac Tτ sint in ratione datâ, quo majores existant eo major erit inclinatio linearum 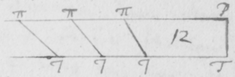 PT ac πτ.
PT ac πτ.
[45]Sicui in potestate est instrumentum aliquod ad quantitates refractionum accuratè mensurandas paratum, nullus dubito quin istius etiam ope seorsim dimetiendo refractiones diversorum generum radiorum, facilè observabit differentias: licèt ego prædictis tanquam manifestissimis acquiescens, non operæ pretium duxerim rem alijs modis experiri. Verùm ut cuique magis pateat quanta sit prædictorum evidentia, quædam quæ exinde scaturiunt notatu dignissima proferre non pigebit.
[46] Sit Fφ (figura ) paries vel operculum fenestræ duobus foraminibus F et φ luci pervium, ijsque digitos duos ab invicem distantibus; et intus disponantur duo Prismata ABC DEG in situ sibi invicem parallelo, at perpendiculari ad lineam Fφ per centra foraminum ductam: quæ duo lucem ingressam refringant ad imagines duas PT et MN in oppositum parietem projiciendas, simili prorsus modo quo factum fuit in experimento priori. Et præterea sint anguli Prismatum 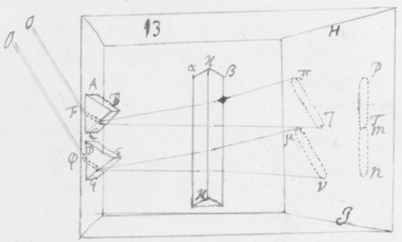 ACB, DGE (comprehensi planis refringentibus) æquales. Quibus ita constitutis, videbis imagines PT et MN in directum jacentes cum extremitatibus earum T et M contiguis. Quod si non eveniat, situs unius e Prismatibus parùm mutandus est donec extremitates contiguas esse cernas, vel fortè nonnihil coincidentes. Purpurâ M et rubore T sic juxta positis, adhibeatur Prisma tertium αβκ, quod primis prismatibus et eorum imaginibus interponatur in situ ad lineam Fφ sive ad imagines dictas PT, MN parallelo: ita nempe ut radios utriusque Prismatis ABC ac DEG tendentes versus PT et MN pariter intercipiat, eosque refringens aliò projiciat, quemadmodum ad πτ ac μν. Adeò ut quæ duobus prismatibus in priori specimine facta sunt, hic videas facta tribus. His ita paratis et constitutis videbis imagines πτ et μν ab invicem disjunctas esse, quæ priùs apud PT et MN fuerunt contiguæ, et in directum positæ: ita quidem ut purpura μ in extremitate imaginis μν magis distet ab imaginibus primis PT et MN quàm rubor τ in extremitate imaginis πτ. Id quod nullo prorsus modo potuisset accidisse, nisi radij ad purpuram generandam apti aliquanto magis refringerentur ex incidentiâ pari quàm radij generantes rubedinem. Etenim cùm radij coloris utriusque pariter incidant in Prisma posterius αβκ; pariter etiam emergerent si æqualiter refringerentur, et exinde depingerent imagines πτ et μν prioribus PT et MN parállelas, et in directum jacentes. Dixi radios utriusque coloris purpurei rubeique pariter incidere in Prisma posterius αβκ: Quod ne moram injiciat alicui, concipiendum est quòd radij FT tantùm inclinantur versus extremitatem ejus K quantùm alteri φM versus extremitatem alteram αβκ: Et sic incident pariter sive ad eosdem angulos, licèt non paralleli. Siquis tamen velit efficere ut incidant etiam paralleli, nihil aliud agendum est quàm ut alterum e prismatibus anterioribus ABC vel DEG circa suum axem paululum convertatur donec inter T et M interiores imaginum extremitates tanta intercedat distantia quanta intersit foraminibus F et φ sive quantam isti rei sufficientem judicaverit, imaginibus ad istam distantiam in directum jacentibus. Et Prismate αβκ deinceps interposito, facilè percipiet quod incidentes parallelè emergent inclinati, tum quòd imagines non ampliùs in directum jacebunt, tum quòd purpura M ad majorem distantiam transferetur quàm rubedo T.
ACB, DGE (comprehensi planis refringentibus) æquales. Quibus ita constitutis, videbis imagines PT et MN in directum jacentes cum extremitatibus earum T et M contiguis. Quod si non eveniat, situs unius e Prismatibus parùm mutandus est donec extremitates contiguas esse cernas, vel fortè nonnihil coincidentes. Purpurâ M et rubore T sic juxta positis, adhibeatur Prisma tertium αβκ, quod primis prismatibus et eorum imaginibus interponatur in situ ad lineam Fφ sive ad imagines dictas PT, MN parallelo: ita nempe ut radios utriusque Prismatis ABC ac DEG tendentes versus PT et MN pariter intercipiat, eosque refringens aliò projiciat, quemadmodum ad πτ ac μν. Adeò ut quæ duobus prismatibus in priori specimine facta sunt, hic videas facta tribus. His ita paratis et constitutis videbis imagines πτ et μν ab invicem disjunctas esse, quæ priùs apud PT et MN fuerunt contiguæ, et in directum positæ: ita quidem ut purpura μ in extremitate imaginis μν magis distet ab imaginibus primis PT et MN quàm rubor τ in extremitate imaginis πτ. Id quod nullo prorsus modo potuisset accidisse, nisi radij ad purpuram generandam apti aliquanto magis refringerentur ex incidentiâ pari quàm radij generantes rubedinem. Etenim cùm radij coloris utriusque pariter incidant in Prisma posterius αβκ; pariter etiam emergerent si æqualiter refringerentur, et exinde depingerent imagines πτ et μν prioribus PT et MN parállelas, et in directum jacentes. Dixi radios utriusque coloris purpurei rubeique pariter incidere in Prisma posterius αβκ: Quod ne moram injiciat alicui, concipiendum est quòd radij FT tantùm inclinantur versus extremitatem ejus K quantùm alteri φM versus extremitatem alteram αβκ: Et sic incident pariter sive ad eosdem angulos, licèt non paralleli. Siquis tamen velit efficere ut incidant etiam paralleli, nihil aliud agendum est quàm ut alterum e prismatibus anterioribus ABC vel DEG circa suum axem paululum convertatur donec inter T et M interiores imaginum extremitates tanta intercedat distantia quanta intersit foraminibus F et φ sive quantam isti rei sufficientem judicaverit, imaginibus ad istam distantiam in directum jacentibus. Et Prismate αβκ deinceps interposito, facilè percipiet quod incidentes parallelè emergent inclinati, tum quòd imagines non ampliùs in directum jacebunt, tum quòd purpura M ad majorem distantiam transferetur quàm rubedo T.
[47]Si tria prismata non præsto sint, experimentum jam recitatum duobus experiri possis, idque modo magis expedito et facili. Sit ABCDE (figura ) Prisma cujus unum latus planum ABDE 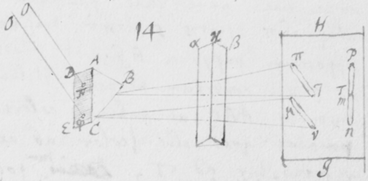 papyro denigratâ tegatur duobus parvis foraminibus F et φ luci perviâ, quorum foraminum situs esto ad longitudinem Prismatis transversus. Tum Prismate hoc ita disposito, ut radij permeantes ista foramina terminentur in oppositum quoddam planum, puta papyrum HI; transferatur ista papyrus ultra citraque donec videas imagines duas PT et MN contiguis extremitatibus in directum conjunctas, ut priùs. Deinde altero Prismate αβκ interposito in situ ad alterum transverso: videbis imagines illas PT et MN ad πτ et μν ita translatas esse ut non amplius jaceant in directum, rubedine τ a PN minùs remotâ quàm purpura μ, sicut in prioribus contingebat.
papyro denigratâ tegatur duobus parvis foraminibus F et φ luci perviâ, quorum foraminum situs esto ad longitudinem Prismatis transversus. Tum Prismate hoc ita disposito, ut radij permeantes ista foramina terminentur in oppositum quoddam planum, puta papyrum HI; transferatur ista papyrus ultra citraque donec videas imagines duas PT et MN contiguis extremitatibus in directum conjunctas, ut priùs. Deinde altero Prismate αβκ interposito in situ ad alterum transverso: videbis imagines illas PT et MN ad πτ et μν ita translatas esse ut non amplius jaceant in directum, rubedine τ a PN minùs remotâ quàm purpura μ, sicut in prioribus contingebat.
[48]Est et aliud ex eodem fonte derivatum specimen haud expertu difficilius aut minoris evidentiæ. Prismate ABC (figura ) juxta foramen F ut prius collocato ; ad distantiam convenientem (veluti duodecim pedum) statuatur aliud Prisma αβκ in situ transverso respectu prioris, vel forte parallelo aut alio quovis pro arbitrio: ita tamen ut anterius Prisma ABC lucem refractam et coloratam projiciat in aliquod ex ejus planis lateribus αδ. Quod quidem latus obducatur papyro 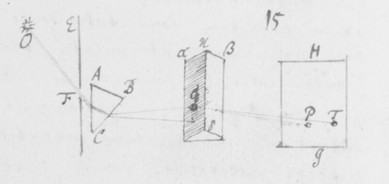 denigratâ, & exiguo foramine G per medium transfossâ, per quod aliqui ex radijs ab anteriori prismate refractis transeant in hoc prisma posterius: ubi cùm rursus refracti fuerint pergant ad papyrum HI abinde decem pedibus vel pluribus distantem. Quibus ita constructis et dispositis in situ illo figatur papyrus HI et prisma posterius αβκ. Denique præ manibus sumatur anterius Prisma ABC non ut moveatur a loco ejus, sed ut motu tantùm angulari nunc huc nunc illuc paululum inclinetur, ut alios atque alios colores successivè trajiciat per foramen G in oppositam papyrum HI. Et videbis quod color quilibet diversus ad locum diversum perget. Veluti cùm ea sit positio Prismatis ABC ut rubeum colorem projiciat in G, si ponatur quod ille color ab altero prismate αβκ refringatur ad T, tum positione Prismatis ABC paululum mutatâ inclinando circa axem donec purpura cadat in G, videbis quod ille color juxta obliquiorem tramitem refringetur, puta ad P. Et pari modo si color aliquis intermedius incidat in G, idem refringetur ad locum ipsis P ac T interjacentem. Quamobrem cùm radij cujuslibet generis pergentes a foramine F positione dato ad foramen G positione datum, et ideò similiter incidentes in prisma posterius αβκ, refringantur ad loca diversa P, T, cæteraque intermedia: constat quòd inæqualiter refringuntur. Et cùm refractus GP observetur magis deflectere ab incidenti FG quàm refractus GT: constat quòd radij purpuram exhibentes magis refringuntur quàm exhibentes ruborem, cæteriq́ue deinceps in ordine intermedio.
denigratâ, & exiguo foramine G per medium transfossâ, per quod aliqui ex radijs ab anteriori prismate refractis transeant in hoc prisma posterius: ubi cùm rursus refracti fuerint pergant ad papyrum HI abinde decem pedibus vel pluribus distantem. Quibus ita constructis et dispositis in situ illo figatur papyrus HI et prisma posterius αβκ. Denique præ manibus sumatur anterius Prisma ABC non ut moveatur a loco ejus, sed ut motu tantùm angulari nunc huc nunc illuc paululum inclinetur, ut alios atque alios colores successivè trajiciat per foramen G in oppositam papyrum HI. Et videbis quod color quilibet diversus ad locum diversum perget. Veluti cùm ea sit positio Prismatis ABC ut rubeum colorem projiciat in G, si ponatur quod ille color ab altero prismate αβκ refringatur ad T, tum positione Prismatis ABC paululum mutatâ inclinando circa axem donec purpura cadat in G, videbis quod ille color juxta obliquiorem tramitem refringetur, puta ad P. Et pari modo si color aliquis intermedius incidat in G, idem refringetur ad locum ipsis P ac T interjacentem. Quamobrem cùm radij cujuslibet generis pergentes a foramine F positione dato ad foramen G positione datum, et ideò similiter incidentes in prisma posterius αβκ, refringantur ad loca diversa P, T, cæteraque intermedia: constat quòd inæqualiter refringuntur. Et cùm refractus GP observetur magis deflectere ab incidenti FG quàm refractus GT: constat quòd radij purpuram exhibentes magis refringuntur quàm exhibentes ruborem, cæteriq́ue deinceps in ordine intermedio.
[49] Siqua forsan oboriatur suspicio, quod ex motu Prismatis ABC foraminibus F ac G interpositi incidentia radiorum diversos colores efficientium tantùm varietur quantùm sufficiat ad efficiendam varietatem locorum P, T, &c: ad quos refringuntur: quamvis motus iste sit exiguus et ineptus huic effectui, tamen ut suspicio illa prorsus eximatur anterius Prisma ABC ad alteras partes foraminis F Solem versus collocandum est, ut radij incidentes in foramen G directè veniant a dicto foramine F. Eo enim pacto cùm foramina F ac G positione determinentur, positio radiorum per utrumque trajectorum determinabitur, eademq́ue accuratè erit omnium incidentia quoscunque colores exhibentium: et tamen diversicolorum refractio non secus peragetur ad loca diversa P, T &c quàm modò explicui.
[50]Cùm veritatem propositam sic fecerim stabilitam, hanc propositionem concludam annotando connexionem et affinitatem quam coloribus et refractionibus interesse dixeram: Nempe ex ostensis non solùm pateat quòd diversa colorum genera cum definitis gradibus refrangibilitatis reciprocantur: sed et ijsdem a[51] experimentis probatur dari radios diversè refrangibiles, et radios diversè refrangibiles esse diversicolores, ijsdemq́ue b[52] probatur e contra radios diversicolores esse diversè refrangibiles, et inde radios diversè refrangibiles dari. Et hinc scopus eorum quæ in primis lectionibus de dispari refrangibilitate radiorum edocui, quoad causas colorum intelligendas multùm illustratur; ut pateat quòd una absque alijs dilucidè tractari nequeant.
<30>[53][54]Posteaquam ostendi radios qui producunt varios colores etiam varias refractiones pati: cogitabam de explicando modo quo colores generantur mediante Prismate. Sed istud quoniam ex præcipuis esse videatur quæ de coloribus dicenda suscepi: satius esse judico me priùs ostendere veritatem tertiæ propositionum quas in postremâ Lectione proposueram, quatenus albedinem concernit; eam nempe ex omnigenis coloribus posse componi; et inde lucem solis albere quòd omnes colores in eâ commisti lateant. Quod cùm ostendero, genesis colorum a Prismatibus postmodum satiùs et majori cum evidentiâ pandetur.
Itaque proponatur jam monstrandum quòd cùm omnes omninò colores qui virtute Prismatum generantur, debitè commiscentur sibi: color albus exinde resultabit. Istud autem cùm semel deprehenderam esse verum, de varijs postea modis cogitabam quibus mistura talis perfectè fieret: ac primò rem aggressus sum cum pluribus Prismatibus ita dispositis ut colores eorum in eundem locum inciderent et sic inter se miscerentur.
[55]Sint ABC, DEF 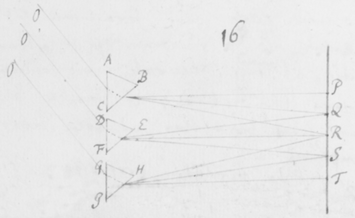 GHI tria Prismata juxta se in situ parallelo ita disposita, ut alterum DEF sit alteris duobus ABC et GHI utrinque vicinissimis intermedium, in morem trium linearum conficientium capitalem literam græcam Ξ. Et lux per unumquodque Prisma liberè transiens excipiatur in papyrum PT pede uno vel duobus postpositam. Coloribus omnium prismatum sic in ipsam PT projectis, convertantur prismata circa proprios axes, et videbis colores istos sibi invicem accedere vel recedere. Quare convertantur donec talis sit eorum situs ut unius Prismatis ABC rubor, et alterius GHI purpura vel color indicus cum viriditate tertij DEF coincidant, sicut vides factum ad R. Et ex istis coloribus ita sibi commixtis albedinem generari cernes, colore purpureo et cæruleo juxta P conspecto, rubeo verò et flavo juxta T, et albo juxta R cæteros intercedente.
GHI tria Prismata juxta se in situ parallelo ita disposita, ut alterum DEF sit alteris duobus ABC et GHI utrinque vicinissimis intermedium, in morem trium linearum conficientium capitalem literam græcam Ξ. Et lux per unumquodque Prisma liberè transiens excipiatur in papyrum PT pede uno vel duobus postpositam. Coloribus omnium prismatum sic in ipsam PT projectis, convertantur prismata circa proprios axes, et videbis colores istos sibi invicem accedere vel recedere. Quare convertantur donec talis sit eorum situs ut unius Prismatis ABC rubor, et alterius GHI purpura vel color indicus cum viriditate tertij DEF coincidant, sicut vides factum ad R. Et ex istis coloribus ita sibi commixtis albedinem generari cernes, colore purpureo et cæruleo juxta P conspecto, rubeo verò et flavo juxta T, et albo juxta R cæteros intercedente.
Cæterùm in istis experiendis juvabit observare sequentia.
[56]Primò, si anguli Prismatum planis refringentibus contenti ACB, DFE et GIH sint inæquales; præstat ut illud Prisma cujus angulus GIH maximus est ponatur versus exteriorem partem anguli contenti radijs incidentibus et refractis: et istud versus interiorem cujus angulus ACB est minimus.
Secundò, aperturæ per quas lux transmittitur per prismata debent esse magnæ. Imò convenit ut transitus luci per tota Prismata pateat, obstaculo nullo adhibito. Neque opus est ut experimentum in tenebris peragatur sicut in alijs quamplurimis requiritur.
Tertiò papyrus PT in quam colores incidunt non nimis distare debet a Prismatibus. Sufficit distantia pedum plus minus duorum. Has autem aperturas et distantiam statuo ut colores eò meliùs commisceantur ad albedinem perfectiorem componendam.
Quartò ut colores ad R faciliùs etiam et satiùs commisceantur, Prisma ABC statuatur imprimis in situ quocunque tali ut radij tum ingredientes tum emergentes refractionem præter propter æqualem patiantur: et in eo situ figatur. Et colores ejus ad distantiam duorum pedum excipiantur, vel ad eam potiùs ubi vides flavum ejus et cæruleum modò contiguos, albedine intermediâ tum evanescente. Postea figatur aliud Prisma GHI in tali situ ut purpura ejus contingat ruborem alterius ABC, non autem coincidat illi: et linea contactus notetur. Deinde tertium Prisma DEF sic fige ut ejus colorum medietas cadat in dictam lineam contactûs, quod ubi contingit facilè cognosces intercipiendo lucem ingressuram cætera Prismata. Denique papyrus PT ultra citraque transferatur paululum donec videas albedinem perfectam in medio colorum ad R generari. Quam quidem albedinem ex varijs coloribus compositam esse constabit intercipiendo colores unius duorumve prismatum priusquam attingant papyrum. Nam loco albedinis eos quos non intercipis colores intueberis.
Denique si velis ut colores adhuc perfectiùs misceantur, possis adhibere plura prismata modò præsto sint: tamen eventus non deerit expectationi si tria tantum adhibeas. Etenim colores cujusque Prismatis seorsim spectati non sunt omninò simplices, sed viridis ejus et rubeus nonnihil miscentur in flavo: et purpureus ac viridis in cæruleo; et sic de reliquis; quemadmodum in sequentibus ostendetur. Et inde fit quod cùm tria tantùm prismata adhibentur, non solùm tres colores rubeus viridis et indicus commisceantur in R, sed etiam cæruleus et flavus unà cum omnibus eorum gradibus intermedijs istam albedinis compositionem ingrediantur.
[57]Verùm cùm tot prismata in situ tam accurato disponere, propter motum solis et alia incommoda difficile forsan et laboriosum simul inveniatur, nisi adhibeatur Machina quædam eâ de causâ fabricata ut ejus ope prismata in desiderato situ figantur: alium propterea modum profero quo ista negotio leviori, idque unico prismate periclitari poteris. Sumatur papyrus vel aliud opacum 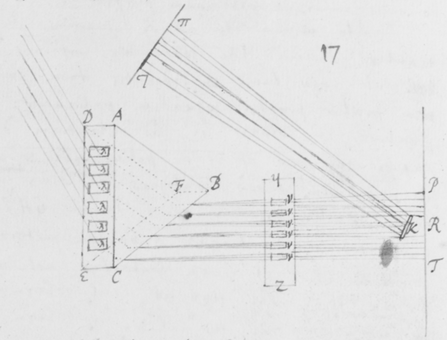 corpus attenuatum in morem laminæ. Et in eo confodiantur oblongæ rimæ sex aut plures parallelæ, quarum latitudines sint æquales distantijs aut ijs paulò majores. Deinde papyrus ista figatur alicui ex planis lateribus prismatis: Sit istud latus papyro obductum ACED (figura ), et rimæ in papyro excisæ literis λ designentur; quarum situs esto parallelus ad EC concursum laterum refringentium prismatis sive verticem ejus. Papyrus autem debet toti isti plano ADEC superinduci, nequa lux alibi transmissa quàm per prædictas rimas perturbet experimentum. Tum Prisma statuatur in luce solis ut radij ejus vel per dictas rimas id ingrediantur vel postquam refracti fuerint per eas egrediantur: et in isto situ figatur. Quo facto sumatur alia papyrus PT quæ sic teneatur a posticâ parte Prismatis ad distantiam duorum triumve digitorum ut in eam lux terminetur; et videbis tot lineas colorum quot sunt oblongæ rimæ λ; quarum linearum cuique tot competent colores quot solent apparere virtute Prismatum. Nempe quælibet rima subit officium unius e prismatibus in experimento priori adhibitis et proprios colores cæruleum rubrum cæterosque generat quasi tot essent prismata quot sunt rimæ: Porro si papyrus PT longiùs differatur a Prismate coloratas istas lineas paulatim dilatari cernes et interjecta spatia minui donec absorbeantur a coloribus jam factis contiguis. Et si papyrus adhuc longius differatur, colores a diversis rimis effecti (rubri cum cæruleis primò deinde alij cum alijs) incipient plus pluśque misceri. Et sic sese paulatim diluent, donec cùm mistura satis absoluta est, convertantur in albedinem, præterquam in eorum extremitatibus P ac T ubi mixtura et confusio fere nulla est. Et isthæc accidunt cùm papyrus PT quasi ad distantiam decem vel duodecim vicibus majorem ipsâ AC vel BC latitudine planorum prisma constituentium, amoveatur. Quod si amoveatur adhuc longiùs, absimilium radiorum commistio fortasse perfectior evadet, sed colores purpurei et cærulei ad P, ac flavi rubeique ad T latiores fient, et interjectum spatium album minuetur, donec totum destruatur ab istis coloribus occupatum.
corpus attenuatum in morem laminæ. Et in eo confodiantur oblongæ rimæ sex aut plures parallelæ, quarum latitudines sint æquales distantijs aut ijs paulò majores. Deinde papyrus ista figatur alicui ex planis lateribus prismatis: Sit istud latus papyro obductum ACED (figura ), et rimæ in papyro excisæ literis λ designentur; quarum situs esto parallelus ad EC concursum laterum refringentium prismatis sive verticem ejus. Papyrus autem debet toti isti plano ADEC superinduci, nequa lux alibi transmissa quàm per prædictas rimas perturbet experimentum. Tum Prisma statuatur in luce solis ut radij ejus vel per dictas rimas id ingrediantur vel postquam refracti fuerint per eas egrediantur: et in isto situ figatur. Quo facto sumatur alia papyrus PT quæ sic teneatur a posticâ parte Prismatis ad distantiam duorum triumve digitorum ut in eam lux terminetur; et videbis tot lineas colorum quot sunt oblongæ rimæ λ; quarum linearum cuique tot competent colores quot solent apparere virtute Prismatum. Nempe quælibet rima subit officium unius e prismatibus in experimento priori adhibitis et proprios colores cæruleum rubrum cæterosque generat quasi tot essent prismata quot sunt rimæ: Porro si papyrus PT longiùs differatur a Prismate coloratas istas lineas paulatim dilatari cernes et interjecta spatia minui donec absorbeantur a coloribus jam factis contiguis. Et si papyrus adhuc longius differatur, colores a diversis rimis effecti (rubri cum cæruleis primò deinde alij cum alijs) incipient plus pluśque misceri. Et sic sese paulatim diluent, donec cùm mistura satis absoluta est, convertantur in albedinem, præterquam in eorum extremitatibus P ac T ubi mixtura et confusio fere nulla est. Et isthæc accidunt cùm papyrus PT quasi ad distantiam decem vel duodecim vicibus majorem ipsâ AC vel BC latitudine planorum prisma constituentium, amoveatur. Quod si amoveatur adhuc longiùs, absimilium radiorum commistio fortasse perfectior evadet, sed colores purpurei et cærulei ad P, ac flavi rubeique ad T latiores fient, et interjectum spatium album minuetur, donec totum destruatur ab istis coloribus occupatum.
[58]In hisce autem experiendis cavendum est ut oblonga foramina λ sint accuratè æqualia et æqualibus distantijs ab invicem dissita, nè luce magis copiosâ per aliquod ingressâ quàm per cætera, colores exinde generati prævaleant cæteris et misturam perfectam conturbent: et sic vice albedinis colores apparebunt hinc illinc more fortuito sparsi. Illa verò distantia rimarum λ ut et earundem latitudo non malè statuitur fore pars digiti circiter duodecima, aut eâ fortè major si prisma satis amplum adhibeas. Quinetiam si cupias ut experimentum sit omnibus numeris absolutum, vice prismatum vitreorum vulgò venalium (quæ sunt nimis gracilia) debes amplioribus uti qualia possis efficere ex laminis vitreis utrinque perpolitis et conjunctis in morem vasculi prismiformis, quod vasculum impleatur aquâ clarissimâ, et undique cemento obturetur. Non multùm refert quænam sit hujus longitudo, sufficit ut sit trium digitorum, sed refringentia latera debent esse quatuor vel sex digitos lata aut ampliùs, ut rimæ præfatæ λ cum distantijs earum fiant majores et plures et magis accuratæ. Sin utaris angustioribus, qualia vulgò venduntur; colores externi juxta P ac T dilatando priùs destruent interjectam albedinem quam perficiatur per remotionem papyri PT. Et illa præterea quæ in totum constant ex vitro, colore aliquo ut viridi vel flavo plerumque tinguntur, et radios ita tingunt in transitu ut albedinem perfectam exhibere nequeant.
[59]Iam verò audire videor objectionem ex receptis philosophorum opinionibus depromptam: Dicat enim aliquis quòd colores revera et propriè loquendo non miscentur sed destruuntur potiùs; idque eâ de causâ quòd umbræ vicinia, quæ necessaria est ad productionem colorum, tollitur cum radij per diversas rimas trajecti commisceri incipiunt; et præterea quòd radijs sic mixtis quorum motus inter se dissentiunt, necesse est ut isti motus destruant alterutros, quibus cessantibus color omnis perit et in albedinem convertitur. Sic Cartesianus aliquis contendat forte quòd cùm globuli miscentur quorum rotationes contrariantur sibi, necesse est ut impediant sese et alternos motus destruant: Et sic alij objiciant alia.
[60]Sed responsio multiplex in promptu est: et imprimis inquam quòd cùm umbræ coloribus interjectæ primùm evanescunt removendo papyrum PT, colores tamen non ideo pereunt neque minimùm immutantur donec incipiant misceri per remotiorem distantiam papyri. Et albedo non producitur donec per distantiam adhuc remotiorem mistura radiorum omnis generis evadat perfecta. Unde confinium umbræ non est necessarium ad colores producendos, neque albedo generatur ex isto sublato.
[61]Secundo colores qui primò omnium miscentur, nimirum purpureus sive violaceus et rubeus videntur esse maximè omnium absimiles, propterea quod adversas colorum extremitates occupant. Quamobrem itáque motus eorum contrarij non destruunt sese neque color albus generatur antequam cæteri etiam colores omnes misceantur?
[62]Tertiò cuique licet observare idque nullo negotio quòd colores non omninò mutantur trajiciendo radios per medium quantumvis luminosum. Sic colores prismatum sunt ijdem sive trajiciantur per spatium illuminatum sive tenebris involutum. Et res omnes eodem modo coloratæ cernuntur, sive conspiciantur cùm lumen solis trajicitur per intermedium spatium sive cùm excluditur. Id quod secus esset si lux in lucem per idem medium transeuntem posset agere. Quinimò si radij duobus prismatibus refracti sese decussent, postquam ab invicem discreti sunt, eosdem colores efficient, quos aliàs efficerent si non omninò miscerentur. Id quod non posset evenire si radij diversis coloribus tincti sibi mutuò per eadem spacia transientibus mutationem aliquam inducerent.
[63]Quarto, cùm in illâ distantiâ papyrum PT fixeris ubi colores albedinem optimè componunt: statuatur alia papyrus YZ ad distantiam duroum vel trium digitorum a prismate, et in eâ notentur lineæ coloratæ; tum exscindantur istæ partes papyri in quas dictæ lineæ cecidêre, factis eo pacto rimis oblongis ν parallelis et æqualibus, ut et æquè latis ac distantibus. Deinde papyrus ista YZ in locum suum restituatur tres digitos circiter a prismate distantem ut per rimas ejus lux colorata trajiciatur ad alteram papyrum PT longinquiorem. Quo facto possis observare quòd si parùm deprimas papyrum YZ ut purpureos colores & cæruleos superioribus labris rimarum ejus impingentes intercipiat, et transmittat cæteros: albedo ad papyrum PT convertetur in rubeum colorem, aut citrium vel flavum. Sin attollas eam ut rubei et flavi labris inferioribus intercipiantur, cæteríque perlabantur; albedo ista convertetur in purpureum indicum et cæruleum. Perinde ut fieri oporteret in mixtura colorum: Nam unis e mixturâ sublatis alteri debent ad propriam speciem et formam restitui.
[64]Quintò, papyro YZ sublatâ, et reliquis stantibus: papyrum alteram PT in meditullio albedinis acu perfora ut lucis ejus albæ portiuncula trajiciatur quam deinceps excipe in aliam papyrum isti PT ad distantiam quatuor vel sex digitorum postpositam: et vice albedinis colores iterum apparebunt. At quomodo colores illi de novo generari potuissent si destruerentur in productione potiùs quàm miscerentur non video. Concedendum est itaque quòd tantùm miscentur: et quòd radij varijs coloribus tincti et promanantes a diversis rimis λ, λ decussant sese in dicto foramine per acum effecto, et postea divergentes ab invicem gradatim segregantur et segregati proprios iterum colores depingunt: quemadmodum posthac fusiùs explicabitur. Ad eundem præterea modum si speculum aliquod planum et exiguum K statuas in medio albedinis ad PT papyrum effectæ, ita quidem ut aliquos ex albificantibus radijs aliorsum, veluti ad πτ reflectat; lux alba sic reflexa degenerabit in colores, quos videre est ad πτ, papyrum objiciendo. Etenim radij tincti cum diversis coloribus et in albedinem ad speculum K commisti, inclinantur ad se invicem propterea quod adveniunt a diversis fissuris λ, λ, λ, λ, λ, λ. Atqui tantùm divergunt a speculo postquam reflectuntur quantùm anteà convergebant. Divergentes itaque paulatim dissocientur ac dissociati proprios colores non secus exhibebunt quàm si nunquam fuerant commisti. Liquet ergo quod in misturâ radiorum diversicolorum suæ dispositiones ad efficiendos varios colores non destruuntur; ut ut albedinem exhibeant dum commisceantur sibi.
[65]Denique vulgò notum est quod ex pulveribus diversicoloribus inter se commixtis color novus emergit; tamen si pulveres isti inspiciantur Microscopijs, omnes videntur tincti cum proprijs coloribus. Adeò ut ex mixturâ pulverum colores proprij non destruantur, sed permiscendo tantùm color novus elicitur. Verùm ijdem planè colores ex mixturâ colorum prismatum ac pulverum producuntur: Sic pulvis cæruleus cum flavo mixtus producit viriditatem, et eadem viriditas etiam producitur ex mixturâ radiorum tinctorum cum cæruleo et flavo. Et proinde non dubium est quin colores novi ex coalescentibus Prismatum coloribus, non facta assimilatione sed mistura tantum, similiter oriantur . Cæterùm ut nullum dubitandi locum relinquerem; effeci ut pulveres colorum principalium quos prismata generant, rubei, flavi, viridis, cærulei et purpurei in proportione certâ miscerentur: et licèt albedo perfecta non prodibat, tamen isti colores ad sensum periêre, et quoddam genus albedinis, fuscum et obscurum, sive mediocre inter albedinem et nigredinem perfectam producebatur. Quod nostro proposito non minùs inservit quàm si albedo perfecta prodijsset, quandoquidem fuscus ille ab albo perfecto tantùm differt quantitate lucis non autem specie coloris, ut exinde pateat, quòd producitur ex albo cum nigredine contemperato. Neque expectandum est, ut mihi videtur, alium quàm fuscum colorem e tali pulverum mistura generari: Nam cùm pulveres colorati intromittant maximam partem lucis, istam ferè solam reflectentes quæ apta est ad exhibendos proprios colores, ut ostendetur postea: eorum mixtura maximam quoque partem lucis intromittet. Unde pro albedine perfectâ talis color generandus est qualis efficitur ex albedine et nigredine mixtis, id est, fuscus. Attamen non eo inficias quin tales fortè pulveres inveniantur, præsertim inter mineralia, qui tantum lucis reflectant ut mixti exhibeant albedinem perfectiorem quàm hactenus vidi e mixturis effectam. Cæterùm quòd pulveres coloribus tantùm quinque præcipuis tinctos miscebam non ideo cogitandum est albedinem ex quinque solis productam fuisse, sed ex omnigenis. Nam in omnium corporum coloribus alij latent principalibus commixti licèt minùs fortes ut a principali colore superati non cernantur. Sic in cæruleo pulvere latent cyaneus et indicus alijque gradus omnes usque ad viridem aut flavum fortassis ex unâ parte, et ad intensum purpureum ex alterâ: Ut ut cæruleus eò solus appareat quòd sit cæteris longè copiosior.
Experientijs hisce admonitus in mentem præterea revocabam quòd corpuscula quæ conspiciuntur in radijs solaribus huc illuc volitantia varios colores exhibent modò quisquam ea diligenter observet in cubiculo quaquaversum luci occluso, præter unicum foramen per quod illuminantur. Et tamen cùm isti pulvisculi in acervum congregantur nullus omninò color apparet præterquam fuscus.
[66]Videtis itaque quòd possibile sit albedinem e mixtura colorum generari. Imò quòd colores prismatum revera non destruantur ad albedinem producendam; sed commisceantur tantum, quandoquidem emergunt immutati cùm radij coeuntes decussavêre et propter divergentiam subsequentem dissociantur iterum. Adhæc cum rei dignitas postulare videatur ut nullus non moveatur lapis, præter modos præcedentes componendi albedinem lubet adhibere tertium et quartum deinde quo prædicta faciliùs experiri possis et magis fortè cum evidentiâ.
Posito quòd 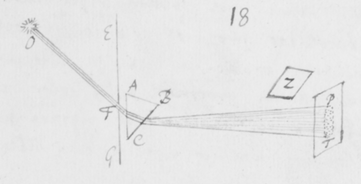 Sol illuceat obscurato cubiculo per unicum tantùm foramen F, (figura ) cui Prisma ABC affigitur, ingressam lucem refringens ad PT: juxta colores in papyrum PT sic projectos teneatur alia papyrus Z ut illuminetur a coloratâ luce quam altera papyrus PT reflectit. Quo facto, papyrus Z sic illuminata radijs omnium colorum confusè reflexis a PT, apparebit alba. De hoc autem specimine maximè luculento et facili juvabit observare sequentia.
Sol illuceat obscurato cubiculo per unicum tantùm foramen F, (figura ) cui Prisma ABC affigitur, ingressam lucem refringens ad PT: juxta colores in papyrum PT sic projectos teneatur alia papyrus Z ut illuminetur a coloratâ luce quam altera papyrus PT reflectit. Quo facto, papyrus Z sic illuminata radijs omnium colorum confusè reflexis a PT, apparebit alba. De hoc autem specimine maximè luculento et facili juvabit observare sequentia.
[67]Primò quòd auferendo papyrum PT ne lucem ampliùs ad Z reflectat: e consequenti defectu lucis in Z cognoscas eam illuminari per solam lucem coloratam a PT reflexam.
Secundò si papyrum Z ipsi PT valdè vicinam teneas, ut una pars ejus magis illuminetur ab uno colore & alia ab alio: ipsa Z non apparebit alba sed ejus partes coloribus istis tingentur quibus sunt vicinissimæ. Sin ipsa Z ad majorem a PT distantiam transferatur ut omnes ejus partes æqualiter ferè ab omnibus coloribus illuminentur: ex illâ colorum mixturâ generabitur albedo.
Denique quòd albedo illa Z non destruendo colores sed tantùm miscendo generatur exinde pateat quod colores PT cernuntur beneficio radiorum non secus oculo mixtim incidentium quam papyro Z. Itaque si colores destruerentur potiùs quàm miscerentur ad Z, etiam destruerentur ad corneam tunicam vel pupillam oculi: ubi tamen certissimum est quòd miscentur tantùm, ut decussantes, postea divergant ad varias partes Retinæ et sic excitent phantasmata propria. Quinimò si radij tincti cum diversis coloribus dum per eadem spatia confusè transeunt possent in se invicem agere et dispositiones mutare quas quilibet habent ad expingendos proprios colores: omnes omnium rerum colores conturbarentur ac se mutuò transmutarent dum per aera transmittuntur; ubique scilicet radijs aliorum corporum omnigenis coloribus tinctorum occurrentes. Et sic in coloribus visibilium nulla esset certitudo, constantia nulla.
[68][69]Quartum præterea modum descripturus quo colores in albedinem misceri possent, pono quòd ABC (figura ) sit Prisma foràs ante foramen F 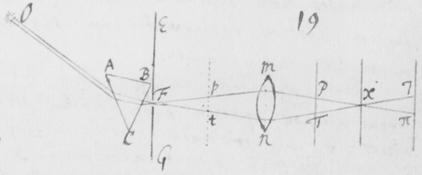 dispositum, quod refractam lucem in obtenebratum cubiculum transmittat versus MN. Tum lentem MN convexam sume cujus focus ad distantiam semipedis aut pedis unius duorumee (quale est objectivum vitrum Perspicilli bipedalis;) et eam statue paulò plus distantem a foramine F quàm focus distat a se: ita scilicet ut lux colorata per eam deinceps trajiciatur, sicut videre est in schemate. Sit autem ejus latitudo sive apertura tanta ut omnes radios transmittat. Deinde cùm lentem in dicto situ stabilitam feceris, ponè statuatur papyrus PT in quam radij bis refracti terminentur. Eamq́ue primò colloca proximè ad lentem, deinde ad majorem distantiam continuato motu transfer, et videbis colores purpureum P rubeuḿque T contrahi et eouśque minui dum omnes convertantur in albedinem, puta ad X quatuor vel sex pedes aut longiùs fortè distantem a lente, pro convexitate ejus vel positione. Deinde si papyrum adhuc longiùs transferas, colores iterum emergent sed in situ contrario, rubeo ad τ conspecto et purpureo ad π. Neque ulla inter eos ad PT et πτ differentia intercedit præterquam quòd situs sit contrarius. Scilicet a lente MN effectum est ut omnes radij venientes ab aliquot punctis foraminis F in totidem iterum punctis congregentur ad papyrum X: Et sic omnes omnium specierum tum purpuram ad P tum rubedinem ad T, tum alios alibi colores efficientum convergunt ad X et ibi confusè miscentur ad albedinem generandam: De quâ imagine albâ et orbiculari monebam supra a[70]. Postea verò cùm sese decussavêre in X, radij PX tendunt ad π et TX ad τ, adeo ut ijdem colores expingantur ad P et π per eosdem radios Pπ, et ijdem ad T et τ per eosdem Tτ, et sic de alijs. Unde liquet iterum quòd dispositiones, radiorum absimilium, ad diversos colores producendos non destruantur per eorum mixturam, quandoquidem eosdem expingunt cùm segregantur quos ante mixturam expingebant.
dispositum, quod refractam lucem in obtenebratum cubiculum transmittat versus MN. Tum lentem MN convexam sume cujus focus ad distantiam semipedis aut pedis unius duorumee (quale est objectivum vitrum Perspicilli bipedalis;) et eam statue paulò plus distantem a foramine F quàm focus distat a se: ita scilicet ut lux colorata per eam deinceps trajiciatur, sicut videre est in schemate. Sit autem ejus latitudo sive apertura tanta ut omnes radios transmittat. Deinde cùm lentem in dicto situ stabilitam feceris, ponè statuatur papyrus PT in quam radij bis refracti terminentur. Eamq́ue primò colloca proximè ad lentem, deinde ad majorem distantiam continuato motu transfer, et videbis colores purpureum P rubeuḿque T contrahi et eouśque minui dum omnes convertantur in albedinem, puta ad X quatuor vel sex pedes aut longiùs fortè distantem a lente, pro convexitate ejus vel positione. Deinde si papyrum adhuc longiùs transferas, colores iterum emergent sed in situ contrario, rubeo ad τ conspecto et purpureo ad π. Neque ulla inter eos ad PT et πτ differentia intercedit præterquam quòd situs sit contrarius. Scilicet a lente MN effectum est ut omnes radij venientes ab aliquot punctis foraminis F in totidem iterum punctis congregentur ad papyrum X: Et sic omnes omnium specierum tum purpuram ad P tum rubedinem ad T, tum alios alibi colores efficientum convergunt ad X et ibi confusè miscentur ad albedinem generandam: De quâ imagine albâ et orbiculari monebam supra a[70]. Postea verò cùm sese decussavêre in X, radij PX tendunt ad π et TX ad τ, adeo ut ijdem colores expingantur ad P et π per eosdem radios Pπ, et ijdem ad T et τ per eosdem Tτ, et sic de alijs. Unde liquet iterum quòd dispositiones, radiorum absimilium, ad diversos colores producendos non destruantur per eorum mixturam, quandoquidem eosdem expingunt cùm segregantur quos ante mixturam expingebant.
[71]Porro si radios cujuśvis coloris intercipias, interponendo corpus aliquod opacum prope lentem MN, et cæteros facias missos: videbis non modò colores interceptos e papyris PT ac πτ tolli, sed et albedinem X destrui, et ejus vice colorem aliquem qualis efficitur per mixturam radiorum præterlabentium generari. Sic si radios intercipias ostendentes rubeum ad N: rubedo T ac τ tolletur et albedo X convertetur in cæruleum. Vel si sistas tum rubeum ad N tum purpureum ad M, et intermedios flavum viridem et cæruleum præterlapsos mittas: ex eorum misturâ viriditas producetur ad X. Et sic prætermittendo quos velis et sistendo alios, pro arbitratu possis experiri mixturas quaslibet et explorare qui color inde generabitur; modò pretium laboris experientiam illam judicaveris.
<41>[72]Verum cùm experimenti hujus dignitas videatur exigere ut summâ cum diligentiâ retegatur et penitiùs explicetur, dum plura de coloribus simul complectitur et exhibet quàm in unico tantùm experimento solent latere: non gravabor copiosiùs ostendere quo pacto radij miscentur ad X, et nonnulla postmodum scitu non indigna patefacere. Itaque concipiantur tales refractiones in Prismate fieri, ut radij incidant in varios circulos ad Lentem MN, qui varios gradus refractionis patiuntur; prout explicui in præcedentibus a[73]. Sitq́ue PQRST (figura ) oblonga imago composita ex isti circulis, 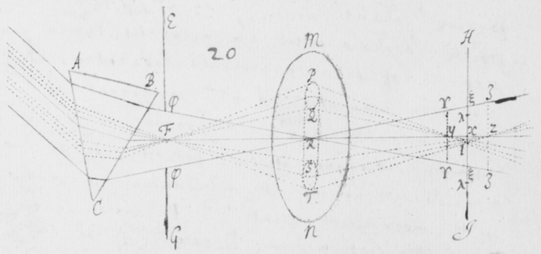 & in lentem projecta: quorum circulorum extremi duo sunto PQ purpureus et ST rubeus. Porrò sit φFφ diameter foraminis per quod lux in lentem trajicitur cujus foraminis punCtum aliquod ut F primò consideremus a quo venientes radij dictos circulos PQ, ST totamque imaginem PT efformant. Et præterea cùm radij quemlibet circulum efformantes sint conformes sibi: ponatur quòd Lens sit tali figurâ prædita ut eos omnes cujusdam e circulis, puta rubei ST versus punctum quoddam Z exactè refringat. Quod fieri posse per lentem convexis Hyperbolis terminatam, ut et per lentes aliter formatas Cartesius in Dioptricâ et Geometriâ suâ edocuit. Est itáque Z focus radiorum FS{,} FT et cæterorum uniformitèr rubeorum, et recta FZ ducta erit axis lentis. Præterea cùm radij FP, FQ, cæteriq́ue conficientes alterum extremum circulum PQ colorem purpureum ostendant & propterea magis refringantur quàm alteri tendentes ad ST; illi ideò convergent ad punctum quoddam aliquantò propinquius quàm Z, veluti ad Y; ut ij facilè percipient, qui nórunt focos lentium esse tantò propinquiores sibi, quantò major est earum vis refractiva. Liquet itáque radios in coloribus et refractionibus absimiles ad diversos focos convergere. Sed cùm eadem Lens pluribus focis haud queat adaptari, et ideò cùm Z supponatur focus in quem omnes radij ad circulum rubeum ST pertinentes exactè conveniant: radij pertinentes ad alterum circulum PQ purpureum, omnes in ejus focum Y exactè convenire nequeunt. Attamen eorum concursus juxta Y in axe tam proximè accuratus erit, ut quoad sensum et experientiam omnem habeatur pro accurato. Quinetiam si lens MN ponatur sphæricè convexa ut neuter focorum Y vel Z strictè loquendo possit esse accuratus, tamen quantum ad præsentia spectat pro accuratis habeantur. Itaque concipiendo quod radij manantes ab ST convergant ad Z et quod alteri manantes a PQ convergant ad Y et ibi decussantes divergant itidem: patebit quòd hi duo radiorum penicilli concurrent et miscebuntur in spatio focis Y et Z intermedio, veluti ad l, modò Lentis centrum R ponatur intermedium circulis PQ et ST. Ad eundem modum radij cæterorum generum convergent in alios focos ipsis Y et Z intermedios, ac tanto propinquiores ipsi Y quanto major est eorum passio refractiva. Sic focus viridiformium radiorum cadet in medio spatio veluti ad X; radijq́ue cæruliformes convenient citiùs inter X et Y, et flaviformes longinquiùs inter X et Z, ac cæteri colores intermedij in spatijs intermedijs: Eorumque penicilli sese decussabunt ultra citraque locum l; ita tamen ut istæ decussationes sint eò densiores quantò sunt ipsi l viciniores, et ut Spatium xl sit minimum per quod omnes radij transeunt manantes ab eodem puncto F. Non dissimili modo radij venientes ab alio quovis puncto foraminis, ut φ, si sint rubriformes convergent ad ζ; sin purpuriformes, ad ϒ; et ad intermedium aliquod punctum si sint intermedij generis et eorum concursus densissimus erit in loco medio veluti ad ξλ. Atque adeò ex radijs ab integro foramine φF manantibus foci maximè refrangibilium jacebunt in superficie quâdam ϒYϒ ad lentem proximâ, foci minimè refrangibilium jacebunt in aliâ superficie ζxζ a lente remotissimâ, focique mediocriter refrangibilium jacebunt in alijs intermedijs superficiebus. Et sic omnes omnium radiorum foci totum spatium ϒζζϒ a superficiebus istis integratum occupabunt, et in eo praecipue penicilli decussabunt & commiscebuntur.
& in lentem projecta: quorum circulorum extremi duo sunto PQ purpureus et ST rubeus. Porrò sit φFφ diameter foraminis per quod lux in lentem trajicitur cujus foraminis punCtum aliquod ut F primò consideremus a quo venientes radij dictos circulos PQ, ST totamque imaginem PT efformant. Et præterea cùm radij quemlibet circulum efformantes sint conformes sibi: ponatur quòd Lens sit tali figurâ prædita ut eos omnes cujusdam e circulis, puta rubei ST versus punctum quoddam Z exactè refringat. Quod fieri posse per lentem convexis Hyperbolis terminatam, ut et per lentes aliter formatas Cartesius in Dioptricâ et Geometriâ suâ edocuit. Est itáque Z focus radiorum FS{,} FT et cæterorum uniformitèr rubeorum, et recta FZ ducta erit axis lentis. Præterea cùm radij FP, FQ, cæteriq́ue conficientes alterum extremum circulum PQ colorem purpureum ostendant & propterea magis refringantur quàm alteri tendentes ad ST; illi ideò convergent ad punctum quoddam aliquantò propinquius quàm Z, veluti ad Y; ut ij facilè percipient, qui nórunt focos lentium esse tantò propinquiores sibi, quantò major est earum vis refractiva. Liquet itáque radios in coloribus et refractionibus absimiles ad diversos focos convergere. Sed cùm eadem Lens pluribus focis haud queat adaptari, et ideò cùm Z supponatur focus in quem omnes radij ad circulum rubeum ST pertinentes exactè conveniant: radij pertinentes ad alterum circulum PQ purpureum, omnes in ejus focum Y exactè convenire nequeunt. Attamen eorum concursus juxta Y in axe tam proximè accuratus erit, ut quoad sensum et experientiam omnem habeatur pro accurato. Quinetiam si lens MN ponatur sphæricè convexa ut neuter focorum Y vel Z strictè loquendo possit esse accuratus, tamen quantum ad præsentia spectat pro accuratis habeantur. Itaque concipiendo quod radij manantes ab ST convergant ad Z et quod alteri manantes a PQ convergant ad Y et ibi decussantes divergant itidem: patebit quòd hi duo radiorum penicilli concurrent et miscebuntur in spatio focis Y et Z intermedio, veluti ad l, modò Lentis centrum R ponatur intermedium circulis PQ et ST. Ad eundem modum radij cæterorum generum convergent in alios focos ipsis Y et Z intermedios, ac tanto propinquiores ipsi Y quanto major est eorum passio refractiva. Sic focus viridiformium radiorum cadet in medio spatio veluti ad X; radijq́ue cæruliformes convenient citiùs inter X et Y, et flaviformes longinquiùs inter X et Z, ac cæteri colores intermedij in spatijs intermedijs: Eorumque penicilli sese decussabunt ultra citraque locum l; ita tamen ut istæ decussationes sint eò densiores quantò sunt ipsi l viciniores, et ut Spatium xl sit minimum per quod omnes radij transeunt manantes ab eodem puncto F. Non dissimili modo radij venientes ab alio quovis puncto foraminis, ut φ, si sint rubriformes convergent ad ζ; sin purpuriformes, ad ϒ; et ad intermedium aliquod punctum si sint intermedij generis et eorum concursus densissimus erit in loco medio veluti ad ξλ. Atque adeò ex radijs ab integro foramine φF manantibus foci maximè refrangibilium jacebunt in superficie quâdam ϒYϒ ad lentem proximâ, foci minimè refrangibilium jacebunt in aliâ superficie ζxζ a lente remotissimâ, focique mediocriter refrangibilium jacebunt in alijs intermedijs superficiebus. Et sic omnes omnium radiorum foci totum spatium ϒζζϒ a superficiebus istis integratum occupabunt, et in eo praecipue penicilli decussabunt & commiscebuntur.
[74]Iam ex hâc descriptione venit observandum quòd cùm papyrus HI teneatur in medio dicti spatij ϒζζϒ, ut in eam radij terminentur ubi densissimus est eorum concursus et mixtura ad albedinem generandam perfectissima: radij viridiformes tendentes ad focos in papyro sitos in eam incident intra literas ξξ, sed rubriformes venientes ab ST, ac tendentes ad focos in superficie ζZζ sitos ut dictum est, incident in papyrum intra literas λλ paulò viciniùs ad I. Et pari modo purpuriformes incident in eundem locum λλ dum tendunt a PQ ad focos sitos in superficie ϒYϒ. Cæteri autem radij cadent in alia spatia inter ξξ & λλ mediocria, ipsíque ξξ tantò viciniora quanto foci eorum minùs absint a papyro. Liquet itaque quòd totum spatium ξXlλ non debet albescere, sed pars ejus tantùm media inter literas ξ et λ interiores sita, ubi scilicet colores omnes commiscentur: Etenim in extremitate ξ versus H radij viridiformes cadunt soli, qui proinde tingent extremitatem istam cum viriditate. Ad alteram autem extremitatem versus I nulla miscetur viriditas sed purpura tantum cum rubore. Qui dicta perpendet etiam facilè percipiet quòd cùm papyrus paululum transferatur ultra citráque, colores alij præter viriditatem apparebunt ad extremitatem imaginis versus H, scilicet inter P et ϒ purpureus apparebit extimus, inter ϒ et ξ cæruleus, et viridis ad ξ, deinde flavus inter ξ et ζ, ac rubeus denique ad ζ et postea perpetuò. Ad alteram autem imaginis extremitatem versus I sitam rubeus erit extimus a T usque ad λ ubi commiscetur purpuræ: Quæ quidem mixtura dat pallidum quendam colorem nunc ad rubeum nunc ad cæruleum nonnihil vergentem pro variâ proportione mistorum. At ultra λ purpura semper conspicietur. Cæterùm cùm distantia interϒ et ζ valde parva sit et multò magis distantia inter X et l sive ξ et λ, hoc est latitudo limbi colorati: propter summam ejus exilitatem conspectui vix patebit, sed totum spatium ξXlλ nisi acriùs observanti apparebit album.
[75]Cùm hæc advertissem, experiebar deinde an responderent præconceptis: et licèt malè successerat primò dum utebar angustâ lente: postea tamen cùm adhibui lentem eâ de causâ latiorem ut angulus XYl sive ξϒλ et inde Xl sive ξλ hoc est latitudo dicti limbi colorati fieret major, quod optabam evenit. Adhibeatur itaque lens cujus latitudo sive apertura sit trium digitorum aut major eo, foci autem longinquitas pro lubitu tuo pedium trium vel quatuor, tum ea collocetur ad distantiam sex vel octo pedum a foramine φFφ, ut colores PQRST in eam prolapsi usque ad extremitates ejus extendantur, nullis tamen præterlabentibus. Deinde papyrus HI ponè collocata transferatur ultra citráque, et ad extremitatem imaginis versus H videbis omnes prismatum colores a purpura ad rubedinem usque gradatim successivos: sed ad alteras imaginis partes versus I, inter purpuram ad ζ et rubedinem ad ϒ conspicuam, neque viriditas neque alius quispiam ex intermedijs coloribus apparebit nisi fortè qui fiunt ex rubeo et purpureo mixtis: Quemadmodum ex eo cognoscas quòd cùm intercipis extremitatem purpuræ, ope corporis opaci juxta lentem ad P interpositi, ille limbus imaginis versus I fiet rubeus; sin extremitas rubedinis ad T intercipiatur, limbus idem fiet purpureus. Et hinc est quòd transitus a purpura ad rubedinem ex hâc parte imaginis fit multò celerior quàm ex alterâ versus H ubi colores omnes interveniunt. Cæterùm cùm dictorum colorum latitudo tam exigua sit (videlicet haud major centesimâ parte digiti,) ut nisi vitra sint benè polita et a venis libera, et insuper experientis diligentia et curiositas solito major, fortè excidet proposito. Quamobrem in majorem evidentiam rei et experiendi copiam addo, quòd si Microscopium sumas atque ita disponas ut papyrum aliquam affixam laminæ super quam objecta collocantur contemplanda, distinctè ampliet; dein ita statuas ut imago lucida ξxlλ incidat in istam papyrum; colores in ejus limbo sic ampliatos videbis manifestos.
[76]Verùm cùm mistura radiorum quoad colores absimilium non sit adeò perfecta in hoc specimine quin ut e coloribus aliqui in extremitate albedinis appareant (licèt tam exigui ut incautus fortè non advertat,) placet insuper observare quod si vice lentis refractariæ speculum concavum accuratè formatum et perpolitum adhibeas, dicta mistura fiet omnibus numeris perfecta. Etenim irregularitas illa quâ refractiones ita perturbantur, in reflectionibus nulla est, sed radij quoscunque colores expingentes et utcunque refrangibiles ad eosdem tamen angulos reflectuntur in quibus incidunt. Quamobrem si MN (fig ) sit speculum Ellipticum 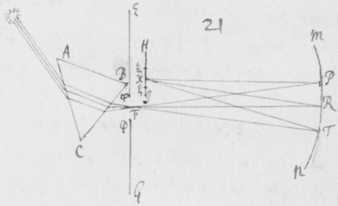 cujus foci sint F et X: radij omnes a puncto F manantes cujuscunque generis sive purpuram ad P, sive rubedinem ad T, sive alios alibi colores quoscunque ad speculum exhibentes, tamen omnes accuratè convenient in eodem puncto X. Quinimò licet speculum MN non sit ex ellipticâ figurâ segmentum sed e sphæricâ: modò semidiameter sphæræ, hoc est distantia ejus a focis prædictis F et X, satis magna sit, puta trium pluriúmve pedum, et distantia focorum valdè parva, puta non plusquam unius digiti: si hæc inquam ponantur, radij ab F manantes adeò propemodum convenient in X ut istud X quoad omnem sensum pro exacto foco habeatur. Et eodem modo radij manantes ab alijs punctis ut φ ipsi F vicinis in alijs ut ξ ipsi X vicinis quàm proximè convenient. Et sic omnes omninò colores reflectentur a speculo PT in unumquodque punctum imaginis ξXξ, totamque exhibebunt albam.
cujus foci sint F et X: radij omnes a puncto F manantes cujuscunque generis sive purpuram ad P, sive rubedinem ad T, sive alios alibi colores quoscunque ad speculum exhibentes, tamen omnes accuratè convenient in eodem puncto X. Quinimò licet speculum MN non sit ex ellipticâ figurâ segmentum sed e sphæricâ: modò semidiameter sphæræ, hoc est distantia ejus a focis prædictis F et X, satis magna sit, puta trium pluriúmve pedum, et distantia focorum valdè parva, puta non plusquam unius digiti: si hæc inquam ponantur, radij ab F manantes adeò propemodum convenient in X ut istud X quoad omnem sensum pro exacto foco habeatur. Et eodem modo radij manantes ab alijs punctis ut φ ipsi F vicinis in alijs ut ξ ipsi X vicinis quàm proximè convenient. Et sic omnes omninò colores reflectentur a speculo PT in unumquodque punctum imaginis ξXξ, totamque exhibebunt albam.
[77]Porro ex his notandum est quòd non solùm albedo ad Focum X e commisturâ radiorum omnis generis producitur, sed et ista ad foramen φFφ effecta cùm lux modò transierit Prisma et nondum aliqui colores apparuêre, quòd ista inquam constat ex simili mixturâ: quandoquidem omnes radij quibuscunque coloribus affecti qui ad punctum quodvis imaginis ξXξ convergunt, ab alio quodam puncto foraminis φFφ manarunt: et sic ijdem radij ad utrumque spatium φFφ et ξXξ miscentur, et utriusque albedinis eadem est compositio.
[78]Atque hæc clariora fient observando primò quòd rei alicujus utcunque figuratæ et applicatæ ad foramen φFφ umbra distinctè projicitur in papyrum radios excipientem ad X. Quinimò bullularum aëris in Prismate latentium (sicut vitris omnibus contingere solet) umbras videbis ad instar macularum in dictam papyrum projectas. Id quod nullo pacto contingere potuisset nisi radij manantes ab aliquot punctis ipsius φFφ in totidem punctis rursus convenirent ad ξXξ. Et licèt non exactè conveniant in ijsdem punctis manantes ab ijsdem, cùm lens refractaria vice speculi adhibeatur, ut in figuris 19 & 20, proinde colores nonnullos generent in confinio lucis et umbræ sicut fusè explicui; tamen spatium, in quod conveniunt tantillum est ut pro puncto sensibili fermè habeatur.
[79]Secundò quòd si lentem in figura ita statuas ut æquidistet a focis ejus F et X in medio posita, ac deinde colores excipias in papyrum PT tum ultra lentem versus X tum citra versus F alternis temporibus admotam: possis observare quòd colores eodem planè modo apparent diminuuntur et in albedinem paulatim convertuntur dum dicta papyrus motu lento et continuo transfertur ad F, atque dum transfertur ad X. Adeò ut divergentia colorum ab F et convergentia ad X omnino similis sit. Pari ratione si papyrus πτ lente moveatur ad X juxta et papyrus PT movetur ad F, ijdem colores in utrâque conspicientur, et eodem modo desinent in albedinem, hoc tantùm excepto quod eorum situs contrariatur propter decussationem radiorum in X. Atque adeò divergentia colorum ab utrisque F et X omninò similis est. Quid itáque concludatur exinde quàm quòd eodem modo commiscentur et ad F antequam divaricârunt ab invicem, et ad X ubi rursus congregantur in albedinem. Sed ut comparatio modò facta evadat illustrior ab instantiâ aliquâ, venit observandum porrò quòd cùm papyrus statuatur ipsi F contigua, & amoveatur deinde versus pt, et postea statuatur ad X et amoveatur versus πτ: quòd, inquam, albedo ad F et X in utroque casu primò degenerabit in colores secundum extremitates ejus, dum in meditullio manet alba. Cujus rei ratio non alia est quàm quòd radij divergentes primò segregantur in confinio lucis et umbræ.
Sic posito quod radij divergant a 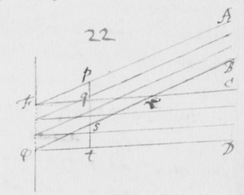 spatio Fφ, (figura ) alij quidem paralleli tendentes ad AB atque alij ad priores inclinati sed inter se paralleli tendentes ad CD. Prima segregatio fiet in extremitatibus juxta lineas FA et φD, ultimaque in medio veluti ad r. Nam lineâ pt inter Fφ et r ductâ, videre est quòd parallelæ ad juxta extremitates pq et st ab invicem segregantur, sed mixtæ transeunt per intermedium spatium qs.
spatio Fφ, (figura ) alij quidem paralleli tendentes ad AB atque alij ad priores inclinati sed inter se paralleli tendentes ad CD. Prima segregatio fiet in extremitatibus juxta lineas FA et φD, ultimaque in medio veluti ad r. Nam lineâ pt inter Fφ et r ductâ, videre est quòd parallelæ ad juxta extremitates pq et st ab invicem segregantur, sed mixtæ transeunt per intermedium spatium qs.
[80]Tertiò sicut lens MN in figura refringendo radios divergentes ab F facit ut convergant ad X et ibi conficiant albedinem: eodem modo si isti radij postquam decussavêre divergentes ab X iterum trajiciantur per aliam lentem μν (figura ) priori similem et similiter positam inter focos ejus X et ξ, (id est, in æquali ab utrisque distantiâ:) colores sic ad ξ 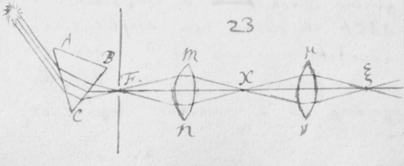 secundâ vice congregati, albedinem rursus component sicut ante composuerant ad X, hoc tantùm interposito discrimine, quòd apparebunt in limbo albedinis ad ξ duplo latiores quàm (e mox ostensis) appareant ad X; atque insuper in situ contrario. At speculis ut dictum est adhibitis quæ lucem aliquoties repercutiant, isti colores erunt nulli: atque adeò penicilli FX et Xξ evadent omnino similes & similis fiet decussatio, et commistura radiorum ad F, X, et ξ. Concludendum est itaque quòd lux, cùm modò trajicitur per prisma, licèt albedinem exhibeat, tamen constat ex radijs heterogeneis confusè mixtis et ab invicem per divergentiam mox discessuris, qui postquam ita segregantur proprijs apparent formis, sin iterum congregantur albedinem rursus componunt, & sic præterea in infinitum.
secundâ vice congregati, albedinem rursus component sicut ante composuerant ad X, hoc tantùm interposito discrimine, quòd apparebunt in limbo albedinis ad ξ duplo latiores quàm (e mox ostensis) appareant ad X; atque insuper in situ contrario. At speculis ut dictum est adhibitis quæ lucem aliquoties repercutiant, isti colores erunt nulli: atque adeò penicilli FX et Xξ evadent omnino similes & similis fiet decussatio, et commistura radiorum ad F, X, et ξ. Concludendum est itaque quòd lux, cùm modò trajicitur per prisma, licèt albedinem exhibeat, tamen constat ex radijs heterogeneis confusè mixtis et ab invicem per divergentiam mox discessuris, qui postquam ita segregantur proprijs apparent formis, sin iterum congregantur albedinem rursus componunt, & sic præterea in infinitum.
[81][82] Imò vero lux non solùm componitur ex omnium colorum radijs ut egreditur prismate et nondum discernitur in colores istos, sed etiam cùm nondum attigerit prisma et antecedenter ad omnem refractionem. Et inde non mirum est quòd cùm segregatur in colores virtute prismatis radios inæqualiter refringentis, et colores iterum commiscentur ope lentis aut alio quovis modo præmonstrato, quòd, inquam, rursus componant albedinem.
[83]Verùm ut hoc discrimen inesse radijs antecedenter ad refractiones ostendam: sit ABC (figura ) prisma quod excipit radios in obscurum cubiculum per foramen F uno digito latum trajectos, eosque refringit ad papyrum vel parietem HI ijs obsistentem apud T. Porrò autem cùm superficies prismatis BC non omnes refringat radios versus 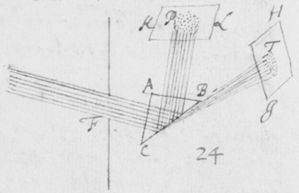 T sed et plurimos reflectat, eos apud P siste cum alia papyro KL in morem albæ imaginis foramini F persimilis terminante. Deinde converte prisma circa axem ejus secundum ordinem literarum ABCA et videbis tum amplitudinem colorum ad T, tum quantitatem lucis ad P augeri perpetuò, donec tandem cum refractio ad planum BC fit maximè obliqua, colores ad T incipiant evanescere et reflecti ad P, purpureus primò, deinde cæruleus viridis et flavus, ac denique ruber. Cujus quidem lucis accessu imago P fiet multò lucidior quàm antea. Interea verò dum colores a T gradatim evanescunt videbis albedinem P paululum mutari & nonnihil vergere ad cæruleum, per accessum nempe purpurei et cærulei qui primò reflectuntur: at postquam cæteri etiam colores viridis flavus et ruber reflectuntur a T, albedo ad P redintegrabitur. Id quod nullo modo accidisse potuisset nisi radijs prout a Sole veniunt discrimen interesse concedatur. Scilicet quòd ex ijs quidem ad efficiendos rubeum et flavum dispositi pertinaciùs et cum minori refractione penetrent superficiem BC et versus T prolabantur, dum alij ad exhibendum purpureum et cæruleum parati superficiem dictam aut penetrent languidiùs majorem refractionem patientes, aut si nequeant penetrare propter nimiam eorum obliquitatem, tum faciliùs et citiùs reflectantur ad P. Ijs primò omnium reflexis quorum potentia ad istam superficiem penetrandam sit minima, id est, purpuriformibus, et cæteris deinde suo ordine prout incidentia fit magis, obliqua, donec rubriformes ultimò reflectantur obliquitate tantâ debilitati ut non sint ampliùs potentes dictæ superficiei resistentiam superare. Atque hæc facilè constabunt ijs qui nôrunt quòd quò major est vis refractiva superficiei cujusvis, eò citiùs et ad minorem obliquitatem radij reflectentur; et quo minor eò magis obliqui penetrabunt.
T sed et plurimos reflectat, eos apud P siste cum alia papyro KL in morem albæ imaginis foramini F persimilis terminante. Deinde converte prisma circa axem ejus secundum ordinem literarum ABCA et videbis tum amplitudinem colorum ad T, tum quantitatem lucis ad P augeri perpetuò, donec tandem cum refractio ad planum BC fit maximè obliqua, colores ad T incipiant evanescere et reflecti ad P, purpureus primò, deinde cæruleus viridis et flavus, ac denique ruber. Cujus quidem lucis accessu imago P fiet multò lucidior quàm antea. Interea verò dum colores a T gradatim evanescunt videbis albedinem P paululum mutari & nonnihil vergere ad cæruleum, per accessum nempe purpurei et cærulei qui primò reflectuntur: at postquam cæteri etiam colores viridis flavus et ruber reflectuntur a T, albedo ad P redintegrabitur. Id quod nullo modo accidisse potuisset nisi radijs prout a Sole veniunt discrimen interesse concedatur. Scilicet quòd ex ijs quidem ad efficiendos rubeum et flavum dispositi pertinaciùs et cum minori refractione penetrent superficiem BC et versus T prolabantur, dum alij ad exhibendum purpureum et cæruleum parati superficiem dictam aut penetrent languidiùs majorem refractionem patientes, aut si nequeant penetrare propter nimiam eorum obliquitatem, tum faciliùs et citiùs reflectantur ad P. Ijs primò omnium reflexis quorum potentia ad istam superficiem penetrandam sit minima, id est, purpuriformibus, et cæteris deinde suo ordine prout incidentia fit magis, obliqua, donec rubriformes ultimò reflectantur obliquitate tantâ debilitati ut non sint ampliùs potentes dictæ superficiei resistentiam superare. Atque hæc facilè constabunt ijs qui nôrunt quòd quò major est vis refractiva superficiei cujusvis, eò citiùs et ad minorem obliquitatem radij reflectentur; et quo minor eò magis obliqui penetrabunt.
[84]De hoc autem experimento juvabit observare sequentia. Primò quòd cùm prædicta variatio albedinis ad P sit admodum parva propter exuberantiam lucis albæ collatæ ad reflexum cæruleum: itáque cavendum est ne prismate utaris quod ex vitro conflatur tincto cum colore aliquo, ne lucem ad P reflexam ita tingat ut difficile sit dictam variationem observare. Præstat adhibere prisma ex laminis vitreis tenuibus et perpolitis confectum et aquâ lympidissimâ repletum.
<50>Secundò licèt mutatio dicta sit parva, tamen satis est ad ostendendum quòd radij retinent eosdem colores cùm reflectuntur quos exhibent cùm trajiciuntur per superficiem BC; siquidem tingunt albedinem P colore suo quantum liceat tam paucis tingere. Colores itáque suos habuêre priùs, et eosdem retinent sive refringantur sive reflectantur: licèt {m}isturis plerumque celati latent donec eruantur (non autem fiunt) virtute Prismatum.
Tertiò ex luce P ad priorem speciem albedinis per reflectionem omnium colorum ab T restitutâ, quid aliud denotatur quàm quòd albedo ista per misturam colorum omnium reproducitur. Scilicet cùm rubor ultimò reflexus admiscetur cæteris coloribus antea reflexis, reflexorum colorum mistura tunc perfecta est ad albedinem componendam, quæ superadditur albedini priùs existente in P.
Quartò, nequa oboriatur suspicio quòd refractiones in superficiebus AC et AB ad ingressum radiorum in Prisma et egressum factæ, possint aliquid conducere ad effectus hosce producendos; juvabit observare quòd effectus ijdem producuntur, cujuscunque licèt magnitudinis statuatur angulus ACB; hoc est, quæcunque sit refractio superficiei AC; modò angulus ABC ponatur ejusdem magnitudinis atque angulus ACB: alias enim pro imagine albâ ad P generabuntur colores. Experimentum itaque nullatenus dependet a refractionibus superficierum AC et AB : imò possis efficere quòd cùm colores partim reflectuntur ad P et partim trajiciuntur ad T, radij perpendiculariter incident in AC emergentq́ue ex AB, et sic neutrâ superficie refringentur; modò statuas angulum ACB ut et ABC esse circiter: et ijdem tamen effectus producentur.
[85]Cæterùm in majorem evidentiam et explicationem modi quo prædicta fiunt, liceat 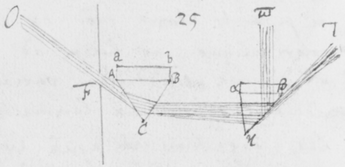 experiri per lucem in colores discretam, quòd purpureus primò et cæteri deinde (quisque suo ordine) reflectuntur. Etenim (in figura ) sint ABC et αβκ duo prismata parallela quorum alterum ABC projicit colores in alterum αβκ ad distantiam duodecim vel plurium pedum. Tum Prismate αβκ circa axem ejus secundum ordinem literarum , converso donec tanta sit obliquitas radiorum in superficiem βκ incidentium ut incipiant ad π reflecti non ampliùs potentes penetrare ad τ; videbis omnes purpuriformes primò reflecti, cæterosque deinde suo ordine.
experiri per lucem in colores discretam, quòd purpureus primò et cæteri deinde (quisque suo ordine) reflectuntur. Etenim (in figura ) sint ABC et αβκ duo prismata parallela quorum alterum ABC projicit colores in alterum αβκ ad distantiam duodecim vel plurium pedum. Tum Prismate αβκ circa axem ejus secundum ordinem literarum , converso donec tanta sit obliquitas radiorum in superficiem βκ incidentium ut incipiant ad π reflecti non ampliùs potentes penetrare ad τ; videbis omnes purpuriformes primò reflecti, cæterosque deinde suo ordine.
[86]Veruntamen quia purpuriformes radij paulò magìs refringuntur in primo prismate ABC, et ideò magis inclinantur ad superficiem βκ secundi Prismatis αβκ quàm cæteri: poterit objici quòd, eâ de causâ primò omnium reflectuntur. Quamobrem (in figura ) duo prismata statuantur non parallela sibi invicem sed in transverso situ, ut omnicolores radij quasi ad eosdem angulos incidant in præfatam superficiem βκ. Quo posito possis observare convertendo prisma posterius 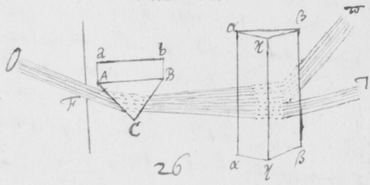 αβκ circa axem ejus secundum ordinem literarum quòd radij purpuriformes primò omnium reflectuntur, et ultimò rubriformes; coloribus ad π continuò translatis prout a τ dispareant.
αβκ circa axem ejus secundum ordinem literarum quòd radij purpuriformes primò omnium reflectuntur, et ultimò rubriformes; coloribus ad π continuò translatis prout a τ dispareant.
[87]Sunt et alij præterea modi quibus experiri liceat quòd ex radijs similiter incidentibus quædam genera penitus reflecti possunt dum alia partim transmittuntur. Quemadmodum si EFG (figura ) sit operculum fenestræ ad F terebratum, et foras statuatur 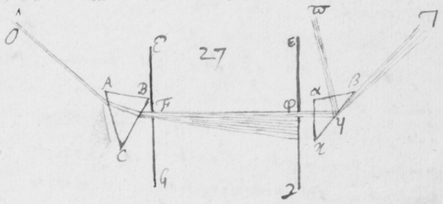 Prisma ABC quod lucem solis foramen F ingressuram intercipiat et refringat versus φ, ad illud φ pedibus ab F duodecim aut longiùs postpositum statuatur opacum corpus εφγ quod lucem sistat, dempto parvo foramine φ per quod aliqua pars lucis, nempe violacea longiùs trajiciatur ad Y. Istud autem φ {n}on sit semisse digiti latius. Deinde præ manibus sumatur aliud Prisma αβκ et ad radios transversè positum statuatur a posticâ parte foraminis φ, circáque axem ejus convertatur donec videas lucem violaceam postquam ab ejus basi βκ obliquissimè refracta fuerit versus τ, totam a τ disparuisse modò, et ad π reflecti. Luce violaceâ tam obliquè ad π reflexâ ut ad τ statim pervasura esset modò ex angulari motu Prismatis secundum ordinem literarum facto, angulus κyφ vel minimùm augeretur: prisma istud αβκ in eo situ figatur. Tum alterum prisma ABC motu circa axem ejus nunc hac nunc illac parùm convertatur, ut colores quos projicit in obstaculum εγ paululum attollantur, eóque pacto omnes successivè transmittantur per foramen φ in prisma posteriusαβκ. Et videbis quod cùm flavedo transmittitur ad Y, illi radij non omnes ad π reflectentur, sed plurimi perrumpent superficiem βκ et ad τ pertingent. Et cum rubor ad Y transmittitur, illi radij fortiùs adhuc perrumpent ut ex copiâ perrumpentis lucis et minori ejus refractione constet. Neque mirum videatur quòd purpuriformes radij sint minùs potentes penetrare superficiem βκ quàm rubriformes; [88]quandoquidem prismatibus eodem modo dispositis, antehac ostendi quòd majorem refractionem patiantur; posito scilicet angulo κYφ tanto ut omnigeni radij possint superficiem βκ penetrare.
Prisma ABC quod lucem solis foramen F ingressuram intercipiat et refringat versus φ, ad illud φ pedibus ab F duodecim aut longiùs postpositum statuatur opacum corpus εφγ quod lucem sistat, dempto parvo foramine φ per quod aliqua pars lucis, nempe violacea longiùs trajiciatur ad Y. Istud autem φ {n}on sit semisse digiti latius. Deinde præ manibus sumatur aliud Prisma αβκ et ad radios transversè positum statuatur a posticâ parte foraminis φ, circáque axem ejus convertatur donec videas lucem violaceam postquam ab ejus basi βκ obliquissimè refracta fuerit versus τ, totam a τ disparuisse modò, et ad π reflecti. Luce violaceâ tam obliquè ad π reflexâ ut ad τ statim pervasura esset modò ex angulari motu Prismatis secundum ordinem literarum facto, angulus κyφ vel minimùm augeretur: prisma istud αβκ in eo situ figatur. Tum alterum prisma ABC motu circa axem ejus nunc hac nunc illac parùm convertatur, ut colores quos projicit in obstaculum εγ paululum attollantur, eóque pacto omnes successivè transmittantur per foramen φ in prisma posteriusαβκ. Et videbis quod cùm flavedo transmittitur ad Y, illi radij non omnes ad π reflectentur, sed plurimi perrumpent superficiem βκ et ad τ pertingent. Et cum rubor ad Y transmittitur, illi radij fortiùs adhuc perrumpent ut ex copiâ perrumpentis lucis et minori ejus refractione constet. Neque mirum videatur quòd purpuriformes radij sint minùs potentes penetrare superficiem βκ quàm rubriformes; [88]quandoquidem prismatibus eodem modo dispositis, antehac ostendi quòd majorem refractionem patiantur; posito scilicet angulo κYφ tanto ut omnigeni radij possint superficiem βκ penetrare.
[89]Iam cùm radij qui citiùs et faciliùs reflectuntur in experimento ad Figuram 24 tradito (nempe purpuriformes) etiam citiùs et faciliùs reflectantur in experimentis duobus novissimè recitatis, cùm eadem ijsdem radijs semper eveniant; liquet quòd hoc non fit ex contingentiâ sed ex prædispositione radiorum, et quòd antecedenter ad omnem reflexionem aut refractionem quidam ad exhibendos quosdam colores sunt apti et facilius reflexibiles, alij verò alijs coloribus et progrediendi viribus afficiuntur. Neque aliud experimentis jam recitatis discrimen interesse videtur, quàm quòd in primo radij omnium formarum, prout a sole adveniunt confusè mixti, incidant in prisma quod rubriformes transmittit et reflectit cæruliformes; in reliquis autem duobus experimentis dissimiles radij priùs discernuntur ab invicem quàm incidant in dictum Prisma.
[90]Adhæc lubet alium adducere modum quo dissimilitudo radiorum in luce solis mixtorum innotescat, non multò dissimilem ei ad Figuram ostenso, sed conspectui jucundiorem et æque scientificum. In Figura Sunto AαBβC 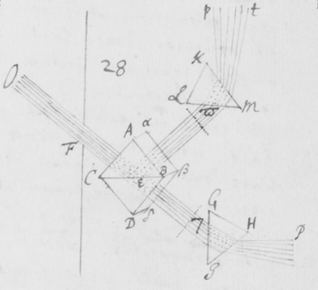 et BβDδC duo prismata ita juxta se posita et colligata, ut duo ex eorum planis CBβ conveniant sibi et coincidant, excepto tantùm quòd nonnihil aeris in morem tenuissimæ laminæ intercedat ijs: Id quòd eveniet ultrò, siquidem haud queas prismata tam arctè constringere quin tantum intercedet aeris quantum proposito sufficiat. Porro in majorem rei evidentiam convenit ut anguli ACB et CBD sint æquales proximè[91], eò ut plana AαC et BβδD fiant parallela, licèt hoc non sit omninò necessarium. His præmissis statuantur dicta prismata juxta foramen F, ut lux ingressa per ea trajiciatur versus τ, primò permeans superficiem AαC, deinde intermediam superficiem BβC, et inde per BβδD prolapsa in papyrum ad τ collocatam, quam albedine tingit tanquam si non omninò transierit prismata, sed vitrum parallelis planis AαC et BβδD terminatum. Præterea cùm intermedia superficies BβC lucem ei incidentem non omnem transmittat ad τ sed multam reflectat, quæ aliquò exibit à prismate ABC per superficiem ejus AαβB, puta versus π: ad illud π statuatur alia papyrus quæ lucem hanc terminet similiter albicantem. Quod ubi feceris, converte prisma quadrangulare (ex duobus triangularibus colligatis confectum) motu lento circa axem ejus secundum ordinem literarum ABDCA: tandeḿque videbis quòd albedo ad π ac τ degenerabit in colores; flavedine primò, deinde rubedine ad τ conspectâ, cæruleo autem colore ad π ; donec post intensissimam rubedinem ad τ color et lux omnis evanescat inde, et cæruleus ad π iterum transformetur in albedinem aliquanto lucidiorem quam antea. Utpote dum prismata circa communem axem, ut dictum est, convertuntur, radiorum in mediam superficiem BβC (hoc est in laminam aeris prismatibus interjectam) prolapsorum incidentia continuò fit obliquior, donec tanta sit eorum obliquitas ut nequeant ampliùs penetrare dictam laminam progredique ad τ, sed ab eâ reflectantur ad π. Quod accidet cùm angulus FεC (obliquitas incidentium) sit graduum ferè quinquaginta. Radij autem purpuriformes minimè omnium potentes penetrare dictam laminam aëream, reflectentur primò, et albedinem priùs reflexam ad π nonnihil tingent eorum colore, dum ex radijs perlabentibus ad τ flavedo imperfecta aut potiùs color inter flavum et viridem mediocris componitur. Postea cæruleus, et viridis deinde reflexus paulo magis tinget lucem in π cum colore cæruleo (licèt admodum diluto propter exuberantiam albedinis commixtæ,) manebitque rubor in τ, qui mox per flavedinis hactenus commixtæ reflectionem fiet intensior, donec ipse etiam denuò reflexus albedinem in π redintegret.
et BβDδC duo prismata ita juxta se posita et colligata, ut duo ex eorum planis CBβ conveniant sibi et coincidant, excepto tantùm quòd nonnihil aeris in morem tenuissimæ laminæ intercedat ijs: Id quòd eveniet ultrò, siquidem haud queas prismata tam arctè constringere quin tantum intercedet aeris quantum proposito sufficiat. Porro in majorem rei evidentiam convenit ut anguli ACB et CBD sint æquales proximè[91], eò ut plana AαC et BβδD fiant parallela, licèt hoc non sit omninò necessarium. His præmissis statuantur dicta prismata juxta foramen F, ut lux ingressa per ea trajiciatur versus τ, primò permeans superficiem AαC, deinde intermediam superficiem BβC, et inde per BβδD prolapsa in papyrum ad τ collocatam, quam albedine tingit tanquam si non omninò transierit prismata, sed vitrum parallelis planis AαC et BβδD terminatum. Præterea cùm intermedia superficies BβC lucem ei incidentem non omnem transmittat ad τ sed multam reflectat, quæ aliquò exibit à prismate ABC per superficiem ejus AαβB, puta versus π: ad illud π statuatur alia papyrus quæ lucem hanc terminet similiter albicantem. Quod ubi feceris, converte prisma quadrangulare (ex duobus triangularibus colligatis confectum) motu lento circa axem ejus secundum ordinem literarum ABDCA: tandeḿque videbis quòd albedo ad π ac τ degenerabit in colores; flavedine primò, deinde rubedine ad τ conspectâ, cæruleo autem colore ad π ; donec post intensissimam rubedinem ad τ color et lux omnis evanescat inde, et cæruleus ad π iterum transformetur in albedinem aliquanto lucidiorem quam antea. Utpote dum prismata circa communem axem, ut dictum est, convertuntur, radiorum in mediam superficiem BβC (hoc est in laminam aeris prismatibus interjectam) prolapsorum incidentia continuò fit obliquior, donec tanta sit eorum obliquitas ut nequeant ampliùs penetrare dictam laminam progredique ad τ, sed ab eâ reflectantur ad π. Quod accidet cùm angulus FεC (obliquitas incidentium) sit graduum ferè quinquaginta. Radij autem purpuriformes minimè omnium potentes penetrare dictam laminam aëream, reflectentur primò, et albedinem priùs reflexam ad π nonnihil tingent eorum colore, dum ex radijs perlabentibus ad τ flavedo imperfecta aut potiùs color inter flavum et viridem mediocris componitur. Postea cæruleus, et viridis deinde reflexus paulo magis tinget lucem in π cum colore cæruleo (licèt admodum diluto propter exuberantiam albedinis commixtæ,) manebitque rubor in τ, qui mox per flavedinis hactenus commixtæ reflectionem fiet intensior, donec ipse etiam denuò reflexus albedinem in π redintegret.
[92]Cæterùm ut hoc specimen evadat illustratius, sumatur aliud prisma GHI quod a posticâ parte prismatum ABCD ita collocetur ut lucem Oετ per ea transmissam refringat versus PT et in colores permutet: violaceo in P, rubeo in T cæterisque in interm{e}dia loca projectis. Tum prismata colligata circa communem axem (ut priùs) rotentur donec lux alba versus τ transmissa incipiat flavescere; et videbis quòd color purpureus in P simul evanescet. Id quòd arguit purpuriformes radios non ampliùs ad prisma GHI pertingere, sed a superficie CBβ primò omnium ad π reflecti; et lucem ετ ideò flavescere quod purpura e misturâ tollitur quâ priùs albedinem exhibuit. Ad eundem modum si prismata ABCD diutiùs rotentur, videbis reliquos colores a π ad τ successivè disparere prout lux ετ plus plusque rubescit; et cùm fit ruberrima, tum solam rubedinem in τ manere. Quod manifestò convincit hanc lucem ετ non aliunde rubescere quàm quòd a radijs aliorum colorum per superficiem CBβ reflexis secernitur.
Simili ratione si cum prismate quarto KLM refringas radios ad π reflexos, et colores eo pacto productos et in album parietem projectos duodecim pedes aut longiùs distantem animadvertas: videbis quòd cùm lux ετ incipiat viridè flavescere, purpura in p, quam prisma hoc elicit e luce επ, plusquam cæteri colores augebitur, per accessum nempe purpuræ quæ tunc in P disparuit: cæterisq́ue deinde coloribus in pt gradatim fiet accessus prout a PT disparent; donec cùm omnis color a PT disparuit, colores ad pt non ampliùs augeantur. Hoc autem discrimen quo violaceus et cæruleus ad pt augmentum suum omne paulo citiùs obtinent quàm rubeus et flavus, tam exile est, ut nisi observator sit attentus, is ægrè advertat.
[93]Ut istis denique finem imponamus, lubet alium adducere modum quo quædam genera radiorum luci solis intermista partim transmitti possint dum alia reflectantur. Nempe si duas laminas vitreas CB (in figura ) planè perpolitas et ad invicem applicatas secundum planitiem earum connectas, eásque vasi RQ aquæ pleno 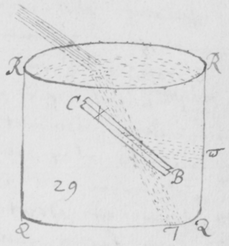 immergas, extremitate superficierum juxta-positarum undique cerâ vel pice priùs obturatâ, ut aqua non interrepat et expellat aërem, qui more laminæ tenuissimæ, ut dictum est, interjacebit vitris. Si hæc, inquam, fiant, possis efficere ut dictorum vitrorum CB talis sit situs , ut (illucente Sole) aer interjectus cæruliformes radios reflectat versus π, et transmittat rubriformes versus τ; atque alias omnes apparentias modò recensitas exhibeat.
immergas, extremitate superficierum juxta-positarum undique cerâ vel pice priùs obturatâ, ut aqua non interrepat et expellat aërem, qui more laminæ tenuissimæ, ut dictum est, interjacebit vitris. Si hæc, inquam, fiant, possis efficere ut dictorum vitrorum CB talis sit situs , ut (illucente Sole) aer interjectus cæruliformes radios reflectat versus π, et transmittat rubriformes versus τ; atque alias omnes apparentias modò recensitas exhibeat.
[94]Cæterùm de hisce modis experiendi notandum venit; primò quòd colores hic producuntur a parallelis superficiebus quarum aliquæ recurvant radios quantum aliæ incurvant, atque adeò quæ mutuos effectus destruerent, siquos in immutando dispositiones radiorum intrinsecas quoad eorum colores, ut opinantur Philosophi, producerent
[95]Secundò quòd lux postquam trajicitur per istas parallelas superficies, licèt alba sit, manifestò tamen constet ex dissimilibus radijs, quandoquidem earum aliqua genera penitus reflecti possunt ad π dum alia ad τ partim trajiciuntur. Et eadem ratione constet albedinem reflexam similiter compositam esse, siquidem, ut dixi, redintegrata est, cum rubor omnium ultimus reflectitur a τ. Quis autem dubitaverit unquam quin lux a Sole directè adveniens sit ejusdem naturæ cum luce reflexâ, vel per parallelas superficies trajectâ, cùm ijdem cujusque sunt effectus, et eædem proprietates omnes. Quælibet in idem quodvis corpus incidens, tingit cum ijsdem coloribus; quælibet, si per prisma trajiciatur eosdem colores ostendit, et eadem in omnibus perficit. Atqui si nil aliud ostenderam quàm quòd lux reflexa vel trajecta per parallela plana (ut dictum est,), albedineḿque exhibens, componitur ex radijs diversorum generum, fuisset aliquid prodijsse tenus; dum causa colorum detegeretur, quos illi deinceps efficerent per prismata trajecti. At quis dubitabit quin causa colorum sit eadem sive lux rectà tendat a sole ad Prisma sive priùs reflexa ut a nubibus aut trajecta per parallela plana, ut per vitream fenestram, adveniat; et ideò quòd in quoquo casu incidentes radij sunt mistura dissimilium. [96]Verùm in summam rei certitudinem, super quàm quòd obvium est advertere, ut liqueat nullam simplicis cujusvis coloris lucem, quoad colorem ejus, reflexionibus speculorum variari posse, ostendam posthac quòd istud refractionibus non potest fieri: Atque adeò (praeter rationes sparsim antedictas[97]) cùm inhærentes dispositiones vel formæ radiorum, quibus apti sunt ad exhibendum colorem aliquem destrui nequeant, vel ullo modo virtute reflectionis aut refractionis mutari, quid aliud concludamus quàm quòd dictæ dispositiones sunt insitæ radijs ab eorum origine, atque ijs, ut dicam, connatæ: licèt non possunt exhibere proprios colores antequam heterogenei ab invicem virtute refractionum secernantur.
[98][99]Hucusque fundamenta struximus, quibus apparentiæ vulgares colorum prismatibus effectorum certissimè possunt explicari. Imò præter alios complures modos eosque magis intricatos, et antehac ignotos, quos ante explicatos habuistis; horum etiam causas tam apertè passim insinuavimus et declaravimus, ut eas non opus esset jam ampliùs attingere nisi proptereà ut methodum propositam retineamus; eas nempe ex principijs antè monstratis scientificè determinandi. Atque has imprimis explicandas apud me proposui non tam propter dignitatem experimentorum, quàm celebritatem, dum sola ferè hactenus de coloribus per prismata generandis innotuêre. Ea verò sunt duplicia: vel cùm colores projiciuntur in corpus aliquod pone prisma locatum, vel cùm objecta mediante prismate cernuntur tincta coloribus.
[100]Ad enarrandum priorem casum primò: Sit ABC 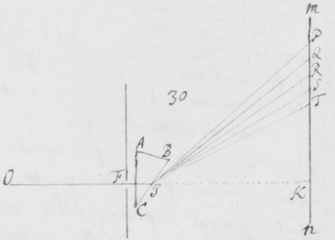 prisma, quod lucem solis OF per foramen F transmissam refringit et refractam projicit in papyrum MN. Et sit OF una ex rectis in quâ radij successivè adveniunt, eaq́ue ponatur perpendicularis ad primam prismatis superficiem AC, incidat in secundam CB ad I, et producatur ad K. Et cùm omnes radij in ipsâ OI advenientes non patiantur eandem refractionem (per Lectiones primam et secundam), ducantur IP{,} IQ, IR, IS, & IT pro quibusdam ex ejus refractis, et alij innumeri subintelligantur intermedij. Plures autem radios in eâdem rectâ successivos siquis ægrè concipiat: vice lineæ OF cogitet exiguum spatium in rebus physicis æquipollens lineæ, in quo plures paralleli radij fluant, sed indefinitè parùm distantes, ut quoad sensum pro coincidentibus habeantur. Quibus præmissis constat ex Lectionibus 4, 5, et 6 quòd isti radij non concipiendi sunt omninò similes, sed mixtura rubriformium, flaviformium, viridiformium, cæruliformium, et purpuriformium, cum omnibus eorum gradibus intermedijs. Sed quia colores isti quinque sunt præcipui, unicum cujusque radium considerabimus. Et quia radius rubriformis est minime, omnium refrangibilis (per Lectionem 3) sit ille IT, nempe cujus angulus refractus KIT est omnium minimus. Porrò cùm radius flaviformis paulo magis refrangibilis est, (per eandem Lectionem 3), erit ejus angulus refractus paulo major, puta quòd sit KIS, et radius IS. Ad eundem modum cæterorum trium radiorum, viridiformis, cæruliformis, et purpuriformis, anguli refracti sunt gradatim adhuc majores (per eandem Lectionem 3{)}; qui proinde radij magis atque magis divaricabunt ab IK puta in IR, IQ et IP. Liquet ergo quòd heterogenei radij in eâdem recta OFI advenientes commixti, segregantur per inæquales refractiones et seorsim incidunt in puncta P, Q, R, S, T. Et seorsim incidentes quisque pro dispositione suâ, vel formâ diversâ, diversum colorem dabit, rubeum ad T, flavum ad S, viridem ad R, cæruleum ad Q et purpureum ad P: Idque ex definitionibus ipsorum, quandoquidem rubriformes radios definio qui cùm soli sunt rubeum colorem efficiunt, et flaviformes qui flavum, et sic de cæteris.
prisma, quod lucem solis OF per foramen F transmissam refringit et refractam projicit in papyrum MN. Et sit OF una ex rectis in quâ radij successivè adveniunt, eaq́ue ponatur perpendicularis ad primam prismatis superficiem AC, incidat in secundam CB ad I, et producatur ad K. Et cùm omnes radij in ipsâ OI advenientes non patiantur eandem refractionem (per Lectiones primam et secundam), ducantur IP{,} IQ, IR, IS, & IT pro quibusdam ex ejus refractis, et alij innumeri subintelligantur intermedij. Plures autem radios in eâdem rectâ successivos siquis ægrè concipiat: vice lineæ OF cogitet exiguum spatium in rebus physicis æquipollens lineæ, in quo plures paralleli radij fluant, sed indefinitè parùm distantes, ut quoad sensum pro coincidentibus habeantur. Quibus præmissis constat ex Lectionibus 4, 5, et 6 quòd isti radij non concipiendi sunt omninò similes, sed mixtura rubriformium, flaviformium, viridiformium, cæruliformium, et purpuriformium, cum omnibus eorum gradibus intermedijs. Sed quia colores isti quinque sunt præcipui, unicum cujusque radium considerabimus. Et quia radius rubriformis est minime, omnium refrangibilis (per Lectionem 3) sit ille IT, nempe cujus angulus refractus KIT est omnium minimus. Porrò cùm radius flaviformis paulo magis refrangibilis est, (per eandem Lectionem 3), erit ejus angulus refractus paulo major, puta quòd sit KIS, et radius IS. Ad eundem modum cæterorum trium radiorum, viridiformis, cæruliformis, et purpuriformis, anguli refracti sunt gradatim adhuc majores (per eandem Lectionem 3{)}; qui proinde radij magis atque magis divaricabunt ab IK puta in IR, IQ et IP. Liquet ergo quòd heterogenei radij in eâdem recta OFI advenientes commixti, segregantur per inæquales refractiones et seorsim incidunt in puncta P, Q, R, S, T. Et seorsim incidentes quisque pro dispositione suâ, vel formâ diversâ, diversum colorem dabit, rubeum ad T, flavum ad S, viridem ad R, cæruleum ad Q et purpureum ad P: Idque ex definitionibus ipsorum, quandoquidem rubriformes radios definio qui cùm soli sunt rubeum colorem efficiunt, et flaviformes qui flavum, et sic de cæteris.
[101]Præterea licèt irradiata linea OF non sit perpendicularis ad planum AC sed utcunque inclinata; tamen flaviformes, et cæteri suo ordine prout sunt magis refrangibiles magis divaricabunt ab incidentibus radijs IK quàm rubriformes, (id quod manifestius est quàm ut jam demonstrem). Quare tum etiam heterogenei segregabuntur per divergentiam ab invicem, et seorsim cadentes colores proprios exhibebunt.
[102]Adhæc si præter unicam irradiatam lineam OI plures alias ei parallelas concipiamus, pari ratione liquebit quod cujusque lineæ flaviformes radij, et reliqui suo ordine magis divaricabunt ab IK quàm rubriformes: ita quidem ut si foramen F sit circulare, pro quinque punctis P, Q, R, S, T tot circuli 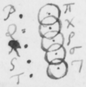 vel Ellipses π{,} χ{,} ρ{,} σ{,} τ ponendæ sint in quas dictarum quinque specierum radij incident. Et sic pro innumeris alijs punctis intermedijs totam lineam PT constituentibus circuli vel Ellipses aliæ ponendæ sunt, quæ component oblongam imaginem rubeam ad τ, purpuream ad π, et coloribus intermedijs ad intermedia loca tinctam.
vel Ellipses π{,} χ{,} ρ{,} σ{,} τ ponendæ sint in quas dictarum quinque specierum radij incident. Et sic pro innumeris alijs punctis intermedijs totam lineam PT constituentibus circuli vel Ellipses aliæ ponendæ sunt, quæ component oblongam imaginem rubeam ad τ, purpuream ad π, et coloribus intermedijs ad intermedia loca tinctam.
[103]Quinetiam denique id ipsum fiet si radij non omnes adveniunt paralleli, sed aliquantulùm inclinati, quemadmodum ijs contingit qui manant a diversis partibus solaris disci. De quâ re satis dictum fuit in Lectione secundâ.
[104]Verùm e re futurum judico, ut experimentum hoc vulgare fusiùs prosequar, et singulas ejus circumstantias attingam. Et primò si radij non transeunt per angustum foramen F, sed ex unicâ tantùm parte limitantur, colores non omnes apparebunt: Verbi gratiâ si corpus aliquod opacum FG (figura ) Soli interponatur et Prismati juxta basem ejus AB, quod umbram projiciat 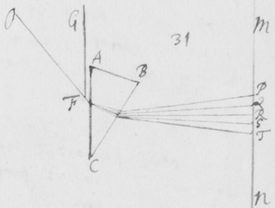 in MP, colores efficiat in spatio PT, et lucem permittat in ipsum NT influere: In PT confinio lucis et umbræ nulli colores generabuntur præter purpureum et cæruleum cum varijs eorum gradibus. Et ratio est quòd ex radijs omnium formarum qui transeunt per extremitatem dicti corporis opaci FG soli purpuriformes propter maximam eorum refractionem possunt ad P usque deflecti; unde color purpureus ibi conspicietur. Deinde cæruliformes, cùm paulò minùs refrangibiles existant, incident in totum spatium NQ, non potentes ulteriùs versus M deflecti quàm ad Q. Atque ita duæ radiorum species eæque solæ incident in Q, et colorem ex purpureo et cæruleo compositum exhibebunt. Præterea viridiformes minùs adhuc refringibiles, in spatio NR non ultra extendentur quàm ad R; flaviformes autem terminabuntur in S. Quare tres tantùm species colorum miscebuntur ad R, et color ex ijs omnibus (nempe ex purpureo cæruleo et viridi) generabitur. At cùm purpureus et viridis commixti producant cæruleum, ut facilè est ex antedictis experiri[105]; liquet colorem ad R non alium fore quàm caeruleum. Deniq́ue cùm radij rubriformes minimè omnium refringuntur ut in spatium NT incidentes non magis deflectantur versus M quàm ad T, liquet quòd in dicto spatio NT fiet mistura colorum omnium, et proinde albescet: sed in ipso S (ubi color omnis dempto rubeo miscetur) cæruleus ad viriditatem nonnihil vergens apparebit, sed maximè dilutus, propterea quòd solus rubor ex albedinis compositione desit.
in MP, colores efficiat in spatio PT, et lucem permittat in ipsum NT influere: In PT confinio lucis et umbræ nulli colores generabuntur præter purpureum et cæruleum cum varijs eorum gradibus. Et ratio est quòd ex radijs omnium formarum qui transeunt per extremitatem dicti corporis opaci FG soli purpuriformes propter maximam eorum refractionem possunt ad P usque deflecti; unde color purpureus ibi conspicietur. Deinde cæruliformes, cùm paulò minùs refrangibiles existant, incident in totum spatium NQ, non potentes ulteriùs versus M deflecti quàm ad Q. Atque ita duæ radiorum species eæque solæ incident in Q, et colorem ex purpureo et cæruleo compositum exhibebunt. Præterea viridiformes minùs adhuc refringibiles, in spatio NR non ultra extendentur quàm ad R; flaviformes autem terminabuntur in S. Quare tres tantùm species colorum miscebuntur ad R, et color ex ijs omnibus (nempe ex purpureo cæruleo et viridi) generabitur. At cùm purpureus et viridis commixti producant cæruleum, ut facilè est ex antedictis experiri[105]; liquet colorem ad R non alium fore quàm caeruleum. Deniq́ue cùm radij rubriformes minimè omnium refringuntur ut in spatium NT incidentes non magis deflectantur versus M quàm ad T, liquet quòd in dicto spatio NT fiet mistura colorum omnium, et proinde albescet: sed in ipso S (ubi color omnis dempto rubeo miscetur) cæruleus ad viriditatem nonnihil vergens apparebit, sed maximè dilutus, propterea quòd solus rubor ex albedinis compositione desit.
[106]Porrò si corpus opacum φγ Soli interponatur et Prismati juxta verticem ejus C, sicut videre est in schemate. Inter obscuratum spatium NT et lucidum PM cernes alios duos colores, rubeum in T et flavum in R; idque propter jam dictas rationes. 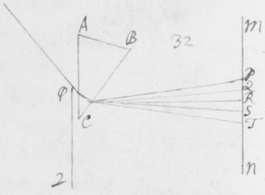 Quippe radij prout apti sunt ad hos ordine colores (rubeum, flavum, viridem, cæruleum, et violaceum) generandos, extenduntur per spatia MT, MS, MR, MQ et MP. Et cùm soli rubriformes extendantur usque ad T, cæteris propter majorem refractionem citiùs terminatis; necesse est ut iste color in T sit rubeus. Item cùm tria radiorum genera in R incidant, color ex istis (nempe rubeo, flavo, et viridi) compositus ibidem cernetur[107]; rubeus autem et viridis flavum constituunt, atque adeò flavus apparebit in R. Præterea cùm omnium formarum radij misceantur in P, et postea perpetuò versus M; spatium istud PM apparebit album. Nec secus constat quòd citrius in S, et in Q flavus ad viriditatem vergens apparebit, sed adeò dilutus tamen, et cæruleo redundans, ut nomen viriditatis non mereatur.
Quippe radij prout apti sunt ad hos ordine colores (rubeum, flavum, viridem, cæruleum, et violaceum) generandos, extenduntur per spatia MT, MS, MR, MQ et MP. Et cùm soli rubriformes extendantur usque ad T, cæteris propter majorem refractionem citiùs terminatis; necesse est ut iste color in T sit rubeus. Item cùm tria radiorum genera in R incidant, color ex istis (nempe rubeo, flavo, et viridi) compositus ibidem cernetur[107]; rubeus autem et viridis flavum constituunt, atque adeò flavus apparebit in R. Præterea cùm omnium formarum radij misceantur in P, et postea perpetuò versus M; spatium istud PM apparebit album. Nec secus constat quòd citrius in S, et in Q flavus ad viriditatem vergens apparebit, sed adeò dilutus tamen, et cæruleo redundans, ut nomen viriditatis non mereatur.
[108]Tertiò si opaca duo 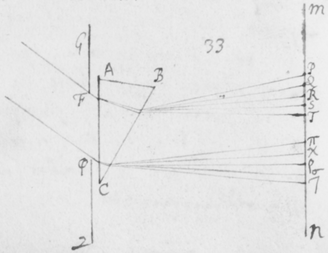 corpora GF et γφ (figura ) Soli et Prismati interponantur, ut radij inter utrumque quasi per oblongam rimam prismati parallelam transeant; atque distantia Fφ sit satis magna: pro utróque termino F et φ generabuntur colores, purpureus nempe ad P et cæruleus ad R per terminum F; atque flavus ad ρ, ac rubeus ad τ per terminum φ, sicut modò explicatum fuit: Eritque Tπ spatium album utrisque coloribus interjectum. Iam si obstacula GF et γφ ad se invicem paululum admoveantur, ut intermedium spatium Fφ evadat angustius, isto pacto spatium album quoque Tτ fiet angustius, donec tandem evanescat, et colores utrinque coeant. Sin spatium Fφ magis adhuc coarctetur, viriditas in medio colorum emerget vice albedinis, quæ jam evanuit. Quæ quidem viriditas antea non apparuit propter commisturam radiorum heterogeneorum, quibus involuta latuit: jam verò heterogeneis istis per obstacula duo sibi propiùs admota alternè interceptis; ea paulatim detegitur, patet, et evadit perfectior; donec (cùm dictum Fφ satis angustum est) ab omni ferè misturâ liberatur, et eruitur, propriâque specie non minùs quàm cæteri colores elucet. Et hinc in transitu colligitur, quod viriditas inter colores medietatem exactè obtinet, non magis ad rubeum vergens quam violaceum, neque ad flavum quam caeruleum . Præterea observandum est quòd cùm præfata albedo Tπ per angustiam spatij Fφ incipit evanescere, intermedij colores paulatim fiunt viciniores, flavus videlicet ad rubeum et cæruleus ad violaceum. Ita ut cùm spatium Fφ fit valde angustum flavus ad rubeum et cæruleus ad violaceum quasi duplo vicinior evadit, quàm cùm amplitudo dicti Fφ permisit albedinem in medio cerni. Et ut quinque colores (viriditate jam internatâ) non occupent plus spatij quam eorum duo priùs occupavêre. Cujus rei ratio patebit ex figuris tribus præcedentibus, contemplanti modum quo flavus ad ρ & cæruleus ad R heterogeneis radijs compositus mutatur in flavum ad S vel σ & cæruleum ad Q vel χ constantem ex solis homogeneis; cæteris e misturâ per angustiam spatij Fφ sublatis.
corpora GF et γφ (figura ) Soli et Prismati interponantur, ut radij inter utrumque quasi per oblongam rimam prismati parallelam transeant; atque distantia Fφ sit satis magna: pro utróque termino F et φ generabuntur colores, purpureus nempe ad P et cæruleus ad R per terminum F; atque flavus ad ρ, ac rubeus ad τ per terminum φ, sicut modò explicatum fuit: Eritque Tπ spatium album utrisque coloribus interjectum. Iam si obstacula GF et γφ ad se invicem paululum admoveantur, ut intermedium spatium Fφ evadat angustius, isto pacto spatium album quoque Tτ fiet angustius, donec tandem evanescat, et colores utrinque coeant. Sin spatium Fφ magis adhuc coarctetur, viriditas in medio colorum emerget vice albedinis, quæ jam evanuit. Quæ quidem viriditas antea non apparuit propter commisturam radiorum heterogeneorum, quibus involuta latuit: jam verò heterogeneis istis per obstacula duo sibi propiùs admota alternè interceptis; ea paulatim detegitur, patet, et evadit perfectior; donec (cùm dictum Fφ satis angustum est) ab omni ferè misturâ liberatur, et eruitur, propriâque specie non minùs quàm cæteri colores elucet. Et hinc in transitu colligitur, quod viriditas inter colores medietatem exactè obtinet, non magis ad rubeum vergens quam violaceum, neque ad flavum quam caeruleum . Præterea observandum est quòd cùm præfata albedo Tπ per angustiam spatij Fφ incipit evanescere, intermedij colores paulatim fiunt viciniores, flavus videlicet ad rubeum et cæruleus ad violaceum. Ita ut cùm spatium Fφ fit valde angustum flavus ad rubeum et cæruleus ad violaceum quasi duplo vicinior evadit, quàm cùm amplitudo dicti Fφ permisit albedinem in medio cerni. Et ut quinque colores (viriditate jam internatâ) non occupent plus spatij quam eorum duo priùs occupavêre. Cujus rei ratio patebit ex figuris tribus præcedentibus, contemplanti modum quo flavus ad ρ & cæruleus ad R heterogeneis radijs compositus mutatur in flavum ad S vel σ & cæruleum ad Q vel χ constantem ex solis homogeneis; cæteris e misturâ per angustiam spatij Fφ sublatis.
[109]Quartò si lux terminetur obstaculo Gγ cujus extremitas perpendiculariter transversa est ad longitudinem Prismatis, colores omninò nulli virtute termini illius generabuntur. Etenim ponamus parallelos 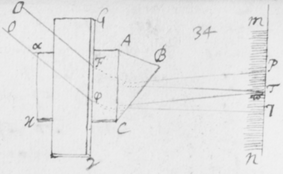 radios OF Oφ cæterosque (in figura ) juxta extremitatem dictam Gγ in Prisma ABC prolapsos, ibidemque refractos esse ad PT et πτ; atque MN esse umbram ipsius Gγ. Iam licèt radij purpuriformes FP et φπ magis refringantur quàm rubriformes FT et φτ, tamen istâ refractione secundum terminum umbræ factâ, ita ut ex dictis radijs nulli magis deflectant versus umbram quàm cæteri; palam est quòd ubicunque purpuriformes incidunt, rubriformes etiam incident in eundem locum: et e contra. Quod idem de radijs intermedijs pari modo concipiatur. Et sic radijs omnium specierum ubique per extremitatem umbræ commixtis, umbra benè definietur sine aliquo colore (præter album vel fuscum ex luce et umbrâ mixtis) conspecto. Sed cavendum est, ne colores per limites prismatis Aα vel Cκ generati habeantur pro generatis a limite Gγ. Quamobrem de prismatibus monendum volo, quòd quæ ex vitro in totum fiunt, ad examen hujus et proxime præcedentis commodè instituendum sunt nimis exigua, propterea quòd colores per extremitatem verticis et basis producti interjectum spatium album haud relinquent satis amplum in quo generatio colorum prædictis modis probetur. Itaque ut prisma conficiatur ex vitris planis et benè politis, qualia ad specula conficienda adhibentur, moneo; quibus in morem cunei connexis et in vasculum dein prismiforme completis, (ut supra dictum,) vasculum istud impleatur aquâ limpidissimâ et occludatur; Et sic prismata ad arbitrium ampla conficias.
radios OF Oφ cæterosque (in figura ) juxta extremitatem dictam Gγ in Prisma ABC prolapsos, ibidemque refractos esse ad PT et πτ; atque MN esse umbram ipsius Gγ. Iam licèt radij purpuriformes FP et φπ magis refringantur quàm rubriformes FT et φτ, tamen istâ refractione secundum terminum umbræ factâ, ita ut ex dictis radijs nulli magis deflectant versus umbram quàm cæteri; palam est quòd ubicunque purpuriformes incidunt, rubriformes etiam incident in eundem locum: et e contra. Quod idem de radijs intermedijs pari modo concipiatur. Et sic radijs omnium specierum ubique per extremitatem umbræ commixtis, umbra benè definietur sine aliquo colore (præter album vel fuscum ex luce et umbrâ mixtis) conspecto. Sed cavendum est, ne colores per limites prismatis Aα vel Cκ generati habeantur pro generatis a limite Gγ. Quamobrem de prismatibus monendum volo, quòd quæ ex vitro in totum fiunt, ad examen hujus et proxime præcedentis commodè instituendum sunt nimis exigua, propterea quòd colores per extremitatem verticis et basis producti interjectum spatium album haud relinquent satis amplum in quo generatio colorum prædictis modis probetur. Itaque ut prisma conficiatur ex vitris planis et benè politis, qualia ad specula conficienda adhibentur, moneo; quibus in morem cunei connexis et in vasculum dein prismiforme completis, (ut supra dictum,) vasculum istud impleatur aquâ limpidissimâ et occludatur; Et sic prismata ad arbitrium ampla conficias.
[110]Quintò, ut 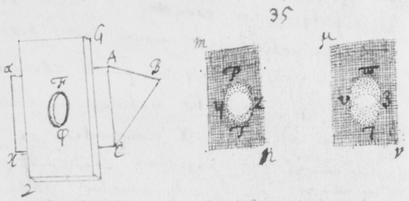 omnia jam uno comprehendam specimine, sit Gγ (figura ) corpus opacum orbiculari foramine Fφ unum duośve digitos lato pertusum, per quod lux in prisma trajiciatur, ubi cùm refracta fuerit, projicitur deinde in papyrum vel quodvis album corpus MN quasi semisse pedis a prismate postpositum, et videbis illuminatum spatium PYTZ rotundum ad modum foraminis Fφ, album in ejus medietate, et duobus semilunulis colorum terminatum, purpureo et cæruleo ad P, flavo autem et rubeo ad T: qui colores paulatim deficiunt versus Y et Z ubi nulli omninò conspiciuntur. Præterea si papyrum ad majorem distantiam paulatim distuleris, velut ad μν; videbis colores distendi et augeri, et intermediam albedinem usque comminui dum prorsus evanescat totumque spatium coloribus rubeo flavo cæruleo et purpureo tinctum appareat. Et papyrum longiùs differendo, viriditas e medio emerget et crescet tum amplitudine spatij tum perfectione speciei: Totumq́ue spatium coloratum distrahetur in oblongam formam. Quorum omnium rationes ex supradictis depromantur.
omnia jam uno comprehendam specimine, sit Gγ (figura ) corpus opacum orbiculari foramine Fφ unum duośve digitos lato pertusum, per quod lux in prisma trajiciatur, ubi cùm refracta fuerit, projicitur deinde in papyrum vel quodvis album corpus MN quasi semisse pedis a prismate postpositum, et videbis illuminatum spatium PYTZ rotundum ad modum foraminis Fφ, album in ejus medietate, et duobus semilunulis colorum terminatum, purpureo et cæruleo ad P, flavo autem et rubeo ad T: qui colores paulatim deficiunt versus Y et Z ubi nulli omninò conspiciuntur. Præterea si papyrum ad majorem distantiam paulatim distuleris, velut ad μν; videbis colores distendi et augeri, et intermediam albedinem usque comminui dum prorsus evanescat totumque spatium coloribus rubeo flavo cæruleo et purpureo tinctum appareat. Et papyrum longiùs differendo, viriditas e medio emerget et crescet tum amplitudine spatij tum perfectione speciei: Totumq́ue spatium coloratum distrahetur in oblongam formam. Quorum omnium rationes ex supradictis depromantur.
[111]Adhæc si corpus opacum quo lux terminata est, collocetur a posticâ parte prismatis, colores eodem planè modo producentur ac priùs; nec quicquam refert quanta intersit prismati et corpori terminanti distantia. Verbi gratiâ si corpus opacum Gγ  perforatum in F absit a prismate ABC ad distantiam pedis unius aut ampliùs; et prisma istud sit satis amplum (videlicet ex vitreis laminis, ut dictum est, confectum) nè lux priùs discernatur in colores quàm permeet dictum foramen F: ista lux alba postquam transijt per ipsum F, non secus degenerabit in colores apud P, Q, R, S, T quàm factum erat in præcedentibus. Scilicet ex solâ schematis contemplatione patebit modus quo radij diversorum generum inæqualiter refracti convergunt a diversis partibus prismatis ad foramen F, ubi (ut et hinc inde versus G et γ) componunt albedinem; sed inibi decussantes divergunt postea, diversique colores in diversa spatia P, Q, R, S, T tendunt. Atque hæc fortè clariora fient experienti quòd cùm radij obstaculo quolibet H ex utravis parte prismatis intercipiantur, e coloribus P Q R S T aliqui tollentur. Si radios nempe vertici C vicinos intercipias tolles purpureum P, vel tolles rubeum T, si intercipias eos basi AB vicinos, et sic de reliquis. Ita ut quoslibet pro arbitrio tuo possis tollere vel facere ut quilibet solus appareat.
perforatum in F absit a prismate ABC ad distantiam pedis unius aut ampliùs; et prisma istud sit satis amplum (videlicet ex vitreis laminis, ut dictum est, confectum) nè lux priùs discernatur in colores quàm permeet dictum foramen F: ista lux alba postquam transijt per ipsum F, non secus degenerabit in colores apud P, Q, R, S, T quàm factum erat in præcedentibus. Scilicet ex solâ schematis contemplatione patebit modus quo radij diversorum generum inæqualiter refracti convergunt a diversis partibus prismatis ad foramen F, ubi (ut et hinc inde versus G et γ) componunt albedinem; sed inibi decussantes divergunt postea, diversique colores in diversa spatia P, Q, R, S, T tendunt. Atque hæc fortè clariora fient experienti quòd cùm radij obstaculo quolibet H ex utravis parte prismatis intercipiantur, e coloribus P Q R S T aliqui tollentur. Si radios nempe vertici C vicinos intercipias tolles purpureum P, vel tolles rubeum T, si intercipias eos basi AB vicinos, et sic de reliquis. Ita ut quoslibet pro arbitrio tuo possis tollere vel facere ut quilibet solus appareat.
[112]Denique si lux ex unicâ tantùm parte pone prisma limitetur, vel si duo statuantur limites, ijque vel ad easdem vel ad oppositas partes prismatis; vel quocunque alio more lux terminetur; modus quo colores exinde generantur ex antedictis facilè patebit; ut jacturam temporis fecero de hâc re plura verba facturus. Quinetiam si duo vel plura prismata quocunque modo inter se disponantur, peritus Optices facilè explorabit causam.
[113][114]Sed antequam hæc penitus dimitto placet insuper annotare sequentia duo: quorum primum esto modus, quo colores duorum prismatum ita commisceantur ut albedinem componant. De qua re perficienda cùm plures antehac modos ostendi, hujus non omninò memini; quippe objectioni, quòd colores non miscentur, sed ex confinio lucis sublato pereunt, et in albedinem evanescunt, in hoc minùs commode tunc satisfecisse potuissem. Sunto ABC et αβκ duo prismata cum angulis 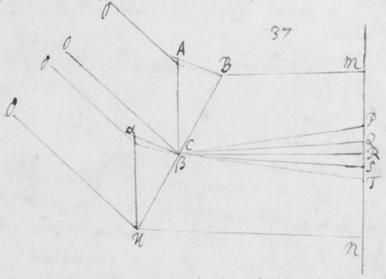 verticalibus ACB et ακβ æqualibus, et ea disponantur in situ parallelo ita ut alterius linea verticalis C cum β extremitate basis alterius conveniat, planis BC et βκ in directum jacentibus. Quo facto si sol transluceat ea in papyrum MN, octo vel duodecim digitos postpositam, colores quidem generabuntur ad M et N per exteriores prismatum terminos β et κ, non autem per interiores C et β, sed medium spatium PT totum apparebit album. Sin alterutrum prisma tollas alterius extremitas C vel β generabit colores ad PT; ac dein si restituas, albedo etiam restituetur. Scilicet albedo ista componitur e coloribus ab extremitate C et β prismatis utriusque prolapsis. Id quod facilè constet ex præfatis. Nam radij purpuriformes ab utroque prismate refracti limitantur in eodem puncto P; ita ut ab uno prismate manantes incidant in PM; ab altero, in PN; et ab utroque simul in totum MN, non secus quàm si omnes ab unico prismate venissent. Eodem modo cæruliformes extenduntur per totum spatium MN: et eorum terminus communis est Q prout manant a diversis prismatibus. Et sic de cæteris. Quare omnigeni radij commiscentur in unaquâque parte spatij PT, et albedinem ideò component. Sin alterutrum prisma tollas, puta ABC, vel lucem ei potiùs occludas; tum radijs rubriformibus ab MT, flaviformibus ab MS, viridiformibus ab MR, cæruliformibus ab MQ, et purpuriformibus ab MP sublatis, manebunt rubriformes in NT, flaviformes in NS, viridiformes in NR, cæruliformes in NQ, et purpuriformes in NP. Adeóque purpureus apparebit in P, et cæruleus in R, ut ostendimus ante[115]. Et simili ratione si lux occludatur alteri prismati αβκ, ne permeet; rubor apparebit in T et flavedo in R.
verticalibus ACB et ακβ æqualibus, et ea disponantur in situ parallelo ita ut alterius linea verticalis C cum β extremitate basis alterius conveniat, planis BC et βκ in directum jacentibus. Quo facto si sol transluceat ea in papyrum MN, octo vel duodecim digitos postpositam, colores quidem generabuntur ad M et N per exteriores prismatum terminos β et κ, non autem per interiores C et β, sed medium spatium PT totum apparebit album. Sin alterutrum prisma tollas alterius extremitas C vel β generabit colores ad PT; ac dein si restituas, albedo etiam restituetur. Scilicet albedo ista componitur e coloribus ab extremitate C et β prismatis utriusque prolapsis. Id quod facilè constet ex præfatis. Nam radij purpuriformes ab utroque prismate refracti limitantur in eodem puncto P; ita ut ab uno prismate manantes incidant in PM; ab altero, in PN; et ab utroque simul in totum MN, non secus quàm si omnes ab unico prismate venissent. Eodem modo cæruliformes extenduntur per totum spatium MN: et eorum terminus communis est Q prout manant a diversis prismatibus. Et sic de cæteris. Quare omnigeni radij commiscentur in unaquâque parte spatij PT, et albedinem ideò component. Sin alterutrum prisma tollas, puta ABC, vel lucem ei potiùs occludas; tum radijs rubriformibus ab MT, flaviformibus ab MS, viridiformibus ab MR, cæruliformibus ab MQ, et purpuriformibus ab MP sublatis, manebunt rubriformes in NT, flaviformes in NS, viridiformes in NR, cæruliformes in NQ, et purpuriformes in NP. Adeóque purpureus apparebit in P, et cæruleus in R, ut ostendimus ante[115]. Et simili ratione si lux occludatur alteri prismati αβκ, ne permeet; rubor apparebit in T et flavedo in R.
[116]In istis autem experiendis requiritur ut anguli ACB et ακβ sint æquales. Id quod tentabis si prismata secundum longitudinem eorum ita connectas ut duo ex planis dictos angulos comprehendentibus puta BC et βκ fiant contigua et reliqua duo AC et ακ sibi opposita. Quo facto 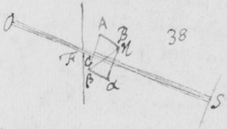 si radij Solis ingressi foramen F, pergant ad eundem locum S cùm trajiciuntur per dicta prismata perpendiculariter ad eorum latera AC et ακ, atque cùm liberè progrediuntur, nullo interjecto obstaculo: tum plana AC et ακ sunt parallela, et anguli ACB et ακβ æquales. Sin istud non eveniat, sunt inæquales: in quo casu notetur præterea, quòd inclinando plana BC et βκ (in figura ) vel ab invicem reclinando, possis albedinem in PT haud secus componere ac si dicti anguli fuissent æquales et plana BC et βκ in directum jacentia.
si radij Solis ingressi foramen F, pergant ad eundem locum S cùm trajiciuntur per dicta prismata perpendiculariter ad eorum latera AC et ακ, atque cùm liberè progrediuntur, nullo interjecto obstaculo: tum plana AC et ακ sunt parallela, et anguli ACB et ακβ æquales. Sin istud non eveniat, sunt inæquales: in quo casu notetur præterea, quòd inclinando plana BC et βκ (in figura ) vel ab invicem reclinando, possis albedinem in PT haud secus componere ac si dicti anguli fuissent æquales et plana BC et βκ in directum jacentia.
[117]Quinetiam possis hoc idem cum unico tantùm prismate perficere, dummodò commiscendi satis magnum sit, puta cujus refringentia latera AC et BC sint sex vel octo digitos lata. Etenim sint FG et φγ duo corpora opaca, plana, rectangula, et ad prismatis planum ACκα secundum planitiem ejus sic applicata 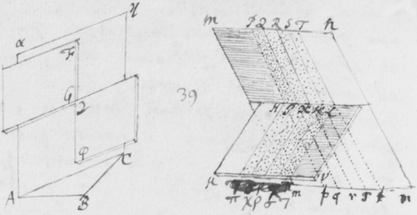 ut eorum angularia puncta G et γ juxta plani istius centrum se mutuò contingant, et latera concurrentia (quorum FG et φγ sint ad axem Prismatis parallela) ex adverso jaceant in directum. Quo facto si lux refracta projiciatur in papyrum MNX pedes quasi duos distantem; obstaculum FG projiciet umbram in MH, purpuram efficiet in PHIQ, ac cæruleum colorem in QILT et permittet lucem in LN. E contra verò obstaculum γφ permittet lucem in Hm, rubedinem efficiet in pHIq, ac flavedinem in qILt, et projiciet umbram in Ln. Dico jam si speculo aliquo μνx colores ex alterutrâ parte lineæ HL, ut HLpt, ita reflectantur ut incidant in papyrum ad eundem locum cum coloribus HLPT ex alterâ parte: color omnis evanescet totumque HLTP apparebit album. Nam purpuriformes radij a prismate ad PHIQ directè tendunt, et cætera quatuor radiorum genera ad eundem locum reflectuntur a speculo incidentes puta in HIχπ: Item purpuriformes & cæruliformes directè tendunt ad QIXR et cætera tria genera illuc reflectuntur ab IXρχ: Et sic de reliquis. Adeò ut omnes omnium generum radij passim per spatium PHLT misceantur, ibidemque componant albedinem. Sed notandum est quòd cùm lux reflectione semper debilitetur, radijs quamplurimis inter reflectendum amissis; exinde forsan eveniat quòd lux directa nonnihil prævalebit reflexæ et color ejus dominabitur, nisi compensatio fiat ita papyrum inclinando ut directa lux paulo obliquiùs in eam incidat quàm reflexa: de quâ re facilè judicium feras ex perfectione albedinis emergentis.
ut eorum angularia puncta G et γ juxta plani istius centrum se mutuò contingant, et latera concurrentia (quorum FG et φγ sint ad axem Prismatis parallela) ex adverso jaceant in directum. Quo facto si lux refracta projiciatur in papyrum MNX pedes quasi duos distantem; obstaculum FG projiciet umbram in MH, purpuram efficiet in PHIQ, ac cæruleum colorem in QILT et permittet lucem in LN. E contra verò obstaculum γφ permittet lucem in Hm, rubedinem efficiet in pHIq, ac flavedinem in qILt, et projiciet umbram in Ln. Dico jam si speculo aliquo μνx colores ex alterutrâ parte lineæ HL, ut HLpt, ita reflectantur ut incidant in papyrum ad eundem locum cum coloribus HLPT ex alterâ parte: color omnis evanescet totumque HLTP apparebit album. Nam purpuriformes radij a prismate ad PHIQ directè tendunt, et cætera quatuor radiorum genera ad eundem locum reflectuntur a speculo incidentes puta in HIχπ: Item purpuriformes & cæruliformes directè tendunt ad QIXR et cætera tria genera illuc reflectuntur ab IXρχ: Et sic de reliquis. Adeò ut omnes omnium generum radij passim per spatium PHLT misceantur, ibidemque componant albedinem. Sed notandum est quòd cùm lux reflectione semper debilitetur, radijs quamplurimis inter reflectendum amissis; exinde forsan eveniat quòd lux directa nonnihil prævalebit reflexæ et color ejus dominabitur, nisi compensatio fiat ita papyrum inclinando ut directa lux paulo obliquiùs in eam incidat quàm reflexa: de quâ re facilè judicium feras ex perfectione albedinis emergentis.
[118]Alterum quod notandum venit est de modo tollendi quoslibet colores in figura 36 per interpositionem corporis H, quantùm nempe ista circumstantia adversatur hypothesibus Philosophorum, quæ de coloribus hucusque fuerunt excogitatae. Ex illis enim positis, refracta lux ad eas semper partes cum cæruleo et violaceo terminanda est, versus quas fit refractio; quandoquidem gyrationes globulorum ex opinione Cartesij, vel partes anteriores pulsuum Ætheris obliquè vibrantis ex aliâ quadam Hypothesi, per viciniam quiescentis Medij ad eas semper partes impediuntur et hebescunt. Attamen ostensum ést ad figuram 36 quòd, obstaculo H ex utrâvis parte prismatis interjecto ut radios ipsius vertici C vicinos intercipiat, possis violaceum et cæruleum tollere et efficere ut viridis vel flavus aut etiam ruber ad eas partes maneat extimus versus quas refractio peragitur. Nec Hypothesis eorum tutior est, qui ponunt colores ex luce et umbrâ mistis componi; cùm eadem videatur mistura quæcunque, licèt color sit extremus ad easdem partes M vel N.
Hujusmodi etiam Hypotheses ex alijs experimentis sparsim occurrentibus everti possent, modò id meo proposito necessarium judicarem: quemadmodum ex illis ubi lucem partim reflecti posse, et partim transmitti docebam[119]; nam lux transmissa dabat flavum vel rubeum, nec tamen ab ullo quiescente Medio, vel tenebris terminabatur.
[120]Cæterum non opus est ut Hypotheses ejusmodi refutem, quæ, ex inventâ tandem veritate, suâ sponte corruent. Satiùs fecero, si proferam experimentum tandem, quo omnia qua de genesi colorum hactenus explicui, non modò probari possunt, sed etiam videri. Quamobrem sit ABCac prisma quod radios per foramen F in obscuratum cubiculum transmissos 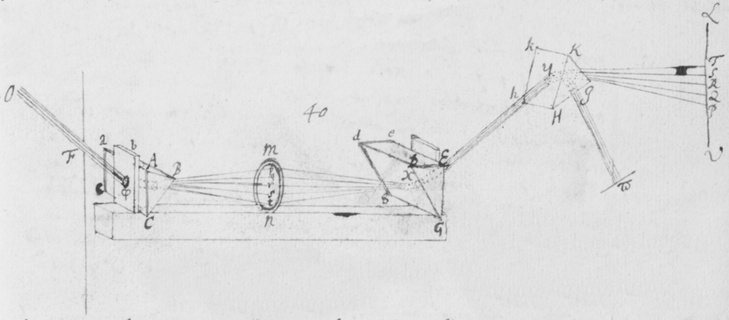 refringat versus lentem MN ut colores quos efficit in p, q{,} r, s, t per lentem deinde trajiciantur ad X et ibidem commisceantur in albedinem sicut in præcedentibus ostendi. Deinde aliud prisma DEGgd priori parallelum ad locum X, ubi albedo redintegrata est, statuatur, quod lucem versus Y refringat. Hujus autem prismatis verticalis angulus Gg sit æqualis angulo verticali Cc prismatis anterioris, aut eo forte minor, et similiter positus ut incidentes radios in parallelismum reducat quos prisma anterius dispersit. His positis observabis an lux ad Y (pedes aliquot distans) trajecta, aeque alba maneat ac fuerit in X, vel sensim abeat in colores. Si penitus appareat alba, tunc prismata cum lente debitè disposuisti: sin aliqui colores ad Y cernantur prisma DEG circa suum axem eo modo parùm converti debet ut colores minuantur; et cùm penitus evanuêre et lux in totum albescit, siste prisma. Quod si nequeas hoc modo efficere quin lux inter transiendum ab X ad Y ex aliquâ sui parte transmigret in colores, lentem MN paulo longiùs a prismate ABC transfer, et loco X rursus invento ubi colores in albedinem accuratissimè convergunt, in eo statue prisma DEF ut priùs, et rursus experire an possis lucem sine coloribus ad Y projicere. Et cùm eo usque mutaveris positiones prismatum et lentis dum effeceris lucem ad Y trajectam quàm minimè possis coloratam, prismata cum lente in eo situ figantur idque vel ope trabis, ut in schemate describitur, vel tubi aut instrumenti cujusvis in eum finem fabricati.
refringat versus lentem MN ut colores quos efficit in p, q{,} r, s, t per lentem deinde trajiciantur ad X et ibidem commisceantur in albedinem sicut in præcedentibus ostendi. Deinde aliud prisma DEGgd priori parallelum ad locum X, ubi albedo redintegrata est, statuatur, quod lucem versus Y refringat. Hujus autem prismatis verticalis angulus Gg sit æqualis angulo verticali Cc prismatis anterioris, aut eo forte minor, et similiter positus ut incidentes radios in parallelismum reducat quos prisma anterius dispersit. His positis observabis an lux ad Y (pedes aliquot distans) trajecta, aeque alba maneat ac fuerit in X, vel sensim abeat in colores. Si penitus appareat alba, tunc prismata cum lente debitè disposuisti: sin aliqui colores ad Y cernantur prisma DEG circa suum axem eo modo parùm converti debet ut colores minuantur; et cùm penitus evanuêre et lux in totum albescit, siste prisma. Quod si nequeas hoc modo efficere quin lux inter transiendum ab X ad Y ex aliquâ sui parte transmigret in colores, lentem MN paulo longiùs a prismate ABC transfer, et loco X rursus invento ubi colores in albedinem accuratissimè convergunt, in eo statue prisma DEF ut priùs, et rursus experire an possis lucem sine coloribus ad Y projicere. Et cùm eo usque mutaveris positiones prismatum et lentis dum effeceris lucem ad Y trajectam quàm minimè possis coloratam, prismata cum lente in eo situ figantur idque vel ope trabis, ut in schemate describitur, vel tubi aut instrumenti cujusvis in eum finem fabricati.
[121]Cum habeas hanc machinam e prismatibus et lente ut dictum est compositam, ope lucis per eam transmissæ cuncta possis experiri quæ hactenus fuerunt tradita. Hæc enim lux XY jubari a Sole directo persimilis est, et easdem omnes apparentias exhibet, ac si a foramine F rectà promanasset, nullam omninò refractionem passa; Adeoq́ue ejusdem esse constitutionis facilè credamus. Et tamen cùm in sua principia componentia, hoc est in radios diversorum generum, apud lentem MN discreta fuerit, facile erit modos examini subjicere quibus posthac in colores converti potest, idque tantùm sistendo hoc vel illud radiorum genus apud MN, ut constitutio lucis XY quoad ejus conversionem in colores pateat.
[122]Quemadmodum si desideretur ut sensui planissimè pateat quòd prisma convertit lucem in colores non transmutando proprietates ejus intrinsecas, sed segregando tantum radios ad excitandum varia colorum phantasmata dispositos, ex quibus lux omnis albens constituitur: nihil aliud agendum est quam ut prisma aliquod HIK ita statuatur ut lucem XY excipiat, et refringendo transmutet in colores P, Q, R, S, T, in papyrum aliquam LV procidentes. Deinde si colorem quemlibet apud lentem MN interposito obstaculo sistas, videbis eundem colorem a papyro LV deficere. Sic purpuram p obstruendo, disparebit purpura P, cæteris coloribus non omninò mutatis, (dempto fortè cæruleo, quatenus aliquid purpuræ commixtum habeat.) Sic viridem r intercipiendo, viridis R evanescet: Et sic de alijs. Atque ita videre est quòd ijdem colores apud papyrum LV et apud lentem MN pertinent ad eosdem radios, ijsque non communicantur a refractione lentis HIK, siquidem præexistebant, segregati quidem ad lentem MN, et congregati in luce XY. Ad eundem modum si cupias experimenta penitiùs rimari, quibus alia genera radiorum omninò reflecti possint, dum alia (licèt similiter incidentia) partim transmittantur: Prisma HIK circa axem ejus converte donec altera pars colorum (violacea nempe et cærulea) postquam obliquissimè refracta fuerit versus LV, abinde penitus dispareat, versus π reflexa; parte tamen alterâ ad LV pervadente. Deinde si dimidium colorum rubedinem versus intercipias ad MN, rubor et flavus disparebunt ab LV, et lux ad π reflexa fiet admodum cærulea. Sin alterum dimidium purpuram versus intercipias, rubor apud LV non mutabitur sed lux in π (propter ablatum purpuream et cæruleum) flavescet aut rubescet. Id quod indicat purpuriformia et cæruliformia radiorum genera penitus ad π reflecti, dum cætera partim refringuntur ad LV. Nec secus alia colorum phænomena, quæ prismata ab immediatâ Solis luce eliciunt, ope lucis hujus XY poteris experiri; et intercipiendo quodvis radiorum genus apud MN, eorum causas intueri.
[123]Siquis autem velit instrumentum quale jam descripsimus ad experimenta hujusmodi instituenda conficere: lentem adhibeat latam tres digitos, et ampliùs, quæ radios parallelos ad focum duos pedes circiter distantem congregat: atque ita prismata distabunt octo pedibus, et conficient instrumentum satis magnum quo omnia strictiùs examini subjiciantur. Quod ad positionem lentis attinet, si prismntum anguli verticales ACB et DGE sint æquales, puto 60 vel , ipsa æqualiter ab utrisque distabit: sin alter angulus sit major altero, lens illi prismati vicinior collocetur cujus angulus verticalis existit major. Et nota quòd jubar XY per spatium eo latius diffunditur quo lens statuitur anteriori prismati ABC vicinior: atque adeò siquando opus sit amplo jubare, debes tantùm efficere, ut lens sit aliquanto vicinior anteriori prismati, quàm posteriori, et adhibere prisma posterius, cujus angulus verticalis sit tanto ferè minor quàm angulus verticalis anterioris. Denique si velis ut colores in lentem illam procidentes sint magis discreti et ab invicem distracti, quàm more jam descripto continget, eâ nempe de causâ ut singula radiorum genera pro lubitu distinctiùs sive magis sejunctim intercipiantur; (Id quod in experimentis nonnullis necessarium duco:) Nihil aliud agendum est, quàm ut lux per duo parva foramina F et φ ab invicem longè distantia priùs trajiciatur quàm incidat in prismata a[124]; Vel ut alia lens non procul ab anteriori prismate collocetur b[125], quæ apta sit ut lucem a longinquo foramine F divergentem, congreget ad alteram subsequentem lentem MN. His enim modis imago colorata apud MN fiet multùm angustior quàm antè, (longitudine ejus vix diminutâ,) et proinde colores ejus erunt minùs commisti.
[126][127][128]Enarratâ colorum genesi quos prismata in longinquum projiciunt, de ijs jam restat dicendum quos exhibent dum transpiciuntur. Quoniam verò de mensurâ refractionum in ordine ad scientiam de opticis instrumentis visionem perficientibus promovendam convenit me disserere, et multæ sint exinde deducendæ propositiones quibus hujusmodi colorum genesis innititur et explicari debet, modò ex solis principijs antecedenter demonstratis (ut in geometriâ solet fieri) velim determinare: ideò non vobis displiceat si de legibus refractionum nonnulla præsternam, et sic res ad mathematicam puram magis accedentes his ad physicam spectantibus interspergam.
[129]Veteres quidem refractiones metiebantur per angulos quos radiùs incidens et refractus cum perpendiculo refringentis plani conficiunt: quasi datam haberent rationem. Ut si GH sit planum refringens 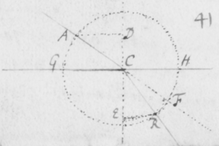 cui ducitur DCE linea perpendicularis ad aliquod ejus punctum C et sit AC radius quilibet incidens in ipsum C, & refractus in CR: supposuêrunt veteres quòd angulus incidentiæ ACD semper esset ad angulum refractionis RCE in eâdem ratione; vel potiùs credidêre suppositionem istam satis accuratam esse, modò dicti anguli sint parvi. Sic in vitro statuebant angulum ACD esse ad angulum RCE ut binarius numerus ad ternarium proximè: sive quòd incidentia ACD ferè tripla sit anguli refracti RCF utroque radio comprehensi. At illa refractionum æstimatio minùs exacta deprehenditur, quàm ut pro fundamento dioptrices debeat statui. Et Cartesius aliam regulam primus excogitavit, quâ istud exactiùs determinaretur. Nempe quòd dictorum angulorum sinus sunt in ratione datâ. In figura 41 si centro C et distantiâ quâlibet AC circulus describatur secans radios præfatos in A et R, et ab istis punctis ad plani perpendiculum DCE demittantur normales AD et RE, ipsarum AD et RE proportio erit eadem perpetuò. Cujus rei veritatem Author non ineleganter demonstrasset modò de causis physicis quas assumpsit nullum dubitandi locum reliquisset. Ut ut, quoniam instrumentis in istum finem accuratè constructis examinârunt aliqui, et veritati (quoad Sensum) exactè convenientem adinvenêrunt: non dubitabimus pro fundamento statuere; hoc solùm adhibito moderamine, quòd cùm is de quibuslibet radijs indifferenter affirmaverit, quasi omnium persimilis fuisset refractio; nos tantùm affirmamus de singulis eorum generibus, ponendo quòd radiorum æque refrangibilium sinus refractionis sunt ut sinus incidentiæ. Concipiamus aliquot genera radiorum secundum lineam AC in figura 14 allapsa esse ad punctum C ibique refracta per superficiem IH, puta mediocriter
cui ducitur DCE linea perpendicularis ad aliquod ejus punctum C et sit AC radius quilibet incidens in ipsum C, & refractus in CR: supposuêrunt veteres quòd angulus incidentiæ ACD semper esset ad angulum refractionis RCE in eâdem ratione; vel potiùs credidêre suppositionem istam satis accuratam esse, modò dicti anguli sint parvi. Sic in vitro statuebant angulum ACD esse ad angulum RCE ut binarius numerus ad ternarium proximè: sive quòd incidentia ACD ferè tripla sit anguli refracti RCF utroque radio comprehensi. At illa refractionum æstimatio minùs exacta deprehenditur, quàm ut pro fundamento dioptrices debeat statui. Et Cartesius aliam regulam primus excogitavit, quâ istud exactiùs determinaretur. Nempe quòd dictorum angulorum sinus sunt in ratione datâ. In figura 41 si centro C et distantiâ quâlibet AC circulus describatur secans radios præfatos in A et R, et ab istis punctis ad plani perpendiculum DCE demittantur normales AD et RE, ipsarum AD et RE proportio erit eadem perpetuò. Cujus rei veritatem Author non ineleganter demonstrasset modò de causis physicis quas assumpsit nullum dubitandi locum reliquisset. Ut ut, quoniam instrumentis in istum finem accuratè constructis examinârunt aliqui, et veritati (quoad Sensum) exactè convenientem adinvenêrunt: non dubitabimus pro fundamento statuere; hoc solùm adhibito moderamine, quòd cùm is de quibuslibet radijs indifferenter affirmaverit, quasi omnium persimilis fuisset refractio; nos tantùm affirmamus de singulis eorum generibus, ponendo quòd radiorum æque refrangibilium sinus refractionis sunt ut sinus incidentiæ. Concipiamus aliquot genera radiorum secundum lineam AC in figura 14 allapsa esse ad punctum C ibique refracta per superficiem IH, puta mediocriter 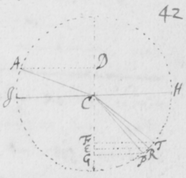 refrangibiles radios in CR, minimè refrangibiles in CT, et minimè refrangibiles in CP; ac innumeros alios gradibus intermedijs plus minùs refringibiles per totum spatium TCP diffusos esse. Iam si ducatur DCG perpendicularis ad planum refringens IH, et centro C, distantiâ quâvis AC circulus ut priùs describatur secans radios dictos in A; P, R, T; atque ex istis punctis demittantur perpendiculares AD; PG, RE, TF pro sinibus angulorum ACD; PCG, RCE, TCF: pono quòd utcunque radij incidant, tamen semper erit AD ad PG in eadem ratione; quâ semel cognitâ regulam habes pro refractione radiorum maxime refrangibilium in eandem superficiem ad angulum quemvis incidentium mensurandâ. Et sic semper erit AD ad TF in eâdem ratione: quâ cognitâ regulam habes quâcum refractio minimè refrangibilium pro quavis incidentiâ determinabitur. Atque idem de ratione ipsius AD ad RE et ad sinum cujusvis intermedij generis concipiatur.
refrangibiles radios in CR, minimè refrangibiles in CT, et minimè refrangibiles in CP; ac innumeros alios gradibus intermedijs plus minùs refringibiles per totum spatium TCP diffusos esse. Iam si ducatur DCG perpendicularis ad planum refringens IH, et centro C, distantiâ quâvis AC circulus ut priùs describatur secans radios dictos in A; P, R, T; atque ex istis punctis demittantur perpendiculares AD; PG, RE, TF pro sinibus angulorum ACD; PCG, RCE, TCF: pono quòd utcunque radij incidant, tamen semper erit AD ad PG in eadem ratione; quâ semel cognitâ regulam habes pro refractione radiorum maxime refrangibilium in eandem superficiem ad angulum quemvis incidentium mensurandâ. Et sic semper erit AD ad TF in eâdem ratione: quâ cognitâ regulam habes quâcum refractio minimè refrangibilium pro quavis incidentiâ determinabitur. Atque idem de ratione ipsius AD ad RE et ad sinum cujusvis intermedij generis concipiatur.
[130]Porro autem cùm sinus PG, RE, TF cæterique datam habeant rationem ad sinum AD, datam quoque rationem inter sese habebunt. Atque adeò si ex unicâ observatione proportionem sinuum PG, RE, TF, et reliquorum ad radios ex eadem incidentiâ refractos pertinentium cognoveris, regulam exinde habebis quacum ex sinu refractionis cujusvis generis radiorum, et in istam superficiem utcunque incidentium dato, cæterorum omnium ex eadem incidentia prolabentium sinus elicias: licèt quænam sit eorum incidentia non innotuerit. Quinimò si omnium AD; TF, RE, PG &c proportiones inter se semel cognoscantur, habito respectu ad eadem media refringentia, regulam habes pro cæteris omnibus exquirendis ex unico quovis unquam dato. Itaque quo rationes istorum sinuum investigentur , convenit ut in aliquo radiorum genere proportio sinus incidentiæ ad sinum refractionis primùm exquiratur: deinde ut proportiones sinuum refractionis pro radijs diversorum generum ad eundem angulum incidentium determinentur.
[131]Ad sinus incidentiæ cum sinubus refractionis conferendos commodum erit, ut medium genus eligatur, puta genus illud radiorum qui viriditatem vel potius colorem viridi et cæruleo intermedium exhibent. Credo enim illos qui refractiones antehac mensuravêre, (sive id factum sit, ut jam dicta Hypothesis Cartesij probaretur sive alijs de causis,) credo illos, inquam, mensuram instituisse ad medietatem refractæ lucis: hoc est si spatium a coloribus occupatum spectemus, ad confinium viridis et cærulei; aut si spectemus quantitatem lucis, ad medietatem viridis. Et præterea punctum istud pro principali foco lentium habendum esse videtur, in quod intermedium genus radiorum convergit: atque etiam siquando de radijs indistinctè disserendum est, ut hactenus apud Opticæ scriptores consueverit, genus mediocre commodiùs quàm extremorum aliquod pro omnibus haberi potest.
[132]Porrò cùm fortè desideretur accuratius examen dictæ regulæ Cartesianæ, quàm antehac instituebatur, dum varia radiorum refrangibilitas experientes latuit: primò dicam id quo pacto non incommodè fiat. Quoniam fluidi pellucidi superficies refringentes facilè possint inclinari ad quemvis datum angulum, quod solido non est concessum, fluida in hunc finem fuerunt adhibita, sed instrumento magis laborioso quàm opus erat, et erroribus fortè magis obnoxio, quàm si omni apparatu privaretur, demptâ trabe cui vasculum aquæ plenum affigitur. Sit itaque HK in figura 15 vectis ligneus, duas trese ulnas longus aut amplius, satis crassus ne ob longitudinem ejus et pondus minimùm inflecti queat, quadrilaterus, rectangulus, et rectus, cum lateribus oppositis exacte parallelis. Tum lamellæ duae HI et KL super unum ejus latus ad angulos 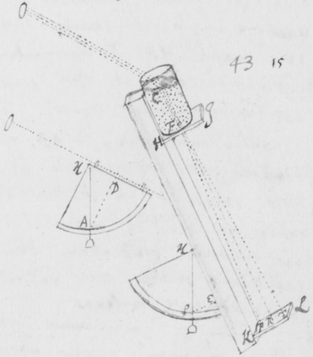 rectos erigantur, KL proximè ad unam extremitatem et HI quasi quatuor digitos ab alterâ distans; quarum longitudo sit trium digitorum quatuore, latitudo autem duorum vel trium. Deinde sumatur vasculum aliquod cylindricum vel prismiforme CF duos tresve digitos latum, longum verò quatuor, vel quinque; ejus basis super lamellam HI figatur cemento aliquo duro ac tenaci et in eo situ firmetur ope trabis HK ultra dictam lamellam HI productæ. Tum trajiciatur ejus fundum in medietate, et lamella simul, parvo foramine F, puta decimâ parte digiti lato: et juxta foramen istud in alterâ lamellâ notetur punctum R, quod æquè distat a trabe ac dicti foraminis centrum; ita scilicet ut linea FR per centrum foraminis ad R ducta sit parallela longitudini trabis. Denique sumatur lamella vitrea plana polita, et uniformiter crassa, eaque applicetur ad planitiem lamellæ HI vasculo CF obversam super foramen F, et cemento figatur ita ut vasculum istud aquæ (quâ repleatur) non sit pervium. Et cum normâ aliquâ fiat periculum an illa vitrea lamella perpendiculariter insistat trabi. Quod si non contingat, corrigatur situs, donec sit exactè perpendicularis. In cujus rei gratiam convenit ut dicta lamella vitrea sit tres vel quatuor digitos longa et lata, quò de situ ejus meliùs judicare liceat. Instrumento hoc sic fabricato, et aquâ vasi CF plusquam ad medietatem ejus infusâ, illud in radijs solaribus ita statuatur, ut in superiori superficie aqueâ refracti, perpendiculariter emergant ad foramen F, rectàque progrediantur versus laminam KL; rubedine ad T, purpurâ ad P, et viridi vel confinio cærulei et viridis ad R incidentibus. Convenit autem ut dicta lamina KL dealbetur, aut albente papyro vestiatur, quò de coloribus judicium certius proferri queat. Interea verò cum Quadrante aliquo amplo, et exactè fabricato εκρ quæratur inclinatio trabis HK ad horizontem, et habebis angulum refractionis εκρ, et ejus sinum ερ. Tum solis altitudo statim inquiratur, ejusque complementum ad erit angulus incidentiæ, et AD sinus. Quibus sinubus ad invicem collatis, et experimento ad diversas Solis altitudines repetito, constabit an sinuum ratio semper sit eadem. Quod si velis ut experimenta varia simul fiant, aut ad minorem incidentiam quàm sit complementum maximæ altitudinis solaris: vice radiorum a sole directè manantium possis adhibere reflexos{.}
rectos erigantur, KL proximè ad unam extremitatem et HI quasi quatuor digitos ab alterâ distans; quarum longitudo sit trium digitorum quatuore, latitudo autem duorum vel trium. Deinde sumatur vasculum aliquod cylindricum vel prismiforme CF duos tresve digitos latum, longum verò quatuor, vel quinque; ejus basis super lamellam HI figatur cemento aliquo duro ac tenaci et in eo situ firmetur ope trabis HK ultra dictam lamellam HI productæ. Tum trajiciatur ejus fundum in medietate, et lamella simul, parvo foramine F, puta decimâ parte digiti lato: et juxta foramen istud in alterâ lamellâ notetur punctum R, quod æquè distat a trabe ac dicti foraminis centrum; ita scilicet ut linea FR per centrum foraminis ad R ducta sit parallela longitudini trabis. Denique sumatur lamella vitrea plana polita, et uniformiter crassa, eaque applicetur ad planitiem lamellæ HI vasculo CF obversam super foramen F, et cemento figatur ita ut vasculum istud aquæ (quâ repleatur) non sit pervium. Et cum normâ aliquâ fiat periculum an illa vitrea lamella perpendiculariter insistat trabi. Quod si non contingat, corrigatur situs, donec sit exactè perpendicularis. In cujus rei gratiam convenit ut dicta lamella vitrea sit tres vel quatuor digitos longa et lata, quò de situ ejus meliùs judicare liceat. Instrumento hoc sic fabricato, et aquâ vasi CF plusquam ad medietatem ejus infusâ, illud in radijs solaribus ita statuatur, ut in superiori superficie aqueâ refracti, perpendiculariter emergant ad foramen F, rectàque progrediantur versus laminam KL; rubedine ad T, purpurâ ad P, et viridi vel confinio cærulei et viridis ad R incidentibus. Convenit autem ut dicta lamina KL dealbetur, aut albente papyro vestiatur, quò de coloribus judicium certius proferri queat. Interea verò cum Quadrante aliquo amplo, et exactè fabricato εκρ quæratur inclinatio trabis HK ad horizontem, et habebis angulum refractionis εκρ, et ejus sinum ερ. Tum solis altitudo statim inquiratur, ejusque complementum ad erit angulus incidentiæ, et AD sinus. Quibus sinubus ad invicem collatis, et experimento ad diversas Solis altitudines repetito, constabit an sinuum ratio semper sit eadem. Quod si velis ut experimenta varia simul fiant, aut ad minorem incidentiam quàm sit complementum maximæ altitudinis solaris: vice radiorum a sole directè manantium possis adhibere reflexos{.}
[133]Cum eandem sinuum incidentiæ et refractionis rationem alicui radiorum generi utcunque in eandem quamvis superficiem incidenti perpetuò competere sat exploratum fuerit, proponatur exquirere rationem illam ad superficiem data quælibet Media disterminantem; idque unico experimento. Si aer sit unum ex datis Medijs, et liquor quilibet alterum, instrumentum novissimè descriptum non incommodè possit adhiberi. Sin Mediorum alterum sit solidum, res expeditè perficitur ad diagramma 16 . In cujus explicationem præmittantur sequentia duo Lemmata.
Lemma 1. In figura 16 Sit ABC prisma ex materiâ quâvis pellucidâ confectum, cujus axis sit horizonti parallelus et perpendicularis ad radios 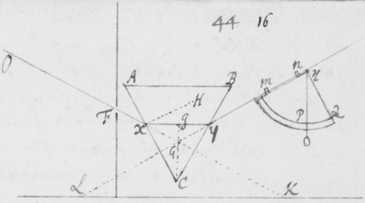 solis, et præterea sit ejus positio talis ut dictos radios OX æque refringat ingredientes ad X et egredientes ad Y: istud autem quo pacto debet fieri, ostensum fuit in conclusione Lectionis 1[134]. Iam dico quòd angulus refractionis ad alterutram refringentem superficiem, ut AC factæ, est æqualis dimidio verticalis anguli prismatici ACB. Scilicet ad punctum incidentiæ X erigatur perpendicularis HX eritque HXY angulus refractionis ad superficiem AC: Porrò demittatur CI perpendicularis in radium XY, et ista bisecabit angulum YCX propterea quod triangulum YCX (ob æqualitatem refractionis in X et Y) sit isosceles. Dico itaque quod angulus XHY et ICX æquantur. Nam angulus AXY = angulo (per 32. 1. Elementa.) Sed anguli AXH et XIC sunt recti; Ergo residui HXY, et ICX æquantur. Q.E.D.
solis, et præterea sit ejus positio talis ut dictos radios OX æque refringat ingredientes ad X et egredientes ad Y: istud autem quo pacto debet fieri, ostensum fuit in conclusione Lectionis 1[134]. Iam dico quòd angulus refractionis ad alterutram refringentem superficiem, ut AC factæ, est æqualis dimidio verticalis anguli prismatici ACB. Scilicet ad punctum incidentiæ X erigatur perpendicularis HX eritque HXY angulus refractionis ad superficiem AC: Porrò demittatur CI perpendicularis in radium XY, et ista bisecabit angulum YCX propterea quod triangulum YCX (ob æqualitatem refractionis in X et Y) sit isosceles. Dico itaque quod angulus XHY et ICX æquantur. Nam angulus AXY = angulo (per 32. 1. Elementa.) Sed anguli AXH et XIC sunt recti; Ergo residui HXY, et ICX æquantur. Q.E.D.
Lemma 2. Adhoc si radius incidens OX et emergens YN indefinitè producantur occurrentes in G, et præterea si recta quævis KL horizonti parallela radijs istis interjiciatur constituens triangulum GKL: Et cùm refractus radius YN tendit sursum si summa angulorum LKX et KLY sumatur, aut eorum differentia cùm iste YN tendit deorsum: Dico quòd illius summæ vel differentiæ dimidium unà cum angulo refractionis HXY æquabitur angulo incidentiæ HXG. Nam dicta summa vel differentia æquatur angulo NGK (per 32{.} 1{.} Elementa,) hoc est angulis . Et cùm triangulum GYX sit isosceles, dictæ summæ vel differentiæ dimidium æquabitur angulo refracto GYX, qui cum angulo refractionis YXH constituit angulum incidentiæ. Q.E.D.
His præmissis problema propositum sic perficitur. Primò mensuretur angulus verticalis Prismatis ACB: et ejus dimidium erit angulus refractionis. Dein Prismate in positione præfatâ disposito, per quod radij trajiciantur ingressi foramen F, ope Quadrantis MNPQ ampli et accurati (puta cujus pinnarum M et N distantia sit pedis unius minimùm) exploretur angulus YLK vel PκQ quem refracti radij YMN cum horizonte constituunt; faciendo ut mediocriter refrangibiles per pinnas M et N, ad distantiam decem aut viginti pedum a prismate trajiciantur: Et simul observetur Solis altitudo XKL. Qui duo anguli addantur, si refracti radij YMN sursum tendant, sicut in schemate describitur; alias minor subtrahatur de majori. Et summæ vel differentiæ dimidium unà cùm angulo refractionis priùs invento erit angulus incidentiæ ut pateat per Lemma secundum. Denique ex angulis incidentiæ et refractionis sic datis, dantur eorum sinus. Q.E.F.
[135]Sic in prismate quodam vitreo dimensus sum angulum ejus maximum ACB et inveni esse : Cujus dimidium HXY est : ejusque sinus 5240, posito sinu 10000. Deinde cùm altitudo Solis OKL observabatur esse , alter angulus MLK a radio YN ad medium viriditatis tendente conflatus erat : quorum summa est ejusq́ue dimidium YXK : quod unà cum angulo refractionis HXY facit angulum incidentiæ: cujus sinus est 8097. denique conferendo sinus jam inventos ut eorum proportio in minimis terminis haberetur; inveni esse ut 11 ad 17 ferè. Quare pro regulâ generali statuendum est, quòd radiorum viriditatem exhibentium sinus incidentiæ ex aere in vitrum quodvis æque refractivum ac illud prisma, sit ad sinum refractionis, ut septendecim ad undecim.
[136]Hujus autem modi commoditas in mensurandis refractionibus ex eo conjicietur, quòd instrumento nullo hic opus sit, dempto Quadrante, et Prismate cujus refractio desideratur; quòd refractionem, dum geminatur, facta ad X et Y, exinde certiùs metiri possis: et quòd facillimum est prisma in desiderato situ disponere, ut supra ostenditur[137]. Imò quòd parvus error a situ desiderato ferè nihili est, dum quoad sensum haud inde mutabitur angulus refractus MGK, ut experienti patebit. Quippe angulus iste tunc minimus est; et quantitatibus per motum generatis, cùm maximæ existant vel minimæ, hoc est in momento regressûs, earum motus ut plurimùm sunt infinitè parvi. Sic verbi gratiâ in figura 17 si centro C describatur circulus λLλ, et extra 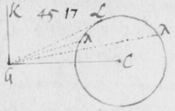 eum sumatur punctum quoddam G, ducaturque GC, et erigatur normalis GK; Deinde si concipiatur quòd punctum λ moveatur uniformiter in illius circuli circumferentiâ, per quod punctum recta quædam Gλ circa centrum G rotata perpetuò transeat: manifestum est quod quo major sit angulus CGλ sive quo minor angulus KGλ, eo minor erit motus angularis ipsius Gλ: et cùm angulus CGλ sit maximus sive angulus KGλ minimus, hoc est in momento regressûs (rectâ Gλ tunc circulum in L tangente) motus ejus erit infinitè parvus et quoad sensum nullus, parvusque error a puncto contactûs L nullam sensibilem variationem in angulis istis KGL et CGL producet. Et ad eundem fere modum parva convolutio prismatis haud omnino mutabit angulum MGK, cùm iste sit minimus sive complementum ejus maximum. Quòd si prisma disponeretur in quovis alio situ quàm hic describitur, (puta cùm radij perpendiculariter ingressi, ad egressum duntaxat refringuntur,) minimus error ab isto desiderato situ multùm mutaret angulum refractum, et sic experientia foret incertitudini, et erroribus multò magis obnoxia.
eum sumatur punctum quoddam G, ducaturque GC, et erigatur normalis GK; Deinde si concipiatur quòd punctum λ moveatur uniformiter in illius circuli circumferentiâ, per quod punctum recta quædam Gλ circa centrum G rotata perpetuò transeat: manifestum est quod quo major sit angulus CGλ sive quo minor angulus KGλ, eo minor erit motus angularis ipsius Gλ: et cùm angulus CGλ sit maximus sive angulus KGλ minimus, hoc est in momento regressûs (rectâ Gλ tunc circulum in L tangente) motus ejus erit infinitè parvus et quoad sensum nullus, parvusque error a puncto contactûs L nullam sensibilem variationem in angulis istis KGL et CGL producet. Et ad eundem fere modum parva convolutio prismatis haud omnino mutabit angulum MGK, cùm iste sit minimus sive complementum ejus maximum. Quòd si prisma disponeretur in quovis alio situ quàm hic describitur, (puta cùm radij perpendiculariter ingressi, ad egressum duntaxat refringuntur,) minimus error ab isto desiderato situ multùm mutaret angulum refractum, et sic experientia foret incertitudini, et erroribus multò magis obnoxia.
[138]In majorem hujus rei copiam, quia dantur aliqui casus ubi refractiones per modos jam descriptos haud possint mensurari, (ut cùm refractio fit ex vitro in mediorum sibi ipsis crystallum, ex aquâ in vitrum, vel ex uno liquore in alium;) Et nequa omninò sit refringens superficies cujus refractio nequit investigari, problema sequens lubet proponere.
Datis refractionibus quas duo media alicui tertio contigua conficiunt, illorum sibi ipsis contiguorum refractionem invenire.
In figura 18 sunto duo media proposita A et B, quorum superficiei disterminantis refractio quæritur, et sit A Medium tertium cujus superficiei ipsis A et B contiguæ refractiones dantur sitque sinus incidentiæ ad sinum refractionis ex Medio C in Medium A sicut I ad R; et sinus incidentiæ ad sinum refractionis ex eodem Medio C in alterum Medium B sicut ι ad ρ. Dico quod est sinus incidentiæ ad sinum refractionis ex Medio B in Medium A.
Verbi gratiâ proponatur investigatio refractionis ex aquâ in vitrum, datâ refractione ex aëre in utrumque. Sitque sinus incidentiæ ex aëre in vitrum ad sinum refractionis ut 17 ad 11, et sinus incidentiæ ex aere in aquam ad sinum refractionis ut 4 ad 3. Quare sinus istos multiplicando reciprocè, erit ut ad , sive ut 51 ad 44 ita sinus incidentiæ ex aquâ in vitrum ad sinum refractionis. Et sic cognitâ refractione ex aere in quævis alia Media proposita, possis adipisci eorum refractioncm inter se: et e contra.
[139]Cæterum demonstratio hujus non est omittenda, in quem finem præsternatur Lemma sequens. Si Media duo proposita A et B in figura 18 concipiantur esse planis parallelis terminata, contigua, et dicto Medio tertio (puta aëre) circundata et radius quilibet ON 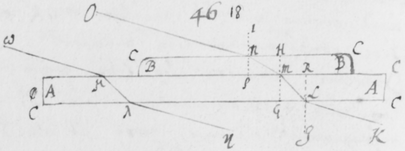 obliquè incidens ad N refringatur primò ad M ac deinde ad L, et emergens pergat ad K: Dico quòd iste radius incidens ON sibi emergenti LK parallelus esse. Cujus quidem assertionis veritas experientiâ patebit. Etenim ponatur Medium A esse vitrum, et Medium B esse aquam, Mediuḿque tertium circundans esse aëra: Et laminæ vitreæ A superficies ρMR tenuiter illinatur aquâ B, et statuatur parallela ad Horizontem, ut aqua consistat uniformiter crassa. Quo facto videbis quod radij per utrumque Medium A et B trajecti tendent ad easdem plagas versus quas tenderent a Sole directi.
obliquè incidens ad N refringatur primò ad M ac deinde ad L, et emergens pergat ad K: Dico quòd iste radius incidens ON sibi emergenti LK parallelus esse. Cujus quidem assertionis veritas experientiâ patebit. Etenim ponatur Medium A esse vitrum, et Medium B esse aquam, Mediuḿque tertium circundans esse aëra: Et laminæ vitreæ A superficies ρMR tenuiter illinatur aquâ B, et statuatur parallela ad Horizontem, ut aqua consistat uniformiter crassa. Quo facto videbis quod radij per utrumque Medium A et B trajecti tendent ad easdem plagas versus quas tenderent a Sole directi.
Præmisso hoc, erigantur ιNρ, HMG, et RLI perpendiculares ad refringentia puncta N, M, et L. Est ergo ι ad ρ ut sinus anguli ONι ad sinum anguli MNρ, sive anguli NMH. Et multiplicando rationem antecedentem per I fiet ad ut sinus de ONι ad sinum de NMH. Porro est I ad R, ut sinus anguli KLI sive ONι, ad sinum anguli MLR sive LMG et multiplicando antecedentem rationem per ι, fiet ad ut sinus de ONι ad sinum de LMG. Iam permutando terminos utriusque proportionis fiet . Et . Et permutando . Q.E.D.
[140][141]Ex hisce sic ostensis problema non inutile proficiscitur, quo refractiones fluidorum: eodem modo metiri possis ac de solidis ostensum : est ad figuram 16: non adhibito instrumento HILK, quod in figura 15 describitur. Scilicet ex laminis vitreis in morem cunei connexis vasculum prismiforme conficiatur, cujus acies sive angulus verticalis sit circiter, vel 90. Istius autem anguli quantitatem exactissimâ mensura cognitam habeto, ejusque dimidij sinum pro sinu refractionis semper statue. Quo peracto, cùm liquoris alicujus vis refractiva desideratur, vasculum cum illo liquore impleatur et in tali situ disponatur, ut acies ejus a concursu refringentium planorum constituta, sit parallela ad Horizontem, et perpendicularis ad radios solares, atque ut illi radij per præfata refringentia plana trajecti refractiones ad ingressum et egressum æquales patiantur. Et ope Quadrantis, ut ostensum erat ad figuram 16, exploretur angulus incidentiæ, cujus sinus ad præfatum sinum refractionis erit ut sinus incidentiæ ad sinum refractionis ex aere in liquorem propositum.
[142]Instantiæ gratiâ, ut aquæ refractionem cognoscerem curavi, ut prisma ligneum conficeretur quale est ABκ, in figura 19 cujus ille angulus ACB, quem pro verticali designabam foret rectus, cæteriq́ue duo semirecti. 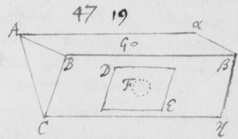 Et effeci ut refringentia plana Aκ et Bκ per Meditullium trajicerentur foramine F parallelo ad basem Aβ, per quod foramen lux itura esset; Et ut tertium planum Aβ foderetur in G usque dum aditus ad foramen F transversè pertingeret. Dein sumptis duabus ex vitro lamellis, quas speculum confractum mihi: subministravit, alteram DE super meditullium plani Bκ cum cæmento fixi, et alteram super meditullium alterius plani Aκ, ut meatus F utrinque clauderetur. Tum aquam pluvialem per orificium G in excavatum spatium infudi, et cum operculo ex subere conciso clausi. Atque adeò aqua duabus vitrejs lamellis ad angulum rectum inclinatis interjecta vices subibat aqueæ prismatis habentis angulum rectum. Eas autem laminas rectum angulum exactè comprehendere ex applicatione normæ cognovi, cujus ideò dimidium pro angulo refractionis habendum est[143]. Hoc prisma dein ita statuebam ad ingressum lucis in obscurum cubiculum, ut eadem foret utrinque refractionis quantitas; et ex altitudine solis, et refractorum radiorum viridiformium inclinatione ad Horizontem, inveni angulum refractum esse . Cujus dimidium unà cum angulo refractionis dabit angulum incidentiæ . Horum verò angulorum et sinus sunt 9434 et 7071 respectu sinûs 10000, quorum quidem numerorum ratio est paulo minor quam Cartesiana 250 ad 187 et paulo major quam 4 ad 3 nempe 4.002 ad 3; quæ tamen a ratione tam parvâ differentiâ recedit, ut error fuerit insensibilis si posuerim esse ut 4 ad 3, idque maximè cùm aquæ refractio non perpetim eadem maneat, sed a caloris vicissitudine nonnihil patiatur variośque densitatis gradus induat: Quod idem et aeri circundanti contingit, qui a vaporibus etiam non solùm variè incrassatur, sed et arctiùs (auctâ Atmosphaeræ gravitate) vel laxiùs comprimitur{.} Adde quòd aquarum ex diversis terrarum regionibus scaturientium aut vi solis in vapores et pluviam deinde conversarum diversæ sint densitates, et internæ dispositiones ad refringendum, ortæ ex varijs mineralium tincturis, quas e locis subterraneis extrahunt, et exhalationibus variè crassis aut copiosis, quæ simul cum vaporibus in altum attolluntur.
Et effeci ut refringentia plana Aκ et Bκ per Meditullium trajicerentur foramine F parallelo ad basem Aβ, per quod foramen lux itura esset; Et ut tertium planum Aβ foderetur in G usque dum aditus ad foramen F transversè pertingeret. Dein sumptis duabus ex vitro lamellis, quas speculum confractum mihi: subministravit, alteram DE super meditullium plani Bκ cum cæmento fixi, et alteram super meditullium alterius plani Aκ, ut meatus F utrinque clauderetur. Tum aquam pluvialem per orificium G in excavatum spatium infudi, et cum operculo ex subere conciso clausi. Atque adeò aqua duabus vitrejs lamellis ad angulum rectum inclinatis interjecta vices subibat aqueæ prismatis habentis angulum rectum. Eas autem laminas rectum angulum exactè comprehendere ex applicatione normæ cognovi, cujus ideò dimidium pro angulo refractionis habendum est[143]. Hoc prisma dein ita statuebam ad ingressum lucis in obscurum cubiculum, ut eadem foret utrinque refractionis quantitas; et ex altitudine solis, et refractorum radiorum viridiformium inclinatione ad Horizontem, inveni angulum refractum esse . Cujus dimidium unà cum angulo refractionis dabit angulum incidentiæ . Horum verò angulorum et sinus sunt 9434 et 7071 respectu sinûs 10000, quorum quidem numerorum ratio est paulo minor quam Cartesiana 250 ad 187 et paulo major quam 4 ad 3 nempe 4.002 ad 3; quæ tamen a ratione tam parvâ differentiâ recedit, ut error fuerit insensibilis si posuerim esse ut 4 ad 3, idque maximè cùm aquæ refractio non perpetim eadem maneat, sed a caloris vicissitudine nonnihil patiatur variośque densitatis gradus induat: Quod idem et aeri circundanti contingit, qui a vaporibus etiam non solùm variè incrassatur, sed et arctiùs (auctâ Atmosphaeræ gravitate) vel laxiùs comprimitur{.} Adde quòd aquarum ex diversis terrarum regionibus scaturientium aut vi solis in vapores et pluviam deinde conversarum diversæ sint densitates, et internæ dispositiones ad refringendum, ortæ ex varijs mineralium tincturis, quas e locis subterraneis extrahunt, et exhalationibus variè crassis aut copiosis, quæ simul cum vaporibus in altum attolluntur.
[144]Problematis hujus de refractionis fluidorum mensurâ sic soluti veritas constabit ex ostenso quod refractionis in hoc prismate ex aquâ et vitris composito eadem est quantitas, quæ foret si vitrum tolleretur, et aqua sola maneret aëre circundata. Sit itaque ABC prisma in figura 20 confectum ex laminis vitreis ACφδ, et BCφε (ut dictum est,) et aquâ δφε repletum; et concipiatur 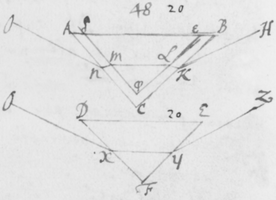 quòd DEF sit aqueum prisma immediatè circundatum aere, et omninò simile aquæ δεφ circumclusæ vitro, similiteŕque positum. Et incidant radij paralleli ON, OX in utrumque; quorum alter ON refractus in N M L et K tendit ad H; alter verò OX refractus in X et Y tendit ad Z. Dico jam quòd emergentes KH et YZ erunt paralleli, atque adeò quòd in utroque prismate tota refractionum quantitas erit eadem. Etenim in figura 18 si radius ωμ ipsi ON parallelus incidat in vitream laminam A, emergatque in λκ, notum est quòd radius λκ erit parallelus ipsi ωμ, hoc est ipsis ωμ et LK; Et cùm λκ et LK sint paralleli, erunt etiam μλ et ML paralleli. Unde liquet propositio, quòd
quòd DEF sit aqueum prisma immediatè circundatum aere, et omninò simile aquæ δεφ circumclusæ vitro, similiteŕque positum. Et incidant radij paralleli ON, OX in utrumque; quorum alter ON refractus in N M L et K tendit ad H; alter verò OX refractus in X et Y tendit ad Z. Dico jam quòd emergentes KH et YZ erunt paralleli, atque adeò quòd in utroque prismate tota refractionum quantitas erit eadem. Etenim in figura 18 si radius ωμ ipsi ON parallelus incidat in vitream laminam A, emergatque in λκ, notum est quòd radius λκ erit parallelus ipsi ωμ, hoc est ipsis ωμ et LK; Et cùm λκ et LK sint paralleli, erunt etiam μλ et ML paralleli. Unde liquet propositio, quòd
Quantitas refractionis ex aëre in Medium quodvis propositum est eadem sive radij immediatè ingrediantur istud Medium ex aëre (ut fit ad ωμλ,) sive priùs permeent aliud Medium interpositum, et parallelis planis terminatum (uti fit ad ONML): Et e contra. Atque idem intellige, cùm vice aeris aliud quodpiam adhibetur Medium.
Quare in figura 20 cùm paralleli radij OX et ON incidant in prismata DFE & ACB similia et similiter posita, refractionis quantitas ex aere in aquam erit eadem sive radij immediatè intrent, ut videre est ad DEF, sive priùs permeent lamellam vitream AδφC: hoc est, radius XY semel refractus erit parallelus ipsi ML bis refracto. Et ob eandem rationem cùm XY et ML sint paralleli, radij emergentes YZ et KH erunt etiam paralleli. Quare cùm radij et incidentes et emergentes sint paralleli, refractio tota prismatis utriusque est eadem. Atque adeò cùm aqueum prisma aëri contiguum propter fluiditatem aquæ fabricari nequeat, ejus vice liceat adhibere vitreum prisma cum aquâ repletum. Q.E.O.
Et sic modus generalis, quo refractiones ex aere in quælibet proposita Media determinentur, ostensus est; facillimus quidem et erroribus minimè obnoxius, præsertim si angulus prismatis sit magnus et exactè cognitus, Quadrans magnus et accuratus, et observatio facta longè post prisma, ubi colores multùm dilatati faciliùs distinguuntur. Et præterea, cùm refractiones inter aerem et Media proposita sic experientijs determinantur; indicata est regula, quâ Mediorum eorundem sibi ipsis contiguorum refractiones eliciantur. Quod satis est in gratiam primi casûs de refractionibus dimetiendis cum in eodem quopiam radiorum genere proportio sinus incidentiæ, et refractionis quæritur, ostendisse.
[145]Prosequendus est jam alter casus, ubi heterogeneorum radiorum refractiones sunt conferendæ; Et proportiones sinuum refractionis investigandæ sunt cùm eorum incidentia supponitur eadem. Id quòd ex ostensis quodammodò præstari potest, sed convenit, ut aliquid ampliùs urgeam. Et quoniam de intermedijs radiorum generibus facilè esset judicium proferre, si modò refractiones extremorum forent cognitæ: satisfecero si radios maxime omnium refrangibiles cum minimè refrangibilibus comparavero. Itaque in figura 21 sit ABC prisma vitreum, ita positum, ut radij tum ingredientes tum egredicntes eandem quantitatem refractionis ut priùs patiantur. Dies autem seligatur 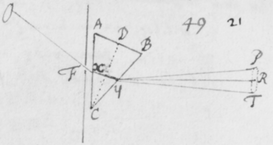 splendidus, et cubiculum esto valde obscurum, ut colores usque ad ultima quæ occupent spatia distinctè satis videri possint. Tunc ad distantiam viginti pedum aut ampliùs a prismate radij excipiantur in papyrum aliquam directè obversam, et spatij a coloribus illuminati (ut PT) longitudo et latitudo mensuretur. Sic prismate adhibito cujus angulus verticalis ACB fuit , et latitudine foraminis radios intromittentis existente quartâ parte digiti: Ad distantiam XP vel XT inveni maximam longitudinem imaginis PT esse circiter et latitudinem . Iam si latitudo hujus imaginis ab ejus longitudine subtrahatur, manebit digiti pro longitudine quam habere debuisset si discus Solis et foraminis F diameter fuissent infinitè parva. Hoc est si radij advenissent omnes in eâdem rectâ OCF. Ista itáque linea subtendit angulum quem radij duo similiter incidentes per inæqualitatem refractionis constituunt, quorum alter maximè omnium similiter incidentium & alter minimè omnium refringitur: qui proinde angulus ex calculo reperietur . Verùm cùm angulus iste binâ refractione ad X et Y conficiatur, et præterea cùm utraque supponatur æqualis; calculus ad hoc negotium satis accuratus ex unicâ tantùm refractione poterit institui, puta quæ conficitur ad latus BC. Etenim si verticalis angulus ACB plano DC bisecetur, et alterum prismatis dimidium DCB vel DCA concipiatur tolli, refractio ad alterum dimidium facta (radijs OF obliquè incidentibus in latus AC et perpendiculariter emergentibus e latere DC, vel perpendiculariter incidentibus in latus DC secundum unicam quandam lineam XY et obliquè emergentibus e latere BC) refractio, inquam, sic ad alterum dimidium facta foret semissis refractionis ad integrum prisma, si modò unicum quodpiam radiorum puta mediocriter refrangibilium genus spectetur{.} Quinetiam si cætera omnia radiorum genera simul spectentur, assertio illa licèt non ampliùs sit absolutè vera, tamen veritati tam proximè accedit, ut quoad sensum et calculum mechanicum pro verâ habeatur. Quamobrem cùm refractiones utrinque ad X et y peractæ computatio geometrica ægriùs institui possit, istud more ad praxin magis accommodato, ut ut mechanico, perficere non verebor, confisus id mihi vitio verti non debere, si dum computationes rebus physicis adhibeo, minutias quæ operam molestè et sine fructu producerent, missas faciam. Refractionem itaque ex unicâ tantum parte prismatis perpendam; Et quoniam omnes radij, demptis viridiformibus, a dimidio ACD bis deberent refringi, et semel tantùm ab altero dimidio DCB, perpendiculariter ingressi latus planum DC secundum lineam XY: itaque in dimidio DCB fiat calculus, hoc est ad latus planum BC; supposito quòd omnibus radijs secundum eandem lineam XY allapsis angulus quem maximè refrangibiles cum minimè refrangibilibus postquam refringerentur a latere BC, constituerent, foret dimidium anguli PYT, hoc est . Iam cùm angulus incidentiæ radij XY ex præmonstratis[146] sit et angulus refractionis mediocris , transferantur hæc omnia in Schema 22 ponendo quòd CB sit superficies disterminans Medium
splendidus, et cubiculum esto valde obscurum, ut colores usque ad ultima quæ occupent spatia distinctè satis videri possint. Tunc ad distantiam viginti pedum aut ampliùs a prismate radij excipiantur in papyrum aliquam directè obversam, et spatij a coloribus illuminati (ut PT) longitudo et latitudo mensuretur. Sic prismate adhibito cujus angulus verticalis ACB fuit , et latitudine foraminis radios intromittentis existente quartâ parte digiti: Ad distantiam XP vel XT inveni maximam longitudinem imaginis PT esse circiter et latitudinem . Iam si latitudo hujus imaginis ab ejus longitudine subtrahatur, manebit digiti pro longitudine quam habere debuisset si discus Solis et foraminis F diameter fuissent infinitè parva. Hoc est si radij advenissent omnes in eâdem rectâ OCF. Ista itáque linea subtendit angulum quem radij duo similiter incidentes per inæqualitatem refractionis constituunt, quorum alter maximè omnium similiter incidentium & alter minimè omnium refringitur: qui proinde angulus ex calculo reperietur . Verùm cùm angulus iste binâ refractione ad X et Y conficiatur, et præterea cùm utraque supponatur æqualis; calculus ad hoc negotium satis accuratus ex unicâ tantùm refractione poterit institui, puta quæ conficitur ad latus BC. Etenim si verticalis angulus ACB plano DC bisecetur, et alterum prismatis dimidium DCB vel DCA concipiatur tolli, refractio ad alterum dimidium facta (radijs OF obliquè incidentibus in latus AC et perpendiculariter emergentibus e latere DC, vel perpendiculariter incidentibus in latus DC secundum unicam quandam lineam XY et obliquè emergentibus e latere BC) refractio, inquam, sic ad alterum dimidium facta foret semissis refractionis ad integrum prisma, si modò unicum quodpiam radiorum puta mediocriter refrangibilium genus spectetur{.} Quinetiam si cætera omnia radiorum genera simul spectentur, assertio illa licèt non ampliùs sit absolutè vera, tamen veritati tam proximè accedit, ut quoad sensum et calculum mechanicum pro verâ habeatur. Quamobrem cùm refractiones utrinque ad X et y peractæ computatio geometrica ægriùs institui possit, istud more ad praxin magis accommodato, ut ut mechanico, perficere non verebor, confisus id mihi vitio verti non debere, si dum computationes rebus physicis adhibeo, minutias quæ operam molestè et sine fructu producerent, missas faciam. Refractionem itaque ex unicâ tantum parte prismatis perpendam; Et quoniam omnes radij, demptis viridiformibus, a dimidio ACD bis deberent refringi, et semel tantùm ab altero dimidio DCB, perpendiculariter ingressi latus planum DC secundum lineam XY: itaque in dimidio DCB fiat calculus, hoc est ad latus planum BC; supposito quòd omnibus radijs secundum eandem lineam XY allapsis angulus quem maximè refrangibiles cum minimè refrangibilibus postquam refringerentur a latere BC, constituerent, foret dimidium anguli PYT, hoc est . Iam cùm angulus incidentiæ radij XY ex præmonstratis[146] sit et angulus refractionis mediocris , transferantur hæc omnia in Schema 22 ponendo quòd CB sit superficies disterminans Medium 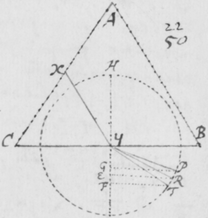 vitreum versus A, et aereum versus F, et quod angulus incidentiæ XYH sit : eritque angulus refractionis RYF ; et angulus PYT , differentia nempe refractionis inter maximè refrangibiles YP et minime refrangibiles YT. Qui angulus a radio YR mediocriter refracto et confinium cærulei ac viridis occupante, bisecatur; Et proin angulus PYR vel RYT erit dimidium totius PYT. Adeóque angulus PYE . Et angulus TYE . Et eorum sinus PG ac TF erunt 81656 & 80481: quorum proportione ad simpliciores numeros redactâ erit TF ad PG ut ad . Ad hunc modum experimenta et calculum cùm sæpius instituerim, horum sinuum proportiones inter terminos 67 ad 66 et 72 ad 71 semper obvenerunt; sed ut plurimùm incidi in proportiones 69 ad 68, ad , & 70 ad 69, quarum tantilla est differentia, ut parvi intersit quænam adhibeatur.
vitreum versus A, et aereum versus F, et quod angulus incidentiæ XYH sit : eritque angulus refractionis RYF ; et angulus PYT , differentia nempe refractionis inter maximè refrangibiles YP et minime refrangibiles YT. Qui angulus a radio YR mediocriter refracto et confinium cærulei ac viridis occupante, bisecatur; Et proin angulus PYR vel RYT erit dimidium totius PYT. Adeóque angulus PYE . Et angulus TYE . Et eorum sinus PG ac TF erunt 81656 & 80481: quorum proportione ad simpliciores numeros redactâ erit TF ad PG ut ad . Ad hunc modum experimenta et calculum cùm sæpius instituerim, horum sinuum proportiones inter terminos 67 ad 66 et 72 ad 71 semper obvenerunt; sed ut plurimùm incidi in proportiones 69 ad 68, ad , & 70 ad 69, quarum tantilla est differentia, ut parvi intersit quænam adhibeatur.
[147]Ratione sinuum refractionis pro extremis radiorum similiter incidentium generibus sic inventâ, eorum comparatio ad sinum incidentiæ simul innotescit, quippe qui paulo ante inventus est 52400, Et conferendo hunc 52400 ad sinus 81656 & 80481, eorum ratio in minoribus numeris reperietur ad & : aut ad 69 & 68 fere. Refractionibus nempe ex vitro in aerem peractis.
[148]Quòd si radij e contra ex aere in vitrum similiter incidant, proportiones sinuum nullo negotio ex jam inventis eruuntur, utpote quæ sunt reciprocæ. Sit I sinus incidentiæ e vitro in aerem, P sinus refractionis maxime refrangibilium radiorum, R mediocriter refrangibilium ac T minime refrangibilium: Dico quòd ex horum reciprocè proportionalibus si ponatur esse sinus incidentiæ ex aere in vitrum erit sinus refractionis maximè refrangibilium radiorum sinus refractionis mediocriter refrangibilium, ac minime refrangibilium{.} Nam cùm sinus incidentiæ radij maxime refrangibilis e vitro in aerem sit I et sinus refractionis P, radij ejus ex aëre in vitrum per easdem lineas retroacti sinus incidentiæ erit P et sinus refractionis I, siquidem jam radius est incidens qui priùs fuerit refractus. Est ergo sinus incidentiæ radij maxime refrangibilis ex aere in vitrum utcunque incidentis ad sinum refractionis ut P ad I hoc est (applicando rationem ad P) ut 1 ad , hoc est (applicando ad I denuò) ut ad . Et simili argumento constabit ejusmodi sinus radij mediocriter refrangibilis esse ut ad et sinus minime refrangibilis ut ad . Liquet ergo quod posito communi sinu incidentiæ erunt , , & singulorum generum respectivè sinus.
[149]Rem numeris illustro. Cùm ad 69 & 68 sit ratio sinus communis incidentiæ ad sinus maximè discrepantium refractionum e vitro in aerem: sinus incidentiæ communis ad sinus refractionum ex aere in vitrum erit ut ad & , sive ( ferè) ad 68 et 69. Hoc est pro radijs maximè refrangibilibus sinus incidentiæ ad sinum refractionis ut 106 ad 68 pro minime refrangibilibus, ut 106 ad 69. [150]Hisce sic determinatis rationes sinuum pro radijs intermedijs facilè determinantur ex cognitis colorum distantijs quas in imagine coloratâ observant{.} Sic radij qui ad cæruleum magis quàm flavum vergunt, cùm in mediam imaginem cadant intermediam rationem sinuum ad vel 106 ad habebunt. Et sic de alijs.
<85>[151][152]Ad eundem modum quo refractiones ad vitrum determinatæ sunt id ipsum posset fieri ad alia Media. Sed e re erit ut regulam jam ostendam, quâ refractionum istarum mensuræ ex sinubus earum sic ad vitrum determinatis, possunt determinari ad quodlibet aliud Medium propositum, idque licèt istud sit alij Medio quàm aeri contiguum. In figura 23 sit AB superficies terminans aerem ex parte F, et vitrum ex parte G, ad cujus aliquod punctum X ducatur linea FxG ei perpendiculariter insistens: et præterea concipiatur rectam IX ad angulum IXA infinitè parvum duci, secundum quam omnes omnium formarum radij supponantur incidere et in X refringi puta mediocriter refrangibiles versus R maximè refrangibiles versus P, et minimè refrangibiles versus T, aliósque intermedios versus intermedias plagas. 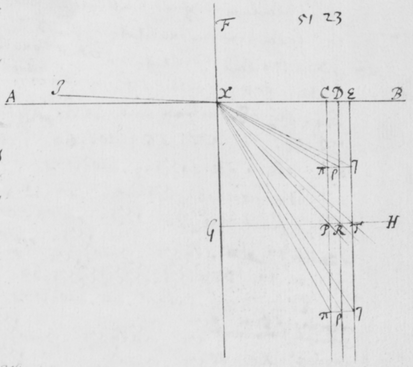 Porrò ducatur linea quævis GH parallela ad lineam incidentiæ IX, hoc est perpendicularis ad FG. Ea verò secet radios in punctis P R ac T, a quibus demittantur PC RD ac TE perpendiculares ad refringentem superficiem AB. His ad vitrum sic determinatis ac descriptis, si aliud quodvis Medium in locum vitri jam concipiatur substitui, cæteris stantibus; et radij alicujus mediocriter refrangibilis secundum lineam IX incidentis ad X refractus Xρ ducatur secans rectam DR in ρ, (Quod fieri suppono, siquidem modum quo mediocriter refrangibilium refractiones ad Media quælibet investigari possint, antehac exposui.) Dein per punctum ρ ducatur recta πτ secans lineas CP et ET in π ac τ perpendiculariter, junganturq́ue πX ac τX: Dico quòd radij maxime refrangibiles secundum dictam lineam IX incidentes refringentur in lineam Xπ, et minimè refrangibiles in lineam Xτ, radijq́ue cujusvis speciei quos vitrum refringebat ad quodlibet punctum rectæ PT, illi ad correspondens punctum rectæ πτ per alterum dictum Medium refringentur quod pro vitro supponitur substitui; istis punctis linearum PT et πτ habitis pro correspondentibus per quæ recta quævis ipsi DR parallela transit. Patet itáque modus quo refractiones quorumvis radiorum ex aëre in quodlibet Medium propositum obliquitate maximâ incidentium determinari poterunt, cognitâ unici tantùm cujusvis radiorum generis in istud Medium refractione. Et proportionibus sinuum ex obliquissima istâ refractione determinatis, eorundem radiorum refractiones dabuntur ad quamlibet aliam datam incidentiam.
Porrò ducatur linea quævis GH parallela ad lineam incidentiæ IX, hoc est perpendicularis ad FG. Ea verò secet radios in punctis P R ac T, a quibus demittantur PC RD ac TE perpendiculares ad refringentem superficiem AB. His ad vitrum sic determinatis ac descriptis, si aliud quodvis Medium in locum vitri jam concipiatur substitui, cæteris stantibus; et radij alicujus mediocriter refrangibilis secundum lineam IX incidentis ad X refractus Xρ ducatur secans rectam DR in ρ, (Quod fieri suppono, siquidem modum quo mediocriter refrangibilium refractiones ad Media quælibet investigari possint, antehac exposui.) Dein per punctum ρ ducatur recta πτ secans lineas CP et ET in π ac τ perpendiculariter, junganturq́ue πX ac τX: Dico quòd radij maxime refrangibiles secundum dictam lineam IX incidentes refringentur in lineam Xπ, et minimè refrangibiles in lineam Xτ, radijq́ue cujusvis speciei quos vitrum refringebat ad quodlibet punctum rectæ PT, illi ad correspondens punctum rectæ πτ per alterum dictum Medium refringentur quod pro vitro supponitur substitui; istis punctis linearum PT et πτ habitis pro correspondentibus per quæ recta quævis ipsi DR parallela transit. Patet itáque modus quo refractiones quorumvis radiorum ex aëre in quodlibet Medium propositum obliquitate maximâ incidentium determinari poterunt, cognitâ unici tantùm cujusvis radiorum generis in istud Medium refractione. Et proportionibus sinuum ex obliquissima istâ refractione determinatis, eorundem radiorum refractiones dabuntur ad quamlibet aliam datam incidentiam.
[153]Hujus autem propositionis certitudinem licèt ab experientijs nondum habeo depromptam , nullus tamen dubito quin satisfaciet omnibus quas de illa licebit facere. Verùm cùm occasio de causis refractionum dicendi lata sit, veritatem ejus ex proprijs fundamentis eruere conabor, contentus interea gratis assumere.
[154]Calculum quod attinet is facilè potest institui ex hac proportionalitate quòd sinus incidentiæ radij IX (hoc est sinus 90graduum) sit ad sinum refractionis (puta quæ facta sit in lineam XR,) sicut XR ad RG. sic ad vitrum erit , et {}. Et . Et inde deducetur quod . Quæ proportiones semel inventæ possunt in eum finem asservari ut earum ope refractiones ad alia Media quàm vitra determinentur . Nam quolibet Medio proposito, sumatur , , & , atque perpendicula CP, DR, & ET erigantur; Tum ex datâ sinuum refractionis radiorum mediocriter refrangibilium proportione, hoc est ex datâ proportione ipsius Xρ ad XD, dabitur punctum ρ et longitudo Dρ, cui æquales sunt Cπ et Eτ. Punctisq́ue π ac τ sic datis dantur rationes ipsarum Xπ et XC, hoc est sinuum incidentiæ et refractionis, pro radijs maxime refrangibilibus, ut et rationes ipsarum Xτ et XE, hoc est sinuum incidentiæ et refractionis, pro radijs minimè refrangibilibus Sic pro superficie aquam et aerem disterminante sinus isti sunt ut 68 ad 90 pro minime refrangibilibus, et ut 68 ad 91 pro maximè refrangibilibus.
[155]Proportionibus linearum XC, XD et XE sic inventis, mensura rcfractionum ejusdem rei ex aëre in Medium quodvis propositum et ad quamlibet incidentiam factarum per aliud insuper Theorema non inelegans determinari potest. In lineâ Fx (figura 24) ad refringens planum AB perpendiculari, sumatur punctum aliquod F quod lucidum fingatur, ac ducatur quælibet Fδ secans AB in δ eáque concipiatur esse mediocriter refrangibilis radius cujus refractus ex aere in Medium propositum esto δM, qui retro-ductus secet ipsam FX in φ. Porrò fiat et . centroque F et intervallis Fε et Fγ describantur circuli secantes AB in ε et γ jungantuŕque Fε, Fγ, φε, φγ, et producantur φε et φγ indefinitè versus N et L. Dico jam si radius minime refrangibilis incidat 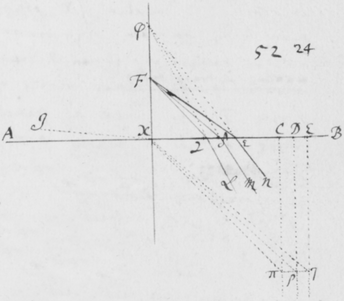 secundum lineam Fε, quòd iste refringetur in lineam εN; Et si maximè refrangibilis incidat secundum Fγ, quòd iste refringetur in ipsam γL. Et sic radij quorumlibet intermediorum generum manantes a puncto F et in puncta sibi correspondentia inter γ et ε incidentes, ita refringentur a Medio proposito quasi manassent omnes a puncto φ: Istis punctis inter C et E atque γ et ε habitis pro correspondentibus, quorum distantiæ ab X et F respectivè, sunt in eâdem ratione cum DX ac δF.
secundum lineam Fε, quòd iste refringetur in lineam εN; Et si maximè refrangibilis incidat secundum Fγ, quòd iste refringetur in ipsam γL. Et sic radij quorumlibet intermediorum generum manantes a puncto F et in puncta sibi correspondentia inter γ et ε incidentes, ita refringentur a Medio proposito quasi manassent omnes a puncto φ: Istis punctis inter C et E atque γ et ε habitis pro correspondentibus, quorum distantiæ ab X et F respectivè, sunt in eâdem ratione cum DX ac δF.
[156]Cujus Theorematis demonstrationi præsternantur duo Lemmata sequentia.
1. [157]Duobus punctis γ, δ in lineâ quâpiam AB (figura 24) sumptis, et alijs duobus φ et F in ejus perpendiculo FX; junctisq́ue φδ, Fδ, φγ, et Fγ: differentia quadratorum a duobus φδ et Fδ concurrentibus ad δ æquabitur differentiæ quadratorum ab alijs duobus φγ et Fγ concurrentibus ad γ. Nam cùm , et ; erit differentia . Et ob eandem rationem est differentia . Quare dictæ differentiæ sic æquales eidem tertio sunt æquales inter se. Q.E.D.
2. [158]Si radius aliquis FG (figura 25) incidat in superficiem AB, et refringatur versus H: Lineâ GH retro-ductâ ut 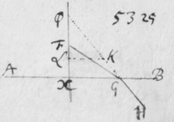 secet perpendiculum FX in φ, dico quod sinus incidentiæ, ad sinum refractionis. Et e contra si sinus incidentiæ . sinum refractionis; erit φγH refractus ipsius FG. Etenim sumatur , et demittatur KL perpendicularis ad FX; quo facto, cùm angulus GFX æquetur angulo incidentiæ et angulus GφX angulo refractionis, erit GX sinus incidentiæ et KL sinus refractionis, habito respectu ad circulum cujus semidiameter sit FG vel φK. Sed est hoc est . Q.E.D.
secet perpendiculum FX in φ, dico quod sinus incidentiæ, ad sinum refractionis. Et e contra si sinus incidentiæ . sinum refractionis; erit φγH refractus ipsius FG. Etenim sumatur , et demittatur KL perpendicularis ad FX; quo facto, cùm angulus GFX æquetur angulo incidentiæ et angulus GφX angulo refractionis, erit GX sinus incidentiæ et KL sinus refractionis, habito respectu ad circulum cujus semidiameter sit FG vel φK. Sed est hoc est . Q.E.D.
[159]His præmissis Theorema propositum sic demonstratur. In Figura 24 ducatur IX obliquissima linea secundum quam radij omnium formarum ex aëre ad punctum X incidere ponantur et in Medium propositum refringi maxime refrangibiles versus π, et minimè refrangibiles versus τ, eosq́ue lineæ ad puncta D, C, et E normaliter erectæ secent in punctis ρ, π, ac τ, ut explicabatur ad Figuram 23. Iam cùm istorum radiorum sinus incidentiæ et refractionis statuantur esse ut Xρ ad XD, Xπ ad XC et Xτ ad XE respectivè; si præterea demonstratum fuerit quod φδ ad Fδ, φγ ad Fγ et φε ad Fε respectivè sunt in eâdem ratione, (hoc est, quod sinus incidentiæ, ad sinum refractionis radiorum mediocriter refrangibilium et sinus incidentiæ ad sinum refractionis radiorum maxime refrangibilium &c) constabit propositum ex Lemmate secundo. Et ad mediocriter refrangibiles quod attinet cùm φδ supponatur refractus ipsius Fδ, erit (per Lemma secundum) φδ ad Fδ ut sinus incidentiæ ad sinum refractionis, hoc est ut Xρ ad XD. Sed eadem proportionalitas in cæteris radiorum generibus jam demonstranda proponitur, puta quòd sit . Scilicet est , ut et , per Hypothesin. Quare permutando et connectendo rationes æquales est . Et quadrando , diminuendoque per terminos æqualis rationis {}. Et augendo per terminos æqualis rationis Denique terminorum radices extrahendo, permutandoq́ue est . Quare φγ sive γL est refractus ipsius Fγ per Lemma secundum. Q.E.D. Et eodem argumento patebit quòd εN sit refractus radij Fε. Déque alijs radijs pro varijs refrangibilitatis gradibus, intermedia spatia variè occupantibus, idem intelligendum est.
<89>[160]De refractionibus superficierum aeri contiguarum mensurandis hæc satis. Quod si desideretur id ipsum ad alias superficies aeri ex neutra parte contiguas fieri, sunto ABβH et αβνμ duo quælibet Media secundum planam superficiem Hβ contigua, et aere circundata. Sitque AB planum ipsi Hβ parallelum, et in eo sumatur punctum X, ad quod ducatur XV perpendicularis et IX obliquissima linea secundum quam (ut jam ante) radij omnium formarum incidant et pro gradu refrangibilitatis refringantur ad P, R, ac T aliaque intermedia loca. Horum radiorum in propositam 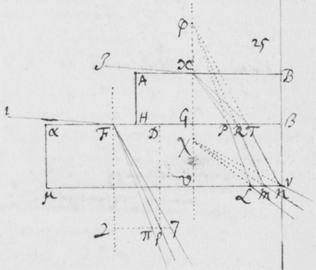 superficiem αβ sic incidentium refractiones jam quæruntur. Atque equidem cùm viridiformium refractiones ad quaslibet superficies fuerint antehac expositæ, radij XR sit RM refractus, et is retro-ducatur donec secet perpendiculum XV in φ. Et insuper ducantur φP, φT et producantur ad L et N. Dico quòd PL erit refractus ipsius XP, ac TN ipsius XT, atque omnes aliarum formarum radij incidentes inter P ac T ita refringentur, ut postea divergant a puncto φ. Concipiatur enim quòd Medium αβνμ longiùs versus αμ producitur quàm Medium ABβH, ita ut ejus plani αHβ pars inter H et α sit aeri contigua, et ad aliquod in eo punctum F ducatur perpendicularis Fγ nec non obliquissima linea ιF, secundum quam radij omnium formarum incidant, et pro gradu refrangibilitatis refringantur ad π, ρ, τ locaque intermedia perinde ut effectum erat ad alterius Medij superficiem AB. Præterea sumatur , et ducatur Dρ ipsi Fγ parallela, ut secet radium Fρ in ρ, unde ργ demittatur ad Fγ normalis, aliośque radios Fπ et Fτ secans in π ac τ. Iam cùm sit , erit etiam et ex ostensis ad figuram 23; Et insuper ex ostensis ad figuram 18 cùm radiorum secundum IX et ιF lineas parallelas incidentium eadem sit refractio in Medium αβνμ, sive immediatè ingrediantur ex aere sicut fit ad F, sive priùs permeent aliud Medium ut ABβH parallelis planis terminatum: sequitur quod radij alterutro modo refracti in dictum Medium αβνμ sunt paralleli radijs homogeneis altero modo in idem Medium refractis; hoc est quod Fπ ad PL, Fρ ad RM et Fτ ad TN sunt paralleli. Quapropter si refracti radij PL, RM, ac TN retro-ducantur donec singuli occurrant perpendiculo GX; cum eo et basibus GP, GR, ac GT constituent triangula similia triangulis γπF, γρF, et γτF, imò et ipsis æqualia, siquidem eorum bases γπ et GP, γρ et GR, γτ et GT sibimet respectivè sunt æquales. Quare cùm horum triangulorum vertices conveniant ad idem punctum F, illorum etiam vertices ad idem aliquod punctum φ convenient. Hoc est radij PL, RM, ac TN ipsorum XP, XR et XT refracti divergent omnes ab eodem puncto φ. Q.E.D.
superficiem αβ sic incidentium refractiones jam quæruntur. Atque equidem cùm viridiformium refractiones ad quaslibet superficies fuerint antehac expositæ, radij XR sit RM refractus, et is retro-ducatur donec secet perpendiculum XV in φ. Et insuper ducantur φP, φT et producantur ad L et N. Dico quòd PL erit refractus ipsius XP, ac TN ipsius XT, atque omnes aliarum formarum radij incidentes inter P ac T ita refringentur, ut postea divergant a puncto φ. Concipiatur enim quòd Medium αβνμ longiùs versus αμ producitur quàm Medium ABβH, ita ut ejus plani αHβ pars inter H et α sit aeri contigua, et ad aliquod in eo punctum F ducatur perpendicularis Fγ nec non obliquissima linea ιF, secundum quam radij omnium formarum incidant, et pro gradu refrangibilitatis refringantur ad π, ρ, τ locaque intermedia perinde ut effectum erat ad alterius Medij superficiem AB. Præterea sumatur , et ducatur Dρ ipsi Fγ parallela, ut secet radium Fρ in ρ, unde ργ demittatur ad Fγ normalis, aliośque radios Fπ et Fτ secans in π ac τ. Iam cùm sit , erit etiam et ex ostensis ad figuram 23; Et insuper ex ostensis ad figuram 18 cùm radiorum secundum IX et ιF lineas parallelas incidentium eadem sit refractio in Medium αβνμ, sive immediatè ingrediantur ex aere sicut fit ad F, sive priùs permeent aliud Medium ut ABβH parallelis planis terminatum: sequitur quod radij alterutro modo refracti in dictum Medium αβνμ sunt paralleli radijs homogeneis altero modo in idem Medium refractis; hoc est quod Fπ ad PL, Fρ ad RM et Fτ ad TN sunt paralleli. Quapropter si refracti radij PL, RM, ac TN retro-ducantur donec singuli occurrant perpendiculo GX; cum eo et basibus GP, GR, ac GT constituent triangula similia triangulis γπF, γρF, et γτF, imò et ipsis æqualia, siquidem eorum bases γπ et GP, γρ et GR, γτ et GT sibimet respectivè sunt æquales. Quare cùm horum triangulorum vertices conveniant ad idem punctum F, illorum etiam vertices ad idem aliquod punctum φ convenient. Hoc est radij PL, RM, ac TN ipsorum XP, XR et XT refracti divergent omnes ab eodem puncto φ. Q.E.D.
[161]Ostenso hoc, sequentia obveniunt notanda. 1. Quòd proportio sinuum incidentiæ et refractionis ad superficiem Hβ factæ, ex his facilè determinantur. Nam pro radijs maxime refrangibilibus sinus isti sunt ut φP ad XP; et pro minime refrangibilibus, ut φT ad XT; &c.
2. Hinc si proportiones sinuum refractionis ex aëre in duo quælibet Media proposita, paribus incidentijs, dentur; proportiones sinuum refractionis ex altero Mediorum in alterum facilè dabuntur: dividendo nempe sinus posterioris Medij per correspondentes sinus anterioris. Sic cùm refractio fit ex aëre in vitrum dicti sinus sunt ut ; et cùm fit ex aere in aquam sunt ut : Ergo cùm fit ex aquâ in vitrum erunt ut , hoc est ut ferè.
3. Si tertium aliquod Medium aëre densius postponatur Medio αβνμ, contingens illud in superficie νμ, quæ concipiatur plana ipsiśque AB et αβ parallela; Et si radij divergentes a puncto φ (sicut modò ostensum erat) in illud incidant ad puncta L, M, et N; postquam in ijsdem refringuntur divergent rursus ab alio quodam puncto χ quod situm est in perpendiculo XG: Et sic præterea in infinitum, quotcunque licèt Media parallelis planis ab invicem discreta sese ordine subsequantur. Quod si aër immediatè succedat Medio αβνμ, punctum istud χ a quo emergentes radij tendunt situm erit ad V in ipsâ refringenti superficie, propterea quòd emergent paralleli ad summè obliquam lineam IX secundum quàm primùm incidebant ex aere, si modò emergere dicantur qui nunquam divaricabunt a refringenti superficie.
<91>4. Si radij ab aliquo puncto F in aere sito divergentes, tendant ad puncta γ, δ, ε, pro more quem ad schema 24 explicui, et per varia deinde plana refringentia ipsiq́ue AB parallela transeant: semper divergent omnes ab eodem aliquo puncto quod situm est in perpendiculo planorum per punctum F transeunte, non secus quàm si incidissent in planum AB advenientes in obliquissimâ lineâ IX. Et longitudines radiorum punctis refringentibus dictóque perpendiculo interceptorum sunt ut sinus incidentiæ et refractionis ad singula plana quæ respectant. Quarum assertionum demonstrationes cùm facilè eruantur e prædictis, prætermitto, nè nimius in hâc re videar. Et sic tandem absolvi quæ de legibus refractionum dicenda esse judicabam; in quibus prolixitatem aliquam materia postulavit. Nam omnia ferè de integro hic tractanda erant, idq́ue sedulò, cùm totius Dioptrices scientia his legibus tanquam fundamentis innitatur.
[162][163]Quod reliquum est in ordine ad explicandas apparentias, quas Prismata exhibent dum objectis interponuntur, id protinus aggredior. Et quibus Philosophia Naturalis magis quàm Mathematica delicio est, licèt hæc fortè supervacanea videantur, habito tantùm ad enarrandam colorum genesin respectu: cùm tamen ad rem opticam necessariò pertineant, quatenus refractiones radiorum refrangibilitate differentium inter se conferri debent, non potui penitùs omittere; et cùm a præsenti negotio non sint aliena, statui hic rebus magis Physicis innectere quò materiæ varietas interstrata tædium relevare possit. Primò itaque refractiones contemplabor in solitariâ superficie factas, deinde refractiones geminatas, quales radijs per inclinata duo plana prismatum transeuntibus eveniunt; ac demum aliqua de constructione oculi, et ejus ad visionem dispositione levitèr attingam.
[164]De radiorum semel refractorum affectionibus:
Et primò de similiter refrangibilibus agitur perfunctoriè.
Propositio 1. Incidentijs æqualibus, refractiones sunt æquales. Nam sinus æqualium incidentiarum sunt æquales (per 26: 1: Elementa), atque adeò sinus refractionum sunt æquales (per 14: 5: Elementa.) Et anguli (per 7: 6: Elementa). Et sic e contra Refractionibus æqualibus, æquales sunt incidentiæ.
Propositio 2. Incidentiâ majori, major est angulus refractionis. Nam sinus incidentiæ majoris est major (15 3 Elementa), et ergo sinus refractionis (14 5 Elementa), et angulus (15 3 Elementa). Similiq́ue ratiocinio constet e contra quod angulo refractionis majori, major convenit angulus incidentiæ.
Corollarium: Si majori incidentiâ minor sit refractio, aut contra: Id fit ob dissimilem refrangibilitatem.
<92>Propositio 3. Si radij homogenei 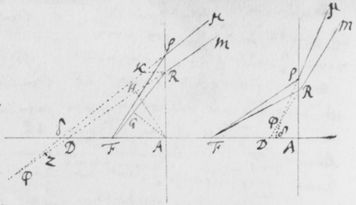 FR, Fρ, manantes a puncto quodam lucido F, refringantur a qualibet plana superficie AR, eorum refracti RM, ρμ ab invicem postea divergent. Nam ab F demittatur FA perpendicularis ad planum AR, et hinc inde producatur donec refractos radios retro-ductos secet in punctis D, ac δ: Eruntque RFA, ρFA anguli incidentiæ; et RDA, ρδA anguli refractionis. Iam cùm sit (ex constructione,) erit etiam (per propositionem 2 præcedentem:) Atque adeò (per propositionem 32 libri 1 Elementorum, et axioma 17) hoc est 2 rectis. Sed radij RD et ρδ ad eas partes concurrent ubi sunt anguli duobus rectis minores (per axioma 13: 1 Elementa), hoc est ad partes versus punctum F; et proinde ad alteras partes versus M et μ tendentes, ab invicem divergent. Q.E.O.
FR, Fρ, manantes a puncto quodam lucido F, refringantur a qualibet plana superficie AR, eorum refracti RM, ρμ ab invicem postea divergent. Nam ab F demittatur FA perpendicularis ad planum AR, et hinc inde producatur donec refractos radios retro-ductos secet in punctis D, ac δ: Eruntque RFA, ρFA anguli incidentiæ; et RDA, ρδA anguli refractionis. Iam cùm sit (ex constructione,) erit etiam (per propositionem 2 præcedentem:) Atque adeò (per propositionem 32 libri 1 Elementorum, et axioma 17) hoc est 2 rectis. Sed radij RD et ρδ ad eas partes concurrent ubi sunt anguli duobus rectis minores (per axioma 13: 1 Elementa), hoc est ad partes versus punctum F; et proinde ad alteras partes versus M et μ tendentes, ab invicem divergent. Q.E.O.
Scholium: Si angulus Rφρ, quem refracti radij comprehendunt ponatur esse infinitè parvus, punctum istud φ erit limes disterminans intersectiones radiorum utrinque jacentium, quas cum radio Rφ vel ρφ efficiunt: Ita scilicet ut cùm refractio fit e Medio rariori in densius, radiorum ad partes puncti R adversus A incidentium refracti secabunt radium φR ad partes puncti φ adversus R, et incidentium inter A et R refracti eundem φR secabunt inter φ et R. E contra verò cùm refractio fit e densiori Medio in rarius, incidentium ad partes ipsius φ adversus R refracti secabunt præfatum φR inter φ et R, et incidentium inter R et A refracti secabunt ad partes ultra φ sive ab R remotas. Porrò cum intersectiones, quas radij utrinque cum φρ efficiunt, sint eò densiores quo sunt viciniores puncto φ ac in illo puncto densissimæ: istud itaque φ pro foco radij φR habendum est sive pro loco imaginis illuc per refractionem translatæ; habito scilicet ad eos solummodo radios respectu qui jacent in plano FAR, quod refringenti plano perpendiculariter insistit, transitque per punctum radians F. Nam alij refracti quorum incidentes jacent in alijs planis per puncta F et R transientibus et obliquis ad refringens planum, radium Rφ nec in puncto φ, nec ullibi omninò secabunt, si eos solummodò excipias quorum incidentes jacent in superficie conicâ cujus axis est AF, vertex F, et semi-angulus AFR: utpote qui omnes præfatum Rφ in puncto D secabunt, quod in axe FA sit positum. Et hujus itaque Rφ centra radiationis præcipuè sunt duo, alterum φ a refractis jacentium in plano FAR effectum, et alterum a refractis jacentium in conicis superficiebus axe DFA angulisque AFR, ADR descriptis. Ad reliquos autem radios quod attinet, aliter circa FR quaquaversum positos, eorum refracti maximè appropinquant radio Rφ alicubi inter D et φ. Adeò ut respectu oculi per cujus pupillæ centrum radius RM transit, locus imaginis per totum spatium φD diffundi debeat. Vel potiùs cùm spatium φD sit unici tantùm puncti F imago, debemus unicum aliquod in eo punctum quod lucis omnis ab eo versus oculum pergentis meditullium occupet, inter puncta D et φ in mediâ circiter distantiâ interjacens, pro sensibili imagine statuere. Puncti verò illius accurata determinatio, cùm omnium radiorum ab F versus oculi pupillam refractorum habenda sit æstimatio, problema solutu difficillimum praebebit nisi Hypothesi alicui saltem verisimili, si non accuratè veræ innitatur assertio. Quemadmodum cùm radij æquè multi a termino D, alijsque vicinis punctis, ac a termino φ alijsque punctis similiter sibi vicinis versus oculum videantur profluere: locus imaginis ita debet in medio istorum terminorum statui, ut angulus quem radij duo a D et φ ad idem quodpiam pupillæ punctum convergentes includunt, a radio ab illo visionis loco ad idem pupillæ punctum pergente quàm proximè semper bisecetur. Quâ Hypothesi admissâ nihil aliud agendum est, quàm ut fiat , et erit Z locus visionis puncti F quæsitus; posito nempe quòd M sit locus oculi. Nam cùm ponatur , erit divisim . Et proinde ductis tribus lineis a φ, D, et Z ad M vel potiùs ad punctum quodpiam huic M indefinitè vicinum, angulus quem externæ duæ continent, ab interjacente lineâ (per 3. 6. Elementa) quàm proximè semper bisecabitur. Cæterùm nè puncti φ positio gratis assumatur, placet illud insuper sequenti Methodo determinare, præsertim cùm in hâc re videatur præcipuum.
Normalibus AG, AH a puncto A in radios dimissis, alterâ AG in incidentem radium FR et alterâ AH in refractum DR, factóque ; punctum φ erit locus objccti F post refractionem visi habito unicè ad radios in plano FAR jacentibus respectu. Scilicet cùm hoc punctum sit limes per interpositionem dirimens ac distinguens intersectiones radiorum utrinque positorum, nè longâ propositionum serie ad hoc demonstrandum opus sit, illorum intersectiones finitis intervallis ab RD distantium vix respiciam, sed radij tantùm indefinitè propinquissimi intersectionem speculando determinabo propositum, siquidem ea ipsa (ut jam dictum est) sit punctum φ, quod quæritur. Et nè demonstratio hæc, quæ (dum nullis ferè fundamentis præmonstratis innititur) longiuscula futura est, vos itaque tædio afficiat, lubet ut in partes aliquot sive conclusiones distinguatur.
Dico igitur imprimis quòd positis quorumlibet uniformium radiorum FR, Fρ, refractis RD, ρδ secantibus perpendiculum FA in D ac δ: . In præcedentibus enim ostensum est (sectio 120) quòd FR & RD sunt ut sinus incidentiæ et refractionis, et sic Fρ ad ρδ habebit eandem rationem. Quare terminos quadrando erit et per conversam rationem rursus per conversam rationem, subintellectâ tamen permutatione, fit . Est autem (per sectionem 119) . Est etiam & , adeoque . Quare est . Et applicando antecedentes ad et consequentes ad prodit . Q.E.O.
Porrò si radiorum FR, Fρ distantia sit indefinitè parva: Dico quod erit . Tunc enim segmenta Rρ, Dδ pro infinitè parvis habenda sunt, sive linæ AD, Aδ, ut et AR, Aρ pro infinitè parùm differentibus, hoc est pro æqualibus. Evadit ergo , et . Et sic vice proportionis jam ante ostensæ oritur . Sive multiplicando priorem rationem per , est .
Tertiò dico, quod est . Nam erectâ RK ad AR normali, quæ secet radium ρμ in K: est , sive , siquidem Aρ et AR, nec non Aδ et AD pro infinitè parùm differentibus habentur. Et priori ratione per multiplicatâ divisâque per AR orietur . Quamobrem cùm supra inventum est , si utriuśque permutatio subintelligatur, patebit esse . et multiplicando per AR permutandoque fit . Est autem . Quare et .
Dico denique Quòd est . Nam cùm sit , erit divisim . At est , et . Quare . Ductisque extremis et medijs in se invicem fit . et applicando ad oritur . Quo in proportionalitatem resoluto prodit . Sed (per 8. 6. Elementa) est ; ut et et proinde et , atque adeò . Q.E.D.
[165]Sed videor actum agere, et his itaque paucis circa radios homogeneos in gratiam sequentium obiter notatis, ut eorum penitior cognitio habeatur, Lectiones, quas Vir Reverendus Dr Barrow de ijs fusè composuit, consulendas esse moneo, deq́ue heterogeneis sive dissimiliter refrangibilibus radijs pergo actutùm disserere.
[166]Propositio 4. Si radij heterogenei manantes a puncto quodam lucido refringantur a qualibet planâ superficie, eorum refracti possunt esse paralleli vel convergentes æquè ac divergentes. Cæterùm placet, ut ad magis particularia descendam a quibus veritas hujus patebit. Et cùm a sinibus incidentiæ et refractionis diversorum generum radiorum ratiocinia pendebunt; posito quòd similiter incidentium communis sinus incidentiæ brevitatis gratiâ vocetur I, sinum refractionis purpuriformium nominabo P, cæruliformium Q, viridiformium R, flaviformium S, et rubiformium T.
Propositio 5. Si sit FT radius extremè rubiformis, ac TB subtendens angulum TAF ducatur ut sit , et agatur FP huic TB 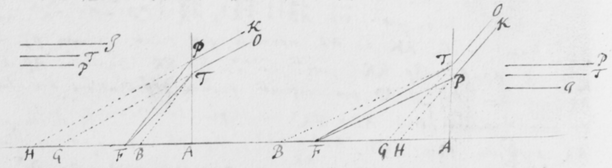 parallela, quæ concipiatur esse radius extremè purpuriformis: Dico quod radiorum Fφ et FT refracti PK ac TO erunt paralleli. Nam radijs PK TO retrorsum ductis donec secent FA in H ac G, erit a[167]. Et præterea cùm b[168], erit ex æquo . Sed est a[169]. Ergo . Atque adeo cùm TB et PF sint parallelæ b[170], erunt etiam TG et PH parallelæ c[171]. Q.E.O.
parallela, quæ concipiatur esse radius extremè purpuriformis: Dico quod radiorum Fφ et FT refracti PK ac TO erunt paralleli. Nam radijs PK TO retrorsum ductis donec secent FA in H ac G, erit a[167]. Et præterea cùm b[168], erit ex æquo . Sed est a[169]. Ergo . Atque adeo cùm TB et PF sint parallelæ b[170], erunt etiam TG et PH parallelæ c[171]. Q.E.O.
Propositio 6. Eodem modo pateat quod innumeri radij intermediarum possunt ita duci inter FP, et FT ut eorum refracti fient ipsis PK ac TO paralleli. Quo posito dico quod illi radij prout a rubedine ad purpuram succedunt, hoc est prout sunt magis ac magis refrangibiles, incident in punctis a P usque ad T continuò successivis. Sic verbi gratiâ fiat . Et ipsis 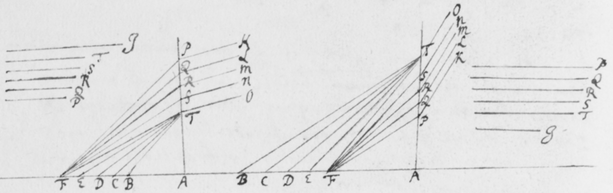 TB, TC, TD ac TE ducantur parallelæ FP, FQ, FR, FS quæ, unà cum FT priùs ductâ concipiantur esse radij coloribus quinque insignioribus purpureo cæruleo{,} viridi{,} flavo et rubeo tincti, et constabit e præcedenti propositione quod eorum refracti PK, QL, RM, SN, TO erunt paralleli: Sed cùm P, Q, R, S ac T ferè sint in Arithmeticâ vel potiùs in Geometricâ proportione, aut saltem sese gradatim superant longitudine, eò quòd sunt sinus refractionum ab invicem gradatim differentium: sequitur quod TB, TC, TD, TE, TF sese etiam longitudine gradatim superabunt, et proinde jacebunt in ordine nominato; et ideò FP, FQ, FR, FS et FT jacebunt in eodem ordine.
TB, TC, TD ac TE ducantur parallelæ FP, FQ, FR, FS quæ, unà cum FT priùs ductâ concipiantur esse radij coloribus quinque insignioribus purpureo cæruleo{,} viridi{,} flavo et rubeo tincti, et constabit e præcedenti propositione quod eorum refracti PK, QL, RM, SN, TO erunt paralleli: Sed cùm P, Q, R, S ac T ferè sint in Arithmeticâ vel potiùs in Geometricâ proportione, aut saltem sese gradatim superant longitudine, eò quòd sunt sinus refractionum ab invicem gradatim differentium: sequitur quod TB, TC, TD, TE, TF sese etiam longitudine gradatim superabunt, et proinde jacebunt in ordine nominato; et ideò FP, FQ, FR, FS et FT jacebunt in eodem ordine.
Propositio 7. Radij nullius extra spatium PT incidentis, refractus potest esse præfatis refractis parallelus: siquidem nullus datur radius magis refrangibilis quàm purpuriformis FPK supponitur, nec minùs refrangibilis quàm rubiformis FTO. Nam si talis refractus ponatur esse ipsi PK cæterisque parallelus; vel incidet ad partes juxta P et sic erit magis refrangibilis quàm FPK ob eandem rationem quâ FPK sit magis refrangibilis quàm FQL; vel incidet ad partes juxta T et sic erit minùs refrangibilis quàm FTO ob eam rationem, qua FTO sit minùs refrangibilis quàm FSN: contra Hypothesin.
Scholium: Verùm hic et in posterum notandum est quòd colorum extremitates nullibi exactè definiuntur, sed insensibili diminutione paulatim deficiunt: adeò ut haud facile sit dicere quis sit eorum terminus vel quanta sit maxima et minima radiorum refrangibilitas. Sed habitu ad experimenta et frequentes colorum apparentias respectu, convenit ut eos solummodò radios consideremus quorum numerus et vigor tantus est ut facilè sentiantur, cæteris ad extremitates summas non adnumeratis. Et sic in præcedentibus calculis, ubi determinavimus esse , cùm refractio fit ex vitro in aerem; ponimus T, et P esse sinus extimorum radiorum, quorum numerus est tantus, ut liquidò feriant sensus; non autem radiorum qui in extremitate summâ tam pauci sunt, ut vix aut nullo modo sentiantur, et ideò non digni ut in æstimationem veniant. Verùm tamen sive illi solùm radij considerentur, quorum copia tanta est ut facilè sentiantur, sive etiam alij adhuc exteriores; semper supponimus P designare sinum refractionis extremorum, qui considerantur ad extremitatem purpuream, ac T sinum eorum ad rubram: hoc est supponimus P designare sinum maximè refrangibilium ex omnibus, qui considerantur, ac T sinum eorum qui ponuntur minimè omnium refrangibiles. Atque has duas radiorum species in præcedentibus potiùs vocavimus extremè quàm intensè purpuriformes et rubiformes, eo quòd sunt omnium colorum extremitates, cùm intensissima sive perfectissima purpura et rubedo non in summis extremitatibus sed circa meditullium purpuræ et rubedinis cernantur.
<98>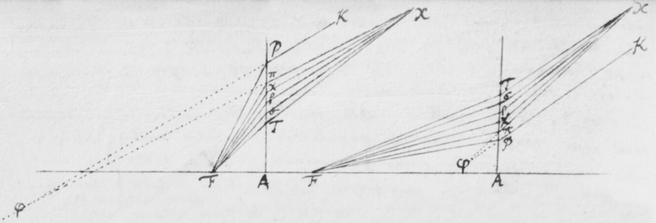
Propositio 8. Radij extremè purpuriformis Fπ intra spatium PT incidentis refractus πX converget ad TX refractum radij FT extremè rubiformis et alicubi ultra refringentem superficiem secabit puta ad X. Nam cùm FP et Fπ sint homogenei a[172], eorum refracti PK, πX divergent ab aliquo puncto velut φ quod citra refringentem superficiem locatum est b[173]. Ergo anguli c[174], hoc est anguli XTπ d[175] e[176] sunt minores duobus rectis. Quibus angulis ultra refringentem superficiem jacentibus, etiam πX ac TX concurrent ultra f[177]. **
**
Propositio 10. Radius intermedij generis cujus refractus transit per dictum punctum X, incidet in refringentem superficiem inter π ac T. Non enim incidet in punctum π, quia tunc eandem refractionem pateretur ac radius intensè purpuriformis, contra Hypothesin quòd sit intermedij generis. Neque incidet extra dictum π versus P quia tunc deberet esse magis refrangibilis quàm præfatus ille purpuriformis FP a[178], habens nempe minorem angulum refractionis ad majorem angulum incidentiæ; Id quod adhuc magis hypothesi contradicit. Et simili discursu patebit etiam, quòd in punctum T vel extra illud ad partes ipsi P adversas non potest incidere. Restat ergo ut transeat inter π ac T.
** Propositio 9. Omnes radij ab F ad X refracti jacent in eodem plano FAX. Nam planum in quo radius incidens et ejus refractus jacent, semper perpendiculare est ad planum refringens: Sed nullum perpendiculare planum transit per puncta F et X praeter FAX. Ergo omnes radij ab F ad X refracti jacent in isto plano.
Propositio 11. Heterogenei radij quorum refracti transeunt per dictum X, cadent in spatium PT in eodem ordine in quo colores eorum sibi invicem a purpurâ ad rubedinem succedunt. Ponatur enim quod cæruliformis radius incidat ad χ, et cùm viriditas sit color inter cæruleum et rubeum intermedius, eodem modo constabit quòd viridiformis radius cadet inter χ ac T, quo ostensum est in præcedenti propositione quod radius quilibet intermediorum generum debeat inter π ac T incidere. Cadat itáque ad ρ. Et cùm flavedo sit color viridi et rubeo interveniens, eodem quo dictum est modo constabit quòd flaviformis radius cadet inter ρ ac T puta ad σ. Atque ita deinceps{.}
Si jam desideretur, ut ex datis punctis F et X, angulus TXπ determinetur: quo id perficiam convenit, ut problema sequens more Lemmatis exponatur.
Problema. Dato puncto planum refringens irradiante, et alio etiam puncto, per quod refractus radius debet transire, positio radiorum, sive refringens punctum quæritur. Sit F punctum radios ejaculans, et R punctum ubi radius refringi debeat ut postmodum transeat per datum X. Ab ijsdem F et X normales FA, et Xα ad refringens planum demittantur. Et facto , cum latere recto VG seorsim describatur Parabola Conica VLν, 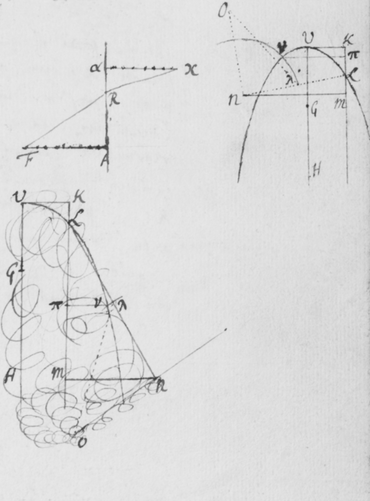 cujus vertex sit V, et axis VGH. Deinde ad axem erigatur a vertice normalis et agatur KM ad axem parallela, quæ secet Parabolam in L, et capiatur LM ejus longitudinis, ut sit . Eique perpendiculariter insistens ad M ducatur MN, ut sit , jungaturque LN et ad ipsam erigatur normalis , et in angulo ONL inscribatur , centróque N et intervallo Nλ describatur circulus, secans Parabolam in ν, unde νπ perpendiculariter ad LM demittatur. Denique si huic νπ sumatur AR æqualis, erit R quæsitum punctum refractionis, quod radios FR, et RX positione determinat. Q.E.F{.}
cujus vertex sit V, et axis VGH. Deinde ad axem erigatur a vertice normalis et agatur KM ad axem parallela, quæ secet Parabolam in L, et capiatur LM ejus longitudinis, ut sit . Eique perpendiculariter insistens ad M ducatur MN, ut sit , jungaturque LN et ad ipsam erigatur normalis , et in angulo ONL inscribatur , centróque N et intervallo Nλ describatur circulus, secans Parabolam in ν, unde νπ perpendiculariter ad LM demittatur. Denique si huic νπ sumatur AR æqualis, erit R quæsitum punctum refractionis, quod radios FR, et RX positione determinat. Q.E.F{.}
Cæterùm cùm hoc idem Problema a Doctore Barrow in Lectione 5 rerum Opticarum eleganter solutum extet, potestis illum consulere, et ideò demonstrationem hujus constructionis brevitatis gratiâ prætermitto. Hoc autem sic præmisso, problematis priùs propositi solutio fit palam . Nempe ut angulus TXπ e datis F et X determinetur nihil aliud agendum est, quàm ut ope problematis jam modò constructi, duo radij cum refractis suis ducantur alter FTX extremè rubriformis, et alter FπX extremè purpuriformis, qui ab F manantes, postquam refracti fuerint, transeant per X.
Scholium: Verùm enim cùm anguli hujus πXT determinatio eò spectet, ut noscatur quanta sit objectorum mediante refractione visorum propter inæquales absimilium radiorum refractiones confusio, perque quantum spatium colores inde emergentes extenduntur (quemadmodum pateat concipiendo F esse punctum lucidum quod oculo in X existente per totum angulare spatium πXT dilatatum ac diffusum appareat:) placet insuper modum ostendere quo quantitas ejus uno intuitu pro quavis puncti X sive oculi a refringenti superficie distantiâ præter propter innotescat, puncto F manente determinato. Concipiatur itáque quòd a dicto F ad idem quodpiam refractivæ superficiei punctum R, radij omnium formarum incidant, quorum extremè rubiformis refringatur versus K et purpuriformis versus O: et radijs hisce retroactis, exquirantur eorum foci, sive puncta Y et Z a quibus radij ejusdem formæ ambobus utrinque vicinissimi divergunt; per Scholium ad Propositionem 3. Tum 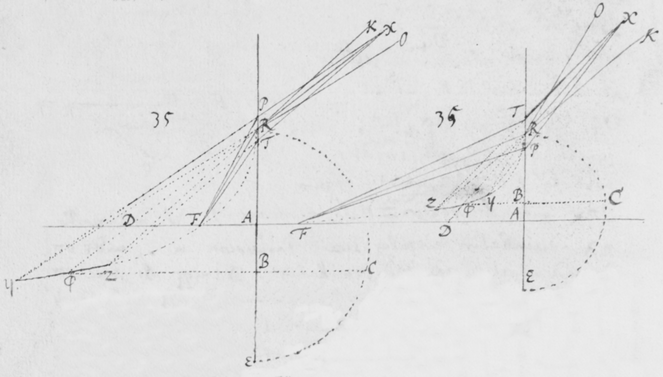 ducto etiam RX refracto radij viridiformis similiter incidentis ab F ad R: dico quòd ubicunque sumatur punctum X in lineâ novissimè ductâ RX, rectæ XY XZ abinde ad puncta Y et Z ductæ comprehendent angulum YXZ quàm proximè æqualem angulo quæsito PXT, extra quem radij pene nulli a puncto F ad punctum X refracti divaricant. Nam cum Y sit focus sive punctum istud a quo radij intensè purpuriformes refracti divaricant qui ab F manantes jacent ex utraque parte radij FRO sibi vicinissimi; Et cùm FPX sit ejusmodi radius: ejus itaque refractus PX tendet ab eo puncto Y, aut saltem ab alio quodam puncto in lineâ RY sito, quod ipsi sit valdè propinquum; siquidem is admodum vicinus est radio FRO licèt non omnium vicinissimus. Et simili ratione pateat quod radij FT extremè rubriformis refractus TX penè tendit a puncto Z quod focus est radij RK. Atque adeò constat quòd angulus YXZ quam-proximè adæquatur angulo PXT extra quem nulli radij punctis F et X interjecti divaricant. Q.E.O.
ducto etiam RX refracto radij viridiformis similiter incidentis ab F ad R: dico quòd ubicunque sumatur punctum X in lineâ novissimè ductâ RX, rectæ XY XZ abinde ad puncta Y et Z ductæ comprehendent angulum YXZ quàm proximè æqualem angulo quæsito PXT, extra quem radij pene nulli a puncto F ad punctum X refracti divaricant. Nam cum Y sit focus sive punctum istud a quo radij intensè purpuriformes refracti divaricant qui ab F manantes jacent ex utraque parte radij FRO sibi vicinissimi; Et cùm FPX sit ejusmodi radius: ejus itaque refractus PX tendet ab eo puncto Y, aut saltem ab alio quodam puncto in lineâ RY sito, quod ipsi sit valdè propinquum; siquidem is admodum vicinus est radio FRO licèt non omnium vicinissimus. Et simili ratione pateat quod radij FT extremè rubriformis refractus TX penè tendit a puncto Z quod focus est radij RK. Atque adeò constat quòd angulus YXZ quam-proximè adæquatur angulo PXT extra quem nulli radij punctis F et X interjecti divaricant. Q.E.O.
Adhæc si describatur linea quædam curva YφZ in quâ foci radiorum omnigenorum jacent secundum lineam FR incidentium et ita refractorum in puncto R ut per totum angulum KRO divaricent: ista curva YφZ non malè assimilabitur objecto lucido cujus angulus visibilis ad oculum in X situm, sit YXZ, et distantia ab eodem oculo ad meditullium ejus æstimata, φX. Sed notum est quòd visibilium apparentes magnitudines penè sunt reciprocè ut eorum distantiæ: Atque adeò longitudines φX penè sunt reciprocè ut anguli YXZ. Instantiæ gratiâ, cùm punctum X in ipsâ refringenti superficie ad R existit apparens longitudo ipsius YZ, erit angulus YRZ sive KRO. Est ergo . Quare puncto φ semel invento, (faciendo nempe quod sit . a[179]) angulus PXT definiens amplitudinem apparentem lucis a puncto PXT refractæ facilè determinatur pro qualibet positione puncti X in linea RX ad arbitrium assumpti.
Ex his palam est, quòd quo longiùs punctum X distat ab R eò minor est angulus KRO et quod nullus est cum X cadit ad infinitam distantiam, maximus autem cùm in ipsâ refringenti superficie cadit, quemadmodum ad R.
Cæterùm curva prædicta in quâ radiorum omnis generis in puncto R refractorum radiationum centra locantur est Cissois vulgaris sive Dioclea, circulo accommodata cujus diameter RE est ad AR ut ad . Nam super diametro RE descripto circulo isto RCE, agatur quævis recta φBC normalis ad RE, circuloque in C et curvâ in φ terminata. Et propter analoga latera similium triangulorum RAD, RBφ, erit . Et applicando posteriorem rationem ad BR fiet . Rursusque ducendo consequentes rationum in Rφ et applicando ad AR orietur . Est autem ut priùs, et consequentibus in DR atque antecedentibus in FR ductis, oritur et vicissim . Quamobrem rationes eidem tertiæ congruentes connectendo, habebitur , ducendóque antecedentes rationum in BR et consequentes AR prodibit et insuper applicando posteriorem rationem ad fiet {.} Sed cum posuerim erit , et proinde ac divisim . Atqui ex naturâ circuli est BC media proportionalis inter BR et BE adeóque est et proinde sive {.} Quod indicat curvam esse Cissoidem sicut ostendendum proposui.
[180]Præcedentia prælibavi ut de modo constaret quo radij difformes ab eodem puncto divergentes possint ab unicâ planâ superficie sic refringi ut ad aliud punctum puta centrum oculi fiant postea convergentes: in quâ re fundatur genesis colorum conspicuorum trans prismata, ut facilè deprehendi potest, et posthac fusiùs explicabitur. Quinetiam ut angulus quem ejusmodi convergentes radij efficiunt promptè noscatur indicavi, adeò ut cuiquam liceret doctrinam a nobis prolatam cum observationibus sensuum in ejusmodi minutijs conferre. Et in hunc finem placuit jam alia his agnata subjungere, quæ obliquitas incidentium radiorum aut Mediorum densitas varia subministret. Imprimis verò Lemma unum atque alterum præsternam.
[181]Lemma 1{.} Quatuor lineis GB, GC, GD, GE (figura 31{)} a dato puncto G ad datam lineam EB ita ductis ut sit : angulus BGC quem minima GB, cum alterutrâ intermediarum GC constituit, major est quàm angulus DGE ab alterâ intermediâ GD et maximâ GE constitutus. Nam centro G radio GE describatur circulus EK et radius 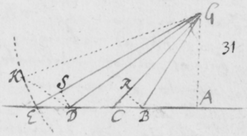 GK ducatur constituens angulum DGK æqualem angulo BGC, et puncta K D jungantur: eruntque triangula GDK, GBC similia propter æquales angulos ad G et latera circa illos proportionalia a[182], nempe Quare , sed b[183]. Ergo linea c[184], et d[185]; hoc est . Q.E.D.
GK ducatur constituens angulum DGK æqualem angulo BGC, et puncta K D jungantur: eruntque triangula GDK, GBC similia propter æquales angulos ad G et latera circa illos proportionalia a[182], nempe Quare , sed b[183]. Ergo linea c[184], et d[185]; hoc est . Q.E.D.
Lemma 2. Positis istis angulis infinitè parvis, ac GA perpendiculari ad lineam EB demissâ: erit . A punctis enim B ac D ad lineas GC, GE demittantur normalia BR ac DS, et erunt anguli præfati ad se invicem ut est ad , ponendo nempe lineas istas BR ac DS æquipollentes esse arcubus infinitè parvis quibus anguli illi subtenduntur. Est autem ex Hypothesi ac dividendo permutandóque . Item propter similia triangula BAG, CRB est , et pari ratione EA vel sive . Quamobrem addendo rationes æquales est (et permutatis terminis posteriorem rationum) (et æquipollenti ratione pro substitutâ) (terminisque ad invicem vicissim applicatis) . Est itáque , hoc est, ut angulus EGD ad angulum CGB. Q.E{.}D.
[186]Propositio 11. Heterogeneis radijs secundum eandem lineam incidentibus, quo obliquior est eorum incidentia cæteris paribus eo major erit differentia refractionis. In figuris 32 et 33 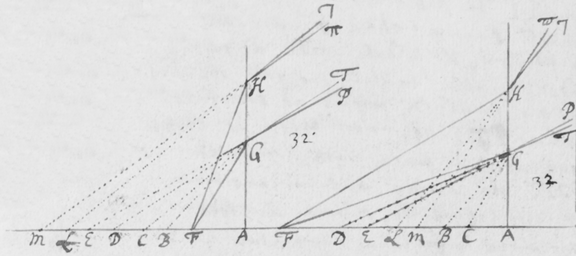 sit FG linea secundum quam duo radij incidunt, quorum alter purpuriformis refringitur versus P, et alter rubiformis versus T, eritque angulus PGT differentia refractionis. Item sit FH linea obliquior quam FG et secundum hanc alij duo ejusmodi radij incidant quorum purpuriformis versus π et rubiformis versus τ refringitur, et similiter erit angulus πHτ eorum differentia refractionis{.} Dico jam quòd . Demittatur enim FA ad refringens planum linea normalis, quæ refractos radios retro-actos in D, E, L et M secet. Et ad hanc a puncto G ducantur lineæ duæ GB, GC ipsis HL et HM parallelæ. Iam cùm tres lineæ GF, GD, GE (ex naturâ refractionis ante descriptâ) sunt in ratione datâ a[187], et alteræ tres HF, HL, HM in eâdem ratione a[188]: proportionales erunt . Sed est , propter similia triangula LMH et BCG. Quare . Adeóque per Lemma 1. Hoc est . Sive . Q.E.D.
sit FG linea secundum quam duo radij incidunt, quorum alter purpuriformis refringitur versus P, et alter rubiformis versus T, eritque angulus PGT differentia refractionis. Item sit FH linea obliquior quam FG et secundum hanc alij duo ejusmodi radij incidant quorum purpuriformis versus π et rubiformis versus τ refringitur, et similiter erit angulus πHτ eorum differentia refractionis{.} Dico jam quòd . Demittatur enim FA ad refringens planum linea normalis, quæ refractos radios retro-actos in D, E, L et M secet. Et ad hanc a puncto G ducantur lineæ duæ GB, GC ipsis HL et HM parallelæ. Iam cùm tres lineæ GF, GD, GE (ex naturâ refractionis ante descriptâ) sunt in ratione datâ a[187], et alteræ tres HF, HL, HM in eâdem ratione a[188]: proportionales erunt . Sed est , propter similia triangula LMH et BCG. Quare . Adeóque per Lemma 1. Hoc est . Sive . Q.E.D.
Scholium: Propositio etiam valet de radijs heterogeneis secundum parallelas lineas incidentibus; Imò et quodammodo valebit cùm incidentia fit secundum lineas inclinatas, ita quidem ut a puncto divergentes refringantur versus aliud punctum. Quemadmodum in figura 34 si linea quævis VX ducatur refringenti superficiei AP parallela, quæ secet perpendiculum ejus FA in V; et FPX, FTX, duos dissimiliter refrangibiles radios a dato puncto F ad quodpiam punctum X in recta VX refractos designent: summa angulorum PFT et PXT pro differentia refractionis habenda est, quæ quidem summa eo major evadet quo radij incidant obliquiores, hoc est quo punctum X longiùs ab V distet. Scilicet angulus PXT qui in rariori Medio existit augebitur ad certum usque terminum, et postea perpetuò diminuetur, donec X ad infinitam usque distantiam amoveatur. At alter angulus PFT in Medio densiori existens ita augebitur in perpetuum, ut utriusque simul sumpti summa etiam semper augeatur. Præterea si punctum X in datâ rectâ ad superficiem AP normali indeterminatum existat, quo radij obliquiùs incidant, hoc est quo punctum X propiùs ad superficiem accedit, angulus quidem PFT eò major evadet ad certum solummodò terminum, et postea rursus diminuetur; sed alter angulus PXT ità semper in tantum augebitur, 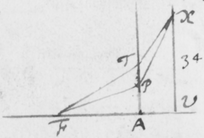 ut utriusque etiam summa, sive tota refractionis differentia augmentum simul in perpetuum adipiscatur. Et eadem plerumque observanda venient, si rectam in qua punctum X indeterminatum existit obliquè positam esse respectu superficiei AP cogites. Aliquando tamen contrarium eveniet. Quemadmodum si positione radij FPX manente datâ, punctum X ad quod alter radiorum FTX, concipiatur esse in lineâ PX indeterminatum: differentia refractionum eo minor evadet, quo dictum X longius amoveatur a P, sive quo radius FTX incidat obliquiùs; angulo ad X semper magis diminuto, quàm alter angulus ad F augetur. Ad eundem modum si vice rectæ VX curvam aliquam pro loco puncti X adhibeas, vel supponas istud X datum esse, et locum ipsius F in densiori Medio indeterminatum esse putes, varia hujusmodi de magnitudine angulorum ad F et X enunciari possent, quorum determinationes non tanti videntur, ut ijs diutiùs incumberem, placuit tamen de illis modò commonuisse, siquidem ad apparentia spatia respiciunt, per quæ colores (unicâ variè obliquâ superficie transpectâ) distendi videntur: quemadmodum et propositio præcedens ad spatia colorum in parietes, aut ejusmodi obstacula trajectorum referenda est .
ut utriusque etiam summa, sive tota refractionis differentia augmentum simul in perpetuum adipiscatur. Et eadem plerumque observanda venient, si rectam in qua punctum X indeterminatum existit obliquè positam esse respectu superficiei AP cogites. Aliquando tamen contrarium eveniet. Quemadmodum si positione radij FPX manente datâ, punctum X ad quod alter radiorum FTX, concipiatur esse in lineâ PX indeterminatum: differentia refractionum eo minor evadet, quo dictum X longius amoveatur a P, sive quo radius FTX incidat obliquiùs; angulo ad X semper magis diminuto, quàm alter angulus ad F augetur. Ad eundem modum si vice rectæ VX curvam aliquam pro loco puncti X adhibeas, vel supponas istud X datum esse, et locum ipsius F in densiori Medio indeterminatum esse putes, varia hujusmodi de magnitudine angulorum ad F et X enunciari possent, quorum determinationes non tanti videntur, ut ijs diutiùs incumberem, placuit tamen de illis modò commonuisse, siquidem ad apparentia spatia respiciunt, per quæ colores (unicâ variè obliquâ superficie transpectâ) distendi videntur: quemadmodum et propositio præcedens ad spatia colorum in parietes, aut ejusmodi obstacula trajectorum referenda est .
Cæterùm ut de mutuis angulorum PGT & πHτ (in figuris 32 et 33) proportionibus habeatur plenior determinatio, dico præterea quod sunt inter se quàm proximè ut lineæ AB et AD segmenta nempe basium triangulorum æquialtorum, quorum alterum EGD constituitur a radijs GP ac GT cum perpendiculo AF concurrentibus, et alterum CGB sit simile triangulo MHL a radijs Hπ et Hτ similiter constituto. Nam anguli EGD, & CGB, si essent infinitè pani, forent inter se ut AB ad AD, per Lemma 2. At isti ex Hvpothesi sunt æquales angulis PGT et πHτ, Quare etiam illi PGT & πHτ modò essent infinitè parvi, forent itidem ut AB ad AD. Cùm itaque semper sint admodum (licèt non infinitè) parvi, sequitur quòd sunt quàm proximè ut AB ad AD. Et pari ratione constat quòd sunt quàm proximè ut AC ad AE. Scilicet eorum ratio has duas rationes semper intercedit; et ideò veritatem adhuc propiùs assequemur adhibendo rationem intermediam, nempe quòd sit PGT ad πHτ ut ad ; vel ut ad proximè.
<106>Propositio 3. Heterogeneis radijs e densiori Medio in rarius secundum eandem datam lineam in superficiem positione datam incidentibus: quo rarius sit Medium in quod radij refringuntur eo major erit differentia refractionis. Sit FL linea secundum quam duo radij 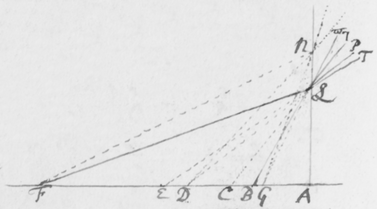 incidunt in superficiem AL quorum maximè refrangibilis refringatur ad P, et minime refrangibilis ad T: Dico quòd si Medium rarius foret adhuc magis rarum ut refringeret maximè refrangibilem radium ad π et minimè refrangibilem ad τ, tunc angulus πLτ foret major angulo PLT. Demittatur enim FA ad refringentem superficiem normalis, quæ secet refractos radios retrorsum ductos in G, C, D, et E. Deinde in refringente superficie quæratur tale punctum N, ut sit , ac DN productus erit refractus radij minimè refrangibilis incidentis ab F ad N a[189]. Iam cùm talis supponitur positio linearum FL et FN, ut radij maximè refrangibilis secundum FL et minimè refrangibilis secundum FN incidentis refracti DL ac DN divergant a puncto D quod situm est in perpendiculo FA: eâ de causâ, licèt raritas Medij in quod refractio peragitur foret alia quàm supponitur, tamen ejusmodi radiorum secundum easdem lineas FN et FL incidentium refracti semper divergerent ab aliquo puncto quod in eadem FA sit positum: quemadmodum in præcedentibus ostensum est b[190]. Sic cùm raritas dicti Medij talis esse supponitur, ut maximè refrangibilis radius secundum FL incidens refringatur a puncto quopiam G, tunc minimè refrangibilis secundum FN incidens refringetur ab eodem G. Sed cùm maxime refrangibilis radius supponebatur a puncto G refringi tunc etiam minimè refrangibilis secundum eandem lineam FL incidens supponebatur refringi a puncto C. Quare est c[191] et præterea cum antea posuerim esse , ex æquo erit . Sed est d[192]. adeoque . Quare si linea quædam BL ita ducatur ut sit erit , propter majorem rationem quam habet ad DL, et insuper erit , eò quòd sit . Et proinde punctum B cadet inter G et C, eritque . Cùm verò sit , aut vicissim , erit e[193]. Et multo magis . Q.E.D.
incidunt in superficiem AL quorum maximè refrangibilis refringatur ad P, et minime refrangibilis ad T: Dico quòd si Medium rarius foret adhuc magis rarum ut refringeret maximè refrangibilem radium ad π et minimè refrangibilem ad τ, tunc angulus πLτ foret major angulo PLT. Demittatur enim FA ad refringentem superficiem normalis, quæ secet refractos radios retrorsum ductos in G, C, D, et E. Deinde in refringente superficie quæratur tale punctum N, ut sit , ac DN productus erit refractus radij minimè refrangibilis incidentis ab F ad N a[189]. Iam cùm talis supponitur positio linearum FL et FN, ut radij maximè refrangibilis secundum FL et minimè refrangibilis secundum FN incidentis refracti DL ac DN divergant a puncto D quod situm est in perpendiculo FA: eâ de causâ, licèt raritas Medij in quod refractio peragitur foret alia quàm supponitur, tamen ejusmodi radiorum secundum easdem lineas FN et FL incidentium refracti semper divergerent ab aliquo puncto quod in eadem FA sit positum: quemadmodum in præcedentibus ostensum est b[190]. Sic cùm raritas dicti Medij talis esse supponitur, ut maximè refrangibilis radius secundum FL incidens refringatur a puncto quopiam G, tunc minimè refrangibilis secundum FN incidens refringetur ab eodem G. Sed cùm maxime refrangibilis radius supponebatur a puncto G refringi tunc etiam minimè refrangibilis secundum eandem lineam FL incidens supponebatur refringi a puncto C. Quare est c[191] et præterea cum antea posuerim esse , ex æquo erit . Sed est d[192]. adeoque . Quare si linea quædam BL ita ducatur ut sit erit , propter majorem rationem quam habet ad DL, et insuper erit , eò quòd sit . Et proinde punctum B cadet inter G et C, eritque . Cùm verò sit , aut vicissim , erit e[193]. Et multo magis . Q.E.D.
Lemma 3. Si a duobus punctis D, G (figura 35) in 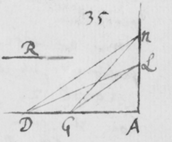 lineâ quâpiam AD sitis, ad alia duo puncta L, N in ejus perpendiculo AN sita ducantur quatuor rectæ DN, DL, GN, GL; ratio ductarum ad punctum remotius N magis accedit ad æqualitatem quàm ratio ductarum ad vicinius punctum L . Sive est . Sit enim , et erit . Quare cùm sit , sive , erit . Verùm est a[194] et ideo . Hoc est sive . Atque adeò cum supponatur , erit . Q.E.D.
lineâ quâpiam AD sitis, ad alia duo puncta L, N in ejus perpendiculo AN sita ducantur quatuor rectæ DN, DL, GN, GL; ratio ductarum ad punctum remotius N magis accedit ad æqualitatem quàm ratio ductarum ad vicinius punctum L . Sive est . Sit enim , et erit . Quare cùm sit , sive , erit . Verùm est a[194] et ideo . Hoc est sive . Atque adeò cum supponatur , erit . Q.E.D.
Lemma 4. Centro A, distantia quavis AD (in figura ) describatur circulus DGγ. 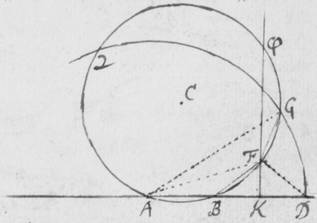 Deinde centro quolibet C distantiâ AC describatur alius circulus secans rectam AD in B et circulum priùs descriptum in G. Tum arcus BG bisecetur in F; et FK demittatur ad BD perpendicularis: His ita constitutis, dico quòd FK sic perpendiculariter demissa dictam BD bisecabit. Iunctis enim AF, AG, BF, FG et FD; in triangulis AFG et AFD anguli ad A sunt æquales propter æquales arcus BF, FG quibus subtenduntur; Item latera circa istos angulos AD et AG sunt æqualia, quippe radij ejusdem circuli. Et aliud latus AF habent commune. Quare etiam tertia latera FG et FD sunt æqualia. Sed est propter æqualitatem arcuum quos subtendunt, adeoque , et triangulum FKB = triangulo FKD, et inde .
Deinde centro quolibet C distantiâ AC describatur alius circulus secans rectam AD in B et circulum priùs descriptum in G. Tum arcus BG bisecetur in F; et FK demittatur ad BD perpendicularis: His ita constitutis, dico quòd FK sic perpendiculariter demissa dictam BD bisecabit. Iunctis enim AF, AG, BF, FG et FD; in triangulis AFG et AFD anguli ad A sunt æquales propter æquales arcus BF, FG quibus subtenduntur; Item latera circa istos angulos AD et AG sunt æqualia, quippe radij ejusdem circuli. Et aliud latus AF habent commune. Quare etiam tertia latera FG et FD sunt æqualia. Sed est propter æqualitatem arcuum quos subtendunt, adeoque , et triangulum FKB = triangulo FKD, et inde .
Corollarium 1. Hinc recta KF, quæ bisecat BD insistens ei normaliter, bisecabit etiam arcus BG circulorum omnium per data duo puncta A et B, transeuntium, et alicubi in G secantium datum circulum DG centro A intervallo AD descriptum. Imò et bisecabit arcus BGγ in altero intersectionis puncto φ.
Corollarium 2. Idem eveniet cùm A et B coincidunt; hoc est cùm circuli AFG tangunt rectam AD in puncto AB. Potest etiam B sumi ad alteras partes ipsius A. In transcursu etiam notetur, quod anguli BFK, BGD, quos circulus ABF cum recta FK et arcu GD efficit, sint æquales{.}
Lemma 5. Lineis quatuor 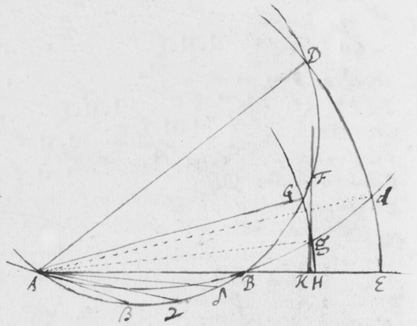 Aβ, AB, Aγ, et AG (figura ) circulo alicui ab eodem circumferentiæ puncto ita inscriptis ut sit , quarum omnium Aβ sit minima: Dico angulum BAG majorem esse angulo BAγ. Describatur enim alius circulus ABgd secans priorem in punctis A et B, Cujus diameter sit ad ejus ABG diametrum sicut AB ad Aβ, centris utrisque ad easdem partes ipsius AB jacentibus. Dein centro A distantiâ AG describe tertium circulum GH secundo occurrentem in g. Et istud g ex constructione jacebit alicubi inter G et H, atque adeò si Ag ducatur erit angulus BAG major angulo BAg. Est autem propterea quòd AB et Ag similiter inscriptæ sint circulo ABg, ac Aβ et Aγ ipsi Aβγ, habentes nempe easdem rationes, et inter se (AG vel Ag) et ad diametros circulorum quibus inscribuntur. Cum ergo sit erit . Q.E.D.
Aβ, AB, Aγ, et AG (figura ) circulo alicui ab eodem circumferentiæ puncto ita inscriptis ut sit , quarum omnium Aβ sit minima: Dico angulum BAG majorem esse angulo BAγ. Describatur enim alius circulus ABgd secans priorem in punctis A et B, Cujus diameter sit ad ejus ABG diametrum sicut AB ad Aβ, centris utrisque ad easdem partes ipsius AB jacentibus. Dein centro A distantiâ AG describe tertium circulum GH secundo occurrentem in g. Et istud g ex constructione jacebit alicubi inter G et H, atque adeò si Ag ducatur erit angulus BAG major angulo BAg. Est autem propterea quòd AB et Ag similiter inscriptæ sint circulo ABg, ac Aβ et Aγ ipsi Aβγ, habentes nempe easdem rationes, et inter se (AG vel Ag) et ad diametros circulorum quibus inscribuntur. Cum ergo sit erit . Q.E.D.
** Corollarium 1. Hinc in eodem quovis radiorum genere, quo major est refractio, eo major erit angulus refractus. In figura 26, ubi est , erit .
Corollarium 2{.} Hinc etiam si sit , multò magis erit . Hoc est in genere, quo majores sunt subtensæ et simul quo major est inæqualitas rationis earum, eo major erit differentia angulorum quos subtendunt. Atque idem de sinibus et eorum angulis, utpote subtensarum et earum angulorum dimidijs intellige.
Lemma 6. Insuper si arcus γδ ipsi βγ capiatur æqualis et AD inscribatur circulo ABD quæ sit ad Aδ sicut AG ad Aγ, cæteris stantibus: dico quòd arcus DG erit arcu GB major. Nam centro A, radio AD describe circulum DdE circulo ABg occurrentem in d et rectæ AB in E. Et Ad ducatur. Iam cùm Ad, Ag et AB circulo ABgd similiter inscribantur atque Aδ, Aγ, et Aβ ipsi Aβγ, erit arcus gd = arcui Bg. Quare demissâ gK ad BE perpendiculari, et productâ donec secet arcum BD in F, ista gK (per Lemma 4) bisecabit tum rectam BE tum arcum BD. At quoniam gF ex constructione jacet extra circulum gG punctum F cadet inter G et D. Quare sive , et multo magis . Q.E.O.
Corollarium 1. Hinc si arcus βδ non tantùm duabus sed quotcunque partibus æqualibus constet, correspondentes partes arcus BD a termino B ad terminum D sese gradatim superabunt longitudine. Adeóque si arcus βγ ad arcum γδ habeat quamcunque rationem commensurabilem; erit , siquidem numeris æqualium partium mensurantium arcus βγ et γδ correspondentes consimiles numeri partium inæqualium constituentium arcus BG ac GD, quarum illæ in GD sunt omnes parte maximâ ipsius BG majores. Quinetiam si βγ ad γδ habeat quamcunque rationem incommensurabilem, erit itidem . Nam rationum similitudines, quæ quantitatibus commensurabilibus indefinitè conveniunt, eo nomine conveniunt etiam incommensurabilibus similiter affectis; quemadmodum ex Euclidea definitione similium rationum ostendi posset, sed faciliùs deprehenditur imaginando quantitates quas vocant incommensurabiles posse mensurari per partes indefinitè parvas, et sic ad naturam commensurabilium præsertim quoad rationum habitudines quodammodò reduci. Concipias itaque arcum βγ in æquales et indefinitè multas partes dividi, et ejusmodi tot sumi quæ minus quàm unâ parte, hoc est indefinitè parùm differunt ab arcu γδ, atque adeò ipsi pro more consueto censeantur æquales. Concipe etiam BD in partes quales ante definivi correspondentes partibus ipsius βδ dividi; et propter tot inæquales partes majores quidem in GD et minores in BG quot sunt æquales in γδ et βγ, erit {.}
Corollarium 2. Hinc præterea componendo sequitur esse . Nec non {.}
Corollarium 3. Consectatur denique quòd 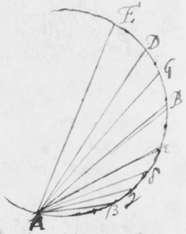 ductis utcunque quatuor subtensis Aβ Aγ, Aδ, Aε (in figura ); et alijs quatuor AB, AG{,} AD, AE quarum singulæ ad priorum singulas eandem rationem observant, (nempe :) Si AE sit omnium maxima et Aβ minima, erit . Nam per Corollarium 1 hujus est , et . Et multò magis . Haud secus pateat esse . Scilicet ex corollario 2 hujus est , ac ; Et multò magis .
ductis utcunque quatuor subtensis Aβ Aγ, Aδ, Aε (in figura ); et alijs quatuor AB, AG{,} AD, AE quarum singulæ ad priorum singulas eandem rationem observant, (nempe :) Si AE sit omnium maxima et Aβ minima, erit . Nam per Corollarium 1 hujus est , et . Et multò magis . Haud secus pateat esse . Scilicet ex corollario 2 hujus est , ac ; Et multò magis .
Denique quæ de subtensis et earum arcubus dicta sunt, possunt etiam de sinibus et eorum arcubus aut angulis intelligi.
[195]Hactenus Lemmata præstravimus, ex quibus aliqua quæ ad refractiones ejusdem alicujus variè incidentium radiorum generis spectant, nullo negotio possent erui: Sed cùm apud alios demonstrata prostent, et a scopo meo videantur aliena, mitto, déque difformium radiorum affectionibus e vestigio pergo dicere.
[196]Propositio 1{.}Heterogeneis radijs secundum eandem lineam incidentibus, quo obliquior sit eorum incidentia cæteris paribus, eo major erit differentia refractionis. &c
<111>Propositio 2. Heterogeneis radijs in superficiem quæcunque Media disterminantem incidentibus; quò magis Media differunt densitate eò major erit inæqualitas rationis sinuum refractionis. In figura Sit Fγ radius e minime refrangibilibus utcunque in superficiem Aγ incidentibus, sitq́ue refractus ejus γλ, qui retroactus secet perpendiculum FA in φ. 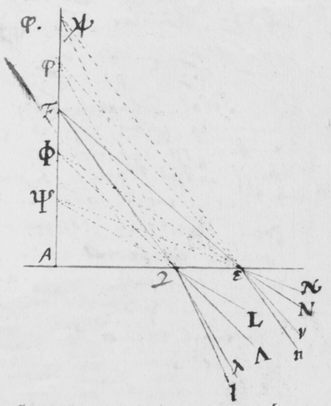 Dein capiatur Aε ut sit Fε ad Fγ in datâ quâdam ratione qualem ante a[197] descripsimus, hâc scilicet conditione ut habito Fε pro radio maximè refrangibili, refractus ejus εν ab eodem φ divergat. . Facto hoc, si pro posteriori Medio aliud utcunque densum rarume substituatur, ejusmodi tamen duo radij secundum easdem rectas Fε, Fγ incidentes semper debent ita refringi ut ab eodem aliquo perpendiculi istius puncto similiter divergant b[199]; quemadmodum a ψ versus l et n, posito quod hoc Medium posterius sit densitatis ab anteriori magis diversæ quàm alterum posterius Medium quod efficiebat divergentes a φ. Ostendendum est itáque quòd major sit inæqualitas rationis sinuum refractionis in posteriori quàm priori casu. Scilicet radij Fγλ sinus incidentiæ est ad sinum refractionis ut φγ ad Fγ c[200], hoc est ut 1 ad . Et sic radij Fεν sinus isti sunt ut 1 ad . Quare sinus refractionum eorundem radiorum sunt inter se ut ad . Et simili discursu constabit quòd radiorum a ψ refractorum consimiles refractionum sinus sunt ut ad . Restat itaque probandum quod inter & major sit disproportio quàm inter et . Hoc est, (cùm sit , d[201]) probandum restat quod sit {.} Scilicet est per Lemma 3, et sumendo reciproca rationum erit ducendoq́ue priorem rationem in Fε et posteriorem in Fγ, orietur et vicissim . Q.E.D.
Dein capiatur Aε ut sit Fε ad Fγ in datâ quâdam ratione qualem ante a[197] descripsimus, hâc scilicet conditione ut habito Fε pro radio maximè refrangibili, refractus ejus εν ab eodem φ divergat. . Facto hoc, si pro posteriori Medio aliud utcunque densum rarume substituatur, ejusmodi tamen duo radij secundum easdem rectas Fε, Fγ incidentes semper debent ita refringi ut ab eodem aliquo perpendiculi istius puncto similiter divergant b[199]; quemadmodum a ψ versus l et n, posito quod hoc Medium posterius sit densitatis ab anteriori magis diversæ quàm alterum posterius Medium quod efficiebat divergentes a φ. Ostendendum est itáque quòd major sit inæqualitas rationis sinuum refractionis in posteriori quàm priori casu. Scilicet radij Fγλ sinus incidentiæ est ad sinum refractionis ut φγ ad Fγ c[200], hoc est ut 1 ad . Et sic radij Fεν sinus isti sunt ut 1 ad . Quare sinus refractionum eorundem radiorum sunt inter se ut ad . Et simili discursu constabit quòd radiorum a ψ refractorum consimiles refractionum sinus sunt ut ad . Restat itaque probandum quod inter & major sit disproportio quàm inter et . Hoc est, (cùm sit , d[201]) probandum restat quod sit {.} Scilicet est per Lemma 3, et sumendo reciproca rationum erit ducendoq́ue priorem rationem in Fε et posteriorem in Fγ, orietur et vicissim . Q.E.D.
Scholium. Demonstratio perinde se habet in literis majusculis (quibus refractiones designavi cùm posterius Medium sit anteriori rarius) si modò vice signi ⫍ ubique subintelligatur signum ⫎ et ⫍ vice ⫎. Notabis insuper quòd in hâc demonstratione posui densitatem posterioris tantum Medij variatam esse, sed eodem recidit si anteriora Media successivè varia adhiberi, posteriori non mutato, sive quod tantundem est si refractiones e posteriori Medio in anterius vicissim peragi concipias: siquidem radijs in superficiem alterutrinq́ue incidentibus consimiles sunt sinuum rationes. Cæterùm de exactâ horum sinuum pro quibuslibet propositis Medijs ratione investigandâ disserui ante, et hanc utique propositionem haud attigissem, nisi id in gratiam quartæ secuturæ fuisset factum.
[202]Propositio 3{.}Heterogeneis radijs e densiori Medio in rarius &c{.}
Propositio 14 15. Heterogeneis radijs e Medio densiori in rarius secundum eandem datam lineam in superficiem positione datam incidentibus: quo densius est Medium e quo radij incidunt eo major erit differentia refractionis. Scilicet (propter majores refractiones) eo majores erunt sinus refractionum respectu dati circuli, ad quem referuntur: & simul eo major erit inæqualitas rationis istorum sinuum (per propositionem 13 :) Adeóque eo major erit differentia angulorum quos subtendunt (per corollarium 2 ad Lemma 5.) Hoc est, eo major differentia refractionis. Q.E.O{.}
<113>[203]Propositio 15 16. Heterogeneis radijs e Medio rariori in densius secundum eandem datam lineam in superficiem positione datam incidentibus: quo rarius est Medium e quo radij incidunt, eo major erit differentia refractionis. Sit AD superficies in quam duo radij secundum eandem datam lineam IX incidunt quorum alter maxime refrangibilis refringatur ad P, et alter minime refrangibilis ad T: Dico quod si Medium ex quo radij incidunt foret adhuc rarius, ut dictos radios magis refringeret, puta maximè refrangibilem versus π, et minimè refrangibilem versus τ; tunc πXτ major angulus evaderet, quàm PXT. Id quod gradatim sic demonstro.
Casus 1. Ponamus primò, quod recta IX, secundum quam radij incidunt sit ad refringentem superficiem obliquissima. Ac ducatur quælibet recta PD eidem superficiei 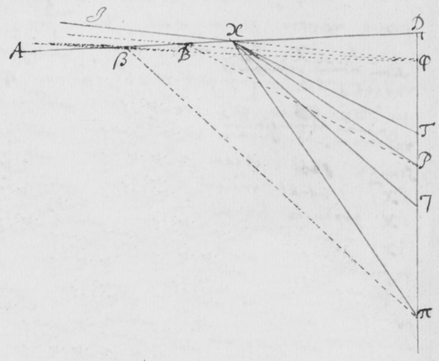 normaliter insistens in D, et secans refractos radios in punctis T, P, τ, π. Et IX producatur donec istam PD secet in φ. Tum in linea AD quæratur punctum quoddam B, hâc lege ut ductis Bφ, BP, fiat . Liquet ergo quod si minime refrangibilis radius incidat in B versus φ tendens, is debet versus P refringi: Quippe cum ex Hypothesi sit [204], hoc est sinus incidentiæ ejus et refractionis, sicut sinus incidentiæ et refractionis alterius maximè refrangibilis radij IXT. Quamobrem si supponamus hosce radios retrocedere, alterum nempe e minimè refrangibilibus a T ad X et alterum a P ad B, et maximè refrangibilem a P ad X; eorum omnium refracti tendunt a puncto φ, siquidem notum est Theorema quod radij secundum refractum ejus retro incidentis, incidens vicissim fit refractus. Iam cùm radij difformes PB PX ab eodem puncto P manantes refringantur ab eodem φ quod situm est in perpendiculo PD, proportione inter PX et PB semel cognitâ, si ab alio quovis ejusdem perpendiculi puncto ad refringentem superficiem duæ ducantur lineæ eandem rationem habentes, hoc est ut altera designans maximè refrangibilem radium sit ad alteram quæ designet minimè refrangibilem, ut PX ad PB: tunc istorum refracti (ex ante monstratis b[205]) divergent ab aliquo etiam puncto quod situ est in eodem perpendiculo PD; utcunque Medium ex parte radij IX supponatur rarum, dummodo Mediorum alterum ex parte radij PX eandem densitatem retineat. Quemadmodum si maximè refrangibilis radius incidat secundum πX et refringatur a φ, Medio scilicet versus IX jam posito rariori quàm ante; tunc rectâ πβ sic ductâ ut sit , radius etiam minimè refrangibilis πβ refringetur ab eodem φ. Unde sequitur esse πβ ad φβ sicut sinus incidentiæ radiorum minimè refrangibilium ad sinum refractionis c[206]. Ast in ratione istorum sinuum est est etiam τX ad φX, eò quòd inflexa IXτ designet radium æqualiter refrangibilem cujus pars IX producta transit per idem φ. Quare est . Cùm verò radius IX supponatur esse ad refringentem superficiem summè obliquus sive in angulo infinitè parvo inclinatus, adeò ut recta Dφ pro infinitè parvâ sive nullâ haberi debeat, sequitur esse , , ac : quos valores pro Xφ, Bφ, et βφ substituendo in supra recensitas proportiones & , emergent et . Ex quibus pateat rectas BP ad XT & βπ ad Xτ parallelas esse, angulośque BPX ad PXT et βπX ad πXτ æquales. Sed ex Hypothesi est . Et proinde .d[207] Hoc est . Q.E.D.
normaliter insistens in D, et secans refractos radios in punctis T, P, τ, π. Et IX producatur donec istam PD secet in φ. Tum in linea AD quæratur punctum quoddam B, hâc lege ut ductis Bφ, BP, fiat . Liquet ergo quod si minime refrangibilis radius incidat in B versus φ tendens, is debet versus P refringi: Quippe cum ex Hypothesi sit [204], hoc est sinus incidentiæ ejus et refractionis, sicut sinus incidentiæ et refractionis alterius maximè refrangibilis radij IXT. Quamobrem si supponamus hosce radios retrocedere, alterum nempe e minimè refrangibilibus a T ad X et alterum a P ad B, et maximè refrangibilem a P ad X; eorum omnium refracti tendunt a puncto φ, siquidem notum est Theorema quod radij secundum refractum ejus retro incidentis, incidens vicissim fit refractus. Iam cùm radij difformes PB PX ab eodem puncto P manantes refringantur ab eodem φ quod situm est in perpendiculo PD, proportione inter PX et PB semel cognitâ, si ab alio quovis ejusdem perpendiculi puncto ad refringentem superficiem duæ ducantur lineæ eandem rationem habentes, hoc est ut altera designans maximè refrangibilem radium sit ad alteram quæ designet minimè refrangibilem, ut PX ad PB: tunc istorum refracti (ex ante monstratis b[205]) divergent ab aliquo etiam puncto quod situ est in eodem perpendiculo PD; utcunque Medium ex parte radij IX supponatur rarum, dummodo Mediorum alterum ex parte radij PX eandem densitatem retineat. Quemadmodum si maximè refrangibilis radius incidat secundum πX et refringatur a φ, Medio scilicet versus IX jam posito rariori quàm ante; tunc rectâ πβ sic ductâ ut sit , radius etiam minimè refrangibilis πβ refringetur ab eodem φ. Unde sequitur esse πβ ad φβ sicut sinus incidentiæ radiorum minimè refrangibilium ad sinum refractionis c[206]. Ast in ratione istorum sinuum est est etiam τX ad φX, eò quòd inflexa IXτ designet radium æqualiter refrangibilem cujus pars IX producta transit per idem φ. Quare est . Cùm verò radius IX supponatur esse ad refringentem superficiem summè obliquus sive in angulo infinitè parvo inclinatus, adeò ut recta Dφ pro infinitè parvâ sive nullâ haberi debeat, sequitur esse , , ac : quos valores pro Xφ, Bφ, et βφ substituendo in supra recensitas proportiones & , emergent et . Ex quibus pateat rectas BP ad XT & βπ ad Xτ parallelas esse, angulośque BPX ad PXT et βπX ad πXτ æquales. Sed ex Hypothesi est . Et proinde .d[207] Hoc est . Q.E.D.
Casus 2. Incidentibus verò radijs angulum definitè magnum cum refringente superficie constituentibus, propositum sic patebit. Sit HX recta secundum quam incidunt, et cum e Medio minùs raro adveniunt sit XM minimè refractus et XN maximè refractus. Cùm verò 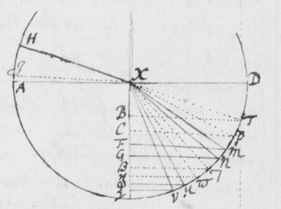 adveniunt e magis raro, sit Xμ minimè refractus et Xν maximè refractus{.} Adhibeantur etiam obliquissimè incidentes radij IX cum eorum refractis XT, XP, Xτ et Xπ, quales jam descripsimus. Ita scilicet ut cùm tanta sit anterioris Medij raritas ut radios HX incurvari faciat versus M et N, tunc etiam consimiles radios IX incurvet versus T et P. Cùm verò tantò major sit ejus raritas ut illos cogat versus μ et ν tunc hosce simul cogat versus τ et π. Sit insuper APD circulus centro X et intervallo quolibet descriptus qui secet hosce refractos radios in T, P, M, N, τ, π, μ, & ν, a quibus ad perpendiculum BX demittantur sinus refractionum TB, PC, MF, NG, τβ, πκ, μφ, νγ. Et ex lege refractionum a[208] patebit esse et et . Et insuper ex Hypothesi et constructione patebit esse TB sinuum istorum maximum et νγ minimum. Adeóque per corollarium 3 Lemmatis 6 est . Et permutando est . Verùm (ex ostensis in casu primo) est . Quare et multò magis erit . Q.E.D.
adveniunt e magis raro, sit Xμ minimè refractus et Xν maximè refractus{.} Adhibeantur etiam obliquissimè incidentes radij IX cum eorum refractis XT, XP, Xτ et Xπ, quales jam descripsimus. Ita scilicet ut cùm tanta sit anterioris Medij raritas ut radios HX incurvari faciat versus M et N, tunc etiam consimiles radios IX incurvet versus T et P. Cùm verò tantò major sit ejus raritas ut illos cogat versus μ et ν tunc hosce simul cogat versus τ et π. Sit insuper APD circulus centro X et intervallo quolibet descriptus qui secet hosce refractos radios in T, P, M, N, τ, π, μ, & ν, a quibus ad perpendiculum BX demittantur sinus refractionum TB, PC, MF, NG, τβ, πκ, μφ, νγ. Et ex lege refractionum a[208] patebit esse et et . Et insuper ex Hypothesi et constructione patebit esse TB sinuum istorum maximum et νγ minimum. Adeóque per corollarium 3 Lemmatis 6 est . Et permutando est . Verùm (ex ostensis in casu primo) est . Quare et multò magis erit . Q.E.D.
Propositio 6. Heterogeneis radijs e Medio rariori in densius secundum eandem lineam in superficiem positione datam incidentibus, quo densius sit Medium in quod radij incidunt eo major erit differentia refractionum ad certum usque terminum, et post eo minor perpetuò. Nam si Medium posterius densitate suâ valdè parùm superet anterius, ita ut refractiones indefinitè parvas efficiat, differentia refractionum erit etiam indefinitè parva, et proinde minor quàm foret si Medium posterius supponeretur densius ut refractiones evaderent majores. Quare aucta Medij posterioris densitate augebitur dicta refractionum differentia. Quod si densitas ejus in infinitum augeatur refractiones etiam quantum poterunt augebuntur, hoc est usque dum omnes refracti radij perpendiculariter emergant, angulis refractionum et eorum differentijs tunc prorsus evanescentibus. Quare differentia refractionum rursus diminuta est donec in nihilum evanuit.
Scholium. Etsi limitis ejus determinatio ubi differentia refractionis evadit maxima plus tædij et laboris administrare possit quam utilitatis cùm tamen alicujus fortè momenti censeatur densitatem Medij cognoscere quod radijs in se refractis colores maximè conspicuos efficiat, non pigebit hunc insuper designare. Idque primò cùm incidentia fit obliquissimè.
Casus 1. Esto IX communis radiorum in superficiem AX quæcunque Media dirimentem obliquissimè incidentium via. Et eorum refracti ut ante sunto Xπ et Xτ . Et agatur recta quævis πτ præfatæ superficiei parallela, quæ radijs istis occurrat in π ac τ; A quibus ad AX demissis perpendicularibus πC, 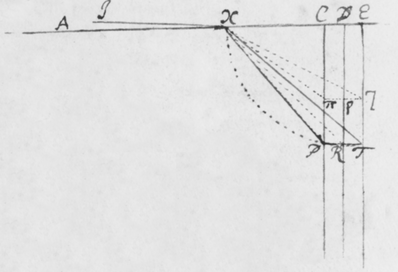 τE, bisecetur CE in D et centro D, distantia DX circulus describatur secans Cπ in P et Eτ in T, junganturque XP et XT. Dico quod cùm ea sit posterioris Medij densitas, ut radiorum secundum IX incidentium maximè refrangibiles ad P et minime refrangibil{es} ad T refringat, tunc angulus PXT, . Etenim utcunque Medium posterius ponatur densum, refracti radij ita lineas CP et ET in punctis π ac τ secabunt ut recta πτ, ipsi AX parallela sit. Quare si ducatur linea Dρ, quæ lineas omnes πτ bisecet, centrum cujuscunque circuli per puncta π ac τ transeuntis semper jacebit in eâdem Dρ. At angulus πXτ est angulus in segmento circuli per puncta π, τ, et X transeuntis; qui ideo erit maximus cùm ejusmodi circulus existit minimus, propterea quòd ratio subtensæ πτ ad circuli dimensiones tunc evadit maxima. Verùm iste circulus fit omnium minimus cùm centrum ejus cadit in D, siquidem pro semidiametro tunc habet XD minimam rectarum quæ ab X ad RD duci possunt. Est ergo angulus πXτ tunc maximus cùm centrum circuli transeuntis per puncta π, τ, et X cadit in D. Adeóque cùm circulus XPT et angulus PXT ejusmodi sint, liquet propositum.
τE, bisecetur CE in D et centro D, distantia DX circulus describatur secans Cπ in P et Eτ in T, junganturque XP et XT. Dico quod cùm ea sit posterioris Medij densitas, ut radiorum secundum IX incidentium maximè refrangibiles ad P et minime refrangibil{es} ad T refringat, tunc angulus PXT, . Etenim utcunque Medium posterius ponatur densum, refracti radij ita lineas CP et ET in punctis π ac τ secabunt ut recta πτ, ipsi AX parallela sit. Quare si ducatur linea Dρ, quæ lineas omnes πτ bisecet, centrum cujuscunque circuli per puncta π ac τ transeuntis semper jacebit in eâdem Dρ. At angulus πXτ est angulus in segmento circuli per puncta π, τ, et X transeuntis; qui ideo erit maximus cùm ejusmodi circulus existit minimus, propterea quòd ratio subtensæ πτ ad circuli dimensiones tunc evadit maxima. Verùm iste circulus fit omnium minimus cùm centrum ejus cadit in D, siquidem pro semidiametro tunc habet XD minimam rectarum quæ ab X ad RD duci possunt. Est ergo angulus πXτ tunc maximus cùm centrum circuli transeuntis per puncta π, τ, et X cadit in D. Adeóque cùm circulus XPT et angulus PXT ejusmodi sint, liquet propositum.
Hinc obiter pateat hunc angulum PXT tunc etiam maximum evadere cùm talis est posterioris Medij densitas ut angulus refractionis mediocriter refrangibilium radiorum XR obliquissimè secundum IX incidentium sit semirectus; et eo minorem perpetim fieri quò iste refractionis angulus a semirecto (excessu vel defectu) magis deviat. Quemadmodum si refractiones ex aere in aquam, in vitrum et in crystallum peractæ conferantur, e calculo patebit quòd cùm angulus incidentiæ sit proximè, tunc angulus refractionis in aquam erit major semirecto, inque vitrum erit minor. Quamobrem aqua minùs densa est et vitrum magis densum quàm ut efficiant angulum PXT maximum. Et proinde cùm crystallum sit adhuc densius , efficiet istum PXT minorem quàm vitrum efficeret. Et sic vitrum etsi minùs refringat, in isthoc tamen casu heterogeneos radios in se refractos magis abinvicem dissipabit quàm crystallum, eóque pacto colores in oppositam ejus superficiem projiciet magis distinctos. Sed hæc sunt expertu difficillima, quòd vitrum et crystallum densitate parùm differant, nec possint haberi satis crassa; et si possent, tum propter maximam crassitiem haud forent satis perspicua.
Casus 2. Quòd si linea secundum quam incidunt radij non sit maximè obliqua, Problema emerget solidum; sed lubet modum ostendere quo conditionibus ejus nonnihil mutatis, ad planum reduci poterit. Sciendum est itáque quod cùm inter extremos seu maxime difformes radios innumeri sint intermedij qui gradibus continuò successivis et infinitè parvis alij magis alijs refringuntur: differentia refractionis extremorum radiorum conflata erit ex consimilibus intermediorum differentijs numero et parvitate infinitis. Iam cognitis proprietatibus istarum infinitè parvarum differentiarum possumus exinde de omnibus simul aggregatis, sive de differentijs finitè parvis quales intercedunt extremorum refractionibus, judicium proferre, præsertim cùm istæ differentiæ sint admodum exiguæ. Sic cognito quòd infinitæ parvæ differentiæ augentur, diminuuntur vel simul maximæ evadunt aut minimæ: concludendum erit quòd omnium summa perinde augetur, diminuitur, vel maxima fit aut minima. Quod si non sint omnes simul maximæ vel minimæ, tamen summa pro maxima aut minima haberi potest, cùm id accidit intermediæ parti. Sic omnium colorum latitudo tunc maxima censeri potest, cum id accidit viriditati. Iam licèt Problema propositum cùm de differentijs finitè parvis agitur existat solidum, si tamen instituatur de differentijs infinitè parvis, ad planum reduci potest. Verùm huic solvendo nolo obnixè incumbere, sed breviter tantùm ostendam quo pacto calculus in hoc et ejusmodi alijs sit ineundus, ut ad æquationem perveniatur, ex quâ maximus angulorum infinitè parvorum possit elici. Et insuper ex eodem fundamento determinabo proportiones differentiarum refractionis respectu diversorum Mediorum, quas in præcedentibus quatuor propositionibus generaliter tantùm descripsi{.}
Primò itaque investiganda est regula vel Æquatio, quâ ex uno utcunque refracto radio dato, refractus alter cum eo constituens angulum infinitè parvum cognosci poterit. Radijs e Medio densitate dato in Medium cujuslibet densitatis secundum obliquissimam lineam IX ut priùs incidentibus, sint XR et Xρ refracti duo, quorum alter XR sit altero Xρ paulo magis refrangibilis, differentiâ tamen infinitè parvâ. Et agatur lineola quævis Rρ his in R et ρ occurrens, et refringenti superficiei parallela. Ad quam superficiem normales etiam RD, ρδ demittantur, quas datam finitamque distantiam ab X, ab invicem verò infinitè parvam habere finges, sed lineolam Rρ, cum radijs per R et ρ transeuntibus plus aut minùs ab XD vergere (quemadmodum in præcedentibus) concipies pro variâ posterioris Medij assumendâ densitate. Iam si recta DR secet radios Xρ in M, et IX in K, cùm infinitè parvum triangulum RMρ sit simile triangulo DMX a quo triangulum KRX non nisi infinitè parvis differentijs RXM et DXK discrepat, quæ dissimilitudinem non inferunt, triangula etiam RMρ et RDX pro similibus haberi debent. Et proinde demissis perpendicularibus KL et RN, erit . Adeóque cum sit (nam est ) erit etiam . Quæ differentia est inter XN sive XR et XM, et inde erit .
Inventa est itaque relatio inter XK, XM, et XR cùm angulus IXA sit infinitè parvus: Quinetiam utcunque IX obliqua ponatur, illæ XK, XM, et XR eandem relationen observabunt, siquidem reciprocè sint ut sinus incidentiæ et refractionis; et proinde inventa est etiam inter eas relatio pro quâvis obliquitate incidentis IX. Atq́ue ita cognitis vel utcunque ad arbitrium assumptis XK et XR, inde XM simul cognoscitur. Quod primò determinandum proposui.
Quamobrem sit IX 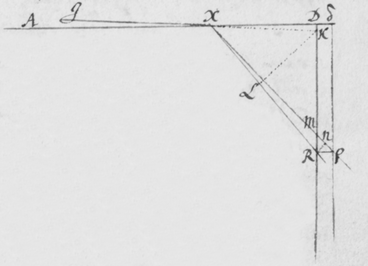 linea datum quemvis angulum AXI cum refringente superficie constituens; cæterisq́ue stantibus, erit . Insuper est . Atque adeò est . Quod si NR dividatur per XR prodibit sinus anguli RXN respectu circuli cujus semidiameter sit unitas. Quare cùm angulus iste et sinus ejus sunt simul maximi, ad maximum angulum determinandum quærenda erit maxima quantitas , hoc est maximum . Sive (factâ per datum divisione) quærendum erit maximum . Id quod per Methodos de maximis et minimis satis notas fieri potest, et prodibit . Cujus æquationis constructio est ejusmodi.
linea datum quemvis angulum AXI cum refringente superficie constituens; cæterisq́ue stantibus, erit . Insuper est . Atque adeò est . Quod si NR dividatur per XR prodibit sinus anguli RXN respectu circuli cujus semidiameter sit unitas. Quare cùm angulus iste et sinus ejus sunt simul maximi, ad maximum angulum determinandum quærenda erit maxima quantitas , hoc est maximum . Sive (factâ per datum divisione) quærendum erit maximum . Id quod per Methodos de maximis et minimis satis notas fieri potest, et prodibit . Cujus æquationis constructio est ejusmodi.
A puncto quolibet 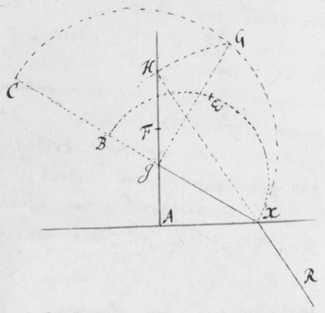 incidentis radij IX demitte perpendiculum IA, et in eo sume . Et XI producto ad B, ut sit , super BX describe semicirculum BEX cui inscribe . Dein XB producto ad C ut sit , super CX describe semicirculum CGX quem in G secet perpendiculum IG super diametro ejus ad I erectum. Denique centro X et intervallo GX describatur arcus GH secans AI productum in H, ducatur HX, et producatur versus R, eritque XR ipsius IX refractus cùm tanta sit posterioris Medij densitas ut differentia refractionis RXM fiat omnium maxima. Quo invento, densitas posterioris Medij talem refractionem efficientis facilè dabitur. Concipe ergo radios XR et Xρ esse mediocriter refrangibiles, diverso tamen gradu , et posterius Medium sic inventum, non modò inter istos, sed et inter extremos seu maxime difformes radios maximam circiter quam potest refractionis differentiam efficiet.
incidentis radij IX demitte perpendiculum IA, et in eo sume . Et XI producto ad B, ut sit , super BX describe semicirculum BEX cui inscribe . Dein XB producto ad C ut sit , super CX describe semicirculum CGX quem in G secet perpendiculum IG super diametro ejus ad I erectum. Denique centro X et intervallo GX describatur arcus GH secans AI productum in H, ducatur HX, et producatur versus R, eritque XR ipsius IX refractus cùm tanta sit posterioris Medij densitas ut differentia refractionis RXM fiat omnium maxima. Quo invento, densitas posterioris Medij talem refractionem efficientis facilè dabitur. Concipe ergo radios XR et Xρ esse mediocriter refrangibiles, diverso tamen gradu , et posterius Medium sic inventum, non modò inter istos, sed et inter extremos seu maxime difformes radios maximam circiter quam potest refractionis differentiam efficiet.
Sin autem hujusmodi differentiarum proportiones ad variam raritatem vel densitatem Mediorum desiderentur, e jam ostensis facilè determinabuntur dummodo ponantur infinitè parvæ. Sic raritate vel densitate posterioris tantùm Medij variatâ ut radij secundum IX incidentes nunc refringantur ad M et R, nunc ad μ et ρ: ductáque qualibet DK ipsi DX normali quæ secet eos in K, M, R, μ et ρ: erit angulus infinitè parvus MXR ad consimilem angulum 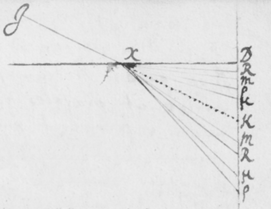 μXρ sicut ad . Quod si raritas vel densitas anterioris Medij varietur, non mutato posteriori Medio: Analysta facilè deprehendet quòd, (in figura ,) sit . Et proinde quod, in figura , sit . Non enim perinde est sive raritas vel densitas anterioris Medij, sive posterioris varietur, ut e præostensis pateat.
μXρ sicut ad . Quod si raritas vel densitas anterioris Medij varietur, non mutato posteriori Medio: Analysta facilè deprehendet quòd, (in figura ,) sit . Et proinde quod, in figura , sit . Non enim perinde est sive raritas vel densitas anterioris Medij, sive posterioris varietur, ut e præostensis pateat.
Propositiones præcedentes ad luminis e longinquo emanantis refringentem diffusionem spectant. In duabus sequentibus agitur de refractione luminis e propinquo manantis.
Propositio 7. Heterogeneis radijs a dato puncto ad datum punctum per superficiem positione datam refractis: quo Medium densius sit magis densum eò major erit eorum ad invicem inclinatio ex parte Medij utriusque ad certum usque terminum, et post erit eo minor. Scilicet cùm densitas ejus haud major sit quàm densitas alterius Medij ut refractio fiat infinitè parva, tum differentia refractionis erit etiam infinitè parva, et proinde augebitur ex auctâ densitate. Quod si densitas ejus in infinitum augeatur tum omnium radiorum in illud incidentium refracti perpendiculariter emergent a[209], et e contra soli perpendiculares possunt ingredi Medium rarius e densiori a[210]. Unde omnes radij a puncto ad punctum refracti tunc pergent in ijsdem lineis, sive coincident, et sic differentia refractionis rursus in nihilum evanescet.
Propositio {8}{18}8. Heterogeneis radijs a dato puncto ad datum punctum per superficiem positione datam refractis: quo Medium rarius sit magis rarum eo major erit eorum ad invicem inclinatio ex parte Medij utriuśque. Sit AT superficies ita refringens difformes radios FTX et FPX , ut manantes ab eodem puncto 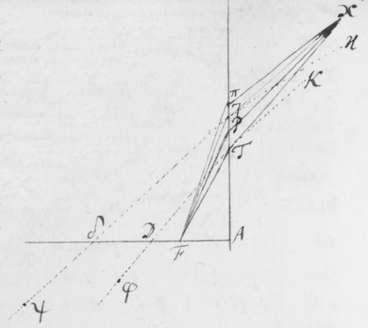 F, in idem rursus ad X conveniant. Dico si Medium posterius esset rarius ut præfatos radios adhuc magis refringeret, puta FTX secundum FτX et FPX secundum FπX; quòd angulus πXτ foret major angulo PXT, ut et angulus πFτ major angulo PFT.
F, in idem rursus ad X conveniant. Dico si Medium posterius esset rarius ut præfatos radios adhuc magis refringeret, puta FTX secundum FτX et FPX secundum FπX; quòd angulus πXτ foret major angulo PXT, ut et angulus πFτ major angulo PFT.
Ad abbreviandam prioris casûs demonstrationem ponamus radios esse quàm minimè difformes ut propter infinitè parvam differentiam refractionis, angulos PXT & πXτ constituant infinitè parvos *[211]. Tum ducatur TK refractus radij conformis ipsi FPX, ut infinitè parvus angulus KTX sit differentia refractionis radiorum secundum eandem lineam FT incidentium. Et pari modo ducatur τκ refractus radij conformis ipsi FπX, ut angulus infinitè parvus κτX existat differentia refractionis radiorum sccundum eandem Fτ incidentium. Liquet ergo quòd cùm Fτ sit obliquior quàm FT atque etiam in Medium densius incidat, erit angulus κτX major angulo KTX. Adhæc producantur XT et Xτ donec in punctis D ac δ secent lineam FA quæ sit plano AT perpendicularis: et ultra producantur ad φ et ψ ita ut sit , et . Et erunt puncta sic inventa φ et ψ foci radiorum FTX et FτX per Propositionem 8 casus 2. a[212]. Et inde ; ut et casus 3 Scholij ad Propositionem 12. b[213]. Istæ quidem proportionalitates non sunt omninò veræ ubi anguli præfati per differentiam refractionis effecti ponuntur esse definitæ alicujus magnitudinis, sed ad veritatem eo magis accedunt quo anguli isti statuuntur minores, adeò ut in angulis infinitè parvis pro accuratè veris haberi debeant. Iam cùm ex Hypothesi sit erit etiam , ut et quemadmodum pateat ex determinatione punctorum ψ et φ supra positâ. Quamobrem est , vel permutando , et componendo . Hoc est substituendo rationes his æquales, . et permutando . Verùm est ut dictum fuit; et ideò multò magìs est . Q.E.D.
Exhinc verò de posteriori etiam casu, quòd semper sit , fiat conjectura, siquidem demonstrationem longè difficiliorem postularet; et his tam multa impendisse verba jamdudum pertæsum est. Hæc itáque de refractionibus solitariæ superficiei sufficiant.
De radiorum bis refractorum affectionibus.
[214]Quòd si gemina sit refractio perinde ut in Prismatibus contingit, quorum phænomena præsertim explicare statui: radiorum sic refractorum passiones e præcedentibus ita manifestæ sunt, ut circa illas parùm negotij superesse videatur. De parallelis quidem superficiebus nihil aliud occurrit observandum, quàm quòd posterior tantùm recurvat radios quantùm prior incurvat. De inclinatis verò sequentia notentur.
20{.} Homogenei radij ad Prisma divergentes, post utramque refractionem divergere pergent. Patet per Propositionem 7 .
Atque idem de parallelis, vel convergentibus radijs intellige quod nempe post utramque refractionem manebunt paralleli vel convergentes.
Scholium Quòd si punctum a quo quilibet indefinitè propinqui post utramque refractionem divergunt, sive locus imaginis trans prisma conspicuæ desideretur, inventio ejus a Scholio ad præfatam Propositionem 8 manifesta est. Sed ut promptiùs fiat conjectura, juvabit adhibere Theorema hocce mechanicum; Quòd imago ad eandem illam circiter distantiam post prisma apparebit, quam habet objectum, cujus est imago, dummodò refractiones hinc, et inde non sint admodum inæquales.
21. Ex heterogeneis radijs ad Prisma divergentibus aliqui post utramque refractionem convergent. Id quod constat e propositionibus 10 & 12. Scilicet ex illis qui in plano ad utraque refringentia plana perpendiculari jacent, magis refrangibiles ex incidentia paulo obliquiori convenient cum minùs refrangibilibus. Atque idem in innumeris alijs ferè planis superficiebus continget.
22{.} E radijs itaque sic a puncto ad punctum sive ab objecto ad oculum refractis, alij ad verticem prismatis gradatim alijs propiores transibunt pro eo ut sint magis atque magis refrangibiles (per propositionem 10 ). Unde colorum ordines definiuntur.
23{.} Quo major est angulus verticalis Prismatis cæteris paribus, differentia refractionis fiet eo major, et inde colorum apparentia distinctior. Et hoc manifestum est e propositione 2 .
24. Quo densior est Prismatis materia, vel quo rarius est medium circumfluum cæteris paribus, eo major erit refractionis differentia, et inde colorum apparentia manifestior. Scilicet posterior casus e propositionibus 14 & 16 patet. Priorem verò ne per propositionem 17 in dubium revocetur, sic ostendo. Concipe magis refrangibilem radium 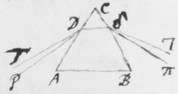 PD et minùs refrangibilem TD sic in Prisma ad idem quodvis punctum D incidere, ut refracti pergant in eadem linea Dδ ac denuò in δ refracti divergant versus π ac τ. Quo posito constat per Propositionem quod angulus πδτ ex auctâ Prismatis densitate augebitur. Deque angulo PDT par est ratio, si modò radij consimiles secundum easdem lineas retrocedere concipiantur. Patet itaque assertio de radijs in Prismate coincidentibus, et inde etiam de parallelis{.}
PD et minùs refrangibilem TD sic in Prisma ad idem quodvis punctum D incidere, ut refracti pergant in eadem linea Dδ ac denuò in δ refracti divergant versus π ac τ. Quo posito constat per Propositionem quod angulus πδτ ex auctâ Prismatis densitate augebitur. Deque angulo PDT par est ratio, si modò radij consimiles secundum easdem lineas retrocedere concipiantur. Patet itaque assertio de radijs in Prismate coincidentibus, et inde etiam de parallelis{.}
Lemma 7. Radijs tribus homogeneis 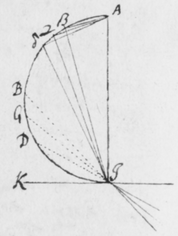 βI, γI, δI e Medio densiori in rarius per superficiem IK refractis; si differentiæ incidentiarum βIγ, γIδ sint æquales, summa refractorum angulorum extremis radijs effectorum erit major duplo anguli refracti per intermedium radium effecti. Hoc est, refractis radijs retro-actis ad B, G, ac D, dico quòd . Etenim descripto quovis circulo ADI tangente refringentem superficiem in I, cujus diameter sit AI, quiq́ue dictos radios secet in β, γ, δ; B, D, G: Quandoquidem anguli βIγ et γIδ sint æquales, erunt etiam arcus βγ, et γδ æquales. Sed ductis Aβ, Aγ, &c: erunt Aβ, Aγ, Aδ sinus incidentiarum, adeoque inter se ut sunt AB, AG, AD sinus refractionum. Quare (per Lemma 6 ) est arcus GD major arcu BG. Et inde . Hoc est , sive . Q.E.D.
βI, γI, δI e Medio densiori in rarius per superficiem IK refractis; si differentiæ incidentiarum βIγ, γIδ sint æquales, summa refractorum angulorum extremis radijs effectorum erit major duplo anguli refracti per intermedium radium effecti. Hoc est, refractis radijs retro-actis ad B, G, ac D, dico quòd . Etenim descripto quovis circulo ADI tangente refringentem superficiem in I, cujus diameter sit AI, quiq́ue dictos radios secet in β, γ, δ; B, D, G: Quandoquidem anguli βIγ et γIδ sint æquales, erunt etiam arcus βγ, et γδ æquales. Sed ductis Aβ, Aγ, &c: erunt Aβ, Aγ, Aδ sinus incidentiarum, adeoque inter se ut sunt AB, AG, AD sinus refractionum. Quare (per Lemma 6 ) est arcus GD major arcu BG. Et inde . Hoc est , sive . Q.E.D.
25. Homogeneis radijs a Prismate refractis, angulus quem incidentes et emergentes comprehendunt tunc maximus evadit cùm æqualis est hinc et inde refractio. Sit ABC Prisma, GRSN radius utrinque ad R et S 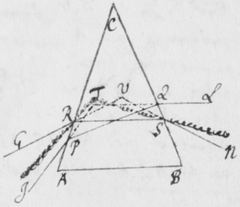 æqualiter refractus, et IPQL alius radius refractus inæqualiter, magis quidem ad P minùs ad Q. Et producantur hi radij donec sibi occurrant, IP et QL in T, GR verò et NS in V. Dico angulum RVS esse majorem angulo PTQ. Quod ut pateat, concipe radios in lineis PQ et RS hinc inde pergentes utrinque egredi Prismate, et sic e Medio densiori in rarius refringi. Iam in triangulis CPQ et CRS, cùm angulus C communis sit, cæterorum angulorum summæ erunt æquales. Et proinde cùm CRS sit Isosceles, duplum anguli CSR æquabitur angulis . Quamobrem radij QP incidentia ad P tanto major est incidentia radij RS ad S, quanto eadem incidentia sit major incidentia radij PQ ad Q. Trium itaq́ue incidentiarum differentiæ sunt æquales, adeoque (juxta Lemma præmonstratum) summa refractorum angulorum per incidentiam maximam et minimam effectorum major erit duplo anguli refracti per incidentiam mediocrem effecti. Hoc est , sive . Itaque cùm in triangulis PTQ et RVS summa angulorum ad Basin PQ sit major summâ eorum ad basin RS, erit angulus verticalis RVS major angulo verticali PTQ. Q.E.D.
æqualiter refractus, et IPQL alius radius refractus inæqualiter, magis quidem ad P minùs ad Q. Et producantur hi radij donec sibi occurrant, IP et QL in T, GR verò et NS in V. Dico angulum RVS esse majorem angulo PTQ. Quod ut pateat, concipe radios in lineis PQ et RS hinc inde pergentes utrinque egredi Prismate, et sic e Medio densiori in rarius refringi. Iam in triangulis CPQ et CRS, cùm angulus C communis sit, cæterorum angulorum summæ erunt æquales. Et proinde cùm CRS sit Isosceles, duplum anguli CSR æquabitur angulis . Quamobrem radij QP incidentia ad P tanto major est incidentia radij RS ad S, quanto eadem incidentia sit major incidentia radij PQ ad Q. Trium itaq́ue incidentiarum differentiæ sunt æquales, adeoque (juxta Lemma præmonstratum) summa refractorum angulorum per incidentiam maximam et minimam effectorum major erit duplo anguli refracti per incidentiam mediocrem effecti. Hoc est , sive . Itaque cùm in triangulis PTQ et RVS summa angulorum ad Basin PQ sit major summâ eorum ad basin RS, erit angulus verticalis RVS major angulo verticali PTQ. Q.E.D.
Lemma 8. Si secundum tres lineas βI, γI, δI æquales angulos βIγ et γIδ continentes, tres radij minimè refrangibiles incidant ad I in superficiem IK, et e Medio rariori in densius refringantur, quorum refracti retrorsum producti sint IB, IG, ID; et præterea si trium maximè refrangibilium radiorum secundum easdem lineas βI, γI, δI incidentium refracti retrorsum producti sint Ib, Ig, Id: Differentia refractionis radiorum quorum incidentia est minima unà cum differentia refractionis eorum quorum incidentia est maxima, major erit quàm dupla differentia refractionis eorum quorum incidentia est mediocris. Hoc est, . Etenim descripto quovis circulo ADI tangente refringentem 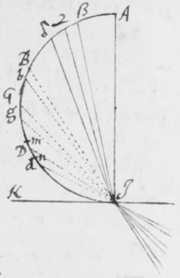 superficiem in I; cujus diameter sit AI, quiq́ue præfatos radios in punctis β, γ, δ; B, b; G, g; D, d secet: concipe subtensas ab A ad quodlibet istorum punctorum duci. Et erunt Aβ, Aγ, Aδ inter se ut sunt AB, AG, AD, atque etiam ut sunt Ab, Ag, Ad. Unde sequitur quod AB, AG, AD inter se sunt ut Ab, Ag, Ad; et præterea (per Lemma 6, ) quòd sit , et . Iam fiat , eritque , et . Item in peripheria AD sume punctum quoddam N sub hac conditione, ut, si concipias AM, AN subtensas duci, sit . Et erunt AB, AG, AM inter se ut sunt Ab, Ag, AN. Adeoque cùm arcus BG ac GM sint æquales, erit summa arcuum (per Lemma 8) major duplo arcu Gg. Sed cùm sit , vel conversè , propter erit . Et utrobique addito arcu Bb, erit . Et multò magis erit duplo arcu Gg: sive . Q.E.O.
superficiem in I; cujus diameter sit AI, quiq́ue præfatos radios in punctis β, γ, δ; B, b; G, g; D, d secet: concipe subtensas ab A ad quodlibet istorum punctorum duci. Et erunt Aβ, Aγ, Aδ inter se ut sunt AB, AG, AD, atque etiam ut sunt Ab, Ag, Ad. Unde sequitur quod AB, AG, AD inter se sunt ut Ab, Ag, Ad; et præterea (per Lemma 6, ) quòd sit , et . Iam fiat , eritque , et . Item in peripheria AD sume punctum quoddam N sub hac conditione, ut, si concipias AM, AN subtensas duci, sit . Et erunt AB, AG, AM inter se ut sunt Ab, Ag, AN. Adeoque cùm arcus BG ac GM sint æquales, erit summa arcuum (per Lemma 8) major duplo arcu Gg. Sed cùm sit , vel conversè , propter erit . Et utrobique addito arcu Bb, erit . Et multò magis erit duplo arcu Gg: sive . Q.E.O.
26. Heterogeneis radijs a Prismate refractis, differentia angulorum quos incidentes cum emergentibus constituunt, tunc minima evadit, cùm 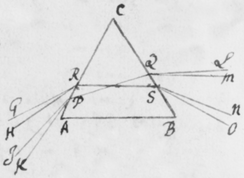 æquales sunt utrobique refractiones. In Prismate ABC sumatur , et RS ducatur, ut et alia quævis linea PQ quæ non sit parallela ad RS. Et concipe radios in Prismate secundum has lineas PQ et RS hinc inde pergentes ad puncta P, Q; R, et S egredi, et maxime refrangibiles versus K, M; H, et O refringi, ac minimè refrangibiles versus I, L; G, et N. Dico quòd refractionum inæqualiter ad P et Q factarum differentiæ simul sumptæ sint majores quàm differentiæ refractionum æqualiter ad R et S factarum simul sumptæ. Nam incidentiarum ad P Q et S differentiæ sunt æquales, ut ostensum erat in Propositione praecedenti. Atque adeò (per Lemma 8) differentia refractionis radiorum difformium ad P ubi maxima est incidentia, unà cum differentia consimili ad Q ubi minima est incidentia, excedit duplum consimilis differentiæ ad S ubi incidentia est mediocris. Hoc est : Sive cùm NSO ac GRH æquentur, . Q.E.D.
æquales sunt utrobique refractiones. In Prismate ABC sumatur , et RS ducatur, ut et alia quævis linea PQ quæ non sit parallela ad RS. Et concipe radios in Prismate secundum has lineas PQ et RS hinc inde pergentes ad puncta P, Q; R, et S egredi, et maxime refrangibiles versus K, M; H, et O refringi, ac minimè refrangibiles versus I, L; G, et N. Dico quòd refractionum inæqualiter ad P et Q factarum differentiæ simul sumptæ sint majores quàm differentiæ refractionum æqualiter ad R et S factarum simul sumptæ. Nam incidentiarum ad P Q et S differentiæ sunt æquales, ut ostensum erat in Propositione praecedenti. Atque adeò (per Lemma 8) differentia refractionis radiorum difformium ad P ubi maxima est incidentia, unà cum differentia consimili ad Q ubi minima est incidentia, excedit duplum consimilis differentiæ ad S ubi incidentia est mediocris. Hoc est : Sive cùm NSO ac GRH æquentur, . Q.E.D.
Scholium. Posui quidem radios e Prismate utrobique egredi; sin pergant ab I et K per P et Q versus L et M, et a G et H per R et S versus N et O, linearum positiones et quantitates angulorum non inde mutabuntur. Et proinde demonstratio præfata tunc etiam valebit. Et propter eandem rationem valebit etiam cùm radij ad Prisma divergentes evadunt in Prismate paralleli. Quod idem de Propositionum 24 et 25 demonstrationibus itidem intellige. Quinetiam in alijs quibuscunque casibus ubi divergunt ante refractionem et post convergunt, vel in Prisma incidunt paralleli; non adeò multùm a parallelismo intra Prisma recedunt unquam, quin ut anguli vel differentiæ angulorum quos incidentes cum emergentibus constituunt, pro ijsdem circiter haberi possint ac si intus essent paralleli; adeóque dictas propositiones ad omnes omninò casus extendi.
27. Si denique, radijs a dato puncto F ad datum punctum X, per Prisma ABC positione datum refractis, desiderentur anguli DFE, GXH quos heterogenei 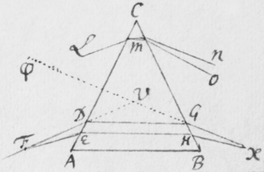 comprehendunt: Problema ex eorum numero est quæ veteres linearia dixêre. At sequens mechanica solutio, quantùm exigunt res practicæ, veritati appropinquat. Finge summam angulorum æqualem esse angulo NMO quem radij duo alteris FD et FE quoad refrangibilitatem consimiles, ac juxta quamvis lineam LM, rectæ angulum DFE bisecanti quàm proximè parallelam incidentes, post binam refractionem constituunt. Et e radijs ad X refractis aliquem GX cum incidente radio FD convenientem in V, produc ad φ, ut sit φ locus imaginis quam objectum F oculo in X constituto exhibet. Dein angulo NMO, ac distantijs φX et φV mechanicè cognitis, dic esse . Et erit GXH quem quæris proximè. Quemadmodum ex ostensis ad Scholium Propositionis 12 quodammodo manifestum est.
comprehendunt: Problema ex eorum numero est quæ veteres linearia dixêre. At sequens mechanica solutio, quantùm exigunt res practicæ, veritati appropinquat. Finge summam angulorum æqualem esse angulo NMO quem radij duo alteris FD et FE quoad refrangibilitatem consimiles, ac juxta quamvis lineam LM, rectæ angulum DFE bisecanti quàm proximè parallelam incidentes, post binam refractionem constituunt. Et e radijs ad X refractis aliquem GX cum incidente radio FD convenientem in V, produc ad φ, ut sit φ locus imaginis quam objectum F oculo in X constituto exhibet. Dein angulo NMO, ac distantijs φX et φV mechanicè cognitis, dic esse . Et erit GXH quem quæris proximè. Quemadmodum ex ostensis ad Scholium Propositionis 12 quodammodo manifestum est.
Cùm refractiones utrobique non sint admodum inæquales res expeditiùs absolvitur per Scholium ad Propositionem 11 fingendo esse vel compositè .
<129>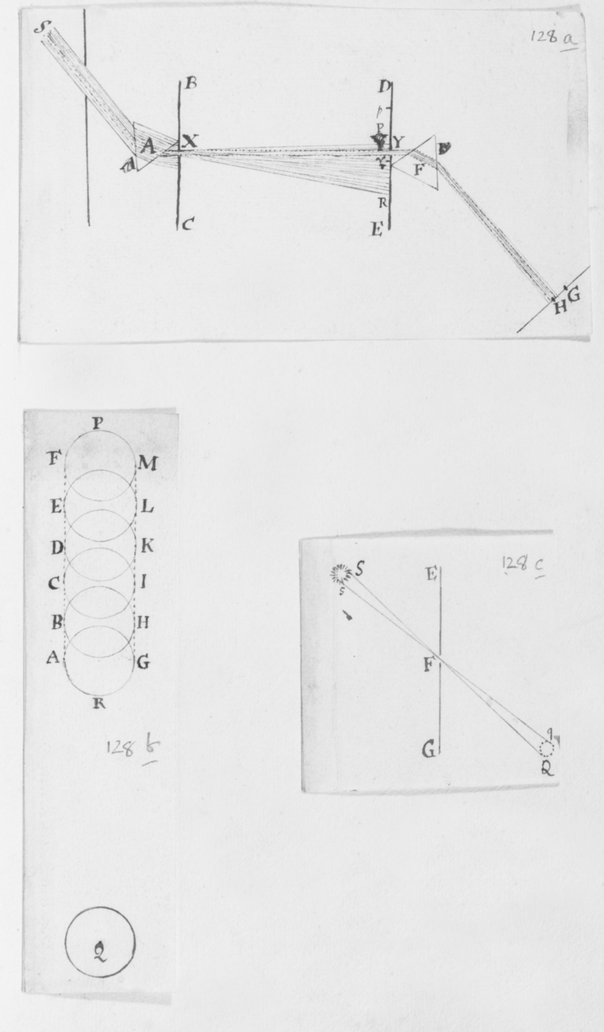
[1] Jan. 1669
[2] Lectio 1
[3] 1. Incepti ratio.
[4] 2. Quòd omnium radiorum non est eadem refrangibilitas.
[5] 3. Probatur experimento vulgari, per longitudinem imaginis coloratæ{.}
[6] 4. Casùs in quo radij æquè refrangibiles faciunt imaginem orbicularem.
[7] 5. Demonstratio istius Casûs. Ejus pars prima.
[8] 6. Lemma ad secundam partem{.}
[9] a. 6.10 Elementa
[10] b. 28.1 Elementa
[11] c. 10.11 Elementa
[12] d. Definitio 3.19 Elementa
[13] e. 4.6 Elementa
[14] 7. Pars secunda.
[15] 8. In isto tamen casu longitudo imaginis plusquam quadruplex est latitudinis: unde varia refrangibilitas convincitur.
[16] 9. Ejusdem rei demonstratio contractior.
[17] 10. Quo pacto Prisma facilè statuatur in situ ad experienda prædicta requisito.
[18] Lectio 2
[19] 11. Imaginis præfatæ figura describitur: quòd partim rectis, partim semicirculis terminatur.
[20] 12. Quomodo talis evadit per orbiculares imagines (quas unumquodque genus radiorum æquè refrangibilium facit) in longum dispositas.
[21] 13. Exinde deducitur experimentum, quo termini recti fiant distinctissimi.
[22] 14. Quare termini circulares semper apparent confusi{.}
[23] 15. Admonitio de figura et situ Lentium et Prismatum{.}
[24] 16. Déque imagine quâdam orbiculari.
[25] 17. Ab imaginis figura aliud etiam experimentum deducitur quo fiat multùm oblongior.
[26] 18. Experimentum istud promovetur.
[27] a Number 16.
[28] 19. Magis adhuc promovetur, per imaginem Stellæ Veneris.
[29] 20. Et applicatur descriptioni refractionis ad Figuram 1 traditæ.
[30] 21. Circumstantiâ variatâ, eidem descriptioni rursus applicatur.
[31] 22. Quod in adductis experimentis refractiones non casu fiunt inæquales, sed ex inæquali refrangibilitate.
[32] 23. Perstringuntur alia experimenta prioribus affinia.
[33] Lectio 3
[34] 24. Dissertatio de coloribus inita.
[35] 25. De opinionibus Philosophorum et imprimis Peripateticorum{.}
[36] 26. De opinionibus aliorum Philosophorum.
[37] 27. Colorum origines et fundamenta generalia describuntur.
[38] 28. Idque quatuor propositionibus{.}
[39] 29. De quibus non hypotheticè et probabiliter, sed ab experimentis aut demonstrativè disserendum esse promittitur.
[40] 30. De primâ propositione agitur perfunctoriè.
[41] vide Figuram 2.
[42] 31. Transitur ad secundam.
[43] 32. Cui probandæ adducitur experimentum.
[44] 33. Experimenti præfati circumstantia notatur.
[45] 34. Idem instrumentis refractiones dimetientibus posse probari. Tamen evidentiam experimenti jam descripti sufficere.
[46] 35. Illud promovetur aliquantum, idque vel tribus prismatibus adhibitis.
[47] 36. Vel contractiùs duobus{.}
[48] 37. Idem aliter promovetur{.}
[49] 38. Quod specimen, circumstantiâ variatâ, fit maximè scientificum.
[50] 39. Conclusio de affinitate cognitionis colorum et refractionum.
[51] a sectiones 3 & 30
[52] b sectio 32 &c
[53] Lectio 4
[54] 40. Transitur ad propositionem tertiam.
[55] 41. Modus componendi albedinem ex coloribus Prismatum{.}
[56] 42. Notanda quædam quò satiùs fiat.
[57] 43. Alius ejusdem rei perficiendæ modus{.}
[58] 44. In illum notæ{.}
[59] 45. Objectio quòd albor ex destructione non misturâ colorum generatur.
[60] 46. Responsio multiplex: Primò Quod illi colores non destruuntur ex umbræ confinio sublato.
[61] 47. Secundò, Neque probabilitèr ex motuum contrarietate.
[62] 48. Tertiò, Quòd radij per idem medium confusè transientes non agunt in se invicem{.}
[63] 49. Quartò, Quòd albor præfatus perit si quilibet color e misturâ tollatur.
[64] 50. Quintò, quòd colores, cùm decussando segregantur iterum, ad propriam speciem redeunt.
[65] 51. Sextò, res illustratur per misturam diversicolorum pulverum. Et quòd ex pulveribus omnium colorum debitè mistis fuscus producitur.
[66] Tertius modus miscendi colores prismatis in albedinem.
[67] 53{.} In eundem notæ.
[68] Lectio 5
[69] 54. Quartus ejusdem rei peragendæ modus, cæteris illustrior.
[70] a Num: 16 et 18
[71] 55. In eundem nota{.}
[72] 56. Quo more radij diversicolores in albentem lentis focum convergunt.
[73] a Num 12
[74] 57. De coloribus in extremitate foci illius, propter exilitatem vix conspicuis.
[75] 58. Dictorum colorum observatio.
[76] 59. Quintus modus albedinem componendi quarto ferè similis.
[77] 60. Lucem egredientem prismate non secus e coloribus (licèt nondum apparentibus) componi, ac postea cum colores in idem spatium congregati sunt.
[78] 61. Probatur ex eo quòd in modo quarto et quinto componendi albedinem, radij non convergunt ad idem spatium nisi qui divergebant ab eodem.
[79] 62. Et quòd divergentia colorum a prismate persimilis est eorum divergentiæ ab albenti lentis foco.
[80] 63. Atque etiam quòd divergentes a dicto foco non secus in alium focum congregari possunt, quàm divergentes a lente{.}
[81] Lectio 6.
[82] 64. Imò lucem e coloribus ante omnem refractionem componi{.}
[83] 65. Ut ex eo pateat quòd aliqui colores reflecti possunt dum alij per prisma trajiciuntur. Hujusque rei experiendæ modus adducitur.
[84] 66. Notandam quædam{.}
[85] 67. In majorem rei evidentiam ostenditur quosdam colores alijs facilius reflecti.
[86] 68. Idem aliter ostenditur, circumstantiâ tantùm variatâ{.}
[87] 69. Idem adhuc aliter.
[88] Sectio 37.
[89] 70. Et proinde cùm e radijs solaribus alij alijs, pro specie colorum quos postmodum exhibent, faciliùs reflectuntur; constat lucem solis ex illis coloribus componi.
[90] 71. Alius modus quo lux solis partim reflecti potest et partim refringi.
[91] Sectio 90
[92] 72. Penitiùs hic ostenditur quinam e radijs solaribus reflectuntur et quinam transmittuntur: atq́ue adeò hoc non casu sed prædispositione radiorum evenire{.}
[93] 73. Tertius modus quo lux solis partim reflecti potest et partim refringi.
[94] 74. Notandum Quòd colores hic fiunt a parallelis superficiebus.
[95] 75. Et quod lux postquam reflexa vel per parallelas superficies trajecta fuit, e coloribus componitur; quam tamen ejusdem naturæ cum immediatâ solis luce credimus.
[96] 76. Conclusio, quòd reflectio vel refractio non mutat radiorum dispositiones; neque adeò discrepantiam quoad colores inducit.
[97] Lectio
[98] Lectio 7
[99] 77. Colorum vulgare phænomenon explicatur.
[100] 78. Supposito quòd plures radij per eandem lineam ex ordine fluunt: Eamque vel perpendicularem anteriori plano prismatis;
[101] 79{.} Vel obliquam utrique.
[102] 80. Vel quòd adveniunt in pluribus lineis, ijsque vel parallelis.
[103] 81. Vel parùm inclinatis.
[104] 82. De varijs phænomeni circumstantijs; Luce juxta basem prismatis terminatâ{.}
[105] Lectiones 4 & 5. Vide etiam Lectionem
[106] 83. Vel juxta verticem ejus{.}
[107] Lectio
[108] 84. Vel utrinque. (Ubi viriditatis productio bella describitur.)
[109] 85. Vel juxta alterutrum triangularem limitem{.}
[110] 86. Vel undique. (Ubi rursus de præfatâ viriditate.)
[111] 87. Vel ad distantiam aliquam a prismate.
[112] 88. Vel alio quovis modo.
[113] Lectio 8
[114] 89. E præfatis modus deducitur albedinem e coloribus componendi{.}
[115] Vide figuras 31 et 32.
[116] 90. Utrum anguli prismatum sint æquales cognoscere.
[117] 91. Alius modus commiscendi colores in albedinem, priori affinis.
[118] 92. Adversus philosophorum Hypotheses notæ.
[119] Numbers 71 & 73.
[120] 93. Instrumentum describitur quocum omnia de coloribus, hactenus tradita dilucidissimè probentur.
[121] 94. Ejus usus describitur.
[122] 95. Et illustratur exemplis.
[123] 96. In constructionem præfati instrumenti notæ quædam.
[124] a Sectio 17
[125] b Sectio 18
[126] Iulio. 1670
[127] Lectio 9
[128] 97. Hactenus ostensis dissertatio de mensurâ refractionum subnectitur.
[129] 98. De mensurâ refractionis dati generis radiorum e quâvis incidentiâ datâ.
[130] 99. De mensurâ refractionum radiorum genere differentium ex eâdem quavis incidentiâ.
[131] 100. Ad sinus incidentiæ et refractionis coferendos adhibetur mediocre genus radiorum.
[132] 101. Modus explorandi sinuum istorum rationes.
[133] 102. Modus explorandi vim refractivam Medij cujusvis aëre circundati, præsertim verò Solidi.
[134] sectio 10.
[135] 103{.} Exemplum in refractione cujusdam generis vitri.
[136] 104{.} Modi præfati commoditas
[137] sectio 10
[138] 105. Regula de investigandâ refractione Mediorum sibi ipsis contiguorum quorum aeri contiguorum refractiones cognoscuntur.
[139] 106. Ejus regulæ demonstratio{.}
[140] Lectio 10
[141] 107. Modus dimetiendi refractiones solidorum, ad fluida accommodantur{.}
[142] Aquæ refractio prout ipse dimensus sum in specimen ejus rei adducitur{.}
[143] Lemma 1. Sectionis 102.
[144] 109{.} Præfatorum Demonstratio{.}
[145] 110. Radiorum diversi generis refractiones conferuntur, et maxima refrangibilitatis differentia investigatur.
[146] Sectio 103
[147] 111. Illarum refractionum sinus ad communem sinum incidentiæ conferuntur.
[148] 112. Radiorum ex oppositis partibus refringentis superficiei incidentium sinus sunt reciprocè proportionales.
[149] 113. Illustratur refractione vitri{.}
[150] E refractionibus extremorum generum facile est de intermedijs conjecturam facere.
[151] Lectio 11
[152] 115. Theoremate ostenditur ut e refractionibus heterogeneorum ad vitrum vel quodvis Medium inter se determinatis, possunt etiam ad alia quælibet Media aeri contigua refractiones (sine novis experimenti molestijs) inter se determinari{.}
[153] 116. De Theorematis illius certitudine.
[154] 117. De proportione quarundam linearum quæ computationi per hoc Theorema instituendæ inserviat.
[155] 118. Aliud ejusdem rei peragenda Theorema{.}
[156] 119. Ad ejus demonstrationem duo Lemmata prælibantur.
[157] Lemma 1. vide figuram præcedentem.
[158] 120. Lemma 2.
[159] 121. Demonstratio.
[160] 122. Heterogeneorum refractiones a superficiebus aeri ex neutra parte contiguis Theoremate etiam determinantur{.}
[161] 123. Theorema illud notis quibusdam promovetur{.}
[162] Lectio 12
[163] 124. Mensuris refractionum sic fuse explicatis ad propositiones exinde scaturientes transitur.
[164] 125. Obviæ quædam conformium radiorum affectiones, sequentibus inserventies, traduntur.
[165] Lectio 13
[166] 126. Difformium radiorum a planâ superficie refractorum affectiones enarrantur
[167] a Sectio 120
[168] b Hypothesis 120
[169] a Sectio 120
[170] b Hypothesis 120
[171] c 7. 6. Elementa
[172] a Hypothesis
[173] b Propositio 3.
[174] c 17. 1 Elementa
[175] d 29. 1 Elementa
[176] e 15. 1 Elementa
[177] f axioma 13. 1 Elementa
[178] a Corollarium propositionis 2
[179] a Scholium propositionis 3.
[180] Lectiones 14 & 15
[181] 127. Lemmata quædam ad prosequendam de difformium radiorum affectionibus doctrinam ponuntur{.}
[182] a. 6. 6 Elementa & Hypothesis
[183] b. 16. 1 Elementa
[184] c. 7. 3 Elementa
[185] d. 25. 1 Elementa
[186] Sequentes duæ propositiones numeris 1 et 3 notatæ hic deleri debent et ad paginas 110 & 112 transferire.
[187] a Sectiones 98 & 99 & sequentes
[188] a Sectiones 98 & 99 & sequentes
[189] a sectio 120
[190] b. sectio 122
[191] c Sectiones 98 & 120
[192] d Lemma 3
[193] e Lemma 1
[194] a sectio 119
[195] 128{.} Continuatur præfatarum affectionum declaratio.
[196] Pete ex paginis 103, 104 & 105
[197] a sectiones 117, 118, 122
[198] a sectiones 117, 118, 122
[199] b sectiones 118 & 122
[200] c sectio 120
[201] d Lemma 3
[202] Pete ex pagina 106.
[203] Lectiones 16 et 17
[204] The contents of this note are only visible in the diplomatic transcript because they were deleted on the original manuscript
[205] b Sectio 118
[206] c Sectio 120
[207] d Corollarium 1 Lemmatis 5
[208] a Sectiones 99 & 110
[209] a Duplex hæc assertio contemplanti sectiones 115 & 118 patebit.
[210] a Duplex hæc assertio contemplanti sectiones 115 & 118 patebit.
[211] * Consule casus 2 scholij ad Propositionem 6.
[212] a Scholium ad propositionem 3, Sectio 125.
[213] b Scholium ad propositionem 11 sectio 126.
[214] Lectio 18.
