Method of Curves and Infinite Series, and application to the Geometry of Curves (Part 2)
Problema 5.
Curvæ alicujus ad datum punctum
curvaturam invenire.
Problema cum primis elegans videtur et ad curvarum scientiam utile. In ejus autem constructionem generalia quædam præmittere convenit.
1{.} Ejusdem circuli eadem est undique curvatura et Inæqualium circulorum curvaturæ sunt reciprocè proportionales diametris. Si alicujus diameter diametro alterius duplo minor est, ejus periferiæ curvatura erit duplo major, si diameter triplo minor est curvatura erit triplo major, &c.
2. Si Circulus Curvam aliquam ad partem concavam in dato puncto tangat, sitque talis magnitudinis ut alius contingens circulus in angulis contactûs proximè punctum istud interscribi nequeat, circulus ille ejusdem est curvitatis ac Curva in isto puncto contactûs. Nam circulus, qui inter curvam et alium circulum juxta punctum contactus interjacet, minus deflectit a curva ejusque curvaturam magis appropinquat quam ille alius circulus; et proinde curvaturam ejus maximè appropinquat inter quem et Curvam non alius quisquam potes intercedere.
3. Itaque centrum curvaminis ad aliquod Curvæ punctum est centrum tangentis circuli æqualiter incurvatæ; et sic radius vel semidiameter curvaminis est pars perpendiculi ad istud centrum terminata.
4{.} Et proportio curvaminis ad diversa ejus puncta e proportione cui curvaminis circulorum æque curvorum sive e reciproca proportione radiorum curvaminis innotescit.
Problema itaque ad hunc locum redijt ut radius vel centrum curvaminis inveniatur{.}
Concipe ergo quod ad tria curvæ puncta δ, D, ac d ducantur perpendicula quorum quæ sunt ad 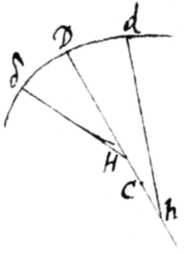 D et δ conveniant in H; et quæ ad D et d, conveniant in h. Et puncto D existente medio si major est curvitas a parte Dδ quam Dd, erit . Sed quo perpendicula δH ac dh propiora sunt intermedio perpendiculo, eò minùs distabunt puncta H et h. Et convenientibus tandem perpendiculis, coalescent. Coalescant autem in puncto C et erit illud C centrum curvaminis ad curvæ punctum D cui perpendicula insistunt. Id quod per se manifestum est.
D et δ conveniant in H; et quæ ad D et d, conveniant in h. Et puncto D existente medio si major est curvitas a parte Dδ quam Dd, erit . Sed quo perpendicula δH ac dh propiora sunt intermedio perpendiculo, eò minùs distabunt puncta H et h. Et convenientibus tandem perpendiculis, coalescent. Coalescant autem in puncto C et erit illud C centrum curvaminis ad curvæ punctum D cui perpendicula insistunt. Id quod per se manifestum est.
Hujus autem C varia sunt symptomata quæ ad ejus determinationem inservire possunt: Quemadmodum 1{.} Quod sit concursus perpendiculorum hinc et inde a DC infinitè parùm distantium.
2{.} Quod perpendiculorum finitè parùm distantium intersectiones hinc et inde dirimit ac disterminat. Ita ut quæ sunt a parte curviori Dδ citiùs ad H conveniant, et quæ sunt ex alterâ minùs curvâ parte Dδ remotiùs conveniant ad h.
3. Si DC dum curvæ perpendiculariter insistat moveri concipiatur, illud ejus punctum C (si demas motum accedendi vel recedendi a puncto insistentiæ C) minimè movebitur sed centri motionis rationem habebit.
4{.} Si centro C intervallo DC circulus describatur, non potest alius describi circulus qui juxta contactum interjacebit.
5. Denique si alterius alicujus tangentis circuli centrum ut H vel h paulatim ad hujus centrum C accedat donec tandem conveniat, tunc aliquod e punctis in quibus circulus ille curvam secavit simul conveniet punctum contactûs D.
Et unumquodque horum Symptomatum ansam præbet diversimodè resolvendi Problema. Nos autem primum tanquam simplicissimum eligemus.
Ad quodlibet Curvæ punctum D 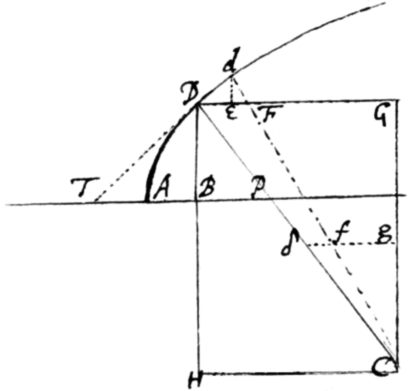 esto DT tangens, DC perpendiculum et C centrum curvaminis ut ante. Sitque AB basis ad quam DB in angulo recto applicatur, et cui DC occurrit in P. Age DG parallelam AB, Et CG perpendiculum, inque eo cape Cg cujuslibet datæ magnitudinis, et age gδ perpendiculum quod occurrat DC in δ: eritque fluxio Basis ad fluxionem Applicatæ. Concipe præterea punctum D per infinitè parvum intervallum Dd in curva promoveri et actis dE ad DG et Cd ad curvam normalibus quarum Cd occurrit DG in F et δg in f; erit DE momentum Basis dE momentum Applicatæ, ac δf contemporaneum momentum rectæ gδ. Estque . Habitis itaque horum momentorum sive quod perinde est fluxionum generantium rationibus, habebitur ratio GC ad datam gC (quippe quæ est DF ad δf,) et inde punctum C determinabitur.
esto DT tangens, DC perpendiculum et C centrum curvaminis ut ante. Sitque AB basis ad quam DB in angulo recto applicatur, et cui DC occurrit in P. Age DG parallelam AB, Et CG perpendiculum, inque eo cape Cg cujuslibet datæ magnitudinis, et age gδ perpendiculum quod occurrat DC in δ: eritque fluxio Basis ad fluxionem Applicatæ. Concipe præterea punctum D per infinitè parvum intervallum Dd in curva promoveri et actis dE ad DG et Cd ad curvam normalibus quarum Cd occurrit DG in F et δg in f; erit DE momentum Basis dE momentum Applicatæ, ac δf contemporaneum momentum rectæ gδ. Estque . Habitis itaque horum momentorum sive quod perinde est fluxionum generantium rationibus, habebitur ratio GC ad datam gC (quippe quæ est DF ad δf,) et inde punctum C determinabitur.
Sit ergo , , , et et erit seu , hujus autem z momentum δf dic (factum nempe ex velocitate et infinite parva quantitate,) eritque momentum , , et inde . Est ergo . Adeoque .
Cùm insuper Basis fluxioni m (ad quam tanquam uniformem fluxionem cæteras referre convenit) liberum sit quancunque velocitatem tribuere; dic esse 1, et erit , et . Et inde , ac {.}
Expositâ itaque quâvis æquatione quâ relatio BD ad AB pro curvâ definiendâ designetur, imprimis quære relationem inter m et n per Problema 1, et interea substitue 1 pro m et z pro n. Dein ex æquatione resultante per idem Problema 1 quære relationem inter m, n, et r et interea substitue 1 pro m et z pro n ut ante. Atque ita per priorem operationem obtinebis valorem z, et per posteriorem obtinebis valorem r; quibus habitis, produc DB ad H versus concavam partem curvæ ut sit , et age HC parallelam AB et perpendiculo DC occurrentem in C, eritque C centrum curvaturæ ad curvæ punctum D. Vel cùm sit , fac , vel .
Exemplum 1. Sic exposita , æquatione ad Hyperbolam cujus latus rectum est a ac transversum ; emerget (per Problema 1) (scriptis nempe 1 pro m et z pro n in æquatione resultante, quæ secus foret ) et hinc denuò prodit scriptis iterum 1 pro m et z pro n. Per priorem est , et per posteriorem . Dato itaque quovis curvæ puncto D et per consequentiam x et y, ex his dabuntur z et r, quibus cognitis fac vel DH, et age HC Quemadmodum si definitè sit , & , adeoque Hyperbolæ conditio: et si assumatur , erit , , & . Invento H, erige HC occurrente perpendiculo DC priùs ducto. Vel quod perinde est fac et age DC curvedinis Radium.
Siquando computationem non admodum perplexam fore censeas, possis indefinitos valores ipsorum r et z in valore CG substituere. Et sic in hoc exemplo per debitam reductionem obtinebis . Cujus tamen DH valor per calculum negativus prodit sicut in exemplo numerali videre est. At hoc tantùm arguit DH ad partes versus B capiendam esse{.} Nam si fuisset affirmativus ad contrarias partes duxisse oporter{et}.
Corollarium. Hinc si signum symbolo præfixum mutetur, ut fiat æquatio ad Ellipsin; erit {.}
At posito ut æquatio fiat ad Parabolam; erit . Indéque . Ex his facilè colligitur radium curvaturæ cujusvis conicæ sectionis valere .
Exemplum 2. Si (æquatio ad Cissoidem Dioclis) exponatur; Per Problema 1 imprimis obtinebitur ; ac deinde . Adeoque est . Et . Dato itaque quolibet Cissoidis puncto et inde x et y, dabuntur z et r: Quibus cognitis fac .
Exemplum 3{.} Si detur æquatio ad Conchoidem, ut supra; Finge , et emerget . Jam harum prior (viz ) per Problema 1 dat (scripto nempe z pro n,) et posterior dat . Et ex his æquationibus rite dispositis determinantur l et z. Ut autem r præterea determinetur, e novissimâ æquatione extermina fluxionem l substituendo et emerget , æquatio quæ fluentes quantitates sine aliquibus earum fluxionibus (prout exigit resolutio Problematis primi) complectitur. Hinc itaque per Problema 1 elicies . Qua æquatione in ordinem redactâ et concinnatâ, dabitur r. Inventis autem z et r fac .
Si penultimam æquationem per z divisisses, exinde postmodum per Problema 1 obtinuisses , æquationem priori simpliciorem pro determinando r.
Dedi quidem hoc exemplum ut modus operandi in surdis æquationibus constaret. At Conchoidis curvatura sic breviùs inveniri potuit. Æquationis partibus quadratis et per divisis, exurgit {.} Et inde per Problema 1 exoritur . sive . Et hinc denuo per Problema 1 exoritur . Per priorem exitum determinatur z, et per posteriorem r.
Exemplum 4. Sit IADF Trochois ad circulum ALE (cujus diameter est AE) accommodata; et ordinatâ BD secante circulum in L, dic , , , , et arcus ejusque arcûs fluxionem dic k. Et imprimis (ducto PL semidiametro) erit Fluxio Basis AB ad fluxionem arcus 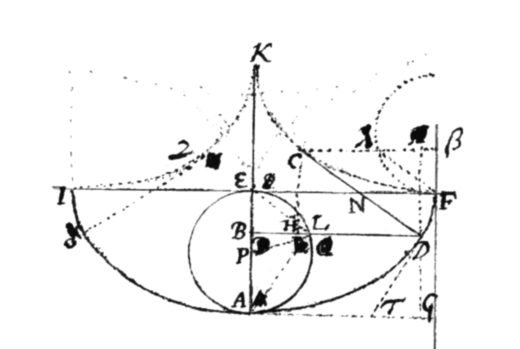 AL ut BL ad PL; hoc est, . Atque adeo .
AL ut BL ad PL; hoc est, . Atque adeo .
Porrò ex natura circuli est . Et inde per Problema 1 , sive .
Adhæc ex natura Trochoidis est arcus AL; adeoque . Et inde per Problema 1, .
Denique pro fluxionibus l et k valores hic substituantur et emerget . Unde per Problema 1 deducitur {.} Et his inventis fac et erige HC.
Corollarium. Cæterum ex his consectatur, 1{.} Quod sit et , sive quod EF in N bisecat CD radium curvaminis. Et hoc patebit substituendo valores r et z jam inventos in æquatione et exitum probè reducendo.
2. Hinc Curva FCK in qua centrum curvaminis indefinite versatur est alia huic æqualis Trochois cujus vertices ad I et F adjacent hujus cuspidibus. Nam circulus Fλ æqualis ALE et similiter positus describatur et agatur Cβ parallela EF circuloque occurrens in λ; et erit arcus Fλ (= arcus ){.}
3. CD quæ recta est ad Trochoidem IAF, contingit Trochoidem IKF in C.
4. Hinc (inversis Trochoidibus) si superioris Trochoidis cuspidi K pondus ad distantiam KA sive filo appensum innitatur, et undulante pondere filum se applicet ad Trochoidis partes KF et KI hinc inde obsistentes ne in rectum distendatur, et cogentes ut ad earum normam dum digreditur a perpendiculo paulatim desuper inflectatur, parte CD sub infimo contactûs puncto manente rectâ: pondus in inferioris Trochoidis perimetro movebitur, utpote cui filum CD semper perpendiculare est.
5. Est itaque tota fili longitudo KA æqualis perimetro Trochoidis KCF, ejusque pars CD æqualis parti perimetri CF.
6. Cum filum circa mobile punctum C tanquam centrum undulando convolvatur; superficies per quam tota CD continuò trajicitur erit ad superficiem per quam pars CN supra rectam IF simul trajicitur ut ad hoc est ut 4 ad 1. Est itaque area CFN quarta pars areæ CFD, et area KCNE quarta pars areæ KCDA.
7. Quinimò cùm subtensa EL sit æqualis et parallela CN, et circa immobile centrum E perinde ac CN circa mobile centrum C circumagitur, æquales erunt superficies per quas simul trajiciuntur; nempe area CFN et circuli segmentum EL. Et inde area NFD tripla erit segmenti istius, ac tota EADF tripla semicirculi{.}
8. Denique cùm pondus D attingit punctum F, totum filum circum Trochoidis perimetrum KCF flectetur, radio curvaminis CD manente nullo. Et proinde Trochois IAF ad ejus cuspidem F curvior est quàm quilibet circulus, et cum tangente BF productâ constituit angulum contactus infinitè majorem quàm circulus cum rectâ potest constituere.
Sunt etiam anguli contactûs Trochoidalibus infinitè majores et illis deinceps alij infinite majores et sic in infinitum, et tamen maximi sunt infinitè minores rectilineis. Sic . . . &c denotant seriem curvarum quarum quælibet posterior cum Basi constituit angulum contactus infinitè majorem quàm prior cùm eadem Basi potest constituere. Estque angulus contactus quem prima constituit, ejusdem generis cum circularibus, et ille quem secunda constituit, ejusdem generis cum Trochoidalibus. Et quamvis subsequentium anguli angulos præcedentium perpetim infinitè superant, tamen anguli rectilinei magnitudinem nunquam possunt assequi.
Ad eundem modum . . . &c denotant seriem linearum quarum subsequentium anguli ad vertices cum basibus confecti sunt angulis præcedentium perpetim infinitè minores. Quinetiam inter angulos contactus duorum quorumlibet ex his generibus possunt alia angulorum se infinite superantium intercedentia genera in infinitum excogitari.
Angulorum verò contactus unum genus esse infinitè majus alio constat cùm unius generis curva utcunque magna inter rectam tangentem et alterius generis curvam quantumvis parvam juxta punctum contactus non potest interjacere: Sive cujus angulus contactus necessariò continet alterius angulum contactûs ut partem totius. Sic curva angulus contactûs quem cum basi constituit, necessario continet angulum contactus curvæ . Qui verò se mutuò superare possunt anguli sunt ejusdem generis, uti de præfatis angulis Trochoidis et hujus curvæ contigit.
Ex his patet curvas in quibusdam punctis posse infinitè rectiores esse vel infinitè curviores quolibet circulo et tamen formam curvarum non ideo amittere. Sed hæc in transitu. ***
< insertion from p 65 >***[1]
Exemplum 5. Esto ED Quadratrix ad circulum centro A descriptum pertinens, ac DB ad AE normaliter demissâ dic . et . Eritque ut supra. quæ æquatio, scriptis 1 pro m et z pro n, fit 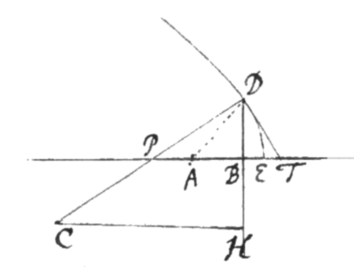 ; Et inde per Problema 1 elicitur . Factâque reductione et scriptis iterum 1 pro m et z pro n, exit . Inventis autem z et r fac , et age HC ut supra.
; Et inde per Problema 1 elicitur . Factâque reductione et scriptis iterum 1 pro m et z pro n, exit . Inventis autem z et r fac , et age HC ut supra.
Si constructionem concinnare placet, perbrevem invenies; nempe ad DT duc normalem DP occurrentem AT in P, et fac esse .
Scilicet est , et . et , et Præterea est , (utpote ,) adeóque . Denique est . Ubi valor negativus tantum arguit CH capiendam esse ad partes DH versus AB.
Eadem methodo Spiralium et aliarum quarumvis Curvarum curvatura calculo brevissimo determinari potest.
Ad curvaturam praæterea, cum curvæ alijs modis ad rectas referuntur, sine prævia reductione determinandam, jam potuit hæc methodus applicari perinde ut in determinando Tangentes factum est. Sed cùm omnes Geometricæ curvæ ut et Mechanicæ (præsertim ubi definientes conditiones ad infinitas æquationes uti post ostendam reducantur) ad rectangulas ordinatas referri possent videor satis præstitisse.
[2] < text from p 63 resumes >Qui plura desiderat haud difficulter proprio Marte supplebit Præsertim si in ejus rei illustrationem ex abundanti methodum pro Spiralibus adjecero.
Esto BK circulus, A centrum ejus, B punctum in circumferentia datum, ADd spiralis, DC perpendiculum ejus, et C centrum curvitatis ad punctum D. Ductâque ADK recta, et ei parallela et 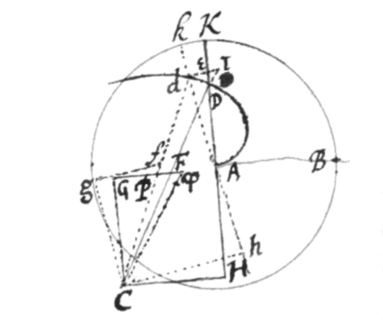 æquali CG, ut et normali GF occurrente CD in F; dic AB vel , , , & . Præterea concipe punctum D per infinitè parvum spatium Dd in spirali moveri, et perinde per d agi semidiatrum Ak, eique parallelam et æqualem Cg, et normalem gf occurentem Cd in f, cui etiam GF occurrit in P; Produc GF ad φ ut sit , et ad AK demitte normalem dE et produc donec cum CD conveniat ad I: Et ipsarum BK, AD, ac Gφ contemporanea momenta erunt Kk, DE, et Fφ, quæ proinde dicentur , , et .
æquali CG, ut et normali GF occurrente CD in F; dic AB vel , , , & . Præterea concipe punctum D per infinitè parvum spatium Dd in spirali moveri, et perinde per d agi semidiatrum Ak, eique parallelam et æqualem Cg, et normalem gf occurentem Cd in f, cui etiam GF occurrit in P; Produc GF ad φ ut sit , et ad AK demitte normalem dE et produc donec cum CD conveniat ad I: Et ipsarum BK, AD, ac Gφ contemporanea momenta erunt Kk, DE, et Fφ, quæ proinde dicentur , , et .
Jam est ubi assumo ut supra. Item adeóque . Præterea . Ad hæc propter , , triangula CPφ et ADd sunt similia, et inde , unde aufer Fφ et restabit . Denique demissa CH normali ad AD est . Vel substituto pro , erit {.}
Et nota quod in hujusmodi computationibus quantitates (ut AD et AE) pro ǽqualibus habeo quarum ratio a ratione aequalitatis non nisi infinitè parùm differt.
Ex his autem prodit hujusmodi Regula: Relatione inter x et y per quamlibet æquationem definitâ, quære relationem fluxionum m et n ope Problematis 1, et substitue 1 pro m et pro n. Deinde ex æquatione prodeunte quære denuò per Problema 1 relationem inter m n et r et iterum substitue 1 pro m. Prior exitus per debitam reductionem dabit n et z et posterior dabit r; quibus cognitis fac , et erige normalem HC spiralis perpendiculo DC priùs ducto occurrentem in C, et erit C centrum curvaminis. Vel quod eodem recidit cape , et age CD.
Exemplum 1. Si detur æquatio ad Spiralem Archimedeam; erit per Problema 1 sive (scripto 1 pro m et pro n) . Et hinc denuò per Problema 1 exit . Quare ex dato quolibet spiralis puncto D et inde longitudine AD sive y, dabuntur et : Quibus cognitis fac . et .
Et hinc facilè deducitur hujusmodi constructio. Produc AB ad Q ut sit , et fac .[3]
Exemplum 2. Si definit relationem inter BK et AD: obtinebis (per Problema 1) , sive , et inde rursus . Est itaque et . Quibus cognitis fac . Vel opere concinnato, fac .
Exemplum 3. Ad eundem modum si determinat relationem BK ad AD, orietur , et . Ex quibus DH, et inde punctum C determinatur ut ante.
Et sic aliarum quarumvis spiralium curvaturam nullo negotio determinabis. Imo et ad horum exemplar Regulas pro quibuslibet curvarum generibus excogitare.
Absolvi tandem Problema sed cum methodum adhibueri{m} a vulgaribus operandi modis satis diversam, et ipsum Problema non sit ex eorum numero quorum contemplatio apud Geometras increbuit: in ablatæ solutionis illustrationem et confirmationem non gravabor aliam solutionem attingere, magis obviam et usitatis in ducendo tangentes methodis affinem. Utpote si centro et intervallo quovis circulus describi concipiatur, qui curvam quamlibet in pluribus punctis secet, et circulus ille contrahetur vel dilatetur donec duo intersectionum puncta conveniant, is curvam ibidem tanget. Et præterea si centrum ejus accedere vel recedere a puncto contactûs fingatur, donec tertium intersectionis punctum cum prioribus in puncto contactûs conveniat, is æque curvus ac Curva in illo puncto contactûs evadet. Quemadmodum in ultimo quinque symptomatum centri curvaminis supra monui, e quorum singulis dixi Problema diversimodè confici potuisse.
Centro itaque C et radio 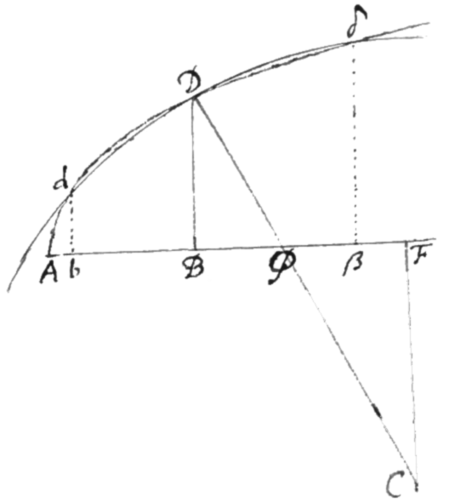 CD describatur circulus secans curvam in punctis d, D, ac δ. Et demissis db, DB, δβ, et CF ad Basin AB normalibus: dic , , , , ac ; et erit , ac ; Quorum quadratorum aggregatum æquatur quadrato DC. Hoc est . Quam {æquationem si pl}acet abbreviare possis fingendo symbolo cuivis , et evadet . Postquam verò t, v, et inveneris si s desideres fac .
CD describatur circulus secans curvam in punctis d, D, ac δ. Et demissis db, DB, δβ, et CF ad Basin AB normalibus: dic , , , , ac ; et erit , ac ; Quorum quadratorum aggregatum æquatur quadrato DC. Hoc est . Quam {æquationem si pl}acet abbreviare possis fingendo symbolo cuivis , et evadet . Postquam verò t, v, et inveneris si s desideres fac .
Proponatur jam quælibet æquatio pro Curva definienda cujus flexuræ quantitatem invenire oportet et ejus ope alterutram quantitatem x vel y extermina et emerget æquatio cujus radices (db, DB, δβ &c si extermines x, vel Ab, AB, Aβ &c si extermines y) sunt ad intersectionum puncta (d, D, δ &c). Et proinde cùm ex istis tres evadent æquales, circulus et curvam continget et erit ejusdem curvitatis ac curva in puncto contactus{.} Æquales autem evadent conferendo æquationem cum alia totidem dimensionum æquatione fictitia cujus tres sunt æquales radices ut docuit Cartesius; vel expeditiùs multiplicando terminos ejus bis per Arithmeticam progressionem.
Exemplum. Sit æquatio ad Parabolam, et exterminato x (substituendo nempe in æquatione superiori valorem ejus ) prodibit
cujus e radicibus y tres debent fieri æquales. Et in hunc finem terminos per Arithmeticam progressionem bis multiplico ut hic videre est, et exit sive . Unde facilè colligitur esse ut supra.
Quamobrem dato quovis Parabolæ puncto D, duc perpendiculum DP et in axe cape et erige normalem FC occurentem DP in C et erit C desideratum centrum curvitatis.
Idem in Ellipsi et Hyperbola præstare possis sed calculo satis molesto, et in alijs curvis utplurimùm fastidiosissimo.
De Quæstionibus quibusdam
cognatis.
Ex hujus Problematis resolutione consectantur aliorum nonnullorum confectiones. Cujusmodi sunt
1. Invenire punctum ubi linea datam habet curvaturam.
Sic in Parabola si punctum quæratur ad quod radius curvaturæ sit datæ longitudinis f: e centro curvaturæ ut prius invento radium determinabis esse , quem pone æqualem f. Et factâ reductione emerget .
2. Invenire punctum rectitudinis.
Punctum rectitudinis voco ad quod radius flexionis infinitus evadit, sive centrum infinitè distans; quale est ad verticem Parabolæ . Et hoc idem plerumque limes est flexionis contrariæ cujus determinationem supra posui. Sed et alia haud inelegans ex hoc Problemate scaturit. [4]Nempe quo longior est radius flexionis eo minor evadit angulus DCd, et pariter momentum δf adeóque fluxio quantitatis z unà diminuitur, ita ut per ejus radij infinitatem prorsus evanescant. Quære ergo fluxionem r et suppone nullam esse{.}
Quemadmodum si limitem flexûs contrarij in Parabola secundi generis cujus ope Cartesius construxit æquationes sex dimensionum determinare oportet. Ad illam Curvam æquatio est . Et hinc per Problema 1 exit ; Quæ, scripto 1 pro m et z pro n, fit : Unde rursus per Problema 1 exit , Et hæc, scripto iterum 1 pro m, z pro n, et 0 pro r, fit . Jam extermina z scribendo pro valorem , in æquatione , et proveniet , sive . 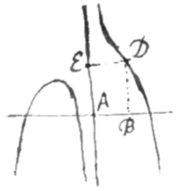 Quamobrem ad punctum A erige perpendiculum , et per E duc ED parallelam AB, et punctum D ubi Parabolæ partem convexo-concavam secuerit erit in confinio flexionis contrariæ.
Quamobrem ad punctum A erige perpendiculum , et per E duc ED parallelam AB, et punctum D ubi Parabolæ partem convexo-concavam secuerit erit in confinio flexionis contrariæ.
Similique methodo alia rectitudinis puncta quæ non interjacent partibus contrariè flexis determinari possunt. Veluti si Curvam definiat, Exinde per Problema 1 imprimis producetur et hinc denuò , Ubi suppone et factâ reductione prodibit . Quamobrem sume et BD normaliter erecta curvæ in desiderato rectitudinis puncto D occurret{.}
<71>3. Invenire punctum flexûs infiniti
Quære radium curvaminis et suppone nullum esse. Sic ad Parabolam secundi generis æquatione definitam, erit radius ille ; qui nullus evadit cùm sit .
4{.} Flexûs maximi minimive punctum determinare.
Ad hujusmodi puncta radius curvaturæ aut maximus aut minimus evadit. Quare centrum curvaturæ ad id temporis momentum nec versus punctum contactus neque ad contrarias partes movetur sed penitus quiescit. Quæratur itaque fluxio Radij CD; vel expeditiùs, quæratur fluxio alterutrius rectæ BH vel AK, et supponatur nulla.
Quemadmodum si de Parabola secundi generis quæstio proponatur: imprimis ad curvaturæ centrum determinandum invenies , adeoque est , dic autem , et erit , unde juxta Problema 1 educitur . Jam vero  [5]l ipsius BH fluxionem suppone nullam esse, et insuper cùm ex hypothesi sit , et inde per Problema 1 , posito substitue pro n, et emerget . Cape ergo . Et BD normaliter erecta occurret curvæ in puncto maximæ curvaturæ. Vel, quod perinde est fac .
[5]l ipsius BH fluxionem suppone nullam esse, et insuper cùm ex hypothesi sit , et inde per Problema 1 , posito substitue pro n, et emerget . Cape ergo . Et BD normaliter erecta occurret curvæ in puncto maximæ curvaturæ. Vel, quod perinde est fac .
Ad eundem modum Hyperbola secundi generis per æquationem designata maximè flectitur in 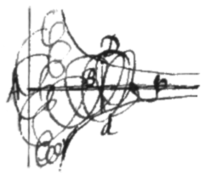 [6] punctis D, d, quæ determinabis sumendo in Basi, et erigendo . eique æqualem Qp ex altera parte et agendo AP et Ap, quæ curvæ occurrent in desideratis punctis D ac d.
[6] punctis D, d, quæ determinabis sumendo in Basi, et erigendo . eique æqualem Qp ex altera parte et agendo AP et Ap, quæ curvæ occurrent in desideratis punctis D ac d.
5. Locum centri curvaminis determinare; sive Curvam describere in quâ centrum istud perpetuo versatur.
Trochoidis centrum curvaminis in alia Trochoide versari ostensum est. Et sic Parabolæ centrum istud in alia secundi generis (quam æquatio definit) Parabola versatur, ut inito calculo facilè constabit.
6. Luce in quamlibet curvam incidente, invenire focum sive concursum radiorum circa quodpiam ejus punctum refractorum.
Curvaturam ad istud Curvæ punctum quære, et centro radioque curvaturæ Circulum describe; Dein quære concursum radiorum a Circulo circa istud punctum refractorum. Nam idem erit concursus refractorum a propositâ Curvâ.
7. His addi potest particularis inventio curvaturæ ad vertices curvarum ubi normaliter secant Bases. Nempe punctum in quo Curvæ perpendiculum cum Basi conveniens ipsam ultimò secuerit, est centrum curvaturæ ejus. Quamobrem habitâ relatione inter Basin x et rectangulum applicatum y et inde (per Problema 1) relationem inter fluxiones m et n; valor ; si in eo scribas 1 pro m et fingas , erit radius curvaturæ.
Sic in Ellipsi , est , qui valor si supponas et consequenter et scribas 1 pro m evadet radius curvaturæ. Et sic ad vertices Hyperbolæ et Parabolæ radius curvaturæ erit etiam dimidium lateris recti.
Atque ita ad Conchoiden æquatione definitam valor ope Problematis 1 invenietur . Qui supponendo , et inde vel evadet , vel radius curvaturæ. [7]Fac ergo , et , et habes curvaturæ centra C et c ad vertices conjugatarum Conchoidum E et e.
<73>Problema 6.
Curvaturæ ad datum Curvæ alicujus punctum
qualitatem determinare.
Per qualitatem Curvaturæ intelligo formam ejus quatenus est plus vel minùs inæquabilis, sive quatenus plus vel minùs variatur in processu per diversas partes Curvæ. Sic interroganti qualis sit circuli curvatura, responderi potest quod sit uniformis, sive invariata; [8]et interroganti qualis sit curvatura Spiralis quæ describitur per motum puncti D cum accelerata celeritate AD in recta AK uniformitèr circa centrum A gyrante progredientis ab A, adeo ut recta AD ad arcum BK dato puncto K descriptum rationem habeat numeri ad Logarithmum ejus, responderi potest quod sit uniformiter variata sive quod sit æquabiliter inæquabilis. Et sic aliæ curvæ in singulis earum punctis aliquales pro curvaturæ variatione denominari possunt.
Quæritur itaque Curvaturæ circa aliquod Curvæ punctum inæquabilitas sive variatio. Qua de causa animadvertendum est 1 Quod ad puncta in similibus curvis similiter posita similis est inæquabilitas sive variatio curvaturæ. 2 Et quod momenta radiorum curvaturæ ad illa puncta sunt proportionalia contemporaneis momentis curvarum, et fluxiones fluxionibus. 3 Atque adeò quod ubi fluxiones illæ non sunt proportionales dissimilis erit inæquabilitas curvaturæ. Utpote major erit inæquabilitas ubi major est ratio fluxionis radij curvaturæ ad fluxionem Curvæ, Adue fluxionum ratio illa non immeritò dici potest index inæquabilitatis sive variationis curvaturæ.
Ad Curvæ alicujus AD puncta D ac d 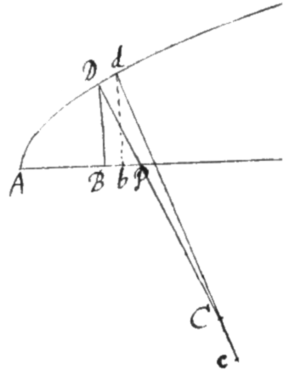 infinitè parùm distantia sunto radij curvaturæ DC ac dc, et existente Dd momento Curvæ erit Cc contemporaneum momentum radij curvaturæ, et index inæquabilitatis curvaturæ. Nempe tanta dicetur inæquabilitas illa, quantam esse indicat rationis illius quantitas. Sive curvatura dicetur tanto dissimilior curvaturæ circuli.
infinitè parùm distantia sunto radij curvaturæ DC ac dc, et existente Dd momento Curvæ erit Cc contemporaneum momentum radij curvaturæ, et index inæquabilitatis curvaturæ. Nempe tanta dicetur inæquabilitas illa, quantam esse indicat rationis illius quantitas. Sive curvatura dicetur tanto dissimilior curvaturæ circuli.
Demissis jam ad quamlibet AB occurrentem DC in P, rectangulis applicatis DB ac db dic , , , , et inde , eritque , et . ac sive supposito . Quamobrem relatione inter x et y per quamlibet æquationem definitâ, et inde juxta Problema 4 & 5 invento perpendiculo DP sive t et radio curvaturæ v, ejusque radij fluxione l per Problema 1; dabitur index inæquabilitatis curvaturæ .
Exemplum 1. Sit (æquatio ad Parabolam{)} et per Problema 4) erit , adeoque . Item per Problema 5 *[9] et . Jam æquationes et , et per Problema 1 dant , et , et . Quibus ordinatis et posito , orientur , vel et . Et sic inventis n, k, et l habebitur index inæquabilitatis curvaturæ.
Quemadmodum si in numeris definiatur , sive , et , erit , , , , et . Adeoque indici inæquabilitatis{.}
Sin autem definiatur , erit , , , et , Adeoque index inæquabilitatis. Quamobrem inæquabilitas Curvaturæ ad punctum a quo ad axin demissa ordinatim applicata æquatur lateri recto Parabolæ dupla est ejus ad punctum a quo demissa ordinatim applicata æquatur dimidio ejusdem lateris recti. Hoc est curvatura in priori casu duplo dissimilior est curvaturæ circuli, quàm in posteriori.
Exemplum 2. Sit , et per Problema 4 erit BP et inde , sive . Item per Problema 5 erit ubi si substituas evadet . Et est . Jam per Problema 1 æquationes et et dant et , et . Et sic invento l, dabitur index inæquabilitatis curvaturæ.
Sic ad Ellipsin , ubi est et si supponatur , erit , , , , et indici inæquabilitatis curvaturæ. Unde patet curvaturam hujus Ellipsis ad hic definitum punctum D, esse duplo minus inæquabilem (sive duplo similiorem curvaturæ circuli,) quàm curvatura Parabolæ ad illud ejus punctum a quo ad axin demissa ordinatim applicata æquatur dimidio ejus lateris recti.
Si conclusiones in his exemplis concinnare placet, ad Parabolam exibit index inæquabilitatis et ad Ellipsin exibit index , et sic ad Hyperbolam , observata analogiâ, erit index . Unde patet quod ad diversa puncta cujusvis Conicæ sectionis seorsim spectatæ curvaminis inæquabilitas est ut rectangulum . Et quod ad diversa puncta Parabolæ est ut ordinatim applicata BD.
Cæterùm cum Parabola sit simplicissima linearum inæquabili curvaturâ flexarum, ejusque curvaturæ inæquabilitas tam levi negotio determinatur (utpote cujus index sit ;) aliarum curvarum curvaturæ ad curvaturam hujus non incommodè referri possunt. Quemadmodum si quæratur qualis sit Ellipsis curvatura ad illud ejus punctum quod definitur assumendo : Quoniam index ejus (ut supra) sit , responderi potest esse similem curvaturæ Parabolæ ad illud ejus punctum inter quod et axin recta ordinatim applicatur.
Sic cum lineæ Spiralis ADE jam ante descriptæ[10] fluxio sit ad fluxionem subtensæ AD in data quadam ratione, puta d ad e: versus partes concavas ejus erige ad AD normalem , et erit P centrum curvaturæ, et sive index inæquabilitatis ejus. Quare Spiralis hæcce curvaturam habet ubique similiter inæquabilem ac Parabola habet in illo ejus puncto a quo demittitur ad axin ordinatim applicata .
Et sic index inæquabilitatis ad quodvis Trochoidis punctum D (fig ) invenietur esse . Quare curvatura ejus ad idem D tam inæquabilis est sive tam dissimilis curvaturæ circuli, quàm curvatura Parabolæ cujusvis ad illud ejus punctum ubi ordinatim applicata æquatur .
Ex his credo sensus Problematis satis elucescet, quo benè perspecto non difficile erit animadvertenti seriem rerum supra traditarum plura exempla de proprio suppeditare et hujusmodi complures alias operandi methodos, prout res exiget, concinnare. Quinetiàm cognata Problemata (ubi perplexa computatione non conteritur et fatigatur,) haud majori difficultate transiget: Cujusmodi sunt, 1{.} Invenire punctum curvæ alicujus ubi vel nullam, vel infinitam, vel maximam aut minimam, vel datam quamvis habeat inæquabilitatem curvaturæ. Sic ad vertices Conicarum sectionum nulla est inæquabilitas curvaturæ, ad cuspidem Trochoidis infinita est, et ad puncta Ellipseos maxima est ubi rectangulum fit maximum, hoc est ubi lineæ diagonales rectanguli Parallelogrammi circumscripti Ellipsin secant cujus latera tangunt illam in principalibus verticibus{.}
2. Curvam alicujus definitæ speciei, puta Conicam Sectionem, determinare, cujus curvaturæ ad aliquod punctum & æqualis sit et similis curvaturæ alterius alicujus curve ad datum punctum ejus.
3. Conicam Sectionem determinare ad cujus punctum aliquod curvatura & lineæ tangentis (respectu axis) positio sit similis curvaturæ ac tangentis positioni alterius alicujus Curvæ ad assignatum punctum ejus. Et hujus problematis usus est ut vice Ellipsium secundi generis quarum refringendi proprietates Cartesius in Geometria demonstravit, Conicæ sectiones idem in refractionibus quàm proximè præstantes subrogari possint. Atque idem de alijs curvis intellige.
<77>Problema 7.
Curvas pro arbitrio multas invenire quarum areæ
per finitas æquationes designari possunt.
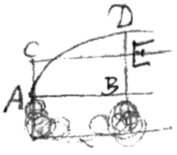 Sit AB basis curvæ, ad cujus initium A erigatur normalis et agatur CE parallela AB, sit etiam DB rectangula applicata occurrens rectæ DE in E et curvæ AD in D. Et concipe has areas ACEB et ADB a rectis BE et BD per AB delatis generari. Et earum incrementa sive fluxiones perpetim erunt ut lineæ describentes BE et BD. Quare parallelogrammum ACEB sive dic x, et curvæ aream ADB dic z: et fluxiones m et r erunt ut BE et BD, adeoque posito erit .
Sit AB basis curvæ, ad cujus initium A erigatur normalis et agatur CE parallela AB, sit etiam DB rectangula applicata occurrens rectæ DE in E et curvæ AD in D. Et concipe has areas ACEB et ADB a rectis BE et BD per AB delatis generari. Et earum incrementa sive fluxiones perpetim erunt ut lineæ describentes BE et BD. Quare parallelogrammum ACEB sive dic x, et curvæ aream ADB dic z: et fluxiones m et r erunt ut BE et BD, adeoque posito erit .
Si jam ad arbitrium assumatur æquatio quævis pro definienda relatione z ad x, exinde per problema 1 elicietur r. Atque ita duæ habebuntur æquationes quarum posterior Curvam definiet et prior aream ejus.
Exempla. Assumatur et inde per Problema 1 elicietur , sive siquidem est .
Assumatur et inde prodibit , æquatio ad Parabolam.
Assumatur , sive , et emerget , sive æquatio iterum ad Parabolam.
Assumatur præterea , sive sive et elicietur sive {.}
Item assumatur sive et elicietur sive Ubi negativus valor ipsius r tantùm denotat BD capiendam esse ad partes contra BE.
Adhæc si assumas , elicies et exterminato z proveniet .
Vel si assumas , dic et erit , et inde per Problema 1 . Item æquatio per Problema 1 dat cujus ope si extermines l fiet .
Si denique assumas , elicies . Quare per assumptam æquationem imprimis quære aream z, ac deinde applicatam r per elicitam{.}
Atque ita ex areis qualescunque effingas semper possis applicatas determinare.
<78>Problema 8.
Curvas pro arbitrio multas invenire quarum
areæ ad aream datæ alicujus Curvæ relationem habent per finitas æquationes
designabilem.
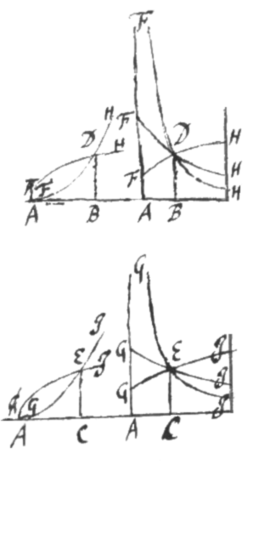 Sit FDH data curva, ac GEI quæsita
Sit FDH data curva, ac GEI quæsita 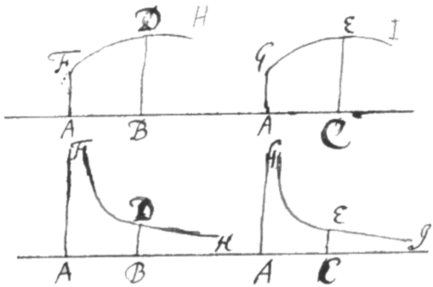 et earum applicatas DB et EC concipe super Basibus AB et AC erectas incedere: Et arearum quas ita transigunt incrementa sive fluxiones erunt ut applicatæ illæ ductæ in earum velocitates incedendi, hoc est in fluxiones basium. Sit ergo , , ac , area , & area , ac arearum fluxiones sint p, et q, nempe p ipsius s, et q ipsius t: Eritque . Quare si supponatur , et , ut supra; erit et inde .
et earum applicatas DB et EC concipe super Basibus AB et AC erectas incedere: Et arearum quas ita transigunt incrementa sive fluxiones erunt ut applicatæ illæ ductæ in earum velocitates incedendi, hoc est in fluxiones basium. Sit ergo , , ac , area , & area , ac arearum fluxiones sint p, et q, nempe p ipsius s, et q ipsius t: Eritque . Quare si supponatur , et , ut supra; erit et inde .
Assumantur itaque duæ quævis æquationes quarum una definiat relationem arearum s ac t, et altera relationem basium x et z et inde per Problema 1 quærantur fluxiones q et r, et statuatur .
Exemplum 1. Data curva AFD sit circulus æquatione designatus, et quærantur aliæ curvæ quarum areæ adæquant aream ejus. Ex hypothesi ergo est et inde . et . Superest ut r determinetur assumendo relationem aliquam inter bases x et z.
Veluti si fingas erit per Problema 1 . Quare substitue pro r et fiet . Est autem , adeoque , æquatio ad curvam cujus area æquatur areæ circuli{.}
Ad eundem modum si fingas , proveniet , et inde et exterminato v et x fiet .
<79>Vel si fingas , proveniet ; et inde .
Atque ita si fingas , ope Problema 1 obtinebitur et inde quæ Curvam Mechanicam designat.
Exemplum 2. Detur iterum Circulus et quærantur Curvæ quarum areae ad aream ejus habeant aliam quamlibet assumptam relationem. Veluti si assumes , et præterea fingas , mediante Problema 1 elicies et . Quare est , et substituto pro p, et pro x fit {.}
Quod si assumas , et , invenies ope Problema 1 et . Adeoque sive . Jam vero pro exterminando l, æquatio per Problema 1 dat et proinde est ubi si supprimas v et x substituendo valores et z, emerget .
Sin assumas , et emerget , et atque adeò , et pro p et x substitutis et fiet æquatio ad Curvam Mechanicam.
Exemplum 3. Ad eundem modum figuræ assumptam relationem ad aliam quamvis datam figuram habentes inveniuntur. Sic datâ Hyperbolâ , si assumas et elicies per Problema 1 et et inde , et substitutis pro p et pro x, proveniet {.}
Atque ita si assumas , et , elicies , et . Est autem et inde . Quare . Jam vero ope Problema 1 dat . Adeóque est et substitutis pro v et pro x, fit .
Exemplum 4. Ad hæc si detur Cissoides ad quam relatæ aliæ figuræ sunt inveniendæ, et ea de causa assumatur , finge ejusque fluxionem k et erit et inde per Problema 1 . Æquatio autem per Problema 1 dat ubi si extermines h fiet . Quare cùm præterea sit erit . Porro ad determinandum z et r assumatur et ope Problema 1 emerget sive . Quare est . Quæ æquatio cùm sit ad circulum, habebitur relatio arearum circuli et Cissoidis.
Atque ita si assumpsisses et prodijsset æquatio denuò ad circulum.
Haud secus si detur curva aliqua Mechanica, possunt aliæ ad eam relatæ curvæ Mechanicæ inveniri, sed ad eliciendum Geometricas convenit ut e rectis ab invicem Geometricè dependentibus aliqua pro Basi adhibeatur, et ut area ad parallelogrammum complementalis quæratur supponendo fluxionem ejus valere Basin ductam in fluxionem ordinatim applicatæ.
Exemplum 5. [11]Sic Trochoide ADF propositâ, refero ad Basin AB et completo parallelogrammo ABDG quæro complementalem superficiem ADG concipiendo descriptam esse per motum rectæ GD, et proinde fluxionem ejus valere illam GB in celeritatem progrediendi ductam, hoc est . Jam cùm AL sit parallela tangenti DT, erit AB ad BL ut fluxio ejusdem AB ad fluxionem applicatæ BD hoc est ut 1 ad l. Quare est , adeóque , Et proinde area ADG describitur fluxione BL; Atque adeo cùm area circularis ALB eadem fluxione describátur æquales erunt.
[12]Pari ratione si concipias ADF esse figuram arcuum sive sinuum versorum, hoc est cujus applicata BD æquatur arcui AL: cùm fluxio arcus AL sit ad fluxionem Basis AB ut PL ad BL, hoc est erit . Adeoque fluxio areæ ADG erit . Quare si ad ipsius AB punctum B recta æqualis in angulo recto applicari concipiatur, illa ad curvam quandam Geometricam terminabitur cujus area Basi AB adjacens æquatur areæ ADG.
Et sic alijs figuris per arcuum circuli, Hyperbolæ vel cujusvis Curvæ ad arcuum istorum sinus rectos vel versos aut alias quasvis geometricè determinabiles rectas lineas in datis angulis applicationem constitutis, æquales Geometric{æ} figuræ inveniri possunt.
[13]Circa Spiralium areas levissimum est negotium. Utpote centro convolutionis A radio quovis AG descripto arcu DG occurrente AF in G et spirali in D; cùm arcus ille ad instar lineæ super Basi AG incedentis describat Spiralis Aream AHDG, ita ut ejus areæ fluxio sit ad fluxionem rectanguli , ut arcus GD ad 1; si rectam GL arcui isti æqualem erigas illa similiter incedendo super eadem AG describet aream ALG æqualem areæ Spiralis AHDG; curvâ EIL existente Geometricâ. Et præterea si subtensa AL ducatur, erit triangulum , adeoque complementalia segmenta ALI et ADH erunt etiam æqualia. Et hæc non tantum Spirali Archimedeæ (ubi AIL evadit Parabola Apolloniana) , sed et alijs quibuscunque conveniunt, adeo ut omnes eodem negotio in æquales Geometricas converti possint.
Possem plura hujus construendi Problematis specimina afferre, sed hæc sufficiant cùm sint adeò generalia ut quicquid hactenus circa curvarum areas inventum fuerit, vel ni fallor inveniri possit, aliquo saltem modo complectantur, et utplurimùm leviori curâ sine solitis ambagibus determinent.
Præcipuus autem hujus & præcedentis Problematis usus est, ut assumptis conicis sectionibus vel quibuslibet notæ magnitudinis curvis, aliæ curvæ quæ cum his conferri possunt, investigentur, et earum definientes æquationes in Catalogum ordinatim disponantur. Et constructo ejusmodi Catalogo, cum curvæ alicujus area quæritur, si æquatio ejus definiens vel immediatè in Catalogo reperiatur, vel in aliam quam Catalogus complectitur transformari potest, exinde cognosces aream ejus. Quinetiam Catalogus ille determinandis Curvarum longitudinibus, centris gravitatum, solidis per convolutionem generatis, solidorum superficiebus, et cuilibet fluenti quantitati per analogam fluxionem generatæ, inservire potest. Ast quomodo formandus sit et utendus in sequente Problemate patebit ubi duplicem exhibuimus. 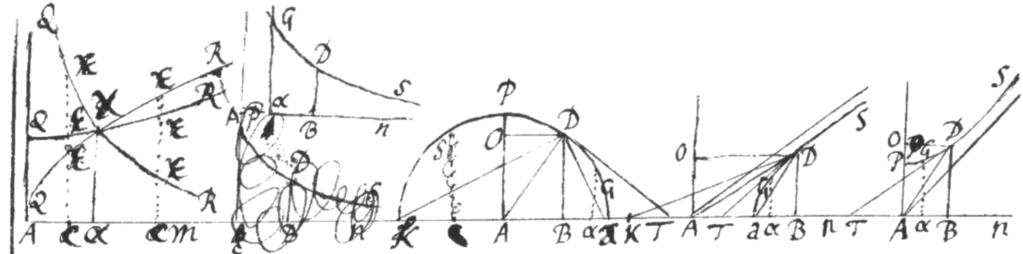
Problema 9.
Propositæ alicujus Curvæ aream determinare{.}
Problematis resolutio in eo fundatur ut quantitatum fluentium relatio ex relatione fluxionum (per Problema 2) eliciatur. Et imprimis si recta BD cujus motu quæsita area AFDB describitur, super basi AB positione datâ erectè incedat, concipe ut supra parallelogrammum ABEC a parte ejus BE unitatem æquante interea describi. Et posita BE fluxione parallelogrammi erit BD fluxio areæ quæsitæ.
Dic ergo , et erit etiam et dic insuper aream , et erit ut et , eo quod sit . Et proin per æquationem definientem BD simul definitur fluxionum ratio , et exinde per Problema 2, Casum 1, elicietur relatio fluentium quantitatum x et z.
Exempla prima. Ubi BD sive r valet simplicem
aliquam quantitatem{.}
Detur vel æquatio nempe ad Parabolam, et (per Problema 2) emerget . Est ergo sive areæ Parabolicæ AFDB{.}
Detur æquatio ad Parabolam secundi generis et (per Problema 2) emerget , hoc est .
Detur sive æquatio ad Hyperbolam secundi generis, et emerget sive : hoc est areæ infinite longæ HDBH ex altera parte applicatæ BD jacentis, ut innuit valor negativus.
Atque ita si detur , emerget {.}
<84>Præterea sit . sive , æquatio iterum ad Parabolam, et proveniet , hoc est {.}
Sit , et fiet , sive .
Sit , et fiet , sive .
Sit , et fiet , sive .
Et sic in alijs.
Exempla secunda. Ubi r valet plures ejusmodi connexas quantitates.
Sit , et fiet {.}
Sit , et fiet .
Sit et fiet .
Exempla 3{.} ubi prævia reductio per divisionem
requiritur.
Detur , æquatio ad Hyperbolam Apollonianam et factâ in infinitum divisione, evadet . Et inde per Problema 2 (ut in secundis exemplis) obtinebitur {.}
Detur et per divisionem elicietur vel etiam {.} Indeque per problema 2, vel .
Detur , et per divisionem evadet et inde per Problema 2, .
<85>Exempla 4. Ubi prævia reductio per extractionem
radicum requiritur.
Detur æquatio nempe ad Hyperbolam et radice ad usque terminos infinitè multos extractâ, evadet Atque inde ut in præcedentibus &c{.}
Ad eundem modum si detur æquatio scilicet ad circulum, obtinebitur {.}
Atque ita si detur æquatio iterum ad circulum proveniet extrahendo radicem adeoque est {.}
Sic æquatio denuò ad circulum per extractionem radicis dat unde per Problema 2 elicitur .
Et sic , per debitam reductionem dat . Unde per Problema 2 fit {.}
Sic denique per extractionem radicis cubicæ dat . Indeque . vel etiam . Indeque .
Exempla 5. Ubi prævia reductio per æquationis affectæ
resolutionem requiritur.
Si curva per æquationem definiatur, extrahe radicem et proveniet . Unde ut in prioribus obtinebitur {.}
Sin sit æquatio ad curvam resolutio dabit triplicem radicem nempe et , et et inde trium correspondentium arearum valores . , ac .
<86>De Curvis Mechanicis hic nihil adjicio, siquidem reductio ad formam Geometricarum post ostenditur.
Cæterum cum sic inventi valores z areis quandoque ad Basis finitam partem AB, quandoque ad partem BH infinitè versus H productam, et quandoque ad utramque partem sitis secundum diversos eorum terminos competant: quò debitus areæ ad quamlibet Basis portionem sitæ valor assignetur, Area illa semper ponenda est æqualis differentiæ valorum z partibus Basis ad initium et finem istius areæ terminatis competentium.
Exempli Gratia. Ad curvam quam æquatio definit inventum est . Jam ut quantitatem areæ bdDB adjacentis parti Basis bB determinem, a valore z qui fit ponendo subduco valorem z 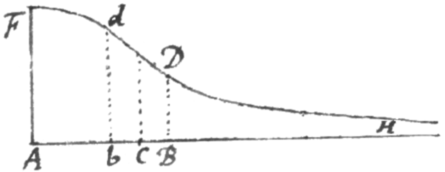 qui fit ponendo , et (distinctionis gratia scriptâ X majuscula pro AB et x minusculâ pro Ab) restat valor areæ illius bdDB. Unde si Ab seu x ponatur nullum habebitur tota area .
qui fit ponendo , et (distinctionis gratia scriptâ X majuscula pro AB et x minusculâ pro Ab) restat valor areæ illius bdDB. Unde si Ab seu x ponatur nullum habebitur tota area .
Ad eandem Curvam inventum est etiam unde rursus juxta præcedentia erit area illa bdDB. Adeoque si AB seu x statuatur infinitum, area adjacens bdH a parte H similiter infinite longa valebit . Siquidem posterior series propter infinitatem denominatorum evanescat.
Ad Curvam æquatione designatam, inventum est . Unde fit . Haec autem evadit infinita sive x fingatur nulla sive X infinita et proinde utraque area AFDB et bdH infinitè magna est, ac solæ partes intermediæ (qualis bdDB) exhiberi possunt. Id quod semper evenit ubi basis x cum in numeratoribus aliquorum tum in denominatoribus aliorum terminorum valoris z reperitur. Ubi vero x in numeratoribus solummodo, ut in primo exemplo, reperitur; valor z competit areæ sitæ ad AB cis parallelè incedentem. Et ubi in denominatoribus tantùm, ut in secundo exemplo; valor ille mutatis omnium terminorum signis, competit areæ omni ultra parallelè incedentem infinitè productæ.
Siquando Curva linea secat Basin inter puncta b et B puta in E, vice areæ habebitur arearum ad diversas Basis partes differentia 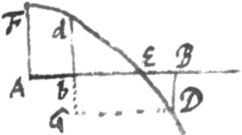 , cui si addatur rectangulum BDGb obtinebitur area dEDG
, cui si addatur rectangulum BDGb obtinebitur area dEDG
Præcipuè autem notandum est quod ubi in valore r terminus aliquis per x unius tantùm dimensionis dividitur, area illi termino correspondens pertinet ad Hyperbolam conicam et proinde per infinitam seriem seorsim exhibenda est; quemadmodum in sequentibus factum.
Sit æquatio ad Curvam et per divisionem fiet . Indeque {.} Et area . Ubi per notas et designo areolas terminis et . Jam ut investigetur, fingo Ab seu x definitam esse et bB indefinitam seu fluentem lineam, quam itaque si dicam y, erit areæ isti Hyperbolicæ adjacenti bB, nempe . Est autem, factâ divisione, &c{.} Adeoque seu . Et proinde tota area quæsita .
Ad eundem modum AB seu X pro definita linea adhiberi potuit et sic prodijsset {.}
Quinetiam si bisecetur bB in C et assumatur AC esse definitæ longitudinis et Cb ac CB indefinitæ. Tum dicto et Cb vel , erit , indeque area Hyperbolica parti Basis bC adjacens . Erit etiam et inde area alteri basis parti CB adjacens {.}
Et harum arearum summa valebit .
Sic æquatione ad Curvam existente, ejus radix erit . Unde fit , et area , hoc est .
Potest autem terminus iste Hyperbolicus utplurimùm com
modè devitari mutando initium Basis, id est, augendo vel minuendo eam per datam aliquam quantitatem. Quemadmodum in exemplo priori ubi erat æquatio ad Curvam, si faciam b esse initium Basis, et fingens Ab cujuslibet esse determinatæ longitudinis puta , pro Basis residuo bB jam scribam x: Hoc est si diminuam Basem per scribendo pro x: evadet , et per divisionem . Unde fit .
Et sic pro initio Basis adhibendo aliud atque aliud ejus punctum, potest area cujusvis curvæ modis infinitis exprimi.
Potuit etiam æquatio in duas series infinitas resolvi prodeunte ubi terminus per x unius tantùm dimensionis divisus non reperitur. Sed hujusmodi series, ubi dimensiones x in unius numeratoribus et alterius denominatoribus infinitè ascendunt, minùs aptæ sunt ex quibus z per computum Arithmeticum obtineri possit, cùm in ejus valore numeri pro speciebus substituuntur.
Instituenti computum hujusmodi numerosum, postquam valor areæ in speciebus habetur, haud aliquid difficile occurret. Tamen in præcedentem doctrinam penitiùs illustrandam exemplum unum et alterum subjungere placuit{.}
Proponatur Hyperbola AD quam æquatio designat, utpote cujus vertex est ad A, et uterque Axis æquatur unitati. Et e præcedentibus Area ejus ADB erit hoc est . Quæ series infinitè producitur multiplicando ultimum terminum continuò per succedaneos terminos hujus progressionis . . . . &c. Nempe primus terminus facit secundum terminum. Hic facit tertium terminum. Hic facit quartum terminum. Et sic in infinitum. Sumatur jam AB cujuslibet longitudinis puta , et 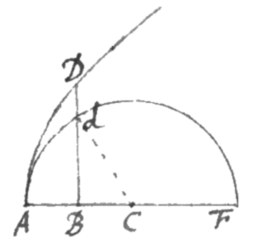 hunc numerum scribe pro x ejusque radicem pro , et primus terminus sive in decimalem fractionem reductus evadit 0,08333333 &c. Hic facit 0,00625 secundum terminum. Hic facit &c tertium terminum. Et sic in infinitum. Terminos autem quos sic gradatim elicio dispono in duas Tabulas affirmativos nempe in unam et negativos in aliam, et addo, ut hic vides.
hunc numerum scribe pro x ejusque radicem pro , et primus terminus sive in decimalem fractionem reductus evadit 0,08333333 &c. Hic facit 0,00625 secundum terminum. Hic facit &c tertium terminum. Et sic in infinitum. Terminos autem quos sic gradatim elicio dispono in duas Tabulas affirmativos nempe in unam et negativos in aliam, et addo, ut hic vides.
.
Dein a summa affirmativorum aufero summam negativorum et restat 0,0893284166257043 quantitas areæ Hyperbolicæ ADB quam quærere oportuit.
Proponatur jam circulus AdF quem æquatio designat, hoc est cujus diameter AF sit unitas, et e præcedentibus area ejus AdB erit {.} In qua serie cùm termini non differant a terminis seriei supra exprimentis aream Hyperbolicam nisi in signis + et −, nihil aliud agendum restat quam ut eosdem numerales terminos cum alijs signis nectamus, subducendo nempe connexas ambarum præfatarum Tabularum summas 0,0898935605036193 a primo termino duplicato 0,1666666666666666 et residuum 0,0767731061630473 erit areæ circularis portio AdB, posito scilicet AB quadrante diametri. Atque ita videre est quod etsi areæ circuli et Hyperbolæ non conferantur ratione geometrica, tamen utraque eodem computo arithmetico prodit.
Inventa circuli portione AdB, exinde tota area facilè eruitur. Nempe radio dC acto, duc Bd seu seu et facti dimidium seu 0,0541265877365274 valebit triangulum CdB, quod adde areæ AdB et habebitur Sector ACd cujus sextuplum 0,7853981633974482 est area tota.
Et hinc obiter exit peripheriæ longitudo 3,1415926535897928, dividendo nempe aream per quadrantem diametri.
Hisce calculum areæ inter Hyperbolam dFD et ejus Asymptoton CA interjectæ subnectimus. Sit C centrum Hyperbolæ et posito , , et ; erit  , et et inde area , et area ac earum summa . Ponamus jam , et Ab vel , existente et : et substituendo hos numeros pro a b et x, primus seriei terminus evadet 0,2, secundus , tertius 0,000004, et sic deinceps ut vides in hac Tabula
, et et inde area , et area ac earum summa . Ponamus jam , et Ab vel , existente et : et substituendo hos numeros pro a b et x, primus seriei terminus evadet 0,2, secundus , tertius 0,000004, et sic deinceps ut vides in hac Tabula
.
Quod si areæ hujus partes Ad et AD seorsim desiderentur subduc minorem AD e majori Ad et restabit . Ubi si 1 scribatur pro a et b, ac pro x, termini in decimales redacti conficient sequentem Tabulam
.
Jam si hæc arearum differentia addatur et auferatur summæ earum priùs inventæ, aggregati dimidium 0,10536,05156,578263 erit major area Ad, et residui dimidium 0,09531,01798,043248 minor AD.
Per easdem Tabulas obtinentur etiam areæ illæ AD et Ad ubi AB et Ab ponuntur sive & si modo numeri in depressiora loca debitè transferantur ut hic videre est
. .
Et sic positis AB & Ab seu et , obtinebitur et .
Ad eundem modum si stantibus CA et , ponantur AB et vel vel elicientur areæ illæ,
Ex inventis hisce areis jam facile est alias per solam additionem et subductionem derivare. Utpote cum sit , arearum pertinentium ad rationes & (hoc est, insistentium partibus Basis et ) summa 0,6931471805599453 erit area AFδβ, existente , ut notum est. Dein cum sit , arearum pertinentium ad et 2 summa 1,0986122886681097 erit area AFδβ, existente . Pariter cùm sit , et , per debitam arearum additionem obtinebitur , existente , et existente . Atque ita cùm sit , et , et , et , et , et , et , et , et . patet aream AFδβ per arearum supra inventarum compositionem inveniri posse, existente ; 1000; 7; aut alio quolibet e recensitis numeris, et stante .Id quod significare volui ut Methodus construendo Logarithmorum Canoni aptissima pateret quæ areas Hyperbolicas (ex quibus Logarithmi facilè deducuntur) tot numeris primis correspondentes, quasi per binas tantum haud molestas operationes determinat. Cæterùm cùm Canon iste ex hoc fonte præ cæteris feliciter depromi videatur, quid si Constructionem ejus coronidis loco perstringam.
Imprimis itaque assumpto 0 pro Logarithmo numeri 1, et 1 pro Logarithmo numeri 10 ut solet, investigandi sunt Logarithmi primorum numerorum 2, 3, 5, 7, 11, 13, 17, 37, dividendo inventas areas Hyperbolicas per 2,3025850929940457 aream nempe correspondentem numero 10, vel quod eodem recidit, multiplicando per ejus reciprocum 0,4342944819032518. Sic enim e.g. Si 0,69314718&c area correspondens numero 2 multiplicetur per 0,43429{&c} facit 0,3010299956639812 Logarithmum numeri 2.
Deinde Logarithmi numerorum omnium in Canone qui ex horum multiplicatione fiunt indagandi sunt per additionem eorum Logarithmorum, ut solet, et loca vacua postmodum interpolanda ope hujus Theorematis. Sit n numerus Logarithmo donandus, x differentia inter illum et proximos numeros hinc inde æqualiter distantes quorum logarithmi habentur ac d semissis differentiæ logarithmorum, et quæsitus Logarithmus numeri n obtinebitur addendo logarithmo minoris numeri. Nam si numeri exponantur per Cp, Cβ et CP. Et existente rectangulo CBD vel ut supra, ac erectis parallelè incedentibus pq et PQ, si n scribatur pro Cβ et x pro βp vel BP erit area pqQP sive ad aream pqδβ sive , ut differentia inter logarithmos extremorum numerorum sive , ad differentiam inter logarithmos minoris et medij, quæ proinde erit , hoc est facta divisione .
Hujus autem seriei duos primos terminos pro Canone construendo sat accuratos existimo etiamsi ad usque quatuordecim vel forte quindecim figurarum loca logarithmi producerentur, si modò numerus logarithmo donandus non sit minor quam 1000. Quod sane calculum haud difficilem præbere potest siquidem x utplurimùm erit unitas vel numerus binarius. Non opus est tamen omnia loca beneficio hujus regular interpolare. Nam logarithmi numerorum qui prodeunt e multiplicatione vel divisione numeri novissimè transacti per numeros quorum logarithmi prius habebantur obtineri possunt per additionem vel subductionem eorum logarithmorum. Quinetiam per differentias logarithmorum et illarum differentiarum secundas differentias tertiasque si opus est, loca vacua expeditiùs impleri possunt, adhibitâ tantùm prædictâ regulâ ubi ad obtinendum illas differentias continuatio aliquot locorum plenorum desideratur.
Eadem methodo Regulæ pro intercalatione Logarithmorum inveniri possunt ubi e tribus numeris dantur logarithmi minoris et medij, vel medij et majoris, idque licet numeri non sint in Arithmetica progressione.
Imò et hujus methodi vestigijs insistendo Regulæ pro construendis artificialium sinuum et Tangentium Tabulis sine adminiculo naturalium haud difficulter depromi possunt. Sed hæc in transitu.
<94>Hactenus Curvarum quæ per æquationes minùs simplices definiuntur Quadraturam mediante reductione in æquationes ex infinite multis terminis simplicibus constantes ostendimus. Cum verò ejusmodi curvæ per finitas etiam æquationes nonnunquam quadrari possint vel saltem comparari cum alijs curvis quarum areæ quodammodo pro cognitis habeantur, quales sunt sectiones conicæ: eapropter sequentes duos Theorematum catalogos in illum usum ope Problematis septimi & octavi ut promisimus constructos, jam visum est adjungere. Horum prior exhibet areas curvarum quæ quadrari possunt, et posterior complectitur curvas quarum areas cum areis conicarum sectionum conferre liceat. In utrisque literæ latinæ d, e, f, g, et h datas quasvis quantitates, x et z bases curvarum, v et y parallelè incedentes , et s ac t areas ut supra denotant. Graecæ autem η et θ quantitati z suffixæ denotant ejusdem z dimensionum numerum sive sit integer vel fractus, sive affirmativus aut negativus. Veluti si sit erit , , sive , vel , & vel . Insuper in valoribus arearum abbreviandi causâ scribitur R vice radicalis illius vel quâ valor incedentis y afficitur.
Catalogus Curvarum aliquot ad rectilineas
figuras relatarum, ope Problematis 7 constructus.
<96>
His adjiciantur sequentia magis generalia Theoremata quibus via ad altiora sternitur.
<97>
Possint et hujusmodi alia adjici, sed ad alterius generis curvas quæ cum Conicis sectionibus conferri possunt jam transeo. Et in hoc Catalogo expositam Curvam linea QEχR (fig ) designatam habes, cujus basis principium sit A, basis AC, parallelè incedens CE areæ principium αχ, et area descripta αχEC. Ejus autem areæ principium sive terminus initialis (quod utplurimùm vel basis principio A insistit, vel ad infinitam distantiam recedit) invenitur quærendo basis longitudinem Aα cùm areæ valor nullus est, et erigendo normalem αχ.
Ad eundem modum Conicam sectionem (fig ) habes designatam linePDG, cujus centrum sit A, vertex a, rectangulæ semidiametri Aa & AP, basis principium A vel a, vel α, basis AB vel aB, vel αB{,} ordinatim applicata BD tangens DT occurrens AB in T, subtensa aD et inscriptum vel ascriptum rectangulum ABDO.
Itaque retentis jam ante definitis literis, erit , , , AB vel , , et ABDP, vel . et præterea siquando ad alicujus areæ determinationem duæ Conicæ Sectiones requiruntur, posterioris area dicetur σ, basis ξ, et parallelè incedens Υ.
Catalogus Curvarum aliquot ad Conicas Sectiones
relatarum ope Problematis 8 constructus.
<98>
< insertion from p 171 >
< text from p 98 resumes >
<99>
<100>
[1] This pag: must bee inserted at the end of pag 59.
[2] pag 60, lin. 6
[3] here a particular figure is required
[4] Fig
[5] 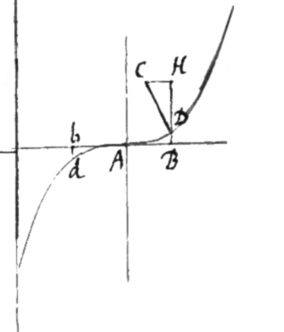
[6] 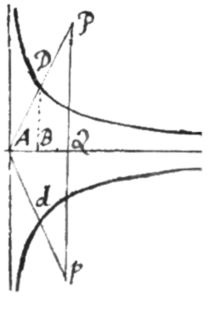
[7] Fig
[8] Fig.
[9] is. fig. for. 5.
[10] pag & fig
[11] Fig
[12] Fig
[13] Fig
