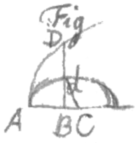Method of Curves and Infinite Series, and application to the Geometry of Curves (Part 3)

<101>

Antequam Theoremata in his Curvarum classibus tradita exemplis illustrare pergam, juvabit observare{.} 1{.} Quòd cùm quantitatum d, e, f, g, h et i signa omnia in æquationibus curvas definientibus affirmativa posuerim, siquando contingant esse negativa in subsequentibus Basis et incedentis linæ Sectionis Conicæ, nec non quæsitæ Areæ valoribus mutari debent{.}

2{.} Numeralium η et θ, ubi negativæ sunt, signa in arearum valoribus sunt etiam mutanda. Quinetiam ipsarum signis mutatis Theoremata novam formam induere possunt{.} Sic in septimo ordine posterioris Catalogi, Theorema tertium, signo ipsius η mutato, evadit $\frac{\mathrm{d}}{{\mathrm{z}}^{\begin{array}{r}-2\mathrm{\eta }\\ +1\end{array}}\sqrt{}\stackrel{\_}{\mathrm{e}+\mathrm{f}{\mathrm{z}}^{-\mathrm{\eta }}}}=\mathrm{y}$. $\frac{1}{{\mathrm{z}}^{-\mathrm{\eta }}}=\mathrm{x}$. &c. hoc est $\frac{\mathrm{d}{\mathrm{z}}^{3\mathrm{\eta }-1}}{\sqrt{}\stackrel{\_}{\mathrm{e}{\mathrm{z}}^{2\mathrm{\eta }}+\mathrm{f}{\mathrm{z}}^{\mathrm{\eta }}}}=\mathrm{y}$. ${\mathrm{z}}^{\mathrm{\eta }}=\mathrm{x}$. $\sqrt{}\stackrel{\_}{\mathrm{f}\mathrm{x}+\mathrm{e}\mathrm{x}\mathrm{x}}=\mathrm{v}$. $\frac{\mathrm{d}}{\mathrm{\eta }\mathrm{e}}in2\mathrm{x}\mathrm{v}-3\mathrm{s}=\mathrm{t}${.} Et sic in alijs.

3. Cujusque ordinis (si secundum prioris Catalogi demas) series utrinque in infinitum continuari potest. Scilicet in tertij quartique ordinis seriebus prioris Catalogi, numeri coefficientes initialium terminorum (2, $-4$, 16, $-96$, 868 &c) generantur multiplicando numeros $-2$, $-4$, $-6$, $-8$, $-10$ &c in se continuò; et subsequentium terminorum coefficientes ex initialibus in tertio <102> ordine derivantur multiplicando gradatim per $-\frac{3}{2}$, $-\frac{5}{4}$, $-\frac{7}{6}$, $-\frac{9}{8}$, $-\frac{11}{10}$ &c, vel in quarto ordine multiplicando per $-\frac{1}{2}$, $-\frac{3}{4}$ $-\frac{5}{6}$, $-\frac{7}{8}$, $-\frac{9}{10}$ &c. Denominatorum verò coefficientes (1, 3, 15, 105 &c) ex ductu numerorum 1, 3, 5, 7, 9 &c in se gradatim oriuntur.

In secundo autem Catalogo series ordinum 1, 2, 3, 4, 9 & 10 ope solius divisionis infinitè producuntur. Sic habito $\frac{\mathrm{d}{\mathrm{z}}^{4\mathrm{\eta }-1}}{\mathrm{e}+\mathrm{f}{\mathrm{z}}^{\mathrm{\eta }}}=\mathrm{y}$, si divisionem ad usque convenientem periodum instituas, orietur exempli gratia $\frac{\mathrm{d}}{\mathrm{f}}{\mathrm{z}}^{3\mathrm{\eta }-1}-\frac{\mathrm{d}\mathrm{e}}{\mathrm{f}\mathrm{f}}{\mathrm{z}}^{2\mathrm{\eta }-1}+\frac{\mathrm{d}\mathrm{e}\mathrm{e}}{{\mathrm{f}}^3}{\mathrm{z}}^{\mathrm{\eta }-1}\frac{-\frac{\mathrm{d}{\mathrm{e}}^3}{{\mathrm{f}}^3}{\mathrm{z}}^{\mathrm{\eta }-1}}{\mathrm{e}+\mathrm{f}{\mathrm{z}}^{\mathrm{\eta }}}=\mathrm{y}${.} Priores tres termini sunt primi ordinis prioris Catalogi et quartus primæ speciei hujus ordinis: unde constat aream valere $\frac{\mathrm{d}}{3\mathrm{\eta }\mathrm{f}}{\mathrm{z}}^{3\mathrm{\eta }}-\frac{\mathrm{d}\mathrm{e}}{2\mathrm{\eta }\mathrm{f}\mathrm{f}}{\mathrm{z}}^{2\mathrm{\eta }}+\frac{\mathrm{d}\mathrm{e}\mathrm{e}}{\mathrm{\eta }{\mathrm{f}}^3}{\mathrm{z}}^{\mathrm{\eta }}-\frac{{\mathrm{e}}^3}{\mathrm{\eta }{\mathrm{f}}^3}\mathrm{s}$; positâ nempe s areâ sectionis conicæ cujus basis x sit $={\mathrm{z}}^{\mathrm{\eta }}$, et incedens applicata $\mathrm{v}=\frac{\mathrm{d}}{\mathrm{e}+\mathrm{f}\mathrm{x}}$.

Quinti autem sextique ordinis series ope duarum Theorematum in quinto ordine prioris Catalogi per debitam Additionem vel subductionem infinitè producuntur, ut et septimi octavique series ope Theorematum in subsequenti sexto ordine; ac undecimi series ope Theorematis in decimo ordine ejusdem prioris Catalogi. Exempli gratia. si præfati quinti ordinis series ultra producenda sit; finge $\mathrm{\theta }=-4\mathrm{\eta }$, et quinti ordinis alterius Catalogi Theorema primum evadet $-8\mathrm{\eta }\mathrm{e}{\mathrm{z}}^{\begin{array}{r}-4\mathrm{\eta }\\ -1\end{array}}-5\mathrm{\eta }\mathrm{f}{\mathrm{z}}^{\begin{array}{r}-3\mathrm{\eta }\\ -1\end{array}}in\frac{1}{2}\sqrt{}\stackrel{\_}{\mathrm{e}+\mathrm{f}{\mathrm{z}}^{\mathrm{\eta }}}=\mathrm{y}$. $\frac{{\mathrm{R}}^3}{{\mathrm{z}}^{4\mathrm{\eta }}}=\mathrm{t}$. Est autem juxta quartum Theorema hujus producendæ seriei, (scripto $-\frac{5\mathrm{\eta }\mathrm{f}}{2}$ pro d,) $-\frac{5\mathrm{\eta }}{2}\mathrm{f}{\mathrm{z}}^{\begin{array}{r}3\mathrm{\eta }\\ -1\end{array}}\sqrt{}\stackrel{\_}{\mathrm{e}+\mathrm{f}{\mathrm{z}}^{\mathrm{\eta }}}=\mathrm{y}$, $\frac{1}{{\mathrm{z}}^{\mathrm{\eta }}}=\mathrm{x}$, $\sqrt{}\stackrel{\_}{\mathrm{f}\mathrm{x}+\mathrm{e}\mathrm{x}\mathrm{x}}=\mathrm{v}$, & $\frac{10\mathrm{f}{\mathrm{v}}^3-15\mathrm{f}\mathrm{f}\mathrm{s}}{12\mathrm{e}}=\mathrm{t}$. Quare subductis prioribus ipsarum y ac t valoribus restabunt $-4\mathrm{\eta }\mathrm{e}{\mathrm{z}}^{\begin{array}{c}-4\mathrm{\eta }\\ -1\end{array}}\sqrt{}\stackrel{\_}{\mathrm{e}+\mathrm{f}{\mathrm{z}}^{\mathrm{\eta }}}=\mathrm{y}$, et $\frac{10\mathrm{d}\mathrm{f}{\mathrm{v}}^3-15\mathrm{f}\mathrm{f}\mathrm{s}}{12\mathrm{e}}-\frac{{\mathrm{R}}^3}{{\mathrm{z}}^{4\mathrm{\eta }}}=\mathrm{t}$. Ipsisque in $\frac{\mathrm{d}}{4\mathrm{\eta }\mathrm{e}}$ ductis, et pro $\frac{{\mathrm{R}}^3}{{\mathrm{z}}^{4\mathrm{\eta }}}$ scripto si placet $\mathrm{x}{\mathrm{v}}^3$, emerget quintum producendæ seriei Theorema $\frac{\mathrm{d}}{{\mathrm{z}}^{\begin{array}{c}4\mathrm{\eta }\\ +1\end{array}}}\sqrt{}\stackrel{\_}{\mathrm{e}+\mathrm{f}{\mathrm{z}}^{\mathrm{\eta }}}=\mathrm{y}$. $\frac{1}{{\mathrm{z}}^{\mathrm{\eta }}}=\mathrm{x}$. $\sqrt{}\stackrel{\_}{\mathrm{f}\mathrm{x}+\mathrm{e}\mathrm{x}\mathrm{x}}=\mathrm{v}$, & $\frac{10\mathrm{d}\mathrm{f}{\mathrm{v}}^3-15\mathrm{d}\mathrm{f}\mathrm{f}\mathrm{s}}{48\mathrm{\eta }\mathrm{e}\mathrm{e}}-\frac{\mathrm{d}\mathrm{x}{\mathrm{v}}^3}{4\mathrm{\eta }\mathrm{e}}=\mathrm{t}$.

4{.} Horum ordinum nonnulli ex alijs etiam possunt aliter derivari, utpote in posteriori Catalogo quintus, sextus, septimus et undecimus ab octavo, ac nonus a decimo, . Adeo ut omisisse potuissem, nisi quod usui esse possint, quamvis non prorsus necessariæ. <103> Nonnullos tamen ordines omisi quos a primo et secundo, nec non a nono decimoque derivasse potuissem, utpote qui denominatoribus magis compositis afficiuntur, et proinde vix ulli unquam usui esse possunt. *^[1]

< insertion from p 101 >

5. Si Curvæ alicujus definiens æquatio ex pluribus æquationibus diversorum ordinum vel diversarum specierum ejusdem ordinis componatur, ejus aream ex areis correspondentibus componere oportet; cavendo tamen ut signis + et − rectè connectantur{.} Nam parallelè incedentes paralleles incedentibus et areæ correspondentes correspondentibus areis non semper sunt simul addendæ vel simul subducendæ; sed aliquando harum summa et illarum differentia sumenda est pro nova linea incedente et area correspondente constituenda. Et hoc fieri debet cùm constituentes areæ positæ sunt ad diversam partem parallelè incedentis . Ut autem hoc incommodum cauti promptiùs devitare possint, singulis arearum valoribus propria signa. (Etiamsi nonnunquam negativa, ut fit in posterioris Catalogi quinto septimóque ordine,) præfixi.

< text from p 103 resumes > < insertion from p 168 >

^[2]6. De Arearum signis observandum est præterea quod $+\mathrm{s}$ vel denotat aream Conicæ sectionis Basi adjacentem esse reliquis quantitatibus in valore t addendam, vel aream ex altera parte ordinatim applicatæ esse subducendam. Et contra $-\mathrm{s}$ ambiguè denotat aream basi adjacentem esse subducendam, vel aream ex altera parte ordinatim applicatæ esse addendam: prout commodum videbitur. Deinde valor ipsius t si affirmativus prodierit, designat aream Curvæ propositæ adjacentem basi ejus: Et contra si fuerit negativus, designat aream ex altera parte ordinatim applicatæ.

7{.} Cæterùm ut Area illa certiùs definiatur, prospiciendum est de limitibus ejus. Et quidem limitum ad Basin, parallelè incedentem, et Curvæ perimetrum, nulla potest esse incertitudo: sed limes initialis sive principium a quo incipit descriptio ejus varias positiones obtinet. In sequentibus exemplis vel est ad initium basis vel ad infinitam distantiam, vel in concursu curvæ cum basi ejus. Sed potest alibi locari. Et ubicunque sit, invenies quærendo illam Basis longitudinem ad quam valor ipsius t evadit nullus, et parallelè incedentem erigendo. Nam erecta illa linea erit limes quæsitus.

8{.} Siqua pars areæ infra basin posita sit, t designabit differentiam ejus et partis supra basin.

9{.} Siquando dimensiones terminorum in valoribus x, v et t nimis altæ vel nimis depressæ obvenerint, ad justum gradum liceat reducere dividendo vel multiplicando toties per datam quamvis quantitatem quæ vices unitatis gerere fingitur, quoties dimensiones illæ sint justo altiores vel depréssiores.

< text from p 103 resumes >

10. Præter præcedentes catalogos possunt etiam Catalogi Curvarum ad alias Curvas in suo genere simplicissimas (ut ad $\sqrt{}\stackrel{\_}{\mathrm{e}+\mathrm{f}{\mathrm{x}}^3}=\mathrm{v}$, vel ad $\mathrm{x}\sqrt{}\stackrel{\_}{\mathrm{e}+\mathrm{f}{\mathrm{x}}^3}=\mathrm{v}$, vel ad $\sqrt{}\stackrel{\_}{\mathrm{e}+\mathrm{f}{\mathrm{x}}^4}=\mathrm{v}$ &c) relatarum construi, eò ut Curvæ cujuslibet propositæ aream ex origine simplicissima possimus derivare, et cum quibus curvis affinitatem habeat cognoscere. Cæterùm præcedentes tandem exemplis aliquot illustremus.

Exemplum 1. Sit QER ejusmodi Conchoidalis 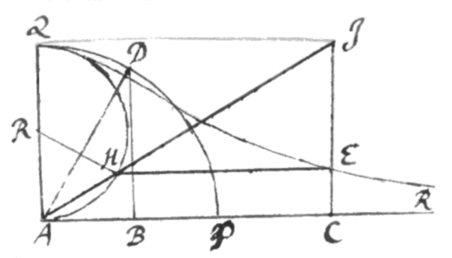ut, Semicirculo QHA descripto et ad diametrum AQ erigatur erecto AC perpendiculo si compleatur parallelogrammum QACI, agatur diagonalis AI semicirculo occurrens in H, et ab H demittatur ad IC normalis HE, punctum E incidat in Curvam. Et quæratur area ACEQ. Dic itaque $\mathrm{AQ}=\mathrm{a}$. $\mathrm{AC}=\mathrm{z}$, $\mathrm{CE}=\mathrm{y}$, et propter continuè proportionales AI, AQ, AH, EC, erit EC, sive $\mathrm{y}=\frac{{\mathrm{a}}^3}{{\mathrm{a}}^2+{\mathrm{z}}^2}$.

Jam ut hæc induat formam æquationum in Catalogis, finge $\mathrm{\eta }=2$ et pro ${\mathrm{z}}^2$ in denominatore scribe ${\mathrm{z}}^{\mathrm{\eta }}$, ac ${\mathrm{a}}^3{\mathrm{z}}^{\frac{1}{2}\mathrm{\eta }-1}$ pro ${\mathrm{a}}^3$ sive ${\mathrm{a}}^3{\mathrm{z}}^{1-1}$ in numeratore, et emerget $\mathrm{y}=\frac{{\mathrm{a}}^3{\mathrm{z}}^{\frac{1}{2}\mathrm{\eta }-1}}{{\mathrm{a}}^2+{\mathrm{z}}^{\mathrm{\eta }}}$, æquatio primæ speciei secundi ordinis posterioris Catalogi; collatisque terminis fit $\mathrm{d}={\mathrm{a}}^3$, $\mathrm{e}={\mathrm{a}}^2$ et $\mathrm{f}=1$; Adeoque $\sqrt{}\frac{{\mathrm{a}}^3}{{\mathrm{a}}^2+{\mathrm{z}}^2}=\mathrm{x}$ $\sqrt{}\stackrel{\_}{{\mathrm{a}}^3-{\mathrm{a}}^2{\mathrm{x}}^2}=\mathrm{v}$, et $\mathrm{x}\mathrm{v}-2\mathrm{s}=\mathrm{t}$.

Ut autem inventi valores x et v ad justum dimensionum numerum reducantur selige datam quamlibet quantitatem, velut a, per quam tanquam unitatem semel multiplicetur ${\mathrm{a}}^3$ in valore x, et in valore v dividatur ${\mathrm{a}}^3$ semel et ${\mathrm{a}}^2{\mathrm{x}}^2$ bis. Et hoc pacto obtinebis $\sqrt{}\frac{{\mathrm{a}}^4}{{\mathrm{a}}^2+{\mathrm{z}}^2}=\mathrm{x}$, $\sqrt{}\stackrel{\_}{{\mathrm{a}}^2-{\mathrm{x}}^2}=\mathrm{v}$, $\mathrm{x}\mathrm{v}-2\mathrm{s}=\mathrm{t}$. Quorum constructio est ejusmodi.

<104>

Centro A intervallo AQ describe quadrantem circuli QDP, in AC cape $\mathrm{AB}=\mathrm{AH}$, erige normalem BD quadranti occurrentem in D, et age AD. Et sectoris ADP duplum æquabitur areæ quæsitæ ACEQ. Est enim $\sqrt{}\frac{{\mathrm{a}}^4}{{\mathrm{a}}^2+{\mathrm{z}}^2}(=$$\sqrt{}\mathrm{AQ}\times \mathrm{EC}=\mathrm{AH})=\mathrm{AB}$ sive x; et $\sqrt{}\stackrel{\_}{{\mathrm{a}}^2-{\mathrm{x}}^2}\left(=\sqrt{}\stackrel{\_}{{\mathrm{AD}}^q-{\mathrm{AB}}^q}\right)=\mathrm{BD}$ sive v; et $\mathrm{x}\mathrm{v}-2\mathrm{s}=2\Delta \mathrm{ADB}-2\mathrm{ABDQ}$ vel etiam $2\Delta \mathrm{ADB}+2\mathrm{BDP}$ hoc est vel $=-2\mathrm{QAD}$ vel $=2\mathrm{DAP}$: quorum valorum affirmativus $2\mathrm{DAP}$ competit areæ ACEQ citra EC, et negativus $2\mathrm{QAD}$ competit areæ RECR ultra EC in infinitum protensæ.

Solutiones Problematum sic inventæ nonnunquam concinnari possunt. Sic in hoc casu actâ RH circuli QHA semidiametro, propter arcus QH, DP æquales, erit sector QRH dimidium sectoris DAP, atque adeò pars quarta superficiei ACEQ.

^[3]Exemplum 2. Sit AGE curva 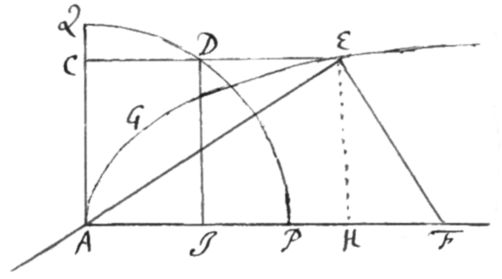quam normæ AEF punctum angulare E describit dum crurum alterum AE interminatum continuò transit per datum punctum A, et alterum EF datæ longitudinis super recta AF positione data prolabitur. Demitte EH ad AF normalem, et comple parallelogrammum AHEC, ac dictis $\mathrm{AC}=\mathrm{z}$, $\mathrm{CE}=\mathrm{y}$, et $\mathrm{EF}=\mathrm{a}$, propter HF, HE, HA continuè proportionales erit HA sive $\mathrm{y}=\frac{{\mathrm{z}}^2}{\sqrt{}\stackrel{\_}{{\mathrm{a}}^2-{\mathrm{z}}^2}}$. Jam ut innotescat area AGEC, finge ${\mathrm{z}}^2={\mathrm{z}}^{\mathrm{\eta }}$, sive $2=\mathrm{\eta }$ et inde fiet $\frac{{\mathrm{z}}^{\frac{3}{2}\mathrm{\eta }-1}}{\sqrt{}\stackrel{\_}{{\mathrm{a}}^2-{\mathrm{z}}^{\mathrm{\eta }}}}=\mathrm{y}$. Ubi cum z sit fractæ dimensionis in numeratore, deprime valorem y dividendo per ${\mathrm{z}}^{\frac{1}{2}\mathrm{\eta }}$ et fiet $\frac{{\mathrm{z}}^{\mathrm{\eta }-1}}{\sqrt{}\stackrel{\_}{{\mathrm{a}}^2{\mathrm{z}}^{-\mathrm{\eta }}-1}}=\mathrm{y}$, æquatio secundæ speciei septimi ordinis posterioris Catalogi. Ac terminis collatis evadet $\mathrm{d}=1$, $\mathrm{e}=-1$, et $\mathrm{f}={\mathrm{a}}^2$. Adeoque ${\mathrm{z}}^2\left(=\frac{1}{{\mathrm{z}}^{-\mathrm{\eta }}}\right)={\mathrm{x}}^2$. $\sqrt{}\stackrel{\_}{{\mathrm{a}}^2-{\mathrm{x}}^2}=\mathrm{v}$ & $\mathrm{s}-\mathrm{x}\mathrm{v}=\mathrm{t}$. Cùm itaque x et z æquentur, et sit $\sqrt{}\stackrel{\_}{{\mathrm{a}}^2-{\mathrm{x}}^2}=\mathrm{v}$ æquatio ad circulum cujus semidiameter est a: centro A intervallo a sive EF describatur circulus PDQ cui occurrat CE in D, et compleatur parallelogrammum ACDI, eritque $\mathrm{AC}=\mathrm{z}$, $\mathrm{CD}=\mathrm{v}$, et area quæsita $\mathrm{AGEC}\left(=\mathrm{s}-\mathrm{x}\mathrm{v}=\mathrm{ACDP}-\mathrm{ACDI}\right)=\mathrm{IDP}$.

Exemplum 3. Sit AGE Cissois ad Circulum ADQ diametro <105> AQ descriptum pertinens. Agatur 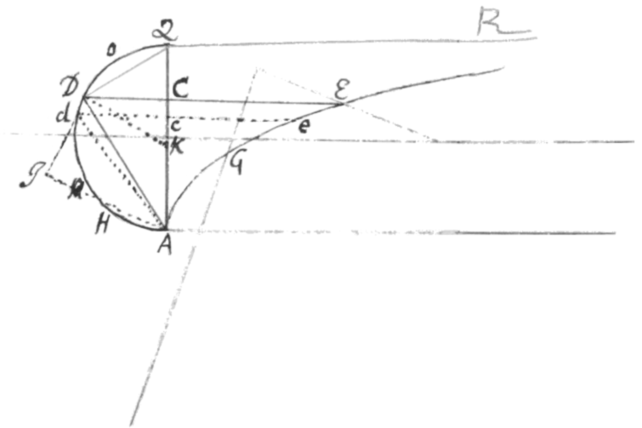DCE diametro normalis et curvis occurrens in D et E. Et nominatis $\mathrm{AC}=\mathrm{z}$, $\mathrm{CE}=\mathrm{y}$ et $\mathrm{AQ}=\mathrm{a}$, propter CD, CA, CE continuè proportionales erit CE $\mathrm{y}=\frac{{\mathrm{z}}^2}{\sqrt{}\stackrel{\_}{\mathrm{a}\mathrm{z}-{\mathrm{z}}^2}}$, ac dividendo per z, fit $\mathrm{y}=\frac{\mathrm{z}}{\sqrt{}\stackrel{\_}{\mathrm{a}{\mathrm{z}}^{-1}-1}}$. Est itaque ${\mathrm{z}}^{-1}={\mathrm{z}}^{\mathrm{\eta }}$ sive $-1=\mathrm{\eta }$ et inde $\frac{{\mathrm{z}}^{-2\mathrm{\eta }-1}}{\sqrt{}\stackrel{\_}{\mathrm{a}{\mathrm{z}}^{\mathrm{\eta }}-1}}=\mathrm{y}$, æquatio tertiæ speciei, septimi ordinis posterioris catalogi. Collatisque terminis fit $\mathrm{d}=1$. $\mathrm{e}=-1$. et $\mathrm{f}=\mathrm{a}$. Adeoque $\mathrm{z}\left(=\frac{1}{{\mathrm{z}}^{\mathrm{\eta }}}\right)=\mathrm{x}$. $\sqrt{}\stackrel{\_}{\mathrm{a}\mathrm{x}-{\mathrm{x}}^2}=\mathrm{v}$. et $3\mathrm{s}-2\mathrm{x}\mathrm{v}=\mathrm{t}$. Quare est $\mathrm{AC}=\mathrm{x}$, $\mathrm{CD}=\mathrm{v}$, et inde $\mathrm{ACDH}=\mathrm{s}$, adeoque $3\mathrm{ACDH}$$4\Delta \mathrm{ADC}\left(=3\mathrm{s}-2\mathrm{x}\mathrm{v}=\mathrm{t}\right)=$ areæ Cissoidali ACEGA. Vel quod perinde est, $3segment:\mathrm{ADHA}=are\ae \mathrm{ADEGA}$. $4seg\mathrm{ADHA}=are\ae \mathrm{AHDEGA}$

Exemplum 4. Esto PE prima Conchoides 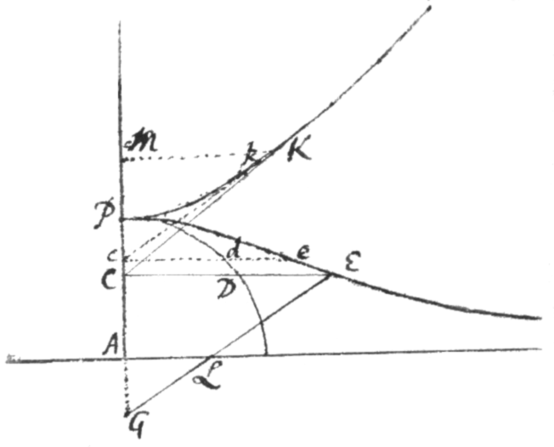Veterum centro G, Asymptoto AL et intervallo LE descripta. Age GAP axin ejus ac demitte EC ordinatim applicatam. Dictisque $\mathrm{AC}=\mathrm{z}$, $\mathrm{CE}=\mathrm{y}$, $\mathrm{GA}=\mathrm{b}$, et $\mathrm{AP}=\mathrm{c}$, propter proportionales $\mathrm{AC}.\mathrm{CE}-\mathrm{AL}\colon\colon \mathrm{GC}.\mathrm{CE}$, erit CE sive $\mathrm{y}=\frac{\mathrm{b}+\mathrm{z}}{\mathrm{z}}\sqrt{}\stackrel{\_}{{\mathrm{c}}^2-{\mathrm{z}}^2}$.

Jam ut ejus area PEC exhinc inveniatur, partes applicatæ CE seorsim considerandæ sunt. Et quidem si illa CE ita dividatur in D ut sit $\mathrm{CD}=\sqrt{}\stackrel{\_}{{\mathrm{c}}^2-{\mathrm{z}}^2}$ ac $\mathrm{DE}=\frac{\mathrm{b}}{\mathrm{z}}\sqrt{}\stackrel{\_}{{\mathrm{c}}^2-{\mathrm{z}}^2}$ erit CD ordinatim applicata circuli centro A intervallo AP descripti: adeoque pars areæ PDC innotescet, et restabit pars altera DPED invenienda. Cùm itaque DE (pars applicatæ quacum describitur) valeat $\frac{\mathrm{b}}{\mathrm{z}}\sqrt{}\stackrel{\_}{{\mathrm{c}}^2-{\mathrm{z}}^2}$, suppone $2=\mathrm{\eta }$, et evadet $\frac{\mathrm{b}}{\mathrm{z}}\sqrt{}\stackrel{\_}{{\mathrm{c}}^2-{\mathrm{z}}^{\mathrm{\eta }}}=\mathrm{DE}$, æquatio primæ speciei quinti ordinis posterioris Catalogi. Collatisque terminis, fiet $\mathrm{d}=\mathrm{b}$ $\mathrm{e}={\mathrm{c}}^2$ et $\mathrm{f}=-1$; atque adeò $\frac{1}{\mathrm{z}}\left(=\sqrt{}\frac{1}{{\mathrm{z}}^{\mathrm{\eta }}}=\mathrm{x}\right)$. $\sqrt{}\stackrel{\_}{-1+\mathrm{c}\mathrm{c}\mathrm{x}\mathrm{x}}=\mathrm{v}$. et $2\mathrm{b}\mathrm{c}\mathrm{c}\mathrm{s}-\frac{\mathrm{b}{\mathrm{v}}^3}{\mathrm{x}}=\mathrm{t}$.

<106>

His inventis redige ad justum dimensionum numerum multiplicando terminos nimis depressos ac dividendo nimis altos per datam quamvis quantitatem. Id quod si fiet per c, prodibit $\frac{{\mathrm{c}}^2}{\mathrm{z}}=\mathrm{x}$. $\sqrt{}\stackrel{\_}{-{\mathrm{c}}^2+{\mathrm{x}}^2}=\mathrm{v}$, & $\frac{2\mathrm{b}\mathrm{s}}{\mathrm{c}}-\frac{\mathrm{b}{\mathrm{v}}^3}{\mathrm{c}\mathrm{x}}=\mathrm{t}$ Et horum constructio est ejusmodi.

Centro A, vertice principali P, et parametro $2\mathrm{AP}$ Hyperbolam PK describe. Deinde a puncto C age rectam CK quæ tangat Hyperbolam in K: et erit ut AP ad $2\mathrm{AG}$ ita area CKPC ad aream quæsitam DPED.

Exemplum 5. Norma GFE ita circa polum G rotante ut ejus punctum angulare F super recta AF positione data continuò prolabatur: concipe curvam PE a puncto quolibet E in crure EF sito describi. Jam ut inveniatur hujus area, demitte GA et EH ad rectam AF perpendiculares et completo parallelogrammo AHEC, dic $\mathrm{AC}=\mathrm{z}$, $\mathrm{CE}=\mathrm{y}$, $\mathrm{AG}=\mathrm{b}$ et $\mathrm{EF}=\mathrm{c}$, et propter proportionals $\mathrm{HF}.\mathrm{EH}\colon\colon$$\mathrm{AG}.\mathrm{AF}$, erit $\mathrm{AF}=\frac{\mathrm{b}\mathrm{z}}{\sqrt{}\stackrel{\_}{\mathrm{c}\mathrm{c}-\mathrm{z}\mathrm{z}}}$. Adeoque CE sive $\mathrm{y}=\frac{\mathrm{b}\mathrm{z}}{\sqrt{}\stackrel{\_}{{\mathrm{c}}^2-{\mathrm{z}}^2}}-\sqrt{}\stackrel{\_}{{\mathrm{c}}^2-{\mathrm{z}}^2}$ Cùm autem $\sqrt{}\stackrel{\_}{\mathrm{c}\mathrm{c}-{\mathrm{z}}^2}$ sit ordinatim applicata circuli semidiametro c descripti: circa centrum A describe talem circulum PDQ, eique CE producta 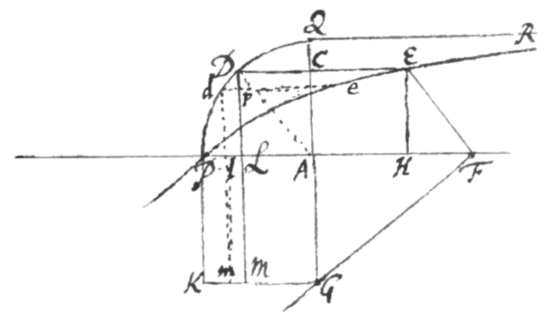occurat in D, et erit $\mathrm{DE}=\frac{\mathrm{b}\mathrm{z}}{\sqrt{}\stackrel{\_}{{\mathrm{c}}^2-{\mathrm{z}}^2}}$: cujus æquationis ope restat area PDEP vel DERQ determinanda. Supponatur ergo $\mathrm{\eta }=2$ et evadet $\mathrm{DE}=\frac{\mathrm{b}{\mathrm{z}}^{\mathrm{\eta }-1}}{\sqrt{}\stackrel{\_}{\mathrm{c}\mathrm{c}-{\mathrm{z}}^{\mathrm{\eta }}}}$ æquatio primæ speciei quarti ordinis prioris catalogi. Et collatis terminis fiet $\mathrm{b}=\mathrm{d}$, $\mathrm{c}\mathrm{c}=\mathrm{e}$, et $-1=\mathrm{f}$; adeoque $-\mathrm{b}\sqrt{}\stackrel{\_}{\mathrm{c}\mathrm{c}-\mathrm{z}\mathrm{z}}\left(=-\mathrm{b}\mathrm{R}\right)=\mathrm{t}$. Jam cum valor t negativus existat, et inde area per t designata jaceat ultra lineam DE; ut ejus limes initialis inveniatur quære illam ipsius z longitudinem qua t evadit nulla et invenies esse c. Quare produc AC ad Q ut sit $\mathrm{AQ}=\mathrm{c}$, et erige applicatam QR et erit DQRED area illa cujus <107> valor jam inventus est $-\mathrm{b}\sqrt{}\stackrel{\_}{\mathrm{c}\mathrm{c}-\mathrm{z}\mathrm{z}}$.

Quod si quantitatem areæ PDE juxta basin AC positæ et cum ea coextensæ desideres, possis ignoto limite QR sic determinare. A valore quem t ad basis longitudinem AC sortita est subduc valorem ejus ad initium basis. hoc est a $-\mathrm{b}\sqrt{}\stackrel{\_}{\mathrm{c}\mathrm{c}-\mathrm{z}\mathrm{z}}$ subduc $-\mathrm{b}\mathrm{c}$ et proveniet quantitas $\mathrm{b}\mathrm{c}-\mathrm{b}\sqrt{}\stackrel{\_}{\mathrm{c}\mathrm{c}-\mathrm{z}\mathrm{z}}$ quam quæris. Comple ergo parallelogrammum PAGK et ad AP demitte normalem DM quæ cum GK occurrat in M et erit parallelogrammum PLMK æquale areæ PDE.

Siquando æquatio curvam aliquam definiens non reperiatur in Catalogis, neque ad simpliciores terminos ope divisionis vel alio pacto reduci possit: transformanda est in alias affinium Curvarum æquationes pro more in Problemate 8 ostenso, donec tandem obvenerit aliqua cujus area ex Catalogis innotescat. Et conatibus omnimodo institutis, si nulla talis obveniat, certum est Curvam propositam neque cum figuris rectilineis neque cum Conicis Sectionibus comparari posse.

Ad eundem modum cùm de Curvis Mechanicis agitur illæ imprimis transformandæ sunt in æquales Geometricas prout in eodem Problema 8 ostensum fuit, ac deinde Geometricarum areæ ex Catalogis eliciendæ. Cujus rei accipe sequens exemplum.

Exemplum 6{.} Proponatur figura arcuum cujusvis Conicæ Sectionis ad sinus rectos applicatorum determinanda. Utpote sit A centrum Conicæ Sectionis, AQ & AR semiaxes, CD ordinatim applicata ad axin AR, et PD perpendiculum ad punctum D. Sit etiam AE dicta figura Mechanica occurrens CD in E, et ex ejus natura præfinita erit CE æqualis arcui QD. Quæritur itaque area AEC, vel parallelogrammo ACEF completo quæritur excessus AEF. In quem finem sit a latus rectum Conicæ Sectionis, et <108> b latus transversum sive $2\mathrm{AQ}$. sit etiam $\mathrm{AC}=\mathrm{z}$, et $\mathrm{CD}=\mathrm{y}$, eritque $\sqrt{}\stackrel{\_}{\frac{1}{4}\mathrm{b}\mathrm{b}+\frac{\mathrm{b}}{\mathrm{a}}\mathrm{z}\mathrm{z}}=\mathrm{y}$ æquatio ad conicam sectionem, ut notum est. Erit etiam $\mathrm{PC}=\frac{\mathrm{b}}{\mathrm{a}}\mathrm{z}$ et inde $\mathrm{PD}=\sqrt{}\stackrel{\_}{\frac{1}{4}\mathrm{b}\mathrm{b}+\frac{\mathrm{b}\mathrm{b}+\mathrm{a}\mathrm{b}}{\mathrm{a}\mathrm{a}}\mathrm{z}\mathrm{z}}$ {.} Atque adeò cùm sit fluxio arcus QD ad fluxionem Basis AC ut PD ad CD, si fluxio basis supponatur 1 erit arcus illius QD, sive applicatæ CE fluxio 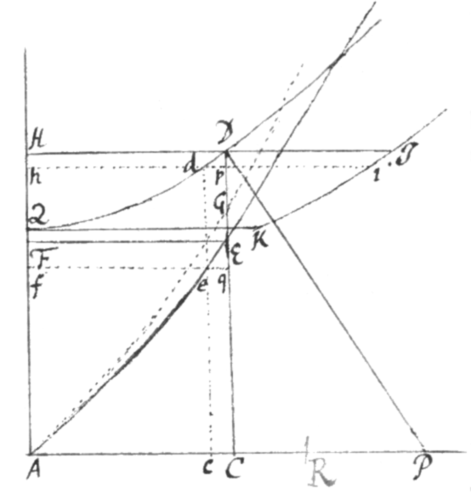$\sqrt{}\frac{\frac{1}{4}\mathrm{b}\mathrm{b}+\frac{\mathrm{b}\mathrm{b}+\mathrm{a}\mathrm{b}}{\mathrm{a}\mathrm{a}}\mathrm{z}\mathrm{z}}{\frac{1}{4}\mathrm{b}\mathrm{b}+\frac{\mathrm{b}}{\mathrm{a}}\mathrm{z}\mathrm{z}}$. Hanc duc in FE sive z et proveniet $\mathrm{z}\sqrt{}\frac{\frac{1}{4}\mathrm{b}\mathrm{b}+\frac{\mathrm{b}\mathrm{b}+\mathrm{a}\mathrm{b}}{\mathrm{a}\mathrm{a}}\mathrm{z}\mathrm{z}}{\frac{1}{4}\mathrm{b}\mathrm{b}+\frac{\mathrm{b}}{\mathrm{a}}\mathrm{z}\mathrm{z}}$ fluxio areæ AEF adeoque si in applicata CD capias $\mathrm{CG}=\mathrm{z}\sqrt{}\frac{\frac{1}{4}\mathrm{b}\mathrm{b}+\frac{\mathrm{b}\mathrm{b}+\mathrm{a}\mathrm{b}}{\mathrm{a}\mathrm{a}}\mathrm{z}\mathrm{z}}{\frac{1}{4}\mathrm{b}\mathrm{b}+\frac{\mathrm{b}}{\mathrm{a}}\mathrm{z}\mathrm{z}}$, area AGC quam illa CG super AC incedens describet, æquabitur areæ AEF, et erit AG curva geometrica. Quæritur itaque area AGC. Et in unc finem substituatur ${\mathrm{z}}^{\mathrm{\eta }}$ pro $\mathrm{z}\mathrm{z}$ in æquatione novissima et evadet ${\mathrm{z}}^{\begin{array}{r}\mathrm{\eta }\\ -1\end{array}}\sqrt{}\frac{\frac{1}{4}\mathrm{b}\mathrm{b}+\frac{\mathrm{b}\mathrm{b}+\mathrm{a}\mathrm{b}}{\mathrm{a}\mathrm{a}}{\mathrm{z}}^{\mathrm{\eta }}}{\frac{1}{4}\mathrm{b}\mathrm{b}+\frac{\mathrm{b}}{\mathrm{a}}{\mathrm{z}}^{\mathrm{\eta }}}=\mathrm{CG}$, æquatio secundæ speciei undecimi ordinis posterioris Catalogi. Et collatis utrobique terminis fit $\mathrm{d}=1$. $\mathrm{e}=\frac{1}{4}\mathrm{b}\mathrm{b}=\mathrm{g}$. $\mathrm{f}=\frac{\mathrm{b}\mathrm{b}+\mathrm{a}\mathrm{b}}{\mathrm{a}\mathrm{a}}$, et $\mathrm{h}=\frac{\mathrm{b}}{\mathrm{a}}$; adeoque $\sqrt{}\stackrel{\_}{\frac{1}{4}\mathrm{b}\mathrm{b}+\frac{\mathrm{b}}{\mathrm{a}}\mathrm{z}\mathrm{z}}=\mathrm{x}$, $\sqrt{}\stackrel{\_}{-\frac{1}{4}\frac{{\mathrm{b}}^3}{\mathrm{a}}+\frac{\mathrm{a}+\mathrm{b}}{\mathrm{a}}\mathrm{x}\mathrm{x}}=\mathrm{v}$ & $\frac{\mathrm{a}}{\mathrm{b}}\mathrm{s}=\mathrm{t}$. Hoc est $\mathrm{CD}=\mathrm{x}$. $\mathrm{DP}=\mathrm{v}$ et $\frac{\mathrm{a}}{\mathrm{b}}\mathrm{s}=\mathrm{t}$. Et inventorum talis est constructio. Ad Q erige QK perpendicularem et æqualem QA et huic parallelam æqualem vero DP age HI per punctum D. Et linea KI in quam HI terminatur erit Sectio Conica areaque comprehensa HIKQ ad aream quæsitam AEF ut b ad a, sive ut PC ad AC.

Nota, si mutes signum b, sectio Conica cujus arcui recta CG æquatur, evadet Ellipsis; et præterea si fiat $\mathrm{b}=-\mathrm{a}$ Ellipsis evadet circulus: In quo casu linea KI fit recta parallela AQ.

<109>

Postquam Curvæ alicujus area sic inventa fuerit; de constructionis demonstratione consulendum est, quacum sine Computo Algebraico quantùm liceat contexta ornetur Theorema ut evadat publicæ notitiæ dignum. Estque demonstrandi methodus generalis quam sequentibus exemplis illustrare conabor.

Demonstratio Constructionis in Exemplo 5. In arcu PQ sume punctum d proximum ad D et age de ac dm parallelas DE ac DM et occurrentes DM et AP in p et l: et erit DEed momentum areæ PDEP et LMmt momentum areæ LMKP. Age semidiametrum AD, et concipe indefinitè exiguum arcum Dd esse instar rectæ et triangula Dpd et ALD erunt similia, adeoque $\mathrm{Dp}.\mathrm{pd}\colon\colon \mathrm{AL}.\mathrm{LD}$. Est autem $\mathrm{HF}.\mathrm{EH}\colon\colon \mathrm{AG}.\mathrm{AF}$, hoc est $\mathrm{AL}.\mathrm{LD}\colon\colon \mathrm{ML}.\mathrm{DE}$. Et proinde $\mathrm{Dp}.\mathrm{pd}\colon\colon \mathrm{ML}.\mathrm{DE}$. Quare $\mathrm{Dp}\times \mathrm{DE}=\mathrm{pd}\times \mathrm{ML}$. Hoc est momentum DEed æquale momento LMml. Et cùm hoc de quibuslibet contemporaneis momentis indeterminatè demonstretur, patet singula momenta areaæ PDEP esse singulis contemporaneis momentis areæ PLMK æqualia, adeoque totas areas ex istis momentis compositas æquari. Q.E.D.

Demonstratio Constructionis in exemplo 3. Esto DEed momentum superficiei AHDE ac AdDA contemporaneum momentum segmenti ADH age semidiametrum DK, et de occurrat AQ in c, estque $\mathrm{Cc}.\mathrm{Dd}\colon\colon \mathrm{DC}.\mathrm{DK}$. Præterea est $\mathrm{DC}.\mathrm{QA}\left(2\mathrm{DK}\right)\colon\colon \mathrm{AC}.\mathrm{DE}$. Adeoque $\mathrm{Cc}.2\mathrm{Dd}\left(\colon\colon \mathrm{DC}.2\mathrm{DK}\right)\colon\colon \mathrm{AC}.\mathrm{DE}$. et $\mathrm{Cc}\times \mathrm{DE}=2\mathrm{Dd}\times \mathrm{AC}\times$. Jam ad periferiæ momentum Dd rectà productum (i.e. ad tangentem circuli) demitte normalem AI et erit AI æqualis AC, adeoque $2\mathrm{Dd}\times \mathrm{AC}\left(=2\mathrm{Dd}\times \mathrm{AI}\right)=4\text{triangulis}\mathrm{ADd}$. Quare $4\text{triang}\mathrm{ADd}$$=\mathrm{Cc}\times \mathrm{DE}=$ momento DEed. Spatij ergo AHDE singula momenta sunt quadrupla momentorum contemporaneorum segmenti ADH et proinde totum illud spatium quadruplum totius segmenti{.} Q.E.D.

Demonstratio constructionis in Exemplo 4. Parallelam CE age indefinitè parùm distantem ce, et Hyperbolæ tangentem Ck ac demitte KM rectam ad AP: Et ex Hyperbolæ natura erit $\mathrm{AC}.\mathrm{AP}\colon\colon \mathrm{AP}.\mathrm{AM}${.} Adeoque ${\mathrm{AG}}^q.{\mathrm{GL}}^q\left(\colon\colon {\mathrm{AC}}^q.{\mathrm{LE}}^q\text{sive}{\mathrm{AP}}^q\right)\colon\colon {\mathrm{AP}}^q.{\mathrm{AM}}^q$ ac divisim ${\mathrm{AG}}^q.{\mathrm{AL}}^q\left({\mathrm{DE}}^q\right)$$\colon\colon {\mathrm{AP}}^q.{\mathrm{AM}}^q-{\mathrm{AP}}^q\left({\mathrm{MK}}^q\right)$. Et inversè $\mathrm{AG}.\mathrm{AP}\colon\colon \mathrm{DE}.\mathrm{MK}$. Est autem <110> areola DEed ad triangulum CKc ut altitudo DE ad semissem altitudinis KM. Hoc est, ut AG ad $\frac{1}{2}\mathrm{AP}$. Quare omnia spatij PDE momenta ad omnia contemporanea momenta spatij PKC sunt ut AG ad $\frac{1}{2}\mathrm{AP}$. Et proinde tota illa spatia sunt in eadem ratione. Q.E.D.

Demonstratio Constructionis in Exemplo 6. Parallelam et proximam CD age cd et occurrentem curvæ AE in e age hi & fe occurrentes DC in p et q. Et erit ex Hypothesi $\mathrm{Dd}=\mathrm{Eq}$ et ex similitudine triangulorum Dpd, DCP erit $\mathrm{Dp}.\mathrm{Dd}\left(\mathrm{Eq}\right)\colon\colon$$\mathrm{CP}.\mathrm{PD}\left(\mathrm{HI}\right)$. Adeoque $\mathrm{Dp}\times \mathrm{HI}=\mathrm{Eq}\times \mathrm{CP}$, et inde $\mathrm{Dp}\times \mathrm{HI}(\text{moment}$$\mathrm{HIih}).\mathrm{Eq}\times \mathrm{AC}(\text{moment}\mathrm{EFfe})\colon\colon \mathrm{Eq}\times \mathrm{CP}.\mathrm{Eq}\times \mathrm{AC}\colon\colon \mathrm{CP}.\mathrm{AC}$. Quare cum PC et AC sint in data ratione lateris transversi ad latus rectum Conicæ Sectionis QD, et arearum HIQK et AEF momenta HIih & EFfe in illâ ratione, erunt ipsæ areæ in eâdem ratione. Q.E.D.

In hujusmodi demonstrationibus observandum est quod quantitates pro æqualibus habeo quarum ratio est æqualitatis. Et ratio æqualitatis censenda est quæ minùs differt ab æqualitate quàm qualibet inæqualis ratio potest assignari. Sic in postremâ demonstratione posui rectangulum $\mathrm{Eq}\times \mathrm{AC}$, sive FEqf æquale spatio FEef quia (propter differentiam Eqe infinite minorem ipsis sive respectu ipsarum nullam) non habent rationem inæqualitatis. Et eadem de causa posui $\mathrm{DP}\times \mathrm{HI}=\mathrm{HIih}$, & sic in alijs.

Hac methodo probandi curvas per æqualitatem vel datam rationem momentorum æquales esse vel datam rationem habere hic usus sum quòd cùm methodis in his rebus usitatis affinitatem habeat; sed magis naturalis videtur quæ genesi superficierum ex fluendi motu innititur. Sic si constructio in Exemplo 2 demonstranda sit; Ex natura circuli est fluxio rectæ ID ad fluxionem rectæ IP, ut AI ad ID: Estque AI ad ID ut ID ad CE ex natura Curvæ AGE: et proinde $\mathrm{CE}\times flux:\mathrm{ID}=\mathrm{ID}\times flux:\mathrm{IP}$. Sed $\mathrm{CE}\times flux:\mathrm{ID}$= fluxioni areæ ACEG, et $\mathrm{ID}\times flux\mathrm{IP}=$ fluxioni areæ PDI. Et propterea areæ illæ æqualiter fluendo genitæ æquales erunt. Q.E.D.

Plenioris illustrationis gratia adjiciam demonstrationem Constructionis qua Cissoidis area in Exemplo 3 determinatur. <111> Lineæ punctim notatæ in schemate deleantur, et agatur DQ et Cissoidis Asymptoton QR: Et ex natura circuli est ${\mathrm{DQ}}^q=\mathrm{AQ}\times \mathrm{CQ}$, et inde per Problema 1 $2\mathrm{DQ}\times flux:\text{ipsius}\mathrm{DQ}=$$\mathrm{AQ}\times flux.\mathrm{CQ}$. Adeoque $\mathrm{AQ}.\mathrm{DQ}\colon\colon 2flux:\mathrm{DQ}.flux:\mathrm{CQ}$. Est et ex natura Cissoidis $\mathrm{ED}.\mathrm{AD}\colon\colon \mathrm{AQ}.\mathrm{DQ}$. Quare $\mathrm{ED}.\mathrm{AD}\colon\colon 2flux:\mathrm{DQ}.flux:\mathrm{CQ}$. Et $\mathrm{ED}\times flux\mathrm{CQ}=$$\mathrm{AD}\times 2flux:\mathrm{DQ}$ sive $=4\times \frac{1}{2}\mathrm{AD}\times flux:\mathrm{DQ}$. Jam cùm DQ perpendicularis sit ad terminum ipsius AD circa A gyrantis, est $\frac{1}{2}\mathrm{AD}\times flux\mathrm{DQ}=$ fluxioni generanti aream ADOQ{.} Est et ejus quadruplum $\mathrm{ED}\times flux\mathrm{CQ}=$ fluxioni generanti Cissoidalem aream QREDO. Et proinde area illa infinitè longa QREDO generatur quadrupla alterius ADOQ. Q.E.D.

Scholium.

Per præcedentes catalogos non tantùm areæ curvarum sed et aliæ cujuscunque generis quantitates analoga fluendi ratione generatæ, e fluxionibus derivari possunt. Idque mediante hoc Theoremate, Quod quantitas cujuscunque generis sit ad unitatem congeneram ut area Curvæ ad unitatem superficialem, si modò fluxio quantitatem illam generans sit ad unitatem sui generis ut fluxio generans aream ad unitatem sui generis, hoc est ut linea super Basi normaliter incedens qua area ilia describitur, ad unitatem linearem. Et proinde si fluxio qualiscunque exponatur per ejusmodi lineam incedentem quantitas ab illa fluxione generata exponetur per aream ab illa incedente descriptam{.} Vel si fluxio per eosdem terminos Algebraicos cum incedente linea exponatur, quantitas generata exponetur per eosdem cum area descripta. Æquatio itaque quæ fluxionem <112> cujuscunque generis exhibet quærenda est in prima collumna Catalogorum, et valor t in ultima collumna indicabit quantitatem generatam.

Quemadmodum si $\sqrt{}\stackrel{\_}{1+\frac{9\mathrm{z}}{4\mathrm{a}}}$ fluxionem cujuscunque generis exhibeat, pone æqualem y, et ut ad formam æquationum in catalogis reducatur substitue ${\mathrm{z}}^{\mathrm{n}}$ pro z, sic enim evadet ${\mathrm{z}}^{\begin{array}{r}\mathrm{\eta }\\ -1\end{array}}\sqrt{}\stackrel{\_}{1+\frac{9}{4\mathrm{a}}{\mathrm{z}}^{\mathrm{\eta }}}=\mathrm{y}$, æquatio primæ speciei tertij ordinis prioris Catalogi et collatis terminis fiet $\mathrm{d}=1$, $\mathrm{e}=1$, $\mathrm{f}=\frac{9}{4\mathrm{a}}$, et inde $\frac{8\mathrm{a}+18\mathrm{z}}{27}\sqrt{}\stackrel{\_}{1+\frac{9\mathrm{z}}{4\mathrm{a}}}\left(=\frac{2\mathrm{d}}{3\mathrm{\eta }\mathrm{f}}{\mathrm{R}}^3\right)=\mathrm{t}$. Est itaque $\frac{8\mathrm{a}+18\mathrm{z}}{27}\sqrt{}\stackrel{\_}{1+\frac{9\mathrm{z}}{4\mathrm{a}}}$ quantitas quæ generatur fluxione $\sqrt{}\stackrel{\_}{1+\frac{9\mathrm{z}}{4\mathrm{a}}}$.

Atque ita si $\sqrt{}\stackrel{\_}{1+\frac{16{\mathrm{z}}^{\frac{2}{3}}}{9{\mathrm{a}}^{\frac{2}{3}}}}$ designet fluxionem, per debita{m} reductionem (extrahendo ${\mathrm{z}}^{\frac{2}{3}}$ e radicali, et scribendo ${\mathrm{z}}^{\mathrm{\eta }}$ pro ${\mathrm{z}}^{-\frac{2}{3}}$) habebitur $\frac{1}{{\mathrm{z}}^{\begin{array}{r}\mathrm{\eta }\\ +1\end{array}}}\sqrt{}\stackrel{\_}{{\mathrm{z}}^{\mathrm{\eta }}+\frac{16}{9{\mathrm{a}}^{\frac{2}{3}}}}=\mathrm{y}$, æquatio secundæ speciei quinti ordinis posterioris Catalogi, et collatis terminis fit $\mathrm{d}=1$, $\mathrm{e}=\frac{16}{9{\mathrm{a}}^{\frac{2}{3}}}$, et $\mathrm{f}=1$, Adeoque ${\mathrm{z}}^{\frac{2}{3}}\left(=\frac{1}{{\mathrm{z}}^{\mathrm{\eta }}}\right)=\mathrm{x}\mathrm{x}$, $\sqrt{}\stackrel{\_}{1+\frac{16\mathrm{x}\mathrm{x}}{9{\mathrm{a}}^{\frac{2}{3}}}}=\mathrm{v}$, et $\frac{3}{2}\mathrm{s}\left(=-\frac{2\mathrm{d}}{\mathrm{\eta }}\mathrm{s}\right)=\mathrm{t}$. Quibus inventis, quantitas per fluxionem $\sqrt{}\stackrel{\_}{1+\frac{16{\mathrm{z}}^{\frac{2}{3}}}{9{\mathrm{a}}^{\frac{2}{3}}}}$ generata innotescet ponendo esse ad unitatem sui generis ut area $\frac{3}{2}\mathrm{s}$ ad unitatem superficialem. Vel quod eodem recidit, ponendo quantitatem t non amplius superficiem significare, sed alterius generis quantitatem quæ est ad unitatem ejusdem generis ut superficies illa ad unitatem superficialem. . Sic posito quod $\sqrt{}\stackrel{\_}{1+\frac{16{\mathrm{z}}^{\frac{2}{3}}}{9{\mathrm{a}}^{\frac{2}{3}}}}$ designet fluxionem linearem imaginor t non ampliùs superficiem sed lineam jam significare, eam nempe quæ ad unitatem linearem est ut area quam t iuxta Catalogos designat ad unitatem superficialem, hoc est eam quæ producitur applicando aream illam ad linearem unitatem. Qua ratione si linearis unitas statuatur e longitudo per præfatam fluxionem generata erit $\frac{3\mathrm{s}}{2\mathrm{e}}$. Et hoc fundamento Catalogi illi ad longitudines curvarum, contenta solidorum & alias quascunque quantitates æque ac areas curvarum determina{n}das applicari possunt.

<113>

De Quæstionibus cognatis.

1. Curvarum areas per Mechanicam approximare.

Methodus est ut duarum pluriumve rectilinearum figurarum valores ita componantur inter se ut valorem areæ curvæ quamproximè constituant. Sic ad circulum AFD quem æquatio $\mathrm{x}-\mathrm{x}\mathrm{x}=\mathrm{r}\mathrm{r}$ designat postquam inventus est areæ AFDB valor $\frac{2}{3}{\mathrm{x}}^{\frac{3}{2}}-\frac{1}{5}{\mathrm{x}}^{\frac{5}{2}}-\frac{1}{28}{\mathrm{x}}^{\frac{7}{2}}-\frac{1}{72}{\mathrm{x}}^{\frac{9}{2}}\text{\&c.}$ quærendi sunt aliquot rectangulorum valores, quales sunt ipsius $\mathrm{BD}\times \mathrm{AB}$ valor $\mathrm{x}\sqrt{}\stackrel{\_}{\mathrm{x}-\mathrm{x}\mathrm{x}}$ sive ${\mathrm{x}}^{\frac{3}{2}}-\frac{1}{2}{\mathrm{x}}^{\frac{5}{2}}-\frac{1}{8}{\mathrm{x}}^{\frac{7}{2}}-\frac{1}{16}{\mathrm{x}}^{\frac{9}{2}}\text{\&c.}$ ac ipsius $\mathrm{AD}\times \mathrm{AB}$ valor $\mathrm{x}\sqrt{}\stackrel{\_}{\mathrm{x}}$ sive ${\mathrm{x}}^{\frac{3}{2}}$. Dein hi valores 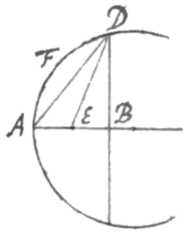per literas quaslibet diversas (quæ numeros indefinitè designent) multiplicandi sunt et addendi summæque termini cum correspondentibus terminis valoris areæ AFDB comparandi, ut quantum liceat evadant æquales. Quemadmodum si per e et f multiplicentur, fiet summa $\begin{array}{r}\mathrm{e}\\ +\mathrm{f}\end{array}{\mathrm{x}}^{\frac{3}{2}}-\frac{\mathrm{e}}{2}{\mathrm{x}}^{\frac{5}{2}}-\frac{\mathrm{e}}{8}{\mathrm{x}}^{\frac{7}{2}}\text{\&c}$ cuius terminis cum terminis hisce $\frac{2}{3}{\mathrm{x}}^{\frac{3}{2}}-\frac{1}{5}{\mathrm{x}}^{\frac{5}{2}}-\frac{1}{28}{\mathrm{x}}^{\frac{7}{2}}\text{\&c}$ collatis, prodit $\mathrm{e}+\mathrm{f}=\frac{2}{3}$, et $-\frac{\mathrm{e}}{2}=-\frac{1}{5}$; Sive $\mathrm{e}=\frac{2}{5}$ et $\mathrm{f}\left(=\frac{2}{3}-\mathrm{e}\right)=\frac{4}{15}$. Adeoque est $\frac{2}{5}\mathrm{BD}\times \mathrm{AB}+\frac{4}{15}\mathrm{AD}\times \mathrm{AB}=\text{areæ}\mathrm{AFDB}$ proximè. Scilicet $\frac{2}{5}\mathrm{BD}\times \mathrm{AB}+\frac{4}{15}\mathrm{AD}\times \mathrm{AB}$ valet $\frac{2}{3}{\mathrm{x}}^{\frac{3}{2}}-\frac{1}{5}{\mathrm{x}}^{\frac{5}{2}}-\frac{1}{20}{\mathrm{x}}^{\frac{7}{2}}$$-\frac{1}{40}{\mathrm{x}}^{\frac{9}{2}}\text{\&c}$ quod ab area AFDB subductum relinquit solummodò errorem $\frac{1}{70}{\mathrm{x}}^{\frac{7}{2}}+\frac{1}{90}{\mathrm{x}}^{\frac{9}{2}}\text{\&c}${.}

Sic bisectâ AB in E, rectanguli $\mathrm{AB}\times \mathrm{DE}$ valor erit $\mathrm{x}\sqrt{}\stackrel{\_}{\mathrm{x}-\frac{3}{4}\mathrm{x}\mathrm{x}}$ sive ${\mathrm{x}}^{\frac{3}{2}}-\frac{3}{8}{\mathrm{x}}^{\frac{5}{2}}-\frac{9}{128}{\mathrm{x}}^{\frac{7}{2}}-\frac{27}{1024}{\mathrm{x}}^{\frac{9}{2}}$ &c Et hoc collatum cum rectangulo $\mathrm{AD}\times \mathrm{AB}$ dat $\frac{8\mathrm{DE}+2\mathrm{AD}}{15}in\mathrm{AB}=$$\text{areæ}\mathrm{AFDB}$, errore tantùm existente $\frac{1}{560}{\mathrm{x}}^{\frac{7}{2}}+\frac{1}{5760}{\mathrm{x}}^{\frac{9}{2}}\text{\&c}$ qui semper minor est quam $\frac{1}{1500}$ totius areæ, etiamsi AFDB ponatur quadrans circuli. Hoc autem Theorema sic enunciari potest. Ut 3 ad 2 ita rectangulum $\mathrm{AB}in\mathrm{DE}$ plus quinta parte differentiæ inter AD ac DE ad aream AFDB proxime.

Atque ita conferendo duo rectangula $\mathrm{AB}\times \mathrm{ED}$ et $\mathrm{AB}\times \mathrm{BD}$, vel omnia tria rectangula inter se, vel adhibendo adhuc alia rectangula <114> possunt aliæ regulæ excogitari, eæque tanto exactiores quo plura rectangula adhibentur. Et idem de area Hyperbolæ ac aliarum curvarum intelligendum est. Imò et per unicum tantùm rectangulum area plerumque commode exhiberi potest, ut in prædicto circulo si capiatur AE ad AB ut $\sqrt{}5$ ad 5, rectangulum $\mathrm{AB}\times \mathrm{ED}$ erit ad aream AFDB ut 3 ad 2, errore tantùm existente $\frac{1}{175}{\mathrm{x}}^{\frac{7}{2}}+$$\frac{11}{2250}{\mathrm{x}}^{\frac{9}{2}}\text{\&c}$.

2. Ex Datâ areâ, Basem et incedentem
lineam determinare.

Ubi area per finitam æquationem exhibetur nihil occurrit difficultatis. Ubi verò per infinitam exhibetur, affecta radix extrahenda est quæ Basem designat. Sic ad Hyperbolam quam æquatio $\frac{\mathrm{a}\mathrm{b}}{\mathrm{a}+\mathrm{x}}=\mathrm{r}$ designat postquam inventum est $\mathrm{z}=\mathrm{b}\mathrm{x}-\frac{\mathrm{b}\mathrm{x}\mathrm{x}}{2\mathrm{a}}+\frac{\mathrm{b}{\mathrm{x}}^3}{3\mathrm{a}\mathrm{a}}\text{\&c}$; ut ex data area z vicissim innotescat Basis x, extrahe radicem affectam et proveniet $\mathrm{x}=\frac{\mathrm{z}}{\mathrm{b}}+\frac{\mathrm{z}\mathrm{z}}{2\mathrm{a}\mathrm{b}\mathrm{b}}+\frac{{\mathrm{z}}^3}{6\mathrm{a}\mathrm{a}{\mathrm{b}}^3}+\frac{{\mathrm{z}}^4}{24{\mathrm{a}}^3{\mathrm{b}}^4}+\frac{{\mathrm{z}}^5}{96{\mathrm{a}}^4{\mathrm{b}}^5}\text{\&c}$ et præterea si incedens r desideretur divide $\mathrm{a}\mathrm{b}$ per $\mathrm{a}+\mathrm{x}$ hoc est per $\mathrm{a}+\frac{\mathrm{z}}{\mathrm{b}}+\frac{\mathrm{z}\mathrm{z}}{2\mathrm{a}\mathrm{b}\mathrm{b}}+\frac{{\mathrm{z}}^3}{6\mathrm{a}\mathrm{a}{\mathrm{b}}^3}\text{\&c}$ et emerget $\mathrm{r}=\mathrm{b}-\frac{\mathrm{z}}{\mathrm{a}}+\frac{\mathrm{z}\mathrm{z}}{2\mathrm{a}\mathrm{a}\mathrm{b}}-\frac{{\mathrm{z}}^3}{6{\mathrm{a}}^3\mathrm{b}\mathrm{b}}+\frac{{\mathrm{z}}^4}{24{\mathrm{a}}^4{\mathrm{b}}^3}\text{\&c}$.

Sic ad Ellipsin quam æquatio $\mathrm{a}\mathrm{x}-\frac{\mathrm{a}}{\mathrm{c}}\mathrm{x}\mathrm{x}=\mathrm{r}\mathrm{r}$ designat, postquam inventa fuerit area $\mathrm{z}=\frac{2}{3}{\mathrm{a}}^{\frac{1}{2}}{\mathrm{x}}^{\frac{3}{2}}-\frac{{\mathrm{a}}^{\frac{1}{2}}{\mathrm{x}}^{\frac{5}{2}}}{5\mathrm{c}}$$-\frac{{\mathrm{a}}^{\frac{1}{2}}{\mathrm{x}}^{\frac{7}{2}}}{28\mathrm{c}\mathrm{c}}-\frac{{\mathrm{a}}^{\frac{1}{2}}{\mathrm{x}}^{\frac{9}{2}}}{72{\mathrm{c}}^3}\text{\&c}$. scribe ${\mathrm{v}}^3$ pro $\frac{3\mathrm{z}}{2{\mathrm{a}}^{\frac{1}{2}}}$ ac t pro ${\mathrm{x}}^{\frac{1}{2}}$, et evadet ${\mathrm{v}}^3={\mathrm{t}}^3-\frac{3{\mathrm{t}}^5}{10\mathrm{c}}-\frac{3{\mathrm{t}}^7}{56\mathrm{c}\mathrm{c}}-\frac{{\mathrm{t}}^9}{48{\mathrm{c}}^3}\text{\&c}$, et extracta radice $\mathrm{t}=\mathrm{v}+\frac{{\mathrm{v}}^3}{10\mathrm{c}}+\frac{81{\mathrm{v}}^5}{1400\mathrm{c}\mathrm{c}}+\frac{1171{\mathrm{v}}^7}{25200{\mathrm{c}}^3}\text{\&c}$. Cujus quadratum $\mathrm{v}\mathrm{v}+\frac{{\mathrm{v}}^4}{5\mathrm{c}}+\frac{22{\mathrm{v}}^6}{175\mathrm{c}\mathrm{c}}+\frac{823{\mathrm{v}}^8}{7875{\mathrm{c}}^3}\text{\&c}$ valet x. Et hoc valore pro x in æquatione $\mathrm{a}\mathrm{x}-\frac{\mathrm{a}}{\mathrm{c}}\mathrm{x}\mathrm{x}=\mathrm{r}\mathrm{r}$ substituto, et extracta radice, proveni{et} $\mathrm{r}={\mathrm{a}}^{\frac{1}{2}}\mathrm{v}-\frac{2{\mathrm{a}}^{\frac{1}{2}}{\mathrm{v}}^3}{5\mathrm{c}}-\frac{38{\mathrm{a}}^{\frac{1}{2}}{\mathrm{v}}^5}{175\mathrm{c}\mathrm{c}}-\frac{407{\mathrm{a}}^{\frac{1}{2}}{\mathrm{v}}^7}{2250{\mathrm{c}}^3}\text{\&c}${.} Adeoque ex data area z et inde v sive $\sqrt{}cub:\frac{3\mathrm{z}}{2{\mathrm{a}}^{\frac{1}{2}}}$, dabitur Basis x et Incedens r. Quæ omnia ad Hyperbolam etiam accommodantur si modo signum quant < insertion from p 155 > itatis c ubique mutetur ubi existit imparium dimensionum. < text from p 114 resumes >

<115>

Problema 10. Curvas pro arbitrio
multas invenire quarum longitudines
per finitas æquationes
designari possunt.

Ad hujus resolutionem via 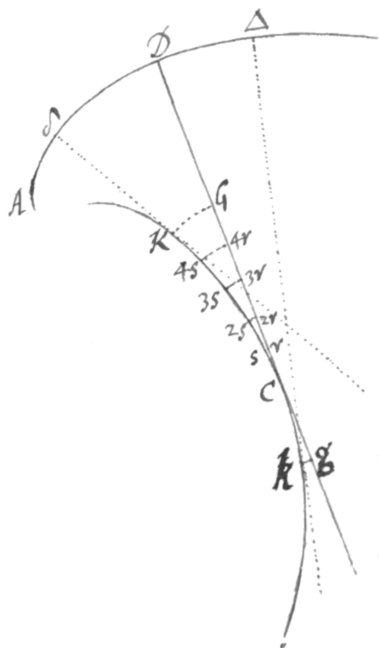per sequentes positiones sternitur.

1. Si recta DC in curvam quamvis AD perpendiculariter insistens moveri concipiatur, singula ejus puncta G, k, r &c describent alias æquidistantes sibique perpendiculares curvas GK, gk, rs &c.

2. Si recta illa hinc inde indefinitè producatur ejus extremitates movebuntur ad contrarias plagas, et punctum quod distinguit inter contrarios motus, quodque ideo dici potest centrum motionis, idem est cum centro curvaturæ quam curva AD habet ad punctum D, ut supra diximus. Istud autem punctum esto C.

3{.} Si lineam AD non circularem esse sed difformiter incurvatam supponamus puta magis curvam in δ et minùs in Δ, illud centrum continuò mutabitur propriùs accedens ad partes magis curvas ut in K et longiùs recedens a partibus minùs curvis ut in k, eoque pacto lineam aliquam qualis KCk describet.

4. Hanc a centro curvaturæ descriptam lineam recta DC continuò tanget. Nam si rectæ illius punctum D moveat versus δ, ejus punctum G quod interea transit ad K et situm est ad eandem partem centri C movebit versus eandem plagam (per Positionem secundam) . Deinde si idem D moveat versus Δ punctum g quod interea transit ad k et situm est ad contrariam partem centri C movebit ad contrariam plagam hoc est ad eandem plagam ad quam G in priori casu movebat <116> dum transijt ad K. Et proinde K et k jacent ad eandem partem rectæ DC. Quare cum K et k indeterminatè pro quibuslibet punctis sumantur, patet totam illam curvam jacere ad eandem partem rectæ DC, proindeque ab illa non secari sed tangi tantùm.

Hic supponitur lineam δDΔ magis curvam esse a parte δ continuò et minùs a parte Δ. Quod si maxima minimáve curvatura fuerit ad ipsum D, tunc recta DC secabit curvam KC, sed in angulo tamen qui sit quovis rectilineo minor. Quod perinde est ac si tangere dicatur. Imo punctum C in hoc casu termi < insertion from p 153 > nus est instar cuspidis, ad quem partes curvæ obliquissimo concursu desinentes se mutuò contingunt, proindeque a recta DC quæ angulum illum contactûs dividit rectius dicatur tangi quàm secari. < text from p 116 resumes >

5. Recta CG æquatur curvæ CK. Nam concipe rectæ illius singula puncta r, 2r, 3r, 4r &c describere curvarum arcus rs, $\mathrm{2r}\mathrm{2s}$, $\mathrm{3r}\mathrm{3s}$ &c interea dum per motum rectæ illius accedant ad curvam CK; et arcus illi, cùm (per Positionem primam) sint perpendiculares ad rectas quæ (per Positionem 4) tangunt curvam CK, erunt etiam perpendiculares ad curvam illam. Quare partes istius CK inter arcus illos interjectæ quæ propter infinitam parvitatem pro rectis haberi possint æquantur intervallis eorundem arcuum, hoc est (per Positionem 1) totidem partibus rectæ CG. Et additis utrinque æqualibus, tota CK aæquabitur toti CG.

Idem constare potest imaginando singulas partes rectæ CG inter movendum successivè applicari ad singulas partes curvæ CK, easque mensurare, perinde ut rotæ super planum per gyros promoventis circumferentia distantiam metitur quam punctum contactûs transigit.

Ex his pateat Problema resolvi posse assumendo pro lubitu curvam quamvis AδDΔ et inde determinando alteram curvam KCk in qua assumptæ centrum curvaturæ versatur. Ad rectam itaque quamvis positione datam AB demissis perpendiculis DB, CL et in AB sumpto quovis puncto A dictisque $\mathrm{AB}=\mathrm{x}$ et $\mathrm{BD}=\mathrm{y}$, pro curva AD definienda assumatur relatio quævis inter x et y et inde per Problema 5 elicietur punctum C quo et curva KC et ejus longitudo GC determinatur.

Exemplum. Sit $\mathrm{a}\mathrm{x}=\mathrm{y}\mathrm{y}$ æquatio ad curvam AD, Parabolam <117> nempe Apollonianam. Et per Problema 5, 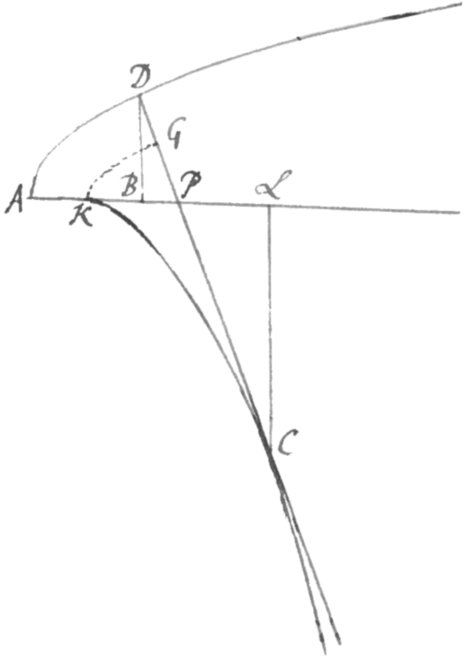invenientur $\mathrm{AL}=\frac{1}{2}\mathrm{a}+3\mathrm{x}$, $\mathrm{CL}=\frac{4{\mathrm{y}}^3}{\mathrm{a}\mathrm{a}}$, ac $\mathrm{DC}=\frac{\mathrm{a}+4\mathrm{x}}{\mathrm{a}}\sqrt{}\stackrel{\_}{\frac{1}{4}\mathrm{a}\mathrm{a}+\mathrm{a}\mathrm{x}}$. Quibus habitis, curva KC determinatur AL et LC et longitudo ejus per DC. Utpote cùm liberum sit ubivis in curva KC assumere puncta K et C, supponamus K esse centrum curvaturæ Parabolæ ad verticem, et positis perinde AB et BD seu x et y nullis evadet $\mathrm{DC}=\frac{1}{2}\mathrm{a}$, estque hæc longitudo AK vel DG quæ subducta a superiori indefinito valore DC relinquit GC seu $\mathrm{KC}=\frac{\mathrm{a}+4\mathrm{x}}{\mathrm{a}}\sqrt{}\stackrel{\_}{\frac{1}{4}\mathrm{a}\mathrm{a}+\mathrm{a}\mathrm{x}}-\frac{1}{2}\mathrm{a}$.

Jam si qualis sit hæc curva quantaque ejus longitudo, non ampliùs habita relatione ad Parabolam scire desideretur; Dic $\mathrm{KL}=\mathrm{z}$ et $\mathrm{LC}=\mathrm{v}$, et erit $\mathrm{z}=\left(=\mathrm{AL}-\frac{1}{2}\mathrm{a}\right)=3\mathrm{x}$ seu $\frac{1}{3}\mathrm{z}=\mathrm{x}$, et $\frac{\mathrm{a}\mathrm{z}}{3}\left(=\mathrm{a}\mathrm{x}\right)=\mathrm{y}\mathrm{y}$, adeoque $4\sqrt{}\frac{{\mathrm{z}}^3}{27\mathrm{a}}\left(=\frac{4{\mathrm{y}}^3}{\mathrm{a}\mathrm{a}}=\mathrm{CL}\right)=\mathrm{v}$. sive $\frac{16{\mathrm{z}}^3}{27\mathrm{a}}=\mathrm{v}\mathrm{v}$. Quod indicat curvam KC esse Parabolam secundi generis. Et pro ejus longitudine prodit $\frac{3\mathrm{a}+4\mathrm{z}}{3\mathrm{a}}\sqrt{}\stackrel{\_}{\frac{1}{4}\mathrm{a}\mathrm{a}+\frac{1}{3}\mathrm{a}\mathrm{z}}-\frac{1}{2}\mathrm{a}$, scribendo $\frac{1}{3}\mathrm{z}$ pro x in valore CG.

Potest etiam Problema resolvi per assumptionem æquationis quæ relationem inter AP et PD (posita nempe P intersectione Basis et Perpendiculi) definiat. Nam dictis $\mathrm{AP}=\mathrm{x}$, et $\mathrm{PD}=\mathrm{y}$, concipe CPD per spatium quàm minimum moveri puta ad locum Cpd, inque CD et Cd sumpto CΔ et Cδ ejusdem cujusvis datæ longitudinis puta 1, et ad CL demissis Δg, δγ perpendiculis quorum Δg (quod dic z) occurrat Cd in f, et completo parallelogrammo gγδe, positisque m, n, et r fluxionibus quantitatum x y et z ut supra; erit $\mathrm{\Delta e}.\mathrm{\Delta f}\left(\colon\colon \mathrm{\Delta e}\times \mathrm{\Delta e}.\mathrm{\Delta \delta }\times \mathrm{\Delta \delta }\colon\colon \mathrm{Cg}\times \mathrm{Cg}.\mathrm{C\Delta }\times \mathrm{C\Delta }\right)\colon\colon \frac{\mathrm{Cg}\times \mathrm{Cg}}{\mathrm{C\Delta }}.\mathrm{C\Delta }$. Et $\mathrm{\Delta f}.\mathrm{Pp}$$\colon\colon \mathrm{C\Delta }.\mathrm{CP}$. Et ex æquo $\mathrm{\Delta e}.\mathrm{Pp}\colon\colon \frac{\mathrm{Cg}\times \mathrm{Cg}}{\mathrm{C\Delta }}.\mathrm{CP}$. Est autem Pp <118> momentum Basis AP cujus additamento evadit Ap, ac Δe contemporaneum momentum perpendiculi Δg cujus ablatione evadit δγ. Adeoque Δe et Pp sunt ut fluxiones 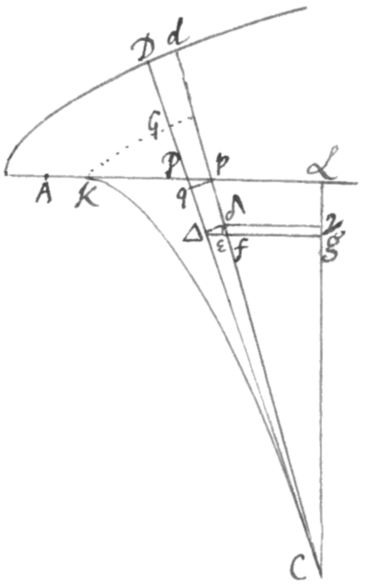linearum $\mathrm{\Delta g}\left(\mathrm{z}\right)$ et $\mathrm{AP}\left(\mathrm{x}\right)$, hoc est ut r et m. Quare $\mathrm{r}.\mathrm{m}\colon\colon \frac{{\mathrm{Cg}}^{quadr}}{\mathrm{C\Delta }}.\mathrm{CP}$. Et proinde cùm sit ${\mathrm{Cg}}^{quadr}\left(={\mathrm{C\Delta }}^{quadr}-{\mathrm{\Delta g}}^{quad}\right)=1-\mathrm{z}\mathrm{z}$, et $\mathrm{C\Delta }=1$, erit $\mathrm{CP}=\frac{\mathrm{m}-\mathrm{m}\mathrm{z}\mathrm{z}}{\mathrm{r}}${.} Et insuper cùm e tribus m, n, et r quamlibet pro uniformi fluxione ad quam cæteræ referantur habere liceat, si ista ponatur m ejusque quantitas unitas, evadet $\mathrm{CP}=\frac{1-\mathrm{z}\mathrm{z}}{\mathrm{r}}$.

Præterea est $\mathrm{C\Delta }\left(1\right).\mathrm{\Delta g}\left(\mathrm{z}\right)\colon\colon \mathrm{CP}.\mathrm{PL}$, et $\mathrm{C\Delta }\left(1\right).\mathrm{Cg}\left(\sqrt{}\stackrel{\_}{1-\mathrm{z}\mathrm{z}}\right)\colon\colon \mathrm{CP}.\mathrm{CL}$, Adeoque fit $\mathrm{PL}=\frac{\mathrm{z}-{\mathrm{z}}^3}{\mathrm{r}}$ et $\mathrm{CL}=\frac{1-\mathrm{z}\mathrm{z}}{\mathrm{r}}\sqrt{}\stackrel{\_}{1-\mathrm{z}\mathrm{z}}$. Ac denique acta pq parallela arcui infinitè parvo Dd seu perpendiculari DC erit Pq momentum ipsius DP cujus additamento evadit dp simul ac AP evadit Ap. Et idcirco Pp et Pq sunt ut fluxiones ipsarum $\mathrm{AP}\left(\mathrm{x}\right)$ et $\mathrm{PD}\left(\mathrm{y}\right)$, hoc est ut 1 et n, Atque adeò cùm propter similia triangula Ppq & CΔg, CΔ ac Δg seu 1 et z sint in eadem ratione erit $\mathrm{n}=\mathrm{z}$. Unde talis evadit Problematis resolutio.

E proposita æquatione quæ relationem inter x et y designet quære relationem fluxionum m et n per Problema 1. Et posito $\mathrm{m}=1$ habebitur valor n cui z æquatur. Dein substituto z pro n ope æquationis novissimæ quære relationes fluxionum m n et r per idem Problema 1, et et iterum substituto 1 pro m obtinebitur valor r. ^[4]Quibus habitis fac $\frac{1-\mathrm{n}\mathrm{n}}{\mathrm{r}}=\mathrm{CP}$, $\mathrm{z}\times \mathrm{CP}=\mathrm{PL}$ et $\mathrm{CP}\times \sqrt{}\stackrel{\_}{1-\mathrm{n}\mathrm{n}}=\mathrm{CL}$; Et erit C ad curvam cujus pars quævis KC æquatur rectæ CG differentiæ nempe tangentium ductarum a punctis C et K perpendiculariter ad curvam Dd.

Exemplum. Sit $\mathrm{a}\mathrm{x}=\mathrm{y}\mathrm{y}$ æquatio quæ relationem inter AP et PD designet et per Problema 1 primò erit $\mathrm{a}\mathrm{m}=2\mathrm{y}\mathrm{n}$ seu <119> $\mathrm{a}=2\mathrm{y}\mathrm{z}$. Deinde $0=2\mathrm{n}\mathrm{z}+2\mathrm{y}\mathrm{r}$ seu $-\frac{\mathrm{z}\mathrm{z}}{\mathrm{y}}=\mathrm{r}$. Indeque fit $\mathrm{CP}=\left(\frac{1-\mathrm{n}\mathrm{n}}{\mathrm{r}}=\right)\mathrm{y}-\frac{4{\mathrm{y}}^3}{\mathrm{a}\mathrm{a}}$, $\mathrm{PL}=\left(\mathrm{z}\times \mathrm{CP}=\right)\frac{1}{2}\mathrm{a}-\frac{2\mathrm{y}\mathrm{y}}{\mathrm{a}}$, et $\mathrm{CL}=\frac{\mathrm{a}\mathrm{a}-4\mathrm{y}\mathrm{y}}{2\mathrm{a}\mathrm{a}}\sqrt{}\stackrel{\_}{4\mathrm{y}\mathrm{y}-\mathrm{a}\mathrm{a}}$. Et a CP ac PL ablatis y et x restat $\mathrm{CD}=-\frac{4{\mathrm{y}}^3}{\mathrm{a}\mathrm{a}}$ et $\mathrm{AL}=\frac{1}{2}\mathrm{a}-\frac{3\mathrm{y}\mathrm{y}}{\mathrm{a}}$. Aufero autem y et x quòd CP et PL ubi valores habent affirmativos cadant ad partes puncti P versus D et A, et tunc diminui debent auferendo affirmativas quantitates PD et AD. Ubi verò negativos valores obtinent, cadent ad contrarias partes puncti P et tunc augeri debent, id quod etiam fit auferendo affirmativas quantitates PD et AD.

Jam ut curvæ in qua punctum C locatur longitudo inter duo quævis puncta K et C noscatur; quæro longitudinem tangentis ad punctum K et aufero a CD. Quemadmodum si K sit punctum ad quod tangens terminatur ubi CΔ et Δg seu 1 et z ponuntur æquales quodque proinde in ipsa basi AP situm est, scribe 1 pro z in æquatione $\mathrm{a}=2\mathrm{y}\mathrm{z}$ et prodit $\mathrm{a}=2\mathrm{y}$. Quare pro y scribe $\frac{1}{2}\mathrm{a}$ in valore CD nempe in $-\frac{4{\mathrm{y}}^3}{\mathrm{a}\mathrm{a}}$, et oritur $-\frac{1}{2}\mathrm{a}$. Estque hæc longitudo tangentis ad punctum K, sive ipsius DG inter quam et superiorem indefinitum valorem CD differentia $\frac{4{\mathrm{y}}^3}{\mathrm{a}\mathrm{a}}-\frac{1}{2}\mathrm{a}$ est GC cui curvæ pars KC æquatur.

Ut insuper pateat qualis sit hæc curva, ab AL (mutato prius signo ut evadat affirmativa) aufer AK quæ erit $\frac{1}{4}\mathrm{a}$ et restabit $\mathrm{KL}=\frac{3\mathrm{y}\mathrm{y}}{\mathrm{a}}-\frac{3}{4}\mathrm{a}$ quam dic t et in valore lineæ CL quam dic v scribe $\frac{4\mathrm{a}\mathrm{t}}{3}$ pro $4\mathrm{y}\mathrm{y}-\mathrm{a}\mathrm{a}$ et prodibit $\frac{2\mathrm{t}}{3\mathrm{a}}\sqrt{}\frac{4}{3}\mathrm{a}\mathrm{t}=\mathrm{v}$. seu $\frac{16{\mathrm{t}}^3}{27\mathrm{a}}=\mathrm{v}\mathrm{v}$ æquatio ad Parabolam secundi generis ut supra.

Siquando relatio inter t et v minùs commodè ad æquationem redigi possit, sufficit investigasse tantùm longitudines PC et PL. Quemadmodum si pro relatione in AP et PD assumatur æquatio $3\mathrm{a}\mathrm{a}\mathrm{x}+3\mathrm{a}\mathrm{a}\mathrm{y}-{\mathrm{y}}^3=0$. Inde per Problema 1 primò prodit $\mathrm{a}\mathrm{a}+\mathrm{a}\mathrm{a}\mathrm{z}-\mathrm{y}\mathrm{y}\mathrm{z}=0$, deinde $\mathrm{a}\mathrm{a}\mathrm{r}-2\mathrm{y}\mathrm{z}\mathrm{z}-\mathrm{y}\mathrm{y}\mathrm{r}=0${.} <120> Atque adeo est $\mathrm{z}=\frac{\mathrm{a}\mathrm{a}}{\mathrm{y}\mathrm{y}-\mathrm{a}\mathrm{a}}$, & $\mathrm{r}=\frac{2\mathrm{y}\mathrm{z}\mathrm{z}}{\mathrm{a}\mathrm{a}-\mathrm{y}\mathrm{y}}$. Unde dantur $\mathrm{PC}=\frac{1-\mathrm{n}\mathrm{n}}{\mathrm{r}}$ & $\mathrm{PL}=\mathrm{z}\times \mathrm{PC}$, quibus punctum C quod ad curvam situm est determinatur. Et longitudo curvǽ inter duo ejusmodi puncta e differentia correspondentium duarum tangentium DC sive $\mathrm{PC}-1$ innotescit.

Exempli gratia. Si ponatur $\mathrm{a}=1$ et ad determinandum aliquod curvæ punctum C sumatur $\mathrm{y}=2$; evadet AP seu {$\mathrm{x}\left(=\frac{{\mathrm{y}}^3-3\mathrm{a}\mathrm{a}\mathrm{y}}{3\mathrm{a}\mathrm{a}}\right)=\frac{2}{3}$}. $\mathrm{z}=\frac{1}{3}$. $\mathrm{r}=-\frac{4}{9}$. $\mathrm{PC}=-2$ & $\mathrm{PL}=-\frac{2}{3}$. Deinde ad aliud punctum C determinandum si sumatur $\mathrm{y}=3$ evadet $\mathrm{AP}=6$. $\mathrm{z}=\frac{1}{8}$. $\mathrm{r}=\frac{-3}{256}$. $\mathrm{PC}=-84$ et $\mathrm{PC}=-10\frac{1}{2}$. Quibus habitis si auferatur y a PC restabit $-4$ in priori casu et $-87$ in secundo casu pro longitudinibus DC quarum differentia 83 est longitudo curvæ inter inventa duo puncta C et C.

Hæc ita intelligenda sunt ubi curva inter puncta duo C et C vel K et C continuatur sine termino quem cuspidi assimilavimus. Sed ubi unus vel plures ejusmodi termini interjacent istis punctis (qui termini inveniuntur per determinationem maximæ aut minimæ PC vel DC) longitudines singularum partium Curvæ inter illos et puncta C vel K seorsim investigari debent et addi.

<121>

Problema 11. Curvas invenire quotascunque quarum longitudines cum propositæ alicujus curvæ longitudine, vel cum area ejus ad datam lineam applicatâ, ope finitarum æquationum comparari possunt.

Peragitur involvendo longitudinem areamve propositæ Curvæ in æquatione quæ in praecedente Problemate assumitur ad determinandam relationem inter AP et PD. Sed ut z et r inde per Problema 1 eliciantur, fluxio longitudinis vel areæ illius priùs investigari debet.

Fluxio longitudinis ejus determinatur ponendo æqualem radici quadraticæ summæ quadratorum a fluxionibus Basis, et perpendiculariter incedentis. Sit enim RN linea perpendiculariter incedens super Basi MN, et QR curva proposita ad quam RN terminatur. Dictisque $\mathrm{MN}=\mathrm{s}$, $\mathrm{NR}=\mathrm{t}$, et $\mathrm{QR}=\mathrm{v}$, et earum fluxionibus 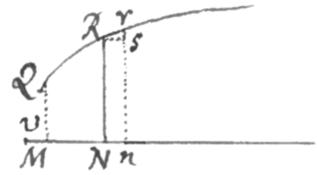p, q, et l respectivè; concipe lineam NR ad locum quam proximum nr promoveri, et demisso ad nr perpendiculo Rs, erunt Rs, sr, et Rr contemporanea momenta linearum MN, NR, et QR quorum additamentis evadunt Mn, nr, et Qr. Et cùm hæc sint inter se ut earundem linearum fluxiones, ac propter angulum rectum Rsr sit $\sqrt{}\stackrel{\_}{\mathrm{Rs}\times \mathrm{Rs}+\mathrm{sr}\times \mathrm{sr}}=\mathrm{Rr}$, erit $\sqrt{}\stackrel{\_}{\mathrm{p}\mathrm{p}+\mathrm{q}\mathrm{q}}=\mathrm{l}$.

Ad determinandas autem fluxiones p et q duæ requiruntur æquationes una quæ definiat relationem inter MN et NR seu s et t, unde relatio inter fluxiones p et q eruenda est, et alia quæ definiat relationem inter MN vel NR ad datam figuram et AP seu x ad quæsitam, unde relatio fluxionis p vel q ad fluxionem m seu 1 innotescit{.}

<122>

Invento l, fluxiones n et r per assumptam tertiam æquationem qua longitudo PD sive y definitur investigandæ sunt, et capienda $\mathrm{PC}=\frac{1-\mathrm{n}\mathrm{n}}{\mathrm{r}}$, $\mathrm{PL}=\mathrm{n}\times \mathrm{PC}$, ac $\mathrm{DC}=\mathrm{PC}-\mathrm{y}$ ut in præcedente Problemate{.}

Exemplum 1. Sit $\mathrm{a}\mathrm{s}-\mathrm{s}\mathrm{s}=\mathrm{t}\mathrm{t}$ æquatio ad datam curvam QR utpote circulum, $\mathrm{x}\mathrm{x}=\mathrm{a}\mathrm{s}$ relatio inter lineas AP et MN, et $\frac{2}{3}\mathrm{v}=\mathrm{y}$ relatio inter longitudinem datæ curvæ QR et rectæ PD. Per primam fit $\mathrm{a}\mathrm{p}-2\mathrm{s}\mathrm{p}=2\mathrm{t}\mathrm{q}$ seu $\frac{\mathrm{a}-2\mathrm{s}}{2\mathrm{t}}\mathrm{p}=\mathrm{q}$ et inde $\frac{\mathrm{a}\mathrm{p}}{2\mathrm{t}}\left(=\sqrt{}\stackrel{\_}{\mathrm{p}\mathrm{p}+\mathrm{q}\mathrm{q}}\right)=\mathrm{l}$. Per secundam fit $2\mathrm{x}=\mathrm{a}\mathrm{p}$ adeoque est $\frac{\mathrm{x}}{\mathrm{t}}=\mathrm{l}$. Et per tertiam fit $\frac{2}{3}\mathrm{l}=\mathrm{n}$ hoc est $\frac{2\mathrm{x}}{3\mathrm{t}}=\mathrm{z}$, dein hinc fit $\frac{2}{3\mathrm{t}}-\frac{2\mathrm{x}\mathrm{q}}{3\mathrm{t}\mathrm{t}}=\mathrm{r}$. Quibus inventis capienda sunt $\mathrm{PC}=\frac{1-\mathrm{n}\mathrm{n}}{\mathrm{r}}$, $\mathrm{PL}=\mathrm{n}\times \mathrm{PC}$, ac $\mathrm{DC}=\mathrm{PC}-\mathrm{y}$ sive $\mathrm{PC}-\frac{2}{3}\mathrm{QR}$. Ubi patet longitudinem datæ curvæ QR inveniri non posse quin simul innotescat longitudo rectæ DC, indeque longitudo curvæ ad quam punctum C cadit. Et contra.

Exemplum 2. Stante $\mathrm{a}\mathrm{s}-\mathrm{s}\mathrm{s}=\mathrm{t}\mathrm{t}$, ponatur $\mathrm{x}=\mathrm{s}$ et $\mathrm{v}\mathrm{v}-4\mathrm{a}\mathrm{x}=4\mathrm{a}\mathrm{y}$. Perque primam invenietur $\frac{\mathrm{a}\mathrm{p}}{2\mathrm{t}}=\mathrm{l}$ ut supra. Per secundam verò $1=\mathrm{p}$, atque adeo $\frac{\mathrm{a}}{2\mathrm{t}}=\mathrm{l}$. Et per tertiam $2\mathrm{l}\mathrm{v}-4\mathrm{a}=4\mathrm{a}\mathrm{n}$, seu (eliminato l) $\frac{\mathrm{v}}{4\mathrm{t}}-1=\mathrm{z}$, dein hinc $\frac{\mathrm{l}}{4\mathrm{t}}-\frac{\mathrm{v}\mathrm{q}}{4\mathrm{t}\mathrm{t}}=\mathrm{r}$.

Exemplum 3. Ponantur tres æquationes $\mathrm{a}\mathrm{a}=\mathrm{s}\mathrm{t}$, $\mathrm{a}+3\mathrm{s}=\mathrm{x}$ et $\mathrm{x}+\mathrm{v}=\mathrm{y}$. Et per primam (quæ Hyperbolam denotat) evadit $0=\mathrm{p}\mathrm{t}+\mathrm{q}\mathrm{s}$, seu $-\frac{\mathrm{p}\mathrm{t}}{\mathrm{s}}=\mathrm{q}$, et inde $\frac{\mathrm{p}}{\mathrm{s}}\sqrt{}\stackrel{\_}{\mathrm{s}\mathrm{s}+\mathrm{t}\mathrm{t}}\left(=\sqrt{}\stackrel{\_}{\mathrm{p}\mathrm{p}+\mathrm{q}\mathrm{q}}\right)=\mathrm{l}$. Per secundam evadit $3\mathrm{p}=1$, adeoque est $\frac{1}{3\mathrm{s}}\sqrt{}\stackrel{\_}{\mathrm{s}\mathrm{s}+\mathrm{t}\mathrm{t}}=\mathrm{l}$. Et per tertiam fit $1+\mathrm{l}=\mathrm{n}$ sive $1+\frac{1}{3\mathrm{s}}\sqrt{}\stackrel{\_}{\mathrm{s}\mathrm{s}+\mathrm{t}\mathrm{t}}=\mathrm{z}$, dein hinc fit $\mathrm{k}=\mathrm{r}$, posita scilicet k fluxione radicalis $\frac{1}{3\mathrm{s}}\sqrt{}\stackrel{\_}{\mathrm{s}\mathrm{s}+\mathrm{t}\mathrm{t}}$, quæ si fingatur æqualis φ sive $\frac{1}{9}+\frac{\mathrm{t}\mathrm{t}}{9\mathrm{s}\mathrm{s}}=\mathrm{\phi }\mathrm{\phi }$, proveniet inde $\frac{2\mathrm{t}\mathrm{q}}{9\mathrm{s}\mathrm{s}}-\frac{2\mathrm{t}\mathrm{t}\mathrm{p}}{9{\mathrm{s}}^3}=2\mathrm{\phi }\mathrm{k}$. Et substituto imprimis $-\frac{\mathrm{p}\mathrm{t}}{\mathrm{s}}$ pro q, deinde $\frac{1}{3}$ pro p, factaque divisione per $2\mathrm{\phi }$, habebitur $-\frac{2\mathrm{t}\mathrm{t}}{27\mathrm{\phi }{\mathrm{s}}^3}=\left(\mathrm{k}=\right)\mathrm{r}$. Inventis n et r cætera peraguntur ut in exemplo primo.

<123>

Quod si, a quovis curvae puncto Q perpendiculum QV ad MN demittatur, & curva invenienda sit cujus longitudo ex longitudine quæ oritur applicando aream QRNV ad datam aliquam lineam innotescat: ponatur illa data linea e, longitudo $\frac{\mathrm{QRNM}}{\mathrm{e}}$ quæ ex applicatione oritur v, et ipsius v fluxio l. Et cùm fluxio areæ QRNV sit ad fluxionem areæ parallelogrammi rectanguli super MN ad altitudinem e constituti ut incedens linea NR seu t qua hæc describitur ad incedentem lineam e qua illud eodem tempore describitur; et longitudinum quæ oriuntur applicando areas illas ad datam e; hoc est linearum v et MN seu s fluxiones l et p sint in eadem ratione, erit $\mathrm{l}=\frac{\mathrm{p}\mathrm{t}}{\mathrm{e}}$. Per hanc itaque regulam valor l inquirendus est, cæteraque ut in præcedentibus exemplis peragenda.

Exemplum 4. Sit QR Hyperbola quam æquatio $\mathrm{a}\mathrm{a}+\frac{\mathrm{a}\mathrm{s}\mathrm{s}}{\mathrm{c}}=\mathrm{t}\mathrm{t}$ definit, et inde juxta Problema 1 evadet $\frac{\mathrm{a}\mathrm{s}\mathrm{p}}{\mathrm{c}}=\mathrm{t}\mathrm{q}$ sive $\frac{\mathrm{a}\mathrm{s}\mathrm{p}}{\mathrm{c}\mathrm{t}}=\mathrm{q}$. Dein si pro alijs duabus æquationibus assumantur $\mathrm{x}=\mathrm{s}$, et $\mathrm{y}=\mathrm{v}$; prior dabit $1=\mathrm{p}$, unde fit $\mathrm{l}\left(=\frac{\mathrm{p}\mathrm{t}}{\mathrm{e}}\right)=\frac{\mathrm{t}}{\mathrm{e}}$; et posterior dabit imprimis $\mathrm{n}=\mathrm{l}$, sive $\mathrm{z}=\frac{\mathrm{t}}{\mathrm{e}}$, dein hinc $\mathrm{r}=\frac{\mathrm{q}}{\mathrm{e}}$, et substituto $\frac{\mathrm{a}\mathrm{s}\mathrm{p}}{\mathrm{c}\mathrm{t}}$ sive $\frac{\mathrm{a}\mathrm{s}}{\mathrm{c}\mathrm{t}}$ pro q evadet $\mathrm{r}=\frac{\mathrm{a}\mathrm{s}}{\mathrm{e}\mathrm{c}\mathrm{t}}$. Inventis n et r fac $\frac{1-\mathrm{n}\mathrm{n}}{\mathrm{r}}=\mathrm{CP}$ et $\mathrm{n}\times \mathrm{CP}=\mathrm{PL}$ ut in præcedentibus, et inde punctum C adeoque curva in quam omnia ejusmodi puncta cadunt determinabitur, cujus curvæ longitudo ex longitudine DC quæ valet $\mathrm{CP}-\mathrm{v}$ innotescet, uti satis ostendimus.

Est et alia Methodus qua Problema resolvitur; quærendo nempe Curvas quarum fluxiones vel æquentur fluxioni Curvæ propositæ, vel ex illius et aliarum linearum fluxionibus componantur. Et hæc aliquando usui esse potest præsertim in convertendo Mechanicas curvas in æquales geometricas. Cujus rei insigne est Exemplum in <124> Spiralibus.

Sit AB recta positione data, BD arcus super 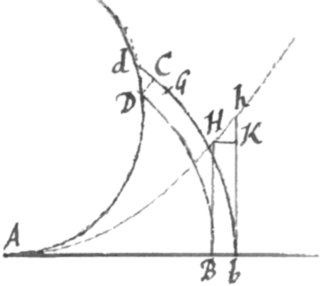AB tanquam Basi incedens ac interea retinens A pro centro, ADd Spiralis ad quam arcus ille perpetim terminatur, bd arcus quam proximus sive locus in quem arcus BD dum incedit proximè movetur, DC perpendicularis ad arcum bd, dG differentia arcuum, AH alia curva spirali AD æqualis, BH recta super AB normaliter incedens ac terminata ad curvam AH, bh locus quam proximus in quem recta illa incedit, et HK perpendicularis ad bh. Et in triangulis infinitè parvis DCd ac HKh, cùm DC et HK æqualia sint eidem tertio Bb, indeque sibi mutuo æqualia, ac Dd et Hh ex Hypothesi sint correspondentes partes æqualium curvarum et inde etiam æqualia, nec non anguli ad C et K recti, tertia etiam latera dC et hK æqualia erunt. Quare cùm insuper sit $\mathrm{AB}.\mathrm{BD}\colon\colon \mathrm{Ab}.\mathrm{bC}\colon\colon$$\mathrm{Ab}-\mathrm{AB}\left(\mathrm{Bb}\right).$$\mathrm{bC}-\mathrm{BD}\left(\mathrm{CG}\right)$. Adeoque $\frac{\mathrm{BD}\times \mathrm{Bb}}{\mathrm{AB}}=\mathrm{CG}$, si hoc auferatur a dG restabit $\mathrm{dG}-\frac{\mathrm{BD}\times \mathrm{Bb}}{\mathrm{AB}}\left(=\mathrm{dC}\right)=\mathrm{hK}$. Dic itaque $\mathrm{AB}=\mathrm{z}$, $\mathrm{BD}=\mathrm{v}$, & $\mathrm{BH}=\mathrm{y}$, et earum fluxiones r, l, et n respectivè; et cùm bB, dG et hK sint earundem contemporanea momenta quorum additamentis evadunt Ab, bd, et bh, et proinde inter se sint ut fluxiones, ideo pro momentis in æquatione novissima substituantur fluxiones, juxta et notæ pro lineis et emerget $\mathrm{l}-\frac{\mathrm{v}\mathrm{r}}{\mathrm{z}}=\mathrm{n}$. Ubi si e fluxionibus r < insertion from p 145 > pro æquabili habeatur et supponatur unitas esse ad quam cæteræ referantur evadet $\mathrm{l}-\frac{\mathrm{v}}{\mathrm{z}}=\mathrm{n}$. < text from p 124 resumes >

Quamobrem data per æquationem aliquam relatione inter AB et BD (sive x et v) qua Spiralis definiatur, dabitur (per Problema 1) fluxio l, et inde etiam fluxio n ponendo æqualem $\mathrm{l}-\frac{\mathrm{v}}{\mathrm{z}}$. Atque hæc per Problema 2 dabit lineam y sive BH cujus est fluxio.

Exemplum 1. Si detur $\frac{\mathrm{z}\mathrm{z}}{\mathrm{a}}=\mathrm{v}$, æquatio nempe ad Spiralem Archimedeam, inde per Problema 1, elicietur $\frac{2\mathrm{z}}{\mathrm{a}}=\mathrm{l}$. A quo aufer $\frac{\mathrm{v}}{\mathrm{z}}$ sive $\frac{\mathrm{z}}{\mathrm{a}}$ et restabit $\frac{\mathrm{z}}{\mathrm{a}}=\mathrm{n}$, et inde per Problema 2 fit $\frac{\mathrm{z}\mathrm{z}}{2\mathrm{a}}=\mathrm{y}$. Quod indicat curvam AH cui hæc spiralis AD æquatur esse Parabolam Apollonianam cujus latus rectum existit $2\mathrm{a}$; sive cujus incedens BH perpetuò æquatur semissi arcus BD.

Exemplum 2. Si proponatur Spiralis quam æquatio ${\mathrm{z}}^3=\mathrm{a}\mathrm{v}\mathrm{v}$ sive $\frac{{\mathrm{z}}^{\frac{3}{2}}}{{\mathrm{a}}^{\frac{1}{2}}}=\mathrm{v}$ definit, emerget per Problema 1 $\frac{3{\mathrm{z}}^{\frac{1}{2}}}{2{\mathrm{a}}^{\frac{1}{2}}}=\mathrm{l}$, A quo si auferatur $\frac{\mathrm{v}}{\mathrm{z}}$ seu $\frac{{\mathrm{z}}^{\frac{1}{2}}}{{\mathrm{a}}^{\frac{1}{2}}}$ restabit <125> $\frac{{\mathrm{z}}^{\frac{1}{2}}}{2{\mathrm{a}}^{\frac{1}{2}}}=\mathrm{n}$ et inde per Problema 2 producetur $\frac{{\mathrm{z}}^{\frac{3}{2}}}{3{\mathrm{a}}^{\frac{1}{2}}}=\mathrm{y}$. Hoc est $\frac{1}{3}\mathrm{BD}=\mathrm{BH}$, existente AH Parabola secundi generis.

Exemplum 3. Si ad Spiralem sit $\mathrm{z}\sqrt{}\frac{\mathrm{a}+\mathrm{z}}{\mathrm{c}}=\mathrm{v}$. Exinde per Problema 1 elicietur $\frac{2\mathrm{a}+3\mathrm{z}}{2\sqrt{}\stackrel{\_}{\mathrm{a}\mathrm{c}+\mathrm{c}\mathrm{z}}}=\mathrm{l}$, A quo si auferatur $\frac{\mathrm{v}}{\mathrm{z}}$ sive $\sqrt{}\frac{\mathrm{a}+\mathrm{z}}{\mathrm{c}}$, restabit $\frac{\mathrm{z}}{2\sqrt{}\stackrel{\_}{\mathrm{a}\mathrm{c}+\mathrm{c}\mathrm{z}}}=\mathrm{n}$. Jam cum quantitas hac fluxione n generata nequeat inveniri per ea quæ in Problema 2 habentur, nisi fiat resolutio in infinitam seriem; juxta tenorem Scholij Problema 9 reduco ad formam æquationum in prima collumna Catalogorum substituendo ${\mathrm{z}}^{\mathrm{\eta }}$ pro z, et evadit $\frac{{\mathrm{z}}^{2\mathrm{\eta }-1}}{2\sqrt{}\stackrel{\_}{\mathrm{a}\mathrm{c}+\mathrm{c}{\mathrm{z}}^{\mathrm{\eta }}}}=\mathrm{n}$, æquatio nempe secundæ speciei quarti ordinis prioris Gatalogi. Et conferendo terminos fit $\mathrm{d}=\frac{1}{2}$, $\mathrm{e}=\mathrm{a}\mathrm{c}$, et $\mathrm{f}=\mathrm{c}$, adeoque $\frac{\mathrm{z}-2\mathrm{a}}{3\mathrm{c}}\sqrt{}\stackrel{\_}{\mathrm{a}\mathrm{c}+\mathrm{c}\mathrm{z}}$$\left(=\mathrm{t}\right)=\mathrm{y}$. Quæ æquatio est ad curvam geometricam AH cui spiralis AD æquatur.

<128>

Problema 12. Curvarum Longitudines
determinare.

Fluxionem curvæ lineæ in superiore Problemate ostendimus æqualem esse radici quadraticæ summæ quadratorum a fluxionibus Basis et perpendiculariter Incedentis. Et proinde si Basis fluxionem pro uniformi ac determinata mensura, nimirum unitate, ad quam cæteræ fluxiones referantur, habeamus, et insuper per æquationem quæ curvam definit quæramus fluxionem Incedentis, habebitur fluxio Curvæ lineæ a qua longitudo ejus per Problema 2 elicienda est.

Exemplum 1. Proponatur Curva FDH quam æquatio $\frac{{\mathrm{z}}^3}{\mathrm{a}\mathrm{a}}+\frac{\mathrm{a}\mathrm{a}}{12\mathrm{z}}=\mathrm{y}$ definit, posito scilicet $\mathrm{z}=$ basi AB, ac $\mathrm{y}=$ incedenti DB: et ex æquatione illa per Problema 1 elicietur $\frac{3\mathrm{z}\mathrm{z}}{\mathrm{a}\mathrm{a}}-\frac{\mathrm{a}\mathrm{a}}{12\mathrm{z}\mathrm{z}}=\mathrm{n}$, existente nimirum 1 pro fluxione ipsius z et n fluxione y. Dein additis fluxionum quadratis fit summa $\frac{9{\mathrm{z}}^4}{{\mathrm{a}}^4}+\frac{1}{2}$$+\frac{{\mathrm{a}}^4}{144{\mathrm{z}}^4}=99$, et extracta radice $\frac{3\mathrm{z}\mathrm{z}}{\mathrm{a}\mathrm{a}}+\frac{\mathrm{a}\mathrm{a}}{12\mathrm{z}\mathrm{z}}=\mathrm{q}$, indeque per Problema 2, $\frac{{\mathrm{z}}^3}{\mathrm{a}\mathrm{a}}+\frac{\mathrm{a}\mathrm{a}}{12\mathrm{z}}=\mathrm{t}$, ubi q fluxionem Curvae ac t longitudinem designat.

Itaque si cujusvis portionis Curvæ hujus puta dD longitudo desideretur a punctis d ac D demitte ad AB perpendicula db ac DB et in valore t substitue quantitates Ab et AB seorsim pro z, ac differentia productorum erit longitudo quæsita dD. Quemadmodum si sit $\mathrm{Ab}=\frac{1}{2}\mathrm{a}$ et $\mathrm{AB}=\mathrm{a}$, scripto $\frac{1}{2}\mathrm{a}$ pro z evadet $\mathrm{t}=-\frac{\mathrm{a}}{24}$, dein scripto a pro z evadet $\mathrm{t}=\frac{11\mathrm{a}}{12}$, a quo si prior valor auferatur restabit $\frac{23\mathrm{a}}{24}$ pro longitudine dD. Vel si Ab tantùm definiatur esse $\frac{1}{2}\mathrm{a}$ et AB spectetur indefinitè, restabit $\frac{{\mathrm{z}}^3}{\mathrm{a}\mathrm{a}}-\frac{\mathrm{a}\mathrm{a}}{12\mathrm{z}}+\frac{\mathrm{a}}{24}=\mathrm{dD}$.

Quod si cupias noscere portionem Curvæ quam t designat, finge valorem t æquari nihilo, et evadet ${\mathrm{z}}^4=\frac{{\mathrm{a}}^4}{12}$, sive <128> $\mathrm{z}=\frac{\mathrm{a}}{\sqrt{}④12}$. Adeoque si sumatur $\mathrm{Ab}=\frac{\mathrm{a}}{\sqrt{}④12}$, et erigatur bd, longitudo arcus dD erit t sive $\frac{{\mathrm{z}}^3}{\mathrm{a}\mathrm{a}}-\frac{\mathrm{a}\mathrm{a}}{12\mathrm{z}}$. Et hæc de alijs curvis generaliter intelligenda sunt.

Ad eundem modum quo hujus longitudinem determinavimus si pro alia Curva definienda proponatur æquatio $\frac{{\mathrm{z}}^4}{{\mathrm{a}}^3}+\frac{{\mathrm{a}}^3}{32\mathrm{z}\mathrm{z}}=\mathrm{y}$ proveniet $\frac{{\mathrm{z}}^4}{{\mathrm{a}}^3}-\frac{{\mathrm{a}}^3}{32\mathrm{z}\mathrm{z}}=\mathrm{t}$, vel si proponatur $\frac{{\mathrm{z}}^{\frac{3}{2}}}{{\mathrm{a}}^{\frac{1}{2}}}-\frac{1}{3}{\mathrm{a}}^{\frac{1}{2}}{\mathrm{z}}^{\frac{1}{2}}=\mathrm{y}$, proveniet $\frac{{\mathrm{z}}^{\frac{3}{2}}}{{\mathrm{a}}^{\frac{1}{2}}}+\frac{1}{3}{\mathrm{a}}^{\frac{1}{2}}{\mathrm{z}}^{\frac{1}{2}}=\mathrm{t}$. Vel generaliter si sit $\mathrm{c}{\mathrm{z}}^{\mathrm{\theta }}+\frac{{\mathrm{z}}^{2-\mathrm{\theta }}}{4\mathrm{\theta }\mathrm{\theta }\mathrm{c}-8\mathrm{\theta }\mathrm{c}}=\mathrm{y}$, ubi θ pro quolibet numero sive integro sive fracto designando adhibetur, erit $\mathrm{c}{\mathrm{z}}^{\mathrm{\theta }}-\frac{{\mathrm{z}}^{2-\mathrm{\theta }}}{4\mathrm{\theta }\mathrm{\theta }\mathrm{c}-8\mathrm{\theta }\mathrm{c}}=\mathrm{t}$.

Exemplum 2. Proponatur curva quam æquatio $\frac{2\mathrm{a}\mathrm{a}+2\mathrm{z}\mathrm{z}}{3\mathrm{a}\mathrm{a}}\sqrt{}\stackrel{\_}{\mathrm{a}\mathrm{a}+\mathrm{z}\mathrm{z}}=\mathrm{y}$ definit, et per Problema 1 obtinebitur $\mathrm{n}=\frac{4{\mathrm{a}}^4\mathrm{z}+8\mathrm{a}\mathrm{a}{\mathrm{z}}^3+4{\mathrm{z}}^5}{3{\mathrm{a}}^4\mathrm{y}}$ sive, exterminato y, $\mathrm{n}=\frac{2\mathrm{z}}{\mathrm{a}\mathrm{a}}\sqrt{}\stackrel{\_}{\mathrm{a}\mathrm{a}+\mathrm{z}\mathrm{z}}$ cuius quadrato adde 1, et summa erit $1+\frac{4\mathrm{z}\mathrm{z}}{\mathrm{a}\mathrm{a}}+\frac{4{\mathrm{z}}^4}{{\mathrm{a}}^4}$, eiusque radix $1+\frac{2\mathrm{z}\mathrm{z}}{\mathrm{a}\mathrm{a}}=\mathrm{q}${.} Unde per Problema 2 obtinetur $\mathrm{z}+\frac{2{\mathrm{z}}^3}{3\mathrm{a}\mathrm{a}}=\mathrm{t}$.

Exemplum 3. Proponatur Parabola secundi generis ad quam æquatio est ${\mathrm{z}}^3=\mathrm{a}\mathrm{a}\mathrm{y}$ seu $\frac{{\mathrm{z}}^{\frac{3}{2}}}{{\mathrm{a}}^{\frac{1}{2}}}=\mathrm{y}$ et inde per Problema 1 elicietur $\frac{3{\mathrm{z}}^{\frac{1}{2}}}{2{\mathrm{a}}^{\frac{1}{2}}}=\mathrm{n}$, adeoque est $\sqrt{}\stackrel{\_}{1+\frac{9\mathrm{z}}{4\mathrm{a}}}$$\left(=\sqrt{}\stackrel{\_}{1+\mathrm{n}\mathrm{n}}\right)=\mathrm{q}$. Jam cùm longitudo per fluxionem q generata nequeat inveniri per Problema 2 absque reductione in infinitam seriem simplicium terminorum, consulo Catalogos ad Problema 9 et juxta ea quæ in Scholio ejus habentur prodit $\mathrm{t}=\frac{8\mathrm{a}+18\mathrm{z}}{27}\sqrt{}\stackrel{\_}{1+\frac{9\mathrm{z}}{4\mathrm{a}}}$.

Et sic Parabolarum ${\mathrm{z}}^5=\mathrm{a}{\mathrm{y}}^4$, ${\mathrm{z}}^7=\mathrm{a}{\mathrm{y}}^6$, ${\mathrm{z}}^9=\mathrm{a}{\mathrm{y}}^8$ &c longitudines inveniri possunt.

Exemplum 4. Proponatur Parabola ad quam æquatio est ${\mathrm{z}}^4=\mathrm{a}{\mathrm{y}}^3$, sive $\frac{{\mathrm{z}}^{\frac{4}{3}}}{{\mathrm{a}}^{\frac{1}{3}}}=\mathrm{y}$, et inde per Problema 1 orietur $\frac{4{\mathrm{z}}^{\frac{1}{3}}}{3{\mathrm{a}}^{\frac{1}{3}}}=\mathrm{n}$. Adeoque $\sqrt{}\stackrel{\_}{1+\frac{16{\mathrm{z}}^{\frac{2}{3}}}{9{\mathrm{a}}^{\frac{2}{3}}}}\left(=\sqrt{}\stackrel{\_}{\mathrm{n}\mathrm{n}+1}\right)=\mathrm{q}$. Quo invento consulo Catalogos juxta Scholium prædictum et facta collatione cum secundo Theoremate quinti ordinis posterioris <129> Catalogi, prodit ${\mathrm{z}}^{\frac{1}{3}}=\mathrm{x}$, $\sqrt{}\stackrel{\_}{1+\frac{16\mathrm{x}\mathrm{x}}{9{\mathrm{a}}^{\frac{2}{3}}}}=\mathrm{v}$, et $\frac{3}{2}\mathrm{s}=\mathrm{t}$. Ubi x designat basem y ordinatim applicatam et s aream Hyperbolæ atque t longitudinem quæ oritur applicando aream $\frac{3}{2}\mathrm{s}$ ad unitatem linearem.

Eadem methodo Parabolarum ${\mathrm{z}}^6=\mathrm{a}{\mathrm{y}}^5$, ${\mathrm{z}}^8=\mathrm{a}{\mathrm{y}}^7$, ${\mathrm{z}}^{10}=\mathrm{a}{\mathrm{y}}^9$ &c longitudines etiam per aream Hyperbolæ determinantur{.}

Exemplum 5. Proponatur Cissois Veterum, et existente ad eam æquatione $\frac{\mathrm{a}\mathrm{a}-2\mathrm{a}\mathrm{z}+\mathrm{z}\mathrm{z}}{\sqrt{}\stackrel{\_}{\mathrm{a}\mathrm{z}-\mathrm{z}\mathrm{z}}}=\mathrm{y}$, inde per Problema 1 elicietur $\frac{-\mathrm{a}-2\mathrm{z}}{2\mathrm{z}\mathrm{z}}\sqrt{}\stackrel{\_}{\mathrm{a}\mathrm{z}-\mathrm{z}\mathrm{z}}=\mathrm{n}$, et consequenter $\frac{\mathrm{a}}{2\mathrm{z}}\sqrt{}\frac{\mathrm{a}+3\mathrm{z}}{\mathrm{z}}\left(=\sqrt{}\stackrel{\_}{\mathrm{n}\mathrm{n}+1}\right)=\mathrm{q}${.} Quæ scribendo ${\mathrm{z}}^{\mathrm{\eta }}$ pro $\frac{1}{\mathrm{z}}$ seu ${\mathrm{z}}^{-1}$ evadit $\frac{\mathrm{a}}{2\mathrm{z}}\left(=\sqrt{}\stackrel{\_}{\mathrm{a}{\mathrm{z}}^{\mathrm{\eta }}+3}\right)=\mathrm{q}$ æquatio primæ speciei quinti ordinis posterioris Catalogi et collatis terminis fiunt $\frac{\mathrm{a}}{2}=\mathrm{d}$, $3=\mathrm{e}$, et $\mathrm{a}=\mathrm{f}$; adeoque $\mathrm{z}\left(=\frac{1}{{\mathrm{z}}^{\mathrm{\eta }}}\right)=\mathrm{x}\mathrm{x}$. $\sqrt{}\stackrel{\_}{\mathrm{a}+3\mathrm{x}\mathrm{x}}=\mathrm{v}$, et $6\mathrm{s}-\frac{2{\mathrm{v}}^3}{\mathrm{x}}\left(=\frac{4\mathrm{d}\mathrm{e}}{\mathrm{\eta }\mathrm{f}}in\frac{{\mathrm{v}}^3}{2\mathrm{e}\mathrm{x}}-\mathrm{s}\right)=\mathrm{t}$. Et adhibita a pro unitate per cujus multiplicationem vel divisionem hæ quantitates ad justum dimensionum numerum reducantur, evadunt $\mathrm{a}\mathrm{z}=\mathrm{x}\mathrm{x}$, $\sqrt{}\stackrel{\_}{\mathrm{a}\mathrm{a}+3\mathrm{x}\mathrm{x}}=\mathrm{v}$, et $\frac{6\mathrm{s}}{\mathrm{a}}-\frac{2{\mathrm{v}}^3}{\mathrm{a}\mathrm{x}}=\mathrm{t}$. Quorum hæc est constructio.

Existente VD Cissoide, AV diametro 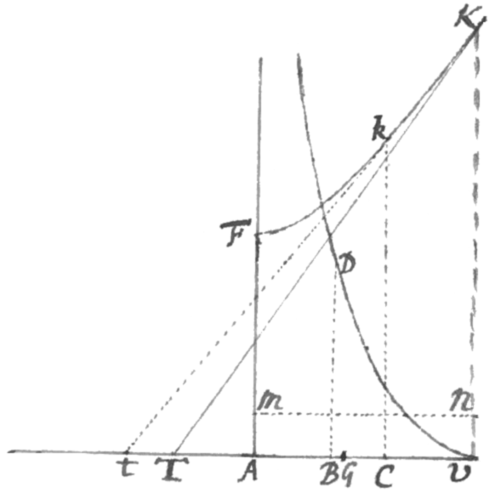circuli ad quem aptatur, AF asymptoto ejus, ac DB perpendiculari ad AV; cum semiaxe $\mathrm{AF}=\mathrm{AV}$, et semiparametro $\mathrm{AG}=\frac{1}{3}\mathrm{AV}$ describatur Hyperbola FkK, et inter AB et AV sumpta AC media proportionali, erigantur ad C et V perpendicula Ck et VK, et agantur kt et KT rectæ tangentes Hyperbolam in k et K et occurrentes AV in t ac T, et ad AV constituatur rectangulum AVNM æquale spatio TKkt; et Cissoidis VD longitudo erit sextupla altitudinis VN{.}

<130>

^[5]Exemplum 6. Existente Ad ellipsi quam æquatio $\sqrt{}\stackrel{\_}{\mathrm{a}\mathrm{z}-2\mathrm{z}\mathrm{z}}$ definit: proponatur curva Mechanica AD talis ut si Bd seu y producatur donec huic curvæ ad D occurrat, sit BD æqualis arcui Ellipticæ Ad. Jam quo hujus longitudo determinetur æquatio $\sqrt{}\stackrel{\_}{\mathrm{a}\mathrm{z}-2\mathrm{z}\mathrm{z}}=\mathrm{y}$ dabit $\frac{\mathrm{a}-4\mathrm{z}}{2\sqrt{}\stackrel{\_}{\mathrm{a}\mathrm{z}-2\mathrm{z}\mathrm{z}}}=\mathrm{n}$. Cujus quadrato si 1 addatur prodit $\frac{\mathrm{a}\mathrm{a}-4\mathrm{a}\mathrm{z}+8\mathrm{z}\mathrm{z}}{4\mathrm{a}\mathrm{z}-8\mathrm{z}\mathrm{z}}$ quadratum fluxionis arcûs Ad, et huic si iterum addatur 1, provenit $\frac{\mathrm{a}\mathrm{a}}{4\mathrm{a}\mathrm{z}-8\mathrm{z}\mathrm{z}}$ cujus radix $\frac{\mathrm{a}}{2\sqrt{}\stackrel{\_}{\mathrm{a}\mathrm{z}-2\mathrm{z}\mathrm{z}}}=\mathrm{n}$ est fluxio curvæ lineæ AD. Ubi si e radicali z et pro ${\mathrm{z}}^{-1}$ scribatur ${\mathrm{z}}^{\mathrm{\eta }}$, habebitur $\frac{\mathrm{a}}{2\mathrm{z}\sqrt{}\stackrel{\_}{\mathrm{a}{\mathrm{z}}^{\mathrm{\eta }}-2}}$ fluxio primæ speciei septimi ordinis posterioris Catalogi; Collatisque terminis exibunt $\mathrm{d}=\frac{1}{2}\mathrm{a}$, $\mathrm{e}=-2$, et $\mathrm{f}=\mathrm{a}$, adeoque $\mathrm{z}\left(=\frac{1}{{\mathrm{z}}^{\mathrm{\eta }}}\right)=\mathrm{x}$, $\sqrt{}\stackrel{\_}{\mathrm{a}\mathrm{x}-2\mathrm{x}\mathrm{x}}=\mathrm{v}$, et $\frac{8\mathrm{s}}{\mathrm{a}}-\frac{4\mathrm{x}\mathrm{v}}{\mathrm{a}}+\mathrm{v}\left(=\frac{8\mathrm{d}\mathrm{e}}{\mathrm{\eta }\mathrm{f}\mathrm{f}}in\mathrm{s}-\frac{1}{2}\mathrm{x}\mathrm{v}-\frac{\mathrm{f}\mathrm{v}}{4\mathrm{e}}\right)=\mathrm{t}$. Quorum constructio est ut, ad Ellipsis centrum C acta recta dC constituatur super AC parallelogrammum æquale sectori ACd, et duplum altitudinis ejus ponatur esse longitudo Curvæ AD.

Exemplum 7. Existente 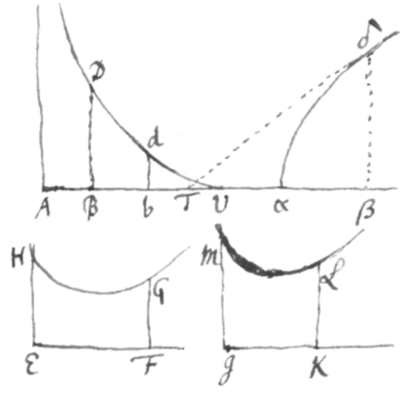$\mathrm{A\beta }=\mathrm{\phi }$, & αδ Hyperbola ad quam æquatio sit $\sqrt{}\stackrel{\_}{-\mathrm{a}+\mathrm{b}\mathrm{\phi }\mathrm{\phi }}=\mathrm{\beta \delta }$, actaque δT tangente ejus; proponatur curva VdD cujus basis AB sit $\frac{1}{\mathrm{\phi }\mathrm{\phi }}$, & normaliter incedens BD longitudo quæ oritur applicando aream αδTα ad unitatem linearem. Jam ut hujus VD longitudo determinetur quæro fluxionem areæ αδTα cum AB uniformiter fluit & invenio esse $\frac{\mathrm{a}}{4\mathrm{b}\mathrm{z}}\sqrt{}\stackrel{\_}{\mathrm{b}-\mathrm{a}\mathrm{z}}$ posita $\mathrm{AB}=\mathrm{z}$ & fluxione ejus unitate. Nam est $\mathrm{AT}=\frac{\mathrm{a}}{\mathrm{b}\mathrm{\phi }}=\frac{\mathrm{a}}{\mathrm{b}}\sqrt{}\mathrm{z}$, ejusque fluxio $\frac{\mathrm{a}}{2\mathrm{b}\sqrt{}\mathrm{z}}$, cujus dimidium ductum in altitudinem βδ seu $\sqrt{}\stackrel{\_}{-\mathrm{a}+\frac{\mathrm{b}}{\mathrm{z}}}$ est fluxio areæ αδT descriptæ per tangentem δT. Quare fluxio illa est $\frac{\mathrm{a}}{4\mathrm{b}\mathrm{z}}\sqrt{}\stackrel{\_}{\mathrm{b}-\mathrm{a}\mathrm{z}}$, atque hæc applicata ad unitatem fit fluxio ⊕ ⊕ incedentis BD. Hujus quadrato $\frac{\mathrm{a}\mathrm{a}\mathrm{b}-{\mathrm{a}}^3\mathrm{z}}{16\mathrm{b}\mathrm{b}\mathrm{z}\mathrm{z}}$ adde 1 quadratum fluxionis ipsius AB et prodit $\frac{\mathrm{a}\mathrm{a}\mathrm{b}-{\mathrm{a}}^3\mathrm{z}+16\mathrm{b}\mathrm{b}\mathrm{z}\mathrm{z}}{16\mathrm{b}\mathrm{b}\mathrm{z}\mathrm{z}}$, cujus radix $\frac{1}{4\mathrm{b}\mathrm{z}}\sqrt{}\stackrel{\_}{\mathrm{a}\mathrm{a}\mathrm{b}-{\mathrm{a}}^3\mathrm{z}+16\mathrm{b}\mathrm{b}\mathrm{z}\mathrm{z}}$ est fluxio curvæ VD. Est autem hæc fluxio primæ speciei sexti ordinis posterioris Catalogi, collatisque terminis <131> exeunt $\frac{1}{4\mathrm{b}}=\mathrm{d}$, $\mathrm{a}\mathrm{a}\mathrm{b}=2$, $-{\mathrm{a}}^3=\mathrm{f}$, $16\mathrm{b}\mathrm{b}=\mathrm{g}$, adeoque $\mathrm{z}=\mathrm{x}$, & $\sqrt{}\stackrel{\_}{\mathrm{a}\mathrm{a}\mathrm{b}-{\mathrm{a}}^3\mathrm{x}+16\mathrm{b}\mathrm{b}\mathrm{x}\mathrm{x}}=\mathrm{v}$ (æquatio ad unam Conicam sectionem, puta HG, cujus area EFGH sit s, existente $\mathrm{EF}=\mathrm{x}$ & $\mathrm{FG}=\mathrm{v}$:) Item $\frac{1}{\mathrm{z}}=\mathrm{\xi }$ & $\sqrt{}\stackrel{\_}{16\mathrm{b}\mathrm{b}-{\mathrm{a}}^3\mathrm{\xi }+\mathrm{a}\mathrm{a}\mathrm{b}\mathrm{\xi }\mathrm{\xi }}=\mathrm{{\rm Y}}$ (æquatio ad aliam Conicam sectionem, puta ML, cujus area IKLM sit σ, existente $\mathrm{IK}=\mathrm{\xi }$ & $\mathrm{KL}=\mathrm{{\rm Y}}$:)Denique $\frac{2\mathrm{a}\mathrm{a}\mathrm{b}\mathrm{b}\mathrm{\xi }\mathrm{{\rm Y}}-{\mathrm{a}}^3\mathrm{b}\mathrm{{\rm Y}}-{\mathrm{a}}^4\mathrm{v}-4\mathrm{a}\mathrm{a}\mathrm{b}\mathrm{b}\mathrm{\sigma }-32\mathrm{a}\mathrm{a}\mathrm{b}\mathrm{b}\mathrm{s}}{64{\mathrm{b}}^4-{\mathrm{a}}^4}=\mathrm{t}$.

Quare ut curvæ VD portionis cujuscunque Dd longitudo noscatur, demitte db normalem ad AB fingeque $\mathrm{Ab}=\mathrm{z}$ & exinde per jam inventa quære t, dein finge $\mathrm{AB}=\mathrm{z}$ et exinde etiam quære t & horum duorum t differentia erit longitudo Dd.

Exemplum 8.Proponatur Hyperbola ad quam æquatio est $\sqrt{}\stackrel{\_}{\mathrm{a}\mathrm{a}+\mathrm{b}\mathrm{z}\mathrm{z}}=\mathrm{y}$ et inde per Problema 1 elicietur $\mathrm{n}=\frac{\mathrm{b}\mathrm{z}}{\mathrm{y}}$ seu $\frac{\mathrm{b}\mathrm{z}}{\sqrt{}\mathrm{a}\mathrm{a}+\mathrm{b}\mathrm{z}\mathrm{z}}$, cujus quadrato adde 1 & summæ radix erit $\sqrt{}\frac{\mathrm{a}\mathrm{a}+\mathrm{b}\mathrm{z}\mathrm{z}+\mathrm{b}\mathrm{b}\mathrm{z}\mathrm{z}}{\mathrm{a}\mathrm{a}+\mathrm{b}\mathrm{z}\mathrm{z}}=\mathrm{q}$. Hanc fluxionem cùm non reperiatur in tabulis reduco in infinitam seriem, & primò per divisionem evadit $\mathrm{q}=\sqrt{}\stackrel{\_}{1+\frac{\mathrm{b}\mathrm{b}}{\mathrm{a}\mathrm{a}}\mathrm{z}\mathrm{z}-\frac{{\mathrm{b}}^3}{{\mathrm{a}}^4}{\mathrm{z}}^4+\frac{{\mathrm{b}}^4}{{\mathrm{a}}^6}{\mathrm{z}}^6-\frac{{\mathrm{b}}^5}{{\mathrm{a}}^8}{\mathrm{z}}^8\text{\&c}}$ dein per extractionem radicis $\mathrm{q}=1+\frac{\mathrm{b}\mathrm{b}}{2\mathrm{a}\mathrm{a}}\mathrm{z}\mathrm{z}-\frac{+4{\mathrm{b}}^3+{\mathrm{b}}^4}{8{\mathrm{a}}^4}{\mathrm{z}}^4$$+\frac{8{\mathrm{b}}^4+4{\mathrm{b}}^5+{\mathrm{b}}^6}{16{\mathrm{a}}^6}{\mathrm{z}}^6\text{\&c}$. Et hinc per Problema 2 obtinetur t seu longitudo Hyperbolæ $=\mathrm{z}+\frac{\mathrm{b}\mathrm{b}}{6\mathrm{a}\mathrm{a}}{\mathrm{z}}^3-\frac{+4{\mathrm{b}}^3+{\mathrm{b}}^4}{40{\mathrm{a}}^4}{\mathrm{z}}^5$$+\frac{8{\mathrm{b}}^4+4{\mathrm{b}}^5+{\mathrm{b}}^6}{112{\mathrm{a}}^6}{\mathrm{z}}^7\text{\&c}${.}

Quod si Ellipsis $\sqrt{}\stackrel{\_}{\mathrm{a}\mathrm{a}-\mathrm{b}\mathrm{z}\mathrm{z}}=\mathrm{y}$ proponatur debet signum ipsius b ubique mutari & habebitur $\mathrm{z}+\frac{\mathrm{b}\mathrm{b}}{6\mathrm{a}\mathrm{a}}{\mathrm{z}}^3$$+\frac{4{\mathrm{b}}^3-{\mathrm{b}}^4}{40{\mathrm{a}}^4}{\mathrm{z}}^5+\frac{8{\mathrm{b}}^4-4{\mathrm{b}}^5+{\mathrm{b}}^6}{112{\mathrm{a}}^6}{\mathrm{z}}^7\text{\&c}$ pro longitudine ejus et posita insuper unitate pro b, emerget $\mathrm{z}+\frac{{\mathrm{z}}^3}{6\mathrm{a}\mathrm{a}}+\frac{3{\mathrm{z}}^5}{40{\mathrm{a}}^4}$$+\frac{5{\mathrm{z}}^7}{112{\mathrm{a}}^6}\text{\&c}$ pro longitudine circuli: cujus seriei numerales coefficientes in infinitum inveniuntur multiplicando continuo per terminos hujus progressionis, $\frac{1\times 1}{2\times 3}.\frac{3\times 3}{4\times 5}.\frac{5\times 5}{6\times 7}.\frac{7\times 7}{8\times 9}.\frac{9\times 9}{10\times 11}\text{\&c}$.

<132>

Exemplum 9. Proponatur denique Quadratrix VDE cujus vertex est V, existente 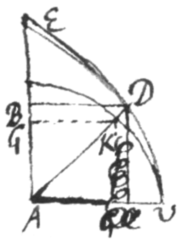A centro et AV semidiametro circuli interioris ad quem aptatur, atque angulo VAE recto. Acta jam recta qualibet AKD secante circulum istum in K, et Quadratricem in D demissisque ad AE normalibus KG, DB; dic AV a{,} AG z, VK x, et BD y, eritque ut in superiore Exemplo, $\mathrm{x}=\mathrm{z}+\frac{{\mathrm{z}}^3}{6\mathrm{a}\mathrm{a}}+\frac{3{\mathrm{z}}^5}{40{\mathrm{a}}^4}+\frac{5{\mathrm{z}}^7}{112{\mathrm{a}}^6}+\text{\&c}$. Extrahe radicem z et emerget $=\mathrm{x}-\frac{{\mathrm{x}}^3}{6\mathrm{a}\mathrm{a}}+\frac{{\mathrm{x}}^5}{120{\mathrm{a}}^4}$$-\frac{{\mathrm{x}}^7}{5040{\mathrm{a}}^6}+\text{\&c}$. Cujus quadratum aufer de ${\mathrm{AK}}^q$ & residui radix $\mathrm{a}-\frac{\mathrm{x}\mathrm{x}}{2\mathrm{a}}+\frac{{\mathrm{x}}^4}{24{\mathrm{a}}^3}-\frac{{\mathrm{x}}^6}{720{\mathrm{a}}^5}+\text{\&c}$ erit GK. Jam cùm ex natura Quadratricis sit AB$=\mathrm{VK}$ sive x, sitque etiam $\mathrm{AG}.\mathrm{GK}\colon\colon \mathrm{AB}.\mathrm{BD}\left(\mathrm{y}\right)$, divide $\mathrm{AB}\times \mathrm{GK}$ per AG et orietur $\mathrm{y}=\mathrm{a}-\frac{\mathrm{x}\mathrm{x}}{3\mathrm{a}}$$-\frac{{\mathrm{x}}^4}{45{\mathrm{a}}^3}-\frac{2{\mathrm{x}}^6}{945{\mathrm{a}}^5}\text{\&c}$. Et inde per Problema 1, $\mathrm{n}=-\frac{2\mathrm{x}}{3\mathrm{a}}-\frac{4{\mathrm{x}}^3}{45{\mathrm{a}}^3}-\frac{4{\mathrm{x}}^5}{315{\mathrm{a}}^5}\text{\&c}$. Cujus quadrato adde 1 et summa radix erit $1+\frac{2\mathrm{x}\mathrm{x}}{9\mathrm{a}\mathrm{a}}+\frac{14{\mathrm{x}}^4}{405{\mathrm{a}}^4}+\frac{604{\mathrm{x}}^6}{12757{\mathrm{a}}^6}+\text{\&c}=\mathrm{q}$. Unde per Problema 2 obtinetur t seu Quadratricis arcus $\mathrm{VD}=\mathrm{x}+\frac{2{\mathrm{x}}^3}{27\mathrm{a}\mathrm{a}}+\frac{14{\mathrm{x}}^5}{2025{\mathrm{a}}^4}+\frac{604{\mathrm{x}}^7}{893025{\mathrm{a}}^6}+\text{\&c}$