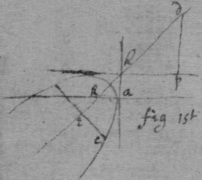Newton's Waste Book (Part 2)

Author: Isaac Newton

Source: MS Add. 4004, ff. 15v-50r, Cambridge University Library, Cambridge, UK

Published online: June 2013

Additional Information
- Notes on the Electronic Edition
  - You are currently reading the normalized version of this text. Normalized transcriptions provide a tidied-up view of the original text. Editorial interventions are applied to expand abbreviations and correct textual mistakes. Additions are silently included within the body text and deleted text is not displayed. Switching to the diplomatic view of this text will show 745 deletions, reveal 447 additions and not apply 1816 editorial regularizations.
- Revision History
  - 14 February 2011
    - Catalogue information compiled from CUL Janus Catalogue by Michael Hawkins
  - 1 September 2011
    - Transcription and encoding of Isaac Newton's text from front to ff. 63r by Daniele Cassisa
  - 10 September 2011
    - Yvonne Santacreu tagged transcription of Barnabas Smith's notes
  - 3 November 2011
    - Transcription and encoding of Isaac Newton's text from ff 64v-198v by Margarita Fernandez-Chas
  - 4 June 2013
    - Proofed by Robert Iliffe
  - 6 June 2013
    - Preliminary audit of XML by Michael Hawkins
- Download NATP00221.xml and schema (advanced users only)
Related Texts
- This document is part of MS Add. 4004
  The previous part of this document is Newton's Waste Book (Part 1) [MS Add. 4004, ff. {cover}-15r]
  The next part of this document is Newton's Waste Book (Part 3) [MS Add. 4004, ff. 50v-198v]

[Diplomatic Text] [Manuscript Images][Catalogue Entry]

<15v>

How to find the axes vertices Diamiters, Centers, or Asymptotes of any Crooked Line supposeing it have them.

^[1] Definitions.

^[2] 3 The Vertex of a crooked line is that point where the crooked line intersect the diameter or axis as at $(a)$

^[3] 4 The Asymptote of crooked lines are such lines which being produced both ways infinitely have noe least distance twixt them & the crooked line & yet {doe} noe where intersect it. or touch it as dδ , dθ .

^[4] 5 Those lines which are limited on all sides as acxkλ are Ellipses of the first, 2^d, 3^d, 4^th kind &c

6 Those which are not ellipses & have noe Asymptotes are Parabolas of the first, 2^d, 3^d, 4^th kind &c. as zkah .

7 Those which have Asymptotes, are Hyperbolas of the 1^st, 2^d, 3^d 4^th kind, &c as (upon) whose asymptotes are βd , γd .

8 There are some lines of a middle nature twixt a Parabola & hyperbola haveing an Asymptote for one of its sides but none for the other as βαγe , one side αγ haveing the asymptote δe , the other side αβ haveing none.

10 If an Ellipsis have 2 axes (as am & xλ ) the longer is the transverse axis (as am ) the shorter is the right axis (as xλ ).

9 If two diameters of the same Ellipsis be ordinately applyed the one to the other the shortest of them is called the right diameter, the longest the transverse one. (as am & xλ ).

1 If all the parallell lines which are terminated by the same or by 2 divers figures, bee bisected by a streight line; that bisecting line is a diameter, & those paralle{l} lines, are lines ordinately applied to that diameter.

2 If those parallell lines intersect the diameter at right angles the diameter is an axis

The center of an Ellipsis is that point where two of its diameters intersect.

The center of two opposite Hyperbolas is that point where two of their diameters intersect one another or else where their Asymptotes intersect.

<16r>

Propositions. The lines ordinately applied to the axis of a crooked line are parallell to the tangent of the crooked line at its vertex.

^[5] Demonstr. Suppose chad a Parab & dc (being ordinately applied to the axis ab ) not parallell to the tangent an but to some other line like ah. If dc bee understood to move towards a db continually decreasing untill it vanish into nothing at the conjuction of the points a & d . & since cb must be equall to ah at the conjuntion of the points a & d . it followeth that cb cannot decrease so as to vanish into nothing at the same time which bd doth & therefore cannot allways be equal to bd .

^[6] Otherwise. if dc is not parallell to the tangent an but to some other line as ah . Then ab doth not bisect all the parallell lines (as oe ) which are terminated by the crooked line cad . & therefore cannot bee its diameter

^[7] 2^dly. If ad is the axis of a crooked line & $cb = y$ , is ordinately applied to ad . that is if $bc = ce = y$ . Then y must be found noe where of odd dimensions in the Equation expressing the nature of the line cod. For (suppose{in}g $y = bc = ce$ to be the unknowne quantity) y hath 2 valors bc & cd equall to one another excepting that the one bc is affirmative, the other ce is negative. which two valors cannot bee exprest by an equation in which y is of odd dimensions for suppose $y y = a a$ . then is $\sqrt{a a} = a$ , since $a \times a = a a$ . & $\sqrt{a a} = - a$ , since $- a \times - a = a a$ . & $y = \sqrt{a a}$ therefore is $y = + a$ , or $y = - a$ . soe if $y^{4} = a^{4}$ . then is $y y = a a$ , & $y = a$ or $y = - a$ but if $y^{3} = a^{3}$ . then $y = \sqrt{c: a^{3}} = a$ . but not $y = \sqrt{c: - a^{3}} = - a$ . soe if $y^{5} = a^{5}$ . then $y = a = \sqrt{qc: a^{5}}$ but not $y = - 5 = \sqrt{qc: - a^{5}}$ . The same reason is cogent in compound equations. as if $y y - 2 x y + x x = a x$ . Then, $y = x \overset{\cup}{O} \sqrt{a x}$ . where though the root $a + \sqrt{a x}$ is affirmative & the roote $a - \sqrt{a x}$ may bee negative yet they can never be equall in length, & though the 2 roots of an equation which differ in signes should bee equally long yet that is when the Equation is fully determined.

^[8] Proposition 4^th. If x is of more dimensions in a quantity not multiplied by x then in one multiplied by it (as in $y^{2} =$ $x y + a a$ ) then y is not parallel to one of the lines Asymptotes. & e contra. Otherwise x & y are parallel to the Asymptotes of the line. et e contra.

Proposition 3^d. If ag is the Asymptote of the crooked line dcf , & $ab = x$ is coincident with it, & $bc = y$ . then in the Equation (expressing the relation twixt x & y ,) x must bee multiplied by y wherever it is of its greatest dimensions. & if ae is an asymptote to the line dcf , & $bc = y$ be parallel to it, & $ab = x$ terminated by it at the point a , then must y be multiplied by x wherever it is of its greatest dimensions. Example: Suppose $a x x + y x x = b^{3}$ . because in these 2 termes $a x x + y x x$ x is of its greatest dimensions; but in one of them (viz: $a x x$ ) it is not multiplyed by y therefore x is not coincident with ag the asymptote. If $y y x x + a y x x$ − $a^{3} x - a^{4} = 0$ . then since x is of its greatest dimensions in $y y x x$ & $a y x x$ onely & is drawne into y in both of them therefore x is coincident with the Asymptote{;} Also since y is of its greatest dimensions in $x x y y$ onely, (which {illeg} multiplied by x ) therefore y is parallel to x {illeg} {terminated} by an Asymptote. &c.

Demonstration If x is coincident with the Asymptote then { $\frac{e e}{o} = x$ } when $o = y$ . i:e: x is infinite when {illeg} {wisheth}. Now suppose $y y x x + a y x x -$ $= a^{4}$ . then if $y = o$ is $x = \frac{a a}{\sqrt{o o + a o}}$ . i:e: x is {illeg} but if $y y x x + a a x x = a^{4}$ . then if $y = o$ it is { $x = \frac{a a}{\sqrt{o o + a a}} = \overset{\cup}{O} a$ }. soe {that} x is finite & therefor{e}{illeg} coincident with the {illeg} de{illeg}{illeg} of {illeg} is like{illeg}

<16v>

^[9] Haveing {an} the nature of a crooked line expresed in algebraicall termes to find its axes if {I}{i} {shave} { anq }

^[10] Draw a line infinitely both ways fix upon some point (as b ) for the begining of one of the unknowne quantitys (which I call x . Then reduce the Equation to such an order (if it bee not already so) that x may be always found in the line bc . with one end fixed at b , & having y making right angles with it at the other end: that end of y which is remote from x , describing the crooked line. which may bee always done without any great difficulty. As may be perceived by these examples.

^[11] Suppose the given Equation was $y^{3} = a x x$ . soe that $bg = x$ . $gd = y$ . dc being perpendicular to bc & the angle dgc being given, the proportion twixt dg & dc is given, which I supose as d to e . then is $d ∶ e ∷ y ∶ \frac{e y}{d}$ $d ∶ e ∷ y ∶ dc = \frac{e y}{d} = w$ . & $\frac{d w}{e} = y$ . ${gc}^{2} \begin{array}{l} = {gd}^{2} - {dc}^{2} \\ = y y - w w \end{array} = \frac{d d w w - e e w w}{e e}$ . or $\frac{g}{c} \sqrt{d d - e e}$ . & $bc = v = \frac{w \sqrt{d d - e e}}{e}$ . Or $\frac{e v - w \sqrt{d d - e e}}{e} = x$ .^[12] Therefore I write $\frac{d^{3} w^{3}}{e^{3}}$ for $y^{3}$ , & $\frac{e e v v - 2 e v w \sqrt{d d - e e} + d d w w - e e w w}{e e}$ for $x x$ in the equation $y^{3} = a x x$ , & soe I have this equation $\frac{d^{3} w^{3}}{e^{3}} = \frac{a e e v v - 2 a e v w \sqrt{d d - e e} + a d d w^{2} - a e e w^{2}}{e e}$ . which expresseth the relation twixt w & v , that is twixt dc & bc , writeing therefore y for dc , & x for bc : I have this equation $d^{3} y^{3} + a e^{3} y y - a e d d y y + 2 a e e x y \sqrt{d d - e e} - a e^{3} x x$

^[13] Soe if x $= bd$ turned about the pole b & y $= dg$ about the pole g describing the crooked line ad by the conjunction at the extremitys. & the equation expresing the relation which they beare to one another is $x x = a y$ . the distance of the poles is given which I call $b = bg$ .^[14] perpendicular to bg I draw $dc = w$ & make $bc = v$ . Then, is $\begin{matrix} {dc}^{2} + {bc}^{2} = {bd}^{2} . \\ w^{2} + v^{2} = x x . \end{matrix}$ $\begin{array}{r} {dc}^{2} + {cg}^{2} = {dg}^{2} . \\ w^{2} + b b - 2 b v + v v = y y . \end{array}$ soe that for $x x = a y$ I write $w^{2} + v^{2} = a \sqrt{w^{2} + b b - 2 b v + v v}$ . Or $w^{4} + 2 w^{2} v^{2} + w^{4} = a a w^{2} + a a b b - 2 a a b v + a a v v$ . which expresseth the relation which bc beareth to dc , & by makeing $bc = x$ , $dc = y$ , it is, $\begin{array}{l} y^{4} & + & 2 x x y y & + & x^{4} & = & 0 \\ - & a a y y & + & 2 a a b x \\ - & a a x x \\ - & a a b b \end{array}$ .

Example 3^d If $bg = x$ be always in the line bc . & fd turning about the pole f & passing by the end of $bg = x$ with its other end d describes the crooked line bdh , soe that calling gd y $x = y$ . then drawing ef & dc perpendicular to bh . $be = a$ , & $ef = b$ are given. & I make $bc = v$ {.} $dc = w$ . then is $eg = x - a$ . $gc = v - x$ . $\begin{matrix} ef ∶ eg ∷ gc ∶ cd . \\ b ∶ x - a ∷ v - x ∶ w . \end{matrix}$ $bw = v x - a v + a x - x x$ . or by extracting the roote $x = \frac{+ a + v}{2} \overset{\cup}{O} \sqrt{\frac{a a + 2 a v + v v - 4 b w}{4}}$ . againe $\begin{matrix} {gc}^{2} + {dc}^{2} = {gd}^{2} \\ v v - 2 v x + x x + w^{2} = y y = x x . \end{matrix}$ . Or $\frac{v v + w^{2}}{2 w} = x = \frac{a + v}{2} \overset{\cup}{O} \sqrt{\frac{a a + 2 a v + v v - 4 b w}{4}}$ . & by transposeing $\frac{a + v}{2}$ to the other side & so squareing both parts $w^{4} - 2 a v w^{2} = 2 a w^{3} + v^{4} - 4 b w v^{2}$ . which equation expresseth the relation twixt $w = dc$ , & v $= bc$ . & so by calling dc y , & bc x , it is, $y^{4} - 2 a x y y + 4 b x x y - x^{4} - 2 a x^{3} = 0$ .

Example 4^th. if $bd = x$ turnes about the pole b , & gd (a given line $= a$ ) slides upon bg with one end & intersecting bd at right angles at the other end describes the crooked line bde by its intersection with bd . then makeing $bc = v$ , $dc = w$ . $\begin{matrix} {bc}^{2} + {dc}^{2} = {bd}^{2} . \\ v^{2} + w^{2} = x^{2} . \end{matrix}$ $\begin{matrix} bc ∶ bd ∷ dc ∶ dg . \\ v ∶ x ∷ w ∶ a . \end{matrix}$ & $\frac{a v}{w} = x$ therefore $v v + w w = \frac{a a v v}{w w}$ or $w^{4} + v v w w = a a v v$ . & so by writing x for v & y for w , I have the relation twixt $x = bc$ & $y = dc$ exprest in this equation $y^{4} + x x y y - a a x x = 0$ .

Or if the relation twixt bd & dg was exprest in this equation (making $dg = y$ . $bd = x$ ) $\begin{matrix} x x y \\ + a y y \end{matrix} = a^{3}$ . then as before $\begin{matrix} {bc}^{2} + {dc}^{2} = {bd}^{2} . \\ v^{2} + w^{2} = x^{2} . \end{matrix}$ $\begin{matrix} {bc}^{} ∶ {bd}^{} ∷ {dc}^{} ∶ {dg}^{} . \\ v^{} ∶ \sqrt{v v + w^{2}} ∷ w^{} ∶ y . \end{matrix}$ therefore $y = \frac{w \sqrt{v v + w^{2}}}{v}$ . first therefore I take away $x x$ by making $\frac{a^{3} - a y y}{y} = x x = v v + w^{2}$ . or by ordering it $a^{3} - a a y - v v y - w w y = 0$ . Then I take away y by substituteing its valor $\frac{w \sqrt{v v + w^{2}}}{v}$ into its roome & it will be $a^{3} - \frac{a w^{2} v^{2} - a w^{4}}{v v} = \frac{v v w \sqrt{v v + w^{2}} + w^{3} \sqrt{v v + w^{2}}}{v}$ . & by squareing both parts. $\begin{matrix} a^{6} v^{4} & - & 2 a^{4} v^{4} w^{2} & - & 2 a^{4} v v w^{4} & + & a a v^{4} w^{4} & - & 2 a a v v w^{6} & + & a a w^{8} & - & v^{8} w w & - & 3 v^{6} w^{4} & = & 0 \\ - & 3 v^{4} w^{6} & - & v v w^{8} \end{matrix}$ . & by writeing x for v & y for w the equation will be $\begin{array}{l} a a y^{8} & + & 2 a a x x y^{6} & + & a a x^{4} y^{4} & - & x^{8} y y & + & a^{6} x^{4} & = & 0 \\ - & x x y^{8} & - & 3 x^{4} y^{6} & - & 3 x^{6} y^{4} & - & 2 a^{4} x^{4} y y \\ - & 2 a^{4} x x y^{4} \end{array}$ .

The like may as easily be performed in any other case.

After the equation is brought to this order observe that if y is noe where of odd dimensions then the line bc (which is coincident with x ) is parte of an axis of the crooked line, as in the 2^d Example. And if x is noe where of odd dimensions (as in this, $a^{4} + y y a a = a a x^{2}$ ) Then from the point b at the begining of x . I draw bk perpendicular to bc which is coincident with the axis of the crooked line. And if neither x nor y bee of unequall dimensions in any terme of the equation then both bk & bc may bee taken for axes of the crooked line or lin{e}s whose nature are expressed by the equation. As in the 4^th Example.

But if y is of odd dimension{s} in the Equation then ordering the Equation according to y see if y is of eaven dimensions in the first te{r}me {illeg} { x } not found in the 2^nd. if so take away the 2^nd terme of the equation & if there result an Equation in which y is noe where of {odd} dim{en}sions. Then I draw ce perpendicular to bc & equall to that quantity which added or substracted from y that might take away the 2^d terme; through the point {illeg} P{illeg} f{illeg}{illeg}{illeg}bee {illeg}.

<17r>

^[15] As in this Example, $y y +$ $2$ $a y$ $- \frac{x^{3}}{a} = 0$ . Then to take away the 2^d terme I make $z - a = y$ . & soe I have, $z z * - a a - \frac{x^{3}}{a} = 0$ . in which z is not of odd dimensions. Then drawing bc for x , dc for y , & de for z : or which is the same (since $z - a = y$ ) I make $ce = - a$ that is I draw dc & ce on 2 contrary sides of the line bc . & through the point e I draw ae parallell to bc & make it the axis of the line dag

^[16] Example the 2^d. $y^{4} - 8 a y y y + 24 a a y^{2} - 3 a x y^{2} - 32 a^{3} y$ $+ 16 a^{4}$ $+ 12 a a x y = 0$ . Then by making $z + 2 a = y$ I take away the 2^d terme. & the Equation $z^{4} * - 3 a x z z * + 12 a^{3} x = 0$ . in which z is onely of eaven dimensions. Then I draw bc for x . dc for y de for, or which is the same (since $z +$ $2$ $a = y$ ) I make $ec = 2 a$ , that is I draw ec & dc on the same side of bc then through the point e parallell to bc I draw ea for the axis of the lines dac d khg .

^[17] In like manner, if x is of odd dimensions in some terme of the Equation, the Axis bk perpendicular to $x = bc$ may bee found. As for Example. $x x +$ { $2$ } $a x - \frac{a^{3}}{a} = 0$ . by makei{ng} $z - \frac{a}{2} = x$ , I take away the 2^d terme and soe have this equation $z z * - \frac{y^{3}}{a} - \frac{a a}{4} = 0$ . therefore I draw $bc = x$ from the fixed point b , & $ce = z$ , or which is the same (since $z - \frac{a}{2} = x$ ) I draw $eb = - \frac{1}{2} a$ , that is I draw eb & bc on two contrary sides of the line k b then throug{h} the point e , parallell to bk I draw ea the axis of the line

^[18] Example 2^d. $x^{4} - 4 a x^{3} + 4 a a x x$ $- a a y y - a a b y = 0$ . by makeing $x = z + a$ I have this Equation $x^{4} - 2 a a z z - a a y y - a a b y + a^{4} = 0$ . In which z is noe where of odd dimensions. therefore assumeing b for the begining of x & making $b
c = x$ , & $ce =$ z , or which is the same I make $be = + a$ , since $x = z + a$ ; that is if bc is affirmative I take be & bc on the same side of the line kb . otherwise I describe them on contrary sides of it. then through the point e parallell to bk I draw eg {an} axis of the lines dbmd & nhr . Againe I order the Equation according to y & it is $\begin{array}{l} a^{2} y y & + & a a b y & - & z^{4} & = & 0 \\ + & 2 a a z z \\ - & a^{4} \end{array}$ . & soe since x is not in the 2^d terme makeing $v - \frac{b}{2} = y$ . I take away the 2^d terme, & it is $\begin{array}{l} a a v v & * & - & \frac{a a b b}{4} & - & z^{4} & = & 0 \\ + & 2 a a z z \\ - & a^{4} \end{array}$ . Therefore I draw $ec = z$ , $dc = y$ , & $df = v$ . or which differs not (since $v - \frac{b}{2} = y$ ) I make $cf = - \frac{b}{2}$ & through the point f parallell to ce I draw { fg } for another axis of the lines dbmd , & ndhdr .

^[19] But if the unknowne quantity ( x or y ) is of odd dimensions in the first terme or if both the unknowne quantitys are in the 2^d terme, or if by these meanes the equation is irreducible to such a forme that x , or, y , or both of them bee of odd dimensions noewhere in the Equation: Then try to find the axes by the following method. Observing by the way that

If $+ x$ begins at the point b & extends towards c in the line sr then $- x$ is taken the contrary way towards s , & all the affirmative lines parallell to sr are drawne the same way which $+ x$ is but the negative lines parallell to sr are drawn the same way with $- x$ as if from the point m I must draw a line $= a$ , I draw it towards n but if from the same point m I must draw a line $= - a$ I draw it towards l . soe if from the point d I must draw $d λ = + b$ , then I draw it towards θ , but if $d λ = - b$ then I draw it towards γ . Againe if $+ y$ is drawne toward p from the line sr , then $- y$ is drawne from the same line sr the contrary way towards o , & those lines which are affected with an affirmative signe & are parallell to y they are drawne the same way which y is but those lines which are negative are drawn the contrary way. as if $a = aπ$ then I draw aπ towards e but if $- a = aπ$ then I draw it towards t . soe if $vμ = + d$ then I draw it from v towards δ, if $vμ = - d$ , I draw it towards w.

A generall rule to find the axes of any line.

^[20] ^[21] Suppose $bc = x$ . $cd = y$ . & kg to be the axis. then parallel to y from the point b to the axis kg draw $bf = c$ . from d the end of y , perpendicular to kg draw $dh = ϩ$ . & make $fh = ϱ$ & suppose $fe ∶ fg ∷ d ∶ e$ . then is $fg = \frac{e x}{d}$ . & $d ∶ e ∷ dh = ϩ ∶ \frac{e ϩ}{d} = dg$ . $\begin{matrix} {dg}^{2} - {dh}^{2} = {gh}^{2} \\ \frac{e e ϩ ϩ}{d d} - ϩ ϩ = {gh}^{2} \end{matrix}$ . $gh = \frac{ϩ \sqrt{e e - d d}}{d}$ $gh = \begin{matrix} - fh & + fg \\ - ϱ & + \frac{e x}{d} \end{matrix} = \frac{ϩ \sqrt{e e - d d}}{d}$ . therefore $\frac{d ϱ + ϩ \sqrt{e e - d d}}{e} = x$ . Againe $ge + ec - dg = dc$ , that is $\sqrt{\frac{e e x x}{d} - x x} + c - \frac{e ϩ}{d} = y$ . or for x writeing its valor, $y = \frac{c e - d ϩ + ϱ \sqrt{e e - d d}}{e}$ . Now assumeing any quantity for e , that I may find the valors of c & d . I substitute these valors of x & y into theire roome in the Equation. as if the equation be $x^{2} - 2 x y + a y + y y = 0$ . by making $e = a$ . the valor of x is $\frac{d ϱ + ϩ \sqrt{a a - d d}}{a}$ & the valor of y is $\frac{a c - d ϩ + ϱ \sqrt{a a - d d}}{a}$ . which 2 valors substituting into their roome in the equation, there results { $\begin{matrix} a a ϩ ϩ & + & 2 d ϩ ϩ \sqrt{a^{2} - d^{2}} & + & 4 d d ϱ ϩ & - & 2 d ϱ ϱ \sqrt{a a - d d} \\ - & 2 a a ϱ ϩ & + & 2 a c ϱ \sqrt{a a - d d} \\ - & a^{2} d ϩ & + & a a ϱ \sqrt{a a - d d} \\ - & 2 a c d ϩ & + & a a ϱ ϱ \\ - & 2 a c ϩ \sqrt{a^{2} - d^{2}} & - & 2 d a c ϱ \\ + & a^{3} c \\ + & a a c c \end{matrix}} = 0$ } Now that I may have an equation in which ϩ is of {2} eaven dimensions o{ne}ly I suppose the 2^d terme $= 0$ & soe have this equation $4 d d ϱ ϩ - 2 a a ϩ ϱ$ $- a a d ϩ - 2 a c d ϩ - 2 a c ϩ \sqrt{a a - d d} = 0$ & that the termes in this {feigned} equation may destiny one another I order it according to { ϱ } & soe suppose each terme $= 0$ . & so I have these equations $4 d d ϱ ϩ - 2 a a ϱ ϩ = 0$ & $- a a d ϩ - 2 a c d ϩ - 2 a c ϩ \sqrt{a a - d d} = 0$ . by the first I find $2 d d = a a$ , or $d = \frac{a a}{\sqrt{2}}$ . by the 2^d $- a a d - 2 a c d - 2 a c \sqrt{a a - d d} = 0$ . & by substituteing the valor of d into its {roome} I find $\frac{a^{3} - 4 a a c}{\sqrt{2}} = 0$ . or $c = \frac{- a}{4}$ therefore from { b } perpendicular to bc I draw $bf = \frac{- a}{4}$ . through the point f parallell to bc I draw $fe = \frac{a}{\sqrt{2}}$ & since $f$ {illeg} $= a$ therefore I draw $ge = \sqrt{a a - \frac{a a}{2}} = \frac{a}{\sqrt{2}}$ . & lastly {illeg}{illeg}the points f & g I draw fg the axis of the crooked line bah .

<17v>

But since there is noe use of those termes in which ϩ is of eaven dimensions the Calculation will bee much abreviated by this following table.

^[22] $x = \sqrt{e e - d d}$ . $y = - d$ . $y y = - 2 c d$ . $y^{3} = - 3 c c d$ . $y^{4} = - 4 c^{3} d$ . $y^{5} = - 5 c^{4} d$ . $y^{6} = - 6 c^{5} d$ &c $x y = c \sqrt{e e - d d}$ . $x y y = c c \sqrt{e e - d d}$ . $x y^{3} = c^{3} \sqrt{e e - d d}$ . $x y^{4} = c^{4} \sqrt{e e - d d}$ . $x y^{5} = c^{5} \sqrt{e e - d d}$ . &c.

^[23] $x x = 2 d \sqrt{e e - d d}$ . $y y = \begin{matrix} - 2 \\ - 1 \times 2 \end{matrix}} d \sqrt{e e - d d}$ . $y^{3} = \begin{matrix} - 6 \\ - 2 \times 3 \end{matrix}} c d \sqrt{e e - d d}$ . $y^{4} = \begin{matrix} - 12 \\ - 3 \times 4 \end{matrix}} c c d \sqrt{e e - d d}$ . $y^{5} = \begin{matrix} - 20 \\ - 4 \times 5 \end{matrix}} c^{3} d \sqrt{e e - d d}$ . $y^{6} = \begin{matrix} - 30 \\ - 5 \times 6 \end{matrix}} c^{4} d \sqrt{e e - d d}$ . $x y = - 2 d d + e e$ . $x y y = - 4 c d d + 2 c e e$ . $x y^{3} = - 6 c c d d + 3 c c e e$ . $x y^{4} = - 8 c^{3} d d + 4 c^{3} e e$ . $x y^{5} = 5 c^{4} e e - 104 d d$ . &c. $x x y = 2 c d \sqrt{e e - d d}$ . $x x y y = 2 c c d \sqrt{e e - d d}$ . $x x y^{3} = 2 c^{3} d \sqrt{e e - d d}$ . $x x y^{4} = 2 c^{4} d \sqrt{e e - d d}$ . $x x y^{5} = 2 c^{5} d \sqrt{e e - d d}$ . &c.

^[24] $x^{3} = 3 d d \sqrt{e e - d d}$ . $y^{3} = - 3 d e e + 3 d^{3}$ . $y^{4} = 2 \times 6 c d^{3} - 2 \times 6 c d e e$ . $y^{5} = 3 \times 10 c c d^{3} - 3 \times 10 c c d e e$ . $y^{6} = 4 \times 15 c^{3} d^{3} - 4 \times 15 c^{3} d e e$ . $x y y = - 3 d d \sqrt{e e - d d} + e e \sqrt{e e - d d}$ . $x y^{3} = - 3 c e e \sqrt{e e - d d} - 9 c d d \sqrt{e e - d d}$ . $x y^{4} = 6 c c e e \sqrt{e e - d d} - 18 c c d d \sqrt{e e - d d}$ . $x y^{5} = 10 c^{3} e e \sqrt{e e - d d} - 30 c^{3} d d \sqrt{e e - d d}$ . &c $x x y = 2 d e e - 3 d^{3}$ . $x x y y = 4 c d e e - 6 c d^{3}$ . $x x y^{3} = 6 c c d e e - 9 c c d^{3}$ . $x x y^{4} = 8 c^{3} d e e - 12 c^{3} d^{3}$ . $x^{3} y = 3 c d d \sqrt{e e - d d}$ . $x^{3} y y = 3 c c d d \sqrt{e e - d d}$ . $x^{3} y^{3} = 3 c^{3} d^{2} \sqrt{e e - d d}$ . $x^{3} y^{4} = 3 c^{4} d d \sqrt{e e - d d}$ .

^[25] $x^{4} = 4 d^{3} \sqrt{e e - d d}$ . $y^{4} = - 1 \times 4 d \sqrt{- e^{6} - 3 e^{4} d d + 3 e e d^{4} - d^{6}}$ . $y^{5} = - 2 \times 10 c d \sqrt{- e^{6} - 3 e^{4} d d + 3 e e d^{4} - d^{6}}$ . $y^{6} = - 3 \times 20 c c d \sqrt{- e^{6} &c}$ : $y^{7} = - 4 \times 35 c^{3} d \sqrt{- e^{6} &c}$ . $x y^{3} = e^{4} \begin{matrix} - 2 d d e e + 1 d^{4} \\ - 3 d d e e + 3 d^{4} \end{matrix}$ . $x y^{4} = 4 c e^{4} \begin{array}{l} - 8 \\ - 12 \end{array} c d d e e \begin{array}{l} + 4 \\ + 12 \end{array} c d^{4}$ . $x y^{5} = 10 c c e^{4} \begin{array}{l} - 20 \\ - 30 \end{array} c c d d e e \begin{array}{l} + 10 \\ + 30 \end{array} c c d^{4}$ . $x y^{6} = 20 c^{3} e^{4} \begin{array}{l} - 40 \\ - 60 \end{array} c^{3} d d e e \begin{array}{l} + 20 \\ + 60 \end{array} c^{3} d^{4}$ &c. $x x y y = \begin{matrix} 1 \times 2 d e e \\ - 4 d^{3} \end{matrix} \sqrt{e e - d d}$ . $x x y^{3} = \begin{matrix} 2 \times 3 c d e e \\ - 12 c d^{3} \end{matrix} \sqrt{e e - d d}$ . $x x y^{4} = \begin{matrix} + 12 c c d e e \\ - 24 c c d^{3} \end{matrix} \sqrt{e e - d d}$ . $x x y^{5} = \begin{matrix} + 20 c^{3} d e e \\ - 40 c^{3} d^{3} \end{matrix} \sqrt{e e - d d}$ . $x^{3} y = 3 d d e e - 4 d^{4}$ . $x^{3} y y = 6 c d d e e - 8 c d^{4}$ . $x^{3} y^{3} = 9 c c d d e e - 12 c c d^{4}$ . $x^{3} y^{4} = 12 c^{3} d d e e - 16 c^{3} d^{4}$ . $x^{4} y = 4 c d^{3} \sqrt{e e - d d}$ . $x^{4} y y = 4 c c d^{3} \sqrt{e e - d d}$ . $x^{4} y^{3} = 4 c^{3} d^{3} \sqrt{e e - d d}$ . $x^{4} y^{4} = 4 c^{4} d^{3} \sqrt{e e - d d}$ .

^[26] $x^{5} = 5 d^{4} \sqrt{e e - d d}$ . $y^{5} = - 1 \times 5 d e^{4} + 10 d^{3} e e - 5 d^{5}$ . $y^{6} = - 2 \times 15 c d e^{4} + 60 c d^{3} e e - 30 c d^{5}$ . $y^{7} = - 3 \times 35 c c d e^{4} + 210 c c d^{3} e e - 105 c c d^{5}$ . $y^{8} = - 4 \times 70 c^{3} d e^{4}$ $+ 560 c^{3} d^{3} e e - 280 c^{3} d^{5}$ &c $x y^{4} = e^{4} \begin{matrix} - 2 d d e e + 1 d^{4} \\ - 4 d d e e + 4 d^{4} \end{matrix} in \sqrt{e e - d d}$ . $x y^{5} = 5 e c e^{4} \begin{matrix} - 10 c d d e e + 5 c d^{4} \\ - 20 c d d e e + 20 c d^{4} \end{matrix} in \sqrt{e e - d d}$ . $x y^{6} = 15 c c e^{4} \begin{matrix} - 30 c c d d e e + 15 c c d^{4} \\ - 60 c c d d e e + 60 c c d^{4} \end{matrix} in \sqrt{e e - d d}$ . $x y^{7} = 35 c^{3} e^{4} \begin{matrix} - 70 c^{3} d d e e + 35 c^{3} d^{4} \\ - 140 c^{3} d d e e + 140 c^{3} d^{4} \end{matrix} in \sqrt{e e - d d}$ . $x x y^{3} = 2 d e^{4} \begin{matrix} - 4 d^{3} e e + 2 d^{5} \\ - 3 d^{3} e e + 3 d^{5} \end{matrix}$ . $x x y^{4} = - 2 \times 4 c d e^{4} \begin{matrix} - 2 \times 8 c d^{3} e e + 8 c d^{5} \\ - 12 c d^{3} e e + 12 c d^{5} \end{matrix}$ . $x x y^{5} = 20 c c d e^{4} \begin{matrix} - 40 c c d^{3} e e + 2 \times 10 c c d^{5} \\ - 30 c c d^{3} e e + 30 c c d^{5} \end{matrix}$ . $x x y^{6} = 40 c^{3} d e^{4} \begin{matrix} - 80 c^{3} d^{3} e e + 2 \times 20 c^{3} d^{5} \\ - 60 c^{3} d^{3} e e + 60 c^{3} d^{5} \end{matrix}$ $x^{3} y y = \begin{matrix} 1 \times 3 d d e e \\ - 5 d^{4} \end{matrix} \sqrt{e e - d d}$ . $x^{3} y^{3} = \begin{matrix} 3 \times 3 d d c e e \\ - 15 c d^{4} \end{matrix} \sqrt{e e - d d}$ . $x^{3} y^{4} = \begin{matrix} 6 \times 3 c c d d e e \\ - 6 \times 5 c c d^{4} \end{matrix} \sqrt{e e - d d}$ . $x^{3} y^{5} = \begin{matrix} 10 \times 3 c^{3} d d e e \\ - 50 c^{3} d^{4} \end{matrix} \sqrt{e e - d d}$ . $x^{3} y^{6} = \begin{matrix} 15 \times 3 c^{4} d d e e \\ - 75 c^{4} d^{4} \end{matrix} \sqrt{e e - d d}$ . $x^{4} y = 1 \times 4 d^{3} e e - 5 d^{5}$ . $x^{4} y y = 2 \times 4 c d^{3} e e - 10 c d^{5}$ . $x^{4} y^{3} = 3 \times 4 c c d^{3} e e - 15 c c d^{5}$ . $x^{4} y^{4} = 4 \times 4 c^{3} d^{3} e e - 20 c^{3} d^{5}$ . $x^{4} y^{5} = 5 \times 4 c^{4} d^{3} e e - 25 c^{4} d^{5}$ . $x^{5} y = 5 c d^{4} \sqrt{e e - d d}$ . $x^{5} y y = 5 c c d^{4} \sqrt{e e - d d}$ . $x^{5} y^{3} = 5 c^{3} d^{4} \sqrt{e e - d d}$ .

^[27] $y^{6} = - 6 \times 1 d \sqrt{e^{10} - 5 e^{8} d d + 10 e^{6} d^{4} - 10 e^{4} d^{6} + 5 e e d^{8} - d^{10}}$ . $y^{7} = - 6 \times 7 d c \sqrt{e^{10} &c}$ : $y^{8} = - 6 \times 28 c c d \sqrt{e^{10} &c}$ : $y^{9} = - 6 \times 84 c^{3} d \sqrt{e^{10} &c}$ : $x y^{5} = 1 \times 1 e^{6} \begin{matrix} - 3 d d e^{4} + 3 d^{4} e e - d^{6} \\ - 5 d d e^{4} + 3 d^{4} e e - 5 d^{6} \end{matrix}$ . $x y^{6} = 1 \times 6 c e^{6} \begin{matrix} - 18 c d d e^{4} + 18 c d^{4} e e - 6 c d^{6} \\ - 6 \times 5 c d d e^{4} + 60 c d^{4} e e - 30 c d^{6} \end{matrix}$ . $x y^{7} = 1 \times 21 c c e^{6} \begin{matrix} - 63 c c e^{4} d d + 63 c c e e d^{4} - 21 c c d^{6} \\ - 21 \times 5 c c e^{4} d d + 210 c c e e d^{4} - 105 c c d^{6} \end{matrix}$ . $x y^{8} = 1 \times 53 c^{3} e^{6} &c$ $x x y^{4} = 2 \times 1 d e^{4} \begin{matrix} - 4 d^{3} e e + 2 d^{5} \\ - 4 d^{3} e e + 4 d^{5} \end{matrix} \sqrt{e e - d d}$ . $x x y^{5} = 2 \times 5 c d e^{4} \begin{matrix} - 20 c d^{3} e e + 10 c d^{5} \\ - 5 \times 4 d^{3} e e + 20 c d^{5} \end{matrix} in \sqrt{e e - d d}$ . $x x y^{6} = 2 \times 15 c c d e^{4} \begin{matrix} - 60 c c d^{3} e e + 30 c c d^{5} \\ - 4 \times 15 c c d^{3} e e + 60 c c d^{5} \end{matrix} \times \sqrt{e e - d d}$ . $x^{3} y^{3} = 3 \times 1 d d e^{4} \begin{matrix} - 6 d^{4} e e + 3 d^{6} \\ - 3 d^{4} e e + 3 d^{6} \end{matrix}$ . $x^{3} y^{4} = 3 \times 4 c d d e^{4} \begin{matrix} - 24 c d^{4} e e + 12 c d^{6} \\ - 3 \times 4 c d^{4} e e + 12 c d^{6} \end{matrix}$ . $x^{3} y^{5} = 3 \times 10 c c d d e^{4} \begin{matrix} - 60 c c d^{4} e e + 30 c c d^{6} \\ - 30 c c d^{4} e e + 30 c c d^{6} \end{matrix}$ . $x^{4} y y = 4 \times 1 d d d e e \begin{matrix} - 4 d^{5} \\ - 2 d^{5} \end{matrix} in \sqrt{e e - d d}$ . $x^{4} y^{3} = 4 \times 3 d^{3} c e e \begin{matrix} - 12 c d^{5} \\ - 6 c d^{5} \end{matrix} in \sqrt{e e - d d}$ . $x^{4} y^{4} = 4 \times 6 c c d^{3} e e \begin{matrix} - 24 c c d^{5} \\ - 12 c c d^{5} \end{matrix} in \sqrt{e e - d d}$ . $x^{4} y^{5} = 4 \times 10 c^{3} d^{3} e e &c$ . $x^{5} y = 1 \times 5 d^{4} e e \begin{matrix} - 5 d^{6} \\ - 1 d^{6} \end{matrix}$ . $x^{5} y y = 5 \times 2 c d^{4} e e \begin{matrix} - 10 c d^{6} \\ - 2 c d^{6} \end{matrix}$ . $x^{5} y^{3} = 5 \times 3 c c d^{4} e e \begin{matrix} - 15 c c d^{6} \\ - 3 c c d^{6} \end{matrix}$ . $x^{5} y^{4} = 5 \times 4 c^{3} d^{4} e e \begin{matrix} - 20 c c d^{6} \\ - 4 c c d^{6} \end{matrix}$ . $x^{6} = 1 \times 6 d^{5} \sqrt{e e - d d}$ . $x^{6} y = 6 c d^{5} \sqrt{e e - d d}$ . $x^{6} y y = 6 c c d^{5} \sqrt{e e - d d}$ . $x^{6} y^{3}$ = $6 c^{3} d^{5} \sqrt{e e - d d}$ . &c.

^[28] $y^{3}$ $- d^{3}$ . $y^{4} = - 4 c d^{3}$ . $y^{5} = - 10 c c d^{3}$ . $y^{6} = - 20 c^{3} d^{3}$ . $y^{7} = - 35 c^{4} d^{3}$ . $y^{8} = - 56 c^{5} d^{3}$ . $x y y = d d \sqrt{e e - d d}$ . $x y^{3} = c d d \sqrt{e e - d d}$ . $x y^{4} = c c d d \sqrt{e e - d d}$ . $x y^{5} = c^{3} d d \sqrt{e e - d d}$ . $x x y = d^{3} - e e d$ . $x x y y = 2 c d^{3} - 2 c e e d$ . $x x y^{3} = 3 c c d^{3} - 3 c c e e d$ . $x x y^{4} = 4 c^{3} d^{3} - 4 c c e e d$ . $x^{3} = e e - d d in \sqrt{e e - d d}$ . $x^{3} y = c e e - c d d \sqrt{e e - d d}$ . $x^{3} y y = c c e e - c c d d in \sqrt{e e - d d}$ . $x^{3} y^{3} = c^{3} \sqrt{e^{6} - 3 e^{4} d d + 3 e e d^{4} - d^{6}}$ .

^[29] $y^{4} =$ $- 1 \times 4 d^{3} \sqrt{e e - d d}$ . $y^{5} = - 5 \times 4 c d^{3} \sqrt{e e - d d}$ . $y^{6} = - 15 \times 4 c c d^{3} \sqrt{e e - d d}$ . $y^{7} = - 35 \times 4 c^{3} d^{3} \sqrt{e e - d d}$ . $x y^{3} = 1 \times 3 d d e e \begin{matrix} - 3 d^{4} \\ - 1 d^{4} \end{matrix}$ . $x y^{4} = 4 \times 3 c d d e e \begin{matrix} - 12 c d^{4} \\ - 4 \times 1 d^{4} \end{matrix}$ . $x y^{5} = 10 \times 3 c c d d e e \begin{matrix} - 30 c c d^{4} \\ - 10 c c d^{4} \end{matrix}$ . $x y^{6} = 20 \times 3 c^{3} d d e e \begin{matrix} - 60 c^{3} d^{4} \\ - 20 c^{3} d^{4} \end{matrix}$ . $x x y y = - 1 \times 2 d e e \begin{matrix} + 2 d^{3} \\ + 2 d^{3} \end{matrix} in \sqrt{e e - d d}$ . $x x y^{3} = - 3 \times 2 c d e e \begin{matrix} + 6 c d^{3} \\ + 6 c d^{3} \end{matrix}$ . $x x y^{4} = - 6 \times 2 c c d e e \begin{matrix} + 12 c c d^{3} \\ + 12 c c d^{3} \end{matrix}$ . $x x y^{5} = - 10 \times 2 c^{3} d e e \begin{matrix} + 20 c^{3} d^{3} \\ + 20 c^{3} d^{3} \end{matrix}$ . $x^{3} y = 1 \times 1 e^{4} \begin{matrix} - 2 d d e e + d^{4} \\ - 3 d d e e + 3 d^{4} \end{matrix}$ . $x^{3} y y = 1 \times 2 c e^{4} \begin{matrix} - 4 c e e d d + 2 d^{4} c \\ - 6 c e e d d + 6 c d^{4} \end{matrix}$ . $x^{3} y^{3} = 3 c c e^{4} \begin{matrix} - 6 c c e e d d + 3 c c d^{4} \\ - 9 c c e e d d + 9 c c d^{4} \end{matrix}$ . $x^{3} y y = 4 c^{3} e^{4} &c.$ $x^{4} = 4 e e d - 4 d^{3} in \sqrt{e e - d d}$ . $x^{4} y = 4 c e e d - 4 c d^{3} in \sqrt{e e - d d}$ . $x^{4} y y = - 4 c c d \sqrt{e^{6} - 3 e^{4} d d + 3 e e d^{4} - d^{6}}$ . $x^{4} y^{3} = - 4 c^{3} d \sqrt{e^{6} &c}$ .

^[30] $y^{5} = - 1 \times 10 e e d^{3} + 10 d^{5}$ . $y^{6} = - 6 \times 10 c e e d^{3} + 60 c d^{5}$ . $y^{7} = - 21 \times 10 c c e e d^{3} + 210 c c d^{5}$ . $y^{8} = - 56 \times 10 c^{3} e e d^{3} + 560 c^{3} d^{5}$ . $x y^{4} = - 1 \times 6 e e d d \begin{matrix} - 6 d^{4} \\ - 4 d^{4} \end{matrix} in \sqrt{e e - d d}$ . $x y^{5} = - 5 \times 6 c e e d d \begin{matrix} - 30 c d^{4} \\ - 20 c d^{4} \end{matrix} in \sqrt{e e - d d}$ . $x y^{6} = - 15 \times 6 c c e e d d \begin{matrix} - 90 c c d^{4} \\ - 60 c c d^{4} \end{matrix} in \sqrt{e e - d d}$ . $\begin{matrix} x x y^{3} = - 1 \times 3 e^{4} d & + 6 e e d^{3} & - 3 d^{5} \\ + 6 e e d^{3} & - 6 d^{5} \\ - 1 d^{5} \end{matrix}$ . $\begin{matrix} x x y^{4} = - 4 \times 3 c e^{4} d & + 24 c e e d^{3} & - 12 c d^{5} \\ + 24 c e e d^{3} & - 24 c d^{5} \\ - 4 c d^{5} \end{matrix}$ . $\begin{matrix} x x y^{5} = - 10 \times 3 c c e^{4} d & + 60 c c e e d^{3} & - 30 c c d^{5} \\ + 60 c c e e d^{3} & - 60 c c d^{5} \\ - 10 c c d^{5} \end{matrix}$ . $\begin{array}{l} x^{3} y y = e^{4} & - 2 d d e e & + d^{4} \\ - 6 d d e e & + 6 d^{4} \\ + 3 d^{4} \end{array} in \sqrt{e e - d d}$ . $\begin{array}{l} x^{3} y^{3} = 3 \times 1 c e^{4} & - 6 c d d e e & + 3 c d^{4} \\ - 18 c d d e e & + 18 c d^{4} \\ + 9 c d^{4} \end{array} in \sqrt{e e - d d}$ . $\begin{array}{l} x^{3} y^{4} = 6 c c e^{4} & - 12 c c d d e e & + 6 c c d^{4} \\ - 36 c c d d e e & + 30 c c d^{4} \\ + 18 c c d^{4} \end{array} in \sqrt{e e - d d}$ . $\begin{array}{l} x^{4} y = 4 d e^{4} & - 9 d^{3} e e & + d^{5} \\ - 6 d^{3} e e & + d^{5} \end{array}$ . $\begin{array}{l} x^{4} y y = 2 \times 4 c d e^{4} & - 16 c d^{3} e e & + 8 c d^{5} \\ - 12 c d^{3} e e & + 12 c d^{5} \end{array}$ . $\begin{array}{l} x^{4} y^{3} = 3 \times 4 c c d e^{4} & - 24 c c d^{3} e e & + 12 c c d^{5} \\ - 18 c c d^{3} e e & + 18 c c d^{5} \end{array}$ . $x^{5} = 10$ {illeg} $d d - 10 d^{4}$ {illeg}{ $\sqrt{e e - d d}$ }. $10 c$ {illeg} $d d - 10 c d^{4}$ {illeg} $\sqrt{e e - d d} = x^{5} y$ . $x^{5} y y = 10$ $c d d \sqrt{e^{6} - 3 e^{4} d d + 3 e e d^{4} - d^{6}}$

<18v>

The use of the precedent table in finding the Axes of crooked Lines, declared by Examples.

^[31] Suppose I had this Equation given, $x x - 2 x y + a y + y y$ . That I may find the axis of the line signified by it, first I observe of how many dimensions one of the unknowne quantities or the rectangle of them both is found at most in the Equation, (as in this Example they have noe more than 2) then I take every quantity in which one of the unknowne quantitys or the rectangle of them both is of soe many dimensions (which in this case are $x x - 2 x y + y y$ .) Then lookeing in the Table, (either amongst the rules of the first or 2^d sort &c) for a rule in which the first quantity is of soe many dimensions I substitute the valors of the unknowne quantitys, found by that rule, into their place in the selected quantitys & supposeing the product $= 0$ , I find the proportion of d to e thereby, that is I find the angle which the axis makes with the unknowne quantity called x . As in this case I take the 2^d Rule of the first sort, & by it I find $x x = 2 d \sqrt{e e - d d}$ . $x y = e e - 2 d d$ . $y y = - 2 d \sqrt{e e - d d}$ . which valors substituting into the roome of the unknown quantitys in these selected termes $x x - 2 x y + y y$ . I have this equation. $2 d \sqrt{e e - d d} - 2 e e + 4 d d - 2 d \sqrt{e e - d d} = 0$ . or, $2 d d = e e$ . & $e = d \sqrt{2}$ so that by assuming any quantity for $e e$ as a I have the valor of d , for $d = \frac{a}{\sqrt{2}}$ . therefore $d ∶ d \sqrt{2} ∷ d ∶ e ∷ \frac{a}{\sqrt{2}} ∶ a ∷ a ∶ a \sqrt{2}$ &c. In the next place that I may find the length of the line $bf = c$ . I take another rule whose first quantity is not of soe many nor of fewer dimensions than one of the unknowne quantitys or the rectangle them both is some where in the Equation. Then select every quantity out of the Equation, the valor of whose unknowne quantity may be found by this rule, & substituting their valors, found thereby, into their places in these selected termes make the product $= 0$ . & find the valor of c thereby. As in this example I must take the first rule of the 1^st sort. By which I find $x y = c \sqrt{e e - d d}$ , $y = - d$ , $y y = - 2 d c$ : but the valor of $x x$ cannot be found by it. therefore I onely take the termes $- 2 x y + a y + y y$ , & by substituting the valors of the unknown quantitys into their roomes I have $- 2 c \sqrt{e e - d d} - a d - 2 d c = 0$ . Then by substituting the about found valors of $d = a$ & $e = \sqrt{2 a a}$ into their places, it is $\overset{\cup}{O} 2 a c + a a + 2 a c$ . Or $+ 2 a c + a a + 2 a c$ . or $c = - \frac{a}{4}$ . Soe that if I make b the beginning of x , & $+ x$ to tend towards c in the line bc , & $+ y$ towards k perpendicularly to bc . then must I draw $bf = - \frac{a}{4}$ from the point b perpendicular to bc ; & $fe = a$ , & parallell to bc ; then $eg = \sqrt{{gf}^{2} - {fe}^{2}}$ $eg = a$ , & parallell to bf . Lastly through the points f & g draw gf the axis of the line sought. Otherwise it may be done thus $eg ∶ ef ∷ - bf ∶ bh$ . therefore I take $bh = \frac{- c d}{\sqrt{e e - d d}} = \frac{a}{4}$ , & through the points f & h $\sqrt{e e - d d} ∶ d ∷ - c ∶ \frac{- c d}{\sqrt{e e - d d}}$ . I draw af the axis sought.

^[32] Example the 2^d. If the Equation bee $x^{3} - a x y + y^{3} = 0$ . the Rule whose first quantity is of as many dimensions as either of the unknowne quantitys in this Equation, is the 3^d of the first sort or the first of the 2^d sort. Selecting therefore onely $x^{3} + y^{3}$ out of the Equation (since in neither of these rules the valor of $x y$ is found) by the 3^d rule of the first sort I find $x^{3} = 3 d d \sqrt{e e - d d}$ , $y^{3} = 3 d^{3} - 3 d e e$ . therefore the selected termes $x^{3} + y^{3} = 3 d d \sqrt{e e - d d} + 3 d^{3} - 3 d e e = 0$ . & $d \sqrt{e e - d d}$ $e e - d d$ . Or, $e e = 2 d d$ . In like manner by the first rule of the 2^d sort tis found $y^{3} = - d^{3}$ . $x^{3} = e e - d d in \sqrt{e e - d d}$ . & therefore $x^{3} + y^{3} =$ $\sqrt{e^{6} - 3 e^{4} d d + 3 e e d^{4} - d^{6}} - d^{3} = 0$ . & $\sqrt{c: e^{6} - 3 e^{4} d d + 3 e e d^{4} - d^{6}} = d d$ . Or $e e = 2 d d$ as before. Soe that $eg ∶ fe ∷ \sqrt{d d - e e} ∶ d ∷ d ∶ d$ . therefore $eg = fe$ . Now that I may find $bf = c$ I take the 2^d Rule of the first sort (whose first quantity $y y$ is of fewer dimensions than $x^{3}$ or $y^{3}$ but not of fewer $x y$ ,) The quantitys in the Equation whose valors are expressed in this rule are $x y$ , & $y^{3}$ for $x y = e e - 2 d d$ . $y^{3} = - 6 c d \sqrt{e e - d d}$ . Soe that I write $- 6 c d \sqrt{e e - d d} - a e e + 2 a d d$ instead of $y^{3} - a x y$ . soe that $c = \frac{2 a d d - a e e}{6 d d \sqrt{e e - d d}}$ . Or since $2 d d - e e = 0$ , it is, $c = \frac{0 \times a}{6 d d} = 0$ . Had I taken the first rule of the first sort I had found $x y = c \sqrt{e e - d d}$ . & $y^{3} = - 3 c d d$ . therefore $y^{3} - a x y = - 3 c c d - a c \sqrt{e e - d d} = 0$ which is right since $c = 0$ . but by this equation c hath other valors for $3 c d - a \sqrt{e e - d d} = 0$ or $3 c \overset{\cup}{O} a = 0$ , & $c = \frac{\overset{\cup}{O} a}{3}$ . &c. Whence observe that for the most {part} it will bee most convenient to find c by that rule whose 1^st quantity hath one dimension lesse than the first quantity of that rule by which the proportion twixt d & e were found.

<20r>

Example the 3^d. If the Equation be $\begin{matrix} x x y y & + & 4 b x y y & + & 4 b b y y & = & 0 \\ - & 2 a x x y & - & 8 a b x y & - & 8 a b b y \\ - & a^{4} \end{matrix}$ . $x x y y$ being of 4 dimensions I take the 4^th rule of the first sort, or the 2^d rule of the 2^d sort. By the 4^th rule of the 1^st sort I find $x x y y = 2 d e e \sqrt{e e - d d} - 4 e^{3} \sqrt{e e - d d}$ & since by that rule I can find the valor of noe other quantity in the Equation I make $x x y y = \begin{matrix} 2 d e e \\ - 4 d^{3} \end{matrix} \sqrt{e e - d d} = 0$ . Which is divisible by d , & $e e - 2 d d$ , & by $\sqrt{e e - d d}$ . therefore either $d = 0$ ; or, $e e - 2 d d = 0$ ; or, $e e - d d = 0$ . The operation is the same if I make use of the 2^d rule of the 2^d sort. Againe I take the 3^d rule of the 1^st sort & by it I find, $x y y = e e \sqrt{e e - d d} - 3 d d \sqrt{e e - d d}$ . $x x y = 2 d e e - 3 d^{3}$ . therefore & $x x y y = 4 c d e e - 6 c d^{3}$ . therefore $\begin{matrix} x x y y \\ - 2 a x x y \end{matrix} + 4 b x y y = \begin{matrix} 4 c d e e - 4 a d e e + 4 b e e \\ - 6 c d^{3} + 6 a d^{3} - 12 b d d \end{matrix} \sqrt{e e - d d} = 0$ . Or $c = a \frac{+ 2 b e e \sqrt{e e - d d} - b b d d \sqrt{e e - d d}}{3 d^{3} - 2 d e e}$ . & if $d = 0$ , then $c = a + \frac{2 b e e \sqrt{e e - d d}}{0}$ . or c is infinitely long. but if $e e - 2 d d = 0$ . then $c = a \overset{\cup}{O} 4 b \overset{\cup}{O} 6 b$ . & if $e e - d d = 0$ , then $c = a$ . Againe I take the first rule of the 2^d sort & by it I find $x x y y = 2 c d^{3} - 2 c d e e$ . $x x y = d^{3} - e e d$ . $x y y = d d \sqrt{e e - d d}$ . therefore $x x y y - 2 a x x y + 4 b x y y = 2 c d^{3} - 2 c d e e - 2 a d^{3} + 2 a e d d + 4 b d d \sqrt{e e - d d} = 0$ Now if $d = 0$ . or if $e e - d d = 0$ , then the termes of this Equation destroy one another soe that the valor of c may not be found thereby. but if $e e - 2 d d = 0$ , then I find $2 c d^{3} - 4 c d^{3} - 2 a d^{3} + 4 a d^{3} + 4 b d d \sqrt{d d} = 0$ . Or $2 c d^{3} = 2 a d^{3} \overset{\cup}{O} 4 b d^{3}$ . Or $c = a \overset{\cup}{O} 2 b$ . Againe I take the 2^d rule of the 1^st sort & by it I find $\begin{matrix} x x y y - 2 a x x y + 4 b x y y \\ + 4 b b y y - 8 a b x y \end{matrix} = 2 c d d \sqrt{e e - d d} - 8 b b d \sqrt{e e - d d} - 4 a c d \sqrt{e e - d d} + 16 d d a b - 8 a b e e - 16 c d d b + 8 c e e b = 0$ . If $d = 0$ then $c c = 2 a c \frac{- 4 c e e b}{0 \times \sqrt{e e}} + 4 b b + \frac{4 a b e e}{0 \sqrt{e e}}$ . or c $a \overset{\cup}{O} \frac{2 e b}{0} \overset{\cup}{O} \sqrt{\frac{4 e e b b}{0 \times 0} \frac{\begin{matrix} + 4 a e b \\ \overset{\cup}{O} 4 a e b \end{matrix}}{0} \begin{matrix} + a a \\ + 4 b b \end{matrix}}$ . that is c is infinitely long as was found before. also it may bee found to bee $8 c e e b - 8 a e e b = 0$ , or $c = a$ but upon this supposition $d = 0$ it was not before found $c = a$ & therefore $c = a$ is false, when $d = 0$ . If $e e - d d = 0$ . then I find $8 a b d d - 8 c b d d = 0$ . or $c = a$ . &c. If $e e - 2 d d = 0$ . then $c c \sqrt{d d} - 4 b b \sqrt{d d} - 2 a c \sqrt{d d} = 0$ . $c = a \overset{\cup}{O} \sqrt{a a - 4 b b}$ . Which valor not being found before I conclude $e e - 2 d d = 0$ to bee false. Lastly by useing the first rule of the first sort I find, $4 b c c \sqrt{e e - d d} - 8 a b c \sqrt{e e - d d} - 8 c d b b + 8 a b b d = \begin{matrix} 4 b x y y + 4 b b y y \\ - 8 a b x y - 8 a b b y \end{matrix} = 0$ . & by supposeing $d = 0$ I have { $c =$ $2 a$ }. & $c = a$ . & if $e e = d d$ , then $c = a$ which being always found upon the supposition $d d = e e$ . I conclude the valor of $d d$ to be $e e$ & of c to be a . & so draw the axis gf parallell to x & distant from it the length of a . But here observe that this might have beene better performed by taking away the 2^d terme of the Equation $\begin{matrix} x x y y & + & 4 b x y y & + & 4 b b y y & = & 0 \\ - & 2 a x x y & - & 8 a b x y & - & 8 a b b y \\ - & a^{4} \end{matrix}$ . Or $x x + 4 b x + 4 b b \frac{- a^{4}}{y y - 2 a y} = 0$ as was observed before.

<21r>

^[33]To find the Diameter or axis of any crooked line which hath it

^[34] Suppose the crooked line to bee $(lgc)$ , the diameter or Axis $(kd)$ , the undetermined quantitys describing the line to be $ab = x$ , $bc = y$ . from the point a (the begining of x), perpendicular to kb draw $ah = pb = c$ , cutting the axis kd in h . parallell to kb draw $hp = x$ . & produce cb soe that it intersect the axis in the point d . & suppose that hp is to hd . as d to e : or that $hd = \frac{e x}{d}$ . & therefore $dp = \frac{x \sqrt{e e - d d}}{d}$ . let ec $= el = ϩ$ be one of those lines which are ordinately applied to the diameter $he = ϩ$ . lastly suppose that ec is to ef as e is to f : then is $ef = f ϩ e$ ; & $fc =$ $\frac{ϩ \sqrt{e e - f f}}{e}$ then $hp ∶ pd ∷ fc ∶ fd$ .
$x ∶ \frac{x \sqrt{e e - d d}}{d} ∷ \frac{ϩ \sqrt{e e - f f}}{f} ∶ \frac{ϩ \sqrt{e^{4} - e e f f - e e d d + d d f f}}{d e} = fd$ & $hd = ϱ - \frac{f ϩ}{e} + \frac{ϩ \sqrt{e^{4} - e e f f - e e d d + d d f f}}{d e} = \frac{e x}{d}$ . & by ordering the Equation it will be, $x =$ $\frac{e d ϱ - d f ϩ + ϩ \sqrt{e^{4} - e e f f - e e d d + d d f f}}{e e}$ . Againe, $d ∶ e ∷ fc ∶ cd = \frac{ϩ \sqrt{e e - f f}}{d}$ . & $dp = \frac{x \sqrt{e e - d d}}{d}$ , $dp + pb - dc = y = \frac{x \sqrt{e e - d d} + dc - ϩ \sqrt{e e - f f}}{d}$ or by substituteing the valor of x into its place it is $y = \frac{e ϱ \sqrt{e e - d d} + f ϩ \sqrt{e e - d d} - d ϩ \sqrt{e e - f f} + e e c}{e e}$ . And that I may abbreviate the termes I make $\sqrt{e e - d d} = t$ ; & $\frac{+ f \sqrt{e e - d d} + d \sqrt{e e - f f}}{e} = v$ ; & so the Equation is $y = \frac{t ϱ - v ϩ + e c}{e}$ . Also by supposeing $s = \frac{\sqrt{e^{4} - e e f f + d d f f - e e d d} - d f}{e}$ , I lessen the termes of the Equation $x = \frac{e d ϱ - d f ϩ + ϩ \sqrt{e^{4} - e e f f - e e d d + d d f f}}{e e}$ , by writeing instead $\frac{d ϱ + s ϩ}{e} = x$ .

Now therefore by substituting these valors of x & y into their stead I take them out of the Equation expressing the relation twixt them soe that then I have an equation expressing the relation twixt ϱ & ϩ . And to that end it will bee convenient to have a table of the squares, cube, squaresquares, square=cubs, rectangles &c of the valors of x & y , After the manner of that which follows.

$x = \frac{d ϱ + s ϩ}{e}$ . $x x = \frac{s s ϩ ϩ + 2 d s ϱ ϩ + d d ϱ ϱ}{e e}$ . $x^{3} = \frac{s^{3} ϩ^{3} + 3 d ϱ s s ϩ ϩ + 3 d d ϱ ϱ s ϩ + d^{3} ϱ^{3}}{e^{3}}$ . $x^{4} = \frac{s^{4} ϩ^{4} + 4 d ϱ s^{3} ϩ^{3} + 6 d d ϱ ϱ s s ϩ ϩ + 4 d^{3} ϱ^{3} s ϩ + d^{4} ϱ^{4}}{e^{4}}$ . $x^{5} = \frac{s^{5} ϩ^{5} + 5 d ϱ s^{4} ϩ^{4} + 10 d d ϱ ϱ s^{3} ϩ^{3} + 10 d^{3} ϱ^{3} s s ϩ ϩ + 5 d^{4} ϱ^{4} s ϩ + d^{5} ϱ^{5}}{e^{5}}$ . &c. $y = \frac{t ϱ - v ϩ + e c}{e}$ . $y y = \frac{\begin{matrix} v v ϩ ϩ & - & 2 t ϱ v ϩ & + & t t ϱ ϱ \\ - & 2 e c v ϩ & + & 2 e c t ϱ \\ + & e e c c \end{matrix}}{e e}$ . $y^{3} = \frac{\begin{matrix} - & v^{3} ϩ^{3} & + & 3 t ϱ v v ϩ ϩ & - & 3 t t ϱ ϱ v ϩ & + & t^{3} ϱ^{3} \\ + & 3 e c v v & - & 6 e c t ϱ v & + & 3 t t ϱ ϱ e c \\ - & 3 e e c c v & + & 3 t ϱ e e c c \\ + & e^{3} c^{3} \end{matrix}}{e^{3}}$ . $\begin{array}{l} y^{4} & = & v^{4} ϩ^{4} & - & 4 t ϱ v^{3} ϩ^{3} & + & 6 t t ϱ ϱ v v ϩ ϩ & - & 4 t^{3} ϱ^{3} v ϩ & + & t^{4} ϱ^{4} \\ - & 4 e c & + & 12 c e t ϱ & - & 12 t t ϱ ϱ c e v & + & 4 c e t^{3} ϱ^{3} \\ + & 6 c c e e & - & 12 c c e e t ϱ v & + & 4 c^{3} e^{3} t ϱ \\ - & 4 c^{3} e^{3} v & + & c^{4} e^{4} \end{array}$ . $\begin{array}{l} y^{5} & = & - & v^{5} ϩ^{5} & + & 5 t ϱ v^{4} ϩ^{4} & - & 10 t t ϱ ϱ v^{3} ϩ^{3} & + & 10 t^{3} ϱ^{3} v v ϩ ϩ & - & 5 t^{4} ϱ^{4} v ϩ & + & t^{5} ϱ^{5} \\ + & 5 c e & - & 20 c e t ϱ & + & 30 t t ϱ ϱ c e & - & 20 c e t^{3} ϱ^{3} & + & 5 c e t^{4} ϱ^{4} \\ - & 10 c c e e & + & 30 c c e e t ϱ & - & 30 c c e e t t ϱ ϱ & + & 10 c c e e t^{3} ϱ^{3} \\ + & 10 c^{3} e^{3} & - & 20 c^{3} e^{3} t ϱ & + & 10 c^{3} e^{3} t^{2} ϱ^{2} \\ - & 5 c^{4} ϱ^{4} & + & 5 c^{4} e^{4} t ϱ \\ + & c^{5} e^{5} \end{array}$ . &c $x y = \frac{\begin{matrix} - & s v ϩ ϩ & + & e ϱ s ϩ & + & d t ϱ ϱ \\ + & e c s & + & d e c ϱ \\ - & d v ϱ \end{matrix}}{e e}$ . $x x y = \frac{\begin{matrix} - & s s v ϩ^{3} & + & s s t ϱ ϩ ϩ & + & 2 e c d s ϱ & + & e c d d ϱ ϱ \\ + & s s e c & + & 2 t d s ϱ ϱ & + & t d d ϱ^{3} \\ - & 2 d s v ϱ & - & d d v \end{matrix}}{e e e}$ . $x^{3} y = \frac{\begin{matrix} - & v s^{3} ϩ^{4} & + & 2 t ϱ s^{3} ϩ^{3} & + & 3 e c d s s ϱ ϩ^{2} & + & 3 e c d d s ϱ ϱ ϩ & + & e c d^{3} ϱ^{3} \\ + & e c s^{3} & + & 3 t d s ϱ^{2} ϩ^{2} & + & 3 t d d s ϱ^{3} & + & t d^{3} ϱ^{4} \\ - & 3 d ϱ s s v & - & 3 d d s v ϱ ϱ & - & d^{3} v ϱ^{3} \end{matrix}}{e^{4}}$ . &c. $x y y = \frac{\begin{matrix} v v s ϩ^{3} & - & 2 t ϱ v s ϩ ϩ & + & s t t ϱ ϱ ϩ & + & t t d ϩ^{3} \\ - & 2 e c v s & + & 2 s t c e ϱ & + & 2 e c t d ϱ^{2} \\ + & d v v ϱ & + & s c c e e & + & e e c c d ϱ \\ - & 2 d t v ϱ ϱ \\ - & 2 d ϱ e c v \end{matrix}}{e^{3}}$ . $x x y y = \frac{\begin{matrix} s s v v ϩ^{4} & - & 2 s s t v ϱ ϩ^{3} & + & s s t t ϱ ϱ ϩ^{2} & + & 2 t t d s ϱ^{3} ϩ & + & d d t t ϱ^{4} \\ - & 2 s s e c v & + & 2 s s e c t ϱ & + & 4 e c t d s ϱ^{2} & + & 2 d d e c t ϱ^{3} \\ + & 2 d s ϱ v v & + & s s e e c c & + & 2 e e c c d s ϱ & + & d d e e c c ϱ ϱ \\ - & 4 d s ϱ ϱ t v & - & 2 d d t v ϱ^{3} \\ - & 4 d s ϱ e c v & - & 2 d d e c v ϱ ϱ \\ + & d d v v \end{matrix}}{e^{4}}$ .
$x y^{3} = \frac{\begin{array}{l} - & s v^{3} ϩ^{4} & + & 3 s t ϱ v v ϩ^{3} & - & 3 s t t ϱ ϱ v ϩ^{2} & + & s t^{3} ϱ^{3} ϩ & + & d t^{3} ϱ^{4} \\ + & 3 s e c v v & - & 6 s e c t ϱ v & + & 3 s t t ϱ ϱ e c & + & 3 d t t ϱ^{3} c e \\ - & d ϱ v^{3} & - & 3 s e e c c v & + & 3 s t ϱ e e c c & + & 3 d t ϱ ϱ c c e e \\ - & 3 d t ϱ ϱ v v & - & 3 d t t ϱ^{3} v \\ + & 3 d e c v v & - & 6 d e c t ϱ ϱ v \\ - & 3 d e e c c v \end{array}}{e^{4}}$ . &c $\begin{matrix} If there bee occasions to doe \\ these opera \overline{co} ns in Equations \\ of 5 or 6 or more dimensions \\ this table may be easily enlarged. \end{matrix}$

As for example. If the relation twixt x & y bee exprest in this Equation, $x x + a x - 2 x y + y y = 0$ . then into the place of $x x$ , x , $x y$ , $y y$ , I substitute their valors found by this table, & there results $\begin{array}{l} + & s s ϩ ϩ & + & 2 d s ϱ ϩ & + & d d ϱ ϱ & = & 0 \\ + & 2 s v & + & a e s & + & a d e ϱ \\ + & v v & - & 2 t s ϱ & - & 2 d t ϱ ϱ \\ - & 2 e d s & - & 2 d e c ϱ \\ + & 2 d v ϱ & + & t t ϱ ϱ \\ - & 2 t ϱ v & + & 2 e c t ϱ \\ - & 2 e c v & + & e e c \end{array}$ . Which Equation expresseth the relation twixt ϱ & ϩ . that is twixt ge & le or ec . Now that $ge = ϱ$ be the diameter & $le = ec = \overset{\cup}{O} ϩ$ be ordinately applied to it, it is required (by Prop 2^d) that in this Equation ϩ be not of odd dimensions. & that may bee soe the quantitys in the 2^d terme which ϩ is {illeg} of {illeg} must {illeg} one another which cannot be unlesse these quantitys destroy one another in which the unknowne quantitys ϱ & ϩ {illeg}are of the {same} <21v> dimensions. Which things being considered it will appeare that I must divide the 2^d terme into two parts, makeing, $\begin{matrix} 2 d s ϱ ϩ & - & 2 t s ϱ ϩ & + & 2 d v ϱ ϩ & = & 0 \\ - & 2 t v ϱ ϩ \end{matrix}$ ; &, $a e s ϩ - 2 e c s ϩ - 2 e v c ϩ = 0$ . & divideing the first by $2 ϱ ϩ$ & the 2^d by $e ϩ$ they will be, $d s - t s - t v + d v = 0$ . Hitherto useing the letters s , t , & v for brevitys sake, I must now write their valors in theire stead (that I may find the length of c , & the proportion of d to e which determine the position of the axis, & also the proportion of e to f which determines the position of the lines applyed to the axis.) & soe {instead} of the Equation $d s - t s - t v + d v = 0$ ; there results, $2 d f \sqrt{e e - d d} = e e f - e e \sqrt{e e - f f} - 2 d d \sqrt{e e - f f}$ . & by squareing both parts & ordering the product it is, $e^{4} - 4 d d e e + 4 d^{4} = 4 d d f \sqrt{e e - f f} - 2 e e f \sqrt{e e - f f}$ . Which is divisible by $2 d d - e e = 0$ , for the quote will bee $2 d d - e e = 2 f \sqrt{e e - f f}$ . & therefore $2 d d = e e$ . Or, $2 d d = e e + 2 f \sqrt{e e - f f}$ . Againe by inserting the valors of s & v into the Equation, $a s - 2 c s - 2 c v = 0$ , there resulteth, $\begin{matrix} + & a \\ - & 2 c \end{matrix} \sqrt{e^{4} - e e d d - e e f f + d d f f} - 2 c f \sqrt{e e - d d} - 2 c d \sqrt{e e - d d} - a d f + 2 c d f = 0$ . & by writing $2 d d$ instead of $e e$ & divideing it by d there resulteth $\begin{matrix} + & a \\ - & 4 c \end{matrix} \sqrt{2 d d - f f} - a f = 0$ Or $\frac{a}{4} \frac{- a f}{4 \sqrt{2 d d - f f}} = c$ . Thus haveing found the proportion of d to e , & the valor of c since there remaines noe more equations by which I may find the proportion of e to f I concluded it to be undetermined, soe that I may assume any proportion betwixt them. As if I make $f = 0$ . Then the angle ceh is a right one & eh the axis of the line, & $c = \frac{a}{4} = ah$ . & $d ∶ \sqrt{2 d d} ∷ d ∶ e ∷ hp ∶ hd$ . or $d ∶ \sqrt{2 d d} ∶ hp ∶ dp$ . that is $hp = dp$ ; As in the 1^st figure.^[35] Or if I make $e e ∶ f f ∷ 2 ∶ 1$ . that is $e e = 2 f f$ . or $f = d$ , then I find that $c = 0$ . that is that the diameter ed intersects the line ap at the point a the begining of x . & that the lines ec are parallell to ma as in the 2^d figure^[36] &c. Soe that by assumeing any proportion twixt ec & ef , that is, supposeing the angle fec of any bigness, the position of the diamiter fa , may be found after the same manner. As If I would have the angle fec to be an angle of 60 degrees. then must $ec = ϩ$ be double to $fe = \frac{1}{2} ϩ$ , & $fc = \sqrt{\frac{3}{4} y y}$ . i.e. $e ∶ f ∷ 2 ∶ 1$ . & $2 d d = e e$ , therefore $\frac{d d}{2} = f f$ . I found before that $\frac{a}{4} \frac{- a f}{4 \sqrt{2 d d - f f}} = c$ . or writeing the valor of f in its roome, tis $\frac{a}{4} \frac{- a \sqrt{\frac{1}{2} d d}}{4 \sqrt{\frac{3 d d}{2}}} = c$ that is $\frac{a}{4} \overset{\cup}{O} \frac{a}{4 \sqrt{3}} = c$ . Or since c must be lesse than $\frac{a}{4}$ it must $\frac{a}{4} - \frac{a}{4 \sqrt{3}} = c = ah$ . & $ph = dp$ since $e e = 2 d d$ . As in the 3^d figure.^[37] But if I would make the angle ceh of 60 degrees then as before $e = 2 f$ , & $\frac{d d}{2} = f f$ , & $\frac{a}{4} \overset{\cup}{O} \frac{a}{4 \sqrt{3}} = c$ , or since c must be greater than $\frac{a}{4}$ tis $\frac{a}{4} + \frac{a}{4 \sqrt{3}} = c$ , as in the 4^th fig. &c.^[38]

Example 2^d. If the Equation expressing the nature of the line be $\begin{array}{l} x^{3} & - & 3 x x y & + & 3 x y y & - & y^{3} & = & 0 \\ - & a y y \end{array}$ .

<23v>

^[39] To find the Axis or Diameter of any crooked Line supposeing it have them.

^[40] ^[41] ^[42] Suppose $bc = x$ ; $cd = y$ ; nad the line whose axis or Diameter is sought; pk its axis or Diameter; a its vertex; $hd = hn = ϩ =$ lines ordinately applied to its Diameter; bm a perpendicular to pc drawne from the point b , i.e. from the begining of x ; $bf = c =$ parte of the line bm intercepted twixt the diameter & pc ; $mh = ϱ =$ a line parallell to bc & drawne from bm to the intersection of fk & nd ; & $he = mf$ & parallell to mf ; & dgh a right angled triangle. $dh ∶ hg ∷ d ∶ f$ &, $mh = fe ∶ he = mf ∷ d ∶ e$ .

Then $d ∶ e ∷ ϩ ∶ \frac{f ϩ}{d} = hg = eq$ . &, $eq + fe = \frac{d ϱ + f ϩ}{d} = x$ . Againe $gd = \sqrt{\frac{d d ϩ^{2} - f f ϩ^{2}}{d d}}$ $d ∶ e ∷ ϱ ∶ he = \frac{e ϱ}{d} = gq$ . &, $gq + qc + dg = cd$ ; or, $\frac{e ϱ + d c + ϩ \sqrt{d d - f f}}{d} = y$ .

Now therefore by substituteing $\frac{d ϱ + f ϩ}{d}$ into the place of x , & $\frac{e ϱ + d c - ϩ \sqrt{d d - f f}}{d}$ into the place of y , & theire squares & cubes &c: into the place of $x^{2}$ , $x^{3}$ , $y^{2} - y^{3}$ &c. I take x & { y } out of the Equation expressing the relation twixt them & Soe have an Equation expressing the relation twixt ϱ & ϩ . And to that end it will be convenient to have a table of the squares, cubes, & rectangles &c: of the valors of x & y , like that which follows.

$\begin{array}{l} \begin{array}{l} \begin{array}{l} d x & = & d ϱ + f ϩ \\ d d x x & = & d d ρ ϱ + 2 d ϱ f ϩ + f f ϩ^{2} \\ d^{3} x^{3} & = & f^{3} ϩ^{3} + 3 f f ϩ ϩ d ϱ + 3 d d ϱ ϱ f ϩ + d^{3} ϱ^{3} \\ d^{4} x^{4} & = & f^{4} ϩ^{4} + 4 d ϱ f^{3} ϩ^{3} + 6 d d ϱ^{2} f^{2} ϩ^{2} + 4 d^{3} ϱ^{3} f ϩ + d^{4} ϱ^{4} \\ d y & = & \begin{matrix} + & ϩ \sqrt{d d - f f} & + & e ϱ \\ + & d c \end{matrix} \\ d d y y & = & \begin{array}{l} + & d d ϩ ϩ & + & 2 e ϱ ϩ \sqrt{d d - f f} & + & e e ϱ ϱ \\ + & 2 d c & + & 2 e d c ϱ \\ + & d d c c \end{array} \end{array} & \begin{matrix} d d x y & = & \begin{array}{l} + & f ϩ^{2} \sqrt{d d - f f} & + & f e ϱ ϩ & + & d e ϱ ϱ \\ + & f d c ϩ & + & d d c ϱ \\ + & d ϱ ϩ \sqrt{d d - f f} \end{array} \\ d^{3} x^{2} y & = & \begin{array}{l} + & f f ϩ^{3} \sqrt{d d - f f} & + & f f e ϱ ϩ^{2} & + & 2 e f ϱ^{2} ϩ & + & d d e ϱ^{3} \\ + & f f d c & + & 2 d d c f ϱ & + & d^{3} c ϱ ϱ \\ + & 2 d f ϱ \sqrt{d d - f f} & + & d d ϱ ϱ \sqrt{d d - f f} \end{array} \\ d^{4} x^{3} y & = & \begin{array}{l} + & f^{3} ϩ^{4} \sqrt{d d - f f} & + & e f^{3} ϱ ϩ^{3} & + & 3 d e f f ϱ ϱ ϩ ϩ & + & 3 d d e f ϱ ϱ ϩ ϩ & + & d^{3} e ϱ^{4} \\ + & d c f^{3} & + & 3 d d c f f ϱ & + & 3 c d^{3} f ϱ ϱ & + & d^{4} c ϱ^{3} \\ + & 3 f f d ϱ \sqrt{d d - f f} & + & 3 d d f ϱ ϱ \sqrt{d d - f f} & + & d^{3} ϱ^{3} \sqrt{d d - f f} \end{array} \end{matrix} \end{array} \\ \begin{array}{l} d^{3} y^{3} & = & \begin{array}{l} \begin{array}{r} d d \\ - f f \end{array} ϩ^{3} \sqrt{d d - f f} & + & 3 d d e ϱ ϩ ϩ & + & 3 e e ϱ ϱ ϩ \sqrt{d d - f f} & + & e^{3} ϱ^{3} \\ + & 3 d d d c & + & 6 e d c ϱ & + & 3 e e d c ϱ^{2} \\ - & 3 f f e ϱ & + & 3 d d c c & + & 3 d d c c e e ϱ \\ - & 3 f f d c & + & d^{3} c^{3} \end{array} \\ d^{4} y^{4} & = & \begin{array}{l} d^{4} ϩ^{4} & + & 4 e ϱ d d ϩ^{3} \sqrt{d d - f f} & + & 6 d d e e ϱ ϱ ϩ ϩ & + & 4 e^{3} ϱ^{3} ϩ \sqrt{d d - f f} & + & e^{4} ϱ^{4} \\ - & 2 d d f f & + & 4 d^{3} c & - & 6 f f e e ϱ ϱ & + & 12 d c e e ϱ ϱ & + & 4 d c e^{3} ϱ^{3} \\ + & f^{4} & - & 4 e ϱ f f & + & 12 d^{3} e c ϱ & + & 12 d d e c ϱ & + & 6 d d c c e e ϱ ϱ \\ - & 4 d c f f & - & 12 d f f e e ϱ & + & 4 d^{3} c^{3} & + & 4 d^{3} c^{3} e ϱ \\ + & 6 d^{4} c c & + & d^{4} c^{4} \\ - & 6 d d f f c c \end{array} \\ d^{3} x y y & = & \begin{array}{l} f d d ϩ^{3} & + & d^{3} ϱ ϩ ϩ & + & e e ϱ ϱ ϩ & + & d e e ϱ^{3} \\ - & f^{3} & - & d f f ϱ & + & 2 c d e f ϱ & + & 2 c d d e ϱ ϱ \\ + & 2 e f ϱ \sqrt{d d - f f} & + & c c d d f & + & c c d^{3} ϱ \\ + & 2 c d f \sqrt{d d - f f} & + & 2 c ϱ^{2} \sqrt{d d - f f} \\ + & 2 c d d ϱ \sqrt{d d - f f} \end{array} \\ d^{4} x x y y & = \\ d^{4} x y^{3} & = \end{array} \end{array}$

As for example if the relation twixt x & y bee exprest by, $x x + a x - 2 x y + y y = 0$ then in stead of $x x$ , { x }, $x y$ , $y y$ , writeing their valors found by this table there resulteth { $\begin{array}{l} d d ϩ ϩ & + & 2 d f ϱ ϩ & + & d d ϱ ϱ & = & 0 \\ + & 2 f ϩ ϩ \sqrt{d d - f f} & + & a d f & + & a d d ϱ \\ - & 2 e f ϱ & - & 2 d e ϱ ϱ \\ - & 2 d c f & - & 2 d d c ϱ \\ - & 2 d ϱ \sqrt{d d - f f} & + & e e ϱ ϱ \\ + & 2 ϱ \sqrt{d d} & + & 2 e d c ϱ \\ - & 2 d c & + & d d \end{array}$ .} Which equation espresseth the relation twixt ϱ & ϩ when any valors are assumed for c , d , e , & f . And if the valors of c , d , e , & f bee such that ϩ is not of odd dimensions in the Equation (that is that the 2^d terme of this Equation be wa{illeg}) then (by Prop: the 2^d) $\overset{\cup}{O} y = hn = hd$ is ord{illeg} <24r> is ordinately applyed to the Diameter pk .Now that the 2^d terme of this Equation vanish it is necessary that those termes destroy one another in which the unknowne quantitys ϱ & ϩ are not diverse nor differ in dimensions. Whence it appeares that I must divide the 2^d terme into 2 parts making $2 d f ϱ ϩ - 2 e f ϱ ϩ - 2 d ϱ ϩ \sqrt{d d - f f} + 2 e ϱ ϩ \sqrt{d d - f f} = 0$ . & $a d f ϩ - 2 d c f ϩ + 2 d c ϩ \sqrt{d d - f f} = 0$ . Or by divideing the first of these by $2 ϱ ϩ$ , & the 2^d by $d ϩ$ . they are, $d f - e f \begin{array}{r} - d \\ + e \end{array} \sqrt{d d - f f} = 0$ , & $a f - 2 c f + 2 c \sqrt{d d - f f} = 0$ . The first being divided by $d - e = 0$ . there results, $f + \sqrt{d d - f f} = 0$ . Therefore one or both these propositions $d = e$ ; $d d = 2 f f$ , is trew. by the 2^d tis found that $\frac{a f}{2 f - 2 \sqrt{d d - f f}} = c$ . Now since by assumeing some quantitys for the valors of d , c , or f I cannot find the valor of e unless by the Equation $d = e$ . therefore I conclude $d = e$ . whence it is not necessary that $d d = 2 f f$ , or the proportion of d to f bee limited soe that by assuming the angle ahd of any bigness I may find the position of the axis ahd . As if I suppose the angle fhd to be a right one (i.e. that ah is the axis of the line) then are the triangles feh & hgd alike, & therefore $fh ∶ fe ∷ dh ∶ gh ∷ \sqrt{d d + e e} ∶ e ∷$ $d ∶ f$ . & $\frac{e d}{\sqrt{d d + e e}} = f$ . Or because $d = e$ . therefore $+ f = \frac{d}{\sqrt{2}}$ . & $c = \frac{a}{4}$ . Soe that I draw $bf = \frac{a}{4}$ . & fq parallell to pb $qk = fq$ & parallell bf & through the points f & k I draw kh the axis of the line nad , as in figure 1^st^[43] So if I would have hd parallell to qk i.e. the angle dhf of 45 degrees. then this evident that $hg = 0 = f$ . & $c = \frac{a f}{2 f \overset{\cup}{O} 2 \sqrt{d d - f f}}$ . Threfore through the point b I draw the axis kh , so that $bq = kq$ , as before. &c. & note that since kh the axis is always parallell to it selfe the line dbn is a parabola.^[44]

^[45] Example the 2^d, $x^{3} + y^{3} = a^{3}$ . Being first to write the valors of $x^{3}$ & $y^{3}$ (found by the precedent table) into their roome, since I have noe neede of those termes in which ϩ is of eaven dimensions I leave them out, & soe for $x^{3} + y^{3} - a^{3} = 0$ I write onely $\begin{array}{l} f^{3} ϩ^{3} & + & d d \sqrt{d d - f f} & + & 3 d d f ϱ ϱ ϩ & + & 6 e d c ϱ ϩ \sqrt{d d - f f} & + & 3 d d c c ϩ \sqrt{d d - f f} & = & 0 \\ - & f f & + & 3 e e ϱ ϱ ϩ \sqrt{d d - f f} \end{array}$ . Then sorting these quantitys together in which the unknowne quantitys are the same there these 4 Equations (the 1^st being divided by $ϩ^{3}$ , the 2^d by $3 ϱ ϩ^{2}$ , the 3^d by $6 ϩ ϱ$ , the 4^th by $3 ϩ$ ) viz: $f^{3} \begin{array}{r} + d d \\ - f f \end{array} \sqrt{d d - f f} = 0$ ; $d d f + e e \sqrt{d d - f f} = 0$ ; $+ c d e \sqrt{d d - f f} = 0$ ; $+ d d c c \sqrt{d d - f f} = 0$ . In the first Equa
tion $f^{3} = \begin{array}{r} - d d \\ + f f \end{array} \sqrt{d d - f f}$ , I extract the cube roote & tis $f = - \sqrt{d d - f f}$ . or $d d = 2 f f$ . In the 2^d $d d f = e e \sqrt{d d - f f}$ , $d d f = e e f$ , or $d = e$ . By the 3^d, $+ c d e \sqrt{d d - f f} = 0$ , or $c = \frac{+ 0}{d e f} = 0$ . & so by the fourth.^[46] Now therefore since $c = 0$ $d =$ e . In the line bq from some point as q perpendicular to bq I draw $kq = + e$ , $= bq = d$ . then from the points k & l through b I draw the line ak which (since it cuts the lines hnd applied to them at right angles) is axis of the lines ndr which appeares in that $d d = 2 f f$ , for therefore ${nt}^{2} = 2 {st}^{2} = {st}^{2} + {ns}^{2}$ , soe that $ns = st$ & nt perpen
dicular to bk .

^[47] Example 3^d If the nature of the given line bee expressed in these termes $x^{3} - 3 x x y + 2 x y y - 2 a y y = 0$ . Then by supplanting the valors of x & y into theire roome & working as before, there will bee, $- f^{3} + 2 f d d - 3 f f \sqrt{d d - f f} = 0$ . & 2^dly $3 d d f - 6 d e f \begin{array}{r} - 3 d d \\ + 4 e d \end{array} \sqrt{d d - f f} = 0$ . & 3^dly $- 6 c d d f + 4 c d e f + 4 c d d \sqrt{d d - f f} - 4 a d e \sqrt{d d - f f} = 0$ . & 4^tly, $2 c c d d f - 4 a c d d \sqrt{d d - f f} = 0$ . The first of these divided by $f = 0$ . is $- f f + 2 d d = 3 f \sqrt{d d - f f}$ . Or squareing & ordering the product tis $10 f^{4} - 13 f f d d + 4 d^{4} = 0$ . Which being $2 f f - d d = 0$ . there results $5 f f - 4 d d = 0$ . Wherefore I conclude one of these 3 to be the valors of f viz: $f = 0 = \sqrt{\frac{d d}{2}} = \sqrt{\frac{4 d d}{5}}$ . Now that I may know which of those is the right valor of f I try them singly, & first suppose $f = 0$ ; If so then by the 4^th Equation $- 4 a c d d \sqrt{d d - f f} = 0$ , therefore $c = 0$ . If $c = 0 = f$ , then in the 3^d Equation all the termes vanish except $- 4 a d e \sqrt{d d} = 0$ : therefore $e = \frac{0}{4 a d \sqrt{d d}} = 0$ . & since $0 = e = f = 0$ , all the termes in the 2^d Equation vanish except except $- 3 d d \sqrt{d d}$ , therefore also $d = 0$ , which since it ought not to bee I conclude that $f = 0$ is false. Therefore I passe the 2^d valor of $f f = \frac{d d}{2}$ , or, $\overset{\cup}{O} f = \sqrt{d d - f f}$ . & soe divideing the 4^th Equation by $2 d d f$ {i{t}} results $c c = \overset{\cup}{O} 2 a c$ . which is divisible by $c = 0$ & by $c \overset{\cup}{O} 2 a = 0$ , Now that I may know which is the right valor of c first I suppose $c = 0$ : & soe all the termes in the Equation vanish except, $4 a d e \sqrt{d d - f f} = 0$ . or, { $e = \frac{0}{4 a d f} = 0$ . } & since $e = 0$ , by the 2^d Equation tis $3 d d f - 3 d d \sqrt{d d - f f} = 0$ or $f = \overset{\cup}{O} \sqrt{d d - f f} = \sqrt{f f} = + \sqrt{d d - f f}$ . {Which things since} they agree I conclude that $f = \sqrt{d d - f f}$ , or $d d = 2 f f$ ; $c = 0$ ; $e = 0$ . Since $e = 0$ {illeg} {illeg} must be parallell to x & {illeg} $c = 0$ {illeg} must bee {coincident} with it. then {illeg} the axis { bc I take some {illeg} {illeg} } & fro{illeg} perpendicular {illeg} {illeg} {illeg}the {illeg}

<24v>

^[48] Example the 4^th. If the Equation bee $b x^{3} + a y x x = a^{4}$ . by takeing onely those termes (of the valors of $x^{3}$ & $y x x$ found by the precedent table) in which ϩ is of odd dimensions, & sorting those together in which the unknowne quantitys are the same & of the same dimensions as before. there will result these Equations. first $b f^{3} + a f f \sqrt{d d - f f} = 0$ . 2^dly $3 d d b f + 2 d d b f + a d d \sqrt{d d - f f} = 0$ . & 3^dly, $2 a d d f c = 0$ . the 1^st is divisible by $f = 0$ , $f b + a \sqrt{d d - f f} = 0$ . To know which of these 2 are the valors of f first I suppose $f = 0$ to be trew, & then all the termes in the 2^d Equation vanish except $a d d \sqrt{d d}$ , or $d d = \frac{0}{a \sqrt{d d}} = 0$ . now since both d & f should never bee $= 0$ therefore I conclude that $f = 0$ is false & so pass to its other valor $f = \frac{- a \sqrt{d d - f f}}{b}$ . or $\frac{- b f}{a} = \sqrt{d d - f f}$ . & soe by the 2^d Equation tis $d d b = - a d e$ . which is divisible by $d = 0$ , $d b + a e = 0$ . If $d b = - a e$ tis $b ∶ - a ∷ e ∶ d ∷ \sqrt{d d - f f} ∶ f$ . & soe the diameter will bee parallel to the lines ordinately applied to it which cannot bee therefore I try the other valor of $d = 0$ . And if $d = 0$ , then the 3^d Equation $2 a d d f c = 0$ vanisheth & soe c cannot bee found & is therefore unlimited. Now since I find noe repugnancys in these Equations $f = \frac{- a \sqrt{d d - f f}}{b}$ , & $d = 0$ , I conclude them trew. & since $d = 0$ . I draw bh perpendicular wc from b the begining of x , which shall bee the Diameters of the lines enm & dpl . then in that diameter I take some point as b or h & from that point draw $gh = + f$ or $th = - f$ , i.e. of any length, & parallell to bc . then from the pointe t or g perpendicular to tg I draw $ts = \frac{a \sqrt{d d - f f}}{b}$ , or $gr = - \frac{a \sqrt{d d - f f}}{b}$ . that is, $- a ∶ b ∷ th ∶ ts ∷ gh ∶ gr$ . & so through the points s & h or h & r I draw sr which shall be parallel to the lines ordinately applied to the Diameter bh .

Example the 5^t. Suppose $x^{3} = a a y$ . Then by selecting those termes out the valors of $x^{3}$ & y in which ϩ is of od dimensions , & sorting them together in which the unknowne quantitys differ not, I have, $f^{3} ϩ^{3} = 0$ ; $3 d d f ϱ ϱ ϩ = 0$ ; & 3^dly $a a d d ϩ \sqrt{d d - f f} = 0$ . by the first $f = 0$ , & therefore the 2^d vanisheth; & the 3^d divided by $a a ϩ$ is, $d d \sqrt{d d - f f} = 0$ ; or $0 = d d d$ . Now since $d = f = 0$ , & the proportion of d to e & the length of c cannot bee found tis evident the line hath noe axis or diameter.

<25r>

November 1664

^[49] ^[50] Observe the Axes, Diameters & position of the lines ordinately applied to them may bee for the most parte easlier obteined by making $bc = x$ . $cd = y$ . $bf = c = cq$ . $mh = ϱ = fe$ . $hd = ϩ = - hn$ . $hd ∶ dg ∷ d ∶ f ∷ ϩ ∶ \frac{f ϩ}{d} = dg$ . the angles bcd , mgd , fqd , mbc , feh , right ones. $fe ∶ he ∷ d ∶ e ∷ ϱ ∶ \frac{e ϱ}{d} = he = gq$ . $qc + gq + gd = cd = \frac{f ϩ + e ϱ + c d}{d} = y$ . $hg = \sqrt{ϩ ϩ - \frac{f f ϩ ϩ}{d d}} = eq$ . $fe + eq = bc = \frac{d ϱ + ϩ \sqrt{d d - f f}}{d} = x$ . Then for readiness in these operations make a table of the squares, cubes, rectangles, &c of these valors of x & y . As was done before $\begin{matrix} \begin{array}{l} \begin{matrix} d x & = & ϩ \sqrt{d d - f f} & + & d ϱ . \end{matrix} \\ \begin{matrix} d d x x & = & d d ϩ ϩ & + & 2 d ϱ ϩ \sqrt{d d - f f} & + & d d ϱ ϱ . \\ - & f f \end{matrix} \\ \begin{array}{l} d^{3} x^{3} & = & d d ϩ^{3} \sqrt{d d - f f} & + & 3 d^{3} ϱ ϩ ϩ & + & 3 d d ϱ ϱ ϩ \sqrt{d d - f f} & + & d^{3} ϱ^{3} . \\ - & f f & - & 3 d f f ϱ ϩ ϩ \end{array} \\ \begin{matrix} d y & = & f ϩ & + & e ϱ & + & c d . \end{matrix} \\ \begin{array}{l} d d y y & = & f f ϩ ϩ & + & 2 e f ϱ ϩ & + & e e ϱ ϱ . \\ + & 2 c d f & + & 2 c d e ϱ \\ + & c c d d \end{array} \\ \begin{array}{l} d^{3} y^{3} & = & f^{3} ϩ^{3} & + & 3 e f f ϱ ϩ ϩ & + & 3 e e f ϱ ϱ ϩ & + & e^{3} ϱ^{3} . \\ + & 3 c d f f & + & 6 c d e f ϱ & + & 3 e e c d ϱ ϱ \\ + & 3 c c d d f & + & 3 c c d d e ϱ \\ + & c^{3} d^{3} \end{array} \end{array} & \begin{array}{l} \begin{array}{l} d d x y & = & f ϩ ϩ \sqrt{d d - f f} & + & d f ϱ ϩ & + & d e ϱ ϱ . \\ + & e ϱ ϩ \sqrt{d d - f f} & + & c d d ϱ \\ + & c d ϩ \sqrt{d d - f f} \end{array} \\ \begin{array}{l} d^{3} x y y & = & f f ϩ^{3} \sqrt{d d - f f} & + & d f f ϱ ϩ ϩ & + & 2 d e f ϱ ϱ ϩ & + & d e e ϱ^{3} . \\ + & 2 c d d f ϱ & + & 2 c d d e ϱ ϱ \\ + & 2 e f ϱ \sqrt{d d - f f} & + & e e ϱ ϱ \sqrt{e e - f f} & + & c c d^{3} ϱ \\ + & 2 c d f \sqrt{d d - f f} & + & 2 c d e ϱ \sqrt{e e - f f} \\ + & c c d d \sqrt{e e - f f} \end{array} \\ \begin{array}{l} d^{3} x x y & = & d d f ϩ^{3} & + & d d e ϱ ϩ ϩ & + & d d e ϱ^{3} . \\ - & f^{3} & - & f f e ϱ & + & c d^{3} ϱ ϱ \\ + & 2 d f ϱ \sqrt{d d - f f} & + & d d f ϱ ϱ ϩ \\ + & c d^{3} & + & 2 d e ϱ ϱ ϩ \sqrt{d d - f f} & &c. \\ - & d c f f & + & 2 c d d ϱ ϩ \sqrt{d d - f f} \end{array} \end{array} \end{matrix}$

^[51] Example If the relation twixt bc & cd be expressed by $\begin{matrix} a y y & - & b x y & + & b b x & = & 0 \\ - & a b y \end{matrix}$ . then by inserting those quantitys (of the valors of x & y found by this table) in which ϩ is of odd dimensions, into place of $y y$ , $x y$ , y , x in this Equation, & supposeing those to destroy one another which are multiplied by the same unknowne quantitys there will bee these 2 Equations $2 a e f - b d f - b e \sqrt{d d - f f} = 0$ , & ∼ $2 a c d f + b c d \sqrt{d d - f f} + b b d \sqrt{d d - f f} - a b d f = 0$ . The 2^d is divisible by $d = 0$ & there ∼ results $2 a c f + b c \sqrt{d d - f f} + b b \sqrt{d d - f f} - a b f = 0$ . Now to try which of these two are true first I suppose $d = 0$ ^[52], & soe the first Equation will bee $2 a e f - b e \sqrt{- f f} = 0$ . which is impossible unlesse $f = 0$ , & then the valors of e & c cannot bee found, Therefore $d = 0$ is false. And therefore by the 2^d Equation $c = \frac{- b b \sqrt{d d - f f} + a b f}{2 a f + b \sqrt{d d - f f}}$ . & by the first $e = \frac{b d f}{2 a f - b \sqrt{d d - f f}}$ . $2 a f \underset{\cap}{O} b \sqrt{d d - f f} ∶ b f d ∷ e ∶$ . & $c = \frac{\underset{\cap}{O} b b \sqrt{d d - f f} + a b f}{2 a f \overset{\cup}{O} b \sqrt{d d - f f}}$ . Whence the proportion twixt d & f that is the angle fhn is undetermined,

^[53] For avoyding mistakes (which might have happened in the 4^th Example where I found $d = 0$ . & $f = \frac{- a \sqrt{d d - f f}}{b}$ ) it will not be amisse to make $hd ∶ dg ∷ f ∶ g ∷ ϩ ∶ \frac{g ϩ}{f} = dg$ . & $fe ∶ he ∷ d ∶ e ∷ ϱ ∶ \frac{e ϱ}{d} = he$ . & soe it will be $\frac{g ϩ}{f} + \frac{e ϱ}{d} + c = y$ . & $\frac{ϱ + ϩ \sqrt{f f - g g}}{f} = x$ . Or, $\frac{d g ϩ + f e ϱ + d f c}{d f} = y$ . & $\frac{f ϱ + ϩ \sqrt{f f - g g}}{f} = x$ . And then observe that it can never happen that $f = 0$ . or $d + e = 0$ . observe alsoe that if $- d ∶ e ∷ g ∶ + \sqrt{f f - g g}$ . then the line fh is the axis, otherwise the diameter of the crooked line. when $d = 0$ the axis is perpendicular to x as also if $c = \frac{a}{0}$ : And then it will be convenient to doe the worke over againe changing the names of x & y {that} is writeing y instead of x & x instead of y .

<26r>

^[54] Haveing the Diameter to find the Vertex of the line.

^[55] Suppose $bc = x$ , or $tr = x$ . cd or $ra = y$ . $bf = c$ . $fq ∶ kq ∷ d ∶ e ∷ fs = br = x ∷ as = y - c$ . that is $e x = d y - d c$ . soe that into the given equation I insert this valor of $x = \frac{d y - d c}{e}$ or of $y = \frac{e x + d c}{d}$ into the place of x or (which may more readily bee done).

^[56] As in the first example I found d $= e$ & the proportion twixt d & f to bee unlimited so that if I would fk to bee the Axis I make $- d ∶ e ∷ f ∶ \sqrt{d d - f f}$ . (vide C) or $f = \sqrt{d d - f f}$ . & there I found $c = \frac{a f}{2 f - 2 \sqrt{d d - f f}}$ . or since $f = - \sqrt{d d - f f}$ it is $c = \frac{a}{4}$ . As may bee seene in that example. Now that I may find the vertex of the line was there exprest in these termes. $x x + a x - 2 x y + y y = 0$ . I suppose $d ∶ e ∷ x ∶ y - c$ . that is $x = y - c$ . or $x = y - \frac{a}{4}$ . or $y = x + \frac{a}{4}$ . & writeing this valor of y into its roome in the Equation $x x + a x - 2 x y + y y = 0$ ; there results $a x + \frac{a a}{16} = 0$ . or $x = - \frac{a}{16}$ . Therefore from the point b I draw $br = - \frac{a}{16}$ . & from the point r I draw the perpendicular rd until it {cut}{cutt} the axis hd , that is, soe that $rd = hd$ . & the point d shall bee the vertex of the Parabola mdo .

^[57] Soe in the 2^d Example of the line $x^{3} + y^{3} = a^{3}$ , it was found $d = e$ . & $c = 0$ . & therefore $y = \frac{e x + d c}{d}$ . or $y = x$ . therefore I write $x^{3}$ for $y^{3}$ in the Equation $x^{3} + y^{3} = a^{3}$ . & it is $2 x^{3} = a^{3}$ . or $x = \frac{a}{\sqrt{c: 2}}$ . therefore I take $br = \frac{a}{\sqrt{c: 2}}$ & soe draw the perpendicular ar , which shall intersect the axis ab at the vertex of the crooked line. ^[58] & then (calling $br = h$ ) it shall be $ar = c + \frac{e h}{d}$ . Soe that in this case $ar = \frac{a}{\sqrt{2}}$ .

^[59] In the 3^d Example the Equation being $x^{3} - 3 x x y + 2 x y y - 2 a y y = 0$ , It was found, $c = 0$ . $d ∶ e ∷ q ∶ 0$ . that is $e = 0$ . therefore $y = \frac{e x + d c}{d} = 0$ . Therefore by writeing 0 instead of y in the Equation all the termes vanish except ∼ $x^{3} = 0$ , or $x = 0 = br$ . & $ar = c + \frac{e h}{d} = 0$ . soe that the vertex of the line $(bdn)$ must bee at the point b .

^[60] But in the 4^th Example, $b x^{3} + a x x y = a^{4}$ . It was found $d ∶ e ∷ 0 ∶$ {1 }{i}. or $d = 0$ . & c was unlimited, I make therefore $c = 0$ . & since the axis is perpendicular to x therefore I insert the valor of x into the equation $(x = \frac{d y - d c}{e} = 0)$ & there results $b 0 0 0 + a 0 0 y = a^{4}$ . or $y = \frac{a^{4} - b 0 0 0}{0 0 a} = \frac{a^{3}}{0 0}$ . Wherefore I conclude the vertex of the line to be infinitely distant from b towards m.

^[61] ☞ If the position of any line (as ts ) be given the point where it intersects the given crooked line dsa may be found by the same manner; for suppose ∼ ar or $ac = x$ . cd or $rs = y$ . & $r x = y y$ . $ta = a$ . $tq = b$ . $pq = d$ . angles tqp , srt , dct right ones; then, to find the point s where the crooked line dsa is intersected by the line fp , I suppose $tq ∶ pq ∷ tr ∶ rs$ . that is, $y = \frac{d a + d x}{b}$ . or $\frac{b y - d a}{d} = x$ . & since by the nature of the line $r x = y y$ . it follows that $y y = \frac{b r y - d a r}{d}$ . & $\frac{d d x x + 2 d d a x + d d a a}{b b} = r x$ . & by extracting the rootes of them. both, $y = \frac{b r}{2 d} \overset{\cup}{O} \sqrt{\frac{+ b b r r - 4 d d a r}{4 d d}}$ . & $x = \frac{b b r}{2 d d} - a \overset{\cup}{O} \sqrt{\frac{b^{4} r r}{4 d^{4}} - \frac{a b b r}{d d}}$ . therefore I take $ar = \frac{b b r}{2 d d} - a \overset{\cup}{O} \frac{b}{d} \sqrt{\frac{b b r r}{4 d d} - a r}$ . & $rs = \frac{b r}{2 d} \overset{\cup}{O} \sqrt{\frac{b b r r}{4 d d} - a a}$ .

By the same manner the intersection by 2 crooked lines may be found.

<27r>

^[62] Having the nature of any lines expressed in Algebraicall termes, to find its Asymptotes if have any

^[63] Suppose rh , & rs the asymptotes of the line dtn . & hd parallel to rs drawne from the Asymptote to the line dtn $bc = x$ . $cd = y$ . $bf = c$ . $fe ∶ he ∷ d ∶ e$ . $hd ∶ dg ∷ f ∶ g$ . $fe = mh = ϱ$ . $hd = ϩ$ . the angles dcb , cbm , dgm , bfq , hef , to bee right ones. then is, $eh = \frac{e ϱ}{d}$ . $dg = \frac{g ϩ}{f}$ . $hg = \frac{ϩ \sqrt{f f - g g}}{f}$ . $dg + gq + qc = \frac{d g ϩ + e f ϱ + d f c}{d f} = y$ . & $fe + eq = \frac{f ϱ + ϩ \sqrt{f f - g g}}{f} = x$ . Now for readiness in operation it bee convenient to have a table of these valors of x & y which will bee the same with that by which the diameters of crooked lines are determined. viz.
$\begin{matrix} \begin{array}{l} f x = f ϱ + ϩ \sqrt{f f - g g} . \\ \begin{array}{l} f f x x & = & f f ϩ ϩ & + & 2 f ϱ ϩ \sqrt{f f - g g} & + & f f ϱ ϱ . \\ - & g g \end{array} \\ \begin{array}{l} f^{3} x^{3} & = & f f \sqrt{f f - g g} ϩ^{3} & + & 3 f f f ϱ ϩ^{2} & + & 3 f f ϱ^{2} ϩ \sqrt{f f - g g} & + & f^{3} ϱ^{3} . \\ - & g g & - & 3 g g f ϱ \end{array} \\ d f y = d g ϩ + e f ϱ + d f c . \\ \begin{array}{l} d d f f y y & = & d d g g ϩ ϩ & + & 2 d e f g ϱ ϩ & + & e e f f ϱ ϱ \\ + & 2 d d c f g & + & 2 c d e f f ϱ \\ + & c c d d f f \end{array} \\ \begin{array}{l} d^{3} f^{3} y^{3} & = & d^{3} g^{3} ϩ^{3} & + & 3 d d e f g g ϱ ϩ ϩ & + & 3 d e e f f g ϱ ϱ ϩ & + & e^{3} f^{3} ϱ^{3} . \\ + & 3 c d^{3} f g g & + & 6 c d d e f f g ϱ & + & 3 c d e e f f ϱ ϱ \\ + & 3 c c d^{3} f f g & + & 3 c c d d e f ϱ \\ + & c^{3} d^{3} f^{3} \end{array} \end{array} & \begin{array}{l} \begin{array}{l} d f f x y & = & d g \sqrt{f f - g g} ϩ ϩ & + & d f g ϱ ϩ & + & e f f ϱ ϱ . \\ + & e f ϱ \sqrt{f f - g g} & + & d c f f ϱ \\ + & c d f \sqrt{f f - g g} \end{array} \\ \begin{array}{l} d f^{3} x x y & = & d f f g ϩ^{3} & + & e f^{3} ϱ ϩ ϩ & + & d g f f ϱ ϱ ϩ & + & e f^{3} ϱ^{3} . \\ - & g g g d & - & e f g g ϱ & + & 2 e f f ϱ ϱ \sqrt{f f - g g} & + & c d f^{3} ϱ ϱ \\ + & c d f^{3} & + & 2 c d f f ϱ \sqrt{f f - g g} \\ - & c d f g g \\ + & 2 d f g ϱ \sqrt{f f - g g} \end{array} \\ \begin{array}{l} d d f^{3} x y y & = & d d g g ϩ^{3} \sqrt{f f - g g} & + & d d f g g ϱ ϩ ϩ & + & 2 d e f f g ϱ ϱ ϩ & + & e e f^{3} ϱ^{3} . \\ + & 2 d e f g ϱ \sqrt{f f - g g} & + & 2 c d d f f g ϱ & + & 2 c d e f^{3} ϱ ϱ \\ + & 2 c d d f g \sqrt{f f - g g} & + & e e f f ϱ ϱ \sqrt{f f - g g} & + & c c d d f^{3} ϱ \\ + & 2 c d e f f ϱ \sqrt{f f - g g} \\ + & c c d d f f \sqrt{f f - g g} \end{array} \end{array} \end{matrix}$ This table may be continued when the nature of the lines are expressed by Equations of 4 or more dimensions. This like the former rules will be beste perceived by Examples than precepts. As

Example the 1^st. To find the asymptotes of the line whose nature is exprest by $r x + \frac{r x x}{q} = y y$ . first I write the valors of x , $x x$ & $y y$ (found by this table) into theire places in the Equation $r x + \frac{r x x}{q} - y y = 0$ . & there results $\begin{matrix} \frac{r f f ϩ ϩ - r g g ϩ ϩ + 2 r f ϱ ϩ \sqrt{f f - g g} + r f f ϱ ϱ}{q f f} \\ \begin{matrix} \frac{\begin{matrix} - & d d g g ϩ ϩ & - & 2 d e f g ϱ ϩ & - & e e f f ϱ ϱ \\ - & c c d d f f & - & 2 d d c f g ϩ & - & 2 c d e f f ϱ \end{matrix}}{d d f f} & \frac{+ r f ϱ + r ϩ \sqrt{f f - g g}}{f} \end{matrix} \end{matrix} = 0$ . or by ordering it, $\begin{matrix} + \frac{r}{q} \\ - \frac{r g g}{q f f} \\ - \frac{g g}{f f} \end{matrix} ϩ ϩ \begin{matrix} + \frac{2 r ϱ \sqrt{f f - g g}}{q f} \\ - \frac{2 e g ϱ}{d f} \\ - \frac{2 c g f}{f} \\ + \frac{r \sqrt{f f - g g}}{f} \end{matrix} ϩ \begin{matrix} + \frac{r ϱ ϱ}{q} \\ - \frac{e e ϱ ϱ}{d d} \\ - \frac{2 c e ϱ}{d} \\ + r ϱ - c c \end{matrix} = 0$ . Or, $\begin{array}{l} + & d d f f r & ϩ ϩ & + & 2 d d f r ϱ \sqrt{f f - g g} & ϩ & + & d d f f r ϱ ϱ \\ - & d d g g r & - & 2 d e f g q ϱ & - & e e f f q ϱ ϱ \\ - & d d g g q & - & 2 c d d f g q & + & d d f f q r ϱ \\ + & d d f q r \sqrt{f f - g g} & - & 2 c d q e f f ϱ \\ - & c c d d f f q \end{array} = 0$ . Now by assumeing any valors for c ; d , e ; f , g . I have, by this equation, the relation which ϱ beares to ϩ , that is which mh beares to hd . But that the valors of c , d , e , f & g , may be such that hr (to which hd is applyed) may be one asymptote & hd parallell to the other, it is necessary (by Proposition 3^d) that neither ϱ nor ϩ bee any where of soe many or of more dimensions, then in those termes in which they multiply one another. Therefore I consider of how many dimensions ϱ is at the most in any terme multiplied by ϩ, & how many ϩ is in any terme multiplied by ϱ ; & find them but of one. & therefore conclude that ϱ & ϩ ought to be found in noe terme in this equation ∼ unlesse where they multiply one another. ^[64]^[65] Moreover tis manifest that the Equation (expresing the nature of the given line) will ever be of one & but of one dimension more than ϱ or ϩ in some termes in which they multiply one another: & therefore this may bee put for a Generall Rule viz. All those termes must destroy one another in which there is not $ϱ ϩ$ & which are of as many, or want but one dimension of being of as many dimensions as the Equation is. Now that these termes destroy one another, tis necessary that those be $= 0$ in which the unknowne quantitys ϱ & ϩ are the same. Upon which considerations it will appeare that in this example I must make, $d d f f r ϩ ϩ - d d g g r ϩ ϩ - d d g g q ϩ ϩ = 0$ . 2^dly, $+ d d f q r \sqrt{f f - g g} ϩ - 2 c d d f g q ϩ = 0$ . thi{rdly} { $d d f f r ϱ ϱ - e e f f q ϱ ϱ = 0$ }. 4^thly $d d f f q r ϱ - 2 c d q e f f ϱ = 0$ . Or by dividing them by those quantitys which {neede} {illeg} $= 0$ . they are $d d r f f - d d g g r - d d g g q = 0$ . 2^dly $d d r \sqrt{f f - g g} - 2 c d d g = 0$ . thirdly, $d d r - e e q = 0$ . 4^thly, $d d q r - 2 c d q e = 0$ . by the 3^d, $d = e \sqrt{\frac{q}{r}}$ . & since tis not $d = 0$ , by the first $f f = g g + \frac{q g g}{r}$ . by the 2^d $c = \frac{r \sqrt{f f - g g}}{2 g}$ . or { $c = g \frac{\sqrt{r q}}{2}$ }. by the 4^th $\frac{d r}{2 e} = c = \frac{\sqrt{r q}}{2}$ . Therefore from the point b I draw bf & $bk = c = \overset{\cup}{O} \frac{\sqrt{r q}}{2}$ . from f I draw fq parallell to bc . from q I draw qv , soe that $fq ∶ qv ∷ d ∶ e ∷ \sqrt{q} ∶ \sqrt{r}$ . & through the points f & v I draw fv which shall be {one} Asymptote then <27v> or which is the same (since tis not $c = 0$ ) I make. $e ∶ d ∷ c ∶ bl = \frac{d c}{e}$ . Or, $bl = \frac{c \sqrt{q}}{\sqrt{r}}$ . & soe draw the asymptote passing through the points l & f . Then from the point k I draw pk parallell to bl & pv parallell to bk soe that (assumeing some other proportion twixt d & e than before if there be any other) $d ∶ e ∷ pk ∶ pv ∷ - \sqrt{q} ∶ \sqrt{r}$ . & soe through the points k & v I draw the other Asymptote. Or since it is not $c = 0$ ; I make $e ∶ d ∷ bk ∶ \frac{d c}{e} = bl = \frac{+ c \sqrt{q}}{r}$ . & soe through the points l & k I draw the other asymptote, which shall be parallell to hd.

Example the 2^d. Suppose the Asymptotes of $x x - y x + a y = 0$ were to bee determined, Since I have noe use of the termes in which is $ϱ ϩ$ I onely select those termes out of the valors of $x x$ , y & $y x$ in which $ϱ ϩ$ is not & sorting them as was before taught I have these equations, 1^st $f f ϩ ϩ - g g ϩ ϩ - - g ϩ ϩ \sqrt{f f - g g} = 0$ 2^dly $a g ϩ - c ϩ \sqrt{f f - g g} = 0$ . 3^dly, $d ϱ ϱ - e ϱ ϱ = 0$ . 4^thly $\frac{a e ϱ}{d} - c ϱ = 0$ . by the third $d = e$ . by the {4^th} $a = c$ . by the 1^st $g = + \sqrt{f f - g g}$ . by the 2^d $c = a$

Example the 3^d, Suppose $x x - a x + b y - y y = 0$ . then by workeing as before I have these Equations, $f f - 2 g g = 0$ . $- a \sqrt{f f - g g} + b g - 2 c g = 0$ . $d d - e e = 0$ . { $b e - a d - 2 c e = 0$ .} by the 4^th $d = \overset{\cup}{O} e$ . by the 1^st $f = \overset{\cup}{O} g \sqrt{2}$ . or { $g = \overset{\cup}{O} \sqrt{f f - g g}$ .} by the 2^d (by supposeing $g = + \sqrt{f f - g g}$ ) tis $\frac{b - a}{2} = c$ : & by the 4^th (by supposeing $d = + e$ ) tis $\frac{b - a}{2} = c$ . But by the 2^d (by supposing $g = - \sqrt{f f - g g}$ ) tis $\frac{a + b}{2} = c$ . & by the 4^th (by supposeing $d = - e$ ) tis $\frac{a + b}{2} = c$ . Whence I conclude that when $c = \frac{b - a}{2}$ then is $d = e$ , & $g = \sqrt{f f - g g}$ ; & when $c = \frac{b + a}{2}$ then $d = - e$ & $g = - \sqrt{f f - g g}$ .

<30v>

^[66] To find the Quantity of crookednesse in lines.

^[67] Suppose $ab = x$ . $be = y$ . $bc = o = gh$ . $bg = c$ . ed & df secants to the crooked line intersecting at d . the angles abe , acf , egd , right ones. & let $r x = y y$ , be the relation twixt x & y . soe that aef is a Parabola. Then $be = \sqrt{r x}$ . $bn = v = \frac{r}{2}$ . $eb ∶ bn ∷ eg ∶ gd$ $\sqrt{r x} ∶ \frac{r}{2} ∷ c + \sqrt{r x} ∶ \frac{c r + r \sqrt{r x}}{2 \sqrt{r x}} = gd = \frac{r}{2} + \frac{c r}{2 \sqrt{r x}}$ . $cf = \sqrt{r x + r o}$ . $cf ∶ cm ∷ fh ∶ hd$ $\sqrt{r x + r o} ∶ \frac{r}{2} ∷ c + \sqrt{r x + r o} ∶ \frac{c r + r \sqrt{r x + r o}}{2 \sqrt{r x + r o}} = hd = \frac{r}{2} - o + \frac{c r}{2 \sqrt{r x}}$ . That is $2 c r \sqrt{r x} + 2 r \sqrt{r r x x + r r o x} = 2 r \sqrt{r r x x + r r o x} - 4 o \sqrt{r r x x + r r o x} + 2 c r \sqrt{r x + r o}$ . Or, Squareing both sides $4 c c r^{3} x = 16 o o r r x x + 16 o^{3} r r x \begin{matrix} - 16 c r r x o \\ - 16 c r r x o \end{matrix} \sqrt{r x} + 4 c c r^{3} x + 4 c c r^{3} o$ that is ( by blotting out $4 c c r^{3} x$ on both sides, divideing the rest by o, & then supposeing $o = bc$ to vanish) $- 16 c r r x \sqrt{r x} + 4 c c r^{3} = 0$ . Or $c = \frac{4 x \sqrt{r x}}{r}$ therefore makeing $ab = x$ . $bg = \frac{4 x \sqrt{r x}}{r}$ . $gd = \frac{bn \times eg}{eb} = \frac{1}{2} r + 2 x$ . & describing a circle with the Radius $de = \sqrt{\frac{16 x^{3}}{r} + 12 x x + 3 r x + \frac{r r}{4}}$ , the circle shall have the same quantity of crookednesse which the Parabola hath at the point e.

^[68] Or thus. If $ab = x$ . $cb = y$ . $bd = v$ . cd & em perpendiculars to the crooked line cma which intersect at the point e . $af = c$ . $fe = d$ . the angles abc , baf , afe , mna right ones.

Suppose $r x = y y$ , expresseth the relation twixt ab & bc . First I find the length of $bd = v$ (see folium 8^th hujus, or Des=Cartes his Geometry pag 40) which is $v = \frac{r}{2}$ . $cb ∶ bd ∷ gc ∶ ge$ . $y ∶ v ∷ c + y ∶ \frac{c v + v y}{y}$ . $ab + ge = x + v + \frac{c v}{y} = d$ . Or $- d y + c v + v y + x y = 0$ . Out of these termes first I take away v by writeing its valor in its roome which in this case is $\frac{1}{2} r$ & there results, $\frac{c r}{2} + \frac{y r}{2} + x y - d y = 0$ . Then I take away either x or y (which may bee easiliest done) by the helpe of the Equation expressing the nature of the li{ne which} is now $r x = y y$ . or $\frac{y y}{r} = x$ . And there results $\frac{c r}{2} + \frac{y r}{2} + \frac{y^{3}}{r} - d y = 0$ . Now tis Evident that when the lines cm & ce are coincident that ce is the radius of a circle which hath the same quantity of crookednesse which the Parabola mca hath at the point c . Wherefore I suppose eb & nm 2 of the rootes of the Equation $2 y^{3} + r r y - 2 d r y + c r r = 0$ , to be equall to one another. & so by Huddenius his method I multiply it $\begin{matrix} 2 y^{3} & + & r r y & - & 2 d r y & + & c r r & = & 0 \\ 3 & 1 & 1 & 0 \end{matrix}$ . & there results, $\frac{6 y y - r r}{2 r} = d$ . againe otherwise $\begin{matrix} 2 y^{3} & + & r r y & - & 2 d r y & + & c r r & = & 0 \\ 2 & 0 & 0 & - 1 \end{matrix}$ , & there results $\frac{4 y^{3}}{r r} = c$ . Soe that if $cb = qa = y$ . then $ab = \frac{y y}{r}$ . $af = \frac{4 y^{3}}{r r}$ . $fe = \frac{6 y y - r r}{2 r}$ . then the circle described by the radius ec shall bee as crooked as the Parabola at the point c

^[69]^[70] The crookednesse of equall portions of circles are as their diameters, reciprocally.

Demonstration. The crookednesse of any whole circle ( bfd , gcme ) amounts to 4 right angles, therefore there is as much crookednesse in the circle bfd as in cmeg . Now supposing the perimeter fbdf is equall to the arch cme , Then as the arch $emc = fdbf$ is to the circumference cmegc , soe is the crookednesse of the arch cme to the crookednesse of the perimeter cmegc , or of bdfb . so is ab to ac .

<31r>

To find the Quantity of crookednesse in lines^[71]

^[72] Suppose ndf & efm perpendiculars to the crooked line adeo , which intersect one another at f . $ac = x$ . $ce = y$ . $cm = v$ . $ag = ch = c$ . $gf = d$ . & the angles abd , ace , mag, agf right ones. Then, $ec = y ∶ cm = v ∷ eh = y - c ∶ hf = \frac{v y - v c}{y}$ . $gf = gh + hf = x + \frac{v y - v c}{y} = d$ . Or $d y - v y + v c - x y = 0$ .

Haveing therefore the relation twixt x & y (as if it be $r x - \frac{r}{q} x x = y y$ ) first I find the valor of v ( see Cartes Geometry pag 40^th. or folium 8^th of this) (as in this Example tis $\frac{1}{2} r - \frac{r x}{q} = v$ ) by which I take v out of the Equation $d y - x y - v y + v c = 0$ , (& in this case there results $d y - x y - \frac{1}{2} r y + \frac{r x y}{q} + \frac{1}{2} r c - \frac{r x c}{q} = 0$ .) then by meanes of the Equation expressing the relation twixt x & y I take out either x or y , which may easliest bee done (as in this example I take out y by writeing $\sqrt{r x - \frac{r x x}{q}}$ in its stead & there results
$\begin{array}{r} + d \\ - x \\ - \frac{r}{2} \\ + \frac{r x}{q} \end{array} \sqrt{r x - \frac{r x x}{q}} = \frac{r c x}{q} - \frac{1}{2} r c$ . Or $\begin{matrix} 2 d q \\ - & 2 x q \\ - & r q \\ + & 2 r x \end{matrix} \sqrt{r x q - r x x} = 2 r c x \sqrt{q} - r c q \sqrt{q}$ . & by squareing both parts $\begin{array}{l} - 1 & 0 & 1 & 2 & - 2 & - 1 & 0 \\ 4 d d q^{3} r x & - & 4 d d q q r x x & + & 8 d q q r x^{3} & - & 4 q q r x^{4} & = & q^{3} r r c c & - & 4 q q r r c c x & + & 4 r r q c c x x \\ - & 4 d q^{3} r r & - & 8 d q^{3} r & - & 8 d q r r & + & 8 q r r \\ + & q^{3} r^{3} & + & 4 d q q r r & + & 4 q^{3} r & - & 4 r^{3} \\ + & 8 d q q r r & - & 4 q q r r \\ + & 4 q^{3} r r & - & 8 q q r r \\ - & q q r^{3} & + & 4 q r^{3} \\ - & 4 q q r^{3} & + & 4 q r^{3} \end{array}$ ) Then if I assume any valors for c & d that is if I determine the point f , I have an Equation by which I can find all the perpendiculars to the crooked line, drawne from the point f . for if I tooke x out of the Equation, the rootes of the Equation will bee all such lines as are drawn from the points of intersection d , e , k , h , to the line ao (as db , ec , &c) but if I tooke y out of the Equation then the roots of the Equation will bee those lines drawne from a to the perpendiculars (as ab , ac , &c. Now by how much the nigher the points d & f are to one another, soe much the lesse difference there will bee twixt the crookednesse of the parte of the line de , & a circle described by the radius df or ef . And should the line df be understood to move untill it bee coincident with ef , taking f for the point where they ceased to intersect at theire coincidence, the circle described by the radius ef , & the crooked line at the point e , would bee alike crooked. And when the 2 lines df & ef are coincident 2 of the rootes of the Equation (viz db & ec , ab & ac ) shall bee equall to one another; Wherefore to find the crookednesse of the line at the point e I suppose the equation to have 2 equall rootes & so ordering it According D: Cartes or Huddenius his Method, the valor of any of these 3 { $\begin{matrix} x \\ y \end{matrix}}$ } c d being given, the valor of the other 2 may be found. ^[73] (as in this Example the valor of x being given I multiply the Equation according to Huddenius method & it is $\begin{matrix} \begin{array}{l} - & 4 d d q^{3} x & + & 8 d q q x^{3} & - & 8 q q x^{4} \\ + & 4 d r q^{3} & - & 8 d q r & + & 16 q r \\ - & r r q^{3} & + & 4 q^{3} & - & 8 r r \\ + & 8 q r r \end{array} \\ \begin{matrix} 4 q q r x & - & 2 q^{3} x \end{matrix} \end{matrix} = c c = \begin{matrix} \begin{array}{l} - & 4 q q x^{4} & + & 8 d q q x^{3} & - & 4 d d q q x x & + & 4 d d q^{3} x \\ + & 8 q r & - & 8 d q r & - & 8 d q^{3} & - & 4 d q^{3} r \\ - & 4 r r & + & 4 q^{3} & + & 12 d q q r & + & q^{3} r r \\ - & 12 q q r & + & 4 q^{3} r \\ + & 8 q r r & - & 5 q q r r \end{array} \\ \begin{matrix} 4 q r x x & - & 4 q q r x & + & q^{3} r \end{matrix} \end{matrix}$ ^[74] Then by divideing both the numerators by x & the denominators by $2 q r x - q q r$ , & so multiplying them {in crucem} & ordering the product it is. { $\begin{array}{l} 4 d d q^{4} & - & 4 q^{4} r d & + & q^{4} r r & = & 0 \\ - & 16 q^{4} x & + & 8 q^{4} r x \\ + & 16 q^{3} r x & - & 8 q^{3} r r x \\ + & 24 q^{3} x x & + & 12 q^{4} x x \\ - & 24 q q r x x & - & 36 q^{3} r x x \\ - & 16 q q x^{3} & + & 24 q q r r x x \\ + & 16 q r x^{3} & - & 24 q^{3} x^{3} \\ + & 56 q q r x^{3} \\ - & 32 q r r x^{3} \\ + & 16 q q x^{4} \\ - & 32 q r x^{4} \\ + & 16 r r d^{4} \end{array}$ }.

Now considering that if q , r , & x bee known, that is, if the Ellipsis eak be determined, & the line ac given{,} there are onely two points in the line (viz: e & k ) to be considered. And the valors of d are ( gf , am , sq ) {such} lines as are drawne from the line gas to the points where the perpendiculars efm kqm intersect (as m ) or to such points where two perpendiculars (as ef & df ) {ceased} to intersect at theire coincidence into one (as f & y ). Therefore {illeg}of the first {illeg} roots I get the valor of the {line} $cm = x + \frac{r}{2} - \frac{r x}{q} = d$ . as {illeg} this Equation by {illeg} that is $d - x + \frac{r}{2} - \frac{r x}{q} = 0$ {illeg} $+ 2 d q - 2 q x + q r - r x = 0$ ; {illeg} there results <31v> $+ 2 d q^{3} - q^{3} r - 6 q^{3} x + 6 q q r x + 12 q q x x - 12 q r x x - 8 q x^{3} + 8 r x^{3} = 0$ .^[75] That is dividi{ng} it by $2 y^{3}$ ; $d = \frac{r}{2} + 3 x - \frac{3 r x - 6 x x}{q} + \frac{6 r x x + 4 x^{3}}{q q} - \frac{4 r x^{3}}{q^{3}}$ . Which Equation expresseth the length of the lines ( $qs = d$ , & $gf = d$ ) which are drawne from the line sag to the points q & f at which the coincident perpendiculars last intersected one another before theire coincidence. Now haveing the length of gf or sq it will not be difficult to find, $c = ag = ch$ , or, $as = cl = c$ ; for it was found before that $d y - v y - x y + v c = 0$ Or $c = \frac{v y + x y - d y}{v}$ . Likewise it will not bee difficult to find ef or kq , for (supposeing $lq = d - x$ ; $hf = d - x$ ; $lc = + c$ ; $hc = - c$ ; $ec = + y$ ; $ck = - y$ . $ef = e$ . or $kq = e$ ) it is, $y y - 2 c y + c c + x x - 2 d x + d d = e e = {\begin{matrix} kq \times kq \\ ef \times ef \end{matrix}$ , Lastly the circle described with the radius ef shall have the same quantity of crookedness which the Ellipsis hath at the point e .

^[76] Example the 2^d. Were I to find the quantity of crookedness at some given point of the line exprest by $r x + \frac{r x x}{q} = y y$ ; I might consider that it differs from the former Example onely in that there I have $\frac{- r x x}{q}$ or $\frac{r x x}{- q}$ , here $\frac{r x x}{q}$ , that is in the former q was negative in this is affirmative. Soe that this operation will bee the same with the former the signe of q being changed soe that it will be found
qf or $hq = d = \frac{r}{2} + 3 x \frac{+ 3 r x + 6 x x}{q} \frac{+ 6 r x x + 4 x^{3}}{q q} \frac{+ 4 r x^{3}}{q^{3}}$ . &c as before.

^[77] Example the 3^d. In the Parabola, $r x = y y$ . & $v = \frac{r}{2}$ . In the above mentioned Equation $d y - x y - v y + v c = 0$ I take out v by write{ing} $\frac{r}{2}$ in its roome & it is $d y - x y \frac{- r y + r c}{2} = 0$ . then I take out y by writeing $\sqrt{r x}$ in its stead $- 2 d \sqrt{r x} + 2 x \sqrt{r x} + r \sqrt{r x} = r c$ . & by squareing both sides, $\begin{matrix} 4 d d x & - & 8 d x x & - & 4 d r x & + & 4 x^{3} & + & 4 r x x & + & r r x & = & r c c \\ 1 & 2 & 1 & 3 & 2 & 1 & 0 \end{matrix}$ . Which is an equation haveing 2 equall roots & therfore multiplied according Huddenius his method soe that $r c c$ be blotted out, & the result divided by x it is, $\begin{matrix} 4 d d & - & 16 d x & + & 12 x x & = & 0 \\ - & 4 d r & + & 8 r x \\ + & r r \end{matrix}$ . Now tis evident that $x = ac$ being determined there are 2 points (viz: e & k ) from which perpendiculars being drawne they intersect one another in the axis at m , wherefore ∼ $am = x + \frac{r}{2}$ is one of the rootes of the Equation & therefore it being divided by $d - x - \frac{r}{2} = 0$ , or by $2 d - 2 x - r = 0$ there results $2 d - 6 x - r = 0$ Or $d = \frac{1}{2} r + 3 x = sq = gf$ . Then into the above found Equation ∼ ∼ $\frac{2 x \sqrt{r x} - 2 d \sqrt{r x} + r \sqrt{r x}}{r} = c$ , I substitut this valor of d & there results $\frac{- 4 x \sqrt{r x}}{r} = c = ag = ch = pf$ . $ef = \frac{r + 4 x}{2 r} \sqrt{r r + 4 r x}$ . Soe that I have $eh = \sqrt{r x} + \frac{4 x \sqrt{r x}}{r}$ . And $hf = \frac{1}{2} r + 2 x$ . & therefore $ef = \sqrt{\frac{1}{4} r r + 3 r x + 12 x x + \frac{16 x^{3}}{r}}$ shall be the Radius of a circle which is as crooked as the Parabola at the point e .

^[78] Or it might have beene done thus, haveing the Equation $d y - x y - \frac{r y + r c}{2} = 0$ , I might have written $\frac{y y}{r}$ in stead of x , & soe have had $\begin{matrix} d y & - & \frac{y^{3}}{r} & - & \frac{r y}{2} & + & \frac{r c}{2} & = & 0 \\ 1 & 3 & 1 & 0 \end{matrix}$ which must have 2 equall roots & therefore by the Method de maximis & minimis I {blott} out $\frac{r c}{2}$ & there results, $d y - \frac{3 y^{3}}{r} - \frac{r y}{2} = 0$ . Or, $d = \frac{r}{2} + \frac{r y y}{r}$ . makeing $ad = y$ , $de = x$ . $cm = v$ . $gf = d$ . $ag = fp = c$ . now if $ad = y$ bee determined it is manifest that there is but one point of the Parabola (viz: e) to bee considered from which the perpendiculars which are drawne doe noe where intersect one another & therefore this equation hath not superfluous rootes like the former.

^[79] Example the 4^th. If it bee supposed that the nature of the line is contained in $r y - y y - r x = 0$ . & if tis $ad = x$ . $y = {\begin{matrix} ed \\ ek \end{matrix}$ . $v = {\begin{matrix} dt \\ dy \end{matrix}$ . fe & jk 2 perpendiculars to the crooked line, f, & q two points where the coincident perpendiculars last intersected $d = {\begin{cases} ap = qs \\ fg \end{cases}$ . $c = {\begin{matrix} pq \\ pf \end{matrix}$ . Then is $v = \frac{r y}{r - 2 y}$ . by which I take v out of the above named Equation $d y - x y - v y + v c = 0$ , & the result being divided by y , it is, $r y + 2 d y - 2 x y - d r + r x - c r$ Or ({illeg} $y = \frac{d r - r x + c r}{r + 2 d - 2 x}$ : Then I substitute this valor of y into its place in Equation $r x + y y - r y$ & there results $r x + \frac{d d r r - 2 d r r x + r r x x + 2 d c r r - 2 c r r x + c c r r}{r r - 4 r x + 4 x x + 4 d d + 4 d r - 3 d x} \frac{r r x - d r r - d r r}{r + 2 d - 2 x} = 0$ . or by ordering it {it} will bee {{illeg} $\begin{array}{l} d^{3} & + & d d x x & + & 4 d d x & - & d d r \\ - & 5 r & + & 6 d r & + & 2 c r \\ + & 2 r r & - & d r r \\ - & c r r \\ 3 & 2 & 1 & 0 \end{array} = 0$ } Which Equation must have {illeg}

<32r>

two equall roots & therefore by ordering it according to Huddenius Method de Maximis & Minimis, I blot out the last terme & the result is $\begin{array}{l} 6 x x & - & 8 d x & + & 2 d d \\ - & 5 r x & + & 3 d r \\ + & r r \end{array} = 0$ . Or $\begin{array}{l} 2 d d & + & 3 d r & + & 6 x x \\ - & 8 d x & - & 5 r x \\ + & r r \end{array} = 0$ . By what was said before tis evident that the perpendicular $(rm)$ drawne from the line asg to the point where the two perpendiculars intersect, is one of the rootes of this Equation.

^[80] And that I may have a general rule to find the line rm (or had there beene 3 or more perpendiculars, to find all those lines which are drawne from the line acrw to every intersection of the perpendiculars) I consider that if $[ac = λv = θb = c]$ be not drawne from the line $[at]$ to the point of intersection $[m]$ ; then d hath two valors as $[vc & bc]$ but if they bee drawne to the point $[m]$ , that is, if they be ∼ coincident with nm ; then the two roots of d are equall to one ∼ another, being the same with the line rm . Likewise if $[aλ = cv = wz = d]$ be drawne from the line aw to the perpendiculars fe , qk {illeg} but not from the point where they ∼ intersect; then hath $[c]$ two roots (as λv , λz ) which will also be equall to one ∼ another & coincident with the line mn , when $(d)$ is the same with $(rm)$ . This being considered; if I would the valor of nm , I must order the affore found Equation (in which x was supposed to have 2 equall roots) according to c & it will bee $\begin{array}{l} r c c & - & r r c & - & d r r & + & 6 d r x & - & 8 d x x \\ - & d d r & + & 4 d d x & + & 4 x^{3} \\ + & 2 r r x & - & 5 r x x \\ 2 & 1 & 0 & 0 & 0 \end{array} = 0$ . which must have 2 equall roots & therefore by Huddenius Method de Maximis & Minimis I take away the last terme & Soe I have, $2 r c c - r r c = 0$ ; or, $c = \frac{r}{2} = nm$ : But if I would have the valor of rm I order the Equation according to the letter d & it is $\begin{array}{l} 4 d d r & - & d r r & + & c c r \\ - & d d r & + & 6 d r x & - & c r r \\ - & 8 d x x & + & 2 r r x \\ + & 4 x^{3} \end{array} = 0$ . which Equation must likewise have two equall roots & therefore takeing away the last terme by Huddenius method de Maximis & Minimis there resulteth this, $\begin{array}{l} 8 d d x & - & d r r \\ - & 2 d d r & + & 6 d r x \\ - & 8 d x x \end{array} = 0$ . Or $d = x - \frac{r}{2} = rm$ & this $(x - \frac{1}{2} r)$ is one of the rootes of the Equation $\begin{array}{l} 2 d d & + & 3 d r & + & 6 x x \\ - & 8 d x & - & 5 r x \\ + & r r \end{array} = 0$ , which was required, therefore I must divide this equation by $d - x + \frac{r}{2} = 0$ . that is by $2 d - 2 x + r = 0$ , & there will result, $d - 3 x + r = 0$ . That is $d = 3 x - r = fg = qs$ . Whence it will not be difficult to find the points q & f & ∼ consequently the lines qk , fe which shall be the radij of circles which have the same quantity of crookednesse the line $(aek)$ hath at the points e & k . Makeing { $c = {\begin{matrix} as \\ ag \end{matrix}$ }.

May 1665

^[81] 1. Note that the crooked line φfγqπ (described by the points q & f ) is always touched by the (perpendicular) kq ; & that in such sort as to bee measured by it{,} they applying themselves the one to the other, point by point; soe that if $aγ = kξ$ the shortest of all the lines qk be substracted from qk there remaines $qξ = qγ$ . By this meanes the length of as many crooked lines may bee found as is desired

2. Also if the line qk is applyed to the crooked line qγ point by point, every point of the line qk (as k ) shall describe lines (as akw) to which qξk is perpendicular.

^[82] 3. The line {qπxfy } is the same (if wka be a Parabola) {Heura{illeg}} found. & {illeg} perpendicular to th{e} line efb , & abd a tangent & the position & {illeg} point {illeg} with the tangent (as if they were inherent in the same {body}) while the tangent gl{illeg} the crooked line ebf, soe that the point { $\begin{matrix} a \\ f \end{matrix}$ {illeg}} describe {illeg} dag{illeg} then from {illeg} draw perpendiculars to the line dag (or {illeg} then shall the {illeg} point c , {illeg} perpendiculars intersect {illeg} the po{illeg} of the {illeg} {illeg} {illeg} {least} {illeg}

<32v>

^[83] The Crookednesse in lines may bee otherwise found as in the following Examples

^[84] In the Parabola aeg suppose e the point where the crookednesse is sought for, & that f is the center & fe the Radius of a Circle equally crooked with the Parabola at e . Then naming the quantitys $ce = y$ . $ap = d$ . $pf = - c$ . $ef = s$ . By the nature of the line $ac = \frac{y y}{r}$ . $ce + pf = eh =$ $y - c$ . { $cp = \frac{y}{r} - d = hf$ }. ${eh}^{2} + {hf}^{2} = {ef}^{2}$ , That is, $\begin{matrix} \frac{y^{4}}{r r} & * & - & \frac{2 d y y}{r} & + & y y & - & c y & \begin{matrix} + & c c \\ + & d d \end{matrix} & = & s s \\ 4 & 2 & 2 & 1 & 0 & 0 \end{matrix}$ which Equation must have 2 equall rootes that ef may be perpendicular to the Parabola & therefore multiplyed according to Huddenius's Method it produceth $\begin{matrix} \frac{2 y^{3}}{r r} & - & \frac{2 d y}{r} & + & y & - & c & = & 0 \\ 3 & 1 & 1 & 0 \end{matrix}$ . Which Equation hath soe many rootes as there can be drawn perpendiculars to the Parabola from the determined point f . And two of these rootes must become equall, that f may bee the center of the required Circle, therefore this equation is to bee multiplyed againe, & it will produce $\frac{6 y^{2}}{r r} - \frac{2 d}{r} + 1 = 0$ that is $\frac{3 y y}{r} + \frac{r}{2} = d$ . Or $3 x + \frac{r}{2} = d$ : As was found in the 3^d precedent example.

^[85] Here observe that in the 1^st of these 3 Equations y hath 4 valors gl , ec , hs & kv . see fig 2^d when d ; c , & s are determined. But d , c , & $y = ec$ being determined $(s)$ hath but one valor $= ef$ . And if d , s , & $y = ec$ bee determined then c hath 2 valors pf & pm. And c, s , & $y = ec$ being determined d hath 2 valors an & ap as that first equation denotes by the dimensions of the quantitys in it. 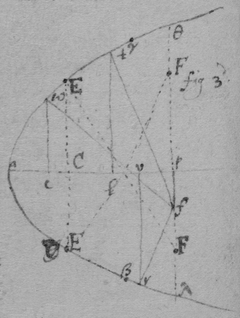By the 2^d of these Equations 2 of the valors of $(y)$ are united by the increasing or diminishing the valor of $d = fe$ &c. first suppose the circle soe little as noe where to intersect the Parabola, it being increased gradually will first touch the Parabola at r (fig 3^d) then ceasing to touch it it intersects it in 2 points g & k (fig 2^d) which two points grow more distant untill it touch the Parabola in t (fig 3^d) which being divided into two intersection points e & h (fig 2d) the points g & e draw nearer untill they conjoyne in the touch point w & soe the circle ceaseth (by still increasing) to touch the Parabola or intersect it unlesse in h & k . Whence from one point f may be drawne 3 perpendiculars fr , fw , ft , to the Parabola twar . And therefore in this 2^d Equation $(y)$ must have 3 valors wc , tl , & vr , when $ap = d$ , & $pf = - c$ , are determined then also hath $(s)$ three valors fr , fw , & ft .

By the 3^d Equation Two of the valors of $(y)$ in the 2^d Equation are united by incresing or diminishing the length of $pf = - c$ . For begining at the point at the point p (from which the 3 perpendiculars fall upon γ , a & β ) if the point f doth gradually move from p , the perpendicular $\{\begin{matrix} ft \\ fw \\ fr \end{matrix}\}$ moves from $\{\begin{matrix} γ \\ a \\ β \end{matrix}\}$ towards $\{\begin{matrix} a \\ γ \\ λ \end{matrix}\}$ Soe that the two perpendiculars = wf & tf will at last conjoyne into one EF , Which shall be the Radius of a Circle as crooked as the Parabola at E .

This 3^d operation might have beene done by making pf determined & by = increasing or diminishing $ap = d$ . That is by destroying the term $- \frac{2 d y}{r}$ in stead of $- c$ in the 2^d Equation. And so might the 2^d Operation beene done otherwise by determining the circle egh , Or taking c or d out of the 1^st Equation instead of $s s$ .

^[86] There is another way of finding the crookednesse in lines & that is not by supposing two perpendiculars ( wf & ft , or wf & fr ). but 3 intersections of a circle with the figure, (fig 2^d h , e , g : or e , g & h ). And then shall $\begin{matrix} x \\ y \end{matrix}}$ have 3 equall valors $\{\begin{matrix} al & , & ac & , & as & . \\ lg & , & fc & , & eh \end{matrix}\}$ Or $\{\begin{matrix} ac & , & al & , & av \\ ce & , & lg & , & vk \end{matrix}\}$ . As if (in the last example I had this equation $\begin{matrix} y^{4} & * & - & 2 d r y y & + & r r y y & - & 2 c y r r & + & c c r r & + & d d r r & - & s s r r & = & 0 \\ 3 & 1 & 1 & 0 & - 1 & - 1 & - 1 \end{matrix}$ . Supposing it to have 3 equall rootes by Huddenius his method tis $\begin{matrix} 3 y^{4} & * & - & 2 d r y y & + & r r y y & - & c c r r & - & d d r r & + & s s r r & = & 0 \\ 4 & 2 & 2 & 0 & 0 & 0 \end{matrix}$ . (Which equation doth not determine the perpendiculars to eag ) as $\frac{2 y^{5}}{r r} * - \frac{2 d y}{r} + y = c$ doth for by { $12 y^{4} - 2 d r y y + r r y y = 0$ }. this I can find the valor of c ( y being determined) but by it I {illeg} neither find the valor of { c } nor till one of them is taken out of the Equation). That Equation multiplyed {illeg} the dimensions of y produceth $6 y^{2} - 2 d r + r r$ Or { $\frac{3 y y}{r} + \frac{r}{2}$ {illeg} $3 x$ {illeg} $= d$ }.

^[87] The same may be done thus. If a circle touch a crooked line at one point & intersect it {illeg}er when two points come together that circle {illeg} to {illeg} or {illeg}

As if $bc = y$ . { $ac = \frac{y y}{r}$ $an = mt = d$ . $pv = o$ {illeg} c{illeg}={illeg} $= \frac{r}{2}$ . {illeg} $- \frac{y y}{r}$ . $\frac{r}{2} ∶ y ∷ \frac{d r - y y}{r} ∶ \frac{2 d r y - y^{2}}{r r} = bq$ }. { $\frac{r}{2} ∶$ {illeg} $+ y ∷$ {illeg} $= d - \frac{y y - 2 o y}{r} ∶ \frac{2 d r y + 2 r o - 2 y^{3} - o y y}{r r} = pg$ . {illeg} may ever bee {illeg}). Then {illeg}} { ${bq}^{2} + {qt}^{2}$ {illeg} $6 y^{4} - 8 d r y y o + r r y y o + 2 d d r r o - d r^{3} o = 0$ . Or $d d = \frac{8 d r y y}{2 r r}$ {illeg}.} Or $d =$ {illeg} Or, {illeg} $d =$ {illeg} which cannot {illeg} T{illeg} by the {illeg} perpendiculars {illeg} by supposeing the circle described by the Radius {illeg} pt & {illeg} to {illeg}

<33r>

^[88] Haveing found (by the former rule) an Equation by which the quantity of crookednesse in any line may bee found to find the greatest or least crookednes of that line.

^[89] In the 4^th Example I had found $gf = qs = d = 3 x - r$ . And by a rule there shewed viz { $\begin{matrix} as \\ ag \end{matrix}} = c = \frac{x y + v y - d y}{v}$ }: It was there found $\begin{array}{l} 4 x^{3} & - & 8 d x x & + & 4 d d x & - & d d r \\ - & 5 r & + & 6 d r & + & c c r \\ + & 2 r r & - & d r r \\ - & c r r \end{array} = 0$ . Now by writeing $3 x - r$ in stead of d & ordering the product according to the letter c it is $\begin{array}{l} c c r & - & c r r & + & 16 x^{3} \\ - & 12 r x x \\ - & 3 r r x \end{array} = 0$ . Or extracting the roote it is $c = \frac{r}{2} \overset{\cup}{O} \sqrt{12 x x - 3 r x + \frac{r r}{4} - 16 \frac{x^{3}}{r}} = {\begin{matrix} as & . \\ ag & . \end{matrix}$ Also by the nature of the line, $\begin{matrix} kd \\ ed \end{matrix}} = y = \frac{r}{2} \overset{\cup}{O} \sqrt{\frac{r r}{4} - r x}$ . Therefore $kh = gl = \{\begin{matrix} kd - sa \\ ga - ed \end{matrix}\} = \sqrt{\frac{r r}{4} - r x} + \sqrt{12 x x - 3 r x + \frac{r r}{4} - \frac{16 x^{3}}{r}}$ . Also $qh = le - fg = r - 2 x$ . And Since ${he}^{2} + {gl}^{2} = {qk}^{2}$ Therefore
$\frac{3 r r}{2} - 8 r x + 16 x x - \frac{16 x^{3}}{r} + 2 \sqrt{12 x x - 3 r x + \frac{r r}{4} - 16 \frac{x^{3}}{r}} \times \sqrt{\frac{r r}{4} - r x} = qk qk = z z$ ; Supposing $qk = z$ The roote of the Surde quantity extracted the Equation is $- \frac{16 x^{3}}{r} + 24 x x - 12 r x + 2 r r = z z$ . Or $16 x^{3} - 24 r x x + 12 r r x - 2 r^{3} + r z z = 0$ . In which Equation the least valor of $z = fe$ is to bee found & that should happen when x hath 2 equall valors or rootes. But because $fe = z$ being determined x can have but one valor $= ad$ the other 2 rootes being imaginary tis impossible that it should have 2 equall rootes: Therefore I take away x out of the Equation by substituting its valor $\frac{r y - y y}{r}$ in its stead & there results $\begin{matrix} 16 y^{6} & - & 48 r y^{5} & + & 24 r r y^{4} & + & 32 r^{3} y^{3} & - & 36 r^{4} y y & + & 12 r^{5} y & - & 2 r^{6} & + & r^{4} z z & = & 0 \\ 6 & 5 & 4 & 3 & 2 & 1 & 0 & 0 \end{matrix}$ . In which equation z or $ef = qk$ being determined y hath 2 valors de & dk the other foure being imaginary & when ef is the longest or shortest that may bee then these two valors become one & then is the line aek more or least crooked. If therefore (that y 's valors become equall) this Equation is multiplyed according to its dimensions there will result $8 y^{5} - 20 y^{4} + 8 r r y^{3} + 8 r^{3} y y - 6 r^{4} y + r^{5} = 0$ . which is divisible by $y - \frac{r}{2} = 0$ , or by $2 y - r = 0$ (for there results $4 y^{4} - 8 r y^{3} + 4 r^{3} y - r^{4} = 0$ ). And if $y = \frac{r}{2}$ , then is $x = \frac{r}{4}$ . Therefore I take $ad = \frac{r}{4}$ & $de = \frac{r}{2}$ & at the point e shall bee the least crookednesse.

Here may bee noted Huddenius his mistake, that if some quantity in an equation designe a maximum or minimum that Equation hath two equall rootes which is false in the equation $16 x^{3} - 24 r x x + 12 r r x - 2 r^{3} + r z z = 0$ . & in all other equations which have but one roote.

Another way. May 1665

^[90] Or because the lines fn & qn described by the points f & q doe touch one another points n from which points onely lines drawne perpendicular to the crooked line kea will bee perpendicular to the point of greatest or least crookednesse: And also since all those are points of greatest or least crookedness to which such perpendiculars are drawne: The difficulty will be to find the point n . Now suppose that $am = d$ be determined then c hath two valors for $\begin{matrix} mf \\ mq \end{matrix}} = c$ . And alsoe y hath two valors for $\begin{matrix} dk \\ de \end{matrix}} = y$ . Alsoe (when am is not parallell to the axis of the line) x hath two (or more) valors $\begin{matrix} ad \\ ad \end{matrix}} = x$ . which valors of c , x , or y become equall if $am = an$ : by which meanes the point n may bee found: Excepting onely when fm , mq , are parallel to the crooked line at n ({ un }{)} ^[91] that is, perpendicular to the streightest or most crooked partes of the line aek . But if $as = c$ be determined, then $d = {\begin{matrix} st & . \\ sf & . \end{matrix}$ $x = {\begin{matrix} av & . \\ ad & . \end{matrix}$ $y = {\begin{matrix} rv & . \\ ed & . \end{matrix}$ (but if $(as)$ is parallel to the axis of the line the two valors of y are equall & soe not usefull). Which valors of d , x, & y become equall if $as = b un$ : excepting onely when as is perpendicular to the most streight or crooked parts of the line ake .

^[92] As for example. In the precedent example it was found $d + r - 3 x = 0$ . But because an or x is parallell to the axis of the line, Therefore substitute either the valors of d or of x into their stead. As if I substitute the valor of $x = \frac{r y - y y}{r}$ into its place it will bee $d + r - 3 y + \frac{3 y y}{r} = 0$ or $\begin{matrix} 3 y y & - & 3 r y & + & r r & + & d r & = & 0 \\ 2 & 1 & 0 & 0 \end{matrix}$ . which must have 2 equall roots & therefore multiplyed according to y 's dimensions tis $6 y y - 3 r y = 0$ . Or $y = \frac{r}{2}$ as before. But if I had substituted d 's valor into its stead it would have beene $\begin{matrix} 16 x^{3} & - & 12 r x x & + & 3 r r x & - & c r r & + & c c r & = & 0 \\ 3 & 2 & 1 & 0 & 0 \end{matrix}$ which {illeg}ving 2 equall roots being rightly ordered is $48 x^{3} - 24 r x^{2} + 3 r r x = 0$ . Or $16 x^{2} - 8 r x + r r = 0$ . Or $4 x - r = 0$ . Or $x = \frac{r}{4} = 0$ , as before.

{In the first} Example of finding the quantity of crookednesse in lines the {illeg} found { $\begin{matrix} 4 r x^{3} \end{matrix}$ {illeg} $\begin{matrix} \frac{x x + 3 r x}{q} & - & 3 x & - & \frac{r}{2} & = & 0 \\ 1 & 1 & 0 \end{matrix}$ }. which {must} have 2 equall rootes & therefore by Hudde{nius} method it is {{illeg} $x x - 4 q x x - 4 q r x + 4 q q x + q q r - q^{3} = 0$ }. Or, $4 x x - 4 q x + q q = 0$ .{illeg} That is $2 x = y$ . or $x =$ {illeg} $= y$ Or {illeg} = {illeg} $= y$ {illeg} that if I take { $us = \frac{r}{2}$ } & {illeg} $} =$ {illeg} $= y$ {illeg} the points {illeg} the greatest or least crookednesse {illeg} the line {illeg} {illeg} crookednesse which {illeg} found

{These Equations} {illeg} superfluous rootes {illeg} often as {illeg} the perpendiculars {illeg} {illeg}

<33v>

The points of greatest or least crookednesse may bee yet otherwise found by an equation of 4 equall rootes. As in the example of the 2^d way of finding the quantity of crookedness in lines it was found $y^{4} * - 2 d r y y + r r y y - 2 c r r y + c c r r + d d r r - s s r r = 0$ . which being compared with an equation like it $y^{4} - 4 e y^{3} + b e e y y - 4 e^{3} y + e^{4} = 0$ . by the 2^d terme tis $4 e y^{3} = 0$ , or $y = 0$ . & $\frac{y y}{r} = \frac{0 0}{r} = 0 = x$ . Soe that the Parabola at the begining is most crooked (at a ).

<38r>

^[93]If the body b move {fro} the line bd & from the point d two lines da , dc bee drawne the motion of the body b from ad is to its motion from dc as $ab ∥ dc$ is to $cb ∥ ad$ .

^[94] Corollary 1. The body b receiving two divers forces from a & c & the force from ba is to the forc{e} from { bc } as ba to bc , then draw $ad ∥ bc$ & $cd ∥ ab$ , the body b shall bee moved in the line bd .

^[95] 2^d Or if the body { b }{ d } is suspended by the {thred} bd & is forced from a to {illeg} & from { c } towards f , then draw $dc ∥ ab$ & $da ∥$ {illeg}, & make $da ∶ ab ∷$ force from c to f ∷ force from {illeg} the body {illeg} {illeg}nd in Equilibrio is b .

{illeg}Corollary 3^d. the force of the body b from d is to its force from a as bd to ba .

<38v>

vide pag: 15. But here observe that unlesse the reflecting line adn bee drawne through the point $(w)$ the center of motion in the whole body aiwn the determination of the motion of adn will not be the same with the determination of the motion of g before reflection (as in the first figure^[96]) but verge from it (as in the 2^d fig^[97]) that is wl & gdi will not bee parallell. For since the chiefe resistan{ce} of the body adn is from its center of motion (prop 32) from w towards d , & not from i towards d , the body g will find more opposition on that side towards the center w , then on the other side towards a & therefore at its reflection it must incline toward v (axiom 120) & not returne in the line dg . But if the body awn presse g towards w then g presseth the body awn towards the contrary parte as from w towards l (axiom 119) & not from w towards m, if $wm ∥ dg$ . But if the line adn pass through the point w (as in fig: 1^st^[98]) then

38 If the superficies abr (fig 3^d^[99]) circulate all its points in the line cd move with equall velocity from c towards d. For make $∠ sfr = tsr = recto$ . & $∠ srf = crt$ & draw $ta ⊥ dc$ than is the motion of the point e from c to the motion of the point f from c as ae to sf. but $ae = sf$ (for triangle rsf similis triangle ret therefore $\frac{er \times sf}{fr} = et$ . also aet similis triangle erf therefore $er ∶ fr ∷ et ∶ ae$ . or, $\frac{er \times ae}{fr} = et = \frac{er \times sf}{fr}$ & $ae = sf$ ) therefore the motion of e from c is equall to the motion of f from c.

39 If the body g reflect on the immoveable surface $(dv)$ at its corner o (fig 4^th^[100]) its parallell motion (viz from d to v ) shall not bee hindered by the surface dv , (viz: if the center of g 's motion were distant from the perpendicular dm an inch at one minute before reflection it shall bee so far distant from it one minute after reflection). For dv is noe ways opposed to motion parallell to it, & a body might $\{\begin{matrix} slide \\ move \end{matrix}\}$ upon it without looseing any motion, & if at the first moment of contact the body g should loose its perpendicular & onely keepe its parallel motion it would (perhaps) continue to slide upon it & not reflect.

40 The body g reflecting on the plaine vd at its corner o all its points in the perpendicular line $op ⊥ vd$ shall move from the plaine vd with the same velocity which before reflection they moved to it. For the point o (prop 9) moves with that velocity backwards which it before did forwards (viz to vd ) & all the other points (prop 38) move with the same velocity from it.

<47r>

^[101] A Method for finding theorems concerning Quæstions de Maximis et minimis. And 1^st Concerning the invention of Tangents to crooked lines.

^[102] Suppose $ab = x$ . $eb = y$ . $bd = v$ . $bc = o$ . $cf = z$ . & $ed = df$ . the nature of the line $a x + x x = y y$ . Then is $ac = x + o$ . $a x + a o + x x + 2 o x + o o = z z$ . $v v + y y = {ed}^{2} = {fd}^{2} = z z + v v - 2 o v + o o$ . Or $y y = o o - 2 o v + z z$ Or $y y = o o - 2 o v + a x + a o + x x + 2 o x + o o$ . & since $a x = y y - x x$ . Therefore $0 = 2 o o - 2 v o + a o + 2 x o$ . Or $2 \times o - 2 v + a + 2 x = 0$ . Now that ed may bee perpendicular to the line tis required that the points e , & f conjoyne, which will happen when $bc = o$ vanisheth into nothing. Therefore in the equation $2 \times o - 2 v + a + 2 x = 0$ . Or $v = o + \frac{a}{2} + x$ , those termes in which $(o)$ is must be blotted out, & there remaines $v = x + \frac{a}{2} = bd$ . which determines the perpendicular ed .

^[103] Hence it appeares that in such like operations those termes may be ever blotted out in which $(o = b)$ is of more than one dimension.

As if the nature of the line was $x^{3} + x x y + x y y = a y y$ . Then since $ac = o + x$ it is $x^{3} + 3 x^{2} o + 3 x o o + o^{3} + x x z + 2 x o z + o o z + x z z + o z z = a z z$ . That is $x^{3} + 3 x^{2} o + x x z + 2 x o z + o o z + x z^{2} + o z^{2} = a z^{2}$ . Also $v v + y y = v v - 2 v o + o o + z z$ . or $y y + 2 v o = z z$ . Therefore
$a y y - x y y - x x y (= x^{3}) + 3 x x o + x x z + 2 x o z + o z z (+ x z z - a z z =) + x y y + 2 v o x - a y y - 2 v o a = 0$ . That is $x x y - 3 x x o - 2 x o z - o z z + 2 v o a - 2 v o x = x x \sqrt{y y + 2 v o}$ . That is (both parts squared & those terms left out in which o is of more than one dimension) $x + y y + \overline{2 x x y in 2 v o a - 2 v o x - 3 x x o - 2 x o z - o z z} = x^{4} y y + 2 v o x^{4}$ Or $y in 2 v o a - 2 v o x - 3 x x o - 2 x o z - o z z = v o x x$ . That is $- 3 x x y - 2 x z y - z z y = v x x + 2 v x y - 2 v a y$ . Now if $bc = o$ vanisheth then is $z = y$ . And consequently $\frac{- 3 x x y - 2 x y y - y^{3}}{x x + 2 x y - 2 a y} = v = \frac{3 x x y + 2 x y y + y^{3}}{2 a y - 2 x y - x x}$ .

^[104] Hence I observe that if in the valor of y there be divers termes in which x is then in the valor of z there are those same termes & also those termes each of them multiplyed by so many units as x hath dimensions in that terme & againe multiplyed by o & divided by x . As if ∼ ∼ ∼ $x^{3} + x x y + x y y - a y y = 0$ . Then, $x^{3} + x x z + x z z - a z z + \frac{3 x^{3} o + 2 x x o z + x o z z}{x} = 0$ . Which operation may bee conveniently symbolized by (ordering the equation according to the dimensions of y ) making some letter (as a . e . m . n . p ) to signifie a terme, & the same letter with some marke (as $\ddot{a}$ , $\ddot{c}$ , $\ddot{e}$ , $\ddot{g}$ , $\ddot{m}$ , $\ddot{n}$ , $\ddot{p}$ &c), to signifie the same terme multiplyed according to the dimensions of x in it as in the former example (supposing $x - a = m$ . $x x = n$ . $x^{3} = p$ .) The nature of the line is ${\begin{matrix} in letters & x y y - a y y + x x y + x^{3} = 0 & x z z - a z^{2} + x^{2} z + x^{3} + \frac{x o z z + 2 x x o z + 3 x^{3} o}{x} = 0 . \\ & \\ in their symbols & m y y + n y + p = 0 & m z z + n z + p + \frac{\ddot{m} z z o + \ddot{n} z o + \ddot{p} o}{x} = 0 . \end{matrix}$ Soe if $\begin{matrix} \underset{︸}{a^{4} + a x^{3} + b b x^{2} - a b b x} & = & y^{4} . \\ m = y^{4} . \end{matrix}$ Then $\begin{matrix} \underset{︸}{3 a o x^{2} + 2 b b o x - a b b o} & + & \underset{︸}{a x^{3} + b b x^{2} - a b b x + a^{4}} & = & z^{4} . \\ \frac{\ddot{m} o}{x} \sim \sim & + & \sim \sim m \sim \sim \sim \sim & = & z^{4} . \end{matrix}$ $\frac{\ddot{m} o}{x} + m = z^{4}$ .

And as any particular Equation may be thus symbolized so divers equations may bee represented by the same caracters as $0 = a + c y + y y e$ may represent all equations in which y is of one & two dimensions

Now if a generall Theoreme be required for drawing tangents to such lines it may bee thus found. $eb = y$ , $bd = v$ , $ab = x$ , $bc = o$ , $fc = z$ , by supposition, $a + c y + e y y = 0$ . Then by observation the 2^d, $a + c z + e z z + \frac{\ddot{a} o + \ddot{c} o z + \ddot{e} o z z}{x} = 0$ . Or, $- c y x - e y y x (= x a) + c z x + e z z x + \ddot{a} o + \ddot{c} o z + \ddot{e} o z z = 0$ . Againe ${eb}^{2} + {bd}^{2} = {cf}^{2} + {cd}^{2}$ that is. $y y + 2 o v = z z$ . Which valor of $z z$ put into its stead in the termes $e z z x$ & $c z x$ in the former Equation the result is $+ c y x - \ddot{a} o - \ddot{c} o z - \ddot{e} o z z - 2 e o v x = c x \sqrt{y y + 2 o v}$ . And both parts squared it is (by the first Observacion) $c c y y x^{2} - 2 c y x \ddot{a} o - 2 c x y \ddot{c} o z - 2 c x y \ddot{e} o z z - 4 c x y e o v x = c^{2} x x y y + 2 c c x x o v$ . Which rightly ordered is $- \ddot{a} y - \ddot{c} y z - \ddot{e} y z z = 2 e x y v + c x v$ . And since the points e & f conjoine to make ed a perpendicular therefore is $z = y$ & consequently $\frac{- \ddot{a} y - \ddot{c} y y - \ddot{e} y^{3}}{c x + 2 e x y} = v$ . Which is the Theorem sought for. As for example were it required to draw a perpendicular to the line whose nature is $\begin{matrix} x^{3} & + & x x y & \begin{array}{l} + & x \\ - & a \end{array} y y & = & 0 . \\ a & + & c y & \begin{array}{l} + & e \end{array} y y & = & 0 . \end{matrix}$ Then is $\frac{- \ddot{a} y - \ddot{c} y y - \ddot{e} y^{3}}{c x + 2 e x y} = \frac{- 3 x^{3} y - 2 x x y y - x y^{3}}{x^{3} + 2 x x y - 2 a x y} = v$ or $v = \frac{3 x x y + 2 x y y + y^{3}}{2 a y - 2 x y - x x}$ .

In like manner to draw tangents to those lines in which y is of 1, 2 & 3 dimensions suppose $a + c y + e y y + g y^{3} = 0$ . Then is by 2^d observacion $- c y x - e y y x - g y^{3} x + \ddot{a} o + c z x +$ {illeg}{illeg} $= 0$ & by writeing the valor of $z = \sqrt{y y + 2 v o}$ ) in its stead in those termes in which {illeg} not (viz {illeg} $+ g z^{3} x$ there results { $c y x + g y^{3} x - \ddot{a} o - \ddot{c} z o - e z^{2} o - g z^{3} o - 2 e x v o = c x + g y y x - 2 v o g x - \sqrt{y y + 2 v o}$ }. {illeg} {illeg} by {illeg} it is
{illeg}{ $2 g o z^{3} = 4 e o v x = c x + g y y x in c x + g y y$ }{illeg} $in y y + 2 v o$ . Or {illeg}{ $+ g y y o v x + 4 v o g x y y$ }. That is { $\frac{- \ddot{a} y - \ddot{c} y y - \ddot{e} y^{3} - \ddot{g} y^{4}}{c x + 2 e x y + 2 g x y y} = v$ }.

By the same proceeding {illeg} of 1, 2, 3 {illeg} dimensions in { $a + c y +$ {illeg} $g y^{3}$ {illeg}} it would be found {illeg} $= v$ . &c {illeg} {illeg}

<47v>

^[105] Having the nature of a crooked line expressed in Algebraicall termes which are not put one parte equall to another but all of them equall to nothing, if each of the termes be multiplyed by soe many units as x hath dimensions in them. & then multiplyed by y & divided by x they shall be a numerator: Also if the signes be changed & each terme be multiplyed by soe many units as y hath dimensions in that terme & then divided by y they shall bee a denominator in the valor of v .

Example 1^st. If $r x + \frac{r x x}{q} - y y = 0$ . Then $\frac{\begin{matrix} 1 & 2 & 0 \\ r x & + & \frac{r}{q} x x & - & y y & in & \frac{y}{x} \end{matrix}}{\begin{matrix} - & r x & - & \frac{r}{q} x x & + & y y & in & \frac{1}{y} \\ 0 & 0 & 2 \end{matrix}} = \frac{r y + 2 \frac{r}{q} x y}{2 y} = \frac{r}{2} + \frac{r}{q} x = v$ . Example 2^d. If $x^{3} + x x y + x y y - a y y = 0$ . Then $\frac{3 x^{3} + 2 x x y + x y y in \frac{y}{x}}{- x x y - 2 x y y + 2 a y^{2} in \frac{1}{y}} = v = \frac{3 x x y + 2 x y y + y^{3}}{- 2 a y - 2 x y - x x}$ . Example 3^d. If $x^{3} + b x x - c d x + b c d + d x y = 0$ . Then $\frac{3 x x y - 2 b x y - c d y + d y y}{- d x} = \frac{2 b y}{d} - \frac{3 x y}{d} + \frac{c y}{x} - \frac{y y}{x} = v$ . And by taking y out of the valor of v then, $v = \frac{2 x^{3}}{d d} - \frac{3 b x x}{d d} + \frac{b b x}{d d} - \frac{2 c x}{d} + \frac{2 b c}{d} + \frac{b c c}{x x} - \frac{b b c c}{x^{3}}$ .^[106]

Note. That haveing $\{\begin{matrix} x \\ y \end{matrix}\}$ given, it will be often more convenient to find $\{\begin{matrix} y \\ x \end{matrix}\}$ by the equation expressing the nature of the line & then having x & y to find v by them both, Then to take $\{\begin{matrix} y \\ x \end{matrix}\}$ out of v 's valor & soe to find it by $\{\begin{matrix} x \\ y \end{matrix}\}$ alone.

The Perpendiculars to crooked lines & also the Theorems ∼ for finding them may otherwis more conveniently be found thus

^[107] Supposing $ab = x$ ; $cb = o$ , $db = v$ , $eb = y$ , $cf = z$ . And if the distance twixt fc & fb , bee imagined to bee infinitely little, that is if the triangle efr is supposed to bee infinitely little then $be ∶ bd ∷ bg ∶ be ∷ re ∶ fr ∷ y ∶ v ∷ o ∶ z - y$ . That is $y z - y y = v o$ . Or $z = y + \frac{v o}{y}$ .

Now suppose the nature of the line bee $r x - \frac{r x x}{q} - y y = 0$ . Then is $r x + r o - r x x - 2 r o x - r r o - z^{2}$ { $= 0$ }

In which equation instead of $r x (= \frac{r x x}{q} + y y)$ & $z z (= y y + 2 v o + \frac{v v o o}{y y})$ write theire valors & the result is $r o - \frac{\begin{matrix} 2 r o x & - & 2 v o q \\ - & r o o \end{matrix}}{q} - \frac{v v o o}{y y} = 0$ . Or $r - \frac{2 r x - r o}{q} - 2 v - \frac{v v o}{y y} = 0$ . but these two termes $r o$ , $\frac{v v o}{y y}$ are infinitely little, that is if compared to finite termes they vanish therefore I blot them out & there rests $\frac{r}{2} - \frac{r x}{q} = v = db$ .

Suppose the nature of the line be $p + q y + r y y = 0$ Then (by observation the 2^d) it is $- q y x - r y y x (= p x) + \ddot{p} o + q z x + \ddot{q} z o + r z z x + \ddot{r} z z o = 0$ . Then writeing the valor of $z (= y + \frac{v o}{y})$ in its stead in these termes $q z x + r z z x$ , There results $\ddot{p} o + \frac{q x v o}{y} + \ddot{q} z o + 2 r x v o + \ddot{r} z z o = 0$ . Or because the difference twixt z & y is infinitely little it is $\frac{\ddot{p} y + \ddot{q} y y + \ddot{r} y^{3}}{- q x - 2 r x y} = v$ .

^[108] And though the angle ebg made by intersection of x & y is not determined whether it acute obtuse or a right one, yet may the line bg bee found after the same manner which determines the position of the tangent eg . For suppose {illeg} $= t$ . cb {illeg} $cb = y$ , $fc = z$ , $ab = x$ , & that $z ∥ y$ . Then (supposing the distance of fc & eb to be {infinit}ely little) it is, $t ∶ y ∷ t + o ∶ y + \frac{o y}{t} = z$ . Now if the nature of the line is $p + q y$ {illeg} $y^{3} =$ {0 } Then is $- q y x - r q^{2} x - s y^{3} x (= p x) + \ddot{p} o + q x z + \ddot{q} o z + r x z^{2} + \ddot{r} o z^{2} + s x z^{3}$ {illeg} And by putting the valor of z into its stead in those terms in which {illeg} results $\ddot{p} o + \frac{q x o y}{t} + \ddot{q} o z + \frac{2 r x o y^{2}}{t} + \ddot{r} o z^{2} + \frac{3 s x o y^{3}}{t} + \ddot{s} o z^{3} = 0$ . Or $t =$ {illeg}

Soe that the variation of the angle ebg makes no variation.

Note that the foundation of this operation of that {illeg} {illeg} pag 131) {illeg} tangents {illeg} But since {illeg} Equation is the sa{illeg} {illeg}stons that it would bee if {illeg} {illeg}

<50r>

To draw perpendiculars to crooked lines in all other cases.

Although the unknowne quantitys x & y are not related to one another as in the precedent rules ( that is soe that y move upon x in a given angle), yet may there be drawne tangents to them by the same method.

^[111] As if

^{[Editorial Note 2]}

^[1]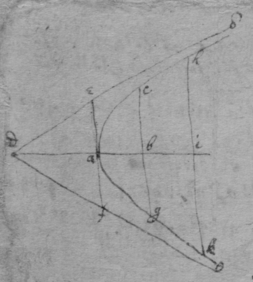

^[2]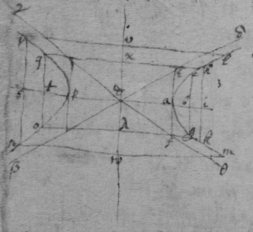

^[3]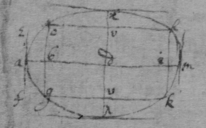

^[4]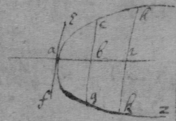

^[5]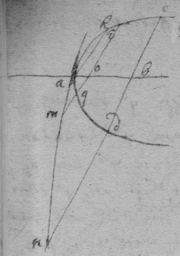

^[6]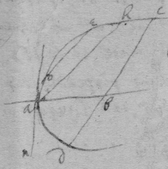

^[7]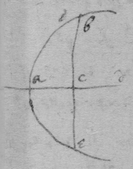

^[8]

^[9] October 1664

^[10]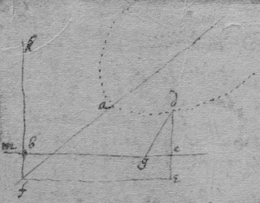

^[11]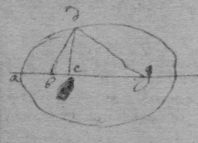

^[12]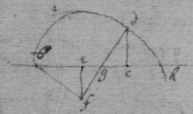

^[13]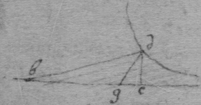

^[14]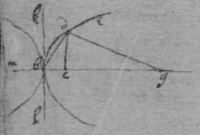

^[15]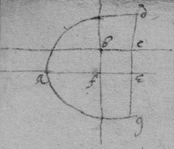

^[16]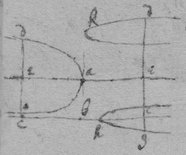

^[17]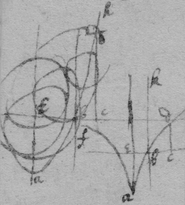

^[18]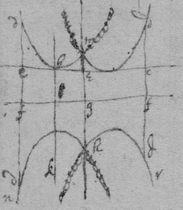

^[19]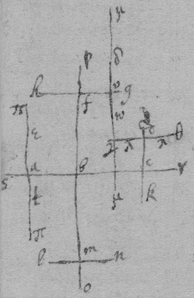

^[20]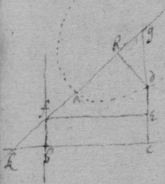

^[21]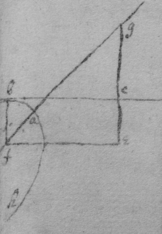

^[22] For the first equation of the first sort

^[23] For the 2^d

^[24] For the 3^d

^[25] For the 4^th

^[26] For the 5^t

^[27] For the 6^t &c

^[28] For the first Equation of the seacond Sort

^[29] For the seacond

^[30] For the 3^d.

^[31]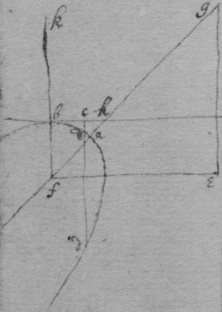

^[32]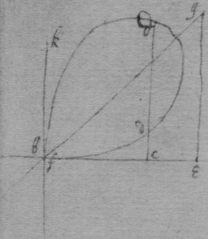

^[33] November 1664

^[34]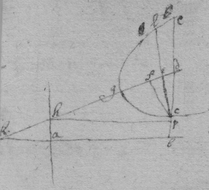

^[35]

^[36]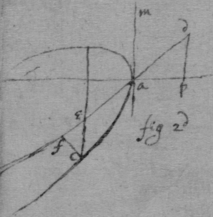

^[37]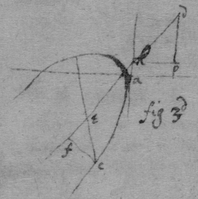

^[38]

^[39] November 1664

^[40] A

^[41]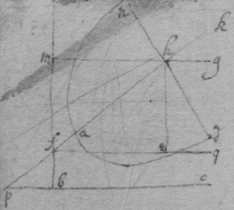

^[42]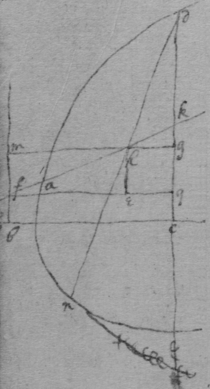

^[43]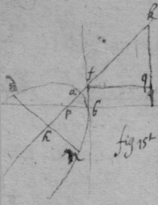

^[44]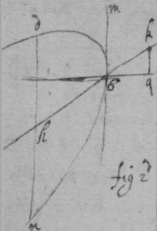

^[45]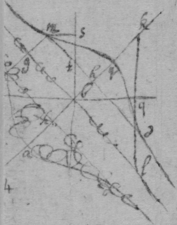

^[46]

^[47]

^[48]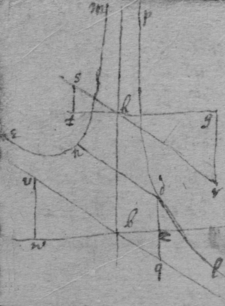

^[49] B

^[50]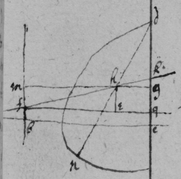

^[51] This line is a streight one the equation being divisible by $b = y = 0$

^[52] Endeavor not to find the quantity d in these cases, but suppose it given^{[Editorial Note 1]}

^{[Editorial Note 1]} There is a line connecting the end of this note to the following one

^[53] Or else C ☞

^[54] December

^[55]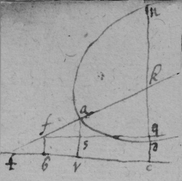

^[56]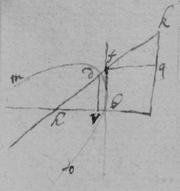

^[57]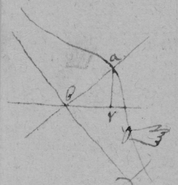

^[58] ☞

^[59]

^[60]

^[61]

^[62] F

^[63]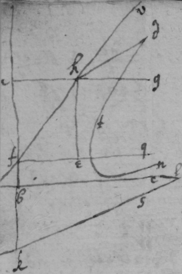

^[64] G

^[65]

^[66] December 1664

^[67]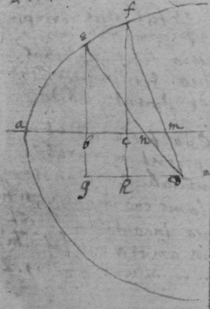

^[68]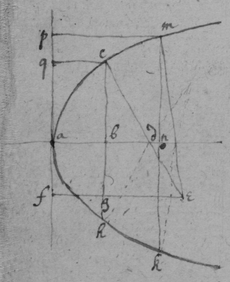

^[69] Theorema

^[70]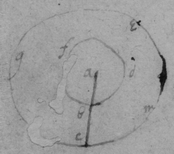

^[71] December 1664.

^[72]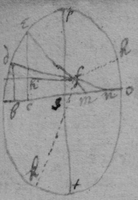

^[73]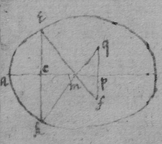

^[74]

^[75]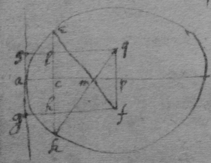

^[76]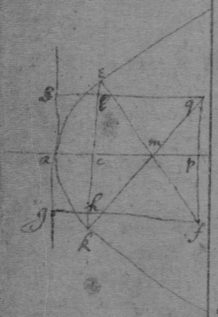

^[77]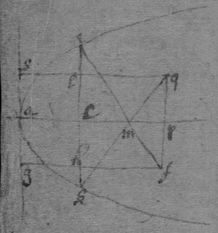

^[78]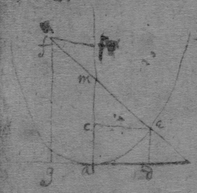

^[79]

^[80]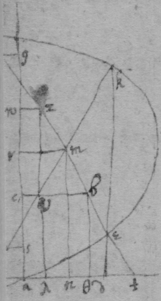

^[81]

^[82]

^[83] Feb 1664

^[84]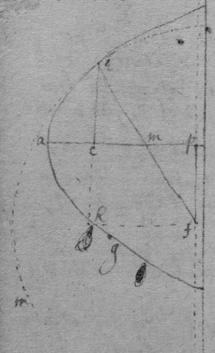

^[85]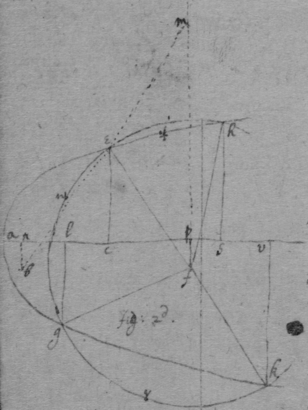

^[86] Another way.

^[87]

^[88] December 1664

^[89]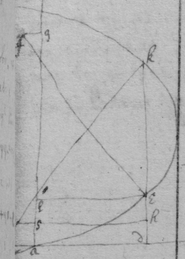

^[90]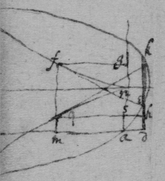

^[91]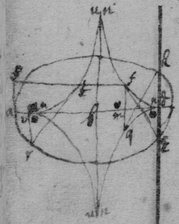

^[92]

^[93]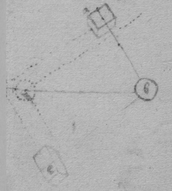

^[94] Of compound force.

^[95]

^[96]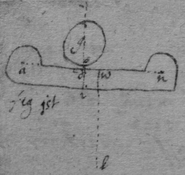

^[97]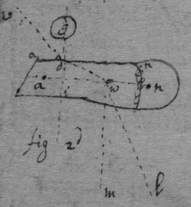

^[98]

^[99]

^[100]

^[101] May 20^th 1665

^[102]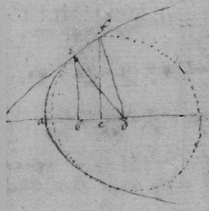

^[103] Observation 1^st

^[104] Observacion 2^d

^[105] An universall theorem for tangents to crooked lines, when $y ⊥ x$ .

^[106] See Des Cartes his Geometry. booke 2^d, pag 42, 46, 47. Or thus, $\begin{matrix} x^{3} & - & b x x & - & c d x & + & d y x & + & b c d \\ 2 & 1 & 0 & 0 & - 1 \end{matrix}$ { $\frac{2 x x y - b x y}{- d x} \frac{+ b c d y}{d x x} = v$ }. And $\frac{b c y}{x x} + \frac{b y}{d} - \frac{2 x y}{d} = v$ .

^[107]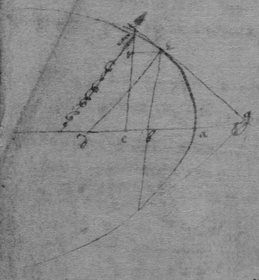

^[108] An universall theorem for drawing tangents to crooked lines when x & y intersect at any determined angle

^[109]

^[110] A=

^[111]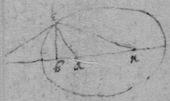

^{[Editorial Note 2]} The rest of the page is damaged.

Newton's Waste Book (Part 2)

How to find the axes vertices Diamiters, Centers, or Asymptotes of any Crooked Line supposeing it have them.

[9] Haveing {an} the nature of a crooked line expresed in algebraicall termes to find its axes if {I}{i} {shave} { anq }

A generall rule to find the axes of any line.

But since there is noe use of those termes in which ϩ is of eaven dimensions the Calculation will bee much abreviated by this following table.

The use of the precedent table in finding the Axes of crooked Lines, declared by Examples.

[39] To find the Axis or Diameter of any crooked Line supposeing it have them.

[54] Haveing the Diameter to find the Vertex of the line.

[66] To find the Quantity of crookednesse in lines.

To find the Quantity of crookednesse in lines[71]