De Analysi per aequationes numero terminorum infinitas
De Analysi per æquationes numero terminorum infinitas.
Methodum generalem quam de curvarum quantitate per infinitam terminorum seriem mensuranda olim excogitaveram, in sequentibus brevitèr explicatam potiùs quàm accuratè demonstratam habes.
Basi AB, curvæ alicujus AD, sit applicata  BD perpendicularis: & vocetur , & ; & sint a, b, c &c quantitates datæ; & m, n numeri integri. Deinde
BD perpendicularis: & vocetur , & ; & sint a, b, c &c quantitates datæ; & m, n numeri integri. Deinde
[1] Reg: I. Si , erit .  Res exemplo patebit. Exemp 1. Si ; hoc est si , & ; erit . Exempl 2. Si erit . Exemp 3. Si , erit . Exemp 4. Si , id est si & , erit
infinitè versus α protensæ; quam calculus ponit negativam propterea quòd jacet ex altera parte lineæ BD. Exemp: 5. Si , erit . Exemp 6. Si
, erit , qualis est area Hyperbolæ utraque parte linea BD.
Res exemplo patebit. Exemp 1. Si ; hoc est si , & ; erit . Exempl 2. Si erit . Exemp 3. Si , erit . Exemp 4. Si , id est si & , erit
infinitè versus α protensæ; quam calculus ponit negativam propterea quòd jacet ex altera parte lineæ BD. Exemp: 5. Si , erit . Exemp 6. Si
, erit , qualis est area Hyperbolæ utraque parte linea BD.
Reg II. Si valor ipsius y ex pluribus istius modi [2] terminis componitur, area etiam componetur ex areis quaæ a singulis terminis emanant.
Hujus Exempla prima sunto. Si  erit . Etenim si semper sit , & ; erit ex præcedenti Regula superficiei AFB descriptæ per lineam BF, & descriptæ per DF; Quare totæ ABD. Sic si erit . Et si , erit .
erit . Etenim si semper sit , & ; erit ex præcedenti Regula superficiei AFB descriptæ per lineam BF, & descriptæ per DF; Quare totæ ABD. Sic si erit . Et si , erit .
Exempla secunda. Si
, erit  . Vel si , erit . Quarum signa si mutaveris habebis affirmativum valorem ( vel ) Superficiei αBD, modò tota cadat supra Basin
. Vel si , erit . Quarum signa si mutaveris habebis affirmativum valorem ( vel ) Superficiei αBD, modò tota cadat supra Basin  ABα; sin aliqua pars cadat infra, (quod fit cùm curva decussat suam Basin inter B & α, ut hic vides in δ,) istâ parte a parte superiori subductâ, habebis valorem differentiæ. Earum verò summam si cupis, quære utramque superficiem seorsim, & adde. Quod idem in reliquis hujus regulæ exemplis notandum volo.
ABα; sin aliqua pars cadat infra, (quod fit cùm curva decussat suam Basin inter B & α, ut hic vides in δ,) istâ parte a parte superiori subductâ, habebis valorem differentiæ. Earum verò summam si cupis, quære utramque superficiem seorsim, & adde. Quod idem in reliquis hujus regulæ exemplis notandum volo.
Exempla tertia. Si , erit superficiei descriptæ. Sed hic notandum est quod dictæ superficiei {partes} sic inventæ jacent ex diverso latere lineæ 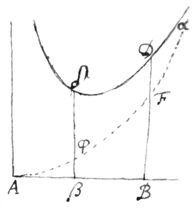 BD: nempe, posito & , erit superficiei per BF descriptæ, & descriptæ per DF. Et hoc semper accidit cum indices rationum basis x in valore superficiei quæsitæ sint varijs signis affectæ. In hujus modi casibus pars aliqua BDδβ superficiei media (quæ sola dari poterit, cùm superficies sit utrinque infinita) sic invenitur. Subtrahe superficiem ad minorem basin Aβ pertinentem a Superficie ad majorem basin AB pertinente & habebis βBDδ superficiem differentiæ basium insistentem. Sic in hoc exemplo, Si & , erit . Enim superficies ad AB pertinens (viz ) erit , sive ; Et superficies ad Aβ pertinens (viz ) erit , sive : Et earum differentia (viz ) erit sive . Eodem modo si , & erit . Sic si , & ; Erit .
BD: nempe, posito & , erit superficiei per BF descriptæ, & descriptæ per DF. Et hoc semper accidit cum indices rationum basis x in valore superficiei quæsitæ sint varijs signis affectæ. In hujus modi casibus pars aliqua BDδβ superficiei media (quæ sola dari poterit, cùm superficies sit utrinque infinita) sic invenitur. Subtrahe superficiem ad minorem basin Aβ pertinentem a Superficie ad majorem basin AB pertinente & habebis βBDδ superficiem differentiæ basium insistentem. Sic in hoc exemplo, Si & , erit . Enim superficies ad AB pertinens (viz ) erit , sive ; Et superficies ad Aβ pertinens (viz ) erit , sive : Et earum differentia (viz ) erit sive . Eodem modo si , & erit . Sic si , & ; Erit .
Denique notari poterit quòd si quantitas in valore ipsius y reperiatur, iste terminus (cùm hyperbolicam superficiem generat) seorsim a reliquis considerandus est. Ut si : Sit , & , ac ; 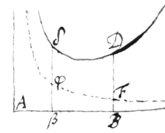 Et erit , utpote quæ ex terminis generatur: quare si reliqua superficies φβFB, quæ Hyperbolica est, ex calculo aliqua sit data, dabitur tota βBDδ.
Et erit , utpote quæ ex terminis generatur: quare si reliqua superficies φβFB, quæ Hyperbolica est, ex calculo aliqua sit data, dabitur tota βBDδ.
[3] Reg III. Sin valor ipsius y vel aliquis ejus terminus sit præcedentibus magis compositus, in terminos simpliciores reducentus est, operando in literis ad eundem modum quo Arithmetici in numeris decimalibus dividunt, radices extrahunt, vel affectas Æquationes solvunt. Et ex istis terminis quæsitam curvæ superficiem per præcedentes regulas dinceps elicies.
Exempla dividendo.
Sit , curvâ nempe exist ente Hyperbolâ: Iam ut æquatio ista a denominatore suo liberetur divisionem sic instituo Et sic vice hujus nova prodit &c serie {istûc}{istâc} infinitè continuatâ. Adeoque per Reg secundam erit area  &c infinitæ etiam seriei, tamen cujus termini pauci initiales erunt in usum aliquem satis exacti cùm x sit aliquoties minor quam b.
&c infinitæ etiam seriei, tamen cujus termini pauci initiales erunt in usum aliquem satis exacti cùm x sit aliquoties minor quam b.
Eodem modo si , dividendo prodibit &c: Unde per Reg 2 erit &c Vel si terminus ponatur in divisore primus, hoc modo : prodibit &c pro valore ipsius y. Unde per Reg 2 erit &c. Priori modo procede cum x sit satis parva, posteriori cùm satis magna supponitur.
Denique si , dividendo prodit &c: Unde erit &c.
Exempla Radicem extrahendo.
Si , radicem sic extraho Unde pro , nova producitur, viz: &c: Et area Hyperbolæ quæsita erit  &c.
&c.
Eodem modo si ejus radix erit &c: Adeóque area circuli  quæsita &c. Vel si ponas , erit radix &c
quæsita &c. Vel si ponas , erit radix &c  Et area quæsita &c: Sive &c.
Et area quæsita &c: Sive &c.
Si , (cujus quadratura dat longitudinem curvæ ellipticæ,) extrahendo radicem utramque, prodit Et dividendo sicut fit in
fractionibus decimalibus, habes Adeóque unam quæsitam
Sed observandum est quod operatio non rarò abbreviatur per debitam Æquationis præparationem. Ut in allato exemplo Si utremque partem fractionis per multiplices prodibit , & reliquum opus perficitur extrahendo radicem numeratoris tantum & dividendo per denominatorem.
Ex hisce credo satis patebit modus reducendi quemlibet valorem ipsius y (quibuscunque) radicibus vel denominatoribus sit perplexus, ut hic videre est ) in series infinitas simplicium terminorum, ex quibus, per Reg 2, quæsita superficies cognoscetur.
Exempla per resolutionem Æquationum affectarum.
[4] Quia tota difficultas in Resolutione latet, modum quo ego utor in æquatione numerali primùm illustrabo. Sit resolvenda: Et sit 2 numerus qui minùs quàm decimâ sui parte differt a radice quæsitâ. Tum pono , & substituo hunc sibi valorem in Æquationem; & inde nova prodit , cujus radix p exquirenda est ut quotienti addatur: Nempe (neglectis ob parvitatem) , sive veritatem 2 prope 1 est; itaque scribo 0,1 in quotiente, & suppono & hunc ejus valorem, ut priùs, substituo, unde prodit . Et cùm ad veritatem prope accedit, sive ferè sit (dividendo nempe donec tot eliciantur figuræ quot locis primæ figuræ hujus & principalis quotientis exclusivè distant,) scribo in inferiori parte quotientis, cùm negativa sit. Et operationem sic produco quosque placuerit. Verùm si ad bis tot figuras tantùm quot in quotiente jam reperiuntur, unâ dempta, operam continuare cupio, pro q substituo in hanc , primo ejus termino propter exilitatem suam neglecto: Et prodit ferè sive (rejecto ,) ferè, quam scribo in negativa parte quotientis. Denique negativam partem quotientis ab affirmativa subducens, habeo 2,09455147 quotientiem quæsitam.
Æquationes plurium dimensionum nihilo seciùs resolvuntur, & operam sub fine, ut hic factum fuit, levabis, si primos ejus terminos gradatim omiseris.
Præterea notandum est qùod in hoc exemplo si dubitarem an ad veritatem satis accederet, pro − finxissem & ejus radicis primam figuram in quotiente scripsissem. Et secundam vel etiam tertiam quotientis figuram sic explorare convenit ubi in æquatione ista ultimò resultante quadratum coefficientis penultimi termini non sit decies major quàm factus ex ultimo termino ducto in coefficientem termini antepenultimi. Imò laborem plerumque minues præsertim in æquationibus plurimarum dimensionum, si figuras omnes quotienti addendas dicto modo (hoc est extrahendo minorem {radicem}{radicum} ex tribus ultimis terminis æquationis novissimè resultantis ) exquiras. Isto enim modo figuras duplo plures qualibet 2 vice in quotiente 1 lucraberis.
<5r>Hæc methodus de resolvendis Æquationibus pervulgata an sit nescio, certè mihi videtur præ reliquis simplex & usui accommodata. Demonstratio ejus ex ipso modo operandi putet, unde cum opus sit in memoriam facilè revocatur. Aequationes in quibus vel aliqui vel nulli termini desint eadem fere facilitate perficit. Et æquatio semper relinquitur cujus radix una cum acquisita quotiente adæquat radicem æquationis primò propositæ: unde examinatio operis hic æque poterit institui ac in reliqua Arithmetica, auferendo nempe quotientem a radice primæ æquationis (sicut Analistis notum est *[5]) ut æquatio ultima vel termini ejus duo tresve ultimi producantur inde. Quicquid laboris hic est in substituendo quantitates unas pro alijs reperietur. Id quod variè possis perficere, at sequentem modum maximè expeditum puto, præsertim cum numeri 2 coefficientes 1 constant ex pluribus figuris. Sit substituenda pro y in hanc : cum ista potest resolvi in hanc formam . Æquatio nova sic generabitur . & . & . & , quæ quærebatur.
His in numeris sic ostensis: Sit æquatio literalis, [6] , resolvenda. Primùm inquiro valorem ipsius y cùm x sit nulla, hoc est, elicio radicem hujus æquationis ; & invenio esse . Itaque scribo in quotiente & supposito , pro y substituo valorem istum, & terminos inde resultantes ( &c) margini appono: Ex quibus assumo ubi p & x seorsim sunt minimarum dimensionum & eas nihilo ferè æquales suppono, sive ferè, sive . Et scribens in quotiente, substituo pro p . Et terminos inde resultantes iterum in margines scribo, ut vides in annexo schemate. Et inde assumo quantitates , in quibus q & x seorsim sunt minimarum dimensionum & fingo ferè, sive ; & adnectens quotienti, substituo pro q ; & sic procedo quousque placuerit.
* Sin duplo tantùm plures quotienti terminos, uno dempto, jungendos adhuc vellem: primo termino æquationis novissimè resultantis misso, & ista etiam parte secundi ubi x est tot dimensionum quot in penultimo termino quotientis; in reliquos terminos margini adscriptos, ut vides, substituo pro q. Et ex ultimis duobus terminis æquationis inde resultantis, facta divisione , Elicio quotienti adnectendas.
Denique quotiens ista per Reg secundam dabit &c pro area quæsita, quæ ad veritatem tanto magis accedit quanto x sit minor. [7] Sin velis ut valor areæ tanto magis veritati accedat quanto x sit major, exemplum esto ; Itaque hanc resoluturus excerpo terminos in quibus x & y vel seorsim vel simul multiplicatæ sunt & plurimarum & æqualium. ubique dimensionum. Et ex ijs quasi nihilo æqualibus radicem elicio, quam invenio esse x , & hanc in quotiente scribo. Vel quod eodem recidit, ex (unitate pro x substitutâ) radicem extraho & eam per x multiplico, & factum in quotiente scribo. Deinde pono , & sic procedo ut in priori exemplo donec habeo quotientem &c, Adeóque aream de qua vide exempla tertia Reg secunda. Lucis gratia dedi hoc exemplum in omnibus idem cum priori, modò x & a sibi invicem ibi substituantur, ut non opus esset aliud resolutionis paradigma hic adjungere.
<6r>Nota quod area limitatur a curva quæ juxta asymptoton aliquam in infinitum serpit; & termini initiales valoris extracti de y , in asymptoton istam semper terminantur: Unde positionem asymptoti facile invenias. Idem semper notandum est cùm area designatur terminis plus plusque divisis per x continuò: præterquam quòd asymptoti rectæ quandóque habeatur Parabola Conica vel alia magis composita.
Sed hunc modum missum faciens, utpote particularem quia non applicabilem curvis in orbem ad instar Ellipsium flexis; de altero modo per exemplum supra ostenso (scilicet quo dimensiones de x in numeratoribus quotientis perpetuò fiunt plures) annotabo sequentia.
1. Si quando accidit quòd valor ipsius y, cùm nullum esse {fingitur}{fingitum} , sit quantitas surda vel penitus ignota, licebit illam litera aliqua^ designare. Ut in exemplo , si radix hujus fuisset surda vel ignota, finxissem quamlibet pro ea ponendam, et resolutionem ut sequitur perfecissem.
Scribens b
in quotiente, suppono
, & istum pro y
substituo, ut vides; unde nova &c resultat, rejectis terminis , qui nihilo sunt æquales propterea quod b supponitur radix hujus . Deinde termini dant quotienti apponendum & substituendum pro p. &c. Completo opere sumo numerum aliquem pro
a
, & hanc , sicut de numerali æquatione ostensum supra, resolvo; &radicem ejus pro
b
substituo.
2. Si dictus valor sit nihil, hoc est si in æquatione resolvenda nullus sit terminus nisi qui per x vel y sit multiplicatus, ut in hac ; tum terminos selego in quibus x seorsim & y etiam seorsim si fieri potest , alias per x multiplicata sit minimarum dimensionum. Et illi dant pro primo termino quotientis, & pro y substituendam. In hâc , licebit primum terminum quotientis vel ex , vel ex elicere.
3 Si valor iste sit imaginarius ut in hoc augeo vel imminuo quantitatem
x
donec dictus valor evadat realis. Sic in annexo schemate cum
nulla est tum
est imaginaria:  Sin minuatur
AC
per datam
AB
ut
BC
fiat
x
; tum posito quod
sit nulla,
erit valore quadruplici (
CE
,
CF
,
CG
&
CH
) realis; quarum radicum (
CE
,
CF
,
CG
, vel
CH
) utravis esto primus terminus quotientis, prout superficies
BEDC
,
BFDC
,
BGDC
, vel
BHDC
desideratur. In alijs etiam easibus, si quando hæsitas, te hoc modo extricabis **.[8]
Sin minuatur
AC
per datam
AB
ut
BC
fiat
x
; tum posito quod
sit nulla,
erit valore quadruplici (
CE
,
CF
,
CG
&
CH
) realis; quarum radicum (
CE
,
CF
,
CG
, vel
CH
) utravis esto primus terminus quotientis, prout superficies
BEDC
,
BFDC
,
BGDC
, vel
BHDC
desideratur. In alijs etiam easibus, si quando hæsitas, te hoc modo extricabis **.[8]
Et hæc de areis curvarum investigandis dicta sufficiant. Imò cùm Problemata de curvarum longitudine, de quantitate & superficie solida, deque centro gravitatis omnia possunt eò tandem reduci ut quǽratur quantitas superficiei planæ linea curva terminatæ, non opus est quicquam de ijs adjungere. In istis autem quo ego operor modo dicam brevissimè.
[9] Sit ABD curva quævis, & AHKB rectangulum  cujus latus AH vel BK est unitas. Et cogita rectam DBK uniformitèr ab AH motam, areas ABD & AK describere; & quòd est momentum quo , & momentum quo ABD gradatim augetur; et quo ex momento BD perpetim dato, possis, per prædictas regulas, aream ABD ipso descriptam investigare, sive cum momento 1 descripta conferre. Iam qua ratione superficies ABD ex momento suo perpetim dato per præcedentes regulas elicitur, eâdem quælibet alia quantitas ex momento suo sic dato elicitur. Exemplo res fiet clarior. Sit [10] circulus cujus arcûs AD longitudo
cujus latus AH vel BK est unitas. Et cogita rectam DBK uniformitèr ab AH motam, areas ABD & AK describere; & quòd est momentum quo , & momentum quo ABD gradatim augetur; et quo ex momento BD perpetim dato, possis, per prædictas regulas, aream ABD ipso descriptam investigare, sive cum momento 1 descripta conferre. Iam qua ratione superficies ABD ex momento suo perpetim dato per præcedentes regulas elicitur, eâdem quælibet alia quantitas ex momento suo sic dato elicitur. Exemplo res fiet clarior. Sit [10] circulus cujus arcûs AD longitudo 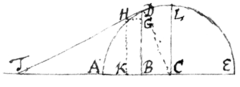 est indaganda. Ducto tangente DHT, & completo indefinitè parvo rectangulo HGBK & posito : Erit ut BK sive GH momentum Basis AB, ad DH momentum árcus . . . . Adeóque sive est momentum arcus AD. Quod reductum fit &c. Quare per regulam secundam longitudo arcus AD est &c. Sive &c. Non secus ponendo CB esse x, & radium CA esse 1, invenies arcum LD esse &c
est indaganda. Ducto tangente DHT, & completo indefinitè parvo rectangulo HGBK & posito : Erit ut BK sive GH momentum Basis AB, ad DH momentum árcus . . . . Adeóque sive est momentum arcus AD. Quod reductum fit &c. Quare per regulam secundam longitudo arcus AD est &c. Sive &c. Non secus ponendo CB esse x, & radium CA esse 1, invenies arcum LD esse &c
Sed notandum est quod unitas ista quæ pro momento ponitur est superficies cùm de solidis, & linea cum de superficiebus, & punctum cum de lineis (ut in hoc exemplo) agitur. Nec vereor loqui de unitate in punctis sive lineis infinitè parvis siquidem, proportiones ibi jam contemplantur Geometræ dum utuntur methodis Indivisibilium.
Ex his fiat conjectura de superficiebus & quantitatibus solidorum ac de centris gravitatum. Verum si e contra ex area vel longitudine [11] &c: curvæ alicujus datæ longitudo Basis AB desideratur, ex æquationibus per præcedentes regulas inventis extrahatur radix de x. Ut si ex area ABDC Hyperbolæ 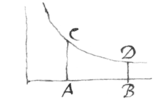 [12] datâ cupio basin AB cognoscere, areâ ista z nominatâ, radicem hujus &c: extraho, neglectis illis terminis in quibus x est plurium dimensionum quam z in quotiente desideratur. Ut si vellem quod z ad quinque tantùm dimensiones in quotiente ascendat, negligo omnes &c, & radicem hujus tantùm extraho. [13] Analysin ut vides exhibui propter adnotanda duo sequentia. 1 Quòd inter substituendum, istos terminos semper omitto quos nulli deinceps usui fore prævideam. Cujus rei regula esto, quòd post primum terminum ex qualibet quantitate sibi collaterali resultantem non addo plures terminos dextrorsum quàm istius primi termini index dimensionis ab indice dimensionis maximæ unitatibus distat. Ut in hoc exemplo ubi maxima dimensio est 5 omisi omnes terminos post
, post
posui unicum, & duos tantùm post
. Cùm radix extrahenda sit parium ubique, vel imparium dimensionum; Hæc esto regula; Quod post primum terminum ex qualibet quantitate sibi collaterali resultantem non addo plures terminos dextrorsum, quàm istius primi termini index dimensionis ab indice dimensionis maximæ binis unitatibus distat; vel ternis unitatibus, si indices dimensionum ipsius x unitatibus ubique ternis a se invicem distant. & sic de reliquis.
[12] datâ cupio basin AB cognoscere, areâ ista z nominatâ, radicem hujus &c: extraho, neglectis illis terminis in quibus x est plurium dimensionum quam z in quotiente desideratur. Ut si vellem quod z ad quinque tantùm dimensiones in quotiente ascendat, negligo omnes &c, & radicem hujus tantùm extraho. [13] Analysin ut vides exhibui propter adnotanda duo sequentia. 1 Quòd inter substituendum, istos terminos semper omitto quos nulli deinceps usui fore prævideam. Cujus rei regula esto, quòd post primum terminum ex qualibet quantitate sibi collaterali resultantem non addo plures terminos dextrorsum quàm istius primi termini index dimensionis ab indice dimensionis maximæ unitatibus distat. Ut in hoc exemplo ubi maxima dimensio est 5 omisi omnes terminos post
, post
posui unicum, & duos tantùm post
. Cùm radix extrahenda sit parium ubique, vel imparium dimensionum; Hæc esto regula; Quod post primum terminum ex qualibet quantitate sibi collaterali resultantem non addo plures terminos dextrorsum, quàm istius primi termini index dimensionis ab indice dimensionis maximæ binis unitatibus distat; vel ternis unitatibus, si indices dimensionum ipsius x unitatibus ubique ternis a se invicem distant. & sic de reliquis.
2 Cùm videam p q vel r &c: in æquatione novissimè resultante esse unius tantùm dimensionis, ejus valorem, hoc est, reliquos terminos quotienti addendos, per divisionem quæro. Ut hic vides factum.
[14] Si ex dato arcu αD sinus AB desideratur; 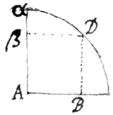 æquationis &c supra inventæ (posito nempe , & ,) radix extracta erit &c. Et præterea si cosinum Aβ ex isto arcu dato cupis, fac &c.
æquationis &c supra inventæ (posito nempe , & ,) radix extracta erit &c. Et præterea si cosinum Aβ ex isto arcu dato cupis, fac &c.
[15] Hic obiter notetur, qd 5 vel 6 terminis istarum radicum cognitis eas plerumque ex analogia observata poteris ad arbitrium producere. Sic hanc &c produces dividendo ultimum terminum per hos ordine numeros &c., Et hanc &c per hos &c & hanc &c per. hos &c Et hanc &c multiplicando per hos &c. Et sic de reliquis.
[16] Et hæc de curvis Geometricis dicta sufficiant. Quin etiam si curva mechanica est Methodum tamen nostram nequaquam respuit. Exemplo sit Trochoides, ADFG
cujus 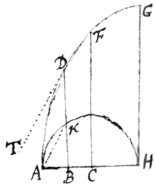 vertex A & axis AH, & AKH rota qua describitur. Et quæratur superficies ABD. Iam posito , ut supra, & ; primò quæro longitudinem ipsius BD. Nempe ex natura Trochoidis , quare tota . Sed est − &c, & (ex prædictis) &c. Ergo tota &c. Et (per Reg 2) &c.
vertex A & axis AH, & AKH rota qua describitur. Et quæratur superficies ABD. Iam posito , ut supra, & ; primò quæro longitudinem ipsius BD. Nempe ex natura Trochoidis , quare tota . Sed est − &c, & (ex prædictis) &c. Ergo tota &c. Et (per Reg 2) &c.
Vel brevius sic: Cùm recta AK tangenti TD parallela sit erit AB ad BK sicut momentum linæ AB, momento linæ BD, hoc est &c. Quare (per Reg 2) &c Et superficies &c.
Non dissimili modo (posito C centro circuli & ) obtinebis aream CBDF &c.
Sit area ABDV Quadratricis VDE (cujus vertex 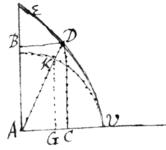 est
V
, &
A
centrum circuli interioris
VK
cui aptatur) invenienda. Ducta qualibet
AKD
demitto perpendiculares
DB
,
DC
,
KG
. Eritque . sive . Verum ex natura Quadratricis erit arcui VK; sive . Quare posito erit &c ex supra ostensis, & &c. Adeóque
Sive, divisione facta, &c & (per Reg 2) &c.
est
V
, &
A
centrum circuli interioris
VK
cui aptatur) invenienda. Ducta qualibet
AKD
demitto perpendiculares
DB
,
DC
,
KG
. Eritque . sive . Verum ex natura Quadratricis erit arcui VK; sive . Quare posito erit &c ex supra ostensis, & &c. Adeóque
Sive, divisione facta, &c & (per Reg 2) &c.
[17] Sic longitudo Quadratricis VD, licet calculo difficiliori, determinabilis est. Nec quicquam hujus modi scio ad quod hæc methodus idque varijs modis, sese non extendit. Imo tangentes ad curvas Mechanicas (si quando id non alias fiat) hujus ope ducantur. Et quicquid Vulgaris Analysis per æquationes ex finito terminorum numero constantes (quando id sit possibile) perficit, hæc per æquationes infinitas semper perficiat: Ut nil dubitaverim nomen Analysis etiam huic tribuere. Ratiocinia nempe in hâc non minùs certa sunt quàm in illâ, nec æquationes minùs exactæ; licet omnes earum terminos nos homines & rationis finitæ nec designare neque ita concipere possumus, ut quantitates inde desideratas exactè cognoscamus: Sicut radices surdæ finitarum æquationum nec numeris nec quavis arte Analytica ita possunt exhiberi ut alicujus quantitas a reliquis distincta & exactè cognoscatur. Geometricè quidem exhiberi possunt, quòd hisce non conceditur: Imò et istis dimensionum duabus tribúsve plurium, ante curvas in Geometriam super inductas, constructio nulla fuit habita. Denique ad Analyticam merito pertinere censeatur cujus beneficio curvarum areæ & longitudines &c (id modò fiat) exactè & Geometricè determinentur. Sed ista narrandi non est locus.
Respicienti, duo præ reliquis demonstranda occurrunt.
[18] 1 Quadratura curvarum simplicium in Reg 1. Sit itaque  curva alicujus ADδ Basis , perpendiculariter applicata & area ut prius. Idem sit , et rectangulum æquale spatio BβδD. Est ergo & . His præmissis, ex relatione inter
x
&
z
ad arbitrium assumptâ quæro
y
isto quem sequentem vides modo.
curva alicujus ADδ Basis , perpendiculariter applicata & area ut prius. Idem sit , et rectangulum æquale spatio BβδD. Est ergo & . His præmissis, ex relatione inter
x
&
z
ad arbitrium assumptâ quæro
y
isto quem sequentem vides modo.
Pro lubitu sumatur sive . Tum pro , & pro substitutis prodibit = (ex natura curvæ) . Et sublatis ( & ) æqualibus, reliquisque per o divisis, restat . Si jam supponamus Bβ esse infinite parvam, sive o esse nihil, erunt v & y æquales & termini per o multiplicati evanescent; quare restabit , sive , sive . Quare e contra si erit .
[19] Vel in genere si ; sive, ponendo & , si z, sive : tum pro x & (sive, quod perinde est, ) pro z substitutis prodit &c &c, reliquis nempe terminis qui tandem evanescerent omissis. Iam sublatis & æqualibus, reliquisque per o divisis, restat . Sive, dividendo per , erit . sive ; vel restituendo pro c & pro p , hoc est m pro & pro , fiet . Quare e contra si erit . Q.E.D.
[20] Hic in transitu notetur modus quo curvæ tot quot placuerit, quarum areæ sunt cognitæ, possunt inveniri; sumendo nempe quamlibet æquationem pro relatione inter aream z & basin x ut inde quæratur applicata y. Ut si supponas , ex calculo invenies . Et sic de reliquis.
[21] Alterum demonstrandum, est literalis æquationum affectarum resolutio. Nempe quòd quòtiens, cum x sit salis parva quo magis producitur eo magis veritati accedit, ut distantia sua (p, q, vel r &c) ab exacto valore ipsius y, tandem evadat minor quavis data quantitate; Et in infinitum producta sit ipsi y æqualis. Quod sic patebit [1: Quoniam ex ultimo termino æquationum quarum p, q, r &c sunt radices, ista quantitas in qua x est minimæ dimensionis (hoc est, plusquam dimidium istius ultimi termini, si supponis x satis parvam) in qualibet operatione perpetuò tollitur; iste ultimus terminus (per 1.10 Elem) tandem evadet minor quavis data quantitate; et prorsus evanescet si opus infinite continuatur. . [Nempe si , erit
x
dimidium omnium &c & dimidium omnium &c. Itaque si erit
x
plusquam  dimidium omnium &c: & plusquam dimidium omnium &c. Sic si erit x plusquam dimidium omnium &c et sic de reliquis. Et numeros coefficientes quod attinet, illi plerumque decrescent perpetuò, vel si quando increscant, tantum opus est ut
x
aliquo {ties}ad huc minor supponatur.
dimidium omnium &c: & plusquam dimidium omnium &c. Sic si erit x plusquam dimidium omnium &c et sic de reliquis. Et numeros coefficientes quod attinet, illi plerumque decrescent perpetuò, vel si quando increscant, tantum opus est ut
x
aliquo {ties}ad huc minor supponatur.
2 Si ultimus terminus alicujus æquationis continuò diminuatur donec tandem evanescat, una ex ejus radicibus etiam diminuetur donec cum ultimo termino simul evanescit{.}
3 Quare quantitates p, q, r &c unus valor continuo decrescit donec tandem, cùm opus in infinitum producitur, penitus evanescat.
4 Sed valores istarum p q vel r &c unà cum quotiente eatenus extractâ adæquant radices æquationis propositæ. (Sic in resolutione æquationis . supra ostensâ percipies &c :) Unde satis liquet propositum quod quotiens infinite producta est una ex valoribus de y.
Idem patebit substituendo quotientem pro y in æquationem propositam. Videbis enim terminos illos sese perpetuò destruere in quibus x est minimarum dimensionum.
[1] Curvarum Simplicium Quadratura
[2] et compositarum ex simplicibus
[3] et aliarum omnium.
[4] Numeralis æquationum affectarum resolutio.
[5] * Geometr Cartesij
[6] Literalis æquationum affectarum resolutio
[7] Alius modus easdem resolvendi.
[8] ** Denique si index rationis de x vel y sit fractio, reduco ad integrum: ut in hoc exemplo . posito , & , resultabit eujus indix est &c sive restituendo &c et quadrando &c.
[9] Applicatio prædictorum ad reliqua istiusmodi Problemata.
[10] Ut ad longitudines curvarum inveniendas
[11] Prædictorum conversum
[12] Ut {invenio}{inven}
[13] Hæc duo priùs adnotanda essent, si tum in mentem venerant cùm de resolutione æquationis literalis hæc verba [Sin duplo tantùm plures quotienti terminos &c] habui.
[14] vel ex data longitudine curvæ.
[15] De serie progressionum continuanda.
[16] Applicatio prædictorum ad curvas Mechanicas
[17] Conclusio, quòd hæc methodus Analytica censenda est.
[18] Præparatio pro regula prima demonstranda.
[19] Demonstratio
[20] Inventio curvarum quæ possunt quadrari.
[21] Demonstratio de resolutione æquationum affectarum.
