On the Refraction Observed in Iceland Spar

Author: Isaac Newton

Source: MS Add. 3970.8, ff. 610r-612r, Cambridge University Library, Cambridge, UK

Published online: May 2009

Additional Information
- Notes on the Electronic Edition
  - You are currently reading the normalized version of this text. Normalized transcriptions provide a tidied-up view of the original text. Editorial interventions are applied to expand abbreviations and correct textual mistakes. Additions are silently included within the body text and deleted text is not displayed. Switching to the diplomatic view of this text will show 116 deletions, reveal 91 additions and not apply 97 editorial regularizations.
- Revision History
  - 1 February 2008
    - Transcription by Yvonne Martin-Portugues
  - 1 March 2009
    - Coding audited and updated to Newton v2.0 DTD by Michael Hawkins
  - 2 May 2009
    - Proofed by Robert Iliffe
  - 6 May 2009
    - Updated to Newton V3.0 (TEI P5 Schema) by Michael Hawkins
- Download NATP00124.xml and schema (advanced users only)

[Diplomatic Text] [Manuscript Images][Catalogue Entry]

<610r>

Besides the Refractions hitherto described, there is a refraction of another kind made in Island-glass, which is a sort of Talc or pellucid stone found in Island, in the form of an {illeg} parallelopiped, clear as crystall splitting in glossy planes parallel to any of its sides, & enduring a violent fire without fusion. The obtuse angles of its sides or surfaces being 101 degr 52′, & the acute ones 78 ^degr 8′ each

If a beam of light fall perpendicularly upon any surface of this glass, this beam in passing through that {surface} shall part into two beams one of which shall go perpendicularly through the glass {illeg} to do according to the rules of Opticks & the other beam shall start {illeg}varicate from the former beam in an angle of about 6° 40′ & when it arrives {illeg} other side of the glass falling upon it obliquely in an angle of 83° 20′ it shall {illeg} perpendicularly out of the glass. And if the beame of light fall upon the first surface of the glass in any oblique {illeg} {this} beame shall there divide into two beames one of which shall be refracted {according} to the known laws of Opticks the sine of incidence being to the sine of refraction {illeg}, & the other shall be refracted according to another law.

This {illeg} {instance} with its wonderfull refraction was first described by Erasmus Bartholine {illeg} more exactly by Hugenius in his Treatise of light written {illeg} ABCDEF represent 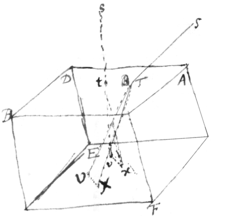a p{illeg} bounded with six parallelogram sides or six {illeg} whose {obtuse} angles are each of them 101° 52′ & their acute ones 68° 8′. And let three of the obtuse angles lye about the solid angle C & other three about the opposite solid angle E the other six solid angles being composed each of them with one obtuse & two acute ones And let the two biggest solid angles C & E composed of three obtuse ones be called the principal solid angles. & the plane which is perpendicular to the refracting surfaces & bisects either of their obtuse angles be called the principal planes. And let ST represent a beam of light falling on the first surface of the glass AB at the point T & being there refracted. This beam ST shall divide it self into two beams TV & TX some of the rays in the beam ST being refracted according to the known law of Opticks & going in the beam TV to the place V in the further surface of the glass the sine of the refraction of these rays being to the sine of their incidence as 3 to 5. And the rest of the rays in the beam ST being refracted according to another law & going in the beam TX to another place X in the further surface of the glass. which place X is thus found.

<610v>

Find the line N which is in such proportion to the thickness of the glass or distance between the two refracting surfaces as the sine of 6° 40′ is to the Radius. Then from the point V upon the further surface of the glass draw he line VK equal to the line N & parallel to the lines which bisect the obtuse angle F of the further surface which is adjacent to one of the lesser solid angles, & you will have to point X to which the beam TX shal go.

Ph. 3 When these two beams of light TV & TX arrive at the further surface of the glass the beam TV which was refracted at the first surface after the usual manner shall be again refracted entirely after the usual manner at the second surface & the beam TX which was refracted after the unusual manner in the first surface shall be again refracted entirely after the unusuall manner in the second so that both these beams shall emerge out of the second surface in lines parallel to the first incident beam ST.

Ph. 4 If two or more pieces of Island glass be placed one after another in such manner that all the surfaces of the latter be parallel to all the corresponding surfaces of the first, the rays which are refracted after the usual manner in the first surface of the first glass will be refracted after the usual manner in all the following surfaces & the rays which are refracted after the unusual manner in the first surface will be refracted after the unusual manner in all the following surfaces. And therefore there is a difference in the rays of light by means of which one sort of rays is constantly refracted after the usuall manner & the other sort constantly after the unusual manner; & this difference was in the rays before their first refraction as well as before the latter refractions because it had the same effect upon them in all the refractions.

Ph. 5 And tho the surfaces of the glasses are any ways inclined to one another yet if their planes of perpendicular refraction be parallel to one another the rays which are refracted after the usual manner in the first surface are refracted after the usual manner in all the following surfaces & the rays which are refracted after the unusual manner in the first surface are refracted after the unusuall manner in all the following surfaces.

Ph. 6. But if the planes of perpendicular refraction of the second glass be at right angles with the planes of perpendicular refraction of the first glass: the rays which are refracted after the usuall manner in passing through the first glass will all of them be refracted after the unusual manner in passing through the second glass & the rays which are refracted after the unusual manner in passing through the first glass will all of them be refracted after the usual manner in passing through the second glass. And therefore there are not two sorts of rays differing in nature from one another one of which is refracted constantly & in all positions after the usual manner & the other constantly & in all positions after the unusual manner The difference in the foregoing experiment was only in the position of the sides of the ray to the coast of unusual refraction For by this experiment it appears that one & the same way is refracted sometimes in the usual & sometimes in the unsual manner according to the position which its sides have to the glass. not according to the position or bigness of the angle of incidence but according to the position of the sides of the ray to the planes of perpendicular refraction of the glass. Let every ray be conceived to have four sides or quadrants two of them opposite to one another which incline the ray to be refracted unusually & other two opposits which do not incline it to

<611v>

And let the planes which are perpendicular to the refracting surfaces of the glass & parallel to the lines which bisect the other {illeg}angles of that parallelogram surface be called the planes of perpendicular refraction. For if a {beam} of light fall perpendicularly upon any surface of this glass it shall at the point of incide{nce} divide into two beames one of which shall go perpendicularly into the glass as it ought to do by the usual rules of Opticks, the other shall start aside & diaricate from the perpendicular ray making with it an angle of 6° 40′, & going through the glass in the plane of perpendicular refraction & bending from the perpendicular towards the sides of the glass which with the refracting plane comprehend one of the two begger solid angles. Let ST represent the beam incident at T perpendicularly on the surface ACBD, & this beam at the point of incidence T shall become divided into {the} beame TV & TX one of which TV shall go perpendicularly into the glass, the other TX shall shall go into it obliquely making with the perpendicular an angle VTX of 6° 40′ [who{se} plane VTX is parallel to the planes of perpendicular refraction] & {illeg} from it in the plane of perpendicular refraction VTX towards th{e} {illeg} of the glass AF & BF which with the refracting surface AB {conteine} the solid angle C which is one of the two biggest solid angles. let the two rays TV & TX fall upon the further side of the glass EF at the points V & X & draw the line VX [& this line VX will be to the thickness of the glass or distance between the planes AB & EF as the tangent of 6 40 to the radius & be parallel to the lines which bisect the obtuse angles E & F of that further side of the glass]

Now let ST represent any other beam of light incident obliquely on {AB} the first surface of the glass AB & let the point of incidence be T & this beam shall also be divided at the point of incidence T into two beams TV & TX one of which TV shal be refracted after the usual manner, the sine of incidence being to the sine of refraction as five to three, Let this beame fall upon the further surface of the glass EF at the point V. Draw the line VX equal & parallel to the line VX. Draw it the same way from V which the line VX lies from V & joyning TX this line TX shall be the other beam of light carried by the unusual refraction from T to V.

When these two beams &c