On the Refraction Observed in Iceland Spar
Besides the Refractions hitherto described, there is a refraction of another kind made in glass Island-glass, wch is a sort of Talc or pellucid stone \or pellucid \{&} fissile/ stone/ found in Island, in the form of an \{bounded} with six p/ /{illeg}\ parallelopiped, easily \clear as crystall/ splitting in p \glossy/ planes parallel to any of its \{six}/ sides, not fusible or not wthout great difficulty \& enduring the \a violent/ fire wthout fusion./ It has six plane sides bounded wth in form of parallelograms whose \The/ obtuse angles are \of its {illeg} sides \or surfaces/ being/ 101 degr 52′, & \the/ acute ones 78 degr 8′ eat|c|h [It has eight solid angles two of wch opposite to one another are \each of them/ bounded wth three of those obtuse angles, the other six wth one obtuse & two acute ones.] This {illeg} strange substance wth its wonderful refraction has been \was first/ described by Erasmus Bartholine & afterwards more exactly by Hugenius in he Treatise De la Lumiere \of light written in French./. Let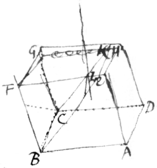 
ABFEHDCG represent the a piece of this glasse, [ABFE its parallelogram base whose opposi obtuse angles at B & E are 101 52 each & acute ones at A & F are 78 each & let ABCD, BCGF, GFEH & AEH be it four |parallelogram| sides standing up this base] bounded with six parallelogram sides AB {&} D, [ABFE, BCD, CBFG, GFEH, HEAD & DCGH,] each of wch whose obtuse angles \[ABF, AEF,/ DAB, DCB, BCG, BFG, FGH, FEH, HEA, HDA, \DCG, DHG]/ are all \each/ of them 101° 52′ & & {sic} their other angles \acute ones/ 78° 8′ each And let \let/ C & E \will/ be the \two opposite/ solid angles bounded each of them wth three pl{a} of those obtuse angles Bisect with the line {illeg} CH bisect the solid \obtuse/ angle \the other six solid angles being bounded each wth one obtuse & acute ones/ From one of those \two/ solid angles suppose (bisect \draw/ the line CH|K| bisecting the angle one of the obtuse angles \about it suppose/ DCG, & complete ye parallelogram BCKL & let this parallelogram be called the principal section of this|e| Glass &] Le
If a beam of light fall perpendicularly upon any surface of this glass, this beam sh{illeg} \in passing through/ that {surface} shall part into two beams one of wch shall go perpendicularly through the glass {illeg} to do according to ye ordina rules of Opticks & the other beam shall start {illeg}varicate from ye former beam in an angle of about 6° 40′ & when it arrives {illeg} other side of the glass falling upon it obliquely in an angle of 83° 20′ it shall {illeg} perpendicularly out of the glass. And if the beame of light fall upon the {illeg} substance with its wonderfull first surface of ye glass in any oblique {illeg} {this} beame shall always \there/ divide into two beames one of wch shall be refracted {according} to the known laws of Opticks the sine of incidence being to ye sine of refraction {illeg}, & the other shall be refracted according to another law.
This {illeg} {instance} wth its wonderfull refraction was first described by Erasmus Bartholine {illeg} more exactly by Hugenius in his book Treatise of light written {illeg} ABCDEF represent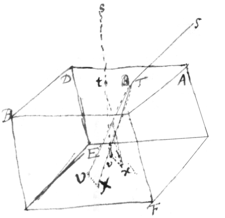 
a p{illeg} bounded wth six pgrā sides \or six {illeg}/ whose {obtuse} angles are each of them 101° 52′ & their acute ones 68° 8′. And let three of thi|e|s obtuse angles lye about the solid angle C & other three about the opposite solid angle E the other six solid angles being composed of \each of them with/ one obtuse & two acute ones And let the two biggest solid angles \C & E/ composed of {illeg}|three| obtuse ones be called the principal solid angles. And |& the plane wch is perpendicular to the refracting surfaces & bisects either of their obtuse angles be called the principal planes.| And let {illeg} ST represent a beam of light falling on ye first surface of the glass AB at ye point T{K} & being there refracted. This beam ST shall divide it self into two beams TV & TX some of the rays in the beam ST being refracted ac according to the known laws of Opticks & going in the beam TV to the place V in the second \further/ surface &|of| the glass & being there the sine of the refraction of these rays being to the sine of their incidence as 3 to 5. And the rest of the rays in the beam ST being refracted according to another law & going in the {illeg}|be|am TX to another place X wch in the further surface of the glass. In ye wch place \X/ is thus found.
Find the line N wch is in such proportion to the thickness of the glass or distance between the two refracting surfaces as the sine of 6° 40′ is to ye Radius. Then from the point V draw the lin upon the further surface of the glass draw he line VK equal to the line N & parallel to the lines wch bisect the obtuse angle \F/ of ye further surface wch is opposite adacent {sic} to one of the lesser solid angles, & you will have to point X to wch the beam TX shal go.
Ph. 4|3| When these two beams of light TV & TX arrive at the further surface of |the glass| the beam TV wch was refracted at ye first surface after the usual manner shall be again refracted \entirely/ after the usual manner at the second {f} surface & the beam \TX/ wch was refracted after the unusual manner in the first surface shall be again refracted \entirely/ after the \un/usuall manner \in the second/ so that both these beams shall emerge out of the second surface in lines parallel to the first incident beam ST.
Ph. 4 If two \or more/ pieces of Island glass be placed one after another in such manner yt all the surfaces of the latter be parallel to all the corresponding surfaces of the f{illeg}|i|r{illeg}|s|t{illeg}, the rays wch are refracted regularly \after the usual manner/ in the first surface \of the first glass/ will be refacted {sic} regularly \after ye usual manner/ in all the following surfaces & the rays wch are refracted after the unusual manner in the first surface will be refacted {sic} after ye unusual manner in all the following surfaces. And {illeg} therefore there is a difference in the rays of light by means of wch one sort {illeg}|o|f rays is constantly refracted regularly & the after ye usuall manner & the other sort \constantly/ after the unusual manner; & this difference was in the rays before their first refraction \as well as before the f{illeg}l latter refractions/ because it had the same effect upon them in all the refractions.
Ph. {illeg}|5| And tho the surfaces of the glasses are any ways inclined to one another yet if their planes of perpendicular refraction be parallel to one another the rays wch are refracted regularly \after ye usual manner/ in the first surface are refracted regularly \after ye usual manner/ in all the following surfaces & the rays wch are refracted after the unusual manner in the first surface shall be \are/ refracted after ye unusuall manner in all the following surfaces.
Ph. 6. But if the planes of perpendicular refraction of the second glass be per at right angles wth the planes of perpendicular refraction of ye first glass: the rays wch are refracted after the usuall manner in passing through the first glass will all of them be refracted after the unusual manner in passing through the second glass & the rays wch are refracted after ye unusual manner in passing through the first {illeg} glass will all of them be refracted after the unusual manner in passing through the second glass. And therefore there are not two sorts of rays \differing in nature from one another/ one of wch \is refracted/ constantly {illeg} /& in all positions\ after the usual manner & the other constantly \& in all positions/ after the unusual manner |The difference in the foregoing experiment was only in the position of the sides of the ray to the coast of unusual refraction For by this expt it appears that| but one & the same way is refracted sometimes regu in the usual & sometimes in the unsual manner according to the position wch it|s| hath \sides have/ to the glass. Let every ray be conceived to be distinguished into four quadrants by two planes crossing one another perpendicularly to |not according to ye position or bigness of the angle of incidence but according to ye position of the sides of ye ray to the planes of perpendicular refraction of| the glass. [|L|et every ray be conceived to to {sic} have four sides or quadrants two of them opposite to one another {illeg} wch incline the ray to be refracted unusually & other two opposits] wch do not incline it to
<611v>And let the planes wch are perpendicular to ye refracting plane \surfaces of the glass/ & parallel to the lines wch bisect the other {illeg}angles |of that plane surface parallelogram surface| be called the planes of perpendicular refraction. For if an {beam} of light fall perpendicularly upon any surface of this glass it shall divide at the point of incide{nce} {illeg} divide into two beames one of wch shall go perpendicularly into the glass \as it ought to do by the usual {illeg} laws of Opticks/ the other shall start aside & as is represented in the annexed scheme where represents \is/ the ray \Beam/ incident perpendicularly ray perpendicularly {illeg} \on/ ye refracting surface, {illeg} the ray {illeg} going perpendicularly into ye glass & the \refracted/ ray refracted divaricating from ye perpendicular by an unusual refractiō the angle in an angle of 6° 40′] as it ought to do by the usua usual rules of Opticks, the other shall start aside & diaricate from the perpendicular ray making with it an angle of 6° 40′, & \&/ going \through ye glass/ in the plane of perpendicular refraction & bending from the perpendicular towards the sides of the glass wch with the refracting plane comprehend one of the two begger solid angles. Let ST represent the beam incident \at T/ perpendicularly on the surface AC{illeg}BD, & TV TX the two be this beam at the point of incidence T shall become divided into {the} beame TV & TX one of wch TV shall go perpendicularly into ye glass, the other TX shall decline from ye perpendicular \shall go into it obliquely/ making with it \the perpendicular/ an angle {illeg} VTX of 6° 40′ & declining whose in the pl which [who{se} plane VTX is parallel to ye planes of the perpendicular refraction] & {illeg} from it in the plane of perpendicular refraction VTX towards th{e} {illeg} of the glass AF & BF wch with the refracting plane surface AB {conteine} the one of the solid angle C wch is one of the two biggest solid angles. let the two rays TV & TX fall upon the further side of the glass EF at ye points V & X & draw the line VX [& this line VX will be to ye thickness of the glass or distance between the planes AB & EF as the tangent of 6 40 to ye radius & be parallel to the lines wch bisect the obtuse angles E & F of that \further/ side of the glass]
Now let ST represent any \other/ beam of light incident obliquely on \{AB}/ ye first surface of the glass AB & let the point of incidence be T & this beam shall {illeg} \also/ be divided at ye point \of incidence/ T into two beams TV & TX one of wch TV shal be refracted after the usual manner, the sine of incidence being to the sine of refraction as five to three, & the Let this beame fall upon the further surface of the glass EF upon at the point V. & Draw the line VX equal & parallel to ye line VX. Draw it the same way from V wch ye line VX lies from V & joyning TX this line TX shall be the other beam of light carried by the unusual refraction from T to V.
When these two beams &c
