Chapter VII
CHAPTER VII.
NEWTON'S HYPOTHESIS OF REFRACTION AND REFLEXION — OF TRANSPARENCY AND OPACITY — HYPOTHESIS OF COLOURS — THE SPECTRUM SUPPOSED TO BE DIVIDED LIKE A MUSICAL STRING — INCORRECTNESS OF THIS SPECULATION — HOOKE'S OBSERVATIONS ON THE COLOURS OF THIN PLATES EXPLAINED BY THE VIBRATIONS PRODUCED IN THE ETHER BY THE LUMINOUS CORPUSCLES — HOOKE CLAIMS THIS THEORY AS CONTAINED IN HIS MICROGRAPHIA — NEWTON'S RESEARCHES ON THE COLOURS OF THIN PLATES — PREVIOUS OBSERVATIONS OF BOYLE — HOOKE'S ELABORATE EXPERIMENTS ON THESE COLOURS — HIS EXPLANATION OF THEM — DR. YOUNG'S OBSERVATIONS UPON IT — NEWTON ACKNOWLEDGES HIS OBLIGATIONS TO HOOKE — NEWTON'S ANALYSIS OF THE COLOURS SEEN BETWEEN TWO OBJECT-GLASSES — CORRECTIONS OF THEM BY MM. PROVOSTAYES AND DESAINS — NEWTON'S THEORY OF FITS OF EASY REFLEXION AND TRANSMISSION — SINGULAR PIIENOMENON IN THE FRACTURE OF A QUARTZ CRYSTAL — NEWTON'S OBSERVATIONS ON THE COLOURS OF THICK PLATES — RECENT EXPERIMENTS ON THE SAME SUBJECT.
In the preceding chapter we have given an account of the first part of Newton's discourse on light and colours, read on the 9th December 1675, and explaining his hypothesis concerning " ether and ethereal substances, and their effects and uses." In the second part of the portion read at the same meeting he proceeds to " the consideration of light" as connected with the supposed ether, that is to the cause of refraction, reflexion, transparency, and opacity.
Regarding the ether as more dense in free space than in solid bodies, and as diminishing in density towards their surface both from without and from within, Newton supposes the incurvation or bending of a ray of light, incident on such a surface, in one direction to produce refraction, and in another to produce reflexion, to be effected within " the space of ether's graduated rarity," or " physical superficies." In the case of refraction, from air to glass, the ray passes from denser into rarer ether, and is incurvated from the perpendicular in its passage through the physical superficies; whereas in reflexion from a dense medium, such as glass into air, it is incurvated upwards or towards the glass, and the incurvation may be such that the ray does not emerge but suffer total reflexion.
In order to account by the agency of ether for the simultaneous refraction and reflexion of light incident upon the same surface of glass or water, Newton supposes " that ether in the confine of two mediums is less pliant and yielding than in other places, and so much the less pliant (or ' more rigidly tenacious') by how much the mediums differ in density." When light therefore, that is small corpuscles, falls upon " this rigid resisting ethereal superficies, it puts it into a vibrating motion, so that the ether therein is continually expanded and compressed by turns." When a ray of light is incident upon it " while it is much compressed, it is too dense and stiff to let the ray pass through, and so reflects it ; but the rays that are incident upon it at other times, when it is either expanded by the interval of two vibrations, or not too much compressed or condensed, go through and are refracted."
When the ether is of the same rarity in every pore, or when the ether is evenly spread by its continual vibrations into all the pores when they do not exceed a certain size, the light will pass freely through the body, or the body will be transparent. But when the pores exceed a certain size, the density of the ether will be greater than that which surrounds it, and the light being refracted or reflected at its superficies, the body will be opaque.
On the 16th December the second portion of Newton's discourse was read, in which he applies his hypothesis to the explanation of colours. For this purpose he supposes the particles of light to have different degrees of "bigness, strength, or power," red having the largest, and violet the least degree of any of these qualities. When light, therefore, is incident on the " refracting superficies," the smallest particles, namely, the violet, will be most incurvated or refracted, and the red the least ; and when these fall upon the refracting superficies of the retina, they will there excite "the sensation of various colours according to their bigness and mixture, the biggest with the strongest colours reds and yellows, the least with the weakest blues and violets, the middle with green, and a confusion of all with white; much after the manner that in the sense of hearing, nature makes use of aerial vibrations of several bignesses to generate sounds of divers tones." Pursuing this idea, " the analogy of nature," he conjectures, " that colour may possibly be distinguished into its principal degrees, red, orange, yellow, green, blue, indigo, and deep violet, on the same ground that sound within an eighth is graduated into tones. In order to test this speculation by experiment, he forms a distinct spectrum, and, " because his own eyes are not very critical in distinguishing colour," he employs a friend to whom he has not communicated his thoughts, to measure the lengths of the different coloured spaces. The differences between the measures thus obtained, he says, " were but little, especially towards the red end, and taking means between these differences, the length of the image (reckoned not by the distance of the verges of the semicircular ends, but by the distance of the centres of those semicircles, or length of the strait sides as it ought to be) was divided in about the same proportion that a string is between the end and the middle to sound the tones in the eighth."
Ingenious as this speculation is, it is contradicted by all the recent discoveries respecting the prismatic spectrum, of which we have given an account in a preceding chapter. It is not even true in the spectrum which Newton himself observed. There are not seven colours in any spectrum, and even if we divide it into such a number of parts, the divisions have no resemblance to those of a musical string.
From the explanation of colours produced by refraction, Newton proceeds to explain those produced by reflexion, namely, the colours of thin plates described by Hooke in his Micrographia. In order to do this, he supposes that the ethereal vibrations excited by a ray move faster than the ray itself, and so " overtake and outrun it, one after another." When light, therefore, is incident upon a thin transparent plate, the waves, excited by its passage through the first surface, overtaking it one after another, till it arrive at the second surface, will cause it to be there reflected or refracted according as the condensed or the expanded part of the wave overtakes it there. If the plate be so thin that the condensed part of the first wave overtakes the ray at the second surface, it must be reflected there ; if double that thickness, so that the following rarefied part of the wave, that is, the space between that and the next wave, overtake it, there it must be transmitted ; if triple the thickness, so that the condensed part of the second wave overtake it, there it must be reflected, and so where the plate is five, seven, or nine times that thickness, it must be reflected by reason of the third, fourth, or fifth wave, overtaking it at the second surface ; but when it is four, six, or eight times that thickness, so that the ray may be overtaken there, by the dilated interval of those waves, it shall be transmitted, and so on; the second surface being made able or unable to reflect according as it is condensed or expanded by the waves.
In this way he explains the coloured rings produced by pressing a convex lens against a plain glass ; and he concludes this portion of his discourse, namely, his " Hypothesis," by applying it to certain phenomena of Inflexion or Diffraction, as observed by Grimaldi.
It was after the reading of this portion of his discourse that Hooke said, " that the main of it was contained in his Micrographia, which Mr. Newton had only carried farther in some particulars," — a remark which led to the correspondence with Oldenburg and Hooke, which — we have given in the preceding chapter.
In the remainder of his discourse, Newton gives an account of his beautiful experiments on the colours of thin plates ; but before we enter upon their consideration, we must notice the previous observations of Boyle and Hooke, in order that we may apportion to Hooke and to Newton the discoveries which they actually made. In the details into which this will lead us, we shall see two great minds striving for victory, — calling forth all their powers to surmount the difficulties which beset them in their path, — deviating from the rigorous process of research which both of them recognised, and perhaps forgetting, in the ardour of their pursuit, some of those courtesies which are now deemed essential in intellectual warfare.
In his book on Colours,[1] Mr. Boyle informs us, that divers, if not all essential oils, as also spirit of wine, when shaken, " have a good store of bubbles, which appear adorned with various and lively colours." He mentions also, that bubbles of soap and turpentine exhibit the same colours, which " vary according to the incidence of the sight and the position of the eye ;" and he had seen a glass-blower blow bubbles of glass, which burst, and displayed " the varying colours of the rainbow, which were exceedingly vivid."
In the year 1664, Hooke published, in his Micrographia,[2] a very interesting chapter of the colours observable in Muscovy glass, (mica,) and other thin bodies, in which he has described many new phenomena.
1. In several parts of plates of mica, he found white specks or flaws diversely coloured with all the colours of the rainbow, the colours being ranged in rings, encompassing, and having the same form as the speck. The colours from the middle of the spot were blue, purple, scarlet, yellow, and green, the same series of colours recurring nine or ten times.
2. By pressing together two pieces of plate-glass with his forefingers and thumbs, he produced the same series of colours as in mica, the colours changing with the thin plate of air between the glasses. The same phenomena were produced by placing different fluids between the plates, the colours being more strong and vivid in proportion as the refractive power of the fluids differed from that of the glass-plates.
3. If the plate of air or fluid is thickest in the middle like a convex lens, or thinnest as in a concave lens, the colours will also be produced, the order of colours in the first case being red, yellow, green, blue, &c. ; and, in the second, quite contrary.
4. As the colours cease when the plates have a certain thickness, so they cease also when the plate has a certain thinness, the colours ending in a white and colourless ring.
5. When we cleave a plate of mica with a needle, we shall come to one of such a thickness as to exhibit a uniform colour, every different degree of thinness below this giving a different colour.
6. When two or three or more of these coloured plates are laid one upon another, they exhibit such compound colours " as one would scarce imagine would be the result of such ingredients." A faint yellow, for example, and a blue, may produce a very deep purple.
7. The same coloured laminæ may be obtained by blowing glass very thin ; and also from bubbles of pitch, rosin, colophony, turpentine, solutions of gums, or any glutinous liquor, such as wort, wine, spirit of wine, oil of turpentine, glare of snails, soap-water, &c.
8. The same colours are produced upon polished steel by gradually tempering or softening it with a sufficient degree of heat. They are also produced on brass, copper, silver, gold, tin, but most conspicuously upon lead ; and the colours that cover the surface of the metal are nothing else than a very thin vitrified part of the heated metal.
9. The same colours are exhibited in animal bodies, as in pearls, mother-of-pearl shells, oyster shells, and almost all other kinds of stony shells. They are seen also in muscles and tendons.
<158>10. If we take any glutinous substance, and run it exceedingly thin upon the surface of a smooth glass, or a polished metalline body, the same colours are produced; "and in general wheresoever you meet with a transparent body thin enough, that is terminated by reflecting bodies of differing refractions from it, there will be a production of these pleasing and lovely colours."
Such is a brief account of Hooke's elaborate inquiry into the colours of thin plates. We shall now consider the theory which he invented to explain them. He considers light as produced by " a very short vibrating motion propagated every way through a homogeneous medium by direct or straight lines extended every way like rays from the centre of a sphere, and with equal velocity, so that the pulse or vibration of the luminous body will generate a sphere which will continually increase, and grow bigger, just after the same manner (though indefinitely swifter) as the waves on the surface of the water do swell into bigger circles about a point of it where, by the sinking of a stone, the motion was begun ; — whence it necessarily follows, that all the parts of these spheres, undulated through a homogeneous medium, cut the rays at right angles." Our author then proceeds to explain how refraction and reflexion take place at the confines of media, in which the " fluid undulating substance" (or ether) has different densities.
In applying this theory to the explanation of the colours of thin plates, he considers it " most evident that the reflexion from the under or farther side of the body, is the principal cause of the production of these colours." Supposing a ray " to fall obliquely on the thin plate, part thereof is reflected back by the first superficies," but, as the body is transparent, another part of the ray is refracted by the first surface, reflected by the second, and refracted again by the first surface, so that after two refractions and one reflexion, there is propagated a kind of fainter ray, whose pulse, by reason of the time spent in passing and repassing between the two surfaces, comes behind the former reflected pulse, so that hereby (the surfaces being so near together that the eye cannot discriminate them from one) this confused or duplicated pulse, whose strongest part precedes, and whose weakest follows, does produce on the retina the sensation of a yellow. If the two reflecting surfaces be yet farther removed asunder, then will the weaker pulse be so far behind, that it may be coincident with the second, third, fourth, fifth, &c., as the plate grows thicker ; " so that if there be a thin transparent body that, from the greatest thinness requisite to produce colours, does, in the manner of a wedge, by degrees grow to the greatest thickness that a plate can be of to exhibit a colour by the reflexion of light from such a body, there shall be generated such a consecution of colours, whose order, from the thin end towards the thick, shall be yellow, red, purple, blue, green, and these so often repeated, as the weaker pulse does lose pace with its primary or first pulse, and is coincident with a second, third, fourth, &c., pulse behind the first. And this, as it is coincident, or follows from the first hypothesis I took of colours, so upon experiment have I found it in multitudes of instances that seem to prove it."
Dr. Thomas Young has quoted nearly the whole of these passages as such an approximation to the true explanation of the colours of thin plates, that if he had not satisfied himself respecting the phenomena of this class of colours, these passages would have led him earlier to a similar opinion. The doctrine of interference is distinctly stated in them, and had Hooke adopted Newton's views of the different refrangibility of light, and applied them to his own theory of the coincidence of pulses, he would have left his rival behind in this branch of discovery.
Relying on the correctness of his views respecting the colours produced by reflexion, Hooke very ingeniously applied the same principle to the colours produced by refraction; and his objection to Newton's doctrine always was, that it was contrary to his theory. It is very obvious that hypotheses, however much they were abjured by the experimental philosophers of that day, were not only invented but admired; and Newton was thus driven to propose a hypothesis to satisfy his friends, he himself declaring that he neither believed it, nor wished them to believe it.
When this hypothesis was read, Hooke, as we have already seen, stated " that the main of it was contained in his Micrographia, which Mr. Newton had only carried farther in some particulars." The reader will, we think, be able to judge, from our abstract of Hooke's theory and observations, of the truth of this remark. We think it substantially true, and do not hesitate to say, that Newton has not done justice to Hooke. Excepting once, in reference to the inflexion of light, Hooke's name is never mentioned. The results of his experiments are made use of, and his theory partly adopted and altered, without any acknowledgment of the one, or notice of the other. In his vindication, read on the 21st December 1675, Newton admits that he made use of some of Hooke's observations ; that he adopted the idea of a vibrating ether ; and he thanks him for his explanation of opacity, and for his notice of the colours of plated bodies. In his interesting reply to Hooke, which we have given in the preceding chapter, he goes much farther, acknowledging that Hooke had added much several ways to Descartes' theory, especially in considering the colours of thin plates, and giving him the credit of two important discoveries, (which we do not find in the Micrographia,) namely, the dilatation of the coloured rings by the obliquation of the eye, and the apparition of a black spot at the contact of two convex glasses, and at the top of a water-bubble. In thus justifying the criticism of Hooke, and throwing some blame on Newton, we revert with pleasure to the noble amends which he made in his private letter, when there was no " intermeddling friend" to pervert the native generosity of his character.
We have hitherto considered only that part of Newton's discourse which contained his hypothesis, and its application to refraction, reflexion, transparency, and opacity. The remaining portions of it were read at the Royal Society on the 20th January, the 3d and the 10th February 1675-6, and contain all the optical discoveries of Newton.
The portion which was read on the 20th January, contained fifteen observations. In the first three of these he describes the arcs and circles of colours, which are exhibited by pressing together the imperfectly flat surfaces of two prisms. The place where they touched was absolutely transparent, appearing like a black spot " when looked upon," and " when looked through" it seemed like a hole in the thin plate of air between the prisms. The arcs and rings were generally of many colours, and about eight or nine in number. By turning the prisms about their common axis, the rings became black and white, and were sometimes about thirty in number. In order to see them distinctly, and without any other colour, it was necessary to hold the eye at a considerable distance from them, and also to view them through a slit or oblong hole narrower than the pupil of the eye.
In order to observe the order of the colours more correctly, and obtain measures of the rings at different thicknesses of the plate of air between the glasses, Newton took two object-glasses, the one a plano-convex for a fourteen feet telescope, and the other a large double convex for one of fifty feet, and having laid upon this the other with its plane side downwards, he pressed them slowly together, and observed the following orders of colours, next to the pellucid or dark central spot.
Order 1st, — Dark spot, violet, blue, white, yellow, and red.
Order 2d, — Violet, blue, green, yellow, and red.
Order 3d, — Purple, blue, green, yellow, and red.
Order 4th, — Green and red.
The succeeding orders became more and more imperfect, " till after three or four more revolutions they ended in perfect whiteness."[3]
When his eye was placed perpendicularly over the glasses, he found the diameter of the first six rings at the most luminous " part of their orbits," to be, when squared in arithmetical progression of the odd numbers, 1, 3, 5, 7, 9, 11, and the diameter of the dark rings between the more luminous ones, when squared, to be in arithmetical progression of the even numbers, 2, 4, 6, 8, 10, 12. When the rings were viewed obliquely, they became bigger, as Hooke had observed, continually swelling as the eye was removed farther from their axis.
"By measuring the diameter of the same ring at several obliquities of the eye, partly by other means, as also by making use of the two prisms for very great obliquities," Newton found its diameter, and consequently the thickness of the air at its perimeter, to be " proportional to the secant of an angle whose sine is a certain mean proportional between the sines of incidence and refraction. And that mean proportional is the first of 106 arithmetical mean proportionals between the sines of incidence and refraction counted from the lesser sine, that is, from the sine of refraction when the refraction is made out of air into water, otherwise from the sine of incidence."[4] That is, the angle to whose secant the thickness of the air is proportional, is one whose sine is to the sine of the real angle of incidence in the constant ratio of
m being the index of refraction of the glass.
In repeating the experiment with the light of a monochromatic lamp, and measuring the angles with great care, and at incidences so great as 85° 21′, MM. Provostayes and Desains obtained the following results. At an incidence of 85° 21′ the diameter of the seventh black ring in millionths of a millimetre, was
| By observation, | 47.53 |
| By Newton's Formula, | 40.11 |
According to the doctrine of interference, the thickness of the plate of air should be proportional to the secant of the angle of incidence, which, in the present case, would give 47.55 for the diameter of the seventh ring, a coincidence with the experiment so remarkable, as to leave no doubt of the truth of the theory.[5]
<164>The difference between Newton's experiment and the result of theory, is so great as to call forth the remark from Sir John Herschel,[6] that " it might be drawn into an argument against the theory, were we sure that the law of refraction at extreme incidences, and with very thin laminæ, does not vary sensibly from that of the proportional sines." The important results obtained by MM. Provostayes and Desains will teach us rather to doubt the accuracy of an unconfirmed experiment, and carefully to repeat it, than to explain it by calling in question a well established law.
By various modes of observation, Newton found the following relations between the diameter of the rings and the thickness of the plate of air : —
| Diameter of the ring,} | 10, , , , , , 14, , , , , 29, 35. |
| Thickness of the plate of air,} | 10, {}, , , 13, , 20, , , 37, , 84, |
Our author next proceeded to examine the effects of homogeneous coloured light, and was thus led to more important results. In place of eight or nine rings which he saw in the open air, he now saw more than twenty. In red light the rings were much larger than in blue and violet. The thickness of the plate of air at which any red ring was produced, was to that at which the same violet ring was produced, as nine to fourteen. The rings were not of various colours, as before, when white light was used, but of the prismatic colour which was employed, and each ring was separated from the other by a dark ring or space. Upon placing a white paper behind the rings, Newton observed rings painted upon it of the same colour with those which were reflected, and of the same size as their intermediate dark space. Hence he concluded that the light which fell on the dark spaces was transmitted through the glasses without any change of colour and that the aerial interval of the glasses according to its various thickness is disposed in some places to reflect, and in others to transmit, the light of any colour, and in the same place to reflect one colour where it transmits another.
From the examination of the colours of thin plates of air, Newton proceeded to that of the colours of thin plates of water, as exhibited in the soap-bubble. Having covered the soap-bubble with a glass shade, he saw its colours emerge in a regular order, like so many concentric rings encompassing the top of it. As the bubble grew thinner by the continual subsidence of the water, the rings dilated slowly and overspread the whole of it, descending to the bottom, where they vanished successively. When the colours had all emerged from the top, there arose in the centre of the rings a small round black spot, like that in the centre of the rings formerly described, dilating it to more than half an inch in breadth till the bubble burst.
Upon examining the rings between the object-glasses, Newton found that when they were only eight or nine in number, more than forty could be seen by viewing them through a prism; and even when the plate of air seemed all over uniformly white, multitudes of rings were disclosed by the prism. The same result was obtained with thin plates of water, mica, and glass.
By means of these interesting observations, Newton proceeds to shew how the system of coloured rings exhibited by white light, are produced by the superposition of the rings belonging to each separate colour in the spectrum, and he constructs a diagram, explaining a method of finding the colours of which the rings are composed at any distance from their centre. He then concludes this part of his discourse with a table shewing, in millionths of an inch, the different thicknesses of plates of air, water, and glass, when they exhibit the different colours in the seven rings or orders of colours. The thicknesses, for example, of air, water, and glass, at which no light is reflected, or at which the black of the first ring is produced, are 2, , millionths of an inch respectively, and the thicknesses at the margin of the seventh ring are 84, 63, and millionths of an inch. This Table, which is known by the name of Newton's Scale of Colours, is of great value in all optical researches, and is constantly referred to by modern writers on Optics.
This celebrated discourse is concluded by nine propositions, shewing how the phenomena of thin transparent plates stand related to the colours of all natural bodies, and how the size of the component parts of such bodies may be conjectured by their colours, — a subject which will be discussed in another chapter.
Such is a brief account of Newton's discoveries respecting the colours of thin plates, and of the hypothesis of ethereal vibrations, by which he proposed to explain them. The experiments from which they were deduced were all made previous to 1675 ; and it does not appear that, during the remaining fifty-two years of his life, he made any other communications on optical subjects to the Royal Society. In the preface to his Treatise on Optics, dated 1704, he tells us that "part of the ensuing discourse about light was written at the desire of some gentlemen of the Royal Society in the year 1675, and then sent to their secretary and read at their meetings ; and the rest was added about twelve years after, to complete the Theory, except the third book and the last proposition of the second, which were since put together out of scattered papers." These additions to the discourse, which were made in 1687, are no doubt his ampler discussion of the theory of the colours of natural bodies, and his theory of fits of easy reflexion and easy transmission, by which he explains the colours of thin plates; and what was since put together out of scattered papers, was the first part of the third book on the inflexion of light, and the fourth part of the second book on the colours of thick plates. An explanation, therefore, of the theory of fits, will form an appropriate conclusion of our account of Newton's discoveries respecting the colours of thin plates.
In the propositions of his Optics, where he explains this theory, Newton does not attempt to assign any cause by which these fits are produced. He does not inquire whether the kind of action or disposition in which they originate " consists in a circulating or vibrating motion of the ray or of the medium, or something else ;" but he says, that those who require a hypothesis, " which, whether it be true or false, he does not consider, may for the present adopt the one previously explained, in which the rays of light, by impinging on any refracting or reflecting surface, excite vibrations in the refracting or reflecting medium or substance," and that the ray is refracted or reflected according as it is in that part of the vibration which conspires with or impedes its motion.[7] A popular idea may be formed of these fits of reflexion and transmission, by supposing that each particle of light, after its emission from a luminous body, revolves round an axis perpendicular to the direction of its motion, and presenting alternately to a refracting surface, which it approaches, an attractive and a repulsive pole, in virtue of which it will be refracted if the attractive pole is nearest the refracting surface, and reflected if the repulsive pole is nearest that surface.
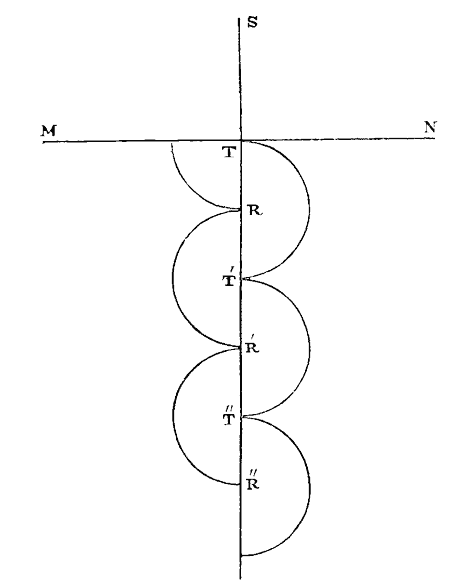
In order to explain this more clearly, let S be a ray of light which falls upon a transparent surface MN, and is transmitted by that surface. It is obvious that it must have been nearer its fit of transmission than its fit of reflexion when it met the surface MN at T ; but whether it was exactly in its fit of transmission, or a little way from it, the theory supposes that it is put by the action of the surface into the same state as if it had begun its fit of transmission at T. Let us now suppose that its fit of reflexion takes place at R, and that these fits recur at T′, R′, T″, R″, &c., so that if there was a second transparent surface at T′ or T″, the ray would be transmitted ; and if there was a second transparent surface at R′, R″, it would be reflected. The spaces TT′, T′T″, are called the intervals of the fits of transmission, and the spaces RR′, R′R″, the intervals of the fits of reflexion. Now, as the spaces TT′ RR′ are equal for light of the same colour it is obvious that the ray R will be transmitted, if the thickness of the body is TT′, T′T″, &c., that is TT′, 2TT′, 3TT′, or any multiple whatever of TT′, the interval of a fit of easy transmission ; and as TT′ is equal to RR′, the ray Rit will be reflected when the thickness of the body is TT′, TT′, TT′, TT′, &c. If the body MN, therefore, were a plate with parallel surfaces, and if the eye were placed above it so as to receive the rays reflected perpendicularly, it would in every case see the first surface MN by the portion of light uniformly reflected from that surface ; but if the thickness of the body were TT′, 2TT′, 3TT′, 4TT′, or 1000TT′, the eye would receive no rays from the second surface, because they would be all transmitted ; and, in like manner, if the thickness were TT′, TT′, TT′, or TT′, the eye would receive all the light reflected from the second surface, because it would be all reflected. When this reflected light meets the first surface MN, on its way back from the second surface, it will be all transmitted, because it is then in its fit of transmission. At intermediate thicknesses, such as TT′, a portion only of the light will be reflected from the second surface, increasing as the thickness increased from TT′ to TT′, and diminishing again as the thickness increased from TT′ to 2TT′.
Let us now suppose that the plate whose surface is MN has its thickness varying like a wedge MNP, Fig. 15, and that the eye is placed above it to receive the light which it reflects. The interval of the fits being TT′, RR′, as before, it is evident that, near the point N, the light that falls upon the second surface tP, will be transmitted, because it is in a fit of transmission, but at the thickness TR the light will be reflected from the second surface at r, because it is then in a fit of reflexion, and again transmitted in returning through the first surface MN. In like manner, the light will be transmitted at t′ and t″, and reflected at r′ and r″, so that the observer will see a series of dark and luminous bands, the middle of the dark ones being at t, t′, t″, and of the luminous ones at r, r′, r″.
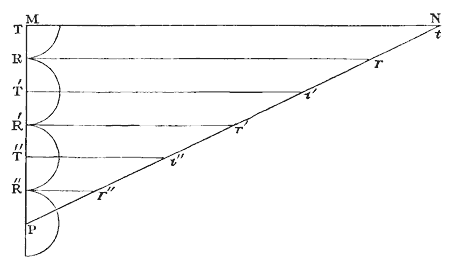
Let us now suppose that the figure is adapted to red light ; then since the length of a fit is greatest in red, least in violet, and of an intermediate size in yellow light, it is obvious that in yellow light there will be a set of dark and luminous bands less than those in the figure, and in violet light another set less than in the yellow. When, therefore, the light incident on the plate is white, all these bands will be superimposed, and form the coloured bands already described. When the thin plate is wedge shaped, the bands will be parallel. When it has the form of a concave lens, like air or vacuity between two object-glasses, the bands will be circular, with the lowest tints in the centre. When it has the form of a convex lens, like the plates of air in mica, the bands will also be circular, with the lowest tints at the margin; and when the thin plate has different thicknesses like a film of blown glass, the bands will have no regular shape, the same thickness giving always the same colour.
The preceding doctrine of fits has always been regarded as an ingenious explanation of the colours of thin plates. It is not given by its author as a theory or a hypothesis, but simply as an expression of the facts which he has observed ; and yet it has to a certain extent the character of a hypothesis, in so far as it assumes that the second surface of the plate does not in every part of it reflect light like the first, whereas in the theory of interference, certain portions thus reflected are destroyed before they reach the eye of the observer.
With the exception of the interesting observations of MM. Provostayes and Desains already referred to, no discovery of any great importance has been made on the subject of thin plates since the time of Newton. We have had occasion to observe a number of curious phenomena in the thin plates of decomposed glass when acting upon light in a state of combination. The colours which they reflect and transmit are not deducible from any theory of light, and have an intimate connexion with the absorption of light by coloured media.[8]
Among natural phenomena illustrative of the colours of thin plates, we have found none more remarkable than one exhibited by the fracture of a large crystal of quartz of a smoky colour, and about two and a quarter inches in diameter. The surface of fracture, in place of being a face of cleavage, or irregularly conchoidal, as we have sometimes seen it, was filamentous like a surface of velvet, and consisted of short fibres so small as to be incapable of reflecting light. Their size could not have been greater than the third of the millionth part of an inch, or one-fourth of the thinnest part of the soap-bubble when it exhibits the black spot where it bursts.[9]
Although Newton did not communicate his observations on the colours of thick plates to the Royal Society in his discourse on light and colours, but " put them together out of scattered papers" some time before the publication of his Optics,[10] yet this is the proper place for bringing them under the notice of the reader.
The colours of thick plates arise from a quantity of light scattered in all directions from the little inequalities or imperfections which exist in the surface of a glass mirror either silvered or unsilvered. In order to observe them, a sunbeam is admitted through a small hole about a third of an inch in diameter into a dark loom. This beam is received perpendicularly on a concavo-convex glass mirror, a quarter of an inch thick, and having each surface ground to a sphere six feet in radius. When the sunbeam passes through a small hole in the middle of a sheet of white paper placed in the centre of the mirror's concavity, the hole is surrounded with four or five coloured rings. The rings resembled those seen by transmission through two object-glasses, but were larger and fainter in their colours. When mirrors of different thicknesses were used, the diameters of the rings were reciprocally as the square roots of the thicknesses ; and in homogeneous light they were largest in the red, and smallest in the violet rays, like those formed by thin plates.
These and other phenomena described by Newton, he explains by taking into consideration the fits of easy reflexion and transmission of the faint scattered light already mentioned. On the undulatory theory that they are explained by the interference of the portions of light scattered at the first surface by the rays in passing and repassing through it.
The Duke de Chaulnes[11] observed similar rings when the surface of the mirror was covered with fine gauze, or with a thin film of milk dried upon it, and Sir. William Herschel[12] noticed analogous colours when hair-powder was scattered in the air before a metallic mirror, on which a beam of light was incident.
When we look through two plates of parallel glass of exactly the same thickness, at a circular disc of light 1° or 2° in diameter, no coloured bands will be seen when the light is incident perpendicularly, and when the plates are parallel. But if we incline them slightly to one another, we shall see, beside the direct image of the luminous body which is crossed with no fringes, a series of lateral images formed by successive reflexions between the surfaces of the plates, which are crossed with fifteen or sixteen highly coloured bands parallel to the common section of the surfaces of the plates. The breadth of these bands is inversely as the inclination of the plates, and at a given inclination their magnitudes are inversely as the thickness of the plates employed.
These brilliant bands, which we have described minutely in a separate memoir,[13] are explicable by the doctrine of fits of easy reflexion and transmission. They have been explained also on the undulatory hypothesis by Dr. Thomas Young,[14] and in greater detail by Sir. John Herschel.[15]
Another species of coloured fringes, produced by the reflexion of a pencil of light between the lenses of a double or a triple achromatic object-glass, is equally explicable by Newton's theory of fits, and by the doctrine of interference. Owing to the curvature of the surfaces which produce them, the forms of the isochromatic lines, or the lines of equal tint, are various and beautiful.[16]
[1] Experiments and Observations touching Colours. Exp. xix. p. 243, London, 1664.
[2] " Micrographia, or some Physiological Descriptions of Minute Bodies made by magnifying-glasses, with Observations and Inquiries thereupon." In many of the copies the date is 1667, but the title-page which bears this date was a trick of the printer, to indicate a second edition, which was never printed. The imprimatur of the President of the Royal Society is Nov. 23, 1664. See Ward's Life of Hooke, in the Lives of the Gresham Professors, p. 190.
[3] The reader will observe that the orders here given, and their colours, differ somewhat from those published nearly thirty years afterwards in his " Optics."
[4] Optics, Book ii. Part i., Obs. 7, 18.
[5] Comptes Rendus, &c. &c., tom. xxv. p. 498. 1850.
[6] Treatise on Light, Art. 670.
[7] It is curious that Newton here makes no mention of an ethereal medium as that in which the vibrations are executed, as he does in his Hypothesis, formerly described. See p. 136.
[8] " On the Connexion between the Phenomena of the Absorption of Light and the Colours of Thin Plates." — Phil. Trans. 1837, p. 245.
[9] Edinburgh Journal of Science, vol. i. p. 108. June 1824.
[10] These observations, thirteen in number, entitled " Observations concerning the Reflections and Colours of thick transparent polished Plates, form the fourth part of the Second Book of Optics.
[11] Mém. Acad. par. 1705.
[12] Phil. Trans. 1807.
[13] Edinburgh Transactions, 1815, vol. vii. p. 435.
[14] Art. Chromatics in Encyclopædia Brittanica.
[15] Treatise on Light, § 688-695.
[16] Edinburgh Transactions, 1832, vol. xii.
