Unarranged fragments, mostly relating to the dispute with Leibniz
Out of Mr Gregories Letter of the 17th of May 1671
This method of infinite Series hath no good successe in the second Segments of round Solids, at least so farre as I can improoue them yet such as it is you shall haue it
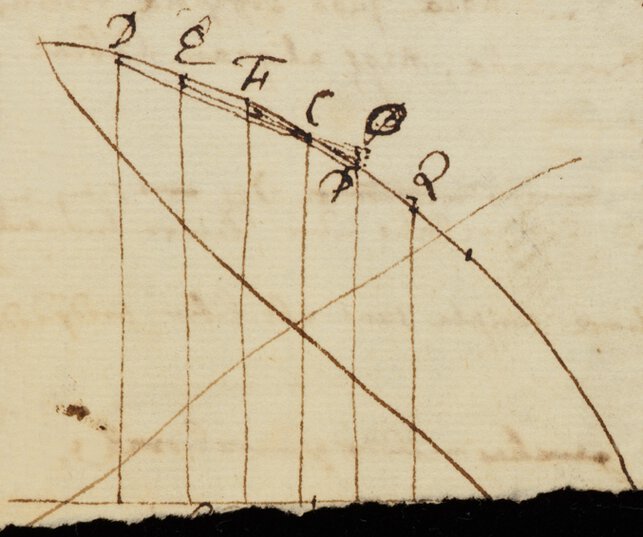
 Sit igitur Ellipsis ADCE, cuius Axis transversus AC. Coniugatus DE; Centrum B, supponatur nunc Sphærois generari ex revolutione Semiellipseos ADC, circa Axem AC, seceturque Sphærois a duobus Planis parallelis, per Puncta K, B, Axi DB normalibus, et a duobus Planis Parallelis per Puncta B, F, axi BC normalibus:
Sit igitur Ellipsis ADCE, cuius Axis transversus AC. Coniugatus DE; Centrum B, supponatur nunc Sphærois generari ex revolutione Semiellipseos ADC, circa Axem AC, seceturque Sphærois a duobus Planis parallelis, per Puncta K, B, Axi DB normalibus, et a duobus Planis Parallelis per Puncta B, F, axi BC normalibus:
Sit , ; eritque pars Sphæroidis KIFB a quatuor dictis Planis comprehensa = in infinitum. This Series is nothing but a Congeries of other Series's all of them being infinite, yet is the best I can haue to this Purpose, I hope Mr Newton hath better, and that with his Leaue yee will informe mee, If you would haue it agree to the Sphære, yee shall only put c in place of r, which will render it more Simple, I can giue such a Series as this for the second Segment of any round Solid, and if you like this, I shall giue a Series for the second Segments of an Hyperbolick Spindle, which I imagine is of greater Consequence than any thing else for Guaging –
p. 11. l. 4.
3dly We do not dispute about the antiquity of the symbols of fluents fluxions & moments Summs & Differences. And yet the symbol used by Mr Newton for fluents or summs is older then the symbol used in the same sense by Mr Leibnitz, & Mr Newton had symbols from fluxions before he wrote his Letter dated 24 Octob 1676, but Mr Leibnitz has none to this day & the rectangles under the fluxions & the letter o used by Mr Newton for moments are older then the symbols dx & dy used in the same sense by MrLeibnitz. . But These are only ways of Notation & signify nothing to the method it self which may be without them. [All the use that can be made of them is to shew that Mr Leibnitz method was as old as the use of the symbols dx & dy & Mr Newtons as old as his use of any symbols for the same things.]
— as in the Principia. In the first Proposition of his book De quadratura Curvarum he used prickt Letters but did not make them necessary to his method. for in the Introduction to that book he described this method at large & illustrated it with various examples without making any use of prickt letters. That book was first printed in the year 1714 but the first Proposition thereof at the request of Dr Wallis was copied & sent to the Dr by Mr Newton in his Letter of 27 August 1692 & printed the next year in the second Volume of the Doctors works. It was made use of upon all occasions, by Mr Newton when he wrote his Principia Philosophiæ And so many things are cited out of it in Mr Newtons Letter of 24 Octob 1676 that one may reasonably conclude that the book was writ before that time. In his Analysis per æquationes &c — — — — — trifling. And if it were not, yet Mr Newton has the advantage as was mentioned above. For prickt letters are put for fluxions which are motions & finite quantities & never signify moments or differences which are infinitely small parts generated by fluxion. Where the symbols of fluxions (whether prickt letters or others are multiplied by the letter o to make them infinitely little the rectangles are put for moments, or where fluxions are considered as the exponents of moments, the symbols of fluxions are put for the exponents of moments, but in such cases the factor o is always understood. This factor Mr Newton always expresses when he is demonstrating a Proposition but when he is only investigating a Proposition he usually neglects to write it down Now Mr Leibnitz has no symbols of fluxions in his method & theref. all Mr Newtons symbols of fluxions are the oldest in the kind. And as for the dx & dy of Mr Leibnitz they are not to be compared with the symbols of fluxions but with the symbols of Moments that is with the rectangles under the symbols of fluxions & the letter o And those rectangles are the oldest being used by Mr Newton in his Analysis sent by Dr Barrow to Mr Collins in Iuly 1669. And tho our great Mathematician tells us that Mr Newton by putting o for the increment of x loses all the advantage of the differential method: the contrary is true. Mr Leibnits by putting dx for the letter o has lost a considerable part of the advantange of Mr Newtons method without adding any thing new to it besides his symbols. For the Method by Mr Leibnitz's way of Notation is not Geometrical nor demonstrative. It is only fitted for investigation, & is not so expedite as Mr Newtons method who in such cases neglects to write down the letter o, & so uses but one letter to represent moments the other being understood. These advantages it has lost, & has added no new ones. For there is nothing that can be done by it but what may be done by Mr Newton's method & that with as much or more dispatch.
But whereas Mr Leibnitz had changed the Letters a & e used by Dr Barrow into dx & dy he tells us in the Acta Eruditorum mensis Iunij 1686 pag 297 that this change was not necessary to the method Malo autem dx & simila adhibere saith he quam literas pro illis quia istud dx est modificatio quædam ipsius x, ut sola quando id fieri opus est litera x cum suis scilicet potestatibus & differentialibus calculum ingredieatur, & relationes transcendentes inter x et aliud exprimantur: Qua ratione etiam lineas transcendentis æquatione Explicare licet. So then Mr Leibnitz by his own confession might have used letters as Dr Barrow did & the method would have been the same, but he chose rather to use the symbols dx & dy as more convenient. And yet from these symbols he gave the method the name of the differential method as if it had been a new method. At which rate a man might put any letter for the Abscissa of a curve & modify the letter variously to represent the Ordinate, the area, the length, the subtangent, & the radius of curvity & call this a new methodu, & give it a new name to extinguish the memory of former authors & make himself famous for inventing a new method of solving all sorts of Problemes relating to curve lines.
<2v>— as in the Principles. Mr Newton seldome uses prickt letters till he has brought Problems to equations & by those equations is to deduce fluxions from fluents or fluents from fluxions. How he deduces fluxions from fluents he has told us in the first Proposition of his book the Quadratura Curvarum & there he uses prickt letters & by them shews how from æquations involving fluents to deduce the first econd & third fluxions of the fluents & so on in infinitum & this he does by one very short rule comprehended in five lines Also in explaining how he extracts a fluent out of an equation involving its fluxions he uses prickt letters & extends the Proposition to the 2d 3d & following fluxions. In his Letter dated 242 Octob 1676 he comprehended his method in these sentences Data æquatione fluentes quotcunque quantitates involvente fluxiones invenire & vice versa. And Vna methodus consistit in extractione fluentis ex æquatione fluxionem ejus involvente, altera &c. When Dr Wallis was printing the second Volume of his works he wrote to Mr Newton to explain those sentences to him & Mr Newton did it by prickt letters sending him a copy of the first Proposition of his book the Quadratura Curvarum & of another Paper This was in the year 1692. In the year 1686 Mr Newton wrote in the Scholium upon the second Lemma of the second book of his Principia Philosophiæ that ten years before upon his writing to Mr Leibnitz about his Method of fluxions comprised in this sentence Data æquatione quotcunque fluentes quantitates involvente Fluxiones invenire & vice versa. Mr Leibnitz wrote back that he had also fallen into such a method & communicated his method scarce differing from Mr Newtons except in the forms of names & symbols. And Mr Newton's symbols here related unto were those of letters with pricks. And indeed in his Letter of 24 Octob 1676 so many things are quoted out of book of Quadratures that one may thence conclude that this book was writ before that letter. But in the Principia Philosophiæ & in the Letters of Mr Newton to Mr Collins & Mr Oldenburg published in the Commercium Epistolicum & in his Analysis he had no where occasion to treat of Equations involving fluents & fluxions. In the Introduction to the book of Quadratures Mr Newton explained the method of fluxions at large & illustrated it with various examples without making any use of letters with pricks. And will our great Mathematician say that Mr Newton did not then understand the Method of fluxions because there are no such Letters in that Introduction
If the net value of the goods were 100li the Queens duty would be 52.2.6 as above, and the summ of the value & duty augmented by the 7th part thereof namely would be the gross value by the candle For the allowance of 6 & per cent in the eighth part of the whole. Say therefore: As in this case the gross value by the candle 173.17.1 is to the Queens duty 52li.2.6d in this case, so is 1 to 0∟299815, & so is the gross value to the Queens duty in all other cases.
Wherefore if you multiply the gross value by the ratio 0∟299815 you will have the Queens duty.
As if the gross value be 100li this multiplied by the said ratio will produce the Queens duty 29li∟9815 or 29l.19.7 The truth of which method will thus appear
China ware sold for 100li
The right method of Computation as is conceived by the Auditors is to find the ratio of the Queens duty to the gross price in any one case & then in all cases to multiply the gross price by that ratio.
Let the net value of the goods be 100li & in this case the Queens duty will be 52l.2.6 as above; & the summ of this value & duty augmented by the 7th part thereof (the the allowance for prompt payment & warehouse room), namely 173li.17s.1d will be the gross value by the candle. And as this value is to the Queens duty in this case so is 1 to ,299815, & so is the gross vales to the Queens duty in any other case.
As if the gross value were 100li, this multiplied by ,299815 will produce the Queens duty 29,9815 that is 29li.19.7.
And if the gross value were 3748li.10s, this multiplied by ,299815 will produce the Queens duty 1123li∟8565, that is 1123li.17s.1d.
Now the truth of this method may be thus proved.
China ware sold for 100li
<4v>Now that 29li.19.7 is the Queens just duty will further appear by the following computation.
The western Churhes in external profession of faith were now macedonians, except that they still used the language of one hypostasis as equipollent to that of one usia & substance. There might be many who believed the holy Ghost to be God but they did not yet begin to speak out. easter Chur / & began to be shy of one anothers communion. For the little Council of Alexandria had agreed that the bishops who had consented to the abolishing of the use of the word usia with its compounds, (except the ringleaders) should not lose their bishopricks if in time they would retract & come over to the Council of Nice. But now the Latines finding themselves strong enough resolved to deprive them all who would not retract so soon as they could get an Emperor for their purpose. And began also to break friendship with the Macedonians & declare for the party of Athanasius against them.
The friendship between the Macedonians & the Churches of Italy & the west lasted, I think, till Pope Damasus called at Rome a Council of 93 bishops who sent Elpidius with a letter to a Council convened at the same time in Illyricum, in which letter they thus describe their faith. When the evil . . . . . . erring bishops. By these words they signify that the communion between the Greek & Latin Churches was not yet broke off. The Churches of the whole Empire whether for or against the consubstantiality of the Son, for or against the Deity of the Holy Ghost, composed hitherto one visible catholick Church, notwithstanding the differences of opinions ☉ & the Latines were meditating to excommunicate & throw out of their communion all those bishops.
The Council of Illyricum having recieved this letter — — — . . . others used that of three. Basil wrote also at the same time by Sabinus to the bishops of Illyricum. For in his 273d Epistle he writes thus: Ego enim cum inciderim in Sabinum diaconum quo nuncio huc ad nos illi [occidentales] usi sunt, ad Illyricos scripsi, ad Italos præterea & Gallos episcopos & nonnullos privatim. These Councils therefore of Rome & Illyricum & Gallia were convened after Basil was made bishop, that is, after Iune 371, & so may be placed in the year 372. For Athanasius heard of them before his death and died in May 373. The controversy therefore about the deity of the holy Ghost which Athanasius had been hitherto labouring to kindle brake out into a flame in the year 372
In another Epistle written this year to the Churches of Italy & Gallia Basil exprest himself in this manner. We are seized with a persecution . . . . . . . . . . . / during the reign of Valens the Christians of the Greek Empire brake into several parties. The generality were those who for the sake of peace contended for the language of the scriptures & in conformity to the Apostles rule of holding fast the form of sound words & to the decree of the Church catholick in the Council of Antioch against Paul of Samosat rejected the use of the word usia with its compounds as novel & tending to faction & sabellianes Paulinianism & forbore the curious inquiries Nicolaitans into the metaphysical nature of as novel & tending to Montanism Paulinianism & Sabellianism, & forbore the curious inquiries of the men of science falsly so called, into the metaphysical nature of the supreme Beings: co contenting themselves with the declaration that the Son was like the father according to the scriptures & for doing so were falsly called Arians by the Saintworshippers For they anathematized as well the novel language of Arius on the one hand as that of the Gnosticks on the other. Next to them in number were the homousiams who owned not the deity of the holy Ghost & were falsly called Macedonians by the Saint worshippers, as if Macedonius was the author of that opinion.
Pag. 12. l 6. + The Postscript not being sent to Mr Newton he did not meddle with it till Mr l'Abbé Conti pressed him to write an Answer that the Postscript & the Answer might both be shewed to the King & the Answer was not writ till after the King had seen the Postscript. This Answer was a follows.
Between Letter 6 & 7 insert this Introduction to the Observations.
The Answer of Mr Leibnitz being sent open to Mr Remond at Paris to be sent from thence to Mr l'Abbe Conti, & copies of Mr Newton's & Mr l@Abbe Conti's Letters being sent also thither. Mr Newton declined to return an answer in writing & only drew up the following Observations to satisfy his frends privately that it was easy to have returned an Answer had it been fit to let Mr Leibnitz go on with his politiques.
At the end of all the Letters add the Paragraph in the German Elogium of Mr Leibnitz.
<6v>Tempus autem quæ quantitas est fluens hic expono per lineam rectam uniformiter crescentem vel ac temporis momentum per particulam lineæ eodem temporis momento genitam, et inde lineam voco quantitatem uniformiter fluentem, et particulam voco momentum ejus, et quantitates alias omnes simul augescentes voco fluentes et earum particulas eodem temporis momento genitas voco fluentium momenta et velocitates augescendi voco quantitatum fluxiones] et particulas singulis temporis momentis genitas nominando momenta — et has motuum vel incrementorum velocitates (ex fluxione temporis) nominando fluxiones
× (i.e. fluxiones pro differentijs)
✝ ubi Leibnitius Inventor nominatur,
pag. 44. lin 17 — de qua sequentia . Anno vero 1676 priores decem olim excogitavi et anno 1676 Propositiones in formam sequentem redegi, undecimam vel eodem anno vel paulo post adjuxi, et duodecimam ex Epistolis anno 1676 scriptis jam addidi.
ut videre licet in Lib. 11, Prop. XIV cas. 3.
Quoniam methodus meus generalis ex methodo fluxionem et methodo Serierum convergentium componitur, et quantitatum in series resolu{t}arum momenta prima secunda, tertia cæteraque sunt correspondentibus serierum terminibus momento temporis genitis proportionalia ideoque in resolutione Problematum nonnunquam usus sum terminis serierum. Sit A quantitas fluens, & quantitas alia fluens. Augeatur quantitas A momento O, et quantitas B evadet . quæ in seriem resoluta fit . Et primæ sunt .
Et ipsius fluxio prima est & hujus fluxio est , Et hujus fluxio
To
Sir Isaac Newton at the Lower Side of Leicester fields
Westminster.
Office {C}
suposd Golden square.
<7v>For Sir Isaac Newton at his house in St Martins street nigh Leîsterffields
These
<6bis(r)>Honored Sir
In obedience to my fathers Commands I am oblig'd to continue here at london for sometime longer Sir Wm Quintin haueing promis'd my friends in the Countrey that I shall be preferd in the Customes, now seeing that I haue Qualified my self for that purpose, & that Iam in expectation dayly to come into Mr Iohn Selbys place at Whitby, he being to be promoted to a Collection in the South, & that now Sir the Welfare of our Family seems much to depend on my good success. Your kindnes has been extraordinary to me, for otherwise Imight haue suffer'd very much. I apply dayly to the Treasury & hope that Mr Iohn Selbys Warrant & mine will be granted us & that how glad I shall be to be in a Condition to support my Dear Father, that has liu'd well in the world Sir you must not think much with me for being so free with you Imust Confess Iue been a great trespasser upon you but Ihope your Goodness will pardon me, & that my Dear father prays dayly you may continue my friend, & not let us sink now, when there is so fair a probability of my getting now into business, Iue' taken abundance of pains & the great fatigue Iue' undergone & hardships here as ar almost inexpressible. I hope I shall demonstrate, when please god I am in business my gratitude to you & how much I am
Honored Sir
His patet me anno 1676 & annis minimùm quinque vel septem prioribus methodum generalem habuisse reducendi Problemata ad æquationes fluxionales. Et ex hujusmodi æquationibus tam affectis quam simplicibus eliciendi quantitates fluentes, et in hac methodo quandoque series pro quantitatibus ignotis assumere et assumptas terminorum coefficientes & indices dignitatum ex conditionibus Problematis determinare, Et inter computandum fluxiones et momenta ex fluentibus & fluentes vicessim ex fluxionibus & momentis deducim & in huic finem me Theoremata plura pro Quadratura figurarum & inventione fluentium per hanc methodum concinnasse, & propter generalem usum hujus methodi in solutionionis problematibus me nomen Analyseos eidem ab anno 1669 imposuisse & huic. affines fuisse methodos Tangentium Gregorij, et Barrovij, propterea quod Methodum Slusij similiter producerent, & Barrovium Analysin meam ut methodum novam ad Collinium misisse.
Brevitate verborum effectum est ut Scholium præcedens male intellectum fuerit, et propterea rem totam fusius enarrabo.
Cum vero D. Leibnitius anno 1684 elementa hujus Analyseos in lucem emitteret & silentio præteriret ea omnia ad hanc methodum spectantia quæ vel ab Oldenburgo acceperat vel in manu Collinij viderat: posui Scholium superius ut inde constaret me primum de hac methodo scripsisse et [elementa ejus in Lemmate præcedente synthetice demonstrata non habuisse aliunde] & Lemma superius ab editis Leibnitianis non fuisse desumptum.
Terminos serirum pro momentis nonnunquam usus sum propter analogiam. Nam hi termini per terminos correspondentes seriei numeralis multiplicati convertuntur in momenta.
<7v>Et his admitus D. Leibnitius compendium hocce in manu Collinij videre potuit. Is enim hoc tempore Collinium de commercio Gregorij et meo consuluit et partem litererum nostrarum in ejus manu vidit & ab Oldenburgo paulo ante postulaverat ut demonstrationem mearum serierum a Collinio procuraret: quæ Demonstratio extabat in hoc Compendio
Analysis vero de qua hic locutus sum eadem est cum Analysi per series cujus compendium Barrovius anno 1669 ad Collinium misit
His respondit D. Leibn. 27 Aug 1676 in hæc verba.
Hoc compendium est Analysis illa per series fluxiones et mom{enta} quam Ionesius edidit.
Hæc est Analysis illa per series, fluxiones et momenta cujus specimen Barrovius noster anno 1669 cum Collinio communicavit ut supra.
<8r>In Epistolis meis 10 Decem 1672 & 24 Octob 1676 datis dixi quantitates surdas methodum meam non morari, Et hanc rem exemplo explicuo in Analysis mea a Ionesio edita, pag. 14. Substituatur utique in æquatione pro quantitate radicale symbolum quodvis; Tractetur symbolum illud ut quantitas fluens; Et completo opere pro symbolo et ejus fluxione scribatur quantitas radicalis et ejus fluxio.
Tempus utique per quantitatem quamcunque uniformiter fluentem fluxionum ejus per unitatem & momentum per literam o Newtonus designat: Aliarum quantitatum fluentes designato per alia symbola et momenta earum per symbola illa ducta in momentum o, e st Areas vero curvarum designat per ordinatas quadrato inclusas. Leibnitius pro fluxionibus nulla habet symbola, pro momentis præfigit symbolis fluentium literam d, et pro Areis præ figit symbolis Ordinatarum literam. Newtonus caculo suo usus est in Analysi quam Barrovius cum Collinio mense Iulio anni 1669 communicavit; et hanc methodum tum in Analysi illa tum alias in Epistolis 10 Decem. 1672, 13 Iun 1676 & 24 Octob 1676 valde generalim esse significavit & verbis partim apertis descripsit partim figuratis celavit, [eamque ad Curvarum areas longitudines, soliditates & curvaturas (sc. per fluxiones secundas) sese extendere, ut et ad inversa Tangentium Problemata aliaque difficiliora, sino vero ad omnia pene dixerat problemat si forte numeralia quædam Diophantæis similia excipiantur.] Leibnitius suam communicare cœpit anno 1677 mense Iunio Et ut suam faceret scripsit in hæc verba. Clarissimi Slusij methodum tangentium nondum esse absolutam celeberrimo Newtono assentior: Et jam a multo tempore rem tangentium longe generalius tractavi scilicet per differentias Ordinatarum. Sed anno tamen superiore methodum differentialem minime invenerat. Scripsit enim 27 Aug. 1676 multa esse adeo mira et implexa ut neque ab æquationibus pendeant neque a Quadraturis: qualia sunt (ea multis alijs) Problemata methodi Tangentium inversæ; quæ etiam Cartesius in potestate non esse fassus est. [Annis 1675 & 1676 D. Leibnitius quadraturam quandam circuli componebat limabat et poliebat vulgari more: sed postea prolixius exponere vulgari more quæ Analysis sua nova paucis exhibet non satis operæ pretium videbatur. Leibn. in Actis Eruditorum Anno 1691 p. 178.]
sed acceptis Newtono Literis anno sequente mense Iunio methodum differentialem ut olim a sc inventam communicare cœpit his verbis. Clarissimi Slusij methodum tangentium nondum esse absolutam celeberrimo Newtono assentior: et jam a multo tempore rem tangentium longe generalius tractavi scilicet per differentias Ordinatarum &c. Quod methodum hanc a multo tempore invenerat probandum est. Nam D. Leibnitius pro se testis esse non potest. Iniqus esset Iudex qui in rebus controversis hominem quemvis pro seipso testem admitteret.
Et vires hase considerat, non ut qualitates , primas causis destitutas aut rebus corporibus essentiales, sed ut qualitates {lats} patent{illeg} quaru{m} causes ignoramus. Et vires considerat ut qualitates primas causis destitutas aut corporibus essentiales sed quarum causes ignoramus.
Sir Isaac Newton
These
<9v>Hon'd Sir,
I take leave to put You in mind of bringing with You to the Royal Society Your Key of the Iron Chest which contains the Common Seal, the Lease being ingross'd and ready for the Seal to be affixt to it.
I am
Your most Obliged and Obedient Servant
Io: Thorpe
Galileo argued that uniform gravity by acting equally in equal times upon a falling body would produce equal velocities of descent in those times, or that the whole force imprest, the whole time of descent & the whole velocity acquired in falling would be proportional to one another; but the whole descent or space described would arise from the time & velocity together & there be in a compound ratio of them both, or as the square of {in ther of there} descent. And if a body ascend, the gravity of the body by acting upon it equally in equal times will take of equal velocities of ascent in those equal times, or that ② the whole force imprest, ① the whole time of ascent to any height ③ & the whole velocity taken of in that time are proportional to one another but not to the space of ascent. The whole space of ascent will arise from the time & velocity together & be in compound ratio of them both, that is, as the square of either of them. And upon these rules of ascending & descending, Galileo demonstrated that projectiles would, in spaces void of resistance, {d}escribe Parabolas. And all Mathematicians (not excepting Mr Leibnitz himself) unanimously agree that he was in the right. And it is proportional but by the space of ascent to which it is not proportionall.
et in epistolis supra impressis significavit methodum suam ad tangentes directe & inverse et ad alia etiam problemata extendere, [et methodum suam in tangentibus directe et inverse per exempla exposuit.] Leibnitius negaverat Tangentes inverse per æquationes & quadraturas tractavi posse sed Lecta Newtoni literis animum advertit ad methodos tangentium & consideratio differentiarum in methodis illis primam lucem ipsi affundit.
methodus determinandi Tangentes per differentias linearum primam lucem affundisse Leibnitio id est methodus Archimedis a Fermatio, Gregorio, Barrowo restituta & promotam, a Newtono ad æquationes quasvis in indeterminatas & motuum velocitates applicata.
Vidit hoc Fermatius antea, determinando punctum flexus contrarij.
Nulla est hæc analogia. Differentiæ non sunt summarum differentiæ, nec relationem habent ad summas nisi quatenus sunt quantitates infinite minores aliunde .
Methodus igitur determinandi Tangentes per differentias primam lucem affuderat Leibnitio (p id est methodus Archimedis a Fermatio Gregorio Barrowo restituta & promota, a Newtono ad quantitatum augmenta generaliter applicata. Hujus methodi exempla in problemate tangentium directo (p ) & inverso (p ) & in Quadratura curvarum p et methodo serierum p Newtonus dederat. Leibnitius ex his deprehendit similitudinem in methodorum p sed] Et ex his D. Leibnitius deprehendit similitudinem methodorum ab initio p
Et His admonitus D. Leibnitius in methodum tangentium per differentias animum intendit (p 46, 47 87, 88) & methodum differentialem Newtonianæ similem esse statim ab initio deprehendit p. 90, 91, 93.
& arcus HC, CP erunt synchroni, et erit decrementum momentaneum ex resist & grav. Est increm momentaneaum ex grav. Ergo decrem. moment. ex resist.
a D Leibnitius hic fatetur se methodum differentialem a methodo determinandi Tangentes per Differentias didicisse Archimedes, Fermatius, Gregorius, & Barrowu{s} methodum Differentiarum ad Tangentes applicuerae: Newtonus methodum a Fermatij acceptam ad æquationes abstractas & proportiones motuum , et per æquationes & proportiones motuum ad problemata quævis quæ per æquationes & proportiones motuum & series tractari possunt applicu{illeg} & se talis methodi compotem esse & methodum Slusij ejusdem corollarium esse significavit in epistolis supra impressis pag & Et cum D. Leibnitius scripsissit methodum inversam tangentium et ab æquationibus & quadraturis non pendere, Newtonus respondit hanc etiam in potestate esse et exemplum generale dedit solutionis per quadraturas ubi datur relatio inter latera duo quævis trianguli quod ab ordinata, tangente & subtangente constituitur. Et tum demum D. Leibnitius his omnibus admo{t}eitus methodum quæsivit per relationem differentiarum ad Tangentes. incidit Et tum demum D. Leibnitius animum advertit ad methodos tangentium, & consideratio Differentiarum in methodis illis primam lucem ipsi affundit Et problemata tangentium inversa aliaque similia ab æquationibus & quadraturis pendere se primam negasse & subinde a Newtono didicisse statim oblitus est Vide p. 65, 85, 86, 93.
Vidi b mox b Hoc antea Fermatius qui, per differentiam primam evanescentem est per osculum determinavit punctum flexus contrarij.
c Et notavi c mirabilem &c c Nulla est hujusmodi analogia Differentiæ non sunt summarum differentiæ; non sunt ejusdem generis quantitates cum summis; sunt ad summas ut momentum ad tempus, vel punctum ad lineam, non ut radix ad potentiam. Leibnitius primam lucem aliunde habuit.
Sic etiam oblitus est literarum Oldenburgi per quas series suas omnes accepit p.
he saith that when he was in London the second time he saw some of my Letters in the hands of Mr Collins cheifly those which related to series & observed that in one of them I acknowledged my ignorance in the dimensions of the vulgar figures except the Cissoid. & that the Committee had omitted this. But being told that this was in my Letter of 24 Octob. 1676 & was published {in} the Commerc. p 74 he acknowledges that it was, & adds that he would cite another insta{nce.} In another of m{y} Letters which he then saw (meaning a Letter dated 1672 & not yet publish{ed} said that I acknowledged that I could not find the second segm{ents} of Sphæroids, & that the Committee had omitted this.
{illeg} were as much as was proper in tha{t} {illeg} it being {illeg} of that book to enter into disputes about {illeg} {M}r Pell at that {illeg} notice of Mercators series for the H{illeg}d Mr Collins had some {illeg}communited mine & Gregories series to the Math{ematicia}ns at home & abroad, {illeg} might meet with some of them either at London or Paris without being {illeg} with Mr Collins.] & might be able to give him notice of
{illeg} .
Provided nevertheless that over & above the summs above mentioned there may be issued yearely out of the coinage monnys of England, the summ of 300li per an' for the salary of the General of the Mint in Scotland, 50li per an' for {t}he salary of the Clerk of the Bullion & 50li per an' in part of the salary {of} the Warden of the said Mint untill the next voidance of their places.
{illeg} in the Scholium Paraph there referred unto I do not find one word to this purpose. On the con{trary} {I} there represent that I sent notice to Mr Leibnitz of my Method {illeg} sent notice to me of his method & left him to make it appear that he had {illeg} method before the date of my Letter, that is, eight months at least before the date {illeg} And by referring to the Letters which passed between Mr Leibnitz & {illeg} before, I left the Reader to consult those Letters & interpret the {illeg} Paragraph thereby. For by those Letter{s} {illeg}ld see that I {illeg} {o}f that Method & the Method of Ser{ies} {illeg} five years before {illeg} {t}hose Letters that is, in the year 16{illeg} {M}r Leibnitz knew nothing
Cum methodus Tangentium Slusij fundaretur in proportione differentiæ Ordinatarum duarum sibi proximarum ad differentiam Abscissarum et anno 1672 ad Collinium scripsissem hanc methodum esse Corollarium methodi generalis quæ citra molestum ullum calculum ad resolvendum abstrusiora problematum genera de curvitatibus, Areis, longitudinibus, centris gravitatis, curvarum &c & ad quantitates surdas minime hæret, exemplar autem hujus Epistolæ anno 1676 ad D. Leibnitium mitteretur; et eodem anno literis alijs ad ipsum missis significarem me compotem esse methodi determinandi maximas & minimas ducendi tangentes quadrandi curvilineas et similia peragendi quæ in terminis surdis æque ac in rationalibus procederet, qu{a}que beneficio serierum ad omnia pene problemata [etiam ad inversa tangentium aliaque difficili ora] se extenderet, [et methodum exemplis illustrarem] respondet D. Leibnitius id sibi non videri; esse enim multa usque ad eo mira et implexa ut neque ab æquationibus pendeant neque ex quadraturs, qualia sunt ex multis alijs problemata methodi tangentius inversæ. Cum autem rescripsissem inversa de Tangentibus problemata esse in potestate, aliaque illis difficiliora & methodum tangentium Slusij ex meis Principijs statim consequi, & similiter quæstiones de maximis & minimis resolvi & quadraturas reddi faciliores & alia similia peragi, et Analysin meam ad surdas quantitates aut ad Curvas suas vocant Mechanicas non hærere, eandem vero exemplis illustrassem sed literis transpositis hanc sententiam involventibus [Data æquatione quotcunque fluentes quantitates involvente fluxione invenire et vice versa] fundamentum ejus celassem: Respondit D. Leibnitius in hæc verba. Clarissimi Slusij Methodum Tangentium [id est methodum per differentias Ordinatarum] nondum esse absolutam Celeberrimo Newtono assentior et jam a multo tempore rem Tangentium longe generalius tractavi, scilicet per differentias Ordinatarum. Deinde methodum suam communicavit a mea vix abludentem præterquam in verborum et notarum formulis. Vtriusque fundamentum continetur in hoc Lemmate.
Hoc fecerunt Gregorius in Prop 7 Geometriæ universalis anno 1668 impressæ et Barrovius in ejus Lect 10 anno 1669 impressa, idque methodo consimili. Idem D. Leibnitius facere potuisset jam a multo tempore. Sed inversa tangentium Problemata differentiales & quadraturas reducere jam anno superiore minime noverat. Vide pag 65 l. 14, 15. Cum vero a Newtono didicerat Clarissimi Slusij methodum Tangentium nondum esse absolutam, sed Corollarium esse methodi generalis quæ extenderet se citra molestum ullum calculum ad abstrusiora problematum genera, etiam ad inversa tangentium problemata aliaque difficiliora, & quæ ad quantitates surdas & Curvas Mechanicas minime hæreret, & cujus ope Quadraturæ redderentur faciliores: cœpit is methodum Tangentium per differentias Ordinatarum ab alijs traditam jam longe generalius tractare quam antea, & novo nomine novisque symbolis ut suam ornare. Quo effectum est
Id est, vel . Et nota quod Differentiæ rectius decerentur partes. Sunt enim partes summarum non autem differentiæ, neque aliaquam habent relationem ad summas nisi quatenus sunt earum partes.
idque semper per quadraturas solas absque methodo generaliore quando datur relatio inter latere trianguli TBC.
Hæc Isagoge et Corollarium Propositionis ultimæ scripta sunt ubi liber prodijt: reliqua ex MS antiquo impressa sant.
idque nonnunquam per quadraturas nonnunquam methodis generalioribus.
 aliaque difficiliora. Vide etiam
aliaque difficiliora. Vide etiam
Simplicior est expressio . quæstiones de maximis et minimis aliasque quasdem determinari, & Problem
Vide etiam pag 30 & pag 47 lin 4
Gregorius ex unica tantum serie Newtonianam methodum invenit & Newtonum tamen inventorem primum libere agnovit: Leibnitius pluribus edoctus, fuit. Vide pag 30 & pag 47 lin 4, 8. & 71, 72.
Hic est tractatus de Analysi per æquationes numero terminorum infinitas supra impressus.
Hinc liquet methodum fluxionum non tantum ante annum 1669 Newtono involuisse sed etiam ad magnum perfectionis gradum eo tempore provectam fuisse.
② In the year 1671 I wrote a Tract concerning the methods of converging series & fluxions jointly but did not finish it, that part of it being wanting which related to the solution of Problems which could not be reduced to quadratures, as I mentioned in my letter to Mr Oldenburg dated 24. Octob 1676 which was published by Dr Wallis in the third Volume of his works. From this Tract I extracted in the year 1676 the following book of Quadratures; & therein I copied from the former Tract without any alteration the Tables set down in the tenth Proposition for squaring some Curves, & comparing them with the Conic Sections. In my Letter to Mr Coll dated 8 Novem. 1676 found by MrIones a mongst his Papers & published by him & dated 8 Novem. 1676 I had relation to this Book in saying Nulla extat Curva — — — adeo generaliter. This relates to Coroll. 2. Prop. 10 of this Book.
③ ∥ This Book was in the hands of Mr Ralpson & Dr Halley in the year 1691 as the former attested in print before his death & the latter still attests. And in the year 1692 at the request of Dr Wallis I sent to him the first Proposition of this Book with examples in first & second fluxions & before the end of the year he printed the the same in the second Volume of {his} Works which Volume came abroad in April 1693. And this was the first time that any Rule was published for finding second third fourth & other differences. But the Book continued in MS till the year 1704. And then in publishing it I wrote a Preface in which I affirmed that I found the method of fluxions gradually in the years 1665 & 1666. For I thought then that I might safely write this because Dr Wallis in the Preface to the first Volume of his works published in spring.
④ In the abovementioned Letter of 24 Octob 1676 at the request of Mr Leibnitz I described how before the Plague which raged in London in the years 1695 & 1696 by considering how to interpole the series of Dr Wallis I found the method of converging series together with the Rule for converting the dignities of Binomials into such series, & that Dr Barrow about the time that the Logarithmotechnia of Mr Mercator came abroad sent to Mr Collins a compendium of these series. A copy of this Compendium in the handwriting of Mr Collins was found by Mr Iones among the papers of Mr Collins & published after it had been collated with the original which Mr Iones borrowed of me for that end. The title thereof was Analysis per series numero terminorum infinitas. And in this Tract there are instances of calculating by the method of fluxions, this method being interwoven with that of Series. & it is therin affirmed that the method of series extends to all Problems & that ejus beneficio curvarum area & longitudinis &c (id modo fiat) exacte & Geometrice determinantur And therefore I then understood the method of Fluxions so far as it is conteined in the first five or six Propositions of the book of Quadratures. And by the Testimony of Dr Barrow & Mr Collins I understood it thus far some years before that time For Mr Collins in a Letter to Mr Strode And how this is done is explained in my said Letter of 24 Octob 1676. & illustrated with examples. And this is not to be done without the method of fluxions so far as it is conteined in the first five or six Propositions of the book of Quadratures. And therefore the method of fluxions so far as it is conteined in those Propositions was known to me when I wrote the said Letter of 24 Octob 1676 & even when I wrote the Analysis per Æquationes numero terminorum infinitas which was in the yeare 1669 it was known to me & by the Testimony of Dr Barrow & Mr Collins it was known to me some years before that. For Mr Collins in a letter to Mr Strode dated 26 Iuly 1672 & published by Order of the R. S. in the Commercium Epistolicum wrote thus. Mense Septembri 1668, Mercator Logarithmotechniam edidit suam, quæ specimen hujus methodi (i.e. serierum infinitarum) in unica tantum figura, nempe Quadraturam Hyperbolæ continet. Haud multo post quam in publicum prodierat Liber, exemplar ejus Cl. Wallisio Oxonium misi qui suam de eo judicium in Actis Philosophicis statim fecit; aliumque Barro{v}i{o} Cantabrigiam qui quasdam Newtoni chartas extemplo remisit: e quibus et ALIIS, quæ OLIM ab Auctore cum Barrovio communicata fuerant, patet illam Methodum a dicto Newtono ALIQVOT ANNIS ANTEA excogitatam & modo universali applicatam fuisse: ita ut ejus ope in quavis Figura Curvilinea proposita quæ una vel pluribus proprietatibus definitur Quadratura vel Area dictæ Figuræ, ACCVRATA SI POSSIBILE SIT, sin minus infinitè vero propinqua, Evolutio vel longitudo lineæ curvæ, Centrum gravitatis Figuræ; solida ejus rotatione genita, & eorum superficies; sine ulla radicum extractione obtineri queant. So then by the testimony of Dr Barrow founded upon papers communicated by me to him from time to time, I had brought the method to the perfection here described, some years before the Logarithmotechnia came abroad. In another Letter, Mr Collins saith, above two years before. By these testimonies it appears therefore that I had the method in the perfection here described before September 1666, that is so far as to square curves exactly when it may be done, or at least by continual approximation, & by consequence that I then understood the method of fluxions so far at least as it is conteined in the first five or six Propositions of the book of Quadratures. Which together with the testimony of Dr Wallis I recon sufficient to justify what I said in the Introduction to this Book.
① In December 1672 upon notice from Mr Collins that Mr Iames Gregory had a improved the methods of tangents of Dr Barrow so as to draw tangents without calcuclation & that Mr Slusius had such another Method which he intended to communicate to Mr Oldenburg, I wrote the following Letter to Mr Collins dated 10 Decem 1672. Ex animo gaudeo D. Barrovij — — — — reducendo eas ad series infinitas. you have here a description of the great extent of the method of fluxions, with an example of it in drawing of Tangents. The method here described was interwoven with another method in which I reduce equations to converging series.
② For in the year 1671 I wrote a Tract concerning the method of
NB. Hunc Librum de Quadraturis MS Halleius & Ralphsonus Anno 1691 manibus suis tractarunt uti posterior publice testatus est et prior adhuc testatur. Propositionem primam cum exemplis in fluxionibus primis & secundis inveniendis D. Wallisius anno 1672 a me accepit & eadem in secundo Volumine operum ejus anno proximo lucem vidit, & prima fuit hujus generis Regula quæ lucem vidit; estqus Regula illa verissima et maxime universalis. In Lemmate secundo libri secundi Principiarum mathematicorum Philosophiæ, Regulam illam synthetice demonstra & in Scholio quod Lemmati subjunxi dixi me Propositionem eandem totidem syllabis posui dixique me eandem prius in Epistola 24 Octob. 1676 ad Oldenburgum data posuisse. Hanc Epistolam D. Wallisius in tertio operum suorum volumine edidit, Et ibi habetur hæc Propositio totidem literis tanquam fundamentum methodi cujusdam ducendi tangentes, determinandi maxima & minima, quadrandi figuras & similia peragendi, in qua non hæret{ur} ad Æquationes Radicalibus unam vel utramque Indefinitam Quantitatem involventibus utcunque affectas. Et eodem fundamento dixi me ad Theoremata quædam generaliora quadrandi curvas pervenisse. Et Theorema primum (sc. ubi posui et exemplis illustravi addidique me pro Trinomijs etiam et alijs quibusdam Regulas quasdam concinasse. Est autem hoc Theorema primum idem cum Propositione quinta libri de Quadraturis, Et Theorema primum pro Trinomijs idem cum Propositione sexta ejusdem libri. Et hæ duæ Propositiones pendent a Propositionibus quatuor primis ejusdem libri. Et propterea methodus fluxionum quatenus continetur in Propositionibus sex primis Libri de Quadraturis mihi innotuit anno 1676. Sed et Propositio septima et octava, ejusdem sunt generis. Nona autem ac decima requirentur ad solutionem Problematis quod posui in Epistola ad D. Collinium Novem. 8 1676 data & ad Ioneso edita verbis sic Latine redditis Nulla extat Figura curvilinea cujus Æquatio — — — haud tamen adeo generaliter. ☉ ☉ Et in eadem Epistola Ordinatæ Curvilinearum quæ cum Ellipsi et Hyperbola comparari possunt eædem ponuntur | habentur ac in Tabula secunda Prop. X libri de Quadraturis. Ideoque Tabula illa (et propterea methodus fluxionum cujus ope Tabula constructa fuit) mihi innotuit anno 1676: immò et annis aliquot antea. Nam dixi in Epistola illa me Theoremata pro Comparatione Curvarum cum Conicis Sectionibus in Catalogum dudum retulisse.
Anno igitur 1676 Methodum fluxionum intellexeram quatenus in Libro hocce de Quadraturis exponitur. Sed et anno 1671 eandem intellexeram Namque in Epistola mea prædicta ad D. Oldenburgum 24 Oct. 1676 scripta, dixi me in Tractatu quem tunc ante quinquennium de Seriebus conscripseram me etia alia præter methodum serierum haud pauca congessisse inter quæ erat methodus ducendi Tangentes quam solertissimus Slusius ante annos duos tresve tecum communicavit; de qua tu (suggerente Collinsio) rescripsisti eandem mihi etiam innotuissi. Diversa ratione in eam incidimus. Et subinde dico me in hanc methodum tangentium incidisse per methodum quandam quæ ad quæstiones de maximis et minimis, de que quadraturis & alijs se extendit & quantitates surdas non moratur, & cujus fundamentum continetur in hac sententia, Data æquatione fluentes quotcunque quantitates involvente, Fluxiones invenire; et vice versa. De his omnibus hic loquor tanquam mihi ante quinquennium cognitis. Sed et in Epistola [ad D. Collinium 10 Decem. 1672 data hanc methodum sic descripsi. Ex animo gaudeo — — — ne grave ducas. Methodus fluxionum hic perspicue describitur. Et præterea, in Epis] eadem
— nec prius cum amicis communicare cœpit quam ab Anglia discesserat, & postquam ab Oldenburgo acceperat, remisit {illeg} acce{illeg} ut Anglis ignotam.
Methodum exhibendi Arcum cujus sinus datus Leibnitius ab Oldenburgo postea quæsivit, Maij 12 1672, ideoque nondum intellexit
p. 38. a Collinius jam ante quadrennium series Newtonianas ante triennium Gregorianas cum amicis communicare cœpit. Leibnitius in Anglia diversabatur anno superiore & hujusmodi series nondum communicaverat, nec prius cum amicis communicare cœpit quam ab Anglia discesserat, Et subinde cum series aliquas ab Oldenburgo acceperat, quas a suis diversas esse tum fatebatur, tandem unam acceptarum remisit Oldenburgo ut Anglis ignotam. Nullas autem communicavit nisi quas ab Oldenburgo acceperat.
b Methodum exhibendi arcum cujus sinus datur Leibnitius ab Oldenburgo postea quæsivit, Maij 12 1676, ideoque nondum habuit. Sola methodus transmutatoria quam postea communicavit non dat arcum ex Sinu, ideoque non est methodus de qua hic agitur, Series forsan duas habere potuit sed methodum qua inventæ sunt nondum habuit.
p. 41. Hanc seriem D. Collins initio anni 1671 a Gregorio acceperat ut supra; D. Leibnitius cum amicis in Gallia opusculum de eadem hoc anno communicare cœpit, celata hac Epistola.
p. 42. a His verbis Leibnitius series acceptas a suis diversas esse testatur et unam tamen acceptarum quasi Anglis ignotam anno proximo pro sua remisit. Miror quænam fuerint ipsius series quibuscum series ab Oldenburgo missas jam comparare non potuit, et quare lucem nunquam viderunt.
p. 42. b Hoc nunquam fecit Leibnitius . . . . . . vindicandi quasi a nemine acceptam quia longe diversam ab ijs quas per Georgium Mohr acceperat Certe series hæc Leibnitio ipso teste non est Leibnitiana quia non diversa ab ijs quas ab Oldenburgo acceperat. Series hasce mirabatur ut valde ingeniosas sed demonstrare nondum potuit Postulat igitur demonstrationem sibi mitti, et ut eandem obtineat, sua ab his longe diversa circa hanc rem meditata promittit.
*** ad verba [Via quadam sic satis singulari] notetur. Leibnitius in Epistola 26 Octob 1674 data dicebat series suas una et eadem methodo inventas esse. & hanc methodum jam vocat viam quandam satis singularum. quas per Mohrum mox accepit. Series per Mohrum acceptas ut valde ingeniosas laudabat sed demonstrre nondum poterat. Postulabat igitur demonstrationem sibi mitti, et ut eandem obtinereat sua ab his longe diversa circa hanc rem meditata promittebat.] Sed series ab Oldenburgianis diversas, et viam singularem qua ejusmodi series prodirent, nunquam communicavit.
. {☾} .
Seriem Gregorianam ab Oldenburgo acceptam Mense Maio a suis distinuerat. Opusculum de hac serie compositum hoc anno cum amicis in Gallia communicare cœpit celata Oldenburgi communicatione. Seriem eandem quasi Anglis ignotam jam promittit se cum Oldenburgo communicaturum, & proximo anno communicavit. Et prætendit se cum amicis in Gallia ante biennium id est anno 1672 communicasse. Prætendebat etiam ante menses quatuordecim
suas in
Series mense Aprili ab Oldenburgo missas, Leibnitius a suis diversas esse agnovit Missarum una erat series Gregorij pro arcu circuli ex tangente alia erat series Newtoni pro arcu ex sinu. Opusculum De serie priore compositum Leibnitius hoc anno cum amicis in Gallia communicare cœpit, Celata Oldenburgi epistola. Et jam promittit se hanc seriem quasi Anglis ignotam cum Oldenburgo communicaturum, et simili fide dicit se eandem jam plusquam biennio abhinc cum Geometris in Gallia communicasse. Seriem alteram easdem laudabat ut novas & valde ingeniosas & ideo postulabat. earum demonstrationem ad se mitti, quasi series nullas ab Oldenburgo prius accepisset. Et hoc parto . . . . . acceperat.
a Quasi Leibnitius nesciret hanc Quadraturam Anglis Gregorianam esse &c innotuisse.
b Anno 1673 Leibnitius in Anglia commorans de hujusmodi seriebus aliquid audire potuit. Anno proximo jactabat se hujusmodi seriem unam atque alteram habere sed nullam cum Anglis communicavit, anno tertio mense Aprili vel Maio accepit ab Oldenburgo ejusmodi series aliquot quas a suis diversa, esse agnovit. Eodem anno opusculum de serierum acceptarum una cum amicis in Gallia communicare cœpit, celata Oldenburgi epistola. Et jam promittit se hanc seriem quasi Anglis ignotam Oldenburgo remissurum.
b Quasi ante Annum easdem non accepisset ab Oldenburgo.
c Opusculum prædictum de Quadratura arithmetica D. Leibnitius polire perrexit.
When Mr Leibnitz published the series o Gregory & such other things as he had notice of from England for preventing disputes & doing justice to every body: he should have acknowledged the correspondence he had kept with Mr Oldenburg & what he had received from England or seen in the hands of Mr Collins relating to the things which he published.
a He omits the greatest part of my method of series & its connexion with the method of Fluxions.
b He gives Mr Fatioo the lye who had seen my ancient papers, & pretends that when I represented that in the year 1671 I wrote a tract on the method of series & another. method founded on this Proposition Data æquatione fluentes quantitates involvente invenire fluxiones & I did not dream of the calculus of fluents & fluxions
c He affirms falsly that I use prict letters for the differential characters For fluxions & differences are quantities of a different kind.
d He places the invention of the methods in the invention of the symbols used in them as if new names & new symbols ought to pass for new inventions.
e He affirms falsly that in my Principles I had frequent occasion to use my calculus of fluxions for after I had invented the Propositions by Analysis I demonstrated them by composition.
f He affirms falsly that in this book there is no footstep of this Calculus for the 2d Lemma of the second book conteins the elements of this calculus And the Scholium upon this Lemma asserts this Calculus to my self.
g Prickt letters appeared in the second volume of the Works of Dr Wallis which was printed in the year 1693 & mentions that what he there printed of this matter he had from me in the year 1692. My Tract of Quadratures was handed about in London in 1691. I made much use of it in writing my book of Principles & composed it many years before but never placed the method in the use of prickt letters: for the Introduction to this book was writ in the year 1704 & conteins a description of the method without the use of prickt letters.
h Incrementum constans ipsius x nunquam notabam per x punctatam uno puncto. Illud noto per ; & ubi est unitas, per o
i Notatio mea per o falso dicitur calculi differentialis commoda destruere. Notatio est elegantior et utilior.
k Regulam circa gradus utiliores falsam non dedi Mathematicus ille eminens erravit. Annon hic est Bernoullius.
l Apparet Leibnitium Anno 1689 ubi scripsit Tentamen De motuum Cœlestium causis, rectam methodum differentiandi differentiali non intellexisse. Rectam methodum Wallisius noster e literis nostris anno 1692 ad eum missis descripsit in secundo Operum volumine anno 1693 in lucem emisso, Eandem recte descripsi in Propositione prima libri de Quadraturis; et hic liber manibus amicorum terebatur anno 1691, & subsidio mihi fuit annis ubi scribebam Principia Philosophiæ et multa ante conscriptus fuit. Et recte capiendo fluxiones fluxionum et momenta momentorum inveni Demonstrationem Theorematis Kepleriani anno 1677 & Curvaturam Curvarum ante annum 1673 ut ex epistola mea 10 Decem 1672 ad Collinium data manifestum est.
a literas punctatas uno duobus tribus &c punctis superpositis non pro dx, d{d}x, d3x; dy, ddy &c nunquam adhibuit. Hæ sunt quantitates diversi generis. Ex verbis ejus nunc adhibet incidit suspicio quod is fuit author Epitomis libri De Quadratura Curvarum in Actis Erudit. anno 1705 impressæ unde nata est hæc controversia.
b In Principijs Naturæ Mathematicis, calculo fluxionum utendi nulla erat occasio. Invent{a} sunt Propositiones per hanc Analysin, demonstratæ vero per synthesin.
c
1 Methodum Serierum a me inventam minuit.
2 Somnia narrat. Ex Epistola 24. Octob. 1676 data certissimum est me fluxionales æquationes per ea tempora habuisse.
3 fallitur. Pro symbolis differentiarum non utor symbolis fluxionum. Hæ sunt quantitates diversi generis.
4 Fallitur. Methodi non consistunt in formulis verborum et symbolorum. In tractatu de quadraturis olim scripto literis punctatis utor, in ejus Præfatione nuper scripta methodum fluxionum absque literis punctatis describo.
5 Falitur. In libro Principiorum nullam habui occasionem utendi calculo fluxionum Propositiones inveni per Analysin demonstravi per synthesin. Analysis tamen ita per Demonstrationes syntheticas ita elucet ut Marchio Hospitalius scripserit librum pene totum ex hac Analysi constare et ipse Leibnitius agnoverit me omnium primum specimine publice dato ostendisse quod partem hujus methodi nobilissimam et latissime patentem haberem: eam utique qua solidum minimæ resistentiæ, Curva celerrimi descensus, Catenaria et Vellaria inventa fuerunt.
6 Fallitur. Nam Lemma secundum libri secundi & Scholium ejus continet elementa hujus calculi.
7 Fallitur. Nam Volumen tertium editum fuit anno 1699. Extant literæ punctatæ in volumine secundo quod impressum fuit anno 1693. Liber autem de Quadraturis in manibus amicorum terebatur anno 1691 et deinceps & in meis dum Principia Philosophiæ scriberem & multo ante compositus fuit.
8. Fallitur. Incrementum constans ipsius x nunquam notabam per punctatum uno puncto. Illud noto per : et ubi est unitas, per o.
9. Fallitur. Notatio mea per o non destruit commodo calculi differentialis se e contra, commodior est.
10 Fallitur. Regulam circa gradus ulteriores veram dedi.
11 Annon Mathematicus ille eminens Bernoullius est? Anne author Epistola seipsum hic citavit.
12 Accusationem probare debuit. Non probata pro calumnia haberi debet.
13 Methodum veram Leibnitius ipse non habuit Anno 1689 ubi scripsit Tentamen suum de motuum cœlestium causis. Post annum 1690 methodus illa cœpit a Leibnitianis intelligi. Anno 1696 Dn. Marchio Hospitalius eandem edidit. Methodum veram Wallisius a me accepit anno 1692 & anno proximo in secundo Operum Volumine edidit. Eadem describitur in Propositione prima libri de Quadraturis olim scripti. A momentis secundis multæ Propositiones in Libris Principiorum pendent. Hujus generis est determinatio Propositionis Keplerianæ quam anno 1677 inveni. Dixi etiam in Epistola 10 Decem 1672 ad Collin{um} data methodum de qua ibi locutus sum, id est methodum fluxionem ad curvaturas Curvarum se extendere. Hæ autem pendent a fluxionibus secundis. Regulam utique Fluxionum primarum intelligenti Regula secundarum latere noti potest cum sit eadem cum Regula primarum ut Propositionem primam Libri de Quadraturis consulenti statim patebit
complaint that Newton in his Principles & book of Quadratures had used fluxions for the differences of Mr Leibnitz the inventor of {ean} {illeg}{thor} as Honoratus Faber substituted progressions of Motion for the method of Cavellerius.
1. It was hoped that a few copies of the following Commercium Epistolicum printed off & sent to Mathematicians who were able to judge of these things, might it have silenced the complaint that Mr Newtons book of Quadratures was a peice of Plagiary: but Mr Leibnitz & his friends have declined answering it, & endeavoured to run the dispute into a squabble about other matters occult qualities, miracles, gravity, attraction sensoriums, the perfection of the world, a vacuum atoms the solving of problems & the like: all which are nothing to the purpose which are nothing to the purpose. And tho Mr Leibnitz is dead, yet this squabbling humour is still continued by some of his friends. And therefore it has been thought fit to publish this Commercium Epistolicum together with the Account given thereof in the Philosophical Transactions for Ianuary 171 & so leave it to posterity to judge of this matter by the ancient Records.
3 Against the credit of these Records it has been objected that the Committee of the R. Society published every thing that made against Mr Leibnitz & omitted every thing that made against Mr Newton. The objection was made by Mr Leibnitz but had nothing more in it then clamour. For in a Postscript of his first Letter to Abbe Conti, for proving this he wrote that in his second voyage into England Mr Collins shewed him part of his correspondence & he observed there that Mr Newton acknowledged his ignorance in many things & said (among other things) that he had found nothing about the dimension of the celebrated curvilinears besides the dimension of the Cissoid But saith he they have supprest all this. And Mr Newton in his Letter to Abbe Conti dated 26 Feb. 171 replied that this passage was not suppressed but published in the Commercium pag 74 lin. 10 & 11. Mr Leibnitz in his Answer written to Abbé Conti Apr. 9 1716 acknowledged that he had been mistaken, but saith he, I'le cite another instance. Mr Newton owned in one of his Letters to Mr Collins that he could not find the content of second sections (or second segments) of Spheroids or such like bodies: & the Commmitte had omitted that. And Mr Newton in his Remarks upon the Letter of Mr Leibnitz replyed that if the Committee had omitted it they would have done right, it being nothing to the point in question, but on the contrary, Mr Collins in a Letter to Mr Iames Gregory the 24th of December 1670, & in an other to Mr Bertet the 21th of Feb. 1671, both printed in the Commercium Epistolicum pag. 24, 26, wrote that his (Mr Newtons) method extended to second segments of round solids. And Mr Oldenburg wrote the same thing to Mr Leibnitz himself the 8th of December 1674. See the Commercium Epistolicum pag 39. So that the accusation was groundless & amounts to nothing more then a piece of railery.
2 The Letters of Mr Leibnitz to Mr Oldenburg are dated 3 Feb. 20 Feb. 30. Mar. 26 Apr. 24 May. 8 Iune, 1673; 15 Iuly, 26 Octob. 1674; 30 March, 20 May, 12 Iuly, 28 Decemb. 1675; 12 May, 27 {O}Aug. 18 Novem 1676 & 21 Iune & 12 Iuly 1677. And these are all except the 3d & the five last entered in the Letters books of the R. S. No 6 pag 35, 34, * 101, 115, 137; & No 7 pag. 93, 110, 213, 235, 149, 189, And the Originals of all these letters except that of 27 Aug. 1676 which was published by Dr Wallis, & that of 18 Novem following are stilll extant in the hand writing of Mr Leibnitz. The Letters of 15 Iuly & 26 Octob. 1674; 12 Iuly & 28 Decem. 1675 & 21 Iune & 12 Iuly 1677 were also published by Dr Wallis. And all these Letters together with the Letters of Mr Oldenburg to Mr Leibnitz copies of which are still preserved make up the continued correspondence between Mr Leibnitz & Mr Oldenburge from Feb 3 167 to the death of Mr Oldenburg excepting that the Letter by which Mr Leibnitz desired a collection of Gregories Letters & that of Mr Oldenburg by which he sent to Mr Leibnitz that collection The Letters of Mr Leibnitz ran upon numbers till Iune 8 . Then Mr Leibnitz began to study the higher Geometry & the correspondence ceased for a time. And the next year in Iuly Mr Leibnitz renewed the correspondence beginning his Letter of Iuly 15th with these words Diu est quod nullas a me habuisti litteras. And from thence forward the correspondence continues without intermission to the death of Mr Oldenburg except that the aforesaid two Letters are wanting [the latter of which is extant but was not published] having nothing in it material to the controversy.] So then the Commercium Epistolicum of Mr with Mr Oldenburg Mr Collins & Mr Newton is here printed entire except those two Letters. For Mr Collins & Mr Newton had no correspondence with him except only by means of Mr Leibnitz.
4 When the Commercium Epistolicum came abroad which was in the end of the year 1712. Mr Leibnitz to avoid answering it pretended all the two next years that he had not seen it, nor was at leasure to examin it, but had referred it the judgment of an able & impartial Mathematician. And the judgment of this Mathematician dated 7 Iune 1713 was inserted into a scurrillous paper dated 29 Iuly 1713 & dispersed over all Europe, without telling the name of the Mathematician or that of the Printer or City where it was printed. [But in the end of the year 1715 & begining of the year following Mr Leibnitz to give the judgment of the Mathematician more credit began to tell the world that it was Mr Iohn Bernoulli & to make this probable he translated the Letter of 13 Iune 1713 into French & in the translation omitted the sentence quemadmodum ab eminente quodam Mathematico dudum notatum est, by which words the author of the Letter cited Mr Iohn Bernoulli as a person different from himself.]
6 In this flying paper it is said that prickt letters appeared first in the third Volume of Dr Wallis his works. And that Mr Newton did not understand how to find second differences till it was commonly understood by others. But this is a misrepresentation. The third Volum e came abroad in 1699. But prickt letters appeared in the second Volume which came abroad in Spring 1683. In this Volume Dr Wallis published the first Proposition of Mr Newtons book of Quadratures illustrated with examples in first & second differences. And this is the first line that any Rule came abroad for finding 2d, 3d, & fourth differences & so on. Dr Wallis published also at the same time the fift Proposition of the Book of Quadratures & represented that he had received these things from Mr Newton by Letters dated Aug 27 & Sept 17 1702. This Proposition depends upon the four preceding Propositions & therefore the first five Propositions of that Book were in being in the year 1692. This Book in MS was in the hands of Dr Halley & Mr Ralpson in the year 1691 as Mr Ralpson has publickly attested & Dr Halley still attests. And this was before the differential method began to make a noise abroad & may suffice to clear this Book from the accusation of plagiary which gave a beginning to these disputes. In the XIVth Proposition of the second Book of Principles you have an instance of solving Problemes by second Differences. And this is the first instance of that kind made publick.
It is true that Mr Leibnitz was the first who published a Rule for first differences. But he should then have acknowledged (as he did in his Letter of 21 Iune 1677 written to Mr Oldenburg) that he knew by Mr Newtons Letters that Mr Newton had a Method which did the same things. Or rather, he should have acknowledged that Mr Newton gave him light into the method. For Dr Wallis in the Preface to the two first volumes of his works published in spring 1695 wrote that the method of fluxions & differential Calculus is one and the same method differing only in some modes of expression & that Mr Newton in his Letters of 13 Iune & 24th Octob 1676 explained to Mr Leibnitz this Method found by him ten years before that time or above; that is, in the year 1666 or before. The editors of the Acta Eruditorum the next year in giving an account of these two Volumes cited a sentence out of this Paragraph & therefore knew of it. And Dr Wallis gave notice of it to Mr Leibnitz himself in a Letter to him dated & printed in the third Volume of his works
The Original Letters & Letter Books from whence the Commercium Epistolicum was printed are still kept in the Archives of the R. S. & & no question is made in England of their sincerity They have also upon occasions been shewed to strangers who have viewed them & collated some of them with the printed Letters to their satisfaction.
It has been Objected with clamour that when Mr Newton wrote the Scholium at the end of the Book of Quadratures he did not understand second differences: but the Objector knew by the first Proposition of the Book that he did understand second differences.
An Account of what has been done
since the publishing of the
Commercium.
The Commercium Epistolicum was published before the end of the year 1712 & no answer has hitherto been given to it: for it is unanswerable. Mr Leibnitz pretended the two first years that being then at Vienna he had not seen the Book, but had written to an able & impartial Mathematician to give his judgment upon it. And the Answer or pretended answer of the Mathematician dated 7 Iune 1713 was inserted into a scurrilous paper dated 29 Iuly following & printed without the name of the author or printer or Mathematician or place where it was printed & the paper was dispersed over Europe: & it was two years & an half before Mr Leibnitz began to tell the word that the Mathematician was Iohn Bernoulli. The Letter ascribed to him was in these words. Videtur N...sis occasionem nactus serierum opus multum promovisse per extractiones radicum, quas primus in usum adhibuit et quidem in ijs excolendis ut verisimile est ab initio omne suum studium posuit; nec credo — — — alijs fuisset familiaris &c Thus far the Mathematician. His first argument against Mr Newton is founded upon a supposition that prickt letters are essential to the method of fluxions, which is not so. In the Introduction to the Book of Quadratures Mr Newton teaches the method of fluxions & illustrates it with examples & yet there is not a prickt letter in all that Introduction. In the second Lemma of the second Book of Principles Mr Newton demonstrated the Elements of the Method of fluxions: & yet there is not a prickt letter in all that Lemma. In his Letters of 10 Decem 1673 & 24 Octob 1676 he wrote that he had a general Method of solving Problems of which the method of Tangents of Slusius was a Corollary & which stuck not at surds & in the latter of these two letters he added that this Method was founded in the sentence Data æquatione fluentes quotcunque quantitates involvente fluxiones invenire & vice versa. And will any impartial man affirm that when Mr Newton wrote those two Letters, he did not so much as dream of the method of deducing fluents from fluxions & fluxions from fluents because there are no prickt letters in those two Letters. Sometimes he used prickt letters & sometimes letters without pricks or other symbols & sometimes he wrote of it without any symbols. What symbols he used in his Analysis per series numero terminorum infinitas has been shewed above. There he used the symbol in the very same sence in which Mr Leibnitz uses the symbol , & therefore in those days he dreamt of the summatory method which is the inverse of the differential. And when Mr Leibnitz was in England the second time he saw Mr Newtons Letter of 24 Octob. 1676 in which this Analysis is mentioned by the name of Compendium serierum, & in the hands of Mr Collins he saw many of the Letters of Mr Newton & Mr Gregory which ran principially upon series & had then an opportunity to ask for this Compendium serierum .
The Mathematician says further that Mr Newton in his Principles of Philosophy had frequent occasion to use prict letters & yet used them not: but the truth is, he had no occasion to use them in that book. For that book is written by composition after the manner of the Ancients: but yet the Analysis by which it was invented shines through the composition; & this was acknowleged formerly both by the marq. de l' Hospital & by Mr Leibnitz himself as has been mentioned above
The Mathematician saith further that prickt letters appeared first in the third volume of the works of Dr Wallis many years after the differential calculus had obteined every where. But he hath misrepresented the matter. The third Volume of Dr Wallis Works came abroad in the year 1699 & prickt letters appeared in his second volume which came abroad in spring 1693, which was two years before Dr Wallis heard that the Differential Method began to be celebrated abroad
The second argument of the Mathematician to prove that the calculus of fluxions was not older then the differential calculus is that Mr Newton did not understand how to find the fluxion of fluxions or difference of differences. And yet the Mathematician knew by the first Proposition of the Book of Quadratures but Newton did understand how to find the difference of differences or second difference & the difference of second differences or third difference & so on in infinitum. And if you look into the Book of Principles lib. 2 Prop. 4 you will see that he there knew how to find the difference of moments or second difference. And I do not meet with any ancienter instance made publick of working in second differences.
Pag. 1. lin. 20. — prima (p. 37, 38.) Add: Et symbola Leibnitij nondum obtinuerunt in Anglia.
Newtonus Tractatum suum de Quadraturis dudum scrip sit quippe Nam plurima ex eo citata sunt in Epistolis 24 Octob. & 8 Novem 1676 (p. 34) In Epistola priore recitantur Ordinatis Curvarum quarum collationem cum Sectionibus Conicis Newtonus tum ante annos quinque (seu anno 1671) in Tabulam retulerat (pag. 178. In Epistola posteriore anno 1711) a Ionesio edita Corollarium secundum Propositionis decimæ fusius enarratur, his verbis. Nulla extat Curva cujus Æquatio ex tribus constat terminis — haud tamen adeo generaliter. Hæc sunt omnium quæ in Libro de Quadraturis habentur difficilima & absque methodo fluxionum aut simili inveniri non potuerunt & abunde satis demonstrant, methodum illam quatenus in Propositionibus decem primis Libra illius habetur, Newtono innotuisse anno 1676 aut & antea.
Object. 1. Newtonus introducit attractiones i.e. qualitates occultas & vult gravitatem ejusmodi esse.
Resp. Quo sensu Newtonus voce attractionis utitur, ostenditur ex ejus supra (pag. 35, 36): libro Principiorum: & plenius patet ex sequentibus. In Introductione ad Sect. XI Lib. 1 Newtonus sic scribit. Qua de causa jam pergo motum exponere corporum se mutuo trahentium, considerando vires centripetas tanquam Attractiones, quamvis fortasse si physice loquamur, verius dicantur impulsus. In Mathematicis jam versamus, & propterea missis disputationibus Physicis, familiari utimur sermone, quo possimus a Lectoribus Mathematicis facilius intelligi. Et in Scholio sub finem hujus Sectionis: Vocem Attractionis hic generaliter usurpo pro corporum conatu quocunque accedendi ad invicem sive conatus ille fiat per ab actione corporum vel se mutuo petentium, vel per spiritus emissos se agitantium, sive is ab actione Ætheris, aut Aeris Medijve cujuscunque seu corporei seu incorporei oriatur corpora innotantia in se invicem utcunque impellentis. Eodem sensu generali usurpo vocem Impulsus, non species virium & qualitates Physicas sed quantitates & proportiones Mathematicas in hoc Tractatu expendaris, ut in Definitionibus explicui In Mathesi investigandæ sunt virium quantitates & rationes illæ quæ ex conditionibus quibuscunque positis consequuntur: deinde ubi in Physicam descenditur, conferendæ sunt hæ rationes cum Phænomenis ut innotescat quænam virium conditiones singulis corporum attractivorum viribus competant
Object. 2. Newtonus asserit Deum habere sensorium
Resp. Newtonus per Sensorium nihil aliud intelligit quam spatium infinitum tanquam locum in quo Deus omnia sentit. Sic enim liquitur de Deo: Is totus est sui similis, totus oculus, totus auris, totus cerebrum, totus brachum, totus vis sentiendi intelligendi et agendi: sed more minime humano, more minime corporeo, more nobis prorsus incognito. Vt cæcus non habet idæam colorum, sic nos ideam non habemus modorum quibus Deus sentit & intelligit omnia. Corpore omni & figura corporeo destituitur: ideoque videri non potest, nec sub specie rei alicujus corporei coli debet.
Object. 3 Newtonus introducit miracula in Philosophiam
Resp. Leibnitius vocat miracula, quæ quotidie eveniunt nemine admirante.
And whereas one of the methods of regression which Mr Newton sent to him at his own request & which upon the first reading he did not know to be his own nor understand he afterwards claimed as his own invention by pretending that he had forgot it till he found it in one of his old Papers: it lies upon him in point of candour & justice either to prove that he found it & forgot it before he wrote to Mr Newton for it or else publickly & in express words to renounce his claim to it for preventing future disputes about it.
It is therefore expected that Mr Leibnitz de renounce all right to this method as first Inventor, as well as to the Differential method of Mouton as second Inventor. For second Inventors have no right. The sole right is in the first Inventor untill another finds out the same thing apart: in which case to take away the right of the first Inventor & divide it between him & that other, would be an Act of Injustice.
Mr Leibnitz in (his Letter of 1711 has opposed his own candor to the arguments of Dr Keill as if it were injustice to question it, that is to refuse his own testimony for himself, & in the same Letter he has in an arbitrary manner without who much as one argument to justifie himself called the candor of Mr Newton for publishing that he found the method of fluxions gradually in the years 1665 & 1666; & now it mutually comes upon him to satisfy the world about his own candor & integrity in the ten or twelve particulars last above mentioned. Nec lex est justior ulla.
And whereas he has in his Theodicee accused Mr Newton of making gravity an occult quality & a miracle & thereby introducing occult qualities & miracles into Philosophy & yet Mr Newton has no where declared any opinion about the cause of gravity: it lies upon him in point of candor & justice to beg Mr Newtons pardon publickly for endeavouring by such indirect & unfair practise to prejudice the world against him. The Philosophy which Mr Newton in his Principles & Opticks has pursued is experimentall & it is not the business of Experimental Philosophy to teach the causes of things any further then they can be proved by experiments. And whereas Mr Leibnitz is of opinion that nothing is done by election without a reason, or in other words that all things are governed by fate & necessity & that God is a supramundane intelligence & the souls of men do not act upon their bodies but all animal motion is performed without any other cause than mechanism & man himself is a meer machine if he would forbear to trouble the world with such conjectures & teach nothing more then he can Prove by experiments his Philosophy would be of better credit.
And whereas Mr Newton sent him at his own request a method of regression which upon the first reading he did not know to be his own nor understand, but so soon as he understood it he claimed it as his own by pretending that he had forgot it untill he found it in his old papers: it lies upon him in point of candor & justice either to prove that he was the first inventor of this method, or to renounce his claim to it for preventing future dispute about it.
None fuller of Miracles & occult qualities than that.
None more occult mysterious miraculous & trifling than that which supposes every thing, proves nothing, & excludes the proof of a Deity from phænomena.
Mr Leibnitz in his Theodicee has accused Mr Newton of introducing occult qualities & miracles into philosophy upon a supposition that he make gravity an occult quality seated in the will of God. And yet Mr Newton in his Optiqus (Quest 22 has written expresly, to the contrary. Qua causa efficiente hæ [gravitatis, virtutisque magneticæ et Electricæ {illeg} vel alterius cujuscunque attractiones peragantur, saith he, in id vero hic non inquiro. Quam ego attractionem appello, fieri sane potest ut ea efficiatur impulsu vel alio aliquo in universum solummodo vim aliquam significare intelligatur qua sit illa vis. Nam ex phænomenis Naturæ illud nos prius edoctos leges & proprietates istius attractionis; quam in id inquirere par sit quanam efficiente causa peragatur attractio. And a little after he mentions the same attractions as forces which by phænomena appear to have a being in nature & tho their causes be not yet known & distinguishes them from occult qualities which are supposed to flow from the specific forms of things And in the beginning of his Principia Philosophiæ speaking of the centripetal forces & attractions he saith: Virium causas et sedes physicas jam non expendo. And a little after: Voces autem attractionis impulsus vel propensionis cujuscunque in centrum, indifferenter & pro se mutuo promiscue usurpo, has vires non Physice sed Mathematice tantum considerando. Vnde cæveat Lector ne per hujusmodi voces cogitet me speciem vel modum actionis causamve aut rationem physicam alicubi definire, vel centris (quæ sunt puncta mathematica) vires vere et physice tribuere, si forte aut centra trahere aut vires centrorum esse dixero.
And whilst Mr Leibnitz has taught that God is intelligentia supramundana & that all animal motion (even that of man) is purely mechanical, & that there no election of any thing without a reason, that is, none at all, but all things are by fate & necessity: it lies upon him to satisfy the world that it may be proved by phænomena that there is a God in whom we live & move & have our being.
And whereas Mr Newton sent him at his own request a method of Regression, which upon the first reading he did not know to be his own, nor understood it, but so soon as he understood it he claimed as his own by pretending that he had found it long before, & had forgot it, as he perceived by his old papers: it lies upon him in point of candor & justice, either to prove that he was the first inventor of this method, or to renounce his claim to it for preventing future disputes.
It is therefore expected that Mr Leibnitz do renounce all right to this method as first inventor, as well as to the Differential Method of Mouton as second Inventor. For second Inventors have no right. The sole right is in the first Inventor untill another finds out the same thing apart: in which case to take away the right of the first Inventor & divide it between him & that other would be an Act of injustice.
✝ For this reason Mr Newton is silent about the cause of gravity, there occurring no experiments or phænomena by which it it could be proved what was the causes thereof. And this he has abundantly declared his Principles, neare the beginning, in these words: Virium causas et sedes Physicas jam non expendo. And a little after: Voces attractionis impulsus vel propensionis cujuscunque in centrum, indifferenter & pro se mutuo promiscue usurpo, has vires non physice sed Mathematice tantum considerando. Vnde caveat Lector ne per hujusmodi voces cogitet me speciem vel modum actionis causamve aut rationem physicam alicubi definir{e} vel centris (quæ sunt puncta mathematica) vires vere & physice tribuere si forte aut centra trahere aut vires centrarum esse dixero. And in the end of his Opticks[1]: Qua causa efficiente hæ attractiones [sc. gravitas visque magnetica et electrica aliæque] peragantur, in id vero hic non inquiro. Quare ego attractionem appella, fieri sane potest ut ea efficiatur impulsu vel alio aliquo modo nobis incognito. Hanc vocem attractionis ita hic accipi velim ut in universum solummodo vim aliquam significare intelligatur qua corpora, ad se mutuo tend{e}nt, cuicunque demum causæ attribuenda sit illa vis. Nam ex phænomenis naturæ illud nos prius edoctos oportet quænam corpora se invicem attrahant & quænam sint leges & proprietates istius attractionis; quam in id inquirere par sit quanam efficiente causa peragutur attractio. And a little affter, he mentions the same attractions as forces which by phænomena appear to have a being in nature & may be usefull in explaining Nature tho their causes be not yet known & distinguishes them from occult qualities which are supposed to flow from the specific forms of things. But And in the Scholium all the end of his Principles, after he has mentioned the properties of gravity he adds: Rationem vero harum gravitatis proporietatum ex Phænomenis &c . . . . non habent. Notwithstanding all this Mr Leibnitz has accused Mr Newton of making gravity an occult quality & a miracle. And therefore It lies upon him in point of candor & justice to beg Mr Newton's pardon publickly for endeavouring by such indirect & unfair practises to prejudice the learned part of Europe against him.
And whereas this Philosophy of Mr Liebnitz is thought by some to weaken all the arguments for a Deity taken from Phænomena, it lies upon him in point of religion either to show that his Philosophy is not of such a nature & to declare that he is not offended with Mr Newton for insisting upon such arguments, or to beg pardon of all mankind who beleive a And yet the Editors of the Acta Eruditorum have accused him of denying that the cause of gravity is mechanical tho he is silent about that cause & have compared an Agent which he calls a subtile Spirit to Dr H Mores hylarcic Principle. tho he is silent about the nature & cause of that Agent, & Mr Leibnitz has accused him of making Gravity an occult quality & a miracle.
The Philosophy which Mr Newton in his Principles & Opticks has pursued is experimental, & it is not the business of experimental Philosophy to teach the causes of things any further then they can be proved by experiments. We are not to fill this Philosophy with opinions which cannot be proved by Phænomena. In this Philosophy Hypotheses have no place unless as conjectures or Questions proposed to be examined. by experiments. For this reason Mr Newton in his Optiques distinguished those things which were made certain by experiments from those things which remained uncertain & which he therefore proposed in the end of his Opticks in the form of Queres. For this reason in the Preface to his Principles, when he had mentioned the Motions of the Planets Comets Moon & Sea as deduced in this book from gravity, he added: Vtinam cætera Naturæ Phænomena ex Principijs Mechanicis eodem argumentandi genere derivare liceret. Nam multa me movent ut nonnihil suspicer ea omnia ex viribus quibusdam pendere posse quibus corporum particulæ per causas nondum cognitas vel in se mutuo impelluntur & secundum figuras regulares cohærent, vel ab invicem fugantur & recedunt: quibus viribus ignotis Philosophi hactenus Naturam frustra tentarunt And in the end of this book in the second Edition, he said that he forbore to describe the effects of this attraction for want of a sufficient number of experiment to determin the laws of its acting. And for the same reason he is silent about the cause of gravity, there occurring no experiments or phænomena by which he might prove what was the cause thereof. And this he hath abundantly declared in his Principles, neare the beginning thereof, in these words: Virium causas et sedes Physicas jam non expendo. And a little after: Voces attractionis, impulsus, vel propensionis cujuscunque in centrum, indifferenter & pro se mutuo promiscue usurpo, has vires non physice sed Mathematice tantum considerando. Vnde caveat Lector ne per hujusmodi voces cogitet me speciem vel modum actionis causamve aut rationem phyiscam alicubi definire vel centris (quæ sunt puncta mathematica) vires vere et physice tribuere, si forte aut centra trahere aut vires centrorum esse dixero. And in the end of his Opticks: Qua causa efficiente hæ attractiones, [sc. gravitas visque magnetica et electrica aliæque] peragantur, hic non inquiro. Quam Ego attractionem appello, fieri sane potest ut ea efficiatur impulsu vel alio aliquo modo nobis incognito. Hanc vocem attractionis ita hic accipi velim ut in universum solummodo vim aliquam significare intelligatur qua corpora ad se mutuo tendant cuicunque demum causæ attribuenda sit illa vis. Nam ex phænomenis naturæ illud nos prius e doctos oportet quænam corpora seinvicem attrahant, & quænam sint leges & proprietates istius attractionis; quam in id inquirere par sit quanam efficiente causa peragatur attractio. And a little after he mentions the same attractions as forces which by Phænomena appear to have a being in nature tho their causes be not yet known, & distinguishes them from occult qualities which are supposed to flow from the specific forms of things. And in the Scholium at the end of his Principles after he had mentioned the properties of gravity, he added: Rationem vero harum gravitatis proprietatum ex Phænomenis nondum potui deducere, & hypotheses non fingo. Quicquid enim ex phænomenis non deducitur Hypothesis vocanda est; & Hypotheses seu Metaphysicæ seu Physicæ seu Qualitatum occultarum seu Mechanicæ in Philosophia experimentali locum non habent. — Satis est quod Gravitas revera existat et agat secundum leges a nobis expositas, et ad corporum cœlestium & maris nostri motus omnes sufficiat. And after all this one would wonder that Mr Newton should be reflected upon for not explaining the cause of gravity by an Hypothesis, as if it were a crime to content himself with certainties established by experiments & phænomena & let uncertainties alone. And yet the Editors of the Acta Eruditorum have accused him of denying that the cause of Gravity is mechanical tho he is silent about that cause, & Mr Leibnitz has accused him ✝[2] of making gravity an occult quality & a miracle It lies upon Mr Leibnitz therefore in point of candor & justice to beg Mr Newtons pardon publickly for endeavouring by such indirect & unfair practises to defame him & prejudice the learned part of Europe against him.
And whereas Mr Leibnitz tells us that God (the God in whom we live & move & have our being) is Intelligentia supramundana, & applys the name of miracles not only to extraordinary & supernatural events but even to the laws of nature if imprest upon her by the will of God, & under the name of miracles excludes all the actions of the first cause from being considered in experimental Philosophy, & teaches that nothing happens without a reason or in other words that there is nothing done by choise but all things are governed by fate & in his Hypothesis of an Harmonia præstabilita asserts that the soul acts not upon the body, but all animal motion, even in man himself, is performed by meere mechanism it lies upon him in point of religion to satisfy the world that his philosophy doth not tend to enervate & explode all the arguments for a supreme governour of the Vniverse taken from Phænomena make him cry out against Mr Newton cries out against Mr Newton for introducing occult qualities & miracles into Philosophy, & applys the name of miracles not only to extraordinary or supernatural events but even to the laws of Nature if imprest upon her by the will of God.
Anno Christi finiente Apogæum Solis Motus medius Solis ab Ap ogæo Motus medius Solis ab Apogæo. Motus medius ☉is ab Æquinoxio.
Here he represents that he knew nothing by Mr Newton's Letters but that he had a certain method of Tangents, but when his Principles came abroad he abundantly understood that he had gone much further in these methods: But he is {since} gone back from what he acknowledged here & tells us that the Principles are written in the manner of the ancients & have nothing of the new Analysis in them, nor make it appear that Mr Newton knew any thing of these methods when he wrote that book. It lies upon therefore in candor & justice to acknowledge that when Mr Newton wrote his Principles he had a method of resolving difficillima et pulcherrima quæque etiam mistæ Matheseos Problemata quæ sine calculo differentiali AVT SIMILI non temere quisquam pari facilitate tractabit. For that book is full of such Problemes & therefore in the judgment of Mr Leibnitz himself could not have been invented sine Calculo Differentiali AVT SIMILI It lies upon him also in candor & justice to acknowledge that before he wrote his Letter of 21 Iune 1677 in which he began first to propose the Differential Method, he did understand by Mr Newtons three Letters above mentioned, that Mr Newton in those days had a method of determining maxima & minima, & finding the tangents areas, lengths curvities, solid contents, centers of gravity of curves & curvilinear figures analytical or mechanical & this without taking away surds, & that this method gave the Areas of Curvilinear figures in Series which in certain cases brake off & became finite, & compared figures with the Conic sections & readily gave the Method of Tangents of Slusius as a branch or Corollary thereof, & gave also the Areas of Curvilinear figures by the help of finite & infinite equations together extended to inverse Problemes of Tangents & others more difficult & even to almost all Problems except perhaps some numeral ones like those of Diophantus. He is also to acknowledge that when Mr Newton told him how general his methods were he could not beleive it but in his Letter of 27 Aug. 1676 represented it improbable. And then it lies upon him to make the world understand why upon publishing his own method he concealed all this & did not candidly tell his Readers what he knew of the Methodus SIMILIS & whose it was. & that it was invented before his own & & seemed incredible to him when he was first told of it, & put him upon considering how to improve the methods of tangents then extant & particularly those of Slusius & Barrow which gave him light into it. For he told Dr Wallis in his Letter of 28 May 1697) that he found this method by observing that Differences answered to Tangents & summs to Quadratures. Epist. ad
And whereas Mr Leibnitz tells us that God (the God in whom we live & move & have our being) is INTELLIGENTIA SVPRAMVNDANA, & applys the name of miracles not only to extraordinary & supernatural events but even to the laws of Nature if imprest upon her by the will of God, so that for atoms to be hard or heavy by the will of God without a mechanical cause would be a miracle & by consequence for atoms or any thing else to exist by the standing will of God would be a standing miracle & thus by the name of miracles excludes all the actions of the first cause from being considered in experimental Philosophy, & in his Hypothesis of an Harmonia præstabilita asserts that the soul acts not upon the body but all animal motion, even in man himself, is performed by mere mechanism: it lies upon him to satisfy mankind that his philosophy doth not tend to enervate & explode all the arguments for a supreme governor of the Vniverse taken from the Phænomena of nature; & that while he asserts that nothing happens without a reason, or in other words that there is nothing done by choise but all things are governed by fate, he doth not mean mechanically, & that his accusing Mr Newton for introducing occult qualities & miracles into Philosophy proceeds not from notions of this kind.
It is true that the Philosophy of these two Gentlemen differ very much. The one teaches that God, (the God in whom we live & move & have our being) is Omnipresent: the other that he is INTELLIGENTIA SVPRAMVNDANA a God that's no where in the world. Whence it follows that he cannot act upon the world without a miracle The {one} beleives that animal motion in man is not purely mechanical; the other that it is, the soul or mind (according to the Hypothesis of an Harmonia præstabilita) never acting upon the body. The one teaches that Philosophers are to argue from Phænomena to the{re} immediate causes thereof & from those causes to the next & so on till we come to the first cause: the other that all the actions of God are miracles & all the laws imprest upon Nature by the will of God are perpetual miracles & occult qualities & therefore not to be considered by Philosophers. But why must it go for a miracle or wonder if God has any thing to do with the world & why must all the arguments for a Deity taken from phænomena be exploded by new hard-names? For certainly Philosophers are to reason without railing, & not to rail without reasoning.
The one sees no reason why God may not chuse by the power of his will in things indifferent: the other teaches that nothing is done without a reason, meaning (I think) that all things are by fate. The one teaches that God (the God in whom we live & move & have our being) is omnipresent: the other &c
The one for want of experiments to decide the question doth not affirm whether the cause of gravity be mechanical or not mechanical the other that it is a miracle if it be not mechanical. The one by way of inquiry attributes it to the will of the creator that the least particles of matter are hard: the other attributes the hardness of matter to conspiring motions & calls it a miracle if the cause of this hardness be other then mechanical. The one doth not affirm that animal motion in man is purely mechanical: the other that it is purely mechanical; the soul or mind (according to the Hypothesis of an Harmonia præstabilita) never acting upon the body; or never without a miracle.
<27v>The one proceeds upon the evidence of Experiment & Phænomena & stops where such evidence is wanting: the other is taken up with Hypotheses & propounds them not to be examined by Experiments but to be received without examination The one doth not presume to say that God cannot chuse to act by the power of his will in matters indifferent: the other affirms that nothing is done without a reason
And why must the laws of Nature be call'd miracles & occult qualities (that
Mr Leibnitz in his Tentamen de motuum Cœlestium causis after he had mentioned Dr Barrows indefinitely little triangle for drawing of tangents & said (according to the Scholium upon Mr Newtons Xth Lemma) that there were infinite degrees of infinites & infinitely littles he tells us: Si motus exponatur per lineam communem quam dato tempore mobile absolvit, impetus seu velocitas exponetur per lineam infinite parvam, & ipsum elementum velocitatis, qualis est gravitatis sollicitatio, vel conatus centrifugus per lineam infinities infinite parvam. Atque hæc Lemmatum loco annotanda duxi pro methodo nostra quantitatum incomparabilium & Analysi infinitorum, tanquam doctrinæ hujus novæ Elementa. And this is all one as to say that if the space described be considered as the fluent, the velocity must be considered as the first fluxion & the variation of the velocity as the second fluxion, & so on This was the foundation of Mr Newton's arguing in his Principles & this (with a little variation of the Language) Mr Leibnits reccons among the Elements of his Analysis. And while Mr Newton's book of Principles is founded upon these Elements & in that book he argues right. : it is certain that when he wrote that book, he understood the elements of the infinitesimal Analysis & had not then forgotten the method of second fluxions.
And Mr Leibnitz himself in his Letter of 21 Iune 1677 in explaining his Method shewed how it gave the method of Tangents of Slusius & proceeded without taking away surds & extended to Quadratures, & then declared himself of opinion that since Mr Newtons method did these things it was of the same kind. Arbitror saith he, qua celare voluit Newtonus de Tangentibus ducendis, ab his non abludere. Quod addit, ex hoc eodem fundamento Quadraturas quoque reddi faciliores me in sententia hac confirmat, nimirum semper figuræ illæ sunt quadrabiles quæ sunt ad æquationem differentialem. And before this Mr Newton told him further in his three Letters above mentioned, that his method determined Maxima & Minima, gave the lengths, & curvities of Curves, & centers of gravity of curvilinear figures, & compared curves with the Conic Sections & squared them by infinite series or æquations which in certain cases brake off & became finite, & by the help of finite & infinite æquations together resolved inverse problems of tangent & others more difficult, & even to almost all Problems except perhaps some numeral ones like those of Diophantus. And When Mr Leibnitz was first told the great extent of the Method, he could not beleive it, but represented it improbable saying Quod dicere videmini plerasque difficultates (exceptis Problematibus Diophantæis) ad Series infinitas reduci; id mihi non videtur. Sunt enim multa usque mira & implexa ut neque ab æquationibus pendeant neque ex Quadraturis: It lies upon him therefore in candor & justice to acknowledge that before he found the Differential method or at least before he wrote his Letter of 21 Iune 1677, he knew all this & wondred at it: And to give an Account why he concealed his knowledge thereof when he published the Differential method as his own & why he did not then let the Germans know what he meant by the methodus SIMILIS, or whose it was, or what he had learnt of it by his correspondence with Mr Oldenb.
And — Analysis extended to almost all sorts of Problemes & represented it so general that Mr Leibnitz himself exprest his disbeleif of it. It lies upon him therefore in candour & justice to aknowledge this & to give an Account why he did not acknowledge any thing thereof when he first published the differential method. For it was not enough to mention a methodus SIMILIS without saying whose it was & of what antiquity & extent according to the notice he had from England.
— I do not know. But this I know that can be on Iudge in this matter. He is too much of a party, Mr Leibnitz objected against Dr Keill that he is Homo novus & rerum anteactarum parum peritus, & the same objection lies against Mr Bernoul{li}
Mr Bernoulli had the differential Method from Mr Leibnitz & is the chief of his disciples, & gave his opinion in the Acta Leipsica before he saw the Commercium Epistolicum at which time he was homo novus & rerum anteactarum parum peritus, as Mr Leibnitz objected against Dr Keil, & what he wrote after he saw the Commercium was in his own defense. [And Mr Leibnitz appealed from the Committee of the Royall Society to the chief man of his party who h{ad]} & his skill in Mathematicks will not mend the matter. He is skilful enough to know that in taxing me with ignorance in second differences he was mistaken & that some errors in Mr Leibnitz his Tentamen de motuum cœlestium causis proceeded from his want of skill in those differences but he has not hitherto acknowledged what he knows.
— & that before the end of the year 1666 I sometimes used letters with one or two pricks for quantities involving first or second fluxions & wrote a small Tract on this subject which was the grownd of that larger Tract which I wrote in the year 1671 both which are still in my custody & are founded upon the first Proposition of the Book of Quadratures explained & demonstrated in a Geometrical manner without prickt letters or other symbols; & that when I wrote the larger of those two Tracts I had made my Analysis composed of the methods of Series & Fluxions together so universal —
And therefore he is the Agressor. In both his Letters to Dr Sloan (that dated 4 Mart. & that dated 29 Decem. 1711, he pressed the R. Socity to condemn Dr Keil & & before I medled in this matter challenged me to declare my opinion. His words in his second letter are: Itaque vestræ æquitati committo, annon coercendæ sint variæ & injustæ [Keilij] vociferationes, quas ipsi Newtono, Viro insigni et gestorum optime conscio, improbari arbitror; ejusque sententiæ suæ libenter daturum Iudicia mihi persuadeo. And therefore he is the aggressor.
P. S.
Mr Leibnitz seems to say that what he formerly allowed concerning my having found a method like his own proceeded from his beleiving me, but since I have retracted what I acknowledged formerly he may be allowed to do the like. especially since the probabilities observed by Bernoulli, , vizt in the Libel above mentioned. Mr Bernoulli may pretend that no Probleme can be solved by the method of fluxions without the use of prict letters & that in the Introduction to the Book of Quadratures the Method of fluxions is not explained because there are no prickt letters in that Introduction, & that in the second Lemma of the second book of the Principia Philosophiæ the Elements of the method of fluxions are not demonstrated because there are no prick letters in it, & that from the sentences set down in my letter of 24 October 1676 viz Data æquatione fluentes involvente fluxiones invenire & vice versa, and Vna methodus consistit in extractione fluentis ex æquatione fluxionem involvente it cannot be inferred that I then knew the first Proposition of the Book of Quadratures had at that time a method of reducing Problems to fluxional equations or of resolving such æquation because there are no prickt letters in those sentences. And that in the Analysis per æquationes numero terminorum infinitas there are no specimens of the Method of fluxions because there are no prickt letters. And that the Proposition in the Schediasma hereunto annexed is no part of the Method of fluxions because it is explained without prickt letters tho it be the very same with the first Proposition in the book of Quadratures upon which the Method of fluxions is founded. But other men will rather inferr from these things that I had the method of fluxions fifty years ago putting such symbols for fluxions as I thought fit, & Mr Leibnitz was of the same mind before he knew what symbols I used, as in his Letter of 21 Iune 1677 where he allowed me a Methodus similis & in the Acta Eruditorum for October 1684 p 473 where he again mentioned a Methodus similis extending to the higher sort of Problemes & in his Letter to me dated 17 Mar 1673 st. n. hereunto annexed wherein he acknowledged of his own accord that by the Principia Philosophiæ I had shewed that I had such a method & added that he also had endeavoured to reduce the difficulter Problems to such an Analysis. And in the Acta Eruditorum for Iune 1686 pag 297 he allowed that in the Differential method one might use letters instead of dx & such like symbols, & thereby left me at liberty to use what symbols I thought fit. And further, I do not put prickt letters for differences or moments as Mr Bernoulli supposes, but for fluxions which are quantities of another kind, the one being infinitely little parts & the other finite velocities of motion. And whereas Mr Leibnitz pretends that since I have retracted what I formerly he may be allowed to do the like; he should have proved that had retracted, & if I had done an ill thing yet that would not authoriz him to do the like. And whereas he questions my credit in what I said of Dr Wallis, he will find the truth of what I said in the Paragraph of this Preface hereunto annexed
Leibnitius eadem fide chartam totam volantem scribere potuit qua citationem prædictam delevit, & verisimile est quod Menkenius eandem prælo commisit. Nam Leibnitius chartas imprimendas ad ipsum mittere solebat. Et Bernoullius Epistolam sine nomine imprimendam ad Leibnitium non misit
In prima sua ad Abbatem de Comitibus Epistola Leibnitius scripsit — — —
Ad hanc Questionem spectat quod D. Wallisius noster Celeberrimus Professor Oxoniensis, Propositionem primam Libri de Quadraturis exemplis in fluxionibus prim{illeg} & secundis in veniendis illustratam. edidit anno 1693 in Volumine secundo Operum suorum pag 392. Et hæc fuit Regula omnium antiquissima quæ lucem vidit pro fluxionibus secundis tertijs quartis cæterisque in infinitum inveniendis Eandem Newtonus demonstravit synthetice in Lemmate secundo Libri secundi Principiorum: cum Propositionem sine Demonstratione prius posuisset in Epistola ad Oldenburgum 24 Octob. 1676 ut ad Leibnitium mitteretur & ibi significasset eandem esse fundamentum methodi generalis de qua scripserat tum ante annos quinque, id est anno 1671. In hujus Propositionis solutione habetur Algorithmus Methodi fluxionum.
Gregorius scripsit ad Collinium 5 Sept. 1671, se ex Barrovij methodis tangentes ducendi methodum generalem & Geometricam ducendi tangentes ad omnes Curvas sine calculo: Slusius se similem methodum habere mense Novembri 1672 scripsit ad Oldenburgum. Et Newtonus ad Collinium 10 Decem 1672 scripsit in hæc verba: Ex animo gaudeo D. Barrovij nostri reverendi Lectiones Mathematicas exteris adeo placuisse, neque parum me juvat intelligere eos [Slusium et Gregorium] in eandem mecum incidisse ducendi Tangentes methodum . Et subinde methodum suam tangentium descripsit, & addidit hanc methodum esse corollarium Methodi generalis solvendi abstrusiora Problemata & non hærere ad quantitates surdas. Epistolas totas Gregorij & Newtoni habes infra in Commercio, & earum Exemplaria Oldenburgus misit ad Leibnitium inter Excerpta ex Gregorij Epistolis 26 Iunij 1676; et Leibnitius Prælectiones Barrovij mense Novembri proximo secum tulit in Germaniam.
 Sunto jam utim Epistola Newtoni seu Abscissa & Ordinata . Et sint earum fluxiones p et q & momenta op et oq, et in AB producta capiatur , erigatur Ordinata EF parallela BC & occurrens Curvæ in F et compleatur parallelogrammum BCGE et erit . Proponatur æquatio quævis quantitates duas fluentes x et y involvens, puta ut in Epistola illa. Multiplicetur omnis æquationis terminus per indicem dignitatis x et productum divisum per x (videlicet ,) vocetur R. Multiplicetur omnis æquationis terminus per indicem dignitatis y & productum divisum per y (videlicet ) vocetur S. Et per Regulam in Epistola illa Newtoni traditam erit subtangens , vel potius propterea quod AB et BD ducantur in partes contrarias. Sed ex methodo tangentium Barrovij est . adeoque . Ergo et facta reductione Hæc est æquatio involvens fluxiones. Et si plures sint quantitates fluentes eadem operatio instituta in singulis dabit æquationem involventem fluxiones omnium. Et hæc Regula illud omne comprehendit quod Leib{nitius} ad Newtonum anno 1677 rescripsit, ut et illud omne quod in Actis Eruditorum anno 1684 in lucem edidit. Exhibet enim hæc Regula solutionem Propositionis, primæ Libri de Quadraturis.
Sunto jam utim Epistola Newtoni seu Abscissa & Ordinata . Et sint earum fluxiones p et q & momenta op et oq, et in AB producta capiatur , erigatur Ordinata EF parallela BC & occurrens Curvæ in F et compleatur parallelogrammum BCGE et erit . Proponatur æquatio quævis quantitates duas fluentes x et y involvens, puta ut in Epistola illa. Multiplicetur omnis æquationis terminus per indicem dignitatis x et productum divisum per x (videlicet ,) vocetur R. Multiplicetur omnis æquationis terminus per indicem dignitatis y & productum divisum per y (videlicet ) vocetur S. Et per Regulam in Epistola illa Newtoni traditam erit subtangens , vel potius propterea quod AB et BD ducantur in partes contrarias. Sed ex methodo tangentium Barrovij est . adeoque . Ergo et facta reductione Hæc est æquatio involvens fluxiones. Et si plures sint quantitates fluentes eadem operatio instituta in singulis dabit æquationem involventem fluxiones omnium. Et hæc Regula illud omne comprehendit quod Leib{nitius} ad Newtonum anno 1677 rescripsit, ut et illud omne quod in Actis Eruditorum anno 1684 in lucem edidit. Exhibet enim hæc Regula solutionem Propositionis, primæ Libri de Quadraturis.
Propositionem quintam libri de Quadraturis Wallisius edidit — — — — ab ipso excogitatam, i.e. anno 1666 aut antea; nec non teste N. Fatio de Duillier qui chartas antiquas Newtoni viderat, & contra seipsum testimonium perhibuit. Et his præmissis legatur jam Recensio Commercij Epistolici & Consulatur Commercium ipsum ubi de factis dubitatur.
Sic inventio fluxionum ex Epistola Newtoni {cf} methodis Tangentium Barrovij & Gregorij a Newtono citati facillime deducitur Et Theorema sic ex Newtoni Epistola derivatum inventio illud omne comprehendit illud omne quod Leibnitius ad Newtonum anno 1677 rescripsit, ut et illud omne quod in Actis Eruditorum anno 1684 de hac methodo in lucem edidit. Exhibet enim hoc Theorema solutionem. Propositionis primæ Libri Newtoni de Quadraturis Idem vêro Newtono innotuisse anno 1686 ut manifestum est ex Lem. 2 Lib. 2 Princip. ut et anno 1676, quemadmodum manifestum est ex Epistolis Newtoni 13 Iunij & 24 Octob. anni illius, ex quibus utique Wallisius scripsit Newtonum methodum exposuisse, Leibnitio. Idem Newtono innotuisse etiam anno 1672 manifestum est ex ijs quæ de Epistola ejus hoc anno scripta, jam dicta fuerunt.
Iudex celando et nomen suum & nomina eorum quos judicat, libellum potius quam sententium judicis dictitat.
a Hæc Epistola, cum celetur et Iudicis et Iudicatim nomen, Libellum defamatorum magis sapit quam probi judicis sententiam.
b Algorithmus habetur &
c In Analysi per series Newtonus utitur
d Nullam habuit occasionem. Propositiones non invenit per synthesin sed per Analysin inventas demonstravit synthetice ut in Geometriam admitterentur.
e Volumen tertium.
f Eodem sensu
g In libro
h Eminens ille
i Recta methodus
ubi Ordinatim Applicata (ceu momentum areæ fluentis) ex æquatione Abscissam et Aream involvente deducitur.
Recueil Tom. 2. p. 4, 5, 36, 52, 53.
In Epistola ad Cometissam de Kilmanseg
Agnovit Oldenburgium ad se mississe des Essays
Ad hanc Quæstionem spectat quod Leibnitius differentias & methodum differentialem vocat quæ Newtonus momenta, Et Methodus momentorum: Et quod methodus fluxionum non magis differt a methodo differentialij quam differt a methodo momentorum. [ Vna et eadem est methodus nisi quatenus Newtoni methodus sit amplior Momenta vel differentiæ sunt partes genitæ quantitatem genitarum, fluxiones sunt velocitates quibus partes illæ generantur. Leibnitius & Newtonus considerant partes , Newtonus considerat etiam velocitates quibus partes generantur. Newtoni methodus complectitur methodum Leibnitij.]
Vna et eadem est methodus quoad differentius vel momenta. Hæc sunt partes quantitatum genitarum. Fluxiones sunt velocitates quibus partes generantur. Vterque considerat partes. Newtonus considerat etiam velocitates quibus partes generantur. Newtoni methodus complectitum methodum Leibnitij.
Leibnitius itaque Epistolam Oldenburgij seriebus refertam accepit Sed Series si fas est credere nunquam contulit cum suis.
Ad hanc Quæstionem spectat quod Leibnitius differentias & methodum differentialem vocat quas Newtonus momenta & methodum momentorum quod methodus momentorum & methodus fluxionum eadem sit. Momenta sunt partes quas Leibnitius differentias vocat, fluxiones sunt velocitates quibus partes generantur. Leibnitius considerat partes, Newtonus considerat etiam velocitates. Newtoni methodus est amplior & Leibnitij methodum complectitur.
Et hæc est Regula ducendi tangentes quam Newtonus in Epistola illa posuit ut partem aliquam vel specimen vel Corollarium Methodi suæ generalis:
Ducatur jam secundum methodum Barrovij a Gregorio promotam Ordinata nova EF priori BC proxima & compleatur parallelogrammum BCGE et pro momentis BE vel CG & GF scribamus p et q et erit . seu et facta reductione prodit . Hæc æquatio ubi duæ tantum sunt fluentes involvit earum momenta. Et ubi plures momenta. {illeg} vel ut Leibnitius loquitur, omnium differentias. Et Theorema hocce quod sic ex specimine in Newtoni Epistola posito facillime deducitur, illud omne comprehendit quod Leibnitius anno 1677 ad Newtonum rescripsit, ut et illud omne quod in Actis Eruditorum anno 1684 in lucem edidit. Hoc Theorema exhibet solutionem Propositionis primæ Libri de Quadraturis, ideoque solutio Propositionis illius anno 1672 Newtono innotuit.
In libro de Analysi per Series Fluxiones ac Differentias anno 1711 a Ionesio edito extat Fragmentum Epistolæ D. Newtoni ad D. Collinium Nove. 8 1676 data ubi Newtonus scribit in hæc verba. Nulla extat Curva cujus æquatio — possint comparo. — Eadem methodus Æquationes quatuor terminorum aliasque complectitur, haud tamen adeo generaliter. Hactenus Newtonus. Hæc autem absque Methodo fluxionum fieri non possunt. Indicant vero methodum quadrandi Curvlineas in libro de Quadraturis expositam, eousque promotam fuisse ante 8 Novem 1676.
In Epistola Newtoni ad Oldenburgum 24 Octob. 1676 ponuntur Ordinatæ Curvilinearum qu{a}rum collationes cum Conicis sectionibus Newtonus in Catalogum tunc olim retulerat. Earundem Curvarum et {E}odem ordine Collationes cum Con. Sect. describuntur in Tabula posteriore in libro de Quadraturis: ideoque Tabula illa composita fuit est methodus quadrandi Curvas eousque producta, annis aliquot ante annum 1676. Id quod absque methodo fluxionum fieri non potuit.
In prædicta Analysi per series quam Barrovius anno 1669 ad Collinium misit Newtonus exponit tempus per abscissam Curvæ fluentem per aream ejus fluxionem fluentis per Ordinatam & momentum ejus per fluxionem ductam in temporis momentum o. Et sub finem Tractatus illus dat specimen calculi. Et Leibnitius methodum serierum Newtoni in Tractatu illo descriptam postulabat a Collinio per literas ad Oldenburgum 12 Maij 1676, potuitque videre proximo mense Octobri ubi in Angliam venit & in manibus Collinij vidit epistolas plures Newtoni Gregorij & aliorum, eas præsertim quæ circa series versabantur ut ipse in epistolis ad D. Abbatem de Comitibus & Cometissam de Kilmansegger agnovit.
Et his præmissis legatur jam Recensio Commercij Epistolici & consulatur Commercium ipsum ubi de factis dubitatur.
✝ Tandem agnovit iterum in Epistola sua ad Cometissam de Kilmansegger, ut supra in Præfatione ostenditur
— Et Mathematicum esse Bernoullium ipsum scripsit, & charta illa volunte denuo dispersæ & Gallice in Hollandia imprimi curavit & Problemata Bernoullij Analystis Anglis solvenda proposuit Et auctorite Bernullij amicos suos rerum mathematicarum inscios contra Newtonum passim ciere conatus est, cum tamen Bernoullius.
Commercium Epist. p. 32, 3{0}, , 39, 42, , 44, 45, 58, 87, 88, 96.
Charta volans in Commer p.
<31v>In Charta illa 29 Iulij 1713 data Leibnitius Epistolam 15 Aprilis 1675 datam qua Oldenburgus series aliquot ad Leibnitium misit et inter alias seriem Gregorij quam Leibnitius postea ut suam edidit in dubium vocare conatus est, dicendo: Tale quiddam Gregorium habuisse ipsi Angli & Scot. Wallisius, Hookius Newtonus & junior Gregorius ultra triginta sex annos ignoraverunt & Leibnitij esse inventum crediderunt. At hæc Epistola in Libro Epistolico Regiæ Societatis asservata, ut et Epistola autographa Leibnitij se series missas recepisse agnoscentis, cum ijsdem epistolis in Commercio editis, coram Comite de Kilmansegger, Abbate de Comitibus, ministris aliquot publicis exterorum Principum & alijs exteirs non paucis Anno 1715 collatæ sunt et ab omnibus agnitæ; & Leibnitius ipse a {an}no proximo in Epistola sua ad D. Cometissam de Kilmansegger 18 Apr. 1716 data & a D. {illeg} Deso Maiseaux edita, idem agnovit narrando historiam epistolis in Commercio editis conformem. Narrat enim quomodo Londinum venit initio anni 1673, cum Oldenburgo amicitiam contraxit, a Pellio nostro apud D. Boyle audivit quod Mercator seriem invenisset pro Hyperbola, librum comparavit & secum asportavit in Galliam, ibi sub Huygenio cœpit meditationes Geometricas gustare, parvo tempore multum profecit, & invenit seriem suam pro circulo, dein sic pergit Nous crûmes que j'etois le primier, qui avois fait quelque chose de tel sur le circle; & j'en écrivis sur ce ton-la a [15 Iulij & 26 Octob] a M. Oldenbourg en 1674 avec qui auparavant je ne telles choses, quoique nous eussiouns échangé deja [Feb. 20, Mart. 30, Apr 26 Maij 24 & Iunij 8] plusieurs Lettres. M. Oldenburg m'ecrit [15 Apr 1675] m'envoya des essays. Cependant le mieu [Londinum missa 27 Aug. 1676] fut asser applaudi [24 Octob. 1676] per Mr Newton même. Il est trouvé par apres [anno 1712] qu'un nomme M. Gregory avoit trove justement la même series que moi. Mais c'est ce qu' j'appris tard. Hic Leibnitius agnoscit se recepisse ab Oldenburgo de essays exempla serierum Newtoni, et inter hæc exempla erat series Gregorij ut in Commercio videre licet. At Newtonus Wallisius Gregorius junior et Hugenius hanc seriem a Gregorio ad Collinium ab Oldenburgo ad Leibnitium missam fuisse, per ea tempora ignorarunt.
Contra fidem epistolarum in Commercio editarum scripsit insuper Leibnitius — videntur
Altamen ut accusationem probaret — — — in Commercio pag. 39.
Cæterum Leibnitius in prima sua ad Abbatem — — — . ostendit
Subinde in prima sua ad
D. Leibnitius autem in proxima — — — — Leibnitius.
Altamen post ejus mortem — — — — referri debet. Et hæc Quæstio est utrum Leibnitius sit inventor Methodi & pro differentijs igitur Leibnitianis Newtonus adhibet semperque [ex quo usus est hac methodo] adhibuit fluxiones, quemadmodum Honoratus Fabrius motuum progressus Cavallerianæ methodo substituit.
Ad hanc Quæstionem spectat quod Algorithmus methodi habiatur in Propositione prima Libri de quadraturis & quod D. Wallisius Propositionem illam cum exemplis inveniendi fluxiones primas et secundas edidit annno 1693 in Volumine secundo operum suorum pag. 393. — id est anno 1671.
Eodem spectat quod Iacobus Gregorius scripsit ad Collinium 5 Sept 1671 — — — — — Propositionis primæ libri de Quadraturis.
Propositionem quintam Libri de Quadraturis — de factis dubitatur.
— si fieri potest. Hoc artificium anno 1669 Newtono innotuisse uti patet ex Analysi per series,[3] immo et annis aliquot antequam Mercatoris Logarithmotechnia prodiret (id est anno 1666 aut antea) teste Barrouus uti patet ex Epistola ✝[4] Collini i ad D. Strode. Propositio illa quinta pendet a quatuor prioribus; ideoque Methodus fluxionum quatenus continetur in Propositionibus quinque primis libri de Quadraturis Newtono innotuit anno 1666 aut antea.
Newtonus incidit in Theoremata sua de refractionibus, & coloribus lucis ineunte anno 1666. Sub idem tempus invenit etiam methodos serierum et fluxionum. De his omnibus scripsit Tractatus anno 1671 ut in lucem mitterentur. Sed anno proximo cum nonnulla communicasset de natura lucis, subortæ statim per diversorum Epistolas objectionibus alijsque refertas, crebræ interpellationes, ipsum prorsus a consilio deterruerunt, et effecerunt ut seipsum argeret imprudentiæ (ut ipsa olim locutus est) quod umbram captando, eatenus perdiderat quietem suam, rem prorsus substantialem. Ab his omnibus igitur edendis abstinuit usque ad annum 1704 et interea aliqua tantum communicavit privatim cum amicis. Librum vero MS de Quadraturis literis punctatis refertum Halleius noster & Ralphsonus anno 1691 manibus suis tractarunt ut alter testatum reliquit & alter adhuc testatur. Eodem libro Newtonus annis 1685 & 1686 inveniendis Principijs Philosophiæ se plurimum usum fuisse profitetur. Et quæ in Epistolis tribus Newtoni anno 1676 scriptis ex eodem citantur, indicant eundem jdem tum in MS extitisse.
Et his præmissis —
Sir Isaac Newton
Bar.
St Martins Street
{illeg}
Kill
Dominus Brunkerus quadravit Hyperbolam per hasce duas series &c et &c. Et hæ series cædam sunt cum seriebus &c et &c ut colligendo summas binorum terminorum patebit. Impressa est autem Brunkeri Quadratura Anno 1668 mense Aprili idque in Actis Philosophicis Num. 34. Et paulo post impressa est Mercatoris Logarithmotechnia cum eadem Quadratura promota. Et mox Gregorius Quadraturam eandem Geometrice demonstravit posita hac prima Propositione. Si fuerint quantitates continue proportionales A, B, C D, E, F, &c numero terminorum infinitæ, quarum prima et maxima A; erit A–B ad A ut A ad summam omnium; hoc enim passu demonstratur apud Geometras. Hæc Gregorius. Per hanc Propositionem Geometricam prodit quadratura Hyperbolæ absque Divisione Arithmetica. Mercator vero Propositionem probavit per Divisionem Arithmeticam. Sed methodum generalem. Quadrandi Curvas per hujusmodi series nec D. Brunker nec Mercator nec Gregorius invenit. Gregorius hujusmodi methodum diu quæsivit & vix tandem sub finem anni 1670 invenire potuit. Newtonus hujusmodi methodum aliquam primus omnium protulit.
Proposuerat Wallisius in Arithmetica sua seriem Curvarum cujus ordinatæ sunt &c et areæ , &c, existente Abscissa x Et quòd si series posterior in locis alternis interpolari possit habebitur area circuli: Invenit Newtonus methodum interpolandi hanc seriem. Et eadem methodo interpolavit seriem potestatum binomij &c. Ponatur utique litera aliqua puta n pro indice binomij, et per Methodum Newtoni prodibit series . ubi n potest esse namerus integer, vel fractus vel surdus affirmativus vel negativus, et a et x nomina quæcunque designant. Et hæc series eadem est cum Regula generali quam Newtonus in Principio Epistolæ suæ primæ cum Leibnitio communicavit. Sic Newtonus pervenit ad methodum generalem quadrandi Curvas quarum ordinatæ sunt binomiorum dignitates quæcunque, sive nomina sint quantitates simplices sive compositæ, et indices dignitatum sint numeri integri vel fracti vel surdi affirmativi vel negativi, ut ex epistolis ejus ad Oldenburgum cum Leibnitio communicandis intelligo. Deinde animadvertit idem per divisiones et extractiones radicum fieri & methodum promovit ad radices æquationum affectarum sive æquationes illæ solas quantitates fluentes involvant sive etiam fluxiones, Et methodum etiam primus invenit assumendi terminos serierum et eosdem per collationem terminorum homogeniorum determinandi. ut ex ijsdem epistolis et alijs ejus scriptis patet.
Leibnitius vero ne unam quidem seriem earum quas sibi arrogorare conatus est primus invenit Methodum perveniendi ad has Series anno 1676 a Newtono accepit, acceptæ nihil unquam addidit. Newtonus methodum et invenit et perfecit.
Quinetiam Regula jam descripta methodum fluxionum quam Leibnitius differentialem vocat in se involvit. Si momentum dignitatis Siquidem Seriei cujuscunque terminus secundus sit momentum termini primi et tertius quartus quintus et reliqui sint ad momenta termini primi in datis rationibus, si modo Binomij nomen secundum sit momentum nominis primi. Verbi gratia sit o momentum fluentis x et quæratur momentum dignitatis , id est quæratur differentia inter & et resolvendo in seriem , secundus seriei terminus erit differentia quæsita. Sit jam p momentum quantitatis fluentis y et quæratur momentum quantitatis fluentis id est quæratur differentia inter et et resolvendo binomia in series et multiplicando series in se mutuo prodibit series cujus secundus terminus est differentia quæsita. Et hæc est methodi quam Leibnitius differentialem vocat Demonstratio omnium brevissima & maxime naturalis. Communicavit igitur Newtonus cum Leibnitio per Epistolam suam primam fundamentum verum methodi differentialis a quo methodus illa sponte fluit et per quod brevissime et optime demonstratur.
Quinetiam sub finem epistolæ secundæ 24 Octob 1676 datæ Newtonus inversa de tangentibus Problemata esse in potestate aliaque illis difficiliora ad quæ solvenda duplici usus est methodo et una concininniore altera generatione & methodum utramque hisce designavit sententijs. Vna methodus consistit in extractione fluentis quantitatis ex æquatione simul involvente fluxionem ejus. Altera tantuum in assumptione seriei pro quantitate qualibet incognita ex qua cætera commode derivari possunt; et in collatione terminorum homologorum æquationis resultantis ad eruendos terminos assumptæ seriei.
dignitate Fluentem e{illeg}re
Hanc seriem anno 1669 Newtono innotuisse patet ex Analysi supra impressa pag 19 lin 19, 20
1 Methodus tam fluxionum quam serierum infirmitarum fundatur in operationibus quatuor vel quinque generallibus quarum hæc est prima. Et per hanc operationem Fluens ex æquatione quacunque non affecta extrahitur eruitur.
2 Operatio secunda generalis qua fluens ex æquatione affecta extrahitur.
p. 636. l. ult. Id est, Data æquatione quotcunque fluentes quantitates involvente invenire fluxiones et vice versa. Solvitur vero sumendo secundos terminos serierum pro momentis primorum. Sit æquatio {illeg} . Solvitur vero per operationem primam in Epistola superiore descriptam sumendo secundos serierum terminos pro momentis primorum. Sit æquatio . Fluant x et y & sit earum momentans & . et fluendi velocitates. et Et erit . Resolvatur binomium in seriem et ablatis æqualibus et y manebunt æqualia et ablatis æqualibus et y manebunt æqualia et , quibus per o divisis fit . Sit æquatio et simili operatione prodibit . Et idem fit in singulis terminis æquationum compositarum. Et hoc est methodi fluxionum fundamentum verum et demonstratio optima brevissima et maxime generalis et Newtono ab initio inotuit ut ex ejus Analysi per æquationes infinitas (pag 3 Reg. 1. & pag 19) manifestum est. Newtonus communicavit cum Leibnitio methodum suam perveniendi ad series infinitas, Leibnitius secundos serierum terminos invenit.
p. 634 l. 11 a Regula prima.
l. 30. b Regula secunda.
p. 636 l. 19 Analysis per æquationes infinitas supra impressa
l 45. Ad verba: Diversa ratione in eam incidimus, nota: Slusius methodum Riccio cujdam tr{i}buit & a se abjudicaret Lemmata ponendo a quibus methodus derivari non potest. Extant Lemmata in Actis Philosophicis Newtonus methodum primus communicavit & verum ejus fundamentum solus posuit. Qui aliter sentit doceat quomodo methodus a Lemmatibus illis derivari possit.
p 635 l. 1 Exemplum generale quadrandi curvas per methodum fluxionem & series infinitas conjunctim. Vid. pag. 18. lin 31.
p. 639. Pag 639 l. 1. Series Newtoniana ex quantitatem indefinitam (id est fluentem) unam vel plures in se semper involvunt, ideoque ad methodum fluxionum perinent.
Ib. lin. 20. Ex his patet Propositiones Newtoni de Quadratura Curvarum ante annum 1676 inventas fuisse.
P. 640. l. 7. NB D. Brunker Hyperbolam per hanc seriem seu per hanc (conjunctis binis terminis) primus quadravit. Mercator quadraturam hanc ampliavit. Gregorius circulum per hanc seriem &c quadravit. Leibnitius hanc Quadraturam ab Oldenburgo accepit. Newtonus quadravit Circulum per hanc seriem
P. 644. l. 17. Id est, Vna methodus ...... assumptæ seriei. Prior methodus est Operatio tertia vel Regula tertia generalis qua Analysis per series infinitas et fluxiones perficitur. Posterior est Regula quarta et ultima. Duæ Primæ Regulæ in epistola priora traduntur et prima quidem dat quantitatem fluentem ex equationibus non affectis, secunda dat Fluentem ex æquationibus affectis fluxionem ejus non involventibus, tertia dat fluentem ex æqu. affectis fluxionem ejus involventibus. Quarta dat fluentes ex omnibus. Hasce quatuor operationes pervenitudi ad fluentes Newtonus ante annum 1676 invenerat. Ab eo tempore his nihil additum est. Newtonum esse harum omnium Regularum inventorem primum nemo dubitat. Et in Regulis hisce quatuor methodus tota fluentium et momentorum tam in Æquationibus infinitis quam in finitis comprehenditur, cum momenta fluentium facile inveniantur per {R}eg 1 ut Supra expositum est.
In Leibnitij Epistolam secundam.
Pag. 648. lin 20. His verbis patet Leibnitium calculum differentialem cum amicus jam primum communicare cæpisse et ponendo fluentem cum ejus momento pro binomio habuisse secundos terminos dignitatum binomij pro momentis vel (ut ipse loquitur) differentijs dignitatum, perinde ut Newtonus antea fecerat. Vide pag 19.
Inveniri possunt plures hujusmodi series assumendo seriem arearum pro lubitu, et inde computando seriem Ordinatarum & methodo Newtoniana sub initio hujus Epistolæ exposita interpolando seriem utramque; vel assumendo seriem quamlibet ordinatarum ad Curvas quæ per finitas æquationes quadrari possunt et interpolando seriem arearum. Et
Methodus prior est tertia in his Epistolis Regula generalis extrahendi quantitates indeterminatas & fluentes & et posterior est Regula quarta. Quantitas fluens Per Regulam primam ex æquationibus non affectis, per secundam ex æquationibus affectis fluxionem non involventibus, per tertiam ex æquationibus affectis fluxionem simul involventibus, per quartam ex conditionibus Problematis eructur et extrahitur. Et momentum fluentis invenitur per Regulam primam ut supra, vel etiam per Ordinatam Curvæ cujus area est ut fluens? Et sic Newtonus Regulis hisce quatuor totam per fluentes & earum momenta Analysin idque in æquationibus tam infinitis quam finitis complexus fuit Et eum esse harum quatuor Regularum inventorem primum nemo dubitat. Analysin eandem alij aliter explicuerunt, nemo ampliorem reddidit, Leibnitius anno sequente proferre cœpit nondum totam protulit,
p. 645 lin. 29. Ad verba a aliter se habere solet. a Id est, ad solutionem Problematis methodus generalis jam descripta sæpe requiritur.
p. 648 lin 19 Ad verba a in posterum. a Cœpit agitur Leibnitius methodum suam differentialem jam primum cum amicis communicare
p 648 lin 28. Ad verba. Idemque est de cæteris potentijs. Ex secundis terminis potentiarum binomij Leibnitius hic colligit differentias. Newtonus quandoque ex secundis terminis potentiarum quandque ex secundo termino seriei potentias omnes involventis momenta colligerat. Eadem est utriusque computandi ratio ut conferenti computationem Leibnitianam hic positam cum computatione Newtoniana in Analysi superius impressa pag 19, statim patebit.
p 649 lin 24 Ad verba celare voluit notetur. Multis docet Leibnitius se in methodum incidisse quæ cum Newtoniana per omnia congruit.
Analysin per fluentes et earum momenta in æquationibus tam infinitis quam finitis Newtonus in his Epistolis ad Regulas quatuor reduxit. P{illeg}r primam trahitur fluens ex Binomijs atque adeo ex æquationibus quibuscunque non affectis et momentum fluentis. simul prodit. Per secundam extrahitur fluens ex æquationibus affectis fluxionem non involventibus, Per tertiam extrahitur fluens ex æquationibus affectis fluxionem simul involventibus. Per quartam extrahit fluens ex conditionibus Problematis. Regulæ duæ primæ in principio Epistolæ superioris apertè traduntur & anno 1665 inventæ sunt (pag: duæ ultimæ in fine hujus occultantur . Harum Regularum Newtonum esse primum inventorem nemo dubitat. Analysin eandem alij aliter explicuerunt, nemo ampliorem reddidit.
In the same Letter of 27 Aug. 1676 after Mr Leibnitz had described his Quadrature of the circle & equilateral Hyperbola, he added: Vicissim ex seriebus Regressuum pro Hyperbola hanc inveni — — — — — quæ in Newtoni Epistola expressa est; scilicet erit . .... Quod regressum ex arcubus attinet incideram ego directe in Regulam, quæ ex dato arcu Sinum complementi exhibet. Nempe sinus Complementi &c. Sed postea quoque deprehendi ex ea illam nobis communicatam pro inveniendo Sinu recto qui est &c posse demonstrari. And yet in the same Letter he desired Mr Newton to explain further to him the extraction of affected roots & the method of regression by which alone these series were to be found. [By this one would think that Mr Leibnitz had found these four series or at least the three first of them by the inverse method of series or method of Regressions, sometime before he received that method in Mr Newtons Letter, & that he now understood that method very well, & yet His words are. Sed desideraverim ut Clarissimus Newtonus nonnulla quoque amplius explicet: ut Originem Theorematis quod initio posuit: Item modum quo quantitates p, q, r in suis operationibus invenit: Ac denique quomodo in Methodo Regressuum se gerat ut cum ex Logarithmo quærit numerum Neque enim explicat quomodo id ex methodo sua derivetur. He pretended to two series for the Two of the four series which he pretended to were for finding the Number from the Log. & yet in the same Letter he desired Mr N. to tell him the method of finding them.
When Mr Newton had received this Letter, he wrote back that all the said four Series had been communicated by him to Mr Leibnitz, the two first being one & the same series in different circumstance, & the third being the excess of the Radius above the versed sine which was communicated. Whereupon Mr Leibnitz desisted from his claim.
When Mr Newton in the same Letter had explained what Mr Leibnitz desired he added two series for faciliating the method of Regressions And Mr Leibnitz in his Answer dated 21 Iunij 1677 desired that Mr Newton would send him in the continuation of those two series But three weeks after in a Letter dated 12th Iuly 1677 he added: Relectis Newtoni literis video id facile non tantum ex ejus extractionibus derivari sed et altera illa methodo sub finem literarum ejus exposita inveniri qua me quoque aliquando usum in veteribus meis schedis reperio. Sed cum in exemplo quod forte in manus meas sumpseram, nihil prodijsset elegans solita impatientia eam porro adhibere neglexisse. In the year 1676 Mr Mohr had given him an elegant Instance of this method of Regressions as above. In the year before that Mr Oldenburg had sent him three or elegant instances of it. In the year before that he pretended to have had a Theoreme for finding the Arc whose sine was given & a Theoreme for finding the sine whose Arc was given would have been an elegant instance. In the year 1668 Vicount Brounker & Mr Mercator published a Theoreme for finding the Logarithm whose Number was given, & the inverse Theorem for finding the Number from the Logarithm given would have been an elegant instance. This Theoreme he wanted & yet he threw away the method of finding it He wanted it so much as to write three lines to Mr Oldenburg for the method of finding this & such like Theorem, & the last time desired expresly that Mr Newton would explain to him quomodo in methodo Regressuum se gerat ut cum ex Logarithmo quærit Numerum. But as soon as he understood the method, it was his own: for he then found in his old papers that he had used it long ago, but had neglected it for want of an elegant instance. A man may forget things & find them again in his old papers, but in cases of right such pretences are not to be regarded without proof. Mr Newton deserved to have been treated with more candour & gratitude.
In the Acta Eruditorum Mensis Ianuarij 1689 pag 37 Mr Leibnitz making mention of the method of Series, represents that Mercator found them by division & Newton enlarged the method by extractions of roots both pure & affected & then adds. A me ut obiter hic dicam, methodo serierum promovendæ, præter transformationem irrationalium linearum in rationales symmetras (voco autem rationales quarum Ordinatæ semper ex abscissis haberi possunt in numeris rationalibus) excogitata est ratio pro curvis transcendenter datis, ubi ne extractio quidem locum habet. Assumo enim seriem arbitrariam, eamque ex legibus problematis tractando obtineo ejus coefficientes. This Transformation of Figures is no part of the method of series. It's only a Lemma towards doing that sometimes by the division of Wallis, which may be always done more readily without it The other method of assuming an arbitrary series is Mr Newton's. In his Letter of 1676 he set it down in this sentence. Altera [methodus consistit] tantum in assumptione seriei pro quantitate qualibet incognita ex qua cætera commode derivari possunt et in collatione terminorum homologorum æquationis resultantis ad eruendos terminos assumptæ seriei. So then Mr Leibnits has no right to the invention of any part of the method of Series.
Yet there is a sort of series the invention of which is due to him, & those he mentions in the end of his Letter dated 3 Feb. 1673. Modum habeo, saith he, summam inveniendi seriei fractionum in infinitum decrescentium, quarum Numerator unitas, nominatores vero numeri Triangulares, aut Pyramidales, aut Triangulo-triangulares &c. And these are found in the following manner.
De serie From the series &c take all the terms but the first & there will remain . De hac serie aufer omnes terminos From this series take all the terms but the first & there will remain & so on. And in generall, any regular series by subducting all the terms but the first or two first or three or four first will give a new series equal to the first or two first or three or four first terms.
This method seems to consist in subducting from any regular series all the terms except the first or two first, or three or four first. From the series , &c subduct all the terms but the first & there will remain And from this series take all the terms but the first & there will remain , &c. And from the first series take all the terms but the two first & there will remain &c And from this series , &c take all the terms but the first & there will remain , &c.
He pretended to two series for finding the number whose Logarithm was given, & yet wanted the method of finding those series. And when Mr Newton had further explained it he desired him again to explain it further & at length when he understood it he wrote back that he had it long ago as he found in his old Papers, but had neglected it for want of an elegant example.
In the year 1675 when he wrote the letter to Mr Collins printed by Dr Wallis he did not use the differential method as he would have done had he then known it.
It does not appear that he discovered his knowing any thing of it before the receipt of Sir Is. Newtons two Letters from Mr Oldenburg A.C. 1676
In those letters Sir Isaac discovered that he knew it & had written a treatise of it five years before. He represented that it was a method which did not stick at fractions & surds, which extended to the Problemes of direct & inverse tangents & others more difficult & gave an instance of its great extent in problemes of Quadratures setting down a general series which ran in infinitum & gave the quadrature in an infinite series when it was not expressible by a finite æquation but when it was expressible by a finite equation, brake off & gave that equation & wrote in the same letter. that this was the first Theoreme of those which he there spake of & therefore he had at that time other Theoremes of a higher kind derived from that method. This Theoreme is the fift in his book of Quadratures & the sixt is of the same kind & doth the same thing in trinomials which the fift doth in binomials & the third & fourth are introductory to the fift & sixt & therefore these four Propositions were then known to him as the result of the method of fluxions: & so were the ninth & tenth with the Tables of quadratures set down in the Scholium of the 10th. For in the second of the two letters above mentioned he did set down the Ordinates of these curves & said that he had tables of all their Quadratures: which Tables could not have been computed without the knowledg of the 9th & 10th Propositions. In the same letters he sets down ænigmatically this Probleme Data æquatione fluentes quotcunque quantitates involvente invenire fluxiones & vice versa. And the first part of this Probleme is the first Problem in the book of quadratures & the second Probleme is a very easy & obvious corollary of the first Probleme or rather it is nothing else then the first Probleme applied to the case of Quadratures & therefor it must be allowed that the Propositions in the book of Quadratures were known to Sir Isaac before the writing of the said two letters to Mr Oldenburg & by consequence that he had then not only invented the method of fluxions but also carried it to a higher pitch then Mr Leibnitz was able to carry it under the name of the differential method during the 30 years which followed before the publishing of the book of Quadratures notwithstanding the light which Mr Newton gave him into it by those two letters. And by all these considerations it is manifest that Mr Newton was the first inventor of the method. And the same thing is further manifest by his little Tract de Analysi per series numero terminorum infinitas written in the year 1669 ✝ ✝ & mentioned in Mr Newtons second Letter to Mr Oldenburg & lately published by Mr Iones. & by the letters of Dr Barrow & others found amongs the papers of Mr Collins & published with that Tract by Mr Iones.
Sir Isaac was therefore the first inventor of this method, & the next question is whether Mr Leibnits was a collateral inventor, or had it from Sir Isaac. [And if he had it not from Sir Isaac by means of the correspondence which he kept with Mr Collins before the receipt of Mr Newton's two letters above mentioned yet a man of his parts might easily have it from those two letters.] For the infinite series described in those letters are nothing else then the the summ of the indefinite or fluent quantity & all its differences. The first term is the fluent quantity, the second is the first difference, the third is the second difference, & so on in infinitum. For By the rule set down in Mr Newtons first Letter the binomium is resolved into this infinite series where the first term being the fluent the second term is its first difference & the third term is its second difference & so on in infinitum.
4 As for the symbols used by Mr Leibnitz they are of a later date . He has no symbols for fluxions: Mr Newtons are the oldest & the only symbols of that kind. The symbols of differences ax & dy are later by eight or ten years then the rectangles under the fluxions & the moment o used by Mr Newton in the same sense. And the symbols of summs , are later by 16 or 20 years then MrNewtons of including the Ordinate or Fluxion in a square to signify the Area or fluent.
5 And if the Methods be compared, Mr Newtons is the more elegant because he uses but one infinitely or indefinitely small quantity signified by the letter o. It is the more Natural & Geometrical because founded upon the rationes primæ quantitatum nascentium which have a being in Geometry, whilst indivisibles & quantitates minimæ or primæ nascentes upon which the differential method is founded have no being. There are rationes primæ quantitatum nascentium but not differentia prima nascentes. Nature generates quantities by continual flux or increase & the ancient Geometers admitted such a generation of areas & solids where they drew one line into another by motion to generate an area & the area into a line to generate a solid. But the summing up of indivisibles to generate an area or solid was never yet admitted into Geometry. Mr Newton's method is also of greater extent being adapted either for finding out a Proposition or for demonstrating it: Mr Leibnitzes is only for finding it out. When the work succeeds not in finite equations Mr Newton has recours to converging series & thereby his method becomes incomparably more universal then that of Mr Leibnitz which is confined to finite equations. And where the law of the fluxions is not known but the fluxions are had only in a few particular cases Mr Newton finds that Law quam proxime by drawing a Curve line through any number of given points & thence deduces the solution of the Probleme; & on this Account also his method is more universal then that of Mr Leibnitz. The method of M. Fermat de maximis & minimis Mr Newton retained & made universal without using any more symbols then one for infinitely small quantities. Dr Barrow began to use more symbols then one for infinitely small quantities drawing of Tangents & Mr Leibnitz changed the Symbols of Dr Barrow into dx & dy & from this Notation gave the method a new name without ever acknowledging himself obliged to the Doctor. Mr Newton made the method general in the years 1665 & 1666, Mr Leibnitz in th{e y}ear 1677. And if Mr Leinits pretends to have found it earlier, it lies upon him to prov{e} {illeg} & to give the world a fair account when & by what means he found it.
Mr Newton published his Treatise of Quadratures in the year 1704. This Treatise was written long before many things being cited out of it in his Letter of 24 Octob 1676. That it might not be taken for a new piece Mr Newton repeated what Dr Wallis had published nine years before without being then contradicted namely that the found the method of fluxions was invented by degrees in the years 1665 & 1666. Herupon the Editors of those Acta in Ianuary 1705 in the style of Mr Leibnitz represend that Mr Leibnitz was the first inventor of the method & that Mr Newton had substituted fluxions for differences . And Mr Keil in an Epistle published in the Philosophical Transactions for May & Iune 1708 retorted the accusation, saying: Fluxionum Arithmeticam sine omni dubio primus invenit D. Newtonus ut cuilibet ejus Epistolas a Wallisio editas legenti facile constabit. Eadem tamen Arithmetica postea mutatis Nomine & Notationis modo, a Domino Leibnitio in Actis Eruditorum edita est. And this was the beginning of the present controversy.
Mr Leibnitz in a Letter to Dr Sloan dated 4 Martij st. n. 1711 gave his reasons against MrKeill & desired that the R. Society would cause Mr Keil to make a publick recantation. Mr Keill chose rather to explain & defend what he had affirmed . And Mr Leibnitz in a second Letter to Dr Sloan dated 29 Decem 1711 instead of making good his accusation insisted only upon his own candor, as if it would be unjust to question it & , [justified what had been published in the Acta Lipsiensia, [& yet allowed that Mr Newton had found the method of fluxions apart though not so early;] called Mr Keil a novice unacquanted with things past & one that acted without author{y} from Mr Newton, & a clamorous man, & said that the Acta Lips. had given every man his due & desired that Mr Newton himself would give his opinion in this matter. He knew that Mr Newton had already given his opinion in the Introduction to his book of Quadratures: but Mr Newton must retract that opinion & allow that Mr Leibnitz was the first Inventor, or not be quiet.
The R. Society therefore having as much authority over Mr Leibnitz as over Mr Keil & being now twice pressed by Mr Leibnitz to interpose & seeing no reason to condemn Mr Keill without inquiring into the matter & that Mr Leibnitz declined to make good his accusation & that neither Mr Newton nor Mr Lebnitz (the only persons alive who remeembred what had passed in these matters 40 years ago) could be witnesses for or against Mr Keil, , appointed a Committee to search old Letters & Papers & report their opinion thereupon, And ordered the Letters & Papers to be published together with the opinion of their Committee, by which opinion Mr Newton had the method
If it be pretended that Mr Leibnitz has not yet produced his reasons for himself: I answer that in all the Letters which passed between him & Dr Wallis about these matters wherein he defended himself as well as he was able, he produced not any one reason to prove either that he had the differential method before the year 1677 or that Mr Newton had it not above ten years before that time. He produced not any one argument against Mr Fatio to prove that Mr Newton was the oldest inventor by many years. He did not then deny that Mr Newton was the first inventor In his first Letter against Mr Keill he produced his reasons against what Mr Keill had said. And after Mr Keil had explained himself & answered those reasons: in his next Letter for want of reason{s} cried out. Quæ D. Ioannes Keillius nuper ad Te scripsit, candorem meum apertius quam ante oppugnant: quem ut ego hac ætate, post tot documenta vitæ, Apologia defendam, & cum homine docto sed novo, & parum perito rerum anteactarum cognitore, nec mandatum habente ab eo cujus interst, tanquam {p}ro Tribunali litigam nemo prudens æquusque probabit. That is, he told the R. S{ociety} that they would be unjust unless they would allow him to be a witness in his own {cas}e.
The first of these shews what was the opinion of Mr Leibnitz before he knew any thing more of my method then what he had from my Letters writ in or before the year 1676 from the Principia Philosophiæ mathematica. The second shews was the tradition in England before we heard that this Method began to be celebrated in Holland as invented by Mr Leibnitz. Among the said Letters & Papers were also several papers written by my self in the years 1664, 1665 & 1666 some of which happen to be dated
Et Commercium Epistolicum oblivioni tradere conæretur tanquam nimis prolixo cui responderet, nec tamen satis prolixum .
Commercio Epistolico respondere recusaret, & convitijs uteretur
Cum D. Leibnitius add{u}e non posset ut vel Commercio Epistolico responderet vel argumenta pro se afferret; cumque præcedentes Epistolas is in Galliam prius mitteret quam earum tertia in Angliam veniret & prætenderet se hoc facere ut testes haberet et alias etiam pro argumentis contumelas adhiberet: Newtonus minime rescripsit sed Observationes sequentes in tertiam illam Epistolam scriptas cum amicis solummodo communicavit.
P. S.
When the Committee of the R. S. published the Commercium Epistolicum the Papers in my custody were not produced, & it will be more usefull to read the progress by which the method was invented. Among my papers written in the years 1664, 1665 & 1666 some happen to be dated: amongst which is that which follows
13 Novem. 1665
Probleme.
An Equation being given &c
Proposition is here set down in these Rules.
<39v>
<39v>
He saith that he formerly beleived me & on that account acknowledged that I had found the method of fluxions apart, but now M. Bernoulli has given him reason to suspect me, he is at liberty to retract. But his Letter to Mr N. dated Mar. 1693 & herunto annexed was written before he had any other notice of my method then from Mr Oldenburgh Mr. Collins & the Principia Philosophiæ, & therefore he is not at liberty to retract.
P. S.
Illustri Viro
ISAAC NEWTON
Godefridus Gulielmus Leibnitius S.P.D.
Quantum tibi . . . . . . Vale. Dabam Hanoveræ Martij 1693.
that time that Mercator published his Logarithmotechnia & this Compendium is the Analysis per Series now extant. I mentioned also that five years before the writing that Letter that is in the year 1671 I had written a Tract concerning the method of series & another method together, & that the other method was founded in this sentence Data æquatione fluentes quotcunque quantitates involvente fluxiones invenire & vice versa.
I suppose he means because he finds no prickt letters there. And by the same way of arguing he & Mr Bernoulli may pretend that they find nothing of the method of fluxions in the Introduction to the Book of Quadratures, tho that Introduction be entirely taken up in describing this Method & illustrating it with Examples [& my saying there that I found this Method in the years 1665 & 1666 gave occasion to this controversy]. In that Introduction I say that I invented (not prickt letters, but) the method of fluxions in the years 1665 & 1666, & describe it there without the use of prickt letters, as I did long before in my Analysis above mentioned. Let the world judge whether the method described in this Introduction & said here to be invented by me gradually in those years be not one & the same method with that described in the said Analysis & communicated by Dr Barrow to Mr Collins 47 years ago & in my Letters of 10 Dec 1672 & 24 Octob 1676 & concerning which I say in my Letter of 13 Iune 1676 that Analysis by my method of series extends to almost all sorts of Problems (except perhaps some numeral ones like those of Diophantus) but becomes not altogether universal without it the help of some further methods, which in next Letter dated 24 Octob 1676 I describe to be the direct & invers methods of fluxions the method I of extracting fluents out of equations involving their fluxions, & the method of assuming arbitrary series. Although I said in that Letter that the of the method of which I wrote a Tract in the year 1671 was founded in this sentence Data æquatione fluentes quotcunque quantitates inolvente fluxiones invenire & vice versa
— & Dr Wallis (Vol 2 Opper. pag 393 lin. 32) has told him that that this method needs no further explication then that which I gave of it in my Letter of 24 Oct. 1676.
That of Mr Leibnitz shew that he understood that I had a Methodus similis before he knew any thing more of it then what he had from my Letters in the year 1676 & from the Principia Philosophiæ: that of Dr Wallis that the tradition that I invented the method [mentioned there by the Doctor] was as old in england as the year 1676, at which time copies of my Letters were sent to him by Mr Oldenburg.
Cum D. Leibnitius Epistolas præcedentes in Galliam prius mitteret quam Responsem ejus in Angliam veniret et Responsum illud convilijs abundaret & Autho; Newtonus minime rescripsit, sed Observationes sequentes in Responsum illud se scriptas cum amicis tantum communicavit.
& convilijs abundaret, et Commercio Epistolico minime responderetur; Newtonus non rescripsit, sed seq. Observationes in Responsum illud a se compositas cum amicis tantum communicavit.
Cum D. Leibnitius Epistolas præcedentes in Galliam prius mitteret quam earum tertia in Angliam veniret, Newtonus minime rescripsit sed Observationes sequentes in tertiam illam scriptas cum amicis tantum communicavit.
Observationes in Epistolam præcedentem.
The force & evidence of the Commercium Epistolicum & of the account here given of that matter stands upon the authority of the ancient Letters & papers partly by Dr Wallis & partly by order of the R. Society the originals of those published by order of the Society are still preserved. If those ancient Letters & Papers are altogether against Mr Leibnitz it is his own fault. If the Notes upon them for enabling the reader to compare them & understand them at one reading, have in any thing misrepresented them, Mr Leibnitz & his friends are at liberty to shew wherein they are misrepresented & to set right the representation. But they are not at liberty to tell stories at discretion without proving what they say. Mr Leibnitz can not be an evidence in his own cause & his friends know nothing of his correspondence with the English in his travells 40 years ago but what they have from him or from the Letters & papers then written & still preserved.
It has been said that Mr Newton in the Scholium at the end of his Book of Quadratures has put the third fourth & fift terms of a converging Series respectively equall to the 2d 3d & 4th differences of the first Term, & therefore did not understand the method of second third & fourth differences. But in the first Proposition of that Book he shewed how to find the first second third & following fluxions in infinitum & therefore when he wrote that Book, which was before the year 1676, he did understand the method of all the fluxions & by consequence of all the Differences. And if he did not understand it when he added that Scholium to the end of the book, which was in the year 1704, it must have been because he had then forgot it. And so the Question is only whether Mr Newton had forgot the method of second differences before the year 1704.
In the tenth Proposition of the second Book of his Principia Philosophiæ in describing some of the uses of the terms of a converging series for solving of Problemes he tells us that if the first term of the series represent the Ordinate  BC of any Curve line ACG, & CBDI be a parallelogram infinitely narrow whose side DI cuts the Curve in G & its tangent CF in F: the second term of the series will represent the line IF, & the third term the line FG. Now the line FG is but half the second difference of the Ordinate And therefore Mr Newton when he wrote his Principia, put the third term of the series equall to half the second difference of the first term & by consequence had not then forgotten the method of second differences. ‡[5]
BC of any Curve line ACG, & CBDI be a parallelogram infinitely narrow whose side DI cuts the Curve in G & its tangent CF in F: the second term of the series will represent the line IF, & the third term the line FG. Now the line FG is but half the second difference of the Ordinate And therefore Mr Newton when he wrote his Principia, put the third term of the series equall to half the second difference of the first term & by consequence had not then forgotten the method of second differences. ‡[5]
In the year 1692 when at the request of Dr Wallis, he sent to him a copy of the explication of the Proposition, Data æquatione fluentes quotcunque quantitates invenire, he gave examples thereof in first second & third fluxions as you may see in the second Volume of the Doctors works pag 391, 392, 393 & 396. And therefore he had not then forgotten the method of second fluxions.
Nor is it likely that in the year 1704 when he added the aforesaid Scholium to the end of the book of Quadratures, he had forgotten both the first Proposition of the book & the last upon which that Scholium was written. If the word [ut] which in that Scholium may have been accidentally omitted between the words [erit] & [ejus] be restored; that scholium will agree with the rest of his writings,
Sir
I beg you will not think mee impertinent in troubling you with this. it is upon the account of the Medall
Proceribus populisque concentientibus
I think it will be better thus
Senatu Populoque sancientibus
Proceres is but a Metaphor {&} is properly the Beams in buildings, and expresses rather cheif Officers than Noblemen
Populos is {rea}d in the plurall number but I think ofter in the singular sancire leges in Tully's word
I am your most obedient Serv
S: Garth
pag. 4.
It has been said that Mr Newton in the Scholium at the end of this book of Quadratures has put the third fourth & fift terms of a converging series respectively equall to the 2d 3d & 4th differences of the first term, & therefore when he wrote that Scholium
Mr Newton in the tenth Proposition of the second book of his Principia Philosophiæ, in describing the use that may be made of the severall terms of a converging series tells us that if the first term of the Series represent the Ordinate of a Curve BC the second will represent the line IF, & the third the line FG. Now the line FG is but half the second difference of the Ordinate, & therefore Mr Newton in applying these series to the solution of Problems did then put the third term equal to half the second difference, as it really is.
Mr Newton therefore when he wrote the Principia Philosophiæ & long before that, when he wrote the first Proposition of his book of Quadratures understood the method of second differences. And if he did not understand it when he wrote the Scholium, which was but tenn years ago, it must be because he has forgot it. But there is no need of saying that he had forgot it: for if the word [ut] which has been twice accidentally omitted between the words [erit] & [ejus] in that scholium be restored, that Scholium will agree with the rest of his writings.
It has been represented that the R. Society have passed sentence without hearing both parties & therefore their sentence is voyd. And indeed Mr Leibnitz pressed them to condemn Mr Keil without hearing both parties; And told them that his own candour could not be questioned without injustice: Which is the same thing as to tell them that they would be unjust if they did not allow Mr Leibnitz to be a witness in his own cause & condemn Mr Keil without hearing both parties. But the R. Society do not act as a Court of Iudicature, nor have they been desired to give their opinion in this matter unless by Mr Leibnitz against Mr Keill.
It has been represented in Germany that Mr Leibnitz first found out the differential Calculus in numbers, & then by inventing the Analysis of infinitesimals translated this Calculus to Geometry. But this is to tell us that he first found out the differential calculus of Mouton & then by inventing the Analysis of infinitesimals translated Moutons calculus to Geometry. The invention of Moutons method is nothing to the purpose. It lies upon him to prove that he invented the Analysis of infinitesimals before the year 1677. In a letter to Dr Wallis dated 28 May 1697 he tells us that the consideration of differences & summs in series of numbers gave him the first light by observing that Differences answered to tangents & summs to quadratures: that is, it put him upon considering Dr Wallis's summatory method of Quadratures & Dr Barrow's differential method of Tangents. But this consideration alone could not give him light into the method of drawing Tangents without sticking at surds & into the universal extent of this method for solving all sorts of Problems. That light he had by his correspondence with Mr Oldenburg as is manifest by what has been said above.
It has been suggested by Mr Leibnitz himself, that the Committee of R. Society published only those papers which made against him & suppressed those that made for him. B
the symbol o, The proportion of the fluxions (which are finite quantities) giving all the other moments. It is more natural & geometrical
And whereas Mr Leibnitz has represented that the use of the letter o is vulgar & destroys the advantages of the Differential Method
The reason of his inconsistency in this matter was his computing by a wonderfull unphilosophical errour, the quantity of impulsive force acquired by a falling body from the quantity of its matter & of the space described by it in falling; recconing the force acquired to be in a compound ratio of the matter & the space together . Now matter is as the weight thereof & the space described is as the square of the line of its falling, & therefore according to Mr Leibnitz the force acquired in falling is in a compound ratio of the weight of the falling body & the square of the time of its falling. And by consequence, where the weight remains the same, the force acquired in falling will be as the square of the time So that if the time of falling be divided into equal parts, & in the first part of the time four degrees of force will be acquired, in the three first parts of time nine degrees of force will be acquired, in the four first parts of time sixteen degrees of force will be acquired, & so on And therefore if in the first part of the time one degree of impulsive force be acquired in the second part of the time three degrees of force will be acquired, in the third part of the time five degrees of force will be acquired in the fourth part of time seven degrees of force will be acquired, & so on. And so the weight or gravity of the body which by its action impresses these impulsive forces upon the body, acts with three times more force in the second part of the time then in the first & with five times more force in the third part of the time then in the first & with seven times more force in the fourth part of the time then in the first, & so on. Which is as much as to say that the falling body grows heavier & heavier as it falls, & becomes three times heavier in the midle of the second part of the time then in the middle of the first & five times heavier in the middle of the third part of the time then in the middle of the first, & so on. Or that the weight of the body is proportional to the time of its falling: And by consequence that in the beginning of the first part of the time the body have no weight at all. Which is contrary to the Hypothesis of uniform gravity & to experience it self.
The Theory of Projectiles invented by Galilæo is founded upon the Hypothesis of uniform gravity, & is generally approved by Mathematicians. Now uniform gravity is that which acts with an uniform force & in equal times by acting with equal forces upon the body communicates equal forces to it. If in the first part of time it communicates one degree of force & gives one degree of velocity to the falling body; in the second part of time by acting as much as in the first, it will communicate another degree of force & give another degree of velocity the falling body; & in the third part of time it will generate a third part of force & a third degree of velocity & so on perpetually: & therefore the time of falling, the force imprest, & the velocity of descent will be always proportional to one one another. But the space described by the falling body arises partly from the time of descent & partly from the velocity of the falling body & therefore will be in a compound ratio of them both or as the square of either of them, & by consequence as the square of the force.
And so if two equal bodies be thrown directly upwards tho one with a velocity double to that of the other, the swifter body will rise four times higher then the other in twice the time & in that time the action of gravity upon it for taking away the force by which it ascends will be double to the action of gravity upon the other body, & therefore the force by which it ascended & which is taken away by that action is only double to the force by which the other body ascended.
A body therefore of one pound weight is not (as Mr Leibnitz supposes in the Acta Eruditorum ad Annum 1686 pag. 162) throw in Vacuo four times as high but sixteen times as high by the same quantity of impulsive force wherewith a body of four pound weight is thrown one foot high. The ground of his error is that he confounds [Acta Erudit: ad Ann. 1686 pag. 162; & ad Ann. 1690 pag. 234; & ad Ann. 1691 pag. 439; & ad Ann. 1695 pag. 155] the spaces described in unequal times by bodies falling downwards or thrown upwards with the spaces described by bodies rising & falling in equal times at the ends of the unequal arms of a ballance. Whereas in the first case the spaces described are as the time & the velocity together, that is, as the square of the velocity: in the second case the times being equal the spaces described are only as the velocities.
And because tis true that in an horizontal place, where gravity neither adds to nor takes from the Velocity, a body of four pound weight will be carried one foot by the same force imprest at once whereby a body of one pound weight will in the same time be carried on four feet: therefore he supposes [Acta Erudit: ad Ann. 1686 pag 162,] that in a perpendicular plane wherein Gravity continually augments or diminishes the velocity in proportion to the time of its acting; a body of four pounds weight will be thrown upwards one foot by the same force imprest at once whereby a body of one pound weight will be carried up four foot; or that a body of One pound weight in falling four foot, will acquire the same impulsive force as a body of four pounds weight in falling one foot. Then which nothing can be more contrary both to reason & experience.
p. 38 l. 14. The Principle upon which he founded his Dynamique is erroneous The forces of equal bodies are not as the spaces by them in unequal times but as the spaces described by them in equal times
P. 44. l. 1. For fluxions write moments. For fluxions are not differences.
P. 46. l. 3. Mr Newton in 1704 in the Introduction to his book of Quadratures published that he found the Method of Fluxions gradually in the years 1665 & 1666, the next year in giving an account of this book in the Acta Lips. for this was called in question & Mr Newton was accused of Plagiary. Mr Keill in 1711 defended him.
P 49. l. 10 This was in pursuit of the charge of Plagiary published in the Acta Lips 1705 as above . Mr Leibnitz was then at Vienna & Copies of the Commercium were sent to him thither by several hands from England. And thereupon he appealed from the judgment of the Committee to that of Mr Bernoulli, desiring him to examin the Book, & pretending that he had not yet seen it himself; & Mr Bernoulli's answer dated 7 Iune 1713 he inserted into a Paper of his own dated 29 Iulij 1713 & caused them to be published without their names, as if written by other persons unconcerned. And Dr Keill answered this Paper in the Iournal Literair.
P. 49. l. 19. The pretence that Mr Leibnitz intended to write a Commercium is a sham. The
P. 52. l. 7. Hoc factum est anno 1673 ad finem vergente.
P. 53. l. 6. Hæc Newtoniana Leibnitiu{ss} non vidit ante annum 1676.
P. 53. l penult. Mr Newton scripsit Lemma II Lib. II Princip. & Scholium subjunctum, non ut methodum Leibnitio concederet sed ut eandem sibi vindicaret.
before his Lectures came abroad, {illeg} — — — — — because {they} did many more things of this kind. [He has not produced the least proof that he knew the method before the year 1677, but on the contrary in his Letter of 27 Aug. 1676 he declared his disbeleif that my methods were so general as I had described & said that many Problems, & among others the inverse Problems of Tangents, could not be reduced to æquations or quadratures; & placed the perfection of Analysis in Analytical Tables of Tangents & the Combinatory Art, saying of the first, Nihil est quod novim in TOTA Analysi momenti majoris; & of the second, Ea vero nihil differt ab ANALYSI ILLA SVPREMA ad cujus intima Cartesius non pervenit: est enim ad eam constituendam opus Alphabeto cogitationum humanarum. And in a Letter from Amsterdam to Mr Oldenburg 28 Novem. 1676 he was thinking to improve the Method of Tangents of Slusius by such a Table of Tangents.] In that Letter he placed the perfection of Analysis in other methods then the differential, & represented it improbable that my methods should be so general as I had affirmed
6. Post verba [Metaphysica in Idæis, Idææ et Philosophia omnis vera in Phænomenis fundantur, & incepit Newtonus a Phænomenis: Momortus ab idæis incipiendum esse clausis oculis & ab hujusmodi somnijs ad phænomena pergendum esse contendit.] adde: Sed audiamus quid Leibnitius ipse cui Author noster cum Bernoullijs duobus tantopere favet, de Metaphysicæ sanæ notionibus olim scripsit. In charta enim quam De Primæ Philosophiæ Emendatione & de Notione Substantiæ scripsit quæque in Actis Lipsicis anno 1694 mense Martio impressa fuit hæc habet. Video plerosque qui Mathematicis doctrinis delectantur — — — — hoc commodo caremus. Hactenus Leibnitius.
11. Post verba [rimari philosophorum est.] adde. In Principiorum editione secunda sub finem, Newtonus scripsit se rationem proprietatum gravitatis ex phænomenis deducere nondum potuisse & Hypotheses se non fingere. Et postquam motus Planetarum Cometarum Æquinoxionem & maris nostri a vi gravitatis per phænomena et mathematicas demonstrationes derivasset subjungit motus particularum corporum a spiritu quodam quo attractio electrica perficetur quam maxime pendere, sed hæc paucis exponi non posse. Et Editores Actorum Lipsiensium (Anno 1714 mense
6. In Metaphysicæ sanæ notionibus.] Metaphysicam sanam intelligit Cartesianam qua utique ab ideis inmatis ad existentiam verum pergitur. Audiamus autem quid Leibnitius de Metaphysicæ sanæ notionibus olim scripsit. Is enim in dissertatione De Primæ Philosophiæ emendatione & de Notione substantiæ in Actis Lipsicis anno 1694 mense Martio impressa, hæc habet. Video, ait, plerosque qui Mathematicis doctrinis delectantur .......... hoc commodo caremus. Hactenus Leibnitius. Metaphysica utique in Idæis, Ideæ & Philosophia omnis vera in Phænomenis fundantur, et incipit Newtonus a Phænomenis: Momortus Idæas non a Phænomenis deducendas esse sed clausis oculis formandas, oculos deinceps apperiendos esse ut phænomena beneficio idæarum clare & distincte videamus.
qu{a} utique Ideæ non deducuntur a phænomenis sed innatæ esse finguntur, non disputatur a Phænomenis de existentia r{eu}m sed extensionem esse corpus & res non extensis existere probatur ab Idæarum in{na}tarum figmentis.
— materiam in forma quacunque positam, ope legum naturæ formas omnes quarem est capax successive assumere tandemque ad illam quæ est hujus mundi devenire; philosophiam omnem naturalem &c
Vires attrahentes, tanquam qualitates occultas a Newtono introductas, Leibnitius in Tractatu de Bonitate Dei alibi hostili animo explodit. Idem hic facit Momortus quasi vires attrahentes in Gallia damnatas: Newtonus induceret At Vires attrahentes in Gallia damnatus Newtonus non inducit — — — per fractonem excitatis.
2B. Demonstratum Vacuum se dedisse.] Medionum maxime fluidorum qualia sunt Aer Aqua et Argentum vivum, resistentiam prope omnem a vi intertiæ partium fluidi oriri & vim inertiæ proportionalem esse densitati fluidi adeoque resistentiam Mediorum summe fluidorum proportionalem esse densitati eorundem Mediorum quamproxime Newtonus ostendit, et legem resistentiæ in talibus fluidis exposuit multisque experimentis confirmavit. In Vacuo Boyliano resistentia corporum cadentium longe minor reperitur quam in aere & si forte aliqua sit, sentiri tamen non potest In spatijs cœlestibus quæ supra Atmosphæram sunt & aere omni magis sunt vacua, resistentiam adhuc minorem esse statuit, Et et ad Philosophiam cœlorum sufficere quod spatia illa medijs resistentibus vacua sint. Ad Medio corporeo non resistente plena sint, Quæstio est ad Philosophiam cœlorum minime spectans Sed ejusmodi tamen, medium corporeum dari Newtonus non credit nisi forte duo sint corporum genera alterum cujus partes vim habent inertiæ, alterum cujus partes vim talem non habent.
5B. In experientia universali nixa] Quanam experientia constat motus omnes animalium et hominis ipsius mere mechanicas esse & omnes cogitandi et volendi actionis a quibus motus isti oriuntur, in motu corporum consistare?
6. In metaphysicæ sanæ notionibus] Metaphysicam sanam intelligit Cartesianam: Qua utique . . . . . . devenire statuit. Sed nec Cartesius alicubi probavit, facultatem cogitandi rem cogitantem esse aut rem omnes extensam extensionem esse, motum corporum in sola translatione relativa sine vi inertia consistere, aut res cogitantes spatio non adesse, seu nullibi esse, aut Ideas nobis innatas esse aut nos nos ideas substantiarum habere. Hæc omnia sunt Hypotheses. Metaphysica in Ideis abstractis fundatur, Philosophia vera in Phænomenis. In Metaphysica clausis oculis disputamus, in Philosophia videmus et a phænomenis veritatis deducimus. Metaphysica a Theogonia Gentium antiquarum originem habuit qua utique Mundum totum animasque mortuorum aut partes esse Dei aut ejus potentias esse finxerunt id est Deum esse rerum omnium naturam: Physica missis gentium religionibus incipit a rebus visis et cognitis et earum rationes & causas investigat, idque per argumenta si fieri potest mathematica.
be found by the same method, & then subjoyns: Nec quicquam hujusmodi scio ad quod hæc methodus idque varijs modis sese non extendit. Imo tangentes ad Curvas Mechanicas (siquando id non alias fiat) hujus ope ducuntur. Et quicquid vulgaris Analysis per æquationes ex finito terminorum numero constantes (quando id sit possibile) perficit, hæc per æquationes infinitas semper perficit: Ut nihil dubitaverim etiam nomen Analysis etiam huic tribuere.
Tempus utique per quantitatem quamcunque uniformiter fluentem, fluxionem ejus per unitatem, et momentum per literam o Newtonus designat. Aliarum quantitatum fluxiones designat is per alia symbola, et momenta earum per symbola illa ducta in momentum o, et areas curvarum per ordinatas quadrato inclusas. D. Leibnitius pro fluxionibus nulla habet symbola, pro momentis literam d præfigit symbolis fluentium, et pro areis literam ∫ præfigit symbolis Ordinatarum. Newtonus calculo suo usus est in Analysi quam Barrovius cum Collinio mense Iulio anni 1669 communicavit; et hanc methodum tum in Octob. 1676 valde generalem esse significavit, & verbis partim apertis differentialem vocat, anno 1676 minime invenerat. Scripsit enim ad Oldenburgum eo anno, Augusti 27, multa esse adeo mira et implexa ut neque ab æquationibus pendeant neque a Quadraturis: qualia sunt (ex multis alijs) problemata methodi Tangentium inversæ, quæ etiam Cartesius in potestate non esse fassus est. At acceptis Newtoni literis, anno sequente in Literis ad Oldenburgum 21 Iunij datis, methodum differentialem ut olim a se inventam communicare cœpit his verbis. Clarissimi Slusij methodum tangentium nondum esse absolutam celeberrimo Newtono assentior: et jam a multo tempore rem tangentium longe generalius tractavi scilicet per differentias Ordinatarum. — Hinc in posterum nominando dy differentiam duarum proimarum y &c. Quod methodum hanc a multo tempore invenerat probandum est. Nam D. Leibnitius pro se testis esse non potest. Iniquissimus esset Iudex qui in rebus controversis hominem quemvis pro seipso testem admitteret.
GEORGIVS D. G. MA. BRIT. FRAN. ET HIB. REX. FIDEI DEFENSOR.
Ecclesia tuta.
And such Letters were writ in the name of the Elders & people; together the people being present at the writing of them, & giving their assent (Act xv. 6, 12, 22, 23:) for the Elders were not to take the oversight of the flock of God as Lords over Gods heritage but, as ensamples to the flock. The Presiden{t} was to act by the advice & with the consent of the Council & the President & Council were to acquainte the people therewith & to advise & teach them & procure their assent for avoiding ill will discord faction & schism.
Fluxionum serierum infinitarum incidisse.
pag tertia, Sed et specimen ejus methodi Collinius cum Gregorio communicavit. Et Anno 1676 Newtonus eandem in epistolis duabus duabus ad D. Oldenburgum datis et ad D. Leibnitium missis, quoad series infinitas fuse explicuit, quoad Fluxiones vero subobscure insinuavit. Scripsit enim in epistolarum secunda Die 24 Octobris data, se tunc compotem fuisse — Et ibidem Theorema subnectit pro Binomijs quod quadraturam finita exhibet æquatione ubi fieri potest, infinita verò ubi quadratura per finitam exhiberi nequit. Quo exemplo satis ostendit methodum fluxionum absque methodo serierum infinitarum perfici non posse Hoc Theorema primum vocat hoc est primum Seriei Theorematum — patebit. Scripsit vero Newtonus methodum ex dictis haud difficile colligi, se vero impræsentia ne fuse exponere cogeretur, eandem his literis transpositis celare (6accdæ13eff7i3l9n404qrr4st12vx. Quæ quidem ordinatæ hanc conficiunt sententiam Data æquatione Fluentes, quotcunque quantitates involventes invenire Fluxiones et vice versa. Et hisce Literis anno 1677 acceptis Leibnitius respondit se in parilem methodum incidisse uti Princip Phil. Natur. Math. pag 253 &c videre licet: cujus tamen explicationem (in cæteris suis inventis publicandis non raro nimis præ properus, uti in Act. Erudit. plus semel conspici queat) ad Annum usque 1684 distulerit.
D. Iacobus Gregorius ex unica Newtoni serie quam a Collinio acceperit, methodum ipsam serierum infinitarum collegit. D. Leibnitius circa annum 1675 Londini fuit, & postea cum Collinio commercium Epistolicum habuit et subinde epistolas Newtoni ab Oldenburgo accepit; & tum demum rescripsit se methodum Newtonianæ non dissimilem habere. Qua ratione in hanc methodum inciderit, ipse novit: nobis sufficit quod Newtonus sit primus ejus inventor. Is inventionem terminorum serierum infinitarum primus docuit, et secundus seriei cujusque terminus est quantitas illa quam Leibnitius differentiam vocat primi termini & cujus adeo inventionem sibi arrogat
Sed et Newtonus hanc methodum longius provexit quam alius {illeg} Ipsam enim ad quadraturam Curvarum per series infinitas quæ in æquationes finitas vertuntur ante {annum} 1676 applicuit.
Ipsam etiam ad æquationes fluxionales — nequeunt. Et methodum generalem jam invenerat extrahendi fluxiones ex æquationibus fluxionalibus.
Methodos insuper universaliores ad comparationes Curvarum quæ geometrice quadrari non possunt eodem tempore tradiderat — subministraverit.
Et has methodos insuper ad enodanda naturæ phænomena in Principijs suis mathematicis adeo feliciter applicuit ut ejus inventis cultores methodi differentialis vix aliquid addiderint. Planetas gravitate sua circum solem in Ellipsibus revolvi ac radijs ad solem ductis areas describere temporibus proportionales, Newtonus ante annum 1677 demonstrare didicit, & demonstrationem cum Societate Regia anno 1684 communicavit. Prodijt hæc demonstratio in lucem anno 1687, et Leibnitius anno 1689 Theorema a Newtonianum, differentiali sed errante, calculo ad incudem revocavit ut suum faceret. Asseruit enim se Theorema illud invenisse, sed in calculo aliquoties erravit, ideoque nihil invenit. Sed nec methodum jam satis didicerat qua Newtonus Principia sua sua mathematica investigavit, ut ex erroribus ejus manifestum est. At ex eo tempore methodum differentialis in quæstionibus difficilioribus enodandis e{nc}ol{eri} cœpit, facto initia a resolutione Problematum de resistentijs mediorum & motibus corporum cœlestium, quæ Newtonus antea tractaverat, ut ex ejus Principijs Mathematicis manifestum est Methodus igitur fluxionum quam Leibnitius differentialem vocat, non prius apud exteros excoli et celebrari cœpit, quàm Newtonus eandem apud nos ad summum fastigium evexerat.
Iustitia hic reddenda est Newtono (cui Geometria Optica et Astronomia multum debent) qui etiam propria Marte aliquid hic [sc. Methodo differentiali] simile habuit uti postea didici [videlicet ex Algeb{ra} Wallisij Anno 1693 impressa]. Verum est quod alijs utitur symbolis: sed quemadmodum ipsa characteristica, ut it dicam, magna pars est artis inventoris, credo quod notra [symbola] plus luminis præbent. Hæc Leibnitius in the Iournal des Sçavans 23 August 1694.
Gregorius in Prop. 7 Geometriæ universalis anno 1668 impressæ et Barrovius in ejus Lect 10 anno 1669 impressa rem tangentium tractaverant per differentias ordinatarum. Idem facere potuisset Leibnitius jam a multo tempore. Methodus Slusij Corollarium est methodi Tangentium per differentias Ordinatarum. Nam Etenim in primo ejus Lemmate differentia dignitatum duarum ejusdem gradus applicata ad differentiam laterum, est differentia infinite parva ordinatarum duarum applicata ad differentiam infinite parvam Abscissarum. Cum igitur Newtonus dixisset Methodum Tangentium Slusij esse unum particulare vel Corollarium potius methodi generalis quæ extenderet se citra molestum ullum calculum . . . . et exemplum dedisset hujus methodi in Serie generali pro quadraturis cœpit Leibnitius methodum Tangentium per differentias Ordinatarum ab alijs traditam jam longe generalius tractare quam antea, et novo nomine novisque symbolis ut suam ornare. Et ne eandem a Newtono didicisse videretur scribit in hæc verba. Clarissimi Slusij methodum Tangentium nondum esse absolutam Newtono assentior. Et jam a multo tempore rem Tangentium longe generalius tractavi scilicet per differentias Ordinatarum. Et cum hanc Methodum mense Octobri Anni 1684 edere cœpisset, scripsit postea se inventum plusquam nonum in annum pressisse. Quod perinde est ac si dixisset se inventum habuisse ante mensem Octobrem anni 1675. Et postea methodum solo suo nomine edidit cœlatis Newtoni literis donec a D. Wallisio ederentur. Et ne parum candi{des} egisse videretur, prætendit se cum Elementa calculi sui edidit anno 1684, nihil aliud de Inventis Newtoni in hoc genere ipsi innotuisse quam quod ipse olim significaverat in literis, posse se Tangentes invenire non sublatis Irrationalibus. Cum tamen ex literis hic impressis constet methodum Differentialem anno 1676 Leibnitio minime innotuisse, anno vero 1677 Leibnitium cognovisse quod methodus Differentiali similis Newtono innotesceret Nam et anno 1684 mense Octobri elementa methodi differentialis edidit sub hoc titulo: Nova methodus pro maximis & minimis itemque tangentibus quæ nec fractas nec irrationales quantitates moratur; & subjuxit: Et hæc quidem initia sunt tantum Geometriæ cujusdam multo sublimicoris difficillima & pulcherrima quæque etiam mistæ Matheseos pertingentis quæ sine calculo nostro differentiali, aut SIMILI, non temere quisquam pari facilitate tractabit. Quid Leibnitius per methodum similem his intelligat sentie{s} Confer{ando} hanc methodi differentialis descriptionem cum simillime descriptione methodi in epistolis tribus Newtoni
Introduction
Pag 7. Instead of necessary to salvation should it not be necessary to communion
P. 21. lin 2, 3. Let the note φ come at the end of the sentence without a parenthesis.
Mint Office. 13 Apr. 1714
Sir
I have considered the inclosed Estimate made upon a Proposal offered to the Lords Commissioners for Trade & Plantations for coyning 1500 Tonns of Copper into half pence & farthings in five years time
minusculis a et b designat He might have added further that in [one & the same book, the book of Quadratures, [Mr Newton sometimes uses letters with pricks sometimes not. For] in the Introduction to the book of Qu some Problemes are solved by the method of fluxions without the use of such Letters with pricks & in the body of the book letters with pricks are made use of: And yet the method is one & the same. Mr Leibnitz confines his method &c
In the second Lemma of the 2d Section of the book Mr Newton demonstrated synthetically the Elements of the method of fluxions & added this Scholium. In literis — Vtriusque continetur in hoc Lemmate. This Scholium referrs to Mr Newtons Letter dated 24 Octob. 1676 Where he distinguishes between the method of series & the method of fluxions & represents that the method of fluxions proceeds in surd quantities as well as rationals & readily gives the Method of Tangents of Slusius &c And in his Letter dated 10 Decemb. 1672 he represents that the method whereof the method of Tangents of Slusius was but a Corollary or branch & which proceeded in æquations affected with surd quantities, was very general & reached to the abstruser sorts of Problems, & particularly to Problemes about the curvature of Curves. Now in solving such Problems by the method of fluxions the second fluxions come under consideration & therefore Mr Newton had extended his method to the second fluxions in or before the yeare 1672, whereas it doth not appear that Mr Leibnitz understood the second differences before the year 1684.
11. 13. When Mr Leibnitz wrote to Mr Oldenburg for the Demonstration of the series for the arc of a circle whose sine was given, Mr Oldenburgh & Mr Collins deire{illeg} Mr Newton to describe his own method of finding it. And thereupon Mr Newton wrote his Letter of 13 Iune 1676: which conteined his method of Series & was sent to Paris Iune 26. [& neare the end of it when he had described his method of Series which he calls infinite equations, he added that Analysis by the assistance of there equations extends to almost all Problems except some numeral ones like those of Diophantus, but becomes not altogether universal without some further methods of reducing Problems to infinite equations & infinite equations to finite ones when it might be done] This Letter together with the extracts of Gregonis Letters was sent to Paris 26 Iune 1676
13 Mr Leibnitz in his Answer dated 27 Aug 1676 in recompense for Mr Newtons method of Series sent back a Theoreme for transmuting figures into one another, & thereby Demonstrated the series of Mr Gregory for finding the arch whose tangent was given. [But this Demonstration was composed without the assistance of the Differential method, & therefore Mr Leibnits had not yet found out that method. For in the Acta Eruditorum Mensis Aprilis pag 178 he wrote Iam Anno 1675 compositum habebam opusculum Quadraturæ Arithmeticæ ab amicis ab illo tempore lectum, sed quod materia sub manibus crescente limare ad editionem non vacavit postquam aliæ occupationes supervenere; præsertim cum nunc prolixius exponere vulgari more quæ Analysis nostra paucis exhibet, non satis operæ pretium videatur And in his Letter of 12 May 1676 he wrote to Mr Oldenburg that he was then polishing this Demonstration to send it to him. And in October following he left Paris being called home by his Prince to be imployed in publick affairs wherby he was no longer a leasure to file & polish this work for the Press vulgari more.
26 In his said Letter of 27 Aug 1676 he added further: Quod dicere videmini plerasque difficultates (exceptis Problematibus Diophantæis ad Series infinitas reduci; id mihi non videtur. Sunt enim multa usque adeo mira et implexa ut neque ab æquationibus pendeant neque ex quadraturis. Qualia sunt (ex multis alijs) Problemata methodi tangentium inversæ. And this also makes it very certain that he had not yet found out the differential method.
27 Mr Newton in his Answer dated 24 Octob. 1676 at the request of Mr Leibnitz gave an account how before the plage which began to rage in Summer 1665 he found the method of series, & upon the coming out of Mercators Logarithmotechnia communicated to Mr Collins by Mr Barrow a Compendium of these series (meaning the Analysis above mentioned) & two years after at the suggestion of Mr Collins wrote a larger Tract on the same subject, joyning with it a Method from which the determination of Maxima & minima & the method of Tangens of Slusius & some others readily flowed, & which stuck not at surds, & was founded upon this Proposition: Data æquatione quotcunque fluentes quantitates involvente fluxiones invenire; et vice versa. This Proposition he wrote down enigmatically & added that it faciliated the Quadratures of Curves & afforded him infinite series which brake off & became finite when the Curve was capable of being squared by a finite equation. And of this he gave an instance by such a Series. By which circumstance it is manifest that this was one of the methods mentioned in his former Letter of 13 Iune where he said that Analysis by the help of series extended to almost all Problemes but became not universal without some further methods of finding infinite series & reducing them back to finite equations
28 In his Letter of Octob 242 1676 he said further that his method extended to inverse Problems of Tangents & others more difficult, & that by a double method which he comprehended in this sentence exprest enigmatically: Vna methodus consistit in extractione fluentis quantitatis ex æquatione simul involvente fluxionem ejus: altera cætera commode derivari possunt, & in collatione terminorum homologorum æquationis resultantis ad cruendos terminos assumptæ seriei.
29
At length Mr Leibnitz in his Letter of 21 Iune 1677 after all this description of Mr Newtons method, began to put in for it as coinventor in these words. Clarissimi Slusij methodum Tangentium nondum esse absolutam Celeberrimo Newtono assentior. Et jam a multo tempore rem tangentium longe generalius tractavi; scilicet per differentias ordinatarum — positis differentijs Abscissarum, si placet, æqualibus. Hinc nominando in posterum proximarum x, patet esse esse &c. Which is the first Lemma of Slusius. What Dr Barrow 8 years before called a & e Mr Leibnits begins now to call & . Hinc nominando in posterum, saith he. And then by a calculation perfectly like that of Mr Gregory & Dr Barrow, he gives an example of drawing Tangents shews how to proceed without sticking at surds, & adds: Arbitror quæ celare voluit Newtonus de Tangentibus ducendis ab his non abludere. Quod addit ex edem fundamento quadraturas quoque reddi faciliores me in hac sententia hac confirmant, nimirum semper figuræ illæ sunt quadrabiles quæ sunt ad æquationes differentialem.
About seven years after Mr Leibnits published this method of Tangents in the differentiall characters in the Acta Eruditorum mensis Octob. 1684, under this Title: Nova methodus pro maximis et minimis itemque tangentibus quæ nec fractas nec irrationales moratur & added: Et hæc quidem initia sunt tantum Geometriæ cujusdam multo sublimioris ad difficillima & pulcherrima quæque etiam mistæ matheseos Problemata pertingentis, quæ sine calculo nostro differentiali aut simili, non temere quisquam pati facilitate tractabit. Compare this with the description which Mr Newton gave of his method in his Letter of 10 Decem. 1672 & you will find the descriptions very much alike. And hitherto Mr Leibnitz prætended only to be coinventor of this general method, as appears by his words, aut simili.
Why he used the symbols & rather then the letters a & e of Dr Barrow, he tells us in the Acta Eruditorum mensis Iunij 1686. Malo autem, saith he, et similia adhibere quam literas pro illis quia istud est modificatio quædam ipsius x, et ita ope ejus talibus & differentijs calculum ingrediatur & relationes transcendentes inter x et aliud exprimantur. Qua ratione etiam lineas transcendentes æquatione explicare licet. Which is as much as to say that he might have used letters but to avoyd defining their signification upon every new occasion he chose rather to use these symbols.
In Autum 1683 Mr Newton sent the Principal Propositions of his Principia Mathematica to London where they were communicated to the R. Society & in the year 1686 he sent up the rest of the book, & two years after an Epitome thereof was printed in the Acta Eruditorum, & the year following Mr Leibnitz published three papers relating to that book In
pricks & secondly because Mr Newton when he wrote his Principia did not understand second differences but represented the constant difference of x not by a prickt letter as he doth at present but by the letter{illeg} o (in a vulgar manner which destroys the advantages of the differential calculus) but has also given a false Rule about the higher degrees of differences. And whether this Mathematician be Mr Leibnitz himself or any other person is not material. He was imployed by Mr Leibnitz & Mr Leibnitz so far approved his paper as to cause it to be published & thereby has made it his own untill he tells the names of the author, & therefore we shall consider this paper at present as writ by Mr Leibnitz
As to the first argument it amounts to this that tho Mr Newton when he wrote his Letter dated 24 Octob 1676 had a method which he comprehended under these sentences: Data æquatione fluentes quotcunque quantitates involvente invenire fluxiones et vice versa: And Vna Methodus [inversa] consistit in extractione fluentis quantitatis ex æquatione fluxionem involvente yet he had not the method of fluxions because he did not in that calculus use letters with pricks. The sophism is evident at the first sight. For Mr Newton doth not place his method in forms of symbols nor confine himself to any particular sort of symbols for fluxions. Where he puts the Areas of Curves for fluents de puts the Ordinates for fluxiones & denotes the fluxions by the symbols of the Ordinates. And where he puts the letters x, y, z fluents, he denotes their fluxions either by other letters, as p, q, r, for AB, CD, EF, or by the same letters in other forms as X, Y, Z, or , , And this he does to this day as is evident by his book of Quadratures, where he uses prickt letters in the first Proposition, the Ordinates of Curves in the last Proposition & other symbols in solving several Problems in the Introduction. When Mr Leibnitz changed the Letters of Dr Barrow into other symbols he did not invent a new method of tangents: he only invented new symbols, & if in the differential method he had used Letters the method would have been the same by his own confession: for he tells us that he might have used Letters. There are no harder Problems yet solved by any man then those found in the Principia Philosophiæ, & Mr Leibnitz himself has told us that the Differential method extends to the abstruser Problems in Geometry such as cannot be solved without this method or another like it & the Marques de L'Hospital has told us that the Principia are full of this calculus. Mr Leibnitz pretends that Mr Newton uses prickt letters instead of , , , &c, & upon this pretence grownds his objection & used the same pretence in the Acta Lipsiensia of Feb A.C. 1705 pag. 1{illeg} But this pretence is a gross mistake . Mr Newton does not use prict letters for differences unless with the coefficient o either exprest or understood. Wherever he uses prickt letters they signify fluxions & Mr Leibnitz has no fluxions in his method. All Mr Newtons symbols for fluxions are the oldest in the kind. The differential symbols appear no older then the year 1677. the rectangles under fluxions & the letter o were used by Mr Newton for moments in or before the year 1669 & are still used by him in the same sense. The symbols for summs , , &c do not appear to have been used by Mr Leibnitz before the year 1686: Mr Newton in the year 1669 inscribed the Ordinate or Fluxion in a square or rectangle to denote the area or fluent. And thus much in answer to the first Objection.
As to the second Objection, Mr Newton in his Analysis, in his Principles, & in his Treatise of Quadratures did put the letter o for the constant increase of the fluent x & uses the same notation to this day. He has not changed the letter o into the mark as is erroneously suggested nor ever did use the make for the letter o. These symbols represent quantities of a different sort. The symbol represents the velocity of increase the letter o a particle generated by increase: the first is always a finite quantity, the second usually supposed infinitely little The first is an unite when x flows uniformly, & must be multiplied by the second either exprest or understood to signify what Mr Leibnits calls .
But Mr Leibnitz adds that Mr Newton formerly represented the constant increase of x by the letter o in the vulgar manner which destroys the advantages of the differential method. If this be true it proves either that Mr Newton has not yet found out the Method of fluxions because he still uses the letter o in the same sence as formerly, or else that the Method of fluxions wants the advantages of the differential, & is nothing more then a vulgar method known to the world before Mr Newton pretended to it. If this be so then Mr Leibnitz has invented nothing but a new name & a new Notation to make a vulgar method his own. For the Method of fluxions as used by Mr Newton has the advantage of the differential in all respects. It is more elegant, because he uses but one infinitely or indefinitely small quantity signified by the letter o. it is more natural & geometrical because founded upon the primæ quantitatum nascentium rationes which have a being in Geometry whilst indivisibles upon which the differential method is founded have no being either in Geometry or in Nature. There are rationes primæ quantitatum nascentium but not quantitates primæ nascentes. Nature generates quantities by continual flux or increase & the ancient Geometers admitted such a generation of areas & solids when they drew one line into another by local motion to generate an area & the area into a line to generate a solid. But the summing up of indivisibles to generate an area or solid was never yet admitted into Geometry. Mr Newton's method is also of a greater extent, being adapted either to the ready finding out of a Proposition or to the Demonstrating it: Mr Leibnits's is only for finding it out. When the work succeeds not in finite equations Mr Newton has recourse to converging series & thereby his method becomes incomparably more universal then that of Mr Leibnits which is confined to finite equations. And where the law of the fluxions is not known but the fluxions are had only in a few particular cases Mr Newton finds that law quamproxime by drawing a Curve line through any number of given points, & thence deduces the solution of the Problem And to this degree of perfection Mr Newton had brought his method before the year 1676 as appears by his Analysis & his Letters of 10 Decem 1672, 13 Iune & 24 Octob. 1676.
Its added that Mr Newton in his Principles of Philosophy gave a false rule about the higher degrees of Differences as had been observed by an eminent Mathematician, meaning Mr Iohn Bernoulli who in the Acta Lipsiensia of Febr. 1713 published that Mr Newton in the Scholium to the 10th Prop of the 2d Book of his Princ. took the terms of a converging series for the first second third & following differences respectively. But Mr Bernoulli is mistaken. Mr Newton affirms no such thing nor meddles with second differences in all that Scholium. In the Scholium of the last Proposition of his book of Quadratures, the word ut has by some mistake been omitted. But the mistake (whether a press-fault or a slip of the pen) might have been easily corrected either by the last Proposition of that book where the series of the first second & following fluxions is described or by the first Proposition of that Book which teaches how to find all the differences successively, or even by the Scholium in the Principia which is found fault with. For there Mr Newton puts the third term of the series equal to that part of the Ordinate which lyes between the Arc & the Tangent & by consequence to half the second difference.
<82r>Mr Leibnitz began his last Letter to Dr Sloan secretary to the R. Society with these words. Quæ D. Ioa{nn}es Keilius nuper ad Te scripsit, candorem meum apertius defendam, & cum homine docto, sed novo, et parum perito rerum anteactarum cognitore, nec mandatum habente ab eo cujus interest, tanquam pro tribunali litigem nemo prudens æquusque probabit. Thus Mr Leibnitz excused himself from making good his charge against Mr Keil & told the R. Society that they would be unjust his candor & allow him to be a witness in his own cause.
Mr Leibnitz has since in opposition to the Report of the Committee, upon a pretence that he was not at leasure to examin the matter himself & had not seen the Commercium, imployed an eminent Mathematician as he pretends, to examin the matter & give his judgment thereupon & the Iudgment of the nameles & therefore pretended Mathematician dated 7 Iuly 1713 he caused to be published. And by this judgment Mr Newton had not the method of fluxions till after the writing of his Principia Philosophiæ, & that for these two reasons. First because in all the Letters in Commercium Epistolicum from which the Committee draw their reasons there is not any instance of Mr Newtons letters with pricks, & secondly
I consider time as flowing or increasing by continual flux & other quantities as increasing continually in time & from that fluxion of time, I give the name of fluxions to the velocitys with which all other quantities increase. Also from the moments of time I give the name of moments to the parts of any other quantities generated in moments of time. I expose time by any quantity flowing uniformly & represent its fluxion by an unit, & the fluxions of other quantities I represent by any other fit symbols, & the fluxions of their fluxions by other fit symbols & the fluxions of those fluxions by others, & their moments generated by those fluxions I represent by the symbols of the fluxions drawn into the letter o & its powers , , &c: vizt their first moments by their first fluxions drawn into the letter o, their second moments by their second fluxions drawn into , & so on. And when I am investigating a truth or the solution of a Probleme I use all sorts of approximations & neglect to write down the letter o, but when I am demonstrating a Proposition I always write down the letter o & proceed exactly by the rules of Geometry without admitting any approximations. And I found the method not upon summs & differences, but upon the solution of this probleme: By knowing the Quantities generated in time to find their fluxions. And this is done by finding not prima momenta but primas momentorum nascentium rationes. This Probleme determins the Tangents of Curves Geometrically, & the Inverse thereof determins their Areas without summing up of their Ordinates.
This Method is derived immediately from Nature her self, that of indivisibles Leibnitian differences or infinitely small quantities not so. For there are no quantitates primæ nascentes or ultimæ evanescentes, there are only rationes primæ quantitatum nascentium or ultimæ evanescentium.
was with difficulty that I was induced to wri{te} {the l}etters of 26 Feb. 1716. So I do not {illeg} consequence that I should part with a quiet life for the sake of it, & therefore I intend to meddle with this controversy no further. / But whatever is done, I do not think this business of such consequence that I should meddle with it any further.
Pag. 219. lin. 22. dele: [Obtinet hæc ratio quamproxime ubi co{illeg} in Medijs rigore aliquo præditis tardissime moventur.] et scribe [In M{illeg} quæ rigore omni vacant, & quorum vis resistendi oritur a sola vi inertiæ partium, resistentiæ corporum sunt in duplicata ratione velocitatum &c]
Pag. 252. lin. 14. Adde Scholium sequens.
It has been said that in the old {illeg} & papers published in the Commer: Epist there are no prickt letters. And indeed I seldom used prickt letters when I considered only first fluxions as in the Introduction to the Book of Quadratures but when I considered also second third & fourth fluxions, as in the body f the book I distinguished them by the number of pricks. In the year 1692 At the request of Dr Wallis I sent him the first Proposition of the Book of Quadratures with th its solution & examples in first & second fluxions copied almost verbatim from the Bo{ok} & the Dr printed them the same year in the second Volume of his works which came abroad the next year. And thence it may be understood that the Book of Quadratures was then in Manuscript. In my Letter of 24 Octob 1676 I sent down the first Proposition of this Book verbatim in an Ænigma, & said that it was the foundation of the method, there concealed & gave me general Theorems for squaring of figures by series which sometimes brake of & became finite & & how it gave me such Series is explained in the first six Propositions of this Book. I know no other way of finding them In the same Letter I copied also many Ordinates of Curves from a Table in the end of the 10th Proposition & upon the 7th 8th 9th & 10th Propositions I wrote to Mr Collins my Letter of 8 Nov. 1676 printed by Mr Iones. And from all this it may be understood that this Book was then in manuscript. And as the notation used in this book is the oldest so it is the best.
② run the dispute into a squable about a Vacuum & Atoms & universal gravity & occult qualities & Miracles & the Sensorium of God & the perfection of the world & the definitions of time & space & the solving of Problems & the Question whethe he did not find the differential Method proprio Marte: all which are nothing to the purpose ×× Mr Iames Gregory after a years study found the method of converging series proprio Marte but did not claim it because he had notice of it from England before he searched for it & by that notice knew that he was not the first inventor. Gregorius autem, said Collins, Newtonum primum ejus inventorem anticipare haud integrum ducit. There is but one proper Question & that is: Who was the first Inventor? Let it be prov{e}d that Mr Leibnitz had the Method before he had any notice of it from England & then let it be further proved that he had it before the date of my Letter of 10 Decem 1672 & by consequence before he learnt the hith{illeg}. In the mean while {illeg}. There is but one proper Question & that is: Who was the first Inventor? All other Questions are prevarications. & t{en} to cloud this question. And untill the Book is answered directly & without prevaricating, I see no need of setting pen to paper any more about this matter. ① If Mr Leibnitz could have made a good objection against the Commercium Epist he might have done it in a short Letter without writing another book as big. But this Book being matter of fact & unanswerable he treated it with opprobious language & indoustrious avoided Answering it & for indoustriously avoided answering it by several excuses & [endeavoured to rund the dispute into a it & for that end] endeavoured to Pay it a{si}de by runing the dispute into a
The Committee of the R. S. said that I had this method above 15 years before Mr Leibnitz began to publish it: [that is, when I wrote the Analysis per æquationes numero terminorum infinitas] And Mr Collins in his Letter to Mr Strode of 26 Iuly 1672 affirmed that by the Analysis per æquationes numero terminorum infinitas & other papers communicated before to Doctor Barrow it appeared that I had the method & applied it generally some years before the Doctor sent that Analysis to Mr Collins, that is, some years before Iuly 1669. And I see no reason why the testimony of Dr Barrow should be questioned in this matter.
The Marquess de l'Hospital recommended the Differential Notation, but had
It was with difficulty that I was drawn to answer Mr Leibnitz. He is dead & The method it self is not of such consequence that I should meddle with this controversy any further.
1 In the Introduction to the following Book I said that I invented the Method of fluxions gradually in the years 1665 & 1666. The first Proposition thereof at the request of Dr Wallis I sent to him in 1692 & it was printed that year in the second Volume of his works, & came abroad in Spring following, & this was the first time that any Rule for finding second third & fourth fluxions & moments came abroad. ③ In the Preface to the first & second Volume of the works of Dr Wallis he affirmed that in my Letters of 13 Iune & 24 Octob. 1676 I explained to Mr L. the Method of fluxions found by me ten years before that time or above.
From Dr Barrows method of Tangents compared with his own Methods Mr Iames Gregory deduced a method of drawing Tangents without calculation & gave notice of it to Mr Collins by a Letter dated 5 Sept. 1670, & upon notice from Mr Collins that Mr Gregory & Mr Slusius had such Methods I wrote to Mr Collins the following Letter dated 10 Decem 1672.
Ex animo gaudeo D. Barrovij amici nostri reverendi Lectiones Mathematicas exteris adeo placuisse — — — ne grave ducas. Thus far my Letter, in which the method of fluxions is with its large extent is sufficiently described, & illustrated with an example of drawing Tangents. And by sying: [Hanc methodum intertexui alteri isti qua Æquationum Exegesin instituo reducendo eas ad series infinitas.] I refer to the method described in the Tract which I wrote in the year 1671, in which I joyned the methods of series & fluxions together as I mentioned in my Letter of 24 Octob. 1676.
In the same Letter I mentioned also that when Mr Mercators Logarithmotechnia came abroad Dr Barrow communicated to Mr Collins a Compendium of my method of Series. And this is the Tract entituled Analysis per series numero terminorum infinitas. The Logarithmotechnia came abroad in September 1668 Mr Collins a few months after sent a copy of it to Dr Barrow who replied that the Method of Series was invented & made general by me about two years before the publication of Mercators Logarithmotechnia & at the same time sent back to Mr Collins the said Tract of Analysis per series. This was in Iuly 1669. In a letter to Mr Bertet dated 21 Feb. 167 Mr Collins represented that about four years before that time I had invented a general method of Analysis meaning the method described in the Analysis per series. [For by the litle Analysis I understood that merely the reduction of quantities into converging series but much more the method of solving all sorts of Problems {illeg} working in æquations which involve converging series when they cannot be solved by finite equations: And this is the method of moments.] And in a Letter to Mr Strode dated 26 Iuly 1672 he said that after he had sent a copy of the Logarithmo- to Dr Barrow at Cambridge, the Doctor quasdam Newton's chartas extemplo remisit: e quibus et alijs quæ prius ab Auctore cum Barrovio de eadem methodo communicata fuerant, patet illam Methodum a dicto Newtono aliquot annis antea excogitatam & modo universali applicatam fuisse: ita ut ejus ope in quavis figura curvilinea proposita quæ una vel pluribus proprietatibus definitur, Quadratura vel Area dictæ figuræ ACCVRATA SI POSSIBILE sit, sin minus infinite vero propinqua, Evolutio vel longitudo lineæ curvæ, Centrum gravitatis figuræ, Solida ejus rotatione genita, et eorum superficies, obtineri queant. Here the words [ACCVRATA SI POSSIBILE SIT] relate to the words in the Analysis [Cujus [methodi] beneficio Curvarum areæ et longitudines &c (ID MODO FIAT) exacte & Geometrice determinentur. Sed ista narrandi non est locus.] How this is done is described in the first six Propositions of the Book of Quadratures. And without the method described in those Propositions it cannot be done. And thus it appears by the testimony of Dr Barrow & Mr Collins grounded upon this & former papers communicated to Dr Barrow that I had the method of moments & fluxions & made it general some years before Iuly 1669 or (as Mr Collins explains himself in his aforsaid Letter to Mr David Gregory,) about two years before the publication of Mr Mercators Logarithmotechnia, that is, in the year 1666. And all this together with the testimony of Dr Wallis mentioned above & that of Mr Fatio published in the year 1699, & the acknowledgement which Mr Leibnitz made in his Letters of 7 Iune 1677 & 7 March 169 may suffice to justify my saying in the Introduction to the book of Quadratures that I found this Method gradually in the years 1665 & 1666
* NB. Hunc Librum in M. S. nostrates Halleius et Ralphsonus in manibus suis triverunt anno 1691, uti Ralphsonus publice testatum reliquit & Halleius adhuc testatur. Propositionem primam exemplis illustratam D. Wallisius in secundo Operum suorum Volumine anno 1692 imprimi Curavit, et sub initio anni sequentis in lucem emisit. Et hæc fuit Regula omnium prima pro fluxionibus secundis, tertijs, et ulterioribus inveniendi quæ lucem vidit, estque Regula verissima brevissima et optima. Eandem Propositionem ijsdem verbis, tanquam fundamentum methodi fluxionum, e Libro quem anno 1672 conscripseram desumptum, posui in Epistola mea 24 Octob. 1676 ad Oldenburgum data, et a Wallisio edita. In eadem Epistola posui Ordinatas Curvarum quas per Methodum fluxionum cum Sectionibus conicis contuleram et in Catalogum anno 1672 retuleram, qui Catalogus in hoc Libro de Quadraturis habetur, et absque methodo momentorum construi non posset. In eadem Epistola posui Propositionem quintam hujus Libri pro Quadratura Curvilinearum quarum Ordinatæ sunt dignitates binomiorum, eandemque exemplis aliquot illustravi, dixique Regulas hujusmodi ad Trinomia et alia magis composita se extendere, et has Regulas Quadraturam accuratam dare quoties fieri potest. Sed et in Analysi per series numero terminorum infinitas mense Iulio anni 1669 a D. Barrovio ad Collinium missa, descripsi methodum momentorum & quomodo Problemata per eandem ad series convergentes deduci possint, et quod hujus beneficio Curvarum areæ et longitudines &c (id modo fiat) exacte et Geometrice determinantur. Ideoque Propositio quinta Libri hujus de Quadraturis tunc mihi innotuit. Et propterea etiam methodum fluxionum et momentorum quatenus in Propositionibus quinque primis habetur, tunc intellexeram. Nam Propositio quinta a quatuor primis dependet.
Sed et testimonio Barrovij et Collinij hæc methodus {mhi} innotuit annis aliquot antea. Nam Collinius in Epistola sua ad Thomam Strode 26 Iulij 1672 data, sic scripsit. Mense Septembri 1668 Mercator Logarithmotechniam edidit suam, quæ specimen hujus methodi [id est serierum infinitarum] in unica tantum figura, nempe Quadraturam Hyperbolæ continet. Haud multo postquam in publicum prodierat liber, exemplar ejus Cl. Wallisio Oxonium mihi — aliumque Barrovio Cantabrigiam, qui quasdam Newtoni Chartas — extemplo remisit: e quibus et ex alijs quæ olim ab Auctore cum Barrovio communicata fuerant, patet illam Methodum a dicto Newtono aliquot annis antea excogitatam et modo universali applicatam fuisse: ita ut ejus ope in quavis Figura curvilinea proposita, quæ una vel pluribus proprietatibus definitur, Quadratura vel area dictæ figuræ ACCVRATA si possibile sit, sin minus infinite vero propinqua; Evolutio vel longitudo Lineæ curvæ; centrum gravitatis Figuræ; solida ejus rotatione genita, & eorum superficies; sine ulla Radicum extractione obtineri queant. Hic verba [Accurata si possibile sit] relationem habent ad series quæ abrumpuntur & finitæ evadunt & sic dant Quadraturam accuratam si sit possibile; adeoque methodus quadrandi curvas descripta in Propositione quinta et sexta Libri huius de Quadraturis & propterea etiam methodus fluxionum quatenus in quinque vel sex prioris hujus Libri Propositionibus continetur, annis aliquot ante mensem Iulij 1669, testibus Barrovio et Collinio, mihi innotuere. Nam et Collinius in Epistola ad Davidem Gregorium Iacobi fratrem 11 Aug. 1676 data scripsit quod ✝ supradicta serierum infinitarum doctrina a Newtono biennio ante excogitata fuit, quam ederetur Mercatoris Logarithmotechnia, et generaliter omnibus figuris applicata. Methodum igitur habui generalem applicandi series ante annum 1667. Quod erat probandum.
The said Doctrine of Infinite series was invented by MrNewton about two years before the publication of Mercators Logarithmotechnia, & generally applied to all Curves. Epist. Collin. ad D. Greg.
Methodum fluxionum anno 1666 aut antea a me inventem fuisse D. Wallisius in Præfatione primi operum suorum Voluminis Anno 1695 in lucem edita commemoravit. Et librum hunc M S. De Quadraturis nostrates Halleius & Ralphsonus Anno 1691 in manibus suis tractaverat uti Ralphsonus publice testatum reliquit, & Halleus adhuc testatur.
Mr Leibnitz agrees with me that the Method of fluxions was obvious. For he saith in his aforesaid Postscript that it would have been easy for me to have found it out if it had been hinted to me. He allows therefore that it would have been easy for him to have found it out if it had bene hinted to him. I affirm that it was hinted to him very plainly, even so plainly that Dr Wallis in the Preface to the two first Volumes of his works published 21 years ago affirmed that in my two Letters of 1676 I explained to Mr Leibnitz the method of fluxions found by me ten years before the writing of those Letters or above.
For I made him understand that I had a general M which gave the method of Tangents of Slusius extended to quadratures of series & other difficulter Problemes & gave me the series for Quadratures which I there set down. The description
For in my Letters of 10 Decem 1672, 13 Iune 1676 & 24 Octob. 1676 I For
For I so far described the method as to make Dr Wallis in the Preface to the two first Volumes of h{is} works printed above 20 years ago, say that in my two Letters &c
He pretend now that when I wrote my book of Principles I had not the method of fluxions because I had frequent occasion of using the calculus of fluxions with prickt letters in composing that book & yet nothing thereof appears it. But this {is} a notorious sophism. The Ancients invented their Propositions by Analysis & Demonstrated them by synthesis, & admitted nothing into Geometry before it was demonstrated synthetically. I followed their example that the Propositions in that book might be admitted into Geometry. For the glory of Geometry is its certainty & nothing is to be admitted into Geometry before it be made as certain plane & evident as art can make it.
— by Mr Iames Bernoulli who published a specimen of this calculus in the Acta Eruditorum for May 1690 pag. 218. And from that time the this method began to be celebrated more & {mo}re in Germany France & Holland — — in England. And this made Mr Leibnitz in the Acta Eruditorum of May 1700 after he had said that no man before me had proved by a specimen made public that he had the method, subjoyn that no man before the Bernoullis & himself had communicated the method.
His meaning seems to have been that he & Bernoulli were the first who had published differentiall calculuations & I was the first who by a published specimen without such calculations had proved that I had the method. For the Propositions in the Book of Principles were invented by the Method of Fluxions but composed & published without the calculations that it might be received into Geometry. For the Ancients admitted nothing into Geometry till it was demonstrated by composition.
In this state things continued &c.
In the same Reply I said that the Method of Fluxions gave me some very general Theoremes for squaring of Curves & there described the first of those Theorem at large & illustrated it with examples. And this Theorem is the fift Proposition of the book of Quadratures & the second of those Theorems is the six Proposition of that book & these two are founded on the four first Propositions And therefore these six Propositions, & by consequence the method of fluxions conteined in them were most certainly known to me in the year 1676 when I wrote that Reply. And the seventh & eighth Propositions of that book are two more of those general Theorems.
In the same Reply I set down the Ordinates of Curves which I had compared with the Conick Sections & said that I had long before those days mad a Catalogue of them. This Cataloge was deduced from the 9th & 10th Propositions of the Book of Quadratures & composed the Scholium upon the 10th Proposition of that Book. And by these things it is evident that the Book of Quadrature & by consequence the method of fluxions described therein was known to me in the year 1676 when I wrote that Letter of Reply & long before. For I had intermitted these studies five years together before I wrote my two Letters of Iune 13th & Octob. 24 1676. And (by what I noted above) it is as certain that Mr Leibnitz when he wrote his Letter of 27 Aug. 1676 knew nothing of the method of reducing Problems to differential Equations.
And if the Manuscript which I wrote in the year 1671 & still held by me, & the Analysis which Dr Barrow communicated to Mr Collins in the year 1669 & which has been lately published from a copy thereof in the hand writing of Mr Colling by Mr Iones who purchased his Library, & with others Manuscript which were writ before the year 1669 & are still in my keeping, be compared with the book of Quadratures it will be found that one & the same method of fluxions is described in them all.
And the Method which Mr Leibnitz calls the summatory method & is also described in them. For the summatory Quantities which Mr Leibnits by præfixing the Letter ∫, in this manner, , , &c I described in my aforesaid Analysis in this manner , &c & in some of my older Manuscripts in this , . & therefore he is not the first inventor of the summatory Method.
Knowing therefore that my method readily gave the Method of tangents of Slusius In his journey therefore from London to Hannover he was considering how to make the method of Tangents of Slusius extend to all sorts as I find by a letter of his dated from Amsterdam Novem. 1676. And the next year finding how to deduce the Method of Slusius from the Differential Method of Tangents published by Dr Barrow in the year 1670, he wrote ba{w}ck in a Letter dated from Hanover 21 Iune 1677
that is the Differential calculation. I invented the Propositions in the Book of Quadratures by the Analysis of Fluxions but demonstrated them Synthetically that they might deserve to be admitted into Geometry according to the Rules of the Ancient Geometers, who to make the science certain demonstrated synthetically what ever they found by the Analysis. And in these synthetical Demonstration the Analysis was so conspicuous that Mr Leibnitz allowed that this Book was a proof that
calling those things miracles which create no wonder, & those things occult quali{ties} whose causes are occult tho the qualities themselves be manifest, & those things the souls of men which do not animate their bodies. His Harmonia præstabilita is a miraclous Hypothesis & contradicts the daily experience of all man kind, every man constantly finding in himself a power of moving his body by his will. He accuses me — — — Epistolicum.
If he acknowledged it before the sentences in cyphers were deciphered, & before he knew how by this method the series set down in that Letter for squaring of curves was invented, or how by the same method the figures whose Ordinates are there, set down were composed with the conick sections, or had seen the Compendium there mentioned which Dr Barrow sent to Mr Collins in the year 1669: he ought much more to acknowledge it now.
In his Letter of 27 Aug 1676 he acknowledged that he received from Mr Oldenburg a packet conteining my Letter of 13 Iune preceding & a parcel of other analytical papers communicated by Mr Collins. That Parcel was to be sent back to Mr Oldenburg & is now in the Custody of the R. Society & therefore was received & sent back. [And I doubt not but he will still acknowledge that he did receive that parcel & packet & therein many extract of Gregories Letters & particularly a copy of Mr Gregories Letter of 15 Feb. 1671 & a copy of my Letter of 10 Decem 1672.] It conteins many extracts of Gregories Letters & particularly his Letter of 15 Feb 1671 & a copy of my Letter of 10 Decem. 1672. And I doubt not but he will still acknowledge that he received this parcel.
L'Abbé Conti
Part of a Letter of Dr Wallis to Mr Leibnitz Iuly 30 1697.
Optaverim item ut tibi vacet tuam Calculum Differentialem, et Newtono suam Fluxionum Methodum, justo ordine exponere; ut quid sit utrique commune et quid intersit discriminis, et utramque distinctius intelligamus.
NB The Doctor here wishes that the method common to us both & the improvement thereof were stated between us; the first as due to me, & the other as due to Mr Leibnitz. And no Answer was returned to this by Mr Leibnitz;
But whilst in his Letters to Dr Wallis he found no fault with him for saying that by my Letters in the year 1676 I explained to Mr Leibnitz the method found by me ten years before or above but yeilded to me so much of the method as was common to us both, & claimed only the improvements that he had made to it: he went on amongst his Friends abroad to call the whole method without distinction his own, & thereby gave occasion to Mr Fatio to write the following Paragraph.
Newtonus scit unus omnium optime, satisque indicavit publice cum sua Mathematica Naturæ Principia publiccaret anno 1687, nova quædam inventa Geometrica quæ ipsi communia mecum fuere, neutrum luci ab altero acceptæ sed meditationibus quemque suis debere, et a me decennio ante exposita fuisse.
NB. The Scholium upon the second Lemma of the second Book of Principles is here referred unto. I wrote that Lemma in the year 1686. And because I had signified to Mr Leibnitz ten years before that I had a method which determined tangents, maxima & minima & other Problems without sticking at surds & included the method of Tangents of Slusius & in {illeg} the method of Tangents of Slusius & faciliated Quadratures, & gave me the Series for Quadratures there mentioned & that I had wrote a Tract of this method & the Method of Series together in the year 1671 & that the Analysis composed of these two methods together reached to invers Problems of T. & others more differencial & was so general as to extend to almost all sorts of Problems except perhaps some numeral ones like those of Diophantus: & the next year when Mr Leibnitz sent me the Elements of such a Method, & in the year 1684 published those Elements without making any mention of the correspondence which had been between us: I added that scholium to secure the Lemma to my self But whether Mr Leibnitz found the Method apart or had light into {it} from me, is a question I did not there meddle with. Nor was it material, the right thing due to the first inventor. But Mr Leibnitz proceds. thus
cujusque specimina quadam dedit in Analysi sua per æquationes numero terminorum infinitas quam Barrovius anno 1669 ad Collinium misit, & in Epistola 10 Decem 1672 ad Collinium missa. Circa mitium.
NB. In the Letters which hereupon followed between Mr
NB. Dr Wallis by his Letter of Dec. 1. 1696 gave notice to Mr Leibnitz of this Paragraph. And Mr Leibnitz made only this exception to it that the methods were not perfectly alike but had some differences which the Doctor should have mentioned if he had known them. [In one of his Letters dated 28 May 1697 he said. Methodum Fluxionum profundissimi Newtoni cognatam esse Methodo meæ Differentiali non tantum adnimadverti postquam opus ejus et tuum prodijt sed etiam professus sum in Actis Eruditorum et alias quoque monui. Id enim candori meo convenire putavi non minus quam ipsius merito Itaque communi nomine designare soleo Analyseos infinitesimalis, quæ latius quam Tetragonistica patet. Interim quemadmodum et Vietæa et Cartesiana methodus Analyseos speciosæ nomine venit, discrimina tamen nonnullis. And in his Letter of 29 Mart. 1967 De te autem queri nanquam mihi in mentem venit; quem facile apparet nostra in Actis Lipsiensibus prodita, non satis vidisse. It never came into his mind to complain of the Doctor's Preface, seing he had not sufficiently seen the improvements made to my method.] For as the Analysis speciosa of Vieta & Cartes differed] He did not deny that in the year 1676 I had explained to him the Method found by me ten years before or above but only contended that he had improved the method] See the Letters published in the third Volume of the Doctors works. Yet Mr Leibnitz persisted amongst his friend to call the method his own & thereby gave occasion to Mr Fatio to write what follows.
— a celeberrimum Virum Leibnitium misit, quæ tamen per aliam quandam methodum generalis redderetur Eodem porro anno — — — fusius patebit. Problema autem in quo fundabatur hæ methodis literis quidem transpositis ad hunc modum celabat — — — et vice versa. Mente Newtoni ex his et alijs percepta, Vir celeberrimus anno proximo rescripsit se in parilem methodum incidisse (ut ex ejus Epistola in tertio Operum Wallisij Volumine videre licet) cujus tamen explicationem — — — distulerit.
<93r>Galileo upon a supposition of uniform gravity shewed that if gravity in a falling body produced one part of velocity in one part of tie it would produce another part of velocity in another part of time & a third part of velocity in a third part of time &c. so that the velocity produced would be always proportional to the time in which it was produced & by consequence to the force producing it. For if uniform gravity impress one part of force in one part of time, it will impress another parts of force in another part of time & a third part of force in a third part of time & so on
NB. Dr Wallis by his Letter of Decem. 1. 1696 gave notice of this Paragraph to Mr Leibnitz; who made only the exception to its that altho the Methods were alike & therefore he called them both by the name of the infinitesimal method yet they differed in some improvements which he had made to it which the Doctor should have mentioned if he had known them . See their Letters published in the third Volume of the Doctors works. After this Mr Leibnitz persisting amongst his friends to call the Method his own gave occasion to Mr Fatio to write what follows.
Out of the Answer of Mr Leibnitz published in the Acta Eruditorum for May. 1700 p. 202.
Certe cùm Elementa calculi mei edidi anno 1684 ne constabat quidem mihi aliud de inventis ejus in hoc genere quam quod ipse olim significaverat in literis posse se tangentes invenire non sublatis irrationalibus; quod Hugenius quoque se posse mihi significavit postea etsi cæterorum istius calculi adhuc expers: sed majora multo consecutum Newtonum, viso demum libro Principiorum ejus satis intellexi.
NB What is here acknowledged & was further acknowledged in his Letter to Mr Oldenburge dated 21 Iune 1677 concerning the likeness of the Methods admits of no retraction.
In this Answer he challenged Mr Fatio to solve the Problem of Bernoulli a series of Curves cutting another series at right angles. Which makes it probable that the solution of this Problem has been ever since reserved for a challenge.
Mr Fatio returned an Answer but the Editors of the Acta Lips. would not print it, & what it was I do not know.
After he had voluntarily in his Letter of 1693 given me the preference speaking of himself as if he also had endeavoured to can pass the same thing. After Dr Wallis had said in his Preface — — & the Editors of the Acta Eruditorum had complained of Dr Wallis for nothing more in the Preface to the two first Volumes of his works besides the words Quod moneo nequis &c & the Doctor had represented that he know nothing more of that Method then that it was of the same kind with mine & the Editors & Mr Leibnitz had acquiesced in that excuse & Mr Leibnitz had acknowledged the likeness of the Methods & pretended to nothing more then the improvements that he had made to it: to call the whole method his own
For the two parts of the sentence set down in my Letter of 24 Octob 1676, vizt Data æqu.—, et vice versa denote
For the sentence [Data æquatione fluentes quotcunque quantitates involvente, invenire fluxiones et vice versa, inserted into my Letter of 24 Octob 1696 as the foundation of the method upon which & the method of series together, I had written a Tract in the year 1671; relates to the direct & inverse methods of fluxions, called by Mr Leibnitz the Differential & the summatory methods. And both these methods, & especially the second, are for enlarging the bounds of Analysis, & extending it to such quantities as transcend the vulgar equations & therefore are by Mr Leibnitz called transcendent; of which kind are the Ordinates of Curves called by Des Cartes Mechanical.
— Wallisij operum volumina primum et secundum prodiere, Hugeniusque curiositati meæ favens locum inde descriptum ad Newtonum pertinentem mihi mature transmisit.
NB. The first part of this Answer should have been made to Dr Wallis, had it agreed with our Letters of 10 Decem 1672, 24 Octob. 1676 & 21 Iune 1677. The second part admits of no retraction upon a pretence that I had deceived him. The third part seems to relate to the place above mentioned in the Preface to the two first Volumes of the Doctors works, concerning the likeness of the Methods. In the same Answer, he acknowledged that I was the first who had proved by a specimen made publick that I had that part of the infinitesimal calculus by which the solidum rotundum minimæ resistentiæ & the Curva celerrimi descensus &c were invented. Mr Fatio returned an Answer to Mr Leibnitz, but the Editors of the Acta would not print it, & what it was I do not know.
The plain meaning of the place was to tell the world that Mr Leibnitz was the first inventor of the method, & that Mr Newtons method could not be well understood without first understanding the Differential method of Mr Leibnitz & therefore Mr Newton uses & ever did use fluxions for the Leibnitian differences even as Fabrius substituted motions for the method of Cavallerius. In the year 1676 he had notice of Mr Newtons method & that Mr Newton had written a Treatise of it five years before & the notice was so plain that he was able the next year when he had found the differential method to compare the methods & see the likeness as appears by his Letter of 21 Iune 1677. And in the year 1684 when he published the elements of his method, he acknowledged another method like his own tho he did not say whose it was, & of what antiquity as he ought to have done. At that time I was writing my Principia Philosophiæ & the book came out in the year 1687 & was the first instance made publick of applying the Method to the higher sort of Problemes. And the next instances made publick were those of Mr Leibnitz De Lineis Opticis de motu projectilium in Medio resistente & de Motuum cœlestium causis, published in the the year 1689 & all of them taken out of the Book of Principles. And the next year the Differential method began to be taken notice of abroad & in the year 1693 Mr Newton received a Letter from Mr Leibnitz wherein he acknowledged that in publishing the book of Principles I made it appear that my Analysis recht beyond the vulgar & said that he also by convenient characters had endeavoured to subject the transcendent Geometry to Anslysis. And hitherto he gave me the preference. In the beginning of the year 1695 Dr Wallis hearing that the method began to be celebrated in Holland under the name of the Differential method inserted into the Preface of the two first Volumes of his works that in the Letter which in the year 1676 had passed between me & Mr Leibnitz I explained to him the method found by me ten years before that time or above & the next year gave notice to Mr Leibnitz of this passage & in the Letters which followed between them Mr Leibnitz did not deny it nor find any fault with what the Doctor had said. In the year 1699 the Doctor published those Letters in the third Volume of his works having received copies of mine from Mr Oldenburg him self & of Mr Leibnitz's from the Library of Mr Collins, & Mr Fatio published the same year that I was the oldest inventor by many years & the next year Mr Leibnitz returned an answer without contradicting him. Dr Wallis died in October 1703 the last of the old men who knew what passed in the days of Mr Oldenburg & hitherto Mr Leibnitz forbore to claim the first invention. This claim was first made by the Passage above mentioned in the Acta Eruditorum for Ianuary 1705. And therefore Mr Leibnitz & his friends are the aggressors & out to prove their claim. If he pretends he's in possession I can tell him that he never was in quiet possession, that I never was out of possession in England, & that what possession he has was got by concealing from his Countrimen his knowledge of what passed between him & me in the year 1676.
— which is wrested against me; it was written not to give away that Lemma to Mr Leibnitz but on the contrary to assert it to my self. Because Mr Leibnitz in publishing the Elements
NB Mr Leibnitz having prepared the way to tell the Doctor what was his method he repeats in his next letter what he had said in the Acta Eruditorum of of Iune 1706 concerning the Analytical inventions of Galilæus, Cavallerius, Fermat, Cartes, Gregory a S. Vincent, Huygens, Wallis, Iames Gregory, Isaac Barrow, Mercator & me:
NB The use which Mr Leibnitz makes of this in his following Letters is to tell the Doctor that his method was not perfectly the same with mine but differed from it by some improvements which he had made. He did not complain of the Doctor for saying that by my Letters in the year 1676 I had explained to him the method found by me ten years before or above but only contend{illeg} that he had improved it by teachin how to reducing transcendent quantities & mechanical Curves to equations & by the {inver}tion of exponential Equations.
NB. Mr Leibnitz in the Acta Eruditorum for October 1684 published the Elements of the Differential method & there mentioned a Methodus similis without saying whose it was & what he knew of it as he ought to have done in point of candor. Afterwards in the Acta Eruditorum for Iune 1686 in giving an Account of the Analytical inventions of Galileo Cavallerius Fermat Cartes, Gregory of St Vincent, Huygens, Wallis, Gregory, Barrow, Mercator & me, he mentioned my general method of Series, but instead of acknowledging what he knew of my infinitesimal Analysis he was silent about it & left me to publish it my self giving {me the} complement that by doing so I, & in this Letter to Dr Wallis he repeats all this instead of doing me justice. And by the same sort of Candor Dr Wallis if he had been silent. without pleading ignorance This fault Mr Leibnitz committed against me at the very same that he & the Editors of the Acta {illeg} would not allow the like in Dr Wallis towards Mr Leibnitz, but made him plead ignorance of what he had omitted.
all this he had notice from London the year before
In the year 1684 Mr Leibnitz published Gregorys series & in the year 1684 he published the Elements of the differential method. Both these he published as his own without letting the world know that he had received any thing from London concerning them. I was then writing the Principia Philosophiæ & this book came abroad in 1687 & was the first specimen made publick of applying the method to the higher sorts of Problems.
In the year 1689 Mr Leibnitz published the principal Propositions of this book as his own in three papers called Epistola de lineis Opticis Schediasma de resistentia Medij & motu Projectilium gravium in Medio resistente & Tentamen de motuum cœlestium causis, pretending that he had found them all before htat book came abroad. And to make the principal Proposition his own adapted to it an erroneous demonstration. And this was the second specimen made publick of applying the method to the higher Problems.
In the years 1696 & 1691, the Differential method began to be celebrated & in the beginning of the year 1695 Dr Wallis hearing that it began to be celebrated in Holland inserted into the Introduction of the two first Volumes of his works that in the Letters which passed between me & Mr Leibnitz in the year 1676 I explained to Mr Leibnitz the method found by me ten years before or above that is in the {year} 1666 or before, & gave notice of this to Mr Leibnitz in a Letter dated 1 Decem. 1696. And the Editors of the Acta Eruditorum in giving an Account of the two volumes of Dr Wallis cited some words out of this passage But neither they nor Mr Leibnitz in the Letters which followed between him & Dr Wallis denyed the truth thereof.
And in the year 1693 I received a Letter from Mr Leibnitz dated 17 March in which he acknowledged that by the book of Principles it appeared that I had a method of doing what the vulgar Analysis would not reach & added that he had also by a convenient notation endeavoured to subject the transcendent Geometry to Analysis. But he did not yet begin to give the preference to himself.
In the beginning of the year 1695 Dr Wallis hearing that the Method began to be celebrated in Holland under the name of the Differential method of Mr Leibnitz inserted into the Introduction of the two first Volumes of his works, a Paragraph importing that in the Letters which passed between me & Mr Leibnitz in the year 1676 I explained to him the method found by me ten years before or above, & gave notise of this Paragraph to Mr Leibnitz in a Letter dated 1 Decem. 1696.
In Iuly 1669 Dr Barrow sent to Mr Collins my Analysis per series numero terminorum infintas conteining my method of series with some specimens of my method of fluxions intermixed. And in the year 1671 I wrote a larger Tract on those methods together.
In the year 1670 Dr Barrow published his method of tangents & Mr Gregory deduced from it the method of Tangents of Slusius & by a letter dated 5 Nov. 1670 gave notice thereof to Mr Collins & in the end of that year fell into my method of series, & in a Letter dated 15 Feb. 167 sent him a Series since claimed by Mr Leibnitz & the series which he had received from me & Gregory he freely communicated to his friends at home & abroad.
In a Letter dated 10 Decem 1672 I sent my method of tangents to Mr Collins & told him that I took it to be the same with that of Gregory & Slusius & that it was a branch or rather a Corollary of a general method of Analysis which extended to the abstruser sorts of Problemes concerning the Curvities, areas, lengths centers of gravity of Curves &c & proceeded without freeing equations from surds & that I had interwoven this method with that other of series, meaning in the tract which I wrote the year before.
In the beginning of the year 1673 Mr Leibnitz was at London & pretended to the Differential method of Mouton & received notice of Mercators series for the Hyperbola & might receive notice of some other series without being acquainted {with it} & going from thence to Paris was instructed in the higher Geometry by Mr Huygens & in the mean time wrote Letters to Mr Oldenburg about other matters dated Mar. 30, Apr. 26, May 24, Iune 8 & the next year in Iuly & October sent notice to Mr Oldenburg that he had found the area or circumference of a circle by a series of numbers, & that by the same method any Arc might be found by the like series whose sine was given tho the proportion of the Arc to the whole circumference was not known. If the proportion was known it gave him the circumference. If it was not known yet it gave him the arc.
In April 1675 he received eight series from Mr Oldenburg amongst which were the series of Gregory for finding the arc by the tangent & the tangent by the arc & mine for finding the Arc by the sine & the sine by the arc. And by his Letter of 20 May 1675 he acknowledged the receipt thereof & said that he was not then at leasure to examin them & compare them with his own which he had found some years before that is, in the year 1673 or before. His own were therefore different from all these, & tho he was not at leasure to examin what was sent him yet he was at leasure to compose a demonstration of one of them & communicate the composition to his friends at Paris without letting them know what he had read.
In his Letter of 12 May 1676 he admired the two series for finding the arc by the sine & the sine by the arc & said that because of their elegance Mr Oldenburg would do him an acceptable favour if he would send him the demonstration thereof, that is, the method of finding them & promised him a recompence & added that Mr Collins could easily satisfy his desire. And all this makes it plane that he had not yet any method of finding these two series.
In my Letter of Iune 13 1676 I sent him my method of series with many examples, & said that Analysis by these series extended to almost all Problemes, but became not altogether universal without some further methods, which I forbore to explain because I began long ago to be weary of these studies, so as to have absteined from them about five years.
Gregory died neare the end of the year 1675 & Mr Collins at the request of Mr Leibnitz & some of the Academy of Sciences, made extracts from Gregoris Letters & gave the collection to Mr Oldenburg with this title, Extracts from Mr Gregories Letters to be lent Mr Leibnitz to peruse who is desired to return the same to you. And the same was sent to him at the same time with my Letter of 13 Iune 1676 & returned some time after to Mr Oldenburg & is still in the custody of the R. Society, & among the Letters conteins that of Gregory dated 5 Novemb. 1670 & 15 Feb. 1671 & that written by me 10 Decem 1672.
Mr Leibnitz in his answer dated 21 Iuly 1676 thanked Mr Oldenburg M Collins & me for what had been sent him, & in requital sent back his method of series by transmutation of figures into other figures in whose equations the Ordinate ascends to no power & therefore may be reduced to an infinite series by the division alone, or to one or two or more powers & then may be reduced to an infinite series by extraction of roots. And this method of transmutation he commended as one of the most valuable things in Analysis, & illustrated it with Gregories series for finding the arc of a circle whose tangent was given, saying that he had communicated it to his friends three years before or above, that is, before 27 Aug. 1673, or soon after his coming to Paris from London. In the same Letter he said that he did not beleive that my method of Infinite series was so general as I had described, because many Problems were so wonderfull & intricate that they could not be reduced to equations or quadratures, such as were (amongst many others) the inverse problems of tangents. And therefore he had not yet found the methods of reducing Problems to series either by the help of differential equations or by assuming arbitrary series.
In my next Letter dated 24 Octob 1676 I replied that five years before (vizt anno 1671) I wrote a Tract about series & another method together which readily gave the method of Tangents of Slusius & stuck not at equations involving surds & extended to quæstions de maximis & minimis & Quadratures & others & couched it in the following sentence exprest enigmatically, Data æquatione quotcunque fluentes quantitates involvente fluxiones invenire & vice versa. I set down a Theoreme also for squaring of curves saying that it was found by this method & mentioned other Theoremes for comparing them with the Conic sections. How these Theoremes follow from this method is explained in the book of Quadratures & without this method it was impossible to find them I said also that my methods extended to inverse Problemes of Tangents & others more difficult & that either by extracting the fluent out of an equation involving its fluxion or by assuming a series at pleasure . I said also that if the relation between any two sides of the right anguled triangle conteined under the ordinate Tangent & Subtangent be defined by any equation, the Probleme may be resolved without my general method but if the Abscissa also entred the vinculum, it used to be otherwise, that is, for the most part to require my general method, which method is the method of series made general by the methods of fluxions & arbitrary series as I said before. This Letter Mr Leibnitz saw in the hands of Mr Collins when he was in London the second time, as he has lately acknowledged in one of his Letters, & after his arrival at Hannover received a copy of it.
In his answer dated 21 Iune 1677 he sent back the method of Tangents published by Dr Barrow in 1670 with the characteristic changes & how this meethod readily gave the method of Slusius as Gregory had notified in his Letter of 5 Novem 1670 & how the method which did this might be improved so as to proceed in equations involving surds & extended to quadratures as I had notified in my Letters of 10 Decem 1672 & 24 Octob 1676. This is all the Differential method which he then sent back to me &
complained that it was too long to be answered & yet should have been longer by printing all the Letters entire
Mr Newton was therefore the first inventor, & whether Mr Leibnitz invented it proprio Marte afterwards or not is a question of no consequence. The first inventor is the inventor & inventoris jura are due only to him. He has the sole right till another finds it out & then to take right from him & share with another would be an Act of injustice, & a great encouragement to pretenders. But however there are great reasons to beleive that Mr Leibnitz did not invent this without receiving some light from Mr Newton.
For it must be observed that wherever Mr Newton in his Letters spake of his general method he understood his Meth'd of Series & Fluents taken together as two parts of one general method. In his Analysis the series are applied to the solution of Problemes by the method of fluents & thereby give new series. In the year 1671 he wrote of both together. The series in his book of Quadratures are derived from the method of fluents & were derived from that method before the year 1676 p. 72. The method of extracting Fluents out of equations involving their Fluxions comprehends both together. The method of assuming the terms of a series & determining them by the conditions of the Problem proceeds by means of the method of fluents. When Mr Newton represented that his method of series extended to the solution of almost all problemes except numeral ones like those of Diophantus, he included inverse problems of Tangents & those problems are not tractable without the method of fluents. And sometimes series are considered as fluents & their second terms as moments. And Mr Newton sometimes derives this method of fluents from the series into which the power of a binomium is resolved p 19. lin. 19, 20.
In the next place it must be observed that Mr Newton at the request of Mr Leibnitz communicated to him freely & plainly one half of this general method the method of Series. p. 45, 49. Mr Gregory by the help of but one series with notice that it was the result of a general method found out the method within the space of a year. Mr Leibnitz pretended to have two series in the year 1674 & had eight others sent him by Mr Oldenburg in April 1675 & took a years time to consider them: but this method being altioris indaginis he could not find it out, but at length requested Mr Oldenb. to procure it from Mr Collins, & at the request of Mr O. & Mr C. Mr N sent it to him. And when he had it he understood it with difficulty & desired Mr Newton to explain some things further.
And for the other half of the method, Mr Leibnitz had a general description of it in Mr Newton's Letters of 10 Decemb 1672, 13 Iune 1676 & 24 Octob 1676, with examples in drawing of Tangents p 30, squaring of curves p 72 & solving inverse problems of tangents p. 86. In being told that it extended to Tangents of mechanical curves, & to quadratures, curvities, & centers of gravity of curves in general & to inverse problems of Tangents he was sufficiently told that it was founded upon the consideration of the small parts of quantity called particles & moments by Mr Newton & indivisibles infinitesimals & Differences by Mr Leibnitz. For there is no other way of considering any of these Problemes then by these particles of quantity. Mr Newton therefore having told Mr Leibnitz one half of his method & made so great a discovery of the other half said that the foundation thereof was obvious (p. 72. l. 1 & put it in cyphers least it should be taken from him.
And now Mr Leibnitz knowing by Mr Newtons Letters that the method of Slusius for drawing tangents was a corollary of Mr Newtons general method (p 39) set his mind upon improving it this method & that by the differences of the Ordinates (p 87, 88) He considered that as the summs of the Ordinates gave the Area , so their differences gave the tangents & thence received the first light into the Differential method (p. 104) & having found it he saw that it answered to the description which Newton had given of his method in drawing of Tangents & that without sticking at surds, in rendring quadratures more easy & in bringing of inverse Problemes of Tangents to Equations & Quadratures p 88, 89, 90, 91 93. In his journey home by London & Amsterdam he was upon another designe of improving Slusius's method of Tangents & extending it to the solution of all sorts of Problemes & this was by calculating a certain Table of Tangents as the most useful & easy method he could then think on (pag 87) This was in Novem. 28 1676 & therefore he had not invented the Differential method at that time. But the perusal of Mr Newtons Letters had given him him a notion that the method of Slusius was capable of being improved into a general method of solving all sort of Problems. In his last letter against Mr Keil (p. 119) he represents that his friends know how he found the Differential method in a very different manner from what Mr Keil surmises & these words imply that he found it after he got home to his friends & by consequence in the year 1677 & most probably not before the receipt of Mr Newtons second Letter. For the publishing of an opusculum upon Mr Greg. series was first suspended by his coming into business, & then laid aside upon his finding the Differential method. p. 42.
Thus much concerning the invention of the Method. And now it may not be amiss to take some notice of the conduct of Mr Leibnitz in this & such like matters.
Dr Pell reprehended him for pretending to Moutons differential method.
Mr Collins reprehended him for intermedling with a what Mr Gregory & Mr Tschurnhause were upon, as appears by a Letter not yet published.
When Mr Tschurnhause had fallen upon the method of assuming the terms of a series & determining them by the conditions of the Probleme Mr Leibnitz took it from him by pretending (without proving) that he had communicated it to Mr Tschurhause ten years before when they were together at Paris, & that Mr Tschurnhause had forgot the communication.
Mr Leibnitz should not have pretended to two series in the year 1674 & afterwards have written to Mr Oldenburg for the method of finding them.
He should not have forgotten the eight series sent him by Mr Oldenburgh & Mr Collins
He should not have taken a years time to consider them upon pretence that he was busy about mechanical things, nor have written to Mr Oldenburg to procure from Mr Collins without Newtons knowledge the method of finding such series when {he} could not find it himself. For by his own rule if he should afterwards have forgott the receipt of the method, Mr Oldenburg & Mr Collins were not to put him in mind of it without authority from Mr Newton.
He should not have communicated to the G{inthent} at Paris an opusculum written upon one of the eight series without letting them know that hed received it from Mr Oldenburgh & Mr Collins.
He should not have promised Mr O. & Mr C. a series of a very different kind from the two which he had received from Mohr, in recompence for Mr Newtons meethod when he meant to send them nothing but one of the eight series which he received from them the year before.
He should not have published that series as his own in the Acta Lipsica without acknowledging whence he had it & that it was {o}{illeg} Mr Gregories series sent by him to Mr Collins in the year 1671.
<97r>He should not have endeavoured to share the method of series with Mr Newton by sending his transmutation of figures for a general method of finding series when he had newly desired Newtons method for want of a general method of his own, the transmutation method not being general till Mr Newton made it so by communicating his extraction of roots, & even then being tedious & of no use.
He should not have laid claim to some of the reciprocal serie sent him by Mr Newton by changing the signes & subducting the versed sine from the Radius when he had no method of finding reciprocal series besides the method sent him by Mr Newton & did not yet understand it.
He should not at the same time have desired Mr Newton to send him his method of reciprocal series & after he had it & with difficulty understood it have written back that he had found it before as he perceived by his old papers but for want of a good example had laid it aside.
When he sent his differential method to Mr Newton he should have acknowledged that he had but newly found it out. And not have described it in such a manner as shows that his aim was then to make himself the first inventor of the method. For men are not to interrupt one anothers proceedings nor to snatch away one anothers inventions.
And when he published an Account of Mr Newton's book of Quadratures & represented that the method of fluxions was from the first beginning thereof substituted & used by Mr N. instead of the Differential method (p ) he had forgot that the very first proposition of the Book was set down in Mr Newton's Letter of 24 Octob 1676 as the foundation of the method of fluxions upon which Mr Newton had written a treatise in the year 1671. And the Mr Keil put him in mind of this, & explained to him that the second Proposition of the book was in the Analysis A.C. 1669 & that the eight following Propositions (which are all founded upon the method of fluents) were found before the writings of the said Letter (pag. 113) & by consequence before Mr Leibnitz understood the differential method: yet Mr Leibnitz has not mended the account that he has given of that Book of Quadratures but represents that his candor is questioned, that at his age after so many documents of his life it is not to be expected that he should defend it by an Apology, & enter into a debate against a young man unacquainted with what passed & not authorized by Mr Newton, & refuses to explain how he came by the differential method, & blames Mr Keil for finding fault with the account given of Mr said book, saying that it is free from detraction & has given every man his due, that is that the method of infinitesimals is due to Mr Leibnitz & the rest of the book to Mr Cheyne & Mr Craige: & nothing to Mr Newton but drudgery & dishonesty in prosecuting other mens inventions as his own.
Seriem mense Maio Anni hujus Leibnitius ab Oldenburgo acceperat & eo tempore suam esse vel non noverat vel non audebat asserere (p 42 lin 8) Gregorius ante quadrennium hanc seriem Collinio misserat, & ante finem anni hujus emortuus est, & Leibnitius opusculum de hac sere compositum cum Gallis communicare jam cœpit p 42. l. 25. Eandem prius cum Gallis ut suam communicasse non constat.
Communicavit forte sed vix ut suam. Nam Quadraturam quam Oldenburgus postea a Leibnitio accepit Leibnitius mense Maio Anni hujus ab ipsissimo Oldenburgo acceperat & eo tempore suam esse vel non noverat vel non audebat asserere (p 42 l 8) ideoque nondum cœperat aperte Gregorius, ante quadrennium eandem Collinio miserat, & hoc anno mortuus est Et Leibnitius opsuculum de hac serie cum Gallis jam communicare cœpit p 42 l 25. Anno 1674 Leibnitius jactabat se hujusmodi series duas habere sed quænam fuerint & unde habuit non constat.
Communicare potuit sed vix ut suam. Nam quadraturam quam cum Oldenburgo postea communicavit, accepitat ab ipsissimo mense Maio hujus Anni & suam esse tunc non novera
Hanc Quadraturam Leibnitius mense Maio A.
Quadraturam quam Leibnitius suam esse.
Quadraturam Gregorij Leibnitius Mense Maio anni hujus ab Oldenburgo acceperat ut supra, et eo tempore suam esse vel non noverat vel non ausus fuerat asserere. At opusculum de eadem ante finem hujus {ann}, Cum Gregorius jam emortuus esset, in Gallia communicare cœpit. Quænam fuerint series duæ quas anno superiore habuit et unde habuit in dubio est. Certe demonstrationem utriusque nondum habuit.
Slusius grounded his method of Tangents upon three Lemmas the two first of which were these
1 Differentia duarum dignitatum ejusdem gradus applicata ad differentiam laterum, dat partes singulares gradus inferioris ex binomio laterum ut .
2 Tot sunt partes singulares ex binomio in gradu quolibet, quot unitates habet exponens Dignitatis immediate superioris; tres nimirum in Quadrato, quatuor in cubo &c When Slusus demonstrates his method by these Theoremes he takes the Difference of two Dignities & the difference of their latera for infinitely small Differences. If Mr Leibnitz when his mind ran upon improving this method of Tangents printed by Slusius had recourse to these Lemmas & at length understood them, he might easily understood that Mr Newtons Theoreme for resolving the dignity of a Binomium into an infinite series was of the same kind with these two Lemmas but much more general & complete & comprehended them as a General comprehends a particular & by consequence that this Theorem had the same relation to Mr Newtons general method which those Lemmas had the particular method published by Slusius. And since he gave the name of Differences to the infinitely small parts of quantity, its very probable that he had that name from the first of these Lemmas of Slusius.
Archimedes began the method of squaring curves & drawing tangents to them by considering the infinitesimals of quantity. Cavallerius & Fermat applied this method to Equations Fermats method was first published by Herigon & Sch{octen}. Gregory, Barrow & Slusius improved it for Tangents Mr Newton made it general extending it to the solution of all sorts of difficulter Problems & notice of his having made it general was sent to Collins Gregory Slusius & others in the year 1669 Mr Leibnits having notice thereof & one half of Newtons method being communicated to him with some descriptions & examples of the other half, fell into the other half A.C. 1677 wrote back to Mr newton as if he had known it long before, pretends to be the first inventor refuses to let the world know plainly the time & manner of his invention conceals what he learnt by his correspondence with Mr Oldenburg & Mr Collin & will not allow young men who were not privy to that correspondence capable of understanding the letters & papers then written , & yet appeals to the judgment of the R. Society amongst whom there is not a man now to be found besides himself who was privy to it.
And tho he had the method of series plainly communicated to him at his own request, yet he cannot forbear putting in for a share in that invention also. In the year 1673 when he was in London the first time, there was not a Mathematician of note in that city who had not heard of the method & seen some of the series & yet soon after his going thence to Paris he could not forbear putting for the first inventor of such a series for the area of the circle. He could not then forbear pretending to two such series both found by one & the same method tho he wanted the demonstration or method of finding them. For one of them was for finding the arc by the sine, this cannot be found by his method of Transmutations & he wrote a little after for the demonstration. When he had received eight such series from Mr O & Mr C. he took time to consider them & compare them with with his own but never produced any other series then what he had received. After a years consideration he wanted the Demosntration or method of finding them dropt the receipt of them & found out a pretence to desire the Demonstration & desired Mr O. to procure him the Demonstration or method of Mr Collins without Mr Newtons leave, tho by his own rule, if they had sent him the Method & he had forgot the receipt of it & claimed it as his own, Mr Oldenburg & Collins were not to contradict him without authority from Mr Newton. Mr O & Mr C. pressed Mr N to send his own method himself. Mr N sent it &
Sir
A copy of your book entituled Clavis Domus Heber was presented to me in your name some months ago & I then desired the person who brought me the present to return my thanks & told him that I did not understood Hebrew. I have looked over it & find the designe very good. The Hebrew tonge is said to be narrow, & the just signification of several words to be almost lost & few books are extant written in the ancient Hebrew , & the designe of recovering the ancient signification of the words must be very commendable: but for want of skill in that tongue I am unable to make a further judgement of the success in this desgne. then I am perswaded that a person of your abilities has wanted the success desired. I am
When Mr Newton in his Letter dated 13 Iune 1676 had explained his method of series, he added: Ex his videre est quantum fines Analyseos per hujusmodi infinitas æquationes ampliantur: quippe quæ earum beneficio ad omnia pene dixeram problemata (si numeralia Diophanti et similia excipias) sese extendit. Non tamen omnino universalis evadit . . . . . tulerit excogitavi. To this Mr Leibnitz in his Letter of 27 Aug. 1676 answered: Quod dicere videmini plerasque difficultates {e}xceptis problematibus Diophantæis) ad Series Infinitas reduci; id mihi non videtur. Sunt enim multa usque adeo mira & implexa ut neque ab æquationibus pendeant neque ex Quadraturis. Qualia sunt (ex multis alijs) Problemata methodi Tangentius inversæ [By this Answer it is absolutely certain that Mr Leibnitz had not yet found out the reduction of problems to æquations or Quadratures by the differential method.] And Mr Newton in his Letter of 24 Octob 1676 replied Vbi dixi, omnia pene Problemata &c . . . . . . . . ad eruendos terminos assumptæ seriei. By the Answer of Mr Leibnitz it is most certain that he had not then found out the reduction of problems to differential æquations & that Mr Newton had then found out the reduction of Problemes to fluxional æquations & finite series [& by their means the Reduction of the inverse problemes of tangents & other more difficult to such equations series & quadratures]
Mr Newton in his Analysis above mentioned in arguing why the method there proposed should be caled Analysis subjoyned: Denique ad Analyticam merito pertinere censeatur, cujus beneficio Curvarum areæ & longitudines &c (id modo fiat) exacte & Geometrice determinentur. Sed ista narrandi non est locus. And in his Letter of Iune 13 1676 he touched upon the same subject saying (as above) neque [vacat] alia quædam tradere quæ circa Reductionem infinitarum serierum in finitas ubi rei natura tulerit excogitavi. And in his Letter of 24 Octob. 1676, he explained this method further saying that by the method which he couched in this sentence Data æquatione quotcunque fluentes quantitates involvente fluxiones invenire & vice versa, he had endeavoured to render the speculation concerning the Quadrature of Curves more simple & had arrived at some very general Theorems & there set down the first of those Theorems & illustrated it several examples. And this is the fift Proposition in his Book of Quadratures & the second of those Theoremes is the sixt Proposition. And these two depend on the four first Propositions of that book & therefore the six first Propositions thereof were understood by him in the year 1669 when Dr Barrow communicated the said Analysis to Mr Collins: which Propositions comprehend the direct method of fluxions & some part of the Inverse method.
Hereupon the Editors of the Acta Lipsiensia the next yeare in Iune (in the Stile of Mr Leibnitz) in giving an account of these two first Volumes of Dr Wallis's works, tooke notice of this clause of the Preface & complained not of the Doctors saying that Mr Newton in his two Letters of 1676 explained to Mr Leibnitz the Method of fluxions found by him ten years before or above, but that while the Doctor mentioned the differential calculus & said that he did it nequis causetur de calculo differentiali nihil ab ipso dictum fuisse, he did not tell the Reader that Mr Leibnitz had this calculus at that time when the Letters passed between him & Mr Newton by means of Mr Oldenburg. And in several Letters which followed thereupon between Mr Leibnitz & Dr Wallis, concerning this matter Mr Leibnitz denyed not that Mr Newton had the method 10 years before the writing of those Letters as Dr Wallis had affirmed, pretended not that he had the differential method so early, brought no proof that he had it before the year 1677 no other proof besides the concession of Mr Newton that he had it so early, ⊡ represented that tho the method, agreed in the main, yet they might differ in some things & challenged to himself only those things wherein (as he conceived) they might differ, namely {illeg} the Notation , or , or , &c. 2ly Differential equations, (tho he had allowed those to Mr Newton in his Letter of 21 Iune 1677) & 3dly exponential Equations.
But after the death of Dr Wallis, Mr Newton repeating what Dr Wallis had published nine years before & Mr Leibnitz & the Editor{s} of the Acta Lipsiensia had not then contradicted those Editors in the style of Mr Leibnitz, began to pretended that Mr Leibnitz was the first Inventor & Mr Newton had substituted fluxions for the Leibnitian differences, And when Mr Keil defended Mr Newton, Mr Leibnitz refused to argue the matter with him pretending that he was a novice unacquainted with what had formerly passed, & a clamorous fellow & had no authority from Mr Newton & appealed to Mr Newton himself, thereby endeavouring to pick a quarrel with him, or force him to retract what he & Dr Wallis had published, & to acknowledge himself a lyar & a plagiary.
The Question lies in a little room. Mr Leibnitz in the year 1676 affirmed that inverse Problems of Tangents were not reducible to equations & was polishing the series of Gregory vulgari more & conjecturing that the method of Slusius might be made general by a Table of Tangents & therefore had not then found the differential calculus. And yet in the beginning of his Letter of 21 Iune 1677 he affirmed that he had found this calculus jam tum a multo tempore. It lies upon him to prove that he had it before the year 1677. For no man is a witness in his own cause. He has published the series of Mr Gregory as his own. It lies upon him to prove that he had it before he received it from Mr Oldenburg. In the year 1674 he pretended to a series for finding the arc by the sine & two years after he desired Mr Oldenburg to procure from Mr Collins the Method of finding that series. It lies upon him to prove that he had found out that series by himself in or before the year 1674. Mr Newton in his Letter of 13 Iune 1674 sent him several series with the methods of finding them & he pretended to have found some of them before the receipt of that Letter: It lies upon him to prove that he had methods of finding them & had found them before. At his own desire Mr Newton sent to him two inverse methods of series & he understood them with great difficulty, & as soon as he understood them he pretended to have found one of them long before & to have forgot it as he perceived by his old papers. It lies upon him to prove that he had every found it before. A year or two after Mr Newton had published his Principia Philosophiæ Mr Leibnitz published three papers relating to the principal Propositions in that book, pretending that he had found them before the publishing of that Book: it lies upon him to prove that he had found them before. He pretended that the Propositions concerning the motion of bodies in resisting Mediums were for the most part found out by him twelve years before while he was yet at Paris that is, before he had the Differential method: it lies upon him to prove it. He pretended to the Proposition that a body revolving in an Ellipsis & with a radius drawn to the lower focus describing equall Areas in equal times, is attracted towards the lower focus by a force which is reciprocally as the square of that radius; his demonstration is erroneous & it lies upon him to prove that he did not some time after the publishing of Mr Newtons Principia try to adapt a Demonstration to that Proposition with a designe rival Mr Newton in the invention of the Proposition. [To commit an error is a pardonable fault incident to humain nature:, but to claim from another man the invention of a Proposition by an erroneous demonstration , is a fault of a higher kind, & Mr Leibnitz is complained of for doing this to make himself a coinventor. His Tentamen de motuum cœlestium causis is full of faults. He is complained of not for those faults but for writing that faulty piece in hast before he understood the subject & doing it as a coinventor without acknowledging that Mr Newton went before him in those matters & gave him light into them. He is complained of for making Dr Barrows method of Tangents his own by changing the notation & giving the method a new name without ever acknowledging himself beholden to Dr Barrow.
Now that you may know what kind of calculation Mr Newton used when in or before the year 1669 when he he wrote this Compendium of Anlysis
By the same way of working the second Rule may be also demonstrated. Or if any æquation whatever be assumed expressing the relation between the Abscissa & Area of a Curve the Ordinate may be found as is mentioned in the next words. And if this Ordinate drawn into an unit be put for the Area of a new Curve the Ordinate of this new Curve may be found by the same method. And so on perpetually. And these Ordinates represent the first second third fourth & following fluxions of the first Area. This was Mr Newtons way of working in those days when he wrote the said Compendium of his Analysis; And by the same way of working he demonstrated the two first Propositions in his Book of Quadratures: & the very same way of working is used by him to this day.
Among the examples &c
It is the more Geometrical & natural because founded upon the rationes primæ quantitatum nascentium which have a being in Geometry whilst indivisibles & quantitates primæ nascentes upon which the Differential method is founded have no being. Nature generates quantities by continual flux or increase & the ancient Geometers admitted such a generation of areas where they drew one line into another by continual motion, to generate an area, & the area into a line to generate a solid. But the summing up of indivisibles to generate an area or solid was never yet admitted into Geometry. Mr Newtons method is adapted either for finding out a Proposition or for demonstrating it, Mr Leibnitz's is only for finding out. When the work succeeds not in finite equations Mr Newtons method has recours to converging series & thereby becomes incomparably more universal then that of Mr Leibnits which is confined to finite equations. And where the Law of the fluxions is not known but the fluxions are had only in a few particular cases Mr Newton finds that law quamproxime by his Differential method, & thence deduces the fluents & solves the Problem, & on this account also his method is more universal then the method of Mr Leibnitz. So then Mr Leibnitz has only a part of Mr Newtons general method, & if he would have that part to be his own, it lies upon him to prove that he had it before the year 1677. All other arguments are in vain. Several Accounts of this Commercium having being given abroad all of them very imperfect: it has been thought fit to publish the Account which follows.
Sir
I received your Book of the second Edition & return you my hearty thanks for the favour of such a present. Its now above eighteen years since I left off the study of Mathematicks & the disuse of thinking upon these things makes it difficult to me to take them into consideration: but however I have run my eye over it & performd & cannot but applaud it much. I wish heartily that France may always flourish with men who improve these sciences. I am
Mr Leibnitz has since [upon a pretence that he was not at leasure & had not seen the Commercium] in opposition to the Report of the Committee [ ] imployed a nameless Mathematician to examin the matter & give his judgment thereupon. And the Mathematician in a Letter to Mr Leibnitz dated 7 Iuly 1713 has dropt the consideration of the ancient records & given his opinion that Mr Newton had not the method of fluxions till after the writing of his Principia Philosophiæ & that for these reasons. First becaus in all the Letters of the Commercium Eipstolicum from which the Committee draw their arguments there is not any instance of Mr Newtons using letters with pricks
— For this is one & the same Proposition with that of deducing the Ordinate from the Area, & the Area from the Ordinate & therefore was known to Mr Newton when he wrote this Analysis. [And he that considers Mr Newtons Book of Quadratures will see that that Book was written for solving this fundamental Proposition, the four first Propositions of that book conteining the direct method, the rest conteining the inverse
In this Compendium Mr Newton represents the uniform fluxion of time or of any exponent of time, by an unit, the moment of time or of its exponent by the letter o, the fluxions of other quantities by any other symbols the moments of those quantities by the rectangles under those symbols & the letter o, & the area of a Curve or fluent by the Ordinate of fluxion inclosed in a square. When he is demonstrating any Proposition he uses the letter o for a finite moment of time or of its exponent & performs the whole calculation by the Geometry of the Ancients without any approximation; & so soon as the calculation is at an end & the Equation is reduced, he supposes that the moment o decreases in infinitum & vanishes. But when he is not demonstrating but only investigating a Proposition, for making dispatch, he supposes the moment o to be infinitely little, & forbears to write it down & uses all manner of approximations which he conceives will produce no error in the conclusion. An example of the first kind you have in the end of this Compendium in demonstrating the first of the three Rules laid down in the beginning of the book, Examples of the second kind you have in the same Compendium in finding the lengths of Curve lines p 15, & in finding the Ordinates areas & lenghts of Mechanical Curves p. 17, 18. And he tells you that by the same method tangents may {be} drawn to Mechanical curves. And in his Letter of 10 Decem. 1672 he adds that Problems about the Curvature of Curves geometrical or mechanical are resolved by the same method. Whence its manifest that he had then extended the method to the second fluxions, if not to the third. For when the Areas of Curves are considered as fluents (as is done in this Analysis) the Ordinates express the first fluxions, the tangents are given by the second fluxions & the curvatures by the third. And indeed the Problem Data æquatione fluentes quantitates involvente fluxiones invenire & vice versa extends to all the fluxions as is manifest by the examples of the solution of that Problem published by Dr Wallis Tom 2. p. 391, 392, 396. Thus the method of Fluxions for investigating Propositions by finite æquations is as universal as the differential method, & exceeds it in the method of demonstrating, being also on that account more geometrical, besides the advantage of working in converging series which makes it incomparably more universal.
But that you may be fully satisfied that Mr Newton used this Method Method of calculating in the year 1669 or before when he wrote the said Compendium I will here set down his ddemonstration of the first Rule above mentioned. Sit Curvæ alicujus – – – – – . erit . Q. E. D. Where note that &c denotes the series into which the dignity is resolved & denotes series into which the dignity is resolved. T
Among the Examples.
And in the Analysis pag. 16 where Mr Newton saith Momentum est superficies cum de solidis & linea cum de superficiebus & punctum cum de lineis agitur, it is all one as if he had said that when solids are considered as fluents, their moments are superficies & the moments of those moments (or second moments) are lines & the moments of those moments (or third moments) are points. And in his Principia Philosophiæ where he frequently considers lines as fluents described by points whose velocities increase or decrease, the velocities are the first fluxions & their increase the second And by the Letters & papers dated between the years 1669 & 1677 inclusive the Committee found that Mr Newton had his method before Iuly 1669 & that nothing occurred by which it could be gathered that Mr Leibnits had any other differential method then Moutons before the year 1677.
⊡ allowed that the methods agreed in the main & said that he therefore used to call them by the common name of the Infinitesimal Analysis, represented that as the methods of Victa & Cærtes were called by the common name of Analysis speciosa & yet differed in some things so perhaps the methods of Mr Newton & himself might differ in some things & challenged to himself only those things wherein as he conceived they might differ; namely first the Notation dy, ddy or d2y, dddy or d3y, , dey; secondly differential equations & thirdly Exponential Equations. The first & third are allowed to Mr Leibnitz, the second Mr Leibnitz in his Letter of 21 Iune 1677 recconned common to Mr Newton & himself.
This was the state of the dispute between Dr Wallis & Mr Leibnitz at that time Mr Leibnis compared Mr Newton & himself to Vieta & Descartes in respect of what was common to their methods And four years after, when Mr Fatio suggested that Mr Leibnitz the second inventor of this calculus might borrow something from Mr Newton the oldest inventor by many years: Mr Leibnitz in his Answer published in the Acta Lipsiensia in May 1700, did not deny that Mr Newton was the oldest inventor by many years nor asserted any thing more to himself then that he had found the method apart or without the assistance of Mr Newton. And in making this defence he added Quam [methodum] ante Dominum Newtonum et Me nullus quod sciam Geometra habuit; uti ante hunc maximi nominis Geometram NEMO specimine publice dato se habere probavit, ante Dominos Bernoullios & Me nullus communicavit. Hitherto therefore Mr Leibnitz did not pretend to be the first inventor
But after the death of Dr Wallis, (the last of the old mathematicians who were acquainted with what had passed between the English & Mr Leibnits 40 or 50 years ago) when Mr Newton in the Introduction to his book of Quadratures repeated what Dr Wallis had publickly affirmed nine years before & Mr Leibnitz & the Editors of the Acta Lipsiensia had not then contradicted: those Editors in the style of Mr Leibnitz began to pretend that Mr Leibnitz was the first Inventor & that Mr Newton had substituted Fluxions for the Leibnitsian differences. And when Mr Keil defended Mr Newton Mr Leibnitz refused to argue the matter with him pretending that he was a novice unacquainted with what had formerly passed, that he had no authority from Mr Newton, that he behaved himself clamorously & that Mr Newton understood the matter better then any body & as he hoped, would not refuse to give his opinion: that is, now Barrow, Gregory, Oldenburg Collins & Wallis who understood this matter were dead, he Mr Leibnitz was resolved to attaque Mr Newton himself & try to run him down by the advantage of his correspondence with the learned abroad or force him to retract what he & Dr Wallis had published & by consequence to acknowledg himself a lyar & a plagiary.
tend to be the first inventor.
Mr Leibnitz deduces the circular motion of the Planets from the Vortex, the motion of ascent & descent from gravity, but has not demonstrated that a Planet will in every revolution ascend & descend by Gravity just once & not oftner.
In a Letter from Hannover dated Martij 1693 Mr Leibnitz wrote thus to Mr Newton Mirifice ampliaveras Geometriam tuis seriebus, sed edito Principiorum opere ostendisti patere tibi etiam quæ Analysi receptæ non subsunt Conatus sum ego quoque notis commodis adhibitis quæ differentias et summas exhibent Geometriam illam quam transcendentem appello, Analysi quodammodo subjicere, nec res male processit. Mr Leibnitz therefore hitherto allowed that Mr Newton had a methodus SIMILIS without pretending that it was derived from the differential.
③ Dr Wallis in the Præface to the two first volumes of his works published in 1695 made this mention of the method. In secundo volumine (inter alia) habetur Newtoni methodus de fluxionibus (ut ille loquitur,) consimilis naturæ cum Leibnitij (ut hic loquitur) Calculo differentiali (quod, qui utramque methodum contulerit, satis animadvertat, utut sub loquendi formulis diversis) quam ego descripsi (Algebræ Cap. 91 &c præsertim Cap. 95) ex binis Newtoni Literis (aut earum alteris) Iunij 13 & Octob. 24 1676 ad Oldenburgum datis, cum Leibnitio tum communicandis (ijsdem fere verbis, saltem leviter mutatis, quæ in illis Literis habentur,) ubi METHODUM HANC LEIBNITIO EXPONIT tum ante DECEM ANNOS, nedum plures [i.e. anno 1666 vel 1665] ab ipso excogitatam. Quod moneo, nequis causetur, de hoc Calculo Differentiali nihil a nobis dictum esse.
② At the request of Dr Wallis, Mr Newton in two Letters dated Aug. 27 & Sept 17 1692 explained at large the solution of these two Problems Data æquationes fluentes quotcunque quantitates involvente fluxiones invenire & Ex æquatione fluxionem radicis involvente, radicem extrahere; & Dr Wallis published the same in the second volume of his works.
① In the Iournal des Sçavans of munday 30 August 1694 Mr Leibnitz in writing of the advantages of the differential Calculus above the ordinary Analysis, said: This justice is to be done to MrNewton (to whom Geometry Optique & Astronomy are much indebted) that also in this affair, he has of himself found something like it, according to what I have since understood It is true that he uses other characters: but as the characteristique it self, as I may speak, is a great part of the Art of invention, I beleive that ours give more light. Thus far Mr Leibnitz, who did not yet know what characters were used by Mr Newton
④ The next year in the Acta Lipsiensia of Iune an Account was given of the two first Tomes of the Mathematical works of Dr Wallis & thereupon followed several Letters between Dr Wallis & Mr Leibnitz, with frequent mention of the method of fluxions & differential method & the account given of them by Dr Wallis, & all this without any complaint against Dr Wallis for saying that Mr Newton in his Letters of 13 Iun. & 24 Octob 1676 explained to Mr Leibnitz this method found ten years before or above. Mr Leibnitz allowed these methods to resemble one another so much that he used to call them by the common name of the infinitesimal method. He only contended that Mr Newton's method & his own might differ in some things, & layd claim to what might be proper to his own but is very confused in describing the same. He pretended to the invention of the differential notation dy, d2y (or ddy) d3y, , dey, & it is his own. But he was not the first who considered the quantities which he calls second differences. Mr Newton had considered them before in determining the curvatures of Curve lines by his method of fluxions. See his Letter to Mr Collins dated 10 Decem. 1672. See also his solution of the two Problemes in the second Tomes of Dr Wallises Works p. 392, 393, 396. Mr Leibnitz pretended also to the invention of Differential equations for expressing the nature of transcendent Curves: but these equations were known before to Mr Newton
For his fundamental Proposition, Data æquatione fluentes quotcunque quantitates involvente fluxiones invenire, is for finding such equations, & his other Problem ex æquatione fluxionem radicis involvente radicem extrahere is for resolving such equations into converging series. A third thing which he claims is the invention of exponential Equations. Mr Newton in his Letter of 24 Octob 1676 proposed equations in which the exponents of the Dignites of indeterminate quantities were frat or surd numbers: Mr Leibnitz in his answer mutualy proposed equations in which the exponents of the Dignities of indeterminate quantities were indeterminate quantities. And these æquations were first proposed by him, but have hitherto been of no use. Mr Leibnitz therefore giving the name of the Infinitesimal method to the methods of himself & Mr Newton so far as he conceived them common to them both, forbore to claime the whole to himself & only claimed some things in which he pretended that he & Mr Newton might differ.
After these things Mr Fatio in the year 1699 represented that Mr Newton was the first Inventor of the Method & Mr Leibnitz answered Certe cum Elementa calculi meam edidi anno 1684, ne constabat quidem mihi aliud de Inventis ejus in hoc genere quam quod ipse olim significaverat in literis, posse se Tangentes invenire non sublatis irrationalibus: quod Hugenius quoque se posse mihi significavit postea, etsi cæterorum istius calculi adhuc expers. Sed majora multo consecutum Newtonum, viso demum libro Principiorum ejus, satis intellexi. Calculum tamen differentiali tam similem abeo exerceri, non ante didicimus quam cum non ita pridem magni Geometræ Iohannis Wallisij operum volumina primum et secundum prodiere:
Et post aliqua: Quam [methodum] ante Dominum Newtonum & me nullus quod sciam Geometra habuit; uti ante hunc maximi nominis Geometram NEMO specimine publice dato se habere probavit: ante Dominos Bernoullios & ME nullus communicavit.
Here it is something acknowledge that no man before Mr Newton & himself had this method, no man before Mr Newton had proved by a public specimen that he had this method. But he should not have said that in the year 1684 when he published the elements of his differential method he knew nothing more of Mr Newton's Inventions of this kind then that he could draw tangents without sticking at surds. ‡ By Mr Newtons Letters he knew certainly that Mr Newtons methods gave the method of Slusius readily & made it more convenient so as not to stick at surds, that in like manner it determined maxima & minima & some other Problems there not named, without sticking at surds, that it rendred Quadratures more easy those figures being always squareable which were at a differential equation; that it gave the Theoreme There described & illustrated with examples for squaring curves by a series which brake off & became finite when the Curve was squarable by a finite equation, & found other Rules for comparing the areas of curves with those of the Conick Sections He knew also that Mr Newtons methods reached to the Curvature of Curves & to their lengths & centers of gravity &c & to the inverse Problems of Tangents, & proceeded in Mechanical Curves as well as others. He knew also that Mr Newtons method of series by the help of his other methods extended to almost all sorts of Problems except some numeral ones like those of Diophantus & that when he wrote his letters of 27 Aug. & Novemb 18 1676 he had not found out the differentiall method, & therefore Mr Newtons methods for doing these things were the older, & yet the next year so soon as he had found out how to extend Dr Barrows method of Tangents to some of these things, he changes the notation gives the method a new name as if it were his own & rivals Mr Newton by writing back that he had found out this new method jam a multo tempore Clarissimi Slusij Methodum tangentium saith he, nondum esse absolutam, celeberrime Newtono assentior. Et jam a multo tempore rem tangentium generalius tractavi scilicet per differentias Ordinatarum. And to this day he has not acknowledged himself obliged either to Dr Barrow or to Mr Newton for any thing. When any man has found out any thing & gives notice of his success to his friend, it is not lawfull for his friend to go about to supplant him by pretending that he had found out the same thing long before, unless he can prove that he had found it out long before. For the very notice may put his friend upon trying to find it out. And if hee can find it out & may be allowed to pretend that he found it out before he received the notice, he is allowed to supplant & robb the first Inventor. It lies upon Mr Leibnitz therefore to prove that he invented the Differential method before the receipt of Mr Newtons Letters In the year 1677 he put in his claim to the differential method in these words Et jam a multo tempore rem tangentium generalius tractavi scilicet per differentias Ordinatarum. It lies upon him to prove his claim.
In the year 1704 Mr Newton published his Treatise of Quadratures The book had been some years before in the hands of some of his friends & thereby he was induced to publish it. And that it might not be taken for a new piece he wrote an Introduction to it wherein he described the method of fluxions upon which it was founded, & represented that he found out that method gradually in the years 1665 & 1666 & the first step to the inverse method was the Quadrature of Curves concerning which he had [olim] long ago written that Tract of Quadratures. In Mr Newtons Letter of 24 Octob. 1676 there are so many things quoted out of that book as may make it evident that the book was then in being. And that the Method of fluxions was found out in the years 1665 & 1666 is nothing more then what Dr Wallis wrote in the Preface to the two first Volumes of his works, saying that Mr Newton in his letters of 13 Iune & 24 Octob. 1676, methodum hanc Leibnitio exponit tum ante decem annos, nedum plures, ab ipso excogitatam. Quod moneo nequis causetur de hoc Calculo Differentiali nihil a nobis dictum esse. The Editors of the Acta Eruditorum in their Account of these two Volumes (written in the style of Mr Leibnitz take notise of this Paragraph & complain that Dr Wallis had here omitted what Mr Leibnitz had performed in the Letters which passed at time between & him & Mr Newton, & Mr Leibnitz himself in the Letters which followed thereupon between him & Dr Wallis, pursued the complaint. But none of them at that time found fault with Dr Wallis for saying that Mr Newton had found the Differential Method 10 years before or above. But now, Dr Wallis being dead, & Mr Leibnitz by an universal correspondence have better established his credit, the Editors of the Acta in Ianuary 1705 in the style of Mr Leibnitz, represent that the method of fluxions was derived from the differential method, & the book of Quadratures was a new piece conteining little or nothing worth mentioning besides what Cheine & Craig had published before. Whereupon Mr Keil in an Epistle published in the Philosophical Transactions in May & Iune A.C. 1708, wrote on the contrary quod fluxionum Arithmeticam, sine omni dubio, primus invenit Dominus Newtonus ut cuilibet ejus Epistolas a Wallisio editas legenti facile constabit. Eadem, tamen Arithmetica postea mutatis Nomine & Notationis modo, a Domino Leibnitsio in Actis Eruditorum edita est. And Mr Leibnitz in a Letter to Dr Sloane Secretary of the Society dated 4 Mart. st. n. 1711 complained thereof to the R. Society, proposing that Mr Keil should make a public recantation.
This Letter being shewed to Mr Newton he was at first concerned that a dispute of this kind should arise being of a quiet disposition & very averse from disputes & careless of fame: but some days after, the Acta Lipsica of Ianuary 1705 being shewn to him & he finding himself there traduced in an artificial manner & represented a Lyar & a Plagiary, he gave leave to Mr Keill to pursue the dispute. And Mr Keil thereupon wrote an answer wherein he explained & justified what he had said. This Letter was read in the R. Society 24 May 1711 & then ordered to be sent to Mr Leibnitz. And Mr Leibnitz returned an answer dated 29 Decem 1711 in which he persisted in his complaint against Mr Keil, justified what was in the Acta Lipsiensia, & pretended that he had found the Differential method above nine years before he published it, that is in the year 1675 or before, & that no body had gone before him in those matters: whence it follows that Dr Wallis & Mr Newton had falsly affirmed that the method of fluxions was found in the years 1665 & 1666. And in both his Letters he appealed to the opinion of Mr Newton, pressing in his last that Mr Newton would declare his opinion in this matter, that is that Mr Newton would retract what he & Dr Wallis had already declared & what Mr Leibnitz durst not deny sixteen years before when Dr Wallis published it & that he would retract what he wrote in his Letter of 24 Octob. 1676 namely that he had written a treatise upon this method & the method of Series together five years before that is in the year 1671, & that he would retract the Analysis written in the year 1669 & published by Mr Iones & acknowledge it to be a spurious piece. All these things Mr Newton was to retract or be quarrelled by Mr Leibnitz for not giving judgment against Mr Keil.
The Royal Society have as much authority over Mr Leibnitz as over Mr Keill, & Mr Leibnitz in accusing Mr Keill obliged himself to justify his accusation least it should be taken for a calumny. And yet Mr Leibnitz in his last letter refused to justify his accusation calling it injustice to expect that one of his age & reputation should defend his candor & pleade to give any reasons for it. And therefore the R. Society considering that the Question depended upon things done 35 or 40 years ago ordered a Committee to search out what old Letters & other Papers were to be met with relating to this matter & report their opinion upon them & then ordered the Papers & the Report of their Committee to be published. [And Mr Leibnitz some months after these things came abroat, pretending that was not a leasure ]
And had invented a great part of Mr Newtons Principia Philosophiæ before he saw that book, & some part of it twelve years before while he was yet at Paris, that is before he had the Differential method. But such pretenses are not to be regarded. No man is a witness in his own c{anp}
& in maintaining it declined to give any reasons for his claim insisted upon his own candor as if it were unjust to question it, pressd that Mr Newton should declare his opinion, as the only man now alive who well understood this matter & refused to contend with any man but Mr Newton as if all younger men were novice & uncapable of understanding the ancient Letters & Papers which remaind upon this subject, & under the person of a nameles Mathematician & two other nameless correspondents has put about a triple Libel against Mr Newton full of railing & injurious accusations without any proof
used letters & tells us that for certain reasons he chose rather to use the symbols dx & dy. He that shall compare Dr Barrows method of Tangents with that of Mr Leibnitz will find them exactly the same except the different Notation & the improvements made to the method by the suggestions of Mr Newton. And what those improvements were will appear by {three} of Mr Newtons Letters dated 10 Decem 1672 13 Iune 1676 & 24 Octob. 1676.
For Mr Newton at the request of Mr Collins sent to him his method of Tangents in a Letter dated 10 Decem 1672. And it proved to be the same – – – – – – sentences set down enigmatically: the first of which was this
Thus Mr Newton in these three Letters represented that his method was very universal, that it gave the method of Slusius as an obvious Corollary & that it proceeded without sticking at surds & faciliated Quadratures. And after all this information Mr Leibnitz in his said Letter of 27 Iune 1677 proposed Dr Barrows method of Tangents with some of these improvements shewing how the method of Slusius easily followed from it, & how it might be managed so as not to stick at surds, & then added: Arbitror quæ celare voluit Newtonus ab his non abludere Quod addit ex hoc eodem fundamento Quadraturas quoque reddi faciliores me in sententia hac confirmat; nimirum semper figuræ illæ sunt quadrabiles quæ sunt ad æquationem differentialem. Thus he concludes that he had got a method like that of Mr Newton. And at length he published this method in the Acta Eruditorum mensis Octobris An. 1684 pag. 467, with this title. Nova methodus pro maximis et minimis itemque tangentibus quæ nec fractas nec irrationales quantitates moratur & singulare pro illis calculi genus per G. G. L. And after he had described his new notation & how to find differential equations (as he calls them) without sticking at fractions or surds: & applied this calculus to Tangents & maxima & minima he subjoyns. Et hæc quidem initia sunt Geometriæ cujusdam multo sublimioris ad difficillima et pulcherrima quæque etiam mistæ matheseos problemata pertingentis, quæ sine calculo nostro differentiali, aut simili, non temere quisquam pari facilitate tractabit.
He published the elements of his Differential method without mentioning any other author then himself or taking any notice of what had passed between him & Mr Newton . And afterwards excused it by saying that before the publishing of Mr Newtons Principia Philosophiæ, he knew nothing more of Mr Newton's method then that it was a method of Tangents which stuck not at surds. p. 104, 107.
Now Mr Leibnitz denyes that he had all this light from Mr Newton or in the time of this correspondence learnt that Mr Newton had a general method of this kind, or any further method then to draw Tangents without sticking at surds{,} (p. 104, 107) & affirms that the method of fluents was always used by Mr Newton in the room of the Differential method. p 108, 119. Mr Keill is thinks otherwise And the R. Society look upon the ancient Letters & Papers here printed as the best evidence now to be had in the Question depending between them.
But Mr Leibnitz denyes that he had all this light from Mr Newton or in the time of this correspondence learnt that Mr Newton had a general method or any further method of this kind then to general method or any further method of this kind then to draw Tangents without sticking at surds which might be done without knowing any thing more of the method p. 104, 107.) And in like manner, after he had conversed wth the mathematicians at London he wrote from Paris as if he had never heard of Mr Newtons method of series & pretended to be the first inventor of two series for the circle (p 38) & the next year when he received eight series from Mr Oldenburg & knew none of them to be his own, he forgot the receipt of them before the end of the year & communicated one of them as his own to his friends at Paris (p 42) & the spring following endeavoured to get the Method from Mr Oldenburg & Mr Collins without the knowledge of Mr Newton (p. 45) tho by his own rule if he should afterwards have forgot the receipt of the method & taken it for his own, Mr Oldenburgh & Mr Collins were not to contradict him without authority from Mr Newton p. 118. And in recompence for Mr Newtons method he promised them his own inventions about the same subject, tho those inventions were nothing else then an Opusculum or discourse upon one of the eight series which he had received the year before from Mr Oldenburg but had forgot the receipt of it. p 42, 45, 61. And when at his own request the received from Mr Newton the method of deriving reciprocal series from one another tho he understood it with difficulty yet he wrote back that he had found it before as he perceived by his old papers but not meeting with an elegant example of its use had neglected it. p. 63 96 And when he published the above mentioned series as his own, (p 97) he had not only forgot that he had received it from Mr Oldenburg but also that the collection of Gregories Letters had been sent him at his own request, amongst which was Gregories Letter of Feb 15 1671 conteining that series then sent to Mr Collins p 25, 47.
As for those Gentlemen who have used the Differential method, & particularly the Marquess de L'Hospital, Mr Varignon & the brothers the two Bernoulli there is nothing in these Letters & papers that can reflect upon them. They were strangers to the correspondence between Mr Leibnits & Mr Oldenburg & are much to be commended for the use & improvements they have made of the infinitesimal method.
And when he
Mr Collins in the beginning of the year 1671 received several series from Mr Gregory with leave, to communicate them to whom he pleased & was very free in doing so. Mr Leibnitz having been at London began soon after to pretend himself the first inventor of two such series, & in the year 1675 had eight series sent him by Collins & Mr Oldenburg, & knew none of them to be his own & yet the same year communicated the last of them to his friends at Paris as his own, the next year sent it back to Mr Oldenburg as his own, & had a copy sent him of the Letter by which Mr Gregory had communicated that series to Mr Collins A.C. 1671 & yet afterwards published that series in the Acta Lipsica as his own without letting the world know that he had it from Mr O. & Mr C. who had it from Gregory.
A year after the receipt of the eight series he pretended to have forgot them & endeavoured to get the method from Mr O. & Mr C without Mr Newtons knowledg; tho if he should also have forget the receipt of the method, & taken it for his own Mr Oldenburg & Mr Collins by his own rule were not to contradict him without authority from Mr Newton.
When Mr Newton sent him his method with some examples of series: he endeavoured to make some copy of the reciprocall series his own in some cases, tho he did not yet understand the method of deriving reciprocal series from one another but at the same time wrote to Mr Newton to explain it. And when he had it, he wrote back that he had found it before as he perceived by his old papers but for want of a good example of its use had neglected it. p. 96.
— tho he now pretends that in the year 1684 when he published the elements of his differential calculus he knew nothing more of Mr Newtons inventions of that sort then what he signified in his Letters, namely that he could draw Tangents without taking away irrationals, which a man might do without knowing any thing more of the Differential method, but afterwards by his Principles found that his method was of much larger extent p 104, 107.
After Mr Leibnitz had conversed with the Mathematicians in London by whom he could not but hear of Mr Newtons method of series he endeavored also to make himself the first inventor of that method by pretending to two series for the circle with the method of finding them (p 38) forgetting the receipt of eight series sent him by Mr Oldenburg (p 40, 41) communicating one of the eight at Paris as his own & sending it back to Mr Oldenburg as his own (p 42, 65) tho he knew it was Gregories (p 47) endeavouring without Mr Newtons leave to get the method from Oldenburg & Collins tho by his own rule if he should afterwards forget the receipt of the method & take it for his own, Mr Oldenburg & Mr Collins were not to contradict him without authority from Mr Newton (p. 45, 118) promising them by way of recompence his own inventions about series of a very different kind from two series brought him from London: which inventions were a discourse upon the series which he had received the year before from Mr O & published at Paris, p. 45) by sending Mr Newton a Proposition like those of Mr Gregory & Dr Barrow for transmuting of figures into one another & thereby squaring one figure by another in some cases & crying it up for a general method & one of the chiefest the chiefest part of Analysis (p. 58) by desiring Mr Newtons method of deriving reciprocal series from one another & when he had & understood it, pretending that he had found it before as he perceived by his old papers, but for want of an elegant example had neglected to use it (p. 63, 96) by publishing in the Acta Lips. the series of Gregory for the circle & Hyperbola as his own without letting the world know that he had from M. O & Mr C. & that it was Gregories series found by Mr Newtons method (p. 97) & by numbring himself in those Acta amongst the inventors of the methods of Series & pretending that Mr Newton allowed that he had a general method p. 98.
If it be said that Mr Newton should have published his methods sooner, it appears by the following letters that he communicated a treatise of it to his friends in 1669 (p. 1, 2) that he was soon after about it (p. 27, 28, 29,) but was discouraged by contentions arising (p 71) & that Mr Leibnitz should not have discouraged him further by pretending to his methods. He might have sent him his differential method, but he should at the same time have acknowledged that he had but newly found it out & that he had found it out by means of the light which he had received into it by Letters, & not have sent it in such a manner as if he had known it long before (p 88) Candid men do not interrupt one anothers proceedings nor endeavour to snatch away one anothers inventions And its further to be considered that the Propositions in Mr Newtons Principia philosophiæ were first published by himself & yet the chief of them were afterwards claimed by Mr Leibnitz p 97.
Mr Newton's writing that he found his general method in the years 1665 & 1666 may go for history where there appears no reason to question it, but it gives him not inventoris jura against any man that can prove he had that general method before the year 1669. Mr Leibnitz's writing that he had improved the method of Slusius into a general method a multo tempore before the date of his Letter 21 Iune 1677 is no argument against another that can prove he had done the same thing before the date of that Letter p 88. When Mr Tschurnhause produced a general method of solving Problemes by assuming the terms of a series & determining them by the conditions of the Probleme, Mr Leibnitz ought not to have pretended publickly without some proof that he communicated that method to Mr Tschurnhause ten years before when they were together at Paris (Acta Lips. 1686. p. 293) Certainly Mr Leibnitz had not that method when he wrote his Letter of Aug. 27 1676 which was but a month or six weeks before he & Tschurnhause parted from one another at Paris. And so when Mr Leibnitz pretends to the first invention of the principal Propositions in Mr Newtons Principia, his pretention without any proof gives him not inventoris jura. It might have gone for history if no body else had published the Propositions before him: but the R. S. cannot take any man for an evidence in his own case. Mr Newton was desired to tell the original of his method, & when he had told it, to prevent contention with Mercator Mr Barrow did not think himself inured by Mr Newtons Analysis. Mr Gregory after he understood Mr Newtons method acknowledged him the first inventor. Mr Leibnitz is the only competitor tho a later man then the other two. Instead of following the example of Mr Newton who voluntarily yeilded the first invention of a Series to Mercator he refuses to yeild the first invention of the infinitesimal method to Mr Newton pretends to have found it out long before he communicated it to him would never say when he first found it out, of late denys that he then knew that Mr Newton had such a general method, heards himself with the first Inventors of the methods of series, claims the first invention of the principal propositions of Mr Newtons Principia Philosophiæ, without offering at any proof, appeals to the R. S. & at the same time refuses to plead before them or bring any proof of what he pretends to, represents that his Letters & those of Mr Newton & Mr Collins printed by Dr Wallis & other quoted by Mr Keil can be understood by young men such as Mr Keill is who were not privy to what passed when the Letters were written, will not allow any man the liberty of opposing him without authority from Sir Isaac Newton, & insists upon the credit of his own candor that is, he would have the R. S. to lay aside the consideration of the ancient Letters & papers of correspondence with Oldenburgh unlesse there be any witnesses now alive that were then privy to what passed between him Mr Oldenburg Mr Collins & Mr Newton & thereby capable of interpreting those Letters; He would the society rely upon the candour of his own testimony for himself without examining into the matter & give judgment accordingly unless Mr Newton who has always avoyded disputes shall have the vanity to enter into a dispute with him about an invention, & undertake to produce living evidence who were privi to all the correspondance between Mr Leibnitz Mr Oldenburg Mr Collins Mr Barro & Mr Gregory 36 years ago.
The first Proposition of the Tract De Quadratura Curvarum (communicated to Dr Wallis in August 1692) extends to the second third & following fluxions, as is manifest by the examples by which it is explained. And this Proposition was known to Mr Newton when he wrote his Principia Philosophiæ, & ten years before when he wrote his Letter dated 24 Octob. 1676, as above, & five years before that, when he wrote a Tract upon the Method of Series in conjunction with another method founded upon this Proposition, as he mentions in his said Letter. And the Inverse of this Proposition, namely to extract Fluents out of equations involving their fluxions, extends also to the second third & following Fluxions as is manifest by what Mr Newton sent to Dr Wallis in August & September 1692 & the Doctor published concerning this matter in the second Volume of his works pag. 396, & it was known to Mr Newton when he wrote his said Letter dated 24 Octob. 1676, that is before Mr Leibnitz knew any thing more of the Differential method then what he found in Dr Barrows method of Tangents.
212s. 240d∷106.120∷
4li. 7. 5
et ibi condensari et convertio in aquam et spiritus humidos, & subinde per lentum calorem in & sales & sulphura et tincturas et limum et argillim & arenam et lapides & coralla & substantias alias terrestres paulatim migrare
Decrescente autem corpore Solis motus medij Planetarum circum solem paulatim tardescent, & crescente Terra motus medium Lunæ circ{u} Terram paulatim augebitur. Et collatis quidem observationibus Eclipsium Babylonicis cum ijs Albategrij et cum hodiernis motum medium Lunæ paulatim accelerari, prumus omnium quod sciam, deprehendit
Ita privatim ut publice Quæritur unde habuit & quando primum habuit.. Methodum differentialem Moutoni Leibnitius habuit anno 1673 & suam esse voluit ‡ ‡ methodum aliam differentialem nondum habuit. Series postea habuit sed quas anno 1675 ab Oldenburgo accepit ab Anglis prius accipere potuisset. Methodum generalem perveniendi ad ejusmodi series anno proximo ab Oldenburgo petivit, a Newtono accepit antea non habuit. Eodem tempore methodum extrahendi radices in speciebus a Newtono accepit qua transmutatio Leibnitiana figurarum in methodum quandam generalem evasit sed inclitem. Per extractiones solas res citius peragitur. Anno 1677 Leibnitius methodum novam differentialem habuit: sed se ante visas Newtoni literas in manu Collinij: utrum hanc viderit nondum constat. 10 Decemb. 1672 & 24 Octob 1676 datas, eam habuisse nondum probavit. Extabat Analysis Newtoni in manu Collinij utrum hanc viderit nondum constat.
Vide pag.
Newtonus et Leibnitius non sunt idonei judices. Ex monumentis antiquis judicium ferendum est.
Quasi methodum Moutoni & series Brounkeri Wallisij et Gregorij, non liceat proprijs authoribus, nisi authoritate ab his accepta, asserere. Huiusmodi Lege lata tutiores redderentur plagiarij. Validius est judicium eorum qui partibus non sunt addicti.
Newtonus habuit anno 1669 ut ex ejus Analysi manifestum est Vtrum Leibnitius hanc Analysin in manu Collinij viderit nondum constat.
Vide pag. Ib: dicitur Newtonum pro differentijs Leibnitianis adhibere semperque adhibuisse fluxiones quemadmodum et Honoratus Fabrius motuum progressus Cavallerianæ methodo substituit: id est Leinitium esse primum inventorem methodi infinitesimalis & Newtonum eandem a Leibnitio habuisse Et hinc natæ sunt inter Leibnitium et Keillium lites
A year or two after Mr Newton had published his Principia Philosophiæ Mr Leibnitz published his Schediasma de Resistentia Medij. conteining Mr Newtons Propositions on that subject put into another dress. To make them his own He introduced the discourse by telling his reader that he found them for the most part at Paris twelve years before & communicated some of them to the Royal Academy & in the end of his discourse he adds: Nobis nunc fundamenta Geometrica jecisse sufficerit in quibus maxima consistebat difficultas. Et fortassis attente consideranti vias quasdam novas vel certe satis antea impeditas aperuisse videbimur. Omnia autem respondent nostræ Analysi infinitorum, hoc est calculo summarum et differentiarum cujus elementa quædam in his Actis dedimus. But he had forgot that when he wrote his Letter of 27 Aug. 1676 which was but a month or six weeks before he left Paris, he
He should have let the world know that six first Propositions in this book & the ninth & 10th with the Quadratures in the scholium to the 10th which depend on the 7th & 8th were known to Mr Newton when he wrote his Letter of Oct. 24 1676, & not have represented them novel & conteining nothing of moment but what had been treated of before by others and already described in the Acta Lipsica in giving account of their works. And particularly he should not have ascribed the vth Proposition to Mr Sheen when he knew that Mr Newton had communicated that Proposition in his said Letter. He should not have complained of Mr Keil as a young man who knew not what formerly passed about these matters For this is to appeal to living witnesses about what passed 36 years ago in Letters between Mr Oldenburg & Mr Leibnitz. Some of the Letters were published by Dr Wallis & most of the rest are now found & published & young men are as able to understand them as old ones. Otherwise the whole society to whom he appeales will be disabled from giving judgment He should not have complained of Mr Keil for writing without authority from Sir Isaac Newton. For e{ve}r mas hath authority to repell injuries from his neighbour without asking leave. He should not lay so great a stress as he seems to do upon inventing without the assistance of the first inventor. For the first Inventor alone hath Inventoris jura till another start up: & then to take away his right & share it with another would be an Act of injustice & an encouragement to pretenders.
But while the Committee have given their opinion for Mr Keil this ought not to reflect upon the Marquis de L'Hospital, Mr Varignion Mr Iohn Bournoull i & his brother or any others who have used the Differential Method. They knew nothing of the method of Fluents till the publishing of Mr Newtons Principia & there Mr Newton forbore to assert his right least it should beget a controversy about an invention which Mr Leibnitz in his Letter of 21th of Iune 1677 began to put in for & Mr Newton ever after declined contending about. They see that the method proposed by Mr Leibnitz was of great use & are much to be commended for the use they have made of it & for improving it even beyond what Mr Leibnits was able to do. They knew nothing of the correspondence of Mr Leibnitz with Mr Oldenberg & Mr Collins. Mr Leibnitz would never let the world know what he learnt from the English by that correspondence. There is scarce a word of it in the Acta Lipsica, & the blame lies only upon him for concealing it.
30.
96.
.
That the series for the length of an arch of the circle by the Tangent which in his Letter of Aug. 1676 he sent to Mr Olden Mr Newton as his own & afterwards published in the Acta Lipsica without mentioning any other Author than himself was communicated to him the year before by Mr Oldenburgh in his Letter of 1675 having been communicated to Mr Oldenburgh by Mr C. & to Mr C. by Mr Gregory in his Letter of 1671, & acknowledged by Mr L. in his Letter of 1675 to be different from his own.
That whereas Mr Leibnitz in the Acta Leipsica published he ought not to be reputed the inventer of any of these series having received some of them from Mr Oldenberg in his Letters of & seen others in Mr Newtons Letters & in a Paper of Mr Gregorys remains composed by Mr Collins at the request of Mr Leibnitz & others of the Academy of Sciences & sent by Mr Oldenb. to the Academy of Sciences to be communicates to Mr Leibnitz, & having written to Mr Oldenberg 1676 to know the Demonstration of some of those series, that is how they were invented, which gave occasion to Mr Newton at the sollicitation of Mr O & Mr C to send him the demonstration in his Letter of 14 Iune 1676.
That in the year 1673 Mr Leibnitz pretended to a differential method of a very different sort namely that of Mr Mouton, & was checkt for it by Dr Pell & thereupon wrote a Letter of excuse dated & therefore at that time had not the differential method which he now pretends to.
That in all the Letters of Mr Leibnitz there appears not the least mention of his present differential method before his Letter of Iune 1677 tho he gloried much in other inventions of less note such as were his instrument for finding the roots of Equations, a series for the area of a circle which after he had received other series from hence he did not communicate, his method of Transmutations derived from those of Dr Barrow & Mr Gregory
That Mr newton in a Letter to Mr Collins. dated A.C. 1672 describing a method of Tangents which proved to be the same with that of Mr Slusius, represented that this method was but a Corollary of a general method of solving difficult problems & it appears to us that this general method was the method of fluxions & that Mr Collins communicated copies of this Letter to Mr Slusius, Mr Churhause & others & sent it in the above mentioned paper to the Academy of Sciences to be communicated to Mr Leibnits a year before Mr Leibnits began to communicate the differential method, & we are of opinion that it was not difficult to collect the method of fluxions from this Letter.
That Mr Newton in his Letter of 24 Octob 1676 mentioning his Letter to Mr Collins of 1672 & that he there represented his method of drawing Tangents to be more general then that of Slusius as not sticking at surd quantities, & to be a Corollary of the general method of which he there spake of, Mr Leibnitz took occasion from thence of describing his differential method, as a method of the same kind, but without acknowledging that he had seen a copy of that Letter to Mr Collins
That Mr Leibnitz before he proposed his differential method knew by Mr Newtons Letter of 28 Octob. 1676 that Mr Newton had the Method of fluxions above 5 years before & that by Mr Newton Tract de Analysi per æquationes numero terminorum infinitas communicated by Dr Barrow to Mr Collins in Iuly 1669 it is manifest that he had the method of fluxions at that time. For he there describes the generation of quantities by motion & gives the name of moments to their incrementa momentanea which Mr Leibnits calls differences & gives an example of calculating by such moments, &
For there the second fluxion is & the second moment or differen & Mr Newton puts the third terme of the series equal not to this difference as
p. 4. l 22. For there the second term of the series to put equal to FG which is but half the second moment or difference. For the differences are & & their difference is .
— But the Society have as much authority over Mr Leibnitz as over Dr Keil [And Mr Leibnitz was as injust in demanding of the Society that they should condemn Dr Keil without offering any reasons against him] & could not in justice condemn Dr Keil without hearing the reasons of the Accuser against him but but might in justice condemn Mr Leibnitz of calumny if he refused to give his reasons & make good his accusation. as he really did. The Society are not to be commanded to condemn any man. Vpon a complaint they have a right to examin the matter between both parties before they give their opinion{s} & for the accuser to decline a fair examination is an argument of calumny. But the Society have not yet given their opinion in this matter. They have only appointed a Committee to search Records & give their opinion upon them, & have ordered the Records & the opinion of their Committee to be published. And I may add that their Committee was numerous & was composed of the ablest Mathematicians & such as were skilled in the hands of Dr Barrow Mr Oldenburgh Mr Collins Mr Leibnitz, Mr Gregory
But Mr Leibnitz tells us that the case was clear & he expected justice: that is, he will be judge in his own case & the Royal Society must be the Executioner. ✝ ✝ He tells us that Mr Keill opposes his reputation which at such an age & after so many documents of his life that he should defend no man that's prudent or just would approve of; that is that he is above all human judicature, that the Society would be injust if they should allow Mr Keil to accuse him as he accused Mr Keil, that they would be unjust if they should {indi}fferently examin the matter between them, that they would be injust if they should not He tells us also that he expected that Mr Newton himself would have done him justice. He knew that Mr Newton had written in the Introduction to the Treatise De Quadratura Curvarum that he found the method of fluxions gradually in the y ears 1665 & 1666 & therefore for Mr Leibnitz to demand the judgment of Mr Newton was to quarrel him. It was to demand that he should either retract what he had printed or expect that Mr Leibnitz would fall foul upon him. And the event has shewed that this was the designe of his demanding Mr Newtons judgment in this matter. Its well known here that Mr Newton kept off these disputes as long as he was able: being much more desirous of a quiet life then of being celebrated for mathematical inventions: but when he was chalenged by Mr Leibnitz in two several Letters, & shewed the was also shewed the Acta Eruditorum he is not to be blamed if in his own defense he consented to the publishing of the ancient Letters in the Commercium Epistolicum that the world might see how he had been treated these forty years together
What these words meant no man could understand who was unacquainted with the correspondence which had passed between him & Mr Newton by means of Mr Oldenburg seven years before. And yet this was all the mention that he then made of that correspondence, thô he ought in justice to have spoken plain.
It has been said that Dr Keill & Mr Newton were the aggressors: whereas the contrary is true. Mr Newton exprest himself displeased at what Dr Keill had published in the Philosophical Transactions least it should create a controversy. This he did long before Mr Leibnitz complained of it, & continued to do so till the complaint arrived. But being then shewed what was published in the Acta Lipsica for Ian 1708 concerning his book of Quadratures, & seing himself there accused of plagiary for affirming that he found the method of fluxions gradually in the years 1665 & 1666 & understanding that what Dr Keill had published was for defending him from that accusation: he gave the Doctor leave to return what answer he pleased to the complaint of Mr Leibnitz. And Mr Leibnitz in his next Letter dated 29 Decem. 1711 persisted in justifying what had been published in the Acta Lipsica, & challenged Mr Newton to declare his opinion in the matter, that is, to retract what he had published or enter into a dispute about it.
Mr Leibnitz in the letters which passed between him & Dr Wallis denyed not that MrNewton
While Mr Newton knew not what was printed in the Acta Lipsica Mr Keil in an Epistle printed — — — edita est.
Mr Newton not having seen what was in the Acta Lipsica exprest himself offended at the printing of this paragraph of Mr Keills Letter, least it should create a controversy. And Mr Leibnitz understanding it in a stronger sense — what he had written, & Mr Newton upon being shewed the Acta Lipsica, gave him leave to do so. And Mr Leibnitz in a second Letter to Dr Sloan — — — — — — ☉ ☉ in that matter. He knew that Mr Keil affirmed nothing more that what Dr Wallis had published thirteen years before without being then contradicted. He knew that Mr Newton had also given his opinion in the matter in the Introduction to his book of Quadratures published before this controversy began: but Dr Wallis was dead, Dr Keill was a Novice & Mr Newton must now be forced to retract that opinion & allow that he had substituted fluxions for differences, or not be quiet. book of Quadratures published before the controversy began: but Mr Newton must retract what he had published — — — — or not be quiet. Mr Leibnitz was therefore the aggressor.
The Royal Society having as much authority.
— means of Mr Oldenburg. And thereupon a correspondence arising between Mr Leibnitz & Dr Wallis, the Doctor in a Letter dated 1 Decem. 1696 & printed in the 3d Volume of his works thus excuses himself for inserting that advertisment without saying more of the Differential method. Calculi Differentialis vel nomen audivisse me non memini nisi postquam utrumque Volumen absolverant operæ, eratque Præfationis (præfigendæ) postremum folium sub Prælo, ejusque typos jam posuerant Typothetæ. Quippe tum me monuerat amicus quidam harum rerum gnarus qui peregre fuerat, tum talem methodum in Belgio prædicari, tum illam cum Newtoni methodo fluxion um quasi coincidere. Quod fecit ut (transmotis typis jam positis) id monitum inseruerim. By this Letter compared with the Monitum it self, Mr Leibnitz could not but understand that it was at that time the opinion of the Mathematicians in England that Mr Newton found the method of fluxions about the same time with the method of converging series. And yet in the Letters which followed hereupon between him & Dr Wallis concerning this matter, he denyed not that Mr Newton had the method of fluxions so early as Dr Wallis affirmed, pretended not that he himself had the differential method so early, brought no proof that he had it before the year 1677 — — — — common to Mr Newton & himself. His words were
This was the state of the dispute between Dr Wallis & Mr Leibnitz at that time. And in the year 1699 Dr Wallis by the leave of Mr Leibnitz inserted into the third Volume of his works the said two Letters together with the three answers of Mr Leibnitz dated 27 Aug. 1676 21 Iune 1677 & 12 Iuly 1677, having procured those answers from the library of Mr Collins.
In the same year (A.C. 1699) Mr Fatio, in his Dissertation on the line of the quickest descent, suggested that Mr Leibnitz the second inventor
His words were. Quod [Newtonus] addit, ex hoc eodem fundamento quadraturas quoque reddi faciliores, me in sententia hac confirmat; nimirum semper figuræ illæ sunt quadrabiles quæ sunt ad æquationem differentialem.
In Ieromes version of the Book of Iudeth, Nebuchadonosor king of the Assyrians is said to have overcome Arphaxed in the 12th year of his reign & to have gone against the western nations in the 13th year. And according this recconing the 12th or 13th year of Nebuchadonosor may fall in with the 8th year of Iosiah. Eupole.
It has been said that the Royal Society gave judgment against Mr Leibnitz without hearing both parties. But this is a mistake. They have not yet given any judgment in the matte{r.} Mr Leibnitz indeed desired the R. Society to condemn Mr Keil without hearing both parties, & by the same sort of justice they might have condemned Mr Leibnitz without hearing both parties. For they have an equal authority over them both. And when Mr Leibnitz declined to make good his charge against Mr Keil, the Society might in justice have censured him for not making it good. But they only appointed a Committee to search out & examin such old Letters & papers as were still extant about these matters & report their opinion how the matter stood according to those letters & papers, [They were not directed to examin Mr Leibnitz or Mr Keill but only to report what they found in the ancient Letters & papers]. And he that compares their Report with those Letters & papers will find it just. The Committee was numerous & skilfull & the Society are satisfied in their fidelity in printing what they found in the ancient Letters & Papers without adding altering or omitting any thing in favour of either party. And the Letters & Papers are sealed up together & by Order of the R. Society kept under lock & key that they may be consulted & compared with the Commercium Epistolicum whenever it shall be desired by persons of Note.
It has been said that Dr Keill & Mr Newton were the aggressors: whereas the contrary is true. It is welll known in England that Mr Newton has of many years neglected these things & endeavoured to decline the very dispute which is now started. He was solicited again & again to let the Letters between him & Mr Leibnitz be printed by Dr Wallis before he gave his consent He exprest himself displeased at what Dr Keill had printed in the Transactions least it should create a controversy. This he did a long time before Mr Leibnitz complained. & ever after that complaint arrived untill he was shewed what was printed in the Acta Eruditorum for Ianuary 1705, & there finding himself accused of plagiary for pretending that he had found the method of fluxions in the years 1665 & 1666, & being made to understand that Mr Keill vindicated him from that accusation he gave Mr Keill leve to return what answer he pleased to the complaint of Mr Leibnits. And when Mr Leibnitz in his Letter of 29 Decem. 1711 persisted in justifying what was printed in the Acta Leipsica, as if the Editors had not detracted from any man but given every man his due; & challenged Mr Newton to declare his opinion in the smaller that is, to retract what he had published or enter into a dispute about it. the R. Society was moved to appoint a Committee to search only & examin the ancient Letters & Papers in their custody concerning this matter, & report their opinion upon them. And whether the Committe has framed a right opinion upon them is left to every to judge.
He forbore to reflect upon him for publishing a considerable part of the Principia Philosophiæ in another dress as if he had found it himself. He forbore to reflect upon him for adapting an erroneous Demonstration to the XIth Proposition of the first Book of the Principles in order to make himself a coinventor thereof. He
Mr Leibnitz therefore had notice of the advertisement
— he did not make a fuller mention of it
— he said so little of it &
Unless you had rather say that Iosiah in the eighth year of his reign, upon his delivery from the the Assyrians began to seek the Lord, & that in the 12th year of his reign upon his delivery from the Scythians, he reformed Iudea from idolatry
This kingdom seems to have been potent & to {have} had wars with the kings of Touran or Scythia beyond the river Oxus with various success, & to have been subdued by Cyaxeres. For while Nebuchadnezzar warred in the west Cyaxeres went eastward against the Provinces of Persia. Whether the Pischdadians whom the Persians reccon to have been their oldest kings were kings of this kingdom of Persia or of the Assyrians I leave to be examined.
Herodotus tells us that the Medes reigned over all Asia beyond the river Halys 128 years together, excepting the time that the Scythians reigned. They lost their dominion to the Medes Anno Nabonass, 211. Subduct 128 years & the reign of the Medes over Armenia & Cappadocia as far as the river Halys will begin Anno Nabonass 83, that is two years after the death of Asserhadon: about which time the nations revolted from the Assyrians. When Cyaxeres expelled the Scythians & overthrew the Assyrian Empire, it may be presumed that he recovered Armenia & Cappodocia as far as the river Halys before he went eastward against the Persians.
Pray let me have the satisfaction of seeing you here on thursday morning next about 10, or 11 a clock, to see me sign some papers of moment, in which you will oblige
Ap: 13th 1714.
Inewton
Cartesius Menti vim attribuit mutandi determinationem motuum corporeorum. Leibnitius {in} hypothesi Harmo{n} præstabilitatæ ne hoc quidem concedit. Similiter plane Author noster in sequentibus
1 As to what the Author of the Latin paper saith of Mr Flamsteed & Mr Hook Mr Newton always acknowledged the use of Mr Flamsteeds Observations Mr Hook being often desired to produce a Demonstration of the Proposition claimed by him was never able to produce one. Mr Leibnitz claimed the same Proposition by an erroneous Demonstration & whether he or Mr Tschurnhause were in the right about a method claimed by them both may be disputed.
2 This Author in the next place complains – – – – – – were fourged.
3 The same Author in the next place ascribes a general method of series to Mr Leibnitz tho this method was found many years before by Mr Newton. And he tells us also that the English & Scotch, Wallis, Hook, Newton Gregory junior, acknowledged 36 yeas ago the series for finding the Arc of a circle by the Tangent to be the Invention of Leibnitz. But he should have complained of Mr Oldenburg for not letting the English & Scotch know that this Series with many others was sent by him to Mr Leibnits in April 1675 And that a collection of Gregories papers were also sent by him to Mr Leibnitz the next year.
4 And in the next place he magnifies an invention called the Exponential calculus without considering that Mr Leibnitz had the hint from Mr Newton & that this Calculus has hitherto been of no use
5 In the last place our Author tells us that the English & Scotch Wallis Hook Newton Gregory junior acknowledge 36 years ago — — in April 1675.
6 In the Remarks it represented that Mr Leibnitz never communicated his reasons to the R. Society of England & so the Society has not examined the reasons on both sides for giving judgment. And upon this pretence the Author of the Remarks gives a contrary judgment to that of the Committee of the R. S. But the truth is Mr Leibnitz absolute refused to give any reasons, calling it injustice to expect that he should defend his candor And the Committee of the R. S. grounded their Report upon ancient & unquestionable Records & published the Records that the justice of their Report might appear to the world. But the Author of the Remarks has laid aside the Records of the first seven years & begins his Report with the year 1676 & 1677, & thereby confesses that he has no way to defend Mr Leibnitz but by laying aside the oldest Records And this makes it necessary to write to you again of these matters & state the matters from the Records themselves in relation to both the Questions that about converging series & that about the differential method
But because Mr Leibnitz & his correspondents or some of them have composed & published in Germany a paper without a name whereby they defame Mr Newton accuse the Committee of the Royal Society of partiality, set aside Records, afirm & deny things without proof endeavour to bring the matter to a squabble [& make it a dispute between England & Germany. (all which are dishonest practises)] I intend to give you hereafter a fuller account of these matters out of the Records themselves.
6 fore aliquando tandem in inter omnes conveniat. At vero hunc in finem in Metaphysicæ sanæ notionibus – – – – Geometræ oportebit] id est sperat Author ut Philosophia Newtoni in Phænomenis per Demonstrationes Mathematicas fundata rejiciatur & omnes tandem conveniant in Philosophia quam Geometræ in Hypothesibus ad notiones Metaphysicæ sanæ aptatis fundabunt Metaphysica in Idæis, Ideæ et Philosophia omnis vera in Phænomenis fundantur, et incipit Newtonus a Phænomenis: incipiendum esse ab Idæis et Hypothesibus vult Author noster. Et metaphysicam sanam intelligit Cartesianam: Qua utique asseritur – – – – – devenire statuit. Sed nec vim aut facultatem cogitandi rem cogitantem esse, aut rem omnem extensam extensionem esse, aut extensionem rem mobilem esse, aut motum corporum in sola translatione relativa sine vi inertiæ, consistere, aut rem cogitantem nulli spatio præsentem esse & et Deum non esse omnipræsentem per substantiam suam aut nos ideas habere substantiarum Cartesius alicubi probavit. Hæc omnia sunt meræ Hypotheses [Metaphysicæ quas clausis oculis ab ideis id est somniando confingimus] Quippe Metaphysicam ab Ideis deducimus clausis oculis & Ideæ non sunt veræ nisi quatenus cum phænomenis congruunt.] Metaphysicæ ab antiqua gentium Theogonia originem habuit, qua utique Deum esse & hujus vel partes vel vires & potentias esse mundum totum argumentis fallacibus statuere, Et usque nunc de Deo et Angelis & essentijs rerum disputant, argumenta capiendo ab Idæis rerum quas oculis clausis formamus, id est somniando.
Series itaque tres prædictas, utpote elegantes, per hanc methodum Regressuum minime invenerat; methodum aliam Regressum non habuerat. Sed nec ipsum hac, methodo in veteribus schedis usum esse concedendum est. Ipse pro se testis esse non potest. Probandum est aliorum inventa sub candoris prætextu nemini coincedendum est.
Tandem D. Leibnitius in Actis Eruditorum Anni 1693 pag. 178 methodum newtoni solvendi Problemata per assumptionem seriei pro quantitate qualibet incognita D. Leibnitius [quam Newtonus Anno 1676 in dum agnovit. Certe Anno 1676 ubi scripsit multa esse invenerat, Newtonus antem hoc anno eandem in Epistola prædicta descripsit ut supra.
Constat igitur quod D. Leibnitius nullum habe{a}t jus in methodum serierum. Nam transmutatio Figurarum quam prætendit nihil aliud est quam Lemma quoddam superfluum in casu particulare, et methodum serierum minime constituit.  nihil aliud est quam Lemma quoddam ad invenienda arearum momenta quod ex quo methodum differentialem invenit evasit inutile.
nihil aliud est quam Lemma quoddam ad invenienda arearum momenta quod ex quo methodum differentialem invenit evasit inutile.
Nam transmutatio figurarum quam jactat non est methodus serierum compergentium sed Lemma quoddam [quo momentum vel incrementum areæ quadrandæ invenerat antequam intelligeret methodum differentialem] quo momentum areæ per seriem quadrandæ prodijt. Quod Lemma post inventionem methodi differentialis nullius amplius fuit usus.
P.S. In Actis Eruditorum anni 1713 quæ jam modo advecta sunt in Angliam, Mense Febr. pag. 94, dicitur quod Newtonus resolvendo dignitatem binomij ex fluente et momento ejus compositi in seriem convergentem sumat terminos seriei successive pro differentialibus ; nempe secundum terminum pro differentia termini primi, tertium pro differentia secunda ejusdem quartum pro differentia tertia &c . At Newtonus hoc non asserit neque ibi de differentialibus vel fluxionibus agit Sit dignitas binomij et series in quam hæc resolvetur erit &c . Sit jam j fluxio quantitatis et o momentum ejus et per ea quæ in Introductione ad Tractatum de quadratura figurarum dicta sunt fluentis fluxio est & fluentis fluxio est et fluentis fluxio est & sic deinceps secunda tertia &c sic deinceps & ejusdem Fluentis momentum primum est secundum tertium & sic porro. Vnde liquet terminos serierum ex mente Newtoni non esse differentiales termini primi sed differentialibus tantum proportionales. Et hoc dicere voluit Newtonus in Scholio Propositionis undecimæ Tractatus illius licet vox [ut] quæ in Scholij lin 3 habetur, & iterari debuisset desit in lin 8 & 11. Dicit enim Newtonus in Scholio illo quod Exponi possunt hæ fluxiones per Curvarum Ordinatas BD, BE, BF, BG, BH. qua quidem Ordinatæ non sunt termini serierum sed terminis tantum proportionales.
Multiplicentur utique termini serierum (incipiendo a termino secundo) per hanc numerorum progressionem &c seu 1, 2, 6, 24, 120 &c Et habebuntur differentiales seu progressio momentorum ex mente Newtoni. Et hinc liquet affinitatem esse longe maximam inter methodum serierum convergentium & methodum fluxionum, ut non mirum sit Newtonum postquam invenisset methodum serierum, statim incidisse in methodum fluxionum et ex utraque methodum unam universalem composuisse. De utraque enim simul scripsit in Epistolis 13 Iunij & 24 Octob 1676 datis, ut et in tractatu quem composuit anno 1671 & in Analysi per æquationes infintas anno 1669 ad D. Collini missa: et in hac Analysi scripsit Momentum esse superficiem cum de solidis, lineam cum de superficiebus & punctum (seu lineam infinite parvam) cum de lineis agitur, quod perinde est ac si scripsisset solidi momentum primum esse superficiem, momentum momenti seu momentum secundum esse lineam, & momentum momenti secundi seu momentum tertium esse punctu.
In the year 1689 {illeg} Mr Leibnitz began to pretend to this method a has been b admonished that it is Mr {illeg} forgets to acknowledg the true author d Act Lips Ann 1689 p. 37 & 1693 p. 178. b Wallis Opera Vol. 2 {p} {illeg} vol 3 p 645 Et Cheynes Fluxionum methodus inversa p. 46.
But when he sent his method to Mr Newton he forgot to ack{nowledge} that he had but newly found it, & that want of it made him of opinion the year before that inverse problems of tangents & such like could not be reduced to equations & quadratures & He forgot to acknowledge his error & that this invention he now perceived that Mr Newtons method which extended to such Problems was more general then he could beleive the year before. He forgot to acknowledge that in the Collection of Gregories Letters & papers which at his own request Mr Collins & Mr Oldenburg sent to him at Paris he found the Copy of Mr Newtons Letter of 10 Decemb. 1672, conteining his method of Tangents & representing it as a branch or corollary of a general method of solving all sorts of Problems & that the agreement of this method of Tangents with that which Slusius published put him upon considering how to enlarge the method of Slusius by the differences of the Ordinates. Mr Newtons Letters of 13 Iune & 24 Octob 1676 gave him light into the Method. And those things are now so far out of his Memory that he has told the world that when he published the elements of his differential method he knew nothing more of Mr Newtons inventions of this sort then what Mr Newton had formerly signified in his Letters namely that he could draw Tangents without taking away irrationalls: which Hugens had signified that he could also do before he understood the infinitesimal method. p. 104, 107.
In like manner when Mr Collins had begun to make known Mr Newtons method of Series to the Mathematicians in London & to & communicate the series Mr Leibnitz about 3 or 4 years after coming to London where he conversed with the Mathematicians, & going thence to Paris wrote from thence as if he had never heard of Mr Newton's method & put in for the invention next after Mercator pretended to be the first inventor of two series for the circle p 38 & the next year when he received eight series from Mr C & Mr O & knew none of them to be his own & forgot the receipt of them before the end of the year & communicated to his friends at Paris an Opusculum upon one of them as his own series (p. 42) & wrote that he had communicated it to the Geometers at Paris above two years before, that is in the year 1673, presently after his coming from London. p 45. And the spring following {illeg} he endeavoured to get the method from Mr O. & Mr C. promising them by way of recompence the series which with seven others he had received from them the year before & published at Paris as his own but represented it a very different series from theirs & that it was the series of which he had writ to them some years before. (p. 45.) But they forbore sending the method after the eight series & earnestly desired Mr N. to send his own method himself, & he did so, & Mr Leibnitz sent back the said series as he had promised. (p 49, 61) For Mr Oldenburg & Mr Collins were not to question his candor without authority from the Executors of Mr Gregory. He still requested wanted Mr Newtons method of deriving reciprocal series from one another, & wrote for it & when he received it, tho he understood it with difficulty yet he wrote back that he had found it before . . . . . . . Collins p. 25. 47. He has forgot also that the Series for Quadratures which breake off in some cases & becomes finite were deduced by Mr Newton from the method of fluents before the writing of the Letters which passed between them in the year 1676, that is, before Mr Leibnitz knew any thing of the differential method, p. 169. & that the method of assuming the terms of a series & determines them by the conditions of the Problem was a part of Mr Newtons general method before the writing of those Letters p. 86. Wallis Vol 2 p
If it appears therefore by the following Letters & Papers
If it appears therefor by the following Letters & Papers that Mr Newton had the method of infinite series in the year 1669 & then applied it generally to the solution of problemes by the method of fluents & that Mr Iames Gregory having notice thereof found out the method of series in the end of the next year & in the beginning of the year following sent to Mr Collins the series for the circle since claimed by Mr Leibnitz: but acknoledged Mr Newton the first inventor of the method. & that Mr Leibnitz in the years 1675, 1676, 1677, received large communications from London relating to these methods whereof he forgot to make acknowledgments, & it doth not appear that he knew any thing of the methods before those communications, & if the pretence of candour & sincerity doth not make any man a witness in his own cause & the pretence of finding things apart without proving the priority of invention is not to be regarded: it remains that Mr Leibnitz either desist from his pretentions to the series of Gregory & from numbring himself amongst the first inventors of the method of series & the method of infinitesimals; or prove that he had the said series & methods before his correspondence with Mr Oldenburg began , before he came into England, before Mr Gregory sent the said series & Dr Barrow the Analysis to Mr Collins
l. 8. for the circle tho he wanted the Demonstration
l. 19. promised to send them some series of his own very different from theirs but sent them the above mentioned series having forgotten that he had received it from them the year before (p. 42, 45, 61) And when he sent his differential method to Mr Oldenburg, he forgot to acknowledge that he had but just invented it & by the invention was convinced that Inverse Problemes of Tangents were reducible to Equations & Quadratures p.
Mr Leibnitz in his Letter of 27 Aug. 1676 wrote thus: Quod dicere videmini plerasque difficultates (exceptis Problematibus Diophantæis) ad Series infinitas reduci; id mihi non videtur. Sunt enim multa usque adeo mira et implexa ut neque ab æquationibus pendeant neque ex quadraturis Qualia sunt ex multis alijs Problemata methodi tangentium inversæ. And when I answered that such Problemes were in my power he replied (in his Letter of 21 Iune 1677) that he conceived that I meant by infinite series but he meant Geometrically. And now he persists in the same reply saying that he meant by vulgar equations. See the Answer to this in the Commercium Epistolicum pag 92.
He saith that one may judge that when he wrote his Letter of Aug 27. 1676 he had some entrance into the differential calculus because he said there that he had solved the Probleme of Beaune certa Analysi a certain Analysis. But what if that Probleme may be solved certa Analysi without the differential method. For no further analysis is requisite then this, That the Ordinate of the Curve desired increases or decreases in Geometrical progression when the Abscissa increases in Arithmetical, & therefore the Abscissa & Ordinate have the same relati on to one another as the Logarithm & its number. And to infer fro this that Mr Leibnitz had entrance into the differential method is as if one should say that Archimedes had entrance into it because he drew tangents to the spiral squared the Parabola, & found the proportion between the sphere & C ilynnder, or that Cavallerius Fermat & Wallis had entrance into it because they did many more things of this kind.
He complains that the Committee have gone out of the way in falling upon the method of series: but he should consider that both methods are but two branches of one general method. I joyned them together in my Analysis. I interwove them in the Tract which I wrote in the year 1671 as I said in my Letters of 10 Decem 1672 & 24 Octob 1676. In my Letter of 13 Iune 1676 I said that my method of Series extended to almost all Problemes but became not general without some other methods meaning the method of fluxions & the method of arbitrary series {—} a method which depends upon that of fluxions, & now to take those other methods from me is to restrain & stint the method of series & make it cease to be general. In my Letter of 24 Octob 1676 I called all these methods together my general method. See the Commercium Epistolicum pag. 86. lin. 16. And If Mr Leibnitz has been tearing this general method in pieces & taking from me first one part & then another part whereby the rest is maimed, he has given a just occasion to the Committee to defend the whole. It is also to be considered that Mr Leibnitz is perpetually at work to make himself a witness in his own cause & it's allowed in all Courts of justice to speak to the credit of the witness.
7 Mr Leibnitz represents that he has been in possession He acknowledges that when he was in London the second time he saw some of my Letters in the hands of MrCollins, & he has quoted two of those which he then saw vizt those written 1672 & 24 Octob 1676. & no doubt he would principally desire to see the Letter which conteined the chief of my series & the Demonstration of the two series which a few months before he entreated Mr Oldenburg to procure from Mr Collins, that is, the Analysis per æquationes numero terminorum infinitas. But he tells us that he never saw where I explained my method fluxions & that he finds nothing of it in the Commercium Epistolicum where that Analysis & my Letters of 10 Decem 1672, 13 Iune 1676 & 24 Octob 1676 are published.
8 He saith also that he never saw where I explain the method claimed by me where he assumes an arbitrary series. If he pleases to look into the Commercium Epistolicum pag. 55, 56 & 86 he will there see that I had that Method when I wrote my Letters of 24 Octob. 1676 & 13 Iune 1676 & five years before. Mr Leibnitz might also find it himself, but not so early; And second Inventors have no right.
Mr Leibnitz published his Schediasma de resistentia Medij et motu projectorum gravium in Medio restente in Ianuary 1689 & concluded it with these words Multa ex his deduci possent praxi accommodata, sed nobis nunc fundamenta Geometrica jecisse sufficerit, in quibus maxima consistebat difficultas. Et fortassis attente consideranti vias quasdem novas et satis antea impeditas aperuisse videbimur. Omnia autem respondent nostræ Analysi infinitorum, hoc est calculo summarum & differentiarum (cujus elementa quædam in his Actis dedimus) communibus quoad licuit verbis hic expresso. This was the first specimen made publick by Mr Leibnits of applying the Differential method to the higher sorts of Problems. And by the words here cited it appears that Mr Leibnitz himself at that time acc ounted it so. And yet this specimen was published a yeare & an half after that of the Principia, & was borrowed from the Principia, & the things in the Book of Principles answer as much to the calculus of fluxions as those in the Schediasma to the calculus of differences, & the differential calculus did not begin to be celebrated before the publication of this specimen.
For as the Ordinate is to the sub-perpendicular (or subtangent to the Ordinate) so is the fluxion of the Abscissa to the fluxion of the ordinate And if you say, As the Perpendicular to the Ordinate so the Radius of Curvity to a fourth proportional & to this 4th Proportional apply a quarter of the summ of the squares of the fluxions of the Abscissa & Ordinate, you will have the second fluxion of the Ordinate.
Schol.
As the Ordinate is to the subperpendicular (or subtangent to the Ordinate) so is the fluxion of the Abscissa to the fluxion of the Ordinat. Let the summ of the squares of the fluxions of the Abscissa & ordinate be applied to a quantity which is to the Ordinate as the Radius of curvity to the Perpendicular, & the Latus will be the second fluxion of the Ordinate. When these fluxions make the Ordinate decrease they must be taken with negative signes. How to reduce the equations which result from hence & to separate the unknown quantities is the business not of this but another method.
Scholium.
Vt Ordinata ad sub-perpendicularem (vel sub-tangens ad Ordinatam) ita est fluxion Abscissæ ad fluxionem Ordinatæ Applicetur summa quadratorum fluxionum Ordinatæ et Abscissæ ad lineam quæ sit ad Ordinatam ut Radius curvitatis ad Perpendicularem, & Latus erit fluxion secunda Ordinatæ. Hæ fluxiones ubi Ordinatam diminuunt, negativæ ponendæ sunt. Non hujus sed alius est methodi æquationes prodeuntes reducere & indeterminatas separare. Problema hocce cum nullius fere sit usus in Actis eruditorum annos plures neglictum et insolutum mansit. Et eadem de causa solutionem ejus non ulterius prosequor.
. Et Vt subtangens ad tangentum ita summa quadratorum fluxionum Ordinatæ et Abscissæ ad rectangulum sub radio curvitatis et fluxione secunda Abscissæ
Scholium
Fluat Abscissa uniformiter & erit, Ordinata ad subperpendicularem (vel subtangens ad Ordinatam) ut fluxio Abscissæ ad fluxionem Ordinatæ, Et Ordinata ad perpendicularem ut fluxio abscissæ ad fluxionem arcus & quadrat{illeg} fluxionis arcus ad rectangulum sub radio curvitatis et fluxione secunda Abscissæ Hæ fluxiones &c
Vpon account of my progress in these matters he procured for me a fellowship in Trinity College in the year 1667 & the Mathematick Professorship two years after.
p. 1. l. ult. purchased of Rob. Barker
p. 3. l 3, 4 blot out the word are or add the word which
He pretends that in my book of Principles pag. 253, 254 I allowed him the invention of the calculus differentialis independently of my own method & that to attribute this invention to my self is contrary to my knowledge there avowed: & yet in all that book I do not find one word to this purpose. In the year 1685 (at which time I was writing that book) Mr Craige brought to me the Acta Eruditorum for October 1684 & desired me to explain to him the elements of the Calculus differentialis conteined therein & I did so & told him that the method was mine as would appear if the Letters which had passed between Mr Leibnitz & me were published & Mr Craige is still alive & remembers this, & therefore I could not mean in the Book of Principles to allow that Mr Leibnitz was either the first inventor or had received no light from me. I was so far from doing this that in the very place which he quotes I did affirm that before he sent me notice of his method I sent him notice of mine & of some of its performances. I gave him this notice in my Letters of 13 Iune & 24 Octob 1676 & he understood it so far as to be able to compare the methods. By his own confession he saw my Letter of 24 October 1676 when he was the second time in London which was eight months before he sent me notice of his method. He had notice of it also by copies of other Letters sent to him at Paris in Iune 1676 in a Collection of Mr Iames Gregories Letters which he certainly received. In this Collection were copies of two Letters of Mr Gregory dated 5 Sept. 1670, & 15 Feb 167 & a copy of my Letter dated 10 Decem 1672, & by these Letters he had notice that Gregory from Barrows differential method of Tangents deduced a method of tangents without calculation in the year 1670 & in l the beginning of the next year found the series for the quadrature of the circle by the tangent & that I had a general method of Analysis which readily gave the same method of tangents of Gregory & Slusius & extended also to the abstruser sorts of Problemes concerning the curvatures areas lengths centers gravity of curves &c and proceeded without fresing equations from surds & that I had written a Tract concerning this method & the method of series together meaning in the year 1671. And by my Letter of 13 Iune 1676 he had notice that my Analysis was so universal as to extend to almost all sorts of Problems . And as the series for the Quadrature of the circle which he sent me back as his own in his Letter of 27 Aug 1676 was Gregories so what he sent me back as his own in his Letter of 21 Iune 1677 concerning the Differential method was nothing more then what the Letters above mentioned had given him notice of a year before And further, Mr Leibnitz by his Letter of 12 May 1676 desired Mr Oldenburg to procure from Mr Collins the demonstration of two of my series meaning the method of finding them, & about the same time he desired also that the aforesaid collection of Gregory Letters might be made & sent to Paris & in October following when he came the second time to London he applied himself to Mr Collins & saw in his hands several of my Letters, as he has acknowledged, & no doubt would then desire chiefly to see my Letter in which I had communicated to him the said two series with the Demonstration which he wanted, that is my Analysis per æquationes numero terminorum infinitas, & therefore saw it. By my Letters of 10 Decem 1672 & 24 Octob. 1676 he could not but know that I had the method of fluxions in the year 1671 & by this Analysis he could not but know that I had this method in the year 1669. And after all this to tell me that in my Book of Principles pag 253 & 254 I allowed him the invention & that to attribute it now to my self is contrary to my knowledg, & that he found it without receiving any light from me & was the first inventor, is very extraordinary.
Mr Mercator lived above 10 or years longer without proceeding further then to the single Quadrature of the Hyperbola. The progress made by Mr Newton shews that he wanted not Mercators assistance. However, for avoyding disputes, he supposes a[7] that my L Brunker invented & Mercator demonstrated the series for the Hyperbola some years before they published it.
The aforesaid treatise of Analysis Mr Newton in his Letter to Mr Oldenburg dated 24 Octob. 1676 mentions in the following manner. Eo ipso tempore &c
When Mr Newton had explained these three Rules & illustrated then with various examples, he layd down the Idea of deducing the area from the Ordinate by considering the Area as a quantity growing or increasing by continual flux & becoming bigger or less accordingly as the increase or flux is swifter or slower And this flux he measured by the length of the Ordinate supposing the Abscissa to increase uniformly in proportion to time. And from the moments of time he gave the names of moments to the momentaneus increases or infinitely small parts of the Abscissa & Area generated in moments of time. The moment of a line he called a point in the sense of Cavallerius tho it be not a gemetrical point but an infinitely short line & the moment of an Area or superficies he called a line in the sense of Cavallerius tho it be not a Geometrical line but an infinitely narrow superficies. And when he considered the Ordinate as the moment of the Area he understood by it the rectangle under the Geometrical Ordinate & a moment of the Abscissa, as in the method of Cavallerius; & assumed an unit for the ordinate of a rectangle proportional to time. Sit ABD saith he, Curva quævis, et ABH rectangulum cujus latus AH vel BK est unitas. Et Cogita rectam DBK  uniformiter ab AH motam areas ABD [curvilineam] & AK [rectangulam] describere; & quod [recta] BK (1) sit momentum quo [area] AK (x) & [recta] BD (y) momentum quo [area curilinea] ABD gradatim augetur; et quod ex momento BD perpetim dato possis, per præcedentes [tres] Regulas, aream ABD ipso descriptam investigare sive cum [ipsius] AK (x) momento 1 descripta conferre. Iam qua ratione superficies ABD ex momento suo perpetim dato per præcedentes Regulas elicitur eadem quælibet alia quantitas ex momento suo sic dato elicietur. Exemplo res fiet clarior. Then he illustrated this with examples & added his method of Regression from the Area or Arc or solid to the Abscissa, & shewed how the same method extends to Mechanical Curves for determining their Ordinates tangents areas, lengths, &c
uniformiter ab AH motam areas ABD [curvilineam] & AK [rectangulam] describere; & quod [recta] BK (1) sit momentum quo [area] AK (x) & [recta] BD (y) momentum quo [area curilinea] ABD gradatim augetur; et quod ex momento BD perpetim dato possis, per præcedentes [tres] Regulas, aream ABD ipso descriptam investigare sive cum [ipsius] AK (x) momento 1 descripta conferre. Iam qua ratione superficies ABD ex momento suo perpetim dato per præcedentes Regulas elicitur eadem quælibet alia quantitas ex momento suo sic dato elicietur. Exemplo res fiet clarior. Then he illustrated this with examples & added his method of Regression from the Area or Arc or solid to the Abscissa, & shewed how the same method extends to Mechanical Curves for determining their Ordinates tangents areas, lengths, &c
Among the examples which he there set down for illustrating this method there are these. Let the Radius of a circle be &c.
Let the versed sine be x & the equations will be
Mr Collins gave Mr Gregory notice of this method
In the year – – – – correspondence with Mr Oldenburgh. In Feb. 167 meeting Dr Pell at Mr Boyle's & pretending to the differential method of Mouton & notwithstanding that he was shewn by Dr Pell that it was Moutons method, persisted in maintaining it to be his own invention by reason that he had found it by himself without knowing what Mouton had done before & had much improved it.
When one of Mr Newtons series was sent to Mr Greg. he first tried to deduce it from his own series combined together, as he mentions in his Letter dated 19 Decem. 1670, And by some such method Mr Leibnitz before he left London seems to have found the summ of a series of fractions decreasing in infinitum whose Numerator is given number & denominators are triangular or pyramidal or triangulo Triangular numbers &c. From the series
And in the year 1682 he published it as his own in the Acta Eruditorum without mentioning that he had received it from Mr Oldenburg. He might carry it with him from London to Paris in the 1673; but that he had the demonstration of it before the year 1675 doth not appear.
He might carry this series from London & communicate it to his friends at Paris above 3 years before he sent it back to Mr Oldenburg: but it doth not appear that he had the Demonstration thereof so early. When found the demonstration, then he wrote his opusculum upon it, & communicated that also to his friends. And he himself has told us that this was in the year 1675. However, it lies upon him to prove that he had this series before he received it from Mr Oldenburg because he did not then know it to be his own.
He had therefore several direc series & by consequence a method of finding them before he invented & forgot the inverse method. And if he had searched his old papers diligently he might have found this method also there [but he wrote for Mr Newtons methods because he had forgot his own.]
Myrina, & saith that when she was Queen of the Amazons in Libya she there conquered the Atlantides & Gorgons & them made a league with Orus the son of Isis (he should have said with Osiris, the hasband of Isis & father of Orus & passing through Ægypt subdued Arabia Syria & Cilicia & came through Phrygia to them mediterranean but passing over into Europe was slain with many of her weomen by the Thracians & Scythians under the conduct of Sipylus a Scythian & Mompsus a Thracian whom Lycurgus king of Thrace had banished. This was that Lycurgus whom Bacchus slew a little before he received this baffle whereby a stop was put to his victories.
This is that Neptune who with Apollo or Orus the Son of Osiris fortified Troy with a wall in the reign of Laomedon the father of Priam, & left many bastard children in Greece & Asia minor some of which were Argonauts as Naplius the son of Amymone, Ancæus the son of Abta, & Erginus, others were contemporary to them, as Amycus whom Pollux slew in the time of the Argonautic expedition, Lycus whom Hercules slew. Corynetes & Procrustes whom Theseus slew Hippothous whom Theseus restored to the kingdom of Cercyon, & Theseus himself
This that Neptune who with Apollo or Orus the Son of Osiris fortified Troy with a wall in the reigne of Laomedon, & left many children in Greece some of which were Argonauts & others were contemporary to them. De flourished therefore one generation before the Argonautic expedition or about 400 years before Solon went into Egypt
Hanc seriem D. Collins initio anni 1671 a Gregorio acceperat ut supra D Leibnitius eandem scripto opusculo ut suam cum amicus in Gallia hoc anno communicare cœpit, celata hac epistola.
pag. 42. His verbis patet series quas D. Leibnitius se ante annos aliquot invenisse professus est a communicatis diversas fuisse.
Pretends that by that corresponde he learnt nothing more of Mr Newtons method then that he had a method of Tangents which stuck not at surds, will not allow that young men who were not privy to that correspondence can understand the Letters & Papers which then passed between the correspondents & some of which have been printed by Dr Wallis.
printed the elements of his method in the Acta Lipsica without mentioning any thing that he learnt by that correspondence or letting the world know that Newton also had such a method, excuses himself by pretending that he then knew nothing of Mr Newtons method being general or extending further then to the drawing of tangents without sticking at surds.
Pro scribere licet . Et sic resistentia erit ad gravitatem ut ad 1 id est ut .
. Decrementum spatij , ex resist & Grav. Incr ex Grav . Decr. ex resist. , ad descens ex Grav . Resist. Grav . 1 .
. .
.
spatium FG cadendo describente generat velocitem qua duplum illud spatium 2FG eodem tempore describi posset ut ex demonstratis Galilæi notum est, id est velocitatem quæ exponitur per spatium 2FG applicatum ad tempus hoc est velocitatem : et in corpore arcum CG generat tantum velocitatem quæ sit ad hanc velocitatem ut ad FG vel FI ad CF, id est velocitatem . Addatur hæc velocitas ad decrementum prædictum & habebitur decrementum velocitatis ex resistentia sola oriundum
And having now got eight or ten series, he endeavoured in May following to get the method also from Mr O. & Mr without the knowledge of Mr Newton tho by his own rule if he should have forgot the receipt of the method they were not to reclaim it without authority from Mr Newton. (p. 118) And for sending him the method he promised them the series of which he had written to them some years before, representing them his own & very different from theirs p 45 but meant one of the eight series which he had received from them the year before p 61. For the series being Gregories they were not to question his candor without authority from the Executors of Mr Gregory. Mr Collins had the Method but forbore to send it after the eight series & he & Mr Oldenburg wrote earnestly to Mr Newton to send his own method himself, & Mr Newton did so, p 49. And a year or two after Mr N. had published his Principia Philosophiæ, Mr And when he pretended that Tschurnhause had this method from him while they were together at Paris (Acta Lips Ann. 1686 he forrgot that at that time he did not know how to continue series or derive reciprocal series from one another (p. 63, 94, 96. A year or two after Mr Newton had published his Principia Philosophiæ Mr Leibnitz publishing three papers relating to it, sometimes complements Mr
. Resist. grav. . . Resist. grav
. . Resist. Grav . velocitas ut id est ut sive ut Densitas ut . Velocitas ut id est ut .
Velocitas autem est ut id est ut GT in et Densitas medij ut resistentia directe et quadratum velocitatis inverse, id est ut directe et inverse, hoc est inverse ut GT. Et Velocitas corporis in puncto quovis G æqualis est velocitatis corporis Parabolam in vacuo describentis cujus vertex est punctum G, diameter GC et latus rectum . . Et velocitas in puncto quovis G eadem est cum velocitate quarum corporis in Parabola pergerat verticem G, diametrum GC & latus rectum
For Isaac newton in German street near St Iames Church
I writ to you about a month a goe and fearing that my letter might be not Come safe to your hands makes me so bold as to troubel you with this to lett you know of my misfortuns for I haueing had a great deal of illness which has been uery Chargable to me humbley disire that you will plleas to asist me in this my great nesesety for my wants is uery great makes me so bold to troubel you about a fortnight sence my husband had all his goods seased by the landlord so sir I humbley disire you that you will be pleased to giue the bearer sumthing for me and she will take care to send it to me my son Thomas marryed her mother sir Humbley beging the fauer that you will be pleased to Answer this I remain sir your humble saruant
Katthern Rastall
For upon all these considerations there is a suspicion that Mr Newtons Series for finding the Arc whose sine is given was communicated to him in England & that in the year 1673 he began to communicate it as his own to some of his Friends at Paris, & the next year wrote of it as his own in his Letters to Mr Oldenburgh in order to get the Demonstration or method of finding it. But the next year when Mr Oldenburgh sent him this & the series of Gregory & several others: he dropt his pretence to this series for want of a Demonstration & took time to compare those series with his own as if he had others different from those sent him. And when he had found a Demonstration of Gregories series, he began to communicate it as his own to his friends & concealed from them the letter by which he had received it from Mr Oldenburgh & pretended to Mr Oldenburgh that he had it a year or two before the receipt of that Letter
And that in his Letters of Iuly 15 & Octob 26 1674, he mentioned but one series for squaring the Circle, & said that the method which gave that series gave hi{m} also a series for any Arc whose sine was given tho the proportion of the Arc to the whole circumference was not known.
What to do upon them, & meeting with a Demonstration of Gregories Series, by a transmutation of figures he supprest Mr Oldenburgh Letter & by vertue of that Demonstration began to communicate to his friends at Paris that Series as invented by himself. For he tells us in the Acta Lipsiensia: for April 1671: Iam anno 1675 compositum habebam opusculum. Quadraturæ Arithmeticæ ab illo tempore lectum & One series he had in the year 1673, & might carry it with him from England to Paris another he began to communicate in the year 1675 The first was for finding the Arc whose sine was given as appears by his Letter of Octob. 26 1674, the second for finding the Arc whos{e} tangent was given as appears by his writings ever since, & it lies upon him to prove that he had this latter series before the year 1675 in which he received it from Mr Oldenburgh.
{illeg}{on} receiving Mr Newton Series again by one George Mohr, {illeg} Mr {O}ldenburgh in such a manner as if he had never seen that series {illeg}e & desired Mr Oldenburgh to procure from Mr Collins Mr Newtons method of finding it. If Mr Leibnits thinks fit to obviate this suspicion he is in the first place to prove that he had Gregories series before he received from Mr Oldenburgh.
Mr Leibnitz in his Letter of 28 May 1697 wrote thus to {illeg} Methodum Fluxionum profundissimi Newtoni cognatam esse methodo meæ differentiali — — professus sum in Actis Eruditorum — Itaque communi nomine designare Soleo Analyseos Infinitesimalis — Interim quemadmodum et Vietæa & Cartesiana methodus Analyseos Speciosæ nomine venit discrimina tamen nonulla supersunt: ita fortasse & Newtoniana & Mea differunt in nonnulli. And in recconing up the differences or improvements which he had made to Mr Newtons method, he added Exponential Equations. But these Equations are owing to his correspondence with the English. Dr Wallis insquaring the circle interpoled the indices of Dignities 0. 1. 2. 3. 4. 5. &c with these fractions &c. Mr Newton introduced into his Analytical computations fract, surd, indefinite & negative indices of Dignities — — its Vsefulness to the world.
Mr Newton in his Letter of October 24. 1676, wrote that he had two Methods
Here also Mr Leibnitz allows that when Mr Newtons Principles of Philosophy came abroad; he understood thereby the affinity that there was between the methods & therefore called them by the common name of the infinitesimal method, & thought himself bound in candor to acknowledge this affinity; & there is still the same obligation upon him in point of candor, And Mr Leibnitz doth not only here acknowledge the affinity of the Methods but also gives the preference to Mr Newtons method in antiquity; representing that as the Analysis in species was invented by Vieta & augmented by Cartes which made some difference between them, so Mr Newtons method & his own might differ in some things. And this subordination & distinction of the methods which he then acknowledged to Dr Wallis, he ought still to acknoledge. The death of that learned Man doth not acquit him from this obligation.
In enumerating the differences which he had added to Mr Newtons method, he names in the second place Differential Equations: but the Letters between them in the year 1676 shew that Mr Newton had such equations at that time & Mr Leibnitz had them not. He names in the third place Exponential Equations: But these Equations are owing to his correspondence with the English. Dr Wallis in the interpolation of series considered fract & negative indices of dignities.
And whereas in his Letter of 28 Decem 1675 he wrote to Mr Oldenburg that he had communicated that series above two years before to his Friends at Paris & written to him sometimes about it, & in his Letter of 12 Maij 1676 said to Mr Oldenburgh that he had writen to him about that Series some years before; & in his Letter to Mr Oldenburgh dated 27 Aug. 1676, that he had communicated that series to his friends above {illeg} three years before that is upon his first coming from London to Paris:: he is desired to tell us how it came to pass that when he received Mr Oldenburghs Letter of Apr. 15. 1675 he did not know this series to be his own, & wrote of it to Mr Oldenburg some years before
In his Letters of Iuly 15 & Octob 26 1674, he tells us of but one series for the whole circumference of a circle, & saith that the method which gave him this series gave him also a series for any Arc whose sine was given, tho the proportion of the Arc to the whole circumference be was not known. This method therefore by the sine of 30 degrees gave him a series for the whole circumference. If he had also a series for the whole circumference deduced from the tangent of 45 degrees he is desired to tell the world what method he had in those days which could give him both those series. For the method by transmutation of figures will not do it
And if in the year 1674 he had the Demonstration of a series for finding any Arch whose sine was | is given: he is desired to tell the world what it was & why in his Letter of May 12. 1676 he desired Mr Oldenburgh to procure from Mr Colling the Demonstration of Mr Newtons series for doing the same thing; & wherein his own series differed from Mr Newton's. For there is a suspicion that the Series which he mentioned in his Letter Octob 26 1674 for finding the Arch whose wsine was given was Mr Newton's & that when he received Mr Oldenburghs Letter of Apr 15. 1675 he durst not challenge it for want of a Demonstration, but took time t{o} consider & examin the several Series which he received in that Letter, before he would
Neque expoduntur occultæ Qualitates quia latent earum caussæ, sed quoniam ipsæ finguntur esse effectuum manifestorum caussæ occultæ, et ex hoc nomine qualitatibus rerum specificis tanquam caussis phænomenων nondum patentibus imposto deterremur a caussis hisce indagandis quasi quidem illæ penitus essent deploratæ postquam magnus ipsæ Philosophus Aristoteles in eas penetrare non poterat. Hoc sensu non ipsa gravitas, sed sola gravitatis causa dici potest, secundum Peripateticos, qualitas occulta, secundum Newtonum vero gravitas est qualitas manifestissima & causa ejus quæ nos latet potest esse substantia
Num. VI, VII, XXII, XLVII, LIII, LVI
Iudicio primarij Mathematici opponitur Iudicium Wallisij, in Præfatione ad operum suorum Volumen primum, anno 1695 editum, de quo D. Leibnitius per ea tempora minime conquestas est.
Eaton bill
for 5 h{illeg}ons hong batt — – 0 – 6 – 10
for 3 peckes of Oats – 0 – 2 – 0
for 1 peck half pe{n}es – 0 – 2 – 0
for a peck of bran – 0 – 0 – 4
0 – 5 – 2
& pretending that after the invention thereof he did not want Mr Newton's extractions.
Mr Newton in his Letter of Iune 13, 1676 represented that his methods of series described in that Letter were not universal without some further methods. And in his Letter of Octob 24. 1676 in describing those further methods wrote that – – – – – thereof & that after he found it he had no further use of Mr Ns Method of extractions. It remains
Mr Leibnitz in the Acta Eruditorum for April 1691 pag 179, wrote thus Cæterum ex seriebus infinitis a me alijsque —
It lies upon him to prove that he invented any one of these series, or else to beg pardon publickly for pretending to other mens inventions.
3dly We do not dispute about the antiquity of the symbols of fluents fluxions & moments, summs & differences used by Mr Newton & Mr Leibnitz these being not necessary to the method, but liable to change. And yet the symbol or used by Mr Newton for a fluent or summ, is older then the symbol used in the same sense by Mr Leibnitz. And some of the symbols of fluxions used by Mr Newton are as old as his Analysis communicated by Dr Barrow to Mr Collins in the year 1669: while Mr Leibnitz has no symbols of fluxions to this day. And the rectangles under the fluxions & the Letter o used by Mr Newton for moments are much older then the symbols dx & dy used by Mr Leibnitz for the same quantities. But all these symbols are only ways of notation & signify nothing to the method it self, which may be without them.
is downright trifling. Letters with pricks are seldome used by Mr Newton unless where he is deducing fluxions from equations involving fluents or fluents from equations involving fluxions. And even in these cases he doth not always use them, but thinks as convenient as any others Aut whatever letters or symbols he puts for fluxions the rectangle under the first fluxion & the letter o he puts for the first moment called the first difference by Mr Leibnitz & the rectangle under the second fluxion & he puts for the second moment & so on. In this sence he used the letter o in his Analysis communicated to Mr Collins in the year 1669 & in his book the Quadratura Curvarum & uses it in the same sense to this day. And the method by this way of notation is as advantageous & universal as by any other.
<124v>And the method by the letter o as it is the oldest so it is as beautifull as advantageous & as universall as by the symbols dx & dy.
Mr Newton has used the letter o these 45 years & above & still uses it, in the same manner & his method thereby is as advantageous & universall as the differential & more Geometrical.
But where there are equations consisting of many terms (as in the first Proposition of the Quadratura Curvarum) he represents the flowing quantities by the letters x y or z & their Fluxions by the same letters with points or by others equipollent And Mr Leibnitz himself in the Acta Eruditorum (A1686 pag ) has confessed that instead of the marks dx & dy he could have used letters.
55000.
88
In the Acta Eruditorum for March 1714 pag. 140 & 141, it's said that Mr Newton denies that the cause of gravity is the mechanical, & that he laies down a certain new Hypothesis concerning a subtile spirit pervading the pores of bodies (perhaps the same with the Hylarctick principle of Dr H. More) & this spirit is represented of less value then Hypotheses are unless it be the Æther or subtile matter of the Cartesians. And yet Mr Newton has no where denyed that the cause of gravity is Mechanical nor affirmed whether that subtile spirit be material or immaterial. nor declared any opinion about their {names} It appears by experiments ( shewed to the R. Society by Mr Hawksby that bodies do attract one another at very small distances in such a sense as he uses the word attraction, & he suspects that this attraction & electrical attraction may be performed by one & the same agent, the body constantly attracting at very small distances without friction, & the attraction being extended to great distances by friction; & this Agent he calls a subtile spirit. But what is this Agent or spirit & what are the laws by which it acts he leaves to be decided by experiments. And we should not have mentioned all this, had not Mr Leibnitz & some of his friends reflected upon Mr Newton for supposing these things & for not explaining the causes of gravity & electric attraction by Hypotheses & by this & other reflexions endeavoured to make the world beleive that Mr Newton in point of philosophy is much inferior to Mr Leibnits & in point of Mathematicks not only to Mr Leibnits but also to Mr Bernoulli & Mr Tschurnhause & therefore not likely to be the first inventor of the method of fluxions.
But whereas some have told us that gravity is seated in the will of God, & Mr Leibnitz has represented that according to this opinion gravity is a miracle {illeg}
Mr Newton in his Letter of 24 Octob. 1676 wrote that he had two methods of resolving Inverse Problems of tangents & such like difficult ones, one of which methods consisted in assuming a Series for any unknown quantity from which all the rest might convenitently be deduced & in the collating the homologous terms of the resulting Equation for determining the terms of the assumed Series. Mr Leibnitz many years after, published this method as his own, claiming to himself the first invention thereof. It remains that he either renounce this claim publickly, or prove that he invented it before Mr Newton wrote his said Letter.
Mr Newton introduced into Analysis the use of fract, surd & indefinite indices of dignities, & in his Letter of 24 Octob. 1676 represented to Mr Leibnitz that his methods extended to the resolution of affected Equations involving dignities whose Indices were fract or surd. Mr Leibnitz in his Answer dated 21 Iune 1677 mutually desired M. Newton to tell him what he thought of the resolution of Equations inolving Dignities whose indices were undetermined, such as were these & . And these Equations he now calls exponential, & represents to the world that he was the first inventor thereof, & magnifies the invention as a great discovery. But he has not yet made a publick acknowledgment of the light which Mr Newton gave him into it, nor told us any use thereof where the indices of dignities are fluents.
One of their statutes is that if any Fellow of the Society, shall contemptuously or contumaciously disobey the Statutes or Orders of the Society, or shall by speaking writing or printing publickly defame the Society or advisedly or malitiously do any thing to the damage & detriment thereof, He shall be ejected out of the Society. And therefore it lies upon Mr Leibnitz to beg the pardon of the Society for defaming him, least they put this statute in execution.
To the Honourable Isaac Newton these
<126r>Sir
Your Honours knowne vnbounded goodness, a Singular Patron & fauorer to all schollars & Learned men, is my sole motive for enterprizeing this small present to your Honour. a Rude & vnpollisht Booke, Begotten in spaine, & brought forth in England. I shall be extremly obliged to your Honours fauor in countenanceing the same, haueing onely a sett N. assigned me for the performance, which I hope to dispose off to those worthy Gentlemen my Benefactors, who did me the fauor, to accept my Translation, the Booke of Common Prayer into spanish, my Indigent circumstances did not permit me to vndertake it on my owne account, I am in all Duty to Command
Sir Your most Obedient servant Felix De Alvarado
Sir Be pleased to Cast an Eye thereon. there being therein, vncommon Varietie I shall not trouble your Honour any more on any account.
p. 12. ✝ The APostill not being sent to Mr Newton he did not meddle with it till M l'Abbé Conti sollicited him to write an Answer that the Postill with his Answer might be shewed to the King.
P. 71. Mr Newton observing that as Mr Leibnitz had appealed from the Commimttee of the R. S. to Mr I. Bernoullj, so he had sent his Apostill as well to Paris as to London & therein boasted of his happiness in disciples & had now again sent all the Letters to Paris that his Answer might be read there first & sent from thence to London: refused to answer Mr Leibnitz any further by Letters & only drew up the following Remarques & shewed them privatly to some of his friends to satisfy that it was easy to have returned an Answer had it been right to let him go on with his politicks
In the following papers you will find Mr Newton in the year 1669 had a method of series which gave the Areas & lengths of Curves &c exactly & Geometrically if it might be: & that by the testimony [pag. lin of Dr Barrow & Mr Collins he had this method some years before, that is in the year 1666 or before . This method is explained & illustrated with examples in Mr Newtons Letter of 242 Oct 1676, in Curves with binomial Ordinates, & said to extend to trinomials &c. And in the fift Proposition of the Book of Quadratures it is explained in a general equation extending to all those cases; & that Proposition involves the knowledge of the four preceding Propositions; & therefore by the testimony of Dr Barrow & Mr Collins, the Method of fluxions, so far at least as it is conteined in the first five Propositions of the book of Quadratures, was known to Mr Newton in the year 1666 or before Dr Wallis attested the same thing in the Preface to the second Volume of his works A.C. 1695 & gave Mr Leibnitz notice thereof by a Letter, & Mr Leibnitz did not then deny it nor complain. In his Letter of 21 Iune 1677 he was searching after the method of which Mr Newton had given him notice. In the year 1684 he published the elements of the Method he had found by that search & acknowledged a Methodus similis which might do the same things. The next year but one Mr Newton demonstrated the elements of his method synthetically in the second Lemma of the second book of his Principles, & in a Scholium represented that
Mr Newton called it the inverse method of fluxions above 40 years ago & you have given it a new name as if you had been the first inventor.
After he had been in England the first time where he might easily meet with some of Newtons & Gregories Series he pretended to have found the series for the Arc by the sine. Then he relinquished that pretence & pretended to have found the series for the arc by the tangent, which was Gregories & wrote for Mr Newtons method of finding the former series, And upon the death of Gregory he wrote also for a Collection of what Gregory had sent to Collins about these things & received it Then he came again into England & consulted Mr Collins aabout these matters & Mr Collins shewed him the originals. And as he wrote for the method of {s}eries which Newton had sent to Collins, that is, for the method contained in the Analysis per æquationes numero terminorum infinitas, & desired it so much as to offer a reward for it, so he had now an opportunity to see the original, And yet this candid Gentleman would never make any publik acknowledgment that
pag. 6. Mr Newton's inverse method of fluxions you have baptized by a new name.
I know that at the request of Mr Leibnitz a collecti{on} of Gregories papers was sent to him in the year 1676 & re{illeg} by him & that in this collection was a copy of Mr Gregory Letter of February 1671, wherein he then sent this & many other series to Mr Collins, & therefore Mr Leibnitz knew that Mr Gregory invented this series in or before the year 1671. I know that Mr Leibnitz soon after coming to London consulted Mr Collins to
had seen these Papers or received any light into these things from England. Let me add that two years after Mr Newtons Book of Principles came abroad, Mr Leibnitz published a great number of his Propositions in other words & pretended to have found them himself & yet the demonstration by which he pretended to have found the chief of them is an Erroneous one. To gave himself a litle to that Proposition he tried to adapte a Demonstration to it, but the Demonstration proves an erroneous one, & the error arises from his want of skill in the Method which he improperly calls differential. After Mr Newton – – –
To Sir Isaack Newton Master of the Mint at his house in
Leicester-street
<130v>Feb: 7th: 1777. Lord Portesmouth.
Tale quiddam Gregorius habuisse, multi extranei agnoverunt ex epistolis Oldenburgi series ad Leibnitium mittentis 15 Apr & 1675 epistola autore, a Leibnitij serie se receptas agnosentis 20 Maij subsequentis: multi inquam extranei id agnoverunt; collatis his Epistolis in Commercio editis cum monumentis antiquis ex quibus edebantur. Et in horum numero erant Comes de Kilmanseggar, Abas de Comitibus & ministri aliquot publici externorum Principum. Et Leibnitius ipse agnovit in Epistola ad D. Ramond 15 Aug. 1676 scripsit quod Le Roi m'a fact la grace de dire ici, que l'Abbé Conti viendra un jour in Allemagne pour me convertir. Et in Epistola sua ad Dominam Kilmansegger 18 Apr. 1716. M. Oldenburg m'ecrivit qu'un M. Newton a Cambridge avoit deja donné des choses semblables, non seulement sur le Cercle mais encore sur toutes sortes d'autres figures scilicet in epistola 26 Octob 1674] et m'enevoya des essais. [scilicet in Epistola 15 Apr 1675] Cependent le mien fuit assez aplandi per M. Newton même sc. in Epist 13 Iun 1676. Il sest trové par après, qu'un nommé M. Gregory avoit trové justment la même series que moi. Mais c'est que j'appris tard. Hæ Epistolæ extant in commercio Epistolico, et in illa 15 Apr. 1675 in qua Oldenburgus misit Leibnitio des essays specimina serierum erat series Gregorij de qua agitur. Hanc seriem a Leibnitio anno 1676 acceptam Newtonus laudavit nescius per ea tempora quod Leibnitius eandem acceperat ab Oldenburgo, Accepit autem bis: primo in Epistola prædicta deinde in excerptis ex Gregorij Epistolis ad ipsum missis 26 Iunij 1676. Et subinde eandem Newtono misit ut suam 27 Aug. 1676 et post annos sex eandem edidit ut suam in Actis Eruditorum celatio omni suo commercio quod habuerat cum Oldenburgo. Et jam conatur se excusare dicendo quod tande agnovit hanc seriem a Gregorio inventam esse
p. Hanc
But in cases of controversy its against the law of all nations to admit any man to be a witness for himself, & therefore his saying that he had found it above three years before must not be taken in evidence It lies upon him to prove it. And if he had found it so long ago yet Gregory had sent it to Collins & Collins had begun to communicate it to others before that time. And if he had found it before that time yet the series is extant in Mr Newton's Analysis. And to prove that he invented it before the month of Iuly 1669. By his Theoreme of Transmutations He taught how to reduce the Area of a circle to area of a curve whose Abscissa is x & Ordinate . The squaring of this Curve by the series was not his invention. Mr N Communicated it to Mr Collins in the said Analysis. pag 6 lin ult. His words are: Eodem modo si sit , dividendo prodibit , &c Vnde (per Regulam secundam) erit [area] , &c. And after all this evidence
After he had commended Mr Newtons series & desired the method of finding them & Mr Newton had gratified him in his request he & his friend Tschurnhause should not have Endeavoured to blow upon it as if it produced series only per accidens & more simple & general principles of Series were to be expected, & pretended to other general methods of reducing quantities to infinite series. He should not have claimed some of Mr Newtons reciprocal series & in the same Letter have desired Mr Newton to send him his method of finding reciprocal series & when the method was sent him & he understood it not & wrote again to have it explained, he should not, as soon as he understood it, have written back to Mr Oldenburgh that he perceived by his old papers that had found it before but laid it aside for want of a good example of its use. He should not have published Mr Gregories series in the Acta Leipsica as his own without letting the world know that he received that Series from Mr O & Mr C. & that Mr G. sent it to Mr C. in the beginning of the year 1671. He should not at the same time have amused the world with a harmony of series without letting them know that one of those series was nothing else then the half of this 1 another nothing else then the half of this &c. as you may perceive by subducting every negative term from the term preceding. He should not have published his differential method in the Acta Leipsica without aknowledging that Mr Newton had a method of
Multiplicationes Divisiones & Extractiones radicum Newtonus commun{illeg} ratione per immutabiles dignitatum indices notavit, Leibni{tius} proposuit indices mutabiles. Vide supra, p. 95.
temp. temp.∷R. . in
.
.
.
.
. Add
in :
ad 2f, seu ad 2ff.
At that time Dr Barrow represented to Mr Collins that by this & other papers which the author had communicated to him before it appeared that Mr Newton had invented this method & applied it universally some years before.
The ancient calendar year of the Greeks consisted therefore of twelve Lunar months each of thirty days & these years & months they corrected from time to time by the courses of the Sun & Moon, omitting a day or two in the month as often as they found the month of 30 days too long for the course of the Moon & adding a month to the year as often as they found the twelve lunar months too short for the return of the four seasons. Hence Thales called the last day of the month the thirtith. And to the And to the ancient calendar year Cleobulus one of the seven wise men had reference in his Parable of one father who had 12 sons each of which had 30 daughters half black & half white. And according to the number of days in this Calendar year, Demetrius Phalareus had 360 statues erected to him by the Athenians, & Cyrus cut the river Giridus into 360 Channels, & the Egyptians recconed their months to consist of 30 days & their year of twelve such months & five additional days. And in the scriptures the three years & an half of Daniel are by Iohn said to be 42 months & 1260 days.
p. 2. l. 7. ad sexdecim et amplius post . l. 8. Progressus vero quos jam fuerat Newtonus
p. 3. l 18, Iones ad fidem exemplaris a se reperti inter Collinij chartas, Collinijque manu exarati, postquam exemplaris fidem ad Autographum — l. 38 Ordinata. l. 39, Area.
p. 5. l. 4. cujusvis Curvæ, ejusdem Curvæ — l. 9. In hoc Compendio suo. l. 11 referentis per rectangulum sub unitate, et litera o comprehensum, vel (quod perinde est) per literam o; subintellecta scilicet unitate; aliarumque— ante jam
p. 13. l. 33. transcribendam, eamque in manibus Collinij D. Leibnitius vidit antequam Londino excederet.
p. 7. l 13 in lucem emitti curavit. lin 34 dele [Et Collinio]. lin 35 excolens. Anno proximo Geometriam altiorem didicere cœpit et ejusdem anni mense Iulio rescripsit mirando quodam se potitum esse —
p 8. l 16. singulari. Per series suas quas ab acceptis hic distinguit, & ante annos aliquot adeoque antequam Geometriam alitorem discere cœperat via quadam singulari inventas prædicat intelligere videtur series jam ante descriptas numerorum fractorum quibus denominatores sunt numeri triangulares vel pyramidales vel triangul-triangulares aut similes.
Et quanquam D. Leibnitius suam de seriebus acceptis sententiam D. Oldenburgo perscribere hic promiserat: cavit tamen posthæc — l. 18 si a numericis jam memoratis discesserimus. l. 19 Dele [quas ad – – – – – conciemasse.]
p. 9 l 9 Quorum votis annuens Newtonus
p. 10. l 8. 1675, et annum fere antequam Geometriam sublimiorem addiscere cœperat.
p. 13 l 9 de Analysi sua (ceu compendio methodi serierum) . l. 33 transcribendam, et Collinius eandem cum Leibnitio communicabat antequam ille
p. 18. l. 27 Et Leibnitio cujus candorem in dubium vocare injustum esset, privilegium concedebatur, candorem aliorum pro lubitu in dubium absque injuria vocandi: Newtonum vero oportebat
p. 3. l. 5 Dele a votre Maitre Leibnits. &. Vide
P. 40 l. 12. for imposturues write
P. 41. l. 12, 13. Plagiaries. read you who can so little defend your self from the imputation it.
P. 46. l. 12. Dele, d'alleurs vous dites que et scribe disant qu'il ne vouloit
Pag 6. l. 11. & p. 7. 11 for l'assembleé write le Commis the Committee
Pag. 44. l. 1, 2. add, unless in telling Dr Wallis that the Letters which had passed between him & Mr Oldenburg were either lost or mislaid in a heap of papers
P 7. l 2. par vos amis & attributed to you
P 8. l. 9. And therefore you may do well to clear your self from being the author of the abusive Synopsis of the Book of Quadratures published in the Acta Eruditorum for Ian. 1705, which has occasioned all this dispute.
P. 11. l. 10. add. since you have passed your judgment upon it.
Pag. 51. lin 17, 18 &c dele Il est vray — — leur Virginité.
Pag 50 lin 10. — — au Mr Leibnitz. N'y dit il pas — &c. Quære.
Sir Isaac Newton
SIR,
YOU are hereby Desired and Summoned to Meet the rest of your Brethren, Members of the Society of the City of London, of and for the Mines, the Mineral, and the Battery Works, at the Mineral-Office-General in Black-fryers, at 2 of the Clock in the after noon on thursday next being the 8th Day of this instant Month of October Anno Dom. 1713. Per Cur' H. H. Stringer Serjeant.
Dated at the Mineral-Office-General the 6th Day of October
Proposuerat Newtonus resolutionem æquationum ubi indices dignitatum sunt fractæ vel surdæ quantitates, p 86: D. Leibnitius vicissim proponit resolutionem æquationum ubi indices dignitatum sunt quantitates indefinitæ.
In hac Analysi quantitates fluentes per symbola quæcunque ut v, x, y z et earum fluxiones per symbola alia quæcunque ut V X Y Z vel p q r s & momenta per fluxiones in coefficientem aliquam perparvam o ductas ut op, oq, or os designari possunt ut mox fit ex demonstratione Regulæ primæ Sed maxima ex parte coefficiens o subintelligitur & eadem symbola pro fluxionibus & momentis promiscue usurpantur et unitas p{tit}ur tam pro momento quantitatis uniformiter fluentis quam pro ejus fluxione ponitur, ut hic fit ubi 1 ponitur pro momento BK.
Huic patet resolutionem dignitatis indefinitæ binomij cujusvis in seriem infinitam Newtono jam tum innotuisse: quæ operatio reductione quantitatum omnium per multiplicationes divisiones et extractiones radicum non affectarum in series infinitas, comprehendit.
Certe D. Leibnitius Anno 1676 negavit Problemata methodi tangentium inversæ et multa alia ab æquationibus aut Quadraturis pendere
Certe cum Newtonus (Anno 1676) dixisset Analysin suam ad omnia pene problemata sese extendere (p. 55, 56) D. Leibnitius respondit Id sibi non videri; esse enim multa usque adeo mira et implexa ut neque ab æquationibus pendeant neque ex quadraturis; Qualia sunt (ex multis alijs) Problemata methodi Tangentium inversæ. Deinde vero, a Newtono admonitas didicit hujusmodi problemata ab æquationibus & quadraturis pendere: et generalem illam Newtoni Analysin in hujusmodi æquationibus fundari statim intellexit. Vide pag 90. lin 26, 27, 28, 29.
Annon D. Leibnitius a Newtono admonitus in hujusmodi æquationes incidit. Vide pag. 30, l. 11. & pag 47. lin 16. & pag 55 lin 29 & 56 lin 1 & pag 65 l 14. pag 72. l. 14. p 85 l 32 & p. 88. l 14. & p. 90 l. 26, 27, 28, 29.
The Answer of Mr Tschurnhause to this paper was received by Mr Oldenburgh the 8th Iune 1675, & entituled Responsum ac scriptum Dn Collinij de Cartesij inventis.
D. Leibnitius series pro Hyperbola & circulo quarum reciprocæ sunt elegantes, ante annos plure habuisse dicitur, series plures reciprocas ante biennium ab Oldenburgo accepit, methodum serierum reciprocarum anno superiore a Newtono postulavit, & hoc anno acceptam ægre intellexit, & eandem tamem primus invenerat: Et quamvis hæc methodus ex arcu daret sinum et tangentem, ex logarithmo daret numerum et serierum omnium exhiberet reciprocas, eandem tamen neglexerat ut inutilem.
② D Leibnitius [ante annos plures seriem habuit Mercatores pro Hyperbola, hujus seriei reciproca est elegantissima Series etiam pro circulo se habuisse dixit quarum reciprocæ solunt e{ssu} ele. Et exemplo tamen eleganti serierum reciprocarum caruit]. ① Series plures reciprocas ante biennium ab Oldenburgo acceperat & Methodum serierum reciprocarum anno superiore a Newtono postulaverat, hoc anno acceptam ægre intellexerat: & eandem tamen invenerat prius. ③ Et quamvis series haberet ante annos plures pro Hyperbola et Circulo et hæc methodus ex arcu daret sinum rectum sinum versum tangentem, cotangentem & secantem & ex logarithmo daret numerum & serierum omnium exhiberet reciprocas, eandem tamen olim inventam neglexerat ut inutilem.
ægre intellexerat & intellectam se olim invenisse ex chartis antiquis mox didicit ex chartis antiquis invenisse. Et quamvis series haberet ante annos plures pro Hyperbola et circulo et hæc methodus
3 D: Leibnitius series reciprocas ante biennium ab Oldenburgo acceperat methodum serierum reciprocarum anno superiore a Newtono postulaverat & hoc anno acceptam ægre intellexerat et eandem tamen prius | pri{mu}s invenerat. Anno 1675 Series plures reciprocas ab Oldenburgo accepit & unius earum ut elegantiam singularem habentis Demonstrationem anno proximo ab Oldenburgo postula vit. p. 45. Seriem pro Quadratura circuli quam anno 1675 cum Gallis ut suam communicabat, id est Gregorianam, anno 1673 sibi notam fuisse scripsit (p 45). ‡ sed methodo inveniendi elegentem hujus reciprocam caruit. Toto fere quadrennio D. Leibnitius methodum serierum reciprocarum desiderabat & tamen prius invenerat & se invenisse oblitus fuerat. (p 25 & 41) sed Leibnitio diu ignota. Toto fere quadrenni{o} Liebnitius methodum serierum reciprocarum desiderabat & tamen prius invenerat, se invenisse oblitus fuerat.
1. Rogatur D. Leibnitius ut hanc ἑνθ{υν}σιν communicet.
2. De methodo generali ex methodis serierum & fluxionum composita Newtonus loquitur in sequentibus p 14, 15, 18, 30. 55, 56, 71 85, 86.
Et quamvis ex arcu daret sinum ex logarithmo numerum & serierum omnium exhiberet reciprocas? eandem tamen neglexerat ut inutilem.
What is said in the following letters & in a Letter of Mr Collins to Mr Newton printed by Dr Wallis concerning the method of tangents being known to Slusius before he printed his Mesolabium was grownded upon a mistake. The letter of Mr Collins dated 18th Iune 1673 runs thus
Quod ad Slusij Methodum de Tangentibus spectat: Erat ea ab ipso bene intellecta quum suum Mesolatio librum edidit, sed noluit tunc publici juris facere ed quod nollet Amico suo Angelo Riccio prævenire. Qui tamen postea declinans ipse studia Mathematica petebat a Slusio scribere, pollicitus est eam D. Oldenburgo transmittere ut Transactionibus Philosophicis inseretur. Ante vero quam huc appulerit scribebam Ego ad Te ut intelligerem quid ea de re tu noveris. Tuumque responsum cum D. Oldenburgo communicabam, ut ipse D. Slusio transmitteret: ut sciat ipse, rem eam esse apud Anglos congitam; utut forte non tam diu neque tam mature ut ipsi fuerit.
Riccius published his Exercitatio Geometrica de Maximis & Minimis at Rome in the year 1666 , & by his third Theoreme for determining Maxima & Minima he teachs how to draw Tangents to some curves. And Slusius in the fourth chapter of his Miscellanies published with his Mesolabium in the year 1668, sets down the Theorem of Riccius & makes this note upon it. Liceret hujus Propositionis usum prolixius extendere, ad determinandas nempe maximas & minimas applicatarum in Curvis, t angentes & similia Verum cum hanc materiam nuper, in Exerciatione sua Geometrica, feliciter aggressus sit Vir Clarissimus Michael Angelus Riccius, doctrina & humanitate singulari, orbi literato notissimus; & justi operis spem faciat: frustra nunc pluribus insisterem cum meliora ac perfectiora ab ipso propediem expectari debeant. And this is that method of Tangens which Slusius when he published his Mesolabium reliquished to his friend Riccius & which Riccius afterwards desired Slusius to publish & Slusius thereupon promised to send to Mr Oldenburg to be published in the Transactions. But the method which Slusius sent afterwards to Mr Oldenburgh to be published was very different from this & floweth not easily either from the Theorem published before by Riccius & Slusius or from the three Lemmas from which Slusius pretended to derive it.
This year Mr Leibnitz Upon notice that Mr Iames Gregory was dead, desired th{illeg} Letters might be collected & sent to Paris & they were collected & sent accordingly, & among them were copies of MrGregories Letters of 5 Sept 1670 & mine of 10 Decem. 1672 & by these Letters Mr Leibnitz had notice that Mr Barrows method of Tangents was capable of improvement so as to give the method of Tangents of Gregory & that the Method of Gregory & Slusius might be improved so as to give my general method of Analysis & that this Analysis proceeded without sticking at surds, & that I had interwoven it with the method of series, vizt in a Tract which I wrote upon this subject in the year 1671. Mr Leibnitz wrote also to Mr Oldenburg for the Demonstration of some of my Series that is the method of finding them & told him that Mr Collins could help him to it, & therefore knew that Mr Collins had my Method, that is my Analysis per series numero terminorum infinitas; for I sent Mr Collins my method in no other Paper then that. At the same time he received also my Letter of 13 Iune 1676 in which I represented the Art of that Analysis by my methods of Series & some other methods (meaning principally the method of fluxions) became so general as to extend to almost all Problemes except perhaps some numeral ones like those of Diophantus. And in October following he came to London & consulting Mr Collins saw in his hands many of mine & Gregories Letters especially those relating to series. He saw also my Letter of 24 Octob. 1676 wherein he had further notice of these things, & while he was in London he met with Dr Barrows Lectures, & in his way from London to Hannover was meditating how to improve the method of Tangents of Slusius, as I gather from his Letter writen from Amsterdam to Mr Oldenburg Novem. 1676.
There was also at the same time an abusive Harang printed agains Dr Keill in the Acta Eruditorum for Iuly 1676 without the name of the author. The Author by calling a formula of Mr I. Bernoulli formulam meam has father it upon that writer but I hear that Mr Bernoulli denies that he wrote it, & I doo not think such papers fit to be answered. [There are some matters of fact not yet fully stated. I have set them down in the inclosed paper, & give you leave to publish it.] For avoiding answering any such Letters & Papers & ridding my hands of ths matter I have herewith sent you a general relation of the matter of fact, & give you leave to print it, & every body to think of it what they please. For I do not think the matter of so much consequence that I should concern my self about it any further.
In my Analysis per æquationes numero terminorum infinitas I said that by this Analysis Curvarum areæ & longitudines &c (id modo fiat) exacte et geometrice determinantur: sed ista narrandi non est locus. And Mr Collins in his Letter to Mr Strode above mentioned, said thias by this Analysis & other things communicated before to Dr Barrow it appeared that I knew this method some years before the Logarithmotechnia of Mercator came abroad so as to find the area of any figure accurately if it may be or at least by approximation in infinitum. And in my Letter of 24 Octob. 1676 I represented that the Quadrature of Curves was improved by the method of fluxions & I had by that Method found some general Theoremes for that end & there set down one of those Theoremes & illustrated it with examples. And in the six first Propositions of the Book of Quadratures I shewed how such Theorems were to be found by that Method, & therefore that Method so far as it is conteined in the first six Propositions of the Book of Quadratures was known to me before I wrote the said Latter & before I wrote the said Analysis & before Mercators Logarithmotechnia came abroad, there being no other Method then that conteined in those six Propositions by which such Theorems could be found.
2. In October 1676 he went from Paris to London & there met with Dr Barrows Lectures & saw my Letter of 24 October 1676. And Mr Iames Bernoulli in the Acta Eruditorum for December 1691 pag. 14, said that the Calculus of Mr Leibnitz – – — – – – – – he never claimed a right to it.
5 Mr Leibnitz published a Schediasma de resistentia Medij & motu projectorum gravium in Medio resistente & in the end of it added Et fortassis attente consideranti vias quasdam novas vel certe satis antea impeditas apperuisse videbimur. Omnia autem respondent nostræ Analysi infinitorum, hoc est, calculo summarum & differentiarū (cujus elementa quædam in his Actis dedimus) communibus quoad licuit verbis hic expresso. And this was the second specimen made public of the use of this method in the difficulter Problemes. And yet it was nothing else than the two first sections of the second book of Principles reduced into another order & form of words.
6 At the request of Dr Wallis — — — — necessary to the Method.
3 The Marquess de l'Hospital in the Preface to his Analysis said that Mr Leibnis had done me justice in the Iournal des Scavans du 30 Aoust 1694 vizt in acknowledging that I found the method proprio Marte. But the Marquess did not then know that I was the first inventor.
7 If it be asked why I did not publish – – – – till the year 1704 And for the same reason I intend to meddle with this matter no more. The inverse Method of fluxions is capable of great improvements, & the improvements are his who finds them out.
It has been represented in Germany that Mr Leibnitz first found out the differentiall calculus in numbers & then by inventing the Analysis of infinitesimals translated this calculus to Geometry. But this is to tell us that he found out the differential calculus of Mouton In the beginning of the year 1673 he pretended to the invention of this differential calculus in numbers & was told by Dr Pell that it was Moutons method & acknowledged what Dr Pell said to be true, & yet defended himself by saying that he found it apart without knowing what Mouton had done before. But if Mouton was the first inventor he had the sole right to the invention till Mr Leibnitz also found it out & he that has once the sole right to an invention is not afterwards to be deprived of any part of his right by sharing it with coinventors.
The Editors of the Acta Eruditorum mense Octob. anni 1685 pag 483 tell us that the quadrature of the circle by the series &c was found out by Mr Leibnitz ten years before or above that is in the year 1675 before the month of October. And Mr Leibnitz tells us in the Acta Erudit. of the next year mense Iunio pag 298, 299, that he found out this Quadrature soon after he began to understand Algebra, but was still forced to do many things by the ambages of figures which he would have done by the compendium of Analysis untill at length he found out his differential calculus. And in a letter to Dr Wallis dated 28 May 1697 he tells us that the consideration of differences & summs in series of numbers gave him the first light , by observing that Differences answered to tangents & summs to quadratures: that is, it put upon upon considering Dr Barrows differential method of Tangents & Dr Wallis's summatory method of Quadratures. And this was some time after the year 1675. But this consideration alone could not give him light into the method of drawing Tangents without sticking at surds nor into the universal extent of this method for solving all sorts of Problemes. That light he had by his correspondence with Mr Oldenburg as is manifest by what has been said above. By that correspondence he received the series of Gregory, & learnt that Mr Newton had a general method, of solving Problems without sticking at surds which method gave the method of tangents of Slusius as an obvious corollary & determined the curvities, areas; convex surfaces; solid contents, & centers of gravity of figures & by the conditions of tangents mutually gave the figures & for squaring of curves gave converging series which brake off & became finite as often as the curve might be squared by a finite equation, & gave rules for comparing of Figures with the areas of the conick sections. This put Mr Leibnitz upon considering how to improve the method of Slusius so as to make it universal as is manifest by his Letter to Mr Oldenburg dated at Amsterdam Nov 1676. And when he began to see how the differential methods of Barrow & Slusius might be improved, he began where Barrow left off as the Marquess de L'Hospital has observed, & to make himself a coinventor changed the notation of Dr Barrow & pretended to have found the method long before writing back to Mr Oldenburgh: Clarissimi Slusij methodum tangentium nondum esse absolutam Celeberrimo Newtono assentior Et jam a multo tempore rem Tangentium generalius tractavi; scilicet per differentiat Ordinatarum: [And then proceeded in that letter to describe this new method & compare it with Newtons as his own invented jam tum a multo tempore,] though it be certain that he was but then beginning to understand it. For when he wrote his Letter of 27 Aug. 1676, & therein represented that he did not beleive that Mr Newtons Methods were so general as he represented them & added: Sunt enim multa usque adeo mira et implexa ut neque ab æquationibus pendeant neque ex quadraturis: qualia sunt, ex multis alijs, Problemata methodi tangentium inversæ its most certain that he understood nothing of this matter. He saith indeed in his Letter to Dr Sloan dated 29 Decem. 1711 Inventum plusquam in nonum in annum pressi, ut nemo me præcurrisse quæri possit. By which words he would have us beleive that he found it before October 1675 & by consequence before the correspondence which he had with Mr Newton by means of Mr Oldenburg. But he is not a witness in his own cause. It lies upon him to prove it. He had Moutons differential method before October 1675: but the differential method now in dispute he had not when he wrote his Letter of 27 Aug 1676 & if he affirms that he had it before May 1677, it lies upon him to prove his assertion. It is not enough to say that he first found the differential method in numbers The Differential method in numbers is not his. Mouton found it before him; & it is but of narrow extent & little use. The question is about the general method of Analysis called the method of moments & fluxions by Mr Newton & the method of infinitesimals & indivisibles by Mr Leibnitz.
To Sir Isaac Newton
☉ A man who knows that he is but the second inventor & endeavours to diminish the right of the first inventor is a Plagiary.
And whereas he represents that he supprest the Invention above nine years & by consequence had it in the year 1675 it lies upon him to prove that he had it when he wrote his Letter to Mr Oldenburg dated 27 Aug. 1676, wherein he affirmed that Problemes of the inverse method of Tangents & many others could not be reduced to Infinite Series nor depended on Equations or Quadratures.
made all that delay that no body might complain of his pretending to step in before them
But we in England give no right to second Inventors. The first Inventor has the sole right – . . . . doth afterward.
And since he has said (in his Letter to Dr Sloan dated 29 Dec. 1711) that he supprest the Method above nine years, before he published it, & it follows from thence that he had it in the year 1675, it lies upon him to prove that he had it when he wrote his Letter to Mr Oldenburgh dated 27 Aug. 1676, wherin he affirmed that Problems of the inverse method of Tangents & many others could not be reduced to Infinite Series nor depended on Equations or Quadratures.
And whereas in the same Letter he has appealed to the judgment of Mr Hugenius as a most intelligent & most uncorrupt judge: he is desired to tell the world whether he believes in his conscience that Mr Hugenius ever heard the cause between both parties or was made acquainted with the commerce between the English & Mr Leibnitz by Letters while he staid at Paris.
It lies upon him also to tell the world what was the series mentioned in his Letter to Mr Old. dated 26 Oct. 1674 by which he found any Arc of a circle whose sine was given, & what was the method by which he found that series, & could not find the series of Mr Newton the Demonstration of which he desired Mr Oldenburg (12 May 1676 to procure from Mr Collins.
<142r>It lies upon him also to tell the world what was the method, by which he found the series of regression for the circle & Hyperbola sent to him by Mr Newton 13 Iune 1676 before he claimed them from Mr Newton by his Letter of 27 Aug. following.
And since he has told us that his friends know how he came by the Differential method; it lies upon him to let the world know how he came by it & at what time.
But since he has complaiend of the R. Society for giving judgment without hearing both parties, he is desired to tell the world whether he beleives in his conscience that Mr Hugenius to whom he appeals as a most intelligent & most uncorrupt judge ever heard the cause between both parties or was made acquainted with what had passed between the English & Mr Leibnitz by Letters during his stay at Paris between the year 1672 & the year 1677.
And Mr Leibnitz himself in a letter to Mr Newton dated from Hanover March 1693 & still extant in his own hand writing, acknowledges the same thing in these words: Mirifice ampliaveras Geometriam tuis seriebus, sed edito Principiorum opere ostendisti patere tibi etiam quæ analysi receptæ non subsunt. Conatus sum ego quoque notis commodis adhibitis quæ differentias et summas exhibent, Geometriam illam quam transcendentem appello, Analysi quodammodo subjicere, nec res male processit.
☉ Dr Wallis had received copies of Mr newtons two Letters of 13 Iune & 24 Octob. 1676 from Mr Oldenburgh & published many things out of them in the second volume of his Works in his Algebra printed in English 1683 & printed in Latin A.C. 1693. And soon after had intimation from Holland to print the Letters intire because Mr Newtons notions of fluxions passed there with applause by the name of the Differential Method of Mr Leibnitz, & thereupon took notice of this matter in the Preface to his first Volume published two years after the second & in a letter dated April. 10th 1695 he wrote thus to Mr Newton about it. I wish you would print the two large Letters of Iune & August [He means Iune & October.] 1676. I had intimation from Holland, as desired there by your friends, that somewhat of that kind were down; because your Notions (of Fluxions) pass there with great applause, by the name of Leibnitz's Calculus Differentialis. I had this intimation when all but part of the Preface to this Volume was printed off; so that I could only insert (while the Press stayd) that short intimation thereof which you there find. You are not so kind to your reputation (& that of the nation) as you might be when you let things of worth lye by you so long, till others carry away the Reputation that is due to you. I have endeavoured to do you justice in that point; and am now sorry that I did not print those two Letters verbatim. ♀ ♀ And in a which Letter to Mr Leibnitz dated 1 Decem. 1676, Dr Wallis thus excuses his inserting the said Paragraph into his Preface without making a further mention of the Differential calculus. Calcul Differentialis vel nomen audivisse me non memini nisi postquam utrumque Volumen absolverant operæ, eratque Præfationis (præfigendæ) postremum folium sub Prelo ejusque typos jam posuerant Typothetæ. Quippe tum me monuerat amicus quidam harum rerum gnarus qui peregre fuerat, tum talem methodum in Belgio prædicari, tum illam cum Newtoni methodo fluxionum quasi coincidere. Quod fecit ut (transmotis typis jam positis) id monitum inseruerim. And in the Letter which followed hereupon
– – – – Mr Leibnitz at that time. By which it may appear that it was then a received notion in England that Mr Newton had found the method of fluxions ten years before the said correspondence between him & Mr Leibnitz or above.
The short Intimation of this matter which Dr Wallis inserted into the Preface of his first Volume was in these words. In secundo Volumine, (inter alia) habitur – – – – – – – nihil a nobis dictum esse.
Hereupon the Editors of the Acta Lips. – – – – to Mr Leibnitz at that time. And in the year 1699 Dr Wallis by the leave of Mr Leibnitz inserted into the 3d Volume of his works the said two Letters together with the three Answers of Mr Leibniz found in the Library of Mr Collins & dated 27 Aug. 1676 & 21 Iune 1677 & 12 Iuly 1677
In the same year (A.C. 1699) Mr Fatio, in his Dissertation on the Line of the quickest descent, suggested that Mr Leibnitz . . . . . before Ianuary 1705
Videamus jam qua facile fuerit ex hoc methodi generalis exempla {illeg} methodo Tangentium Barrovij collato methodum ipsam generalem deducere
Methodus vero generalis ex hoc ejus specimine vel exemplo sic deducitur
Et hinc Wallisius in Præfatione ad Volumen secundum operum suorum dixit quod Newtonus Literis suis 13 Iunij & 24 Octob. (scribendo quod Methodus sua generalis prompte et absque æquationum reductione daret methodum Tangentium Slusij & methodum suam Leibnitio explicuisset. & methodum Tangentium Slusij inde fluere idque absque æquationum reductione dixisset Leibnitius utique in itinere suo ex Gallia {Anglia} in Germaniam Methodo tangentium Slusij amplianda cogitabat, ut ex Epistola ejus ad Oldenburgum Amstelodami Novem. data manifestum est. Et proximo mense Iunij rescripsit Clarissimi Slusij Methodum Tangentium nondum esse absolutam Celeberrimo Newtono assentior. Deinde in eadem Epistola descripsit methodum tangentium Barrovij et quomodo ex hac methodo Barrovij Methodus Tangentium Slusij deduci posset, & quod methodus sic inventa exhiberi posset ubi plures sunt literæ indeterminatæ quam duæ et ea{æ} ratione procedere non sublatis irrationalibus. Hoc totum est quod Leibnitius ea tempore descripsit. Et hoc {t}otum e{go} Epistola Newtoni 1672 f{er}ille consequi jam ostensum Viderit itaque Lector annon Newtonus methodum habuerit anno 1672 & annon Leibnitius (qui anno 1673 altiorem Geometriam cœpit discere) post annos quatuor ex Newtoni Litteris lucem aliquam acceperit. Et horum vestigijs institit ubi rescripsit
Idem consequitur ex epistolis Newtoni anno 1676 scripto si cum methodo Tangentium Slusij conferantur, ut Wallisius in Præfatione ad Operum suorum Volumen primum notavit.
Qu. 1. Whether is it right to set a president for discouraging Manufactures by taxing them?
Qu. 2. Whether is it worth the while to do this for a tax scarce exceeding twelve or fifteen thousand pounds per an'
Qu. 3. Whether, after the Lords have rejected a Bill for lowering the fineness of Plate, is it right to tack this to a money bill, & will not the Lords reject it.
Qu. 4. Whether some of the Goldsmiths should not be consulted about the plurality of Diets, standard & the marks thereof.
& auctoritate Bernoullij amicos suos rerum mathematicarum inscios contra Newtonum passim ciere conatus est: cum tamen Bernoullius
Eodem spectat etiam quod in Epistola Newtoni ad Oldenburgium 24 Octob. 1676 data, des{c}iptæ exiant Ordinatæ — cum conicis sectionibus referuntur in
Newtonus in Epistola sua ad Oldenburgum 24 Octob 1676 data, ubi solutione{m} Problema aliquot generali nominasset subjungit: Fundamentum harum operationum, satis OBVIVM quidem quoniam jam non possum explicationem ejus proseque sic potius celavi 6accdæ &c. Celavit ut obvium ne subriperetur. Quam vero fuit obvium & quam facile subripi potuit, sic patebit. Iacobus Gregorius scripsit ad Collinium.
Quæritur, non quis methodum totam invenit, (nam tota nondum inventa est sed quis methodum invenit quatenus in scriptis a Newtono editis habetur. Qui aliquid addiderit is jus habebit in partes additas.
Sed et L. ipse anno proximo in Epistola sua ad Con. de Kilm 18 Apr data & a Des Maizeaux edita idem agnovit narrando quod cum ipse de serie quam pro circulo invenerat ad Oldenburgium scriberet (viz per Epistolas 15 Iulij & 26 Octob. 1674;] Oldenburgius responderet (vizt 8 Decem 1674) quod Newtonus quidem Cantabrigiensis jam antea similia dedisset non solum pro circulo sed etiam pro omni figurarum aliarum genere & [ & ipsi mitteret des essais,] ipsi mitteret serierum specimina. His verbis Leibnitius Hoc non obstante, ait, series mea satis laudata fuit per Newtonum ipsum. Postea inventum est Gregorium quendam eandem etiam seriem invenisse: sed hoc didici tarde. Hæc Leibnitius. Literas utique multa fruge Algebraica refertas acceperat, sed tunc præter ordinarias curas Mechanicis imprimis negotijs distractus, non potuit examinare series quas Oldenburgius miserat, ac cum suis compare: ut ipse tunc rescripsit. Et Newtonus Wallisius & junior Gregorius hanc seriem a Gregorio ad Collinium & ab Oldenburgio ad Leibnitium fuisse missam, per ea tempora ignorabat
Hæc epistola in Galliam prius missa fuit quam in Angliam veniret, et et eidem subjunctum erat Problema Bernoullij quod Leibnitius olim proposerat D. Fatio solvendum, [Iam vero Leibni{uj} postulabat ab Abbate ut is suo nomine proponeret idem Analystis Anglis. ✝ ✝ et præterea Eodem tempore Leibnitius Epistolam volantur Iudicis Mathematici edi curavit in Hollandia tanquam [jam cœpit amicis suis scribere quod judex ille Mathematicus erat ipse a Bernoullio scriptam, et amicis subinde cœpit scribere quod Bernoullius erat ejusdem auctor. Sic Quæstio dirimenda erat authoritate Bernoullij et Iudicis constituti & Problemata proponentis ab Analystis Anglis solvenda. Newtonus autem qui ignorabat Epistolam ad Abbatem cum hoc Problemate per Galliam in Angliam venisse, inductus fuit ab Abbate ut eidem responderet et Re- Epistola ad Abbatem 26 Feb 171 data scripsit quod Consessus R. Societatis Hoc artificium Newtono innotuit anno 1676 uti patet per Epistolam ejus eo anno 24 Octob ad Oldenburgum scriptam, immo et anno 1669 ut affirmatur Newtonus autem qui ignorabat Epistolam cum hoc Problemate per Galliam in Angliam venisse impulsus fuit ab Abb te &c ut eidem responderet et responso suo ad Abbatem 26 Feb 171 dato scripsit quod Concessus
1 Motum harmonicum Planetarum Assumpsit, (in Tentaminis artic non probavit {illeg} {illeg} Vide Tentaminis Artic. 6. 2. Vim centrifugam simi verso angulo proportionalem esse Lebn. Artic 11 assumpsit contra veritatem: et inde circulationis Motum paracentrium Planetarum a differentia virium centrifugarum & centripetarum (quæ nullæ est) oriri fixit Artic 15, 21, 25. Et Ex errantibus Articulis 12 et 15 deduxit Artic 19. At Propositiones Mathematicæ sic inveniri non solent
Methodum differentialem Moutoni Leibnitius habuit anno 1673 & suam esse voluit. Methodum aliam differentialem nondum habuit. Series postea habuit sed quas anno 1675 ab Oldenburgo accepit, ab alijs prius accipere potuisset. Methodum generalem perveniendi ad ejusmodi series anno proximo ab Oldenburgo petijt, a Newtono accepit, antea non habuit. Methodum extrahendi radices in speciebus a Newtono simul accept qua transmutatio figurarum in methodum quandam generalem evasit, sed inutilem. Per extractiones solas res citius peragitur. Anno 1677 methodum novam differentialem habuit ac tantam methodi hujus antiquitatem Editores jactant, majorem non asserunt.
3 Inde deduxit vim centrifugum mobilis harmonice circulantis esse in ratione radiorum reciproca triplicata (Artic 12). Newtonus autem demonstravit hanc vim mobilis in Ellipsis circa focum harmonice circulantis esse ratione radiorum reciproce duplicata. Par Motum paracentricum . . . . . . (quæ nulla est) Leibnitius oriri finxit (in Artic 15, 21, 25.) Et ex errantibus Articulis 12 et 15 deduxit Artic. 19 Crenda sunt hæc et Propositiones Mathematicæ sic inveniri non solent.
Motum Cometarum Leibnitius non attigit, Planetæ et Cometæ ijsdem legibus revolvuntur apud Newtonum. Vortices alicubi harmonice alibi non harmonice moveri Leibnitius pro lubitu finxit: harmonicæ circulationi obstant vortices Satellitum Saturni Iovis {ac} Terræ Motibus Cometarum Vortices non favent. Motum harmonicum Planetarum Leibnitius non probavit sed in Tentaminis Artic 6 assumpsit. : Newtonus motum harmonicum corporum omnium in centrum immotum attractorum demonstravit. Motum circulationis & motum paracentricum Leibnitius nunc a diversis causis nunc ab eadem deducit Newtonus utrumque ab eadem causa (pro simplicitate naturæ semper deducit. Vim centrifugam . . . .
a A relatione Differentiarum ad Tangentes Leibnitius se methodum differentialem habuisse hic fatetur, id est a methodo determinandi tangents per differentias Archimedes Fermatius Gregorius, Barrowus methodum differentiarum ad Tangentes applicuere Newtonus hanc methodum ducendi tangentes aux it & præterea ad Quadraturas Curvarum & alia problematum genera , applicuit & valde generalem reddidit, & idem significavit in Epistolis suis ad Collinium A. C 1672 & Oldenburgum A.C. 1676. Scripsit mox Leibnitius methodum inversam tangentium ab æquationibus et quadraturis non pendere & respondit Newtonus methodum hanc inversam etiam in potestate esse. Quibus omnibus admonitas. Leibnitius in eandem methodum incidit, ut ex verbis ejus hic positis cum epistola ejus ad Oldenburgum anno 1677 scripta collatis manifestum est. Vide supra pag.
b Nulla est hujusmodi analogia Differentiæ non sunt differentiæ summarum Leibnitius primam lucem methodi aliunde habuit.
.
* Quasi Leibnitius hoc non advertisset anno 1677, ubi primum incidit in methodum Newtoni. Vide Literas ejus supra impressas p. 90, 91. Certe Methodum Newtoni ante annum 1671 inventam fuisse, Leibnitius ex Literis ejus intellexerat; sed in Actis Lipsientibus hoc nunquam agnovit. Vide supra p. 70, 71, 72. Sic et se ab Oldenburgo series Newtonianas et Gregorianas in eunte anno 1675 accepisse, statim oblitus est. Vide p. 40, 41, 42, 45. Et methodum serierum se ab Oldenburgo postulasse & a Newtono accepisse, statum oblitus est Vide p. 45, 62, 98. Et problemata tangentium inversa ab æquationibus et quadraturis pendere se primum negasse & sub{in}de a Newtono didicisse, statim oblitus est Vide p 65, 85, 86, 93.
✝ Methodum fluxionum & methodum Differentialem esse unam et eandem methodum Leibnitius hic agnoscit; ideoque se communi nomine del a se designari Analyseos Infinitesimalis designare solere, licet in nonnullis differre possint, ut Analysis speciosa Dietæ & eæ Cartesij in nonnullis differunt. Quæritur quis sit Analyseos hujus Infinitesimalis inventor primus & siquid alter alterius inventis addiderit.
** Methodus Fatetur hic Leibnitius Tangentium per Differentias primam lucem ipsi affudisse id est methodus Archimedis a Fermatio Gregorio Barrovio restitutam & promotam, a Newtono ad quantitatum augmenta momentanea generaliter applicatam. Hujus methodi exempla in problemate tangentium directo (p 30) & inverso (p 86) in Quadraturis (p 72) & in Methodo serierum (p 15, 18, 19) Newtonus dederat, Et his admonitus D. Leibnitius in methodum tangentium animum intendit (p 46, 47, 87 88) & differentias in methodum generalem formavit (p. 88 89) & Newtonianæ similem esse esse statim ab initio vidit, p. 90, 91, 93.
** Fermatius determinando punctum flexus contrarij, hoc antea vidit.
‖ Nulla est hæc analogia. Differentiæ non sunt summarum differentiæ sed quantitatum augmenta infinite parva.
<146v>Hanc methodum tangentium Leibnitius animo revolvit (p 46, 47, 87, 88) generalem reddit (p 88, 89) & Newtonianæ similem esse statim videt, p. 90, 91, 93. Fermatij Gregorij Barrovij a Newtono ad quantitatum augmenta momentarea generaliter applicatam. Hanc Methodum tangentium . . . .
hoc est methodum quam Archimedes, Fermatius, Gregorius Barrovius coluere, Newtonus ad quantitatum augmenta momentanea generaliter applicuit. Hancce tangentium methodum Leibnitius animo revolvit (p 47, 87, 88) generalem reddit (p 88 89 & Newtonianæ similem esse statim vidit p 90, 91, 93.
a Gregorio editam anno 1668 in Mercatori{s} quam etiam Gregorius edidit anno 1668 in Mercatoris Quadratura demonstrata Prop. V.)
of as general extent for solving the same sorts of problems, & that Mr Newtons method was the older being found in or before the year 1671. He should not afterwards have pretended that when he published the elements of his differential method he knew nothing further of Mr Newtons method then that it was a method of drawing tangents without sticking at surds: but when his Principia Philosophiæ came abroad he then began to understand that his method was much more general. He should not two years after this book came abroad, three years after it was sent to the R. Society to be printed & above five years after the principal of those Propositions were communicated to the R. S. have published three papers for making himself the inventor of the principal of those Propositions & the first that had opened new ways of Geometry? For Mathematicians say that he had added nothing of truth to Mr Newtons Propositions that his thre papers are of no use but to make himself an inventor & that he has derived some of Mr Newtons Propositions from precarius Hypotheses & erroneous calculations instead of inventing them. When he undertook to give an Account of Mr Newton's book of Quadratures in the Acta Leipsica he should not have given an Account of his own method instead of Mr Newtons. He should not have represented his own method the older & Mr Newtons a substitute for he knew by his correspondence with Mr O. & by the letters published & interpreted by Dr Wallis that Mr Newton had the Method of Fluents in the year 1671.
Mr Leibnitz tells me that I knew the author of the Letter of 7 Iune 1713 inserted into the defamatory paper & blames me for calling him a Mathematician or pretended Mathematician — but because I did not know whether he was Mr Iohn Bernoulli or was only pretended to be him. For that Mathematician
& understanding by the same Letters that the method of tangents printed by Slusius agreed with Mr Newtons & was a Corollary of Mr Newtons general method (p. 30) he set his mind upon improving this method of tangents so as to bring it to a general method For in his journey home from Paris by London & Amsterdam he was upon a project of extending it to the solution of all sorts of problems by calculating a certain Table of Tangents as the most easy & useful way he could then think of & wrote of this designe to Mr Oldenburg in a Letter dated at Amsterdam 28 Nov. 1676 (pag 87) & therefore he had not then invented the differential method but was endeavouring to find out such a general method as Mr N. had described. In his last letter against Mr Keil (p 119) he represents that his friends know how he found this method in a very different manner from what . . . . . . . & then laid aside upon his finding that method p. 42. Now Mr Newton had told him that his method extended to Tangents of Mechanical Curves & to Quadratures Curvities & centers of gravity & of Curves in general & to inverse problemes of Tangents, & he was thereby sufficiently informed that the method was founded upon the consideration of the small particles of quantity called particles augmentas momentanea & moments by Mr Newton & infinitesimals indivisibles & Differences by Mr Leibnitz. For there is no other way of resolving any of those sorts of Problems then by considering these particles of quantity. And this consideration [especially after the receipt of Mr Newtons second Letter, was sufficient to make him lay aside his designe of calculating Tables of tangents &] might make him begin to think upon the methods of Slusius Barrow Gregory & Fermat who drew tangents by the proportion of the augmenta of the ordinates to the augmenta of the Abscissas. For he tells us that he found out the differential method by considering how to draw tangents by the differences of the Ordinates & how thereby to render the Method of Slusi{us} more general (p. 88.) & considered that as the summs of the Ordinates gave the Area so their differences gave the tangents & thence received the first light into the Differential method (p. 104) And with Slusius he gave the name of Differences to the moments of dignities. And when he had found the method he saw that it answered to the description which Mr Newton had given of his method in drawing of Tangents in rendring Problems of Quadratures more easy, & in bringing Problemes of Tangents to Equations & Quadratures p 88, 89, 90, 81, 93.
In his last letter against Mr Keil (p. 119) he represents that his friends know how he found the differential method in a very different manner from what Mr Keil surmised, & these words imply that he found it after he got home to his friends & by consequence in the year 1677. And most probably he found it upon the receipt of Mr Newton second Letter which gave him new light into it. For the publishing an opusculum upon a Series of Mr Gregory sent him by Mr Oldenburg was first suspended by his coming into business & then laid aside upon his finding the differential method p. 42.
Archimedes began the method of squaring curves & drawing tangents to them by considering the infinitesimals of quantity. Cavallerius & Fermat applied this method to Equations. Fermats method was first published by Herigon & Schooten Gregory Barrow & Slusius improved it for Tangents. Newton about the same time made it general, extending it (in conjunction with the method of series) to the solution of all sorts of difficulter Problemes Collins, Gregory, Slusius & others had notice of this general method in the year 1669. Leibnitz was in London in the year 1673 & there claimed the Differential method of Mouton. At that time there was not a mathematician of note in that city who was not acquainted with Collins & had not heard of the method & seen some of the series produced by it. & After he was gone thence to Paris he began to put in for first inventor of two series for the circle ( ) said they were both found by the same method (p ) & yet wrote afterwards for the Demonstration or method of finding one of them (p. .) In April 1675 Collins & Oldenburg sent him eight series found by this method, & he then knew none of them to be his own, or at least did not think it adviseable then to own any of them, but took time to consider them & compare them with his own & yet this same year he communicated the last of them ✝ as his own to his friends at Paris who knew not that he had received them from London.. The next spring one Mohr shewed him two series he had from Collins & then Leibnitz wrote to Oldenburg to procure him the Demonstration from Collins promising them a recompence & this he did without putting them in mind to ask Mr Newtons leave, tho by his own rule if he had got the Demonstration, that is, Mr Newtons method of Series, & claimed it as his own, Mr Oldenburg & Mr Collins were not to contradict him without authority from Mr Newton. Those two series were the same with the two first of the eight sent him by Mr Oldenberg, but he pretended to have forgot the receipt of those, & not to have seen the two before Mr Mohr brought them to him. Mr Oldenburgh & Mr Collins upon considering the matter, forbore to send him the method without Mr Newton's knowledge & wrote earnestly to Mr Newton to send it himself & MrNewton did so.
Mr Leibnitz had been now two or three years in quest of the method of series, & one of his essays was to subduct the negative termes from the affirmative in these & such like Progressions. &c. &c & thereby he came to these series &c &c. A quarter of the first series & half the second series, together with the last of the eight series sent him by Oldenburg made a harmony which he sent back to Mr Oldenburg to be communicated to Mr Newton in recompence for his method. For Mr Leibnitz knew that Mr Oldenburg & Mr Collins were not to make a discovery without authority from the Executors of Mr Gregory who had sent that series to Mr Collins in the year 1671, & was now dead.
In further recompence for Mr Newtons method Mr Leibnitz sent him method of his own by transmutation of figures, recommending it for a very general method of series, tho he wanted Mr Newton's method for finding the two series of Mohr, & Mathematition say that his transmutations are of little or no use & did not amount to general method before Mr Newton made it.
And tho he still wanted the method of deriving reciprocal series from one another & desired Mr Newton to send it to him (p 63): yet he could not forbear claiming some series from Mr Newton which were the result of that method. p. 61, 62 And when Mr Newton sent him the Method tho he understood it with difficulty, he wrote back that he had found it before, as he perceived by his old papers, but for want of a good example of its use had neglected it. p 96.
Newtons knowing any thing of the method, till Mr Newton by publishing his Principles convinced every body that he understood the method very well & how to make use of it & that it scarce differed from the differential method except in words & symbols, & the publishing of the correspondence by Dr Wallis justified that notion & made it appear beyond question that the method of fluents was in substance the same with the differential method. And then Mr Leibnitz pretended that he understood nothing of this when he published the elements of the differential method, nor then knew any thing more of Mr Newton's method then that it was a method of Tangents which stuck not at radicals & which any man might have without having the differential method p. 104, 107.
promising to recompence them with his own series very different from those of Mohr & this he did without desiring Mr Newtons leave, tho by his own rule if he had got the Demonstration . . . . . . . . . . & Mr Newton did so, & Mr Leibnitz in requital sent him back a harmony of series, one of which . . . . . . . . . Mr Newton's method in the year 1671 or before.
In further recompence . . . . . . . . . . had neglected it. p. 96.
he published the elements of it in the Acta Lipsica that is in the year 1674 or the beginning of the year following p. 119, And here his memory fails him againe for in those days he wrote his opusculum vulgari more & continued to polish it for the press till he fell into lasiness & found out his infinitesimal Analysis & was then of opinion that inverse problems of Tangents were not reducible to equations or quadratures, as has been said above.
Now if the plea of reputation candor & sincerity doth not make any man a witness in his own cause, & the pretence of finding things apart without proving the priority of invention is not to be regarded, & the allowance of either of these pretences would be unjust & prove an endless encouragement to pretenders; If the following Letters & Papers be well attested, & by them it appears that Mr Newton had the method of infinite series & fluxions in the years 1669 & 1671 & then applied it generally to the solution of Problems by the method of fluents & in the year 1671 wrote a larger treatise upon both those methods conjoined,] & that Mr Iames Gregory
His first endeavour was to make himself the inventor of the method of series. In the begining of the year 1673 when there was not a Mathematician of note in London who was not acquainted with Collins & had not heard of the method of Slusius he went from L. thence to Paris & pretended there to be the first inventor of two series for the circle both found by one & the same method ( 38) & In April 1675 Collins & Oldenburg sent him eight others: For he then knew none of the eight to be his own but took time to consider them & compare them with his own (p 40, 42) & yet the very same year he communicated to his friends at Paris an Opusculum written upon the last of the eight as his own series without letting them know that he had received it from England. p 41, 42. & the next year pretended to have forgot the receipt of the eight series, & desired Mr Oldenburg to procure him the Method from Mr Collins, calling it the demonstration of two series shewed him by one Mohr p. 45, & promised to recompence them with his own invention of series very different from those of Mohr, saying that they were the series of which he had written to him some years before p. 45. But when Mr Oldenburg received them they proved to be a harmony of series, one of which was the last of the eight series which Mr Oldenburgh had sent him the year before & the others were different & served only to make up the harmony being found by subducting the negative terms from the preceding affirmative ones in these & such like progressions & . The first progression gives this series . The second gives this And a quarter of the first series & half of the second & the series sent him by Oldenburg compose the harmony. p. 61. And tho the series sent him by Mr Oldenburg was sent by Mr Gregory to Mr Collins in the beginning of the year 1671 & a copy of Mr Gregory's letter was sent to Mr Leibnitz in summer 1676 whereby he could not but know that the series was Gregorys (p 47 yet he published it in the Acta Leipsica as his own without letting the world know that he received it from Oldenburg & Collins & that Collins had it from Gregory who found it by Newtons method in the in the beginning of the year 1671 or before.
A yeare or two after the publishing of Mr Newtons Principia Philosophiæ Mr Leibnitz having been long from home in a
And [wherin he prætended to have found the principall Propositions in Mr Newtons said book relating to the motions of the Planets] mathematicians say that in writing his Tentamen de motuum cœlestium causis he forgot to reexamin the process of finding his 19th Proposition which is the chief of Mr Newtons Propositions relating to the motions of the Planets & that no man could find that Proposition by such an erroneous process as he has set down. Errors are easily committed in calculations They blame him not for committing them but for pretending to find Mr Newtons Proposition by them, & publishing them hastily with a designe to make that Proposition his own. They blame him not for committing some errors in his first essay, but for adapting calculation to Mr Newtons Propopsition with intention to make it his own: but for adapting a calculation to another man's Proposition with a designe to make himself the first inventor, tho by the errors of the calculation it appears that he did not invent it. & yet allowing that Mr Newton by himself attained to principles like the differential method [& that Mr Keil is a young man unacquainted with things done before his time] by which allowance he seems to mean that although Mr Newton had the method of fluents in the year 1676 when he wrote his two Letters of 13 Iune & 24 Octob. & had not at that time heard of the Differential method, yet the differential method is the older., being known to Mr Leibnitz above nine years before
That the R. Society is satisfied in the fidelity of their Committee in printing no papers but such as appeared to them to be genuine & in omitting none which in their opinion made for Mr Leibnitz & particularly they are satisfied that the three Letters to Mr Collins in Iuly & Aug. 1669 found in the hand of Dr Barrow & the copy of the Analysis referred to in those Letters & found in the hand of Mr Collins are genuine, & that the Letter of Mr Iames Gregory to Mr Collins dated 15 Feb. 167 & found in the hand of the author & copied in the hand of Mr Collins, & the Letter of Mr Oldenburg to Mr Leibnitz dated 15 Apr 1675 & found in english in the hand writing of Mr Collins & in Latin in one of the letter Books of the R. Society (being translated into Latin by Mr Oldenburgh & the Answer of Mr Leibnitz dated from Paris 20 May 1675 & the Letter of Mr Leibnitz to Mr Oldenburgh dated from Paris 12 May 1676 & found in the hand writing of Mr Leibnitz among the ancient papers left by Mr Oldenburgh in the custody of the R. Society with notes on the back side in the hand of Mr Oldenburg & the Letter of Mr Newton to Mr Collins 10 Decem 1672 found in the hand of the author among the Papers of Mr Collins with a copy thereof in the hand of Mr Collins, & the Collection of the papers of Mr Iames Gregory sent to Mr Leibnitz at Paris 1676 & found in the hand of Mr Collins are all of them genuine. And we see no reason to doubt of the sincerity of any of the Letters published by Dr Wallis. And since Mr Leibnitz proposes to print a further Commercium Epistolicum if for giving credit to the Letters in his custody he pleases to take attested copies of such letters as he intends to publish & send the Originalls to any of the forreign ministers here, or to any other friend to be examined before a Committee of the R. S. by such as know the hands of Mr Oldenburgh, Mr Collins, Mr Newton, Mr Gregory, Dr Wallis, Dr Barrow &c, & to let attested copies be taken of them here: the Originals shall be returned with attested copies of any Letters in our custody which his friends shall think material to be published by him: by which means those Letters which he shall publish will become authentick & of indisputable credit & authority. which
A letter from Mr Leibnitz which being produced wherin he represents his inclination to publish a further Commercium Epistolicum which may serve for an history in Literatur & desires copies of such Letters as are in our hands to be published with those in his own custody: if for preventing disputes about the credit of the Originals he pleases after he has taken attested copies of them in his own custody, to send your Originals to any foreign Minister or other friend in England to be eximined before a Committee of the R. S. by such as know the hands of Mr Oldenburge, Mr Collins, Mr Gregory, Dr Wallis, &c & to let attested copies be taken of them here: the Originalls shall be returned, with attested copies of any letters in our custody which his friends shall desire, the Originalls of all the Letters & MSS in our custody printed or to be printed being also examined
4 Slusius in November 1672 gave notice of his new method of tangents to Mr O & communicated it to him in Ianuary following & founded it on three Lemmas the first of which was this. Differentia duarum Dignitatum ejusdem gradus applicata ad Differentiam Laterum dat partes singulares gradus inferioris ex binomio laterum. In general Let be the infinitely small difference of y & x & n the index of the dignity & the difference of will be :
5 Mr Newton being at that time desired by Mr Oldenburg to communicate his Method of Tangents, sent it to him in a letter dated 10 Decem 1672. [It proved to be the same with that of Slusius. And the same method was communicated by Hudden to Schooten in the year 1659. But Mr Newton deduced it from a Method much more general. For when he had described it he subjoyns] And subjoyned Hoc est unum particulare vel Corollarium potius Methodi Generalis . . . . . . . surdis sunt immunes. Newtons method of Tangents proved to be the same with that of Slusius. And it appeares since that the same method was communicated by Hudde to Schooten in 1659. But their methods were not so general as Newtons.
12 Mr Oldenburg 15 Apr 1675 sent to Mr Leibnitz several series one of which was that of Mr Gregory for finding the arch of a circle whose tangant is given. And Mr Leibnitz by his Letter of 20th May following owned the receipt of the Letter. Towards the end of the year Mr Gregory died & Mr Collins the next year at the request of Mr Leibnitz & some others collected extrats out of Mr Gregories Letters & Papers & sent them to Mr Oldenburg to be sent to Mr Leibnitz at Paris & returned back after they had been perused there. They were sent a little before the 11th of August 1676 as Mr Collins mentioned in a letter of that date written to the brother of the said Gregory. And Mr Tschurnhause being then at Paris in his Letter to Mr Old. dated 1 Sept 1676, has this reference to the Collection. Similia porro, saith he, quæ in hac re præstitit eximius Geometra Gregorius memoranda certe sunt, si quidem optimæ famæipsius consulturi sunt qui ipsius relicta MSS luci publicæ ut exponantur operam navabunt. In this Collection was a
6 Dr Wallis in his Arithmetick published A. 1657, Chap. 33 Prop. 68, tought how to reduce the fraction by perpet. divis. into the series .
7 Vicount Brounker squared the Hyperbola by this series that is, by this joyning every two terms into one. This was published in the Philosophical Transactions in April 1668.
8 Mercator by the Division of Dr Wallis demonstrated the Quadratures of Vicount Brounker after another manner & published it the same year about September.
9 The next year in August Dr Barrow communicated to Mr Collins the Analysis per Æquationes numero terminorum infinitas which is the first Tract in this Collection of Mr Iones. And Mr Collins thenceforward communicated several things out of it to his friends, [& one of the series for the Circle he communicated to Mr Iame Greg]
10 Mr Gregory having by a series sent to him by Mr Collins found Mr Newtons method of Series sent back to Mr Collins in the begining of the year 1671 several other series, & gave Mr Collins leave to communicate them freely. One of those series was for the arc of a circle whose tangent was given vizt
11 Mr Leibnitz was at London in the years 1671 1672 & 1673 till March & then went to Paris, & in 1674 wrote to Mr Oldenburg (15 Iuly) that he had a wonderful Theoreme which gave him the area of a circle or of any sector thereof in a series of rational numbers produced continually in infinitum & 26 October that by one & the same method he could find either the whole circumference or any arch whose sine was given tho the proportion of the arc to the whole circumference was not known. If the proportion was known this method or Wonderful Theorem gave him the whole circumference: if not it gave him at least the Arc. And in his Letter of May 12 1676 he desired Mr Oldenburg to help him to the demonstration of the Theorem, that is to Mr Newtons method of finding it
* Vpon reading this Letter before the R. Society, Mr Newton represented that these last words reflected upon the Committee of the R. S. as if they had printed things partially, & that as he did not print the Commercium Epistolicum himself but left it to the Committee to print what they thought fit least he should seem to make himself a witness in his own cause, so he did not think Mr Leibnitz a proper person to print a Commercium in his own cause. But if he had any ancient Letters which he had received from England & pleased to send the Originals to any friend in England who might produce them to be examined before the R. S. by such as knew the hands , & to let attested copies be taken of them: the Originals should be returned & the Letters might then be printed either in the Transactions or in Germany as Mr Committee to themselves in publishing the Commercium Epistolicum, represented further that he could have supplied the Committee with some ancient Letters of moment then in his own custody but forbore to do it least he should seem to make himself a witness in his own cause. And to prove the truth of what he said, he produced two original Letters written to himself the one by Mr Leibnitz from Hanover Mar. 1693, the other by Dr Wallis from Oxford 10 Apr. 1695 which direct{o} to a Passage in the Preface to the first Volume of his works where the Doctor (Homo vetus & intelligentissimus) gives his opinion very fully in this matter. And these two Letters, after they had been examined before the R. S. by persons who knew the hands were read to them , & left in their Archives & thence copied by Mr Newton in the Appendix to his Remarks printed above pag 100 & 105.
NB Vpon the reading of this Letter to the R. Society Mr Newton represented that he was so far from printing the Commercium Epistolicum himself that he did not so much as deliver to the Committee of the Society the Letters which he had in his own custody. And to prove this produced a letter of Mr Leibnitz dated & another of Dr Wallis dated both which after the hands had been examined were deposited in the Archives of the Society.
Here instead of proving his accusation against Dr Keill which he was bound to do in justice, he tells the R. Society that they are imprudent & unjust unless they will allow him to be a witness in his own cause against the Doctor And yet in that is to say the Royal Society are imprudent & unjust unless they will allow him to a witness in his own cause against Dr Keill.
Here again he reflects upon the prudence & justice of the R. S. telling them that: they are imprudent & injust if they suffer his candor to be questioned while he himself is questioning the candor of others. They are unjust unless they allow him (post tot documenta vitæ) to be a witness in his own cause, contrary to the laws of all nations.
7 Mr Leibnitz indeed was the first who published the invention of first differences. but he published nothing but what he might deduce from Mr Newtons Letters. For in Mr Newtons Letter to Mr Collins dated 10 Decem 1672, a copy of which was sent to him by Mr Old. among the extracts of Gregories Letters 26 Iune 1676, Mr Newton described a method of Tangents which he conjectured to be the same with the methods of Gregory & Slusius, & said that it was a branch or Corrollary of a general Method of solving the abstruser Problems without any troblesome calculus & without stopping at surds. And the method of tangents be described by the following example. Pone CB applicatam ad AB in quovis angulo dato terminarj ad quamvis Curvam CA, & dicatur AB x & BC y, habitudoque inter x et y exprimatur qualibet æquatione puta ,  qua ipsa determinatur Curva. Regula ducendi tangentem hæc est. Multiplica æquationis terminos per quamlibet progressionem Arithmeticam juxta dimensiones y, puta ; ut et juxta dimensiones x, puta Prius productum erit Numerator, et posterius divisum per x denominator Fractionis quæ exprimet longitudinem [subtangentis] BD ad cujus extremitatem D ducenda est Tangens CD. Est ergo longitudo . This far Mr Newton. And this is as much as to say that as all the terms of the æquation multiplied by the indices of the dignities of the abscissa x & divided by the abscissa x are to all the terms of the æquation multiplied by the indices of the dignities of the ordinate y & divided by the ordinate y, so is the Ordinate y=BC to the subtangent BD, & (by the method of tangents of Dr Barrow) so is dy to dx. And by multiplying the extremes & means you have the equation . [Or .] And this is as much as to say that if you multiply every term of the Æquation by the index of the dignities of x in that term & by & then multiply every terms by the indices of the dignity of y therin & by dy & put the summ of all the terms produced equall to O you will have an Equation involving the differences of x & y vizt. And is the solution of the first Proposition of Book of Quadratures when there are but two indeterminate quantities. And when there are more, the same operation applied to them all gives the solution. And this is the solution of the Proposition Data æquatione fluentes quotcunque quantitates involvente invenire fluxiones. which is the first Proposition of the Book of Quadratures. which was set down in Mr Newtons Letter of 24 Iune 1676 & published in his Book of Principles. And therefore Mr Newton understood the solution of this Proposition in the year 1672, & Mr Leibnitz had sufficient light into it from the copy of the said Letter in the year 1676, besides the light which he received into it from Mr Newtons Letters of Iune 13 & Octob. 24. 1676. And what he published in the Acta Eruditorum in the year 1684 amounts to nothing more then the solution of this Proposition. I cited Dr Barrow's method of Tangents because Mr Leibnitz procured the Doctors Lectures when he was in London the second time, & carried them with him into Germany; & in his Letter of 21 Iune 1677 deduced from thence the method of Tangents of Slusius as Gregory had done before. For Gregory tells us this in his Letter to Collins 5 Sept. 1670, a coppy of which was sent to Mr Leibnitz in the Excerpta of Gregories Letters 26 Iune 1676.
qua ipsa determinatur Curva. Regula ducendi tangentem hæc est. Multiplica æquationis terminos per quamlibet progressionem Arithmeticam juxta dimensiones y, puta ; ut et juxta dimensiones x, puta Prius productum erit Numerator, et posterius divisum per x denominator Fractionis quæ exprimet longitudinem [subtangentis] BD ad cujus extremitatem D ducenda est Tangens CD. Est ergo longitudo . This far Mr Newton. And this is as much as to say that as all the terms of the æquation multiplied by the indices of the dignities of the abscissa x & divided by the abscissa x are to all the terms of the æquation multiplied by the indices of the dignities of the ordinate y & divided by the ordinate y, so is the Ordinate y=BC to the subtangent BD, & (by the method of tangents of Dr Barrow) so is dy to dx. And by multiplying the extremes & means you have the equation . [Or .] And this is as much as to say that if you multiply every term of the Æquation by the index of the dignities of x in that term & by & then multiply every terms by the indices of the dignity of y therin & by dy & put the summ of all the terms produced equall to O you will have an Equation involving the differences of x & y vizt. And is the solution of the first Proposition of Book of Quadratures when there are but two indeterminate quantities. And when there are more, the same operation applied to them all gives the solution. And this is the solution of the Proposition Data æquatione fluentes quotcunque quantitates involvente invenire fluxiones. which is the first Proposition of the Book of Quadratures. which was set down in Mr Newtons Letter of 24 Iune 1676 & published in his Book of Principles. And therefore Mr Newton understood the solution of this Proposition in the year 1672, & Mr Leibnitz had sufficient light into it from the copy of the said Letter in the year 1676, besides the light which he received into it from Mr Newtons Letters of Iune 13 & Octob. 24. 1676. And what he published in the Acta Eruditorum in the year 1684 amounts to nothing more then the solution of this Proposition. I cited Dr Barrow's method of Tangents because Mr Leibnitz procured the Doctors Lectures when he was in London the second time, & carried them with him into Germany; & in his Letter of 21 Iune 1677 deduced from thence the method of Tangents of Slusius as Gregory had done before. For Gregory tells us this in his Letter to Collins 5 Sept. 1670, a coppy of which was sent to Mr Leibnitz in the Excerpta of Gregories Letters 26 Iune 1676.
10 In the end of the year 1715 Mr Leibnitz in the Postscript of a Letter to Abbe Conti wrote thus: They that have writ against me have made no difficulty to attack my candour by interpretations forced & ungrounded: they shall not have the pleasure to see me answer to the slender to reasons of a sort of men who use me so ill &c. If this was the case he should have shewn by some instances wherein they had misinterpreted the originall Letters. The Notes upon the Letters are of no authority but what they derive from the Letters. And the Reader is judge of that. Neither the Letters nor the Notes upon them have hitherto been answered & therefore they are now published as unanswerable
11 Mr Newton in his Answer to the said Postscript dated 26 Feb. 171 pressed Mr Leibnitz in these words. Mr Leibnitz has hitherto refused to answer, knowing well that it is impossible to answer to matters of fact. For a pretence to his silence he alledges at present that he has not seen the Book, & that he has not leasure to examin it, but has desired a famous Mathematician to do it &c. And Mr Leibnitz in his Answer to Mr Newtons Letter, 9 Apr. 1716 still excused himself from answering saying: For writing an answer from point to point, to the work published against me, it would require a work as big at least as that one must enter into a great detail of the quantity of minutes which passed 30 or 40 years ago, wherof I remember but little; I must search my old Letters, many of which are lost, besides that for the most part I kept no minutes of my own, & the rest are buried in a great heap of papers which I cannot search out without a great deal of time & patience. But I have no leasure to do it, being charged at present with business of quite another nature. Thus far Mr Leibnitz. He had time to keep a large correspondence by Letters & enter into Metaphysical disputes: but had no time to shew any defect or flaw in flaws in the Epistles or Notes upon them . However, upon his death which happened in November following his friends gave out quod Commercio Epistolico Anglorum aliud quoddam suum idemque amplius opponere decreverat as you may see in his Elogium printed in the Acta Eruditorum for Iuly 1717.
4B. In the flying Paper above mentioned Mr Leibnitz wrote: Certe aut miram ejus [Newtoni] oblivionem esse oportet aut magnam contra conscientiæ testimonium iniquitatem, si accusationem (ut ex indulgentia colligas) probat, qua quidam ejus asseclæ etiam seriem, quæ arcus circularis magnitudinem ex tangente exhibet, a Gregorio hausisse Lei. . . . um volunt. And Mr Newton in his Letter to Abbe Conti dated 26 Feb 1617 to be communicated to him, pressed him about this matter in these words. In his Letter of 20 May 1675 he acknowledged — — — dated 15 Feb. 1671 (your self being one of them) These Letters were compared with the print Baron Kilmanseg being present. And Mr Leibniz in his Letter to Madam Kilmansegg 19 Apr 1716 in mentioning this series endeavoured to excuse himself by saying that Mr Newton himself applauded it. It was found afterwards that one named Mr Gregory had found just same series with him But that was what he understood late. He was therefore at length satisfied by these Letters that Gregory had found the same series. Abbe Conti & several other Gentlemen (amongst whom was Count Kilmansegg) having viewed the Originals & compared them with the printed copies: Mr Leibnitz in a letter to the Countess did not think fit to question what had been approved, but endeavoured to excuse himself as well as he could, as if he had not read the Letters of Mr Oldenburg when he first reccived them. So then the credit of the Letters in the Commercium is still safe.
<154r>8 Mr Leibnitz in a Letter to Mr Chamberlain dated from Vienna 25 Aug. 1714 wrote that it being probable that there were still some Letters that regarded him among those of Mr Oldenburg & Mr Collins, which were not yet published, he desired that the R. S. would give order to communicate them to him. For, said he, when I return to Hannover, I may also publish a Commercium epistolicum which may serve for Histoire Litteraire. I shall be disposed no less to publish the Letters which may be alledged against me then those that favour me & leave the jugment to the publick. But upon reading this to the Society, it was represented that these words reflected upon their Committee & that as they had not referred it to him but to a Committee of other persons to Collect & publish the ancient Letters so Mr Leibnitz was not to be made a juge in his one cause. That If he had any ancient letters relating to this matter they ought to be examined & allowed by other people before they were printed. That they might send him attested copies of any Letters, but were not to part with the Originals, & that he himself had Originall letters relating to this matter, but did not produce then to the Committee because he would not make himself a witness in his own cause. And to prove this he produced two old Letters one of Mr Leibnitz dated March 1693 & another of Dr Wallis dated 10 April 1695, both written to himself. And the Letters being examined before the R. Society by those who knew the hands, were laid up in their Archives.
9 In the end of the year 1715 & beginning of the next year Mr Leibnitz — – – – – different from himself. By this citation he is a witness that Mr Iohn Bernoulli was not the author. By printing the Letter in Latin with this citation Mr Leibnitz is a witness that Bernoully was not the author. And Mr Bernoulli by affirming per omnia humanitatis sacra that he wrote no such Letter is a third witness. And the style & contents of the whole flying paper points at Mr Leibnitz for the author thereof. For the word illaudibiles is peculiar to Mr Leibnitz. No body but Mr Leibnitz could know what passed between him & Mr Huygens at Paris 38 years before. Mr Leibnitz in the year 1684 published the elements of the method by Addition Substraction Multiplication & Division & called this the Algorithm of his method. And the Mathematician objects that ♁♁ that he did not beleive that Mr Newton when he wrote his Principles & before, did so much as dream of his calculus of fluxions & fluents or the reduction thereof to general Analytical operations ad instar Algorithmi vel Regularum Arithemticarum. The word Algorithmus in this sence is peculiar to Mr Leibnitz & the Argument goes beyond what Bernoulli ever affirmed. And if Mr Bernoulli had been the author of the Letter of 7th Ione it would have been act of plagiary in Mr Leibnitz to leave out the sentence in which Bernoulli is cited by the author. Mr Leibnitz by correcting has confessed it to be his own.
<154v>5 In this flying Paper it is represented that when the ancient Epistles published in the Commercium Epistolicum were written Mr Newton did not so much asdream of the Method of fluxions because there are no prickt Letters in all the Commercium; no not in this Principia Philosophia. And is not this as trifling as if one should say that when Mr Newton wrote his Introduction to his Book of Quadratures in which he explains the method of Fluxions in words at length & illustrated his explanation with examples in solving of Problems, he did not so much as dream of the method of Fluxions, because there are no prickt letters in all that Introduction. And when he wrote the second Lemma of this second Book of Principles & added a Scholium in which he said that the foundation of the Method of fluxions was conteined in that Lemma & that in his correspondence with Mr Leibnitz in the year 1676 he had couched it in this sentence ; Data æquatione fluentes quotcunque quantitates involvente fluxiones invenire et vice versa: he did not so muc{h} as dreame of the method of fluxions when he wrote those things because ther are no prict letters in what he then wrote. When he wrote his Analysis per series which Dr Barrow in the year 1669 sent to Mr Collins he used the symbol in the very same sense in which Mr Leibnitz afterwards used the symbol , & the symbols ov, , oy, in the very same sense in which Mr Leibnitz afterwards used the symbols dx, dz & therefore in the year 1664 did at least dream of the method which Mr Leibnitz afterwards called summatory & differential.
I said in my Letter of 24 Octob 1676 that I wrote a Tract five years before concerning the method of Series & another method together, & said then that the other method proceeded without sticking at surds, & was founded on this Proposition: Data æquatione fluentes quotcunque quantitates involvente, Fluxiones invenire; & vice versa. And the two parts of this Proposition imply the direct & inverse methods of fluxions, called by Mr Leibnitz the differential & summatory methods. And in that Letter I said further that the method there spoken of, extended to Problems about maxima & minima, & about tangents directly & inversely, & Quadratures & to some other Problems; & gave me the general Series there set down for Quadratures & other Series of like nature. And in my Letter of 10 Decem. 1672 (a copy of which was sent by Mr Oldenburge to Mr Leibnitz & came to his hands) I mentioned some other sorts of Problems, & particularly those of finding the curvatures of Curves, & the tangents of Mechanical Curves. And in my Letter of 13 Iune 1676 I said that my Analysis (composed of the method of Series & other methods vizt the methods of fluxions & arbitrary series) extended to almost all sorts of Problems except perhaps some numeral ones like those of Diophantus. And Mr Leibnitz in his Letter of Aug. 27. 1676 replyed that he did not beleive that my method could be so general, or extend to inverse Problemes of tangents & many others: All those things are old. And if all this, & the Analysis per series numero terminorum infinitas, & with my Letter to Mr Collins Novem 8 1676 published by Mr Iones, & the consent of the Book of Quadratures with all the rest, & with my Letter to Mr Collins Novem 8 1676 published by Mr Iones, be not sufficient security: no man must hereafter venture to Communicate any thing in writing, before he has secured it to himself by publishing it in print. And if after such a concession as Mr Leibnitz made in these his Letters now recited & printed seventeen years ago, men may be allowed to go back upon any pretence whatever: even printing will be no security after witnesses are dead.
Part of a Letter of Dr Wallis to Mr Leibnitz Iuly 30. 1697
Optaverim item ut tibi vacet tuum Calculum Differentialem & Newtono suam Fluxionum Methodum, justo ordine exponere; ut quid sit utrique commune et quid intersit discriminis, et utramque distinctius intelligamus.
NB The doctor here wishes that the common method as due to me & the improvements as due to Mr Leibnitz were stated between us. And Mr Leibnitz returned no answer to this but under the colour of having improved the method went on to call it his own, & at length when my witnesses were dead, & he thought himself strong enough in disciples fell foul upon Dr Keill for saying nothing more then what Dr Wallis had said before without being complained of. And in his Letter of 29 Decem 1711 claimed a right to the whole method & pressed that I would declare my opinion in this matter; that is that I would retract what I had published in the Introduction to the book of Quadaratures & what Dr Wallis had published in the Preface to the two first Volumes of his Works, & what Mr Leibnitz himself had in those days conceded to the Doctor.
The next year Mr Leibnitz acknowledged that I was the first that had proved by a specimen made publick, that I had that part of the Method whereby the Solidum minimæ resistentiæ, the linea celerrimi descensus & the Curva Catenaria & velaria were invented.
And after all this when I wrote the Introduction to the Book of Quadratures which (to the best of my memory) was in the year 1703 or 1704 I did not suspect that I should be called to account for saying there that I invented the Method of fluxions by degrees in the year 1665 & 1666; the seven or eight years after be required to give my opinion in this matter, in order to make me retract, & be put to all this trouble in defending my self.
The next year Mr Leibnitz in his Answer to Mr Fatio
Out of the Answer of Mr Leibnitz published in the Acta Lipsiensia for May 1700
Certe cum Elementa – – – – satis intelli. — prodiere.
NB Let the first part of this sentence be compared with my Letters of 10 Decem 1672, & 24 Octob 1676 both which came to his hands & with his own Letter of 21 Iune 1677: & let the latter part thereof be compared with his Letter of March 1693 printed above, & with his concession that I was the first who had proved by a specimen made publick, that I had that part of the infinitesimall Calculus by which the Solidum rotundum minimæ resistentiæ & the Curva celerrimi descensus, were invented.
After all this, when I wrote the Introduction
NB. The first part of this Answer should have been made to Dr Wallis had it been consonant to our Letters of 10 Decem. 1672, 24 Octob. 1676 & 21 Iune 1677. The second part admits of no retraction upon a pretence that I had deceived him. The third part seems to relate to the place above mentioned in the Preface to the first & second Volumes of the Doctor worth concerning the likeness of the methods. In the same Answer he acknowledged that I was the first who had proved by a specimen made publick that I had that part of the infinitesimal calculus by which the Solidum rotundum minimæ resistentiæ & the Curva Celerrimi descenses &c were invented. Mr Fatio returned an Answer to Mr Leibnitz but the Editors of the Acta would not print it, & what it was I do not know.
— & then challenged Mr Fatio to solve the Probleme of Mr Bernoulli for finding a Series of Curves which should cut another given series at right angles. Which makes it probable that M. Bernoulli hath ever since reserved the solution of that Problem for a challeng.
Consessus Arbitrorum Delectorum a Societate Regia, ad quam D. Leibnitius provocaverat ad Calcem hujusce Commercij Epistolicis annexas. Ea est ut sequitur, occasione nata ex Vindicatione hujus Inventionis suo proprio Autori a D. Iohanne Keill nunc Professore apud Oxonienses & [Literis D. Leibnitij a Regia Societate remedium petentis, nempe ut ipsis Iudicibus, Keilius] publice sententiam suam] et provocatione D. Leibnitij ad judicium R. Societatis.
2 In my Letter of 24 Octob 1676 I represented that five years before that time that is in the year 1671 I wrote a Book of this Method & the method of series together but for the sake of quiet desisted from my designe of publishing it, The Book is still in being, & conteins a very plain description of those two methods. The first Proposition of the Book of Relatione quantitatum fluentium inter se data fluxionum relationem determinare. In the year 1684 Mr Craig desired me to explain to him the elements of the differential calculus then newly printed in the Acta Eruditorum. I did so & told him that it was my method in another dress as would appear if the Letters which past between me & Mr Leibnitz seven or eight years before should be published & Mr Craig is still alive & remembers this. Dr Wallis in the Preface to the two first Volumes of his works printed in spring 1695 wrote that in those Letters I had explained to Mr Leibnitz the Method, found by me 10 years before or above that is in the year 1666 or before. In the Account of these two Volumes published in the Acta Eruditorum the next year this passage was taken notice of & not contradicted. Dr Wallis in a letter dated 1 Decem. 1696 gave notice of this passage to Mr Leibnitz, & in the Letters which followed between them it was not contradicted. Dr Wallis in the 3d Volume of his workes published the Letters which had passed between me & Mr Leibnitz in the years 1676 & 1677. And Mr Fatio the same year (viz 1699) published that I was the oldest inventor by many years & confirmed his opinion by what he had seen in my manuscripts, & Mr Leibnitz in his answer did not contradict him And all this was done without any encouragement from me. In the year 1704 I published (in the Introduction to my book of Quadratures) that I found the method of fluxions by degrees in the years 1665 & 1666. For this was not yet disputed. But Dr Wallis being now dead, the Leibnitians in the Acta Eruditorum for Ianuary 1705 in giving an Account of the Introduction to this book published the Passage above mentioned, & there by the world was told that I did not invent the method so early nor write a book upon it in the year 1671 nor mention it in my Letters of 13 Iune & 24 Octob 1676 was the first inventor but had & 10 Decem 1672 nor always used fluxions for the Leibnitian differences even as Faber had substituted motions for the method of Cavallerius. With this Accusation the dispute began, & Mr Leibnitz has made this accusation his own by saying in his Letter of 29 Decem. 1711 Frustra ad Exemplum Actorum Lipsiensium [Keilius] provocat ut sua dicta excuset; in illis enim circa hanc rem quicquam cuiquam detractum non reperio sed potius passim suum cuique tributum. In the same Letter he refused to contend with Dr Keill because the Dr was not authorised by me, & desired that I would give my opinion in this matter, that is, that I would either condemn Dr Keill & retract what Dr Wallis Mr Fatio & I had published some years before or enter into the lists with him as he expresses himself in his last letter. And by this attaque he [has given Dr Wallis Mr Fatio & me the lye & charged me with plagiary & ought to prove the accusation upon pain of being deemed guilty of calumny] is the aggressor
Dr Wallis affirmed that Mr Newton explained to Mr Leibnits in the year 1676, Mr Newton never allowed that Mr Leinitz had the Differential method before the year 1677. And Mr Leibnitz himself in the Acta Eruditorum for April 1691 pag 178 acknowledged that he found it after he returned home from Paris to enter upon business. And as for the pretended method of infinite series it is of little or no use. I do not know that any other use has been made of it then to colour over the pretence of Mr Leibnitz to the Series of Mr Gregory.
Mr Leibnitz in his Answer to Mr Fatio printed in the Acta Eruditorum for the year 1700 pag. 203, wrote thus. Spee [Newtonus] scit unus omnium optime, satisque indicavit publice cum sua Mathematica Naturæ Principia publicaret, Anno 1687 nova quædam inventa Geometrica quæ ipsi communia mecum fuere NEVTRVM LVCI AB ALTERO ACCETPÆ, sed meditationibus quemque suis debere, & a me decennio ante [i.e. anno 1677] exposita fuisse. In the Book here referred unto Mr Newton did not acknowledge that Mr Leibnitz found this Method without receiving light from the three above mentioned Letters, & Dr Wallis told him the contrary without being confuted or contradicted; & if he had found it without the assistance of Mr Newton, yet second inventors have no right.
Mr Leibnitz in his aforesaid Answer to Mr Fatio , wrt also. Certe cum elementa — — — — satis intellexi. Here he again acknowledged that the Book of Principles gave him great light into Mr Newton Method: & yet he now denyes that this book conteins any thing of that Method in it. Here he pretended that before that book came abroad he knew nothing more of Mr Newtons inventions then that he had a certain method of Tangents, & that by that book he received the first light into Mr Newtons method of fluxions. But in his Letter of Iune 21 1677 he acknowledged that Mr Newtons method extend also to Quadratures & was like his own. His words are: Arbitror quæ — — — differentialem. Mr Newton had in his three Letters above mentioned (copies of which MrLeibnitz had received from Mr Oldenburgh) represented his method so general as by the help of Equations both finite & infinite to determin maxima & minima, tangents, areas, solid contents, centers of gravities , lenghts & curvities of Curve lines & curvilinear figures even without taking away radicals & to extend to the Curves usually called Mechanical, & to inverse Problems of tangents & others more difficult, & to almost all Problemes except perhaps some numeral ones like those of Diophantus. And Mr Leibnitz in his Letter of 27 Aug. 1677 represented that he could not beleive that Mr Newtons method was so general. Mr Newton in the first of the three Letters had set down his method of Tangents deduced from this general method & illustrated with an example, & said that this Method of Tangents was but a branch or corollary of his general method, & that he took the method of Tangents of Slusius to be of the same kind; & thereupon Mr Leibnitz in his return from Paris through England & Holland into Germany was considering how to improve the method of Tangents of Slusius & extend it to all sorts of Problems, as we have shewed above out of his Letters. ② Mr Newton in the last of the said three Letters added that his Method gave Theoremes for Quadratures by series which brake off & became finite when the Quadrature might be expressed in a finite equation, & set down the first Theorem with several examples. ① Mr Newton in his second Letter shewed how to resolve any dignity of a Binomium into a series, & its well known that if the second term of the Binomium be indefinitely small, the second term of the series will be the first difference of the Dignity, & the following terms will be proportional to the following Differences. ② Mr Newton also in the last — — examples. And after Mr Newton had made so large an explanation of his method, & Mr Leibnitz had got light into it, & in his Letter of Iune 21 explained how the method which he was fallen into answered to the discription which Mr Newton had given of his Method in drawing Tangents, giving the Method of Slusius, proceeding without taking away fractions & surds & faciliating Quadratures: to tell the Germans that when he first published his Differential he knew nothing more of Mr Newtons Inventions then that he had a certain method of Tangents is very extraordinary, & wants an explanation.
When Mr Leibnitz first published his Differential Method – – – – – some years before the year 1676. It was not enough to mention a methodus similis without saying – – – – candor & justice.
The Editors of the Acta Eruditorum have represented that Mr
[1] Quest 22.
[3] vid Com Epist. pag
[4] {Vid} Comm: Epist. p.
[5] ‡ In writing that book he had frequent occasion to consider the increase or decrease of the velocities with which quantities are generated & argues right about it That increase or decrease is the second fluxion of the quantity, & therefore he had not then forgotten the method of second fluxions.

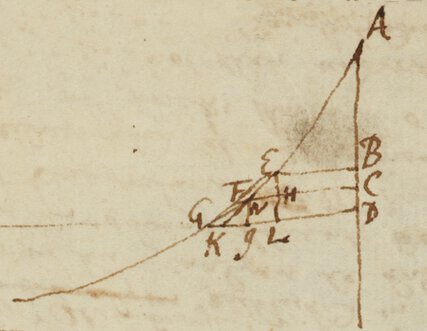 . . . . . .
. . . . . .  . . . . . . . Or .
. . . . . . . Or .