Unpublished Appendix to 'methodus': Problem IX

<33>

innititur: quæque magis perspicua et ornata evadet si fundamenta quædam pro more methodi syntheticæ præsternantur; qualia sunt haec.

< insertion from between the lines >

Axiomata.

< text from p 33 resumes >

Axioma 1. Quæ fluxionibus æqualibus simul generantur sunt æqualia.

Axioma 2. Quæ fluxionibus in data ratione simul generantur, sunt in ratione fluxionum.

Nota , simul generari intelligo quæ tota eodem tempore generantur.

Axioma 3. Fluxio totius æquatur fluxionibus partium simul sumptis.

Ubi nota quod profluxiones affirmativè ac defluxiones negativè ponendæ sint.

< insertion from lower down the right margin > < text from p 33 resumes > < insertion from higher up the right margin >

Axioma 4. Fluxiones sunt ut momenta contemporanea fluxionibus istis generata.

< text from p 33 resumes > < insertion from lower down the right margin >

Axioma 4. Momenta contemporanea sunt ut fluxiones.

< text from p 33 resumes >

Theoremata.

Theorema 1. Positis quatuor perpetuò proportionalibus fluentibus quantitatibus: summa extremarum reciprocè ductarum in suas fluxiones æquatur summæ mediarum reciprocè ductarum in suas fluxiones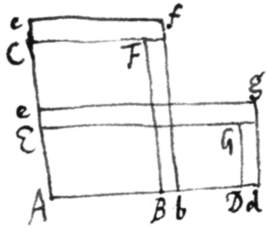. <34> /> {.} Sit $\mathrm{AB}.\mathrm{AD}\colon\colon \mathrm{AE}.\mathrm{AC}$, et erit $\mathrm{AB}\times fl:\mathrm{AC}+\mathrm{AC}\times fl:\mathrm{AB}=\mathrm{AD}\times fl:\mathrm{AE}$$+\mathrm{AE}\times fl:\mathrm{AD}$. Nam augeantur hæ lineæ momentis suis Bb, Dd, Ee, Cc fluendo, & propter perpetuam earum proportionalitatem, adeoque rectangula ab extremis et medijs constituta perpetuo æqualia nempe $\mathrm{AF}=\mathrm{AG}$ & $\mathrm{Af}=\mathrm{Ag}$; augmenta rectangulorum istorum BFCf & DGEg æqualia erunt: hoc est $\mathrm{Ab}\times \mathrm{Cc}\left(\mathrm{Cf}\right)$$+\mathrm{AC}\times \mathrm{Bb}\left(\mathrm{bF}\right)=\mathrm{Ad}\times \mathrm{Ee}\left(\mathrm{Eg}\right)+\mathrm{AE}\times \mathrm{Dd}\left(\mathrm{dG}\right)$. * < insertion from the left margin > * sive $\mathrm{Ab}+\mathrm{AC}\times \frac{\mathrm{Bb}}{\mathrm{Cc}}=\mathrm{Ad}\times \frac{\mathrm{Ee}}{\mathrm{Cc}}+\mathrm{AE}\times \frac{\mathrm{Dd}}{\mathrm{Cc}}$. Adeoque cùm fluxiones sint ut momenta quantitatum ab istis continuò generata, hoc est $\frac{\mathrm{Bb}}{\mathrm{Cc}}=\frac{fl\mathrm{AB}}{fl\mathrm{AC}}${,} $\frac{\mathrm{Ee}}{\mathrm{Cc}}=\frac{fl\mathrm{AE}}{fl\mathrm{AC}}$ & $\frac{\mathrm{Dd}}{\mathrm{Cc}}=\frac{fl\mathrm{AD}}{fl\mathrm{AC}}$, erit $\mathrm{Ab}+\mathrm{AC}\times \frac{fl\mathrm{AB}}{fl\mathrm{AC}}=\mathrm{Ad}\times \frac{fl\mathrm{AE}}{fl\mathrm{AC}}+\mathrm{AE}\times \frac{fl\mathrm{AD}}{fl\mathrm{AC}}$. Sive $\mathrm{Ab}\times fl\mathrm{AC}+\mathrm{AC}\times fl\mathrm{AB}=\mathrm{Ad}\times fl\mathrm{AE}+\mathrm{AE}\times fl\mathrm{AD}$. < text from p 34 resumes > Decrescant jam rectangula Af et Ag donec in prima rectangula AF & AG redierint, & tunc Ab evadet AB atque Ad evadet AD. Quare in ultimo istius infinitè parvæ defluxionis momento, hoc est in primo momento fluxionis quadrangulorum AF et AG quando incipiunt augeri vel diminui, erit $\mathrm{AB}\times fl:\mathrm{AC}+\mathrm{AC}\times fl\mathrm{AB}=$$\mathrm{AD}\times fl\mathrm{AE}+\mathrm{AE}\times fl\mathrm{AD}$. Q.E.D.

Corollarium 1. Positis tribus continuè proportionalibus, summa extremarum reciproce ductarum in suas fluxiones æquatur duplo mediæ ductæ in suam fluxionem. Sit $\mathrm{A}.\mathrm{B}\colon\colon \mathrm{B}.\mathrm{C}$ et erit $\mathrm{A}\times fl:\mathrm{C}+\mathrm{C}\times fl:\mathrm{A}(=$^*[1]$\mathrm{B}\times fl:\mathrm{B}+\mathrm{B}\times fl\mathrm{B})$$=2\mathrm{B}\times fl\mathrm{B}$.

Corollarium 2. Positis tribus continuè proportionalibus $\mathrm{A}.\mathrm{B}.\mathrm{C}$ si summa extremarum sit data quantitas, fluxio minoris extremæ erit ad fluxionem mediæ ut duplum mediæ ad differentiam extremarum. $2\mathrm{B}.\mathrm{C}-\mathrm{A}\colon\colon fl\mathrm{A}.fl\mathrm{B}$. Nam cùm $\mathrm{A}+\mathrm{C}$ ex Hypothesi non fluat, ^*[2] erit $fl:\mathrm{A}+fl:\mathrm{C}=0$, sive <35> /> $fl\mathrm{C}=-fl\mathrm{A}$. adeoque $\mathrm{A}\times fl:\mathrm{C}=-\mathrm{A}\times fl\mathrm{A}$. Quare $\stackrel{\_}{\mathrm{C}-\mathrm{A}}\times fl\mathrm{A}$$\left(=\mathrm{A}\times fl:\mathrm{C}+\mathrm{C}\times fl\mathrm{A}\right)$^*[3]$=2\mathrm{B}\times fl\mathrm{B}$, hoc est $2\mathrm{B}.\mathrm{C}-\mathrm{A}\colon\colon fl\mathrm{A}.fl\mathrm{B}$.

Corollarium 3{.} Sin differentia extremarum detur, fluxio alterutrius extremæ erit ad fluxionem mediæ, ut duplum mediæ ad summam extremarum. $2\mathrm{B}.\mathrm{A}+\mathrm{C}\colon\colon fl\mathrm{A}.fl\mathrm{B}$. Demonstratur ut Corollarium 2.

Corollarium 4. Quod si summa primæ et secundæ quantitatis detur, erit fluxio secundæ ad fluxionem tertiæ ut prima ad duplum secundæ auctum tertia. $\mathrm{A}.2\mathrm{B}+\mathrm{C}\colon\colon fl\mathrm{B}.fl\mathrm{C}$. Nam cùm ex Hypothesi $\mathrm{A}+\mathrm{B}$ non fluat, ^*[4] erit $fl\mathrm{A}+fl\mathrm{B}=0$ sive $fl\mathrm{B}=-fl\mathrm{A}$, adeoque $\mathrm{C}\times fl\mathrm{B}=-\mathrm{C}\times fl\mathrm{A}$. Quare $\mathrm{A}\times fl\mathrm{C}$$\left(=2\mathrm{B}\times fl\mathrm{B}-\mathrm{C}\times fl\mathrm{A}\right)=2\stackrel{\_}{\mathrm{B}+\mathrm{C}}\times fl\mathrm{B}$; hoc est $\mathrm{A}.2\mathrm{B}+\mathrm{C}\colon\colon fl:\mathrm{B}${$.$}$fl:\mathrm{C}$.

Corollarium 5. Si denique differentia primæ et secundæ datur erit fluxio alterutrius ad fluxionem tertiæ ut prima ad duplum secundæ diminutum tertia. $\mathrm{A}.2\mathrm{B}-\mathrm{C}$$\colon\colon fl\mathrm{B}.fl\mathrm{C}$. Demonstratur ut Corollarium 4.

Corollarium 6. Positis quotcuncue continuè proportionalibus, quarum una sit data quantitas & cæteræ fluentes: fluxiones fluentium erunt inter se ut fluentes illæ ductæ in numerum terminorum quibus distant a dato illo termino. Sint $\mathrm{A}.\mathrm{B}.\mathrm{C}.\mathrm{D}.\mathrm{E}.\mathrm{F}.$ continuè proportionales et si datur C, erit $-2\mathrm{A}.-\mathrm{B}.\mathrm{D}.2\mathrm{E}.3\mathrm{F}\colon\colon fl\mathrm{A}.fl:\mathrm{B}.fl\mathrm{D}.fl\mathrm{E}${$.$}$fl\mathrm{F}$. Nam propter $\mathrm{C}.\mathrm{D}.\mathrm{E}∺$, est $\mathrm{C}\times fl\mathrm{E}+\mathrm{E}\times fl\mathrm{C}=$$2\mathrm{D}\times fl\mathrm{D}$, per Corollarium 1. At ex Hypothesi $fl\mathrm{C}=0$. Ergo $\mathrm{C}\times fl:\mathrm{E}=2\mathrm{D}\times fl\mathrm{D}$. hoc est $fl\mathrm{D}.fl\mathrm{E}\left(\colon\colon \mathrm{C}.2\mathrm{D}\right)\colon\colon \mathrm{D}.2\mathrm{E}$.

Iterum quia $\mathrm{D}.\mathrm{E}.\mathrm{F}∺$, erit $\mathrm{D}\times fl:\mathrm{F}+\mathrm{F}\times fl:\mathrm{D}=$$\mathrm{E}\times 2fl\mathrm{E}$. sive $\mathrm{D}\times fl\mathrm{F}=$$\mathrm{E}\times 2fl:\mathrm{E}-\mathrm{F}\times fl:\mathrm{D}$. Sed e jam ostensis est $fl\mathrm{D}.fl\mathrm{E}\left(\colon\colon \mathrm{D}.2\mathrm{E}\right)$$\colon\colon \mathrm{E}.2\mathrm{F}$. Ergo $\mathrm{F}\times fl\mathrm{D}=\frac{1}{2}\mathrm{E}\times fl\mathrm{E}$. adeoque $\mathrm{D}\times fl\mathrm{F}=$$\frac{3}{2}\mathrm{E}\times fl\mathrm{E}$. Et $fl:\mathrm{E}.fl:\mathrm{F}\left(\colon\colon 2\mathrm{D}.3\mathrm{E}\right)\colon\colon 2\mathrm{E}.3\mathrm{F}$. Atque ita in cæteris.

<36>

Corollarium 7. Si fluentes duæ quantitates se multiplicant fluxio Facti componitur ex fluxionibus factorum alterne ductis in factores. $Fl:\mathrm{A}\mathrm{B}=\mathrm{B}\times fl\mathrm{A}+\mathrm{A}\times fl\mathrm{B}${.} Nam $1.\mathrm{A}\colon\colon \mathrm{B}.\mathrm{A}\mathrm{B}$. Ergo per Theorema 1.

Corollarium 8. Si fluens quantitas per fluentem quantitatem dividitur: fluxio Quoti prodit auferendo fluxionem divisoris multiplicatam per dividuum, a fluxione dividui multiplicata per divisorem & dividendo residuum per quadratum divisoris. $Fl:\frac{\mathrm{B}}{\mathrm{A}}=\frac{\mathrm{A}\times fl:\mathrm{B}-\mathrm{B}\times fl:\mathrm{A}}{\mathrm{A}\mathrm{A}}$. Nam $\mathrm{A}.1\colon\colon \mathrm{B}.\frac{\mathrm{B}}{\mathrm{A}}$. Ergo per Theorema 1, $\mathrm{A}\times fl\frac{\mathrm{B}}{\mathrm{A}}+\frac{\mathrm{B}}{\mathrm{A}}\times fl\mathrm{A}=1\times fl:\mathrm{B}$, nam $\mathrm{B}\times fl:1$ nihil est. Aufer utrobique $\frac{\mathrm{B}}{\mathrm{A}}\times fl\mathrm{A}$ et residuum divide per A, et prodibit $fl:\frac{\mathrm{B}}{\mathrm{A}}=\frac{\mathrm{A}\times fl\mathrm{B}-\mathrm{B}\times fl\mathrm{A}}{\mathrm{A}\mathrm{A}}$.

Corollarium 9. Fluxio radicis est ad fluxionem potestatis alicujus ut radix ad potestatem illam multiplicatam per numerum dimensionum $fl:\mathrm{A}.fl{\mathrm{A}}^3$$\colon\colon \mathrm{A}.3{\mathrm{A}}^3$. vel $fl:\sqrt{}3:\mathrm{A}.fl:\mathrm{A}\colon\colon \sqrt{}3:\mathrm{A}.3\mathrm{A}$ & sic in alijs potestatibus. Patet per Corollarium 6.

Theorema 2. In triangulo quovis perpetim rectangulo cujus latera quomodocunque fluunt summa laterum ductorum in suas fluxiones æquatur hypotenusæ ductæ in fluxionem suam. Sit $\mathrm{A}\mathrm{A}+\mathrm{B}\mathrm{B}=\mathrm{C}\mathrm{C}$ et erit $\mathrm{A}\times fl:\mathrm{A}+\mathrm{B}\times fl:\mathrm{B}=\mathrm{C}\times fl:\mathrm{C}$ Nam per Corollarium 9 Theorematis 1 est $fl:\mathrm{A}.fl:\mathrm{A}\mathrm{A}\left(\colon\colon \mathrm{A}.2\mathrm{A}\mathrm{A}\right)${∷}$1.2\mathrm{A}$, adeoque $fl:\mathrm{A}\mathrm{A}=2\mathrm{A}\times fl\mathrm{A}$. Eadem ratione $fl\mathrm{B}\mathrm{B}=$$2\mathrm{B}\times fl\mathrm{B}$ & $fl\mathrm{C}\mathrm{C}=2\mathrm{C}\times fl:\mathrm{C}$. Quare cum $\mathrm{A}\mathrm{A}+\mathrm{B}\mathrm{B}$$=\mathrm{C}\mathrm{C}$ atque adeo per Axiomata 1 & 3 $fl:\mathrm{A}\mathrm{A}+fl:\mathrm{B}\mathrm{B}=fl:\mathrm{C}\mathrm{C}$ erit $2\mathrm{A}\times fl\mathrm{A}+2\mathrm{B}\times fl\mathrm{B}=2\mathrm{C}\times fl\mathrm{C}$. Quod dimidiatum fit $\mathrm{A}\times fl\mathrm{A}+\mathrm{B}\times fl\mathrm{B}=\mathrm{C}\times fl\mathrm{C}$. Q.E.D.

Corollarium 1. Si crus alterutrum sit data quantitas, erit fluxio alterius cruris ad fluxionem hypotenusæ ut hypotenusa ad crus illud alterum. Detur A, et erit $\mathrm{C}.\mathrm{B}\colon\colon fl:\mathrm{B}.fl:\mathrm{C}$, nam $\mathrm{B}\times fl\mathrm{B}=\mathrm{C}\times fl\mathrm{C}$ propterea quòd $\mathrm{A}\times fl\mathrm{A}$ nihil sit.

Corollarium 2. Si hypotenusa datur, erit profluxio unius <37> /> cruris ad defluxionem alterius ut illud alterum crus ad crus primum. Detur C, et erit $\mathrm{B}.\mathrm{A}\colon\colon fl:\mathrm{A}.fl:\mathrm{B}$ propterea quod $\mathrm{C}\times fl:\mathrm{C}$ nihil sit.

Theorema 4. Si recta circa datum punctum 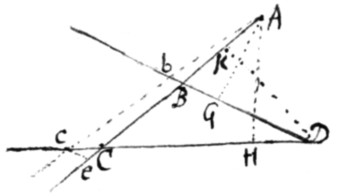gyrans, secet alias duas positione datas & ad commune punctum terminatas rectas: fluxiones earum quæ positione dantur, erunt ut illæ rectæ ductæ in conterminas partes lineæ gyrantis.      Circa datum punctum A gyret recta AC, & inter gyrandum secet ea rectas positione datas DC ac DB in punctis C et B. Dico esse $\mathrm{DB}\times \mathrm{AB}.\mathrm{DC}\times \mathrm{AC}\colon\colon$$fl\mathrm{DB}.fl\mathrm{DC}$. Sit enim Abc positio rectæ gyrantis in proximo temporis momento, hoc est Cc momentum rectæ DC et Bb contemporaneum momentum rectæ DB; et ipsi DB parallela agatur ce occurrens AC in e: et propter similia triangula CBD, Cec, erit $\mathrm{DC}.\mathrm{DB}\colon\colon \mathrm{Cc}.\mathrm{ce}$. Dein propter similia triangula Aec, ABb, erit $\mathrm{Ac}.\mathrm{Ab}\colon\colon \mathrm{ec}.\mathrm{Bb}$, et additis rationibus $\mathrm{DC}\times \mathrm{Ac}.\mathrm{DB}\times \mathrm{Ab}\colon\colon \mathrm{Cc}.\mathrm{Bb}\colon\colon$ (per axioma 4) $fl:\mathrm{DC}.fl:\mathrm{DB}$. Coeant jam lineæ infinitè parùm distantes Ac & AC, et in momento concursus evadet $\mathrm{DC}\times \mathrm{AC}.\mathrm{DB}\times \mathrm{AB}\colon\colon fl:\mathrm{DC}.fl:\mathrm{DB}$. Q.E.D.

Corollarium 1{.} Iisdem positis, et ab A demissis ad DB et DC normalibus AG et AH: erit primo $\mathrm{DC}\times \mathrm{AC}.\mathrm{DB}\times \mathrm{BG}\colon\colon fl:\mathrm{DC}.$$fl:\mathrm{AB}$. Nam per Corollarium 1 Theorematis 2, est $\mathrm{AB}.\mathrm{BG}\colon\colon fl:\mathrm{DB}.fl:\mathrm{AB}$. sive $\mathrm{DB}\times \mathrm{AB}.\mathrm{DB}\times \mathrm{BG}\colon\colon fl:\mathrm{DB}.fl\mathrm{AB}$, et supra erat $\mathrm{DC}\times \mathrm{AC}.$$\mathrm{DB}\times \mathrm{AB}\colon\colon fl:\mathrm{DC}.fl\mathrm{DB}$. Ergo ex æquo $\mathrm{DC}\times \mathrm{AC}.\mathrm{DB}\times \mathrm{BG}\colon\colon$$fl:\mathrm{DC}.fl:\mathrm{AB}$.

Corollarium 2. Erit secundo $\mathrm{DC}\times \mathrm{CH}.\mathrm{DB}\times \mathrm{BG}\colon\colon fl\mathrm{DC}.fl\mathrm{AB}$. Nam per Corollarium 1 Theorematis 2 est $\mathrm{CH}.\mathrm{AC}\left(\text{vel}\mathrm{DC}\times \mathrm{CH}.\mathrm{DC}\times \mathrm{AC}\right)\colon\colon fl\mathrm{AC}.$$fl\mathrm{DC}$. Et supra erat $\mathrm{DC}\times \mathrm{AC}.\mathrm{DB}\times \mathrm{BG}\colon\colon fl\mathrm{DC}.fl\mathrm{AB}$. Ergo ex æquo $\mathrm{DC}\times \mathrm{CH}.\mathrm{DB}\times \mathrm{BG}\colon\colon fl\mathrm{AC}.fl\mathrm{AB}$.

Theorema 3{.} Si Trianguli alicujus Basis et longitudine et positione detur, vertex autem sit ad rectam positione datam; demisso ab alterutro termino basis ad rectam illam positione datam perpendiculo, quod occurrat opposito cruri trianguli, erit fluxio ejus oppositi cruris ad fluxionem alterius cruris ut illud alterum crus ad partem hujus cruris inter verticem trianguli et perpendiculum illud situm. Sit AB basis trianguli, C vertex, DE locus verticis, et <38> /> BE perpendiculariter demissa ad DC occurrat AC in F, eritque $\mathrm{BC}.\mathrm{FC}\colon\colon fl\mathrm{AC}.fl\mathrm{BC}$. Nam ab A ad DE 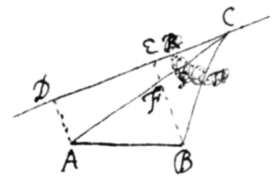demisso perpendiculo AD, erit (per Corollarium 1. Theorematis 2) $\mathrm{BC}.\mathrm{EC}\colon\colon fl\mathrm{EC}.fl\mathrm{BC}$, et $\mathrm{DC}.\mathrm{AC}(\text{sive}$$\mathrm{EC}.\mathrm{FC})\colon\colon fl\mathrm{AC}.fl\mathrm{BC}=fl\mathrm{EC}$. Ergo ex æquo perturbatè $\mathrm{BC}.\mathrm{FC}\colon\colon fl\mathrm{AC}.fl\mathrm{BC}$. Q.E.D.

Corollarium 1{.} Est $fl:\mathrm{AC}$ ad $fl:\mathrm{BC}$ ut cosinus anguli ACD ad cosinum angulum BCD. Nam cosinus isti sunt ut BC ad FC.

Corollarium 2. Si punctum A infinitè 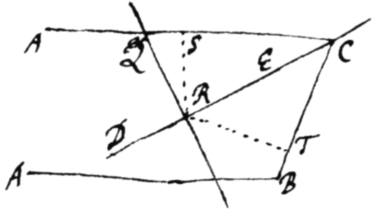distet a B, hoc est si AC sit ipsi AB parallela, age quamvis RQ occurentem AC in Q, sitque RQ positione data, et demisso ad BC normali RT, erit $\mathrm{TC}.\mathrm{QC}\colon\colon fl:\mathrm{BC}.fl\mathrm{QC}$. Nam demisso insuper ad QC normali RS, erit per Corollarium 1, $\mathrm{TC}.\mathrm{SC}\colon\colon fl:\mathrm{BC}.fl\mathrm{AC}=fl:\mathrm{SC}$, & propter datam rationem SC ad QC erit per axioma 2 $\mathrm{SC}.\mathrm{QC}\colon\colon fl:\mathrm{SC}.fl:\mathrm{QC}$. Ergo additis rationibus $\mathrm{TC}.$$\mathrm{QC}\colon\colon fl:\mathrm{BC}.fl:\mathrm{QC}$. Q.E.D.

Hujusmodi alia Theoremata non inutilia proponi possent: sed ad fluxiones superficierum festinamus.

Theorema 5. Si recta quævis motu 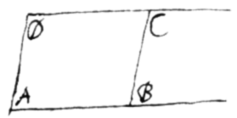parallelo per aream aliquam, a duabus parallelis & positione datis rectis terminatam transferatur: erit fluxio areæ ut fluxio alterutrius rectæ parallelæ. Sint AB, DC rectæ parallelæ, & BC recta per spatium interjectum ADCB in data inclinatione ABC translata et AD terminus a quo incipit transferri; et erit $fl:\mathrm{ADCB}$ ut $fl\mathrm{AB}$. Nam area BD est ut longitudo AB Quare per Axioma 2 $fl:\mathrm{BD}$ ut $fl:\mathrm{AB}$.

Scholium. Si angulus ABC rectus sit, tum quemadmodum statui solet $\mathrm{BD}=\mathrm{AB}\times \mathrm{BC}$, sic nos statuemus <39> /> $fl\mathrm{BD}=fl\mathrm{AB}\times \mathrm{BC}$ hoc est (per Corollarium 7 Theorematis 1) $=\mathrm{BC}\times fl\mathrm{AB}$. Sed hic sicut per $\mathrm{AB}\times \mathrm{BC}$ non intelligitur linea sed productum arithmeticum quod exprimit numerum unitatum in area BD ex Hypothesi quod unitas superficialis sit quadratum cujus latera sunt unitates lineares: sic in hoc Scholio per $\mathrm{BC}\times fl\mathrm{AB}$ non intelligitur fluxio linearis sed fluxio generans productum arithmeticum quod exprimit numerum unitatum superficialium in BD ex Hypothesi quod momentum basis fluentis ductum in datam altitudinem parallelogrammi facit momentum parallelogrammi.

Theorema 6. Si recta quævis motu 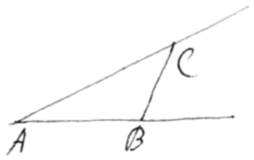parallelo transferatur per aream alijs duabus positione datis et non parallelis rectis terminatam, erit fluxio areæ ut fluxio alterutrius rectæ positione datæ ducta in rectam mobilem. Transferatur BC per spatium CAB rectis AC AB positione datis terminatum: et erit $fl:\mathrm{CAB}$ ut $\mathrm{BC}\times fl:\mathrm{AB}$. Etenim triangulum CAB est ut ${\mathrm{AB}}^q$. ergo, per Axioma 2, fl: trianguli CAB est ut $fl{\mathrm{AB}}^q$. Sed per Corollaria 6 & 9, Theorema 1, $fl{\mathrm{AB}}^q$ est ut $2\mathrm{AB}\times fl\mathrm{AB}$ hoc est cùm $2\mathrm{AB}$ et BC sint in data ratione, ut $\mathrm{BC}\times fl\mathrm{AB}$.

Scholium. Si angulus ABC rectus sit, potest juxta Scholium præcedens, poni $fl\mathrm{CAB}=\frac{1}{2}\mathrm{BC}\times fl:\mathrm{AB}$.

Theorema 7{.} Si recta circa datum punctum gyrans, continuò terminetur ad aliam rectam positione datam: erit fluxio spatij a gyrante recta descripti, ut fluxio alterius rectæ. Gyret recta CB 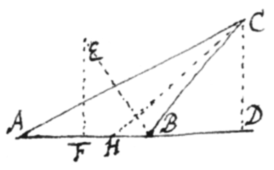circa punctum C sitque CA terminus a quo incipit gyrare, et AB recta ad quam terminatur, et erit area ABC ut recta AB; adeoque (per Axioma 2) $fl\mathrm{ABC}$ ut $fl\mathrm{AB}$.

Scholium. Demisso ad AB normali CD, erit (juxta Scholium Theorematis 5) $\frac{1}{2}\mathrm{CD}\times fl:\mathrm{AB}=fl\mathrm{ABC}$, quia $\frac{1}{2}\mathrm{CD}\times \mathrm{AB}=\mathrm{ABC}$.

<40>

Theorema 8. Iisdem positis, si ab alio insuper quovis dato puncto recta perpetim ducatur ad concursum priorum rectarum, et a primo puncto ad hanc rectam demittatur linea perpendicularis terminata ad rectam positione datam: erit fluxio hujus novæ rectæ ducta in lineam perpendicularem, ut fluxio areæ a prima recta descriptæ.

A dato E agatur EB, et ad hanc perpendicularis CH occurrens AB in H, eritque $\mathrm{CH}\times fl:\mathrm{EB}$, ut $fl:\mathrm{ABC}$. Nam demisso ad AB normali EF, erit per Corollarium 1 Theorematis 2, $fl\mathrm{AB}\left(fl:\mathrm{FB}\right).fl:\mathrm{EB}\colon\colon \mathrm{EB}.\mathrm{FB}$. (hoc est propter similia triangula EBF, HCD) $\colon\colon \mathrm{HC}.\mathrm{CD}$. Ergo $\mathrm{CD}\times fl:\mathrm{AB}=\mathrm{HC}\times fl:\mathrm{EB}$. Quare cùm CD datum sit, adeoque $\mathrm{CD}\times fl:\mathrm{AB}$ ut $fl:\mathrm{AB}$, sitque etiam (per Theorema 7) $fl\mathrm{AB}$ ut $fl\mathrm{ABC}$, erit $\mathrm{HC}\times fl\mathrm{EB}$ ut $fl\mathrm{ABC}$.

Scholium. Est et per Scholium superius $\frac{1}{2}\mathrm{HC}\times fl\mathrm{EB}=fl\mathrm{ABC}$$\left(=\frac{1}{2}\mathrm{CD}\times fl\mathrm{AB}\right)=fl\mathrm{ABC}$. Et insuper in eo temporis momento quo contingit angulum EBC rectum esse, est $\frac{1}{2}\mathrm{BC}\times fl:\mathrm{EB}$$=fl:\mathrm{ABC}$ quia tunc HC et BC coincidunt.

Theorema 9. Si recta circa datum punctum gyrans, secet alias duas positione datas rectas: superficierum inter datum punctum et rectas positione datas isto motu generatarum fluxiones erunt ut quadrata longitudinum generantium. Sit A datum 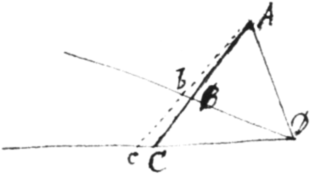punctum circa quod AC gyrat, sintque BD et CD rectæ positione datæ, & AD principium a quo AC incipit gyrare, et erit $fl:\mathrm{ADB}.fl\mathrm{ADC}\colon\colon {\mathrm{AB}}^q.{\mathrm{AC}}^q$. Sit enim Abc positio rectæ gyrantis in proximo temporis momento, et triangula infinitè parva ABb, ACc erunt momenta superficierum ADB, ADC, adeoque ut ipsarum fluxiones. Sed per 15. 6. Elementarum ista triangula sunt ut $\mathrm{AB}\times \mathrm{Ab}$ ad $\mathrm{AC}\times \mathrm{Ac}$: Quæ ratio, si Abc retro volvatur donec redeat in AC, in ultimo ejus regressûs momento, hoc est in primo momento progressûs ubi AC incipit <41> pergere ad Ac evadit ${\mathrm{AB}}^q$ ad ${\mathrm{AC}}^q$. Q.E.D.

Theorema 10. Si recta positione data tangat curvam positione datam et utraque secentur ab alia utcunque motâ rectâ: fluxiones curvæ illius & tangentis ejus in eo temporis momento æquales erunt, quo mota illa linea secat utramque in puncto contactû;s. Esto curva RS, Tangens ejus AB punctum contactûs C 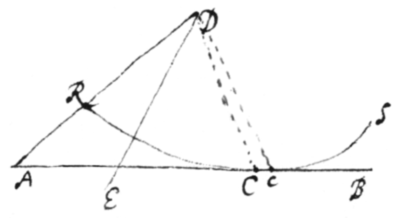et linea mobilis DE: dico fluxiones linearum RC et AC æquales evadere quando DE pertingit ad C. Nam in RC sumatur arcus infinitè parvus Cc, & cum hæc juxta Hypothesin Archimedeam pro recta haberi possit, produc eam utrinque in directum, sitque ea producta AB propterea quod ipsa AB tantùm tangat curvam. RS itaque et AB commune habent momentum Cc, & proinde eandem fluxionem dum DE transit per illud momentum. Q.E.D.

Corollarium. Hinc omnia quæ in Theorematibus 3 et 4 de fluxionibus rectarum positione datarum demonstrata sunt, conveniunt etiam fluxionibus curvarum quas rectæ illæ tangunt in intersectione cum linea mobili.

Theorema 12. Si recta illa DE circa datum punctum D convoluta, describat duas superficies quarum una DRC terminatur ad curvam RC, altera DAC ad tangentem curvæ AC: fluxiones illarum superficierum æquales erunt in eo temporis momento quo recta circumacta transit per punctum contactus C . Nempe $fl\mathrm{DRC}=fl\mathrm{DAC}$ quia tunc commune est utriusque momentum CDc.

Corollarium{.} Hinc omnia quæ in Theorematibus 7, 8 & 9 de fluxionibus superficierum rectis positione datis terminatarum demonstrata sunt, conveniunt etiam fluxionibus superficierum terminatarum curvis positione datis quas rectæ illæ tangunt.

<42>

Theorema 13. Si recta mobilis perpetuò tangat curvam, punctum contactûs in omni temporis momento erit centrum circa quod recta 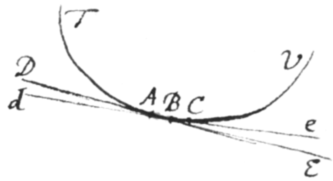in illo momento volvitur. Concipe Curvam TV lineolis parvitate et multitudine infinitis constare quarum duæ sunto AB & BC. Hasce produc utrinque in directum, nempe AB ad D et E et BC ad d et e, et manifestum est quod tangens mobilis in eo temporis momento quo volvitur de loco DE in locum de, convertitur circa punctum contactus B, propterea quod istud B sit communis intersectio locorum DE ac de.

Corollarium 1. Hinc omnia quæ in Theorematibus 3, 4, 7, 8, 9, 10, 11 de recta circa datum punctum ceu centrum volvente demonstrata sunt, conveniunt etiam rectæ perpetuò tangenti curvam lineam positione datam, si modò punctum contactûs circa quod recta illa in momento contactûs illius convolvitur, vicem centri dati gerere concipiatur. Et proinde sigillatim{.}

Corollarium 2. S

<45>

cruris ad defluxionem alterius ut illud alterum crus ad crus primum. Detur C, et erit $\mathrm{B}.\mathrm{A}\colon\colon fl:\mathrm{A}.fl\mathrm{B}$ propterea quod $\mathrm{C}\times fl:\mathrm{C}$ nihil sit.

<46> diametri A, turn ab altero diametri termino B demisso BC normali ad AC, erit fluxio segmenti ACE ut dimidium fluxionis perpendiculi BC ductum in AC: vel juxta Scholium $fl:\mathrm{ACE}=\frac{1}{2}\mathrm{AC}\times fl\mathrm{BC}$.

Jactis hisce demonstrationum fundamentis, methodus tenendi demonstrationes, uno et altero exemplo constabit. Proponatur itaque constructio in Exemplo secundo demonstranda. Per Corollarium 2 Theorematis 1, est $fl:\mathrm{ID}$ ad $fl:\mathrm{IP}$ ut AI ad ID. Estque AI ad ID ut ID ad CE ex natura Curvæ AGE. Et proinde $\mathrm{CE}\times fl:\mathrm{ID}=\mathrm{ID}\times fl:\mathrm{IP}$. Sed (per Scholium Theorematis 3) $\mathrm{CE}\times fl\mathrm{ID}=$ fluxioni areæ ACEG, et $\mathrm{ID}\times fl:\mathrm{IP}=$ fluxioni areæ PDI. et proinde areæ illæ per Axioma 1 æquantur. Q.E.D.

Proponatur denuò constructio qua Cissoidis area in Exemplo 3 determinatur. Ad hanc autem demonstrandam, lineæ punctim notatæ in schemate deleantur et agantur DQ, AE et Cissoidis Asymptoton QR. Iam propter $\mathrm{AQ},\mathrm{DQ},\mathrm{CQ}∺$, est (per Corollarium 2 Theorematis 1) $fl\mathrm{DQ}.$$fl\mathrm{CQ}\colon\colon \mathrm{DQ}.2\mathrm{CQ}$. Et propter similia triangula QDC, DEA, est $\mathrm{DQ}.2\mathrm{CQ}\colon\colon \mathrm{ED}.2\mathrm{AD}$. Ergo $fl\mathrm{DQ}.fl\mathrm{CQ}\colon\colon \mathrm{ED}.2\mathrm{AD}$. & $\mathrm{ED}\times fl\mathrm{CQ}=2\mathrm{AD}\times fl:\mathrm{DQ}$ sive = $4\times \frac{1}{2}\mathrm{AD}\times fl\mathrm{DQ}$. Sed per Corollarium 1, Theorema 3, est $\frac{1}{2}\mathrm{AD}\times fl\mathrm{DQ}$= fluxioni generanti aream ADOQ, est et ejus quadruplum $\mathrm{ED}\times fl\mathrm{CQ}=$ fluxioni generanti Cissoidalem aream QREDO. Et proinde per Axioma 2 area illa infinite longa QREDO generatur quadrupla alterius ADOQ. Q.E.D.

Denique ad demonstrandam constructionem areæ Conchoidalis in Exemplo 4; Ubi demonstraveris ut supra quod sit $\mathrm{AG}.\mathrm{AP}\colon\colon \mathrm{DE}.\mathrm{MK}$, sic procede. Est autem (per Corollarium 2, Theorema 3) $\mathrm{MK}\times fl\mathrm{PC}=fl:\mathrm{are\ae \; PKC}$ & $\mathrm{DE}\times fl\mathrm{PC}$$=fl\mathrm{are\ae \; DPE}$. Ergo $fl\mathrm{PKC}.fl\mathrm{DPE}\left(\colon\colon \mathrm{MK}.\mathrm{DE}\right)\colon\colon$$\mathrm{AP}.\mathrm{AG}$. Adeoque per Axioma 2 Areæ PKC et DPE sunt in eadem ratione.