Newton's Demonstration that planets move in ellipses
Hypoth. 1. Bodies move uniformly in straight lines unless so far as they are retarded by the resistence of the Medium or disturbed by some other force.
Hyp. 2. The alteration of motion is ever proportional to the force by which it is altered.
Hyp. 3. Motions imprest in two different lines, if those lines be taken
in proportion to the motions & completed into a parallelogram, compose a motion whereby the diagonal of the Parallelogram shall be
described in the same time in which the sides thereof would have
been described by those compounding motions apart. The 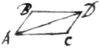 motions AB & AC compound the motion AD.
motions AB & AC compound the motion AD.
Prop. 1.
If a body move in vacuo & be continually attracted toward an immoveable center, it shall constantly move in one & the same plane, & in that plane describe equal areas in equall times.
Let A be the center towards which the body 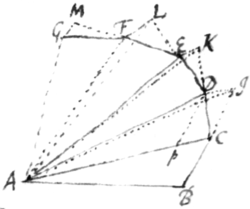 is attracted, & suppose the attraction acts not
continually but by discontinued impressions
made at equal intervalls of time which
intervalls we will consider as physical
moments. Let BC be the right line in which
it begins to move from B & which it describes with uniform
motion in the first physical moment before the attraction
make its first impression upon it. At C let it be attracted
towards the center A by one impuls or impression of force, &
let CD be the line in which it shall move after that impuls.
Produce BC to I so that CI be equall to BC & draw ID
parallel to CA & the point D in which it cuts CD shall be the
place of the body at the end of the second moment. And because
the bases BC CI of the triangles ABC, ACI are equal those
two triangles shall be equal. Also because the triangles ACI, ACD
stand upon the same base AC & between two parallels they shall
be equall. And therefore the triangle ACD described in the second
moment shall be equal to the triangle ABD described in the first
moment. And by the same reason if the body at the end of the
2d, 3d, 4th, 5t & following moments be attracted by single impulses in D, E, F, G &c describing the line DE in the 3d moment, EF in
the 4th, FG in the 5t &c: the triangle AED shall be equall
to the triangle ADC & all the following triangles AFE, AGF &
to the preceding ones & to one another. And by consequence
the areas compounded of these equall triangles (as ABE, AEG,
ABG &c) are to one another as the times in which they
are described. Suppose now that the moments of time be diminished in length & encreased in number in infinitum, so that
the impulses or impressions of the attraction may become continuall & that the line BCDEFG by the infinite number &
infinite littleness of its sides BC, CD, DE &c may become a
curve one: & the body by the continual attraction shall describe areas of this Curve ABE, AEG, ABG & proportionall to
the times in which they are described. W. W. to be Dem.
is attracted, & suppose the attraction acts not
continually but by discontinued impressions
made at equal intervalls of time which
intervalls we will consider as physical
moments. Let BC be the right line in which
it begins to move from B & which it describes with uniform
motion in the first physical moment before the attraction
make its first impression upon it. At C let it be attracted
towards the center A by one impuls or impression of force, &
let CD be the line in which it shall move after that impuls.
Produce BC to I so that CI be equall to BC & draw ID
parallel to CA & the point D in which it cuts CD shall be the
place of the body at the end of the second moment. And because
the bases BC CI of the triangles ABC, ACI are equal those
two triangles shall be equal. Also because the triangles ACI, ACD
stand upon the same base AC & between two parallels they shall
be equall. And therefore the triangle ACD described in the second
moment shall be equal to the triangle ABD described in the first
moment. And by the same reason if the body at the end of the
2d, 3d, 4th, 5t & following moments be attracted by single impulses in D, E, F, G &c describing the line DE in the 3d moment, EF in
the 4th, FG in the 5t &c: the triangle AED shall be equall
to the triangle ADC & all the following triangles AFE, AGF &
to the preceding ones & to one another. And by consequence
the areas compounded of these equall triangles (as ABE, AEG,
ABG &c) are to one another as the times in which they
are described. Suppose now that the moments of time be diminished in length & encreased in number in infinitum, so that
the impulses or impressions of the attraction may become continuall & that the line BCDEFG by the infinite number &
infinite littleness of its sides BC, CD, DE &c may become a
curve one: & the body by the continual attraction shall describe areas of this Curve ABE, AEG, ABG & proportionall to
the times in which they are described. W. W. to be Dem.
Prop. 2.
If a body be attracted towards either focus of an Ellipsis & the quantity of the attraction be such as suffices to make the body revolve in the circumference of the Ellipsis: the attraction at the two ends of the Ellipsis shall be reciprocally as the squares of the body in those ends from that focus.
Let AECD be the Ellipsis, A, C its two 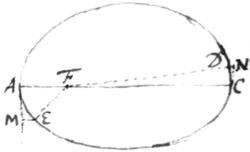 ends or vertices, F that focus towards which
the body is attracted, & AFE, CFD
areas which the body with a ray drawn
from that focus to its center, describes
at both ends in equal times: & those areas
by the foregoing Proposition must be equal because proportionall to the times: that is the rectangles &
must be equal supposing the arches AE & CD
to be so very short that they may be taken for right lines
& therefore AE is to CD as FC to FA. Suppose now
that AM & CN are tangents to the Ellipsis at its two ends
A & C & that EM & DN are perpendiculars let fall from the
points E & D upon those tangents: & because the Ellipsis is
alike crooked at both ends those perpendiculars EM & DN will
be to one another as the squares of the arches AE & CD, &
therefore EM is to DN as FCq to FAq. Now in the times
that the body by means of the attraction moves in the arches AE & CD from A to E & from C to D it would without attraction
move in the tangents from A to M & from C to N. Tis by the
force of the attractions that the bodies are drawn out of the tangents from M to E & from N to D & therefore the attractions
are as those distances ME & ND, that is the attraction at the end of the Ellipsis A
is to the attraction at the other end of the Ellipsis C as ME to
ND & by consequence as FCq to FAq. W. w. to be dem.
ends or vertices, F that focus towards which
the body is attracted, & AFE, CFD
areas which the body with a ray drawn
from that focus to its center, describes
at both ends in equal times: & those areas
by the foregoing Proposition must be equal because proportionall to the times: that is the rectangles &
must be equal supposing the arches AE & CD
to be so very short that they may be taken for right lines
& therefore AE is to CD as FC to FA. Suppose now
that AM & CN are tangents to the Ellipsis at its two ends
A & C & that EM & DN are perpendiculars let fall from the
points E & D upon those tangents: & because the Ellipsis is
alike crooked at both ends those perpendiculars EM & DN will
be to one another as the squares of the arches AE & CD, &
therefore EM is to DN as FCq to FAq. Now in the times
that the body by means of the attraction moves in the arches AE & CD from A to E & from C to D it would without attraction
move in the tangents from A to M & from C to N. Tis by the
force of the attractions that the bodies are drawn out of the tangents from M to E & from N to D & therefore the attractions
are as those distances ME & ND, that is the attraction at the end of the Ellipsis A
is to the attraction at the other end of the Ellipsis C as ME to
ND & by consequence as FCq to FAq. W. w. to be dem.
Lemma. 1.
If a right line touch an Ellipsis in any point thereof & parallel to that tangent be drawn another right line from the center of the Ellipsis which shall intersect a third right line drawn from the touch point through either focus of the Ellipsis: the segment of the last named right line lying between the point of intersection & the point of contact shall be equal to half the long axis of the Ellipsis.
Let APBQ be the Ellipsis; AB its 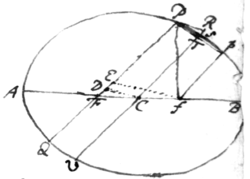 long axis; C its center; F, f its Foci;
P the point of contact; PR the tangent;
CD the line parallel to the tangent,
& PD the segment of the line FP.
I say that this segment shall be equal
to AC.
long axis; C its center; F, f its Foci;
P the point of contact; PR the tangent;
CD the line parallel to the tangent,
& PD the segment of the line FP.
I say that this segment shall be equal
to AC.
For joyn Pf & draw fE parallel to CD & because Ff is bisected in C, FE shall be bisected in D & therefore 2PD shall be equal to the summ of PF & PE that is to the summ of PF & Pf, that is to AB & therefore PD shall be equal to AC. W. W. to be Dem.
Lemma. 2.
Every line drawn through either Focus of any Ellipsis & terminated at both ends by the Ellipsis is to that diameter of the Ellipsis which is parallel to this line as the same Diameter is to the long Axis of the Ellipsis.
Let APBQ be the Ellipsis, AB its long Axis, F, f its foci, C its center, PQ the line drawn through its focus F, & VCS its diameter parallel to PQ & PQ will be to VS as VS to AB.
For draw fp parallel to QFP & cutting the Ellipsis in p. Joyn Pp cutting VS in T & draw PR which shall touch the Ellipsis in P & cut the diameter VS produced in R & CT will be to CS as CS to CR, as has been shewed by all those who treat of the Conic sections. But CT is the semisumm of FP & fp that is of FP & FQ & therefore 2CT is equal to PQ. Also 2CS is equal to VS & (by the foregoing Lemma) 2CR is equal to AB. Wherefore PQ is to VS as VS to AB. W. W. to be Dem.
Corol. .
Lem. 3.
If from either focus of any Ellipsis unto any point in the perimeter of the Ellipsis be drawn a right line & another right line doth touch the Ellipsis in that point & the angle of contact be subtended by any third right line drawn parallel to the first line: the rectangle which that subtense conteins with the same subtense produced to the other side of the Ellipsis is to the rectangle which the long Axis of the Ellipsis conteins with the first line produced to the other side of the Ellipsis as the square of the distance between the subtense & the first line is to the square of the short Axis of the Ellipsis.
Let AKBL be the Ellipsis, AB 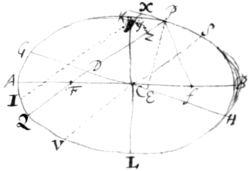 its long Axis, KL its short Axis, C its
center, F, f its foci, P the point of
the perimeter, PF the first line PQ
that line produced to the other side
of the Ellipsis PX the tangent, XY the
subtense produced to the other side of
the Ellipsis & YZ the distance between
this subtense & the first line. I say that
the rectangle YXI is to the rectangle as YZq to KLq
its long Axis, KL its short Axis, C its
center, F, f its foci, P the point of
the perimeter, PF the first line PQ
that line produced to the other side
of the Ellipsis PX the tangent, XY the
subtense produced to the other side of
the Ellipsis & YZ the distance between
this subtense & the first line. I say that
the rectangle YXI is to the rectangle as YZq to KLq
For let VS be the diameter of the Ellipsis parallel to the first line PF & GH another diameter parallel to the tangent PX, & the rectangle YXI will be to the square of the tangent PXq as the rectangle SCV to the rectangle GCH that is as SVq to GHq. This a property of the Ellipsis demonstrated by all that write of the conic sections. And they have also demonstrated that all the Parallelogramms circumscribed about an Ellipsis are equall. Whence the rectangle is equal to the rectangle & consequently GH is to KL as AB that is (by Lem. 1) 2PD to 2PE & in the same proportion is PX to YZ. Whence PX is to GH as YZ to KL & PXq to GHq as YZq to KLq. But YXI was to PXq as SVq that is (by Cor. Lem. 2) to GHq, whence invertedly YXI is to as PXq to GHq & by consequence as YZq to KLq. W. w. to be Dem.
Prop. III.
If a body be attracted towards either focus of any Ellipsis & by that attraction be made to revolve in the Perimeter of the Ellipsis: the attraction shall be reciprocally as the square of the distance of the body from that focus of the Ellipsis.
Let P be the place of the body in the Ellipsis
at any moment of time & PX the tangent in which the body
would move uniformly were it not attracted & X the place
in that tangent at which it would arrive in any given part
of time & Y the place in the perimeter of the Ellipsis
at which the body doth arrive in the same time by means of
the attraction. Let us suppose the time to be divided into
equal parts & that those parts are very little ones so that
they may be considered as physical moments & that the attraction acts not continually but by intervalls once in the beginning of every physical moment & let the first action be
upon the body in P, the next upon it in Y & so on perpetually, so that the body may move from P to Y in the chord
of the arch PY & from Y to its next place in the Ellipsis in the chord of the next arch & so on for ever. And
because the attraction in P is made towards F & diverts
the body from the tangent PX into the chord PY so that
in the end of the first physical moment it be not found
in the place X where it would have been without the attraction but in Y being by the force of the attraction in P
translated from X to Y: the line XY generated by the
force of the attraction in P must be proportional to that
force & parallel to its direction that is parallel to PF
Produce XY & PF till they cut the Ellipsis 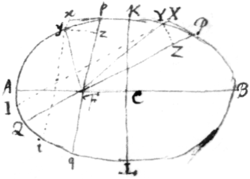 in I & Q. Ioyn FY & upon FP let fall
the perpendicular YZ & let AB be the
long Axis & KL the short Axis of the
Ellipses. And by the third Lemma YXI
will be to as YZq to KLq
& by consequence YX will be equall to
.
in I & Q. Ioyn FY & upon FP let fall
the perpendicular YZ & let AB be the
long Axis & KL the short Axis of the
Ellipses. And by the third Lemma YXI
will be to as YZq to KLq
& by consequence YX will be equall to
.
And in like manner if py be the chord of another Arch py which the revolving body describes in a physical moment of time & px be the tangent of the Ellipsis at p & xy the subtense of the angle of contact drawn parallel to pF, & if pF & xy produced cut the Ellipsis in q & i & from y upon pF be let fall the perpendicular yz: the subtense yx shall be equal to . And therefore YX shall be to yx as to , that is as to
And because the lines PY py are by the revolving body described in equal times, the areas of the triangles PYF pyF must be equal by the first Proposition; & therefore the rectangles & are equal, & by consequence YZ is to yz as pF to PF. Whence is to as to And therefore YX is to yx as to .
And as we told you that XY was the line generated in a physical moment of time by the force of the attraction in P, so for the same reason is xy the line generated in the same quantity of time by the force of the attraction in p. And therefore the attraction in P is to the attraction in p as the line XY to the line xy, that is as to
Suppose now that the equal lines in which the revolving body describes the lines PY & py become infinitely little, so that the attraction may become continual & the body by this attraction revolve in the perimeter of the Ellipsis: & the lines PQ, XI as also pq, xi becoming coincident & by consequence equal, the quantities & will become & . And therefore the attraction in P will be to the attraction in p as to , that is reciprocally as the squares of the distances of the revolving bodies from the focus of the Ellipsis. W. W. to be Dem.
