De Munde Systemate (Liber Tertius) (1726)
DE
MUNDI SYSTEMATE.
LIBER TERTIUS.
IN libris præcedentibus principia philosophiæ tradidi, non tamen philosophica sed mathematica tantum, ex quibus videlicet in rebus philosophicis disputari possit. Hæc sunt motuum & virium leges & conditiones, quæ ad philosophiam maxime spectant. Eadem tamen, ne sterilia videantur, illustravi scholiis quibusdam philosophicis, ea tractans quæ generalia sunt, & in quibus philosophia maxime fundari videtur, uti corporum densitatem & resistentiam, spatia corporibus vacua, motumque Lucis & sonorum. Superest ut ex iisdem principiis doceamus constitutionem systematis mundani. De hoc argumento composueram librum tertium methodo populari, ut a pluribus legeretur. Sed quibus principia posita satis intellecta non fuerint, ii vim consequentiarum minime percipient, neque præjudicia deponent, quibus a multis retro annis insueverunt: & propterea ne res in disputationes trahatur, summam libri illius transtuli in propositiones, more mathematico, ut ab iis solis legantur qui principia prius evolverint. Veruntamen quoniam propositiones ibi quam plurimæ occurrant, quæ lectoribus etiam mathematice doctis moram nimiam injicere possint, auctor esse nolo ut quisquam eas omnes evolvat; suffecerit siquis definitiones, leges motuum & sectiones tres priores libri primi sedulo legat, dein transeat ad hunc librum de mundi systemate, & reliquas librorum priorum propositiones hic citatas pro lubitu consulat.
REGULÆ
PHILOSOPHANDI.
REGULA I.
Causas rerum naturalium non plures admitti debere, quam quæ & veræ sint & earum phænomenis explicandis sufficiant.
DIcunt utique philosophi: Natura nihil agit frustra, & frustra fit per plura quod fieri potest per pauciora. Natura enim simplex est & rerum causis superfluis non luxuriat.
REGULA II.
Ideoque effectuum naturalium ejusdem generis eædem assignandæ sunt causæ, quatenus fieri potest.
Uti respirationis in homine & in bestia; descensus lapidum in Europa & in America; lucis in igne culinari & in sole; reflexionis lucis in terra & in planetis.
REGULA III.
Qualitates corporum quæ intendi & remitti nequeunt, quæque corporibus omnibus competunt in quibus experimenta instituere licet, pro qualitatibus corporum universorum habendæ sunt.
Nam qualitates corporum non nisi per experimenta innotescunt, ideoque generales statuendæ sunt quotquot cum experimentis generaliter quadrant; & quæ minui non possunt, non possunt auferri. Certe contra experimentorum tenorem somnia temere confingenda non sunt, nec a naturæ analogia recedendum est, cum ea simplex esse soleat & sibi semper consona. Extensio corporum non nisi per sensus innotescit, nec in omnibus sentitur: sed quia sensibilibus omnibus competit, de universis affirmatur. Corpora plura dura esse experimur. Oritur autem durities totius a duritie partium, & inde non horum tantum corporum quæ sentiuntur, sed aliorum etiam omnium particulas indivisas esse duras merito concludimus. Corpora omnia impenetrabilia esse non ratione sed sensu colligimus. Quæ tractamus, impenetrabilia inveniuntur, & inde concludimus impenetrabilitatem esse proprietatem corporum universorum. Corpora omnia mobilia esse, & viribus quibusdam (quas vires inertiæ vocamus) perseverare in motu vel quiete, ex hisce corporum visorum proprietatibus colligimus. Extensio, durities, impenetrabilitas, mobilitas & vis inertiæ totius oritur ab extensione, duritie, impenetrabilitate, mobilitate & viribus inertiæ partium: & inde concludimus omnes omnium corporum partes minimas extendi & duras esse & impenetrabiles & mobiles & viribus inertiæ præditas. Et hoc est fundamentum philosophiæ totius. Porro corporum partes divisas & sibi mutuo contiguas ab invicem separari posse, ex phænomenis novimus, & partes indivisas in partes minores ratione distingui posse ex mathematica certum est. Utrum vero partes illæ distinctæ & nondum divisæ per vires naturæ dividi & ab invicem separari possint, incertum est. At si vel unico constaret experimento quod particula aliqua indivisa, frangendo corpus durum & solidum, divisionem pateretur: concluderemus vi hujus regulæ, quod non solum partes divisæ separabiles essent, sed etiam quod indivisæ in infinitum dividi possent.
Denique si corpora omnia in circuitu terræ gravia esse in terram, idque pro quantitate materiæ in singulis, & lunam gravem esse in terram pro quantitate materiæ suæ, & vicissim mare nostrum grave esse in lunam, & planetas omnes graves esse in se motuo, & cometarum similem esse gravitatem in solem, per experimenta & observationes astronomicas universaliter constet: dicendum erit per hanc regulam quod corpora omnia in se mutuo gravitant. Nam & fortius erit argumentum ex phænomenis de gravitate universali, quam de corporum impenetrabilitate: de qua utique in corporibus cœlestibus nullum experimentum, nullam prorsus observationem habemus. Attamen gravitatem corporibus essentialem esse minime affirmo. Per vim insitam intelligo solam vim inertiæ. Hæc immutabilis est. Gravitas recedendo a terra, diminuitur.
REGULA IV.
In philosophia experimentali, propositiones ex phænomenis per inductionem collectæ, non obstantibus contrariis hypothesibus, pro veris aut accurate aut quamproxime haberi debent, donec alia ocurrerint phænomena, per quæ aut accuratiores reddantur aut exceptionibus obnoxiæ.
Hoc fieri debet ne argumentum inductionis tollatur per hypotheses.
PHÆNOMENA.
PHÆNOMENON I.
Planetas circumjoviales, radiis ad centrum jovis ductis, areas describere temporibus proportionales, eorumque tempora periodica, stellis fixis quiescentibus, esse in ratione sesquiplicata distantiarum ab ipsius centro.
COnstat ex observationibus astronomicis. Orbes horum planetarum non differunt sensibiliter a circulis jovi concentricis, & motus eorum in his circulis uniformes deprehenduntur. Tempora vero periodica esse in sesquiplicata ratione semidiametrorum orbium consentiunt astronomi; & idem ex tabula sequente manifestum est.
Satellitum jovialium tempora periodica.
| 1d. 18h. 27′. 34″. | 3d. 13h. 13′. 42″. | 7d. 3h. 42′. 36″. | 16d. 16h. 32′. 9″. |
Distantiæ satellitum a centro jovis.
Elongationes satellitum jovis & diametrum ejus D. Pound micrometris optimis determinavit ut sequitur. Elongatio maxima heliocentrica satellitis quarti a centro jovis micrometro in tubo quindecim pedes longo capta fuit, & prodiit in mediocri jovis a terra distantia 8′. 16″ circiter. Ea satellitis tertii micrometro in telescopio pedes 123 longo capita fuit, & prodiit in eadem jovis a terra distantia 4′. 42″. Elongationes maximæ reliquorum satellitium in eadem jovis a terra distantia ex temporibus periodicis prodeunt 2′. 56″. , & 1′. 51″. .
Diameter jovis micrometro in telescopio pedes 123 longo sæpius capta fuit, & ad mediocrem jovis a sole vel terra distantiam reducta, semper minor prodiit quam 40″, nunquam minor quam 38″, sæpius 39″. In telescopiis brevioribus hæc diameter est 40″ vel 41″. Nam lux jovis per inæqualem refrangibilitatem nonnihil dilatatur, & hæc dilatatio minorem habet rationem ad diametrum jovis in longioribus & perfectoribus {sic} telescopiis quam in brevioribus & minus perfectis. Tempora quibus satellites duo, primus ac tertius, transibant per corpus jovis, ab initio ingressus ad initium exitus, & ab ingressu completo ad exitum completum, observata sunt ope telescopii ejusdem longioris. Et diameter jovis in mediocri ejus a terra distantia prodiit per transitum primi satellitis , & per transitum tertii . Tempus etiam quo umbra primi satellitis transiit per corpus jovis observatum fuit, & inde diameter jovis in mediocri ejus a terra distantia prodiit 37″ circiter. Assumamus diametrum ejus esse quamproxime; & elongationes maximæ satellitis primi, secundi, tertii, & quarti æquales erunt semidiametris jovis 5,965, 9,494, 15,141, & 26,63 respective.
PHÆNOMENON II.
Planetas circumsaturnios, radiis ad saturnum ductis, areas describere temporibus proportionales, & eorum tempora periodica, stellis fixis quiescentibus, esse in ratione sesquiplicata distantiarum ab ipsius centro.
Cassinus utique ex observationibus suis distantias eorum a centro saturni & periodica tempora hujusmodi esse statuit.
Satellitum saturniorum tempora periodica.
1d. 21h. 18′. 27″. 2d. 17h. 41′. 22″. 4d. 12h. 25′. 12″. 15d. 22h. 41′. 14″. 79d. 7h. 48′. 00″.
<392>Distantiæ satellitum a centro saturni in semidiametris annuli.
| Ex observationibus | 1. | 2. | 3. | 8. | 24. |
| Ex temporibus periodicis. | 1,93. | 2,47. | 3,45. | 8. | 23,35. |
Quarti satellitis elongatio maxima a centro saturni ex observationibus colligi solet esse semidiametrorum acto quamproxime. At elongatio maxima satellitis hujus a centro saturni, micrometro optimo in telescopio Hugeniano pedes 123 longo capta, prodiit semidiametrorum octo cum septem decimis partibus semidiametri. Et ex hac observatione & temporibus periodicis, distantiæ satellitum a centro saturni in semidiametris annuli sunt 2,1. 2,69. 3,75. 8,7. & 25,35. Saturni diameter in eodem telescopio erat ad diametrum annuli ut 3 ad 7, & diameter annuli diebus Maii 28 & 29 anni 1719. prodiit 43″. Et inde diameter annuli in mediocri saturni a terra distantia est 42″, & diameter saturni 18″. Hæc ita sunt in telescopiis longissimis & optimis, propterea quod magnitudines apparentes corporum cœlestium in longioribus telescopiis majorem habeant proportionem ad dilatationem lucis in terminis illorum corporum quam in brevioribus. Si rejiciatur lux omnis erratica, manebit diameter saturni haud major quam 16″.
PHÆNOMENON III.
Planetas quinque primarios mercurium, venerem, martem, jovem & saturnum orbibus suis solem cingere.
Mercurium & venerem circa solem revolvi ex eorum phasibus lunaribus demonstratur. Plena facie lucentes ultra solem siti sunt; dimidiata e regione solis; falcata cis solem, per discum ejus ad modum macularum nonnunquam transeuntes. Ex martis quoque plena facie prope solis conjunctionem, & gibbosa in quadraturis, certum est, quod is solem ambit. De jove etiam & saturno idem ex eorum phasibus semper plenis demonstratur: hos enim luce a sole mutuata splendere ex umbris satellitum in ipsos projectis manifestum est.
<393>PHÆNOMENON IV.
Planetarum quinque primariorum, & vel solis circa terram vel terræ circa solem tempora periodica, stellis fixis quiescentibus, esse in ratione sesquiplicata mediocrium distantiarum a sole.
Hæc a Keplero inventa ratio in confesso est apud omnes. Eadem utique sunt tempora periodica, eædemque orbium dimensiones, sive sol circa terram, sive terra circa solem revolvatur. Ac de mensura quidem temporum periodicorum convenit inter astronomos universos. Magnitudines autem orbium Keplerus & Bullialdus omnium diligentissime ex observationibus determinaverunt: & distantiæ mediocres, quæ temporibus periodicis respondent, non differunt sensibiliter a distantiis quas illi invenerunt, suntque inter ipsas ut plurimum intermediæ; uti in tabula sequente videre licet.
Planetarum ac telluris tempora periodica circa solem respectu fixarum, in diebus & partibus decimalibus diei.
| ♄ | ♃ | ♂ | ♁ | ♀ | ☿ |
| 10759,275. | 4332,514. | 686,9785. | 365,2565. | 224,6176. | 87,9692. |
Planetarum ac telluris distantiæ mediocres a sole.
| ♄ | ♃ | ♂ | ♁ | ♀ | ☿ | |
| Secundum Keplerum | 951000. | 519650. | 152350. | 100000. | 72400. | 38806. |
| Secundum Bullialdum | 954198. | 522520. | 152350. | 100000. | 72398. | 38585. |
| Secundum tempora periodica | 954006. | 520096. | 152369. | 100000. | 72333. | 38710. |
De distantiis mercurii & veneris a sole disputandi non est locus, cum hæ per eorum elongationes a sole determinentur. De distantiis etiam superiorum planetarum a sole tollitur omnis disputatio per eclipses satellitum jovis. Etenim per eclipses illas determinatur positio umbræ quam jupiter projicit, & eo nomine habetur jovis longitudo heliocentrica. Ex longitudinibus autem heliocentrica & geocentrica inter se collatis determinatur distantia jovis.
<394>PHÆNOMENON V.
Planetas primarios, radiis ad terram ductis, areas describere temporibus minime proportionales; at radiis ad solem ductis, areas temporibus proportionales percurrere.
Nam respectu terræ nunc progrediuntur, nunc stationarii sunt, nunc etiam regrediuntur: At solis respectu semper progrediuntur, idque propemodum uniformi cum motu, sed paulo celerius tamen in periheliis ac tardius in apheliis, sic ut arearum æquabilis sit descriptio. Propositio est astronomis notissima, & in jove apprime demonstratur per eclipses satellitum, quibus eclipsibus heliocentricas planetæ hujus longitudines & distantias a sole determinari diximus.
PHÆNOMENON VI.
Lunam radio ad centrum terræ ducto, aream tempori proportionalem describere.
Patet ex lunæ motu apparente cum ipsius diametro apparente collato. Perturbatur autem motus lunaris aliquantulum a vi solis, sed errorum insensibiles minutias in hisce phænomenis negligo.
PROPOSITIONES.
PROPOSITIO I. THEOREMA I.
Vires, quibus planetæ circumjoviales perpetuo retrahuntur a motibus rectilineis & in orbibus suis retinentur, respicere centrum jovis, & esse reciproce ut quadrata distantiarum locorum ab eodem centro.
PAtet pars prior propositionis per phænomenon primum, & propositionem secundam vel tertiam libri primi: & pars posterior per phænomenon primum, & corollarium sextum propositionis quartæ ejusdem libri.
Idem intellige de planetis qui saturnum comitantur, per phænomenon secundum.
PROPOSITIO II. THEOREMA II.
Vires, quibus planetæ primarii perpetuo retrahuntur a motibus rectilineis, & in orbibus suis retinentur, respicere solem, & esse reciproce ut quadrata distantiarum ab ipsius centro.
Patet pars prior propositionis per phænomenon quintum, & propositionem secundam libri primi: & pars posterior per phænomenon quartum, & propositionem quartam ejusdem libri. Accuratissime autem demonstratur hæc pars propositionis per quietem apheliorum. Nam aberratio quam minima a ratione duplicata (per Corol. 1. Prop. xlv. Lib. i.) motum apsidum in singulis revolutionibus notabilem, in pluribus enormem efficere deberet.
<396>PROPOSITIO III. THEOREMA III.
Vim qua luna retinetur in orbe suo, respicere terram, & esse reciproce ut quadratum distantiæ locorum ab ipsius centro.
Patet assertionis pars prior per phænomenon sextum, & propositionem secundam vel tertiam libri primi: & pars posterior per motum tardissimum lunaris apogæi. Nam motus ille, qui singulis revolutionibus est graduum tantum trium & minutorum trium in consequentia, contemni potest. Patet enim (per corol 1. prop. xlv. lib. i.) quod si distantia lunæ a centro terræ sit ad semidiametrum terræ ut D ad 1; vis a qua motus talis oriatur, sit reciproce ut , id est, reciproce ut ea ipsius D dignitas cujus index est , hoc est, in ratione distantiæ paulo majore quam duplicata inverse, sed quæ partibus propius ad duplicatam quam ad triplicatam accedit. Oritur vero ab actione solis (uti posthac dicetur) & propterea hic negligendus est. Actio solis quatenus lunam distrahit a terra, est ut distantia lunæ a terra quamproxime; ideoque (per ea quæ dicuntur in corol. 2. prop. xlv. lib. i.) est ad lunæ vim centripetam ut 2 ad 357,45 circiter, seu 1 ad . Et neglecta solis vi tantilla, vis reliqua qua luna retinetur in orbe erit reciproce ut . Id quod etiam plenius constabit conferendo hanc vim cum vi gravitatis, ut fit in propositione sequente.
Corol. Si vis centripeta mediocris qua luna retinetur in orbe augeatur primo in ratione ad , deinde etiam in ratione duplicata semidiametri terræ ad mediocrem distantiam centri lunæ a centro terræ: habebitur vis centripeta lunaris ad superficiem terræ, posito quod vis illa descendendo ad superficiem terræ perpetuo augeatur in reciproca altitudinis ratione duplicata.
PROPOSITIO IV. THEOREMA IV.
Lunam gravitare in terram, & vi gravitatis retrahi semper a motu rectilineo, & in orbe suo retineri.
Lunæ distantia mediocris a terra in syzygiis est semidiametrorum terrestrium, secundum Ptolemæum & plerosque astronomorum 59, secundum Vendelinum & Hugenium 60, secundum Copernicum , secundum Streetum , & secundum Tychonem . Ast Tycho, & quotquot ejus tabulas refractionum sequuntur, constituendo refractiones solis & lunæ (omnino contra naturam lucis) majores quam fixarum, idque scrupulis quasi quatuor vel quinque, auxerunt parallaxin lunæ scrupulis totidem, hoc est, quasi duodecima vel decima quinta parte totius parallaxeos. Corrigatur iste error, & distantia evadet quasi semidiametrorum terrestrium, fere ut ab aliis assignatum est. Assumamus distantiam mediocrem sexaginta semidiametrorum in syzygiis; & lunarem periodum respectu fixarum compleri diebus 27, horis 7, minutis primis 43, ut ab astronomis statuitur; atque ambitum terræ esse pedum Parisiensium 123249600, uti a Gallis mensurantibus definitum est: & si luna motu omni privari fingatur ac dimitti, ut urgente vi illa omni, qua (per corol. prop. iii.) in orbe suo retinetur, descendat in terram; hæc spatio minuti unius primi cadendo describet pedes Parisienses . Colligitur hoc ex calculo vel per propositionem xxxvi libri primi, vel (quod eodem recidit) per corollarium nonum propositionis quartæ ejusdem libri, confecto. Nam arcus illius quem luna tempore minuti unius primi, medio suo motu, ad distantiam sexaginta semidiamtrorum terrestrium describat, sinus versus est pedum Parisiensium circiter, vel magis accurate pedum 15. dig. 1. & lin. . Unde cum vis illa accedendo ad terram augeatur in duplicata distantiæ ratione inversa, ideoque ad superficiem terræ major sit partibus quam ad lunam; corpus vi illa in regionibus nostris cadendo, describere deberet spatio minuti unius primi pedes Parisienses , & spatio minuti unius secundi pedes , vel magis accurate pedes 15. dig. 1. & lin. . Et eadem vi gravia revera descendunt in terram. Nam penduli, in latitudine Lutetiæ Parisiorum ad singula minuta secunda oscillantis, longitudo est pedum trium Parisiensium & linearum , ut observavit Hugenius. Et altitudo, quam grave tempore minuti unius secundi cadendo describit, est ad dimidiam longitudinem penduli hujus in duplicata ratione circumferentiæ circuli ad diametrum ejus (ut indicavit etiam Hugenius) ideoque est pedum Parisiensium 15. dig. 1. lin. . Et propterea vis qua luna in orbe suo retinetur, si descendatur in superficiem terræ, æqualis evadit vi gravitatis apud nos, ideoque (per reg. i. & ii.) est illa ipsa vis quam nos gravitatem dicere solemus. Nam si gravitas ab ea diversa esset, corpora viribus utrisque conjunctis terram petendo duplo velocius descenderent, & spatio minuti unius secundi cadendo describerent pedes Parisienses : omnino contra experientiam.
Calculus hic fundatur in hypothesi quod terra quiescit. Nam si terra & luna moveantur circum solem, & interea quoque circum commune gravitatis centrum revolvantur: manente lege gravitatis distantia centrorum lunæ ac terræ ab invicem erit semidiametrorum terrestrium circiter; uti computationem ineunti patebit. Computatio autem iniri potest per prop. lx. lib. i.
Scholium.
Demonstratio propositionis sic fusius explicari potest. Si lunæ plures circum terram revolverentur, perinde ut fit in systemate saturni vel jovis: harum tempora periodica (per argumentum inductionis) observarent legem planetarum a Keplero detectam, & propterea harum vires centripetæ forent reciproce ut quadrata distantiarum a centro terræ, per prop. i. hujus. Et si earum infima esset parva, & vertices altissimorum montium prope tangeret: hujus vis centripeta qua retineretur in orbe, gravitates corporum in verticibus illorum montium (per computationem præcedentem) æquaret quamproxime, efficeretque ut eadem lunula, si motu omni quo pergit in orbe suo privaretur, defectu vis centrifugæ qua in orbe permanserat, descenderet in terram, idque eadem cum velocitate qua gravia cadunt in illorum montium verticibus, propter æqualitatem virium quibus descendunt. Et si vis illa qua lunula illa infima descendit, diversa esset a gravitate, & lunula illa etiam gravis esset in terram more corporum in verticibus montium: eadem lunula vi utraque conjuncta duplo velocius descenderet. Quare cum vires utræque, & hæ corporum gravium, & illæ lunarum, centrum terræ respiciant, & sint inter se similes & æquales, eædem (per reg. i. & ii.) eandem habebunt causam. Et propterea vis illa, qua luna retinetur in orbe suo, ea ipsa erit quam nos gravitatem dicere solemus: idque maxime ne lunula in vertice montis vel gravitate careat, vel duplo velocius cadat quam corpora gravia solent cadere.
<399>PROPOSITIO V. THEOREMA V.
Planetas circumjoviales gravitare in jovem, circumsaturnios in saturnum, & circumsolares in solem, & vi gravitatis suæ retrahi semper a motibus rectilineis, & in orbibus curvilineis retineri.
Nam revolutiones planetarum circumjovialium circa jovem, circumsaturniorum circa saturnum, & mercurii ac veneris reliquorumque circumsolarium circa solem sunt phænomena ejusdem generis cum revolutione lunæ circa terram; & propterea (per reg. ii.) a causis ejusdem generis dependent: præsertim cum demonstratum sit quod vires, a quibus revolutiones illæ dependent, respiciant centra jovis, saturni ac solis, & recedendo a jove, saturno & sole decrescant eadem ratione ac lege, qua vis gravitatis decrescit in recessu a terra.
Corol. 1. Gravitas igitur datur in planetas universos. Nam venerem, mercurium cæterosque esse corpora ejusdem generis cum jove & saturno, nemo dubitat. Et cum attractio omnis per motus legem tertiam mutua sit, jupiter in satellites suos omnes, saturnus in suos, terraque in lunam, & sol in planetas omnes primarios gravitabit.
Corol. 2. Gravitatem, quæ planetam unumquemque respicit, esse reciproce ut quadratum distantiæ locorum ab ipsius centro.
Corol. 3. Graves sunt planetæ omnes in se mutuo per corol. 1. & 2. Et hinc jupiter & saturnus prope conjunctionem se invicem attrahendo, sensibiliter perturbant motus mutuos, sol perturbat motus lunares, sol & luna perturbant mare nostrum, ut in sequentibus explicabitur.
Scholium.
Hactenus vim illam qua corpora cœlestia in orbibus suis retinentur centripetam appellavimus. Eandem jam gravitatem esse constat, & propterea gravitatem in posterum vocabimus. Nam causa vis illius centripetæ, qua luna retinetur in orbe, extendi debet ad omnes planetas per reg. i, ii. & iv.
<400>PROPOSITIO VI. THEOREMA VI.
Corpora omnia in planetas singulos gravitare, & pondera eorum in eundem quemvis planetam, paribus distantiis a centro planetæ, proportionalia esse quantitati materiæ in singulis.
Descensus gravium omnium in terram (dempta saltem inæquali retardatione quæ ex aëris perexigua resistentia oritur) æqualibus temporibus fieri, jamdudum observarunt alii; & accuratissime quidem notare licet æqualitatem temporum in pendulis. Rem tentavi in auro, argento, plumbo, vitro, arena, sale communi, ligno, aqua, tritico. Comparabam pyxides duas ligneas rotundas & æquales. Unam implebam ligno, & idem auri pondus suspendebam (quam potui exacte) in alterius centro oscillationis. Pyxides ab æqualibus pedum undecim filis pendentes constituebant pendula, quoad pondus, figuram, & aëris resistentiam omnino paria: & paribus oscillationibus, juxta positæ, ibant una & redibant diutissime. Proinde copia materiæ in auro (per corol. 1. & 6. prop. xxiv. Lib. II.) erat ad copiam materiæ in ligno, ut vis motricis actio in totum aurum ad ejusdem actionem in totum lignum; hoc est, ut pondus ad pondus. Et sic in cæteris. In corporibus ejusdem ponderis differentia materiæ, quæ vel minor esset quam pars millesima materiæ totius, his experimentis manifesto deprehendi potuit. Jam vero naturam gravitatis in planetas eandem esse atque in terram, non est dubium. Elevari enim fingantur corpora hæc terrestria ad usque orbem lunæ, & una cum luna motu omni privata demitti, ut in terram simul cadant; & per jam ante ostensa certum est quod temporibus æqualibus describent æqualia spatia cum luna, ideoque quod sunt ad quantitatem materiæ in luna, ut pondera sua ad ipsius pondus. Porro quoniam satellites jovis temporibus revolvuntur quæ sunt in ratione sesquiplicata distantiarum a centro jovis, erunt eorum gravitates acceleratrices in jovem reciproce ut quadrata distantiarum a centro jovis; & propterea in æqualibus a jove distantiis, eorum gravitates acceleratrices evaderent æquales. Proinde temporibus æqualibus ab æqualibus altitudinibus cadendo, describerent æqualia spatia; perinde ut fit in gravibus, in hac terra nostra. Et eodem argumento planetæ circumsolares, ab æqualibus a sole distantiis dimissi, descensu suo in solem æqualibus temporibus æqualia spatia describerent. Vires autem, quibus corpora inæqualia æqualiter accelerantur, sunt ut corpora; hoc est, pondera ut quantitates materiæ in planetis. Porro jovis & ejus satellitum pondera in solem proportionalia esse quantitatibus materiæ eorum patet ex motu satellitum quam maxime regulari; per corol. 3. prop. lxv. lib. i. Nam si horum aliqui magis traherentur in solem, pro quantitate materiæ suæ, quam cæteri: motus satellitum (per corol. 2. prop. lxv. lib. i.) ex inæqualitate attractionis perturbarentur. Si, paribus a sole distantiis, satelles aliquis gravior esset in solem pro quantitate materiæ suæ, quam jupiter pro quantitate materiæ suæ, in ratione quacunque data, puta d ad e: distantia inter centrum solis & centrum orbis satellitis, major semper foret quam distantia inter centrum solis & centrum jovis in ratione subduplicata quam proxime; uti calculo quodam inito inveni. Et si satelles minus gravis esset in solem in ratione illa d ad e, distantia centri orbis satellitis a sole minor foret quam distantia centri jovis a sole in ratione illa subduplicata. Ideoque si in æqualibus a sole distantiis, gravitas acceleratrix satellitis cujusvis in solem major esset vel minor quam gravitas acceleratrix jovis in solem, parte tantum millesima gravitatis totius; foret distantia centri orbis satellitis a sole major vel minor quam distantia jovis a sole parte distantiæ totius, id est, parte quinta distantiæ satellitis extimi a centro jovis: quæ quidem orbis eccentricitas foret valde sensibilis. Sed orbes satellitum sunt jovi concentrici, & propterea gravitates acceleratrices jovis & satellitum in solem æquantur inter se. Et eodem argumento pondera saturni & comitum ejus in solem, in æqualibus a sole distantiis, sunt ut quantitates materiæ in ipsis: & pondera lunæ ac terræ in solem vel nulla sunt, vel earum massis accurate proportionalia. Aliqua autem sunt per corol. 1. & 3. prop. v.
Quinetiam pondera partium singularum planetæ cujusque in alium quemcunque sunt inter se ut materia in partibus singulis. Nam si partes aliquæ plus gravitarent, aliæ minus, quam pro quantitate materiæ: planeta totus, pro genere partium quibus maximæ abundet, gravitaret magis vel minus quam pro quantitate materiæ totius. Sed nec refert utrum partes illæ externæ sint vel internæ. Nam si verbi gratia corpora terrestria, quæ apud nos sunt, in orbem lunæ elevari fingantur, & conferantur cum corpore lunæ: si horum pondera essent ad pondera partium externarum lunæ ut quantitates materiæ in iisdem, ad pondera vero partium internarum in majori vel minori ratione, forent eadem ad pondus lunæ totius in majori vel minori ratione: contra quam supra ostensum est.
Corol. 1. Hinc pondera corporum non pendent ab eorum formis & texturis. Nam si cum formis variari possent; forent majora vel minora, pro varietate formarum, in æquali materia: omnino contra experientiam.
Corol. 2. Corpora universa, quæ circa terram sunt, gravia sunt in terram; & pondera omnium, quæ æqualiter a centro terræ distant, sunt ut quantitates materiæ in iisdem. Hæc est qualitas omnium in quibus experimenta instituere licet, & propterea per reg. iii. de universis affirmanda est. Si æther aut corpus aliud quodcunque vel gravitate omnino destitueretur, vel pro quantitate materiæ suæ minus gravitaret, quoniam id (ex mente Aristotelis, Cartesii & aliorum) non differt ab aliis corporibus nisi in forma materiæ, posset idem per mutationem formæ gradatim transmutari in corpus ejusdem conditionis cum iis, quæ pro quantitate materiæ quam maxime gravitant, & vicissim corpora maxime gravia, formam illius gradatim induendo, possent gravitatem suam gradatim amittere. Ac proinde pondera penderent a formis corporum, possentque cum formis variari, contra quam probatum est in corollario superiore.
Corol. 3. Spatia omnia non sunt æqualiter plena. Nam si spatia omnia æqualiter plena essent, gravitas specifica fluidi quo regio aëris impleretur, ob summam densitatem materiæ, nil cederet gravitati specificæ argenti vivi, vel auri, vel corporis alterius cujuscunque densissimi; & propterea nec aurum neque aliud quodcunque corpus in aëre descendere posset. Nam corpora in fluidis, nisi specifice graviora sint, minime descendunt. Quod si quantitas materiæ in spatio dato per rarefactionem quamcunque diminui possit, quidni diminui possit in infinitum?
Corol. 4. Si omnes omnium corporum particulæ solidæ sint ejusdem densitatis, neque sine poris rarefieri possint, vacuum datur. Ejusdem densitatis esse dico, quarum vires inertiæ sunt ut magnitudines.
Corol. 5. Vis gravitatis diversi est generis a vi magnetica. Nam attractio magnetica non est ut materia attracta. Corpora aliqua magis trahuntur, alia minus, plurima non trahuntur. Et vis magnetica in uno & eodem corpore intendi potest & remitti, estque nonnunquam longe major pro quantitate materiæ quam vis gravitatis, & in recessu a magnete decrescit in ratione distantiæ non duplicata, sed fere triplicata, quantum ex crassis quibusdam observationibus animadvertere potui.
PROPOSITIO VII. THEOREMA VII.
Gravitatem in corpora universa fieri, eamque proportionalem esse quantitati materiæ in singulis.
Planetas omnes in se mutuo graves esse jam ante probavimus, ut & gravitatem in unumquemque seorsim spectatum esse reciproce ut quadratum distantiæ locorum a centro planetæ. Et inde consequens est, (per prop. lxix. lib. i. & ejus corollaria) gravitatem in omnes proportionalem esse materiæ in iisdem.
Porro cum planetæ cujusvis A partes omnes graves sint in planetam quemvis B, & gravitas partis cujusque sit ad gravitatem totius, ut materia partis ad materiam totius, & actioni omni reactio (per motus Legem tertiam) æqualis sit; planeta B in partes omnes planetæ A vicissim gravitabit, & erit gravitas sua in partem unamquamque ad gravitatem suam in totum, ut materia partis ad materiam totius. Q.E.D.
Corol. 1. Oritur igitur & componitur gravitas in planetam totum ex gravitate in partes singulas. Cujus rei exempla habemus in attractionibus magneticis & electricis. Oritur enim attractio omnis in totum ex attractionibus in partes singulas. Res intelligetur in gravitate, concipiendo planetas plures minores in unum globum coire & planetam majorem componere. Nam vis totius ex viribus partium componentium oriri debebit. Siquis objiciat quod corpora omnia, quæ apud nos sunt, hac lege gravitare deberent in se mutuo, cum tamen ejusmodi gravitas neutiquam sentiatur: respondeo quod gravitas in hæc corpora, cum sit ad gravitatem in terram totam ut sunt hæc corpora ad terram totam, longe minor est quam quæ sentiri possit.
Corol. 2. Gravitatio in singulas corporis particulas æquales est reciproce ut quadratum distantiæ locorum a particulis. Patet per corol. 3. prop. lxxiv. lib. i.
PROPOSITIO VIII. THEOREMA VIII.
Si globorum duorum in se mutuo gravitantium materia undique in regionibus, quæ a centris æqualiter distant, homogenea sit: erit pondus globi alterutrius in alterum reciproce ut quadratum distantiæ inter centra.
Postquam invenissem gravitatem in planetam totum oriri & componi ex gravitatibus in partes; & esse in partes singulas reciproce proportionalem quadratis distantiarum a partibus: dubitabam an reciproca illa proportio duplicata obtineret accurate in vi tota ex viribus pluribus composita, an vero quam proxime. Nam fieri posset ut proportio, quæ in majoribus distantiis satis accurate obtineret, prope superficiem planetæ ob inæquales particularum distantias & situs dissimiles, notabiliter erraret. Tandem vero, per prop. lxxv. & lxxvi. libri primi & ipsarum corollaria, intellexi veritatem propositionis de qua hic agitur.
Corol. 1. Hinc inveniri & inter se comparari possunt pondera corporum in diversos planetas. Nam pondera corporum æqualium circum planetas in circulis revolventium sunt (per corol. 2. Prop. iv. lib. i.) ut diametri circulorum directe & quadrata temporum periodicorum inverse; & pondera ad superficies planetarum, aliasve quasvis a centro distantias, majora sunt vel minora (per hanc propositionem) in duplicata ratione distantiarum inversa. Sic ex temporibus periodicis veneris circum solem dierum 224 & horarum , satellitis extimi circumjovialis circum jovem dierum 16 & horarum , satellitis Hugeniani circum saturnum dierum 15 & horarum , & lunæ circum terram dierum 27. hor. 7. min. 43, collatis cum distantia mediocri veneris a sole & cum elongationibus maximis heliocentricis satellitis extimi circumjovialis a centro jovis 8′. 16″. satellitis Hugeniani a centro saturni 3′. 4″, & lunæ a centro terræ 10′. 33″. computum ineundo inveni quod corporum æqualium & a centro solis, jovis, saturni ac terræ æqualiter distantium pondera sint in solem, jovem, saturnum ac terram ut 1, , & respective, & auctis vel diminutis distantiis, pondera diminuuntur vel augentur in duplicata ratione: pondera æqualium corporum in solem, jovem, saturnum ac terram in distantiis 10000, 997, 791 & 109 ab eorum centris, atque ideo in eorum superficiebus, erunt ut 10000, 943, 529 & 435 respective. Quanta sint pondera corporum in superficie lunæ dicetur in sequentibus.
Corol. 2. Innotescit etiam quantitas materiæ in planetis singulis. Nam quantitates materiæ in planetis sunt ut eorum vires in æqualibus distantiis ab eorum centris, id est, in sole, jove, saturno ac terra sunt ut 1, , , & respective. Si parallaxis solis statuatur major vel minor quam 10″. , debebit quantitas materiæ in terra augeri vel diminui in triplicata ratione.
Corol. 3. Innotescunt etiam densitates planetarum. Nam pondera corporum æqualium & homogeneorum in sphæras homogeneas sunt in superficiebus sphærarum ut sphærarum diametri, per prop. lxxii. lib. i. ideoque sphærarum heterogenearum densitates sunt ut pondera illa applicata ad sphærarum diametros. Erant autem veræ solis, jovis, saturni ac terræ diametri ad invicem ut 10000, 997, 791, & 109, & pondera in eosdem ut 10000, 943, 529 & 435 respective, & propterea densitates sunt ut 100, , 67, 400. Densitas terræ quæ prodit ex hoc computo non pendet a parallaxi solis, sed determinatur per parallaxin lunæ, & propterea hic recte definitur. Est igitur sol paulo densior quam jupiter, & jupiter quam saturnus, & terra quadruplo densior quam sol. Nam per ingentem suum calorem sol rarescit. Luna vero densior est quam terra, ut in sequentibus patebit.
Corol. 4. Densiores igitur sunt planetæ qui sunt minores, cæteris paribus. Sic enim vis gravitatis in eorum superficiebus ad æqualitatem magis accedit. Sed & densiores sunt planetæ, cæteris paribus, qui sunt soli propiores; ut jupiter saturno, & terra jove. In diversis utique distantiis a sole collocandi erant planetæ ut quilibet pro gradu densitatis calore solis majore vel minore frueretur. Aqua nostra, si terra locaretur in orbe saturni, rigesceret, si in orbe mercurii in vapores statim abiret. Nam lux solis, cui calor proportionalis est, septuplo densior est in orbe mercurii quam apud nos: & thermometro expertus sum quod septuplo solis æstivi calore aqua ebullit. Dubium vero non est quin materia mercurii ad calorem accommodetur, & propterea densior sit hac nostra; cum materia omnis densior ad operationes naturales obeundas majorem calorem requirat.
PROPOSITIO IX. THEOREMA IX.
Gravitatem pergendo a superficiebus planetarum deorsum decrescere in ratione distantiarum a centro quam proxime.
Si materia planetæ quoad densitatem uniformis esset, obtineret hæc propositio accurate: per prop. lxxiii. lib. i. Error igitur tantus est, quantus ab inæquabili densitate oriri possit.
PROPOSITIO X. THEOREMA X.
Motus planetarum in cœlis diutissime conservari posse.
In scholio propositionis xl. lib. ii. ostensum est quod globus aquæ congelatæ, in aëre nostro libere movendo & longitudinem semidiametri suæ describendo, ex resistentia aëris amitteret motus sui partem . Obtinet autem eadem proportio quam proxime in globis utcunque magnis & velocibus. Jam vero globum terræ nostræ densiorem esse, quam si totus ex aqua constaret, sic colligo. Si globus hicce totus esset aqueus, quæcunque rariora essent quam aqua, ob minorem specificam gravitatem emergerent & supernatarent. Eaque de causa globus terreus aquis undique coopertus, si rarior esset quam aqua, emergeret alicubi, & aqua omnis inde defluens congregaretur in regione opposita. Et par est ratio terræ nostræ maribus magna ex parte circumdatæ. Hæc si densior non esset, emergeret ex maribus, & parte sui pro gradu levitatis extaret ex aqua, maribus omnibus in regionem oppositam confluentibus. Eodem argumento maculæ solares leviores sunt quam materia lucida solaris cui supernatant. Et in formatione qualicunque planetarum, ex aqua materia omnis gravior, quo tempore massa fluida erat, centrum petebat. Unde cum terra communis suprema quasi duplo gravior sit quam aqua, & paulo inferius in fodinis quasi triplo vel quadruplo aut etiam quintuplo gravior reperiatur: verisimile est quod copia materiæ totius in terra quasi quintuplo vel sextuplo major sit quam si tota ex aqua constaret; præsertim cum terram quasi quadruplo densiorem esse quam jovem jam ante ostensum sit. Quare si jupiter paulo densior sit quam aqua, hic spatio dierum triginta, quibus longitudinem 459 semidiametrorum suarum describit, amitteret in medio ejusdem densitatis cum aëre nostro motus sui partem fere decimam. Verum cum resistentia mediorum minuatur in ratione ponderis ac densitatis, sic ut aqua, quæ partibus levior est quam argentum vivum, minus resistat in eadem ratione; & aer, qui partibus 860 levior est quam aqua, minus resistat in eadem ratione: si ascendatur in cœlos ubi pondus medii, in quo planetæ moventur, diminuitur in immensum, resistentia prope cessabit. Ostendimus utique in scholio ad prop. xxii. lib. ii. quod si ascenderetur ad altitudinem milliarium ducentorum supra terram, aër ibi rarior foret quam ad superficiem terræ in ratione 30 ad 0,0000000000003998, seu 75000000000000 ad 1 circiter. Et hinc stella jovis in medio ejusdem densitatis cum aere illo superiore revolvendo, tempore annorum 1000000, ex resistentia medii non amitteret motus sui partem decimam centesimam millesimam. In spatiis utique terræ proximis, nihil invenitur quod resistentiam creet præter aërem exhalationes & vapores. His ex vitro cavo cylindrico diligentissime exhaustis gravia intra vitrum liberrime & sine omni resistentia sensibili cadunt; ipsum aurum & pluma tenuissima simul demissa æquali cum velocitate cadunt, & casu suo describendo altitudinem pedum quatuor sex vel octo simul incidunt in fundum, ut experientia compertum est. Et propterea si in cœlos ascendatur aëre & exhalationibus vacuos, planetæ & cometæ sine omni resistentia sensibili per spatia illa diutissime movebuntur.
<408>HYPOTHESIS I.
Centrum systematis mundani quiescere.
Hoc ab omnibus concessum est, dum aliqui terram, alli solem in centro systematis quiescere contendant. Videamus quid inde sequatur.
PROPOSITIO XI. THEOREMA XI.
Commune centrum gravitatis terræ, solis & planetarum omnium quiescere.
Nam centrum illud (per legum corol. iv.) vel quiescet vel progredietur uniformiter in directum. Sed centro illo semper progrediente, centrum mundi quoque movebitur contra hypothesin.
PROPOSITIO XII. THEOREMA XII.
Solem motu perpetuo agitari, sed nunquam longe recedere a communi gravitatis centro planetarum omnium.
Nam cum (per corol. 2. prop. viii.) materia in sole sit ad materiam in jove ut 1067 ad 1, & distantia jovis a sole sit ad semidiametrum solis in ratione paulo majore; incidet commune centrum gravitatis jovis & solis in punctum paulo supra superficiem solis. Eodem argumento cum materia in sole sit ad materiam in saturno ut 3021 ad 1, & distantia saturni a sole sit ad semidiametrum solis in ratione paulo minore: incidet commune centrum gravitatis saturni & solis in punctum paulo infra superficiem solis. Et ejusdem calculi vestigiis insistendo si terra & planetæ omnes ex una solis parte consisterent, commune omnium centrum gravitatis vix integra solis diametro a centro solis distaret. Aliis in casibus distantia centrorum semper minor est. Et propterea cum centrum illud gravitatis perpetuo quiescit, sol pro vario planetarum situ in omnes partes movebitur, sed a centro illo nunquam longe recedet.
Corol. Hinc commune gravitatis centrum terræ, solis & planetarum omnium pro centro mundi habendum est. Nam cum terra, sol & planetæ omnes gravitent in se mutuo, & propterea, pro vi gravitatis suæ, secundum leges motus perpetuo agitentur: perspicuum est quod horum centra mobilia pro mundi centro quiescente haberi nequeunt. Si corpus illud in centro locandum esset in quod corpora omnia maxime gravitant (uti vulgi est opinio) privilegium istud concedendum esset soli. Cum autem sol moveatur, eligendum erit punctum quiescens, a quo centrum solis quam minime discedit, & a quo idem adhuc minus discederet, si modo sol densior esset & major, ut minus moveretur.
PROPOSITIO XIII. THEOREMA XIII.
Planetæ moventur in ellipsibus umbilicum habentibus in centro solis, & radiis ad centrum illud ductis areas describunt temporibus proportionales.
Disputavimus supra de his motibus ex phænomenis. Jam cognitis motuum principiis, ex his colligimus motus cœlestes a priori. Quoniam pondera planetarum in solem sunt reciproce ut quadrata distantiarum a centro solis; si sol quiesceret & planetæ reliqui non agerent in se motuo, forent orbes eorum elliptici, solem in umbilico communi habentes, & areæ describerentur temporibus proportionales (per prop. i. & xi. & corol. 1. prop. xiii. lib. i.) actiones autem planetarum in se motuo perexiguæ sunt (ut possint contemni) & motus planetarum in ellipsibus circa solem mobilem minus perturbant (per prop. lxvi. lib. i.) quam si motus isti circa solem quiescentem peragerentur.
Actio quidem jovis in saturnum non est omnino contemnenda. Nam gravitas in jovem est gravitatem in solem (paribus distantiis) ut 1 ad 1067; ideoque in conjunctione jovis & saturni, quoniam distantia saturni a jove est ad distantiam saturni a sole fere ut 4 ad 9, erit gravitas saturni in jovem ad gravitatem saturni in solem ut 81 ad seu 1 ad 211 circiter. Et hinc oritur perturbatio orbis saturni in singulis planetæ hujus cum jove conjunctionibus adeo sensibilis ut ad eandem astronomi hæreant. Pro vario situ planetæ in his conjunctionibus, eccentricitas ejus nunc augetur nunc diminuitur, aphelium nunc promovetur nunc forte retrahitur, & medius motus per vices acceleratur & retardatur. Error tamen omnis in motu ejus circum solem a tanta vi oriundus (præterquam in motu medio) evitari fere potest constituendo umbilicum inferiorem orbis ejus in communi centro gravitatis jovis & solis (per prop. lxvii. lib. i.) & propterea ubi maximus est, vix superat minuta duo prima. Et error maximus in motu medio vix superat minuta duo prima annuatim. In conjuctione autem jovis & saturni gravitates acceleratrices solis in saturnum, jovis in saturnum & jovis in solem sunt fere ut 16, 81 & seu 156609, ideoque differentia gravitatum solis in saturnum & jovis in saturnum est ad gravitatem jovis in solem ut 65 ad 156609 seu 1 ad 2409. Huic autem differentiæ proportionalis est maxima saturni efficacia ad perturbandum motum jovis, & propterea perturbatio orbis jovialis longe minor est quam ea saturnii. Reliquorum orbium perturbationes sunt adhuc longe minores, præterquam quod orbis terræ sensibiliter perturbatur a luna. Commune centrum gravitatis terræ & lunæ, ellipsin circum solem in umbilico positum percurrit, & radio ad solem ducto areas in eadem temporibus proportionales describit, terra vero circum hoc centrum commune motu menstruo revolvitur.
PROPOSITIO XIV. THEOREMA XIV.
Orbium aphelia & nodi quiescunt.
Aphelia quiescunt, per prop. xi. lib. i. ut & orbium plana, per ejusdem libri prop. i. & quiescentibus planis quiescunt nodi. Attamen a planetarum revolventium & cometarum actionibus in se invicem orientur inæqualitates aliquæ, sed quæ ob parvitatem hic contemni possunt.
Corol. 1. Quiescunt etiam stellæ fixæ, propterea quod datas ad aphelia nodosque positiones servant.
Corol. 2. Ideoque cum nulla sit earum parallaxis sensibilis ex terræ motu annuo oriunda, vires earum ob immensam corporum distantiam nullos edent sensibiles effectus in regione systematis nostri. Quinimo fixæ in omnes cœli partes æqualiter dispersæ contrariis attractionibus vires mutuas destruunt, per prop. lxx. lib. i.
<411>Scholium.
Cum planetæ soli propiores (nempe mercurius, venus, terra, & mars) ob corporum parvitatem parum agant in se invicem: horum aphelia & nodi quiescent, nisi quatenus a viribus jovis, saturni, & corporum superiorum turbentur. Et inde colligi potest per theoriam gravitatis, quod horum aphelia moventur aliquantulum in consequentia respectu fixarum, idque in proportione sesquiplicata distantiarum horum planetarum a sole. Ut si aphelium martis in annis centum conficiat 33′. 20″ in consequentia respectu fixarum; aphelia terræ, veneris, & mercurii in annis centrum conficient 17′. 40″, 10′. 53″, & 4′. 16″ respective. Et hi motus, ob parvitatem, negliguntur in hac propositione.
PROPOSITIO XV. PROBLEMA I.
Invenire orbium principales diametros.
Capiendæ sunt hæ in ratione subsesquiplicata temporum periodicorum, per prop. xv. lib. i. deinde sigillatim augendæ in ratione summæ massarum solis & planetæ cujusque revolventis ad primam duarum medie proportionalium inter summam illam & solem, per. prop. lx. lib. i.
PROPOSITIO XVI. PROBLEMA II.
Invenire orbium eccentricitates & aphelia.
Problema confit per prop. xviii. lib. i.
PROPOSITIO XVII. THEOREMA XV.
Planetarum motus diurnos uniformes esse, & librationem lunæ ex ipsius motu diurno oriri.
Patet per motus legem 1, & corol. 22. prop. lxvi. lib. i. Jupiter utique respectu fixarum revolvitur horis 9. 56′, mars horis 24. 39′. venus horis 23 circiter, terra horis 23. 56′, sol diebus & luna diebus 27. 7 hor. 43′. Hæc ita se habere ex phænomenis manifestum est. Maculæ in corpore solis ad eundem situm in disco solis redeunt diebus circiter, respectu terræ; ideoque respectu fixarum sol revolvitur diebus circiter. Quoniam vero lunæ circa axem suum uniformiter revolventis dies menstruus est; hujus facies eadem ulteriorem umbilicum orbis ejus semper respiciet quamproxime, & propterea pro situ umbilici illius deviabit hinc inde a terra. Hæc est libratio lunæ in longitudinem. Nam libratio in latitudinem orta est ex latitudine lunæ & inclinatione axis ejus ad planum elipticæ. Hanc librationis lunaris theoriam D. N. Mercator in astronomia sua initio anni 1676 edita, ex literis meis plenius exposuit. Simili motu extimus saturni satelles circa axem suum revolvi videtur, eadem sui facie saturnum perpetuo respiciens. Nam circum saturnum revolvendo, quoties ad orbis sui partem orientalem accedit, ægerrime videtur, & plerumque videri cessat: id quod evenire potest per maculas quasdam in ea corporis parte quæ terræ tunc obvertitur, ut Cassinus notavit. Simili etiam motu satelles extimus jovialis circa axem suum revolvi videtur, propterea quod in parte corporis jovi aversa maculam habeat quæ tanquam in corpore jovis cernitur ubicunque satelles inter jovem & oculos nostros transit.
PROPOSITIO XVIII. THEOREMA XVI.
Axes planetarum diametris quæ ad eosdem axes normaliter ducuntur minores esse.
Planetæ sublato omni motu circulari diurno figuram sphæricam, ob æqualem undique partium gravitatem, affectare deberent. Per motum illum circularem fit ut partes ab axe recedentes juxta æquatorem ascendere conentur. Ideoque materia si fluida sit ascensu suo ad æquatorem diametros adaugebit, axem vero descensu suo ad polos diminuet. Sic jovis diameter (consentientibus astronomorum observationibus) brevior deprehenditur inter polos quam ab oriente in occidentem. Eodem argumento, nisi terra nostra paulo altior esset sub æquatore quam ad polos, maria ad polos subsiderent, & juxta æquatorem ascendendo, ibi omnia inundarent.
PROPOSITIO XIX. PROBLEMA III.
Invenire proportionem axis planetæ ad diametros eidem perpendiculares.
Norwoodus noster circa annum 1635 mensurando distantiam pedum Londinensium 905751 inter Londinum & Eboracum, & observando differentiam latitudinum 2 gr. 28′ collegit mensuram gradus unius esse pedum Londinensium 367196, id est, hexapedarum Parisiensium 57300.
Picartus mensurado arcum gradus unius & 22′. 55″ in meridiano inter Ambianum & Malvoisinam, invenit arcum gradus unius esse hexapedarum Parisiensium 57060. Cassinus senior mensuravit distantiam in meridiano a villa Collioure in Roussilion ad observatorium Parisiense; & filius ejus addidit distantiam ab observatorio ad turrem urbis Dunkirk. Distantia tota erat hexapedarum , & differentia latitudinum villæ Collioure & urbis Dunkirk erat graduum octo & 31′. . Unde arcus gradus unius prodit hexapedarum Parisiensium 57061. Et ex his mensuris colligitur ambitus terræ pedum Parisiensium 123249600, & semidiameter ejus pedum 19615800, ex hypothesi quod terra sit sphærica.
In latitudine Lutetiæ Parisiorum corpus grave tempore minuti unius secundi cadendo describit pedes Parisienses 15 dig. 1 lin. ut supra, id est, lineas . Pondus corporis diminuitur per pondus aëris ambientis. Ponamus pondus amissum esse partem undecimam millesimam ponderis totius, & corpus illud grave cedendo in vacuo describet altitudinem linearum 2174 tempore minuti unius secundi.
Corpus in circulo ad distantiam pedum 19615800 a centro, singulis diebus sidereis horarum 23. 56′. 4″ uniformiter revolvens tempore minuti unius secundi describet arcum pedum 1433,46, cujus sinus versus est pedum 0,0523656, seu linearum 7,54064. Ideoque vis, qua gravia descendunt in latitudine Lutetiæ, est ad vim centrifugam corporum in æquatore a terræ motu diurno oriundam, ut 2174 ad 7,54064.
Vis centrifuga corporum in æquatore terræ est ad vim centrifugam, qua corpora directe tendunt a terra in latitudine Lutetiæ graduum 48. 50′. 10″, in duplicata ratione radii ad sinum complementi latitudinis illius, id est, ut 7,54064 ad 3,267. Addatur hæc vis ad vim qua gravia descendunt in latitudine illa Lutetiæ, & corpus in latitudine illa via tota gravitatis cadendo, tempore minuti unius secundi describet lineas 2177,267, seu pedes Parisienses 15 dig. 1 & lin. 5,267. Et vis tota gravitatis in latitudine illa erit ad vim centrifugam corporum in æquatore terræ ut 2177,267 ad 7,54064 seu 289 ad 1.
Unde si APBQ figuram terræ designet jam non amplius sphæricam revolutione ellipseos circum axem minorem PQ genitam, sitque ACQqca canalis aquæ plena, a polo Qq ad centrum Cc, & inde ad æquatorem Aa pergens: debebit pondus aquæ in canalis crure ACca, esse ad pondus aquæ in crure altero QCcq ut 289 ad 288, eo quod vis centrifuga ex circulari motu orta partem unam e ponderis partibus 289 sustinebit ac detrahet, & pondus 288 in altero 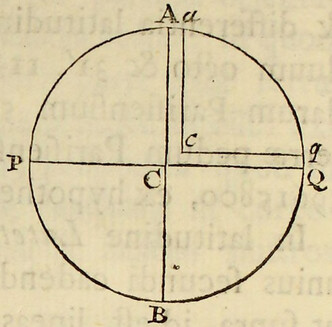 crure sustinebit reliquas. Porro (ex propositionis xci. corol. 2. lib. i.) computationem ineundo, invenio quod si terra constaret ex uniformi materia, motuque omni privaretur, & esset ejus axis PQ ad diametrum AB ut 100 ad 101: gravitas in loco Q in terram foret ad gravitatem in eodem loco Q in sphæram centro C radio PC vel QC descriptam, ut 126 ad 125. Et eodem argumento gravitas in loco A in sphæroidem, convolutione ellipseos APBQ circa axem AB descriptam, est ad gravitatem in eodem loco A in sphæram centro C radio AC descriptam, ut 125 ad 126. Est autem gravitas in loco A in terram media proportionalis inter gravitates in dictam sphæroidem & sphæram: propterea quod sphæra, diminuendo diametrum PQ in ratione 101 ad 100, vertitur in figuram terræ; & hæc figura diminuendo in eadem ratione diametrum tertiam, quæ diametris duabus AB, PQ perpendicularis est, vertitur in dictam sphæroidem; & gravitas in A, in casu utroque, diminuitur in eadem ratione quam proxime. Est igitur gravitas in A in sphæram centro C radio AC descriptam, ad gravitatem in A in terram ut 126 ad , & gravitas in loco Q in sphæram centro C radio QC descriptam, est ad gravitatem in loco A in sphæram centro C radio AC descriptam, in ratione diametrorum (per prop. lxxii. lib. i.) id est, ut 100 ad 101. Conjungantur jam hæ tres rationes, 126 ad 125, 126 ad & 100 ad 101: & fiet gravitas in loco Q in terram ad gravitatem in loco A in terram, ut ad , seu ut 501 ad 500.
crure sustinebit reliquas. Porro (ex propositionis xci. corol. 2. lib. i.) computationem ineundo, invenio quod si terra constaret ex uniformi materia, motuque omni privaretur, & esset ejus axis PQ ad diametrum AB ut 100 ad 101: gravitas in loco Q in terram foret ad gravitatem in eodem loco Q in sphæram centro C radio PC vel QC descriptam, ut 126 ad 125. Et eodem argumento gravitas in loco A in sphæroidem, convolutione ellipseos APBQ circa axem AB descriptam, est ad gravitatem in eodem loco A in sphæram centro C radio AC descriptam, ut 125 ad 126. Est autem gravitas in loco A in terram media proportionalis inter gravitates in dictam sphæroidem & sphæram: propterea quod sphæra, diminuendo diametrum PQ in ratione 101 ad 100, vertitur in figuram terræ; & hæc figura diminuendo in eadem ratione diametrum tertiam, quæ diametris duabus AB, PQ perpendicularis est, vertitur in dictam sphæroidem; & gravitas in A, in casu utroque, diminuitur in eadem ratione quam proxime. Est igitur gravitas in A in sphæram centro C radio AC descriptam, ad gravitatem in A in terram ut 126 ad , & gravitas in loco Q in sphæram centro C radio QC descriptam, est ad gravitatem in loco A in sphæram centro C radio AC descriptam, in ratione diametrorum (per prop. lxxii. lib. i.) id est, ut 100 ad 101. Conjungantur jam hæ tres rationes, 126 ad 125, 126 ad & 100 ad 101: & fiet gravitas in loco Q in terram ad gravitatem in loco A in terram, ut ad , seu ut 501 ad 500.
Jam cum (per corol. 3. prop. xci. lib. i.) gravitas in canalis crure utrovis ACca vel QCcq sit ut distantia locorum a centro terræ si crura illa superficiebus transversis & æquidistantibus distinguantur in partes totis proportionales, erunt pondera partium singularum in crure ACca ad pondera partium totidem in crure altero, ut magnitudines & gravitates acceleratrices conjunctim; id est, ut 101 ad 100 & 500 ad 501, hoc est, ut 505 ad 501. Ac proinde si vis centrifuga partis cujusque in crure ACca ex motu diurno oriunda, fuisset ad pondus partis ejusdem ut 4 ad 505, eo ut de pondere partis cujusque, in partes 505 diviso, partes quatuor detraheret; manerent pondera in utroque crure æqualia, & propterea fluidum consisteret in æquilibrio. Verum vis centrifuga partis cujusque est ad pondus ejusdem ut 1 ad 289, hoc est, vis centrifuga quæ deberet esse ponderis pars est tantum pars . Et propterea dico, secundum regulam auream, quod si vis centrifuga faciat ut altitudo aquæ in crure ACca superet altitudinem aquæ in crure QCcq parte centesima totius altitudinis: vis centrifuga faciet ut excessus altitudinis in crure ACca sit altitudinis in crure altero QCcq pars tantum . Est igitur diameter terræ secundum æquatorem ad ipsius diametrum per polos ut 230 ad 229. Ideoque cum terræ semidiameter mediocris, juxta mensuram Picarti, sit pedum Parisiensium 19615800, seu milliarium 3923,16 (posito quod milliare sit mensura pedum 5000) terra altior erit ad æquatorem quam ad polos excessu pedum 85472, seu milliarium . Et altitudo ejus ad æquatorem erit 19658600 pedum circiter, & ad polos 19573000 pedum.
Si planeta vel major sit vel minor quam terra manente ejus densitate ac tempore periodico revolutionis diurnæ, manebit proportio vis centrifugæ ad gravitatem, & propterea manebit etiam proportio diametri inter polos ad diametrum secundum æquatorem. At si motus diurnus in ratione quacunque acceleretur vel retardetur, augebitur vel minuetur vis centrifuga in duplicata illa ratione, & propterea differentia diametrorum augebitur vel minuetur in eadem duplicata ratione quamproxime. Et si densitas planetæ augeatur vel minuatur in ratione quavis, gravitas etiam in ipsum tendens augebitur vel minuetur in eadem ratione, & differentia diametrorum vicissim minuetur in ratione gravitatis auctæ vel augebitur in ratione gravitatis diminutæ. Unde cum terra respectu fixarum revolvatur horis 23. 56′, jupiter autem horis 9. 56′, sintque temporum quadrata ut 29 ad 5, & revolventium densitates ut 400 ad : differentia diametrorum jovis erit ad ipsius diametrum minorem ut ad 1, seu 1 ad quamproxime. Est igitur diameter jovis ab oriente in occidentem ducta, ad ejus diametrum inter polos ut ad quamproxime. Unde cum ejus diameter major sit 37″, ejus diameter minor quæ polis interjacet, erit 33″. . Pro luce erratica addantur 3″ circiter, & hujus planetæ diametri apparentes evadent 40″ & 36″. : quæ sunt ad invicem ut ad quamproxime. Hoc ita se habet ex hypothesi quod corpus jovis sit uniformiter densum. At si corpus ejus sit densius versus planum æquatoris quam versus polos, diametri ejus possunt esse ad invicem ut 12 ad 11, vel 13 ad 12, vel forte 14 ad 13. Et Cassinus quidem anno 1691 observavit, quod jovis diameter ab oriente in occidentem porrecta diametrum alteram superaret parte sui circiter decima quinta. Poundus autem noster telescopio pedum 123 longitudinis & optimo micrometro, diametros jovis anno 1719, mensuravit ut sequitur.
| Tempora. | Diam. max. | Diam. min. | Diametri ad invicem. | |||||
| dies | hor. | part. | part. | |||||
| Jan. | 28 | 6 | 13,40 | 12,28 | ut | 12 | ad | 11 |
| Mar. | 6 | 7 | 13,12 | 12,20 | 13 | 12 | ||
| Mar. | 9 | 7 | 13,12 | 12,08 | 12 | 14 | ||
| Apr. | 9 | 9 | 12,32 | 11,48 | 14 | 13 | ||
Congruit igitur theoria cum phænomenis. Nam planetæ magis incalescunt ad lucem solis versus æuatores suos, & propterea paulo magis ibi decoquuntur quam versus polos.
Quinetiam gravitatem per rotationem diurnam terræ nostræ minui sub æquatore, atque ideo terram ibi altius surgere quam ad polos (si materia ejus uniformiter densa sit) patebit per experimenta pendulorum quæ recensentur in propositione sequente.
<417>PROPOSITIO XX. PROBLEMA IV.
Invenire & inter se comparare pondera corporum in terræ hujus regionibus diversis.
Quoniam pondera inæqualium crurum canalis aqueæ ACQqca æqualia sunt; & pondera partium, cruribus totis proportionalium & similiter in totis sitarum, sunt ad invicem ut pondera totorum, ideoque etiam æquantur inter se; erunt pondera æqualium & in cruribus similiter sitarum partium reciproce ut crura, id est, reciproce ut 230 ad 229. Et par est ratio homogeneorum & æqualium quorumvis & in canalis cruribus similiter sitorum corporum. Horum pondera sunt reciproce ut crura, id est, reciproce ut distantiæ corporum a centro terræ. Proinde si corpora in supremis canalium partibus, sive in superficie terræ consistant; erunt pondera eorum ad invicem reciproce ut distantiæ eorum a centro. Et eodem argumento pondera, in aliis quibuscunque per totam terræ superficiem regionibus, sunt reciproce ut distantiæ locorum a centro; & propterea, ex hypothesi quod terra sphærois sit, dantur proportione.
Unde tale confit theorema, quod incrementum ponderis pergendo ab æquatore ad polos, sit quam proxime ut sinus versus latitudinis duplicatæ, vel quod perinde est, ut quadratum sinus recti latitudinis. Et in eadem circiter ratione augentur arcus graduum latitudinis in meridiano. Ideoque cum latitudo Lutetiæ Parisiorum sit 48gr. 50′, ea locorum sub æquatore 00gr. 00′, & ea locorum ad polos 90gr. & duplorum sinus versi sint 11334, 00000 & 20000, existente radio 10000, & gravitas ad polum sit ad gravitatem sub æquatore ut 230 ad 229, & excessus gravitatis ad polum ad gravitatem sub æquatore ut 1 ad 229: erit excessus gravitatis in latitudine Lutetiæ ad gravitatem sub æquatore, ut ad 229, seu 5667 ad 2290000. Et propterea gravitates totæ in his locis erunt ad invicem ut 2295667 ad 2290000. Quare cum longitudines pendulorum æqualibus temporibus oscillantium sint ut gravitates, & in latitudine Lutetiæ Parisiorum longitudo penduli singulis minutis secundis oscillantis sit pedum trium Parisiensium & linearum , vel potius ob pondus aëris : longitudo penduli sub æquatore superabitur a longitudine synchroni penduli Parisiensis, excessu lineæ unius & 87 partium millesimarum lineæ. Et simuli computo confit tabula sequens.
<418>Constat autem per hanc tabulam, quod graduum inæqualitas tam parva sit, ut in rebus geographicis figura terræ pro sphærica haberi possit: præsertim si terra paulo densior sit versus planum æquatoris quam versus polos.
Jam vero astronomi aliqui in longinquas regiones ad observationes astronomicas faciendas missi, observarunt quod horologia oscillatoria tardius moverentur prope æquatorem quam in regionibus nostris. Et primo quidem D. Richer hoc observavit anno 1672 in insula Cayennæ. Nam dum observaret transitum fixarum per meridianum mense Augusto, reperit horologium suum tardius moveri quam pro medio motu solis, existente differentia 2′. 28″ singulis diebus. Deinde faciendo ut pendulum simplex ad minuta singula secunda per horologium optimum mensurata oscillaret, notavit longitudinem penduli simplicis, & hoc fecit sæpius singulis septimanis per menses decem. Tum in Galliam redux contulit longitudinem hujus penduli cum longitudine penduli Parisiensis (quæ erat trium pedum Parisiensium, & octo linearum cum tribus quintis partibus lineæ) & reperit breviorem esse, existente differentia lineæ unius cum quadrante.
Postea Halleius noster circa annum 1677 ad insulam Sanctæ Hellenæ navigans, reperit horologium suum oscillatorium ibi tardius moveri quam Londoni, sed differentiam non notavit. Pendulum vero brevius reddidit plusquam octava parte digiti, seu linea una cum semisse. Et ad hoc efficiendum, cum longitudo cochleæ in ima parte penduli non sufficeret, annulum ligneum thecæ cochleæ & ponderi pendulo interposuit.
Deinde anno 1682 D. Varin & D. Des Hayes invenerunt longitudinem penduli singulis minutis secundis oscillantis in observatorio regio Parisiensi esse ped. 3. lin. . Et in insula Gorea eadem methodo longitudinem penduli synchroni invenerunt esse ped. 3. lin. , existente longitudinum differentia lin. 2. Et eodem anno ad insulas Guadaloupam & Martinicam navigantes, invenerunt longitudinem penduli synchroni in his insulis esse ped. 3. lin. .
Posthac D. Couplet filius anno 1697 mense Julio, horologium suum oscillatorium ad motum solis medium in observatorio regio Parisiensi sic aptavit, ut tempore satis longo horologium cum motu solis congrueret. Deinde Ulyssipponem navigans invenit quod mense Novembri proximo horologium tardius iret quam prius, existente differentia 2′. 13″ in horis 24. Et mense Martio sequente Paraibam navigans invenit ibi horologium suum tardius ire quam Parisiis, existente differentia 4′. 12″ in horis 24. Et affirmat pendulum ad minuta secunda oscillans brevius fuisse Ulyssipponi lineis & Paraibæ lineis quam Parisiis. Rectius posuisset differentias esse & . Nam hæ differentiæ differentiis temporum 2′. 13″, & 4′. 12″ respondent. Crassioribus hujus observationibus minus fidendum est.
<420>Annis proximis (1699 & 1700) D. Des Hayes ad Americam denuo navigans, determinavit quod in insulis Cayennæ & Granadæ longitudo penduli ad minuta secunda oscillantis, esset paulo minor quam ped 3. lin. , quodque in insula S. Christophori longitudo illa esset ped. 3. lin. , & quod in insula S. Dominici eadem esset ped. 3. lin. 7.
Annoque 1704. P. Feuelleus invenit in Porto-belo in America longitudinem penduli ad minuta secunda oscillantis, esse pedum trium Parisiensium & linearum tantum , id est, tribus fere lineis breviorem quam Lutetiæ Parisiorum, sed errante observatione. Nam deinde ad insulam Martinicam navigans, invenit longitudinem penduli isochroni esse pedum tantum trium Parisiensium & linearum .
Latitudo autem Paraibæ est 6gr. 38′ ad austrum, & ea Porto beli 9gr. 33′ ad boream, & latitudines insularum Cayennæ, Goreæ, Guadaloupæ, Martinicæ, Granadæ, Sancti Christophori, & Sancti Dominici sunt respective 4gr. 55′, 14gr. 40′, 14gr. 00′, 14gr. 44′, 12gr. 6′, 17gr. 19′, & 19gr. 48′ ad boream. Et excessus longitudinis penduli Parisiensis supra longitudines pendulorum isochronorum in his latitudinibus observatas sunt paulo majores quam pro tabula longitudinum penduli superius computata. Et propterea terra aliquanto altior est sub æquatore quam pro superiore calculo, & densior ad centrum quam in fodinis prope superficiem, nisi forte calores in zona torrida longitudinem pendulorum aliquantulum auxerint.
Observavit utique D. Picartus quod virga ferrea, quæ tempore hyberno ubi gelabant frigora erat pedis unius longitudine, ad ignem calefacta evasit pedis unius cum quarta parte lineæ. Deinde D. de la Hire observavit quod virga ferrea quæ tempore consimili hyberno sex erat pedum longitudinis, ubi soli æstivo exponebatur evasit sex pedum longitudinis cum duabus tertiis partibus lineæ. In priore casu calor major fuit quam in posteriore, in hoc vero major fuit quam calor externarum partium corporis humani. Nam metalla ad solem æstivum valde incalescunt. At virga penduli in horologio oscillatorio nunquam exponi solet calori solis æstivi, nunquam calorem concipit calori externæ superficiei corporis humani æqualem. Et propterea virga penduli in horologio tres pedes longa, paulo quidem longior erit tempore æstivo quam hyberno, sed excessu quartam partem lineæ unius vix superante. Proinde differentia tota longitudinis pendulorum quæ in deversis regionibus isochrona sunt, diverso calori attribui non potest. Sed neque erroribus astronomorum e Gallia missorum tribuenda est hæc differentia. Nam quamvis eorum observationes non perfecte congruant inter se, tamen errores sunt adeo parvi ut contemni possint. Et in hoc concordant omnes, quod isochrona pendula sunt breviora sub æquatore quam in observatorio regio Parisiensi, existente differentia non minore quam lineæ unius cum quadrante, non majore quam linearum . Per observationes D. Richeri in Cayenna factas differentia fuit lineæ unius cum quadrante. Per eas D. Des Hayes differentia illa correcta prodiit lineæ unius cum semisse vel unius cum tribus quartis partibus lineæ. Per eas aliorum minus accuratas prodiit eadem quasi duarum linearum. Et hæc discrepantia partim ad erroribus observationum, partim a dissimilitudine partium internarum terræ & altitudine montium, & partim a diversis aëris caloribus, oriri potuit.
Virga ferrea pedes tres longa, tempore hyberno in Anglia, brevior est quam tempore æstivo, sexta parte lineæ unius, quantum sentio. Ob calores sub æquatore auferatur hæc quantitas de differentia lineæ unius cum quadrante a Richero observata, & manebit linea : quæ cum linea per theoriam jam ante collecta probe congruit. Richerus autem observationes in Cayenna factas, singulis septimanis per menses decem iteravit, & longitudines penduli in virga ferrea ibi notatas cum longitudinibus ejus in Gallia similiter notatis contulit. Quæ diligentia & cautela in aliis observatoribus defuisse videtur. Si hujus observationibus fidendum est, terra altior erit ad æquatorem quam ad polos excessu milliarum septendecim circiter, ut supra per theoriam prodiit.
<422>PROPOSITIO XXI. THEOREMA XVII.
Puncta æquinoctialia regredi, & axem terræ singulis revolutionibus annuis nutando bis inclinari in eclipticam & bis redire ad positionem priorem.
Patet per corol. 20. prop. lxvi. lib. i. Motus tamen iste nutandi perexiguus esse debet, & vix aut ne vix quidem sensibilis.
PROPOSITIO XXII. THEOREMA XVIII.
Motus omnes lunares, omnesque motuum inæqualitates ex allatis principiis consequi.
Planetas majores, interea dum circa solem feruntur, posse alios minores circum se revolventes planetas deferre, & minores illos in ellipsibus, umbilicos in centris majorum habentibus, revolvi debere patet per prop. lxv. lib. i. Actione autem solis perturbabuntur eorum motus multimode, iisque adficientur inæqualitatibus quæ in luna nostra notantur. Hæc utique (per corol. 2, 3, 4, & 5. prop. lxvi.) velocius movetur, ac radio ad terram ducto describit aream pro tempore majorem, orbemque habet minus curvum, atque ideo propius accedit ad terram, in syzygiis quam in quadraturis, nisi quatenus impedit motus eccentricitatis. Eccentricitas enim maxima est (per corol. 9. prop. lxvi.) ubi apogæum lunæ in syzygiis versatur, & minima ubi idem in quadraturis consistit; & inde luna in perigæo velocior est & nobis propior, in apogæo autem tardior & remotior in syzygiis quam in quadraturis. Progreditur insuper apogæum, & regrediuntur nodi, sed motu inæquabili. Et apogæum quidem (per corol. 7 & 8 prop. lxvi.) velocius progreditur in syzygiis suis, tardius regreditur in quadraturis, & excessu progressus supra regressum annuatim fertur in consequentia. Nodi autem (per corol. 2. prop. lxvi.) quiescunt in syzygiis suis & velocissime regrediuntur in quadraturis. Sed & major est lunæ latitudo maxima in ipsius quadraturis (per corol. 10. prop. lxvi.) quam in syzygiis: & motus medius tardior in perihelio terræ (per corol. 6. prop. lxvi.) quam in ipsius aphelio. Atque hæ sunt inæqualitates insigniores ab astronomis notatæ.
<423>Sunt etiam aliæ quædam a prioribus astronomis non observatæ inæqualitates, quibus motus lunares adeo perturbantur, ut nulla hactenus lege ad regulam aliquam certam reduci potuerint. Velocitates enim seu motus horarii apogæi & nodorum lunæ, & eorundem æquationes, ut & differentia inter eccentricitatem maximam in syzygiis & minimam in quadraturis, & inæqualitas quæ variatio dicitur, augentur ac diminuuntur annuatim (per corol. 14. prop. lxvi.) in triplicata ratione diametri apparentis solaris. Et variatio præterea augetur vel diminuitur in duplicata ratione temporis inter quadraturas quam proxime (per corol. 1 & 2. lem. x. & corol. 16. prop. lxvi. Lib. i.) sed hæc inæqualitas in calculo astronomico ad prostaphæresin lunæ referri solet, & cum ea confundi.
PROPOSITIO XXIII. PROBLEMA V.
Motus inæquales satellitum jovis & saturni a motibus lunaribus derivare.
Ex motibus lunæ nostræ motus analogi lunarum seu satellitum jovis sic derivantur. Motus medius nodorum satellitis extimi jovialis, est ad motum medium nodorum lunæ nostræ, in ratione composita ex ratione duplicata temporis periodici terræ circa solem ad tempus periodicum jovis circa solem, & ratione simplici temporis periodici satellitis circa jovem ad tempus periodicum lunæ circa terram (per corol. 16. prop. lxvi. lib. i.) ideoque annis centum conficit nodus iste 8gr. 24′. in antecedentia. Motus medii nodorum satellitum interiorum sunt ad motum hujus, ut illorum tempora periodica ad tempus periodicum hujus (per idem corollarium) & inde dantur. Motus autem augis satellitis cujusque in consequentia est ad motum nodorum ipsius in antecedentia, ut motus apogæi lunæ nostræ ad hujus motum nodorum, (per idem corol.) & inde datur. Diminui tamen debet motus augis sic inventus in ratione 5 ad 9 vel 1 ad 2 circiter, ob causam quam hic exponere non vacat. Æquationes maximæ nodorum & augis satellitis cujusque fere sunt ad æquationes maximas nodorum & augis lunæ respective, ut motus nodorum & augis satellitum tempore unius revolutionis æquationum priorum, ad motus nodorum & apogæi lunæ tempore unius revolutionis æquationum posteriorum. Variatio satellitis e jove spectati, est ad variationem lunæ, ut sunt ad invicem toti motus nodorum temporibus quibus satelles & luna ad solem revolvuntur, per idem corollarium; ideoque in satellite extimo non superat 5″. .
PROPOSITIO XXIV. THEOREMA XIX.
Fluxum & refluxum maris ab actionibus solis ac lunæ oriri.
Mare singulis diebus tam lunaribus quam solaribus bis intumescere debere ac bis defluere patet per corol. 19. & 20. prop. lxvi. lib. i. ut & aquæ maximam altitudinem, in maribus profundis & liberis, appulsum luminarium ad meridianum loci minori quam sex horarum spatio sequi, uti fit in maris Atlantici & Æthiopici tractu toto orientali inter Galliam & promontorium Bonæ Spei ut & in maris Pacifici littore Chilensi & Peruviano: in quibus omnibus littoribus æstus in horam circiter secundam, tertiam vel quartam, incidit, nisi ubi motus ab oceano profundo per loca vadosa propagatus usque ad horam quintam sextam septimam aut ultra retardatur. Horas numero ab appulsu luminaris utriusque ad meridianum loci, tam infra horizontem quam supra, & per horas diei lunaris intelligo vigesimas quartas partes temporis quo luna motu apparente diurno ad meridianum loci revertitur. Vis solis vel lunæ ad mare elevandum maxima est in ipso appulsu luminaris ad meridianum loci. Sed vis eo tempore in mare impressa manet aliquamdiu & per vim novam subinde impressam augetur, donec mare ad altitudinem maximam ascenderit, id quod fiet spatio horæ unius duarumve sed sæpius ad littora spatio horarum trium circiter, vel etiam plurium si mare sit vodasum.
Motus autem bini, quos luminaria duo excitant, non cernentur distincte, sed motum quendam mixtum efficient. In luminarium conjunctione vel oppositione conjungentur eorum effectus, & componetur fluxus & refluxus maximus. In quadraturis sol attollet aquam ubi luna deprimit, deprimetque ubi sol attollit; & ex effectuum differentia æstus omnium minimus orietur. Et quoniam, experientia teste, major est effectus lunæ quam solis, incidet aquæ maxima altitudo in horam tertiam lunarem circiter. Extra syzygias & quadraturas, æstus maximus qui sola vi lunari incidere semper deberet in horam tertiam lunarem, & sola solari in tertiam solarem, compositis viribus incidet in tempus aliquod intermedium quod tertiæ lunari propinquius est; ideoque in transitu lunæ a syzygiis ad quadraturas, ubi hora tertia solaris præcedit tertiam lunarem, maxima aquæ altitudo præcedet etiam tertiam lunarem, idque maximo intervallo paulo post octantes lunæ; & paribus intervallis æstus maximus sequetur horam tertiam lunarem in transitu lunæ a quadraturis ad syzygias. Hæc ita sunt in mari aperto. Nam in ostiis fluviorum fluxus majores cæteris paribus tardius ad ἀκμὴν venient.
Pendent autem effectus luminarium ex eorum distantiis a terra. In minoribus enim distantiis majores sunt eorum effectus, in majoribus minores, idque in triplicata ratione diametrorum apparentium. Igitur sol tempore hyberno, in perigæo existens, majores edit effectus, efficitque ut æstus in syzygiis paulo majores sint, & in quadraturis paulo minores (cæteris paribus) quam tempore æstivo; & luna in perigæo singulis mensibus majores ciet æstus quam ante vel post dies quindecim, ubi in apogæo versatur. Unde fit ut æstus duo omnino maximi in syzygiis continuis se mutuo non sequantur.
Pendet etiam effectus utriusque luminaris ex ipsius declinatione seu distantia ab æquatore. Nam si luminare in polo constitueretur, traheret illud singulas aquæ partes constanter, sine actionis intensione & remissione, ideoque nullam motus reciprocationem cieret. Igitur luminaria recedendo ab æquatore polum versus, effectus suos gradatim amittent, & propterea minores ciebunt æstus in syzygiis solstitialibus quam in æquinoctialibus. In quadraturis autem solstitialibus majores ciebunt æstus quam in quadraturis æquinoctialibus; eo quod lunæ jam in æquatore constitutæ effectus maxime superat effectum solis. Incidunt igitur æstus maximi in syzygias & minimi in quadraturas luminarium, circa tempora æquinoctii utriusque. Et æstum maximum in syzygiis comitatur semper minimus in quadraturis, ut experientia compertum est. Per minorem autem distantiam solis a terra, tempore hyberno quam tempore æstivo, fit ut æstus maximi & minimi sæpius præcedant æquinoctium vernum quam sequantur, & sæpius sequantur autumnale quam præcedant.
Pendent etiam effectus luminarium ex locorum latitudine. Designet ApEP tellurem aquis profundis undique coopertam; C centrum ejus; P, p polos; AE æquatorem; F locum quemvis extra æquatorem; Ff parallelum loci; Dd parallelum ei respondentem ex altera parte æquatoris; L locum quem luna tribus ante horis occupabat; H locum telluris ei perpendiculariter subjectum; h locum huic oppositum; K, k loca inde gradibus 90 distantia, CH, Ch maris altitudines maximas mensuratas a centro telluris; & CK, Ck altitudines minimas: & si axibus Hh, Kk describatur ellipsis, deinde ellipseos hujus revolutione circa axem majorem Hh describatur sphærois HPKhpk; designabit hæc figuram 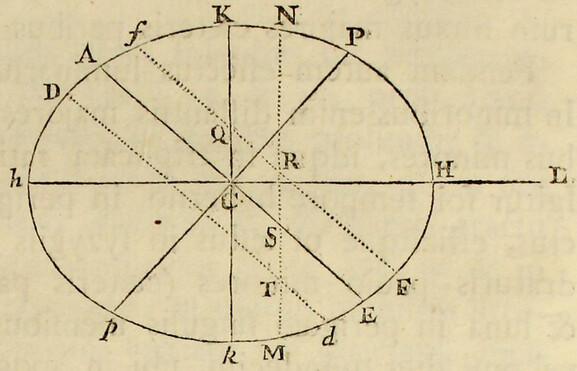 maris quam proxime, & erunt CF, Cf, CD, Cd altitudines maris in locis F, f, D, d. Quinetiam si in præfata ellipseos revolutione punctum quodvis N describat circulum NM, secantem parallelos Ff, Dd in locis quibusvis R, T, & æquatorem AE in S; erit CN altitudo maris in locis omnibus R, S, T, sitis in hoc circulo. Hinc in revolutione diurna loci cujusvis F, affluxus erit maximus in F, hora tertia post appulsum lunæ ad meridianum supra horizontem; postea defluxus maximus in Q hora tertia post occasum lunae; dein affluxus maximus in f hora tertia post appulsum lunæ ad meridianum infra horizontem; ultimo defluxus maximus in Q hora tertia post ortum lunæ; & affluxus posterior in f erit minor quam affluxus prior in F. Distinguitur enim mare totum in duos omnino fluctus hemisphæricos, unum in hemisphærio KHk ad boream vergentem, alterum in hæmisphærio opposito Khk; quos igitur fluctum borealem & fluctum australem nominare licet. Hi fluctus semper sibi mutuo oppositi veniunt per vices ad meridianos locorum singulorum, interposito intervallo horarum lunarium duodecim. Cumque regiones boreales magis participant fluctum borealem, & australes magis australem, inde oriuntur æstus alternis vicibus majores & minores, in locis singulis extra æquatorem, in quibus luminaria oriuntur & occidunt. Æstus autem major, luna in verticem loci declinante, incidet in horam circiter tertiam post appulsum lunæ ad meridianum supra horizontem, & luna declinationem mutante vertetur in minorem. Et fluxuum differentia maxima incidet in tempora solstitiorum; præsertim si lunæ nodus ascendens versatur in principio arietis. Sic experientia compertum est, quod æstus matutini tempore hyberno superent vespertinos & vespertini tempore æstivo matutinos, ad Plymuthum quidem altitudine quasi pedis unius, ad Bristoliam vero altitudine quindecim digitorum: observantibus Colepressio & Sturmio.
maris quam proxime, & erunt CF, Cf, CD, Cd altitudines maris in locis F, f, D, d. Quinetiam si in præfata ellipseos revolutione punctum quodvis N describat circulum NM, secantem parallelos Ff, Dd in locis quibusvis R, T, & æquatorem AE in S; erit CN altitudo maris in locis omnibus R, S, T, sitis in hoc circulo. Hinc in revolutione diurna loci cujusvis F, affluxus erit maximus in F, hora tertia post appulsum lunæ ad meridianum supra horizontem; postea defluxus maximus in Q hora tertia post occasum lunae; dein affluxus maximus in f hora tertia post appulsum lunæ ad meridianum infra horizontem; ultimo defluxus maximus in Q hora tertia post ortum lunæ; & affluxus posterior in f erit minor quam affluxus prior in F. Distinguitur enim mare totum in duos omnino fluctus hemisphæricos, unum in hemisphærio KHk ad boream vergentem, alterum in hæmisphærio opposito Khk; quos igitur fluctum borealem & fluctum australem nominare licet. Hi fluctus semper sibi mutuo oppositi veniunt per vices ad meridianos locorum singulorum, interposito intervallo horarum lunarium duodecim. Cumque regiones boreales magis participant fluctum borealem, & australes magis australem, inde oriuntur æstus alternis vicibus majores & minores, in locis singulis extra æquatorem, in quibus luminaria oriuntur & occidunt. Æstus autem major, luna in verticem loci declinante, incidet in horam circiter tertiam post appulsum lunæ ad meridianum supra horizontem, & luna declinationem mutante vertetur in minorem. Et fluxuum differentia maxima incidet in tempora solstitiorum; præsertim si lunæ nodus ascendens versatur in principio arietis. Sic experientia compertum est, quod æstus matutini tempore hyberno superent vespertinos & vespertini tempore æstivo matutinos, ad Plymuthum quidem altitudine quasi pedis unius, ad Bristoliam vero altitudine quindecim digitorum: observantibus Colepressio & Sturmio.
Motus autem hactenus descripti mutantur aliquantulum per vim illam reciprocationis aquarum, qua maris æstus, etiam cessantibus uminarium {sic} actionibus, posset aliquamdiu perseverare. Conservatio hæcce motus impressi minuit differentiam æstuum alternorum; & æstus proxime post syzygias majores reddit, eosque proxime post quadraturas minuit. Unde sit {sic} ut æstus alterni ad Plymuthum & Bristoliam non multo magis differant ab invicem quam altitudine pedis unius vel digitorum quindecim; utque æstus omnium maximi in iisdem portubus, non sint primi a syzygiis, sed tertii. Retardantur etiam motus omnes in transitu per vada, adeo ut æstus omnium maximi, in fretis quibusdam & fluviorum ostiis, sint quarti vel etiam quinti a syzygiis.
Porro fieri potest ut æstus propagetur ab oceano per freta diversa ad eundem portum, & citius transeat per aliqua freta quam per alia: quo in casu æstus idem, in duos vel plures successive advenientes divisus, componere possit motus novos diversorum generum. Fingamus æstus duos æquales a diversis locis in eundem portum venire, quorum prior præcedat alterum spatio horarum sex, incidatque in horam tertiam ab appulsu lunæ ad meridianum portus. Si luna in hocce suo ad meridianum appulsu versabatur in æquatore, venient singulis horis senis æquales affluxus, qui in mutuos refluxus incidendo eosdem affluxibus æquabunt, & sic spatio diei illius efficient ut aqua tranquille stagnet. Si luna tunc declinabat ab æquatore, fient æstus in oceano vicibus alternis majores & minores, uti dictum est; & inde propagabuntur in hunc portum affluxus bini majores & bini minores, vicibus alternis. Affluxus autem bini majores component aquam altissimam in medio inter utrumque, affluxus major & minor faciet ut aqua ascendat ad mediocrem altitudinem in medio ipsorum, & inter affluxus binos minores aqua ascendet ad altitudinem minimam. Sic spatio viginti quatuor horarum, aqua non bis ut fieri solet, sed semel tantum perveniet ad maximam altitudinem & semel ad minimam; & altitudo maxima, si luna declinat in polum supra horizontem loci, incidet in horam vel sextam vel tricesimam ab appulsu lunæ ad meridianum, atque luna declinationem mutante mutabitur in defluxum. Quorum omnium exemplum in portu regni Tunquini ad Batsham sub latitudine boreali 20gr. 50′. Halleius ex nautarum observationibus patefecit. Ibi aqua die transitum lunæ per æquatorem sequente stagnat, dein luna ad boream declinante incipit fluere & refluere, non bis, ut in aliis portubus, sed semel singulis diebus; & æstus incidit in occasum lunæ, defluxus maximus in ortum. Cum lunæ declinatione augetur hic æstus, usque ad diem septimum vel octavum, dein per alios septem dies iisdem gradibus decrescit, quibus antea creverat; & luna declinationem mutante cessat, ac mox mutatur in defluxum. Incidit enim subinde defluxus in occasum lunæ & affluxus in ortum, donec luna iterum mutet declinationem. Aditus ad hunc portum fretaque vicina duplex patet, alter ab oceano Sinensi inter continentem & insulam Luconiam, alter a mari Indico inter continentem & insulam Borneo. An æstus spatio horarum duodecim a mari Indico, & spatio horarum sex a mari Sinensi per freta illa venientes, & sic in horam tertiam & nonam lunarem incidentes, componant hujusmodi motus; sitne alia marium illorum conditio, observationibus vicinorum littorum determinandum relinquo.
Hactenus causas motuum lunæ & marium reddidi. De quantitate motuum jam convenit aliqua subjungere.
PROPOSITIO XXV. PROBLEMA VI.
Invenire vires solis ad perturbandos motus Lunæ.
Designet S solem, T terram, P lunam, CADB orbem lunæ. In 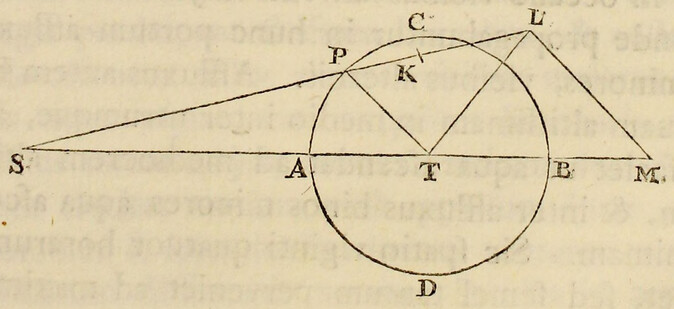 SP capiatur SK æqualis ST; sitque SL ad SK in duplicata ratione SK ad SP, & ipsi PT agatur parallela LM; & si gravitas acceleratrix terræ in solem exponatur per distantiam ST vel SK, erit SL gravitas acceleratrix lunæ in solem. Ea componitur ex partibus SM, LM, quarum LM & ipsius SM pars TM perturbat motum lunæ, ut in libri primi prop. lxvi. & ejus corollariis expositum est. Quatenus terra & luna circum commune gravitatis centrum revolvuntur, perturbabitur etiam motus terræ circa centrum illud a viribus consimilibus; sed summas tam virium quam motuum referre licet ad lunam, & summas virium per lineas ipsis analogas TM & ML designare. Vis ML in mediocri sua quantitate est ad vim centripetam, qua luna in orbe suo circa terram quiescentem ad distantiam PT revolvi posset, in duplicata ratione temporum periodicorum lunæ circa terram & terræ circa solem (per corol. 17. prop. lxvi. lib. i.) hoc est, in duplicata ratione dierum 27. hor. 7. min. 43. ad dies 365. hor. 6. min. 9. id est, ut 1000 ad 178725, seu 1 ad . Invenimus autem in propositione quarta quod, si terra & luna circa commune gravitatis centrum revolvantur, earum distantia mediocris ab invicem erit semidiametrorum mediocrium terræ quamproxime. Et vis qua luna in orbe circa terram quiescentem, ad distantiam PT semidiametrorum terrestrium revolvi posset, est ad vim, qua eodem tempore ad distantiam semidiametrorum 60 revolvi posset, ut ad 60; & hæc vis ad vim gravitatis apud nos ut 1 ad quamproxime. Ideoque vis mediocris ML est ad vim gravitatis in superficie terræ, ut ad , seu 1 ad 638092,6. Inde vero & ex proportione linearum TM, ML, datur etiam vis TM: & hæ sunt vires solis quibus lunæ motus perturbantur. Q.E.I.
SP capiatur SK æqualis ST; sitque SL ad SK in duplicata ratione SK ad SP, & ipsi PT agatur parallela LM; & si gravitas acceleratrix terræ in solem exponatur per distantiam ST vel SK, erit SL gravitas acceleratrix lunæ in solem. Ea componitur ex partibus SM, LM, quarum LM & ipsius SM pars TM perturbat motum lunæ, ut in libri primi prop. lxvi. & ejus corollariis expositum est. Quatenus terra & luna circum commune gravitatis centrum revolvuntur, perturbabitur etiam motus terræ circa centrum illud a viribus consimilibus; sed summas tam virium quam motuum referre licet ad lunam, & summas virium per lineas ipsis analogas TM & ML designare. Vis ML in mediocri sua quantitate est ad vim centripetam, qua luna in orbe suo circa terram quiescentem ad distantiam PT revolvi posset, in duplicata ratione temporum periodicorum lunæ circa terram & terræ circa solem (per corol. 17. prop. lxvi. lib. i.) hoc est, in duplicata ratione dierum 27. hor. 7. min. 43. ad dies 365. hor. 6. min. 9. id est, ut 1000 ad 178725, seu 1 ad . Invenimus autem in propositione quarta quod, si terra & luna circa commune gravitatis centrum revolvantur, earum distantia mediocris ab invicem erit semidiametrorum mediocrium terræ quamproxime. Et vis qua luna in orbe circa terram quiescentem, ad distantiam PT semidiametrorum terrestrium revolvi posset, est ad vim, qua eodem tempore ad distantiam semidiametrorum 60 revolvi posset, ut ad 60; & hæc vis ad vim gravitatis apud nos ut 1 ad quamproxime. Ideoque vis mediocris ML est ad vim gravitatis in superficie terræ, ut ad , seu 1 ad 638092,6. Inde vero & ex proportione linearum TM, ML, datur etiam vis TM: & hæ sunt vires solis quibus lunæ motus perturbantur. Q.E.I.
PROPOSITIO XXVI. PROBLEMA VII.
Invenire incrementum horarium areæ quam luna, radio ad terram ducto, in orbe circulari describit.
Diximus aream, quam luna radio ad terram ducto describit, esse tempori proportionalem, nisi quatenus motus lunaris ab actione solis turbatur. Inæqualitatem momenti, vel incrementi horarii hic investigandam proponimus. Ut computatio facilior reddatur, fingamus orbem lunæ circularem esse, & inæqualitates omnes negligamus, ea sola excepta, de qua hic agitur. Ob ingentem vero solis distantiam, ponamus etiam lineas SP, ST sibi invicem parallelas esse. Hoc pacto vis LM reducetur semper ad mediocrem suam quantitatem TP, ut & vis TM ad mediocrem suam quantitatem . Hæ vires (per legum corol. 2.) componunt vim TL; & hæc vis, si in radium TP demittatur perpendiculum LE, resolvitur in vires TE, EL, quarum TE, agendo semper secundum radium TP, nec accelerat nec retardat descriptionem areæ TPC radio illo TP factam; & EL agendo secundum perpendiculum, accelerat vel retardat ipsam, quantum accelerat vel retardat lunam. Acceleratio illa lunæ, in transitu ipsius a quadratura C ad conjunctionem A, singulis temporis 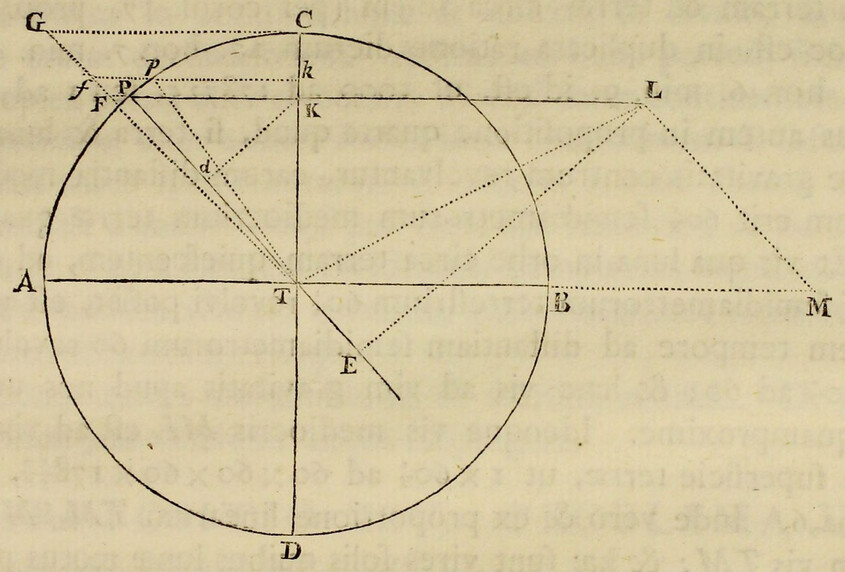 momentis facta, est ut ipsa vis accelerans EL, hoc est, ut . Exponatur tempus per motum medium lunarem, vel (quod eodem fere recidit) per angulum CTP, vel etiam per arcum CP. Ad CT erigatur normalis CG ipsi CT æqualis. Et diviso arcu quadrantali AC in particulas innumeras æquales Pp, &c. per quas æuales totidem particulæ temporis exponi possint, ductaque pk perpendiculari ad CT, jungatur TG ipsis KP, kp productis occurrens in F & f; & erit FK æqualis TK, & Kk erit ad PK ut Pp ad Tp, hoc est in data ratione, ideoque seu area FKkf, erit ut id est ut EL; & composite, area tota GCKF ut summa omnium virium EL tempore toto CP impressarum in lunam, atque ideo etiam ut velocitas hac summa genita, id est, ut acceleratio descriptionis areæ CTP, seu incrementum momenti. Vis qua luna circa terram quiescentem ad distantiam TP, tempore suo periodico CADB dierum 27. hor. 7. min. 43. revolvi posset, efficeret ut corpus, tempore CT cadendo, describeret longitudinem , & velocitatem simul acquireret æqualem velocitati, qua luna in orbe suo movetur. Patet hoc per corol. 9. prop. iv. lib. i. Cum autem perpendiculum Kd in TP demissum sit ipsius EL pars tertia, & ipsius TP seu ML in octantibus pars dimidia, vis EL in octantibus, ubi maxima est, superabit vim ML in ratione 3 ad 2, ideoque erit ad vim illam, qua luna tempore suo periodico circa terram quiescentem revolvi posset, ut 100 ad seu 11915, & tempore CT velocitatem generare deberet quæ esset pars velocitatis lunaris, tempore autem CPA velocitatem majorem generaret in ratione CA ad CT seu TP. Exponatur vis maxima EL in octantibus per aream rectangulo æqualem. Et velocitas, quam vis maxima tempore quovis CP generare posset, erit ad velocitatem quam vis omnis minor EL eodem tempore generat, ut rectangulum ad aream KCGF: tempore autem toto CPA, velocitates genitæ erunt ad invicem ut rectangulum & triangulum TCG, sive ut arcus quadrantalis CA ad radium TP. Ideoque (per prop. ix. lib. v. elem.) velocitas posterior, toto tempore genita, erit pars velocitatis lunæ. Huic lunæ velocitati, quæ areæ momento mediocri analoga est, addatur & auferatur dimidium velocitatis alterius; & si momentum mediocre exponatur per numerum 11915, summa seu 11965 exhibebit momentum maximum areæ in syzygia A, ac differentia seu 11865 ejusdem momentum minimum in quadraturis. Igitur areæ temporibus æqualibus in syzygiis & quadraturis descriptæ, sunt ad invicem ut 11965 ad 11865. Ad momentum minimum 11865 addatur momentum, quod sit ad momentorum differentiam 100 ut trapezium FKCG ad triangulum TCG (vel quod perinde est, ut quadratum sinus PK ad quadratum radii TP, id est ut Pd ad TP) & summa exhibebit momentum areæ, ubi luna est in loco quovis intermedio P.
momentis facta, est ut ipsa vis accelerans EL, hoc est, ut . Exponatur tempus per motum medium lunarem, vel (quod eodem fere recidit) per angulum CTP, vel etiam per arcum CP. Ad CT erigatur normalis CG ipsi CT æqualis. Et diviso arcu quadrantali AC in particulas innumeras æquales Pp, &c. per quas æuales totidem particulæ temporis exponi possint, ductaque pk perpendiculari ad CT, jungatur TG ipsis KP, kp productis occurrens in F & f; & erit FK æqualis TK, & Kk erit ad PK ut Pp ad Tp, hoc est in data ratione, ideoque seu area FKkf, erit ut id est ut EL; & composite, area tota GCKF ut summa omnium virium EL tempore toto CP impressarum in lunam, atque ideo etiam ut velocitas hac summa genita, id est, ut acceleratio descriptionis areæ CTP, seu incrementum momenti. Vis qua luna circa terram quiescentem ad distantiam TP, tempore suo periodico CADB dierum 27. hor. 7. min. 43. revolvi posset, efficeret ut corpus, tempore CT cadendo, describeret longitudinem , & velocitatem simul acquireret æqualem velocitati, qua luna in orbe suo movetur. Patet hoc per corol. 9. prop. iv. lib. i. Cum autem perpendiculum Kd in TP demissum sit ipsius EL pars tertia, & ipsius TP seu ML in octantibus pars dimidia, vis EL in octantibus, ubi maxima est, superabit vim ML in ratione 3 ad 2, ideoque erit ad vim illam, qua luna tempore suo periodico circa terram quiescentem revolvi posset, ut 100 ad seu 11915, & tempore CT velocitatem generare deberet quæ esset pars velocitatis lunaris, tempore autem CPA velocitatem majorem generaret in ratione CA ad CT seu TP. Exponatur vis maxima EL in octantibus per aream rectangulo æqualem. Et velocitas, quam vis maxima tempore quovis CP generare posset, erit ad velocitatem quam vis omnis minor EL eodem tempore generat, ut rectangulum ad aream KCGF: tempore autem toto CPA, velocitates genitæ erunt ad invicem ut rectangulum & triangulum TCG, sive ut arcus quadrantalis CA ad radium TP. Ideoque (per prop. ix. lib. v. elem.) velocitas posterior, toto tempore genita, erit pars velocitatis lunæ. Huic lunæ velocitati, quæ areæ momento mediocri analoga est, addatur & auferatur dimidium velocitatis alterius; & si momentum mediocre exponatur per numerum 11915, summa seu 11965 exhibebit momentum maximum areæ in syzygia A, ac differentia seu 11865 ejusdem momentum minimum in quadraturis. Igitur areæ temporibus æqualibus in syzygiis & quadraturis descriptæ, sunt ad invicem ut 11965 ad 11865. Ad momentum minimum 11865 addatur momentum, quod sit ad momentorum differentiam 100 ut trapezium FKCG ad triangulum TCG (vel quod perinde est, ut quadratum sinus PK ad quadratum radii TP, id est ut Pd ad TP) & summa exhibebit momentum areæ, ubi luna est in loco quovis intermedio P.
Hæc omnia ita se habent, ex hypothesi quod sol & terra quiescunt, & luna tempore synodico dierum 27. hor. 7. min. 43. revolvitur. Cum autem periodus synodica lunaris vere sit dierum 29. hor. 12. & min. 44, augeri debent momentorum incrementa in ratione temporis, id est, in ratione 1080853 ad 1000000. Hoc pacto incrementum totum, quod erat pars momenti mediocris, jam fiet ejusdem pars . Ideoque momentum areæ in quadratura lunæ erit ad ejus momentum in syzygia ut ad , seu 10973 ad 11073, & ad ejus momentum, ubi luna in alio quovis loco intermedio P versatur, ut 10973 ad , existente videlicet TP æquali 100.
Area igitur, quam luna radio ad terram ducto singulis temporis particulis æqualibus describit, est quam proxime ut summa numeri 219,46 & sinus versi duplicatæ distantiæ lunæ a quadratura proxima, in circulo cujus radius est unitas. Hæc ita se habent ubi variatio in octantibus est magnitudinis mediocris. Sin variatio ibi major sit vel minor, augeri debet vel minui sinus ille versus in eadem ratione.
PROPOSITIO XXVII. PROBLEMA VIII.
Ex motu horario lunæ invenire ipsius distantiam a terra.
Area, quam luna radio ad terram ducto singulis temporis momentis describit, est ut motus horarius lunæ & quadratum distantiæ lunæ a terra conjunctim; & propterea distantia lunæ a terra est in ratione composita ex subduplicata ratione areæ directe & subduplicata ratione motus horarii inverse. Q.E.I.
Corol. 1. Hinc datur lunæ diameter apparens: quippe quæ sit reciproce ut ipsius distantia a terra. Tentent astronomi quam probe hæc regula cum phænomenis congruat.
Corol. 2. Hinc etiam orbis lunaris accuratius ex phænomenis quam antehac definiri potest.
<433>PROPOSITIO XXVIII. PROBLEMA IX.
Invenire diametros orbis in quo luna, sine eccentricitate, moveri deberet.
Curvatura trajectoriæ, quam mobile, si secundum trajectoriæ illius perpendiculum trahatur, describit, est ut attractio directe & quadratum velocitatis inverse. Curvaturas linearum pono esse inter se in ultima proportione sinuum vel tangentium angulorum contactuum ad radios æquales pertinentium, ubi radii illi in infinitum diminuuntur. Attractio autem lunæ in terram in syzygiis est excessus gravitatis ipsius in terram supra vim solarem (vide fig. pag. 428.) qua gravitas acceleratrix lunæ in solem superat gravitatem acceleratricem terræ in solem vel ab ea superatur. In quadraturis autem attractio illa est summa gravitatis lunæ in terram & vis solaris KT, qua luna in terram trahitur. Et hæ attractiones, si dicatur N, sunt ut & quam proxime; seu ut & . Nam si gravitas acceleratrix lunæ in terram exponatur per numerum 178725, vis mediocris ML, quæ in quadraturis est PT vel TK & lunam trahit in terram, erit 1000, & vis mediocris TM in syzygiis erit 3000; de qua, si vis mediocris ML subducatur, manebit vis 2000 qua luna in syzygiis distrahitur a terra, quamque jam ante nominavi . Velocitas autem lunæ in syzygiis A & B est ad ipsius velocitatem in quadraturis C & D, ut CT ad AT & momentum areæ quam luna radio ad terram ducto describit in syzygiis ad momentum ejusdem areæ in quadraturis conjunctim, i.e. ut ad . Sumatur hæc ratio bis inverse & ratio prior semel directe, & fiet curvatura orbis lunaris in syzygiis ad ejusdem curvaturam in quadraturis ut ad , i.e. ut ad
Quoniam figura orbis lunaris ignoratur, hujus vice assumamus ellipsin DBCA, in cujus centro T terra collocetur, & cujus axis major DC quadraturis, minor AB syzygiis interjaceat. Cum autem planum ellipseos hujus motu angulari circa terram revolvatur, & trajectoria cujus curvaturam consideramus describi debet in plano 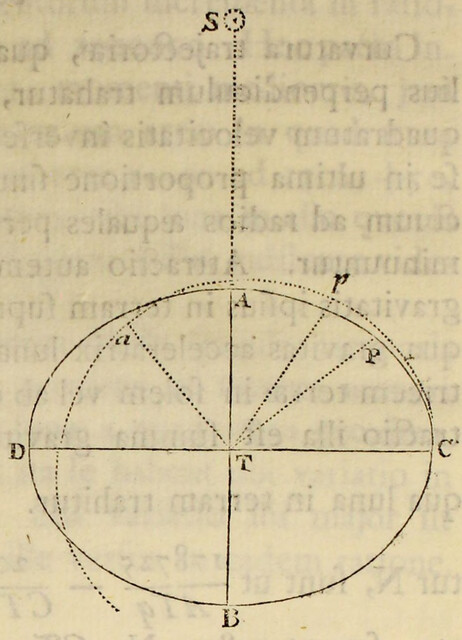 quod omni motu angulari omnino destituitur: consideranda erit figura, quam luna in ellipsi illa revolvendo describit in hoc plano, hoc est figura Cpa, cujus puncta singula p inveniuntur capiendo punctum quodvis P in ellipsi, quod locum lunæ repræsentet, & ducendo Tp æqualem TP, ea lege ut angulus PTp æqualis sit motui apparenti solis a tempore quadraturæ C confecto; vel (quod eodem fere recidit) ut angulus CTp sit ad angulum CTP ut tempus revolutionis synodicæ lunaris ad tempus revolutionis periodicæ seu 29d. 12h. 44′, ad 27d. 7h. 43′. Capiatur igitur angulus CTa in eadem ratione ad angulum rectum CTA, & sit longitudo Ta æqualis longitudini TA; & erit a apsis ima & C apsis summa orbis hujus Cpa. Rationes autem ineundo invenio quod differentia inter curvaturam orbis Cpa in vertice a, & curvaturam circuli centro T intervallo TA descripti, sit ad differentiam inter curvaturam ellipseos in vertice A & curvaturam ejusdem circuli, in duplicata ratione anguli CTP ad angulum CTp; & quod curvatura ellipseos in A sit ad curvaturam circuli illius, in duplicata ratione TA ad TC; & curvatura circuli illius ad curvaturam circuli centro T intervallo TC descripti, ut TC ad TA; hujus autem curvatura ad curvaturam ellipseos in C, in duplicata ratione TA ad TC; & differentia inter curvaturam ellipseos in vertice C & curvaturam circuli novissimi, ad differentiam inter curvaturam figuræ Tpa in vertice C & curvaturam ejusdem circuli, in duplicata ratione anguli CTp ad angulum CTP. Quæ quidem rationes ex sinubus angulorum contactus ac differentiarum angulorum facile colliguntur. His autem inter se collatis, prodit curvatura figuræ Cpa in a ad ipsius curvaturam in C, ut ad . Ubi numerus designat differentiam quadratorum angulorum CTP & CTp applicatam ad quadratum anguli minoris CTP, seu (quod perinde est) differentiam quadratorum temporum 27d. 7h. 43′, & 29d. 12h. 44′, applicatam ad quadratum temporis 27d. 7h. 43′.
quod omni motu angulari omnino destituitur: consideranda erit figura, quam luna in ellipsi illa revolvendo describit in hoc plano, hoc est figura Cpa, cujus puncta singula p inveniuntur capiendo punctum quodvis P in ellipsi, quod locum lunæ repræsentet, & ducendo Tp æqualem TP, ea lege ut angulus PTp æqualis sit motui apparenti solis a tempore quadraturæ C confecto; vel (quod eodem fere recidit) ut angulus CTp sit ad angulum CTP ut tempus revolutionis synodicæ lunaris ad tempus revolutionis periodicæ seu 29d. 12h. 44′, ad 27d. 7h. 43′. Capiatur igitur angulus CTa in eadem ratione ad angulum rectum CTA, & sit longitudo Ta æqualis longitudini TA; & erit a apsis ima & C apsis summa orbis hujus Cpa. Rationes autem ineundo invenio quod differentia inter curvaturam orbis Cpa in vertice a, & curvaturam circuli centro T intervallo TA descripti, sit ad differentiam inter curvaturam ellipseos in vertice A & curvaturam ejusdem circuli, in duplicata ratione anguli CTP ad angulum CTp; & quod curvatura ellipseos in A sit ad curvaturam circuli illius, in duplicata ratione TA ad TC; & curvatura circuli illius ad curvaturam circuli centro T intervallo TC descripti, ut TC ad TA; hujus autem curvatura ad curvaturam ellipseos in C, in duplicata ratione TA ad TC; & differentia inter curvaturam ellipseos in vertice C & curvaturam circuli novissimi, ad differentiam inter curvaturam figuræ Tpa in vertice C & curvaturam ejusdem circuli, in duplicata ratione anguli CTp ad angulum CTP. Quæ quidem rationes ex sinubus angulorum contactus ac differentiarum angulorum facile colliguntur. His autem inter se collatis, prodit curvatura figuræ Cpa in a ad ipsius curvaturam in C, ut ad . Ubi numerus designat differentiam quadratorum angulorum CTP & CTp applicatam ad quadratum anguli minoris CTP, seu (quod perinde est) differentiam quadratorum temporum 27d. 7h. 43′, & 29d. 12h. 44′, applicatam ad quadratum temporis 27d. 7h. 43′.
Igitur cum a designet syzygiam lunæ, & C ipsius quadraturam, proportio jam inventa eadem esse debet cum proportione curvaturæ orbis lunæ in syzygiis ad ejusdem curvaturam in quadraturis, quam supra invenimus. Proinde ut inveniatur proportio CT ad AT, duco extrema & media in se invicem. Et termini prodeuntes ad applicati, fiunt . Hic pro terminorum AT & CT semisumma N scribo 1, & pro eorundem semidifferentia ponendo x, fit , & : quibus in æquatione scriptis, & æquatione prodeunte resoluta, obtinetur x æqualis 0,00719, & inde semidiameter CT fit 1,00719, & semidiameter AT 0,99281, qui numeri sunt ut & quam proxime. Est igitur distantia lunæ a terra in syzygiis ad ipsius distantiam in quadraturis (seposita scilicet eccentricitatis consideratione) ut ad , vel numeris rotundis ut 69 ad 70.
PROPOSITIO XXIX. PROBLEMA X.
Invenire variationem lunæ.
Oritur hæc inæqualitas partim ex forma elliptica orbis lunaris, partim ex inæqualitate momentorum areæ, quam luna radio ad terram ducto describit. Si luna P in ellipsi DBCA circa terram in centro ellipseos quiescentem moveretur, & radio TP ad terram ducto describeret aream CTP tempori proportionalem; esset autem ellipseos semidiameter maxima CT ad semidiametrum minimam TA ut 70 ad 69: foret tangens anguli CTP ad tangentem anguli motus medii a quadratura C computati, ut ellipseos semidiameter TA ad ejusdem semidiametrum TC seu 69 ad 70. Debet autem descriptio areæ CTP, in progressu lunæ a quadratura ad syzygiam, ea ratione accelerari, ut ejus momentum in syzygia lunæ sit ad ejus momentum in quadratura ut 11073 ad 10973, utque excessus momenti in loco quovis intermedio P supra momentum in quadratura sit ut quadratum sinus anguli CTP. Id quod satis accurate fiet, si tangens anguli CTP diminuatur in subduplicata ratione numeri 10973 ad numerum 11073, id est, in ratione numeri 68,6877 ad numerum 69. Quo pacto tangens anguli CTP jam erit ad tangentem motus medii ut 68,6877 ad 70, & angulus CTP in octantibus, ubi motus medius 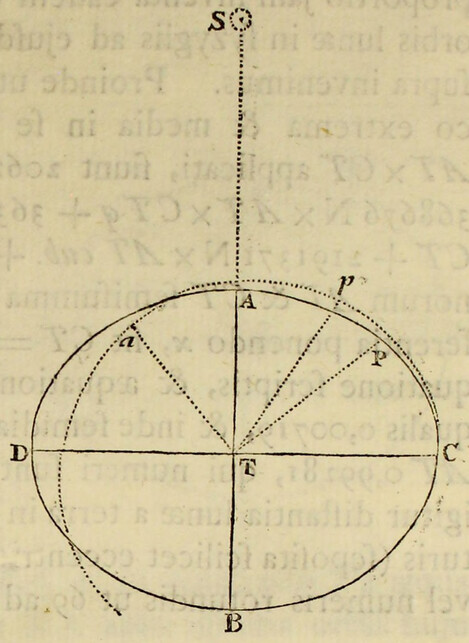 est 45gr. invenietur 44gr. 27′. 28″. qui subductus de angulo motus medii 45gr. relinquit variationem maximam 32′. 32″. Hæc ita se haberent si luna, pergendo a quadratura ad syzygiam, describeret angulum CTA graduum tantum nonaginta. Verum ob motum terræ, quo sol in consequentia motu apparente transfertur, luna, priusquam solem assequitur, describit angulum CTa angulo recto majorem in ratione temporis revolutionis lunaris synodicæ ad tempus revolutionis periodicæ, id est, in ratione 29d. 12h. 44′. ad 27d. 7h. 43′. Et hoc pacto anguli omnes circa centrum T dilatantur in eadem ratione, & variatio quæ secus esset 32′. 32″, jam aucta in eadem ratione, fit 35′. 10″.
est 45gr. invenietur 44gr. 27′. 28″. qui subductus de angulo motus medii 45gr. relinquit variationem maximam 32′. 32″. Hæc ita se haberent si luna, pergendo a quadratura ad syzygiam, describeret angulum CTA graduum tantum nonaginta. Verum ob motum terræ, quo sol in consequentia motu apparente transfertur, luna, priusquam solem assequitur, describit angulum CTa angulo recto majorem in ratione temporis revolutionis lunaris synodicæ ad tempus revolutionis periodicæ, id est, in ratione 29d. 12h. 44′. ad 27d. 7h. 43′. Et hoc pacto anguli omnes circa centrum T dilatantur in eadem ratione, & variatio quæ secus esset 32′. 32″, jam aucta in eadem ratione, fit 35′. 10″.
Hæc est ejus magnitudo in mediocri distantia solis a terra, neglectis differentiis, quæ a curvatura orbis magni, majorique solis actione in lunam falcatam & novam quam in gibbosam & plenam, oriri possint. In aliis distantiis solis a terra, variatio maxima est in ratione quæ componitur ex duplicata ratione temporis revolutionis synodicæ lunaris (dato anni tempore) directe, & triplicata ratione distantiæ solis a terra inverse. Ideoque in apogæo solis, variatio maxima est 33′. 14″, & in ejus perigæo 37′. 11″, si modo eccentricitas solis sit ad orbis magni semidiametrum transversam ut ad 1000.
Hactenus variationem investigavimus in orbe non eccentrico, in quo utique luna in octantibus suis semper est in mediocri sua distantia a terra. Si luna propter eccentricitatem suam, magis vel minus distat a terra quam si locaretur in hoc orbe, variatio paulo major esse potest vel paulo minor quam pro regula hic allata: sed excessum vel defectum ab astronomis per phænomena determinandum relinquo.
PROPOSITIO XXX. PROBLEMA XI.
Invenire motum horarium nodorum lunæ in orbe circulari.
Designet S solem, T terram, P lunam, NPn orbem lunæ, Npn vestigium orbis in plano eclipticæ; N, n, nodos, nTNm lineam nodorum infinite productam; PI, PK; perpendicula demissa in lineas ST, Qq; Pp perpendiculum demissum in planum eclipticæ; A, B syzygias lunæ in plano elipticæ; AZ perpendiculum in lineam nodorum 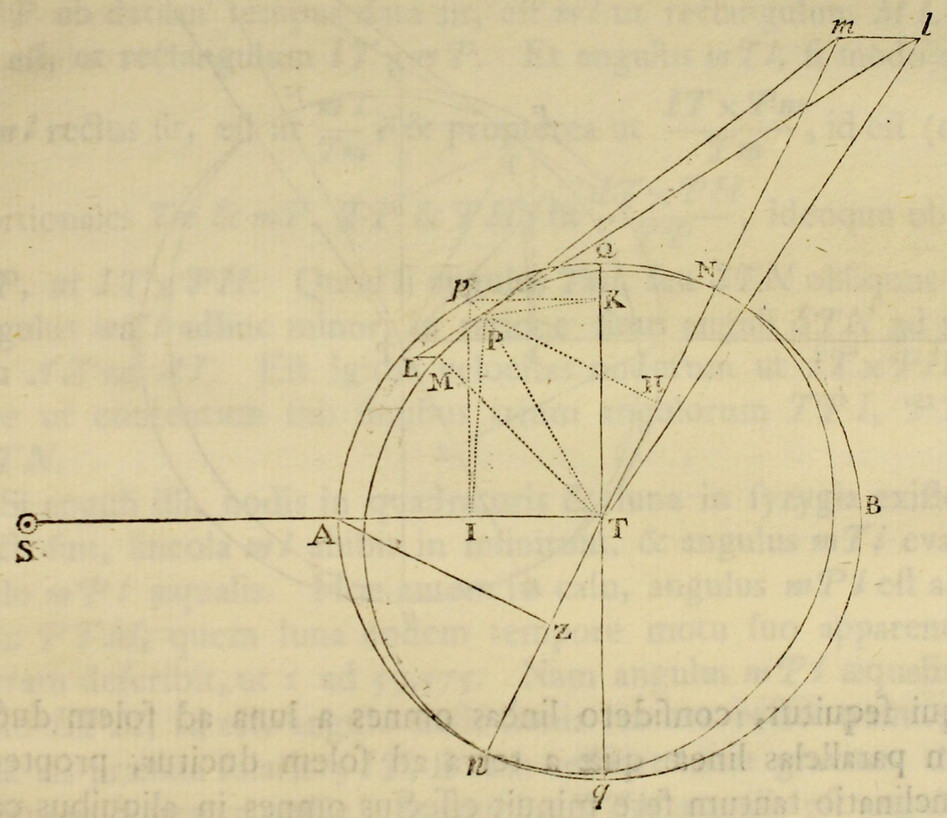 Nn; Q, q quadraturas lunæ in plano elipticæ, & pK perpendiculum in lineam Qq quadraturis interjacentem. vis solis ad perturbandum motum lunæ (per prop. xxv.) duplex est, altera lineæ LM in schemate propositionis illius, altera linæ MT proportionalis. Et luna vi priore in terram, posteriore in solem secundum lineam rectæ ST a terra ad solem ductæ parallelam trahitur. Vis prior LM agit secundum planum orbis lunaris, & propterea situm plani nil mutat. Hæc igitur negligenda est. Vis posterior MT qua planum orbis lunaris perturbatur eadem est cum vi vel . Et hæc vis (per prop. xxv.) est ad vim qua luna in circulo circa terram quiescentem tempore suo periodico uniformiter revolvi posset, ut ad radium circuli multiplicatum per numerum 178,725, sive ut IT ad radium multiplicatum per 59,575. Cæterum in hoc calculo, & eo
Nn; Q, q quadraturas lunæ in plano elipticæ, & pK perpendiculum in lineam Qq quadraturis interjacentem. vis solis ad perturbandum motum lunæ (per prop. xxv.) duplex est, altera lineæ LM in schemate propositionis illius, altera linæ MT proportionalis. Et luna vi priore in terram, posteriore in solem secundum lineam rectæ ST a terra ad solem ductæ parallelam trahitur. Vis prior LM agit secundum planum orbis lunaris, & propterea situm plani nil mutat. Hæc igitur negligenda est. Vis posterior MT qua planum orbis lunaris perturbatur eadem est cum vi vel . Et hæc vis (per prop. xxv.) est ad vim qua luna in circulo circa terram quiescentem tempore suo periodico uniformiter revolvi posset, ut ad radium circuli multiplicatum per numerum 178,725, sive ut IT ad radium multiplicatum per 59,575. Cæterum in hoc calculo, & eo 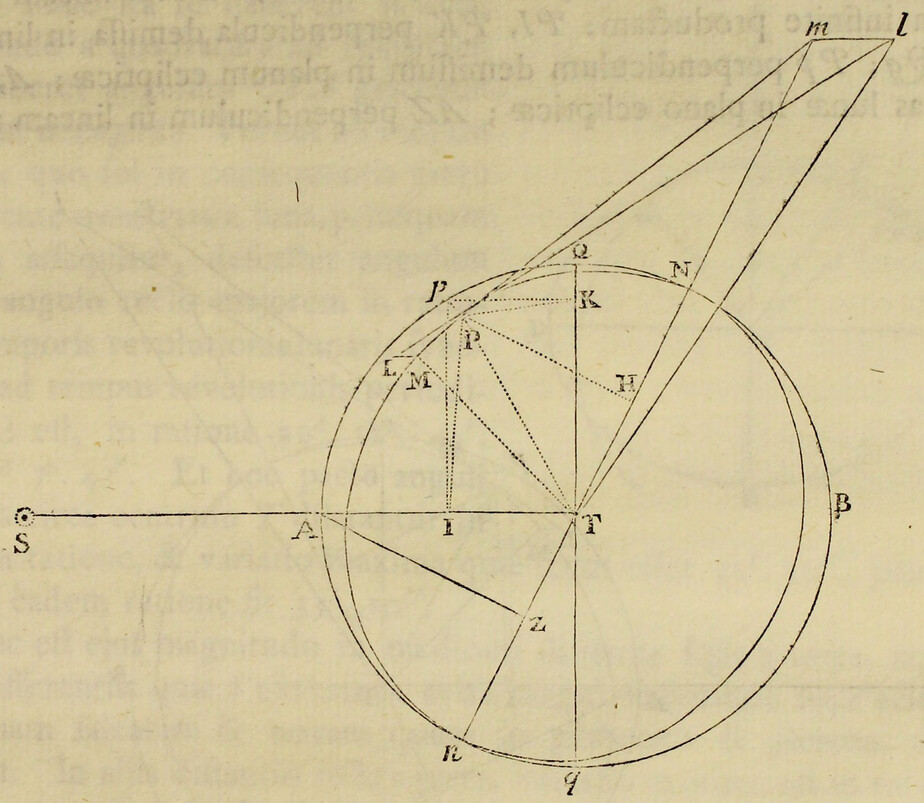 omni qui sequitur, considero lineas omnes a luna ad solem ductas tanquam parallelas lineæ quæ a terra ad solem ducitur, propterea quod inclinatio tantum fere minuit effectus omnes in aliquibus casibus, quantum auget in aliis; & nodorum motus mediocres quærimus, neglectis istiusmodi minutiis, quæ calculum nimis impeditum redderent.
omni qui sequitur, considero lineas omnes a luna ad solem ductas tanquam parallelas lineæ quæ a terra ad solem ducitur, propterea quod inclinatio tantum fere minuit effectus omnes in aliquibus casibus, quantum auget in aliis; & nodorum motus mediocres quærimus, neglectis istiusmodi minutiis, quæ calculum nimis impeditum redderent.
Designet jam PM arcum, quem Luna dato tempore quam minimo describit, & ML lineolam cujus dimidium luna, impellente vi præfata , eodem tempore describere posset. Jungantur PL, MP, & producantur eæ ad m & l, ubi secent planum eclipticæ; inque Tm demittatur perpendiculum PH. Et quoniam recta ML parallela est plano eclipticæ, ideoque cum recta ml quæ in plano illo jacet concurrere non potest, & tamen jacent hæ rectæ in plano communi LMPml; parallelæ erunt hæ rectæ, & propterea similia erunt triangula LMP, lmP. Jam cum MPm sit in plano orbis, in quo luna in loco P movebatur, incidet punctum m in lineam Nn per orbis illius nodos N, n ductam. Et quoniam vis qua dimidium lineolæ LM generatur, si tota simul & semel in loco P impressa esset, generaret lineam illam totam; & efficeret ut luna moveretur in arcu, cujus chorda esset LP, atque ideo transferret lunam de plano MPmT in planum LPlT; motus angularis nodorum a vi illa genitus, æqualis erit angulo mTl. Est autem ml ad mP ut ML ad MP, ideoque cum MP ob datum tempus data sit, est ml ut rectangulum , id est, ut rectangulum . Et angulus mTl, si modo angulus Tml rectus sit, est ut , & propterea ut , id est (ob proportionales Tm & mP, TP & PH) ut , ideoque ob datam TP, ut . Quod si angulus Tml, seu STN obliquus sit, erit angulus mTl adhuc minor, in ratione sinus anguli STN ad radium, seu AZ ad AT. Est igitur velocitas nodorum ut , sive ut contentum sub sinubus trium angulorum TPI, PTN & STN.
Si anguli illi, nodis in quadraturis & luna in syzygia existentibus, recti sint, lineola ml abibit in infinitum, & angulus mTl evadet angulo mPl æqualis. Hoc autem in casu, angulus mPl est ad angulum PTM, quem luna eodem tempore motu suo apparente circa terram describit, ut 1 ad 59,575. Nam angulus mPl æqualis est angulo LPM, id est, angulo deflexionis lunæ a recto tramite, quem sola vis præfata solaris , si tum cessaret lunæ gravitas, dato illo tempore generare posset; & angulus PTM æqualis est angulo deflexionis lunæ a recto tramite, quem vis illa, qua luna in orbe suo retinetur, si tum cessaret vis solaris , eodem tempore generaret. Et hæ vires, ut supra diximus, sunt ad invicem ut 1 ad 59,575. Ergo cum motus medius horarius lunæ respectu fixarum sit 32′. 56″. . , motus horarius nodi in hoc casu erit 33″. . . . Aliis autem in casibus motus iste horarius erit ad 33″. . . . ut contentum sub sinubus angulorum trium TPI, PTN, & STN (seu distantiarum lunæ a quadratura, lunæ a nodo, & nodi a sole) ad cubum radii. Et quoties signum anguli alicujus de affirmativo in negativum, deque negativo in affirmativum mutatur, debebit motus regressivus in progressivum & progressivus in regressivum mutari. Unde fit ut nodi progrediantur quoties luna inter quadraturam alterutram & nodum quadraturæ proximum versatur. Aliis in casibus regrediuntur, & per excessum regressus supra progressum singulis mensibus feruntur in antecedentia.
Corol. 1. Hinc si a dati arcus quam minimi PM terminis P & M ad lineam quadraturas jungentem Qq demittantur perpendicula PK, Mk, eademque producantur donec secent lineam nodorum Nn in D & d; erit motus horarius nodorum ut area MPDd & quadratum lineæ AZ conjunctim. Sunto enim PK, PH & AZ prædicti tres 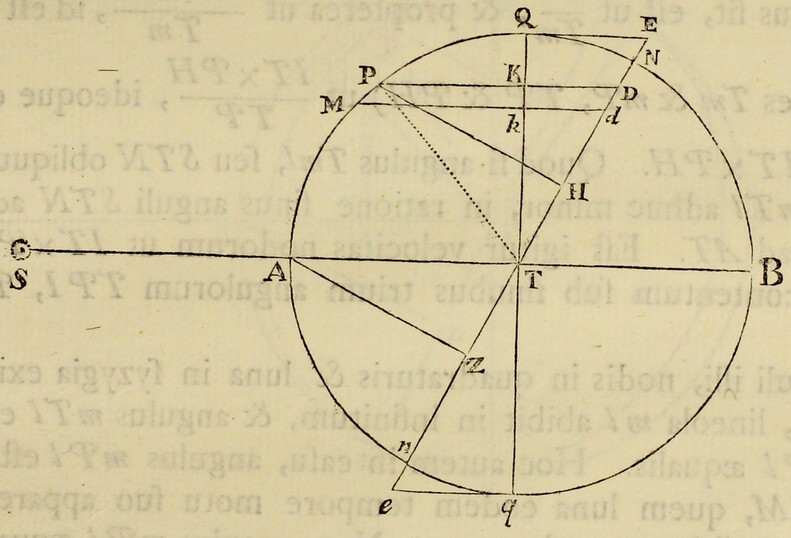 sinus. Nempe PK sinus distantiæ lunæ a quadratura, PH sinus distantiæ lunæ a nodo, & AZ sinus distantiæ nodi a sole: & erit velocitas nodi ut contentum . Est autem PT ad PK ut PM ad Kk, ideoque ob datas PT & PM est Kk ipsi PK proportionalis. Est & AT ad PD ut AZ ad PH, & propterea PH rectangulo proportionalis, & conjunctis rationibus, est ut contentum , & ut id est, ut area PDdM, & conjunctim. Q.E.D.
sinus. Nempe PK sinus distantiæ lunæ a quadratura, PH sinus distantiæ lunæ a nodo, & AZ sinus distantiæ nodi a sole: & erit velocitas nodi ut contentum . Est autem PT ad PK ut PM ad Kk, ideoque ob datas PT & PM est Kk ipsi PK proportionalis. Est & AT ad PD ut AZ ad PH, & propterea PH rectangulo proportionalis, & conjunctis rationibus, est ut contentum , & ut id est, ut area PDdM, & conjunctim. Q.E.D.
Corol. 2. In data quavis Nodorum positione, motus horarius mediocris est semissis motus horarii in syzygiis lunæ, ideoque est ad 16″. . . . ut quadratum sinus distantiæ nodorum a syzygiis ad quadratum radii, sive ut ad Nam si luna uniformi cum motu perambulet semicirculum QAq, summa omnium arearum PDdM, quo tempore luna pergit a Q ad M, erit area QMdE quæ ad circuli tangentem QE terminatur; & quo tempore luna attingit punctum n, summa illa erit area tota EQAn quam linea PD describit, dein luna pergente ab n ad q, linea PD cadet extra circulum, & aream nqe ad circuli tangentem qe terminatam describet; quæ, quoniam nodi prius regrediebantur, jam vero progrediuntur, subduci debet de area priore, & cum æqualis sit areæ QEN, relinquet semicirculum NQAn. Igitur summa omnium arearum PDdM, quo tempore luna semicirculum describit, est area semicirculi; & summa omnium quo tempore luna circulum describit est area circuli totius. At area PDdM, ubi luna versatur in syzygiis, est rectangulum sub arcu PM & radio PT; & summa omnium huic æqualium arearum, quo tempore luna circulum describit, est rectangulum sub circumferentia tota & radio circuli; & hoc rectangulum, cum sit æquale duobus circulis, duplo majus est quam rectangulum prius. Proinde nodi, ea cum velocitate uniformiter continuata quam habent in syzygiis lunaribus, spatium duplo majus describerent quam revera describunt; & propterea motus mediocris quocum, si uniformiter continuaretur, spatium a se inæquabili cum motu revera confectum describere possent, est semissis motus quem habent in syzygiis lunæ. Unde cum motus horarius maximus, si nodi in quadraturis versantur, sit 33″. . . , motus mediocris horarius in hoc casu erit 16″. . . . Et cum motus horarius nodorum semper sit ut & area PDdM conjunctim, & propterea motus horarius nodorum in syzygiis lunæ ut & area PDdM conjunctim, id est (ob datam aream PDdM in syzygiis descriptam) ut erit etiam motus mediocris ut atque adeo hic motus, ubi nodi extra quadraturas versantur, erit ad 16″. . . . ut ad Q.E.D.
<442>PROPOSITIO XXXI. PROBLEMA XII.
Invenire motum horarium nodorum lunæ in orbe elliptico.
Designet Qpmaq ellipsim, axe majore Qq, minore ab descriptam, QAqB circulum circumscriptum, T terram in utriusque centro communi, S solem, p lunam in ellipsi motam, & pm arcum quem data temporis particula quam minima describit, N & n nodos 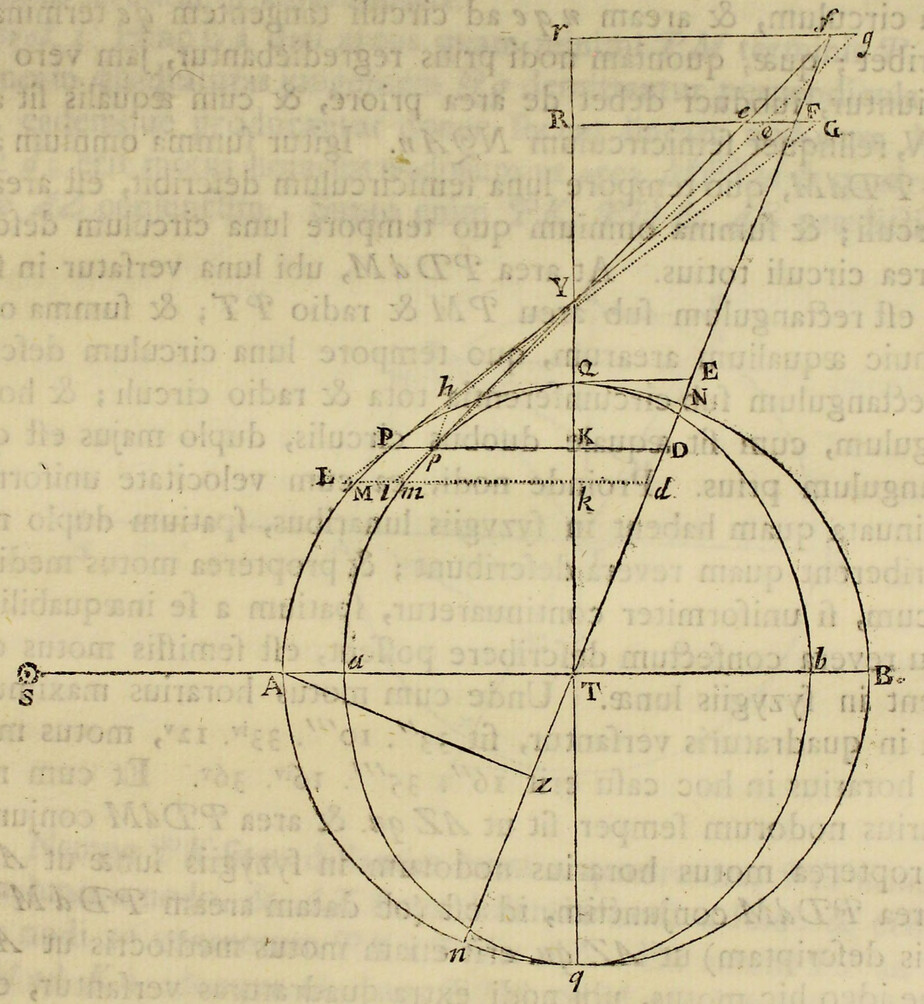 linea Nn junctos, pK & mk perpendicula in axem Qq demissa & hinc inde producta, donec occurrant circulo in P & M, & lineæ nodorum in D & d. Et si luna, radio ad terram ducto, aream describat tempori proportionalem, erit motus horarius nodi in ellipsi ut area pDdm & conjunctim.
linea Nn junctos, pK & mk perpendicula in axem Qq demissa & hinc inde producta, donec occurrant circulo in P & M, & lineæ nodorum in D & d. Et si luna, radio ad terram ducto, aream describat tempori proportionalem, erit motus horarius nodi in ellipsi ut area pDdm & conjunctim.
Nam si PF tangat circulum in P, & producta occurrat TN in F, & pf tangat ellipsin in p & producta occurrat eidem TN in f, conveniant autem hæ tangentes in axe TQ ad Y; & si ML designet spatium quod luna in circulo revolvens, interea dum describit arcum PM, urgente & impellente vi prædicta , seu motu transverso describere posset, & ml designet spatium quod luna in ellipsi revolvens eodem tempore, urgente etiam vi seu , describere posset; & producantur LP & lp donec occurrant plano eclipticæ in G & g; & jungantur FG & fg, quarum FG producta secet pf, pg & TQ in c, e & R respective, & fg producta secet TQ in r. Quoniam vis seu in circulo est ad vim seu in ellipsi, ut PK ad pK, seu AT ad aT; erit spatium ML vi priore genitum, ad spatium ml vi posteriore genitum, ut PK ad pK, id est, ob similes figuras PYKp & FYRc, ut FR ad cR. Est autem ML ad FG (ob similia triangula PLM, PGF) ut PL ad PG, hoc est (ob parallelas Lk, PK, GR) ut pl ad pe, id est (ob similia triangula plm, cpe) ut lm ad ce; & inverse ut LM est ad lm, seu FR ad cR, ita est FG ad ce. Et propterea si fg esset ad ce ut fY ad cY, id est, ut fr ad cR (hoc est ut fr ad FR & FR ad cR conjunctim, id est, ut fT ad FT & FG ad ce conjunctim) quoniam ratio FG ad ce utrinque ablata relinquit rationes fg ad FG & fT ad FT, foret fg ad FG ut fT ad FT; atque ideo anguli, quos FG & fg subtenderent ad terram T, æquarentur inter se. Sed anguli illi (per ea quæ in præcedente propositione exposuimus) sunt motus nodorum, quo tempore luna in circulo arcum PM, in ellipsi arcum pm percurrit: & propterea motus nodorum in circulo & ellipsi æquarentur inter se. Hæc ita se haberent, si modo fg esset ad ce ut fY ad cY, id est, si fg æqualis esset . Verum ob similia triangula fgp, cep, est fg ad ce ut fp ad cp; ideoque fg æqualis est ; & propterea angulus, quem fg revera subtendit, est ad angulum priorem, quem FG subtendit, hoc est, motus nodorum in ellipsi ad motum nodorum in circulo, ut hæc fg seu ad priorem fg seu , id est, ut ad , seu fp ad fY & cY ad cp, hoc est, si ph ipsi TN parallela occurrat FP in h, ut Fh ad FY & FY ad FP; hoc est, ut Fh ad FP seu Dp ad DP, ideoque ut area Dpmd ad aream DPMd. Et propterea, cum (per corol. 1. prop. xxx.) area posterior & conjunctim proportionalia sint motui horario Nodorum in Circulo, erunt area prior & AZq conjunctim proportionalia motui horario nodorum in ellipsi. Q.E.D.
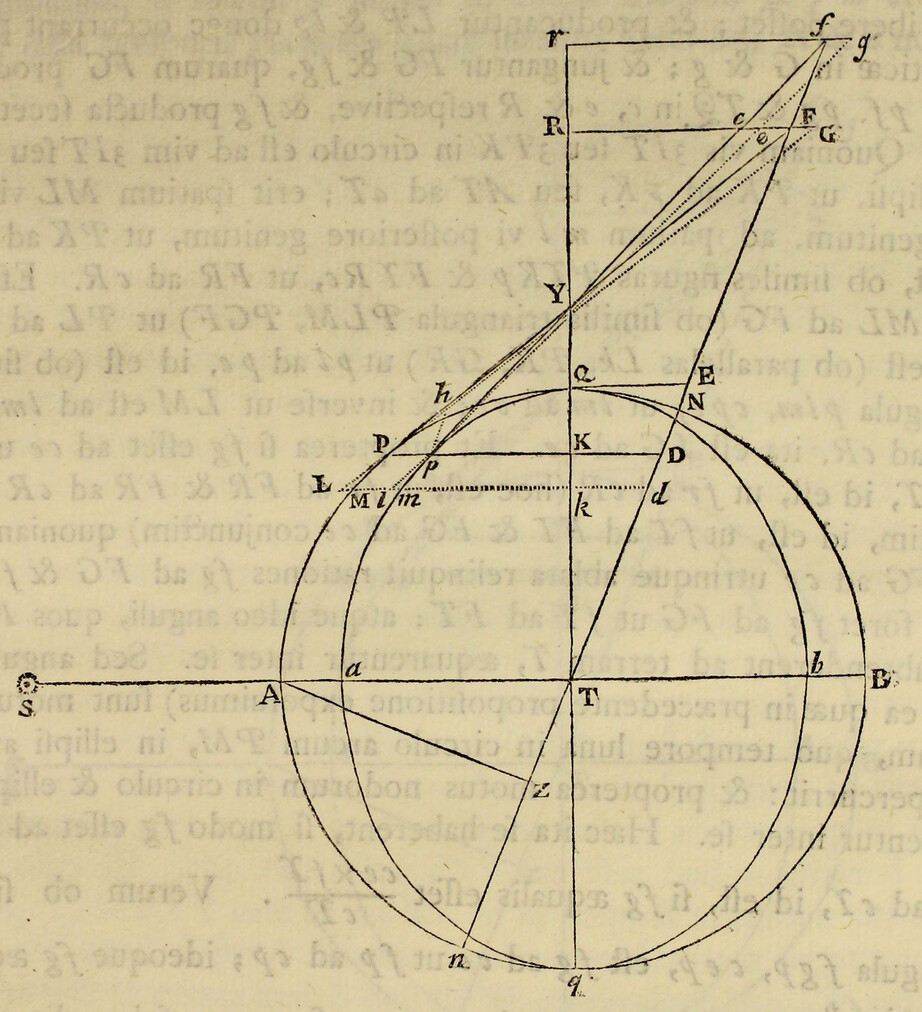
Corol. Quare cum, in data nodorum positione, summa omnium arearum pDdm, quo tempore luna pergit a quadratura ad locum quemvis m, sit area mpQEd, quæ ad ellipseos tangentem QE terminatur; & summa omnium arearum illarum, in revolutione integra, sit area ellipseos totius: motus mediocris nodorum in ellipsi erit ad motum mediocrem nodorum in circulo, ut ellipsis ad circulum, id est ut Ta ad TA, seu 69 ad 70. Et propterea, cum (per corol. 2. prop. xxx.) motus mediocris horarius nodorum in circulo sit ad 16″. . . . ut ad si capiatur angulus 16″. . . . ad angulum 16″. . . . ut 69 ad 70, erit motus mediocris horarius nodorum in ellipsi ad 16″. . . . ut ad ; hoc est, ut quadratum sinus distantiæ nodi a sole ad quadratum radii.
Cæterum luna, radio ad terram ducto, aream velocius describit in syzygiis quam in quadraturis, & eo nomine tempus in syzygiis contrahitur, in quadraturis producitur; & una cum tempore motus nodorum augetur ac diminuitur. Erat autem momentum areæ in quadraturis lunæ ad ejus momentum in syzygiis ut 10973 ad 11073; & propterea momentum mediocre in octantibus est ad excessum in syzygiis, defectumque in quadraturis, ut numerorum semisumma 11023 ad eorundem semidifferentiam 50. Unde cum tempus lunæ in singulis orbis particulis æqualibus sit reciproce ut ipsius velocitas, erit tempus mediocre in octantibus ad excessum temporis in quadraturis, ac defectum in syzygiis, ab hac causa oriundum, ut 11023 ad 50 quam proxime. Pergendo autem a quadraturis ad syzygias, invenio quod excessus momentorum areæ in locis singulis, supra momentum minimum in quadraturis, sit ut quadratum sinus distantiæ lunæ a quadraturis quam proxime; & propterea differentia inter momentum in loco quocunque & momentum mediocre in octantibus, est ut differentia inter quadratum sinus distantiæ lunæ a quadraturis & quadratum sinus graduum 45, seu semissem quadrati radii; & incrementum temporis in locis singulis inter octantes & quadraturas, & decrementum ejus inter octantes & syzygias, est in eadem ratione. Motus autem nodorum, quo tempore luna percurrit singulas orbis particulas æquales, acceleratur vel retardatur in duplicata ratione temporis. Est enim motus iste, dum luna percurrit PM, (cæteris paribus) ut ML, & ML est in duplicata ratione temporis. Quare motus nodorum in syzygiis, eo tempore confectus quo luna datas orbis particulas percurrit, diminuitur in duplicata ratione numeri 11073 ad numerum 11023; estque decrementum ad motum reliquum ut 100 ad 10973, ad motum vero totum ut 100 ad 11073 quam proxime. Decrementum autem in locis inter octantes & syzygias, & incrementum in locis inter octantes & quadraturas, est quam proxime ad hoc decrementum, ut motus totus in locis illis ad motum totum in syzygiis & differentia inter quadratum sinus distantiæ lunæ a quadratura & semissem quadrati radii ad semissem quadrati radii conjunctim. Unde si nodi in quadraturis versentur, & capiantur loca duo æqualiter ab octante hinc inde distantia, & alia duo a syzygia & quadratura iisdem intervallis distantia, deque decrementis motuum in locis duabus inter syzygiam & octantem, subducantur incrementa motuum in locis reliquis duobus, quæ sunt inter octantem & quadraturam; decrementum reliquum æquale erit decremento in syzygia: uti rationem ineunti facile constabit. Proindeque decrementum mediocre, quod de nodorum motu mediocri subduci debet, est pars quarta decrementi in syzygia. Motus totus horarius nodorum in syzygiis, ubi luna radio ad terram ducto aream tempori proportionalem describere supponebatur, erat 32″. . . Et decrementum motus nodorum, quo tempore luna jam velocior describit idem spatium diximus esse ad hunc motum ut 100 ad 11073; ideoque decrementum illud est . . , cujus pars quarta . . . motui horario mediocri superius invento 16″. . . . subducta, relinquit 16″. . . . motum mediocrem horarium correctum.
Si nodi versantur extra quadraturas, & spectentur loca bina a syzygiis hinc inde æqualiter distantia; summa motuum nodorum, ubi luna versatur in his locis, erit ad summam motuum, ubi luna in iisdem locis & nodi in quadraturis versantur, ut ad Et decrementa motuum, a causis jam expositis oriunda, erunt ad invicem ut ipsi motus, ideoque motus reliqui erunt ad invicem ut ad & motus mediocres ut motus reliqui. Est itaque motus mediocris horarius correctus, in dato quocunque nodorum situ, ad 16″. . . . ut ad ; id est, ut quadratum sinus distantiæ nodorum a syzygiis ad quadratum radii.
<447>PROPOSITIO XXXII. PROBLEMA XIII.
Invenire motum medium nodorum lunæ.
Motus medius annuus est summa motuum omnium horariorum mediocrium in anno. Concipe nodum versari in N, & singulis horis completis retrahi in locum suum priorem, ut non obstante motu suo proprio, datum semper servet situm ad stellas fixas. Interea vero solem S, per motum terræ, progredi a nodo, & cursum annuum apparentem uniformiter complere. Sit autem Aa arcus datus quam minimus, quem recta TS ad solem semper ducta, intersectione sui & circuli NAn, dato tempore quam minimo describit: & motus horarius mediocris (per jam ostensa) erit ut , id est (ob proportionales AZ, ZY) ut rectangulum sub AZ & ZY, hoc est, ut 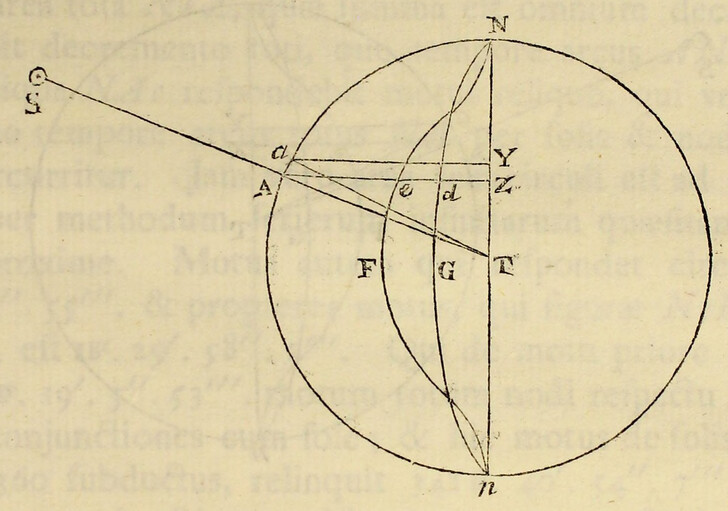 area AZYa. Et summa omnium horariorum motuum mediocrium ab initio, ut summa omnium arearum aYZA, id est, ut area NAZ. Est autem maxima AZYa æqualis rectangulo sub arcu Aa & radio circuli; & propterea summa omnium rectangulorum in circulo toto ad summam totidem maximorum, ut area circuli totius ad rectangulum sub circumferentia tota & radio; id est, ut 1 ad 2. Motus autem horarius, rectangulo maximo respondens, erat 16″. . . . Et hic motus, anno toto sidereo dierum 365. hor. 6. min. 9. fit 39gr. 38′. 7″. . Ideoque hujus dimidium 19gr. 49′. 3″. est motus medius nodorum circulo toti respondens. Et motus nodorum, quo tempore sol pergit ab N ad A, est ad 19gr. 49′. 3″. . ut area NAZ ad circulum totum.
area AZYa. Et summa omnium horariorum motuum mediocrium ab initio, ut summa omnium arearum aYZA, id est, ut area NAZ. Est autem maxima AZYa æqualis rectangulo sub arcu Aa & radio circuli; & propterea summa omnium rectangulorum in circulo toto ad summam totidem maximorum, ut area circuli totius ad rectangulum sub circumferentia tota & radio; id est, ut 1 ad 2. Motus autem horarius, rectangulo maximo respondens, erat 16″. . . . Et hic motus, anno toto sidereo dierum 365. hor. 6. min. 9. fit 39gr. 38′. 7″. . Ideoque hujus dimidium 19gr. 49′. 3″. est motus medius nodorum circulo toti respondens. Et motus nodorum, quo tempore sol pergit ab N ad A, est ad 19gr. 49′. 3″. . ut area NAZ ad circulum totum.
Hæc ita se habent ex hypothesi quod nodus horis singulis in locum priorem retrahitur, sic ut sol anno toto completo ad nodum eundem redeat a quo sub initio digressus fuerat. Verum per motum nodi fit ut sol citius ad nodum revertatur, & computanda jam est abbreviatio temporis. Cum sol anno toto conficiat 360 gradus, & nodus motu maximo eodem tempore conficeret 39gr. 38′. 7″. , seu 39,6355 gradus; & motus mediocris nodi in loco quovis N sit ad ipsius motum mediocrem in quadraturis suis, ut ad : erit motus solis ad motum nodi in N, ut ad ; id est, ut {sic} ad Unde si circuli totius circumferentia 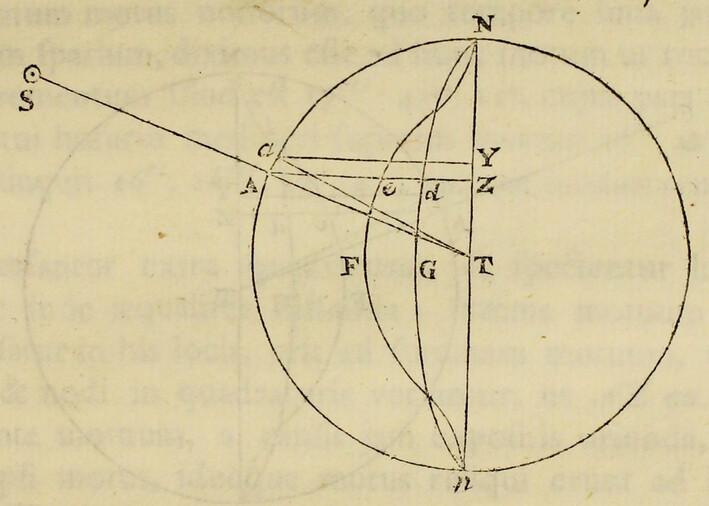 NAn dividatur in particulas æquales Aa, tempus quo sol percurrat particulam Aa, si circulus quiesceret, erit ad tempus quo percurrit eandem particulam, si circulus una cum nodis circa centrum T revolvatur, reciproce ut {sic} ad {sic}. Nam tempus est reciproce ut velocitas qua particula percurritur, & hæc velocitas est summa velocitatum solis & nodi. Igitur si tempus, quo sol sine motu nodi percurreret arcum NA, exponatur per sectorem NTA, & particula temporis quo percurreret arcum quam minimum Aa, exponatur per sectoris particulam ATa; & (perpendiculo aY in Nn demisso) si in AZ capiatur dZ, ejus longitudinis ut sit rectangulum dZ in ZY ad sectoris particulam ATa ut ad ; id est, ut sit dZ ad ut ad ; rectangulum dZ in ZY designabit decrementum temporis ex motu nodi oriundum, tempore toto quo arcus Aa percurritur. Et si punctum d tangit curvam NdGn, area curvilinea NdZ erit decrementum totum, quo tempore arcus totus NA percurritur; & propterea excessus sectoris NAT supra aream NdZ erit tempus illud totum. Et quoniam motus nodi tempore minore minor est in ratione temporis, debebit etiam area AaYZ diminui in eadem ratione. Id quod fiet si capiatur in AZ longitudo eZ, quæ sit ad longitudinem AZ ut ad . Sic enim rectangulum eZ in ZY erit ad aream AZYa ut decrementum temporis, quo arcus Aa percurritur, ad tempus totum quo percurreretur, si nodus quiesceret: & propterea rectangulum illud respondebit decremento motus nodi. Et si punctum e tangat curvam NeFn, area tota NeZ, quæ summa est omnium decrementorum, respondebit decremento toti, quo tempore arcus AN percurritur; & area reliqua NAe respondebit motui reliquo, qui verus est nodi motus, quo tempore arcus totus NA per solis & nodi conjunctos motus percurritur. Jam vero vero area semicirculi est ad aream figuræ NeFn, per methodum serierum infinitarum quæsitam, ut 793 ad 60 quamproxime. Motus autem qui respondet circulo toti erat 19gr. 49′. 3″. . & propterea motus, qui figuræ NeFn duplicatæ respondet, est 1gr. 29′. 58″. . Qui de motu priore subductus relinquit 18gr. 19′. 5″. . motum totum nodi respectu fixarum inter sui ipsius conjunctiones cum sole; & hic motus de solis motu annuo graduum 360 subductus, relinquit 341gr. 40′. 54″. . motum solis inter easdem conjunctiones. Iste autem motus est ad motum annuum 360gr ut nodi motus jam inventus 18gr. 19′. 5″. . ad ipsius motum annuum, qui propterea erit 19gr. 18′. 1″. . Hic est motus medius nodorum in anno sidereo. Idem per tabulas astronomicas est 19gr. 21′. 21″. . Differentia minor est parte trecentesima motus totius, & ab orbis lunaris eccentricitate & inclinatione ad planum eclipticæ oriri videtur. Per eccentricitatem orbis motus nodorum nimis acceleratur, & per ejus inclinationem vicissim retardatur aliquantulum, & ad justam velocitatem reducitur.
NAn dividatur in particulas æquales Aa, tempus quo sol percurrat particulam Aa, si circulus quiesceret, erit ad tempus quo percurrit eandem particulam, si circulus una cum nodis circa centrum T revolvatur, reciproce ut {sic} ad {sic}. Nam tempus est reciproce ut velocitas qua particula percurritur, & hæc velocitas est summa velocitatum solis & nodi. Igitur si tempus, quo sol sine motu nodi percurreret arcum NA, exponatur per sectorem NTA, & particula temporis quo percurreret arcum quam minimum Aa, exponatur per sectoris particulam ATa; & (perpendiculo aY in Nn demisso) si in AZ capiatur dZ, ejus longitudinis ut sit rectangulum dZ in ZY ad sectoris particulam ATa ut ad ; id est, ut sit dZ ad ut ad ; rectangulum dZ in ZY designabit decrementum temporis ex motu nodi oriundum, tempore toto quo arcus Aa percurritur. Et si punctum d tangit curvam NdGn, area curvilinea NdZ erit decrementum totum, quo tempore arcus totus NA percurritur; & propterea excessus sectoris NAT supra aream NdZ erit tempus illud totum. Et quoniam motus nodi tempore minore minor est in ratione temporis, debebit etiam area AaYZ diminui in eadem ratione. Id quod fiet si capiatur in AZ longitudo eZ, quæ sit ad longitudinem AZ ut ad . Sic enim rectangulum eZ in ZY erit ad aream AZYa ut decrementum temporis, quo arcus Aa percurritur, ad tempus totum quo percurreretur, si nodus quiesceret: & propterea rectangulum illud respondebit decremento motus nodi. Et si punctum e tangat curvam NeFn, area tota NeZ, quæ summa est omnium decrementorum, respondebit decremento toti, quo tempore arcus AN percurritur; & area reliqua NAe respondebit motui reliquo, qui verus est nodi motus, quo tempore arcus totus NA per solis & nodi conjunctos motus percurritur. Jam vero vero area semicirculi est ad aream figuræ NeFn, per methodum serierum infinitarum quæsitam, ut 793 ad 60 quamproxime. Motus autem qui respondet circulo toti erat 19gr. 49′. 3″. . & propterea motus, qui figuræ NeFn duplicatæ respondet, est 1gr. 29′. 58″. . Qui de motu priore subductus relinquit 18gr. 19′. 5″. . motum totum nodi respectu fixarum inter sui ipsius conjunctiones cum sole; & hic motus de solis motu annuo graduum 360 subductus, relinquit 341gr. 40′. 54″. . motum solis inter easdem conjunctiones. Iste autem motus est ad motum annuum 360gr ut nodi motus jam inventus 18gr. 19′. 5″. . ad ipsius motum annuum, qui propterea erit 19gr. 18′. 1″. . Hic est motus medius nodorum in anno sidereo. Idem per tabulas astronomicas est 19gr. 21′. 21″. . Differentia minor est parte trecentesima motus totius, & ab orbis lunaris eccentricitate & inclinatione ad planum eclipticæ oriri videtur. Per eccentricitatem orbis motus nodorum nimis acceleratur, & per ejus inclinationem vicissim retardatur aliquantulum, & ad justam velocitatem reducitur.
PROPOSITIO XXXIII. PROBLEMA XIV.
Invenire motum verum nodorum lunæ.
In tempore quod est ut area , (in fig. præced.) motus iste est ut area NAe, & inde datur. Verum ob nimiam calculi difficultatem, præstat sequentem problematis constructionem adhibere. Centro C, intervallo quovis CD, describatur circulus BEFD. Producatur DC ad A, ut sit AB ad AC ut motus medius ad semissem motus veri mediocris, ubi nNodi sunt in quadraturis, id est, ut 19gr. 18′. 1″. . ad 19gr. 49′. 3″. , atque adeo BC ad AC ut motuum differentia 0gr. 31′. 2″. , ad motum posteriorem 19gr. 49′. 3″. . hoc est, ut 1 ad ; dein per punctum D ducatur infinita Gg, quæ tangat circulum in D; & si capiatur angulus BCE vel BCF æqualis duplæ distantiæ solis a loco nodi, per motum medium invento; & agatur AE vel AF secans perpendiculum DG in G; & capiatur angulus qui sit ad motum totum nodi inter ipsius syzygias (id est, ad 9gr. 11′. 3″.) ut tangens DG ad circuli BED circumferentiam totam; atque angulus iste (pro quo angulus DAG 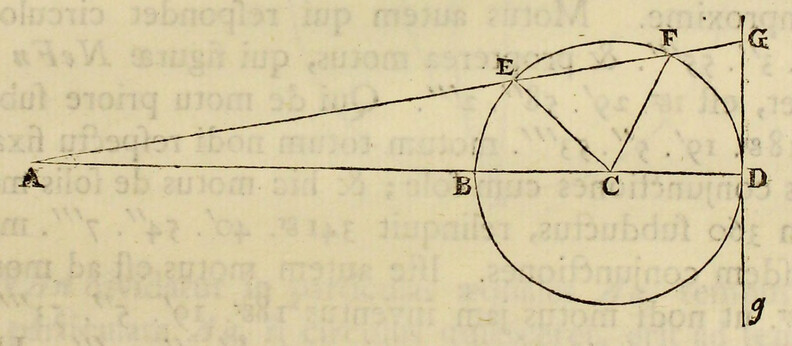 usurpari potest) ad motum medium nodorum addatur ubi nodi transeunt a quadraturis ad syzygias, & ab eodem motu medio subducatur ubi transeunt a syzygiis ad quadraturas; habebitur eorum motus verus. Nam motus verus sic inventus congruet quam proxime cum motu vero qui prodit exponendo tempus per aream , & motum nodi per aream NAe; ut rem perpendenti & computationes instituenti constabit. Hæc est æquatio semestris motus nodorum. Est & æquatio menstrua, sed quæ ad inventionem latitudinis lunæ minime necessaria est. Nam cum variatio inclinationis orbis lunaris ad planum eclipticæ duplici inæqualitati obnoxia sit, alteri semestri, alteri autem menstruæ; hujus menstrua inæqualitas & æquatio menstrua nodorum ita se mutuo contemperant & corrigunt, ut ambæ in determinanda latitudine lunæ negligi possint.
usurpari potest) ad motum medium nodorum addatur ubi nodi transeunt a quadraturis ad syzygias, & ab eodem motu medio subducatur ubi transeunt a syzygiis ad quadraturas; habebitur eorum motus verus. Nam motus verus sic inventus congruet quam proxime cum motu vero qui prodit exponendo tempus per aream , & motum nodi per aream NAe; ut rem perpendenti & computationes instituenti constabit. Hæc est æquatio semestris motus nodorum. Est & æquatio menstrua, sed quæ ad inventionem latitudinis lunæ minime necessaria est. Nam cum variatio inclinationis orbis lunaris ad planum eclipticæ duplici inæqualitati obnoxia sit, alteri semestri, alteri autem menstruæ; hujus menstrua inæqualitas & æquatio menstrua nodorum ita se mutuo contemperant & corrigunt, ut ambæ in determinanda latitudine lunæ negligi possint.
Corol. Ex hac & præcedente propositione liquet quod nodi in syzygiis suis quiescunt, in quadraturis autem regrediuntur motu horario 16″. . Et quod æquatio motus nodorum in octantibus sit 1gr. 30′. Quæ omnia cum phænomenis cœlestibus probe quadrant.
Scholium.
Alia ratione motum nodorum J. Machin Astron. Prof. Gresham. & Hen. Pemberton M. D. seorsum invenerunt. Hujus methodi mentio quædam alibi facta est. Et utriusque chartæ, quas vidi, duas propositiones continebant, & inter se in utrisque congruebant. Chartam vero D. Machin, cum prior in manus meas venerit, hic adjungam.
De Motu Nodorum Lunæ.
PROPOSITIO I.
"Motus solis medius a nodo, definitur per medium proportionale geometricum, inter motum ipsius solis medium, & motum illum mediocrem quo sol celerrimè recedit a nodo in quadraturis.
"Sit T locus ubi terra, Nn linea nodorum lunæ ad tempus quodvis datum, KTM huic ad rectos angulos ducta, TA recta circum centrum revolvens ea cum velocitate angulari qua sol & nodus a se invicem recedunt, ita ut angulus inter rectam quiescentem Nn & revolventem TA, semper fiat æqualis distantiæ locorum solis & nodi. Jam si recta quævis TK dividatur in partes TS & SK quæ sint ut motus solis horarius medius ad motum horarium mediocrem nodi in quadraturis, & ponatur recta TH media proportionalis inter partem TS & totam TK, hæc recta inter reliquas proportionalis erit motui medio solis a nodo.
<452>"Describatur enim circulus NKnM centro T & radio TK, eodemque centro & semiaxibus TH & TN describatur ellipsis NHnL, & in tempore quo sol a nodo recedit per arcum Na, si ducatur recta Tba, area sectoris NTa exponet summam motuum nodi & solis in eodem tempore. Sit igitur arcus aA quam minimus quem recta Tba præfata lege revolvens in datâ temporis particula uniformiter describit, & sector quam minimus TAa erit ut summa velocitatum qua sol & nodus tum temporis seorsim feruntur. Solis autem velocitas ferè uniformis est, utpote cujus parva 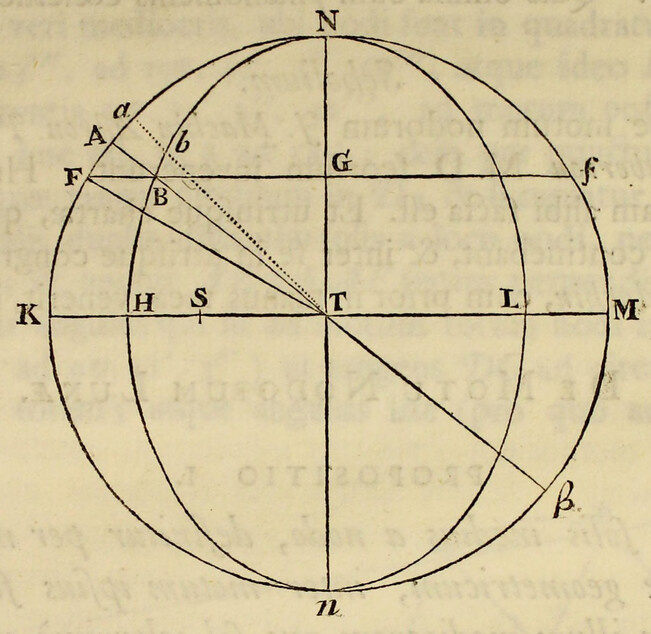 inæqualitas vix ullam inducit in medio nodorum motu varietatem. Altera pars hujus summæ nempe velocitas nodi in mediocri sua quantitate, augetur in recessu a syzygiis in duplicata ratione sinus distantiæ ejus a sole; per Coroll. Prop. 31. Lib. 3tii Princip. & cum maxima est in quadraturis ad solem in K, eandem rationem obtinet ad solis velocitatem ac ea quam habet SK ad TS hoc est ut (differentia quadratorum ex TK & TH vel) rectangulum KHM ad TH quadratum. Sed ellipsis NBH dividit sectorem ATa summæ harum duarum velocitatum exponentem, in duas partes ABba & BTb ipsis velocitatibus proportionales. Producatur enim BT ad circulum in β, & a puncto B demittatur ad axem majorem perpendicularis BG, quæ utrinque producta ocurrat circulo in punctis F & f, & quoniam spatium ABba est ad sectorem TNb ut rectangulum ABβ ad BT quadratum (rectangulum enim illud æquatur differentiæ quadratorum ex TA & TB ob rectam Aβ æqualiter & inæqualiter sectam in T & B.) Hæc igitur ratio ubi spatium ABba maximum est in K, eadem erit ac ratio rectanguli KHM ad HT quadratum, sed maxima nodi mediocris velocitas erat ad solis velocitatem in hac ratione. Igitur in quadraturis sector ATa dividitur in partes velocitatibus proportionales. Et quoniam rectang. KHM est ad HT quadr. ut FBf ad BG quad. & rectangulum ABβ æquatur rectangulo FBf. Erit igitur areola ABba ubi maxima est ad reliquum sectorem TBb, ut rectang. ABβ ad BG quadr. Sed ratio harum areolarum semper erat ut ABβ rectang. ad BT quadratum; & propterea areola ABba in loco A minor est simili areola in quadraturis, in duplicata ratione BG ad BT hoc est in duplicata ratione sinus distantiæ solis a nodo. Et proinde summa omnium areolarum ABba nempe spatium ABN erit ut motus nodi in tempore quo sol digreditur a nodo per arcum NA. Et spatium reliquum nempe sector ellipticus NTB erit ut motus solis medius in eodem tempore. Et propterea quoniam annuus motus nodi medius, is est qui fit in tempore quo sol periodum suam absolverit, motus nodi medius a sole erit ad motum ipsius solis medium, ut area circuli ad aream ellipseos, hoc est ut recta TK ad rectam TH mediam scilicet proportionalem inter TK & TS; vel quod eodem redit ut media proportionalis TH ad rectam TS.
inæqualitas vix ullam inducit in medio nodorum motu varietatem. Altera pars hujus summæ nempe velocitas nodi in mediocri sua quantitate, augetur in recessu a syzygiis in duplicata ratione sinus distantiæ ejus a sole; per Coroll. Prop. 31. Lib. 3tii Princip. & cum maxima est in quadraturis ad solem in K, eandem rationem obtinet ad solis velocitatem ac ea quam habet SK ad TS hoc est ut (differentia quadratorum ex TK & TH vel) rectangulum KHM ad TH quadratum. Sed ellipsis NBH dividit sectorem ATa summæ harum duarum velocitatum exponentem, in duas partes ABba & BTb ipsis velocitatibus proportionales. Producatur enim BT ad circulum in β, & a puncto B demittatur ad axem majorem perpendicularis BG, quæ utrinque producta ocurrat circulo in punctis F & f, & quoniam spatium ABba est ad sectorem TNb ut rectangulum ABβ ad BT quadratum (rectangulum enim illud æquatur differentiæ quadratorum ex TA & TB ob rectam Aβ æqualiter & inæqualiter sectam in T & B.) Hæc igitur ratio ubi spatium ABba maximum est in K, eadem erit ac ratio rectanguli KHM ad HT quadratum, sed maxima nodi mediocris velocitas erat ad solis velocitatem in hac ratione. Igitur in quadraturis sector ATa dividitur in partes velocitatibus proportionales. Et quoniam rectang. KHM est ad HT quadr. ut FBf ad BG quad. & rectangulum ABβ æquatur rectangulo FBf. Erit igitur areola ABba ubi maxima est ad reliquum sectorem TBb, ut rectang. ABβ ad BG quadr. Sed ratio harum areolarum semper erat ut ABβ rectang. ad BT quadratum; & propterea areola ABba in loco A minor est simili areola in quadraturis, in duplicata ratione BG ad BT hoc est in duplicata ratione sinus distantiæ solis a nodo. Et proinde summa omnium areolarum ABba nempe spatium ABN erit ut motus nodi in tempore quo sol digreditur a nodo per arcum NA. Et spatium reliquum nempe sector ellipticus NTB erit ut motus solis medius in eodem tempore. Et propterea quoniam annuus motus nodi medius, is est qui fit in tempore quo sol periodum suam absolverit, motus nodi medius a sole erit ad motum ipsius solis medium, ut area circuli ad aream ellipseos, hoc est ut recta TK ad rectam TH mediam scilicet proportionalem inter TK & TS; vel quod eodem redit ut media proportionalis TH ad rectam TS.
PROPOSITIO II.
"Dato motu medio nodorum lunæ invenire motum verum.
"Sit angulus A distantia solis a loco nodi medio, sive motus medius solis a nodo. Tum si capiatur angulus B cujus tangens sit ad tangentem anguli A ut TH ad TK, hoc est in subduplicata ratione motus mediocris horarii solis ad motum mediocrem horarium solis a nodo in quadraturis versante; erit idem angulus B distantia solis a loco nodi vero. Nam jungatur FT & ex demonstratione propositionis superioris erit angulus FTN distantia solis a loco nodi medio, angulus autem ATN distantia a loco vero, & tangentes horum angulorum sunt inter se ut TK ad TH.
"Coroll. Hinc angulus FTA est æquatio nodorum lunæ, sinusque hujus anguli ubi maximus est in octantibus, est ad radium ut KH ad . Sinus autem hujus æquationis in loco quovis alio A est ad sinum maximum, ut sinus summæ angulorum ad radium: hoc est fere ut sinus duplæ distantiæ solis a loco nodi medio (nempe ) ad radium.
Scholium.
"Si motus nodorum mediocris horarius in quadraturis sit 16″. . hoc est in anno toto sidereo 39°. 38′. 7″. . erit TH ad TK in subduplicata ratione numeri 9,0827646 ad numerum 10,0827646, hoc est ut 18,6524761 ad 19,6524761. Et propterea TH ad HK ut 18,6524761 ad 1. hoc est ut motus solis in anno sidereo ad motum nodi medium 19°. 18′, 1″. .
"At si motus medius nodorum Lunæ in 20 annis Julianis sit 386°. 50′. 15″. sicut ex observationibus in theoria lunæ adhibitis deducitur: motus medius nodorum in anno sidereo erit 19°. 20′ 31″. . Et TH erit ad HK ut 360gr. ad 19°. 20′. 31″. . hoc est ut 18,61214 ad 1. unde motus mediocris horarius nodorum in quadraturis evadet 16″. . Et æquatio nodorum maxima in octantibus 1°. 29′. 57″.
PROPOSITIO XXXIV. PROBLEMA XV.
Invenire variationem horariam inclinationis orbis lunaris ad planum eclipticæ.
Designent A & a syzygias; Q & q quadraturas; N & n nodos; P locum lunæ in orbe suo; p vestigium loci illius in plano eclipticæ, & mTl motum momentaneum nodorum ut supra. Et si ad lineam Tm demittatur perpendiculum PG, jungatur pG, & producatur ea donec occurrat Tl in g, & jungatur etiam Pg: erit angulus PGp inclinatio orbis lunaris ad planum eclipticæ, ubi luna versatur in P; & angulus Pgp inclinatio ejusdem post momentum temporis completum; ideoque angulus GPg variatio momentanea inclinationis. Est autem hic angulus GPg ad angulum GTg ut TG ad PG & Pp ad PG conjunctim. Et propterea si pro momento temporis substituatur hora; cum angulus GTg (per prop. xxx.) sit ad angulum 33″. 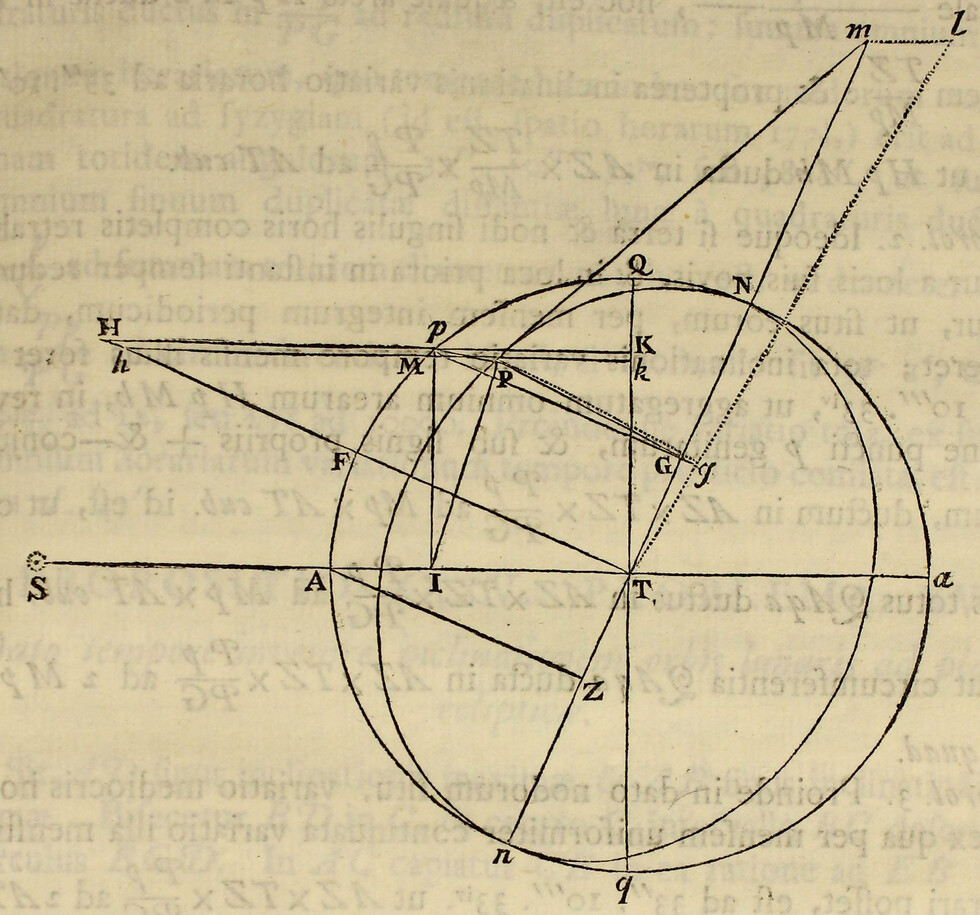 . . ut ad erit angulus GPg (seu inclinationis horaria variatio) ad angulum 33″. . ut ad Q.E.I.
. . ut ad erit angulus GPg (seu inclinationis horaria variatio) ad angulum 33″. . ut ad Q.E.I.
Hæc ita se habent ex hypothesi quod luna in orbe circulari uniformiter gyratur. Quod si orbis ille ellipticus sit, motus mediocris nodorum minuetur in ratione axis minoris ad axem majorem; uti supra expositum est. Et in eadem ratione minuetur etiam inclinationis variatio.
<456>Corol. 1. Si ad Nn erigatur perpendiculum TF, sitque pM motus horarius lunæ in plano eclipticæ; & perpendicula pK, Mk in QT demissa & utrinque producta occurrant TF in H & h: erit IT ad AT ut Kk ad Mp, & TG ad Hp ut TZ ad AT, ideoque æquale , hoc est, æquale areæ HpMh ductæ in rationem : & propterea inclinationis variatio horaria ad 33″. . . ut HpMh ducta in ad
Corol. 2. Ideoque si terra & nodi singulis horis completis retraherentur a locis suis novis, & in loca priora in instanti semper reducerentur, ut situs eorum, per mensem integrum periodicum, datus maneret; tota inclinationis variatio tempore mensis illius foret ad 33″. . , ut aggregatum omnium arearum HpMh, in revolutione puncti p genitarum, & sub signis propriis + & − conjunctarum, ductum in ad id est, ut circulus totus QAqa ductus in ad hoc est, ut circumferentia QAqa ducta in ad
Corol. 3. Proinde in dato nodorum situ, variatio mediocris horaria, ex qua per mensem uniformiter continuata variatio illa menstrua generari posset, est ad 33″. . . ut ad , sive ut ad , id est (cum Pp sit ad PG ut sinus inclinationis prædictæ ad radium, & sit ad ut sinus duplicati anguli ATn ad radium quadruplicatum) ut inclinationis ejusdem sinus ductus in sinum duplicatæ distantiæ nodorum a sole, ad quadruplum quadratum radii.
Corol. 4. Quoniam inclinationis horaria variatio, ubi nodi in quadraturis versantur, est (per hanc propositionem) ad angulum 33″. . ut ad id est, ut ad ; hoc est, ut sinus duplicatæ distantiæ lunæ à quadraturis ductus in ad radium duplicatum: summa omnium variationum horariarum, quo tempore luna in hoc situ nodorum transit a quadratura ad syzygiam (id est, spatio horarum ,) erit ad summam totidem angulorum 33″. . , seu 5878″, ut summa omnium sinuum duplicatæ distantiæ lunæ à quadraturis ducta in ad summam totidem diametrorum; hoc est, ut diameter ducta in ad circumferentiam; id est, si inclinatio sit 5gr. 1′, ut ad 22, seu 278 ad 10000. Proindeque variatio tota, ex summa omnium horariarum variationum tempore prædicto conflata, est 163″, seu 2′. 43″.
PROPOSITIO XXXV. PROBLEMA XVI.
Dato tempore invenire inclinationem orbis lunaris ad planum eclipticæ.
Sit AD sinus inclinationis maximæ, & AB sinus inclinationis minimæ. Bisecetur BD in C, & centro C, intervallo BC describatur circulus BGD. In AC capiatur CE in ea ratione ad EB quam  EB habet ad : et si dato tempore constituatur angulus AEG æqualis duplicatæ distantiæ nodorum à quadraturis, & ad AD demittatur perpendiculum GH: erit AH sinus inclinationis quæsitæ.
EB habet ad : et si dato tempore constituatur angulus AEG æqualis duplicatæ distantiæ nodorum à quadraturis, & ad AD demittatur perpendiculum GH: erit AH sinus inclinationis quæsitæ.
Nam æquale est . Ideoque cum detur, est ut AH. Designet jam AEg duplicatam distantiam nodorum à quadraturis post datum aliquod momentum temporis completum, & arcus Gg ob datum 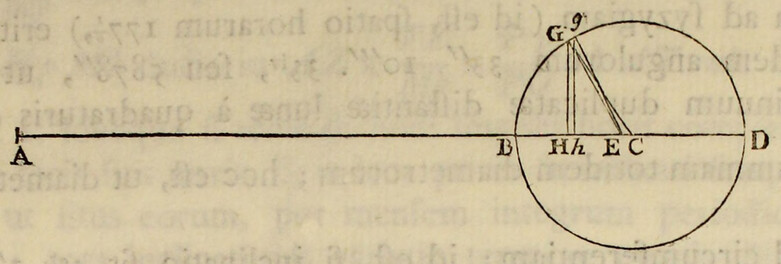 angulum GEg erit ut distantia GE. Est autem Hh ad Gg ut GH ad GC, & propterea Hh est ut contentum , seu ; id est, ut seu , id est, ut AH & sinus anguli AEG conjunctim. Igitur si AH in casu aliquo sit sinus inclinationis, augebitur ea iisdem incrementis cum sinu inclinationis, per Corol. 3. Propositionis superioris, & propterea sinui illi æqualis semper manebit. Sed AH, ubi punctum G incidit in punctum alterutrum B vel D, huic sinui æqualis est, & propterea eidem semper æqualis manet. Q.E.D.
angulum GEg erit ut distantia GE. Est autem Hh ad Gg ut GH ad GC, & propterea Hh est ut contentum , seu ; id est, ut seu , id est, ut AH & sinus anguli AEG conjunctim. Igitur si AH in casu aliquo sit sinus inclinationis, augebitur ea iisdem incrementis cum sinu inclinationis, per Corol. 3. Propositionis superioris, & propterea sinui illi æqualis semper manebit. Sed AH, ubi punctum G incidit in punctum alterutrum B vel D, huic sinui æqualis est, & propterea eidem semper æqualis manet. Q.E.D.
In hac demonstratione supposui angulum BEG, qui est duplicata distantia nodorum à quadraturis, uniformiter augeri. Nam omnes inæqualitatum minutias expendere non vacat. Concipe jam angulum BEG rectum esse, & in hoc casu Gg esse augmentum horarium duplæ distantiæ nodorum & solis ab invicem; & inclinationis variatio horaria in eodem casu (per Corol. 3. Prop. novissimæ) erit ad 33″. . . ut contentum sub inclinationis sinu AH & sinu anguli recti BEG, qui est duplicata distantia nodorum a sole, ad quadruplum quadratum radii; id est, ut mediocris inclinationis sinus AH ad radium quadruplicatum; hoc est (cum inclinatio illa mediocris sit quasi 5gr. ) ut ejus sinus 896 ad radium quadruplicatum 40000, sive ut 224 ad 10000. Est autem variatio tota, sinuum differentiæ BD respondens, ad variationem illam horariam ut diameter BD ad arcum Gg; id est, ut diameter BD ad semicircumferentiam BGD & tempus horarum , quo nodus pergit à quadraturis ad syzygias, ad horam unam conjunctim; hoc est, ut 7 ad 11 & ad 1. Quare si rationes omnes conjungantur, fiet variatio tota BD ad 33″. . . ut ad 110000, id est, ut 29645 ad 1000, & inde variatio illa BD prodibit 16′, .
Hæc est inclinationis variatio maxima quatenus locus lunæ in orbe suo non consideratur. Nam inclinatio, si nodi in syzygiis versantur, nil mutatur ex vario situ lunæ. At si nodi in quadraturis consistunt, inclinatio minor est ubi luna versatur in syzygiis, quam ubi ea versatur in quadraturis, excessu 2′. 43″; uti in propositionis superioris Corollario quarto indicavimus. Et hujus excessus dimidio 1′. variatio tota mediocris BD in quadraturis lunaribus diminuta fit 15′. 2″, in ipsius autem syzygiis aucta fit 17′. 45″. Si Luna igitur in syzygiis constituatur, variatio tota in transitu nodorum a quadraturis ad syzygias erit 17′. 45″: ideoque si inclinatio, ubi nodi in syzygiis versantur, sit 5gr. 17′. 20″; eadem, ubi nodi sunt in quadraturis, & luna in syzygiis, erit 4gr. 59′. 35″. Atque hæc ita se habere confirmatur ex observationibus.
Si jam desideretur orbis inclinatio illa, ubi luna in syzgiis & nodi ubivis versantur; fiat AB ad AD ut sinus graduum 4. 59′. 35″ ad sinum graduum 5. 17′. 20″, & capiatur angulus AEG æqualis duplicatæ distantiæ nodorum à quadraturis; & erit AH sinus inclinationis quæsitæ. Huic orbis inclinationi æqualis est ejusdem inclinatio, ubi luna distat 90gr. à nodis. In aliis lunæ locis inæqualitas menstrua, quam inclinationis variatio admittit, in calculo latitudinis lunæ compensatur, & quodammodo tollitur per inæqualitatem menstruam motus nodorum (ut supra diximus) ideoque in calculo latitudinis illius negligi potest.
Scholium.
Hisce motuum lunarium computationibus ostendere volui, quod motus lunares per theoriam gravitatis a causis suis computari possint. Per eandem theoriam inveni præterea quod æquatio annua medii motus lunæ oriatur a varia dilatatione orbis lunæ per vim solis, juxta Corol. 6. Prop. lxvi. Lib. I. Hæc vis in perigæo solis major est, & orbem lunæ dilatat; in apogæo ejus minor est, & orbem illum contrahi permittit. In orbe dilatato luna tardius revolvitur, in contracto citius; & æquatio annua, per quam hæc inæqualitas compensatur, in apogæo & perigæo solis nulla est, in mediocri solis a terra distantia ad 11′. 50″ circiter ascendit, in aliis locis æquationi centri solis proportionalis est; & additur medio motui lunæ ubi terra pergit ab aphelio suo ad perihelium, & in opposita orbis parte subducitur. Assumendo radium orbis magni 1000 & eccentricitatem terræ , hæc æquatio, ubi maxima est, per theoriam gravitatis prodiit 11′. 49″. Sed eccentricitas terræ paulo major esse videtur, & aucta eccentricitate hæc æquatio augeri debet in eadem ratione. Sit eccentricitas , & æquatio maxima erit 11′. 51″.
Inveni etiam quod in perihelio terræ, propter majorem vim solis, apogæum & nodi lunæ velocius moventur quam in aphelio ejus, idque in triplicata ratione distantiæ terræ a sole inverse. Et inde oriuntur æquationes annuæ horum motuum æquationi centri solis proportionales. Motus autem solis est in duplicata ratione distantiæ terræ a sole inverse, & maxima centri æquatio quam hæc inæqualitas generat, est 1gr. 56′. 20″ prædictæ solis eccentricitati congruens. Quod si motus solis esset in triplicata ratione distantiæ inverse, hæc inæqualitas generaret æquationem maximam 2gr. 54′. 30″. Et propterea æquationes maximæ, quas inæqualitates motuum apogæi & nodorum lunæ generant, sunt ad 2gr. 54′. 30″ ut motus medius diurnus apogæi, & motus medius diurnus nodorum lunæ sunt ad motum medium diurnum solis. Unde prodit æquatio maxima medii motus apogæi 19′. 43″, & æquatio maxima medii motus nodorum 9′. 24″. Addditur vero æquatio prior & subducitur posterior, ubi terra pergit a perihelio suo ad aphelium: & contrarium fit in opposita orbis parte.
Per theoriam gravitatis constitit etiam quod actio solis in lunam paulo major sit ubi transversa diameter orbis lunaris transit per solem, quam ubi eadem ad rectos est angulos cum linea terram & solem jungente: & propterea orbis lunaris paulo major est in priore casu quam in posteriore. Et hinc oritur alia æquatio motus medii lunaris, pendens a situ apogæi lunæ ad solem, quæ quidem maxima est cum apogæum lunæ versatur in octante cum sole; & nulla cum illud ad quadraturas vel syzygias pervenit: & motui medio additur in transitu apogæi lunæ a solis quadratura ad syzygiam, & subducitur in transitu apogæi a syzygia ad quadraturam. Hæc æquatio, quam semestrem vocabo, in octantibus apogæi, quando maxima est, ascendit ad 3′. 45″ circiter, quantum ex phænomenis colligere potui. Hæc est ejus quantitas in mediocri solis distantia a terra. Augetur vero ac diminuitur in triplicata ratione distantiæ solis inverse, ideoque in maxima solis distantia est 3′. 34″, & in minima 3′. 56″ quamproxime: ubi vero apogæum lunæ situm est extra octantes, evadit minor; estque ad æquationem maximam, ut sinus duplæ distantiæ apogæi lunæ a proxima syzygia vel quadratura ad radium.
Per eandem gravitatis theoriam actio solis in lunam paulo major est ubi linea recta per nodos lunæ ducta transit per solem, quam ubi linea illa ad rectos est angulos cum recta solem ac terram jungente. Et inde oritur alia medii motus lunaris æquatio, quam semestrem secundam vocabo, quæque maxima est ubi nodi in solis octantibus versantur, & evanescit ubi sunt in syzygiis vel quadraturis, & in aliis nodorum positionibus proportionalis est sinui duplæ distantiæ nodi alterutrius a proxima syzygia aut quadratura: additur vero medio motui lunæ si sol distat a nodo sibi proximo in antecedencia, subducitur si in consequentia, & in octantibus, ubi maxima est, ascendit ad 47″ in mediocri solis distantia a terra, uti ex theoria gravitatis colligo. In aliis solis distantiis hæc æquatio, maxima in octantibus nodorum est reciproce ut cubus distantiæ solis a terra, ideoque in perigæo solis ad 49″ in apogæo ejus ad 45″ circiter ascendit.
Per eandem gravitatis theoriam apogæum lunæ progreditur quam maxime ubi vel cum sole conjungitur vel eidem opponitur, & regreditur ubi cum sole quadraturam facit. Et eccentricitas fit maxima in priore casu & minima in posteriore, per Corol. 7, 8 & 9. Prop. lxvi. Lib. I. Et hæ inæqualitates per eadem Corollaria permagnæ sunt, & æquationem principalem apogæi generant, quam semestrem vocabo. Et æquatio maxima semestris est 12gr. 18′ circiter, quantum ex observationibus colligere potui. Horroxius noster lunam in ellipsi circum terram, in ejus umbilico inferiore constitutam, revolvi primus statuit. Halleius centrum ellipseos in epicyclo locavit, cujus centrum uniformiter revolvitur circum terram. Et ex motu in epicyclo oriuntur inæqualitates jam dictæ in progressu & regressu apogæi & quantitate eccentricitatis. Dividi intelligatur distantia mediocris lunæ a terra in partes 100000, & referat T terram & TC eccentricitatem mediocrem lunæ partium 5505. Producatur TC ad B, ut sit CB sinus æquationis maximæ semestris 12gr. 18′ ad radium TC, & circulus BDA centro C, intervallo CB descriptus erit epicyclus ille in quo centrum orbis lunaris locatur & secundum ordinem literarum BDA revolvitur. Capiatur angulus BCD æqualis duplo argumento annuo, seu duplæ distantiæ veri loci solis ab apogæo lunæ semel æquato, & erit CTD æquatio semestris apogæi lunæ 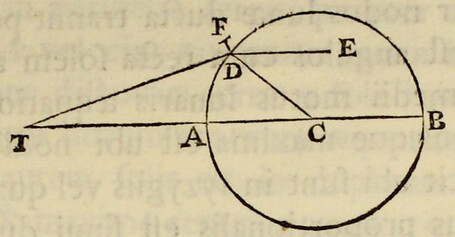 & TD eccentricitas orbis ejus in apogæum secundo æquatum tendens. Habitis autem lunæ motu medio & apogæo & eccentricitate, ut & orbis axe majore partium 200000; ex his eruetur verus lunæ locus in orbe & distantia ejus a terra, idque per methodos notissimas.
& TD eccentricitas orbis ejus in apogæum secundo æquatum tendens. Habitis autem lunæ motu medio & apogæo & eccentricitate, ut & orbis axe majore partium 200000; ex his eruetur verus lunæ locus in orbe & distantia ejus a terra, idque per methodos notissimas.
In perihelio terræ, propter majorem vim solis, centrum orbis lunæ velocius movetur circum centrum C quam in aphelio, idque in triplicata ratione distantiæ terræ a sole inverse. Ob æquationem centri solis in argumento annuo comprehensam, centrum orbis lunæ velocius movetur in epicyclo BDA in duplicata ratione distantiæ terræ a sole inverse. Ut idem adhuc velocius moveatur in ratione simplici distantiæ inverse; ab orbis centro D agatur recta DE versus apogæum lunæ, seu rectæ TC parallela, & capiatur angulus EDF æqualis excessui argumenti annui prædicti supra distantiam apogæi lunæ a perigæo solis in consequentia; vel quod perinde est, capiatur angulus CDF æqualis complemento anomaliæ veræ solis ad gradus 360. Et sit DF ad DC ut dupla eccentricitas orbis magni ad distantiam mediocrem solis a terra, & motus medius diurnus solis ab apogæo lunæ ad motum medium diurnum solis ab apogæo propio conjunctim, id est, ut ad 1000 & 52′. 27″. ad 59′. 8″. conjunctim, sive ut 3 ad 100. Et concipe centrum orbis lunæ locari in puncto F, & in epicyclo, cujus centrum est D, & radius DF, interea revolvi dum punctum D progreditur in circumferentia circuli DABD. Hac enim ratione velocitas, qua centrum orbis lunæ in linea quadam curva circum centrum C descripta movebitur, erit reciproce ut cubus distantiæ solis a terra quamproxime, ut oportet.
Computatio motus hujus difficilis est, sed facilior reddetur per approximationem sequentem. Si distantia mediocris lunæ a terra sit partium 100000, & eccentricitas TC sit partium 5505 ut supra: recta CB vel CD invenietur partium , & recta DF partium . Et hæc recta ad distantiam TC subtendit angulum ad terram quem translatio centri orbis a loco D ad locum F generat in motu centri hujus: & eadem recta duplicata in situ parallelo ad distantiam superioris umbilici orbis lunæ a terra, subtendit eundem angulum, quem utique translatio illa generat in motu umbilici, & ad distantiam lunæ a terra subtendit angulum quem eadem translatio generat in motu lunæ, quique propterea æquatio centri secunda dici potest. Et hæc æquatio, in mediocri lunæ distantia a terra, est ut sinus anguli, quem recta illa DF cum recta a puncto F ad lunam ducta continet quamproxime, & ubi maxima est evadit 2′. 25″. Angulus autem quem recta DF & recta a puncto F ad lunam ducta comprehendunt, invenitur vel subducendo angulum EDF ab anomalia media lunaæ, vel addendo distantiam lunæ a sole ad distantiam apogeæi lunæ ab apogæo solis. Et ut radius est ad sinum anguli sic inventi, ita 2′. 25″. sunt ad æquationem centri secundam, addendam, si summa illa sit minor semicirculo, subducendam si major. Sic habebitur ejus longitudo in ipsis luminarium syzygiis.
Cum atmosphæra terræ ad usque altitudinem milliarium 35 vel 40 refringat lucem solis, & refringendo spargat eandem in umbram terræ, & spargendo lucem in confinio umbræ dilatet umbram: ad diametrum umbræ, quæ per parallaxim prodit, addo minutum unum primum in eclipsibus lunæ, vel minutum unum cum triente.
<464>Theoria vero lunæ primo in syzygiis, deinde in quadraturis, & ultimo in octantibus per phænomena examinari & stabiliri debet. Et opus hocce aggressurus motus medios solis & lunæ ad tempus meridianum in observatorio regio Grenovicensi, die ultimo mensis Decembris anni 1700. st. vet. non incommode sequentes adhibebit: nempe motum medium solis ♑ 20gr. 43′. 40″, & apogæi ejus ♋ 7gr. 44′. 30″, & motum medium lunæ ♒ 15gr. 21′. 00″, & apogæi ejus ♓ 8gr. 20′. 00″, & nodi ascendentis ♌ 27gr. 24′. 20″; & differentiam meridianorum observatorii hujus & observatorii regii Parisiensis 0hor. 9min. 20sec. motus autem medii lunæ & apogæi ejus nondum satis accurate habentur.
PROPOSITIO XXXVI. PROBLEMA XVII.
Invenire vim solis ad mare movendum.
Solis vis ML seu PT, in quadraturis lunaribus, ad perturbandos motus lunares, erat (per Prop. xxv. hujus) ad vim gravitatis apud nos, ut 1 ad 638092,6. Et vis seu in syzygiis lunaribus est duplo major. Hæ autem vires, si descendatur ad superficiem terræ, diminuuntur in ratione distantiarum a centro terræ, id est, in ratione ad 1; ideoque vis prior in superficie terræ est ad vim gravitatis ut 1 ad 38604600. Hac vi mare deprimitur in locis, quæ 90 gradibus distant a sole. Vi altera, quæ duplo major est, mare elevatur & sub sole & in regione soli opposita. Summa 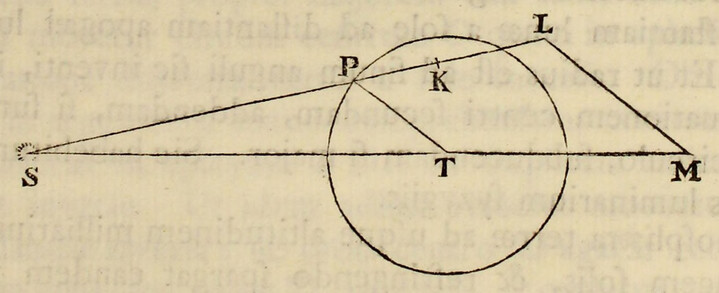 virium est ad vim gravitatis ut 1 ad 12868200. Et quoniam vis eadem eundem ciet motum, sive ea deprimat aquam in regionibus quæ 90 gradibus distant a sole, sive elevet eandem in regionibus sub sole & soli oppositis, hæc summa erit tota solis vis ad mare agitandum; & eundem habebit effectum, ac si tota in regionibus sub sole & soli oppositis mare elevaret, in regionibus autem quæ 90 gradibus distant a sole nil ageret.
virium est ad vim gravitatis ut 1 ad 12868200. Et quoniam vis eadem eundem ciet motum, sive ea deprimat aquam in regionibus quæ 90 gradibus distant a sole, sive elevet eandem in regionibus sub sole & soli oppositis, hæc summa erit tota solis vis ad mare agitandum; & eundem habebit effectum, ac si tota in regionibus sub sole & soli oppositis mare elevaret, in regionibus autem quæ 90 gradibus distant a sole nil ageret.
Hæc est vis solis ad mare ciendum in loco quovis dato, ubi sol tam in vertice loci versatur quam in mediocri sua distantia a terra. In aliis solis positionibus vis ad mare attollendum, est ut sinus versus duplæ altitudinis solis supra horizontem loci directe & cubus distantiæ solis a terra inverse.
Corol. cum vis centrifuga partium terræ a diurno terræ motu oriunda, quæ est ad vim gravitatis ut 1 ad 289, efficiat ut altitudo aquæ sub æquatore superet ejus altitudinem sub polis mensura pedum Parisiensium 85472, ut supra in prop. xix; vis solaris de qua egimus, cum sit ad vim gravitatis ut 1 ad 12868200, atque ideo ad vim illam centrifugam ut 289 ad 12868200 seu 1 ad 44527, efficiet ut altitudo aquæ in regionibus sub sole & soli oppositis superet altitudinem ejus in locis, quæ 90 gradibus distant a sole, mensura tantum pedis unius Parisiensis & digitorum undecim cum tricesima parte digiti. Est enim hæc mensura ad mensuram pedum 85472 ut 1 ad 44527.
PROPOSITIO XXXVII. PROBLEMA XVIII.
Invenire vim lunæ ad mare movendum.
Vis lunæ ad mare movendum colligenda est ex ejus proportione ad vim solis, & hæc proportio colligenda ex proportione motuum maris, qui ab his viribus oriuntur. Ante ostium fluvii Avonæ ad lapidem tertium infra Bristolium, tempore verno & autumnali totus aquæ ascensus in conjunctione & oppositione luminarium, observante Samuele Sturmio, est pedum plus minus 45, in quadraturis autem est pedum tantum 25. Altitudo prior ex summa virium, posterior ex earundem differentia oritur. Solis igitur & lunæ in æquatore versantium & mediocriter a terra distantium sunto vires S & L, & erit ad ut 45 ad 25, seu 9 ad 5.
<466>In portu Plymuthi æstus maris ex observatione Samuelis Colepressi ad pedes plus minus sexdecim altitudine mediocri attollitur, ac tempore verno & autumnali altitudo æstus in syzygiis superare potest altitudinem ejus in quadraturis pedibus septem vel octo. Si maxima harum altitudinum differentia sit pedum novem, erit ad ut ad seu 41 ad 23. Quæ proportio satis congruit cum priore. Ob magnitudinem æstus in portu Bistoliæ, observationibus Sturmii magis fidendum esse videtur, ideoque donec aliquid certius constiterit, proportionem 9 ad 5 usurpabimus.
Cæterum ob aquarum reciprocos motus, æstus maximi non incidunt in ipsas luminarium syzygias, sed sunt tertii a syzygiis ut dictum fuit, seu proxime sequuntur tertium lunæ post syzygias appulsum ad meridianum loci, vel potius (ut a Sturmio notatur) sunt tertii post diem novilunii vel plenilunii, seu post horam a novilunio vel plenilunio plus minus duodecimam, ideoque incidunt in horam a novilunio vel plenilunio plus minus quadragesimam tertiam. Incidunt vero in hoc portu in horam septimam circiter ab appulsu lunæ ad meridianum loci; ideoque proxime sequuntur appulsum lunæ ad meridianum, ubi luna distat a sole vel ab oppositione solis gradibus plus minus octodecim vel novemdecim in consequentia. Æstas & hyems maxime vigent, non in ipsis solstitiis, sed ubi sol distat a solstitiis decima circiter parte totius circuitus, seu gradibus plus minus 36 vel 37. Et similiter maximus æstus maris oritur ab appulsu lunæ ad meridianum loci, ubi luna distat a sole decima circiter parte motus totius ab æstu ad æstum. Sit distantia illa graduum plus minus . Et vis solis in hac distantia lunæ a syzygiis & quadraturis, minor erit ad augendum & ad minuendum motum maris a vi lunæ oriundum, quam in ipsis syzygiis & quadraturis, in ratione radii ad sinum complementi distantiæ hujus duplicatæ seu anguli graduum 37, hoc est, in ratione 10000000 ad 7986355. Ideoque in analogia superiore pro S scribi debet .
Sed & vis lunæ in quadraturis, ob declinationem lunæ ab æquatore, diminui debet. Nam Luna in quadraturis, vel potius in gradu post quadraturas, in declinatione graduum plus minus 22. 13′ versatur. Et luminaris ab æquatore declinantis vis ad mare movendum diminuitur in duplicata ratione sinus complementi declinationis quamproxime. Et propterea vis lunæ in his quadraturis est tantum . Est igitur ad ut 9 ad 5.
Præterea diametri orbis, in quo luna sine eccentricitate moveri deberet, sunt ad invicem ut 69 ad 70; ideoque distantia lunæ a terra in syzygiis est ad distantiam ejus in quadraturis ut 69 ad 70, cæteris paribus. Et distantiæ ejus in gradu a syzygiis, ubi æstus maximus generatur, & in gradu a quadraturis, ubi æstus minimus generatur, sunt ad mediocrem ejus distantiam ut 69,098747 & 69,897345 ad . Vires autem lunæ ad mare movendum sunt in triplicata ratione distantiarum inverse, ideoque vires in maxima & minima harum distantiarum sunt ad vim in mediocri distantia ut 0,9830427 & 1,017522 ad 1. Unde fit ad ut 9 ad 5. Et S ad L ut 1 ad 4,4815. Itaque cum vis solis sit ad vim gravitatis ut 1 ad 12868200, vis lunæ erit ad vim gravitatis ut 1 ad 2871400.
Corol. 1. Cum aqua vi solis agitata ascendat ad altitudinem pedis unius & undecim digitorum cum tricesima parte digiti, eadem vi lunæ ascendet ad altitudinem octo pedum & digitorum , & vi utraque ad altitudinem pedum decem cum semisse, & ubi luna est in perigæo ad altitudinem pedum duodecim cum semisse & ultra, præsertim ubi æstus ventis spirantibus adjuvatur. Tanta autem vis ad omnes maris motus excitandos abunde sufficit, & quantitati motuum probe respondet. Nam in maribus quæ ab oriente in occidentem late patent, uti in mari Pacifico, & maris Atlantici & Æthiopici partibus extra tropicos, aqua attolli solet ad altitudinem pedum sex, novem, duodecim vel quindecim. In mari autem Pacifico, quod profundius est & latius patet, æstus dicuntur esse majores quam in Atlantico & Æthiopico. Etenim ut plenus sit æstus, latitudo maris ab oriente in occidentem non minor esse debet quam graduum nonaginta. In mari Æthiopico, ascensus aquæ intra tropicos minor est quam in zonis temperatis, propter angustiam maris inter Africam & australem partem Americæ. In medio mari aqua nequit ascendere, nisi ad littus utrumque & orientale & occidentale simul descendat: cum tamen vicibus alternis ad littora illa in maribus nostris angustis descendere debeat. Ea de causa fluxus & refluxus in insulis, quæ a littoribus longissime absunt, perexiguus esse solet. In portubus quibusdam, ubi aqua cum impetu magno per loca vadosa, ad sinus alternis vicibus implendos & evacuandos, influere & effluere cogitur, fluxus & refluxus debent esse solito majores, uti ad Plymuthum & pontem Chepstowæ in Anglia; ad montes S. Michælis & urbem Abrincatuorum (vulgo Auranches) in Normannia; ad Cambaiam & Pegu in India orientali. His in locis mare, magna cum velocitate accedendo & recedendo, littora nunc inundat nunc arida relinquit ad multa millaria. Neque impetus influendi & remeandi prius frangi potest, quam aqua attollitur vel deprimitur ad pedes 30, 40, vel 50 & amplius. Et par est ratio fretorum oblongorum & vadosorum, uti Magellanici & ejus quo Anglia circundatur. Æstus in hujusmodi portubus & fretis per impetum cursus & recursus supra modum augetur. Ad littora vero quæ descensu præcipiti ad mare profundum & apertum spectant, ubi aqua sine impetu effluendi & remeandi attolli & subsidere potest, magnitudo æstus respondet viribus solis & lunæ.
Corol. 2. Cum vis lunæ ad mare movendum sit ad vim gravitatis ut 1 ad 2871400, perspicuum est quod vis illa sit longe minor quam quæ vel in experimentis pendulorum, vel in staticis aut hydrostaticis quibuscunque sentiri possit. In æstu solo marino hæc vis sensibilem edit effectum.
Corol. 3. Quoniam vis lunæ ad mare movendum est ad solis vim consimilem ut 4,4815 ad 1, & vires illæ (per corol. 14. prop. lxvi. lib. i.) sunt ut densitates corporum lunæ & solis & cubi diametrorum apparentium conjunctim; densitas lunæ erit ad densitatem solis ut 4,4815 ad 1 directe, & cubus diametri lunæ ad cubum diametri solis inverse: id est (cum diametri mediocres apparentes lunæ & solis sint 31′. & 32′. 12″) ut 4891 ad 1000. Densitas autem solis erat ad densitatem terræ ut 1000 ad 4000; & propterea densitas lunæ est ad densitatem terræ ut 4891 ad 4000 seu 11 ad 9. Est igitur corpus lunæ densius & magis terrestre quam terra nostra.
<469>Corol. 4. Et cum vera diameter lunæ ex observationibus astronomicis sit ad veram diametrum terræ ut 100 ad 365; erit massa lunæ ad massam terræ ut 1 ad 39,788.
Corol. 5. Et gravitas acceleratrix in superficie lunæ erit quasi triplo minor quam gravitas acceleratrix in superficie terræ.
Corol. 6. Et distantia centri lunæ a centro terræ erit ad distantiam centri lunæ a communi gravitatis centro terræ & lunæ, ut 40,788 ad 39,788.
Corol. 7. Et mediocris distantia centri lunæ a centro terræ in octantibus lunæ erit semidiametrorum maximarum terræ quamproxime. Nam terræ semidiameter maxima suit pedum Parisiensium 19658600, & mediocris distantia centrorum terræ & lunæ, ex hujusmodi diametris {sic} constans, æqualis est pedibus 1187379440. Et hæc distantia (per corollarium superius) est ad distantiam centri lunæ a communi gravitatis centro terræ & lunæ, ut 40,788 ad 39,788: ideoque distantia posterior est pedum 1158268534. Et cum luna revolvatur, respectu fixarum, diebus 27, horis 7, & minutis primis ; sinus versus anguli, quem luna tempore minuti unius primi describit, est 12752341, existente radio 1000,000000,000000. Et ut radius est ad hunc sinum versum, ita sunt pedes 1158268534 ad pedes 14,7706353. Luna igitur vi illa, qua retinetur in orbe, cadendo in terram, tempore minuti unius primi describet pedes 14,7706353. Et augendo hanc vim in ratione ad , habebitur vis tota gravitatis in orbe lunæ per Corol. Prop. III. Et hac vi luna cadendo tempore minuti unius primi describet pedes 14,8538067. Et ad sexagesimam partem distantiæ lunæ a centro terræ id est ad distantiam pedum 197896573 a centro terræ, corpus grave tempore minuti unius secundi cadendo describet etiam pedes 14,8538067. Ideoque ad distantiam pedum 19615800, quæ sunt terræ semidiameter mediocris, grave cadendo describet pedes 15,11175, seu pedes 15, dig. 1, & lin. . Hic erit descensus corporum in latitudine graduum 45. Et per tabulam præcedentem in prop. xx. descriptam, descensus erit paulo major in latitudine Lutetiæ Parisiorum existente excessu quasi partium lineæ. Gravia igitur per hoc computum in latitudine Lutetiæ cadendo in vacuo describent tempore unius secundi pedes Parisienses 15, dig. 1, & lin. circiter. Et si gravitas minuatur auferendo vim cetrifugam, quæ oritur a motu diurno terræ in illa latitudine; gravia ibi cadendo describent tempore minuti unius secundi pedes 15, dig. 1, & lin. . Et hac velocitate gravia cadere in latitudine Lutetiæ supra ostensum est ad prop. iv, & xix.
Corol. 8. Distantia mediocris centrorum terræ & lunæ in syzygiis lunæ est sexaginta semidiametrorum maximarum terræ, dempta tricesima parte semidiametri circiter. Et in quadraturis lunæ distantia mediocris eorundem centrorum est semidiametrorum terræ. Nam hæ duæ distantiæ sunt ad distantiam mediocrem lunæ in octantibus ut 69 & 70 ad per prop. xxviii.
Corol. 9. Distantia mediocris centrorum terræ & lunæ in syzygiis lunæ est sexaginta semidiametrorum mediocrium terræ cum decima parte semidiametri. Et in quadraturis lunæ distantia mediocris eorundem centrorum est sexaginta & unius semidiametrorum mediocrium terræ, dempta tricesima parte semidiametri.
Corol. 10. In syzygiis lunæ parallaxis ejus horizontalis mediocris in latitudinibus graduum 0, 30, 38, 45, 52, 60, 90, est 57′. 20″, 57′. 16″, 57′. 14″, 57′. 12″, 57′. 10″, 57′. 8″, 57′. 4″ respective.
In his computationibus attractionem magneticam terræ non consideravi, cujus utique quantitas perparva est & ignoratur. Siquando vero hæc attractio investigari poterit, & mensuræ graduum in meridiano, ac longitudines pendulorum isochronorum in diversis parallelis, legesque motuum maris, & parallaxis lunæ cum diametris apparentibus solis & lunæ ex phænomenis accuratius determinatæ fuerint: licebit calculum hunc omnem accuratius repetere.
PROPOSITIO XXXVIII. PROBLEMA XIX.
Invenire figuram corporis lunæ.
Si corpus lunare fluidum esset ad instar maris nostri, vis terræ ad fluidum illud in partibus & citimis & ultimis elevandum esset ad vim lunæ, qua mare nostrum in partibus & sub luna & lunæ oppositis attollitur, ut gravitas acceleratrix lunæ in terram ad gravitatem acceleratricem terræ in lunam, & diameter lunæ ad diametrum terræ conjunctim; id est, ut 39,788 ad 1 & 100 ad 365 conjunctim, seu 1081 ad 100. Unde cum mare nostrum vi lunæ attollatur ad pedes , fluidum lunare vi terræ attolli deberet ad pedes 93. Eaque de causa figura lunæ sphærois esset, cujus maxima diameter producta transiret per centrum terræ, & superaret diametros perpendiculares excessu pedum 186. Talem igitur figuram luna affectat, eamque sub initio induere debuit. Q.E.I.
Corol. Inde vero fit ut eadem semper lunæ facies in terram obvertatur. In alio enim situ corpus lunare quiescere non potest, sed ad hunc situm oscillando semper redibit. Attamen oscillationes, ob parvitatem virium agitantium, essent longe tardissimæ: adeo ut facies illa, quæ terram semper respicere deberet, possit alterum orbis lunaris umbilicum (ob rationem in prop. xvii allatam) respicere, neque statim abinde retrahi & in terram converti.
LEMMA I.
Si APEp terram designet uniformiter densam, centroque C & polis P, p & æquatore AE delineatam; & si centro C radio CP describi intelligatur sphæra Pape; sit autem QR planum, cui recta a centro solis ad centrum terræ ducta normaliter insistit; & terræ totius exterioris PapAPepE, quæ sphæra modo descripta altior est, particulæ singulæ conentur recedere hinc inde a plano QR, sitque conatus particulæ cujusque ut ejusdem distantia a plano: Dico primo, quod tota particularum omnium in æquatoris circulo AE, extra globum uniformiter per totum circuitum in morem annuli dispositarum, vis & efficacia ad terram circum centrum ejus rotandam, sit ad totam particularum totidem in æquatoris puncto A, quod a plano QR maxime distat, consistentium vim & efficaciam, ad terram consimili motu circulari circum centrum ejus movendam, ut unum ad duo. Et motus iste circularis circum axem, in communi sectione æquatoris & plani QR jacentem, peragetur.
<472>Nam centro K diametro IL describatur semicirculus INLK. Dividi intelligatur semicircumferentia INL in partes innumeras æquales, & a partibus singulis N ad diametrum IL demittantur sinus NM. Et summa quadratorum ex sinibus omnibus NM æqualis erit summæ quadratorum ex sinibus KM, & summa utraque æqualis erit summæ quadratorum ex totidem semidiametris KN; ideoque summa quadratorum ex omnibus NM, erit duplo minor quam summa quadratorum ex totidem semidiametris KN.
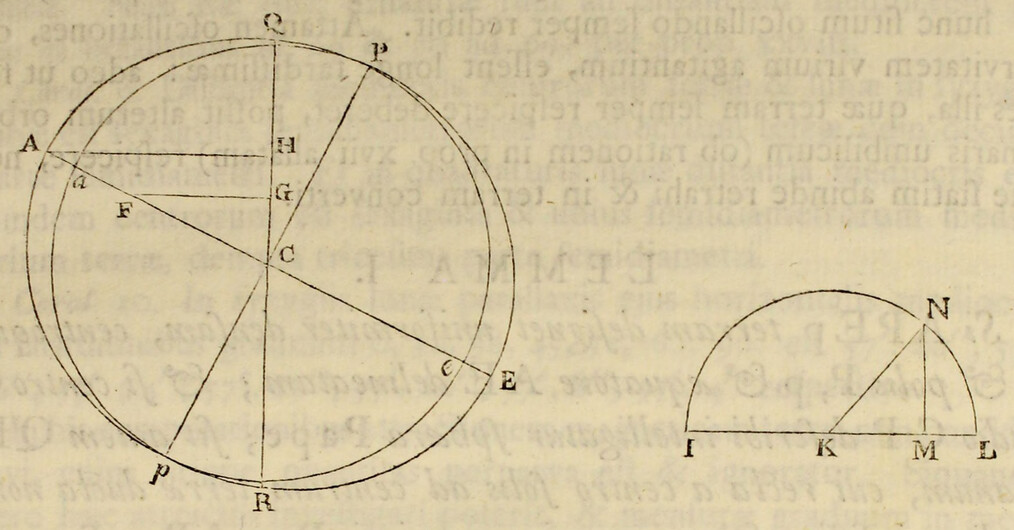
Jam dividatur perimeter circuli AE in particulas totidem æquales, & ab earum unaquaque F ad planum QR demittatur perpendiculum FG, ut & a puncto A perpendiculum AH. Et vis, qua particula F recedit a plano QR, erit ut perpendiculum illud FG per hypothesin, & hæc vis ducta in distantiam CG erit efficacia particulæ F ad terram circum centrum ejus convertendam. Ideoque efficacia particulæ in loco F, erit ad efficaciam particulæ in loco A, ut ad , hoc est, ut ad ; & propterea efficacia tota particularum omnium in locis suis F erit ad efficaciam particularum totidem in loco A, ut summa omnium ad summam totidem , hoc est (per jam demonstrata) ut unum ad duo. Q.E.D.
Et quoniam particulæ agunt recedendo perpendiculariter a plano QR, idque æqualiter ab utraque parte hujus plani: eædem convertent circumferentiam circuli æquatoris, eique inhærentem terram, circum axem tam in plano illo QR quam in plano æquatoris jacentem.
LEMMA II.
Iisdem positis: dico secundo quod vis & efficacia tota particularum omnium extra globum undique sitarum, ad terram circum axem eundem rotandam, sit ad vim totam particularum totidem, in æquatoris circulo AE uniformiter per totum circuitum in morem annuli dispositarum, ad terram consimili motu circulari movendam, ut duo ad quinque.
Sit enim IK circulus quilibet minor Æquatori AE parallelus, sintque L, l particulæ duæ quævis æquales in hoc circulo extra globum Pape sitæ. Et si in planum QR, quod radio in solem ducto perpendiculare est, demittantur perpendicula LM, lm: vires totæ, quibus particulæ illæ fugiunt planum QR, proportionales erunt perpendiculis illis LM, lm. Sit autem recta Ll plano Pape paralella & 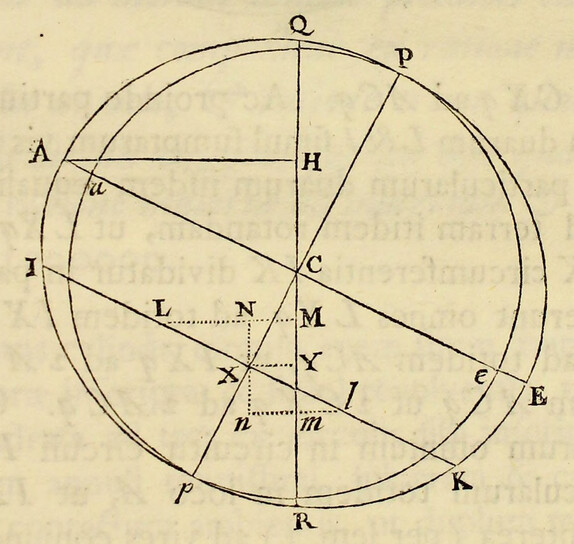 bisecetur eadem in X, & per punctum X agatur Nn, quæ parallela sit plano QR & perpendiculis LM, lm ocurrat in N ac n, & in planum QR demittatur perpendiculum XY. Et particularum L & l vires contrariæ, ad terram in contrarias partes rotandam, sunt ut & , hoc est, ut & , seu & : & harum differentia est vis particularum ambarum simul sumptarum ad terram rotandam. Hujus differentiæ pars affirmativa seu est ad particularum duarum ejusdem magnitudinis in A consistentium vim , ut ad . Et pars negativa seu ad particularum earundem in A consistentium vim
bisecetur eadem in X, & per punctum X agatur Nn, quæ parallela sit plano QR & perpendiculis LM, lm ocurrat in N ac n, & in planum QR demittatur perpendiculum XY. Et particularum L & l vires contrariæ, ad terram in contrarias partes rotandam, sunt ut & , hoc est, ut & , seu & : & harum differentia est vis particularum ambarum simul sumptarum ad terram rotandam. Hujus differentiæ pars affirmativa seu est ad particularum duarum ejusdem magnitudinis in A consistentium vim , ut ad . Et pars negativa seu ad particularum earundem in A consistentium vim 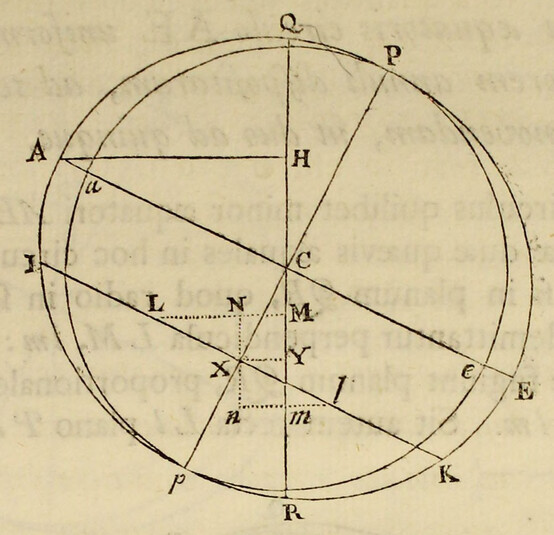 , ut ad . Ac proinde partium differentia, id est, particularum duarum L & l simul sumptarum vis ad terram rotandam est ad vim particularum duarum iisdem æqualium & in loco A consistentium ad terram itidem rotandam, ut ad . Sed si circuli IK circumferentia IK dividatur in particulas innumeras æquales L, erunt omnes ad totidem ut 1 ad 2 (per lem i.) atque ad totidem , ut ad ; & totidem ad totidem ut ad . Quare vires conjunctæ particularum omnium in circuitu circuli IK sunt ad vires conjunctas particularum totidem in loco A, ut ad : & propterea (per lem. i.) ad vires conjunctas particularum totidem in circuitu circuli AE, ut ad .
, ut ad . Ac proinde partium differentia, id est, particularum duarum L & l simul sumptarum vis ad terram rotandam est ad vim particularum duarum iisdem æqualium & in loco A consistentium ad terram itidem rotandam, ut ad . Sed si circuli IK circumferentia IK dividatur in particulas innumeras æquales L, erunt omnes ad totidem ut 1 ad 2 (per lem i.) atque ad totidem , ut ad ; & totidem ad totidem ut ad . Quare vires conjunctæ particularum omnium in circuitu circuli IK sunt ad vires conjunctas particularum totidem in loco A, ut ad : & propterea (per lem. i.) ad vires conjunctas particularum totidem in circuitu circuli AE, ut ad .
Jam vero si sphæræ diameter Pp dividatur in partes innumeras æquales, quibus insistant circuli totidem IK; materia in perimetro circuli cujusque IK erit ut : ideoque vis materiæ illius ad terram rotandam, erit ut in . Et vis materiæ ejusdem, si in circuli AE perimetro consisteret, esset ut in . Et propterea vis particularum omnium materiæ totius, extra globum in perimetris circulorum omnium consistentis, est ad vim particularum totidem in perimetro circuli maximi AE consistentis, ut omnia in ad totidem in , hoc est, ut omnia in ad totidem in , id est, ut omnia ad totidem , hoc est, ut tota quantitas fluens, cujus fluxio est , ad totam quantitatem fluentem, cujus fluxio est ; ac proinde per methodum fluxionum, ut ad , id est, si pro CX scribatur tota Cp vel AC, ut ad . hoc est, ut duo ad quinque. Q. E. D.
LEMMA III.
Iisdem positis: dico tertio quod motus terræ totius circum axem jam ante descriptum, ex motibus particularum omnium compositus, erit ad motum annuli prædicti circum axem eundem, in ratione, quæ componitur ex ratione materiæ in terra ad materiam in annulo, & ratione trium quadratorum ex arcu quadrantali circuli cujuscunque ad duo quadrata ex diametro; id est, in ratione materiæ ad materiam & numeri 925275 ad numerum 1000000.
Est enim motus cylindri circum axem suum immotum revolventis ad motum sphæræ inscriptæ & simul revolventis, ut quælibet quatuor æqualia quadrata ad tres ex circulis sibi inscriptis: & motus cylindri ad motum annuli tenuissimi, sphæram & cylindrum ad communem eorum contactum ambientis, ut duplum materiæ in cylindro ad triplum materiæ in annulo; & annuli motus iste circum axem cylindri uniformiter continuatus, ad ejusdem motum uniformem circum diametrum propriam, eodem tempore periodico factum, ut circunferentia circuli ad duplum diametri.
<476>HYPOTHESIS II.
Si annulus prædictus terra omni reliqua sublata, solus in orbe terræ, motu annuo circa solem ferretur, & interea circa axem suum, ad planum eclipticæ in angulo graduum inclinatum, motu diurno revolveretur: idem foret motus punctorum æquinoctialium, sive annulus iste fluidus esset, sive is ex materia rigida & firma constaret.
PROPOSITIO XXXIX. PROBLEMA XX.
Invenire præcessionem æquinoctiorum.
Motus mediocris horarius nodorum lunæ in orbe circulari, ubi nodi sunt in quadraturis, erat 16″. . . , & hujus dimidium 8″. . . . (ob rationes supra explicatas) est motus medius horarius nodorum in tali orbe; fitque anno toto sidereo 20gr. 11′. 46″. Quoniam igitur nodi LLunæ in tali orbe conficerent annuatim 20gr. 11′. 46″. in antecedentia; & si plures essent lunæ, motus nodorum cujusque (per corol. 16. prop. lxvi. Lib. i.) forent ut tempora periodica; si luna spatio diei siderei juxta superficiem terræ revolveretur, motus annuus nodorum foret ad 20gr. 11′. 46″ ut dies sidereus horarum 23. 56′. ad tempus periodicum lunæ dierum 27. 7 hor. 43′; id est, ut 1436 ad 39343. Et par est ratio nodorum annuli lunarum terram ambientis; sive lunæ illaeæ se mutuo non contingant, sive liquescant & in annulum continuum formentur, sive denique annulus ille rigescat & inflexibilis reddatur.
Fingamus igitur quod annulus iste, quoad quantitatem materiæ, æqualis sit terræ omni PapAPepE quæ globo Pape superior est; (Vid. fig. pag. 474.) & quoniam globus iste est ad terram illam superiorem ut ad id est (cum terræ diameter minor PC vel aC sit ad semidiametrum majorem AC ut 229 ad 230) ut 52441 ad 459; si annulus iste terram secundum æquatorem cingeret & uterque simul circa diametrum annuli revolveretur, motus annuli esset ad motum globi interioris (per hujus lem. iii.) ut 459 ad 52441 & 1000000 ad 925275 conjunctim, hoc est, ut 4590 ad 485223; ideoque motus annuli esset ad summam motuum annuli ac globi, ut 4590 ad 489813. Unde si annulus globo adhæreat, & motum suum, quo ipsius nodi seu puncta æquinoctialia regrediuntur, cum globo communicet: motus qui restabit in annulo erit ad ipsius motum priorem, ut 4590 ad 489813; & propterea motus punctorum æquinoctialium diminuetur in eadem ratione. Erit igitur motus annuus punctorum æquinoctialium corporis ex annulo & globo compositi ad motum 20gr. 11′. 46″, ut 1436 ad 39343 & 4590 ad 489813 conjunctim, id est, ut 100 ad 292369. Vires autem quibus nodi lunarum (ut supra explicui) atque ideo quibus puncta æquinoctialia annuli regrediuntur (id est vires in fig. pag. 437 & 438) sunt in singulis particulis ut distantiæ particularum a plano QR, & his viribus particulæ illæ planum fugiunt; & propterea (per lem. ii.) si materia annuli per totam globi superficiem in morem figuræ PapAPepE ad superiorem illam terræ partem constituendam spargeretur, vis & efficacia tota particularum omnium ad terram circa quamvis æquatoris diametrum rotandam, atque ideo ad movenda puncta æquinoctialia, evaderet minor quam prius in ratione 2 ad 5. Ideoque annuus æquinoctiorum regressus jam esset ad 20gr. 11′. 46″, ut 10 ad 73092: ac proinde fieret 9″. .
Cæterum hic motus, ob inclinationem plani æquatoris ad planum eclipticæ minuendus est, idque in ratione sinus 91706 (qui sinus est complementi graduum ) ad radium 100000. Qua ratione motus iste jam fiet 9″. . Hæc est annua præcessio æquinoctiorum a vi solis oriunda.
Vis autem lunæ ad mare movendum erat ad vim solis, ut 4,4815 ad 1 circiter. Et vis lunæ ad æquinoctia movenda est ad vim solis in eadem proportione. Indeque prodit annua æquinoctiorum præcessio a vi lunæ oriunda 40″. , ac tota præcessio annua a vi utraque oriunda 50″. . Et hic motus cum phænomenis congruit. Nam præcessio æquinoctiourum ex observationibus astronimicis est annuatim minutorum secundorum plus minus quinquaginta.
Si altitudo terræ ad æquatorem superet altitudinem ejus ad polos, milliaribus pluribus quam , materia ejus rarior erit ad circumferentiam quam ad centrum: & præcessio æquinoctiorum ob altitudinem illam augeri, ob raritatem diminui debet.
Descripsimus jam systema solis, terræ, lunæ, & planetarum: superest ut de cometis nonnulla adjiciantur.
<478>LEMMA IV.
Cometas esse luna superiores & in regione planetarum versari.
Ut defectus parallaxeos diurnæ extulit cometas supra regiones sublunares, sic ex parallaxi annua convincitur eorum descensus in regiones planetarum. Nam cometæ, qui progrediuntur secundum ordinem signorum, sunt omnes sub exitu apparitionis aut solito tardiores aut retrogradi, si terra est inter ipsos & solem; at justo celeriores si terra vergit ad oppositionem. Et contra, qui pergunt contra ordinem signorum sunt justo celeriores in fine apparitionis, si terra versatur inter ipsos & solem; & justo tardiores vel retrogradi, si terra sita est ad contrarias partes. Contingit hoc maxime ex motu terræ in vario ipsius situ, perinde ut fit in planetis, qui pro motu terræ vel conspirante vel contrario nunc retrogradi sunt, nunc tardius progredi videntur, nunc vero celerius. Si terra pergit ad eandem partem cum cometa, & motu angulari circa solem tanto celerius fertur, ut recta per terram & cometam perpetuo ducta convergat ad partes ultra cometam, cometa e terra spectatus, ob motum suum tardiorem apparet esse retrogradus; sin terra tardius fertur, 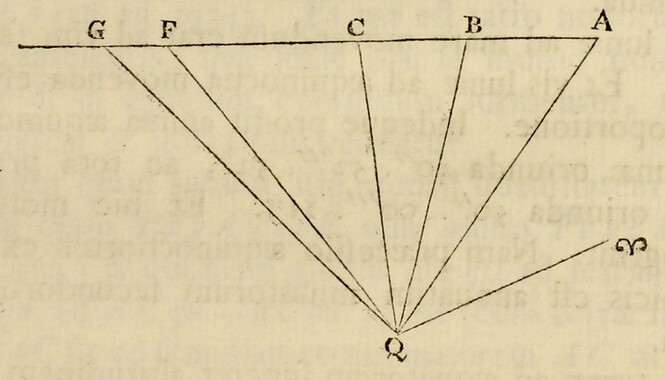 motus cometæ (detracto motu terræ) fit saltem tardior. At si terra pergit in contrarias partes, cometa exinde velocior apparet. Ex acceleratione autem vel retardatione vel motu retrogrado distantia cometæ in hunc modum colligitur. Sunto γQA, γQB, γQC observatæ tres longitudines cometæ sub initio motus, sitque γQF longitudo ultimo observata, ubi cometa videri desinit. Agatur recta ABC, cujus partes AB, BC rectis QA & QB, QB & QC interjectæ, sint ad invicem ut tempora inter observationes tres primas. Producatur AC ad G, ut sit AG ad AB ut tempus inter observationem primam & ultimam ad tempus inter observationem primam & secundam, & jungatur QG. Et si cometa moveretur uniformiter in linea recta, atque Terra vel quiesceret, vel etiam in linea recta uniformi cum motu progrederetur; foret angulus γQG longitudo cometæ tempore observationis ultimæ. Angulus igitur FQG, qui longitudinum differentia est, oritur ab inæqualitate motuum cometæ ac terræ. Hic autem angulus, si terra & cometa in contrarias partes moventur, additur angulo γQG, & sic motum apparentem cometæ velociorem reddit: sin cometa pergit in easdem partes cum terra, eidem subducitur, motumque cometæ vel tardiorem reddit, vel forte retrogradum; uti modo exposui. Oritur igitur hic angulus præcipue ex motu terræ, & idcirco pro parallaxi cometæ merito habendus est, neglecto videlicet ejus incremento vel decremento nonnullo, quod a cometæ motu inæquabili in orbe proprio oriri possit. Distantia
motus cometæ (detracto motu terræ) fit saltem tardior. At si terra pergit in contrarias partes, cometa exinde velocior apparet. Ex acceleratione autem vel retardatione vel motu retrogrado distantia cometæ in hunc modum colligitur. Sunto γQA, γQB, γQC observatæ tres longitudines cometæ sub initio motus, sitque γQF longitudo ultimo observata, ubi cometa videri desinit. Agatur recta ABC, cujus partes AB, BC rectis QA & QB, QB & QC interjectæ, sint ad invicem ut tempora inter observationes tres primas. Producatur AC ad G, ut sit AG ad AB ut tempus inter observationem primam & ultimam ad tempus inter observationem primam & secundam, & jungatur QG. Et si cometa moveretur uniformiter in linea recta, atque Terra vel quiesceret, vel etiam in linea recta uniformi cum motu progrederetur; foret angulus γQG longitudo cometæ tempore observationis ultimæ. Angulus igitur FQG, qui longitudinum differentia est, oritur ab inæqualitate motuum cometæ ac terræ. Hic autem angulus, si terra & cometa in contrarias partes moventur, additur angulo γQG, & sic motum apparentem cometæ velociorem reddit: sin cometa pergit in easdem partes cum terra, eidem subducitur, motumque cometæ vel tardiorem reddit, vel forte retrogradum; uti modo exposui. Oritur igitur hic angulus præcipue ex motu terræ, & idcirco pro parallaxi cometæ merito habendus est, neglecto videlicet ejus incremento vel decremento nonnullo, quod a cometæ motu inæquabili in orbe proprio oriri possit. Distantia 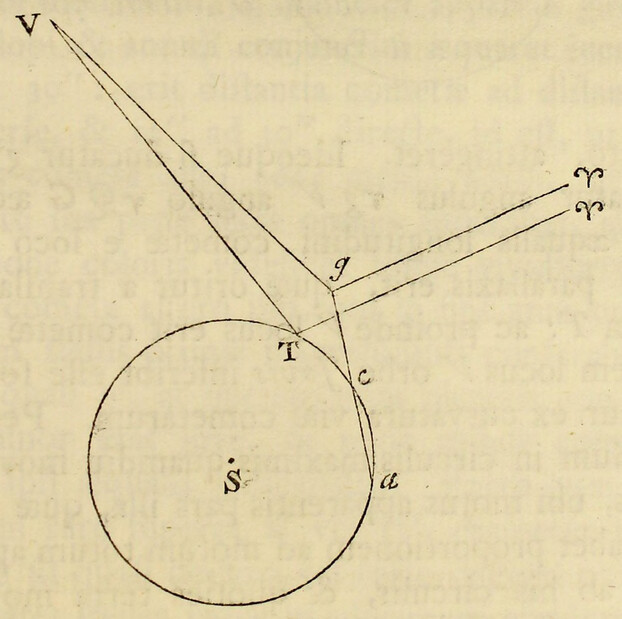 vero cometæ ex hac parallaxi sic colligitur. Designet S solem, acT orbem magnum, a locum terræ in observatione prima, c locum terræ in observatione tertia, T locum terræ in observatione ultima, & Tγ lineam rectam versus principium arietis ductam. Sumatur angulus γTV æqualis angulo γQF, hoc est, æqualis longitudini cometæ ubi terra versatur in T. Jungatur ac, & producatur ea ad g, ut sit ag ad ac ut AG ad AC, & erit g locus quem terra tempore observationis ultimæ, motu in recta ac uniformiter
vero cometæ ex hac parallaxi sic colligitur. Designet S solem, acT orbem magnum, a locum terræ in observatione prima, c locum terræ in observatione tertia, T locum terræ in observatione ultima, & Tγ lineam rectam versus principium arietis ductam. Sumatur angulus γTV æqualis angulo γQF, hoc est, æqualis longitudini cometæ ubi terra versatur in T. Jungatur ac, & producatur ea ad g, ut sit ag ad ac ut AG ad AC, & erit g locus quem terra tempore observationis ultimæ, motu in recta ac uniformiter 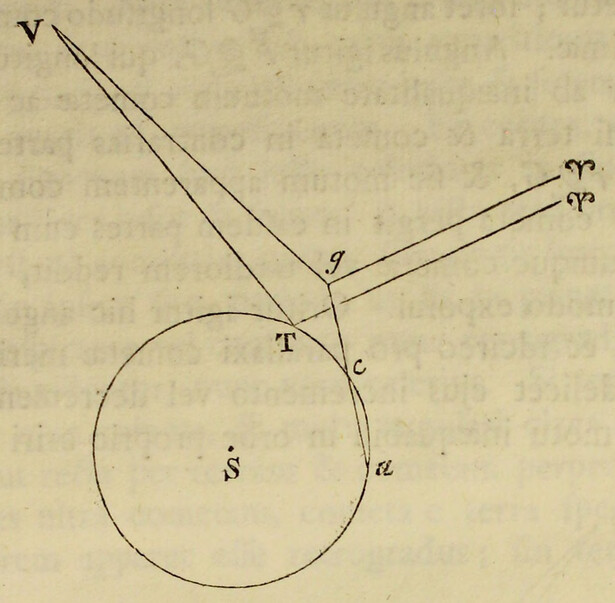 continuato, attingeret. Ideoque si ducatur gγ ipsi Tγ parallela, & capiatur angulus γgV angulo γQG æqualis, erit hic angulus γgV æqualis longitudini cometæ e loco g spectati; & angulus TVg parallaxis erit, quæ oritur a translatione terræ de loco g in locum T: ac proinde V locus erit cometæ in plano eclipticæ. Hic autem locus V orbe Jovis inferior esse solet.
continuato, attingeret. Ideoque si ducatur gγ ipsi Tγ parallela, & capiatur angulus γgV angulo γQG æqualis, erit hic angulus γgV æqualis longitudini cometæ e loco g spectati; & angulus TVg parallaxis erit, quæ oritur a translatione terræ de loco g in locum T: ac proinde V locus erit cometæ in plano eclipticæ. Hic autem locus V orbe Jovis inferior esse solet.
Idem colligitur ex curvatura viæ cometarum. Pergunt hæc corpora propemodum in circulis maximis quamdiu moventur celerius; at in fine cursus, ubi motus apparentis pars illa, quæ a parallaxi oritur, majorem habet proportionem ad motum totum apparentem, deflectere solent ab his circulis, & quoties terra movetur in unam partem, abire in partem contrariam. Oritur hæc deflexio maxime ex parallaxi, propterea quod respondet motui terræ; & insignis ejus quantitas, meo computo, collocavit disparentes cometas satis longe infra jovem. Unde consequens est quod in perigæis & periheliis, ubi propius adsunt, descendunt sæpius infra orbes martis & inferiorum planetarum.
Confirmatur etiam propinquitas Cometarum ex luce capitum. Nam corporis cœlestis a sole illustrati & in regiones longinquas abeuntis, diminuitur splendor in quadruplicata ratione distantiæ: in duplicata ratione videlicet ob auctam corporis distantiam a sole, & in alia duplicata ratione ob diminutam diametrum apparentem. Unde si detur & lucis quantitas & apparens diameter cometæ, dabitur distantia, dicendo quod distantia sit ad distantiam planetæ, in ratione diametri ad diametrum directe & ratione subduplicata lucis ad lucem inverse. Sic minima capillitii cometæ anni 1682 diameter, per tubum opticum sexdecim pedum a Flamstedio observata & micrometro mensurata, æquabat 2′. 0″; nucleus autem seu stella in medio capitis vix decimam partem latitudinis hujus occupabat, ideoque lata erat tantum 11″ vel 12″. Luce vero & claritate capitis superabat caput cometæ anni 1680, stellasque primæ vel secundæ magnitudinis æmulabatur. Ponamus saturnum cum annulo suo quasi quadruplo lucidiorem fuisse: & quoniam lux annuli propemodum æquabat lucem globi intermedii, & diameter apparens globi sit quasi 21″, ideoque lux globi & annuli conjunctim æquaret lucem globi, cujus diameter esset 30″: erit distantia cometæ ad distantiam saturni ut 1 ad inverse, & 12″ ad 30″ directe, id est, ut 24 ad 30 seu 4 ad 5. Rursus cometa anni 1665 mense aprili, ut auctor est Hevelius, claritate sua pene fixas omnes superabat, quinetiam ipsum saturnum, ratione coloris videlicet longe vividioris. Quippe lucidior erat hic cometa altero illo, qui in fine anni præcedentis apparuerat, & cum stellis primæ magnitudinis conferebatur. Latitudo capillitii erat quasi 6′, at nucleus cum planetis ope tubi optici collatus plane minor erat jove, & nunc minor corpore intermedio saturni, nunc ipsi æqualis judicabatur. Porro cum diameter capillitii cometarum raro superet 8′ vel 12′, diameter vero nuclei, seu stellæ centralis sit quasi decima vel forte decima quinta pars diametri capillitii, patet stellas hasce ut plurimum ejusdem esse apparentis magnitudinis cum planetis. Unde cum lux eorum cum luce saturni non raro conferri possit, eamque aliquando superet; manifestum est, quod cometæ omnes in periheliis vel infra saturnum collocandi sint, vel non longe supra. Errant igitur toto cœlo, qui cometas in regionem fixarum prope ablegant: qua certe ratione non magis illustrari deberent a sole nostro, quam planetæ, qui hic sunt, illustrantur a stellis fixis.
Hæc disputavimus non considerando obscurationem cometarum per fumum illum maxime copiosum & crassum, quo caput circundatur, quasi per nubem obtuse semper lucens. Nam quanto obscurius redditur corpus per hunc fumum, tanto propius ad solem accedat necesse est, ut copia lucis a se reflexæ planetas æmuletur. Inde verisimile fit cometas longe infra sphæram saturni descendere, uti ex parallaxi probavimus. Idem vero quam maxime confirmatur ex caudis. Hæ vel ex reflexione fumi sparsi per æthera, vel ex luce capitis oriuntur. Priore casu minuenda est distantia cometarum, ne fumus a capite semper ortus per spatia nimis ampla incredibili cum velocitate & expansione propagetur. In posteriore referenda est lux omnis tam caudæ quam capillitii ad nucleum capitis. Igitur si concipiamus lucem hanc omnem congregari & intra discum nuclei coarctari, nucleus ille jam certe, quoties caudam maximam & fulgentissimam emittit, Jovem ipsum splendore suo multum superabit. Minore igitur cum diametro apparente plus lucis emittens, multo magis illustrabitur a sole, ideoque erit soli multo proprior. Quinetiam capita sub sole delitescentia, & caudas cum maximas tum fulgentissimas instar trabium ignitarum nonnunquam emittentia, eodem argumento infra orbem veneris collocari debent. Nam lux illa omnis si in stellam congregari supponatur, ipsam venerem ne dicam veneres plures conjunctas quandoque superaret.
Idem denique colligitur ex luce capitum crescente in recessu cometarum a terra solem versus, ac decrescente in eorum recessu a sole versus terram. Sic enim cometa posterior anni 1665 (observante Hevelio) ex quo conspici cœpit, remittebat semper de motu suo apparente, ideoque præterierat perigæum; splendor vero capitis nihilominus indies crescebat, usque dum cometa radiis solaribus obtectus desiit apparere. Cometa anni 1683 (observante eodem Hevelio) in fine mensis julii, ubi primum conspectus est, tardissime movebatur, minuta prima 40 vel 45 circiter singulis diebus in orbe suo conficiens. Ex eo tempore motus ejus diurnus perpetuo augebatur usque ad Sept. 4. quando evasit graduum quasi quinque. Igitur toto hoc tempore cometa ad terram appropinquabat. Id quod etiam ex diametro capitis micrometro mensurata colligitur: quippe quam Hevelius reperit Aug. 6. esse tantum 6′. 5″ inclusa coma, at Sept. 2. esse 9′. 7″. Caput igitur initio longe minus apparuit quam in fine motus, at initio tamen in vicinia solis longe lucidius extitit quam circa finem, ut refert idem Hevelius. Proinde toto hoc tempore, ob recessum ipsius a sole, quoad lumen decrevit, non obstante accessu ad terram. Cometa anni 1618 circa medium mensis Decembris, & iste anni 1680 circa finem ejusdem mensis, celerrime movebantur, ideoque tunc erant in perigæis. Verum splendor maximus capitum contigit ante duas fere septimanas, ubi modo exierant de radiis solaribus; & splendor maximus caudarum paulo ante, in majore vicinitate solis. Caput cometæ prioris, juxta observationes Cysati, Decem. 1. majus videbatur stellis primæ magnitudinis, & Decem. 16. (jam in perigæo existens) magnitudine parum, splendore seu claritate luminis plurimum defecerat. Jan. 7. Keplerus de capite incertus finem fecit observandi. Die 12 mensis Decemb. conspectum & a Flamstedio observatum est caput cometæ posterioris in distantia novem graduum a sole; id quod stellæ tertiæ magnitudinis vix concessum fuisset. Decemb. 15 & 17 apparuit idem ut stella tertiæ magnitudinis, diminutum utique splendore nubium juxta solem occidentem. Decemb. 26. velocissime motus, inque perigæo propemodum existens, cedebat ori pegasi, stellæ tertiæ magnitudinis. Jan. 3. apparebat ut stella quartæ, Jan. 9. ut stella quintæ, Jan. 13. ob splendorem lunæ crescentis disparuit. Jan. 25. vix æquabat stellas magnitudinis septimæ. Si sumantur æqualia a perigæo hinc inde tempora, capita quæ temporibus illis in longinquis regionibus posita, ob æquales a terra distantias, æqualiter lucere debuissent, in plaga solis, maxime splenduere, ex altera perigæi parte evanuere. Igitur ex magna lucis in utroque situ differentia, concluditur magna solis & cometæ vicinitas in situ priore. Nam lux cometarum regularis esse solet, & maxima apparere ubi capita velocissime moventur, atque ideo sunt in perigæis; nisi quatenus ea major est in vicinia Solis.
<484>Corol. 1. Splendent igitur cometæ luce solis a se reflexa.
Corol. 2. Ex dictis etiam intelligitur cur cometæ tantopere frequentant regionem solis. Si cernerentur in regionibus longe ultra saturnum, deberent sæpius apparere in partibus soli oppositis. Forent enim terræ viciniores, qui in his partibus versarentur; & sol interpositus obscuraret cæteros. Verum percurrendo historias cometarum, reperi quod quadruplo vel quintuplo plures detecti sunt in hemisphærio solem versus, quam in hemisphærio opposito, præter alios proculdubio dubio non paucos, quos lux solaris obtexit. Nimirum in descensu ad regiones nostras neque caudas emittunt, neque adeo illustrantur a sole, ut nudis oculis se prius detegendos exhibeant, quam sint ipso jove propiores. Spatii autem tantillo intervallo circa solem descripti pars longe major sita est a latere terræ, quod solem respicit; inque parte illa majore cometæ, soli ut plurimum viciniores, magis illuminari solent.
Corol. 3. Hinc etiam manifestum est, quod cœli resistentia destituuntur. Nam cometæ vias obliquas & nonnunquam cursui planetarum contrarias secuti, moventur omnifariam liberrime, & motus suos, etiam contra cursum planetarum diutissime conservant. Fallor ni genus planetarum sint, & motu perpetuo in orbem redeant. Nam quod scriptores aliqui meteora esse volunt, argumentum a capitum perpetuis mutationibus ducentes, fundamento carere videtur. Capita cometarum atmosphæris ingentibus cinguntur; & atmosphæræ inferne densiores esse debent. Unde nubes sunt, non ipsa cometarum corpora, in quibus mutationes illæ visuntur. Sic terra si e planetis spectaretur, luce nubium suarum proculdubio splenderet, & corpus firmum sub nubibus prope delitesceret. Sic cingula jovis in nubibus planetæ illius formata sunt, quæ situm mutant inter se, & firmum jovis corpus per nubes illas difficilius cernitur. Et multo magis corpora cometarum sub atmosphæris & profundioribus & crassioribus abscondi debent.
<485>PROPOSITIO XL. THEOREMA XX.
Cometas in sectionibus conicis umbilicos in centro solis habentibus moveri, & radiis ad solem ductis areas temporibus proportionales describere.
Patet per corol. 1. prop. xiii. libri primi, collatum cum prop. viii, xii, & xiii. libri tertii.
Corol. 1. Hinc si cometæ in orbem redeunt; orbes erunt ellipses, & tempora periodica erunt ad tempora periodica planetarum in axium principalium ratione sesquiplicata. Ideoque cometæ maxima ex parte supra planetas versantes, & eo nomine orbes axibus majoribus describentes, tardius revolventur. Ut si axis orbis cometæ sit quadruplo major axe orbis saturni, tempus revolutionis cometæ erit ad tempus revolutionis saturni, id est, ad annos 30, ut (seu 8) ad 1, ideoque erit annorum 240.
Corol. 2. Orbes autem erunt parabolis adeo finitimi, ut eorum vice parabolæ sine erroribus sensibilibus adhiberi possint.
Corol. 3. Et propterea (per corol. 7. prop. xvi. lib. i.) velocitas cometæ omnis, erit semper ad velocitatem planetæ cujusvis circa solem in circulo revolventis, in subduplicata ratione duplæ distantiæ planetæ a centro solis, ad distantiam cometæ a centro solis quamproxime. Ponamus radium orbis magni, seu ellipseos in qua terra revolvitur semidiametrum maximam esse partium 100000000: & terra motu suo diurno mediocri describet partes 1720212, & motu horario partes . Ideoque cometa in eadem telluris a sole distantia mediocri, ea cum velocitate quæ sit ad velocitatem telluris ut ad 1, describet motu suo diurno partes 2432747, & motu horario partes . In majoribus autem vel minoribus distantiis, motus tum diurnus tum horarius erit ad hunc motum diurnum & horarium in subduplicata ratione distantiarum reciproce, ideoque datur.
Corol. 4. Unde si latus rectum parabolæ quadruplo majus sit radio orbis magni, & quadratum radii illius ponatur esse partium 100000000: area quam cometa radio ad solem ducto singulis diebus describit, erit partium , & singulis horis area illa erit partium . Sin latus rectum majus sit vel minus in ratione quavis, erit area diurna & horaria major vel minor in eadem ratione subduplicata.
LEMMA V.
Invenire lineam curvam generis parabolici, quæ per data quotcunque puncta transibit.
Sunto puncta illa A, B, C, D, E, F, &c. & ab iisdem ad rectam quamvis positione datam HN demitte perpendicula quotcunque AH, BI, CK, DL, EM, FN.
Cas. 1. Si punctorum H, I, K, L, M, N æqualia sunt intervalla HI, IK, KL, &c. collige perpendiculorum AH, BI, CK, &c. differentias primas b, , , , , &c. secundas c, , , , &c. tertias d, , , &c. id est, ita ut sit , , , , , &c. dein 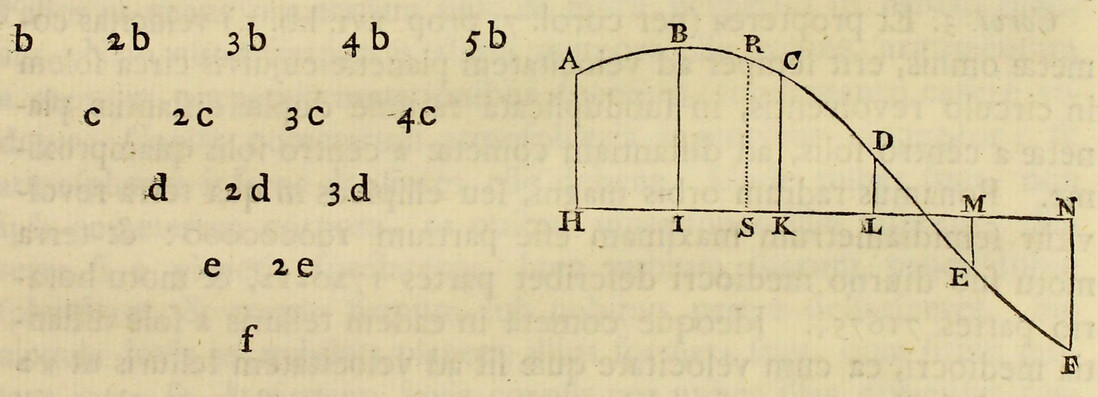 &c. & sic pergatur ad differentiam ultimam, quæ hic est f. Deinde erecta quacunque perpendiculari RS, quæ fuerit ordinatim applicata ad curvam quæsitam: ut inveniatur hujus longitudo, pone intervalla HI, IK, KL, LM, &c. unitates esse, & dic , , in , in , in , in ; pergendo videlicet ad usque penultimum perpendiculum ME, & præponendo signa negativa terminis HS, IS, &c. qui jacent ad partes puncti S versus A, & signa affirmativa terminis SK, SL, &c. qui jacent ad alteras partes puncti S. Et signis probe observatis, erit , &c.
&c. & sic pergatur ad differentiam ultimam, quæ hic est f. Deinde erecta quacunque perpendiculari RS, quæ fuerit ordinatim applicata ad curvam quæsitam: ut inveniatur hujus longitudo, pone intervalla HI, IK, KL, LM, &c. unitates esse, & dic , , in , in , in , in ; pergendo videlicet ad usque penultimum perpendiculum ME, & præponendo signa negativa terminis HS, IS, &c. qui jacent ad partes puncti S versus A, & signa affirmativa terminis SK, SL, &c. qui jacent ad alteras partes puncti S. Et signis probe observatis, erit , &c.
Cas. 2. Quod si punctorum H, I, K, L, &c. inæqualia sint intervalla HI, IK, &c. collige perpendiculorum AH, BI, CK, &c. differentias primas per intervalla perpendiculorum divisas b, , , , ; secundas per intervalla bina divisa {sic} c, , , , &c. tertias per intervalla terna divisas d, , , &c. quartas per intervalla quaterna divisas e, , &c. & sic deinceps; id est, ita ut sit , , &c. dein , , , &c. postea , , &c. Inventis differentiis, dic , , p in , q in , r in , s in ; pergendo scilicet ad usque perpendiculum penultimum ME, & erit ordinatim applicata , &c.
Corol. Hinc areæ curvarum omnium inveniri possunt quamproxime. Nam si curvæ cujusvis quadrandæ inveniantur puncta aliquot, & parabola per eadem duci intelligatur: erit area parabolæ hujus eadem quamproxime cum area curvæ illius quadrandæ. Potest autem parabola per methodos notissimas semper quadrari Geometrice.
LEMMA VI.
Ex observatis aliquot locis cometæ invenire locum ejus ad tempus quodvis intermedium datum.
Designent HI, IK, KL, LM tempora inter observationes (in fig. præced.) HA, IB, KC, LD, ME observatas quinque longitudines cometæ, HS tempus datum inter observationem primam & longitudinem quæsitam. Et si per puncta A, B, C, D, E duci intelligatur curva regularis ABCDE; & per lemma superius inveniatur ejus ordinatim applicata RS, erit RS longitudo quæsita.
Eadem methodo ex observatis quinque latitudinibus invenitur latitudo ad tempus datum.
<488>Si longitudinum observatarum parvæ sint differentiæ, puta graduum tantum 4 vel 5; suffecerint observationes tres vel quatuor ad inveniendam longitudinem & latitudinem novam. Sin majores sint differentiæ, puta graduum 10 vel 20, debebunt observationes quinque adhiberi.
LEMMA VII.
Per datum punctum P ducere rectam lineam BC, cujus partes PB, PC, rectis duabus positione datis AB, AC abscissæ, datam habeant rationem ad invicem.
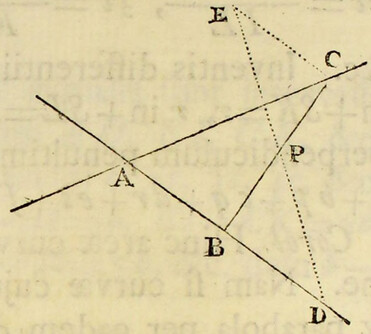
A puncto illo P ad rectarum alterutram AB ducatur recta quævis PD, & producatur eadem versus rectam alteram AC usque ad E, ut sit PE ad PD in data illa ratione. Ipsi AD parallela sit EC; & si agatur CPB, erit PC ad PB ut PE ad PD. Q.E.F.
LEMMA VIII.
Sit ABC parabola umbilicum habens S. Chorda AC bisecta 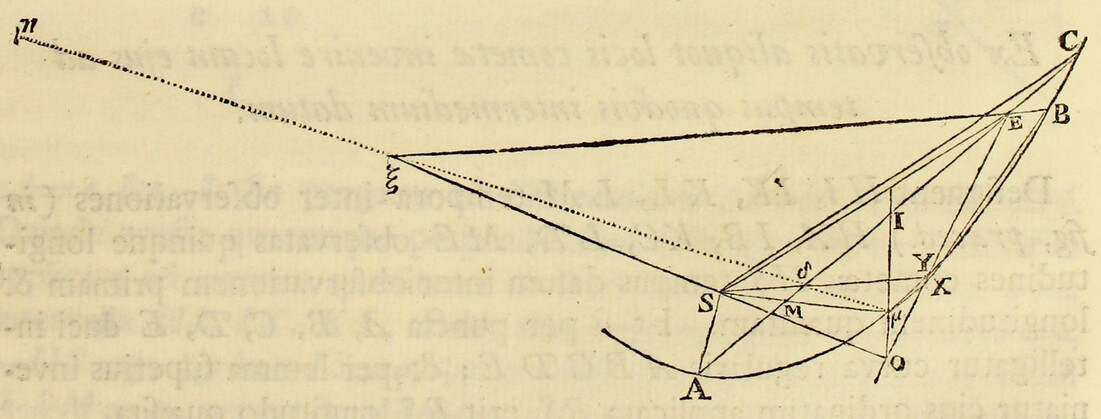 in I abscindatur segmentum ABCI, cujus diameter sit Iμ & vertex μ. In Iμ producta capiatur μO æqualis dimidio ipsius Iμ. Jungatur OS, & producatur ea ad ξ, ut sit Sξ æqualis . Et si cometa B moveatur in arcu CBA, & agatur ξB secans AC in E: dico quod punctum E abscindet de chorda AC segmentum AE tempori proportionale quamproxime.
in I abscindatur segmentum ABCI, cujus diameter sit Iμ & vertex μ. In Iμ producta capiatur μO æqualis dimidio ipsius Iμ. Jungatur OS, & producatur ea ad ξ, ut sit Sξ æqualis . Et si cometa B moveatur in arcu CBA, & agatur ξB secans AC in E: dico quod punctum E abscindet de chorda AC segmentum AE tempori proportionale quamproxime.
Jungatur enim EO secans arcum parabolicum ABC in Y, & agatur μX quæ tangat eundem arcum in vertice μ, & actæ EO occurrat in X; & erit area curvilinea AEXμA ad aream curvilineam ACYμA ut AE ad AC. Ideoque cum triangulum ASE sit ad triangulum ASC in eadem ratione, erit area tota ASEXμA ad aream totam ASCYμA ut AE ad AC. Cum autem ξO sit ad SO ut 3 ad 1, & EO ad XO in eadem ratione, erit SX ipsi EB parallela: & propterea si jungatur BX, erit triangulum SEB triangulo XEB æquale. Unde si ad aream ASEXμA addatur triangulum EXB, & de summa auferatur triangulum SEB, manebit area ASBXμA areæ ASEXμA æqualis, atque ideo ad aream ASCYμA ut AE ad AC. Sed areæ ASBXμA æqualis est area ASBYμA quamproxime, & hæc area ASBYμA est ad aream ASCYμA, ut tempus descripti arcus AB ad tempus descripti arcus totius AC. Ideoque AE est ad AC in ratione temporum quamproxime. Q.E.D.
Corol. Ubi punctum B incidit in parabolæ verticem μ, est AE ad AC in ratione temporum accurate.
Scholium.
Si jungatur μξ secans AC in δ, & in ea capiatur ξn quæ sit ad μB ut ad : acta Bn secabit chordam AC in ratione temporum magis accurate quam prius. Jaceat autem punctum n ultra punctum ξ, si punctum B magis distat a vertice principali parabolæ quam punctum μ; & citra, si minus distat ab eodem vertice.
<490>LEMMA IX.
Rectæ Iμ & μM & longitudo æquantur inter se.
Nam est latus rectum parabolæ pertinens ad verticem μ.
LEMMA X.
Si producatur ad N & P, ut μN sit pars tertia ipsius μI, & SP sit ad SN ut SN ad Sμ. Cometa, quo tempore describit arcum AμC, si progrederetur ea semper cum velocitate quam habet in altitudine ipsi SP æquali, describeret longitudinem æqualem chordæ AC.
Nam si cometa velocitate, quam habet in μ, eodem tempore progrederetur uniformiter in recta, quæ parabolam tangit in μ; area, quam radio ad punctum S ducto describeret, æqualis esset areæ parabolicæ ASCμ. Ideoque contentum sub longitudine in tangente descripta & longitudine Sμ esset ad contentum sub longitudinibus AC & SM, ut area ASCμ ad triangulum ASC, id est, ut SN 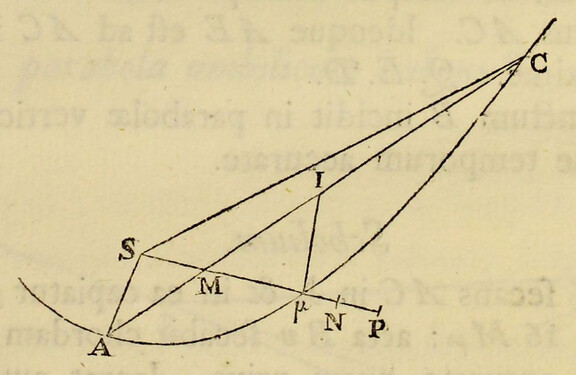 ad SM. Quare AC est ad longitudinem in tangente descriptam, ut Sμ ad SN. Cum autem velocitas cometæ in altitudine SP sit (per corol. 6 prop. xvi. lib. i.) ad ejus velocitatem in altitudine Sμ, in subduplicata ratione SP ad Sμ inverse, id est, in ratione Sμ ad SN; longitudo hac velocitate eodem tempore descripta, erit ad longitudinem in tangente descriptam, ut Sμ ad SN. Igitur AC & longitudo hac nova velocitate descripta, cum sint ad longitudinem in tangente descriptam in eadem ratione, æquantur inter se. Q.E.D.
ad SM. Quare AC est ad longitudinem in tangente descriptam, ut Sμ ad SN. Cum autem velocitas cometæ in altitudine SP sit (per corol. 6 prop. xvi. lib. i.) ad ejus velocitatem in altitudine Sμ, in subduplicata ratione SP ad Sμ inverse, id est, in ratione Sμ ad SN; longitudo hac velocitate eodem tempore descripta, erit ad longitudinem in tangente descriptam, ut Sμ ad SN. Igitur AC & longitudo hac nova velocitate descripta, cum sint ad longitudinem in tangente descriptam in eadem ratione, æquantur inter se. Q.E.D.
Corol. Cometa igitur ea cum velocitate, quam habet in altitudine , eodem tempore describeret chordam AC quamproxime.
LEMMA XI.
Si cometa motu omni privatus de altitudine SN seu demitteretur, ut caderet in solem, & ea semper vi uniformiter continuata urgeretur in solem, qua urgetur sub initio; idem semisse temporis, quo in orbe suo describat arcum AC, descensu suo describeret spatium longitudini Iμ æquale.
Nam cometa, quo tempore describat arcum parabolicum AC, eodem tempore ea cum velocitate, quam habet in altitudine SP (per lemma novissimum) describet chordam AC, ideoque (per corol. 7. prop. xvi. lib. i.) eodem tempore in circulo, cujus semidiameter esset SP, vi gravitatis suæ revolvendo, describeret arcum, cujus longitudo esset ad arcus parabolici chordam AC, in subduplicata ratione unitatis ad binarium. Et propterea eo cum pondere, quod habet in solem in altitudine SP, cadendo de altitudine illa in solem, describeret semisse temporis illius (per corol. 9. prop. iv. lib. i.) spatium æquale quadrato semissis chordæ illius applicato ad quadruplum altitudinis SP, id est, spatium . Unde cum pondus cometæ in solem in altitudine SN sit ad ipsius pondus in solem in altitudine SP, ut SP ad Sμ: cometa pondere quod habet in altitudine SN eodem tempore, in solem cadendo, describet spatium , id est, spatium longitudini Iμ vel Mμ æquale. Q.E.D.
<492>PROPOSITIO XLI. PROBLEMA XXI.
Cometæ in parabola moti trajectoriam ex datis tribus observationibus determinare.
Problema hocce longe difficillimum multimode aggressus, composui problemata quædam in libro primo, quæ ad ejus solutionem spectant. Postea solutionem sequentem paulo simpliciorem excogitavi.
Seligantur tres observationes æqualibus temporum intervallis ab invicem quamproxime distantes. Sit autem temporis intervallum illud, ubi cometa tardius movetur, paulo majus altero, ita videlicet ut temporum differentia sit ad summam temporum, ut summa temporum ad dies plus minus sexcentos; vel ut punctum E (in fig. lem. viii.) 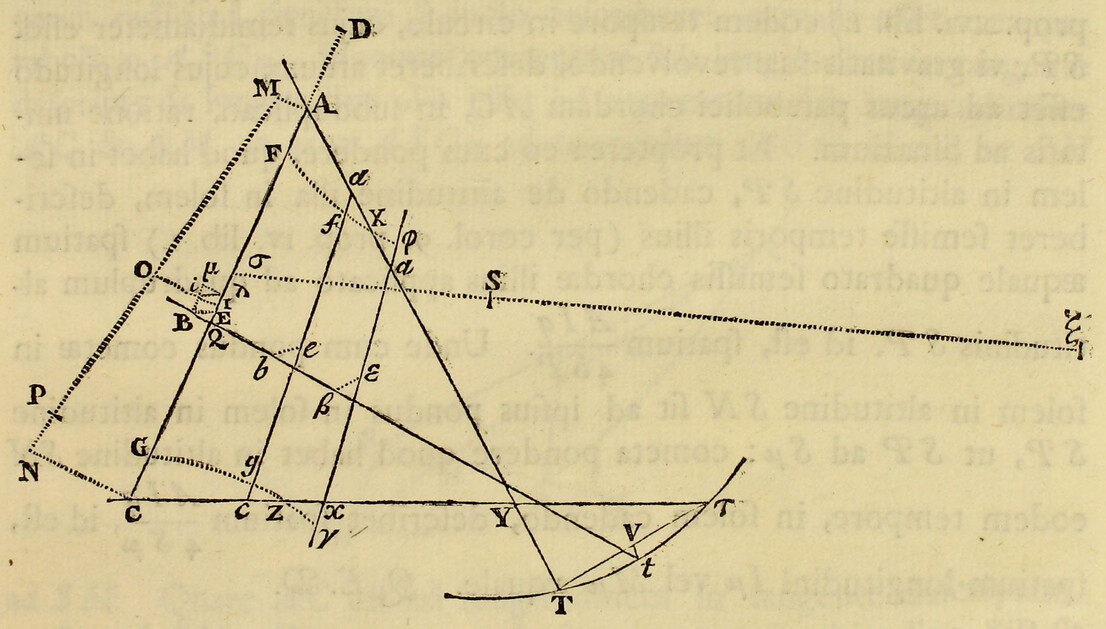 incidat in punctum M quamproxime, & inde aberret versus I potius quam versus A. Si tales observationes non præsto sint, inveniendus est novus cometæ locus per lemma sextum.
incidat in punctum M quamproxime, & inde aberret versus I potius quam versus A. Si tales observationes non præsto sint, inveniendus est novus cometæ locus per lemma sextum.
Designent S solem, T, t, τ tria loca terræ in orbe magno, TA, tB, τC observatas tres longitudines cometæ, V tempus inter observationem primam & secundam, W tempus inter secundam ac tertiam, X longitudinem quam cometa toto illo tempore ea cum velocitate, quam habet in mediocri telluris a sole distantia, describere posset, quæque (per corol. 3. prop. xl. lib. iii.) invenienda est, & tV perpendiculum in chordam Tτ. In observata longitudine media tB sumatur utcunque punctum B pro loco cometæ in plano eclipticæ, & inde versus solem S ducatur linea BE, quæ sit ad sagittam tV, ut contentum sub SB & St quad. ad cubum hypotenusæ trianguli rectanguli, cujus latera sunt SB & tangens latitudinis cometæ in observatione secunda ad radium tB. Et per punctum E agatur (per hujus lem. vii.) recta AEC, cujus partes AE, EC, ad rectas TA & τC terminatæ, sint ad invicem ut tempora V & W: & erunt A & C loca cometæ in plano eclipticæ in observatione prima ac tertia quamproxime, si modo B sit locus ejus recte assumptus in observatione secunda.
Ad AC bisectam in I erige perpendiculum Ii. Per punctum B age occultam Bi ipsi AC parallelam. Junge occultam Si secantem AC in λ, & comple parallelogrammum iIλμ. Cape Iσ æqualem , & per solem S age occultam σξ æqualem . Et deletis jam literis A, E, C, I, a puncto B versus punctum ξ duc occultam novam BE, quæ sit ad priorem BE in duplicata ratione distantiæ BS ad quantitatem . Et per punctum E iterum duc rectam AEC eadem lege ac prius, id est, ita ut ejus partes AE & EC sint ad invicem, ut tempora inter observationes V & W. Et erunt A & C loca cometæ magis accurate.
Ad AC bisectam in I erigantur perpendicula AM, CN, IO, quorum AM & CN sint tangentes latitudinum in observatione prima ac tertia ad radios TA & τC. Jungatur MN secans IO in O. Constituatur rectangulum iIλμ ut prius. In IA producta capiatur ID æqualis . Deinde in MN versus N capiatur MP, quæ sit ad longitudinem supra inventam X in subduplicata ratione mediocris distantiæ telluris a sole (seu semidiametri orbis magni) ad distantiam OD. Si punctum P incidat in punctum N; erunt A, B, C tria loca cometæ, per quæ orbis ejus in plano eclipticæ describi debet. Sin punctum P non incidat in punctum N; in recta AC capiatur CG ipsi NP æqualis, ita ut puncta G & P ad easdem partes rectæ NC jaceant.
Eadem methodo, qua puncta E, A, C, G, ex assumpto puncto B inventa sunt, inveniantur ex assumptis utcunque punctis aliis b & β puncta nova e, a, c, g, & ε, α κ, γ. Deinde si per G, g, γ ducatur circumferentia circuli Ggγ secans rectam τC in Z: erit Z locus cometæ in plano eclipticæ. Et si in AC, ac, ακ capiantur AF, af, αφ ipsis CG, cg, κγ respective æquales, & per puncta F, f, 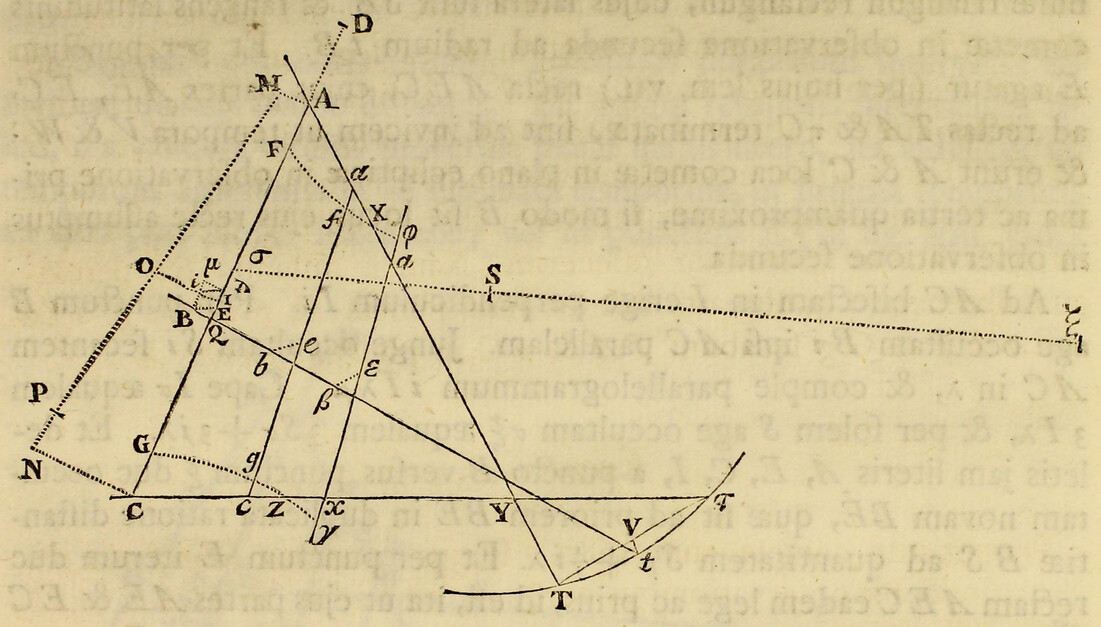 φ ducatur circumferentia circuli Ffφ secans rectam AT in X; erit punctum X alius cometæ locus in plano eclipticæ. Ad puncta X & Z erigantur tangentes latitudinum cometæ ad radios TX & τZ; & habebuntur loca duo cometæ in orbe proprio. Denique (per prop. xix. Lib. i.) umbilico S, per loca illa duo describatur parabola, & hæc erit trajectoria cometæ. Q.E.I.
φ ducatur circumferentia circuli Ffφ secans rectam AT in X; erit punctum X alius cometæ locus in plano eclipticæ. Ad puncta X & Z erigantur tangentes latitudinum cometæ ad radios TX & τZ; & habebuntur loca duo cometæ in orbe proprio. Denique (per prop. xix. Lib. i.) umbilico S, per loca illa duo describatur parabola, & hæc erit trajectoria cometæ. Q.E.I.
Constructionis hujus demonstratio ex lemmatibus consequitur: quippe cum recta AC secetur in E in ratione temporum, per lemma vii, ut oportet per lem. viii: & BE per lem. xi. sit pars rectæ BS vel Bξ in plano eclipticæ arcui ABC & chordæ AEC interjecta; & MP (per corol. lem. x.) longitudo sit chordæ arcus, quem cometa in orbe proprio inter observationem primam ac tertiam describere debet, ideoque ipsi MN æqualis fuerit, si modo B sit verus cometæ locus in plano eclipticæ.
Cæterum puncta B, b, β non quælibet, sed vero proxima eligere convenit. Si angulus AQt in quo vestigium orbis in plano eclipticæ descriptum secat rectam tB, præterpropter innotescat; in angulo illo ducenda erit recta occulta AC, quæ sit ad in subduplicata ratione SQ ad St. Et agendo rectam SEB, cujus pars EB æquetur longitudini Vt, determinabitur punctum B quod prima vice usurpare licet. Tum recta AC deleta & secundum præcedentem constructionem iterum ducta, & inventa insuper longitudine MP; in tB capiatur punctum b, ea lege, ut si TA, τC se mutuo secuerint in Y, sit distantia Yb ad distantiam YB in ratione composita ex ratione MP ad MN & ratione subduplicata SB ad Sb. Et eadem methodo inveniendum erit punctum tertium β; si modo operationem tertio repetere lubet. Sed hac methodo operationes duæ ut plurimum suffecerint. Nam si distantia Bb perexigua obvenerit, postquam inventa sunt puncta F, f & G, g, actæ rectæ Ff & Gg secabunt TA & τC in punctis quæsitis X & Z.
Exemplum.
Proponatur cometa anni 1680. Hujus motum a Flamstedio observatum & ex observationibus computatum, atque ab Halleio ex iisdem observationibus correctum, tabula sequens exhibet.
<496>| Cometæ | ||||||||||||||||||
| Tem. appar | Temp. verum | Long. Solis. | Longitudo. | Lat. bor. | ||||||||||||||
| h. | ′ | h. | ′ | ″ | ° | ′ | ″ | ° | ′ | ″ | ° | ′ | ″ | |||||
| 1680. | Dec. | 12 | 4. | 46 | 4. | 46. | 0 | ♑ | 1. | 51. | 23 | ♑ | 6. | 32. | 30 | 8. | 28. | 0 |
| 21 | 6. | 32 | 6. | 36. | 59 | 11. | 6. | 44 | ♒ | 5. | 8. | 12 | 21. | 42. | 13 | |||
| 24 | 6. | 12 | 6. | 17. | 52 | 14. | 9. | 26 | 18. | 49. | 23 | 25. | 23. | 5 | ||||
| 26 | 5. | 14 | 5. | 20. | 44 | 16. | 9. | 22 | 28. | 24. | 13 | 27. | 0. | 52 | ||||
| 29 | 7. | 55 | 8. | 3. | 2 | 19. | 9. | 43 | ♓ | 13. | 10. | 41 | 28. | 9. | 58 | |||
| 30 | 8. | 2 | 8. | 10. | 26 | 20. | 21. | 9 | 17. | 38. | 20 | 28. | 11. | 53 | ||||
| 1681 | Jan. | 5 | 5. | 51 | 6. | 1. | 38 | 26. | 22. | 18 | ♈ | 8. | 48. | 53 | 26. | 15. | 7 | |
| 9 | 6. | 49 | 7. | 0. | 53 | ♒ | 0. | 29. | 2 | 18. | 44. | 4 | 24. | 11. | 56 | |||
| 10 | 5. | 54 | 6. | 6. | 10 | 1. | 27. | 43 | 20. | 40. | 50 | 23. | 43. | 52 | ||||
| 13 | 6. | 56 | 7. | 8. | 55 | 4. | 33. | 20 | 25. | 59. | 48 | 22. | 17. | 28 | ||||
| 25 | 7. | 44 | 7. | 58. | 42 | 16. | 45. | 36 | ♉ | 9. | 35. | 0 | 17. | 56. | 30 | |||
| 30 | 8. | 7 | 8. | 21. | 53 | 21. | 49. | 58 | ♉ | 13. | 19. | 51 | 16. | 42. | 18 | |||
| Feb. | 2 | 6. | 20 | 6. | 34. | 51 | 24. | 46. | 59 | 15. | 13. | 53 | 16. | 4. | 1 | |||
| 5 | 6. | 50 | 7. | 4. | 41 | 27. | 49. | 51 | 16. | 59. | 6 | 15. | 27. | 3 | ||||
His adde observationes quasdam e nostris.
| Temp. appar. | Cometæ Longitudo. | Cometæ Lat. bor. | ||||
| 1681. | Febr. | 25 | ♉ | |||
| 27 | ||||||
| Mar. | 1 | |||||
| 2 | ||||||
| 5 | ||||||
| 7 | ♊ | |||||
| 9 | ||||||
Hæ observationes telescopio septupedali, & micrometro filisque in foco telescopii locatis peractæ sunt: quibus instrumentis & positiones fixarum inter se & positiones cometæ ad fixas determinavimus. Designet A stellam quartæ magnitudinis in sinistro calcaneo Persei (Bayero ο) B stellam sequentem tertiæ magnitudinis in sinistro pede (Bayero ζ) & C stellam sextæ magnitudinis (Bayero n) in talo ejusdem pedis, ac D, E, F, G, H, I, K, L, M, N, O, Z, α, β, γ, δ stellas alias minores in eodem pede. Sintque p, P, Q, R, S, T, V, X, loca cometæ in observationibus supra descriptis: & existente distantia AB partium , erat AC partium , BC , AD , BD , CD , AE , CE , DE , AI , BI , CI , DI , AK , BK 43, CK , FK 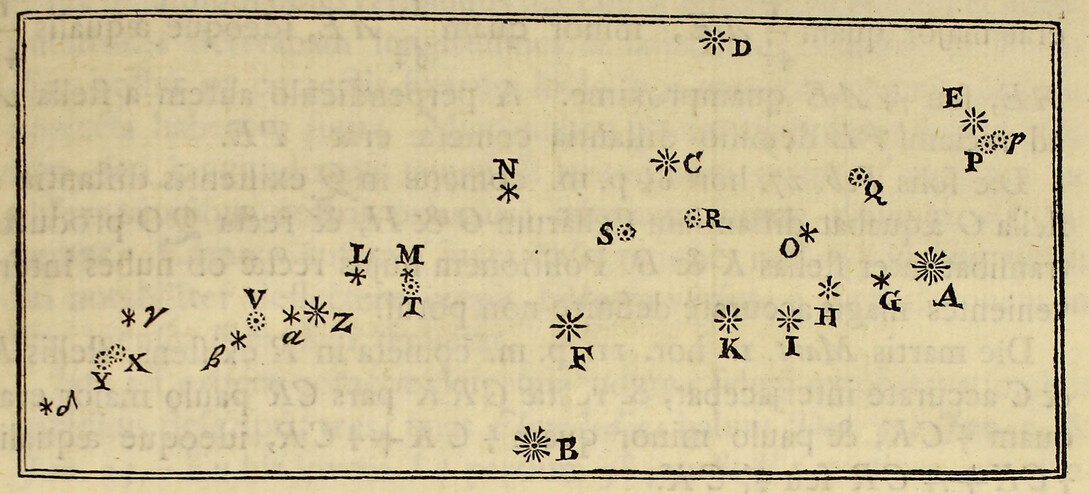 29, FB 23, FC , AH , DH , BN , CN , BL , NL . HO erat ad HI ut 7 ad 6 & producta transibat inter stellas D & E, sic ut distantia stellæ D ab hac recta esset . LM erat ad LN ut 2 ad 9 & producta transibat per stellam H. His determinabantur positiones fixarum inter se.
29, FB 23, FC , AH , DH , BN , CN , BL , NL . HO erat ad HI ut 7 ad 6 & producta transibat inter stellas D & E, sic ut distantia stellæ D ab hac recta esset . LM erat ad LN ut 2 ad 9 & producta transibat per stellam H. His determinabantur positiones fixarum inter se.
Tandem Poundius noster iterum observavit positiones harum fixarum inter se, & earum longitudines & latitudines in tabulam sequentem retulit.
| Fixarum | Longitudines. | Lat. boreæ. | Fixarum | Longitudines. | Lat. boreæ. | |||||||||||
| ° | ′ | ″ | ° | ′ | ″ | ° | ′ | ″ | ° | ′ | ″ | |||||
| A | ♉ | 26. | 41. | 50 | 12. | 8. | 36 | L | ♉ | 29. | 33. | 34 | 12. | 7. | 48 | |
| B | 28. | 40. | 23 | 11. | 17. | 54 | M | 29. | 18. | 54 | 12. | 7. | 20 | |||
| C | 27. | 58. | 30 | 12. | 40. | 25 | N | 28. | 48. | 29 | 12. | 31. | 9 | |||
| E | 26. | 27. | 17 | 12. | 52. | 7 | Z | 29. | 44. | 48 | 11. | 57. | 13 | |||
| F | 28. | 28. | 37 | 11. | 52. | 22 | α | 29. | 52. | 3 | 11. | 55. | 48 | |||
| G | 26. | 56. | 8 | 12. | 4. | 58 | β | ♊ | 0. | 8. | 23 | 11. | 48. | 56 | ||
| H | 27. | 11. | 45 | 12. | 2. | 1 | γ | 0. | 40. | 10 | 11. | 55. | 18 | |||
| I | 27. | 25. | 2 | 11. | 53. | 11 | δ | 1. | 3. | 20 | 11. | 30. | 42 | |||
| K | 27. | 42. | 7 | 11. | 53. | 26 | ||||||||||
Positiones vero cometæ ad has fixas observabam ut sequitur.
Die veneris Feb. 25. st. vet. hor. p. m. cometæ in p existentis distantia a stella E erat minor quam , major quam , ideoque æqualis proxime; & angulus ApE nonnihil obtusus erat, sed fere rectus. Nempe si demitteretur ad pE perpendiculum ab A, distantia cometæ a perpendiculo illo erat .
Eadem nocte hora , cometæ in P existentis distantia a stella E erat major quam , minor quam , ideoque æqualis , seu quamproxime. A perpendiculo autem a stella A ad rectam PE demisso distantia cometæ erat {sic}.
Die solis Feb. 27. hor. p. m. cometæ in Q existentis distantia a stella O æquabat distantiam stellarum O & H, & recta QO producta transibat inter stellas K & B. Positionem hujus rectæ ob nubes intervenientes magis accurate definire non potui.
Die martis Mart. 1. hor. 11. p. m. cometa in R existens, stellis K & C accurate interjacebat, & rectæ CRK pars CR paulo major erat quam , & paulo minor quam , ideoque æqualis seu .
Die mercurii Mart. 2. hor. 8. p. m. cometæ existentis in S distantia a stella C erat quamproxime. Distantia stellæ F a recta CS producta erat ; & distantia stellæ B ab eadem recta, erat quintuplo major quam distantia stellæ F. Item recta NS producta transibat inter stellas H & I, quintuplo vel sextuplo propior existens stellæ H quam stellæ I.
Die saturni Mart. 5. hor. p. m. cometa existente in T, recta MT æqualis erat , & recta LT producta transibat inter B & F, quadruplo vel quintuplo propior F quam B, auferens a BF quintam vel sextam ejus partem versus F. Et MT producta transibat extra spatium BF ad partes stellæ B, quadruplo propior existens stellæ B quam stellæ F. Erat M stella perexigua quæ per telescopium videri vix potuit, & L stella major quasi magnitudinis octavæ.
Die lunæ Mart. 7. hor. p. m. cometa existente in V, recta Vα producta transibat inter B & F, auferens a BF versus F , & erat ad rectam Vβ ut 5 ad 4. Et distantia cometæ a recta αβ erat .
Die mercurii Mart. 9. hora . p. m. cometa existente in X, recta γX æqualis erat , & perpendiculum demissum a stella δ ad rectam γX erat .
Eadem nocte hora 12, cometa existente in Y, recta γY æqualis erat , aut paulo minor, puta , & perpendiculum demissum a stella δ ad rectam γY æqualis erat vel circiter. Sed cometa ob viciniam horizontis cerni vix potuit, nec locus ejus tam distincte ac in præcedentibus definiri.
Ex hujusmodi observationibus per constructiones figurarum & computationes derivabam longitudines & latitudines cometæ, & Poundius noster ex correctis fixarum locis loca cometæ correxit, & loca correcta habentur supra. Micrometro parum affabre constructo usus sum, sed longitudinum tamen & Latitudinum errores (quatenus ex observationibus nostris oriantur) minutum unum primum vix superant. Cometa autem (juxta observationes nostras) in fine motus sui notabiliter deflectere cœpit boream versus, a parallelo quem in fine Mensis Februarii tenuerat.
Jam ad orbem cometæ determinandum; selegi ex observationibus hactenus descriptis tres, quas Flamstedius habuit Dec. 21, Jan. 5, & Jan. 25. Ex his inveni St partium 9842,1 & Vt partium 455, quales 10000 sunt semidiameter orbis magni. Tum ad operationem primam assumendo tB partium 5657, inveni SB 9747, BE prima vice 412, Sμ 9503, iλ 413: BE secunda vice 421, OD 10186, X 8528,4 MP 8450, MN 8475, NP 25. Unde ad operationem secundam collegi distantiam tb 5640. Et per hanc operationem inveni tandem distantias TX 4775 & τZ 11322. Ex quibus orbem definiendo, inveni nodos ejus descendentem in ♋ & ascendentem in ♑ 1gr. 53′; inclinationem plani ejus ad planum eclipticæ 61gr. ; verticem ejus (seu perihelium cometæ) distare a nodo 8gr. 38′, & esse in ♐ 27gr. 43′ cum latitudine australi 7gr. 34′; & ejus latus rectum esse 236,8, areamque radio ad solem ducto singulis diebus descriptam 93585, quadrato semediametri orbis magni posito 100000000; cometam vero in hoc orbe secundum seriem signorum processisse, & Decemb. 8d. 0h. 4′. p. m. in vertice orbis seu perihelio fuisse. Hæc omnia per scalam partium æqualium & chordas angulorum ex tabula sinuum naturalium collectas determinavi graphice; construendo schema satis amplum, in quo videlicet semidiameter orbis magni (partium 1000) æqualis esset digitis pedis Anglicani.
Tandem ut constaret an cometa in orbe sic invento vere moveretur, collegi per operationes partim arithmeticas partim graphicas loca cometæ in hoc orbe ad observationum quarundam tempora: uti in tabula sequente videre licet.
<500>Postea vero Halleius noster orbitam per calculum arithmeticum, accuratius determinavit, quam per descriptiones linearum fieri licuit; & retinuit quidem locum nodorum in ♋ & ♑ 1gr. 53′, & inclinationem plani orbitæ ad eclipticam 61gr. , ut & tempus perihelii cometæ Decemb. 8d. 0h. 4′: distantiam vero perihelii a nodo ascendente in orbita cometæ mensuratam invenit esse 9gr. 20′, & latus rectum parabolæ esse 2430 partium, existente mediocri solis a terra distantia partium 100000. Et ex his datis, calculo itidem arithmetico accurate instituto, loca cometæ ad observationum tempora computavit, ut sequitur.
Apparuit etiam hic cometa mense Novembri præcedente & Coburgi in Saxonia a Dno. Gottfried Kirch observatus est diebus mensis hujus quarto, sexto & undecimo, stylo veteri; & ex positionibus ejus ad proximas stellas fixas ope telescopii nunc bipedalis nunc decempedalis satis accurate observatis, ac differentia longitudinum Coburgi & Londini graduum undecim & locis fixarum a Poundio nostro observatis, Halleius noster loca cometæ determinavit ut sequitur.
Novem. 3d. 17h. 2′, tempore apparente Londini, cometa erat in ♎ 29gr. 51′ cum lat. bor. 1gr. 17′. 45″.
Novem. 5d. 15h. 58′ cometa erat in ♍ 3gr. 23′ cum lat. bor. 1gr. 6′.
Novem. 10d. 16h. 31′ cometa æqualiter distabat a stellis leonis σ ac τ Bayero; nondum vero attigit rectam easdem jungentem, sed parum abfuit ab ea. In stellarum catalogo Flamstediano σ tunc habuit ♍ 14gr. 15′ cum lat. bor. 1gr. 41′ fere, τ vero ♍ 17gr. , cum lat. austr. 0gr. 34′. Et medium punctum inter has stellas fuit ♍ 15gr. , cum lat. bor. 0gr. . Sit distantia cometæ a recta illa 10′ vel 12′ circiter, & differentia longitudinum cometæ & puncti illius medii erit 7′, & differentia latitudinum , circiter. Et inde cometa erat in ♍ 15gr. 32′ cum lat. bor. 26′ circiter.
Observatio prima ex situ cometæ ad parvas quasdam fixas abunde satis accurata fuit. Secunda etiam satis accurata fuit. In tertia, quæ minus accurata fuit, error minutorum sex vel septem subesse potuit, & vix major. Longitudo vero cometæ in observatione prima, quæ cæteris accuratior fuit, in orbe prædicto parabolico computata erat ♌ 29gr. 30′. 22″. latitudo borealis 1gr. 25′. 7″. & distantia ejus a sole 115546.
Porro Halleius observando quod cometa insignis intervallo annorum 575 quater apparuisset, scilicet mense Septembri post cædem Julii Cæsaris, anno Christi 531 Lampadio & Oreste Coss. anno Christi 1106 mense Februario, & sub finem anni 1680, idque cum cauda longa & insigni (præterquam quod sub mortem Cæsaris, cauda ob incommodam telluris positionem minus apparuisset:) quæsivit orbem ellipticum cujus axis major esset partium 1382957, existente mediocri distantia telluris a sole partium 10000: in quo orbe utique cometa annis 575 revolvi possit. Et ponendo nodum ascendentem in ♋ 2gr. 2′; inclinationem plani orbis ad planum eclipticæ 61gr. 6′. 48″; perihelium cometæ in hoc plano ♐ 22gr. 44′. 25″; tempus æquatum perihelii Decem. 7d. 23h. 9′; distantiam perihelii a nodo ascendente in plano eclipticæ 9gr. 17′. 35″; & axem conjugatum 18481,2: computavit motum cometæ in hoc orbe elliptico. Loca autem ejus tam ex observationibus deducta quam in hoc orbe computata exhibentur in tabula sequente.
Observationes cometæ hujus a principio ad finem non minus congruunt cum motu cometæ in orbe jam descripto, quam motus planetarum congruere solent cum eorum theoriis, & congruendo probant unum & eundem fuisse cometam, qui toto hoc tempore apparuit, ejusque orbem hic recte definitum fuisse.
In tabula præcedente omisimus observationes diebus Novembris 16, 18, 20 & 23 ut minus accuratas. Nam cometa his etiam temporibus observatus fuit. Ponthæus utique & socii, Novem. 17. st. vet. hora sexta matutina Romæ, id est, hora 5. 10′ Londini, filis ad fixas applicatis, cometam observarunt in ♎ 8gr. 30′ cum latitudine australi 0gr. 40′. Extant eorum observationes in tractatu, quem Ponthæus de hoc cometa in lucem edidit. Cellius, qui aderat & observationes suas in epistola ad D. Cassinum misit, cometam eadem hora vidit in ♎ 8gr. 30′ cum latitudine australi 0gr. 30′. Eadem hora Galletius Avenioni (id est, hora matutina 5. 42 Londini) cometam vidit in ♎ 8gr sine latitudine, Cometa autem per theoriam jam fuit in ♎ 8gr. 16′. 45″ cum latitudine australi 0gr. 53′. 7″.
Nov. 18. hora matutina 6. 30′ Romæ (id est, hora 5, 40′ Londini) Ponthæus cometam vidit in ♎ 13gr. 30′ cum latitudine australi 1gr. 20′. Cellius in ♎ 13gr. 30′ cum latitudine australi 1gr. 00′. Galletius autem hora matutina 5. 30′ Avenioni cometam vidit in ♎ 13gr. 00′, cum latitudine australi 1gr. 00′. Et R. P. Ango in academia Flexiensi apud Gallos, hora quinta matutina (id est, hora 5. 9′ Londini) cometam vidit in medio inter stellas duas parvas, quarum una media est trium in recta linea in virginis australi manu, Bayero ψ, & altera est extrema alæ Bayero θ. Unde cometa tunc fuit in ♎ 12gr. 46′ cum latitudine australi 50′. Eodem die Bostoniæ in Nova-Anglia in latitudine graduum, hora quinta matutina, (id est Londini hora matutina 9. 44′) cometa visus est prope ♎ 14gr, cum latitudine australi 1gr. 30′, uti a cl. Halleio accepi.
Nov. 19. hora mat. Cantabrigiæ, cometa (observante juvene quodam) distabat a spica ♍ quasi 2gr boreazephyrum versus. Erat autem spica in ♎ 19gr. 23′. 47″ cum lat. austr. 2gr. 1′. 59″. Eodem die hor. 5. mat. Bostoniæ in Nova-Anglia, cometa distabat a spica ♏ {sic} gradu uno, differentia latitudinum existente 40′. Eodem die in insula Jamaica, cometa distabat a spica intervallo quasi gradus unius. Eodem die D. Arthurus Storer ad fluvium Patuxent prope Hunting Creek in Maryland, in confinio Virginiæ in lat. , hora quinta matutina (id est, hora 10a Londini) cometam vidit supra spicam ♏ {sic}, & cum spica propemodum conjunctum, existente distantia inter eosdem quasi . Et ex his observationibus inter se collatis colligo quod hora 9. 44′ Londini cometa erat in ♎ 18gr. 50′ cum latitudine australi 1gr. 25′ circiter. Cometa autem per theoriam jam erat in ♎ 18gr. 52′. 15″ cum latitudine australi 1gr. 26′. 54″.
Nov. 20. D. Montenarus astronomiæ professor Paduensis, hora sexta matutina Venetiis (id est, hora 5. 10′ Londini) cometam vidit in ♎ 23gr. cum latitudine australi 1gr. 30′. Eodem die Bostoniæ, distabat cometa a spica ♍, 4gr. longitudinis in orientem, ideoque erat in ♎ 23gr. 24′ circiter.
Nov. 21. Ponthæus & socii hor. mat. cometam observarunt in ♎ 27gr. 50′ cum latitudine australi 1gr. 16′, Cellius in ♎ 28gr. Ango hora quinta matutina in ♎ 27gr. 45′. Montenarus in ♎ 27gr. 51′. Eodem die in insula Jamaica cometa visus est prope principium scorpii, eandemque circiter latitudinem habuit cum spica virginis, id est, 2gr. 2′. Eodem die ad horam quintam matutinam Ballasoræ in India Orientali, (id est ad horam noctis præcedentis 11. 20′ Londini) capta est distantia cometæ a spica ♍ 7gr. 35′ in orientem. In linea recta erat inter spicam & lancem, ideoque versabatur in ♎ 26gr. 58′ cum lat. australi 1gr. 11′ circiter; & post horas 5 & 40′ (ad horam scilicet quintam matutinam Londini) erat in ♎ 28gr. 12′ cum lat. austr. 1gr. 16′. Per theoriam vero cometa jam erat in ♎ 28gr. 10′. 36″, cum latitudine australi 1gr. 53′. 35″.
Novem. 22. Cometa visus est a Montenaro in ♏ 2gr. 33′. Bostoniæ autem in Nova-Anglia apparuit in ♏ 3gr circiter, eadem fere cum latitudine ac prius, id est, 1gr. 30′. Eodem die ad horam quintam matutinam Ballasoræ cometa observabatur in ♏ 1gr. 50′; ideoque ad horam quintam matutinam Londini cometa erat in ♏ 3gr. 5′ circiter. Eodem die Londini hora mat. Hookius noster cometam vidit in ♏ 3gr. 30′ circiter, idque in linea recta quæ transit per spicam virginis & cor leonis, non exacte quidem, sed a linea illa paululum deflectentem ad boream. Montenarus itidem notavit quod linea a cometa per spicam ducta, hoc die & sequentibus transibat per australe latus cordis leonis, interposito perparvo intervallo inter cor leonis & hanc lineam. Linea recta per cor leonis & spicam virginis transiens, eclipticam secuit in ♍ 3gr. 46′; in angulo 2gr. 51′. Et si cometa locatus fuisset in hac linea in 3gr ejus latitudo fuisset 2gr. 26′. Sed cum cometa consentientibus Hookio & Montenaro, nonnihil distaret ab hac linea boream versus, latitudo ejus fuit paulo minor. Die 20 ex observatione Montenari, latitudo ejus propemodum æquabat latitudinem spicæ ♍, eratque 1gr. 30′ circiter, & consentientibus Hookio, Montenaro & Angone perpetuo augebatur, ideoque jam sensibiliter major erat quam 1gr. 30′. Inter limites autem jam constitutos 2gr. 26′ & 1gr. 30′, magnitudine mediocri latitudo erit 1gr. 58′ circiter. Cauda cometæ, consentientibus Hookio & Montenaro, dirigebatur ad spicam ♍, declinans aliquantulum a stella ista, juxta Hookium in austrum, juxta Montenarum in boream; ideoque declinatio illa vix fuit sensibilis, & cauda æquatori fere parallela existens, aliquantulum deflectebatur ab oppositione solis boream versus.
Nov. 23. st. vet. hora quinta matutina Noriburgi (id est hora Londini) D. Zimmerman cometam vidit in ♏ 8gr. 8′, cum latitudine australi 2gr. 31′, captis scilicet ejus distantiis a stellis fixis.
Nov. 24. Ante ortum solis cometa visus est a Montenaro in ♏ 12gr. 52′, ad boreale latus rectæ quæ per cor leonis & spicam virginis ducebatur, ideoque latitudinem habuit paulo minorem quam 2gr. 38′. Hæc latitudo, uti diximus, ex observationibus Montenari, Angonis & Hookii, perpetuo augebatur; ideoque jam paulo major erat quam 1gr. 58′; & magnitudine mediocri, sine notabili errore, statui potest 2gr. 18′. Latitudinem Ponthæus & Galletius jam decrevisse volunt, & Cellius & observator in Nova Anglia eandem fere magnitudinem retinuisse, scilicet gradus unius vel unius cum semisse. Crassiores sunt observationes Ponthæ & Cellii, eæ præsertim quæ per azimuthos & altitudines capiebantur, ut & eæ Galletii: meliores sunt eæ quæ per positiones cometæ ad fixas a Montenaro, Hookio, Angone & observatore in Nova-Anglia, & nonnunquam a Ponthæo & Cellio sunt factæ. Eodem die ad horam quintam matutinam Ballasoræ cometa observabatur in ♏ 11gr. 45′; ideoque ad horam quintam matutinam Londini erat in ♏ 13gr circiter. Per theoriam vero cometa jam erat in ♏ 13gr. 22′. 42″.
Nov. 25. Ante ortum solis Montenarus cometam observavit in ♏ circiter. Et Cellius observavit eodem tempore quod cometa erat in linea recta inter stellam lucidam in dextro femore virginis & lancem australem libræ, & hæc recta secat viam cometæ in ♏ 18gr. 36′. Per theoriam vero cometa jam erat in ♏ . circiter.
Congruunt igitur hæ observationes cum theoria quatenus congruunt inter se, & congruendo probant unum & eundem fuisse cometam, qui toto tempore a quarto die Novembris ad usque nonum Martii apparuit. Trajectoria cometæ hujus bis secuit planum eclipticæ, & propterea non fuit rectilinea. Eclipticam secuit non in oppositis cœli partibus, sed in fine virginis & principio capricorni, intervallo graduum 98 circiter; ideoque cursus cometæ plurimum debatur {sic} a circulo maximo. Nam & mense Novembri cursus ejus tribus saltem gradibus ab ecliptica in austrum declinabat, & postea mense Decembri gradibus 29 vergebat ab ecliptica in septentrionem partibus duabus orbitæ, in quibus cometa tendebat in solem & redibat a sole, angulo apparente graduum plus triginta ab invicem declinantibus, ut observavit Montenarus. Pergebat hic cometa per signa novem, a leonis scilicet ultimo gradu ad principium geminorum, præter signum leonis per quod pergebat antequam videri cœpit; & nulla alia extat theoria, qua cometa tantam cœli partem motu regulari percurrat. Motus ejus fuit maxime inæquabilis. Nam circa diem vigesimum Novembris descripsit gradus circiter quinque singulis diebus; dein motu retardato inter Novemb. 26 & Decemb. 12, spatio scilicet dierum quindecim cum semisse, descripsit gradus tantum 40; postea vero motu iterum accelerato, descripsit gradus fere quinque singulis diebus, antequam motus iterum retardari cœpit. Et theoria, quæ motui tam inæquabili per maximam cœli partem probe respondet, quæque easdem observat leges cum theoria planetarum, & cum accuratis observationibus astronomicis accurate congruit, non potest non esse vera.
Cæterum trajectoriam quam cometa descripsit, & caudam veram 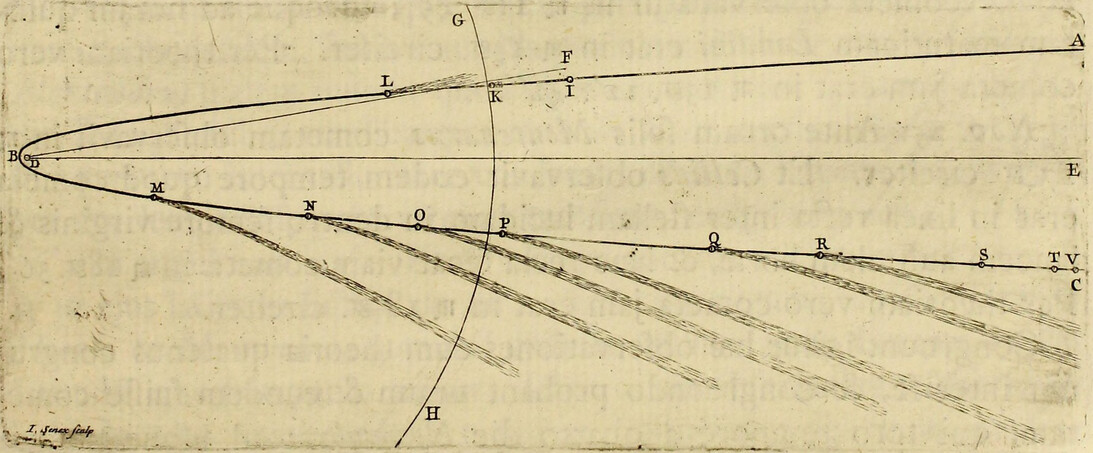 quam singulis in locis projecit, visum est annexo schemate in plano trajectoriæ delineatas exhibere: ubi ABC denotat trajectoriam cometæ, D solem, DE trajectoriæ axem, DF lineam nodorum, GH intersectionem sphæræ orbis magni cum plano trajectoriæ, I locum cometæ Nov. 4. Ann. 1680, K locum ejusdem Nov. 11, L locum Nov. 19, M locum Dec. 12, N locum Dec. 21, O locum Dec. 29, P locum Jan. 5 sequent. Q locum Jan. 25, R locum Feb. 5, S locum Feb. 25, T locum Mar. 5, & V locum Mar. 9. Observationes vero sequentes in cauda definienda adhibui.
quam singulis in locis projecit, visum est annexo schemate in plano trajectoriæ delineatas exhibere: ubi ABC denotat trajectoriam cometæ, D solem, DE trajectoriæ axem, DF lineam nodorum, GH intersectionem sphæræ orbis magni cum plano trajectoriæ, I locum cometæ Nov. 4. Ann. 1680, K locum ejusdem Nov. 11, L locum Nov. 19, M locum Dec. 12, N locum Dec. 21, O locum Dec. 29, P locum Jan. 5 sequent. Q locum Jan. 25, R locum Feb. 5, S locum Feb. 25, T locum Mar. 5, & V locum Mar. 9. Observationes vero sequentes in cauda definienda adhibui.
Nov. 4 & 6. Cauda nondum apparuit. Nov. 11. Cauda jam cœpta non nisi semissem gradus unius longa tubo decempedali visa fuit. Nov. 17. Cauda gradus amplius quindecim longa Ponthæo apparuit. Nov. 18. Cauda 30gr longa, solique directe opposita in Nova-Anglia cernebatur, & protendebatur usque ad stellam ♂, quæ tunc erat in ♍ 9gr. 54′. Nov. 19. In Mary-land cauda visa fuit gradus 15 vel 20 longa. Dec. 10. Cauda (observante Flamstedio) transibat per medium distantiæ inter caudam serpentis Ophiuchi & stellam δ in aquilæ australi ala, & desinebat prope stellas A, ω, b in Tabulis Bayeri. Terminus igitur erat in ♑ , cum latitudine boreali circiter. Dec. 11. Cauda surgebat ad usque caput sagittæ (Bayero α, β,) desinens in ♑ 26gr. 43′ cum latitudine boreali 38gr. 34′. Dec. 12. Cauda transibat per medium sagittæ, nec longe ultra protendebatur, desinens in ♒ 4gr, cum latitudine boreali circiter. Intelligenda sunt hæc de longitudine caudæ clarioris. Nam luce obscuriore, in cœlo forsan magis sereno, cauda Dec. 12, hora 5. 40′ Romæ (observante Ponthæo) supra cygni uropygium ad gradus 10 sese extulit; atque ab hac stella ejus latus ad occasum & boream min. 45. destitit. Lata autem erat cauda his diebus gradus 3, juxta terminum superiorem, ideoque medium ejus distabat a stella illa 2gr. 15′ austrum versus, & terminus superior erat in ♓ 22gr, cum latitudine boreali 61gr. Et hinc longa erat cauda 70gr circiter. Dec. 21. Eadem surgebat fere ad cathedram Cassiopeiæ, æqualiter distans a β & Schedir, & distantiam ab utraque distantiæ earum ab invicem æqualem habens, ideoque desinens in ♈ 24gr, cum latitudine . Dec. 29. Cauda tangebat Scheat sitam ad sinistram, & intervallum stellarum duarum in pede boreali Andromedæ accurate complebat, & longa erat 54gr; ideoque desinebat in ♉ 19gr, cum latitudine 35gr. Jan. 5. Cauda tetigit stellam π in pectore Andromedæ ad latus ejus dextrum, & stellam μ in ejus cingulo ad latus sinistrum; & (juxta observationes nostras) longa 40gr; curva autem erat & convexo latere spectabat ad austrum. Cum circulo per solem & caput cometæ transeunte angulum confecit graduum 4 juxta caput cometæ; at juxta terminum alterum inclinabatur ad circulum illum in angulo 10 vel 11 graduum & chorda caudæ cum circulo illo continebat angulum graduum octo. Jan. 13. Cauda luce satis sensibili terminabatur inter Alamech & Algol, & luce tenuissima desinebat e regione stellæ κ in latere Persei. Distantia termini caudæ a circulo solem & cometam jungente erat 3gr. 50′, & inclinatio chordæ caudæ ad circulum illum . Jan. 25 & 26. Cauda luce tenui micabat ad longitudinem graduum 6 vel 7; & nocte una & altera sequente ubi cœlum valde serenum erat, luce tenuissima & ægerrime sensibili attingebat longitudinem graduum duodecim & paulo ultra. Dirigebatur autem ejus axis ad lucidam in humero orientali aurigæ accurate, ideoque declinabat ab oppositione solis boream versus in angulo graduum decem. Denique Feb. 10. caudam oculis armatis aspexi gradus duos longam. Nam lux prædicta tenuior per vitra non apparuit. Ponthæus autem Feb. 7. se caudam ad longitudinem graduum 12 vidisse scribit. Feb. 25 & deinceps cometa sine cauda apparuit.
Orbem jam descriptum spectanti & reliqua cometæ hujus phænomena in animo revolventi, haud difficulter constabit, quod corpora cometarum sunt solida, compacta, fixa ac durabilia ad instar corporum planetarum. Nam si nihil aliud essent quam vapores vel exhalationes terræ, solis & planetarum, cometa hicce in transitu suo per viciniam solis statim dissipari debuisset. Est enim calor solis ut radiorum densitas, hoc est, reciproce ut quadratum distantiæ locorum a sole. Ideoque cum distantia cometæ a centro solis Decemb. 8. ubi in perihelio versabatur, esset ad distantiam terræ a centro solis ut 6 ad 1000 circiter, calor solis apud cometam eo tempore erat ad calorem solis æstivi apud nos ut 1000000 ad 36, seu 28000 ad 1. Sed calor aquæ ebullientis est quasi triplo major quam calor quem terra arida concipit ad æstivum solem, ut expertus sum: & calor ferri candentis (si recte conjector) quasi triplo vel quadruplo major quam calor aquæ ebullientis; ideoque calor, quem terra arida apud cometam in perihelio versantem ex radiis solaribus concipere posset, quasi 2000 vicibus major quam calor ferri candentis. Tanto autem calore vapores & exhalationes, omnisque materia volatilis statim consumi ac dissipari debuissent.
Cometa igitur in perihelio suo calorem immensum ad solem concepit, & calorem illum diutissime conservare potest. Nam globus ferri candentis digitum unum latus, calorem suum omnem spatio horæ unius in aëre consistens vix amitteret. Globus autem major calorem diutius conservaret in ratione diametri, propterea quod superficies (ad cujus mensuram per contactum aëris ambientis refrigeratur) in illa ratione minor est pro quantitate materiæ suæ calidæ inclusæ. Ideoque globus ferri candentis huic terræ æqualis, id est, pedes plus minus 40000000 latus, diebus totidem, & idcirco annis 50000, vix refrigesceret. Suspicor tamen quod duratio caloris, ob causas latentes, augeatur in minore ratione quam ea diametri: & optarim rationem veram per experimenta investigari.
Porro notandum est quod cometa mense Decembri, ubi ad solem modo incaluerat, caudam emittebat longe majorem & splendidiorem quam antea mense Novembri, ubi perihelium nondum attigerat. Et universaliter caudæ omnes maximæ & fulgentissimæ e cometis oriuntur statim post transitum eorum per regionem solis. Conducit igitur calefactio cometæ ad magnitudinem caudæ. Et inde colligere videor quod cauda nihil aliud sit quam vapor longe tenuissimus, quem caput seu nucleus cometæ per calorem suum emittit.
Cæterum de cometarum caudis triplex est opinio; eas vel jubar esse solis per translucida cometarum capita propagatum, vel oriri ex refractione lucis in progressu ipsius a capite cometæ in terram, vel denique nubem esse seu vaporem a capite cometæ jugiter surgentem & abeuntem in partes a sole aversas. Opinio prima eorum est qui nondum imbuti sunt scientia rerum opticarum. Nam jubar solis in cubiculo tenebroso non cernitur, nisi quatenus lux reflectitur e pulverum & fumorum particulis per aërem semper volitantibus: ideoque in aëre fumis crassioribus infecto splendidius est, & sensum fortius ferit; in aëre clariore tenuius est & ægrius sentitur: in cœlis autem sine materia reflectente nullum esse potest. Lux non cernitur quatenus in jubare est, sed quatenus inde reflectitur ad oculos nostros. Nam visio non fit nisi per radios qui in oculos impingunt. Requiritur igitur materia aliqua reflectens in regione caudaeæ, ne cœlum totum luce solis illustratum uniformiter splendeat. Opinio secunda multis premitur difficultatibus. Caudæ nunquam variegantur coloribus: qui tamen refractionum solent esse comites inseparabiles. Lux fixarum & planetarum distincte ad nos transmissa demonstrat medium cœleste nulla vi refractiva pollere. Nam quod dicitur fixas ab Ægyptiis comatas nonnunquam visas fuisse, id, quoniam rarissime contingit, ascribendum est nubium refractioni fortuitæ. Fixarum quoque radiatio & scintillatio ad refractiones tum oculorum tum aëris tremuli referendæ sunt: quippe quæ admotis oculo telescopiis evanescunt. Aëris & ascendentium vaporum tremore fit, ut radii facile de angusto pupillæ spatio per vices detorqueantur, de latiore autem vitri objectivi apertura neutiquam. Inde est quod scintillatio in priori casu generetur, in posteriore autem cesset: & cessatio in posteriore casu demonstrat regularem transmissionem lucis per cœlos sine omni refractione sensibili. Nequis contendat quod caudæ non soleant videri in cometis, cum eorum lux non est satis fortis, quia tunc radii secundarii non habent satis virium ad oculos movendos, & propterea caudas fixarum non cerni: sciendum est quod lux fixarum plus centum vicibus augeri potest mediantibus telescopiis, nec tamen caudæ cernuntur. Planetarum quoque lux copiosior est, caudæ vero nullae: cometæ autem sæpe caudatissimi sunt, ubi capitum lux tenuis est & valde obtusa. Sic enim cometa anni 1680, mense Decembri, quo tempore caput luce sua vix æquabat stellas secundæ magnitudinis, caudam emittebat splendore notabili usque ad gradus 40, 50, 60 vel 70 longitudinis & ultra: postea Jan. 27 & 28 caput apparebat ut stella septimæ tantum magnitudinis, cauda vero luce quidem pertenui sed satis sensibili longa erat 6 vel 7 gradus, & luce obscurissima, quæ cerni vix posset, porrigebatur ad gradum usque duodecimum vel paulo ultra: ut supra dictum est. Sed & Feb. 9. & 10 ubi caput nudis oculis videri desierat, caudam gradus duos longam per telescopium contemplatus sum. Porro si cauda oriretur ex refractione materiæ cœlestis, & pro figura cœlorum deflecteretur de solis oppositione, deberet deflexio illa in iisdem cœli regionibus in eandem semper partem fieri. Atqui cometa anni 1680 Decemb. 28 hora p. m. Londini, versabatur in ♓ 8gr. 41′, cum latitudine boreali 28gr. 6′, sole existente in ♑ 18gr. 26′. Et cometa anni 1577, Dec. 29 versabatur in ♓ 8gr. 41′ cum latitudine boreali 28gr. 30′, sole etiam existente in ♑ 18gr. 26′ circiter. Utroque in casu terra versabatur in eodem loco, & cometa apparebat in eadem cœ parte: in priori tamen casu cauda cometæ (ex meis & aliorum observationibus) declinabat angulo graduum ab oppositione solis aquilonem versus; in posteriore vero (ex observationibus Tychonis) declinatio erat graduum 21 in austrum. Igitur repudiata cœlorum refractione, superest ut phænomena caudarum ex materia aliqua reflectente deriventur.
Caudas autem a capitibus oriri & in regiones a sole aversas ascendere confirmatur ex legibus quas observant. Ut quod in planis orbium cometarum per solem transeuntibus jacentes, deviant ab oppositione solis in eas semper partes, quas capita in orbibus illis progredientia relinquunt. Quod spectatori in his planis constituto apparent in partibus a sole directe aversis; digrediente autem spectatore de his planis, deviatio paulatim sentitur, & indies apparet major. Quod deviatio cæteris paribus minor est ubi cauda obliquior est ad orbem cometæ, ut & ubi caput cometæ ad solem propius accedit; præsertim si spectetur deviationis angulus juxta caput cometæ. Præterea quod caudæ non deviantes apparent rectæ, deviantes autem incurvantur. Quod curvatura major est ubi major est deviatio, & magis sensibilis ubi cauda cæteris paribus longior est: nam in brevioribus curvatura ægre animadvertitur. Quod deviationis angulus minor est juxta caput cometæ, major juxta caudæ extremitatem alteram, atque ideo quod cauda convexo sui latere partes respicit a quibus fit deviatio, quæque in recta sunt linea a sole per caput cometaeæ in infinitum ducta. Et quod caudæ quæ prolixiores sunt & latiores, & luce vegetiore micant, sint ad latera convexa paulo splendidiores & limite minus indistincto terminatæ quam ad concava. Pendent igitur phænomena caudæ a motu capitis, non autem a regione cœli in qua caput conspicitur; & propterea non fiunt per refractionem cœlorum, sed a capite suppeditante materiam oriuntur. Etenim ut in aëre nostro fumus corporis cujusvis igniti petit superiora, idque vel perpendiculariter si corpus quiescat, vel oblique si corpus moveatur in latus; ita in cœlis, ubi corpora gravitant in solem, fumi & vapores ascendere debent a sole (uti jam dictum est) & superiora vel recta petere, si corpus fumans quiescit; vel oblque, si corpus progrediendo loca semper deserit a quibus superiores vaporis partes ascenderant. Et obliquitas ista minor erit ubi ascensus vaporis velocior est: nimirum in vicinia solis & juxta corpus fumans. Ex obliquitatis autem diversitate incurvabitur vaporis columna: & quia vapor in columnæ latere præcedente paulo recentior est, ideo etiam is ibidem aliquanto densior erit, lucemque propterea copiosius reflectet, & limite minus indistincto terminabitur. De caudarum agitationibus subitaneis & incertis, deque earum figuris irregularibus, quas nonnulli quandoque describunt, hic nihil adjicio; propterea quod vel a mutationibus aëris nostri, & motibus nubium caudas aliqua ex parte obscurantium oriantur; vel forte a partibus viæ lacteæ, quæ cum caudis praeætereuntibus confundi possint, ac tanquam earum partes spectari.
Vapores autem, qui spatiis tam immensis implendis sufficiant, ex cometarum atmosphæris oriri posse, intelligetur ex raritate aëris nostri. Nam aër juxta superficiem terraeæ spatium occupat quasi 850 partibus majus quam aqua ejusdem ponderis, ideoque aëris columna cylindrica pedes 850 alta ejusdem est ponderis cum aquæ columna pedali latitudinis ejusdem. Columna autem aëris ad summitatem atmosphæræ assurgens æquat pondere suo columnam aquæ pedes 33 altam circiter; & propterea si columnæ totius aëreæ pars inferior pedum 850 altitudinis dematur, pars reliqua superior æquabit pondere suo columnam aquæ altam pedes 32. Inde vero (per regulam multis experimentis confirmatam, quod compressio aëris sit ut pondus atmosphæræ incumbentis, quodque gravitas sit reciproce ut quadratum distantiæ locorum a centro terræ) computationem per corol. prop. xxii. lib. II. ineundo, inveni quod aër, si ascendatur a superficie terræ ad altitudinem semidiametri unius terrestris, rarior sit quam apud nos in ratione longe majori, quam spatii omnis infra orbem saturni ad globum diametro digiti unius descriptum. Ideoque globus aëris nostri digitum unum latus, ea cum raritate quam haberet in altitudine semidiametri unius terrestris, impleret omnes planetarum regiones usque ad sphæram saturni & longe ultra. Proinde cum aër adhuc altior in immensum rarescat; & coma seu atmosphæra cometæ, ascendendo ab illius centro, quasi decuplo altior sit quam superficies nuclei, deinde cauda adhuc altius ascendat, debebit cauda esse quam rarissima. Et quamvis ob longe crassiorem cometarum atmosphæram, magnamque corporum gravitationem solem versus, & gravitationem particularum aëris & vaporum in se mutuo, fieri possit ut aër in spatiis cœlestibus inque cometarum caudis non adeo rarescat; perexiguam tamen quantitatem aëris & vaporum ad omnia illa caudarum phænomena abunde sufficere, ex hac computatione perspicuum est. Nam & caudarum insignis raritas colligitur ex astris per eas translucentibus. Atmosphæra terrestris luce solis splendens, crassitudine sua paucorum milliarium, & astra omnia & ipsam lunam obscurat & extinguit penitus: per immensam vero caudarum crassitudinem, luce pariter solari illustratam, astra minima sine claritatis detrimento translucere noscuntur. Neque major esse solet caudarum plurimarum splendor, quam aëris nostri in tenebroso cubiculo latitudine digiti unius duorumve lucem solis in jubare reflectentis.
Quo temporis spatio vapor a capite ad terminum caudæ ascendit, cognosci fere potest ducendo rectam a termino caudæ ad solem, & notando locum ubi recta illa trajectoriam secat. Nam vapor in termino caudæ, si recta ascendat a sole, ascendere cœpit a capite, quo tempore caput erat in loco intersectionis. At vapor non recta ascendit a sole, sed motum cometæ, quem ante ascensum suum habebat, retinendo, & cum motu ascensus sui eundem componendo, ascendit oblique. Unde verior erit problematis solutio, ut recta illa quæ orbem secat, parallela sit longitudini caudæ, vel potius (ob motum curvilineum cometæ) ut eadem a linea caudæ divergat. Hoc pacto inveni quod vapor, qui erat in termino caudæ Jan. 25, ascendere cœperat a capite ante Dec. 11, ideoque ascensu suo toto dies plus 45 consumpserat. At cauda illa omnis quæ Dec. 10 apparuit, ascenderat spatio dierum illorum duorum, qui a tempore perihelii cometæ elapsi fuerant. Vapor igitur sub initio in vicinia solis celerrime ascendebat, & postea cum motu per gravitatem suam semper retardato ascendere pergebat; & ascendendo augebat longitudinem caudæ: cauda autem, quamdiu apparuit, ex vapore fere omni constabat, qui a tempore perihelii ascenderat; & vapor, qui primus ascendit, & terminum caudæ composuit, non prius evanuit quam ob nimiam suam tam a sole illustrante quam ab oculis nostris distantiam videri desiit. Unde etiam caudæ cometarum aliorum, quæ breves sunt, non ascendunt motu celeri & perpetuo a capitibus & mox evanescunt, sed sunt permanentes vaporum & exhalationum columnæ, a capitibus lentissimo multorum dierum motu propagatæ, quæ, participando motum illum capitum quem habuere sub initio, per cœlos una cum capitibus moveri pergunt. Et hinc rursus colligitur spatia cœlestia vi resistendi destitui; utpote in quibus non solum solida planetarum & cometarum corpora, sed etiam rarissimi caudarum vapores motus suos velocissimos liberrime peragunt ac diutissime conservant.
Ascensum caudarum ex atmosphæris capitum & progressum in partes a sole aversas Keplerus ascribit actioni radiorum lucis materiam caudæ secum rapientium. Et auram longe tenuissimam in spatiis liberrimis actioni radiorum cedere, non est a ratione prorsus alienum, non obstante quod substantiæ crassæ impeditissimis in regionibus nostris a radiis solis sensibiliter propelli nequeant. Alius particulas tam leves quam graves dari posse existimat, & materiam caudarum levitare, perque levitatem suam a sole ascendere. Cum autem gravitas corporum terrestrium sit ut materia in corporibus, ideoque servata quantitate materiæ intendi & remitti nequeat, suspicor ascensum illum ex rarefactione materiæ caudarum potius oriri. Ascendit fumus in camino impulsu aëris cui innatat. Aër ille per calorem rarefactus ascendit, ob diminutam suam gravitatem specificam, & fumum implicatum rapit secum. Quidni cauda cometæ ad eundem modum ascenderit a sole? Nam radii solares non agitant media, quæ permeant, nisi in reflexione & refractione. Particulæ reflectentes ea actione calefactæ calefacient auram ætheream cui implicantur. Illa calore sibi communicato rarefiet, & ob diminutam ea raritate gravitatem suam specificam, qua prius tendebat in solem, ascendet & secum rapiet particulas reflectentes ex quibus cauda componitur: Ad ascensum vaporum conducit etiam, quod hi gyrantur circa solem & ea actione conantur a sole recedere, at solis atmosphæra & materia cœlorum vel plane quiescit, vel motu solo quem a solis rotatione acceperint, tardius gyratur. Hæ sunt causæ ascensus caudarum in vicinia solis, ubi orbes curviores sunt, & cometæ intra densiorem & ea ratione graviorem solis atmosphæram consistunt, & caudas quam longissimas mox emittunt. Nam caudæ, quæ tunc nascuntur, conservando motum suum & interea versus solem gravitando, movebuntur circa solem in ellipsibus pro more capitum, & per motum illum capita semper comitabuntur & iis liberrime adhærebunt. Gravitas enim vaporum in solem non magis efficiet ut caudæ postea decidant a capitibus solem versus, quam gravitas capitum efficere possit ut hæc decidant a caudis. Communi gravitate vel simul in solem cadent, vel simul in ascensu suo retardabuntur; ideoque gravitas illa non impedit, quo minus caudæ & capita positionem quamcunque ad invicem a causis jam descriptis aut aliis quibuscunque facillime accipiant & postea liberrime servent.
Caudæ igitur, quæ in cometarum periheliis nascuntur, in regiones longinquas cum eorum capitibus abibunt, & vel inde post longam annorum seriem cum iisdem ad nos redibunt, vel potius ibi rarefactæ paulatim evanescent. Nam postea in descensu capitum ad solem caudæ novæ breviusculæ lento motu a capitibus propagari debebunt, & subinde in periheliis cometarum illorum, qui ad usque atmosphæram solis descendunt, in immensum augeri. Vapor enim in spatiis illis liberrimis perpetuo rarescit ac dilatatur. Qua ratione fit ut cauda omnis ad extremitatem superiorem latior sit quam juxta caput cometæ. Ea autem rarefactione vaporem perpetuo dilatatum diffundi tandem & spargi per cœlos universos, deinde paulatim in planetas per gravitatem suam attrahi, & cum eorum atmosphæris misceri rationi consentaneum videtur. Nam quemadmodum maria ad constitutionem terræ hujus omnino requiruntur, idque ut ex iis per calorem solis vapores copiose satis excitentur, qui vel in nubes coacti decidant in pluviis, & terram omnem ad procreationem vegitabilium irrigent & nutriant; vel in frigidis montium verticibus condensati (ut aliqui cum ratione philosophantur) decurrant in fontes & flumina: sic ad conservationem marium & humorum in planetis requiri videntur cometæ, ex quorum exhalationibus & vaporibus condensatis, quicquid liquoris per vegetationem & putrefactionem consumitur & in terram aridam convertitur, continuo suppleri & refici possit. Nam vegetabilia omnia ex liquoribus omnino crescunt, dein magna ex parte in terram aridam per putrefactionem abeunt, & limus ex liquoribus putrefactis perpetuo decidit. Hinc moles terræ aridæ indies augetur, & liquores, nisi aliunde augmentum sumerent, perpetuo decrescere deberent, ac tandem deficere. Porro suspicor spiritum illum, qui aëris nostri pars minima est sed subtilissima & optima, & ad rerum omnium vitam requiritur, ex cometis præcipue venire.
Atmosphæræ cometarum in descensu eorum in solem excurrendo in caudas, diminuuntur, & (ea certe in parte quæ solem respicit) angustiores redduntur: & vicissim in recessu eorum a sole, ubi jam minus excurrunt in caudas, ampliantur; si modo phænomena eorum Hevelius recte notavit. Minimæ autem apparent, ubi capita jam modo ad solem calefacta in caudas maximas & fulgentissimas abiere, & nuclei fumo forsan crassiore & nigriore in atmosphærarum partibus infimis circundantur. Nam fumus omnis ingenti calore excitatus crassior & nigrior esse solet. Sic caput cometæ, de quo egimus, in æqualibus a sole ac terra distantiis obscurius apparuit post perihelium suum quam antea. Mense enim Decembri cum stellis tertiæ magnitudinis conferri solebat, at mense Novembri cum stellis primæ & secundæ. Et qui utrumque viderant, majorem describunt cometam priorem. Nam juveni cuidam Cantabrigiensi, Novem. 19, cometa hicce luce sua quamtumvis plumbea & obtusa, æquabat spicam virginis, & clarius micabat quam postea. Et Montenaro Nov. 20. st. vet. cometa apparebat major stellis primæ magnitudinis, existente cauda duorum graduum longitudinis. Et D. Storer literis, quæ in manus nostras incidere, scripsit caput ejus mense Decembri, ubi caudam maximam & fulgentissimam emittebat, parvum esse & magnitudine visibili longe cedere cometæ qui mense Novembri ante solis ortum apparuerat. Cujus rei rationem esse conjectabatur, quod materia capitis sub initio copiosior esset, & paulatim consumeretur.
Eodem spectare videtur, quod capita cometarum aliorum, qui caudas maximas & fulgentissimas emiserunt, apparuerint subobscura & exigua. Nam anno 1668 Mart. 5. st. nov. hora septima vespertina R.P. Valentinus Estancius, Brasiliæ agens, cometam vidit horizonti proximum ad occasum solis brumalem, capite minimo & vix conspicuo, cauda vero supra modum fulgente, ut stantes in littore speciem ejus e mari reflexam facile cernerent. Speciem utique habebat trabis splendentis longitudine 23 graduum, ab occidente in austrum vergens, & horizonti fere parallela. Tantus autem splendor tres solum dies durabat, subinde notabiliter decrescens; & interea decrescente splendore aucta est magnitudine cauda. Unde etiam in Lusitania quartam fere cœli partem (id est gradus 45) occupasse dicitur ab occidente in orientem splendore cum insigni protensa; nec tamen tota apparuit, capite semper in his regionibus infra horizontem delitescente. Ex incremento caudæ & decremento splendoris manifestum est, quod caput a sole recessit, eique proximum fuit sub initio, pro more cometæ anni 1680. Et in chronico Saxonico similis legitur cometa anni 1106, cujus stella erat parva & obscura (ut ille anni 1680) sed splendor qui ex ea exivit valde clarus & quasi ingens trabs ad orientem & aquilonem tendebat, ut habet Hevelius ex Simeone Dunelmensi Monacho. Apparuit initio mensis Februarii, ac deinceps circa vesperam, ad occasum solis brumalem. Inde vero & ex situ caudæ colligitur caput fuisse soli vicinum. A sole, inquit Matthæus Parisiensis, distabat quasi cubito uno, ab hora tertia [rectius sexta] usque ad horam nonam radium ex se longum emittens. Talis etiam erat ardentissimus ille cometa ab Aristotele descriptus Lib. i. Meteor. 6. cujus caput primo die non conspectum est, eo quod ante solem vel saltem sub radiis solaribus occidisset, sequente vero die quantum potuit visum est. Nam quam minima fieri potest distantia solem reliquit, & mox occubuit. Ob nimium ardorem [caudæ scilicet] nondum apparebat capitis sparsus ignis, sed procedente tempore (ait Aristoteles) cum [cauda] jam minus flagraret, reddita est [capiti] cometæ sua facies. Et splendorem suum ad tertiam usque cœli partem [id est, ad 60gr] extendit. Apparuit autem tempore hyberno [an. 4. olymp. 101.] & ascendens usque ad cingulum orionis ibi evanuit. Cometa ille anni 1618, qui e radiis solaribus caudatissimus emersit, stellas primæ magnitudinis æquare vel paulo superare videbatur, sed majores apparuere cometæ non pauci, qui caudas breviores habuere. Horum aliqui jovem, alii venerem vel etiam lunam æquasse traduntur.
Diximus cometas esse genus planetarum in orbibus valde eccentricis circa solem revolventium. Et quemadmodum e planetis non caudatis minores esse solent, qui in orbibus minoribus & soli propioribus gyrantur, sic etiam cometas, qui in periheliis suis ad solem propius accedunt, ut plurimum minores esse, ne solem attractione sua nimis agitent, rationi consentaneum videtur. Orbium vero transversas diametros & revolutionum tempora periodica, ex collatione cometarum in iisdem orbibus post longa temporum intervalla redeuntium, determinanda relinquo. Interea huic negotio propositio sequens Lumen accendere potest.
PROPOSITIO XLII. PROBLEMA XXII.
Inventam cometæ trajectoriam corrigere.
Operatio 1. Assumatur positio plani trajectoriaeæ, per propositionem superiorem inventa; & seligantur tria loca cometæ observationibus accuratissimis definita, & ab invicem quam maxime distantia; sitque A tempus inter primam & secundam, ac B tempus inter secundam ac tertiam. Cometam autem in eorum aliquo in perigæo versari convenit, vel saltem non longe a perigæo abesse. Ex his locis apparentibus inveniantur per operationes trigonometricas, loca tria vera cometæ in assumpto illo plano trajectoriæ. Deinde per loca illa inventa, circa centrum solis ceu umbilicum, per operationes arithmeticas, ope prop. xxi. Lib. i. institutas, describatur sectio conica: & ejus areæ, radiis a sole ad loca inventa ductis terminatæ, sunto D & E; nempe D area inter observationem primam & secundam, & E area inter secundam ac tertiam. Sitque T tempus totum, quo area tota velocitate cometæ per prop. xvi. lib. i. inventa describi debet.
Oper. 2. Augeatur longitudo nodorum plani trajectoriæ, additis ad longitudinem illam 20′ vel 30′, quæ dicantur P; & servetur plani illius inclinatio ad planum eclipticæ. Deinde ex prædictis tribus cometæ locis observatis inveniantur in hoc novo plano loca tria vera, ut supra: deinde etiam orbis per loca illa transiens, & ejusdem areæ duæ inter observationes descriptæ, quæ sint d & e, nec non tempus totum t, quo area tota describi debeat.
Oper. 3. Servetur longitudo nodorum in operatione prima, & augeatur inclinatio plani trajectoriæ ad planum eclipticæ, additis ad inclinationem illam 20′ vel 30′, quæ dicantur Q. Deinde ex observatis prædictis tribus cometæ locis apparentibus inveniantur in hoc novo plano loca tria vera, orbisque per loca illa transiens, ut & ejusdem areæ duæ inter observationes descriptæ, quæ sint δ & ε, & tempus totum τ, quo area tota describi debeat.
<519>Jam sit C ad 1 ut A ad B, & G ad 1 ut D ad E, & g ad 1 ut d ad e, & γ ad 1 ut δ ad ε; sitque S tempus verum inter observationem primam ac tertiam; & signis + & − probe observatis quærantur numeri m & n, ea lege, ut sit , & æquale . Et si in operatione prima I designet inclinationem plani trajectoriæ ad planum eclipticæ, & K longitudinem nodi alterutrius: erit vera inclinatio plani trajectoriæ ad planum eclipticæ, & vera longitudo nodi. Ac denique si in operatione prima, secunda ac tertia, quantitates R, r & ρ designent latera recta trajectoriæ, & quantitates , , ejusdem latera transversa respective: erit verum latus rectum, & verum latus transversum trajectoriæ quam cometa describit. Dato autem latere transverso datur etiam tempus periodicum cometæ. Q.E.I.
Cæterum cometarum revolventium tempora periodica, & orbium latera transversa, haud satis accurate determinabuntur, nisi per collationem cometarum inter se, qui diversis temporibus apparent. Si plures cometæ, post æqualia temporum intervalla, eundem orbem descripsisse reperiantur, concludendum erit hos omnes esse unum & eundem cometam, in eodem orbe revolventem. Et tum demum ex revolutionum temporibus dabuntur orbium latera transversa, & ex his lateribus determinabuntur orbes elliptici.
In hunc finem computandæ sunt igitur cometarum plurium trajectoriæ, ex hypothesi quod sint parabolicæ. Nam hujusmodi trajectoriæ cum phænomenis semper congruent quamproxime. Id liquet, non tantum ex trajectoria parabolica cometæ anni 1680, quam cum observationibus supra contuli, sed etiam ex ea cometæ illius insignis, qui annis 1664 & 1665 apparuit, & ab Hevelio observatus fuit. Is ex observationibus suis longitudines & latitudines hujus cometæ computavit, sed minus accurate. Ex iisdem observationibus Halleius noster loca cometæ hujus denuo computavit, & tum demum ex locis sic inventis trajectoriam cometæ determinavit. Invenit autem ejus nodum ascendentem in ♊ 21gr. 13′. 55″, inclinationem orbitæ ad planum eclipticæ 21gr. 18′. 40″, distantiam perihelii a nodo in orbita 49gr. 27′. 30″. Perihelium in ♌ 8gr. 40′. 30″ cum latitudine austrina heliocentrica 16gr. 1′. 45″. Cometam in perihelio Novem. 24d. 11h. 52′ p. m. tempore æquato Londini, vel 13h. 8′ Gedani, stylo veteri, & latus rectum parabolæ 410286, existente mediocri terræ a sole distantia 100000. Quam probe loca cometæ in hoc orbe computata congruunt cum observationibus, patebit ex tabula sequente ab Halleio supputata.
Mense Februario anni ineuntis 1665, stella prima arietis, quam in sequentibus vocabo γ, erat in ♈ 28gr. 30′. 15″ cum latitudine boreali 7gr. 8′. 58″. Secunda arietis erat in ♈ 29gr. 17′. 18″ cum latitudine boreali 8gr. 28′. 16″. Et stella quædam alia septimæ magnitudinis, quam vocabo A, erat in ♈ 28gr. 24′. 45″ cum latitudine boreali 8gr. 28′. 33″. Cometa vero Feb. 7d. 7′. 30″ Parisiis (id est Feb. 7d 8′. 37″ Gedani) st. vet. triangulum constituebat cum stellis illis γ & A rectangulum ad γ. Et distantia cometæ a stella γ æqualis erat distantiæ stellarum γ & A, id est 1gr. 19′. 46″ in circulo magno, atque ideo ea erat 1gr. 20′. 26″ in paralello latitudinis stellæ γ. Quare si de longitudine stellæ γ detrahatur longitudo 1gr. 20′. 26″, manebit longitudo cometæ ♈ 27gr. 9′. 49″. Auzoutius ex hac sua observatione cometam posuit in ♈ 27gr. 0′. circiter. Et ex schemate, quo Hookius motum ejus delineavit, is jam erat in ♈ 26gr. 59′. 24″. Ratione mediocri posui eundem in ♈ 27gr. 4′. 46″. Ex eadem observatione Auzoutius latitudinem cometæ jam posuit 7gr & 4′ vel 5′ boream versus. Eandem rectius posuisset 7gr. 3′. 29″, existente scilicet differentia latitudinum cometæ & stellæ γ æquali differentiæ longitudinum stellarum γ & A.
Feb. 22d. 7h. 30′ Londini, id est Feb. 22d. 8h. 46′ Gedani, distantia cometæ a stella A, juxta observationem Hookii a seipso in schemate delineatam, ut & juxta observationes Auzoutii a Petito in schemate delineatas, erat pars quinta distantiæ inter stellam A & primam arietis, seu 15′. 57″. Et distantia cometæ a linea jungente stellam A & primam arietis erat pars quarta ejusdem partis quintæ, id est 4′. Ideoque cometa erat in ♈ 28gr. 29′. 46″, cum lat. bor. 8gr. 12′. 36″.
Mart. 1d. 7h. 0′ Londini, id est Mart. 1d. 8h. 16′ Gedani, cometa observatus fuit prope secundam arietis, existente distantia inter eosdem ad distantiam inter primam & secundam arietis, hoc est ad 1gr. 33′, ut 4 ad 45 secunduum Hookium, vel ut 2 ad 23 secundum Gottignies. Unde distantia cometæ a secunda arietis erat 8′. 16″ secundum Hookium, vel 8′. 5″ secundum Gottignies, vel ratione mediocri 8′. 10″. Cometa vero secundum Gottignies jam módo prætergressus fuerat secundam arietis quasi spatio quartæ vel quintæ partis itineris uno die confecti, id est 1′. 35″ circiter (quocum satis consentit Auzoutius) vel paulo minorem secundum Hookium, puta 1′. Quare si ad longitudinem primæ arietis addatur 1′, & ad latitudinem ejus 8′. 10″, habebitur longitudo cometæ ♈ 29gr. 18′, & latitudo borealis 8gr. 36′. 26″.
Mart. 7d. 7h. 30′ Parisiis (id est Mart. 7d. 8h. 37′ Gedani) ex observationibus Auzoutii distantia cometæ a secunda arietis æqualis erat distantiæ secundæ arietis a stella A, id est 52′. 29″. Et differentia longitudinum cometæ & secundæ arietis erat 45′ vel 46′, vel ratione mediocri 45′. 30″. Ideoque cometa erat in ♉ 0gr. 2′. 48″. Ex schemate observationum Auzoutii, quod Petitus construxit, Hevelius deduxit latitudinem cometæ 8gr. 54′. Sed sculptor viam cometæ sub finem motus ejus irregulariter incurvavit, & Hevelius in schemate observationum Auzoutii a se constructo incurvationem irregularem correxit, & sic latitudinem cometæ fecit esse 8gr. 55′. 30″. Et irregularitatem paulo magis corrigendo, latitudo evadere potest 8gr. 56′, vel 8gr. 57′.
Visus etiam fuit hic cometa Martii die 9, & tunc locari debuit in ♉ 0gr. 18′, cum lat. bor. 9gr. circiter.
Apparuit hic cometa menses tres, signaque fere sex descripsit, & uno die gradus fere viginti confecit. Cursus ejus a circulo maximo plurimum deflexit, in boream incurvatus; & motus ejus sub finem ex retrogrado factus est directus. Et non obstante cursu tam insolito, theoria a principio ad finem cum observationibus non minus accurate congruit, quam theoriæ planetarum cum eorum observationibus congruere solent, ut inspicienti tabulam patebit. Subducenda tamen sunt minuta duo prima circiter, ubi cometa velocissimus fuit; id quod fiet auferendo duodecim minuta secunda ab angulo inter nodum ascendentem & perihelium, seu constituendo angulum illum 49gr. 27′ 18″. Cometæ utriusque (& hujus & superioris) parallaxis annua insignis fuit, & inde demonstratur motus annuus terræ in orbe magno.
Confirmatur etiam theoria per motum cometæ, qui apparuit anno 1683. Hic fuit retrogradus in orbe, cujus planum cum plano eclipticæ angulum fere rectum continebat. Hujus nodus ascendens (computante Halleio) erat in ♍ 23gr. 23′; inclinatio orbitæ ad eclipticam 83gr. 11′; perihelium in ♊ 25gr. 29′. 30″; distantia perihelia a sole 56020, existente radio orbis magni 100000, & tempore perihelii Julii 2d. 3h. 50′. Loca autem cometæ in hoc orbe ab Halleio computata, & cum locis a Flamstedio observatis collata, exhibentur in tabula sequente.
<523>Confirmatur etiam theoria per motum cometæ retrogradi, qui apparuit anno 1682. Hujus nodus ascendens (computante Halleio erat in ♉ 21gr. 16′. 30″. Inclinatio orbitæ ad planum eclipticæ 17gr. 56′. 0″. Perihelium in ♒ 2gr. 52′. 50″. Distantia perihelia a sole 58328, existente radio orbis magni 100000. Et tempus æquatum perihelii Sept. 4d. 7h. 39′. Loca vero ex observationibus Flamstedii computata, & cum locis per theoriam computatis collata, exhibentur in tabula sequente.
Confirmatur etiam theoria per motum retrogradum cometæ, qui apparuit anno 1723. Hujus nodus ascendens (computante D. Bradleo, astronomiæ apud Oxonienses professore Saviliano) erat in ♈ 14gr. 16′. Inclinatio orbitæ ad planum eclipticæ 49gr. 59′. Perihelium in ♉ 12gr. 15′. 20″. Distantia perihelia a sole 998651, existente radio orbis magni 1000000, & tempore æquato perihelii Septem. 16d. 16h. 10′. Loca vero cometæ in hoc orbe a Bradleo computata, & cum locis a seipso & patruo suo D. Poundio, & a D. Halleio observatis collata exhibentur in tabula sequente.
His exemplis abunde satis manifestum est, quod motus cometarum per theoriam a nobis expositam non minus accurate exhibentur, quam solent motus planetarum per eorum theorias. Et propterea orbes cometarum per hanc theoriam enumerari possunt, & tempus periodicum cometæ in quolibet orbe revolventis tandem sciri, & tum demum orbium ellipticorum latera transversa & apheliorum altitudines innotescent.
Cometa retrogradus qui apparuit anno 1607, descripsit orbem, cujus nodus ascendens (computante Halleio) erat in ♉ 20gr. 21′; inclinatio plani orbis ad planum eclipticæ erat 17gr. 2′; perihelium erat in ♒ 2gr. 16′; & distantia perihelia a sole erat 58680, existente radio orbis magni 100000. Et cometa erat in perihelio Octob. 16d. 3h. 50′. Congruit hic orbis quamproxime cum orbe cometæ, qui apparuit anno 1682. Si cometæ hi duo fuerint unus & idem, revolvetur hic cometa spatio annorum 75, & axis major orbis ejus erit ad axem majorem orbis magni, ut : ad 1, seu 1778 ad 100 circiter. Et distantia aphelia cometæ hujus a sole, erit ad distantiam mediocrem terræ a sole, ut 35 ad 1 circiter. Quibus cognitis, haud difficile fuerit orbem ellipticum cometæ hujus determinare. Atque hæc ita se habebunt si cometa, spatio annorum septuaginta quinque, in hoc orbe posthac redierit. Cometæ reliqui majori tempore revolvi videntur & altius ascendere.
Cæterum cometæ, ob magnum eorum numerum, & magnam apheliorum a sole distantiam, & longam moram in apheliis, per gravitates in se mutuo nonnihil turbari debent, & eorumm eccentricitates & revolutionum tempora nunc augeri aliquantulum, nunc diminui. Proinde non est expectandum ut cometa idem in eodem orbe, & iisdem temporibus periodicis accurate redeat. Sufficit si mutationes non majores obvenerint, quam quæ a causis prædictis oriantur.
Et hinc ratio redditur cur cometæ non comprehendantur zodiaco more planetarum, sed inde migrent & motibus variis in omnes cœlorum regiones ferantur. Scilicet eo fine, ut in apheliis suis, ubi tardissime moventur, quam longissime distent ab invicem, & se mutuo quam minime trahant. Qua de causa cometæ, qui altius descendunt, ideoque tardissime moventur in apheliis, debent altius ascendere.
Cometa, qui anno 1680 apparuit, minus distabat a sole in perihelio suo quam parte sexta diametri solis; & propter summam velocitatem in vicinia illa, & densitatem aliquam atmosphæræ solis, resistentiam nonnullam sentire debuit, & aliquantulum retardari, & propius ad solem accedere: & singulis revolutionibus accedendo ad solem, incidet is tandem in corpus Solis. Sed & in aphelio ubi tardissime movetur, aliquando per attractionem aliorum cometarum retardari potest, & subinde in solem incidere. Sic etiam stellæ fixæ, quæ paulatim expirant in lucem & vapores, cometis in ipsas incidentibus refici possunt, & novo alimento accensæ pro stellis novis haberi. Hujus generis sunt stellæ fixæ, quæ subito apparent, & sub initio quam maxime splendent, & subinde paulatim evanescunt. Talis fuit stella in cathedra Cassiopeiæ quam Cornelius Gemma octavo Novembris 1572, lustrando illam cœli partem nocte serena minime vidit; at nocte proxima (Novem. 9.) vidit fixis omnibus splendidiorem, & luce sua vix cedentem veneri. Hanc Tycho Brahæus vidit undecimo ejusdem mensis ubi maxime splenduit; & ex eo tempore paulatim decrescentem & spatio mensium sexdecim evanescentem observavit. Mense Novembri, ubi primum apparuit, venerem luce sua æquabat. Mense Decembri nonnihil diminuta jovem æquare videbatur. Anno 1573, mense Januario minor erat jove & major Sirio, cui in fine Februarii & Martii initio evasit æqualis. Mense Aprili & Maio stellis secundæ magnitudinis, Junio, Julio & Augusto stellis tertiæ magnitudinis, Septembri, Octobri & Novembri stellis quartæ, Decembri & anni 1574, mense Januario stellis quintæ, & mense Februario stellis sextæ magnitudinis æqualis videbatur, & mense Martio ex oculis evanuit. Color illi ab initio clarus, albicans ac splendidus, postea flavus, & anni 1573 mense Martio rutilans instar martis aut stellæ aldebaran; Maio autem albitudinem sublividam induxit, qualem in saturno cernimus, quem colorem usque in finem servavit, semper tamen obscurior facta. Talis etiam fuit stella in dextro pede serpentarii, quam Kepleri discipuli anno 1604, die 30 Septembris st. vet. apparere cœpisse observarunt, & luce sua stellam jovis superasse, cum nocte præcedente minime apparuisset. Ab eo vero tempore paulatim decrevit, & spatio mensium quindecim vel sexdecim ex oculis evanuit. Tali etiam stella nova supra modum splendente Hipparchus ad fixas observandas & in catalogum referendas excitatus fuisse dicitur. Sed fixæ, quæ per vices apparent & evanescunt, quæque paulatim crescunt, & luce sua fixas tertiæ magnitudinis vix unquam superant, videntur esse generis alterius, & revolvendo partem lucidam & partem obscuram per vices ostendere. Vapores autem qui ex sole & stellis fixis & caudis cometarum oriuntur, incidere possunt per gravitatem suam in atmospheæras planetarum & ibi condensari & converti in aquam & spiritus humidos, & subinde per lentum calorem in sales, & sulphura, & tincturas, & limum, & lutum, & argillam, & arenam, & lapides, & coralla, & substantias alias terrestres paulatim migrare.
SCHOLIUM GENERALE.
Hypothesis vorticum multis premitur difficultatibus. Ut planeta unusquisque radio ad solem ducto areas describat tempori proportionales, tempora periodica partium vorticis deberent esse in duplicata ratione distantiarum a sole. Ut periodica planetarum tempora sint in proportione sesquiplicata distantiarum a sole, tempora periodica partium vorticis deberent esse in sesquiplicata distantiarum proportione. Ut vortices minores circum saturnum, jovem & alios planetas gyrati conserventur & tranquille natent in vortice solis, tempora periodica partium vorticis solaris deberent esse æqualia. Revolutiones solis & planetarum circum axes suos, quæ cum motibus vorticum congruere deberent, ab omnibus hisce proportionibus discrepant. Motus cometarum sunt summe regulares, & easdem leges cum planetarum motibus observant, & per vortices explicari nequeunt. Feruntur cometæ motibus valde eccentricis in omnes cœlorum partes, quod fieri non potest, nisi vortices tollantur.
Projectilia, in aëre nostro, solam aëris resistentiam sentiunt. Sublato aëre, ut fit in vacuo Boyliano, resistentia cessat, siquidem pluma tenuis & aurum solidum æquali cum velocitate in hoc vacuo cadunt. Et par est ratio spatiorum cœlestium, quæ sunt supra atmosphæram terræ. Corpora omnia in istis spatiis liberrime moveri debent; & propterea planetæ & cometæ in orbibus specie & positione datis secundum leges supra expositas perpetuo revolvi. Perseverabunt quidem in orbibus suis per leges gravitatis, sed regularem orbium situm primitus acquirere per leges hasce minime potuerunt.
Planetæ sex principales revolvuntur circum solem in circulis soli concentricis, eadem motus directione, in eodem plano quamproxime. Lunæ decem revolvuntur circum terram, jovem & saturnum in circulis concentricis, eadem motus directione, in planis orbium planetarum quamproxime. Et hi omnes motus regulares originem non habent ex causis mechanicis; siquidem cometæ in orbibus valde eccentricis, & in omnes cœlorum partes libere feruntur. Quo motus genere cometæ per orbes planetarum celerrime & facillime transeunt, & in apheliis suis ubi tardiores sunt & diutius morantur; quam longissime distant ab invicem, ut se mutuo quam minime trahant. Elegantissima hæcce solis, planetarum & cometarum compages non nisi consilio & dominio entis intelligentis & potentis oriri potuit. Et si stellæ fixæ sint centra similium systematum; hæc omnia simili consilio constructa, suberunt Unius dominio: præsertim cum lux fixarum sit ejusdem naturæ ac lux solis, & systemata omnia lucem in omnia invicem immittant. Et ne fixarum systemata per gravitatem suam in se mutuo cadant, hic eadem immensam ab invicem distantiam posuerit.
<528>Hic omnia regit non ut anima mundi, sed ut universorum dominus. Et propter dominium suum, dominus deus [1]Παντοκράτωρ dici solet. Nam deus est vox relativa & ad servos refertur: & deitas est dominatio dei, non in corpus proprium, uti sentiunt quibus deus est anima mundi, sed in servos. Deus summus est ens æternum, infinitum, absolute perfectum: sed ens utcunque perfectum sine dominio non est dominus deus. Dicimus enim deus meus, deus vester, deus Israelis, deus deorum, & dominus dominorum: sed non dicimus æternus meus, æternus vester, æternus Israelis, æternus deourum; non dicimus infinitus meus, vel perfectus meus. Hæ appellationes relationem non habent ad servos. Vox deus passim[2] significat dominum: sed omnis dominus non est deus. Dominatio entis spiritualis deum constituit, vera verum, summa summum, ficta fictum. Et ex dominatione vera sequitur deum verum esse vivum, intelligentem & potentem; ex reliquis perfectionibus summum esse, vel summe perfectum. Æternus est & infinitus, omnipotens & omnisciens, id est, durat ab æterno in æternum, & adest ab in infinitum: omnia regit; & omnia cognoscit, quæ fiunt aut fieri possunt. Non est æternitas & infinitas, sed æternus & infinitus; non est duratio & spatium, sed durat & adest. Durat semper & adest ubique, & existendo semper & ubique, durationem & spatium constituit. Cum unaquæque spatii particula sit semper, & unumquodque durationis indivisibile momentum ubique, certe rerum omnium fabricator ac dominus non erit nunquam, nusquam. Omnis anima sentiens diversis temporibus, & in diversis sensuum, & motuum organis eadem est persona indivisibilis. Partes dantur successivæ in duratione, coexistentes in spatio, neutræ in persona hominis seu principio ejus cogitante; & multo minus in substantia cogitante dei. Omnis homo, quatenus res sentiens, est unus & idem homo durante vita sua in omnibus & singulis sensuum organis. Deus est unus & idem deus semper & ubique. Omnipræsens est non per virtutem solam, sed etiam per substantiam: nam virtus sine substantia subsistere non potest. In ipso[3] continentur & moventur universa, sed sine mutua passione. Deus nihil patitur ex corporum motibus: illa nullam sentiunt resistentiam ex omnispræsentia dei. Deum summum necessario existere in confesso est: Et eadem necessitate semper est & ubique. Unde etiam totus est sui similis, totus oculus, totus auris, totus cerebrum, totus brachium, totus vis sentiendi, intelligendi, & agendi, sed more minime humano, more minime corporeo, more nobis prorsus incognito. Ut cæcus non habet ideam colorum, sic nos ideam non habemus modorum, quibus deus sapientissimus sentit & intelligit omnia. Corpore omni & figura corporea prorsus destituitur, ideoque videri non potest, nec audiri, nec tangi, nec sub specie rei alicujus corporei coli debet. Ideas habemus attributorum ejus, sed quid sit rei alicujus substantia minime cognoscimus. Videmus tantum corporum figuras & colores, audimus tantum sonos, tangimus tantum superficies externas, olfacimus odores solos, & gustamus sapores; intimas substantias nullo sensu, nulla actione reflexa cognoscimus; & multo minus ideam habemus substantiæ dei. Hunc cognoscimus solummodo per proprietates ejus & attributa, & per sapientissimas & optimas rerum structuras & causas finales, & admiramur ob perfectiones; veneramur autem & colimus ob dominium. Colimus enim ut servi, & deus sine dominio, providentia, & causis finalibus nihil aliud est quam fatum & natura. A cæca necessitate metaphysica, quæ utique eadem est semper & ubique, nulla oritur rerum variatio. Tota rerum conditarum pro locis ac temporibus diversitas, ab ideis & voluntate entis necessario existentis solummodo oriri potuit. Dicitur autem deus per allegoriam videre, audire, loqui, ridere, amare, odio habere, cupere, dare, accipere, gaudere, irasci, pugnare, fabricare, condere, construere. Nam sermo omnis de deo a rebus humanis per similitudinem aliquam desumitur, non perfectam quidem, sed aliqualem tamen. Et hæc de deo; de quo utique ex phænomenis disserere, ad philosophiam naturalem pertinet.
<530>Hactenus phænomena cælorum & maris nostri per vim gravitatis exposui, sed causam gravitatis nondum assignavi. Oritur utique hæc vis a causa aliqua, quæ penetrat ad usque centra solis & planetarum, sine virtutis diminutione; quæque agit non pro quantitate superficierum particularum, in quas agit (ut solent causæ mechanicæ) sed pro quantitate materiæ solidæ; & cujus actio in immensas distantias undique extenditur, decrescendo semper in duplicata ratione distantiarum. Gravitas in solem componitur ex gravitatibus in singulas solis particulas, & recedendo a sole decrescit accurate in duplicata ratione distantiarum ad usque orbem saturni, ut ex quiete apheliorum planetarum manifestum est, & ad usque ultima cometarum aphelia, si modo aphelia illa quiescant. Rationem vero harum gravitatis proprietatum ex phænomenis nondum potui deducere, & hypotheses non fingo. Quicquid enim ex phænomenis non deducitur, hypothesis vocanda est; & hypotheses seu metaphysicæ, seu physicæ, seu qualitatum occultarum, seu mechanicæ, in philosophia experimentali locum non habent. In hac philosophia propositiones deducuntur ex phænomenis, & redduntur generales per inductionem. Sic impenetrabilitas, mobilitas, & impetus corporum & leges motuum & gravitatis innotuerunt. Et satis est quod gravitas revera existat, & agat secundum leges a nobis expositas, & ad corporum cælestium & maris nostri motus omnes sufficiat.
Adjicere jam liceret nonnulla de spiritu quodam subtilissimo corpora crassa pervadente, & in iisdem latente; cujus vi & actionibus particulæ corporum ad minimas distantias se mutuo attrahunt, & contiguæ factæ cohærent; & corpora electrica agunt ad distantias majores, tam repellendo quam attrahendo corpuscula vicina; & lux emittitur, reflectitur, refringitur, inflectitur, & corpora calefacit; & sensatio omnis excitatur, & membra animalium ad voluntatem moventur, vibrationibus scilicet hujus spiritus per solida nervorum capillamenta ab externis sensuum organis ad cerebrum & a cerebro in musculos propagatis. Sed hæc paucis exponi non possunt; neque adest sufficiens copia experimentorum, quibus leges actionum hujus spiritus accurate determinari & monstrari debent.
FINIS.
[1] Id est Imperator universalis.
[2] Pocockus noster vocem dei deducit a voce Arabica du, (& in casu obliquo di,) quæ dominum significat. Et hoc sensu principes vocantur dii, Psalm. lxxxiv. 6. & Joan. x. 45. Et Moses dicitur deus fratris Aaron, & deus regis Pharaoh (Exod. iv. 16. & vii 1.) Et eodem sensu animæ principum mortuorum olim a gentibus vocabantur dii, sed falso propter defectum dominii.
[3] Ita sentiebant veteres, ut Pythagoras apud Ciceronem, de Natura deorum, lib. 1. Thales, Anaxagoras, Virgilius Georgic. lib. iv. v. 220, & Æneid. lib 6. v. 721. Philo Allegor. lib. 1. sub initio. Aratus in Phænom. sub initio. Ita etiam scriptores sacri ut Paulus in Act. xvii. 27, 28. Johannes in Evang. xiv. 2. Moses in Deut. iv. 39. & x. 14. David Psal. cxxxix. 7, 8, 9. Solomon 1 Reg. viii. 27. Job xxii. 12, 13, 14. Jeremias xxiii. 23, 24. Fingebant autem idololatræ solem, lunam, & astra, animas hominum & alias mundi partes esse partes dei summi & ideo colendas sed falso.
