The Second Book of Opticks. Part II (1704)
THE
SECOND BOOK
OF
OPTICKS.
PART II.
Remarks upon the foregoing Observations.
HAving given my Observations of these Colours, before I make use of them to unfold the Causes of the Colours of natural Bodies, it is convenient that by the simplest of them, such as are the 2d, 3d, 4th, 9th, 12th, 18th, 20th, and 24th, I first explain the more expounded. And first to shew how the Colours in the fourth and eighteenth Observations are produced, let there be taken in any right line from the Point Y,[Image 1] the Lengths YA, YB, YC, YD, YE, YF, YG, YH, in proportion to one another, as the Cube-roots of the Squares of the numbers, , , , , , {}, , 1, whereby the lengths of a musical Chord to sound all the Notes in an Eighth are represented; that is, in the proportion of the numbers 6300, 6814, 7114, 7631, 8255, 8855, 9243, 10000. And at the Points A, B, C, D, E, F, G, H, let perpendiculars Aα, Bβ, &c. be erected, by whose intervals the extent of the several Colours set underneath against them, is to be represented. Then divide the line Aα in such proportion as the numbers 1, 2, 3, 5, 6, 7, 9, 10, 11, &c. set at the points of division denote. And through those divisions from Y draw Lines 1I, 2K, 3L, 5M, 6N, 7O, &c.
Now if A2 be supposed to represent the thickness of any thin transparent Body, at which the outmost violet is most copiously reflected in the first Ring, or Series of Colours, then by the 13th Observation HK, will represent its thickness, at which the utmost red is most copiously reflected in the same Series. Also by the 5th and 16th Observations, A6 and HN will denote the thicknesses at which those extreme Colours are most copiously reflected in the second Series, and A10 and HQ the thicknesses, at which they are most copiously reflected in the third Series, and so on. And the thickness at which any of the intermediate Colours are reflected most copiously, will, according to the 14th Observation, be defined by the distance of the line AH from the intermediate parts of the lines 2K, 6N, 10Q, &c. against which the names of those Colours are written below.
But further, to define the latitude of these Colours in each Ring or Series, let A 1 design the least thickness, and A3 the greatest thickness, at which the extreme violet in the first Series is reflected, and let HI, and HL, design the like limits for the extreme red, and let the intermediate Colours be limited by the intermediate parts of the Lines 1I, and 3L, against which the names of those Colours are written, and so on: But yet with this caution, that the reflexions be supposed strongest at the intermediate Spaces, 2K, 6N, 10Q, &c. and from thence to decrease gradually towards these limits, 1I, 3L, 5M, 7O, &c. on either side; where you must not conceive them to be precisely limited, but to decay indefinitely. And whereas I have assigned the same latitude to every Series, I did it, because although the Colours in the first series seem to be a little broader than the rest, by reason of a stronger reflexion there, yet that inequality is so insensible as scarcely to be determined by Observation.
Now according to this description, conceiving that the rays originally of several Colours are by turns reflected at the Spaces 1I L3, 5M, O7, 9P R11, &c. and transmitted at the Spaces AHI1, 3LM5, 7OP9, &c. it is easy to know what Colour must in the open Air be exhibited at any thickness of a transparent thin body. For if a Ruler be applied parallel to AH, at that distance from it by which the thickness of the body is represented, the alternate Spaces 1IL3, 5MO7, &c. which it crosseth will denote the reflected original Colours, of which the Colour exhibited in the open Air is compounded. Thus if the constitution of the green in the third Series of Colours be desired, apply the Ruler as you see at πρσφ, and by its passing through some of the blue at π and yellow at σ, as well as through the green at ρ, you may conclude that the green exhibited at that thickness of the body is principally constituted of original green, but not without a mixture of some blue and yellow.
<34>By this means you may know how the Colours from the center of the Rings outward ought to succeed in order as they were described in the 4th and 18th Observations. For if you move the Ruler gradually from AH through all distances, having passed over the first space which denotes little or no reflexion to be made by thinnest substances, it will first arrive at 1 the violet, and then very quickly at the blue and green, which together with that violet compound blue, and then at the yellow and red, by whose further addition that blue is converted into whiteness, which whiteness continues during the transit of the edge of the Ruler from I to 3, and after that by the successive deficience of its component Colours, turns first to compound yellow, and then to red, and last of all the red ceaseth at L. Then begin the Colours of the second Series, which succeed in order during the transit of the edge of the Ruler from 5 to O, and are more lively than before, because more expanded and severed. And for the same reason, instead of the former white there intercedes between the blue and yellow a mixture of orange, yellow, green, blue and indico, all which together ought to exhibit a dilute and imperfect green. So the Colours of the third Series all succeed in order; first, the violet, which a little interferes with the red of the second order, and is thereby inclined to a reddish purple; then the blue and green, which are less mixed with other Colours, and consequently more lively than before, especially the green: Then follows the yellow, some of which towards the green is distinct and good, but that part of it towards the succeeding red, as also that red is mixed with the violet and blue of the fourth Series, whereby various degrees of red very much inclining to purple are compounded. This violet and blue, which should succeed this red, being mixed with, and hidden in it, there succeeds a green. And this at first is much inclined to blue, but soon becomes a good green, the only unmixed and lively Colour in this fourth Series. For as it verges towards the yellow, it begins to interfere with the Colours of the fifth Series, by whose mixture the succeeding yellow and red are very much diluted and made dirty, especially the yellow, which being the weaker Colour is scarce able to shew it self. After this the several Series interfere more and more, and their Colours become more and more intermixed, till after three or four more revolutions (in which the red and blue predominate by turns) all sorts of Colours are in all places pretty equally blended, and compound an even whiteness.
And since by the 15th Observation the rays endued with one Colour are transmitted, where those of another Colour are reflected, the reason of the Colours made by the transmitted Light in the 9th and 20th Observations is from hence evident.
If not only the order and species of these Colours, but also the precise thickness of the plate, or thin body at which they are exhibited, be desired in parts of an Inch, that may be also obtained by assistance of the 6th or 16th Observations. For according to those Observations the thickness of the thinned Air, which between two Glasses exhibited the most luminous parts of the first six Rings were , , , , parts of an Inch. Suppose the Light reflected most copiously at these thicknesses be the bright citrine yellow, or confine of yellow and orange, and these thicknesses will be Gμ, Gν, Gξ, Gο, Gτ. And this being known, it is easy to determine what thickness of Air is represented by Gφ, or by any other distance of the Ruler from AH.
But further, since by the 10th Observation the thickness of Air was to the thickness of Water, which between the same Glasses exhibited the same Colour, as 4 to 3, and by the 21th Observation the Colours of thin bodies are not varied by varying the ambient medium; the thickness of a Bubble of Water, exhibiting any Colour, will be of the thickness of Air producing the same Colour. And so according to the same 10th and 21th Observations the thickness of a plate of Glass, whose refraction of the mean refrangible ray, is measured by the proportion of the Sines 31 to 20, may be of the thickness of Air producing the same Colours; and the like of other mediums. I do not affirm, that this proportion of 20 tO 31, holds in all the rays; for the Sines of other sorts of rays have other proportions. But the differences of those proportions are so little that I do not here consider them. On these Grounds I have composed the following Table, wherein the thickness of Air, Water, and Glass, at which each Colour is most intense and specifick, is expressed in parts of an Inch divided into ten hundred thousand equal parts.
<37>The thickness of coloured Plates and Particles of
| Air. | Water. | Glass. | ||
| Very Black | {} | |||
| Black | 1 | {} | ||
| Beginning of Black | 2 | |||
| Their Colours of the first Order, | Blue | |||
| White | ||||
| Yellow | ||||
| Orange | 8 | 6 | ||
| Red | 9 | |||
| Violet | ||||
| Indico | ||||
| Blue | 14 | 9 | ||
| Green | ||||
| Their Colours of the first Order, | Yellow | |||
| Orange | 13 | |||
| Bright Red | ||||
| Scarlet | ||||
| Purple | 21 | {} | ||
| Indico | ||||
| Blue | {} | |||
| Of the third Order, | Green | {} | ||
| Yellow | ||||
| Red | 29 | |||
| Bluish Red | 32 | 24 | ||
| Bluish Green | 34 | 22 | ||
| Of the fourth Order, | Green | |||
| Yellowish Green | 36 | 27 | ||
| Red | 26 | |||
| Of the fifth Order, | Greenish Blue | 46 | ||
| Red | 34 | |||
| Of the sixth Order, | Greenish Blue | 44 | 38 | |
| Red | 65 | 42 | ||
| Of the seventh Order, | Greenish Blue | 71 | {} | |
| Ruddy White | 77 | {} |
Now if this Table be compared with the 6th Scheme, you will there see the constitution of each Colour, as to its Ingredients, or the original Colours of which it is compounded, and thence be enabled to judge of its intenseness or imperfection; which may suffice in explication of the 4th and 18th Observations, unless it be further desired to delineate the manner how the Colours appear, when the two Object-Glasses are lay'd upon one another. To do which, let there be described a large Arc of a Circle, and a streight Line which may touch that Arc, and parallel to that Tangent several occult Lines, at such distances from it, as the numbers set against the several Colours in the Table denote. For the Arc, and its Tangent, will represent the superficies of the Glasses terminating the interjacent Air; and the places where the occult Lines cut the Arc will show at what distances from the Center, or Point of contact, each Colour is reflected.
There are also other uses of this Table: For by its assistance the thickness of the Bubble in the 19th Observation was determined by the Colours which it exhibited. And so the bigness of the parts of natural Bodies may be conjectured by their Colours, as shall be hereafter shewn. Also, if two or more very thin plates be lay'd one upon another, so as to compose one plate equalling them all in thickness, the resulting Colour may be hereby determined. For instance, Mr. Hook in his Micrographia observes, that a faint yellow plate of Muscovy-glass lay'd upon a blue one, constituted a very deep purple. The yellow of the first Order is a faint one, and the thickness of the plate exhibiting it, according to the Table is , to which add 9, the thickness exhibiting blue of the second Order, and the sum will be , which is the thickness exhibiting the purple of the third Order.
To explain, in the next place, the Circumstances of the 2d and 3d Observations; that is, how the Rings of the Colours may (by turning the Prisms about their common Axis the contrary way to that expressed in those Observations) be converted into white and black Rings, and afterwards into Rings of Colours again, the Colours of each Ring lying now in an inverted order; it must be remembered, that those Rings of Colours are dilated by the obliquation of the rays to the Air which intercedes the Glasses, and that according to the Table in the 7th Observation, their dilatation or increase of their diameter is most manifest and speedy when they are obliquest. Now the rays of yellow being more refracted by the first superficies of the said Air than those of red, are thereby made more oblique to the second superficies, at which they are reflected to produce the coloured Rings, and consequently the yellow Circle in each Ring will be more dilated than the red; and the excess of its dilatation will be so much the greater, by how much the greater is the obliquity of the rays, until at last it become of equal extent with the red of the same Ring. And for the same reason the green, blue and violet, will be also so much dilated by the still greater obliquity of their rays, as to become all very nearly of equal extent with the red, that is, equally distant from the center of the Rings. And then all the Colours of the same Ring must be coincident, and by their mixture exhibit a white Ring. And these white Rings must have black and dark Rings between them, because they do not spread and interfere with one another as before. And for that reason also they must become distincter and visible to far greater Numbers. But yet the violet being obliquest will be something more dilated in proportion to its extent than the other Colours, and so very apt to appear at the exterior verges of the white.
Afterwards, by a greater obliquity of the rays, the violet and blue become more sensibly dilated than the red and yellow, and so being further removed from the center of the Rings, the Colours must emerge out of the white in an order contrary to that which they had before, the violet and blue at the exterior limbs of each Ring,and the red and yellow at the interior. And the violet, by reason of the greatest obliquity of its rays, being in proportion most of all expanded, will soonest appear at the exterior limb of each white Ring, and become more conspicuous than the rest. And the several Series of Colours belonging to the several Rings, will, by their unfolding and spreading, begin again to interfere, and thereby render the Rings less distinct, and not visible to so great numbers.
If instead of the Prisms the Object-glasses be made use of, the Rings which they exhibit become not white and distinct by the obliquity of the Eye, by reason that the rays in their passage through that Air which intercedes the Glasses are very nearly parallel to those Lines in which they were first incident on the Glasses, and consequently the rays endued with several Colours are not inclined one more than another to that Air, as it happens in the Prisms.
There is yet another circumstance of these Experiments to be considered, and that is why the black and white Rings which when viewed at a distance appear distinct, should not only become confused by viewing them near at hand, but also yield a violet Colour at both the edges of every white Ring. And the reason is, that the rays which enter the Eye at several parts of the Pupil, have several obliquities to the Glasses, and those which are most oblique, if considered apart, would represent the Rings bigger than those which are the least oblique. Whence the breadth of the perimeter of every white Ring is expanded outwards by the obliquest rays, and inwards by the least oblique. And this expansion is so much the greater by how much the greater is the difference of the obliquity; that is, by how much the Pupil is wider, or the Eye nearer to the Glasses. And the breadth of the violet must be most expanded, because the rays apt to excite a sensation of that Colour are most oblique to a second, or further superficies of the thin'd Air at which they are reflected, and have also the greatest variation of obliquity, which makes that Colour soonest emerge out of the edges of the white. And as the breadth of every Ring is thus augmented, the dark intervals must be diminished, until the neighbouring Rings become continuous, and are blended, the exterior first, and then those nearer the Center, so that they can no longer be distinguish'd apart, but seem to constitute an even and uniform whiteness.
Among all the Observations there is none accompanied with so odd circumstances as the 24th. Of those the principal are, that in thin plates, which to the naked Eye seem of an even and uniform transparent whiteness, without any terminations of shadows, the refraction of a Prism should make Rings of Colours appear, whereas it usually makes Objects appear coloured only there where they are terminated with shadows, or have parts unequally luminous; and that it should make those Rings exceedingly distinct and white, although it usually renders Objects confused and coloured. The cause of these things you will understand by considering, that all the Rings of Colours are really in the plate, when viewed with the naked Eye, although by reason of the great breadth of their circumferences they so much interfere and are blended together, that they seem to constitute an even whiteness. But when the rays pass through the Prism to the Eye, the orbits of the several Colours in every Ring are refracted, some more than others, according to their degrees of refrangibility: By which means the Colours on one side of the Ring (that is on one side of its Center) become more unfolded and dilated, and those on the other side more complicated and contracted. And where by a due refraction they are so much contracted, that the several Rings become narrower than to interfere with one another, they must appear distinct, and also white, if the constituent Colours be so much contracted as to be wholly coincident. But, on the other side, where the orbit of every Ring is made broader by the further unfolding of its Colours, it must interfere more with other Rings than before, and so become less distinct.
To explain this a little further, suppose the concentrick Circles AV, and BX,[Image 2] represent the red and violet of any order, which, together with the intermediate Colours, constitute any one of these Rings. Now these being viewed through a Prism, the violet Circle BX, will by a greater refraction be further translated from its place than the red AV, and so approach nearer to it on that side, towards which the refractions are made. For instance, if the red be translated to av, the violet may be translated to bx, so as to approach nearer to it at x than before, and if the red be further translated to av, the violet may be so much further translated to bx as to convene with it at x, and if the red be yet further translated to αY, the violet may be still so much further translated to βξ as to pass beyond it at ξ, and convene with it at e and f. And this being understood not only of the red and violet, but of all the other intermediate Colours, and also of every revolution of those Colours, you will easily perceive how those of the same revolution or order, by their nearness at xv and Yξ, and their coincidence at xv, e and f, ought to constitute pretty distinct Arcs of Circles, especially at xv, or at e and f, and that they will appear severally at xv, and at xv exhibit whiteness by their coincidence, and again appear several at Yξ, but yet in a contrary order to that which they had before, and still retain beyond e and f. But, on the other side, at ab, ab, or αβ, these Colours must become much more confused by being dilated and spread so, as to interfere with those of other Orders. And the same confusion will happen at Yξ between e and f, if the refraction be very great, or the Prism very distant from the Object-Glasses: In which case no parts of the Rings will be seen, save only two little Arcs at e and f, whose distance from one another will be augmented by removing the Prism still further from the Object-Glasses: And these little Arcs must be distinctest and whitest at their middle, and at their ends, where they begin to grow confused they must be coloured. And the Colours at one end of every Arc must be in a contrary order to those at the other end, by reason that they cross in the intermediate white; namely their ends, which verge towards Yξ, will be red and yellow on that side next the Center, and blue and violet on the other side. But their other ends which verge from Yξ will on the contrary be blue and violet on that side towards the Center, and on the other side red and yellow.
Now as all these things follow from the Properties of Light by a mathematical way of reasoning, so the truth of them may be manifested by Experiments. For in a dark room, by viewing these Rings through a Prism, by reflexion of the several prismatique Colours, which an assistant causes to move to and fro upon a Wall or Paper from whence they are reflected, whilst the Spectator's Eye, the Prism and the Object-Glasses (as in the 13th Observation) are placed steddy: the position of the Circles made successively by the several Colours, will be found such, in respect of one another, as I have described in the Figures abxv, or abxv, or αβξY. And by the same method the truth of the Explications of other Observations may be examined.
By what hath been said the like Phænomena of Water, and thin plates of Glass may be understood. But in small fragments of those plates, there is this further observable, that where they lye flat upon a Table and are turned about their Centers whilst they are viewed through a Prism, they will in some postures exhibit waves of various Colours, and some of them exhibit these waves in one or two Positions only, but the most of them do in all positions exhibit them, and make them for the most part appear almost all over the plates. The reason is, that the superficies of such plates are not even, but have many cavities and swellings, which how shallow soever do a little vary the thickness of the plate. For at the several sides of those cavities, for the reasons newly described, there ought to be produced waves in several postures of the Prism. Now though it be but some very small, and narrower parts of the Glass, by which these waves for the most part are caused, yet they may seem to extend themselves over the whole Glass, because from the narrowest of those parts there are Colours of several Orders that is of several Rings, confusedly reflected, which by refraction of the Prism are unfolded, separated, and according to their degrees of refraction, dispersed to several places, so as to constitute so many several waves, as there were divers orders of Colours promiscuously reflected from that part of the Glass.
These are the principal Phænomena of thin Plates or Bubbles, whose explications depend on the properties of Light, which I have heretofore delivered. And these you see do necessarily follow from them, and agree with them, even to their very least circumstances; and not only so, but do very much tend to their proof. Thus, by the 24th Observation, it appears, that the rays of several Colours made as well by thin Plates or Bubbles, as by refractions of a Prism, have several degrees of refrangibility, whereby those of each order, which at the reflexion from the Plate or Bubble are intermixed with those of other orders, are separated from them by refraction, and associated together so as to become visible by themselves like Arcs of Circles. For if the rays were all alike refrangible, 'tis impossible that the whiteness, which to the naked sence appears uniform, should by refraction have its parts transposed and ranged into those black and white Arcs.
It appears also that the unequal refractions of difform rays proceed not from any contingent irregularities; such as are veins, an uneven polish, or fortuitous position of the pores of Glass; unequal and casual motions in the Air or Æther, the spreading, breaking, or dividing the same ray into many diverging parts, or the like. For, admitting any such irregularities, it would be impossible for refractions to render those Rings so very distinct, and well defined, as they do in the 24th Observation. It is necessary therefore that every ray have its proper and constant degree of refrangibility connate with it,according to which its refraction is ever justly and regularly performed, and that several rays have several of those degrees.
And what is said of their refrangibility may be also understood of their reflexibility, that is of their dispositions to be reflected some at a greater, and others at a less thickness, of thin Plates or Bubbles, namely, that those dispositions are also connate with the rays, and immutable; as may appear by the 13th, 14th, and 15th Observations compared with the fourth and eighth.
By the precedent Observations it appears also, that whiteness is a dissimilar mixture of all Colours, and that Light is a mixture of rays indued with all those Colours. For considering the multitude of the Rings of Colours, in the 3d, 12th and 24th Observations, it is manifest that although in the 4th and 18th Observations there appear no more than eight or nine of those Rings, yet there are really a far greater number, which so much interfere and mingle with one another, as after those eight or nine revolutions to dilute one another wholly, and constitute an even and sensibly uniform whiteness. And consequently that whiteness must be allowed a mixture of all Colours, and the Light which conveys it to the Eye must be a mixture of rays indued with all those Colours.
But further, by the 24th Observation, it appears, that there is a constant relation between Colours and Refrangibility, the most refrangible rays being violet, the least refrangible red, and those of intermediate Colours having proportionably intermediate degrees of refrangibility. And by the 13th, 14th and 15th Observations, compared with the 4th or 18th, there appears to be the same constant relation between Colour and Reflexibility, the violet being in like circumstances reflected at least thicknesses of any thin Plate or Bubble, the red at greatest thicknesses, and the intermediate Colours at intermediate thicknesses. Whence it follows, that the colorifique dispositions of rays are also connate with them and immutable, and by consequence that all the productions and appearances of Colours in the World are derived not from any physical change caused in Light by refraction or reflexion, but only from the various mixtures or separations of rays, by virtue of their different Refrangibility or Reflexibility. And in this respect the Science of Colours becomes a Speculation as truly mathematical as any other part of Optiques. I mean so far as they depend on the nature of Light, and are not produced or altered by the power of imagination, or by striking or pressing the Eyes.
[Image 1] Fig. 5. {sic} 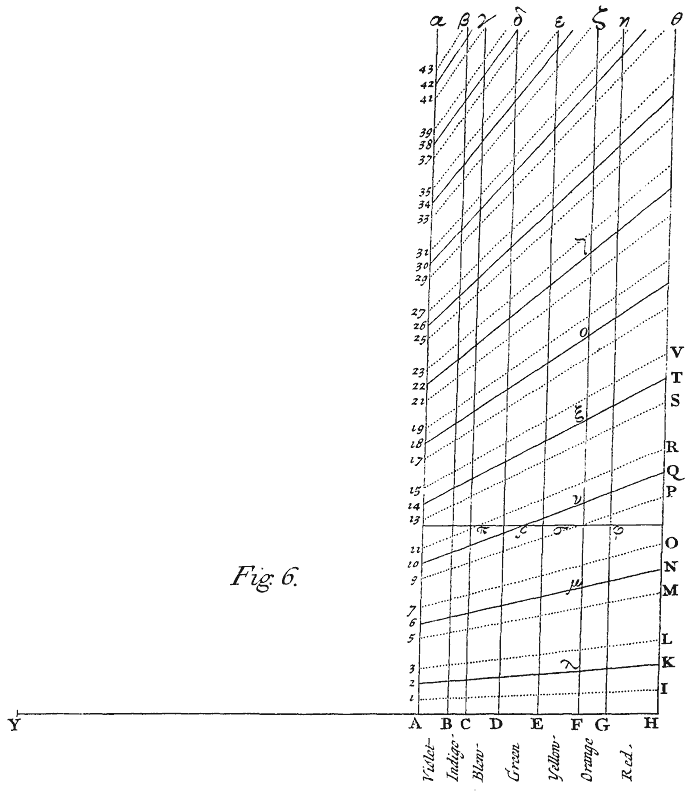
[Image 2] Fig. 7. 
