The Second Book of Opticks. Part I (1704)
THE
SECOND BOOK
OF
OPTICKS.
PART I.
Observations concerning the Reflexions, Refractions, and Colours of thin transparent Bodies.
IT has been observed by others that transparent Substances, as Glass, Water, Air, &c. when made very thin by being blown into Bubbles, or otherwise formed into Plates, do exhibit various Colours according to their various thinness, although at a greater thickness they appear very clear and colourless. In the former Book I forbore to treat of these Colours, because they seemed of a more difficult consideration, and were not necessary for establishing the Properties of Light there discoursed of. But because they may conduce to further discoveries for completing the Theory of Light, especially as to the constitution of the parts of natural Bodies, on which their Colours or Transparency depend; I have here set down an account of them. To render this Discourse short and distinct, I have first described the principal of my Observations, and then considered and made use of them. The Observations are these.
OBS. I.
Compressing two Prisms hard together that their Sides (which by chance were a very little convex)might somewhere touch one another: I found the place in which they touched to become absolutely transparent, as if they had there been one continued piece of Glass. For when the Light fell so obliquely on the Air, which in other places was between them,as to be all reflected; it seemed in that place of contact to be wholly transmitted, insomuch that when looked upon, it appeared like a black or dark Spot, by reason that little or no sensible Light was reflected from thence, as from other places; and when looked through it seemed (as it were) a hole in that Air which was formed into a thin Plate, by being compressed between the Glasses. And through this hole Objects that were beyond might be seen distinctly, which could not at all be seen through other parts of the Glasses where the Air was interjacent. Although the Glasses were a little convex, yet this transparent Spot was of a considerable breadth, which breadth seemed principally to proceed from the yielding inwards of the parts of the Glasses, by reason of their mutual pressure. For by pressing them very hard together it would become much broader than otherwise.
<3>OBS. II.
When the Plate of Air, by turning the Prisms about their common Axis, became so little inclined to the incident Rays, that some of them began to be transmitted, there arose in it many slender Arcs of Colours which at first were shaped almost like the Conchoid, as you see them delineated in the first Figure.[Image 1] And by continuing the motion of the Prisms, these Arcs increased and bended more and more about the said transparent Spot, till they were completed into Circles or Rings incompassing it, and afterwards continually grew more and more contracted.
These Arcs at their first appearance were of a violet and blue Colour, and between them were white Arcs of Circles, which presently by continuing the motion of the Prisms became a little tinged in their inward Limbs with red and yellow, and to their outward Limbs the blue was adjacent. So that the order of these Colours from the central dark Spot, was at that time white, blue, violet; black; red, orange, yellow, white, blue, violet, &c. But the yellow and red were much fainter than the blue and violet.
The motion of the Prisms about their Axis being continued, these Colours contracted more and more, shrinking towards the whiteness on either side of it, until they totally vanished into it. And then the Circles in those parts appeared black and white, without any other Colours intermixed. But by further moving the Prisms about, the Colours again emerged out of the whiteness, the violet and blue at its inward Limb, and at its outward Limb the red and yellow. So that now their order from the central Spot was white, yellow, red; black; violet, blue, white, yellow, red, &c. contrary to what it was before.
OBS. III.
When the Rings or some parts of them appeared only black and white, they were very distinct and well defined, and the blackness seemed as intense as that of the central Spot. Also in the borders of the Rings, where the Colours began to emerge out of the whiteness, they were pretty distinct, which made them visible to a very great Multitude. I have sometimes numbered above thirty Successions (reckoning every black and white Ring for one Succession) and seen more of them, which by reason of their smalness I could not number. But in other Positions of the Prisms, at which the Rings appeared of many Colours, I could not distinguish above eight or nine of them, and the exterior of those were very confused and dilute.
In these two Observations to see the Rings distinct, and without any other Colour than black and white, I found it necessary to hold my Eye at a good distance from them. For by approaching nearer, although in the same inclination of my Eye to the plane of the Rings, there emerged a blueish Colour out of the white, which by dilating it self more and more into the black rendered the Circles less distinct, and left the white a little tinged with red and yellow. I found also by looking through a slit or oblong hole, which was narrower than the Pupil of my Eye, and held close to it parallel to the Prisms, I could see the Circles much distincter and visible to a far greater number than otherwise.
OBS. IV.
To observe more nicely the order of the Colours which arose out of the white Circles as the Rays became less and less inclined to the plate of Air; I took two Object Glasses, the one a Plano-convex for a fourteen-foot Telescope, and the other a large double convex for one of about fifty-foot; and upon this, laying the other with its plane-side downwards, I pressed them slowly together,to make the Colours successively emerge in the middle of the Circles, and then slowly lifted the upper Glass from the lower to make them successively vanish again in the same place. The Colour, which by pressing the Glasses together emerged last in the middle of the other Colours, would upon its first appearance look like a Circle of a Colour almost uniform from the circumference to the center, and by compressing the Glasses still more, grow continually broader until a new Colour emerged in its center, and thereby it became a Ring encompassing that new Colour. And by compressing the Glasses still more, the Diameter of this Ring would increase, and the breadth of its Orbit or Perimeter decrease until another new Colour emerged in the center of the last: And so on until a third, a fourth, a fifth, and other following new Colours successively emerged there, and became Rings encompassing the innermost Colour, the last of which was the black Spot. And, on the contrary, by lifting up the upper Glass from the lower, the diameter of the Rings would decrease, and the breadth of their Orbit increase, until their Colours reached successively to the center; and then they being of a considerable breadth, I could more easily discern and distinguish their Species than before. And by this means I observed their Succession and Quantity to be as followeth.
Next, to the pellucid central Spot made by the contact of the Glasses succeeded blue, white, yellow, and red, the blue was so little in quantity that I could not discern it in the circles made by the Prisms, nor could I well distinguish any violet in it, but the yellow and red were pretty copious, and seemed about as much in extent as the white, and four or five times more than the blue. The next Circuit in order of Colours immediately encompassing these were violet, blue, green, yellow, and red, and these were all of them copious and vivid, excepting the green, which was very little in quantity, and seemed much more faint and dilute than the other Colours. Of the other four, the violet was the least in extent, and the blue less than the yellow or red. The third Circuit or Order was purple, blue, green, yellow, and red; in which the purple seemed more reddish than the violet in the former Circuit, and the green was much more conspicuous, being as brisque and copious as any of the other Colours, except the yellow; but the red began to be a little faded, inclining very much to purple. After this succeeded the fourth Circuit of green and red. The green was very copious and lively, inclining on the one side to blue, and on the other side to yellow. But in this fourth Circuit there was neither violet, blue, nor yellow, and the red was very imperfect and dirty. Also the succeeding Colours became more and more imperfect and dilute, till after three or four Revolutions they ended in perfect whiteness. Their Form, when the Glasses were most compressed so as to make the black Spot appear in the Center, is delineated in the Second Figure[Image 2]; where a, b, c, d, e: f, g, h, i, k: l, m, n, o, p: q, r: s, t: v, x: y denote the Colours reck'ned in order from the center, black, blue, white, yellow, red: violet, blue, green, yellow, red: purple, blue, green, yellow, red: green, red: greenish blue, red: greenish blue, pale red: greenish blue, reddish white.
OBS. V.
To determine the interval of the Glasses, or thickness of the interjacent Air, by which each Colour was produced, I measured the Diameters of the first six Rings at the most lucid part of their Orbits, and squaring them, I found their Squares to be in the Arithmetical Progression of the odd Numbers, 1. 3. 5. 7. 9. 11. And since one of these Glasses was Plain, and the other Spherical, their Intervals at those Rings must be in the same Progression. I measured also the Diameters of the dark or faint Rings between the more lucid Colours, and found their Squares to be in the Arithmetical Progression of the even Numbers, 2. 4. 6. 8. 10. 12. And it being very nice and difficult to take these measures exactly; I repeated them at divers times at divers parts of the Glasses, that by their Agreement I might be confirmed in them. And the same method I used in determining some others of the following Observations.
OBS. VI.
The Diameter of the sixth Ring at the most lucid part of its Orbit was parts of an Inch, and the Diameter of the Sphere on which the double convex Object-Glass was ground was about 102 Feet, and hence I gathered the thickness of the Air or Aereal Interval of the Glasses at that Ring. But some time after, suspecting that in making this Observation I had not determined the Diameter of the Sphere with sufficient accurateness, and being uncertain whether the Plano-convex Glass was truly plain, and not something concave or convex on that side which I accounted plain; and whether I had not pressed the Glasses together, as I often did, to make them touch. (For by pressing such Glasses together their parts easily yield inwards, and the Rings thereby become sensibly broader than they would be, did the Glasses keep their Figures.) I repeated the Experiment, and found the Diameter of the sixth lucid Ring about parts of an Inch. I repeated the Experiment also with such an Object-Glass of another Telescope as I had at hand. This was a double convex ground on both sides to one and the same Sphere, and its Focus was distant from it Inches. And thence, if the Sines of incidence and refraction of the bright yellow Light be assumed in proportion as 11 to 17, the Diameter of the Sphere to which the Glass was figured will by computation be found 182 Inches. This Glass I laid upon a flat one, so that the black Spot appeared in the middle of the Rings of Colours without any other pressure than that of the weight of the Glass. And now measuring the Diameter of the fifth dark Circle as accurately as I could, I found it the fifth part of an Inch precisely. This measure was taken with the points of a pair of Compasses on the upper surface on the upper Glass, and my Eye was about eight or nine Inches distance from the Glass, almost perpendicularly over it, and the Glass was of an Inch thick, and thence it is easy to collect that the true Diameter of the Ring between the Glasses was greater than its measured Diameter above the Glasses in the proportion Of 80 to 79 or thereabouts, and by consequence equal to parts of an Inch, and its true Semi-diameter equal to parts. Now as the Diameter of the Sphere (182 Inches) is to the Semi-diameter of this fifth dark Ring ( parts of an Inch) so is this Semi-diameter to the thickness of the Air at this fifth dark Ring; which is therefore or parts of an Inch, and the fifth part thereof; viz. the th part of an Inch, is the thickness of the Air at the first of these dark Rings.
The same Experiment I repeated with another double convex Object-glass ground on both sides to one and the same Sphere. Its Focus was distant from it Inches, and therefore the Diameter of that Sphere was 184 Inches. This Glass being laid upon the same plain Glass, the Diameter of the fifth of the dark Rings, when the black Spot in their center appeared plainly without pressing the Glasses, was by the measure of the Compasses upon the upper Glass parts of an Inch, and by consequence between the Glasses it was . For the upper Glass was of an Inch thick, and my Eye was distant from it 8 Inches. And a third proportional to half this from the Diameter of the Sphere is parts of an Inch. This is therefore the thickness of the Air at this Ring, and a fifth part thereof, viz. the th part of an Inch is the thickness thereof at the first of the Rings, as above.
I tryed the same thing by laying these Object-Glasses upon flat pieces of a broken Looking-glass, and found the same measures of the Rings: Which makes me rely upon them till they can be determined more accurately by Glasses ground to larger Spheres, though in such Glasses greater care must be taken of a true plain.
These Dimensions were taken when my Eye was placed almost perpendicularly over the Glasses, being about an Inch, or an Inch and a quarter, distant from the incident rays, and eight Inches distant from the Glass; so that the rays were inclined to the Glass in an Angle of about 4 degrees. Whence by the following Observation you will understand, that had the rays been perpendicular to the Glasses, the thickness of the Air at these Rings would have been less in the proportion of the Radius to the Secant of 4 degrees, that is of 10000. Let the thicknesses found be therefore diminished in this proportion, and they will become and , or (to use the nearest round number) the th part of an Inch. This is the thickness of the Air at the darkest part of the first dark Ring made by perpendicular rays, and half this thickness multiplied by the progression, 1, 3, 5, 7, 9, 11, &c. gives the thicknesses of the Air at the most luminous parts of all the brightest Rings, viz. , , , , &c. their arithmetical means , , , &c. being its thicknesses at the darkest parts of all the dark ones.
OBS. VII.
The Rings were least when my Eye was placed perpendicularly over the Glasses in the Axis of the Rings: And when I viewed them obliquely they became bigger, continually swelling as I removed my Eye further from the Axis. And partly by measuring the Diameter of the same Circle at several obliquities of my Eye, partly by other means, as also by making use of the two Prisms for very great obliquities, I found its Diameter, and consequently the thickness of the Air at its perimeter in all those obliquities to be very nearly in the proportions expressed in this Table.
| Angle of Incidence on the Air. | Angle of Refraction into the Air. | Diameter of the Ring. | Thickness of the Air. |
| Deg. Min. | |||
| 00 00 | 00 00 | 10 | 10 |
| 06 26 | 10 00 | ||
| 12 45 | 20 00 | ||
| 18 49 | 30 00 | {} | |
| 24 30 | 40 00 | {} | 13 |
| 29 37 | 50 00 | ||
| 33 58 | 60 00 | 14 | 20 |
| 35 47 | 65 00 | ||
| 37 19 | 70 00 | ||
| 38 33 | 75 00 | 37 | |
| 39 27 | 80 00 | ||
| 40 00 | 85 00 | 29 | |
| 40 11 | 90 00 | 35 |
In the two first Columns are expressed the obliquities of the incident and emergent rays to the plate of the Air, that is, their angles of incidence and refraction. In the third Column the Diameter of any coloured Ring at those obliquities is expressed in parts, of which ten constitute that Diameter when the rays are perpendicular. And in the fourth Column the thickness of the Air at the circumference of that Ring is expressed in parts of which also ten constitute its thickness when the rays are perpendicular.
And from these measures I seem to gather this Rule: That the thickness of the Air is proportional to the secant of an angle, whose Sine is a certain mean proportional between the Sines of incidence and refraction. And that mean proportional, so far as by these measures I can determine it, is the first of an hundred and six arithmetical mean proportionals between those Sines counted from the Sine of refraction when the refraction is made out of the Glass into the plate of Air, or from the Sine of incidence when the refraction is made out of the plate of Air into the Glass.
OBS. VIII.
The dark Spot in the middle of the Rings increased also by the obliquation of the Eye, although almost insensibly. But if instead of the Object-Glasses the Prisms were made use of, its increase was more manifest when viewed so obliquely that no Colours appeared about it. It was least when the rays were incident most obliquely on the interjacent Air, and as the obliquity decreased it increased more and more until the coloured Rings appeared, and then decreased again, but not so much as it increased before. And hence it is evident, that the transparency was not only at the absolute contact of the Glasses, but also where they had some little interval. I have sometimes observed the Diameter of that Spot to be between half and two fifth parts of the Diameter of the exterior circumference of the red in the first circuit or revolution of Colours when viewed almost perpendicularly; whereas when viewed obliquely it hath wholly vanished and become opake and white like the other parts of the Glass; whence it may be collected that the Glasses did then scarcely, or not at all, touch one another, and that their interval at the perimeter of that Spot when viewed perpendicularly was about a fifth or sixth part of their interval at the circumference of the said red.
OBS. IX.
By looking through the two contiguous Object-Glasses, I found that the interjacent Air exhibited Rings of Colours, as well by transmitting Light as by reflecting it. The central Spot was now white, and from it the order of the Colours were yellowish red; black; violet, blue, white, yellow, red; violet, blue, green, yellow, red, &c. But these Colours were very faint and dilute unless when the Light was trajected very obliquely through the Glasses: For by that means they became pretty vivid. Only the first yellowish red, like the blue in the fourth Observation, was so little and faint as scarcely to be discerned. Comparing the coloured Rings made by reflexion, with these made by transmission of the Light; I found that white was opposite to black, red to blue, yellow to violet, and green to a compound of red and violet. That is, those parts of the Glass were black when looked through, which when looked upon appeared white, and on the contrary. And so those which in one case exhibited blue, did in the other case exhibit red. And the like of the other Colours. The manner you have represented in the third Figure[Image 3], where AB, CD, are the surfaces of the Glasses contiguous at E, and the black lines between them are their distances in arithmetical progression, and the Colours written above are seen by reflected Light, and those below by Light transmitted.
OBS. X.
Wetting the Object-Glasses a little at their edges, the water crept in slowly between them, and the Circles thereby became less and the Colours more faint: Insomuch that as the water crept along one half of them at which it first arrived would appear broken off from the other half, and contracted into a less room. By measuring them I found the proportions of their Diameters to the Diameters of the like Circles made by Air to be about seven to eight, and consequently the intervals of the Glasses at like Circles, caused by those two mediums Water and Air,are as about three to four. Perhaps it may be a general Rule, That if any other medium more or less dense than water be compressed between the Glasses, their intervals at the Rings caused thereby will be to their intervals caused by interjacent Air, as the Sines are which measure the refraction made out of that medium into Air.
OBS. XI
When the water was between the Glasses, if I pressed the upper Glass variously at its edges to make the Rings move nimbly from one place to another, a little white Spot would immediately follow the center of them, which upon creeping in of the ambient water into that place would presently vanish. Its appearance was such as interjacent Air would have caused, and it exhibited the same Colours. But it was not Air, for where any bubbles of Air were in the water they would not vanish. The reflexion must have rather been caused by a subtiler medium, which could recede through the Glasses at the creeping in of the water.
OBS. XII.
These Observations were made in the open Air. But further to examine the effects of coloured Light falling on the Glasses, I darkened the Room, and viewed them by reflexion of the Colours of a Prism cast on a Sheet of white Paper, my Eye being so placed that I could see the coloured Paper by reflexion in the Glasses, as in a Looking-glass. And by this means the Rings became distincter and visible to a far greater number than in the open Air. I have sometimes seen more than twenty of them, whereas in the open Air I could not discern above eight or nine.
<16>OBS. XIII.
Appointing an assistant to move the Prism to and fro about its Axis, that all the Colours might successively fall on that part of the Paper which I saw by reflexion from that part of the Glasses, where the Circles appeared, so that all the Colours might be successively reflected from the Circles to my Eye whilst I held it immovable, I found the Circles which the red Light made to be manifestly bigger than those which were made by the blue and violet. And it was very pleasant to see them gradually swell or contract accordingly as the Colour of the Light was changed. The interval of the Glasses at any of the Rings when they were made by the utmost red Light, was to their interval at the same Ring when made by the utmost violet, greater than as 3 to 2, and less than as 13 to 8,by the most of my Observations it was as 14 to 9. And this proportion seemed very nearly the same in all obliquities of my Eye; unless when two Prisms were made use of instead of the Object-Glasses. For then at a certain great obliquity of my Eye, the Rings made by the several Colours seemed equal, and at a greater obliquity those made by the violet would be greater than the same Rings made by the red. The refraction of the Prism in this case causing the most refrangible rays to fall more obliquely on that plate of the Air than the least refrangible ones. Thus the Experiment succeeded in the coloured Light, which was sufficlently strong and copious to make the Rings sensible. And thence it may be gathered, that if the most refrangible and least refrangible rays had been copious enough to make the Rings sensible without the mixture of other rays, the proportion which here was 14 to 9 would have been a little greater, suppose or {} to 9.
OBS. XIV.
Whilst the Prism was turn'd about its Axis with an uniform motion, to make all the several Colours fall successively upon the Object-Glasses, and thereby to make the Rings contract and dilate: The contraction or dilatation of each Ring thus made by the variation of its Colour was swiftest in the red, and slowest in the violet, and in the intermediate Colours it had intermediate degrees of celerity. Comparing the quantity of contraction and dilatation made by all the degrees of each Colour, I found that it was greatest in the red; less in the yellow, still less in the blue, and least in the violet. And to make as just an estimation as I could of the proportions of their contractions or dilatations, I observed that the whole contraction or dilatation of the Diameter of any Ring made by all the degrees of red, was to that of the Diameter of the same Ring made by all the degrees of violet, as about four to three, or five to four, and that when the Light was of the middle Colour between yellow and green, the Diameter of the Ring was very nearly an arithmetical mean between the greatest Diameter of the same Ring made by the outmost red, and the least Diameter thereof made by the outmost violet: Contrary to what happens in the Colours of the oblong Spectrum made by the refraction of a Prism, where the red is most contracted, the violet most expanded, and in the midst of all the Colours is the confine of green and blue. And hence I seem to collect that the thicknesses of the Air between the Glasses there, where the Ring is successively made by the limits of the five principal Colours (red, yellow, green, blue, violet) in order (that is, by the extreme red, by the limit of red and yellow in the middle of the orange, by the limit of yellow and green, by the limit of green and blue, by the limit of blue and violet in the middle of the indigo, and by the extreme violet) are to one another very nearly as the six lengths of a Chord which found the notes in a sixth Major, sol, la, mi, fa, sol, la. But it agrees something better with the Observation to say, that the thicknesses of the Air between the Glasses there, where the Rings are successively made by the limits of the seven Colours, red, orange, yellow, green, blue, indigo, violet in order, are to one another as the Cube Roots of the Squares of the eight lengths of a Chord, which found the notes in an eighth, sol, la, fa, sol, la, mi, fa, sol; that is, as the Cube Roots of the Squares of the Numbers, 1, , , , , , {}, .
OBS. XV.
These Rings were not of various Colours like those made in the open Air, but appeared all over of that prismatique Colour only with which they were illuminated. And by projecting the prismatique Colours immediately upon the Glasses, I found that the Light which fell on the dark Spaces which were between the Coloured Rings, was transmitted through the Glasses without any variation of Colour. For on a white Paper placed behind, it would paint Rings of the same Colour with those which were reflected, and of the bigness of their immediate Spaces. And from thence the origin of these Rings is manifest; namely, That the Air between the Glasses, according to its various thickness, is disposed in some places to reflect, and in others to transmit the Light of any one Colour (as you may see represented in the fourth Figure[Image 4]) and in the same place to reflect that of one Colour where it transmits that of another.
OBS. XVI.
The Squares of the Diameters of these Rings made by any prismatique Colour were in arithmetical progression as in the fifth Observation. And the Diameter of the sixth Circle, when made by the citrine yellow, and viewed almost perpendicularly, was about parts of an Inch, or a little less, agreeable to the sixth Observation.
The precedent Observations were made with a rarer thin medium, terminated by a denser, such as was Air or Water compressed between two Glasses. In those that follow are set down the appearances of a denser medium thin'd within a rarer, such as are plates of Muscovy-glass, Bubbles of Water, and some other thin substances terminated on all sides with Air.
<20>OBS. XVII.
If a Bubble be blown with Water first made tenacious by dissolving a little Soap in it, 'tis a common Observation, that after a while it will appear tinged with a great variety of Colours. To defend these Bubbles from being agitated by the external Air (whereby their Colours are irregularly moved one among another, so that no accurate Observation can be made of them,) as soon as I had blown any of them I covered it with a clear Glass, and by that means its Colours emerged in a very regular order, like so many concentrick Rings incompassing the top of the Bubble. And as the Bubble grew thinner by the continual subsiding of the Water, these Rings dilated slowly and over-spread the whole Bubble, descending in order to the bottom of it, where they vanished successively. In the mean while, after all the Colours were emerged at the top, there grew in the Center of the Rings a small round black Spot, like that in the first Observation, which continually dilated it self till it became sometimes more than or of an Inch in breadth before the Bubble broke. At first I thought there had been no Light reflected from the Water in that place, but observing it more curiously, I saw within it several smaller round Spots, which appeared much blacker and darker than the rest, whereby I knew that there was some reflexion at the other places which were not so dark as those Spots. And by further Tryal I found that I could see the Images of some things (as of a Candle or the Sun) very faintly reflected, not only from the great black Spot, but also from the little darker Spots which were within it.
Besides the aforesaid coloured Rings there would often appear small Spots of Colours, ascending and descending up and down the sides of the Bubble, by reason of some inequalities in the subsiding of the Water. And sometimes small black Spots generated at the sides would ascend up to the larger black Spot at the top of the Bubble, and unite with it.
OBS. XVIII.
Because the Colours of these Bubbles were more extended and lively than those of the Air thin'd between two Glasses, and so more easy to be distinguished, I shall here give you a further description of their order, as they were observed in viewing them by reflexion of the Skies when of a white Colour, whilst a black Substance was placed behind the Bubble. And they were these, red, blue; red, blue; red, blue; red, green; red, yellow, green, blue, purple; red, yellow, green, blue, violet; red, yellow, white, blue, black.
The three first Successions of red and blue were very dilute and dirty, especially the first, where the red seemed in a manner to be white. Among these there was scarce any other Colour sensible besides red and blue, only the blues (and principally the second blue) inclined a little to green.
The fourth red was also dilute and dirty, but not so much as the former three; after that succeeded little or no yellow, but a copious green, which at first inclined a little to yellow, and then became a pretty brisque and good willow green, and afterwards changed to a bluish Colour; but there succeeded neither blue nor violet.
The fifth red at first inclined very much to purple, and afterwards became more bright and brisque, but yet not very pure. This was succeeded with a very bright and intense yellow, which was but little in quantity, and soon changed to green: But that green was copious and something more pure, deep and lively, than the former green. After that followed an excellent blue of a bright sky-colour, and then a purple, which was less in quantity than the blue, and much inclined to red.
The sixth red was at first of a very fair and lively Scarlet, and soon after of a brighter Colour, being very pure and brisque, and the best of all the reds. Then after a lively orange followed an intense bright and copious yellow, which was also the best of all the yellows, and this changed first to a greenish yellow, and then to a greenish blue; but the green between the yellow and the blue, was very little and dilute, seeming rather a greenish white than a green. The blue which succeeded became very good, and of a very bright sky-colour, but yet something inferior to the former blue; and the violet was intense and deep with little or no redness in it. And less in quantity than the blue.
In the last red appeared a tincture of scarlet next to violet, which soon changed to a brighter Colour, inclining to an orange; and the yellow which followed was at first pretty good and lively, but afterwards it grew more dilute, until by degrees it ended in perfect whiteness. And this whiteness, if the Water was very tenacious and well-tempered, would slowly spread and dilate it self over the greater part of the Bubble; continually growing paler at the top, where at length it would crack in many places, and those cracks, as they dilated, would appear of a pretty good, but yet obscure and dark sky-colour; the white between the blue Spots diminishing, until it resembled the threds of an irregular Net-work, and soon after vanished and left all the upper part of the Bubble of the said dark blue Colour. And this Colour, after the aforesaid manner, dilated it self downwards, until sometimes it hath overspread the whole Bubble. In the mean while at the top, which was of a darker blue than the bottom, and appeared also full of many round blue Spots, something darker than the rest, there would emerge one or more very black Spots, and within those other Spots of an intenser blackness, which I mentioned in the former Observation; and these continually dilated themselves until the Bubble broke.
If the Water was not very tenacious the black Spots would break forth in the white, without any sensible intervention of the blue. And sometimes they would break forth within the precedent yellow, or red, or perhaps within the blue of the second order, before the intermediate Colours had time to display themselves.
By this description you may perceive how great an affinity these Colours have with those of Air described in the fourth Observation, although set down in a contrary order, by reason that they begin to appear when the Bubble is thickest, and are most conveniently reckoned from the lowest and thickest part of the Bubble upwards.
OBS. XIX.
Viewing in several oblique positions of my Eye the Rings of Colours emerging on the top of the Bubble, I found that they were sensibly dilated by increasing the obliquity, but yet not so much by far as those made by thin'd Air in the seventh Observation. For there they were dilated so much as, when viewed most obliquely, to arrive at a part of the plate more than twelve times thicker than that where they appeared when viewed perpendicularly; whereas in this case the thickness of the Water, at which they arrived when viewed most obliquely, was to that thickness which exhibited them by perpendicular rays, something less than as 8 to 5. By the best of my Observations it was between 15 and to 10, an increase about 24 times less than in the other case.
Sometimes the Bubble would become of an uniform thickness all over, except at the top of it near the black Spot, as I knew, because it would exhibit the same appearance of Colours in all positions of the Eye. And then the Colours which were seen at its apparent circumference by the obliquest rays, would be different from those that were seen in other places, by rays less oblique to it. And divers Spectators might see the same part of it of differing Colours, by viewing it at very differing obliquities. Now observing how much the Colours at the same places of the Bubble, or at divers places of equal thickness, were varied by the several obliquities of the rays; by the assistance of the 4th, 14th, 16th and 18th Observations, as they are hereafter explained, I collect the thickness of the Water requisite to exhibit any one and the same Colour, at several obliquities, to be very nearly in the proportion expressed in this Table.
| Incidence on the Water. | Refraction into the Water. | Thickness of the Water. |
| Deg. Min. | Deg. Min. | |
| 00 00 | 00 00 | 10 |
| 15 00 | 11 11 | |
| 30 00 | 22 1 | |
| 45 00 | 32 2 | |
| 60 00 | 40 30 | 13 |
| 75 00 | 46 25 | |
| 90 00 | 48 35 |
In the two first Columns are expressed the obliquities of the rays to the Superficies of the Water, that is, their Angles of incidence and refraction. Where I suppose that the Sines which measure them are in round numbers as 3 to 4, though probably the dissolution of Soap in the Water, may a little alter its refractive Vertue. In the third Column the thickness of the Bubble, at which any one Colour is exhibited in those several obliquities, is expressed in parts, of which ten constitute its thickness when the rays are perpendicular.
I have sometimes observed, that the Colours which arise on polished Steel by heating it, or on Bell-metal, and some other metalline substances, when melted and poured on the ground, where they may cool in the open Air, have, like the Colours of Water-bubbles, been a little changed by viewing them at divers obliquities, and particularly that a deep blue, or violet, when viewed very obliquely, hath been changed to a deep red. But the changes of these Colours are not so great and sensible as of those made by Water. For the Scoria or vitrified part of the Metal, which most Metals when heated or melted do continually protrude, and send out to their surface, and which by covering the Metals in form of a thin glassy skin, causes these Colours, is much denser than Water; and I find that the change made by the Obliquation of the Eye is least in Colours of the densest thin Substances.
OBS. XX.
As in the ninth Observation, so here, the Bubble, by transmitted Light, appeared of a contrary Colour to that which it exhibited by reflexion. Thus when the Bubble being looked on by the Light of the Clouds reflected from it, seemed red at its apparent circumference, if the Clouds at the same time, or immediately after, were viewed through it, the Colour at its circumference would be blue. And, on the contrary, when by reflected Light it appeared blue, it would appear red by transmitted Light.
OBS. XXI.
By wetting very thin plates of Muscovy-glass, whose thinness made the like Colours appear, the Colours became more faint and languid; especially by wetting the plates on that side opposite to the Eye: But I could not perceive any variation of their species. So then the thickness of a plate requisite to produce any Colour, depends only on the density of the plate, and not on that of the ambient medium. And hence, by the 10th and 16th Observations, may be known the thickness which Bubbles of Water, or Plates of Muscovy-glass, or other substances, have at any Colour produced by them.
OBS. XXII.
A thin transparent Body, which is denser than its ambient medium, exhibits more brisque and vivid Colours than that which is so much rarer; as I have particularly observed in the Air and Glass. For blowing Glass very thin at a Lamp-furnace, those plates incompassed with Air did exhibit Colours much more vivid than those of Air made thin between two Glasses.
OBS. XXIII.
Comparing the quantity of Light reflected from the several Rings, I found that it was most copious from the first or inmost, and in the exterior Rings became gradually less and less. Also the whiteness of the first Ring was stronger than that reflected from those parts of the thinner medium were without the Rings; as I could manifestly perceive by viewing at a distance the Rings made by the two ObjectGlasses; or by comparing two Bubbles of Water blown at distant times, in the first of which the whiteness appeared, which succeeded all the Colours, and in the other, the whiteness which preceded them all.
OBS. XXIV.
When the two Object-Glasses were lay'd upon one another, so as to make the Rings of the Colours appear, though with my naked Eye I could not discern above 8 or 9 of those Rings, yet by viewing them through a Prism I have seen a far greater multitude, insomuch that I could number more than forty, besides many others, that were so very small and close together, that I could not keep my Eye steddy on them severally so as to number them, but by their extent I have sometimes estimated them to be more than an hundred. And I believe the Experiment may be improved to the discovery of far greater numbers. For they seem to be really unlimited, though visible only so far as they can be separated by the refraction, as I shall hereafter explain.
But it was but one side of these Rings, namely, that towards which the refraction was made, which by that refraction was rendered distinct, and the other side became more confused than when viewed by the naked Eye, insomuch that there I could not discern above one or two, and sometimes none of those Rings, of which I could discern eight or nine with my naked Eye. And their Segments or Arcs, which on the other side appeared so numerous, for the most part exceeded not the third part of a Circle. If the Refraction was very great, or the Prism very distant from the Object-Glasses, the middle part of those Arcs became also confused, so as to disappear and constitute an even whiteness, whilst on either side their ends, as also the whole Arcs furthest from the center, became distincter than before, appearing in the form as you see them designed in the fifth Figure.[Image 5]
The Arcs, where they seemed distinctest, were only white and black successively, without any other Colours intermixed. But in other places there appeared Colours, whose order was inverted by the refraction in such manner, that if I first held the Prism very near the Object-Glasses, and then gradually removed it further off towards my Eye, the Colours of the 2d, 3d, 4th, and following Rings shrunk towards the white that emerged between them, until they wholly vanished into it at the middle of the Arcs, and afterwards emerged again in a contrary order. But at the ends of the Arcs they retained their order unchanged.
I have sometimes so lay'd one Object-Glass upon the other, that to the naked Eye they have all over seemed uniformly white, without the least appearance of any of the coloured Rings; and yet by viewing them through a Prism, great multitudes of those Rings have discovered themselves. And in like manner plates of Muscovy-glass, and Bubbles of Glass blown at a Lamp-furnace, which were not so thin as to exhibit any Colours to the naked Eye, have through the Prism exhibited a great variety of them ranged irregularly up and down in the form of waves. And so Bubbles of Water, before they began to exhibit their Colours to the naked Eye of a By-stander, have appeared through a Prism, girded about with many parallel and horizontal Rings; to produce which effect, it was necessary to hold the Prism parallel, or very nearly parallel to the Horizon, and to dispose it so that the rays might be refracted upwards.
[Image 1] Fig. 1. 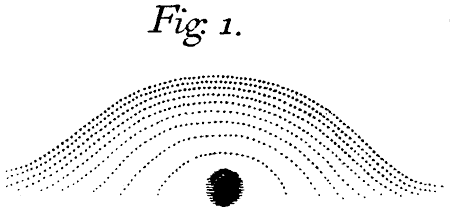
[Image 2] Fig. 2. 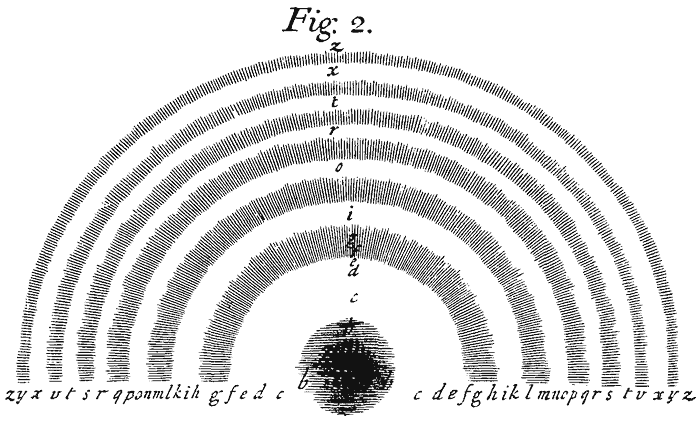
[Image 3] Fig. 3. 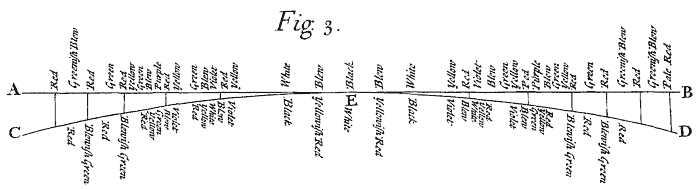
[Image 4] Fig. 4. 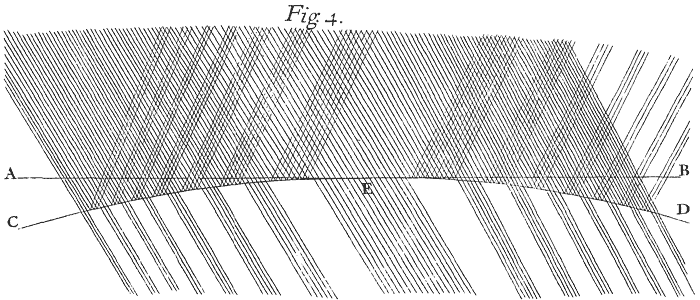
[Image 5] Fig. 5. 
