Copy of an extract of a letter to John Collins, dated 10 December 1672

<45r>

Extractum
Ex Domini Newtoni Epistola, datâ Cantabrigia Dec. 10. 1672. ad Dominum Collinium.

Perquam gaudeo, Domini Barrovij Lectiones Mathematicas adeo acceptus esse Mathematicis exteris; nec {parvùm} me afficiebat, quod intelligerem, illos in eandem mecum nicidisse methodum Tangentes ducendi. Quam ipsorum methodum {conjùram}, hoc Exemplo videbis;

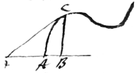
Suppone CB, applicatam ad AB in quolibet angulo dato, terminari ad quamvis curvam AC, et AB appellato x, et BC y, relatio inter x et y exprimatur æquatione qualibet, puta $${\mathrm{x}}^3-2\mathrm{x}\mathrm{x}\mathrm{y}+\mathrm{b}\mathrm{x}\mathrm{x}-\mathrm{b}\mathrm{b}\mathrm{x}+\mathrm{b}\mathrm{y}\mathrm{y}-{\mathrm{y}}^3=0$$ quâ ipsâ determinatur curva. Ad ducendam Tangentem Regula hæc est: Multiplica terminos æquationis per quamvis progressionem Arithmeticam juxta dimensiones y, puta hoc modo; $$\begin{array}{ccccccccccc}0& & 1& & 0& & 0& & 2& & 3\\ {\mathrm{x}}^3& -& 2\mathrm{x}\mathrm{x}\mathrm{y}& +& \mathrm{b}\mathrm{x}\mathrm{x}& -& \mathrm{b}\mathrm{b}\mathrm{x}& +& \mathrm{b}\mathrm{y}\mathrm{y}& -& {\mathrm{y}}^3\\ 3& & 2& & 2& & 1& & 0& & 0\end{array}$$ Productum primum erit Numerator, et postremum divisum per x, erit Denominator fractionis, quæ exprimit longitudinem BD, ad cujus finem ducanda est Tangens;
{&} Longitudo BD est $\frac{-2\mathrm{x}\mathrm{x}\mathrm{y}+2\mathrm{b}\mathrm{y}\mathrm{y}-3{\mathrm{y}}^3}{3\mathrm{x}\mathrm{x}-4\mathrm{x}\mathrm{y}+2\mathrm{b}\mathrm{x}-\mathrm{b}\mathrm{b}}$.

Hoc est unum particulare, sive potius Corollarium generali methodi, quæ seipsam extendit, absque modesto ullo calculo {non} solum {ad} ducendum Tangentes ad omnes Curvas, sive Geometricas, sive Mechanicas, vel quodmodocunque relatas ad lineas Rectas, vel <45v> ad alias Curvas, sed etiam ad resolvenda alia problemata abstrusioris familiæ de curvitate, areis, longitudinibus, centris gravitatis Curvarum etc. Neque (ut Huddenij methodus de maximis et minimis, adeoque nec ut Slusij nova methodus de Tangentibus, ut arbitror) limitatur ad æquationes quæ immunes sunt á quantitatis surdis. Methodum hanc intertexui illi alteri, operandi {scilicet} in Æquationibus eas ad series infinitas reducendo. Memini, me aliquando, occasione datâ, dixisse Domino Barrovio, {cum} in procinctu erat lectiones suas edendi, instructum me esse istiusmodi methodo Tangentes ducendi; sed aliis rebus impediebar, quò minus tum temporis {cum} ipsi describerem.

Circa resolvendas, Cardani regularum beneficio, Æquationes ejusmodi quæ habent 3 radices possibiles; Exempla strui possunt ad libitum; verùm nisi Brasserùs {directu{m}}{direct{um}} ostendat methodum id præstandi, quod Fergusonus non facit non admittetur esse scientifica. Quâ ratione id præstandum sit directé, ex occasione forsan ostendam.

<45ar>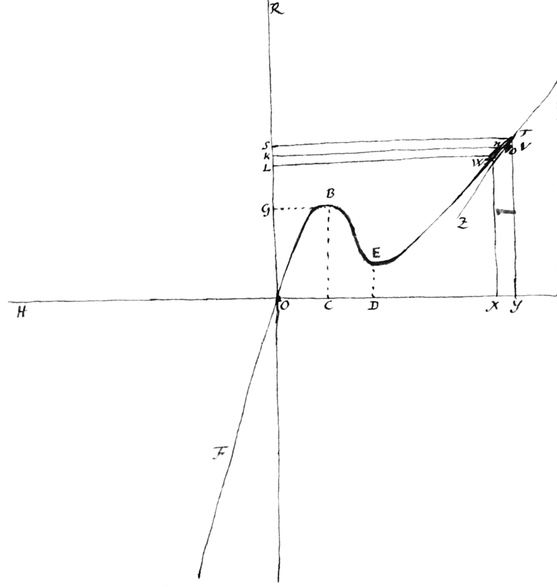

In hac æquatione
${\mathrm{z}}^3-21\mathrm{z}\mathrm{z}+120\mathrm{z}$

$\begin{array}{cccc}& & & \text{Resolvenda.}\\ \text{Radices}& 1& —& 120\hfill \\ & 2& —& 164\hfill \\ & 3& —& 198\hfill \\ & 4& —& 225\hfill \\ & 5& —& 200\hfill \\ & 6& —& 180\hfill \\ & 7& —& 154\hfill \\ & 8& —& 128\hfill \\ & 9& —& 108\hfill \\ & 10& —& 100\hfill \\ & 11& —& 110\hfill \end{array}$

Resolvenda supponuntur punctata deorsùm ab O versus R et radices excitatæ tanquam {ordinatæ} ad ea, per <45av> quarum summitates transit Locus æquationis FOBE.

Radices Limitum sunt $\mathrm{GB}=4$. Resolvendo sive Limite ad eas BC, existente 225: Atque radix alterius Limitis est $\mathrm{OD}=10$; cujus Resolvendum $\mathrm{DE}=100$.

Jam verò, quandoquidem Curva hæc habet flexuras, Domini Tschurnhaus rogandus est, ut suam Tangentium Doctrinam ita adaptet, ut portionem quam ducit, ducatur à pede ordinatæ C ad D, ubi demum cumque id accidit, non verò ab O ad H, vel alioqui sursum vel deorsim a linea ROS.

Si $\left.\begin{array}{c}\mathrm{OL}\\ \mathrm{OS}\end{array}\right\}$ sit Resovendum, radix est $\left\}\begin{array}{c}\mathrm{LW}\\ \mathrm{ST}\end{array}\right\}$. Has inventas supponimus per operationem tentativam. At supposito, Resovendum datum esse OK, ad quod requiritur radix. Supposito, Chordam TW ductam, liquet, KN nimis parvam esse ad id ut sit radix, et ducto tangente TZ, KO nimis magna est; quâ ratione propinqua sit approximatio. At inter B et E est aliud punctum flexûs contrarij.