Copy of a letter from Newton to Henry Oldenburg, dated 13 June 1676

<1r>

June 13^th 1676.

Dignissime {Vir}

{Quanquam D. Leibnitij, modestia} in excerptis quæ ex Epistola ejus ad me {nuper misisti nostratibus} multum tribuat circa speculationem {quandam infinitarum} serierum de quâ jam cœpit esse rumor: nullus dubito tamen quin ille, non tantum (quod asserit) methodum reducendi quantitates quascunque in ejusmodi series, sed et varia compendia, fortè nostris similia, si non et meliora, adinvenerit. Quoniam tamen ea scire pervelit quæ ab Anglis hâc in re inventa sunt, et ipse ante annos aliquot in hanc speculationem inciderim: ut votis ejus aliqua saltern ex parte satisfacerem iam, nonnulla eorum quæ mihi occurrerunt, ad te transmisi.

Fractiones in infinitas series reduco per divisionem et quantitates radicales per Extractionem radicum, perindè instituendo operationes istas in speciebus ac {in}stitui solent in decimalibus numeris. Hæc sunt fundamenta harum reductionum; sed extractiones radicum multum abbreviantur per hoc Theorema.

${\left.\overline{\mathrm{P}+\mathrm{P}\mathrm{Q}}\right\}}^{\frac{\mathrm{m}}{\mathrm{n}}}={\mathrm{P}}^{\frac{\mathrm{m}}{\mathrm{n}}}+\frac{\mathrm{m}}{\mathrm{n}}\mathrm{A}\mathrm{Q}+\frac{\mathrm{m}-\mathrm{n}}{2\mathrm{n}}\mathrm{B}\mathrm{Q}+\frac{\mathrm{m}-2\mathrm{n}}{3\mathrm{n}}\mathrm{C}\mathrm{Q}+\frac{\mathrm{m}-3\mathrm{n}}{4\mathrm{n}}\mathrm{D}\mathrm{Q}+\text{\&c}$.
Ubi $\mathrm{P}+\mathrm{P}\mathrm{Q}$ significat quantitatem cujus radix vel etiam dimentio quævis vel radix dimensionis investiganda est. P primum terminum quantitatis ejus, Q reliquos terminos divisos per primum, & $\frac{\mathrm{m}}{\mathrm{n}}$ numeralem indicem dimensionis ipsius $\mathrm{P}+\mathrm{P}\mathrm{Q}$ sive dimentio illa integra sit, sive (ut ita loquar) fracta, sive affermativa, sive negativa. Nam sicut Analystæ pro $\mathrm{a}\mathrm{a}$ $\mathrm{a}\mathrm{a}\mathrm{a}$ &c scribere solent ${\mathrm{a}}^2$, ${\mathrm{a}}^3$, sic ego pro $\sqrt{}\mathrm{a}$, $\sqrt{}{\mathrm{a}}^3$, $\sqrt{}c.{\mathrm{a}}^5$ &c scribo ${\mathrm{a}}^{\frac{1}{2}}$, ${\mathrm{a}}^{\frac{3}{2}}$, ${\mathrm{a}}^{\frac{5}{3}}$, & pro $\frac{1}{\mathrm{a}}$, $\frac{1}{\mathrm{a}\mathrm{a}}$, $\frac{1}{{\mathrm{a}}^3}$ scribo ${\mathrm{a}}^{-1}$, ${\mathrm{a}}^{-2}$, ${\mathrm{a}}^{-3}$. Et sic pro $\frac{\mathrm{a}\mathrm{a}}{\sqrt{}\mathrm{c:}\overline{{\mathrm{a}}^3+\mathrm{b}\mathrm{b}\mathrm{x}}}$ scribo $\mathrm{a}\mathrm{a}\times {\left.\overline{{\mathrm{a}}^3+\mathrm{b}\mathrm{b}\mathrm{x}}\right\}}^{-\frac{1}{3}}$, & pro $\frac{\mathrm{a}\mathrm{a}\mathrm{b}}{\genfrac{}{}{0ex}{}{\phantom{.}}{\sqrt{}\mathrm{c:}\overline{{\mathrm{a}}^3+\mathrm{b}\mathrm{b}\mathrm{x}\times {\mathrm{a}}^3+\mathrm{b}\mathrm{b}\mathrm{x}}}}$ scribo $\mathrm{a}\mathrm{a}\mathrm{b}\times {\left.\overline{{\mathrm{a}}^3+\mathrm{b}\mathrm{b}\mathrm{x}}\right\}}^{-\frac{2}{3}}$: in quo ultimo casu si ${\left.\overline{{\mathrm{a}}^3+\mathrm{b}\mathrm{b}\mathrm{x}}\right\}}^{-\frac{2}{3}}$ conciapiatur esse ${\left.\overline{\mathrm{P}+\mathrm{P}\mathrm{Q}}\right\}}^{\frac{\mathrm{m}}{\mathrm{n}}}$ in Regulâ; erit $\mathrm{P}={\mathrm{a}}^3$, $\mathrm{Q}=\frac{\mathrm{b}\mathrm{b}\mathrm{x}}{{\mathrm{a}}^3}$, $\mathrm{m}=-2$, & $\mathrm{n}=3$. Denique pro terminis inter operandum inventis in Quoto, usurpo A, B, C, D &c nempe A pro primo termino ${\mathrm{P}}^{\frac{\mathrm{m}}{\mathrm{n}}}$, B pro secundo $\frac{\mathrm{m}}{\mathrm{n}}\mathrm{A}\mathrm{Q}$ & sic deinceps. Cæterum usus Regulæ patebit Exemplis.

Exempl: 1. Est $\sqrt{}\overline{\phantom{|}\mathrm{c}\mathrm{c}+\mathrm{x}\mathrm{x}\phantom{|}}\left(\text{seu}{\left.\overline{\mathrm{c}\mathrm{c}+\mathrm{x}\mathrm{x}}\right\}}^{\frac{1}{2}}\right)=\mathrm{c}+\frac{\mathrm{x}\mathrm{x}}{2\mathrm{c}}-\frac{{\mathrm{x}}^4}{8{\mathrm{c}}^3}+\frac{{\mathrm{x}}^6}{16{\mathrm{c}}^5}-\frac{5{\mathrm{x}}^8}{128{\mathrm{c}}^7}$$+\frac{7{\mathrm{x}}^{10}}{256{\mathrm{a}}^9}+\text{\&c.}$. Nam in hoc casu est $\mathrm{P}=\mathrm{c}\mathrm{c}$, $\mathrm{Q}=\frac{\mathrm{x}\mathrm{x}}{\mathrm{c}\mathrm{c}}$, $\mathrm{m}=1$, $\mathrm{n}=2$, $\mathrm{A}\left(={\mathrm{P}}^{\frac{\mathrm{m}}{\mathrm{n}}}={\left.\overline{\mathrm{c}\mathrm{c}}\right\}}^{\frac{1}{2}}\right)=\mathrm{c}$. $\mathrm{B}\left(=\frac{\mathrm{m}}{\mathrm{n}}\mathrm{A}\mathrm{Q}\right)=\frac{\mathrm{x}\mathrm{x}}{2\mathrm{c}}$. $\mathrm{C}\left(=\frac{\mathrm{m}-\mathrm{n}}{2\mathrm{n}}\mathrm{B}\mathrm{Q}\right)=\frac{-{\mathrm{x}}^4}{8{\mathrm{c}}^3}$, & sic deinceps.

Exempl: 2. Est $\sqrt{}⑤\overline{{\mathrm{c}}^5+{\mathrm{c}}^4\mathrm{x}-{\mathrm{x}}^5}\left(\text{i.e.}{\left.\overline{{\mathrm{c}}^5+{\mathrm{c}}^4\mathrm{x}-{\mathrm{x}}^5}\right\}}^{\frac{1}{5}}\right)=\mathrm{c}+\frac{{\mathrm{c}}^4\mathrm{x}-{\mathrm{x}}^5}{5{\mathrm{c}}^4}\frac{-2{\mathrm{c}}^8\mathrm{x}\mathrm{x}+4{\mathrm{c}}^4{\mathrm{x}}^6}{25{\mathrm{c}}^9}$$\frac{-2{\mathrm{x}}^{10}}{25{\mathrm{c}}^9}+\text{\&c.}$ ut patebit substituendo in allatam Regulam, 1 pro m, 5 pro n, ${\mathrm{c}}^5$ pro {P, & $\frac{{\mathrm{c}}^4\mathrm{x}-{\mathrm{x}}^5}{{\mathrm{c}}^5}$} pro Q. Potest etiam $-{\mathrm{x}}^5$ substitui pro P, & $\frac{{\mathrm{c}}^4\mathrm{x}+{\mathrm{c}}^5}{-{\mathrm{x}}^5}$ pro Q, et tunc <1v> evadet $\sqrt{}⑤\overline{{\mathrm{c}}^5+{\mathrm{c}}^4\mathrm{x}-{\mathrm{x}}^5}=-\mathrm{x}${$+\frac{{\mathrm{c}}^4\mathrm{x}+{\mathrm{c}}^5}{5{\mathrm{x}}^4}+\frac{2{\mathrm{c}}^8\mathrm{x}\mathrm{x}+4{\mathrm{c}}^9\mathrm{x}+{\mathrm{c}}^{10}}{25{\mathrm{x}}^9}+\text{\&c}$}. Prior modus eligendus est si x valde {parvum sit, posterior si valde} magnum.

Exempl: 3. Est $\frac{\mathrm{N}}{\sqrt{}③\overline{{\mathrm{y}}^3-\mathrm{a}\mathrm{a}\mathrm{y}}}${$\left(\text{hoc est}{\mathrm{N}\times \left.\overline{{\mathrm{y}}^3-\mathrm{a}\mathrm{a}\mathrm{y}}\right\}}^{-\frac{1}{3}}\right)=\mathrm{N}\times$}$\frac{1}{\mathrm{y}}+\frac{\mathrm{a}\mathrm{a}}{3{\mathrm{y}}^3}+\frac{2{\mathrm{a}}^4}{9{\mathrm{y}}^5}+\frac{7{\mathrm{a}}^6}{81{\mathrm{y}}^7}+\text{\&c.}$ Nam $\mathrm{P}={\mathrm{y}}^3$. $\mathrm{Q}=\frac{-\mathrm{a}\mathrm{a}}{\mathrm{y}\mathrm{y}}$. $\mathrm{m}=-1$. $\mathrm{n}=3$. {$\mathrm{A}\left(={\mathrm{P}}^{\frac{\mathrm{m}}{\mathrm{n}}}={\mathrm{y}}^{3\times \frac{-1}{3}}\right)$}$={\mathrm{y}}^{-1}$. hoc est $\frac{1}{\mathrm{y}}$. $\mathrm{B}\left(=\frac{\mathrm{m}}{\mathrm{n}}\mathrm{A}\mathrm{Q}=\frac{-1}{3}\times \frac{1}{\mathrm{y}}\times \frac{-\mathrm{a}\mathrm{a}}{\mathrm{y}\mathrm{y}}\right)=\frac{\mathrm{a}\mathrm{a}}{3{\mathrm{y}}^3}\text{\&c}$.

Exempl: 4. Radix cubica ex quadrato-quadrato ipsius $\mathrm{d}+\mathrm{e}$ (hoc est $\left.{\left.\overline{\mathrm{d}+\mathrm{e}}\right\}}^{\frac{4}{3}}\right)$ Est ${\mathrm{d}}^{\frac{4}{3}}+\frac{4\mathrm{e}{\mathrm{d}}^{\frac{1}{3}}}{3}+\frac{2\mathrm{e}\mathrm{e}}{9{\mathrm{d}}^{\frac{2}{3}}}-\frac{4{\mathrm{e}}^3}{81{\mathrm{d}}^{\frac{5}{3}}}+\text{\&c}$. Nam $\mathrm{P}=\mathrm{d}$. $\mathrm{Q}=\frac{\mathrm{e}}{\mathrm{d}}$. $\mathrm{m}=4$. $\mathrm{n}=3$. $\mathrm{A}\left(={\mathrm{P}}^{\frac{\mathrm{m}}{\mathrm{n}}}\right)=$${\mathrm{d}}^{\frac{4}{3}}$ &c.

Eodem modo simplices etiam potestates eliciuntur. Ut si quadrato-cubus ipsius $\mathrm{d}+\mathrm{e}\left(\text{hoc est}{\left.\overline{\mathrm{d}+\mathrm{e}}\right\}}^5\text{, seu}{\left.\overline{\mathrm{d}+\mathrm{e}}\right\}}^{\frac{5}{1}}\right)$ desideretur: erit juxta Regulam $\mathrm{P}=\mathrm{d}$. $\mathrm{Q}=\frac{\mathrm{e}}{\mathrm{d}}$. $\mathrm{m}=5$ & $\mathrm{n}=1$; adeoque $\mathrm{A}\left(={\mathrm{P}}^{\frac{\mathrm{m}}{\mathrm{n}}}\right)={\mathrm{d}}^5$, $\mathrm{B}\left(=\frac{\mathrm{m}}{\mathrm{n}}\mathrm{A}\mathrm{Q}\right)=5{\mathrm{d}}^4\mathrm{e}$, & sic $\mathrm{C}=10{\mathrm{d}}^3\mathrm{e}\mathrm{e}$, $\mathrm{D}=10\mathrm{d}\mathrm{d}{\mathrm{e}}^3$, $\mathrm{E}=5\mathrm{d}{\mathrm{e}}^4$, $\mathrm{F}={\mathrm{e}}^5$, & $\mathrm{G}\left(=\frac{\mathrm{m}-5\mathrm{n}}{6\mathrm{n}}\mathrm{F}\mathrm{Q}\right)=0$. Hoc est ${\left.\overline{\mathrm{d}+\mathrm{e}}\right\}}^5={\mathrm{d}}^5+5{\mathrm{d}}^4\mathrm{e}+10{\mathrm{d}}^3\mathrm{e}\mathrm{e}+10\mathrm{d}\mathrm{d}{\mathrm{e}}^3+5\mathrm{d}{\mathrm{e}}^4+{\mathrm{e}}^5$.

Quinetiam Divisio, sive simplex sit, sive repetita, per eandem Regulam perficitur. Ut si $\frac{1}{\mathrm{d}+\mathrm{e}}$, $\left(\text{hoc est}{\left.\overline{\mathrm{d}+\mathrm{e}}\right\}}^{-1}\text{sive}{\left.\overline{\mathrm{d}+\mathrm{e}}\right\}}^{\frac{-1}{1}}\right)$ in seriem simplicium terminorum resolvendum sit: erit juxta Regulam $\mathrm{P}=\mathrm{d}$. $\mathrm{Q}=\frac{\mathrm{e}}{\mathrm{d}}$. $\mathrm{m}=-1$. $\mathrm{n}=1$. & $\mathrm{A}\left(={\mathrm{P}}^{\frac{\mathrm{m}}{\mathrm{n}}}={\mathrm{D}}^{\frac{-1}{1}}\right)={\mathrm{d}}^{-1}$ seu $\frac{1}{\mathrm{d}}$. $\mathrm{B}\left(=\frac{\mathrm{m}}{\mathrm{n}}\mathrm{A}\mathrm{Q}=-1\times \frac{1}{\mathrm{d}}\times \frac{\mathrm{e}}{\mathrm{d}}\right)=-\frac{\mathrm{e}}{\mathrm{d}\mathrm{d}}$, & sic $\mathrm{C}=\frac{\mathrm{e}\mathrm{e}}{{\mathrm{d}}^3}$, $\mathrm{D}=\frac{-{\mathrm{e}}^3}{{\mathrm{d}}^4}$ &c Hoc est $\frac{1}{\mathrm{d}+\mathrm{e}}=\frac{1}{\mathrm{d}}-\frac{\mathrm{e}}{\mathrm{d}\mathrm{d}}+\frac{\mathrm{e}\mathrm{e}}{{\mathrm{d}}^3}-\frac{{\mathrm{e}}^3}{{\mathrm{d}}^4}+\text{\&c}$.

Sic et ${\left.\overline{\mathrm{d}+\mathrm{e}}\right\}}^{-3}$ (hoc est unitas ter divisa per $\mathrm{d}+\mathrm{e}$ vel semel per cubum ejus,) evadit $\frac{1}{{\mathrm{d}}^3}-\frac{3\mathrm{e}}{{\mathrm{d}}^4}+\frac{6\mathrm{e}\mathrm{e}}{{\mathrm{d}}^5}-\frac{10{\mathrm{e}}^3}{{\mathrm{d}}^6}+\text{\&c}$.

Et $\mathrm{N}\times {\left.\overline{\mathrm{d}+\mathrm{e}}\right\}}^{-\frac{1}{3}}$ hoc est N divisum per radicem cubicam ipsius $\mathrm{d}+\mathrm{e}$ evadit $\mathrm{N}\times \frac{1}{{\mathrm{d}}^{\frac{1}{3}}}-\frac{\mathrm{e}}{3{\mathrm{d}}^{\frac{4}{3}}}+\frac{2\mathrm{e}\mathrm{e}}{9{\mathrm{d}}^{\frac{7}{3}}}-\frac{14{\mathrm{e}}^3}{81{\mathrm{d}}^{\frac{10}{8}}}+\text{\&c}$

Et $\mathrm{N}\times {\left.\overline{\mathrm{d}+\mathrm{e}}\right\}}^{-\frac{3}{5}}$ (hoc est N divisum per radicem quadrato-cubicam ex cubo ipsius $\mathrm{d}+\mathrm{e}$, sive $\left.\frac{\mathrm{N}}{\sqrt{}⑤\overline{{\mathrm{d}}^3+3\mathrm{d}\mathrm{d}\mathrm{e}+3\mathrm{d}\mathrm{e}\mathrm{e}+{\mathrm{e}}^3}}\right)$ evadit $\mathrm{N}\times \frac{1}{{\mathrm{d}}^{\frac{3}{5}}}-\frac{3\mathrm{e}}{5{\mathrm{d}}^{\frac{9}{5}}}+\frac{12\mathrm{e}\mathrm{e}}{25{\mathrm{d}}^{\frac{13}{5}}}-\frac{52{\mathrm{e}}^3}{125{\mathrm{d}}^{\frac{18}{5}}}\text{\&c}$.

Per eandem Regulam Genesses Potestatum, Divisiones per potestates aut per quantitates radicales, et extractiones radicum altiorum in numeris etiam commodè instituuntur.

Extractiones Radicum affectarum in speciebus imitantur earum extractiones in numeris, sed methodus Vietæ et Oughtredi nostri huic negotio minus idonea est, quapropter aliam excogitare adactus sum cujus specimen exhibent sequentia Diagrammata ubi dextra columna prodit substituendo in mediâ columnâ valores ipsorum y, p, q, r &c in sinistra columnâ expressos. Prius Diagramma exhibet resolutionem hujus numeralis æquationis ${\mathrm{y}}^3-2\mathrm{y}-5=0$; Et hic in supremis numeris pars negativa Radicis subducta de parte affirmativa relinquit absolutam Radicem $2\underset{‾}{|09455148}$: et posterius Diagramma exhibet resolutionem hujus liter{ariæ} æquationis ${\mathrm{y}}^3+\mathrm{a}\mathrm{x}\mathrm{y}+\mathrm{a}\mathrm{a}\mathrm{y}-{\mathrm{x}}^3-2{\mathrm{a}}^3=0$.

<2r>

$\begin{array}{l}\begin{array}{rrr}\phantom{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_}& \phantom{.\_\_\_\_\_\_\_\_\_\_\_\_\_.}& \phantom{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_}\\ \begin{array}{c}\end{array}& \begin{array}{r}\\ \\ \end{array}& \begin{array}{l}\\ \\ \end{array}\hfill \\ \begin{array}{c}\end{array}& \begin{array}{c}\\ & \end{array}& \begin{array}{l}\\ \begin{array}{r}\left(\begin{array}{cc}+& \mathrm{2,10000000}\\ -& \mathrm{0,00544852}\end{array}\right.\\ \begin{array}{cc}+& \mathrm{2,09455148}\end{array}\end{array}\hfill \end{array}\hfill \end{array}\\ \begin{array}{rrr}\phantom{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_}& \phantom{.\_\_\_\_\_\_\_\_\_\_\_\_\_.}& \phantom{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_}\\ \begin{array}{c}2+\mathrm{p}=\mathrm{y}\end{array}& \begin{array}{r}{\mathrm{y}}^3\\ -2\mathrm{y}\\ -5\end{array}& \begin{array}{llllllll}+& 8& +& 12\mathrm{p}& +& 6\mathrm{p}\mathrm{p}& +& {\mathrm{p}}^3\\ -& 4& -& \phantom{0}2\mathrm{p}\\ -& 5\end{array}\hfill \\ \begin{array}{c}\end{array}& \begin{array}{c}\\ \phantom{{\mathrm{p}}^3}\text{summa}\phantom{{\mathrm{p}}^3}\end{array}& \begin{array}{l}\\ -& 1& +& 10\mathrm{p}& +& 6\mathrm{p}\mathrm{p}& +& {\mathrm{p}}^3\end{array}\hfill \end{array}\\ \begin{array}{rrr}\phantom{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_}& \phantom{.\_\_\_\_\_\_\_\_\_\_\_\_\_.}& \phantom{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_}\\ \begin{array}{r}+\mathrm{0,1}+\mathrm{q}=\mathrm{p}\end{array}& \begin{array}{r}+{\mathrm{p}}^3\\ +6\mathrm{p}\mathrm{p}\\ +10\mathrm{p}\\ -1\end{array}& \begin{array}{llllllll}+& \mathrm{0,001}& +& \phantom{0}\mathrm{0,03}\mathrm{q}& +& \mathrm{0,3}\mathrm{q}\mathrm{q}& +& {\mathrm{q}}^3\\ +& \mathrm{0,06}\phantom{1}& +& \phantom{0}\mathrm{1,2}\phantom{0\mathrm{q}}& +& 6\phantom{\mathrm{,3}\mathrm{q}\mathrm{q}}\\ +& 1\phantom{\mathrm{,001}}& +& \mathrm{10,}\phantom{0\mathrm{q}}\\ -& 1\end{array}\hfill \\ \begin{array}{c}\end{array}& \begin{array}{c}\\ \phantom{{\mathrm{q}}^3}\text{summa}\phantom{{\mathrm{q}}^3}\end{array}& \begin{array}{r}\\ \phantom{+}& \mathrm{0,061}& +& \mathrm{11,23}\mathrm{q}& +& \mathrm{6,3}\mathrm{q}\mathrm{q}& +& {\mathrm{q}}^3\end{array}\hfill \end{array}\\ \begin{array}{rrr}\phantom{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_}& \phantom{.\_\_\_\_\_\_\_\_\_\_\_\_\_.}& \phantom{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_}\\ \begin{array}{c}-\mathrm{0,0054}+\mathrm{r}=\mathrm{q}\end{array}& \begin{array}{r}+{\mathrm{q}}^3\\ +\mathrm{6,3}\mathrm{q}\mathrm{q}\\ +\mathrm{11,23}\mathrm{q}\\ +\mathrm{0,061}\end{array}& \begin{array}{lllllll}-& \mathrm{0,0000001}& +& \phantom{0}\mathrm{0,000}\mathrm{r}& \phantom{+}& \text{\&c}& \phantom{{\mathrm{q}}^3}\\ +& \mathrm{0,0001837}& -& \phantom{0}\mathrm{0,068}& \phantom{\mathrm{q}}\\ -& \mathrm{0,060642}\phantom{0}& +& \mathrm{11,23}& \phantom{\mathrm{q}}\\ +& \mathrm{0,061}\end{array}\hfill \\ \begin{array}{c}\end{array}& \begin{array}{c}\\ \phantom{{\mathrm{q}}^3}\text{summa}\phantom{{\mathrm{q}}^3}\end{array}& \begin{array}{r}\\ -& \mathrm{0,0005416}& +& \mathrm{11,162}\mathrm{r}\end{array}\hfill \end{array}\\ \begin{array}{rrr}\phantom{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_}& \phantom{.\_\_\_\_\_\_\_\_\_\_\_\_\_.}& \phantom{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_}\\ \begin{array}{c}-\mathrm{0,00004852}+\mathrm{s}=\mathrm{r}\end{array}& \phantom{.\_\_\_\_\_\_\_\_\_\_\_\_\_.}& \phantom{\_}\end{array}\\ \phantom{\_}\end{array}$

$\begin{array}{c}\begin{array}{l}\phantom{\_}\\ \begin{array}{rrr}\phantom{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_}& \phantom{.\_\_\_\_\_\_\_\_\_\_\_\_\_.}& \phantom{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_}\\ \begin{array}{c}\end{array}& \begin{array}{r}\\ \\ \end{array}& \begin{array}{l}\\ \\ \end{array}\hfill \\ \begin{array}{c}\end{array}& \begin{array}{c}\\ \end{array}& \left(\mathrm{a}-\frac{\mathrm{x}}{4}+\frac{\mathrm{x}\mathrm{x}}{64\mathrm{a}}+\frac{131{\mathrm{x}}^3}{512\mathrm{a}\mathrm{a}}+\frac{509{\mathrm{x}}^4}{16384{\mathrm{a}}^3}\text{\&c}\right.\hfill \end{array}\\ \begin{array}{rrr}\phantom{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_}& \phantom{.\_\_\_\_\_\_\_\_\_\_\_\_\_.}& \phantom{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_}\\ \begin{array}{c}\mathrm{a}+\mathrm{p}=\mathrm{y}\end{array}& \begin{array}{c}{\mathrm{y}}^3\end{array}& \begin{array}{llllllll}\phantom{+}& {\mathrm{a}}^3& +& 3\mathrm{a}\mathrm{a}\mathrm{p}& +& 3\mathrm{a}\mathrm{p}\mathrm{p}& +& {\mathrm{p}}^3\end{array}\hfill \\ \begin{array}{c}\end{array}& \begin{array}{c}+\mathrm{a}\mathrm{x}\mathrm{y}\end{array}& \begin{array}{llll}+& \mathrm{a}\mathrm{a}\mathrm{x}& +& \mathrm{a}\mathrm{x}\mathrm{p}\end{array}\hfill \\ \begin{array}{c}\end{array}& \begin{array}{c}+\mathrm{a}\mathrm{a}\mathrm{y}\end{array}& \begin{array}{llll}+& {\mathrm{a}}^3& +& \mathrm{a}\mathrm{a}\mathrm{p}\end{array}\hfill \\ \begin{array}{c}\end{array}& \begin{array}{c}-{\mathrm{x}}^3\end{array}& \begin{array}{l}-{\mathrm{x}}^3\end{array}\hfill \\ \begin{array}{c}\end{array}& \begin{array}{c}-2{\mathrm{a}}^3\end{array}& \begin{array}{l}-2{\mathrm{a}}^3\end{array}\hfill \\ \phantom{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_}& \phantom{.\_\_\_\_\_\_\_\_\_\_\_\_\_.}& \phantom{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_}\end{array}\\ \begin{array}{rrr}\phantom{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_}& \phantom{.\_\_\_\_\_\_\_\_\_\_\_\_\_.}& \phantom{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_}\\ \begin{array}{c}-\frac{1}{4}\mathrm{x}+\mathrm{q}=\mathrm{p}\end{array}& \begin{array}{c}{\mathrm{p}}^3\end{array}& \begin{array}{llllll}-& \frac{1}{64}{\mathrm{x}}^3& +& \frac{3}{16}\mathrm{x}\mathrm{x}\mathrm{q}& & \text{\&c}\end{array}\hfill \\ \begin{array}{c}\end{array}& \begin{array}{c}+3\mathrm{a}\mathrm{p}\mathrm{p}\end{array}& \begin{array}{llllll}+& \frac{3}{16}\mathrm{a}\mathrm{x}\mathrm{x}& -& \frac{3}{2}\mathrm{a}\mathrm{x}\mathrm{q}& +& 3\mathrm{a}\mathrm{q}\mathrm{q}\end{array}\hfill \\ \begin{array}{c}\end{array}& \begin{array}{c}+\mathrm{a}\mathrm{x}\mathrm{p}\end{array}& \begin{array}{llll}-& \frac{1}{4}\mathrm{a}\mathrm{x}\mathrm{x}& +& \mathrm{a}\mathrm{x}\mathrm{q}\end{array}\hfill \\ \begin{array}{c}\end{array}& \begin{array}{c}+4\mathrm{a}\mathrm{a}\mathrm{p}\end{array}& \begin{array}{l}-\mathrm{a}\mathrm{x}\mathrm{x}+4\mathrm{a}\mathrm{a}\mathrm{q}\end{array}\hfill \\ \begin{array}{c}\end{array}& \begin{array}{c}+\mathrm{a}\mathrm{a}\mathrm{x}\end{array}& \begin{array}{l}+\mathrm{a}\mathrm{a}\mathrm{x}\end{array}\hfill \\ \begin{array}{c}\end{array}& \begin{array}{c}-{\mathrm{x}}^3\end{array}& \begin{array}{l}-{\mathrm{x}}^3\end{array}\hfill \\ \phantom{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_}& \phantom{.\_\_\_\_\_\_\_\_\_\_\_\_\_.}& \phantom{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_}\end{array}\\ \begin{array}{rrr}\phantom{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_}& \phantom{.\_\_\_\_\_\_\_\_\_\_\_\_\_.}& \phantom{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_}\\ \begin{array}{c}+\frac{\mathrm{x}\mathrm{x}}{64\mathrm{a}}+\mathrm{r}=\mathrm{q}\end{array}& \begin{array}{c}3\mathrm{a}\mathrm{q}\mathrm{q}\end{array}& \begin{array}{llll}+& \frac{3{\mathrm{x}}^4}{4096\mathrm{a}}& & \text{\&c}\end{array}\hfill \\ \begin{array}{c}\end{array}& \begin{array}{c}+\frac{3}{16}\mathrm{x}\mathrm{x}\mathrm{q}\end{array}& \begin{array}{llll}+& \frac{3{\mathrm{x}}^4}{1024\mathrm{a}}& & \text{\&c}\end{array}\hfill \\ \begin{array}{c}\end{array}& \begin{array}{c}-\frac{1}{2}\mathrm{a}\mathrm{x}\mathrm{q}\end{array}& \begin{array}{llll}-& \frac{1}{128}{\mathrm{x}}^3& -& \frac{1}{2}\mathrm{a}\mathrm{x}\mathrm{r}\end{array}\hfill \\ \begin{array}{c}\end{array}& \begin{array}{c}+4\mathrm{a}\mathrm{a}\mathrm{q}\end{array}& \begin{array}{llll}+& \frac{1}{16}\mathrm{a}\mathrm{x}\mathrm{x}& +& 4\mathrm{a}\mathrm{a}\mathrm{r}\end{array}\hfill \\ \begin{array}{c}\end{array}& \begin{array}{c}-{\mathrm{x}}^3\end{array}& \begin{array}{l}-{\mathrm{x}}^3\end{array}\hfill \\ \begin{array}{c}\end{array}& \begin{array}{c}-\frac{65}{64}{\mathrm{a}}^3\end{array}& \begin{array}{l}-\frac{65}{64}{\mathrm{a}}^3\end{array}\hfill \\ \begin{array}{c}\end{array}& \begin{array}{c}-\frac{1}{16}\mathrm{a}\mathrm{a}\mathrm{x}\end{array}& \begin{array}{l}-\frac{1}{16}\mathrm{a}\mathrm{a}\mathrm{x}\end{array}\hfill \\ \phantom{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_}& \phantom{.\_\_\_\_\_\_\_\_\_\_\_\_\_.}& \phantom{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_}\end{array}\\ \phantom{\_}\end{array}\\ \left.\phantom{\frac{0}{0^0}}+4\mathrm{a}\mathrm{a}-\frac{1}{2}\mathrm{a}\mathrm{x}\right)+\frac{131}{128}{\mathrm{x}}^3-\frac{15{\mathrm{x}}^4}{4096\mathrm{a}}\left(+\frac{131{\mathrm{x}}^3}{512\mathrm{a}\mathrm{a}}+\frac{509{\mathrm{x}}^4}{16384{\mathrm{a}}^3}\right.\text{.}\phantom{\frac{0}{0^0}}\end{array}$

In prior Diagrammate primus terminus valoris ipsorum p, q, r, in prima columnâ invenitur dividendo primum terminum summæ proximè superioris per coefficientem secundi termini ejusdem summæ ut $-1$ per 10 aut 0,061 per 11,23 et mutando signum quoti.: et idem terminus eodem ferè modo invenitur in secundo diagrammate. Sed Verùm hic præcipua difficultas est in inventione primi termini radicis: methodo um generali em qua id perficitur, {anc} brevitatis gratia prætereo, ut et alia quædam quæ ad concinnandam operationem spectant. Neque enim hic compendia tradere vacat, dicam tantum in genere quod radix cujusvis æquationis semel extracta pro regula resolvendi consimiles æquationes asservari possit; quodque ex pluribus ejusmodi regulis, regulam generaliorem plerumque efformare liceat; & quod radices omnes, sive simplices sint sive affectæ, modis infinitis extrahi {p}ossint, de quorum simplicioribus itaque semper consulendum est.

<2v>

Quomodo ex æquationibus, {sic ad infinitas series reductis, ar}eæ & longitudines curvarum, cont{en}ta et sup{erficies solidorum, vel quorum}libet segmentorum figurarum quarumvis eoru{mque centra gravitatis deter}minantur, & quomodo etiam Curvæ omnes Mechanicæ {ad ejusmodi æquation}es infinitarum serierum reduci possint, indeque Prob{lemata circa ill}as resolvi perinde ac si geometricæ essent, nimis longum foret describere. Sufficiat cerit specimina quædam talium Problematum recensuisse: inque ijs brevitatis gratia literas A, B, C, D &c pro terminis seriei, sicut sub initio, nonnunquam usurpabo.

1. Si ex dato sinu recto vel sinu verso arcus desideretur: sit radius r & sinus rectus x eritque arcus $=\mathrm{x}+\frac{{\mathrm{x}}^3}{6\mathrm{r}\mathrm{r}}+\frac{3{\mathrm{x}}^5}{40{\mathrm{r}}^4}+\frac{5{\mathrm{x}}^7}{112{\mathrm{r}}^6}+\text{\&c}$. hoc est $=\mathrm{x}+\frac{1\times 1\times \mathrm{x}\mathrm{x}}{2\times 3\times \mathrm{r}\mathrm{r}}\mathrm{A}+\frac{3\times 3\mathrm{x}\mathrm{x}}{4\times 5\mathrm{r}\mathrm{r}}\mathrm{B}+\frac{5\times 5\mathrm{x}\mathrm{x}}{6\times 7\mathrm{r}\mathrm{r}}\mathrm{C}+\frac{7\times 7\mathrm{x}\mathrm{x}}{8\times 9\mathrm{r}\mathrm{r}}\mathrm{D}+\text{\&c}$. Vel sit d diameter & x sinus versus, et erit arcus $={\mathrm{d}}^{\frac{1}{2}}{\mathrm{x}}^{\frac{1}{2}}+\frac{{\mathrm{x}}^{\frac{3}{2}}}{6{\mathrm{d}}^{\frac{1}{2}}}+\frac{3{\mathrm{x}}^{\frac{5}{2}}}{40{\mathrm{d}}^{\frac{3}{2}}}+\frac{5{\mathrm{x}}^{\frac{7}{2}}}{112{\mathrm{d}}^{\frac{5}{2}}}+\text{\&c}$ hoc est $=\sqrt{}\mathrm{d}\mathrm{x}in1+\frac{\mathrm{x}}{6}+\frac{3\mathrm{x}\mathrm{x}}{40\mathrm{d}}+\frac{5{\mathrm{x}}^3}{112\mathrm{d}\mathrm{d}}+\text{\&c}$.

2. Si vicissim ex dato arcu desiderentur sinus: sit radius r et arcus z, eritque sinus rectus $=\mathrm{z}-\frac{{\mathrm{z}}^3}{6\mathrm{r}\mathrm{r}}+\frac{{\mathrm{z}}^5}{120{\mathrm{r}}^4}-\frac{{\mathrm{z}}^7}{5040{\mathrm{r}}^6}+\frac{{\mathrm{z}}^9}{36288{\mathrm{r}}^8}-\text{\&c}$, hoc est $=\mathrm{z}-\frac{\mathrm{z}\mathrm{z}}{2\times 3\mathrm{r}\mathrm{r}}\mathrm{A}-\frac{\mathrm{z}\mathrm{z}}{4\times 5\mathrm{r}\mathrm{r}}\mathrm{B}-\frac{\mathrm{z}\mathrm{z}}{6\times 7\mathrm{r}\mathrm{r}}\mathrm{C}-\text{\&c}$; Et sinus versus $=\frac{\mathrm{z}\mathrm{z}}{2\mathrm{r}}-\frac{{\mathrm{z}}^4}{24{\mathrm{r}}^3}$$+\frac{{\mathrm{z}}^6}{720{\mathrm{r}}^5}-\frac{{\mathrm{z}}^8}{4032{\mathrm{r}}^7}+\text{\&c}$, hoc est $\frac{\mathrm{z}\mathrm{z}}{1\times 2\mathrm{r}}-\frac{\mathrm{z}\mathrm{z}}{3\times 4\mathrm{r}\mathrm{r}}\mathrm{A}-\frac{\mathrm{z}\mathrm{z}}{5\times 6\mathrm{r}\mathrm{r}}\mathrm{B}-\frac{\mathrm{z}\mathrm{z}}{7\times 8}\mathrm{C}$.

3. Si arcus capiendus sit in ratione datâ ad alium arcum: esto circuli diameter $=\mathrm{d}$, Chorda arcûs dati $=\mathrm{x}$, & arcus quæsitus ad arcum illum datum ut n ad 1; eritque arcûs quæsiti chorda $=\mathrm{n}\mathrm{x}+\frac{1-\mathrm{n}\mathrm{n}}{2\times 3\mathrm{d}\mathrm{d}}\mathrm{x}\mathrm{x}\mathrm{A}+\frac{9-\mathrm{n}\mathrm{n}}{4\times 5\mathrm{d}\mathrm{d}}\mathrm{x}\mathrm{x}\mathrm{B}+\frac{25-\mathrm{n}\mathrm{n}}{6\times 7\mathrm{d}\mathrm{d}}\mathrm{x}\mathrm{x}\mathrm{C}$$+\frac{36-\mathrm{n}\mathrm{n}}{8\times 9\mathrm{d}\mathrm{d}}\mathrm{x}\mathrm{x}\mathrm{D}+\frac{49-\mathrm{n}\mathrm{n}}{10\times 11\mathrm{d}\mathrm{d}}\mathrm{x}\mathrm{x}\mathrm{E}+\text{\&c}$. Ubi nota quod si n est numerus impar, series desinet esse infinita, & evadet eadem quæ prodit per vulgarem Algebram ad multiplicandum datum angulum per istum numerum n.

4. Si in axe alterutro AB ellipseos ADB (cujus centrum C & axis alter DH) detur punctum aliquod E circa quod recta EG occurrens Ellipsi in G motu angulari feratur, & ex datâ area sectoris Ellipticæ BEG quæratur recta GF quæ à puncto G ad axem AB normaliter demittitur: esto $\mathrm{BC}=\mathrm{q}$, $\mathrm{DC}=\mathrm{r}$, $\mathrm{EB}=\mathrm{t}$, ac duplum areæ $\mathrm{BEG}=\mathrm{z}$; & erit $\mathrm{GF}=\frac{\mathrm{z}}{\mathrm{t}}-\frac{\mathrm{q}{\mathrm{z}}^3}{6\mathrm{r}\mathrm{r}{\mathrm{t}}^4}+\frac{10\mathrm{q}\mathrm{q}-\mathrm{q}\mathrm{q}\mathrm{t}}{120{\mathrm{r}}^4{\mathrm{t}}^7}{\mathrm{z}}^5$$\frac{-280{\mathrm{q}}^3+504\mathrm{q}\mathrm{q}\mathrm{t}-225\mathrm{q}\mathrm{t}\mathrm{t}}{5040{\mathrm{r}}^6{\mathrm{t}}^{10}}{\mathrm{z}}^7+\text{\&c}$. Sic itaque Astronomicum illud Kepleri Problema resolvi potest.

5. In eâdem Ellipsi si statuatur $\mathrm{CD}=\mathrm{r}$, $\frac{{\mathrm{CB}}^q}{\mathrm{CD}}=\mathrm{c}$, & $\mathrm{CF}=\mathrm{x}$, erit arcus Ellipticus $\begin{array}{lllllllllllllll}\mathrm{DG}& =& \mathrm{x}& +& \frac{1}{6\mathrm{c}\mathrm{c}}{\mathrm{x}}^3& +& \frac{1}{10\mathrm{r}{\mathrm{c}}^3}{\mathrm{x}}^5& +& \frac{1}{14\mathrm{r}\mathrm{r}{\mathrm{c}}^4}{\mathrm{x}}^7& +& \frac{1}{18{\mathrm{r}}^3{\mathrm{c}}^5}{\mathrm{x}}^9& +& \frac{1}{22{\mathrm{r}}^4{\mathrm{c}}^6}{\mathrm{x}}^{11}& +& \text{\&c}\\ & & & & & -& \frac{1}{40{\mathrm{c}}^4}& -& \frac{1}{28\mathrm{r}{\mathrm{c}}^5}& -& \frac{1}{24\mathrm{r}\mathrm{r}{\mathrm{c}}^6}& -& \frac{1}{22{\mathrm{r}}^3{\mathrm{c}}^7}\\ & & & & & & & +& \frac{1}{112{\mathrm{c}}^6}& +& \frac{1}{48\mathrm{r}{\mathrm{c}}^7}& +& \frac{3}{88\mathrm{r}\mathrm{r}{\mathrm{c}}^8}\\ & & & & & & & & & -& \frac{5}{1152{\mathrm{c}}^8}& -& \frac{5}{352\mathrm{r}{\mathrm{c}}^9}\\ & & & & & & & & & & & +& \frac{7}{2816{\mathrm{c}}^{10}}\end{array}$
Hic numerales coefficientes supremorum terminorum $\left(\frac{1}{6}.\frac{1}{10}.\frac{1}{14}\text{\&c}\right)$ sunt in musica progressione, & numerales coefficientes omnium inferiorum in unaquaque columna prodeunt multiplicando continuò <3r> Numeralem coefficientem supremi termini per terminos hujus progressionis $\frac{\frac{1}{2}\mathrm{n}-1}{2}.\frac{\frac{3}{3}\mathrm{n}-3}{4}.\frac{\frac{5}{4}\mathrm{n}-5}{6}.\frac{\frac{7}{5}\mathrm{n}-7}{8}.\frac{\frac{9}{6}\mathrm{n}-9}{10}.\text{\&c}$: ubi n significat numerum dimensionum ipsius c in denominatore istius supremi termini. E:g: ut terminorum infra $\frac{1}{22{\mathrm{r}}^4{\mathrm{c}}^6}$, numerales coefficientes inveniantur, pono $\mathrm{n}=6$, ducoque $\frac{1}{22}$ (numeralem coefficientem ipsius $\frac{1}{22{\mathrm{r}}^4{\mathrm{c}}^6}$) $in\frac{\frac{1}{2}\mathrm{n}-1}{2}$ hoc est $in1$; et prodit $\frac{1}{22}$ numeralis coefficiens termini proximè inferior{is;} dein duco hunc $\frac{1}{22}in\frac{\frac{3}{3}\mathrm{n}-3}{4}$ sive $in\frac{\mathrm{n}-3}{4}$ hoc est $in\frac{3}{4}$ & prodit $\frac{3}{88}$ numeralis coefficiens tertij termini in ista columna. Atque ita $\frac{3}{88}\times \frac{\frac{5}{4}\mathrm{n}-5}{6}$ facit $\frac{5}{352}$ num: coeff: quarti termini & $\frac{5}{352}\times \frac{\frac{7}{5}\mathrm{n}-7}{8}$ facit $\frac{7}{2816}$ numeralem coefficientem infimi termini. Idem in alijs ad infinitum usque columnis præstari potest, adeoque valor ipsius DG per hanc regulam pro lubitu produci.
Ad hæc si BF dicatur x, sitque r latus rectum Ellipseos & $\mathrm{e}=\frac{\mathrm{r}}{\mathrm{AB}}$; erit arcus Ellipticus
$\begin{array}{ccc}\begin{array}{c}\\ \begin{array}{c}\mathrm{BG}=\sqrt{}\mathrm{r}\mathrm{x}in\end{array}\end{array}& \begin{array}{c}\\ \begin{array}{ccccccccccc}\begin{array}{c}\begin{array}{lll}1& +& 2& \phantom{\sqrt{}}\\ & -& \frac{3}{2}\mathrm{e}\end{array}\}\\ 3\mathrm{r}\end{array}& \mathrm{x}\phantom{\sqrt{}}& & \begin{array}{c}\begin{array}{ll}-& 2\phantom{\sqrt{}}\\ +& 3\mathrm{e}\\ -& \frac{5}{8}\mathrm{e}\mathrm{e}\end{array}\}\\ 5\mathrm{r}\mathrm{r}\end{array}& \mathrm{x}\mathrm{x}\phantom{\sqrt{}}& & \begin{array}{c}\begin{array}{ll}+& 4\phantom{\sqrt{}}\\ -& 9\mathrm{e}\\ +& \frac{23}{4}\mathrm{e}\mathrm{e}\\ -& \frac{7}{16}{\mathrm{e}}^3\end{array}\}\\ 7{\mathrm{r}}^3\end{array}& {\mathrm{x}}^3\phantom{\sqrt{}}& & \begin{array}{c}\begin{array}{ll}-& 10\phantom{\sqrt{}}\\ +& 30\mathrm{e}\\ -& \frac{123}{4}\mathrm{e}\mathrm{e}\\ +& \frac{91}{8}{\mathrm{e}}^3\\ -& \frac{45}{128}{\mathrm{e}}^4\end{array}\}\\ 9{\mathrm{r}}^4\end{array}& {\mathrm{x}}^4\phantom{\sqrt{}}\end{array}\end{array}& \begin{array}{c}\\ \begin{array}{c}+\text{\&c.}\phantom{\sqrt{}}\end{array}\end{array}\end{array}$
Quare si ambitus totius Ellipseos desideretur: biseca CB in F, & quære arcum DG per prius Theorema & arcum GB per posterius.

6 Si vice versa ex dato arcu Elliptico DG quæratur sinus ejus CF, tum dicto $\mathrm{CD}=\mathrm{r}$, $\frac{{\mathrm{CB}}^q}{\mathrm{CD}}=\mathrm{c}$, & arcu illo $\mathrm{DG}=\mathrm{z}$ erit
$\begin{array}{lllllllllll}\mathrm{CF}& =& \mathrm{z}& -& \frac{1}{6\mathrm{c}\mathrm{c}}{\mathrm{z}}^3& -& \frac{1}{10\mathrm{r}{\mathrm{c}}^3}{\mathrm{z}}^5& -& \frac{1}{14\mathrm{r}\mathrm{r}{\mathrm{c}}^4}{\mathrm{z}}^7& -& \text{\&c.}\\ & & & & & +& \frac{13}{120{\mathrm{c}}^4}& +& \frac{71}{420\mathrm{r}{\mathrm{c}}^5}\\ & & & & & & & -& \frac{493}{5040{\mathrm{c}}^6}\end{array}$
Quæ autem de Ellipsi dicta sunt, omnia facilè accommodantur ad Hyperbolam: mutatis tantum signis ipsorum c & e ubi sunt {ea} imparium dimentionum.

7. Præterea si sit CE Hyperbola cujus Asymptoti AD, AF rectum angulum FAD constituant & ad AD erigantur utcunque perpendicula BC, DE occurrentia Hyperbolæ in C & E, & AB dicatur a, BC b, & area BCED z, erit $\mathrm{BD}=\frac{\mathrm{z}}{\mathrm{b}}+\frac{\mathrm{z}\mathrm{z}}{2\mathrm{a}\mathrm{b}\mathrm{b}}+\frac{{\mathrm{z}}^3}{6\mathrm{a}\mathrm{a}{\mathrm{b}}^3}+\frac{{\mathrm{z}}^4}{24{\mathrm{a}}^3{\mathrm{b}}^4}+\frac{{\mathrm{z}}^5}{120{\mathrm{a}}^4{\mathrm{b}}^5}\text{\&c}$: ubi coefficientes denominatorum prodeunt multiplicando terminos hujus arithmeticæ progressionis, $1,2,3,4,5\text{\&c}$ in se continuò. Et hinc ex Logarithmo dato potest numerus ei competens inveniri.

8. Esto VDE Quadratrix cujus vertex V, existente A centro & AE semidiametro circuli ad quem aptatur, & angulo, VAE recto. Demissoque ad AE perpendiculo quovis DB & acta Quadratricis tangente DT occurrente axi ejus AV in T: dic $\mathrm{AV}=\mathrm{a}$, & $\mathrm{AB}=\mathrm{x}$, eritque <3v> $\mathrm{BD}=\mathrm{a}-\frac{\mathrm{x}\mathrm{x}}{3\mathrm{a}}-\frac{{\mathrm{x}}^4}{45{\mathrm{a}}^3}-\frac{2{\mathrm{x}}^6}{945{\mathrm{a}}^5}-\text{\&c.}$ Et $\mathrm{VT}=\frac{\mathrm{x}\mathrm{x}}{3\mathrm{a}}+\frac{{\mathrm{x}}^4}{15{\mathrm{a}}^3}+\frac{2{\mathrm{x}}^6}{189{\mathrm{a}}^5}+\text{\&c.}$ Et area AVDB$=\mathrm{a}\mathrm{x}-\frac{{\mathrm{x}}^3}{9\mathrm{a}}-\frac{{\mathrm{x}}^5}{225{\mathrm{a}}^3}-\frac{2{\mathrm{x}}^7}{6615{\mathrm{a}}^5}-\text{\&c}$ Et arcus $\mathrm{VD}=\mathrm{x}+\frac{2{\mathrm{x}}^3}{27\mathrm{a}\mathrm{a}}+\frac{14{\mathrm{x}}^5}{2025{\mathrm{a}}^4}+\frac{604{\mathrm{x}}^7}{893025{\mathrm{a}}^6}+\text{\&c}$. Unde vicissim ex dato BD, vel VT, aut areâ AVDB arcuve VD, per resolutionem affectarum æquationum erui potest x seu AB.

9 Esto Denique AEB sphæroides, revolutione Ellipseos AEB circa axem AB genita, & recta planis quatuor, AB per axem transeunte, DC parallelo AB, CDE perpendiculariter bisecante axem, et FC parallelo CE: sitque recta $\mathrm{CB}=\mathrm{a}$. $\mathrm{CE}=\mathrm{c}$. $\mathrm{CF}=\mathrm{x}$. & $\mathrm{FG}=\mathrm{y}$; et sphæroideos segmentum CDFG, dictis quatuor planis comprehensum erit.
$\begin{array}{rrrrrrrrrrrrrrrr}+2\mathrm{c}\mathrm{x}& \mathrm{y}& & -\frac{\mathrm{x}}{3\mathrm{c}}& {\mathrm{y}}^3& & -\frac{\mathrm{x}}{20{\mathrm{c}}^3}& {\mathrm{y}}^5& & -\frac{\mathrm{x}}{56{\mathrm{c}}^5}& {\mathrm{y}}^7& & -\frac{5\mathrm{x}}{576{\mathrm{c}}^7}& {\mathrm{y}}^9& & \hfill -\text{\&c}\hfill \\ -\frac{\mathrm{c}{\mathrm{x}}^3}{3\mathrm{a}\mathrm{a}}& & & -\frac{{\mathrm{x}}^3}{18\mathrm{c}\mathrm{a}\mathrm{a}}& & & -\frac{{\mathrm{x}}^3}{40{\mathrm{c}}^3\mathrm{a}\mathrm{a}}& & & -\frac{5{\mathrm{x}}^3}{336{\mathrm{c}}^5\mathrm{a}\mathrm{a}}& & & \hfill -\text{\&c.}\hfill \\ -\frac{\mathrm{c}{\mathrm{x}}^5}{20{\mathrm{a}}^4}& & & -\frac{{\mathrm{x}}^5}{40\mathrm{c}{\mathrm{a}}^4}& & & -\frac{3{\mathrm{x}}^5}{160{\mathrm{c}}^3{\mathrm{a}}^4}& & & \hfill -\text{\&c.}\hfill \\ -\frac{\mathrm{c}{\mathrm{x}}^7}{56{\mathrm{a}}^6}& & & -\frac{5{\mathrm{x}}^7}{336\mathrm{c}{\mathrm{a}}^6}& & & \hfill -\text{\&c}\hfill \\ -\frac{5\mathrm{c}{\mathrm{x}}^9}{576{\mathrm{a}}^7}& & & \hfill -\text{\&c.}\hfill \\ \hfill -\text{\&c.}\hfill \end{array}$
Ubi numerales coefficientes supremorum terminorum $\left[2,\frac{-1}{\phantom{-}3},\frac{-1}{20},\frac{-1}{56},\frac{-5}{576}\text{\&c}\right]$ in infinitum producuntur multiplicando primum coefficientem 2 continuò per terminos hujus progressionis $\frac{-1\times 1}{\phantom{-}2\times 3}.\frac{1\times 3}{4\times 5}.\frac{3\times 5}{6\times 7}.\frac{5\times 7}{8\times 9}.\frac{7\times 9}{10\times 11}.\text{\&c}$. Et numerales coefficientes terminorum in unaquaque coluna descendentium in infinitum producuntur multiplicando continuò coefficientem supremi termini in prima columna per eandem progressionem, in secunda autem per terminos hujus $\frac{1\times 1}{2\times 3}.\frac{3\times 3}{4\times 5}.\frac{5\times 5}{6\times 7}.\frac{7\times 7}{8\times 9}.\frac{9\times 9}{10\times 11}\text{\&c}$; in tertia per terminos hujus $\frac{3\times 1}{2\times 3}.\frac{5\times 3}{4\times 5}.\frac{7\times 5}{6\times 7}.$$\frac{9\times 7}{8\times 9}.\text{\&c}$, in quarta per terminos huius $\frac{5\times 1}{2\times 3}.\frac{7\times 3}{4\times 5}.\frac{9\times 5}{6\times 7}.\text{\&c}$, in quinta per terminos huius $\frac{7\times 1}{2\times 3}.\frac{9\times 3}{4\times 5}.\frac{11\times 5}{6\times 7}.\text{\&c}$ Et sic in infinitum. Et eodem modo segmenta aliorum solidorum designari, & valores eorum aliquando commodè per series quasdem numerales in infinitum produci possu{n}t.

Ex his videre est quantum fines Analyseos per hujusmodi infinitas æquationes ampliantur: quippe quæ earum beneficio, ad omnia, penè dixerim, problemata (si numeralia Diophanti et similia excipias) sese extendit Non tamen omninò universalis evadit, nisi per ulteriores quasdem methodos eliciendi series infinitas. Sunt enim quædam Problemata in quibus non liceat ad series infinitas per divisionem vel extractionem radicum simplicium affectarumve pervenire: sed quomodo in istis casibus procedendum sit jam non vacat dicere; ut neque alia quædam tradere quæ circa reductionem infinitarum serierum in finitas, ubi rei natura tulerit, excogitari. Nam parcius scribo, quod hæ speculationes diu mihi fastidio esse cœperunt, adeò ut ab ijsdem jam per quinque ferè annos abstinuerim. Unum tamen addam: quòd postquam Problema aliquod ad infinitam æquationem deducitur, possint indè variæ approximationes in usum Mechanicæ nullo ferè negotio formari, quæ per alias methodos quæsitæ, multo labore temporisque dispendio constare solent. Cujus rei Exemplo esse possunt Tractatus Hugenij aliorumque de Quadraturâ circuli. Nam ut ex datâ arcûs chorda A, & dimidij arcûs chorda D arcum illum proxime assequarim, finge arcum illum esse Z, et circuli radium r; juxtaque superiora erit A (nempe duplum sinûs dimidij z) $=\mathrm{z}-\frac{{\mathrm{z}}^3}{4\times 6\mathrm{r}\mathrm{r}}+\frac{{\mathrm{z}}^5}{4\times 4\times 120{\mathrm{r}}^4}-\text{\&c}$. <4r> Et $\mathrm{B}=\frac{1}{2}\mathrm{z}-\frac{{\mathrm{z}}^3}{2\times 16\times 6\mathrm{r}\mathrm{r}}+\frac{{\mathrm{z}}^5}{2\times 16\times 16\times 120{\mathrm{r}}^4}-\text{\&c}$. Duc jam B in numerum fictitium n & producto aufer A, & residui secundum terminum (nempe $\left.-\frac{\mathrm{n}{\mathrm{z}}^3}{2\times 16\times 6\mathrm{r}\mathrm{r}}+\frac{{\mathrm{z}}^3}{4\times 6\mathrm{r}\mathrm{r}}\text{,}\right)$ eo ut evanescat, pone $=0$, indeque emerget $\mathrm{n}=8$, & erit $8\mathrm{B}-\mathrm{A}=3\mathrm{z}\ast -\frac{3{\mathrm{z}}^5}{64\times 120{\mathrm{r}}^4}+\text{\&c}$: hoc est $\frac{8\mathrm{B}-\mathrm{A}}{3}=\mathrm{z}$ errore tantum existente $\frac{{\mathrm{z}}^5}{7680{\mathrm{r}}^4}-\text{\&c}$ in excessu. Quod est Theorema Hugenianum.

Insuper si in arcûs Bb sagittâ AD indefinitè productâ 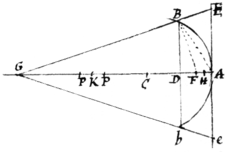quæratur punctum G à quo actæ rectæ GB, Gb abscindant tangentem Ee quamproximè æqualem arcui isti: esto circuli centrum C diameter $\mathrm{AK}=\mathrm{d}$, & sagitta $\mathrm{AD}=\mathrm{x}$ et erit DB $\left(=\sqrt{}\overline{\mathrm{d}\mathrm{x}-\mathrm{x}\mathrm{x}}\right)={\mathrm{d}}^{\frac{1}{2}}{\mathrm{x}}^{\frac{1}{2}}-\frac{{\mathrm{x}}^{\frac{3}{2}}}{2{\mathrm{d}}^{\frac{1}{2}}}-\frac{{\mathrm{x}}^{\frac{5}{2}}}{8{\mathrm{d}}^{\frac{3}{2}}}-\frac{{\mathrm{x}}^{\frac{7}{2}}}{16{\mathrm{d}}^{\frac{5}{2}}}-\text{\&c}$. Et $\mathrm{AE}\left(=\mathrm{AB}\right)={\mathrm{d}}^{\frac{1}{2}}{\mathrm{x}}^{\frac{1}{2}}+\frac{{\mathrm{x}}^{\frac{3}{2}}}{6{\mathrm{d}}^{\frac{1}{2}}}+\frac{3{\mathrm{x}}^{\frac{5}{2}}}{40{\mathrm{d}}^{\frac{3}{2}}}+\frac{5{\mathrm{x}}^{\frac{7}{2}}}{112{\mathrm{d}}^{\frac{5}{2}}}+\text{\&c}$. Et $\mathrm{AE}-\mathrm{DB}.\mathrm{AD}\colon\colon \mathrm{AE}.\mathrm{AG}$. Quare $\mathrm{AG}=\frac{3}{2}\mathrm{d}-\frac{1}{5}\mathrm{x}-\frac{12\mathrm{x}\mathrm{x}}{175\mathrm{d}}-\text{vel}+\text{\&c}$. Finge ergo $\mathrm{AG}=\frac{3}{2}\mathrm{d}-\frac{1}{5}\mathrm{x}$, & vicissim erit $\mathrm{DG}\left(\frac{3}{2}\mathrm{d}-\frac{6}{5}\mathrm{x}\right).\mathrm{DB}\colon\colon \mathrm{DA}.\mathrm{AE}-\mathrm{DB}$. Quare $\mathrm{AE}-\mathrm{DB}=\frac{2{\mathrm{x}}^{\frac{3}{2}}}{3{\mathrm{d}}^{\frac{1}{2}}}+\frac{{\mathrm{x}}^{\frac{5}{2}}}{5{\mathrm{d}}^{\frac{3}{2}}}+\frac{23{\mathrm{x}}^{\frac{7}{2}}}{300{\mathrm{d}}^{\frac{5}{2}}}+\text{\&c}$. Adde AB et prodit $\mathrm{AE}={\mathrm{d}}^{\frac{1}{2}}{\mathrm{x}}^{\frac{1}{2}}+$$\frac{{\mathrm{x}}^{\frac{3}{2}}}{6{\mathrm{d}}^{\frac{1}{2}}}+\frac{3{\mathrm{x}}^{\frac{5}{2}}}{40{\mathrm{d}}^{\frac{3}{2}}}+\frac{17{\mathrm{x}}^{\frac{7}{2}}}{1200{\mathrm{d}}^{\frac{5}{2}}}+\text{\&c}$. Hoc aufer de valore ipsius AE supra habito et restabit error $\frac{16{\mathrm{x}}^{\frac{7}{2}}}{525{\mathrm{d}}^{\frac{5}{2}}}+\mathrm{vel}-\text{\&c}$. Quare in AG cape AH quintam partem AD , & $\mathrm{KG}=$HC; & actæ GBE, Gbe abscindent tangentem Ee quamproximè æqualem arcui Bab errore tantum existente $\frac{16{\mathrm{x}}^3}{525{\mathrm{d}}^3}\sqrt{}\mathrm{d}\mathrm{x}+\mathrm{vel}-\text{\&c}$; multo minore scilicet quam in Theoremate Hugenij. Quod si fiat $7\mathrm{AK}.3\mathrm{AH}\colon\colon \mathrm{DH}.\mathrm{n}$, & capiatur $\mathrm{KG}=\mathrm{CH}-\mathrm{n}$ erit error adhuc multò minor.

Atque ita si circuli segmentum aliquod BAb per Mechanicam designandum esset: primò reducerem aream istam in infinitam seriem; puta hanc $\mathrm{BbA}=$ $\frac{4}{3}{\mathrm{d}}^{\frac{1}{2}}{\mathrm{x}}^{\frac{3}{2}}-\frac{2{\mathrm{x}}^{\frac{5}{2}}}{5{\mathrm{d}}^{\frac{1}{2}}}-\frac{{\mathrm{x}}^{\frac{7}{2}}}{14{\mathrm{d}}^{\frac{3}{2}}}-\frac{{\mathrm{x}}^{\frac{9}{2}}}{36{\mathrm{d}}^{\frac{5}{2}}}-\text{\&c}$; dein quærerem constructiones mechanicas quibus hanc seriem proximè assequere; cujusmodi sunt hæc.

Age rectam AB, & erit segmentum $\mathrm{BbA}=\overline{\frac{2}{3}\mathrm{AB}+\mathrm{BD}}\times \frac{4}{5}\mathrm{AD}$ proximè, existente scilicet errore tantum $\frac{{\mathrm{x}}^3}{70\mathrm{d}\mathrm{d}}\sqrt{}\mathrm{d}\mathrm{x}+\text{\&c}$, in defectu: vel proximiùs erit segmentum illud, (bisecto AD in F et acta recta BF,) $=\frac{4\mathrm{BF}+\mathrm{AB}}{15}\times 4\mathrm{AD}$, existente errore solummodo $\frac{{\mathrm{x}}^3}{560\mathrm{d}\mathrm{d}}\sqrt{}\mathrm{d}\mathrm{x}+\text{\&c}$. qui semper minor est quàm $\frac{1}{1500}$ totius segmenti, etiamsi segmentum illud ad usque semicirculum augeatur.

Sic et in Ellipsi BAb cujus vertex A, axis alteruter AK, et latus rectum AP, cape $\mathrm{PG}=\frac{1}{2}\mathrm{AP}+\frac{19\mathrm{AK}-21\mathrm{AP}}{10\mathrm{AK}}\times \mathrm{AP}$; in Hyperbola verò cape $\mathrm{PG}=\frac{1}{2}\mathrm{AP}+\frac{19\mathrm{AK}+21\mathrm{AP}}{10\mathrm{AK}}\times \mathrm{AP}$: & acta recta GBE abscindet tangentem AE quamproximè æqualem arcui Elliptico vel Hyperbolico AB, dummodo ar{cus} ille non sit nimis magnus. Et pro area segmenti Hyperbolici BbA, in DP cape $\mathrm{DM}=\frac{3{\mathrm{AD}}^q}{4\mathrm{AK}}$, & ad D & M erige perpendicula Dβ, MN occurrentia semicirculo super diametro AP descripto, eritque 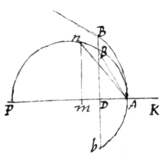$\frac{4\mathrm{AN}+\mathrm{A\beta }}{15}\times 4\mathrm{AD}=\mathrm{BbA}$ proximè vel proximius propius erit $\frac{21\mathrm{AN}+4\mathrm{A\beta }}{75}\times 4\mathrm{AD}=\mathrm{BbA}$, si modoò capiatur $\mathrm{DM}=\frac{5{\mathrm{AD}}^q}{7\mathrm{AK}}$.