The Lawes of Motion
The Lawes of Motion
How solitary bodyes are moved.
Sect: 1[1]. There is an uniform extension, space, or expansion continued every way without bounds: in which all bodyes are, each in severall parts of it: which parts of space possesse {illeg} adequately filled by them are their places. And their passing out of one place or part of space into another, through all the intermediate space is their motion. Which motion is done with more or lesse velocity accordingly as tis done through more or lesse space in equal times or through equall spaces in more or lesse time. But the motion it selfe & the force to persevere in that motion is more or lesse accordingly as the factus of the bodys bulk into its velocity is more or lesse. And that force is equivalent to that motion which it is able to beget or destroy.
2[2]. The motion of a body tends one way 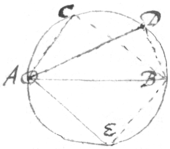 directly & severall other ways obliqly. As if the body A move directly towards the point B it also moves obliquely towards all the lines BC, BD, BE & which passe through that point B: & shall arrive to them all at the same time. Whence its velocity towards them is in such proportion as its distance from them that is, as AB, AC, AD, AE &c.
directly & severall other ways obliqly. As if the body A move directly towards the point B it also moves obliquely towards all the lines BC, BD, BE & which passe through that point B: & shall arrive to them all at the same time. Whence its velocity towards them is in such proportion as its distance from them that is, as AB, AC, AD, AE &c.
3[3]. If a body A move towards B with  the velocity R, & by the way hath some new force done to it which had the body rested would have propel{e}d it towards C with the velocity S. Then making AB∶AC∷R∶S, & Completing the Parallelogram BC the body shall move in the Diagonall AD & arrive at the point D with this compound motion in the same time it would have arrived at the point B with its single motion.
the velocity R, & by the way hath some new force done to it which had the body rested would have propel{e}d it towards C with the velocity S. Then making AB∶AC∷R∶S, & Completing the Parallelogram BC the body shall move in the Diagonall AD & arrive at the point D with this compound motion in the same time it would have arrived at the point B with its single motion.
4[4] In every body there is a certaine point, called its center of motion about which if the body bee any way circulated the endeavours of its parts every way from the center are exactly counterpoised by opposite endeavours. And the progressive motion of the body is the same with the motion of this its center which always moves in a streight line & uniformly when the body is free from occursions with other bodys. And so doth the common center of two bodys; which is found by dividing the distance twixt their propper centers in reciprocall proportion to their bulk. And so the common center of 3 or more bodys &c. And all the lines passing through these centers of motion are axes of motion.
5[5]. The angular quantity of a bodys circular 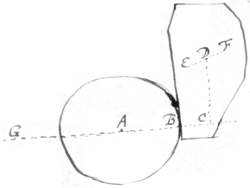 motion & velocity is more or lesse accordingly as the body makes one revolution in more {or} lesse time but the reall quantity of its circular motion is more or lesse accordingly as the body hath more or lesse power & force to persevere in that motion; which motion divided by the bodys bulke is the reall quantity of its circular velocity. Now to know the reall quantity of a bodys circular motion & velocity about any given axis EF; Suppose it hung upon the two end E & F of that axis as upon two poles: And that another globular body of the same bignesse, whose center is A, is so placed that the circulating body shall hit it in the point F & strike it away in the line BAG (which lyeth in the same plane with one of the circles described about the axis EF) & thereby just loose all its owne motion. Then hath the Globe gotten the same quantity of progressive motion & velocity which the other had of circular, its velocity being the same with that of the point C which describes a circle touching the line BG. The Radius DC of which circle I may therefore call the radius of Circular motion or velocity about that axis EF. And the circle described with the said Radius of Circulation in that plane which cuts the axis EF perpendicularly in the center of motion I call the Equator of circulation about that axis, and those circles which passe through the poles, meridians &c.
motion & velocity is more or lesse accordingly as the body makes one revolution in more {or} lesse time but the reall quantity of its circular motion is more or lesse accordingly as the body hath more or lesse power & force to persevere in that motion; which motion divided by the bodys bulke is the reall quantity of its circular velocity. Now to know the reall quantity of a bodys circular motion & velocity about any given axis EF; Suppose it hung upon the two end E & F of that axis as upon two poles: And that another globular body of the same bignesse, whose center is A, is so placed that the circulating body shall hit it in the point F & strike it away in the line BAG (which lyeth in the same plane with one of the circles described about the axis EF) & thereby just loose all its owne motion. Then hath the Globe gotten the same quantity of progressive motion & velocity which the other had of circular, its velocity being the same with that of the point C which describes a circle touching the line BG. The Radius DC of which circle I may therefore call the radius of Circular motion or velocity about that axis EF. And the circle described with the said Radius of Circulation in that plane which cuts the axis EF perpendicularly in the center of motion I call the Equator of circulation about that axis, and those circles which passe through the poles, meridians &c.
6[6]. A body circulates about one axis (as PC) 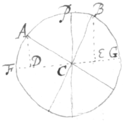 directly & about severall other axes (as AC, BC, &c) obliquely. And the angular quantity of its circulations about those axes (PC, AC, BC &c) are as the sines (PC, AD, BE, &c) of the angles which those axes make with the Equator (FG) of the principall & direct axis (PC).
directly & about severall other axes (as AC, BC, &c) obliquely. And the angular quantity of its circulations about those axes (PC, AC, BC &c) are as the sines (PC, AD, BE, &c) of the angles which those axes make with the Equator (FG) of the principall & direct axis (PC).
7[7]. If a body circulates about the axis AC with 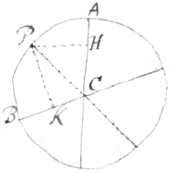 the angular quantity of velocity R: & some new force is done to it, which, if the body had rested, would have made it circulate about another axis BC, with the angular quantity of velocity S. Then in the plane of the two axes, & in one of those two opposite angles (made by the axes) in which the two circulations are contrary one to another, (as in the angle ACB). I find such a point P from which the perpendic{la}rs (PK, PH) let fall to those axes bee reciprocally proportional to the angular velocitys about those axes, (that is PK∶PH∷R∶S). And drawing the line PC, it shall bee the new axis about which the compound motion is performed. And the summe of & when the perpendiculars PH & PK fall on divers sides of the axis PC, otherwise their difference, is the angular quantity of circulation about that axis: Which in the angle tends contrary to the circulation about the axis
the angular quantity of velocity R: & some new force is done to it, which, if the body had rested, would have made it circulate about another axis BC, with the angular quantity of velocity S. Then in the plane of the two axes, & in one of those two opposite angles (made by the axes) in which the two circulations are contrary one to another, (as in the angle ACB). I find such a point P from which the perpendic{la}rs (PK, PH) let fall to those axes bee reciprocally proportional to the angular velocitys about those axes, (that is PK∶PH∷R∶S). And drawing the line PC, it shall bee the new axis about which the compound motion is performed. And the summe of & when the perpendiculars PH & PK fall on divers sides of the axis PC, otherwise their difference, is the angular quantity of circulation about that axis: Which in the angle tends contrary to the circulation about the axis
8[8]. Every body keepes the same reall quantity of circular motion & velocity so long as tis not opposed by other bodys. And it keeps the same axis too if the endeavour from the axis which the two opposite quarters twixt the Equator & every meridian of motion have, bee exactly counterpoised by the opposite endeavours of the 2 side quarters; & then also its axis doth always keepe parallel to it selfe. But if the said endeavours from the axis bee not exactly counterpoised by such opposite endeavours: then for want of such counterpoise the prevalent parts shall by little & little get further from the axis & draw nearer & nearer to such a Counterpoise, but shall never bee exactly counterpoised. And as the axis is continually moved in the body, so it continually moves in the space too with some kind or other of spirall motion; always drawing nearer & nearer to a center or parallelisme with it selfe, but never attaining to it. Nay tis so far from ever keeping parallel to it selfe, that it shall never bee twice in the same position.
How Bodys are Reflected.
9[9]. Suppose the bodys A & α did move in 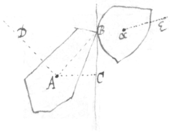 the lines DA & Eα till they met in the point B: that BC is the plane which toucheth them in the point of contact B: that the velocity of the Body A towards the said plane of contact is B, & the motion AB; & that the change which is made by reflection in that velocity & motion is X & AX. Suppose also that from the body A its center of motion two lines are drawne the one AB to the point of contact the other AC to the plane of Contact: that the intercepted line BC is F: that the axis of motion which is perpendicular to the plane ABC & its Equator are called the axis & Equator of reflected circulation: that the radius of that Equator is G: that the reall quantity of velocity about that axis is D, & the AD: that the change which reflection {m}akes in that velocity & motion is y & AY: And that the correspondent lines & motions of the other body α are β, αβ, ξ, αξ, φ, γ, δ, αδ, ν & αν. Lastly for brevity sake suppose that . And . Observing that at the time of reflection if in either body the center of motion doth move from the plane of contact, or those parts of it nearest the point of contact doe circulate from the plane of contact: then the said motion is to bee esteemed negative & the signe of its velocity B, β, D or δ must bee made negative in the valor of Q.
the lines DA & Eα till they met in the point B: that BC is the plane which toucheth them in the point of contact B: that the velocity of the Body A towards the said plane of contact is B, & the motion AB; & that the change which is made by reflection in that velocity & motion is X & AX. Suppose also that from the body A its center of motion two lines are drawne the one AB to the point of contact the other AC to the plane of Contact: that the intercepted line BC is F: that the axis of motion which is perpendicular to the plane ABC & its Equator are called the axis & Equator of reflected circulation: that the radius of that Equator is G: that the reall quantity of velocity about that axis is D, & the AD: that the change which reflection {m}akes in that velocity & motion is y & AY: And that the correspondent lines & motions of the other body α are β, αβ, ξ, αξ, φ, γ, δ, αδ, ν & αν. Lastly for brevity sake suppose that . And . Observing that at the time of reflection if in either body the center of motion doth move from the plane of contact, or those parts of it nearest the point of contact doe circulate from the plane of contact: then the said motion is to bee esteemed negative & the signe of its velocity B, β, D or δ must bee made negative in the valor of Q.
10[10]. The velocitys B, β, D & δ & they only are directly opposed & changed in Reflection; & that according to these rules . . . & . Which mutations X ξ Y & ν tend all of them from the plane of Contact. And these four rules I gather thus: The whole velocity of the two points of contact towards one another perpendicularly to the plane of contact is Q (arising partly from the bodys progressive velocity B & β & partly from their circular D & δ): And the same points are reflected one from another with the same quantity of such velocity. So that the whole change of all that their velocity which is perpendicular to the plane of contact is Q. Which change must bee distributed amongst the foure opposed velocitys B, β D & δ proportionably to the easinesse (or smallnesse of resistance) with which those velocitys are changed, that is, proportionably to , , , & . Soe that . that is . . . & .
11[11]. Now if any two reflecting bodys A & α, with the quantity of their progressive & angular motions; & their position at their meeting & consequently their point & plane of contact &: be given: to know how those bodys shall bee reflected, First find B & β by sec 2. Then the lines F & φ & the axis of reflected circulation by sec 9. & their Radij G & γ by sec 5. Then their angular quantity of velocity about the axes of reflected circulation by sec 6, & the reall quantity D & δ by sec 5. Then P & Q by sec 9 Then X, ξ, Y & ν by sec 10. Then the bodys new progressive determinations & velocitys by sec 3. Then the angular quantity of that circulation (Y & ν) which is generated by reflection by sec 5. And lastly the new axes & angular quantity of velocity about them by sec 7.
Some Observations about Motion.
Only those bodyes which are absolutely hard are exactly reflected acording to those rules. Now the bodyes here amongst us (being an aggregate of smaller other bodyes) haue a relenting softnesse & springynesse, which makes their contact be for some time & in more points then one. And the touching surfaces during the time of contact doe slide one upon another more or lesse or not at all acording to their roughnesse. And few or none of these bodyes haue a springynesse soe strong, as to force them one from another with the same vigor that they came together. Besides that their motions are continually impeded & slackened by the mediums in which they move. Now hee that would prescribe rules for the reflections of these compound bodies, must consider in how many points the two bodies touch at their meeting, the position & pression of every point, which their planes of contact &c: & how all these are varyed every moment during the time of contact by the more or lesse relenting softnesse or springynesse of those bodies & their various slidings. And also what effect the air or other mediums compressed betwixt the bodies may haue.
2 These are some cases of Reflections of bodies absolutely hard to which these rules extend not: As when two bodies meet with their angular point, or in more points then one at once; Or with their superficies. But these cases are rare.
3 In all reflections of any bodies what ever this rule is true that the common center of two or more bodies changeth not its state of motion or rest by the reflection of those bodies one amongst another.
4 Motion may be lost by reflection. As 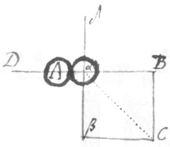 if two equall Globes A & α with equall motions from D & δ done in the perpendicular lines DA & δα, hit one another when the center of the body α is in the line DA. Then the body A shall loose all its motion & yet the motion of α is not doubled. For completing the square Bβ, the body α shall move in the Diagonall αC, & arrive at C but at the same time it would haue arrived at β without reflection. see the third section.
if two equall Globes A & α with equall motions from D & δ done in the perpendicular lines DA & δα, hit one another when the center of the body α is in the line DA. Then the body A shall loose all its motion & yet the motion of α is not doubled. For completing the square Bβ, the body α shall move in the Diagonall αC, & arrive at C but at the same time it would haue arrived at β without reflection. see the third section.
5 Motion may be gained by reflection. For if the body α return with the same motion back again from C to α. The two bodyes A & α after reflection shall regain the same equall motions in the lines AD & αδ (though backwards) which they had at first.
[1] Of Place motion velocity & force.
[2] with what velocity a body moves severall ways at once.
[3] How two progressive motions are joyned into one.
[4] Of centers & axes of motion & the motion of those centers.
[5] Of circular motion and velocity about those axes.
[6] With what velocity a body circulates about severall axes at once.
[7] How two circular motions are joyned into one.
[8] In what cases a circulating body persevere in the same state & in what it doth not.
[9] Some names & letters defined.
[10] The Rule for Reflection
[11] The conclusion. In what method the precedent rules must be used.
