The October 1666 Tract on Fluxions
☞ Note that if there happen to bee in any equation either a fraction or surde quantity or a Mechanichall one, (i:e: which cannot bee Geometrically computed, but is expressed by the area or length or gravity or content of some curve line or sollid, &c) To find in what proportion the unknowne quantitys increase or decrease doe thus. 1 Take two letters the one (as ξ) to signify that quantity, the other (as π) its motion of increase or decrease: And making an equation betwixt the letter (ξ) & the quantity signifyed by it, find thereby (by prop 7 if the quantity bee Geometricall, or by some other meanes if it bee mechanicall) the valor of the other letter (π). 2 Then substituting the letter (ξ) signifying that quantity, into its place in the maine Equation esteeme that letter (ξ) as an unknowne quantity & performe the worke of seaventh proposition; & into the resulting Equation instead of those letters ξ & π substitute theire valors. And soe you have the Equation required.
Example 1. To find p & q the motions of x & y whose relation is, . first suppose , Or . & thereby find π the motion of ξ, viz: (by prop 7) . Or . Secondly in the Equation , writing ξ in stead of , the result is , whereby find the relation of the motions p, q, & π: viz (by prop 7) . In which Equation instead of ξ & π writing theire valors, the result is, . which was required to.
[which equation multiplyed by , is . & in stead of , writing its valor , it is . Or . Which conclusion will also bee found by taking the surde quantity out the given Equation for both parts being squared it is . & therefore (by prop 7) , as before.]
☞ Note also that it may bee more convenient (setting all the termes on one side of the Equation) to put every fractionall, irrationall & mechanicall terme, as also the summe of the rationall termes, equall severally to some letter: & then to find the motions corresponding to each of those letters the sume of which motions is the Equation required.
Example the 2d. If is the relation twixt x & y, whose motions p & q are required. I make ; ; & . & the motions of τ, φ, & ξ being called β, γ, & δ; the first Equation , gives (by prop 7) . the second , gives ; Or . & the Third , gives, ; Or . Lastly , is the Equation sought.
Example 3d. If . be=y. & the superficies abc=z 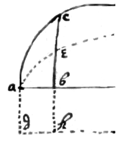 suppose that , is the relation twixt x, y & z, whose motions are p, q, & r: & that p & q are desired. The Equation gives (by prop 7), . Now drawing dh∥ab⊥ad=1−bh. I consider the superficies abhd=ab×bh=x×1=x, & abd=z doe increase in the proportion of bh to bc: that is, 1∶
∷p∶r. Or . Which valor of r being substituted into the Equation , gives . which was required.
suppose that , is the relation twixt x, y & z, whose motions are p, q, & r: & that p & q are desired. The Equation gives (by prop 7), . Now drawing dh∥ab⊥ad=1−bh. I consider the superficies abhd=ab×bh=x×1=x, & abd=z doe increase in the proportion of bh to bc: that is, 1∶
∷p∶r. Or . Which valor of r being substituted into the Equation , gives . which was required.
How to proceede in other cases (as when there are cube rootes, surde denominators, rootes within rootes (as &c: in the equation) may bee easily deduced from what {ha}th bee{n} already said.
<49r>October 1666.
To resolve Problems by Motion these following Propositions are sufficient
1 If the body a in the Perimeter of the cirkle or sphære adc 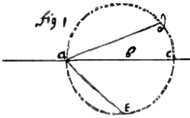 moveth towards its center b, its velocity to each point ( d, c, e,) of that circumference is as the chords (ad, ac, ae) drawne from that body to those points are.
moveth towards its center b, its velocity to each point ( d, c, e,) of that circumference is as the chords (ad, ac, ae) drawne from that body to those points are.
2 If the △s adc, aec, are alike viz ad = ec &c (though in divers plaines) & 3 bodys 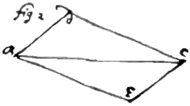 move from the point a uniformely & in equall times the first to d, the 2d to e, the 3d to c; Then is the thirds motion compounded of the motion of the first & second.
move from the point a uniformely & in equall times the first to d, the 2d to e, the 3d to c; Then is the thirds motion compounded of the motion of the first & second.
3. All the points of a Body keeping Parallel to it selfe are in equall velocity.
4. If a body move onely circularly | angularly about some axis, the velocity of its points are as their distance from that axis.
5. The motions of all bodys are either parallel or angular, or mixed of them both, after the same manner that the motion towards c (Prop 2) is compounded of those towards d & e. And in mixed motion any line may bee taken for the axis (or if a line or superficies move in plano, any point in that plane may bee taken for the center) of the angular motion
6 If the lines ae, ah being moved doe continually intersect; I describe 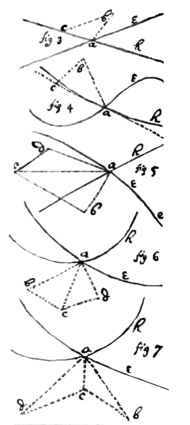 the trapezium abcd, & its diagonall ac: & say that, the proportion & position of these five lines ab, ad, ac, cb, cd, being determined by requisite data; shall designe the proportion & position of these five motions; viz: of the point a fixed in the line ae & moveing towards b, of the point a fixed in the line ah & moveing towards d; of the intersection point a moveing in the plaine abcd towards c, (for those five lines are ever in the same plaine, though ae & ah may chanch onely to touch that plaine in their intersection point a); of the intersection point a moveing in the line ae parallely to cb & according to the order of the letters c, b; & of the intersection point a move{ing} in the line ah parallely to cd & according to the order of the {lett}ers c, d.
the trapezium abcd, & its diagonall ac: & say that, the proportion & position of these five lines ab, ad, ac, cb, cd, being determined by requisite data; shall designe the proportion & position of these five motions; viz: of the point a fixed in the line ae & moveing towards b, of the point a fixed in the line ah & moveing towards d; of the intersection point a moveing in the plaine abcd towards c, (for those five lines are ever in the same plaine, though ae & ah may chanch onely to touch that plaine in their intersection point a); of the intersection point a moveing in the line ae parallely to cb & according to the order of the letters c, b; & of the intersection point a move{ing} in the line ah parallely to cd & according to the order of the {lett}ers c, d.
Note that one of the lines as ah (fig 3d & 4th) resting, the points d & a are coincident, & the point c shall bee in the line ah if it bee streight (fig 3), otherwise in its tangent (fig 4th)
7. Haveing an equation expressing the relation twixt two or 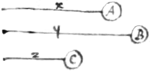 more lines x, y, z &c: described in the same time by two or more moveing bodys A, B, C, &c. the relation of their velocitys p, q, r, &c may bee thus found, viz: Set all the termes on one side of the Equation that they become equall to nothing. And first multiply each terme by so many times as x hath dimensions in that terme. Secondly multiply each terme by so many times as y hath dimensions in it. Thirdly (if there be 3 unknowne quantitys) multiply each terme by so many times as z hath dimensions in that terme. (& if there bee still more unknowne quantitys doe like to every unknowne quantity). The summe of all these products shall bee equall to nothing. which Equation gives the relation of the velocitys p, q, r, &c Or thus. Translate all the termes to one side of the equation, & multiply them being ordered according to x by this progression, {illeg} &c. or being ordered by the dimensions of y multiply them by this,: &c. The sume of these products shall bee equall to nothing, which equation gives the relation of their velocitys p, q, &c.
more lines x, y, z &c: described in the same time by two or more moveing bodys A, B, C, &c. the relation of their velocitys p, q, r, &c may bee thus found, viz: Set all the termes on one side of the Equation that they become equall to nothing. And first multiply each terme by so many times as x hath dimensions in that terme. Secondly multiply each terme by so many times as y hath dimensions in it. Thirdly (if there be 3 unknowne quantitys) multiply each terme by so many times as z hath dimensions in that terme. (& if there bee still more unknowne quantitys doe like to every unknowne quantity). The summe of all these products shall bee equall to nothing. which Equation gives the relation of the velocitys p, q, r, &c Or thus. Translate all the termes to one side of the equation, & multiply them being ordered according to x by this progression, {illeg} &c. or being ordered by the dimensions of y multiply them by this,: &c. The sume of these products shall bee equall to nothing, which equation gives the relation of their velocitys p, q, &c.
Or more Generally the Equation may bee multiplyed by the terme of these progressions &c. And &c. (a & b signifying any two numbers whither rationall or irrationall
8. If two Bodys A & B, by their velocitys p & q describe the lines x & y. & an Equation bee given expressing the relation twixt one of the lines x, & y ratio of their motions q & p; To find the other line y.
Could this bee ever done all problems whatever might bee resolved. But by the following rules it may bee very often done. (Note that ±m & ±n are logarithmes or numbers signifying the dimensions of x.)
ffirst get that valor of . Which if it bee rationall & its Denominator consist of but one terme: Multiply that valor by x & divide each terme of it by the logarithme of x in that terme the quote shall bee the valor of y. As if . Then is . Or if . Then is . (Soe if . Then is . soe that y is infinite. But note that in this case x & y increase in the same proportion that numbers & their logarithmes doe, y being like a logarithme added to an infinite number . But if x bee diminished by c, as if =, y is also diminished by the infinite number & becomes finite like a logarithme of the number x. & so x being given, y may bee mechanichally found by a Table of logarithmes, as shall bee hereafter showne.)
Secondly. But if the denominator of the valor of consist of more termes than one, it may bee reduced to such a forme that the denominator of each parte of it shall have but one terme, unlesse that parte bee : Soe that y may bee then found by the precedent rule. Which reduction is thus performed, viz: 1st, If the denominator bee not a+bx, nor all its termes multiplyed by x or xx, or x3, &c; Increase or diminish x untill the last terme of the Denominator vanish. 2dly, And when all the termes in the Denominator are multiplyed by x, xx, or x3 &c: Divide the numerator by the Denominator (as in Decimall numbers) untill the Quotient consist of such parts none of whose Denominators are so multiplyed by x, x2 & begin the Division in those termes in which x is of its fewest dimensions unlesse the Denominator be a+bx . If then the termes in the valor of bee such as was before required the valor of y may bee found by the first parte of this Prop: onely it must bee so much diminished or increased as it was before increased or diminished by increasing or diminishing x. But if the denominator of any terme consist of more termes than one, unlesse that terme bee . First find those parts of y's valor which correspond to the other parts of its valor. & then by the preceding reductions &c: seeke the parte of y's valor answering to this parte of its valor.
Example 1st. If . Then by Division tis . (as may appeare by multiplication.) Therefore (by 1st parte of this Prop:) tis . ( signifys that parte of the valor of y which is correspondent to the terme of the valor of , which may bee found by a Table of logarithmes as may hereafter appeare.)
Example 2d. If . I suppose x=z−a. Or . And by Division , (as may appeare by multiplication.) And substituteing x+a into the place of z, tis . And Therefore (by parte 1st of Prop 8) .
But sometimes The last terme of the Denominator cannot bee taken away, (as if the Denominator bee aa+xx. or a4+x4 or a4+bbxx+x4 &c) And then it will bee necessary to have in readinesse some examples with such Denominators to which all other cases of like denomination may bee by Division reduced. As if . Make bxx=z, Then is .
. Make bx3=z, Then is .
. Make bx4=z, Then is . &c. In Generall if . Make bxn=z, & then is . Also if . Make & then is . That is, if ; I make x=zz, & . Or if . Make , & □=CDV=y 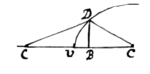
Thirdly If the valor of is irrationall being a square roote, The simplest cases may bee reduced to these following examples.
1. If . Then .
2. If . Then
3. If . Then .
4. If . Then .
5. If . Then .
1. If . Then .
2. If . Then .
3. If . Then .
4. If . Then is .
5. If . Then .
<50v>1. If . Then .
1. If . Then is .
2. If . Then is .
3. If . Then .
4 . −630a3+
1. If . Then is .
2. . Then is .
3. If . Then is .
4. If . Then
2 If, . Make xn=zz. And then is .
3. If, . Make xn=z. Then is .
4. If, . Make xn=z. Then, .
5. If . Make xn=z. then is .
1 If . Make xn=zz. then is .
1 If . Make . then is
2 If . Make . then is .
3 If . Make . then is .
If . Make xn=z. Then is .
If . Make . Then is
If . Then is .
If . Make . Then is .
<52r>
1.
●□::Note 2. that●is to□::3.●□:: as the ordinately applyed line bc 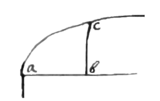 in some of the Conick sections: is to its corresponding superficies abc, the axis ab being in like manner related to z. But all those areas (& consequently □, □, □) may bee Mechanichally found either by a Table of logarithmes or signes & Tangents. And I have beene therefore hitherto content to suppose them knowne, as the basis of most of the precedent propositions.
in some of the Conick sections: is to its corresponding superficies abc, the axis ab being in like manner related to z. But all those areas (& consequently □, □, □) may bee Mechanichally found either by a Table of logarithmes or signes & Tangents. And I have beene therefore hitherto content to suppose them knowne, as the basis of most of the precedent propositions.
Note also that if the C Valor of consists of severall parts each part must bee considered severally, as if: . Then is □ . & □ . Therefore □.
Note also that of the denominator of the valor of consist of both rationall & surde quantitys or of two or more surde quantitys First take those surde quantitys out of the denominator, & then seeke (y) by the precedent theoremes
But this eighth Proposition may bee ever thus resolved mechanichally. viz: Seeke the Valor of as if you were resolving the equation in Decimall numbers either by Division or Extraction of rootes or Vieta's Analyticall resolution of powers; This operation may bee continued at pleasure, the farther the better. & from each terme ariseing from this operation may bee deduced a parte of the valor of y, (by parte the 1st of this prop).
Example 1. If . Then by division is &c. And consequently &c.
Example 2. If . Extract the roote & 'tis &c (as may appeare by squareing both parts). Therefore (by 1st parte of Prop 8) &c.
Example 3. If
<52v>But the Demonstrations of hath beene said must not bee wholly omitted.
Prop 7 Demonstrated. 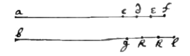
Lemma. If two bodys A, B, move uniformely the oneother from ab to c, d, e, f,g, h, k, l, &c: in the same time. Then are the lines ac,bg, & cd,gh, & de,hk, & ef,kl, &c: as their velocitys p.q. And though they move not uniformely yet are the infinitely little lines which each moment they describe, as their velocitys which they have while they describe them. As if the body A with the velocity p describe the infinitely little line (cd=)p×o in one moment, in that moment the body B with the velocity q, will describe the line (gh=)q×o. For p:q::po:qo. Soe that if the described lines bee (ac=)x, & (bg=)y, in one moment, they will bee (ad=)x+po, & (bh=)y+qo in the next.
Demonstr: Now if the equation expressing the relation twixt the lines x & y bee x3−abx+a3−dyy=0. I may substitute x+po & y+qo into the place of x & y; because (by the lemma) they as well as x & y, doe signify the lines described by the bodys A & B. By doeing so there results x3+3poxx+3ppoox+p3o3−dyy−2dqoy−dqqoo=0−abx−abpo+a3. But x3−abx+a3−dyy=0 (by supp). Therefore there remaines onely 3poxx+3ppoox+p3o3−abpo−2dqoy−dqqoo=0. Or dividing it by o tis 3px2+3ppox+p3oo−abp−2dqy−dqqo=0. Also those termes are infinitely little in which o is . Therefore omitting them there rests 3pxx−abp−2dqy=0. The like may bee done in all other equations.
Hence I observe. First that those termes ever vanish which are not multiplyed by o, they being the propounded equation. Secondly those termes also vanish in which o is of more than one dimension, because they are infinitely lesse than those in which o is but of one dimension. Thirdly the still remaining termes, being divided by o will have that forme which, by the 1st rule in Prop 7th, they should have (as may partly appeare by the second termes of Mr Oughtreds latter Analiticall table).
After the sàme manner may this 7th Prop: bee demonstrated: there being 3 or more unknowne quantitys (x, y, z, &c
Prop 8th is the Converse of this 7th Prop. & may bee therefore Analytically demonstrated by it.
Prop 1st Demonstrated. If some body A move in the right line 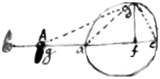 gafc from g towards c. From any point d draw df⊥ac. & call, df=a. fg=x, dg=y. Then is aa+xx−yy=0. Now by Prop 7th, may the proportion of (p) the velocity of that body towards f; to (q) its velocity towards d bee found viz 2xp−2yq=0. Or x∶y∷q∶p. That is gf∶gd∷ its velocity to d: its velocity towards f or c. & when the body A is at a, that is when the points g & a are coincident then is ac∶ad∷ad∶af∷ velocity to c∶ velocity to d.
gafc from g towards c. From any point d draw df⊥ac. & call, df=a. fg=x, dg=y. Then is aa+xx−yy=0. Now by Prop 7th, may the proportion of (p) the velocity of that body towards f; to (q) its velocity towards d bee found viz 2xp−2yq=0. Or x∶y∷q∶p. That is gf∶gd∷ its velocity to d: its velocity towards f or c. & when the body A is at a, that is when the points g & a are coincident then is ac∶ad∷ad∶af∷ velocity to c∶ velocity to d.
Prop 2d, Demonstrated. From the points d & e draw df⊥ac⊥ge. 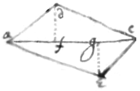 And let the firsts bodys velocity to d bee called ad, the seconds to e bee ae, & the 3ds toward c bee ac. Then shall the firsts velocity towards c bee af (by Prop 1): & The seconds towards c is ag, (prop 1). but af=gc (for △adc=△aec, & △adf =△gec. by sup). Therefore ac=ag+gc =ag+af. That is the velocity of the third body towards c is equall to the summ of the velocitys of the first & second body towards c.
And let the firsts bodys velocity to d bee called ad, the seconds to e bee ae, & the 3ds toward c bee ac. Then shall the firsts velocity towards c bee af (by Prop 1): & The seconds towards c is ag, (prop 1). but af=gc (for △adc=△aec, & △adf =△gec. by sup). Therefore ac=ag+gc =ag+af. That is the velocity of the third body towards c is equall to the summ of the velocitys of the first & second body towards c.
The former Theorems Applyed to Resolving of Problems.
Prob. 1. To draw Tangents to crooked lines.
Seeke (by prop 7th; or 3d, 4th & 2d, &c) the motions of those streight lines to which the crooked line is cheifely referred, & with what velocity they increase or decrease: & they shall give (by prop 6t, or 1st or 2d) the motion of the point describing the crooked line; which motion is in its tangent.
Tangents to Geometricall lines.
Example 1. If the crooked line fac is described by the 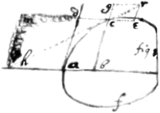 intersection of two lines cb & dc the one moveing parallely, viz: cb∥ad, & dc∥ab; soe that if ab=x, & bc=y=ad, Their relation is x4−3y+10ax3+ayxx−2y3x+a4−y4=0. To draw the tangent hcr; I consider that the point c fixed in the line cb moves towards e parallely to ab (for so doth the line cb (by supp:) & consequently all its points): also the point c fixed in the line dc moves towards g parallely to ad (by sup): therefore I draw ce∥ab & cg∥ad, & in such proportion as the motions they designe & so draw er∥cb, & gr∥dc, & the diagonall cr, (by Prop 6), that is, if the velocity of the line cb, (that is the celerity of the increasing of ab, or dc; or the velocity of the point c from d) bee called p, & the velocity of the line cd bee called q; I make ce∶gc∷p∶q(∷ce∶er∷hb∶cb.) & the point c shall move in the diagonall line cr (by prop 6) which is therefore the required tangent Now the relation of p & q may bee found by the foregoing Equation (p signifying the increase of x, & q of y) to bee 4px3−9pyxx+30paxx+2payx−2py3−3qx3+qaxx−6qyyx−4qy3=0. by Prop 7 And therefore . which determines the tangent hc
intersection of two lines cb & dc the one moveing parallely, viz: cb∥ad, & dc∥ab; soe that if ab=x, & bc=y=ad, Their relation is x4−3y+10ax3+ayxx−2y3x+a4−y4=0. To draw the tangent hcr; I consider that the point c fixed in the line cb moves towards e parallely to ab (for so doth the line cb (by supp:) & consequently all its points): also the point c fixed in the line dc moves towards g parallely to ad (by sup): therefore I draw ce∥ab & cg∥ad, & in such proportion as the motions they designe & so draw er∥cb, & gr∥dc, & the diagonall cr, (by Prop 6), that is, if the velocity of the line cb, (that is the celerity of the increasing of ab, or dc; or the velocity of the point c from d) bee called p, & the velocity of the line cd bee called q; I make ce∶gc∷p∶q(∷ce∶er∷hb∶cb.) & the point c shall move in the diagonall line cr (by prop 6) which is therefore the required tangent Now the relation of p & q may bee found by the foregoing Equation (p signifying the increase of x, & q of y) to bee 4px3−9pyxx+30paxx+2payx−2py3−3qx3+qaxx−6qyyx−4qy3=0. by Prop 7 And therefore . which determines the tangent hc
☞ Hence may bee observed this Generall Theorem for Drawing Tangents to crooked lines thus referred to streight ones; that is, to such lines in which y=bc is ordinately applyed to x=ab at any given angle abc. viz: Multiply the termes of the Equation ordered according to the dimensions of y, by any Arithmeticall progression which product shall bee the Numerator: Againe change the signes of the Equation & ordering it according to x, multiply the termes by any Arithmeticall progression & the product divided by x shall bee the Denominator of the valor of hb, that is, of x produced from y to the tangent hc.
As if . 2.1.0.Then firstyy∗=0−rx0.-1.-2., produceth 2yy, or, 2rx−2xx. Secondly 2.1.0.Secondly+rx−yy produceth . Therefore . Or else .
Example 2. If the crooked line chm bee describe by 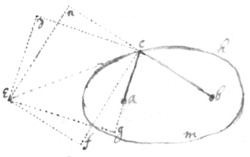 the intersection of two lines ac, bc circulating about their centers a & b, soe that if ac=x, & bc=y; their relation is x3−abx+cyy=0. To draw the tangent ec I consider that the point c fixed in the line bc moves towards f in the line cf⊥bc (for the tangent to a circle is perpendicular to its radius). also the point c fixed in the line ac moves towards d in the line cd⊥ac & from those lines cd & cf I draw two others de∥cg & ef∥bc which must bee in such proportion one to another as the motions represented by them (prop 6), that is (prop 6) as the motions of the intersection point c moveing in the lines ca & cb
the intersection of two lines ac, bc circulating about their centers a & b, soe that if ac=x, & bc=y; their relation is x3−abx+cyy=0. To draw the tangent ec I consider that the point c fixed in the line bc moves towards f in the line cf⊥bc (for the tangent to a circle is perpendicular to its radius). also the point c fixed in the line ac moves towards d in the line cd⊥ac & from those lines cd & cf I draw two others de∥cg & ef∥bc which must bee in such proportion one to another as the motions represented by them (prop 6), that is (prop 6) as the motions of the intersection point c moveing in the lines ca & cb 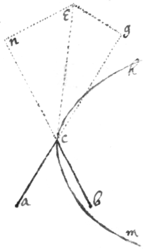 to or from the centers a & b; that is, (the celerity of the increase of x being called p, & of y being q), de∶ef∷p∶q. Then shall the diagonall ce bee the required tangent. Or which is the same, (for △ecg=△ecd, & △ecf=△ecn,) I produce ac & bc to g & n, so that cg∶cn∷p∶q. & then draw ne⊥bn, & ge⊥ag; & the tangent diagonall ce to their intersection point e. Now the relation of p & q may bee found by the given Equation to bee, 3pxx−pab+2qcy=0 (by prop 7) Or 2cy∶ab−3xx∷p∶q∷cg∶cn, whichdetermins the tangent ce.
to or from the centers a & b; that is, (the celerity of the increase of x being called p, & of y being q), de∶ef∷p∶q. Then shall the diagonall ce bee the required tangent. Or which is the same, (for △ecg=△ecd, & △ecf=△ecn,) I produce ac & bc to g & n, so that cg∶cn∷p∶q. & then draw ne⊥bn, & ge⊥ag; & the tangent diagonall ce to their intersection point e. Now the relation of p & q may bee found by the given Equation to bee, 3pxx−pab+2qcy=0 (by prop 7) Or 2cy∶ab−3xx∷p∶q∷cg∶cn, whichdetermins the tangent ce.
But note that if p, or q be negative cg or cn must bee drawn from c towards a or b, but from a or b if affirmative.
Hence tis easy to pronounce a Theorem for Tangents in such like cases & the like may bee done in all other cases however Geometricall lines bee referred to streight ones.
Tangents to Mechanichall lines
Example the 3d. If the Quadratrix kbf is described by the 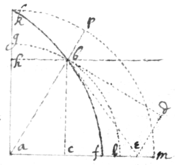 intersection (b) of the two lines hb & ap, the one hp∥ma moving uniformly from k to a, whilest the other ap circulates from k to m about the center a. Draw the circle gbl with the Rad. ab; & make bl=bd⊥ab∥de; & to the intersection point e of the lines am & ed draw eb which shall touch the Quadratrix in b. For suppose the motion of the point p fixed in the line ap, towards m to bee pm, then the motion of the point b fixed in the line ab, towards d is bl=bd, (prop 4), & the motion of the line bh towards ca, & therefore of the point b fixed in it towards c (prop 3) is ha=bc (by supp): Also ce∥bh & ed∥ap (sup). Therefore (by Prop 6) is the intersection point b of those two lines ap & hb, moves in the diagonall eb, & consequently eb toucheth the Quadratrix in b.
intersection (b) of the two lines hb & ap, the one hp∥ma moving uniformly from k to a, whilest the other ap circulates from k to m about the center a. Draw the circle gbl with the Rad. ab; & make bl=bd⊥ab∥de; & to the intersection point e of the lines am & ed draw eb which shall touch the Quadratrix in b. For suppose the motion of the point p fixed in the line ap, towards m to bee pm, then the motion of the point b fixed in the line ab, towards d is bl=bd, (prop 4), & the motion of the line bh towards ca, & therefore of the point b fixed in it towards c (prop 3) is ha=bc (by supp): Also ce∥bh & ed∥ap (sup). Therefore (by Prop 6) is the intersection point b of those two lines ap & hb, moves in the diagonall eb, & consequently eb toucheth the Quadratrix in b.
Example 4th
<54v>Prob 2d. To find the quantity of crookednesse of lines.
Lemma. The crookednesse of equall parts of circles are as their diameters reciprocally. For the crookednesse of a whole circle (acdea, bfghmb) amounts to 4 right angles. Therefore there is not more crookednesse in one whole circle acdea than in another 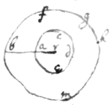 bfghmb. Suppose the perimeter acde=bfgh. Then tis, ar∶br∷ bfgh=acde∶bfghmb∷ crookednesse of bfgh∶crookednesse of bfghmb=crookednesse of acdea.
bfghmb. Suppose the perimeter acde=bfgh. Then tis, ar∶br∷ bfgh=acde∶bfghmb∷ crookednesse of bfgh∶crookednesse of bfghmb=crookednesse of acdea.
Resolution. Find That point fixed in the crooked line's perpendicular which is then in least motion, for it is the center of a circle which passing through the given point is of equall crookednesse with the line at that given point. Now, since the crooked line's tangent & perpendicular &c: (at that moment) circulate about that center; I observe, 1st that every point fixed in the Tangent or Perpendicular, or whose position to them is determined, doth describe a curve line to which the right line drawne from that center is perpendicular, & is also the radius of a circle of equall crookedness with it: 2dly that the motion of every such point is as its distance from that center; & so are the motions of the intersection point, in which any radius drawn from that center intersects two parallel lines.
Example 1. If cb=y is ordinately applyed to ab=x 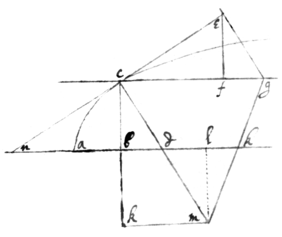 at a right angle abc, nc being tangent & mc perpendicular to the curve line ac: I seeke the motion of two points c & d fixed in the perpendicular cd; or (which is better & to the same purpose) I draw cg∥ab, & seeke the motions of the two intersection points c & d in which the perpendicular cd intersects those fixed lines cfg, & abdk: & then draw cg & dk in such proportion as those motions are, & the line gkm drawn by their ends shall intersect the perpendicular cd in the required center m: mc being the radius of a circle of equall crookednesse with the curve line ac at the point c. Now, Making △cegfe= & like △ncdbc, suppose the motion of the line cb & consequently of the points c & b fixed in it & moveing towards f & k, to bee p=nb=cf: Then is ce=cn the motion of the point c in which bc intersects the tangent ne (by Prop 6), that is of the point c fixed in the perpendicular cd, & moveing in the tangent ne: & therefore cg=nd=p+bd(=p+v if bd=v), is the motion of the intersection point c towards g in which point the perp: cd intersects cg (by Prop 6). If also the motion of the intersection point d from the point b (that is the velocity of the increase of v) bee called r, then is dk=nb+r=p+r soe that, cg−dk∶cd∷cg∶cm; that is, . Also . Lastly the motion of the point c from b, (that is the velocity with which y=cb increaseth) will bee q=cb=y.
at a right angle abc, nc being tangent & mc perpendicular to the curve line ac: I seeke the motion of two points c & d fixed in the perpendicular cd; or (which is better & to the same purpose) I draw cg∥ab, & seeke the motions of the two intersection points c & d in which the perpendicular cd intersects those fixed lines cfg, & abdk: & then draw cg & dk in such proportion as those motions are, & the line gkm drawn by their ends shall intersect the perpendicular cd in the required center m: mc being the radius of a circle of equall crookednesse with the curve line ac at the point c. Now, Making △cegfe= & like △ncdbc, suppose the motion of the line cb & consequently of the points c & b fixed in it & moveing towards f & k, to bee p=nb=cf: Then is ce=cn the motion of the point c in which bc intersects the tangent ne (by Prop 6), that is of the point c fixed in the perpendicular cd, & moveing in the tangent ne: & therefore cg=nd=p+bd(=p+v if bd=v), is the motion of the intersection point c towards g in which point the perp: cd intersects cg (by Prop 6). If also the motion of the intersection point d from the point b (that is the velocity of the increase of v) bee called r, then is dk=nb+r=p+r soe that, cg−dk∶cd∷cg∶cm; that is, . Also . Lastly the motion of the point c from b, (that is the velocity with which y=cb increaseth) will bee q=cb=y.
As if the nature of the crooked line bee x3−axy+ayy=0. Then is (by examp: 1. Prob: 1.), & (for nb∶bc∷bc∶bd) Soe that 3xxy−ayy−axv+2ayv=0. & therefore (by Prop 7) 6pxy−pav−2qay+3qxx+2qav−rax+2ray=0 & substituting , & , & y, into the places of p, v, & q in this equation The product will bee . Or . And therefore . Also . Soe that . That is . Which Equation gives the point k & consequently the point m. for km∥abk.
☞ But in such cases where y is ordinately applyed to x at right angles, From the consideration of the Equation ; Or rather : may the following Theoreme bee pronounced. To which purpose let X signify the given Equation, that is, all the algebraicall termes (expressing the nature of the given line) considered as equall to nothing & not some of them to others. Let X· signify those termes ordered according to the dimensions of x & then multiplyed by any arithmeticall progression Let X· signify those termes ordered according to the dimensions of y & then multiplyed by any Arithmeticall progression. Let :X signify those termes ordered by x & then multiplyed by any two arithmeticall progressions one of them being greater than the other by a terme. Let X: signify those termes ordered by y & then multiplied by any two Arith: Progr: differing by a terme. Let ·X· signify those termes ordered according to x, & then multiplyed by the greater of the progressions which multiplyed :X; & then ordered by y & multiplyed by the greater progression which multiplyed X:. Then (observing that all these progressions have the same difference & proceede the same way in respect of the dimension of x & y) will the 3 Theorems bee
1st. .
2d. .
3d. radio circuli æqualis curvitatis cum curva ac in puncto c.
As if the line bee x3−axy+ayy=0. Then is ·X=3x3−axy. X·=−axy+2ayy. :X=6x3=3×2.1×0. x−1.
:X=6x3=x3−axy+ayy. 0x−1.1×0.2×1.X:=2ayy=x3−axy+ayy & 3×0.1×1.0×2.·X·=−axy=x3−axy+ayy. Which valors of ·X, X· &c being substituted into their places in the first rule, the result is;
. Which being conveniently reduced is
. As was found before.
.
Or suppose the line is a Conick section whose nature . Then is ·X=rx+ 210 = xx+rx−yy . 0312 X·=−2yy= xx+rx∗−y . 2×1.1×0.0x−1. :X=xx= xx+rx−yy . 0x−1.0x−1.1×0.2×1. X:=−2yy= xx+rx∗−yy . 2×01×00×2 ·X·=0= xx+rx−yy . Which valors of ·X, ·X, :X, &c being substituted into their places in the first Theoreme, give . Or (since 4qryy−4qrrx−4rrxx=0) tis, . So by the second Theoreme tis . Or +2x+ . And so by the 3d Theoreme, tis . Or . Or .
Note that the curvity of any curve whose ordinates are inclined from right to oblique angles , as the curvity of a circle whose ordinates are in like manner inclined so as to make it becom an Ellipsis.
Prob: To find the points of curves where they have a given degree of curvity.
<56r>Prob 3d. To find the points distinguishing twixt the concave & convex
portions of crooked lines.
Resolution. The lines are not crooked at those points: & therefore the radius cm determining the crookednesse at that point must bee infinitely greate. To which purpose I put the denominator of its valor (in rule the 3d) to bee equall to nothing, & so have this Theoreme ·X·XX:−2·XX··X·+X·X·:X=0. Or better perhaps .
Example, was this point to be found in the Concha whose nature is +bb x4+2bx3+ccxx−2bccx−bbcc=0. +yy . Then is ·X=2x4+2bx3+2bccx+2bbcc. X·=2xxyy=X: :X=2x4−4bccx−bbbcc. ·X·=0. Which valors subrogated into the Theoreme, they produce 2x4+2bx3+2bccx+2bbcc+ . And subrogating −bb −x4−2bx3−ccxx +2bccx+bbcc the valor of xxyy into its stead & twice reducing the Equation by the divisor x+b. Tis x3+bcc+ . Or x4+4bx3+3bbxx−2bccx−2bbcc=0. Which being againe reduced by x+b=0. Tis x3+3bxx−2bcc=0. See Geometr: Chart: pag: 259.
<56v>Probl: 4. To find the points at which lines are most or least crooked.
Resol: At those points the afforesaid radius cm neither increaseth nor decreaseth. So that the center m in that moment doth absolutely rest, & therefore neither the line bk nor al doth increase or diminish, that is, ck & bl doe soe much increase or diminish as y & x (lb & ab) doe diminish or increase. Or in a word the point m resteth. Find therefore the motion of al or cm or lm & suppose it nothing.
Thus to find the point of least crookednesse in the curve x3=ccy By the rule in prob 2 I make ·X=3x3. X·=−ccy. :X=6x3. X:=0 & ·X·equals;0 & thence obteine , or which is least when or . And then therefore happens the greatest crookednesse
In like manner if the curve be xxy=a3 The rule gives ·X=2a3 X·=a3 :X=−6a3 X:;=0=·X· And thence which is least when .
Soe if the curve bee x3=byy. Then is ·X=3x3. X·=−2byy. :X=6x3 X:=−2yyc. ·X·=0. And therefore ck=3y+ , which hath no least nor the curve any least crookednesse.
<57r>Prob 5t. To find the nature of the crooked line whose area is expressed by any given equation.
That is, the nature of the area being given to find the nature of the crooked line whose area it is.
Resol. If the relation of ab=x, &  abc=y bee given &
abc=y bee given & 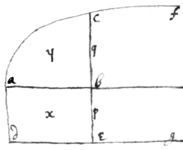 the relation of ab=x, & bc=q bee required (bc being ordinately applyed at right angles to ab). Make de∥ab⊥ad∥be=1. & then is □abed=x. Now supposing the line cbe by parallel motion from ad to describe the two superficies ae=x, & abc=y; The velocity with which they increase will bee, as be to bc: that is, the motion by which x increaseth being be=p=1, the motion by which y increaseth will bee bc=q. which therefore may bee found by prop: 7th. viz:
.
the relation of ab=x, & bc=q bee required (bc being ordinately applyed at right angles to ab). Make de∥ab⊥ad∥be=1. & then is □abed=x. Now supposing the line cbe by parallel motion from ad to describe the two superficies ae=x, & abc=y; The velocity with which they increase will bee, as be to bc: that is, the motion by which x increaseth being be=p=1, the motion by which y increaseth will bee bc=q. which therefore may bee found by prop: 7th. viz:
.
Example 1. If . Or −4rx3+9yy=0. Then is . Or rx=qq & therefore abc is the Parabola whose area abc is .
Example 2d. If x3−ay+xy=0. Then is . Or
Example 3d. If . Then is . Or if axm=bxn; then is .
Note that by this probleme may bee gathered a Catalogue of all those lines which can bee squared. And therefore it will not bee necessary to shew how this Probleme may bee resolved in other cases in which q is not ordinately applye{d} to x at right angles.
Prob 6. The nature of any Crooked line being given, to find other lines whose areas may bee compared to the area of that given line.
Resol: Suppose the given line to be ac & its area abc=s, 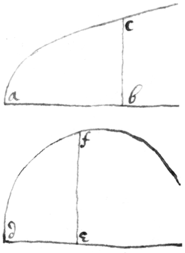 the sought line df & its area def=t; & that bc=z is ordinately applyed to ab=x, & ef=v to de=y, soe that ∠abc=∠def; & that the velocitys with which ab & de increase (that is, the velocity of the points b & e, or of the lines bc & ef moving from a & d) bee called p & q. Then may the ordinately applyed lines bc & ef multiplyed by their velocitys p & q, (that is pz & qv) signify the velocitys with which the areas abc=s & def=t increase. Now the relation of the areas s & t (taken at pleasure) gives the relation of the motions pz & qv describing those areas, by Proposition the 7th.; Also the relation of the lines ab=x & de=y (taken at pleasure) gives the relation of p & q, by Prop 7th: which two equations, together with the given Equation expressing the nature of the line ac, give the relation of de=y & ef=v that is the desired nature of the line df.
the sought line df & its area def=t; & that bc=z is ordinately applyed to ab=x, & ef=v to de=y, soe that ∠abc=∠def; & that the velocitys with which ab & de increase (that is, the velocity of the points b & e, or of the lines bc & ef moving from a & d) bee called p & q. Then may the ordinately applyed lines bc & ef multiplyed by their velocitys p & q, (that is pz & qv) signify the velocitys with which the areas abc=s & def=t increase. Now the relation of the areas s & t (taken at pleasure) gives the relation of the motions pz & qv describing those areas, by Proposition the 7th.; Also the relation of the lines ab=x & de=y (taken at pleasure) gives the relation of p & q, by Prop 7th: which two equations, together with the given Equation expressing the nature of the line ac, give the relation of de=y & ef=v that is the desired nature of the line df.
Example 1. As if ax+bxx=zz is the nature of the line ac: & at pleasure I assume s=t to be the relation of the areas abc & def; & x=yy to bee the relation of the lines ab & de. Then is pz=qv (prop 7), & p=2qy (by prop 7). Therefore 2yz=v (by the 2 last Equations), & =zz=ax+bxx=ayy+by4. or vv=4ay4+4by6. & : Which is the nature of the line def whose area def is equall to the area abc, supposing .
<57v>Example 2. If ax+bxx=zz as before; & I assume, as+bx=t, & x=yy. Then is apz+bp=qv (by prop 7), & p=2qy. 2azy+2by=v=2by+2ay . Or v=2by+2ayy ; The required nature of the line def.
Example 3d. If : & at pleasure I assume , & xx−a=y. Then is 4ccay+ccyy=aass+2aast+aatt, And (by prop 7) 4ccaq+8ccyq=2aaspz+2aatpz+2aasqv+2aatqv= . & (by prop 7) 2px=q. Therefore . But . & , Therefore . That is ca+2cy=2cy+ . Or .
Example 4th. If ax+bxx=zz as before & I assume ss=t, & x=yy. Then is 2spz=qv, & p=2qy (by prop 7) Therefore . Where note that in this case the line is a Mechanicall one because s the area of the line ax+bxx=zz canott bee Geometrically found. The like is to bee observed in other such like cases.
Probl: 7. The Nature of any Crooked line being given to find its area when it may bee. Or more generally, two crooked lines being given to find the relation of their areas, when it may bee.
Resolution. In the figure of the fift probleme Let abc=y represent the area of the given line acf; cb=q the motion describing that area; abed=x another area which is equall to the basis ab=x of that given line acf, (viz: supposing ab∥de⊥be∥ad=1); & be=p=1 the motion describing that other area. Now haveing (by supp) the relation twixt ab=x=abed, & bc=q= given, I seeke the area abc=y by the Eight proposition
Example 1. If the nature of the line bee, . I looke in the tables of the Eight proposition for the Equation corresponding to this Equati{on} which I find to bee , (For if instead of c, a, b, n I write a, aa, −1, 2, it will be .) And against it is the equation . And substituting a, aa, −1, 2 into the places of c, a, b, n it will bee, the required area.
Example 2. If
. Because there are two termes in the valor of bc I consider them severally & first I find the area correspondent to the terme
, or
; To bee
, or
, by prop: 8. part 1. Secondly to find the area corresponding to the other terme I looke the Equation (in prop 8. part 3) corresponding to it which is , (for if instead of c, a, b, n, I write eeb, −1, a, −1, it will bee
, Or
): Against which is the Equation
. In which writing eeb, −1, a, −1, instead of c, a, b, n, the result will bee
; Or,
which is the 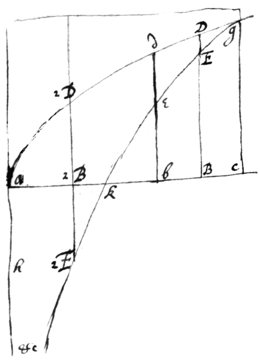 area corresponding to that other terme. Now to see how these areas stand related one to another I draw the annexed scheme, in which is ab=x.
.
. &
. Soe that
is the superficies corresponding to the first terme bd, which because it is affirmative must bee extended (or lye) from the line bd towards a. Also the other superficies correspondent to the 2d terme de, being negative must lye on the other side bd from a, which is therefore
. Lastly if x=ab=r Then is
. &
. And if aB=x=s, then is
, And
. Soe that,
. &
& substracting DdeE from bBDd there remaines
. which is the required Area of the given line &cfkeEg. Where note that for the quantitys r=ab & s=aB taking any numbers you may thereby finde the area bBdD correspond to their difference bB.
area corresponding to that other terme. Now to see how these areas stand related one to another I draw the annexed scheme, in which is ab=x.
.
. &
. Soe that
is the superficies corresponding to the first terme bd, which because it is affirmative must bee extended (or lye) from the line bd towards a. Also the other superficies correspondent to the 2d terme de, being negative must lye on the other side bd from a, which is therefore
. Lastly if x=ab=r Then is
. &
. And if aB=x=s, then is
, And
. Soe that,
. &
& substracting DdeE from bBDd there remaines
. which is the required Area of the given line &cfkeEg. Where note that for the quantitys r=ab & s=aB taking any numbers you may thereby finde the area bBdD correspond to their difference bB.
Note that sometimes one parte of the Area may bee Affirmative & the other negative. as if a2B=r, & ab=s. Then is b2B2Ee=kbe−k2B2E= =b2B2Ee=kbe−k2B2E.
<59r>Prob 9. To find such crooked lines whose lengths may bee found &also to find theire lengths.
Lemma 1. If to any crooked immovable line acg 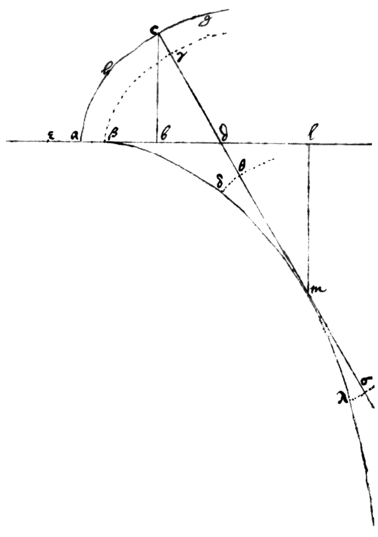 the streight line dcmσ moves to & fro perpendicularly every point of the said line cdmσ (as γ, θ, σ, &c) shall describe a curve line (as βγ, δθ, λσ, &c) all which will bee perpendicular to the said line cdmσ, & also parallel one to another & to the line acg.
the streight line dcmσ moves to & fro perpendicularly every point of the said line cdmσ (as γ, θ, σ, &c) shall describe a curve line (as βγ, δθ, λσ, &c) all which will bee perpendicular to the said line cdmσ, & also parallel one to another & to the line acg.
2. If acg bee not a circle, there may bee drawne some curve line βδmλ, which the moving line cdmδ will always touch in some point or other (as at m) & to which therefore all the curve lines βγ, δθ, λσ, &c: are perpendiculars.
3. Soe that every point (γ, θ, m, σ, &c:) of the line cdmσ, when it begineth or ceaseth to touch the curve line βδmλ, doth then move perpendicularly to or from it: & therefore the line γdmσ doth not at all slide upon the curve line βδmλ, but exactly measure it by applying it selfe to it point by point: & therefore the correspondent parts of the said lines are equall (viz: βm=γm. δm=θm. δλ=θσ. &c).
Resol. Take any Equation for the nature of the crooked line acg, & by the 2d probleme find the center m of its crookedness at c. That point m is a point of the required curve line βδmλ. For that point m whereat cdmσ the perpendicular to acg doth touch the curve line βδmλ is lesse moved than any other point of the said perpendicular, being as it were the hinge & center upon | about which the perpendicular turneth | moveth at that moment.
Example 1. If acg is a Parabola whose nature (supposing ab=x⊥bc=y) is rx=yy. By Theoreme the 1st of Problem 2d I find cb+lm=y+ . By the 2d Theoreme, bl=2x+r. And by the 3d Theoreme . Soe that supposing ab=r. bl=3x=z. . The relation twixt v & z will bee 27rvv=16z3, (for r4vv=16y6=16y3x3=) which is the nature of the required line βδmλ. And since cγ=aβ=r. Therefore . is the length of its parte βδm.
Example 2. Soe if aa=xy, is the nature of the line acg. By the afforesaid Theoreme I find, cb+lm=; &, ; whereby the nature of the curve line βδmλ is determined. And lastly I find which determine its length.
<59v>Prob: 10. Any curve line being given to find other lines whose lengths may be compared to its length or to its area, & to compare them.
Resolution. Take any Equation for the 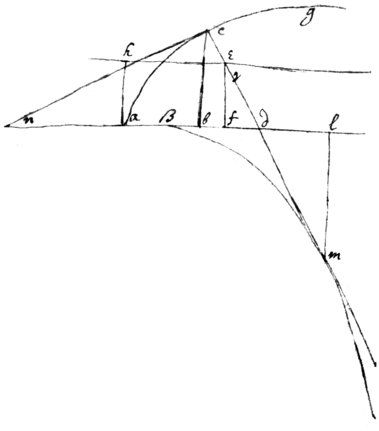 relation twixt ad & the perpendicular cd=y (whither that relation bee expressed by an Equation or whither it bee the same which some streight line beares to a curved one or to its superficies &c). Then (by prop 7) find the relation twixt the increase or decrease (p & q) of the lines ad=x, & dc=y. & say (by prop 6) that q∶p∷dc∶dn=
. And soe is the triangle dnc (rectanguled at c) given & consequently the Nature of the curve line acg to which dc is perpendicular, & cn a tangent.
relation twixt ad & the perpendicular cd=y (whither that relation bee expressed by an Equation or whither it bee the same which some streight line beares to a curved one or to its superficies &c). Then (by prop 7) find the relation twixt the increase or decrease (p & q) of the lines ad=x, & dc=y. & say (by prop 6) that q∶p∷dc∶dn=
. And soe is the triangle dnc (rectanguled at c) given & consequently the Nature of the curve line acg to which dc is perpendicular, & cn a tangent.
Now the center (m) of the perpendiculars motion (which gives the nature & length of the required curve line βm) may be found as in the 2d or 9th Probleme, But more conveniently thus. Draw any fixed line he∥ad⊥ah=a=ef⊥ad. Also call fd=v. & the increase or decrease of (fd) call r. And the increase or decrease of the motions p & q, call β & γ Now considering that the motion (p+r) of the intersection point e in the line he is to the motion (p) of the intersection point (d) in the line (ad), as (em) is to (dm) (see prob 2); That is that the difference (r) of those motions is to the motion (p) of the point (b) soe is (ed) to (dm): First I find the valor of v. viz ∶q∷cn∶cd∷ef=a∶fd=v= . Or aaqq+vvqq−vvpp=0. Secondly by this Equation I find the valor of r, viz: (by Prob 7), 2aaqγ+2vvqγ+2rvqq−2rvpp−2vvpβ=0. Thirdly . Lastly supposing the motion p to bee uniforme that its increase or decrease β may vanish, & also substituting ppzz the valor of aaqq+vvqq in its stead in the Denominator of dm, the result will bee , if p=1. And to find the lines dl & ml, say −p∶q∷dm∶dl= . &
Soe that by the equation expressing the relation twixt x & y first I finde q & then γ. which two give me &c.
Example 1. If the relation twixt x & y bee supposed to bee yy−ax=0. Then (by Prop 7) I find, first 2qy−ap=0, Or 2qy−a=0. & secondly 2γy+2qq=0. And substituting these valors of & γ= in their stead in the Equation , &c: The results will bee . . & . (And adding cd=−y to dm, & ad=x = to dl, the result is cm= . & al= .) Which determine the nature & crookednesse of the line βm. (For if aβ= . βl=z. lm=v. The relation twixt z & v will bee 16z3=27rvv. The length of βm being . as before was found).
Example the 2d. If x=ad⊥dk=
, is the nature of the 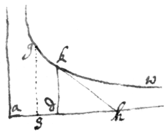 crooked line (the Hyperbola) gkw: And I would find other crooked lines (βm) whose lengths may bee compared with the area sdkg (calling as=b⊥gs) of that crooked line gkw. I call that area sdkg=ξ, & its motion θ. Now since 1∶dk∷p∶θ, (see prob 5. & the Note on prop 7 in Example 3); Therefore dk×p=dk=θ=
. This being knowne I take at pleasure any Equation, in which ξ is, for the valor of cd=y.
crooked line (the Hyperbola) gkw: And I would find other crooked lines (βm) whose lengths may bee compared with the area sdkg (calling as=b⊥gs) of that crooked line gkw. I call that area sdkg=ξ, & its motion θ. Now since 1∶dk∷p∶θ, (see prob 5. & the Note on prop 7 in Example 3); Therefore dk×p=dk=θ=
. This being knowne I take at pleasure any Equation, in which ξ is, for the valor of cd=y.
As 1st suppose ay=ξ, That (by prop 7) gives aq=θ= , Or qx=a; which also (by prop 7) gives γx+qp=0. Which valors of q= , & γ= ; by helpe of the Theorems &c: doe give . . & . which determines the nature of the required curve line βm. The length of that portion of it which is intercepted twixt the point m & the curve line acg being −cm=cd+dm= , Or mc= .
☞ [Note that in this case although the area sdkg=ξ cannot bee Geometrically found & therefore the line acg is a Mechanicall one yet the desired line βm is a Geometricall one. And the like will happen in all other such like cases, when in the Equation taken at pleasure to expresse the relation twixt x, y, & ξ; neither x, y, nor ξ doe multiply or divide one another, nor it selfe, nor is in any denominator or roote, except x which may multiply it selfe & bee in denominators & rootes, when y or ξ are not in those fractions or rootes & herein onely doth this excell the precedent 9th probleme. Such is this Equation aξ−aby+ax3+ . &c: But not this ξξ=a3y. nor ξ=xy. &c]
Secondly suppose ξ=xy. that (by prop 7) give θ=y+xq= , Or xy+xxq=aa, & that (by prop 7) gives y+qx+2qx+γxx=0. Which two valors of , And ; by meanes of the Theoremes , , & ; doe determine the nature & length of the desired curve line βm.
Example the 3d. In like manner to find curve lines whose lengths may bee compared to the length gk of the said curve (Hyperbola) gkw. Call gk=ξ, & its motion θ. Now, drawing kh the tangent to gkw at k, I consider that ad=x & gk=ξ doe increase in the proportion of dh to kh; that is, dh∶kh∷p∶θ. Now finding (by prob 1) that dh=−x, & ; therefore is . Which being found, I take any equation, in which ξ is, for the valor of cd=y. & then worke as in the precedent Example.
Note that by this or the Ninth Probleme may bee gathered a Catalogue of whatever lines, whose lengths can bee Geometrically found.
<60v>Prob 12. To find the Length of any given crooked line when it may bee.
Resolution. The length of any streight line to which the curve line is cheifly related being called (x), the length of the curve line (y), & theire motions (p & q) first (by prob 1) get an equation expressing the relation twixt x & , & then seeke the valor of (y) by the Eight proposition. [Or find a curve line whose area is equall to the length of the given line, by Prob 11. And then find that area by Prob 7.]
<61r>Prob 11. To find curve lines whose Areas shall bee Equall (or have any other given relation) to the length of any given Curve line drawn into a given right line
Resolution. The length of any streight line, to which the given curve line is cheifely referred, being called x, the length of the curve line y, & their motions of increase p & q. The valor of (found by the first probleme) being ordinately applyed at right angles to x, gives the nature of a curve line whose area is equall to (y) the length of the curve line.
And this Line thus found gives (by prob 6) other lines. whose areas have any given relation to the length (y) of the given curve line
<61v>Prob 13. To find the nature of a Crooked line whose length is expressed
by any given Equation, (when it may bee done).
Resolution. Suppose ab=x, bc=y, ac=z. & their motions p, q, r. 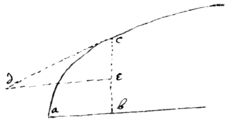 And let the relation twixt x & z bee supposed given. Then (by prop 8) finding the relation twixt p & r make
. (For drawing cd tangent to ac at c & de⊥cb⊥ab: the lines de, ec, dc, shall bee as p, q, r. but
, & therefore
). Lastly, the ratio twixt x & being thus knowne, seeke y (by prop 8). Which relation twixt ab=x & bc=y determines the nature of the crooked line ac=z.
And let the relation twixt x & z bee supposed given. Then (by prop 8) finding the relation twixt p & r make
. (For drawing cd tangent to ac at c & de⊥cb⊥ab: the lines de, ec, dc, shall bee as p, q, r. but
, & therefore
). Lastly, the ratio twixt x & being thus knowne, seeke y (by prop 8). Which relation twixt ab=x & bc=y determines the nature of the crooked line ac=z.
Of Gravity.
Definition. 1. I call that point the center of Motion in any Body, which always rests when or howsoever that Body circulates without progressive motion. It would always bee the same with the center of Gravity were the Rays of Gravity parallel & not converging towards the center of the Earth.
Def: 2 And the right lines passing through that point I call the axes of Motion or Gravity.
Lemma 1 The place & distance of Bodys is determinded by their center of Gravity. Which is the middle point of a right line circle or Parallelogram:
Lemma 2 Those weights doe equiponderate whose quantitys are reciprocally proportionall to their distances from the common axis of Gravity, supposing their centers of Gravity to bee in the same plaine with that common axis of Gravity.
Prob To find the center of Gravity in rectilinear plaine figures 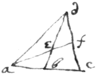
1. In the Triangle acd make ab=bc, & cd=fd. & draw db, & af, their intersection point (e) is its center of Gravity.
In the Trapezium abdc, draw ad & cb. Ioyne the centers of 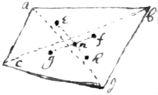 Gravity e & h, f & g of the opposite triangles acb & dcb, bad & adc with the lines eh, fg. Their intersection point n is the center of Gravity in the Trapezium. (And so of Pentagons, hexagones &c)
Gravity e & h, f & g of the opposite triangles acb & dcb, bad & adc with the lines eh, fg. Their intersection point n is the center of Gravity in the Trapezium. (And so of Pentagons, hexagones &c)
Prob: To find such plaine figures which are equiponderate to any given plaine figure in respect of an axis of Gravity in any given position.
Resol That the natures & positions of the given 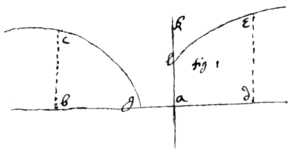 curvilinear plaine (gbc,) & sought plaine (bde) bee such that they may equiponderate in respect of the axis (ak;) I suppose x=ab⊥bc=z, & y=ad⊥de=v to bee either perpendicular or parallel or coincident to the said axis ak: And the motions whereby x & y doe increase or decrease (i:e: the motions
curvilinear plaine (gbc,) & sought plaine (bde) bee such that they may equiponderate in respect of the axis (ak;) I suppose x=ab⊥bc=z, & y=ad⊥de=v to bee either perpendicular or parallel or coincident to the said axis ak: And the motions whereby x & y doe increase or decrease (i:e: the motions 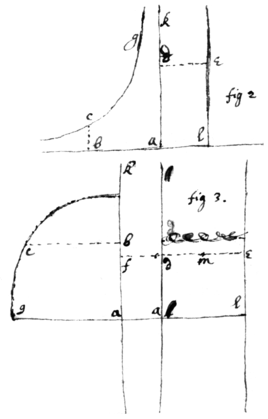 of bc, & de to or from the point a) I call p & q. Now the ordinatly applyed lines bc=z, & de=v, multiplyed into their motion p & q (that is, pz, & qv) may signify the infinitly little parts of those areas (acb, & lde) which each moment they describe; which infinitly little parts doe equiponderate (by Lemma 1 & 2), if they multiplied by their distances from the axis ak doe make equall products. (that is; pxz=qyv, in fig 1: pxz=qvv in fig 2: pzz=qv×fm, in fig 3; supposing dm=me. &) And if all the respective infinitly little parts doe equiponderate the superficies must do so too.
of bc, & de to or from the point a) I call p & q. Now the ordinatly applyed lines bc=z, & de=v, multiplyed into their motion p & q (that is, pz, & qv) may signify the infinitly little parts of those areas (acb, & lde) which each moment they describe; which infinitly little parts doe equiponderate (by Lemma 1 & 2), if they multiplied by their distances from the axis ak doe make equall products. (that is; pxz=qyv, in fig 1: pxz=qvv in fig 2: pzz=qv×fm, in fig 3; supposing dm=me. &) And if all the respective infinitly little parts doe equiponderate the superficies must do so too.
Now therefore, (the relation of x & z being given by the nature of the curve line cg,) I take at pleasure any Equation for the relation twixt x & y, & thereby (by prop 7) find p & q, & so by the precedent Theorem find the relation twixt y & v, for the nature of the sought plaine lde.
Exam: 1. If cg (fig 2) is an Hyperbola, soe that aa=xz. & I suppose 2x=y. then is 2p=q (prop 7). & paa=pxz=qvv=pvv. Or aa=vv. or a=v=de. Soe that le is a streight line, & lde a parallelogram, which equiponderates with the Hyperbola cgkabc (infinitly extended towards gk) if 2ab=ad. al×al=ab×bc.
<62v>Example 2. If cg (fig 3) is a circle whose nature is, . & I suppose at pleasure 3aax−x3=6aay. Then (by prop 7) I find 3aap−3xxp=6aaq. And therefore paa−pxx= =qv×fm=(if fd=a,) . Or . Or 2aa=vv+av. Or ; . Soe that le is a streight line & alde a parallelogram
Example 3. If abcg is a parallelogram (fig 4) whose nature 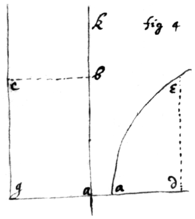 is, a=z. & I suppose at pleasure x=yy−b. Then (by prop 7) tis p=2qy. Therefore aap=aaqy=pzz=qvy. Or aa=v. Soe that aed is a parallelogram.
is, a=z. & I suppose at pleasure x=yy−b. Then (by prop 7) tis p=2qy. Therefore aap=aaqy=pzz=qvy. Or aa=v. Soe that aed is a parallelogram.
Or if I suppose at pleasure, x=y3−b. Then is (prop 7) p=3qyy. & therefore aap= aaqyy=pzz=qvy. Or 3aay=2v.
Or if I suppose x=y4−b. then is p=4qy3 & 2aayy=v. so that aed is a Parabola. [Soe if xx=y5. then is 2px=5qy4. &, =ap=pzz=qvy. Or 5aaqy =4qvy. & 25a4y=16vv. soe that aed is a Parabola.]
Example 4 If gbc (fig 1) is an Hyperbola whose nature is xx−aa= zz. & I suppose x=y+b. Then (by prop 7) is p=q. Therefore =pxz=qyv=pyv. Or . Or in . &c.
Or if I suppose xx=2y. Then is 2px=2q. Therefore =pxz=qyv. Or (xx−aa=)2y−aa=yyvv.
Or if I suppose xx=yy+aa. Then (prop 7) is 2px=2qy. Therefore qyz=pxz=qyv. Or . & y=v; so that aed is a triangle
Note that This Probleme may bee resolved although the lines x, z, y, v, & ak have any other given inclination one to another, but the precedent cases may suffice
Note also that if I take a Parallelogram for the knowne superficies (as in the 3d Example I may thereby gather a Catalogue of all such curvilinear superficies whose weight in respect of the axis, may bee knowne.
Note also I might have shewn how to find lines whose weights in respect of any axis are not onely equall but have also any other given proportion one to another. And then have made two Problems instead of this, as I did in Probl: 5 & 6: 9 & 10.
<63r>Prob 15. To find the Gravity of any given plaine in respect of any axis, given in position
when it may bee done.
Resol: Suppose ek to bee the Axis of Gravity, acb the given plaine, 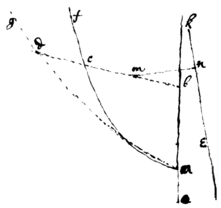 cb=y, & db=z to bee ordinatly applyed at any angles to ab=x. Bisect cb at m & draw mn⊥ek. Now, since [cb×mn] is the gravity of the line [cb], (by lem 1 & 2); if I make cb×mn=db=z, every line db shall designe the Gravity of its correspondent line cb, that is, the superficies adb shall designe the Gravity of the superficies acb. Soe that finding the quantity of that superficies adb (by prob 7) I find the gravity of the superficies acb.
cb=y, & db=z to bee ordinatly applyed at any angles to ab=x. Bisect cb at m & draw mn⊥ek. Now, since [cb×mn] is the gravity of the line [cb], (by lem 1 & 2); if I make cb×mn=db=z, every line db shall designe the Gravity of its correspondent line cb, that is, the superficies adb shall designe the Gravity of the superficies acb. Soe that finding the quantity of that superficies adb (by prob 7) I find the gravity of the superficies acb.
Example 1 If ac is a Parabola; soe that, 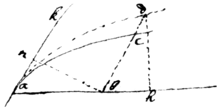 rx=yy, & the axis ak is ∥ dcb. &, nb⊥ak, & , ab∶nb∷d∶e. Then is bc×nb=y×
. Or eerx3=ddzz, is the nature of the curve line ad. whose area (were abd a right angle would be
but now it) is
, (by prob 7) which is the weight of the area acb in respect of the axis ak.
rx=yy, & the axis ak is ∥ dcb. &, nb⊥ak, & , ab∶nb∷d∶e. Then is bc×nb=y×
. Or eerx3=ddzz, is the nature of the curve line ad. whose area (were abd a right angle would be
but now it) is
, (by prob 7) which is the weight of the area acb in respect of the axis ak.
Examp: 2 If ac is a Circle
Prob 16. To find the Axes of Gravity of any Plaines
Resol. Find the quantity of the Plaine (by Prob 7) which call A & the quantity of its gravity in respect of any axis (by prob 15) which call B. & parallell to that axis draw a line whose distance from it shall bee . That line shall bee an Axis of Gravity of the given plain
Or If you cannot find the quantity of the plane: Then 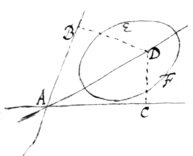 find its gravitys in respect of two divers axes (AB & AC) which gravitys call C & D. & though (A) the intersection of those axes draw a line AD with this condition that the distances (DB & DC) of any one of its points (D) from the said axes (AB & AC), bee in such proportion as to the gravitys of the plane. That line (AD) shall bee an axis of gravity of the said plane EF.
find its gravitys in respect of two divers axes (AB & AC) which gravitys call C & D. & though (A) the intersection of those axes draw a line AD with this condition that the distances (DB & DC) of any one of its points (D) from the said axes (AB & AC), bee in such proportion as to the gravitys of the plane. That line (AD) shall bee an axis of gravity of the said plane EF.
Prob 17 To find the Center of Gravity of any Plaine, when it may bee
Resol Find two axes of Gravity by the precedent Prop, & their common intersection is the Center of Gravity desired. If the figure have any knowne Diameter that may bee taken for one of its axes of Gravity.
