De Motu Corporum (Liber Secundus) (1687)
DE
MOTU CORPORUM
Liber SECUNDUS.
SECT. I.
De Motu corporum quibus resistitur in ratione velocitatis.
Prop. I. Theor. I.
Corporis, cui resistitur in ratione velocitatis, motus ex resistentia amissus est ut spatium movendo confectum.
NAm cum motus singulis temporis particulis amissus sit ut velocitas, hoc est ut itineris confecti particula: erit componendo motus toto tempore amissus ut iter totum. Q.E.D.
Corol. Igitur si corpus gravitate omni destitutum in spatiis liberis sola vi insita moveatur, ac detur tum motus totus sub initio, tum etiam motus reliquus post spatium aliquod confectum, dabitur spatium totum quod corpus infinito tempore describere potest. Erit enim spatium illud ad spatium jam descriptum ut motus totus sub initio ad motus illius partem amissam.
<237>Lemma. I.
Quantitates differentiis suis proportionales, sunt continue proportionales.
Sit A ad A-B ut B ad B-C & C ad C-D &c. & dividendo fiet A ad B ut B ad C & C ad D &c. Q.E.D.
Prop. II. Theor. II.
Si corpori resistitur in ratione velocitatis, & sola vi insita per Medium similare moveatur, sumantur autem tempora æqualia: velocitates in principiis singulorum temporum sunt in progressione Geometrica, & spatia singulis temporibus descripta sunt ut velocitates.
Cas. 1. Dividatur tempus in particulas æquales, & si ipsis particularum initiis agat vis resistentiæ impulsu unico, quæ sit ut velocitas, erit decrementum velocitatis singulis temporis particulis ut eadem velocitas. Sunt ergo velocitates differentiis suis proportionales, & propterea (per Lem. I. Lib. II.) continue proportionales. Proinde si ex æquali particularum numero componantur tempora quælibet æqualia, erunt velocitates ipsis temporum initiis, ut termini in progressione continua, qui per saltum capiuntur, omisso passim æquali terminorum intermediorum numero. Componuntur autem horum terminorum rationes ex æqualibus rationibus terminorum intermediorum æqualiter repetitis, & propterea sunt æquales. Igitur velocitates his terminis proportionales, sunt in progressione Geometrica. Minuantur jam æquales illæ temporum particulæ, & augeatur earum numerus in infinitum, eo ut resistentiæ impulsus redditur continuus, & velocitates in principiis æqualium temporum, semper continue proportionales, erunt in hoc etiam Casu continue proportionales. Q.E.D.
<238>Cas. 2. Et divisim velocitatum differentiæ, hoc est earum partes singulis temporibus amissæ, sunt ut totæ: Spatia autem singulis temporibus descripta sunt ut velocitatum partes amissæ, (per Prop. I. Lib. II.) & propterea etiam ut totæ. Q.E.D.
Corol. Hinc si Asymptotis rectangulis ADC, CH describatur Hyperbola BG, sintque AB, DG ad Asymptoton AC perpendiculares, & exponatur tum corporis velocitas tum resistentia Medii, ipso motus initio, per lineam quamvis 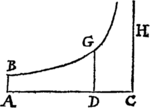 datam AC, elapso autem tempore aliquo per lineam indefinitam DC: exponi potest tempus per aream ABGD, & spatium eo tempore descriptum per lineam AD. Nam si area illa per motum puncti D augeatur uniformiter ad modum temporis, decrescet recta DC in ratione Geometrica ad modum velocitatis, & partes rectæ AC æqualibus temporibus descriptæ decrescent in eadem ratione.
datam AC, elapso autem tempore aliquo per lineam indefinitam DC: exponi potest tempus per aream ABGD, & spatium eo tempore descriptum per lineam AD. Nam si area illa per motum puncti D augeatur uniformiter ad modum temporis, decrescet recta DC in ratione Geometrica ad modum velocitatis, & partes rectæ AC æqualibus temporibus descriptæ decrescent in eadem ratione.
Prop. III. Prob. I.
Corporis, cui dum in Medio similari recta ascendit vel descendit, resistitur in ratione velocitatis, quodque ab uniformi gravitate urgetur, definire motum.
Corpore ascendente, exponatur 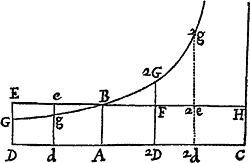 gravitas per datum quodvis rectangulum BC, & resistentia Medii initio ascensus per rectangulum BD sumptum ad contrarias partes. Asymptotis rectangulis AC, CH, per punctum B describatur Hyperbola secans perpendicula DE, de in G, g; & corpus ascendendo, tempore DG gd, describet spatium EG ge, tempore DGBA spatium ascensus totius EGB, tempore AB 2G 2D spatium descensus BF 2G, atque tempore 2D 2G 2g 2d spatium descensus 2 GF 2e 2g: & velocitates corporis (resistentiæ Medii proportionales) in horum temporum periodis erunt ABED, ABed, nulla, ABF 2D, AB 2e 2d respective; atque maxima velocitas, quam corpus descendendo potest acquirere, erit BC.
gravitas per datum quodvis rectangulum BC, & resistentia Medii initio ascensus per rectangulum BD sumptum ad contrarias partes. Asymptotis rectangulis AC, CH, per punctum B describatur Hyperbola secans perpendicula DE, de in G, g; & corpus ascendendo, tempore DG gd, describet spatium EG ge, tempore DGBA spatium ascensus totius EGB, tempore AB 2G 2D spatium descensus BF 2G, atque tempore 2D 2G 2g 2d spatium descensus 2 GF 2e 2g: & velocitates corporis (resistentiæ Medii proportionales) in horum temporum periodis erunt ABED, ABed, nulla, ABF 2D, AB 2e 2d respective; atque maxima velocitas, quam corpus descendendo potest acquirere, erit BC.
Resolvatur enim rectangulum AH in rectangula innumera Ak, Kl, Lm, Mn, &c. quæ sint ut incrementa velocitatum æqualibus totidem temporibus facta; & erunt nihil, Ak, Al, Am, An, &c. ut velocitates totæ, atque adeo (per Hypothesin) ut resistentia Medii in 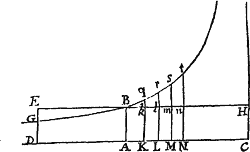 principio singulorum temporum æqualium. Fiat AC ad AK vel ABHC ad ABkK, ut vis gravitatis ad resistentiam in principio temporis secundi, deque vi gravitatis subducantur resistentiæ, & manebunt ABHC, KkHC, LlHC, NnHC, &c. ut vires absolutæ quibus corpus in principio singulorum temporum urgetur, atque adeo (per motus Legem II.) ut incrementa velocitatum, id est, ut rectangula Ak, Kl, Lm, Mn &c; & propterea (per Lem. I. Lib. II.) in progressione Geometrica. Quare si rectae Kk, Ll, Mm, Nn &c. productæ occurrant Hyperbolæ in q, r, s, t &c. erunt areæ ABqK, KqrL, LrsM, MstN &c. æquales, adeoque tum temporibus tum viribus gravitatis semper æqualibus analogæ. Est autem area ABqK (per Corol. 3 Lem. VII. & Lem. VIII. Lib. I.) ad aream Bkq ut K.q ad seu AC ad , hoc est ut vis gravitatis ad resistentiam in medio temporis primi. Et simili argumento areæ qKLr, rLMs, sMNt, &c. sunt ad areas qklr, rlms, smnt &c. ut vires gravitatis ad resistentias in medio temporis secundi, tertii, quarti, &c. Proinde cum areæ æquales BAKq, qKLr, rLMs, sMNt, &c. sint viribus grauitatis analogæ, erunt areæ Bkq, qklr, rlms, smnt, &c. resistentiis in mediis singulorum temporum, hoc est, (per
principio singulorum temporum æqualium. Fiat AC ad AK vel ABHC ad ABkK, ut vis gravitatis ad resistentiam in principio temporis secundi, deque vi gravitatis subducantur resistentiæ, & manebunt ABHC, KkHC, LlHC, NnHC, &c. ut vires absolutæ quibus corpus in principio singulorum temporum urgetur, atque adeo (per motus Legem II.) ut incrementa velocitatum, id est, ut rectangula Ak, Kl, Lm, Mn &c; & propterea (per Lem. I. Lib. II.) in progressione Geometrica. Quare si rectae Kk, Ll, Mm, Nn &c. productæ occurrant Hyperbolæ in q, r, s, t &c. erunt areæ ABqK, KqrL, LrsM, MstN &c. æquales, adeoque tum temporibus tum viribus gravitatis semper æqualibus analogæ. Est autem area ABqK (per Corol. 3 Lem. VII. & Lem. VIII. Lib. I.) ad aream Bkq ut K.q ad seu AC ad , hoc est ut vis gravitatis ad resistentiam in medio temporis primi. Et simili argumento areæ qKLr, rLMs, sMNt, &c. sunt ad areas qklr, rlms, smnt &c. ut vires gravitatis ad resistentias in medio temporis secundi, tertii, quarti, &c. Proinde cum areæ æquales BAKq, qKLr, rLMs, sMNt, &c. sint viribus grauitatis analogæ, erunt areæ Bkq, qklr, rlms, smnt, &c. resistentiis in mediis singulorum temporum, hoc est, (per 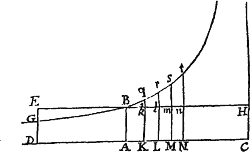 Hypothesin) velocitatibus, atque adeo descriptis spatiis analogæ. Sumantur analogarum summæ, & erunt areæ Bkq, Blr, Bms, Bnt, &c. spatiis totis descriptis analogæ necnon areæ ABqK, ABrL, ABsM, ABtN, &c. temporibus. Corpus igitur inter descendendum, tempore quovis ABrL, describit spatium Blr, & tempore LrtN spatium rlnt. Q.E.D. Et similis est demonstratio motus expositi in ascensu. Q.E.D.
Hypothesin) velocitatibus, atque adeo descriptis spatiis analogæ. Sumantur analogarum summæ, & erunt areæ Bkq, Blr, Bms, Bnt, &c. spatiis totis descriptis analogæ necnon areæ ABqK, ABrL, ABsM, ABtN, &c. temporibus. Corpus igitur inter descendendum, tempore quovis ABrL, describit spatium Blr, & tempore LrtN spatium rlnt. Q.E.D. Et similis est demonstratio motus expositi in ascensu. Q.E.D.
Corol. 1. Igitur velocitas maxima, quam corpus cadendo potest acquirere, est ad velocitatem dato quovis tempore acquisitam, ut vis data gravitatis qua perpetuo urgetur, ad excessum vis hujus supra vim qua in fine temporis illius resistitur.
Corol. 2. Tempore autem aucto in progressione Arithmetica, summa velocitatis illius maximæ ac velocitatis in ascensu (atque etiam earundem differentia in descensu) decrescit in progressione Geometrica.
Corol. 3. Sed & differentiæ spatiorum, quæ in æqualibus temporum differentiis describuntur, decrescunt in eadem progressione Geometrica.
Corol. 4. Spatium vero a corpore descriptum differentia est duorum spatiorum, quorum alterum est ut tempus sumptum ab initio descensus, & alterum ut velocitas, quæ etiam ipso descensus initio æquantur inter se.
<241>Prop. IV. Prob. II.
Posito quod vis gravitatis in Medio aliquo similari uniformis sit, ac tendat perpendiculariter ad planum Horizontis; definire motum Projectilis, in eodem resistentiam velocitati proportionalem patientis.
E loco quovis D egrediatur Projectile secundum lineam quamvis rectam DP, & per longitudinem DP exponatur ejusdem velocitas sub initio motus. A puncto P ad lineam Horizontalem DC demittatur perpendiculum PC, & secetur DC in A ut sit DA ad AC ut resistentia Medii ex motu in altitudinem sub initio orta, ad vim gravitatis; vel (quod perinde est) ut sit rectangulum sub DA & DP 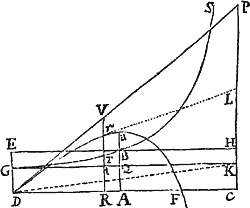 ad rectangulum sub AC & PC ut resistentia tota sub initio motus ad vim Gravitatis. Describatur Hyperbola quævis GTBS secans erecta perpendicula DG, AB in G & B; & compleatur parallelogrammum DGKC, cujus latus GK secet AB in Q. Capiatur linea N in ratione ad QB qua DC sit ad CP; & ad rectæ DC punctum quodvis R erecto perpendiculo RT, quod Hyperbolæ in T, & rectis GK, DP in t & V occurrat; in eo cape Vr æqualem tGT / N, & Projectile tempore DRTG perveniet ad punctum r, describens curvam lineam DraF, quam punctum r semper tangit; perveniens autem ad maximam altitudinem a in perpendiculo AB, & postea semper appropinquans ad Asymptoton PLC.. Estque velocitas ejus in puncto quovis r ut Curvæ Tangens rL.Q.E.D.
ad rectangulum sub AC & PC ut resistentia tota sub initio motus ad vim Gravitatis. Describatur Hyperbola quævis GTBS secans erecta perpendicula DG, AB in G & B; & compleatur parallelogrammum DGKC, cujus latus GK secet AB in Q. Capiatur linea N in ratione ad QB qua DC sit ad CP; & ad rectæ DC punctum quodvis R erecto perpendiculo RT, quod Hyperbolæ in T, & rectis GK, DP in t & V occurrat; in eo cape Vr æqualem tGT / N, & Projectile tempore DRTG perveniet ad punctum r, describens curvam lineam DraF, quam punctum r semper tangit; perveniens autem ad maximam altitudinem a in perpendiculo AB, & postea semper appropinquans ad Asymptoton PLC.. Estque velocitas ejus in puncto quovis r ut Curvæ Tangens rL.Q.E.D.
Est enim N ad QB ut DC ad CP seu DR ad RV, adeoque RV æqualis , & Rr (id est seu ) æqualis . Exponatur jam tempus per aream RDGT, & (per Legum Corol. 2.) distinguatur motus corporis in duos, unum ascensus, alterum ad latus. Et cum resistentia sit ut motus, distinguetur etiam hæc in partes duas partibus motus proportionales & contrarias: ideoque longitudo a motu ad latus descripta erit (per Prop. II. hujus) ut linea DR, altitudo vero (per Prop. III. hujus) ut area , hoc est ut linea Rr. Ipso autem motus initio area RDGT aequalis est rectangulo , ideoque linea illa Rr (seu ) tunc est ad DR ut (seu QB) ad N, id est ut CP 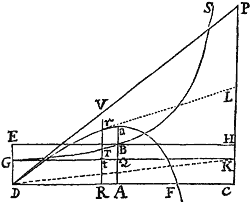 ad DC; atque adeo ut motus in altitudinem ad motum in longitudinem sub initio. Cum igitur Rr semper sit ut altitudo, ac DR semper ut longitudo, atque Rr ad DR sub initio ut altitudo ad longitudinem: necesse est ut Rr semper sit ad DR ut altitudo ad longitudinem, & propterea ut corpus moveatur in linea DraF, quam punctum r perpetuo tangit. Q.E.D.
ad DC; atque adeo ut motus in altitudinem ad motum in longitudinem sub initio. Cum igitur Rr semper sit ut altitudo, ac DR semper ut longitudo, atque Rr ad DR sub initio ut altitudo ad longitudinem: necesse est ut Rr semper sit ad DR ut altitudo ad longitudinem, & propterea ut corpus moveatur in linea DraF, quam punctum r perpetuo tangit. Q.E.D.
Corol. 1. Hinc si Vertice D, Diametro DE deorsum producta, & latere recto quod sit ad 2 DP ut resistentia tota, ipso motus initio, ad vim gravitatis, Parabola construatur: velocitas quacum corpus exire debet de loco D secundum rectam DP, ut in Medio uniformi resistente describat Curvam DraF, ea ipsa erit quacum exire debet de eodem loco D, secundum eandem rectam DR, ut in spatio non resistente describat Parabolam. Nam Latus rectum Parabolæ hujus, ipso motus initio, est & Vr est seu . Recta autem, quæ, si duceretur, Hyperbolam GTB tangeret in G, parallela est ipsi DK, ideoque Tt est , & N erat . Et propterea Vr est , id est (ob proportionales DR & DC, DV & DP) . & Latus rectum prodit , id est (ob proportionales QB & CK, DA & AC) , adeoque ad 2 DP ut ad ; hoc est ut resistentia ad gravitatem. Q.E.D.
Corol. 2. Unde si corpus de loco quovis D, data cum velocitate, secundum rectam quamvis positione datam DP projiciatur, & resistentia Medii ipso motus initio detur, inveniri potest Curva DraF, quam corpus idem describet. Nam ex data velocitate datur latus rectum Parabolæ, ut notum est. Et sumendo 2 DP ad latus illud rectum ut est vis Gravitatis ad vim resistentiæ, datur DP. Dein secando DC in A, ut sit ad in eadem illa ratione Gravitatis ad resistentiam, dabitur punctum A. Et inde datur Curva DraF.
Corol. 3. Et contra, si datur curva DraF, dabitur & velocitas corporis & resistentia Medii in locis singulis r. Nam ex data ratione ad , datur tum resistentia Medii sub initio motus, tum latus rectum Parabolæ: & inde datur etiam velocitas sub initio motus. Deinde ex longitudine tangentis rL, datur & huic proportionalis velocitas, & velocitati proportionalis resistentia in loco quovis r.
Corol. 4. Cum autem longitudo sit ad latus rectum Parabolæ ut gravitas ad resistentiam in D; & ex aucta Velocitate augeatur resistentia in eadem ratione, at latus rectum Parabolæ augeatur in ratione illa duplicata: patet longitudinem augeri in ratione illa simplici, adeoque velocitati semper proportionalem esse, neque ex angulo CDP mutato augeri vel minui, nisi mutetur quoque velocitas.
Corol. 5. Unde liquet methodus determinandi Curvam DraF ex Phænominis quamproxime, & inde colligendi resistentiam & velocitatem quacum corpus projicitur. Projiciantur corpora duo similia & æqualia eadem cum velocitate, de loco D, secundum angulos diversos CDP, cDp (minuscularum literarum locis subintellectis) & cognoscantur loca F, f, ubi incidunt in horizontale planum DC. Tum assumpta quacunque longitudine pro DP vel Dp, fingatur quod resistentia in D sit ad gravitatem in ratione qualibet, & exponatur ratio illa per longitudinem quamvis SM. Deinde per computationem, ex longitudine illa assumpta DP, inveniantur longitudines DF, Df, ac de ratione per calculum inventa, auferatur ratio eadem per experimentum inventa, & exponatur differentia per 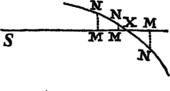 perpendiculum MN. Idem fac iterum ac tertio, assumendo semper novam resistentiæ ad gravitatem rationem SM, & colligendo novam differentiam MN. Ducantur autem differentiæ affirmativæ ad unam partem rectæ SM, & negativæ ad alteram; & per puncta N, N, N agatur curva regularis NNN secans rectam SMMM in X, & erit SX vera ratio resistentiæ ad gravitatem, quam invenire oportuit. Ex hac ratione colligenda est longitudo DF per calculum; & longitudo quæ sit ad assumptam longitudinem DP ut modo inventa longitudo DF ad longitudinem eandem per experimentum cognitam, erit vera longitudo DP. Qua inventa, habetur tum Curva Linea DraF quam corpus describit, tum corporis velocitas & resistentia in locis singulis.
perpendiculum MN. Idem fac iterum ac tertio, assumendo semper novam resistentiæ ad gravitatem rationem SM, & colligendo novam differentiam MN. Ducantur autem differentiæ affirmativæ ad unam partem rectæ SM, & negativæ ad alteram; & per puncta N, N, N agatur curva regularis NNN secans rectam SMMM in X, & erit SX vera ratio resistentiæ ad gravitatem, quam invenire oportuit. Ex hac ratione colligenda est longitudo DF per calculum; & longitudo quæ sit ad assumptam longitudinem DP ut modo inventa longitudo DF ad longitudinem eandem per experimentum cognitam, erit vera longitudo DP. Qua inventa, habetur tum Curva Linea DraF quam corpus describit, tum corporis velocitas & resistentia in locis singulis.
Scholium.
Cæterum corpora resisti in ratione velocitatis Hypothesis est magis Mathematica quam Naturalis. Obtinet hæc ratio quamproxime ubi corpora in Mediis rigore aliquo præditis tardissime moventur. In Mediis autem quæ rigore omni vacant (uti posthac demonstrabitur) corpora resistuntur in duplicata ratione velocitatum. Actione corporis velocioris communicatur eidem Medii quantitati, tempore minore, motus major in ratione majoris velocitatis, adeoque tempore æquali (ob majorem Medii quantitatem perturbatam) communicatur motus in duplicata ratione major, estque resistentia (per motus Legem 2. & 3.) ut motus communicatus. Videamus igitur quales oriantur motus ex hac lege Resistentiæ.
SECT. II.
De motu corporum quibus resistitur in duplicata ratione velocitatum.
Prop. V. Theor. III.
Si corpori resistitur in velocitatis ratione duplicata, & sola vi insita per Medium similare movetur, tempora vero sumantur in progressione Geometrica a minoribus terminis ad majores pergente: dico quod velocitates initio singulorum temporum sunt in eadem progressione Geometrica inverse, & quod spatia sunt æqualia quae singulis temporibus describuntur.
Nam quoniam quadrato velocitatis proportionalis est resistentia Medii, & resistentiæ proportionale est decrementum velocitatis; si tempus in particulas innumeras æquales dividatur, quadrata velocitatum singulis temporum initiis erunt velocitatum earundem differentiis proportionales. Sunto temporis particulæ illæ AK, KL, LM, &c. in recta 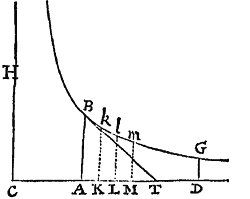 CD sumptæ, & erigantur perpendicula AB, Kk, Ll, Mm, &c. Hyperbolæ BKlmG, centro C Asymptotis rectangulis CD, CH, descriptæ occurrentia in B, k, l, m, &c. & erit AB ad Kk ut CK ad CA, & divisim ad Kk ut AK ad CA, & vicissim ad AK ut Kk ad CA, adeoque ut ad . Unde cum AK & dentur, erit ut ; & ultimo, ubi coeunt AB & Kk, ut ABq. Et simili argumento erunt , , &c. ut Kkq., Llq. &c. Linearum igitur AB, Kk, Ll, Mm quadrata sunt ut earundem differentiæ, & idcirco cum quadrata velocitatum fuerint etiam ut ipsarum differentiæ, similis erit ambarum progressio. Quo demonstrato, consequens est etiam ut areæ his lineis descriptæ sint in progressione consimili cum spatiis quæ velocitatibus describuntur. Ergo si velocitas initio primi temporis AK exponatur per lineam AB, & velocitas initio secundi KL per lineam Kk, & longitudo primo tempore descripta per aream AKkB, velocitates omnes subsequentes exponentur per lineas subsequentes Ll, Mm, &c. & longitudines descriptæ per areas Kl, Lm, &c. & composite, si tempus totum exponatur per summam partium suarum AM, longitudo tota descripta exponetur per summam partium suarum AMmB. Concipe jam tempus AM ita dividi in partes AK, KL, LM, &c. ut sint CA, CK, CL, CM, &c. in progressione Geometrica, & erunt partes illæ in eadem progressione, & velocitates AB, Kk, Ll, Mm, &c. in progressione eadem inversa, atque spatia descripta Ak, Kl, Lm, &c. æqualia. Q.E.D.
CD sumptæ, & erigantur perpendicula AB, Kk, Ll, Mm, &c. Hyperbolæ BKlmG, centro C Asymptotis rectangulis CD, CH, descriptæ occurrentia in B, k, l, m, &c. & erit AB ad Kk ut CK ad CA, & divisim ad Kk ut AK ad CA, & vicissim ad AK ut Kk ad CA, adeoque ut ad . Unde cum AK & dentur, erit ut ; & ultimo, ubi coeunt AB & Kk, ut ABq. Et simili argumento erunt , , &c. ut Kkq., Llq. &c. Linearum igitur AB, Kk, Ll, Mm quadrata sunt ut earundem differentiæ, & idcirco cum quadrata velocitatum fuerint etiam ut ipsarum differentiæ, similis erit ambarum progressio. Quo demonstrato, consequens est etiam ut areæ his lineis descriptæ sint in progressione consimili cum spatiis quæ velocitatibus describuntur. Ergo si velocitas initio primi temporis AK exponatur per lineam AB, & velocitas initio secundi KL per lineam Kk, & longitudo primo tempore descripta per aream AKkB, velocitates omnes subsequentes exponentur per lineas subsequentes Ll, Mm, &c. & longitudines descriptæ per areas Kl, Lm, &c. & composite, si tempus totum exponatur per summam partium suarum AM, longitudo tota descripta exponetur per summam partium suarum AMmB. Concipe jam tempus AM ita dividi in partes AK, KL, LM, &c. ut sint CA, CK, CL, CM, &c. in progressione Geometrica, & erunt partes illæ in eadem progressione, & velocitates AB, Kk, Ll, Mm, &c. in progressione eadem inversa, atque spatia descripta Ak, Kl, Lm, &c. æqualia. Q.E.D.
Corol. 1. Patet ergo quod si tempus exponatur per Asymptoti partem quamvis AD, & velocitas in principio temporis per ordinatim applicatam AB; velocitas in fine temporis exponetur per ordinatam DG, & spatium totum descriptum per aream Hyperbolicam adjacentem ABGD; necnon spatium quod corpus aliquod eodem tempore AD, velocitate prima AB, in Medio non resistente describere posset, per rectangulum. .
Corol. 2. Unde datur spatium in Medio resistente descriptum, capiendo illud ad spatium quod velocitate uniformi AB in Medio non resistente simul describi posset, ut est area Hyperbolica ABGD ad rectangulum .
Corol. 3. Datur etiam resistentia Medii, statuendo eam ipso motus initio æqualem esse vi uniformi centripetæ, quæ, in cadente corpore, tempore AC, in Medio non resistente, generare posset velocitatem AB. Nam si ducatur BT quæ tangat Hyperbolam in B, & occurrat Asymptoto in T; recta AT æqualis erit ipsi AC, & tempus exponet quo resistentia prima uniformiter continuata tollere posset velocitatem totam AB.
Corol. 4. Et inde datur etiam proportio hujus resistentiæ ad vim gravitatis, aliamve quamvis datam vim centripetam.
Corol. 5. Et viceversa, si datur proportio resistentiæ ad datam quamvis vim centripetam, datur tempus AC, quo vis centripeta resistentiæ æqualis generare possit velocitatem quamvis AB; & inde datur punctum B per quod Hyperbola Asymptotis CH, CD describi debet; ut & spatium ABGD, quod corpus incipiendo motum suum cum velocitate illa AB, tempore quovis AD, in Medio similari resistente describere potest.
Prop. VI. Theor. IV.
Corpora Sphaerica homogenea & æqualia, resistentiis in duplicata ratione velocitatum impedita, & solis viribus insitis incitata, temporibus quæ sunt reciproce ut velocitates sub initio, describunt semper æqualia spatia, & amittunt partes velocitatum proportionales totis.
Asymptotis rectangulis CD, CH descripta Hyperbola quavis BbEe secante perpendicula 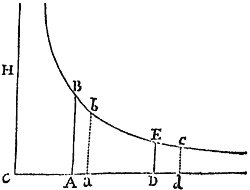 AB, ab, DE, de, in B, b, E, e, exponantur velocitates initiales per perpendicula AB, DE, & tempora per lineas Aa, Dd. Est ergo ut Aa ad Dd ita (per Hypothesin) DE ad AB, & ita (ex natura Hyperbolæ) CA ad CD; & componendo, ita Ca ad Cd. Ergo areæ ABba, DEed, hoc est spatia descripta æquantur inter se, & velocitates primæ AB, DE sunt ultimis ab, de, & propterea (dividendo) partibus etiam suis amissis AB-ab, DE-de proportionales. Q.E.D.
AB, ab, DE, de, in B, b, E, e, exponantur velocitates initiales per perpendicula AB, DE, & tempora per lineas Aa, Dd. Est ergo ut Aa ad Dd ita (per Hypothesin) DE ad AB, & ita (ex natura Hyperbolæ) CA ad CD; & componendo, ita Ca ad Cd. Ergo areæ ABba, DEed, hoc est spatia descripta æquantur inter se, & velocitates primæ AB, DE sunt ultimis ab, de, & propterea (dividendo) partibus etiam suis amissis AB-ab, DE-de proportionales. Q.E.D.
Prop. VII. Theor. V.
Corpora Sphærica quibus resistitur in duplicata ratione velocitatum, temporibus quæ sunt ut motus primi directe & resistentiæ primæ inverse, amittent partes motuum proportionales totis, & spatia describent temporibus istis in velocitates primas ductis proportionalia.
Namque motuum partes amissæ sunt ut resistentiæ & tempora conjunctim. Igitur ut partes illæ sint totis proportionales, debebit resistentia & corpus conjunctim esse ut motus. Proinde tempus erit ut Motus directe & resistentia inverse. Quare temporum particulis in ea ratione sumptis, corpora amittent semper particulas motuum proportionales totis, adeoque retinebunt velocitates in ratione prima. Et ob datam velocitatum rationem, describent semper spatia quæ sunt ut velocitates primæ & tempora conjunctim. Q.E.D.
Corol. 1. Igitur si æquivelocia corpora resistuntur in duplicata ratione diametrorum, Globi homogenei quibuscunque cum velocitatibus moti, describendo spatia diametris suis proportionalia, amittent partes motuum proportionales totis. Motus enim Globi cujusque erit ut ejus velocitas & Massa conjunctim, id est ut velocitas & cubus diametri; resistentia (per Hypothesin) erit ut quadratum diametri & quadratum velocitatis conjunctim; & tempus (per hanc Propositionem) est in ratione priore directe & ratione posteriore inverse, id est ut diameter directe & velocitas inverse; adeoque spatium (tempori & velocitati proportionale) est ut diameter.
Corol. 2. Si æquivelocia corpora resistuntur in ratione sesquialtera diametrorum: Globi homogenei quibuscunque cum velocitatibus moti, describendo spatia in sesquialtera ratione diametrorum, amittent partes motuum proportionales totis. Nam tempus augetur in ratione resistentiæ diminutæ, & spatium augetur in ratione temporis.
Corol. 3. Et universaliter, si æquivelocia corpora resistuntur in ratione dignitatis cujuscunque diametrorum, spatia quibus Globi homogenei, quibuscunque cum velocitatibus moti, amittent partes motuum proportionales totis, erunt ut cubi diametrorum ad dignitatem illam applicata. Sunto diametri D & E; & si resistentiæ sint ut Dn & En , spatia quibus amittent partes motuum proportionales totis, erunt ut D3-n & E3-n. Igitur describendo spatia ipsis D3-n & E3-n proportionalia, retinebunt velocitates in eadem ratione ad invicem ac sub initio.
Corol. 4. Quod si Globi non sint homogenei, spatium a Globo densiore descriptum augeri deber in ratione densiratis. Motus enim sub pari velocitate major est in ratione densitatis, & tempus (per hanc Propositionem) augetur in ratione motus directe, ac spatium descriptum in ratione temporis.
Corol. 5. Et si Globi moveantur in Mediis diversis, spatium in Medio, quod cæteris paribus magis resistit, diminuendum erit in ratione majoris resistentiæ. Tempus enim (per hanc Propositionem) diminuetur in ratione resistentiæ, & spatium in ratione temporis.
Lemma. II.
Momentum Genitæ æquatur momentis Terminorum singulorum generantium in eorundem laterum indices dignitatum & coefficientia continue ductis.
Genitam voco quantitatem omnem quæ ex Terminis quibuscunque in Arithmetica per multiplicationem, divisionem & extractionem radicum; in Geometria per inventionem vel contentorum & laterum, vel extremarum & mediarum proportionalium absque additione & subductione generatur. Ejusmodi quantitates sunt Facti, Quoti, Radices, rectangula, quadrata, cubi, latera quadrata, latera cubica & similes. Has quantitates ut in determinatas & instabiles, & quasi motu fluxuve perpetuo crescentes vel decrescentes hic considero, & eorum incrementa vel decrementa momentanea sub nomine momentorum intelligo: ita ut incrementa pro momentis addititiis seu affirmativis, ac decrementa pro subductitiis seu negativis habeantur. Cave tamen intellexeris particulas finitas. Momenta, quam primum finitæsunt magnitudinis, desinunt esse momenta. Finiri enim repugnant aliquatenus perpetuo eorum incremento vel decremento. Intelligenda sunt principia jamjam nascentia finitarum magnitudinum. Neque enim spectatur in hoc Lemmate magnitudo momentorum, sed prima nascentium proportio. Eodem recidit si loco momentorum usurpentur vel velocitates incrementorum ac decrementorum, (quas etiam motus, mutationes & fluxiones quantitatum nominare licet) vel finitæ quævis quantitates velocitatibus hisce proportionales. Termini autem cujusque Generantis coefficiens est quantitas, quæ oritur applicando Genitam ad hunc Terminum.
Igitur sensus Lemmatis est, ut si quantitatum quarumcunque perpetuo motu crescentium vel decrescentium A, B, C, &c. Momenta, vel mutationum velocitates dicantur a, b, c, &c. momentum vel mutatio rectanguli AB fuerit , & contenti ABC momentum fuerit : & dignitatum , , , , , , , , , & momenta , , , {,} , , ,,, & respective. Et generaliter ut dignitatis cujuscunque momentum fuerit aA. Item ut Genitæ momentum fuerit ; & Genitæ momentum ; & Genitæ sive momentum : & sic in cæteris. Demonstratur vero Lemma in hunc modum.
<252>Cas. 1. Rectangulum quodvis motu perpetuo auctum AB, ubi de lateribus A & B deerant momentorum dimidia & , fuit in , seu ; & quam primum latera A & B alteris momentorum dimidiis aucta sunt, evadit in seu . De hoc rectangulo subducatur rectangulum prius, & manebit excessus . Igitur laterum incrementis totis a & b generatur rectanguli incrementum .Q.E.D.
Cas. 2. Ponatur AB æquale G, & contenti ABC seu GC momentum (per Cas. 1.) erit , id est (si pro G & g scribantur AB & ) . Et par est ratio contenti sub lateribus quotcunque. Q.E.D.
Cas. 3. Ponantur A, B, C æqualia; & ipsius , id est rectanguli AB, momentum erit , ipsius autem , id est contenti ABC, momentum erit . Et eodem argumento momentum dignitatis cujuscunque est . Q.E.D.
Cas. 4. Unde cum in A sit 1, momentum ipsius ductum in A, una cum ducto in a erit momentum ipsius 1, id est nihil. Proinde momentum ipsius seu est . Et generaliter cum in sit 1, momentum ipsius ductum in An una cum in erit nihil. Et propterea momentum ipsius seu erit . Q.E.D.
Cas. 5. Et cum in sit A, momentum ipsius in erit a, per Cas. 3: ideoque momentum ipsius erit sive . Et generaliter si ponatur æqualem B, erit æquale , ideoque æquale , & æquale seu , adeoque æquale b, id est æquale momento ipsius . Q.E.D.
Cas. 6. Igitur Genitæ cujuscunque momentum est momentum ipsius ductum in , una cum momento ipsius ducto in , id est ; idque sive dignitatum indices m & n sint integri numeri vel fracti, sive affirmativi vel negativi. Et par est ratio contenti sub pluribus dignitatibus. Q.E.D.
Corol. 1. Hinc in continue proportionalibus, si terminus unus datur, momenta terminorum reliquorum erunt ut iidem termini multiplicati per numerum intervallorum inter ipsos & terminum datum. Sunto A, B, C, D, E, F continue proportionales; & si detur terminus C, momenta reliquorum terminorum erunt inter se ut -2A, -B, D, 2E, 3F.
Corol. 2. Et si in quatuor proportionalibus duæ mediæ dentur, momenta extremarum erunt ut cædem extremæ. Idem intelligendum est de lateribus rectanguli cujuscunque dati.
Corol. 3. Et si summa vel differentia duorum quadratorum detur, momenta laterum erunt reciproce ut latera.
Scholium.
In literis quæ mihi cum Geometra peritissimo G. G. Leibnitio annis abhinc decem intercedebant, cum significarem me compotem esse methodi determinandi Maximas & Minimas, ducendi Tangentes, & similia peragendi, quæ in terminis surdis æque ac in rationalibus procederet, & literis transpositis hanc sententiam involventibus [Data æquatione quotcunque fluentes quantitates involvente, fluxiones invenire, & vice versa] eandem celarem: rescripsit Vir Clarissimus se quoque in ejusmodi methodum incidisse, & methodum suam communicavit a mea vix abludentem præterquam in verborum & notarum formulis. Utriusque fundamentum continetur in hoc Lemmate.
Prop. VIII. Theor. VI.
Si corpus in Medio uniformi, Gravitate uniformiter agente, recta ascendat vel descendat, & spatium totum descriptum distinguatur in partes æquales, inque principiis singularum partium (addendo resistentiam Medii ad vim gravitatis, quando corpus ascendit, vel subducendo ipsam quando corpus descendit) colligantur vires absolutæ; dico quod vires illae absolutæ sunt in progressione Geometrica.
Exponatur enim vis gravitatis per datam lineam AC; resistentia per lineam indensinitam AK; vis absoluta in descensu corporis per differentiam KC; velocitas corporis per lineam AP (quæ sit media proportionalis inter AK & AC, ideoque in dimidiata ratione resistentiæ) incrementum resistentiæ data temporis particula factum per lineolam KL, & contemporaneum velocitatis incrementum per lineolam PQ; & centro C Asymptotis rectangulis CA, CH describatur Hyperbola quævis BNS, erectis perpendiculis AB, KN, LO, PR, QS occurrens in B, N, O, R, S. Quoniam AK est ut APq., erit hujus momentum KL ut illius momentum 2APQ, id est ut AP in KC. Nam velocitatis incrementum PQ, per motus Leg. 2. proportionale est vi generanti KC. Componatur ratio ipsius KL cum ratione ipsius KN, & fiet rectangulum ut ; hoc est, ob datum rectangulum , ut AP. Atqui areæ Hyperbolicæ KNOL ad rectangulum ratio ultima, ubi coeunt puncta K & L, est æqualitatis. Ergo area illa Hyperbolica evanescens est ut AP. Componitur igitur area tota Hyperbolica ABOL ex particulis KNOL velocitati AP semper proportionalibus, & propterea spatio velocitate ista descripto proportionalis est. Dividatur jam area illa in partes æquales 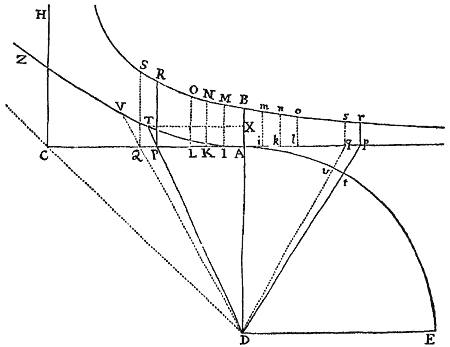 ABMI, IMNK, KNOL, &c. & vires absolutæ AC, IC, KC, LC, &c. erunt in progressione Geometrica. Q.E.D. Et simili argumento, in ascensu corporis, sumendo, ad contrariam partem puncti A, æquales areas ABmi, imnk, knol, &c. constabit quod vires absolutæ AC, iC, kC, lC, &c. sunt continue proportionales. Ideoque si spatia omnia in ascensu & descensu capiantur æqualia; omnes vires absolutæ lC, kC, iC, AC, IC, KC, LC, &c. erunt continue proportionales. Q.E.D.
ABMI, IMNK, KNOL, &c. & vires absolutæ AC, IC, KC, LC, &c. erunt in progressione Geometrica. Q.E.D. Et simili argumento, in ascensu corporis, sumendo, ad contrariam partem puncti A, æquales areas ABmi, imnk, knol, &c. constabit quod vires absolutæ AC, iC, kC, lC, &c. sunt continue proportionales. Ideoque si spatia omnia in ascensu & descensu capiantur æqualia; omnes vires absolutæ lC, kC, iC, AC, IC, KC, LC, &c. erunt continue proportionales. Q.E.D.
Corol. 1. Hinc si spatium descriptum exponatur per aream Hyperbolicam ABNK; exponi possunt vis gravitatis, velocitas corporis & resistentia Medii per lineas AC, AP & AK respective; & vice versa.
Corol. 2. Et velocitatis maximæ, quam corpus in infinitum descendendo potest unquam acquirere, exponens est linea AC.
Corol. 3. Igitur si in data aliqua velocitate cognoscatur resistentia Medii, invenietur velocitas maxima, sumendo ipsam ad velocitatem illam datam in dimidiata ratione, quam habet vis Gravitatis ad Medii resistentiam illam cognitam.
Corol. 4. Sed & particula temporis, quo spatii particula quam minima NKLO in descensu describitur, est ut rectangulum . Nam quoniam spatium NKLO est ut velocitas ducta in particulam temporis; erit particula temporis ut spatium illud applicatum ad velocitatem, id est ut rectangulum quam minimum applicatum ad AP. Erat supra KL ut . Ergo particula temporis est ut , vel quod perinde est, ut . Q.E.D.
Corol. 5. Eodem argumento particula temporis, quo spatii particula nklo in ascensu describitur, est ut .
Prop. IX. Theor. VII.
Positis jam demonstratis, dico quod si Tangentes angulorum sectoris Circularis & sectoris Hyperbolici sumantur velocitatibus proportionales, existente radio justæ magnitudinis: erit tempus omne ascensus futuri ut sector Circuli, & tempus omne descensus præteriti ut sector Hyperbolæ.
Rectæ AC, qua vis gravitatis exponitur, perpendicularis & æqualis ducatur AD. Centro D semidiametro AD describatur tum circuli Quadrans AtE, tum Hyperbola rectangula AVZ axem habens AX, verticem principalem A & Asymptoton DC. Jungantur Dp, DP, & erit Sector circularis AtD ut tempus ascensus omnis futuri; & Sector Hyperbolicus ATD ut tempus descensus omnis præteriti.
Cas 1. Agatur enim Dvq abscindens Sectoris ADt & trianguli ADp momenta, seu particulas quam minimas simul descriptas 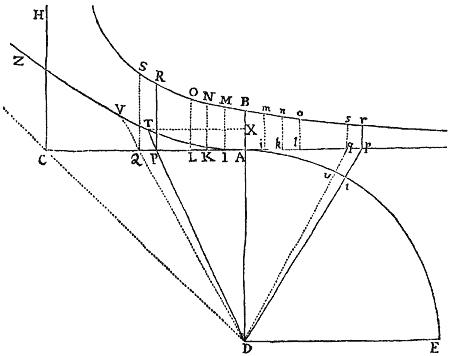 tDv & pDq. Cum particulæ illæ, ob angulum communem D, sunt in duplicata ratione laterum, erit particula tDv ut . Sed pD quad. est id est seu ; & qDp est . Ergo Sectoris particula vDt est ut , id est, per Corol. 5, Prop. VIII. ut particula temporis. Et componendo fit summa particularum omnium tDv in Sectore ADt, ut summa particularum temporis singulis velocitatis decrescentis Ap particulis amissis pq respondentium, usque dum velocitas illa in nihilum diminuta evanuerit; hoc est, Sector totus ADt est ut ascensus totius futuri tempus. Q.E.D.
tDv & pDq. Cum particulæ illæ, ob angulum communem D, sunt in duplicata ratione laterum, erit particula tDv ut . Sed pD quad. est id est seu ; & qDp est . Ergo Sectoris particula vDt est ut , id est, per Corol. 5, Prop. VIII. ut particula temporis. Et componendo fit summa particularum omnium tDv in Sectore ADt, ut summa particularum temporis singulis velocitatis decrescentis Ap particulis amissis pq respondentium, usque dum velocitas illa in nihilum diminuta evanuerit; hoc est, Sector totus ADt est ut ascensus totius futuri tempus. Q.E.D.
Cas. 2. Agatur DQV abscindens tum Sectoris DAV, tum trianguli DAQ particulas quam minimas TDV & PDQ; & erunt hæ particulæ ad invicem ut DTq. ad DPq. id est (si TX & AP parallelæ sint) ut DXq. ad DAq. vel TXq. ad APq. & divisim ut DXq.-TXq. ad ADq.-APq. Sed ex natura 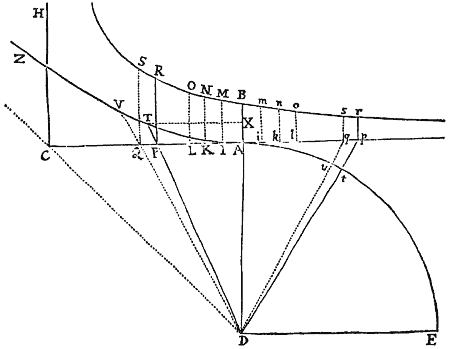 Hyperbolæ est ADq., & per Hypothesin APq. est . Ergo particulæ sunt ad invicem ut ADq. ad ; id est ut AD ad seu AC ad CK: ideoque Sectoris particula TDV est , atque adeo ob datas AC & AD, ut PQ / CK; & propterea per Corol. 5. Prop. VIII. Lib. II. ut particula temporis incremento velocitatis PQ respondens. Et componendo fit summa particularum temporis, quibus omnes velocitatis AP particulæ PQ generantur, ut summa particularum Sectoris ADT, id est tempus totum ut Sector totus. Q.E.D.
Hyperbolæ est ADq., & per Hypothesin APq. est . Ergo particulæ sunt ad invicem ut ADq. ad ; id est ut AD ad seu AC ad CK: ideoque Sectoris particula TDV est , atque adeo ob datas AC & AD, ut PQ / CK; & propterea per Corol. 5. Prop. VIII. Lib. II. ut particula temporis incremento velocitatis PQ respondens. Et componendo fit summa particularum temporis, quibus omnes velocitatis AP particulæ PQ generantur, ut summa particularum Sectoris ADT, id est tempus totum ut Sector totus. Q.E.D.
Corol. 1. Hinc si AB æquetur quartæ parti ipsus AC, spatium ABRP, quod corpus tempore quovis ATD cadendo describit, erit ad spatium quod corpus semisse velocitatis maximæ AC, eodem tempore uniformiter progrediendo describere potest, ut area ABRP, qua spatium cadendo descriptum exponitur, ad aream ATD qua tempus exponitur. Nam cum sit AC ad AP ut AP ad AK, erit 2APQ æquale (per Corol 1. Lem. II. hujus) adeoque KL ad PQ ut 2AP ad AC, & inde LKN ad seu DPQ ut ad . Sed erat DPQ ad DTV ut CK ad AC. Ergo ex æquo LKN est ad DTV ut ad ; id est, ob æquales CKN & , ut AP ad AC; hoc est ut velocitas corporis cadentis ad velocitatem maximam quam corpus cadendo potest acquirere. Cum igitur arearum ABKN & AVD momenta LKN & DTV sunt ut velocitates, erunt arearum illarum partes omnes simul genitæ ut spatia simul descripta, ideoque areæ totæ ab initio genitæ ABKN & AVD ut spatia tota ab initio descensus descripta. Q.E.D.
Corol. 2. Idem consequitur etiam de spatio quod in ascensu describitur. Nimirum quod spatium illud omne sit ad spatium, uniformi cum velocitate AC eodem tempore descriptum, ut est area ABnk ad Sectorem ADt.
Corol. 3. Velocitas corporis tempore ATD cadentis est ad velocitatem, quam eodem tempore in spatio non resistente acquireret, ut triangulum APD ad Sectorem Hyperbolicum ATD. Nam velocitas in Medio non resistente foret ut tempus ATD, & in Medio resistente est ut AP, id est ut triangulum APD. Et velocitates illae initio descensus æquantur inter se, perinde ut areæ illæ ATD, APD.
<260>Corol. 4. Eodem argumento velocitas in ascensu est ad velocitatem, qua corpus eodem tempore in spatio non resistente omnem suum ascendendi motum amittere posset, ut triangulum ApD ad Sectorem circularem AtD; sive ut recta Ap ad arcum At.
Corol. 5. Est igitur tempus quo corpus in Medio resistente cadendo velocitatem AP acquirit, ad tempus quo velocitatem maximam AC in spatio non resistente cadendo acquirere posset, ut Sector ADT ad triangulum ADC: & tempus, quo velocitatem Ap in Medio resistente ascendendo possit amittere, ad tempus quo velocitatem eandem in spatio non resistente ascendendo posset amittere, ut arcus At ad ejus Tangentem Ap.
Corol. 6. Hinc ex dato tempore datur spatium ascensu vel descensu descriptum. Nam corporis in infinitum descendentis datur velocitas maxima, per Corol. 2. & 3. Theor. VI, Lib. II. indeque datur & spatium quod semisse velocitatis illius dato tempore describi potest, & tempus quo corpus velocitatem illam in spatio non resistente cadendo posset acquirere. Et sumendo Sectorem ADT vel ADt ad triangulum ADC in ratione temporum; dabitur tum velocitas AP vel Ap, tum area ABKN vel ABkn, quæ est ad Sectorem ut spatium quæsitum ad spatium jam ante inventum.
Corol. 7. Et regrediendo, ex dato ascensus vel descensus spatio ABnk vel ABNK, dabitur tempus ADt vel ADT.
Prop. X. Prob. III.
Tendat uniformis vis gravitatis directe ad planum Horizontis, sitque resistentia ut medii densitas & quadratum velocitatis conjunctim: requiritur tum Medii densitas in locis singulis, quæ faciat ut corpus in data quavis linea curva moveatur, tum corporis velocitas in iisdem locis.
Sit AK planum illud plano Schematis perpendiculare; ACK linea curva; C corpus in ipsa motum; & FCf recta ipsam tangens in C. Fingatur autem corpus C nunc progredi ab A ad K per lineam illam ACK, nunc vero regredi per eandem lineam; & in progressu impediri a Medio, in regressu æque promoveri, sic ut in iisdem locis eadem 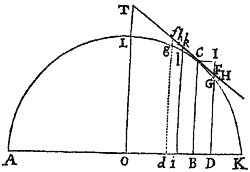 semper sit corporis progredientis & regredientis velocitas. Æqualibus autem temporibus describat corpus progrediens arcum quam minimum CG, & corpus regrediens arcum Cg; & sint CH, Ch longitudines æquales rectilineæ, quas corpora de loco C exeuntia, his temporibus, absque Medii & Gravitatis actionibus describerent: & a punctis C, G, g ad planum horizontale AK demittantur perpendicula CB, GD, gd, quorum GD ac gd tangenti occurrant in F & f. Per Medii resistentiam fit ut corpus progrediens, vice longitudinisCH, describat solummodo longitudinem CF; & per vim gravitatis transfertur corpus de F in G: adeoque lineola HF vi resistentiæ, & lineola FG vi gravitatis simul generantur. Proinde (per Lem. X. Lib. I.) lineola FG est ut vis gravitatis & quadratum temporis conjunctim, adeoque (ob datam gravitatem) ut quadratum temporis; & lineola HF ut resistentia & quadratum temporis, hoc est ut resistentia & lineola FG. Et inde resistentia fit ut HF directe & FG inverse, sive ut . Hæc ita se habent in lineolis nascentibus. Nam in lineolis finitæ magnitudinis hæ rationes non sunt accuratæ.
semper sit corporis progredientis & regredientis velocitas. Æqualibus autem temporibus describat corpus progrediens arcum quam minimum CG, & corpus regrediens arcum Cg; & sint CH, Ch longitudines æquales rectilineæ, quas corpora de loco C exeuntia, his temporibus, absque Medii & Gravitatis actionibus describerent: & a punctis C, G, g ad planum horizontale AK demittantur perpendicula CB, GD, gd, quorum GD ac gd tangenti occurrant in F & f. Per Medii resistentiam fit ut corpus progrediens, vice longitudinisCH, describat solummodo longitudinem CF; & per vim gravitatis transfertur corpus de F in G: adeoque lineola HF vi resistentiæ, & lineola FG vi gravitatis simul generantur. Proinde (per Lem. X. Lib. I.) lineola FG est ut vis gravitatis & quadratum temporis conjunctim, adeoque (ob datam gravitatem) ut quadratum temporis; & lineola HF ut resistentia & quadratum temporis, hoc est ut resistentia & lineola FG. Et inde resistentia fit ut HF directe & FG inverse, sive ut . Hæc ita se habent in lineolis nascentibus. Nam in lineolis finitæ magnitudinis hæ rationes non sunt accuratæ.
Et simili argumento est fg ut quadratum temporis, adeoque ob æqualia tempora æquatur ipsi FG; & impulsus quo corpus regrediens urgetur est ut . Sed impulsus corporis regredientis & resistentia progredientis ipso motus initio æquantur, adeoque & ipsis proportionales & æquantur; & propterea ob æquales fg & FG, æquantur etiam hf & HF, suntque adeo CF, CH (vel Ch) & Cf in progressione Arithmetica, & inde HF semidifferentia est ipsarum Cf & CF; & resistentia quæ supra fuit ut , est ut .
Est autem resistentia ut Medii densitas & quadratum velocitatis. Velocitas autem ut descripta longitudo CF directe & tempus inverse, hoc est ut , adeoque quadratum velocitatis ut . Quare resistentia, ipsique proportionalis est ut Medii densitas & conjunctim; & inde Medii densitas ut directe & inverse, id est ut . Q.E.D.
Corol. 1. Et hinc colligitur, quod si in Cf capiatur Ck æqualis CF, & ad planum horizontale AK demittatur perpendiculum ki, secans curvam ACK in l; fiet Medii densitas ut {.} Erit enim fC ad kC ut seu ad , & divisim fk ad kC, id est ad CF ut ad ; hoc est (si ducatur terminus uterque in ) ut ad , sive ad . Nam ratio prima nascentium & est æqualitatis. Scribatur itaque pro ; & Medii densitas, quæ fuit ut evadet ut .
<263>Corol. 2. Unde cum 2 HF & æquentur, & FG & kl (ob rationem æqualitatis) componant 2 FG; erit 2 HF ad CF ut ad 2FG; & inde HF ad FG, hoc est resistentia ad gravitatem, ut rectangulum CF in ad 4
Corol. 3. Et hinc si curva linea desiniatur per relationem inter basem seu abscissam AB & ordinatim applicat am BC; (ut moris est) & valor ordinatim applicatæ resolvatur in seriem convergentem: Problema per primos seriei terminos expedite solvetur: ut in Exemplis sequentibus.
Exempl. 1. Sit Linea ACK semicirculus super diametro AK descriptus, & requiratur Medii densitas quæ faciat ut Projectile in hac linea moveatur.
Bisecetur semicirculi diameter AK in O; & dic OK n, OB a, BC e, & BD vel Bi o: & erit DGq. seu æquale seu ; & radice per methodum nostram extracta, fiet &c. Hic scribatur nn pro ee+aa & evadet &c.
Hujusmodi Series distinguo 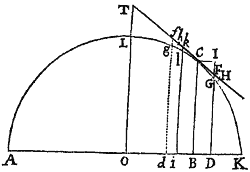 in terminos successivos in hunc modum. Terminum primum appello in quo quantitas infinite parva o non extat; secundum in quo quantitas illa extat unius dimensionis; tertium in quo extat duarum, quartum in quo trium est, & sic in infinitum. Et primus terminus, qui hic est e, denotabit semper longitudinem ordinatæ BC insistentis ad indefinitæ quantitatis initium B; secundus terminus qui hic est , denotabit differentiam inter BC & DF, id est lineolam IF, quæ abscinditur complendo parallelogrammum BCID, atque adeo positionem Tangentis CF semper determinat: ut in hoc casu capiendo IF ad IC ut est ad o seu a ad e. Terminus tertius, qui hic est designabit lineolam FG, quæ jacet inter Tangentem & Curvam, adeoque determinat angulum contactus FCG, seu curvaturam quam curva linea habet in C. Si lineola illa FG finitæ est magnitudinis, designabitur per terminum tertium una cum subsequentibus in infinitum. At si lineola illa minuatur in infinitum, termini subsequentes evadent infinite minores tertio, ideoque negligi possunt. Terminus quartus, qui hic est , exhibet variationem Curvaturæ; quintus variationem variationis, & sic deinceps. Unde obiter patet usus non contemnendus harum Serierum in solutione Problematum, quæ pendent a Tangentibus & curvatura Curvarum.
in terminos successivos in hunc modum. Terminum primum appello in quo quantitas infinite parva o non extat; secundum in quo quantitas illa extat unius dimensionis; tertium in quo extat duarum, quartum in quo trium est, & sic in infinitum. Et primus terminus, qui hic est e, denotabit semper longitudinem ordinatæ BC insistentis ad indefinitæ quantitatis initium B; secundus terminus qui hic est , denotabit differentiam inter BC & DF, id est lineolam IF, quæ abscinditur complendo parallelogrammum BCID, atque adeo positionem Tangentis CF semper determinat: ut in hoc casu capiendo IF ad IC ut est ad o seu a ad e. Terminus tertius, qui hic est designabit lineolam FG, quæ jacet inter Tangentem & Curvam, adeoque determinat angulum contactus FCG, seu curvaturam quam curva linea habet in C. Si lineola illa FG finitæ est magnitudinis, designabitur per terminum tertium una cum subsequentibus in infinitum. At si lineola illa minuatur in infinitum, termini subsequentes evadent infinite minores tertio, ideoque negligi possunt. Terminus quartus, qui hic est , exhibet variationem Curvaturæ; quintus variationem variationis, & sic deinceps. Unde obiter patet usus non contemnendus harum Serierum in solutione Problematum, quæ pendent a Tangentibus & curvatura Curvarum.
Præterea CF est latus quadratum ex CIq. & IFq. hoc est ex BDq. & quadrato termini secundi. Estque æqualis duplo termini tertii, & æqualis duplo quarti. Nam valor ipsius DG convertitur in valorem ipsius il, & valor ipsius FG in valorem ipsius kl, scribendo Bi pro BD, seu pro . Proinde cum &c. erit &c. Et horum summa est , differentia . Terminum quintum & sequentes hic negligo, ut infinite minores quam qui in hoc Problemate considerandi veniant. Itaque si designetur Series universaliter his terminis &c. erit CF æqualis , æqualis , & æqualis . Pro CF, & scribantur hi earum valores, & Medii densitas quæ erat ut jam fiet ut . Deducendo igitur Problema unumquodque ad seriem convergentem, & hic pro Q, R & S scribendo terminos seriei ipsis respondentes; deinde etiam ponendo resistentiam Medii in loco quovis G esse ad Gravitatem ut ad , & velocitatem esse illam ipsam quacum corpus, de loco C secundum rectam CF egrediens, in Parabola, diametrum CB & latus rectum habente, deinceps moveri posset, solvetur Problema.
Sic in Problemate jam solvendo, si scribantur seu pro , pro R, & pro S, prodibit Medii densitas ut , hoc est (ob datam n) ut seu , id est ut Tangentis longitudo illa CT, quæ ad semidiametrum OL ipsi AK normaliter insistentem terminatur; 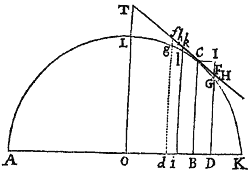 & resistentia erit ad gravitatem ut a ad n, id est ut OB ad circuli semidiametrum OK, velocitas autem erit ut . Igitur si corpus C certa cum velocitate, secundum lineam ipsi OK parallelam, exeat de loco L, & Medii densitas in singulis locis C sit ut longitudo tangentis CT, & resistentia etiam in loco aliquo C sit ad vim gravitatis ut OB ad OK; corpus illud describet circuli quadrantem LCK. Q.E.I.
& resistentia erit ad gravitatem ut a ad n, id est ut OB ad circuli semidiametrum OK, velocitas autem erit ut . Igitur si corpus C certa cum velocitate, secundum lineam ipsi OK parallelam, exeat de loco L, & Medii densitas in singulis locis C sit ut longitudo tangentis CT, & resistentia etiam in loco aliquo C sit ad vim gravitatis ut OB ad OK; corpus illud describet circuli quadrantem LCK. Q.E.I.
At si corpus idem de loco A secundum lineam ipsi AK perpendicularem egrederetur, sumenda esset OB seu a ad contrarias partes centri O, & propterea signum ejus mutandum esset, & scribendum pro . Quo pacto prodiret Medii densitas ut . Negativam autem densitatem (hoc est quæ motus corporum accelerat) Natura non admittit, & propterea naturaliter fieri non potest ut corpus ascendendo ab A describat circuli quadrantem AL. Ad hunc effectum deberet corpus a Medio impellente accelerari, non a resistente impediri.
Exempl. 2. Sit linea ALCK Parabola, axem habens OL horizonti AK perpendicularem, & requiratur Medii densitas quæ faciat ut projectile in ipsa moveatur.
Ex natura Parabolæ, rectangulum ADK æquale est rectangulo sub ordinata DG & recta aliqua data: hoc est, si dicantur recta illa b, AB a, AK c, BC e & BD o; rectangulum in c-a-o seu æquale est rectangulo b in DG, adeoque DG æquale . Jam scribendus esset hujus seriei secundus terminus pro Qo, & ejus coefficiens pro Q; tertius item terminus pro Roo, & ejus coefficiens pro R. Cum vero plures non sint termini, debebit quarti termini coefficiens S evanescere, & propterea quantitas . cui Medii densitas proportionalis est, nihil erit. Nulla igitur Medii densitate movebitur Projectile in Parabola, uti olim demonstravit Galilæus. Q.E.I.
Exempl. 3. Sit linea AGK Hyperbola, Asymptoton habens NX plano horizontali AK perpendicularem; & quæratur Medii densitas quæ faciat ut Projectile moveatur in hac linea.
Sit MX Asymptotos altera, ordinatim applicatæ DG pro ductæ occurrens in V, & ex natura Hyperbolæ, rectangulum 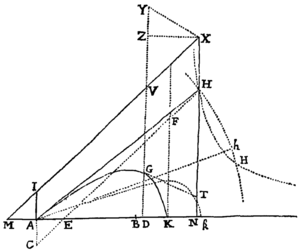 XV in VG dabitur. Datur autem ratio DN ad VX, & propterea datur etiam rectangulum DN in VG. Sit illud bb; & completo parallelogrammo DNXZ, dicatur BN a, BD o, NX c, & ratio data VZ ad ZX vel DN ponatur esse . Et erit DN æqualis , VG æqualis , VZ æqualis m / n/a-o, & GD seu NX-VZ-VG æqualis . Resolvatur terminus in seriem convergentem &c. & fiet GD æqualis &c. Hujus seriei terminus secundus usurpandus est pro Qo, tertius cum signo mutato pro , & quartus cum signo etiam mutato pro , eorumque coefficientes & scribendæ sunt, in Regula superiore, pro Q, R & S. Quo facto prodit medii densitas ut seu id est, si in VZ sumatur VY æqualis VG, ut . Namque sunt ipsarum XZ & ZY quadrata. Resistentia autem invenitur in ratione ad Gravitatem quam habet XY ad YG, & velocitas ea est quacum corpus in Parabola pergeret verticem G diametrum DG & latus rectum habente. Ponatur itaque quod Medii densitates in locis singulis G sint reciproce ut distantiæ XY, quodque resistentia in loco aliquo G sit ad gravitatem ut XY ad YG; & corpus de loco A justa cum velocitate emissum describet Hyperbolam illam AGK. Q.E.I.
XV in VG dabitur. Datur autem ratio DN ad VX, & propterea datur etiam rectangulum DN in VG. Sit illud bb; & completo parallelogrammo DNXZ, dicatur BN a, BD o, NX c, & ratio data VZ ad ZX vel DN ponatur esse . Et erit DN æqualis , VG æqualis , VZ æqualis m / n/a-o, & GD seu NX-VZ-VG æqualis . Resolvatur terminus in seriem convergentem &c. & fiet GD æqualis &c. Hujus seriei terminus secundus usurpandus est pro Qo, tertius cum signo mutato pro , & quartus cum signo etiam mutato pro , eorumque coefficientes & scribendæ sunt, in Regula superiore, pro Q, R & S. Quo facto prodit medii densitas ut seu id est, si in VZ sumatur VY æqualis VG, ut . Namque sunt ipsarum XZ & ZY quadrata. Resistentia autem invenitur in ratione ad Gravitatem quam habet XY ad YG, & velocitas ea est quacum corpus in Parabola pergeret verticem G diametrum DG & latus rectum habente. Ponatur itaque quod Medii densitates in locis singulis G sint reciproce ut distantiæ XY, quodque resistentia in loco aliquo G sit ad gravitatem ut XY ad YG; & corpus de loco A justa cum velocitate emissum describet Hyperbolam illam AGK. Q.E.I.
Exempl. 4. Ponatur indefinite, quod linea AGK Hyperbola sit, centro X Asymptotis MX, NX ea lege descripta, ut constructo rectangulo XZDN cujus latus ZD secet Hyperbolam in G & Asymptoton ejus in V, fuerit VG reciproce ut ipsius ZX vel DN dignitas aliqua NDn, cujus index est numerus n: & quæratur Medii densitas, qua Projectile progrediatur in hac curva.
Pro DN, BD, NX scribantur A, O, C respective, sitque VZ ad ZX vel DN ut dade, & VG æqualis , & erit DN æqualis , , in , & GD seu æqualis . Resolvatur terminus ille in seriem infinitam &c. ac fiet GD æqualis &c. Hujus seriei terminus secundus usurpandus est pro Qo, tertius pro , quartus pro . Et inde Medii densitas , in loco quovis G, fit , adeoque si in VZ capiatur VY æqualis , est reciproce ut XY. Sunt enim & in ipsarum XZ & ZY quadrata. Resistentia autem in eodem loco G fit ad Gravitatem ut S in ad , id est XY ad . Et velocitas ibidem ea ipsa est quacum corpus projectum in Parabola pergeret, verticem G, diametrum GD & Latus rectum seu habente. Q.E.I.
Scholium.
Quoniam motus non sit in Parabola nisi in Medio non resistente, in Hyperbolis vero hic descriptis sit per resistentiam perpetuam; perspicuum est quod linea, quam Projectile in Medio uniformiter resistente describit, propius accedit ad Hyperbolas hasce quam ad Parabolam. Est utique linea illa Hyperbolici generis, sed quæ circa verticem magis distat ab Asymptotis; in partibus a vertice remotioribus propius ad ipsas accedit quam pro ratione Hyperbolarum quas hic descripsi. Tanta vero non est inter has & illam differentia, quin illius loco possint hæ in rebus practicis non incommode adhiberi. Et utiliores forsan futuræ sunt hæ, quam Hyperbola magis accurata & simul magis composita. Ipsæ vero in usum sic deducentur.
Compleatur parallelogrammum XYGT, & ex natura harum Hyperbolarum facile colligitur quod recta GT tangit Hyperbolam in G, ideoque densitas Medii in G est reciproce ut tangens GT, & velocitas ibidem ut , resistentia autem ad vim gravitatis ut GT ad .
Proinde si corpus de loco A secundum rectam AH projectum describat Hyperbolam AGK, & AH producta occurrat Asymptoto NX in H, actaque AI occurrat alteri Asymptoto MX in I: erit Medii densitas in A reciproce ut AH, & corporis velocitas ut , ac resistentia ibidem ad Gravitatem ut AH ad in AI. Unde prodeunt sequentes Regulæ.
Reg. 1. Si servetur Medii densitas in A & mutetur angulus NAH, manebunt longitudines AH, AI, HX. Ideoque si longitudines illæ in aliquo casu inveniantur, Hyperbola deinceps ex dato quovis angulo NAH expedite determinari potest.
Reg. 2. Si servetur tum angulus NAH tum Medii densitas in A, & mutetur velocitas quacum corpus projicitur; servabitur longitudo AH, & mutabitur AI in duplicata ratione velocitatis reciproce.
Reg. 3. Si tam angulus NAH quam corporis velocitas in A, gravitasque acceleratrix servetur, & proportio resistentiæ in A ad gravitatem motricem augeatur in ratione quacunque: augebitur proportio AH ad AI in eadem ratione, manente Parabolæ latere recto, eique proportionali longitudine ; & propterea minuetur AH in eadem ratione, & AI minuetur in ratione illa duplicata. Augetur vero proportio resistentiæ ad pondus, ubi vel gravitas specifica sub æquali magnitudine fit minor, vel Medii densitas major, vel resistentia, ex magnitudine diminuta, diminuitur in minore ratione quam pondus.
Reg. 4. Quoniam densitas Medii prope verticem Hyperbolæ minor est quam in loco A, ut servetur densitas mediocris, debet ratio minimæ tangentium GT ad Tangentem AH inveniri, & densitas in A, per Regulam tertiam, diminui in ratione paulo minore quam semisummæ Tangentium ad Tangentem AH.
Reg. 5. Si dantur longitudines AH, AI, & describenda sit figura AGK: produc HN ad X, ut sit HX æqualis facto sub & AI; centroque X & Asymptotis MX, NX per punctum A describatur Hyperbola, ea lege ut sit AI ad quamvis VG ut ad .
Reg. 6. Quo major est numerus n, eo magis accuratæ sunt hae Hyperbolæ in ascensu corporis ab A, & minus accuratæ in ejus descensu ad G; & contra. Hyperbola Conica mediocrem rationem tenet, estque cæteris simplicior. Igitur si Hyperbola sit hujus generis, & punctum K, ubi corpus projectum incidet in rectam quamvis AN per punctum A transeuntem, quæratur: occurrat producta AN Asymptotis MX, NX in M & N, & sumatur NK ipsi AM æqualis.
Reg. 7. Et hinc liquet methodus expedita determinandi hanc Hyperbolam ex Phænominis. Projiciantur corpora duo similia & æqualia eadem velocitate, in angulis diversis HAK, hAK, incidentque in planum Horizontis in K & k; & no tetur proportio AK ad Ak. Sit ea d ad e. Tum erecto cujusvis longitudinis perpendiculo AI, assume utcunque longitudinem AH vel Ah, & inde collige graphice longitudines AK, Ak, per Reg. 6. Si ratio AK ad Ak sit eadem cum ratione d ad e, longitudo AH recte assumpta fuit. Sin minus cape in recta infinita SM longitudinem SM æqualem assumptæ AH, & erige perpendiculum MN æquale rationum differentiæ ductæ in rectam quamvis datam. Simili methodo ex assumptis pluribus longitudinibus AH invenienda sunt plura puncta N: & tum demum si per omnia agatur Curva linea regularis NNXN, 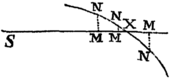 hæc abscindet SX quæsitæ longitudini AH æqualem. Ad usus Mechanicos sufficit longitudines AH, AI easdem in angulis omnibus HAK retinere. Sin figura ad inveniendam resistentiam Medij accuratius determinanda sit, corrigendæ sunt semper hæ longitudines per Regulam quartam.
hæc abscindet SX quæsitæ longitudini AH æqualem. Ad usus Mechanicos sufficit longitudines AH, AI easdem in angulis omnibus HAK retinere. Sin figura ad inveniendam resistentiam Medij accuratius determinanda sit, corrigendæ sunt semper hæ longitudines per Regulam quartam.
Reg. 8. Inventis longitudinibus AH, HX; si jam desideretur positio rectæ AH, secundum quam Projectile data illa cum velocitate emissum 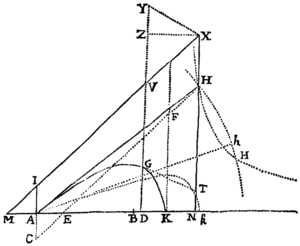 incidit in punctum quodvis K: ad puncta A & K erigantur rectæ AC, KF horizonti perpendiculares, quarum AC deorsum tandat, & æquetur ipsi AI seu . Asymptotis AK, KF describatur Hyperbola, cujus Conjugata transeat per punctum C, centroque A & intervallo AH describatur Circulus secans Hyperbolam illam in puncto H; & projectile secundum rectam AH emissum incidet in punctum K. Q.E.I. Nam punctum H, ob datam longitudinem AH, locatur alicubi in circulo descripto. Agatur CH occurrens ipsis AK & KF, illi in C, huic in F, & ob parallelas CH, MX & æquales AC, AI, erit AE æqualis AM, & propterea etiam æqualis KN. Sed CE est ad AE ut FH ad KN, & propterea CE & FH æquantur. Incidit ergo punctum H in Hyperbolam Asymptotis AK, KF descriptam, cujus conjugata transit per punctum C, atq adeo reperitur in communi intersectione Hyperbolæ hujus & circuli descripti. Q.E.D. Notandum est autem quod hæc operatio perinde se habet, sive recta AKN horizonti parallela sit, sive ad horizontem in angulo quovis inclinata: quodque ex duabus intersectionibus H, H duo prodeunt anguli NAH, NAH, quorum minor eligendus est; & quod in Praxi mechanica sufficit circulum semel describere, deinde regulam interminatam CH ita applicare ad punctum C, ut ejus pars FH, circulo & rectæ FK interjecta, æqualis sit ejus parti CE inter punctum C & rectam HK sitæ.
incidit in punctum quodvis K: ad puncta A & K erigantur rectæ AC, KF horizonti perpendiculares, quarum AC deorsum tandat, & æquetur ipsi AI seu . Asymptotis AK, KF describatur Hyperbola, cujus Conjugata transeat per punctum C, centroque A & intervallo AH describatur Circulus secans Hyperbolam illam in puncto H; & projectile secundum rectam AH emissum incidet in punctum K. Q.E.I. Nam punctum H, ob datam longitudinem AH, locatur alicubi in circulo descripto. Agatur CH occurrens ipsis AK & KF, illi in C, huic in F, & ob parallelas CH, MX & æquales AC, AI, erit AE æqualis AM, & propterea etiam æqualis KN. Sed CE est ad AE ut FH ad KN, & propterea CE & FH æquantur. Incidit ergo punctum H in Hyperbolam Asymptotis AK, KF descriptam, cujus conjugata transit per punctum C, atq adeo reperitur in communi intersectione Hyperbolæ hujus & circuli descripti. Q.E.D. Notandum est autem quod hæc operatio perinde se habet, sive recta AKN horizonti parallela sit, sive ad horizontem in angulo quovis inclinata: quodque ex duabus intersectionibus H, H duo prodeunt anguli NAH, NAH, quorum minor eligendus est; & quod in Praxi mechanica sufficit circulum semel describere, deinde regulam interminatam CH ita applicare ad punctum C, ut ejus pars FH, circulo & rectæ FK interjecta, æqualis sit ejus parti CE inter punctum C & rectam HK sitæ.
Quæ de Hyperbolis dicta sunt facile applicantur ad Parabolas. Nam si XAGK. Parabolam designet quam recta XV tangat in 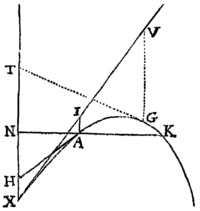 vertice X, sintque ordinatim applicatæ IA, VG ut quælibet abscissarum XI, XV dignitates , ; agantur XT, TG, HA, quarum XT parallela sit VG, & TG, HA parabolam tangant in G & A: & corpus de loco quovis A, secundum rectam AH productam, justa cum velocitate projectum, describet hanc Parabolam, si modo densitas Medij, in locis singulis G, sit reciproce ut tangens GT. Velocitas autem in G ea erit quacum Projectile pergeret, in spatio non resistente, in Parabola Conica, verticem G, diametrum VG deorsum productam, & latus rectum . Et resistentia in G erit ad vim Gravitatis ut TG ad 3nn-3n / n-2 VG. Vnde si NAK lineam horizontalem designet, & manente tum densitate Medij in A, tum velocitate quacum corpus projicitur, mutetur utcunque angulus NAH; manebunt longitudines AH, AI, HX, & inde datur Parabolæ vertex X, & positio rectæ XI, & sumendo VG ad IA ut ad , dantur omnia Parabolae puncta G, per quae Projectile transibit.
vertice X, sintque ordinatim applicatæ IA, VG ut quælibet abscissarum XI, XV dignitates , ; agantur XT, TG, HA, quarum XT parallela sit VG, & TG, HA parabolam tangant in G & A: & corpus de loco quovis A, secundum rectam AH productam, justa cum velocitate projectum, describet hanc Parabolam, si modo densitas Medij, in locis singulis G, sit reciproce ut tangens GT. Velocitas autem in G ea erit quacum Projectile pergeret, in spatio non resistente, in Parabola Conica, verticem G, diametrum VG deorsum productam, & latus rectum . Et resistentia in G erit ad vim Gravitatis ut TG ad 3nn-3n / n-2 VG. Vnde si NAK lineam horizontalem designet, & manente tum densitate Medij in A, tum velocitate quacum corpus projicitur, mutetur utcunque angulus NAH; manebunt longitudines AH, AI, HX, & inde datur Parabolæ vertex X, & positio rectæ XI, & sumendo VG ad IA ut ad , dantur omnia Parabolae puncta G, per quae Projectile transibit.
SECT. III.
De motu corporum quæ resistuntur partim in ratione velocitatis, partim in ejusdem ratione duplicata.
Prop. XI. Theor. VIII.
Si corpus resistitur partim in ratione velocitatis, partim in velocitatis ratione duplicata, & sola vi insita in Medio similari movetur, sumantur autem tempora in progressione Arithmetica: quantisates velocitatibus reciproce proportionales, quadam quantitate auctæ, erunt in progressione Geometrica.
Centro C, Asymptotis rectangulis CADd & CH describatur Hyperbola BEeS, & Asymptoto CH parallelæ sint AB, DE, de. In Asymptoto CD dentur puncta A, G: Et fi tempus exponatur per aream Hyperbolicam ABED uniformiter crescentem; dico quod velocitas exponi potest per longitudinem DF, cujus reciproca GD una cum data CG componat longitudinem CD in progressione Geometrica crescentem.
<275>Sit enim areola DEed datum temporis incrementum quam minimum, & erit Dd reciproce ut DE, adeoque directe ut CD. Ipsius autem decrementum, quod (per hujus Lem. II.) est , erit ut seu , id est, ut . 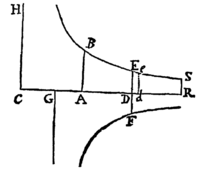 Igitur tempore ABED per additionem datarum particularum EDde uniformiter crescente, decrescit in eadem ratione cum velocitate. Nam decrementum velocitatis est ut resistentia, hoc est (per Hypothesin) ut summa duarum quantitatum, quarum una est ut velocitas, altera ut quadratum velocitatis; & ipsius decrementum est ut summa quantitatum & , quarum prior est ipsa , & posterior est ut
. Proinde , ob analogum decrementum, est ut velocitas. Et si quantitas GD ipsi > reciproce proportionalis quantitate data CG augeatur, summa CD, tempore ABED uniformiter crescente, crescet in progressione Geometrica. Q.E.D.
Igitur tempore ABED per additionem datarum particularum EDde uniformiter crescente, decrescit in eadem ratione cum velocitate. Nam decrementum velocitatis est ut resistentia, hoc est (per Hypothesin) ut summa duarum quantitatum, quarum una est ut velocitas, altera ut quadratum velocitatis; & ipsius decrementum est ut summa quantitatum & , quarum prior est ipsa , & posterior est ut
. Proinde , ob analogum decrementum, est ut velocitas. Et si quantitas GD ipsi > reciproce proportionalis quantitate data CG augeatur, summa CD, tempore ABED uniformiter crescente, crescet in progressione Geometrica. Q.E.D.
Corol. 1. Igitur si datis punctis A, G, exponatur tempus per aream Hyperbolicam ABED, exponi potest velocitas per ipsius GD reciprocam .
Corol. 2. Sumendo autem GA ad GD ut velocitatis reciproca sub initio, ad velocitatis reciprocam in fine temporis cujus vis ABED, invenietur punctum G. Eo autem invento, velocitas ex dato quovis alio tempore inveniri potest.
Prop. XII. Theor. IX.
Iisdem positis, dico quod si spatia descripta sumantur in progressione Arithmetica, velocitates data quadam quantitate auctæ erunt in progressione Geometrica.
In Asymptoto CD detur punctum R, & erecto perpendiculo RS, quod occurrat Hyperbolæ in S, exponatur descriptum spatium per aream Hyperbolicam RSED; & velocitas erit ut longitudo GD, quæ cum data CG componit longitudinem CD, in Progressione Geometrica decrescentem, interea dum spatium RSED augetur in Arithmetica.
Etenim ob datum spatii incrementum EDde, lineola Dd, quæ decrementum est ipsius GD, erit reciproce ut ED, adeoque directe ut CD, hoc est ut summa ejusdem GD & longitudinis datæ CG. Sed velocitatis decrementum, tempore sibi reciproce proportionali, quo data spatii particula DdeE describitur, est ut resistentia & tempus conjunctim, id est directe ut summa duarum quantitatum, quarum una est velocitas, altera ut velocitatis quadratum, & inverse ut velocitas; adeoque directe ut summa dearum quantitatum, quarum una datur, altera est ut velocitas. Igitur decrementum tam velocitatis quam lineæ GD, est ut quantitas data & quantitas decrescens conjunctim, & propter analoga decrementa, analogæ semper erunt quantitates decrescentes: nimirum velocitas & linea GD. Q.E.D.
Corol. 1. Igitur si velocitas exponatur per longitudinem GD, spatium descriptum erit ut area Hyperbolica DESR.
Corol. 2. Et si utcunque assumatur punctum R, invenietur punctum G, capiendo GD ad GR ut est velocitas sub initio ad velocitatem post spatium quodvis ABED descriptum. Invento autem puncto G, datur spatium ex data velocitate, & contra.
<277>Corol. 3. Unde cum, per Prop. XI. detur velocitas ex dato tempore, & per hanc Propositionem detur spatium ex data velocitate; dabitur spatium ex dato tempore: & contra.
Prop. XIII. Theor. X.
Posito quod corpus ab uniformi gravitate deorsum attractum recta ascendit vel descendit, & resistitur partim in ratione velocitatis, partim in ejusdem ratione duplicata: dico quod si Circuli & Hyperbolæ diametris parallelæ rectæ per conjugatarum diametrorum terminos ducantur, & velocitates sint ut segmenta quædam parallelarum a dato puncto ducta, Tempora erunt ut arearum Sectores, rectis a centro ad segmentorum terminos ductis abscissi: & contra.
Cas. 1. Ponamus primo quod corpus ascendit, centroque D & semidiametro quovis DB describatur circuli quadrans BETF, 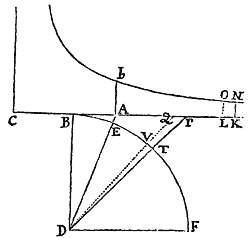 & per semidiametri DB terminum B agatur infinita BAP, semidiametro DF parallela. In ea detur punctum A, & capiatur segmentum AP velocitati proportionale. Et cum resistentiæ pars aliqua sit ut velocitas & pars altera ut velocitatis quadratum, fit resistentia tota in P ut . Jungantur DA, DP circulum secantes in E ac T, & exponatur gravitas per DA quadratum, ita ut sit gravitas ad resistentiam in P ut DAq. ad : & tempus ascensus omnis futuri erit ut circuli sector EDTE.
& per semidiametri DB terminum B agatur infinita BAP, semidiametro DF parallela. In ea detur punctum A, & capiatur segmentum AP velocitati proportionale. Et cum resistentiæ pars aliqua sit ut velocitas & pars altera ut velocitatis quadratum, fit resistentia tota in P ut . Jungantur DA, DP circulum secantes in E ac T, & exponatur gravitas per DA quadratum, ita ut sit gravitas ad resistentiam in P ut DAq. ad : & tempus ascensus omnis futuri erit ut circuli sector EDTE.
Agatur enim DVQ, abscindens & velocitatis AP momentum PQ, & Sectoris DET momentum DTV dato temporis momento respondens: & velocitatis decrementum illud PQ erit ut summa virium gravitatis DBq. & resistentiæ , id est (per Prop. 12. Lib. II. Elem.) ut DP quad. Proinde area DPQ, ipsi PQ proportionalis, est ut DP quad; & area DTV, (quæ est ad aream DPQ ut DTq. ad DPq.) est ut datum DTq. Decrescit igitur area EDT uniformiter ad modum temporis futuri, per subductionem datarum particularum DTV, & propterea tempori ascensus futuri proportionalis est. Q.E.D.
Cas. 2. Si velocitas in ascensu corporis exponatur per longitudinem AP ut prius, & resistentia ponatur esse ut , & si vis gravitatis minor sit quam quæ per DAq. exponi possit; capiatur BD ejus longitudinis, ut sit gravitati proportionale, 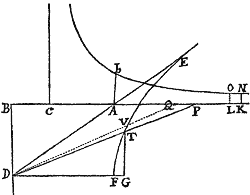 sitque DF ipsi DB perpendicularis & æqualis, & per verticem F describatur Hyperbola FTVE cujus semidiametri conjugatæ sint DB & DF, quæque secet DA in E, & DP, DQ in T & V; & erit tempus ascensus futuri ut Hyperbolæ sector TDE.
sitque DF ipsi DB perpendicularis & æqualis, & per verticem F describatur Hyperbola FTVE cujus semidiametri conjugatæ sint DB & DF, quæque secet DA in E, & DP, DQ in T & V; & erit tempus ascensus futuri ut Hyperbolæ sector TDE.
Nam velocitatis decrementum PQ, in data temporis particula factum, est ut summa resistentiæ & gravitatis id est ut Est autem area DTV ad aream DPQ ut DTq. ad DPq. adeoque, si ad DF demittatur perpendiculum GT, ut GTq. seu ad BDq. utque GDq. ad PBq. & divisim ut DFq. ad Quare cum area DPQ sit ut PQ, id est ut erit area DTV ut datum DFq. Decrescit igitur area EDT uniformiter singulis temporis particulis æqualibus, per subductionem particularum totidem datarum DTV, & propterea tempori proportionalis est. Q.E.D.
Cas. 3. Sit AP velocitas in descensu corporis, & resistentia, & vis gravitatis, existente angulo DAB recto. 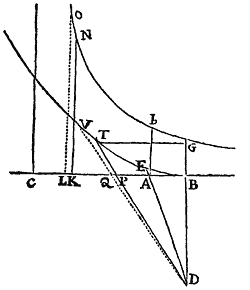 Et si centro D, vertice principali B, describatur Hyperbola rectangula BETV secans productas DA, DP & DQ in E, T & V; erit Hyperbolæ hujus sector DET ut tempus descensus.
Et si centro D, vertice principali B, describatur Hyperbola rectangula BETV secans productas DA, DP & DQ in E, T & V; erit Hyperbolæ hujus sector DET ut tempus descensus.
Nam velocitatis incrementum PQ, eique proportionalis area DPQ, est ut excessus gravitatis supra resistentiam, id est ut seu Et area DTV est ad arcam DPQ ut DTq. ad DPq. adeoque ut GTq. seu ad BPq. utque GDq. ad BDq. & divisim ut BDq. ad Quare cum area DPQ sit ut erit area DTV ut datum BDq. Crescit igitur area EDT uniformiter singulis temporis particulis æqualibus, per additionem totidem datarum particularum DTV, & propterea tempori descensus proportionalis est. Q.E.D.
Corol. Igitur velocitas AP est ad velocitatem quam corpus tempore EDT, in spatio non resistente, ascendendo amittere vel descendendo acquirere posset, ut area trianguli DAP ad aream sectoris centro D, radio DA, angulo ADT descripti; ideoque ex dato tempore datur. Nam velocitas in Medio non resistente, tempori atque adeo Sectori huic proportionalis est; in Medio resistente est ut triangulum; & in Medio utroque ubi quam minima est, accedit ad rationem æqualitatis, pro more Sectoris & Trianguli.
Prop. XIV. Prob. IV.
Iisdem positis, dico quod spatium ascensu vel descensu descriptum, est ut summa vel differentia areæ per quam tempus exponitur, & areæ cujusdam alterius quæ augetur vel diminuitur in progressione Arithmetica; si vires ex resistentia & gravitate compositæ sumantur in progressione Geometrica.
Capiatur AC (in Fig. tribus ultimis,) gravitati, & AK resistentiæ proportionalis. Capiantur autem ad easdem partes puncti A si corpus ascendit, aliter ad contrarias. Erigatur Ab quæ sit ad DB ut DBq. ad 4BAC: & area AbNK augebitur vel diminuetur in progressione Arithmetica, dum vires CK in progressione Geometrica sumuntur. Dico igitur quod distantia corporis ab ejus altitudine maxima sit ut excessus arev AbNK supra aream DET.
Nam cum AK sit ut resistentia, id est ut ; assumatur data quævis quantitas Z, & ponatur AK æqualis ; & (per hujus Lem. II.) erit ipsius AK momentum KL æquale seu , & areæ AbNK momentum KLON æquale seu
Cas. 1. Jam si corpus ascendit, sitque gravitas ut existente BET circulo, (in Fig. Cas. 1. Prop. XIII.) linea AC, quæ gravitati proportionalis est, erit & DPq. seu erit seu : ideoque area DTV erit ad aream DPQ ut DTq. vel DBq. ad .
<281>Cas. 2. Sin corpus ascendit, & gravitas sit ut linea AC (Fig. Cas. 2. Prop. XIII.) erit & DTq. erit ad DPq. ut DFq. seu DBq. ad seu id est ad seu . Ideoque area DTV erit ad aream DPQ ut DBq. ad .
Cas. 3. Et eodem argumento, si corpus descendit, & propterea gravitas sit ut & linea AC (Fig. Cas. 3. Prop. præced.) æquetur erit area DTV ad aream DPQ ut DBq. ad : ut supra.
Cum igitur areæ illæ semper sint in hac ratione; si pro area DTV, qua momentum temporis sibimet ipsi semper æquale exponitur, scribatur determinatum quodvis rectangulum, puta , erit area DPQ, id est ; ad ut CK in Z ad BDq. Atque inde fit PQ in BD cub. æquale , & areæ AbNK momentum KLON superius inventum, fit . Auferatur æreae DET momentum DTV seu , & restabit . Est igitur differentia momentorum, id est momentum differentiæ arearum, æqualis ; & propterea (ob datum ) ut velocitas AP, id est ut momentum spatii quod corpus ascendendo vel descendendo describit. Ideoque differentia arearum & spatium illud proportionalibus momentis crescentia vel decrescentia, & simul incipientia vel simul evanescentia sunt proportionalia. Q.E.D.
Corol. Igitur si longitudo aliqua V sumatur in ea ratione ad arcum ET, quam habet linea DA ad lineam DE; spatium quod corpus ascensu vel descensu toto in Medio resistente describit, erit ad spatium quod in Medio non resistente eodem tempore describere posset, ut arearum illarum differentia ad , ideoque ex dato tempore datur. Nam spatium in Medio non resistente est in duplicata ratione temporis, sive ut , & ob datas BD & AB, ut . Tempus autem est ut DET seu , & harum arearum momenta sunt ut ductum in momentum ipsius V & ductum in momentum ipsius ET, id est, ut in & , sive ut & . Et propterea momentum areæ est ad momentum differentiæ arearum DET & AKNb, ut ad sive ut ad AP; adeoque, ubi V & AP quam minimæ sunt, in ratione æqualitatis. Æqualis igitur est area quam minima differentiæ quam minimæ arearum DET & AKNb. Unde cum spatia in Medio utroque, in principio descensus vel fine ascensus simul descripta accedunt ad æqualitatem, adeoque tunc sunt ad invicem ut area & arearum DET & AKNb differentia; ob eorum analoga incrementa necesse est ut in æqualibus quibuscunque temporibus sint ad invicem ut area illa & arearum DET & AKNb differentia. Q.E.D.
SECT. IV.
De Corporum circulari Motu in Mediis resistentibus.
LEM. III.
Sit PQRr Spiralis quæ secet radios omnes SP, SQ, SR, &c. in æqualibus angulis. Agatur recta PT quætangat eandem in puncto quovis P, secetque radium SQ in T; & ad Spiralem erectis perpendiculis PO, QO concurrentibus in O, jungatur SO. Dico quod fi puncta P & Q accedant ad invicem & coeant, angulus PSO evadet rectus, & ultima ratio rectanguli ad PQ quad. erit ratio æqualitatis.
Etenim de angulis rectis OPQ, OQR subducantur anguli æquales SPQ, SQR, & manebunt anguli æquales OPS, OQS. Ergo circulus qui transit per 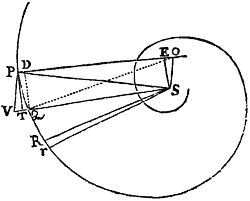 puncta O, S, P transibit etiam per punctum Q. Coeant puncta P & Q, & hic circulus in loco coitus PQ tanget Spiralem, adeoque perpendiculariter secabit rectam OP. Fiet igitur OP diameter circuli hujus, & angulus OSP in semicirculo rectus. Q.E.D.
puncta O, S, P transibit etiam per punctum Q. Coeant puncta P & Q, & hic circulus in loco coitus PQ tanget Spiralem, adeoque perpendiculariter secabit rectam OP. Fiet igitur OP diameter circuli hujus, & angulus OSP in semicirculo rectus. Q.E.D.
Ad OP demittantur perpendicula QD, SE, & linearum rationes ultimæ erunt hujusmodi: TQ ad PD ut TS vel PS ad PE, seu PO ad PS. Item PD ad PQ ut PQ ad PO. Et ex æquo perturbate TQ ad PQ ut PQ ad PS. Unde fit PQq. æqualis . Q.E.D.
<284>Prop. XV. Theor. XI.
Si Medii densitas in locis singulis sit reciproce ut distantia locorum a centro immobili, sitque vis centripeta in duplicata ratione densitatis: dico quod corpus gyrari potest in Spirali, quæ radios omnes a centro illo ductos intersecat in angulo dato.
Ponantur quæ in superiore Lemmate, & producatur SQ ad V, ut sit SV æqualis SP. Temporibus æqualibus describat corpus arcus quam minimos PQ & QR, sintque areæ PSQ, QSr æquales. Et quoniam vis centripeta, qua corpus urgetur in P est reciproce ut SPq. & 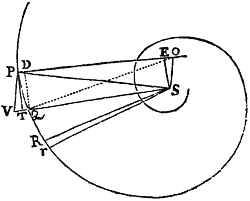 (per Lem. X. Lib. I.) lineola TQ, quæ vi illa generatur, est in ratione composita ex ratione hujus vis & ratione duplicata temporis quo arcus PQ describitur, (Nam resistentiam in hoc casu, ut infinite minorem quam vis centripeta negligo) erit id est (per Lemma novissimum) , in ratione duplicata temporis, adeoque tempus est ut , & corporis velocitas qua arcus PQ illo tempore describitur ut seu , hoc est in dimidiata ratione ipsius SP reciproce. Et simili argumento velocitas, qua arcus QR describitur, est in dimidiata ratione ipsius SQ reciproce. Sunt autem arcus illi PQ & QR ut velocitates descriptrices ad invicem, id est in dimidiata ratione SQ ad SP, sive ut SQ ad ; & ob æquales angulos SPQ, SQr & æquales areas PSQ, QSr, est arcus PQ ad arcum Qr ut SQ ad SP. Sumantur proportionalium consequentium differentiæ, & fiet arcus PQ ad arcum Rr ut SQ ad , seu ; nam punctis P & Q coeuntibus, ratio ultima ; ad fit æqualitatis. In Medio non resistente areae æquales PSQ, QSr (per Theor. I. Lib. I.) temporibus æqualibus describi deberent. Ex resistentia oritur arearum differentia RSr, & propterea resistentia est ut lincolæ Qr decrementum Rr collatum cum quadrato temporis quo generatur. Nam lineola Rr (per Lem. X. Lib. I.) est in duplicata ratione temporis. Est igitur resistentia ut . Erat autem PQ ad Rr ut SQ ad , & inde fit ut sive ut Namque punctis P & Q coeuntibus, SP & SQ coincidunt; & ob similia triangula PVQ, PSO, fit PQ ad ut OP ad . Est igitur ut resistentia, id est in ratione densitatis Medii in P & ratione duplicata velocitatis conjunctim. Auferatur duplicata ratio velocitatis, nempe ratio , & manebit Medii densitas in P ut . Detur Spiralis, & ob datam rationem OS ad OP, densitas Medii in P erit ut . In Medio igitur cujus densitas est reciproce ut distantia a centro SP, corpus gyrari potest in hac Spirali. Q.E.D.
(per Lem. X. Lib. I.) lineola TQ, quæ vi illa generatur, est in ratione composita ex ratione hujus vis & ratione duplicata temporis quo arcus PQ describitur, (Nam resistentiam in hoc casu, ut infinite minorem quam vis centripeta negligo) erit id est (per Lemma novissimum) , in ratione duplicata temporis, adeoque tempus est ut , & corporis velocitas qua arcus PQ illo tempore describitur ut seu , hoc est in dimidiata ratione ipsius SP reciproce. Et simili argumento velocitas, qua arcus QR describitur, est in dimidiata ratione ipsius SQ reciproce. Sunt autem arcus illi PQ & QR ut velocitates descriptrices ad invicem, id est in dimidiata ratione SQ ad SP, sive ut SQ ad ; & ob æquales angulos SPQ, SQr & æquales areas PSQ, QSr, est arcus PQ ad arcum Qr ut SQ ad SP. Sumantur proportionalium consequentium differentiæ, & fiet arcus PQ ad arcum Rr ut SQ ad , seu ; nam punctis P & Q coeuntibus, ratio ultima ; ad fit æqualitatis. In Medio non resistente areae æquales PSQ, QSr (per Theor. I. Lib. I.) temporibus æqualibus describi deberent. Ex resistentia oritur arearum differentia RSr, & propterea resistentia est ut lincolæ Qr decrementum Rr collatum cum quadrato temporis quo generatur. Nam lineola Rr (per Lem. X. Lib. I.) est in duplicata ratione temporis. Est igitur resistentia ut . Erat autem PQ ad Rr ut SQ ad , & inde fit ut sive ut Namque punctis P & Q coeuntibus, SP & SQ coincidunt; & ob similia triangula PVQ, PSO, fit PQ ad ut OP ad . Est igitur ut resistentia, id est in ratione densitatis Medii in P & ratione duplicata velocitatis conjunctim. Auferatur duplicata ratio velocitatis, nempe ratio , & manebit Medii densitas in P ut . Detur Spiralis, & ob datam rationem OS ad OP, densitas Medii in P erit ut . In Medio igitur cujus densitas est reciproce ut distantia a centro SP, corpus gyrari potest in hac Spirali. Q.E.D.
Corol. 1. Velocitas in loco quovis P ea semper est quacum corpus in Medio non resistente gyrari potest in circulo, ad eandem a centro distantiam SP.
Corol 2. Medii densitas, si datur distantia SP, est ut , sin distantia illa non datur, ut . Et inde Spiralis ad quamlibet Medii densitatem aptari potest.
Corol. 3. Vis resistentiæ in loco quovis P, est ad vim centripetam in eodem loco ut ad OP. Nam vires illæ sunt ut lineæ Rr & TQ seu ut & quas simul generant, hoc est ut & PQ, seu & OP. Data igitur Spirali datur proportio resistentiæ ad vim centripetam, & vice versa ex data illa proportione datur Spiralis.
Corol. 4. Corpus itaque gyrari nequit in hac spirali, nisi ubi vis resistentiæ minor est quam dimidium vis centripetæ. Fiat resistentia æqualis dimidio vis centripetæ & Spiralis conveniet cum linea recta PS, inque hac recta corpus descendet ad centrum, dimidia semper cum velocitate qua probavimus in superioribus in casu Parabolæ (Theor. X. Lib. I.) descensum in Medio non resistente fieri. Unde tempora descensus hic erunt dupla majora temporibus illis atque adeo dantur.
Corol. 5. Et quoniam in æqualibus a centro distantiis velocitas eadem est in Spirali PQR atque in recta SP, & longitudo Spiralis ad longitudinem rectæ PS est in data ratione, nempe in ratione OP ad OS; tempus descensus in Spirali erit ad tempus descensus in recta SP in eadem illa data ratione, proindeque datur.
Corol. 6. Si centro S intervallis duobus datis describantur duo circuli; numerus revolutionum quas corpus intra circulorum circumferentias complere potest, est ut , sive ut Tangens anguli quem Spiralis continet cum radio PS; tempus vero revolutionum earundem ut , id est reciproce ut Medii densitas.
Corol. 7. Si corpus, in Medio cujus densitas est reciproce ut distantia locorum a centro, revolutionem in Curva quacunque AEB circa centrum illud fecerit, & Radium primum AS in codem angulo secuerit in B quo prius in A, idque cum velocitate quæ fuerit ad velocitatem suam primam in A reciproce in dimidiata ratione distantiarum 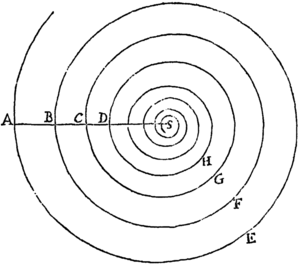 a centro (id est ut BS ad mediam proportiona lem inter AS & CS:) corpus illud perget innumeras consimiles revolutiones BFC, CGD, &c. facere, & intersectionibus distinguet Radium AS in partes AS, BS, CS, DS &c. continue proportionales. Revolutionum vero tempora erunt ut Perimetri orbitarum AEB, BFC, CGD &c. directe, & velocitates in principiis A, B, C, inverse; id est ut , , . Atque tempus totum, quo corpus perveniet ad centrum, erit ad tempus revolutionis primæ ut summa omnium continue proportionalium , , pergentium in infinitum, ad terminum primum ; id est ut terminus ille primus ad differentiam duorum primorum , & quam proxime ut ad AB. Unde tempus illud totum expedite invenitur.
a centro (id est ut BS ad mediam proportiona lem inter AS & CS:) corpus illud perget innumeras consimiles revolutiones BFC, CGD, &c. facere, & intersectionibus distinguet Radium AS in partes AS, BS, CS, DS &c. continue proportionales. Revolutionum vero tempora erunt ut Perimetri orbitarum AEB, BFC, CGD &c. directe, & velocitates in principiis A, B, C, inverse; id est ut , , . Atque tempus totum, quo corpus perveniet ad centrum, erit ad tempus revolutionis primæ ut summa omnium continue proportionalium , , pergentium in infinitum, ad terminum primum ; id est ut terminus ille primus ad differentiam duorum primorum , & quam proxime ut ad AB. Unde tempus illud totum expedite invenitur.
Corol. 8. Ex his etiam præterpropter colligere licet motus corporum in Mediis, quorum densitas aut uniformis est, aut aliam quamcunque legem assignatam observat. Centro S intervallis continue proportionalibus SA, SB, SC &c. describe circulos quotcunque, & statue numerum revolutionum inter perimetros duorum quorum vis ex his circulis, in Medio de quo egimus, esse ad numerum revolutionum inter eosdem in Medio proposito, ut Medii propositi densitas mediocris inter hos circulos ad Medii, de quo egimus, densitatem mediocrem inter eosdem quam proxime; Sed & in eadem quoque ratione esse Tangentem anguli quo Spiralis præfinita, in Medio de quo egimus, secat radium AS, ad tangentem anguli quo Spiralis nova secat radium eundem in Medio proposito: Atque etiam ut sunt eorundem angulorum secantes ita esse tempora revolutionum omnium inter circulos eosdem duos quam proxime. Si hæc fiant passim inter circulos binos, continuabitur motus per circulos omnes. Atque hoc pacto haud difficulter imaginari possimus quibus modis ac temporibus corpora in Medio quocunque regulari gyrari debebunt.
Corol. 9. Et quamvis motus excentrici in Spiralibus ad formam Ovalium accedentibus peragantur; tamen concipiendo Spiralium illarum singulas revolutiones eisdem ab invicem intervallis distare, iisdemque gradibus ad centrum accedere cum Spirali superius descripta, intelligemus etiam quomodo motus corporum in hujusmodi Spiralibus peragantur.
Prop. XVI. Theor. XII.
Si Medii densitas in locis singulis sit reciproce ut dignitas aliqua distantiæ locorum a centro, sitque vis centripeta reciproce ut distantia in dignitatem illam ducta: dico quod corpus gyrari potest in Spirali, quæ radios omnes a centro illo ductos intersecat in angulo dato.
Demonstratur eadem methodo cum Propositione superiore. Nam si vis centripeta in P sit reciproce ut distantiæ SP dignitas quælibet cujus index est ; colligetur ut supra, quod tempus quo corpus describit arcum quemvis PQ erit ut & resistentia in P ut sive ut , adeque ut . Et propterea densitas in P est reciproce ut SPn .
Scholium.
Cæterum hæc Propositio & superiores, quæ ad Media inæqualiter densa spectant, intelligendæ sunt de motu corporum adeo parvorum, ut Medii ex uno corporis latere major densitas quam ex altero non consideranda veniat. Resistentiam quoque cæteris paribus densitati proportionalem esse suppono. Unde in Mediis quorum vis resistendi non est ut densitas, debet densitas eo usque augeri vel diminui, ut resistentiæ vel tollatur excessus vel defectus suppleatur.
Prop. XVII. Prob. V.
Invenire & vim centripetam & Medii resistentiam qua corpus in data Spirali data lege revolvi potest. Vide Fig. Prop. XV.
Sit spiralis illa PQR. Ex velocitate qua corpus percurrit arcum quam minimum PQ dabitur tempus, & ex altitudine TQ, quæ est ut vis centripeta & quadratum temporis, dabitur vis. Deinde ex arearum, æqualibus temporum particulis confectarum PSQ & QSR, differentia RSr, dabitur corporis retardatio, & ex retardatione invenietur resistentia ac densitas Medii.
Prop. XVIII. Prob. VI.
Data lege vis centripetæ, invenire Medii densitatem in locis singulis, qua corpus datam Spiralem describet.
Ex vi centripeta invenienda est velocitas in locis singulis, deinde ex velocitatis retardatione quærenda Medii densitas: ut in Propositione superiore.
<290>Methodum vero tractandi hæc Problemata aperui in hujus Propositione decima, & Lemmate secundo; & Lectorem in hujusmodi perplexis disquisitionibus diutius detenere nolo. Addenda jam sunt aliqua de viribus corporum ad progrediendum, deque densitate & resistentia Mediorum, in quibus motus hactenus expositi & his affines peraguntur.
SECT. V.>
De Densitate & compressione Fluidorum, deque Hydrostatica.
Definitio Fluidi.
Fluidum est corpus omne cujus partes cedunt vi cuicunque illatæ, & cedendo facile movetur inter se.
Prop. XIX. Theor. XIII.
Fluidi homogenei & immoti, quod in vase quocunque immoto clauditur & undique comprimitur, partes omnes (seposita Condensationis, gravitatis & virium omnium centripetarum consideratione) æqualiter premuntur undique, & absque omni motu a pressione illa orto permanent in locis suis.
Cas. 1. In vase sphærico ABC claudatur & uniformiter comprimatur fluidum undique: dico quod ejusdem pars nulla ex illa pressione movebitur. Nam si pars aliqua D moveatur, necesse est ut omnes ejusmodi partes, ad eandem a centro distantiam undique consistentes, simili motu simul moveantur; atque hoc adeo quia similis & æqualis est omnium pressio, & motus omnis exclusus supponitur, nisi qui a pressione illa oriatur. Atqui non possunt omnes ad centrum propius accedere, nisi fluidum ad centrum condensetur; contra Hypothesin. Non possunt longius ab eo recedere nisi fluidum ad circumferentiam condensetur; etiam contra Hypothesin. Non possunt servata sua a centro distantia moveri in plagam quamcunque quia pari ratione movebuntur  in plagam contrariam; in plagas autem contrarias non potest pars eadem eodem tempore moveri. Ergo fluidi pars nulla de loco suo movebitur. Q.E.D.
in plagam contrariam; in plagas autem contrarias non potest pars eadem eodem tempore moveri. Ergo fluidi pars nulla de loco suo movebitur. Q.E.D.
Cas. 2. Dico jam quod fluidi hujus partes omnes sphaericæ æqualiter premuntur undique: sit enim EF pars sphærica fluidi, & si hæc undique non premitur æqualiter, augeatur pressio minor, usque dum ipsa undique prematur æqualiter; & partes ejus, per casum primum, permanebunt in locis suis. Sed ante auctam pressionem permanebunt in locis suis, per casum eundum primum, & additione pressionis novæ movebuntur de locis suis, per definitionem Fluidi. Quæ duo repugnant. Ergo falso dicebatur quod Sphæra EF non undique premebatur æqualiter. Q.E.D.
Cas. 3. Dico præterea quod diversarum partium sphæricarum æqualis sit pressio. Nam partes sphaericæ contiguæ se mutuo premunt æqualiter in puncto contactus, per motus Legem III. Sed & per Casum secundum, undique premuntur eadem vi. Partes igitur duæ quævis sphæricæ non contiguæ, quia pars sphærica intermedia tangere potest utramque, prementur eadem vi. Q.E.D.
Cas. 4. Dico jam quod fluidi partes omnes ubique premuntur æqualiter. Nam partes duæ quævis tangi possunt a partibus Sphæricis in punctis quibuscunque, & ibi partes illas Sphæricas æqualiter premunt, per Casum 3. & vicissim ab illis æqualiter premuntur, per Motus Legem Tertiam. Q.E.D.
Cas. 5. Cum igitur fluidi pars quælibet GHI in fluido reliquo tanquam in. vase claudatur, & undique prematur æqualiter, partes autem ejus se mutuo æqualiter premant & quiescant inter se; manifestum est quod Fluidi cujuscunque GHI, quod undique premitur æqualiter, partes omnes se mutuo premunt æqualiter, & quiescunt inter se. Q.E.D.
Cas. 6. Igitur si Fluidum illud in vase non rigido claudatur, & undique non prematur æqualiter, cedet idem pressioni fortiori, per Definitionem Fluiditatis.
Cas. 7. Ideoque in vase rigido Fluidum non sustinebit pressionem fortiorem ex uno latere quam ex alio, sed eidem cedet, idque in momento temporis, quia latus vasis rigidum non persequitur liquorem cedentem. Cedendo autem urgebit latus oppositum, & sic pressio undique ad æqualitatem verget. Et quoniam Fluidum, quam primum a parte magis pressa recedere conatur, inhibetur per resistentiam vasis ad latus oppositum; reducetur pressio undique ad æqualitatem in momento temporis absque motu locali; & subinde, partes fluidi per Casum quintum, se mutuo prement æqualiter, & quiescent inter se. Q.E.D.
Corol. Unde nec motus partium fluidi inter se, per pressionem fluido ubivis in externa superficie illatam, mutari possunt nisi, quatenus aut figura superficiei alicubi mutatur, aut omnes fluidi partes intensius vel remissius sese premendo difficilius vel facilius labuntur inter se.
Prop. XX. Theor. XIV.
Si Fluidi Sphærici, & in æqualibus a centro distantiis homogenei, fundo sphærico concentrico incumbentis partes singulæ versus centrum totius gravitent; sustinet fundum pondus Cylindri, cujus basis æqualis est superficiei fundi, & altitudo eadem quæ Fluidi incumbentis.
Sit DHM superficies fundi, & AEI superficies superior fluidi. Superficiebus sphæricis innumeris BFK, CGL distinguatur fluidum in Orbes concentricos æqualiter crassos; & concipe vim gravitatis agere solummodo in superficiem superiorem Orbis cujusque, & æquales esse actiones in æquales partes superficierum omnium. Premitur ergo superficies suprema AE vi simplici gravitatis propriæ, qua & omnes Orbis supremi partes & superficies secunda BFK (per Prop. XIX.) premuntur. Premitur præterea superficies secunda BFK vi propriæ gravitatis, quæ addita vi priori facit pressionem duplam.  Hac pressione & insuper vi propriæ gravitatis, id est pressione tripla, urgetur superficies tertia CGL. Et similiter pressione quadrupla urgetur superficies quarta, quintupla quinta & sic deinceps. Pressio igitur qua superficies unaquæque urgetur, non est ut quantitas solida fluidi incumbentis, sed ut numerus Orbium ad usque summitatem fluidi; & æquatur gravitati Orbis insimi multiplicatæ per numerum Orbium: hoc est gravitati solidi cujus ultima ratio ad Cylindrum præfinirum, (si modo Orbium augeatur numerus & minuatur crassitudo in infinitum, sic ut actio gravitatis a superficie infima ad supremam continua reddatur) fiet ratio æqualitatis. Sustinet ergo superficies infima pondus cylindri præfiniti. Q.E.D. Et simili argumentatione patet Propositio, ubi gravitas decrescit in ratione quavis assignata distantiæ a centro, ut & ubi Fluidum sursum rarius est, deorsum densius. Q.E.D.
Hac pressione & insuper vi propriæ gravitatis, id est pressione tripla, urgetur superficies tertia CGL. Et similiter pressione quadrupla urgetur superficies quarta, quintupla quinta & sic deinceps. Pressio igitur qua superficies unaquæque urgetur, non est ut quantitas solida fluidi incumbentis, sed ut numerus Orbium ad usque summitatem fluidi; & æquatur gravitati Orbis insimi multiplicatæ per numerum Orbium: hoc est gravitati solidi cujus ultima ratio ad Cylindrum præfinirum, (si modo Orbium augeatur numerus & minuatur crassitudo in infinitum, sic ut actio gravitatis a superficie infima ad supremam continua reddatur) fiet ratio æqualitatis. Sustinet ergo superficies infima pondus cylindri præfiniti. Q.E.D. Et simili argumentatione patet Propositio, ubi gravitas decrescit in ratione quavis assignata distantiæ a centro, ut & ubi Fluidum sursum rarius est, deorsum densius. Q.E.D.
Corol. 1. Igitur fundum non urgetur a toto fluidi incumbentis pondere, sed eam solummodo ponderis partem sustinet quæ in Propositione describitur; pondere reliquo a fluidi figura fornicata sustentato.
Corol. 2. In æqualibus autem a centro distantiis eadem semper est pressionis quantitas, sive superficies pressa sit Horizonti parallela vel perpendicularis vel obliqua; sive fluidum a superficie pressa sursum continuatum surgat perpendiculariter secundum lineam rectam, vel serpit oblique per tortas cavitates & canales, easque regulares vel maxime irregulares, amplas vel angustissimas. Hisce circumstantiis pressionem nil mutari colligitur, applicando demonstrationem Theorematis hujus ad Casus singulos Fluidorum.
<294>Corol. 3. Eadem Demonstratione colligitur etiam (per Prop. XIX.) quod fluidi gravis partes nullum, ex pressione ponderis incumbentis, acquirunt motum inter se, si modo excludatur motus qui ex condensatione oriatur.
Corol. 4. Et propterea si aliud ejusdem gravitatis specificæ corpus, quod sit condensationis expers, submergatur in hoc fluido, id ex pressione ponderis incumbentis nullum acquiret motum: non descendet, non ascendet, non cogetur figuram suam mutare. Si Sphæricum est manebit sphæricum, non obstante pressione; si quadratum est manebit quadratum: idque sive molle sit, sive fluidissimum; sive fluido libere innatet, sive fundo incumbat. Habet enim fluidi pars quælibet interna rationem corporis submersi, & par est ratio omnium ejusdem magitudinis, figuræ & gravitatis specificæ submersorum corporum. Si corpus submersum servato pondere liquesceret & indueret formam fluidi; hoc, si prius ascenderet vel descenderet vel ex pressione figuram novam indueret, etiam nunc ascenderet vel descenderet vel figuram novam induere cogeretur: id adeo quia gravitas ejus caeteræque motuum causæ permanent. Atqui, per Cas. 5. Prop. XIX. jam quiesceret & figuram retineret. Ergo & prius.
Corol. 5. Proinde corpus quod specifice gravius est quam Fluidum sibi contiguum subsidebit, & quod specifice levius est ascendet, motumque & figuræ mutationem consequetur, quantum excessus ille vel defectus gravitatis efficere possit. Namque excessus ille vel defectus rationem habet impulsus, quo corpus, alias in æquilibrio cum fluidi partibus constitutum, urgetur; & comparari potest cum excessu vel defectu ponderis in lance alterutra libræ.
Corol. 6. Corporum igitur in fluidis constitutorum duplex est Gravitas: altera vera & absoluta, altera apparens, vulgaris & comparativa. Gravitas absoluta est vis tota qua corpus deorsum tendit: relativa & vulgaris est excessus gravitatis quo corpus magis tendit deorsum quam fluidum ambiens. Prioris generis Gravitate partes fluidorum & corporum omnium gravitant in locis suis: ideoque conjunctis ponderibus componunt pondus totius. Nam totum omne grave est, ut in vasis liquorum plenis experiri licet; & pondus totius æquale est ponderibus omnium partium, ideoque ex iisdem componitur. Alterius generis gravitate corpora non gravitant in locis suis, id est inter se collata non prægravant, sed mutuos ad descendendum conatus impedientia permanent in locis suis, perinde ac si gravia non essent. Quæ in Aere sunt & non prægravant, Vulgus gravia non judicat. Quæ prægravant vulgus gravia judicat, quatenus ab Aeris pondere non sustinentur. Pondera vulgi nihil aliud sunt quam excessus verorum ponderum supra pondus Aeris. Unde & vulgo dicuntur levia, quæ sunt minus gravia, Aerique praegravanti cedendo superiora petunt. Comparative levia sunt non vere, quia descendunt in vacuo. Sic & in Aqua, corpora, quæ ob majorem vel minorem gravitatem descendunt vel ascendunt, sunt comparative & apparenter gravia vel levia, & eorum gravitas vel levitas comparativa & apparens est excessus vel defectus quo vera eorum gravitas vel superat gravitatem aquæ vel ab ea superatur. Quæ vero nec prægravando descendunt, nec prægravanti cedendo ascendunt, etiamsi veris suis ponderibus adaugeant pondus totius, comparative tamen & in sensu vulgi non gravitant in aqua. Nam similis est horum Casuum Demonstratio.
Corol. 7. Quæ de gravitate demonstrantur, obtinent in aliis quibuscunque viribus centripetis.
Corol. 8. Proinde si Medium, in quo corpus aliquod movetur, urgeatur vel a gravitate propria, vel ab alia quacunque vi centripeta, & corpus ab eadem vi urgeatur fortius: differentia virium est vis illa motrix, quam in præcedentibus Propositionibus ut vim centripetam consideravimus. Sin corpus a vi illa urgeatur levius, differentia virium pro vi centrifuga haberi debet.
Corol. 9. Cum autem fluida premendo corpora inclusa non mutent eorum Figuras externas, patet insuper, per Corollaria Prop. XIX. quod non mutabunt situm patium internarum inter se: proindeque, si Animalia immergantur, & sensatio omnis a motu partium oriatur; nec lædent corporibus immersis, nec sensationem ullam excitabunt, nisi quatenus hæc corpora a compressione condensari possunt. Et par est ratio cujuscunque corporum Systematis fluido comprimente circundati. Systematis partes omnes iisdem agitabuntur motibus, ac si in vacuo constituerentur, ac solam retinerent gravitatem suam comparativam, nisi quatenus fluidum vel motibus earum nonnihil resistat, vel ad easdem compressione conglutinandas requiratur.
Prop. XXI. Theor. XV.
Sit Fluidi cujusdam densitas compressioni proportionalis, & partes ejus a vi centripeta distantiis suis a centro reciproce proportionali deorsum trahantur: dico quod si distantiae illæ sumantur continue proportionales, densitates fluidi in iisdem distantiis erunt etiam continue proportionales.
Designet ATV fundum Sphæricum cui fluidum incumbit, S centrum, SA, SB, SC, SD, SE, &c. distantias continue proportionales. Erigantur perpendicula AH, BI, CK, DL, EM, &c. quæ sint ut densitates Medii in locis A, B, C, D, E; & specificæ gravitates in iisdem locis erunt ut , , , &c. vel, quod perinde est, ut , , &c. Finge primum 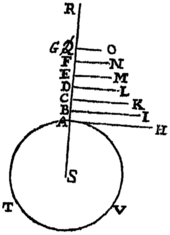 has gravitates uniformiter continuari ab A ad B, a B ad C, a C ad D &c. factis per gradus decrementis in punctis B, C, D &c. Et hæ gravitates ductæ in altitudines AB, BC, CD &c. conficient pressiones AH, BI, CK, quibus fundum ATV (juxta Theorema XIV.) urgetur. Sustinet ergo particula A pressiones omnes AH, BI, CK, DL, pergendo in infinitum; & particula B pressiones omnes præter primam AH; & particula C omnes præter duas primas AH, BI; & sic deinceps: adeoque particulæ primæ A densitas AH est ad particulv secundæ B densitatem BI ut summa omnium , in infinitum, ad summam omnium &c. Et BI densitas secundæ B, est ad CK densitatem tertiæ C, ut summa omnium , &c. ad summam omnium , &c. Sunt igitur summæ illæ differentiis suis AH, BI, CK, &c. proportionales, atque adeo continue proportionales per hujus Lem. I. proindeque differentiæ AH, BI, CK, &c. summis proportionales, sunt etiam continue proportionales. Quare cum densitates in locis A, B, C sint ut AH, BI, CK, &c. erunt etiam hæ continue proportionales. Pergatur per saltum, & (ex æquo) in distantiis SA, SC, SE continue proportionalibus, erunt densitates AH, CK, EM continue proportionales. Et eodem argumento in distantiis quibusvis continue proportionalibus SA, SD, SQ densitates AH, DL, QO erunt continue proportionales. Coeant jam puncta A, B, C, D, E, &c. eo ut progressio gravitatum specificarum a fundo A ad summitatem Fluidi continua reddatur, & in distantiis quibusvis continue proportionalibus SA, SD, SQ, densitates AH, DL, QT, semper existentes continue proportionales, manebunt etiamnum continue proportionales. Q.E.D.
has gravitates uniformiter continuari ab A ad B, a B ad C, a C ad D &c. factis per gradus decrementis in punctis B, C, D &c. Et hæ gravitates ductæ in altitudines AB, BC, CD &c. conficient pressiones AH, BI, CK, quibus fundum ATV (juxta Theorema XIV.) urgetur. Sustinet ergo particula A pressiones omnes AH, BI, CK, DL, pergendo in infinitum; & particula B pressiones omnes præter primam AH; & particula C omnes præter duas primas AH, BI; & sic deinceps: adeoque particulæ primæ A densitas AH est ad particulv secundæ B densitatem BI ut summa omnium , in infinitum, ad summam omnium &c. Et BI densitas secundæ B, est ad CK densitatem tertiæ C, ut summa omnium , &c. ad summam omnium , &c. Sunt igitur summæ illæ differentiis suis AH, BI, CK, &c. proportionales, atque adeo continue proportionales per hujus Lem. I. proindeque differentiæ AH, BI, CK, &c. summis proportionales, sunt etiam continue proportionales. Quare cum densitates in locis A, B, C sint ut AH, BI, CK, &c. erunt etiam hæ continue proportionales. Pergatur per saltum, & (ex æquo) in distantiis SA, SC, SE continue proportionalibus, erunt densitates AH, CK, EM continue proportionales. Et eodem argumento in distantiis quibusvis continue proportionalibus SA, SD, SQ densitates AH, DL, QO erunt continue proportionales. Coeant jam puncta A, B, C, D, E, &c. eo ut progressio gravitatum specificarum a fundo A ad summitatem Fluidi continua reddatur, & in distantiis quibusvis continue proportionalibus SA, SD, SQ, densitates AH, DL, QT, semper existentes continue proportionales, manebunt etiamnum continue proportionales. Q.E.D.
Corol. Hinc si detur densitas Fluidi in duobus locis, puta A & E, colligi potest ejus densitas 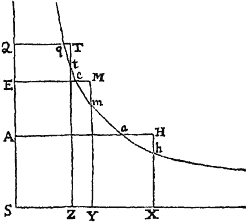 in alio quovis loco Q. Centro S, Asymptotis rectangulis SQ, SX describatur Hyperbola secans perpendicula AH, EM, QT in a, e, q, ut & perpendicula HX, MY, TZ ad asymptoton SX demissa in h, m, & t. Fiat area ZYmtZ ad aream datam YmhX ut area data EeqQ ad aream datam EeaA; & linea Zt producta abscindet lineam QT densitati proportionalem. Namque si lineæ SA, SE, SQ sunt continue proportionales, erunt areæ EeqQ, EeaA æquales, & inde areæ his proportionales YmtZ, XhmY etiam æquales & lineæ SX, SY, SZ id est AH, EM, QT continue proportionales, ut oportet. Et si lineæ SA, SE, SQ obtinent alium quemvis ordinem in serie continue proportionalium, lineæ AH, EM, QT, ob proportionales areas Hyperbolicas, obtinebunt eundem ordinem in alia serie quantitatum continue proportionalium.
in alio quovis loco Q. Centro S, Asymptotis rectangulis SQ, SX describatur Hyperbola secans perpendicula AH, EM, QT in a, e, q, ut & perpendicula HX, MY, TZ ad asymptoton SX demissa in h, m, & t. Fiat area ZYmtZ ad aream datam YmhX ut area data EeqQ ad aream datam EeaA; & linea Zt producta abscindet lineam QT densitati proportionalem. Namque si lineæ SA, SE, SQ sunt continue proportionales, erunt areæ EeqQ, EeaA æquales, & inde areæ his proportionales YmtZ, XhmY etiam æquales & lineæ SX, SY, SZ id est AH, EM, QT continue proportionales, ut oportet. Et si lineæ SA, SE, SQ obtinent alium quemvis ordinem in serie continue proportionalium, lineæ AH, EM, QT, ob proportionales areas Hyperbolicas, obtinebunt eundem ordinem in alia serie quantitatum continue proportionalium.
Prop. XXII. Theor. XVI.
Sit Fluidi cujusdam densitas compressioni proportionalis, & partes ejus a gravitate quadratis distantiarum suarum a centro reciproce proportionali deorsum trahantur: dico quod si distantiæ sumantur in progressione Musica, densitates Fluidi in his distantiis erunt in progressione Geometrica.
Designet S centrum, & SA, SB, SC, SD, SE distantias in Progressione Geometrica. Erigantur perpendicula AH, BI, CK, &c. quæ sint ut 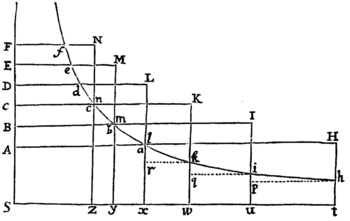 Fluidi densitates in locis A, B, C, D, E, &c. & ipsius gravitates specicæ in iisdem locis erunt , ,, &c. Finge has gravitates uniformiter continuari, primam ab A ad B, secundam a B ad C, tertiam a C ad D, &c. Et hæ ductæ in altitudines AB, BC, CD, DE, &c. vel, quod perinde est, in distantias SA, SB, SC, &c. altitudinibus illis proportionales, conficient exponentes pressionum , , , &c. Quare cum densitates sint ut harum pressionum summæ, differentiæ densitatum , , &c. erunt ut summarum differentiæ , , , &c. Centro S Asymptotis SA, SX describatur Hyperbola quævis, quæ secet perpendicula AH, BI, CK, &c. in a, b, c; ut & perpendicula ad Asymptoton SX demissa Ht, Iu, Kw in h, i, k; & densitatum differentiæ tu, uw, &c. erunt ut , , &c. Et rectangula , , &c. seu tp, uq. &c. ut , , &c. id est ut Aa, Bb &c. Est enim ex natura Hyperbolæ SA ad AH vel St, ut th ad Aa, adeoque æquale Aa. Et simili argumento est æqualis Bb, &c. Sunt autem Aa Bb, Cc, &c. continue proportionales, & propterea differentiis suis , , &c. proportionales; ideoque differentiis hisce proportionalia sunt rectangula tp, uq, &c. ut & summis differentiarum vel summæ rectangulorum , vel . Sunto ejusmodi termini quam plurimi, & summa omnium differentiarum, puta , erit summæ omnium rectangulorum, puta zthn, proportionalis. Augeatur numerus terminorum & minuantur distantiæ punctorum A, B, C, &c. in infinitum, & rectangula illa evadent æqualia areæ Hyperbolicæ zthn, adeoque huic areæ proportionalis est differentia . Sumantur jam distantiæ quælibet, puta SA, SD, SF in Progressione Musica, & differentiæ , erunt æquales; & propterea differentiis hisce proportionales areæ thlx, xlnz æquales erunt inter se, & densitates St, Sx, Sz, id est AH, DL, FN, continue proportionales. Q.E.D.
Fluidi densitates in locis A, B, C, D, E, &c. & ipsius gravitates specicæ in iisdem locis erunt , ,, &c. Finge has gravitates uniformiter continuari, primam ab A ad B, secundam a B ad C, tertiam a C ad D, &c. Et hæ ductæ in altitudines AB, BC, CD, DE, &c. vel, quod perinde est, in distantias SA, SB, SC, &c. altitudinibus illis proportionales, conficient exponentes pressionum , , , &c. Quare cum densitates sint ut harum pressionum summæ, differentiæ densitatum , , &c. erunt ut summarum differentiæ , , , &c. Centro S Asymptotis SA, SX describatur Hyperbola quævis, quæ secet perpendicula AH, BI, CK, &c. in a, b, c; ut & perpendicula ad Asymptoton SX demissa Ht, Iu, Kw in h, i, k; & densitatum differentiæ tu, uw, &c. erunt ut , , &c. Et rectangula , , &c. seu tp, uq. &c. ut , , &c. id est ut Aa, Bb &c. Est enim ex natura Hyperbolæ SA ad AH vel St, ut th ad Aa, adeoque æquale Aa. Et simili argumento est æqualis Bb, &c. Sunt autem Aa Bb, Cc, &c. continue proportionales, & propterea differentiis suis , , &c. proportionales; ideoque differentiis hisce proportionalia sunt rectangula tp, uq, &c. ut & summis differentiarum vel summæ rectangulorum , vel . Sunto ejusmodi termini quam plurimi, & summa omnium differentiarum, puta , erit summæ omnium rectangulorum, puta zthn, proportionalis. Augeatur numerus terminorum & minuantur distantiæ punctorum A, B, C, &c. in infinitum, & rectangula illa evadent æqualia areæ Hyperbolicæ zthn, adeoque huic areæ proportionalis est differentia . Sumantur jam distantiæ quælibet, puta SA, SD, SF in Progressione Musica, & differentiæ , erunt æquales; & propterea differentiis hisce proportionales areæ thlx, xlnz æquales erunt inter se, & densitates St, Sx, Sz, id est AH, DL, FN, continue proportionales. Q.E.D.
Corol. Hinc si dentur Fluidi densitates duæ quævis, puta AH & CK, dabitur area thkw harum differentiæ tw respondens; & inde invenietur densitas FN in altitudine quacunque SF, sumendo aream thnz ad aream illam datam thkw ut est differentia ad differentiam .
Scholium
Simili argumentatione probari potest, quod si gravitas particularum Fluidi diminuatur in triplicata ratione distantiarum a centro; & quadratorum distantiarum SA, SB, SC, &c. reciproca (nempe ,, ) sumantur in progressione Arithmeca; densitates AH, BI, CK, &c. erunt in progressione Geometrica. Et si gravitas diminuatur in quadruplicata ratione distantiarum, & cuborum distantiarum reciproca (puta , , , &c.) sumantur in progressione Arithmetica; densitates AH, BI, CK, &c. erunt in progressione Geometrica. Et sic in infinitum. Rursus si gravitas particularum Fluidi in omnibus distantiis eadem sit, & distantiæ sint in progressione Arithmetica, densitates erunt in progressione Geometrica, uti Vir Cl. Edmundus Halleius invenit. Si gravitas sit ut distantia, & quadrata distantiarum sint in progressione Arithmetica, densitates erunt in progressione Geometrica. Et sic in infinitum. Hæc ita se habent ubi Fluidi compressione condensati densitas est ut vis compressionis, vel, quod perinde est, spatium a Fluido occupatum reciproce ut hæc vis. Fingi possunt aliæ condensationis leges, ut quod cubus vis comprimentis sit ut quadrato-quadratum densitatis, seu triplicata ratio Vis æqualis quadruplicatæ rationi densitatis. Quo in casu, si gravitas est reciproce ut quadratum distantiae a centro, densitas erit reciproce ut cubus distantiæ. Fingatur quod cubus vis comprimentis sit ut quadrato-cubus densitatis, & si gravitas est reciproce ut quadratum distantiæ, densitas erit reciproce in sesquiplicata ratione distantiæ. Fingatur quod vis comprimens sit in duplicata ratione densitatis, & gravitas reciproce in ratione duplicata distantiæ, & densitas erit reciproce ut distantia. Casus omnes percurrere longum esset.
Prop. XXIII. Theor. XVII.
Particulæ viribus quæ sunt reciproce proportionales distantiis centrorum suorum se mutuo fugientes componunt Fluidum Elasticum, cujus densitas est compressioni proportionalis. Et vice versa, si Fluidi ex particulis se mutuo fugientibus compositi densitas sit ut compressio, vires centrifugæ particularum sunt reciproce proportionales distantiis centrorum.
Includi intelligatur Fluidum in spatio cubico ACE, dein compressione redigi in spatium cubicum minus ace; & particularum similem situm inter se in utroque  spatio obtinentium distantiæ erunt ut cuborum latera AB, ab; & Medii densitates reciproce ut spatia continentia AB cub. & ab cub. In latere cubi majoris ABCD capiatur quadratum DP æquale lateri cubi minoris db; & ex Hypothesi, pressio qua quadratum DP urget Fluidum inclusum, erit ad pressionem qua latus illud quadratum db urget Fluidum inclusum, ut Medii densitates ad invicem, hoc est ab cub. ad AB cub. Sed pressio qua quadratum DB urget Fluidum inclusum, est ad pressionem qua quadratum DP urget idem Fluidum, ut quadratum DB ad quadratum DP, hoc est ut AB quad. ad ab quad. Ergo ex æquo pressio qua latus DB urget Fluidum, est ad pressionem qua latus db urget Fluidum, ut ab ad AB. Planis FGH, fgh per media cuborum ductis distinguatur Fluidum in duas partes, & hæ se mutuo prement iisdem viribus, quibus premuntur a planis AC, ac, hoc est in proportione ab ad AB: adeoque vires centrifugæ, quibus hæ pressiones sustinentur, sunt in eadem ratione. Ob eundem particularum numerum similemque situm in utroque cubo, vires quas particulæ omnes secundum plana FGH, fgh exercent in omnes, sunt ut vires quas singulæ exercent in singulas. Ergo vires, quas singulæ exercent in singulas secundum planum FGH in cubo majore, sunt ad vires quas singulæ exercent in singulas secundum planum fgh in cubo minore ut ab ad AB, hoc est reciproce ut distantiæ particularum ad invicem. Q.E.D.
spatio obtinentium distantiæ erunt ut cuborum latera AB, ab; & Medii densitates reciproce ut spatia continentia AB cub. & ab cub. In latere cubi majoris ABCD capiatur quadratum DP æquale lateri cubi minoris db; & ex Hypothesi, pressio qua quadratum DP urget Fluidum inclusum, erit ad pressionem qua latus illud quadratum db urget Fluidum inclusum, ut Medii densitates ad invicem, hoc est ab cub. ad AB cub. Sed pressio qua quadratum DB urget Fluidum inclusum, est ad pressionem qua quadratum DP urget idem Fluidum, ut quadratum DB ad quadratum DP, hoc est ut AB quad. ad ab quad. Ergo ex æquo pressio qua latus DB urget Fluidum, est ad pressionem qua latus db urget Fluidum, ut ab ad AB. Planis FGH, fgh per media cuborum ductis distinguatur Fluidum in duas partes, & hæ se mutuo prement iisdem viribus, quibus premuntur a planis AC, ac, hoc est in proportione ab ad AB: adeoque vires centrifugæ, quibus hæ pressiones sustinentur, sunt in eadem ratione. Ob eundem particularum numerum similemque situm in utroque cubo, vires quas particulæ omnes secundum plana FGH, fgh exercent in omnes, sunt ut vires quas singulæ exercent in singulas. Ergo vires, quas singulæ exercent in singulas secundum planum FGH in cubo majore, sunt ad vires quas singulæ exercent in singulas secundum planum fgh in cubo minore ut ab ad AB, hoc est reciproce ut distantiæ particularum ad invicem. Q.E.D.
Et vice versa, si vires particularum singularum sunt reciproce ut distantiæ, id est reciproce ut cuborum latera AB, ab; summæ virium erunt in eadem ratione, & pressiones laterum DB, db ut summæ virium; & pressio quadrati DP ad pressionem lateris DB ut ab quad. ad AB quad. Et ex æquo pressio quadrati DP ad pressionem lateris db ut ab cub. ad AB cub. id est vis compressionis ad vim compressionis ut densitas ad densitatem. Q.E.D.
Scholium.
Simili argumento si particularum vires centrifugæ sin reciproce in duplicata ratione distantiarum inter centra, cubi virium comprimentium erunt ut quadrato-quadrata desitatum. Si vires centrifugæ sint reciproce in triplicata vel quadruplicata ratione distantiarum, cubi virium comprimentium erunt ut quadratocubi vel cubo-cubi densitatum. Et universaliter, si D ponatur pro distantia, & E pro densitate Fluidi compressi, & vires centrifugæ sint reciproce ut distantiæ dignitas quælibet Dn, cujus index est numerus n; vires comprimentes erunt ut latera cubica Dignitatis , cujus index est numerus : & contra. Intelligenda vero sunt hæc omnia de particularum Viribus centrifugis quæ terminantur in particulis proximis, aut non longe ultra diffunduntur. Exemplum habemus in corporibus Magneticis. Horum Virtus attractiva terminatur fere in sui generis corporibus sibi proximis. Magnetis virtus per interpositam laminan ferri contrahitur, & in lamina fere terminatur. Nam corpora ulteriora non tam a Magnete quam a lamina trahuntur. Ad eundem modum si particulæ fugant alias sui generis particulas sibi proximas, in particulas autem remotiores virtutem nullam nisi forte per particulas intermedias virtute illa auctas exerceant, ex hujusmodi particulis componentur Fluida de quibus actum est in hac propositione. Quod si particulæ cujusque virtus in infinitum propagetur, opus erit vi majori ad æqualem condensationem majoris quantitatis Fluidi. Ut si particula unaquæque vi sua, quæ sit reciproce ut distantia locorum a centro suo, fugat alias omnes particulas in infinitum; Vires quibus Fluidum in vasis similibus æqualiter comprimi & condensari possit, erunt ut quadrata diametrorum vasorum: ideoque vis, qua Fluidum in eodem vase comprimitur, erit reciproce ut latus cubicum quadrato-cubi densitatis. An vero Fluida Elastica ex particulis se mutuo fugantibus constent, Quæstio Physica est. Nos proprietatem Fluidorum ex ejusmodi particulis constantium Mathematice demonstravimus, ut Philosophis ansam præbeamus Quaestionem illam tractandi.
SECT. VI.
De Motu & resistentia Corporum Funependulorum.
Prop. XXIV. Theor. XVIII.
Quantitates materiæ in corporibus funependulis, quorum centra oscillationum a centro suspensionis æqualiter distant, sunt in ratione composita ex ratione ponderum & ratione duplicata temporum oscillationum in vacuo.
Nam velocitas, quam data vis in data materia dato tempore generare potest, est ut vis & tempus directe, & materia inverse. Quo major est vis vel majus tempus vel minor materia, eo major generabitur velocitas. Id quod per motus Legem secundam manifestum est. Jam vero si pendula ejusdem sint longitudinis, vires motrices in locis a perpendiculo æqualiter distantibus sunt ut pondera: ideoque si corpora duo oscillando describant arcus æquales, & arcus illi dividantur in partes æquales; cum tempora quibus corpora describant singulas arcuum partes correspondentes sint ut tempora oscillationum totarum, erunt velocitates ad invicem in correspondentibus oscillationum partibus, ut vires motrices & tota oscillationum tempora directe & quantitates materiæ reciproce: adeoque quantitates materiæ ut vires & oscillationum tempora directe & velocitates reciproce. Sed velocitates reciproce sunt ut tempora, atque adeo tempora directe & velocitates reciproce sunt ut quadrata temporum, & propterea quantitates materiæ sunt ut vires motrices & quadrata temporum, id est ut pondera & quadrata temporum. Q.E.D.
Corol. 1. Ideoque si tempora sunt æqualia, quantitates materiæ in singulis corporibus erunt ut pondera.
Corol. 2. Si pondera sunt æqualia, quantitates materiæ erunt ut quadrata temporum.
Corol. 3. Si quantitates materiae aequantur, pondera erunt reciproce ut quadrata temporum.
Corol. 4. Unde cum quadrata temporum cæteris paribus sint ut longitudines pendulorum; si & tempora & quantitates materiæ æqualia sunt, pondera erunt ut longitudines pendulorum.
Corol. 5. Et universaliter, quantitas materiæ pendulæ est ut pondus & quadratum temporis directe, & longitudo penduli inverse.
Corol. 6. Sed & in Medio non resistente quantitas Materiæ pendulæ est ut pondus comparativum & quadratum temporis directe & longitudo penduli inverse. Nam pondus comparativum est vis motrix corporis in Medio quovis gravi, ut supra explicui; adeoque idem præstat in tali Medio non resistente atque pondus absolutum in vacuo.
<305>Corol. 7. Et hinc liquet ratio tum comparandi corpora inter se, quoad quantitatem materiæ in singulis, tum comparandi pondera ejusdem corporis in diversis locis, ad cognoscendam variationem gravitatis. Factis autem experimentis quam accuratissimis inveni semper quantitatem materiæ in corporibus singulis corum ponderi proportionalem esse.
Prop. XXV. Theor. XIX.
Corpora Funependula quæ in Medio quovis resistuntur in ratione momentorum temporis, quæque in ejusdem gravitatis specificæ Medio non resistente moventur, oscillationes in Cycloide eodem tempore peragunt, & arcuum partes proportionales simul describunt.
Sit AB Cycloidis arcus, quem corpus D tempore quovis in Medio non resistente oscillando describit. Bisecetur idem in C, ita ut C sit infimum ejus punctum; & erit vis acceleratrix qua corpus urgetur in loco quovis D vel d vel E ut longitudo arcus CD vel Cd vel CE. Exponatur vis illa per eundem arcum; & cum resistentia sit ut momentum temporis, adeoque detur, exponatur eadem per datam arcus Cycloidis partem CO, & sumatur arcus Od in ratione 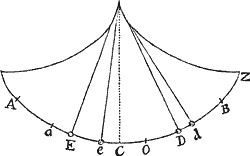 ad arcum CD quam habet arcus OB ad arcum CB: & vis qua corpus in d urgetur in Medio resistente, cum sit excessus vis Cd supra resistentiam CO, exponetur per arcum Od, adeoque erit ad vim qua corpus D urgetur in Medio non resistente, in loco D, ut arcus Od ad arcum CD; & propterea etiam in loco B ut arcus OB ad arcum CB. Proinde si corpora duo, D, d exeant de loco B, & his viribus urgeantur: cum vires sub initio sint ut arcus CB & OB, erunt velocitates primæ & arcus primo descripti in eadem ratione. Sunto arcus illi BD & Bd, & arcus reliqui CD, Od erunt in eadem ratione. Proinde vires ipsis CD, Od proportionales manebunt in eadem ratione ac sub initio, & propterea corpora pergent arcus in eadem ratione simul describere. Igitur vires & velocitates & arcus reliqui CD, Od semper erunt ut arcus toti CD, OB, & propterea arcus illi reliqui simul describentur. Quare corpora duo D, d simul pervenient ad loca C & O, alterum quidem in Medio non resistente ad locum C, & alterum in Medio resistente ad locum O. Cum autem velocitates in C & O sint ut arcus CB & OB; erunt arcus quos corpora ulterius pergendo simul describunt, in eadem ratione. Sunto illi CE & Oe. Vis qua corpus D in Medio non resistente retardatur in E est ut CE, & vis qua corpus d in Medio resistente retardatur in e est ut summa vis Ce & resistentiæ CO, id est ut Oe; ideoque vires, quibus corpora retardantur, sunt ut arcubus CE, Oe proportionales arcus CB, OB; proindeque velocitates in data illa ratione retardatæ manent in eadem illa data ratione. Velocitates igitur & arcus iisdem descripti semper sunt ad invicem in data illa ratione arcuum CB & OB; & propterea si sumantur arcus toti AB, aB in eadem ratione, corpora D, d simul describent hos arcus, & in locis A & a morum omnem simul amittent. Isochronæ sunt igitur oscillaciones totæ, & arcubus totis BA, BE proportionales sunt arcuum partes quælibet BD, Bd vel BE, Be quæ simul describuntur. Q.E.D.
ad arcum CD quam habet arcus OB ad arcum CB: & vis qua corpus in d urgetur in Medio resistente, cum sit excessus vis Cd supra resistentiam CO, exponetur per arcum Od, adeoque erit ad vim qua corpus D urgetur in Medio non resistente, in loco D, ut arcus Od ad arcum CD; & propterea etiam in loco B ut arcus OB ad arcum CB. Proinde si corpora duo, D, d exeant de loco B, & his viribus urgeantur: cum vires sub initio sint ut arcus CB & OB, erunt velocitates primæ & arcus primo descripti in eadem ratione. Sunto arcus illi BD & Bd, & arcus reliqui CD, Od erunt in eadem ratione. Proinde vires ipsis CD, Od proportionales manebunt in eadem ratione ac sub initio, & propterea corpora pergent arcus in eadem ratione simul describere. Igitur vires & velocitates & arcus reliqui CD, Od semper erunt ut arcus toti CD, OB, & propterea arcus illi reliqui simul describentur. Quare corpora duo D, d simul pervenient ad loca C & O, alterum quidem in Medio non resistente ad locum C, & alterum in Medio resistente ad locum O. Cum autem velocitates in C & O sint ut arcus CB & OB; erunt arcus quos corpora ulterius pergendo simul describunt, in eadem ratione. Sunto illi CE & Oe. Vis qua corpus D in Medio non resistente retardatur in E est ut CE, & vis qua corpus d in Medio resistente retardatur in e est ut summa vis Ce & resistentiæ CO, id est ut Oe; ideoque vires, quibus corpora retardantur, sunt ut arcubus CE, Oe proportionales arcus CB, OB; proindeque velocitates in data illa ratione retardatæ manent in eadem illa data ratione. Velocitates igitur & arcus iisdem descripti semper sunt ad invicem in data illa ratione arcuum CB & OB; & propterea si sumantur arcus toti AB, aB in eadem ratione, corpora D, d simul describent hos arcus, & in locis A & a morum omnem simul amittent. Isochronæ sunt igitur oscillaciones totæ, & arcubus totis BA, BE proportionales sunt arcuum partes quælibet BD, Bd vel BE, Be quæ simul describuntur. Q.E.D.
Corol. Igitur motus velocissimus in Medio resistente non incidit in punctum infimum, C, sed reperitur in puncto illo O, quo arcus totus descriptus aB bisecatur. Et corpus subinde pergendo ad a, iisdem gradibus retardatur quibus antea accelerabatur in desensu suo a B ad O.
<307>Prop. XXVI. Theor. XX.
Corporum Funependulorum, quæ resistuntur in ratione velocitatum, oscillationes in Cycloide sunt Isochronæ.
Nam si corpora duo a centris suspensionum æqualiter distantia, oscillando describant arcus inæquales, & velocitates in arcuum partibus correspondentibus sint ad invicem ut arcus toti: resistentiæ velocitatibus proportionales erunt etiam ad invicem ut iidem arcus. Proinde si viribus motricibus a gravitate oriundis, quæ sint ut iidem arcus, conferantur vel addantur hæ resistentiæ, erunt differentiæ vel summæ ad invicem in eadem arcuum ratione: cumque velocitatum incrementa vel decrementa sint ut hæ differentiæ vel summæ, velocitates semper erunt ut arcus toti: Igitur velocitates, si sint in aliquo casu ut arcus toti, manebunt semper in eadem ratione. Sed in principio motus, ubi corpora incipiunt descendere & arcus illos describere, vires, cum sint arcubus proportionales, generabunt velocitates arcubus proportionales. Ergo velocitates semper erunt ut arcus toti describendi, & propterea arcus illi simul describentur. Q.E.D.
Prop. XXVII. Theor. XXI.
Si corpora Funependula resistuntur in duplicata ratione velocitatum, differentiæ inter tempora oscillationum in Medio resistente ac tempora oscillationum in ejusdem gravitatis specificæ Medio non resistente, erunt arcubus oscillando descriptis proportionales, quam proxime.
Nam pendulis æqualibus in Medio resistente describantur arcus inæquales A, B; & resistentia corporis in arcu A, erit ad resistentiam corporis in parte correspondente arcus B, in duplicata ratione velocitatum, id est ut Aquad. ad Bquad. quam proxime. Si resistentia in arcu B esset ad resistentiam in arcu A ut rectangulum AB ad Aquad. tempora in arcubus A & B forent æqualia per Propositionem superiorem. Ideoque resistentia Aquad. in arcu A, vel AB in arcu B, efficit excessum temporis in arcu A supra tempus in Medio non resistente; & resistentia BB efficit excessum temporis in arcu B supra tempus in Medio non resistente. Sunt autem excessus illi ut vires efficientes AB & BB quam proxime, id est ut arcus A & B. Q.E.D.
Corol. 1. Hinc ex oscillationum temporibus, in Medio resistente in arcubus inæqualibus factarum, cognosci possunt tempora oscillationum in ejusdem gravitatis specificæ Medio non resistente. Nam si verbi gratia arcus alter sit altero duplo major, differentia temporum erit ad excessum temporis in arcu minore supra tempus in Medio non resistente, ut differentia arcuum ad arcum minorem.
Corol. 2. Oscillationes breviores sunt magis Isochronæ, & brevissimæ iisdem temporibus peraguntur ac in Medio non resistente, quam proxime. Earum vero quæ in majoribus arcubus fiunt, tempora sunt paulo majora, propterea quod resistentia in descensu corporis qua tempus producitur, major sit pro ratione longitudinis in descensu descriptæ, quam resistentia in ascensu subsequente qua tempus contrahitur. Sed & tempus oscillationum tam brevium quam longarum nonnihil produci videtur per motum Medii. Nam corpora tardescentia paulo minus resistuntur pro ratione velocitatis, & corpora accelerata paulo magis quam quæ uniformiter progrediuntur: id adeo quia Medium, eo quem a corporibus accepit motu, in eandem plagam pergendo, in priore casu magis agitatur, in posteriore minus; ac proinde magis vel minus cum corporibus motis conspirat. Pendulis igitur in descensu magis resistit, in ascensu minus quam pro ratione velocitatis, & ex utraque causa tempus producitur.
Prop. XXVIII. Theor. XXII.
Si corpus Funependulum in Cycloide oscillans resistitur in ratione momentorum temporis, erit ejus resistentia ad vim gravitatis ut excessus arcus descensu toto descripti supra arcum ascensu subsequente descriptum, ad penduli longitudinem duplicatam.
Designet BC arcum descensu descriptum, Ca arcum ascensu descriptum, & Aa differentiam arcuum: & stantibus quæ in Propositione XXV. constructa & demonstrata sunt, erit vis qua corpus oscillans urgetur in loco quovis D, ad uim resistentia ut arcus CD ad arcum CO, qui semissis est differentiæ illius Aa. Ideoque vis qua corpus oscillans urgetur in Cycloidis principio seu puncto altissimo, id est vis gravitatis, erit ad resistentiam ut arcus Cycloidis inter punctum illud supremum & punctum insimum C ad arcum CO; id est (si arcus duplicentur) ut Cycloidis totius arcus, seu dupla penduli longitudo, ad arcum Aa. Q.E.D.
Prop. XXIX. Prob. VII.
Posito quod corpus in Cycloide oscillans resistitur in duplicata ratione velocitatis: invenire resistentiam in locis singulis.
Sit Ba (Fig. Prop. XXV.) arcus oscillatione integra descriptus, sitque C infimum Cycloidis punctum, & CZ semissis arcus Cycloidis totius, longitudini Penduli æqualis; & quæratur resistentia corporis in loco quovis 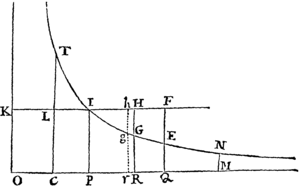 D. Secetur recta infinita OQ in punctis O, C, P, Q ea lege ut (si erigantur perpendicula OK, CT, PI, QE, centroque O & Asymptotis OK, OQ describatur Hyperbola TIGE secans perpendicula CT, PI, QE in T, I & E, & per punctum I agatur KF occurrens Asymptoto OK in K, & perpendiculis CT & QE in L & F) fuerit area Hyperbolica PIEQ ad aream Hyperbolicam PITC ut arcus BC descensu corporis descriptus ad arcum Ca ascensu descriptum, & area IEF ad aream ILT ut OQ ad OC. Dein perpendiculo MN abscindatur area Hyperbolica PINM quæ sit ad aream Hyperbolicam PIEQ ut arcus CZ ad arcum BC descensu descriptum. Et si perpendiculo RG abscindatur area Hyperbolica PIGR, quæ sit ad aream PIEQ ut arcus quilibet CD ad arcum BC descensu toto descriptum: erit resistentia in loco D ad vim gravitatis, ut area ad aream PIENM.
D. Secetur recta infinita OQ in punctis O, C, P, Q ea lege ut (si erigantur perpendicula OK, CT, PI, QE, centroque O & Asymptotis OK, OQ describatur Hyperbola TIGE secans perpendicula CT, PI, QE in T, I & E, & per punctum I agatur KF occurrens Asymptoto OK in K, & perpendiculis CT & QE in L & F) fuerit area Hyperbolica PIEQ ad aream Hyperbolicam PITC ut arcus BC descensu corporis descriptus ad arcum Ca ascensu descriptum, & area IEF ad aream ILT ut OQ ad OC. Dein perpendiculo MN abscindatur area Hyperbolica PINM quæ sit ad aream Hyperbolicam PIEQ ut arcus CZ ad arcum BC descensu descriptum. Et si perpendiculo RG abscindatur area Hyperbolica PIGR, quæ sit ad aream PIEQ ut arcus quilibet CD ad arcum BC descensu toto descriptum: erit resistentia in loco D ad vim gravitatis, ut area ad aream PIENM.
Nam cum vires a gravitate oriundæ quibus corpus in locis Z, B, D, a urgetur, sint ut arcus CZ, CB, CD, Ca, & arcus illi sint ut areæ PINM, PIEQ, PIGR, PITC; exponatur tum arcus tum vires per has areas respective. Sit insuper Dd spatium quam minimum a corpore descendente descriptum, & exponatur idem per aream quam minimam RGgr parallelis RG, rg comprehensam; & producatur rg ad h, ut sint GHhg, & RGgr contemporanea arearum IGH, PIGR decrementa. Et areæ incrementum , seu , erit ad areæ PIGR decrementum RGgr seu , ut ad RG; adeoque ut ad seu : hoc est (ob æqualia , , , PIHR & ) ut ad OPIK. Igitur si area dicatur Y, atque areæ PIGR decrementum RGgr detur, erit incrementum areæ Y ut .
Quod si V designet vim a gravitate oriundam arcui describendo CD proportionalem, qua corpus urgetur in D; & R pro resistentia ponatur: erit vis tota qua corpus urgetur in D, adeoque ut incrementum velocitatis in data temporis particula factum. Est autem resistentia R (per Hypothesin) ut quadratum velocitatis, & inde (per Lem. II.) incrementum resistentiæ ut velocitas & incrementum velocitatis conjunctim, id est ut spatium data temporis particula descriptum & conjunctim; atque adeo, si momentum spatii detur, ut ; id est, si pro vi V scribatur ejus exponens PIGR, & resistentia R exponatur per aliam aliquam aream Z, ut .
Igitur area PIGR per datorum momentorum subductionem uniformiter decrescente, crescunt area Y in ratione , & area Z in ratione . Et propterea si areæ Y & Z simul incipiant & sub initio aequales sint, hae per additionem aequalium momentorum pergent esse æquales, & æqualibus itidem momentis subinde decrescentes simul evanescent. Et vicissim, si simul incipiunt & simul evanescunt, æqualia habebunt momenta & semper erunt æquales: id adeo quia si resistentia Z augeatur, velocitas una cum arcu illo Ca, qui in ascensu corporis describitur, diminuetur; & puncto in quo motus omnis una cum resistentia cessat propius accedente ad punctum C, resistentia citius evanescet quam area Y. Et contrarium eveniet ubi resistentia diminuitur.
Jam vero area Z incipit desinitque ubi resistentia nulla est, hoc est, in principio & fine motus, ubi arcus CD, CD arcubus CB & Ca æquantur, adeoque ubi recta RG incidit in rectas QE & CT. Et area Y seu incipit desinitque ubi nulla est, adeoque ubi & IGH æqualia sunt: hoc est (per constructionem) ubi recta RG incidit in rectam QE & CT. Proindeque areæ illæ simul incipiunt & simul evanescunt, & propterea semper sunt æquales. Igitur area æqualis est areæ Z, per quam resistentia exponitur, & propterea est ad aream PINM per quam gravitas exponitur, ut resistentia ad gravitatem. Q.E.D.
<312>Corol. 1. Est igitur resistentia in loco infimo C ad vim gravitatis, ut area ad aream PINM.
Corol. 2. Fit autem maxima, ubi area PIHR est ad aream IEF ut OR ad OQ. Eo enim in casu momentum ejus (nimirum ) evadit nullum.
Corol. 3. Hinc etiam innotescit velocitas in locis singulis: quippe quæ est in dimidiata ratione resistentiæ, & ipso motus initio æquatur velocitati corporis in eadem Cycloide absque omresistentia oscillantis.
Cæterum ob difficilem calculum quo resistentia & velocitas per hanc Propositionem inveniendæ sunt, visum est Propositionem sequentem subjungere, quæ & generalior sit & ad usus Philosophicos abunde satis accurata.
Prop. XXX. Theor. XXIII.
Si recta aB æqualis sit Cycloidis arcui quem corpus oscillando describit, & ad singula ejus puncta D erigantur perpendicula DK, quæ sint ad longitudinem Penduli ut resistentia corporis in arcus punctis correspondentibus ad vim gravitatis: dico quod differentia inter arcum descensu toto descriptum, & arcum ascensu toto subsequente descriptum, ducta in arcuum eorundam semisummam, æqualis erit areæ BKaB a perpendiculis omnibus DK occupatæ, quamproxime.
Exponatur enim tum Cycloidis arcus oscillatione integra descriptus, per rectam illam sibi æqualem aB, tum arcus qui describeretur in vacuo per longitudinem AB. Bisecetur AB in C, & punctum C repræsentabit infimum Cycloidis punctum, & erit CD ut vis a gravitate oriunda, qua corpus in C secundum Tangentem Cycloidis urgetur, eamque habebit rationem ad longitudinem Penduli quam habet vis in D ad vim gravitatis. Exponatur igitur vis illa per longitudinem CD, & vis gravitatis per longitudinem penduli; & si in DE capiatur DK in ea ratione ad longitudinem penduli quam habet resistentia ad gravitatem, erit DK exponens resistentiæ. Centro C & intervallo CA vel CB construatur semicirculus, BEeA. Describet autem corpus tempore quam minimo spatium Dd, & erectis perpendiculis DE, de circumferentiæ occurrentibus in E & e, erunt hæc ut velocitates quas corpus in vacuo, 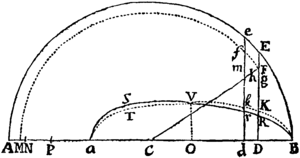 descendendo a puncto B, acquireret in locis D & d. Patet hoc per Prop. LII. Lib. I. Exponantur itaque hæ velocitates per perpendicula illa DE, de; sitque DF velocitas quam acquirit in D cadendo de B in Medio resistente. Et si centro C & intervallo CF describatur circulus FfM occurrens rectis de & AB in f & M, erit M locus ad quem deinceps absque ulteriore resistentia ascenderet, & df velocitas quam acquireret in d. Unde etiam si Fg designet velocitatis momentum quod corpus D, describendo spatium quam minimum Dd, ex resistentia Medii amittit, & sumatur CN æqualis Cg: erit N locus ad quem corpus deinceps absque ulteriore resistentia ascenderet, & MN erit decrementum ascensus ex velocitatis illius amissione oriundum. Ad df demittatur perpendiculum Fm, & velocitatis DF decrementum fg a resistentia DK genitum, erit ad velocitatis ejusdem incrementum fma vi CD genitum, ut vis generans DK ad vim generantem CD. Sed & ob similia triangula Fmf, Fhg, FDC, est fm ad Fm seu Dd, ut CD ad DF, & ex æquo Fg ad Dd ut DK ad DF. Item Fg ad Fh ut CF ad DF; & ex æquo perturbate Fh seu MN ad Dd ut DK ad CF. Sumatur DR ad ut DK ad CF, & erit MN ad Dd ut DR ad ; ideoque summa omnium , id est , æqualis erit summæ omnium id est areæ BRrSa, quam rectangula omnia seu DRrd componunt. Bisecentur Aa & aB in P & O, & erit seu OB æqualis CP, ideoque DR est ad DK ut CP ad CF vel CM, & divisim KR ad DR ut PM ad CP. Ideoque cum punctum M, ubi corpus versatur in medio oscillationis loco O, incidat circiter in punctum P, & priore oscillationis parte versetur inter A & P, posteriore autem inter P & a, utroque in casu æqualiter a puncto P in partes contrarias errans: punctum K circa medium oscillationis locum, id est e regione puncti O, puta in V, incidet in punctum R; in priore autem oscillationis parte jacebit inter R & E, & in posteriore inter R & D, utroque in casu æqualiter a puncto R in partes contrarias errans. Proinde area quam linea KR describit, priore oscillationis parte jacebit extra aream BRSa, posteriore intra eandem, idque dimensionibus hinc inde propemodum æquatis inter se; & propterea in casu priore addita areæ BRSa, in posteriore eidem subducta, relinquet aream BKTa areæ BRSa cqualem quam proxime. Ergo rectangulum seu AaO, cum sit æquale areæ BRSa, erit etiam æquale areæ BKTa quamproxime. Q.E.D.
descendendo a puncto B, acquireret in locis D & d. Patet hoc per Prop. LII. Lib. I. Exponantur itaque hæ velocitates per perpendicula illa DE, de; sitque DF velocitas quam acquirit in D cadendo de B in Medio resistente. Et si centro C & intervallo CF describatur circulus FfM occurrens rectis de & AB in f & M, erit M locus ad quem deinceps absque ulteriore resistentia ascenderet, & df velocitas quam acquireret in d. Unde etiam si Fg designet velocitatis momentum quod corpus D, describendo spatium quam minimum Dd, ex resistentia Medii amittit, & sumatur CN æqualis Cg: erit N locus ad quem corpus deinceps absque ulteriore resistentia ascenderet, & MN erit decrementum ascensus ex velocitatis illius amissione oriundum. Ad df demittatur perpendiculum Fm, & velocitatis DF decrementum fg a resistentia DK genitum, erit ad velocitatis ejusdem incrementum fma vi CD genitum, ut vis generans DK ad vim generantem CD. Sed & ob similia triangula Fmf, Fhg, FDC, est fm ad Fm seu Dd, ut CD ad DF, & ex æquo Fg ad Dd ut DK ad DF. Item Fg ad Fh ut CF ad DF; & ex æquo perturbate Fh seu MN ad Dd ut DK ad CF. Sumatur DR ad ut DK ad CF, & erit MN ad Dd ut DR ad ; ideoque summa omnium , id est , æqualis erit summæ omnium id est areæ BRrSa, quam rectangula omnia seu DRrd componunt. Bisecentur Aa & aB in P & O, & erit seu OB æqualis CP, ideoque DR est ad DK ut CP ad CF vel CM, & divisim KR ad DR ut PM ad CP. Ideoque cum punctum M, ubi corpus versatur in medio oscillationis loco O, incidat circiter in punctum P, & priore oscillationis parte versetur inter A & P, posteriore autem inter P & a, utroque in casu æqualiter a puncto P in partes contrarias errans: punctum K circa medium oscillationis locum, id est e regione puncti O, puta in V, incidet in punctum R; in priore autem oscillationis parte jacebit inter R & E, & in posteriore inter R & D, utroque in casu æqualiter a puncto R in partes contrarias errans. Proinde area quam linea KR describit, priore oscillationis parte jacebit extra aream BRSa, posteriore intra eandem, idque dimensionibus hinc inde propemodum æquatis inter se; & propterea in casu priore addita areæ BRSa, in posteriore eidem subducta, relinquet aream BKTa areæ BRSa cqualem quam proxime. Ergo rectangulum seu AaO, cum sit æquale areæ BRSa, erit etiam æquale areæ BKTa quamproxime. Q.E.D.
Corol. Hinc ex lege resistentiæ & arcuum Ca, CB defferentia Aa, colligi potest proportio resistentiæ ad gravitatem quam proxime.
Nam si uniformis sit resistentia DK, figura aBKkS rectangulum erit sub Ba & DK, & inde rectangulum sub & Aa. æqualis erit rectangulo sub Ba & DK, & DK æqualis erit . Quare cum DK sit exponens resistentiæ, & longitudo penduli exponens gravitatis, erit resistentia ad gravitatem ut ad longitudinem Penduli; omnino ut in Propositione XXVIII. demonstratum est.
Si resistentia sit ut velocitas, Figura aBKkS Ellipsis erit quam proxime. Nam si corpus, in Medio non resistente, oscillatione integra describeret longitudinem BA, velocitas in loco quovis D foret ut circuli diametro AB descripti ordinatim applicata DE. Proinde cum Ba in Medio resistente & BA in Medio non resistente, æqualibus circiter temporibus describantur; adeoque velocitates in singulis ipsius Ba punctis, sint quam proxime ad velocitates in punctis correspondentibus longitudinis BA, ut est Ba ad BA; erit velocitas DK in Medio resistente ut circuli vel Ellipseos super diametro Ba descripti ordinatim applicata; adeoque figura BKVTa Ellipsis, quam proxime. Cum resistentia velocitati proportionalis supponatur, sit OV exponens resistentiæ in puncto Medio O; & Ellipsis, centro O, semiaxibus OB, OV descripta, figuram aBKVT, eique æquale rectangulum , æquabit quam proxime. Est igitur ad ut area Ellipseos hujus ad : id est Aa ad OV ut area semicirculi, ad quadratum radii sive ut 11 and 7 circiter: Et propterea: ad longitudinem penduli ut corporis oscillantis resistentia in O ad ejusdem gravitatem.
Quod si resistentia DK sit in duplicata ratione velocitatis, figura BKTVa Parabola erit verticem habens V & axem OV, ideoque æqualis erit duabus tertiis partibus rectanguli sub Ba & OV quam proxime. Est igitur rectangulum sub & Aa æquale rectangulo sub & OV, adeoque OV aequalis , & propterea corporis oscillantis resistentia in O ad ipsius gravitatem ut ad longitudinem Penduli.
Atque has conclusiones in rebus practicis abunde satis accuratas esse censeo. Nam cum Ellipsis vel Parabola congruat cumfigura BKVTa in puncto medio V, hæc si ad partem alterutram BKV vel VTa excedit figuram illam, deficiet ab eadem ad partem alteram, & sic eidem æquabitur quam proxime.
Prop. XXXI. Theor. XXIV.
Si corporis oscillantis resistentia in singulis arcuum descriptorum partibus proportionalibus augeatur vel minuatur in data ratione; differentia inter arcum descensu descriptum & arcum subsequente ascensu descriptum, augebitur vel diminuetur in eadem ratione quamproxime.
Oritur enim differentia illa ex retardatione Penduli per resistentiam Medii, adeoque est ut retardatio tota eique proportionalis resistentia retardans. In superiore Propositione rectangulum sub recta & arcuum illorum CB, Ca differentia Aa, æqualis erat areæ BKT. Et area illa, si maneat longitudo aB, augetur vel diminuitur in ratione ordinatim applicatarum DK; hoc est in ratione resistentiæ, adeoque est ut longitudo aB & resistentia conjunctim. Proindeque rectangulum sub Aa & est ut aB & resistentia conjunctim, & propterea Aa ut resistentia. Q.E.D.
Corol. 1. Unde si resistentia sit ut velocitas, differentia arcuum in eodem Medio erit ut arcus totus descriptus: & contra.
Corol. 2. Si resistentia sit in duplicata ratione velocitatis, differentia illa erit in duplicata ratione arcus totius; & contra.
Corol. 3. Et universaliter, si resistentia sit in triplicata vel alia quavis ratione velocitatis, differentia erit in eadem ratione arcus totius; & contra.
Corol. 4. Et si resistentia sit partim in ratione simplici velocitatis, partim in ejusdem ratione duplicata, differentia erit partim in ratione arcus totius & partim in ejus ratione duplicata; & contra. Eadem erit lex & ratio resistentiæ pro velocitate, quæ est differentiæ illius pro longitudine arcus.
Corol. 5. Ideoque si, pendulo inæquales arcus successive describente, inveniri potest ratio incrementi ac decrementi resistentiæ hujus pro longitudine arcus descripti, habebitur etiam ratio incrementi ac decrementi resistentiæ pro velocitate majore vel minore.
SECT. VII.
De Motu Fluidorum & resistentia Projectilium.
Prop. XXXII. Theor. XXV.
Si corporum Systemata duo ex æquali particularum numero constent & particulæ correspondentes similes sint, singulæ in uno Systemate singulis in altero, ac datam habeant rationem densitatis ad invicem, & inter se temporibus proportionalibus similiter moveri incipiant, (eæ inter se quæ in uno sunt Systemate & eæ inter se quæ sunt in altero) & si non tangant se mutuo quæ in eodem sunt Systemate, nisi in momentis reflexionum, neque attrahant vel fugent se mutuo, nisi viribus acceleratricibus quæ sint ut particularum correspondentium diametri inverse & quadrata velocitatum directe: dico quod Systematum particulæ ille pergent inter se temporibus proportionalibus similiter moveri; & contra.
Corpora similia temporibus proportionalibus inter se similiter moveri dico, quorum situs ad invicem in fine temporum illorum semper sunt similes: puta si particulæ unius Systematis cum alterius particulis correspondentibus conferantur. Unde tempora erunt proportionalia, in quibus similes & proportionales figurarum similium partes a particulis correspondentibus describuntur. Igitur si duo sint ejusmodi Systemata, particulæ correspondentes, ob similitudinem incæptorum motuum, pergent similiter moveri usque donec sibi mutuo occurrant. Nam si nullis agitantur viribus, progredientur uniformiter in lineis rectis per motus Leg. I. Si viribus aliquibus se mutuo agitant, & vires illæ sint ut particularum correspondentium diametri inverse & quadrata velocitatum directe; quoniam particularum situs sunt similes & vires proportionales, vires totæ quibus particulæ correspondentes agitantur, ex viribus singulis agitantibus (per Legum Corollarium secundum) compositaeæ, similes habebunt determinationes, perinde ac si centra inter particulas similiter sita respicerent; & erunt vires illæ totæ ad invicem ut vires singulæ componentes, hoc est ut correspondentium particularum diametri inverse, & quadrata velocitatum directe: & propterea efficient ut correspondentes particulæ figuras similes describere pergant. Hæc ita se habebunt per Corol. 1.2, & 7. Prop. IV. si modo centra illa quiescant. Sin moveantur, quoniam ob translationum similitudinem, similes manent eorum situs inter Systematum particulas; similes inducentur mutationes in figuris quas particulæ describunt. Similes igitur erunt correspondentium & similium particularum motus usque ad occursus suos primos, & propterea similes occursus, & similes reflexiones, & subinde (per jam ostensa) similes motus inter se, donec iterum in se mutuo inciderint, & sic deinceps in infinitum. Q.E.D.
Corol. 1. Hinc si corpora duo quævis, quæ similia sint & ad Systematum particulas correspondentes similiter sita, inter ipsas temporibus proportionalibus similiter moveri incipiant, sintque eorum densitates ad invicem ut densitates correspondentium particularum: hæc pergent temporibus proportionalibus similiter moveri. Est enim eadem ratio partium majorum Systematis utriusque atque particularum.
Corol. 2. Et si similes & similiter positæ Systematum partes omnes quiescant inter se: & earum duæ, quæ cæteris majores sint, & sibi mutuo in utroque Systemate correspondeant, secundum lineas similiter sitas simili cum motu utcunque moveri incipiant: hæ similes in reliquis systematum partibus excitabunt motus, & pergent inter ipsas temporibus proportionalibus similiter moveri; atque adeo spatia diametris suis proportionalia describere.
<319>Prop. XXXIII. Theor. XXVI.
Iisdem positis, dico quod Systematum partes majores resistuntur in ratione composita ex duplicata ratione velocitatum suarum & duplicata ratione diametrorum & ratione densitatis partium Systematum.
Nam resistentia oritur partim ex viribus centripetis vel centrifugis quibus particulæ systematum se mutuo agitant, partim ex occursibus & reflexionibus particularum & partium majorum. Prioris autem generis resistentiaeæ sunt ad invicem ut vires totae motrices a quibus oriuntur, id est ut vires totæ acceleratrices & quantitates materiæ in partibus correspondentibus; hoc est (per Hypothesin) ut quadrata velocitatum directe & distantiæ particularum correspondentium inverse & quantitates materiæ in partibus correspondentibus directe: ideoque (cum distantiæ particularum systematis unius sint ad distantias correspondentes particularum alterius, ut diameter particulæ vel partis in systemate priore ad diametrum particulæ vel partis correspondentis in altero, & quantitates materiæ sint ut densitates partium & cubi diametrorum) resistentiæ sunt ad invicem ut quadrata velocitatum & quadrata diametrorum & densitates partium Systematum. Q.E.D. Posterioris generis resistentiæ sunt ut reflexionum correspondentium numeri & vires conjunctim. Numeri autem reflexionum sunt ad invicem ut velocitates partium correspondentium directe, & spatia inter eorum reflexiones inverse. Et vires reflexionum sunt ut velocitates & magnitudines & densitates partium correspondentium conjunctim; id est ut velocitates & diametrorum cubi & densitates partium. Et conjunctis his omnibus rationibus, resistentiæ partium correspondentium sunt ad invicem ut quadrata velocitatum & quadrata diametrorum & densitates partium conjunctim. Q.E.D.
Corol. 1. Igitur si systemata illa sint Fluida duo Elastica ad modum Aeris, & partes eorum quiescant inter se: corpora autem duo similia & partibus fluidorum quoad magnitudinem & densitatem proportionalia, & inter partes illas similiter posita, secundum lineas similiter positas utcunque projiciantur; vires autem motrices, quibus particulæ Fluidorum se mutuo agitant, sint ut corporum projectorum diametri inverse, & quadrata velocitatum directe: corpora illa temporibus proportionalibus similes excitabunt motus in Fluidis, & spatia similia ac diametris suis proportionalia describent.
Corol. 2. Proinde in eodem Fluido projectile velox resistitur in duplicata ratione velocitatis quam proxime. Nam si vires, quibus particulæ distantes se mutuo agitant, augerenter in duplicata ratione velocitatis, projectile resisteretur in eadem ratione duplicata accurate; ideoque in Medio, cujus partes ab invicem distantes sese viribus nullis agitant, resistentia est in duplicata ratione velocitatis accurate. Sunto igitur Media tria A, B, C ex partibus similibus & æqualibus & secundum distantias æquales regulariter dispositis constantia. Partes Mediorum A & B fugiant se mutuo viribus quæ sint ad invicem ut T & V, illæ Medii C ejusmodi viribus omnino destituantur. Et si corpora quatuor æqualia D, E, F, G in his Mediis moveantur, priora duo D & E in prioribus duobus A & B, & altera duo F & G in tertio C; sitque velocitas corporis D ad velocitatem corporis E, & velocitas corporis F ad velocitatem corporis G, in dimidiata ratione virium T ad vires V; resistentia corporis D erit ad resistentiam corporis E, & resistentia corporis F ad resistentiam corporis G in velocitatum ratione duplicata; & propterea resistentia corporis D erit ad resistentiam corporis F ut resistentia corporis E ad resistentiam corporis G. Sunto corpora D & F æquivelocia ut & corpora E & G; & augendo velocitates corporum D & F in ratione quacunque, ac diminuendo vires particularum Medii B in eadem ratione duplicata, accedet Medium B ad formam & conditionem Medii C pro lubitu, & idcirco resistentiæ corporum æqualium & æquivelocium E & G in his Mediis, perpetuo accedent ad æqualitatem, ita ut earum differentia evadat tandem minor quam data quævis. Proinde cum resistentiæ corporum D & F sint ad invicem ut resistantiæ corporum E & G, accedent etiam hæ similiter ad rationem æqualitatis. Corporum igitur D & F, ubi velocissime moventur, resistantiæ sunt æquales quam proxime: & propterea cum resistentia corporis F sit in duplicata ratione velocitatis, erit resistentia corporis D in eadem ratione quam proxime. Q.E.D.
Corol. 3. Igitur corporis in Fluido quovis Elastico velocissime moventis eadem fere est resistentia ac si partes Fluidi viribus suis centrifugis destituerentur, seque mutuo non fugerent: si modo Fluidi vis Elastica ex particularum viribus centrifugis oriatur.
Corol. 4. Proinde cum resistentiæ similium & æquivelocium corporum, in Medio cujus partes distantes se mutuo non fugiunt, sint ut quadrata diametrorum, sunt etiam æquivelocium & celerrime moventium corporum resistentiæ in Fluido Elastico ut quadrata diametrorum quam proxime.
Corol. 5. Et cum corpora similia, æqualia & æquivelocia, in Mediis ejusdem densitatis, quorum particulæ se mutuo non fugiunt, sive particulæ illæ sint plures & minores, sive pauciores & majores, in æqualem materiæ quantitatem temporibus æqualibus inpingant, eique æqualem motus quantitatem imprimant, & vicissim (per motus Legem tertiam) æqualem ab eadem reactionem patiantur, hoc est, æqualiter resistantur: manifestum est etiam quod in ejusdem densitatis Fluidis Elasticis, ubi velocissime moventur, æquales sint eorum resistentiæ quam proxime; sive Fluida illa ex particulis crassioribus constent, sive ex omnium subtilissimis constituantur. Ex Medii subtilitate resistentia projectilium celerrime motorum non multum diminuitur.
Corol. 6. Cum autem particulæ Fluidorum, propter vires quibus se mutuo fugiunt, moveri nequeant quin simul agitent particulas alias in circuitu, atque adeo dissicilius moveantur inter se quam si viribus istis destituerentur; & quo majores sint earum vires centrifugæ, eo difficilius moveantur inter se: manifestum esse videtur quod projectile in tali Fluido eo difficilius movebitur, quo vires illæ sunt intensiores; & propterea si corporis velocissimi in superioribus Corollariis velocitas diminuatur, quoniam resistentia diminueretur in duplicata ratione velocitatis, si modo vires particularum in eadem ratione duplicata diminuerentur; vires autem nullatenus diminuantur, manifestum est quod resistentia diminuetur in ratione minore quam duplicata velocitatis.
Corol. 7. Porro cum vires centrifugæ eo nomine ad augendam resistentiam conducant, quod particulæ motus suos per Fluidum ad majorem a se distantiam per vires illas propagent; & cum distantia illa minorem habeat rationem ad majora corpora: manifestum est quod augmentum resistentiæ ex viribus illis oriundum in corporibus majoribus minoris sit momenti; & propterea, quo corpora sint majora eo magis accurate resistentia tardescentium decrescet in duplicata ratione velocitatis.
Corol. 8. Unde etiam ratio illa duplicata magis accurate obtinebit in Fluidis quæ, pari densitate & vi Elastica, ex particulis minoribus constant. Nam si corpora illa majora diminuantur, & particulæ Fluidi, manente ejus densitate & vi Elastica, diminuantur in eadem ratione; manebit eadem ratio resistantiæ quæ prius: ut ex præcedentibus facile colligitur.
Corol. 9. Hæc omnia ita se habent in Fluidis, quorum vis Elastica ex particularum viribus centrifugis originem ducit. Quod si vis illa aliunde oriatur, veluti ex particularum expansione ad instar Lanæ vel ramorum arborum, aut ex alia quavis causa, qua motus particularum inter se redduntur minus liberi: resistantia, ob minorem Medii fluiditatem, erit major quam in superioribus Corollariis.
<323>Prop. XXXIV. Theor. XXVII.
Quæ in præcedentibus duabus Propositionibus demonstrata sunt, obtinent ubi particulæ Systematum se mutuo contingunt, si modo particulæ illæ sint summe lubricæ.
Concipe particulas viribus quibusdam se mutuo fugere, & vires illas in accessu ad superficies particularum augeri in insinitum, & contra, in recessu ab iisdem celerrime diminui & statim evanescere. Concipe etiam systemata comprimi, ita ut partes eorum se mutuo contingant, nisi quatenus vires illæ contactum impediunt. Sint autem spatia per quæ vires particularum diffunduntur quam angustissima, ita ut particulæ se mutuo quam proxime contingant: & motus particularum inter se iidem erunt quam proxime ac si se mutuo contingerent. Eadem facilitate labentur inter se ac si essent summe lubricæ, & si impingant in se mutuo reflectentur ab invicem ope virium præfatarum, perinde ac si essent Elasticæ. Itaque motus erunt iidem in utroque casu, nisi quatenus perexigua particularum sese non contingentium intervalla diversitatem efficiant: quæ quidem diversitas diminuendo particularum intervalla diminui potest in infinitum. Jam vero quæ in præcedentibus duabus Propositionibus demonstrata sunt, obtinent in particulis sese non contingentibus, idque licet intervalla particularum, diminuendo spatia per quæ vires diffunduntur, diminuantur in infinitum. Et propterea eadem obtinent in particulis sese contingentibus, exceptis solum differentiis quæ tandem differentiis quibusvis datis minores evadant. Dico igitur quod accurate obtinent. Si negas, assigna differentiam in casu quocunque. Atqui jam probatum est quod differentia minor sit quam data quævis. Ergo differentia falso assignatur, & propterea nulla est. Q.E.D.
Corol. 1. Igitur si Systematum duorum partes omnes quiescant inter se, exceptis duabus, quæ cæteris majores sint & sibi mutuo correspondeant inter cæteras similiter sitæ. Hæ secundum lineas similiter positas utcunque projectæ similes excitabunt motus in Systematibus, & temporibus proportionalibus pergent spatia similia & diametris suis proportionalia describere; & resistentur in ratione composita ex duplicata ratione velocitatum & duplicata ratione diametrorum & ratione densitatis Systematum.
Corol. 2. Unde si Systemata illa sint Fluida duo similia, & eorum partes duæ majores sint corpora in iisdem projecta: sint autem Fluidorum particulæ summe lubricæ, & quoad magnitudinem & densitatem proportionales corporibus: pergent corpora temporibus proportionalibus spatia similia & diametris suis proportionalia describere, & resistentur in ratione Corollario superiore definita.
Corol. 3. Proinde in eodem Fluido Projectile magnitudine datum resistitur in duplicata ratione velocitatis.
Corol. 4. At si particulæ Fluidi non sint summe lubricæ, vel si viribus quibuscunque se mutuo agitant, quibus motuum libertas diminuitur: Projectilia tardiora difficilius superabunt resistentiam, & propterea magis resistentur quam in velocitatis ratione duplicata.
Prop. XXXV. Theor. XXVIII.
Si Globus & Cylindrus æqualibus diametris descripti, in Medio raro & Elastico, secundum plagam axis Cylindri, æquali cum velocitate celerrime moveantur: erit resistentia Globi duplo minor quam resistentia Cylindri.
Nam quoniam resistentia (per Corol. 3. Prop. XXXIII.) eadem est quam proxime ac si partes Fluidi viribus nullis se mutuo fugerent, supponamus partes Fluidi ejusmodi viribus destitutas per spatia omnia uniformiter dispergi. Et quoniam actio Medii in corpus eadem est (per Legum Corol. 5.) sive corpus in Medio quiescente moveatur, five Medii particulæ eadem cum velocitate impingant in corpus quiescens: consideremus corpus tanquam quiescens, & videamus quo impetu urgebitur a Medio movente. Designet igitur ABKI corpus Sphæricum centro C semidiametro 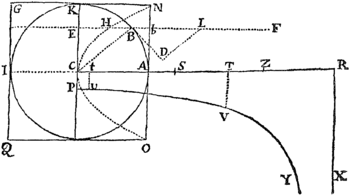 CA descriptum, & incidant particulæ Medii data cum velocitate in corpus illud Sphæricum, secundum rectas ipsi AC parallelas: Sitque FB ejusmodi recta. In ea capiatur LB semidiametro CB æqualis, & ducatur BD quæ Sphæram tangat in B. In AC & BD demittantur perpendiculares BE, DL, & vis qua particula Medii, secundum rectam FB oblique incidendo, Globum ferit in B, erit ad vim qua particula eadem Cylindrum ONGQ axe ACI circa Globum descriptum perpendiculariter feriret in b, ut LD ad LB vel BE ad BC. Rursus efficacia hujus vis ad movendum globum secundum incidentiæ suæ plagam FB vel AC, est ad ejusdem efficaciam ad movendum globum secundum plagam determinationis suæ, id est secundum plagam rectæ BC qua globum directe urget, ut BE ad EC. Et conjunctis rationibus, efficacia particulæ, in globum secundum rectam FB oblique incidentis, ad movendum eundem secundum plagam incidentiæ suæ, est ad efficaciam particulæ ejusdem secundum eandem rectam in cylindrum perpendiculariter incidentis, ad ipsum movendum in plagam eandem, ut BE quadratum ad BC quadratum. Quare si ad cylindri basem circularem NAO erigatur perpendiculum bHE, & sit bE æqualis radio AC, & bH æqualis , erit bH ad bE ut effectus particulæ in globum ad effectum particulæ in cylindrum. Et propterea Solidum quod a rectis omnibus bH occupatur erit ad solidum quod a rectis omnibus bE occupatur, ut effectus particularum omnium in globum ad effectum particularum omnium in Cylindrum. Sed solidum prius est Parabolois vertice V, axe CA & latere recto CA descriptum, & solidum posterius est cylindrus Paraboloidi circumscriptus: & notum est quod Parabolois sit semissis cylindri circumscripti. Ergo vis tota Medii in globum est duplo minor quam ejusdem vis tota in Cylindrum. Et propterea si particulæ Medii quiescerent, & cylindrus ac globus æquali cum velocitate moverentur, foret resistentia globi duplo minor quam resistentia cylindri. Q.E.D.
CA descriptum, & incidant particulæ Medii data cum velocitate in corpus illud Sphæricum, secundum rectas ipsi AC parallelas: Sitque FB ejusmodi recta. In ea capiatur LB semidiametro CB æqualis, & ducatur BD quæ Sphæram tangat in B. In AC & BD demittantur perpendiculares BE, DL, & vis qua particula Medii, secundum rectam FB oblique incidendo, Globum ferit in B, erit ad vim qua particula eadem Cylindrum ONGQ axe ACI circa Globum descriptum perpendiculariter feriret in b, ut LD ad LB vel BE ad BC. Rursus efficacia hujus vis ad movendum globum secundum incidentiæ suæ plagam FB vel AC, est ad ejusdem efficaciam ad movendum globum secundum plagam determinationis suæ, id est secundum plagam rectæ BC qua globum directe urget, ut BE ad EC. Et conjunctis rationibus, efficacia particulæ, in globum secundum rectam FB oblique incidentis, ad movendum eundem secundum plagam incidentiæ suæ, est ad efficaciam particulæ ejusdem secundum eandem rectam in cylindrum perpendiculariter incidentis, ad ipsum movendum in plagam eandem, ut BE quadratum ad BC quadratum. Quare si ad cylindri basem circularem NAO erigatur perpendiculum bHE, & sit bE æqualis radio AC, & bH æqualis , erit bH ad bE ut effectus particulæ in globum ad effectum particulæ in cylindrum. Et propterea Solidum quod a rectis omnibus bH occupatur erit ad solidum quod a rectis omnibus bE occupatur, ut effectus particularum omnium in globum ad effectum particularum omnium in Cylindrum. Sed solidum prius est Parabolois vertice V, axe CA & latere recto CA descriptum, & solidum posterius est cylindrus Paraboloidi circumscriptus: & notum est quod Parabolois sit semissis cylindri circumscripti. Ergo vis tota Medii in globum est duplo minor quam ejusdem vis tota in Cylindrum. Et propterea si particulæ Medii quiescerent, & cylindrus ac globus æquali cum velocitate moverentur, foret resistentia globi duplo minor quam resistentia cylindri. Q.E.D.
Scholium.
Eadem methodo figuræ aliæ inter se quoad resistentiam comparari possunt, eæque inveniri quæ ad motus suos in Mediis resistentibus continuandos aptiores sunt. Ut si base circulari CEBH, quæ centro O, radio OC describitur, & altitudine  OD, construendum sit frustum coni CBGF, quod omnium eadem basi & altitudine constructorum & secundum plagam axis sui versus D progredientium frustorum minime resistatur: biseca altitudinem OD in Q & produc, OQ ad S ut sit QS æqualis QC, & erit S vertex coni cujus frustum quæritur.
OD, construendum sit frustum coni CBGF, quod omnium eadem basi & altitudine constructorum & secundum plagam axis sui versus D progredientium frustorum minime resistatur: biseca altitudinem OD in Q & produc, OQ ad S ut sit QS æqualis QC, & erit S vertex coni cujus frustum quæritur.
Unde obiter cum angulus CSB semper sit acutus, consequens est, quod si solidum ADBE convolutione figuræ Ellipticæ vel Ovalis ADBE circa axem AB facta generetur, & tangatur figura generans a rectis tribus FG, GH, HI in punctis F, B & I, ea lege ut GH sit perpendicularis ad axem in puncto contactus B, & FG, HI cum eadem GH contineant angulos FGB, BHI graduum 135: solidum, quod convolutione figuræ ADFGHIE circa axem eundem CB generatur, minus resistitur quam solidum prius; si modo utrumque secundum plagam axis sui AB progrediatur, & utriusque terminus B præcedat. Quam quidem propositionem in construendis Navibus  non inutilem futuram esse censeo.
non inutilem futuram esse censeo.
Quod si figura DNFB ejusmodi sit ut, si ab ejus puncto quovis N ad axem AB demittatur perpendiculum NM, & a puncto dato G ducatur recta GR quæ parallela sit rectæ figuram tangenti in N, & axem productum secet in R, fuerit MN ad GR ut GRcub. ad Solidum quod figuræ hujus revolutione circa axem AB facta describitur, in Medio raro & Elastico ab A versus B velocissime movendo, minus resistetur quam aliud quodvis eadem longitudine & latitudine descriptum Solidum circulare.
Prop. XXXVI. Prob. VIII.
Invenire resistentiam corporis Sphærici in Fluido raro & Elastico velocissime progredientis. (Vide Fig. Pag. 325.)
Designet ABKI corpus Sphæricum centro C semidiametro CA descriptum. Producatur CA primo ad S deinde ad R, ut sit AS pars tertia ipsius CA, & CR sit ad CS ut densitas corporis Sphærici ad densitatem Medii. Ad CR erigantur perpendicula PC, RX, centroque R & Asymptotis CR, RX describatur Hyperbola quævis PVY. In CR capiatur CT longitudinis cujusvis, & erigatur perpendiculum TV abscindens aream Hyperbolicam PCTV, & sit CZ latus hujus areæ applicatæ ad rectam PC. Dico quod motus quem globus, describendo spatium CZ, ex resistentia Medii amittet, erit ad ejus motum totum sub initio ut longitudo CT ad longitudinem CR quamproxime.
<328>Nam (per motuum Legem tertiam) motus quem cylindrus GNOQ circa globum descriptus impingendo in Medii particulas amitteret, æqualis est motui quem imprimeret in easdem particulas. Ponamus quod particulæ singulæ reflectantur a cylindro, & ab eodem ea cum velocitate resiliant, quacum cylindrus ad ipsas accedebat. Nam talis erit reflexio, per Legum Corol. 3. si modo particulæ quam minime sint, & vi Elastica quam maxima reflectantur. Velocitas igitur quacum a cylindro resiliunt, addita velocitati cylindri componet totam velocitatem duplo majorem quam velocitas cylindri, & propterea motus quem cylindrus ex reflexione particulæ cujusque amittit, erit ad motum totum cylindri, ut particula duplicata ad cylindrum. Proinde cum densitas Medii sit ad densitatem cylindri ut CS ad CR; si Ct sit longitudo tempore quam minimo a cylindro descripta, erit motus eo tempore amissus ad motum totum cylindri ut ad . Ea enim est ratio materiæ Medii, a cylindro protrusæ & reflexæ, ad massam cylindri. Unde cum globus sit duæ tertiæ partes cylindri, & resistentia globi (per Propositionem superiorem) sit duplo minor quam resistentia cylindri: erit motus, quem globus describendo longitudinem L amittit, ad motum totum globi, ut ad , sive ut Ct ad CR. Erigatur perpendiculum tv Hyperbolæ occurrens in v, & (per Corol. 1. Prop. V. Lib. II) si corpus describendo longitudinem areæ CtvP proportionalem, amittit motus sui totius CR partem quamvis Ct, idem describendo longitudinem areae CTVP proportionalem, amittet motus sui partem CT. Sed longitudo Ct æqualis est , & longitudo OZ (per Hypothesin) æqualis est , adeoque longitudo Ct est ad longitudinem CZ ut area CPvt ad aream CPVT. Et propterea cum globus describendo longitudinem quam minimam Ct amittat motus sui partem, quæ sit ad totum ut Ct ad CR, is describendo longitudinem aliam quamvis CZ, amittet motus sui partem quæ sit ad totum ut CT ad CR. Q.E.D.
Corol. 1. Si detur corporis velocitas sub initio, dabitur tempus quo corpus, describendo spatium Ct, amittet motus sui partem Ct: & inde, dicendo quod resistentia sit ad vim gravitatis ut ista motus pars amissa ad motum, quem gravitas Globi eodem tempore generaret; dabitur proportio resistentiæ ad gravitatem Globi.
Corol. 2. Quoniam in his determinandis supposui quod particulæ Fluidi per vim suam Elasticam quam maxime a Globo reflectantur, & particularum sic reflexarum impetus in Globum duplo major sit quam si non reflecterentur: manifestum est quod in Fluido, cujus particulæ vi omni Elastica aliaque omni vi reflexiva destituuntur, corpus Sphæricum resistentiam duplo minorem patietur; adeoque eandem velocitatis partem amittendo, duplo longius progredietur quam pro constructione Problematis hujus superius allata.
Corol. 3. Et si particularum vis reflexiva neque maxima sit neque omnino nulla, sed mediocrem aliquam rationem teneat: resistentia pariter, inter limites in constructione Problematis & Corollario superiore positos, mediocrem rationem tenebit.
Corol. 4. Cum corpora tarda paulo magis resistantur quam pro ratione duplicata velocitatis: hæc describendo longitudinem quamvis CZ amittent majorem motus sui partem, quam quæ sit ad motum suum totum ut CT ad CR.
Corol. 5. Cognita autem resistentia corporum celerrimorum, innotescet etiam resistentia tardorum; si modo lex decrementi resistentiæ pro ratione velocitatis inveniri potest.
<330>Prop. XXXVII. Prob. IX.
Aquæ de vase dato per foramen effluentis definire motum.
Si vas impleatur aqua, & in fundo perforetur ut aqua per foramen defluat, manifestum est quod vas sustinebit pondus aquæ totius, dempto pondere partis illius quod foramini perpendiculariter imminet. Nam si foramen obstaculo aliquo occluderetur, obstaculum sustineret pondus aquæ sibi perpendiculariter incumbentis, & fundum vasis sustineret pondus aquæ reliquæ. Sublato autem obstaculo, fundum vasis eadem aquæ pressione eodemve ipsius pondere urgebitur ac prius; & pondus quod obstaculum sustinebat, cum jam non sustineatur, faciet ut aqua descendat & per foramen defluat.
Unde consequens est, quod motus aquæ totius effluentis is erit quem pondus aquæ foramini perpendiculariter incumbentis generare possit. Nam aquæ particula unaquæque pondere suo, quatenus non impeditur, descendit, idque motu uniformiter accelerato; & quatenus impeditur, urgebit obstaculum. Obstaculum illud vel vasis est fundum, vel aqua inferior defluens; & propterea ponderis pars illa, quam vasis fundum non sustinet, urgebit aquam defluentem & motum sibi proportionalem generabit.
Designet igitur F aream foraminis, A altitudinem aquæ foramini perpendiculariter incumbentis, P pondus ejus, AF quantitatem ejus, S spatium quod dato quovis tempore T in vacuo libere cadendo describeret, & V velocitatem quam in fine temporis illius cadendo acquisierit: & motus ejus acquisitus æqualis erit motui aquæ totius eodem tempore effluentis. Sit velocitas quacum effluendo exit de foramine, ad velocitatem V ut d ad e; & cum aqua velocitate V describere posset spatium , aqua effluens eodem tempore, velocitate sua , describere posset spatium . Et propterea columna aquæ cujus longitudo sit & latitudo eadem quæ foraminis, posset eo tempore defluendo egredi de vase, hoc est columna . Quare motus , qui fiet ducendo quantitatem aquæ effluentis in velocitatem suam, hoc est motus omnis tempore effluxus illius genitus, æquabitur motui . Et si æquales illi motus applicenter ad FV; fiet æqualis A. Unde est dd ad ee ut A ad , & d ad e in dimidiata ratione ad S. Est igitur velocitas quacum aqua exit e foramine, ad velocitatem quam aqua cadens, & tempore T cadendo describens spatium S acquireret, ut altitudo aquæ foramini perpendiculariter incumbentis, ad medium proportionale inter altitudinem illam duplicatam & spatium illud S, quod corpus tempore T cadendo describeret.
Igitur si motus illi sursum vertantur; quoniam aqua velocitate V ascenderet ad altitudinem illam S de qua deciderat; & altitudines (uti notum est) sint in duplicata ratione velocitatum: aqua effluens ascenderet ad altitudinem . Et propterea quantitas aquæ effluentis, quo tempore corpus cadendo describere posset altitudinem , æqualis erit columnæ aquæ totius AF foramini perpendiculariter imminentis.
Cum autem aqua effluens, motu suo sursum verso, perpendiculariter surgeret ad dimidiam altitudinem aquæ foramini incumbentis; consequens est quod si egrediatur oblique per canalem in latus vasis, describet in spatiis non resistentibus Parabolam cujus latus rectum est altitudo aquæ in vase supra canalis orificium, & cujus diameter horizonti perpendicularis ab orificio illo ducitur, atque ordinatim applicatæ parallelæ sunt axi canalis.
Hæc omnia de Fluido subtilissimo intelligenda sunt. Nam si aqua ex partibus crassioribus constet, hæc tardius effluet quam pro ratione superius assignata, præsertim si foramen angustum sit per quod effluit.
<332>Denique si aqua per canalem horizonti parallelum egrediatur; quoniam fundum vasis integrum est, & eadem aquæ incumbentis pressione ubique urgetur ac si aqua non efflueret; vas sustinebit pondus aquæ totius, non obstante effluxu, sed latus vasis de quo effluit non sustinebit pressionem illam omnem, quam sustineret si aqua non efflueret. Tolletur enim pressio partis illius ubi perforatur: quæ quidem pressio æqualis est ponderi columnæe aquæ, cujus basis foramini æquatur & altitudo eadem est quæ aquæ totius supra foramen. Et propterea si vas, ad modum corporis penduli, filo prælongo a clavo suspendatur, hoc, si aqua in plagam quamvis secundum lineam horizontalem effluit, recedet semper a perpendiculo in plagam contrariam. Et par est ratio motus pilarum, quæ Pulvere tormentario madefacto implentur, &, materia in flammam per foramen paulatim expirante, recedunt a regione flammæ & in partem contrariam cum impetu feruntur.
Prop. XXXVIII. Theor. XXIX.
Corporum Sphæricorum in Mediis quibusque Fluidissimis resistentiam in anteriore superficie definire.
Defluat aqua de vase Cylindrico ABCD, per canalem Cylindricum EFGH, in vas inferius IKLM; & inde effluat per vasis marginem IM. Sit autem margo ille ejusdem altitudinis cum vasis superioris fundo CD, eo ut aqua per totum canalem uniformi cum motu descendat; & in medio canalis collocetur Globus P, sitque PR altitudo aquæ supra Globum, & SR ejusdem altitudo supra fundum vasis. Sustineatur autem Globus filo tenuissimo TV, lateribus canalis hinc inde affixo. Et manifestum est per proportionem superiorem, quod quantitas aquæ dato tempore defluentis erit ut amplitudo foraminis per quod defluit; hoc est, si Globus tollatur, ut canalis orificium: sin Globus adsit, ut spatium undique inter Globum & canalem. Nam velocitas aquæ defluentis (per superiorem Propositionem) ea erit quam corpus cadendo, & casu suo describendo dimidiam aquæ altitudinem SR, acquirere posset: adeoque eadem est sive Globus tollatur, sive adsit. Et propterea aqua defluens erit ut amplitudo spatii per quod transit. Certe transitus aquæ per spatium angustius facilior esse nequit quam per spatium amplius, & propterea velocitas  ejus ubi Globus adest, non potest esse major quam cum tollitur: ideoque major aquæ quantitas, ubi Globus adest, non effluet quampro ratione spatii per quod tran sit. Si aqua non sit liquor subtilissimus & fluidissimus, hujus transitus per spatium angustius, ob crassitudinem particularum, erit aliquanto tardior: at liquorem fluidissimum esse hic supponimus. Igitur quantitas aquæ, cujus descensum Globus dato tempore impedit, est ad quantitatem aquæ quæ, si Globus tolleretur, eodem tempore descenderet, ut basis Cylindri circa Globum descripti ad orificium canalis; sive ut quadratum diametri Globi ad quadratum diametri cavitatis canalis. Et propterea quantitas aquæ cujus descensum Globus impedit, æqualis est quantitati aquæ, quæ eodem tempore per foramen circulare in fundo vasis, basi Cylindri illius æquale, descendere posset, & cujus descensus per fundi partem quamvis circularem basi illi æqualem impeditur.
ejus ubi Globus adest, non potest esse major quam cum tollitur: ideoque major aquæ quantitas, ubi Globus adest, non effluet quampro ratione spatii per quod tran sit. Si aqua non sit liquor subtilissimus & fluidissimus, hujus transitus per spatium angustius, ob crassitudinem particularum, erit aliquanto tardior: at liquorem fluidissimum esse hic supponimus. Igitur quantitas aquæ, cujus descensum Globus dato tempore impedit, est ad quantitatem aquæ quæ, si Globus tolleretur, eodem tempore descenderet, ut basis Cylindri circa Globum descripti ad orificium canalis; sive ut quadratum diametri Globi ad quadratum diametri cavitatis canalis. Et propterea quantitas aquæ cujus descensum Globus impedit, æqualis est quantitati aquæ, quæ eodem tempore per foramen circulare in fundo vasis, basi Cylindri illius æquale, descendere posset, & cujus descensus per fundi partem quamvis circularem basi illi æqualem impeditur.
Jam vero pondus aquæ, quod vas & Globus conjunctim sustinent, est pondus aquæ totius in vase, præter partem illam quæ aquam defluentem accelerat, & ad ejus motum generandum sufficit, quæque, per Propositionem superiorem, æqualis est ponderi columnæ aquæ cujus basis æquatur spatio inter Globum & canalem per quod aqua defluit, & altitudo eadem cum altitudine aquæ supra fundum vasis, per lineam SR designata. Vasis igitur fundum & Globus conjunctim sustinent pondus aquæ totius in vase sibi ipsis perpendiculariter imminentis. Unde cum fundum vasis sustineat pondus aquæ sibi perpendiculariter imminentis, reliquum est ut Globus etiam sustineat pondus aquae sibi perpendiculariter imminentis{.} Globus quidem non sustinet pondus aquæ illius stagnantis & sibi absque omni motu incumbentis, sed aquæ defluenti resistendo impedit effectum tanti ponderis; adeoque vim aquæ defluentis sustinet ponderi illi æqualem. Nam impedit descensum & effluxum quantitatis aquæ quem pondus illud accurate efficeret si Globus tolleretur. Aqua pondere suo, quatenus descensus ejus impeditur, urget obstaculum omne, ideoque obstaculum, quatenus descensum aquæ impedit, vim sustinet æqualem ponderi quo descensus ille efficeretur. Globus autem descensum quantitatis aquæ impedit, quem pondus columnæ aquæ sibi perpendiculariter incumbentis efficere posset; & propterea vim aquæ decurrentis sustinet ponderi illi æqualem. Actio & reactio aquæ per motus Legem tertiam æquantur inter se, & in plagas contrarias diriguntur. Actio Globi in aquam descendentem, ad ejus descensum impediendum, in superiora dirigitur, & est ut descendendi motus impeditus, eique tollendo adæquate sufficit: & propterea actio contraria aquæ in Globum æqualis est vi quæ motum eundem vel tollere vel generare possit, hoc est ponderi columnæ aquæ, quæ Globo perpendiculariter imminet & cujus altitudo est RS.
Si jam canalis orificium superius obstruatur, sic ut aqua descendere nequeat, Globus quidem, pondere aquæ in canali & vase inferiore IKLM stagnantis, premetur undique; sed non obstante pressione illa, si ejusdem sit specificæ gravitatis cum aqua, quiescet. Pressio illa Globum nullam in partem impellet. Et propterea ubi canalis aperitur & aqua de vase superiore descendit, vis omnis, qua Globus impellitur deorsum, orietur ab aquæ illius descensu, atque adeo æqualis erit ponderi columnæ aquæ, cujus altitudo est RS & diameter eadem quæ Globi. Pondus autem istud, quo tempore data quælibet aquæ quantitas per foramen basi Cylindri circa Globum descripti a quale, sublato Globo effluere posset, sufficit ad ejus motum omnem generandum; atque adeo quo tempore aqua in Cylindro uniformiter decurrendo describit duas tertias partes diametri Globi, sufficit ad motum omnem aqua Globo æqualis generandum. Nam Cylindrus aquæ, latitudine Globi & duabus tertiis partibus altitudinis descriptus, Globo æquatur. Et propterea aquæ currentis impetus in Globum quiescentem, quo tempore aqua currendo describit duas tertias partes diametri Globi, si uniformiter continuetur, generaret motum omnem partis Fluidi quæ Globo æquatur.
Quæ vero de aqua in canali demonstrata sunt, intelligenda sunt etiam de aqua quacunque fluente, qua Globus quilibet in ea quiescens urgetur. Quæque de aqua demonstrata sunt obtinent etiam in Fluidis universis subtilissimis. De his omnibus idem valet argumentum.
Jam vero per Legum Corol. 5, vis Fluidi in Globum eadem est, sive Globus quiescat & Fluidum uniformi cum velocitate moveatur, sive Fluidum quiescat & Globus eadem cum velocitate in partem contrariam pergat. Et propterea resistentia Globi in Medio quocunque Fluidissimo uniformiter progredientis, quo tempore Globus duas tertias partes diametri suæ describit, æqualis est vi, quæ in corpus ejusdem magnitudinis cum Globo & ejusdem densitatis cum Medio uniformiter impressa, quo tempore Globus duas tertias partes diametri suæ progrediendo describit, velocitatem Globi in corpore illo generare posset. Tanta est resistentia Globi in superficiei parte praecedente. Q.E.D.
Corol. 1. Si solidum Sphæricum in ejusdem secum densitatis Fluido subtilissimo libere moveatur, & inter movendum eadem vi urgeatur a tergo atque cum quiescit; ejusdem resistentia ea erit quam in Corollario secundo Propositionis xxxvi. descripsimus. Unde si computus ineatur, patebit quod solidum dimidiam motus sui partem prius amittet, quam progrediendo descripserit longitudinem diametri propriæ; Quod si inter movendum minus urgeatur a tergo, magis retardabitur: & contra, si magis urgeatur, minus retardabitur.
Corol. 2. Hallucinantur igitur qui credunt resistentiam projectilium per infinitam divisionem partium Fluidi in infinitum diminui. Si Fluidum sit valde crassum, minuetur resistentia aliquantulum per divisionem partium ejus. At postquam competentem Fluiditatis gradum acquisiverit, (qualis forte est Fluiditas Aeris vel aquæ vel argenti vivi) resistentia in anteriore superficie solidi, per ulteriorem partium divisionem non multum minuetur. Nunquam enim minor futura est quam pro limite quem in Corollario superiore assignavimus.
Corol. 3. Media igitur in quibus corpora projectilia sine sensibili motus diminutione longissime progrediuntur, non solum Fluidissima sunt, sed etiam longe rariora quam sunt corpora illa quæ in ipsis moventur: nisi forte quis dixerit Medium omne Fluidissimum, impetu perpetuo in posticam projectilis partem facto, tantum promovere motum ejus quantum impedit & resistit in parte antica. Et motus quidem illius, quem projectile imprimit in Medium, partem aliquam a Medio circulariter lato reddi corpori a tergo verisimile est. Nam & experimentis quibusdam factis, reperi quod in Fluidis satis compressis pars aliqua redditur. Omnem vero in casu quocunque reddi nec rationi consentaneum videtur, neque cum experimentis hactenus a me tentatis bene quadrat. Fluidorum enim utcunque subtilium, si densa sint, vim ad solida movenda resistendaque permagnam esse, & quomodo vis illius quantitas per experimenta determinetur, plenius patebit per Propositiones duas quae sequuntur.
Lemmma IV.
Si vas Sphæricum Fluido homogeneo quiescente plenum a vi impressa moveatur in directum, motuque progressivo semper accelerato ita pergat ut interea non moveatur in orbem: partes Fluidi inclusi, æqualiter participando motum vasis, quiescent inter se. Idem obtinebit in vase figuræ cujuscunque. Res manifesta est, nec indiget demonstratione.
Prop. XXXIX. Theor. XXX.
Fluidum omne quod motu accelerato ad modum venti increbescentis progreditur, & cujus partes inter se quiescunt, rapit omnia ejusdem densitatis innatantia corpora, & secum cum eadem velocitate defert.
Nam per Lemma superius si vas Sphæricum, rigidum, Fluidoque homogeneo quiescente plenum, motu paulatim impresso progrediatur; Fluidi motum vasis participantis partis omnes semper quiescent inter se. Ergo si Fluidi partes aliquæ congelarentur, pergerent hæ quiescere inter partes reliquas. Nam quoniam partes omnes quiescunt inter se, perinde est sive fluidæ sint, sive aliquæ earum rigescant. Ergo si vas a vi aliqua extrinsecus impressa moveatur, & motum suum imprimat in Fluidum: Fluidum quoque motum suum imprimet in sui ipsius partes congelatas easque secum rapiet. Sed partes illæ congelatæ sunt corpora solida ejusdem densitates cum Fluido; & par est ratio Fluidi, sive id in vase moto claudatur, sive in spatiis liberis ad modum venti spiret. Ergo Fluidum omne quod motu progressivo accelerato fertur, & cujus partes inter se quiescunt, solida quæcunque ejusdem densitatis inclusa, quæ sub initio quiescebant, rapit secum, & una moveri cogit. Q.E.D.
Prop. XL. Prob. X.
Invenire resistentiam solidorum Sphæricorum in Mediis Fluidissimis densitate datis.
In Fluido quocunque dato inveniatur resistentia ultima solidi specie dati, cujus magnitudo in infinitum augetur. Dein dic: ut ejus motus amissus, quo tempore progrediendo longitudinem semidiametri suæ describit, est ad ejus motum totum sub initio, ita motus quem solidum quodvis datum, in Fluido eodem jam facto subtilissimo, describendo diametri suæ longitudinem amitteret, est ad ejus motum totum sub initio quamproxime. Nam si particulæ minimæ Fluidi subtiliati eandem habeant proportionem eundemque situm ad solidum datum in eo movens, quem particulæ totidem minimæ Fluidi non subtiliati habent ad solidum auctum; sintque particulæ Fluidi utriusque summe lubricæ, & viribus centrifugis centripetisque omnino destituantur; incipiant autem solida temporibus quibuscunque proportionalibus in his Fluidis similiter moveri: pergent eadem similiter moveri, adeoque quo tempore describunt spatia semidiametris suis æqualia, amittent partes motuum proportionales totis; idque licet partes Medii subtiliati minuantur, & magnitudo solidi in Medio non subtiliato moventis augeatur in infinitum. Ergo ex resistentia solidi aucti in Medio non subtiliato, dabitur per proportionem superiorem resistentia solidi non aucti in Medio subtiliato. Q.E.I.
Si particulæ non sunt summe lubricæ, supponendum est quod in utroque; Fluido sunt æqualiter lubricæ, eo ut ex defectu lubricitatis resistentia utrinque æqualiter augeatur: & Propositio etiamnum valebit.
<339>Corol. 1. Ergo si ex aucta solidi Sphærici magnitudine augeatur ejus resistentia in ratione duplicata; resistentia solidi Sphærici dati ex diminuta magnitudine particularum Fluidi, nullatenus minuetur.
Corol. 2. Sin resistentia, augendo solidum Sphæricum, augeatur in minore quam duplicata ratione diametri: eadem diminuendo particulas Fluidi, diminuetur in ratione qua resistentia aucta deficit a ratione duplicata diametri.
Corol. 3. Unde perspicuum est quod solidi dati resistentia per divisionem partium Fluidi non multum diminui potest. Nam resistentia solidi aucti debebit esse quam proxime ut quantitas materiæ fluidæ resistentis, quam solidum illud movendo protrudit & a locis a se invasis & occupatis propellit: hoc est ut spatium Cylindricum per quod solidum movetur, adeoque in duplicata ratione semidiametri solidi quamproxime.
Corol. 4. Igitur propositis duobus Fluidis, quorum alterum ab altero quoad vim resistendi longissime superatur: Fluidum quod minus resistit est altero rarius; suntque Fluidorum omnium vires resistendi prope ut eorum densitates; præsertim si solida sint magna, & velociter moveantur, & Fluidorum æqualis sit compressio.
Scholium Generale.
Quæ hactenus demonstrata sunt tentavi in hunc modum. Globum ligneum pondere unciarum Romanarum , diametro digitorum Londinensium fabricatum, filo tenui ab unco satis firmo suspendi, ita ut inter uncum & centrum oscillationis Globi distantia esset pedum . In filo punctum notavi pedibus decem & uncia una a centro suspensionis distans; & e regione puncti illius collocavi Regulam in digitos distinctam, quorum ope notarem longitudines arcuum a Pendulo descriptas. Deinde numeravi oscillationes quibus Globus quartam motus sui partem amitteret. Si pendulum deducebatur a perpendiculo ad distantiam duorum digitorum, & inde demittebatur; ita ut toto suo descensu describeret arcum duorum digitorum, totaque oscillatione prima, ex descensu & ascensu subsequente composita, arcum digitorum fere quatuor: idem oscillationibus 164 amisit octavam motus sui partem, sic ut ultimo suo ascensu describeret arcum digiti unius cum tribus partibus quartis digiti. Si primo descensu descripsit arcum digitorum quatuor, amisit octavam motus partem oscillationibus 121; ita ut ascensu ultimo describaret arcum digitorum . Si primo descensu descripsit arcum digitorum octo, sexdecim, triginta duorum vel sexaginta quatuor, amisit octavam motus partem oscillationibus 69, , ; respective. Igitur differentia inter arcus descensu primo & ascensu ultimo descriptos, erat in casu primo, secundo, tertio, quarto, quinto, sexto, digitorum , , 1, 2, 4, 8 respective. Dividantur eæ differentiæ per numerum oscillationum in casu unoquoque; & in oscillatione una mediocri, qua arcus digitorum , 15, 30, 60, 120 descriptus fuit, differentia arcuum descensu & subsequente ascensu descriptorum, erit , , , , , partes digiti respective. Hæ autem in majoribus oscillationibus sunt in duplicata ratione arcuum descriptorum quam proxime; in minoribus vero paulo majores quam in ea ratione, & propterea (per Corol. 2. Prop. xxxi. Libri hujus) resistentia Globi, ubi celerius movetur, est in duplicata ratione velocitatis quamproxime; ubi tardius, paulo major quam in ea ratione: omnino ut in Corollariis Propositionis xxxii. demonstratum est.
Designet jam V velocitatem maximam in oscillatione quavis, sintque A, B, C quantitates datæ, & fingamus quod differentia arcuum sit . Et cum velocitates maximæ in prædictis sex Casibus, sint ut arcuum dimidiorum , , , 15, 30, 60 chordæ, atque adeo ut arcus ipsi quam proxime, hoc est ut numeri , 1, 2, 4, 8, 16: scribamus in Casu secundo quarto & sexto numeros 1, 4, & 16 pro ; & prodibit arcuum differentia æqualis in Casu secundo; & æqualis in casu quarto; & æqualis in casu sexto. Unde si per has æquationes determinemus quantitates A, B, C; habebimus Regulam inveniendi differentiam arcuum pro velocitate quacunque data.
Cæterum cum velocitates maximæ sint in Cycloide ut arcus oscillando descripti, in circulo vero ut semissium arcuum illorum chordæ, adeoque paribus arcubus majores sint in Cycloide quam in circulo, in ratione semissium arcuum ad eorundem chordas; tempora autem in circulo sint majora quam in Cycloide in velocitatis ratione reciproca: ut ex resistentia in circulo inveniatur resistentia in Trochoide, debebit resistentia augeri in duplicata circiter ratione arcus ad chordam, ob velocitatem in ratione illa simplici auctam; & diminui in ratione chordæ ad arcum, ob tempus (seu durationem resistentiæ qua arcuum differentia prædicta generatur) diminutum in eadem ratione: id est (si rationes conjungamus) debebit resistentia augeri in ratione arcus ad chordam circiter. Hæc ratio in casu secundo est 6283 ad 6279, in quarto 125666 ad 12533, in sexto 25132 ad 24869. Et inde resistentia , , & evadunt , & , id est in numeris decimalibus 0, 004135, 0, 056486 & 0, 8363. Unde prodeunt æquationes , 004135: , 05648 & , 8363. Et ex his per debitam terminorum collationem & reductionem Analyticam fit , 0002097, , 0008955 & , 0030298. Est igitur differentia arcuum ut 0, , ,: & propterea cum per Corol. Prop. xxx. resistentia Globi in medio arcus oscillando descripti, ubi velocitas est V, sit ad ipsius pondus ut ad longitudinem Penduli; si pro A, B & C scribantur numeri inventi, fiet resistentia Globi ad ejus pondus, ut 0, , , ad longitudinem Penduli inter centrum suspensionis & Regulam, id est ad 121 digitos. Unde cum V in casu secundo designet 1, in quarto 4, in sexto 16: erit resistentia ad pondus Globi in casu secundo ut 0.003029 ad 121, in quarto ut 0.042875 ad 121, in sexto ut 0.63013 ad 121.
Arcus quem punctum in filo notatum in Casu sexto descripsit, erat seu digitorum. Et propterea cum radius esset 121 digitorum, & longitudo penduli inter punctum suspensionis & centrum Globi esset 126 digitorum, arcus quem centrum Globi descripsit erat digitorum. Quoniam corporis oscillantis velocitas maxima ob resitentiam Aeris non incidit in punctum infimum arcus descripti, sed in medio fere loco arcus totius versatur: hæc eadem erit circiter ac si Globus descensu suo toto in Medio non resistente describeret arcus illius partem dimidiam digitorum idque in Cycloide, ad quam motum penduli supra reduximus: & propterea velocitas illa æqualis erit velocitati quam Globus, perpendiculariter cadendo & casu suo describendo altitudinem arcus illius Sinui verso æqualem, acquirere posset. Est autem sinus ille versus in Cycloide ad arcum istum ut arcus idem ad penduli longitudinem duplam 252, & propterea aequalis digitis 15, 278. Quare velocitas ea ipsa est quam corpus cadendo & casu suo spatium 15, 278 digitorum describendo acquirere posset. Unde cum corpus tempore minuti unius secundi cadendo (uti per experimenta pendulorum determinavit Hugenius) describat pedes Parisienses , id est pedes Anglicos seu digitos , & tempora sint in dimidiata ratione spatiorum; Globus tempore minut. 16 tert. 38 quart. cadendo describet 15, 278 digitos, & velocitatem suam prædictam acquiret; & propterea cum eadem velocitate uniformiter continuata describet eodem tempore longitudinem duplam 30, 556 digitorum. Tali igitur cum velocitate Globus resistentiam patitur, quæ sit ad ejus pondus ut 0, 63013 ad 121, vel (si resistentiæ pars illa sola spectetur quæ est in velocitatis ratione duplicata) ut 0, 58172 ad 121.
Experimento autem Hydrostatico inveni quod pondus Globi hujus lignei esset ad pondus Globi aquei magnitudinis ejusdem, ut 55 ad 97: & propterea cum 121 sit ad 213, 4 in eadem ratione, erit resistentia Globi aquei pr278fata cum velocitate progredientis ad ipsius pondus ut 0, 58172 ad 213, 4, id est ut 1 ad . Unde cum pondus Globi aquei, quo tempore Globus cum velocitate uniformiter continuata describat longitudinem pedum 30, 556, velocitatem illam omnem in Globo cadente generare posset; manifestum est quod vis resistentiæ uniformiter continuata tollere posset velocitatem minorem in ratione 1 ad , hoc est velocitatis totius partem . Et propterea quo tempore Globus, ea cum velocitate uniformiter continuata, longitudinem semidiametri suæ seu digitorum describere posset, eodem amitteret motus sui partem .
Numerabam etiam oscillationes quibus pendulum quartam motus sui partem amisit. In sequente Tabula numeri supremi denotant longitudinem arcus descensu primo descripti, in digitis & partibus digiti expressam: numeri medii significant longitudinem arcus ascensu ultimo descripti; & loco infimo stant numeri oscillationum. Experimentum descripsi tanquam magis accuratum quam cum motus pars tantum octava amitteretur. Calculum tentet qui volet.
| Descensus Primus | 2 | 4 | 8 | 16 | 32 | 64 |
| Ascensus ultimus | 3 | 6 | 12 | 24 | 48 | |
| Num. Oscillat. | 374 | 272 |
Postea Globum plumbeum, diametro digitorum duorum & pondere unciarum Romanarum suspendi filo eodem, sic ut inter centrum Globi & punctum suspensionis intervallum esset pedum , & numerabam oscillationes quibus data motus pars amitteretur. Tabularum subsequentium prior exhibet numerum oscillationum quibus pars octava motus totius cessavit; secunda numerum oscillationum quibus ejusdem pars quarta amissa fuit.
| Descensus primus | 1 | 2 | 4 | 8 | 16 | 32 | 64 |
| Ascensus Ultimus | 7 | 14 | 28 | 56 | |||
| Numerus Oscillat. | 226 | 228 | 193 | 140 | 53 | 30 |
| Descensus primus | 1 | 2 | 4 | 8 | 16 | 32 | 64 |
| Ascensus ultimus | 3 | 6 | 12 | 24 | 48 | ||
| Numerus Oscillat. | 510 | 518 | 420 | 318 | 204 | 121 | 70 |
In Tabula priore seligendo ex observationibus tertiam, quintam & septimam, & exponendo velocitates maximas in his observationibus particulatim per numeros 1, 4, 16 respective, & generaliter per quantitatem V ut supra: emerget in observatione prima , in secunda , in tertia aequ. . Quæ æquationes per reductiones superius expositas dant, , 000145, , 000217 & , 0009. Et inde prodit resistentia Globi cum velocitate V moventis, in ea ratione ad pondus suum unciarum , quam habet 0, , , ad Penduli longitudinem 121 digitorum. Et si spectemus eam solummodo resistentiæ partem quæ est in duplicata ratione velocitatis, hæc erit ad pondus Globi ut 0, ad 121 digitos. Erat autem hæc pars resistentiæ in experimento primo ad pondus Globi lignei unciarum ut 0, ad 121: & inde fit resistentia Globi lignei ad resistentiam Globi plumbei (paribus eorum velocitatibus) ut in 0, 00227235 ad in 0, 007675, id est ut 130309 ad 17719 seu ad 1. Diametri Globorum duorum erant & 2 digitorum, & harum quadrata sunt ad invicem ut & 4, seu & 1 quamproxime. Ergo resistentiæ Globorum æquivelocium erant in minore ratione quam duplicata diametrorum. At nondum consideravimus resistentiam fili, quæ certe permagna erat, ac de pendulorum inventa resistentia subduci debet. Hanc accurate definire non potui, sed majorem tamen inveni quam partem tertiam resistentiæ totius minoris penduli, & inde didici quod resistentiæ Globorum, dempta fili resistentia, sunt quamproxime in dimidiata ratione diametrorum. Nam ratio ad , id est 7 ad seu ad 1, non longe abest a diametrorum ratione duplicata ad 1.
Cum resistentia fili in Globis majoribus minoris sit momenti, tentavi etiam experimentum in Globo cujus diameter erat digitorum. Longitudo penduli inter punctum suspensionis & centrum oscillationis erat digitorum , inter punctum suspensionis & nodum in filo dig. Arcus primo penduli descensu a nodo descriptus, 32 dig. arcus ascensu ultimo post oscillationes quinque ab eodem nodo descriptus, 28 dig. Summa arcuum seu arcus totus oscillatione mediocri descriptus, 30 dig. Differentia arcuum 4 dig. Ejus pars decima seu differentia inter descensum & ascensum in oscillatione mediocri dig. Ut radius ad radium , ita arcus totus 60 dig. oscillatione mediocri a Nodo descriptus, ad arcum totum , oscillatione mediocri a centro Globi descriptum: & ita differentia ad differentiam novam 0, 4475. Si longitudo penduli, manente longitudine arcus descripti, augeretur in ratione 126 ad , velocitas ejus diminueretur in ratione illa dimidiata; & arcuum descensu & subsequente ascensu descriptorum differentia 0, 4475 diminueretur in ratione velocitatis, adeoque evaderet 0, 4412. Deinde si arcus descriptus augeretur in ratione ad , differentia ista 0, 4412 augeretur in duplicata illa ratione, adeoque, evaderet 1, 509. Hæc ita se haberent, ex hypothesi quod resistentia Penduli esset in duplicata ratione velocitatis. Ergo si pendulum describeret arcum totum digitorum, & longitudo ejus inter punctum suspensionis & centrum oscillationis esset 126 digitorum, differentia arcuum descensu & subsequente ascensu descriptorum foret 1, 509 dig. Et hæc differentia ducta in pondus Globi penduli, quod erat unciarum 208, producit 313, 9. Rursus ubi pendulum superius ex Globo ligneo constructum, centro oscillationis, quod a puncto suspensionis digitos 126 distabat, describebat arcum totum digitorum, differentia arcuum descensu & ascensu descriptorum fsuit in seu , quæ ducta in pondus Globi, quod erat unciarum , producit 48, 55. Duxi autem differentias hasce in pondera Globorum ut invenirem eorum resistentias. Nam differentiæ oriuntur ex resistentiis, suntque ut resistentiæ directe & pondera inverse. Sunt igitur resistentiæ ut numeri 313, 9 & 48, 55. Pars autem resistentiæ Globi minoris, quæ est in duplicata ratione velocitatis, erat ad resistentiam totam ut 0, 5817. ad 0, 63013, id est ut 44, 4 ad 48, 55; & pars resistentiæ Globi majoris propemodum æquatur ipsius resistentiæ toti, adeoque partes illæ sunt ut 313, 9 & 44, 4 quamproxime, id est ut 7, 07 ad 1. Sunt autem Globorum diametri & ; & harum quadrata & sunt ut 7, 38 & 1, id est ut Globorum, resistentiæ 7, 07 & 1 quamproxime. Differentia rationum haud major est quam quæ ex fili resistentia oriri potuit. Igitur resistentiarum partes illæ quæ sunt (paribus Globis) ut quadrata velocitatum, sunt etiam (paribus velocitatibus) ut quadrata diametrorum Globorum; & propterea (per Corollaria Prop. XL. Libri hujus) resistentia quam Globi majores & velociores in aere movendo sentiunt, haud multum per infinitam aeris divisionem & subtiliationem diminui potest, proindeque Media omnia in quibus corpora multo minus resistuntur, sunt aere rariora.
Cæterum Globorum, quibus usus sum in his experimentis, maximus non erat perfecte Sphæricus, & propterea in calculo hic allato minutias quasdam brevitatis gratia neglexi; de calculo accurato in experimento non satis accurato minime sollicitus. Optarim itaque (cum demonstratio vacui ex his dependeat) ut experimenta cum Globis & pluribus & majoribus & magis accuratis tentarentur. Si Globi sumantur in proportione Geometrica, puta quorum diametri sint digitorum 4, 8, 16, 32; ex progressione experimentorum colligetur quid in Globis adhuc majoribus evenire debeat.
Jam vero conferendo resistentias diversorum fluidorum inter se tentavi sequentia. Arcam ligneam paravi longitudine pedum quatuor, latitudine & altitudine pedis unius. Hanc operculo nudatam implevi aqua fontana, fecique ut immersa pendula in medio aquæ oscillando moverentur. Globus autem plumbeus pondere unciarum, diametro digitorum, movebatur ut in Tabula sequente descripsimus, existente videlicet longitudine penduli a puncto suspensionis ad punctum quoddam in filo notatum 126 digitorum, ad oscillationis autem centrum digitorum.
| Arcus descensu primo a puncto in filo notato descriptus digitorum. | 64 | 32 | 16 | 8 | 4 | 2 | 1 | ||
| Arcus ascensu ultimo descriptus digitorum. | 48 | 24 | 12 | 6 | 3 | ||||
| Arcuum differentia motui amisso proportionalis, digitorum. | 16 | 8 | 4 | 2 | 1 | ||||
| Numerus oscillationum in aqua. | 3 | 7 | |||||||
| Numerus oscillationum in aere. | 287 | 535 |
In experimento columnæ quartæ, motus æquales oscillationibus 535 in aere, & in aqua amissi sunt. Erant autem oscillationes in aere paulo celeriores quam in aqua, nimirum in ratione 44 ad 41. Nam oscillationes in aqua, & in aere simul peragebantur. Et propterea si oscillationes in aqua in ea ratione accelerarentur ut motus pendulorum in Medio utroque fierent æquiveloces, numerus oscillationum in aqua, quibus motus idem ac prius amitteretur (ob resistentiam auctam in ratione illa duplicata & tempus diminutum in ratione eadem simplici) diminueretur in eadem illa ratione 44 ad 41, adeoque evaderet in seu . Paribus igitur Pendulorum velocitatibus motus æquales in aere oscillationibus 535 & in aqua oscillationibus amissi sunt; ideoque resistentia penduli in aqua est ad ejus resistentiam in aere ut 535 ad . Hæc est proportio resistentiarum totarum in Casu columnæ quartæ.
Designet jam resistentiam Globi in aere cum velocitate V moventis, & cum velocitas maxima, in Casu columnæ, quartæ sit ad velocitatem maximam in casu columnæ primæ ut 1 ad 8, & resistentia in Casu columnæ quartæ ad resistentiam in Casu columnæ primæ in ratione arcuum differentiæ in his casibus, ad numeros oscillationum applicatæ, id est ut ad ;, seu ut ; ad 4280: scribamus in his Casibus 1 & 8 pro velocitatibus, atque ; & 4280 pro resistentiis, & fiet & seu , indeque per reductionem æquationum proveniet & & ; atque adeo resistentia ut quamproxime. Quare in Casu columnaæe quartæ ubi velocitas erat 1, resistentia tota est ad partem suam quadrato velocitatis proportionalem, ut seu , ad ; & idcirco resistentia penduli in aqua est ad resistentiæ partem illam in aere quæ quadrato velocitatis proportionalis est, quæque sola in motibus velocioribus consideranda venit, ut ad & 535 ad conjunctim, id est ut 637 ad 1. Si penduli in aqua oscillantis filum totum fuisset immersum, resistentia ejus fuisset adhuc major; adeo ut penduli in aere oscillantis resistentia illa quæ velocitatis quadrato proportionalis est, quæque sola in corporibus velocioribus consideranda venit, sit ad resistentiam ejusdem penduli totius, eadem cum velocitate in aqua oscillantis, ut 800 vel 900 ad 1 circiter, hoc est ut densitas aquæ ad densitatem aeris quamproxime.
In hoc calculo sumi quoque deberet pars illa resistentiæ penduli in aqua, quæ esset ut quadratum velocitatis, sed (quod mirum forte videatur) resistentia in aqua augebatur in ratione velocitatis plusquam duplicata. Ejus rei causam investigando, in hanc incidi, quod Arca nimis angusta esset pro magnitudine Globi penduli, & motum aquæ cedentis præ angustia sua nimis impediebat. Nam si Globus pendulus, cujus diameter erat digiti unius, immergeretur, resistentia augebatur in duplicata ratione velocitatis quamproxime. Id tentabam construendo pendulum ex Globis duobus, quorum inferior & minor oscillaretur in aqua, superior & major proxime supra aquam filo assixus esset, & in Aere oscillando, adjuvaret motum penduli eumque diuturniorem redderet. Experimenta autem hoc modo instituta se habebant ut in Tabula sequente describitur.
| Arcus descensu primo descriptus | 16 | 8 | 4 | 2 | 1 | ||
| Arcus ascensu ultimo descriptus. | 12 | 6 | 3 | ||||
| Arcuum diff. motui amisso proportionalis | 4 | 2 | 1 | ||||
| Numerus Oscillationum | 34 | 53 |
Resistentia hic nunquam augetur in ratione velocitatis plusquam duplicata. Et idem in pendulo majore evenire verisimile est, si modo Arca augeatur in ratione penduli. Debebit tamen resistentia tam in aere quam in aqua, si velocitas per gradus in infinitum augeatur, augeri tandem in ratione paulo plusquam duplicata, propterea quod in experimentis hic descriptis resistentia minor est quam pro ratione de corporibus velocissimis in Libri hujus Prop. xxxvi & xxxviii. demonstrata. Nam corpora longe velocissima spatium a tergo relinquent vacuum, ideoque resistentia quam sentiunt in partibus præcedentibus, nullatenus minuetur per pressionem Medii in partibus posticis.
Conferedo resistentias Mediorum inter se, effeci etiam ut pendula ferrea oscillarentur in argento vivo. Longitudo fili ferrei erat pedum quasi trium, & diameter Globi penduli quasi tertia pars digiti. Ad filum autem proxime supra Mercurium affixus erat Globus alius plumbeus satis magnus ad motum per duli diutius continuandum. Tum vasculum, quod capiebat quasi libras tres argenti vivi, implebam vicibus alternis argento vivo & aqua communi, ut pendulo in Fluido utroque successive oscillante invenirem proportionem resistentiarum: & prodiit resistentia argenti vivi ad resistentiam aquæ ut 13 vel 14 ad 1 circiter: id est ut densitas argenti vivi ad densitatem aquæ. Ubi Globum pendulum paulo majorem adhibebam, puta cujus diameter esset quasi vel partes digiti, prodibat resistentia argenti vivi in ea ratione ad resistentiam aquæ quam habet numerus 12 vel 10 ad 1 circiter. Sed experimento priori magis fidendum est, propterea quod in his ultimis vas nimis angustum fuit pro magnitudine Globi immersi. Ampliato Globo, deberet etiam vas ampliari. Constitueram quidem hujusmodi experimenta in vasis majoribus & in liquoribus tum Metallorum fusorum, tum aliis quibusdam tam calidis quam frigidis repetere: sed omnia experiri non vacat, & ex jam descriptis satis liquet resistentiam corporum celeriter motorum densitati Fluidorum in quibus moventur proportionalem esse quamproxime. Non dico accurate. Nam Fluida tenaciora pari densitate proculdubio magis resistunt quam liquidiora, ut oleum frigidum quam calidum, calidum quam aqua pluvialis, aqua quam Spiritus vini. Verum in liquoribus qui ad sensum satis fluidi sunt, ut in Aere, in aqua seu dulci seu falsa, in Spiritibus vini, Terebinthi & Salium, in Oleo a fœcibus per destillationem liberato & calefacto, Oleoque Vitrioli & Mercurio, ac Metallis liquefactis, & siqui sint alii, qui tam Fluidi sunt ut in vasis agitati motum impressum diutius conservent, effusique liberrime in guttas decurrendo resolvantur, nullus dubito quin regula allata satis accurate obtineat: præsertim si experimenta in corporibus pendulis & majoribus & velocius motis instituantur.
Quare cum Globus aqueus in aere movendo resistentiam patiatur qua motus sui pars , interea dum longitudinem semidiametri suæ describat (ut jam ante ostensum est) tollatur, sitque densitas aeris ad densitatem aquæ ut 800 vel 850 ad 1 circiter, consequens est ut hæc Regula generaliter obtineat. Si corpus quodlibet Sphæricum in Medio quocunque satis Fluido moveatur, & spectetur resistentiæ pars illa sola quæ est in duplicata ratione velocitatis, haec pars erit ad vim quæ totum corporis motum, interea dum corpus idem longitudinem duarum ipsius semidiametrorum motu illo uniformiter continuato describat, vel tollere posset vel eundem generare, ut densitas Medii ad densitatem corporis quamproxime. Igitur resistentia quasi triplo major est quam pro lege in Corollario primo Propositionis xxxviii. allata; & propterea partes quasi duae tertiæ motus illius omnis quem Globi partes anticæ movendo imprimunt in Medium, restituuntur in Globi partes posticas a Medio in orbem reduente, inque spatium irruente quod Globus alias vacuum post se relinqueret. Unde si velocitas Globi eousque augeatur ut Medium non posset adeo celeriter in spatium illud irruere, quin aliquid vacui a tergo Globi semper relinquatur, resistentia tandem evadet quasi triplo major quam pro Regula generali novissime posita.
Hactenus experimentis usi sumus oscillantium pendulorum, eo quod eorum motus facilius & accuratius observari & mensurari possint. Motus autem pendulorum in gyrum actorum & in orbem redeundo circulos describentium, propterea quod sint uniformes & eo nomine ad investigandam resistentiam datæ velocitati competentem longe aptiores videantur, in consilium etiam adhibui. Faciendo enim ut pendulum circulariter latum duodecies revolveretur, notavi magnitudines circulorum duorum, quos prima & ultima revolutione descripsit. Et inde collegi velocitates corporis sub initio & fine. Tum dicendo quod corpus, velocitate mediocri describendo circulos duodecim mediocres, amitteret velocitatum illarum differentiam, collegi resistentiam qua differentia illa eo omni corporis per circulos duodecim itinere amitti posset; & resistentia inventa, quanquam hujus generis experimenta minus accurate tentare licuit, probe tamen cum præcedentibus congruebat.
Denique cum receptissima Philosophorum ætatis hujus opinio sit, Medium quoddam æthereum & longe subtilissimum extare, quod omnes omnium corporum poros & meatus liberrime permeet; a tali autem Medio per corporum poros fluente resistentia oriri debeat: ut tentarem an resistentia, quam in motis corporibus experimur, tota sit in eorum externa superficie, an vero partes etiam internæ in superficiebus propriis resistentiam notabilem sentiant, excogitavi experimentum tale. Filo pedum undecim longitudinis, ab unco chalybeo satis firmo, mediante annulo chalybeo, suspendebam pyxidem abiegnam rotundam, ad constituendum pendulum longitudinis prædictæ. Uncus sursum præacutus erat acie concava, ut annulus arcu suo superiore aciei innixus liberrime moveretur. Arcui autem inferiori annectebatur filum. Pendulum ita constitutum deducebam a perpendiculo ad distantiam quasi pedum sex, idque secundum planum aciei unci perpendiculare, ne annulus, oscillante Pendulo, supra aciem unci ultro citroque laberetur. Nam punctum suspensionis in quo annulus uncum tangit, immotum manere debet. Locum igitur accurate notabam, ad quem deduxeram pendulum, dein pendulo demisso notabam alia tria loca ad quæ redibat in fine oscillationis primæ, secundæ ac tertiæ. Hoc repetebam sæpius, ut loca illa quam potui accuratissime invenirem. Tum pyxidem plumbo & gravioribus, quæ ad manus erant, metallis implebam. Sed prius ponderabam pyxidem vacuam, una cum parte sili quæ circum pyxidem volvebatur ac dimidio partis reliquæ quæ inter uncum & pyxidem pendulam tendebatur. (Nam filum tensum dimidio ponderis sui pendulum a perpendiculo digressum semper urget.) Huic ponderi addebam pondus aeris quam pyxis capiebat. Et pondus totum erat quasi pars septuagesima octava pyxidis metallorum plenæ. Tum quoniam pyxis Metallorum plena, pondere suo tendendo filum, augebat longitudinem penduli, contrahebam filum ut penduli jam oscillantis eadem esset longitudo ac prius. Dein pendulo ad locum primo notatum distracto ac dimisso, numerabam oscillationes quasi septuaginta & septem, donec pyxis ad locum secundo notatum rediret, totidemque subinde donec pyxis ad locum tertio notatum rediret, atque rursus totidem donec pyxis reditu suo attingeret locum quartum. Unde concludo quod resistentia tota pyxidis plenæ non majorem habebat proportionem ad resistentiam pyxidis vacuæ quam 78 ad 77. Nam si æquales essent ambarum resistentiæ, pyxis plena ob vim suam insitam septuagies & octies majorem vi insita pyxidis vacui, motum suum oscillatorium tanto diutius conservare deberet, atque adeo completis semper oscillationibus 78 ad loca illa notata redire. Rediit autem ad eadem completis oscillationibus 77.
Designet igitur A resistentiam pyxidis in ipisius superficie externa, & B resistentiam pyxidis vacuæ in partibus internis; & si resistentiæ corporum æquivelocium in partibus internis sint ut materia, seu numerus particularum quæ resistuntur: erit resistentia pyxidis plenæ in ipsius partibus internis: adeoque pyxidis vacuæ resistentia tota erit ad pyxidis plenæ resistentiam totam ut 77 ad 78, & divisim ad ut 77, ad 1, indeque ad B ut ad 1, & divisim A ad B ut 5928 ad 1. Est igitur resistentia pyxidis vacuæ in partibus internis quinquies millies minor quam ejusdem resistentia in externa superficie, & amplius. Sic disputamus ex hypothesi quod major illa resistentia pyxidis plenæ oriatur ab actione Fluidi alicujus subtilis in Metallum inclusum. At causam longe aliam esse opinor. Nam tempora oscillationum pyxidis plenæ minora sunt quam tempora oscillationum pyxidis vacuæ, & propterea resistentia pyxidis plenæ in externa superficie major est, pro ipsius velocitate & longitudine spatii oscillando descripti, quam ea pyxidis vacuæ. Quod cum ita sit, resistentia pyxidum in partibus internis aut nulla erit aut plane insensibilis.
<354>Hoc experimentum recitavi memoriter. Nam charta, in qua illud aliquando descripseram, intercidit. Unde fractas quasdam numerorum partes, quæ memoria exciderunt, omittere compulsus sum. Nam omnia denuo tentare non vacat. Prima vice, cum unco infirmo usus essem, pyxis plena citius retardabatur. Causam quærendo, reperi quod uncus infirmus cedebat ponderi pyxidis, & ejus oscillationibus obsequendo in partes omnes flectetabur. Parabam igitur uncum firmum, ut punctum suspensionis immotum maneret, & tunc omnia ita evenerunt uti supra descripsimus.
Eadem methodo qua invenimus resistentiam corporum Sphæricorum in Aqua & argento vivo, inveniri potest resistentia corporum figurarum aliarum; & sic Navium figuræ variæ in Typis exiguis contructæ inter se conferri, ut quænam ad navigandum aptissimæ sint, sumptibus parvis tentetur.
SECT. VIII.
De Motu per Fluida propagato.
Prop. XLI. Theor. XXXI.
Pressio non propagatur per Fluidum secundum lineas rectas, nisi ubi particulæ Fluidi in directum jacent.
Si jaceant particulæ a, b, c, d, e in linea recta, potest quidem pressio directe propagari ab a ad e; at  particula e urgebit particulas oblique positas f & g oblique, & particulæ illæ f & g non sustinebunt pressionem illatam, nisi fulciantur a particulis ulterioribus h & k; quatenus autem fulciuntur, premunt particulas fulcientes; & hæ non sustinebunt pressionem nisi fulciantur ab ulterioribus l & m easque premant, & sic deinceps in infinitum. Pressio igitur, quam primum propagatur ad particulas quæ non in directum jacent, divaricare incipiet & oblique propagabitur in infinitum; & postquam incipit oblique propagari, si inciderit in particulas ulteriores, quæ non in directum jacent, iterum divaricabit; idque toties, quoties in particulas non accurate in directum jacentes inciderit. Q.E.D.
particula e urgebit particulas oblique positas f & g oblique, & particulæ illæ f & g non sustinebunt pressionem illatam, nisi fulciantur a particulis ulterioribus h & k; quatenus autem fulciuntur, premunt particulas fulcientes; & hæ non sustinebunt pressionem nisi fulciantur ab ulterioribus l & m easque premant, & sic deinceps in infinitum. Pressio igitur, quam primum propagatur ad particulas quæ non in directum jacent, divaricare incipiet & oblique propagabitur in infinitum; & postquam incipit oblique propagari, si inciderit in particulas ulteriores, quæ non in directum jacent, iterum divaricabit; idque toties, quoties in particulas non accurate in directum jacentes inciderit. Q.E.D.
Corol. Si pressionis a dato puncto per Fluidum propagatæ pars aliqua obstaculo intercipiatur, pars reliqua quæ non intercipitur divaricabit in spatia pone obstaculum. Id quod sic etiam  demonstrari potest. A puncto A propagetur pressio quaquaversum, idque si fieri potest secundum lineas rectas, & obstaculo NBCK perforato in BC, intercipiatur ea omnis, præter partem Coniformem APQ, quæ per foramen circulare BC transit. Planis transversis de, fg, hi distinguatur conus APQ in frusta & interea dum conus ABC, pressionem propagando, urget frustum conicum ulterius degf in superficie de, & hoc frustum urget frustum proximum fgih in superficie fg, & frustum illud urget frustum tertium, & sic deinceps in infinitum; manifestum est (per motus Legem tertiam) quod frustum primum defg, reactione frusti secundi fghi, tantum urgebitur & premetur in superficie fg, quantum urget & premit frustum illud secundum. Frustum igitur degf inter Conum Ade & frustum fhig comprimitur utrinque, & propterea (per Corol. 6. Prop. XIX.) figuram suam servare nequit, nisi vi eadem comprimatur undique. Eodem igitur impetu quo premitur in superficiebus de, fg conabitur cedere ad latera df, eg; ibique (cum rigidum non sit, sed omnimodo Fluidum) excurret ac dilatabitur, nisi Fluidum ambiens adsit, quo conatus iste cohibeatur. Proinde conatu excurrendi premet tam Fluidum ambiens ad latera df, eg quam frustum fghi eodem impetu; & propterea pressio non minus propagabitur a lateribus df, eg in spatia NO, KL hinc inde, quam propagatur a superficie fg versus PQ.Q.E.D.
demonstrari potest. A puncto A propagetur pressio quaquaversum, idque si fieri potest secundum lineas rectas, & obstaculo NBCK perforato in BC, intercipiatur ea omnis, præter partem Coniformem APQ, quæ per foramen circulare BC transit. Planis transversis de, fg, hi distinguatur conus APQ in frusta & interea dum conus ABC, pressionem propagando, urget frustum conicum ulterius degf in superficie de, & hoc frustum urget frustum proximum fgih in superficie fg, & frustum illud urget frustum tertium, & sic deinceps in infinitum; manifestum est (per motus Legem tertiam) quod frustum primum defg, reactione frusti secundi fghi, tantum urgebitur & premetur in superficie fg, quantum urget & premit frustum illud secundum. Frustum igitur degf inter Conum Ade & frustum fhig comprimitur utrinque, & propterea (per Corol. 6. Prop. XIX.) figuram suam servare nequit, nisi vi eadem comprimatur undique. Eodem igitur impetu quo premitur in superficiebus de, fg conabitur cedere ad latera df, eg; ibique (cum rigidum non sit, sed omnimodo Fluidum) excurret ac dilatabitur, nisi Fluidum ambiens adsit, quo conatus iste cohibeatur. Proinde conatu excurrendi premet tam Fluidum ambiens ad latera df, eg quam frustum fghi eodem impetu; & propterea pressio non minus propagabitur a lateribus df, eg in spatia NO, KL hinc inde, quam propagatur a superficie fg versus PQ.Q.E.D.
Prop. XLII. Theor. XXXII.
Motus omnis per Fluidum propagatus divergit a recto tramite in spatia immota.
Cas. 1. Propagetur motus a puncto A per foramen BC, pergatque (si fieri potest) in spatio conico BCQP, secundum lineas rectas divergentes a puncto C. Et ponamus primo quod motus iste sit undarum in superficie stagnantis aquæ. Sintque de, fg, hi, kl, &c. undarum singularum partes altissimæ, vallibus totidem intermediis ab invicem distinctæ Igitur quoniam aqua in undarum jugis altior est quam in Fluidi partibus immotis LK, NO, defluet eadem de jugorum terminis e, g, i, l, &c. d, f, h, k, &c. hinc inde versus KL & NO: & quoniam in undarum vallibus depressior est quam in Fluidi partibus immotis KL, NO; defluet eadem de partibus illis immotis undarum valles. Defluxu priore undarum juga, posteriore valles hinc inde dilatantur & propagantur versus KL & NO. Et quoniam motus undarum ab A versus PQ fit per continuum defluxum jugorum in valles proximos, adeoque celerior non est quam pro celeritate descensus & descensus aquæ hinc inde versus KL & NO eadem velocitate peragi debet; propagabitur dilatatio undarum hinc inde versus KL & NO, eadem velocitate qua undæ ipsæ ab A versus PQ recta progrediuntur. Proindeque spatium totum hinc inde versus KL & NO ab undis dilatatis rfgr, shis, tklt, vmnv, &c occupabitur. Q.E.D. Hæc ita se habere quilibet in aqua stagnante experiri potest.
Cas. 2. Ponamus jam quod de, fg, hi, kl, mn designent pulsus a puncto A per Medium Elasticum successive propagatos.  Pulsus propagari concipe per successivas condensationes & rarefactiones Medii, sic ut pulsus cujusque pars densissima Sphæricam occupet superficiem circa centrum A descriptam, & inter pulsus successivos æqualia intercedant intervalla. Designent autem lineæ de, fg, hi, kl, &c. densissimas pulsuum partes per foramen BC propagatas. Et quoniam Medium ibi densius est quam in spatiis hinc inde versus KL & NO, dilatabit sese tam versus spatia illa KL, NO utrinque sita, quam versus pulsuum rariora intervalla; eoque pacto rarius semper evadens e regione intervallorum ac densius e regione pulsuum, participabit eorundem motum. Et quoniam pulsuum progressivus motus oritur a perpetua relaxatione partium densiorum versus antecedentia intervalla rariora; & pulsus eadem celeritate sese in Medii partes quiescentes KL, NO hinc inde relaxare debent; pulsus illi eadem celeritate sese dilatabunt undique in spatia immota KL, NO, qua propagantur directe a centro A; adeoque spatium totum KLON occupabunt. Q.E.D. Hoc experimur in sonis, qui vel domo interposita audiuntur, vel in cubiculum per fenestram admissi sese in omnes cubiculi partes dilatant, inque angulis omnibus audiuntur, non reflexi a parietibus oppositis sed a fenestra directe propagati.
Pulsus propagari concipe per successivas condensationes & rarefactiones Medii, sic ut pulsus cujusque pars densissima Sphæricam occupet superficiem circa centrum A descriptam, & inter pulsus successivos æqualia intercedant intervalla. Designent autem lineæ de, fg, hi, kl, &c. densissimas pulsuum partes per foramen BC propagatas. Et quoniam Medium ibi densius est quam in spatiis hinc inde versus KL & NO, dilatabit sese tam versus spatia illa KL, NO utrinque sita, quam versus pulsuum rariora intervalla; eoque pacto rarius semper evadens e regione intervallorum ac densius e regione pulsuum, participabit eorundem motum. Et quoniam pulsuum progressivus motus oritur a perpetua relaxatione partium densiorum versus antecedentia intervalla rariora; & pulsus eadem celeritate sese in Medii partes quiescentes KL, NO hinc inde relaxare debent; pulsus illi eadem celeritate sese dilatabunt undique in spatia immota KL, NO, qua propagantur directe a centro A; adeoque spatium totum KLON occupabunt. Q.E.D. Hoc experimur in sonis, qui vel domo interposita audiuntur, vel in cubiculum per fenestram admissi sese in omnes cubiculi partes dilatant, inque angulis omnibus audiuntur, non reflexi a parietibus oppositis sed a fenestra directe propagati.
Cas. 3. Ponamus denique quod motus cujuscunque generis propagetur ab A per foramen BC: & quoniam propagatio ista non fit nisi quatenus partes Medii centro A propiores urgent commoventque partes ulteriores; & partes quæ urgentur Fluidæ sunt, ideoque recedunt quaquaversum in regiones ubi minus premuntur: recedent eaedem versus Medii partes omnes quiescentes, tam laterales KL & NO, quam anteriores PQ, eoque pacto motus omnis, quam primum per foramen BC transiit, dilatari incipiet, & abinde tanquam a principio & centro in partes omnes directe propagari. Q.E.D.
Prop. XLIII. Theor. XXXIII.
Corpus omne tremulum in Medio Elastico propagabit motum pulsuum undique in directum; in Medio vero non Elastico motum circularem excitabit.
<359>Cas. 1. Nam partes corporis tremuli vicibus alternis eundo & redeundo, itu suo urgebunt & propellent partes Medii sibi proximas, & urgendo compriment easdem & condensabunt; dein reditu suo sinent partes compressas recedere & sese expandere. Igitur partes Medii corpori tremulo proximæ ibunt & redibunt per vices, ad instar partium corporis illius tremuli: & qua ratione partes corporis hujus agitabant hasce Medii partes, hæ similibus tremoribus agitatæ agitabunt partes sibi proximas, eæque similiter agitatæ agitabunt ulteriores, & sic deinceps in infinitum. Et quemadmodum Medii partes primæ eundo condensantur & redeundo relaxantur, sic partes reliquæ quoties eunt condensabuntur, & quoties redeunt sese expandent. Et propterea non omnes ibunt & simul redibunt (sic enim determinatas ab invicem distantias servando non rarefierent & condensarentur per vices) sed accedendo ad invicem ubi condensantur, & recedendo ubi rarefiunt, aliquæ earum ibunt dum aliæ redeunt; idque vicibus alternis in infinitum. Partes autem euntes & eundo condensatæ, ob motum suum progressivum quo feriunt obstacula, sunt pulsus; & propterea pulsus successivi a corpore omni tremulo in directum propagabuntur; idque æqualibus circiter ab invicem distantiis, ob æqualia temporis intervalla, quibus corpus tremoribus suis singulis singulos pulsus excitat. Q.E.D. Et quanquam corporis tremuli partes eant & redeant secundum plagam aliquam certam & determinatam, tamen pulsus inde per Medium propagati sese dilatabunt ad latera, per Propositionem præcedentem; & a corpore illo tremulo tanquam centrocommuni, secundum superficies propemodum Sphæricas & concentricas, undique propagabuntur. Cujus rei exemplum aliquod habemus in Undis, quæ si digito tremulo excitentur, non solum pergent hinc inde secundum plagam motus digiti, sed, in modum circulorum concentricorum, digitum statim cingent & undique propagabuntur. Nam gravitas undarum supplet locum vis Elasticæ.
Quod si Medium non sit Elasticum: quoniam ejus partes a corporis tremuli partibus vibratis pressæ condensari nequeunt, propagabitur motus in instanti ad partes ubi Medium facillime cedit, hoc est ad partes quas corpus tremulum alioqui vacuas a tergo relinqueret. Idem est casus cum casu corporis in Medio quocunque projecti. Medium cedendo projectilibus, non recedit in infinitum, sed in circulum eundo pergit ad spatia quæ corpus relinquit a tergo. Igitur quoties corpus tremulum pergit in partem quamcunque, Medium cedendo perget per circulum ad partes quæ corpus relinquit, & quoties corpus regreditur ad locum priorem, Medium inde repelletur & ad locum suum priorem redibit. Et quamvis corpus tremulum non sit firmum, sed modis omnibus flexile, si tamen magnitudine datum maneat, quoniam tremoribus suis nequit Medium ubivis urgere, quin alibi eidem simul cedat; efficiet ut Medium, recedendo a partibus ubi premitur, pergat semper in Orbem ad partes quae eidem cedunt.
Corol. Hallucinantur igitur qui credunt agitationem partium flammæ ad pressionem per Medium ambiens secundum lineas rectas propagandam conducere. Debebit ejusmodi pressio non ab agitatione sola partium flammæ sed a totius dilatatione derivari.
Prop. XLIV. Theor. XXXIV.
Si Aqua in canalis cruribus erectis KL, MN vicibus alternis ascendat & descendat; construatur autem Pendulum cujus longitudo inter punctum suspensionis & centrum oscillationis æquetur semissi longitudinis aquæ in Canali: dico quod aqua ascendet & descendet iisdem temporibus quibus pendulum oscillatur.
Longitudinem aquæ mensuro secundum axes canalis & crurum, eandem summæ horum axium æquando. Designent igitur AB, CD mediocrem altitudinem aquæ in crure utroque; & ubi aqua in crure KL ascendit ad altitudinem EF, descenderit aqua in crure MN ad altitudinem GH. Sit autem P corpus pendulum, VP filum, V punctum suspensionis, SPQR Cyclois quam Pendulum describat, P ejus punctum infimum, PQ arcus altitudini AE æqualis. Vis, qua motus aquæ alternis vicibus  acceleratur & retardatur, est excessus ponderis aquæ in alterutro crure supra pondus in altero, ideoque ubi aqua in crure KL ascendit ad EF, & in crure altero descendit ad GH, vis illa est pondus duplicatum aquæ EABF, & propterea est ad pondus aquæ totius ut AE seu PQ ad VP seu PR. Vis etiam, qua pondus P in loco quovis Q acceleratur & retardatur in Cycloide, est ad ejus pondus totum, ut ejus distantia PQ a loco infimo P, ad Cycloidis longitudinem PR. Quare aquæ & penduli, æqualia spatia AE, PQ describentium, vires motrices sunt ut pondera movenda; ideoque vires illæ, si aqua & pendulum in principio, æquali cum velocitate moveantur; pergent eadem temporibus æqualiter movere, efficientque ut motu reciproco simul eant & redeant. Q.E.D.
acceleratur & retardatur, est excessus ponderis aquæ in alterutro crure supra pondus in altero, ideoque ubi aqua in crure KL ascendit ad EF, & in crure altero descendit ad GH, vis illa est pondus duplicatum aquæ EABF, & propterea est ad pondus aquæ totius ut AE seu PQ ad VP seu PR. Vis etiam, qua pondus P in loco quovis Q acceleratur & retardatur in Cycloide, est ad ejus pondus totum, ut ejus distantia PQ a loco infimo P, ad Cycloidis longitudinem PR. Quare aquæ & penduli, æqualia spatia AE, PQ describentium, vires motrices sunt ut pondera movenda; ideoque vires illæ, si aqua & pendulum in principio, æquali cum velocitate moveantur; pergent eadem temporibus æqualiter movere, efficientque ut motu reciproco simul eant & redeant. Q.E.D.
Corol. 1. Igitur aquæ ascendentis & descendentis, sive motus intensior sit sive remissior, vices omnes sunt Isochronæ.
Corol. 2. Si longitudo aquæ totius in canali sit pedum Parisiensium , aqua tempore minuti unius secundi descendet, & tempore minuti alterius secundi ascendet; & sic deinceps vicibus alternis in infinitum. Nam pendulum pedum longitudinis, tempore minuti unius secundi oscillatur.
<362>Corol. 3. Aucta autem vel diminuta longitudine aquæ, augetur vel diminuitur tempus reciprocationis in longitudinis ratione dimidiata.
Prop. XLV. Theor. XXXV.
Vndarum velocitas est in dimidiata ratione latitudinum.
Consequitur ex constructione Propositionis sequentis.
Prop. XLVI. Prob. XI.
Invenire velocitatem Vndarum.
Constituatur Pendulum cujus longitudo inter punctum suspensionis & centrum oscillationis æquetur latitudini Undarum: & quo tempore pendulum illud oscillationes singulas peragit, eodem Undæ progrediendo latitudinem suam propemodum conficient.
Undarum latitudinem voco mensuram transversam quæ vel vallibus imis vel summis culminibus interjacet. Designet ABCDEF superficiem aquæ stagnantis, undis successivis ascendentem ac descendentem, sintque A, C, E, &c. undarum culmina, & B, D, F, &c. valles intermedii. Et quoniam motus undarum fit per aquæ successivum ascensum & descensum, sic ut ejus partes A, C, E, &c. quæ nunc infimæ sunt, mox fiant altissimæ; & vis motrix, qua partes altissimæ descendunt & infimæ ascendunt, est pondus aquæ elevatæ; alternus ille ascensus & descensus analogus erit motui reciproco aquæ in canali, easdemque temporis leges observabit: & propterea (per Prop. XLIV) si distantiæ inter undarum loca altissima A, C, E, & infima B, D, F æquentur duplæ penduli longitudini, partes altissimæ A, C, E tempore oscillationis unius evadent infimæ, & tempore oscillationis alterius denuo ascendent. Igitur inter transitum Undarum singularum tempus erit oscillationum duarum; hoc est Unda describet latitudinem suam, quo tempore pendulum illud bis oscillatur; sed eodem tempore pendulum, cujus longitudo quadrupla est, adeoque æquat undarum latitudinem, oscillabitur semel. Q.E.D.
Corol. 1. Igitur Undæ, quæ pedes Parisienses latæ sunt, tempore minuti unius secundi progrediendo latitudinem suam conficient; adeoque tempore minuti unius primi percurrent pedes , & horæ spatio pedes 11000 quam proxime.
Corol. 2. Et undarum majorum vel minorum velocitas augebitur vel diminuetur in dimidiata ratione latitudinis.
Hæc ita se habent ex Hypothesi quod partes aquæ recta ascendunt vel recta descendunt; sed ascensus & descensus ille verius fit per circulum, ideoque tempus hac Propositione non nisi quamproxime definitum esse affirmo.
Prop. XLVII. Theor. XXXVI.
Pulsuum in Fluido Elastico propagatorum velocitates sunt in ratione composita ex dimidiata ratione vis Elasticæ directe & dimidiata ratione densitatis inverse; si modo Fluidi vis Elastica ejusdem condensationi proportionalis esse supponatur.
Cas. 1. Si Media sint homogenea, & pulsuum distantiæ in his Mediis æquentur inter se, sed motus in uno Medio intensior sit: contractiones & dilatationes partium analogarum erunt ut iidem motus. Accurata quidem non est hæc proportio. Verum tamen nisi contractiones & dilatationes sint valde intensæ, non errabit sensibiliter, ideoque pro Physice accurata haberi potest. Sunt autem vires Elasticæ motrices ut contractiones & dilatationes; & velocitates partium æqualium simul genitæ sunt ut vires. Ideoque æquales & correspondentes pulsuum correspondentium partes, itus & reditus suos per spatia contractionibus & dilatationibus proportionalia, cum velocitatibus quæ sunt ut spatia, simul peragent: & propterea pulsus, qui tempore itus & reditus unius latitudinem suam progrediendo conficiunt, & in loca pulsuum proxime præcedentium semper succedunt, ob æqualitatem distantiarum, æquali cum velocitate in Medio utroque progredientur.
<364>Cas. 2. Sin pulsuum distantiæ seu longitudines sint majores in uno Medio quam in altero; ponamus quod partes correspondentes spatia latitudinibus pulsuum proportionalia singulis vicibus eundo & redeundo describant: & æquales erunt earum contractiones & dilatationes. Ideoque si Media sint homogenea, æquales erunt etiam vires illæ Elasticæ motrices quibus reciproco motu agitantur. Materia autem his viribus movenda, est ut pulsuum latitudo; & in eadem ratione est spatium per quod singulis vicibus eundo & redeundo moveri debent. Estque tempus itus & reditus unius in ratione composita ex ratione dimidiata materiæ & ratione dimidiata spatii, atque adeo ut spatium. Pulsus autem temporibus itus & reditus unius eundo latitudines suas conficiunt, hoc est, spatia temporibus proportionalia percurrunt; & propterea sunt æquiveloces.
Cas. 3. In Mediis igitur densitate & vi elastica paribus, pulsus omnes sunt æquiveloces. Quod si Medii vel densitas vel vis Elastica intendatur, quoniam vis motrix in ratione vis Elasticae, & materia movenda in ratione densitatis augetur; tempus quo motus iidem peragantur ac prius, augebitur in dimidiata ratione densitatis, ac diminuetur in dimidiata ratione vis Elasticæ. Et propterea velocitas pulsuum erit in ratione composita ex ratione dimidiata densitatis Medii inverse & ratione dimidiata vis Elasticæ directe. Q.E.D.
Prop. XLVIII. Theor. XXXVII.
Pulsibus per Fluidum propagatis, singulæ Fluidi particulæ, motu reciproco brevissimo euntes & redeuntes, accelerantur semper & retardantur pro lege oscillantis Penduli.
Designent AB, BC, CD, &c. pulsuum successivorum æquales distantias; ABC plagam motus pulsuum ab A versus B propagati; E, F, G puncta tria Physica Medii quiescentis, in recta AC ad æquales ab invicem distantias sita; Ee, Ff, Gg, spatia æqualia perbrevia per quæ puncta illa motu reciproco singulis vibrationibus eunt & redeunt; ε, φ, γ loca quævis intermedia eorundem punctorum; & EF, FG lineolas Physicas seu Medii partes lineares punctis illis interjectas, & successive translatas in loca εφ, φγ & ef,fg. Rectæ Ee æqualis ducatur recta PS. Bisecetur eadem in O, centroque O & intervallo OP describatur circulus SIPi. Per  hujus circumferentiam totam cum partibus suis exponatur tempus totum vibrationis unius cum ipsius partibus proportionalibus; sic ut completo tempore quovis PH vel PHSh, si demittatur ad PS perpendiculum HL vel hl, & capiatur Ee æqualis PL vel Pl, punctum Physicum E reperiatur in ε. Hac lege punctum quodvis E eundo ab E per ε ad e, & inde redeundo per ε ad E iisdem accelerationis ac retardationis gradibus, vibrationes singulas peraget cum oscillante Pendulo. Probandum est quod singula Medii puncta Physica tali motu agitari debeant. Fingamus igitur Medium tali motu a causa quacunque cieri, & videamus quid inde sequatur.
hujus circumferentiam totam cum partibus suis exponatur tempus totum vibrationis unius cum ipsius partibus proportionalibus; sic ut completo tempore quovis PH vel PHSh, si demittatur ad PS perpendiculum HL vel hl, & capiatur Ee æqualis PL vel Pl, punctum Physicum E reperiatur in ε. Hac lege punctum quodvis E eundo ab E per ε ad e, & inde redeundo per ε ad E iisdem accelerationis ac retardationis gradibus, vibrationes singulas peraget cum oscillante Pendulo. Probandum est quod singula Medii puncta Physica tali motu agitari debeant. Fingamus igitur Medium tali motu a causa quacunque cieri, & videamus quid inde sequatur.
In circumferentia PHSh capiantur æquales arcus HI, IK vel hi, ik, eam habentes rationem ad circumferentiam totam quam habent æquales rectæ EF, FG ad pulsuum intervallum totum BC. Et demissis perpendiculis IM, KN vel im, kn; quoniam puncta E, F, G motibus similibus successive agitantur, si PH vel PHSk sit tempus ab initio motus puncti E, erit PI vel PHSi tempus ab initio motus puncti F, &  PK vel PHSh tempus ab initio motus puncti G; & propterea Eε, Fφ, Gγ erunt ipsis PL, PM, PN in itu punctorum, vel ipsis Pn, Pm, Pl in punctorum reditu, æquales respective. Unde εγ in itu punctorum æqualis erit EG-LN, in reditu autem æqualis EG+ln. Sed εγ latitudo est seu expansio partis Medii EG in loco εγ, & propterea expansio partis illius in itu, est ad ejus expansionem mediocrem ut ad EG; in reditu autem ut seu ad EG. Quare cum sit LN ad KH ut IM ad radium OP, & EG ad BC ut HK ad circumferentiam PHShP, & vicissim EG ad HK ut BC ad circumferentiam PHShP; id est (si circumferentia dicatur Z) ut ad OP, & ex æquo LN ad EG ut IM ad : erit expansio partis EG in loco εγ ad expansionem mediocrem quam habet in loco suo primo EG, ut ad in itu, utque ad in reditu. Unde si dicatur V, erit expansio partis EG, punctive Physici F, ad ejus expansionem mediocrem in itu, ut ad V, in reditu ut ad V; & ejusdem vis elastica ad vim suam elasticam medioin itu, ut ad ; in reditu ut ad . Et eodem argumento vires Elasticæ punctorum Physicorum E & G in itu, sunt ut & ad ; & virium differentia ad Medii vim elasticam mediocrem, ut ad . Hoc est (si ob brevitatem pulsuum supponamus HK & KN indefinite minores esse quantitate V) ut ad , sive ut
ad V. Quare cum quantitas V detur, differentia virium est ut , hoc est (ob proportionales ad HK & OM ad OI vel OP,
PK vel PHSh tempus ab initio motus puncti G; & propterea Eε, Fφ, Gγ erunt ipsis PL, PM, PN in itu punctorum, vel ipsis Pn, Pm, Pl in punctorum reditu, æquales respective. Unde εγ in itu punctorum æqualis erit EG-LN, in reditu autem æqualis EG+ln. Sed εγ latitudo est seu expansio partis Medii EG in loco εγ, & propterea expansio partis illius in itu, est ad ejus expansionem mediocrem ut ad EG; in reditu autem ut seu ad EG. Quare cum sit LN ad KH ut IM ad radium OP, & EG ad BC ut HK ad circumferentiam PHShP, & vicissim EG ad HK ut BC ad circumferentiam PHShP; id est (si circumferentia dicatur Z) ut ad OP, & ex æquo LN ad EG ut IM ad : erit expansio partis EG in loco εγ ad expansionem mediocrem quam habet in loco suo primo EG, ut ad in itu, utque ad in reditu. Unde si dicatur V, erit expansio partis EG, punctive Physici F, ad ejus expansionem mediocrem in itu, ut ad V, in reditu ut ad V; & ejusdem vis elastica ad vim suam elasticam medioin itu, ut ad ; in reditu ut ad . Et eodem argumento vires Elasticæ punctorum Physicorum E & G in itu, sunt ut & ad ; & virium differentia ad Medii vim elasticam mediocrem, ut ad . Hoc est (si ob brevitatem pulsuum supponamus HK & KN indefinite minores esse quantitate V) ut ad , sive ut
ad V. Quare cum quantitas V detur, differentia virium est ut , hoc est (ob proportionales ad HK & OM ad OI vel OP, 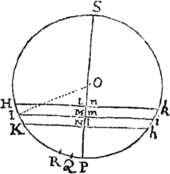 datasque HK & OP) ut OM; id est, si Ff bisecetur in Ω, ut Ωφ. Et eodem argumento differentia virium Elasticarum punctorum Physicorum ε & γ, in reditu lineolæ Physicæ εγ est ut Ωφ. Sed differentia illa (id est excessus vis Elasticæ puncti ε supra vim elasticam puncti γ,) est vis qua interjecta Medii lineola Physica εγ acceleratur; & propterea vis acceleratrix lineolæ Physicæ εγ est ut ipsius distantia a Medio vibrationis loco Ω. Proinde tempus (per Prop. XXXVIII. Lib. I.) recte exponitur per arcum PI; & Medii pars linearis εγ lege præscripta movetur, id est lege oscillantis Penduli: estque par ratio partium omnium linearium ex quibus Medium totum componitur. Q.E.D.
datasque HK & OP) ut OM; id est, si Ff bisecetur in Ω, ut Ωφ. Et eodem argumento differentia virium Elasticarum punctorum Physicorum ε & γ, in reditu lineolæ Physicæ εγ est ut Ωφ. Sed differentia illa (id est excessus vis Elasticæ puncti ε supra vim elasticam puncti γ,) est vis qua interjecta Medii lineola Physica εγ acceleratur; & propterea vis acceleratrix lineolæ Physicæ εγ est ut ipsius distantia a Medio vibrationis loco Ω. Proinde tempus (per Prop. XXXVIII. Lib. I.) recte exponitur per arcum PI; & Medii pars linearis εγ lege præscripta movetur, id est lege oscillantis Penduli: estque par ratio partium omnium linearium ex quibus Medium totum componitur. Q.E.D.
Corol. Hinc patet quod numerus pulsuum propagatorum idem sit cum numero vibrationum corporis tremuli, neque multiplicatur in eorum progressu. Nam lineola Physica εγ, quamprimum ad locum suum primum redierit, quiescet; neque deinceps movebitur, nisi vel ab impetu corporis tremuli, vel ab impetu pulsuum qui a corpore tremulo propagantur, motu novo cieatur. Quiescet igitur quamprimum pulsus a corpore tremulo propagari desinunt.
Prop. XLIX. Prob. XII.
Datis Medii densitate & vi Elastica, invenire velocitatem pulsuum.
Fingamus Medium ab incumbente pondere, pro more Aeris nostri comprimi, sitque A altitudo Medii homogenei, cujus pondus adæquet pondus incumbens, & cujus densitas eadem sit cum densitate Medii compressi, in quo pulsus propagantur. Constitui autem intelligatur Pendulum, cujus longitudo inter punctum suspensionis & centrum oscillationis sit A; & quo tempore pendulum illud oscillationem integram ex itu & reditu compositam peragit, eodem pulsus eundo conficiet spatium circumferentiæ circuli radio A descripti æquale.
Nam stantibus quæ in Propositione superiore constructa sunt, si linea quævis Physica, EF singulis vibrationibus describendo spatium PS, urgeatur in extremis itus & reditus cujusque locis P & S, a vi Elastica quæ ipsius ponderi æquetur; peraget hæc vibrationes singulas quo tempore eadem in Cycloide, cujus Perimeter tota longitudini PS æqualis est, oscillari posset: id adeo quia vires æquales æqualia corpuscula per æqualia spatia simul impellent. Quare cum oscillationum tempora sint in dimidiata ratione longitudinis pendulorum, & longitudo penduli æquetur dimidio arcui Cycloidis totius; foret tempus vibrationis unius ad tempus oscillationis Penduli cujus longitudo est A, in dimidiata ratione longitudinis seu PO ad longitudinem A. Sed vis Elastica qua lineola Physica EG, in locis suis extremis P, S existens, urgetur, erat (in demonstratione Propositionis superioris) ad ejus vim totam Elasticam ut ad V, hoc est (cum punctum K jam incidat in P) ut HK ad V: & vis illa tota, hoc est pondus incumbens, qua lineola EG comprimitur, est ad pondus lineolæ ut ponderis incumbentis altitudo A ad lineolæ longitudinem EG; adeoque ex æquo, vis qua lineola EG in locis suis P & S urgetur, est ad lineolæ illius pondus ut ad . Quare cum tempora, quibus aequalia corpora per æqualia spatia impelluntur, sint reciproce in dimidiata ratione virium, erit tempus vibrationis unius urgente vi illa Elastica, ad tempus vibrationis urgente vi ponderis, in dimidiata ratione ad , atque adeo ad tempus oscillationis Penduli cujus longitudo est A, in dimidiata ratione ad & PO ad A conjunctim; id est (cùm fuerit, in superiore Propositione, V æqualis , & HK æqualis ) in dimidiata ratione ad seu ad hoc est in ratione ad , seu BC ad . Sed tempore vibrationis unius ex itu & reditu compositæ, pulsus progrediendo conficit latitudinem suam BC. Ergo tempus quo pulsus percurrit spatium BC, est ad tempus oscillationis unius ex itu & reditu compositæ, ut BC ad , id est ut BC ad circumferentiam circuli cujus radius est A. Tempus autem, quo pulsus percurret spatium BC, est ad tempus quo percurret longitudinem huic circumferentiæ æqualem, in eadem ratione; ideoque tempore talis oscillationis pulsus percurret longitudinem huic circumferentiæ æqualem. Q.E.D.
Prop. L. Prob. XIII.
Invenire pulsuum distantias.
Corporis, cujus tremore pulsus excitantur, inveniatur numerus Vibrationum dato tempore. Per numerum illum dividatur spatium quod pulsus eodem tempore percurrere possit, & pars inventa erit pulsus unius latitudo. Q.E.I.
Schol.
Spectant Propositiones novissimæ ad motum Lucis & Sonorum. Lux enim cum propagetur secundum lineas rectas, in actione sola (per Prop. XLI. & XLII.) consistere nequit. Soni vero propterea quod a corporibus tremulis oriantur, nihil aliud sunt quàm aeris pulsus propagati, per Prop. XLIII. Confirmatur id ex tremoribus quos excitant in corporibus objectis, si modò vehementes sint & graves, quales sunt soni Tympanorum. Nam tremores celeriores & breviores difficilius excitantur. Sed & sonos quosvis, in chordas corporibus sonoris unisonas impactos, excitare tremores notissimum est. Confirmatnr etiam ex velocitate sonorum. Nam cùm pondera specifica Aquæ pluvialis & Argenti vivi sint ad invicem ut 1 ad circiter, & ubi Mercurius in Barometro altitudinem attingit digitorum Anglicorum 30, pondus specificum Aeris & aquæ pluvialis sint ad invicem ut 1 ad 850 circiter: erunt pondera specifica aeris & argenti vivi ut 1 ad 11617. Proinde cum altitudo argenti vivi sit 30 digitorum, altitudo aeris uniformis, cujus pondus aerem nostrum subjectum comprimere posset, erit 34850 digitorum seu pedum Anglicorum 29042. Estque hæc altitudo illa ipsa quam in constructione superioris Problematis nominavimus A. Circuli radio 29042 pedum descripti circumferentia est pedum 182476. Et cum Pendulum digitos longum, oscillationem ex itu & reditu compositam, tempore minutorum duorum secundorum, uti notum est, absolvat; pendulum pedes 29042, seu digitos 348500, longum, oscillationem consimilem tempore minutorum secundorum absolvere debebit. Eo igitur tempore sonus progrediendo conficiet pedes 182476, adeoque tempore minuti unius secundi pedes 968. Scribit Mersennus, in Balisticæ suæ Prop. XXXV. se factis experimentis invenisse quod sonus minutis quinque secundis hexapedas Gallicas 1150 (id est pedes Gallicos 6900) percurrat. Unde cum pes Gallicus sit ad Anglicum ut 1068 ad 1000, debebit sonus tempore minuti unius secundi pedes Anglicos 1474 conficere. Scribit etiam idem Mersennus Robervallum Geometram clarissimum in Obsidione Theodonis observasse tormentorum fragorem exauditum esse post 13 vel 14 ab igne viso minuta secunda, cùm tamen vix dimidiam Leucam ab illis Tormentis abfuerit. Continer Leuca Gallica hexapedas 2500, adeoque sonus tempore 13 vel 14 secundorum, ex Observatione Robervalli, confecit pedes Parisienses 7500, ac tempore minuti unius secundi pedes Parisienses 560, Anglicos verò 600 circiter. Multum differunt hæ Observationes ab invicem, & computus noster medium locum tenet. In porticu Collegii nostri pedes 208 longa, sonus in termino alterutro excitatus quaterno recursu Echo quadruplicem efficit. Factis autem experimentis inveni quod singulis soni recursibus pendulum quasi sex vel septem digitorum longitudinis oscillabatur, ad priorem soni recursum eundo & ad posteriorem redeundo. Longitudinem penduli satis accuratè definire nequibam: sed longitudine quatuor digitorum, oscillationes nimis celeres esse, ea novem digitorum nimis tardas judicabam. Unde sonus eundo & redeundo confecit pedes 416 minore tempore quàm pendulum digitorum novem, & majore quàm pendulum digitorum quatuor oscillatur; id est minore tempore quàm minutorum tertiorum, & majore quàm ; & propterea tempore minuti unius secundi conficit pedes Anglicos plures quàm 866 & pauciores quàm 1272, atque adeò velocior est quàm pro Observatione Robervalli, ac tardior quàm pro Observatione Mersenni. Quinetiam accuratioribus postea Observationibus definivi quod longitudo penduli major esse deberet quàm digitorum quinque cum semisse, & minor quàm digitorum octo; adeoque quòd sonus tempore minuti unius secundi confecit pedes Anglicos plures quàm 920 & pauciores quàm 1085. Igitur motus sonorum, secundum calculum Geometricum superius allatum, inter hos limites consistens, quadrat cum Phænomenis, quatenus hactenus tentare licuit. Proinde cùm motus iste pendeat ab aeris totius densitate, consequens est quod soni non in motu ætheris vel aeris cujusdam subtilioris, sed in aeris totius agitatione consistat.
Refragari videntur experimenta quædam de sono in vasis aere vacuis propagato, sed vasa aere omni evacuari vix possunt; & ubi satis evacuantur soni notabiliter imminui solent; Ex. gr. Si aeris totius pars tantùm centesima in vase maneat, debebit sonus esse centuplo languidior, atque adeò non minus audiri quàm si quis sonum eundem in aere libero excitatum audiendo, subinde ad decuplam distantiam à corpore sonoro recederet. Conferenda sunt igitur corpora duo æqualiter sonora, quorum alterum in vase evacuato, alterum in aere libero consistat, & quorum distantiæ ab auditore sint in dimidiata ratione densitatum aeris: & si sonus corporis prioris non superat sonum posterioris objectio cessabit.
Cognita sonorum velocitate, innotescunt etiam intervalla pulsuum. Scribit Mersennus (Lib. I. Harmonicorum Prop. IV.) se (factis experimentis quibusdam quæ ibidem describit) invenisse quod nervus tensus vicibus 104 recurrit spatio minuti unius secundi, quando facit Unisonum cum organica Fistula quadrupedali aperta vel bipedali obturata, quam vocant Organarii C fa ut. Sunt igitur pulsus 104 in spatio pedum 968, quos sonus tempore minuti secundi describit: adeoque pulsus unus occupat spatium pedum circiter; id est duplam circiter longitudinem fistulæ. Unde verisimile est quòd latitudines pulsuum, in omnium apertarum fistularum sonis, æquentur duplis longitudinibus fistularum.
Porrò Soni cessante motu corporis sonori statim cessant, neque diutiùs audiuntur ubi longissimè distamus à corporibus sonoris. quàm cum proximè absumus, patet ex Corollario Propositionis XLVIII. Libri hujus. Sed & cur soni in Tubis Stenterophonicis valde augentur, ex allatis principiis manifestum est. Motus enim omnis reciprocus singulis recursibus à causa generante augeri solet. Motus autem in Tubis dilatationem sonorum impedientibus tardiùs amittitur & fortius recurrit, & propterea à motu novo singulis recursibus impresso magis augetur. Et hæc sunt præcipua Phænomena Sonorum.
SECT. IX.
De motu Circulari Fluidorum.
Hypothesis.
REsistentiam, quæ oritur ex defectu lubricitatis partium Fluidi, cæteris paribus, proportionalem esse velocitati, qua partes Fluidi separantur ab invicem.
Prop. LI. Theor. XXXVIII.
Si Cylindrus solidus infinitè longus in fluido uniformi & infinito circa axem positione datum uniformi cum motu revolvatur, & ab hujus impulsu solo agatur Fluidum in Orbem, perseveret autem fluidi pars unaquæque uniformiter in motu suo; dico quod tempora periodica partium fluidi sunt ut ipsarum distantiæ ab axe cylindri.
Sit AFL cylindrus uniformiter 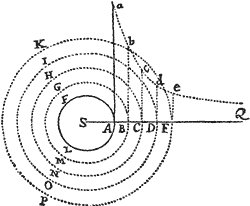 circa axem S in orbem actus, & circulis concentricis BGM, CHN, DIO, EKP, &c. distinguatur fluidum in orbes cylindricos innumeros concentricos solidos ejusdem crassitudinis. Et quoniam homogeneum est Fluidum, impressiones contiguorum orbium in se mutuò factæ, erunt (per Hypothesin) ut eorum translationes ab invicem & superficies contiguæ in quibus impressiones fiunt. Si impressio in Orbem aliquem major est vel minor, ex parte concava quàm ex parte convexa, prævalebit impressio fortior, & motum Orbis vel accelerabit vel retardabit prout in eandem regionem cum ipsius motu, vel in contrariam dirigitur. Proinde ut Orbis unusquisque in motu suo uniformiter perseveret, debent impressiones ex parte utraque sibi invicem æquari, & fieri in regiones contrarias. Unde cùm impressiones sunt ut contiguæ superficies & harum translationes ab invicem, erunt translationes inversè ut superficies, hoc est inversè ut superficierum distantiæ ab axe. Sunt autem differentiæ motuum angularium circa axem ut hæ translationes applicatæ ad distantias, sive ut translationes directè & distantiæ inversè hoc est (conjunctis rationibus) ut quadrata distantiarum inversè. Quare si ad infinitæ rectæ SABCDEQ partes singulas erigantur perpendicula Aa, Bb, Cc, Dd, Ee, &c. ipsarum SA, SB, SC, SD, SE, &c. quadratis reciprocè proportionalia, & per terminos perpendicularium duci intelligatur linea curva Hyperbolica; erunt summæ distantiarum, hoc est motus toti angulares, ut respondentes summæ linearum Aa, Bb, Cc, Dd, Ee: id est, si ad constituendum Medium uniformiter fluidum orbium numerus augeatur & latitudo minuatur in infinitum, ut areæ Hyperbolicæ his summis Analogæ AaQ, BbQ, CcQ, DdQ, EeQ, &c. & tempora motibus angularibus reciprocè proportionalia erunt etiam his areis reciprocè proportionalia. Est igitur tempus periodicum particulæ cujusvis D reciprocè ut area DdQ, hoc est (per notas Curvarum quadraturas) directè ut distantia SD. Q.E.D.
circa axem S in orbem actus, & circulis concentricis BGM, CHN, DIO, EKP, &c. distinguatur fluidum in orbes cylindricos innumeros concentricos solidos ejusdem crassitudinis. Et quoniam homogeneum est Fluidum, impressiones contiguorum orbium in se mutuò factæ, erunt (per Hypothesin) ut eorum translationes ab invicem & superficies contiguæ in quibus impressiones fiunt. Si impressio in Orbem aliquem major est vel minor, ex parte concava quàm ex parte convexa, prævalebit impressio fortior, & motum Orbis vel accelerabit vel retardabit prout in eandem regionem cum ipsius motu, vel in contrariam dirigitur. Proinde ut Orbis unusquisque in motu suo uniformiter perseveret, debent impressiones ex parte utraque sibi invicem æquari, & fieri in regiones contrarias. Unde cùm impressiones sunt ut contiguæ superficies & harum translationes ab invicem, erunt translationes inversè ut superficies, hoc est inversè ut superficierum distantiæ ab axe. Sunt autem differentiæ motuum angularium circa axem ut hæ translationes applicatæ ad distantias, sive ut translationes directè & distantiæ inversè hoc est (conjunctis rationibus) ut quadrata distantiarum inversè. Quare si ad infinitæ rectæ SABCDEQ partes singulas erigantur perpendicula Aa, Bb, Cc, Dd, Ee, &c. ipsarum SA, SB, SC, SD, SE, &c. quadratis reciprocè proportionalia, & per terminos perpendicularium duci intelligatur linea curva Hyperbolica; erunt summæ distantiarum, hoc est motus toti angulares, ut respondentes summæ linearum Aa, Bb, Cc, Dd, Ee: id est, si ad constituendum Medium uniformiter fluidum orbium numerus augeatur & latitudo minuatur in infinitum, ut areæ Hyperbolicæ his summis Analogæ AaQ, BbQ, CcQ, DdQ, EeQ, &c. & tempora motibus angularibus reciprocè proportionalia erunt etiam his areis reciprocè proportionalia. Est igitur tempus periodicum particulæ cujusvis D reciprocè ut area DdQ, hoc est (per notas Curvarum quadraturas) directè ut distantia SD. Q.E.D.
Corol. 1. Hinc motus angulares particularum fluidi sunt reciprocè ut ipsarum distantiæ ab axe Cylindri, & velocitates absolutæ sunt æquales.
Corol 2. Si fluidum in vase cylindrico longitudinis infinitæ contineantur, & cylindrum alium interiorem contineat, revolvatur autem cylindrus uterque circa axem communem, sintque revolutionum tempora ut ipsorum semidiametri, & perseveret fluidi pars unaquæque in motu suo: erunt partium singularum tempora periodica ut ipsarum distantiæ ab axe cylindrorum.
<375>Corol. 3. Si cylindro & fluido ad hunc modum motis addatur vel auferatur communis quilibet motus angularis; quoniam hoc novo motu non mutatur attritus mutuus partium fluidi, non mutabuntur motus partium inter se. Nam translationes partium ab invicem pendent ab attritu. Pars quælibet in eo perseverabit motu, qui attritu utrinque in contrarias partes facto, non magis acceleratur quàm retardatur.
Corol. 4. Unde si toti cylindrorum & fluidi Systemati auferatur motus omnis angularis cylindri exterioris, habebitur motus fluidi in cylindro quiescente.
Corol. 5. Igitur si fluido & cylindro exteriore quiescentibus, revolvatur cylindrus interior uniformiter, communicabitur motus circularis fluido, & paulatim per totum fluidum propagabitur; nec prius desinet augeri quàm fluidi partes singulæ motum Corollario quarto definitum acquirant.
Corol. 6. Et quoniam fluidum conatur motum suum adhuc latius propagare, hujus impetu circumagetur etiam cylindrus exterior nisi violenter detentus; & accelerabitur ejus motus quoad usque tempora periodica cylindri utriusque æquentur inter se. Quod si cylindrus exterior violenter detineatur, conabitur is motum fluidi retardare, & nisi cylindrus interior vi aliqua extrinsecùs impressa motum illum conservet, efficiet ut idem paulatim cesset.
Quæ omnia in aqua profunda stagnante experiri licet.
Prop. LII. Theor. XXXIX.
Si Sphæra solida, in fluido uniformi & infinito, circa axem positione datum uniformi cum motu revolvatur, & ab hujus impulsu solo agatur fluidum in orbem; perseveret autem fluidi pars unaquæque uniformiter in motu suo: dico quod tempora periodica partium fluidi erunt ut quadrata distantiarum à centro Sphæræ. Fig. Prop. LI.
Cas. 1. Sit AFL sphæra uniformiter circa axem S in orbem acta, & circulis concentricis BGM, CHN, DIO, EKP, &c. distinguatur fluidum in orbes innumeros concentricos ejusdem crassitudinis. Finge autem orbes illos esse solidos; & quoniam homogeneum est fluidum, impressiones contiguorum Orbium in se mutuò factæ, erunt (per Hypothesin) ut eorum translationes ab invicem & superficies contiguæ in quibus impressiones fiunt. Si impressio in orbem aliquem major est vel minor ex parte concava quàm ex parte convexa, prævalebit impressio fortior, & velocitatem Orbis vel accelerabit vel retardabit, prout in eandem regionem cum ipsius motu vel in contrariam dirigitur. Proinde ut orbis unusquisque in motu suo perseveret uniformiter, debebunt impressiones ex parte utraque sibi invicem æquari, & fieri in regiones contrarias. Unde cum impressiones sint ut contiguæ superficies & harum translationes ab invicem; erunt translationes inversè ut superficies, hoc est inversè ut quadrata distantiarum superficierum à centro. Sunt autem differentiæ motuum angularium circa axem ut hæ translationes applicatæ ad distantias, sive ut translationes directè & distantiæ inversè hoc est (conjunctis rationibus) ut cubi distantiarum inversè. Quare si ad rectæ infinitæ SABCDEQ partes singulas erigantur perpendicula Aa, Bb, Cc, Dd, Ee, &c. ipsarum SA, SB, SC, SD, SE, &c. cubis reciprocè proportionalia, erunt summæ distantiarum, hoc est, motus toti angulares, ut respondentes summæ linearum Aa, Bb, Cc, Dd, Ee: id est (si ad constituendum Medium uniformiter fluidum, numerus Orbium augeatur & latitudo minuatur in infinitum) ut areæ Hyperbolicæ his summis analogæ AaQ, BbQ, CcQ, DdQ, EeQ, &c. Et tempora periodica motibus angularibus reciprocè proportionalia erunt etiam his areis reciprocè proportionalia. Est igitur tempus periodicum orbis cujusvis DIO reciprocè ut area DdQ, hoc est, (per notas Curvarum quadraturas) directè ut quadratum distantiæ SD. Id quod volui primò demonstrare.
Cas. 2. A centro Sphæræ ducantur infinitaeæ rectæ quam plurimæ, quæ cum axe datos contineant angulos, æqualibus differentiis se mutuò superantes; & his rectis circa axem revolutis concipe orbes in an nulos innumeros secari; & annulus unusquisque habebit annulos quatuor sibi contiguos, unum interiorem, alterum exteriorem & duos laterales. Attritu interioris & exterioris non potest annulus unusquisque, nisi in motu juxta legem casus primi facto, æqualiter & in partes contrarias urgeri. Patet hoc ex demonstratione casus primi. Et propterea annulorum series quælibet à globo in infinitum rectà pergens movebitur pro lege casus primi, nisi quatenus impeditur ab attritu annulorum ad latera. At in motu hac lege facto, attritus annulorum ad latera nullus est, neque adeò motum, quo minus hac lege fiat, impediet. Si annuli, qui à centro æqualiter distant, vel citiùs revolverentur vel tardiùs juxta polos quàm juxta æquatorem; tardiores accelerarentur, & velociores retardarentur ab attritu mutuo, & sic vergerent semper tempora periodica ad æqualitatem, pro lege casus primi. Non impedit igitur hic attritus quo minus motus fiat secundum legem casus primi, & propterea lex illa obtinebit: hoc est annulorum singulorum tempora periodica erunt ut quadrata distantiarum ipsorum à centro globi. Quod volui secundo demonstrare.
Cas. 3. Dividatur jam annulus unusquisque sectionibus transversis in particulas innumeras constituentes substantiam absolutè & uniformiter fluidam; & quoniam hæ sectiones non spectant ad legem motus circularis, sed ad constitutionem fluidi solummodo conducunt, perseverabit motus circularis ut priùs. His sectionibus annuli omnes quamminimi asperitatem & vim attritus mutui aut non mutabunt aut mutabunt æqualiter. Et manente causarum proportione manebit effectuum proportio, hoc est proportio motuum & periodicorum temporum. Q.E.D. Cæterum cum motus circularis, & abinde orta vis centrifuga, major sit ad Eclipticam quàm ad polos; debebit causa aliqua adesse qua particulæ singulæ in circulis suis retineantur, ne materia quæ ad Eclipticam est recedat semper à centro & per exteriora Vorticis migret ad polos, indeque per axem ad Eclipticam circulatione perpetua revertatur.
Corol. 1. Hinc motus angulares partium fluidi circa axem globi sunt reciprocè ut quadrata distantiarum à centro globi, & velocitates absolutæ reciprocè ut eadem quadrata applicata ad distantias ab axe.
Corol. 2. Si globus in fluido quiescente similari & infinito circa axem positione datum uniformi cum motu revolvatur, communicabitur motus fluido in morem Vorticis, & motus iste paulatim propagabitur in infinitum; neque prius cessabit in singulis fluidi partibus accelerari, quàm tempora periodica singularum partium sint ut quadrata distantiarum à centro globi.
Corol. 3. Quoniam Vorticis partes interiores ob majorem suam velocitatem atterunt & urgent exteriores, motumque ipsis ea actione perpetuò communicant, & exteriores illi eandem motus quantitatem in alios adhuc exteriores simul transferunt, eaque actione servant quantitatem motus sui planè invariatam; patet quod motus perpetuò transfertur à centro ad circumferentiam Vorticis, & per infinitatem circumferentiæ absorbetur. Materia inter sphæricas duas quasvis superficies Vortici concentricas nunquam accelerabitur, eò quod motum omnem à materia interiore acceptum transfert semper in exteriorem.
Corol. 4. Proinde ad conservationem Vorticis constanter in eodem movendi statu, requiritur principium aliquod activum à quo globus eandem semper quantitatem motus accipiat quam imprimit in materiam vorticis. Absque tali principio necesse est ut globus & Vorticis partes interiores, propagantes semper motum suum in exteriores, neque novum aliquem motum recipientes, tardescant paulatim & in orbem agi desinant.
Corol. 5. Si globus alter huic Vortici ad certam ab ipsius centro distantiam innataret, & interea circa axem inclinatione datum vi aliqua constanter revolveretur; hujus motu raperetur fluidum in vorticem: & primò revolveretur hic vortex novus & exiguus una cum globo circa centrum alterius, & interea latiùs serperet ipsius motus, & paulatim propagaretur in infinitum, ad modum vorticis primi. Et eadem ratione qua hujus globus raperetur motu vorticis alterius, raperetur etiam globus alterius motu hujus, sic ut globi duo circa intermedium aliquod punctum revolverentur, seque mutuò ob motum illum circularem fugerent, nisi per vim aliquam cohibiti. Postea si vires constanter impressæ, quibus globi in motibus suis perseverant, cessarent, & omnia legibus Mechanicis permitterentur, languesceret paulatim motus globorum (ob rationem in Corol. 3. & 4. assignatam) & vortices tandem conquiescerent.
Corol. 6. Si globi plures datis in locis circum axes positione datos certis cum velocitatibus constanter revolverentur, fierent vortices totidem in infinitum pergentes. Nam globi singuli, eadem ratione qua unus aliquis motum suum propagat in infinitum, propagabunt etiam motus suos in infinitum, adeò ut fluidi infiniti pars unaquæque eo agitetur motu qui ex omnium globorum actionibus resultat. Unde vortices non definientur certis limitibus, sed in se mutuò paulatim excurrent; globique per actiones vorticum in se mutuò perpetuò movebuntur de locis suis; uti in Lemmate superiore expositum est; neque certam quamvis inter se positionem servabunt, nisi per vim aliquam retenti. Cessantibus autem viribus illis quæ in globos constanter impressæ conservant hosce motus, materia ob rationem in Corollario tertio & quarto assignatam paulatim requiescet & in vortices agi desinet.
Corol. 7. Si Fluidum similare claudatur in vase sphærico, ac globi in centro consistentis uniformi rotatione agatur in vorticem, globus autem & vas in eandem partem circa axem eundem revolvantur, sintque eorum tempora periodica ut quadrata semidiametrorum: partes fluidi non prius perseverabunt in motibus suis sine acceleratione & retardatione, quàm sint eorum tempora periodica ut quadrata distantiarum à centro vorticis. Alia nulla Vorticis constitutio potest esse permanens.
Corol. 8. Si vas, Fluidum inclusum & globus servent hunc motum, & motu præterea communi angulari circa axem quemvis datum revolvantur; quoniam hoc motu novo non mutatur attritus partium fluidi in se invicem, non mutabuntur motus partium inter se. Nam translationes partium inter se pendent ab attritu. Pars quælibet in eo perseverabit motu, quo fit ut attritu ex uno latere non magis tardetur quàm acceleretur attritu ex altero.
<380>Corol. 9. Unde si vas quiescat ac detur motus globi, dabitur motus fluidi. Nam concipe planum transire per axem globi & motu contrario revolvi; & pone tempus revolutionis hujus esse ad summam hujus temporis & temporis revolutionis globi, ut quadratum semidiametri vasis ad quadratum semidiametri globi: & tempora periodica partium fluidi respectu plani hujus erunt ut quadrata distantiarum suarum à centro globi.
Corol. 10. Proinde si vas vel circa axem eundem cum globo, vel circa diversum aliquem, data cum velocitate quacunque moveatur, dabitur motus fluidi. Nam si Systemati toti auferatur vasis motus angularis, manebunt motus omnes iidem inter se qui prius, per Corol. 8. Et motus isti per Corol. 9. dabuntur.
Corol. 11. Si vas & fluidum quiescant & globus uniformi cum motu revolvatur, propagabitur motus paulatim per fluidum totum in vas, & circumagetur vas nisi violenter detentum, neque prius desinent fluidum & vas accelerari, quàm sint eorum tempora periodica æqualia temporibus periodicis globi. Quod si vas vi aliqua detineatur vel revolvatur motu quovis constanti & uniformi, deveniet Medium paulatim ad statum motus in Corollariis 8.9 & 10 definiti, nec in alio unquam statu quocunque perseverabit. Deinde verò si, viribus illis cessantibus quibus vas & globus certis motibus revolvebantur, permittatur Systema totum Legibus Mechanicis; vas & globus in se invicem agent mediante fluido, neque motus suos in se mutuò per fluidum propagare prius cessabunt, quàm eorum tempora periodica æquantur inter se, & Systema totum ad instar corporis unius solidi simul revolvatur.
Scholium.
In his omnibus suppono fluidum ex materia quoad densitatem & fluiditatem uniformi constare. Tale est in quo globus idem eodem cum motu, in eodem temporis intervallo, motus similes & æquales, ad æquales semper à distantias, ubivis in fluido constitutus, propagare possit. Conatur quidem materia per motum suum circularem recedere ab axe Vorticis, & propterea premit materiam omnem ulteriorem. Ex hac pressione fit attritus partium fortior & separatio ab invicem difficilior; & per consequens diminuitur materiæ fluiditas. Rursus si partes fluidi sunt alicubi crassiores seu majores, fluiditas ibi minor erit, ob pauciores superficies in quibus partes separentur ab invicem. In hujusmodi casibus deficientem fluiditatem vel lubricitate partium vel lentore aliave aliqua conditione restitui suppono. Hoc nisi fiat, materia ubi minùs fluida est magis cohærebit & segnior erit, adeoque motum tardiùs recipiet & longiùs propagabit quàm pro ratione superiùs assignata. Si figura vasis non sit Sphaæica, movebuntur particulæ in lineis non circularibus sed conformibus eidem vasis figuræ, & tempora periodica erunt ut quadrata mediocrium distantiarum à centro quamproximè. In partibus inter centrum & circumferentiam, ubi latiora sunt spatia, tardiores erunt motus, ubi angustiora velociores; neque tamen particulæ velociores petent circumferentiam. Arcus enim describent minus curvos, & conatus recedendi à centro non minus diminuetur per decrementum hujus curvaturæ, quàm augebitur per incrementum velocitatis. Pergendo à spatiis angustioribus in latiora recedent paulò longiùs à centro, sed isto recessu tardescent; & accedendo postea de latioribus ad angustiora accelerabuntur, & sic per vices tardescent & accelerabuntur particulæ singulæ in perpetuum. Hæc ita se habebunt in vase rigido. Nam in fluido infinito constitutio Vorticum innotescit per Propositionis hujus Corollarium sextum.
Proprietates autem Vorticum hac Propositione investigare conatus sum, ut pertentarem siqua ratione Phænomena cœlestia per Vortices explicari possint. Nam Phænomenon est quod Planetarum circa Jovem revolventium tempora periodica sunt in ratione sesquialtera distantiarum à centro Jovis; & eadem Regula obtinet in Planetis qui circa Solem revolvuntur. Obtinent autem hæ Regulæ in Planetis utrisque quam accuratissimè, quatenus observationes Astronomicæ hactenus prodidêre. Ideoque si Planetæ illi à Vorticibus circa Jovem & Solem revolventibus deferantur, debebunt etiam hi Vortices eadem lege revolvi. Verum tempora periodica partium Vorticis prodierunt in ratione duplicata distantiarum à centro motus: neque potest ratio illa diminui & ad rationem sesquialteram reduci, nisi vel materia vorticis eo fluidior sit quo longius distat à centro, vel resistentia, quæ oritur ex defectu lubricitatis partium fluidi, ex aucta velocitate qua partes fluidi separantur ab invicem, augeatur in majori ratione quàm ea est in qua velocitas augetur. Quorum tamen neutrum rationi consentaneum videtur. Partes crassiores & minus fluidæ (nisi graves sint in centrum) circumferentiam petent; & verisimile est quod, etiamsi Demonstrationum gratia Hypothesin talem initio Sectionis hujus proposuerim ut Resistentia velocitati proportionalis esset, tamen Resistentia in minori sit ratione quàm ea velocitatis est. Quo concesso tempora periodica partium Vorticis erunt in majori quàm duplicata ratione distantiarum ab ipsius centro. Quod si vortices (uti aliquorum est opinio) celeriùs moveantur prope centrum, dein tardiùs usque ad certum limitem, tum denuò celeriùs juxta circumferentiam; certè nec ratio sesquialtera neque alia quævis certa ac determinata obtinere potest. Viderint itaque Philosophi quo pacto Phænomenon illud rationis sesquialteræ per Vortices explicari possit.
Prop. LIII. Theor. XL.
Corpora quæ in Vortice delata in orbem redeunt ejusdem sunt densitatis cum Vortice, & eadem lege cum ipsius partibus (quoad velocitatem & cursus determinationem) moventur.
Nam si vorticis pars aliqua exigua, cujus particulæ seu puncta physica datum servant situm inter se, congelari supponatur: hæc, quoniam neque quoad densitatem suam, neque quoad vim insitam aut figuram suam mutatur, movebitur eadem lege ac prius: & contra, si Vorticis pars congelata & solida ejusdem sit densitatis cum reliquo vortice, & resolvatur in fluidum; movebitur hæc eadem lege ac prius, nisi quatenus ipsius particulæ jam fluidæ factæ moveantur inter se. Negligatur igitur motus particularum inter se, tanquam ad totius motum progressivum nil spectans, & motus totius idem erit ac prius. Motus autem idem erit cum motu aliarum Vorticis partium à centro æqualiter distantium, propterea quod solidum in Fluidum resolutum fit pars Vorticis cæteris partibus consimilis. Ergo solidum, si sit ejusdem densitatis cum materia Vorticis, eodem motu cum ipsius partibus movebitur, in materia proximè ambiente relative quiescens. Sin densius sit, jam magis conabitur recedere à centro Vorticis quàm priùs; adeoque Vorticis vim illam, qua priùs in Orbita sua tanquam in æquilibrio constitutum retinebatur, jam superans, recedet à centro & revolvendo describet Spiralem, non amplius in eundem Orbem rediens. Et eodem argumento si rarius sit, accedet ad centrum. Igitur non redibit in eundem Orbem nisi sit ejusdem densitatis cum fluido. Eo autem in casu ostensum est, quod revolveretur eadem lege cum partibus fluidi à centro Vorticis æqualiter distantibus. Q.E.D.
Corol. 1. Ergo solidum quod in Vortice revolvitur & in eundem Orbem semper redit, relativè quiescit in fluido cui innatat.
Corol. 2. Et si vortex sit quoad densitatem uniformis, corpus idem ad quamlibet à centro Vorticis distantiam revolvi potest.
Scholium.
Hinc liquet Planetas à Vorticibus corporeis non deferri. Nam Planetæ secundum Hypothesin Copernicæam circa Solem delati revolvuntur in Ellipsibus umbilicum habentibus in Sole & radiis ad Solem ductis areas describunt temporibus proportionales. At partes Vorticis tali motu revolvi nequeunt. Designent AD, BE, CF, orbes tres circa Solem S descriptos, quorum extimus CF circulus fit Soli concentricus, & interiorum duorum Aphelia sint A, B, & Perihelia D, E. Ergo corpus quod revolvitur in orbe CF, radio ad Solem ducto areas temporibus proportionales describendo, movebitur uniformi cum motu. Corpus autem quod revolvitur in Orbe BE, tardiùs movebitur in Aphelio B & velociùs in Perihelio C, secundum leges Astronomicas; cum tamen secundum leges Mechanicas materia Vorticis in spatio angustiore inter A & C velociùs moveri debeat quàm in spatio latiore inter D & F; id est in Aphelio velociùs quàm in Perihelio. Quæ duo repugnant inter se. Sic 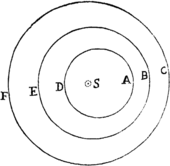 in principio Signi Virginis, ubi Aphelium Martis jam versatur, distantia inter orbes Martis & Veneris est ad distantiam eorundem orbium in principio Signi Piscium ut tria ad duo circiter, & propterea materia Vorticis inter Orbes illos in principio Piscium debet esse velocior quàm in principio Virginis in ratione trium ad duo. Nam quo angustius est spatium per quod eadem Materiæ quantitas eodem revolutionis unius tempore transit, eo majori cum velocitate transire debet. Igitur si Terra in hac Materia cœlesti relativè quiescens ab ea deferretur, & una circa Solem revolveretur, foret hujus velocitas in principio Piscium ad ejusdem velocitatem in principio Virginis in ratione sesquialtera. Unde Solis motus diurnus apparens in principio Virginis major esset quàm minutorum primorum septuaginta, & in principio Piscium minor quàm minutorum quadraginta & octo: cum tamen (experientia teste) apparens iste Solis motus major sit in principio Piscium quàm in principio Virginis, & propterea Terra velocior in principio Virginis quàm in principio Piscium. Itaque Hypothesis Vorticum cum Phænomenis Astronomicis omninò pugnat, & non tam ad explicandos quàm ad perturbandos motus cœlestes conducit. Quomodo verò motus isti in spatiis liberis absque Vorticibus peraguntur intelligi potest ex Libro primo, & in Mundi Systemate pleniùs docebitur.
in principio Signi Virginis, ubi Aphelium Martis jam versatur, distantia inter orbes Martis & Veneris est ad distantiam eorundem orbium in principio Signi Piscium ut tria ad duo circiter, & propterea materia Vorticis inter Orbes illos in principio Piscium debet esse velocior quàm in principio Virginis in ratione trium ad duo. Nam quo angustius est spatium per quod eadem Materiæ quantitas eodem revolutionis unius tempore transit, eo majori cum velocitate transire debet. Igitur si Terra in hac Materia cœlesti relativè quiescens ab ea deferretur, & una circa Solem revolveretur, foret hujus velocitas in principio Piscium ad ejusdem velocitatem in principio Virginis in ratione sesquialtera. Unde Solis motus diurnus apparens in principio Virginis major esset quàm minutorum primorum septuaginta, & in principio Piscium minor quàm minutorum quadraginta & octo: cum tamen (experientia teste) apparens iste Solis motus major sit in principio Piscium quàm in principio Virginis, & propterea Terra velocior in principio Virginis quàm in principio Piscium. Itaque Hypothesis Vorticum cum Phænomenis Astronomicis omninò pugnat, & non tam ad explicandos quàm ad perturbandos motus cœlestes conducit. Quomodo verò motus isti in spatiis liberis absque Vorticibus peraguntur intelligi potest ex Libro primo, & in Mundi Systemate pleniùs docebitur.
