History of the Method of Fluxions

<146r>

The History of the Method of \Series/ Fluxions & Moments.

D^r Wallis in his Opus Arithmeticum published A.C. 1657 cap 33 Prop. 68 reduced the fraction $\frac{\mathrm{A}}{1-\mathrm{R}}$ by perpetual division into the series AR ${\mathrm{AR}}^2+{\mathrm{AR}}^3+{\mathrm{AR}}^4+$&c

M^r Newton in the beginning of the year 1665 found out the reduction of any Dignity of ay Binonial into a series. And by this Reduction the Binomial ${\overline{)\mathrm{P}+\mathrm{P}\mathrm{Q}}}^{\frac{\mathrm{m}}{\mathrm{n}}}$ becomes ${\mathrm{P}}^{\frac{\mathrm{m}}{\mathrm{n}}}+\frac{\mathrm{m}}{\mathrm{n}}\mathrm{A}\mathrm{Q}+\frac{\mathrm{m}-\mathrm{n}}{2\mathrm{n}}\mathrm{B}\mathrm{Q}+\frac{\mathrm{m}-2\mathrm{n}}{3\mathrm{n}}\mathrm{C}\mathrm{Q}+\frac{\mathrm{m}-3\mathrm{n}}{4\mathrm{n}}\mathrm{D}\mathrm{Q}+\mathrm{\&c}$. Vbi $\mathrm{P}+\mathrm{PQ}$ significat Binomium, $\frac{\mathrm{m}}{\mathrm{n}}$ P primum terminum binomij. Q reliquos terminos divisos per primum. Et $\frac{\mathrm{m}}{\mathrm{n}}$ indicem dignitatis ipsius $\mathrm{P}+\mathrm{P}\mathrm{Q}$.

In the \wir\n/ter between/ beginning of the years \1664 &/ 1665 \{rson}/ M^r Newton \(now S^r Isaac Newton)/ by trying to interpole a series of D^r Wallis, found for squaring the circle [Yet y^e radius of a circle be 1 & the sine \Abscissa/ of an Arch be x & the Ordinates $\sqrt{1-\mathrm{x}\mathrm{x}}$ & the Area of the segment described by the Ordinate while x increases will be $\mathrm{x}-\frac{\frac{1}{3}{\mathrm{x}}^3}{3}-\frac{\frac{1}{8}{\mathrm{x}}^5}{5}-$] M^r found out the series for squaring the circle & Hyperbola & their segments. Let the radius of a circle be 1 & the Abscissa x & the Ordinate $\sqrt{1-\mathrm{x}\mathrm{x}}$ & the segment described by the Ordinate while the Abscissa increases will be $\mathrm{x}-\frac{1}{6}{\mathrm{x}}^3-\frac{1}{40}{\mathrm{x}}^5-\frac{1}{112}{\mathrm{x}}^7-\frac{5}{1152}{\mathrm{x}}^9-\mathrm{\&c}$. And if $\sqrt{1+\mathrm{x}\mathrm{x}}$ be y^e rectangular Ordinate of the Hyperbola the segment will be $\mathrm{x}+\frac{1}{6}{\mathrm{x}}^3-\frac{1}{40}{\mathrm{x}}^5+\frac{1}{112}{\mathrm{x}}^7-\frac{5}{1152}{\mathrm{x}}^9+\mathrm{\&c}$. And at the same time he found out also the reducing of di the dignities of Binomials into converging series, & the extraction of roots both single & affected in such series, & before the end next winter he found, the solution of this Probleme Data Æquatione fluentes quotcun quantitates involvente fluxiones invenire. Per fluxiones intelligo velocitates quibus quantitates (quas fluentes voco) augentur vel mutantur. Sit x \Abscissa/ $\mathrm{AB}=\mathrm{x}$ Abscissa figuræ curvilineæ ABC, et $\mathrm{BC}=\mathrm{y}$ Ordinata ejusdem Figuræ cujuscun curvilineæ ACB Abscissa AB vocetur x, & Ordinata \rectangula/ BC vocetur y, & Area ACB 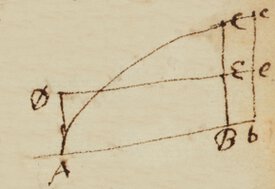vocetur z] And th the next winter he found his Theory of refractions & colours & in the next year he found how to proceed in his method of fluxions w^thout stopping at fractions or surds. And

And that time Vicount Brounker squared the Hyperbola by this series $\frac{1}{1\times 2}+\frac{1}{3\times 4}+\frac{1}{5\times 6}+\frac{1}{7\times 8}+\mathrm{\&c}$, that is by this $1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\frac{1}{6}+\frac{1}{7}-\frac{1}{8}+\mathrm{\&c}$, conjoyning every two terms into one. And the Quadrature was published in the Philosophical Transactions for April 1668.

Ejus anni mense Septembri D. Mercator published a Demonstration \his Logarithmotechnia with a/ Demonstration of this Quadrature by the Division of this Quadrature D^r Wallis. And soon after that M^r Iames Gregory published a Demonstration Geometrical Demonstration thereof. And these Books were a few months after sent by M^r Iohn Collins to D^r Barrow at Cambridge & by D^r Barrow communicated in May or Iune 1669 to M^r Newton. Whereupon D^r Barrow \mutually/ sent to M^r Collins a Tract of M^r Newtons entituled Analysis per series numero terminorum infinitas. And in this Analysis the \Author/ shews first \first/ how to reduce the Ordinates of Curvilinear figures into converging series & how by those series to square the Figures. And then he shews how by his method of fluxions to apply this method of Series to the solution of almost all \other/ Problems [about the lengths of Curves the solid contents & superficies of solides, the center] And then adds. [|(|Nec quicquam hujus modi scio ad quod hæc Methodus id varijs modis \se non extendit/ Et quicquid vulgaris Analysis per Æquationes finitas ex finito terminorum numero constantes, (quando id sit possibile) perfici, hæc per æquationes infinitas semper perficiat: ut nil dubitaverim momen Analyseos huic etiam tribuere. Ratiocinia nempe in hac non sunt minus certo sunt quam in illa, nec æquationes minus <146v> exactæ. Deni ad Analytican merito pertinere censeatur, cujus beneficio Curvarum areæ & longitudines &c (id modo fiat) exacte et Geometrice determinentur: Sed ista narrandi non est locus. These last words refer to a method, w^ch is explained in a Letter of M^r Newton to M^r Oldenburg dated 24 Octob. 1676 & more fully in the 5^th Proposition of M^r Newtons Tract de Quadratura Curvarum, & \this method/ is not to be attained without the knowledge of the in & conteined in the first four Propositions of the Bo four preceding Propositions of that Book. And therefore, M^r Newton in the year 1669 had the Method under the Method of fluxions so far as it is conteined in the first four or five Propositions of that Book of Quadratures.

And by the testimony of D^r Barrow & M^r Collins he had it some years before Mercators Logarithmotechnia came abroad. For M^r Collins in a Letter to M^r Strode dated 26 Iuly 1672 writes thus. Haud multo postquam [Mercatoris Logarithmotechnia] in lucem prodijt in publicum prodierat [Mercatoris Logarithmotechnia,] exemplar ejus — Barrovio Cantabrigiam misi, qui quasdam Newtoni chartas [sc. Analysin prædictam per series] extemplo remisit: e quibus et alijs ex alijs quæ OLIM ab auctore cum Barrovio communicata fuerant, patet illam Methodum a dicto Newtono al ALIQVOT ANNIS ANTEA excogitatam et modo universali applicatam fuisse; ita ut ejus ope in quavis Figura curvilinea proposita quæ una cum vel pluribus proprietatibus definitur Quadratura vel Area dictæ figuræ, accurata|ACCVRATA| si possibile sit, sin minus infinite vero propinqua; evolutio vel longitudo lineæ curvæ Centrum gravitatis figuræ, Solida ejus rotatione genita et eorum superficies; sine ulla radicum extractione [per series] obtineri queant. M^r Newton therefore in the year 1676 had the Method of fluxions so far at the least as is is conteined in the first four or five Propositions of the Book of Quadratures.

In the above mentiond Analysis M^r Newton put any letters as x y z for fluents, & any others as p, q, r sometimes represents fluents by the Areas of Curves, fluxions by their ordinates, time by their common Abscissa, moments uniformly increasing, & moments th a moment of time by a any small part of the Abscissa & moments of the fluents by the Ordinates drawn into the moment of time, And & sometimes the moments of time is not exprest but understood by the Ordinates alone, the moment of time being not exprest but understood. And sometimes he denotes the flux|e|nt by the fluxion encompassed with a square. As if $\frac{\mathrm{a}\mathrm{a}}{64\mathrm{x}}$ be the fluxion a be a given quantity & x be the time & $\frac{\mathrm{a}\mathrm{a}}{64\mathrm{x}}$ the fluxion, he represents the fluent by $\boxed{\frac{\mathrm{a}\mathrm{a}}{64\mathrm{x}}}$

Pag. 182 lin 16 add: except that he doth not confine himself to any set form of symbols.

Pag. 194. lin. 6. This letter of M^r Newton dated Octob. 24 1676 was seen by M^r Collins in Dec \Leibnitz as soon as it came to London that before/ the end of that month For M^r Collins \Leibnitz/ was then at London in his way from Paris into Germany: But he did \not/ stay to take a copy of that {illeg} \long/ Letter along with him. Yet he had time to visit M^r Collins & in hands saw who shewed him many Letters of M^r Newton M^r Gregory & others w^ch ran principally upon series. And it doth not yet appear that he did not then see the A Demonstration of the two \of the two series/ w^ch he desired M^r Oldenburg to procure from M^r Collins & by consequence the Analysis per series numero terminorum infinitas. And that time he procured D^r Barrows Lectures & carried \them/ w^th him into Germany. And when M^r Oldenburg heard that he was arrived at Hannover he sent to him a copy of M^r Newtons Letters of Ianu October 24.

<147v>

Pag. 186. lin. 3. add. For by the Demonstration of finding these two series w^ch he desired M^r Oldenburg to procure from M^r Collins, saying that M^r Collins could easily supply him therewith, he meant the method of finding them conteined in the Analysis per series numero terminorum infinitas

Pag. 197. lin. 15. add. And while he knew th by M^r Newtons Letters that M^r Newton had such a method before the year 1677, he ought not to have published the differential method as his own before he ha without mentioning that correspondence & mention making a candid an acknowledgement as he made in that Letter, of M^r Newtons having in \before/ those days a method like the differential, as he made thereof in that Letter.

In Feb. 1682 M^r Leibnitz published the series of M^r Leibnitz Iames Gregory in the Acta Eruditorum as his own without making any mention of his having received it from M^r Oldenburg & M^r Collins In November\October/ 1682 ––– & 1676. But it was impossible for foreigners to understand this. M^r Leibnits ought to have acknowledged that he undestood by my Letters that I had a Methodus similis w^ch did all this. In the Acta Eruditorum of Iune Pag 198 lin. 32. post Lemmate add. The designe of this Lemm Scholium was not to give away Lemma but to put M^r Leibnitz in mind of the correspondence by w^ch he making a publick \& candid/acknowledgment of this correspondence by \w^ch he had w^th/ w^th M^r Newton \in the year 1696/ by means of M^r Oldenburg [& of what he had learnt by that correspondence], before he l proceeded any further to claim the differential mathod exclusively of M^r Newton For in these Letters w^ch in the year 1676 passed between them, & in another Letter dated 10 Decemb 1672, a copy of w^ch was sent to M^r Oldenburg in Leibnitz in the year 1676, as is mentioned above

Pag. 199. lin.5. Insert. D^r Halley & M^r Ralpson had the Book of Quadratures \in MS/ in their hands in the year 1691 as M^r Ralpson has attested publickly & D^r Halley still attests

Pag. 199|8|. lin 5|1| add insert. M^r Leibnitz published in the Acta Eruditorum for 1689 In Iune anno 1689 M^r Leibnitz Anno 1684 \1683/ ad finem vergente Newtonus \cum Societate Regia (Rogante Halleio)/ \In may 1684 M^r Newton published not \made known that/ he had demonstrated the Proposition of Kepler from the principle of gravity {w^ch} & in autum following sent/ demonstrationem Propositionis Kepleri \communicavit/ Quod |nempe| Planetæ moventur in Ellipsibus & radijs ad Solem \in/ inferiore foco positum ductis areas describunt temporibus proportionales; |& in|sub| Autumno subsequente Demonstrationem ad Halleium misit qui eandem cum Societate Regia mox communicavit.| et Hookius noster qui mecum \cum Newtono/ hac de re contendisse dicitur, nunquam protulit Demonstrationem aliquam. Mathematicus enim non erat.

Anno 1686 mense Maio circiter Newtonus Princip Philosophiæ Naturalis Principia Mathematica ad Societatem Regiam misit ut imprimeretur Et liber ille mense Martio anni proximi \proximi {illeg}/ lucem vidit. This book is full of such Problems as – – – – – – – he acknowledged the same thing

Pag. [198. lin 1]. \or Pag. 197 lin 15/ insert. In spring 1684 M^r Newton made known th to \some/ Mathematicians that he had demonstrated from the Principle of Gravity the Proposition of Gravity fro the Proposition of Kepler that that the Planets move in Ellipsis & with rays drawn to the Sun placed in the lower focus of the Ellipsis describe areas proportionall to the times. And in Autum following he sent it \the Demonstration/ to D^r Halley who communicated it to the R. Society \with some other Propositions concerning the heaven: & the R. S. desired that the/ M|D^r| Hook said there \upon to {apermigh}/ have /be printed; & M^r Newton thereupon began to write his Book of Principles M^r Hook is\ contended with M^r Hook Newton about this matter: but he never produced any Demonstration \of the Proposition/. For he was not skilled in Mathematicks & the Vpon the receipt of the Paper which conteined the Demonstration \of Keplers/ was not to be found without the Method of fluxions.

In November 1684 M^r Leibnitz published       in his letters of 1672 & 1676. But it was impossible from foreigners to understand this by the words here published. M^r Leibnitz ought to have acknowledged the in express words that he understood by his \late/ correspondence with M^r Oldenburg that M^r Newton had a methodus similis. ☉+ < insertion from f 147r > ☉+ He sa On the contrary He < text from f 147v resumes > < insertion from f 146v > ☉+ On the contrary he published in the Acta Eruditorum for May 1700 pag 203, that when he published the Elements of his Calculus < text from f 147v resumes > He

In the Acta Eruditorum of Iune 1686 M^r Leibnitz acknowledged pag. 297 M^r Leibnitz added         more brevity.

Anno 1686 mense Maio Newtonus Philosophiæ naturalis PrincipioMathematica ad Societatem Regiam misit ut imprimeretur. Et liber ille Mense Martio anni proximi lucem vidit. This book is full of Problems        he acknowledged the same thing. Certe, saith he, cum edidi calculi mei edidi anno 1684 ne constabat quidem mihi aliud de inventis ejus in hoc genere quod olim ipse significaverat in literis, posse se tangentes <147r> invenire non sublatis irrationalibus, quod Hygenius quo se posse mihi significavit postea, etsi cœterorum illius Calculi ad huc expers: sed majore multo consecutum Newtonum, viso denum libro Principiorum ejus satis intellexi. And a little after, pag. 206 lin. 5. Non hic de problemate menti valde diffusa circa maxima et minima fuit actum: quam ante Newtonum et me nullus, quod sciam, Geometra habuit, uti ante hunc maximi nominis Geometram nemo specimine publice dato se habere probavit This method is a principal b part of the Method of fluxions being the method by w^ch the Curva cellerimi descensus was found out by M^r Newton & Probleme proposed by M^r Bernoulli Probleme de Curva celerimi descensus proposed \by M^r Bernoulli/ to all the world, was solved, & M^r Leibnitz here acknowledges that M^r Newton by finding the solid of least resistance had proved that he had this method when he wrote his book of Principles. Vide Scholium in Prop. XXXIV Lib.II.

Pag. 199. lin 5|4|. add. D^r Halley & M^r Ralpson had the Book of Quadratures in MS in their hands in the year 1691 as M^r Ralpson has attestested publick ly & D^r Halley still attests

<148r>

2 Of the Method of fluxions & moments

If any equation involve tow unknown quantities suppose x & y, to find when either of them, suppose y is greater or least, Fermat put the letter o fir the indefinitely small difference of two valors of the other quantity x, & substituting x+o for x, has a knew equation, & by reducting these two equations & making the difference o decrease & vanish finds the greatest or least quantity y. This was his method de maximis & minimis; & by this method he drew Perpendiculars to curve lines. A specimen of this method was published by M^r I Schooten in his Commentary upon y^e Geometry of Des Cartes 1659.

M^r Iames Gregory in y^e 7^th Proposition of his Geometriæ Pars universalis published in 1668 puts the letter o for the difference of two Abscissas & draws a right line through the ends of the Ordinates, & that this line may become the tangent of the Curve makes the difference o decrease & vanish.

D^r Barrow in his 10^th Geometrical Lecture published Anno 1670, to find Tangents to curves puts the Letters a & e for the indefinitely small Differences of the Abscissas & Ordinates, brings the Probleme to an equation, rejects all the terms of the Equation in w^ch a & e are either wanting or of more dimensions then one, & by the proportion of a to e draws the Tangent, & this method readily gives the method of Slusius.

Newton at the request of M^r Collins h sent him his method of Tangents in a Letter dated 10 Decem. 1672. It proved to be the same with the method of Slusius, but was sent as a Corollary of a general method of solving Problems: w^ch method in drawing of tangents agreed with those of Gregory & Barrow.

Slusius sent his method to M^r Oldenburg in Ianuary 1673. It was founded on three Lemmas, the first of w^ch was this. Differentia duarum Dignitatum ejusdem g{ra}dus applicata ad d|D|ifferentiam Laterum dat partes singulares gradus inferioris ex binomio Laterum; ut $\frac{{\mathrm{y}}^3-{\mathrm{x}}^3}{\mathrm{y}-\mathrm{x}}=\mathrm{y}\mathrm{y}+\mathrm{yx}+\mathrm{x}\mathrm{x}$

And M^r Leibnitz in his Letter dated 21 Iune 1677 drew tangents by putting \the symbols/ dy & dx for the \letters/ a & e of D^r Barrow. [And by this notation the example in the first Lemma of Slusius {illeg} viz^t $\frac{{\mathrm{y}}^3-{\mathrm{x}}^3}{\mathrm{y}-\mathrm{x}}=\mathrm{y}\mathrm{y}+\mathrm{yx}+\mathrm{x}\mathrm{x}$ became $\frac{d{\mathrm{y}}^3}{d\mathrm{y}}=3\mathrm{y}\mathrm{y}$, or $d{\mathrm{y}}^3=3\mathrm{y}\mathrm{y}d\mathrm{y}$ & in general the Lemma became $d{\mathrm{y}}^{\mathrm{n}}=\mathrm{n}{\mathrm{y}}^{\mathrm{n}-1}d\mathrm{y}$; & in this notation is the convers of this is the first Rule of the Analysis per Æquationes numero terminorum infinitas]

When M^r Newton in his Letter of {illeg} 10 Decem. 1672 had described his method of Tangents, he added. Hoc est unum particulare vel Corollarium potius Methodi generalis quæ extendit se citra molestum ullum calculum non modo ad ducendum Tangentes ad quasvis Curvas sive Geometricas sive mechanicas vel quomodo cun rectas lineas aliasve Curvas respicientes verum etiam ad resolvendum alia abstrusi <148v> ora Problematum genera de Curvitatibus Areis Longitudinibus, centris gravitatis Curvarum &c. Ne (quemadmodum Huddenij methodus de maximis et minimis) ad solae restringitur æquationes illas quæ surdis quantitatibus sunt immunes. And in his Letter dated 13 Iune 1676, after he had described his method of series he added: Ex his videre est quantum fines Analyseos per hujus modi Æquationes infinitas ampliantur: quippe quæ earum beneficio ad omnia pene dixerim problemata, si numeralia Diophanti et similia excipias, sese extendit: non tamen omnino universalis evadit nisi per ulteriores quasdam methodos eliciendi series infinitas        Sed quomodo in istis casibus procedendum sit non vacat dicere: ut ne alia quædam tradere quæ circa reductionem serierum infinitarum in finitas ubi rei natura tulerit, excogitavi. And in his Letter dated 24 Octob. 1676, he represented that a Tract which he wrote five years before upon the method of Series, was for the most part taken up with other things.That there was in it the method of Slusius built upon another \foundation/w^ch gave that method readily, even without a particular demonstration, & made it more general so as not to stick at surdes; the Tangent not withstanding surdes being speedily drawn without any reduction of the Equation w^ch would often render the work immense. And that the same manner of working held in Questions de Maximis & Minimis & some others w^ch in that Letter he forbore to speak of. And that upon the same foundation the Quadrature of Curves became more easy, an example of w^ch he gave in a series which brake off & became finite when the Quadrature might be done by a finite equation. And that this method extended to inverse problemes of Tangents & others more difficult. But the foundation of this method he concealed in sentences set down enigmatically, the first of w^ch was this: Data æquatione quotcun fluentes quantitates involvente, fluxiones invenire, & vice versa

For Here M^r Newton considers not quantities as composed of indivisibles but as generated \after the manner proposed/ by local motion, {illeg} after the manner \used by/ of the Ancients. They considered rectangles as generated by drawing one side into the th other that is by moving one side upon the other to describe the area of the rectangle: & in like manner M^r Newton considers the areas of curves as generated by drawing the Ordinate into the Abscissa, & all in determinate quantities he considers as generated by continual increase And from the flowing of time & the moments thereof, he gives the name of floxing quantities to all quantities w^ch increase in time, & that of fluxions to the velocities of their increase & that of moments to their parts generated in equal moments of time. T He considers time as flowing uniformly, & {illeg} exposes or represents it by any other quantity w^ch is considered as flowing uniformly: \& its fluxion by an unit. And the/ And for \And/th The moments of time \or of its exponent/ he considers as equal to one another, & for d represents one of t this \such a/ moment by the Letter o or by any other letter or mark \drawn into an unit/. The \other/ \other/ flowing quantities he represents by any \other/ letters or marks & most commonly by the letters at the end of the alphabet. Their fluxions he represents by any other letters <149r> or marks, or by the same letters in a different form or di magnitude or distin otherwise distinguished. T And their moments he represents by their fluxions drawn into a moment of time. Fluxions are not moments but finite quantities of another kind. \They are motions/ & to make them become moments M^r Newtons multiplies them by th \a/ moments of the exponent of time. When M^r Newton is demonstrating any Proposition he considers the moment of time \in the sense of the vulgar/ as indefinitely small but not infinitely small, & by that means performs the whole work in finite figures \or schemes/ by the Geometry of lucid & Apollonius with exactly without any approximation: And when he has brought the work to an equation & reduced the equation to the simplest form, he supposes the moment to decrease & vanish, & from the terms w^ch remain, he deduces the Demonstration. An example of this you have in his Demonstration of the Construction of the first Proposition of his Book of Quadratures. \viz^t Data æquatione fluentes quotcun quantitates involvente invenire fluxiones/ And another example you have in his demonstration of the first of the three Lemmas upon which he grownded his Treatise intituled Analysis per æquationes numero terminorum infinitas. [And by these examples it is sufficiently manifest that he had found out this method of fluxions before he wrote the composed those Demonstrations] But when he is only investigating any truth or the solution of any Problem he supposes the moment of time to be infinitely little in the sense of Philosophers, & uses works in figures \or schemes/ infinitely small & uses any approximations, \w^ch he conceives will make no error in the conclusion/ as by putting the arc the & sine chord, sine & tangent equal to one another, & for the more \greater/ dispatch \he/ neglects to write down the {illeg} moment o.

In thi|e| Analysis per æquat above mentioned w^ch D^r Barrow sent to M^r Collins in the year 1669, his principall designe was to describe the method of series: but that method being inseparably conjoyned with the method of fluxions, he touches upon this method in the following manner When he described the three Lemmas upon \w^ch/ he founded this Analysis in squaring of Curves, he proceeded touched upon the method of fluxions in the following manner. Et hæc de areis Curvarum investigandis

<149v>

D^r Wallis by various steps arrived at thi|e| 59^th Proposition of his Arithmetica Infinitorum published 1655. And that Proposition (in other language) is this. Let the Abscissa of any curvilinear figure be x & the Ordinate b erected at right angles by y, & let m & n be numbers & $\frac{\mathrm{m}}{\mathrm{n}}$ be the index of thes\any/ dignity of the abscissa; & if the Ordinate y be equal to this dignity the area of the curve will be $\frac{\mathrm{m}}{\mathrm{n}}{\mathrm{x}}^{\frac{\mathrm{m}-\mathrm{n}}{\mathrm{n}}}$ $\frac{\mathrm{n}}{\mathrm{m}+\mathrm{n}}{\mathrm{x}}^{\frac{\mathrm{m}+\mathrm{n}}{\mathrm{n}}}$ And This is the first Proposion of\Lemma Rule upon w^ch in/ M^r Newtons Analysis per æquationes numero terminorum infinitas. And the se\co/nd is that when y^e Ordinate \of a Curve/ is composed of several such Ordinates the Area is composed of several such areas.

D^r Wallis published his Arithmetica infinitorum in y^e year 1655 & by the 59^th Proposition of that Book if m & n be numbers & the Abscissa of any Curve \Curvilinear figure/ be called x & \putting m & n forbe numbers) &/ the Ordinate erected at right angles by ${\mathrm{x}}^{\frac{\mathrm{m}}{\mathrm{n}}}$ the area of the figure shall be $\frac{\mathrm{n}}{\mathrm{m}+\mathrm{n}}{\mathrm{x}}^{\frac{\mathrm{m}+\mathrm{n}}{\mathrm{n}}}$. This is assumed by M^r Newton as the first Rule upon w^ch he founds his Analysis.

And by the 108^th Proposition of the same book & several other Propositions w^ch follow therein, if the Ordinate be composed of two or more such Ordinates \taken/ w^th their signes + or − the area will be composed of two or more such areas taken w^th their signes + or −. and this is assumed by M^r Newton as the second Rule upon w^ch he founds his Analysis.

And in the same Arithmetica Infinitorum D^r Wallis squared a series of Curves whose ordinates were $1. 1-{\mathrm{x}}^2. {\overline{)1-{\mathrm{x}}^2}}^2. {\overline{)1-{\mathrm{x}}^2}}^3. {\overline{)1-{\mathrm{x}}^2}}^4$. & shewed that if the series of their Areas could be interpoled in the middle places the interpolation would give the Quadratures of y^e circle.

And in his Opus Arithmeticum published A.C. 1657 cap. 33 Prop. 68, he reduced the fraction $\frac{\mathrm{A}}{1-\mathrm{R}}$ by perpetual division into y^e series $\mathrm{A}+\mathrm{A}\mathrm{R}+\mathrm{A}{\mathrm{R}}^2+\mathrm{A}{\mathrm{R}}^3+\mathrm{A}{\mathrm{R}}^4+\mathrm{\&c}$

M^r Newton A.C. 1665

Vicount Brunker squared y^e Hyperb. . . . . in April 1668.

Mercator soon after published a demonstration . . . . numero terminorum infinitas

For M^r Newton A.C. 1665 upon reading the Arithmetica infinitorum of D^r Wallis & considering how to interpole the series of Areas above mentioned, found the infinite\converging/ series for y^e Arc whose sine is given & pursuing the method of interpolation he found also the Quadrature of interpolation all Curves whose Ordinates are the dignities of binomials affected w^ch indices whole or fract or surd, affirmative or negative, together with the resolution of a binomial into a converging series; as at the request of M^r Leibnitz he has explained at large in his Letter dated 24 Octob. 1686 & long since printed by D^r Wallis The two first terms This resolution of a binomial into a converging series together w^th the quadrature of the Curve whose Ordinate is y^e the binomial he has explained at large in his Letter dated 13 Iune 1676 & set down the two first terms of the series in his Analysis above mentioned follows from this general Quadrature, but M^r Newton supposes that M|y|^r L' Brounker might find & Mercator demonstrate \some two or three years/ that Quadrature above or three \four/ \some/ years before they published their performance.

[This Analysis is the first piece published in printed in the Commercium. It is the It was sent to M^r Collins in Iuly 1669 as appears by the dates of three of D^r Barrows Letters still extant. And M^r Newton in his Letter dated 24 Octob. 1676 mentions it in this manner. Eo ipso tem <149r> pore quo Liber [Mercatoris] prodijt communicatum est per amicum D. Barrow (hunc matheseos Professorem Cantab) cum D. Collinio, compendi um quoddam Methodi harum serierum, in quo significaveram areas & Longitudines Curvarum omnium & solidorum superficies & con tenta, ex datis Rectis; et vice versa ex his datis Rectas determinary posse: et methodum illustraveram diversis seriebus. And M^r Collins\Oldenburg/ in a Letter to M^r Strode Slusius dated 14 Sept. 1669, cites sev & entred in the b Letterbook of y^e R. Society, \in giving an account of it/ cites several sentences out of it. And M^r Collins in a Letter to M^r Strode makes this mention dated 26 Iuly 1672 mention of it. Exemplus ejus [Logarithmotechnia]          si cum meridiana clasitate conferatur.

Now This Analysis or Compendium conteins a general method composed of two methods the one converging series, the other of moments & fluxions.] In this Compendium.

<150r>

An Account of the Analysis per Quantitatum Series Fluxiones ac Differentias cum Enumeratione Linearum tertij Ordinis, published by M^r Iones.

|15|1|| If any Equation contein two unknown indeterminate quantities suppose x & y; to find either of them \suppose x/ when y^e other is greatest or least. Des Cartes teaches that the quantity to be found \suppose x/ will in that case have two of its roots become equal. Fermat for the difference of those two roots before they become equal, puts the letter o, & thereby has two equations in both w^ch the other \two other/ quantitys \y/ ought to be one & the same. THen by exterminating that other quantity & reducing the equations & putting the two roots suppose x & x+o equal, that is, by putting the difference o equal to nothing he finds the quantity x, & by this method draws perpendiculars to Curves & resolves other Problemes by maxima & minima.

|16 12| Iames Gregory in the 7^th Proposition of his Geometriæ pars Vniversalis published 1678 puts the letter o upon for the difference of the Ordinates, & that this line may become the Tangent of the Curve, makes the difference o vanish.

|17|3|| Barrow in his 10^th Lecture published 1669, to find Tangents, puts the letters a & e for the differences of the two Abscissass & two Ordinates, conceives a right line \to be/ drawn through the ends of the Ordinates, brings the Probleme to an equation rejects all the terms of the equation in w^ch either a & e are either wanting or of more dimensions then one & by the proportion of a to e draws the Tangent.

\A method of Tangents was communicated by M^r Hudde to M^r Schortem in November 1659 to be kept secret, & Slusius also & Newton fell upon the same method/

|14| Slusius founded his method of Tangents on three Lemmas the first of w^ch was this. Differentia duarum dignitarum ejusdem gradus applicata ad Differentiam laterum dat partes singulares gradus inferioris ex binomio laterum, ut $\frac{{\mathrm{y}}^3-{\mathrm{x}}^3}{\mathrm{y}-\mathrm{x}}=\mathrm{y}\mathrm{y}+\mathrm{y}\mathrm{x}+\mathrm{x}\mathrm{x}$. That is, in the language of M^r Leibnitz, $\frac{d{\mathrm{y}}^{\mathrm{n}}}{d\mathrm{y}}=\mathrm{n}{\mathrm{y}}^{\mathrm{n}-1}$ or $d{\mathrm{y}}^{\mathrm{n}}=\mathrm{n}d\mathrm{y}{\mathrm{y}}^{\mathrm{n}-1}$

|16|5|| A month before Slusius sent his Method to M^r Oldenburgh Newton at y^e request of Oldenburgh \M^r Collins/ sent his in a letter dated 10 Decem. 1672, w^ch \method/ proved the same w^th that of Slusius; & added in the latter part of his Letter, \&/ added these wrods concerning & \added/ Hoc est unum particulare vel Corollarium potius methodi generalis, quæ extendit se citra molestum ullum calculum non modo ad decendum Tangentes ad quasvis Curvas sive Geometricas sive Mechanicas vel quomocun rectas lineas aliasve Curvas respicientes; verum etiam ad resolvendum alia abstrusiora Problematum genera de Curvitatibus, Areis Longitudinibus, Areis Centris gravitatis Curvarum &c. Ne quemadmodum Huddenij Methodus de Maximis et Minimis ad solas restringitur quantitates illas quæ quantitatibus surdis sunt immunes. T And a copy of this Letter was sent to M^r Leibnitz among the extracts of Gregories Letters above mentioned, Iun 26.

The same method of Tangents was communicated by Hudde to Schooten in the year 1659 to be kept secret, & accord

|16| M^r Leibnitz \being then at London/ in the beginning of the next year \1673/ pretended to y^e invention of the Differential method of Mouton & being reprehended for it by D^r Pell, persisted in making himself coinventor of that method, & it appears not that he had any other Differential method at that time.

When M^r Leibnitz wrote

<150v>

26 B

28 M^r Leibnitz in a letter to M^r Oldenburg dated 28\18/ Novem 1676 Methodus Tangentium a{s} lusip pe publicata nondum rei fastigium tenet potest aliquid amplius prœstari in es genere quod maximi foret usus ad omnis generis Problemata: etiam ad meam (sine extractionibus Æquationum ad Series Reductionem. Nimirum posset brevis calculari quæ calculari circa Tangentes Tabula, eou continuanda donec progressio Tabulæ apparet, ut eam scilicet quis, quous libuerit, sine calculo continuare possit.

<152r>

3. Of the Method of Fluxions & Moments

All quantities being indivisible in finitum M^r Newton conceived it more agreable to nature to consider quantities as increasing by \continual/ motion then by opposition of indivisible parts, & from the fluxion & moments of time, he gave the names of fluxions to the velocity|i|es wherewith quantities increase & that of moments to their indefinitely small parts by w^ch generated by motion in moments of time. The fluxion of time or of any quantity increasing or flowing uniformely by which the fluxion of time is represented or exposed, he represents by a given quantity & most commonly by an unit & for the moment of such a s time or its exponent he \usualy/ puts the letter o.For the \other increasing or/ flowing quantities he puts or\which he calls/ fluents he puts any symbol & for their fluxions any other symbols & for their moments the symbols of their fluxions drawn into the moment o. Fluxions are finite quantities & to make them signify indefinitely or infinitely small parts of fluents he multiplies them by the indefinitely or infinitely small moments of time. When he is demonstrating any Proposition he uses this Notation \the letter o in this sense/ & t considers the moment of time \it/ as indefinitely small & performs the whole operation in finite figures by the Geometry of Euclide. But when he is \only/ investigating a Proposition, he \usually/ considers the moment o as infinitely little & for making dispatch neglects to write it down, & proceeds in the calculation by any in figures in by any approximations

But as for the Method of fluxions it was certainly known to M^r Newton when he wrote his Letter to M^r Oldenburg dated 24 Octob. 1676. For in that Letter he exprest it of œnigmatically by these sentences comprehended it in these sentences. Data æquatione \quotcun/ fluentes quantitates involvente fluxiones invenire et vice versa. Et|A|nd said that this was the foundation of the method upon w^ch in conjunction w^th the method of Series he had writ a treatise five years before viz^t in the year 1671

In the mean time time it is be remains to be considered whether M^r Leibnitz after M^r Newton had told him {illeg} that in his Letter of 24 in three several \Letters/ sent to him described several \the/ characted|r|s of his method & told him that in the year 1671 he had wrote a treatise of it

In the mean time, when M^r Leibnitz Newton Leibnitz had seen three of M^r Newtons Letters in w^ch the characters & universality of his met Newton had told M^r Leibnitz that he in y^e year 1671 he had wrote a treatise of the Method & of the method of Series together, when & of another method together, when he had concealed this metho in three Letters w^ch came to the hands of M^r Leibitz described the characters & universality of this method other method so far as to make \enable/ M^r Leibnitz understand that {illeg} it did not abludere from y^e differential method but was a methodus similis \to compare it with the Differential & see that they did not ab invicem abludere but were similes/, when he had concealed the foundation of this method so far a sym in an enigmatical sentence c \it/ in an Ænigma \to hide it/ not from honest men but from plagiaries

Now if after M^r Newton had told M^r Leibnitz that in the year 1671 he had a method of wrote a treatise of the method of Series & of another method together, after he had in three Letters w^ch came to the hands of M^r Leibnitz described the characters & universality of this \other/ method so far as to enable M^r Leibnitz to compare it with the differrential method & say that they did not abinvicem abluder but were similes, after M^r Newton had concealed the foundation of it in an Ænigma to hid it not from honest men but from plagiaries: the Question is, whether M^r Newton should not have Leibnitz should not rather have invited M^r New & encouraged M^r Newton to have published his method then have rivalled him & claimed the method from him by saying &

<152v>

My computation of the time between y^e burning of the first Temple & building of y^e 2^d is this.

Pharoah Nechoh reigned over Phenicia & \&/ Syrea \cava & Namath/ as far as Euphrates the three first years of Iehojakim 2 King {3}3

In y^e year Nebuchadnezzar \(having \newly/ conquered Assyria)/ came against him & besieged Ierusalem & in the 4^th year beat him at Euphrates & took from him all Syria & Phœnicia from y^e river of Egypt to y^e river Euphrates & reigned in his stead, the first year of Nebuchadnezzar over those countries being y^e 4^th of Iehojakim. But whether he took Ierusalem in the thrid or fourth year doth not appear. Dan. 1,1. Ier 46, 2

And Nebuchadnezzar continued w^th his army in those parts \to conquer the nations round about (Ier 25.9,11) &/ to f recover to Babylon whatever had \lately/ belonged to {Nineveh} \Assyria/ & settle his new conquests untill he heard of the death of his father w^ch was in y^e fift or sixt year of Iehojakim, & then hasted to Babylon to succeed his father in the whole kingdom leaving his army captains to follow w^th \the captives, & in the 43^th year of his reign counted from the death of his father he/ his army & the captives. \died {Eupolamug &}/ Berosus apud Euseb l.9 c.39,40 By y^e Canon of Ptolomy he succeded his father A. Nabonass 144 &died A. Nabonass 187. But the Iews recconed \not/ by the in years {illeg} \of Nabonassar/

Iehojakim reigne eleven years & Iehojakim three months being captivated in y^e end of y^e eleventh year or beginning of y^e 12^th (2 Chrom 36. 10.) And the 12^th year was the first year of his successor Ie Zedekiah & the first year of the captivity of Iehojakin, F the years of this captivity beginned w^th the reigh of Zedekiah. The Iews recconed by Lumisolar years the Babylonian Astronomers by the years of Nibonassar.

In the 37^th year of this captivity, that is in y^e 45^th year of y^e reign of Nebuchadnezzar recconned \by Lumisolar years/ from the 4^th year of Iehojakim inclusively, Nebuchadnezzar died, & was succeeded by his son Evilmerodach. 2 King. 25. 27 \Ier. 52. 31/ And in y^e end of the year 25^th day of y^e 12^th month of the year brought his friend Iehojakim out of prison \2 King. 25. 27 Ier. 52. 31/. It is not likely that after he came to y^e throne he would lett his great friend Iehojakim stay long in prison & therefore it's reasonable to beleive that Nebuchadnezzar died \in the end of winter/ neare the end of the 35 45^th year of his reign accordingly \& by consequence/ the recconing of y^e Iew And this was in y^e beginning of y^e year of Nebuchadnez Nabonassar 186|7| And by consequence \therefore/ Iehojakim \therefore/ began his reign in the year of Nabonassar 139, & Nebuchadnezzar in y^e year year of Nabonassar 142 according to y^e Iewish account, & \one or about about/ two years after \that/ he succeded his father at Babylon & reigned 43 years form y^e death of his father, according to the recconing of the Chaldeans, & Canon of Ptolomy, & 44 years & some months according to y^e recconing of the Chaldeans Iews.

And according to this recconing account There Iews had fasted just 70 in y^e 5^t month for y^e burning of y^e City just 7 & in y^e 7^th month for y^e death of Gedaliah just 70 years befoer y^e 9^th month of y^e 4^th year of Darius Hystaspis \2 King. 25. 1 Zech 7. 1/ And in y^e end eleventh month of y^e 2^d year of Darius there had had \Gods/ indignation against y^e cities of Iudah \had lasted/ just 70 years, the indignation beginning in the \tenth month of the/ ninth year of Zedekiah \And so it really was/ on the 10^thmon See 2 King 25. 2 & Ier 34. 7 & Zech 1.12, & 7.1. This recconing therefore \And these agrees two recconing/agrees with /exactly\ with scripture & concerned thereby the computation here set down

And as for y^e D^rs Not being able to y^e digest the opinion that Zechary \might/ begin to prophesy w^thin 16 years after his grand fathers death; can he \not/ digest y^e opinions that 4 generations have been alive together in France, the King & three Dauphins? that \And/ Can he digest the opinions that Zembbabel & Ioshuah might govern I the Iews 118 years together, & that there might be men alive in y^e 2^d year of Darius Hystaspis Nothus, who remembered the first Temple w^ch had been burnt 165 years before?

The Iews were to serve the King of Babylon 70 years. They be & after 70 years were accomplished at Babylon they were to return to their own land (Ier 25. 12 & 29. 10). They began to serve him in y^e first year of his reign over them which was the fourth year of Iehojakim \A. Nabonass. 142./ They returned from \remained in/ captivity until the reign of the kingdom of Persia, & in y^e first year of Cyrus king of Persia (A. Nabonass. 212) they returned home (2 Chron. 36. 20,21,22) But D^r Alex places y^e 4^th year of Iehojakim & 1^st of Nebuchadnezzar two years later.

<152r>

My computation is therefore favored by 4 argum^ts taken from scripture 1^st y^e death of Nebuchadnezzar in y^e 37^th year of Iehojakins captivity. 2^dly the fasting 70 years. 3^dly the indignation upon y^e cities of Iudah 70 years & 4^thly the serving the king of Babylon 70 years.

<153r>

Ex mente Newtoni, primus annus Nebuchadnezzaris juxta Iudœos fuit 4^tus Iehojakimi. juxta Chaldæos \Iudæos et/ non secundus sed sextus \junta Chaldæos/. Et regnavit Nebuchadnezzar \ille/ annos 48 a morte Patris, annos vero 44 & menses aliquot a quarto Iehojakim \inclusive/. Obijt enim & filio Euilm erodacho regnum reliquit anno 37^mo captivitatis Iehojachin, sev \hoc est, anno 37/ regni Zedekiæ ed est. anno 48^vo regni Iehojakim, ed est \et propterea/ anno 45^to regni proprij cum ab \quod capit/ anno 4^to Iehojakimi incipientis inclusive.

Et intra annum ung unum generationes quator {Iaclvus} conquer \surisse eatitisseo/ quam ( \(sc/ Regem Galliæ scilicet & tres Delphinos) \concoquer possum proba{biliest} est &/ quam aliquos in vivis esse fuisse qui Regem nostrum Henricum Octavum de facie norant.

Observations upon y^e Notes of y^e R^nd D^r Alix.

The D^r \in y^e firs 2^d Paragaph/ supposes y^t I place y^e 1^st year of Nebuchadnezzar according to the Chaldees, upon y^e 2^d of Iehojakim, disputes against this opinion & in the 6^t Paragraph concludes that I erred in placing the destruction of Ierusalem upon the 17^th year of Nebuchadn. w^ch fell upon according to the Chaldees. But if I placed y^e taking of Ierusalem upon y^e 17^th year of Nebuchadn. dated from y^e death of his father according to the Chaldees, I placed the death of his father & first year of his reign upon the not upon y^e 2^d but uopn y^e sixt year of Iehojakim.

Evilmerodach succeeded his father Nbuchadnezzar in y^e 37^th year of Iehojakins captivity (2 King 25. 27) The years of this captivity & the years of the reign of Zedekiah have y^e same epocha. Add y^e eleven years of Iehojakim & ther the death of Nebuchnezzar will fall upon the 48^th of year of Iehojakim recconed from the first year of his reign inclusively. Take away the three first years of Iehojakins &the death of Nebuchadnezzar will fall upon y^e 45^th year of his reign recconed from y^e 4^th year of Iehojakim inclusively. Whereas Nebuchadnezzar reigned but 43 years \from y^e death of his father/ according to y^e Canon.

During the three first years of Iehojakim, the king of Egypt reigned over Palestine & Cœlosyria. Nebuchadnezzar came against him in y^e 3^d year of Iehojakim & captivated some of the Iews & the next year beat him at Carchemish & took from him all Syria & Palest{ine} \from Euphrates/ to y^e borders of Egypt (2 King. 24.7) & reigned in his stead. And when the war was fully ended Nebuchadnezzar heard of the death of his father & returned in hast to Babylon to succeed him, leaving his Captains to follow with his army & the captives according to Berosus.

His reign therefore might have a double beginning, the first when he succeeded Pharaoh Nechoh in Syria & Palestine & the neighbouring coasts of Arabia \& Hamath/, the second when he succeeded his father at Babylon the first \commonly/ used by the people of Syria & Phenicia, the second by these in Balonia.

Lin 4. lige, annis tardius scil. a 6^to Iehojakimi \(vide lin 28)/ Lin 9, lege A. Nabonass 160 Ne lin: 11 An Ezekiel in Chaldœa inter captivos usus sit annis Nabonassari? Lin 13 Anno|is| 10 dantur regno Iehojakimi, 12 regno Zedekiœ. Nam regnum Zedeckiæ cœpit cum annis captivitatis Iehojakin. Lin 14 \lije/ 1 37 ad finem vergente ab ipsius deportatione, Lin A ultimo Nebuchadnezzaris quo Evilmerodach regnare cœpit. Lin 6. Nebuchadnezzar ex er citur anno 3^o Iehojakimi Hieroslyma obsedisse dicitur, eodem anno cœpissa non dicitur. L. 22. non Suppano, Pharaonem cœsum anno quarto Iehojakimi & Nebuchadnezzarum eidem in regno Syria et Palestine \tune/ successisse, L. 30 patri vero mortua successisse post bellum finitum. Lin 50 Quatuor fuerunt generationes eodem tempore in Gallia Rex ipse et tres Delphini.

Iddo In the first year of Cyrus \Iddo/ might be ass old as the present\present/ king of France & Z solary as oldn then \his Grandson/ the King of Spain. But could

<153v>

You have seen how M^r Newton in his Letters of 10 Decemb. 1672 13 Iune 1676 & 24 Octob. 1676 represented that he had a very general method by w^ch he drew Tangents after the manner of Slusius determined maxima & minima, squared curvilinear figures \determined their center of gravity/ found the lengths of crooked lines & the quantity of their crookedness, measured the surfaces & solid contents of round solids, determined the inverse Problemes of tangents & other more difficult, & wrought in transcendent curves as well as others reduced difficulties to infinite equations where t|a|ll could they could not be overcome in finite ones, & applied equations finite or infinite to the solution of almost all Problemes except perhaps some numeral ones like those of Diophantus. Vpon this method & the method of Slusius together he said that he in his Letter of 24 Octob. 1676 that he had wrote a Tract five years before, & in the same Letter he said that comprehend wrote down the foundation of this method ænigmatically in this sentence Data æquatione quotcun fluentes quantitates involvente thinking that he had said too much of it & described it too plainly, that it might not be taken from him he wrote down the foundation of ænigmatically in this sentence Data æquatione quotcun fluentes quantitates involvente Fluxiones invenire; & vice versa. And in the second Lemma of the second book of his Principia Philosophiæ when \he had/ demonstrated Geometricaly the elements of this method he added in a Scholium. In literis quæ mihi cum Geometra peritissima annis abhinc decem interecedebant cum significarem me compotem esse methodi determinandi maximas & minimas ducendi Tangentes & similia peragendi quæ in terminis surdis æque ac in rationalibus procederet, & literis transpositis hanc sententiam involventibus [Data æquatione quotcun fluentes quantitates involvente fluxiones invenire, & vice versa] eandem celarem, rescripsit Vir Clarissimus se quo in ejusmodi methodu incidisse, & methodum suam communicavit a mea vix abludentem præterquam in verborum et notarum formulis. Vbius fundamentum \contineter/ in hoc Lemmate The method of fluxions was therefore known to M^r Newton when he wrote the said three Letters

And in the last of those Letters he represents that he wrote of Trac it in a Tract w^ch he composed upon the method of series five years before, that is, in the year 1671.

And in the Compendium w^ch he wrote \communicated to D^r Barrow & M^r Collins/ two years before that there sufficient footsteps of his knowing it at that time.

<154r>

An account of the Analysis per quantitatum series fluxiones ac differentias cum enumeratione linearum tertij Ordinis published by M^r Iones

\This Analysis is f/ If any equation conteining two indeterminate quantities {illeg}fial the less \suppose x & y/ to find |e|on|ith|e|r| of them * when the other * is greatest or least, Fermat supposes \D. Cartes teaches/ that y^e first \the quantity to be found {illeg} will/ in that case will have two roo of its roots become equal. \Fermat/ For the difference of thos two roots \before they become equal/ Fermat puts the letter o, & thereby has two equations in \both/ w^ch the other quantity ought to be \one &/ the same. Then by {this} putting this exterminating that other quantity & reducing the equations, & putting the two roots \suppose/ x & $\mathrm{x}+\mathrm{o}$ equal, that is, by putting the difference o equal to nothing, he finds the quantity x. And this method he applies to y dra \And by this method draws perpendiculars to curves &/ & resolves such other Problemes as are to be resolved by finding when quantities are greatest or least

Iames Gregory in his the 7^th Proposition of his Geometriæ pars Vniversalis \published 1678/ puts the letter o for the difference of two Abscissas & thereby finds the difference of two Ordinates & by proportion of these differences & draws a line right line through the ends of the Ordinates, & that this line may become the Tangent of the curve makes the difference o vanish

Barrow \in his 10^th Lecture published 1669 to fin to find Tangents/ puts the letters a & e for the differences of the Abscissa & Ordinate, & draws a right line through the ends of the Ordinates, & then makes brings the probleme to an equation, rejects all the terms of the Equation in w^ch a & e are either wanting or of more dimensions then one, & by the proportion of a to e draws the Tangent.

Leibnits in the year 1677, chan for y^e letters a & e, substituted the symbols dx & dy, & drew tangents after the same manner with Barrow. This method he Newton in \Iuly/ the year 1669 published his comm afterwards published in the Acta Eruditorum & two years aft mensis Octobris & 1684, & in the conclusion added. Et hæc quidem initia sunt \tantum/ Geometriæ cujusdam multo sublimioris ad difficillima & pulcherrima quæ Problemata etiam mistæ matheseos Problemata, quæ sine calculo nostro differentiali, aut simili, non temere quisquam pari facilitate tractabit. By the words aut simili he means a Newtons method as is evident by his letter of 21 Iune 1677. For he had notice of this method by three of M^r of M^r Newtons letters dated 10 Decem. 16673. 13 Iune 1676 & \24 Octob 1676 by M^r Oldenberg/ & communicated to him \by M^r Oldenburgh/. Whe he changed the letters dx a & e into dx & dy he tells us two years after in y^e Acta Eruditorum 16 mensis Iunij 1686 M Malo autem, dx & saith he, dx et similia ad hibere quam literas pro illis quia istud dx est modifactio quædam ipsius x, & ita ope ejus fit ut sola quando id fieri opus est litera x, cum suis scilicet potestatibus & differentijs calculum ingrediatur & relationes transcendentes inter x et aliud exprimantur. Qua ratione etiam lineas transcendentes inter x et ali æquatione explicare licet. That is, If he had used letters he must have defined their \signification/ upon partial every new occasion, & to avoyd that trouble he chose rather to use y^e symbols dx & dy & define them once for all. For there is nothing that can be done by the symbols dx, dy, &c \dz/ but may be done by letters or any other symbols after their signification is defined. |He also put the letter d before the ordinate of a Curve to signify the area of the Curve or summ of the Ordinates in the method of Cavallerius. For Fluxions he has no proper symbol.|

In the meane time M^r Newton in Iuly 1669 communicated to D^r Barrow & D^r Barrow to M^r Iohn Collins a \short/ Tract intituled Analysis per æquatione numero terminorum infinitas w^ch is the first Tract in the Collection of M^r Iones. In w^ch|this| \Tract/ he shews how to reduce finite equations to infinite ones when there shall be occasion, & by the help of the moments of quantities to apply these æquations both finite & infinite to the solution of the harder Problems. And this is the Geometria multo sublimior ad difficillima et pulcherrim ad quæ Problemata, spoken of by M^r Leibnits seven fifteen years after: excepting that it is more universal & more demonstrative then y^e one of M^r L.

In this Analysis M^r Newton \represents the area of a curve by inclosing the Ordinate in \a square &// considers quantities as increasing or flowing by continual motion in time, & represents time by any quantity w^ch increases or flows uniformely or in proportion to time & from the fluxion & moments of time gives the names of fluxions & moments \to the velocities of flowing & momentaneous increases/ of other quantities in time. For the \flowing/ quantities he puts any symbols letters or symbols & for their fluxions he puts any other \letters or/ symbols & for the fluxion of time or of its exponent he \usually/ puts an unit, & for the a moment of time whether infl infinitely \little/ or only indefinitely little he puts frequently \usually/ puts the letter o, & for the moments of other quantities generated in that moment of time, he puts the fact or content under their fluxions, & that moment of time And for an area of any Curve described by the Ordinate of the Curve he puts the Ordinate with a square about it. M^r L \drawn into one another. When he is demonstrating any Proposition he always uses the letter/ o or some other symbol, for an indefinitely small <154v> quantity \or particle of time/ & so soon as the proceeds in finite quantities & finite figures \by Euclides Geometry/ to the end of the calculation \without any error or approximation or error/, & then supposes the indefinitely small quantitys to be decrease in finitum & vanish or become nothing. But when he is only investigating a truth or the solution of a Probleme he supposes the moment o to be infinitely little & proceeds in the calculation by such approximations as he thinks will create no error in the conclusion, as by putting arches & their chords sines & tangents for one another. And for making dispatch he forbeares to write down the letter o putting the symbol of the fluxion \alone/ for the moment \of the fluxion/, but understanding that symbol to be multiplied by the moment o wheneve to make it infinitely little whenever it signifies a moment. For fluxions or velocities are finite quantities but moments are infinitely little. In the book of Quadratures \& some other papers/ M^r

M^r Leibnitz uses no proper symbols for fluxions, but when he considers any quantity as the ordinate of a Curve he puts the letter s before it to signify y^e area described by that Curve & M^r Newton long before did the same thing

This Tract of Analysis is founded on three Newton uses th any letters for sy fluents & the same letters with pricks up above them for \their/ fluxions. In other Paper M^r Newton uses sometimes the same letters in a different magnitude or form sometimes other letters, sometimes lines represented by two capital letters. For he doth not confine his method to any particular sort of symbol, of {illeg} fluxions. M^r Leibnitz hath no proper symbols for of fluxions. A But methods consist not in names & symbols. What ever be the symbols the methods may be \are/ the same if the do the same things & after the same & after the same manner of working.

This Tract of Analysis is founded on three Rules, The two first of w^ch are equipollent . . . . .

<155r>

2 Off the Differential Method

In|f| any equation involveing two unknown quantities suppose x & y, to find when either of them suppose y is greatest or least, Fermat puts o for the difference of two roots \valors/ of the other quantity \x/, &substituting x+o for x has a new equation, & by reducing these two equations & making the quan difference o become infinitely little & vanish finds the greatest or least quantity y. This was his method de maximis & minimis, & by this method he drew Perpendiculars to Curve Lines.

M^r Iames Gregory in the 7^th Proposition of his Geometriæ pars universalis published 166|7| puts the Letter o for the difference of two Abscissas & draws a right line through the ends of the Ordinates & that this line may become the Tangent of the Curve makes the difference o vanish.

D^r Barrow in his 10^th Lecture published 166|7|0, to find Tangents to Curves, puts the Letters a & e for the \indefinitely small/ Differences of the Abscissas & Ordinates draws a right line through the ends of the Ordinates, \by the conditions of the Curve/ brings the Probleme to an Equation, rejects all the terms of the Equation in w^ch a & e are either wanting or of more dimensions then one & by the proportion of a to e draws the Tangent. And this method readily gives the method of Slusius.

Slusius founded his method of Tangents on three Rules Lemmas the first of w^ch was this. Differentia duarum dignitatum ejusdem gradus applicata ad Differentiam Laterum dat partes singulares gradus inferioris ex binomio laterum, ut $\frac{{\mathrm{y}}^3-{\mathrm{x}}^3}{\mathrm{y}-\mathrm{x}}=\mathrm{y}\mathrm{y}+\mathrm{y}\mathrm{x}+\mathrm{x}\mathrm{x}$

M^r Newton at the request of M^r Collins sent him his method of Tangents in a Letter dated 10 Decem. 17|6|72. It proved to be the same with the method of Slusius, but was sent as a Corollary of a general method \of solving Problems/: w^ch method in drawing of Tangents agreed|s| with that\ose/ of D^r Barrow Gregory & Barrow.

Slusius for sent his method to M^r Oldenburg in Ianuary 1673. It was founded on three Lemmas, the first of w^ch was this. Differentia duarum dignitatum ejusdem gradus applicata ad Differentiam Laterum dat partes singulares gradus inferioris ex binomio laterum; ut $\frac{{\mathrm{y}}^3-{\mathrm{x}}^3}{\mathrm{y}-\mathrm{x}}=\mathrm{y}\mathrm{y}+\mathrm{y}\mathrm{x}+\mathrm{x}\mathrm{x}$

M^r Leibnitz for $\frac{{\mathrm{y}}^3-{\mathrm{x}}^3}{\mathrm{y}-\mathrm{x}}=\mathrm{y}\mathrm{y}+\mathrm{y}\mathrm{x}+\mathrm{x}\mathrm{x}$, wrote $\frac{d{\mathrm{y}}^3}{d\mathrm{y}}=3\mathrm{y}\mathrm{y}$, putting dy & dx for the a & e of D^r Barrow. For in his Letter of 21 Iune 1677 in w^ch he first proposed his method of Tangents, he wrote thus Clarissimi Slusij methodum Tangentium nondum esse absolutam celeberrimo Newtono assentior: et jam a multo temporerem Tangentium longe generalius tractavi, scilicet per differentias Ordinatarum. And a little after he added. Hinc nominando dy differentiam duarum proximarum y & dx differentiam duarum proximarum x; patet $d{\mathrm{y}}^2$ esse $2\mathrm{y}d\mathrm{y}$, & $d{\mathrm{y}}^3$ esse $3{\mathrm{y}}^2$ et ita porro. Which is the first Lemma of Slusius. Then putting y for the Abscissa & x for the Ordinate of a Curve he feigns \assumes/ an equation expressing the relation between them, & to find the Tangent to this Curve he substitutes in this equation the Abscissa x|y|+ dx|y| for x|y| & the Ordinate $\mathrm{x}+d\mathrm{x}$ for x, & in doing this he writes down first those terms in w^ch dy & dx are not, & draws a line under them. Then under that line he writes down those terms in w^ch dy & dx are but of one dimension, & draws a line under them. And under that line he writes down those terms in w^ch dy & dx are either severally or joyntly of more dimensions then one. And then he adds: Vbi abjectis illis quæ sunt supra lineam primam lineam, quippe nihilo æqualibus per æquationem primam; et abjectis illis quæ sunt infra secundam quia <155v> in illis duæ infinitæ parvæ in se invicem ducuntur, restabit tantum quicquid reperitur inter lineam primam et secundam. Then after he had shewn by what remained between the lines to draw the tangent, he added: Quod coincidit cum Regula Slusiana, ostendit eam statim occurrere hanc methodum intelligenti. By hanc methodum therefore he did not understand the method of Slusius but another method w^ch readily gave the method of Slusius; & this was the method of D^r Barrow. For D^r Barrow thus described his own method. He proposes to compute an equation from any conditions of the Curve & in doing this \prescribes these Rules/ saith: Primo inter computandum omnes abjicio terminos \saith he/ in quibus ipsarum a vel e potestas habetur, vel in quibus ipsæ ducuntur in se. Etenim isti termini nihil valebunt. Secundo post æquationem constitutam omnes abjicio terminos literis constantes quantitates notas seu determinatas designantibus, aut in quibus non habentur a vel e. Etenim illi termini semper ad unam æquationis partem adducti nibilum adæquabunt. These were D^r Barrows Rules & these Rules are followed by M^r Leibnitz who sets between two lines the terms that are to be retained & the term above the upper line \& below the lower/ those two sorts of terms that by D^r Barrows Rules are to be rejected, & rejects them accordingly.

And that this was the original of M^r Leibnitz method of Tangents is further confirmed by what he wrote in the Acta Eruditorum mensis Iunij 1686 pag 299. Malo autem, saith he, dx et similia adhibere quam literas pro illis quia istud dx est modificatio quædam ipsius x et ita ope ejus fit ut quando sola quando id fieri opus est litera x cum suis scilicet potestatibus & differentialibus calculum ingrediatur & relationes transcendentes æquatione explicare licet. D^r Barrow used the letters a & e. M^r Leibnitz allows that Letters \he/ might have used \Letters/ but tells us that \for certain reasons/ he chose rather to use the symbols dx & dy. for the reasons here set down |But he should have told us that he us whence he had the method. He should have acknowledged that he used D^r Barrows method of Tangents, excepting that for certain reasons he had changed the letters a & e used by D^r Barrow, into y^e symbols dx & dy. For he had seen D^r Barrows Lectures.|

M^r Leibnitz first published his method of Tangents in the Acta Eruditorum mensis Octobris An. 1684, pag.467, with this Title                Nova Methodus pro maximis et minimis item tangentibus quæ nec fractas nec irrationales quantitates moratur, & singulare pro        illis calculi genus, per G.G.L. And in the end of it he added Et hœc quidem initia sunt tantum Geometriæ cujusdam multo sublimioris ad difficillima et pulcherrima quæ etiam mistæ matheseos problemata pertingentis, quæ sine calculo nostro differentiali, aut simili, non temere quisquam pari facilitate tractabit. It remains that we enquire how M^r Leibnitz came to know that this method of tangents stuck not at fractions or surds & that it was the found \conteined the was the/ principles of a far more sublimer Geometry reaching to all the most difficult & curious Problems in Mathematicks & what was the Calculus similis here hinted at.

At the request of M^r Collins M^r Newton sent to him his Method of Tangents in a Letter dated 10 Decem. 1672. It proved to be the same with that w^ch Slusius about five weeks after sent to M^r Oldenburg but was derived from a more general Principles. For when M^r Newton had described it, he subjoyned in the same Letter Hoc est unum particulare vel Corollarium potius Methodi generalis quæ extendit se citra molestum ullum calculum non modo ad ducendum Tangentes ad quasvis Curvas sive Geometricas sive Mechanicas, vel quomodocun rectas lineas aliasve Curvas respicientes; verum etiam ad resolvendum alia abstrusiora Problematum generade curvitatibus, Areis, Longitudinibus centris gravitatis Curvarum &c Neque (quemadmodum Huddenij methodus de maximis & minimis) ad solas restringitus æquationes illas quæ surdis quantitatibus sunt immunes. And a Copy of this Letter was sent by M^r Oldenburg Iune 26^th 1676, to M^r Leibnitz at Paris amongst the extracts of M^r Gregories Letters collected by M^r Collins as above.

<156r>

And M^r Newton in his Letter of dated 13 Iune 1676 & sent by M^r Oldenburg to Paris Iune 26, taught how to resolve any dignity of an binomium into a converging series, the second terme of w^ch Series by the method of D^r Barrow readily gives the first term Lemma of Slusius together with his wole method. And after he had in that Letter described his method of Series, he subjoyned: Ex his videre est quantum fines Analyseos per hujusmodi æquationes infinitas ampliantur: quippe quæ earum beneficio ad omnia pene dixerim problemata, si numeralia Diophanti et similia excipias, sese extendit: non tamen omnino universalis evadit nisi per ulteriores quasdam methodus eliciendi series infinitas . . . . . . Sed quomodo in istis casibus procedendum sit non vacat dicere: ut ne alia quædam tradere quæ circa reductionem serierum infinitarum in finitas ubi rei natura tulerit, excogitabi.

And in his Letter dated 2{illeg}|4| Octob. 1676, he represented how the Tract w^ch he wrote five years before upon the method of Series, was for the most part taken up w^th other things. That there was in it the method of Slusius built upon another foundation w^ch gave that method readily, even without a particular Demonstration, & made it more general so as not to stick at surdes; the tangent, not withstanding surdes, being speedily drawn without any reduction of the Equation w^ch would often render the work immense. And that the same manner of working held in Questions de Maximis & Minimis & some others, w^ch in that Letter he forbore to speak of. And that upon the same foundation the Quadratures of Curves became more easy, And he set down an instance of the force of this method in an infinite series for squaring of Curves w^ch brake off & became \a/ finite equation when the light be \example of w^ch he gave in a Series/ w^ch brake of and became finite when the Quadrature might be done by a finite equation. And that that this method extended to inverse problems of Tangents & others more difficult. But the foundation of this method he concealed in sentences set down œnigmatically: the first of w^ch was this. Data æquatione fluentes quotcun æquationes involvente fluxiones invenire, & vice versa.

Thus M^r Newton in these three Letters represented that his method was very universal, that it gave the method of Slusius as an obvious Corollary, & that it proceeded w^thout sticking at surds & facilitted Quadratures. And after all this information M^r Leibnitz in his Letter of 27 Iune 1677 proposed his differential calculus in these words Clarissimi Slusij Methodum tangentium nondum esse absolutam Celeberrimo Newtono assentior. Et jam a multa tempore rem Tangentium longe generalius tractavi, scilicet per differentias Ordinatarum. Then he defines his new Notation, saying: Hinc in posterum nominando in posterum dy differentiam duarum proximarum y, &c. Then he gives an example of drawing Tangents by the method changing the a & e of D^r Barrow into dy & dx, & observes how the method of Slusius follows from it, & how it is to be improved so as not to stick at surds, & then adds Arbitror quæ celare voluit Newtonus ab his non abludere. Quod addit ex hoc eodem fundamento Quadraturas quo reddi faciliores me in sententia hac confirmat; nimirum semper figuræ illæ sunt quadrabiles quæ sunt ad æquationem differentialem. Thus he concludes that he had now got a method like that of M^r Newton, & therefor in the Acta Eruditorum by y^e calculus similis meant M^r Newtons method.

<156v>

But he tells us: Et jam a multo tempore rem tangentium longe generalius tractavi, scilicet per differentias Ordinatarum. If he means that he had used D^r Barrows method of Tangents jam a multo tempore, tis nothing to his purpose. But if he means that he had improved it into a general method jam a multo tempore, it lies upon him to prove it. For by the law of all nations, in cases of controversy no man can be a witness for himself. And for any man to insist upon his own candour with a designe to be admitted a witness for himself is a demonstration of his want of candour. If there had been no competition in the case he might have been credited without doing injustice to any man: but he is here putting in his claim to the methods of D^r Barrow & M^r Newton, & therefore by the law of all nations it lies upon him to prove his assertion. In the mean time these Arguments make against him.

In the beginning of the year 1672 he claimed the differential method of Mouton as his own & was reprehended for it by D^r Pell, & yet persisted in maintaining that he had invented it apart & much improved it, but he did not yet pretend to any other Differential method.

In the year 1675 he composed a small work upon the Quadrature of the circle vulgari more because he had not yet found out his new Analysis. For in the Acta Eruditorum mensis Aprilis 1691 pag 178 he wrote thus. Iam anno 1675 compositum habebam opusculum Quadraturæ Arithmeticæ ab amicis ab illo tempore lectum, sed quod materia sub manibus crescente limare ad editionem non vacavit post quam aliæ occupationes supervenere; præsertim cum nunc prolixius exponere vulgari more quæ Analysis nostra nova paucis exhibet non satis operæ pretium videatur. The matter grew under his hands till other affairs came on, that is, till he was called hom to be imployed in publick affairs \which happened in October & November 1676,/; & after that when he had found his new Analysis w^ch exprest that Quadrature in few words, he did not think it worth his while to o on with his composition vulgari more.

In his Letter to M^r Oldenburg dated 12 May 1676 he wrote that he was polishing the Demonstration of this Quadrature; & he sent it to him in his Letter of 27 August. 1676 composed vulgari more without the help of his new Analysis: & therefore he had not yet found out that method.

In the same Letter of 27 August 1676, when M^r Newton had said that his Analysis by the help of infinite equations extended to the solution of almost all Problems, he replied: Id mihi non videtur. Sunt enim multa us adeo miro et implexa ut ne ab Æquationibus pendeant ne ex Quadraturis. Qualia sunt (ex multis alijs) Problemata methodi Tangentium inversæ. Which is a Demonstration that he had not yet found out the Differential method

After he had received M^r Newtons a copy of M^r Netons Letter of 10 Decem. 1672 whereby he had notice that the method of Tangents published soon after by Slusius was but a \branch or/ Corollary of a general method for solving of Problems; his mind ran upon improving that Method, as appears by his Letter to M^r Oldenburg from Amsterdam dated $\frac{18}{28}$ N Novemb. 1676 For there he wrote: Methodus Tangentium a Slusio publicata nondum rei fastigium tenet. Potest aliquid amplius præstari in eo genere quod maximi foret usus ad omnis generis Problemata. Nimirum posset brevis quædam calculari circa Tangentes Tabula, eous continuanda donec progressio Tabula apparet. Amstelodami cum Huddenio locutus sum. Amplior Methodus tangentium a Slusio publicata dudum illi fuit nota. Amplior ejus methodus est quam quæ a Slusio fuit publicata. And these were the improvements of the Method of Slusius w^ch then occured to M^r Leibnitz.

But when he had received M^r Newtons Letter dated 24 Octob. 1676, which gave him further light into the \true/ improvement, he wrote back: Clarissimi Slusij methodum Tangentium nondum esse absolutam Celeberrimo Newtono assentior. And: Hinc nominando in posterum dy differentiam duarum proximarum y &c He had now fixed his Notation & began \here/ to communicate it: And if he would have his method of an earlier date, he is in point of candor to prove it & by y^e law of all nations to prove it.

<157r>

M^r Leibnitz for $\frac{{\mathrm{y}}^3-{\mathrm{x}}^3}{\mathrm{x}-\mathrm{y}}=\mathrm{y}\mathrm{y}+\mathrm{y}\mathrm{x}+\mathrm{x}\mathrm{x}$, wrote $\frac{d{\mathrm{y}}^3}{d\mathrm{y}}=3\mathrm{y}\mathrm{y}$, or rather finding the method of D^r Barrow to be more v founder upon clearer & & more general principles {illeg} changed his a & e into dx & dy.

In the year 16 beginning of the year 1673 he {illeg} claimed the differential method of Mouton as his own but being \& was/ reprehended for it by D^r Pell amp; yet persisted in making him maintaining that he had invented it apart & much improved it,; but did not yet pretend to any other differential method.

In the year 1675 he composed a compend \small/ work upon the Quadrature of the Hyperbola Circle vulgari more because he had not yet found out his new Analysis. For in the Acta Eruditorum mensis Aprilis 1691 pag 178, he writes thus. Iam anno 1675 compositum habebam opusculum Quadraturæ Arithmetiticæ ab amicis ab illo tempore lectum, sed quod materia sub manibus crescente limare ad editionem non vacavit postquam alij|æ| occupationes supervenere; præsertim cum nunc prolixius exponere vulgari more quæ Analysis nostra nova paucis exhibet, non satis operæ pretium videatur. Interim insignes quidam Mathematic{illeg} The matter grew under his hands till other business aff affairs, & after that, when other business came on he had fonud his new Analysis \by w^ch exprest it in few words/ he did not think it \any longer/ worth his \while to/ to expound propose it prolixly in the vulgari more He returned home by England & Holland in November & October & November \& December/ 1676 & therefore found the Differential method after that time.

In his Letter to M^r Oldenburg dated 12 May 1676 he wrote to M^r Oldenburg that he was polishing the Demonstration of this method, & he sent it it to him in his Letter of 27 Aug. 1676 composed more vulgari without the help of his Analysis nove: A therefore he had not yet found out that method.

In his Letter of 27 Aug

In the same Letter of 27 Aug 1676 he when M^r Newton had said that his Analysis by the help of co infinite equations extended to the solution of almost all Problemes except those of num he replied Id mihi non non videtur. Sunt enim multa us adeo mira & implexa ut ne ab Æquationibus pendeant ne ex Quadraturis. Qualia sunt (ex multis alijs) problemata methodi tangentium inversæ. Which is a Demonstration that he had not yet found out the Differential method.

In his Letter to M^r Oldenburg $\frac{18}{28}$ Novem. 1676 he was upon improving the method of Slusius by getteng a Table of Tangents to be computed, which was another method of improving it. t

In his Letter to M^r Oldenburg $\frac{18}{28}$ Novem. 1676, he w^ch was about four months after he had received a copy of M^r Newtons letter of 10 Decem. 1672 concerning the method of Tangents

[In Iuly \or Aug/ 1676 he received a copy of M^r Newtons letter of 10 December 1672 concerning the representing that the method of Tangents there set down (w^ch proved to be y^e same w^th that of Slusius) was a Co branch or Corollary of a very general method &] in his letter from to M^r Oldenburg from Amsterdam dated $\frac{18}{28}$ Novem. 1676, he wrote Methodus tangentium a Slusio publicata nondum rei fastigium tenet. Potest aliquid amplius prœstari in eo genere quod maximi foret usus ad omnis generis Problemata: [etiam ad meam (sine extractionibus) Æquationum ad series reductionem]. Nimirum posset brevis quædam calculari circa Tangentes Tabula eous continuanda donec progressio Tabulæ apparet. And this was the improvement of the method of Slusius w^ch his mind then ran upon.

The next year upon his arrival at Hannover he fell into public

And M^r Newton in his Letter of . . . . after taught how to resolve \the |any| dignity of / a binomium into a converging series \the second/, \term of/ {illeg} which \series/ by the method of D^r Barrow gives the first Lemma of Slusius \together w^th his whole method/. And after he had described this method of series he subjoyned: Ex his videre est the reduction of infinite equations into finite ones when it might be,

And whereas he had said in his Letter of 13 Iune 1676 that his method of series became not universal w^thout some other methods, \& that w^ch he then forbore to describe as also what he had invented concerning/ he \here/ set down the foundation of those methods in sentences exprest enigmatically w^ch & gave a series for squaring of figures w^ch brake off & gave the quadrature in a finite equation w^ch it might be.

<157v>

M^r Newton at the request of M^r Collins sent him his method of Tangents in a Letter dated 10 Decem. 1672. It proved to be the same w^th that of \w^ch/ Slusius but founded upon another Principle sent to M^r Oldenburg about five weeks after but founded upon another principle \the method of fluxions w^ch in drawing of Tangents agrees with the method of D^r Barrow./. [If x be the Abscissa & v the o xⁿ\=y/ the ordinate & x the Abscissa be increased by an indefinitely small quantity o so as to become x+o the ordinate will be ${\overline{)\mathrm{x}+\mathrm{o}}}^{\mathrm{p}}$ w^ch being reduced into an infinite series become ${\mathrm{x}}^{\mathrm{p}}+\mathrm{p}\mathrm{o}{\mathrm{x}}^{\mathrm{p}-1}+\mathrm{\&c}$ as is set down in M^r Newton Analysis pag 19. And by D^r Barrows rules if all the terms be rejected in w^ch o is either wanting or of more dimensions then one there will remain $\mathrm{p}\mathrm{o}{\mathrm{x}}^{\mathrm{p}-1}$ for the diffe increase of the ordinate. Therefore the subtangent is to the Ordinate as o the increase of the abscissa to $\mathrm{p}\mathrm{o}{\mathrm{x}}^{\mathrm{p}-1}$ the increase of the Ordinate that is as 1 to p{illeg}x{illeg} $\mathrm{p}{\mathrm{x}}^{\mathrm{p}-1}$, & by consequence the subtangent is is $\frac{1}{\mathrm{p}}\mathrm{x}${illeg} $\frac{\mathrm{y}}{\mathrm{p}\mathrm{x}\mathrm{p}-1}$ or $\frac{\mathrm{y}\mathrm{x}}{\mathrm{p}\mathrm{x}\mathrm{p}}$

If z be y^e Abscissa \of a Curve &/ x the Ordinate, & ${\mathrm{z}}^{\mathrm{n}}=\mathrm{x}$ the equation, &

M^r Newton by interpolation of series

This method readily gives the method of Slusius]

M^r Newton in his Letter \M^r O. stated/ of 24 Novem. 171 1676. wrote that the had explained his method of Tangents in a Tract written 5 years before \viz^t A. 1671/ that it flowed readily was the same with the method communicated by Slusius, that it but flowed from a fountain w^ch gave it readily without needing a D particular Demonstration, & that it stuck not at radicals, {or surds} & by w^ch exten & w^ch in like manner extended to the solution of determining of maxima & minima & some other {P} sorts of Problems & rendred Quadratures of Curves more easy & stuck not at surds & was comprehended concealed in this sentence exprest enigmatically: Data æquatione quotcun fluentes quantitates involvente fluxiones invenire, & vice versa.

Thus M^r Newton in these three Letters described \represented that/ his method to as very universal, |t|h{e}|a||t| gave \that it gave/ the method of Slusius as an obvious Corollary, & not to st \& that it/ proceed|ed| in Problems of Tangents & of maxima & minima with &|c| some others w^thout sticking at surds & to faciliate|d| quadratures. And after all this \information/ M^r Leibnits in his Letter of 21 Iune 1677 proposed his differentiall calculus in these words Clarissimi Slusij Methodum Tangentium nondum esse absolutam New Celeberrimo Newtono assentior

In the meane time these arguments make against him.

business, w^ch hindered him from finishing his Nova Analys Arithmetical Quadrature of the circle compos for the Press until he found his New Analysis w^ch made him not think it worth the while to pub finish what he had composed \been composing/ vulgari more.

But after \when/ he had received M^r Newtons Letter dated 24 Octob. 1676 w^ch gave him further light into the true improvement: he [wrote back Clarissimi Slusij methodum tangentium nondum esse absolutam Celeberrimo Newtono assentior. And & And: Hinc nominando imposterum dy differentiam duarum] And fixed his differential no{]} beg notation & began to communicate it writing Hinc nominando wrote back: Clarissimi Slusij methodum tangentium nondum esse absolutam celeberrimo Newtono assentior. \And/ Hinc nominando in posterum dy differentiam duarum {illeg} proximarum y &c: [This is the first mention of this method in his Letters & if he would have his method differential method \it/ of an earlier date he is bound in point of candour to prove it.] Here he fixed his notation & began to communicate it. And if he would have his \method/ of an earlier date he is bound to communicate it in point of candour to prove it.

<158r>

M^r Leibn as may appear by the following comparison

The calculation by the method of M^r Leib D^r Barrow

$\begin{array}{c}\underline{\mathrm{a}+\mathrm{b}\mathrm{y}+\mathrm{c}\mathrm{x}+\mathrm{d}\mathrm{y}\mathrm{x}+\mathrm{e}\mathrm{y}+\mathrm{f}{\mathrm{x}}^2+\mathrm{g}{\mathrm{y}}^2\mathrm{x}+\mathrm{h}\mathrm{y}{\mathrm{x}}^2\text{ \&c}}\\ \phantom{\mathrm{a}}\phantom{+}\mathrm{b}\mathrm{a}+\mathrm{c}\mathrm{e}+\mathrm{d}\mathrm{y}\mathrm{e}+2\mathrm{e}\mathrm{y}\mathrm{a}+2\mathrm{f}\mathrm{x}\mathrm{e}+2\mathrm{g}\mathrm{x}\mathrm{y}\mathrm{e}+2\mathrm{h}\mathrm{x}\mathrm{y}\mathrm{e}\text{ \&c}\\ \underline{\phantom{\mathrm{a}}\phantom{+}\phantom{\mathrm{b}\mathrm{a}}\phantom{+}\phantom{\mathrm{c}\mathrm{e}}+\mathrm{d}\mathrm{x}\mathrm{a}\phantom{+}\phantom{2\mathrm{e}\mathrm{a}\mathrm{a}}\phantom{+}\phantom{2\mathrm{f}\mathrm{x}\mathrm{e}}+\mathrm{g}{\mathrm{y}}^2\mathrm{a}+\mathrm{h}{\mathrm{x}}^2\mathrm{a}\text{ \&c}}\\ \phantom{\mathrm{a}}\phantom{+}\phantom{\mathrm{b}\mathrm{a}}\phantom{+}\phantom{\mathrm{c}\mathrm{e}}+\mathrm{d}\mathrm{a}\mathrm{e}+\mathrm{e}\mathrm{a}\mathrm{a}+\mathrm{f}\mathrm{e}\mathrm{e}+\mathrm{g}\mathrm{x}\mathrm{a}\mathrm{a}+\mathrm{h}\mathrm{y}\mathrm{e}\mathrm{e}\phantom{\text{ \&c}}\\ \phantom{\mathrm{a}}\phantom{+}\phantom{\mathrm{b}\mathrm{a}}\phantom{+}\phantom{\mathrm{c}\mathrm{e}}\phantom{+}\phantom{\mathrm{d}\mathrm{a}\mathrm{e}}\phantom{+}\phantom{\mathrm{e}\mathrm{a}\mathrm{a}}\phantom{+}\phantom{\mathrm{f}\mathrm{e}\mathrm{e}}+2\mathrm{g}\mathrm{y}\mathrm{a}\mathrm{e}+2\mathrm{h}\mathrm{x}\mathrm{e}\mathrm{a}\text{ \&c}\\ \phantom{\mathrm{a}}\phantom{+}\phantom{\mathrm{b}\mathrm{y}}\phantom{+}\phantom{\mathrm{c}\mathrm{e}}\phantom{+}\phantom{\mathrm{d}\mathrm{a}\mathrm{e}}\phantom{+}\phantom{\mathrm{e}\mathrm{a}\mathrm{a}}\phantom{+}\phantom{\mathrm{f}\mathrm{e}\mathrm{e}}+\mathrm{g}\mathrm{e}\mathrm{a}\mathrm{a}+\mathrm{h}\mathrm{a}\mathrm{e}\mathrm{e}\phantom{\text{ \&c}}\end{array}\}=0$

The calculation by the Method of D^r M^r Leibnitz

$\frac{\mathrm{a}+\mathrm{b}\mathrm{y}+\mathrm{c}\mathrm{x}+\mathrm{d}\mathrm{y}\mathrm{x}+\mathrm{e}{\mathrm{y}}^2+\mathrm{f}{\mathrm{x}}^2+\mathrm{g}{\mathrm{y}}^2\mathrm{x}+\mathrm{h}\mathrm{y}{\mathrm{x}}^2\text{\&c}}{\begin{array}{c}\mathrm{b}\mathrm{d}\mathrm{y}+\mathrm{c}\mathrm{d}\mathrm{x}+\mathrm{d}\mathrm{y}\mathrm{d}\mathrm{x}+22\mathrm{y}\mathrm{d}\mathrm{y}+2\mathrm{f}\mathrm{x}\mathrm{d}\mathrm{x}+2\mathrm{g}\mathrm{x}\mathrm{y}\mathrm{d}\mathrm{y}+\\ +\mathrm{d}\mathrm{x}\mathrm{d}\mathrm{y}+\mathrm{g}{\mathrm{y}}^2\mathrm{d}\mathrm{x}+\end{array}}$

This put M^r Leibnitz upon considering the method of Slusius & how it might be improved. For in his Letter to M^r Oldenburg \dated/ from Amsterdam $\frac{18}{28}$ Novem 1676 he wrote thus. Methodus tangentium |a| slusij|o| publicata nondum rei fastigium tenet. Potest aliquid amplius præstari in eo genere quod maximi foret usus ad omnis generis Problemata. Nimirum posset brevis quædam calculari circa Tangentes Tabula, eous continuanda donec progressio Tabulæ apparet. And a little after: Methodus tangentium |a| slusij|o| publicata dudum Huddenio fuit nota Amplior ejus methodus est quam quæ a slusio fuit publicata. B By it appears that he He was not yet master of the right way of improving it, but this winter or in spring following began to understand it.

M^r Newton in his Letter dated — — — others more difficult.

And after all this description of an universal method, M^r Leibnitz at length \w^ch stuck not at surds/ |&| whereof the method of Tangents \published by Slusius/ was but a branch or Corollary M^r Leibnitz at length found but w^ch was derived from a bette \more general/ principle M^r Leibnitz [at length [fell upon the differential method of \{dawing}/ Tangents & found that it was capable of these b{illeg} those improvements \mentioned by M^r Newton/ &] in his Letter of 21 Iune 1677 proposed \his differential method/ in these words Clarissimo Newtono Slusij Methodum Tangentium nondum esse absolutam Celeberrimo Newtono assentior. Et jam a multo tempore rem Tangentium longe generalius tractavi, scilicet per differentias Ordinatarum. And Then explaining what he meant by these differences he added \proposes his notation new notation/ Hinc nominando in posterum dy differentiam duarum proximarum y &c {illeg} This \And this/ was the beginning of his notation. A \And/ Then he goes on to shew how by this method |with D^r Barrows method shewing how| Tangents may be drawn, allowing to y^e \{illeg}on{s}{illeg} keeping/ the|reby| Rules of D^r Barrow \above mentioned/ & how the Method of Slusius follows from it & how it as M^r Newton had notified, how & as M^r Newton had notified & how it \is to be improved so as not to/ sticks not at Tang surds, & then adds Arbitror quæ celare voluit Newtonus ab his non abludere. Quod addit, ex hoc eodem fundamento Quadraturas quo reddi faciliores me in sententia hac confirmat, nimirum \semper/ figuræ illæ sunt quadrabiles quæ sunt ad æquationem differentialem. Thus he concludes that he had now got a method like that of M^r Newton & therefore in the Acta Eruditorum by the caculus {sic} similis me\aa/nt me \the like method w^ch/ M^r Newtons method had had partly described openly & partly concealed M^r Newtons method.

But he tells us: Et jam a multo tempore rem Tangentium longe generalius tractavi scilicet per differentias Ordinatarum. If he means that he had used D^r Barrows {so} method of Tangents jam a multo tempore, tis nothing to his purpose. But if he means that he had improved it into a general method jam a multo tempore: it lies upon to prove it. For by the law of all nations, in cases of controversy no man can be a witness for himself. And for any man to insist upon it upon it upon any {fue}tence of d{illeg} \integrity/ {illeg}|{r}| candor \his own candor with a designe to be a of integrity witnes for himsel{f}/, is a demonstration of his want of candor {illeg} integ candor|.| & integrity If there were \had been/ no competition in the case, he might have been credited without doing injustice to any body: but he is here putting in his claim to the methods of D^r Barrow & M^r Newton & therefore by the laws of all nations must put in his \prove his/ assertion

<158v>

p. 88. pro nota * Idem fecit &c scribe

* Gregorius in Prop. 7 Geometriæ universalis anno 1668 impressæ et Barrovius rem langentium tractavit per differentias ordinatarum. Barrovius in ejus Lect 10 anno 1669 impressa idem fecit, sed, paulo generalius. Methodus T Slusius methodum \suam/ tangentium fundavit in hoc Lemmate: Differentia duarum Dignitatum ejusdem gradus applicata ad differentiam laterum [id est Differentia duarum Ordinatam dat partes singulares gradus inferioris ex binomio laterum, ut $\frac{{\mathrm{y}}^3-{\mathrm{x}}^3}{\mathrm{y}-\mathrm{x}}=\mathrm{y}\mathrm{y}+\mathrm{y}\mathrm{x}+\mathrm{x}\mathrm{x}$. Et hic applicando hoc Theore Lemma ad rem Tangentium subintelligat \appliunt per/ differentias infinite parvas. Newtonus in Literis \Epistola/ {illeg} 10 Decem. ad Collinium datis {illeg} c missa data et hoc an {a} anno superrore circa mensem inter 14 Aug Iun & 11 Aug. {illeg}d{illeg} circa mensem Iulium {an a} circa mensem Iulium ad D. Leibnitium missa fuit fuerat ad Leib superiore \data cujus exemplar inter Collectiones Gregorianas anno D./ Oldenburgus anno superiore ad D. Leibnitium miserat, scripsit methodum Tangentium Slusij esse particulare quodd|a|am vel potius Corollarium potius Methodi generalis quæ extend{it}\eret/ se citra molestum ullum calculum ad Tangentes curvarum tam Mechanicaru resolvendum alia abstrusiora Problematum genera de Curvitatibus, Areis, Longitudinibus, centris gravitatis curvarum &c et ad quantitates surdas & Curvas Mechanicas minime hæreret. Et in epistola 13 Iunij 1676 ad D. Leibnitium itidem missa scripserat Analysin suam beneficio serierum ad omnia pene Problemata sese extendere. D. Leibnitius tandem respondit id sibi non videri; esse enim multa us adeo mira & implexa ut ne ab æquationibus pendeant ne ex quadraturis, qualia sunt (ex multis alijs) Problemata methodi tangentiū inversæ. Newtonus rescripsit inversa tangentium Problemata esse in potestate alia illis difficiliora, I{illeg} Et methodum Tangentium flusij a suis principijs {illeg} statim consequi id generalius cum methodus sua quantitates surdas minime moraretur, & eodem modo se rem habere in quæstionibus de æ ma{illeg}|x|imis et minimis alijs quibusdam & eodem fundamento quadraturm Curvarum faciliorem reddi simpliciorem redd{illeg}|i| & cujus exempla quædam dedit sed fundamentum ipsum literis transpositis {illeg} celavit hanc sententiam involventibus. Data Æquatione quotcun fluentes quantitates invol vente fluxiones invenire; et vice versa. Et D. Leibnitius his omnibus admonitus \ne a Newtono aliquid didicisse videretur,/ tandem respondit in hæc verba: Clarissimi Slusij methodum Tangentium nondum esse absolutam Celeberrimo Newtono assentior; et jam a multo tempore rem Tangentium longe generalius tractavi, scilicet per differentias ordinatarum. Et in epistola 29 Decem. 1711 data, addidit, se inventum plusquam nonum in annū pressisse: Quasi habuisset ante mensem Octobren {sic} anni 1675 ideo a Newtono nil didicisset me nil didicisset.

Ad Notam * pag 90 adde. Certe D. Leibnitius similitudinem methodorum non tantum jam intellexerat & sed etiam postea \anno 1684 mense Octobri |postea|/ ubi methodum differentialis elementa in lucem emisit sub hoc titulo: Nova methodus pro maximis et minimis, item tangentibus, quæ nec fractas nec irrationales moratur, & subjiunxit: Et hæc methodus quidam initia sunt tantum Geometriæ cujusdam multo sublimioris {illeg}|a|d difficillima & pulcherrima quæ etiam mistæ Matheseos pertingentis quæ sine calculo nostro differentiali, aut SIMILI, non temere quisquam pari facilitate tractabit. Vide Acta Eruditorum Mensis Octob. pag 467, 473. Conferatur hæc methodi {L}|d|ifferentialis descriptio cum descriptione consimili methodi fluxionem in Epistolis tribus Newtoni ad D. Leibnititum {sic} missis, ut similitudinem metho{r}|d|orum Leibnitio{illeg} cognitam videas.

<159r>

The History of the Method of Moments or Differenc called Differences by M^r Leibnitz.

In the Introduction to Book of Quadratures published A.C. 1704 M^r Newton wrote that he found the Method of fluxions gradually in the years 1665 & 1666, & tho this was not so much as D^r Wallis said nine years before in the Preface to the first volume of his works without being then contradicted, yet in the Acta Eruditorum for Ianuary 1705, in giving an Account of this Book M^r Leibnitz is called the Inventor; & from thence is deduced this conclusion: Pro differtijs {sic} igitur Leibnitianis Newtonus adhibet semper [pro ijsdem] adhibuit fluxiones — iijs tum in Principijs n|N|aturæ Mathematicis tum in alijs postea editis [pro differentijs illis] eleganter est usus quemadmodum et Honoratus Fabrius in sua Synopsi Geometrica motuum progressus Cavallerianæ methodo substituit. D^r Wallis was homo vetus & rerum anteactarum peritissimmus \informed himself of these matters from the beginning/, being very inquisitive in Mathematicall affairs, & having received from M^r Oldenburg M^r cópies of M^r Newtons \my two/ Letters of 13 Iune & 24 Octob. 1676 when they were newly written. and \in the said Preface/ he said that in those Letters I \M^r Newton/ |I| had explained to M^r Leibnitz the Method found by hi{illeg}|m|e ten years before or above; meaning that M^r Newton|I| had found the Method above ten years before M^r Leibnitz, & that he |I| had so far discovered it to M^r Leibnitz \him/ by those Letters, as to leave it easy to find out the rest. And even before M^r N|L|eibnitz had the Method, M^r Newton \I said/ in one of those Letters (that of 24 Octob 1676) said \that/ the foundation of the Method was obvious, & therefore, since he |I| had not then leasure to describe it at large, he |I| would conceale it in an Ænigma. This he |I| did, not to make a mystery of it, but to prevent its being taken from him \me/ because it was obvious. And in that Ænigma he |I| set down the first Proposition of the book of Quadratures because it was obvious in the very words of the Proposition; & therefore had this Proposition with the Method founded upon it where he |I| wrote that Enigma: or rather, because the very words of the Ænigma \Proposition/ are copied in the Ænigma, it argues that the Book of Quadratures was then before him|e|, & so was written before M^r Leibnitz had the Method. This Book is said to have bee \was/ extracted out of older papers. In the said Letter of 24 Octob. 1676 M^r Newton |I| set down a series for squaring of figures w^ch in some cases breaks off & becomes finite & illustrated it with examples & said that he |I| found this & some other Theorems of the same kind by the method whose foundation was comprehended in that Ænigma, that is, by the method of fluxions. And how I found them I explained in the first six Propositions of the Book of Quadratures, & do not know any other method by which they could be found: & therefore when I wrote that Letter I had the Method of fluxions so far as it is conteined in those six Propositions. After I had finished the Book & \while/ the 7^th 8^th 9^th & 10^th Propositions were fresh in memory I wrote upon them to M^r I. Collins that Letter w^ch was dated 8 Novem 1676 & being found amongst his Papers was published by M^r Iones. The <160r> Theoremes at the end of the tenth Proposition for comparing curvilinear figures with the Conic sections were known to m are mentined in th my said Letter of 24 Octob 1676, & all the Ordinates of the figures are there copied in the second part of the Table are there copied from the Book. And therefore the Book was then before me. To understand the two Letters of Octob 24 & Novem 8 1676 & how to perform the things & find the Theorems mentioned in them requires skill in all the Method of fluxions so far as it is comprehended in all the first ten Propositions of the Book. And the eleventh & last Proposition depends upon a series of first second third & fourth fluxions.

The first Proposition of this Book & its solution illustrated with examples in first & second fluxions &c was at the request of D^r Wallis sent to him \almost verbatim/ in a Letter dated 27 Aug. 1692, & printed by him that year in the second Volume of his works, which came abroad the next year, A.C. 1693. And thus the Rule for finding second third & fourth fluxions there set down was published some years before the Rule for finding second third & fourth differences & was at least seventeen years before in manuscript before it was published. In the Ind|t|roduction to this Book the method of fluxions is taught without the use of prickt letters; for I seldom used prickt Letters when I considered only first fluxions: but when I considered also second third & fourth fluxions I distinguished them by the number of pricks. And this notation is not only the oldest but is also the most expedite, tho it was not known to the Marquess de l'Hospital when he recommended the differential Notation.

In my Analysis per æquationes numero terminorum infinitas communicated by D^r Barrow to M^r Collins in Iuly 1669, I said that my Method by series gave the areas of Curvilinear figures exactly when it might be, that is, by the Series breaking off & becoming finite: & thence it appears that when I wrote that Analysis, I had the Method of fluxions so far, at least, as it is conteined in the first six Propositions of the Book of Quadratures; tho those Propositions were not then drawn up in the \very/ words of the Book. In that Tract of Analysis I represented time by a line increasing or flowing uniformly & a moment of time by a particle of the line generated in the moment of time, & thence I called the particles a moment of the line; & the particles of all other quantities generated in the same moment of this line time I called the moments of those quantities; & the fact under the rectangular Ordinate & a moment of the Abscissa I considered as the moment of the rectiline \cursa (rectilinear or/ curvilinear) area described by that Ordinate moving uniformly upon the Abscissa. For a moment of time I put the letter o, & thence computed the moments of the other quantities generated in the moment of time, & for those moments put any other symbols. And for the Area of a figure I sometimes put the Ordinate included in a square. And by considering how to deduce moments from increasing quantities & quantities from their moments, I deduced areas \Ordinates/ of figures from their Ordinates \Areas/ & Ordinates \the Areas/ from the areas \Ordinates/: w^ch is the same thing with deducing <161r> fluxions from fluents & fluents from fluxions. And in the end of the Book I demonstrated by this sort of calculus the first of the three Rules set down in the beginning thereof. And a|i|n this Rule for the index of a Dignity I put an indefinite quantity affirmative or negative integer or fract, for the inden & thereby introduced indefinite indices \of Dignities/ into Analysis. And applying this Method of Moments not only to finite equations but also to equations involving converging series I gave this Tract the name of Analysis per æquationes numero terminorum infinitas.

<163r>

The history of the Differential Method.

M^r Collins having received from me & M^r Iames Gregory several series for squaring the Circle & Conic Sections, was very free in communicating them to the Mathematicians both at home & abroad in {illeg} the years \1670,/ 1671 & 1672 & M^r Leibnitz was in London in the beginning of the year 1673 & went from thence to Paris in the beginnin end of February \carrying Mercators Logarithmotechnia along with him/ & kept a correspondence w^th M^r Oldenburg till Iune following about Arithmetical Questions, being not yet acquainted with the higher Geometry. Then he intermitted his correspondence till Iuly 1674 & in the mean time studied the higher Geometry {illeg} beginning with the Horologium oscillatorium of M^r Huygens w^ch came abroad in April 1673. His following correspondence was about converging series till spring 1676. And I And then upon the news of M^r Iames Gregories death, he wrote for a collection of M Gregories Papers, & the Demonstration of my Series, meaning my Method of finding them & p promised M^r Oldenburg a reward for my Method & directed him to M^r Collins for the same told him that M^r Collins could help him to it. I suppose he meant my Analysis per Series numero terminorum infinitas. For that was the only Paper in w^ch I \had/ sent my Method of Series to M^r Collins.

Thereupon M^r Collins drew up as well Extracts out of Gregories Letters, & the Collection was sent to Paris In Iune following \to be returned & it is now in the Archives of the R. Society/; but instead of sending a copy of my Analysis, he & M^r Oldenburg jointly sollicited me to send what \the Method w^ch/ M^r Leibnitz desired, & thereupon I wrote my Letter to M^r Olde of 13 Iune 1676, w^ch \& this/ was sent to him at the same time with the Collection. In this Collection was a copy of a Letter of M^r Iames Gregory to M^r Collins dated 15 Feb. 167{6}|{8}| 16$\frac{70}{71}$ w^ch conteins several Series one of w^ch was that famous one for finding the Arc whose sin tangent is given: w^ch series had been also sent by M^r Oldenburg to M^r Gregory \Leibniz/ the year before & the receipt thereof acknowledged. There was also in the same Collection a copy of a Letter of M^r Gregory to M^r Collins dated Sept 5. 1670 in w^ch Gregory wri|o|tes that by \improving/ the method of Tangents of Barrow he had found a method of Tangents w^thout calculation. There was also in the same Collection a copy of a Letter which I had writ to M^r Collins above thre years before. The Letter was dated 10 Decem 1672, & is as follows. Ex animo gaudeo – – me grave ducas. And \copies of/ these two last Letters had be were communicated also by M^r Oldenburg to M^r T{illeg}hurn Tschunhause in Iune 1675.

In my letter of 13 Iune 1675|6| I had said (with relation to the Method described in my Analysis per æquationes numero terminorum infintas,) {illeg} Ex his videre est quantum fines Analyseos per hujusmodi series infinitas æquationes ampliantur: quippe quæ earū beneficio, ad omnia pene dixerim problema (si numeralia Diophanti & similia excipias) sese extendit. And M^r Leibnitz in his Answer dated 27 Aug. 1676, replied: Quod dicere videmini pleras difficultates (exceptis Problematibus Diophænteis) ad series Infinitas reduci; id m{h}|i|hi non videtur. Sunt enim multa us adeo mira et implexa ut ne <164r> ab Æquationibus pendeant, neque ex quadraturis. Qualia sunt (ex multis alijs) Problemata methodi Tangentium inversæ. In the same Letter he placed the perfection of Analysis not in the Differential method but in another Analysis method composed of Analytical Tables of tangents & the Combinatory Art. Nihil est, said he, quod norim in totā Analysi momenti majoris. And a little after: Ea vers nihil differt ab Analysis|i| illa SVPREMA, ad eujus intima Cartesius non pervenit. Est enim ad eam constituendam opus Alphabeto cogitationum humanarum. This was the top of his skill at that time & therefore he had not yet found out the differential method /nor had hitherto used fluxions for {h}is differences.\

In October 1676 he cane {sic} to London a second time & there met with D^r Barrows Lectures, & saw my Letter of Octob. 24. 1676 \& therein had fresh notice of my Compendium of Series or Analysis com/ & consulting M^r Collins saw in his hands many of mine & Gregories Letters, especially those relating to series, & therein had fresh notice of my Compendium of Series or Analysis communicated by D^r Barrow to M^r Collins, & consulting M^r Collins saw in his hands many of mine & Gregories Letters, especially those relating to series & in his way home from London was meditating how to improve the method of Tangents of Slusius as appears by his Letter to M^r Oldenburgh dated from Amsterdam $\frac{18}{28}$ Novem. 1676. And the next year in a letter to M^r Oldenburgh dated 21 Iune he sent hither his new Method with this Introduction. Clarissimi Slusij Methodum Tangentium nondum esse absolutam celeberrimo Newtono assentior. And in describing this Method he abbreviated D^r Barrows method of Tangents by new symbols & shewed how it might be improved by the so as to the Method of Slusius (w^ch was the same with that of Gregory) & to proceed in equations involving surds; & then subjoyned: Arbitror quæ celare voluit Newtonus de tangentibus ducendis ab his non abludere. Quod addit, ex eodem fundamento Quadraturas reddi faciliores me in sententia hac confirmat. This was the first time that he began to communicate his differential Method & therefore I had not hitherto used fluxions for \his/ Differences; nor can the assertion be true Pro differentijs Leibnitianis Newtonus semper adhibuit fluxiones.

M^r Iames Bernoulli in the Acta eruditorum for December 1691 pag. 14 said that the Calculus of M^r Leibnitz was founded in that of D^r Barrow & differed not from it except in the notation of differentials & some compendium of operation. And the Marquess de l'Hospital in the Preface to his Analysis of infinite petits published A.C. 1696, represented that where D^r Barrow left off M^r Leibnitz proceeded, & that the improvement w^ch he made to the Doctors Analysis consisted in excluding fractions & surds: but the Marquiss did not then know that M^r Leibnitz had notice of this improvement from me by two Letters above mentioned, dated 10 Decemb. 1672 & 24 Octob. 1676, a copy of the first being sent to h im in Iune 1676. After he had notice that such an improvement was to be made, he might find it proprio Marte, but \by/ that notice knew that I had h it before him. And in his Letter of |2|1{illeg} Iune 1677 he confessed that he had such notice.

In the Acta Eruditorum for October 1684 M^r Leibnitz published the Elements of the differential Method as his own without mentioning the correspondence w^ch he had formerly had with the English \me/ <164v> about these matters. He mentioned indeed a Methodus similis; but whose that Method was or what he knew of it he did not say, as he should have done. And this his silence put me upon a necessity of writing the Scholium upon the second Lemma of the second Book of Principles, least it should be thought that I borrowed that Lemma from M^r Leibnitz

<163v>

\— but {s}aid/ {illeg} that I had interwoven it with the method of infinite series & that being tyred w^th these speculations I had absteined from them five years, that {illeg} & therefore had this method above five years before & had that is before the year 1671. And that it was so general as to reach almost all Problems except \perhaps some numeral ones like/ those of Diophantus. And

& therein \he/ was again told that the foundati I had a \my/ Method of working w^ch readily gave me the method of tangets of Slusius directly & immediatediately {sic} so as to need no demonstration thereof & that stuck not at equations equations affected with radicals involving one or both indeterminate quantities, & proceeded in the same manner in questions about maxima & minima & \in some/ others w^ch I did not there mention, & faciliated Quadratures & gave me general The\re/mes for that end \Quadratures/, one of w^ch I there set down & illustratd w^th examples & that I had wrote a tract of it upon |th|it|s| \method/ & the method of series together five years before with a designe to print it together w^th a tract about light & colours.

In my Letter of Octob 24 I

After things M^r Leibnitz in the year 1684 published thi|e| elements of this method of {illeg} as his own without making any mention of the foregoing correspondence

<164v>

The first Proposition of the Book of Quadratures is certai{illeg}|n|ly the foundation of the method of fluxions. This This Proposition was comprehended verbatim in the ænigma \by/ w^ch in my Letter of Octob. 24 1676 I set down \concealed/ the foundation of the Method th there spoken of & therefore that method was the method of fluxions. In that Letter I said that I had written a Tract of|n| this Method & the Method of series together five years before but did not finish it nor meddle any more with these things till the year 1676 \being tyred with them. {sic}/. And in my Letter of Iune 13 I wrote to the same purpose. \And this is the Method w^ch I described in my Letter of Decem 10^th 1672./ In my Letter of Octob. 24 1676 I said also that Analysis per Series \Æquationes/ numero terminorum infinitas I said that of that method of Analysis \the method there described/: Deni ad Analyticam merito pertinere censeatur, cujus beneficio Curvarum areæ & longitudines &c (id modo fiat) exacte & Geometrice determinentur. Sed ista narrandi non est locus. This was done \effected/ by series which in these \some/ cases break off & become finite, as you may understand by the Letter of M^r Collins to M^r Strode Iuly 26, 1672. And therefore when I wrote \before D^r Barrow sent/ that Analysis to M^r Collins, that is before Iuly 1669 I had the method of fluxions so far at the least as it is conteined in the first six Propositions of the Book of Quadratures.

I sent him also the method of extracting fluents out of the method of equations involving fluxions, w^ch t{illeg}|o| the best of my memory was composed in the year 1671.

M^r Leibnitz never was in quiet possession abroad nor I out of possession in England. He has been told again & again that he was not the first iinventer|o|r {sic} & never would answer directly to this point, but only pretendeth answered indirectly by pretending that he found it apart, & that gave it to him in the Scholium upō the 2^d Lemma of y^e 2^d Book of Principles

< insertion from the bottom of the page > In a Paper dated 29 Iuly 1713 & written by one who used the \Leibnitian/ phrase illaudabil{i} laudis amore & knew what M^r Leibnitz did at Paris 40 years before I was \singled out &/ treated very reproachfully. And this was to make me appear. {illeg}|And| in his Postscript to Mr. l'Abbe Cont \written in Autumn. 16|7|/15 singled out & treated in a very provoking manner. to make me appear. And when I was prevaid|l|ed with to return an Answer \to this Postscript/ he declared in his Letter to Abbé Conti of Apr. {illeg}9^th 1716 to Mr. l' Abbé Conti that he had resolved not to \would by no means/ enter the lists with my forlorn hop{e} (meaning M^r Keill & M^r Coles &c) but since I was willing to appear my self he would give me satisfaction. Nothing {w}|c|ould satisfy \content/ him but to make me appear & give \declare/ my opinion, & now I have declared it, I leave every body ta {sic} his own opinion, out of a desire to be quiet. < text from f 164v resumes > The Editors of the Acta Eruditorum {illeg} |of| Iune 1696 \for silencing D^r Wallis it {illeg}\{illeg}/{illeg}{t}/ pretending|ed| that I had ackno\w/ledged both publickly & privately that in the year 1676 {or} about 20 years before or above \in the year 1676 or before/ M^r Leibnitz had the Differential calculus & Infinite Series & general methods for them + < insertion from the bottom of the page > + & yet I never \{all of} {illeg}/ heard of his having the differential calculus before Iune 1677, nor \in those days/ knew of M^r Oldenburghs letter of Apr. 15 1675 \nor of \a {illeg} of/ {illeg}tegories Letter of 15 Feb. 1671 sent to M^r Leibn in frane 1676/ by \both/ w^ch he received his infinite series from England, & \nor/ looked upon his method of Series to be general < text from f 164v resumes > , {illeg} \Afterwards/ M^r Leibnitz in his Letters \to D^r Sloan/ of 4 March {st. n.} 177 & 29 Decem S^t. n. 1711 \declared answering D^r Keill &/ pressed me to declare my opinion, \& declined answering D^r Keill, & × < insertion from the bottom of the page > × & in the defamatory libel dated 29 Iulij 1713 berated me very (written by one who knew what passed between M^r Leibnitz & his friends at Paris) forty years before) < text from f 164v resumes > / & in his Letter of Apr 29 to Mr. l'Abbe Conte|i| he declared that he would not enter the lists w^th my forlorn hope (meaning Keill & M^r Coats) but since I was willing to appear my self he would give me satisfaction. Nothing would satisfy him but to make me appear & declare my opinion & now I have declared it, I {illeg} am resolved to be silent

<165r>

The History of the Method of \Moments/ Fluxions & Moments approaching Series.

In the Introduction to Book of Quadratures \published A.C. 1704/ I wrote that I invented the Method of fluxions gradually in the years 1665 & 1666, & tho this was not so much as D^r Wallis said \nine years before/ in the Preface to the first volume of his works without being then contradicted, yet the in the Acta Eruditorum for Ianuary 1705 M^r Leibnitz in giving an Account of this Book M^r Leibnitz is called the Inventor, meaning the first Inventor. For \And/ from thence is deduced this conclusion. Pro differentijs igitur Leibnitianis Newtonus adhibet semper [pro ijsdem] adhibuit fluxiones — iijs tum in Principijs Naturæ Mathematicis, tum in alijs postea editis [pro differentijs illis] eleganter est usus, quemadmodum et Honoratus Fabrius in sua Synopsi Geometrica, motuum progressus Cavallerianæ methodo substituit. D^r Wallis was homo vetus & rerum anteactarum peritissimus \being inquisitive in these matters &/ having received from M^r Oldenburg copies of my two Letters of 13 Iune & 24 Octob. when 1676 when they \were/ newly written. \And/ he said that I had ex in those Letters I had explained to M^r Leibnitz the method found by me ten years before or above, meaning I suppose that I \had it above ten years before him &/ had so far discovered it \to him by those Letters/ as to leave it easy to find out the rest. And this is nothing more than what I said in \{illeg}so{illeg}/ the {illeg} Letter |And in one of those Letter w^ch {illeg} before he had it {illeg} before he began to write of it)| \that/ of 24 Octob 1676,) \we/ /I said\ that the foundation of the Method was \very/ obvious & therefore I (since I had not leasure to describe it at large) I would conceale it in an Ænigma. |This I did not to make a mystery of it but to prevent its being taken from me because it was obvious. And in| In {sic} That Ænigma I set down the first Proposition of the book of Quadratur{es} in the very same words \of the Proposition ‖ < insertion from the left margin > ‖ & therefore had this Proposition with the method founded upon it when I wrote the said Letter. Or rather; because the very words of the Proposition are copied in the Ænigma, it argues that the Book of Quadratures was then before me. < text from f 165r resumes > / For this was written that year being {d} \Book was then before me, being newly written. It was/ extracted for that|e| most part out of a Tract w^ch I wrote in the year 1671 \but left unfinished & out of/ & some other older papers. In the \said/ Letter of 24 Octob. 1676 I set down a series for squaring of figures w^ch in some cases breaks off & becomes finite, & illustrated it with examples & said that I found that|is| & some other Theorems of the same kind by the method whose foundation was comprehended in that Ænigma, that is, by the Method of fluxions. And how I found them I explained in the first six Propositions of the Book of Quadratures: & I do not know any other method by which they could be found: & therefore when I wrote that Letter I understood \had/ the Method of fluxions so far as it is conteined in those six Propositions. When \After/ I had finished the Book & the 7^th 8^th 9^th & 10 Propositions were fresh in memory I wrote upon them to M^r Iohn Collins that Letter w^ch was dated 8 Novem. 1676, & being found amongst his Papers of M^r Iohn Collins was published by M^r Iones. The Theorems at the end of the tenth Proposition for comparing curvilinear figures with the Conic sections were known to me also when \before/ I wrote the said Letter of 24 Octob 1676, \they being there mentioned & all/ the Ordinates of the Figures being there set down. \copied from y^e Book in due order./ [Those Theoremes were copied from the Tract w^ch I wrote in the year 1671.] To understand these two Letters & how \to/ performe the things & find the Theorems conteined in them requires skill in all the Method of fluxions so far as it is conteined comprehended in all the first ten Propositions of the Book. And the eleventh & last depends upon a series of first second third & fourth fluxions.

The first Proposition of this Book with \and/ its solution illustrated with examples was at the request of D^r Wallis communicated \sent/ to him in a Letter dated 27 Aug. 1692 & printed by him almost verbatim that year in the second Volume of his works w^ch came abroad the next year, A.C. 1693. And thus the Rule for finding second third & fourth fluxions there set down was published some years before the {illeg}|R|ule for finding second third & fourth differences, & was at least eighteen \seventeen/ years before in manuscript \before it {illeg} was published {illeg}/. In the Introduction to this Book the method of fluxions is taught without the use of prickt letters: for I seldome used prickt letters when I considered only first fluxions. But when I considered also second third & fourth fluxions I distinguished them by the number of pricks. And this notatio{illeg}|n| is not only <166r> the oldest but is also the most expedite, tho it was not known to the Marque{ss} de l'Hospital when he recommended the differential Notation.

In my Analysis per æquationes numero terminorum infinitas communicated by D^r Barrow to M^r Collins in the year \Iuly/ 1669, I said that my Method by series gave the areas of Curvilinear figures exactly when it {illeg} might be, \(that is, by the series breaking off & becoming finite,)/ & thence it appears that when I wrote that Analysis I had the Method of fluxions so far at the least as it is conteined in the first six Propositions of the Book of Quadratures, \though those Propositions were not then drawn up in the words of the Book./

In that Tract I represented time by a line increasing \or flowing/ uniformly & a moment of time by a particle of the line generated in the moment of time, & thence I called the particle a moment of the line, & the particles of all other quantities generated in the same moment of the L{in} time I called the moments of those quantities, & the fact under the rectangular Ordinate & a moment of the Abscissa I considered as the moment of the curvilinear area described by that Ordinate moving uniformly upon the Abscissa. ☉ < insertion from higher up f 165v > ☉ For a moment of time I put the letter o, & thence computed the moments of the other quantities generated in the moment of time \& for those moments put any other symbols./ And for the Area of a figure I sometimes put the Ordinate included in a square. < text from f 166r resumes > And by considering how to deduce moments from \increasing/ quantities & \those/ quantities from \their/ moments I deduced areas of figures from their ordinates & their Ordinates from their areas: which is the same thing with deducing fluents from fluxions {illeg}|f|rom fluents & fluents from fluxions For the area I \something/ put the Ordinate included in a square & \And/ in the end of y^e Book I demonstrated by this sort of calculus the first of the three Rules set down in the beginning thereof. And applying this method \of moments/ not only to finite equations but also to \equations involving/ converging series, considered as equations consisting of an infinite number of terms, I gave this Tract the name of Analysis per æquationes numero terminorum infinitas. And ^✝ < insertion from f 165v > And shewing \also/ thereby to find the Ordinates & Areas of Mechanical Curves &c [that their lengths & tangets may be found by the same Method;] I said: Nec quicquam hujusmodi scio ad quod hæc methodus id varijs modis sese noli extendit. Imo . . . & quiquid vulgaris Analysis per æquationes ex finito terminorum numero constantes (quando id sit possibile) perficit, hæc per æquationes infinitas semper perfici\e/t. And in my Letter of 13 Iune 1676 I said of this Analysis: Ex his &c < text from f 166r resumes > And in my Letter of 13 Iune 1676 I said of this Analysis: Ex his videre est quantum fines Analyseos per hujusmodi infinitas æquationes ampliantur: Quippe{illeg} quæ earum beneficio ad omnia pene dixerim Problemata (si numeralia Diophanti et similia excipias) sese eatendit. |And M^r Leibnitz in his Letter of 27 Aug. 1676 replied that he did not believe that ⊡| < insertion from f 165v > ⊡ my method was so general \the inverse Problems of Tang^ts & many others not being reducible to Equations or Quadratures. B|A|nd in the same Letter he/ & placed the perfection of Analysis \not in this Method but in a Method composed/ of Analytical Tables of Tangents & the Combinatory Art, saying of the one; Nihil est quod norim in tota Analysi momenti majoris: & of the other; Ea vero nihil differt ab Analysi illa suprema, ad cujus intima, quantum judicare possum, Cartesius non pervenit. Est enim ad eam constituendam opus Alphabeto cogitionum humanarum. This was the top of his Analytical skill at that time. < text from f 166r resumes >

M^r Collins in {illeg} a Letter to M^r Strode dated 26 Iuly 1672 gave this account of these Methods. Mense Septembri 1668 Mercator Logarithmotechniam edidit suam, quæ specimen hujus methodi (i.e. Serierum infinitarum) in unica tantum figura, nempe quadraturam Hyperbolæ, continet. Haud multo postquam prodierat liber, exemplar ejus Cl. Wallisio Oxonium misi, qui suum de eo judicium in Actis Philosophicis statim fecit: alium Barrovio Cantabrigiam, qui quasdam Newtoni Chartas – – – extemplo remisit: E quibus et ex alijs, quæ olim ab Auctore cum Barrovio communicata fuerant, patet illam Methodum a dicto Newtono aliquot annis antea excogitatam et modo universali applicatam fuisse: ita ut ejus ope in quavis figura Curvilinea proposita quæ una vel pluribus proprietatibus definitur, Quadratura vel area dictæ figuræ, accurata si possibile sit, sin minus, infinite vero propinqua; evolutio vel longitudo lineæ curvæ; Centrum gravitatis figuræ; solida ejus rotatione genita, et eorum superficies, id non obstantibus radicalibus, \quæ eam non morantur,/ obtineri queant. ✝ < insertion from f 165v > ✝ Postquam intellexerat D. Gregorius hanc methodum, a D. Mercatore in Logarithmotechnia usurpatam, et Hyperbolæ quadrandæ adhibitam quam audauxerat ipse Gregorius, jam universalem redditam esse, omnibus figuris applicatam; acri studio eandem acquisivit, multum in ea enodanda desudavit. Vter D. Newtonus & D. Gregorius in animo habet hanc Methodum exornare: D. Gregorius autem D. Newtonum primum ejus inventorem anticipare haud integrum ducit. < text from f 166r resumes > So then by the testimony of D^r Barrow grounded upon papers w^ch I had communicated to him from time to time I had the method here described some years before the Doctor sent my Analysis to M^rCollins, that is, some years before Iuly 1669. And this is sufficient to justify what I said in the Introduction to the Book of Quadratures, viz^t that I found the Method gradually in the years 1665 & 1666. D^r Barrow then read his Lectures about motion, & that might put me upon taking these things into consideration. I found \the Method of Series in the beginning of the year 1665 the method of Moments soon after * < insertion from f 165v > * If it be asked why I did not publish this method sooner, it was for the same reason that I did not publish the Theory of colours sooner. I found the method of series in the beginning of the year 1665 & the method of fluents & moments soon after & the theory of colours in the beginning of the year 1666, & in the year 1671 was about < text from f 166r resumes > / the Theory of colours also in the beginning of the year 1666, & in the year 1671 was about to publish it {sic} /them all\ together with the Methods of Series & fluxions: but for a reason mentioned in my Lettter {sic} of 24 Octob. 1676, I desisted till the year 1704, excepting that some of my Letters were published before by D^r Wallis & M^r Oldenburg.]

<166v>

The first line that M^r Leibnitz began to communicate the differential Method was {illeg} his Letter of 27 Iune 1677, & therefore the Editors of the Acta eruditorum calumniated me \accused me falsly/ in saying Pro differentijs Leibnit{oanis} Newtonus adhibet semper adhibuit fluxiones: And \they &/ their adherents ought to have proved the accusation.

In one of those Letters (that of 24 Octob. 1676)

<167r>

And Account of the Method of Fluxions found until M^r Leibnitz had notice of it in the year 1676 inclusively.

The method of fluxions is this. M^r Newton considers two or {illeg} more quantities as \flowing or/ growing \in magnitude/ by continuall increase in the same line, & the velocities of their increase he calls their fluxions, & their parts generated in moments of time he calls their moments, the names of fluxions & moments being taken from the fluxion & moments of time. For the flowing quantities \or fluents/ he puts any symbols as z, y, x, & for their fluxions he puts any other symbols or even the same symbols distinguished by their magnitude or by form or by any mark as $\stackrel{.}{\mathrm{z}}$, $\stackrel{.}{\mathrm{y}}$, $\stackrel{.}{\mathrm{x}}$. But one of the fluents he \usually/ considers as flowing uniformly or in proportion to time, & \usually/ puts an unit for its fluxion & the letter o for its moment. And for the moments of the other fluents he puts their fluxions multiplied b{illeg} letter o multiplied by their fluxions Foras 1 the fluxion of time \(or of {illeg}|the| exponent) {illeg}/ is to $\stackrel{.}{\mathrm{z}}$ the fluxion of z, so is o the moment of time to $\stackrel{.}{\mathrm{z}}\mathrm{o}$ the moment of z. When he is demonstrating any Proposition he takes the moment o for o in the sense of the vulgar for an indefinitely \(not infinitely)/ small part of time, & performs the whole operation in finite figures by the Geometry of the Ancients without any approximation, & when the calculation is finished & the Equation reduced, he supposes that y^e moment van of the equation vanish i{n} w^ch are affected with the moment o & by \from/ the remaining terms d{illeg} draws his conclusion. But when he is only investigating a {illeg} truth, he supposes the moment o to be infinitely little, & for making dispatch neglects to write it down, it {illeg}works in figures infinitely small by all manner of approximations w^ch he conceives will make no error in the conclusion. The first way is \sure &/ exact the secon{d} expedite\./{illeg}, & both are according natural

In his Letter dated 24 Octob 1676 M^r comprehended this|e| method of fluxions in this sentence. Data æquatione fluentis quotcun fluentes quantitates involvent{e} invenire fluxiones & vice versa. And how to deduce fluxions from æquations is involving their fluents is taught in the first Proposition of his Book of Quadratures. The Rule there delivered is this Multiplicetur omnis æquationis terminus per indicem dignitatis quantitatis cujus fluentis quam involvit & in singulis multiplicationibus mutetur dignitatis latus in fluxionem suam & aggre{t}|g|atum factorum omnium sub proprijs signis erit æquatio nova. This Rule w^th its Examples M^r Newton copied & sent to D^r Wallis in his Letters & sent to D^rWallis in his \two/ Letters dated Aug. 27, & Sep. 17, 1692 & therefore \the method was invented &/ the book of Quadratures was written before that time. The Rule teaches the inventio Proposition relates to the 2^d 3^d & 4^th Fluxions as well as to the first. For

As every Fluent has its fluxion so every fluxion may be so every fluxion may be considered as a fluent & have its fluxion, And hence a & this is called the second fluxion of the first fluxion|ent|, & the fluxion of the second fluxion may be called the third fluxion & so on. And the like is to be understood of moments. The moment of the first moment is the second moment of the fluent & the moment of the second moment is the third moment & so on.

How to deduce fluxions from \equations involving/ their fluents is taught in the first Proposition of M^r Newtons book of Quadratures. The Rule there described \delivered/ is this. Multiplicetur omni æquationis terminus per indicem dignitatis quantitatis cuc|j|us fluentis quam involvit & in singulis multiplicationis|b|us mutetur dignitatis latur|s| in fluxionem suam, & aggregatum factorum omnium sub proprijs signis erit æquatio nova. This Rule The first mul{ti}plication gives This single Rule gives all the fluxions. The first multiplication gives the first fluxions the second gives the second fluxion{illeg}s & so on, as you may perceive by \is explained in the/ {illeg}|ex|amples of the Rule.

This Proposition with the solution & the Examples is see was copied by M^r Newton & in his Letters dated Aug 27 & Sept. 17, 1692 sent to D^r Wallis & the next year printed by D^r Wallis in his works the second Volume of his works pag. 392 ,|&| 393 & therefore the book of Quadratures was writ before that time.

The M^r Newton in his Letter dated 24 Octob. 1676 comprehended the method of Fluxions is this sentence Data æquatione quotcun fluentes quantitates involvente invenire fluxiones & vice versa. And the fift Proposition of the book of Quadratures was set down at length & s in the same Letter & {was} \& said to be/ deduced from the same method of Fluxions & called the first {illeg} \Theorem/ in a series of such Propositions. Whence the sixt Proposition of the book of Quadratures was also then known to M^r Newton it being the second of the series. And so were the third & fourth Propositions, how these two Propositions were found out by the method of fluxions is fully set down in the first <167v> six Propositions of y^e book of Quadratures. \And therefore/ These six Propositions were therefore known to M^r Newton when wh in the year 1676; & so were some others that follow in the same book as may be gathered from what is cited out of them in the same Letter & in another Letter written by M^r Newton to M^r Collins & pub Nov. 8. 1676 & publis{hed} by M^r Iones. And by so many things quoted out of the book of Quadratures it may be concluded that in the year 1676, it may be concluded that the boo{k} of Quadratures (except the Introduction & last Scholium) was written before that year. For indeed the designe of the book was to make a step towards the inverse method of fluxions.

Another step was made by the solution of this Probleme, Extracere fluentem quantitatem ex æquatione simul involvente fluxionem ejus. |Ex æquatione fluxionem radicis involvente radicem extrahere.| The solution whereof was me sent to D^r Wallis by M^r Newton in his Letter of {sic} dated Sept 17^th 1692 & published by the D^r in the second volume of his work pag. 394. And at the end of the example there set down it was noted M^r Newto{n} that note affirmed \added/ that by the same method the roots of equations might involving the second third {illeg} fourth {illeg} fluxions & other fluxions \($\stackrel{..}{\mathrm{y}}$ $\stackrel{.}{\stackrel{..}{\mathrm{y}}}$ $\stackrel{..}{\stackrel{..}{\mathrm{y}}}$ &c)/ might be extracted. And this method was known to M^r Newton in the year 1676 as appears by his Letter then dated 24 Octob. where he saith Inversa de Tangentibus Problemata sunt in potestate alia illis diffilicilora. Ad quæ solvenda usus sum duplici methodo; una concinniori altera generaliori. Vna methodus consistit in extractione fluentis quantiatis ex æquatione simul involvente fluxionem ejus: altera &c.

And by these things its manifest that M^r Newton in the year 1676 understood the method of fluxions direct & inverse (including the second & had then extended it to the 2^d 3^d 4^th & other fluxions.

And tho he sometimes uses prickt letters for fluxions yet he doth not confine himself to those symbols. In the first Proposition of his book of Quadratures he uses such letters: in the Introduction to y^e book he desembles the method & gives examples of solving Problemes by it w^thout making any use of such Letters.

M^r Newton in his Letter dated 24 {illeg}|O|ctob 1676 represented that five years before, viz^t A.C. 1671, he wrote a treatise of the method of |the method of| infinite series & of another method w^ch readily gave the method of Tangents of Slusius & stuck not at \surds/ & w^ch was founded in this sentence Data æquatione \quotcun/ fluentes quantitates involvente invenire fluxiones & contra vice versa. And in a Letter to M^r Collins dated 10 Decem. 1672 \(which was/ some weeks before Slusius sent his method of Tangets into England) he described the same method of Tangets as a Corollary of the ge or branch of the \his/ general metho{d} w^ch stuck not at Tangents surds & said that this general metho w^ch was therefore his method of fluxions. And he said of this method that it extended to the solution \abstruser sort/ of Problems about the Curvatures areas, lengths, centers of gravities of Curves &c & {illeg} \succeeded/ in Mechanical Curves as well as others. And By its succeeding in M{illeg} By its determining the Curvatures of Curves you may know So then he understood the method of fluxions in those days, & by his applying it to Problems about the Curvature of Curves you may know that he had then extended it to the consider{a}tion of the second fluxions. The sentence  < insertion from f 168r >  The sentence, Data æquatione quotcun fluentes quantitates involvente, fluxiones invenire; & vice versa, being the foundation of the method upon w^ch he wrote in the year 1671 & relating to the second third & following Fluxions as well as to the first, & being one & the same method in them all, it must be allowed that in the year 1671 his method extended to all the fluxions. For after the very same manner that this method, being applied to any equation gives a new æquation involving the first fluxions of the fluents, if it be applied to this new one it gives another new one involving their second fluxions, & so on perpetually. < text from f 167v resumes >

In this Analysis per Æquationes numero terminorum infinitas was founded upon three Rules. The first Rule was this. Let a be a given quantity, x the ab{illeg} of a Curve, y the Ordinate, & $\frac{\mathrm{m}}{\mathrm{n}}$ {illeg}, a {illeg}y $\frac{\mathrm{m}}{\mathrm{n}}$ any number whole \the index of a dignity whole/ or broken affirmative or negative. And if the Ordinate be $\mathrm{a}{\mathrm{x}}^{\frac{\mathrm{m}}{\mathrm{n}}}=\mathrm{y}$ the area of the Curve will be $\frac{\mathrm{a}\mathrm{n}}{\mathrm{m}+\mathrm{n}}{\mathrm{x}}^{\frac{\mathrm{m}+\mathrm{n}}{\mathrm{n}}}$. That is (as M^r Newton afterwards explains) if the fluxion be $\mathrm{a}{\mathrm{x}}^{\frac{\mathrm{m}}{\mathrm{n}}}$ the fluent will be a $\frac{\mathrm{n}\mathrm{a}}{\mathrm{m}+\mathrm{n}}{\mathrm{x}}^{\mathrm{m}+\mathrm{n}}$ {illeg} And this Rule he demonstrates in the end of his book Analysis by the method of fluxions after the very same manner that {i}{illeg} the Introduction to his book of Quadratues he Demonstrated \found/ the inverse thereof \by that method/ viz^t that if the fluent be ${\mathrm{x}}^{\mathrm{n}}$ the fluxion will be $\mathrm{n}{\mathrm{x}}^{\mathrm{n}-1}$. His Demonstration is this. Let the Abscissa of any Curve ADδ be $\mathrm{AB}=\mathrm{x}$, the perpendicular ordinate $\mathrm{BD}=\mathrm{y}$ the area $\mathrm{ABD}=\mathrm{z}$, the moment of the Abscissa $\mathrm{B\beta }=\mathrm{o}$, the moment <170r> of the Area $\mathrm{B\beta \delta D}=\mathrm{o}\mathrm{\upsilon }=\mathrm{BD}\times \mathrm{BK}=rectangulo\mathrm{B\beta HK}$, the side of this rectangle BK being called υ. And the Abscissa AB will be $\mathrm{x}+\mathrm{o}$ & the Area $\mathrm{AB\delta }\text{will be}=2+\mathrm{o}\mathrm{\upsilon }$. Now \since/ if $\frac{\mathrm{n}}{\mathrm{m}+\mathrm{n}}\times \mathrm{a}\mathrm{x}\frac{\mathrm{m}+\mathrm{n}}{\mathrm{n}}=\mathrm{z}$, (as is sub or putting $\frac{\mathrm{x}\mathrm{a}}{\mathrm{m}+\mathrm{n}}=\mathrm{c}$ & $\mathrm{m}+\mathrm{n}=\mathrm{p}$, since $\mathrm{c}{\mathrm{x}}^{\frac{\mathrm{p}}{\mathrm{n}}}=\mathrm{z}$, or ${\mathrm{c}}^{\mathrm{n}}{\mathrm{x}}^{\mathrm{p}}={\mathrm{z}}^{\mathrm{n}}$, if $\mathrm{x}+\mathrm{o}$ be written for x & $\mathrm{z}+\mathrm{o}\mathrm{\upsilon }$ be written for z you will have $\mathrm{c}\mathrm{n}$ in ${\mathrm{x}}^{\mathrm{p}}+\mathrm{p}\mathrm{o}{\mathrm{x}}^{\mathrm{p}-1}+\mathrm{\&c}={\mathrm{z}}^{\mathrm{n}}+\mathrm{n}\mathrm{o}\mathrm{\upsilon }{\mathrm{z}}^{\mathrm{n}-1}+\mathrm{\&c}$ the following terms of these two series being omitted because they would vanish in the conclusion \b makin diminishing o in infinitum & making it vanish./ of th{illeg} Now if you reject \the equal quantities/ ${\mathrm{c}}^{\mathrm{n}}$ in ${\mathrm{x}}^{\mathrm{p}}$ & ${\mathrm{z}}^{\mathrm{n}}$ {be d}a & divide the remainder by o the you will have {c} ${\mathrm{c}}^{\mathrm{n}}\mathrm{p}{\mathrm{x}}^{\mathrm{p}+1}=\mathrm{n}\mathrm{\upsilon }{\mathrm{z}}^{\mathrm{n}-1}(=\frac{\mathrm{n}\mathrm{y}{\mathrm{z}}^{\mathrm{n}}}{\mathrm{z}}=\frac{\mathrm{n}\mathrm{y}{\mathrm{c}}^{\mathrm{n}}{\mathrm{x}}^{\mathrm{p}}}{\mathrm{z}})$ or|&| dividing both parts of y^e equation by ${\mathrm{c}}^{\mathrm{n}}{\mathrm{x}}^{\mathrm{p}}$ you will have {illeg} $\mathrm{p}{\mathrm{x}}^{\mathrm{-1}}=\frac{\mathrm{n}\mathrm{y}}{\mathrm{z}}$ or $\mathrm{p}\mathrm{c}{\mathrm{x}}^{\frac{\mathrm{p}-\mathrm{n}}{\mathrm{n}}}=\mathrm{n}\mathrm{y}$. And by restoring $\frac{\mathrm{a}\mathrm{a}}{\mathrm{m}+\mathrm{n}}$ for c & $\mathrm{m}+\mathrm{n}$ for p that is m for $\mathrm{p}-\mathrm{n}$ you & na for pc you have $\mathrm{a}{\mathrm{x}}^{\frac{\mathrm{m}}{\mathrm{n}}}=\mathrm{y}$. Whence on the contrary if $\mathrm{a}{\mathrm{x}}^{\frac{\mathrm{m}}{\mathrm{n}}}\text{ be }=\mathrm{y}$ then $\frac{\mathrm{n}}{\mathrm{m}+\mathrm{n}}\mathrm{a}{\mathrm{x}}^{\frac{\mathrm{m}+\mathrm{n}}{\mathrm{n}}}\text{ will be }=\mathrm{z}$. Q. E. D.

If this Demonstration \{o}{illeg}e calculation/ be compared with that in the Introduction to the {illeg} the {sic} book of Quadratures you will find them perfectly of the same kind They both procced by resolving the dignity of a Binomium into a converging series & {illeg} shewing that the second when the second term of the binomium is the moment of the first, the second term of the series is the moment of the dignity. But third term of the series is double to y^e moment of the second & the fourth is triple to the moment of the third.

The second Rule upon w^ch M^r Newton founds his Analysis is that if the area of a Curve be described by an Ordinate composed of several parts the whole area shall be composed by \all/ y^e Areas described by those parts. And the third is {sic} And the third Rule is to reduce the compound Ordinates of Curves into such parts w^ch describe such areas as may be found by the first Rule. {illeg}|A|nd after several examples of squaring Curves by this method, he described the method of fluxions for finding the Areas, Le\n/gths, su convex surfaces, & solid contents & centers of gravity of {illeg} curve\lines/ & curvilinear figures.

Let ABD represent a curvilinear figure {illeg} & all AB{KK} a rectangle described w^th the \rectangular/ Ordinate BD moving uniformly \from A towards B/ upon the Absciss AB,|(|x) & ABKH a rectangle described in the same time with the given Ordinate BK \moving uniformly upon the same Absciss/. And let the Ordinates BK(1) & BD(y) be considered as the moments of the {illeg} by w^ch th{e}|ose| Areas ABHK (x) & ABD are in {illeg} continually increased And let c conceive that you can by the three foregoing Rules, from the moment BD deduce

Sit ABD Curva quævis et AHKB rectangulum — dum utuntur methodis Indivisibilium.

Here several things are to be observed, as first that when he takes a point for y^e moment of a line & a line for the moment of a superficies, he takes a point for an infinitely short line & a line for an infinitely narrow superficies as in the method of Cavallerius. And therefore in pulling the ordinates BK|D| & BD|K| for the moments of the areas ABD & ABKH, he takes the Ordinates for infinitely narrow parallelogramms whose bases are the infinitely short parts or moments of the Abscissa AB. Let the moment of the Abscissa (x) be called o & the moments of the Areas ABKH & ABD will be $1\times \mathrm{o}$ & $\mathrm{y}\times \mathrm{o}$, or o & $\mathrm{y}\mathrm{o}$ And this M^r Newton expresses in the end of his Analysis in demonstrating the first Rule. But where his|e| is only investigating the solutions of Problems he neglects to write down the moment o as was said above.

Its to be further observed that in the sense here described he considers a superficies as the moment of a solid, a line as the moment of a supf|e|rficies & a point as the moment of a line: w^ch consideration gives the notion of \first/ second & third moments, a point being \the moment of a superf line &/ the moment of the moment of a superficies {illeg} & the moment of the moment of the moment of of a solid, that is the first moment of a line, the second moment of a superficies & the third moment of a solid.

Its to be observed also that in this Analysis M^r Newton teaches how to find <170v> as many Curves as you please w^ch may be squared. And this is the second Proposition in the book of Quadratures, & is performed by assuming any equation expressing the relation between the Abscissa & area & of the Curve & finding the relation between their fluxion of the Area \relation of their fluxions/ by the first Proposition, Whence & putting the fluxion of the Ordinate for the Area for the Ordinate, the fluxion of the Abscissa being an unit. And this makes it appear that the two first Propositions of the book of Quadratures were known to M^r Newton when he wrote his Analysis w^ch was in in the in or before the year 1669 when he wrote his Analysis.

It is to be observed also that M^r Newton in the same Analysis affirms that by the help of this method \of this Method that Ejus beneficio/ Curvarum areæ & longitudines &c (id modo fiat) exacte et Geometricæ determinantur. Sed ista narrandi non est locus. And this referrs to the fift & sixt Propositions of the book of Quadratures & shews that the first six Propositions of that book were known to M^r Newton in or before the year 1669. For the fift & sixt Propositions depend upon the third & fourth & those upon the first & second.

It is still further to be observed that M^r in the same Analysis M^r Newton uses the symbol $\boxed{\frac{\mathrm{a}\mathrm{a}}{64\mathrm{x}}}$ to express the area of a Curve whose Ordinate is $\frac{\mathrm{a}\mathrm{a}}{64\mathrm{x}}$ & M^r Leibnits expresses the same thing by the symbol $\int \frac{\mathrm{a}\mathrm{a}}{64\mathrm{x}}$, but this symbol is of later date

And lastly \Also/ the relation between the method of Series & the method of fluxions deserves to be observed. For let th any dignity of any binomium whose second term is the fluxion of the first term be resolved into a series the & the first term of

It is also to be observed that when M^r Newton wrote the said Analysis he understood the resolution of the \any/ dignity of any Binomium into a{illeg} converging series. For in the Demonstration of the first Rule he set down the two first terms of the series. Let the dignity be ${\stackrel{-}{\mathrm{x}+\mathrm{o}}}^{\mathrm{p}}$ & the series will be ${\mathrm{x}}^{\mathrm{p}}+\mathrm{p}\mathrm{o}{\mathrm{x}}^{\mathrm{p}-1}+\mathrm{p}\times \frac{\mathrm{p}-1}{2}\times \mathrm{o}\mathrm{o}{\mathrm{x}}^{\mathrm{p}-2}+\mathrm{p}{\mathrm{x}}^{\frac{\mathrm{p}-1}{2}}\times \frac{\mathrm{p}-2}{3}\times {\mathrm{o}}^3{\mathrm{x}}^{\mathrm{p}-3}+\mathrm{\&c}$ the two first terms of w^ch series were set down in the Analysis.

And lastly \further/ it is to be noted that when M^r Newton wrote that Analysis he had noted the observed the great relation which the method of converging series have to one ano & that of fluxions have to one another. For he every where applys the method of series to y^e solution of Problems by the method of fluxions & {illeg} \by the method of Series/ demonstrates the first Rule w^ch is the foundation of the method of fluxions, & fi determin finds the second term of the series to be the moment of the first by reason of this relation between the methods he had \then/ composed one general method of them both. [This relation is further manifest by comparing the terms of the series above me comparing the terms of y^e series above mentioned with the first second & third moments of the first term. For if the terms of the series (beginning w^th the second term) be multiplied by this series of numbers, they be 1. 1×2. 1×2×3. &c they become the moments. And this affinity M^r Newton took some no For the second term of the series is the moment of the first term & the third term is half the moment \moment/ of the second, & the 4^th is a third part of the moment of the third & so on: as is manifest by the first Rule in the Analysis & by the Demonstration thereof & by what is said in several places of the book of Quadratures.

And it may be observed in the last place that M^r Newton by taking \putting fract & negative numbers/ \for/ the indices of Dignities in the first Rule of his Analysis & in the Dignities w^ch he teaches to resolve into a binomia converging series, reduced the operations of multiplication Division & extraction of roots to one common \Rule or/ way of common way of considering them, & thereby very much enlarged the bounds of Analysis]

<168r>

M^r Newton in a Letter \written/ to M^r Collins & dated 10 Decem 1672, that is, some weeks before Slusius sent his Method of Tangents into England, described the same method of Tangents & represented it a branch or Corollary of his general method w^ch