Copy of a letter to John Collins, dated 9 April 1672
By Mr Newton to Mr Collins.
< text from f 46r resumes > < insertion from the left margin of f 46r >By Mr Newtons Answer to Mr Gregories Letter of March: 7: 1673.
< text from f 46r resumes > < insertion from the top right of p 46a >(Entd LB. 6. 71.)
< text from f 46r resumes >Cambridge Apr. 9. 1673.
Sr
Having perused Mr Gregorys candid reply, I have thought good to send you these further considerations upon the differences that still are betweene us. And first that a well polish't plate reflects at the obliquity of 45 degrees more truly then direct \ones/ seemes to me very certaine, For the flatt tubercula or shallow valleys, such as may be the remaines of scratches almost worne out, will cause the least errors in the oblig|q|uest rays which fall on all sides the hill, excepting on the midle of the foreside \and backside/ of it, that is where the hill incli{illeg}|n|es directly towards or directly from the ray; For if the ray fall on that section of the hill, its error is in all obliquitys just double to the hills declivity: but if it fall on any other part of the hill its error is lesse then double, if it be an obl{illeg}|iqu|e ray, and that so much the lesse, by how mu{illeg}|ch| the ray is obliquer; but if it be a direct ray, its error is just double to the declivity and therefore {greatest|r|}{greatest} in \that/ case. I presume Mr. Gregory, if you think it convenient to transmitt this to him, will easily apprehend me.
F|H|or|w| the charge may b|e|varied {sic}, 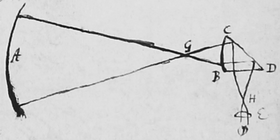 at pleasure in my Telescope, |will| appear by this figure, where A represents the great Concave, E the Eye-Glasse, and BCD a Prisme of Glasse or Crystall whose sides BC & BD are not flat but spherically convex, so that \ye/ rays which come from G the focus of the great concave A, may by the refraction of the first side {illeg} \BC/ be reduced into parallelism, and after reflection from the base CD be made by the refraction of the next side BD to converge to the focus of the Eye-Glass H. The Telescop{e} being thus formed it appears how the charge may be altered by varying the distances of the glasses and speculum.
at pleasure in my Telescope, |will| appear by this figure, where A represents the great Concave, E the Eye-Glasse, and BCD a Prisme of Glasse or Crystall whose sides BC & BD are not flat but spherically convex, so that \ye/ rays which come from G the focus of the great concave A, may by the refraction of the first side {illeg} \BC/ be reduced into parallelism, and after reflection from the base CD be made by the refraction of the next side BD to converge to the focus of the Eye-Glass H. The Telescop{e} being thus formed it appears how the charge may be altered by varying the distances of the glasses and speculum.
As for the objection that Mr. Gregorys Telescope{illeg} will be either overcharged or have too small an Angle of vision &c I apprehend that the difference betweene us lyes in limiting the aperture of the Eye-glass. Mr. Gregory puts it equall to that of the \little/ Concave, but I should rather determine it by this proportion; That if a midle point be taken between the \E{illeg}|y-| {sic}/glass and its focus, the apertures of the Eye-glasse and concave be proportionall to their distances from that point. That is, suppose AB the little concave, EF the eye-glass, GH their common 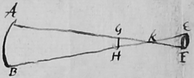 focus or image, and K the meane distance between GH and EF; from the Extremitys of AB draw AK and BK {illeg}|b|utting on the Eye-Glass at F and E, and EF shall be its aperture. The reason \of/ this limitation is, that the superfluous light, which comes on all sides of the speculum AB to the space GH in which the picture of the object is made, may fall besides ye Eye-glass. For if it should passe through it to the Eye-glass|,| it would exceedingly blend those parts of the picture with which ti's mixed; and such are those parts of it which extend themselves be{illeg}|yo|nd the lines AK, BK. As I remember I said in my former letter that the scattering light which falls on the Eye-glass will disturb the vision; and this is to be understood of any straggling light which comes not from the picture; but if it come from the picture to the Eye-glass, the disturbance will be much gr{illeg}|e|ater so as not to be allowed of. Against the first I see no very convenient remedy, & against the last none but as{illeg}|si|gning a small aperture to the Eye-glasse; supposing the Telescope is used in the day-time or in twy-light, or to view the moon or any starr very near her or near the brighter planets. And if for this reason the aperture be limited by {an|m|}{m|an|}y rule, the Angle of vision will become very small as I limited; \affirmed;/ for instance in that case where Mr. Gregory in his Postscript puts it above 20 degrees, it will be reduced to lesse then halfe a degree. yet {sic} I confesse there is a way by which the angle of vision may be somthing inlarged, but it will not be very considerably, unless the Eye-glasse be also deeper charged.
focus or image, and K the meane distance between GH and EF; from the Extremitys of AB draw AK and BK {illeg}|b|utting on the Eye-Glass at F and E, and EF shall be its aperture. The reason \of/ this limitation is, that the superfluous light, which comes on all sides of the speculum AB to the space GH in which the picture of the object is made, may fall besides ye Eye-glass. For if it should passe through it to the Eye-glass|,| it would exceedingly blend those parts of the picture with which ti's mixed; and such are those parts of it which extend themselves be{illeg}|yo|nd the lines AK, BK. As I remember I said in my former letter that the scattering light which falls on the Eye-glass will disturb the vision; and this is to be understood of any straggling light which comes not from the picture; but if it come from the picture to the Eye-glass, the disturbance will be much gr{illeg}|e|ater so as not to be allowed of. Against the first I see no very convenient remedy, & against the last none but as{illeg}|si|gning a small aperture to the Eye-glasse; supposing the Telescope is used in the day-time or in twy-light, or to view the moon or any starr very near her or near the brighter planets. And if for this reason the aperture be limited by {an|m|}{m|an|}y rule, the Angle of vision will become very small as I limited; \affirmed;/ for instance in that case where Mr. Gregory in his Postscript puts it above 20 degrees, it will be reduced to lesse then halfe a degree. yet {sic} I confesse there is a way by which the angle of vision may be somthing inlarged, but it will not be very considerably, unless the Eye-glasse be also deeper charged.
Why I ass{illeg}|i|gn a concave with an Eye-glass to magnifie small objects (in Transact: pag. {illeg} \3080./) and yet an Eye-glass without such a concave to magnifie the image of the great concave wch is equivalent to a small object, is, because that image doth not require to be magnified so much as an object by a microscope, and further because the Angle of the penicill of rays which flow from any point of the small object, that the object may appear sufficiently luminous, ought to be as great as possible; and a concave will with equall distinctnesse reflect ye rays at a greater angle of the penicill then in a Le{illeg}|n|s; but in the Telescope the Angles of those penicills are not so great as to transcend the limits at w{illeg}|hic|h an Eye-glasse may with suf{fi}cient distinctnesse refract them, and therefore in these Instruments I chose to lay all the stress of magnifying upon the Eye-glasses as it is well capable of{illeg}, and the excesse only upon ye concave.
Concerning my citation of Mr. Gregory against Mons Cassegrain the force of it lies only in the inference that Opti instruments most probably according to Mons Cassegrains design had been tryed by reflexion; which I thinke I might well inferr, without haveing regard to the specifick figure of the speculum which Mr. Gregory there spake of. And therefore I think it cannot be said, that I made him speake of spherick figures where his meaning was of hyperbolick and Elliptick ones: but if I should be \so/ understood, because I put the figure of the great concave to be sphericall, wh{illeg}|e|rever I specifie it, I know not why I might not by way of consequence make that interpretation. for {sic} it is not probable, that any man would attempt Hyperbolick & Elliptick figures of speculums untill the event of sphericall ones had been first tryed.
And accordingly the tryall of Mr. Gregory wth Mr. Reive was by a sphericall figure. which {sic} trial although I am now satisfyed that it was made v{illeg}|e|ry rudely, yet by the information which I had of it when I wrote the letter at large \#/ |# about M. Cassegrains designe, I apprehended it to have beene made wth great diligence and curiosity, as I signified in my former letter at large|. And this I hope may excuse me for speakeing of it in the Transactions as if it had beene {illeg}|tr|yed with more accuracy then really it was. And thus much concerning the Telescope.
The design of the burning speculum appears to me very plausible and worthy of being put in practise: what Artists may thinke of it I know not, but the greatest difficultie in the practise that occurrs to me is to proportion the two surfaces so, that the force of both may be in the same point according to the Theory,|.| But perhaps it is not necessary to be so curious, for it seems to me that the effect would scarce be sensibly less if both sides should be ground to the concave and gage of the same tool. I suppose you have received a letter from {illeg}|me| sent last weeke to signify my rec{illeg}|e|ipt of the bookes you sent in Queeres &c. It comes now into my mind that when I sent Mr. Pitts 4łł for Kinkhuysen he further urged a promise of some copies. when {sic} you have opportunity you will oblige me to remember him that his proposall was either 4łł absolutly or 3łł with some copies. I must joyn with Mr. G{illeg}|r|egory in admiring Mr. Horrox. And this all at present from
Sr
Yor humble servant
I Newton
