Incomplete copy of de Quadratura Curvarum
Tractatus de Quadratura Curvarum
Quo tempore incidi in methodum serierum interminatarum convergentium necesse habui mutare notationem quæ tunc in usu erat et pro , , , , , , {,} , &c. scribere , , , , , , , , &c Hac enim ratione computationes magis uniformes et expeditæ, et theoremata magis generalia evaserunt. Qua de causa etiam exponentes dignitatum indefinite designavi cum Slusio in hunc modum , , ponendo dignitatum exponentes μ et ν et similes pro numeris quibusvis integris an fractis, affirmativis an negativis. Quas quidam Notarum formulas, cum jam in usu esse cœperint non opus est ut fusius exponam.
Quantitates indeterminatas ut motu perpetuo crescentes vel decrescentes id est ut fluentes vel defluentes in sequentibus considero designoqꝫ literis z, y, x, v, et earum fluxiones seu celeritates crescendi noto iisdem literis punctatis , , , , sunt et harum fluxionum fluxiones seu mutationes magis aut min us celeres quas ipsorum z, y, x, v fluxiones secundus nominare licet et sic designare , , , ; et harum fluxiones primas seu ipsarum z, y, x, v fluxiones tertias, sic , , , ; et Quartas sic , , , . Et quemadmodum , , , sunt fluxiones quantitatum , , , , et hæ sunt fluxiones quantitatum , , , ; et hæ sunt fluxiones quantitatum primarum z, y, x, v; Sic hæ quantitates considerari possunt ut fluxiones aliarum quas sic designabo , , , , et hæ ut fluxiones aliarum , , , , et hæ ut fluxiones aliarum , , , . Designavit igitur , , z, , , , , , &c seriem quantitatum quarum quælibet posterior est fluxio præcedentis et quælibet prior est fluens quantitas fluxionem habens subsequentem. Similis est series , , , , ; ut et series , , , , , , ; Et Notandum est quod quantitatis quælibet prior in his seriebus est area figuræ Curvilineæ cujus ordinatim applicata rectangula est quantitas posterior et abscissa z: uti area Curvæ cujus ordinata est et abscissa z. Hanc aream sic etiam designo vel etiam sic z. Hanc aream sic etiam designo . Quo autem spectant hæc omnia patebit in Propositionibus quæ sequuntur.
Prop. I. Prob: I
Data æquatione quotcunqꝫ fluentes Quantitates involvente
invenire fluxiones.
Solutio
Multiplicetur omnis æquationis terminus per Indicem dignitatis quantitatis cujusqꝫ fluentis quam involvit, et in singulis multiplicationibus mutetur dignitatis latus {illeg}|i|n suam fluxionem et aggregatum factorum omnium sub propriis signis exit nova æquatio.
Explicatio.
Sunto a, b, c, d, &c quantitates determinatæ et immu{illeg}|t|abiles et proponatur æquatio quavis quantitates fluentes z, y, x, &c involvens, uti Multiplicentur termini primo per Indices Dignitatum x et in singulis multiplicationibus pro dignitatis latere seu x unius dimensionis scribatur et summa factorum erit . Idem fiat in y et prodibit . Idem fiat in z et prodibit , ponatur summa factorum æqualis nihilo et habebitur æquatio Dico quod hac æquatione definitur relatio fluxionum.
Demonstratio.
Nam sit o quantitas infinite parva et sunto , , quantitatum z, y, x momenta, id est incrementa momentanea Synchrona. Et si quantitates fluentes jam sunt z, y, et x hæ post momentum temporis incrementis suis infinite parvis , , auctæ evadent , , , quaæ in æquatione prima pro z, y, et x scriptæ dant æquationem . Subducatur æquatio prior et residuum divisum per o erit . Minuatur Quantitas o in infinitum ut momenta fiant infinitiss{illeg}|i|me parva, et neglectis terminis evanescentibus restabit Quod erat demonstrandum.
Explicatio plenior.
Ad eundem modum si æquatio esset produceretur Ubi si fluxionem tollere velis, pone , et erit et per hanc propo seu , hoc est et inde .
Et per operationem repetitam pergitur ad fluxiones secundas, tertias et sequentes. Sit æquatio et fiat per operationem primam . per secundam . per Tertiam
Ubi vero sic pergitur ad fluxiones secundas tertias et sequentes convenit quantitatem aliquam ut uniformiter fluentem considerare et pro ejus fluxione prima unitatem scribere, pro secunda vero et sequentibus nihil. Sit æquatio ut supra et fluat z uniformiter sitqꝫ ejus fluxio Unitas et fiet per operationem primam , per secundam , per tertiam
In hujus autem generis æquationibus concipindi|u|m est quod fluxiones in singulis terminis sint ejusdem ordinis, id est, vel omnes primi ordinis , vel omnes secundi , , , , vel omnes tertii , , , , , , &c. Et ubi res aliter se habet complendus est ordo per subintellectas fluxiones quantitatis uniformiter fluentis. Sic æquatio novissima complendo ordinem tertium sit
Termini æquationis primæ ut Genitores terminorum æquationis cujus vis alterius quæ per hanc propositionem ex prima prodit et termini ex eodem Genitore nati, ut fratres vel Socii considerari possunt. Innotescunt fratres et ex fratribus Genitor, mutando fluxiones in fluentes quantitates. Sic in æquatione Novissima termini omnes præter ultimum mutando fluxiones in fluentes quantitates evadunt , ideoqꝫ fratres sunt et genitorem habent in , et terminus ultimus qui solitarius est, eadem ratione migrat in Genitorem ; hic m et n pro coefficientibus determinatis indefinite ponuntur, et inveniri possunt quærendo fratres ex his genitoribus et comparando cum fratribus datis: Sic ex genitore prodeunt fratres , , , , , qui cum fratribus datis collati dant .
Prop: II. Prob: II.
Invenire curvas quæ quadrari possint
Sit ABC figura invenienda, BC ordinatim applicata 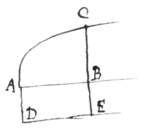 rectangula et AB abscissa; producatur BC ad E, ut sit et compleatur parallelogrammum ABDE. et arearum ABC, ABDE fluxiones erunt ut BC ad BC {sic}; Assumatur igitur æquatio quævis qua relatio arearum definiatur et inde dabitur relatio ordinatarum BC et BC {sic} per prop. I Q.E.I. Hujus rei exempla habentur in propositionibus duabus sequentibus.
rectangula et AB abscissa; producatur BC ad E, ut sit et compleatur parallelogrammum ABDE. et arearum ABC, ABDE fluxiones erunt ut BC ad BC {sic}; Assumatur igitur æquatio quævis qua relatio arearum definiatur et inde dabitur relatio ordinatarum BC et BC {sic} per prop. I Q.E.I. Hujus rei exempla habentur in propositionibus duabus sequentibus.
Prop. III. Theor. I
Si pro abscissa AB et area AE seu promiscuo scribatur z, et si pro scribatur R sit autem area Curvæ erit ordinatim applicata
Demonstratio.
Nam si sit erit per Prop: 1 Pro in primo æquationis termino et in secundo scribe et et fiet . Erat autem &c et inde per prop I fit huic ductæ in adde et summa ducta in , si modo pro scribatur BE sive 1, fiet . Q.E.D.
Prop IV. Theor II
Si Curvæ Abscissa AB sit z et si pro scribatur R et pro scribatur S: sit autem area curvæ : erit ordinatim applicata.
<87r>
Demonstratur ad modum præcedentis propositionis cum scilicet ordinatim applicata sit .
Prop V. Theor. III.
Si Curvæ Abscissa AB sit z, et pro scribatur R. Sit autem ordinatim applicata et ponatur . , , &c erit area . Ubi A, B, C, D, &c. denotant totas Coefficientes datas terminorum singolorum in serie cum signis suis + et −, nempe A primi termini cofficientem {sic} , B secundi coefficientem , C tertii coefficientem et sic deinceps.
Demonstratio.
Sunto juxta propositionem tertiam Curvarum Ordinatæ et earundum /Areæ\
Et si summa ordinatarum ponatur æqualis ordinatæ , summa Arearum æqualis erit Areæ Curv{illeg}|æ| cujus ista est Ordinata; Æquentur igitur Ordinatarū termini correspondentes et fiat , , . et inde . , ac pariter et sic deinceps in infinitum. Pone jam . . &c et in Area scribe ipsorum A, B, C, &c valore inventos et prodibit series proposita. Quod erat Demonstrandum.
Et nota quod Ordinata omnis duplici modo in seriem resolvitur. Nam Index η vel affirmativus esse potest vel negativus. Proponatur Ordinata . Hæc vel sic scribi potest vel sic . In casu priori est {.} , , , , , , \/, , . . . . In posteriori est . . . . . . {.} . . . . . . Tentandus est casus uterqꝫ et si Serierum alterutra ob terminos tandem deficientes abrumpitur ac terminatur, habebitur area Curvæ in terminis finitis. Sic in exemplo hujus priore casu scribendo in serie Valores ipsorum a, b, c, e, f, g, h, λ, θ, r, s, t, u, termini omnes post primum evanescunt {illeg}|i|n infinitum et Area Curvæ prodit . Et hæc Area ob signum negativum adjacet abscissæ ultra ordinatam productæ. Nam area omnis affirmativa adjacet t{a}m abscissæ quam ordinatæ, negativa vero cadit ad contrarias partes ordinatæ et adjacet abscissæ productæ. Hoc modo Series alterutra et nonnumquam utraqꝫ semper terminatur & finita evadit, si curva Geometrice quadrari potest. At si Curva talem Quadraturam non admittit, series utraqꝫ continuabitur in infinitum, et earum altera converget et aream dabit approximando, præterquam ubi r (propter aream infinitam) vel nihil est vel numerus integer et negativus, vel ubi equalis est unitati. Si minor est unitate converget Series, in qua index η affirmativus est: Sin unitate major est converget series altera. In uno casu area adjacet abscissæ in altero adjacet abscissæ ultra ordinatam productæ
Nota insuper quod si Ordinata contentum est sub factore Rationali Q et factore surdo irreducibili , et factoris surdi latus R non dividit factorem Rationalem Q; erit et . Sin factoris Surdi latus R dividit factorem rationalem semel erit et : Si dividit bis erit et . Si ter erit et et sic deinceps.
