Letter from Newton to John Collins, dated 20 August 1672

<1r>

Cambridge Aug 20 1672.

S^r

Since yo^r last I have tryed the calculation for finding by an infinite series the content of y^e second segments of an Ellipsoid. The first series y^t I met with was this $\begin{array}{ccccccccc}\begin{array}{r}\phantom{\frac{\mathrm{b}}{0}}2\mathrm{r}\mathrm{b}\\ -\frac{{\mathrm{b}}^3}{3\mathrm{r}}\\ -\frac{{\mathrm{b}}^5}{20{\mathrm{r}}^3}\\ -\frac{{\mathrm{b}}^7}{56{\mathrm{r}}^5}\\ \text{\&c}\end{array}\}& \mathrm{a}\phantom{\frac{\mathrm{b}}{0}}& \begin{array}{r}\phantom{\frac{0}{0}}-\frac{\mathrm{b}}{3\mathrm{r}}\\ -\frac{{\mathrm{b}}^3}{18{\mathrm{r}}^3}\\ -\frac{{\mathrm{b}}^5}{40{\mathrm{r}}^5}\\ \text{\&c}\end{array}\}& {\mathrm{a}}^3\phantom{\frac{0}{0}}& \begin{array}{r}\phantom{\frac{\mathrm{b}}{0}}-\frac{\mathrm{b}}{20{\mathrm{r}}^3}\\ -\frac{{\mathrm{b}}^3}{40{\mathrm{r}}^5}\\ \text{\&c}\end{array}\}& {\mathrm{a}}^5\phantom{\frac{0}{0}}& \begin{array}{r}\phantom{\frac{\mathrm{b}}{0}}-\frac{\mathrm{b}}{56{\mathrm{r}}^5}\\ \text{\&c}\end{array}& {\mathrm{a}}^7\phantom{\frac{0}{0}}& \begin{array}{r}\phantom{\frac{\mathrm{b}}{0}}\text{\&c.}\end{array}\end{array}$ Which upon comparison proved y^e same w^th M^r Gregories & therefore I have exprest it in y^e same letters. I tryed two or thre others, but could fine {sic} none more simple. Wherefore since I understand your designe is to get a rule for guageing vessells, I|t|his Problem having so bad success for y^t end I shall in its stead present you w^th this following expedient.

Let AFDA represent the vessell viewed endwise 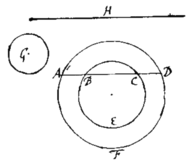its perimeter at the middle being AFD, |&| at y^e end BEC, & y^e top of y^e liquor ABCD. Also let G be a circle whose semidiameter is equall y|t|o y^e difference of y^e semidiameters of y^e other two circles AFD & BEC, & H the whole length of y^e vessel. Find by a table or instrument composed for that purpose, the segments AFD, & BEC, & the w{illeg}|h|ole circle G; & $\frac{2}{3}\mathrm{AFD}+\frac{1}{3}\mathrm{BEC}-\frac{1}{15}\mathrm{G}in\mathrm{H}$ shall be the whole quantity of the liquor {illeg} in y^e vessel. This rule is not exact but approaches the content of y^e Parabolick spindle exactly enough for practice when the {illeg}top of y^e liquor buts upon y^e end of y^e vessell. If y^e vessel be just half full tis exact; if more then half full, tis something to little; if lesse yⁿ half full, too much.

The approximating y^e roots of affected Æquations by Gunters line is thus. Let y^e æquation for instance be ${\mathrm{x}}^3-7\mathrm{x}\mathrm{x}+16\mathrm{x}-12=0$: to resolve w^ch place thre of Gunters {illeg}|R|ulers BF, CG, & DH parallel & equally distant from one another, & to any line AE w^ch crosseth then all apply y^e number 1 of the |t|f|h|ir{s}t|d| {illeg}|R|uler DH, y^e number 7 of y^e second, CG, & y^e number 16 of y^e first BF, accordingly as y^e coefficients of y^e æquation are. Then in y^e cross line taking y^e point A as far from B as B is from C apply any ruler to that point A, about w^ch whilst you turne it slowly observe the numbers where it cuts the other rulers untill you see y^e summ of y^e other numbers on the first & third ruler equall to y^e \sum of y^e/ resolvend 12 & the number on y^e other ruler, w^ch when it happens the number on y^e 3^d ruler shall be y^e cube of y^e desired root. Thus in this case you see $8+32=12+28$, & therefore 8 the number on y^e 3^d ruler is y^e cube of y^e desired root w^ch consequently is 2.

The application of this to any æquations of higher di <1v> mensions is obvious. As a{illeg}|ls|o so to proportion y^e rulers BF, CG, DH, &c y^t y^e line AK may be carried over them with parrallel motion.

The description of a Conick section w^ch shall pass through five given points is this. Let the five points be A, B, C, D, & E any three of w^ch joyn to as A, B, & C joyn to make y^e a rectilinear triangle ABC, to any two angles of w^ch \as A & B/ apply {illeg} two sectors, their poles to y^e angular points, & their leggs to the sides of y^e triangle. And so dispose them that they may turne freely abouth their poles A & B without varying the angles they are thus set at. Which done, apply to y^e other two points D & E successively their two leggs \PQ & RS/ w^ch were before applyed to C (w^ch leggs for distinction sake may be called their describing leggs & t{illeg}|he| other two \MN & TV/ w^ch were applyed to AB, their describing \directing/ leggs,) & marke the intersections of their directing leggs, w^ch intersections suppose to be F when y^e application was made to D, & G when made to E. Draw the right line FG & produce it infinitely both ways. And then if you move the rulers in such manner that their directing leggs doe continually intersect one another at the line GF, the intersection of their other leggs shall describe the conic section w^ch will pass through all the said five given points. {illeg}

If three of the given points lye {illeg} in the same streight line tis impossible for any conick section to pass through them all, And in that case you shall have instead {illeg} \thereof/ two streight lines.

Much after the same manner a Con. Sect. may be described w^ch shall pass through 4 given points & touch a given line, or pass through 3 given points & toug|c|h two given lines, whether those lines be right or curved. &c

I presume it will not be an unpleasing speculation to yo^r Mathematicians to find out y^e Demonstration of this Theorem. As also to determin the center{s}{}, diameters, axes, vertices, & Asymptotes of y^e Con. sect. thus described or to describe a Parabola w^ch shall pass through 4 given points. And there I omit them.

I herewith send you a set of Problems for construing æquations w^ch that I might not forget them I heretofore set down rudely as you'le find. And therefore I think 'em not fit to be seen by any but yo^r selfe, w^ch therefore you may return when you have perused them. How y^e afforesaid descriptions are to be applyed to thof y^e Conick sections are to be applyed to these constructions I need not tell you.

Borellius, of whom you desire my opinion, I esteem among the middle sort of Authors. I find not that he hath added any thing considerable to y^e science{s} of motion but onely proved things already evidently known. Nor hath he done y^t w^thout some Paralogisms, as in y^e proofs of y^e 207|9|^th, 212^th, & 260^th Propositio{ns.} And some of them are not onely proved parallogistically but are also fals as <2r> the 233^d & those y^t depend on it, but yet he may be of good i|u|se to young students in Mechanicks.

S^r I shall trouble you no further at p^rsent, but subscribe my self

yo^r very humble servant

I. Newton

<2v>

These to M^r John Collins

|M^r Newton about the Log^mes Rulers and Mouvable angles|

|From N^o. 4 of the selected papers.|