Mathematical Notebook
Of ye extraction of \Pure/ Square Cubick. Square-square & square-cubick rootes &c.
Let ye number whose roote is to bee extracted bee pointed bec makeing ye first point under ye {ut|n|ite} & comprizeing soe many numbers under each point as ye number hath dimensions as if ye number be square-cube tis thus pointed
Then then then t out of ye figures of ye first point next ye left hand extract ye \greatest/ roote proper to ye power of ye number & set yt downe in ye m{illeg}|Quo|tient wch is ye firt{illeg} {sic} side & is called A. (as ye roote quintuplicate of 5708 is , & quintuplicate is 3125 ) yn takeing yt roote duely multiplied out of ye number (as 3125 out of 5708 ) wth ye rest of ye numbers to ye next point. |seeke| {illeg}|y|e seacond side wch is found by divideing yt number by another number made out of ye first side (wch is called ye Divisor) & this second side I name E. (thus by divideing 258363524 by /qq\\ / after such a mane {sic} yt may be conteined in ye number ye product of yt division shall be E =
The extraction of ye sqare {sic} roote
The extraction of ye cube roote
The extraction of ye square square roote
The extraction of ye Square-Cube roote
Note yt ye 3d 4th 5th & other figures are found by ye same mann{illeg}|e|r yt ye seacond figure is found onely makeing all ye figures found to stand for A ye first side & {illeg} ye figure sought for e or ye 2d side
And if ye number {propounded} be {t} roote is found inexpressible in whole numbers yt|n| adding ciphers & pointing them f{illeg}rom ye unite towards ye right \{kind}/ as was before exp{illeg}|l|ained & soe hold on ye worke in decimalls.
As for ye Divisors they are easily found by ye 2d Table of Powers from a Binomial roote.
If ye {illeg} Number bee of 6.7.8.9.10 &c dimensions The roote may be extracted after ye same manner
Of ye Exta{illeg}|c|tion {sic} of R{illeg}|o|otes in Affected powers.
The manner of ye extraction of rootes in pure & affected powers is verry {sic} much alike, \especially/ when ye affected powers are decently prepared, yt is, when theire affections are not over large & those altogether either affirmative or negative, & ye power affirmative, affirmations & negations so mixt yt there be noe ambiguity & all fractions & Asymmetry taken away
All ye figures in ye coeffents {sic} & affected power are to be pointed (af{illeg}|t|er ye manner before eplained {sic} in ye Analisis of pure powers) according to ye degree of theire dimensions & the worke onely differs from yt in pure powers yt in yt {illeg}|ye| coefficients enter into ye divisors
Let ye first side be called A. ye 2d be called E. ye Roote of ye equation B{L} ye coefficients &c ye Power &c & ye Operation follows
The analysis of Cubick Equations.
<4v>
But ye Coëfficient maybe greater yn ye Power soe yt it cannot be substracted from it wch argues yt ye Cube {illeg} more propperly affects yn is affected. In this case ye coëfficient must descend towards ye unite soe many points untill it may be substracted, & soe many points as ye coëfficient is devolved soe many pricks {illeg}|mu|st be blotted out towards ye left hand in ye power affected. As ye Example shews
=
{illeg} /
.
\
<5r>
To place ye unite of ye coefficient in its right place in respect of ye power make so many pricks above as there are under ye power begining at ye unit, & if ye coefficient be one dimension lesse yn ye power make a prick on every figure if 2 dimensions les yn every other figure of 3 dimensions lesse make it one each third figure &c
If there be many coefficients in ye equation each must be placed according to this rule.
Sometimes ye coefficient is under a negative sine as & ye Analysis is as follows
But sometimes ye square coëfficient hath more paires of figures yn ye cube to be analysed, \hath/ & yn \there is/ præfixing so many ciphers to ye cube as figures are wanting, ye first side will not much differ from ye square roote of ye coefficient. as
<5v>
Sometimes though there be as many 2 figures in the coefficient as 3 figures \in/ ye cube affected yet ye coëfficient may be so greate as to deceive an uwary {sic} Analist As in this . where ye roote of 64 is 8 wch cubed is 512 wch added to 153 makes 665 thē whose \roote/ ye number immediately greater is 9 wch make is ye first sid {sic} .
But if ye coefficient had beene affirmative, yn not ye aggregate of ye facts but ye difference must be taken as in this. .
Since ye roote of 64 is 8 . wch cubed is 512 . & . ye roote of wch is . The like is observable in equations of higher powers
If ye Cube be affected wth a negative sine as . Then ye Equation is expressible of 2 rootes: whereof is less ye other greater yn {i} ye square of one is lesse & the square of ye other is greater ther|n|e . & therefore one roote is lesse ye other greater then . & in this equation are two rootes whereof one is greater ye other lesse then .
☞
Suppose in ye former \cubick/ equation ye lesse roote be 12. yn . or else . & . where is ye greater roote.
And in ye latter equation if ye lesse \greater/ roote be 27. & , c. or | | . {illeg} . If there be 4 cubes continully {sic} proportionall whose greate extreame is . & ye aggregate of ye 3 rest is 8072 & ye lesse extreame, therefore {illeg} | | . ye roote of wch ./is\ 8 ye other roote of ye equation
☞ Or haveing one roo{illeg}|t|e of an equation ye e|E|quation may be lessoned {sic} by division thus {illeg}| | or {illeg} {illeg} | | . & one roote is 12 . therefore divide this equation by & the Quote is an equation conteing {sic} ye ot{illeg}|h|er roote viz: .
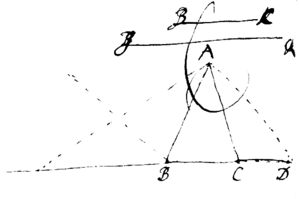
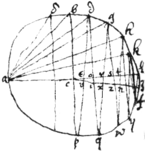
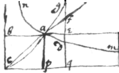
Propositiones Geometricæ. Franc: Vietæ.
prop 1
pro{illeg}|p| 2
prop 3. If . then ∺
prop 3. To find two mene {sic} proportionalls {twixt}
Bc
&
IK
. On ye center
a wth the Rad
ai
describe 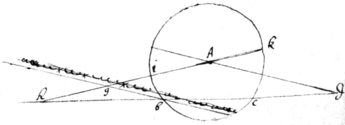 the circle
ibck
. inscribe
b
{illeg}
|
c
|
. draw
da
through ye
center &
bg
parallel to it. draw
hk
through
A
soe yt
. &
.
∺
the circle
ibck
. inscribe
b
{illeg}
|
c
|
. draw
da
through ye
center &
bg
parallel to it. draw
hk
through
A
soe yt
. &
.
∺

Prop: 4
I{illeg}f . yn ye Angle {illeg} / c \ be is tripple to ye Angle abd .
Prop 5
{illeg}|I|f .
Prop 6
Prop 7

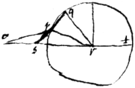
prop 9 If{illeg} . & or . then
<8v>Prop 10
If & . yn be is a side of a 7 equall sided & angled figure. or .
prop 10
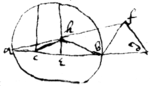
If . & aef a right angle & ab pas {sic} through ye center then . And if then ae is perpendicular to ef . is ye difference of ye extreames & is ye difference of ye meanes. wch given ye proportionall lines may be found &c.

prop 11
\Pse{illeg}|u|domesolabium wherby/ To find 2 meane proportionalls. {illeg} If, . they be inscribed in the {illeg}|c|ircle acbd the diam : being . If twixt g {illeg} | i | & {illeg} | i | h two meane proportionalls are sought on ye same center f wth ye Rad : describe gkhl & inscribe a line kl parallel to cd cutting ab in ye point e | i | & . Examine it.
[1]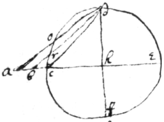
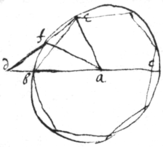
prop 12
If & ac bisected in b & bd bee drawne rd is i|ye| side of a pentagon wch may be inscribed in defcro
prop 13.
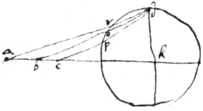
If rd be the side of a & pd ye side of an ye arch rp divided equally in o , od will be {illeg}|th|e side of an to be inscribed in ye circle ord & ye arch RP is bisected \rightly divided/ by Bisecting ye Line ac . /Examine it\
<9r>Of Angular sections.
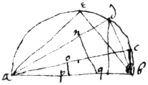
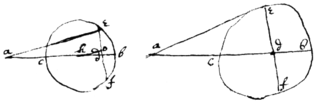
prop 14
If . Then or, . But ye angles anq , aop are right ones and {illeg} | e | {illeg} | = |
prop 15
If \ye angle/ . or . & anq , aop are right ang\les/ then . or the triang: unequall.
prop 16.
In 2 rectang: triang: acb & aed , if ye first have an acute angle cab submultiple to the acute angle eab of ye 2d triang aeb ye si{illeg}|d|es of ye seacond have this proportion. Suppose ye Hypoten of ye first tri: be z . ye base b . ye Cathetus c .
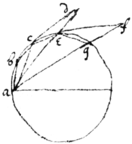
Prop 17. I{illeg}|f| {\∠/} &c: & . & &c then &c /& & &c. {nam} △ cde & cba , efg & eac &c: = & sim. \
Prop.18.
If &c Then &c & if from ʒ to ye center be drawne cʒ then &c & Ergo &c.
<9v>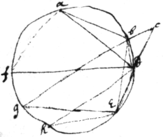
Prop 19
If &c. &. are greater y t |n| ye semiperiphery: then, {illeg} & dh is ye greatest, db ye least line drawn from d to these points , , , . yn {illeg} | | .
Prop 20
Out of ye 18th & 19th {illeg} Prop: To divide An angle into any number of pts in ye figure of ye 18th prop:
\
/
z
.
ah
is ye greatest of ye inscribed lines
: now
z
/{illeg}\
∷
|
∶
|
{illeg}
|
.
|
therfore
.
&
. And
. therfore
Likewise
. &
{illeg}
n
{illeg}/tenth &\
Prop 21
out of ye 17th Theor.: in ye figure whereof if
ab
{\:/} ye least inscribed line
. &
ac
ye next line bee
B
. then
. &
&
&
&
{sic}
.
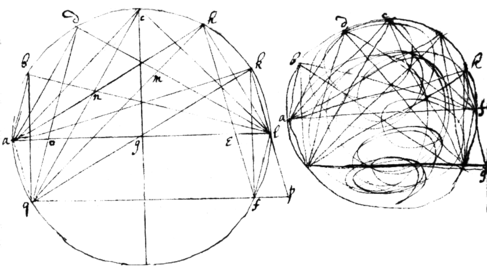
Prop 22.
If . Then And &c ) Soe that Rad{illeg} ye Periph: divided into any number of pts. &c. & &c.
hence Prop 23.
In ye former scheame If al {illeg} . . & / {illeg} | b | ) lc{−}kl{=}dl{−}\h/ therefore . & ye base of ye 4th triang: &{c} ye perpendicular ( {illeg} | bl | ) of ye 5t tri: &{c} base of ye 6t triang. perpendic of the 7th tri base of ye 8th tri. perp: of ye 9th tri:
<10v>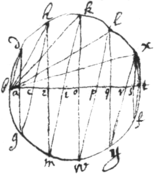
Prop 24:
If {illeg}|
bd
|
b
{illeg}
g
&c: {illeg}|t|hen
&
&
&c: & then
therefore
.
againe
&c
Therefore
.
& since, as
Therefore
. And
to all ye perpen
dicular & transverse line
. that is
|
(
{illeg} \5/ {illeg}
)
|
.
Prop 24
If in ye circle
cfgh
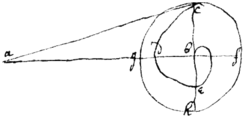 be inscribed ye helix
bedc
a|&|
ac
touch it in ye point
c
then
to ye circumference.
be inscribed ye helix
bedc
a|&|
ac
touch it in ye point
c
then
to ye circumference.
Prop 25
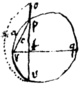
If apcr be les yn halfe ye circle. & . & to ye vrap : then 4 times ye section /rapc\
Prop 26
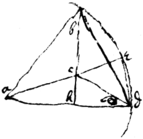
If & bh perpendicular to ad fro {sic} ye angle {illeg} | b |. . yn . & ed is ye side of a heptagon
Prop 27.
If a line be cut by extreame & meane proportion ye lesse {illeg}|s|egment almos{illeg}|t| is to ye whole line as ye diameter is to of 5 times the periphery divided by 6 .
Prop 28
Si secetur linea per extremam & mediam proportionem er{illeg}|i|t proximè, ut tota line{illeg}a plus minori segmento ad {tot} bis totam lineam, ita quæ potest quadrato sesquialterum semidiametri, ad latus quadrati circulo equalis.
linea secta sit
100,000
. minus segmentū
38,197
. Semidiametrū
100,000
, quæ potest quadrato sesquialterū semidiametri paulo maior est quam
122,474
. Radix Peripheriæ,
177,245
.
Prop 28.
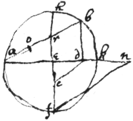
If . & to ye side of a decagon; & fn parallell to cd yn en shall be almost equall to ye fourth ꝑte of a circle for af {sic} is divided in extreame & meane propor in ye point c . & hf Perimeter|hbk|fa ; by ye 27th prop: & .
Prop 29.
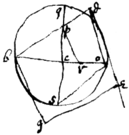
If . & co is divided by extreame & meane proportion in r . & od parallell to rp then db is ye side of a square = to o|t|he area of ye circle. for be|y| ye 28th prop: As ({illeg} .
Prop 30
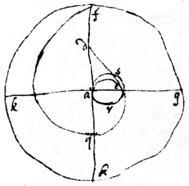
If ye line dc touch ye helix in ye line ag . & ye line hf toucheth ye beginning of it in ye center a & then shall bee equall to perim: asr . & ac being ye Diam: ye tri: acd area of ye triang acd = to ye area of ye circle asr
Prop 31
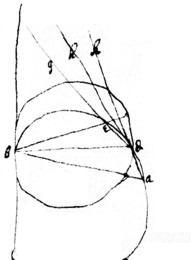
If
bed
be a square of one revolution of an
helix & ye angle
& through ye points
a
,
d
, in ye helix be drawne ye line
adk
& through ye points
ed
{sic}
in ye Helix be drawne
edg
. & ye angle
kdg
bisected by
dh
; then
dh
shall almost touch ye helix in
d
. {illeg}|&| it shall be soe much ye nigher a touch line by how much ye angles
ebd
dba
are lesser.
Prop 32
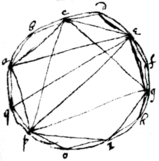
If many Polygons be inscribed in a circle ye number of theire sides increaseing in a double proportion. & theire apotomies, or ye t|b|ase \of/ a tri: whose cathetus is a leg of ye Polygon & hypotenusa is ye {illeg}|D|iam (as ye apotome of ye Polygō
cgp
is
ce
. of
pacegi
is
ae
&c) if ye Apotome of ye sides of ye first Polygō be called
b
. |of| ye 2d
. |of| ye 3d
. of ye 4th
. of ye 5t
of ye Sixt
. & ye diameter be z then And ye first Pol{illeg}ygon be
. ye 2d
. ye 3d
. ye fourth
. ye 5t
ye sixt
. ye {illeg} 7th
&c then
.
& p{illeg}
. &
. &
. & . &
&c
To know how many elections may bee made of \divers ways/ things, whereof some of ym are equall, \may bee ordered./ . as of . doe thus { } { } the number of changes, in order.
To know how many elections may bee made doe thus therefore there are elections in .
Propositiones Geometricae Ex Schootenij
Sectionibus miscellaneis.
Sectio 1ma
To know how many changes 6 Bells,
or how divers conjuctions ye 7 planets can make ♄ ♃ ♂ ☉ ♀ ☿ ☾. or how many divisors
hath, or how man{e {sic}} divers compositions ye 24 le{illeg}|t|ers {sic} can make &c the examples following show.
\
\
31
/
/
wch shows yt in 7 letters 127 el{illeg}e|ec|tions may be made. yt 7 Planets may be conjoyned 120 divers ways. yt
. hath 128 divisors for an unite is one of {y}&
; are ye number of changss {sic} in six bells.
Sec 2
To know how many things & of wt sort they are wch may be chosen 15 ways. . & {illeg}4{illeg} \ . that 4 things all unequall/ m{illeg}|a|y be varyed 15 ways. also. {illeg}|&|. 5 things whereof 3 are equall viz: {illeg}|&| . . & 6 thins {sic} whereof 3 & 3 are eaquall {sic} as . may be varied 15 ways. & . . & 8 things whereof 7 are = may be varyed 15 ways. as . . . 2 wherefore 15 alike things &c |as a \15/|. 2 wt things vary 23 ways. & 24 admitts a {illeg}|7| fold divisor therefore ye multitude of things sought may be 7 fold but since 43 is a primary number (viz wch cannot bee divided) . . therefore onely 42 like things can be varyed 42 ways as .
Sec 3
Every quantity hath one divisor more yt it hath aliquote pts (yt is pts greater yn an unite \of whole numbers./). How to find a quantity haveing a given multitude of divisors or ali{illeg}|q|uote{illeg} pts: suppose its aliq: pts must be 15. & \soe/ by ye former section may be varyed 15 ways. therefore they shall have 15 aliquote pts & 16 divisors. but since onely 42 like things (as ) ca{illeg}|n| be varyed 42 ways therefore oenely {sic} hath 42 aliquote pts & 43 divisors. &c
Sec 4
To find ye least numbers haveing a given multitude of divisors & aliquote pts instead of soe many letters in the former sec: put soe many p{illeg} least primary numbers & take ye least result from ym. as from ye former example: that is or | | &c. {illeg} now. . & . &c therefore \ / are \is/ ye least number{s} haveing 16 divisors.
Sec: 5 conteines a table of Primary numbers.
Sec 6
To find progressions constituteing rectangular triangles wth sides rationall ye examples \following/ shew. take two numbers as . yn since ye product is eaved|n| double it viz:
. &
4
is ye numerato\r/ yn
& since
3
is od multiply it by the difference of ye termes:
&
3
is ye denominator. & ye first terme
. yn since (1) ye difference of ye termes is od multiply it by
4
.
&
per 2 majore terminum.
(the former numerato\{r}/) numerator 2d. yn
3 (ye former denom) added to. {illeg}|
2
| (ye double square of ye diff: of ye termes because ye square (1) is o{illeg}|d|d) ye 2d denominator. I ad anothe example take yn 1st numerator. yn & since
4
is eaven halfe 4 {illeg} 1st denom. & ye 1st {illeg} \halfe/ is (diff: of ye termes)
& ye first denom is 4. ye first terme{illeg} . yn becaus ye diff of ye termes is eaven
2 & & . yn . & ye 2d terme & now {illeg}|t|er{illeg}|m|es may be had by Arithmeticall proportion. thus.
or
&c |&| or
&c thus may other progressions be obteined. For ye use take ye numerator for one leg & ye denom for another & ye Hypoten: will be rationall as in
or . & in this
or .
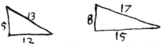
If ye {illeg}|s|uposed number{illeg}|s| be . yn . . & . . so yt . yn {illeg}be . . {illeg}. |&| . . . & ye 2 first termes or . Agai{illeg}|n|e, if ye numbers be . . & . . therefore . yn . . & . . therfore is ye 2d & ye progres may be continued, as . & &c.
Sec 7
To find a {number} wch divided by 7
leaves
2
. by 11
leaves 1
. by 13
leaves 9
. the least common divisor of is {illeg} \1001
/. divide {illeg} \1001
/ twice by each & consider ye remainder of ye {illeg}|s|eacond division thus.
. because
1
is left
105
is ye multiplier.
. since
1
is left
70
is ye multiplier.
since more yn
1
is left (viz:
2
) multiply
2
till it divided by 5 leaves (
1
)
. therefore
is ye multiplyere.
since more yn
1
is left
1 Since more yn 1 is left (viz 3) multiply 3 till it divided by 7 leavs 1 . therfore ye multiplier .
2 Since more yn 1 is left (viz: 3 ) therfore ye multipl: .
3 If but 1 had ben|e|ne left 77 had beene divisor but now . therfore is multiplyer. . now the number sough {sic} is thus found.
< insertion from the center right of f 13r >< text from f 13r resumes >
Lastly did|v|{illeg}|i|de
by ye least com. divis:
whe{illeg}|r|efore
100 ye number left is ye number sought.
Sec 8.
Touching ye Method of weights suppose a man have weigs {sic} of pounds &c by ym all intermediate pounds may be thus weighed &c or is|f| his wights {sic} be all weights may be supplyed thus. &c Note yt weight marked wth − signifie ye wigh {sic} to be put in ye opposite scale ballance.
{illeg}|S|ec. 9.
To find numeri amicabiles that is 2 numbers whose aliquote pts are mutually equall to theire wholes. take this Des-Cartes his rule
If , or any other number producc|e|d out of 2 {illeg} \a{illeg}|s|/ &c (viz &c .|)| bee such a number yt 1 taked|n| out of it triple there rests a primary number{,} & yt if {illeg} 1 taken f{illeg}|r|om it sextuple there rests a primary number, & if 1 taken from its square octodecuple a primary number rests: yn multiply this last prime number by ye assumed number doubled & ye product is one amicable number & ye aliquote pts of {illeg} it make ye other Example. if 2 be taken. numero primario primo. numero primario scdo. numero primario tertio. , one amicable number, & ye 2 former prime numbers \ × one another & ye product/ ye double of ye assumed number viz . Thus from 8 . & 64 &c. may be deduced amicable numbers.
Sec 1{illeg}|0|
To find triangles whose sides, segments of theire bases, & Perpendiculars are expressible by rationall numbers 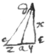 1st if ye perpendic: is without ye tri: let
.
.
. {illeg}
. .
. &
.
.
.
.
. puting any numbers for
a
,
b
, &
x
;
y
&
z
may be found. then
.
. wch reduced to ye common denominator
; & yt cast away.
. {illeg}
.
.
.
.
.
1st if ye perpendic: is without ye tri: let
.
.
. {illeg}
. .
. &
.
.
.
.
. puting any numbers for
a
,
b
, &
x
;
y
&
z
may be found. then
.
. wch reduced to ye common denominator
; & yt cast away.
. {illeg}
.
.
.
.
.
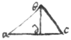
In like manner if ye perpendicular fall wthin side. . . . . . .
Also by ye conjunction & disjunction of 2 triangles it may be found yt . {illeg} . {illeg} . {illeg} . . For if . . that is . . . Likewise . . . ye least quanti{illeg}|t|y divisible by & , being divided by ym, leaves a & x wch must {illeg} multiply ye bases & hy{illeg}|p|otenusas. If ye perpendic: fall wthout ye legs may be thus exprest . . . . .
Sec 11
To ma{illeg}|k|e yt two such tri: be of ye same base & altitude. Suppose an equation twixt ye bases & pependiculars {sic} of ye 2 last tri: as .
.
. or & . Suppose
. {illeg}|o|r
. let
greater yn
.
.
.
& consequently
Sec 1{illeg}|4| differs not from Cap 19: prob 18 Ou{illeg}|g|htred.
Sec: 15 Of P{illeg}|o|lygons or multangular num{illeg}|b|ers
\The sum̄e of all ye tearms|e|s in/ an arithmet: progres: increasing from {illeg} \an/ unite by 1 compseth {sic} tra|i|{illeg} triangles. by 2 , composes □s. by 3 , composes pentangles. by 4 , hexang: &c {illeg}ke as compos {sic} ye triangles &c likewise compose &c So compose ye quintangles &c. If ye first term{e} ye excess {illeg}|o|f the progression . The sume of ye termes \to ye polygon/ ye multitude of ye termes to ye side of ye Polygon. {illeg} given to find {illeg} Suppos {sic} t given to find {illeg}z. or in trigons. in 4gons. in 5gons. in 6go in {illeg}|7|{illeg}|g|ons. in 8gons. in 9gons. &{c} {illeg}|&| z given t is found thus in tri. in 4go , in 5gons. { } { } in 6gons &c. As {illeg} ye side 12 of a tri given. ye &c & if be octangled. .
July 4th 1699. By consulting an accompt of my expenses at Cambridge in th{illeg}|e| {illeg}|y|ears 1663 & 1664 I find that in ye year 1664 a little before Christmas I being then Senior Sophister, I borrowed bought Schooten's Miscellanies & Carte's's Geometry (having read this Geometry & Oughtred's \Clavis/ above half a year before) & borrowed Wallis's works & by consequence made these Annotations out of Schooten & Wallis in winter between the years 1664 & 1665. At wch time I found the method of Infinite Is series. And in summer 169|6|5 being d|f|orced from Cambrid{illeg}|g|e by the Plague I computed ye area of ye Hyperbola a{illeg}|t| Boothby in Lincolnshire to I{illeg} two & fifty figures by the same method. Is. Newton
Annotations out of Dr Wallis his Arithmetica infinitorum.
|1| A primanary series of {illeg}|q|uantys {sic} is arithmetically proportionall, as . & its index is 1
|A| Secundanary series i|a|re those whose rootes are arithmetically proportionall; as . & its index is 2
A Tertianary, quartanary, quintanary series of quantitys are those whose cube, square square, square cube rootes are Arithmetically Proportionall as . / . / . &c Their indices being &c.
3 Subsecunda\na/ry, sub{illeg}|t|ertianary, series &c: are those whose squares, cubes, &c are arithmetically proportionall, as . &c. Theire indices being {illeg} &c.
2 Primary Secundanary, tertianare|y| series &c are said to bee reciprocally proportionall ({illeg} yt is to ye sam {sic} se{illeg} increasing) which continually decrease as. . . . Their indices being negative as .
4 The indices of compound \or mixt of rationall & irrati{illeg}{onall} \series// series, by multiplying or dividing ye indices of ye simple series may bee found as in a subsecundanary progression cube{illeg}|d|
ye index is
. So in ye cube rootes of a secundanary progression,
&c. ye index is
. so in irrationall reciprocal progressions
, ye index is
.

Now su{illeg}|p|pose ye line ac be divided into an infinite number of equall pts &c, from each of wch are drawne perpendiculars \parallels/ &c. wch wch ino|c|rease continually in so{illeg}|m|e of ye foregoeing prg|o|gressions or in some progresion {sic} compounded of ym, all those lines may be taken for ye surface bqnac , & to know wt proportion \all/ those lines have that superficies hath to ye superficies ambc yt is wt proportion all those lines have to soe may equal to ye greatest of ym, I say as ye index of ye progression increased by an unite is to an unite soe is ye square abcm to ye area of ye crooked line. As if abc is a parabola ye lines &c ao|r|e a subsecundanary series (for ) whos {sic} index is wch added to an unite is Therefore so is ye square ambc to ye area of ye Parab. ({illeg}|ye| names of ye lines are {illeg} {illeg}|&|c . &c . . .) T{illeg}|h|e case is ye same if abc bee supposed a sollid, as suppose it{illeg}|s| {nature} t a Parabolicall conoides. yn since ye nature of it is . designes ye squares &c: all wch taken together are equivalent to ye Sollid. & those □s increase in ye same proportion wch . or x doth. yt is they are a primanary series whose index i{illeg}|s| 1 to wch (according to ye rule I ad an unite & tis 2. Therefor 1 {illeg} soe are all ye □s of ye Primary series to soe many □s equall to ye greatest of yt series. & soe is ye conoides to a cilinder of ye same altid|t|ude.
<16r>Also if a superficies be compounded of 2 or more of these series, Their area is as easily found as if ye nature of ye line bee {illeg}, {illeg} y {illeg} , or {illeg} or {illeg} . &c. Their areas will bee to ye parallelograms {ar|b|o{illeg}|u|t} them as {illeg}|2 | to {illeg}|3 |, as 8 to 15 , as 48 to 105 &c. but if I put in ye intermediate termes in these last named lines th{illeg}|e|ir order will bee , , , . . ; &c: & since these lines observe a geometricall progression their areas must observe some kind of progression. of wch every other terme is given viz . T{b}{l}wixt wch {illeg}|t|ermes if ye intermediate termes can bee found ye 2nd □ will give ye area of ye line , ye circle. Soe likwise {sic} in this progression of lines {illeg}| y | . {illeg}| y | . . &c: ye progression of their areas {illeg} is &c. ye 2nd if it can bee found givs {sic} ye area of ye ○ for as its denominator to its numerator so is ye □ of ye diameter to ye area of a semicircle. If th{illeg}|i|s last progresion {sic} bee multiplyed by ye respective termes in ye progress & it may bee diminished ye reslut {sic} being soe yt in this progression {illeg} &c: if b can be found yn, {illeg} ye □ of ye diameter to ye area of ye circle is as ye denominator of b to its numerator. Likewise ye 1st series of areas may be diminished by multiplying each terme by its correspondent terme in this progression &c: & it will become, . &c. In wch if a can bee found yn as ye denom of a to its num: so ye □ of ye Radius is a semicircle, yt making ye radius . . The same \kinds of/ changes may bee performed |by| other p any other progressions, as \by division/ by ye geometricall progression & ye {illeg}|fi|rst series of areas becomes &c viz ye same wth ye 2d series. Also these changes may be done by addition or substraction of mutuall termes in 2 proportions. Soe yt ye most convenient way \may be/ be chosen, {illeg}|w|he|r|by to reduce any series of proportions to ye most convent {sic} forme.
Now if it be propounded to find thes{illeg}e mi{illeg}|d|dle termes, f|i| |I|t w{illeg}|i|ll {illeg}|b|ee convenient to d|f|ind how the given proportion may bee deduced from an Arithmeticall, Geometricall, or some other familiar proportion, viz whose meane termes may be found, as this progression deduceth its originall from this {illeg}| A | & in wch A is an infinine {sic} number .
It will also be convenient to find what relatiō all ye other meanes have to ye first soe yt if ye first bee had all ye other may bee deduced thence. As in this case suppose ye 1st meane to bee a . The progression will bee deducing its originall from {illeg}|&| from this . &c {+} (note yt ye proportions of th{illeg}|e|se te|m|eane termes to oneano {sic}ther, or to , are found f by finding ye proportion of ye circle to ye line &c).
In this case to find ye quantity
a
: it may be
considered yt .
{illeg}
{illeg}
.
.
Naming ye termes in ye progress: 1st observe yt
&c ye proportions still {illeg}|de|creasing & therere|f|ore {sic} yt in &c: ye latter terme is lesse yn ye former; & therefore
or /
\
. Also
. Therefore
Therefore
. And So by ye /same reasoning.\
&c. Thus {illeg}|W|allis doth it. but it ma{illeg}|y| bee done thus.
Therefore
.
yt is
&c. By ye same reasoning
Or
.
Note yt a is greater yn these two summes.
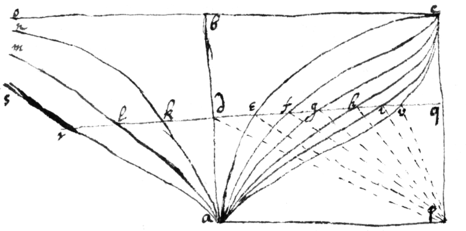
Having ye signe of any angle to find ye angle or to find ye content of any segmnt of a circle
Suppose ye circle to be
aec its \se{illeg}|m|i/diameter
. ye given sine
, viz: ye signe of ye angle
epa
. ye segment sought
eapq
.
abcp
the □ of its Radius. & yt,
&c are continally {sic} proportionall. Then is . .
{illeg}
. .
. . . . &c & since all the{illeg} ordinately applyed lines in these figures
&c are geometr{illeg}|i|cally proportionall their areas
&c will observe some proportion amongst one another. To find wch proportion, 1st
. 2dly
afc is a parab: therefore . also since tis
, therefore . |Also|
, therefore {illeg}/\ . & by ye same proceeding ye proportion may bee still continued after this manner
. &c.
And if ye meane termes be inserted it will bee
or
The first letters \
x
/ run in this {illeg} progression
&c. ye 2d \/ in this
&c ye 3d
in this
\
/
. ye 4th
th{illeg}|i|s
Now if the meane ter{illeg}|m|es in these progressions can bee callculated ye first of ym gives ye area aeqp.
Which is thus done
Soe yt &c. is ye area, apqe
yt is &c:
The progression may be deduced from hence
. &c
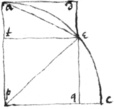 Soe yt if {illeg}|ye| given sine bee .
& if ye Radius . Then is ye superficies
&c:
And ye area &c. By wch meanes ye angle
ape is easily found for .
Soe yt if {illeg}|ye| given sine bee .
& if ye Radius . Then is ye superficies
&c:
And ye area &c. By wch meanes ye angle
ape is easily found for .
The same may bee thus done.
. Or . . . And . &c. as in this order . &c Which progression wth their intermediate termes {illeg}|may| bee thus exhibited. By{illeg} wch it may appeare yt if . . yn &c. And ye area aep given gives ye angle ape for Likewise ye angle ape given its sign ma{illeg}|y| bee found hereby |&c| Note yt &c that is {illeg}|&|c. According to this progression &c. Note also yt ye segment . &c. .
<19v>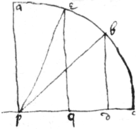
If . . . yn ye areas of ye lines in this progression. & (supposeing also . &c
To squar{illeg}|e| ye Hyperbola.
Epitome Geometriæ
So if nadm is an Hyperbola. & . . &c . & . . . . . . &c. There {sic} squares are. . &c As in ye following table. By whose first terme is represented ye square of ye Hyperbola, viz yt it is
<20v>cui addendum
And so ye summe will bee
wch is ye quantity of ye area
adpq
. If . &
&
.
In like manner if I make
. The opperacon followeth.
wch is ye quantity of ye area
apqd
if
. and
. . a |b | + y | z| {illeg} y |z| . a |b| − y |z| {illeg} . y |z| . y |z|− a |b| {illeg} y |z|− || . {illeg} {illeg} . {illeg} {illeg}|y| ξ . . . . .
. . |Or.| . &. then . or if abn is \a/ right angle. & | {illeg} | / \
<21v> <22r>. . {illeg}. . . . . d {illeg}| n | . . . & . Or . . . {illeg} \ al / &. {illeg} . whence or {illeg} / \ &c: as before onely varying ye signes at εεn & εεξ . . . . . .
<22v>Dr Wi|a|llis in a letter to {illeg}|S|r Kenelme Digby promiseth ye squareing of ye Hyperbola by finding a meane propor{illeg}|t|ion twixt 1 , & in the progression &c.
The resolution of cubick equations out of Dr Wallis in his dedication before Meibomius confuted
suppose . yn . or \+ /{illeg} . that is ma{illeg}|k|ing {illeg}. yn . & . yn × |=| . Againe suppose {illeg}| y | b | a | {illeg}| e | Then {illeg}| | Againe suppose . yn . yt is making , & , yn .
Then in the first o{illeg}|f| th|e|se . or
.
or
. Therefore
.
{illeg}|&| . & by y{illeg}|e| \same/ reason where ye irrationall quantitys have. divers signes other{illeg}|w|ise would bee false. Soe that
. is a rule for resolving ye equation
, when it hath but one roote yt is when it may be generated according to the supposition
. &c. By ye same reason
. may be resolved by this rule
.
But here of|b|serve yt Dr Wallis would h|A|rgue yt since in the first of these two cases fsometimetimes (viz when ye equation hath 3 \reall/ rootes) y {sic} first rule faile|th| as it were imposs|i|ble {sic} for ye equation to have rootes when yet it hath, therefore ye fault is in Algebra. & therefore when Anal{illeg}|i|ses Analysis leads us to an imposs|i|bility {sic} wee ought not to conclude ye thing \absolutely/ imposible, untill wee have tryed all ye ways yt may bee.
But let me answer yt ye fault is {illeg}i{illeg}|not| in ye Analysis in this example, but \in/ his opperation. for {illeg} when ye equation , hath 3 root{illeg}|s| hee supposeth it to have but one roote viz . but sin{illeg}|c|e ye Equation cannot be then generated according to yt supposition it is impose|i|ble {sic} it should be relolved {sic} by it.
<23v>In like manner hee s{illeg}|a|yeth yt Algebra representehteth a thing possible when tis not so as in this examl|p|le, in ye △ abc, make . .  Then to find , worke |thus,| {illeg}
. {illeg}|t|herefore
. or . In wch oppera{illeg}|c|on all things proceede as possible though they are not soe for
ac
is greater yn .
Then to find , worke |thus,| {illeg}
. {illeg}|t|herefore
. or . In wch oppera{illeg}|c|on all things proceede as possible though they are not soe for
ac
is greater yn .
yet I answer yt if ye opperation & conclusion be compared together ye absurdity will appeare. for in ye equation or . but it is impossible yt a □ number should be negative.
Thus is impossible. square it & tis . Againe, & tis . Extract ye roote & tis or . wch is possible. The reason of this proceeding Event is yt hath two possible rootes viz . . & two impossible viz: . .
Thus ye valors of are , , , , , , , .
<24r>Dr Wallis in a letter to Sr Kenelme Digby teacheth how to find ye center of gra{illeg}|v|ity in divers lines first when their position is as in 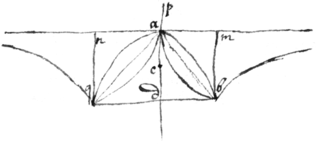 this figure.
this figure.
Suppose ad ye Axis, a their vertex & as 1 to ye series of ye progresion cons. Then saying, as 1 to ye index of ye line increased by an unite (vide pag {illeg}|2|da) so cd to ca Then c is their center of gravity.
The Demonstracon.
Let p bee ye index of ye series according to wch ye odinately aplyed lines (parallell to db) increase, yn {illeg} {illeg} area of ye line ∶ to nmbq . ye distances of those ordinate lines from ye vertex a are equall to ye intercepted diameters & therefore a primanary series \(whos index is 1. / & since supposing a ye center of ye ballance ye whole weight of ye surface or figure is composed of its magnitude & distance from ye center and therefore ye index of all its moments or whole weight is , viz: ye aggregate of ye other two. Therefore as all its mom moments (or ye \weight of the/ figure in its site in respect of ye center a are to soe many of ye greatest (or to ye weight of ye ▭ nmbq hung on ye point d ) soe is 1, to . and if , then nmbq hung on ye point q shall counterballance ye figure in its site &c therefore if {illeg} , {illeg}|c | shall be ye center of gravity of those figures.
Also as the figure is now put extending infinitely towards δ if {p }. {illeg}|m | being ye center of qnbd yn c shall bee ye center of gravity of ye whole figure qndbδ .
Demonstration
<24v>sincce {sic} ye lines parallell to aδ increase in series reciprocl|a|lly proportionall their index is & since ye halfe{illeg}|s| of those lines increas {sic} in ye same proportion their index is . whose extremitys or middle points of ye whole lines (suposing a ye center of ye ballance) are theire centers of gravity, their distances from a being proportionall to ye lines whose centers they are & consequently their index is & since all ye moments (or whole weight of ye figure) increase in a proportion compounded of ye proportion of ye magnitudes & distances of ye lines from ye center a, they will be in a du{illeg}|p|licate proportion of ye lines magnitudes that is a series reciprocall series whose index is . Therefore ye figure is t{illeg}|o| ye inscribed parallelogram as 1 to . & all its moments or w{illeg}|h|ole weight of the Para in this its site to {illeg}|t|he weight of ye pgr as 1 to . Therefore if, , the paralelogra {sic} hanging on ye point p s{illeg}|h|all counterballanc{e} ye whole figure in its site &c: whence ye point c may be found easily, {illeg} viz .
Of Refractions.
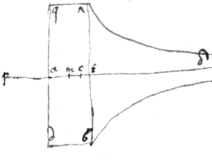
1 If ye {illeg} ray ac
bee refracted at the center  of ye circle
acdg
towards
d
& . Then suppose . {illeg}|S|ee Cartes Dioptricks
of ye circle
acdg
towards
d
& . Then suppose . {illeg}|S|ee Cartes Dioptricks
2 If there be an hyperbola 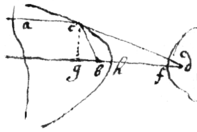 whose \the/ distance of whose foci
bd
are to its transverse axis
hf
as
d
to
e
. Then ye ray {illeg}|i|s refracted to ye exterior focus . See C: Dioptr
whose \the/ distance of whose foci
bd
are to its transverse axis
hf
as
d
to
e
. Then ye ray {illeg}|i|s refracted to ye exterior focus . See C: Dioptr
3 Having ye proportion of d to e, or. . The Hyperbola{illeg} may bee thus described.
1 Upon ye centers a, b 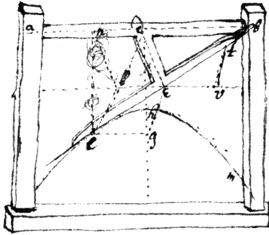 let ye instrument adbtec bee moved in wch instrumnt observe yt ad
{illeg}
c
{illeg}
et
& yt the beame
cet
is not in ye same plane wth
adbe
but intersects it at ye angle
tev
soe yt if
, then
. Or . Also make
, i.e half ye t{illeg}|r|ansverse diamet{er.} Then place \the fiduciall side of/ plate
chm
in the same plaine wth
ab
. & moving ye instrument
adbect
to & fro its edge
cet shall cut or weare its {illeg} into ye shape of ye desired Parabola. Or the plate
chm
may bee filed away untill ye edg {sic}
cet exactly touch it everywhere.
let ye instrument adbtec bee moved in wch instrumnt observe yt ad
{illeg}
c
{illeg}
et
& yt the beame
cet
is not in ye same plane wth
adbe
but intersects it at ye angle
tev
soe yt if
, then
. Or . Also make
, i.e half ye t{illeg}|r|ansverse diamet{er.} Then place \the fiduciall side of/ plate
chm
in the same plaine wth
ab
. & moving ye instrument
adbect
to & fro its edge
cet shall cut or weare its {illeg} into ye shape of ye desired Parabola. Or the plate
chm
may bee filed away untill ye edg {sic}
cet exactly touch it everywhere.
2 By the same proceeding Des=Cartes concave Hyperbolicall wheele may bee described by beeing turned wth a chissell {illeg}| d |tec whose edge is a streight line inclined to the edge \axis/ of the mandrill by ye ∠ tev wch angle is found by making .
3 By the same reason a wheele ma{illeg}|y| be turned Hyperbolically concave ye Hyperbola being convex. Or a Plate may bee turned Hyperbolically concave
<26v>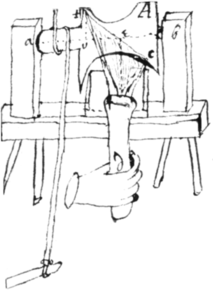 Also Des=Cartes his Convex wheele \
B
/ may be turned {illeg}|o|r {ground} trew a concave wheele \
A
/ being made use of instead
Also Des=Cartes his Convex wheele \
B
/ may be turned {illeg}|o|r {ground} trew a concave wheele \
A
/ being made use of instead  of a patterne
of a patterne
5 In turning the concave wheele
A
it will \perhaps/ bee best to weare it wth a stone
p
& let {illeg}|t|he streight edged chissell d serve for a patterne. And it may bee convenient to grind ye stone (or iron &c {illeg}) p into ye fas{illeg}|h|ion 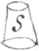 of a cone S That it may fit ye hollow of the wheele A. The angle of wch conce {sic} being
a right one or something greater it will almost grind the wheele to a {illeg}tre{illeg} figur Same done by helpe of a Cone.
of a cone S That it may fit ye hollow of the wheele A. The angle of wch conce {sic} being
a right one or something greater it will almost grind the wheele to a {illeg}tre{illeg} figur Same done by helpe of a Cone.
6
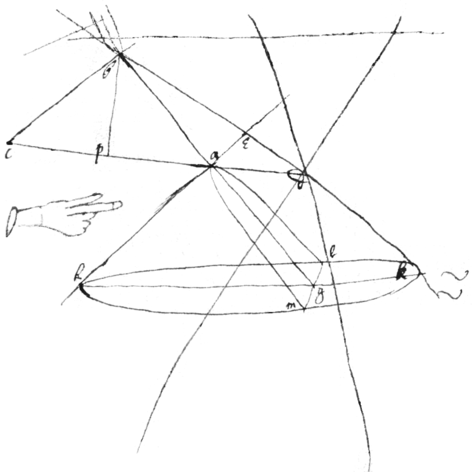 Draw ;
ac & cb of any length or intersecting one another at any angles. to make up the triangl{illeg}{e} abc
. [Suppose yt ac bee called b, & that
{illeg} then is
d
the distance of ye foci]. produc{e} ac to d
soe that . Then draw bk through ye point d, & draw eh
parallell to
bc
, lastly wth the sides
he
,
ek
& angle
hek
describe the cone
heklm
. Then produce
ba
to
g
&c \indefinitely/ & ag
being ye axis of a section
mal
shall be ye sought Par Hyperbola
Draw ;
ac & cb of any length or intersecting one another at any angles. to make up the triangl{illeg}{e} abc
. [Suppose yt ac bee called b, & that
{illeg} then is
d
the distance of ye foci]. produc{e} ac to d
soe that . Then draw bk through ye point d, & draw eh
parallell to
bc
, lastly wth the sides
he
,
ek
& angle
hek
describe the cone
heklm
. Then produce
ba
to
g
&c \indefinitely/ & ag
being ye axis of a section
mal
shall be ye sought Par Hyperbola
7 Since the proportion of cb to ab & ∠ cba is not deter{illeg}|m|ined it will be most convenient to make . & . And then there will bee little danger of error at ye vertex of the {illeg}|Hy|perbola. And ye calculation is readier for drawing , Then is & . Soe that soe yt ye is {illeg} easily found.
9 Halving such a cone smo|o|thly pollished wthin & wthout, by the helpe of a square set ye plate perpendicular {illeg}|t|o one side hae the fiduciall edge being distant from ye vertex the length of & if ye edge of ye plaine every where tou{illeg}ch the cone, tis trew.
10 The exact distance \/ of ye plate from the vertex of ye cone neede not bee much regarded for that changeth onely the shape \bigness/ not ye shape of ye figure.
[By ye broken lookinglasse I find in glasse refraction, yt {illeg}. These are insensib almost insensibly different from truth . Or {illeg} /\ . Or
For ye Ellipsid|s|
<27v>The former demonstrated.
Lemma. If in ye Opposite Hyperbolas one of
abc
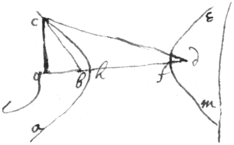 edf
(one of wch are to bee described) supposing . . . & {illeg} point & gc terminated by ye hyperbola Then is . b
d
|
h
|
.
. d
|b|
.
. . . And since af
. /Or
\ Therefore . Both ꝑts of wch □ed & ordered ye result is . That is .
edf
(one of wch are to bee described) supposing . . . & {illeg} point & gc terminated by ye hyperbola Then is . b
d
|
h
|
.
. d
|b|
.
. . . And since af
. /Or
\ Therefore . Both ꝑts of wch □ed & ordered ye result is . That is .
Desciption {sic} ye 1st demonstrated \Synthetically/. See yt Scheame
Naming ye quantitys {illeg} {illeg} ∶ e{illeg} tv Nameing ye quantitys \{illeg}/ . . . . . . {illeg}. Also , therefore That is . As in ye lem̄a
The Same demonstrated synthe \Analy/tically.
Nameing ye quantitys, {illeg}|a |. . . . . . Supose yt {illeg} .
<28r>Then is . That is . Therefore ye line chm is a Conick Section & since is greater yn tis an Hyperbola, wch yt it may bee {illeg} ye same wth yt in ye lemma, Their correspondnt termes are to bee compared together & soe I find yt . & by ye 1st =tion . Or . yt is . by ye 2nd . And by substituting into the place of {illeg}|A|nd ordering it tis {illeg}2{illeg} . Or . Therefore if I take . & . then shall chm bee ye Para|Hyper|bola desired Q:E:D.
The 2d 3d 4th & 5th Propositions are manifest from this
The 6th Description demonstrated Syntheticaly The quantity named are . 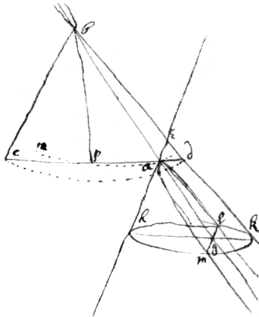
☞ Instead of ye 6th & 7th Descriptions wch are false use these
6 Draw 2 concentrick circles (na & cd) wth ye Radij e & d. Then from ye comon center b draw 2 lines bc & at the given angle of then draw a line cad thr from c throug by ye end of ye Rad & to ye intersection of yt line wth ye circle draw & so the ∠ of is found.
<28v>Or wch is the same {illeg} make . & then if yt cone is sought make the ∠ cba being given, make . Then is . & soe ye is knowne & also , & . Buf But if ye of ye section is sought y{illeg}|e| cone b|e|ing given yn make . And it will bee . & soe is given also . &
{illeg}|I|n generall observe yt in any cone cut any ways . & {illeg}|b|.
7. DesCartes his wheele \thus described/ cut by any plaine produceth one of ye Conick=Sections.
Description ye 6th Demonstrated. Synthetically.
Call, {illeg} . . {illeg} . . . . . . . \./ Therefore . by ordering ye result of /. \ wch is like yt in the lemma.
The 7th Proposition may be easyly demonstrated {illeg} after the same manner.
If the two \equall/ cones
bad bcd intersect the 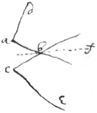 one the other soe yt their intersection shall bee one of ye Conick sections as they had each beene intersected by the plane
bf
.
one the other soe yt their intersection shall bee one of ye Conick sections as they had each beene intersected by the plane
bf
.
To describe ye Parabola (& other figures after ye same manner) pretty exactly.
Thake a squire cbe , soe yt (for then the{illeg} circle described by will bee as crooked as ye Parabola at the vertex d ). Divide ye other leg of ye Squire into any number of pts, Then get a plate of Br{illeg}|a|sse &c: lkfd streight & eaven. And taking one point d for ye vertex of it & another point c for ye Squire to move{illeg}n soe yt , & wearein{illeg}|g| away ye edge of the plate untill (ye {illeg}|S|quire being erected) . the squire touching ye plate at a . thus shall ye edge adf become Parabolicall. wth ye Rad: ab describe a circle adg & by that {meanes} it may bee knowne when . \Instead of ye leg be a/ Demonstraco\circle may be used/ Supose . then {illeg}. Then is {illeg} {illeg} {illeg} cq {illeg} . & . {illeg}|A|nd . & . Demonstracon. . . . . & . Q.E.D.
Another description of ye Parabola y|w|e {sic} ye compasses. Make . Make 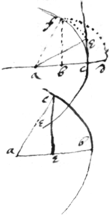 & . Make , & then shall
f
be a point in ye Parabola.
& . Make , & then shall
f
be a point in ye Parabola.
Another. {illeg}|M|ake . | | & ye point c shall bee in ye parabola. This like ye first by calculation may bee made use of in other lines.
The manner whereby any kind of \little/ lines may {illeg}be described very accurately. And that the same Instrument serve for all lines (though never so small) differing in quantity but not{illeg} in qual{illeg}ity.
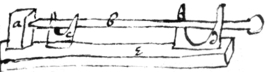 Make ye plate d of ye figure requ{illeg}|ir|ed (by some of ye former meanes) the larger the better. Then hold the streight \steele/ staffe b again{illeg}|st| the center a & {roule}{route} i{illeg}|t| to {illeg}|&| fro it shall grind c into ye same figure but soe much lesse as ac is lesse yn ad.
Make ye plate d of ye figure requ{illeg}|ir|ed (by some of ye former meanes) the larger the better. Then hold the streight \steele/ staffe b again{illeg}|st| the center a & {roule}{route} i{illeg}|t| to {illeg}|&| fro it shall grind c into ye same figure but soe much lesse as ac is lesse yn ad.
 Soe if ye glass c bee fastened upon ye mandrill f, it may be ground acording to ye sollid f{illeg} figure d by ye helpe of a stick of steele (as a cilind cone) {illeg} whose cuspis is in ye hole a upon wch it is moved as on a center. when ye stick cone b leanes uppon ye vertices of d & c it must be perpendicular to the mandrill f. Perhaps it may be convenient to cause ye cone b to turne about its axis. Or it may bee {illeg} better {illeg} instead of ye nutt at a wth a hole in it to make a sharpe pointed nutt, & instead of ye cilinder /cone\ b to make use of a broad plate to cover a, c & d & move every way upon them
Soe if ye glass c bee fastened upon ye mandrill f, it may be ground acording to ye sollid f{illeg} figure d by ye helpe of a stick of steele (as a cilind cone) {illeg} whose cuspis is in ye hole a upon wch it is moved as on a center. when ye stick cone b leanes uppon ye vertices of d & c it must be perpendicular to the mandrill f. Perhaps it may be convenient to cause ye cone b to turne about its axis. Or it may bee {illeg} better {illeg} instead of ye nutt at a wth a hole in it to make a sharpe pointed nutt, & instead of ye cilinder /cone\ b to make use of a broad plate to cover a, c & d & move every way upon them
Another way to describe lines on plates
Suppose ye plate bee abc, whose edg {sic} boc is to be made into ye fashion of a given crooked line suppoes {sic} is its vertex & yt a circle described wth ye {illeg}|R|adius eo would bee as crooked as ye given line at its vertex. A{illeg}gaine suppose two streight rulers mn & pq to bee very trew & steddyly fastened together 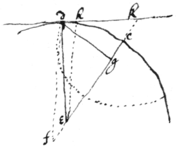 wch must a \very/ little incline ye one to ye other, soe as that being produced they would meete at ar. Then are ye lines {illeg}, & given.
wch must a \very/ little incline ye one to ye other, soe as that being produced they would meete at ar. Then are ye lines {illeg}, & given.
Suppose yn ye point d in ye crooked line is to bee found yn is dc given by supposition, & {illeg} consequently (supposing dk to bee a tangent) . . . . {illeg}. {illeg} . . & (if ) then is . being thus foun{illeg}|d|, supposing yt , then I take . that is . {illeg} haveing thus found ye point e lay ye plate twixt two rule the two rulers so yt ye point of it, fall upon ye point e yn should ye line mn touch ye plate in d. But note yt .
In both telescopes & microscopes tis most convenient to have a convex glasse next ye eye for by that meanes ye angle of vision will bee much greater yn it will bee wth a concave one (though both doe magnifie alike). If ye convex glasse be Hyperbolicall (&c) make it soe bigg yt ye penecilli may crosse in ye pupill; yt is, ye exterior focus will be as far distant from ye vertex as ye eye is. let ye glass bee as thinn yt ye as may bee yt ye eye bee not to{illeg}|o| farr {sic} from ye vertex yet {sic} it should bee about as thick as ye distance of ye interior focus from ye vertex.
And by this meanes also, (ye focus of ye objectglasse being within ye telescope twixt ye glasses) there may bee placed at {illeg}|t|hat {illeg}|f|ocus ye edge of a steele ruler accurately divided into equall parts (to measure ye diameters or distances of starrs &c) wch should bee soe made yt by a pinne or handle it may be placed i{illeg}|n| any posture & in any parte of ye focus, wthout otherwise altering ye Telescope in observations.
Note that were not ye glasses faulty they would not onely magnify objects but render vision more distinct; each of the penicilli passing through (perhaps but) the 10th, 20th or 100th part{illeg}|e| of ye pupill must bee more exactly refracted to one point {illeg} of ye Tunica Retina yn in ordinary visio in wch each of ye penicill{illeg}|i| spreads over all the pupill.
☞ Note also that 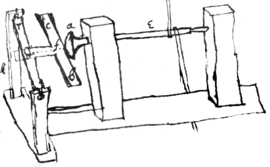 yt ye glasse a
may be ground Parabolic \Hyperbolicall/ by ye line cb, if it turne on ye mandrill e whilst c{illeg}|b
| turnes on ye axis rd being inclined to it as was shewed before. If the edge bee not durable enough, inough instead thereof use a long small cilinder: wch I conceive to bee the best way, of{illeg} all. For a Cilinder of all sollids is most easily made exact (being
yt ye glasse a
may be ground Parabolic \Hyperbolicall/ by ye line cb, if it turne on ye mandrill e whilst c{illeg}|b
| turnes on ye axis rd being inclined to it as was shewed before. If the edge bee not durable enough, inough instead thereof use a long small cilinder: wch I conceive to bee the best way, of{illeg} all. For a Cilinder of all sollids is most easily made exact (being 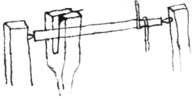 turned, as in the figure, by a gage untill its thicknesse bee every where equall). 2 the Cilinder may bee made {illeg} to slip up & downe & turne round whereby it will not onely grinde ye glase crosse wise to take of all hubbes, but also ye glasse & cilinder will grinde ye one ye other truer & truer. All ye difficulty is in placing ye axis rd perpendicular to the Mandrill ae \& vertex to vertex/, wch yet may bee done exactly severall ways. & untill yn the glasse & Cilinder will not fit. & should ye axis not intersect ye glasse would bee still Hyperbolicall except a point at the vertex of it. The same instrument may also serve for severall glasses onely making df longer or shorter. Let the Cilinder han{g} over the glasse.
turned, as in the figure, by a gage untill its thicknesse bee every where equall). 2 the Cilinder may bee made {illeg} to slip up & downe & turne round whereby it will not onely grinde ye glase crosse wise to take of all hubbes, but also ye glasse & cilinder will grinde ye one ye other truer & truer. All ye difficulty is in placing ye axis rd perpendicular to the Mandrill ae \& vertex to vertex/, wch yet may bee done exactly severall ways. & untill yn the glasse & Cilinder will not fit. & should ye axis not intersect ye glasse would bee still Hyperbolicall except a point at the vertex of it. The same instrument may also serve for severall glasses onely making df longer or shorter. Let the Cilinder han{g} over the glasse.
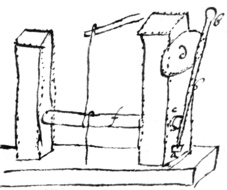
To Grinde Sphæricall optick Glasses
If ye glasse is to bee ground sphærically 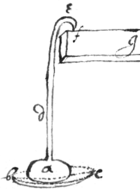 hollow: naile a steele plate to ye beame , on ye upper side: In wch make a center hole for ye steele point of ye shaft : to wch shaft fasten a plugg of stone or leade or leather &c: (wth wch you intend to grinde ye glasse ): wch shaft & plugg being swung to & fro upon ye center f will grind ye glasse bc sphærically hollow.
hollow: naile a steele plate to ye beame , on ye upper side: In wch make a center hole for ye steele point of ye shaft : to wch shaft fasten a plugg of stone or leade or leather &c: (wth wch you intend to grinde ye glasse ): wch shaft & plugg being swung to & fro upon ye center f will grind ye glasse bc sphærically hollow.
The manner whereby 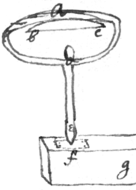 glasses may bee ground sf|p|hærically convex may appeare by ye annexed {illeg} figure (being ye former way inverted). Also ye plugg , in ye figure, is ground sphærically
glasses may bee ground sf|p|hærically convex may appeare by ye annexed {illeg} figure (being ye former way inverted). Also ye plugg , in ye figure, is ground sphærically
But if this way bee not exact enough yet hereby may bee {grownd}{ground} plates of mettall well nigh sphæricall, And by those plates may bee ground glasses after ye usual manner; If a circular hoope of steele \/ bee put about ye edge of ye glasse to keepe it 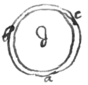 from grinding away at ye edges faster yn in ye middle.
from grinding away at ye edges faster yn in ye middle.
But the best way of all will bee to ti{illeg}|u|rne ye glass circularly upon a mandrill whilest ye plate is steadily rubbed upon it or else to turne ye plate upon a mandrill whilest ye glasse is rubbed upon it \or let sometimes ye one, sometimes ye other bee turned./: & by this meanes they will either of them weare the other to a truely sphericall forme. but however let there bee a hoope or of some mettall wch {illeg}|w|eares more difficultly then glasse to defend ye glasse from wearing more at its edges then in ye middle. Perhaps it may doe well \first/ to weare ye plate sphæricall by ye hoope alone wthout the glasse.
The same meanes may bee used for gr{illeg}|i|nding plaine glasses.
Let not an object glasse bee ground sphærically convex on both sides, but sphaerically convex on one side & concave or plaine \plane or but a little convex ~/ on ye other, & turne ye convexest side towards ye object.
If the Glasses of a Telescope bee not truely ground, how to find where the fault is, & consequently to rectify it.
 Take two plates
abfh, dgkh of {illeg} wood or brasse i{illeg}|at| ye midst of ye sides of wch {boare} two very small holes \c & e/ (viz whose diameters are about ye {illeg}|2|0th or {illeg}|3|0th pte of an inch, that they may transmit but soe much light as may serve to see {illeg}|ye| edge of ye sunne or a starre of ye first magnitude)
Take two plates
abfh, dgkh of {illeg} wood or brasse i{illeg}|at| ye midst of ye sides of wch {boare} two very small holes \c & e/ (viz whose diameters are about ye {illeg}|2|0th or {illeg}|3|0th pte of an inch, that they may transmit but soe much light as may serve to see {illeg}|ye| edge of ye sunne or a starre of ye first magnitude)
Also make two 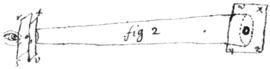 other plates rs, & tv like ye former but ye holes in ym must be as small as can bee (viz \about/ ye 100th pte of an inch in diameter or lesse). For ye small end of ye tube
other plates rs, & tv like ye former but ye holes in ym must be as small as can bee (viz \about/ ye 100th pte of an inch in diameter or lesse). For ye small end of ye tube
Also make an\o/ther plate wzxy wth a hole in \the midst of/ it about ye 5th or sixt pte of an inch in diameter (viz equall to ye diameter of ye pupill of ye eye or eyeglasse). Make ye like \plate A/ (but wth a very small hole) for ye eyeglaess {sic})
First cover ye object glasse wth ye plates af, & gh distant about ye ye holes in ym being distant about ye sixt parte of an inch; & placed neare ye center of ye object glasse. Also cover ye eye glasse wth ye plate A soe yt its hole exactly respect ye center of ye eye glasse then turne ye tube to a Starre wch will appeare like two starrs if ye tube bee two {sic} long or short, wch bee shortned or lengthned untill there appeare but one, And then is ye Tube of a good distance length for ye vertices of ye Glasses.
Secondly remove those plates, and instead thereof cover ye object glasse wth ye plate wz, its hole exactly respecting ye center of ye glasse. (Fig 2)

If ye Glasses of a Telescope bee not truely ground The{illeg}|ir|e errors may bee may bee thus found.
Because an error is much more easily discernable in ye object glasse yn in ye eye {sic} glasse let us first suppose ye eye glasse to bee ground true towards its center, (tis exact enough if it be sphericall, & not Hyperbolicall), & so wee may find & rectifie ye errors of ye object glasse.
First make a thin plate of brasse & in the center of it a Small hole (whose diameter perhaps may bee about ye 50th or 100dth parte of an inch. {illeg}|W|ith wch plate cover ye eye glass ye center of it respecting ye center of ye glasse.
Secondly make two other plates the one B wth two holes \as/ neare to its edge as may bee their{e}{} distance being about ye 5t {sic} pte of an inch or lesse, & ye other C wth one hole close to ye midst of its edge. Let ye diameters of these 3 holes bee about a 20th pte of an inch or lesse. And theire edges must bee true that they may slide one upon another, & yet not let ye suns rays passe through, to wch purpose make ym oblique. Wth these two plates cover ye object glase {sic} (first stopping ye hole of C \ye holes of ye other plate respecting ye center of ye glasse/ & looke at a stare (or ye edge of ye sunne &c) & if ye object appeare double (like two starrs &c) make ye Tube longer or shorter untill it appeare single. Then open ye hole of C , & ye plate B being fixed, slide ye plate C up & downe still looking at ye starre, When then appeares but one starre yt part of ye glasse under ye hole of C is truely ground in respect of ye 2 parts of ye glasse under ye two holes of B. But {no} when ye starre appeares double. And ye position of ye starre caused by ye hole of {illeg} C in repect {sic} of ye starre caused by ye holes of B, shews ye error of ye incli wch way ye glasse under ye hole of C is erroneously inclined; the distance of ye two starres giving ye quantity of yt inclinati error.
Thus ye errors of ye of object glasse bein{g} found in every place of it they may bee all rectified, & found againe, & againe rectified, untill they almost or altogether vanish.
Then may ye eye=glasse bee rectified much after ye same manner, in every parte of it, & if it bee necessary ye object glasse may bee aganie {sic} rectified & againe ye eye=glasse untill ye Teles{illeg}|c|ope bee as perfect as ye workeman can make: Whome perhaps experience & other may teach by this & ye former rules to make telescopes as perfect as {illeg} {illeg}men can \hope to/ make them.
These glasses may also bee rectified whilst on ye Mandrill by observing ye images mab|d|e by reflection from ye vertex & all other ꝑts of ye glasse wt proportion they have one to another & how much they are longer yn broader in one place then another. &c.
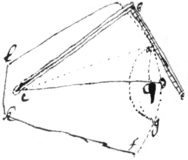
Theoremata varia. Circa angulorum æqualitates.
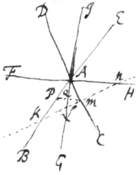
si ang DAB
=
|&| DAE
bisecentur a rectis FH
et IG
et ducatur quævis KLMN
. Erit
1. \{illeg}
/ Euclid 6 3
2.
A
{illeg}+. Scho{illeg}|{o}|te de {concis} /{æqu{is}}\
3. posito .
 Si in angulo quovis PAQ inseribantur æquales
AB, BC, CD, DE, EF, FG, GH &c anguli BA{illeg}
erit angulus
CBQ
dul|p|lus {illeg} \
DCP/ tripl,
ED
|| quadr
FEQ
quint,
GFQ
sext,
HGP
sept.
IHQ
oct &c. Horu vero angulorum positi|o| ra{illeg}|di|o AB {illeg} sinus erunt
Bβ
,
Cχ
&c cosinus
AB
,
Bχ
,
Cδ
&c. Ergo si , & erit \
/
. .
.
&c
Si in angulo quovis PAQ inseribantur æquales
AB, BC, CD, DE, EF, FG, GH &c anguli BA{illeg}
erit angulus
CBQ
dul|p|lus {illeg} \
DCP/ tripl,
ED
|| quadr
FEQ
quint,
GFQ
sext,
HGP
sept.
IHQ
oct &c. Horu vero angulorum positi|o| ra{illeg}|di|o AB {illeg} sinus erunt
Bβ
,
Cχ
&c cosinus
AB
,
Bχ
,
Cδ
&c. Ergo si , & erit \
/
. .
.
&c
To find the sume of ye squares cu{bes} &c. of ye rootes of an equation
If a , bg , c , d , e , f &c be the rootes of ye equation . yn is {illeg} {illeg} &c &c {illeg} = { } &c: .
As on ye other leafe excepting some signes here changed.
< text from f 80v resumes > <81r>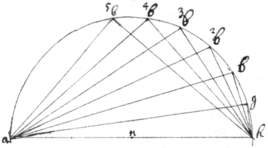
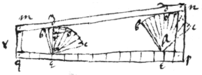
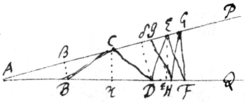
Of Angular sections
Suppose . . & . & yt ye arches {illeg} hg, gb, bb are equall. By ye following Equations an angle \bah/ may bee divided into any number of partes.
This scheame is ye forme\r/ inversed. 
Suppose ye perifery {illeg} \ bgh / to bee a & ye whole perifery to bee p. The line bh subtends these arches. a. . . . . . . . . . . . . &c: All wch are bisected, trisected, quadrisected, quintuse{illeg}|c|ted &c after same manner. |As for example|
The rootes of ye equation . are 3. The first whereof subtends ye arches . . . . . . &c. The second subtends ye arches . . . . . &c. The 3d . . . . &c.
Soe ye rootes of ye equation ~ , doe ye first subtend ye arches . . &c: ye 2d . . . ye 3d . . &c. ye 4th . . &c ye 5t . . . &c.
Hence may appeare ye reason of ye number of rootes in these equations & yt ye points of ye circuference {sic} \to wch they are extended/ æquidistant. & by ye lower scheme may bee known wch rootes are affirmative & wch negative.
The numerall cöefficients of ye afforesaid equations may bee deduced from this progression (if .) &c. As if x . ye ꝑression . And ye coefficients .
1663 /4 January.
All ye parallell lines wch can be understoode to bee drawne uppon any superficies are equiv{illeg}|a|lent to it, as  all ye lines drawne from to may be used instead of ye superficies
all ye lines drawne from to may be used instead of ye superficies
If all ye parallell lines drawne uppon any superficies be multiplied by another line they produce a Sollid like yt wch relults {sic} from ye superficies drawne into ye lame {sic} line  as if either al{illeg}|l| ye lines in ye superficies or if ye superficies oac be drawne into ye line they both produce ye same lollid {sic} whence All ye parallell superficies wch {illeg} can bee understoode to bee in any sollid are equivalent to yt Sollid. And If all ye lines in any triangle, wch are parallell to one of ye sides, be squ\a/red there results a Pyramid. if those in a square, there results a cube. If those in a crookelined figure there resuts {sic} a sollid wth 4 sides {illeg} terminated & bended after according to ye fasshion {sic} of ye crookelined figure{.}
as if either al{illeg}|l| ye lines in ye superficies or if ye superficies oac be drawne into ye line they both produce ye same lollid {sic} whence All ye parallell superficies wch {illeg} can bee understoode to bee in any sollid are equivalent to yt Sollid. And If all ye lines in any triangle, wch are parallell to one of ye sides, be squ\a/red there results a Pyramid. if those in a square, there results a cube. If those in a crookelined figure there resuts {sic} a sollid wth 4 sides {illeg} terminated & bended after according to ye fasshion {sic} of ye crookelined figure{.}
If each line in one superficies bee drawne into each correspondent line in another superficies as in aebk, & omnc  if . . . &c. they produce a sollid whos {sic} opposite sides are fashioned by one of ye superfic as {illeg} figure|Sollid|
fpsrg. where all ye lines drawne from fr {illeg} to ps are equall to all equall to all the correspondent lines drawne from ow to mx. & those drawne from fg to fr are equall to ye correspondent lines drawne from qz to vz.
if . . . &c. they produce a sollid whos {sic} opposite sides are fashioned by one of ye superfic as {illeg} figure|Sollid|
fpsrg. where all ye lines drawne from fr {illeg} to ps are equall to all equall to all the correspondent lines drawne from ow to mx. & those drawne from fg to fr are equall to ye correspondent lines drawne from qz to vz.
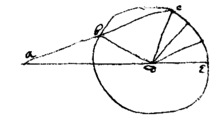
Theorema. 1
If in the Circle abcdeP there be 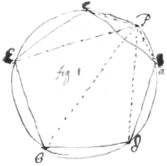 inscribed any Poligon abcde wth an odd number of sides, & from{illeg} any point in ye circumference P there bee drawne lines Pe, Pa, Pb, Pc, Pd to e{illeg}|v|ery corner of ye Pol{illeg}ygon: ye summ of every other line {illeg} is equall to ye summ of ye rest, {illeg}
. & soe are their cubes . unless ye figure be a Tri/gon\
inscribed any Poligon abcde wth an odd number of sides, & from{illeg} any point in ye circumference P there bee drawne lines Pe, Pa, Pb, Pc, Pd to e{illeg}|v|ery corner of ye Pol{illeg}ygon: ye summ of every other line {illeg} is equall to ye summ of ye rest, {illeg}
. & soe are their cubes . unless ye figure be a Tri/gon\
Theor 2
If from{illeg} ye points of ye Polygon 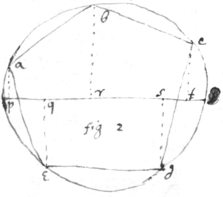 then {illeg}|b|ee drawne perpendicular ap, br, ct, ds, {illeg}
to any Diameter pt: ye summe of ye Pe{illeg}|r|pendiculars on one side ye Diameter is {equall}{equal} to their summe on ye other . & soe is ye summe of their cubes (unlesse wn ye figure is a Trigon), . & of theire square cubes (except wn ye figure is a Trigon or Pentagon. &c.
then {illeg}|b|ee drawne perpendicular ap, br, ct, ds, {illeg}
to any Diameter pt: ye summe of ye Pe{illeg}|r|pendiculars on one side ye Diameter is {equall}{equal} to their summe on ye other . & soe is ye summe of their cubes (unlesse wn ye figure is a Trigon), . & of theire square cubes (except wn ye figure is a Trigon or Pentagon. &c.
Theor {illeg}|3|
If ye 2 circles (fig 1 & 2) be equall wth like Poligo{illeg}{ns} inscribed, & Pa in fig {illeg}|1| be assumed double to pa in fig 2. then are all ye ye other corresponding lines in fig 1 double to those in fig 2 viz , , , .
To square ye Parabola
In ye Parabola cae suppose ye 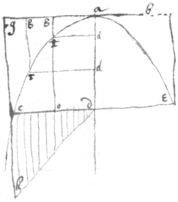 Parameter . . . & or . Now suppose every ye lines called x doe increase in arithmeticall proportion all ye x's taken together ye supp make ye superficies dch wch is halfe a square let every line drawne from cd to hd be square & they produce {illeg}|a| Pyramid equall to every . wch if divided by {illeg}y
r {illeg} there remaines every equall to every {illeg}|e|quall to every or all ye lines drawne from
ag
to
accc
equall to ye superficies
ag
{illeg}|
| equall to a 3d pte of ye superficies
adcg & ye superficie .
Parameter . . . & or . Now suppose every ye lines called x doe increase in arithmeticall proportion all ye x's taken together ye supp make ye superficies dch wch is halfe a square let every line drawne from cd to hd be square & they produce {illeg}|a| Pyramid equall to every . wch if divided by {illeg}y
r {illeg} there remaines every equall to every {illeg}|e|quall to every or all ye lines drawne from
ag
to
accc
equall to ye superficies
ag
{illeg}|
| equall to a 3d pte of ye superficies
adcg & ye superficie .
Otherwise. suppose . . . & ye lines x increasing in arithmeticall proportion every x is equall to \4 times/ ye superficies wch drawne into b produceth ye sollid but if every x be squarered {sic} {illeg}|t|hey poduce {sic} a {illeg}|p|yramid equall to . wherefore every equall to every equall to ye superfies|ci|es adce drawne into r & to cade as before.
<83v>
* & ⊛
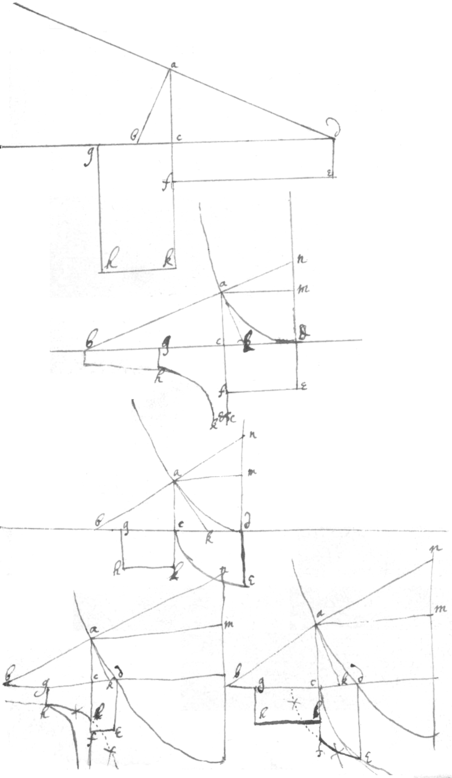
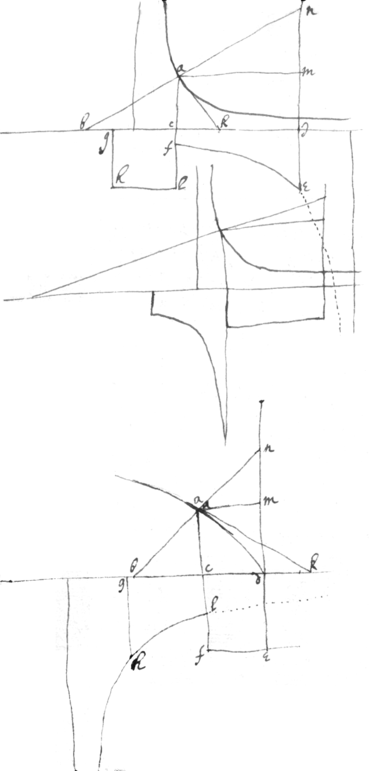
<84r>To Square ye Hyperbola
In ye Hyperbola eqaw. suppose . . \{}/ . \/\/\/ ||. & . {illeg}. |In wch equation| Every x \taken together/ is equall to ye triangle aβb \equall to / & eve{illeg}|r|y {illeg}|ta|k{illeg}en together is a pyramid . Every y taken together is equall to ye superficies If yn . every is equall to ye solid nglmhs. If ye angle mhk is a right one & if {illeg}, then all ye lin that is if ye triangle . every {illeg}|y | will be equall to ye sollid mhstk Joyne these two sollids together as in . *
⊛ Againe Suppose every x taken together to be equall to ye superficies aef , {illeg} ye line squared is {illeg} every composeth a Sollid like a|n| quarter \eighth pte/ whereof (wch is equall to every ) being like \/ xyzv; xv will be equall to ♊ {illeg}|♓ | {illeg} . & {illeg}km . whence ye {illeg} covexe {sic} superficies xyv of ye figure xyvz will fitly joyne wth ye concave superficies mst of ye figure shmkt . If every x is equall to ye superficies aef , every y shall be equall to ye triangle . every every & therefor ye Sollid . Joyne ye Sollid shmkt to yxvz & there resulteth from wch againe substract & there remaines ye sollid wch substract from ye sollid & there remaines b wch being divided by . there remaines to ye superficies abe
<85r>The squareing of severall croked {sic} lines of ye Seacond kind.
 In a \any two/ crooked lines I call ye Parameter or right side \of ye greater./ . \but of ye lesse / Transverse side . ye right axis as
cf
\or
.
/ y
Transverse axis as
fe
{illeg} y, \or/ fd
z.
In a \any two/ crooked lines I call ye Parameter or right side \of ye greater./ . \but of ye lesse / Transverse side . ye right axis as
cf
\or
.
/ y
Transverse axis as
fe
{illeg} y, \or/ fd
z.
Suppose in{illeg} ye Parab: : . & in : . . . . . Or . if . . make . . . . & therefore ye square of ye crooked line (when ye line is p|s|upposed to {sic} close wth ye line cf ) whose nature is exprest by ye foregoing Equation.
 2 . . . . {illeg} \/
{illeg}−
\/
. . {illeg}y or, {illeg} \r/{illeg}b\/b\/. Or {illeg}
2 . . . . {illeg} \/
{illeg}−
\/
. . {illeg}y or, {illeg} \r/{illeg}b\/b\/. Or {illeg}
 3 . . . . {illeg} .
3 . . . . {illeg} .
. . . {illeg}
<87r>
4 In ye Hyperbola Parabola  . .
{illeg}
. .
\{
}/
=
{illeg}
zc. . Since all all
. . all
therefore
bgpf
.
. .
{illeg}
. .
\{
}/
=
{illeg}
zc. . Since all all
. . all
therefore
bgpf
.
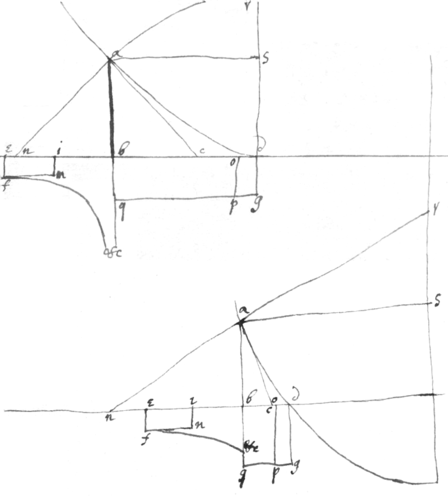 <88r>
<88r>
{illeg}| |. . . . Then shall : be the axis of gravity in & bqgd.
 <89r>
<89r>
In ye 1st figure.
. . . {illeg} . {illeg} or . Suppose ye swiftnesse of de ∶ to ye swiftnesse of gh . . .
Fig 2d {sic}. 3d.
d | θ |. its {illeg}|s|wiftnesse it {sic} swifnes {sic} ∷ | | | × | | |{illeg} \ ∷ / . . . .
Fig 4
motion of ye point a from c ∶ motion of ye point a from m ∷ increasing of ∶increasing of cd ∷motion of gh ∶ motion of de. &c as before.
These are to find such figures cghk, cfed, as doe equiponderate in respect of ye axis acfk.
Reasonings concerning chance.
If by one of ye equall chances a, I gaine p, by ye chance the equall chances \ a , b , c , &c/ are such yt one of ym must necessarily happen, & yt if one of ye chances a happen I gaine p thereby, or q by one of ye chances b , or r by one of ye chances c . My chance or expectation is worth
1 If p is ye number of chances by \one of/ wch I may gaine a, & q those by \one of/ wch I may gaine b, & r those by one of which I may gaine c; soe yt those chances are \all/ equall & one of them must necessarily happen: My hopes or chance is worth . |The same is true if p, q, r signify |an|y|y|{e} proportion of chances for a, b, c.|
2. If I bargaine for more yn one cha{illeg}c|n|ce (viz: yt after I have taken ye gaines by my first chance, from the stake ; I will venter another chance at ye remaining stake &c) my second lott is worth {illeg} A . My third lot is worth . My Fourth lot is worth . My Fift lot is worth . My sixt lot is worth . &c
As if 6 me{illeg}|n| cast a die soe yt he gaines a who throws a cise first: since there is but one point \chance/ to gaine a & 5 to gaine nothing at each cast, I make . & . Therefore by the The first mans lot is worth The 2ds is worth . The thirds is worth . The 4d|t|hs is The fifts lot is worth . The Sixts lot is . &c. Soe yt their lots are as {illeg}| 5 | 4 | 3 | 3 | 1 | 25 .
Soe yt if I cast a die two or more times tis to 5 yt I cast a c{illeg}|i|s{illeg}|e| at ye first cast & 11 to 25 yt I throw it at two casts, & 91 to 125 yt I cast it at thrice, & 671 to 625 yt I cast it once in 4 trialls, & 4651 to 3125 yt I cast it once in 4|5| times. &c
3. If I bargaine to cast severall sorts of of {sic} lots successively at ye same stake ye valor of each lot is thus found viz: The first prop: gives ye valor of ye f{illeg}|ir|st lot; wch valor being destructed from ye stake, ye remainder is ye stake of ye 2d lot wch therefore may bee also found by ye first prop: &c.
As if {illeg}|I| gaine a by throwing 12 at ye first cast, or 11 at ye 2d or 10 at ye 3d &c wth two dice. Since at ye first cast there is but one chance for a (viz 12 ) & 35 for nothing Therefore its valor is (by Prop 1). & ye stake{illeg} for ye 2d cast is . Now since there is|ar|e two chances for i{illeg}|t| (viz: ⚅⚄ & ⚄⚅) at ye 2d cast & 34 for 0 at ye 2d cast therefore its valor is . as ye stake for ye 3d chance lot is f{illeg}|o|r wch there are 3 chances (f{illeg}|vi|z ⚄⚄, ⚅⚃, ⚃⚅, {sic}) & 33 for nothing Therefore its valor is .
<91r>4 If I bargaine wth one or two more to cast lots in order untill one of us by an assigned lott shall win ye stake a: Since ye chances may succede infinitly I onely consider ye first revolution of them The valor of each mans \whole/ expectation being in such proportion one to another as ye valors of their lots in one revolution. & ye valors of each mans f{illeg}|ir|st lot being to ye valor of his whole expectation as ye summe of ye valors of their f{illeg}|irs|t lots to ye stake a.
As if I contend wth another yt who first throws 12 wth 2 dice shall h{illeg}|a|ve a, I haveing ye dice. {illeg}|M|y first lot is worth (by second prop 1), The 2d \his first/ lot is worth . And . for ye two first lots make one revolution because {illeg} I have ye same lot If I throw a 2d time yt I had at ye first. Therefore is my interest in ye stake.
If or bargaine bee soe yt there is some lott at ye beginning of or play wch returnes not in ye {illeg} after revolutions, detract ye valor of those irregular lotts from ye stake & ye rest shall bee ye stake of ye regular lots wch follow & revolve successively. As if I contend wth another yt who first casts 11 must have a , onely I have {ye} first cast for 12. My first lot is worth . & ye stake for or after throws is . his firts lot being . & my next lot . soe yt his share in ye stake is to mine as . Soe yt my share in it is . To wch adding {illeg} ye valor of my f{illeg}|i|rst lot viz: , ye summe is , my interest in ye stake a at ye begining.
5 If ye Proportion of {illeg}|t|he chances for any stake bee irrationall {illeg}|t|he interest in the stake may bee found after ye same manner. As if ye Radij ab
,
ac
, divide ye \horizontall/ circle \
bcd
/ into two pts
abec
& abdc
in such proportion as |2
| to  . And if a ball falling perpendicularly upon ye center
a
doth tumble into ye portion
abec
I winn : {illeg}|b|ut if into ye other portion, I win
b
. my hopes is worth .
. And if a ball falling perpendicularly upon ye center
a
doth tumble into ye portion
abec
I winn : {illeg}|b|ut if into ye other portion, I win
b
. my hopes is worth .
Soe if a die bee not a Regular body but a Parallelipipi|e|don or otherwise unequall sided, it may bee found how much one side is cast is more easily gotten then another.
☞ 6 Soe yt ye facility of ye chances & ye stake belonging to each chance being knowne ye worth of of {sic} the lott may bee ever found by ye precedent precepts. And if they bee not both immediatly found known they must bee sought before ye valor of ye lott can bee found.
As if I want two games at Irish & my adversary three to win a , & I would know ye value of my interest in ye stake my first lot {illeg} can gaine me nothing but ye advantage of another lot, & therefore to know its vallue I must first find ye value of yt other lot &c. First therefore if wee each wanted one lot to win a or interest in it would bee equall viz my lot worth . \2dly/ If I want thr{illeg} lo two {illeg} \one/ games & my adversary one|two|, {illeg} & I gaine ye next game yn I gaine a but if I loose it I onely gaine an{illeg} equall lot for a at ye {illeg}|n|ext game wch is worth , Therefore my interest in ye stake is . 3dly If I want one game & my adversary {illeg}|t|hree & I gaine ye next game I get a; but if I loose it, then I want one game & my adversary but two, yt is I get : Therefore (there being one chance for a & one for ) my interest in ye stake is . 4thly If I want 2 games & my adversary 3; & I win I get . but if I loose I get for or chances will then bee equall; Therefore my interest in ye stake is . Soe if I want {illeg}| 1 | games & my adversary 4 my interest in a is . If I want two and hee 4 , it is . If I want 3 and hee 4 it is . If I 1 and hee 5 , it is: . If I 2 and hee 5 it is . If I 3 and hee 5 it is . If I 4 and hee 5 , it is: . |(|The like may bee done if 3 or more play together. |(|as if one wants one game, another 3 a third 4: Their lots are as . &c.|)| As also if their lots bee of divers sorts.|)|
By this meanes also some of ye precedent questions may bee resolved. as if I have two throws for a cise to win a , wth one die; If I have missed my first lot alredy {sic}, I have at my second cast five chances for nothing. & one for a . therefore yt cast is worth . Soe yt \in/ my first cast I had five chances for & one for a , wch therefore is worth (wth my 2d cast) is worth . That is tis {illeg} to 11 to 25 whith {sic} yt I cast a cise at once in two throws. as before
By this meanes also my lot may bee known if I am to draw 4 cards of severall sorts out of 40 cards {illeg}| 1 | 0 of each s{illeg}i|or|t.
Or if out of two white & 3 black stones I am blindfold to chose a white & a black one.
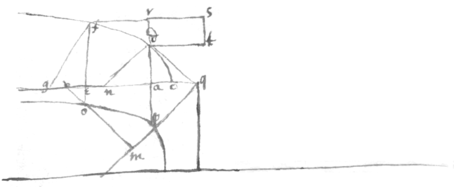
 Equation
Equation
An equation given; & \if/ either \both/
x
, &
y
, be of a /have\ divers quan dimensions, try if ye roote \of one of y
/ may be extracted: {illeg} whereby ye  may often be diminished riduced to finer termes & sometimes to finer dimensions if it can {illeg} \{illeg}/ ye line & {illeg} If a quantity wherein
x
|
y
| is not is divided by {illeg}|
x
| in ye {illeg}q{illeg} {illeg}g line equall to
x
. yt crooked cannot be squared.
may often be diminished riduced to finer termes & sometimes to finer dimensions if it can {illeg} \{illeg}/ ye line & {illeg} If a quantity wherein
x
|
y
| is not is divided by {illeg}|
x
| in ye {illeg}q{illeg} {illeg}g line equall to
x
. yt crooked cannot be squared.
The line
cdf
is a Parab. \
/\
/\
/\
/ge. . .
.
{illeg}.
. {illeg} . .
.
.
. or supposeing
x|y|. {illeg}
& |
|. {illeg} wch shews ye nature of ye crooked line po. now if . yn . for supposeing
eo
moves uniformely from
ap
, &
rs
moves from
dt
wth motion decreaseing in ye ꝑportio yt ye line
eo doth shorten. Suppos &
x
|
y
|.
. then . suppose . yn
. Or
. Or
+
. Or suppose
. yn . Or
+
/
−
\ |
| Or . Or, if
y
|
r
|.
y
|
x
|. &
\
/{illeg}
−
{illeg}a
|y
|. Or . \/. {illeg}y
x
|ʒ
|.
x
|
ʒ
|.
x
|
ʒ
| {illeg}
. .
r
. . .
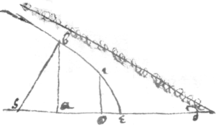 Or
Or
.
Let . a {illeg} y {illeg}/{illeg}\ . . . {illeg} a {illeg} 2 {illeg} v {illeg} {illeg} {illeg} + / − \ {illeg} + .
. + {illeg} {illeg}. . . {illeg}. .
<94v>To square those lines in wch is y onely
If y is in but one terme onely of ye Equation (as . or,
) resolve ye Eq: into ye proport (as
. or,
.) If ye line hath Assymptotes
. .
{illeg} \ / ad. = divided by it produceth. + / − \
<95v>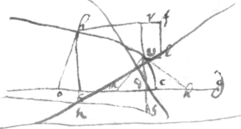
By ye Squares of ye simplest lines to square lines more compound. 1s {sic} those whein y.
find ye valor of y. If ye number of ye termes in ye denom: thereof be neither &c. ye line cannot be squared If it have but one terme tis squared by finding ye square of \{illeg} each/ particular terme in ye valor of y & yn adding all those squares together. Example 1st. . & . Then makeing y equall to each particular terme. . or whose □ is . & . whose □ is Ad {sic} these 2 □s together & they (viz: ) are the □ of ye line . Againe + \ − / a | b |. Or . yn disjoynting ye valor of y. . . Or , whose □ is . , whose □ . {illeg}| |, whose □ . which 3 □s (viz ) is ye □ {illeg} taken together are ye square sought for. And these lines may bee ever squared unless in ye valor of y there bee found , , , &c. for ye Squareing of yt line depends on ye squareing of ye Hyperbola. As in ye line {illeg}| x |{illeg} / \ .
<96r>. . . . . . . . . . \ / . . . make that is . & . wch expresseth ye nature of ye crooked line ns . & . .
2dly. I{illeg}|f| it have 2|3| termes. bee
termes See if it may be reduced to
dimensions by addin{illeg}|g| or subtracting a{illeg} knowne quantity to or from
x
. Example.
. wch (makeing
) i{illeg}|s| thus red{illeg}|u|ced
{illeg}
−
{illeg}
. Or
{illeg}
{illeg}
y
{illeg}
/\ . . {illeg}. . . {illeg}
An Equation expressing ye nature of ye line
ns
.
 <103r>
<103r>
. . . . . . . . . { Ad } . . . . &c: . x |s| . . . wch shewes ye nature of another crooked line yt may be squared.
<104r> <104v>
. . . . . . . . . . . . . . . . /. \ . . . . . . . . . . . . . . .
This table shews ye distance of any two notes As ye distance of C & E is B , or a 3d, or 3,863137 halfe notes. Of B & E tis a 4th, or 4,98045 halfe notes. of B & F tis 6,097763 halfe notes, or {illeg} greater yn a 5t ♭, by 0,095526 halfe notes &c.
<105r>By ye helpe of concordant notes all ye notes in ye Gam ut may bee thus tuned viz:
First tune ye 8ths, &c.
Seacondly tune 5ts to ym both above ym & below them .
Thirdly tune 3ds to ym both above ym & below them .
Fourthly from each rise a fift for & fall a 5t for .
Fiftly from rise a fift for {illeg} & fall a fift for .
Sixtly from ris| | rise a fift for & from fall a fift for .
Seaventhly from each rise a fift for . The rest as are supplyed by 8ths viz to &c.
<105v>November 20. 1665.
<106r>
{illeg}. \ 2,635483 74 |69 | / . . . . {illeg} . \{illeg}/
. . . /\ F . \ / . . . = . . Ff . . perhaps is better yn .
<106v><107r>
 By this table may bee knowne ye distance of any t{illeg}|wo| notes whither a {trew} second of ye lesse, second, third f
ye lesse, a third fourth &c: As to know ye distance twixt
A
re
&
B
sol
re
I follow ye pricked stroke from
A
to
D
or from
D
to
A
where I find it crossed by a black crooked line & {illeg}o \against it/,
a Fourth
written, therefore I conclude A re
& D la sol distant a true fourth.
By this table may bee knowne ye distance of any t{illeg}|wo| notes whither a {trew} second of ye lesse, second, third f
ye lesse, a third fourth &c: As to know ye distance twixt
A
re
&
B
sol
re
I follow ye pricked stroke from
A
to
D
or from
D
to
A
where I find it crossed by a black crooked line & {illeg}o \against it/,
a Fourth
written, therefore I conclude A re
& D la sol distant a true fourth.
And Thus to find ye distance of B mi & D la sol re I follow ye prick line from ye top B to ye right hand side thence to ye bottom B thence towards ye left hand side untill I come {over} D. Or (wch is ye same) I follow ye prick{t}{{illeg}} line from ye top D to {illeg}|th|e left hand side thence to ye bottom D, thence toward ye right hand side untill I come just over B, where{illeg} I find ye pricked line to be crossed by a  stroke & against it to bee written on ye upper line
a tenth
, on the lower
stroke & against it to bee written on ye upper line
a tenth
, on the lower  a ninth
therefore tis
a tenth minor
exactly. But if it
a ninth
therefore tis
a tenth minor
exactly. But if it
. . {illeg} {illeg} . . {illeg}
<108v>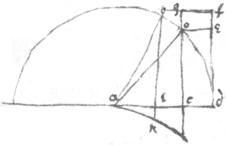
<109r>
The 10 \3/ meanes are best there being an imperfect 5t in ye {illeg}|ou|tward extreame & a trit{illeg}|o|nus in ye inmost. Modi
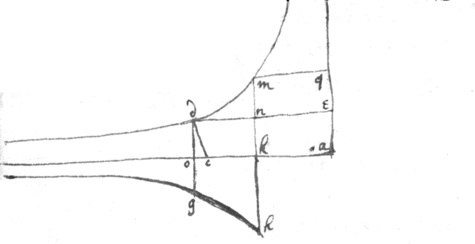
 <110r>
<110r>
In ye Para|Hyper|bola dm
. suppose . . {illeg} a secant. {illeg}|v
| . . {illeg}|
y
|
. . . . . . wch equation continues ye nature of ye crooked line gh. Now supposeng {sic} ye line og always moves over ye same superficies in ye same {illeg}|t|ime, it will increase in {illeg} motion from kh in ye same proportion yt it decreaseth in lenght \&/ ye line ne
will move uniformely through from |(||)|, soe yt ye space . suppose . . . & .
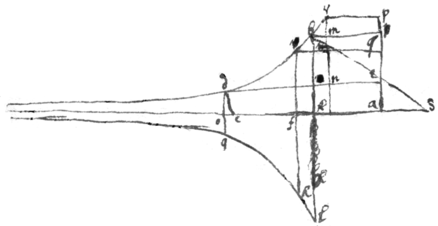
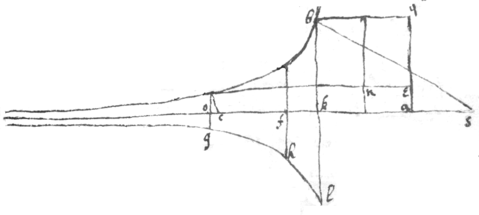
In ye order of ye musicall {illeg}|t|ones ye 2 halfe notes may not {illeg} \be/ together 1st because every note would yn bee distant 3 tones from some other wch is most ungratefull 2dly whole notes ought to bee interposed to moderate their harsh{illeg}|nes|se. 3dly since {illeg}|th|eir {sic} must bee a 5t to ye gr{illeg}|ou|nd: these notes must bee next either next ye ground or its 5t wch would make ym harsh & yt they \wee/ could not gradually passe to or from them.
Neither ought they to be distant but one tone for ye 2d reason {afforesd} & because they will bee more consonant by ye absense of more 2|3| tons {sic} &c if they be distant 2 tones yet perhaps they may not bee wholly uselesse. S{illeg}|ee| {illeg} ye last modes.
A catalogue of ye 12 Musicall modes in theire order of gratefulnesse.
<111r>suppose ye line {illeg}|l|ast found to be md . . . . . . . . . to find at wt point : . . {illeg} . . . |. | . . {illeg} \ 2 / . wch shews ye nature of ye line . & or . suppose . {illeg} x . . .
Suppose {illeg}||. {illeg} {illeg} Suppose . . . . . . . . . . . {illeg}= . {illeg}|a|. . . . .
<111v> tone max; m{illeg}|ed|î: minimꝰ. {illeg} {illeg} {illeg}, , tone {maj me:mi.}
.
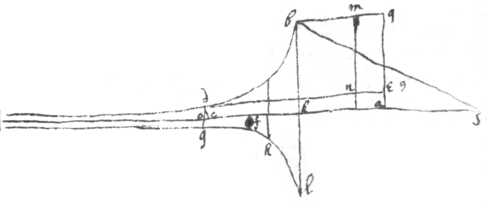
 <112r>
<112r>
Suppose againe ye last line whose nature is comprisd {sic} in this equation {illeg}|y
|{illeg}. . . . . . . to find where
{illeg} 6|3|. 6|3|. \{illeg}/ . \ / {illeg}. {illeg} \/ a. . . .
<112v>
. . . .
1st. . g{illeg} . . . . . . . ton s. . per sup. et fg Modus / \ harum \vocum/ optimus respectu fundamenti.
\ harum \vocum/ optimus respectu fundamenti.
2d. \
/ . . . . . . . And if . . Then & ye voyces in respect of their base /{ground}\ are \best/ 
3d. . . . . . . {illeg} & if , yn . whence  These differ in yt this hath but 2 exact
& this but 2 exact /thirds\
These differ in yt this hath but 2 exact
& this but 2 exact /thirds\
If in ye 1st case . yn / \ If in ye 2d case then
\ If in ye 2d case then 
<113r>
Likewise supposing ye line . . \/ . . . . . &c whence supposeing x to be a line increasing in arithmeticall proportion from ye quantity of ye line untill it be as long as b. ye superfices resulting out of &c is found {illeg} as follows.
.
. .
. . &c
1 Of ye Key or Ground sound. 2dly, Of its . 3dly, of their divisions into & & , illustrated by ye division of a corde. 4thly, {illeg}|T|he order of ye con{illeg}|c|ords in respect of gratefulnes deduced thence & from other considerations. 5thy {sic} ye degrees deduced thence & of the{illeg} proportion of ye concords & degrees i.e. ye logarrithmes of their strings. 6 Of ye various ordering of ye degrees \& distance of ye halfe notes/ , ye keys fift being onely stable 7 Of ye moodes ariseing thence & their dignity; explained by one line, &c. 8thly, How ye tones major & minor are best ordered in every Moode. 9thly of passing from one moode to another explained by 3 lines 10 How ye notes major and minor to be
ordered for yt purpose.
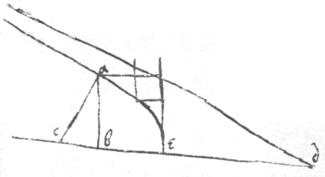
in ye Par|Hyp|a {sic}\r/b: . . . {illeg}+ {illeg}{illeg}| x |{illeg}+ {illeg}x{illeg}{illeg} {illeg}|r | .
<115v>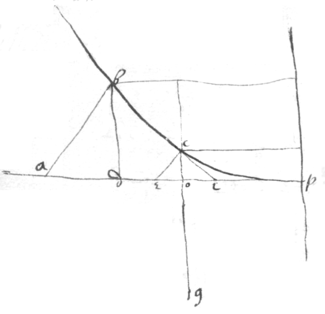
A Method whereby to square those crooked lines wch may be squared.
That a line may be squared Geometrically tis required may be yt its area may be expressed in generall by some equation in wch there is an unknowne quantity, so yt this quantity being determined ye area thereof {illeg}(comprehended by ye cr|o|oked line, ye two lines (whose intersections describe ye crooked line), & another streight line{illeg} wch guides these two lines in theire motion wn they describe it{illeg}) \to wch all ye points in ye crooked line are referred)/ is limited & {by} may bee {illeg}{b}|f|ound by ye same equation. Also {every} every such equation must be of two dimension\s/ because it expresseth ye quanti{f}|t|y of a superficies.
That an super equation expresse ye area of a straight /crooked\ line tis required yt ye superficie{s} increase in |an|{illeg} |un|equall proportion, yt when ye line (considered as unknowne) increaseth {equall} in arithmeticall proportion, wherefore (suppo\s/ ing x always to signifie ye unknowne quantity: a, b, c, &c; {illeg}|t|o signifie ye quanitys {sic} gi{illeg}|v|en) ax, or xx either alone or ade|d|ed to any other supperficiess, serve not to find ye area of any crooked line wch may not be found wth out ym. {How}
<120v>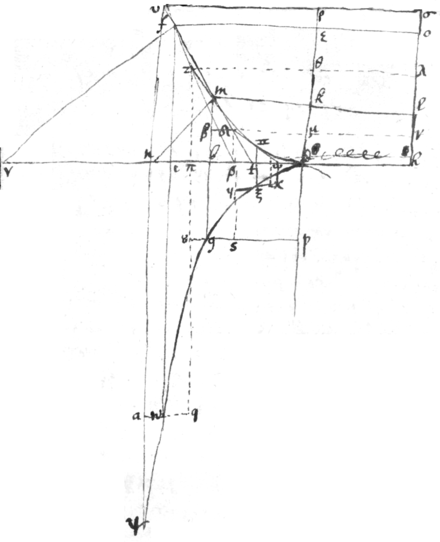 <121r>
<121r>
Prop:
Haveing an equation of 2 dimensions to find wt crooke line it is {wch} whose are{illeg}|a| it doth expresse, suppose ye equation is . nameing ye quantitys; a = dh = kl. {illeg} bg = y. db = mk = x = gp. ye{illeg} superficies supose ye square dkhl {illeg}is equall to ye superficies gbd; yn , & . wch is an equation expressing ye nature of ye line fmd.
I|N|ext making nm={illeg}|s| \a line wch cutteth {f} dmf at right ang angles/. nd=v. \6/ . & . {illeg}|N|ow supposeing, mb:b{illeg}|n|::dh:bg. that is that is, . || Which is ye nature of ye line dgw & ye area , makeing db=x. dh={illeg}|a|. or. , determing {sic} ({illeg}|d|i) to be ({illeg}|x|). &c
The Demonstration whereof is as followeth
Suppose ω♊♌, ♌mz, zfv; &c are tangents of {illeg}|y|e line dmf. & from theire intersections z, ♌, v, draw va, zq. ♌s. ωx, parallel & fr{illeg}|o|m theire touch points draw fw, mg, ♊ξ. all parallell to {mg} kp. also from ye same point of intersection draw vσ, {mf} zλ, ♌{illeg},|ν|. ωζ {sic}.
<122r>And nb:bm::bm:bt::bg:kl::B{m}:B♌. And mb:nb::bt:bm::kl|♌|B:Bm::kl:bg. wherefore ♌B×bg=Bm×kl. {illeg}|th|at is ye rectangle klνμ=bρsg. And. πρs♉=θλνμ. in like manner it may be demonstrated yt ;aqπν {sic}=θλσρ, & ρωxy=μdν{illeg}|h|. &c so yt ye rectangle ρshd is equall to any number of such like squares inscribed {twixt} ye line ny & ye point d, wch squares if they bee infinite in number, they will bee equall to ye superficies dnywgξ.
This being demonstrated tha{illeg}|t| I may shunne confusion in {ye} squareing ye {illeg}|l|ines of every sort {illeg}|I| shall use this method to /in.\ distinguish|ing| ym. viz: first such lines whose area is exprest by equations in wch ye unknowne quantity is numerator, & yt 1st all ye sines being affirmative, 2dly mixed.
|2dly| {L}>|l|ines whose area is exprest by quantitys in wch ye unknowne quantity is divisor, & those 1st under affirmative sines, 2d under mixt one's |3| lines squared by equations mixt of ye 2 former kinds, whose quantitys are all 1s affirmative 2dly mixt.
<124r>The squareing of those lines whose area is exprest by affirmative quantitys in which ye unknowne quantity is {n}umeral{\e/}
Soe yt ye nature of every crooked line, whose {illeg}|a|rea is compounded of ye area of 2 or more of ye former lines, {illeg}|o|r of ye difference of \ye area of/ 2 or more of ye former lines, is exprest by an equation compounded or 2 or more of ye equations expresing ye nature of {illeg}|th|ose lines.
<124v>
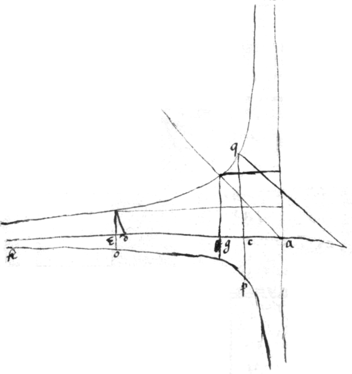 <125r>
<125r>
The squareing those lines whose area is exprest by an equation in wch ye unknown quantity is denominator.
<126r>
Note yt the lines whose nature is expres{illeg}|t| by ye {2}|4| latter sorts of equations, are ye same wth the lines of ye 2 former sorts. D{illeg}|o|ubtfull.
<127r><128r> <129r>
<130r> <131r>
.
<132r> <132v> <133r> <133v> <134v>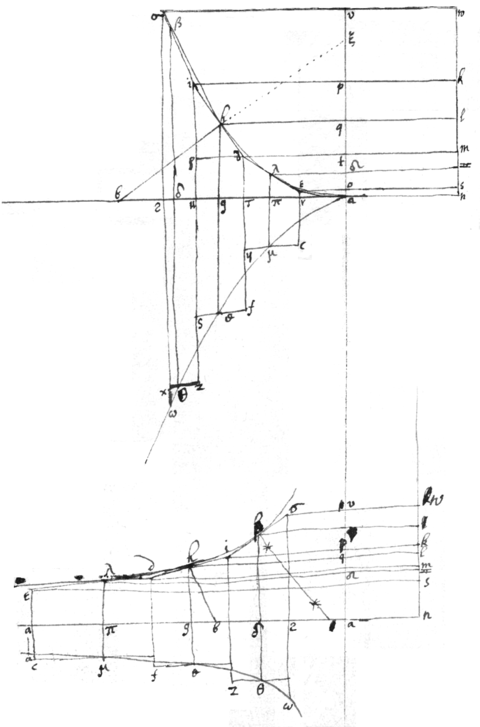 <135r>
<135r>
A Method whereby to square such crooked lines as may be squared.
If ye crooked lines σha \& aoθ/ are of such a nature that (supposeing [gh] parallell to [qa], & [bh] perpendic: to σha & [an] a given line) gh∶bg∷an∶ge. Then ye area [age]=[qlna] ye rectangle made by [an] & [gh].
Demonstration.
Suppose σi, id, de, &c; are tangents of σha, from whose intersections or ends are drawne, ec, dv|f|, iz, σ{illeg}|w|, &{c}{illeg} & from whose touch points are drawne βθ, ho, λμ, &c: all parallel to av. From ye said intersections draw sw, ik, {illeg}|d|m, es, &c. paralle{illeg}|l| {illeg}|t|o bn. {illeg}|Sin|ce gh∶bg∷{illeg}|p|d∶ip∷an∶ge. pd×ge=iν×an. that is □pkmt=□uτfs. by ye same reason {illeg}|t|mso= =τνcy; & vpkw=ζuzx &c: Thus also it may be prooved yt ye ▭vwna{illeg} is equall to any{illeg}|y| number of such li{illeg}|k|e ▭s wch> inscribed twixt ye lin{illeg}|e| ζω & ye point i|a|, wch if they be infinite are equall t{illeg}|o| superficies ζaω=vwna .also {illeg}gπμo. {illeg}=ql♊♌. &c.
Prop 1
To find ye line whose area is exprest by any given equac|t|ion. Suppose ye equatiō is . {is} nameing ye quantitys a=an. x=ag. . bh=s. kge. ba=v. |{illeg} equaco hath 2 equall rootes & is therefore multiplied according to Huddenius his Meth{illeg}| . Wherefore if . therefore aoω is a Para{illeg}|b|: &
<135v>Also if ye Equation be . Then makeing . . . |wch multiplied by Huddenius his method by reasō of z equall rootes.| . Lastly, . wch last equation expresseth ye nature of ye line aθo, whose surface .
Note yt line I call yt line [x] to wch both ye lines \σha & aoω/ have respect & increaseth & dimi{n}isheth wthout moveing over any superficies as π{a}|α|, ga, &c. but yt line to wch but one line h{illeg}|a|th respect I call [y as go, πμ: or [z] as gh, πλ, &c.
If .(m & n being numbers yt signifie ye dimensions of x & y), then , ye area of ye line {illeg}|aμo|. And if . is . ye area of yt line.
<136r>The squareing of ye simplest lines in wch y is but of one dimension.
The square of ye simplest lines in wch y is of 2 dimensions.
4y
The square of those where y is of 3 dimensions onely.
<138r>Of Musick.
1. First some \one/ sound must bee pitched upon, to wch all ye musick must bee more especially refered yn to any other sound, (as number to an unit) let this sound be called ye Cliffe or Key of ye song.
2. Then consider {illeg} ye sound wch is one or two or thre 8ths above or below yt key (for Musick seldome takes a larger compasse yn 3 8ths) The cheife of {illeg}|w|ch is ye 8th next above ye Key. 3.Each of these Eights are alike divided into ꝑ{illeg}|t|s, t|f|or ye ꝑ{illeg}|t|s of ye higher eight are {of}an Eight abo{illeg}|v|e their correspondent ꝑts {illeg}|o|f ye lower eight. so yt ye ꝑts of one Eight knowne give all ye rest, ye other Eights being but a repetition of yt. {illeg}|in| {illeg}|{a}|more base or treble sound. (Hence s{illeg}|o|me call an 8th ye largest consonant.) Let this division of an 8th bee called ye Mode of ye song.
4. This Eight i{illeg}|s| first divided into a 5t & 4th, ye fift being next above ye Key; to wch it{illeg} adds so much sweetnesse yt should this fift bee omitted in any song, ye Key would {illeg}|i|mparte its name & nature {illeg}|t|o some sound w{illeg}|ch| ha{illeg}|th| a fift above it. And since all ha{illeg}|r|mony w{illeg}|t|hout a fi{illeg}|f|t is flat, therefore the key must necessarily have a fift above i{illeg}|t|. ✝ ✝ here annex a discourse of ye motion of strings sounding an 8t 5t & 4th & of ye Logarithmes of those strings, or distances of ye notes.
< text from f 138r resumes >5. An 8th is next divided into a third major & 6t minor, & lastly into a 3d minor & 6t major. * * these are all ye concords conteined in an Eight. Hereto annex a discour{illeg}|se| of ye 3ds & 6ts
The notes in order of concordance
Eight. 5t. 3d maj. 4th. 6t maj. 3d min. 6t min. 2d maj. 7th maj 7th min. 2d min. 5t min. But as too suddaine a change from lesse to greater light offfends ye eye by reason yt, ye \spirits rarified by the/ augmented motion of ye light too violently stretch ye optick nerve: soe ye suddaine passing f{illeg}|r|om grave to acute sounds is not so pleasant as if it were done by degrees, for there \because/ of two {sic} greate a change of motion made \thereby/ in the auditory spirits ♀.|✝| ✝{illeg}|A|nd as a man \suddainely/ com̄e|i|ng from greater to lesse light, cannot discerne objects thereby so well, as when if he came to it by degrees or as when hee hath staid some whi{illeg}|l|e in ye lesser light (by reason yt ye motion of ye spirits in ye optick nerve caused by ye greater \light/, doth, untill it bee allayed; {illeg} disturbe \& as it were drowne/ ye motion motion of ye weaker light) soe if {illeg}|t|he slower motion of ye lower sound immediately succede ye m{illeg}|uch| more smart motion of ye higher its impression {illeg} \on ye auditory spirits — being then/ less perceptible, ye consonance \lower sound/ must bee {more} less pleasant yt {had} if moved ye step had beene graduated, thus that coldness | warmth is \{illeg}/ pleasant to a hot | cold man which is imperceptible to ye same man cold | hot. Thus a little {illeg}|h|eate is at ye first un\ least /perceptible to one newly come from a greater. Coroll: 1. The distance of sounds adds to ye imperfection of their concordance. Cor: 2: Tis better to descend yn ascend by {illeg}|le|apes ye first makeing ye highest sound harsher, ye seacond makeing ye lower \one{illeg}|ly|/ lesse perceptible. Which graduation may be thus don.
{illeg}|6|. The prime ꝑts of an 8th are a 5t & 4th: of a 4th fift are a 3d major & 3d minor: wch two consist ye first of a tone major & tone minor, ye 2d of a tone major {illeg}|&| semitone. A 4th consists of a tone major, minor {illeg}|&| semitone. Soe yt an eight consists of th{illeg}|r|e tone majors, 2 tone minors, & 2 semitones. [The tones might be againe divided into tones & tones, but they would bee of noe use for tones tones & tones \being discor{illeg}|d|s/ can onely serve to move {illeg}|b|y from concord to concord wch if done by tones & tones ye number of discords twixt each concord{illeg} would much m{illeg}|o|re bee harsh yn ye concord would {illeg}|b|ee pleasan{illeg}|t|, besides tones & tones are harshe{illeg}|r|{illeg} discords by far yn tones, & experience speakes yt an 8th run over by notes is unpleasant]. {y}|Y|et perhaps or notes passed over very hastily wth a larger stay upon ye concords twixt wch they are, might bee delightfull. {illeg}|But| since they are such discords, inserted as 'twere by accident /{illeg}\ {illeg}|o|nely to graduate concords, & soe quickly slipt o{illeg}|v|er, ye sen{illeg}|c|e cannot perceive any error or exactnesse in ym, & therefore \bee they usefull yet/ to treate of ym would be lost labor]
7. The degrees (viz 2 tone majors, a tone minor & semitone in {illeg}|y|e{illeg} 5t & a tone major, a tone minor & semitone in a 4th) are \12/ severall ways ordered in ye 8th wch orders are called m|M|odes, generally, because they see \much/ limit ye tune as to prevent \partes of ye tune from/ discords sounds wth ye key, wth its 5t {one} wth one another, \of one wth another/ particularly bes|c|ause tunes framed by divers of them differ in their aires or Modes.
8. These modes are 3 fold, {illeg}|v|iz: 6 in wch ye notes are distant 2 tones: foure in wch they are distant one tone: & 2 in wch they are together. The last two are of small or noe use, because every note \sound/ is distant 3 tones from some other \excepting yt there are but 2 {illeg}|f|ifts/. Also thos notes are two harsh to come together much more to bee annext to ye Key or its fift. Neither is the seacond sort very useful for one of ye notes are annexed {illeg}|ei|ther to the Key or its 5t or 8t, also 4 of its ꝑts \sounds/ are distant 3 notes \& but 4 of them are distant a fift/ from some other: whereas there are but 2 in {illeg}|t|hose of ye first sort \distant {those} notes & six of them distant fifts from other sounds./; the harshnes of ye notes being there also more moderated by their distance. And therefore ye first 6 are yet in use.
<139v>9. The following table may expresse ye 12 Modes in their order of Elegancy. In wch ye tone major & minor are not distinguished, their difference being too little to make new modes by their \order/ changed, though thereby th{illeg}|e|y may add much grace or harshnesse to any particular mode.
This order may be thus evinced. The first Mode excells ye 2d, by reason of ye Note's being more equally \{distantly}/ /convent\ placed twixt ye Key & its fift, {it}|it| lesse detracting from ye fift {illeg} \because/ of its greater distance from it. Also ye key hath its 3d major & ye fift its 3d minor in ye i|1|st mode, but contrarily in ye 2d mode ye key hath its 3d minor & ye 5t its 3d major. The 3d {m} sweetness of ye key in ye 3d mode is still more diminished by haveing ye n{illeg}|o|te imediate{illeg}|e|ly below it & its 8ts. The 4th Mode succedes as partakeing of ye 3ds def{f}ect; ye sweetnesse of its key's 5t, & consequently of its key, being \also/ diminished by ye note {a}|i|mmediately above it. The 5t mode succeds because to ye imperfections of ye 4th this is added yt its first note is next above ye key \& its fifts have tritones/. The 6t mode is yet more unpleasant for both ye key, its 5ts, & eights have a note next below them: Al{illeg}|s|o ye key & its eights have tritones above & below them. Other reasons might {illeg}|b|ee added for this order, & also for ye order of ye six{illeg}|t| last modes; & it might \perhaps bee/ shown yt ye 7th mode may bee as usefull as ye Sixt, but that would {illeg}|b|ee tedious. Note, yt sometime a note is put out of its place for some particular reason (as to prevent a greater discord &c) but yt seemes soe rare & acci{illeg}|d|entall to ye song{illeg} as not to change its aire or constitute a new mode.
10. The tones major & minor may bee six severall ways ordered in each mode but ye best way generally is to make ye first \seacond/ third & fift a{illeg} tone major, the \first/ 2d & 4th a tone minor; especially in a solitary voyce. \{illeg} & but 10 severall ways in all ye six first modes./ |.| the first is by makeing ye distances, pq, rs, vo, to bee a {illeg} tone major/s\ op, & st, to bee tone minors. In this order there are five 5ts{illeg}, {illeg} 4th 3 third majors, & 3 third minors \in an 8th/. Thus is ye 3d 5t & first mode best ordered, & thus may ye 4th & 6t moode bee ordered but not ye 2d \well/ for its \keys/ fift will |yn|bee {illeg}|oo| {illeg}|fla|t. The 2d way is by putting ye {illeg}|t|one minor twix{illeg}|t|, o & p, r & s. This order makes also 5 fif{illeg}|t|{illeg}s, thre 3d {illeg} majors & 3 3d minors, in each 8th. And by it \thus/ may ye 4th, 6t, & 2d Moode bee \best/ ordered; the 3d & 5t moode may bee {illeg} also ordered thus, but not ye first \not well/, for ye Keys 5t will |yn| bee too flatt. The 3d way is by putting ye {illeg} \minor/ note in v|b|etwixt r & s, v & o. & thus each 8th will have five fifts, 2 third majors & 2 minor thirds. The 4th 6t & 2d moode may v|b|ee well thus ordered ye {3}|1|d|s|t & 5t not so well & ye 3d {illeg}|w|orst of all. The 4th Order is by putting ye minor tone {illeg}|t|wi{illeg}|x|t p & q, s & t & thus each 8th hath 5 5|f|ifts, 2 minor 3ds, & 2d moode bee ordered well, v|b|ut ye 6t & 4th moode not well. The other six orders are l{illeg}|e|sse convenient to ye Moodes. Note yt, In every 8th there are 6 5ts, 3 major thirds & 4 minor thirds whereof one or more of them are mad{e} too flat {illeg}|o|r sharpe {illeg}|b|y about ye 10th ꝑte of a note, {illeg}|b|ut in this computation I onely reckon ye exact concords Esteeming yt order most \more/ perfect whose sounds agree in {ye} most \more of ye/ exa{illeg}|c|t concords. Note also yt every order Eight hath soe many exact 4ths, 6t minors & third majors as it hath 5ts, 6|3|t|d| majors & 3d minors their complents to an 8th.
{illeg}|11| |12|. It m{illeg}|ay| bee required sometimes {illeg}|t|o raise or let fall ye voyce in singing wch is best done by r{illeg}i|a|sising or depressing ye {illeg}|ke|y of {illeg}|y|{illeg}|e| song a fif{illeg}|t|, (if an 8{illeg}|t| be too greate), for yt will v|b|ee consonant wth ye former sound wch is now become (for ye present) gratefull to ye eare. Also instruments are usually tuned one a fif{illeg}|t| abov{illeg}|e| another \if the keys of severall parts being a fift one above another/; & a tune might bee pricked for too high a voy{illeg}|c|e in one ꝑte of ye Gamut & {illeg}|t|oo {illeg}|b|ase a voyce if removed an 8th lower. {illeg}|H|ence ariseth a comparison of ye same moode wth it selfe placed a fift higher. The precedent scheme may serve {illeg}|t|o represent any of ye six modes set \repeated/ six times wth ye distance of a fif{illeg}|t| twixt each, according {illeg}|t|o ye order of ye left hand figures. T|B|ut they cannot bee soe repeated more yn 3 times, unlesse {illeg}|w|ith |more| discord yn harmony.
Any of ye 6 Moodes \with its eights/ may bee represented by any of t{illeg}|he|se 3 orders of letters for ye key being o they re present ye first Moode, & ye second it being, s, & ye 3d if it be r &c: Also ye first ranke being lowest ye 2d a fif{illeg}|t| above {illeg}|it| & ye 3d a fift above yt,|this|{wh} scheame may represent {illeg}|an|y of ye Modes wth ye same mode one or 2 fifts above or below it.
<142r>|12| 11. These degrees have of old beene e{illeg}|x|pressed by |ye| Six notes, vt, re, mi, fa, sol, la, the 7th note being omitted as be{illeg}|i|ng a discord to ye key in ye first moode. But of late ye usuall notes are sol, {illeg}|l|a, mi, fa, sol, la, fa, hitherto expressed by ye letters o, p. q. r. s.t. v. Tis generally best (by se{illeg}|e| 10) to make from the distance from sol to {illeg}|l|a, to be a minor tone, from la to mi & fa to sol a major tone, & a semitone from la to fa /& mi to fa\. Onely in ye 2d Mode make sol & la /{illeg}\ {illeg}|&| mi to bee distant a major tone, fa to be dis a minor tone from sol els ye fift to ye key will bee too flat. Or thus if ye key bee f, a, b, or c make ye distances twixt g & a, c & d to bee a minor tone if ye key bee d or e make ye distances from f to g & c to d a minor tone, but if it be {illeg}|g| make {a−}g a−g=d−c=g−f.
<143r>13. Tis usuall to passe from{illeg} one moode to another in ye midst of a song wch how & to wt moode it may be done will appeare by ye precedent scheme. For the 3 rankes may si{illeg}|g|nifie any {of ye} three k Moodes wch have one common key, as F is the key of ye first third & sixt Moode, {illeg}|G| ye key of ye first 2d & 4th mood &c: And wee may passe from any of those Moodes to another wch in yt scheme have ye same key. But this transition is better done from one key to ye key next it, yn to ye remoter key. Neither may it bee done twixt any other Moodes {illeg} as twixt ye fi{illeg}|r|st & fift \or 3d & 4th/ by reason of their great difference, wch would soe change ye aire of ye song as to make ye ꝑts of it rather seeme divers songs.
14. It may app{illeg}|1|0) yt if the key bee f, or b, or e, ye the {tra} transition may be best done ye moode \degrees of ye Moode/ being ordered ye first way. If ye key bee {illeg}|a| or d ye 2d order is best. If ye key bee g ye 3d order is best, & the fourth ye key being c. But in generall, if ye degrees bee ordered ye {illeg}|4|d|t|h way in ye 2d Moode & ye 1st way in all ye rest, this transition will \may/ bee well {illeg}|d|one|.| {illeg}
15. from ye consideration of pa{illeg}|s|sing from one moode to another in ye same song \two other moodes may bee usefull/ ye one whereof wan{illeg}|t|s ye {illeg}|k|ey ye other its fift, but these defects are ꝑly supplyed by their use in ye former {illeg} ꝑte of ye song, whereby such {an} \the {eare} retaining the/ imp{illeg}{illeg}|r|ession \of their {sweetnes}/ may be made in ye song as thereby eare yt made \the eares retaining the impression of/ their sweetness made {illeg}|b|y ye former ꝑte of ye song. q is ye key of one moode & v ye key's 5t in |ye| other moode.
<147r>A Method whereby to find ye areas of Those Lines wch can bee squared.
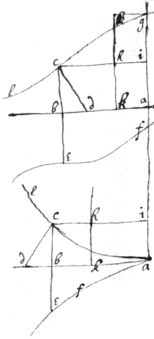
Prop: 1st. If ab=x{illeg} \{illeg}/ ⊥y=be. cb=z. bd=v{illeg} secant=cd. m & n are numbers expressing ye dimensions of x, y, or z. a, b, c, d,|&c:|are knowne quantitys, & . yn . And in generall what ever ye relation t{illeg}|w|ixt x & z bee, make all ye termes equall to nothing, multiply each terme by so ma{illeg}|n|y times zz as x hath dimensions in yt terme, for a Numerator: yn multiply each {illeg}|t|erme by soe ma{illeg}|n|y times −x as z hath dimensions in yt terme f{illeg}|o|r a denominator in ye valor of v.
Prop: 2d. If hi=r. & rv=zy. yn hi & be describe equall) spaces hi{illeg}|g|k, {illeg}|o|r hiak & abef. that is abef=aik{h}
Prop: 3d. If . Or . yn is ye area of ye line aef. And if : yn is
Demonst{illeg}|ra|con.
For . Therefore Suppose akhi is a paralllelogram {sic} & equall to . yn is . & (prop i) . & (prop 2d) rv=zy. yt is .
Pr
<148r>Prop: 4th. If . yn is
And in generall if ye valor of y consists of severall termes so yt x hath more ye one \is not of divers/ dimensions in ye denominator /{illeg}\ of any \no/ terme, are is not of divers dimensions in ye denominator of any terme, yn multiply each terme by x & divide it by ye number of ye dimensions of x, all those produc{illeg}|t|s shall bee ye area{illeg} of ye given line: supposeing al{illeg}|s|o yt either none or all {illeg}|y|e signes of those t{illeg}ermes are changed by this operation. For i{illeg}|f| some bee changed & others bee not ye area is infinite \they proeed {sic} divers ways & joyne no{illeg}|t|/, & yn ye quantitys {illeg} y or x must be increased or diminished or otherwise altered.
The reason of this is|p|rop: is, yt ye {illeg}|a|rea described by {illeg}|y| is also described by {illeg}|it|s parts yt is by ye termes of its va{illeg}|l|or, & wt areas those termes describe appeares by prop 3d.
Prop 5t. The progressions in this Table may bee designed by these g{illeg}|e|omet: lines. Whereby also any intermediate termes may bee found.
The distance of ye terme b from ye terme a being called x. y & the quantity of yt termes being y. & each terme being distant an unit from ye next. The nature of wch table is such yt ye sum̄e of any figure & ye figure above it is equall to ye figure after it. & the nature of ye lines are such yt ye precedent \any/ figure; multiplyed by ye dimen number of dimensions of x in ye first terme, being {illeg}|s|ubstracted from ye figure following |it|, is equall to ye figure under yt following figure. And yt ye numbers of y may be deduced hence 1×2×3×4×5×6×7 &c.
<149r>Prop 6t. If . This Progression &c gives all ye quantitys downward, in ye preceding {illeg}|t|able. As if m=3. n=1. {illeg} the {illeg}|qu|antitys downward are . . &c yt is 1. 3. 3. 1. 0. &c. So if . yt . &c. are ye terms downward.
Prop {illeg}|7|th. .{As} . &c As may bee deduced from {illeg}|&|c.
Prop 8th. The truth of this Prop: appeareth by compareing it wth ye two former as also by calculation if is a whole & affirmative number, or b over lesse yn an|a| unit
Prop 8th. . &c. As may bee dedu{illeg}|c|ed from &c.
The truth of this appeares also by ye 5t & 6t proposition, or by calculation If a>b.
The truth of these two prop: is also thus demonstrated If I divide, 1 by a+b as in decimall {illeg}|f|ractions & find ye quote &c as appeareth also by multiplying both ꝑts by a+b. So {illeg}if|I| extract ye {no{illeg}|t|e} of a2+b as if they were decimall numbers & find &c, as also may appeare by squareing both ꝑts
<152r> \1./{illeg}|I|f two bodys {illeg}|c|, {illeg}|d| describe ye streight li{illeg}|n|es {illeg}|a|c, bd, in ye same time, (calling ac=x, bd=y, p=motion of c, q=motion of d) & if I have an equation expressing ye relation of ac=x & bd=y whose termes are all put equall to nothing. I multiply ye equation each terme of yt equation by so many times py \{illeg}|o|r / as x hath dimensions in {illeg}|it|, & againe also by soe many times {illeg}|q|x \o{illeg}|r| / as {illeg}|y| hath dimensions in it. the sum̄e of these products is an equation expresing ye motions relations of ye motions of {illeg}|c| & {illeg} |d|. |Example if yn .|
\1./{illeg}|I|f two bodys {illeg}|c|, {illeg}|d| describe ye streight li{illeg}|n|es {illeg}|a|c, bd, in ye same time, (calling ac=x, bd=y, p=motion of c, q=motion of d) & if I have an equation expressing ye relation of ac=x & bd=y whose termes are all put equall to nothing. I multiply ye equation each terme of yt equation by so many times py \{illeg}|o|r / as x hath dimensions in {illeg}|it|, & againe also by soe many times {illeg}|q|x \o{illeg}|r| / as {illeg}|y| hath dimensions in it. the sum̄e of these products is an equation expresing ye motions relations of ye motions of {illeg}|c| & {illeg} |d|. |Example if yn .|
2. If an equation expressing ye relation of their motions bee given, tis more difficult & someti{illeg}|m|es Geometrically impossible, thereby to find ye relation of ye spaces described by those motions.
<152v>If . _______then .
— — — — — — — — — — — — — — — — —
As if m=3. n=2. yn , & . Soe if , yn m=-3. n=2. & . If ye valor of q{illeg} consisteth of severall such termes, consider each terme severall y. as if . ye first terme gives ye 2d . therefore .
In generall multiply ye valor of q|y| by x & divide {it} by ye logra each terme of it by ye logarithm{a}|e| of x, in yt {illeg}|t|er{illeg}|m|e: if y{e}|t| equation \valor of q/ consist of simple termes.
{illeg}
. . . . . . ____________ or thus . . And ij . Or thus . .
<153r>Or more ge{rda}lly generally, in|in| . And . .
<153v> <156r>
sit ab=x. bc=y. d{illeg}|f|=z, de=v. {illeg} ______
<156v> <157r>note {illeg}|y|t these are compounde{illeg}|d| onely of ye first simplest Areas:
<157v> <158r> <159r><160r>
Tha{illeg}|t| is.
multiply ye valor of {illeg}|y|. by x, & each divide yt each terme in yt valor by soe many units as x hath dimensions in yt terme, ye product is ye area.
cui eodem modo
<160v><161r>
<161v>
<162r> <162v> <163r>
[1] prop 12. 13 & I think 11 are trew onely mechanically.