Newton's Demonstration that planets move in ellipses

<1r>

Hypoth. 1. Bodies move uniformly in straight lines unless so far as they are retarded by the resistence of y^e Medium or disturbed by some other force.

Hyp. 2. The alteration of motion is ever proportional to y^e force by w^ch it is altered.

Hyp. 3. Two Motions imprest in \two/ different lines, if those lines be taken in proportion to the motions & completed into a parallelogram, compose a motion whereby the diagonal of y^e Parallelogram shall be described in the same time in w^ch y^e sides thereof would have been described by those compounding motions apart. The 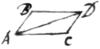motions AB & AC compound the motion AD.

Prop. 1.

If a body move in vacuo & be continually attracted toward an immoveable center, it shall constantly move in one & the same plane, & in that plane describe equal areas in equall times.

Let A be y^e center towards w^ch y^e body 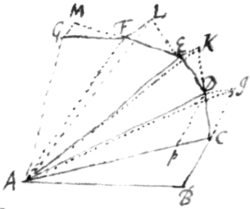is attracted, & suppose y^e attraction acts not continually but by discontinued impressions made at equal intervalls of time w^ch intervalls we will consider as physical moments. Let BC be y^e right line in w^ch it begins to move from B & {illeg} w^ch it describes w^th uniform motion in the first physical moment before y^e attraction make its first impression upon it. At C let it be attracted towards y^e center A w^th|by| one impuls or impression of force, & let CD be y^e line in w^ch it shall move after that impuls. Produce BC to I so that CI be equall to BC & draw ID parallel to CA & the point D in w^ch it cuts CD shall be y^e place of y^e body at the end of y^e second moment. And because the bases BC CI of the triangles ABC, ACI are equal those two triangles shall be equal. Also because the triangles ACI, ACD stand upon the same base AC & between two parallels they shall be equall. And therefore the triangles ACD described in the second moment shall be equal to y^e triangle ABD described in the first moment. And by the same reason if the body at y^e end of the 2^d, 3^d, 4^th, 5^t & following moments be attracted by single impulses in <1r> D, E, F, G &c describing the line DE in y^e 3^d moment, EF in the 4^th, FG in y^e 5^t &c: the triangle AED shall be equall to the triangle ADC & all the following triangles AFE, AGF & to the preceding ones & to one another. And by consequence the areas compounded of these equall triangles (as ABE, AEG, ABG &c) are to one another as the {l}ines times in w^ch they are described. Suppose now that the moments of time be diminished in length & encreased in number in infinitum, so y^t the impulses or impressions of y^e attraction may become continuall & that y^e line BCDEFG by y^e infinite number & infinite littleness of its sides BC, CD, DE &c may become a curve one: & the body by the continual attraction shall describe areas of this Curve ABE, AEG, ABG & proportionall to the times in w^ch they are described. W. W. to be Dem.

Prop. 2.

If a body be attracted towards either focus of an Ellipsis & the quantity of the attraction be such as suffices to make y^e body revolve in the circumference of the Ellipsis: the attraction at y^e two ends of the Ellipsis shall be reciprocally as the squares of the body in those ends from that focus.

Let AECD be the Ellipsis, A, C its two 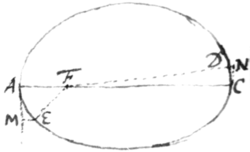ends or vertices, F that focus towards w^ch the body is attracted, & AFE, CFD areas w^ch the body with a ray drawn from that focus to its center, describes at both ends in equal times: & those areas by the foregoing Proposition must be equal because proportionall to the times: that is the rectangles $\frac{1}{2}\mathrm{AF}\times \mathrm{AE}$ & $\frac{1}{2}\mathrm{FC}\times \mathrm{DC}$ must be equal supposing the arches AE & CD to be so very short that they may be taken for right lines & therefore AE is to CD as FC to FA. Suppose now that AM & CN are tangents to the Ellipsis at its two ends A & C & that EM & DN are perpendiculars let fall from the points E & D upon those tangents: & because the Ellipsis is alike crooked at both ends those perpendiculars EM & DN will be to one another as the squares of the arches AE & CD, & therefore EM is to DN as FC^q to FA^q. Now in the times that the body by means of the attraction moves in the arches AE <2r> & CD from A to E & from C to D it would without attraction move in the tangents from A to M & from C to N. Tis by y^e force of the attractions that the bodies are drawn out of the tangents from M to E & from N to D & therefore the attractions are as those distances ME & ND, \that is the attraction/ at the end of the Ellipsis A is to the attraction at y^e other end of y^e Ellipsis C as ME to ND & by consequence as FC^q to FA^q. W. w. to be dem.

Lemma. 1.

If a right line touch an Ellipsis in any point thereof & parallel to that tangent be drawn another right line from the center of the Ellipsis w^ch shall intersect a third right line drawn from y^e touch point through either focus of the Ellipsis: the segment of the last named right line lying between y^e point of intersection & y^e point of contact shall be equal to half y^e long axis of y^e Ellipsis.

Let APBQ be the Ellipsis; AB its 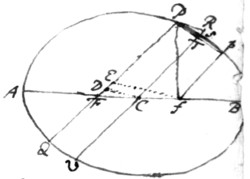long axis; C its center; F, f its Foci; P the point of contact; PR the tangent; CD the line parallel to the tangent, & PD the segment of the line FP. I say that this segment shall be equal to AC.

For joyn PF Pf & draw fE parallel to CD & because Ff & F{illeg} {are} \is/ bisected in C, & {illeg} FE shall be bisected in D & therefore ²PD shall be equal to half the summ of PF & PE that is to half the summ of PF & Pf, that is to AB & therefore PD shall be equal to AC. W. W. to be Dem.

Lemma. 2.

Every line drawn through either Focus of any Ellipsis & terminated at both ends by the Ellipsis is to that diameter of the Ellipsis w^ch is parallel to this line as the same Diameter is to the long Axis of the Ellipsis.

Let APBQ be y^e Ellipsis, AB its long Axis, F, f its foci, C its center, PQ y^e line drawn through its focus F, & VCS its diameter parallel to PQ & PQ will be to VS as VS to AB.

For draw FP \fp/ parallel to QFP & cutting the Ellipsis in p. Joyn Pp cutting VS in T & draw PR w^ch shall touch the <2v> Ellipsis in P & cut the diameter VS produced in R & CT will be to CS as CS to CR, as has been shewed by all those who treat of y^e Conic sections. But CT is y^e semisumm of FP & fp that is of FP & FQ & therefore 2CT is equal to PQ. Also 2CS is equal to VS & (by y^e foregoing Lemma) 2CR is equal to AB. Wherefore PQ is to VS as VS to AB. W. W. to be Dem.

Corol. $\mathrm{AB}\times \mathrm{PQ}={\mathrm{VS}}^{\mathrm{q}}=4{\mathrm{CS}}^{\mathrm{q}}$.

Lem. 3.

If from either focus F of any Ellipsis unto any point in the perimeter of the Ellipsis be drawn a right line & another right line doth touch y^e Ellipsis in that point & the angle of contact be subtended by any third right line drawn parallel to the first line: the rectangle w^ch that subtense conteins w^th the same subtense produced to the other side of the Ellipsis is to the rectangle w^ch the long Axis of the Ellipsis conteins w^th y^e first line produced to the other side of the Ellipsis as the square of the distance between the subtense & the first line is to the square of the short Axis of the Ellipsis.

Let AKBL be the Ellipsis, AB 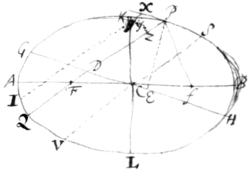its long Axis, KL its short Axis, C its center, F, f its foci, P y^e point of the perimeter, PF y^e first line PQ that line produced to the other side of the Ellipsis PX the tangent, XY y^e subtense produced to y^e other side of the Ellipsis & YZ the distance between this subtense & the first line. I say that the rectangle YXI is to the rectangle $\mathrm{AB}\times \mathrm{PQ}$ as YZ^q to KL^q

For let VS be the diameter of the Ellipsis parallel to the first line PF & GH another diametrer parallel to y^e tangent PX, & the rectangle YXI will be to the square of the tangent PX^q as the rectangle SCV to y^e rectangle GCH that is as SV^q to GH^q. This a property of the Ellipsis demonstrated by all that write of the conic sections. And they have also demonstrated that all the Parallelogramms circumscribed about an Ellipsis are equall. Whence the rectangle $2\mathrm{PE}\times \mathrm{GH}$ is equal to y^e rectangle $\mathrm{AB}\times \mathrm{KL}$ & consequently GH is to KL as AB that is (by Lem. 1) 2PD to 2PE & in the same proportion is PX to YZ. Whence GH PX is to GH as YZ to KL & PX^q to GH^q as YZ^q to KL^q. But PX^q was to GH^q as <3r> YXI was to PX^q as SV^q {illeg} that is (by Lem Cor. Lem. 2) $\mathrm{AB}\times \mathrm{PQ}$ to GH^q, whence invertedly YXI is to $\mathrm{AB}\times \mathrm{PQ}$ as PX^q to GH^q & by consequence as YZ^q to KL^q. W. w. to be Dem.

Prop. III.

If a body be attracted towards either focus of any Ellipsis & by that attraction be made to revolve in the Perimeter of y^e Ellipsis: the attraction shall be reciprocally as the square of the distance of the body from that focus of the Ellipsis.

Let P be the place of the body at {any} in the Ellipsis at any moment of time & PX the tangent in w^ch the body would move uniformly were it not attracted & X y^e place in that tangent at w^ch it would arrive in any given part of time & Y the place in the perimeter of the Ellipsis at w^ch the body doth arrive in the same time by means of the attraction. Let us suppose the time to be divided into equal parts & that those parts are very little ones so y^t they may be considered as physical moments & y^t y^e attraction acts not continually but by intervalls only once in the beginning of every physical moment & let y^e first action be upon y^e body in P, the next upon it in Y & so on perpetually, so y^t y^e body may move from P to Y in the chord of y^e arch PY & from Y to its next place in y^e Ellipsis in the chord of y^e next arch & so on for ever. And because the attraction in P is made towards F & diverts the body from y^e tangent PX into y^e chord PY so that in the end of the first physical moment it be not found in the place X where it would have been without y^e attraction but in Y being by y^e force of y^e attraction in P translated from X to Y: the line XY generated by the force of y^e attraction in P must be proportional to that force & parallel to its direction that is parallel to PF Produce XY & PF till they cut the Ellipsis 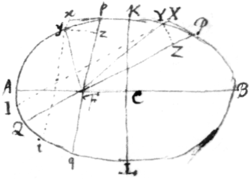in I & Q. Ioyn FY & upon FP let fall the perperpendicular {sic} YZ & let AB be the long Axis & KL y^e short Axis of y^e Ellipses. And by the third Lemma YXI will be to $\mathrm{AB}\times \mathrm{PQ}$ as YZ^q to KL^q & by consequence YX will be equall to $\frac{\mathrm{AB}\times \mathrm{PQ}\times {\mathrm{YZ}}^{\mathrm{q}}}{\mathrm{XI}\times {\mathrm{KL}}^{\mathrm{q}}}$.

And in like manner if py be the chord of another Arch py w^ch the revolving body describes in a physical moment of time & px be the tangent of the Ellipsis at p & xy the subtense of <3v> the angle of contact drawn parallel to pF, & if pF & xy produced cut y^e Ellipsis in q & i & from y upon pF be let fall the perpendicular yz: the subtense yx shall be equal to $\frac{\mathrm{AB}\times \mathrm{pq}\times {\mathrm{yz}}^{\mathrm{quad.}}}{\mathrm{xi}\times {\mathrm{KL}}^{\mathrm{quad.}}}$ . And therefore YX shall be to yx as $\frac{\mathrm{AB}\times \mathrm{PQ}\times {\mathrm{YZ}}^{\mathrm{q}}}{\mathrm{XI}\times {\mathrm{KL}}^{\mathrm{q}}}$ to $\frac{\mathrm{AB}\times \mathrm{pq}\times {\mathrm{yz}}^{\mathrm{quad.}}}{\mathrm{xi}\times {\mathrm{KL}}^{\mathrm{quad.}}}$ , that is as $\frac{\mathrm{PQ}}{\mathrm{XI}}{\mathrm{YZ}}^{\mathrm{q}}$ to $\frac{\mathrm{pq}}{\mathrm{xi}}{\mathrm{yz}}^{\mathrm{quad.}}$

And because the lines PY py are by the revolving body described in equal times, the areas of the triangles PYF pyF must be equal by the first Proposition; & therefore the rectangles $\mathrm{PF}\times \mathrm{YZ}$ & $\mathrm{PF}\times \mathrm{yz}$ are equal, & by consequence YZ is to yz as pF to PF. Whence $\frac{\mathrm{PQ}}{\mathrm{XI}}{\mathrm{YZ}}^{\mathrm{q}}$ is to $\frac{\mathrm{pq}}{\mathrm{xi}}{\mathrm{yz}}^{\mathrm{quad.}}$ as $\frac{\mathrm{PQ}}{\mathrm{XI}}{\mathrm{pF}}^{\mathrm{quad.}}$ {illeg} to $\frac{\mathrm{pq}}{\mathrm{xi}}{\mathrm{PF}}^{\mathrm{quad.}}$ And therefore YX is to yx as $\frac{\mathrm{PQ}}{\mathrm{XI}}{\mathrm{pF}}^{\mathrm{quad}}$ to $\frac{\mathrm{pq}}{\mathrm{xi}}{\mathrm{PF}}^{\mathrm{quad.}}$.

And as we told you that XY was the line generated in a physical moment of time by y^e force of the attraction in P, so for the same reason is xy the line generated in the same quantity of time by the force of the attraction in p. And therefore the attraction in P is to the attraction in p as the line XY to the line xy, that is as $\frac{\mathrm{PQ}}{\mathrm{XI}}{\mathrm{pF}}^{\mathrm{quad}}$ to $\frac{\mathrm{pq}}{\mathrm{xi}}{\mathrm{PF}}^{\mathrm{quad.}}$

Suppose now that the equal lines in w^ch the revolving body describes the lines PY & py become infinitely little, so that the attraction may become continual & the body by this attraction revolve in the perimeter of the Ellipsis: & the lines PQ, XI as also pq, xi becoming coincident & by consequence equal, the quantities $\frac{\mathrm{PQ}}{\mathrm{XI}}{\mathrm{pF}}^{\mathrm{quad}}$ & $\frac{\mathrm{pq}}{\mathrm{xi}}{\mathrm{PF}}^{\mathrm{quad.}}$ will become ${\mathrm{pF}}^{\mathrm{quad}}$ & ${\mathrm{PF}}^{\mathrm{quad}}$. And therefore the attraction in P will be to the attraction in p as ${\mathrm{pF}}^{\mathrm{q}}$ to ${\mathrm{PF}}^{\mathrm{q}}$, that is reciprocally as the squares of the distances of the revolving bodies from the focus of the Ellipsis. W. W. to be Dem.