An account of the Commercium Epistolicum

<67r>

An Account of the Commercium Epistolicum.^[1]

This book is composed of ancient Letters & Papers written by D^r Barrow, M^r Greg. M^r Collins M^r Newton M^r Leibnitz M^r Oldenburg & others, still extant in their hands or in the looks of the R. Society as they were coppied in the days of M^r Oldenburg. And the truth thereof has been examined & reported by a Committee of the R. Society & the Society acquiesce in the Report.

The occasion of this Committee was this. In the Acta Eruditorum published at Leipsic for the month of Ianuary 1704 in Account was given of two Tracts of M^r Newton concerning the species & magnitude of Curvilinear Figures. And in this Account M^r Newton was represented to have substituted fluxions for the Leibnitian differences as Honoratus Faber had substituted motion for the method of Cavellerius, that is, that M^r Newton had not found the method of fluxions in the years 1665 & 1666 as he had affirmed, but had deduced it from the method of M^r Leibnitz & only put it into another form. M^r Keil observing that this paper with divers others pub{illeg}lished in the name of the editors, was writ in the style of M^r Leibnitz, & that M^r Newton was hereby sued with plagiary & falshood took occasion in a paper published in the Transactions A.C. 1708 to write that M^r Newton without all doubt was the first who found out the Arithmetick of fluxions as will easily appear to any man who shall read his Letters published by D^r Wallis : but M^r Leibnitz afterwards having changed the name & manner of notation, published the same in the Acta Eruditorum. M^r Leibnitz afterwards in a letter to D^r Sloan dated 4 March 1711 complained of this to the R. Society, & that he never hea{r}{d} of the name nor saw the characters used by M^r Newton before they were published by D^r Wallis, & proposed to the Society that M^r Keil should testify openly that he had no intention to cast an imputation upon M^r Leibnitz as if he had learnt his differential method from another & attributed it to himself. M^r Keil refused to recant & chose rather to return an Answer whereas he represented that what he wrote was occasioned by the Acta Lipiensia & explained his meaning to be not that M^r Leibnitz knew the name or notation used by M^r Newton but only that M^r Newton was the first inventor & in two Letters written to M^r Oldenburg & by M^r Oldenburg communicated to M^r Leibnitz, had sufficiently described it to a man of a perspications understanding from whence M^r L. had or might have the principles of his calculus, & not being able to learn the names & notation used by M^r Newton did impose his own. An{d} for this his opinion D^r Keil subjoyned his reasons grounded upon several passages taken out of M^r Newtons said Letters & out of his Letter of 10 Decemb. 1672 & his Analysis per æquationes numero terminurum infinitas communicated to M^r Iohn Collins A.C. 1669. And M^r Leibnitz replied that his candor was more openly attact then before; which that he in such an old age after so many proofs of his life should defend with an Apology, & contend with a man who was learned but a novice, & unacquainted with what what had formerly been done, nor authorized by the person concerned, no prudent or just man would approve of. That what was in the Acta Leipsiensia detracted from no man, but every where gave every man his due. That he did not make hast to assert the differential <68r> method to himself but kept it secret above nine years before he began to publish it, that he left it to the equity of the Society to restrain vain & unjust clamours, which he beleived were displeasing to M^r Newton himself. & was persuaded that M^r Newton would declare as much.

The R. Society being thus twice appealed unto, & there being no witnesses now alive (For M^r Leibnitz could not be witness for hirmself nor Newton for M^r Keil), the Society appointed a Committe to search out ancient Letters & papers & letter books left by M^r Oldenburg in the custody of the society or otherwise extant, & to examin what might relate to this matter & report their opinion thereupon: & the Committe made the following Report.

Whe have consulted to be made publick

Whereupon the R. Society ordered the collection of epistles & many scripts with the Report of their Committee & what else might occurr in the Acta Eruditorum proper to clear up this matter to be made publick. And the same were accordingly published under the Title of Commercium Epistolicum.

The Letters & MSS themselvers are of unquestionable authority the Originals of most of them & authentic copies of the rest being still preserved. or long since published by D^r Wallis. And the first paper in this collection is a Tract

M^r Leibnitz in his lettter of Iune 21th 1677 wrote that he agreed with M^r Newton that Slusius'es method of Tangents was not yet perfect & that he himself had of a long time handled the business of Tangents much more generally, namely by the difference of the Ordinates, & then described his Differential method as if he had found it long before : & in his letter of 29 Decemb 1711 that he had found it above 9 years before he began to publish it, that is that he found it before Octob. 1675. For he published it in Octob. 1684. communicated by D^r Barrow to M^r Collins in the year 1669 as appears by three letters of D^r Barrow still extant & by the Letters of M^r Collins M^r Gregory, M^r Bertet, M^r Borellus, M^r Vernon, M^r Strode, & by M^r Oldenburgs Letter to M^r Slusius dated 14 Sept 1669 This Tract was first printed by M^r Iones from a copy found in the hand writing of M^r Collins, then reprinted in the Commercium from the same copy. It conteins an account of the method of reducing æquations into infinite series, & of applying those series to the quadrature of curves by meanes of three Rules set down in the beginning & to other Problems by meanes of Quadratures & of the method of motions or fluxions & moments, & to the inverse of those Problemes by extracting the affected roots the series & to Mechanical curves in finding their Ordinates tangents, areas, lengths, &c. And And after M^r Newton had shewed how it extended to these Problems he adds that he knows nothing to which this method doth not extend & that after various manners. And by its universality & the exactness of its reasoning justifies his giving it the name of Analysis : especially since by the help of it, the Areas & lengths of Curves &c may be determined exactly {&} Geometrically when it is practicable. How to do this he describes not here but gives an instance of it in his letter of Octob. 24. 1676 then communicated to M^r Leibnits & printed in this Commercium p.72, 73. Thus M^r Newton before the year 1669 that is above 44 years ago had carried his Analysis to a higher pitch & made it of a more universal extent, then any other person what so ever hath been able hitherto able to carry the differential method. For the method of series & moments together make and Analysis <69r> much more universal then the method of moments alone. And the conclusions are as exact if you continue the series in infinitum as the conclusions arein vulgar Analysis by finite equations if you extract the roots of those Equations in infinitum.

Now tho it was not M^r Newton designe in this Tract to explain the Analysis of moments any further then in relation to its use in working by infinite series, yet by what is here said of it, it appeares that he was then master of it. F he considers the Area of a curve as generated & described by the Ordinate moving upon the Abscissa with an uniform motion & thereby describing it & calls the Ordinate the moment of the area, & where several areas are so described by several Ordinates he considers the several Ordinates as the moments of the several areas, & where an abscissa increases uni formly he represents the moment by a given quantity & particularly by an unit, & proposes to find the areaat all time by having by the moment thereof at all times. And then adds that by the same method that an Area may be deduced from its moment any other quantity may be deduced from its moment. Where by it is manifest that he had at that time the method of deducing quantities of any sort from their moments. {Vide} pag 14 Commercy : An instance of this he gives in finding the lengths of Curves & adds that the like may be done for their superficies & solid contents & centers of gravity, & on the contrary he gives examples of deducing the Abscissa from the Area or Length of a Curve & of extending the method to Mechanical Curves, & of finding such curves as may be squared. All which shew that M^r Newton had at that time the method of moments direct & inverse so far as relates to this Analysis by series. And in his letter of Decem. 10 1672 he represents that the method of Tangents there described was but a particular or rather a Corollary of a general method which without any troublesome calculation extended it self not only to the drawing tangents to any Curves Geometrical or Mechanical or in any manner whatever related to right lines but also to other more obstruse sorts of Problemes concerning the curvities, areas, lengths, centers of gravities &c of curvilinear figures, & this without sticking at æquations affected with surd quantities. All which is as much as to say that M^r Newton method of moments whereof his method of Tangents was a Corrollary extended to all sorts of æquations whether finite or consisting of an infinite number of terms, rational or affected with surd quantities, & dispatcht the known sorts of Problems in the Mechanical Curves as well as in called Geometrical.

And in the first of his two letters written to M^r Oldenberg A.C. 1676 & by him communicated to M^r Leibnitz, speaking again of this method said that Analysis by the help of series was so much inlarged as to extend to almost all sorts of problems (except numeral ones like those of Diophantus,) but did not become general without some further methods of reducing problems to series : <70r> And in his second Letter making mention of the method by which he drew tangents determined maxima & minima, squared curves, &c, he comprehended this method in the following sentence exprest œnigmatically. Data æquatione quotcung fluentes quantitates involvente, fluxiones invenire, & vice versa. And this is the general method mentioned in his aforesaid Letter of 1672. And by his saying there that he had this method he determined the curvitures of curves it is manifest that he had then extended it to the second fluxions

M^r Newton had therefore in those days a method of considering indeterminate quanties as growing by continual increase, & putting some symbols for those quantities, & others for the velocities of their increase which velocities he calls their fluxions & the rectangle of their fluxions & the moment o for their particles generated in every moment of time which particles he calls their moments, & deriving the fluxions from the quantities or the quantities from the fluxions as the nature of the Question should require. For that he had symbols for these quantities in the manifest by his Analysis above mentioned For towards the end of that Analysis (pag. 19) he puts some letters as x & z for fluents & others as y or v for fluxions & where the fluxion is uniform he represents it by an unit & drawing the fluxions into an indefinitely small quantity o, he puts the rectangles oy, ov ox or o for the moments. And a little before where $\frac{\mathrm{aa}}{\mathrm{64x}}$ is the Ordinate of a Curve he puts $\frac{\mathrm{a}\mathrm{a}}{64\mathrm{x}}$ for the area generated by that Ordinate. And by the like notation z is the area of any curve whose ordinate is z, & z is the ordinate of any curve whose area is z of any & if z be put for any fluent represented by an area or capable of being so represented its fluxion will be z & its moment oz, & for the fluxi of z or second fluxion of of z may be put v or any other letter or mark.

And this much at least concerning the method of fluxions & series appears from the papers extant in the Commercium & written by M^r Newton & communicated to his friends before M^r Leibnitz began to speak of his differential method.

When M^r Collins had received the Analysis above mentioned from D^r Barrow he communicated the series therein set down to his friends & particularly to M^r Iames Gregory who thereby within the space of about a year found out the method & sent back to M^r Collins several other series found thereby, & M^r Collins communicated those also very freely to his friends having M^r Gregories leave to do so. All which appears by the Letters of M^r Collins & M^r Gregory printed in the Commercium.

In the mean time M^r Leibnitz spent some time at London, & in the year 1671 printed there his Hypothesis Physica nova, & in his Dedication thereof to the R. Society mentions his correspondence with M^r Oldenburg; & in the beginning <71r> of the year 1673 being reprehended by D^r Pell for pretending to the differential method of Mons^r Mouton he wrote an apology for himself to M^r Oldenburg extant in the Commercium, & soon after went from London to Paris being about that time chosen fellow of the R. Society. And the next year in Iuly & October wrote to M^r Oldenburg representing that Vicount Brounker & N. Mercator had found an infinite series of rational numbers equal to the area of an Hyperbola, but no man had hitherto found a progression of rational numbers which being continued in infinitum became exactly equal to the Circle But he had now found such a series & durst venture to say that he was the first who had done it. And that this series discovered certain harmonies between the circle & Hyperbola & as he had found the proportion of the circumference to the Diameter in such a series so by the same method the valor of any Arch whose sine was given might be exhibited Geometrically by such a series without knowing the length of the whole circumference, or the proportion of the Arc to the whole circumference. By one & the same method therefore he found either the whole circumference or any part of it & by consequence had got M^r Newtons series described in his Analysis pag 15, viz if x be the sine of an arc in a circle whose radius is 1, the arch will be $\mathrm{x}+\frac{1}{6}{\mathrm{x}}^3+\frac{3}{40}{\mathrm{x}}^5+\frac{5}{112}{\mathrm{x}}^7$ &c. For this series gives the arch of ${30}^{\mathrm{gr}}=\frac{1}{2}+\frac{1}{48}+\frac{3}{1280}+\frac{5}{14336}+\mathrm{\&c}$ & this series multiplied by 3 gives the Quadrantal arch, which multiplied by $\frac{1}{2}$ gives the area of a circle whose diameter in an unit. And must be the series of rational numbers here boasted of by M^r Leibnitz the summ of whose terms is exactly equal to the area of a circle. For this series is found by the same method whereby the Arch is given by the sine, & M^r Leibnitz at that time boasted of no more series then one for the area of the circle. M^r Leibnitz had therefore obteined M^r Newtons series of find the arc by the sine, but the Demonstration of M^r Newton"s series or method of finding it he had not yet obteined : for he wrote to M^r Oldenburg for it about two years after.

In the mean time M^r Oldenburg in his Letter dated Aprill 15 1675 sent eight series to M^r Leibnitz which he had received from M^r Collins. One of them was M^r Newtons series for finding the arc by the sine. Another was his series for finding the sine by the arc. And the two last were M^r Gregories for finding the the tangent by the arc & the arc by the tangent. This Letter came to the hands of M^r Leibnitz, for he wrote an Answer to it dated 20 May 1675, & the asnwer was in these words Literas tuas multa fruge Algebraica refertas accepi pro quibus tibi et doctissimo Collinio gratias ago. Cum nunc præter ordinarias Curas Mechanicis imprimis negotijs distrahar non potui examinare series quas misistis ac cum meis comparare. Vbi fecero per scribam tibi sententiam meam : nam aliquot jam anni sunt quod inveni meas via quadam sic satis singulari. Collinium ipsum magni facio quoniam omnes pura Matheseos partes ab ipso egregie cultas video. Thus M^r Leibnitz know none of the series <72r> sent to him by M^r Oldenburg to be his own, but pretended to have some others found some years before : which others he has not been able to produce to this day. Hence forward therefore he quitted his claim to the series for finding the arc by the sine : for he wanted the Demonstration to support his claim. But the next year having received by another hand the series for finding the arc by the sine & the inverse thereof for finding the by sine by the arc he wrote to M^r Oldenberg for the Demonstration or method of finding them. His Letter was dated 12 May 1676 & began in this manner Cum Georgius Mohr Danus in Geometria & Analysi versatissimus nobis attulerit communicatam sibi a Doctissimo Collinio vestro expressionem relationis inter arcum et sinum per infinitas series sequentes. Posito sinu x, Arcu z, Radio 1 $\mathrm{z}=\mathrm{x}+\frac{1}{6}{\mathrm{x}}^3+\frac{3}{40}{\mathrm{x}}^5+\frac{5}{112}{\mathrm{x}}^7+\frac{35}{1152}{\mathrm{x}}^9+\mathrm{\&c}$ $\mathrm{x}=\mathrm{z}-\frac{1}{6}{\mathrm{z}}^3+\frac{1}{120}{\mathrm{z}}^5$ $-\frac{1}{5040}{\mathrm{z}}^7+\frac{1}{362880}{\mathrm{z}}^9$ − &c Hæc, inquam, cum nobis attulerit ille quæ mihi valde ingeniosa videntur, & posterior imprimis series elegantiam singularem habeat, ideo rem gratam mihi feceris, Vir Clarissime, si Demonstrationem transmiseris. Habebis vicissium me ab his longe diversa circa hanc rem meditata de quibus jam aliquot abhinc annis ad te perscripsisse credo, demonstratione tamen non addita quam nunc polio.

M^r Leibnitz had now so far forgot M^r Oldenbergs letter of April i15^th 1675 that he did not so much as remember that he had seen these two series before they received them from M^r Mohr, tho they were sent him in that Letter. Nor did he remember that the series which he was now polishing & adorning with a demonstration, was sent him in that letter & that he did not then know it to be his own. Or else perhaps when he had found the Demonstration transmutation of figures & kew how to deduce that series from such a transmutation, he might reccon himself a collateral inventor as in the case of Mounton's differential method. For he began the last year 1675 to communicate to his friends a discourse which he had written upon this Quadrature as appears by his words published in the Acta Eruditorum for April 1691. The words are these. Iam anno 1675 compositum habebam opusculum Quadraturæ Arithmeticæ ab Amicis ab illo tempore lectum, sed quod materia sub manibus erescente, limare ad editionem non vacavit postquam aliæ occupationes supervenere præsentim com nunc prolixius exponere. vulgari more quæ Analysis nostra nova paucis exhibet non satis operæ pretium videatur. These words are a confession that he did not find out his Differential Analysis till he had done polishing this Opusculum & began to be taken up with business of another nature. He was polishing it when he wrote his letter of May 12 1676 & sent it to M^r Oldenburg in his letter of Aug 27^th 1676, & returned home by London & Holland in October & November to be imployed in publick affairs

And that the Differential method was not yet found out is demonstrated also by what M^r Leibnitz wrote to M^r Oldenberg in his Letter of 27 Aug 1676 <73r> Neither doth he describe his way of considering quantities as binomials & reducting their powers & radicals & the reciprocals thereof into infinite series by one & the same general Rule : but yet he sett Down the beginning of those series & thereby it appears that he had then found out that Rule. see the Commercium pag. 19 lin 19, 20 & pag 499 lin 22.

In his Analysis therefore his method universal, he applis these series to the solution of all sorts of Problems by considering quantities as growing or increasing by continual motion or flux, & giving the name of moments to their parts generated in equal moments of time, he puts any symbols for the increasing quantities & any others for the velocities of their increase & by drawing or multipliying these velocities into a moment of time he represents their moments. And when he considers any one of the increasing quantities as increasing uniformly or in proportion to time, he puts an unit for the velocity of its increase & that unit multiplied by a moment of time for its moment. So when he represents the growing quantities by the areas of Figure, he represents the velocities of their growth or flux by the ordinates of the figures & time by the Abscissa drawn into a given ordinate, for the length of which he puts an unit, & the moments of these flowing quantities he represents by the Ordinate drawn into the moment of the Abscissa the exponent of time. in which they are generated. So in this Tract when the Ordinate or velocity of increase or flux is $\frac{\mathrm{a}\mathrm{a}}{64\mathrm{x}}$, he represents the area or fluent by the symbol $\frac{\mathrm{a}\mathrm{a}}{64\mathrm{x}}$ & where the fluxion is 1 oy v or yo he represents the moment by o, oy, ov And by the like notation if the Ordinates or fluxions be v, x, y, z the fluents will be v, x, y, z & the moments ov, ox, oy, oz. Also when he fluent is x or z he puts y or v for the fluxion & oy or ov for the moment, & this way of notation he demonstrates the first of his three Rules above mentioned. And by these ways of notation he reserves to himself a liberty of putting any symbols for the fluents, any other symbols for the fluxions & the symbols of the fluxions multiplied by o for the moments By this means he performed all his computations in this method without any other infinitely small quantity then the moment o (as in demonstrating the first of the said three Rules in this Tract & in demonstrating the first Proposition in his book of Quadratures) he considered the symbol o as infinite quantity & performed the whole operation by vulgar Geometry without considering any one quantity as infinitely small & when the computation was brought to an end & the equation reduced : he considered the quantity o as decreasing till it vanish ed & thereby had a new equation which determined what he sought. And this way of working he calls his methods rationum primarum & ultimarum. But if he was minded not to work demonstratively to make dispatch by such approximations as would breed no error in the conclusion, he supposed the quantity o to be infinitely little, & this way of working his method of Moments And both these ways of working are his general method which he calls his method of fluxions. And by these methods he applied his series so generally to the solution of Problemes as to say in his Analysis that he knew of no Problems about figures Geometrical or Mechanical to which <74r> this method did not extend & that after various manners

And as by this Tract of Analysis it appeasr that M^r Newton had then applied this method generally to the solution of Problemes by seires : so by his Letter to M^r Collins dated Decem. 10 1672 & printed in the Commercium it appears that he had then applied it generally to the solution of Problems by finite equations. For in this Letter M^r Newton having described his method of Tangents which proved to be the same with that of Slusius, he added that this method was but a particular or rather a Corollary of a general method which without any toublesome calculation extended itself not only to the drawing of Tangents to any Curves Geometrical or Mechanical or in any manner whatever related to right lines, but also to other more abstrase sorts of Problemes concerning the curvities areas lengths centers of gravities of curves &c & this without sticking at equations affected with irrational quan tities. And thus much concerning the method of series & fluxions appears out of what M^r Newton wrote before the end of the year 1672 : at which time M^r Leibnitz had not begun to write any thing about either series or the Differential method.

When M^r Collins had received M^r Newtons Analysis he communicated one of the series to M^r Iames Gregory who after a years consideration fell upon the same method & sent some other series back to M^r Collins in the beginning of the year 1671 & gave M^r Collins leave to communicate them to whom he pleased. And M^r Collins was very free in communicating the series which he had received from them both as appears by the Letters published in the Commercium.

M^r Leibnitz was at London in the year 1671 & there printed his Hypothesis Physica nova & in his Dedication thereof the R. Society mentioned his correspondence with M^r Oldenburg, & in the beginning of the year 1673 claimed the differential method of Mons^r Mouton pretending that he had found it apart without the assistance of Mouton & had much improved it, & soon after went from London to Paris & the next year A.C. 1674 wrote to M^r Oldenburg that he had found a series of rational numbers equal to the circle & by the same method any arch might be found in such a series without knowing its proportion to the whole circumference. Which is as much as to say that by the sine of an arch whose proportion to the whole circumference was known he had found a series of rational numbers for the whole circumference & by the same method could find a series for any arc tho its proportion to the whole circumference was not known. By the method of finding these particular series in rational numbers he means a general series which by assuming the sine in a rational number gives the arc in a series of rational numbers. And this general series was not found out by M^r Leibnitz for he wrote afterwards to M^r Oldenburg to procure from M^r Collins the Demonstration thereof meaning M^r Newtons method for finding it.

The next year viz^t A.C. 1675 in April M^r Oldenburg having received eight series from M^r Collins sent the to M^r Leibnitz then at Paris Two of them were M^r Newtons for finding the Arc by the sine & the sine by the arc, & other two were M^r Gregories for finding the arc by the tangent & the tangent by the <75r> arc. But M^r Leibnitz knew none of the eight series to be his own For his answer dated at Paris May 20 1675 began in these words : Literas tuas multa fruge Algebraica refertas accepi, pro quibus tibi et doctissimo Collinio gratias ago. Cum nunc præter ordinarias curas Mechanicis imprimis negotijs distrahar, non potui examinare series quas misistis ac cum meis comparare. Vbi fecero, perscribam tibi sententian meam: nam aliquot jam anni sunt quod inveni meas via quadam sic satis singulari. These series were in general terms those of M^r Leibintz in particular numbers. And tho he had got the general series for finding the arc whose sine was given, yet he wanted the Demonstration. But having found a demonstration of the series for the arc whose tangent was given he began this year to communicate it to his friends at Paris as he himself has told us in the Acta Eruditorum mense Aprili anni 1691 pag 178 in these words Iam anno 1675 compositum habebam opusculum Quadraturæ Arithmeticæ ab amicis ab illo tempore lectum sed quod, materia sub manibus crescente limare ad editionem non vacavit postquam aliæ occupationes supervenere; præsertim com nunc prolixius exponere vulgari more, quæ Analysis nostra nova paucis exhibet, non satis operæ pretium videatur. M^r Leibnitz therefore had not yet found his new Analysis nor did it out till after he had done filing & polishing this Opusculum in order to publish it.

The next year when M^r Leibnitz had again received two of the aforesaid eight sries by another hand, he took occasion from thence as if he had forgot that he had receved them before, to write to M^r Oldenburg for the Demonstration of them Parisijs 12 Maij anno 1676: Cum Georgius Mohr Danus in Geometria et Analysi versatissimus, nobis attulerit communicatam sibi a Doctissimo Collinio vestro expressionem relationis inter Arcum et sinum per infinitas series sequentes: Posito sinu x, arcu z, Radio 1.
$\mathrm{z}=\mathrm{x}+\frac{1}{6}{\mathrm{x}}^3+\frac{3}{40}{\mathrm{x}}^5+\frac{5}{112}{\mathrm{x}}^7+\frac{35}{1152}{\mathrm{x}}^9+\mathrm{\&c}$ $\mathrm{x}=\mathrm{z}-\frac{1}{6}{\mathrm{z}}^3+\frac{1}{120}{\mathrm{x}}^5-\frac{1}{5040}{\mathrm{x}}^7-\frac{1}{362880}{\mathrm{x}}^9$ + &c
Hæc, inquam cum nobis attulerit ille, quæ mihi valde ingeniosa videntur, et posterior imprimis series elegantiam quadam singularem habeat ideo rem gratam mihi feceris, Vir Clarissime si DEMONSTRATIONEM transmiseris. Habebis vicissium mea ab his longe diversa circa hanc rem meditata, de quibus jam aliquot abhinc annis ad te perscripsisse credo, demonstratione non addita quam nunc POLIO. By the Demonstration he understands M^r Newtons method: & by his continuing still to polish his Quadrature by the transmutation of figures, it appears that he had not yet found out his new Analysis.

This summer between the 14^th of Iune & 11^th of August M^r Oldenburg sent to M^r Leibnitz at Paris a collection of the Letters & papers of M^r Iames Gregory newly dead. The Collection was made by M^r Collins under this title. Extracts from M^r Gregories Letters to be lent to Mon^s Leibnitz to peruse who is desired to return the same to you. M^r Collins in a letter to M^r David Gregory the brother of M^r Iames dated 11^th Aug. 1711, wrote that they were such. And M^r Tsc{aurn}hause then at Paris {new them af} in a letter to M^r Oldenburg dated 1 Sept. 1676 has this sentence relating to them : Similia porro quæ in hac re præstitit eximius ille Geometra Gregorius [sc. quod series infinitas memoranda certe sunt & quidem optimæ famæ ipsius consultiri, qui ipsus relicta Manuscripta luci publicæ ut exponantur operam navabunt. The collection was therefore received at PAris & sent back, being lately found of M^r Iames Gregory dated 15 Feb. 16701 in which was the series for finding the arc from the Tangent given & another for the tangent from the Arc given. [And yet M^r Leibnitz goes on still to claim the first of these two series <76r> There was also a copy of M^r Newton's Letter of 10 Decemb. 1672, in which the extent of this general method his was described & his method of tangents which proved to be the same with that of Slusius, was described plainly & said to be a branch or Corollary of that general method. And about the same time a letter of M^r Newtons dated 13 Iune 1676 was sent to M^r Leibnitz in which at the requese of M^r Leibnitz he describes his method of infinite series & in the end of which he subjoyns: Ex his videre est quantum fines Analyseos per hujusmodi infinitas æquationes ampliantur : Quippe quæ earum beneficio, ad omnia pene dixerim problemata (si numeralia Diophanti et similia excipias) sese extendit: non tamen omnino universalis evadit nisi per ulteriores quasdam methodos eliciendi series infinitas

And to this M^r Leibnitz in his Letter of 27 Aug. returned answer : Quod dicere videmini, plerasque difficultates exceptis Problematibus Diophantæis) ad series infinitas reduci, id mihi non videtur sunt enim multa usque adeo mira et implexa ut NEQVE AB ÆQVATIONIBVS PENDEANT NEQVE EX QVADRATVRIS, qualia sunt (ex multis alijs) Problemata mathodi tangentium inversa. From which words its most evident that M^r Leibnitz did not yet understand the differential method.

M^r Newton in his Reply dated 24 Octob 1676 making mention of a Tract composed 5 years before but not finished, & of the method of Tangents set down therein & communicated to M^r Collins two or three years before (viz^t in the Letter of 10 Decemb. above mentioned) & how this method which was the same with that of Slusius, flowed readily from his Principles & stuck not at surd quantities questions de, & that the same Principles extended in like manner to the determining Maximas & Minimas & some others & to the Quadratures of Curves which thereby became more easy : he gave some instances of the power of this method in squaring Curves & in letters put out of order, set down the foundation of this Analysis in this sentence, Data Æquatione fluentes quotcunque quantitates involvente fluxiones invenire & vice versa. And towards the end of the Letter he adds that the inverse problemes of Tangents & other more difficult were in his power: for resolving of which he used a double method, one more concise the other more general, which methods he set down in in transposed letters comprehending these sentences Vna methodus consistit in extractione fluentis quantitatis ex æquatione fluxionem ejus involvente: altera tantum in assumptione seriei pro quantitate qualibet incognita ex qua cætera commodederi vari possunt, et in collatione terminorum homologorum æquationis resultantis ad eruendos terminos assumptæ seriei.

And now M^r Leibnitz being convinced that M^r Newtons method <77r> was much more general then he had apprehended, & extended to inverse problems of tangents & others more difficult & stuck not at surd, & in direct problems of Tangents was of the same kind with the Method of Slusius; & in squaring the Curves gave very general & useful Theoremes he wrote back in his Letter of 21 Iune 1677, Clarissimi Slusij methodum tangentium nondum esse absolutam Celeberrino Newtono assentior, et jam a multo tempore rem tangentium longe generalius tractovi scilicat per differentias Ordinotarum.

M^r Iames Gregory in the 7^th Proposition of his Geometria Vniversalis printed in the year 1668 handed the business of Tangents by the differences of the Ordinates. D^r Barrow in his tenth Lecture printed in the year 1669 did the like in a manner something more general. Slusius founded his method of Tangents in this Lemma Differentia duarum dignitatum data ehusdem generis applicata ad Differentiam laterum dat partes singulares gradus inferioris ex binomio laterum, ut$\frac{{\mathrm{y}}^3-{\mathrm{x}}^3}{\mathrm{y}-\mathrm{x}}$ = yy + yx + xx. And these are the differences of M^r Leibnitz. $\frac{{\mathrm{y}}^3-{\mathrm{x}}^3}{\mathrm{y}-\mathrm{x}}$ in the characters of M^r Leibnitz is $\frac{{\mathrm{dy}}^3}{\mathrm{dy}}$ = 3yy, or ${\mathrm{dy}}^3$ = 3yydy & so of other dignities ${\mathrm{dy}}^4=4{\mathrm{y}}^3\mathrm{dy}$, ${\mathrm{dy}}^5=5{\mathrm{y}}^4\mathrm{dy}$, ${\mathrm{dx}}^2=2\mathrm{x}\mathrm{dx}$, M^r Newton's admonition that the Method of Tangents of Slusius was but a branch or corollary of a very generall method was sufficient to put him upon con sidering the method of Slusius with the Lemmas upon which it was grounded. The first Lemma was sufficient to give him the elements & notation & every the name of the differential method & the universality of M^r Newtons Method was sufficient to put him upon applying this differential method to the abstruser Problems, & M^r Newton's saying that his method extended to the finding of curvature of curves was sufficient to put him upon considering the second differences.

^✝ < insertion from f 77v > And that M^r Leibintz received light into the differential method from what M^r Newton wrote of his general method whereof the method of Tangents of Slusius was but a branch or corollary may be gathered even from his own words. For in his Letter to D^r Wallis dated 28 May 1697 he wrote Mihi consideratio Differentiarum & summarum primam lucem affuderat cum animadverterem Differentias Tangentibus & Summas Quadraturis respondere. Vidi mox Differentias Differentiarum in Geometria Osculis exprimi. M^r Newtonus (in his Letter dated 10 Decem 1672 wrote) curvitates curvarum (id est circulorum deosculantium) per methodum suam determinari M^r Leibnitz writes of his in{ven}tion anno 1677 Vidi mox Differentias Differentiarum in Geometria Osculis exprimi.

M^r Newton in the beginning of his Letter dated 13 Iune 1676 sent M^r Leibnitz a Theorem for reducing any dignity of aBinomials into a series Let the Binomials be x+o, the indew of the dignity n, the dignity ${\overline{)\mathrm{x}+\mathrm{o}}}^{\mathrm{n}}$ & the series will be ${\mathrm{nox}}^{\mathrm{n}-1}+{\mathrm{x}}^{\mathrm{n}}+\frac{\mathrm{n}\mathrm{n}-\mathrm{n}}{2}\mathrm{o}\mathrm{o}{\mathrm{x}}^{\mathrm{n}-2}+\mathrm{\&c}$. Therefore (x-o)ⁿ−${\overline{)\mathrm{x}+\mathrm{o}}}^{\mathrm{n}}-{\mathrm{x}}^{\mathrm{n}}=\mathrm{n}\mathrm{o}{\mathrm{x}}^{\mathrm{n}-1}+\frac{\mathrm{n}\mathrm{n}-\mathrm{n}}{2}\mathrm{o}\mathrm{o}{\mathrm{x}}^{\mathrm{n}-2}$. That is in the language of M^r Leibintz ${\mathrm{dx}}^{\mathrm{n}}={\mathrm{n}\mathrm{x}}^{\mathrm{n}-1}\mathrm{dx}+\frac{\mathrm{n}\mathrm{n}-\mathrm{n}}{2}{\mathrm{x}}^{\mathrm{n}-2}\mathrm{dxdx}$ &c. In this series if all the terms except the first be omitted as being infinitely less then the first, there will remain ${\mathrm{dx}}^{\mathrm{n}}={\mathrm{nx}}^{\mathrm{n}-1}\mathrm{dx}$. Or $\frac{{\mathrm{dx}}^{\mathrm{n}}}{\mathrm{dx}}={\mathrm{nx}}^{\mathrm{n}-1}$ And this is the first Lemma of Slusius. M^r Leibnitz therefore had not only from M^r Newtons Letters the notice that M^r Newtons general method was founded upon the same principle with the Method of Tangents of Slusius, the one being a breanch or corollary of the other, but also sent him a series the two first terms of which was the very principle upon which his general method was founded.

And its further observable that by the two first terms of this series M^r Newton in his Analysis per æquationes numero terminorum infinitas, demonstrated the first Rule in that Analysis. Which Rule is the inverse off the first Lemma of Slusius,

‖ < insertion from f 77v > ‖ If it be said that M^r Leibnitz might find his differential some other way without the help of M^r Newton, thats not the question, but whether he had not light enough into it from M^r Newton, & whether M^r Newton had it not before him. < text from f 77v resumes > Now when M^r Leibnitz had said, as above : Et jam a multo tempore rem generalius tractavi, scilicet per differentias Ordinatarum he goes on &c < text from f 77r resumes > When therefore he had said Et jam a multo tempore rem tangentium longe generalius tractavi scilicet per differentias ordinatarum, he does on to describe his method by the difference of two Ordnates & the difference of two abscissas & then adds. Hinc nominando in posterum dy differentiam duarum proximarum y & dx duarum proximarum x patet $d{\mathrm{y}}^2$ esse 2ydy & ${\mathrm{dy}}^3$ esse $3{\mathrm{y}}^2\mathrm{dy}$ & ita porro: which is the very Lemma of Slusius. And here by the words hinc nominando posterum it may be concluded that he began at this very time to communicate his differential method in writing.

Then he sets down as example of drawing Tangents by this Method & concludes with these words : Quod coincidit cum Regula Slusij, ostendite eam statim occurrere hanc methodum intelligenti. And this is the first argument that he gives for the similitude of this differential method & M^r Newtons.

Then he explains how his method is like that of M^r Newtons in that it sticks not at surd quantities, & subjoyns Arbitror quæ celare voluit Newtonus de Tangentibus ducendis ab his non abludere. Quod <78r> addit ex hoc eodem fundamento quadraturas quoque reddi faciliores me in sententia hac confirmat, nimirum semper figuræ illæ sunt quadrabiles quæ sunt ad æquationem differentialem

And in October 1684 when M^r Leibnitz first published the elements of his calculus differentialis, he made this the title of his paper Nova methodus pro Maximis et Minimis itemque Tangentibus quæ nec irrationales moratur & after he had described the elements of his calculus he subjoyned : Et hæc quidem initia sunt tantum Geometriæ cujusdam multo sublimioris ad difficillima & pulcherrima quæque etiam mistæ matheseos pertingentis quæ sine calculo nostro differentiali, aut SIMILI, non temere quisquam pari facilitate tractabit. Compare this description of the differential method with the like description which M^r Newton in his three Letters of 10 Decemb 1672, 13 Iune 1676 & 24 Octob 1676 had given of his general method; & with the comparison which M^r Leibnitz in his Letter of 21^th of Iune 1677 makes between M^r Newtons method & his own. & then you will see what method M^r Leibinitz understood by his words, aut SIMILI.

And two years after in another paper published in the Acta Eruditorum in Iune 1686 under this title De Geometria recondita & Analysi indivisibilium atque infinitarum Addenda. he has these words Porro quoniam ad problemata transcendentia, ubicunque dimensiones tangentesque occurrunt, calculo tractanda, vix quicquam utilius brevius universalius fingi potest calculo meo differentiali seu Analysi indivisibilium atque infinitorum, cujus exiguum tantum velut specimen sive Corollarium continetur in methodo mea Tangentium in Achis Octob. 84 edita. Which description agrees so exactly with the description which Newton in his letter 10 Decemb. 1672, had given of his method, as if that Letter had then been before the eyes of M^r Leibnitz

In the same paper he writes that before he was acquainted with the vulgar Algebra he found out many Theoremes a part of which he afterwars met with in the works of the Gregories & Barrow. And after he was acquainted with the Vulgar Algebra he found out his Arithmetical Quadrature, & at length he found out his calculus differentialis or Analysis indivisibilium aut infinitorum which being once discovered whatsoever he had before admired in these matters, became a play & jeast. Which agrees with what was said above of his having the advantages of the words of M^r Gregory & D^r Barrow, of his beginning to communicate Gregories quadrature in his own name in the year 1675 & of his finding the differential method in the year 1677.

In the same paper in speaking of his way of notation he writes. Malo autem dx et similia adhibere quam literas pro illis, quia istud dx est modificatio quædam ipsius x, et ita ope ejus fit, ut sola quando id fieri opus est litera x cum suis scilicet potestatibus & differentialibus calculum ingrediatur, et relationes transcendentes inter x et aliud exprimantur. Qua ratione etiam lineas transcendentes æquatione explicare licet. Here M^r Leibnitz allows that in his differential method he might have represented the differences by letters (as D^r Barrow did) but he chose rather to represent them by the symbols dx, dy &c this being more <79r> convenient for representing transcental curves by an equation By his own confession therefore, the differential method is one & the same method whether the differences be represented by letters or by any other marks such as are dx, dy, dz . And therefore M^r Newton might use any other sort of Notation without using another method. The invention the method does not lye in the invention of this or that sort of notation but any sort of notation may be used without varying the method, & the method called by M^r Leibnitz the differential method may be M^r Newtons tho the Notation dx, dy, dz be M^r Leibnitz. The area of a curve whose Ordinate is $\frac{\mathrm{aa}}{\mathrm{64x}}$ M^r Leibnitz represents by this mark $\int \frac{\mathrm{a}\mathrm{a}}{64\mathrm{x}}$, M^r Newton in his Analysis by this $\frac{\mathrm{a}\mathrm{a}}{64\mathrm{x}}$. The difference of Notation makes no difference in the method. But M^r Newtons notation being much older then that of M^r Leibnitz makes him the first inventor of the method. When fluents are represented by the areas of Curves & their fluxions by the Ordinates, if any letters as v, x, y, z be put for the Ordinates the fluents will be v, x, y, z & by this way of notation transcendental curves may be exprest in equations as well as by the Notation of M^r Leibnitz. M^r Newton in the end of his Analysis put some letters for fluents & others for their fluxions, M^r Leibnitz allows that he could have done the same thing in his differential method : but Newtons being used by him in & perhaps before the year 1669 gives him priority of invention. M^r Leibnitzhas now confined the method to a particular sort of Notation, M^r Newton has not confined it to any sort of Notation but left it all liberty to use what symbols any man shall think fit. In his Tract of Quadratures & some other papers published by D^r Wallis he has used the symbols $\stackrel{.}{\mathrm{v}}$, $\stackrel{.}{\mathrm{x}}$, $\stackrel{.}{\mathrm{y}}$, $\stackrel{.}{\mathrm{z}}$; but he has not confined his method to those symbols. In his Procipies he has put greater letters for fluents & & small ones for fluxions. And whatever symbols are used, if their signification be ones described they will be sufficient to express transcendent Curves by equations, & whatever else can be exprest be the symbols of M^r Leibnitz.

But its to be observed that in M^r Newtons method there are symbols for fluents & others for fluxions & that the symbols for fluxions multiplied by the letter o which he uses for a moment of time become his symbols of moments or differences: but in the Differential method there are no symbols of fluxions (for fluxions are finite quantities) & therefore M^r Newtons notation is more complete & comprehensive. Its further to be observed that M^r Newton can use the letter o as a finite quantity whenever he pleases & there by perform the whole computation in finite quantities by the Geometry of Euclide, & make his conclusions demonstratively certain: M^r Leibnitz's method wants this advantage his differences dx, dy, dz being always considered as infinitely small. And its still further to be considered that when M^r Newton's method preceeds not in finite equations he can work in infinite series & thereby apply his method to almost all sort of Problems: whereas the working by infinite series is no part of the Analysis of <80r> M^r Leibnitz So Then the method of M^r Newton in the year 1669 when he communicated his Analysis to D^r Barrow & by D^r Barrow to M^r Collins was more extensive & complete in its notations, more demonstrative in its way of working, & more universal in its application to Problems then that of M^r Leibnitz is at present, or perhaps can even be made without borrowing from M^r Newton. And further, M^r Newton's way of considing quantities as increasing by various degrees of velocity is agreable to the nature of things; that of considering them as composed of indivisibles is forced ungeometrical, there being then no indivisibles in Geometry. In his Theoria motus abstract (pag 8) he gives this definition of a point. Punctum, saith he, non est cujus pars nulla est, nec cujus pars non consideratur, sed cujus extensio nulla est, seu cujus partes sunt indistantes, cujus magnitudo est inconsiderabilis, inassignabilis, minor quam quæ ratione, nisi infinita ad aliam sensibilem exponi possit, minor quam quæ dari potest atque hoc est fundamentum Methodi Cavallerianæ. Whether Euclid or M^r Leibnitz are in the right you may understand by considering that two solids touch one another in a superficies without penetrations of dimensions, two surfaces cur one another in Euclids line & two lines cut one another in Euclids point. But according to M^r Leibnitz two solids touch one another in a skin whose depth or thickness is indivisible & penetrate one anothers dimensions to the depth of that skin. And upon this notion of indivisibles he has founded the method of Cavallerius & his own. Cavallerius & Leibnitz might found their methods upon such an Hypothesis, but the Hypotheses is not Geometrical. The differences of M^r Leibnitz which he calls indivisibles, are in various proportions to one another, & frequently they are incommensurable & by consequence divisible in infinitum. For two unequal incommensurable quantities may be subducted from one another in finitum. The language of indivisibles is not Geometrical & a language not Geometrical ought not to be introduced into Geometry.

The symbols by which M^r Newton represents fluxions are the oldest symbols for that sort of quantities: for M^r Leibnitz has not yet any symbols for fluxions. The symbols by which M^r Newton represents moments (viz^t the rectangles of fluxions & a moment of time) are older then those of M^r Leibnitz for differences, being used by M^r Newton in his Analysis communicated to M^r Collins in the year 1669. And M^r Leibnitz in giving an account of this Analysis in the Acta Eruditorum for February 1712 represents the notation by the letter o was used before by Fermat & others in such cases M^r Newton in honour of Fermat, Gregory & other who used it has kept to their notation as far as was M^r Leibnitz has departed from the old way of Notation without any necessity & brought in a new one tending to extinguish the memory of those that went before him & make himself the sole inventor. And therefore its an Act of justice to the memory of those that went before him to keep the use of the letter o,

<80v>

The dispute between M^r Leibintz & M^r Keil. The last Letter was written by M^r Leibnitz & is printed in the Acta Leipsica & M^r Leibnitz has refused to

<81r>

An Account of the Commercium Epistolicum D. Ioannis Collinij & aliorum De Analysi promota.^[2]

1 This Commercium is composed of several Letters & Papers put together in order of time & copied from such originals as are described in the title of every Letter & Paper a Committe of the R. Society being appointed to examin the truth of the Originals & compare the copies therewith. We shall here give you an Account of the matter they contein.

✝

2 M^r Newton in his Letter of 24 Octob 1676 represented that a little before the plague (which raged in London in 1665) he found his method of series, upon the coming abroad of M^r Mercators Logarithm {otechnia} communicated to M^r Collins by D^r Barrow a Compendium of that Method, entituled Analysi Æquationes numero terminorum infinitas & two years after wrote a larger Tract upon the same method with a designe to have published it but upon disputes arising about his Theory of Colours for the sake of quiet left off before he had finished the Tract, & intermitted the further considerration of these things till the writing of his Letter of Iune 13 1676. [He represented also that in the same Tract was a method by which he drew Tangents after the manner of Slusius, determined a maxima & minima, squared Curves, & found converging series for squaring them which gave their squares in finite equations when it was practicable &c & that his method stuck not at surd quantities, & was couched in the solution of his Probleme Data æquatione quotcunque fluentes quantitates involvente fluxiones invenire & vice versa.

3 For solving this Problem the Book De Quadratura Curvarum was composed. And tho it was printed but lately, yet if be compared with M^r Newtons Letter of 24 Octob 1676 it will appear to have been found out before the writing of that letter & by consequence five years before or above, M^r Newton having then absteined five years from these studies. The first Proposition is mentioned expresly in that Letter viz^t Data æquatione fluentes quotcunque quantitates involvente fluxiones invenire. The Second is thus mentioned in the Compendium written A. 1669.^[3] Hinc in transitu notetur modus quo Curvæ quotcunque quarum areæ sunt cognitæ possunt inveniri The fift is set down at large & illustrated with examples of the Theorems for squaring of Curves, & the sixt is the second of that sort, & these two depend on the four first, & therefore all the six first Propositions were found out five years before the writing of that Letter or above. For the 5^t & sixt are also touched upon in the said Compendium in these words. cujus [methodi] beneficio Curvarum areæ & longitudines &c (id modo fiat) exacte et Geometrice determinantur. Sed ista narrandi non est locus^[4] Which words are thus explained by M^r Colling in his Letter to M^r Strode dated 26 Iuly 1672. Ejus [methodi] ope in quavis figura curvilinea proposita quæ una vel pluribus Proprietatibus definitur, Quadratura vel Area dictæ Figuræ accurata si possibile sit, sin minus infinite vero propinqua — obtineri queat. The fift & sixt Propositions of the book of Quadratures were known to M^r Newton when he wrote the said Compendium. <81v>

And some things are mentioned out of the second Corollary & Scholium of the 10^th Proposition in his letter of 24 Octob, & 8^th Novemb. 1676, & by consequence that Proposition & the three preceding on which it depends were also known to M^r Newton in those days.

4 Now the Analysis conteined in those Tracts & Letters is composed of the Method of Series & the method of fluxions conjoyned into one general method. The method of Series is set down very plainly in the Compendium & in the Letter of 13 Iune 1676. But with the difference that the reduction of fractions & surds into infinite series by division & extraction of roots described at large in the Compendium is omitted in the letter of 13 Iune & the reduction of the dignity of any Binomium into an infinite series is described at large in the Letter of 13 Iune 1676 & only touched upon in the Compendium by setting down the two first Terms of the series, viz^t ${\mathrm{x}}^{\mathrm{p}}+{\mathrm{pox}}^{\mathrm{p}-1}$ &c & ${\mathrm{z}}^{\mathrm{n}}+{\mathrm{noyz}}^{\mathrm{n}-1}$ &c.^[5]

5 The method of fluxions conteined in these Tract & Letters is this. M^r Newton considers quantities as increasing continually in time, gives the name of fluxions to the velocities of their increase & that of moments to their parts generated in moments of time. The fluxion of time or of any quantity by which Time is represented & exposed he represents by an unit, & a moment of time he represents by the letter o or by any constant letter taken for dn indefinitely or infinitely small quantity. For indeterminate or flowing quantities he puts any of Letter or symbols & for their fluxions any others, & for their moments he puts their fluxions multiplied by a moment of time. If he is demonstrating a Proposition he puts the moment o for an indefinitely (not infinitely) small part of time & performs the whole operation in finite quantities & finite figures accuratly by vulgar Geometry without any approximation & when the calculation is over he a^[6] supposes the moment o to become infinitely small & vanish into nothing, & by the quantities which remain in the equation, he gathers the last ratios of the fluxions But if he is only investigating a truth, he frequently supposes the moment o & the figures to be infinitely little, proceeds in the calculation by any approximations which he reccons will produce no errors in the conclusion, & for making dispatch neglects to write down the letter o. The first way is Demonstrative, the second more liable to errors, but quicker for saving of time & labour. These modes of computations are described in the Introduction & three first Propositions of his Quadratura Curvarum & the same are used by him in his Compendium.

For the Compendium is founded upon three Rules the two first of which amount to this Proposition. Ordinata Curvæ ex dignitatibus Abscissæ conflata, invenire Aream. And the thing was to reduce the Ordinates of Curves into converging series by divisi{on} or extraction of roots simple or affected. When he had illustrated these Rules by various precepts & examples, & particularly in squaring the circle & conique sections by converging series, he added. Et hac de areis Curvarum investigandis dicta sufficiant. Imo cum Problemata <82r> omnia de Curvarum Longitudine, de quantitate et superficie solidorum deque Centro Gravitatis, possunt eo tandem reduci ut quæratur quantitas superficiei planæ linea curva terminatæ; non opus est quicquam de ijs adjungere. In istis autem quo Ego operor modo, diam brevissime.

7Sit ABD Curva quævis, & AHKB rectangulum cujus latus AH vel BK est unitas. Et cogita rectam DBK uniformiter ab AH motam areas ABD et AK describere; et quod BK (1) sit momentum quo AK (x) & BD (y) momentum quo ABD gradatim augetur; et quod ex momento BD perpetim 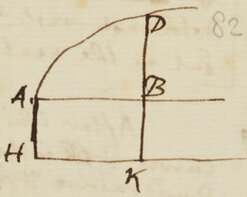dato possis, per præcedentes Regulas, aream ABD ipso descriptam investigare, sive cum AK (x) momento 1 descripta, confere ‖ < insertion from the bottom of f 81v > ‖ Here M^r Newton tells us that the three Rules set down in the begining of the Compendium were the foundation of this method of Moments for squaring of Curves, the Ordinate of any curve being considered as the moment of its area And this is as much as to say that in this Compendium where he proposed to <82v> find the Ordinate of a Curve by the Area or the Area by the Ordinate he understands the same thing as afterwards in his Letter of 24 Octob. 1676 where he proposes Data æquatione fluentes quantitas involvente fluxiones invenire & vice versa. For in this Compendium he doth not restrain the method of moments to the Quadrature of Curves but in the next words he adds : Iam qua ratione &c < text from f 82r resumes > Iam qua ratione superficies ABD. ex momento suo perpetim dato per præcedentes Regulas elicitur eâdem quælibet alia quantitas. Ex momento suo sic dato elicietur. Here he supposes the line AB to increase or flow in proportion to time, & the areas AK & ABD to increase or flow in proportion to the Ordinates $\mathrm{BK}=1$ & $\mathrm{BD}=\mathrm{y}$ & represents their moments or particles generated in moments of time by the line BK & BD & proposes to derive any qantities generated from their moments after the same manner that he derived the areas of curves by the thre Rules from their Ordinat{es} considered as the moments of the Areas. Then he sets down an example of finding the length of an arch of a circle whose sine is given & adds : Sed notandum est quod unitas esta quæ pro momento ponitur est superficies cum de solidis, & linea cum de superficiebus & punctum cum de lineis agitur. Nex vereor loqui de punctis sive lineis infinite parvis, siquidem proportiones ibi jam contemplantur Geometræ dum utuntur methodis Indivisibilium.

8 When therefore he puts a point for the moment of a line by a point he means a line infinitely short, & so when he puts a line for the moment of a surface he meanes by it a surface infinitely narrow, & when he puts a surface for the moment of a solid he means by it a solid infinitely thin. And therefore when he calls the line BK (1) the moment of the rectangular surface AK, & the line BD (y) the moment of the surface ABD, by the lines BK (1) & BD (x) he understands surfaces infinitely narrow, that is, rectangles whose altitudes are BK (1) & BD (y) & bases infinitely short lines generated in moments of time. Let those infinitely short lines answering to moments of time, be represented by the letter o & the moment BK (1) & BD (y) will be $\mathrm{o}\times 1$ & $\mathrm{o}\times \mathrm{y}$, or o & oy. This way of notation he uses neare the end of the Compendium where he is demonstrating the first Rule, but in teaching only the art of investigation, he neglects to write down down the letter o

<82v>

9 After this description of the Method, he applies it to trancendent curves & instances in finding the Ordinate & area of the Trochois & Quadratrix he adds: Nec quicquam hujus modi seo ad quod hæc methodus idque varijs modis, sese non extendit. Imo tangentes ad Curvas Mechanicas (siquando id nono alias fiat, hujus ope ducuntur et quicquid Vulgaris Analysis per æquationes ex finito terminorum numero constantes (quando id sit possibile perficit, hæc per æquationes infinitas semper perficit: ut nil dubitaverim nomen Analysis etiam huic tribuere. And in the last place he demonstrates the first of the three Rules by the method of moments using the very same sort of calculation with that by which he demonstrates the first Proposition in his nook of Quadratures.

10 When therefore he wrote this Compendium he had a general method of Analysis which consisted in applying Equations both finite & infinite to the solution of Problems by the method of moments, & this method was that described in his book of Quadratures

4 Mercator soon after published a Demonstration of this Quadrature by the Division of D^r Wallis, & M^r I. Gregory soon after that published a Geometrical Demonstration thereof, & these books being sent a few months after by D^r Collins to D^r Barrow, the Doctor naturally sent to M^r Collins the Compendium above mentioned. This was in Iuly 1669. The title of this Tract was Analysis per æquatione numero terminorum infinitas. It conteined a general method of squaring all curves by such equations or convergens series, & of solving such other Problems as by the vulgar Analysis were untractable. Amongst the examples of this new Analysis were these. Let the Radius of a circle be 1, the arc z, & the sine thereof x, & the equations for finding the arc whose sine is given the sine whose arc is given will be these.

$\mathrm{z}=\mathrm{x}+\frac{1}{6}{\mathrm{x}}^3+\frac{3}{40}{\mathrm{x}}^5+\frac{5}{112}{\mathrm{x}}^7+\frac{35}{6}{\mathrm{x}}^9+$ &c

$\mathrm{x}=\mathrm{z}-\frac{1}{6}{\mathrm{z}}^3+\frac{1}{120}{\mathrm{z}}^5-\frac{1}{5040}{\mathrm{z}}^7+\frac{1}{362880}{\mathrm{z}}^9-$ &c

5 M^r Iames Gregory having received one of M^r Newtons series from M^r Collins, after some consideration found M^r Newtons method of series in December 1670 & in the beginning of the next year (15 Feb 1671) sent M^r Collins some other Theorems of the same kind, amongst which was this. Let the radius be r, the arc a & the tangent t, & the equation for finding the arc whose tangent is given will be $\mathrm{a}=\mathrm{t}-\frac{{\mathrm{t}}^3}{3{\mathrm{r}}^2}+\frac{5^5}{5{\mathrm{r}}^4}-\frac{{\mathrm{t}}^7}{7{\mathrm{r}}^6}+\frac{{\mathrm{t}}^9}{9{\mathrm{r}}^8}-$ &c

These Theorems M^r Gregory gave M^r Collins full liberty to communicate to whom he pleased & M^r Collins was very free in communicating what he had received both from M^r Newton & from M^r Gregory.

<85r>

An Account of the book entituled
Commercium Epistolicum Collinij et aliorum
De Analysi promota.

This Commercium is composed of several Letters & Papers put together in order of time & copied from such Originals as are described in the Title of every Letter & Paper; a Committee of the R. Society being appointed to examin the sincerity of the Originals & compare therewith the copies taken from them. It ☉+ < insertion from f 85v > ☉+ It relates to a general method of resolving finite æquations into infinite ones & applying these æquations, both finite & infinite to the solution of Problems by the method of moments & fluxions. We will first give an account of that part of the method which consists in resolving finite equations into infinite ones & squaring curvilinear figures thereby. By infinite equations are ment such as involve a series of terms converging or approaching the truth nearer & nearer in infinitum so as at length to differ from the truth less then by any given quantity which can be assigned & if continued in infinitum, to leave no difference.

D^r Wallis in his Opus Arithmeticum published A.C 1657 cap 33 Prop. 68, reduced the fraction $\frac{\mathrm{A}}{1-\mathrm{R}}$ by perpetual division into the series A + AR + ${\mathrm{AR}}^2+{\mathrm{AR}}^3+{\mathrm{AR}}^4+$&c

Vicount Brounker squared the Hyperbola by this series $\frac{1}{1\times 2}+\frac{1}{3\times 4}+\frac{1}{5\times 6}+\frac{1}{7\times 8}+\mathrm{\&c}$, that is by this $1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\frac{1}{6}+\frac{1}{7}-\frac{1}{8}$ &c conjoyning every two terms into one. And the Quadrature was published in the Transactions in April 1668.

M^r Mercator soon after published a Demonstration of this Quadrature by the division of D^r Wallis, & soon after that M^r Iames Gregory published a Geometrical Demonstration thereof. And these books were a few months after (viz^t in May or Iune 1669) sent by M^r Iohn Collins to D^r Barrow at Cambridge & by D^r Barrow comunicated to M^r Newton. Where upon D^r Barrow mutually sent to M^r Collins a Tract of M^r Newton entituled Analysis per æquatione numero terminorum infinitas. And this is the first piece published in the Commercium

M^r Newton in a Letter dated < text from f 85r resumes > M^r Newton in his ^a[7]Letter dated 24 Octob. 1676 makes this mention of it. Eo ipso tempore quo Mercatoris Logarithmotechnia prodijt communicatum est per amicum D. Barrow (tunc matheseos Professorem Cantab) cum D. Collinio Compendium quoddam harum serierum, in quo significaveram Areas & Longitudines Curvarum omnium & solidorum superficies & contenta ex datis rectis; et vice versa ex his datis Rectas determinari posse: & methodum indicatam illustraveram diversis seriebus. M^r Collins ☉ < insertion from f 85v > ☉ M^r Collins in the years 1669, 1670, 1671, 1672 gave notice of this Compendium to M^r Iames Gregory in Scotland M^r Bertet & M^r Vernon then at Paris, M^r Alphonsus Borelli in Italy, M^r Strode M^r Townsend M^r Oldenburg, & others in England as appears by his Letters.^[8] And M^r Oldenburg in a letter dated 14 Sept 1669 & entred in the Letter book of the R. Society gave notice of it to M^r Francis Slusius at Liege. & cited several sentences out of it. M^r Collins in a Letter to M^r Iames Gregory dated 25 novem. 1669,^[9] speaks thus of the method conteined in it. Barrovius provinciam suam publice prælegendi remisit cuidam nomine Newtono Cantabrigiensi, cujus tanquam visi acutissimo ingenio præditi, in Præfatione Prælectionum Opticarum, meminit: quippe antequam ederetur Mercatoris Logarithmotechnia, eandem methodum adinvenerat, eamque ad omnes curvas generalitur, et ad Circulum, diversimode applicarat And in a letter to M^r David Gregory dated 11 August 1676,^[10] he < text from f 85r resumes > in his ^b[11] Letter to M^r David Gregory dated 11 Aug. 1676 mentions it in this manner. Paucos post menses quam editi sunt hi libri (viz^t Mercatoris Logarithmotechnia & Exercitationes Geometricæ Gregorij) missi sunt ad Barrovium Cantabrigiæ. Ille autem responsum dedit hanc infinitarum serierum doctrinam a Newtono ✝ Two years before the publication of M^r Mercators Logarithmotechni. Vide Iones biennium ante excogitatam fuisse quam ederetur Mercatoris Logarithmotechnia & generaliter omnibus figuris applicatam, simulque transmisit D. Newtoni opus manuscriptum. The last of the said two books came out towards the end of year 1668, & D^r Barrow sent the said Compendium to M^r Collins in Iuly following as appears by ^c[12]three of D^r Barrows Letters And in a ^d[13]Letter to M^r Strode dated 26 Iuly 1672 M^r Collins wrote thus of it. Exemplar ejus [Logarithmotechniæ] misi Barrovio Cantabrigiam qui quasdam Newtoni chartas extemplo remisit: E ^e[14]quibus et alijs, quæ olim ab Authore cum Barrovio communicata fuerant, patet illam methodum a dicto Newtono aliquot annis antea excogitatam et modo universali applicatan fuisse: ita ut ejus ope in quavis Figura Curvilinea proposita, quæ una vel pluribus proprietatibus definitur Quadratura vel Area dictæ figuræ, accurata si possibile sit minus infinite vero propinqua, Evolutio vel longitudo Linea Curvæ; centrum gravitatis figuræ, solida ejus rotatione genita & eorum superficies; sine ulla radicum extractione obtineri queant. Postquam intellexerat D. Gregorius hanc methodum a D. Mercatore in Logarithmotechnia usurpatam & Hyperbolæ quadrandæ adhibitam redditam esse, omnibusque figuris applicatam; acri studio eandem acquisivit multumque in ea <86r> enodanda desudavit. Vterque D. Newtonus & Gregorius in animo habet hanc methodum exornare: D. Gregorius autem ducit. And in another Letter written to M^r Oldenburg to be commnicated to M^r Leibnitz & dated 14 Iune 1676, M^r Collins adds: Hujus autem methodi ea præsentia ut cum tam late patet o nullam &c

This Tract was first printed by M^r Iones being found by him among the papers & in the hand writing of M^r Collins & collated with the original remaining in the hand of M^r Newton. It conteins the above mentioned general method of Analysis teaching how to resolve finite equations into infinite ones & how by the method of fluxions & moments to apply equations both finite & infinite to the solution of all Problems. It begins where D^r Wallis left off, & founds the method of Quadratures upon three Rules.

D^r Wallis published his Arithmetica Infinitorum in the year 1655, & by the 59^th Proposition of that Book, if the Abscissa of any Curvilinear figure be called x, & m & n be numbers, & the Ordinate erected at right angles be ${\mathrm{x}}^{\mathrm{m}/\mathrm{n}}$, the area of the figure shall be $\frac{\mathrm{n}}{\mathrm{m}+\mathrm{n}}{\mathrm{x}}^{\frac{\mathrm{m}+\mathrm{n}}{\mathrm{n}}}$. And this is assumed by M^r Newton aas the first Rule upon which he founds his Quadrature of Curves. D^r Wallis demonstrated this Proposition by steps in many Propositions, & then collected all the Propositions into one by a Table of the cases M^r Newton in the end of his Compendium demonstrated it at once by his method of moments.

By the 108^th Proposition of the said Arithmetica infinitorum & by several other Propositions which follow therein; if the Ordinate be composed of two or more Ordinates taken with their signes + & −, the area shall be composed of two or more areas taken with their sines + or − respectively. And this is assumed by M^r Newton as the second Rule upon which he founds his method of Quadratures.

M^r Newton in his Letter to M^r Oldenburg dated 13 Iune 1676 & communicated to M^r Leibnitz taught how to reduce any dignity of any binomial into a converging series & how by that series to square the Curve whose Ordinate is that dignity. And being desired by M^r Leibnitz to explain the original of this Theoreme he replied in his Letter dated 24 Octob 1676 that a little before the plague (which raged in London in the years 1665 & 1666) upon reading the Arithmetica infinitorum of D^r Wallis, & considering how to interpole the series x, $\mathrm{x}-\frac{1}{3}{\mathrm{x}}^3\mathrm{,}\mathrm{x}-\frac{2}{3}{\mathrm{x}}^3+\frac{1}{5}{\mathrm{x}}^5\mathrm{,}\mathrm{x}-\frac{3}{3}{\mathrm{x}}^3$ $+\frac{3}{5}{\mathrm{x}}^5-\frac{1}{7}{\mathrm{x}}^7$, & he found the area of a circle to be the series $\mathrm{x}-\frac{\frac{1}{2}{\mathrm{x}}^3}{3}-\frac{\frac{1}{8}{\mathrm{x}}^5}{5}$ $\frac{\frac{1}{16}{\mathrm{x}}^7}{7}-\frac{\frac{5}{128}{\mathrm{x}}^9}{9}$, &c, And by pursuing the method of interpolation he found the Theoreme above mentioned. And by meanes of this Theoreme he found the reduction of fractions & surds into converging series by division & extraction of roots, & then proceeded to the extraction of affected roots. And the Reduction of the Ordinates of Curves into converging series by these operations where the Quadrature of Curves does not otherwise succeed in his third Rule.

The time when these things were invented is confirmed by <87r> what M^r Collins wrote upon the credit of D^r Barrow wrote in his Letters to M^r Strode & M^r Townley,^[15] in these words In September 1668 M^r Mercator published his Logarithmotechnia containing a specimen of this method in one only Figure, to wi in the Quadrature of the Hyperbola. Not long after the Book came out I sent one of them to D^r Wallis at Oxford, who forthwith gave his sense of it in the Philosophical Transactions. Another of them I sent to D^r Barrow at Cambridge [viz^t in Iune following] who forthwith sent me up some papers of M^r Newton . . . . . . . by which & former communications made thereof from the Author to the Doctor it appears that the said method was invented some years before by the said M^r Newton & generally applied, &c. And in his Letter to M^r David Gregory dated 11 Aug. 1676 he wrote that the Doctrine of infinite series was invented by M^r Newton about two years before the publication of M^r Mercators Logarithmotechnia & generally applied to all curves. It was not invented & generally applied not at once but by degrees in the years 1665 & 1666. But for avoiding disputes M^r Newton supposes that my Lord Brounker might invent & Mercator demonstrate the series for the Hyperbola two or three years before they published it.

These three Rules being laid down & illustrated with this Compendium among the examples for illustrating the method &c various examples, M^r Newton proceeds to describe his method of moments. And for understanding the description he gives of it, I shall first describe the method which he now uses. He considers quantities not as aggregated of indivisibles but as growing & increasing by continual motion & hence calls them fluent quantities.. The velocity of the increase he calls the fluxion of the quantities, & the momentaneus increases or parts generated in moments of times he calls the moments of the fluent quanties, the names of fluxion & moments being taken from the fluxion & moments of time. He exposes time by any quantity which flows uniformly & puts an unit or some other given quantity for its fluxion & the letter o or any other convenient mark he puts for its moment. For the other fluents he puts any other letters most commonly the letter at the end of the Alphabet. For their fluxions he puts any other letters or marks or even the same letters differing in form or magnitude or distinguished in any other manner. And for their moments he puts their fluxions drawn into a moment of time. When he is demonstrating any proposition he always expresses the moment of time & considers it in the sense of the vulgar as indefinitely small but not infinitely small & so performs the whole operation in finite figures or schemes by Geometry of Euclide & Apollonius exactly without any approximation, And in the end of the computation supposes the moment of time to decrease in infinitum & vanish. But when he is only investigating a truth or the solution of a Problem, he supposes the moment of time & the schemes to be infinitely small & uses any approximations which he thinks will create no error in the conclusion (as by putting the arch & it chord sine & tangent equal to one another) & for making dispatch he neglects to write down the symbol of the moment This is his method of fluxions & moments at present. This was his method when he wrote his book of Quadratures as is manifest by his demonstration of the first Proposition thereof. And this was his method when he wrote his Analysis per equationes numero terminorum infinitas, as is manifest by the the demonstration of the first of his three Rules in the end of that tract & by the description which gives of the method used in that Tract in that Tract in the following words.

Sit ABD curva quævis, et AHKB rectangulum cujus latus AH 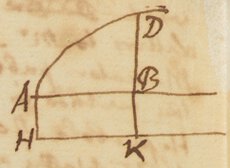<87v> <88r> vel BK est unitas et cogita rectam DBK uniformiter ab H notam, areas ABD, & AK describere; & quod BK (1) sit momentum quo AK (x), et BD (y) momentum quo ABD gradatim augetur; et quod ex momento BD perpetim Dato possis per præcedentes [tres] Regulas, aream ABD ipso descriptam investigare, sive cum [crea] AK (x) momento 1 descripta confere. Iam qua ratione superficies ABD ex momento suo perpetim dato, per prœcedentes [tres] Regulas elicitur, eadem quælibet alia quantitas ex momento suo sic dato elicitur. Exemplo res fiet clarior &c.

Here M^r Newton considers quantities as increasing by continual motion or flux, & represents them by the areas of figures ABKH & ABD described by their Ordinates BK & BD moving forward upon the Abscissa AB with an uniform motion. And their moments he represents by their Ordinates BK & BD, putting an unit for BK. 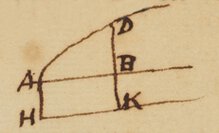And a little after he adds: Sed notandum est quod unitas ista quæ pro momento ponitur est superficies cum de solidis, & linea cum de superficiebus & punctum cum de lineis ( agitur. Nec vereor loqui de unitate in punctis, sive lineis infinite parvis, siquidem proportiones ibi jam contemplantur Geometræ, dum utuntur methodis indivisibilium. When therefore M^r Newton considers a point as the moment of a line he understands by it not Euclids point but an infinitely little part of the line, & when he considers a line as a moment of a superficies he understands not Euclids line but an infinitely narrow superficies. And therefore when he represents the moments of the area ABKH & ABD by their Ordinates BK & BD he understands by those ordinates not geometrical lines in the sense of Euclide, but physical lines in the sense of those who use the method of Indivisibles, that is rectangles infinitely narrow or whose altitudes are the Geometrical lines BK & BD. Let one of those infinitely short parts be called o & the moments of the Areas ABKH & ABD will be oxBK & oxBD. In this manner M^r Newton expresses the moments of areas when
<89r>
when he is demonstrating a Proposition as may be seen in the end of this Tract where he demonstrates the first of the three Rules but where he is only investigating this he considers the Ordinates as physical lines infinitely narrow, as in the method of Cavallesius, & puts them for the moments of the areas.

After M^r Newton had illustrated this method with examples in finding the lengths of Arithmetical Curves & the Ordinates areas & lengths of transcendent curves & deduced abscissas from their given areas or lengths & observed that by the same method the curved superficies & solid contents of curves may be found he subjoyns Nec quicquam hujus modi scio ad quod hæc methodus idque varijs modis sese non extendit. Imo tangents ad curvas Mechanicas (siquando id non alias fiat) hujus ope ducuntu. Et quicquid vulgaris Analysis per æquationes ex finito terminorum numero constantes (quando id sit possibile) perficit, hæc per æquationes infinitas semper perficit; et nil dubitaverum nomen Analyseos etiam huic tribuere. And subjoyning his reasons why this method should be called an Analysis he adds: Denique ad Analyticam merito pertinere censeatur cujus beneficio Curvarum areæ et longitudines & (id modo fiat) exacte et Geometrice determinentur sed ista narrandi non est locus. By these last words its manifest that he had then carried this method further then is described in this compendium. And what he means by those words he explains in his Letters dated 13 Iune & 24 Octob 1676. In the first of those Letters he writes thus. Ex his videre est quantum fines Analyseos per hujusmodi æquationes ampliantur: Quippe quæ earem beneficio, ad omnia <90r> pene dixerim problemata (si numeralia Diophanti et similia excipias) sese extendit. Non tamen omnino universalis evadit nisi per alteriores methodos eliciendi series infinitas. Sunt enim quædam Problemata in quibus non licent ad series Infinitas per divisionem vel extractionem Radicum simplicium affectarumve pervinise. Sed quomodo in istis casibus procedendum sit, jam non vacat dicere; ut neque alia quædam tradere quæ circa Reductionem Infinitarum Serierum infinitas ubi rei natura tulerit, excogitavi. Nam parcius scribo quod hæ speculationes diu mihi fastidio esse cœperunt; adeo ut ab ijsdem jam peae per quinque fere annos abstinuerim. How he proceeded in those cases where division & extraction of roots were useless he tells in his next letter dated 24 Octob 1676 setting down a double method in these two sentences exprest enigmatically Vna methodus consistit in extractione fluentis quantitatis ex æquatione simul involuente fluxionem ejus: altera tantum in assumptione Seriei pro quantitate qualibet incognita ex quæ cætera commode derivari possunt & in collatione terminorum homologorum æquationis resultantis ad eruendos terminos assumptæ seriei. He assumes not the whole series at once but after he has assumed & determined the two or three first terms of the series, he assumes & determins the fourth therm & then the fift & so onHow he proceeded in the Reduction of Problemes by means ofinfinite series to finite æquations he describes in the same letter. But I should first tell you that he there represents, that after he had for some time intermitted the consideration of the method of infinite series he wrote a treatise thereon in the year 1671 with a designe to publish the same; that this Tract conteined also his method of Tangents & maxima & minima &c without sticking at surds & was founded upon the following Proposition Data æquatione quotcunque fluentes quantitates involvente fluxiones invenire, & vice versa; & that upon this foundation he endeavoured to render the Quadrature of Curves more easy, & arrived at certain Theoremes the first of which he there sets down, & illustrates with examples. This Theoreme conteins the Quadrature of a certain sort of Curve by an infinite series which breaks of & becomes finite wherever the Quadrature can be performed by a finite equation. It is the fift Proposition of his book of Quadratures & the sixt Proposition in the second Theoreme of this kind, & these two Propositions are grownded upon the four first Propositions of that book, & therefore all the six first Propositions of that book were understood by M^r Newton in the year 1669 when D^r Barrow communicated the Compendium of the method to M^r Collins. The first Proposition of that Book is Data æquatione fluentes quotcunque æquationes involvente, invenire fluxiones; & M^r Newton in his said Letter dated 24 Octob 1676 tells us that this was the foundation of the method upon which he had written a trasise five years before. The second in this Invenire Curvas quadrari possunt, & this is all one with the first & is mentioned in the Compendium in these words. Hinc in transitur notetur modus quo Curvæ quotcunque quarum areæ sunt cognitæ possunt inveniri; sumendo nempe quamlibet æquationem pro relatione inter aream z & basin x ut inde quæratur applicata y. Vt si supponas $\sqrt{\mathrm{aa}+\mathrm{xx}}=\mathrm{z}$, ex calculo invenies $\frac{\mathrm{x}}{\sqrt{\mathrm{aa}+\mathrm{xx}}}=\mathrm{y}$ Et sic de reliquis The fift & six are sufficiently described by M^r Newton in his Letter dated 13 Iune & 24 Octob. 1676 as invented five years before or above, & also in the Compendium where speaking of his method of converging series, he saith. Denique ad Analyticam merito pertinere cenceatur cujus beneficio curvarum areæ & longitudines &c (id modo fiat) exacte et geometrice determinentur

<91r>

An Account of the Commercium Epistolicum Collinij & aliorum De Analysi promota

This Commercium is composed of several Letters & Papers put together in order of time, & copied from such Originals as are described in the Title of every Letter & Paper, a Committee of the R. Society being appointed to examin the truth about the Originals & compare the Copies therewith. We shall here give you an Account of the matter they contein.

D^r Wallis in his Opus Arithmeticum published A. 1657 lap 33, Prop. 68, reduced the fraction $\frac{\mathrm{A}}{1-\mathrm{R}}$ by perpetual division into the series $\mathrm{A}+\mathrm{A}\mathrm{R}+\mathrm{A}{\mathrm{R}}^2+\mathrm{A}{\mathrm{R}}^3+\mathrm{A}{\mathrm{R}}^4+$&c.

Vicount Brunker squared the Hyperbola by this Series $\frac{1}{1\times 2}+\frac{1}{3\times 4}+\frac{1}{5\times 6}+\frac{1}{7\times 8}+$&c, that is by this $1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\frac{1}{6}+\frac{1}{7}-\frac{1}{8}+$&c conjoyning every two terms into one. And the Quadrature was published in the Philosophical Transactions in Aprill 1668.

Mercator soon after published a Demonstration of this Quadrature by the Division of D^r Wallis, & M^r Iames Gregory soon after that published a Geometrical Demonstration there of And these books were a few months after sent by M^r Collins to D^r Barrow at Cambridge. And upon the receipt of them D^r Barrow mutually sent to M^r Collins a Tract of M^r Newtons entituled Analysis per æquationes numero terminorum infinitas which is the first Tract in the Commercium. This is related by D^r Barrow & M^r Collins in several Letters still extant in their hands & by M^r Newton his Letter of 13 Iune 1676 where he calls this Tract a Compendium of his method of Series. It was sent to M^r Collins in Iuly 1669, & conteined

— In this C{om}pendium among the examples for illustrating the Method were these. Let the radius of a circle be 1, the arc z & the sine x, & the Equations for finding the arc whose sine is given & the sine whose arc is given will be $\mathrm{z}=\mathrm{x}+\frac{1}{6}{\mathrm{x}}^3$ $\mathrm{x}=\mathrm{z}-\frac{1}{6}{\mathrm{z}}^3$
And M^r I. Gregory having after a years study found out a method in December 1670, about two months after in a Letter dated 15 Feb. 1671 sent several Theorems to M^r Collins. with leave to communicate them freely: amongst which Theorems were these. Let the radius be r, the arc a & the tangent t, & the equations for finding the arc whose tangent is given & the tangent whose arc is given will be $\mathrm{a}=\mathrm{t}-\frac{{\mathrm{t}}^3}{{\mathrm{r}}^2}+\frac{{\mathrm{t}}^5}{5{\mathrm{r}}^4}-\frac{{\mathrm{t}}^7}{7{\mathrm{r}}^6}+\frac{{\mathrm{t}}^9}{9{\mathrm{r}}^8}-\mathrm{\&c}$ $\mathrm{t}=\mathrm{a}+\frac{{\mathrm{a}}^3}{3{\mathrm{r}}^2}+\frac{2{\mathrm{a}}^5}{15{\mathrm{r}}^4}+\frac{17{\mathrm{a}}^7}{915{\mathrm{r}}^6}+\frac{62{\mathrm{a}}^9}{2835{\mathrm{r}}^8}+\mathrm{\&c}$

And M^r Collins was very free in communicating to his mathematical friends what he had received from M^r Newton & M^r Gregory as appears by his Letters to Slusius, Bertet, Townley Borellius, Vernon, Strode, Oldenburg.^[16]

In the year 1671 M^r Leibnitz published two Tracts at London the one dedicated to the Royal Society the other dedicated to the Academy of Sciences at Paris & in the Dedication of the first he mentioned his correspondence with M^r Oldenburg.

But M^r Leibnitz never took any further notice of his having received these series, nor how his own differed from them, nor ever producer any other series then those which he received in this Letter or numeral ones derived from them And what he did with Gregories Series – – – lectum &c. By a Theorem for transmuting figures into one another he had now found a Demonstration of this Series, but still wanted the Demonstration of the rest & meeting with a pretence to ask for it he wrote to M^r Oldennburg the following Letter dated

Cum Georgio Mohr Danus . . . . desiderio meo. By the word inquam one would think that he had never seen these two series before & that his diversa circa hanc rem meditata was something else then one of the series which he had received from M^r O.

Vpon this Letter M^r Oldenburg & M^r Collins wrote pressingly to M^r Newton desiring that he himself would describe his own method to be communicated to M^r Leibnitz. Whereupon M^r Newton wrote his Letter of 13 Iune 1676 describing the Method of Series as he had done before in the Compendium above mentioned, but with this difference. There he described at large the reduction of fractions & radicals into series by division & extraction of roots & only set down the two first terms of the series to which the dignity of a Binomial might be reduced here he described at large the reduction of the dignity of a Binomial into a series & only touched upon the Reduction by Division & Extraction of roots. This Letter was sent away to Paris with other papers from M^r Collins on 26 Iune 1676.

For M^r Iames Gregory died in the latter end of the year 1675 - - - - who is desired to return the same. And that they were sent accorddingly as affirmed by M^r Collins in his letter to M^r David Gregory the brother of the deceased dated 11 Aug. 1676, & appears further by the Answers of M^r Leibnitz & M^r Tschurnhause. The Answer of M^r Leibnitz dated 27 Aug. 1676 begins thus Literæ tuæ die 26 Iuly datæ plura ac memorabilium circa rem Analyticam continent quam multa volumina spissa de his rebus edita. Quare tibi pariter ac Clarissimis Viris Newtono ac Collinio gratias ago qui nos participes tot meditationum egregiarum esse voluisstis. And towards the end of the Letter he had answered M^r Newtons Letter he proceeds thus. Ad alia tuarum Litterarum venio - - - - - aptissimus &c And M^r Tschurnhause in his Answer dated 1 Sept. 1676 after he had done with M^r Newtons Letter concludes thus. Similia porro - - - - - - navabunt. Now in this Collection was a copy of the Letter of M^r Iames Gregory dated 15 Feb 1671 wherein he sent to M^r Collins the the series above mentioned for finding the Arc whose tangent was given But yet M^r Leibnitz persisted in his designe of making himself the inventor of that series. And tho he had now received it twice from M^r Oldenburg sent it back to him with an useless Demonstration by way of recompence for M^r Newtons method, pretending that he had found it some years before. And he endeavoured also to claim from M^r Newton the three or four following series tho he had no method for finding them before the receipt of M^r Newtons letter, & did not yet understand the method by which alone they were to be found, but desired M^r Newton to explain it further. Let $1-\mathrm{m}$

The three first of those series he pretended to have found sometimes before the receipt of M^r Newtons Letter, & the fourth he derived from the third as a Corollary thereof.

In the first part of this Letter where he speaks of Newtons Series he saith that he looked over them cursorily to see if he could find the Series of M^r Leibnitz for squaring the circle or Hyperbola. If he had carefully searched for it in the extracts of Gregories Letters collected by M^r Collins he would there have found it in M^r Gregories Letter of 15 Feb 1671. For that Letter is still extant among these extractsin the hand writing of M^r Collins.

And yet M^r Leibnitz though he had now twice received this series from M^r Oldenburg, sent it back to him as his own to be communicated to M^r Newton in requital for the Method of Series pretending that he had found it out three years before or above In The same Letter in which he sent this series back to M^r Oldenburg & which was dated 27 Aug. 1676, he endeavoured also to claim the three following series from M^r Newton

These three series he pretended to have found by his own methods before <92r> the receipt of M^r Newtons Letter method. And yet they are not to be found without the inverse methods of series or methods of Regress, to which M^r Leibnitz was a stranger before the receipt of that Method | Letter. And even then he did not understand what he had received, but wrote to M^r Oldenburg for a further explication of it. Sed desideraverim, saith he, ut Clarissimus Newtonus nonnulla quoque amplius explicet; ut Originem Theorematis . . . . . . derivetur.

M^r Leibnitz for $\frac{{\mathrm{y}}^3-{\mathrm{x}}^3}{\mathrm{y}-\mathrm{x}}=\mathrm{y}\mathrm{y}+\mathrm{y}\mathrm{x}+\mathrm{x}\mathrm{x}$ wrote $\frac{d{\mathrm{y}}^3}{d\mathrm{y}}=3\mathrm{y}\mathrm{y}$, or rather finding the method {of} D^r Barrow to be founded upon clearer & more general principles, for his a & e he wrote dx & dy. For in his Letter of 21 Iune 1677 in which he first proposed his differential method, he wrote thus. Clarississimi Slusij methodum Tangentium nondum esse absolutam celeberrimo Newtono essentior: et jam a multo tempore rem Tangentium longe generalius tractavi, sciliect per differentias Ordinatarum. And a little after he adds Hinc nominando dy differentiam duarum proximarum Ore y & dx differentiam duarum proximarum x; patet $d{\mathrm{y}}^2$ esse $2\mathrm{y}d\mathrm{y}$ & $d{\mathrm{y}}^3$ esse $3{\mathrm{y}}^{2}d\mathrm{y}$ & ita porro: Which is the first Lemma of Slusius. Then putting y for the Abscissa & x for the Ordinate of a Curve he proposes this relation between them $\mathrm{a}+\mathrm{b}\mathrm{y}+\mathrm{c}\mathrm{x}+\mathrm{d}\mathrm{y}\mathrm{x}$ & $\mathrm{c}{\mathrm{c}}^2+\mathrm{f}{\mathrm{x}}^3+\mathrm{g}{\mathrm{y}}^2\mathrm{x}+\mathrm{h}\mathrm{y}\mathrm{x}\mathrm{x}⁤\mathrm{\&c}=0$ in a a curve whose tangent is to be drawn, & therein substituting $\mathrm{x}+d\mathrm{x}$ for x & $\mathrm{y}+d\mathrm{y}$ for y, & writes down first those terms in which dx & dy are not found with a line under them, then under that line he writes down those terms in which dx & dy are but of one dimension & draws another line & under that line he writes down those terms in which dx & dy are of more dimentions then one. And then adds: Vbi abjectis illis quæ sunt supra primam lineam qu ippe nihilo æqualibus per æquationem primam & abjectis illis quæ sunt infra secundam quia in illis duæ infinite parvæ in se invicem ducuntur, restabit tantum quicquid repesitur inter lineam primam et secundam. The after he had shewn by what remained between the lines to draw the tangent he added Quod coincidit cum Regula Slusiana, ostenditque eam statim occurrere hanc Methodum intelligenti. By hanc Methodum therefore he did not understand the method of Slusius but another Method which readily gave the method of Slusius; & this was the Method of D^r Barrow. For D^r Barrow thus describes his own method. 1 Inter computandum omnes abjicio terminos in quibus ipsarum a vel e potestas habetur, vel in quibus ipsæ ducuntur in se. etenim isti termini nihil valebunt 2 Post æquationem constitutam omnes abjicio terminos literis constantes quantitates notas seu determinatas designantibus, aut in quibus non habentur a vel e. Etenim illi termini semper ad unam æquationis partem adducti nihilum adæquabunt. These were D^r Barrows Rules, & these Rules are followed by M^r Leibnitz who sets between two lines the terms that are to be retained & above the upper line & below the lower those two sorts of terms that by D^r Barrows two Rules are to be rejected & rejects them accordingly. And that this was the original of M^r Leibnitz method of Tangents is farther confirmed by what he wrote in the Acta Eruditorum mensis Iunij 1686 pag 297. Malo autem, saith he, dx et similia adhibere quam literas pro illis, quia istud dx est modificatio quædam ipsius x &c ita ope ejus fit ut sola quando id fieri opus est litera cum suis scilicet potestatibus & differentialibus calculum ingrediatur & relationes transcendentes inter x & aliud exprimantur. Qua ratione etiam lineas transcendentes æquatione explicare licet. D^r Barrow used the letters a & e. M^r Leibnitz tells us that he chose rather to use the symbols dx & dy for the reasons here set down. And if his calculations in drawing of tangents be compared with those of D^r Barrow they will be found the same without any other difference then that of the symbols.

M^r Leibnitz first published this Method of tangents in the Acta Eruditorum mensis Octobis A. 1684 p. 467 with this title Nova methodus pro <92v> maximis et minimis itemque tangentibus quæ nec fractas nec irrationales quantitates moratur, & singulare pro illis calculi genus per G.G.L And in the end of it he added. Et hæc quidem initia sunt tantum Geometriæ cujusdam multo sublimioris ad difficillima et pulcherrima quæque etiam mistæ Matheseos Problemata pertingentis quæ sine calculo nostro differentiali; aut simili, non temere quisquam pari facilitate tractabit. It remains that we enquire how M^r Leibnitz came to know that this method of tangents stuck not at fractions or surds, & that it was the principles of a far sublimer Geometry reaching to all the most difficult & valuable Problemes in Mathematicks & what was the calculus similis here hinted at.

At the request of M^r Collins M^r Newton sent him his method of Tangents in a letter dated 10 Decem. 1672. It proved to be the same with that which Slusius about five weeks after sent to M^r Oldenburg but was derived from a better principle. For when M^r Newton had described it he subjoyned in the same Letter. Hoc est unum particulare vel Corollarium potius Methodi Generalis quæ extendit se utra molestum ullum calculum non modo ad ducendum Tangentes ad quasvis Curvas sive Geometricas sive Mechanicas - - - - - - surdis sunt immunes. And a copy of this Letter was sent by M^r Old. Iune 26 1676 to M^r Leibnits at Paris amongst the extracts of M^r Gregories Letters collected by M^r Collins as above, the same being still extant among them in the hand of M^r Collins.

And M^r Newton in his Letter of 13 Iune 1676 & sent by M^r Oldenburg to Paris Iune 26, after he had described his method of Series, subjoyned Ex his videre est quantum fines Analyseos per hujusmodi æquationes infinitas ampliantur: quippe quæ earum beneficio, ad omnia pene dixerim problemata, si numeralia Diophanti et similia excipias sese extendit: non tamen omnino universalis evadit nisi per ulteriores quasdam methodos eliciendi series infinitas — Sed quomodo in illis casibus procedendum sit jam non vacat dicere: ut neque alia quædam tradere quæ circa reductionem serierum infinitarum in finitas ubi rei natura tulerit, excogitavi.

And in his Letter dated 24 Octob. 1676 he represented how the Tract which he wrote five years before upon the method of series, was for the most part taken up by other things. That there was in it the method of Tangents of Slusius built upon another foundation which gave the method readily even without a particular Demonstration & made it more general so as not to stick at any surds, the Tangent being speedily drawn without any Reduction of the Equation which would often render the work immense. And that the same manners of working held in Questions de Maximus & Minimis & some other which in the said Letter he forbore to speake of. And that upon the same foundation the Quadratures of Curves became more easy: an example of which he gave in a Series which brake off & became finite when the Quadrature might be done by a finite equation. And that this method extended to inverse Problems of Tangents & others more difficult.

<93r>

An Account of the Book entituled Commercium Epistolicium Collinij et aliorum De Analysi promota.^[17]

This Commercium is composed of several Letters & Papers put together in order of time & copied from such Originals as are described in the title of every Letter & Paper; a Committee of the R. Society being appointed to examin the sincerity of the Originals & compare the copies therewith.

The first piece is a small Tract of M^r Newtons intituled Analysis per æquationes numero terminorum infinitas. M^r Newton in his Letter dated 24 Oct 1676 makes this mention of it. Eo ipso tempore quo Mercatoris Logarithmotechnia prodijt, communicatum est per amicum D. Barrow (tunc Matheseos Professorem Cantab) cum D. Collinio Compendium quoddam harum serierum, in quo significaveram Areas & Longitudines Curvarum omnium & Solidorum superficies et contenta, ex datis rectis; et vice versa ex his datis Rectas determinari posse: et Methodum ibi indicatam illustraveram diversis seriebus. M^r Collins in his Letter to M^r David Gregory dated 11 Aug. 1676 mentions it in this manner Paucos post menses quam editi sunt hi libri (viz^t Mercatoris Logarithmotechnia & Exercitationes Geometricæ Gregorij) missi sunt ad Barrovium Cantabrigiæ. Ille autem responsum dedit hanc infinitarum serierum doctrinam jam ante biennium a D. Isaaco Newton inventam fuisse & quibusvis figuris generaliter applicatam, simulque transmisit D. Newtoni opus manuscriptum. The last of the said books came out towards the end of the year 1668 & D^r Barrow sent the said Compendium to M^r Collins in Iuly following as appears by three of D^r Barrows Letters still extant. And And M^r Collins {}(who the same year & the thre or four years following gave notice of it to several of his friends, as appears by his Letters published in the Commercium) wrote thus of it to M^r Strode in a letter dated 26 Iuly 1672. Exemplar ejus [Logarithmotechnia] misi Barrovio . . . . . . . si cum meridiana claritate conferatur. Also M^r Oldenburg in a Letter to M^r Slusius dated 14 Septem 1669 & entred in the letter book of the R. S. gives an Account of it & cites several things out of it. This Tract was first printed by M^r Iones being found by him among the papers & in the hand writing of M^r Collins. It conteins a general method of Analysis teaching how to resolve finite equationes into infinite ones & how by the method of fluxions & moments to apply æquations both finite & infinite to the solution of all Problemes. It begins with three Rules or Lemmas. D^r Wallis published . . . . . . . . founds his said Analysis And the third Rule is to reduce fractions radicals & the roots of converging series . . . . . . . . . give the Quadrature of the circle. And M^r Newton A.C. 1665 by considering how to interpole this series found the series for the Arc whose sine is given. And by pursuing the method of interpolation found also the series for the dignities of Binomials set down in the beginning of his Letter dated 13 Iune 1676 the two first terms of which series are set down also in the latter end of the said Compendium. The time & manner of this invention M^r Newton, at the request of M^r Leibnitz, has described in his Letter dated 24 Octob. 1676. And the time is confirmed by M^r Collins in his ^✝[18]Letter to M^r Townley where he saith that in September 1668 M^r Mercator published his Logarithmotechnia, one of which he soon sent to D^r Barrow, who thereupon sent him up some papers of M^r Newtons, by which & former communications made thereof by the Author to the Doctor, it appears that the said method was invented some years before by the said M^r Newton & generally applied.

<93v>

1 Of the method of converging series.

D^r Wallis published his Arithmetica infinitorum in the year 1655 & by the 59^th Proposition of that book; if the Abscissa of any curvilinear figure be called x & m & n be numbers, & the Ordinate erected at right angles be ${\mathrm{x}}^{\frac{\mathrm{m}}{\mathrm{n}}}$: the area of the figure shall $\frac{\mathrm{n}}{\mathrm{m}+\mathrm{n}}{\mathrm{x}}^{\frac{\mathrm{m}+\mathrm{n}}{\mathrm{n}}}$. And this is assumed by M^r Newton as the first Rule upon which he founds his Analysis per series numero terminorum infinitas | quadrature of Curves.

By the 108^th Proposition of the said Arithmetica Infinitorum & by several other Propositions which follow therein; if the Ordinate be composed of two or more such Ordinates taken with their signes + or −, the area shall be composed of two or more such areas taken with their signes + or − respectively. And this is assumed by M^r Newton as the second Rule upon which he founs his said Analysis.

In the same Arithmetica Infinitorum D^r Wallis squared a series of Curves whose Ordinates were $1. 1-{\mathrm{x}}^2. {\overline{)1-{\mathrm{x}}^2}}^2. {\overline{)1-{\mathrm{x}}^2}}^3. {\overline{)1-{\mathrm{x}}^2}}^4$ &c. and shewed that if the series of their areas could be interpoled in the middle places the interpolation would give the Quadrature of the circle

And in his opus Arithmeticum published A.C. 1657 cap. 33 Prop. 68 he reduced the fraction $\frac{\mathrm{A}}{1-\mathrm{R}}$ by perpetual division into the series $\mathrm{A}+\mathrm{A}\mathrm{R}+\mathrm{A}{\mathrm{R}}^2+\mathrm{A}{\mathrm{R}}^3+\mathrm{A}{\mathrm{R}}^4+\mathrm{\&c}$.

M^r Newton (as he represented to M^r Leibnitz A.C. 1655 upon reading the Arithmetica infinitorum of D^r Wallis & considering how to interpole the series of Areas above mentioned, found the infinite series for the Arc whose Sine is given And pursuing the method of interpolation he found also the Quadrature of all Curves whose Ordinates are the dignities of binomials affected with indices whole fract or surd, affirmative or negative; as at the request of M^r Leibnitz, he has explained at large in his Letter dated 24 Octob. 1676 & long since printed by D^r Wallis.

Vicount Brounker squared the Hyperbola by this series $\frac{1}{1\times 2}+\frac{1}{3\times 4}+\frac{1}{5\times 6}+\frac{1}{7\times 8}+\mathrm{\&c}$: that is by this $1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\frac{1}{6}+\frac{1}{7}-\frac{1}{8}+\mathrm{\&c}$, conjoyning every two terms into one. And this Quadrature was published in the Phil. Transactions in April 1668.

M^r Mercator soon after published a demonstration of this Quadrature by the Division of D^r Wallis above described, & soon after that M^r Iames Gregory published a Geometric demonstration thereof. And these books were a few months after sent by M^r Collins to D^r Barrow at Cambridge & by D^r Barrow communicated to M^r Newton & thereupon D^r Barrow mutually sent to M^r Collins a Tract of M^r Newton's entituled Analysis per æquationes numero terminorum infinitas. For M^r Newton had improved his invention into a general method of Analysis: but M^r Mercator proceeded no further then to demonstrate my Lord Brunker's Quadrature by the Division of D^r Wallis tho he lived many years after. Neither did M^r Gregory think of improving it into a method till he had notice of what M^r Newton had done.

This Analysis is the first piece printed in the Commercium. It is the Compendium mentioned in M^r Newtons Letter dated Octob. 24 1676, & was sent to M^r Collins in Iuly 1669 as appears by the dates of three of D^r Barrow's Letters still extant. And M^r Collins &c.

<94r>

^[19] An Account of the Book entituled
Commercium Epistolicum D. Iohannis Collinij & aliorum De Analysi promota.

This Commercium is composed of several Letters & Papers put together in order of time & copied from such Originals as are described in the Title of every Letter & Paper; a Committee of the R. Society being appointed to examin the sincerity of the Originals & compare the Copies therewith. We shall here give you an Account of the matters they contein under these four Heads. 1 Of the method of converging Series. 2 Of the method of fluxions & moments 3 Of the Differential method. 4 Of the three Papers entituled Epistola de Lineis Opticis, Schediasma de resistrentia Medij, & Tentamen de motuum cœlestium causis.

1 Of the Method of converging Series.

M^r Newton in his Letter of 24 Octob. 1676^[20] represented that a little before the plague (which raged in London in 1665) he found his method of Series & upon the coming abroad of M^r Mercators Logarithmotechnia communicated to M^r Iohn Collins by D^r Barrow a Compendium of that Method, & five years before the writing of his Letter (that is A. 1671) wrote a larger tract upon that method with a designe to have published it; but upon disputes arising about his Theory of colours, for the sake of quiet left off before he had finished the Tract & intermitted the further consideration of these matters till the writing of his Letter of Iune 13^th 1676.^[21]

D^r Wallis in his Opus Arithmeticum published A. 1657, cap. 33, Prop. 68, reduced the fraction $\frac{\mathrm{A}}{1-\mathrm{R}}$ by perpetual division into the series $\mathrm{A}+\mathrm{A}\mathrm{R}+\mathrm{A}{\mathrm{R}}^2+\mathrm{A}{\mathrm{R}}^3+\mathrm{A}{\mathrm{R}}^4+\mathrm{\&c}$.

Vicount Brounker squared the Hyperbola by this series $\frac{1}{1\times 2}+\frac{1}{3\times 4}\times \frac{1}{5\times 6}+\frac{1}{7\times 8}+\mathrm{\&c}$, that is by this $1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\frac{1}{6}+\frac{1}{7}-\frac{1}{8}+\mathrm{\&c}$ conjoyning every two terms into one. And the Quadrature was published in the Ph. Transactions in April 1668.^[22]

N. Mercator soon after published a Demonstration of this Quadrature by the Division of D^r Wallis, & soon after that M^r Iames Gregory published a Geometrical Demonstration thereof. And these books were a few months after, sent by M^r Collins to D^r Barrow at Cambridge^[23] & by D^r Barrow communicated to M^r Newton.

Whereupon D^r Barrow mutually received from M^r Newton & sent to M^r Collins a Tract of M^r Newtons entituled Analysis per æquationes numero terminorum infinitas. And this is the Compendium above mentioned & the first Tract in the Commercium. It was sent to M^r Collins in Iuly 1669 as appears by the dates of three of D^r Barrows Letters still extant.^[24] And M^r Collins in his Letter to M^r Strode dated 26 Iulij 1672^[25] makes this mention thereof: Exemplar ejus [Logarithmotechniæ] misi Barrovio Cantabrigiam qui quasdam Newtoni chartas extemplo remisit: E ^a[26]quibus & alijs, quæ olim ab Auctore cum Barrovio communicata fuerant, patet illam Methodum a dicto Newtono aliquot annis antea excogitatam & modo universali applicatam fuisse: ita ut ejus ope in quavis Figura Curvilinea proposita, quæ una vel pluribus proprietatibus definitur Quadratura vel Area dictæ figuræ, accurata si possibile sit, sin minus infinite vero propinqua; Evolutio vel longitudo Lineæ curvæ; centrum gravitatis Figuræ, solida ejus rotatione genita & eorum superficies; sine ulla radium extractione obtineri queant. Postquam intellexerat D. Gregorius hanc methodum a D. Mercatore in Logarithmotechnia usurpatam, & Hyperbolæ qudrandæ adhibitam, quamque adauxerat ipse Gregorius, jam universalem redditam esse omnibusque Figuris applicatam; acsi studio eandem acquisivit, multumque in ea enodanda desudavit. Vterque D. Newtonus & Gregorius in animo habet hanc methodum exornare: D. Gregorius autem D. Newtonum <94v> primum ejus Inventorem anticipare haud integrum ducit. And in another Letter written to M^r Oldenburg to be communicated to M^r Leibnitz & dated 14 Iune 1676,^[27] M^r Collins adds: Hujus autem Methodi ea est præstantia, ut cum tam late pateat, ad multam hæreat difficultatem. Gregorium autem aliosque in ea fuisse opinione arbitror, ut quicquid uspiam antea de hac re innotuit, quasi dubia diluculi lux fuit, si cum meridiana claritate conferatur.

In this Compendium among the examples for illustrating the method, were these. Let the Radius of a circle be 1, the arc z, & the sine x & the Equations for finding the arc whose sine is given & the sine whose arc is given, will be
$\mathrm{z}=\mathrm{x}+\frac{1}{6}{\mathrm{x}}^3+\frac{3}{40}{\mathrm{x}}^5+\frac{5}{112}{\mathrm{x}}^7+\frac{35}{1152}{\mathrm{x}}^9+\mathrm{\&c}$
$\mathrm{x}=\mathrm{z}-\frac{1}{6}{\mathrm{z}}^3+\frac{1}{120}{\mathrm{z}}^5-\frac{1}{5040}{\mathrm{z}}^7+\frac{1}{362880}{\mathrm{z}}^9-\mathrm{\&c}$.

M^r Collins gave M^r Gregory notice of this method in autumn 1669 & M^r Gregory by the help of one of M^r Newtons Series aftter a years study found the method in December 1670, & two months after in a letter dated 15 Feb 1671 sent several Theorems found thereby to M^r Collins with leave to communicate them freely. And M^r Collins was very free in communicating what he had received both from M^r Newton & M^r Gregory as appears by his Letters printed in the Commercium. Amongst the series which M^r Gregory sent in the said Letter were these two. Let the radius of a circle be r the arc a & the tangent t & the equations for finding the arc whose tangent is given & the tangent whose arc is given will be these $\mathrm{a}=\mathrm{t}-\frac{{\mathrm{t}}^3}{3{\mathrm{r}}^2}+\frac{{\mathrm{t}}^5}{5{\mathrm{r}}^4}-\frac{{\mathrm{t}}^7}{7{\mathrm{r}}^6}+\frac{{\mathrm{t}}^9}{9{\mathrm{r}}^8}-\mathrm{\&c}$
$\mathrm{t}=\mathrm{a}+\frac{{\mathrm{a}}^3}{3{\mathrm{r}}^2}+\frac{{\mathrm{2a}}^5}{15{\mathrm{r}}^4}+\frac{{\mathrm{17a}}^7}{315{\mathrm{r}}^6}+\frac{{\mathrm{62a}}^9}{2835{\mathrm{r}}^8}+\mathrm{\&c}$

In this year (1671) M^r Leibnitz published two Tracts at London the one dedicated to the R. Society, the other dedicated to the Academy of Sciences at Paris, & in the dedication of the first mentioned his correspondence with M^r Oldenburg. He staid in London conversing with M^r Oldenburgh, M^r Boyle D^r Pell, M^r Collins &c till February or March 1673 & then went to Paris, & continuing his correspondence with M^r Oldenburg & M^r Collins wrote the next year in Iuly tht he had a wonderfull Theoreme which gave the Area of a Circle or any Sector thereof exactly in a series of rational numbers, & in October that he had found the circumference of a circle in a series of very simple numbers, & that by the same method [ so he calls the said Theoreme] any Arc whose sine was given might be found in a like series tho the proportion to the whole circumference be not known. His Theoreme therefore was for finding any Sector or Arc whose sine was given. If the proportion of the Arc to the whole circumference was not known, the Theoreme or Method gave him only the Arc: if it was known it gave him also the whole Circumference & therefore it was the first of M^r Newtons two Theorems above mentioned. But the Demonstration of this Theoreme M^r Leibnitz wanted & therefore he had not invented the Theoreme himself but had received it from some other hand. For in his Letter of 12 May 1676 he desired M^r Oldenburg to procure the Demonstration from M^r Collins, meaning the method by which M^r Newton had invented it.

M^r Oldenburg in a Letter dated 15 April 1675, sent to M^r Leibnitz eight of M^r Newtons & M^r Gregories series amongst which were M^r Newtons two series above mentioned for finding the Arc whose sine was given & the sine whose Arc was given & <95r> M^r Gregories Series above mentioned for finding the Arc whose Tangent was given, & the Tangent whose Arc was given. And M^r Leibnitz in his answer dated 20 May 1675 acknowledged the receipt of this Letter in these words: Literas tuas multa fruge Algebraica refertas accepi pro quibus tibi et doctissimo. Collinio gratias ago. Cum nunc præter ordinarias curas Mechanicis imprimis negotijs distrahar non potui examinare series quos misistis, ac cum meis comparare. Vbi fecero perscribam tibi sententiam meam: nam aliquot jam anni sunt quod inveni meas via quadam sic singulari.

But M^r Leibnitz never took any further notice of his having received these Series, nor how his own differed from them, nor ever produced any other Series as his own then those which he had received in this Letter, or numeral series derived from them in particular cases. And what he did with Gregories series for finding the Arc whose Tangent is given he has told us in the Acta Eruditorum mensis Aprili 1691 pag. 178. Iam Anno 1675, saith he, compositum habebam opusculum Quadraturæ Arithmeticæ ab amicis ab illo tempore lectum &c. By a Theoreme for transmuting of figures like those of M^r Gregory & D^r Barrow he had now found a Demonstration of this series, or way of inventing it, & therefore communicated it as his own; but still wanted M^r Newtons method for Demonstrating the rest: & meeting with a pretence to ask for it, he wrote to M^r Oldenburg the following Letter dated at Paris 12 May 1676.

Cum Georgius Mohr Danus nobis attulerit communicatam sibi a Doctissimo Collonio vestro expressionem rationis inter Arcum & sinum per infinitas series sequentes: Posito Sinu x, Arcu z, Radio 1.
$\mathrm{z}=\mathrm{x}+\frac{1}{6}{\mathrm{x}}^3+\frac{3}{40}{\mathrm{x}}^5+\frac{5}{112}{\mathrm{x}}^7+\frac{35}{1152}{\mathrm{x}}^9+\mathrm{\&c}$
$\mathrm{x}=\mathrm{z}-\frac{1}{6}{\mathrm{z}}^3+\frac{1}{120}{\mathrm{z}}^5-\frac{1}{5040}{\mathrm{z}}^7+\frac{1}{362880}{\mathrm{z}}^9-\mathrm{\&c}$
Hæc INQVAM, cum nobis attulerit ille, quæ mihi valde ingeniosa videntur, & posterior imprimis series elegantiam quandam singularem habeat: ideo rem gratam mihi feceris, Vir Clarissime, si demonstrationem transmiseris. Habebis vicissim mea his longe diversa circa hanc rem meditata, de quibus jam aliquot abhinc annis ad te perscripisse credo, demonstratione tamen non addita quam nunc polio. Oro ut Cl. Collinio multam a me salutem dicas: is facile tibi materiam suppeditabit satisfaciendi desiderio meo. Here the word INQVAM one would think that he had never seen these two series before & that his diversa circa hanc rem meditata were something else then one of the Series which he had received from M^r Oldenburg the year before, & a Demonstration thereof which he was now polishing to make the present an acceptable recompence for M^r Newtons method.

Vpon the receipt of this Letter M^r Collins & M^r Oldenburg wrote pressingly to M^r Newton desiring that he himself would describe his own Method to be communicated to M^r Leibnitz. Whereupon M^r Newton wrote his Letter of 13^th Iune 1676, describing therein the method of series as he had done before in the compendium above mentioned; but with this difference. There he described at large the reduction of fractions & radicals into series by division & extraction of roots, & only set down the two first terms of the series into which the dignity of a binomial might be reduced, here he described at large the reduction of the dignity of a binomial into a Series & only touched upon the reduction by division & extraction of roots. And Among the examples there were series for finding the Number whose Logarithm is given & for finding the right sine & versed sine whose arc is given. This Letter was sent to Paris Iune 26^th 1676 together with a M{/}S drawn up by M^r Collins conteining extracts of M^r Iames Gregories Letters.

For M^r I. Gregory died neare the end of the year 1675, & M^r Collins at the request of M^r Leibnitz & some others of the Academy of <95v> Sciences drew up extracts of his Letters, & the Collection is still extant in the hand writing of M^r Collins with this title. Extracts from M^r Gregories Letters to be lent M^r Leibnitz to peruse who is desired to return the same to you. And that they were sent is affirmed by M^r Collins in his Letter to M^r David Gregory the brother of the deceased dated 11 August. 1676, & further by the Answers of M^r Leibnitz & M^r Tschurnhause.

The Answer of M^r Leibnitz directed to M^r Oldenburg & dated 27 Aug. 1676 begins thus, Literæ tuæ die 26 Iulij datæ ac memorabiliora circa rem Analyticam continent quam multa volumina spissa de his rebus edita. Quare tibi pariter ac Clarissimis viris Newtono ac Collonio gratias ago qui nos participes tot meditationum egregiarum esse voluistis. And towards the end of the Letter, after he had done with the contents of M^r Newton's Letter he proceeds thus. Ad alia tuarum Literarum venio quæ doctissimus Collinius communicare gravatus non est. Vellem adjecisset appropinquationis Gregorianæ linearis Demonstrationem. Credo tamen aliam haberi simpliciorem, etiam in infinitum euntem, quæ fiat sine ulla bisectione anguli, imo sine supposita circuli constructione; solo rectarum ductu. Vellem Gregoriana omnia conservari. Fuit enim his certe studijs promovendis aptissimus. And the Answer of M^r Tschurnhause dated 1 Sept. 1676, after he had done with M^r Newton's Letter about Series concludes thus. Similia porro quæ in hac re præstitit eximius ille Geometra Gregorius memoranda certe sunt, et quidem optimæ famæ ipsius consulturi, qui ipsius relicta Manuscripta luci publicæ ut exponantur operam navabunt. In the first part of this Letter where M^r Tschurnhause speaks of M^r Newton's Series, he saith that he looked over them cursorily to see if he could find the Series of M^r Leibnitz for squaring the circle or Hyperbola. If he had searched for it in the extracts of Gregories Letters he might have found it in the Letter of 15 Feb. 1671 above mentioned. For the MS of those extracts with that Letter therein is still extant in the hand writing of M^r Collins.

But yet M^r Leibnits having found a new Demonstration of that series, persisted in his design of making himself the inventor thereof. and tho he had now received it twice from M^r Oldenburg yet in his Letter of 27 August 1676 he sent it back to him by way of recompence for M^r Newtons method, pretending that he had found it three years before or above; that is, two years before he received it in M^r Oldenburghs Letter of April 15^th 1675; at which time he did not know it to be his own, as appears by his Answer of May 20^th 1675 above mentioned. But in cases of controversy its against the law of all nations to admit any man to be a witness for himself, & his affirming that he had found it above three years before must not be taken in evidence. It lies upon him to prove it. And if he had found it so long ago yet Gregory had sent it to Collins & Collins had begun to communicate it before that time And to give himself a cleare title to that series it lies upon him to prove further that he had invented it even before the month of Iuly 1669. For by his Theoreme of Transmutations he found only how to reduce the Area of a Circle to the Area of a Curve whose abscissa is x & Ordinate $\frac{1}{1+\mathrm{x}\mathrm{x}}=\mathrm{y}$. The squaring of this Curve by the series $\mathrm{x}-\frac{1}{3}{\mathrm{x}}^3+\frac{1}{5}{\mathrm{x}}^5-\frac{1}{7}{\mathrm{x}}^7+\frac{1}{9}{\mathrm{x}}^9$, &c was not his invention. M^r Newton in the year 1669 communicated it to M^r Collins in the said Analysis pag. 6, lin. ult. His words are: Eodem modo <96r> si sit $\frac{1}{1+\mathrm{x}\mathrm{x}}=\mathrm{y}$, dividendo prodibit $\mathrm{y}=1-{\mathrm{x}}^2+{\mathrm{x}}^4-{\mathrm{x}}^6+{\mathrm{x}}^8$, &c Vnde (per Regulam secundam) erit [area] $\mathrm{ABDC}=\mathrm{x}-\frac{1}{3}{\mathrm{x}}^3+\frac{1}{5}{\mathrm{x}}^5-\frac{1}{7}{\mathrm{x}}^7+\frac{1}{9}{\mathrm{x}}^9$, &c

In the Acta Eruditorum mensis Ianuarij 1689 pag. 37 M^r Leibnitz making mention of the method of series, represents that Mercator found them by division & Newton enlarged the method by extractions of roots both pure & affected, & then adds: A me ut obiter hic dicam, methodo serierum promovendæ præter transformationem irrationalium linearum in rationales symmetras (voco autem rationales quarum Ordinatæ semper ex abscissis haberi possunt in numeris rationalibus) excogita est ratio pro curvis transcendentibus datis, ubi ne extractio quidem lacum habet. Assumo enim seriem arbitrariam, eamque ex legibus problematis tractando obtineo ejus coefficientes. Mercator used the Division of D^r Wallis & found not one new series. The Transmutation of figures is no part of the method of series. It is only a Lemma for doing that in some few cases without the extraction of roots which may be more readily done by the extraction of roots. The other method of assuming an arbitrary series is M^r Newton's. In his Letter of 24 Octob 1676, he set it down in this sentence. Altera [methodus consistit] tantum in assumptione seriei pro quantitate qualibet incognita ex qua cætera commode derivari possint et in collatione terminorum homologorum æquationis resultatis ad eruendos terminos assumptæ seriei.

In the same Letter of 27 Aug. 1676, after M^r Leibnitz had described his quadrature of the circle & equilateral Hyperbola, he added: ^[28]Vicissim ex seriebus regressum pro Hyperbola hanc inveni. Si sit numerus aliquis unitate manor $1-\mathrm{m}$ ejusque logarithmus Hyperbolicus l. Erit $\mathrm{m}=\frac{\mathrm{l}}{1}-\frac{{\mathrm{l}}^2}{1\times 2}+\frac{{\mathrm{l}}^3}{1\times 2\times 3}-{\mathrm{l}}^{4}1\times 2\times 3\times 4$ &c. Si numerus sit major unitata, ut $1+\mathrm{n}$, tunc pro eo inveniendo mihi etiam prodijt Regula, quæ ex dato arcu Sinum complementi exhibet. Nempe sinus Complementi $=1-\frac{{\mathrm{a}}^2}{1\times 2}+\frac{{\mathrm{a}}^4}{1\times 2\times 3\times 4}-\mathrm{\&c}$. Sed posteæ quoque deprehendi ex ea, illam nobis communicatam pro inveniendo sinu recto qui est $\frac{\mathrm{a}}{1}-\frac{{\mathrm{a}}^3}{1\times 2\times 3}+\frac{{\mathrm{a}}^5}{1\times 2\times 3\times 4\times 5}+\mathrm{\&c}$ posse demonstrari. Thus M^r Leibnitz put in for the coinvention of these four series, tho the method of finding them was sent him at his own request, & he did not yet understand it. For in the same Letter he desired M^r Newton to explain it further His words are. Sed desideraverim ut clarissimus Newtonus nonnulla quoque amplius explicet; ut Originem Theorematis quod initio ponit: Item Modum quo quantitates p, q, r in suis Operationibus invenit: Ac denique quomodo in methodo Regressuum se gerat, ut cum ex Logarithmo quærit Numerum. Neque enim explicat quomodo id ex methodo sua derivetur. He pretended to have found two series for the Number whose Logarithm was given & yet in the same Letter desired M^r Newton to explain to him the method of finding those very two series.

When M^r Newton had received this Letter he wrote back that all he said four Series had been communicated by him to M^r Leibnitz, the two first being one & the same series in which the letter <96v> l was put for the Logarithm with its sine + or −, & the third being the excess of the Radius above the versed sine for which a series had been sent him. Whereupon M^r Leibnitz desisted from his claim. But when M^r Newton had further explained his methods of Regression, M^r Leibnitz in his Letter of 12 Iuly 1677 replied that he found by his old papers that he had formerly used one of those methods; but in the example which he had then by chance made use of, there being produced nothing elegant, he had out of his usual impatience neglect to use it any further. But he is not a witness in his own case. It lies upon him to prove that he had it in his old papers. Otherwise the method must go for M^r Newton's. Could M^r Leibnitz reject & forget inverse method of series, as useless? Could he have an elegant direct series which would not have given him an elegant example?

Yet there is an invention of series due to M^r Leibnitz It is of such series whose terms may be all summed up. The method consists in subducting from any regular series all the Terms except the first, or two first, or three or four first. From the series $\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\mathrm{\&c}$ subduct all the terms but the first & there will remain $1=\frac{1}{1\times 2}+\frac{1}{2\times 3}+\frac{1}{3\times 4}+\frac{1}{4\times 5}+\mathrm{\&c}$. And from this series take all the terms but the first & there will remain $\frac{1}{2}=\frac{2}{1\times 2\times 3}+\frac{2}{2\times 3\times 4}+\frac{2}{3\times 4\times 5}+\frac{2}{4\times 5\times 6}+\mathrm{\&c}$. And from the first series take all the terms but the two first & there will remain $\frac{3}{2}=\frac{2}{1\times 3}+\frac{2}{2\times 4}+\frac{2}{3\times 5}+\frac{2}{4\times 6}+\mathrm{\&c}$. And from this series $\frac{1}{1}+\frac{1}{3}+\frac{1}{5}+\frac{1}{7}+\frac{1}{9}+\mathrm{\&c}$ take all the terms but the first & there will remain $1=\frac{2}{1\times 3}+\frac{2}{3\times 5}+\frac{2}{5\times 7}+\frac{2}{7\times 9}+\mathrm{\&c}$

The third Rule is to resolve fractions & radicals into converging series by division & extraction of roots simple or affected, & then by the first & second Rules to find the areas belonging to the several terms of the Ordinate.

M^r Newton in his Letter dated 13 Iune 1676 set down a Theoreme for resolving any dignity of any binomial into a converging series, & the two first terms of this series are set down in the end of the above-mentioned Compendium: which shews that the Theorem was known to him in the year 1669. This Theoreme suffices for the reduction of all fractions & unaffected radicals into converging series. M^r Newton being desired by M^r Leibnitz to tell him the original of this Theorem wrote back in his Letter of 24 Octob. 1676 that a little before the plague which raged in London 1665 upon reading the Arithmetica infinitorum of D^r Wallis & trying to interpole this series $\mathrm{x}. \mathrm{x}-\frac{1}{3}{\mathrm{x}}^3. \mathrm{x}-\frac{2}{3}{\mathrm{x}}^3+\frac{1}{5}{\mathrm{x}}^5. \mathrm{x}-\frac{3}{3}{\mathrm{x}}^3+\frac{3}{5}{\mathrm{x}}^5-\frac{1}{7}{\mathrm{x}}^7$. &c he found first the series for the area of the segment of a circle & by pursuing the method of interpolation he found the said Theorem for resolving the dignity of a binomial into a converging series, & thereby of squaring all curves whose Ordinates could be resolved into such series. And soon after he observed that the same series might be found by perpetual division & by extraction of unaffected roots. And pursuing this method he found out also the extraction of affected roots described in the said compendium, & the extraction of fluent quantities out of Equations involving their fluxions mentioned in his Epistle dated 24 Octob. 1676, & the Resolution of Problemes into converging series by assuming the terms of the series & determining them gradually by the conditions of the Probleme

Now that he