Letter from John Keill to Newton, c. 23–24 February 1715

<69r>

Honoured Sir

I returned but last week to Oxford, but whilst I was in Northampton Shire I began to think on M^r Leibnitz's problem, and I think I have hit upon the Solution of it, it not being difficult to any that understand Fluxions, The method I used was this

Suppose a series of curves of the same nature which have all the same Axis AB and Vertex A. Let AI 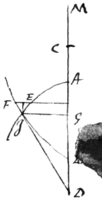be one of them and BI the curve which cuts it at right angles, Because the curve AI is given its subnormal GD will be given, But this subnormal is the subtangent of the curve BI. therefore $\mathrm{FE}:\mathrm{EI}\colon\colon \mathrm{IG}:\mathrm{GD}$. that is calling AG x and IG y: $\stackrel{·}{\mathrm{y}}:-\stackrel{·}{\mathrm{x}}\colon\colon \mathrm{y}:\mathrm{GD}$. (here $\stackrel{·}{\mathrm{x}}$ must be negative for when y increases x decreases, by this Analogy I got an equation and from the equation I obtain a value of the Latus Rectum. This value of the latus Rectum I put in its Room in the equation which expresses the nature of the curve proposed and I have a new equation expressed by x y and their fluxions which gives the nature of the curve required. For example suppose the curve AI a Parabola whose equation is $2\mathrm{l}\mathrm{x}=\mathrm{y}\mathrm{y}$ then $\mathrm{GD}=\mathrm{l}$ and $\stackrel{·}{\mathrm{y}}:-\stackrel{·}{\mathrm{x}}\colon\colon \mathrm{y}\frac{-\stackrel{·}{\mathrm{x}}\mathrm{y}}{\mathrm{y}}=\mathrm{l}$
this value of l being put in the equation for the parabola gives $\frac{-2\mathrm{x}\stackrel{·}{\mathrm{x}}\mathrm{y}}{\stackrel{·}{\mathrm{y}}}=\mathrm{y}\mathrm{y}$ and $-2\mathrm{x}\stackrel{·}{\mathrm{x}}=\mathrm{y}\stackrel{·}{\mathrm{y}}$ hence ${\mathrm{a}}^2-{\mathrm{x}}^2=\frac{1}{2}{\mathrm{y}}^2$ or $2{\mathrm{a}}^2-2{\mathrm{x}}^2={\mathrm{y}}^2$ Hence the curve BI is an Ellipse whose Greater Axis is double in Power to its lesser. If the curves Proposed are Hyperbolas, whose center is C transverse Axis $\mathrm{AM}=2\mathrm{a}$, their equation is $\frac{2\mathrm{l}\mathrm{a}\mathrm{x}+\mathrm{l}{\mathrm{x}}^2}{2\mathrm{a}}={\mathrm{y}}^2$ and the Subnormal is $\frac{\mathrm{l}\mathrm{a}+\mathrm{l}\mathrm{x}}{2\mathrm{a}}={\mathrm{y}}^2$ and $\stackrel{·}{\mathrm{y}}:-\stackrel{·}{\mathrm{x}}\colon\colon \mathrm{y}:\frac{\mathrm{l}\mathrm{a}+\mathrm{l}\mathrm{x}}{2\mathrm{a}}$ hence $\mathrm{l}=-\frac{2\mathrm{a}\mathrm{y}\stackrel{·}{\mathrm{x}}}{\overline{\mathrm{a}+\mathrm{x}}\times \stackrel{·}{\mathrm{y}}}$ which value of l being put in the equation of the Hyperbola gives $\frac{-4{\mathrm{a}}^2\mathrm{y}\mathrm{x}\stackrel{·}{\mathrm{x}}-2\mathrm{a}\mathrm{y}{\mathrm{x}}^2\stackrel{·}{\mathrm{x}}}{2\mathrm{a}\times \overline{\mathrm{a}+\mathrm{x}}\times \stackrel{·}{\mathrm{y}}}={\mathrm{y}}^2$ and $\frac{-{\mathrm{x}}^2\stackrel{·}{\mathrm{x}}-2\mathrm{a}\mathrm{x}\stackrel{·}{\mathrm{x}}}{\mathrm{x}+\mathrm{a}}=\mathrm{y}\stackrel{·}{\mathrm{y}}$ that is $-\mathrm{x}\stackrel{·}{\mathrm{x}}-\mathrm{a}\stackrel{·}{\mathrm{x}}+\frac{{\mathrm{a}}^2\stackrel{·}{\mathrm{x}}}{\mathrm{a}+\mathrm{x}}=\mathrm{y}\stackrel{·}{\mathrm{y}}$ or $\frac{2{\mathrm{a}}^2\stackrel{·}{\mathrm{x}}}{\mathrm{a}+\mathrm{x}}=2\mathrm{x}\stackrel{·}{\mathrm{x}}+2\mathrm{a}\stackrel{·}{\mathrm{x}}+2\mathrm{y}\stackrel{·}{\mathrm{y}}$ and taking the Fluents we have Fluent $\frac{2{\mathrm{a}}^2\stackrel{·}{\mathrm{x}}}{\mathrm{a}+\mathrm{x}}$ + a Given quantity $={\mathrm{x}}^2+2\mathrm{a}\mathrm{x}+{\mathrm{y}}^2$. From which we draw the followin construction. at the center C Asymptotes CA CE describe the hyperbola LGH whose rectangle inscribed is $=2{\mathrm{a}}^2$. make BF perpendicular to BA and = to it. and make up the rectangle MF in AB take any point N and let NO be a mean proportional {between} NA and NM, at the center O with the Radius OP whose Square is equal to the rectangle MF minus the Hyperbolick space BNGR describe the Arch PQ and let NG produced meet with it in P the point P will be the curve required.

<69v>

The curve will be an oval Figure whose greatest Ordinate is at A. M^r Stirling an undergraduate here has likewise solved the Problem, I have also received the solution of this and several other Problems from M^r Pemberton. If you please you may put mine in the Transactions I am Sir

your most obliged Humble Servant

John Keill

For
The Honoured
Sir Isaac Newton
at his house in S^t Martins Street
near Leicester Fields

Westminster