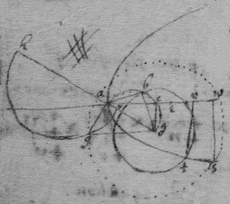Newton's Waste Book (Part 3)
How to Draw Tangents to Mechanicall Lines
Lemma.
1[Editorial Note 1] [1] If one body move from a to b in the same time in which another moves from a to c & a 3d body move from a with motion compounded of those two it shall (completeing the parallelogram abcd ) move to d in the same time. For those motion would severally {carry} it the one from a to c the other from c to d &c
[2] 2 In the description of any Mechanicall line what ever, there may bee found two such motions which compound or make up the motion of the point describeing it, whose ∼ motion being by them found by the Lemma, its determinacon shall bee in a tangent to the mechanicall line.
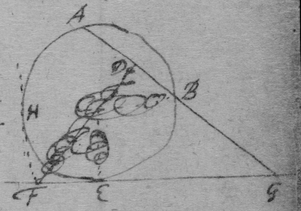
[3] Example the 1st. If abe is an helix, described by the point b the line ab increasing uniformely whilest it also circulates uniformely about the center a Let the radius of the circle dmbd bee ab. & let {dmb } measure the quantity of the giration of ab (viz ad touching the helix at the center) let bf be a tangent to the circle dmbd . then is the motion of the point b towards c to its motion towards f , as ab , to dmb . therefore make . & (by the Lemma) the diagonall bg shall touch the helix in b. Or make . & . the diagonall bg shall touch the helix. (the length of bf may be thus found viz; .)
[4] Example the 2d. If the center of a globe moves uniformely in a streight line parallel to eh, whilest the Globe uniformely girates. Each point in the Globe will describe a Trochoides: to which a the point b I thus draw a tangent. Draw the radii ab & bc perpendicular to it then is the circular motion of the point b determined in the line bc , & its progressive in bf . If therefore I make to as the circular motion of the point b to its progressive the Diagonall (by the Lemma) bg shall touch the Trochoides in b . As if the Globe roule upon the plaine eh , & I make . & . then doth the Diagonall bg touch the Trochoides. (Or be , passing through the point in which the globe & plaine touch, is a perpendicular to the {Trochoides}.
[6] [Scholium. The tangents of Geometricall lines may be found by their descriptions {after} the same manner. As the Ellipsis (whose foci are a & f ) being described by the thred abf the thred ab lengthens so much as the thred bf shortens, or the point b moves equally from a & to f. Therefore I take . & . & the diagonall bg will touch the Ellipsis in b ]. (This should follow the 3d Example's substitute) See folium 57.
[7] Although the nature of a Mechanicall line is not knowne from its description but from some other principle yet may a tangent be drawne to it by the same method.
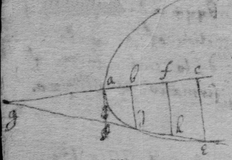
As if be is an Hyperbola. tad its asymptote & . & . to draw a tangent to the line ghm , I consider that, increasing of acdf ∶ increasing of abde ∷ increase of gp ∶ increase of ph ∷ motion of the point h towards k ∶ motion of h towards r , if . Therefore I make {} . & the diagonall hs or wh shall touch the line ghm . Or if . . . . then doth xhs touch the line ghm at h .
Tangents to mechanicall lines may sometimes bee found by finding such a point which is immoveable in respect of the line described & also doth {{illeg}vary} in distance from the describing point. for the {Sicunf{illeg}} through that point. Thus in the Trochoides when the point toucheth the plaine eh tis immoveable, & tis ever equidistant from the describing point b ({illeg} both of them fin{illeg} points in the Globe). Therefore the line {illeg} drawne {from} the describeing point to the touch point of the Globe & plaine is perpendicular to {the} trochoides. But in the spirall though the point {illeg} is {illeg} from that {illeg}.
[8] Instead {in the} third example {illeg} {illeg} {illeg}. Therefore absolute & whole motion of b towards c (or acf ) ∶ whole motion of b towards d (or ed ). Soe that makeing . {} & . The point b will be moved to the line ce & ed in same times which cannot bee unlesse it move to e (their common intersection). The point b therefore move in the line be which doth therefore touch the Quadratrix at b : (The same is done by makeing . & drawing the tangent be through the common intersection of ed & aem .)
To resolve Problems by motion the 6 following propositions are necessary & suffcient.
May 16. 1666.
[13] If the body a in the perimeter of the circle or sphære adce moveth towards its center b . its velocity to each point of that circumference is as the cordes ad , ac , ae , drawne from that body to those points are.
Prop 2. If the triangles adc , aec are alike though in diverse planes; & 3 bodys move from the point a uniformely & in equall times, the first to d , the 2d to e , the 3d to c : then is the 3d's motion compounded of the motion of the 1st & {2d.}
Note that by a body is meant its center of gravity.
Prop. 3. All the points of a body keeping parallel to it selfe are in equall motion.
Prop. 4. If a body onely move circularly about some axis, the motion of its points are as their distances from that axis. Call these 2 simple motions
Prop. 5. If the motion of a body is considered as mixed of simple motions: the motions of all its points are compounded of their simple motions, so as the motion towards c (in prop 2d) is compounded of the motion towards d & e .
Note that all motion is reducible to one of these 3 cases: & in the 3d case any line may bee taken for {the} axis (or if a line or superficies {move} in plano any point of that plaine may bee taken for the center) of motion.
[14] Prop. 6. If the lines {illeg} ah being moved doe continually intersect; I describe the Trapezium abcd {illeg} its diagonall ac : & say that the proportion & position of these five lines ab , ad , ac , cb , cd being determined by {requisite data} they shall designe the proportion & position of these 5 motions: {illeg} of the point a fixed in the {illeg} moveing towards b ; of the point a fixed in the line ah {illeg} moveing towards d ; of the intersection point a moveing in the plaine abcd towards c (for those 5 lines are {illeg} in the same plaine though {illeg} & ah may only touch the plaine in their intersection point): of the intersection point a moveing in the line ae parallely to cb & according to the order of the letters c , b : & of the {inter}section point a moveing in the line ah parallelly to cd & according to the order of those {illeg}
[15] Note that a streight line is said to designe the position of curved motion in any point {illeg} if toucheth the line described by the motion in that point, (as ab , ad , ac ), or {illeg} tis parallell to such a {illeg} (as ad , {illeg}). Note also that one line ah resting (as in Fig 3 & 4) the points d & a are coincident & the point c shall bee in the line ah if {illeg} bee streight (fig 3), otherwise in its tangent ac (fig 4) {illeg}. Haveing an equation expressing the relation of two lines x & y described by two bodys A & B whose motions {illeg} q ; Translate {illeg} the termes to one side & multiply them, being ordered according to x {illeg} {illeg} progression { } &c: & being ordered by the dimensions of y multiply those by {illeg} {illeg} &c. the summa of those products {illeg} equation expressing the relation {illeg} {illeg} motions p & q .
To draw a tangent to the Ellipsis
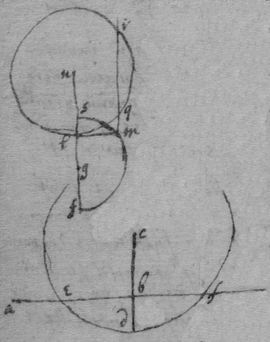
[16] Suppose the Ellipsis to be described by the thred acb , & that ce is its tangent. Since the thred ac is diminished with the same velocity that be increaseth, that is, that the point c hath the same motion towards a & d , the angles dce , ace , must bee equall, by prop 1. And, so of the other {conicks}.
To draw a Tangent to the Concha.
[17] Suppose that gae , glc , alf are the rulers by which the concha is usually described, & that , & . And (since equality is more simple than proportionality) suppose that is the velocity of the point c towards b , or of n towards m . Then is nt the circular motion of the point n about g (prop 1); & lr the circular motion of the point l fixed in the ruler ng , ( prop 4). And lg is the motion of the intersection point l (that is, the velocity of the point c ) moveing in the line glnc from g (prop 6). Now since a two fold velocity of the point c is known nemely cb toward b & lg towards d , make ; & the motion of the point c shall bee in the line fc the diameter of the circle passing through the points bcdf (prop 1) & therefore tangent to the Concha.
To find the point c which distinguisheth twixt the concave & convex portion of the Concha.
[18] Those things in the former proposition being supposed, make triangle gfh like gnt or lbc : & ∼ , & draw kf . Now had the line fd onely parallel motion directed by gd or rf , (since ) the motion of all its points would bee fr , (prop 3): & if it had onely circular motion about g , the motion of the point f fixed in that line df would bee fh (prop 4): But the motion of the point f is compounded of those two simple motions, & is therefore fk (prop 5 & 2); & the motion of the intersection point f made by the lines af df , & moveing in af , shall bee fp , (prop 6). Now if the line cf touch the concha in the required point, tis easily conceived that the motion of the intersection point f is infinitely little; & therefore that the points p & f are coincident, df & fk being one streight line, & the triangles gdf , fkh being alike.
Which may bee thus calculated. Make . . . then is . . . & . Therefore . Or .
In stead of the ordinary method de Maximis et minimis, it will be as convenient (& perhaps more naturall) to use ∼ This; Namely To find the motion of that line or quantity ∼ ∼ ∼ & suppose it equall to nothing, or infinitely small. But then the motion to which tis compared must bee finite. That is, the unknowne quantitys ought not to bee at their greates or least, both at once.
[19] Example, In the triangle bcd , the side bc being given & fixed. the side dc being given & circulateing about the center c , I would know when bd is the shortest it may bee. I call . . . . then is . & . & . or . & . (prop 7). And makeing , tis . Or . (For q signifieing the motion of d towards bc may bee finite though, p , its motion towards b doth perish). Wherefore . or . . . . are the greatest & the least valors of the line bd .
Should I have taken , instead of . The effect would not have followed because both the motions p & q would have vanished at once in the point {e}. But I might have taken the tangent dm for y , or any other line which wou{ld} {illeg} coincidere with bc at its being greatest or least.
[20] Example 2d. If {ne} is the Conchoid (. . . .) fo{illeg} em parallell to it. Then is . & . & . et ponatur p esse motus puncti m & q esse motus puncti c versus b . Erit (prop {6}{)} {illeg}{illeg} . supposeing (For when am is the least that {illeg}{illeg} bee the point c is that which distinguisheth twixt the concave & convex porti{on} of the Conchoid, & then the motion q vanisheth.) it will bee . . & . Or .
Concerning Equations when the ratio of their rootes is considered.
[21] If two of the rootes of an Equation are in proportion the one to the other as
a
to
b
Then multiplying the termes of the Equation by this progression
:&c
. &c. ( or by the same progression augmented or diminished by any quantity, as if it bee augmented by
a
it will bee
. &c. Or were it augmented by
it would be
). Then shall the roote which is correspondent to
be a roote of the resulting equation: but inverting the order of the progression, that roote which is correspondent to
shall bee a roote of the equation resulting from such multiplication.
As for example did I know that two of the rootes of the Equation were in proportion as 1 to 2 & would I have the lesser roote (viz that which is correspondent to 1) I make . . And soe the progression will bee . &c Or . &c by adding 2 . Or by adding one more it will bee . &c. By any of which progressions the Equation may bee multiplyed, as by the 1st, . Which produceth . Or by the 3d . Which produceth . Or by the first Otherwise by destroying the 1st terme. . Which produceth . &c the rootes of which products are, viz: of the first , & . Of the last , & . There I conclude 3 to be the lesse, & consequently 6 the greater of those rootes of the Equation . which are in double proportion But was the greater of those rootes desired then inverting the progression it would bee . Or . The first producing whose rootes are , . The 2d produceth whose rootes are , . And consequently 6 is the greater & 3 the lesse of the rootes in duplicate propor{tion.}
[22] If in the circle adef af is the diameter, ah a perpendicular to the end of it from which I would draw , which should intersect circle in the points d & e soe that bee triple to , that is he quadruple to hd . Then calling . . . The equation expressing the relation twixt x & y is . the rootes of which equation must be quadruple the one to the other: Therefore would I find the lesse roote I make . . And the progression will bee, . &c. by which the Equation being multiplyed the product is . Or . Therefore drawing , Or . from the point b , or c raise the perpendicular db , or ce. & soe draw hde.
Would I have dbec to be a square that is . Then to find hd I call it x & . Soe that the lesse roote is to the greater as x to . Making therefore , , The progression will be . By which the Equation , must be multiplyed. & it produceth . Or Or . & consequently . that is . And . Or . And consequently . Or it might have beene done thus. x substracted from the precedent progression it will be, . &c by which the Equation being multiplyed produceth . Or . And by extracting the roote, . And therefore {} Or . Or . That is . And . And therefore { }.
Reductions of Equations may bee perhaps performed by this method
[23] As in that problem recited by Des Cartes pag 83, viz: The square ad & the right line s being given , to produce ac to e , soe that ef drawn towards the point b may bee equall to the given line s . Putting for the unknowne quantity. , & . The Equation will bee . which having 4 rootes the Equation must have 4 divers resolutions; that is the lines ac , cd , produced both ways indefinitely, there may bee 4 divers lines drawne through the point b , whose parts intercepted twixt the crosse lines lace , mdch , are equall to the given line s : And they are bih lbk , nbm . And therefore the rootes of this equation are (two affirmative) df , dh , (& two negative) dh , dm . Because , , Therefore , , , . Soe that . That is one roote of this equation is to another as x to . Therefore I may multiply this Equation by this progression . And there resulteth . That is . Or, . Which result is the same with the first Equation the reason of which is, that if I make then is . Or if , then is . Or if , then is . Or if then is . Soe that the relation twixt all the rootes being reciprocally the same & not distinguishing one roote from another, tis noe wonder if they bee all indifferently expressed in the resulting Equation. Otherwise the reduction must have succeeded.
Suppose 3 rootes of an Equation are in proportion to each other as a
, b
, c
. Then if that roote which is correspondent to
a
be required, multiply the termes of the Equation by any of these Progressions
1
. 2 . 3 . &c.
As if 3 of the rootes of this Equation were to one another as . And g would find the roote which is correspondent to 1 . Then I make , , , & soe I may have by the first progression this . By the 2d; . &c. By the first of which the Equation being multiplyed produceth . That is . Or . & . Or were it multiplyed by the 2d progression thus . It would produce . Or . Soe that g being the least roote, the other two rootes must be & .
If it be desired to know the length of y & z in this equation when the rootes are in proportion as I multiply it by the precedent progression & the results are . Or . And . Or . . Or . And consequently .
Likewise were the proportion of 4 or 5 or more rootes given I might set down progressions to find them but it will bee better to set downe the method of finding {those}{these} progressions, And it is this. Suppose two of the rootes of an Equation {illeg} That Equation will bee of this forme , or of some forme {illeg} of it; And if a corresponds to the desired roote of the Equation this equation {illeg} will bee of this forme . Then assuming two termes ({illeg} { }) {illeg} third {illeg} progression {illeg} { } by which {illeg} {illeg} multiplyed produceth Or { }. And {illeg} {illeg} termes of the {illeg} {illeg}
<56r>Soe that I have thus much of the progression . And by the same proceding might continue it or get termes on the other side of the cipher. As if I multiply the Equation by this progression there is produced . Or . And . Againe multiplying the Equation by . It is . Or , And . Soe that I have thus much of the progression viz: .
The proceeding is same when the proportion of 3 rootes to one another are given, but there may bee some difference when the ciphers are far distant, as there bee three termes betwixt them, then the operation may be done thus. Let the quantitys, which beare such proportion to one another as the rootes doe bee, a, b, c . let a correspond to the roote which must be knowne And then that Equation will bee of this forme, . or else compounded of it. Then assuming some quantity (as a ) for one of the termes of the progression & placing it conveniently, (as it {no{illeg}} equidistant from the ciphers) feigne two other quantitys as z , y , for the deficient termes and the progression will bee . By which I multiply the Equation . Or . Soe that I have the progression, by which I againe multiply the Equation & there results . Or . which valor of z substituted into its place in the valor y There will bee thus much of the progression .
The same done otherwise.
Did I know that 2 of the rootes of this Equation , were in proportion as 3, . Then I suppose one roote to be
, the other
That is . . By one of which I divide the Equation as first by And the operation is;
. Againe I divide the Quotient by the other roote . Thus
. By the last division I have this equation . Or . And . Therefore the rootes of the Equation are, . .
If I would have
y
&
z
of such a length that the rootes of this equation
. be in proportion as , , . I suppose , . . And soe first divide the Equation by
. Againe I divide this product
by . Lastly were it necessary I should have again divided this quote by the 3d supposed roote of the Equation (viz {illeg}). By the 2d {operation}
. Or
. And by the first
. Or {
} Soe that If I make {illeg} the rootes of this Equation
should bee {illeg}
[24] [25] .R. An Equation being given, expressing the Relation of two or more lines x, y, z, & described in the same line by two or more moveing bodys A, B, C &c to find the relation of their velocitys p, q, r &c:
Resolution.
Sett all the termes on one side of the Equation that they become equall to nothing. And first Multiply each terme by soe many times as x hath dimensions in that terme. Seacondly multiply each terme by soe many times as y hath dimensions in --> it. Thirdly multiply each terme by soe many times as z hath dimensions in it &c. The summe of all these products shall be equall to nothing. Which Equation gives the relation of p, q, r &c.
[26] Or more generally thus. Order the Equation according to the dimensions of x , & (putting a & b for any two numbers whither rationall or not) multiply the termes of it by any parte of this progression viz : : Also order the Equation according to y & multiply the termes of it by this progression: . Also order it according to the dimensions of z & multiply its termes by this progression viz . The summe of all these products shall bee equall to nothing. Which Equation gives the relation of p, q,r &c.
Example 1st. If the propounded Equation bee . By the precedent rule the first operation will produce . The seacond produceth . Which two added together make . (Now suppose a yarde to bee an unit & that A hath moved 3 yardes, then (by the 1st equation) B hath moved two; i.e. , . And at that time by the last Equation . Or velocity of A ∶ velocity of B . Onely if x increaseth then y decreaseth, that is, A & B move contrary ways because p & q are affected with divers signes).
Example the 2d. If the Equation bee . The first operation will produce . Or . The second produceth . The third . The summe of which is . (Note that in this Example there being three unknowne quantitys x , y , z , There must be two of them & two velocitys supposed thereby to find the 3d quantity & the third velocity. Or else there must be some other equation expressing the relation of two of these x , y , z . (as in the first example) whereby one quantity & one velocity being supposed the other quantity & velocity may be found & then by this 2d Example the 3d quantity & the 3d velocity may bee found)
Example 3d, Of the more generall rule. If the Equation bee . the first operation gives Or . the 2d gives . The summe of which two products is equall to nothing. &c.
Demonstration.
[27] Lemma. If two bodys move uniformely the from to in the same line then are the lines & & &c as their velocitys .And though they move not uniformly yet are the infinitely little lines which each moment they describe as their velocitys are which they have while they describe them. As if the body A with the velocity p describe the infinitely little line o in one moment. In the moment the body B with the velocity q will describe the line . For . Soe that if the described {lines} be x & y in one moment, they will bee & , in the next. [or better . &c]
Now if the Equation expressing the relation of the lines x & y be . I may substitute & into the place of x & y because (by the lemma) they as well as x & y doe signifie the lines described by the bodys A & B . By doeing so there results . But by supposition: there remaines therefore . On divideing it by o tis . Also those termes in which o is infinitely lesse then those in which o is not therefore blotting them out there {rests} . Or .
Hence may bee observed: First, that those termes ever vanish in which o is not because they are the propounded Equation. Secondly the remaining Equation being divided by o those termes also vanish in which o still remaines because they are infinitely little. Thirdly that the still remaining termes will ever have that forme which by the first {root}{rule} they should have. [{illeg} partly appeare by Oughtreds Analyticall table].
The {rule} may bee demonstrated after the same manner if there 3 or more unknowne quantitys x, y, z {&c.}
By helpe of the preceding probleme divers others may bee readily resolved.
[28] 1. To draw tangents to crooked lines (however they bee related to streight ones).
Resolution
Find (by the preceding rule) in what proportion those two lines to which the crooked line {chiefly} related doe increase or decrease: produce them in that proportion from the given point in the crooked line {at} those ends draw lines in which those ends are {enclosed} to move through whose intersection the tangent shall passe.
Example 1st. If . . & . Then is . (by the former rule) Therefore I draw . The point g is inclined to move in a parallel to abc & the point e in a parallel to aik (for bg & ie (by supposition) moves parallel to them selves the upon ) Therefore I draw & . & through the intersection I draw hdf touching the crooked line at d . Soe that .
Hence may bee pronounced those theorems in Fol 47
[30] Example the 2d. If . . (which move about the centers a & b as in the Hyperbola or Ellipsis by a thred) And the equation bee . then is . or . therefore I make . (note that I draw cd & cB the one forward the other {backward} because p & q have contrary signes) the points d & B are inclined to move the one in a perpendicular to acd the other to bBc (for they move in circles whose centers are a & b ) therefore I draw & & the tangent ce through the point e .
[31] 2. Hitherto may bee reduced the manner of drawing tangents in mechanicall lines. see Fol 50.
[32] 3. To find the quantity of crookednes in Geometricall lines.
Resolution
[33] Find that point of the perpendicular to the crooked line which is in least motion, let that bee the center of a circle which passing through the given point shall bee of equall crookednesse with the line at that point. This point of least motion may bee found divers ways, as First. From any two points in the perpendicular to the crooked line draw 2 parallel lines in such proportion as the perpendicular moves over them: through their ends draw another line which shall intersect the perpendicular in the point required.
As if . . the tangent of the crooked line. . & as the motion of b from a to the motion of e from a so kb to ef . Then, drawing dfg through the points d & f , cg in the radius of a circle as crooked as line acl at c .
Example. Suppose . then is . . And . velocity of b from a , velocity of y 's increase velocity of v 's increase. therefore , or (since ) tis . Lastly (or . if { {illeg} }) that is . . & .
Hence may bee pronounced those theorems in Fol 49.
Addition connects affirmative numbers into an affirmation sume, & negative ones into a negative
one. as
Substraction takes the lesse number from the greater, the difference having the same signe prefixed which the greater number {hats} as . .
Multiplication adds one factor soe often to it selfe as there are units in the other, & if the signes of the factors bee the same the product is affirmative, if divers tis negative. As to multiply by doe thus Or thus . Or thus . Thus to multiply by the operation will bee Alsoe 465 multiplyed by will produce
Division takes the number which signifies how often the divisor the divisor, the sign of which number or Quote is affirmative if the dividend & divisor have not divers signes, but negative if they have. For if . then , Or . Suppose 34545 to be divided by 47 . First get a Table of the Divisor drawn into the 9 first units as defg . cut at the bottome close to the figures. Then looke which of those 9 quantitys are most like the dividend. As in this case the 7th 329 is therefore substract it from the dividend 34545 , & there will remaine , & then set downe its caracteristick 7 in the quote. I make a prick twixt those figures which have or might have beene altered & those which could not bee altered by the subtraction, & the places of the pricks will skew the places of the figures in the quotient. Againe I substract 141 from &c: & set 3 in the quote &c.
The resolution of the affected Equation . Or First having found two or 3 of the first figures of the desired roote viz (which may bee done either by rationall of Logarithmicall tryalls as Me Oughtred hath thought, or Geometrically by descriptions of lines, or by an instrument consisting of 4 or 5 or more lines of numbers made to slide by one another which may be oblong but better circular.) this knowne parte of the root I call g, the other unknowne parte I call y then is . Then prosecute the Resolution after this manner (making . . &c.) . . . by supposing . Againe supposing Then . . . . That is the . & the difference twixt this & the former valor of x is 0,2 . Therefore make . Then is &c. the first figure of which being added to the last valor of x makes . Then with this valor of x presecuting the operation as before tis . . which valor of substracted from the precedent valor of the {difference} is . Also the {difference} twixt tis & the precedent valor of x is 0,007 . Therefore I make {}. That is {illeg}
[34]
Of the construction of Problems.
[35] If the equation to be resolved bee . Or yy−ay+bb=0 in which the roote of the last terme (viz b) is knowne, they may bee conveniently resolved by D. Cartes his rules. Otherwise the rootes of that terme must bee first extracted as in this yy−py+q=0. Where I take . & soe describing the circle smf erect lm⊥ln & from m the point of intersection draw mr∥ln. the rootes of the Equation shall bee mq & mr. ln being the radius & n the center of the circle
Or it may bee done thus. Let the Equation bee . Then in the indefinite line af take . erect the perpendicular db=c. And from the point & towards b draw with which radius describe the circle edf & ae, af shall bee the rootes of the Equation. When note that any quantity may be taken for c, Soe that the operacion may thereby be made convenient, & to that purpose the difference twixt db & dc must bee as little as may bee(that is twixt & 4cc) soe that the circle intersect not (ef) over obliquely nor the circle be over greate.
[36] As if I had this Equation yy+6y−9=0 Or yy=−6y+9. Then must I make . Then if I make c=6 it will bee . Therefore I take . . . And soe describing the circle efc, I have one affirmative roote af, another negative ae. Or had I taken any other convenient valor for c as 1, or 3. or 4 the line ae & af would still have bene the same.
Had I this equation yy−8=0. or yy=8. Then is . Or makeing c=2; tis: dc=3. Soe that since p is wanting I take ab=0. ad=c=2 dc=3. & describing a circle the rootes will bee ea, af.
Note that if dc is negative or not greater then the circle cannot intersect the line eaf & therefore the rootes of the equation are immmagina{rie}.
< insertion from f 67v >[37] Or they may bee construed by drawing streight lines onely thus. Let the Equation be . or First I divide aa+b into square numbers (as {for} of them as may bee) (It may ever bee divided (though not) into (the fewest) squares by taking the greatest {square} out of aa+b & the greatest out of the remainder &c) as if in numbers the Equation were yy=2y+4 Or . I take the square 4 out of 5 & there rests 1 which is also a square. Then I draw ab . & . & make ab⊥bc. soe is . to which I add ad=1. & soe is .
Were the Equation yy=−4y+34. Or . Then is 38−36=2. 2−1=1. & 38=36+1+1 which are square numbers. Therefore I make . . & draw . & draw . from which take ab=2, & there rests .
Were the Equation . Or . Find & before, &c:
< text from f 67v resumes > <68r>[38] If the Probleme be sollid it may bee readily resolved by the intersection of the Parabola & circle as D: Cartes hath shewed If it bee of 5 or 6 dimensions it may bee resolved by the intersection of the line y3−byy−cdy+bcd+dxy=0. Or y3−byy+bcd+dxy=0 & the circle when pp={illeg} 4q. & q & v affirmative. as D: C: hath explained. Or it might beee done by the intersection of a circle & one of these lines, viz y3+byy−hx=0 when the equation is reduced to such a forme that pp=4q. Or this y3+byy+gy−hx=0. Or this y3+gy−hx={0}, s being affirmative & p=0. Or this y3+d−fyx=0 when p=0, & q & v affirmative. &c.
[39] But all Equations in Generall may bee resolved by the line a2x=y3, after this manner. First (making a=1) describe the line x=y3 uppon a plate. (as cadce. Then in which ab=x. bc=y). Then suppose the Equation to bee resolved bee y9*+my7+ny6+py5+qy4+ry3+syy+tq+v=0. (in which the letters m, n, p &c: signifie the [40] knowne quantitys of each terme affected with its signe + or −). I describe another line cdce, whose nature (making ab=x, bc=y) is the exprest & letting fall perpendicula{r} from every point where these two lines intersect as, df eg, they shall bee the rootes of the propounded eqation.
In like manner was the Equation to bee resolved y10*+my8+my7+py6+qy5+ry4+sy3+ty2+ry+w=0 the nature of the line cdce would bee . Or else it might bee . Or had I this Equation y10+{l}y9+my8+ny7+py6+qy5+ry4+sy3+ty2+vy+w=0. The nature of the line cdce would bee, . Or, . Or it might bee, . If the resolved Equation have fewer dimensions that is if some of the ultimate termes as, w, v, t &c: (or intermediate termes as m, n &c be blotted out: Or if the Equation have more than 10 dimensions{th}e nature of the lines cdce to bee described may be known by the same manner observing the order of the progression
Tis evident alsoe that there are 3 divers lines by which any Probl: may bee resolved unless some of them {chanch} to be the same, the easiest whereof is to bee chosen. It appeares also how Equations of 2 & 3 dimensions may be resolved by drawing streight lines; of 4, 5, & 6 by describing some conick section; of 7, 8, 9, by describing a line of 3 dimensions; of 10, 11, 12, by a line of 4 dimensions, &c: but yet y is never above 2 dimensions & consequently all these lines may bee described by the rule & compasses.
Had I this line y4=x. described on a plate & this Equation to bee resolved viz: y13+ly12*+ny10+py9+qy8+ry7+sy6+ty5+vy4+wy3+ayy+by+c=0. It might bee resolved by describing the line whose nature is . A line of the 2d sort. Whereas by the preceding rule was required that a line of the 3d sort should have [41] beene described. And here observe that taking the square number which is next greater than the number of the dimensions of the resolvend equation. That Equation may bee resolved by lines, the number of whose dimensions is not greater than the roote of the square number. And the rectangle of those numbers which signifie how many dimensions th{e} lines have, may always bee greater or equall but never lesse than the number of dimensions of the resolvend Equations. For the number of points in which two lines may intersect can never bee [42] greater than the rectangle of the numbers of theire dimensions. And they always intersect in soe many points, excepting those which are immaginarie onely. Soe that all Equations guished into sorts.) {St} will often bee very intricate to resolve Equations of many dimensions by the simplest line by which they may be resolved & also for the most part will regaine a description of two lines for every probleme. And then {if maybe often} {illeg} end to use two lines whereas {illeg} compound the other more simple & {illeg} As perhaps an Equation of 16 dimension may bee more speedily resolved by two lines {illeg} of 6 dimensions then by two lines {illeg} 4 dimensions.
<68v>[43] But it will not bee {amisse} to shew more particularly how these resolutions may bee performed. And that firs by the parabola
Suppose therefore I had the parabola x=yy exactly described & would resolve {illeg} plaine probleme the Equation yy+ky+l=0. I take ag=l. gf=k. fh=1=lateri recto Parab: & so draw the line gh & from the intersection points d, e, draw db, ec perpendicular to the axis gc. which shall bee the rootes of the Equation which are affirmative when they fall on the contrary side to fh, but negative if on the same, as in this case.
[44] But were I to resolve a sollid problem the Equation being of 4 dimensions, I take away the 2d terme, makeing it of this forme y4*+lyy+my+n=0. Then take . . Then perpendicular to ap draw af=aq. Also draw fk∥ap, & from the point of intersection k draw kh=n. lastly draw kr⊥ap, & with the radius wr upon the center q describe the circle tsm. (or, which is the same, take . & soe erecting the perpendicular rw, with the Radius rw describe the circle tsm) & from the points where it intersects the Parabola let fall perpendiculars to the axis, (tv, nm) they shall bee the rootes of the Equation the affirmative ones falling on the contrary side to pq. when m is affirmative.
[45] If I would resolve the cubick Equation y3+ky2+ly+m=0 (which multiplyed by y−k=0 produceth ) I make . . . fk∥ae⊥af=aq. kd=km. And with the radius cg upon the center q describe the circle wf. Or else doe thus (since k is one of the rootes of the Equation ) make k=ab+ar & draw bw∥ae (or make ar=kk, & wr⊥ap) & describe a circle with the radius wq. Then letting fall perpendiculars from the intersection points, they (being the rootes of the Equation ) shall all, except wr=k, bee the rootes of the Equation y3+kyy+ly+m.
This operation will bee much shortened when the 2d terme is wanting for {that} since k=0. it will bee . . & aq the radius of the circle.
[46] And if the last terme {vanish} that is if I would resolve this equation yy+ky+l=0. by the intersection of a circle & parabola. I must take . . . & soe with the radius aq upon the center q describe a circle, & the perpendiculars from the intersection points to the axis (a, tv) are the rootes excepting one which is equall to k.
<69r>[47] If I had the crooked line described fig 1st[48] whose nature is x=y3, & would resolve the Equation y3*+lyy+m=0. (calling ad=x, dg=y; Or a=-x. ce=-y) I take ab=m. bd=l. df=1. & df⊥bd & draw bf infinitely both ways. From the intersection points (as e) letting fall perpendiculars, they shall bee the rootes of the Equation y3*+lyy+m. as ce which in this case is negative because on that side on which y is negative.
Would I resolve this equation yy+ky+l=0. (which multiplyed by y-k produceth ) I take ab=kl, (fig 2d)[49] bδ=l, δd=kk. df=1, & soe through the points b & f draw the streight line bfλ (Or which is the same take ab=kl. k=ah⊥ab. & draw hλ∥ab untill it intersect the crooked line in λ (i. e. untill hλ=k3 & soe through the points λ & b draw λbfe). Then from the intersection points to the axis letting fall perpendiculars they (being the rootes of the Equation .) shall all, except βλ=k, be the rootes of the Equation yy+ky+l=0.
[50] Would I resolve the Equation z4+az3+bzz+cz+d=0. It may bee done by a circle thus. Multiply it by this Equation zz−az+aa−b=0, & it will produce , Of this forme z6**+mz3+nzz+pz+q=0. In which (n) ought to be affirmative, & if it bee not, then augment or diminish the rootes of the Equation z4+az3+bzz+cz+d=0. & then repeate the operacion again untill there bee an Equation of this forme z6**+mz3+nzz+pz+q=0 in which n is affirmmative. Then (dividing this equation by it is therefore) take . . & with the radius , describe the circle dk & the perpendiculars (as dh ck) multiplyed by shall bee the rootes of the Equation.
Theoremata Optica.
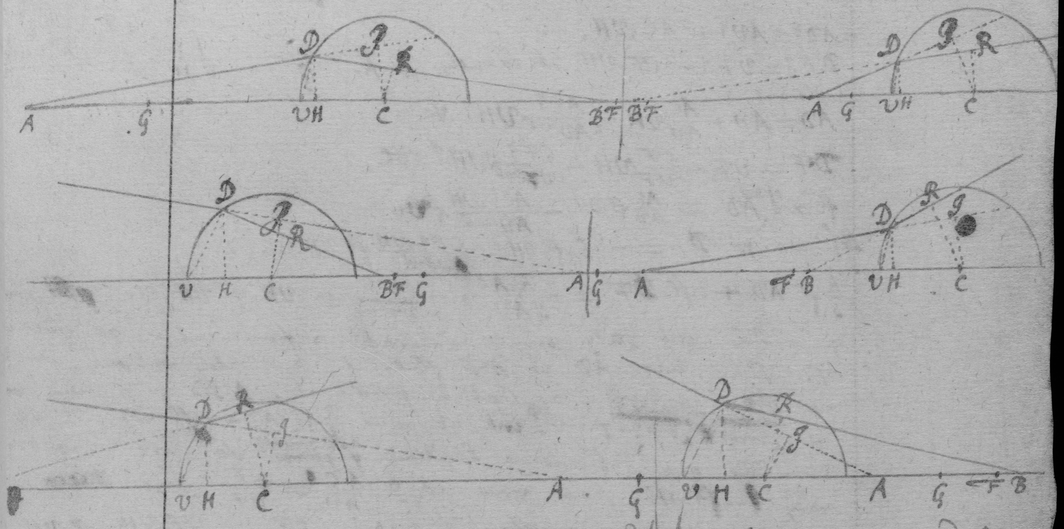
Si radius divergens a puncto dato A vel convergens ad punctum idem A incidit in Sphæram CVD ad punctum D, sit sphæræ centrum C, & secet AC producta sphæram in V et radium refractum DR in B: a punctis D et C ad AB, AD, BD demitte normales DH, CI, CR; sit sinus incidentiæ ad sinum refractionis seu Ci ad CR ut I ad R; et facto R,AC.I,AV∷CF.VF. erit F focus, seu locus imaginis puncti A radios quaquaversum emittentis.
2do A puncto v versus A cape VG ad VA ut est R ad I et error radij refracti DR a loco imaginis in axe AV, seu distantia punctorum B et F erit , sive quamproxime.
3. Ubi punctum infinite distat ita ut radius incidens parallelus sit axi, pro AC scrito AV, et pro FG scripto (nam hæ jam sunt æquipollentia) error BF {fist} , vel , vel .
4. Si radius non refringitur sed reflectitur a superficie sphærica VD, eadem regula obtinet si modo ponatur S.R∷ 1.-1. et perinde capiatur VG ad contrarias partes VA f{illeg} ipsi VA æqualis. Erit enim{adh}uc error  . vel AVq×CV. ACF×FG∷VH.FG.
. vel AVq×CV. ACF×FG∷VH.FG.
Hujus autem Theorematis inventio totis est.
. 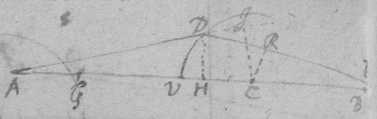 . Et extractis radicibus, &c &c fluxio ipsius &c Defluxio ipsius &c in VH, fl VH &c Qu{illeg} si nihil esset radij omnes accuratè refrigerentur ad focu{illeg} F. Tunc enim AD et DF fluerent in data ratione, jux{illeg} ea quæ Cartesins in Optica probavit: {'} Sed qui{a} nihil non est, error {obliquitatis} superficiei erit VD ut illud . Et ut error ille sive defluxio a legitima obliquitate ita error angular radij refracti. Jam vero est Ergo error angularis radij refracti est ut in , fl VH. Vel etiam ut in , fl VH seu ut , in fl VH seu , posito fl VH=1 & . Dat{ur} autem ratio ad ergo substituto posteriore fiet error ille ut . Duc in VFq et error in axe FB erit ut qua{illeg}do circuli radius determinatur. Divide per radium circuli et fiet ut error BF in omni casu. Dato igitur errore illo in uno casu datur in omni. At in eo casu ubi est radius incidens axi parallelus datur error {e}odem cum quantitate ergo semper idem est cum hac quantitate.
. Et extractis radicibus, &c &c fluxio ipsius &c Defluxio ipsius &c in VH, fl VH &c Qu{illeg} si nihil esset radij omnes accuratè refrigerentur ad focu{illeg} F. Tunc enim AD et DF fluerent in data ratione, jux{illeg} ea quæ Cartesins in Optica probavit: {'} Sed qui{a} nihil non est, error {obliquitatis} superficiei erit VD ut illud . Et ut error ille sive defluxio a legitima obliquitate ita error angular radij refracti. Jam vero est Ergo error angularis radij refracti est ut in , fl VH. Vel etiam ut in , fl VH seu ut , in fl VH seu , posito fl VH=1 & . Dat{ur} autem ratio ad ergo substituto posteriore fiet error ille ut . Duc in VFq et error in axe FB erit ut qua{illeg}do circuli radius determinatur. Divide per radium circuli et fiet ut error BF in omni casu. Dato igitur errore illo in uno casu datur in omni. At in eo casu ubi est radius incidens axi parallelus datur error {e}odem cum quantitate ergo semper idem est cum hac quantitate.

me.Ce∷d.y. mO.CO∷e.y. . . DO.DR∷Dq.Dp d, Cq, Cp−Cm=e, Cp, Cq-Cm. d, Ce, CO−Cm=e, CO, mC+Ce . d−e=f. . =Cm
<71a(v)> [Editorial Note 2]Probl.
Habita Lente plano-convexa, invenire tum convexitatem, tum refractionem vitri.
{Sit} Lens RS, ejus  superficies plana RTS, convexa RVS axis KF{.} Lentis superficie plana solem respiciente, observentur imaginum sola{ntum} a radijs {tum} trajectis tum reflexis convergentibus in charta obversa distinctissimè pict{æ}rum loci duo F et G; F locus imaginis trajectæ G locus reflexæ: et mensurentur quam accuratissime distantiæ VF, TG, ut et crassities vitri TV. Dein fac ut VF+2TV ad VF−2GT, {ita} sinus incidentiæ ex aere in vitrum ad sinum refractionis, {ita} KT ad GT et erit 2KV radius circuli RVS
superficies plana RTS, convexa RVS axis KF{.} Lentis superficie plana solem respiciente, observentur imaginum sola{ntum} a radijs {tum} trajectis tum reflexis convergentibus in charta obversa distinctissimè pict{æ}rum loci duo F et G; F locus imaginis trajectæ G locus reflexæ: et mensurentur quam accuratissime distantiæ VF, TG, ut et crassities vitri TV. Dein fac ut VF+2TV ad VF−2GT, {ita} sinus incidentiæ ex aere in vitrum ad sinum refractionis, {ita} KT ad GT et erit 2KV radius circuli RVS
Probl.
Habita Lente quavis convexo-convexa, ve{illeg} etiam convexa-concava cujus concavitas convexit{illeg} multo minor, invenire tum refractionem vitri, tum convexit{illeg} Lentis.
Sit Lens RS, 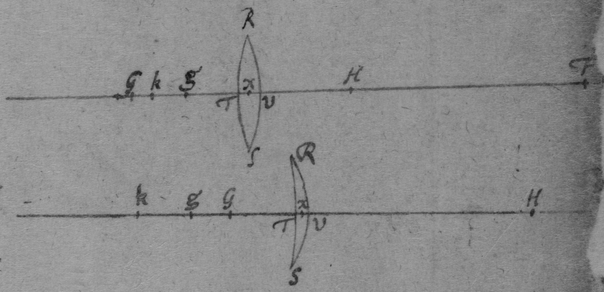 superficies magis convexa RVS, minus convexa vel concava RTS, axis KF, vertices V ac T. Lentis hujus superficie minus convexa vel concava RTS solem directe respiciente, observentur quam accuratissim{e} sol{em} imaginis in charta obversa distinctissimè pictæ ta{tam} trajectæ locus F quam reflexæ locus G, et mensure{illeg} distantiæ VF, TG, et crassities vitri TV. Dein alter{illeg} Lentis superficie RVS solem respiciente observetur qu{æ} locus imaginis reflexæ H et mensuretur distantia V{H} quæ est imaginis illius a vitro. Biseca TV in X. Et fac . Et . Et . Et {L}{illeg} plano-convexa ex consimili vitr{o} confect{æ} cujus vertices sunt T, V, et convexitas versus F {sita} æqu{illeg} summæ convex{itatum} RTS, RVS in fig. 1 vel differentiæ convexitatis et concavitatis in fig. 2, pro{jectis} solis imaginem refractam ad locum priorem F, reflexam vero ad locum quamproximè. Unde †[51] si fiat (juxta Problema prius) VF−2g{T} gT∷VF+2TV.KT erit sinus incidentiæ ex aere in vitrum ad sinum refractionis ut KT ad gT, vel ut KF ad VF. {Sec} ista ratio{.} Sec ad R, et erit radius circuli {RVS} sit ista {C}{illeg}{−}{illeg}{−}{illeg}{D}{illeg}{−}
superficies magis convexa RVS, minus convexa vel concava RTS, axis KF, vertices V ac T. Lentis hujus superficie minus convexa vel concava RTS solem directe respiciente, observentur quam accuratissim{e} sol{em} imaginis in charta obversa distinctissimè pictæ ta{tam} trajectæ locus F quam reflexæ locus G, et mensure{illeg} distantiæ VF, TG, et crassities vitri TV. Dein alter{illeg} Lentis superficie RVS solem respiciente observetur qu{æ} locus imaginis reflexæ H et mensuretur distantia V{H} quæ est imaginis illius a vitro. Biseca TV in X. Et fac . Et . Et . Et {L}{illeg} plano-convexa ex consimili vitr{o} confect{æ} cujus vertices sunt T, V, et convexitas versus F {sita} æqu{illeg} summæ convex{itatum} RTS, RVS in fig. 1 vel differentiæ convexitatis et concavitatis in fig. 2, pro{jectis} solis imaginem refractam ad locum priorem F, reflexam vero ad locum quamproximè. Unde †[51] si fiat (juxta Problema prius) VF−2g{T} gT∷VF+2TV.KT erit sinus incidentiæ ex aere in vitrum ad sinum refractionis ut KT ad gT, vel ut KF ad VF. {Sec} ista ratio{.} Sec ad R, et erit radius circuli {RVS} sit ista {C}{illeg}{−}{illeg}{−}{illeg}{D}{illeg}{−}
et {poni} debet .
Exempli gratia. In Telescopij cujusdam vitro objectivo observabam VF=13ped.11digit. . Et . Seu VF=167dig. VH=1,8125dig. TG=28,8125dig. TV=0,2222 &c dig.. Adeo . . . Unde prodit A= 0,00023{84} dig. B=0,0348{127}dig. gx=28,7256dig. . VF+2TV=167,{444}4&c VF−2gT= 109,771. Ergo 167,444. 109,771∷I.R. vel in minoribus numeris 29.19∷I.R aut magis accuratè ∷ I.R. =17161dig=1430ped. Unnde alterius RVS semidiameter erat quasi 7ped 4dig. At hæc ita se habebant in vitro objectivo Telescopij Doctoris Babington.
In altero Telescopio quad erat in archivis Academiæ, measura{ve} distantiam imaginis trajectæ a vitro objectivo VF=14ped3{gis} .
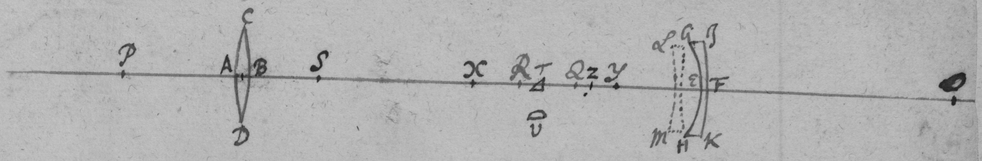
Telescopij novi delineatio
Vitrum objectivum CD parallelos radios refringat versus O. Imago O per refractionem concavæ superficiei GEH transferatur ad P, et inde per reflexionem superficiei specularis ad Q, et inde per refractionem secundam superficiei GEH ad R ubi a speculo obliquo T detorquetur per vitrum oculare perexiguum V ad oculum.
Sit imaginis translatio angularis ab O ad P et a P ad S tanta quanta corrigendis vitri objectivi refractionibus erroneis ab inæquali refrangibilitate ortis sufficit et erit angularis translatio imaginis a Q ad R tanta quanta est a P ad S, et punctum S invenietur faciendo ut sit BE.EO∷EO.ES.
Sit X centrum circuli specularis JFK et Y centrum circuli refrigentis concavi GEH. Et quoniam imaginis angulares translationes PX, XQ æquales sunt, ut et PS, QR; erunt etiam translationes SX, RX æquales: adeo si fiat ES.SX∷ER. RX, vel ES+SX.SX∷EX.RX, ex dato puncto X habebitur ultimæ imaginis locus R, e cujus regione consistet oculus.
Sit insuper Y centrum superficiei concavæ GEH, et quoniam est EP.EQ∷PX.QX, et I×OE.R×OY∷EP.YP. et I×ER.R×YR∷QE.QY: inde derivabitur hæc conclusio. Fac . . Et habebitur circuli GEH centrum Y. Ubi nota quod usurpo pro ratione sinus incidentiæ ex aere in vitrum ad sinum refractionis: et suppono insuper vitri crassitiem EF ad instar nihili esse.
Ghetaldus in his Promotus Archimedes computes the weights of the following equall bodys to bee in the proportions following.
If Sphæres bee made of the following metalls each of whose diameters are one foote their weights will bee as followeth. Note that 1libra=12′. 1′=24″. 1″=24‴
Or
A Sphære of tinn whose diameter is six inches weighs Thirty and Eight pounds. The following line being {6} of Ghetaldus his inches, which is half the Roman foot by Villalpandus account from the Far{nesian urn}. Soe that the weight of a circumscribed cilinder is 57 lib & of such a cilinder of water lb. And of a circumscribed cube (viz whose side is 6 inches)is li. Or more exactly {-.} that is . Or more exactly And such a cube of water libra or more exactly 9,80752lib. & a foot cube of water libra or more exactly 78,46016libra.
The {P}es Regius Gallorum, the Rhinlandick foot, the old Roman foot, & the English foot are as {illeg} But by the Farnesian Urn printed by Villalpand the French royal foot is to {illeg} old {illeg} foot as 12 to 11 or perhaps 11 to 10. The urn conteined a longius of water weighing 10 Roman pounds of 12 {illeg} Gaffendus by weighing found it contein 7 french pounds of 16 ounces. Eight such vessels make a Roman foot cube called a Quadrantal or Amphora Romana weighing 56 French pounds. A cubic French Foot of water by Mersennus trial weighed 74libra, by the vulgar estimat{illeg} {} or 72, suppose 72 & two meane proportional{s} between 7{2} & {56} will be as to 23 or 12 to {11}. Suppose 74{libra} two {meane} will be {as} 11 to 10 or 12 to & this is {the} proportion of the french foot to the Roman. {illeg} Royal French foot {illeg} {illeg} 12. . {11} {illeg} . {illeg} . {illeg} ({illeg} The Roman {illeg} to the {horary} foot as 8 to 9. {illeg} 9 {illeg} {illeg} .
<77v>Some Problems of Gravity & levity &c
[52] Prob 1. To find the proportion of the weights of two equall bodys the one being sollid the other liquid. Resp. If the Sollid body A bee heavier than the liquid B weigh it in the aire & in the liquid Body B; & the difference of those two weights is the weight of soe much water as is equall to that sollid body & so much {wyer} as {deppend} in the {water}. But if it bee lighter than the liquid body B, hang a heavier body C to it, that will sinke it; & weigh them first the body A being in the air & C in the liquid body, 2dly both A & C being in the liquid body; & the difference of these weights is the weight of so much water as is equall to A (& also to soe much thred wyer or hayre as was weighed both in the water & air.)
[53] Note that the weight of soe much water as is equall to that parte of the wyer (to which A & C are fastened) which was weighed both in the air & water, bee subducted from the whole weight of the water & the remaining weight shall bee the weight of the water required.
__________________________________________________________________________________________________________________________
Or Thus, Make the scoale B as light as may bee, yet soe that it will sinke it selfe in the liquid body CC, & sinke the body A also, if A chance to bee lighter than CC. Suppose that f the weight of scoale B in the water, & g in the aire; & that e is the weight of B+A in the water, & d in the aire: then is d−g+f−e the weight of soe much water as is equall to A. Note that the water must reach {'}at both weighings to the same point {illeg} of the wyer & that the wyer bee as small as may bee.
Cor: Hence the proportion of weights of all bodys sollid or liquid or both may bee gathered. & wee may hence deduce tables of the weights of equall bodys, & of the quantitys of bodys equally heavy.
[54] Prob 2. Two bodys {illeg} D & E given to find the proportion of their quantity. Weigh them in the scale B, let their weight & the weight of the scale in the air bee h & k, in the water, m & n then is D{illeg} E∷h−g+f−m:k−g+f−n. For their weight in air is h−g, & k−g; in the water m−f & n−f. &c.
[55] Prob 3. A compound body cd being given to find the weights & proportions, of its two compounding parts c & d. Answer. a & c, b & d, are of the same matter. That the weights of the 5 bodys a, b, cd, c, d, in the aire are e, f, n, m, n−m; & in the water g, h, q, p, q−p. Then is . & . The{re}fore . Or the weight of C in the aire. Also . & . & . & (Prob 1). feq−hen+hgn−fgq:gfn−efq+ehq−ghn∷c:d. And, gfn+ehq−ehn−gfq:efq+ghn−ehn−gfq∷c+d:{c}.
[56] Prob{:} 4. A body f compounded of 3 severall sorts of matter d, e, f−d−e, begin given{:} with the proportion of the weight of the two bodys d & e as {1} to r. To find the weight of the body d. Resp. Suppose that the bodys a & d, b & e, c & f−d−e are of the same matter; & that the weight of the bodys a, b, c, f, d, e, f−d−e, in the aire are g, h, k, p, x, rx, p−x−rx{;} & in the water l, m, n, v, s, t, v−s−t. Then is g:l∷x:s. & h:m∷rx:t. & k:n∷p−x−rx:v−s−t. Therefore . And ghkv−ghnp=hklx+gkmrx−ghnx−ghnrx. Or .
If the weights g=h=k, (as may bee either by experience or calculacion (see coroll: Prob 1) Then is . Now because gold is usually allayed by mixing with it brasse & silver of each an equall weight; suppose that a & d are brasse, b & e silver, c & f−d−e gold, & that x=rx, or r=1. Then is the weight of the brasse or silver in the masse f, & the weight of the gold in it.
<78r>Descriptio cujusdam generis curvarum
secundi ordinis.
Concipe lineas PED datum angulum PED continentes ita moveri ut una earum EP perpetuo transeat per polum P positione datum, et altera ED datæ longitudinis existens perpetuò tang{a}t rectam AB positione 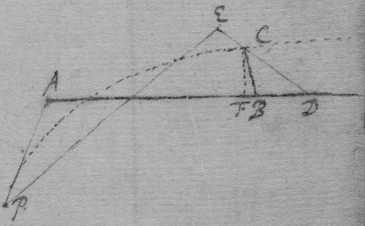 datam . Age PA constituentem angulum PAD æqualem angulo PED sit CD æqualis AP et quodvis punctum C in recta ED. datum describet curvam secundi ordinis.
datam . Age PA constituentem angulum PAD æqualem angulo PED sit CD æqualis AP et quodvis punctum C in recta ED. datum describet curvam secundi ordinis.
Age CB constituentem angulum CBD æqualem angulo PED, et ad AD demitte normalem CF. et dictis . DC=c. CE=b. AB=x BC=y. et posito 1. E∷BC.BF, erit
Et nota quod ubi angulus PED rectus est, et recta ED bisecatur in C, curva erit cissoides veterum.
<80r>A Method Whereby to Square lines Mechanichally.
[57] Prop 1. Supposing ab=x⊥bc=y. If the valor of y (in the Equation expressing the relation twixt x & y) consist of simple termes, Multiply {each} terme by x, & divide it by the number of the dimensions of x in that terme, & the quote shall signify the area acb.
Example. If ax=yy. Or . then is . Soe if . then is . Soe if . then is Soe if . then is .
Prop 2. If any terme in the valor of y bee a compound ter{illeg} Reduce it to simple ones by Division or Extraction of Rootes or by Vie{s} Method of Resolving Affected Equations, as you would doe in Decimall Numbers; & then find the Area by Prop 1st.
Example. If . bee divided as in decimall fractions it produce{illeg} &c. & by the 1 Proposition . the Hyperbolas Area.
As if a=1=b=ab=bc. & x=0,1=be The Calculation is as followeth,

The summe of these two summes is equall to {the area} dbfc, supposing ad={0,9}. And their difference {is equall to} the area bche, supposing ae=1,1. & ab=1=bc∥df∥he. {that is}
<80v>In the manner If a=b=1=ab=bc. & x=0,2=be. The calculatio is as followeth
The summe of these two summes is Equall to theArea dbfc, supposing ad=0.8. And their Difference is equall to the area bche, supposing ae=1,2. & 1=ab=bc∥df∥he. {that is}
{illeg} such respect to the superficies bcfd{,} bche {the numbers} {illeg} {(viz as the lines ad} {illeg} {illeg} {illeg}
Soe that since 10×100=1000 &c. 10×1,1=11 &c. The Superficies answering to these lines{,} 2. 3. 9. 11. & their products (of one of them multiplying another) may bee found. Viz. if ab=1=bc⊥ab{illeg}
If the line ak is Then, the superficies bcgh is
______________________________________________________________________________________________________________________________________________________
Having already found the areas correspondent to the lines 1,1. 0,9. 1,2. 0,8. tis easy by the help of those operations to ding the areas correspondent to the lines 1,01. 1,001. 1,0001. &c: 0,99. 0,999. 0,9999. &c: 1,02. 1,002 &c: 0,98. 0,998. 0,9998. &c. And since . &c. Therefore the areas correspond{ent} to the lines 7. 13. 17. &c: are easily found, as followeth. Viz: if x=0.02. Then
The sume & difference of which two summes give the areas bcfd, bche as before. That is
And since . & . Therefore
{If the} line {c}k is The superficies bcgk is
___________________________________________________________________________________________________________________________________________________
{illeg}if x=0,001. The operation is as followeth{.} {Where} {illeg} . & . Therefore {illeg}ak is {illeg} {illeg}
<81v>Which Area may bee otherwise thus found supposing x=db=-0,0016. Viz.
As was found before excepting that their differenc is e in the two last figures is 28. Which agreement could scarce thus happen in more than 50 figures, were not the reas, corresponding to the lines 2. 3. 5. 7. 13. &c, calculated {aright} in so many figures.
Octob. 1676.
Memorandum. The letters baccdæ13eff7i3lgn4049 rr458t12vx in my second epistle to M. Leibnitz contein this sentence Data æquatione quotcun fluentes quantitates involvente, fluxiones invenire: et vice versâ.
The other letters in the same Epistle, viz: 5accdæ10effhui4l3m 9nboqqr{8}s11t9v3x: 11ab3cdd10eæg10ill4m7n603p3q6r5511t8vx, 3acæ 4egh5i4l4m5n80q4r3s6t4v aaddæ5eüjmmnnooprrr5sttuv, express this sentence. Una Methodus consistit in extraction{e} fluentis quantitatis ex æquatione simul involvente fluxionem ejus. Altera tantum in assumptionæ {seriei} pro quantitate qualibet incognita ex qua cætera commodè derivari posunt, et in collatione terminorum homologorum æquationis resultantis ad eruendos terminos assumptæ {seriei}.
The use of these differences is for composing rules to find the differences of {the terms of a table which {illeg} to be interpoled by the contiuall addition of those differences & also following a geo {illeg}}
<82v>Prob.
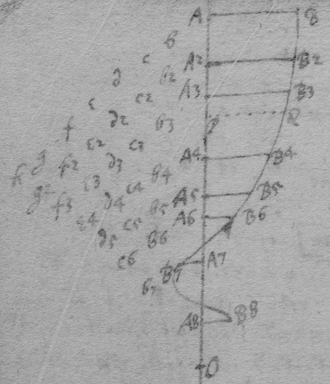
 Recta aliqua AA9 in æquales quotcun partes AA2 A2A3, A3A4, A4A5, &c divisa et ad puncta divisorum erectis parallelis AB, A2B2, A3B3 &c: invenire curvam geometricam quæ per omnium erectarum extremitates B, B2, B3 &c transibit.
Recta aliqua AA9 in æquales quotcun partes AA2 A2A3, A3A4, A4A5, &c divisa et ad puncta divisorum erectis parallelis AB, A2B2, A3B3 &c: invenire curvam geometricam quæ per omnium erectarum extremitates B, B2, B3 &c transibit.
Erectarum AB, A2B2. A3B3 &c quære differentias primas b, b2, b3, &c secundas c, c2, c3 &c tertias d, d2, d3 &c & sic deincep{s} us dum veneris ad ultimam differentiam i. Tunc incipiendo ab ultima differentia excerpe medias differentias in alternis differentiarum et arithmetica media inter duas medias reliquorum ordinum.
Cas 1
{Igitur} Si numerus prignorum. terminorum A, A2, A3, &c sit impar medius {servimus} eorum erit ultimus terminus series ejus k, l, m, &c. Et tunc sic pergendum erit. Sit numerus primerum terminorum 9 et erit k=i, {&c} pergendo us ad seriem primorum terminorum AB, A2B2, A3B3, &c. Sint hæc k, l, m, n, o, p, q, r, s &c quorum ultimu{m} significet ultimam differentiam, penultimum medium arithmeticum inter duas penultimas differentias, antepenultimu{m} mediam trium antepenultimarum differentarum, & sic deinceps us ad primum quod erit vel medius terminorum A, A2, A3, vel arithmeticum medium inter duos medios. Prius accidit ubi numerus terminorum A, A2, A3 & est impar, posterius ubi par.
Cas. 1.
In casu priori sit A5B5 iste medius terminus, hoc est A5B5=k, , c4=m, , e3=0, , g2=q, i=s. Et erecta ordinatim applicata PQ die A5P=x, due terminus hujus progressionis &c. in se continuo Et orientur termini 1. x. &c per quos si termini seriei k, l, m, n, o, p &c respectivè multiplicentur, aggregatum factorum &c erit longitudo ordinatim applicatǽ PQ
Cas 2.
In casu posteriori sint A4B4, A5B5 duo medij termini, hoc est =k, b4=l, , d3=n, e2+e3={o}, f2=p, & h=r{.} Et erecta ordinatim applicata PQ, biseca A5A5 in O {et} d{illeg} OP=x due terminos hujus progressionis &c in se continuo. Et orientur termini &c per quos si termini seriei k, l, m, n, o, p &c respectivè multiplicentur, aggregatum factorum &c erit longitudo ordinatim, applicat{illeg} PQ.
Sed hic notandum est j. Quod intervalla AA2, A2A3, A3A4, &c hic supponuntur esse unitates, Et quod differentiæ colligi debent {illeg}ferendo inferiores quantitates de superioribus A2B2de AB, A3B3de A2B2, b2 de b &c, faciendo AB−A2B2=b{,} A2B2−A3B3=b2{,} b−b2=c &c adeo quando differentia illa {hoc modo} {illeg} negativæ sig{m}a{-}earum {ubi mutandp sunt}.
<83r>For taking of unknowne quantitys out of intricat Equations it may be convenient to have severall formes. Now suppose x, was to be taken out of the Equations ax3+bxx+cx+d=0 & fx3+gxx+hx+k=0.
I feighe the 3 valors of x in the first Equation to bee -r, -s, & -t. {illeg} is [. . . . & that is] the summe of the rootes is {;} of their squares is of their cubes is ; of their rectangles is &c that is,] supposing a=1, every r is b every rr=bb−2c. every r3=b3−3bc+3d, rs=c, rrs=bc-3d, r3s=bbc−2cc−bd. rrss=cc−2bd. r3ss=bcc−2bbd−cd. r3s3=c3−3bcd+3dd. rst=d. rrst=bd. r3st=bbd−2cd. rrsst=cd. r3sst=bcd−3dd. r3s3t=ccd−2bdd. rrsstt=dd. r3sstt=bdd.r3s3tt=cdd. r3s3t3=d3
— — — — — — — — — — — — — — — — —
Or thus, every r4=b. rs4=c. rr4=bb−2c. rst4=d. rrs4=bc−3d. r34=b3−3bc+3d. rrst4=bd. rrss=cc-2bd. r3s4=bbc-2cc-bd. r44=b4−4bbc+4bd+2cc. rrsst4=cd. r3st4=bbd−2cd. rrrss4=bcc−dc−2b{b}d. rrsstt4=dd. r3sst4=bcd−3dd. *r3sstt4=bdd. r3s3t4=ccd−2bdd. r3s3tt4=cdd. r3s3t34=d3. *r3s34=c3−3bcd+3dd.
Now supposing k (or any other quantity of the second Equation) to bee an unknow{ne} quantity, it must have 3 severall valors by reason of the 3 valors of x in the first Equation, & therefore x being taken away, h will bee of three dimensions in the resulting equation.
The 3 valors of h are +fr3−grr+hr=k. & fs3−gss+hs=k & ft3−gtt+ht={k.} Which I multiply into one another that they may produce an equation expressing the 3 fold valor of k: out of which equation I take out r, s, t by writing b for their summe c for the summe of their rectangles rs+rt+st. bc−3d for the summe of all theire rectangles of this for{me rrs} (viz: for rrs+rrt+rss+rtt+rtt+sst+stt) &c as in the Table. Which substitution may bee most briefly done in the said multiplication, thus; writing a to make up six dimensions
For solving this Problem generally Datis quotcun punctis Curvam describere quǽ per omnia transibit: Note these differences
Prob
Curvam Geometricam describere quæ per
data quotcun puncta transibit.
 Sint ista puncta B, B2, B3, B4, B5, B6 B7 &c. Et ad rectam quamvis AA7 demitte perpendicula BA, B2A2, B3A3 &c Et fac , , , , {,} . . Deinde . . &c. Tunc . . &c. Tunc . . &c. Sic pergendum est ad ultimam differentiam. Differentijs sic collectis & divisis per intervalla ordinati{illeg} applicatorum: in alter{eris} earum columnis sive seriem vel ordinibus excerpe medias incipiendo ab ultima et in reliquis columnis excerpe media arithmetica inter duas medias, pergendo us ad seriem primorum terminorum AB, A2B2, &c. Sunto hæc k, l, m, n, o, p, q, r &c quorum ultimus terminus significet ultimam diff. penultimus mediam arithmeticum inter duas penultimas, antepenultimus mediam trium antepenultimarum &c. Et primus {illeg} erit medias ordinatim applicata si numerus datorum punctorum est impar, vel medium aritthmeticum inter duas medias si numerus earum est par.
Sint ista puncta B, B2, B3, B4, B5, B6 B7 &c. Et ad rectam quamvis AA7 demitte perpendicula BA, B2A2, B3A3 &c Et fac , , , , {,} . . Deinde . . &c. Tunc . . &c. Tunc . . &c. Sic pergendum est ad ultimam differentiam. Differentijs sic collectis & divisis per intervalla ordinati{illeg} applicatorum: in alter{eris} earum columnis sive seriem vel ordinibus excerpe medias incipiendo ab ultima et in reliquis columnis excerpe media arithmetica inter duas medias, pergendo us ad seriem primorum terminorum AB, A2B2, &c. Sunto hæc k, l, m, n, o, p, q, r &c quorum ultimus terminus significet ultimam diff. penultimus mediam arithmeticum inter duas penultimas, antepenultimus mediam trium antepenultimarum &c. Et primus {illeg} erit medias ordinatim applicata si numerus datorum punctorum est impar, vel medium aritthmeticum inter duas medias si numerus earum est par.
Cas 1
In casu priori sit A4B4 ista media ordinatim applicata, hoc est A4B4=k, . c3=m, , e2=0. f+f2=p. g=q. Et erecta ordinatim applicata PQ et in basi AA5 sumpto quovis puncto O dic OP=x, et duc in {se}gradatim terminos hujus progressionis &c et ortam progressionem asserva. Vel quod perinde est duc terminos hujus progressionis &c in se gradatim et terminos ex ortos duc respective in terminos hujus progressionis . &c et orientur termini intermedij: tota progressione existente &c Vel dic OA=α, OA2=β, OA3=γ{,} OA4=δ, OA5=e, OA6=ζ, OA7=η , . . Et ex progressione collige ter{min}os e quibus multiplicatis per 1. x−θ. x−μ. x−λ &c collige alios terminos intermedios tota serie prode{ants} 1. x−δ. xx−δ−θx+δθ. x3−δ−2θxx++γε+δθx−{γ.} Per cujus terminos multiplica terminos seriei k. l. m, n. o &c et aggregatum productorum k+x−δ×l+xx−δ−θ×m &c erit longitudo ordinatim applicata PQ.
Cas. 2.
In casu posteriori sint A4B4 et A5B5 dua media ordinatim applicata hoc est {.} b4=l. . d3=n. . f2=p{illeg} Et {illeg} k, m, {illeg}, o, {illeg} & coefficientes orientur en multiplicatione terminorum hujus progressiones {illeg} &c et ubiquorum coefficientes en multiplicatione {illeg} {illeg} {c}ujus progressionis .
. &c Hoc est erit &c=Ordinatim applicatæ . Sive dic . =ρ. . . =ν. . . Et erit k+πl+ρm+σn+τo+νp+φq χr+ψs=PQ.
<84v>Prob
Of Equations,
Every equation hath soe many roots as dimensions of which some may be true some false & some imaginary or impossible.
If there bee some imaginary then the true & false rootes may be knowne by the signes of the Equations termes: Namely there are soe many true rootes as variations of signes & soe many false ones as successions of the same signes. When any termes are wanting supply their{e} voyd places with ±0.
But if any because imaginary roots are properly neither true nor false roots bee imaginary, this r{oote} soe far admitts of exception. Thus the signes of this Eq: x3−pxx+3ppx−p3=0. show it to have three true roots, wherefore if it bee multiplyed by x+2a=0 the resulting equation x4+px3+ppxx+6p3−q3x−2pq3=0 should have thre true rootes & a false one, but the signes shew it to have three false & one true. I conclude therefore that the two roots which in the one case appeare true, & in other false are neither, but imaginary; & that of the other two roots one is true {the} other false.
Hence it appeares that to know the particular constitution of any Equation it is {chi{illeg}fely} necessary to understand what imaginary roots it hath. And this in some of the simplest Equations is easily discovered, thus in xx±ax+bb=0, both roots are imaginary if 4bb<aa, otherwis both reall. And thus in px3−apx−q=0 two roots are imaginary if 4p3<27qq, otherwise all reall. But to give accurate rules for determining the number of these roots in all sorts of Equations would bee a thing not onely very difficult, but uselesse, because in Equations of many dimensions the rules would bee more intricate & laborious to put in practise then to solve the Equations either by lines or numbers. Soe that the accurate determination{s} of those roots is for the most part {esilyest} acquired by solving the Equations.
But yet because the discovery of these roots is very usefull I shall lay downe rules whereby they may bee many times discovered at first sight, & almost always without much labour.
First then the number of impossible roots is always eaven. If one bee impossible there must bee two, if three there must bee foure &c. And hence Equations of odd dim{en}sions must have one roote reall at least.
Secondly the number of reall roots of any Equation are not more then the number of its termes.  Thus x4−2x+3=0 {illeg} have all foure roots reall & therefore must have two imaginary.
Thus x4−2x+3=0 {illeg} have all foure roots reall & therefore must have two imaginary.  Thus x5−3x4+4=0 can have but thre reall roots & two must bee imaginary. Hence are to bee excepted equations which {want} all their odd termes as x6−2x4+3xx−2=0. And in {illeg} like cases write y for xx. And so many terme roots as duct y3−2yy+3y−2=0 hath {times} soe many reall roots, halfe true halfe false, & four times soe imaginary ones the other x6−2x4+3xx−2=0 shall have.
Thus x5−3x4+4=0 can have but thre reall roots & two must bee imaginary. Hence are to bee excepted equations which {want} all their odd termes as x6−2x4+3xx−2=0. And in {illeg} like cases write y for xx. And so many terme roots as duct y3−2yy+3y−2=0 hath {times} soe many reall roots, halfe true halfe false, & four times soe imaginary ones the other x6−2x4+3xx−2=0 shall have.
Thirdly, if under the termes of any Equation you set a progression of {fractions} each having the dimension of the terme above it for its {illeg} & number {denominating} that terme first second third &c for its denominator & {illeg} if {illeg} {illeg} any {illeg} together so that the rectangle of the first {illeg} multiplyed {viz the fraction} {illeg} first {illeg} square of the {illeg} terme multipl{illeg} by {the fraction} {illeg} conclude there are two imaginary roots {illeg} if {illeg} one {illeg} in all throughout the equation conclude also there are two imaginary roots at least. If equall in all cases throughout the Equation, conclude that all the roots of the equation are equall. If it be greater or equal to it in two places of the equation & not in all places betwixt conclude there are foure imaginary roots at least. If it bee greater or equall to it in three places of the equation & not in all places betwixt, conclude there are six imaginary roots at least. And soe of the rest.
Thus if the Equat be x3−3xx+4x−2=0. Th en the progress is . & because , I conclude there are two roots imaginary at least.
there are two imaginary roots.
conclude two rootes are imaginary.
imaginary roots at least, also by the three last termes (1) therefore all 4 roots are imaginary unlesse the like happen in the three middle termes. I try therefore & find & soe can conclude but two rootes imaginary.
Therefore I conclude all four roots imaginary.
are two imaginary roots{.} Also the 3d 4th & 5t terme give therefore since by the 2d 3d & 4th terme tis I conclude ther are 4 roots imaginary. Also by the 4th 5t & 6t termes I find but thence nothing can be concluded because those three termes are of the same condition with the 3d 4th & 5t termes which immediately precede them. Lastly I find by the three last termes ; And by the termes pr{e}ceding them . Therefore I conclude there are two more imaginary roots; that is in all 6 & but one reall.
Thus in litterall Equations, if , because 1×3ppx{illeg} therefore what ever numbers are taken for p and q two roots shall bee imaginary. And soe of the rest.
This rule may be otherwise thus exprest. Over the termes of the equation set a series of fractions each having the dimensions of the terme under it for its numerator, & the number denominating the terme first, second {third} &c for its denominator. Then in every three termes observe{illeg} whither the square of the middle terme multiplyed by the fraction above be greater equall or lesse than the factus of the {terme} before & after it multiplyed by the fraction over the terme before it. If greater write the signe + underneath; if equal or lesse write the signe − underneath the middle terme & lastly set + under the first terme of the equation. Then observe how many changes there are from + to − & conclude that there are soe many pa{ires} of imaginary roots{.} unlesse all the roots bee equall
Thus hath 2: & hath 4 {illeg} many {roots}
If you would bee more exact set downe after their signes the differences of the said squares & rectangles . And then if you see three differences together with the same signe soe that the square of the meane diff bee less then the rectangle of the other two change the signe of the said meane difference
If you would bee yet more exact, augment the roots of the Equatio the more the better, & at least soe much as to make them all true. then set the afforesaid differences with their signes underneath as before. And under them the progression of fractions squares. Then if you see three differences together with the same signe soe that the square of the middle difference multiplyed by the fraction under it bee not greater than the rectangle of the other two differences multiplyed by the fraction under the first: change the signe of the middle difference.
Any Equation being propounded, set down a series of so many fractions as the Equation hath dimensions, whose numerators & denominators are a progression of units backward & forward. Divide each fraction by that preceding it & set the quotes in order overal the middle termes of the Equation. Then observe of every middle terme whither it square multiplyed by the fraction over it bee greater equall or lesse than the rectangle of the two termes on either hand. If greater write + underneath, if equall or lesse write −. Lastly set + under the first & last terme & there shall bee soe many impossible roots as there are changes of signes. Unlesse it happen that all the roots are equall, for &c:
Thus if x5−4x4+x3−2xx−5x−4=0. The series of fractions will bee And dividing by & by &c there results to bee set over the middle termes of the equation th{illeg}s the third : therefore I write −. In the 4th (-20) therfore I write +. In the 5t therefore I write +. lastly under the first & last terme I write +. And soe finding two changes of termes I conclude two roots to bee impossible.
<86v>Sometimes there may bee impossible not by this meanes discovered, which if you suspect, augment or diminish the roots of the Equation a little, not soe much as to make them all affirmative or all negative, or at most not much more. & try the rule againe. And if there bee any impossible roots twill rarely happen that they shall not bee discovered at two or three such tryalls. Nor can there bee an Equation whose impossible roots may not bee thus discovered.
Thus if x3−3ppx−3p3=0, in which noe impossible appeare I put x=y−p & the result is y3−3pyy−p3=0 in which two appeare, Or if I put x=y−2p the result is y3−6pyy+9ppy−5p3=0 in which also two appeare.
Thus if , I set the signes + & − under it as before and find two imaginary roots & to try if it have any more I suppose x=y+1 & the result is x5+6x4+10x3+9xx+5x+0
Now by this rule false roots may bee often discovered at first sight; as if you see a terme wanting twixt two others of the same signes, or if it bee greater there either of those two or its square then their rectangle; conclude there is a paire of impossible roots at least & set the signe − under that terme also set the signe + on either side the term {wanting}. As in this . In which it appears there are 4 if not 6 impossible roots
If there bee two or more termes wanting set signes under them successively to begining with a negative{illeg} only end with an affirmative if the terms on either hand have contrary signes. As in so in The first shows 4, the last two roots imaginary: Soe{.} in which hath {8} roots imaginary
<88r>To reduce severall equations by divisors of {three} dimensions.
Get the divisors of 6 or 7 or 8 such numbers as were described before. Add & sustract them from 29. 8. 1. 0. -1. -8. -27. Take any three numbers out of the {three} middle ranks, r, s. t. Make -s=c. . Then see if you can find 4a+2b+c in the rank preceding these & 9a+3b+c in the rank preceding that also 4a−2b+c in the rank following these & 9a−3b+c in the rank after that{;} if you can try the division by x3−axx+bx−c.
Or better multiply all the numbers in the middle rank by 5 & 10. Let s, {o} {v} signify the products, out of the two ranks on either side take any two eaven or two odd numbers Let those be r & t. Then making . observe if you can find 4m+2n+any s in the rank preceding those or 4m−2n+any s in the rank following those & then 9m+3n+any v in the 2d rank preceding those & 9m−3n+any v in the 2d rank following them. If so try the division by .
Or yet better. Do not add & subduct the divisors from 9, 4, 1, 0, 1, 4, 9 but try if of those in the first & last rank the difference of any two eaven or two odd ones be divisible by 6. Call that difference G & the summ of the same terms H. Then try in the middle collumn there be any term which subducted from H, or added to it produces a number divisible by 9. Call that term + c if it be subducted or − c if added. [Then try if in that column next before or after the middlemost which has fewest divisors there be any te{rm} {illeg} which added to or subducted from produces a number divisible by 9] & the summ or difference K, & putting , & G −=b. Try if you can find 8−4a+2b−c on the 2d rank above the middle one or 8+4a+2b+c in the 2d rank ra{illeg} below it. If so try the division by x3−ax2+bx−c. Or thus against those divisors added & subducted from 27. 8. 1. 0. 1. 8. 27. set 9a+ {illeg}b+c. 4a+2b+c. a+b+c. c. a−b+c. 4a−2b+c. 9a−3b+c. then choose the three ranks of the fewest terms & in them those numbers one in each by which get the valor of a, b, & c. & those gotten will give you numbers to be sought in the other ranks, which if you find there try the division by x3−axx−bx−c. otherwise lose there other numbers out of the same 3 ranks, & doe so till you have gone through all variety.
Note that if the last term of the æquation be p the last but one q, Then if c & have a common divisor which divides {n}ot q, that c is to be rejected. Also if or be greater then the greatest term of the æquation that b or a is to be rejected.
Or thus best. Let the numbers which arose by substituting 2. 1. 0. -1. -2 for x be G. H. I. K. L. If I end not in 5 or {0} substitute 10 & -10 for x & let the numbers arising be F. & M{illeg} but if I end in 5 or 0 & H or K do not, increase or decrease the root of the æquation by an unit. Do so also if {H} be an eaven number and H or K an odd one with fewer divisors & then substitute 10 {&} -10 for x{.}
<88v>How numeral æquations are to be
reduced by divisors of 3 or 4 or more dimensions
Substitute 5, {6}, 3, 2, 1, 0, -1, -2, -3, -{illeg}, -5 & also 4 & -4 if need be, for x, & suppose the resulting terms, be F, G, H, I, K, L, M, N, O, P, Q. Find all their divisors set those of F & Q together by pairs whose last figures are equal or differ by 5. Gather the summs & differences of these pairs. Let summ of any two be R, the tenth parts of their difference S if their last figures, ✝✝ And if the æquation be not of more than 5 dimensions so that it must be divisible (if at all) by a divisor of 2 dimensions set down xx∓Sx to be tried for such a divisor. Where R & S must have the same signes if the divisor of F was greater then the divisor of K otherwise contrary signes. Quadruple the divisors of L. & if the two last figures of any one be the same with the two last figures of 2R, take it from 2R. Let the residue divided by 100, be T. Or if the two last figures of any one added to the two last figures of 2R make 100 add it to 2R & let the summ divided by 100 be T & let the number whose quadruple is added to or subducted from 2R be a And if the æquation be of 6 or 7 dimensions & no more set down x3+Txx+{S-25}+a to be tried Where note that S & T must be negative if they were found so above & a must be negative if it was added to 2R to make T, or els ffirmative if it was subducted. & the same is to be observed of the signes in the following operations.
But if the æquation be of more then 7 dimensions then look among the divisors of K for a number which added to or subducted from S+T+a gives a number divisible by 24. This number divided by 24, call v & the divisor which gave it call β And set down to be tried for a divisor if the æquation be not of more then 9 dimensions. Where {v} must be negative if if it was so above.
But if the æquation be of more then 9 dimension then Cook among the divisors of M for a number which added to or subducted from −S+T+a gives a number divisible by 24. This number divided by 24 call W & the divisor which gave it {γ}. And set down to be tried for a divisor if the æquation be not of more then 11 dimensions or supposed divisible by {−} Divisor of not more {than} 5 dimensions At ita in infinitum pergitur
Now the trial of these divisors is this suppose the divisor be a+bx+cxx+dx3+ex4+fx5 &c And observe if {illeg} be among the divisors of L{,} if this Divisor ascend but to {two} dimensions{;} & a+b+c+1 among the divisors of K if {illeg}ascend but to two or 3 dimensions & a−b+c{−d−1} {illeg} divisors of {illeg} if it ascend but to 2, 3 or 4
dimensions & a+2b+4c+d+e+1 among the divisors of I if it ascend not to more then 5 dimensions & a−2b+4c −d+e−f+1 among the divisors of N if it ascend to no more then six dimensions & a+3b+9c+27d+81e+243f+&c among the divisor of H if it ascend not to more then 7 dimensions, & so in infinitum In all which put c=1 & d, e, f = 0 if the divisor be of 2 dimensions or d=1 & e, f, = 0 if of 3 dimensions, & so on.[58] And when you have tried all the divisors which may be found by this {rale}, {&} rejected those which will not hold this trial: if there remain more or if the æquation be not divisible by any of those which remaine, you may conclude the æquation irreducible by any rational divisor.
<89v>Veterum Loca solida restituta.
Cartesius de hujus Problematis confectione se jactitat quasi aliquid præstitistet a Veteribus tantopere quæsitumm, cujus gratia putat Apollonium libros suos de Conicis sectionibus scripsisse. Sed cum tanti viri pace r{e}m Veteres: neutiquam latuisse cred{ide}rius{.} Docet enim Pappus modum ducendi Ellipsim per quin data puncta et eadem est ratio in cæteris Con. sect. Et si Veteres norint ducere Conic{i}s sectionem per quin data puncta, quis {nori} videt eos cognovisse compositionem loci solidi{.} Imo vero eorum methodus longe elegantior est Cartisiana. Ille rem peregit per calculum Algebraicum qui in verba (pro more Veterum scriptorum) resolutus Adeo prolixum et perplexum evaderet ut nauscum crearet ne{illeg} posset intelligi. At illi rem peregerunt per simplices quasdam Analogias, nihil judicantes lectu dignum quod aliter scribereter, & proinde celantes Analysin per quam Constructiones invenerunt. Ut pateat hanc rem eos non latuisse, conabor inventum restituere insistendo vestigijs Problematis Pappiani. In cum finem propono hæc Problemata.
[59] 1 Conicam sectionem per tria data puncta ABC describere quæ datum centrum O habebit. A duobus punctis AB ad centrum O age rectas AO BO et produc AO ad OP ut sit OP=AO. A tertio puncto C age CS parallelam AO et occurrentem OB in S et cape ST ad , et erit punctum T ad curvam. Biseca TC in V, et ipsi OV parallelam age CR occurrentem AO in R erit CR ordinatim applicata ad diametrum AP. Et latus rect{um} erit ad AP ut RCq ad AR×AP{.} Figura existente Ellipsi si punctum R cadit intra A et P, aliter Hyperbola.
[60]2 Per data quinque puncta A, B, C, D, E Conicam Sectionem describere Junge duo puncta AC et alia duo BE sit jungentium intersectio K. Ipsis AC BE age parallelas Dg DG occurrentis BE, AC in punctis H et F, et facto , puncta G et I erunt ad curvam. Biseca ergo ID et AC in m et n ut et BE ac GD in p et q et actarum mn, pq intersectio O erit centrum Conicæ sectionis. Habito autem centro, describe figuram per puncta A, B, C ut supra, Quod si mn et pq parallelæ sint Figura erit Parabola, . Quo casu produc PQ ad V ut sit BPq.GQq ∷PV.QV. et erit PV diameter V vertex et latus rectum figuræ .
[61] His præmissis nihil aliud restat agendum in compositio loci solidi quam ut quin puncta quæramus per quæ figur{a} transibit. Id quod in Problemat{e} Veterum facillimum est{.} Su{illeg} AT, ST, AG, SG quatuor positione datæ rectæ et ad hac ducendæ sint in datis angulis a puncto aliquo communi C {a}liæ quat{uor} CD, CF, CB, CH ea lege ut rectangulum duarum primarum CD ×CF dat{a}m habeat rationem ad rectangulum reliquarum CB×CH curva in qua punctum C perpetim reperitur transibit per intersectiones datarum A, G, S, T, nam ubi FC nulla est, rectangul{u}m FC×CD nullum erit adeo et rectangulum CD×CH, et {illeg} rectarum CD, CH. Si CD{;} punctum C incidet adT, si CH{;} ad S. At ita ubi CD nulla est punctum C incidet {vel in A vel in G.} Dantur ita quatror puncta A, G, S, T {illeg} et sola restat quinta investiganda. Id quod facillimum est. Nam per punctum A agatur recta quævis AC et in ea quaratur punctum C quod Problemati satisfaciet. Jam adeo ratio DC ad BC, et proinde etiam ratio CH ad FC siquidem ratio DC×CH ad BC×FC detur. Age ergo rectam SC ea lege ut sit CH ad FC in ratione ista data, et hæc secabit rectam AC in puncto quæsito C. Eadem lege unum era {puncto} invenire possunt sed uno aliquo invento {habebimus} quin puncta quæ {Conicam Sectionem jaxta} præcedentia determinando Problemati satisfaciunt.
Et hæc videtur methodus naturalissim{e} solvend problem{a} non {factum} quod ad{illeg}dum simpl{illeg} {sit} pars Problemat{illeg} {illeg} {{illeg}} ab ipso Cartesio proponitur) est invenire punctum aliquod (data{m} habens conditionem deinde cum infinita sint ejusmodi puncta, determinare locum in quo ista omnia reperiuntur. Quid autem magis naturale quam reducere difficultates hujus posteri oris partis ad difficultates prioris determinando locum ex paucis punctis inventis. Proinde cum veteribus constiterit rati ducendi conicam sectionem per quin data puncta, nullus dubitaverim eos hoc medio loca Solida composuisse.
< text from f 89v resumes >Problema
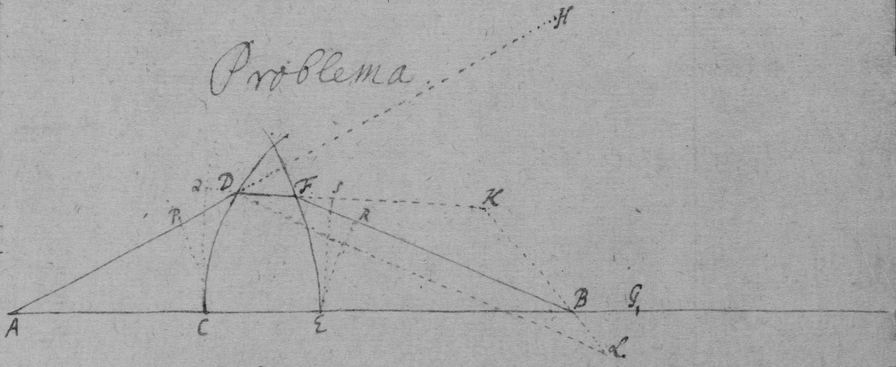
Data quavis refringente superficie CD quæ radios a puncto A divergentes quomodocun refringat: invenire aliam superficiem EF quæ refractos omnes DF convergere faciet ad aliud punctum B.
Junge AB. Eam secent refringentes superficies in C et E. Et posito d ad e ut sinus incidentiæ ex medio ACD in medium EDC ad sinum refractionis, produc AB ad G ut sit BG.CE∷d−e.e, & AD ad H ut sit AH=AG, et DF ad K ut sit DK.DH∷e.d. Junge KB et centro D radio DH describe circulum occurrentem KB productæ in L. Ipsi DL parallelam age BF et erit F punctum superficiei EF quæ radios omnes ADF convergere faciet ad punctum B. Nam de fluxio DF est ad fluxionem AD+BF ut e ad d: adeo CE−DF.AD+BF−AC−BE ∷e.d.
Haud secus Problema resolvitur ubi tres sunt vel plures refringentes superficies.
De resolutione Quæstionum circa numeros.
Primo numeri quæsili redigendi sunt ad æquationem secundum conditiones quæstionis, Deinde exponendi sunt per basem et ordinatam curvæ lineæ quam æquatio illa designabit. 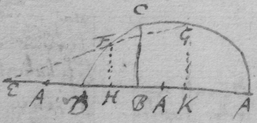 Sit curva ista DC et numeri AB, BC, curva existente tali ut numerus BC ordinatim applicatus ad numerum AB in dato angulo ABC semper terminetur ad eam. Deinde inquirenda erunt puncta curvæ quæ efficient numeros AB, BC rationales. Casus autem in quibus hoc fieri deprehendo sunt sequentes.
Sit curva ista DC et numeri AB, BC, curva existente tali ut numerus BC ordinatim applicatus ad numerum AB in dato angulo ABC semper terminetur ad eam. Deinde inquirenda erunt puncta curvæ quæ efficient numeros AB, BC rationales. Casus autem in quibus hoc fieri deprehendo sunt sequentes.
1. Si numeri in æquatione non ultra gradum quadraticum ascendant ita ut curva sit Conica {s}actio: et detur aliquod punctum F in curv{æ} quo efficitur ut numeri AH. HF. sint rationales ex hoc unico exemplo regula generalis sic elicietur. In AH cape HE cujusvis rationalis longitudinis, age EF, secet hæc curvam in G et demissa GH parallela CB numeri AK, KG erunt rationales. Si punctum F reperitur in linea AH, FH existente nullâ, tunc cape HN cujusvis rationalis longitudinis, Erige NE parallelam BC, & cujusvis etiam rationalis longitudinis. 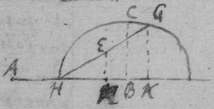 Age HE occurrentem curvæ in G et erunt AK KG rationales.
Age HE occurrentem curvæ in G et erunt AK KG rationales.
Quoniam {ita} hic unicum s{a}{illeg}tem exemplum requiritur, primo inquarendum est ejusmodi exemplum, dein regula generalis inde elicietur ut supra. Exempl{i} autem inveniend hec erit methodus{.} ni melior occurrat. Sit æquatio axx+bxy+cyy+dx+ey+y=0 ubi x et y designant numeros. Et si terminus f desit, punctum istud erit A. Si x in æquatione axx+dx+f=0 sit rationale puncta duo erunt in AB. Si cyy+ey+f sit rationale puncta duo erunt in recta quæ ducitur ab A parallela BC. Si bb−4ac sit quadratus numerus affirmativus tunc curva erit Hyperbola Et recta ducta a puncto A vel B parallela Asymptoto secans curvam in G exhibebit numeros AK GK rationales. Sunt alij innumeri casus quibus enumerandis non immoror
2 Si æquatio ascendit ad tres dimensiones, et tria habentur exemplo rationalia non in arithmetica progressione possunt inde innumera alia reperiri sint enim P, Q, R puncta Curva ad ista exempla  Junge PR, RQ, PQ et punctum S, T, Y ubi PR, RQ, PQ secant curvam dabunt alios tres numeros. Dein junge QS et punctum x quo QS secat curvam dabit aluim numerum. et Sic in infinitum.
Junge PR, RQ, PQ et punctum S, T, Y ubi PR, RQ, PQ secant curvam dabunt alios tres numeros. Dein junge QS et punctum x quo QS secat curvam dabit aluim numerum. et Sic in infinitum.
[62] Punctum B circumferentiam contingit a quo si duæ agantur rectæ una ad datum punctum A altera in dato angulo c ad rectam positione dat{u}m & ad dat{u}m punctum terminatam DC, quadratum prioris ABq æquales sit rectangulo sub abscissa ac data DC×E
Vel sic. Si ABq=FC×E punctum B contingit circ.
< text from f 91v resumes >Loca plana.
1. Si datur linea AB, et angulus ACB, punctum 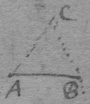 est in circulo per A et B transeunte.
est in circulo per A et B transeunte.
2. Si dantur puncta A, B et ratio AC ad BC punctum  C est in circulo Et si C est in circulo recta BC vergit ad locum B.
C est in circulo Et si C est in circulo recta BC vergit ad locum B.
3 Si a dato puncto A ad rectam positione datam BD ducatur r{ec}ta quævis AB et in ea {illeg}atur punctum C {si} ea lege ut detur rectangulum BAC punct{u}m C est in circulo, transeunte per A
4 Si detur punctum A et rectangulum BAC vel BA×DC 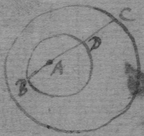 et punctum B ac D est ad circulus, etiam punctum C erit ad circulum.
et punctum B ac D est ad circulus, etiam punctum C erit ad circulum.
5 Si detur punctum A et proportio AB ad AC vel AD ad DC. et punctum B est ad circulum etiam C erit ad circulum. Sin punctus B est ad rectam erit C a rectam
6 Si dentur puncta duo A, B et differentia quadratorum ACq−BCq punctum C est ad rectam 
7 Si dentur puncta duo A, B et summa quadratorum ACq+ BCq C erit ad Circulum 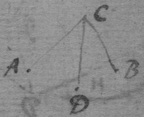
8 Si dentur puncta plura A, B, D et quadratorum ex lineis AC, DC, BC vel quadratorum quæ ad ipsa sunt in datis, rationibus summa vel quod subducendo aliqua ab alijs restat vel proportio aggregati unius ad aggregatus aliud, punctus C erit in circulo.
10 Si dantur puncta B, D, E et productam BD secat 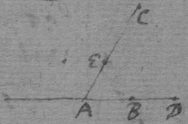 quævis EC in A, et sit rectangulum EAC æquale rectangulo BAD erit punctum C ad circulum.
quævis EC in A, et sit rectangulum EAC æquale rectangulo BAD erit punctum C ad circulum.
11. Si dantur puncta E, D et concurrant 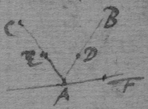 rectæ CE BD ad rectas positione datam AF et rectangulorus. EAC, DAB differentia vel nulla est vel æqualis rectangulo sub AF et recta data: sit autem punctum B ad circulus erit punctus C ad circulum.
rectæ CE BD ad rectas positione datam AF et rectangulorus. EAC, DAB differentia vel nulla est vel æqualis rectangulo sub AF et recta data: sit autem punctum B ad circulus erit punctus C ad circulum.
12 Si detur quadrilaterum ADE quod 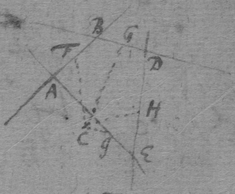 in circulo inscribi potest, et a puncto C ad latera ejus ducantur in datis angulis rectæ quatuor CF, CG, CH CI ita ut rectangulus sub duabus CG×CI datam habeat rationem ad rectangulus sub alijs duabus CF×CH, et in uno aliquo casu punctus C est in circumferentia circuli transeuntis per ABDE, semper erit in circulo illo
in circulo inscribi potest, et a puncto C ad latera ejus ducantur in datis angulis rectæ quatuor CF, CG, CH CI ita ut rectangulus sub duabus CG×CI datam habeat rationem ad rectangulus sub alijs duabus CF×CH, et in uno aliquo casu punctus C est in circumferentia circuli transeuntis per ABDE, semper erit in circulo illo
A{ff}ini{a} sunt 1, 2, 6, 7, 8. Item 3, 4, 5. Item 10. 11
13 Si dentur puncta A, B. Et circulus 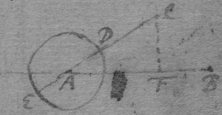 centro A radio dato AD descriptus utcun secetu{illeg}r {an} D et E a ducta AC ac demittatur normalis CF, sit autem rectangulum DCE=2ABF punctum C erit in circulo.
centro A radio dato AD descriptus utcun secetu{illeg}r {an} D et E a ducta AC ac demittatur normalis CF, sit autem rectangulum DCE=2ABF punctum C erit in circulo.
Si trapezij ABDE anguli A ac D recti sint et 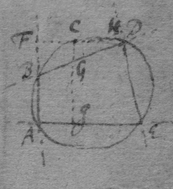 ad AB et AE{.} demittantur perpendicula CF CI a puncto quovis C secantia BD ac DE in H et G et fuerit rectangulum FCH=GCI erit punctum C in circulo transeunte per puncta ABDE. Et viceversa. {I}dem eveniet si ad latera singula {illeg} a puncto C demittantur perpendicula
ad AB et AE{.} demittantur perpendicula CF CI a puncto quovis C secantia BD ac DE in H et G et fuerit rectangulum FCH=GCI erit punctum C in circulo transeunte per puncta ABDE. Et viceversa. {I}dem eveniet si ad latera singula {illeg} a puncto C demittantur perpendicula
[63] Si {i}n circulo quovis ABCD inscrib{a}tur trapezium A B C, D, et a circumferentiæ puncto quovis E ad latera trapezij ducantur lineæ EF, EG, EH, EI constituentes cum lateribus conterminis AB, BC parallelogrammum EFBG et cum alijs duobus lateribus conterminis AD, DC parallelogrammum EHDC. quod sub ductis ad opposita duo latera continetur rectangulum GE×EH æquale est rectangulo EF ×EC sub ductis ad reliqua duo latera contento.
NB Idem eveniet si puncto E ad latera trapezij demittantur pependicula. Ut et si duct{illeg} ad duo latera contermina [64] EH, EC ad AD, CD æquales angulos EHD, ECD vel EHA, ECD cum ipsis conficiant et ductæ ad altera duo latera EF EG æquales angulos cum ipsis.
Et hinc si ductæ quosvis angulos conficiant cum lateribus trapezij, et rectangula GEH, FEI sunt in data ratione facile est cognoscere utrum punctum E sit in circus ferentia circuli. Nam ad latera duo opposita AB, CD, duc EK, EL in angulis EKB ELD in quibus ad altera duo latera duct{a} sunt lineæ æqualibus. Verbi grati{a} EK in angulo AKE=ang CGE et EL in angulo DLE =ang DHE. Et se ratio rectanguli FEI ad rectangulum GEH componitur ex ratione FE ad KE et EI ad EL ita ut rectangula KEL GEH æqualia sint, erit punctum E in circulo secus non erit in circulo.
[65] Si ABE sit circulus et detur A & rectangulum BAC erit punctum C in recta. Et si punctus C in recta sit converget recta CA ad datus punctus A. Et in fig 2 si datur rectang BAC erit C in circulo.
[66] Si linearum AD, BD, CE poli ABC in linea recta sunt, et puncta intersectionum duo DE lineas rectas describunt tertia intersectio F lineam rectam describet. Idem eveniet si linea DE parallela est lineæ BC. Ut et si puncta ABC non sint in directum si modo loca punctorum D, E se secant in recta BC.
[67] Si dati anguli DBA, DCA circa polos B, C volvantur et angulis ABD, ACD æquales capiantur CBF BCF sit punctum D in recta transeunte per punctum F vel etiam in conica sectione transeunte per puncta tria BCF erit punctum A in recta. Et si D in recta sit non transeunte per punctus F aut in con. sectione transeunte per duo E tribus punctis B, C, F, non autem per omnia tria, punctus A erit in conica sectione. Si per unicum tantum E tribus punctis BFC transit conica sectio, punctum A erit in curva primi gradus tertij gener{is} Si per nullum erit primi generis quarti gradus.
< insertion from the bottom of the page >[68] Si circ{illeg} dua {illeg}E AD se secuerint in A et per A agatur recta ACDB et {illeg} CD ad DB {illeg} in circulo transeunte {illeg} intersecti{illeg} {illeg} priorum.
Si recta CD {illeg} {datas} {illeg} {data {illeg}} {illeg} et secetur {illeg} cujus {data} est ratio {illeg}
{Si secetur punctum} {illeg} AD, BD, CD {illeg} vel AB, BC {illeg} {illeg} agei B circulum {illeg}
< text from f 92v resumes >[69] Datis positione lineis AE BE et punctis AB: Si recta quævis CD secat alteras in C, D ea lege et rectangulum AC, BD æquætur dato rectangulo AE×BE, compl{e} parall{o}logrammum AEBP et locus ad quem recta CP vergit erit punctum P.
[70] Si AB datur positione et longitudine & AD BC longitudine sint CE DE æquales cape AF.BF∷AD.BC et CD verget ad datum locum puncti F.
[71] Si a datis punctis A, B ductæ AC, BC datam habeant summam vel differentiam N: Duc CD parallelam AB et in ratione ad AC quam habet N ad AB et punctum D erit in recta quæ perpendicularis est ad AB. Debet vero CD ad plagam versus A duci ubi datur summæ AC+BC, ad plagam versus B ubi datur differentia. AC−BC vel BC−AC.
[72] Si datur circulus ABD et rectangulum ACB punctus C erit in circulo idem habens centrum cum circulo ABD
[73] Si per data puncta AB transit circulus secans in E rectam ipsi AB perpendicularem et arcui BE æqualis sit arcus EF erit F in circulo cujus centrum est A et si F in tali circulo sit, et bisecetur BF in E erit E in recta.
De Loco rectil{í}neo.
Si locus crura duo infinita opposita habet, et non plura, aut rectus est, aut tertij, quinti, septimi vel imparis alicujus generis curva linea.
Si rectæ locum tangentis plaga determinat est rectus est locus.
Si recta nulla ad plagam infiniti cruris tendens potest locum secare rectus est locus.
Si per datum loci punctum recta transiens non potest locus alibi secare rectus est locus.
Si a loci puncto quovis ad rectas duas positione datas in datis angulis demittantur aliæ duæ rectæ, et progrediendo per additionem subductionem et rationes datas, alterutra demissarum ex altera assumpta vel utra ex assumpta tertia determinari potest rectus est locus.
Si in recta quavis ad datam non infiniti cruris plagam tendente determinabile est loci punctus per simplicem Geometri{illeg} rectus est locus.
Si rectæ per punctum datus extra locum transeuntis et loci intersectio determinabilis est per simplicem Geometriam, rectus est locus.
Si rectæ cujusvis assignatæ et loci intersectio determinabilis est per simplicem Geometriam rectus est locus.
<93v>[74] 1 A datis punctis A, B ductæ conveniant AC BC in C et si dentur ipsorum A, B, {illeg} summa vel differentia (loc. C solid.) proportio (loc. circ) differentia quadratorum (rect{)} summa quadratorum vel aliud quodvis compositum ex quadratis (circ) rectangulum (lineare) Area ABC (rect) angulus ACB (circ) differentia angulorum B−A vel summa 2B+C ( Hyperb & rect{illeg} diff B−C vel summa 2B+A vel 2C+A (vel lineare ) 2A=B vel {et}. 3A+C (Hyperb.) 2A=C (Lin {illeg}) 2C=A (Lin {illeg}) A =B (rect) B=C (circ)
[75] 2 Detur AD positione et ang. DAC et punctus B. Et si dentur etiam ipsorum AC BC summa, differentia (Parab erit C in) Proportio (loc. sol.) differentia quadratorum (Parab) summa quadratorum vel aliud quodvis compositum ex quadratis (Loc solid) rectangulum (Lineare)
[76]
Quæstionum solutio Geometrica.
1 Angulum datum DAB recta datæ longitudinis  CB subtendere quæ ad datum punctum P converget Cape PQ=CD et Q erit in circulo cujus centrum P radius PQ. Age QR∥AD et PRD∥AB et erit PD.DC=AD−QR∷ ∷PR.QR. Ergo Q in conica sectione est. Pone QR infinitum et erit AD−QR.QR∷PD.PR. seu PR =−PD. Pone PR infinitus et erit PD+PR.PR∷AD.QR ergo AD=QR. et AB Asymptotos. Cap{e} ergo PS=PD et per S parallelam AD age alteram Asymtoton & {his} Asymptotis per punctus P describe Hyperb{o}lam secantem circulum prædictus in Q.
CB subtendere quæ ad datum punctum P converget Cape PQ=CD et Q erit in circulo cujus centrum P radius PQ. Age QR∥AD et PRD∥AB et erit PD.DC=AD−QR∷ ∷PR.QR. Ergo Q in conica sectione est. Pone QR infinitum et erit AD−QR.QR∷PD.PR. seu PR =−PD. Pone PR infinitus et erit PD+PR.PR∷AD.QR ergo AD=QR. et AB Asymptotos. Cap{e} ergo PS=PD et per S parallelam AD age alteram Asymtoton & {his} Asymptotis per punctus P describe Hyperb{o}lam secantem circulum prædictus in Q.
2 Inter circulum PDF et rectam DF 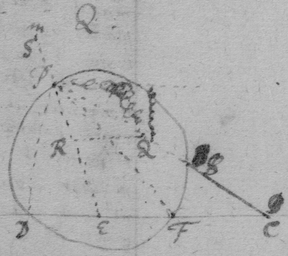 ponere rectam datæ longitudinis BC quæ ad punctum P in circumferentia circuli datum converget. Biseca DF in E. Age PD,PE,PF. Cape PQ=BC. Age QR ∥DC & occurrentem PE in R. Et erit PR.PE∷PQ(BC).PC∷RQ.EC. Et Seu BC,PR.PE,RQ−PR,EF∷ Ergo Q locatur in Conica sectione cujus diameter PR, ordinata {PR}. Sit RQ=0, erit PR=0 et In EP producta cape ergo et erit S centrum et P vertex figuræ. Pone PR infinitus et erit PEq,RQq=PRq,EFq, seu PE{,}RQ=±EF,PR. Quare per S ipsis PD,PS age parallelas et hæ erunt Asymptoti figuræ His igitur Asymptotis per punctum P describe Hyperbolam, ut et centro P radio PQ circulum & per eorum intersectionem Q age rectam PC.
ponere rectam datæ longitudinis BC quæ ad punctum P in circumferentia circuli datum converget. Biseca DF in E. Age PD,PE,PF. Cape PQ=BC. Age QR ∥DC & occurrentem PE in R. Et erit PR.PE∷PQ(BC).PC∷RQ.EC. Et Seu BC,PR.PE,RQ−PR,EF∷ Ergo Q locatur in Conica sectione cujus diameter PR, ordinata {PR}. Sit RQ=0, erit PR=0 et In EP producta cape ergo et erit S centrum et P vertex figuræ. Pone PR infinitus et erit PEq,RQq=PRq,EFq, seu PE{,}RQ=±EF,PR. Quare per S ipsis PD,PS age parallelas et hæ erunt Asymptoti figuræ His igitur Asymptotis per punctum P describe Hyperbolam, ut et centro P radio PQ circulum & per eorum intersectionem Q age rectam PC.
Corol. si ang. PEC rectus est Problema planus erit. Nam circuli centrum incidit in axem figuræ.
3 A dato puncto P rectam PC ducere cujus 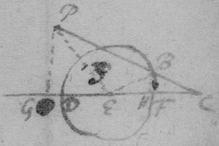 pars BC inter circulum et productam diametrum DF æquabitur semi diametro EF. Age EF ac demitte ⊥ PG,BH. Est EH. HB∷GC(GE+2EH).GP. Ergo punctum B in Hyperbola est. Pone EH=0 et erit HB×GE=0 adeo HB=0. Quare Hyperbola transit per punctum E. Pone EH infinitus et erit EH.HB∷2EH.GP. Ergo . Pone HB infinitus et erit EH.GE∷HB.−GP−2HB∷HB.−2HB Ergo . Quare biseca PE in S et per S age Asymtotos parallelas EH et HB et per punctum E vel P describe Hyperbolam secantem circul{u}m in {D}. Et per B age PC.
pars BC inter circulum et productam diametrum DF æquabitur semi diametro EF. Age EF ac demitte ⊥ PG,BH. Est EH. HB∷GC(GE+2EH).GP. Ergo punctum B in Hyperbola est. Pone EH=0 et erit HB×GE=0 adeo HB=0. Quare Hyperbola transit per punctum E. Pone EH infinitus et erit EH.HB∷2EH.GP. Ergo . Pone HB infinitus et erit EH.GE∷HB.−GP−2HB∷HB.−2HB Ergo . Quare biseca PE in S et per S age Asymtotos parallelas EH et HB et per punctum E vel P describe Hyperbolam secantem circul{u}m in {D}. Et per B age PC.
Corol. Hinc si ang PEG semirectus erit PE axis Hyperbola adeo Problema in eo casu planum.
Quæstionum solutio Geometrica
1 Datis trianguli cujuvis angulo latere et summa vel differentia {re}liquorum laterum datur triangulum{,} Detur latus AB 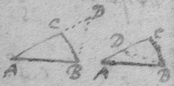 reliquorum laterum AC+BC summa vel differentia AD. Si angulus datus dato lateri conterminus est, sit iste A. Et dabitur triangulum DAB. Angulorum vero CDB ABD differentia in priori casu summa in posteriori est ang ABC.
reliquorum laterum AC+BC summa vel differentia AD. Si angulus datus dato lateri conterminus est, sit iste A. Et dabitur triangulum DAB. Angulorum vero CDB ABD differentia in priori casu summa in posteriori est ang ABC.
Si{t} angulus datus dato lateri oponitur, sit iste C dabitur triangulum CDB specie. In triangulo autem ADB datis lateribus AB AD et ang D datur ang ABD. Unde datur Ang ABC ut ante.
2 Data differentia segmentorum basis summa vel differentia laterum et uno angulorum datur triangulum. Nam si datur summa laterum dabitur ratio differentiæ laterum ad basin si differentia debitur ratio summæ laterum ad basin. Ex ratione utravis & uno angulorum per problema superius datur triangulus specie. et ex data ratione differentiæ segmentorum basis ad latera dantur latera.
3 Data summa vel differentia laterum uno angulorum et ratione basis ad perpendiculum: ex duobus posterioribus dabitur triangulus specie ex priori dabitur etiam magnitudine.
4 Data summa vel differentia laterum uno angulorum et area: ex area rectangulum laterum datum angulum comprehendent{ur}. Si istorum summa vel diff. datur a quadrato summæ aufer duplum rectangulus vel ad quadratum differentiæ {laterus} adde et habebitur priori casu quadratus differenti{æ} posteriori quamdratus summæ laterum: Ex datis autem summa ac differentia laterum dantur latera. Si angulus datus basi conterminus est problema erit solidum.
5 Datis angulo A latera AC vel BC et differentia segmentorum basis AD 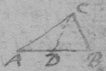 dabitur triangulum ADC ut et angulus B quod est complementus est anguli ADC.
dabitur triangulum ADC ut et angulus B quod est complementus est anguli ADC.
Si detur angulus verticalis C laterum alterutra AC vel BC et segmento basis AC: quiescant BC,AC et punctum D in {circulo} erit radio CB centro C descripto. Ut et in Chonchoide Polo {B} asymptoto AC intervallo AD descripta.
Vel sic. Dato angulo AC{B} datur summa ang: A+B. seu A+CDB Aufer hoc de duobus rectis ac dabitur differentia ang ADC−A. Unde datur triang. per sequ. Prob.
7 Datis basi & differentia angulorum ad basin una cum latere alteratro vel summa differentia ratione laterum aut summa vel differentia {□lo} laterum aut area, perpendiculo vel segm{en}tato basis aut summa vel differentia lateris alterutrius et perpendicula vel segment{i} basis. &c Datur triang. Nam data basi et angulorum ad Basem differentia, {illeg} C erit ad Hyperbolam; et ex dato tertio, punctum C erit ad recta aut circulus aut conican aliquam sectionem.
8 Ubi datar angulus verticalis et differentia segmentorum basis et tertium aliquod, habebitur aliud triangulum ADC ubi datur {illeg} differentia angulorum ad basem, et tertium aliquod.
9 Dat{illeg} basi ratione laterum et tertio quovis ut ⊥ segment{illeg} basis{,} angulo aliquo{,} ratione ⊥ ad lat{eri} {peh} ad segmentum D{tis} {illeg}. Nam {illeg} data {illeg} lat. Dat{ur} circulos {illeg} {illeg}
<96r>Quæstionum solutio Geometrica.
Prob 1
Circulum ABE per data duo puncta A, B describere quæ rectam FG positione datam continget.
Sit E punctum contactus. Produc AB donec occurrat FG in G et erit EG medium proprortionale inter datas AG,BG.
Prob. 2
Circulum ABE per datum punctum A describere  qui recta duas FE, FH continget.
qui recta duas FE, FH continget.
Recta FD biseca angulum HFE. Ad FD demitte normalem AD et produc ad B ut sit DB=AD et per puncta A, D describe circulum ut prius qui contingat rectam FE.
Prob. 3
Circulum ABE per data duo puncta A, B describere qui alium circulum positione datum EKL continget.
Puta factumSit punctum contactus E. Linea contingens 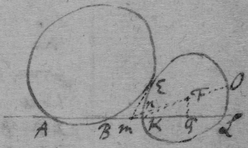 EM. et erit AM×BM=EMq=MK×ML. Divide ergo BK in M ut sit AM.MK∷ML.MB. Cape ME medium proportionale inter AM et BM et centro M radio ME describe circulum. Hic secabit circulum EKL in puncto contactus E. Recta autem BK sic secatur in M. Est AM= AB+MB. MK=BK−MB.ML=BL−MB. ergo AB+MB.BK−MB∷BL−MB. MB. Et componendo AB+BK(AK).BK−MB∷BL.MB. et inverse AK. BL∷BK−MB.MB. et rersus componendo AK+BL.BL∷BK.MB.
EM. et erit AM×BM=EMq=MK×ML. Divide ergo BK in M ut sit AM.MK∷ML.MB. Cape ME medium proportionale inter AM et BM et centro M radio ME describe circulum. Hic secabit circulum EKL in puncto contactus E. Recta autem BK sic secatur in M. Est AM= AB+MB. MK=BK−MB.ML=BL−MB. ergo AB+MB.BK−MB∷BL−MB. MB. Et componendo AB+BK(AK).BK−MB∷BL.MB. et inverse AK. BL∷BK−MB.MB. et rersus componendo AK+BL.BL∷BK.MB.
. Seu 2AG.BL∷BK:MB. {Unde} cum sit BL.BO∷BN.BK, erit 2AG.BN∷BN.BM. Quæ solutio versalis est.
Prob 4
Circulum BDE per datum punctum B describere 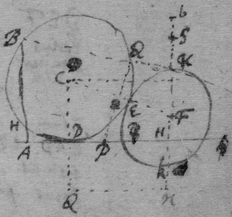 qui datum circulus & rectam lineam AD postione datam continget.
qui datum circulus & rectam lineam AD postione datam continget.
AB est 2CD−AH. NF est 2CQ−NS posito CQ=CF=CS. AB−NF est 2CD−AH−2CQ+NS . Adde 2DQ, erit AB+DQ−HF=NS−AH= . Dividenda est ita data AH in D ita ut dato{illeg} æquale sit, nempo dato AB(Hb)+DQ−HF, seu bk. DH= AH−AD.DHq=AHq−2DAH+ADq.{AH} −2DAH+ADq−. . Fact AB−HK.AH∷BA.AV. & AH. . ADq−DA+ AVq=AV×PV{P}AD{−}AV −AD+AV=AD{×}PV =DV. Age ergo BK occurre{nt}em AH in VHK ad {H}A versus A si {HK} {illeg} versus {b} aliter {illeg} A {illeg} ad bk {illeg} {illeg}
<96v>Nota etiam quod Problematis quatuor sunt casus quorum duo sunt impossibiles ubi circulus datus et recta data se mutuò secant. Casus impossibiles sunt ubi punctum v cadit inter A et P.
Vel in {a}ng GED agatur GD datam per A transiens posito 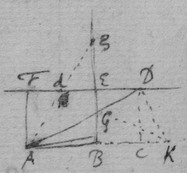 AE quadrato, quære summam radicum Fd, FD Ad AD erige ⊥ DK erit AK summa illa, et CDq+CKq(DKq)+GDq=GKq Aufer BGq seu CKq et restabit CDq+GDq=BKq Datur ergo summa AK. Quare cum ang ADK rectus; super diametro AK describe circulus secantem FE in D, d
AE quadrato, quære summam radicum Fd, FD Ad AD erige ⊥ DK erit AK summa illa, et CDq+CKq(DKq)+GDq=GKq Aufer BGq seu CKq et restabit CDq+GDq=BKq Datur ergo summa AK. Quare cum ang ADK rectus; super diametro AK describe circulus secantem FE in D, d
Super datis rectis tribus AB, CD, EF, 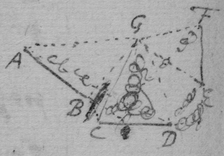 tria constituere triangula quorum vertices erunt ad idem punctum G et anguli ad vertices AGB, CGD, EGF æquales.
tria constituere triangula quorum vertices erunt ad idem punctum G et anguli ad vertices AGB, CGD, EGF æquales.
Vel sic. super lineis AB, CD, EF describe similia segmenta quorumvis circulorum satis magnorum ita ut se mutuo secent compl{illeg} segm. ad circulos {illeg}. Per intersectionem circulorum AB, CD age rectam, ut et aliam rectam per intersectionem circulorum CD, FE: nam hæ rectæ se secabunt in puncto G
The Problem in Schooten de tribus baculis may be solved more easily by supposing the Ellipsis to be a circle first & then 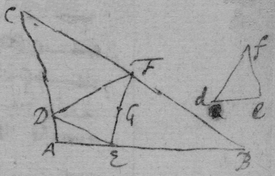 reducing it to the desired circle.
reducing it to the desired circle.
In triangulo dato ABC aliud triangulum DEF dato def simile inscribere cujus latus EF transibit per datum punctum G. Nemper verticis trianguli DEF locus est linea recta.
In data conica sectione ABCDE, trapezium ACDB inscribere cujus anguli duo oppositi 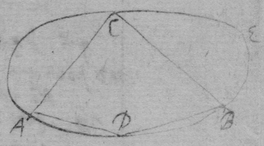 CAD CBD dantur et data puncta A et B consistunt. Vizt si locus puncti D est conica sectio locus punctis c erit linea recta.
CAD CBD dantur et data puncta A et B consistunt. Vizt si locus puncti D est conica sectio locus punctis c erit linea recta.
[77] Ex observationibus proprijs Cometæ anni 1680.
A stella major et orientalior duarum in australi pede Persei, B stella minor earundem. AB stellarum distantia 1gr.46′6″. α, β, γ &c loca Comet{æ}
Observationes Cometæ habitæ ab Academia Physicomathematica Romana anno 1680 et 1681, a Ponthæo æditæ.
Observationes ejusdem cometæ habitæ a R. P Ango in Fleche
Novem 28 hor. 5 matitin. in medio erat inter stellas duas exiguas quarum una est minima trium quæ sunt in manu australi Virginis altera est in extremitate alce: Adeo longitudo Cometæ jam erat ≏ 13, Latitudo australis 50′.
Decem 1. hora 5 matutina. erat in Libra 27. 45′
Observationes Venetijs habitæ a M. Montenaro.
Novem 30 hora post occasum solis duodecima Cometa erat in ≏ 23gr cum lat Aust. 1gr 30′
Decem 1, hor 5 matutina erat in 27. 51 ≏.
Decem 2 erat in ♏ 2. 33
Decem 4 erat in ♎ 12. 52
Credidit M. Montenari latitudinem ad us finem harum observationem augæri.
Observationes Hevelij destituti instrumentis
Anno 1680 Decem. 2 Cometa erat in ≏ 25 cum lat. Austr. 5gr
Decem 3 {Arc}te ortum ☉is hora sexta erat in ♏ 4 cum lat. austr 4gr.
Decem 4 mane hor 6 20′ erat in ♏ 10 cum lat austr. 3gr.
<98v>Observationes Cometæ Mense Novembri anni 1680
Canterburiæ per Artificem quendam nomine Hill, instrumento cujus radius erat 4 pedum Die Veneris Novemb 11 tempore matutino, Cometa inventus est in ♍ 12gr cum lat. Boreali 2gr. Locus ☉is ♏ 29gr. 53′
Romæ per Marcum Antonium Cellium observationes hæ factæ sunt.
Romeæ per Galletium hæ
Cantabrigiæ per juvenem quendam Cometa observatus est Novemb 19 juxta spicam Virginis, quasi duobus gradibus supra stellam illam, sive ad boream, circa horam quartam vel quintam matutinam. Et cauda extendebatur ad us stellam illam primæ magnitudinis quæ cauda Leonis dicitur.
Observationes Parisijs habitæ Cometæ subsequentis 1680 & 1681.
[78]
Ejusdem posterioris Cometæ Observationes Grenovici habitæ
Observationes de Cauda Cometæ prioris
Novemb 19 Cometa juxta spicam virginis existens caudam projiciebat ad us caudam Leonis, spectante juvenes quodam.
Postea caudam per meridiem versus occidentem projici longam satis & ad horizontem obliquam capite vel sub horizonte vel pone ædificia delitescente vidit Humf. Bab. S. T. D.
De cauda Cometæ posterioris
Decemb 8 stylo veteris Hallius noster tempore matutino Parisias versus iter faciens prope Bolonian ante ortum solis Caudam vidit Cometæ quasi perpendiculariter ex horizonte surgentem, ut ipse retulit in epistola quadam citante Flamstedio. Unde Cometa inquit Flamstedius tunc borealem habeb{a}t latitudinem & cum solenondum conjunctus fuerat. Apparebat autem cauda lat{æ} divergens et {illeg} ex corpore {illeg} egressa aer prius {illeg} quam {illeg} {illeg} {illeg} {{illeg}} {illeg}
♀ Decemb 10. duabus horis post occasum Solis, {illeg}bat cauda per medium distantiæ inter caudam serpentis Ophi{illeg}cha et stellam (Bayero δ) in ala austrina Aquilæ. Desinebat vero ad stellas tres exiguas (Bayero Awb) in eductione caudæ Aquilæ ejusdem, id est in linea jungente stellas secundæ magnitudinis in eductione colli Aquilæ, et estellam tertiæ quæ penultima est in cauda ejus, ac stellæ illi penultim{æ} [duplo quidem] propior existebat qu{à}m alteri in eductione colli. Flamstedius in Epistolis ad nos datis. Desinebat igitur cauda in ♑ cum lat. bor. circiter
♄ Decemb 11 post occasum Solis cauda instar jubaris apparuit ab horizonte erecti et lunâ latioris. Post crepusculi cessationem ex tendebat ad us stellas duas quartæ m{æ}gnitudinis (Bayero α, β,) in capite seu glyphidæ Sagittæ. (Flam{st}. ib.) adeo desinebat in ♑ 26gr 43′ cum lat bor. 38gr 34′.
☉ Decemb. 12. Quamprimum non obscura facta est, cauda transibat per medium sagittæ, ne ultra medium longè extendebat. (Flam{st} ib) L{in}quebat igitur stellas 5tæ et 6tæ magnitudinis, δ et ζ in tribulo sagittæ, quasi 40′ ad occidentem, et ultra per 3grad circiter vel fort{æ} 4 extendens desinebat in ♒ 4 cum lat bor circiter vel 43. Desinebat uti e regione superior{is} duarum informium 4tæ magnitudinis quæ supra sagittam sunt {illeg} non et ultra extendebat. Nam cauda ensiformis nobis visa {illeg} sagittam paul{o} longius superare quam Flamstedio, in viam lacteam {illeg} nihil extendens & termino acuto paulatim languescens. Caeter {illeg} in A{s}trola{b}io Flamstedij, cauda hac nocte desinit accurat ad stellas duas exiguas prædictas in tribulo sagittæ.
☿ Decemb 15 hor lucida Aquilæ erat in medio caudæ fere Ancon item austrinus Aquilæ erat {illeg} {illeg} {medio} caudæ fere prope terminum ejus ad latus australe vergens. (Ipse ego & {Bainbro} et ellis part{im} ex observa{tione} partim ex circu{s} {stansijs}) Erat autem cauda 50 grad. longa ({illeg} {steed} epist. 1) {nec tutren} tenuem extremitatem ejus propter Lunæ novel splendorem oliquam apparuise probabila est.
< insertion from the left margin of f 99r >Decemb. 16 hor 5 P.M. Cometa existente in ♑ 17 cum lat. bor. 15gr circiter] cauda lucidam Aquilæ (quæ nocte superiori erat in medio ejus) latere suo boreali {illeg} tangebat, aut quasi; ut et lucidam in {ancone} austrino cygni tangebat eodem latere aut quasi Tota Caudæ longitudo erat 60 grad: feré, latitudo 2 gradus. (Observator quidam Scotus.) Unde Cauda terminabatur in long. ♓ 10 vel 12 circiter 9 lat. bor. 53.
Decem. 19 Hor P.M. Transibat cauda per Delphini caput dein latere suo boreali stellam penultimam in austrina ala Cygni stringebat, tendans inde versus lucidam in Cassiopeiæ cathedra et quasi 60 gradus longa existens ({illeg} observator Scotus) vel potius 63 aut 64 grad ut ex alijs colligo, si non et paullo ultra. Desinebat igitur in ♈ 6 cum lat. bor. 52 vel {illeg} .
Decem 17 cauda inferiùs duos gradus lata {,} superius non-nihil latior, ad caput Cepher extendebat. Decem 22 cauda grad longa ad Cassiopeiam us extendit: ({minor tamem} & {minor} {quam intra} ob D{illeg} splendorem apparuit. Decem 23 caud{a} tenuis et {illeg} per Cassiosu {illeg} extendit, 72gr Conica{illeg} existens circiter. Decem 28 {illeg} orta {illeg} fortior et clarior apparuit {illeg} sed 56gr. {illeg} inter Ala{illeg} {et lum{illeg}} ge{illeg} in femure Andromedæ ad us Persei caput extendit? (Observator quidam Hamburguesis, qui præ cæteris caudam longam ad ultimam {illeg} descripsisse videtur.
< text from f 99r resumes >♄ Decem 18 Cauda linquebat stellas Delphini ad dextra{m}. P{enulti}{ma in Ala} austrina Cygni. (quæ tertiæ magnitudinis est et in Tabulis Bayeri {ζ} diatur) llunat per caudam quarta parte latitudinis cauda{illeg} a latere australi ejus distans. erminus ejus {illeg} habebut multitudinem seu distantiam ab horizonte cum {stellas} quibus {illeg} extrema cauda cygni, Bayero dictis ♊. De{illeg} {igitur} {illeg} ♓ {illeg} lat bor 52gr. 20′.
♂ Dec 21 In cauda stella nulla apparuit sed {cauda} incuvata {illeg} versus {illeg} ad {illeg} onminò {illeg} in loco qui {illeg} seu pectore Cassiopeiæ et alia tertiæ magnitudinis stella in summa fere cathedra prope brachium dextrum (Bayero β dicta) triangulum æquilaterum constituit, tantum ab utra distans quantum {utra} ab invicem, (Flamsted. epist. {s}{ubs.}) adeo in long. ♓ 23gr.54′ lat 47gr 24′ desinebat. Cauda jam 70 adas fere longa duas Cata tendebat versus intervallum inter {schedir} et lucidam cathedræ({illeg} Epist. 2). In Astrolabio vero Flamstedij, Ar{is} caudæ productus secabat ab intervallo inter caput & pectus Cassiopeiæ tertiam ejus partem versus pectus, desinebat autem e regione schedir. Transibat axis ille per caput Delphini, dimidio gradu a stellis duab{us} orientalibus in capite equiculum versus distans. Dein a distantia ultimarum duarum in ala austrina cygni auferebat quin nonas partes distantiæ illius versus stellam ultimam in ala. Postea a spatio inter terminum catenæ Andromadæ & stellam proximam in capite Cephei auferebat tertiam partem distantiæ illius versus terminum caten{æ}
♀ Decem 24 Cauda transibat per medium intervallum stellarum duarum borealium in manu superiori Andromedæ et vix ultra Schedir extendebat (Flamst. Epist. post.) Desinebat igitur in long. ♉ 4 vel 5gr, lat. gr. In Astrolabio Flamstedij cauda desinebat e regione pectoris Andromadæ. Transibat autem (sed on rect{æ}) per medium punctum inter genu dextrum seu australe Pegasi et stellam illam informem ad pedem dextrum quartæ magnitudinis cujus Long ♒ 29 55 lat bor 36. 11. Dein per pr{æ}dictas stellas duas in manu superiori Andromedæ. Juxta Astrolabium stellæ duæ {γ}, δ invictu equiculi, et Cometa triangulum rectangulum constituebant Angulus rectus erat ad stellam occidentaliorem γ. Cometa boream versus distabat ab hac stella tertia parte distantiæ stellarum.
☉ Dec 26 Genu sinistrum Pegasi (quæ stella tertiæ magnitudinis et Bayero dicitur {η} erat inmedio caudæ Flamst. Epist. {ult}.). Sed hac nocte et præc{æ}dent{e} caudæ terminus ob Lunæ splendorem haud satis definiri potuit (Flamst. epist. 2.) Unde die 24 gradus unus forte et alter ad caudæ longitudinem addi debet. Cauda vero hactenus semper curva apparuit, sed non valde curva. Convera sui parte austr{um} respiciebat: qua etiam parte lucidior et distinctiùs terminata apparuit quam altera.
♂ Decem 28 Cauda 56grad longa distantiam inter Alamac et lucidam in femure Cassiopeiæ bisecans ultra pergebat ad us Persei Caput (Observat Hamburgens.)
☿ Decem 29 Cauda tangebat Scheat sitam ad sinistam & intervallum stellar{is} in pede boreali Andromadæ accur{a}te complebat (Flamsteed epist ult Decem 30, hora Situs erat humerus Pegasi seu scheat in latere australi caudæ ita ut per caudam l{a}ceret, a termino caudæ quinta circiter vel sexta parte latitudinus caudæ distans. Implebat autem cauda quasi vel intervalli inter Scheat & genu sinistrum Pegasi (Bayero {η}) Stella φ in femure boreali Andromedæ erat in medio caudæ bisecabat axis caudæ intervallum stellarum in pede Boreali Andromadæ, & cauda intervallum illud plusquam implebat. Desinebat vero in medio loco inter stellam τ quintæ magnitudinis in capite Persei & extemam in borealis pede Andromadæ, sive inter stellam γ tertiæ magnitudinis in humero boreali Persei & punctum qu{a} distantia duarum in pede boreali Andromadæ bisecantur. (Ego.) Unde caudæ longitudo tota erat gr Deflectio caudæ ab oppositione ☉is, seu angulus quem linea jungens caput et extremitatem caudæ effecit cum linea jungente solem & cometam, 5gr. Latitudo caudæ juxta duas λ, μ in pectore Pegasi (hoc est 5gr a capite Cometæ) erat distanti{a} duarum illarum stellarum una cum triente distantiæ (nempe 1gr {30′} circiter). Ejusdem juxta humerum Pegasi (seu gr a capite) latitudo erat dimidium distantiæ humen illius et Pegasi genu sinistri orientalis, adeo 2gr 30′ circitem. Ejusdem inter {illeg}put Andromadæ et annulum qui est in termino catenæ, (hoc est gr a capite) latitudo caudæ erat quinta par{illeg} distantiæ stellarum illarum feré adeo{illeg} {illeg} {illeg} caudæ latitudo adhuc {illeg} {illeg} aliquantulum us ad extremitatem fere, ita ut tandem evaderet 5gr vel paullo major (Ego).
♃ Decem 30 hor {8} Scheat sita erat e latere caudæ ad dextram, et australior duarum in boreali pede Andromedæ erat in medio caudæ. (Flamsteed. [79] Idem et ego observabam hora 9.) Ultra vero hanc stellam australiorem cauda quasi ad 7gr vel gr extendebat circiter(Ego)
☾ Jan 3 Hor Cauda transibat per medium intervalli inter Alamac et australiorem in pede boreali Andromadæ & partes distantiæ stellarum (id est grad) ibi (hoc est 30gr a capite) lata erat. Tendebat verus lucidam in latere Persei sed magis accuratè versus stellam {ι} quartæ magnitudinis in dorso Persei lucidæ proximam quæ tamen sex vel decem minutis circiter distabat ab axe austrum versus. Desinebat verò cauda e regione {a} medij luce inter stellam illam quarta magnitudinis, et aliam ejusdem magnitudinis in humero dextro seu clypeo Persei quæ Bayero θ dicitur. Desinebat igitur in ♉ 22gr. 27′ & lat. bor. 30gr 50′. Si borealiorum duarum μν in angulo Andromadæ distantia dividatur in tres partes æquales & una pars sumatur versus mediam trium in angulo μ, ibi erat medium caudæ (hoc est in ♈ 25g. 4′ lat 30gr 52′) et ibi hoc est 18gr a capite) latitudo ejus æquabat distantiam stellarum illarum, vel paullo superabat adeo erat✝[80] 2gr 6′ circiter. Ex his colligitur caudam curvam fuisse & convexo sui latere austrum respexisse concavo boream. Cauda jam haud multò lucidior erat quam partes lucidiores viæ hacteæ, si partes capiti proximas excipias, et quidem per ultimos duodecim vel quindecim gradus non erat illis u lucidior. Caput jam multo magis conspicuum erat quam cauda at Decemb 15 cauda maximè conspicua erat caput vero instar stellæ adeò exiguæ apparuit (a crepusculo; scilicet et luce lunari obscuratum) ut nudis oculis ne quidem videre possem quamvis adstantes digitum ad eam intenderent. Longitudo caudæ 41gr. Distantia termini caudæ a circulo solem et cometas jungente 4gr 30′ ′. Delinatio caudæ ab oppositione ☉is 7gr.
♂ Jan 4 Hor {9} Cauda juxta caput Cometæ tendebat versus lucidam in eductione cruris sinistri Persei, sed postea vergebat ad lucidam in latere Persei et ubi aer admodum defæcatus erat, et meo et {illeg}{sinetium} judicio extendebat ad us stellam {ι} in dorso Persei. Axis caudæ non transibat per stellam {ι}, sed paucis minutis australior existens, dirigebatur {illeg} accurate versus. Media {illeg}rium in cingulo lucidam in eductione cruris Persei Alge{illeg}b. dictam. vel potius versus punctum 5′ aut 6′ australius. Andromadæ erat in medio caudæ. Latitudo caudæ e regione capitis Andromadæ erat partes distantiæ medij caudæ a capite Andromadæ: Inter Alamac et lucidiorem in altero pede Andromadæ æquabat vel potius partes distantiæ stellarum illarum: Juxta cingulum Andromadæ æquabat distantiam duarum obscuriorem in cingulo. Caudæ limes australis lucidior erat et distinctius terminata, item convexior quam li{mes} borealis. Limes borealis ferè recta erat vel potius nonnihil concava. Caput in centro lucidius, inde ad circumferentiam paulatim languescens, apparebat per tubum duodecim pedum sine stella aliqua vel globo lucido in centro, simill{imum vero stellæ} alicui vel planetæ per nubem lucente ita crassam ut stella distinctè cerni nequeat. Totius lucis in capite diameter erat 12′ vel 14′ circiter. Caput nudis oculis instar stellæ quartæ magnitudinis apparebat. Nox hæc superiori clarior erat & Cometa longius distabat ab horizonte. Unde omnia melius definiebam. (Ego) Hinc distantia termini caudæ a circulo jungente solem et cometam 4gr 45′ Angulus quem cauda juxta caput{.} Cometæ efficiebat cum circulo illo gr, juxta terminum caudæ 10 vel 11gr, quem chorda caudæ efficiebat cum eodem circulo 8gr. Longitudo caudæ 42gr{.} Latitudo e {illeg} capitis Andromadæ (hoc est 3gr a capite cometæ) 1gr 15′ circiter juxta cingulum Andromedæ (hoc est gr a capite) 2gr {illeg} Inter lucid{illeg} stellas in pedibus Androm{e}dæ hoc est (28gr a capite) grad.
☿Jan 5. Stella π in pectore Andromadæ {illeg} caudam ad {illeg} {illeg} {illeg} ad dextram Flamsteed epist. ult.
<100v>♃ Jan 6 hor cauda transibat per medium prima et secundæ in cingulo Andromadæ, sed ob aeris crassiliem ultra lineam jungentem Alamach & lucidiorem in altero pede Andromadæ cerni non pouit, quamvis aer non ita crassus esset quin stellæ quartæ magnitudinis apparerent. Caput cometæ cum tota luce sua vix æquabat stellam quartæ magnitudinis.
♄ Jan 8 hor 8 Cauda, quæ ex australi latere lucidior distinctior & nonnihil convexa erat, a capite incipiens primùm tendebat versus Mirach (seu primam in cingulo Andromadæ) quæ sita erat in medio ejus nisi quod sex vel octo minutis circiter distabat ab ipso medio versus austrum: Postea flectebatur versus Alamach qua sita in ipso medio ejus. Ultra Alamach ad tres vel quatuor gradus luce languescente extendebatur: nec ultra facilè cernebatur quamvis aer adeo clarus esset ut stellæ sextæ magnitudinis apparerent. Aliquando tamen ubi aer solito clarior erat subobscura caudæ vestigia cernebantur us ad lineam jungentem stellas {ι, χ} in tergo et latere dextro Persei & nonnunquam us ad medium locum inter hanc lineam et stellas duas exiguas σ, ψ in cibasi Persei, & semel quidem paulo ultra ita ut stellarum illarum exiguarum citeriorem σ videretur attingere. Nam versus stellas illas duas σψ accuratè tendebat. (Ego) Hinc longitudo caudæ minima erat 24gr circiter, media , maxima 35 & semel 36 vel 37′. Distantia termini caudæ a circulo solem et cometam jungente 5gr. Inclinatio caudæ ad hunc circulum juxta caput cometæ 7gr 30′ juxta extremitatem alteram 10gr40′ Inclinatio chordæ caudæ ad eundem circulum 9gr 10′. Caput cum tota sua luce stellis quartæ magnitudinis cassit eas quintæ paullo superavit. Diameter totius lucis circa caput 12′ Lux caudæ semper argentei erat coloris sed jam per totam caudam obscura valde.
☉ Jan 9 hora Caudæ longitudo constans erat 15gr vel 16gr extendebatur enim paullo ultra Alamach seu pedem australem Andromadæ. Aliquando tamen ubi aer erat solito clarior luce tenui superare visa est dimidiam distantiam inter Alamach & præfatas duas stellas σψ in cibasi Persei ad quaru citeriorem σ nocte superiori semel extendebat, ita ut longitudo ejus tunc esset 24gr circiter (Ego) Caud{æ} ad latus boreale tetigit Mirach, desis{illeg} verò ad υτ in femore genu Andromadæ. Flamsteed Epist ult.
☾ Jan 10 hora 6, 8, 10, cauda desinebat ad Alamach{.} Aliquando tamen ubi aer erat solito clarior, luce suboscura se extendebat ad stellam {χ} in australi lateri Persei, vel potius ad puctum duodecim vel quindecim minutis borealiorem quàm stella illa. Seribit Flamstedius caudam hac nocte desysse sub Alamech, directam vero fuisse versus stellam illam illam {χ} in latere Persei, id est si recta producas; at ob curvaturas cauda ubi eo us visibilis extitit deflectebat a {χ} ad punctum 12′ vel 15′ borealiorem.
♂ Jan 11 hora 8, 9, 10 cauda satis distincta erat ad us Alamech, et paulo ultra, subobscura ad us stellam præfactam exignam {χ} in latere Persei, ubi terminabatur axe caudæ per stellam transeunte. Distantia termini caudæ a circulo solem et Cometas jungente erat igitur 3gr{.} 50′. Inclinatio chodæ caudæ ad circulum illum gr. At distantia illa et inclinatio pa{u}llo majores extitissent si modo cauda æqu{e} longe in sig{illeg} Persei visibiliter extendisset ac aute {illeg} Caput jam cum tota sua luce stellas quinta magnitudinis æquabat.
♃ Jan 13 Cauda luce perobscura desinebat e regione stellæ præfatæ {χ} in latere Persei, luce satis sensibili inter Alamach {illeg}t Algol. terminabatur.
{illeg} Jan 23 & 24{cometam rursus} {beneficio sensibili impetus} vidi {sed} Cauda ejus {ob Linea} splendorem {netiquam} apparuit caput ejus inter nubecula {illeg}cunda apparuit reliquo ca{illeg}o haud lucidioris ut sentiri ægre {illeg}rit.
{illeg} Jan 25 {Luna sub horizonte} cauda cometæ denuò sensibilis {illeg} potuit ad {longitudinem gradus} {illeg} {vel septem.} {illeg} {illeg} sequente ad longitudinem graduum
12 aut paullo ultra sed luce obscurissima et {a}gerrim{à} sensibili: Tali uti luce extendebatur ad lineam jungentem Algol & Pleiadas. Dirigebatur vero axis ejus ad lucidam in humero orientali Auriga accuratà. Unda deviatio caudæ ab oppositione solis boream versus 10gr.Caput Cometæ cum ommi sua luce stellam septimæ magnitudinis æquare videbatur, aut {non {illeg}} superare.
 Jan 30 Caudæ non nisi vestigia quædam obscurissima restabant quæ tamen tam is oculis quam armatis sentin potuete extrudebantur hæcce caudæ vestigia luce magis sensibili ad lineam jungentem Algol et stellas informes in nube arietis, luce minus sensibili ad us lineam jungentem Algol & Pleiadas {Quinimò} nonnunquam sentire visus sum vestigia quædam lucis rarissim{æ} ad us lineam jungentem Algol et stellam 3 tertia magnitudinis in australi pede Persei. Tendebat vero axis reliquiarum caudæ inter genu lucidum Persei & lucidam in humero orientali Aurigæ, nempe versus punctum triente gradus australius quam lucida illa in humero circiter, ade ab oppositione solis deflexit 10gr 4{illeg} circiter. Caput Cometæ cum omni sua luce stellis septima magnitudinis cessit. Ex hoc tempore caudam nudis oculis observare destiti. Telescopio vero septupedali caudam vida us ad Feb 10{illeg} quo tempore duos circiter gradus longa videbatur, & versus punc{illeg} grada uno et altero australius quam lucida in humero orient{a}li Aurigæ dirigi, magis et magis ab oppositione solis deflectens. Posthæ cometam a Feb. 25 ad Mart. 9 demò vidi sed sine cauda. Nam et caput ipsum jam adeo tenue evaserat ut ope Tubi septupedalis cum apertura duarum unciarum cerni vix posset.
Jan 30 Caudæ non nisi vestigia quædam obscurissima restabant quæ tamen tam is oculis quam armatis sentin potuete extrudebantur hæcce caudæ vestigia luce magis sensibili ad lineam jungentem Algol et stellas informes in nube arietis, luce minus sensibili ad us lineam jungentem Algol & Pleiadas {Quinimò} nonnunquam sentire visus sum vestigia quædam lucis rarissim{æ} ad us lineam jungentem Algol et stellam 3 tertia magnitudinis in australi pede Persei. Tendebat vero axis reliquiarum caudæ inter genu lucidum Persei & lucidam in humero orientali Aurigæ, nempe versus punctum triente gradus australius quam lucida illa in humero circiter, ade ab oppositione solis deflexit 10gr 4{illeg} circiter. Caput Cometæ cum omni sua luce stellis septima magnitudinis cessit. Ex hoc tempore caudam nudis oculis observare destiti. Telescopio vero septupedali caudam vida us ad Feb 10{illeg} quo tempore duos circiter gradus longa videbatur, & versus punc{illeg} grada uno et altero australius quam lucida in humero orient{a}li Aurigæ dirigi, magis et magis ab oppositione solis deflectens. Posthæ cometam a Feb. 25 ad Mart. 9 demò vidi sed sine cauda. Nam et caput ipsum jam adeo tenue evaserat ut ope Tubi septupedalis cum apertura duarum unciarum cerni vix posset.
Interim ubi me Cometam nudis oculis observasse affirmo nolim credas Myopem vitro concavo c{æ}nisse quo visio redderet distincta. Tali vitro, sed optimo, semper usus sum.
Cæterum cauda quoad directionem, has observabat leges. Ad singulas observationes per caput cometæ et extremitat caudæ in globo due circulos maximos se secantis in A B C D E &c Divide segmenta AB, BC, CD &c in ratione tempo{illeg} inter observationes utrobi factas intercedentium. Per puncta divisio{nus} duc un superficie globi lineam uniformem quæ segmenta illa AB{,} BC, CD &c in punctis divisionum contengat, et in omni casu circulus per caput co{illeg} & extremitatem caudæ ductus tanget linem illam, uniformem {quam} proximè. Unde cauda, dato tempore, quoad positionem duci potest. {illeg} vero quod segmenta AB, BC, CD, DE &c divisa per sum{illeg} temporum duorum observationes utrobi factas intercedentium (AB{illeg} summam temporis pr{e}imi et sedi, BC per summam temporis secun{dam} tertij &c seu AB per tempus inter observationem primam ac tertiam BC per tempus inter secundam at quartam CD per tempus {illeg} tertiam et quintam &c) debent esse in progressione seu geome{tri}ca seu arithmetica alia aut alia quavis regulan. Et {illeg} hinc collatis inter se observationibus cognosci potest an situs caudæ fuerit rect{è} observatus.
Si inter capellam et polum eclipticæ sumatur punctum tribus gradibus distans a capella, cauda Cometæ, a Decem 15 ad Jan 8 versus punctum illud satis accuratè, dirigebatur pra{illeg}tim circa Dec 18, 25, Jan 4.
Si in globo ducatur circulus maximus qui sel{illeg} ecliplipticam {illeg}  20gr in angulo 54gr transiens per stellam α {illeg} ala septentrionali sagillæ, dem per stellam θ quarttæ magnitudinis {illeg} orientali brachio cassiopeiæ, deni per stellam {illeg} in tergo Persei aut per punctum gradus circiter australius: Cauda Cometæ {ab imd} ad us Jan {:} 4, imd ad Jan 8 salis accuratè terminabatur. Excipe tantum a Dec 15 ad Dec 26 ubi lux ten{uior} in extremitate caudæ ob Lan{illeg} splendorem videri {suon} potuit. Si tam{illeg} caudæ longitudines {F}lam stedianæ juxta observationes{illeg} Hamburg ens{illeg} no{nn}ibil augeantur. {illeg} upon {circulo} b{illeg} alt{eri} {illeg} que{illeg} proxime. A longittudine caud{a} aufer dimidiam latitudinem, et habebitur longitudo correcta. circulus termino hujus longitudinis descriptus secat eclipticam in
20gr in angulo 54gr transiens per stellam α {illeg} ala septentrionali sagillæ, dem per stellam θ quarttæ magnitudinis {illeg} orientali brachio cassiopeiæ, deni per stellam {illeg} in tergo Persei aut per punctum gradus circiter australius: Cauda Cometæ {ab imd} ad us Jan {:} 4, imd ad Jan 8 salis accuratè terminabatur. Excipe tantum a Dec 15 ad Dec 26 ubi lux ten{uior} in extremitate caudæ ob Lan{illeg} splendorem videri {suon} potuit. Si tam{illeg} caudæ longitudines {F}lam stedianæ juxta observationes{illeg} Hamburg ens{illeg} no{nn}ibil augeantur. {illeg} upon {circulo} b{illeg} alt{eri} {illeg} que{illeg} proxime. A longittudine caud{a} aufer dimidiam latitudinem, et habebitur longitudo correcta. circulus termino hujus longitudinis descriptus secat eclipticam in  gr in angulo 54gr circiter. Via cometæ secat eclipticam in
gr in angulo 54gr circiter. Via cometæ secat eclipticam in  21 in angulo 30gr circiter. Ubi hæc via præfatum circulus correctum secat, hoc est in
21 in angulo 30gr circiter. Ubi hæc via præfatum circulus correctum secat, hoc est in  20gr 4′ & latitudine boreali 40′ circiter, ibi erit punctum per quod planum, in quo comet{æ} movit, transire debet. Secuit igitur planum illud eclipticam in
20gr 4′ & latitudine boreali 40′ circiter, ibi erit punctum per quod planum, in quo comet{æ} movit, transire debet. Secuit igitur planum illud eclipticam in  20 vel 20 circiter.
20 vel 20 circiter.
Cauda Decem 10, 11, 12, angustior apparuit, Decem 15 paullo latior, Decem 29 & 30 {illeg}ultòlatior, ut et Jan 3 & 4. Uns{e} remoti{o}r a nobi{s} fuit extremitas caudæ Decem 10, 11, 12 quam Decem 29, 30, & Jan 3, 4, cauda in regiones ulti{illeg} & nobis aversas pergen{se}.
Halleius mihi narravit se iter Parisias instituentem Dec 8 stylo veteri cauda{m} cometæ vidisse perpendiculariter ex horizonte surgentem ad instar trabis igne{ce} ad longitudinem decem vel ma{illeg}iore qui{m} decim graduum paulo ante ortum solis. Quod cauda hæc non prius disperetet quam sol oriens inciperet conspici: ad solis aute{m} fulgorem mo{x} evanesceret. Et quod Cauda e corpore solis exire videretur, ita ut caput cometæ esset soli proximum. Deni quod ipse quid esset ipse quid esset hoc Phænomenon nesciret donec Cometa e radijs solis egressus se omnibus conspicuum exhiberet.
Monsieur Richer sent by the French King to make observations in the Island of Cayenna (north Lat 5gr) having before he went thither set his clock exactly at Paris, found then ({viz} at Cayenna) that it went too slow so as every day to loose two minutes & an half for many days together & after his clock had stood & went again it lost 2 minutes every day as before. Whence Mister Halley concluded that the Pendulum was to be shortned in the proportion of to to make the clock go true at Cayenna. In Goree the Observation was less exact. They there found
Decem 12 Caput per Telescopium Flamstedio apparuit Iovè minus nec rotundum quidem sed inæquale ad instar quadorati cujus anguli fortuitò & irregulariter diffracti fuissent. Lumen capitis jam fuscum admodum & lumine saturnio multis gradibus deterius.
Decem 21 Caput per Telescopium apparuit ut locus nubilosus in cælo nudis oculis apparere solet: excepto quod per faciem ejus puncta quædam lucida sed exigna valdè irregulariter spargebantur. Capitis diameter erat plusquam minuti unius sed non bene terminata nec lucida sed nebulosa
Decem 26 Caput nudis oculis minus apparuit quam Os Pegasi & pallidius, per Telescopium ut ante, nisi quod puncta lucida min{illeg} distincta erant. Exinde caput minus & tenuius perpetuò evasit. Hæc Flamstedius epist. ult.
Ex Hookij Cometa edito ann 1678.
Apr 21 1677 Cometa ab Hookio vesus est inter basem trianguli et stellas informes in nube Aristis, in recta linea jungente{m} Cor Cassiopeiæ & Alamak. Distubat ab Alamak austr{illeg} versus distantiæ cinguli & pedum Andromadæ. Cauda æquabat distantia ejus ab Alamak, & dirigebatur accurate verus stellam in nasu Cassiopei{æ} quartæ magnitudinis. Unde caput dirigebatur non versus solem qui erat in ♉ 11gr sed versus ♉ 14gr. Caput æquabat stellam prim{æ} magnitudinis & lumine magis {fi}sco. Stella in medio capitis (per Telescopium qumidecim pedum conspecta) æque lucida apparebat{illeg} ac ♄ ubi prope horizontem versatur. Rotunda erat, sed non distin{illeg} definita. Diameter ejus erat 25″. Comæ verò loti{us} caput ambientis latitudo seu diameter 4′ 10″. id est decuplo major quam diameter capitis. Angustior erat coma et melius terminata solem versus.
Apr 23 Cometa erat in medio puncto inter Algol et l{illeg}idem informium in nube Aristis, nempe in ♉ 14 lat. bor. 17gr. Unde orientem versus movebat{e}r sed in linea nonnihil ad austrum deflectente. Caud{illeg} recta erat et versus stellam tertiæ magnitudinis in femore {illeg} Cassiopeiæ dirigebatur quasi 7 vel 8 gr longa existens. Caput it versus ♉ 17 dirigebatur, sole tamen existente in ♉ 13 .
Capitis lumen densum erat et compactum & saturno fer{illeg} æquale, caput tamen limbo æquabili ut saturnus non definitum. Et capitis partes aliquæ lucidiores erant aliæ mius lucidæ. Hæ non pr{o}rsus permanentes sed notabiliter mutabiles sese ostentabatis.
< insertion from the left margin of f 103r >Imo Hevelius in schemate quidem {v}iam cometæ infra {rostros} corvi {desibit} at in observationibus non item. Dicit erum, Decemb , 5h mat. cometam properostrum corvi a se detectum esse a rostro illo {favonium} versus vix gradu distantur. {Vidit} calculum Hevelius
Vidit {i}tem Hevelius Cometam Dec {per unam tam} {illeg} {illeg} {punctorum} Cometa{m}. Et ocul Leporis & se{illeg} Cometam pau{cis} {illeg} ante posteriorem observationem supra oculus Leporis ad distantiam {illeg} circiter transi{ti}sse, unde infra humerum {L}eporis transivit & fere tegit. Hevelius præterea cometam pa{rs}im quamdiu cometa magnam hab{ui}t latitudinem australem australiorem po{int} quam Auroutius. Fortè quod Auroutius refractiones neglexit vel pro{illeg}oribus habuit.
< text from f 103r resumes >Cometæ anni 1664 observationes optimæ in lucem edita sunt Hevelij, Ægidij Francisci de Gottignies in urb{e} Roma Professoris & M{illeg} Petiti Pariciensis qui Observationes Au{r}antij edidit. Hevelius tamen Gottignies viam Cometæ illius infra stellam in rostro corvi descri{illeg} Petitus autem (quo{cum} consentit Hugenius in observationibus quibus{illeg} ab Hookio visis) viam ejus supra stellam illam seu ad boream status Hevelius præterea ubi fere australiorem facit viam cometæ quam Petitus et Gottignies, & verbi gratia, cùm illi viam sup{r}am stul{illeg} tertiæ magnitudinis in humero dextro Leporis describunt, {nie} p{o}mit infra. Gottignies in prima sua tabula statuit Cometam in ♊ 4 lat austr 33 in secunda in ♊ 4 lat austr 34 ut{rum} eodem tempore nempe decem anno 1664.
Coma Cometæ anni 1677 juxta nostrum seu stellam in {illeg}capite, lucid{illeg} {illeg} e latere nuclei quod soli oppo{c}ebitu{r} lucidior er{illeg} {illeg} {illeg}rca reliqos partes nuclei: quæ quidem part{illeg} lucidior {illeg} {illeg}llium {illeg}euda Constituebunt nes capitis {esil}{illeg} apparuit in c{u}ada ne regio soli opposita {obseumor} suit quam regio soli obversa ut opporteret si caput cometæ corpus opacum esset & lucis expers. Nucleus vero cum coma come{illeg} anni 1664 collatus minorem rationem ad comam obtinebat sub finem ubi Cometa longi{es} a {Sole} recesserat.
Via cometæ anni 1664 & 1665 juxta
delineationem Hookij.
[81]  Longitudines & latitudines subse
Longitudines & latitudines subse
quentium stellarum, ex catalogo
Tychomico, ad annum completum
1664 collectæ
Distat inquit Auroutius stella A a secundæ ♈tis dextram versus 45′ vel 46′ a prima vero 1gr20′ Angulo recto existente qui a lune{illeg}s ad stellam illam a prima et secunda ♈tis ductis continetur. Ait et Hevelius stellam distare 46′ a secunda ♈tis & 1gr 15 vel 20′ a prima. A prima ♈tis niquit Auroutius Cometa Feb ‡[82] tanto spatio distitit quanto ab eadem stell{u}la A removetur ho{c} est 1gr 20′. Unde concludit Auroutius Cometæ Longitudinem {trinc} fuisse 27gr circ. & Lat. boreal. 7gr 4′ vel 5′.
Feb ait Auroutius Cometa 12 vel 13 movebatur a priori loco et 9 {pringles} propior factus est prima ♈tis. Feb & aut circiter cometa a primæ ♈tis in minima fuit distantia, quæ distantia erat ad summum 50′, {in}quit idem Auroutius, Porro cometa in Mart 7stylo novo, {ait} Auroutius, cometa non ultra 7′ vel 8′ uno die movebatur.
Juxta Observationem R. P Gottignies, Cometa Ma{rt } jam modo prætergressus fuerat Corn{u} sinistrum ♈tis quasi spatio qu{i} vel quintæ partis itineris uno die confecti id est 1′ 30″ vel 2{′} circiter: quo{c}um satis consentiunt Hookius et Auroutius. Ad Distantia primæ et s{e}dæ ♈tis, quæ est 1gr 33′, Gottignies in delineation{e} s{ua} {pinil} distantiam cometæ a seda ♈is esse ut 4 ad 4, Hook ut {4} ad 45, Petitus ut 2 ad 17 sed Petitus in delineationibus suis hand satis asse{c}utus est mente{s} Aurouutij, facil cometam propius {uei}essisse ad stellam A quam ad primam ♈tis contra qui facit Hookios {&} Gottignies. Sit ergo distantia illa distanti{æ} primæ et secunda ♈tis hoc est 8′ 16″ circiter & cometæ longitudos {ea} tempori{bus} {set} Mart {1} Rora 8′ {illeg}esp er{i}t 1′ circiter major quam longitudo secunda ♈tis adeo in ♈{,} 29gr 18′ 30″ Latitudo verò {1}8{′} 1{5}″ m{illeg}quam latitudo ejusdem stellæ adeo{illeg} {illeg} 37′ 15″.
<104r>Cometæ anni 1661 loca ex Hevelio
Maxima Cometæ latitudo Australis 49gr 33′ vel 49gr et locus maximæ latitudin{i} in ♋ 27 gr. Ut ex circulo maximo per loca duo cometæ transeunte ex pluribus observatiionibus colligitur. Securit autem Cometa eclipticam in ♈ 28gr 58′ id Jan 15 hora 9 P. M circiter in angulo. Comet{æ} Decemb 28 pro ratione calurarum observationem latitudinem 3′ vel 4′ justominorem habere videtur. Cætera quoad latitudinem inter se bene consentiment. Et hinc latitudo maxima cometæ forte 49gr 35′ vel 36′ melius statuitur, quam 49 33′.
Decem Cometa detecta prope rastrus Corvi Favonius versus vix gr ab eo distans.
Decem hor 2 vel 3 mat cometa transibat 20′ supra oculum Leporis. hor 8 vesp cometa infra stellas in eridano (dictam tertiam a primo flera) a semigradum ferè {libe}{ro}tum versus incedebat, sic ut hora 10 com{m}a{in} suam decurta{se}per stellam istam in ea tunc clare emicantem projiceret.
hora 4 vesp. Cometa jam modo mandibulam fere occultarat, non tamen occultabat ommino ub aliqui volunt, nam hora 9 Mandibula in ipsa cauda apparuit. Hora 9 Cometa inter Mandibula et stellam in ore C{a}ti in linea fere recta apparuit.
hor 7 vel 8 vesp circiter Cometa cus Mandibula et illa in {co}re triangulus æquilaterum ferè constituit
Et postea Cometa inter mandibulum et Caput Andromedæ existente, Cæpit Hevelius distantiam ab utra stella ut cognosceret an summa distantiarum æquabat distantiam stellarum Inde motum Cometæ quoad progressum in orbita sua exhinc accurat{è} determinavit, præsentim sub initio mensis February.
Cometa distabat una, sui diametro ab inferior{e} duarum stillularum {,} quæ eaudem quo distantiam ferè habebunt ab vivic{è} nempe 2′ circiter vel 3′ {illeg}. Bin{e} illa stellæ limbo orientali comet{illeg} ad hærebant. Inferior et lucidior {binarum} vix {tola}de limbo exi{illeg}{et} superior maxima sui parte suo ten{e}t maxima {illeg} adeita latebat ut ea propt{illeg}{us} etisem mino{rs} et obser{illeg} videretur{.} Inferior igitur a capite cometico plane {tecta} fuerat superior le{m} hu{m} stri{ns}cerat. hor. 7 vesp Cometæ limbus a hinis illis stell{æ} una cometæ diametro distabat H{av}e Hevelius. Unde colligit comet{æ}m vix ultra 6 jam per diem movisse. Movebatur autem, inquit, sursum ita ut longitudo ejus vix quicquam mutaretur.
Di{x}i latitudinem Cometæ Decemb 18 insto minorem esse per 3{′} vel 7′, imò non consentit cum cæteris observationibus nisi 8 {minus} augeatur. Pro 49gr24′ lat. Aust. {scribe} igitur 49gr32′ lat austr. et maximam Cometa latitudinem 49gr 4{0}′ in ♋ 27gr45′. A, B, C, D, E, F, G are the stars in the greater  {ev}ain. L, m, n, s, t stars in the Bears right hinder leg. H, J, K stars in his head & {illeg} neck. Anno 1682 Sept
{ev}ain. L, m, n, s, t stars in the Bears right hinder leg. H, J, K stars in his head & {illeg} neck. Anno 1682 Sept
On Satturday at {1}h 20′ after midnight I saw the comet in V in a right line with the stars F & s, distant from the star s twice as far as that star was from the star t. The tayle pointed directly towards the star K in the eye or cheek, & was about six degrees long reaching of the way to that star.
Sunday at 9h 20′ before midnight the comet was in X. Xs & sn were equal & a little greater then Xn. ms, mX & 1Xs were equal. Xs was equal to 3st The tai{l}e ended over against the middle of st & produced cut of or of qr towards q.
Munday at 8h 40′ at {n}ight vYo were in a right line Yo=1st. The taile ended over against mn or alittle beyond those stars suppose about a degree beyond. & pointed towards a little star p not noted (I think) in the globe.
Tuesday at 9h. 0′ The comet was in Z. oZ was a little greater then DE almost as great as CD. The comet passed about 8′ or 10′ above the star o which is a little scarce noted in the globes. The tayle was crooked, the convex side southward was sensibly brighter{,} then the concave side. The head in this & the former observations scarce so luminous as a star of the first magnitude but more luminous then one of the 2d. The taile went exactly in the middle between the stars m & L or a very little nearer to m & pointed almost at the Pole star, vizt as much below it as the middle star in the little Beares taile was above it & reached up within a degree or two to over against it or very nearely. The tayle produced would have wiped the star A with its north concave side.
Problemamm solutiones juxta sequentes
Regul{a}s
Reg. 1. Circumspicera quid ex datis consequatur ut ex pluribus datis facilius assequamur quod propositum est. Item circumspicere quomodo schemata constmantur ut en datis aliquid colligamus. In hune cognoscendæ sunt proportionalium legès et transmutationes, eo quod Geometria{,} proportionales ob simplicitatem magis quam per æquationes amat progredi. Cognoscendæ s{u}nt etiam Figurarum proprietates quæ in elementis sunt & determinationes simpliciores: Et quando triangula vel quadrangula dantur specie, quando specie et magnitudine Determinatæ item sectiones vete{r}e{m} quæ sunt æquationes recentio{r}us in promptu ess{e} debent. Ut et Locorum determinationes. Nam Geometria tota nihil {a}loud est quam inventio punctorum per intersectiones Locorum.
[83] Sectio determinatæ dici potest simplex duplex triplex &c {proud} in uno, duobus, tribus punctis &c fit, vel ut recentis loq{uca}ntur prout æquatio unius duarum trius dimensionum est.
Si secanda sit recta data AB in x ita sit ut Ae.Ax &c ∷Bx.De. vel rectangulum AxB sequetur dato rectangulo AeD: sit angulus BAD rectus. Biseca BD in C. Centro C radio Ce describe circulo secantem AB in x. At hoc modo construi potest omnis æquatio quadratica. Sed rem longius prosecutus est Apollonius.
Igitur is in recta aliqua dantur  tri{o} puncta A, B, F et secanda sit recta in x ita ut sit Ae.Ax∷Bx. Fx componendo vel dividendo erit Ae.ex∷Bx.BF unde solvetur Problema uti prius.
tri{o} puncta A, B, F et secanda sit recta in x ita ut sit Ae.Ax∷Bx. Fx componendo vel dividendo erit Ae.ex∷Bx.BF unde solvetur Problema uti prius.
Si in recta dentur quat{r}or puncta 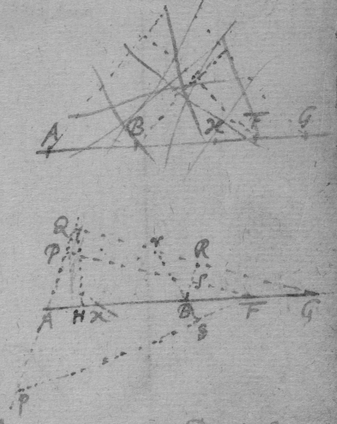 A, B, F, G et seconda sit recta in x ita ut rectangulum AxB, sit ad rectangulus FxG in data ratione AH ad HG, erige perpendiculum HQ quod sit medium proportionale inter AH et HG. I{u}nge AQ, GQ. super BF constitue triangulum BSF simile triangulo{,} AQG et ad easdem partes rectæ AG si punctum x quæritur vel inter A et B vel inter F et G, {A}liter ad partes contrarias. Super diametro PR describe circulum secantem rectam AG in x
A, B, F, G et seconda sit recta in x ita ut rectangulum AxB, sit ad rectangulus FxG in data ratione AH ad HG, erige perpendiculum HQ quod sit medium proportionale inter AH et HG. I{u}nge AQ, GQ. super BF constitue triangulum BSF simile triangulo{,} AQG et ad easdem partes rectæ AG si punctum x quæritur vel inter A et B vel inter F et G, {A}liter ad partes contrarias. Super diametro PR describe circulum secantem rectam AG in x
Addo si recta secanda sit in x ita ut rectangulus AxB sit ad diferentiam inter rectangulam FxG & rectangulum datum mXn: seca{illeg} rectam illum in T et V ita ut {illeg}rectangula{illeg} {{illeg}}{illeg} {illeg}T{G} {illeg} F{QG} {secunda} {æquater} dato {illeg}rectangulo M{illeg} Dein {r}ursus seca in x ita ut rectangulum AxB sit ad rectangulum TxV in ratione illa data.
Si recta secanda est in X ita ut rectangulum AxB sit ad summam rectanguli FxG et rectanguli dati mXn. Erit dividendo AxB÷mXn ad FxG in ratione data et inverse FxG ad AxB÷mXn in ratione data. Qui casus est superioris propositionis.
Ad ho{c} casus facil{e} est cæteros reducere.
"Signo verò ± additionem et subductionem abiguè denoto.
Geometria.
Lib. 1.
[84] Problemata pro numero solutionum quas admittunt distinguntur in gradus. Qu{æ} uni{c} tantum admittunt solutionem sunt primi gradus, quæ secundi, quæ tres tertij, & sic in reliquis. Ut si data recta AB producenda est ad D ita ut punctum D dao intervallo [85] distet a puncto aliquæ C quod in sublimi datur: Solvetur problema si centro C et intervallo isto dato describatur circulus datam illam rectam secans. Et duplici intersectione in D et dprodibit duplex ejus solutio, . Ad utrum vis enim punctum D vel d produci potest recta AB. Quod ostendit Problema secundi gradus esse.
[86] Quantitates autem quibus quæstioni respondetur aliquando directæ & positivæ sunt aliquando retrorsæ vel subductitiæ quas et negativas vocant. Ut si datum illud intervallum {B}C majus sit quam distantia BC ita ut circulus rectam illam sectet in Δ et δ, respondebitur quæstioni directe producendo AB ad δ et contrario modo ducendo BΔ retrorsum. Directas quantitates notamus præfigendo signum + retrorsas præfigendo signum −: ut in his, + Bδ & BΔ. Et ubi neutrum signum proæfigitur quantitas directa est. His signis etiam additionem et subductionem significamus. Ut in AB + Bδ & AB − BA ubi Bδ addi, BΔ subduci intelligitur. IISigno
[87] Hœ quantitates quibus {sestijoni } respondemus aliquando etiam impossibile evadunt; Ut in hoc casu quantitates BD et Bd ubi intervallum CD minus assignatur quam ut circulus rectam AB secare possit. Et quando duæ vel forte quatuor aut plure{illeg} {etiam servant plures} impossibiles sunt (nam numerus impossibilium semper est par) gradus Problematis non æstimabitur ex numero solarum realium sed ex numero omnium, id est omnium qui in quocun casu Problematis generaliter propositi r{e}abes evadere possunt. Problema verò generaliter proponi dico in quo quantitates nullæ ita. limitantur quin possint additis vel subductis datis majores vel minores sumi . Ut si inter A et B inveniendæ sint duæ mediæ proportionales x et y, unica tantum est hujus solutio realis, nec tamen ideo primi erit gradus Problema. Nam si omnes ejus termini{.} exprimantur & datis quibusvis CD quotquot aliquo modo limitantur, C, D, &c augeantur vel diminuantur, Problem{a} generaliter enunciabitur hoc modo Invenire quantitates x et y ita ut sin A ad x & x + C ad et ± D ad B in eadem ratione. Hujus generalis problematis tres possunt esse solutiones reales, adeo casus ejus ubi C, D, nulla sunt id est ubi x et {illeg} med{o}sunt proportionales inter A et B, problema {illeg} grad{es} quamvis duæ ex solutionibus hic evaserint impossi{illeg} {illeg} in {omtres} ejusdem sunt gradus cum genera{illeg} {illeg} {illeg}forte per conditiones {quesdein de quibus} {illeg} {illeg} ad gradum aliqu{aor} inferiorem a
Si linea A ducitur in lineam B rectangulum genitum signamus scribendo A×B vel AB et si id rursus ducatur in lineam C parallel{i}pipedum genitum signat{rus} scribendo A×B×C vel ABC Latus vero quod oritur applicando rectangulum illud ad lineam quamvis D sic notamus . Et sic in reliquis. Sed et exposita linea aliqua ad quam tanquam mensuram universalem aliæ omnes lineæ referant{ur} scribimus A×B vel AB at{it} AB designandum quartam proportionales ab hac linea ubi duæ mediæ sunt A et B et A 'B 'C ad designandam etiam quartam ab eadem linea ubi A ' et C sunt duæ mediæ et sic in infinitum. Et si linea illa sit prima continuè proportionalium et alia quævis A secunda tertiam designamus AA vel A1vel A2 quartam sic A{c} vel A3 quintam sic A99 vel A4 A duarum, tri{sun}, quatuor {q}uim {f}rationum et sic A est [ intelligendo A dimidiæ rationis seu media proportion inter mensura{m} universalem et A quadratum, cubum, quadrato-quadratus, quadrato-cubum, cubocubum de A et sic in infinitum. Nam et quadratum et cubum super latere A constitutum designamus ijsdem notis ac tertium quartum{,} proportionalem. Unde et reliquis proportionalibus per analogiam nomina dantur . Quæ et analogicè etiam dicuntur dimensiones ac potestates lineæ A. Sic A4 dicitur A quatuor dimentionus vel A potestatis quadrato-quadraticæ quamvis revera nihil utra trinam dimensionem et potestatem cubicam in Geometria reperiatur. Et simili analogia dicimus proportionales A9, Ac, A99 generari ducendo A in se et A9 in A et Ac in A. Et quartam proportionalem AB generari ducendo A in B. Et vicissi A99 applicatum ad A producere Ac et AB applicatum ad B producere A, applicatum vero ad C producere .] Deni ad designandum tum latus quadrati æqualis areæ A'B tum medium proportionale inter mensuram universalem et A'B scribo vel et ad designandus tum latus cubicum solidi A'B'C−B'C9 t perimum e duo bus medijs proportionalibus inter mensuram universalem et A'B'C−B'C9 scrio vel & ad hujus quadratum designandum scribo . Eadem notarum ratio in magis compositis tenenda est.
Certe Veteras Inter has scientias maximam esse affinitatem animadverterunt, ita ut ex analogia termino{;} geometricos quadrati cubi et similium in Arithmeticam introducerent et Euclides libros Arithmeticos miscerea{illeg} Geometricis; sed Geometriam tamen quæ scientiarum Mathematica{rum} regina est terminis exoticis contaminare noluerunt. Inventa est uti Geometria ut ejus succinctis operationibus in terris metiendis effugeremus tæ{dium} computi Arithmetici Proinde ut {est sed} computis quantum fieri potest vacare debet, sic etiam a computi nominibus ne horum usu ad rem significatam plus nomio invitenur sei entiam nobilissimam contra institu{cid} ejus cum Arithmetica tandem confundamus. Hae igitur in re reprehendi non debiam si Veteres sequar.
[88] Geometria per intersectiones linearum solvit omnia Problemata, singulas ejusdem problematis solutiones per totidem intersectiones una vice exhibens Nam solutionum omnium eadem est lex et natura ita ut una Geometricè exhiberi non possit qu{in} reliquæ eadem constructione simul prodeant. Unde fit ut ad constructionem cujus Problematis lineæ duæ adhiberi debent quæ se mutu{ò} in tot punctis secare possunt quot Problema admittit solutiones. Ad constructiones omnium problematum primi gradus sufficiunt lineæ rectæ ad eas secundi requiruntur recta et circulus vel duo circuli ad eas tertij requiritur linea magis complexa quæ rectam aut circulum in tribus punctis ad minimum secare possit et sic in infinitum.
[89] Et hinc pro numero punctorum in quibus linea quævis a linea recta secari potest, oritur distinctio linearum in gradus. Primi gradus vel ordinis est linea quam recta in unico tantum puncto secare potest vel cujus intersectionem cum imperata quavis recta determinare Problema est primi gradus. et hujusmodi s{unt} solæ rectæ lineæ. Secundi linea est cujus intersectionem cum recta quavis determinare Problema est secundi gradus et hujusmodi sunt circulus et lineæ illæ omnes quas Comicas Sectiones appellant. Tertij verò gradus linea est cujus intersectionem cum recta determinare problema est tertij gradus est {lissoida} Veterum et sic in infinitum. Lineæ vero quas recta in punctis infinitis secare potest (qualls sunt Spiralis Quadratrix Trochoides & similes) meritò dicentur ordinis ultimi
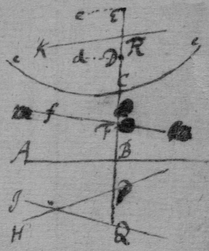
[90] Concipe rectam BC parallelo motu ad latus  ferri et interea secare rectas quotcun positione dat{a}s AB in B, mF in F HP in P, IQ in Q, KR in R et punctis in ea mobilibus C, D, E, F alias lineas cc, dd, ee, ff describere. Determinari autem concipiantur longitudines BC, BD, BE, BF hac semper lege ut sint AB ad BC et PC ad BD et QD ad BE et RE ad BF in eadem ratione. Et si linea dD ad quam ratio secunda desinit recta est, tunc linea cC ad quam prima desinit erit secundi generis et aliquando primi nes ulla est linea secundi generis quæ non potest hoc modo exhiberi. Sin linea eE ad quam ratio tertia desinit recta assumitur{;} linea vel ad quam prima desinit erit tertij generis et aliquando secundi vel primi . Quod si linea fF ad quam quarta ratio desinit recta statuatur tunc linea cC ad quam prima de{sinit e}rit aut qua{rt}i {aut} inferioris alicujus generis. Et sic novas in infinitum lin{eas designa}re licet, et numerus rationum gradum altissimum lineæ cC semp{er æqua}bit. Tot enim punctis &
ferri et interea secare rectas quotcun positione dat{a}s AB in B, mF in F HP in P, IQ in Q, KR in R et punctis in ea mobilibus C, D, E, F alias lineas cc, dd, ee, ff describere. Determinari autem concipiantur longitudines BC, BD, BE, BF hac semper lege ut sint AB ad BC et PC ad BD et QD ad BE et RE ad BF in eadem ratione. Et si linea dD ad quam ratio secunda desinit recta est, tunc linea cC ad quam prima desinit erit secundi generis et aliquando primi nes ulla est linea secundi generis quæ non potest hoc modo exhiberi. Sin linea eE ad quam ratio tertia desinit recta assumitur{;} linea vel ad quam prima desinit erit tertij generis et aliquando secundi vel primi . Quod si linea fF ad quam quarta ratio desinit recta statuatur tunc linea cC ad quam prima de{sinit e}rit aut qua{rt}i {aut} inferioris alicujus generis. Et sic novas in infinitum lin{eas designa}re licet, et numerus rationum gradum altissimum lineæ cC semp{er æqua}bit. Tot enim punctis &
non pluribus possibile est Curvam illam cC a recta BC secari quot sunt rationes. Nam si verbi gratia tres sint rationes et linea BC detur positione dabuntur AB BE, BP, BQ et BC invenienda erit ea lege ut sit AB.BC ∷BC+BP.BD∷BD+BQ.BE quod Problema triplicem admittere solutionem ex superioribus constat adeo linea BC triplex est. Tria igitur et non plura possunt esse puncta C in quibus recta BC occurr{i}tt Curvæ cC, proinde Curva illa tertij est generis.
Facilius autem imaginamur has curvas ubi per motus locales linearum inter se cohærentium tanquam per organa quædam describi concipimus. Ut si regulæ PC PD datum angulum CPD continentes volvantur circa datum punctum P quod in anguli 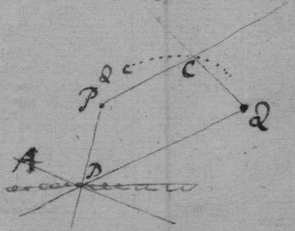 illius vertice est et similitur regulæ QC QD datum angulum Q continentes circa punctum Q ea lege ut regulæ PQ, QD se mutuo semper secent ad rectam aliquam lineam positione datam AD et interea reliquarum regularum PC, QC intersectio C motu suo lineam cC designet: Erit hæc cC linea secundi gradus et aliquando primi. Et hac ratione possunt omnes lineæ secundi gradus designari. Deinde si loco rectæ AD substituatur linea aliqua secundi generis per neutrum punctorum PQ transiens et regularum intersectio D in hac movere cocipiatur, altera intersectio C, designabit lineam quarsi gradus aut etiam tertij. . Qua ratione et omnes tertij gradus lineæs quarum commoda aliqua descriptio organica hactemus reperta fuit designare liceat. At ita ad lineas superiorum generum pergitur, Quod idem fiet si regularum {.}duæPC, PD non volvantur circa polum P sed parallelo motu ferantur ita ut concursus earum P pergat in recta aliqua positione data. Sed Et ad majorem designandi copiamvice rectarum regularum adhiberi possunt curvæ.
illius vertice est et similitur regulæ QC QD datum angulum Q continentes circa punctum Q ea lege ut regulæ PQ, QD se mutuo semper secent ad rectam aliquam lineam positione datam AD et interea reliquarum regularum PC, QC intersectio C motu suo lineam cC designet: Erit hæc cC linea secundi gradus et aliquando primi. Et hac ratione possunt omnes lineæ secundi gradus designari. Deinde si loco rectæ AD substituatur linea aliqua secundi generis per neutrum punctorum PQ transiens et regularum intersectio D in hac movere cocipiatur, altera intersectio C, designabit lineam quarsi gradus aut etiam tertij. . Qua ratione et omnes tertij gradus lineæs quarum commoda aliqua descriptio organica hactemus reperta fuit designare liceat. At ita ad lineas superiorum generum pergitur, Quod idem fiet si regularum {.}duæPC, PD non volvantur circa polum P sed parallelo motu ferantur ita ut concursus earum P pergat in recta aliqua positione data. Sed Et ad majorem designandi copiamvice rectarum regularum adhiberi possunt curvæ.
[91] Lineam vero ut cC in qua punctum aliquod indeterminatum ut C perpetuò reperitur veteres dixerunt puncti illius locus et quoniam problematum constructiones pendebant a descriptione duorum locorum puncti quæsiti in quorum intersection{es} situm inveniretur, ideo. Veteres ad hujusmodi locorum compositionem ut loquebantur id est ad eorum inventiorum ac determinationem summis viribus intebuntur. Duo autem hic requiruntur. Primum ut sa{illeg} datis loci conditionibus, sciamus {æqualis} sit et quomodo describendus deinde ut in quolibet problemata loca inveniamus quæ {simplicissima sunt} et facillis{illeg}à determinari ac describi {possint} sed {illeg} quam {hec de} his agamus proprietates {curvarum cognoscendæ sunt.} Insigniores sunt hæ.
[92] Si para{illeg} quotcun quavis A{G}, DF, G{S} {illeg} agantur {illeg} curvam {illeg} in {tot} punctis A, B, C ac D, E, F, G, H, quot curva {illeg} {illeg} a recti secari potest Dein tertia agatur recta {illeg} prioribus ita secans in K et {of} utrius parts vel summa 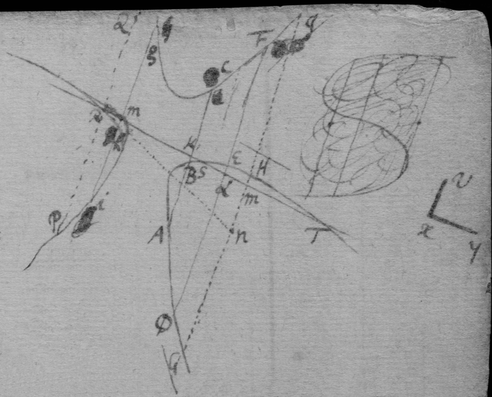 partium ad curvam extensarum ex uno latere æqualis sit parti vel summæ partium ad curvam extensarum ex altero latera, vizt KA+KB=KC et LD=LE+LF: tunc partes etiam reliquarum parallelarum hinc inde æquales erunt MG=MH +MI.
partium ad curvam extensarum ex uno latere æqualis sit parti vel summæ partium ad curvam extensarum ex altero latera, vizt KA+KB=KC et LD=LE+LF: tunc partes etiam reliquarum parallelarum hinc inde æquales erunt MG=MH +MI.
Quinetiam si datis positione rectis vx, xy parallela du{æ} IG, RT utrun ducantur secantes se mutuo in M curvam vero in tot punctis quot rectæ curvam ejus generis secare potest {puncta} in G, H, I et R, S, T contentum sub omnibus partibus unius rectæ inter curvam et alteram rectam sitis MG, MH, MI erit ad contentum sub omnibus ejusmodi partibus alterius rectæ MR, MS, MT in data ratione. Et hinc recta duci potest [93] quæ curvam quamvis descriptam in puncto imperato tanget{.} {secetve} in dat angulo Sit illud punctum {R}. Per quod age duas quasvis rectas RP, RT, se secantes in et uni earum RI parallela {I}G secantem altera RT in M quæ omnes etiam secent Curvam in pleno numero punctorum P, R, Q; R, S, T; G, H, I. In IG cape MN ita ut sit contentum sub PR, QR, MN ad contentum sub GM, HM, IM ut contentum sub RS, RT ad contentum sub MS, MT et acta RN tanget curvam in R, si modo RN capiatur in in eo angulo PRM qu{e}m curva secat. Nam concipe m{,}ξ parallelam {ess}{illeg} PQ et ad eam accedere interea d{illeg} secat curvam in g, h, i et evanescentium, RM, MN {illeg} erit ea quæ est RM ad MN ubi RN {illeg} curvam. {Est autem } contentum sub gMhM , {iN} ad contentum sub GM, HM, IM ut contentum sub MR, MS MT ad contentum sub MR, MS, MT. Hic pro ratione RM ad MR substitu{atur} {illeg} {inter} rationem NM ad MR et coalescentibus {lineas} PQ {et} ig scrib{o} R pro M, Q pro g et P pro i et incides in proportione qu{ar} tangentem RN determinavimus.
Cæterum hæ lineæ utplurimum crura habent in infinitus serpentia quæ aut Hyperbolici sunt generis aut Parabolici. Concipe punctum B secundum lineæ curv{æ} crus AB  delatum abire in infinitum et interea curvam a linea mobili BC semper tangi. Incidat autem semper a puncto atiquo G in tangentem illam perpendiculum GC, et ubi punctum B in infinitus abit si GC fit infinite longum tangente BC prorsus evanescente crus illud AB Parabolicum est, sed si GC non fit infinitè longum, crus Hyperbolicūm est et tangens in ultima positione seu recta illa (uti DE) quacum tangens ultimò convenit, cruris illius Asymptotos appelatur. Crus vero infinitum semper habet socium suum qui nunc ad eandem nunc ad opposit{u}m plagam tendit. Et paris Hyperbolici semper eadem est Asymptotos. Est hæc Assymptotorum insignis proprietas, quod si curva cujusvis generis plenè Hyperbolica secetur a recta in pleno numero punctorum G, H, I et recta illa secet etiam omnes
delatum abire in infinitum et interea curvam a linea mobili BC semper tangi. Incidat autem semper a puncto atiquo G in tangentem illam perpendiculum GC, et ubi punctum B in infinitus abit si GC fit infinite longum tangente BC prorsus evanescente crus illud AB Parabolicum est, sed si GC non fit infinitè longum, crus Hyperbolicūm est et tangens in ultima positione seu recta illa (uti DE) quacum tangens ultimò convenit, cruris illius Asymptotos appelatur. Crus vero infinitum semper habet socium suum qui nunc ad eandem nunc ad opposit{u}m plagam tendit. Et paris Hyperbolici semper eadem est Asymptotos. Est hæc Assymptotorum insignis proprietas, quod si curva cujusvis generis plenè Hyperbolica secetur a recta in pleno numero punctorum G, H, I et recta illa secet etiam omnes 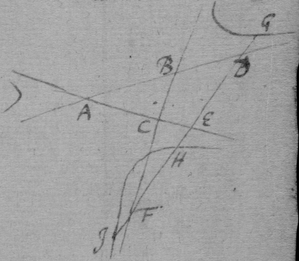 Asymptotos puta AB, AC, BC in D, E, et F pars vel summa partium rectæ Asymptoto vel ab Asymptotis ad crura totidem versus unam plagam extens{a}rum æqualis est parti vel summæ partium similium a reliquis Asymptotis versus alteram plagam ad reliqua crura tendentium DG=EH+FG, vel EG+FH=DI. Curvam verò plenè Hyperbolicam voco qua alia ejus generis cruva non potest habere plura paria crurum Hyperbolicorum. Habet autem tria paria si sit tertij generis quatuor si quarti et sic deinceps.
Asymptotos puta AB, AC, BC in D, E, et F pars vel summa partium rectæ Asymptoto vel ab Asymptotis ad crura totidem versus unam plagam extens{a}rum æqualis est parti vel summæ partium similium a reliquis Asymptotis versus alteram plagam ad reliqua crura tendentium DG=EH+FG, vel EG+FH=DI. Curvam verò plenè Hyperbolicam voco qua alia ejus generis cruva non potest habere plura paria crurum Hyperbolicorum. Habet autem tria paria si sit tertij generis quatuor si quarti et sic deinceps.
[95]Ex crurum infinitorum numero et et diversitate {}endet distinctio curvarum in species principales. Sunt autem alia crura conspirantia seu ad eandem plagam tendenti{æ}, alia divergentia seu vergentia in oppositas plagas et utra rursus {vel} ad easdem partes convexa vel ad contrarias. Par crurum Parabolicorum {illeg} Hyperbolicorum conspirantium æquipollet duobus paribus Hyperbolicorum divergentium, et Par Parabolicorum divergentium æquipollet tribus: saltem in curvis tertij generis. Unde sci{ri} potest quot crura cujusvis generis curva quævis habere potest Ut si curva terti generis habebt par sive Parabolicum sive Hyperbolicum conspirans: non habebit misi aliud par Hyperbolic{u}m divergens. Sed et Ellipses conjugatæ considerandæ sunt quæ et aliquando in puncta conjugata contra{punctur} , aliquando prorsus evanescente: Asymptotorum item situs an parallelæ sunt vel {inclinatus et aliæ} quædam differentia {illeg} notæ {illeg} est. De lineis enim superiorum generum fase disserere non est instituti. {illeg} nec in demonstrandis quæ dicta sunt tempus {illeg} tantum quæ de lineis secundi {illeg} ab Apollonio {illeg} demonstram habentur
ita commemorare ut eadem lineis etiam superiorum generum competere insinuarem.
[96] Cæterum quoniam cognitio determinatio ac curvarum maximè pendet a cruribus infinitis, hæc autem cum eorum Asymptotis noscuntur ex tangentibus; tum etiam qui{a} tangentium inventio post{hec} alijs inservient usibus: methodum jam subjungam ducendi rectas quæ curvas quasvis nondum descriptas postquam describuntur tangent. Sed notæ quibus in operationibus Geometricis utimu{r} sunt prius expicandæ.
[97] Ubi linea aliqua AB ducitur in aliam lineam CD rectangulum genitum significamus scribendo AB'CD et si id rursus ducatur, in tertiam lineam EF ad experimendum parallelipipedum genitum scribimus AB'CD'EF. Latus verò quod oritur applicando rectangulum illud ad lineam quamvis GH sic notamus . At ita in alijs. Sed et exposita linea aliqua ad quam tanquam mensuram universalem aliæ omnes (ut fit in decimo Elementorum) referantur scribimus AB'CD ad designandam quartam proportionalem ab hac linea ubi mediæ du{æ} sunt AB et CD et AB'CD'EF ad designandam etiam quartam ab eadem linea ubi mediæ duæ AB'CD et EF et sic in infinitum. Et si linea illa sit prima continuè proportionalium et alia quævis AB secunda, tertiam sic designamus AB2, quartam sic AB3, quintam sic AB4 at ita deinceps. Et inter lineam illam et aliam quamvis AB notamus mediam proportionalem sic AB, primam e duabus medijs proportionalibus sic AB secundam sic AB. similiter
denotat tum latus quadrati æqualis rectangulo AB'CD tum mediam proportionale inter mensuram illam universalem et AB'CD vel quod perinde est inter AB et CD. Sed AB'CD est quarta proportionalis a mensura illa {pem}ubi mediæ sunt AB et CD. Et has quantitates nominibus usitatis significamus præterquam quod a vocabulis Arithmeticis certas ob rationes cum veteribus abstinendum esse duximus. Porro quantitates compositæ eodem modo signantur. Si {c} A+B'C−D denotat rectangulum sub A+B et C−D et R±S2 quadratum ipsius A±B. Quæ quantitates etiam partibus juxta secundam Elementorum in se ductis sic scribintur A'C+B'C−A'D−B'D et R2±2R'S+S2. Ubi notes quod pars positiva ducta in subductitiam vel subductitia in positivam producit subductitiam duæ vero subductitiæ in se ductæ producunt positivam.  secentur AB AD parallelis BD, EG ita ut sit AB ad AD ut AE ad AG et posita AB mensura illa ad quam lineæ omnes referuntur AG erit AD'AE. Diminuatur AE donec evanes{cet} et postea evadat retrors{a} Ae et A G simul diminuetur evanescet & convertitur in retror{s}am A{G}. Diminuatur
secentur AB AD parallelis BD, EG ita ut sit AB ad AD ut AE ad AG et posita AB mensura illa ad quam lineæ omnes referuntur AG erit AD'AE. Diminuatur AE donec evanes{cet} et postea evadat retrors{a} Ae et A G simul diminuetur evanescet & convertitur in retror{s}am A{G}. Diminuatur
etiam AD donec evenescat et postea retrorsa evadat Ad et retrorsa Ag simul diminuetur evanescet et et convertetur in directam Aα. Duæ igitur retrorsæ Ae, Ad by retrorsam id est directam Aα efficiunt.
[98] Notis proscognitis præmittenda est etiam methodus determinandi fluxiones linearum et fluxionum plagas. Per Fluxionem intelligo celeritatem incrementi vel decrementio lineæ cujusvis indeterminatæ ubi lineæ aliquæ super alias in descriptione curvarum moveri concipiantur et inter movendum augeri vel diminui aut motu punctorum describi. Unde et indeterminatas illas quantitates fluentes nominare licebit. Proponantur datæ aliquot quantitates A, B, C, D, et fluentes V X, Y, Z quarum fluxiones respectivè designent minusculæ v, x, y, z. et requiratur fluxio linea alicujus quæ ex his fit ut linea X'Y. 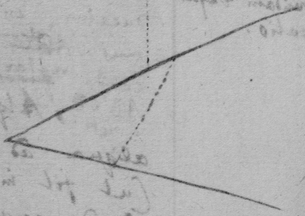 Maneat primum X et fluat Y donec ipsa fiat Z et XY fiat XZ et quia Y et XY fluendo non mutant rationem fluxiones earum erunt ut ipsæ hoc est ut 1 ad X. Unde cum fluxio Y sit y fluxio XY erit Xy. Maneat jam Z et fluat X donec ipsa fiat V et XZ fiat VZ et fluxio XZ eri{t} Zx ut in casu priore. Fluant jam X et Y simul priore ut XV una vice fiat VZ et quia fluxio Xy sufficit ad mutandum XY in XZ et fluxio Zx ad mutandum XZ in VZ Fluxio tota qua XY mutatur in VZ erit Xy+Zx. Pone V æqualem X et Z æqualem Y ut fit ipso fluendi initio et fluxio initialis ipsius XY erit Xy+Yx.
Maneat primum X et fluat Y donec ipsa fiat Z et XY fiat XZ et quia Y et XY fluendo non mutant rationem fluxiones earum erunt ut ipsæ hoc est ut 1 ad X. Unde cum fluxio Y sit y fluxio XY erit Xy. Maneat jam Z et fluat X donec ipsa fiat V et XZ fiat VZ et fluxio XZ eri{t} Zx ut in casu priore. Fluant jam X et Y simul priore ut XV una vice fiat VZ et quia fluxio Xy sufficit ad mutandum XY in XZ et fluxio Zx ad mutandum XZ in VZ Fluxio tota qua XY mutatur in VZ erit Xy+Zx. Pone V æqualem X et Z æqualem Y ut fit ipso fluendi initio et fluxio initialis ipsius XY erit Xy+Yx.
Proponatur jam factum XYZ et ponendo XY=V erit XYZ=VZ. Cujus fluxio juxta casum priore{s} est Vz+Zv.Sed et ob XY=V est Xy+Y{X}=v. Pro V et v {sublimus} æquipollentia et Vz+Zv hoc est fluxio ipsius XYZ fiet XYz+XZy+YZx. Et progressionis modum observando colligitur universalitur quod facti cujuscun fluxio invenietur substituendo sigillatim in facto illo pro unoquo{} factore {fluxionem} ejus et {sumendo resublantium} terminorum aggregatum. Qu{ot} regula
Simili argumentatione fluxio ipsius XYZ invenietur XYz+XZy+YZx et fluxio ipsius VXYZ invenietur VXYz +VXZy+VYZx+XYZv et sic in infinitum flu{xio} fasti semper invenietur substituendo sigillatim pro unoquo factore fluxionem ejus et sumendo resultantiun terminorum aggregatam. Quæ regula
etiam obtinet ubi aliqui factores æquales sunt. Ut si X et y æquales ut XY valeat X2 ejus fluxio Xy+ Yx fiet 2Xx. Et similiter ipsius X3 fluxio est 3X2x et ipsius X2Z fluxio X2z+2XZx. At ita in compositis fluxio ipsius AX−3X2 est Ax−6Xx Nam fluxiones partium simul sumptæ sunt fluxio totius.
In lateribus applicatorum ad fluentia methodus hæc est Proponatur latus . Pone ipsum æquale V et erit XX=YV adeo 2Xx=Yv+Vy nam fluentium semper æqualium fluxiones æquales sunt. Aufer utrobi Vy et reliquum divisum per Y nempe erit v. Est autem v ipsius V id est ipsius fluxio quam invenire oportuit.
Similis est methodus in lateribus {quadraticis}, {cubicin} alijs. . Proponatur latus AX-X2|. Pone ipsum æquale V, et erit AX-X2=V2 adeo Ax−2Xx=2Vv, et .
< insertion from lower down f 135v > < text from f 136r resumes >.
In figuris pro significanda fluxione lineæ alicujus pono lineam ileam literis minusculis: ut bc pro significanda fluxione lineæ BC. Angulorum verò fluxiones expono per fluxiones arcuum quibus subtenduntur ad datam distantiam. Et distantiam illam quæcun tandem assumatur designe per literam R; fluxionem arcus per angulum literis minusculis serpentum, opposit{a}m ordinatat{i}m applicatam in hoc circuloid est {s} sinum cujus arcus per literam s angulo præfixam distantiam ordinatæ {illeg} {centro} id est sinum complemen{illeg} {rationis} per literam s angulo præfixam & horum senuum fluxio s per literas easdem s it {'s}angulo minusculis literis not{illeg}o {præteras}. Sit ABC angulus quilibet {flucus} DC arcus {s}uo ad {datam} {distantis} Bc subtendit{c} 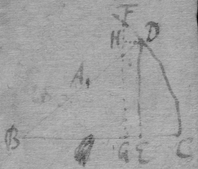 & DE [ sinus ejus et significabit sustantiam illam datam BC vel BD, {I} vel abc fluxio{n}e arcus CD, sB lineam DE, s'B lineam BE{&}sb s'b earum fluxiones
& DE [ sinus ejus et significabit sustantiam illam datam BC vel BD, {I} vel abc fluxio{n}e arcus CD, sB lineam DE, s'B lineam BE{&}sb s'b earum fluxiones
Illud etiam præmittenduni est, fluxionem arcus esse ad fluxionem sinus ejus ut Radius ad sinum complementi et ad defluxionem sinus complementi ut radius ad sinum. ad sb ut R ad s'B et b ad−s'b ut R ad sB. Fluant enim omnes aliquantulum donec CD fiat CF, DE fiat FG et CE fiat CG et ipso fluendi initio fluxiones erunt ut augmenta incipientia FD, FH, HD id est ut BD, BE, DE.
His præmissis proponatur triangulum aliquod  ABC et demissis ad latera singula perpendiculis AE, BF, CG ut sA ad sB ita BF, ad AE & ita BC ad AC adeo sA'AC=sB'BC. Ergo sA'ac+AC'sa
ABC et demissis ad latera singula perpendiculis AE, BF, CG ut sA ad sB ita BF, ad AE & ita BC ad AC adeo sA'AC=sB'BC. Ergo sA'ac+AC'sa 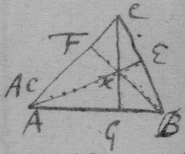 =sB'bc+BC'sb. Sed sa.a∷s'A.R∷AG.Ac Ergo AC'sa=AG'a. Et eodem modo est BC'sb= BG'b. Quare sA'ac+AG'a=sB'bc+BG'b. Quo theoremate conferre possumus fluxiones angulorum duorum et laterum oppositorum trianguli cujuscun et ex tribus cognitis invenire quartam.
=sB'bc+BC'sb. Sed sa.a∷s'A.R∷AG.Ac Ergo AC'sa=AG'a. Et eodem modo est BC'sb= BG'b. Quare sA'ac+AG'a=sB'bc+BG'b. Quo theoremate conferre possumus fluxiones angulorum duorum et laterum oppositorum trianguli cujuscun et ex tribus cognitis invenire quartam.
** Et cum summa trium angulorum detur adeo aggregatum fluxiorum omnium nullum sit, vel quod perinde est duorum fluxio æqualis sit defluxioni tertij si pro +BG'b scribas −BG'a+c, & idem utrobi auferas fiet sA'ac+AB'a+BG'c=sB'bc, Theorema ad comparandas fluxiones duorum angulorum totidem laterum quorum unum angulis illis in terijcitur.
Rursus * est R.s'A∷AC.AG seu s'A'AC=R'AG. Ergo s'A'ac+AC's'a=R'ag. Est et (per Præmissa) a.−s'a vel −a.s'a∷R.sA∷AC.CG. Ergo pro AC's'a scribendo −CG'a, fit s'A'ac−CG'a=R'ag. Eodem modo est s'B'bc−CG'b=R'bg. Et æqualibus æqualia addendo fit s'A'ac+s'B'bc−CG'a+b=R'ab. Ob datam summa trium angulorum pro a+b scribe −c et fit s'A'ac+s'B'bc+CG'c=R'ab. Theorema ad comparandas fluxiones trium laterum et anguli cujusvis.
< insertion from f 137v >Simili argumentatione possunt alia Theoremata colligi [100] ubi perpendicula triangulorum et segmenta basium aliæve lineæ considerantur. Sic AC'ac−BC'bc+BG'ab=AB'ag Theorema est ubi latera tria et segmentum basis considerantur, et, posito X commmunni trium perpendiculorum intersectione, est BX'ac +AX'bc=GX'ab+AB'gc Theorema ubi agitur de lateribus ut perpendiculo. Sed hæc non prosequor. Satis est investigandi methodum aperuisse.
[101] Horum verò Theorematum beneficio possumus in propositus {illeg} quibus{illeg} figuris fluxiones linearum et angulorum haud secus ac in computo trigonometric{os} lias ab alijs colligere donec ad quæsitam pervenimus. Ut si dentur positione lineæ AB, AD, DE et BC data longitudinis moveatur perpetuo subtendæts angulum A et producta secans rectam ED in E, et ex cognita vel desideretur fluxio lineæ EC: primum in trianguli ABC per secundum Theorematum invenietur sA'ac+BG'c=0 evanescunt enim termi{ni}
< text from f 138r resumes >
.
[102]
De mottum plaga et celeritate
Propo
<145r>In figuris hæc est methodus. Puncti mobilis considero semper motus diversos juxta diversas plagas quarum principalis sit via puncti. Et hos motus expono vel saltem exponi imaginor describendo per punctum illud circulum quemvis cujus centrum sit in via illa et in singulis plagis ducendo rectas us ad hunc circulum. Ut si punctum A moveaur in linea BA, per illud A decribo circulum quemvis cujus centrum sit in BA et cui illa BA aliæq lineæ quævis CA, DA, EA occurrant in F, G, H, I, et linearum partes intra circulus AF, AG, AH, AI erunt inter se ut motus puncti A in illarum plagis. Adeo ut si motus puncti A a B exponitur per AF, motus ejus a C exponatur per AG et sic in reliquis: Aut quod perinde est si fluxio lineæ BA ex parte termini A exponitur per AF, aliarum linearum CA, DA ad idem mobile punctum A semper desinentium fluxiones ex parte termini illius A exponantur per AG AH, et lineæ EA defluxio per AI. Unde ex cogniis motibus duorum punctorum ad quæ linea quævis utrin terminatur, cognoscetur et exponi potest ejus fluxio absoluta: quippe quæ summa est fluxiorum ejus ad utrum terminum, vel excessus fluxionis ad unum terminum supra defluxionem ad alterum.
Porro motus punctorum circa 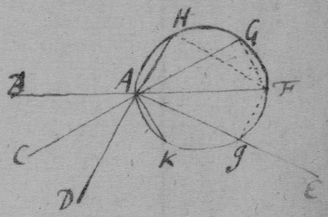 polos quosvis ijdem sunt et easdem habent exponentes ac motus in plagis perpendicularibus ad radios. Sic motus puncti A cirum quemvis in linea CA situm exponens est normalis AK circulo occurrens in K. Expositis vereo duorum punctorum rectæ cujusvis motibus circumpolaribus, recta alia per terminos exponentium acta secabit rectam illam in Polo suo. Et per harum exponentium rationem ad radios id est ad distantias suas a Polo, exponere licebit motum angularem hujus rectæ seu fluxionem angulorum quos ea cum rectis positione datis continet.
polos quosvis ijdem sunt et easdem habent exponentes ac motus in plagis perpendicularibus ad radios. Sic motus puncti A cirum quemvis in linea CA situm exponens est normalis AK circulo occurrens in K. Expositis vereo duorum punctorum rectæ cujusvis motibus circumpolaribus, recta alia per terminos exponentium acta secabit rectam illam in Polo suo. Et per harum exponentium rationem ad radios id est ad distantias suas a Polo, exponere licebit motum angularem hujus rectæ seu fluxionem angulorum quos ea cum rectis positione datis continet.
Et ut ex motibus punctorum invenire et exponi possunt fluxiones linearum et angulorum sec vice versa ex horum fluxionibus colligere licet motus punctorum. Nimirum considerando lineam AF in qua punctum quodvis A movetur ut exponentem motus ejus, et exponentis illus terminum ulteriorem F ut metam ad quam punctum illud A tendit{,} et lineas omnes FA, FG, FH, FI per metam transient{i}s ut {loca} rectæ ex inventione duorum ejusmodi locorum, meta quas {illeg} utrasque inter intersectione est determinabitur. Loca verò si invenientur. Quando mobile punctum ex assumptione duarum quarum vis vel plurium {illeg} determinatum et stabile redditur, invenien{dus} est motus quem punctum illud haberet si una quantitatum assumeretur et alterius tantum vel reliquarum fluxio maneret et motûs illius quoad plagam et quantitatem exponens ducenda est. Cognoscenda est etiam plaga motus quem punctum idem haberet si vice versa illa una quantitas flueret et altera vel reliquæ assumerentur. Et in plaga illa per terminum exponentis acta recta erit unus {illeg} locis metæ.
Hoc modo a motibus punctorum ad fluxiones quantitatus et vicissim ab harum fluxionibus ad illorum motus pergelicebit donec quoadus libuerit perventum sit. Et ubi exponens motus puncti curvam propositam describentis inventa est, hæc et cuevam in puncto illo tanget et exponens erit fluxionis ejus. Sed res exemplis clarior fiet.
A mobili puncto A qua curva quævis 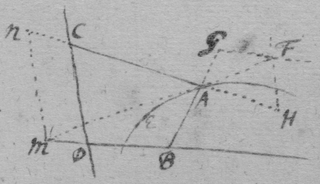 EA describitur ad rectas duas positione datas DB, DC in datis angulis ducuntur rectæ duæ AB AC et ductarum relatio ad invicem habetur. Ducenda est recta quæ curvam hanc tangat in A.
EA describitur ad rectas duas positione datas DB, DC in datis angulis ducuntur rectæ duæ AB AC et ductarum relatio ad invicem habetur. Ducenda est recta quæ curvam hanc tangat in A.
Ut hot fiat exponentur ductarum fluxiones per AG et AH. Jam quia punctum A, assumptione fluentium DB, BA determinatur, et ubi earum una DB assumitur et altera BA solummodo fluit, linea AG exponens est tam motus puncti quam fluxionis lineæ BA, ubi vero vice versa altera BA assumitur el prior DB fluit punctum A movetur in plaga lineæ DB, recta GF quæ per exponentis terminum G in plaga lineæ DB parallela ducitur erit unus locus Metæ. Et simili argumento recta HF quæ per exponentis AH terminum H in plaga lineæ DC ducitur erit alias locus Metæ. Et locorum intersectio F metam dabit ad quam tangens quæsita AF ducenda est. Quam conclusionem sic concinnare licebit. Lecet tangens rectam DB in M et ipsi DC parallela agatur MN occurrens AC in N et AB, AM, AN erunt inter se ut AG, AF, AH, adeo vice exponentium AG, AH adhiberi possunt AB, AN: qua ratione longitudo AN at adeo punctum M ad quod tangens duci debet invenietur.
Ut is relatio inter AB et AC sit quod rectangulum sub AC et data quavis recta R æquales sit quadrato AB2, æquales erunt etiam horum fluxiones R' ac & 2AB'ab{.} Hic Pro fluxionibus ac et ab substitue earum exponentes AH, AHvel potius harum vice lineas AN, AB, et fiet R'AN=2AB2. Unde R'AN et 2R'AC æquales sunt utpote eidem 2AB2 æquales; adeo AN=2AC. Cape ergo CN=AC&Per N ipsi CD parallelam age NM occurrentem DB in M et recta AM curvam propositam tanget in A.
Hand secus si ad definendam relationem inter AB et AC ponatur R'AC−AC2 esse ad AB2 in data ratione, colligentur horum fluxiones R'ac−2AC'ac & 2AC'ab & 2AB'ab, et inde R'AN−2AC'AN in eadem ratione. Unde R'AC−AC2 & æqualia erunt, utpote eandem rationem ad AB2 habentia. Caiatur ergo AN ad AC ut R-AC ad et, actâ MN parallelâ CD, habebitur tangens AM. Porrò Curvæ EA hc sit propietas ut si a dato circulo FK per data puncta P, Q  ducantur rectæ duæ LI, LK, concurrentes ad dat{illeg} circulum EL, ponatur AB æqualis LG et AC æqualis LK: ducantur circulorum tangentes IM KN, LR et fluxio arcus ER exponatur per LR cujusvis{.} longitudinis. Super diametro LR describatur circulus secans PL productam in S et QL in T{,} et erit LS exponens fluxionis rectæ PL et LT exponens fluxionis retrogradæ rectæ QL. Erigantur normales LV ad LP et LX ad LQ
ducantur rectæ duæ LI, LK, concurrentes ad dat{illeg} circulum EL, ponatur AB æqualis LG et AC æqualis LK: ducantur circulorum tangentes IM KN, LR et fluxio arcus ER exponatur per LR cujusvis{.} longitudinis. Super diametro LR describatur circulus secans PL productam in S et QL in T{,} et erit LS exponens fluxionis rectæ PL et LT exponens fluxionis retrogradæ rectæ QL. Erigantur normales LV ad LP et LX ad LQ
occurrentes circulo LTR in V et X et erunt hæ exponentes motuum puncti L circa polos P et Q. Erigantur etiam normales YI ad PI et ZK ad QK ita ut sit YI ad IP ut VL ad LP et ZK ad KQ ut XL ad LQ et erunt hæ exponentes motuum punctorum I et K circa polos eosdem P et Q. Concipe per puncta I et Y circulum describi cujus centrum sit in tangente IM et pariter per puncta K et Z alium circulus cujus centrum sit in tangente KN, et horum circulorum diametri IM KN exponentes erunt motuum punctorum I et K in circumferentia circuli JK: item YM æqualis erit exponenti fluxionis lunæ PI et ZN æqualis exponenti fluxionis totius IL et TL+ZN exponens fluxionis retrogradæ totius KL. Cape ergo AG=SL+YM et AH=LF+ZN, sed of fluxionem retrogradam ipsius LK vel AC cape AH ad partes ipsius A versus C, et HF acta parallela DC secabit GF actam parallelam DB in Meta F ad quam tangens quæsita AF duci debet.
Quod si vice rectarum LI, LK adhibeantur circulorum arcus EL, FK ponendo AB æqualem arcui EL et AC æqualem arcui FK, tunc AG sumenda erit æqualis LR et AH æqualis KN, eo quod LR exponens sit fluxionis arcus EL et KN exponens defluxionis arcus FK, et actæ GF, HF ut prius tangentem determinabunt. Ne problema difficilius erit si vice circulorum EL FK adhibeantur aliæ quævis curvæ lineæ quarum tangentes LR, KN ductæ habentur. Sed et alijs modis innumerris relatio inter AB et AC exprimi potest, imò et vice rectarum DB, DC curvæ quvis adhiberi ad quas AB, AC ducantur in datis plagis et quarum tangentes ad puncta B et C sint DB et DC.
Ducatur verò jam linea DB, DC non in datis plagis sed ad data puncta B et C, et earum 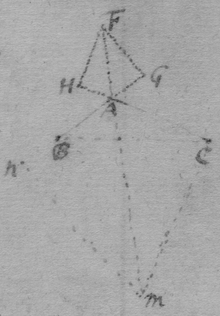 fluxiones exponantur per AG et AH. Et quoniam assumptione anguli ABC et longitudinis BA determinatur punctum A, et ubi angulus ille solummodo assumitur exponens motus puncti A est linea AG, ubi vero e{illeg} tra angulus ille fluit et longitudo BA ass{mi}tur plaga motus puncti A perpendicularis est ad BA, recta GF in plaga illa per exponentis terminum G ducta erit unus locus {metæ}. Et simili argumento recta HF per {t}erminum exponentis AH in plaga perpendiculari ad CA ducta erit alius locus
fluxiones exponantur per AG et AH. Et quoniam assumptione anguli ABC et longitudinis BA determinatur punctum A, et ubi angulus ille solummodo assumitur exponens motus puncti A est linea AG, ubi vero e{illeg} tra angulus ille fluit et longitudo BA ass{mi}tur plaga motus puncti A perpendicularis est ad BA, recta GF in plaga illa per exponentis terminum G ducta erit unus locus {metæ}. Et simili argumento recta HF per {t}erminum exponentis AH in plaga perpendiculari ad CA ducta erit alius locus
Metæ. Et meta in utro loco consistens erit in eorum inter sectione F, adeo AF ad intersectionem illam ducta curvam motu puncti A descriptam tanget in A.
Ut si ea sit natura curva hujus ut summa vel differentia fluentis AB et datæ cujusvis R sit ad fluentem AC in data ratione (qui casus est quatuor Ovalium Cartesij) fluxiones illarum AB et AC erunt in eadem data ratione, adeo si in plagis fluxionum illarum capiantur AG AH vel quod perinde est si in plagis contrarijs capiantur An et AC in illa ratione et ad terminos captarum erigantur perpendicula concurrentia in F vel M acta AF vel AM curvam propositam tanget in A. Unde si ratio illa æqualitatis (qui casus est Hyperbolæ et Ellipsis) tangens bisecabit angulum CAN.
Ponamus jam super plano immobili in quo puncta P et K et recta infinita KD positione data habentur, planum mobile BCA curva aliqua CA terminatum, ita ferri ut recta BC in eo data semper coincidat cum recta KD, et interea secum trahere regulam PB per punctum suum B perpetuo transeuntem et circa polum P rotantem , & ejus intersectione cum termino suo curvilineo CA describere curvam lineam PAL in plano immobili{,} et requiratur hujus curvæ tangens ad punctum quodvis A. Quoniam 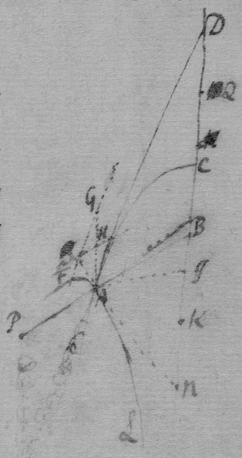 assumptione rectæ KC et curvæ CA det{u}rminatur punctum A assumatur solummodo curva AC et sit CQ exponens fluxionis lineæ KC et huic parællela et æqualis AG exponens erit motus puncti A, et GF duct{o} in plaga motus quem punctum A haberet si vice versa KC assumeretur et curva CA solummodo flueret id est ducta parallela rectæ AD qu{æ} curvam AC tangit in A, erit unus locus metæ. Rursus quoniam punctum A assumptione longitudinis KB et proportionis PA ad PB determinatur, assumamus solummodo proportionem illam et punctum movebit in linea AG erit motus ejus ad motum puncti B ut PA ad PB. Exponatur ergo motus ejus per AH quæ sit ad alterius exponentem id est ad CQ vel AG ut PA ad PB, et per punctum H in plaga motus
assumptione rectæ KC et curvæ CA det{u}rminatur punctum A assumatur solummodo curva AC et sit CQ exponens fluxionis lineæ KC et huic parællela et æqualis AG exponens erit motus puncti A, et GF duct{o} in plaga motus quem punctum A haberet si vice versa KC assumeretur et curva CA solummodo flueret id est ducta parallela rectæ AD qu{æ} curvam AC tangit in A, erit unus locus metæ. Rursus quoniam punctum A assumptione longitudinis KB et proportionis PA ad PB determinatur, assumamus solummodo proportionem illam et punctum movebit in linea AG erit motus ejus ad motum puncti B ut PA ad PB. Exponatur ergo motus ejus per AH quæ sit ad alterius exponentem id est ad CQ vel AG ut PA ad PB, et per punctum H in plaga motus
quem haberet punctum A si vice versa KB assumeretur et ratio PA ad PB flueret, id est parallela PB acta recta HF erit alter locus metæ. Habetis autem duobus metæ locis habetur Meta in eorum intersectione F una cum tangente AF quæ ad metam duci debet. Quæm conclusionem si concinare animus est, produc tangentem donec secet BK in N, et ob similes figuras AFGH, NADB erit BN ad BD ut AH ad HG hoc est ut AP ad AB
Ut si Curva CA Parabola sit cujus vertex C diameter CK ordinatim applicata AI, (quo casu AL Parabola erit Cartesij) imprimis ducenda erit AD quæ Parabolam CA tangat in A quod fiet si capiatur CD æqualis CI, dein capiend{à} est BN ad BD ut AP ad AB et acta AN tanget curvam AL in A.
Quod si AC circulus sit centro B descriptus, quo casu AL Conchoides erit Veterum, erigenda est 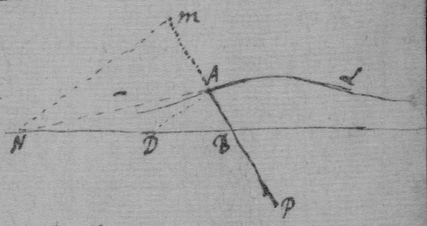 ad AP normalis AD occurrens BN in D, hàc enim circulum illum tanget. Dein capienda est BN ad BD ut AP ad AB. Vel brevius capienda est BM=AP et erigenda normalis MN occurrens BD in N et acta AN figuram AL tanget in A.
ad AP normalis AD occurrens BN in D, hàc enim circulum illum tanget. Dein capienda est BN ad BD ut AP ad AB. Vel brevius capienda est BM=AP et erigenda normalis MN occurrens BD in N et acta AN figuram AL tanget in A.
[105] pag 130' post verba [ - Meritò dicentur ordinis ultimi] adde [Editorial Note 3]
Genera Line{a}rum ejusdem {O}rdinis Si linea aliqua oculo extra planum ejus sito spectetur per planum translucidum, et in plano illo locus ejus apparens vel (ut voce mathematica utamur) projectio notetur, erit linea projecta ejusdm ordinis cum projiciente. Si projiciens est recta projectio erit recta, si curva est quæ rectam secare potest in duobus vel pluribus punctis, projectios ejus projectionem rectæ in totidem punctis secare potest. Et hinc habita linea aliqua cujusvis ordinis possunt aliæ plures ejusdem ordinis inde derivari. Sic Veteres ex circulo derivarunt omnes secundi ordinis figuras et inde Conicas sectiones nominarunt, considerantes spatium illud solidium quod radijs per circuli spretati perimetrum transeuntibus terminatur ut conum quem planum figuræ projectæ secat. Sic et figuræ superiorum ordinum possunt omnes a simplicioribus quibusdam ejusdem ordinis figuris per successivas projectiones derivari et inde distingui in genera coordinata positis illis ejusdem esse generis quæ ab eadem figura derivantur. Nam hæ omnes & solæ in se mutuò per projectiones transeunt et ea ratione cognotæ sunt, a cæteris verò in quas non transeunt alienæ. Hac lege unicum tantum est genus linearum secundi ordinis, eo quod omnes derivantur a circulo: at ordinis tertij genera sunt quin.
[106] In recta infinita EAB dentur puncta 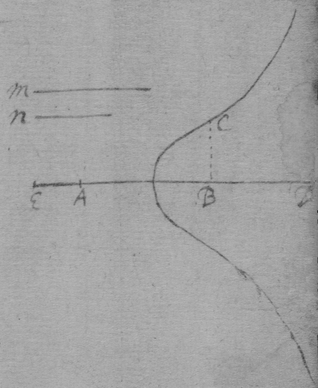 duo A, E et ad tertium quodvis ejus punctum B in dato angulo erigatur ordinata. BC cujus quadratum, si præterea dentur rectæ duæ M et N, æquale fuerit . Et curva linea ad quam hujusmodi recta omnis BC terminatur erit Parabola a{illeg}ta Parabolæ casus sunt quin principales; primus et simplicissimus ubi linea N nulla est: Secundus ac tertius ubi N negativè ponitur et præterea AE est , et secundus quidem ubi AE capitur ab A versus D seu versus alas figuræ, tertius verò ubi AE capitur ad contrarias partes ipsius A: Quartus et quintus sunt ubi AB est atrius{,} cujusvis longitudinis {illeg} ubi Parabola illa secas lineam utrin {illeg} puncto quintus verò {illeg} tribus{.} Primo casu habetur Parabola Neiliana cujus uti longitudinem ubi {illeg} {Neilius noster primus} invenit: secundo haetur, Parabola {illeg} {illeg} longitudinis parabola {campani} formis {illeg} {um} habens conjuga{illeg} {um:} {puncto parabola cum jam formis} solitaria quinto Parabola {illeg} {sum} Ellipsi habens conjugata quæ si in punctum {contragitur} {illeg} illud conjugatum in casu tertio. Et hæ qum figuræ cum profi{illeg} {illeg} cons{illeg} qum {fen}era curvarum tertij ordinis quinta nulla {ipsius} generis pro{si}cit aliquam alterius omnes verò quæ {illeg}generis per successivas projecti{illeg} in se mutuò {illeg} et eadem ratione curvæ superiorum ordinum distinguuntur in genera.
duo A, E et ad tertium quodvis ejus punctum B in dato angulo erigatur ordinata. BC cujus quadratum, si præterea dentur rectæ duæ M et N, æquale fuerit . Et curva linea ad quam hujusmodi recta omnis BC terminatur erit Parabola a{illeg}ta Parabolæ casus sunt quin principales; primus et simplicissimus ubi linea N nulla est: Secundus ac tertius ubi N negativè ponitur et præterea AE est , et secundus quidem ubi AE capitur ab A versus D seu versus alas figuræ, tertius verò ubi AE capitur ad contrarias partes ipsius A: Quartus et quintus sunt ubi AB est atrius{,} cujusvis longitudinis {illeg} ubi Parabola illa secas lineam utrin {illeg} puncto quintus verò {illeg} tribus{.} Primo casu habetur Parabola Neiliana cujus uti longitudinem ubi {illeg} {Neilius noster primus} invenit: secundo haetur, Parabola {illeg} {illeg} longitudinis parabola {campani} formis {illeg} {um} habens conjuga{illeg} {um:} {puncto parabola cum jam formis} solitaria quinto Parabola {illeg} {sum} Ellipsi habens conjugata quæ si in punctum {contragitur} {illeg} illud conjugatum in casu tertio. Et hæ qum figuræ cum profi{illeg} {illeg} cons{illeg} qum {fen}era curvarum tertij ordinis quinta nulla {ipsius} generis pro{si}cit aliquam alterius omnes verò quæ {illeg}generis per successivas projecti{illeg} in se mutuò {illeg} et eadem ratione curvæ superiorum ordinum distinguuntur in genera.
[107] Quinetiam per casus Projectionum distinguuntur genera linearum in species. Nomine{nuis} planum illud Horizontem quod per oculum transit et plano lineæ projectæ parallelum est, et lineam illam Horizontalem in qua Horizon secat planum lineæ projicientis. Et linea omnis projiciens dubit tot projectionum species quot sunt casus positionum lineæ Horizontalis. Si linea Horizontalis alicubi secat projicientem intersectio illa generabit in projectione cruræ duo Hyperbolici generis cirva eandem Asymptoton ad oppositas plagas in infinitum tendentia, id ex eodem Asymptoti latere si intersectio sit in puncto flexus contrarij, aliter ex latere diverso, et Asymptotos erit projectio rectæ quæ curvam projicientem tangit in puncto intersectionis, tot ejusmodi crurum paria in projectione quot sunt intersectiones lineæ Horizontalis cum projiciente. Unde linea secundi ordinis non nisi duo paria crurum Hyperbolicorum habere potest, Linea tertij ordinis non trisi tria paria {L}inea quarti quatuor &c; et earum Asymptoti tris vel plures se secabunt in uno punct{o} si tangentes se secant in uno, {illeg} {illeg}bus vel pluribus; & si Projicit{u}r {illeg} {senel} vel {illeg} {illeg} secat in puncto dec{crissatioris,} {illeg} duæ {illeg} parallelæ {erunt}.
Si Linea Horizontalis {illeg} ge{n}erunt crura duo Parabol{illeg} generis ad eadem pla{illeg} in infi{tum} {illeg} et concavis partibus {illeg} {illeg}picientia, {insi} ubi cont{illeg} {illeg} est {illeg} puncto {illeg}casa crura Parab{illeg} ad mod{illeg} celerum {illeg} oppo{illeg} et ex eodem latere {concave} erunt {illeg} vertice {cento} curva alicujus {illeg} quum obliquissimè tangit Projicie{n}tem seu ut {projiriè} {illeg} angulo contactus crura Parabolica {illeg} ad pla{gas} oppositas {ut si} di{illeg} latere concavæ erunt, at si tangit ipsam {illeg} angulo qui rectilineo æqualis sit contactas ille generabit crura duo Hyperbolica ex eodem latere ejusdem Asumptoti ad eandem plagam in infinitum tendentia.
Si linea Horizontalis et Asymptotos Projicientis crura Hyperbolica quæ circa Asymptoton illam sunt, convertentur in Parabolica: Et vice versa si linea Horizontalis tendit ad plagam crurum Parabolicorum crura illa convertentur in Hyperbolica. Omnia vero crura infinita quæ non tendunt ad plagam lineæ horizontalis in omni casu evanescunt.
Si deni Linea Horizontalis transit per punctum conjugatum, generabitur curva linea cujus punctum conjugatum in infinitum abijt. Et ne punctum conjugatum infinite distans absurdum videatur scias projectiones hujus curvæ haberæ puncta conjugata finitè distantia quæ sunt puncti illius infinitè distantis projectiones.
At hæ sunt mutationes li curvarum linearum quæ projectione fiunt: quarum casus omnes et eorum complexiones siquis ad curvam aliquam projicientem enumeraverit, is simul enumerabit linearum species omnes quæ sunt ejusdem generis cum projiciente: saltem si in lineis altiorum ordinum Projicius satis latè sumitur.
[108] Sic ubi Projiciens est circulus, Linea Horizontalis hunc circulum aut secabit in duobus punctis aut tanget in uno aut tota cadet extra circulum, et perinde Projectio aut quatuor habebit infinita crura Hyperbolica aut duo Parabolica aut nullum. Unde hujus ordinis tres erunt species Hyperbla Parabola et Ellipsis præter Circulum. At in generibus linearum tertij ordinis casus sunt plures
In primo Genere
[109] 1. Si oculus infinitè distat, vel si planum projectionis plano projicientis parallelum est, projectio erit Parabola ejusdem speciei cum projiciente id est Parabola cuspidata quam Neilianam nominavimus. .
2. Si Linea Horizontalis transit per verticem cuspidatum Projicientis id in angulo contactus, Projectio erit Parabola Wallisiana, habens crura duo Parabolica ad oppositas plagas in infinitum tendentia et ex diverso latere concava. et centrum in puncto flexus contrarij.
3. Si linea illa Horizontalis transit per verticem cuspidatum et tendit ad plagam infinitorum crurum Projicientis Projectio erit Crux Hyperbolica librata, habens duas Hyperbolas ex eodem habere unius Asymptoti ex diverso alterius. Libratam vero {vaco} {illeg} curvam quæ diametrum {illeg} rectiineam habet ordinatas {illeg}inde æquales terminantem: non {illeg} quæ {illeg}
4. Si linea illa transi{bis} {illeg} cuspidatum tendit ad aliam quamvis plagam: Projectio {illeg} hyperbolica non lineata habens Hyperbolas duas {duarum} duo crura ex diverso latere unius {illeg} ad {eandem plagam} altera duo ex diverso latere {deterius} {illeg}proti ad plagas oppositas tendunt.
5. Si tendit ad plagam crurum infinitorum et Projicientem nec secat nec tangit Projectio erit Cisso{i}s librata, et uno casu Cissois
{Veterum}
6. Si tendit ad plagam crurum infinitorum et secat Projicientem in duobus punctis Projectio erit Hyperbola triplex librata cuspidatæ. Hyperbolarum una quæ cuspidata erit jacebit extra angulum Asymptotorum alteræ duæ non cuspidatæ jacebunt intra.
7 Si secat Projicientem in unico tantum puncto et non transit per cuspidem ejus Projectio erit Cissois circa Asympotom torta.
8 Si tangit Projicientem extra cuspidem, at adeo in alio etiam puncto secat Projectio erit Crux Parabolica cuspidata. Ejus crura duo Parabolica tendunt ad eandem plagam et concavitate se mutuò respiciunt, in vertice verò non junguntur sed postquam convergendo unum eorum processit in cuspidem, divergunt {denuò} et ad plagas oppositas cruribus Hyperbolicis ex diverso latere ejusdem Asymptoti in infinitum tendunt.
9 Si secat Projicientem in tribus punctis Projectio erit Hyperbola triplex cuspidata non librata. Hyperbolarum illa quæ cuspidata est jacebit extra angulum Asymptotorum suarum, altera jacebit intra, tertia uno crure jacebit {i}ntra altero extra.
In secundo Genere.
1. Si oculus infinite distat vel si plana Projectionis et Projicientis parallela sint, Projectio erit ejusdem species cum Projiciente id est Parabola nodosa.
2. Si linea Horizontalis tendit ad plagam crurum infinitorum Projicientis et Projicientem nec secat nec tangit Projectio erit Cissois nodosa librata.
3. Sin Projicientem tangit in vertice Projectio erit Crux Parabolica nodosa librata
4. Si secat eam inter vertiem et nodum projicietur Hyperbola triplex librata cum nodo in pari Hyperbolarum.
5. Si secat in ipso nodo, Projectio erit Hyperbola triplex librata duas ex tribus asymptotis parallelas habens.
6 Si secat ultra nodum versus crura infinita Projectio erit Hyperbola triplex librata cum nodo in impari Hyperbola.
7. Quod si linea Horizontalis non tendit ad plagam crurum infinitorum et occurrit Projicienti in unico tantum puncto, Projectio erit Cissois nodosa circa Asymptoton torta
8. Si præterea tangit Projicientem inter verticem et nodum projicientur Crux Parabolica nodosa {,} non {librata,} clausa in vertice.
11. Si secat {eam bis} ad partes {nodi} versus vertic{e}m {et} semel alicubi projicietur Hyperbolæ triplex {non} librati cum nodo in pari Hyperbolarum
12. Si secat {illeg} ad {illeg}versus verticem et bis in nodo projicietur Hyperbola triplex non {illeg} Asymp{totos} parallelas habens, {illeg}Hyperbolam concavo {illeg} habens {illeg} et præterea {illeg} in {illeg} contrario si{illeg} modo linea Horizon {illeg} secat Projicientem in ipso vertice.
13. Si secat eam bis in nodo et semel cum sum versus crura infinita Projectio erit Hyperbola triplex non librata duas ex Asumptotis parallelas habens et inter eas Hyperbolam ad easdem partes ommino concavam.
.
Si Secas Projicientem in tribus punctis extra nodum versus crura infinita, Projectio erit Hyperbola triplex non bifida nodum habens in {illeg}Hyperbola{illeg}
9 Si tangit eam {bis} {illeg} nodo Projectio erit Parabola Carte{illeg}.
10. Si {tangit} eam ultra {illeg} projectio erit Crux Parabolica nodosa{,} non librata sep{illeg} {illeg}vertice
<158r>In tertio genere.
1. Si oculus infinite distat vel si plana projectionis et projicientis parallela sint, projectio est, ejusdem speciei cum projiciente id est Parabola campaniformis cum puncto conjugato.
2. Si Linea Horizontalis vel tendit ad plagam crurum infinitorum vel transit per flexum contrarium Projicientis et præterea transit ultra punctum conjugatum Projectio erit Concha librata punctum habens conjugatum ad convexitatum verticis.
3 Sin transit per punctum conjugatum, orietur Concha librata cum puncto conjugato ad infinitam distantiam.
4 Si transit inter punctum conjugatum et Projicientem Projectio est Concha librata punctum conjugatum habens ad concavitatem verticis
5 Si tangit Projicientem fit Crux Parabolica librata cum vertice aperto et puncto conjugato ultra verticem.
6 Si secat Projicientem inter verticem et puncta flexus contrarij fit Hyperbola triplex librata cum flexibus contrarijs in pari Hyperbolerum et puncto conjugato inter tres Asymptotos.
7 Si secat Projicientem in utro flexu contrario fit Hyperbola triplex, trifariam librata, sine flexu contrario, cum puncto conjugato in centro trianguli Asymptotis inclusi, quod centrum est
8 Si secat Projicientem ad alteras partes alterutrius vel utrius flexus contrarij fit Hyperbola triplex librata cum flexibus contrarijs in impari Hyperbola et puncto conjugato inter tres Asymptotos.
9 Quod si linea Horizontalis nec tendit ad plagam crurum infinitorum nec transit per flexum contrarium{;} transit verò per punctum conjugatum, fit Concha flexu contrario circa Asymptoton torta cujus punctum conjugatem in infinitum abit quæ insuper centrum habebit in flexu contrario si modò linea Horizontalis transit per verticem Projicientis.
10 Sin transit ultra vel citra punctum conjugatum et Projicientem secat in unico tantum puncto extra flexus contrarios Projectio erit Concha flexu contrario circa Asymptoton torta cum puncto conjugato ad finitam distantiam.
11 Quod si tangit Projicientem Crux Parabolica non librata aperta in ver{sus} Asymp{toto} conjugado
12 Si deni secat Projicientem in tribus punctis projicitur Hyperbola triplex non {librata} {cum puncto} conjugato {inter} tres Asympto{tos.} Et una Hyperbolarum {illeg} ultra Asymptotos sua altera {secet} uno {illeg} {ultra} {illeg}
In quart{illeg} {genere}
Species 1. 2. 3. 4. 5. 6. 7. 8. 9 {illeg}dem {serit} {illeg} {describuntur} ac in Genere tertio species 1. 2. 5. 6. 7. 8. 10. 11. 12 respectivé, nisi quod projectiones hic non (habent punctum conjugatum. Et {illeg} 4. 5. 6. 9 casus sunt implicissimi ubi tres Asymptoti in unico puncto concurr{u}nt.
In quinto genere.
Species 1. 2. 6. 7. 8. 9. 10. 11. 14. 15 ijsdem verbis describuntur ac in Genere tertio species 1. 2. 4. 5. 6. 7. 8. 10. 11. 12 nisi quod loco puncti conjugati Ellipsis conjugata ponenda est.
3. Si linea Horizontalis vel ad plagam infinitorum crurum tendeus vel per punctum flexus contrarij transiens tangit Ellipsin ad partem exteriorem Projectio erit Parabola librata cum Concha quæ convexitate sua Parabolam respicit.
4 Sin secat Ellipsin Projectio erit Hyperbola duplex librata, cum concha interjecta: cujus casus est simplicissimus ubi tres concurrunt in eodem puncto.
5 Quod si tangit Ellipsin ad partes interiores seu versus Parabolam campaniformem Projectio erit Parabola librata cum concha quæ concavitate sua Parabolam respicit.
12. Si tangit Ellipsin et non tendit ad plagam infinitorum crurum nec transit per flexum contrarium Projectio erit Parabola non librata cum concha flexu contrario circa Asymptoton torta.
13. Si secat Ellipsin in duobus punctis et alibi in tertio extra flexum contrarium; Projectio erit Hyperbola duplex non librata cum Concha flexu contrario circa Asymptoton torta: et præterea centrum habebit in flexu illa contrario si linea horizontalis per tres Projicientis vertices transit; quo casu tres etiam asymptoti per centrum illud transibunt.
At hæ sunt species linearum tertij ordinis quarum formas et particulares conditiones fusius describere non operæ pretium duxi quoniam has ubi opus est Geometræ speculando formam situm et conditiones Lineæ Projicientis haud difficulter colligent. Mal{u}i paucis inventionem
generaliorum proprietatum linearum aperire. U
Considero igitur quod quæ conveniunt duabus linearum speciebus convenire solent generi et quæ conveniunt duobus generibus convenire solent ordini et quæ conveniunt duobus ordinibus observato progressionis tenore convenire solent ordinibus universis: demide quod combinatio simpliciorum linearum quarum ordines conjuncti ascendunt ad ordinem superiorem vicem obire potest lineæ illius ordinis superioris U combinatio duarum linearum primi ordinis vicem lineæ secundi {,} combinatio trium, quatuor vel pluris vicem {linearum} Vertij quarti {ut} superioris ordinis combinatio {unius linea primi superiores } secundi ordinis vicem {illeg} tertijs ordinis et sic in {illeg}lineas. Nam linea superioris ordinis {sæpe} transit {illeg} combinationem {illeg} simpliciorum et combinatio cujusvis ordinis {illeg} {illeg} recta {illeg} linea {tenævis} ejusdem ordinis {illeg} igitur proprietates combinatio {illeg} incipiendo {a simplicioribus} {illeg} considero proprietates {rectarum} combinatorium {in infinitorum deinde} proprietates circuli vel alterus cujusvis non curvæ {illeg}{: cum} rectis in infinitum. {Nam quæ} duabus combinationum {illeg} {per ordinis universos} inveni{illeg}, {fieri} vix potest {illeg} conveniant lineis et linearum combinationibus universis.
Porismata
[110] 5 Si a duobus datis punctis A, B, C ad rectam Dz positione datam inflectantur duæ rectæ Bz, Cz secantes rectam Ay [111] positione datam sit Ay et parallela Dz, habebunt Ax, Ay, xy datas rationes ad invicem.
Est enim Ax.Dz∷AB.DB∷dat.dat et Dz.Ay∷DC.AC∷ dat.dat. Ergo a[112] Ax.Ay∷dat.dat et b[113] Ay.xy∷dat.dat. Q.E.D.
6 Si a duobus datis punctis A, B, C ad punctum tertium z concurrant duæ recta Bz, Cz secantes rectam Ay positione datam in x et y et habeat Ax ad Ay datam rationem tanget punctum z rectam positione datam.
Agatur enim Dz ipsi Ay parallela. Et quia Ax Dz∷AB.DB et Dz.Ay∷DC.AC et conjunctis rationibus Ax.Ay∷ AB×DC.DB×AC. datur ratio AB×DC ad DB×AC sed datur etiam ratio AB ad AC ergo datur ratio DC ad DB et divisim ratio DC ad datam BC at adeo datur punctum D. Datur etiam angulus D et proinde rect{as} Dz quam punctum z tangit datur positione. Q. E. D.
7 Si a duobus datis punctis B,C ad rectam positione datam Dz inflectantur rectæ duæ Bz, Cz secantes rectam Ay ipsi Dz parallelam in punctis x et y et detur ratio Ax ad Ay datur Ay positione.
Nam ob parallelas Ay, Dz sit Ax.Ay∷AB×DC.DB×AC ut supra. Ergo datur ratio AB×DC∷DB×AC sed datur etiam ratio DC ad DB ergo et ratio AB ad AC, ut et AB ad BC . Et inde of datam BC datur AB. Dato autem tum puncto A tum angulo BAy datur positione Ay. Q. E. D.
8 Si a dato puncto B agatur recta Bz secare parallela duas positione datas in x et z capiatur autem Ay et Ax in data ratione et jungatur zy converget zy ad datum punctum C.
Est enim Ax ad Dz ut AB ad DB hoc est in dat{a} ratione et Ax ad Ay in data ratione adeoa[114] Dz ad Ay in dat{a} ratione sed est DC ad AC {in eadem ratione ergo} divisim ratio D{C} ad AD dat{illeg} {illeg} datur et inde {illeg} {punctum} {illeg}
9. {illeg}sdem {positios dantur} {illeg} zy {illeg} yC.
Nam{illeg} zy.yC∷DA.AC. {illeg}
10. {Easdem positios dantur ratione {illeg}} {illeg} yxz, AxB, DzB, DAxz,DAyz, BzC, ByC, ACy seu Dz {in datum.}
[115] P
Porism. 1 Si a datis duobus punctis B, C ad rectam Az positione datam [116] concurrentes rectæ secent in punctis x, y rectam Ay a dato puncto A ipsi BC parallelam ductam, erit Ax ad Ay in data ratione
Nam si Az producta occurrat BC in D erit Ax.xy∷DB.BC ∷dat.dat Q. E. D.
Porism 2 Et si a datis duobus punctis B, C ductæ rectæ Bz, Cz secent Ay in data ratione, punctum z tanget rectam positione datam.
Age rectam zAD occurrrentem BC in D et erit Ax.xy∷DB.BC ergo datur ratio DB ad BC. Ergo datur punctus D.
Porism 3 Et si a dato puncto B agatur Bxz occurrens rectis positione datis Ax, Az in x et z detur autem ratio Ax ad xy. inclinabit zy ad datum punctum C.
Per B Ipsi Ay parallela, agatur DBC occurrens rectis zA, zy in D et C. Ergo a[117] datur linea DB. Est .DB.BC∷Ax.xy . Ergo datur BC. Ergo datur punctum C. Q. E. D.
[118] Porism 4 Si a datis punctis B, C concurrentes rectæ Bz Cz secent in v et y rectas a datis punctis In rectas ipsi BC parallelas ductas Iv, ny Sit Iv ad ny in data ratione tanget punctum z rectam positione datam.
Age BI occurrentem ny in L et erit Iv ad Lx ut IB ad LB hoc est in data ratione Ergo Lx est ad ny in data ratione. In eadem ratione capiatur KL ad Kn et erit Kx ad Ky in eadem data ratione. Ergo (per Porism 2) punctum z tangit rectam zK positione datam. Q. E. D.
[119] Porism. 11. Si a datis punctis B, C concurrant rectæ duæ Bz Cz secantes rectas positione datas Ax Ay in dat{a} ratione jaceant autem puncta ABC in directum, punctum z tangit rectam positione datam.
Cas. 1. Junge xy et triangulum Axy dabitur {illeg}. Jam si xy parallela sit ipsi BC, produc{illeg} xy ad E {ut} sit E{x} ad xy {et} AB ad BC et concurrent{es} {illeg} {rectæ} A {illeg} {illeg} puncto z Atqui {illeg} {datam} {illeg} Ax ad xy {illeg} {Ex} ad {illeg} datur ratio Ex {Ax}{. Ergo} {illeg} {illeg} Ax {illeg} {et} recta AE positione. {Ergo} {illeg}positione datas. Q. E. D.
[120] Cas. 2. Sin {illeg} {perfectio} {illeg}. due vy ipsi BC par{illeg} {et ob } {illeg} {speciefiguram Avx} {illeg} ratio Av ad Ax In {ista} rationes fac {ut} sit AC ad EC nec non in ratione{m} EC ad Av {ut} sit DC ad DB et dabitur punctum D. Ipsis Ax Ay {age} parallelas DC Dn occurrent{es} Bz Cz in {illeg} et n. Converte{m} rationem {nomissimam} et fiet EC DC∷AB.DB∷ Ax.DO Ergo {illeg} sit Av.Ax∷AC.EC et Ax.DO.∷{illeg}.DC erit {denægno} Av.DO∷AC.DC. Sed {in} eadem ratione est Ay.Dn ergo {illeg} Avn {illeg} DOn . Ergo On parallela est BC. et
[121] ratio DO ad Dn datur. Ergo (per cas 1) punctum z tangit rectam positione datam. Q. E. D.
Cas 3. Si datur ratio Ax ad ay age AT ipsi ay parallelam et dabitur ratio AT ad ay: quippe quæ eadem sit rationi AC ad aC. Ergo datur ratio Ax ad AT. Ergo per cas 2 punctum z tangit rectam positione data. Q. E. D.
Porisma
I{y}sdem positis si Ax est ad ay ut datum data parte ipsius Ax auctum vel diminutum ad datum, tangit punctum z rectam positione datam.
<186r>The pricked circle is the Moon according to the parallex of M.C. 46′.20″. And so the digits by the type are 11.43′. which were observed 11.22. The luminous part alwayes seemeth broader than it is.
{In this Type the Sun standeth as in the former, for the time is the same. Now because then was the greatest Observation, it is manifest that the ☾ was then at s, k not at q where the Tables place it. the Tables gô give the ☾ 9' too must in Longitude, as you may measure with your compasses in this Type.}
[Editorial Note 4] <A1191v> [Editorial Note 5]
[Editorial Note 5]
Eclipse of the Sun observed at Ecton A.D. 1652. marrs 29.h.10.32′. mins tempore apparente; sed tempore æqualis 10.26′. Digits eclipsed 11.22′.
This type agreeth with the Tables of M. lunitia & the Rudolphim. the other type repesenteth the observation
For the Altitude of the Sun
Ut rad. ab sim. anguli orientis: ita sinus distantiæ ☉ a Decendente ad sim alt. ☉ 41.50′.
In the same manner I find the altitude of the next superiour degree in the Ecliptic to be 41.54′. & the altitude of the next inferiour degree to be 41.45′. The one being 4′ more than the Suns altitude, & the other 5′ lesse; I take the meane &c. for the distance of the Almicenters, sc. of the Almic. of the Sun, & the Almic. that cutts the Ecliptic either one degree before the Sun, or one degree behind him. & this number I keep
Now I trace a line (AB) for the moones Orbit. & because the Eclipse hapneth in the 9th degree from ♌ I prick that degree behoren 8 & 9 from a scale of one degree, or from my Sector set for the purpose, by where I can measure with my compasses to the 6 part of a minute. The Lat. of 8°. is 43′.58″. I take it into my compasses from my Scale or Sector & setting one foot in 8 of the Orbit with the other I draw the arch about h. & the Lat. of 9° being 49′.20″ I take likewise & setting one foot in 9 of the Orbit I draw a second arch below the Orbit. & by the outsides of these arches I draw the Ecliptic in his true situation.
Then from 8 in the Orbit I let fall a perpendicular (8h) upon the Ecliptic. which perpendicular falleth short of 8 in the Ecliptic by the quantity of the Reduction, which here is h 8 being 2′.03″. set 8 therefore in the Ecliptic so much to the left hand (s.s.s.) from the perpendic. & 60 minutes furtherest 9.
Then I prick the center of the Sun upon the Ecliptic 30′.34″. from 8 toward 9. & I prick the ☾ in her Orbit 41′.06″ from 8 toward 9.
From the Sun measure one degree in the Ecliptic bd. Take in your compasses the . before {illeg}ned for this purpose, & setting one foot in d, with the other draw the arch at e. & laying a ruler to the Sun & to the outside of this arch draw a strait line which shall be the Almicenter of the Sun. Then from the Sun raise a perpendicular at right angles with the said Almicenter, & it shall be the Azimuth of the Sun. & draw a parallell thereto through the Moones {illeg}in her Orbit, & that shall be the Azimuth of the Moones.
I measure from the Ecliptic downward in the Suns Azimuth so much as his parallax of {altit.} comes to (which here is 45″) & there set the apparent center of the sun (as at c) & there upon with his semidiameter 15′.12″ I draw his circle. Also from the Moones place in her Orbit {her} Azimuth I measure her parallax of alt. and (m n being 46′.20″. according to my Tables & where the parallax ends prick the moones apparent center (at n. ) & there{illeg} with her semidiameter (16′.10″.) describe her circle.
{illeg} you a perfect type in which you may measure with your compasses what you will and if you would know the posture of the Luminaryes an hours or half or quarter {illeg} or before prick the points of 8 & 9 into another paper. & by these points draw {illeg} {illeg} then rectifie the places of the Sun & moone by adding or subtracting the {illeg} {illeg}here you must a{illeg} {illeg} orient angle, & altitude of the Sun {illeg} {illeg} the distance of the {illeg} {illeg} labour of {illeg} {illeg}
<1191r>
ed=x=distantiæ solis a planeta Rad=gb=a. abg=medio motai. b=hb cosinui medii motus ab aplelio. af=q= diametro màximo ellipseos=be+ed. bc bd=c=distantiæ focorum. eb=q−x. qq−2qx+xx−zz=xx−zz+2cz−cc. .. & therfor{{illeg}} 2bcq−2bcx=aqq+acc−2aqx. . . . . . . Therefore soe is cd to de. & is the secant of the angle edc.
In the Ellipsis of the Earths motion, ad:df∷ diameter of ☉ at f: Diamet of him at a. Or ad:de∷Diam{illeg} of ☉ at e:Diam of ☉ at a &c. & by this meanes the foci of the Ellipsis may be found.
Haveing the Aphelion viz ∠akl, the middle motion of the ☉ viz ∠eba+∠akl & the ☉s apparent place viz: ∠edp, taking any quantity for af to find the distances of the foci bd Na{illeg} the given quantitys bg={r}d=Rad=a. gh=b. rs=c. bd=x. eb=y. af=q. bh=e. d{s}=d. Then, . . . . . .
Or if the angle (edb) bee right, & af=q. bg=a. bd=x. eb=y. gh=c. then . . . . . . As for example if the difference twixt the middle & apparent place of ☉ when he is at e that is the ∠bhg bee 2degr..2′.54″.. The signe of it 357425, the cosine 9993609=gh, & the rad=gb=af=10000000. Then is & ∠edb=90 degrees. . that is, af:bd∷10000000:178770. And this is the exactest way to find the Ellipsis of ☉. For in March & September when ☉ is about 90d 2′ 54″ of his meane motion from his Apogæ he may perhaps be observed to bee 90d from his Apogæ of his apparent motion. That is the ∠bgh=2d.2′.54″. when ∠edb=90d.
Having the middle motion of a planet in its orbe viz , abe+fka. ba+ad=af=q=Radio. bh=b. . bg=a. be=x Then . . . . . Or . &, to the distance of a planet from ☉. also , & . Making af=bg=q=radio for brevitys sake, than to the secant of the angle eda. Or thus, to the cosine of the angle eda. Note that after the first operacon the calculacion will bee very short. for haveing once found 2cqq & cc+qq I call, cqq=m. & . Soe that in all other operacons wherein m & n vary not as in the same planet the equation is , soe that the middle motion & consequent{e} (b) being given sd the cosine of eda is readily found. By this meanes the ☉s place in the Ecliptick may always bee found This equation may be ordered so that n, or {e} be a decimall {illeg}
[Editorial Note 1] Newton numbered the first two paragraphs to indicate their order within the text. These paragraphs have been moved in our transcription according to Newton's numbering.
[1] 
[2] November 8th 1665.
[3] 
[4] 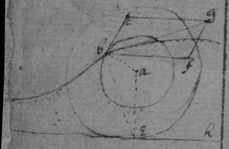
[5] 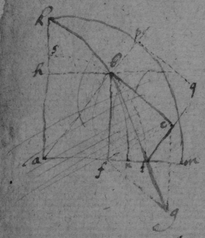
[6] 
[7] 
[8] 
[9] 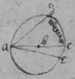
[10] 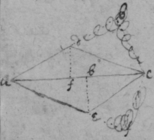
[11] 
[12] 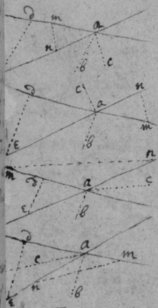
[13] 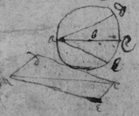
[14] 
[15] 
[16] 
[17] 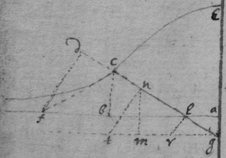
[18] 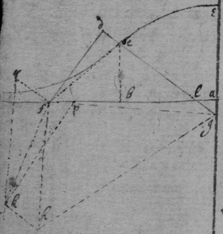
[19] 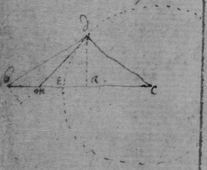
[20] 
[21] May. 1665.
[22] 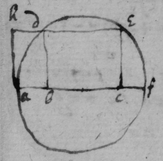
[23] 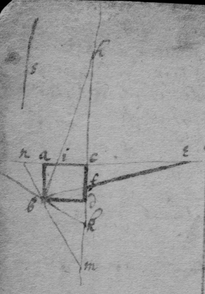
[24] November the 13th
[25] {To} find the velocitys of bodys by the lines they de{scr}ibe.
[26] 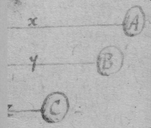
[27] 
[28] Of tangents to Geometricall lines.
[29] 
[30] 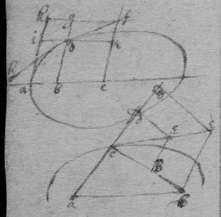
[31] Of tangents to Mechanicall lines.
[32] Of the crookednesse of Geometricall lines.
[33] 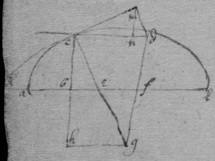
[34] May 30th 1665
[36] 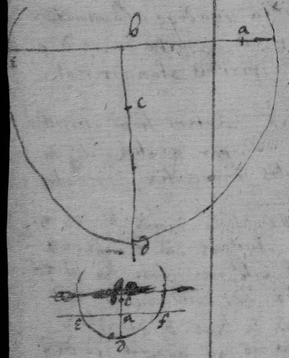
[37] 
[38] The construction of sollid — & Linear Problems
[39] 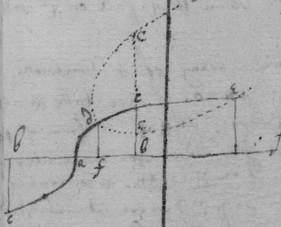
[40] A Generall rule wherby any Probleme may bee resolved.
[41] By what lines a Problem may bee resolved.
[42] In how many points two lines may intersect.
[45] 
[46] 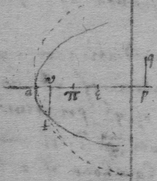
[47] Constructions performed by a Parabola of the 2d kind. x=y3
[48] 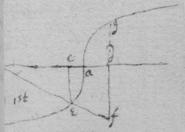
[49] 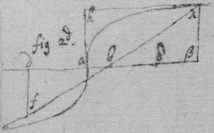
[50] 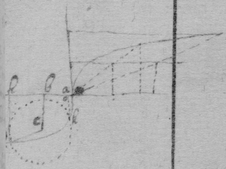
[Editorial Note 2] Written upside down at the bottom of the page.
[51] † juxta proxima præce{illeg}us, erit VF−2gT {ad} VF+2TV {ut} sinus refrationis ad sinum inciden{tiæ}.
[52] 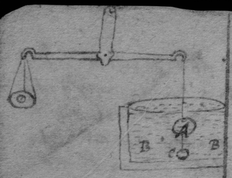
[53] 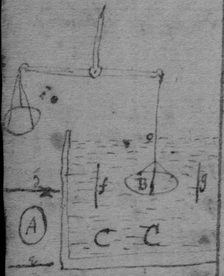
[54] 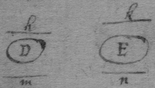
[55] 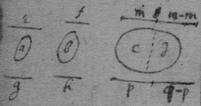
[56] 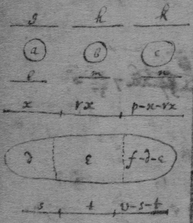
[57] 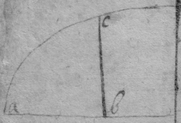
[58] {illeg} equall, otherwise {illeg} they differ by {illeg} 5 let the differen{ce} of the numbers be {illeg} R & the {illeg} tenth part of their Summ S.
[59] 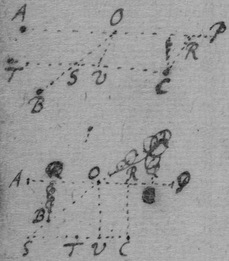
[60] 
[61] 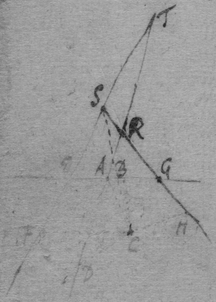
[62] 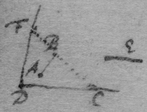
[63] 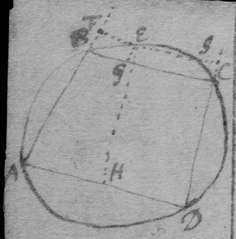
[64] 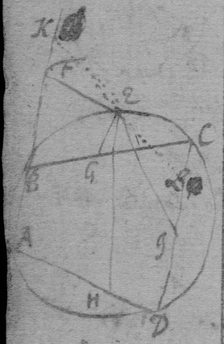
[65] 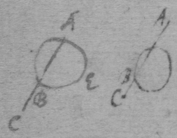
[66] 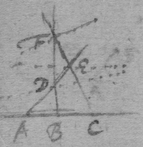
[67] 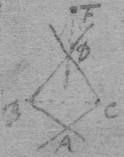
[68] 
[69] 
[70] 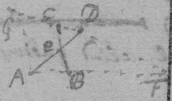
[71] 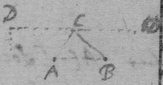
[72] 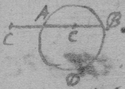
[73] 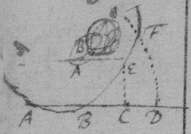
[74] 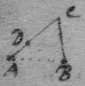
[75] 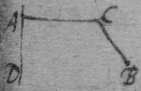
[76] 
[77] 
[78] {illeg} Jan: 6. 5hor. 34′
[79] {Decem} 1st Epist. 2)
[80] ✝ 9?
[81] Nota. distantia Cometæ {illeg} stella B Feb 7 juxta Hookium fuit pars distantiæ primæ et {Sedæ} Arietis id, est {5}′ 12″ seu . Situs autem erat cometa in medio inter stellas B et C.
[83] 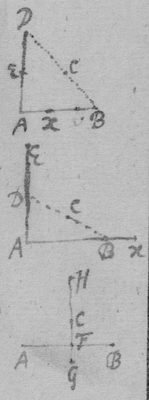
[84] I Gradus Problematum:
[85] 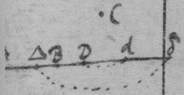
[86] II Quantitates positivæ et subductitiæ cum earum notis
[87] III Quantitates im{p}ossibiles.
[88] IV Quibus lineijs problemata solvuntur{.}
[89] V Ordines Linearum.
[90] Modus exprimendi lineas
[91] Locus linearis puncti vagi.
[92] Curvarum proprietates generales.
[93] Tangentes ad Curvas descriptas ducere.
[94] De cruribus infinitis et Asymptotis curvarum.
[95] Quomodo curare in species distinguendæ
[96] De curvarum tangentibus
[97] Notarum quarundam explicatio.
[98] Fluxiones quantitatum.
[99] 
[100] 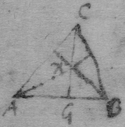
[101] 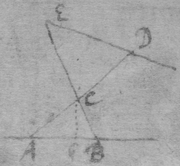
[102] 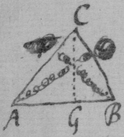
[103] 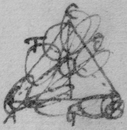
[104] Exempla prima
[105] The contents of this note are only visible in the diplomatic transcript because they were deleted on the original manuscript
[Editorial Note 3] This edit was later made to the text on f. 130r by Newton.
[106] Exemplum in {lineis} tertij ordi{s}.
[107] Species Linearum ejusdem Generis.
[108] Exemplum in lineis secundi ac tertij ordinis.
[109] The contents of this note are only visible in the diplomatic transcript because they were deleted on the original manuscript
[110] 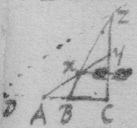
[111] 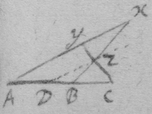
[112] a 8. Dat.
[113] b 5 Dat
[114] a 8 Dat
[115] 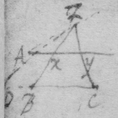
[116] 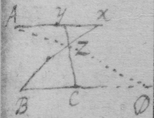
[117] a 30 Dat
[118] 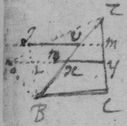
[119] 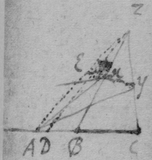
[120] 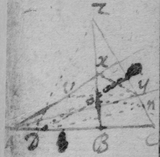
[121] 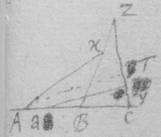
[Editorial Note 4] The following paragraph is written upsidedown at the bottom of the page
[Editorial Note 5] The following paragraph is written upsidedown at the bottom of the page

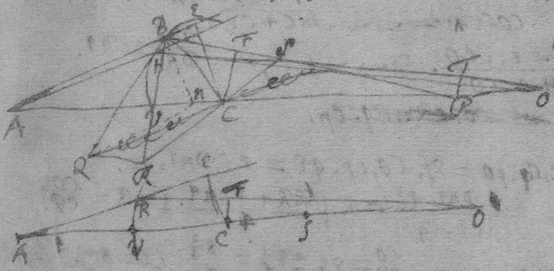 Be.BCBF∷Bn.BQ.BR. B
Be.BCBF∷Bn.BQ.BR. B