Letter from Isaac Newton to Henry Oldenburg, dated 24 October 1676
vir Dignissime
Quanta cum voluptate legi Epistolas Clarissimorum virorum D. Leibnitij & D. Tschurnhausij vix dixerim. Perelegans sane est Leibnitij methodus perveniendi ad series convergentes, & satis ostendisset {sola satis ostendit} ingenium authoris [etsi nihil aliud scripsisset ] sed {et}quæ alibi per Epistolam sparguntur suo nomine dignissima, efficiunt etiam ut ab eo speremus maxima. Diversitas modorum quibus eodem tenditur, eò magis placuit quòd mihi cum tres methodi perveniendi ad ejusmodi series {nobis} innotuerant, [ adeo ut novam nobis communicandam vix expectarem ] Leibnitiano illa ab {isti{illeg}} omnibus {plane} diversa est unam e meis prius descripsi jam addo aliam, illam scilicet quâ primum incidi in has series: nam incidi in eas antequam scirem divisiones et extractiones radicum quibus jam utor et hujus explicatione pendendum est fundamentum Theorematis sub initio Epistolæ prioris positi quod D. Leibnitius a me desiderat. [ sub initio studiorum meorum Mathematicorum ubi incideram in opera Celeberrimi Wallisij nostri, considerando series quarum intercalatione ipse exhibet aream Circuli et Hyperbolæ, utpote quod in serie curvarum quarum basis sive axis communis sit x, et ordinatim applicatæ, . Si areæ alternarum quæ sunt
interpolari possent, haberemus areas intermediarum quarum prima est circulus: ad has interpolandas notabam, quod in omnibus primus terminus esset x, quodque secundi termini essent in Arithmeticâ progressione, et proinde quod duo primi termini serierum intercalandarum deberent esse ad reliquas intercalandas considerabam quod denominatores erant in Arithmeticâ progressione, adeoque solæ numeratorum coefficientes numerales restabant investigandæ hæ autem in alternis datis areis erant figuræ potestatum numeri 11 H[1]; nempe harum hoc est primo 1, deinde . tertio . quarto . quinto . quærebam itaque quomodo in his seriebus, ex datis duabus primis figuris reliquæ derivari possent, et inveni quod posita secunda figura, m, reliquæ producerentur per continuam multiplicationem terminorum hujus seriei . Exempli gratiâ sit et erit hoc est 6 tertius terminus, et hoc est 4, quartus, et , hoc est, 1, quintus et, , hoc est, 0, sextus, quo series in hoc casu terminatur. hanc regulam itaque applicui ad series interserendas et cùm pro circulo secundus terminus esset , posui , et prodierunt termini sive id est , sive id est , sive id est & sic in infinitum. unde cognovi desideratam aream segmenti circularis esse . et eadem ratione prodierunt etiam interserendæ areæ reliquarum curvarum, ut et area Hyperbolæ et cæterarum alternarum in hac serie &c et eadem est ratio intercalandi alias series idque per intervalla duorum pluriumve terminorum simul deficientium. hic fuit primus meus ingressus in has meditationes: qui memoria sanè exciderat nisi oculos in adversaria quædam ante paucas septimanas retulissem. [ Ubi vero hæc didiceram mox considerabam terminos . hoc est, : eodem modo interpolari posse ac areas ab ipsis generatas: et ad hoc nihil aliud requiri quam omissionem denominatorum in terminis exprimentibus areas; hoc est coefficientes terminorum quantitatis intercalandæ , vel vel generaliter , prodire per continuam multiplicationem terminorum hujus seriei , Adeoque e.g. valeret Et valeret Et valeret , Sic itaque innotuit mihi generalis reductio radicalium in infinitas series per regulam illam quam posui initio epistolæ prioris, antequam scirem extractionem radicum. sed hâc cognitâ non potuit altera me, dia latere nam ut probarem has operationes multiplicavi in se, & factum est terminis reliquis in infinitum evanescentibus per continuationem seriei. Atque ita bis in se ductum produxit etiam . Quod ut certa fuit harum conclusionum demonstratio sic me manu duxit ad tentandum è converso, nam {utnam} hæ series quas sic constitit esse radices quantitatis non possent inde extrahi more Arithmetico, et res benè successit. Operationis {for}ma in quadraticis radicibus hæc erat
Unde et simul patefactus est ad resolutionem affectarum æquationum. Nam {faceo} Divisiones quarum utique specimen {præclarum} N. Mercator sub idem tempus excogitavit & mox cum laude omnium ædidit.
< text from f 2r resumes >His perspectis neglexi penitus interpolationem serierum et has operationes tanquam fundamenta magis genuina solummodo adhibui nec latuit reductio per divisionem res utique facilior Sed et resolutionem affectarum ǽquationum mox aggressus sum qua simul ordinatim applicatæ vicissim ex areis curvarum vel arcubus datis innotuere. nam regressio ad hæc nihil indigeat præter resolutionem æquationum quibus areæ vel arcus ex datis rectis dabantur: eo tempore pestis ingruens coegit me hinc fugere et alia cogitare, addidi tamen subinde condituram quandam Logarithmorum ex areâ hyperbolæ, quam hic subjungo Sit dFD Hyperbola cujus centrum C, vertex F, & quadratum 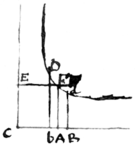 interjectum cape AB, Ab hinc inde sive 0,1, et erectis perpendiculis BD, bd ad Hyperbolam terminatis, erit semisumma spatiorum AD et et semidifferentia quaæ reductæ ic se habent
interjectum cape AB, Ab hinc inde sive 0,1, et erectis perpendiculis BD, bd ad Hyperbolam terminatis, erit semisumma spatiorum AD et et semidifferentia quaæ reductæ ic se habent
horum summa 0.1053605156577 est Ad — et differentia 0.0953101798043 est AD. et eadem ratione positis AB, Ab hinc inde , obtinebitur , et habitis sic Logarithmis Hyperbolicis numerorum quatuor decimalium 0.8, 0,9, 1,1, & 1,2. cum sit , et 0,8 et 0.9 sint minores unitate, adde Logarithmos illorum ad duplum Logarithmi , et habebis 0,6931471805597 Logarithmum Hyperbolicum numeri 2. cujus triplo adde log (siquidem sit ) et habebis 2,3025850929933 logarithmum numeri 10. indeque per additionem simul prodeunt Logarithmi numerorum 9 et 11; adeoque omnium primorum horum Logarithmi in promptu sunt. Insuper ex solâ depressione numerorum superioris computi per loca decimalia et additione obtinentur Logarithmi decimalium 0.98, 0 99, 1.01, 1.02 ut et horum 0.998, 0.999, 1.001 1.002, et inde per additionem et substractionem prodeunt Logarithmi primorum {&c} qui una cum superioribus per Log. numeri 10 divisi evadunt veri Logarithmi in Tabulam inserendi sed hoc postea propiùs obtinui, pudet dicere ad quot figurarum loca hæ computationes otiosus eo tempore perduxi, nam tunc sanè nimis delectabar inventis hisce, sed ubi prodiit ingeniosa illa Nicolai Mercatoris Logarithmotechnia (quem suppono sua primum invenisse) cœpi ea minus curare suspicatus, vel eum nosse extractionem radicum æquam ac divisionem fractionum, vel alios saltem divisione patefacta inventuros reliqua, priusquam ego ætatis essem maturæ ad scribendum, eo ipso tamen tempore quo liber iste prodiit communicatum est per amicum (D. Barrow tunc matheseos Professore) ad D. Collinsio compendium quoddam methodi harum serierum in quo significaveram areas et Longitudines curvarum omnium et solidorum superficies et contenta, ex datis rectis vice versâ ex his datis rectas determinari posse et methodum ibi judicatâ indicatâ illustraveram diversis seriebus [ Suborta deinde inter nos epistolari consuetudine D. Collinsius vir in rem mathematicam promovendam natus non destitit suggerere ut hæc publici juris facerem & ante annos quinque cum suadentibus amicis, consilium ceperam edendi Tractatum de refractione Lucis et coloribus quem tunc in promptu habebam; cœpi de his seriebus iterum cogitare & tractatum de iis etiam conscripsi ut utrumque simul ederem, sed ex occasione Telescopii catadioptrici epistolâ ad te missâ quâ breviter explicui conceptus meos de naturâ lucis inopinatum quiddam effecit ut mei interesse sentirem ad te festinanter scribere de impressione istius Epistolæ et subortæ statim per diversorum epistolas objectionibus aliisque refertas, crebræ interpellationes me prorsus a consilio deterruerunt et effecerunt ut me arguerem imprudentiæ quod umbram captando eatenus perdideram quietem meam, rem prorsus substantialem. [ Sub id tempus Gregorius ex unicâ tantâ serie quadam è meis quam D. Collinsius ad eum transmiserat, post multam considerationem (ut ad Collinsium rescripsit) pervenit ad eandem methodum, & tractatum de eâ reliquit quem speramus ab amicis ejus editum iri. Siquidem pro ingenio quo pollebat non potuit non adjicere de suo multa nova quæ rei mathematicæ interest ut non pereant. ipse autem tractatum meum non penitus absolveram ubi destiti à proposito, neque in hunc usque diem mens rediit ad reliqua adjicienda Deerat quippe pars ea qua decreveram explicare modum solvendi Problemata quæ ad Quadraturas reduci nequeunt licet aliquid de fundamento ejus posuissem.
Cæterum in tractatu isto series infinitæ non magnam partem obtinebant alia haud pauca congessi inter quæ erat methodus ducendi tangentes quam Solertissimus Slusius ante annos duos tresve tibi communicavit de quâ tu (suggerente Collinsio) rescripsisti eandem mihi etiam innotuisse diversâ ratione in eam incidimus. nam res non eget demonstratione prout ego operor. habito meo fundamento nemo potuit tangentes aliter ducere nisi volens de recta viâ deviaret. Quinetiam non hic hæretur ad æquationes radicalibus unam vel utramque indefinitam quantitatem involventibus utcunque affectas, sed absque aliquâ talium æquationum reductione (quæ opus plerumque redderet immensum) tangens confestim ducitur: et eodem modo se res habet in quæstionibus de maximis et minimis alijsque quibusdam de quibus jam non loquor fundamentum harum operationum satis obvium quidam: quoniam jam non possum explicationem ejus prosequi sic potius celavi 6accd et 13eff.713l9n4o4orr4s8t112vx hoc fundamento conatus Sum etiam reddere speculationes de Quadraturâ curvarum simpliciores perervenique ad Theoremata quædam generalia. et ut candide agam ecce primum Theorema. [ Ad curvam aliquam sit ordinatim applicata termino diametri Seu basis z normaliter insistens ubi litteræ d, e, f denotant quaslibet quantitates datas, et θ, η, λ indices potestatum sive dignitatum quantitatum Quibus affixæ sunt. fac , , , et , et area curvæ erit . literis denotantibus terminos proxime antecedentes nempe A terminum , B terminum &c hæc series ubi r fractio est vel numerus negativus continuatur in infinitum ubi vero r integer est et affirmativus continuatur ad tot terminos tantum quot sunt unitates in eodem r et sic exhibet Geometricam Quadraturam curvæ rem exemplis illustro.
Exemp. 1. proponatur Parabola cujus ordinatim applicata sit . hæc in formam regulæ reducta fit . Quare est d . . . . adeoque . . . et area quæsita , hoc est, . et sic in genere si ponatur ordinatim applicata, prodibit area .
Exemplum Secundum Sit ordinatim applicata hæc per reductionem fit , vel etiam in priori casu est . . . . . . Adeoque {potius } Erratum {propter simplum} cum sit . hoc est . . et area curvæ = id est . In secundo autem casu est . . . . . . id est . . et Area hoc est area his casibus diversimodè exhibetur Quatenus computatur a diversis finibus, Quorum assignatio per hos inventos valores arearum facilis est.
Exemp: 3. Sit ordinatim applicata hoc est per reductionem ad debitam formam vel vel et erit in priori casu . . . . . . Adeoque quare cum r non sit numerus affirmativus procedo ad alterum casum hic est . . . . . . adeoque ...[2]. s . , seu , . Et area hoc est .
Exemp: 4. Sit denique Ordinatim applicata hæc ad formam regulæ reducta fit Indeque est . . . . . . ...[3]. . et Area , id est .
<4r>Quod si res non successisset in hoc casu existente r vel fractione vel numero negativo, tunc tentassem alterum casum purgando terminum in ordinatim applicatâ a coefficiente hoc est reducendo ordinatim applicatam ad hanc formam et si in neutro casu fuisset numerus integer et affirmativus conclusissem curvam ex earum numero esse quæ non possunt Geometricè quadrari nam quantum animadverto, hæc regula exhibet in finitis æquationibus areas omnium Geometricam quadraturam admittentium Curvarum quarum ordinatim applicatæ constant ex potestatibus radicibus vel quibuslibet dignitatibus binomij cujuscunque licèt non directe ubi index dignitatis est numerus integer: [ At quando hujusmodi curva aliqua non potest Geometricè quadrari sunt ad manus alia Theoremata pro comparatione ejus cum conicis sectionibus vel saltem cum aliis figuris simplicissimis quibuscum potest comparari ad quod sufficit etiam hoc ipsum unicum jam descriptum Theorema si debite continuatur. pro Trjnomijs etiam et alijs quibusdam, regulas {nonullas} quasdem continuari sed in simplicioribus vulgoque celebratis figuris vix aliquid relatu dignum reperi quod evasit aliorum conatus nisi forte longitudo Cissoidis ejusmodi censeatur. Eam sic construitur determino. Sit VD, Cissois, AV, diameter circuli ad quem aptatur V, vertex, AF Asymptoton ejus, ac DB perpendiculare quodvis ad AV demissum cum semiaxe et semiparametro describatur Hyperbola FkK, et inter AB et AV sumpta AC: media proportionali erigantur ad C et V perpendicula Ck et VK hyperbolæ occurrentia in k & K et 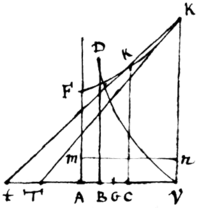 agantur rectæ KT et kt tangentes hyperbolam in eisdem K & k et occurrentes AV, in T, ac, t, et ad AV constituatur rectangulum AVnm æquale spatio TK,kt et cissoidis VD longitudo erit sextupla altitudinis Vn demonstratio perbrevis est [ sed ad infinitas series redeo.
agantur rectæ KT et kt tangentes hyperbolam in eisdem K & k et occurrentes AV, in T, ac, t, et ad AV constituatur rectangulum AVnm æquale spatio TK,kt et cissoidis VD longitudo erit sextupla altitudinis Vn demonstratio perbrevis est [ sed ad infinitas series redeo.
Quamvis multa restent investiganda circa modos approximandi, & diversa serierum genera quæ possunt ad id conducere, tamen vix cum D. Tschurnhausio speraverim dari posse aut simpliciora aut magis generalia fundamenta reducendi quantitates ad hoc genus serierum de quo agimus quam sunt divisiones et extractiones radicum quibus Leibnitius et ego utimur saltem non generaliora quia pro Quadraturâ et ενθυνεσ ὲνθυνσ curvarum ac similibus nullæ possunt dari series ex hisce simplicibus terminis Algebraicis (unicam tantum indefinitam quantitatem involventibus) constantes quas non licet hac methodo colligere nam non possunt esse plures hujusmodi convergentes series ad idem determinandum quam sunt indefinitæ quantitates ex quarum potestatibus series conflentur et ego quidem ex adhibitâ quacunque indefinitâ quantitate seriem novi colligere et idem credo Leibnitio in potestate esse, nam quamvis meâ methodo liberum sit eligere pro conflandâ serie quantitatem quandam quamlibet indefinitam a quâ quæsitum dependeat, et methodum us quam ipse nobis communicavit determinata videatur ad electionem talium indefinitarum quantitatum quibus opus comodè deduci potest ad fractiones quæ per solam divisionem evadant series infinitæ, tamen aliæ quæcunque indefinitæ quantitates pro seriebus conflandis adhiberi possunt per methodum istam quâ affectæ æquationes resolvuntur in proprijs terminis, hoc est conficiendo seriem ex solis terminis quæ æquatio involvit, præterea non video cur dicitur his divisionibus et extractionibus problemata resolvi per accidens siquidem hæ operationes eodem modo se habeant ad hoc genus Algebræ, ac vulgares operationes Arithmeticæ ad Algebram vulgo notam [ quod autem ad simplicitatem methodi attinet nolim fractiones et radicales absque præviâ reductione semper resolvi in series infinitas. Sed ubi perplexæ quantitates occurrunt tentandæ sunt omnimodæ reductiones, sive id fiat, augendo, minuendo, multiplicando, vel dividendo quantitates indefinitas sive per methodum transmutatoriam Leibnitii aut alio quocunque modo qui occurrat, et tunc resolutio in series per divisionem et extractionem opportune adhibebitur hic autem præcipuè intendum est, ut denominatores fractionum & quantitates in vinculo radicum reducantur ad quam paucissimas & minime compositas, et ad tales etiam quæ in seriem abeant citissimè convergentem, et si radices neque convertantur in fractiones neque deprimantur nam per regulam initio alterius epistolæ, extractio altissimarum radicum æque simplex et facilis est ac extractio radicis Quadraticæ vel divisio, et series quæ per divisionem eliciuntur solent minimè omnium convergere, [ hactenus de seriebus unicam indefinitam quantitatem involventibus locutus sum sed possunt etiam perspecta methodo series ex duabus vel pluribus assignatis indefinitis quantitatibus pro arbitrio confici [ Quinetiam beneficio ejusmodi methodi possunt series ad omnes figuras efformari Gregorianis ad circulum et hyperbolam editis affines hoc est quarum ultimus terminus exhibebit quæsitam aream [ sed calculum hic onerosiorem nolim lubens subire. [ possunt denique series ex terminis compositis eadem methodo constitui Quemadmodum si sit ordinatim applicata curvæ alicujus pone et ex binomio extractâ radice prodibit &c. cujus seriei omnes termini quadrari possunt per Theorema jam ante descriptum, sed hæc minoris facio quod ubi series simplices non sunt satis tractabiles aliam nondum communicatam methodum habeo qua pro lubitu acceditur ad quæsitum. E jus fundamentum est commoda expedita et generalis solutio hujus problematis Curvam Geometricm describere quæ per data quotcunque puncta transibit. docuit Euclides descriptionem Circuli per tria data puncta potest etiam conica Sectio describi per quinque data puncta. et curva trium dimensionum per octo septem data puncta hæc statim Geometricè fiunt nullo calculo interposito, sed superius problema est alterius generis, et quamvis primâ fronte intractabile videatur tamen res aliter se habet est enim ferè ex pulcherrimis quæ solvere desiderem [ Seriei à D. Leibnitio pro quadraturâ Curvarum Sectionum proposita affinia sunt Theoremata quædam quæ pro comparatione curvarum cum Conicis sectionibus in catalogum dudum retuli possum utique cum conicis sectionibus Geometricè comparare curvas omnes quarum ordinatim applicatæ sunt vel &c aut vel , vel, aut vel &c aut aut &c vel vel aut vel &c.
Hic d, e, f, g significant quasvis datas quantitates cum suis signis + & − affectas, z, axem vel basem curvæ, et η, , , , , indices potestatum vel dignitatum z, sive sint affirmativi vel negativi sive integri vel fracti, et singula bina Theoremata sunt duo primi termini seriei in infinitum progredientis in tertio et quarto debet esse non majus quam nisi e et g sint contrarii signi in cæteris nulla est limitatio. (harum aliqua nempe secundum, tertium, quartum, quintum & decimum tertium) ex areis duarum conicarum Sectionum conjunctis constant; aliæ quædam (ut nonum decimum et duodecimum) sunt aliter satis compositæ, et omnia quidem in continuatione progressionum cito evadunt compositissima; adeo ut vix per transmutationes figurarum quibus Gregorius et alii usi sunt absque ulteriori fundamento inveniri posse putem. ego quidem haud quicquam generale in his obtinere potui antequam abstraherem a contemplatione figurarum, et rem totam ad simplicem considerationem solarum ordinatim applicatarum reducerem; sed cum hæc et his generaliora sint in potestate, non dubitabitur credo de binomialibus longè facilioribus quæ in his continentur, et prodeunt ponendo tantum literam aliquam e, vel f vel , et vel 2 et si series in quas ista resolvuntur non posuerim in Epistolâ priori, intentus non in omnia particularia enumeranda, sed in illustrandam methodum per unam et alteram in singulis rerum generibus instantiam, quæ ad ostendendam ejus generalitatem sufficere videbatur [ cæterum hæc Theoremata dant series plusquam uno modo nam primum si ponatur , et evadit : unde prodit series nobis communicata, sed si ponatur et inde tandem obtinemus hanc seriem pro longitudine quadrantalis arcus cujus chorda est unitas vel quod perinde est hanc pro longitudine dimidii ejus, et has forte quia æque simplices sunt ac alteræ, et magis convergunt non repudiabitis. sed ego rem aliter æstimo illud enim melius quod utilius est, et problema minori labore solvit, sic quamvis hæc æquatio appareat simplicior hacce tamen in confesso est posteriorem revera simpliciorem esse, propterea quod radicem ejus Geometra facilius eruit; et ob hanc rationem series pro obtinendis arcubus circuli, vel (quod eodem recidit) pro obtinendis sectoribus conicarum Sectionum, pro optimis habeo quæ componuntur ex potestatibus sinuum. nam siquis vellet per simplex computum hujus seriei colligere longitudinem Quadrantis ad viginti figurarum loca decimalia, opus esset 5000000000 terminis seriei circiter, ad quorum calculum milleni anni requirerentur et res tardius obtineretur per tangentem 45 gradium. sed adhibito sinu recto grad. quinquaginta quinque vel sexaginta termini hujus seriei , sufficerent, quorum computatio tribus ut opinor vel quatuor diebus absolvi posset; et tamen hic non est optimus modus computandi totam peripheriam; nam series ex sinu recto triginta grad. vel ex sinu verso graduum conflata multo citius dabit arcum suum, cujus sextuplum vel duodecuplum est tota peripheria: neque majori labore eruitur area totius circuli ex segmento cujus sagitta est quadrans diametri ejus computi specimen, siquidem ad manus est, visum fuit apponere, et una adjungere aream hyperbolæ quæ eodem calculo prodit. posito axe transverso , & sinu verso seu segmenti sagitta erit semisegmentum
&c hæc autem series sic in infinitum producitur sit , , , . , et erit semisegmentum eorumque semisumma et semidifferentia his ita præparatis assumo quadrantem nempe axis, et prodit . . . et sic procedo usque dum venero ad terminum depressissimum qui potest ingredi opus, deinde hos terminos per respectivè divisos, dispono in duas tabulas, ambiguos cum primo in unam et negativos in aliam, et addo ut hic vides
tunc a priori summa aufero posteriorem et restat 0,0893284166257043 area semisegmenti hyperbolici. Addo etiam ejusdem summas & aggregatum aufero à primo termino duplicato 0,1666666666666666, et restat 0.0767731061630478 3 {&} area semisegmenti circularis huic addo triangulum istud quo completur in sectorem hoc est , seu 0,0541265877365274 et habeo sectorem sexaginta graduum 0,1308996938995747 cujus sextuplum 0,7853981633974482 est area totius circuli, quæ divisa per quadrantem diametri dat totam peripheriam 3,1415926535897928 [ Si artes alias adhibuissem potui per eundem numerum terminorum seriei pervenisse ad multa plura loca figurarum puta viginti quinque ut amplius sed animus fuit hic ostendere quid per simplex seriei computum præstari posset Quod sane haud difficile est cum in omni opere multiplicatores ac divisores magnâ ex parte non majores quam 11 & nunquam majores quam 41 adhibere opus sit. per seriem Leibnitii etiam si ultimo loco dimidium termini adjiciatur et alia quædam similia artificia adhibeantur potest computum produci ad multas figuras; ut et ponendo summam terminorum esse ad totam seriem , ut ad 2, Sed optimus ejus usus videtur esse quando vel conjungitur cum duabus alijs persimilibus et citissime convergentibus seriebus, vel sola adhibetur ad computandum arcum 30 grad. posita tangente tunc enim series illa evadit quæ cito convergit vel si conjunges cum alijs seriebus, pone circuli diametrum , et , et area totius circuli erit hic consideravimus series quatenus adhibentur ad computandum totum circulum, sed quando computandæ sunt partes ejus tunc quælibet series habet proprium usum et in suo genere optima est si datur tangens satis parva, vel satis magna, non recurrendum erit ad sinum aliquem ut inde computetur arcus, neque vice versa series dato congruens est æquatio pro solvendo proprio problemate credo Cl. Leibnitium dum posuit seriem pro determinatione cosinus {complementi} ex arcu dato, vix animo um advertisse ad seriem meam pro determinatione sinus versi ex eodem arcu siquidem hæc idem sunt, {hæ eædem} sunt. neque observasse videtur morem meum generaliter usurpandi literas pro quantitatibus cum signis suis + et − affectis dum dividit hanc seriem nam cum area hyperbolicâ BE hic significata per z sit affirmativa vel negativa prout jaceat ex unâ vel alterâ parte ordinatim applicatæ BC  Si area illa in numeris data sit l, & l substituatur in serie pro z orietur vel , vel . prout sit affirmativa vel negativa hoc est posito . Et l Logarithmo hyperbolico numerus ei correspondens erit , si l sit affirmativus et si l sit negativus hoc modo fugio multiplicationem Theorematum quæ alias in nimiam molem crescerent, nam v.g. illud unicum Theorema quod supra posui pro quadratura curvarum resolvendum esset in 32 Theoremata si pro signorum varietate multiplicaretur. præterea quæ habentur de inventione numeri unitate majoris per datum Logarithmum hyperbolicum ope seriei potius quam ope seriei . nondum satis percipio. nam si unus terminus adjiciatur amplius ad seriem posteriorem quam ad priorem posterior magis appropinquabit et minor est labor computare unam vel duas primas figuras adjecti hujus termini, quam dividere unitatem per prodeuntem Logarithmum hyperbolicum ad multa figurarum loca extensum ut inde habeatur Logarithmus hyperbolicus Quæsitus, utraque igitur series (si duas dicere fas sit) officio suo fungatur, potest tamen series ex dimidiá parte terminorum constans optimè adhiberi siquidem hæc dabit semidifferentiam duorum numerorum, ex quâ et rectangulo dato, uterque datur, sic et ex serie &c datur semisumma numerorum, indeque etiam numeri. unde prodit relatio serierum inter se, quâ ex unâ datâ dabitur altera Theorema de inventione arcus ex dato cosino ponendo radium 1, cosinum c, et arcum minus appropinquat quam primâ fronte videtur posito quidem sinu verso v, error erit potest fieri ut ad . Ita chorda ad arcum, et error erit tantum circiter qui semper minor est, quam minuta secunda, dum arcus non sit major quam , et singulis etiam bisectionibus diminuitur 128 vicibus
Si area illa in numeris data sit l, & l substituatur in serie pro z orietur vel , vel . prout sit affirmativa vel negativa hoc est posito . Et l Logarithmo hyperbolico numerus ei correspondens erit , si l sit affirmativus et si l sit negativus hoc modo fugio multiplicationem Theorematum quæ alias in nimiam molem crescerent, nam v.g. illud unicum Theorema quod supra posui pro quadratura curvarum resolvendum esset in 32 Theoremata si pro signorum varietate multiplicaretur. præterea quæ habentur de inventione numeri unitate majoris per datum Logarithmum hyperbolicum ope seriei potius quam ope seriei . nondum satis percipio. nam si unus terminus adjiciatur amplius ad seriem posteriorem quam ad priorem posterior magis appropinquabit et minor est labor computare unam vel duas primas figuras adjecti hujus termini, quam dividere unitatem per prodeuntem Logarithmum hyperbolicum ad multa figurarum loca extensum ut inde habeatur Logarithmus hyperbolicus Quæsitus, utraque igitur series (si duas dicere fas sit) officio suo fungatur, potest tamen series ex dimidiá parte terminorum constans optimè adhiberi siquidem hæc dabit semidifferentiam duorum numerorum, ex quâ et rectangulo dato, uterque datur, sic et ex serie &c datur semisumma numerorum, indeque etiam numeri. unde prodit relatio serierum inter se, quâ ex unâ datâ dabitur altera Theorema de inventione arcus ex dato cosino ponendo radium 1, cosinum c, et arcum minus appropinquat quam primâ fronte videtur posito quidem sinu verso v, error erit potest fieri ut ad . Ita chorda ad arcum, et error erit tantum circiter qui semper minor est, quam minuta secunda, dum arcus non sit major quam , et singulis etiam bisectionibus diminuitur 128 vicibus
Series applicari posset ad computationem tabulæ segmentorum ut observat vir clarissimus; sed res optimè absolvitur per canonem sinuum utpote cognitâ quadrantis areâ per continuas additiones nonæ partis ejus, habebis sectores ad singulos decem gradus in semicirculo, deinde per continuam additionem decimæ partis hujus habebis sectores ad gradus, et sic ad decimas partes graduum et ultra procedi potest, tunc radio existente 1 ab uno quoque sectore et ejus complemento ad 180 grad. aufer dimidium communis sinûs recti & relinquentur segmenta in tabulam referenda cæterum quamvis series hic non prosint in aljis tamen locum obtinent, et quoniam hoc ad earum usum spectat, non gravabor in aliquibus attingere: [ constructionem Logarithmorum non aliunde peti debere credetis forte, ex hoc simplici processu qui ab istis pendet, per methodum supra traditam quærantur Logarithmi hyperbolici numerorum 10, 0.98, 0.99, 1.01, 1.02. id quod fit spatio unius et alterius horæ, deinde divisis Logarithmis quatuor posteriorum per Logarithmum numeri 10, et addito indice 2 prodibunt veri Logarithmi numerorum 98, 99, 100, 101, 102 in tabulam inserendi, hi per dena intervalla interpolandi sunt, et exibunt Logarithmi omnium numerorum inter 980 et 1020 et omnibus inter 980 et 1000 iterum per dena intervalla interpolatis habebitur tabula eatenus constructa, tunc ex his colligendi erunt Logarithmi omnium primorum numerorum, et eorum multiplicium minorum quam 100 ad quod nihil requiritur præter additionem et substractionem siquidem sit.
. . . . . . . . . . . . . . . . 59. . . . . . . . . et habitis sic Logarithmis omnium numerorum minorum quam 100 restat tantum hos etiam semel atque iterum per dena intervalla interpolare [ constructionis tabulæ sinuum à quâ pendet tota res trigonometrica fundamentum optimum est continua additio dati anguli ad seipsum vel ad alium datum utpote in angulo addendo bAE inscribantur HI, IK, KL, LM, MN, NO, OP, &c. 
æquales radio AB: et ad opposita latera demittantur perpendicula BE, HQ, IR, KS, LT, MV, NX, OY, &c. et angulorum HIQ, IKH, KLI, LMK &c. differentiæ erunt angulus A, sinus HQ, IR, KS &c. et cosinus IQ, KR, LS, &c. detur jam aliquis eorum LMK, et cæteri sic eruentur, Ad SV et MV: demitte perpendicula Ta et Kb, et (propter similia triangula ABE, TLa, KMb, ALT, AMV &c) erit . Et unde dantur sinus et cosinus KS, MV, SL, LV, et simul patet ratio continuandi progressiones, nempè &c &c. Et retrò &c. ponè ergo , et fac , . . , &c. Sed nodus est inventio sinus et cosinus anguli A, et hic subveniunt series nostræ, utpote cognito ex superioribus Quadrantalis arcus longitudine 1.57079, &c et simul quadrato ejus 2.4694 &c divide quadratum hoc per quadratum numeri exprimentis rationem 90 grad. ad angulum A et quoto dicto z, tres vel quatuor primi termini huius seriei &c dabunt cosinum istius anguli A, sic primo quæri potest angulus 5 grad et inde tabulam computari ad quinos gradus ac deinde interpolari ad gradus vel dimidios gradus per eandem methodum, nam non convenit progredi per nimios saltus, duæ tertiæ partes tabulæ sic computatæ dant reliquam tertiam partem per additionem vel substractionem more noto, siquidem posito KT cosinu 60 grad. sit , et , tunc ad decimas, et centesimas partes graduum pergendum est per aliam methodum substitutis tamen prius Logarithmis sinum inventorum, si ejus generis tabula desideretur ad computum tabularum Astronomicarum Kepleri posui fundamentum quoddam in alterâ Epistolâ ejus seriei tres primi termini et aliquando duo sufficiunt, sed ad diversas partes Ellipseos diversæ ejusm
odi series aptari debent, vel potius tales series computandæ sunt quæ ex datâ areâ Sectoris Elliptici BGE, immediatè exhibeant aream sectoris circuli cujus angulus est BEG, radius CB, et habitis hisce, computum earum ad duos tres vel fortè quatuor terminos beneficio Logarithmorum haud gravius erit quam solita resolutio tot triangulorum in aliis hypothesibus imo forte minus grave si series prius debitæ concinnentur siquidem unus Logarithmus è tabulâ petitus determinet omnes istos terminos, addendo ipsum et ejus multiplices ad Logarithmos datorum coefficientium in promptu habitos, quæ de hoc genere tabularum dicuntur ad alias transferri possunt ubi ratiocinia Geometrica locum non obtinent sufficit autem per has series computare triginta vel viginti aut fortè pauciores terminos tabulæ in debitis distantijs, termini intermedii facilè interseruntur per methodum quandam quam in usum calculatorum ferè hic descripsissem, sed pergo ad alia [ quæ Cl. Leibnitius à me desiderat explicanda ex parte supra descripsi Quod vero attinet ad inventionem terminorum p, q, r, in extractione radicis affectæ primum p sic eruo, descripto angulo recto BAC, latera ejus BA, AC. divido in 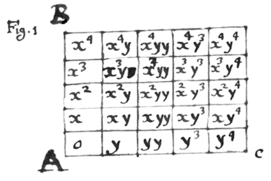 partes æquales {quo{illeg}} et inde normales erigo distribuentes angulare spatium in æqualia parallelogramma quæ concipio denominata esse à dimensionibus duarum indefinitarum specierum puta x et y, regulariter ascendentium a termino A prout vides inscriptas eas in fig. 1 ubi y denotat radicem
partes æquales {quo{illeg}} et inde normales erigo distribuentes angulare spatium in æqualia parallelogramma quæ concipio denominata esse à dimensionibus duarum indefinitarum specierum puta x et y, regulariter ascendentium a termino A prout vides inscriptas eas in fig. 1 ubi y denotat radicem 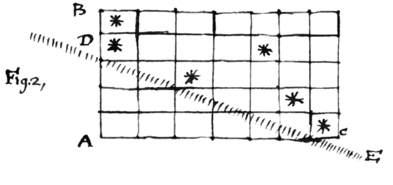 extrahendam et x alterum indefinitam quantitatem ex cujus potestatibus series constituenda est. Deinde cum æquatio aliqua proponitur, parallelogramma singulis ejus terminis respondentia insignio notâ aliquâ, et regulâ ad duo vel forte plura ex insignitis parallelogrammis applicata, quorum unum sit infimum in columnâ sinistra {seu} juxta {latum} AB, et aliud in columna quavis {alia} dextrorsum reperiatur, cæteraque omnia ad quaæ regula non applicatur supra eam jaceant seligo terminos æquationis per parallelogramma contingentia regulam designatos et ex {his tanquam} nihilo æqualibus quæro quantitatem addendam Quotienti.
extrahendam et x alterum indefinitam quantitatem ex cujus potestatibus series constituenda est. Deinde cum æquatio aliqua proponitur, parallelogramma singulis ejus terminis respondentia insignio notâ aliquâ, et regulâ ad duo vel forte plura ex insignitis parallelogrammis applicata, quorum unum sit infimum in columnâ sinistra {seu} juxta {latum} AB, et aliud in columna quavis {alia} dextrorsum reperiatur, cæteraque omnia ad quaæ regula non applicatur supra eam jaceant seligo terminos æquationis per parallelogramma contingentia regulam designatos et ex {his tanquam} nihilo æqualibus quæro quantitatem addendam Quotienti.
Sic ad extrahendam radicem y ex parallelogramma hujus terminis respondentia signo notâ aliquâ ∗ ut vides in fig 2. Dein applico regulam DE ad inferiorem è locis signatis in sinistrâ columnâ, eamque ab inferioribus ad superiora dextrorsum gyrare facio donec alium similiter vel fortè plura è reliquis signatis locis coeperit attingere videoque loca sic attacta esse , et è terminis itaque tanquam nihilo æqualibus (et insuper si placet reductis ad : ponendo ), quæro valorem y et invenio quadruplicem , − , : et . Horum valorem quemlibet pro primo termino Quotientis accipere licet prout è radicibus quampiam extrahere decretum est. sic æquatio quam resolvebam in priori epistolâ dat . et inde : proximè cum itaque a sit primus terminus valoris y pono p pro cæteris omnibus in infinitum et substituo obvenient hic aliquando difficultates nonnullæ, sed ex ijs credo D. Leibnitius se proprio marte extricabit subsequentes vero termini p , &c. eodem modo ex æquationibus secundis tertiis cæterisque eruuntur quo primus y prima, sed cura leviori quia cæteri termini valoris y solent prodire dividendo terminum involventem infimam potestatem indefinitæ quantitatis x per coefficientem lateris aut s.
Intellexti credo ex superioribus regressionem ab areis curvarum ad lineas rectas fieri per hanc extractionem radicis affectæ sed duo alii sunt modi quibus idem perficio, eorum unus affinis est computationibus quibus colligebam approximationes sub finem alterius Epistolæ et intelligi potest per hoc exemplum, proponatur æquatio ad aream hyperbolæ , et partibus ejus multiplicatis in se emerget . . . . Iam de z aufero et restat huic addo et fit . #[5] et fit quamproxime. Sive .
[ eodem modo series de una indefinita quantitate in aliam transferri possunt quemadmodum si posito r radio circuli, x sinu recto arcus z, et longitudine arcus istius, atque hanc seriem è sinu recto ad tangentem vellem transferre, quæro longitudinem tangentis et reduco in infinitam seriem quâ dictâ t, colligo potestates ejus . . aufero autem t de z, et restat Addo , et fit . aufero , et restat quamproximè quare est z=. Sed siquis in usus trigonometricos me jussisset exhibere expressionem arcus per tangentem, eam non hoc circuitu sed directâ methodo quæsivissem per hoc genus computi colliguntur etiam series ex duabus vel pluribus indefinitis quantitatibus constantes, et radices affectarum æquationum magnâ ex parte extrahuntur, sed ad hunc posteriorem usum adhibeo potius methodum in alterâ Epistolâ descriptam tanquam generaliorem, et (regulis pro Elisione superfluorum terminorum habitis) paulo magis expeditam, pro regressione vero ab areis ad lineas rectas & similibus, possunt hujusmodi Theoremata adhiberi.
Theorema 1 sit et vicissim erit . ex gratia proponatur æquatio ad aream hyperbolæ et substitutis in regulâ 1 pro a, pro b, pro c, pro d, et pro e, vicissim exurget &c Theorema 2 sit . et vicissim erit . exempli gratia proponatur æquatio ad arcum circuli et substitutis in regulâ 1 pro a, pro b, pro c, pro d &c orietur [ alterum modum regrediendi ab areis ad lineas rectas celare statui [ ubi dixi omnia pene Problemata solubilia existere, volui de ijs præsertim intelligi circa quæ mathematici se hactenus occuparunt vel saltem in quibus ratiocinia mathematica locum aliquem obtinere possunt nam alia sane adeo perplexis conditionibus implicata excogitare liceat ut non satis comprehendere valeamus et multo minus tantarum computationum onus sustinere quod ista requirerent attamen ne nimium dixisse videor inversa de tangentibus problemata sunt in potestate aliaque illis difficiliora ad quæ solvenda usus sum duplici methodo una concinniori altera generaliori utramque visum est impræsentia literis transpositis consignare ne propter alios idem obtinentes institutum in aliquibus mutare cogerer 5accd et 10effh1114t3m9x6oqqr8snt9v3x: 11ab3cdd10e et g10ill4m7n6o3p3q6rsSnt8vx.3ac et 4egh5i4tmsn8oq4r386t4vaadd et eeeeeiiimmnnooprrrsssssttuu Inversum hoc problema de tangentibus quando tangens inter punctum contactus et axem figuræ est datæ longitudinis, non indiget his methodis, est tamen curva illa mechanica cujus determinatio pendet ab area {et periferia} hyperbolæ. ejusdem generis, est etiam problema quando pars axis inter tangentem et ordinatim appli
catam datur longitudine, sed hos casus vix numeraverim inter ludos naturæ Q nam si in triangulo rectangulo quod ab illa axis parte, ac tangente & ordinatim applicata constituitur, relatio duorum quorumlibet laterum per æquationem quamlibet definiatur, problema solvi poterit absque meâ methodo generali sed ubi pars axis ad punctum aliquod positione datum terminata ingreditur vinculum tunc res aliter se habere solet.
Communicatio Resolutionis affectarum æquationum per methodum Leibnitii pergrata erit juxta et explicatio quomodo hæc se gerat ubi indices potestatis sunt fractiones ut in hac æquatione , aut surdæ quantitates ut in hac , ubi & non designant coefficientes ipsius x, sed indices potestatis seu dignitatis ejus; et indicem dignitatis binomii . res credo mea methodo patet aliter descripsissem sed meta tandem prolixæ huic epistolæ ponenda est, literæ sane excellentissimi Leibnitii valdè dignæ erant quibus fusius hoc responsum darem et volui hac vice copiosior esse, quia credidi amœniora tua negotia severiori hocce scribendi genere non debere a me crebro interpellari.
[1] H Intellige {sic} in {sequent}
[2] ...
[3] ...{in} ?
[4] ...{in} ?
[5] # Aufero , et restat addo
