De Motu Corporum (Liber Primus) (1687)
DE
MOTU CORPORUM
Liber PRIMUS
SECT I.
De Methodo Rationum primarum & ultimarum, cujus ope sequentia demonstrantur.
LEMMA I.
QVantitates, ut & quantitatum rationes, quæ ad æqualitatem dato tempore constanter tendunt & eo pacto propius ad invicem accedere possunt quam pro data quavis differentia; fiunt ultimo æquales.
Si negas, sit earum ultima differentia D. Ergo nequeunt propius ad æqualitatem accedere quam pro data differentia D: contra hypothesin.
<27>Lemma II.
Si in figura quavis Aa cE rectis Aa, AE, & curva AcE comprehensa, inscribentur parallelogramma quotcunque Ab, Bc, Cd, &c. sub basibus AB, BC, CD, &c. 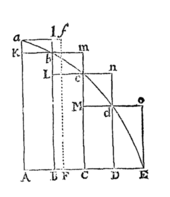 æqualibus, & lateribus Bb, Cc, Dd, &c. figuræ lateri Aa parallelis comenta; & compleantur parallelogramma aKbl, bLcm, cMdn, &c, Dein horum parallelogrammorum latitudo minuatur, & numerus augeatur in infinitum: dico quod ultimæ rationes, quas habent ad se invicem figura inscripta AKbLcMdD, circumscripta AalbmcndoE, & curvilinea AabcdE, sunt rationes æqualitatis.
æqualibus, & lateribus Bb, Cc, Dd, &c. figuræ lateri Aa parallelis comenta; & compleantur parallelogramma aKbl, bLcm, cMdn, &c, Dein horum parallelogrammorum latitudo minuatur, & numerus augeatur in infinitum: dico quod ultimæ rationes, quas habent ad se invicem figura inscripta AKbLcMdD, circumscripta AalbmcndoE, & curvilinea AabcdE, sunt rationes æqualitatis.
Nam figuræ inscriptæ & circumscriptæ differentia est summa parallelogrammorum , hoc est (ob æquales omnium bases) rectangulum sub unius basi Kb & altitudinum summa Aa, id est rectangulum ABla. Sed hoc rectangulum, eo quod latitudo ejus AB in infinitum minuitur, sit minus quovis dato. Ergo, per Lemma I, figura inscripta & circumscripta & multo magis figura curvilinea intermedia fiunt ultimo æquales. Q.E.D.
Lemma III.
Eædem rationes ultimæ sunt etiam æqualitatis, ubi parallelogramomrum latitudines AB, BC, CD, &c. sunt inæquales, & omnes minuuntur in infinitum.
Sit enim AF æqualis latitudini maximæ, & compleatur parallelogrammum FAaf. Hoc erit majus quam differentia figuræ inscriptæ & figuræ circumscriptæ, at latitudine sua AF in infinitum diminuta, minus fiet quam datum quodvis rectangulum.
Corol. 1. Hinc summa ultima parallelogrammorum evanescentium coincidit omni ex parte cum figura curvilinea.
Corol. 2. Et multo magis figura rectilinea, quæ chordis evanescentium arcuum ab, bc, cd, &c. comprehenditur, coincidit ultimo cum figura curvilinea.
Corol. 3. Ut & figura rectilinea quæ tangentibus eorundem arcuum circumscribitur.
Corol. 4. Et propterea hæ figuræ ultimæ (quoad perimetros acE,) non sunt rectilineæ, sed rectilinearum limites curvilinci.
Lemma IV.
Si in duabus figuris AacE, PprT, inscribantur (ut supra) duæ parallelogrammorum series, sitque idem amborum numerus, & ubi latitudines in infinitum diminuuntur, rationes ultimæ parallelogrammorum in una figura ad parallelogramma in altera, singulorum ad singula, sint eædem; dico quod figuræ duæ AacE, PprT, sunt ad invicem in eadem illa ratione.
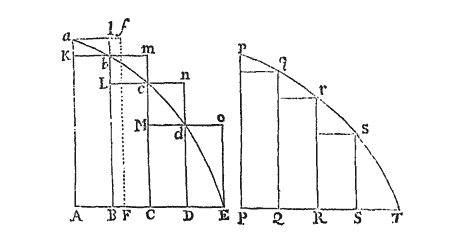
Etenim ut sunt parallelogramma singula ad singula, ita (componendo) fit summa omnium ad summam omnium, & ita figura ad figuram; existente rimirum figura priore (per Lemma III.) ad summam priorem, & posteriore figura ad summam posteriorem in ratione æqualitatis.
Corol. Hinc si duæ cujuscunque generis quantitates in eundem partium numerum utcunque dividantur, & partes illæ, ubi numerus earum augetur & magnitudo diminuitur in infinitum, datam obtineant rationem ad invicem, prima ad primam, secunda ad secundam cæteræque suo ordine ad cæteras; erunt tota ad invicem in eadem illa data ratione. Nam si in Lemmatis hujus figuris sumantur parallelogramma inter se ut partes, summæ partium semper erunt ut summæ parallelogrammorum; atque adeo, ubi partium & parallelogrammorum numerus augetur & magnitudo diminuitur in infinitum, in ultima ratione parallelogrammi ad parallelogrammum, id est (per hypothesin) in ultima ratione partis ad partem.
Lemma V.
Similium figurarum latera omnia, quæ sibi mutuo respondent, sunt proportionalia, tam curvilinea quam rectilinea, & areæ sunt in duplicata ratione laterum.
Lemma VI.
Si arcus quilibet positione datus AB subtendatur chorda AB, & in puncto aliquo A, in medio curvaturæ 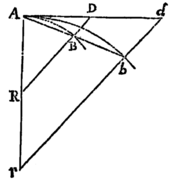 continuæ, tangatur a recta utrinque producta AD; dein puncta A, B ad invicem accedant & coeant; dico quod angulus BAD sub chorda & tangente contentus minuetur in infinitum & ultimo evanescet.
continuæ, tangatur a recta utrinque producta AD; dein puncta A, B ad invicem accedant & coeant; dico quod angulus BAD sub chorda & tangente contentus minuetur in infinitum & ultimo evanescet.
Nam producatur AB ad b & AD ad d, & punctis A, B coeuntibus, nullaque adeo ipsius Ab parte AB jacente amplius intra curvam, manifestum est quod hæc recta Ab, vel coincidet eum tangente Ad, vel ducetur inter tangentem & curvam. Sed casus posterior est contra naturam Curvaturæ, ergo prior obtinet. Q.E.D.
Lemma. VII.
Iisdem positis, dico quod ultima ratio arcus, chordæ & tangentis ad invicem est ratio æqualitatis. Vide Fig. Lem. 6 & 8 vi.
Nam producantur AB & AD ad b & d & secanti BD parallela agatur bd. Sitque arcus Ab similis arcui AB. Et punctis A, B coeuntibus, angulus dAb, per Lemma superius, evanescet; adeoque rectæ Ab, Ad & arcus intermedius Ab coincident, & propterea æquales erunt. Unde & hisce semper proportionales rectæ AB, AD, & arcus intermedius AB rationem ultimam habebunt æqualitatis. Q.E.D.
Corol. 1. Unde si per B ducatur tangenti parallela BF rectam quamvis AF per A transeuntem 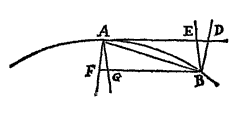 perpetuo secans in F, hæc ultimo ad arcum evanescentem AB rationem habebit æqualitatis, eo quod completo parallelogrammo AFBD, rationem semper habet æqualitatis ad AD.
perpetuo secans in F, hæc ultimo ad arcum evanescentem AB rationem habebit æqualitatis, eo quod completo parallelogrammo AFBD, rationem semper habet æqualitatis ad AD.
Corol. 2. Et si per B & A ducantur plures rectæ BE, BD, AF, AG, secantes tangentem AD & ipsius parallelam BF, ratio ultima abscissarum omnium AD, AE, BF, BG, chordæque & arcus AB ad invicem erit ratio æqualitatis.
Corol. 3. Et propterea hæ omnes lineæ in omni de rationibus ultimis argumentatione pro se invicem usurpari possunt.
Lemma VIII.
Si rectæ datæ AR, BR cum arcu AB, chorda AB & tangente AD,triangula tria ARB, ARB, ARD constituunt, dein puncta A, B accedunt ad invicem: dico quod ultima forma triangulorum evanescentium est similitudinis, & ultima ratio æqualitatis.
<31>Nam producantur AB, AD, AR ad b, d & r. Ipsi RD agatur parallela rbd, & arcui AB similis ducatur arcus Ab. Coeuntibus punctis A, B, angulus bAd 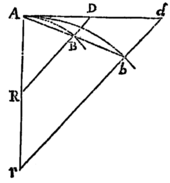 evanescet, & propterea triangula tria rAb, rAb, rAd coincident, suntque eo nomine similia & æqualia. Unde & hisce semper similia & proportionalia RAB, RAB, RAD fient ultimo sibi invicem similia & æqualia. Q.E.D.
evanescet, & propterea triangula tria rAb, rAb, rAd coincident, suntque eo nomine similia & æqualia. Unde & hisce semper similia & proportionalia RAB, RAB, RAD fient ultimo sibi invicem similia & æqualia. Q.E.D.
Corol. Et hinc triangula illa in omni de rationibus ultimis argumentatione pro se invicem usurpari possunt.
Lemma IX.
Si recta AE & Curva AC positione datæ se mutuo secent in angulo dato A, & ad rectam illam in 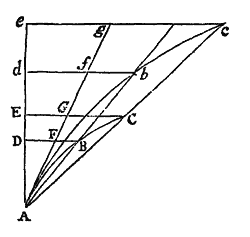 alio dato angulo ordinatim applicentur BD, EC, curvæ occurrentes in B, C; dein puncta B, C accedant ad punctum A: dico quod areæ triangulorum ADB, AEC erunt ultimo ad invicem in duplicata ratione laterum.
alio dato angulo ordinatim applicentur BD, EC, curvæ occurrentes in B, C; dein puncta B, C accedant ad punctum A: dico quod areæ triangulorum ADB, AEC erunt ultimo ad invicem in duplicata ratione laterum.
Etenim in AD producta capiantur Ad, Ae ipsis AD, AE proportionales, & erigantur ordinatæ db, ec ordinatis DB, EC parallelæ & proportionales. Producatur AC ad c, ducatur curva Abc ipsi AbC similis, & recta Ag tangatur curva utraque in A; & secantur ordinatim applicatæ in F, G, f, g. Tum coeant puncta B, C cum puncto A, & angulo c Ag evanescente, coincident areæ curvilineæ Abd, Ace cum rectilincis Afd, Age, adeoque per Lemma V, erunt in duplicata ratione laterum Ad, Ae: Sed his areis proportionales semper sunt areæ ABD, ACE, & his lateribus latera AD, AE. Ergo & areæ ABD, ACE sunt ultimo in duplicata ratione laterum AD, AE. Q.E.D.
Lemma X.
Spatia, quæ corpus urgente quacunque vi regulari describit, sunt ipso
motus initio in duplicata ratione temporum.
Exponantur tempora per lineas AD, AE, & velocitates genitæ per ordinatas DB, EC, & spatia his velocitatibus descripta erunt ut areæ ABD, ACE his ordinatis descriptæ, hoc est ipso motus initio (per Lemma IX) in duplicata ratione temporum AD, AE. Q.E.D.
Corol. 1. Et hinc facile colligitur, quod corporum similes similium figurarum partes temporibus proportionalibus describentium errores, qui viribus æqualibus in partibus istis ad corpora similiter applicatis generantur, & mensurantur a locis figurarum, ad quæ corpora temporibus ijsdem proportionalibus absque viribus istis pervenirent, sunt ut quadrata temporum in quibus generantur quam proxime.
Corol. 2. Errores autem qui viribus proportionalibus similiter applicatis generantur, sunt ut vires & quadrata temporum conjunctim.
Lemma XI.
Subtensa evanescens anguli contactus est ultimo in ratione duplicata subtensæ arcus contermini.
Cas. 1. Sit arcus ille AB, tangens ejus AD, subtensa anguli contactus ad tangentem perpendicularis BD, subtensa arcus AB. Huic subtensæ AB & tangenti AD perpendiculares erigantur AG, BG, concurrentes in G; dein accedant puncta D, B, G, ad puncta d, b, g, sitque I intersectio linearum BG, AG ultimo facta ubi puncta D, B accedunt usque ad A. Manifestum est quod distantia G I minor esse potest quam assignata quævis. Est autem (ex natura circulorum per puncta ABG, Abg transeuntium) AB quad. 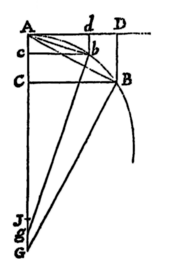 æquale æquale , adeoque ratio AB quad. ad Ab quad. componitur ex rationibus AG ad Ag & BD ad bd. Sed quoniam IG assumi potest minor longitudine quavis assignata, fieri potest ut ratio AG ad Ag minus differat a ratione æqualitatis quam pro differentia quavis assignata, adeoque ut ratio AB quad. ad Ab quad. minus differat a ratione BD ad bd quam pro differentia quavis assignata. Est ergo, per Lemma I, ratio ultima AB quad. ad Ab quad. æqualis rationi ultimæ BD ad bd. Q.E.D.
æquale æquale , adeoque ratio AB quad. ad Ab quad. componitur ex rationibus AG ad Ag & BD ad bd. Sed quoniam IG assumi potest minor longitudine quavis assignata, fieri potest ut ratio AG ad Ag minus differat a ratione æqualitatis quam pro differentia quavis assignata, adeoque ut ratio AB quad. ad Ab quad. minus differat a ratione BD ad bd quam pro differentia quavis assignata. Est ergo, per Lemma I, ratio ultima AB quad. ad Ab quad. æqualis rationi ultimæ BD ad bd. Q.E.D.
Cas. 2. Inclinetur jam BD ad AD in angulo quovis dato, & eadem semper erit ratio ultima BD ad bd quæ prius, adeoque eadem ac AB quad. ad Ab quad. Q.E.D.
Cas. 3. Et quamvis angulus D non detur, tamen anguli D,d ad æqualitatem semper vergent & propius accedent ad invicem quam pro differentia quavis assignata, adeoque ultimo æquales erunt, per Lem. I. & propterea lineæ BD, bd in eadem ratione ad invicem ac prius. Q.E.D.
Corol. 1. Unde cum tangentes AD, Ad, arcus AB, Ab & eorum sinus BC, bc fiant ultimo chordis AB, Ab æquales; erunt etiam illorum quadrata ultimo ut subtensæ BD, bd.
Corol. 2. Triangula rectilinea ADB, Adb sunt ultimo in triplicata ratione laterum AD, Ad, inque sesquiplicata laterum DB, db: Utpote in composita ratione laterum AD & DB, Ad & db existentia. Sic & triangula ABC, Abc sunt ultimo in triplicata ratione laterum BC, bc.
Corol. 3. Et quoniam DB, db sunt ultimo parallela & in duplicata ratione ipsarum AD, Ad; erunt areæ ultimæ curvilineæ ADB, Adb (ex natura Parabolæ) duæ tertiæ partes triangulorum rectilineorum ADB, Adb, & segmenta AB, Ab partes tertiæ eorundem triangulorum. Et inde hæ areæ & hæc segmenta erunt in triplicata ratione tum tangentium AD, Ad; tum chordarum & arcuum AB, Ab.
Scholium.
Cæterum in his omnibus supponimus angulum contactus nec infinite majorem esse angulis contactuum, quos circuli continent cum tangentibus suis, nec iisdem infinite minorem; hoc est curvaturam ad punctum A, nec infinite parvam esse nec infinite magnam, seu intervallum AI finitæ esse magnitudinis. Capi enim potest DB ut : quo in casu circulus nullus per punctum A inter tangentem AD & curvam AB duci potest, proindeque angulus contactus erit infinite minor circularibus. Et simili argumento si fiat DB successive ut , , , , , habebitur series angulorum contactus pergens in infinitum, quorum quilibet posterior est infinite minor priore. Et si fiat DB successive ut , , , , , , &c. habebitur alia series infinita angulorum contactus, quorum primus est ejusdem generis cum circularibus, secundus infinite major, & quilibet posterior infinite major priore. Sed & inter duos quosvis ex his angulis potest series utrinque in infinitum pergens angulorum intermediorum inseri, quorum quilibet posterior erit infinite major priore. Ut si inter terminos & inseratur series , , , , , , , , , Et rursus inter binos quosvis angulos hujus seriei inseri potest series nova angulorum intermediorum ab invicem infinitis intervallis differentium. Neque novit natura limitem.
Quæ de curvis lineis deque superficiebus comprehensis demonstrata sunt, facile applicantur ad solidorum superficies curvas & contenta. Præmisi vero hæc Lemmata ut effugerem tædium deducendi perplexas demonstrationes, more veterum Geometrarum, ad absurdum. Contractiores enim redduntur demonstrationes per methodum indivisibilium. Sed quoniam durior est indivisibilium Hypothesis; & propterea Methodus illa minus Geometrica censetur, malui demonstrationes rerum sequentium ad ultimas quantitatum evanescentium summas & rationes, primasque nascentium, id est, ad limites summarum & rationum deducere, & propterea limitum illorum demonstrationes qua potui breuitate præmittere. His enim idem præstatur quod per methodum indivisibilium, & principiis demonstratis jam tutius utemur. Proinde in sequentibus, siquando quantitates tanquam ex particulis constantes consideravero, vel si pro rectis usurpavero lineolas curvas, nolim indivisibilia sed evanescentia divisibilia, non summas & rationes partium determinatarum, sed summarum & rationum limites semper intelligi, vimque talium demonstrationum ad methodum præcedentium Lemmatum semper revocari.
Objectio est, quod quantitatum evanescentium nulla sit ultima proportio; quippe quæ, antequam evanuerunt, non est ultima, ubi evanuerunt, nulla est. Sed & eodem argumento æque contendi posset nullam esse corporis ad certum locum pergentis velocitatem ultimam. Hanc enim, antequam corpus attingit locum, non esse ultimam, ubi attigit, nullam esse. Et responsio facilis est. Per velocitatem ultimam intelligi eam, qua corpus movetur neque antequam attingit locum ultimum & motus cessat, neque postea, sed tunc cum attingit, id est illam ipsam velocitatem quacum corpus attingit locum ultimum & quacum motus cessat. Et similiter per ultimam rationem quantitatum evanescentium intelligendam esse rationem quantitatum non antequam evanescunt, non postea, sed quacum evanescunt. Pariter & ratio prima nascentium est ratio quacum nascuntur. Et summa prima & ultima est quacum esse (vel augeri & minui) incipiunt & cessant. Extat limes quem velocitas in fine motus attingere potest, non autem transgredi. Hæc est velocitas ultima. Et par est ratio limitis quantitatum & proportionum omnium incipientium & cessantium. Cumque hic limes sit certus & definitus, Problema est vere Geometricum eundem determinare. Geometrica vero omnia in aliis Geometricis determinandis ac demonstrandis legitime usurpantur.
Contendi etiam potest, quod si dentur ultimæ quantitatum evanescentium rationes, dabuntur & ultimæ magnatudines; & sic quantitas omnis constabit ex indivisibilibus, contra quam Euclides de incommensurabilibus, in libro decimo Elementorum, demonstravit. Verum hæc Objectio falsæ innititur hypothesi. Ultimæ rationes illæ quibuscum quantitates evanescunt, revera non sunt rationes quantitatum ultimarum, sed limites ad quos quantitatum sine limite decrescentium rationes semper appropinquant, & quas propius assequi possunt quam pro data quavis differentia, nunquam vero transgredi, neque prius attingere quam quantitates diminuuntur in infinitum. Res clarius intelligetur in infinite magnis. Si quantitates duæ quarum data est differentia augeantur in infinitum, dabitur harum ultima ratio, nimirum ratio æqualitatis, nec tamen ideo dabuntur quantitates ultimæ seu maximæ quarum ista est ratio. Igitur in sequentibus, siquando facili rerum imaginationi consulens, dixero quantitates quam minimas, vel evanescentes vel ultimas, cave intelligas quantitates magnitudine determinatas, sed cogita semper diminuendas sine limite.
SECT. II.
De Inventione Virium Centripetarum.
Prop. I. Theorema. I.
Areas quas corpora in gyros acta radiis ad immobile centrum virium ductis describunt, & in planis immobilibus consistere, & esse temporibus proportionales.
Dividatur tempus in partes æquales, & prima temporis parte describat corpus vi insita rectam AB. Idem secunda temporis parte, si nil impediret, recta pergeret ad c, (per Leg. I) describens lineam Bc æqualem ipsi AB, adeo ut radiis AS, BS, cS ad centrum actis, 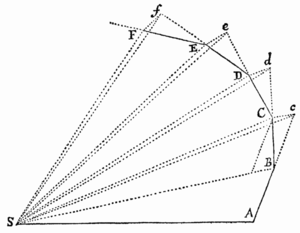 confectæ forent æquales areæ ASB, BSc. Verum ubi corpus venit ad B, agat viscentripeta impulsu unico sed magno, faciatque corpus a recta Bc deflectere & pergere in recta BC. Ipsi BS parallela agatur cC occurrens BC in C, & completa secunda temporis parte, corpus (per Legum Corol. 1) reperietur in C, in eodem plano cum triangulo ASB. Junge SC, & triangulum SBC, ob parallelas SB, Cc, æquale erit triangulo SBc, atque adeo etiam triangulo SAB. Simili argumento si vis centripeta successive agat in C, D, E, &c. faciens ut corpus singulis temporis particulis singulas describat rectas CD, DE EF, &c. jacebunt hæ in eodem plano, & triangulum SCD triangulo SBC & SDE ipsi SCD & SEF ipsi SDE æquale erit. Æqualibus igitur temporibus æquales areæ in plano immoto describuntur: & componendo, sunt arearum summæ quævis SADS, SAFS inter se, ut sunt tempora descriptionum. Augeatur jam numerus & minuatur latitudo triangulorum in infinitum, & eorum ultima perimeter ADF, (per Corollarium quartum Lemmatis tertii) erit linea curva; adeoque vis centripeta qua corpus de tangente hujus curvæ perpetuo retrahitur, aget indesinenter; areæ vero quævis descriptæ SADS, SAFS temporibus descriptionum semper proportionales, erunt iisdem temporibus in hoc casu proportionales. Q.E.D.
confectæ forent æquales areæ ASB, BSc. Verum ubi corpus venit ad B, agat viscentripeta impulsu unico sed magno, faciatque corpus a recta Bc deflectere & pergere in recta BC. Ipsi BS parallela agatur cC occurrens BC in C, & completa secunda temporis parte, corpus (per Legum Corol. 1) reperietur in C, in eodem plano cum triangulo ASB. Junge SC, & triangulum SBC, ob parallelas SB, Cc, æquale erit triangulo SBc, atque adeo etiam triangulo SAB. Simili argumento si vis centripeta successive agat in C, D, E, &c. faciens ut corpus singulis temporis particulis singulas describat rectas CD, DE EF, &c. jacebunt hæ in eodem plano, & triangulum SCD triangulo SBC & SDE ipsi SCD & SEF ipsi SDE æquale erit. Æqualibus igitur temporibus æquales areæ in plano immoto describuntur: & componendo, sunt arearum summæ quævis SADS, SAFS inter se, ut sunt tempora descriptionum. Augeatur jam numerus & minuatur latitudo triangulorum in infinitum, & eorum ultima perimeter ADF, (per Corollarium quartum Lemmatis tertii) erit linea curva; adeoque vis centripeta qua corpus de tangente hujus curvæ perpetuo retrahitur, aget indesinenter; areæ vero quævis descriptæ SADS, SAFS temporibus descriptionum semper proportionales, erunt iisdem temporibus in hoc casu proportionales. Q.E.D.
Corol. 1. In mediis non resistentibus, si areæ non sunt temporibus proportionales, vires non tendunt ad concursum radiorum.
Corol. 2. In mediis omnibus, si arearum descriptio acceleratur, vires non tendunt ad concursum radiorum, sed inde declinant in consequentia.
Pro. II. Theor. II.
Corpus omne quod, cum movetur in linea aliqua curva, & radio ducto ad punctum vel immobile, vel motu rectilineo uniformiter progrediens, describit areas circa punctum illud temporibus proportionales, urgetur a vi centripeta tendente ad idem punctum
Cas. 1. Nam corpus omne quod movetur in linea curva, detorquetur de cursu rectilineo per vim aliquam in ipsum agentem. (per Leg. 1.) Et vis illa qua corpus de cursu rectilineo detorquetur & cogitur triangula quam minima SAB, SBC, SCD &c. circa punctum immobile S, temporibus æqualibus æqualia describere, agit in loco B secundum lineam parallelam ipsi cC (per Prop. 40 Lib. I Elem. & Leg. II.) hoc est secundum lineam BS, & in loco C secundum lineam ipsi dD parallelam, hoc est secundum lineam CS, &c. Agit ergo semper secundum lineas tendentes ad punctum illud immobile S. Q.E.D.
Cas. 2. Et, per Legum Corollarium quintum, perinde est sive quiescat superficies in qua corpus describit figuram curvilineam, sive moveatur eadem una cum corpore, figura descripta & puncto suo S uniformiter in directum.
Scholium.
Urgeri potest corpus a vi centripeta composita ex pluribus viribus In hoc casu sensus Propositionis est, quod vis illa quæ ex omnibus componitur, tendit ad punctum S. Porro si vis aliqua agat secundum lineam superficiei descriptæ perpendicularem, hæc faciet corpus deflectere a plano sui motus, sed quantitatem superficiei descriptæ nec augebit nec minuet, & propterea in compositione virium negligenda est.
Prop. III. Theor. III.
Corpus omne quod, radio ad centrum corporis alterius utcunque moti ducto, describit areas circa centrum illud temporibus proportionales, urgetur vi composita ex vi centripeta tendente ad corpus alterum & ex vi omni acceleratrice, qua corpus alterum urgetur.
Nam (per Legum Corol. 6.) si vi nova, quæ æqualis & contraria sit illi qua corpus alterum urgetur, urgeatur corpus utrumque secundum lineas parallelas, perget corpus primum describere circa corpus alterum areas easdem ac prius: vis autem qua corpus alterum urgebatur, jam destruetur per vim sibi æqualem & contrariam, & propterea (per Leg. 1.) corpus illud alterum vel quiescet vel movebitur uniformiter in directum, & corpus primum, urgente differentia virium, perget areas temporibus proportionales circa corpus alterum describere. Tendit igitur (per Theor. 2.) differentia virium ad corpus illud alterum ut centrum. Q.E.D.
<40>Corol. 1. Hinc si corpus unum radio ad alterum ducto describit areas temporibus proportionales, atque de vi tota (sive simplici, sive ex viribus pluribus, juxta Legum Corollarium secundum, composita,) qua corpus prius urgetur, subducatur (per idem Legum Corollarium) vis tota acceleratrix qua corpus alterum urgetur; vis omnis reliqua qua corpus prius urgetur tendet ad corpus alterum ut centrum.
Corol. 2. Et si areæ illæ sunt temporibus quamproxime proportionales, vis reliqua tendet ad corpus alterum quamproxime.
Corol. 3. Et vice versa, si vis reliqua tendit quamproxime ad corpus alterum, erunt areæ illæ temporibus quamproxime proportionales.
Corol. 4. Si corpus radio ad alterum corpus ducto describit areas quæ, cum temporibus collatæ, sunt valde inæquales, & corpus illud alterum vel quiescit vel movetur uniformiter in directum; actio vis centripetæ ad corpus illud alterum tendentis, vel nulla est, vel miscetur & componitur cum actionibus admodum potentibus aliarum virium: Visque tota ex omnibus, si plures sunt vires, composita, ad aliud (sive immobile sive mobile) centrum dirigitur, circum quod æquabilis est arearum descriptio. Idem obtinet ubi corpus alterum motu quocunque movetur, si modo vis centripeta sumatur, quæ restat post subductionem vis totius agentis in corpus illud alterum.
Scholium
Quoniam æquabilis arearum descriptio Index est centri quod vis illa respicit qua corpus maxime afficitur, corpus autem vi ad hoc centrum tendente retinetur in orbita sua, & motus omnis circularis recte dicitur circa centrum illud fieri, cujus vi corpus retrahitur de motu rectilineo & retinetur in Orbita: quidni usurpemus in sequentibus æquabilem arearum descriptionem ut Indicem centri circum quod motus omnis circularis in spatiis liberis peragitur?
<41>Prop. IV. Theor. IV.
Corporum quæ diversos circalos æquabili motu describunt, vires centripetas ad centra eorundem circulorum tendere, & esse inter se ut arcuum simul descriptorum quadrata applicata ad circulorum radios.
Corpora B, b in circumferentiis circulorum BD, bd gyrantia, simul describant arcus BD, bd. Quoniam sola vi insita describerent tangentes BC, bc his arcubus æquales, manifestum est quod vires centripetæ sunt quæ 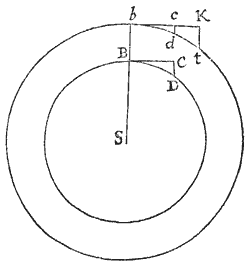 perpetuo retrahunt corpora de tangentibus ad circumferentias circulorum, atque adeo hæ sunt ad invicem in ratione prima spatiorum nascentium CD, cd: tendunt vero ad centra circulorum per Theor. II, propterea quod areæ radiis descriptæ ponuntur temporibus proportionales. Fiat figura tkb figuræ DCB similis, & per Lemma V, lineola CD erit ad lineolam kt ut arcus BD ad arcum bt: nec non, per Lemma XI; lineola nascens tk ad lineolam nascentem dc ut bt quad. ad bd quad. & ex æquo lineola nascens DC ad lineolam nascentem dc ut ad bd quad. seu quod perinde est, ut ad adeoque (ob æquales rationes ) ut ad Q.E.D.
perpetuo retrahunt corpora de tangentibus ad circumferentias circulorum, atque adeo hæ sunt ad invicem in ratione prima spatiorum nascentium CD, cd: tendunt vero ad centra circulorum per Theor. II, propterea quod areæ radiis descriptæ ponuntur temporibus proportionales. Fiat figura tkb figuræ DCB similis, & per Lemma V, lineola CD erit ad lineolam kt ut arcus BD ad arcum bt: nec non, per Lemma XI; lineola nascens tk ad lineolam nascentem dc ut bt quad. ad bd quad. & ex æquo lineola nascens DC ad lineolam nascentem dc ut ad bd quad. seu quod perinde est, ut ad adeoque (ob æquales rationes ) ut ad Q.E.D.
Corol. 1. Hinc vires centripetæ sunt ut velocitatum quadrata applicata ad radios circulorum.
Corol. 2. Et reciproce ut quadrata temporum periodicorum applicata ad radios ita sunt hæ vires inter se. Id est (ut cum Geometris loquar) hæ vires sunt in ratione composita ex duplicata ratione velocitatum directe & ratione simplici radiorum inverse: necnon in ratione composita ex ratione simplici radiorum directe & ratione duplicata temporum periodicorum inverse.
Corol. 3. Unde si tempora periodica æquantur, erunt tum vires centripetæ tum velocitates ut radii, & vice versa.
Corol. 4. Si quadrata temporum periodicorum sunt ut radii, vires centripetæ sunt æquales, & velocitates in dimidiata ratione radiorum: Et vice versa.
Corol. 5. Si quadrata temporum periodicorum sunt ut quadrata radiorum, vires centripetæ sunt reciproce ut radii, & velocitates æquales: Et vice versa.
Corol. 6. Si quadrata temporum periodicorum sunt ut cubi radiorum, vires centripetæ sunt reciproce ut quadrata radiorum; velocitates autem in radiorum dimidiata ratione: Et vice versa.
Corol. 7. Eadem omnia de temporibus, velocitatibus & viribus, quibus corpora similes figurarum quarumcunque similium, centraque similiter posita habentium, partes describunt, consequuntur ex Demonstratione præcedentium ad hosce casus applicata.
Scholium
Casus Corollarii sexti obtinet in corporibus cælestibus (ut seorsum colligerunt etiam nostrates Wrennus, Hockius & Halleus) & propterea quæ spectant ad vim centripetam decrescentem in duplicata ratione distantiarum a centris decrevi susius in sequentibus exponere.
Porro præcedentis demonstrationis beneficio colligitur etiam proportio vis centripetæ ad vim quamlibet notam, qualis est ea gravitatis. Nam cum vis illa, quo tempore corpus percurrit arcum BC, impellat ipsum per spatium CD, quod ipso motus initio æquale est quadrato arcus illius BD ad circuli diametrum applicato; & corpus omne vi eadem in eandem semper plagam continuata, describat spatia in duplicata ratione temporum: Vis illa, quo tempore corpus revolvens arcum quemvis datum describit, efficiet ut corpus idem recta progrediens describat spatium quadrato arcus illius ad circuli diametrum applicato æquale; adeoque est ad vim gravitatis ut spatium illud ad spatium quod grave cadendo eodem tempore describit. Et hujusmodi Propositionibus Hugenius, in eximio suo Tractatu de Horologio oscillatorio, vim gravitatis cum revolventium viribus centrifugis contulit.
Demonstrari etiam possunt præcedentia in hunc modum. In circulo quovis describi intelligatur Polygonum laterum quotcunque Et si corpus in Polygoni lateribus data cum velocitate movendo, ad ejus angulos singulos a circulo reflectatur; vis qua singulis reflexionibus impingit in circulum erit ut ejus velocitas, adeoque summa virium in dato tempore erit ut velocitas illa & numerus reflexionum conjunctim, hoc est (si Polygonum detur specie) ut longitudo dato illo tempore descripta & longitudo eadem applicata ad Radium circuli, id est ut quadratum longitudinis illius applicatum ad Radium; adeoque si Polygonum lateribus infinite diminutis coincidat cum circulo, ut quadratum arcus dato tempore descripti applicatum ad radium. Hæc est vis qua corpus urget circulum, & huic æqualis est vis contraria qua circulus continuo repellit corpus centrum versus.
Prop. V. Prob. I.
Data quibuscunque in locis velocitate, qua corpus figuram datam viribus ad commune aliquod centrum tendentibus describit, centrum illud invenire.
Figuram descriptam tangant rectæ tres PT, TQV, VR in punctis totidem P, Q, R, concurrentes in T & V. Ad tangentes erigantur perpendicula PA, QB, RC, velocitatibus corporis in punctis illis P, Q, R a quibus eriguntur reciproce proportionalia; id est ita ut sit PA ad QB ut velocitas in Q ad velocitatem in P, & QB ad RC ut velocitas in R ad velocitatem in Q. Per perpendiculorum terminos A, B, C ad angulos rectos ducantur AD, DBE, EC concurrentia in D & E: Et actae TD, VE concurrent in centro quæsito S.
Nam cum corpus in P & Q 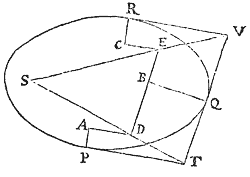 radiis ad centrum ductis areas describat temporibus proportionales, sintque areæ illæ simul descriptæ ut velocitates in P & Q ductæ respective in perpendicula a centro in tangentes PT, QT demissa: Erunt perpendicula illa ut velocitates reciproce, adeoque ut perpendicula AP, BQ directe, id est ut perpendicula a puncto D in tangentes demissa. Unde facile colligitur quod puncta S, D, T sunt in una recta. Et simili argumento puncta S, E, V sunt etiam in una recta; & propterea centrum S in concursu rectarum TD, VE versatur. Q.E.D.
radiis ad centrum ductis areas describat temporibus proportionales, sintque areæ illæ simul descriptæ ut velocitates in P & Q ductæ respective in perpendicula a centro in tangentes PT, QT demissa: Erunt perpendicula illa ut velocitates reciproce, adeoque ut perpendicula AP, BQ directe, id est ut perpendicula a puncto D in tangentes demissa. Unde facile colligitur quod puncta S, D, T sunt in una recta. Et simili argumento puncta S, E, V sunt etiam in una recta; & propterea centrum S in concursu rectarum TD, VE versatur. Q.E.D.
Pro. VI. Theor. V.
Si corpus P revolvendo circa centrum S, describat lineam quamvis curvam APQ, tangat vero recta ZPR curvam illam in puncto quovis P, & ad tangentem ab alio quovis curvæ puncto Q agatur QR distantiæ SP parallela, ac demittatur QT perpendicularis ad distantiam SP: Dico quod vis centripeta sit reciproce ut solidum , si modo solidi illius ea semper sumatur quantilas quæ ultimo fit 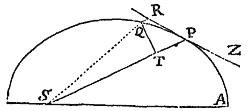 ubi coeunt puncta P & Q.
ubi coeunt puncta P & Q.
Namque in figura indefinite parva QRPT lineola nascens QR, data tempore, est ut vis centripeta (per Leg. II.) & data vi, ut quadratum temporis (per Lem. X.) atque adeo, neutro dato, ut vis centripeta & quadratum temporis conjunctim, adeoque vis centripeta ut lineola QR directe & quadratum temporis inverse. Est autem tempus ut area SPQ, ejusve dupla , id est ut SP & QT conjunctim, adeoque vis centripeta ut QR directe atque SP quad. in QT quad. inverse, id est ut inverse. Q.E.D.
Corol. Hinc si detur figura quævis, & in ea punctum ad quod vis centripeta dirigitur; inveniri potest lex vis centripetæ quæ corpus in figuræ illius perimetro gyrari faciet. Nimirum computandum est solidum huic vi reciproce proportionale. Ejus rei dabimus exempla in problematis sequentibus.
Prop. VII. Prob. II.
Gyretur corpus in circumferentia circuli, requiritur lex vis centripetæ tendentis ad punctum aliquod in circumferentia datum.
Esto circuli circumferentia SQPA, centrum vis centripetæ S, corpus in circumferentia latum 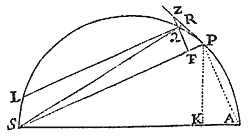 P, locus proximus in quem movebitur Q. Ad diametrum SA & rectam SP demitte perpendicula PK, QT, S per Q ipsi SP parallelam age LR occurrentem circulo in L & tangenti PR in R, & coeant TQ, PR in Z. Ob similitudinem triangulo um ZQR, ZTP, SPA erit RP quad. (hoc est QRL) ad QT quad. ut SA quad. ad SP quad. Ergo æquatur QT quad. Ducantur hæc æqualia in , & punctis P & Q coeuntibus, scribatur SP pro RL Sic fiet æquale Ergo (per Corol. Theor. V.) vis centripeta reciproce est ut , id est (ob datum SA quad) ut quadrato-cubus distantiæ SP. Quod erat inveniendum.
P, locus proximus in quem movebitur Q. Ad diametrum SA & rectam SP demitte perpendicula PK, QT, S per Q ipsi SP parallelam age LR occurrentem circulo in L & tangenti PR in R, & coeant TQ, PR in Z. Ob similitudinem triangulo um ZQR, ZTP, SPA erit RP quad. (hoc est QRL) ad QT quad. ut SA quad. ad SP quad. Ergo æquatur QT quad. Ducantur hæc æqualia in , & punctis P & Q coeuntibus, scribatur SP pro RL Sic fiet æquale Ergo (per Corol. Theor. V.) vis centripeta reciproce est ut , id est (ob datum SA quad) ut quadrato-cubus distantiæ SP. Quod erat inveniendum.
Prop. VIII. Prob. III.
Moveatur corpus in circulo PQA: ad hunc effectum requiritur lex vis centripetæ tendentis ad punctum adeo longinquum, ut lineæ omnes PS, RS ad id ductæ, pro parallelis haberi possint.
A circuli centro C agatur semidiameter CA parallelas istas perpendiculariter secans in M & N, & jungantur CP. Ob similia triangula CPM, & TPZ, vel 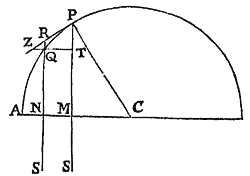 (per Lem. VIII.) TPQ, est CPq. ad PMq. ut PQq. vel (per Lem. VII.) PRq. ad QTq. & ex natura circuli rectangulum æquale est PR quadrato. Coeuntibus autem punctis P, Q sit aequlis . Ergo est CP quad. ad PM quad. ut ad QT quad. adeoque æquale , æquale . Est ergo (per Corol. Theor. V.) vis centripeta reciproce ut hoc est (neglecta ratione determinata ) reciproce ut PM cub. Q.E.I.
(per Lem. VIII.) TPQ, est CPq. ad PMq. ut PQq. vel (per Lem. VII.) PRq. ad QTq. & ex natura circuli rectangulum æquale est PR quadrato. Coeuntibus autem punctis P, Q sit aequlis . Ergo est CP quad. ad PM quad. ut ad QT quad. adeoque æquale , æquale . Est ergo (per Corol. Theor. V.) vis centripeta reciproce ut hoc est (neglecta ratione determinata ) reciproce ut PM cub. Q.E.I.
Scholium.
Et simili argumento corpus movebitur in Ellipsi vel etiam in Hyperbola vel Parabola, vi centripeta quæ sit reciproce ut cubus ordinatim applicatæ ad centrum virium maxime longinquum tendentis.
Prop. IX. Prob. IV.
Gyretur corpus in spirali PQS secante radios omnes SP SQ, &c. in angulo dato: Requiritur lex  vis centripetæ tendentis ad centrum spiralis.
vis centripetæ tendentis ad centrum spiralis.
Detur angulus indefinite parvus PSQ, & ob datos omnes angulos dabitur specie figura SQRT. Ergo datur ratio , estque ut QT, hoc est ut SP. Mutetur jam utcunque angulus PSQ, & recta QR angulum contactus QPR subtendens mutabitur (per Lemma XI.) in duplicata ratione ipsius PR vel QT. Ergo manebit eadem quæ prius, hoc est ut SP. Quare est ut SP cub. id est (per Corol. Theor. V.) vis centripeta ut cubus distantiæ SP.Q.E.I.
Lemma XII.
Parallelogramma omnia circa datam Ellipsin descripta esse inter se æqualia. Idem intellige de Parallelogrammis in Hyperbola circum diametros ejus descriptis.
Constat utrumque ex Conicis.
<48>Prop. X. Prob. V.
Gyretur corpus in Ellipsi: requiritur lex vis centripetæ tendentis ad centrum Ellipseos.
Sunto CA, CB 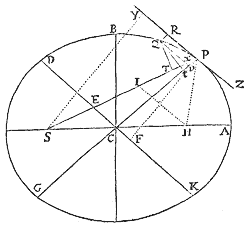 semiaxes Ellipseos; GP, DK diametri conjugatæ; PF, Qt perpendicula ad diametros; Qv ordinatim applicata ad diametrum GP; & si compleatur parallelogrammum QvRP, erit (ex Conicis) PvG ad Qv quad. ut PC quad. ad CD quad. & (ob similia triangula Qvt, PCF) Qv quad. est ad Qt quad. ut PC quad. ad PF quad. & conjunctis rationibus, PvG ad Qt quad. ut PC quad. ad CD quad. & PC quad. ad PF quad. id est vG ad ut PC quad. ad . Scribe QR pro Pv, & (per Lemma xii.) pro , nec non (punctis P & Q coeuntibus) pro vG, & ductis extremis & medijs in se mutuo, fiet æquale Est ergo (per Corol. Theor. V.) vis centripeta reciproce ut , id est (ob datum ) ut , hoc est, directe ut distantia PC. Q.E.I.
semiaxes Ellipseos; GP, DK diametri conjugatæ; PF, Qt perpendicula ad diametros; Qv ordinatim applicata ad diametrum GP; & si compleatur parallelogrammum QvRP, erit (ex Conicis) PvG ad Qv quad. ut PC quad. ad CD quad. & (ob similia triangula Qvt, PCF) Qv quad. est ad Qt quad. ut PC quad. ad PF quad. & conjunctis rationibus, PvG ad Qt quad. ut PC quad. ad CD quad. & PC quad. ad PF quad. id est vG ad ut PC quad. ad . Scribe QR pro Pv, & (per Lemma xii.) pro , nec non (punctis P & Q coeuntibus) pro vG, & ductis extremis & medijs in se mutuo, fiet æquale Est ergo (per Corol. Theor. V.) vis centripeta reciproce ut , id est (ob datum ) ut , hoc est, directe ut distantia PC. Q.E.I.
Corol. 1. Unde vicissim si vis sit ut distantia, movebitur corpus in Ellipsi centrum habente in centro virium, aut forte in circulo, in quem Ellipsis migrare potest.
Corol. 2. Et æqualia erunt revolutionum in Figuris universis circa centrum idem factarum periodica tempora. Nam tempora illa in Ellipsibus similibus æqualia sunt per Corol. 3 & 7 Prop. IV: In Ellipsibus autem communem habentibus axem majorem, sunt ad invicem ut Ellipseon areæ totæ directe & arearum particulæ simul descriptæ inverse; id est ut axes minores directe & corporum velocitates in verticibus principalibus inverse, hoc est ut axes illi directe & ordinatim applicatæ ad axes alteros inverse, & propterea (ob æqualitatem rationum directarum & inversarum) in ratione æqualitatis.
Scholium.
Si Ellipsis, centro in infinitum abeunte, vertatur in Parabolam, corpus movebitur in hac Parabola, & vis ad centrum infinite distans jam tendens, evadet æquabilis. Hoc est Theorema Galilei. Et si Conisectio Parabolica, inclinatione plani ad conum sectum mutata, vertatur in Hyperbolam, movebitur corpus in hujus perimetro, vi centripeta in centrifugam versa.
SECT. III.
De motu Corporum in Conicis Sectionibus excentricis.
Prop. XI. Prob. VI.
Revolvatur corpus in Ellipsi: Requiritur lex vis centripetæ tendentis ad umbilicum Ellipseos.
Esto Ellipseos superioris umbilicus S. Agatur SP secans Ellipseos tum diametrum DK in E, tum ordinatim applicatam Qv in x, & compleatur parallelogrammum QxPR. Patet EP æqualem esse semiaxi 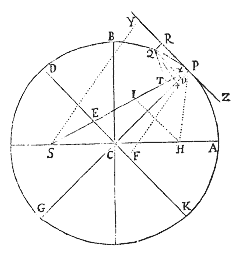 majori AC, eo quod acta ab altero Ellipseos umbilico H linea HI ipsi EC parallela, (ob æquales CS, CH) æquentur ES, EI, adeo ut EP semisumma sit ipsarum PS, PI, id est (ob parallelas HI, PR & angulos æquales IP R, HPZ) ipsorum PS, PH, quæ conjunctim axem totum 2 AC adæquant. Ad SP demittatur perpendicularis QT, & Ellipseos latere recto principali (seu) dicto L, erit ad ut QR ad Pv; id est ut PE (seu AC) ad PC: & ad GvP ut L ad Gv; & GvP ad Qv quad. ut CP quad. ad CD quad; & (per Lem. VIII.) Qv quad. ad Qx quad. punctis Q & P coeuntibus, est ratio æqualitatis, & Qx quad. seu Qv quad. est ad QT quad. ut EP quad. ad PF quad, id est ut CA quad. ad PF quad. sive (per Lem. XII.) ut CD quad. ad CB quad. Et conjunctis his omnibus rationibus, sit ad QT quad. ut AC ad ad ad ad CBq. id est ut ad sive ut ad Gv. Sed punctis Q & P coeuntibus, æquantur & Gv. Ergo & his proportionalia & QT quad. æquantur. Ducantur hæc a qualia in & fiet æquale Ergo (per Corol. Theor. V.)vis centripeta reciproce est ut id est reciproce in ratione duplicata distantiæ SP.Q.E.I
majori AC, eo quod acta ab altero Ellipseos umbilico H linea HI ipsi EC parallela, (ob æquales CS, CH) æquentur ES, EI, adeo ut EP semisumma sit ipsarum PS, PI, id est (ob parallelas HI, PR & angulos æquales IP R, HPZ) ipsorum PS, PH, quæ conjunctim axem totum 2 AC adæquant. Ad SP demittatur perpendicularis QT, & Ellipseos latere recto principali (seu) dicto L, erit ad ut QR ad Pv; id est ut PE (seu AC) ad PC: & ad GvP ut L ad Gv; & GvP ad Qv quad. ut CP quad. ad CD quad; & (per Lem. VIII.) Qv quad. ad Qx quad. punctis Q & P coeuntibus, est ratio æqualitatis, & Qx quad. seu Qv quad. est ad QT quad. ut EP quad. ad PF quad, id est ut CA quad. ad PF quad. sive (per Lem. XII.) ut CD quad. ad CB quad. Et conjunctis his omnibus rationibus, sit ad QT quad. ut AC ad ad ad ad CBq. id est ut ad sive ut ad Gv. Sed punctis Q & P coeuntibus, æquantur & Gv. Ergo & his proportionalia & QT quad. æquantur. Ducantur hæc a qualia in & fiet æquale Ergo (per Corol. Theor. V.)vis centripeta reciproce est ut id est reciproce in ratione duplicata distantiæ SP.Q.E.I
Eadem brevitate qua traduximus Problema quintum ad Parabolam, & Hyperbolam, liceret idem hic facere: verum ob dignitatem Problematis & usum ejus in sequentibus, non pigebit casucæteros demonstratione confirmare.
Prop. XII. Prob. VII.
Moveatur corpus in Hyperbola: requiritur lex vis centripetæ tendentis ad umbilicum figuræ.
Sunto CA, CB semi-axes Hyperbolæ; PG, KD diametri conjugatæ; PF, Qt perpendicula ad diametros; & Qv ordinatim applicata ad diametrum GP. Agatur SP secans tum diametrum DK in E, tum ordinatim applicatam Qv in x, & compleatur parallelogrammum QRPx. Patet EP æqualem esse semiaxi transverso AC, eo quod, acta ab altero Hyperbolæ umbilico H linea HI ipsi EC parallela, ob æquales CS, CH, æquentur ES, EI; adeo ut EP semidifferentia sit ipsarum PS, PI, id est (ob parallelas HI, PR & angulos æquales IPR, HPZ) ipsarum PI, PH, quarum differentia axem totum adæquat. Ad SP demittatur perpendicularis QT. Et Hyperbolæ latere recto principali (seu ) dicto L, erit ad ut QR ad Pv, id est, ut PE (seu AC) ad PC; Et ad GvP ut L ad Gv; & GvP ad Qvq. ut CPq. 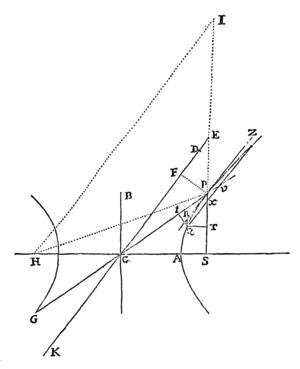 ad CDq; & (per Lem. VIII.)Qvq. ad Qxq, punctis Q & P coeuntibus fit ratio æqualitatis; & Qxq. seu Qvq. est ad QTq. ut EPq. ad PFq, id est ut CAq. ad PFq, sive (per Lem. XII.) ut CDq. ad CBq: & conjunctis his omnibus rationibus fit ad QTq. ut AC ad PC+L ad Gv+CPq. ad CDq.+CDq. ad CBq: id est ut (seu ) ad sive ut 2 PC ad Gv, sed punctis Q & P coeuntibus æquantur . Ergo & his proportionalia æquantur. Ducantur hæc æqualia in & fiet æquale Ergo (per Corol. Theor. V.) vis centripeta reciproce est ut , id est in ratione duplicata distantiæ SP.Q.E.I.
ad CDq; & (per Lem. VIII.)Qvq. ad Qxq, punctis Q & P coeuntibus fit ratio æqualitatis; & Qxq. seu Qvq. est ad QTq. ut EPq. ad PFq, id est ut CAq. ad PFq, sive (per Lem. XII.) ut CDq. ad CBq: & conjunctis his omnibus rationibus fit ad QTq. ut AC ad PC+L ad Gv+CPq. ad CDq.+CDq. ad CBq: id est ut (seu ) ad sive ut 2 PC ad Gv, sed punctis Q & P coeuntibus æquantur . Ergo & his proportionalia æquantur. Ducantur hæc æqualia in & fiet æquale Ergo (per Corol. Theor. V.) vis centripeta reciproce est ut , id est in ratione duplicata distantiæ SP.Q.E.I.
Eodem modo demonstratur quod corpus, hac vi centripeta in centrifugam versa, movebitur in Hyperbola conjugata.
Lemma XIII.
Latus rectum Parabolæ ad verticem quemvis pertinens, est quadruplum distantiæ verticis illius ab umbilico figuræ. Patet ex Conicis.
Lemma XIV.
Perpendiculum quod ab umbilico Parabolæ ad tangentem ejus demittitur, medium est proportionale inter distantias umbilici a puncto contactus & a vertice principali figuræ.
Sit enim APQ Parabola, S umbilicus ejus, A vertex principalis, P punctum 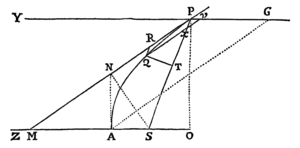 contactus, PO ordinatim applicata ad diametrum principalem, PM tangens diametro principali occurrens in M, & SN linea perpendicularis ab umbilico in tangentem. Jungatur AN, & ob æquales MS & SP, MN & NP, MA & AO, parallelæ erunt rectæ AN & OP, & inde triangulum SAN rectangulum erit ad A & simile triangulis æqualibus SMN, SPN, Ergo PS est ad SN ut SN ad SA. Q.ED.
contactus, PO ordinatim applicata ad diametrum principalem, PM tangens diametro principali occurrens in M, & SN linea perpendicularis ab umbilico in tangentem. Jungatur AN, & ob æquales MS & SP, MN & NP, MA & AO, parallelæ erunt rectæ AN & OP, & inde triangulum SAN rectangulum erit ad A & simile triangulis æqualibus SMN, SPN, Ergo PS est ad SN ut SN ad SA. Q.ED.
Corol. 1. PSq. est ad SNq. ut PS ad SA.
Corol. 2. Et ob datam SA, est SNq. ut PS.
Corol. 3. Et concursus tangentis cujusvis PM cum recta SN quæ ab umbilico in ipsam perpendicularis est, incidit in rectam AN, quæ Parabolam tangit in vertice principali.
<54>Prop. XIII. Prob. VIII.
Moveatur corpus in perimetro Parabolæ: requiritur Lex vis centripetæ tendentis ad umbilicum hujus figuræ.
Maneat constructio Lemmatis, sitqque P corpus in perimetro Parabolæ, & a loco Q in quem corpus proxime movetur, age ipsi SP Parallelam QR & perpendicularem QT, necnon Qv tangenti parallelam & occurentem tum diametro YPG in v, tum distantiæ SP in x. Jam ob similia triangula Pxv, MSP & æqualia unius latera SM, SP, æqualia sunt alterius latera Px seu QR & Pv. Sed, ex Conicis, quadratum ordinatæ Qv æquale est rectangulo sub latere recto & segmento diametri Pv, id est (per Lem. XIII.) rectangulo seu ; & punctis P & Q coeuntibus, ratio Qv ad Qx (per Lem. 8.) fit æqualitatis. Ergo Qxq. eo in 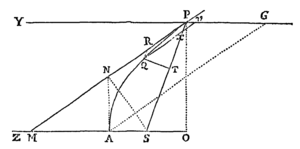 casu, æquale est rectangulo . Est autem (ob æquales angulos QxT, MPS, PMO) Qxq. ad QTq. ut PSq. ad SNq. hoc est (per Corol. I. Lem. XIV.) ut PS ad AS, id est ut ad , & inde (per Prop. 9. Lib. V Elem.) QTq. & æquantur. Ducantur hæc æqualia in , & fiet æquale : & propterea (per Corol. Theor. V.) vis centripeta est reciproce ut , id est, ob datam , reciproce in duplicata ratione distantiæ SP.Q.E.I.
casu, æquale est rectangulo . Est autem (ob æquales angulos QxT, MPS, PMO) Qxq. ad QTq. ut PSq. ad SNq. hoc est (per Corol. I. Lem. XIV.) ut PS ad AS, id est ut ad , & inde (per Prop. 9. Lib. V Elem.) QTq. & æquantur. Ducantur hæc æqualia in , & fiet æquale : & propterea (per Corol. Theor. V.) vis centripeta est reciproce ut , id est, ob datam , reciproce in duplicata ratione distantiæ SP.Q.E.I.
Corol. I. Ex tribus novissimis Propositionibus consequens est, quod si corpus quodvis P, secundum lineam quamvis rectam PR, quacunque cum velocitate exeat de loco P, & vi centripeta quæ sit reciproce proportionalis quadrato distantiæ a centro, simul agitetur; movebitur hoc corpus in aliqua sectionum Conicarum umbilicum habente in centro virium; & contra.
Corol. II. Et si velocitas, quacum corpus exit de loco suo P, ea sit, qua lineola PR in minima aliqua temporis particula describi possit, & vis centripeta potis sit eodem tempore corpus idem movere per spatium QR: movebitur hoc corpus in Conica aliqua sectione cujus latus rectum est quantitas illa quæ ultimo sit ubi lineolæ PR, QR in infinitum diminuuntur. Circulum in his Corollariis refero ad Ellipsin, & casum excipio ubi corpus recta descendit ad centrum.
Prop. XIV. Theor. VI.
Si corpora plura revolvantur circa centrum commune, & vis centripeta decrescat in duplicata ratione distantiarum a centro; dico quod Orbium Latera recta sunt in duplicata ratione arearum quas corpora, radiis ad centrum ductis, eodem tempore describunt.
Nam per Corol. II. Prob. VIII. Latus rectum L æquale est quantitati quæ ultimo fit ubi coeunt puncta P & Q. Sed linea minima QR, dato tempore, est ut vis centripeta generans, hoc est (per Hypothesin) reciproce ut SPq. Ergo est ut hoc est, latus rectum L in duplicata ratione areæ Q.E.D.
Corol. Hinc Ellipseos area tota, eique proportionale rectangulum sub axibus, est in ratione composita ex dimidiata ratione lateris recti & integra ratione temporis periodici.
<56>Prop. XV. Theor. VII.
Iisdem positis, dico quod tempora periodica in Ellipsibus sunt in ratione sesquiplicata transversorum axium.
Namque axis minor est medius proportionalis inter axem majorem (quem transversum appello) & latus rectum, atque adeo rectangulum sub axibus est in ratione composita ex dimidiata ratione lateris recti & sesquiplicata ratione axis transversi. Sed hoc rectangulum, per Corollarium Theorematis Sexti, est in ratione composita ex dimidiata ratione lateris recti & integra ratione periodici temporis. Dematur utrobique dimidiata ratio lateris recti & manebit sesquiplicata ratio axis transversi æqualis rationi periodici temporis. Q.E.D.
Corol. Sunt igitur tempora periodica in Ellipsibus eadem ac in circulis, quorum diametri æquantur majoribus axibus Ellipseon.
Prop. XVI. Theor. VIII.
Iisdem positis, & actis ad corpora lineis rectis, quæ ibidem tangant orbitas, demissisque ab umbilico communi ad has tangentes perpendicularibus: dico quod velocitates corporum sunt in ratione composita ex ratione perpendiculorum inverse & dimidiata ratione laterum rectorum directe. VideFig. Prop. X. & XI.
Ab umbilico S ad tangentem PR demitte perpendiculum SY & velocitas corporis P erit reciproce in dimidiata ratione quantitatis Nam velocitas illa est ut arcus quam minimus PQ in data temporis particula descriptus, hoc est (per Lem. VII.) ut tangens PR, id est (ob proportionales PR ad QT & SP ad SY) ut , sive ut SY reciproce & directe; estque ut area dato tempore descripta, id est, per Theor. VI. in dimidiata ratione lateris recti Q.E.D.
Corol. 1. Latera recta sunt in ratione composita ex duplicata ratione perpendiculorum & duplicata ratione velocitatum.
Corol. 2. Velocitates corporum in maximis & minimis ab umbilico communi distantiis, sunt in ratione composita ex ratione distantiarum inverse & dimidiata ratione laterum rectorum directe. Nam perpendicula jam sunt ipsæ distantiæ.
Corol. 3. Ideoque velocitas in Conica sectione, in minima ab umbilico distantia, est ad velocitatem in circulo in eadem a centro distantia, in dimidiata ratione lateris recti ad distantiam illam duplicatam.
Corol. 4. Corpurum in Ellipsibus gyrantium velocitates in mediocribus distantiis ab umbilico communi sunt eædem quæ corporum gyrantium in circulis ad easdem distantias, hoc est (per Corol. VI. Theor. IV.) reciproce in dimidiata ratione distantiarum. Nam perpendicula jam sunt semi-axes minores, & hi sunt ut mediæ proportionales inter distantias & latera recta. Componatur hæc ratio inverse cum dimidiata ratione laterum rectorum directe, & fiet ratio dimidiata distantiarum inverse.
Corol. 5. In eadem vel æqualibus figuris, vel etiam in figuris inæqualibus, quarum latera recta sunt æqualia, velocitas corporis est reciproce ut perpendiculum demissum ab umbilico ad tangentem
Corol. 6. In Parabola, velocitas est reciproce in dimidiata ratione distantiæ corporis ab umbilico figuræ, in Ellipsi minor est, in Hyperbola major quam in hac ratione. Nam (per Corol. 2 Lem. XIV.) perpendiculum demissum ab umbilico ad tangentem Parabolæ est in dimidiata ratione distantiæ.
Corol. 7. In Parabola, velocitas ubique est ad velocitatem corporis revolventis in circulo ad eandem distantiam, in dimidiata ratione numeri binarii ad unitatem; in Ellipsi minor est, in Hyperbola major quam in hac ratione. Nam per hujus Corollarium secundum, velocitas in vertice Parabolæ est in hac ratione, & per Corollaria sexta hujus & Theorematis quarti, servatur eadem proportio in omnibus distantiis. Hinc etiam in Parabola velocitas ubique æqualis est velocitati corporis revolventis in circulo ad dimidiam distantiam, in Ellipsi minor est, in Hyperbola major.
Corol. 8. Velocitas gyrantis in Sectione quavis Conica est ad velocitatem gyrantis in circulo in distantia dimidii lateris recti Sectionis, ut distantia illa ad perpendiculum ab umbilico in tangentem Sectionis demissum. Patet per Corollarium quintum.
Corol. 9. Unde cum (per Corol. 6. Theor. IV.) velocitas gyrantis in hoc circulo sit ad velocitatem gyrantis in circulo quovis alio, reciproce in dimidiata ratione distantiarum; fiet ex æquo velocitas gyrantis in Conica sectione ad velocitatem gyrantis in circulo in eadem distantia, ut media proportionalis inter distantiam illam communem & semissem lateris recti sectionis, ad perpendiculum ab umbilico communi in tangentem sectionis demissum.
Prop. XVII. Prob. IX.
Posito quod vis centripeta sit reciproce proportionalis quadrato distantiæ a centro, & quod vis illius quantitas absoluta sit cognita; requiritur linea quam corpus describit, de loco dato cum data velocitate secundum datam rectam egrediens.
Vis centripeta tendens ad punctum S ea sit quæ corpus p in orbita quavis data pq gyrare faciat, & cognoscatur hujus velocitas in loco p. De loco P secundum lineam PR exeat corpus P cum data velocitate, & mox inde, cogente vi centripeta, deflectat illud in Conisectionem PQ. Hanc igitur recta PR tanget in P. Tangat itidem recta aliqua pr orbitam pq in p, & si ab S ad eas tangentes demitti intelligantur perpendicula, erit (per Corol. 1. Theor. VIII.) latus rectum Conisectionis ad latus rectum orbitæ datæ, in ratione composita ex duplicata ratione perpendiculorum & duplicata ratione velocitatum, atque adeo datur. Sit istud L. Datur 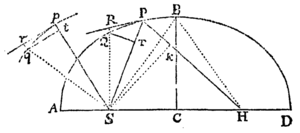 præterea Conisectionis umbilicus S. Anguli RPS complementum ad duos rectos fiat angulus RPH, & dabitur positione linea PH, in qua umbilicus alter H locatur. Demisso ad PH perpendiculo SK, & erecto semiaxe conjugato BC, est (per Prop. 13. Lib. II. Elem.) Addantur utrobique & fiet , seu SP+PH ad PH ut 2 SP+2 KP ad L. Unde datur PH tam longitudine quam positione. Nimirum si ea sit corporis in P velocitas, ut latus rectum L minus fuerit quam 2 SP+2 KP, jacebit PH ad eandem partem tangentis PR cum linea PS, adeoque figura erit Ellipsis, & ex datis umbilicis S, H, & axe principali SP+PH, dabitur: Sin tanta sit corporis velocitas ut latus rectum L æquale fuerit 2SP+2 KP, longitudo PH infinita erit, & propterea figura erit Parabola axem habens SH parallelum lineæ PK, & inde dabitur. Quod si corpus majori adhuc cum velocitate de loco suo P exeat, capienda erit longitudo PH ad alteram partem tangentis, adeoque tangente inter umbilicos pergente, figura erit Hyperbola axem habens principalem æqualem differentiæ linearum SP & PH, & inde dabitur. Q.E.I.
præterea Conisectionis umbilicus S. Anguli RPS complementum ad duos rectos fiat angulus RPH, & dabitur positione linea PH, in qua umbilicus alter H locatur. Demisso ad PH perpendiculo SK, & erecto semiaxe conjugato BC, est (per Prop. 13. Lib. II. Elem.) Addantur utrobique & fiet , seu SP+PH ad PH ut 2 SP+2 KP ad L. Unde datur PH tam longitudine quam positione. Nimirum si ea sit corporis in P velocitas, ut latus rectum L minus fuerit quam 2 SP+2 KP, jacebit PH ad eandem partem tangentis PR cum linea PS, adeoque figura erit Ellipsis, & ex datis umbilicis S, H, & axe principali SP+PH, dabitur: Sin tanta sit corporis velocitas ut latus rectum L æquale fuerit 2SP+2 KP, longitudo PH infinita erit, & propterea figura erit Parabola axem habens SH parallelum lineæ PK, & inde dabitur. Quod si corpus majori adhuc cum velocitate de loco suo P exeat, capienda erit longitudo PH ad alteram partem tangentis, adeoque tangente inter umbilicos pergente, figura erit Hyperbola axem habens principalem æqualem differentiæ linearum SP & PH, & inde dabitur. Q.E.I.
Corol. 1 Hinc in omni Conisectione ex dato vertice principali D, latere recto L, & umbilico S, datur umbilicus alter H capiendo DH ad DS ut est latus rectum ad differentiam inter latus rectum & 4DS. Nam proportio SP+PH ad PH ut 2SP ad L, in casu hujus Corollarii, fit DS+DH ad DH ut 4DS ad L, & divisim DS ad DH ut 4 DS−L ad L.
Corol. 2. Unde si datur corporis velocitas in vertice principali D, invenietur Orbita expedite, capiendo scilicet latus rectum ejus, ad duplam distantiam DS, in duplicata ratione velocitatis hujus datæ ad velocitatem corporis in circulo ad distantiam DS gyrantis: (Per Corol. 3. Theor. VIII. )dein DH ad DS ut latus rectum ad differentiam inter latus rectum & 4 DS.
Corol. 3. Hinc etiam si corpus moveatur in Sectione quacunque Conica, & ex orbe suo impulsu quocunque exturbetur; cognosci potest orbis in quo postea cursum suum peraget. Nam componendo proprium corporis motum cum motu illo quem impulsus solus generaret, habebitur motus quocum corpus de dato impulsus loco, secundum rectam positione datam, exibit.
Corol. 4. Et si corpus illud vi aliqua extrinsecus impressa continuo perturbetur, innotescet cursus quam proxime, colligendo mutationes quas vis illa in punctis quibusdam inducit, & ex seriei analogia, mutationes continuas in locis intermediis æstimando.
SECT. IV.
De Inventione Orbium Ellipticorum, Parabolicorum & Hyperbolicorum ex umbilico dato.
Lemma XV.
Si ab Ellipseos vel Hyperbolæ cujusvis umbilicis duobus S, H, ad punctum quodvis tertium V inflectantur rectæ duæ SV, HV, quarum una HV æqalis sit axi transverso figuræ, altera SV a perpendiculo TR in se demisso bisecetur in T; perpendiculum illud TR sectionem Conicam alicubi tangit: & 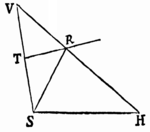 contra, si tangit, erit VH æqualis axi figuræ.
contra, si tangit, erit VH æqualis axi figuræ.
Secet enim VH sectionem conicam in R, & jungatur SR. Ob æquales rectas TS, TV, æquales erunt anguli TRS, TRV. Bisecat ergo RT angulum VRS & propterea figuram tangit: & contra. Q.E.D.
Prop. XVIII. Prob. X.
Datis umbilico & axibus transversis describere Trajectorias Ellipticas & Hyperbolicas, quæ transibunt per puncta data, & rectas positione datas contingent.
Sit S communis umbilicus figuraram; AC longitudo axis transversi Trajectoriæ cujusvis; P punctum per quod Trajectoria debet transire; & TR recta quam debet tangere. Centro P intervallo AB−SP,si orbita sit Ellipsis, vel AB+SP, si ea sit Hyperbola, describatur circulus HG. Ad tangentem TR demittatur perpendiculum ST, & producatur ea ad V, ut sit TV æqualis ST; centroque V & intervallo AC describatur circulus FH. Hac methodo sive dentur duo puncta 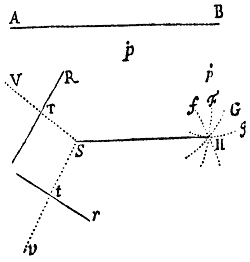 P, p, sive duæ tangentes TR, tr, sive punctum P & tangens TR, describendi sunt circuli duo. Sit H eorum intersectio communis, & umbilicis S, H, axe illo dato describatur Trajectoria. Dico factum. Nam Trajectoria descripta (eo quod PH+SP in Ellipsi, & PH−SP in Hyperbola æquatur axi) transibit per punctum P, & (per Lemma superius) tanget rectam TR. Et eodem argumento vel transibit eadem per puncta duo P,p, vel tanget rectas duas TR, tr. Q.E.F.
P, p, sive duæ tangentes TR, tr, sive punctum P & tangens TR, describendi sunt circuli duo. Sit H eorum intersectio communis, & umbilicis S, H, axe illo dato describatur Trajectoria. Dico factum. Nam Trajectoria descripta (eo quod PH+SP in Ellipsi, & PH−SP in Hyperbola æquatur axi) transibit per punctum P, & (per Lemma superius) tanget rectam TR. Et eodem argumento vel transibit eadem per puncta duo P,p, vel tanget rectas duas TR, tr. Q.E.F.
Prop. XIX. Prob. XI.
Circa datum umbilicum Trajectoriam Parabolicam describere, quæ transibit per puncta data, & rectas positione datas continget.
Sit S umbilicus, P punctum & TR tangens trajectoriæ describendæ. Centro P, intervallo PS describe 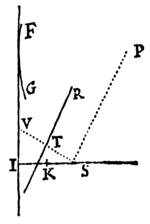 circulum FG. Ab umbilico ad tangentem demitte perpendicularem ST, & produc eam ad V, ut fit TV æqualis ST. Eodem modo describendus est alter circulus fg,si datur alterum punctum p; vel inveniendum alterum punctum v, si datur altera tangens tr; dein ducenda recta IF quæ tangat duos circulos FG, fg si dantur duo puncta P, p; vel transeat per duo puncta V,v, si dantur duæ tangentes TR, tr, vel tangat circulum PG & transeat per punctum V si datur punctum P & tangens TR. Ad FI demitte perpendicularem SI, eamque biseca in K, & axe SK, vertice principali K describatur Parabola. Dico factum. Nam Parabola ob æquales SK & IK, SP & FP transibit per punctum P; & (per Lemmatis XIV. Corol. 3.) ob æquales ST & TV & angulum rectum STR, tanget rectam TR.Q.E.F.
circulum FG. Ab umbilico ad tangentem demitte perpendicularem ST, & produc eam ad V, ut fit TV æqualis ST. Eodem modo describendus est alter circulus fg,si datur alterum punctum p; vel inveniendum alterum punctum v, si datur altera tangens tr; dein ducenda recta IF quæ tangat duos circulos FG, fg si dantur duo puncta P, p; vel transeat per duo puncta V,v, si dantur duæ tangentes TR, tr, vel tangat circulum PG & transeat per punctum V si datur punctum P & tangens TR. Ad FI demitte perpendicularem SI, eamque biseca in K, & axe SK, vertice principali K describatur Parabola. Dico factum. Nam Parabola ob æquales SK & IK, SP & FP transibit per punctum P; & (per Lemmatis XIV. Corol. 3.) ob æquales ST & TV & angulum rectum STR, tanget rectam TR.Q.E.F.
Prop. XX. Prob. XII.
Circa datum umbilicum Trajectoriam quamvis specie datam describere, quæ per data puncta transibit & rectas tanget positione datas.
Cas. 1. Dato umbilico S, describenda sit Trajectoria ABC per puncta duo B, C. Quoniam Trajectoria datur specie, dabitur ratio axis transversi ad 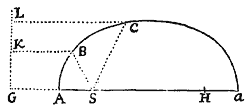 distantiam umbilicorum. In ea ratione cape KB ad BS, & LC ad CS. Centris B, C, intervallis BK, CL, describe circulos duos, & ad rectam KL, quæ tangat eosdem in K & L, demitte perpendiculum SG, idemque seca in A & a, ita ut sit SA ad AG & Sa ad aG, ut est SB ad BK, & axe Aa, verticibus A, a, describatur Trajectoria. Dico factum. Sit enim H umbilicus alter figuræ descriptæ, & cum sit SA ad AG ut Sa ad aG, erit divisim Sa−SA seu SH ad aG−AG seu Aa in eadem ratione, adeoque in ratione quam habet axis transversus figuræ describendæ ad distantiam umbilicorum ejus; & propterea figura descripta est ejusdem speciei cum describenda. Cumque sint KB ad BS & LC ad CS in eadem ratione, transibit hæc Figura per puncta B, C, ut ex Conicis manifestum est.
distantiam umbilicorum. In ea ratione cape KB ad BS, & LC ad CS. Centris B, C, intervallis BK, CL, describe circulos duos, & ad rectam KL, quæ tangat eosdem in K & L, demitte perpendiculum SG, idemque seca in A & a, ita ut sit SA ad AG & Sa ad aG, ut est SB ad BK, & axe Aa, verticibus A, a, describatur Trajectoria. Dico factum. Sit enim H umbilicus alter figuræ descriptæ, & cum sit SA ad AG ut Sa ad aG, erit divisim Sa−SA seu SH ad aG−AG seu Aa in eadem ratione, adeoque in ratione quam habet axis transversus figuræ describendæ ad distantiam umbilicorum ejus; & propterea figura descripta est ejusdem speciei cum describenda. Cumque sint KB ad BS & LC ad CS in eadem ratione, transibit hæc Figura per puncta B, C, ut ex Conicis manifestum est.
Cas. 2. Dato umbilico S, describenda sit Trajectoria quæ rectas duas TR, tr alicubi contingat. Ab umbilico in tangentes demitte perpendicula ST, St & produc eadem ad V, v, ut sint TV, tv æquales TS, ts. Biseca Vv 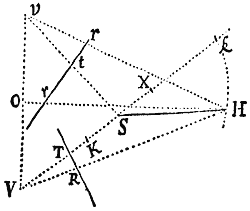 in O,& erige perpendiculum infinitum OH, rectamqueVS infinite productam seca in K & k ita, ut sit VK ad KS & Vk ad kS ut est Trajectoriæ describendæ axis transversus and umbilicorum distantiam. Super diametro Kk describatur circulus secans rectam OH in H; & umbilicis S, H, axe transverso ipsam VH æquante, describatur Trajectoria. Dico factum. Nam biseca Kk in X, & junge HX, HS, HV, Hv. Quoniam est VK ad KS ut Vk ad kS; & composite ut VK+Vk ad KS+kS; divisimque ut Vk−VK ad kS−KS id est ut 2 VX ad 2 KX & 2KX ad 2SX, adeoque ut VX ad HX & HX ad SX, similia erunt triangula VXH, HXS, & propterea VH erit ad SH ut VX ad XH, adeoque ut VK ad KS. Habet igitur Trajectoria descriptæ axis transversus VH eam rationem ad ipsius umbilicorum distantiam SH, quam habet Trajectoriæ describendæ axis transversus ad ipsius umbilicorum distantiam, & propterea ejusdem est speciei. Insuper cum VH, vH æquentur axi transverso, & VS, vS a rectis TR, tr perpendiculariter bisecentur, liquet, ex Lemmate XV, rectas illas Trajectoriam descriptam tangere. Q.E.F.
in O,& erige perpendiculum infinitum OH, rectamqueVS infinite productam seca in K & k ita, ut sit VK ad KS & Vk ad kS ut est Trajectoriæ describendæ axis transversus and umbilicorum distantiam. Super diametro Kk describatur circulus secans rectam OH in H; & umbilicis S, H, axe transverso ipsam VH æquante, describatur Trajectoria. Dico factum. Nam biseca Kk in X, & junge HX, HS, HV, Hv. Quoniam est VK ad KS ut Vk ad kS; & composite ut VK+Vk ad KS+kS; divisimque ut Vk−VK ad kS−KS id est ut 2 VX ad 2 KX & 2KX ad 2SX, adeoque ut VX ad HX & HX ad SX, similia erunt triangula VXH, HXS, & propterea VH erit ad SH ut VX ad XH, adeoque ut VK ad KS. Habet igitur Trajectoria descriptæ axis transversus VH eam rationem ad ipsius umbilicorum distantiam SH, quam habet Trajectoriæ describendæ axis transversus ad ipsius umbilicorum distantiam, & propterea ejusdem est speciei. Insuper cum VH, vH æquentur axi transverso, & VS, vS a rectis TR, tr perpendiculariter bisecentur, liquet, ex Lemmate XV, rectas illas Trajectoriam descriptam tangere. Q.E.F.
Cas. 3. Dato umbilico S describenda sit Trajectoria quæ rectam TR tanget in puncto dato R. In rectam TR demitte perpendicularem ST, & produc eandem ad V, ut sit TV æqualis ST. Junge VR, & rectam VS infinite productam seca in K & k, ita ut sit VK ad SK & Vk ad Sk ut Ellipseos describendæ axis transversus ad distantiam umbilicorum; circuloque super diametro Kk descripto, secetur producta recta VR in H, & umbilicis S, H, axe transverso rectam HV æquante, describatur Trajectoria. Dico factum. Namque VH esse 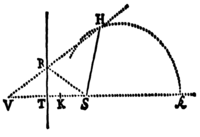 ad SH ut VK ad SK, atque adeo ut axis transversus Trajectoriæ describendæ ad distantiam umbilicorum ejus, patet ex demonstratis in Casu secundo, & propterea Trajectoriam descriptam ejusdem esse speciei cum describenda: rectam vero TR qua angulus VRS bisecatur, tangere Trajectoriam in puncto R, patet ex Conicis Q.E.F.
ad SH ut VK ad SK, atque adeo ut axis transversus Trajectoriæ describendæ ad distantiam umbilicorum ejus, patet ex demonstratis in Casu secundo, & propterea Trajectoriam descriptam ejusdem esse speciei cum describenda: rectam vero TR qua angulus VRS bisecatur, tangere Trajectoriam in puncto R, patet ex Conicis Q.E.F.
Cas. 4. Circa umbilicum S describenda jam sit Trajectoria APB, quæ tangat rectam TR, transeatque per punctum quodvis P extra tangentem datum, quæque similis sit figuræ a p b, axe 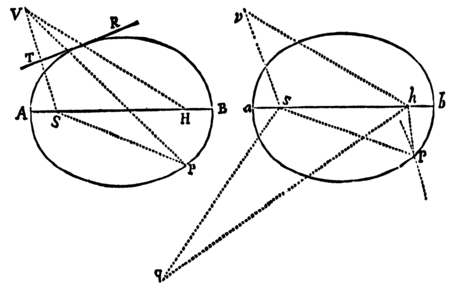 transverso ab & umbilicis s, b descriptæ. In tangentem TR demitte perpendiculum ST, & produc idem ad V, ut sit TV æqualis ST. Angulis autem VSP, SVP fac angulos hsq, shq æquales; centroque q & intervallo quod sit ad ab ut SP ad VS describe circulum secantem figuram apb in p. Junge sp & age SH quæ sit ad sh ut est SP ad sp, quæque angulum PSH angulo psh & angulum VSH angulo psq æquales constituat. Denique umbilicis S,H, axe distantiam VH æquante, describatur sectio conica.
transverso ab & umbilicis s, b descriptæ. In tangentem TR demitte perpendiculum ST, & produc idem ad V, ut sit TV æqualis ST. Angulis autem VSP, SVP fac angulos hsq, shq æquales; centroque q & intervallo quod sit ad ab ut SP ad VS describe circulum secantem figuram apb in p. Junge sp & age SH quæ sit ad sh ut est SP ad sp, quæque angulum PSH angulo psh & angulum VSH angulo psq æquales constituat. Denique umbilicis S,H, axe distantiam VH æquante, describatur sectio conica. 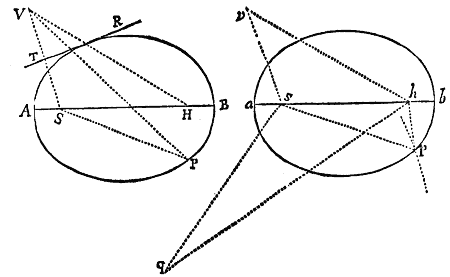 Dico factum. Nam si agatur sv quæ sit ad sp ut est sh ad sq, quæque constituat angulum vsp angulo hsq & angulum vsh angulo psq æquales, triangula svh, spq erunt similia, & propterea vh erit ad pq ut est sh ad sq, id est (ob similia triangula VSP, hsq) ut est VS ad SP seu ab ad pq. Æquantur ergo vh & ab. Porro ob similia triangula VSH, vsh, est VH ad SH ut vh ad sh, id est, axis Conicæ sectionis jam descriptæ ad ilius umbilicorum intervallum, ut axis ab ad umbilicorum intervallum sh, & propterea figura jam descripta similis est figuræ apb. Transit autem hæc figura per punctum P, co quod triangulum PSH simile sit triangulo psh; & quia VH æquatur ipsius axi & VS bisecatur perpendiculariter a recta TR, tangit eadem rectam TR. Q.E.F.
Dico factum. Nam si agatur sv quæ sit ad sp ut est sh ad sq, quæque constituat angulum vsp angulo hsq & angulum vsh angulo psq æquales, triangula svh, spq erunt similia, & propterea vh erit ad pq ut est sh ad sq, id est (ob similia triangula VSP, hsq) ut est VS ad SP seu ab ad pq. Æquantur ergo vh & ab. Porro ob similia triangula VSH, vsh, est VH ad SH ut vh ad sh, id est, axis Conicæ sectionis jam descriptæ ad ilius umbilicorum intervallum, ut axis ab ad umbilicorum intervallum sh, & propterea figura jam descripta similis est figuræ apb. Transit autem hæc figura per punctum P, co quod triangulum PSH simile sit triangulo psh; & quia VH æquatur ipsius axi & VS bisecatur perpendiculariter a recta TR, tangit eadem rectam TR. Q.E.F.
Lemma XVI.
A datis tribus punctis ad quartum non datum inflectere tres rectas quarum differentiæ vel dantur vel nullæ sunt.
Cas. 1. Sunto puncta illa data A, B, C & punctum quartum Z, quod invenire oportet: Ob datam differentiam linearum AZ, BZ, locabitur punctum Z in Hyperbola cujus umbilici sunt A & B, & axis transversus differentia illa data. Sit axis ille MN. Cape PM ad MA ut est MN ad AB, & erecto PR perpendicular ad AB, demissoque ZR perpendiculari ad PR, erit ex natura hujus Hyperbolæ ZR ad AZ ut est MN ad AB. Simili discursu punctum Z locabitur in alia Hyperbola, cujus umbilici sunt A, C & axis transversus differentia inter AZ & CZ, ducique potest QS ipsi AC perpendicularis, ad quam si ab Hyperbolæ hujus puncto quovis Z demittatur normalis ZS, hæc fuerit ad AZ ut est differentia inter AZ & CZ ad AC. Dantur ergo rationes ipsarum ZR & ZS ad AZ, & idcirco datur earundem ZR & ZS ratio ad invicem; adeoque 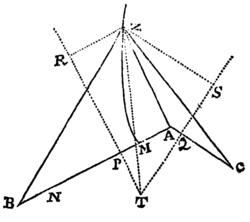 rectis RP, SQ concurrentibus in T, locabitur punctum Z in recta TZ positione data. Eadem Methodo per Hyperbolam tertiam, cujus umbilici sunt B & C & axis transversus differentia rectarum BZ, CZ, inveniri potest alia recta in qua punctum Z locatur. Habitis autem duobus locis rectilineis, habetur punctum quæsitum Z in earum intersectione.Q.E.I.
rectis RP, SQ concurrentibus in T, locabitur punctum Z in recta TZ positione data. Eadem Methodo per Hyperbolam tertiam, cujus umbilici sunt B & C & axis transversus differentia rectarum BZ, CZ, inveniri potest alia recta in qua punctum Z locatur. Habitis autem duobus locis rectilineis, habetur punctum quæsitum Z in earum intersectione.Q.E.I.
Cas. 2. Si duæ ex tribus lineis, puta AZ & BZ æquantur, punctum Z locabitur in perpendiculo bisecante distantiam AB, & locus alius rectilineus invenietur ut supra. Q.E.I.
<68>Cas. 3. Si omnes tres æquantur, locabitur punctum Z in centro circuli per puncta A, B, C transeuntis. Q.E.I.
Solvitur etiam hoc Lemma problematicum per Librum. Tactionum Apollonii a Vieta restitutum.
Prop. XXI. Prob. XIII.
Trajectoriam circa datum umbilicum describere, quæ transibit per puncta data & rectas positione datas continget.
Detur umbilicus S, punctum P, & tangens TR, & inveniendus sit umbilicus alter H. Ad tangentem demitte perpendiculum ST, & produc idem ad Y, ut sit TY æqualis ST, & erit YH æqualis axi transverso. Junge SP, HP, & erit SP differentia inter HP & axem transversum. Hoc modo si dentur plures tangentes TR, vel plura puncta P, devenietur semper ad lineas totidem YH, vel PH, a dictis punctis Y vel P ad umbilicum H ductas, quæ vel æquantur axibus, vel datis longitudinibus SP differunt ab iisdem, atque adeo quæ vel æquantur 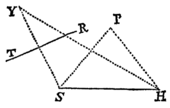 sibi invicem, vel datas habent differentias; & inde, per Lemma superius, datur umbilicus ille alter H. Habitis autem umbilicis una cum axis longitudine ( quæ vel est YH, vel si Trajectoria Ellipsis est, ; sin Hyperbola, ) habetur Trajectoria. Q.E.I.
sibi invicem, vel datas habent differentias; & inde, per Lemma superius, datur umbilicus ille alter H. Habitis autem umbilicis una cum axis longitudine ( quæ vel est YH, vel si Trajectoria Ellipsis est, ; sin Hyperbola, ) habetur Trajectoria. Q.E.I.
Scholium.
Casus ubi dantur tria puncta sic solvitur expeditius. Dentur puncta B, C, D. Junctas BC, CD produc ad E, F, ut sit EB ad EC ut SB ad SC,& FC ad FD ut SC ad SD. Ad EF ductam & productam demitte normales SG, BH, inque GS infinite producta cape GA ad AS & Ga ad aS ut est HB ad BS; & erit A vertex, & Aa axis transversus Trajectoriæ: quæ, perinde ut GA minor, æqualis vel major fuerit quam AS, erit Ellipsis, Parabola vel Hyperbola; puncto 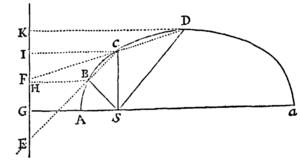 a in primo casu cadente ad eandem partem lineæ GK cum puncto A; in secundo casu abeunin infinitum; in tertio cadente ad contrariam partem lineæ GK. Nam si demittantur ad GF perpendicula CI, DK, erit IC ad HB ut EC ad EB, hoc est ut SC ad SB; & vicissim IC ad SC ut HB ad SB, seu GA ad SA. Et simili argumento probabitur esse KD ad SD in eadem ratione. Jacent ergo puncta B, C, D in Conisectione circa umbilicum S ita descripta, ut rectæ omnes ab umbilico S ad singula Sectionis puncta ductæ, sint ad perpendicula a punctis iisdem ad rectam GK demissa in data illa ratione.
a in primo casu cadente ad eandem partem lineæ GK cum puncto A; in secundo casu abeunin infinitum; in tertio cadente ad contrariam partem lineæ GK. Nam si demittantur ad GF perpendicula CI, DK, erit IC ad HB ut EC ad EB, hoc est ut SC ad SB; & vicissim IC ad SC ut HB ad SB, seu GA ad SA. Et simili argumento probabitur esse KD ad SD in eadem ratione. Jacent ergo puncta B, C, D in Conisectione circa umbilicum S ita descripta, ut rectæ omnes ab umbilico S ad singula Sectionis puncta ductæ, sint ad perpendicula a punctis iisdem ad rectam GK demissa in data illa ratione.
Methodo haud multum dissimili hujus problematis solutionem tradit Clarissimus Geometra De la Hire, Conicorum suorum Lib. VIII. Prop XXV.
SECT. V.
Inventio Orbium ubi umbilicus neuter datur.
Lemma XVII.
Si a datæ conicæ sectionis puncto quovis P, ad Trapezii alicujus ABCD, in Conica illa sectione inscripti, latera quatuor infinite producta AB, CD, AC, DB, totidem rectæ PQ, PR, PS, PT in datis angulis ducantur, singulæ 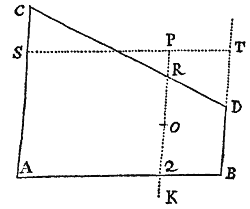 ad singula: rectangulum ductarum ad opposita duo latera , erit ad rectangulum ductarum ad alia duo latera opposita in data ratione.
ad singula: rectangulum ductarum ad opposita duo latera , erit ad rectangulum ductarum ad alia duo latera opposita in data ratione.
Cas. 1. Ponamus imprimis lineas ad opposita latera ductas parallelas esse alterutri reliquorum laterum, puta PQ & PR lateri AC, & PS ac PT lateri AB. Sintque insuper latera duo ex oppositis, puta AC & BD, parallela. Et recta quæ bisecat parallela illa latera erit una ex diametris Conicæ sectionis, & bisecabit etiam RQ. Sit O punctum in quo RQ bisecatur, & erit PO ordinatim applicata ad diametrum illam. Produc PO ad K ut sit OK æqualis PO, & erit OK ordinatim applicata ad contrarias partes diametri. Cum igitur puncta A, B, P & K sint ad Conicam sectionem,& PR secet AB in dato angulo, erit (per Prop. 17 & 18 Lib. III Apollonii) rectangulum PQK ad rectangulum AQB in data ratione. Sed QK & PR æquales sunt, utpote æqualium OK, OP, & OQ, OR differentiæ, & inde etiam rectangula PQK & æqualia sunt; atque adeo rectangulum est ad rectangulum AQB, hoc est ad rectangulum in data ratione. Q.E.D.
Cas. 2. Ponamus jam Trapezii latera opposita AC & BD non esse parallela. Age Bd parallelam AC & occurrentem tum rectæ ST in t, tum Conicæ sectioni in d. Junge Cd secantem PQ in r, & ipsi PQ parallelam age DM 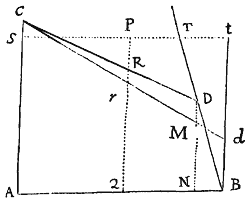 secantem Cd in M & AB in N. Jam ob similia triangula BTt, DBN, est Bt seu PQ ad Tt ut DN ad NB. Sic & Rr est ad AQ seu PS ut DM ad AN. Ergo ducendo antecedentes in antecedentes & consequentes in consequentes, ut rectangulum PQ in Rr est ad rectangulum Tt in PS, ita rectangulum NDM est ad rectangulum ANB, & (per Cas. 1) ita rectangulum QPr est ad rectangulum SPR, ac divisim ita rectangulum QPR est ad rectangulum .Q.E.D.
secantem Cd in M & AB in N. Jam ob similia triangula BTt, DBN, est Bt seu PQ ad Tt ut DN ad NB. Sic & Rr est ad AQ seu PS ut DM ad AN. Ergo ducendo antecedentes in antecedentes & consequentes in consequentes, ut rectangulum PQ in Rr est ad rectangulum Tt in PS, ita rectangulum NDM est ad rectangulum ANB, & (per Cas. 1) ita rectangulum QPr est ad rectangulum SPR, ac divisim ita rectangulum QPR est ad rectangulum .Q.E.D.
Cas. 3. Ponamus denique lineas quatuor PQ, PR, PS, PT 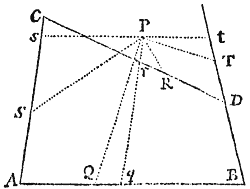 non esse parallelas lateribus AC, AB, sed ad ea utcunque inclinatas. Earum vice age Pq, Pr parallelas ipsi AC; & Ps, Pt parallelas ipsi AB; & propter datos angulos triangulorum PQq, PRr, PSs, PTt, dabuntur rationes PQ ad Pq, PR ad Pr, PS ad Ps & PT ad Pt, atque adeo rationes compositæ PQ in PR ad Pq in Pr, & PS in PT ad Ps in Pt. Sed, per superius demonstrata, ratio Pq in Pr ad Ps in Pt data est: Ergo & ratio PQ in PR ad PS in PT. Q.E.D.
non esse parallelas lateribus AC, AB, sed ad ea utcunque inclinatas. Earum vice age Pq, Pr parallelas ipsi AC; & Ps, Pt parallelas ipsi AB; & propter datos angulos triangulorum PQq, PRr, PSs, PTt, dabuntur rationes PQ ad Pq, PR ad Pr, PS ad Ps & PT ad Pt, atque adeo rationes compositæ PQ in PR ad Pq in Pr, & PS in PT ad Ps in Pt. Sed, per superius demonstrata, ratio Pq in Pr ad Ps in Pt data est: Ergo & ratio PQ in PR ad PS in PT. Q.E.D.
Lemma XVIII.
Iisdem positis, si rectangulum ductarum ad opposita duo latera Trapezii sit ad rectangulum ductarum ad reliqua duo latera in data ratione; punctum P, a quo lineæ ducuntur, tanget Conicam sectionem circa Trapezium descriptam.
Per puncta A, B, C, D & aliquod infinitorum punctorum P, puta p, concipe Conicam sectionem describi: dico punctum P hanc semper tangere. Si negas, 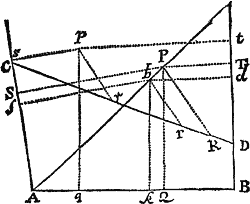 junge AP secantem hanc Conicam sectionem alibi quam in P si fieri potest, puta in b. Ergo si ab his punctis p & b ducantur in datis angulis ad latera Trapezii rectæ pq, pr, ps, pt & bk, br, bſ, bd; erit ut ad ita (per Lemma XVII) ad & ita (per hypoth. ) ad . Est & propter similitudinem Trapeziorum bkAſ, PQAS, ut bk ad bſ ita PQ ad PS. Quare applicando terminos prioris propositionis ad terminos correspondentes hujus, erit br ad bd ut PR ad PT. Ergo Trapezia æquiangula Drbd, DRPT similia sunt, & eorum diagonales Db, DP propterea coincidunt. Incidit itaqueb in intersectionem rectarum AP, DP adeoque coincidit cum puncto P. Quare punctum P, ubicunque sumatur, incidit in assignatam Conicam sectionem. Q.E.D.
junge AP secantem hanc Conicam sectionem alibi quam in P si fieri potest, puta in b. Ergo si ab his punctis p & b ducantur in datis angulis ad latera Trapezii rectæ pq, pr, ps, pt & bk, br, bſ, bd; erit ut ad ita (per Lemma XVII) ad & ita (per hypoth. ) ad . Est & propter similitudinem Trapeziorum bkAſ, PQAS, ut bk ad bſ ita PQ ad PS. Quare applicando terminos prioris propositionis ad terminos correspondentes hujus, erit br ad bd ut PR ad PT. Ergo Trapezia æquiangula Drbd, DRPT similia sunt, & eorum diagonales Db, DP propterea coincidunt. Incidit itaqueb in intersectionem rectarum AP, DP adeoque coincidit cum puncto P. Quare punctum P, ubicunque sumatur, incidit in assignatam Conicam sectionem. Q.E.D.
Corol. Hinc si rectæ tres PQ, PR, PS a puncto communi P ad alias totidem positione datas rectas AB, CD, AC, singulæ ad singulas, in datis angulis ducantur, sitque rectangulum sub duabus ductis ad quadratum tertii, PS quad. in data ratione: punctum P, a quibus rectæ ducuntur, locabitur in sectione Conica quæ tangit lineas AB, CD in A & C & contra. Nam coeat linea BD cum linea AC manente positione trium AB, CD, AC; dein coeat etiam linea PT cum linea PS: & rectangulum evadet PS quad. rectæqueAB, CD quæ curvam in punctis A & B, C & D secabant, jam Curvam in punctis illis coeuntibus non amplius secare possunt sed tantum tangent.
Scholium.
Nomen Conicæ sectionis in hoc Lemmate late sumitur, ita ut sectio tam rectilinea per verticem Coni transiens, quam circularis basi parallela includatur. Nam si punctum p incidit in rectam, qua quævis ex punctis quatuor A, B, C, D junguntur, Conica sectio vertetur in geminas rectas, quarum una est recta illa in quam punctum p incidit, & altera recta qua alia duo ex punctis quatuor junguntur. Si trapezii anguli duo oppositi simul sumpti æquentur duobus rectis, & lineæ quatuor PQ, PR, PS, PT ducantur ad latera ejus vel perpendiculariter vel in angulis quibusvis æqualibus, sitque rectangulum sub duabus ductis æquale rectangulo sub duabus aliis , Sectio conica evadet Circulus. Idem fiet si lineæ quatuor ducantur in angulis quibusvis & rectangulum sub duabus ductis sit ad rectangulum sub aliis duabus ut rectangulum sub sinubus angulorum S, T, in quibus duæ ultimæ PS, PT ducuntur, ad rectangulum sub sinubus angulorum Q, R,in quibus duæ primæ PQ, PR ducuntur. Cæteris in casibus Locus puncti P erit aliqua trium figurarum quæ vulgo nominantur Sectiones Conicæ. Vice autem TrapeziiABCD substitui potest quadrilaterum cujus latera duo opposita se mutuo instar diagonalium decussant. Sed & e punctis quatuor A, B, C, D possunt unum vel duo abire in infinitum, eoque pacto latera figuræ quæ ad puncta illa convergunt, evadere parallela: quo in casu sectio conica transibit per cætera puncta, & in plagas parallelarum abibit in infinitum.
Lemma XIX.
Invenire punctum P, a quo si rectæ quatuor PQ, PR, PS, PT ad alias totidem positione datas rectas AB, CD, AC, BD singulæ ad singulas in datis angulis ducantur, rectangulum sub duabus ductis, ,sit ad rectangulum sub aliis duabus, ,in data ratione.
Lineæ AB, CD, ad quas rectæ duæ PQ, PR, unum rectangulorum continentes ducuntur, conveniant cum aliis duabus positione datis lineis in punctis 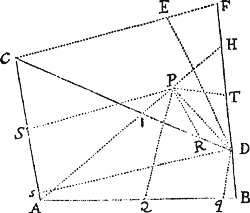 A, B, C, D. Ab eorum aliquo A age rectam quamlibet AH, in qua velis punctum P reperiri. Secet ea lineas oppositas BD, CD, nimirum BD in H & CD in I, & ob datos omnes angulos figuræ, dabuntur rationes PQ ad PA & PA ad PS, adeoque ratio PQ ad PS. Auferendo hanc a data ratione ad , dabitur ratio PR ad PT, & addendo datas rationes PI ad PR, & PT ad PH dabitur ratio PI ad PH atque adeo punctum P. Q.E.I.
A, B, C, D. Ab eorum aliquo A age rectam quamlibet AH, in qua velis punctum P reperiri. Secet ea lineas oppositas BD, CD, nimirum BD in H & CD in I, & ob datos omnes angulos figuræ, dabuntur rationes PQ ad PA & PA ad PS, adeoque ratio PQ ad PS. Auferendo hanc a data ratione ad , dabitur ratio PR ad PT, & addendo datas rationes PI ad PR, & PT ad PH dabitur ratio PI ad PH atque adeo punctum P. Q.E.I.
Corol. 1. Hinc etiam ad Loci punctorum infinitorum P punctum quodvis D tangens duci potest. Nam chorda PD ubi puncta P ac D conveniunt, hoc est, ubi AH ducitur per punctum D, tangens evadit. Quo in casu, ultima ratio evanescentium IP & PH invenietur ut supra. Ipsi igitur AD duc parallelam CF, occurrentem BD in F, & in ea ultima ratione sectam in E, & DE tangens erit, propterea quod CF & evanescens IH parallelæ sunt, & in E & P similiter sectæ.
Corol. 2. Hinc etiam Locus punctorum omnium P definiri potest. Per quodvis punctorum A, B, C, D, puta A, duc Loci tangentem AE, & per aliud quodvis punctum B duc tangenti parallelam BF occurrentem Loco 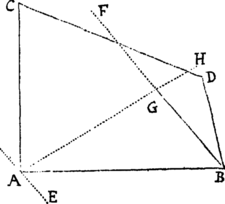 in F. Invenietur autem punctum F per Lemma superius. Biseca BF in G, & acta AG diameter erit ad quam BG & FG ordinatim applicantur. hæc AG occurrat Loco in H, & erit AH latus transversum, ad quod latus rectum est ut BGq. ad AGH. Si AG nullibi occurrit Loco, linea AH existente infinita, Locus erit Parabola & latus rectum ejus Sin ea alicubi occurrit, Locus Hyperbola erit ubi puncta A & H sita sunt ad easdem partes ipsius G: & Ellipsis, ubi G intermedium est, nisi forte angulus AGB rectus sit & insuper BG quad. æquale rectangulo AGH, quo in casu circulus habebitur.
in F. Invenietur autem punctum F per Lemma superius. Biseca BF in G, & acta AG diameter erit ad quam BG & FG ordinatim applicantur. hæc AG occurrat Loco in H, & erit AH latus transversum, ad quod latus rectum est ut BGq. ad AGH. Si AG nullibi occurrit Loco, linea AH existente infinita, Locus erit Parabola & latus rectum ejus Sin ea alicubi occurrit, Locus Hyperbola erit ubi puncta A & H sita sunt ad easdem partes ipsius G: & Ellipsis, ubi G intermedium est, nisi forte angulus AGB rectus sit & insuper BG quad. æquale rectangulo AGH, quo in casu circulus habebitur.
Atque ita Problematis veterum de quatuor lineis ab Euclide incæpti & ab Apollonio continuati non calculus, sed compositio Geometrica, qualem Veteres quærebant, in hoc Corollario exhibetur.
Lemma XX.
Si parallelogrammum quodvis ASPQ angulis duobus oppositis A & P tangit sectionem quamvis Conicam in punctis A & P, & lateribus unius angulorum illorum infinite productis AQ, AS occurrit eidem sectioni Conicæ in B & C; a punctis autem occur suum B & C ad quintum quodvis sectionis Conicæ punctum D agantur rectæ duæ B D,C D occurrentes alteris duobus infinite productis parallelogrammi lateribus PS, PQ in T & R: erunt semper abscissæ latcrum partes PR & PT ad invicem in data ratione. Et contra, si partes illæ abscissæ sunt ad invicem in data ratione, punctum D tanget Sectionem Conicam per puncta quatuor A, B, P, transeuntem.
Cas. 1. Jungantur BP, CP & a puncto D agantur rectae duæ DG, DE, quarum prior 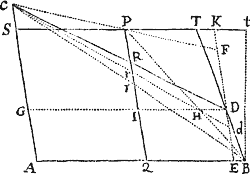 DG ipsi AB parallela sit & occurrat PB, PQ, CA in H, I, G; altera DE parallela sit ipsi AC & occurrat PC, PS, AB in F,K,E: & erit (per Lemma XVII.) rectangulum ad rectangulum in ratione data. Sed est PQ ad DE seu IQ, ut PB ad HB, adeoque ut PT ad DH; & vicissim PQ ad PT ut DE ad DH. Est & PR ad DF ut RC ad DC, adeoque ut IG vel PS ad DG, & vicissim PR ad PS ut DF ad DG; & conjunctis rationibus sit rectangulum ad rectangulum ut rectangulum ad rectangulum , atque adeo in data ratione. Sed dantur PQ & PS & propterea ratio PR ad PT datur. Q.E.D.
DG ipsi AB parallela sit & occurrat PB, PQ, CA in H, I, G; altera DE parallela sit ipsi AC & occurrat PC, PS, AB in F,K,E: & erit (per Lemma XVII.) rectangulum ad rectangulum in ratione data. Sed est PQ ad DE seu IQ, ut PB ad HB, adeoque ut PT ad DH; & vicissim PQ ad PT ut DE ad DH. Est & PR ad DF ut RC ad DC, adeoque ut IG vel PS ad DG, & vicissim PR ad PS ut DF ad DG; & conjunctis rationibus sit rectangulum ad rectangulum ut rectangulum ad rectangulum , atque adeo in data ratione. Sed dantur PQ & PS & propterea ratio PR ad PT datur. Q.E.D.
Cas. 2. Quod si PR & PT ponantur in data ratione ad invicem, tunc simili ratiocinio regrediendo, sequetur esse rectangulum ad rectangulum in ratione data, adeoque punctum D (per Lemma XVIII.) contingere Conicam sectionem transeuntem per puncta A, B, P, C. Q.E.D.
Corol. 1. Hinc si agatur BC secans PQ in r, & PT capiatur Pt in ratione ad Pr quam habet PT ad PR, erit Bt Tangens Conicæ sectionis ad punctum B. Nam concipe punctum D coire cum puncto B ita ut, chorda BD evanescente, BT Tangens evadet; & CD ac BT coincident cum CB & Bt.
Corol. 2. Et vice versa si Bt sit Tangens, & ad quodvis Conicæ sectionis punctum D conveniant BD, CD; erit PR ad PT ut Pr ad Pt. Et contra, si sit PR ad PT ut Pr ad Pt, convenient BD, CD ad Conicæ sectionis punctum aliquod D.
Corol. 3. Conica sectio non secat Conicam sectionem in punctis pluribus quam quatuor. Nam, si fieri potest, transeant duæ Conicæ sectiones per quinque puncta A, B, C, D, P, easque secet recta BD in punctis D, d, & ipsam PQ secet recta Cd in r. Ergo PR est ad PT ut Pr ad PT, hoc est, PR & Pr sibi invicem æquantur, contra Hypothesin.
Lemma XXI.
Si rectæ duæ mobiles & infinitæ BM, CM per data puncta B, C, ceu polos ductæ, 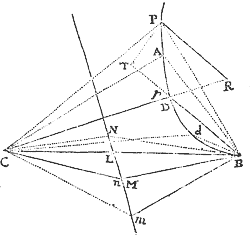 concursu suo M describant tertiam positione datam rectam MN; & aliæ duæ infinitæ rectæ BD, CD cum prioribus duabus ad puncta illa data B, C datos angulos MBD, MCD efficientes ducantur; dico quod hæ duæ BD, CD concursu suo D describent sectionem Conicam. Et vice versa, si rectæ BD, CD concursu suo D describant Sectionem Conicam per punctaB, C, A transeuntem, & harum concursus tunc incidit in ejus punctum aliquod A, cum alieræ duæ BM, CM coincidunt cum linæ BC, punctum M continget rectam positione datam.
concursu suo M describant tertiam positione datam rectam MN; & aliæ duæ infinitæ rectæ BD, CD cum prioribus duabus ad puncta illa data B, C datos angulos MBD, MCD efficientes ducantur; dico quod hæ duæ BD, CD concursu suo D describent sectionem Conicam. Et vice versa, si rectæ BD, CD concursu suo D describant Sectionem Conicam per punctaB, C, A transeuntem, & harum concursus tunc incidit in ejus punctum aliquod A, cum alieræ duæ BM, CM coincidunt cum linæ BC, punctum M continget rectam positione datam.
Nam in recta MN detur punctum N, & ubi punctum mobile M incidit in immotum N, incidat punctum mobile D in immotum P. Junge CN, 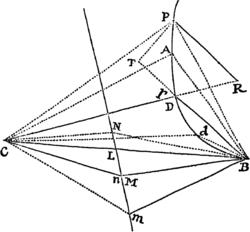 BN, CP, BP, & a puncto P age rectas PT, PR occurrentes ipsis BD, CD in T & R, & facientes angulum BPT æqualem angulo BNM & angulum CPR æqualem angulo CNM. Cum ergo ( ex Hypothesi ) æquales sint anguli MBD, NBP, ut & anguli MCD, NCP: aufer communes NBD & MCP,& restabunt æquales NBM & PBT, NCM & PCR: adeoque triangula NBM, PBT similia sunt, ut & triangula NCM, PCR. Quare PT est ad NM ut PB ad NB, & PR ad NM ut PC ad NC. Ergo PT & PR datam habent rationem ad NM, proindeque datam rationem inter se, atque adeo, per Lemma XX, punctum P ( perpetuus rectarum mobilum BT & CR concursus ) contingit sectionem Conicam. Q.E.D.
BN, CP, BP, & a puncto P age rectas PT, PR occurrentes ipsis BD, CD in T & R, & facientes angulum BPT æqualem angulo BNM & angulum CPR æqualem angulo CNM. Cum ergo ( ex Hypothesi ) æquales sint anguli MBD, NBP, ut & anguli MCD, NCP: aufer communes NBD & MCP,& restabunt æquales NBM & PBT, NCM & PCR: adeoque triangula NBM, PBT similia sunt, ut & triangula NCM, PCR. Quare PT est ad NM ut PB ad NB, & PR ad NM ut PC ad NC. Ergo PT & PR datam habent rationem ad NM, proindeque datam rationem inter se, atque adeo, per Lemma XX, punctum P ( perpetuus rectarum mobilum BT & CR concursus ) contingit sectionem Conicam. Q.E.D.
Et contra, si punctum D contingit sectionem Conicam transeuntem per puncta B, C, A, & ubi rectæ BM, CM coincidunt cum recta BC, punctum illud D incidit in aliquod sectionis punctum A; ubi vero punctum D incidit successive in alia duo quævis sectionis puncta p, P, punctum mobile M incidit successive in puncta immobilia n, N: per eadem n, N agatur recta nN, & hæc erit Locus perpetuus puncti illius mobilis M. Nam, si fieri potest, versetur punctum M in linea aliqua curva. Tanget ergo punctum D sectionem Conicam per puncta quinque C, p, P, B, Atranseuntem, ubi punctum M perpetuo tangit lineam curvam. Sed & ex jam demonstratis tanget etiam punctum D sectionem Conicam per eadem quinque puncta C, p, P, B, A transeuntem, ubi punctum M perpetuo tangit lineam rectam. Ergo duæ sectiones Conicæ transibunt per eadem quinque puncta, contra Corol. 3. Lem. XX. Igitur punctum M versari in linea curva absurdum est. Q.E.D.
Prop. XXII. Prob. XIV.
Trajectoriam per data quinque puncta describere.
Dentur puncta quinque A, B, C, D, P. Ab eorum aliquo Aad alia duo quævis B, C, quæ poli nominentur, age rectas AB, AC hisque parallelas TPS, 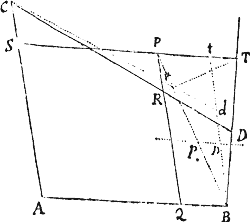 PRQ per punctum quartum P. Deinde a polis duobus B, C age per punctum quintum D infinitas duas BDT, CRD,novissime ductis TPS, PRQ ( priorem priori & posteriorem posteriori ) occurentes in T & R. Denique de rectis PT, PR, acta recta tr ipsi TR parallela, abscinde quas vis Pt, Pr ipsis PT, PR proportionales, & si per earum terminos t, r & polos B, C actæ Bt, Cr concurrant in d, locabitur punctum illud d in
PRQ per punctum quartum P. Deinde a polis duobus B, C age per punctum quintum D infinitas duas BDT, CRD,novissime ductis TPS, PRQ ( priorem priori & posteriorem posteriori ) occurentes in T & R. Denique de rectis PT, PR, acta recta tr ipsi TR parallela, abscinde quas vis Pt, Pr ipsis PT, PR proportionales, & si per earum terminos t, r & polos B, C actæ Bt, Cr concurrant in d, locabitur punctum illud d in 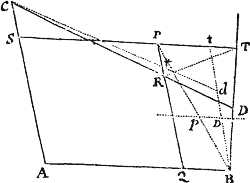 Trajectoria quæsita. Nam punctum illud d (per Lem. XX) versatur in Conica Sectione per puncta quatuor A, B, P, C transeunte; & lineis Rr, Tt evanescentibus, coit punctum d cum puncto D. Transit ergo sectio Conica per puncta quinque A, B C, D, P. Q.E.D.
Trajectoria quæsita. Nam punctum illud d (per Lem. XX) versatur in Conica Sectione per puncta quatuor A, B, P, C transeunte; & lineis Rr, Tt evanescentibus, coit punctum d cum puncto D. Transit ergo sectio Conica per puncta quinque A, B C, D, P. Q.E.D.
Idem aliter.
E punctis datis junge 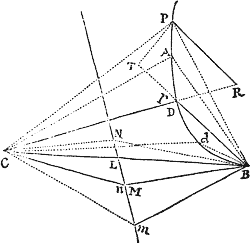 tria quævis A, B, C, & circum duo eorum B, C ceu polos, rotando angulos magnitudine datos ABC, ACB, applicentur crura BA, CA primo ad punctum D, deinde ad punctum P, & notentur puncta M, N in quibus altera crura BL, CL casu utroque se decussant. Agatur recta infinita MN, & rotentur anguli illi mobiles circum polos suos B, C, ea lege ut crurum BA, CA, vel BD, CD intersectio, quæ jam sit d, Trajectoriam quæsitam PADdB delineabit. Nam punctum d per Lem. XXI continget sectionem Conicam per puncta B, C transeuntem & ubi punctum m accedit ad puncta L, M, N, punctum d (per constructione) accedet ad puncta A, D, P. Describetur itaque sectio Conica transiens per puncta quinque A, B, C, D, P. Q.E.F.
tria quævis A, B, C, & circum duo eorum B, C ceu polos, rotando angulos magnitudine datos ABC, ACB, applicentur crura BA, CA primo ad punctum D, deinde ad punctum P, & notentur puncta M, N in quibus altera crura BL, CL casu utroque se decussant. Agatur recta infinita MN, & rotentur anguli illi mobiles circum polos suos B, C, ea lege ut crurum BA, CA, vel BD, CD intersectio, quæ jam sit d, Trajectoriam quæsitam PADdB delineabit. Nam punctum d per Lem. XXI continget sectionem Conicam per puncta B, C transeuntem & ubi punctum m accedit ad puncta L, M, N, punctum d (per constructione) accedet ad puncta A, D, P. Describetur itaque sectio Conica transiens per puncta quinque A, B, C, D, P. Q.E.F.
Corol. 1. Hinc rectæ expedite duci possunt quæ trajectoriam in punctis quibusvis datis B, C tangent. In casu utrovis accedat punctum d ad punctum C & recta Cd evadet tangens quæsita.
Corol. 2. Unde etiam Trajectoriarum centra, diametri & latera recta inveniri possunt, ut in Corollario secundo Lemmatis XIX
Schol.
Constructio in casu priore evadet paulo simplicior jungendo BP, & in ea si opus est producta, capiendo Bp ad BP ut est PR ad PT, & per p agendo rectam infinitam pD ipsi SPT parallelam, inque ea capiendo semper pD æqualem Pr, & agendo rectas BD, Cr concurrentes in d. Nam cum sint Pr ad Pt, PR ad PT, pB ad PB, pD ad Pt in eadem ratione, erunt pD & Pr semper æquales. Hac methodo puncta Trajectoriæ inveniuntur expeditissime, nisi mavis Curvam, ut in casu secundo, describere Mechanice.
Prop. XXIII. Prob. XV.
Trajectoriam describere quæ per data quatour puncta transibit, & rectam contingent positione datam.
Cas. 1. Dentur tangens HB, punctum contactus B, & alia tria puncta C, D, P. Junge BC, & agendo PS parallelam BH, & PQ parallelam BC, comple parallelogrammum BSPQ. Age BD secantem SP in 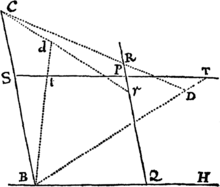 T, & CD secantem PQ in R. Denique agendo quamvis tr ipsi TR parallelam, de PQ, PS abscinde Pr, Pt ipsis PR, PT proportionales respective; & actarum Cr, Bt concursus d (per Corol. 2. Lem. XX) incidet semper in Trajectoriam describendam.
T, & CD secantem PQ in R. Denique agendo quamvis tr ipsi TR parallelam, de PQ, PS abscinde Pr, Pt ipsis PR, PT proportionales respective; & actarum Cr, Bt concursus d (per Corol. 2. Lem. XX) incidet semper in Trajectoriam describendam.
Idem aliter.
Revolvatur tum angulus magnitudine datus CBH circa polum B, tum radius 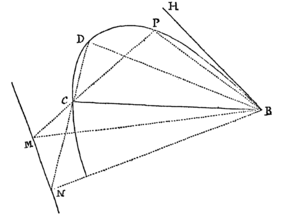 quilibet rectilineus & utrinque productus DC circa polum C. Notentur puncta M, N in quibus anguli crus BC secat radium illum ubicrus alterum BH concurrit cum eodem radio in punctis D & P. Diende ad actam infinitam MN concurrant perpetuo radius ille CP vel CD & anguli crus CB, & cruris alterius BH concursus cum radio delineabit Trajectoriam quæsitam.
quilibet rectilineus & utrinque productus DC circa polum C. Notentur puncta M, N in quibus anguli crus BC secat radium illum ubicrus alterum BH concurrit cum eodem radio in punctis D & P. Diende ad actam infinitam MN concurrant perpetuo radius ille CP vel CD & anguli crus CB, & cruris alterius BH concursus cum radio delineabit Trajectoriam quæsitam.
Nam si in constructionibus Problematis superioris accedat punctum A ad punctum B, lineæ CA & CB coincident, & linea AB in ultimo suo situ fiet tangens BH, atque adeo constructiones ibi positæ evadent eædem cum constructionibus hic descriptis Delineabit igitur cruris BH concursus cum radio sectionem Conicam per puncta C, D, P transeuntem, & rectam BH tangentem in puncto B. Q.E.F.
Cas. 2. Dentur puncta quatuor B, C, D, P extra tangentem HI sita. Junge bin a BD, CP concurrentia in G, tangentique occurrentia in H & I. Secetur 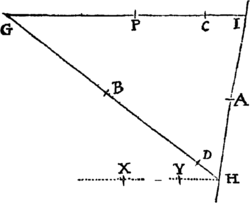 tangens in A, ita ut sit HA ad AI, ut est rectangulum sub media proportionali inter BH & HD & media proportionali inter CG & GP, ad rectangulum sub media proportionali inter PI & IC & media proportionali inter DG & GB, & erit A punctum contactus. Nam si rectæ PI parallela HX trajectoriam secet in punctis quibusvis X & Y: erit (ex Conicis) HA quad. ad AI quad. ut rectangulum XHY ad rectangulum BHD (seu rectangulum CGP ad rectangulum DGB) & rectangulum BHD ad rectangulum PIC conjunctim. Invento autem contactus puncto A, describetur Trajectoria ut in casu primo. Q.E.F. Capi autem potest punctum A vel inter puncta H & I, vel extra; & perinde Trajectoria dupliciter describi.
tangens in A, ita ut sit HA ad AI, ut est rectangulum sub media proportionali inter BH & HD & media proportionali inter CG & GP, ad rectangulum sub media proportionali inter PI & IC & media proportionali inter DG & GB, & erit A punctum contactus. Nam si rectæ PI parallela HX trajectoriam secet in punctis quibusvis X & Y: erit (ex Conicis) HA quad. ad AI quad. ut rectangulum XHY ad rectangulum BHD (seu rectangulum CGP ad rectangulum DGB) & rectangulum BHD ad rectangulum PIC conjunctim. Invento autem contactus puncto A, describetur Trajectoria ut in casu primo. Q.E.F. Capi autem potest punctum A vel inter puncta H & I, vel extra; & perinde Trajectoria dupliciter describi.
Prop. XXIV. Prob. XVI.
Trajectoriam describere quæ transibit per data tria puncta & rectas duas positione datas continget.
Dentur tangentes HI, KL & puncta B, C, D. Age BD tangentibus occurrentem in punctis H, K, & CD tangentibus occurrentem in punctis I, L. Actas ita seca in R & S, ut sit HR ad KR ut est media proportionalis 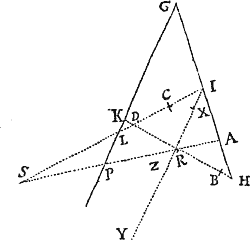 inter BH & HD ad mediam proportionalem inter BK & KD; & IS ad LS ut est media proportionalis inter CI & ID ad mediam proportionalem inter CL & LD. Age RS secantem tangentes in A & P, & erunt A & P puncta contractus. Nam si per punctorum H, I, K, L quodvis I agatur recta IY tangenti KL parallela & occurrens curvæ in X & Y, & in ea sumatur IZ media proportionalis inter IX & IY: erit, ex Conicis, rectangulum XIY (seu IZ quad.) ad LP quad. ut rectangulum CID ad rectangulum CLD; id est (per constructionem) ut SI quad. ad SL quad. atque adeo IZ ad LP ut SI ad SL. Jacent ergo puncta S, P, Z in una recta. Porro tangentibus concurrentibus in G, erit (ex Conicis) rectangulum XIY (seu IZ quad.) ad IA quad. ut GP quad. ad GA quad., adeoque IZ ad IA ut GP ad GA. Jacent ergo puncta P, Z & A in una recta, adeoque puncta S, P & A sunt in una recta. Et eodem argumento probabitur quod puncta R, P & A sunt in una recta. Jacent igitur puncta contactus A & P in recta SR. Hisce autem inventis, Trajectoria describetur ut in casu primo Problematis superioris. Q.E.F.
inter BH & HD ad mediam proportionalem inter BK & KD; & IS ad LS ut est media proportionalis inter CI & ID ad mediam proportionalem inter CL & LD. Age RS secantem tangentes in A & P, & erunt A & P puncta contractus. Nam si per punctorum H, I, K, L quodvis I agatur recta IY tangenti KL parallela & occurrens curvæ in X & Y, & in ea sumatur IZ media proportionalis inter IX & IY: erit, ex Conicis, rectangulum XIY (seu IZ quad.) ad LP quad. ut rectangulum CID ad rectangulum CLD; id est (per constructionem) ut SI quad. ad SL quad. atque adeo IZ ad LP ut SI ad SL. Jacent ergo puncta S, P, Z in una recta. Porro tangentibus concurrentibus in G, erit (ex Conicis) rectangulum XIY (seu IZ quad.) ad IA quad. ut GP quad. ad GA quad., adeoque IZ ad IA ut GP ad GA. Jacent ergo puncta P, Z & A in una recta, adeoque puncta S, P & A sunt in una recta. Et eodem argumento probabitur quod puncta R, P & A sunt in una recta. Jacent igitur puncta contactus A & P in recta SR. Hisce autem inventis, Trajectoria describetur ut in casu primo Problematis superioris. Q.E.F.
Lemma XXII.
Figuras in alias ejusdem generis figuras mutare.
Transmutanda sit figura quævis HGI. Ducantur pro lubitu rectæ duæ parallelæ AO, BL tertiam quamvis positione datam AB secantes in A 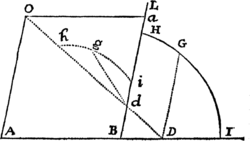 & B, & a figuræ puncto quovis G, ad rectam AB ducatur GD, ipsi OA parallela. Deinde a puncto aliquo O in linea OA dato ad punctum D ducatur recta OD, ipsi BL occurrens in d; & a puncto occursus erigatur recta gd, datum quemvis angulum cum recta BL continens, atque eam habens rationem ad Od quam habet GD ad OD; & erit g punctum in figura nova hgi puncto G respondens. Eadem ratione puncta singula figuræ primæ dabunt puncta totidem figuræ novæ. Concipe igitur punctum G motu continuo percurrere puncta omnia figuræ primæ, & punctum g motu itidem continuo percurret puncta omnia figuræ novæ & eandem describet. Distinctionis gratia nominemus DG ordinatam primam, dg ordinatam novam; BD abscissam primam, Bd abscissam novam; O polum, OD radium abscindentem, OA radium ordinatum primum & Oa (quo parallelogrammum OABa completur) radium ordinatum novum.
& B, & a figuræ puncto quovis G, ad rectam AB ducatur GD, ipsi OA parallela. Deinde a puncto aliquo O in linea OA dato ad punctum D ducatur recta OD, ipsi BL occurrens in d; & a puncto occursus erigatur recta gd, datum quemvis angulum cum recta BL continens, atque eam habens rationem ad Od quam habet GD ad OD; & erit g punctum in figura nova hgi puncto G respondens. Eadem ratione puncta singula figuræ primæ dabunt puncta totidem figuræ novæ. Concipe igitur punctum G motu continuo percurrere puncta omnia figuræ primæ, & punctum g motu itidem continuo percurret puncta omnia figuræ novæ & eandem describet. Distinctionis gratia nominemus DG ordinatam primam, dg ordinatam novam; BD abscissam primam, Bd abscissam novam; O polum, OD radium abscindentem, OA radium ordinatum primum & Oa (quo parallelogrammum OABa completur) radium ordinatum novum.
Dico jam quod si punctum G tangit rectam lineam positione datam, punctum g tanget etiam lineam rectam positione datam. Si punctum G tangit Conicam sectionem, punctum g tanget etiam conicam sectionem. Conicis sectionibus hic circulum annumero. Porro si punctum G tangit lineam tertii ordinis Analytici, punctum g tanget lineam 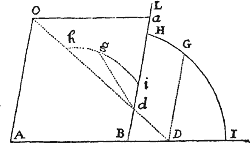 tertii itidem ordinis; & sic de curvis lineis superiorum ordinum: Lineæ duæ erunt ejusdem semper ordinis Analytici quas puncta G, g tangunt. Etenim ut est ad ad OA ita sunt Od ad OD, dg ad DG, & AB ad AD; adeoque AD æqualis est & DG æqualis est . Jam si punctum D tangit rectam lineam, atque adeo in æquatione quavis, qua relatio inter abscissam AD & ordinatam DG habetur, indeterminatæ illæ AD & DG ad unicam tantum dimensionem ascendunt, scribendo in hac æquatione pro AD, & pro DG, producetur æquatio nova, in qua abscissa nova ad & ordinata noua dg ad unicam tantum dimensionem ascendent, atque adeo quæ designat lineam rectam. Sin AD & DG (vel earum alterutra) ascendebant ad duas dimensiones in æquatione prima, ascendent itidem ad & dg ad duas in æquatione secunda. Et sic de tribus vel pluribus dimensionibus. Indeterminatæ ad, dg in æquatione secunda & AD, DG in prima ascendent semper ad eundem dimensionum numerum, & propterea lineæ, quas puncta G, g tangunt, sunt ejusdem ordinis Analytici.
tertii itidem ordinis; & sic de curvis lineis superiorum ordinum: Lineæ duæ erunt ejusdem semper ordinis Analytici quas puncta G, g tangunt. Etenim ut est ad ad OA ita sunt Od ad OD, dg ad DG, & AB ad AD; adeoque AD æqualis est & DG æqualis est . Jam si punctum D tangit rectam lineam, atque adeo in æquatione quavis, qua relatio inter abscissam AD & ordinatam DG habetur, indeterminatæ illæ AD & DG ad unicam tantum dimensionem ascendunt, scribendo in hac æquatione pro AD, & pro DG, producetur æquatio nova, in qua abscissa nova ad & ordinata noua dg ad unicam tantum dimensionem ascendent, atque adeo quæ designat lineam rectam. Sin AD & DG (vel earum alterutra) ascendebant ad duas dimensiones in æquatione prima, ascendent itidem ad & dg ad duas in æquatione secunda. Et sic de tribus vel pluribus dimensionibus. Indeterminatæ ad, dg in æquatione secunda & AD, DG in prima ascendent semper ad eundem dimensionum numerum, & propterea lineæ, quas puncta G, g tangunt, sunt ejusdem ordinis Analytici.
Dico præterea quod si recta aliqua tangat lineam curvam in figura prima; hæc recta translata tanget lineam curvam in figura nova: & contra. Nam si Curvæ puncta quævis duo accedunt ad invicem & coeunt in figura prima, puncta eadem translata coibunt in figura nova, atque adeo rectæ, quibus hæc puncta junguntur simul, evadent curvarum tangentes in figura utraque. Componi possent harum assertionum Demonstrationes more magis Geometrico. Sed brevitati consulo.
Igitur si figura rectilinea in aliam transmutanda est, sussicit rectarum intersectiones transferre, & per easdem in figura nova lineas rectas ducere. Sin curvilineam transmutare oportet, transferenda sunt puncta, tangentes & aliæ rectæ quarum ope Curva linea definitur. Inservit autem hoc Lemma solutioni difficiliorum Problematum, transmutando figuras propositas in simpliciores. Nam rectæ quævis convergentes transmutantur in parallelas, adhibendo pro radio ordinato primo AO lineam quamvis rectam, quæ per concursum convergentium transit: id adeo quia concursus ille hoc pacto abit in infinitum, lineæ autem parallelæ sunt quæ ad punctum infinite distans tendunt. Postquam autem Problema solvitur in figura nova, si per inversas operationes transmutetur hæc figura in figuram primam, habebitur Solutio quæsita.
Utile est etiam hoc Lemma in solutione Solidorum problematum. Nam quoties duæ sectiones conicæ obvenerint, quarum intersectione Problema solvi potest, transmutare licet unum earum in circulum. Recta item & sectio Conica in constructione planorum problematum vertuntur in rectam & circulum.
Prop. XXV. Prob. XVII.
Trajectoriam describere quæ per data duo puncta transibit & rectas tres continget positione datas.
Per concursum tangentium quarumvis duarum cum se invicem, & concursum tangentis tertiæ cum recta illa, quæ per puncta duo data transit, age rectam infinitam; eaque adhibita pro radio ordinato primo, transmutetur figura, per Lemma superius, in figuram novam. In hac figura tangentes illæ duæ evadent parallelæ, & tangens tertia fiet parallela rectæ per puncta duo transeunti. Sunto 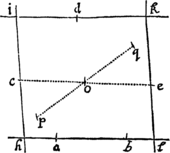 hi, kl tangentes duæ parallelæ, ik tangens tertia, & hl recta huic parallela transiens per puncta illa a, b, per quæ Conica sectio in hac figura nova transire debet, & parallelogrammum hikl complens. Secentur rectæ hi, ik, kl in c, d & e, ita ut sit hc ad latus quadratum rectanguli ahb, ic ad id, & ke ad kd ut est summa rectarum hi & kl ad summam trium linearum quarum prima est recta ik, & alteræ duæ sunt latera quadrata rectangulorum ahb & alb: Et erunt c, d, e puncta contactus. Etenim, ex Conicis, sunt hc quadratum ad rectangulum ahb, & ic quadratum ad id quadratum, & ke quadratum ad kd quadratum, & el quadratum ad alb rectangulum in eadem ratione, & propterea hc ad latus quadratum ipsius ahb, ic ad id, ke ad kd & el ad latus quadratum ipsius alb sunt in dimidiata illa ratione, & composite, in data ratione omnium antecedentium hi & kl ad omnes consequentes, quæ sunt latus quadratum rectanguli ahb & recta ik & latus quadratum rectanguli alb. Habentur igitur ex data illa ratione puncta contactus c, d, e, in figura nova. Per inversas operationes Lemmatis novissimi transferantur hæc puncta in figuram primam & ibi, per casum primum Problematis XIV, describetur Trajectoria. Q.E.F. Cæterum perinde ut puncta a, b jacent vel inter puncta h, l, vel extra, debent puncta c, d, e vel inter puncta h, i, k, l capi, vel extra. Si punctorum a, b alterutrum cadit inter puncta h, l, & alterum extra, Problema impossibile est.
hi, kl tangentes duæ parallelæ, ik tangens tertia, & hl recta huic parallela transiens per puncta illa a, b, per quæ Conica sectio in hac figura nova transire debet, & parallelogrammum hikl complens. Secentur rectæ hi, ik, kl in c, d & e, ita ut sit hc ad latus quadratum rectanguli ahb, ic ad id, & ke ad kd ut est summa rectarum hi & kl ad summam trium linearum quarum prima est recta ik, & alteræ duæ sunt latera quadrata rectangulorum ahb & alb: Et erunt c, d, e puncta contactus. Etenim, ex Conicis, sunt hc quadratum ad rectangulum ahb, & ic quadratum ad id quadratum, & ke quadratum ad kd quadratum, & el quadratum ad alb rectangulum in eadem ratione, & propterea hc ad latus quadratum ipsius ahb, ic ad id, ke ad kd & el ad latus quadratum ipsius alb sunt in dimidiata illa ratione, & composite, in data ratione omnium antecedentium hi & kl ad omnes consequentes, quæ sunt latus quadratum rectanguli ahb & recta ik & latus quadratum rectanguli alb. Habentur igitur ex data illa ratione puncta contactus c, d, e, in figura nova. Per inversas operationes Lemmatis novissimi transferantur hæc puncta in figuram primam & ibi, per casum primum Problematis XIV, describetur Trajectoria. Q.E.F. Cæterum perinde ut puncta a, b jacent vel inter puncta h, l, vel extra, debent puncta c, d, e vel inter puncta h, i, k, l capi, vel extra. Si punctorum a, b alterutrum cadit inter puncta h, l, & alterum extra, Problema impossibile est.
Prop. XXVI. Prob. XVIII.
Trajectoriam describere quæ transibit per punctum datum & rectas quatuor positione datas continget.
Ab intersectione communi duarum quarumlibet tangentium ad intersectionem communem reliquarum duarum agatur recta infinita, & eadem pro radio ordinato primo adhibita, transmutetur figura (per Lem. XXII) in figuram novam, & Tangentes binæ, quæ ad radium ordinatum concurrebant, jam evadent parallelæ. Sunto illæ hi & kl, ik & hl continentes parallelogrammum hikl. Sitque p punctum in hac nova figura, puncto in figura prima dato respondens. Per figuræ centrum O agatur pq, & existente Oq æquali Op, erit q punctum alterum per quod sectio Conica in hac figura nova transire debet. Per Lemmatis XXII operationem inversam transferatur hoc punctum in figuram primam, & ibi habebuntur puncta duo per quæ Trajectoria describenda est. Per eadem vero describi potest Trajectoria illa per Prob. XVII. Q.E.F.
Lemma XXIII.
Si rectæ duæ positione datæ AC, 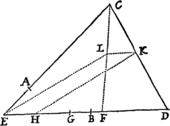 BD ad data puncta A, B terminentur, datamque habeant rationem ad invicem, & recta CD, qua puncta indeterminata C, D junguntur, secetur in ratione data in K: dico quod punctum K locabitur in recta positione data.
BD ad data puncta A, B terminentur, datamque habeant rationem ad invicem, & recta CD, qua puncta indeterminata C, D junguntur, secetur in ratione data in K: dico quod punctum K locabitur in recta positione data.
Concurrant enim rectæ, AC, BD in E, & in BE capiatur BG ad AE ut est BD ad AC, sitque FD æqualis EG, & erit EC ad GD, hoc est ad EF ut AC ad BD, adeoque in ratione data, & propterea dabitur specie ttiangulum EFC. Secetur CF in L in ratione CK ad CD, & dabitur 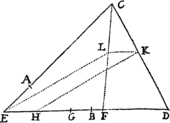 etiam specie triangulum EFL, proindeque punctum L locabitur in recta EL positione data. Junge LK, & ob datam FD & datam rationem LK ad FD, dabitur LK. Huic æqualis capiatur EH, & erit ELKH parallelogrammum. Locatur igitur punctum K in parallelogrammi latere positione dato HK. Q.E.D.
etiam specie triangulum EFL, proindeque punctum L locabitur in recta EL positione data. Junge LK, & ob datam FD & datam rationem LK ad FD, dabitur LK. Huic æqualis capiatur EH, & erit ELKH parallelogrammum. Locatur igitur punctum K in parallelogrammi latere positione dato HK. Q.E.D.
Lemma. XXIV.
Si rectæ tres tangant quamcunque conisectionem, quarum duæ parallelæ sint ac dentur positione; dico quod sectionis semidiameter hisce duabus parallela, sit media proportionalis 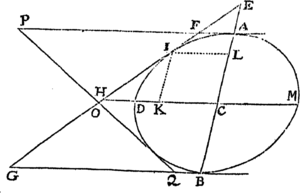 inter harum segmenta, punctis contactuum & tangenti tertiæ interjecta.
inter harum segmenta, punctis contactuum & tangenti tertiæ interjecta.
Sunto AF, GB parallelæ duæ Conisectionem ADB tangentes in A & B; EF recta tertia Conisectionem tangens in I, & occurrens prioribus tangentibus in F & G ; sitque C D semidiameter Figuræ tangentibus parallela: Dico quod AF, CD, BG sunt continue proportionales.
Nam si diametri conjugatæ, AB, DM tangenti FG occurrant in E & H, seque mutuo secent in C, & compleatur parallelogrammum IKCL; erit ex natura sectionum Conicarum, ut EC ad CA ita CA ad LC, & ita divisim EC−CA ad CA−CL seu EA ad AL, & composite EA ad EA+AL seu EL ut EC ad EC+CA seu EB; adeoque (ob similitudinem triangulorum EAF, ELI, ECH, EBG) AF ad LI ut CH ad BG. Est itidem ex natura sectionum Conicarum LI seu CK ad CD ut CD ad CH, atque adeo ex æquo perturbate AF ad CD ut CD ad BG. Q.E.D.
Corol. 1. Hinc si tangentes duæ FG, PQ tangentibus parallelis AF, B G occurrant in F & G,P & Q, seque mutuo secent in O, erit (ex æquo perturbate ) AF ad BQ ut AP ad BG, & divisim ut FP ad GQ, atque adeo ut FO ad OG.
Corol. 2. Unde etiam rectæ duæ PG, FQ per puncta P & G, F & Q ductæ, concurrent ad rectam ACB per centrum figuræ & puncta contactuum A, B transeuntem.
Lemma XXV.
Si parallelogrammi latera quatuor infinite producta tangant sectionem quamcunque Conicam, 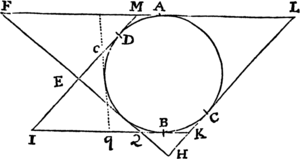 & abscindantur ad tangentem quamvisquintam; sumantur autem abscissæ terminatæ ad angulos oppositos parallelogrammi: dico quod abscissa unius lateris sit ad latus illud, ut pars lateris contermini inter punctum contactus & latus tertium, ad abscissam lateris hujus contermini.
& abscindantur ad tangentem quamvisquintam; sumantur autem abscissæ terminatæ ad angulos oppositos parallelogrammi: dico quod abscissa unius lateris sit ad latus illud, ut pars lateris contermini inter punctum contactus & latus tertium, ad abscissam lateris hujus contermini.
Tangant parallelogrammi MIKL latera quatuor ML, IK, KL, MI sectionem Conicam in A, B, C, D, & secet tangens quinta FQ hæc latera in F, Q, H & E: dico quod sit ME ad MI ut BK ad KQ, 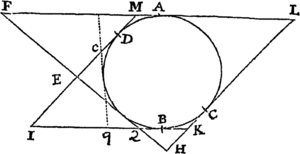 & KH ad KL ut AM ad MF. Nam per Corollarium Lemmatis superioris, est ME ad EI ut AM seu BK ad BQ, & componendo ME ad MI ut BK ad KQ. Q.E.D. Item KH ad HL ut BK seu AM ad AF, & dividendo KH ad KL ut AM ad MF. QE.D.
& KH ad KL ut AM ad MF. Nam per Corollarium Lemmatis superioris, est ME ad EI ut AM seu BK ad BQ, & componendo ME ad MI ut BK ad KQ. Q.E.D. Item KH ad HL ut BK seu AM ad AF, & dividendo KH ad KL ut AM ad MF. QE.D.
Corol. 1. Hinc si parallelogrammum IKLM datur, dabitur rectangulum , ut & huic æquale rectangulum . Æquantur enim rectangula illa ob similitudinem triangulorum KQH, MFE.
Corol. 2. Et si sexta ducatur tangens eq tangentibus KI, MI occurrens in e & q, rectangulum æquabitur rectangulo , eritque KQ ad Me ut Kq ad ME, & divisim ut Qq ad Ee.
Corol. 3. Unde etiam si Eq, eQ jungantur & bisecentur, & recta per puncta bisectionum agatur, transibit hæc per centrum Sectionis Conicæ. Nam cum sit Qq ad Ee ut KQ ad Me, transibit eadem recta per medium omnium Eq, eQ, MK; (per Lemma XXIII) & medium rectæ MK est centrum Sectionis.
Prop. XXVII. Prob. XIX.
Trajectoriam describere quæ rectas quinque positione datas continget.
Dentur positione tangentes ABG, BCF, GCD, FDE, EA. Figuræ quadrilateræ sub quatuor quibusvis contentæ AB FE diagonales AF, BE biseca, & (per Cor. 3. Lem. XXV) recta per puncta bisectionum acta transibit per centrum Trajectoriæ. Rursus figuræ quadrilateræ BGDF, sub alijs quibusvis quatuor tangentibus 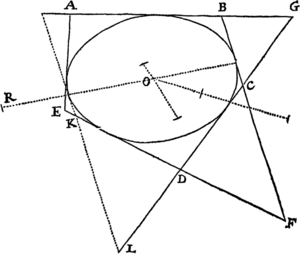 contentæ, diagonales (ut ita dicam) BD, GF biseca, & recta per puncta bisectionum acta transibit per centrum sectionis. Dabitur ergo centrum in concursu bisecantium. Sit illud O. Tangenti cuivis BC parallelam age KL, ad eam distantiam ut centrum O in medio inter parallelas locetur, & acta KL tanget trajectoriam describendam. Secet hæc tangentes alias quasvis duas CD, FDE in L & K. Per tangentium non parallelarum CL, FK cum parallelis CF, KL concursus C & K, F & L age CK, FL concurrentes in R, & recta OR ducta & producta secabit tangentes parallelas CF, KL in punctis contactuum. Patet hoc per Corol. 2. Lem. XXIV. Eadem methodo invenire licet alia contactuum puncta, & tum demum per Casum 1. Prob. XIV. Trajectoriam describere. Q.E.F.
contentæ, diagonales (ut ita dicam) BD, GF biseca, & recta per puncta bisectionum acta transibit per centrum sectionis. Dabitur ergo centrum in concursu bisecantium. Sit illud O. Tangenti cuivis BC parallelam age KL, ad eam distantiam ut centrum O in medio inter parallelas locetur, & acta KL tanget trajectoriam describendam. Secet hæc tangentes alias quasvis duas CD, FDE in L & K. Per tangentium non parallelarum CL, FK cum parallelis CF, KL concursus C & K, F & L age CK, FL concurrentes in R, & recta OR ducta & producta secabit tangentes parallelas CF, KL in punctis contactuum. Patet hoc per Corol. 2. Lem. XXIV. Eadem methodo invenire licet alia contactuum puncta, & tum demum per Casum 1. Prob. XIV. Trajectoriam describere. Q.E.F.
Schol.
Problemata, ubi dantur Trajectoriarum vel centra vel Asymptoti, includuntur in præcedentibus. Nam datis punctis & tangentibus una cum centro, dantur alia totidem puncta aliæque tangentes a centro ex altera ejus parte æqualiter distantes. Asymptotos autem pro tangente habenda est, & ejus terminus infinite distans (si ita loqui fas sit) pro puncto contactus. Concipe tangentis cujusvis punctum contactus abire in infinitum, & tangens vertetur in Asymptoton, atque constructiones Problematis XV & Casus primi Problematis XIV vertentur in constructiones Problematum ubi Asymptoti dantur.
Postquam Trajectoria descripta est, invenire licet axes & umbilicos ejus hac methodo. In constructione & Figura Lemmatis XXI, fac ut angulorum mobilium 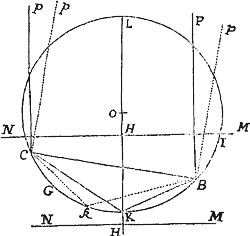 PBN, PCN crura BP, CP quorum concursu Trajectoria describebatur sint sibi invicem parallela, eumque servantia situm revolvantur circa polos suos B, C in figura illa. Interea vero describant altera angulorum illorum crura CN, BN, concursu suo K vel k, circulum IBKGC. Sit circuli hujus centrum O. Ab hoc centro ad Regulam MN, ad quam altera illa crura CN, BN interea concurrebant dum Trajectoria describebatur, demitte normalem OH circulo occurrentem in K & L. Et ubi crura illa altera CK, BK concurrunt ad punctum istud K quod Regulæ propius est, crura prima CP, BP parallela erunt axi majori; & contrarium eveniet si crura eadem concurrunt ad punctum remotius L. Unde si detur Trajectoriæ centrum, dabuntur axes. Hisce autem datis, umbilici sunt in promptu.
PBN, PCN crura BP, CP quorum concursu Trajectoria describebatur sint sibi invicem parallela, eumque servantia situm revolvantur circa polos suos B, C in figura illa. Interea vero describant altera angulorum illorum crura CN, BN, concursu suo K vel k, circulum IBKGC. Sit circuli hujus centrum O. Ab hoc centro ad Regulam MN, ad quam altera illa crura CN, BN interea concurrebant dum Trajectoria describebatur, demitte normalem OH circulo occurrentem in K & L. Et ubi crura illa altera CK, BK concurrunt ad punctum istud K quod Regulæ propius est, crura prima CP, BP parallela erunt axi majori; & contrarium eveniet si crura eadem concurrunt ad punctum remotius L. Unde si detur Trajectoriæ centrum, dabuntur axes. Hisce autem datis, umbilici sunt in promptu.
Axium vero quadrata sunt ad invicem ut KH ad LH, & inde facile est Trajectoriam specie datam per data quatuor puncta describere. Nam si duo ex punctis datis constituantur poli C, B, tertium dabit angulos mobiles PCK, PBK. Tum ob datam specie Trajectoriam, dabitur ratio OH ad OK, centroque O & intervallo OH describendo circulum, & per punctum quartum agendo rectam quæ circulum illum tangat, dabitur regula MN cujus ope Trajectoria describetur. Unde etiam vicissim Trapezium specie datum (si casus quidam impossibiles excipiantur) in data quavis sectione Conica inscribi potest.
Sunt & alia Lemmata quorum ope Trajectoriæ specie datæ datis punctis & tangentibus, describi possunt. Ejus generis est quod, si recta linea per punctum quodvis positione datum ducatur, quæ datam Conisectionem in punctis duobus intersecet, & intersectionum intervallum bisecetur, punctum bisectionis tanget aliam Conisectionem ejusdem speciei cum priore, atque axes habentem prioris axibus parallelos. Sed propero ad magis utilia.
Lemma XXVI.
Trianguli specie & magnitudine dati tres angulos ad rectas totidem positione datas, quæ non sunt omnes parallelæ, singulos ad singulas ponere.
Dantur positione tres rectæ infinitæ AB, AC, BC, & oportet triangulum DEF ita locare, ut angulus ejus D lineam AB, angulus E lineam AC, & angulus F lineam BC tangat. Super DE, DF & EF describe tria circulorum segmenta DRE, DGF, EMF, quæ capiant angulos 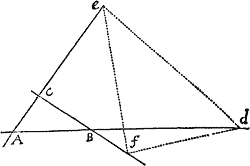 angulis BAC, ABC, ACB æquales respective. Describantur autem hæc segmenta ad eas partes linearum DE, DF, EF ut literæ DRED eodem ordine cum literis BACB, literæ DGFD eodem cum literis ABCA, & literæ EMFE eodem cum literis ACBA in orbem redeant: deinde compleantur hæc segmenta in circulos. Secent circuli duo priores se mutuo in G, sintque centra eorum
angulis BAC, ABC, ACB æquales respective. Describantur autem hæc segmenta ad eas partes linearum DE, DF, EF ut literæ DRED eodem ordine cum literis BACB, literæ DGFD eodem cum literis ABCA, & literæ EMFE eodem cum literis ACBA in orbem redeant: deinde compleantur hæc segmenta in circulos. Secent circuli duo priores se mutuo in G, sintque centra eorum 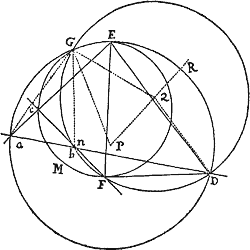 P & Q. Junctis GP, PQ, cape Ga ad AB ut est GP ad PQ, & centro G, intervallo Ga describe circulum, qui secet circulum primum DGE in a. Jungatur tum aD secans circulum secundum DFG in b, tum aE secans circulum tertium GEc in c. Et compleatur figura abcDEF similis & æqualis figuræ ABCdef. Dico factum.
P & Q. Junctis GP, PQ, cape Ga ad AB ut est GP ad PQ, & centro G, intervallo Ga describe circulum, qui secet circulum primum DGE in a. Jungatur tum aD secans circulum secundum DFG in b, tum aE secans circulum tertium GEc in c. Et compleatur figura abcDEF similis & æqualis figuræ ABCdef. Dico factum.
Agatur enim Fc ipsi aD occurrens in n. Jungantur aG, bG, PD, QD & producatur PQ ad R. Ex constructione est angulus EaD æqualis angulo CAB, & angulus EcF æqualis angulo ACB, adeoque triangulum anc triangulo ABC æquiangulum. Ergo angulus anc seu FnD angulo ABC, adeoque angulo FbD æqualis est, & propterea punctum n incidit in punctum b. Porro angulus GPQ, qui dimidius est anguli ad centrum GPD, æqualis est angulo ad circumferentiam GaD; & angulus GQR, qui dimidius est complementi anguli ad centrum GQD, æqualis est angulo ad circumferentiam GbD, adeoque eorum complementa PQG, abG æquantur, suntque ideo triangula GPQ, Gab similia, & Ga est ad ab ut GP ad PQ; id est (ex constructione) ut Ga ad AB. Æquantur itaque ab & AB & propterea triangula abc, ABC, quæ modo similia esse probavimus, sunt etiam æqualia. Unde cum tangant insuper trianguli DEF anguli D, E, F trianguli abc latera ab, ac, bc respective, compleri potest figura ABC def figuræ abc DEF similis & æqualis, atque eam complendo solvetur Problema. Q.E.F.
Corol. Hinc recta duci potest cujus partes longitudine datæ rectis tribus positione datis interjacebunt. Concipe Triangulum DEF, puncto D ad latus EF accedente, & lateribus DE, DF in directum positis, mutari in lineam rectam, cujus pars data DE, rectis positione datis AB, AC, & pars data DF rectis positione datis AB, BC interponi debet; & applicando constructionem præcedentem ad hunc casum solvetur Problema.
Prop. XXVIII. Prob. XX.
Trajectoriam specie & magnitudine datam describere, cujus partes datæ rectis tribus positione datis interjacebunt.
Describenda sit Trajectoria quæ sit similis & æqualis lineæ curvæ DEF, quaque a rectis tribus AB, AC, BC positione datis, in partes datis hujus partibus DE & EF similes & æquales secabitur.
Age rectas DE, EF, DF, & trianguli hujus DEF pone angulos 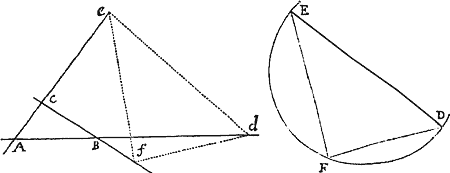 D, E, F ad rectas illas positione datas: (per Lem. XXVI) Dein circa triangulum describe Trajectoriam curvæ DEF similem & æqualem. Q.E.F.
D, E, F ad rectas illas positione datas: (per Lem. XXVI) Dein circa triangulum describe Trajectoriam curvæ DEF similem & æqualem. Q.E.F.
Lemma XXVII.
Trapezium specie datum describere cujus anguli ad rectas quatuor positione datas (quæ neque omnes parallelæ sunt, neque ad commune punctum convergunt) singuli ad singulas consistent.
Dentur positione rectæ quatuor ABC, AD, BD, CE, quarum prima secet secundam in A, tertiam in B, & quartam in C: & describendum sit Trapezium fghi quod sit Trapezio FGHI simile, & cujus angulus f, angulo dato F æqualis, tangat rectam ABC, cæterique anguli g, h, i cæteris angulis datis G, H, I æquales tangant cæteras lineas AD, BD, CE respective. Jungatur FH, & super FG, FH, FI describantur totidem circulorum segmenta FSG, FTH, FVI; quorum primum FSG capiat angulum æqualem angulo BAD, secundum FTH capiat angulum æqualem angulo CBE; ac tertium FVI capiat angulum æqualem angulo AC E. Describi autem debent segmenta ad eas partes linearum FG, FH, FI, ut literarum FSGF idem sit ordo circularis qui literarum BADB, utque literæ FTHF eodem ordine cum literis CBEC, & literæ FVIF eodem cum literis ACEA in orbem redeant. Compleantur segmenta in circulos, sirque P centrum circuli primi FSG, & Q centrum secundi FTH. Jungatur & utrinque 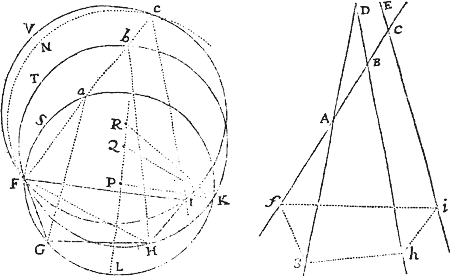 producatur PQ, & in ea capiatur QR in ea ratione ad PQ quam habet BC ad AB. Capiatur autem QR ad eas partes puncti Q ut literarum P, Q, R idem sit ordo circularis atque literarum A, B, C: centroque R & intervallo RF describatur circulus quartus FNc secans circulum tertium FVI in c. Jungatur Fc secans circulum primum in a & secundum in b. Agantur aG, bH, cI, & figuræ abcFGHI similis constituatur figura ABCfghi: Eritque Trapezium fghi illud ipsum quod constituere oportuit.
producatur PQ, & in ea capiatur QR in ea ratione ad PQ quam habet BC ad AB. Capiatur autem QR ad eas partes puncti Q ut literarum P, Q, R idem sit ordo circularis atque literarum A, B, C: centroque R & intervallo RF describatur circulus quartus FNc secans circulum tertium FVI in c. Jungatur Fc secans circulum primum in a & secundum in b. Agantur aG, bH, cI, & figuræ abcFGHI similis constituatur figura ABCfghi: Eritque Trapezium fghi illud ipsum quod constituere oportuit.
Secent enim circuli duo primi FSG, FTH se mutuo in K. Jungantur PK, QK, RK, aK, bK, cK & producatur QP ad L. Anguli ad circumferentias FaK, FbK, FcK sunt semisses angulorum FPK, FQK, FRK ad centra, adeoque angulorum illorum dimidiis LPK, LQK, LRK æquales. Est ergo figura PQRK figuræ abcK æquiangula & similis, & propterea ab est ad bc ut PQ ad QR, id est ut AB ad BC. Angulis insuper FaG, FbH, FcI æquantur fAg, fBh, fCi per constructionem. 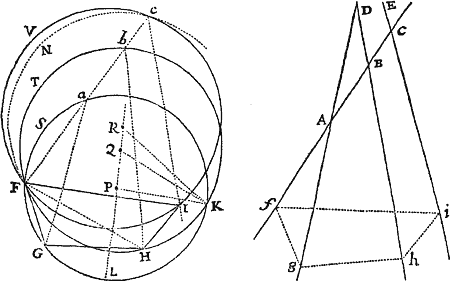 Ergo figuræ abc FGHI figura similis ABCfghi compleri potest. Quo facto Trapezium fghi constituetur simile Trapezio FGHI & angulis suis f, g, h, i tanget rectas AB, AD, BD, CE. Q.E.F.
Ergo figuræ abc FGHI figura similis ABCfghi compleri potest. Quo facto Trapezium fghi constituetur simile Trapezio FGHI & angulis suis f, g, h, i tanget rectas AB, AD, BD, CE. Q.E.F.
Corol. Hinc recta duci potest cujus partes, rectis quatuor positione datis dato ordine interjectæ, datam habebunt proportionem ad invicem. Augeantur anguli FGH, GHI usque eo, ut rectæ FG, GH, HI in directum jaceant, & in hoc casu construendo Problema, ducetur recta fghi cujus partes fg, gh, hi, rectis quatuor positione datis AB & AD, AD & BD, BD & CE interjectæ, erunt ad invicem ut linea FG, GH, HI, eundemque servabunt ordinem inter se. Idem vero sic fit expeditius.
<101>Producantur AB ad K, & BD ad L, ut sit BK ad AB ut HI ad GH; & DL ad BD ut GI ad FG; & jungatur KL occurrens rectæ CE in i. Producatur iL ad M, ut sit LM ad iL ut GH ad HI, & agatur tum MQ ipsi LB parallela rectæque AD occurrens in g, tum gi secans AB, BD in f, h. Dico factum.
Secet enim Mg rectam 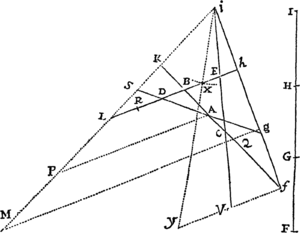 AB in Q, & AD rectam KL in S, & agatur AP, quæ sit ipsi BD parallela & occurat iL in P, & erunt Mg ad Lh (Mi ad Li, gi ad hi, AK ad BK) & AP ad BL in eadem ratione. Secetur DL in R ut sit DL ad RL in eadem illa ratione, & ob proportionales gS ad gM, AS ad AP, & DS ad DL, erit ex
æquo ut gS ad Lh ita AS ad BL & DS ad RL; & mixtim, BL−RL ad Lh−BL ut AS−DS ad gS−AS. Id est BR ad Bh ut AD ad Ag, adeoque ut BD ad gQ. Et vicissim BR ad BD ut Bh ad gQ seu fh ad fg. Sed ex constructione est BR ad BD ut FH ad FG. Ergo fh est ad fg ut FH ad FG. Cum igitur sit etiam ig ad ih ut Mi ad Li, id est, ut IG ad IH, patet lineas FI, fi in g & h, G & H similiter sectas esse. Q.E.F.
AB in Q, & AD rectam KL in S, & agatur AP, quæ sit ipsi BD parallela & occurat iL in P, & erunt Mg ad Lh (Mi ad Li, gi ad hi, AK ad BK) & AP ad BL in eadem ratione. Secetur DL in R ut sit DL ad RL in eadem illa ratione, & ob proportionales gS ad gM, AS ad AP, & DS ad DL, erit ex
æquo ut gS ad Lh ita AS ad BL & DS ad RL; & mixtim, BL−RL ad Lh−BL ut AS−DS ad gS−AS. Id est BR ad Bh ut AD ad Ag, adeoque ut BD ad gQ. Et vicissim BR ad BD ut Bh ad gQ seu fh ad fg. Sed ex constructione est BR ad BD ut FH ad FG. Ergo fh est ad fg ut FH ad FG. Cum igitur sit etiam ig ad ih ut Mi ad Li, id est, ut IG ad IH, patet lineas FI, fi in g & h, G & H similiter sectas esse. Q.E.F.
In constructione Corollarii hujus postquam ducitur LK secans CE in i, producere licet iE ad V, ut sit EV ad iE ut FH ad HI, & agere Vf parallelam ipsi BD. Eodem recidit si centro i, intervallo IH describatur circulus secans BD in X, producatur iX ad Y, ut sit iY æqualis IF, & agatur Yf ipsi BD parallela.
Prop. XXIX. Prob. XIX.
Trajectoriam specie datam describere, quæ a rectis quatuor positione datis in partes secabitur, ordine, specie & proportione datas.
Describenda sit Trajectoria fghi, quæ similis sit lineæ curvæ FGHI, & cujus partes fg, gh, hi illius partibus FG, GH, HI similes & 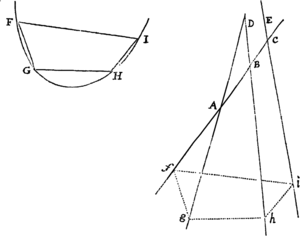 proportionales, rectis AB & AD AD & BD, BD & EC positione datis, prima primis, secunda secundis, tertia tertiis interjaceant. Actis rectis FG, GH, HI, FI, describatur Trapezium fghi quod sit Trapezio FGHI simile & cujus anguli f, g, h, i tangant rectas illas positione datas AB, AD, BD, CE singuli singulas dicto ordine. Dein (per Lem. XXVII) circa hoc Trapezium describatur Trajectoria curvæ lineæ FGHI consimilis.
proportionales, rectis AB & AD AD & BD, BD & EC positione datis, prima primis, secunda secundis, tertia tertiis interjaceant. Actis rectis FG, GH, HI, FI, describatur Trapezium fghi quod sit Trapezio FGHI simile & cujus anguli f, g, h, i tangant rectas illas positione datas AB, AD, BD, CE singuli singulas dicto ordine. Dein (per Lem. XXVII) circa hoc Trapezium describatur Trajectoria curvæ lineæ FGHI consimilis.
Scholium.
Construi etiam potest hoc Problema ut sequitur. Junctis FG, GH, HI, FI produc GF ad V, jungeque FH, IG, & angulis FGH, VFH fac angulos CAK, DAL æquales. Concurrant AK, AL cum recta BD in K & L, & inde agantur KM, LN, quarum KM constituat angulum AKM æqualem angulo GHI, sitque ad AK ut est HI ad GH; & LN constituat angulum ALN æqualem angulo FHI, sitque ad AL ut HI ad FH. Ducantur autem AK, KM, AL, LN ad eas partes linearum AD, AK, AL, ut literæ CAKMC, ALK, DALND eodem ordine cum literis FGHIF in orbem redeant, & acta MN occurrat rectæ 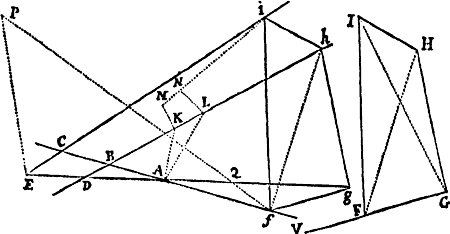 CE in i. Fac angulum iEP æqualem angulo IGF, sitque PE ad Ei ut FG ad GI; & per P agatur QPf, quæ cum recta AED contineat angulum PQE æqualem angulo FIG, rectæque AB occurrat in f, & jungatur fi. Agantur autem PE & PQ ad eas partes linearum CE, PE, ut literarum PEiP & PEQP idem sit ordo circularis qui literarum FGHIF, & si super linea fi eodem quoque literarum ordine constituatur Trapezium fghi Trapezio FGHI simile, & circumscribatur Trajectoria specie data, solvetur Problema.
CE in i. Fac angulum iEP æqualem angulo IGF, sitque PE ad Ei ut FG ad GI; & per P agatur QPf, quæ cum recta AED contineat angulum PQE æqualem angulo FIG, rectæque AB occurrat in f, & jungatur fi. Agantur autem PE & PQ ad eas partes linearum CE, PE, ut literarum PEiP & PEQP idem sit ordo circularis qui literarum FGHIF, & si super linea fi eodem quoque literarum ordine constituatur Trapezium fghi Trapezio FGHI simile, & circumscribatur Trajectoria specie data, solvetur Problema.
Hactenus de orbibus inveniendis. Superest ut motus corporum in orbibus inventis determinemus.
SECT. VI.
De inventione motuum in Orbibus datis.
Prop. XXX. Prob. XXII.
Corporis in data Trajectoria Parabolica moventis, invenire locum ad tempus assignatum.
Sit S umbilicus & A vertex principalis Parabolæ, sitque area Parabolica APS, quæ radio SP, vel post excessum corporis de vertice descripta fuit, vel ante 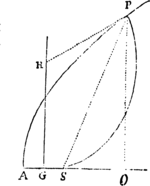 appulsum ejus ad verticem describenda est. Innotescit area illa ex tempore ipsi proportionali. Biseca AS in G, erigeque perpendiculum GH æquale 3 M, & circulus centro H, intervallo HS descriptus secabit Parabolam in loco quasito P. Nam demissa ad axem perpendiculari PO, est Et deleto utrinque HGq. fiet seu scribe , & applicatis terminis omnibus ad , ductisque in , fiet . Sed GH erat 3 M, & inde est . Ergo area APS æqualis est .Q.E.D.
appulsum ejus ad verticem describenda est. Innotescit area illa ex tempore ipsi proportionali. Biseca AS in G, erigeque perpendiculum GH æquale 3 M, & circulus centro H, intervallo HS descriptus secabit Parabolam in loco quasito P. Nam demissa ad axem perpendiculari PO, est Et deleto utrinque HGq. fiet seu scribe , & applicatis terminis omnibus ad , ductisque in , fiet . Sed GH erat 3 M, & inde est . Ergo area APS æqualis est .Q.E.D.
Corol. 1. Hinc GH est ad AS, ut tempus quo corpus descripsit arcum AP ad tempus quo corpus descripsit arcum inter verticem A & perpendiculum ad axem ab umbilico S erectum.
Corol. 2. Et circulo ASP per corpus movens perpetuo transeunte, velocitas puncti G est ad velocitatem quam corpus habuit in vertice A, ut 3 ad 8; adeoque in ea etiam ratione est linea GH ad lineam rectam quam corpus tempore motus sui ab A ad P, ea cum velocitate quam habuit in vertice A, describere posset.
Corol. 3. Hinc etiam viceversa inveniri potest tempus quo corpus descripsit arcum quemvis assignatum AP. Junge AP & ad medium ejus punctum erige perpendiculum rectæ GH occurrens in H.
Lemma XXVIII.
Nulla extat figura Ovalis cujus area, rectis pro lubitu abscissa, possit per æquationes numero terminorum ac dimensionum finitas generaliter inveniri.
Intra Ovalem detur punctum quodvis, circa quod ceu polum revolvatur perpetuo linea recta, & interea in recta illa exeat punctum mobile de polo, pergatque semper ea cum velocitate, quæ sit ut rectæ illius intra Ovalem longitudo. Hoc motu punctum illud describet Spiralem gyris infinitis. Jam si area Oualis per finitam æquationem inveniri potest, invenietur etiam per eandem æquationem distantia puncti a polo, quæ huic areæ proportionalis est, adeoque omnia Spiralis puncta per æquationem finitam inveniri possunt: & propterea rectæ cujusvis positione datæ intersectio cum spirali inveniri etiam potest per æquationem finitam. Atqui recta omnis infinite producta spiralem secat in punctis numero infinitis, & æquatio, qua incersectio aliqua duarum linearum in venitur, exhibet earum intersectiones omnes radicibus totidem, adeoque ascendit ad tot dimensiones quot sunt intersectiones. Quoniam circuli duo se mutuo secant in punctis duobus, intersectio una non invenitur nisi per æquationem duarum dimensionum, qua intersectio altera etiam inveniatur. Quoniam duarum sectionum Conicarum quatuor esse possunt intersectiones, non potest aliqua earum generaliter inveniri nisi per æquationem quatuor dimensionum, qua omnes simul inveniantur. Nam si intersectiones illæ seorsim quærantur, quoniam eadem est omnium lex & conditio, idem erit calculus in casu unoquoque & propterea eadem semper concsusio, quæ igitur debet omnes intersectiones simul complecti & indifferenter exhibere. Unde etiam intersectiones Sectionum Conicarum & curvarum tertiæ potestatis, eo quod sex esse possunt, simul prodeunt per æquationes sex dimensionum, & intersectiones duarum curvarum tertiæ potestatis, quia novem esse possunt, simul prodeunt per æquationes dimensionum novem. Id nisi necessario fieret, reducere liceret Problemata omnia Solida ad Plana, & plusquam solida ad solida. Eadem de causa intersectiones binæ rectarum & sectionum Conicarum prodeunt semper per æquationes duarum dimensionum; ternæ rectarum & curvarum tertiæ potestatis per æquationes trium, quaternæ rectarum & curvarum quartæ potestatis per æquationes dimensionum quatuor, & sic in infinium. Ergo intersectiones numero infinitæ rectarum, propterea quod omnium eadem est lex & idem calculus, requirunt æquationes numero dimensionum & radicum infinitas, quibus omnes possunt simul exhiberi. Si a polo in rectam illam secantem demittatur perpendiculum, & perpendiculum una cum secante revolvatur circa polum, intersectiones spiralis transibunt in se mutuo, quæque prima erat seu proxima, post unam revolutionem secunda erit, post duas tertia, & sic deinceps: nec interea mutabitur a quatio nisi pro mutata magnitudine quantitatum per quas positio secantis determinatur. Unde cum quantitates illæ post singulas revolutiones redeunt ad magnitudines primas, æquatio redibit ad formam primam, adeoque una eademque exhibebit intersectiones omnes, & propterea radices habebit numero infinitas, quibus omnes exhiberi possunt. Nequit ergo intersectio rectæ & spiralis per æquationem finitam generaliter inveniri, & idcirco nulla extat Ovalis cujus area, rectis imperatis abscissa, possit per talem æquationem generaliter exhiberi.
Eodem argumento, si intervallum poli & puncti, quo spiralis describitur, capiatur Ovalis perimetro abscissæ proportionale, probari potest quod longitudo perimetri nequit per finitam æquationem generaliter exhiberi.
Corollarium.
Hinc area Ellipseos, quæ radio ab umbilico ad corpus mobile ducto describitur, non prodit ex dato tempore per æquationem finitam, & propterea per descriptionem Curuarum Geometrice rationalium determinari nequit. Curvas Geometrice rationales appello quarum puncta omnia per longitudines æquationibus definitas, id est, per longitudinum rationes complicatas, determinari possunt; cæterasque (ut Spirales, Quadratrices, Trochoides) Geometrice irrationales. Nam longitudines quæ sunt vel non sunt ut numerus ad numerum (quemadmodum in decimo Elementorum) sunt Arithmetice rationales vel irrationales. Aream igitur Ellipseos tempori proportionalem abscindo per Curvam Geometrice irrationalem ut sequitur.
Prop. XXXI. Prob. XXIII.
Corporis in data Trajectoria Elliptica moventis invenire locum ad tempus assignatum.
Ellipseos APB sit A vertex principalis, S umbilicus, O centrum, sitque P corporis locus inveniendus. Produc OA ad G ut sit OG ad OA ut OA ad OS. Erige perpendiculum GH, centroque O & intervallo OG describe circulum EFG, & super regula GH, ceu fundo, progrediatur rota GEF revolvendo circa axem suum, & interea puncto suo A describendo Trochoidem ALI. Quo facto, cape GK in ratione ad rotæ perimetrum GEFG, ut est tempus quo corpus progrediendo ab A descripsit arcum AP, ad tempus 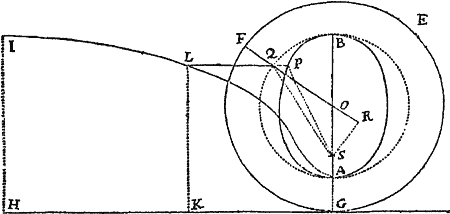 revolutionis unius in Ellipsi. Erigatur perpendiculum KL occurrens Trochoidi in L, & acta LP ipsi KG parallela occurret Ellipsi in corporis loco quæsito P.
revolutionis unius in Ellipsi. Erigatur perpendiculum KL occurrens Trochoidi in L, & acta LP ipsi KG parallela occurret Ellipsi in corporis loco quæsito P.
Nam centro O, intervallo OA describatur semicirculus AQB, & arcui AQ occurrat LP producta in Q, junganturque SQ, OQ. Arcui EFG occurrat OQ in F, & in eandem OQ demittatur perpendiculum SR. Area APS est ut area AQS, id est, ut differentia inter sectorem OQA & triangulum OQS, sive ut differentia rectangulorum & , hoc est, ob datam , ut differentia inter arcum AQ & rectam SR, adeoque (ob æqualitatem rationum SR ad sinum arcus AQ, OS ad OA, OA ad OG, AQ ad GF, & divisim AQ−SR ad GF− sin. arc. AQ) ut GK differentia inter arcum GF & sinum arcus AQ. Q.E.D.
<109>Scholium.
Cæterum ob difficultatem describendi hanc curvam præstat constructiones vero proximas in praxi Mechanica adhibere. Ellipseos cujusvis APB sit AB axis major, O centrum, S umbilicus, OD semiaxis minor, & AK dimidium lateris recti. Secetur AS in G, ut sit AG ad AS ut BO ad BS; & quæratur longitudo L, quæ sit ad ut est AO quad. ad rectangulum . Bisecetur OG in C, centroque C & intervallo CG describatur semicirculus GFO. Denique capiatur angulus GCF in ea ratione ad angulos quatuor 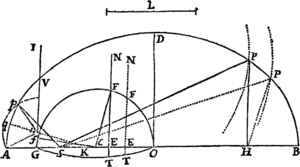 rectos, quam habet tempus datum, quo corpus descripsit arcum quæsitum AP, ad tempus periodicum seu revolutionis unius in Ellipsi: Ad AO demittatur normalis FE, & producatur eadem versus F ad usque N, ut sit EN ad longitudinem L, ut anguli illius sinus EF ad radium CF; centroque N & intervallo AN descriptus circulus secabit Ellipsin in corporis loco quæsito P quam proxime.
rectos, quam habet tempus datum, quo corpus descripsit arcum quæsitum AP, ad tempus periodicum seu revolutionis unius in Ellipsi: Ad AO demittatur normalis FE, & producatur eadem versus F ad usque N, ut sit EN ad longitudinem L, ut anguli illius sinus EF ad radium CF; centroque N & intervallo AN descriptus circulus secabit Ellipsin in corporis loco quæsito P quam proxime.
Nam completo dimidio temporis periodici, corpus P semper reperietur in Apside summa B, & completo altero temporis dimidio, redibit ad Apsidem imam, ut oportet. Ubi vero proxime abest ab Apsidibus, ratio prima nascentium sectorum ASP, GCF, & ratio ultima evanescentium BSP & OCF, eadem est rationi Ellipseos totius ad circulum totum. Nam punctis P, F & N incidentibus in loca p, f & n axi AB quam proximis; ob æquales An, pn, recta nq, quæ ad arcum Ap perpendicularis est, adeoque concurrit cum axe in puncto K, bisecat arcum Ap. Proinde est Ap ad Gn ut AK ad GK, & Ap ad Gn ut 2 AK ad GK. Est & Gn ad Gf ut EN ad EF, seu L ad CF, id est, ut ad CF, seu ad , & ex æquo Ap ad Gf ut ad ad , id est, ut ad , hoc est, ob æqualia > & ODq. ut ad . Proinde est ad ut ad , seu ad CGq. id est, sector nascens ASp ad sectorem nascentem GCf ut ad CGq. & propterea ut area Ellipseos totius ad aream circuli totius. Q.E.D. Argumento prolixiore probari potest analogia ultima in Sectoribus evanescentibus BSP, OCF: ideoque locus puncti P prope Apsides satis accurate 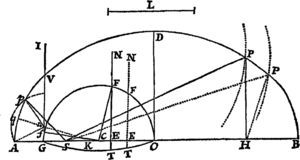 inventus est. In quadraturis error quasi quingentesimæ partis areæ Ellipseos totius vel paulo major obvenire solet: qui tamen propemodum evanescet per ulteriorem Constructionem sequentem.
inventus est. In quadraturis error quasi quingentesimæ partis areæ Ellipseos totius vel paulo major obvenire solet: qui tamen propemodum evanescet per ulteriorem Constructionem sequentem.
Per puncta G, O, duc arcum circularem GTO justæ magnitudinis; dein produc EF hinc inde ad T & N ut sit EN ad FT ut L ad CF; centroque N & intervallo AN describe circulum qui secet Ellipsin in P, ut supra. Arcus autem GTO determinabitur quærendo ejus punctum aliquod T; quod constructionem in illo casu accuratam reddet.
Si Ellipseos latus transversum multo majus sit quam latus rectum, & motus corporis prope verticem Ellipseos desideretur, (qui casus in Theoria Cometarum incidit,) educere licet e puncto G rectam GI axi AB perpendicularem, & in ea ratione ad GK quam habet area AVPS ad rectangulum ; dein centro I & intervallo AI circulum describere. Hic enim secabit Ellipsim in corporis loco quæsito P quamproxime. Et eadem constructione (mutatis mutandis) conficitur Problema in Hyperbola. Hæ autem constructiones demonstrantur ut supra, & si Figura (vertice ulteriore B in infinitum abeunte) vertatur in Parabolam, migrant in accuratam illam constructionem Problematis. XXII.
Si quando locus ille P accuratius determinandus sit, inveniatur tum angulus quidam B, qui sit ad angulum graduum 57,29578 quem arcus radio æqualis subtendit, ut est umbilicorum distantia SH ad Ellipseos diametrum AB; tum etiam longitudo quædam L, quæ sit ad radium in eadem ratione inverse. Quibus semel inventis, Problema deinceps confit per sequentem Analysin. Per constructionem 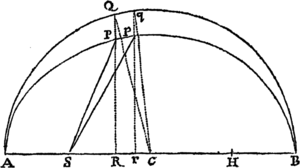 superiorem (vel utcunque conjecturam faciendo) cognoscatur corporis locus P quam proxime. Demissaque ad axem Ellipseos ordinatim applicata PR, ex proportione diametrorum Ellipseos, dabitur circuli circumscripti AQB ordinatim applicata RQ, quæ sinus est anguli ACQ existente AC radio. Sufficit angulum illum rudi calculo in numeris proximis invenire. Cognoscatur etiam angulus tempori porportionalis, id est, qui sit ad quatuor rectos ut est tempus quo corpus descripsit arcum AP, ad tempus revolutionis unius in Ellipsi. Sit angulus iste N. Tum capiatur & angulus D ad angulum B, ut est sinus iste anguli ACQ ad Radium, & angulus E ad angulum , ut est longitudo L ad longitudinem eandem L cosinu anguli diminutam, ubi angulus iste recto minor est, auctam ubi major. Postea capiatur tum augulus F ad angulum B, ut est sinus anguli ad radium, tum angulus G ad angulum ut est longitudo L ad Longitudinem eandem cosinu anguli diminutam ubi angulus iste recto minor est, auctam ubi major. Tertia vice capiatur angulus H ad angulum B, ut est sinus anguli ACQ+E+G ad radium; & angulus I ad angulum N−ACQ−E−G+H, ut est longitudo L ad eandem longitudinem cosinu anguli diminutam, ubi angulus iste recto minor est, auctam
superiorem (vel utcunque conjecturam faciendo) cognoscatur corporis locus P quam proxime. Demissaque ad axem Ellipseos ordinatim applicata PR, ex proportione diametrorum Ellipseos, dabitur circuli circumscripti AQB ordinatim applicata RQ, quæ sinus est anguli ACQ existente AC radio. Sufficit angulum illum rudi calculo in numeris proximis invenire. Cognoscatur etiam angulus tempori porportionalis, id est, qui sit ad quatuor rectos ut est tempus quo corpus descripsit arcum AP, ad tempus revolutionis unius in Ellipsi. Sit angulus iste N. Tum capiatur & angulus D ad angulum B, ut est sinus iste anguli ACQ ad Radium, & angulus E ad angulum , ut est longitudo L ad longitudinem eandem L cosinu anguli diminutam, ubi angulus iste recto minor est, auctam ubi major. Postea capiatur tum augulus F ad angulum B, ut est sinus anguli ad radium, tum angulus G ad angulum ut est longitudo L ad Longitudinem eandem cosinu anguli diminutam ubi angulus iste recto minor est, auctam ubi major. Tertia vice capiatur angulus H ad angulum B, ut est sinus anguli ACQ+E+G ad radium; & angulus I ad angulum N−ACQ−E−G+H, ut est longitudo L ad eandem longitudinem cosinu anguli diminutam, ubi angulus iste recto minor est, auctam 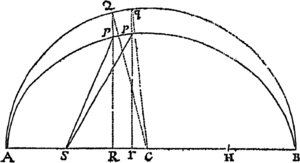 ubi major. Et sic pergere licet in infinitum. Denique capiatur angulus ACq æqualis angulo ACQ+E+G+I &c. & ex cosinu ejus Cr & ordinata pr, quæ est ab sinum qr ut Ellipseos axis minor ad axem majorem, habebitur corporis locus correctus p. Siquando angulus N−ACQ+D negativus est, debet signum + ipsius E ubique mutari in −, & signum − in +. Idem intelligendum est de signis ipsorum G & I, ubi anguli N−ACQ−E+F, & N−ACQ−E−G+H negative prodeunt. Convergit autem series infinita ACQ+E+G+I quam celerrime, adeo ut vix unquam opus fuerit ultra progredi quam ad terminum secundum E. Et fundatur calculus in hoc Theoremate, quod area APS sit ut differentia inter arcum AQ & rectam ab umbilico S in Radium CQ perpendiculariter demissam.
ubi major. Et sic pergere licet in infinitum. Denique capiatur angulus ACq æqualis angulo ACQ+E+G+I &c. & ex cosinu ejus Cr & ordinata pr, quæ est ab sinum qr ut Ellipseos axis minor ad axem majorem, habebitur corporis locus correctus p. Siquando angulus N−ACQ+D negativus est, debet signum + ipsius E ubique mutari in −, & signum − in +. Idem intelligendum est de signis ipsorum G & I, ubi anguli N−ACQ−E+F, & N−ACQ−E−G+H negative prodeunt. Convergit autem series infinita ACQ+E+G+I quam celerrime, adeo ut vix unquam opus fuerit ultra progredi quam ad terminum secundum E. Et fundatur calculus in hoc Theoremate, quod area APS sit ut differentia inter arcum AQ & rectam ab umbilico S in Radium CQ perpendiculariter demissam.
Non dissimili calculo conficitur Problema in Hyperbola. Sit ejus centrum C, Vertex A, Umbilicus S & Asymtotos CK. Cognoscatur quantitas areæ APS tempori proportionalis. Sit ea A, & fiat conjectura de positione rectæ SP, quæ aream illam abscindat quamproxime. Jungatur CP, & 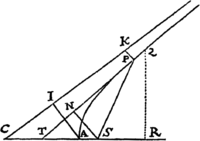 ab A & P ad Asymptoton agantur AI, PK Asymptoto alteri parallelæ, & per Tabulam Logarithmorum dabitur Area AIKP, eique æqualis area CPA, quæ subducta de triangulo CPS relinquet aream APS. Applicando arearum A & APS semidifferentiam vel ad lineam SN, quæ ab umbilico S in tangentem PT perpendicularis est, orietur longitudo PQ. Capiatur autem PQ inter A & P, si area APS major sit area A, secus ad puncti P contrarias partes: & punctum Q erit locus corporis accuratius. Et computatione repetita invenietur idem accuratius in perpetuum.
ab A & P ad Asymptoton agantur AI, PK Asymptoto alteri parallelæ, & per Tabulam Logarithmorum dabitur Area AIKP, eique æqualis area CPA, quæ subducta de triangulo CPS relinquet aream APS. Applicando arearum A & APS semidifferentiam vel ad lineam SN, quæ ab umbilico S in tangentem PT perpendicularis est, orietur longitudo PQ. Capiatur autem PQ inter A & P, si area APS major sit area A, secus ad puncti P contrarias partes: & punctum Q erit locus corporis accuratius. Et computatione repetita invenietur idem accuratius in perpetuum.
Atque his calculis Problema generaliter confit Analytice. Verum usibus Astronomicis accommodatior est calculus particularis qui sequitur. Existentibus AO, OB, OD semiaxibus Ellipseos, (Vide fig. pag. 109.110.) & L ipsius latere recto, quære tum angulum Y, cujus Tangens sit ad Radium ut est semiaxium differentia AO−OD ad eorum summam AO+OD; tum angulum Z, cujus tangens sit ad Radium ut rectangulum sub umbilicorum distantia SH & semiaxium differentia AO−OD ad triplum rectangulum sub OQ semiaxe minore & differentia inter semiaxem majorem & quartam partem lateris recti. His angulis semel inventis, locus corporis sic deinceps determinabitur. Sume angulum T proportionalem tempori quo arcus BP descriptus est, seu motui medio ( ut loquuntur ) æqualem; & angulum V ( primam medii motus æquationem ) ad angulum Y ( æquationem maximam primam ) ut est sinus anguli T duplicati ad radium; atque angulum X ( æquationem secundam ) ad angulum Z ( æquationem maximam secundam ) ut est sinus versus anguli T duplicati ad radium duplicatum, vel ( quod eodem recidit ) ut est quadratum sinus anguli T ad quadratum Radii. Angulorum T, V, X vel summæ T+X+V, si angulus T recto minor est, vel differentiæ T+X−V, si is recto major est rectisque duobus minor, æqualem cape angulum BHP ( motum medium æquatum; ) & si HP occurrat Ellipsi in P, acta SP abscindet aream BSP tempori proportionalem quamproxime. Hæc Praxis satis expedita videtur, propterea quod angulorum perexiguorum V & X ( in minutis secundis, si placet, positorum ) figuras duas tresve primas invenire sufficit. Invento autem angulo motus medii æquati BHP, angulus veri motus HSP & distantia SP in promptu sunt per methodum notissimam Dris. Sethi Wardi Episcopi Salisburiensis mihi plurimum colendi,
Hactenus de motu corporum in lineis curvis. Fieri autem potest ut mobile recta descendat vel recta ascendat, & quæ ad istiusmodi motus spectant, pergo jam exponere.
SECT. VII.
De Corporum Ascensu & Descensu Rectilineo.
Prop. XXXII. Prob. XXIV.
Posito quod vis centripeta sit reciproce proportionalis quadrato distantiæ locorum a centro, spatia definire quæ corpus recta cadendo datis temporibus describit.
Cas. 1. Si corpus non cadit perpendiculariter describet id sectionem aliquam Conicam cujus umbilicus inferior congruit cum centro. Id ex Propositionibus XI, XII, XIII & earum Corollariis constat. Sit sectio illa Conica ARPB 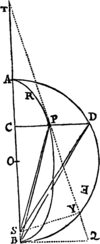 & umbilicus inferior S. Et primo si Figura illa Ellipsis est, super hujus axe majore AB describatur semicirculus ADB, & per corpus decidens transeat recta DPC perpendicularis ad axem; actisque DS, PS erit area ASD areæ ASP atque adeo etiam tempori proportionalis. Manente axe AB minuatur perpetuo latitudo Ellipseos, & semper manebit area ASD tempori proportionalis. Minuatur latitudo illa in infinitum, & orbe APB jam coincidente cum axe AB & umbilico S cum axis termino B, descendet corpus in recta AC, & area ABD evadet tempori proportionalis. Dabitur itaque spatium AC, quod corpus de loco A perpendiculariter cadendo tempore dato describit, si modo tempori proportionalis capatur area ABD, & a puncto D ad rectam AB demittatur perpendicularis DC. Q.E.I.
& umbilicus inferior S. Et primo si Figura illa Ellipsis est, super hujus axe majore AB describatur semicirculus ADB, & per corpus decidens transeat recta DPC perpendicularis ad axem; actisque DS, PS erit area ASD areæ ASP atque adeo etiam tempori proportionalis. Manente axe AB minuatur perpetuo latitudo Ellipseos, & semper manebit area ASD tempori proportionalis. Minuatur latitudo illa in infinitum, & orbe APB jam coincidente cum axe AB & umbilico S cum axis termino B, descendet corpus in recta AC, & area ABD evadet tempori proportionalis. Dabitur itaque spatium AC, quod corpus de loco A perpendiculariter cadendo tempore dato describit, si modo tempori proportionalis capatur area ABD, & a puncto D ad rectam AB demittatur perpendicularis DC. Q.E.I.
Cas. 2. Sin figura superior RPB Hyperbola est, describatur ad eandem diametrum principalem AB Hyperbola rectangula BD: & quoniam areæ CSP, CBfP, SPfB sunt ad areas CSD, CBED, SDEB, singulæ ad singulas, in data ratione altitudinum CP, CD; & area SPfB 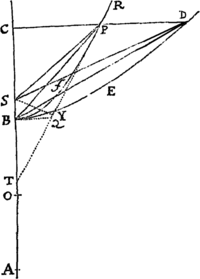 proportionalis est tempori quo corpus P movebitur per arcum PB, erit etiam area SDEB eidem tempori proportionalis. Minuatur latus rectum Hyperbolæ RPB in infinitum manente latere transverso, & coibit arcus PB cum recta CB, & umbilicus S cum vertice B & recta SD cum recta BD. Proinde area BDEB proportionalis erit tempori quo corpus C recto descensu describit lineam CB. Q.E.I.
proportionalis est tempori quo corpus P movebitur per arcum PB, erit etiam area SDEB eidem tempori proportionalis. Minuatur latus rectum Hyperbolæ RPB in infinitum manente latere transverso, & coibit arcus PB cum recta CB, & umbilicus S cum vertice B & recta SD cum recta BD. Proinde area BDEB proportionalis erit tempori quo corpus C recto descensu describit lineam CB. Q.E.I.
Cas. 3. Et simili argumento si figura RPB Parabola est, & eodem vertice principali B describatur alia Parabola BED, quæ semper maneat data, interea dum Parabola prior in cujus perimetro corpus P movetur, diminuto & in nihilum redacto ejus Latere recto, conveniat cum linea CB; fiet segmentum Parabolicum BDEB proportionale tempori quo corpus illud P vel C descendet ad centrum B. Q.E.I.
Prop. XXXIII. Theor. IX.
Positis jam inventis, dico quod corporis cadentis velocitas in loco quovis C est ad velocitatem corporis centro B intervallo BC circulum describentis, in dimidiata ratione quam CA, distantia corporis a Circuli vel Hyperbolæ vertice ulteriore A, habet ad figuræ semidiametrum principalem .
<117>Namque ob proportionales CD, CP, linea AB communis est utriusque figuræ RPB, DEB diameter. Bisecetur eadem in O, & agatur recta PT quæ tangat figuram RPB in P, atque etiam secet communem illam diametrum AB (si opus est productam) in T; sitque SY ad hanc rectam & BQ ad 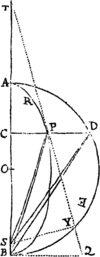 hanc diametrum perpendicularis, atque figuræ RPB latus rectum ponatur L. Constat per Cor. 9. Theor. VIII. quod corporis in linea RPB circa centrum S moventis velocitas in loco quovis P sit ad velocitatem corporis intervallo SP circa idem centrum circulum describentis in dimidiata ratione rectanguli ad SY quadratum. Est autem ex Conicis ACB ad CPq. ut 2 AO ad L, adeoque æquale L. Ergo velocitates illæ sunt ad invicem in dimidiata ratione ad SY quad. Porro ex Conicis est CO ad BO ut BO ad TO, & composite vel divisim ut CB ad BT. Unde dividendo vel componendo fit BO−uel+CO ad BO ut CT ad BT, id est AC ad AO ut CP ad BQ; indeque æquale est . Minuatur jam in infinitum figuræ RPB latitudo CP, sic ut punctum P coeat cum puncto, C, punctumque S cum puncto B, & linea SP cum linea BC, lineaque SY cum linea BQ; & corporis jam recta descendentis in linea CB velocitas fiet ad velocitatem corporis centro B interuallo BC circulum describentis, in dimidiata ratione ipsius ad SYq. hoc est (neglectis æqualitatis rationibus SP ad BC & BQq. ad SYq.) in dimidiata ratione AC ad AO. Q.E.D.
hanc diametrum perpendicularis, atque figuræ RPB latus rectum ponatur L. Constat per Cor. 9. Theor. VIII. quod corporis in linea RPB circa centrum S moventis velocitas in loco quovis P sit ad velocitatem corporis intervallo SP circa idem centrum circulum describentis in dimidiata ratione rectanguli ad SY quadratum. Est autem ex Conicis ACB ad CPq. ut 2 AO ad L, adeoque æquale L. Ergo velocitates illæ sunt ad invicem in dimidiata ratione ad SY quad. Porro ex Conicis est CO ad BO ut BO ad TO, & composite vel divisim ut CB ad BT. Unde dividendo vel componendo fit BO−uel+CO ad BO ut CT ad BT, id est AC ad AO ut CP ad BQ; indeque æquale est . Minuatur jam in infinitum figuræ RPB latitudo CP, sic ut punctum P coeat cum puncto, C, punctumque S cum puncto B, & linea SP cum linea BC, lineaque SY cum linea BQ; & corporis jam recta descendentis in linea CB velocitas fiet ad velocitatem corporis centro B interuallo BC circulum describentis, in dimidiata ratione ipsius ad SYq. hoc est (neglectis æqualitatis rationibus SP ad BC & BQq. ad SYq.) in dimidiata ratione AC ad AO. Q.E.D.
Corol. Punctis B & S coeuntibus, fit TC and ST ut AC ad AO.
Prop. XXXIV. Theor. X.
Si figura BED Parabola est, dico quod corporis cadentis velocitas in loco quovis C æqualis est velocitati qua corpus centro b dimidio intervalli sui BC circulum 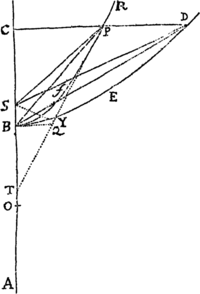 uniformiter describere potest.
uniformiter describere potest.
Nam corporis Parabolam RPB circa centrum S describentis velocitas in loco quovis S (per Corol. 7. Theor. VIII) æqualis est velocitati corporis dimidio intervalli SP circulum circa idem S uniformiter describentis. Minuatur Parabolæ latitudo CP in infinitum eo, ut arcus Parabolicus CP cum recta CB, centrum S cum vertice B, & interuallum SP cum intervallo CP coincidat, & constabit Propositio. Q.E.D.
Prop. XXXV. Theor. XI.
Iisdem positis, dico quod area figuræ DES, radio indefinito SD descripta, æqualis sit areæ quam corpus, radio dimidium lateris recti figuræ DES æquante, circa centrum S uniformiter gyrando, eodem tempore describere potest.
Nam concipe corpus C quam minima temporis particula lineolam Cc cadendo describere, & interea corpus aliud K, uniformiter in circulo OKk circa centrum S gyrando, arcum Kk describere. Erigantur perpendicula CD, cd occurrentia figuræ DES in D, d. Jungantur SD, SK, Sk & ducatur Dd axi AS occurrens in T, & ad eam demittatur perpendiculum SY.
Cas. 1 Jam si figura DES Circulus est vel Hyperbola, bisecetur ejus transversa diameter AS in O, & erit 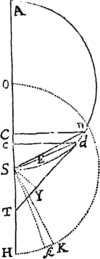 SO dimidium Lateris recti. Et quoniam est TC ad TD ut Cc ad Dd, & TD ad TS ut CD ad SY, erit ex æquo TC ad TS ut ad . Sed per Corol. Prop. 33. est TC ad ST ut AC ad AO, puta si in coita punctorum D, d capiantur linearum rationes ultimæ. Ergo AC est ad AO, id est ad SK, ut ad S. Porro corporis descendentis velocitas in C est ad velocitatem corporis circulum intervallo SC circa centrum S describentis in dimidiata ratione AC ad AO vel SK (per Theor IX.) Et hæc velocitas ad velocitatem corporis describentis circulum OKk in dimidiata ratione SK ad SC per Cor. 6. Theor. IV. & ex æquo velocitas prima ad ultimam, hoc est lineola Cc ad arcum Kk in dimidiata ratione AC ad SC, id est in ratione AC ad CD. Quare est æquale , & propterea AC ad SK ut ad , indeque > æquale , & æquale , id est area KSk æqualis areæ SDd. Singulis igitur temporis particulis generantur arearum duarum particulæ KSk, SDd, quæ, si magnitudo earum minuatur & numerus augeatur in infinitum, rationem obtinent æqualitatis, & propterea (per Corollarium Lemmatis IV) areæ totæ simul genitæ sunt semper æquales. Q.E.D.
SO dimidium Lateris recti. Et quoniam est TC ad TD ut Cc ad Dd, & TD ad TS ut CD ad SY, erit ex æquo TC ad TS ut ad . Sed per Corol. Prop. 33. est TC ad ST ut AC ad AO, puta si in coita punctorum D, d capiantur linearum rationes ultimæ. Ergo AC est ad AO, id est ad SK, ut ad S. Porro corporis descendentis velocitas in C est ad velocitatem corporis circulum intervallo SC circa centrum S describentis in dimidiata ratione AC ad AO vel SK (per Theor IX.) Et hæc velocitas ad velocitatem corporis describentis circulum OKk in dimidiata ratione SK ad SC per Cor. 6. Theor. IV. & ex æquo velocitas prima ad ultimam, hoc est lineola Cc ad arcum Kk in dimidiata ratione AC ad SC, id est in ratione AC ad CD. Quare est æquale , & propterea AC ad SK ut ad , indeque > æquale , & æquale , id est area KSk æqualis areæ SDd. Singulis igitur temporis particulis generantur arearum duarum particulæ KSk, SDd, quæ, si magnitudo earum minuatur & numerus augeatur in infinitum, rationem obtinent æqualitatis, & propterea (per Corollarium Lemmatis IV) areæ totæ simul genitæ sunt semper æquales. Q.E.D.
Cas. 2. Quod si figura DES Parabola sit, invenietur ut supra esse ad ut TC ad ST, hoc est ut 2 ad 1, adeoque æqualem esse . Sedcorporis cadentis velocitas in C æqualis est velocitati 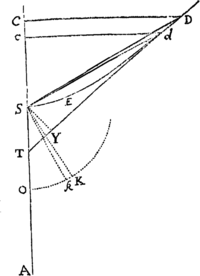 qua circulus intervallo uniformiter describi possit. (per Theor. X.) Et hæc velocitas ad velocitatem qua circulus radio SK describi possit, hoc est, lineola Cc ad arcum Kk est in dimidiata ratione SK ad , id est, in ratione SK ad , per Corol. 6. Theorem. IV. Quare est æquale , adeoque æquale , hoc est, area KSk æqualis Areæ SDd, ut supra. Quod erat demonstrandum.
qua circulus intervallo uniformiter describi possit. (per Theor. X.) Et hæc velocitas ad velocitatem qua circulus radio SK describi possit, hoc est, lineola Cc ad arcum Kk est in dimidiata ratione SK ad , id est, in ratione SK ad , per Corol. 6. Theorem. IV. Quare est æquale , adeoque æquale , hoc est, area KSk æqualis Areæ SDd, ut supra. Quod erat demonstrandum.
Prop. XXXVI. Prob. XXV.
Corporis de loco dato A cadentis determinare tempora 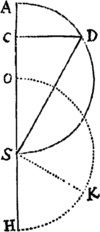 descensus.
descensus.
Super diametro AS (distantia corporis a centro sub initio) describe semicirculum ADS, ut & huic æqualem semicirculum OKH circa centrum S. De corporis loco quovis C erige ordinatim applicatam CD. Junge SD, & areæ ASD æqualem constitue Sectionem OSK. Patet per Theor. XI, quod corpus cadendo describet spatium AC eodem tempore quo corpus aliud uniformiter circa centrum S gyrando, describere potest arcum OK. Quod erat faciendum.
Prop. XXXVII. Prob. XXVI.
Corporis de loco dato sursum vel deorsum projecti definire tempora ascensus vel descensus.
<121>Exeat corpus de loco dato G secundum lineam ASG cum velocitate quacunque. In duplicata ratione hujus velocitatis ad uniformem in circulo velocitatem, qua corpus ad intervallum datum SG circa centrum S revolvi posset, cape CA 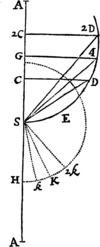 ad . Si ratio illa est numeri binarii ad unitatem, punctum A cadet ad infinitam distantiam, quo in casu Parabola uertice S, axe SC, latere quovis recto describenda est. Patet hoc per Theorema X. Sin ratio illa minor vel major est quam 2 ad 1, priore casu Circulus, posteriore Hyperbola rectangula super diametro SA describi debet. Patet per Theorema IX. Tum centro S, intervallo æquante dimidium lateris recti, describatur circulus HKk, & ad corporis ascendentis vel descendentis loca duo quævis G, C, erigantur perpendicula GI, CD occurrentia Conicæ Sectioni vel circulo in I ac D. Dein junctis SI, SD, fiant segmentis SEIS, SEDS Sectores HSK, HSk æquales, & per Theorema XI. corpus G describet spatium GC eodem tempore quo corpus K describere potest arcum Kk. Q.E.F.
ad . Si ratio illa est numeri binarii ad unitatem, punctum A cadet ad infinitam distantiam, quo in casu Parabola uertice S, axe SC, latere quovis recto describenda est. Patet hoc per Theorema X. Sin ratio illa minor vel major est quam 2 ad 1, priore casu Circulus, posteriore Hyperbola rectangula super diametro SA describi debet. Patet per Theorema IX. Tum centro S, intervallo æquante dimidium lateris recti, describatur circulus HKk, & ad corporis ascendentis vel descendentis loca duo quævis G, C, erigantur perpendicula GI, CD occurrentia Conicæ Sectioni vel circulo in I ac D. Dein junctis SI, SD, fiant segmentis SEIS, SEDS Sectores HSK, HSk æquales, & per Theorema XI. corpus G describet spatium GC eodem tempore quo corpus K describere potest arcum Kk. Q.E.F.
Prop. XXXVIII. Theor. XII.
Posito quod vis centripeta proportionalis sit altitudini seu distantiæ locorum a centro, dico quod cadentium tempora, velocitates & spatia descripta sunt arcubus arcuumque sinibus 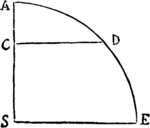 versis & sinibus rectis respective proportionales.
versis & sinibus rectis respective proportionales.
Cadat corpus de loco quovis A secundum rectam AS; & centro virium S, intervallo AS, describatur circuli quadrans AE, sitque CD sinus rectus arcus cujusvis AD, & corpus A, tempore AD, cadendo describet spatium AC, inque loco C acquisierit velocitatem CD. Demonstratur eodem modo ex Propositione X. quo Propositio XXXII. ex Propositione XI. demonstrata fuit. Q.E.D.
Corol. 1. Hinc æqualia sunt tempora quibus corpus unum de loco A cadendo provenit ad centrum S, & corpus aliud revolvendo describit arcum quadrantalem ADE.
Corol. 2. Proinde æqualia sunt tempora omnia quibus corpora de locis quibusvis ad usque centrum cadunt. Nam revolventium tempora omnia periodica (per Corol. 3. Prop. IV.) æquantur.
Prop. XXXIX. Prob. XXVII.
Posita cujuscunque generis vi centripeta, & concessis figurarum curvilinearum quadraturis, requiritur corporis recta ascendentis vel descendentis tum velocitas in locis singulis, tum tempus quo corpus ad locum quemvis perveniet: Et contra.
De loco quovis A in recta ADEC cadat corpus E, deque loco ejus E erigatur semper perpendicularis EG, vi centripetæ in loco illo ad centrum C tendenti proportionalis: 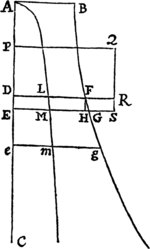 Sitque BFG linea curva quam punctum G perpetuo tangit. Coincidat autem EG ipso motus initio cum perpendiculari AB, & erit corporis velocitas in loco quovis E ut areæ curvilineæ ABGE latus quadratum. Q.E.I. In EG capiatur EM lateri quadrato areæ ABGE reciproce proportionalis, & sit ALM linea curva quam punctum L perpetuo tangit, & erit tempus quo corpus cadendo describit lineam AE ut area curvilinea ALME. Quod erat Inveniendum.
Sitque BFG linea curva quam punctum G perpetuo tangit. Coincidat autem EG ipso motus initio cum perpendiculari AB, & erit corporis velocitas in loco quovis E ut areæ curvilineæ ABGE latus quadratum. Q.E.I. In EG capiatur EM lateri quadrato areæ ABGE reciproce proportionalis, & sit ALM linea curva quam punctum L perpetuo tangit, & erit tempus quo corpus cadendo describit lineam AE ut area curvilinea ALME. Quod erat Inveniendum.
Etenim in recta AE capiatur linea quam minima DE datæ longitudinis, sitque DLF locus lineæ EMG ubi corpus versabatur in D; & si ea sit vis centripeta, ut area ABGE latus quadratum sit ut descendentis velocitas, erit area ipsa in duplicata ratione velocitatis, id est, si pro velocitatibus in D & E scribantur V & V+I, erit area ABFD ut , & area ABGE ut , & divisim area , adeoque ut , id est, si primæ quantitatum nascentium rationes sumantur, longitudo DF ut quantitas , adeoque etiam ut quantitatis hujus dimidium . Est autem tempus quo corpus cadendo describit lineolam DE, ut lineola illa directe & velocitas V inverse, estque vis ut velocitatis incrementum I directe & tempus inverse, adeoque si primæ nascentium rationes sumantur, ut , hoc est, ut longitudo DF. Ergo vis ipsi DF proportionalis facit corpus ea cum velocitate descendere quæ sit ut areæ ABGE latus quadratum Q.E.D.
Porro cum tempus, quo quælibet longitudinis datæ lineola DE describatur, sit ut velocitas, adeoque ut areæ ABFD latus quadratum inverse; sitque DL, atque adeo area nascens DLME, ut idem latus quadratum inverse: erit tempus ut area DLME, & summa omnium temporum ut summa omnium arearum, hoc est (per Corol. Lem. IV.) tempus totum quo linea AE describitur ut area tota AME. Q.E.D.
Corol. 1. Si P sit locus de quo corpus cadere debet, ut, urgente aliqua uniformi ui centripeta nota (qualis vulgo supponitur gravitas) velocitatem acquirat in loco D æqualem velocitati quam corpus aliud vi quacunque cadens acquisivit eodem loco D, & in perpendiculari DF capiatur DR, quæ sit ad DF ut vis illa uniformis ad vim alteram in loco D, & compleatur rectangulum PDRQ, eique æqualis abscindatur area ABFD; erit A locus de quo corpus alterum cecidit. Namque completo rectangulo EDRS, cum sit area ABFD ad aream DFGE ut VV ad , adeoque ut ad I, id est, ut semissis velocitatis totius ad incrementum velocitatis corporis vi inæquabili cadentis; & similiter area PQRD ad aream DRSE ut semissis velocitatis totius ad incrementum velocitatis corporis 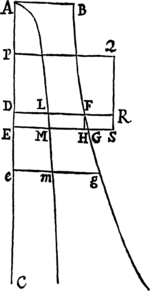 uniformi vi cadentis; fintque incrementa illa (ob æqualitatem temporum nascentium) ut vires generatrices, id est ut ordinatim applicatæ DF, DR, adeoque ut areæ nascentes DFGE, DRSE; erunt (ex æquo) areæ totæ ABFD, PQRD ad invicem ut semisses totarum velocitatum, & propterea (ob æqualitatem velocitatum) æquantur.
uniformi vi cadentis; fintque incrementa illa (ob æqualitatem temporum nascentium) ut vires generatrices, id est ut ordinatim applicatæ DF, DR, adeoque ut areæ nascentes DFGE, DRSE; erunt (ex æquo) areæ totæ ABFD, PQRD ad invicem ut semisses totarum velocitatum, & propterea (ob æqualitatem velocitatum) æquantur.
Corol. 2. Unde si corpus quodlibet de loco quocunque D data cum velocitate vel sursum vel deorsum projiciatur, & detur lex vis centripetæ, invenietur velocitas ejus in alio quovis loco e, erigendo ordinatam eg, & capiendo velocitatem illam ad velocitatem in loco D ut est latus quadratum rectanguli PQRD area curvilinea DFge vel aucti, si locus e est loco D inferior, vel diminuti, si is superior est, ad latus quadratum rectanguli solius PQRD, id est ut ad .
Corol. 3. Tempus quoque innotescet erigendo ordinatam em reciproce proportionalem lateri quadrato ex PQRD+vel−DFge, & capiendo tempus quo corpus descripsit lineam De ad tempus quo corpus alterum vi uniformi cecidit a P & cadendo pervenit ad D, ut area curvilinea DLme ad rectangulum . Namque tempus quo corpus vi uniformi descendens descripsit lineam PD est ad tempus quo corpus idem descripsit lineam PE in dimidiata ratione PD ad PE, id est (lineola DE jamjam nascente) in ratione PD ad seu ad , & divisim, ad tempus quo corpus idem descripsit lineolam DE ut ad DE, adeoque ut rectangulum ad aream DLME; estque tempus quo corpus utrumque descripsit lineolam DE ad tempus quo corpus alterum inæquabili motu descripsit lineam De ut area DLME ad aream DLme, & ex æquo tempus primum ad tempus ultimum ut rectangulum ad aream DLme.
SECT. VIII.
De Inventione Orbium in quibus corpora viribus quibuscunque centripetis agitata revolventur.
Prop. XL. Theor. XIII.
Si corpus, cogente vi quacunque centripeta, moveatur utcunque, & corpus aliud recta ascendat vel descendat, suntque eorum velocitates in aliquo æqualium altitudinum casu æquales, velocitates corum in omnibus altitudinibus erunt æquales.
Descendat corpus aliquod ab A per D, E, ad centrum C, & moveatur corpus aliud a V in linea curva VIKk. Centro C intervallis quibusvis describantur circuli concentrici DI, EK rectæ AC in D & E, curvæque VIK in I & K occurentes. Jungatur IC occurrens ipsi KE in N; & in IK demittatur perpendiculum NT; sitque circumferentiarum circulorum intervallum DE vel IN quam minimum, & habeant corpora in D & I velocitates æquales. Quoniam distantiæ CD, CI æquantur, erunt vires centripetæ in D & I æquales. Exponantur hæ vires per æquales lineolas DE, IN; & si vis una IN, per Legum Corol. 2. resolvatur in duas NT & IT, vis NT, agendo secundum lineam NT corporis cursui ITK perpendicularem, nil mutabit velocitatem corporis in cursu illo, sed retrahet solummodo corpus a cursu rectilineo, facietque ipsum de Orbis tangente perpetuo deflectere, inque via curvilinea ITKk progredi. In hoc effectu producendo vis illa tota consumetur: vis autem altera IT, secundum corporis cursum agendo, tota accelerabit illud, ac dato tempore quam minimo accelerationem generabit sibi ipsi proportionalem. Proinde corporum in D & I accelerationes æqualibus temporibus factæ 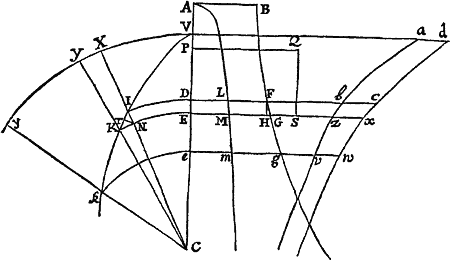 (si sumantur linearum nascentium DE, IN, IK, IT, NT rationes primæ) sunt ut lineæ DE, IT: temporibus autem inæqualibus ut lineæ illæ & tempora conjunctim. Tempora ob æqualitatem velocitatum sunt ut viæ descriptæ DE & IK, adeoque accelerationes, in cursu corporum per lineas DE & IK, sunt ut DE & IT, DE & IK conjunctim, id est ut DE quad. & rectangulum. Sed rectangulum æquale est IN quadrato, hoc est, æquale DE quadrato, & propterea accelerationes in transitu corporum a D & I ad E & K æquales generantur. Æquales igitur sunt corporum velocitates in E & K & eodem argumento semper reperientur æquales in subsequentibus æqualibus distantiis. Q.E.D. Sed & eodem argumento corpora æquivelocia & æqualiter a centro distantia, in ascensu ad æquales distantias æqualiter retardabuntur. Q.E.D.
(si sumantur linearum nascentium DE, IN, IK, IT, NT rationes primæ) sunt ut lineæ DE, IT: temporibus autem inæqualibus ut lineæ illæ & tempora conjunctim. Tempora ob æqualitatem velocitatum sunt ut viæ descriptæ DE & IK, adeoque accelerationes, in cursu corporum per lineas DE & IK, sunt ut DE & IT, DE & IK conjunctim, id est ut DE quad. & rectangulum. Sed rectangulum æquale est IN quadrato, hoc est, æquale DE quadrato, & propterea accelerationes in transitu corporum a D & I ad E & K æquales generantur. Æquales igitur sunt corporum velocitates in E & K & eodem argumento semper reperientur æquales in subsequentibus æqualibus distantiis. Q.E.D. Sed & eodem argumento corpora æquivelocia & æqualiter a centro distantia, in ascensu ad æquales distantias æqualiter retardabuntur. Q.E.D.
Corol. 1. Hinc si corpus vel funipendulum oscilletur, vel impedimento quovis politissimo & perfecte lubrico cogatur in linea curva moveri, & corpus aliud recta ascendat vel descendat, sintque velocitates eorum in eadem quacunque altitudine æquales: erunt velocitates eorum in aliis quibuscunque æqualibus altitudinibus æquales. Namque impedimento vasis absolute lubrici idem præstatur quod vi transversa NT. Corpus eo non retardatur, non acceleratur, sed tantum cogitur de cursu rectilineo discedere.
Corol. 2. Hinc etiam si quantitas P sit maxima a centro distantia, ad quam corpus vel oscillans vel in Trajectoria quacunque revolvens, deque quovis trajectoriæ puncto, ea quam ibi habet velocitate sursum projectum ascendere possit; sitque quantitas A distantia corporis a centro in alio quovis Orbis puncto, & vis centripeta semper sit ut ipsius A dignitas quælibet , cujus Index n−1 est numerus quilibet n unitate diminutus; velocitas corporis in omni altitudine A erit ut , atque adeo datur. Namque velocitas ascendentis ac descendentis (per Prop. XXXIX.) est in hac ipsa ratione.
Prop. XLI. Prob. XXVIII.
Posita cujuscunque generis vi centripeta & concessis figurarum curvilinearum quadraturis, requiruntur tum Trajectoriæ in quibus corpora movebuntur, tum tempora motuum in Trajectoriis inventis.
Tendat vis quælibet ad centrum C & invenienda sit Trajectoria VITKk. Detur circulus VXY centro C intervallo quovis CV descriptus, centroque eodem describantur alii quivis circuli ID, KE trajectoriam secantes in I & K rectamque CV in D & E. Age tum rectam CNIX secantem circulos KE, VY in N & X, tum rectam CKY occurrentem circulo VXY in Y. Sint autem puncta I & K sibi invicem vicinissima, & pergat corpus ab V per I, T & K ad k; sitque A altitudo illa de qua corpus aliud cadere debet ut in loco D velocitatem acquirat æqualem velocitati corporis prioris in I; & stantibus quæ in Propositione XXXIX, quoniam lineola IK, dato tempore quam minimo descripta, est ut velocitas atque adeo ut latus quadratum areæ ABFD, & triangulum ICK 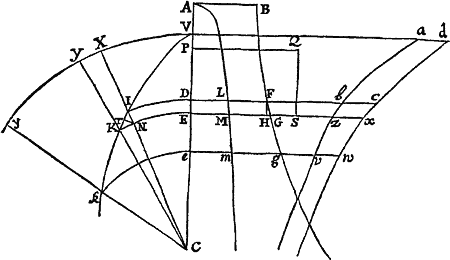 tempori proportionale datur, adeoque KN est reciproce ut altitudo IC, id est, si detur quantitas aliqua Q, & altitudo IC nominetur A, ut ; quam nominemus Z. Ponamus eam esse magnitud inem ipsius Q ut sit in aliquo casu ad Z ut est IK ad KN, & erit semper ad Z ut IK ad KN, & ABFD ad ZZ ut IK quad. ad KN quad. & divisim ABFD−ZZ ad ZZ ut IN quad. ad KN quad. adeoque ad Z ut IN ad KN, & propterea æquale . Unde cum sit ad in duplicata ratione YC ad KC, erit rectang. æquale . Igitur si in perpendiculo DF capiantur semper Db, Dc ipsis & æquales respective, & describantur curvæ lineæ ab, cd quas puncta, b, c perpetuo tangunt; deque puncto V ad lineam AC erigatur perpendiculum Vad abscindens areas curvilineas VDba, VDdc, & erigantur etiam ordinatæ Ez, Ex: quoniam rectangulum seu DbzE æquale est dimidio rectanguli , seu triangulo ICK; & rectangulum seu DcxE æquale est dimidio rectanguli YX in CX, seu triangulo XCY; hoc est, quoniam, arearum VDba, VIC æquales semper sunt nascentes particulæ DbzE, ICK, & arearum VDcd, VCX æquales semper sunt nascentes particulæ DExc, XCY, erit area genita VDba æqualis areæ genitæ VIC, adeoque tempori proportionalis, & area genita VDdc æqualis Sectori genito VCX. Dato igitur tempore quovis ex quo corpus discessit de loco V, dabitur area ipsi proportionalis VDba, & inde dabitur corporis altitudo CD vel CI; & area VDcd, eique æqualis Sector VCX una cum ejus angulo VCI. Datis autem angulo VCI & altitudine CI datur locus I, in quo corpus completo illo tempore reperietur. Q.E.I.
tempori proportionale datur, adeoque KN est reciproce ut altitudo IC, id est, si detur quantitas aliqua Q, & altitudo IC nominetur A, ut ; quam nominemus Z. Ponamus eam esse magnitud inem ipsius Q ut sit in aliquo casu ad Z ut est IK ad KN, & erit semper ad Z ut IK ad KN, & ABFD ad ZZ ut IK quad. ad KN quad. & divisim ABFD−ZZ ad ZZ ut IN quad. ad KN quad. adeoque ad Z ut IN ad KN, & propterea æquale . Unde cum sit ad in duplicata ratione YC ad KC, erit rectang. æquale . Igitur si in perpendiculo DF capiantur semper Db, Dc ipsis & æquales respective, & describantur curvæ lineæ ab, cd quas puncta, b, c perpetuo tangunt; deque puncto V ad lineam AC erigatur perpendiculum Vad abscindens areas curvilineas VDba, VDdc, & erigantur etiam ordinatæ Ez, Ex: quoniam rectangulum seu DbzE æquale est dimidio rectanguli , seu triangulo ICK; & rectangulum seu DcxE æquale est dimidio rectanguli YX in CX, seu triangulo XCY; hoc est, quoniam, arearum VDba, VIC æquales semper sunt nascentes particulæ DbzE, ICK, & arearum VDcd, VCX æquales semper sunt nascentes particulæ DExc, XCY, erit area genita VDba æqualis areæ genitæ VIC, adeoque tempori proportionalis, & area genita VDdc æqualis Sectori genito VCX. Dato igitur tempore quovis ex quo corpus discessit de loco V, dabitur area ipsi proportionalis VDba, & inde dabitur corporis altitudo CD vel CI; & area VDcd, eique æqualis Sector VCX una cum ejus angulo VCI. Datis autem angulo VCI & altitudine CI datur locus I, in quo corpus completo illo tempore reperietur. Q.E.I.
Corol. 1. Hinc maximæ minimaeque corporum altitudines, id est Apsides Trajectoriarum expedite inveniri possunt. Incidunt enim Apsides in puncta illa in quibus recta IC per centrum ducta incidit perpendiculariter in Trajectoriam VIK: id quod fit ubi rectæ IK & NK æquantur, adeoque ubi area ABFD æqualis est ZZ.
Corol. 2. Sed & angulus KIN, in quo Trajectoria alibi secat lineam illam IC, ex data corporis altitudine IC expedite invenitur, nimirum capiendo sinum ejus ad radium ut KN ad IK, id est ut Z ad latus quadratum areæ ABFD.
Corol. 3. Si centro C & vertice principali V describatur sectio quælibet Conica VRS, & a quovis ejus puncto R agatur Tangens RT occurrens axi infinite producto CV in puncto T; dein juncta CR ducatur recta CP, quæ æqualis sit abscissæ CT, angulumque VCP 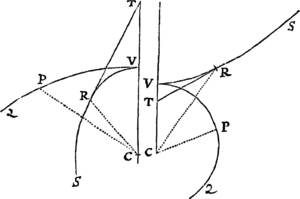 Sectori VCR proportionalem constituat; tendat autem ad centrum C vis centripeta cubo distantiæ locorum a centro reciproce proportionalis, & exeat corpus de loco V justa cum velocitate secundum lineam rectæ CV perpendicularem: progredietur corpus illud in Trajectoria quam punctum P perpetuo tangit; adeoque si conica sectio CVRS Hyperbola sit, descendet idem ad centrum: Sin ea Ellipsis sit, ascendet illud perpetuo & abibit in infinitum. Et contra, si corpus quacunque cum velocitate exeat de loco V, & perinde ut incæperit vel oblique descendere ad centrum, vel ab eo oblique ascendere, figura CVRS vel Hyperbola sit vel Ellipsis, inveniri potest Trajectoria augendo vel minuendo angulum VCP in data aliqua ratione. Sed et vi centripeta in centrifugam versa, ascendet corpus oblique in Trajectoria VPQ quæ invenitur capiendo angulum VCP Sectori Elliptico CVRC proportionalem, & longitudinem CP longitudini CT æqualem: ut supra. Consequuntur hæc omnia ex Propositione præcedente, per Curvæ cujusdam quadraturam, cujus inventionem ut satis facilem brevitatis gratia missam facio.
Sectori VCR proportionalem constituat; tendat autem ad centrum C vis centripeta cubo distantiæ locorum a centro reciproce proportionalis, & exeat corpus de loco V justa cum velocitate secundum lineam rectæ CV perpendicularem: progredietur corpus illud in Trajectoria quam punctum P perpetuo tangit; adeoque si conica sectio CVRS Hyperbola sit, descendet idem ad centrum: Sin ea Ellipsis sit, ascendet illud perpetuo & abibit in infinitum. Et contra, si corpus quacunque cum velocitate exeat de loco V, & perinde ut incæperit vel oblique descendere ad centrum, vel ab eo oblique ascendere, figura CVRS vel Hyperbola sit vel Ellipsis, inveniri potest Trajectoria augendo vel minuendo angulum VCP in data aliqua ratione. Sed et vi centripeta in centrifugam versa, ascendet corpus oblique in Trajectoria VPQ quæ invenitur capiendo angulum VCP Sectori Elliptico CVRC proportionalem, & longitudinem CP longitudini CT æqualem: ut supra. Consequuntur hæc omnia ex Propositione præcedente, per Curvæ cujusdam quadraturam, cujus inventionem ut satis facilem brevitatis gratia missam facio.
Prop. XLII. Prob. XXIX.
Data lege vis centripetæ, requiritur motus corporis de loco dato data cum velocitate secundum datam rectam egressi.
Stantibus quæ in tribus Propositionibus præcedentibus: exeat corpus de loco I secundum lineolam IT, ea cum velocitate quam corpus aliud, vi aliqua uniformi centripeta, de loco P cadendo acquirere posset in D: sitque hæc vis uniformis ad vim qua corpus primum urgetur in I, ut DR ad DF. Pergat autem corpus versus k; centroque C & intervallo Ck describatur circulus ke occurrens rectæ PD in e, & erigantur curvarum ALMm, BFGg, abzvdcxw ordinatim applicatæ em, eg, ev, ew. Ex dato rectangulo PDRQ, dataque lege vis centripetæ qua corpus primum agitatur, dantur curvæ lineæ BFGg, ALMm, per constructionem Problematis XXVII. & ejus Corol. 1. Deinde ex dato angulo CIT datur proportio nascentium IK, KN, & inde, per constructionem Prob. XXVIII, datur quantitas Q, una cum curvis lineis abzv, dcxw: adeoque completo tempore quovis Dbve, datur tum corporis altitudo Ce vel Ck, tum area Dcwe, eique æqualis Sector XCy, angulusque XCy & locus k in quo corpus tunc versabitur. Q.E.I.
Supponimus autem in his Propositionibus vim centripetam in recessu quidem a centro variari secundum legem quamcunque quam quis imaginari potest, in æqualibus autem a centro distantiis esse undique eandem. Atque hactenus corporum in Orbibus immobilibus consideravimus. Superest ut de motu eorum in Orbibus qui circa centrum virium revolvuntur adjiciamus pauca.
SECT. IX.
De Motu Corporum in Orbibus mobilibus, deque motu Apsidum.
Prop. XLIII. Prob. XXX.
Efficiendum est ut corpus in Trajectoria quacunque circa centrum virium revolvente perinde moveri possit, atque corpus aliud in eadem Trajectoria quiescente.
In Orbe VPK positione dato revolvatur corpus P pergendo a V versus K. A centro C agatur semper Cp, quæ sit ipsi CP æqualis, angulumque VCp angulo VCP proportionalem constituat; & area quam linea Cp describit erit ad aream VCP quam linea CP describit, ut velocitas 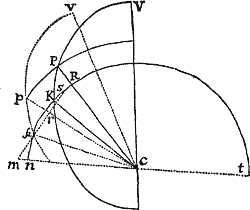 lineæ describentis Cp ad velocitatem lineæ describentis CP; hoc est, ut angulus VCp ad angulum VCP, adeoque in data ratione, & propterea tempori proportionalis. Cum area tempori proportionalis sit quam linea Cp in plano immobili describit, manifestum est quod corpus, cogente justæ quantitatis vi centripeta, revolvi possit una cum puncto p in curva illa linea quam punctum idem p ratione jam exposita describit in plano immobili. Fiat angulus VCv angulo PCp, & linea Cv lineæ CV, atque figura vCp figuræ VCP æqualis, & corpus in p semper existens movebitur in perimetro figuræ revolventis vCp, eodemque tempore describet arcum ejus vp quo corpus aliud P arcum ipsi similem & æqualem VP in figura quiescente VPK describere potest. Quæratur igitur, per Corollarium Propositionis VI, vis centripeta qua corpus revolvi possit in curva illa linea quam punctum p describit in plano immobili, & solvetur Problema. Q.E.F.
lineæ describentis Cp ad velocitatem lineæ describentis CP; hoc est, ut angulus VCp ad angulum VCP, adeoque in data ratione, & propterea tempori proportionalis. Cum area tempori proportionalis sit quam linea Cp in plano immobili describit, manifestum est quod corpus, cogente justæ quantitatis vi centripeta, revolvi possit una cum puncto p in curva illa linea quam punctum idem p ratione jam exposita describit in plano immobili. Fiat angulus VCv angulo PCp, & linea Cv lineæ CV, atque figura vCp figuræ VCP æqualis, & corpus in p semper existens movebitur in perimetro figuræ revolventis vCp, eodemque tempore describet arcum ejus vp quo corpus aliud P arcum ipsi similem & æqualem VP in figura quiescente VPK describere potest. Quæratur igitur, per Corollarium Propositionis VI, vis centripeta qua corpus revolvi possit in curva illa linea quam punctum p describit in plano immobili, & solvetur Problema. Q.E.F.
Prop. XLIV. Theor. XIV.
Differentia virium, quibus corpus in Orbe quiescente, & corpus aliud in eodem Orbe revolvente æqualiter moveri possunt, est in triplicata ratione communis altitudinis inverse.
Partibus orbis quiescentis VP, PK sunto similes & æquales orbis revolventis partes vp, pk. A puncto k in rectam pC demitte perpendiculum kr, idemque produc ad m, ut sit mr ad kr ut angulus VCp ad angulum VCP. Quoniam corporum altitudines PC & pC, KC & kC semper æquantur, manifestum est quod si corporum in locis P & p existentium distinguantur motus singuli (per Legum Corol. 2.) in binos, (quorum hi versus centrum, sive secundum lineas PC, pC; alteri prioribus transversi secundum lineas ipsis PC, pC perpendiculares determinantur) motus versus centrum erunt æquales, & motus transversus corporis p erit ad motum transversum corporis P, ut motus angularis lineæ pC ad motum angularem lineæ PC, id est ut angulus VCp ad angulum VCP. Igitur eodem tempore quo corpus P motu suo utroque pervenit ad punctum K, corpus p æquali in centrum motu æqualiter movebitur a P versus C, adeoque completo illo tempore reperietur alicubi in linea mkr, quæ per punctum k in lineam pC perpendicularis est; & motu transverso acquiret distantiam a linea pC, quæ sit ad distantiam quam corpus alterum acquirit a linea PC, ut est hujus motus transversus ad motum transversum alterius. Quare cum kr æqualis sit distantiæ quam corpus alterum acquirit a linea pC, sitque mr ad kr ut angulus VCp ad angulum VCP, hoc est, ut motus transversus corporis p ad motum transversum corporis P, manifestum est quod corpus p completo illo tempore reperietur in loco m. Hæc ita se habebunt ubi corpora P & p æqualiter secundum lineas pC & PC moventur, adeoque æqualibus viribus secundum lineas illas urgentur. Capiatur autem angulus pCn ad angulum pCk ut est angulus VCp ad angulum VCP, sitque nC æqualis kC, & corpus p completo illo tempore revera reperietur in n; adeoque vi majore urgetur, si modo angulus mCp 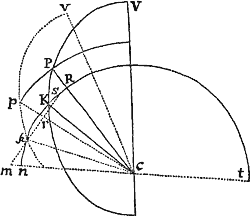 angulo kCp major est, id est si orbis Vpk movetur in consequentia, & minore, si orbis regreditur; estque virium differentia ut locorum intervallum mn, per quod corpus illud p ipsius actione, dato illo temporis spatio transferri debet. Centro C intervallo Cn vel Ck describi intelligetur circulus secans lineas mr, mn productas in s & t, & erit rectangulum æquale rectangulo , adeoque mn æquale . Cum autem triangula pCk, pCn dentur magnitudine, sunt kr & mr, earumque differentia mk & summa ms reciproce ut altitudo pC, adeoque rectangulum est reciproce ut quadratum altitudinis pC. Est & mt directe ut , id est ut altitudo pC. Hæ sunt primæ rationes linearum nascentium; & hinc fit , id est lineola nascens mn, eique proportionalis virium differentia reciproce ut cubus altitudinis pC. Q.E.D.
angulo kCp major est, id est si orbis Vpk movetur in consequentia, & minore, si orbis regreditur; estque virium differentia ut locorum intervallum mn, per quod corpus illud p ipsius actione, dato illo temporis spatio transferri debet. Centro C intervallo Cn vel Ck describi intelligetur circulus secans lineas mr, mn productas in s & t, & erit rectangulum æquale rectangulo , adeoque mn æquale . Cum autem triangula pCk, pCn dentur magnitudine, sunt kr & mr, earumque differentia mk & summa ms reciproce ut altitudo pC, adeoque rectangulum est reciproce ut quadratum altitudinis pC. Est & mt directe ut , id est ut altitudo pC. Hæ sunt primæ rationes linearum nascentium; & hinc fit , id est lineola nascens mn, eique proportionalis virium differentia reciproce ut cubus altitudinis pC. Q.E.D.
Corol. 1. Hinc differentia virium in locis P & p vel K & k est ad vim qua corpus motu circulari revolvi posset ab r ad k, eodem tempore quo corpus P in orbe immobili describit arcum PK, ut ad rk quadratum; hoc est si capiantur datæ quantitates F, G in ea ratione ad invicem quam habet angulus VCP ad angulum VCp, ut Gq.−Fq. ad Fq. Et propterea, si centro C intervallo quovis CP vel Cp describatur Sector circularis æqualis areæ toti VPC, quam corpus P tempore quovis in orbe immobili revolvens radio ad centrum ducto descripsit, differentia virium, quibus corpus P in orbe immobili & corpus p in orbe mobili revolvuntur, erit ad vim centripetam qua corpus aliquod radio ad centrum ducto Sectorem illum, eodem tempore quo descripta sit area VPC, uniformiter describere potuisset, ut Gq.−Fq. ad Fq. Namque sector ille & area pCk sunt ad invicem ut tempora quibus describuntur.
Corol. 2. Si orbis VPK Ellipsis sit umbilicum habens C & Apsidem summam V; eique similis & æqualis ponatur Ellipsis vpk, ita ut sit semper pc æqualis PC, & angulus VCp sit ad angulum VCP in data ratione G ad F; pro altitudine autem PC vel pc scribatur A, & pro Ellipseos latere recto ponatur 2 R: erit vis qua corpus in Ellipsi mobili revolvi potest, ut & contra. Exponatur enim vis qua corpus revolvatur in immota Ellipsi per quantitatem , & vis in V erit . Vis autem qua corpus in circulo ad distantiam CV ea cum velocitate revolvi posset quam corpus in Ellipsi revolvens habet in V, est ad vim qua corpus in Ellipsi revolvens urgetur in Apside V, ut dimidium lateris recti Ellipseos ad circuli semidiametrum CV, adeoque valet : & vis quæ sit ad hanc ut ad Fq., valet : estque hæc vis (per hujus Corol. 1.) differentia virium quibus corpus P in Ellipsi immota VPK, & corpus p in Ellipsi mobili vpk revolvuntur. Unde cum (per hanc Prop.) differentia illa in alia quavis altitudine A sit ad seipsam in altitudine CV ut ad , eadem differentia in omne altitudine A valebit . Igitur ad vim qua corpus revolvi potest in Ellipsi immobili VPK, addatur excessus & componetur vis tota qua corpus in Ellipsi mobili vpk iisdem temporibus revolvi possit.
Corol. 3. Ad eundem modum colligetur quod, si orbis immobilis VPK Ellipsis sit centrum habens in virium centro C; eique similis, æqualis & concentrica ponatur Ellipsis mobilis vpk, sitque Ellipseos hujus latus rectum, & latus transversum, atque angulus VCp semper sit ad angulum VCP ut G ad F; vires quibus corpora in Ellipsi immobili & mobili temporibus æqualibus revolvi possunt, erunt ut respective.
Corol. 4. Et universaliter, si corporis altitudo maxima CV nominetur T, & radius curvaturæ quam Orbis VPK habet in V, id est radius circuli æqualiter curvi, nominetur R, & vis centripeta qua corpus in Trajectoria quacunque immobili VPK revolvi potest, in loco V dicatur , atque aliis in locis P indefinite dicatur X, altitudine CP nominata A, & capiatur G ad F in data ratione anguli VCp ad angulum VCP: erit vis centripeta qua corpus idem eosdem motus in eadem Trajectoria vpk circulariter mota temporibus iisdem peragere potest, ut summa virium
Corol. 5. Dato igitur motu corporis in Orbe quocunque immobili, augeri vel minui potest ejus motus angularis circa centrum virium in ratione data, & inde inveniri novi orbes immobiles in quibus corpora novis viribus centripetis gyrentur.
Corol. 6. Igitur si ad rectam CV positione datam erigatur perpendiculum VP longitudinis indeterminatæ, jungaturque PC, & ipsi æqualis agatur Cp, constituens angulum VCp, qui sit ad angulum VCP in data ratione; vis qua corpus 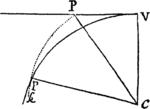 gyrari potest in Curva illa Vpk quam punctum p perpetuo tangit, erit reciproce ut cubus altitudinis Cp. Nam corpus P, per vim inertiæ, nulla alia vi urgente, uniformiter progredi potest in recta VP. Addatur vis in centrum C, cubo altitudinis CP vel Cp reciproce proportionalis, & (per jam demonstrata) detorquebitur motus ille rectilineus in lineam curvam Vpk. Est autem hæc Curva Vpk eadem cum Curva illa VPQ in Corol. 3. Prop. XLI inventa, in qua ibi diximus corpora hujusmodi viribus attracta oblique ascendere.
gyrari potest in Curva illa Vpk quam punctum p perpetuo tangit, erit reciproce ut cubus altitudinis Cp. Nam corpus P, per vim inertiæ, nulla alia vi urgente, uniformiter progredi potest in recta VP. Addatur vis in centrum C, cubo altitudinis CP vel Cp reciproce proportionalis, & (per jam demonstrata) detorquebitur motus ille rectilineus in lineam curvam Vpk. Est autem hæc Curva Vpk eadem cum Curva illa VPQ in Corol. 3. Prop. XLI inventa, in qua ibi diximus corpora hujusmodi viribus attracta oblique ascendere.
Prop. XLV. Prob. XXXI.
Orbium qui sunt Circulis maxime finitimi requiruntur motus Apsidum.
Problema solvitur Arithmetice faciendo ut orbis, quem corpus in Ellipsi mobili, ut in Propositionis superioris Corol. 2. vel 3. revolvens, describit in plano immobili, accedat ad formam orbis cujus Apsides requiruntur, & quærendo Apsides orbis quem corpus illud in plano immobili describit. Orbes autem eandem acquirent formam, si vires centripetæ quibus describuntur, inter se collatæ, in æqualibus altitudinibus reddantur proportionales. Sit punctum V Apsis summa, & scribantur T pro altitudine maxima CV, A pro altitudine quavis alia CP vel Cp, & X pro altitudinum differentia CV−CP; & vis qua corpus in Ellipsi circa umbilicum ejus C (ut in Corollario 2.) revolvente movetur, quæque in Corollario 2. erat ut id est ut , substituendo T−X pro A, erit ut . Reducenda similiter est vis alia quævis centripeta ad fractionem cujus denominator sit A cub., & numeratores, facta homologorum terminorum collatione, statuendi sunt analogi. Res Exemplis patebit.
Exempl. 1. Ponamus vim centripetam uniformem esse, adeoque ut , sive (scribendo T−X pro A in Numeratore) ut ; & collatis Numeratorum terminis correspondentibus, nimirum datis cum datis & non datis cum non datis, fiet ad T cub. ut −Fq.X ad sive ut −Fq. ad Jam cum Orbis ponatur circulo quam maxime finitimus, coeat orbis cum circulo; & ob factas R, T æquales, atque X in infinitum diminutam, rationes ultimæ erunt RGq. ad T cub. ut −Fq. ad seu Gq. ad Tq. ut Fq. ad & vicissim G quadrat. ad F quadrat. ut T quad. ad id est, ut 1 ad 3; adeoque G ad F, hoc est angulus VCp ad angulum VCP, ut 1 ad . Ergo cum corpus in Ellipsi immobili, ab Apside summa ad Apsidem imam descendendo conficiat angulum VCP (ut ita dicam) graduum 180; corpus aliud in Ellipsi mobili, atque adeo in orbe immobili de quo agimus, ab Abside summa ad Apsidem imam descendendo conficiet angulum VCp graduum : id adeo ob similitudinem orbis hujus, quem corpus agente uniformi vi centripeta describit, & orbis illius quem corpus in Ellipsi revolvente gyros peragens describit in plano quiescente. Per superiorem terminorum collationem similes redduntur hi orbes, non universaliter, sed tunc cum ad formam circularem quam maxime appropinquant. Corpus igitur uniformi cum vi centripeta in orbe propemodum circulari revolvens, inter Apsidem summam & Apsidem imam conficiet semper angulum graduum, seu ad centrum; perveniens ab Apside summa ad Apsidem imam, ubi semel confecit hunc angulum, & inde ad Apsidem summam rediens, ubi iterum confecit eundem angulum, & sic deinceps in infinitum.
Exempl. 2. Ponamus vim centripetam esse ut altitudinis A dignitas quælibet seu ubi significant dignitatum indices quoscunque integros vel fractos, rationales vel irrationales, affirmativos vel negativos. Numerator ille seu in seriem indeterminatam per Methodum nostram Serierum convergentium reducta, evadit &c. Et collatis hujus terminis cum terminis Numeratoris alterius , fit ad ut ad &c. Et sumendo rationes ultimas ubi orbes ad formam circularem accedunt, fit ad ut ad , seu ad ut ad , & vicissim ad ut ad id est ut 1 ad n; adeoque G ad F, id est angulus VCp ad angulum VCP, ut 1 ad . Quare cum angulus VCP, in descensu corporis ab Apside summa ad Apsidem imam in Ellipsi confectus, sit graduum 180, conficietur angulus VCp, in descensu corporis ab Apside summa ad Apsidem imam in Orbe propemodum circulari, quem corpus quodvis vi centripeta dignitati proportionali describit, æqualis angulo graduum ; & hoc angulo repetito corpus redibit ab Apside ima ad apsidem summam, & sic deinceps in infinitum. Ut si vis centripeta sit ut distantia corporis a centro, id est ut A seu , erit n æqualis 4 & æqualis 2; adeoque angulus inter Apsidem summam & Apsidem imam æqualis seu Completa igitur quarta parte revolutionis unius corpus perveniet ad Apsidem imam, & completa alia quarta parte ad Apsidem summam, & sic deinceps per vices in infinitum. Id quod etiam ex Propositione X. manifestum est. Nam corpus urgente hac vi centripeta revolvetur in Ellipsi immobili, cujus centrum est in centro virium. Quod si vis centripeta sit reciproce ut distantia, id est directe ut seu , erit , adeoque inter Apsidem summam & imam angulus erit graduum seu 127 & propterea corpus tali vi revolvens, perpetua anguli hujus repetitione, vicibus alternis ab Apside summa ad imam & ab ima ad summam perveniet in æternum. Porro si vis centripeta sit reciproce ut Latus quadrato-quadratum undecimæ dignitatis Altitudinis, id est reciproce ut , adeoque directe ut seu ut erit n æqualis , & æqualis & propterea corpus de Apside summa discedens & subinde perpetuo descendens, perveniet ad Apsidem imam ubi complevit revolutionem integram; dein perpetuo ascensu complendo aliam revolutionem integram, redibit ad Apsidem summam: & sic per vices in æternum.
<141>Exempl. 3. Assumentes m & n pro quibusvis indicibus dignitatum Altitudinis, & b, c pro numeris quibusvis datis, ponamus vim centripetam effe ut , id est ut seu (per eandem Methodum nostram Serierum convergentium) ut & collatis numeratorum terminis, fiet RGq.−RFq.+TFq. ad , ut ad &c. Et sumendo rationes ultimas quæ prodeunt ubi orbes ad formam circularem accedunt, fit Gq. ad , ut Fq. ad , & vicissim Gq. ad Fq. ut ad . Quæ proportio, exponendo altitudinem maximam CV seu T Arithmetice per unitatem, fit Gq. ad Fq. ut b+c ad mb+nc, adeoque ut 1 ad . Unde est G ad F, id est angulus VCp ad angulum VCP, ut 1 ad . Et propterea cum angulus VCP inter Apsidem summam & Apsidem imam in Ellipsi immobili sit erit angulus VCp inter easdem Apsides, in Orbe quem corpus vi centripeta quantitati proportionali describit, æqualis angulo graduum . Et eodem argumento si vis centripeta sit ut , angulus inter Apsides invenietur graduum. Nec secus resolvetur Problema in casibus difficilioribus. Quantitas cui vis centripeta proportionalis est, resolvi semper debet in series convergentes denominatorem habentes A cub. Dein pars data Numeratoris hujus RGq.−RFq.+TFq.−Fq.X ad partem non datam in eadem ratione ponendaæ sunt: Et quantitates superfluas delendo, scribendoque unitatem pro T, obtinebitur proportio G ad F.
Corol. 1. Hinc si vis centripeta sit ut aliqua altitudinis dignitas, inveniri potest dignitas illa ex motu Apsidum; & contra-Nimirum si motus totus angularis, quo corpus redit ad Apsidem eandem, sit ad motum angularem revolutionis unius, seu graduum 360, ut numerus aliquis m ad numerum alium n, & altitudo nominetur A: erit vis ut altitudinis dignitas illa , cujus Index est . Id quod per Exempla secunda manifestum est. Unde liquet vim illam in majore quam triplicata altitudinis ratione decrescere non posse: Corpus tali vi revolvens deque Apside discedens, si cæperit descendere, nunquam perveniet ad Apsidem imam seu altitudinem minimam, sed descendet usque ad centrum, describens curvam illam lineam de qua egimus in Corol. 3. Prop. XLI. Sin cæperit illud de Apside discedens vel minimum ascendere, ascendet in infinitum, neque unquam perveniet ad Apsidem summam. Describet enim curvam illam lineam de qua actum est in eodem Corol. & in Corol. 6. Prop. XLIV. Sic & ubi vis in recessu a centro decrescit in majori quam triplicata ratione altitudinis, corpus de Apside discedens, perinde ut cæperit descendere vel ascendere, vel descendet ad centrum usque vel ascendet in infinitum. At si vis in recessu a centro vel decrescat in minori quam triplicata ratione altitudinis, vel crescat in altitudinis ratione quacunque Corpus nunquam descendet ad centrum usque sed ad Apsidem imam aliquando perveniet: & contra, si corpus de Apside ad Apsidem alternis vicibus descendens & ascendens nunquam appellat ad centrum, Vis in recessu a centro aut augebitur, aut in minore quam triplicata altitudinis ratione decrescet: & quo citius corpus de Apside ad Apsidem redierit, eo longius ratio virium recedet a ratione illa triplicata. Ut si corpus revolutionibus 8 vel 4 vel 2 vel de Apside summa ad Apsidem summam alterno descensu & ascensu redierit, hoc est, si fuerit m ad n ut 8 vel 4 vel 2 vel ad 1, adeoque ualeat vel vel vel , erit vis ut vel vel vel , id est reciproce ut vel vel vel . Si corpus singulis revolutionibus redierit ad Apsidem eandem immotam, erit, m ad n ut 1 ad 1, adeoque æqualis seu , & propterea decrementum virium in ratione duplicata altitudinis, ut in præcedentibus demonstratum est. Si corpus partibus revolutionis unius vel tribus quartis, vel duabus tertiis, vel una tertia, vel una quarta, ad Apsidem eandem redierit, erit m ad n ut vel vel vel ad 1, adeoque æqualis vel vel vel , & propterea Vis aut reciproce ut vel , aut directe ut vel . Denique si Corpus pergendo ab Apside summa ad Apsidem summam confecerit revolutionem integram, & præterea gradus tres, adeoque Apsis illa singulis corporis revolutionibus confecerit in Consequentia gradus tres, erit m ad n ut ad adeoque erit æquale , & propterea Vis centripeta reciproce ut seu . Decrescit igitur Vis centripeta in ratione paulo majore quam duplicata, sed quæ vicibus propius ad duplicatam quam ad triplicatam accedit.
Corol. 2. Hinc etiam si corpus, vi centripeta quæ sit reciproce ut quadratum altitudinis, revolvatur in Ellipsi umbilicum habente in centro virium, & huic vi centripetæ addatur vel auferatur vis alia quævis extranea; cognosci potest (per Exempla tertia) motus Apsidum qui ex vi illa extranea orietur: & contra. Ut si vis qua corpus revolvitur in Ellipsi sit ut , & vis extranea ablata ut , adeoque vis reliqua ut ; erit (in Exemplis tertiis) A æqualis 1 & n æqualis 4, adeoque angulus revolutionis inter Apsides æqualis angulo graduum . Ponatur vim illam extraneam esse 357.45 vicibus minorem quam vis altera qua corpus revolvitur in Ellipsi, id est c esse , & evadet seu 180.7602, id est Igitur corpus de Apside summa discedens, motu angulari perveniet ad Apsidem imam, & hoc motu duplicato ad Apsidem summam redibit: adeoque Apsis summa singulis revolutionibus progrediendo conficiet
Hactenus de motu corporum in orbibus quorum plana per centrum virium transeunt. Superest ut motus etiam determinemus in planis excentricis. Nam Scriptores qui motum gravium tractant, considerare solent a scensus & descensus ponderum, tam obliquos in planis quibuscunque datis, quam perpendiculares: & pari jure motus corporum viribus quibuscunque centra petentium, & planis excentricis innitentium hic considerandus venit. Plana autem supponimus esse politissima & absolute lubrica ne corpora retardent. Quinimo in his demonstrationibus, vice planorum quibus corpora incumbunt quasque tangunt incumbendo, usurpamus plana his parallela, in quibus centra corporum moventur & orbitas movendo describunt. Et eadem lege motus corporum in superficiebus curvis peractos subinde determinamus.
SECT. X.
De Motu Corporum in Superficiebus datis, deque Funipendulorum Motu reciproco.
Prop. XLVI. Prob. XXXII.
Posita cujuscunque generis vi centripeta, datoque tum virium centro tum plano quocunque in quo corpus revolvitur, & concessis Figurarum curvilinearum quadraturis: requiritur motus corporis de loco dato data cum velocitate secundum Rectam in Plano illo datam egressi.
Sit S centrum virium, SC distantia minima centri hujus a plano dato, P corpus de loco P secundum rectam PZ egrediens, Q corpus idem in Trajectoria 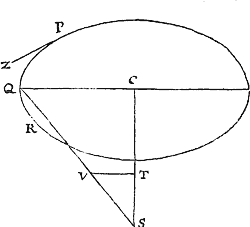 sua revolvens, & PQR Trajectoria illa in plano dato descripta, quam invenire oportet. Jungantur CQ QS, & si in QS capiatur SV proportionalis vi centripetæ qua corpus tra hitur versus centrum S, & agatur VT quæ sit parallela CQ & occurrat SC in T: Vis SV resolvetur (per Legum Corol. 2.) in vires ST, TV; quarum ST trahendo corpus secundum lineam plano perpendicularem, nil mutat motum ejus in hoc plano. Vis autem altera TV, agendo secundum positionem plani, trahit corpus directe versus punctum C in plano datum, adeoque facit illud in hoc plano perinde moveri ac si vis ST tolleretur, & corpus vi sola TV revolveretur circa centrum C in spatio libero. Data autem vi centripeta TV qua corpus Q in spatio libero circa centrum datum C revolvitur, datur per Prop. XLII. tum Trajectoria PQR quam corpus describit, tum locus Q in quo corpus ad datum quodvis tempus versabitur, tum denique velocitas corporis in loco illo Q; & contra. Q.E.I.
sua revolvens, & PQR Trajectoria illa in plano dato descripta, quam invenire oportet. Jungantur CQ QS, & si in QS capiatur SV proportionalis vi centripetæ qua corpus tra hitur versus centrum S, & agatur VT quæ sit parallela CQ & occurrat SC in T: Vis SV resolvetur (per Legum Corol. 2.) in vires ST, TV; quarum ST trahendo corpus secundum lineam plano perpendicularem, nil mutat motum ejus in hoc plano. Vis autem altera TV, agendo secundum positionem plani, trahit corpus directe versus punctum C in plano datum, adeoque facit illud in hoc plano perinde moveri ac si vis ST tolleretur, & corpus vi sola TV revolveretur circa centrum C in spatio libero. Data autem vi centripeta TV qua corpus Q in spatio libero circa centrum datum C revolvitur, datur per Prop. XLII. tum Trajectoria PQR quam corpus describit, tum locus Q in quo corpus ad datum quodvis tempus versabitur, tum denique velocitas corporis in loco illo Q; & contra. Q.E.I.
Prop. XLVII. Theor. XV.
Posito quod vis centripeta proportionalis sit distantiæ corporis a centro; corpora omnia in planis quibuscunque revolventia describent Ellipses, & revolutiones temporibus æqualibus peragent; quæque moventur in lineis rectis ultro citroque discurrendo, singulas eundi & redeundi periodos iisdem temporibus absolvent.
Nam stantibus quæ in superiore Propositione; vis SV qua corpus Q in plano quovis PQR revolvens trahitur versus centrum S est ut distantia SQ; 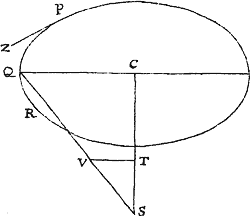 atque adeo ob proportionales SV & SQ, TV & CQ, vis TV qua corpus trahitur versus punctum C in Orbis plano datum, est ut distantia CQ. Vires igitur, quibus corpora in plano PQR versantia trahuntur versus punctum C, sunt pro ratione distantiarum æquales viribus quibus corpora undiquaque trahuntur versus centrum S; & propterea corpora movebuntur iisdem temporibus in iisdem figuris in plano quovis PQR circa punctum C, atque in spatiis liberis circa centrum S, adeoque (per Corol. 2. Prop. X. & Corol. 2. Prop. XXXVIII.) temporibus semper æqualibus, vel describent Ellipses in plano illo circa centrum C, vel periodos movendi ultro citroque in lineis rectis per centrum C in plano illo ductis, complebunt. Q.E.D.
atque adeo ob proportionales SV & SQ, TV & CQ, vis TV qua corpus trahitur versus punctum C in Orbis plano datum, est ut distantia CQ. Vires igitur, quibus corpora in plano PQR versantia trahuntur versus punctum C, sunt pro ratione distantiarum æquales viribus quibus corpora undiquaque trahuntur versus centrum S; & propterea corpora movebuntur iisdem temporibus in iisdem figuris in plano quovis PQR circa punctum C, atque in spatiis liberis circa centrum S, adeoque (per Corol. 2. Prop. X. & Corol. 2. Prop. XXXVIII.) temporibus semper æqualibus, vel describent Ellipses in plano illo circa centrum C, vel periodos movendi ultro citroque in lineis rectis per centrum C in plano illo ductis, complebunt. Q.E.D.
Scholium.
His affines sunt ascensus ac descensus corporum in superficiebus curvis. Concipe lineas curvas in plano describi, dein circa axes quosvis datos per centrum virium transeuntes revolvi, & ea revolutione superficies curvas describere; tum corpora ita moveri ut eorum centra in his superficiebus perpetuo reperiantur. Si corpora illa oblique ascendendo & descendendo currant ultro citroque peragentur eorum motus in planis per axem transeuntibus, atque adeo in lineis curvis quarum revolutione curvae illæ superficies genitæ sunt. Istis igitur in casibus sufficit motum in his lineis curvis considerare.
Prop. XLVIII. Theor. XVI.
Si rota globo extrinsecus ad angulos rectos insistat, & more rotarum revolvendo progrediatur in circulo maximo; longitudo itineris curvilinei, quod punctum quodvis in rotæ perimetro datum, ex quo globum tetigit, confecit, erit ad duplicatum sinum versum arcus dimidii qui globum ex eo tempore inter eundem tetigit, ut summa diametrorum globi & rotæ ad semidiametrum globi.
Prop. XLIX. Theor XVII.
Si rota globo concavo ad rectos angulos intrinsecus insistat & revolvendo progrediatur in circulo maximo; longitudo itineris curvilinei quod punctum quodvis in Rotæ Perimetro datum, ex quo globum tetigit, confecit, erit ad duplicatum sinum versum arcus dimidii qui globum toto hoc tempore inter eundum tetigit, ut differentia diametrorum globi & rotæ ad semidiametrum globi.
Sit ABL globus, C centrum ejus, BPV rota ei insistens, E centrum rotæ, B punctum contactus, & P punctum datum in perimetro rotæ. Concipe hanc Rotam pergere in circulo maximo  ABL ab A per B versus L, & inter eundum ita revolvi ut arcus AB, PB sibi invicem semper æquentur, atque punctum illud P in Perimetro rotæ datum interea describere viam curvilineam AP. Sit autem AP via tota curvilinea descripta ex quo Rota globum tetigit in A, & erit viæ hujus longitudo AP ad duplum sinum versum arcus , ut ad CB. Nam recta CE (si opus est producta) occurrat Rotæ in V, junganturque CP, BP, EP, VP, & in CP productam demittatur Normalis VF. Tangant PH, VH circulum in P & V concurrentes in H, secetque PH ipsam VF in G, & ad VP demittantur Normales GI, HK. Centro item C & intervallo quovis describatur circulus nom secans rectam CP in n, Rotæ perimetrum Bp in o & viam curvilineam AP in m, centroque V & intervallo Vo describatur circulus secans VP productam in q.
ABL ab A per B versus L, & inter eundum ita revolvi ut arcus AB, PB sibi invicem semper æquentur, atque punctum illud P in Perimetro rotæ datum interea describere viam curvilineam AP. Sit autem AP via tota curvilinea descripta ex quo Rota globum tetigit in A, & erit viæ hujus longitudo AP ad duplum sinum versum arcus , ut ad CB. Nam recta CE (si opus est producta) occurrat Rotæ in V, junganturque CP, BP, EP, VP, & in CP productam demittatur Normalis VF. Tangant PH, VH circulum in P & V concurrentes in H, secetque PH ipsam VF in G, & ad VP demittantur Normales GI, HK. Centro item C & intervallo quovis describatur circulus nom secans rectam CP in n, Rotæ perimetrum Bp in o & viam curvilineam AP in m, centroque V & intervallo Vo describatur circulus secans VP productam in q.
Quoniam Rota eundo semper revolvitur circa punctum contactus B, manifestum est quod recta BP perpendicularis est ad lineam illam curvam AP, quam Rotæ punctum P describit, atque adeo quod recta VP tanget hanc curvam in puncto P. Circuli nom radius sensim auctus æquetur tandem distantiæ CP, & ob similitudinem figuræ evanescentis Pnomq & figuræ PFGVI, ratio ultima lineolarum evanescentium Pm, Pn, Po, Pq, id est ratio incrementorum momentaneorum curvæ AP, rectæ CP & arcus circularis BP, ac decrementi rectæ VP, eadem erit quæ linearum PV, PF, PG, PI respective. Cum autem VF ad CF & VH ad CV perpendiculares sunt, angulique HVG, VCF propterea æquales; & angulus VHP, (ob angulos quadrilateri HVEP ad V & P rectos,) complet angulum VEP ad duos rectos, adeoque angulo CEP æqualis est, similia erunt triangula VHG, CEP; & inde fiet ut EP ad CE ita HG ad HV seu HP, & ita KI ad KP, & divisim ut CB ad CE ita PI ad PK, & duplicatis consequentibus ut CB ad ita PI ad PV. Est igitur decrementum lineæ VP, id est incrementum lineæ BV−VP, ad incrementum lineæ curvæ AP in data ratione CB ad , & propterea (per Corol. Lem. IV.) longitudines BV−VP & AP incrementis illis genitæ sunt in eadem ratione. Sed existente BV radio, est VP cosinus anguli VPB seu , adeoque BV−VP sinus versus ejusdem anguli, & propterea in hac Rota cujus radius est , erit BV−VP duplus sinus versus arcus . Ergo AP est ad duplum sinum versum arcus ut ad CB. Q.E.D.
<150>Lineam autem AP in Propositione priore Cycloidem extra Globum, alteram in posteriore Cycloidem intra Globum distinctionis gratia nominabimus.
Corol. 1. Hinc si describatur Cyclois integra ASL & bisecetur ea in S, erit longitudo partis PS ad longitudinem VP (quæ duplus est sinus anguli VBP, existente EB radio) ut ad CB, atque adeo in ratione data.
Corol. 2. Et longitudo semiperimetri Cycloidis AS æquabitur lineæ rectæ, quæ est ad Rotæ diametrum BV ut ad CB.
Corol. 3. Ideoque longitudo illa est ut rectangulum BEC, si modo Globi detur semidiameter.
Prop. L. Prob. XXXIII.
Facere ut Corpus pendulum oscilletur in Cycloide data.
Intra Globum QVS centro C descriptum detur Cyclois QRS bisecta in R & punctis suis extremis Q & S superficiei Globi hinc inde occurrens. Agatur CR bisecans arcum QS in O, & producatur ea ad A, ut sit CA ad CO ut CO ad CR. Centro C intervallo CA describatur Globus exterior ABD, & intra hunc globum Rota, cujus diameter sit AO, describantur duæ semicycloides AQ, AS, quæ globum interiorem tangant in Q & S & globo exteriori occurrant in A. A puncto illo A, filo APT longitudinem AR æquante, pendeat corpus T, & ita intra semicycloides AQ, AS oscilletur, ut quoties pendulum digreditur a perpendiculo AR, filum parte sui superiore AP applicetur ad semicycloidem illam APS, versus quam peragitur motus, & circum eam ceu obstaculum flectatur, parteque reliqua PT cui semicyclois nondum objicitur, protendatur in lineam rectam; & pondus T oscillabitur in Cycloide data QRS. Q.E.F.
Occurrat enim filum PT tum Cycloidi QRS in T, tum circulo QOS in V, agaturque CV occurrens circulo ABD in B; & ad fili partem rectam PT, e punctis extremis P ac T, erigantur perpendicula PB, TW, occurrentia rectæ CV in B & W. Patetenim ex genesi Cycloidis, quod perpendicula illa PB, TW abscindent de CV longitudines VB, VW rotarum diametris OA, OR æquales, atque adeo quod punctum B incidet in circulum ABD. Est igitur TP ad VP (duplum sinum anguli VBP existente radio) ut BW ad BV, seu AO + OR ad AO, id est (cum sint CA ad CO, CO ad CR & divisim AO ad OR proportionales,) ut CA + CO  seu ad CA. Proinde per Corol. 1. Prop. XLIX. longitudo PT æquatur Cycloidis arcui PS, & filum totum APT æquatur Cycloidis arcui dimidio APS, hoc est (per Corollar. 2. Prop. XLIX longitudini AR. Et propterea vicissim si filum manet semper æquale longitudini AR movebitur punctum T in Cycloide QRS. Q.E.D.
seu ad CA. Proinde per Corol. 1. Prop. XLIX. longitudo PT æquatur Cycloidis arcui PS, & filum totum APT æquatur Cycloidis arcui dimidio APS, hoc est (per Corollar. 2. Prop. XLIX longitudini AR. Et propterea vicissim si filum manet semper æquale longitudini AR movebitur punctum T in Cycloide QRS. Q.E.D.
Corol. Filum AR æquatur Cycloidis arcui dimidio APS.
Prop. LI. Theor. XVIII.
Si vis centripeta tendens undique ad Globi centrum C sit in locis singulis ut distantia loci cujusque a centro, & hac sola vi agente Corpus oscilletur (modo jam descripto) in perimetro Cycloidis QRS: dico quod oscillationum utcunque inæqualium æqualia erunt Tempora
Nam in Cycloidis tangentem TW infinite productam cadat perpendiculum CX & jungatur CT. Quoniam vis centripeta qua corpus T impellitur versus C est ut distantia CT, (per Legum Corol. 2.) resolvitur in partes CX, TX, quarum CX impellendo corpus directe a P distendit filum PT & per cujus resistentiam tota cessat, nullum alium edens effectum; pars autem altera TX urgendo corpus transversim seu versus X, directe accelerat motum ejus in Cycloide; manifestum est quod corporis acceleratio huic vi acceleratrici proportionalis sit singulis momentis ut longitudo TX, id est, ob datas CV, WV iisque proportionales TX, TW, ut longitudo TW, hoc est (per Corol. 1. Prop. XLIX.) ut longitudo arcus Cycloidis TR. Pendulis igitur duabus APT, Apt de perpendiculo AR inæqualiter deductis & simul dimissis, accelerationes eorum semper erunt ut arcus describendi TR, tR. Sunt autem partes sub initio descriptæ ut accelerationes, hoc est ut totæ sub initio describendæ, & propterea partes quæ manent describendæ & accelerationes subsequentes his partibus proportionales sunt etiam ut totæ; & sic deinceps. Sunt igitur accelerationes atque adeo velocitates genitæ & partes his velocitatibus descriptæ partesque describendæ, semper ut totæ; & propterea partes describendæ datam servantes rationem ad invicem simul evanescent, id est corpora duo oscillantia simul pervenient ad perpendiculum AR. Cumque vicissim ascensus perpendiculorum de loco infimo R, per eosdem arcus Trochoidales motu retrogrado facti, retardentur in locis singulis a viribus iisdem a quibus descensus accelerabantur, patet velocitates ascensuum ac descensuum per eosdem arcus factorum æquales esse, atque adeo temporibus æqualibus fieri; & propterea cum Cycloidis partes duæ RS & RQ ad utrumque perpendiculi latus jacentes sint similes & æquales, pendula duo oscillationes suas tam totas quam dimidias iisdem temporibus semper peragant. Q.E.D.
<153>Prop. LII. Prob. XXXIV.
Definire & velocitates Pendulorum in locis singulis, & Tempora quibus tum oscillationes totæ, tum singulæ oscillationum partes peraguntur.
Centro quovis G, intervallo GH Cycloidis arcum RS æquante, describe semicirculum HKMG semidiametro GK bisectum. Et si vis centripeta distantiis locorum a centro proportionalis tendat ad centrum G, sitque ea in perimetro HIK æqualis vi centripetæ in perimetro globi QOS (Vide Fig. Prop. L. & LI.) ad ipsius centrum tendente; & eodem tempore quo pendulum T dimittitur e loco supremo S, cadat corpus aliquod L ab H ad G: quoniam vires quibus corpora urgentur  sunt æquales sub initio & spatiis describendis TR, GL semper proportionales, atque adeo, si æquantur TR ad LG, æquales in locis T & L; patet corpora illa describere spatia ST, HL æqualia sub initio, adeoque subinde pergere æqualiter urgeri, & æqualia spatia describere. Quare, per Prop. XXXVIII., tempus quo corpus describit arcum ST est ad tempus oscillationis unius, ut arcus HI (tempus quo corpus H perveniet ad L) ad semicirculum HKM (tempus quo corpus H perveniet ad M.) Et velocitas corporis penduli in loco T est ad velocitatem ipsius in loco infimo R, (hoc est velocitas corporis H in loco L ad velocitatem ejus in loco G, seu incrementum momentaneum lineæ HL ad incrementum momentaneum lineæ HG, arcubus HI, HK æquabili fluxu crescentibus) ut ordinatim applicata LI ad radium GK, sive ut ad SR. Unde cum in Oscillationibus inæqualibus describantur æqualibus temporibus arcus totis Oscillationum arcubus proportionales, habentur ex datis temporibus & velocitates & arcus descripti in Oscillationibus universis. Quæ erant primo invenienda.
sunt æquales sub initio & spatiis describendis TR, GL semper proportionales, atque adeo, si æquantur TR ad LG, æquales in locis T & L; patet corpora illa describere spatia ST, HL æqualia sub initio, adeoque subinde pergere æqualiter urgeri, & æqualia spatia describere. Quare, per Prop. XXXVIII., tempus quo corpus describit arcum ST est ad tempus oscillationis unius, ut arcus HI (tempus quo corpus H perveniet ad L) ad semicirculum HKM (tempus quo corpus H perveniet ad M.) Et velocitas corporis penduli in loco T est ad velocitatem ipsius in loco infimo R, (hoc est velocitas corporis H in loco L ad velocitatem ejus in loco G, seu incrementum momentaneum lineæ HL ad incrementum momentaneum lineæ HG, arcubus HI, HK æquabili fluxu crescentibus) ut ordinatim applicata LI ad radium GK, sive ut ad SR. Unde cum in Oscillationibus inæqualibus describantur æqualibus temporibus arcus totis Oscillationum arcubus proportionales, habentur ex datis temporibus & velocitates & arcus descripti in Oscillationibus universis. Quæ erant primo invenienda.
Oscillentur jam funipendula duo corpora in Cycloidibus inæqualibus & earum semiarcubus æquales capiantur rectæ GH, gh, centrisque G, g & intervallis GH, gh describantur semicirculi HZKM, hzkm. In eorum diametris HM, hm capiantur lineolæ æquales HY, hy, & erigantur normaliter YZ, yz circumferentiis occurrentes in Z & z. Quoniam corpora pendula sub initio motus versantur in circumferentia globi QOS, adeoque a viribus æqualibus urgentur in centrum, incipiuntque directe versus centrum moveri, spatia simul confecta æqualia erunt sub initio. Urgeantur igitur corpora H, h a viribus iisdem in H & h, sintque  HY, hy spatia æqualia ipso motus initio descripta, & arcus HZ hz denotabunt æqualia tempora. Horum arcuum nascentium ratio prima duplicata est eadem quæ rectangulorum GHY, ghy, id est, eadem quæ linearum GH, gh; adeoque arcus capti in dimidiata ratione semidiametrorum denotant æqualia tempora. Est ergo tempus totum in circulo HKM, Oscillationi in una Cycloide respondens, ad tempus totum in circulo hkm Oscillationi in altera Cycloide respondens, ut semiperiferia HKM ad medium proportionale inter hanc semiperiferiam & semiperiferiam circuli alterius hkm, id est in dimidiata ratione diametri HM ad diametrum hm, hoc est in dimidiata ratione perimetri Cycloidis primæ ad perimetrum Cycloidis alterius, adeoque tempus illud in Cycloide quavis est (per Corol. 3. Prop. XLIX.) ut latus quadratum rectanguli BEC contenti sub semidiametro Rotæ, qua Cyclois descripta fuit, & differentia inter semidiametrum illam & semidiametrum globi. Q.E.I. Est & idem tempus (per Corol. Prop. L.) in dimidiata ratione longitudinis fili AR.Q.E.I.
HY, hy spatia æqualia ipso motus initio descripta, & arcus HZ hz denotabunt æqualia tempora. Horum arcuum nascentium ratio prima duplicata est eadem quæ rectangulorum GHY, ghy, id est, eadem quæ linearum GH, gh; adeoque arcus capti in dimidiata ratione semidiametrorum denotant æqualia tempora. Est ergo tempus totum in circulo HKM, Oscillationi in una Cycloide respondens, ad tempus totum in circulo hkm Oscillationi in altera Cycloide respondens, ut semiperiferia HKM ad medium proportionale inter hanc semiperiferiam & semiperiferiam circuli alterius hkm, id est in dimidiata ratione diametri HM ad diametrum hm, hoc est in dimidiata ratione perimetri Cycloidis primæ ad perimetrum Cycloidis alterius, adeoque tempus illud in Cycloide quavis est (per Corol. 3. Prop. XLIX.) ut latus quadratum rectanguli BEC contenti sub semidiametro Rotæ, qua Cyclois descripta fuit, & differentia inter semidiametrum illam & semidiametrum globi. Q.E.I. Est & idem tempus (per Corol. Prop. L.) in dimidiata ratione longitudinis fili AR.Q.E.I.
Porro si in globis concentricis describantur similes Cycloides: quoniam earum perimetri sunt ut semidiametri globorum & vires in analogis perimetrorum locis sunt ut distantiæ locorum a communi globorum centro, hoc est ut globorum semidiametri, atque adeo ut Cycloidum perimetri & perimetrorum partes similes, aqualia erunt tempora quibus perimetrorum partes similes Oscillationibus similibus describuntur, & propterea Oscillationes omnes erunt Isochronæ. Cum igitur Oscillationum tempora in Globo dato sint in dimidiata ratione longitudinis AR, atque adeo (ob datam AC) in dimidiata ratione numeri , id est in ratione integra numeri ; & hic numerus servata ratione AR ad AC (ut fit in Cycloidibus similibus) idem semper maneat, & propterea in globis diversis, ubi Cycloides sunt similes, sit ut tempus: manifestum est quod Oscillationum tempora in alio quovis globo dato, atque adeo in globis omnibus concentricis sunt ut numerus , id est, in ratione composita ex dimidiata ratione longitudinis fili AR directe & dimidiata ratione semidiametri globi AC inverse. Q.E.I
Denique si vires absolutæ diversorum globorum ponantur inæquales, accelerationes temporibus æqualibus factæ, erunt ut vires. Unde si tempora capiantur in dimidiata ratione virium inverse, velocitates erunt in eadem dimidiata ratione directe, & propterea spatia erunt æqualia quæ his temporibus describuntur. Ergo Oscillationes in globis & Cycloidibus omnibus, quibuscunque cum viribus absolutis factæ, sunt in ratione quæ componitur ex dimidiata ratione longitudinis Penduli directe, & dimidiata ratione distantiæ inter centrum Penduli & centrum globi inverse, & dimidiata ratione vis absolutæ etiam inverse, id est, si vis illa dicatur V, in ratione numeri .Q.E.I.
Corol. 1. Hinc etiam Oscillantium, cadentium & revolventium corporum tempora possunt inter se conferri. Nam si Rotæ, qua Cyclois intra globum describitur, diameter constituatur æqualis semidiametro globi, Cyclois evadet linea recta per centrum globi transiens, & Oscillatio jam erit descensus & subsequens ascensus in hac recta. Unde datur tum tempus descensus de loco quovis ad centrum, tum tempus huic æquale quo corpus uniformiter circa centrum globi ad distantiam quamvis revolvendo arcum quadrantalem describit. Est enim hoc tempus (per Casum secundum) ad tempus semioscillationis in Trochoide quavis APS ut ad .
Corol. 2. Hinc etiam consectantur quæ D. C. Wrennus & D. C. Hugenius de Cycloide vulgari adinvenerunt. Nam si globi diameter augeatur in infinitum, mutabitur ejus superficies Sphærica in planum, visque centripeta aget uniformiter secundum lineas huic plano perpendiculares, & Cyclois nostra abibit in Cycloidem vulgi. Isto autem in casu, longitudo arcus Cycloidis, inter planum illud & punctum describens, æqualis evadet quadruplicato sinui verso dimidii arcus Rotæ inter idem planum & punctum describens; ut invenit D. C. Wrennus: Et pendulum inter duas ejusmodi Cycloides in simili & æquali Cycloide temporibus æqualibus Oscillabitur, ut demonstravit Hugenius. Sed & descensus gravium, tempore Oscillationis unius, is erit quem Hugenius indicavit.
Aptantur autem Propositiones a nobis demonstratæ ad veram constitutionem Terræ, quatenus Rotæ eundo in ejus circulis maximis describunt motu clavorum Cycloides extra globum; & Pendula inferius in fodinis & cavernis Terræ suspensa, in Cycloidibus intra globos Oscillari debent, ut Oscillationes omnes evadant Isochronæ. Nam gravitas (ut in Libro tertio docebitur) decrescit in progressu a superficie Terræ, sursum quidem in duplicata ratione distantiarum a centro ejus, deorsum vero in ratione simplici.
Prop. LIII. Prob. XXXV.
Concessis figurarum curvilinearum Quadraturis, invenire vires quibus corpora in datis curvis lineis Oscillationes semper Isochronas peragent.
Oscilletur corpus  T in curva quavis linea STRQ, cujus axis sit OR transiens per virium centrum C. Agatur TX quæ curvam illam in corporis loco quovis T contingat, inque hac Tangente TX capiatur TY æqualis arcui TR. Nam longitudo arcus illius ex figurarum Quadraturis per Methodos vulgares innotescit. De puncto Y educatur recta YZ Tangenti perpendicularis. Agatur CT perpendiculari illi occurrens in Z, & erit vis centripeta proportionalis rectæ TZ.Q.E.I.
T in curva quavis linea STRQ, cujus axis sit OR transiens per virium centrum C. Agatur TX quæ curvam illam in corporis loco quovis T contingat, inque hac Tangente TX capiatur TY æqualis arcui TR. Nam longitudo arcus illius ex figurarum Quadraturis per Methodos vulgares innotescit. De puncto Y educatur recta YZ Tangenti perpendicularis. Agatur CT perpendiculari illi occurrens in Z, & erit vis centripeta proportionalis rectæ TZ.Q.E.I.
Nam si vis, qua corpus trahitur de T versus C, exponatur per rectam TZ captam ipsi proportionalem, resolvetur hæc in vires TY, YZ; quarum YZ trahendo corpus secundum longitudinem fili PT, motum ejus nil mutat, vis autem altera TY motum ejus in curva STRQ directe accelerat vel directe retardat. Proinde cum hæc sit ut via describenda TR, accelerationes corporis vel retardationes in Oscillationum duarum (majoris & minoris) partibus proportionalibus describendis, erunt semper ut partes illæ, & propterea facient ut partes illæ simul describantur. Corpora autem quæ partes totis semper proportionales simul describunt, simul describent totas. Q.E.D.
Corol. 1. Hinc si corpus T filo rectilineo AT a centro A pendens, describat arcum circularem STRQ, & interea urgeatur secundum lineas parallelas deorsum a vi aliqua, quæ sit ad vim uniformem gravitatis, ut arcus TR ad ejus sinum TN: æqualia erun Oscillationum singularum tempora. Etenim ob parallelas TZ, AR, similia erunt triangula ANT, TYZ; & propterea TZ erit ad AT ut TY ad TN; hoc est, si gravitatis vis uniformis exponatur per longitudinem datam AT, vis TZ, qua Oscillationes evadent Isochronæ, erit ad vim gravitatis AT, ut arcus TR ipsi TY æqualis ad arcus illius sinum TN.
Corol. 2. Igitur in Horologiis, si vires a Machina in Pendulum ad motum conservandum impressæ ita cum vi gravitatis componi possint, ut vis tota deorsum semper sit ut linea quæ oritur applicando rectangulum sub arcu TR & radio AR, ad sinum TN, Oscillationes omnes erunt Isochronæ.
Prop. LIV. Prob. XXXVI.
Concessis figurarum curvilinearum quadraturis, invenire tempora quibus corpora vi qualibet centripeta in lineis quibuscunque curvis in plano per centrum virium transeunte descriptis, descendent & ascendent.
Descendat enim corpus de loco quovis S per lineam quamvis curvam STtR in plano per virium centrum C transeunte datam. Jungatur CS & dividatur cadem in partes innumeras æquales, sitque Dd partium illarum aliqua. Centro C, intervallis CD, Cd describantur circuli DT, dt, Lineæ curvæ STtR occurrentes in T & t. Et ex data tum lege vis centripetæ, tum altitudine CS dequa corpus cecidit; dabitur velocitas corporis in alia quavis altitudine CT, per Prop. XXXIX. Tempus autem, quo corpus describit lineolam Tt, est ut lineolæ hujus  longitudo (id est ut secans anguli tTC) directe, & velocitas inverse. Tempori huic proportionalis sit ordinatim applicata DN ad rectam CS per punctum D perpendicularis, & ob datam Dd erit rectangulum , hoc est area DNnd, eidem tempori proportionale. Ergo si SNn sit curva illa linea quam punctum N perpetuo tangit, erit area SNDS proportionalis tempori quo corpus descendendo descripsit lineam ST; proindeque ex inventa illa area dabitur tempus. Q.E.I.
longitudo (id est ut secans anguli tTC) directe, & velocitas inverse. Tempori huic proportionalis sit ordinatim applicata DN ad rectam CS per punctum D perpendicularis, & ob datam Dd erit rectangulum , hoc est area DNnd, eidem tempori proportionale. Ergo si SNn sit curva illa linea quam punctum N perpetuo tangit, erit area SNDS proportionalis tempori quo corpus descendendo descripsit lineam ST; proindeque ex inventa illa area dabitur tempus. Q.E.I.
Prop. LV. Theor. XIX.
Si corpus movetur in superficie quacunque curva, cujus axis per centrum virium transit, & a corpore in axem demittatur perpendicularis, eique parallela & æqualis ab axis puncto quovis ducatur: dico quod parallela illa aream tempori proportionalem describet.
Sit BSKL superficies curva, T corpus in ea revolvens, STtR Trajectoria quam corpus in eadem describit, S initium Trajectoriæ, OMNK axis superficiei curvæ, TN recta a corpore in axem perpendicularis, OP huic parallela & æqualis a puncto O quod in axe datur educta, AP vestigium Trajectoriæ a puncto P in lineæ volubilis OP plano AOP descriptum, A vestigii initium puncto S respondens, TC recta a corpore ad centrum ducta; TG pars ejus vi centripetæ qua corpus urgetur in centrum C proportionalis; TM recta ad superficiem curvam perpendicularis; TI pars ejus vi pressionis qua corpus urget superficiem, vicissimque urgetur versus M a superficie, proportionalis; PHTF recta axi parallela per corpus transiens,  & GF, IH rectæ a punctis G & I in parallelam illam PHTF perpendiculariter demissæ. Dico jam quod area AOP, radio OP ab initio motus descripta, sit tempori proportionalis. Nam vis TG (per Legum Corol. 2.) resolvitur in vires TF, FG; & vis TI in vires TH, HI: Vires autem TF, TH agendo secundum lineam PF plano AOP perpendicularem mutant solummodo motum corporis quatenus huic plano perpendicularem. Ideoque motus ejus quatenus secundum positionem plani factus, hoc est motus puncti P, quo Trajectoriæ vestigium AP in hoc plano describitur, idem est ac si vires TF, TH tollerentur, & corpus solis viribus FG, HI agitaretur, hoc est idem ac si corpus in plano AOP vi centripeta ad centrum O tendente & summam virium FG & HI æquante, describeret curvam AP. Sed vi tali describetur area AOP (per Prop. I.) tempori proportionalis. Q.E.D.
& GF, IH rectæ a punctis G & I in parallelam illam PHTF perpendiculariter demissæ. Dico jam quod area AOP, radio OP ab initio motus descripta, sit tempori proportionalis. Nam vis TG (per Legum Corol. 2.) resolvitur in vires TF, FG; & vis TI in vires TH, HI: Vires autem TF, TH agendo secundum lineam PF plano AOP perpendicularem mutant solummodo motum corporis quatenus huic plano perpendicularem. Ideoque motus ejus quatenus secundum positionem plani factus, hoc est motus puncti P, quo Trajectoriæ vestigium AP in hoc plano describitur, idem est ac si vires TF, TH tollerentur, & corpus solis viribus FG, HI agitaretur, hoc est idem ac si corpus in plano AOP vi centripeta ad centrum O tendente & summam virium FG & HI æquante, describeret curvam AP. Sed vi tali describetur area AOP (per Prop. I.) tempori proportionalis. Q.E.D.
Corol. Eodem argumento si corpus a viribus agitatum ad centra duo vel plura in eadem quavis recta CO data tendentibus, describeret in spatio libero lineam quamcunque curvam ST, foret area AOP tempori semper proportionalis.
Prop. LVI. Prob. XXXVII.
Concessis figurarum curvilinearum Quadraturis, datisque tum lege vis centripetæ ad centrum datum tendentis, tum superficie curva cujus axis per centrum illud transit; invenienda est Trajectoria quam corpus in eadem superficie describet, de loco dato, data cum velocitate versus plagam in superficie illa datam egressum.
Stantibus quæ in superiore Propositione constructa sunt, exeat corpus de loco S in Trajectoriam inveniendam STtR, & ex data ejus velocitate in altitudine SC dabitur ejus velocitas in alia quavis altitudine TC. Ea cum velocitate, dato tempore quam minimo, describat corpus Trajectoriæ suæ particulam Tt, sitque Pp vestigium ejus plano AOP descriptum. Jungatur Op, & circelli centro T intervallo Tt in superficie curva descripti sit PpQ vestigium Ellipticum in eodem plano OAPp descriptum. Et ob datum magnitudine & positione circellum, dabitur Ellipsis illa PpQ. Cumque area POp sit tempori proportionalis, atque adeo ex dato tempore detur, dabitur Op positione, & inde dabitur communis ejus & Ellipseos intersectio p, una cum angulo OPp, in quo Trajectoriæ vestigium APp secat lineam OP. Inde autem invenietur Trajectoriæ vestigium illud APp, eadem methodo qua curva linea VIKk in Propositione XLI. ex similibus datis inventa fuit. Tum ex singulis vestigii punctis P erigendo ad planum AOP perpendicula PT superficiei curvæ occurrentia in T, dabuntur singula Trajectoriæ puncta T.Q.E.I.
SECT. XI.
De Motu Corporum Sphæricorum viribus centripetis se mutuo petentium.
Hactenus exposui motus corporum attractorum ad centrum immobile, quale tamen vix extat in rerum natura. Attractiones enim fieri solent ad corpora; & corporum trahentium & attractorum actiones semper mutuæ sunt & æquales, per Legem tertiam: adeo ut neque attrahens possit quiescere neque attractum, si duo sint corpora, sed ambo (per Legum Corollarium quartum) quasi attractione mutua, circum gravitatis centrum commune revolvantur: & si plura sint corpora (quæ vel ab unico attrahantur vel omnia se mutuo attrahant) hæc ita inter se moveri debeant, ut gravitatis centrum commune. vel quiescat vel uniformiter moveatur in directum. Qua de causa jam pergo motum exponere corporum se mutuo trahentium, considerando vires centripetas tanquam Attractiones, quamvis fortasse, si physice loquamur, verius dicantur Impulsus. In Mathematicis enim jam versamur, & propterea missis disputationibus Physicis, familiari utimur sermone, quo possimus a Lectoribus Mathematicis facilius intelligi.
Prop. LVII. Theor. XX.
Corpora duo se invicem trahentia describunt, & circum commune centrum gravitatis, & circum se mutuo, figuras similes.
Sunt enim distantiæ a communi gravitatis centro reciproce proportionales corporibus, atque adeo in data ratione ad invicem, & componendo, in data ratione ad distantiam totam inter corpora. Feruntur autem hæ distantiæ circum terminos suos communi motu angulari, propterea quod in directum semper jacentes non mutant inclinationem ad se mutuo. Lineæ autem rectæ, quæ sunt in data ratione ad invicem, & æquali motu angulari circum terminos suos feruntur, figuras circum eosdem terminos (in planis quæ una cum his terminis vel quiescunt vel motu quovis non angulari moventur) describunt omnino similes. Proinde similes sunt figuræ quæ his distantiis circumactis describuntur. Q.E.D.
Prop. LVIII. Theor. XXI.
Si corpora duo viribus quibusvis se mutuo trahunt, & interea revolvuntur circa gravitatis centrum commune: dico quod figuris, quas corpora sic mota describunt circum se mutuo, potest figura similis & æqualis, circum corpus alterutrum immotum, viribus iisdem describi.
Revolvantur corpora S, P circa commune gravitatis centrum C, pergendo de S ad T deque P ad Q. A dato puncto s ipsis SP, TQ æquales & parallelæ ducantur semper sp, sq; & curva pqv quam punctum p, revolvendo circum punctum immotum s, describit, 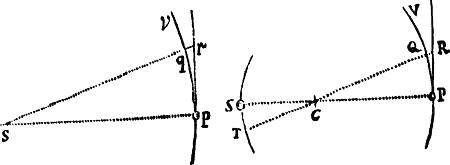 erit similis & æqualis curvis quas corpora S, P describunt circum se mutuo: proindeque (per Theor. XX.) similis curvis ST & PQV, quas eadem corpora describunt circum commune gravitatis centrum C: id adeo quia proportiones linearum SC, CP & SP vel sp ad invicem dantur.
erit similis & æqualis curvis quas corpora S, P describunt circum se mutuo: proindeque (per Theor. XX.) similis curvis ST & PQV, quas eadem corpora describunt circum commune gravitatis centrum C: id adeo quia proportiones linearum SC, CP & SP vel sp ad invicem dantur.
Cas. 1. Commune illud gravitatis centrum C, per Legum Corollarium quartum, vel quiescit vel movetur uniformiter in directum. Ponamus primo quod id quiescit, inque s & p locentur corpora duo, immobile in s, mobile in p, corporibus S & P similia & æqualia. Dein tangant rectæ PR & pr curvas PQ & pq in P & p, & producantur CQ & sq ad R & r. Et ob similitudinem figurarum CPRQ, sprq, erit RQ ad rq ut CP ad sp, adeoque in data ratione. Proinde si vis qua Corpus P versus Corpus S, atque adeo versus centrum intermedium C attrahitur, esset ad vim qua corpus p versus centrum s attrahitur in eadem illa ratione data, hæ vires æqualibus temporibus attraherent semper corpora de tangentibus PR, pr ad arcus PQ, pq, per intervalla ipsis proportionalia 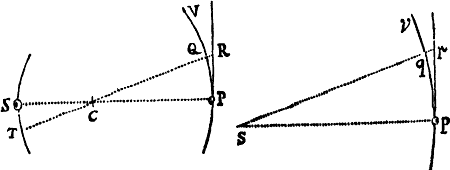 RQ, rq; adeoque vis posterior efficeret ut corpus p gyraretur in curva pqv, quæ similis esset curvæ PQV, in qua vis prior efficit ut corpus P gyretur, & revolutiones iisdem temporibus complerentur. At quoniam vires illæ non sunt ad invicem in ratione CP ad sp, sed (ob similitudinem & æqualitatem corporum S & s, P & p, & æqualitatem distantiarum SP, sp) sibi mutuo æquales, corpora æqualibus temporibus æqualiter trahentur de Tangentibus; & propterea ut corpus posterius p trahatur per intervallum majus rq, requiritur tempus majus, idque in dimidiata ratione intervallorum; propterea quod, per Lemma decimum, spatia ipso motus initio descripta sunt in duplicata ratione temporum. Ponatur igitur velocitas corporis p esse ad velocitatem corporis P in dimidiata ratione distantiæ sp ad distantiam CP, eo ut temporibus quæ sint in eadem dimidiata ratione describantur arcus PQ, pq, qui sunt in ratione integra: Et corpora P, p viribus æqualibus semper attracta describent circum centra quiescentia C & s figuras similes PQV, pqv, quarum posterior pqv similis est & æqualis figuræ quam corpus P circum corpus mobile S describit. Q.E.D.
RQ, rq; adeoque vis posterior efficeret ut corpus p gyraretur in curva pqv, quæ similis esset curvæ PQV, in qua vis prior efficit ut corpus P gyretur, & revolutiones iisdem temporibus complerentur. At quoniam vires illæ non sunt ad invicem in ratione CP ad sp, sed (ob similitudinem & æqualitatem corporum S & s, P & p, & æqualitatem distantiarum SP, sp) sibi mutuo æquales, corpora æqualibus temporibus æqualiter trahentur de Tangentibus; & propterea ut corpus posterius p trahatur per intervallum majus rq, requiritur tempus majus, idque in dimidiata ratione intervallorum; propterea quod, per Lemma decimum, spatia ipso motus initio descripta sunt in duplicata ratione temporum. Ponatur igitur velocitas corporis p esse ad velocitatem corporis P in dimidiata ratione distantiæ sp ad distantiam CP, eo ut temporibus quæ sint in eadem dimidiata ratione describantur arcus PQ, pq, qui sunt in ratione integra: Et corpora P, p viribus æqualibus semper attracta describent circum centra quiescentia C & s figuras similes PQV, pqv, quarum posterior pqv similis est & æqualis figuræ quam corpus P circum corpus mobile S describit. Q.E.D.
Cas. 2. Ponamus jam quod commune gravitatis centrum, una cum spatio in quo corpora moventur inter se, progreditur uniformiter in directum; &, per Legum Corollarium sextum, motus omnes in hoc spatio peragentur ut prius, adeoque corpora describent circum se mutuo figuras easdem ac prius, & propterea figuræ pqv similes & æquales. Q.E.D.
Corol. 1. Hinc corpora duo viribus distantiæ suæ proportionalibus se mutuo trahentia, describunt (per Prop. X.) & circum commune gravitatis centrum, & circum se mutuo, Ellipses concentricas: & vice versa, si tales figuræ describuntur, sunt vires distantiæ proportionales.
Corol. 2. Et corpora duo viribus quadrato distantiæ suæ reciproce proportionalibus describunt (per Prop. XI, XII, XIII.) & circum commune gravitatis centrum & circum se mutuo sectiones conicas umbilicos habentes in centro circum quod figuræ describuntur. Et vice versa, si tales figuræ describuntur, vires centripetæ sunt quadrato distantiæ reciproce proportionales.
Corol. 3. Corpora duo quævis circum gravitatis centrum commune gyrantia, radiis & ad centrum illud & ad se mutuo ductis, describunt areas temporibus proportionales.
Prop. LIX. Theor. XXII.
Corporum duorum S & P circa commune gravitatis centrum C revolventium tempus periodicum esse ad tempus periodicum corporis alterutrius P, circa alterum immotum S gyrantis & figuris quæ corpora circum se mutuo describunt figuram similem & æqualem describentis, in dimidiata ratione corporis alterius S, ad summant corporum S+P.
<166>Namque ex demonstratione superioris Propositionis, tempora quibus arcus quivis similes PQ & pq describuntur, sunt in dimidiata ratione distantiarum CP & SP vel sp, hoc est, in dimidiata ratione corporis S ad summam corporum S+P. Et componendo, summæ temporum quibus arcus omnes similes PQ & pq describuntur, hoc est tempora tota quibus figuræ totæ similes describuntur, sunt in eadem dimidiata ratione. Q.E.D.
Prop. LX. Theor. XXIII.
Si corpora duo S & P, viribus quadrato distantiæ suæ reciproce proportionalibus se mutuo trahentia, revoluntur circa gravitatis centrum commune: dico quod Ellipseos, quam corpus alterutrum P hoc motu circa alterum S describit, Axis transversus erit ad axem transversum Ellipseos, quam corpus idem P circa alterum quiescens S eodem tempore periodico describere posset, ut summa corporum duorum S+P ad primam duarum medie proportionalium inter hanc summan & corpus illud alterum S.
Nam si descriptæ Ellipses essent sibi invicem æquales, tempora periodica, per Theorema superius, forent in dimidiata ratione corporis S ad summam corporum S+P. Minuatur in hac ratine tempus periodicum in Ellipsi posteriore, & tempora periodica evadent æqualia, Ellipseos autem axis transversus per Theorema VII. minuetur in ratione cujus hæc est sesquiplicata, id est in ratione, cujus ratio S ad S+P est triplicata; adeoque ad axem transversum Ellipseos alterius, ut prima duarum medie proportionalium inter S+P & S ad S+P. Et inverse, axis transversus Ellipseos circa corpus mobile descriptæ erit ad axem transversum descriptæ circa immobile, ut S+P ad primam duarum medie proportionalium inter S+P & S. Q.E.D.
<167>Prop. LXI. Theor. XXIV.
Si corpora duo viribus quibusvis se mutuo trahentia, neque alias agitata vel impedita, quomodocunque moveantur; motus eorum perinde se habebunt ac si non traherent se mutuo, sed utrumque a corpore tertio in communi gravitatis centro constituto viribus iisdem traheretur: Et Virium trahentium eadem erit Lex respectu distantiæ corporum a centro illo communi atque respectu distantiæ totius inter corpora.
Nam vires illæ, quibus corpora se mutuo trahunt, tendendo ad corpora, tendunt ad commune gravitatis centrum intermedium, adeoque eædem sunt ac si a corpore intermedio manarent. Q.E.D.
Et quoniam data est ratio distantiæ corporis utriusvis a centro illo communi ad distantiam corporis ejusdem a corpore altero, dabitur ratio cujusvis potestatis distantiæ unius ad eandem potestatem distantiæ alterius; ut & ratio quantitatis cujusvis, quæ ex una distantia & quantitatibus datis utcunque derivatur, ad quantitatem aliam, quæ ex altera distantia & quantitatibus totidem datis datamque illam distantiarum rationem ad priores habentibus similiter derivatur. Proinde si vis, qua corpus unum ab altero trahitur, sit directe vel inverse ut distantia corporum ab invicem; vel ut quælibet hujus distantiæ potestas; vel denique ut quantitas quævis ex hac distantia & quantitatibus datis quomodocunque derivata: erit eadem vis, qua corpus idem ad commune gravitatis centrum trahitur, directe itidem vel inverse ut corporis attracti distantia a centro illo communi, vel ut eadem distantiæ hujus potestas, vel denique ut quantitas ex hac distantia & analogis quantitatibus datis similiter derivata. Hoc est Vis trahentis eadem erit Lex respectu distantiæ utriusque. Q.E.D.
<168>Prop. LXII. Prob. XXXVIII.
Corporum duorum quæ viribus quadrato distantiæ suæ reciproce proportionalibus se mutuo trahunt, ac de locis datis demittuntur, determinare motus.
Corpora, per Theorema novissimum, perinde movebuntur, ac si a corpore tertio in communi gravitatis centro constituto traherentur; & centrum illud ipso motus initio quiescet (per Hypothesin) & propterea (per Legum Corol. 4.) semper quiescet. Determinandi sunt igitur motus Corporum (per Probl. XXV.) perinde ac si a viribus ad centrum illud tendentibus urgerentur, & habebuntur motus corporum se mutuo trahentium. Q.E.I.
Prop. LXIII. Prob. XXXIX.
Corporum duorum quæ viribus quadrato distantiæ suæ reciproce proportionalibus se mutuo trahunt, deque locis datis, secundum datas rectas, datis cum velocitatibus exeunt, determinare motus.
Ex datis corporum motibus sub initio, datur uniformis motus centri communis gravitatis, ut & motus spatii quod una cum hoc centro movetur uniformiter in directum, nec non corporum motus initiales respectu hujus spatii. Motus autem subsequentes (per Legum Corollarium quintum & Theorema novissimum) perinde fiunt in hoc spatio, ac si spatium ipsum una cum communi illo gravitatis centro quiesceret, & corpora non traherent se mutuo, sed a corpore tertio sito in centro illo traherentur. Corporis igitur alterutrius in hoc spatio mobili de loco dato, secundum datam rectam, data cum velocitate exeuntis, & vi centripeta ad centrum illud tendente correpti, determinandus est motus per Problema nonum & vicesimum sextum: & habebitur simul motus corporis alterius e regione. Cum hoc motu componendus est uniformis ille Systematis spatii & corporum in eo gyrantium motus progressivus supra inventus, & habebitur motus absolutus corporum in spatio immobili. Q.E.I.
Prop. LXIV. Prob. XL.
Viribus quibus Corpora se mutuo trahunt crescentibus in simplici ratione distantiarum a centris: requiruntur motus plurium Corporum inter se.
Ponantur imprimis corpora duo T & L commune habentia gravitatis centrum D. Describent hæc per Corollarium primum Theorematis XXI. Ellipses centra habentes in D, quarum magnitudo ex Problemate V. innotescit.
Trahat jam corpus tertium S priora duo T & L viribus acceleratricibus ST, SL, & ab  ipsis vicissim trahatur. Vis ST per Legum Corol. 2. resolvitur in vires SD, DT; & vis SL in vires SD, DL. Vires autem DT, DL, quæ sunt ut ipsarum summa TL, atque adeo ut vires acceleratrices quibus corpora T & L se mutuo trahunt, additæ his viribus corporum T & L, prior priori & posterior posteriori, componunt vires distantiis DT ac DL proportionales, ut prius, sed viribus prioribus majores; adeoque (per Corol. 1. Prop. X. & Corol. 1 & 7. Prop. IV.) efficiunt ut corpora illa describant Ellipses ut prius, sed motu celeriore. Vires reliquæ acceleratrices SD & SD, actionibus motricibus & , quæ sunt ut corpora, trahendo corpora illa æqualiter & secundum lineas TI, LK ipsi DS parallelas, nil mutant situs earum ad invicem, sed faciunt ipsa æqualiter accedere ad lineam IK; quam ductam concipe per medium corporis S, & lineæ DS perpendicularem. Impedietur autem iste ad lineam IK accessus faciendo ut Systema corporum T & L ex una parte, & corpus S ex altera, justis cum velocitatibus, gyrentur circa commune gravitatis centrum C. Tali motu corpus S (eo quod summa virium motricium , distantiæ CS proportionalium, trahitur versus centrum C) describit Ellipsin circa idem C; & punctum D ob proportionales CS, CD describet Ellipsin consimilem, e regione. Corpora autem T & L viribus motricibus & , (prius priore, posterius posteriore) æqualiter & secundum lineas parallelas TI & LK (ut dictum est) attracta, pergent (per Legum Corollarium quintum & sextum) circa centrum mobile D Ellipses suas describendo, ut prius. Q.E.I.
ipsis vicissim trahatur. Vis ST per Legum Corol. 2. resolvitur in vires SD, DT; & vis SL in vires SD, DL. Vires autem DT, DL, quæ sunt ut ipsarum summa TL, atque adeo ut vires acceleratrices quibus corpora T & L se mutuo trahunt, additæ his viribus corporum T & L, prior priori & posterior posteriori, componunt vires distantiis DT ac DL proportionales, ut prius, sed viribus prioribus majores; adeoque (per Corol. 1. Prop. X. & Corol. 1 & 7. Prop. IV.) efficiunt ut corpora illa describant Ellipses ut prius, sed motu celeriore. Vires reliquæ acceleratrices SD & SD, actionibus motricibus & , quæ sunt ut corpora, trahendo corpora illa æqualiter & secundum lineas TI, LK ipsi DS parallelas, nil mutant situs earum ad invicem, sed faciunt ipsa æqualiter accedere ad lineam IK; quam ductam concipe per medium corporis S, & lineæ DS perpendicularem. Impedietur autem iste ad lineam IK accessus faciendo ut Systema corporum T & L ex una parte, & corpus S ex altera, justis cum velocitatibus, gyrentur circa commune gravitatis centrum C. Tali motu corpus S (eo quod summa virium motricium , distantiæ CS proportionalium, trahitur versus centrum C) describit Ellipsin circa idem C; & punctum D ob proportionales CS, CD describet Ellipsin consimilem, e regione. Corpora autem T & L viribus motricibus & , (prius priore, posterius posteriore) æqualiter & secundum lineas parallelas TI & LK (ut dictum est) attracta, pergent (per Legum Corollarium quintum & sextum) circa centrum mobile D Ellipses suas describendo, ut prius. Q.E.I.
Addatur jam corpus quartum 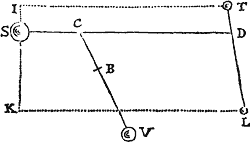 V, & simili argumento concludetur hoc & punctum C Ellipses circa omnium commune centrum gravitatis B describere; manentibus motibus priorum corporum T, L & S circa centra D & C, sed paulo acceleratis. Et eadem methodo corpora plura adjungere licebit. Q.E.I.
V, & simili argumento concludetur hoc & punctum C Ellipses circa omnium commune centrum gravitatis B describere; manentibus motibus priorum corporum T, L & S circa centra D & C, sed paulo acceleratis. Et eadem methodo corpora plura adjungere licebit. Q.E.I.
Hæc ita se habent ubi corpora T & L trahunt se mutuo viribus acceleratricibus majoribus vel minoribus quam trahunt corpora reliqua pro ratione distantiarum. Sunto mutuæ omnium attractiones acceleratrices ad invicem ut distantiæ ductæ in corpora trahentia, & ex præcedentibus facile deducetur quod corpora omnia æqualibus temporibus periodicis Ellipses varias, circa omnium commune gravitatis centrum B in plano immobili describunt. Q.E.I.
Prop. LXV. Theor. XXV.
Corpora plura quorum vires decrescunt in duplicata ratione distantia rum ab eorundem centris, moveri posse inter se in Ellipsibus, & radiis ad umbilicos ductis Areas describere temporibus proportionales quam proxime.
In Propositione superiore demonstratus est casus ubi motus plures peraguntur in Ellipsibus accurate. Quo magis recedit lex virium a lege ibi posita, eo magis corpora perturbabunt mutuos motus, neque fieri potest ut corpora secundum legem hic positam se mutuo trahentia moveantur in Ellipsibus accurate, nisi servando certam proportionem distantiarum ab invicem. In sequentibus autem casibus non multum ab Ellipsibus errabitur.
Cas. 1. Pone corpora plura minora circa maximum aliquod ad varias ab eo distantias revolvi, tendantque ad singula vires absolutæ proportionales iisdem corporibus. Et quoniam omnium commune gravitatis centrum (per Legum Corol. quartum.) vel quiescet vel movebitur uniformiter in directum, fingamus corpora minora tam parva esse, ut corpus maximum nunquam distet sensibiliter ab hoc centro; & maximum illud vel quiescet vel movebitur uniformiter in directum, absque errore sensibili; minora autem revolventur circa hoc maximum in Ellipsibus, atque radiis ad idem ductis describent areas temporibus proportionales; nisi quatenus errores inducuntur, vel per errorem maximi a communi illo gravitatis centro, vel per actiones minorum corporum in se mutuo. Diminui autem possunt corpora minora usque donec error iste & actiones mutuæ sint datis quibusvis minores, atque adeo donec orbes cum Ellipsibus quadrent, & areæ respondeant temporibus, absque errore qui non sit minor quovis dato. Q.E.O.
Cas. 2. Fingamus jam Systema corporum minorum modo jam descripto circa maximum revolventium, aliudve quodvis duorum circum se mutuo revolventium corporum Systema progredi uniformiter in directum, & interea vi corporis alterius longe maximi & ad magnam distantiam siti urgeri ad latus. Et quoniam æquales vires acceleratrices, quibus corpora secundum lineas parallelas urgentur, non mutant situs corporum ad invicem, sed ut Systema totum, servatis partium motibus inter se, simul transferatur efficiunt: manifestum est quod ex attractionibus in corpus maximum, nulla prorsus orietur mutatio motus attractorum inter se, nisi vel ex attractionum acceleratricum inæqualitate, vel ex inclinatione linearum ad invicem, secundum quas attractiones fiunt. Pone ergo attractiones omnes acceleratrices in corpus maximum esse inter se reciproce ut quadrata distantiarum, & augendo corporis maximi distantiam, donec rectarum ab hoc ad reliqua ductarum minores sint differentiæ & inclinationes ad invicem quam datæ quævis, perseverabunt motus partium Systematis inter se absque erroribus qui non sint quibusvis datis minores. Et quoniam, ob exiguam partium illarum ab invicem distantiam, Systema totum ad modum corporis unius attrahitur, movebitur idem hac attractione ad modum corporis unius; hoc est, centro suo gravitatis describet circa corpus maximum, Sectionem aliquam Conicam (viz. Hyperbolam vel Parabolam attractione languida, Ellipsim fortiore,) & Radio ad maximum ducto, verret areas temporibus proportionales, absque ullis erroribus, nisi quas partium distantiæ (perexiguæ sane & pro lubitu minuendæ) valeant efficere. Q.E.O.
Simili argumento pergere licet ad casus magis compositos in infinitum.
Corol. 1. In casu secundo; quo propius accedit corpus omnium maximum ad Systema duorum vel plurium, eo magis turbabuntur motus partium Systematis inter se, propterea quod linearum a corpore maximo ad has ductarum jam major est inclinatio ad invicem, majorque proportionis inæqualitas.
Corol. 2. Maxime autem turbabuntur, ponendo quod attractiones acceleratrices partium Systematis versus corpus omnium maximum, non sint ad invicem reciproce ut quadrata distantiarum a corpore illo maximo; præsertim si proportionis hujus inæqualitas major sit quam inæqualitas proportionis distantiarum a corpore maximo: Nam si vis acceleratrix, æqualiter & secundum lineas parallelas agendo, nil perturbat motus inter se, necesse est ut ex actionis inæqualitate perturbatio oriatur, majorque sit vel minor pro majore vel minore inæqualitate. Excessus impulsuum majorum agendo in aliqua corpora & non agendo in alia, necessario mutabunt situnreorum inter se. Et hæc perturbatio addita perturbationi, quæ ex linearum inclinatione & inæqualitate oritur, majorem reddet perturbationem totam.
Corol. 3. Unde si Systematis hujus partes in Ellipsibus vel Circulis sine perturbatione insigni moveantur, manifestum est, quod eædem a viribus acceleratricibus ad alia corpora tendentibus, aut non urgentur nisi levissime, aut urgentur æqualiter & secundum lineas parallelas quamproxime.
Prop. LXVI. Theor. XXVI.
Si corpora tria, quorum vires decrescunt in duplicata ratione distantiarum, se mutuo trahant, & attractiones acceleratrices binorum quorumcunque in tertium sint inter se reciproce ut quadrata distantiarum; minora autem circa maximum in plano communi revolvantur: Dico quod interius circa intimum & maximum, radiis ad ipsum ductis, describet areas temporibus magis proportionales, & figuram ad formam Ellipseos umbilicum in concursu radiorum habentis magis accedentem, si corpus maximum his attractionibus agitetur, quam si maximum illud vel a minoribus non attractum quiescat, vel multo minus vel multo magis attractum aut multo minus aut multo magis agitetur.
Liquet fere ex demonstratione Corollarii secundi Propositionis præcedentis; sed argumento magis distincto & latius cogente sic evincitur.
Cas. 1. Revolvantur corpora minora P & Q in eodem plano circa maximum S, quorum P describat orbem interiorem PAB, & Q exteriorem QE. Sit QK mediocris distantia corporum P & Q; & corporis P versus Q attractio acceleratrix in mediocri illa distantia exponatur per eandem. In duplicata ratione QK ad QP capiatur QL ad QK, & erit QL attractio acceleratrix corporis P versus Q in distantia quavis QP. Junge PS, eique parallelam age LM occurrentem QS in M, & attractio QL resolvetur (per Legum Corol. 2.) in attractiones QM, LM. Et sic urgebitur corpus P vi acceleratrice triplici: una tendente ad S & oriunda a mutua attractione corporum S & P. Hac vi sola corpus P, circum corpus S sive immotum, sive hac attractione agitatum, describere deberet & areas, radio PS temporibus proportionales, & Ellipsin cui umbilicus est in centro corporis S. Patet hoc per Prob. VI. & Corollaria Theor. XXI. Vis altera est attractionis LM, quæ 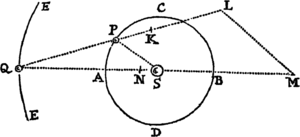 quoniam tendit a P ad S, superaddita vi priori coincidet cum ipsa, & sic faciet ut areæ etiamnum temporibus proportionales describantur per Corol. 3. Theor. XXI. At quoniam non est quadrato distantiæ PS reciproce proportionalis, componet ea cum vi priore vim ab hac proportione aberrantem, idque eo magis quo major est proportio hujus vis ad vim priorem, cæteris paribus. Proinde cum (per Corol. 1. Prob. VIII. & Corol. 2. Theor XXI.) vis qua Ellipsis circa umbilicum S describitur tendere debeat ad umbilicum illum, & esse quadrato distantiæ PS reciproce proportionalis; vis illa composita aberrando ab hac proportione, faciet ut Orbis PAB aberret a forma Ellipseos umbilicum habentis in S; idque eo magis quo major est aberratio ab hac proportione; atque adeo etiam quo major est proportio vis secundæ LM ad vim primam, cæteris paribus. Jam vero vis tertia QM, trahendo corpus P secundum lineam ipsi QS parallelam, componet cum viribus prioribus vim quæ non amplius dirigitur a P in S, quæque ab hac determinatione tanto magis aberrat, quanto major est proportio hujus tertiæ vis ad vires priores, cæteris paribus; atque adeo quæ faciet ut corpus P, radio SP, areas non amplius temporibus proportionales describet, atque aberratio ab hac proportionalitate ut tanto major sit, quanto major est proportio vis hujus tertiæ ad vires cæteras. Orbis vero PAB aberrationem a forma Elliptica præfata hac vis tertia duplici de causa adaugebit, tum quod non dirigitur a P ad S, tum etiam quod non sit proportionalis quadrato distantiæ PS. Quibus intellectis, manifestum est quod areæ temporibus tum maxime fiunt proportionales, ubi vis tertia, manentibus viribus cæteris, fit minima; & quod Orbis PAB tum maxime accedit ad præfatam formam Ellipticam, ubi vis tam secunda quam tertia, sed præcipue vis tertia, sit minima, vi prima manente.
quoniam tendit a P ad S, superaddita vi priori coincidet cum ipsa, & sic faciet ut areæ etiamnum temporibus proportionales describantur per Corol. 3. Theor. XXI. At quoniam non est quadrato distantiæ PS reciproce proportionalis, componet ea cum vi priore vim ab hac proportione aberrantem, idque eo magis quo major est proportio hujus vis ad vim priorem, cæteris paribus. Proinde cum (per Corol. 1. Prob. VIII. & Corol. 2. Theor XXI.) vis qua Ellipsis circa umbilicum S describitur tendere debeat ad umbilicum illum, & esse quadrato distantiæ PS reciproce proportionalis; vis illa composita aberrando ab hac proportione, faciet ut Orbis PAB aberret a forma Ellipseos umbilicum habentis in S; idque eo magis quo major est aberratio ab hac proportione; atque adeo etiam quo major est proportio vis secundæ LM ad vim primam, cæteris paribus. Jam vero vis tertia QM, trahendo corpus P secundum lineam ipsi QS parallelam, componet cum viribus prioribus vim quæ non amplius dirigitur a P in S, quæque ab hac determinatione tanto magis aberrat, quanto major est proportio hujus tertiæ vis ad vires priores, cæteris paribus; atque adeo quæ faciet ut corpus P, radio SP, areas non amplius temporibus proportionales describet, atque aberratio ab hac proportionalitate ut tanto major sit, quanto major est proportio vis hujus tertiæ ad vires cæteras. Orbis vero PAB aberrationem a forma Elliptica præfata hac vis tertia duplici de causa adaugebit, tum quod non dirigitur a P ad S, tum etiam quod non sit proportionalis quadrato distantiæ PS. Quibus intellectis, manifestum est quod areæ temporibus tum maxime fiunt proportionales, ubi vis tertia, manentibus viribus cæteris, fit minima; & quod Orbis PAB tum maxime accedit ad præfatam formam Ellipticam, ubi vis tam secunda quam tertia, sed præcipue vis tertia, sit minima, vi prima manente.
Exponatur corporis S attractio acceleratrix versus Q per lineam QN; & si attractiones acceleratrices QM, QN æquales essent, hæ trahendo corpora S & P æqualiter & secundum lineas parallelas, nil mutarent situm eorum ad invicem. Iidem jam forent corporum illorum motus inter se (per Legum Corol. 6.) ac si hæ attractiones tollerentur. Et pari ratione si attractio QN minor esset attractione QM, tolleret ipsa attractionis QM partem QN, & maneret pars sola MN, qua temporum & arearum proportionalitas & Orbitæ forma illa Elliptica perturbaretur. Et similiter si attractio QN major esset attractione QM, oriretur ex differentia sola MN perturbatio proportionalitatis & Orbitæ. Sic per attractionem QN reducitur semper attractio tertia superior QM ad attractionem MN, attractione prima & secunda manentibus prorsus immutatis: & propterea areæ ac tempora ad proportionalitatem, & Orbita PAB ad formam præfatam Ellipticam tum maxime accedunt, ubi attractio MN vel nulla est, vel quam fieri possit minima; hoc est ubi corporum P & S attractiones acceleratrices, factæ versus corpus Q, accedunt quantum fieri potest ad æqualitatem; id est ubi attractio QN non est nulla, neque minor minima attractionum omnium QM, sed inter attractionum omnium QM maximam & minimam quasi mediocris, hoc est, non multo major neque multo minor attractione QK. Q.E.D.
Cas. 2. Revolvantur jam corpora minora P, Q circa maximum S in planis diversis, & vis LM, agendo secundum lineam PS in plano Orbitæ PAB sitam, eundem habebit effectumac prius, neque corpus P de plano Orbitæ suæ deturbabit. At vis altera NM, agendo secundum lineam quæ ipsi QS parallela est, (atque adeo, quando corpus Q versatur extra lineam Nodorum, inclinatur ad planum Orbitæ PAB;) præter perturbationem motus in longitudinem jam ante expositam, inducet perturbationem motus in latitudinem, trahendo corpus P de plano suæ Orbitæ. Et hæc perturbatio in dato quovis corporum P & S ad invicem situ, erit ut vis illa generans MN, adeoque minima evadet ubi MN est minima, hoc est (uti jam exposui) ubi attractio QN non est multo major neque multo minor attractione QK. Q.E.D.
Corol. 1. Ex his facile colligitur quod si corpora plura minora P, Q, R &c. revolvantur circa maximum S: motus corporis intimi P minime perturbabitur attractionibus exteriorum, ubi corpus maximum S pariter a cæteris, pro ratione virium acceleratricum, attrahitur & agitatur atque cæteri a se mutuo.
Carol. 2. In Systemate vero trium corporum S, P, Q; si attractiones acceleratrices binorum quorumcunque in tertium sint ad invicem reciproce ut quadrata distantiarum, corpus P radio PS aream circa corpus S velocius describet prope conjunctionem A & oppositionem B, quam prope quadraturas C, D. Namque vis omnis qua corpus P urgetur & corpus S non urgetur, quæque non agit secundum lineam PS, accelerat vel retardat descriptionem areæ, perinde ut ipsa in antecedentia vel in consequentia dirigitur. Talis est vis NM, hæc in transitu corporis P a C ad A tendit in antecedentia, motumque accelerat; dein usque ad D in consequentia, & motum retardat; tum in antecedentia usque ad B, & ultimo in conseqentia transeundo a B ad C.
Corol. 3. Et eodem argumento patet quod corpus P, cæteris paribus, velocius movetur in Conjunctione & Oppositione quam in Quadraturis.
Corol. 4. Orbita corporis P cæteris paribus curvior est in quadraturis quam in Conjunctione & Oppositione. Nam corpora velociora minus deflectunt a recto tramite. Et præterea vis NM, in Conjunctione & Oppositione, contraria est vi qua corpus S trahit corpus P, adeoque vim illam minuit; corpus autem P minus deflectet a recto tramite, ubi minus urgetur in corpus S.
Corol. 5. Unde corpus P, cæteris paribus, longius recedet a corpore S in quadraturis, quam in Conjunctione & Oppositione. Hæc ita se habent excluso motu Excentricitatis. Nam si Orbita corporis P excentrica sit, Excentricitas ejus (ut mox in hujus Corol. 9. ostendetur) evadet maxima ubi Apsides sunt in Syzygiis; indeque fieri potest ut corpus P, ad Apsidem summam appellans, absit longius a corpore S in Syzygiis quam in Quadraturis.
Corol. 6. Quoniam 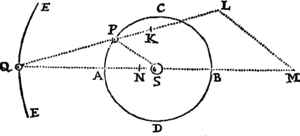 vis centripeta corporis centralis S, qua corpus P retinetur in Orbe suo, augetur in quadraturis per additionem vis LM, ac diminuitur in Syzygiis per ablationem vis KL, & ob magnitudinem vis KL, magis diminuitur quam augeatur; est autem vis illa centripeta (per Corol. 2, Prop. IV.) in ratione composita ex ratione simplici radii SP directe & ratione duplicata temporis periodici inverse: patet hanc rationem compositam diminui per actionem vis KL, adeoque tempus periodicum, si maneat Orbis radius SP, augeri, idque in dimidiata ratione qua vis illa centripeta diminuitur: auctoque adeo vel diminuto hoc Radio, tempus periodicum augeri magis, vel diminui minus quam in Radii hujus ratione sesquiplicata, per Corol. 6. Prop. IV. Si vis illa corporis centralis paulatim languesceret, corpus P minus semper & minus attractum perpetuo recederet longius a centro S; & contra, si vis illa augeretur, accederet propius. Ergo si actio corporis longinqui Q, qua vis illa diminuitur, augeatur ac diminuatur per vices, augebitur simul ac diminuetur Radius SP per vices, & tempus periodicum augebitur ac diminuetur in ratione composita ex ratione sesquiplicata Radii & ratione dimidiata qua vis illa centripeta corporis centralis S per incrementum vel decrementum actionis corporis longinqui Q diminuitur vel augetur.
vis centripeta corporis centralis S, qua corpus P retinetur in Orbe suo, augetur in quadraturis per additionem vis LM, ac diminuitur in Syzygiis per ablationem vis KL, & ob magnitudinem vis KL, magis diminuitur quam augeatur; est autem vis illa centripeta (per Corol. 2, Prop. IV.) in ratione composita ex ratione simplici radii SP directe & ratione duplicata temporis periodici inverse: patet hanc rationem compositam diminui per actionem vis KL, adeoque tempus periodicum, si maneat Orbis radius SP, augeri, idque in dimidiata ratione qua vis illa centripeta diminuitur: auctoque adeo vel diminuto hoc Radio, tempus periodicum augeri magis, vel diminui minus quam in Radii hujus ratione sesquiplicata, per Corol. 6. Prop. IV. Si vis illa corporis centralis paulatim languesceret, corpus P minus semper & minus attractum perpetuo recederet longius a centro S; & contra, si vis illa augeretur, accederet propius. Ergo si actio corporis longinqui Q, qua vis illa diminuitur, augeatur ac diminuatur per vices, augebitur simul ac diminuetur Radius SP per vices, & tempus periodicum augebitur ac diminuetur in ratione composita ex ratione sesquiplicata Radii & ratione dimidiata qua vis illa centripeta corporis centralis S per incrementum vel decrementum actionis corporis longinqui Q diminuitur vel augetur.
Corol. 7. Ex præmissis consequitur etiam quod Ellipseos a corpore P descriptæ axis seu Apsidum linea, quoad motum angularem progreditur & regreditur per vices, sed magis tamen progreditur, & in singulis corporis revolutionibus per excessum progressionis fertur in consequentia. Nam vis qua corpus P urgetur in corpus S in Quadraturis, ubi vis MN evanuit, componitur ex vi LM & vi centripeta qua corpus S trahit corpus P. Vis prior LM, si augeatur distantia PS, augetur in eadem fere ratione cum hac distantia, & vis posterior decrescit in duplicata illa ratione, adeoque summa harum virium decrescit in minore quam duplicata ratione distantiæ PS, & propterea, per Corol. 1. Prop. XLV. facit Augem seu Apsidem summam regredi. In Conjunctione vero & Oppositione, vis qua corpus P urgetur in corpus S differentia est inter vim qua corpus S trahit corpus P & vim KL; & differentia illa, propterea quod vis KL augetur quamproxime in ratione distantiæ PS, decrescit in majore quam duplicata ratione distantiæ PS, adeoque per Corol. 1. Prop. XLV. facit Augem progredi. In locis inter Syzygias & Quadraturas, pendet motus Augis ex causa utraque conjunctim, adeo ut pro hujus vel alterius excessu progrediatur ipsa vel regrediatur. Unde cum vis KL in Syzygiis sit quasi dupla vis LM in quadraturis, excessus in tota revolutione erit penes vim KL, transferetque Augem singulis revolutionibus in consequentia. Veritas autem hujus & præcedentis Corollarii facilius intelligetur concipiendo Systema corporum duorum S, P corporibus pluribus Q, Q, Q &c. in Orbe QE consistentibus, undeque cingi. Namque horum actionibus actio ipsius S minuetur undique decrescetque in ratione plusquam duplicata distantiæ.
Corol. 8. Cum autem pendeat Apsidum progressus vel regressus a decremento vis centripetæ facto in majori vel minori quam duplicata ratione distantiæ SP, in transitu corporis ab Apside ima ad Apsidem summam; ut & a simili incremento in reditu ad Apsidem imam; atque adeo maximus sit ubi proportio vis in Apside summa ad vim in 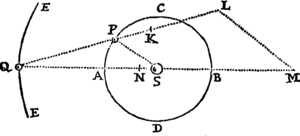 Apside ima maxime recedit a duplicata ratione distantiarum inversa: manifestum est quod Apsides in Syzygiis suis, per vim ablatitiam KL seu NM−LM, progredientur velocius, inque Quadraturis suis tardius recedent per vim addititiam LM. Ob diuturnitatem vero temporis quo velocitas progressus vel tarditas regressus continuatur, fit hæc inæqualitas longe maxima.
Apside ima maxime recedit a duplicata ratione distantiarum inversa: manifestum est quod Apsides in Syzygiis suis, per vim ablatitiam KL seu NM−LM, progredientur velocius, inque Quadraturis suis tardius recedent per vim addititiam LM. Ob diuturnitatem vero temporis quo velocitas progressus vel tarditas regressus continuatur, fit hæc inæqualitas longe maxima.
Corol. 9. Si corpus aliquod vi reciproce proportionali quadrato distantiæ suæ a centro, revolveretur circa hoc centrum in Ellipsi, & mox, in descensu ab Apside summa seu Auge ad Apsidem imam, vis illa per accessum perpetuum vis novæ augeretur in ratione plusquam duplicata distantiæ diminutæ: Manifestum est quod corpus, perpetuo accessu vis illius novæ impulsum semper in centrum, magis vergeret in hoc centrum, quam si urgeretur vi sola crescente in duplicata ratione distantiæ diminutæ, adeoque Orbem describeret Orbe Elliptico interiorem, & in Apside ima propius accederet ad centrum quam prius. Orbis igitur, accessu hujus vis novæ, fiet magis excentricus. Si jam vis, in recessu corporis ab Apside ima ad Apsidem summam, decresceret iisdem gradibus quibus ante creverat, rediret corpus ad distantiam priorem, adeoque si vis decrescat in majori ratione, corpus jam minus attractum ascendet ad distantiam majorem & sic Orbis Excentricitas adhuc magis augebitur. Igitur si ratio incrementi & decrementi vis centripetæ singulis revolutionibus augeatur, augebitur semper Excentricitas, & e contra, diminuetur eadem si ratio illa decrescat. Jam vero in Systemate corporum S, P, Q, ubi Apsides orbis PAB sunt in quadraturis, ratio illa incrementi ac decrementi minima est, & maxima fit ubi Apsides sunt in Syzygiis. Si Apsides constituantur in quadraturis ratio prope Apsides minor est, & prope Syzygias major quam duplicata distantiarum, & ex ratione illa majori oritur Augis motus velocissimus, uti jam dictum est. At si consideretur ratio incrementi vel decrementi totius in progressu inter Apsides, hæc minor est quam duplicata distantiarum. Vis in Apside ima est ad vim in Apside summa in minore quam duplicata ratione distantiæ Apsidis summæ ab umbilico Ellipseos ad distantiam Apsidis imæ ab eodem umbilico: & e contra, ubi Apsides constituuntur in Syzygiis, vis in Apside ima est ad vim in Apside summa in majore quam duplicata ratione distantiarum. Nam vires LM in quadraturis additæ viribus corporis S componunt vires in ratione minore, & vires KL in Syzygiis subductæ viribus corporis S relinquunt vires in ratione majore. Est igitur ratio decrementi & incrementi totius in transitu inter Apsides, minima in quadraturis, maxima in Syzygiis: & propterea in transitu Apsidum a quadraturis ad Syzygias perpetuo augetur, augetque Excentricitatem Ellipsieos; inque transitu a Syzygiis ad quadraturas perpetuo diminuitur, & Excentricitatem diminuit.
Corol. 10. Ut rationem ineamus errorum in latitudinem, fingamus planum Orbis QES immobile manere; & ex errorum exposita causa manifestum est, quod ex viribus NM, ML, quæ sunt causa illa tota, vis ML agendo semper secundum planum Orbis PAB, nunquam perturbat motus in latitudinem, quodque vis NM ubi Nodi sunt in Syzygiis, agendo etiam secundum idem Orbis planum, non perturbat hos motus; ubi vero sunt in Quadraturis eos maxime perturbat, corpusque P de plano Orbis sui perpetuo trahendo, minuit inclinationem plani in transitu corporis a quadraturis ad Syzygias, augetque vicissim eandem in transitu a Syzygiis ad quadraturas. Unde fit ut corpore in Syzygiis existente inclinatio evadat omnium minima, redeatque ad priorem magnitudinem circiter, ubi corpus ad Nodum proximum accedit. At si Nodi constituantur in Octantibus post quadraturas, id est inter C & A, D & B, intelligetur ex modo expositis quod, in transitu corporis P a Nodo alterutro ad gradum inde nonagesimum, inclinatio plani perpetuo minuitur; deinde in transitu per proximos 45 gradus, usque ad quadraturam proximam, inclinatio augetur, & postea denuo in transitu per alios 45 gradus, usque ad nodum proximum, diminuitur. Magis itaque diminuitur inclinatio quam augetur, & propterea minor est semper in nodo subsequente quam in præcedente. Et simili ratiocinio inclinatio magis augetur quam diminuitur, ubi nodi sunt in Octantibus alteris inter A & D, B & C. Inclinatio igitur ubi Nodi sunt in Syzygiis est omnium maxima. In transitu eorum a Syzygiis ad quadraturas, in singulis corporis ad Nodos appulsibus, diminuitur, fitque omnium minima ubi nodi sunt in quadraturis & corpus in Syzygiis: dein creseit iisdem gradibus quibus antea decreverat, Nodisque ad Syzygias proximas appulsis ad magnitudinem primam revertitur.
Corol. 11. Quoniam corpus P ubi nodi sunt in quadraturis perpetuo trahitur de plano Orbis sui, idque in partem versus Q, in transitu suo a nodo C per Conjunctionem A ad nodum D; & in contrariam partem in transitu a nodo D per Oppositionem B ad nodum C; manifestum est quod in motu suo a nodo C, corpus perpetuo recedit ab Orbis sui plano primo CD, usque dum perventum est ad nodum proximum; adeoque in hoc nodo longissime distans a plano illo primo CD, transit per planum Orbis QES, non in plani illius Nodo altero D, sed in puncto quod inde vergit ad partes corporis Q, quodque proinde novus est Nodi locus in anteriora vergens. Et simili argumento pergent Nodi recedere in transitu Corporis de hoc nodo in nodum proximum. Nodi igitur in quadraturis constituti perpetuo recedunt, in Syzygiis (ubi motus in latitudinem nil perturbatur) quiescunt; in locis intermediis conditionis utriusque participes recedunt tardius, adeoque semper vel retrogradi vel stationarii singulis revolutionibus feruntur in antecedentia.
Corol. 12. Omnes illi in his Corollariis descripti errores sunt paulo majores in conjunctione Corporum P, Q quam in eorum Oppositione, idque ob majores vires generantes NM & ML.
Corol. 13. Cumque rationes horum Corollariorum non pendeant a magnitudine corporis Q, obtinent præcedentia omnia, ubi corporis Q tanta statuitur magnitudo ut circa ipsum revolvatur corporum duorum S & P Systema. Et ex aucto corpore Q, auctaque adeo ipsius vi centripeta, a qua errores corporis P oriuntur, evadent errores illi omnes (paribus distantiis) majores in hoc casu quam in altero, ubi corpus Q circum Systema corporum P & S revolvitur.
Corol. 14 Cum autem vires NM, ML, ubi corpus Q longinquum est, sint quamproxime ut vis QK & ratio PS ad QS conjunctim, hoc est, si detur tum distantia PS, tum corporis Q vis absoluta, ut QS cub. reciproce; sint autem vires illæ NM, ML causæ errorum & effectuum omnium de quibus actum est in præcedentibus Corollariis: manifestum est quod effectus illi omnes, stante corporum S & P Systemate, sint quamproxime in ratione composita ex ratione directa vis absolutæ corporis Q & ratione triplicata inversa distantiæ QS. Unde si Systema corporum S & P revolvatur circa corpus longinquum Q, vires illæ NM, ML & earum effectus erunt (per Corol. 2. & 6. Prop. IV.) reciproce in duplicata ratione temporis periodici. Et inde si magnitudo corporis Q proportionalis sit ipsius vi absolutæ, erunt vires illæ NM, ML & earum effectus directe ut cubus diametri apparentis longinqui corporis Qe corpore S spectati, & vice versa. Namque hæ rationes eædem sunt atque ratio superior composita.
Corol. 15. Et quoniam si, manentibus Orbium QE & PAB forma, proportionibus & inclinatione ad invicem, inutetur eorum magnitudo, & si corporum Q & S vel maneant vel mutentur vires in data quavis ratione, hæ vires (hoc est vis corporis S, qua corpus P de recto tramite in Orbitam PAB deflectere, & vis corporis Q, qua corpus idem P de Orbita illa deviare cogitur) agunt semper eodem modo & eadem proportione: necesse est ut similes & proportionales sint effectus omnes & proportionalia effectuum tempora; hoc est, ut errores omnes lineares sint ut Orbium diametri, angulares vero iidem qui prius, & errorum linearium similium vel angularium æqualium tempora ut Orbium tempora periodica.
Corol. 16. Unde, si dentur Orbium formæ & inclinatio ad invicem, & mutentur utcunque corporum magnitudines, vires & distantiæ; ex datis erroribus & errorum temporibus in uno Casu colligi possunt errores & errorum tempora in alio quovis, quam proxime: Sed brevius hac Methodo. Vires NM, ML cæteris stantibus sunt ut Radius SP, & harum effectus periodici (per Corol. 2, Lem. X) ut vires & quadratum temporis periodici corporis P conjunctim. Hi sunt errores lineares corporis P; & hinc errores angulares e centro S spectati (id est tam motus Augis & Nodorum, quam omnes in longitudinem & latitudinem errores apparentes) sunt in qualibet revolutione corporis P, ut quadratum temporis revolutionis quam proxime. Conjungantur hæ rationes cum rationibus Corollarii 14. & in quolibet corporum S, P, Q Systemate, ubi P circum S sibi propinquum, & S circum Q longinquum revolvitur, errores angulares corporis P, de centro S apparentes, erunt, in singulis revolutionibus corporis illius P, ut quadratum temporis periodici corporis P directe & quadratum temporis periodici corporis S inverse. Et inde motus medius Augis erit in data ratione ad motum medium Nodorum; & motus uterque erit ut tempus periodicum corporis P directe & quadratum temporis periodici corporis S inverse. Augendo vel minuendo Excentricitatem & Inclinationem Orbis PAB non mutantur motus Augis & Nodorum sensibilitur, nisi ubi eædem sunt nimis magnæ.
Corol. 17. Cum autem linea LM nunc major sit nunc minor quam radius PS, Exponatur vis mediocris LM per radium illum PS, & erit hæc ad vim mediocrem QK vel QN (quam exponere licet per QS) ut longitudo PS ad longitudinem QS. Est autem vis mediocris QN vel QS, qua corpus retinetur in orbe suo circum Q, ad vim qua corpus P retinetur in Orbe suo circum S, in ratione composita ex ratione radii QS ad radium PS, & ratione duplicata temporis periodici corporis P circum S ad tempus periodicum corporis S circum Q. Et ex æquo, vis mediocris LM, ad vim qua corpus P retinetur in Orbe suo circum S (quave corpus idem P eodem tempore periodico circum punctum quodvis immobile S ad distantiam PS revolvi posset) est in ratione illa duplicata periodicorum temporum. Datis igitur temporibus periodicis una cum distantia PS, datur vis mediocris LM; & ea data datur etiam vis MN quamproxime per analogiam linearum PS, MN.
Corol. 18. Iisdem legibus quibus corpus P circum corpus S revolvitur, fingamus corpora plura fluida circum idem S ad æquales ab ipso distantias moveri; deinde ex his contiguis factis conflari annulum fluidum, rotundum ac corpori S concentricum; & singulæ annuli partes, motus suos omnes ad legem corporis P peragendo, propius accedent ad corpus S, & celerius movebuntur in Conjunctione & Oppositione ipsarum & corporis Q, quam in Quadraturis. Et Nodi annuli hujus seu intersectiones ejus cum plano Orbitæ corporis Q vel S, quiescent in Syzygiis; extra Syzygias vero movebuntur in antecedentia, & velocissime quidem in Quadraturis, tardius aliis in locis. Annuli quoque inclinatio variabitur, & axis ejus singulis revolutionibus oscillabitur, completaque revolutione ad pristinum situm redibit, nisi quatenus per præcessionem Nodorum circumfertur.
Corol. 19. Fingas jam globum corporis S ex materia non fluida constantem ampliari & extendi usque ad hunc annulum, & alveo per circuitum excavato continere Aquam, motuque eodem periodico circa axem suum uniformiter revolvi. Hic liquor per vices acceleratus & retardatus (ut in superiore Lemmate) in Syzygiis velocior erit, in Quadraturis tardior quam superficies Globi, & sic fluet in alveo refluetque ad modum Maris. Aqua revolvendo circa Globi centrum quiescens, si tollatur attractio Q, nullum acquiret motum fluxus & refluxus. Par est ratio Globi uniformiter progredientis in directum & interea revolventis circa centrum suum (per Legum Corol. 5) ut & Globi de cursu rectilineo uniformiter tracti (per Legum Corol. 6.) Accedat autem corpus Q, & ab ipsius inæquabili attractione mox turbabitur Aqua. Etenim major erit attractio aquæ propioris, minor ea remotioris. Vis autem LM trahet aquam deorsum in Quadraturis, facietque ipsam descendere usque ad Syzygias; & vis KL trahet eandem sursum in Syzygiis, sistetque descensum ejus & faciet ipsam ascendere usque ad Quadraturas.
Corol. 20. Si annulus jam rigeat & minuatur Globus, cessabit motus fluendi & refluendi; sed Oscillatorius ille inclinationis motus & præcessio Nodorum manebunt. Habeat Globus eundem axem cum annulo, gyrosque compleat iisdem temporibus, & superficie sua contingat ipsum interius, eique inhæreat; & participando motum ejus, compages utriusque Oscillabitur & Nodi regredientur. Nam Globus, ut mox dicetur, ad suscipiendas impressiones omnes indifferens est. Annuli Globo orbati maximus inclinationis angulus est ubi Nodi sunt in Syzygiis. Inde in progressu Nodorum ad Quadraturas conatur is inclinationem suam minuere, & isto conatu motum imprimit Globo toti. Retinet Globus motum impressum usque dum annulus conatu contrario motum hunc tollat, imprimatque motum novum in contrariam partem: Atque hac ratione maximus decrescentis inclinationis motus fit in Quadraturis Nodorum, & minimus inclinationis angulus in Octantibus post Quadraturas; dein maximus reclinationis motus in Syzygiis & maximus angulus in Octantibus proximis. Et eadem est ratio Globi annulo nudati, qui in regionibus æquatoris vel altior est paulo quam juxta polos, vel constat ex materia paulo densiore. Supplet enim vicem annuli iste materiæ in æquatoris regionibus excessus. Et quanquam, aucta utcunque Globi hujus vi centripeta, tendere supponantur omnes ejus partes deorsum, ad modum gravitantium partium telluris, tamen Phænomena hujus & præcedentis Corollarii vix inde mutabuntur.
Corol. 21. Eadem ratione qua materia Globi juxta æquatorem redundans efficit ut Nodi regrediantur, atque adeo per hujus incrementum augetur iste regressus, per diminutionem vero diminuitur & per ablationem tollitur; si materia plusquam redundans tollatur, hoc est, si Globus juxta æquatorem vel depressior reddatur vel rarior quam juxta polos, orietur motus Nodorum in consequentia.
Corol. 22. Et inde vicissim ex motu Nodorum innotescit constitutio Globi. Nimirum si Globus polos eosdem constanter servat & motus fit in antecedentia, materia juxta æquatorem redundat; si in consequentia, deficit. Pone Globum uniformem & perfecte circinatum in spatiis liberis primo quiscere; dein impetu quocunque oblique in superficiem suam facto propelli, & motum inde concipere partim circularem, partim in directum. Quoniam Globus iste ad axes omnes per centrum suum transeuntes indifferenter se habet, neque propensior est in unum axem, unumve axis situm, quam in alium quemvis; perspicuum est quod is axem suum axisque inclinationem vi propria nunquam mutabit. Impellatur jam Globus oblique in eadem illa superficiei parte qua prius, impulsu quocunque novo; & cum citior vel serior impulsus effectum nil mutet, manifestum est quod hi duo impulsus successive impressi eundem producent motum ac si simul impressi fuissent, hoc est eundem ac si Globus vi simplici ex utroque (per Legum Corol. 2.) composita impulsus fuisset, atque adeo simplicem, circa axem inclinatione datum. Et par est ratio impulsus secundi facti in locum alium quemvis in æquatore motus primi; ut & impulsus primi facti in locum quemvis in æquatore motus, quem impulsus secundus absque primo generaret; atque adeo impulsuum amborum factorum in loca quæcunque: Generabunt hi eundem motum circularem ac si simul & semel in locum intersectionis æquatorum motuum illorum, quos seorsim generarent, fuissent impressi. Globus igitur homogeneus & perfectus non retinet motus plures distinctos, sed impressos omnes componit & ad unum reducit, & quatenus in se est, gyratur semper motu simplici & uniformi circa axem unicum inclinatione semper invariabili datum. Sed nec vis centripeta inclinationem axis, aut rotationis velocitatem mutare potest. Si Globus plano quocunque per centrum suum & centrum in quod vis dirigitur transeunte dividi intelligatur in duo hemisphæria, urgebit semper vis illa utrumque hemiphærium æqualiter, & propterea Globum quoad motum rotationis nullam in partem inclinabit. Addatur vero alicubi inter polum & æquatorem materia nova in formam montis cumulata, & hæc, perpetuo conatu recedendi a centro sui motus, turbabit motum Globi, facietque polos ejus errare per ipsius superficiem, & circulos circum se punctumque sibi oppositum perpetuo describere. Neque corrigetur ista vagationis enormitas, nisi locando montem illum vel in polo alterutro, quo in Casu, per Corol. 21, Nodi æquatoris progredientur; vel in æquatore, qua ratione, per Corol. 20, Nodi regredientur; vel denique ex altera axis parte addendo materiam novam, qua mons inter movendum libretur: & hoc pacto Nodi vel progredientur, vel recedent, perinde ut mons & hæcce nova materia sunt vel polo vel æquatori propiores.
<188>Prop. LXVII. Theor. XXVII.
Positis iisdem attractionum legibus, dico quod corpus exterius Q, circa interiorum P, S commune Gravitatis centrum C, radiis ad centrum illud ductis, describit areas temporibus magis proportionales & Orbem ad formam Ellipseos umbilicum in centro eodem habentis magis accedentem, quam circa corpus intimum & maximum S, radiis ad ipsum ductis, describere potest.
Nam corporis Q attractiones versus S & P componunt ipsius attractionem absolutam, quæ magis dirigitur in corporum S & P commune gravitatis centrum C, quam in corpus maximum S, quæque quadrato distantiæ QC magis est proportionalis reciproce, quam quadrato distantiæ QS: ut rem perpendenti facile constabit.
Prop. LXVIII. Theor. XXVIII.
Positis iisdem attractionum legibus, dico quod corpus exterius Q circa interiorum P & S commune gravitatis centrum C, radiis ad centrum illud ductis, describit areas temporibus magis proportionales, & Orbem ad formam Ellipseos umbilicum in centro eodem habentis magis accedentem, si corpus intimum & maximum his attractionibus perinde atque cætera agitetur, quam si id vel non attractum quiescat, vel multo magis aut multo minus attractum aut multo magis aut multo minus agitetur.
Demonstratur eodem fere modo cum Prop. LXVI, sed argumento prolixiore, quod ideo prætereo. Suffecerit rem sic æstimare. Ex demonstratione Propositionis novissimæ liquet centrum in quod corpus Q conjunctis viribus urgetur, proximum esse communi centro gravitatis illorum duorum. Si coincideret hoc centrum cum centro illo communi, & quisceret commune centrum gravitatis corporum trium; describerent corpus Q ex una parte, & commune centrum aliorum duorum ex altera parte, circa commune omnium centrum quiescens, Ellipses accuratas. Liquet hoc per Corollarium secundum Propositionis LVIII. collatum cum demonstratis in Prop. LXIV. & LXV. Perturbatur iste motus Ellipticus aliquantulum per distantiam centri duorum a centro in quod tertium Q attrahitur. Detur præterea motus communi trium centro, & augebitur perturbatio. Proinde minima est perturbatio, ubi commune trium centrum quiescit, hoc est ubi corpus intimum & maximum S lege cæterorum attrahitur: sitque major semper ubi trium commune illud centrum, minuendo motum corporis S, moveri incipit & magis deinceps magisque agitatur.
Corol. Et hinc si corpora plura minora revolvantur circa maximum, colligere licet 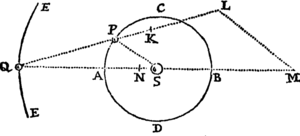 quod Orbitæ descriptæ propius accedent ad Ellipticas, & arearum descriptiones fient magis æquabiles, si corpora omnia viribus acceleratricibus, quæ sunt ut eorum vires absolutæ directa & quadrata distantiarum inverse, se mutuo trahent agitentque, & Orbitæ cujusque umbilicus collocetur in communi centro gravitatis corporum omnium interiorum (nimirum umbilicus Orbitæ primæ & intimæ in centro gravitatis corporis maximi & intimi; ille Orbitæ secundæ, in communi centro gravitatis corporum duorum intimorum; iste tertiæ, in communi centro gravitatis trium interiorum & sic deinceps) quam si corpus intimum quiescat & statuatur communis umbilicus orbitarum Omnium.
quod Orbitæ descriptæ propius accedent ad Ellipticas, & arearum descriptiones fient magis æquabiles, si corpora omnia viribus acceleratricibus, quæ sunt ut eorum vires absolutæ directa & quadrata distantiarum inverse, se mutuo trahent agitentque, & Orbitæ cujusque umbilicus collocetur in communi centro gravitatis corporum omnium interiorum (nimirum umbilicus Orbitæ primæ & intimæ in centro gravitatis corporis maximi & intimi; ille Orbitæ secundæ, in communi centro gravitatis corporum duorum intimorum; iste tertiæ, in communi centro gravitatis trium interiorum & sic deinceps) quam si corpus intimum quiescat & statuatur communis umbilicus orbitarum Omnium.
Prop. LXIX. Theor. XXIX.
In Systemate corporum plurium A, B, C, D &c. si corpus aliquod A trahit cætera omnia B, C, D &c. viribus acceleratricibus quæ sunt reciproce ut quadrata distantiarum a trahente; & corpus aliud B trahit etiam cætera A, C, D &c. viribus quæ sunt reciproce ut quadrata distantiarum a trahente: erunt absolutæ corporum trahentium A, B vires ad invicem, ut sunt ipsa corpora A, B, quorum sunt vires.
Nam attractiones acceleratrices corporum omnium B, C, D versus A, paribus distantiis, sibi invicem æquantur ex hypothesi, & similiter attractiones acceleratrices corporum omnium versus B, paribus distantiis, sibi invicem æquantur. Est autem absoluta vis attractiva corporis A ad vim absolutam attractivam corporis B, ut attractio acceleratrix corporum omnium versus A ad attractionem acceleratricem corporum omnium versus B, paribus distantiis; & ita est attractio acceleratrix corporis B versus A, ad attractionem acceleratricem corporis A versus B. Sed attractio acceleratrix corporis B versus A est ad attractionem acceleratricem corporis A versus B, ut massa corporis A ad massam corporis B; propterea quod vires motrices, quæ (per Definitionem secundam, septimam & octavam) ex viribus acceleratricibus in corpora attracta ductis oriuntur, sunt (per motus Legem tertiam) sibi invicem æquales. Ergo absoluta vis attractiva corporis A est ad absolutam vim attractivam corporis B, ut massa corporis A ad massam corporis B. Q.E.D.
Corol. 1. Hinc si singula Systematis corpora A, B, C, D, &c. seorsim spectata trahant cætera omnia viribus acceleratricibus quæ sint reciproce ut Quadrata distantiarum a trahente; erunt corporum illorum omnium vires absolutæ ad invicem ut sunt ipsa corpora.
<191>Corol. 2. Eodem argumento, si singula Systematis corpora A, B, C, D &c. seorsim spectata trahant cætera omnia viribus acceleratricibus quæ sunt vel reciproce vel directe in ratione dignitatis cujuscunque distantiarum a trahente, quæve secundum legem quamcunque communem ex distantiis ab unoquoque trahente definiuntur; constat quod corporum illorum vires absolutæ sunt ut corpora.
Corol. 3. In Systemate corporum, quorum vires decrescunt in ratione duplicata distantiarum, si minora circa maximum in Ellipsibus umbilicum communem in maximi illius centro habentibus quam fieri potest accuratissimis revolvantur, & radiis ad maximum illud ductis describant areas temporibus quam maxime proportionales: erunt corporum illorum vires absolutæ ad invicem, aut accurate aut quamproxime in ratione corporum; & contra. Patet per Corol. Prop. LXVIII. collatum cum hujus Corol, 1.
Scholium.
His Propositionibus manuducimur ad analogiam inter vires centripetas & corpora centralia, ad quæ vires illæ dirigi solent. Rationi enim consentaneum est, ut vires quæ ad corpora diriguntur pendeant ab eorundem natura & quantitate, ut sit in Magneticis. Et quoties hujusmodi casus incidunt, æstimandæ erunt corporum attractiones, assignando singulis eorum particulis vires proprias, & colligendo summas virium. Vocem attractionis hic generaliter usurpo pro corporum conatu quocunque accedendi ad invicem, sive conatus iste fiat ab actione corporum vel se mutuo petentium, vel per Spiritus emissos se invicem agitantium, sive is ab actione Ætheris aut Aeris mediive cujuscunque seu corporei seu incorporei oriatur corpora innatantia in se invicem utcunque impellentis. Eodem sensu generali usurpo vocem impulsus, non species virium & qualitates physicas, sed quantitates & proportiones Mathematicas in hoc Tractatu expendens: ut in Definitionibus explicui. In Mathesi investigandæ sunt virium quantitates & rationes illæ, quæ ex conditionibus quibuscunque positis consequentur: deinde ubi in Physicam descenditur, conferendæ sunt hæ rationes cum Phænomenis, ut innotescat quænam virium conditiones singulis corporum attractivorum generibus competant. Et tum demum de virium speciebus, causis & rationibus physicis tutius disputare licebit. Videamus igitur quibus viribus corpora Sphærica, ex particulis modo jam exposito attractivis constantia, debeant in se mutuo agere, & quales motus inde consequantur.
SECT. XII.
De Corporum Sphæricorum Viribus attractivis.
Prop. LXX. Theor. XXX.
Si ad Sphæricæ superficiei puncta singula tendant vires æquales centripetæ decrescentes in duplicata ratione distantiarum a punctis: dico quod corpusculum intra superficiem constitutum his viribus nullam in partem attrahitur.
Sit HIKL superficies illa Sphærica, & P corpusculum intus constitutum. Per P agantur ad hanc superficiem lineæ duæ HK, IL, arcus quam minimos HI, KL intercipientes; & ob triangula HPI, LPK (per Corol. 3. Lem. VII.) similia, arcus illi erunt distantiis HP, LP proportionales, & superficiei Sphæricæ particulæ quævis, ad HI & KL rectis per punctum P transeuntibus undique terminatæ, erunt in duplicata illa ratione. Ergo vires harum particularum in corpus P exercitæ sunt inter se æquales. Sunt enim ut particulæ directe & quadrata distantiarum inverse. Et hæ duæ rationes componunt rationem 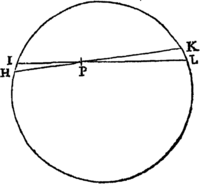 æqualitatis. Attractiones igitur in contrarias partes æqualiter factæ se mutuo destruunt. Et simili argumento attractiones omnes per totam Sphæricam superficiem a contrariis attractionibus destruuntur. Proinde corpus P nullam in partem his attractionibus impellitur. Q.E.D.
æqualitatis. Attractiones igitur in contrarias partes æqualiter factæ se mutuo destruunt. Et simili argumento attractiones omnes per totam Sphæricam superficiem a contrariis attractionibus destruuntur. Proinde corpus P nullam in partem his attractionibus impellitur. Q.E.D.
Prop. LXXI. Theor. XXXI.
Iisdem positis, dico quod corpusculum extra Sphæricam superficiem constitutum attrahitur ad centrum Sphæræ, vi reciproce proportionali quadrato distantiæ suæ ab eodem centro.
Sint AHKB, ahkb æquales duæ superficies Sphæricæ, centris S, s, diametris AB, ab descriptæ, & P, p corpuscula sita extrinsecus in diametris illis productis. Agantur a corpusculis lineæ 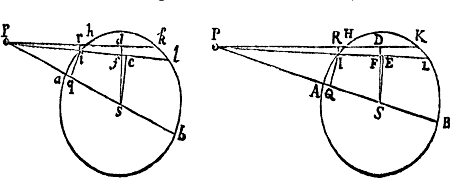 PHK, PIL, phk, pil, auferentes a circulis maximis AHB, ahb, æquales arcus quam minimos HK, hk & HL, hl: Et ad eas demittantur perpendicula SD, sd; SE, se; IR, ir; quorum SD, sd secent PL, pl in F & f. Demittantur etiam ad diametros perpendicula IQ, iq; & ob æquales DS & ds, ES & es, & angulos evanescentes DPE & dpe, lineæ PE, PF & pe, pf & lineolæ DF, df pro æqualibus habeantur: quippe quarum ratio ultima, angulis illis DPE, dpe simul evanescentibus, est æqualitatis. His itaque constitutis, erit PI ad PF ut RI ad DF, & pf ad pi ut DF vel df ad ri; & ex æquo ad ut RI ad ri, hoc est (per Corol. 3. Lem. VII.) ut arcus IH ad arcum ih. Rursus PI ad PS ut IQ ad SE, & ps ad pi ut SE vel se ad iq; & ex æquo ad ut IQ ad iq. Et conjunctis rationibus ad ,
PHK, PIL, phk, pil, auferentes a circulis maximis AHB, ahb, æquales arcus quam minimos HK, hk & HL, hl: Et ad eas demittantur perpendicula SD, sd; SE, se; IR, ir; quorum SD, sd secent PL, pl in F & f. Demittantur etiam ad diametros perpendicula IQ, iq; & ob æquales DS & ds, ES & es, & angulos evanescentes DPE & dpe, lineæ PE, PF & pe, pf & lineolæ DF, df pro æqualibus habeantur: quippe quarum ratio ultima, angulis illis DPE, dpe simul evanescentibus, est æqualitatis. His itaque constitutis, erit PI ad PF ut RI ad DF, & pf ad pi ut DF vel df ad ri; & ex æquo ad ut RI ad ri, hoc est (per Corol. 3. Lem. VII.) ut arcus IH ad arcum ih. Rursus PI ad PS ut IQ ad SE, & ps ad pi ut SE vel se ad iq; & ex æquo ad ut IQ ad iq. Et conjunctis rationibus ad , 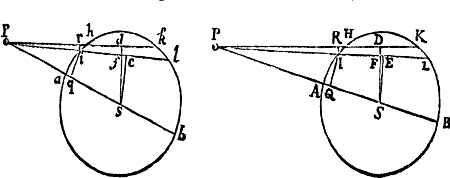 ut ad ; hoc est, ut superficies circularis, quam arcus IH convolutione semicirculi AKB circa diametrum AB describet, ad superficiem circularem, quam arcus ih convolutione semicirculi akb circa diametrum ab describet. Et vires, quibus hæ superficies secundum lineas ad se tendentes attrahunt corpuscula P & p, sunt (per Hypothesin) ut ipsæ superficies applicatæ ad quadrata distantiarum suarum a corporibus, hoc est, ut ad . Suntque hæ vires ad ipsarum partes obliquas quæ (facta per Legum Corol. 2 resolutione virium) secundum lineas PS, ps ad centra tendunt, ut PI ad PQ, & pi ad pq; id est (ob similia triangula PIQ & PSF, piq & psf) ut PS ad PF & ps ad pf. Unde ex æquo fit attractio corpusculi hujus P versus S ad attractionem corpusculi p versus s, ut ad , hoc est ut ps quad. ad PS quad. Et simili argumento vires, quibus superficies convolutione arcuum KL, kl descriptæ trahunt corpuscula, erunt ut ps quad. ad PS quad.; inque eadem ratione erunt vires superficierum omnium circularium in quas utraque superficies Sphærica, capiendo semper sd=SD & se=SE, distingui potest. Et per Compositionem, vires totarum superficierum Sphæricarum in corpuscula exercitæ erunt in eadem ratione. Q.E.D.
ut ad ; hoc est, ut superficies circularis, quam arcus IH convolutione semicirculi AKB circa diametrum AB describet, ad superficiem circularem, quam arcus ih convolutione semicirculi akb circa diametrum ab describet. Et vires, quibus hæ superficies secundum lineas ad se tendentes attrahunt corpuscula P & p, sunt (per Hypothesin) ut ipsæ superficies applicatæ ad quadrata distantiarum suarum a corporibus, hoc est, ut ad . Suntque hæ vires ad ipsarum partes obliquas quæ (facta per Legum Corol. 2 resolutione virium) secundum lineas PS, ps ad centra tendunt, ut PI ad PQ, & pi ad pq; id est (ob similia triangula PIQ & PSF, piq & psf) ut PS ad PF & ps ad pf. Unde ex æquo fit attractio corpusculi hujus P versus S ad attractionem corpusculi p versus s, ut ad , hoc est ut ps quad. ad PS quad. Et simili argumento vires, quibus superficies convolutione arcuum KL, kl descriptæ trahunt corpuscula, erunt ut ps quad. ad PS quad.; inque eadem ratione erunt vires superficierum omnium circularium in quas utraque superficies Sphærica, capiendo semper sd=SD & se=SE, distingui potest. Et per Compositionem, vires totarum superficierum Sphæricarum in corpuscula exercitæ erunt in eadem ratione. Q.E.D.
Prop. LXXII. Theor. XXXII.
Si ad Sphæræ cujusvis puncta singula tendant vires æquales centripetæ decrescentes in duplicata ratione distantiarum a punctis, ac detur ratio diametri Sphæræ ad distantiam corpusculi a centro ejus; dico quod vis qua corpusculum attrahitur proportionalis erit semidiametro Sphæræ.
Nam concipe corpuscula duo seorsim a Sphæris duabus attrahi, & distantias a centris proportionales esse diametris, Sphæras autem resolvi in particulas similes & similiter positas ad corpuscula. Hinc attractiones corpusculi unius, factæ versus singulas particulas Sphæræ unius, erunt ad attractiones alterius versus analogas totidem particulas Sphæræ alterius, in ratione composita ex ratione particularum directe & ratione duplicata distantiarum inverse. Sed particulæ sunt ut Sphæræ, hoc est in ratione triplicata diametrorum, & distantiæ sunt ut diametri, & ratio prior directe una cum ratione posteriore bis inverse est ratio diametri ad diametrum. Q.E.D.
Corol. 1. Hinc si corpuscula in circulis circa Sphæras ex materia æqualiter attractiva constantes revolvantur, sintque distantiæ a centris Sphærarum proportionales earundem diametris; tempora periodica erunt æqualia.
<196>Corol. 2. Et vice versa, si tempora periodica sunt æqualia; distantiæ erunt proportionales diametris. Constant hæc duo per Corol. 3. Theor. IV.
Prop. LXXIII. Theor. XXXIII.
Si ad sphæræ alicujus datæ puncta singula tendant æquales vires centripetæ decrescentes in duplicata ratione distantiarum a punctis: dico quod corpusculum intra Sphæram constitutum attrahitur vi proportionali distantiæ suæ ab ipsius centro.
In Sphæra ABCD, centro S descripta, locetur corpusculum P, & centro eodem S intervallo SP concipe Sphæram interiorem PEQF describi. Manifestum est, per  Theor. XXX. quod Sphæricæ superficies concentricæ, ex quibus Sphærarum differentia AEBF componitur, attractionibus per attractiones contrarias destructis, nil agunt in corpus P. Restat sola attractio Sphæræ interioris PEQF. Et per Theor. XXXII. hæc est ut distantia PS.Q.E.D.
Theor. XXX. quod Sphæricæ superficies concentricæ, ex quibus Sphærarum differentia AEBF componitur, attractionibus per attractiones contrarias destructis, nil agunt in corpus P. Restat sola attractio Sphæræ interioris PEQF. Et per Theor. XXXII. hæc est ut distantia PS.Q.E.D.
Scholium.
Superficies ex quibus solida componuntur, hic non sunt pure Mathematicæ, sed Orbes adeo tenues ut eorum crassitudo instar nihili sit; nimirum Orbes evanescentes ex quibus Sphæra ultimo constat, ubi Orbium illorum numerus augetur & crassitudo minuitur in infinitum, juxta Methodum sub initio in Lemmatis generalibus expositam. Similiter per puncta, ex quibus lineæ, superficies & solida componi dicuntur, intelligendæ sunt particulæ æquales magnitudinis contemnendæ.
<197>Prop. LXXIV. Theor. XXXIV.
Iisdem positis, dico quod corpusculum extra Sphæram constitutum attrahitur vi reciproce proportionali quadrato distantiæ suæ ab ipsius centro.
Nam distinguatur Sphæra in superficies Sphæricas innumeras concentricas, & attractiones corpusculi a singulis superficiebus oriundæ erunt reciproce proportionales quadrato distantiæ corpusculi a centro, per Theor. XXXI. Et componendo, fiet summa attractionum, hoc est attractio Sphæræ totius, in eadem ratione. Q.E.D.
Corol. 1. Hinc in æqualibus distantiis a centris homogenearum Sphærarum, attractiones sunt ut Sphæræ. Nam per Theor. XXXII. si distantiæ sunt proportionales diametris Sphærarum, vires erunt ut diametri. Minuatur distantia major in illa ratione, & distantiis jam factis æqualibus, augebitur attractio in duplicata illa ratione, adeoque erit ad attractionem alteram in triplicata illa ratione, hoc est in ratione Sphærarum.
Corol. 2. In distantiis quibusvis attractiones sunt ut Sphæræ applicatæ ad quadrata distantiarum.
Corol. 3. Si corpusculum extra Sphæram homogeneam positum trahitur vi reciproce proportionali quadrato distantiæ suæ ab ipsius centro, constet autem Sphæra ex particulis attractivis; decrescet vis particulæ cujusque in duplicata ratione distantiæ a particula.
Prop. LXXV. Theor. XXXV.
Si ad Sphæræ datæ puncta singula tendant vires æquales centripetæ decrescentes in duplicata ratione distantiarum a punctis, dico quod Sphæra quævis alia similaris attrahitur vi reciproce proportionali quadrato distantiæ centrorum.
Nam particulæ cujusvis attractio est reciproce ut quadratum distantiæ ejus a centro Sphæræ trahentis, (per Theor. XXXI,) & propterea eadem est ac si vis tota attrahens manaret de corpusculo unico sito in centro hujus Sphæræ. Hæc autem attractio tanta est quanta foret vicissim attractio corpusculi ejusdem, si modo illud a singulis Sphæræ attractæ particulis eadem vi traheretur qua ipsas attrahit. Foret autem illa corpusculi attractio (per Theor XXXIV) reciproce proportionalis quadrato distantiæ ejus a centro Sphæræ; adeoque huic æqualis attractio Sphæræ est in eadem ratione. Q.E.D.
Corol. 1. Attractiones Sphærarum, versus alias Sphæras homogeneas, sunt ut Sphæræ trahentes applicatæ ad quadrata distantiarum centrorum suorum a centris earum quas attrahunt.
Corol. 2. Idem valet ubi Sphæra attracta etiam attrahit. Namque hujus puncta singula trahent singula alterius, eadem vi qua ab ipsis vicissim trahuntur, adeoque cum in omni attractione urgeatur (per Legem 3.) tam punctum attrahens, quam punctum attractum, geminabitur vis attractionis mutuæ, conservatis proportionibus.
Corol. 3. Eadem omnia, quæ superius de motu corporum circa umbilicum Conicarum Sectionum demonstrata sunt, obtinent ubi Sphæra attrahens locatur in umbilico & corpora moventur extra Sphæram.
Corol. 4. Ea vero quæ de motu corporum circa centrum Conicarum Sectionum demonstrantur, obtinent ubi motus peraguntur intra Sphæram.
Prop. LXXVI. Theor. XXXVI.
Si Sphæræ in progressu a centro ad circumferentiam (quod materiæ densitatem & vim attractivam) utcunque dissimilares, in progressu vero per circuitum ad datam omnem a centro distantiam sunt undique similares, & vis attractiva puncti cujusque decrescit in duplicata ratione distantiæ corporis attracti: dico quod vis tota qua hujusmodi Sphæra una attrahit aliam sit reciproce proportionalis quadrato distantiæ centrorum.
<199>Sunto Sphæræ quotcunque concentricæ similares AB, CD, EF &c. quarum interiores additæ exterioribus componant materiam densiorem versus centrum, vel subductæ relinquant tenuiorem; & hæ, per Theor. XXXV, trahent Sphæras alias quotcunque concentricas similares GH, IK, LM, &c. singulæ singulas, viribus reciproce proportionalibus quadrato distantiæ SP. Et componendo vel dividendo, summa virium illarum omnium, vel excessus aliquarum supra alias, hoc est, vis qua Sphæra tota ex concentricis quibuscunque vel concentricarum differentiis composita AB, trahit totam ex concentricis quibuscunque vel concentricarum differentiis  compositam GH, erit in eadem ratione. Augeatur numerus Sphærarum concentricarum in infinitum sic, ut materiæ densitas una cum vi attractiva, in progressu a circumferentia ad centrum, secundum Legem quamcunque crescat vel decrescat: & addita materia non attractiva compleatur ubivis densitas deficiens, eo ut Sphæræ acquirant formam quamvis optatam; & vis qua harum una attrahet alteram erit etiamnum (per argumentum superius) in eadem illa distantiæ quadratæ ratione inversa. Q.E.D.
compositam GH, erit in eadem ratione. Augeatur numerus Sphærarum concentricarum in infinitum sic, ut materiæ densitas una cum vi attractiva, in progressu a circumferentia ad centrum, secundum Legem quamcunque crescat vel decrescat: & addita materia non attractiva compleatur ubivis densitas deficiens, eo ut Sphæræ acquirant formam quamvis optatam; & vis qua harum una attrahet alteram erit etiamnum (per argumentum superius) in eadem illa distantiæ quadratæ ratione inversa. Q.E.D.
Corol. 1. Hinc si ejusmodi Sphæræ complures sibi invicem per omnia similes se mutuo trahant; attractiones acceleratrices singularum in singulas erunt in æqualibus quibusvis centrorum distantiis ut Sphæræ attrahentes.
Corol. 2. Inque distantiis quibusvis inæqualibus, ut Sphæræ attrahentes applicatæ ad quadrata distantiarum inter centra.
<200>Corol. 3. Attractiones vero motrices, seu pondera Sphærarum in Sphæras erunt, in æqualibus centrorum distantiis, ut Sphæræ attrahentes & attractæ conjunctim, id est, ut contenta sub Sphæris per multiplicationem producta.
Corol. 4. Inque distantiis inæqualibus, ut contenta illa applicata ad quadrata distantiarum inter centra.
Corol. 5. Eadem valent ubi attractio oritur a Sphæræ utriusque virtute attractiva, mutuo exercita in Sphæram alteram. Nam viribus ambabus geminatur attractio, proportione servata.
Corol. 6. Si hujusmodi Sphæræ aliquæ circa alias quiescentes revolvantur, singulæ circa singulas, sintque distantiæ inter centra revolventium & quiescentium proportionales quiescentium diametris; æqualia erunt tempora periodica.
Corol. 7. Et vicissim, si tempora periodica sunt æqualia, distantiæ erunt proportionales diametris.
Corol. 8. Eadem omnia, quæ superius de motu corporum circa umbilicos Conicarum Sectionum demonstrata sunt, obtinent ubi Sphæra attrahens, formæ & conditionis cujusvis jam descriptæ, locatur in umbilico.
Corol. 9. Ut & ubi gyrantia sunt etiam Sphæræ attrahentes, conditionis cujusvis jam descriptæ.
Prop. LXXVII. Theor. XXXVII.
Si ad singula Sphærarum puncta tendant vires centripetæ proportionales distantiis punctorum a corporibus attractis: dico quod vis composita, qua Sphæræ duæ se mutuo trahent, est ut distantia inter centra Sphærarum.
Cas 1. Sit ABCD Sphæra, S centrum ejus, P corpusculum attractum, PASB axis Sphæræ per centrum corpusculi transiens, EF, ef plana duo quibus Sphæra secatur, huic axi perpendicularia, & hinc inde æqualiter distantia a centro Sphæræ; Gg intersectiones planorum & axis, & H punctum quodvis in plano EF. Puncti H vis centripeta in corpusculum P secundum lineam PH exercita est ut distantia PH, & (per Legum Corol. 2.) secuncundum lineam PG, seu versus centrum S, ut longitudo PG. Igitur punctorum omnium in plano EF, hoc est plani totius vis, qua corpusculum P trahitur versus centrum S, est ut numerus punctorum ductus in distantiam PG: id est ut contentum sub plano ipso EF & distantia illa PG. Et similiter vis plani ef, qua corpusculum P trahitur versus centrum S, est ut planum illud ductum in distantiam suam Pg; sive ut huic æquale planum EF ductum in distantiam illam Pg; & summa virium plani utriusque ut planum EF ductum in 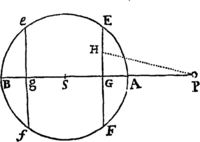 summam distantiarum PG+Pg, id est, ut planum illud ductum in duplam centri & corpusculi distantiam PS, hoc est, ut duplum planum EF ductum in distantiam PS, vel ut summa æqualium planorum EF+ef ducta in distantiam eandem. Et simili argumento, vires omnium planorum in Sphæra tota, hinc inde æqualiter a centro Sphæræ distantium, sunt ut summa planorum ducta in distantiam PS, hoc est, ut Sphæra tota ducta in distantiam centri sui Sa corpusculo P. Q.E.D.
summam distantiarum PG+Pg, id est, ut planum illud ductum in duplam centri & corpusculi distantiam PS, hoc est, ut duplum planum EF ductum in distantiam PS, vel ut summa æqualium planorum EF+ef ducta in distantiam eandem. Et simili argumento, vires omnium planorum in Sphæra tota, hinc inde æqualiter a centro Sphæræ distantium, sunt ut summa planorum ducta in distantiam PS, hoc est, ut Sphæra tota ducta in distantiam centri sui Sa corpusculo P. Q.E.D.
Cas. 2. Trahat jam corpusculum P Sphæram ACBD. Et codem argumento probabitur quod vis, qua Sphæra illa trahitur, erit ut distantia PS. Q.E.D.
Cas 3. Componatur jam Sphæra altera ex corpusculis innumeris P; & quoniam vis, qua corpusculum unumquodque trahitur, est ut distantia corpusculi a centro Sphæræ primæ ducta in Sphæram eandem, atque adeo eadem est ac si prodiret tota de corpusculo unico in centro Sphæræ; vis tota qua corpuscula omnia in Sphæra secunda trahuntur, hoc est, qua Sphæra illa tota trahitur, eadem erit ac si Sphæra illa traheretur vi prodeunte de corpusculo unico in centro Sphæræ primæ, & propterea proportionalis est distantiæ inter centra Sphærarum. Q.E.D.
Cas. 4. Trahant Sphæræ se mutuo, & vis geminata proportionem priorem servabit. Q.E.D.
Cas, 5. Locetur jam corpusculum p intra Sphæram ACBD, & quoniam vis plani ef in corpusculum est ut contentum sub plano illo & distantia pg; & vis contraria plani EF ut contentum sub plano illo & distantia pG; erit vis ex utraque composita ut differentia contentorum, hoc est, ut summa æqualium planorum ducta in. semissem differentiæ distantiarum, id est, ut summa illa ducta in pS, distantiam 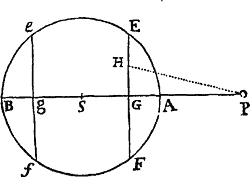 corpusculi a centro Sphæræ. Et simili argumento attractio planorum omnium EF, ef in Sphæra tota, hoc est attractio Sphæræ totius, est ut summa planorum omnium, seu Sphæra tota, ducta in pS distantiam corpusculi a centro Sphæræ. Q.E.D.
corpusculi a centro Sphæræ. Et simili argumento attractio planorum omnium EF, ef in Sphæra tota, hoc est attractio Sphæræ totius, est ut summa planorum omnium, seu Sphæra tota, ducta in pS distantiam corpusculi a centro Sphæræ. Q.E.D.
Cas. 6. Et si ex corpusculis innumeris p componatur Sphæra nova intra Sphæram priorem ACBD sita, probabitur ut prius, quod attractio, sive simplex Sphæræ unius in alteram, sive mutua utriusque in se invicem, erit ut distantia centrorum pS. Q.E.D.
Prop. LXXVIII. Theor. XXXVIII.
Si Sphæræ in progressu a centro ad circumferentiam sint utcunque dissimilares & inæquabiles, in progressu vero per circuitum ad datam omnem a centro distantiam sint undique similares; & vis attractiva puncti cujusque sit ut distantia corporis attracti: dico quod vis tota qua hujusmodi Sphæræ duæ se mutuo trahunt sit proportionalis distantiæ inter centra Sphærarum.
<203>Demonstratur ex Propositione præcedente, eodem modo quo Propositio LXXVII. ex Propositione LXXV. demonstrata fuit.
Corol. Quæ superius in Propositionibus X. & LXIV. de motu corporum circa centra Conicarum Sectionum demonstrata sunt, valent ubi attractiones omnes fiunt vi Corporum Sphæricorum, conditionis jam descriptæ, suntque corpora attracta Sphæræ conditionis ejusdem.
Scholium.
Attractionum Casus duos insigniores jam dedi expositos; nimirum ubi vires centripetæ decrescunt in duplicata distantiarum ratione, vel crescunt in distantiarum ratione simplici; efficientes in utroque Casu ut corpora gyrentur in Conicis Sectionibus, & componentes corporum Sphæricorum vires centripetas eadem lege in recessu a centro decrescentes vel crescentes cum seipsis. Quod est notatu dignum. Casus cæteros, qui conclusiones minus elegantes exhibent, sigillatim percurrere longum esset: Malim cunctos methodo generali simul comprehendere ac determinare, ut sequitur.
Lemma XXIX.
Si describantur centro S circulus quilibet AEB, (Vide Fig. Prop. sequentis) & centro P circuli duo EF, ef, secantes priorem in E, e, lineamque PS in F, f; & ad PS demittantur perpendicula ED, ed: dico quod si distantia arcuum EF, ef in infinitum minui intelligatur, ratio ultima lineæ evanescentis Dd ad lineam evanescentem Ff ea sit, quæ lineæ PE ad lineam PS.
Nam si linea Pe secet arcum EF in q; & recta Ee, quæ cum arcu evanescente Ee coincidit, producta occurrat rectæ PS in T; & ab S demittatur in PE normalis SG: ob similia triangula EDT, edt, EDS; erit Dd ad Ee ut DT ad ET seu DE ad ES, & ob triangula Eqe, ESG (per Lem. VIII. & Corol. 3. Lem. VII.) similia, erit Ee ad qe seu Ff, ut ES ad SG, & ex æquo Dd ad Ff ut DE ad SG; hoc est (ob similia triangula PDE, PGS) ut PE ad PS. Q.E.D.
Prop. LXXIX. Theor. XXXIX.
Si superficies ob latitudinem infinite diminutam jamjam evanescens EFfe, convolutione sui circa axem PS, describat solidum Sphæricum concavo-convexum, ad cujus particulas singulas æquales tendant æquales vires centripetæ: dico quod vis, qua solidum illud trahit corpusculum situm in P, est in ratione composita ex ratione solidi & ratione vis qua particula data in loco Ff traheret idem corpusculum.
Nam si primo consideremus vim superficiei Sphæricæ FE, quæ convolutione arcus FE generatur, & linea de ubivis secatur in r; erit superficiei 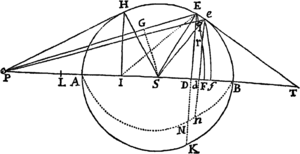 pars annularis, convolutione arcus rE genita, ut lineola Dd, manente Sphæræ radio PE, (uti demonstravit Archimedes in Lib. de Sphæra & Cylindro.) Et hujus vis secundum lineas PE vel Pr undique in superficie conica sitas exercita, ut hæc ipsa superficiei pars annularis; hoc est, ut lineola Dd, vel quod perinde est, ut rectangulum sub dato Sphæræ radio PE & lineola illa Dd: at secundum lineam PS ad centrum S tendentem minor, in ratione PD ad PE, adeoque ut . Dividi jam intelligatur linea DF in particulas innumeras æquales, quæ singulæ nominentur Dd; & superficies FE dividetur in totidem æquales annulos, quorum vires erunt ut summa omnium , hoc est, cum lineolæ omnes Dd sibi invicem æquentur, adeoque pro datis haberi possint, ut summa omnium PD ducta in Dd, id est, ut sive vel ductum in Dd; hoc est, si negligatur data , ut DE quad. Ducatur jam superficies FE in altitudinem Ff; & fiet solidi EFfe vis exercita in corpusculum P ut puta si detur vis quam particula aliqua data Ff in distantia PF exercet in corpusculum P. At si vis illa non detur, fiet vis solidi EFfe ut solidum & vis illa non data conjunctim. Q.E.D.
pars annularis, convolutione arcus rE genita, ut lineola Dd, manente Sphæræ radio PE, (uti demonstravit Archimedes in Lib. de Sphæra & Cylindro.) Et hujus vis secundum lineas PE vel Pr undique in superficie conica sitas exercita, ut hæc ipsa superficiei pars annularis; hoc est, ut lineola Dd, vel quod perinde est, ut rectangulum sub dato Sphæræ radio PE & lineola illa Dd: at secundum lineam PS ad centrum S tendentem minor, in ratione PD ad PE, adeoque ut . Dividi jam intelligatur linea DF in particulas innumeras æquales, quæ singulæ nominentur Dd; & superficies FE dividetur in totidem æquales annulos, quorum vires erunt ut summa omnium , hoc est, cum lineolæ omnes Dd sibi invicem æquentur, adeoque pro datis haberi possint, ut summa omnium PD ducta in Dd, id est, ut sive vel ductum in Dd; hoc est, si negligatur data , ut DE quad. Ducatur jam superficies FE in altitudinem Ff; & fiet solidi EFfe vis exercita in corpusculum P ut puta si detur vis quam particula aliqua data Ff in distantia PF exercet in corpusculum P. At si vis illa non detur, fiet vis solidi EFfe ut solidum & vis illa non data conjunctim. Q.E.D.
Prop. LXXX. Theor. XL.
Si ad Sphæræ alicujus AEB, centro S descriptæ, particulas singulas æquales tendant æquales vires centripetæ, & ad Sphæræ axem AB, in quo corpusculum aliquod P locatur, erigantur de punctis singulis D perpendicula DE, Sphæræ occurentia in E, & in ipsis capiantur longitudines DN, quæ sint ut quantitas & vis quam Sphæræ particula sita in axe ad distantiam PE exercet in corpusculum P conjunctim: dico quod vis tota, qua corpusculum P trahitur versus Sphæram, est ut area comprehensa sub axe Sphæræ AB & linea curva ANB, quam punctum N perpetuo tangit.
Etenim stantibus quæ in Lemmate & Theoremate novissimo constructa sunt, concipe axem Sphæræ AB dividi in particulas innumeras æquales Dd, & Sphæram totam dividi in totidem laminas Sphæricas concavo-convexas EFfe; & erigatur perpendiculum dn. Per Theorema superius, vis qua lamina EFfe trahit corpusculum P est ut & vis particulæ unius ad distantiam PE vel PF exercita conjunctim. Est autem per Lemma novissimum, Dd ad Ff ut PE ad PS, & inde Ff æqualis ; & æquale Dd in , & propterea vis laminæ EFfe est ut Dd in & vis particulæ ad distantiam PF exercita conjunctim, hoc est (ex Hypothesi) ut , seu area evanescens DNnd. Sunt igitur laminarum omnium vires in corpus P exercitæ, ut areæ omnes DNnd, hoc est Sphæræ vis tota ut area tota ABNA. Q.E.D.
Corol. 1. Hinc si vis centripeta ad particulas singulas tendens, eadem semper maneat in omnibus distantiis, & fiat DN ut : erit vis tota qua corpusculum a Sphæra attrahitur, ut area ABNA.
Corol. 2. Si particularum vis centripeta sit reciproce ut distantia corpusculi a se attracti, & fiat DN ut : erit vis qua corpusculum P a Sphæra tota attrahitur ut area ABNA.
Corol. 3. Si particularum vis centripeta sit reciproce ut cubus distantiæ corpusculi a se attracti, & fiat DN ut : erit vis qua corpusculum a tota Sphæra attrahitur ut area ABNA.
Corol. 4. Et universaliter si vis centripeta ad singulas Sphæræ particulas tendens ponatur esse reciproce ut quantitas V, fiat autem DN ut ; erit vis qua corpusculum a Sphæra tota attahitur ut area ABNA.
Prop. LXXXI. Prob. XLI.
Stantibus jam positis, mensuranda est area ABNA.
A puncto P. ducatur recta PH Sphæram tangens in H, & ad axem PAB demissa Normali HI, bisecetur PI in L; & erit (per Prop. 12, Lib. 2. Elem.) PEq. æquale . Est autem SEq. seu SHq. (ob similitudinem triangulorum SPH, SHI) æquale rectangulo PSI. Ergo PEq. æquale est contento 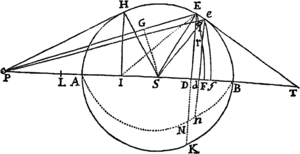 sub , hoc est, sub , id est, sub . Porro DE quad æquale est seu id est, . Nam seu (per Prop. 6. Lib. 2. Elem) æquatur rectangulo ALB. Scribatur itaque pro DEq. & quantitas , quæ secundum Corollarium quartum Propositionis præcedentis est ut longitudo ordinatim applicatæ DN, resolvet sese in tres partes : ubi si pro V scribatur ratio inversa vis centripetæ, & pro PE medium proportionale inter ; tres illæ partes evadent ordinatim applicatæ linearum totidem curvarum, quarum areæ per Methodos vulgatas innotescunt. Q.E.F.
sub , hoc est, sub , id est, sub . Porro DE quad æquale est seu id est, . Nam seu (per Prop. 6. Lib. 2. Elem) æquatur rectangulo ALB. Scribatur itaque pro DEq. & quantitas , quæ secundum Corollarium quartum Propositionis præcedentis est ut longitudo ordinatim applicatæ DN, resolvet sese in tres partes : ubi si pro V scribatur ratio inversa vis centripetæ, & pro PE medium proportionale inter ; tres illæ partes evadent ordinatim applicatæ linearum totidem curvarum, quarum areæ per Methodos vulgatas innotescunt. Q.E.F.
Exempl. 1. Si vis centripeta ad singulas Sphæræ particulas tendens sit reciproce ut distantia; pro V scribe distantiam PE, dein pro PEq., & fiet DN ut Pone DN æqualem duplo ejus : & ordinatæ pars data ducta in longitudinem AB describet aream rectangulam ; & pars indefinita LD ducta normaliter in eandem longitudinem per motum continuum, ea lege ut inter movendum crescendo vel descrescendo æquetur semper longitudini LD, describet aream , id est, aream ; quæ subducta de area priore relinquit aream . Pars autem tertia ducta itidem per motum localem normaliter in eandem longitudinem, describet aream Hyperbolicam; quæ subducta de area relinquet aream quæsitam ABNA. Unde talis emergit Problematis  constructio. Ad puncta, L, A, B erige perpendicula Ll, Aa, Bb, quorum Aa ipsi LB, & Bb ipsi LA æquetur. Asymptotis Ll, LB, per puncta a, b describatur Hyperbola ab. Et acta chorda ba claudet aream aba areæ quæsitæ ABNA æqualem.
constructio. Ad puncta, L, A, B erige perpendicula Ll, Aa, Bb, quorum Aa ipsi LB, & Bb ipsi LA æquetur. Asymptotis Ll, LB, per puncta a, b describatur Hyperbola ab. Et acta chorda ba claudet aream aba areæ quæsitæ ABNA æqualem.
Exempl. 2. Si vis centripeta ad singulas Sphæræ particulas tendens sit reciproce ut cubus distantiæ, vel (quod perinde est) ut cubus ille applicatus ad planum quodvis datum; scribe pro V, dein pro P q.; & fiet DN ut id est (ob continue proportionales PS, AS, SI) ut . Si ducantur hujus partes tres in longitudinem AB, prima generabit aream Hyperbolicam; secunda aream ; tertia aream , id est . De prima subducatur summa secundæ ac tertiæ, &  manebit area quæsita ABNA. Unde talis emergit Problematis constructio. Ad puncta L, A, S, B erige perpendicula Ll, Aa, Ss, Bb, quorum Ss ipsi SI æquetur, perque punctum s Asymptotis Ll, LB describatur Hyperbola asb occurrens perpendiculis Aa, Bb in a & b; & rectangulum
subductum de area Hyperbolica AasbB relinquet aream quæsitam ABNA.
manebit area quæsita ABNA. Unde talis emergit Problematis constructio. Ad puncta L, A, S, B erige perpendicula Ll, Aa, Ss, Bb, quorum Ss ipsi SI æquetur, perque punctum s Asymptotis Ll, LB describatur Hyperbola asb occurrens perpendiculis Aa, Bb in a & b; & rectangulum
subductum de area Hyperbolica AasbB relinquet aream quæsitam ABNA.
Exempl. 3. Si Vis centripeta, ad singulas Sphæræ particulas tendens, decrescit in quadruplicata ratione distantiæ a particulis, scribe pro V, dein pro PE, & fiet DN ut . Cujus tres partes ductæ in longitudinem AB, producunt Areas totidem, viz. . Et hæ post debitam reductionem, subductis posterioribus de priori, evadunt . Igitur vis tota, qua corpusculum P in Sphæræ centrum trahitur, est ut , id est reciproce ut . Q.E.I.
<210>Eadem Methodo determinari potest attractio corpusculi siti intra Sphæram, sed expeditius per Theorema sequens.
Prop. LXXXII. Theor. XLI.
In Sphæra centro S intervallo SA descripta, si capiantur SI, SA, SP continue proportionales: dico quod corpusculi intra Sphæram in loco quovis I attractio est ad attractionem ipsius extra Sphæram in loco P, in ratione composita ex dimidiata ratione distantiarum a centro IS, PS & dimidiata ratione virium centripetarum, in locis illis P & I, ad centrum tendentium.
Ut si vires centripetæ particularum Sphæræ sint reciproce ut distantiæ corpusculi a se attracti; vis, qua corpusculum situm in I trahitur a Sphæra tota, erit ad vim qua trahitur in P, in ratione composita 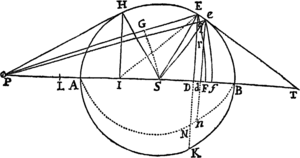 ex dimidiata ratione distantiæ SI ad distantiam SP & ratione dimidiata vis centripetæ in loco I, a particula aliqua in centro oriundæ, ad vim centripetam in loco P ab eadem in centro particula oriundam, id est, ratione dimidiata distantiarum SI, SP ad invicem reciproce. Hæ duæ rationes dimidiatæ componunt rationem æqualitatis, & propterea attractiones in I & P a Sphæra tota factæ æquantur. Simili computo, si vires particularum Sphæræ sunt reciproce in duplicata ratione distantiarum, colligetur quod attractio in I sit ad attractionem in P, ut distantia SP ad Sphæræ semidiametrum SA: Si vires illæ sunt reciproce in triplicata ratione distantiarum, attractiones in I & P erunt ad invicem ut SP quad. ad SA quad.; si in quadruplicata, ut SP cub. ad SA cub. Unde cum attractio in P, in hoc ultimo casu, inventa fuit reciproce ut , attractio in I erit reciproce ut , id est (ob datum SA cub.) reciproce ut PI. Et similis est progressus in infinitum. Theorema vero sic demonstratur.
ex dimidiata ratione distantiæ SI ad distantiam SP & ratione dimidiata vis centripetæ in loco I, a particula aliqua in centro oriundæ, ad vim centripetam in loco P ab eadem in centro particula oriundam, id est, ratione dimidiata distantiarum SI, SP ad invicem reciproce. Hæ duæ rationes dimidiatæ componunt rationem æqualitatis, & propterea attractiones in I & P a Sphæra tota factæ æquantur. Simili computo, si vires particularum Sphæræ sunt reciproce in duplicata ratione distantiarum, colligetur quod attractio in I sit ad attractionem in P, ut distantia SP ad Sphæræ semidiametrum SA: Si vires illæ sunt reciproce in triplicata ratione distantiarum, attractiones in I & P erunt ad invicem ut SP quad. ad SA quad.; si in quadruplicata, ut SP cub. ad SA cub. Unde cum attractio in P, in hoc ultimo casu, inventa fuit reciproce ut , attractio in I erit reciproce ut , id est (ob datum SA cub.) reciproce ut PI. Et similis est progressus in infinitum. Theorema vero sic demonstratur.
Stantibus jam ante constructis, & existente corpore in loco quovis P, ordinatim applicata DN inventa fuit ut . Ergo si agatur IE, ordinata illa ad alium quemvis locum I, mutatis mutandis, evadet ut . Pone vires centripetas, e Sphæræ puncto quovis E manantes, esse ad invicem in distantiis IE, PE, ut ad , (ubi numerus n designet indicem potestatum PE & IE) & ordinatæ illæ fient ut , quarum ratio ad invicem est ut ad . Quoniam ob similia triangula SPE, SEI, fit IE ad PE ut IS ad SE vel SA; pro ratione IE ad PE scribe rationem IS ad SA; & ordinatarum ratio evadet ad . Sed PS ad SA dimidiata est ratio distantiarum PS, SI; & ad dimidiata est ratio virium in distantiis PS, IS. Ergo ordinatæ, & propterea areæ quas ordinatæ describunt, hisque proportionales attractiones, sunt in ratione composita ex dimidiatis illis rationibus. Q.E.D.
<212>Prop. LXXXIII. Prob. XLII.
Invenire vim qua corpusculum in centro Sphæræ locatum ad ejus segmentum quodcunque attrahitur.
Sit P corpus in centro Sphæræ, & RBSD segmentum ejus plano RDS & superficie Sphærica RBS contentum. Superficie Sphærica EFG centro P descripta 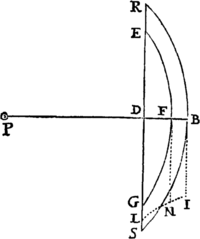 secetur DB in F, ac distinguatur segmentum in partes BREFGS, FEDG. Sit autem superficies illa non pure Mathematica, sed Physica, profunditatem habens quam minimam. Nominetur ista profunditas O, & erit hæc superficies (per demonstata Archimedis) ut . Ponamus præterea vires attractivas particularum Sphæræ esse reciproce ut distantiarum dignitas illa cujus Index est n; & vis qua superficies FE trahit corpus P erit ut . Huic proportionale sit perpendiculum FN ductum in O; & area curvilinea BDLIB, quam ordinatim applicata FN in longitudinem DB per motum continuum ducta describit, erit ut vis tota qua segmentum totum RBSD trahit corpus P. Q.E.I.
secetur DB in F, ac distinguatur segmentum in partes BREFGS, FEDG. Sit autem superficies illa non pure Mathematica, sed Physica, profunditatem habens quam minimam. Nominetur ista profunditas O, & erit hæc superficies (per demonstata Archimedis) ut . Ponamus præterea vires attractivas particularum Sphæræ esse reciproce ut distantiarum dignitas illa cujus Index est n; & vis qua superficies FE trahit corpus P erit ut . Huic proportionale sit perpendiculum FN ductum in O; & area curvilinea BDLIB, quam ordinatim applicata FN in longitudinem DB per motum continuum ducta describit, erit ut vis tota qua segmentum totum RBSD trahit corpus P. Q.E.I.
Prop. LXXXIV. Prob. XLIII.
Invenire vim qua corpusculum, extra centrum Sphæræ in axe segmenti cujusvis locatum, attrahitur ab eodem segmento.
A segmento EBK trahatur corpus P (Vide Fig. Prop. 79. 80. 81.) in ejus axe ADB locatum. Centro P intervallo PE describatur superficies Sphærica EFK, qua distinguatur segmentum in partes duas EBKF & EFKD. Quæratur vis partis prioris per Prop. LXXXI. & vis partis posterioris per Prop. LXXXIII.; & summa virium erit vis segmenti totius EBKD. Q.E.I.
Scholium.
Explicatis attractionibus corporum Sphæricorum, jam pergere liceret ad leges attractionum aliorum quorundam ex particulis attractivis similiter constantium corporum; sed ista particulatim tractare minus ad institutum spectat. Suffecerit Propositiones quasdam generaliores de viribus hujusmodi corporum, deque motibus inde oriundis, ob eorum in rebus Philosophicis aliqualem usum, subjungere.
SECT. XIII.
De Corporum etiam non Sphæricorum viribus attractivis.
Prop. LXXXV. Theor. XLII.
Si corporis attracti, ubi attrahenti contiguum est, attractio longe fortior sit, quam cum vel minimo intervallo separantur ab invicem: vires particularum trahentis, in recessu corporis attracti, decrescunt in ratione plusquam duplicata distantiarum a particulis.
Nam si vires decrescunt in ratione duplicata distantiarum a particulis; attractio versus corpus Sphæricum, propterea quod (per Prop. LXXIV.) sit reciproce ut quadratum distantiæ attracti corporis a centro Sphæræ, haud sensibiliter augebitur ex contactu; atque adhuc minus augebitur ex contactu, si attractio in recessu corporis attracti decrescat in ratione minore. Patet igitur Propositio de Sphæris attractivis. Et par est ratio Orbium Sphæricorum concavorum corpora externa trahentium. Et multo magis res constat in Orbibus corpora interius constituta trahentibus, cum attractiones passim per Orbium cavitates ab attractionibus contrariis (per Prop. LXX.) tollantur, ideoque vel in ipso contactu nullæ sunt. Quod si Sphæris hisce Orbibusque Sphæricis partes quælibet a loco contactus remotæ auferantur, & partes novæ ubivis addantur: mutari possunt figuræ horum corporum attractivorum pro lubitu, nec tamen partes additæ vel subductæ, cum sint a loco contactus remotæ, augebunt notabiliter attractionis excessum qui ex contactu oritur. Constat igitur Propositio de corporibus figurarum omnium. Q.E.D.
Prop. LXXXVI. Theor. XLIII.
Si particularum, ex quibus corpus attractivum componitur, vires in recessu corporis attracti decrescunt in triplicata vel plusquam triplicata ratione distantiarum a particulis: attractio longe fortior erit in contactu, quam cum attrahens & attractum intervallo vel minimo separantur ab invicem.
Nam attractionem in accessu attracti corpusculi ad hujusmodi Sphæram trahentem augeri in infinitum, constat per solutionem Problematis XLI. in Exemplo secundo ac tertio exhibitam. Idem, per Exempla illa & Theorema XLI inter se collata, facile colligitur de attractionibus corporum versus Orbes concavo-convexos, sive corpora attracta collocentur extra Orbes, sive intra in eorum cavitatibus. Sed & addendo vel auferendo his Sphæris & Orbibus ubivis extra locum contactus materiam quamlibet attractivam, eo ut corpora attractiva induant figuram quamvis assignatam, constabit Propositio de corporibus universis. Q.E.D.
<215>Prop. LXXXVII. Theor. XLIV.
Si corpora duo sibi invicem similia & ex materia æqualiter attractiva constantia seorsim attrahant corpuscula sibi ipsis proportionalia & ad se similiter posita: attractiones acceleratrices corpusculorum in corpora tota erunt ut attractiones acceleratrices corpusculorum in eorum particulas totis proportionales & in totis similiter positas.
Nam si corpora distinguantur in particulas, quæ sint totis proportionales & in totis similiter sitæ; erit, ut attractio in particulam quamlibet unius corporis ad attractionem in particulam correspondentem in corpore altero, ita attractiones in particulas singulas primi corporis ad attractiones in alterius particulas singulas correspondentes; & componendo, ita attractio in totum primum corpus ad attractionem in totum secundum. Q.E.D.
Corol. 1. Ergo si vires attractivæ particularum, augendo distantias corpusculorum attractorum, decrescant in ratione dignitatis cujusvis distantiarum: attractiones acceleratrices in corpora tota erunt ut corpora directe & distantiarum dignitates illæ inverse. Ut si vires particularum decrescant in ratione duplicata distantiarum a corpusculis attractis, corpora autem sint ut A cub. & B cub. adeoque tum corporum latera cubica, tum corpusculorum attractorum distantiæ a corporibus, ut A & B: attractiones acceleratrices in corpora erunt ut id est, ut corporum latera illa cubica A & B. Si vires particularum decrescant in ratione triplicata distantiarum a corpusculis attractis; attractiones acceleratrices in corpora tota erunt ut id est aquales. Si vires decrescunt in ratione quadruplicata, attractiones in corpora erunt ut id est reciproce ut latera cubica A & B. Et sic in cæteris.
<216>Corol. 2. Unde vicissim, ex viribus quibus corpora similia trahunt corpuscula ad se similiter posita, colligi potest ratio decrementi virium particularum attractivarum in recessu corpusculi attracti; si modo decrementum illud sit directe vel inverse in ratione aliqua distantiarum.
Prop. LXXXVIII. Theor. XLV.
Si particularum æqualium corporis cujuscunque vires attractivæ sint ut distantiæ locorum a particulis: vis corporis totius tendet ad ipsius centrum gravitatis; & eadem erit cum vi globi ex materia consimili & æquali constantis & centrum habentis in ejus centro gravitatis.
Corporis RSTV particulæ A, B trahant corpusculum aliquod Z viribus quæ, si particulæ æquantur inter se, sint ut distantiæ AZ, BZ; sin particulæ statuantur 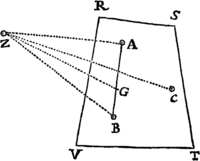 inæquales, sint ut hæ particulæ in distantias suas AZ, BZ respective ductæ. Et exponantur hæ vires per contenta illa . Jungatur AB, & secetur ea in G ut sit AG ad BG ut particula B ad particulam A; & erit G commune centrum gravitatis particularum A & B. Vis per Legum Corol. 2. resolvitur in vires , & vis in vires . Vires autem , ob proportionales A ad B & BG ad AG, æquantur, adeoque, cum dirigantur in partes contrarias, se mutuo destruunt. Restant vires . Tendunt hæ ab Z versus centrum G, & vim componunt; hoc est, vim eandem ac si particulæ attractivæ A & B consisterent in eorum communi gravitatis centro G, globum ibi componentes.
inæquales, sint ut hæ particulæ in distantias suas AZ, BZ respective ductæ. Et exponantur hæ vires per contenta illa . Jungatur AB, & secetur ea in G ut sit AG ad BG ut particula B ad particulam A; & erit G commune centrum gravitatis particularum A & B. Vis per Legum Corol. 2. resolvitur in vires , & vis in vires . Vires autem , ob proportionales A ad B & BG ad AG, æquantur, adeoque, cum dirigantur in partes contrarias, se mutuo destruunt. Restant vires . Tendunt hæ ab Z versus centrum G, & vim componunt; hoc est, vim eandem ac si particulæ attractivæ A & B consisterent in eorum communi gravitatis centro G, globum ibi componentes.
Eodem argumento si adjungatur particula tertia C; & componatur hujus vis cum vi tendente ad centrum G, vis inde oriunda tendet ad commune centrum gravitatis globi illius G & particulæ C; hoc est, ad commune centrum gravitatis trium particularum A, B, C; & eadem erit ac si globus & particula C consisterent in centro illo communi, globum majorem ibi componentes. Et sic pergitur in infinitum. Eadem est igitur vis tota particularum omnium corporis cujuscunque RSTV ac si corpus illud, servato gravitatis centro, figuram globi indueret. Q.E.D.
Corol. Hinc motus corporis attracti Z idem erit ac si corpus attrahens RSTV esset Sphæricum: & propterea si corpus illud attrahens vel quiescat, vel progrediatur uniformiter in directum, corpus attractum movebitur in Ellipsi centrum habente in attrahentis centro gravitatis.
Prop. LXXXIX. Theor. XLVI.
Si corpora sint plura ex particulis æqualibus constantia, quarum vires sunt ut distantiæ locorum a singulis; vis ex omnium viribus composita, qua corpusculum quodcunque trahitur, tendet ad trahentium commune centrum gravitatis, & eadem erit ac si trahentia illa, servato gravitatis centro communi, coirent & in globum formarentur.
Demonstratur eodem modo, atque Propositio superior.
Corol. Ergo motus corporis attracti idem erit ac si corpora trahentia, servato communi gravitatis centro, coirent & in globum formarentur. Ideoque si corporum trahentium commune gravitatis centrum vel quiescit, vel progreditur uniformiter in linea recta, corpus attractum movebitur in Ellipsi, centrum habente in communi illo trahentium centro gravitatis.
<218>Prop. XC. Prob. XLIV.
Si ad singula circuli cujuscunque puncta tendant vires centripetæ decrescentes in quacunque distantiarum ratione: invenire vim qua corpusculum attrahitur ubivis in recta quæ ad planum circuli per centrum ejus perpendicularis consistit.
Centro A intervallo quovis AD, in plano cui recta AP perpendicularis est, describi intelligatur circulus; & invenienda sit vis qua corpus quodvis P in eundem attrahitur. A circuli puncto quovis E ad corpus attractum P agatur recta PE: In recta PA capiatur PF ipsi PE æqualis, 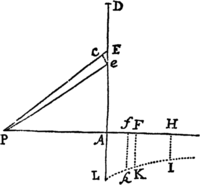 & erigatur Normalis FK, quæ sit ut vis qua punctum E trahit corpusculum P. Sitque IKL curva linea quam punctum K perpetuo tangit. Occurrat eadem circuli plano in L. In PA capiatur PH æqualis PD, & erigatur perpendiculum HI curvæ prædictæ occurrens in I; & erit corpusculi P attractio in circulum ut area AHIL ducta in altitudinem AP. Q.E.I.
& erigatur Normalis FK, quæ sit ut vis qua punctum E trahit corpusculum P. Sitque IKL curva linea quam punctum K perpetuo tangit. Occurrat eadem circuli plano in L. In PA capiatur PH æqualis PD, & erigatur perpendiculum HI curvæ prædictæ occurrens in I; & erit corpusculi P attractio in circulum ut area AHIL ducta in altitudinem AP. Q.E.I.
Etenim in AE capiatur linea quam minima Ee. Jungatur Pe, & in PA capiatur Pf ipsi Pe æqualis. Et quoniam vis, qua annuli punctum quodvis E trahit ad se corpus P, ponitur esse ut FK, & inde vis qua punctum illud trahit corpus P versus A est ut , & vis qua annulus totus trahit corpus P versus A, ut annulus & conjunctim; annulus autem iste est ut rectangulum sub radio AE & latitudine Ee, & hoc rectangulum (ob proportionales PE & AE, Ee & cE) æquatur rectangulo seu ; erit vis qua annulus iste trahit corpus P versus A ut conjunctim, id est, ut contentum , sive ut area FKkf ducta in AP. Et propterea summa virium, quibus annuli omnes in circulo, qui centro A & intervallo AD describitur, trahunt corpus P versus A, est ut area tota AHIKL ducta in AP. Q.E.D.
Corol. 1. Hinc si vires punctorum descrescunt in duplicata distantiarum ratione, hoc est, si sit FK ut , atque adeo area AHIKL ut ; erit attractio corpusculi P in circulum ut , id est, ut .
Corol. 2. Et universaliter, si vires punctorum ad distantias D sint reciproce ut distantiarum dignitas quælibet , hoc est, si sit FK ut , adeoque area AHIKL ut ; erit attractio corpusculi P in circulum ut .
Corol. 3. Et si diameter circuli augeatur in infinitum, & numerus n sit unitate major; attractio corpusculi P in planum totum infinitum erit reciproce ut , propterea quod terminus alter evanescet.
Prop. XCI. Prob. XLV.
Invenire attractionem corpusculi siti in axe solidi, ad cujus puncta singula tendunt vires centripetæ in quacunque distantiarum ratione decrescentes.
<220>In solidum ADEFG trahatur corpusculum P, situm in ejus axe AB. Circulo quolibet RFS ad hunc axem perpendiculari secetur hoc solidum, & in ejus diametro FS, in plano aliquo PALKB per axem transeunte, capiatur (per Prop. XC.) longitudo FK vi qua corpusculum P in circulum illum attrahitur proportionalis. Tangat autem 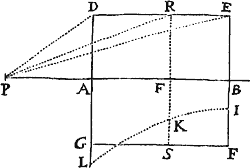 punctum K curvam lineam LKI, planis extimorum circulorum AL & BI occurrentem in A & B; & erit attractio corpusculi P in solidum ut area LABI. Q.E.D.
punctum K curvam lineam LKI, planis extimorum circulorum AL & BI occurrentem in A & B; & erit attractio corpusculi P in solidum ut area LABI. Q.E.D.
Corol. 1. Unde si solidum Cylindrus sit, parallelogrammo ADEB circa axem AB revoluto descriptus, & vires centripetæ in singula ejus puncta tendentes sint reciproce ut quadrata distantiarum a punctis: erit attractio corpusculi P in hunc Cylindrum ut BA−PE+PD. Nam ordinatim applicata FK (per Corol. 1. Prop. XC) erit ut . Hujus pars 1 ducta in longitudinem AB, describit aream ; & pars altera ducta in longitudinem PB, describit aream 1 in (in quod ex curvæ LKI quadratura facile ostendi potest:) & similiter pars eadem ducta in longitudinem PA describit aream 1 in , ductaque in ipsarum PB, PA differentiam AB describit arearum differentiam 1 in auferatur contentum postremum 1 in PE−PD, & restabit area LABI æqualis 1 in AB−PE+PD. Ergo vis huic areæ proportionalis est ut AB−PE+PD.
Corol. 2. Hinc etiam vis innotescit qua Sphærois AGBCD attrahit corpus quodvis P, exterius in axe suo AB situm. Sit NKRM Sectio Conica cujus ordinatim applicata ER, ipsi PE perpendicularis, æquetur semper longitudini PD, quæ ducitur ad punctum illud D, in quo applicata ista Sphæroidem secat. A Sphæroidis verticibus A, B ad ejus axem AB erigantur perpendicula AK, BM ipsis 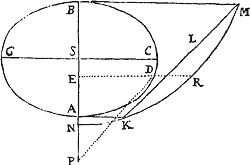 AP, BP æqualia respective, & propterea Sectioni Conicæ occurrentia in K & M; & jungantur KM auferens ab eadem segmentum KMRK. Sit autem Sphæroidis centrum S & semidiameter maxima SC: & vis qua Sphærois trahit corpus P erit at vim qua Sphæra, diametro AB descripta, trahit idem corpus, ut ad . Et eodem computando fundamento invenire licet vires segmentorum Sphæroidis.
AP, BP æqualia respective, & propterea Sectioni Conicæ occurrentia in K & M; & jungantur KM auferens ab eadem segmentum KMRK. Sit autem Sphæroidis centrum S & semidiameter maxima SC: & vis qua Sphærois trahit corpus P erit at vim qua Sphæra, diametro AB descripta, trahit idem corpus, ut ad . Et eodem computando fundamento invenire licet vires segmentorum Sphæroidis.
Corol. 3. Quod si corpusculum intra Sphæroidem in data quavis ejusdem diametro collocetur; attractio 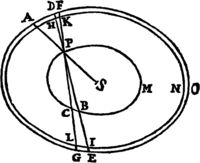 erit ut ipsius distantia a centro. Id quo facilius colligetur hoc argumento. Sit AGOF Sphærois attrahens, S centrum ejus & P corpus attractum. Per corpus illud P agantur tum semidiameter SPA, tum rectæ duæ quævis DE, FG Sphæroidi hinc inde occurrentes in D & E, F & G: Sintque PCM, HLN superficies Sphæroidum duarum interiorum, exteriori similium & concentricarum, quarum prior transeat per corpus P & secet rectas DE & FG in B & C, posterior secet easdem rectas in H, I & K, L. Habeant autem Sphæroides omnes axem communem, & erunt rectarum partes hinc inde interceptæ DP & BE, FP & CG, DH & IE, FK & LG sibi mutuo æquales; propterea quod rectæ DE, PB & HI bisecantur in eodem puncto, ut & rectæ FG, PC & KL. Concipe jam DPF, EPG designare Conos oppositos, angulis verticalibus DPF, EPG infinite parvis descriptos, & lineas etiam DH, EI infinite parvas esse; & Conorum particulæ Sphæroidum superficiebus abscissæ DHKF, GLIE, ob æqualitatem linearum DH, EI, erunt ad invicem ut
erit ut ipsius distantia a centro. Id quo facilius colligetur hoc argumento. Sit AGOF Sphærois attrahens, S centrum ejus & P corpus attractum. Per corpus illud P agantur tum semidiameter SPA, tum rectæ duæ quævis DE, FG Sphæroidi hinc inde occurrentes in D & E, F & G: Sintque PCM, HLN superficies Sphæroidum duarum interiorum, exteriori similium & concentricarum, quarum prior transeat per corpus P & secet rectas DE & FG in B & C, posterior secet easdem rectas in H, I & K, L. Habeant autem Sphæroides omnes axem communem, & erunt rectarum partes hinc inde interceptæ DP & BE, FP & CG, DH & IE, FK & LG sibi mutuo æquales; propterea quod rectæ DE, PB & HI bisecantur in eodem puncto, ut & rectæ FG, PC & KL. Concipe jam DPF, EPG designare Conos oppositos, angulis verticalibus DPF, EPG infinite parvis descriptos, & lineas etiam DH, EI infinite parvas esse; & Conorum particulæ Sphæroidum superficiebus abscissæ DHKF, GLIE, ob æqualitatem linearum DH, EI, erunt ad invicem ut 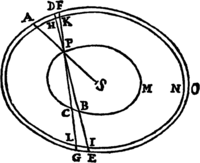 quadrata distantiarum suarum a corpusculo P, & propterea corpusculum illud æqualiter trahent. Et pariratione, si superficiebus Sphæroidum innumerarum similium concentricarum & axem communem habentium dividantur spatia DPF, EGCB in particulas, hæ omnes utrinque æqualiter trahent corpus P in partes contrarias. Æquales igitur sunt vires coni DPF & segmenti Conici EGCB, & per contrarietatem se mutuo destruunt. Et par est ratio virium materiæ omnis extra Sphæroidem intimam PCBM. Trahitur igitur corpus P a sola Sphæroide intima PCBM, & propterea (per Corol. 3. Prop. LXXII.) attractio ejus est ad vim, qua corpus A trahitur a Sphæroide tota AGOD, ut distantia PS ad distantiam AS. Q.E.I.
quadrata distantiarum suarum a corpusculo P, & propterea corpusculum illud æqualiter trahent. Et pariratione, si superficiebus Sphæroidum innumerarum similium concentricarum & axem communem habentium dividantur spatia DPF, EGCB in particulas, hæ omnes utrinque æqualiter trahent corpus P in partes contrarias. Æquales igitur sunt vires coni DPF & segmenti Conici EGCB, & per contrarietatem se mutuo destruunt. Et par est ratio virium materiæ omnis extra Sphæroidem intimam PCBM. Trahitur igitur corpus P a sola Sphæroide intima PCBM, & propterea (per Corol. 3. Prop. LXXII.) attractio ejus est ad vim, qua corpus A trahitur a Sphæroide tota AGOD, ut distantia PS ad distantiam AS. Q.E.I.
Prop. XCII. Prob. XLVI.
Dato corpore attractivo, invenire rationem decrementi virium centripetarum in ejus puncta singula tendentium.
E corpore dato formanda est Sphæra vel Cylindrus aliave figura regularis, cujus lex attractionis, cuivis decrementi rationi congruens (per Prop. LXXX. LXXXI. & XCI.) inveniri potest. Dein factis experimentis invenienda est vis attractionis in diversis distantiis, & lex attractionis in totum inde patefacta dabit rationem decrementi virium partium singularum, quam invenire oportuit.
Prop. XCIII. Theor. XLVII.
Si solidum ex una parte planum, ex reliquis autem partibus infinitum, constet ex particulis æqualibus æqualiter attractivis, quarum vires in recessu a solido decrescunt in ratione potestatis cujusvis distantiarum plusquam quadraticæ, & vi solidi totius corpusculum ad utramvis plani partem constitutum trahatur: dico quod solidi vis illa attractiva, in recessu ab ejus superficie plana, decrescet in ratione potestatis, cujus latus est distantia corpusculi a plano, & Index ternario minor quam Index potestatis distantiarum.
Cas. 1. Sit LGl planum quo Solidum terminatur. Jaceat autem solidum ex parte plani hujus versus I, inque plana innumera mHM, nIN &c. ipsi GL 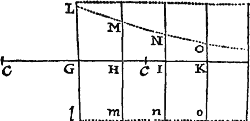 parallela resolvatur. Et primo collocetur corpus attractum C extra solidum. Agatur autem CGHI planis illis innumeris perpendicularis, & decrescant vires attractivæ punctorum solidi in ratione potestatis distantiarum, cujus index sit numerus n ternario non minor. Ergo (per Corol. 3. Prop. XC) vis qua planum quodvis mHM trahit punctum C est reciproce ut . In plano mHM capiatur longitudo HM ipsi reciproce proportionalis, & erit vis illa ut HM. Similiter in planis singulis lGL, nIN, oKO &c, capiantur longitudines GL, IN, KO &c. ipsis . reciproce proportionales; & vires planorum eorundem erunt ut longitudines captæ, adeoque summa virium ut summa longitudinum, hoc est, vis solidi totius ut area GLOK in infinitum versus OK producta. Sed area illa per notas quadraturarum methodos est reciproce ut , & propterea vis solidi totius est reciproce ut Q.E.D.
parallela resolvatur. Et primo collocetur corpus attractum C extra solidum. Agatur autem CGHI planis illis innumeris perpendicularis, & decrescant vires attractivæ punctorum solidi in ratione potestatis distantiarum, cujus index sit numerus n ternario non minor. Ergo (per Corol. 3. Prop. XC) vis qua planum quodvis mHM trahit punctum C est reciproce ut . In plano mHM capiatur longitudo HM ipsi reciproce proportionalis, & erit vis illa ut HM. Similiter in planis singulis lGL, nIN, oKO &c, capiantur longitudines GL, IN, KO &c. ipsis . reciproce proportionales; & vires planorum eorundem erunt ut longitudines captæ, adeoque summa virium ut summa longitudinum, hoc est, vis solidi totius ut area GLOK in infinitum versus OK producta. Sed area illa per notas quadraturarum methodos est reciproce ut , & propterea vis solidi totius est reciproce ut Q.E.D.
Cas. 2. Collocetur jam corpusculum C ex parte plani lGL intra solidum, & capiatur 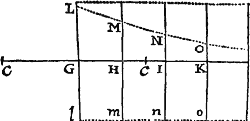 distantia CK æqualis distantiæ CG. Et solidi pars LGloKO, planis parallelis lGL, oKO terminata, corpusculum C in medio situm nullam in partem trahet, contrariis oppositorum punctorum actionibus se mutuo per æqualitatem tollentibus. Proinde corpusculum C sola vi solidi ultra planum OK siti trahitur. Hæc autem vis (per Casum primum) est reciproce ut , hoc est (ob æquales CG, CK) reciproce ut . Q.E.D.
distantia CK æqualis distantiæ CG. Et solidi pars LGloKO, planis parallelis lGL, oKO terminata, corpusculum C in medio situm nullam in partem trahet, contrariis oppositorum punctorum actionibus se mutuo per æqualitatem tollentibus. Proinde corpusculum C sola vi solidi ultra planum OK siti trahitur. Hæc autem vis (per Casum primum) est reciproce ut , hoc est (ob æquales CG, CK) reciproce ut . Q.E.D.
Corol. 1. Hinc si solidum LGIN planis duobus infinitis parallelis LG, IN utrinque terminetur; innotescit ejus vis attractiva, subducendo de vi attractiva solidi totius infiniti LGKO vim attractivam partis ulterioris NIKO, in infinitum versus KO productæ.
Corol. 2. Si solidi hujus infiniti pars ulterior, quando attractio ejus collata cum attractione partis citerioris nullius pene est momenti, rejiciatur: attractio partis illius citerioris augendo distantiam decrescet quam proxime in ratione potestatis .
Corol. 3. Et hinc si corpus quodvis finitum & ex una parte planum trahat corpusculum e regione medii illius plani, & distantia inter corpusculum & planum collata cum dimensionibus corporis attrahentis perexigua sit, constet autem corpus attrahens ex particulis homogeneis, quarum vires attractivæ decrescunt in ratione potestatis cujusvis plusquam quadruplicatæ distantiarum; vis attractiva corporis totius decrescet quamproxime in ratione potestatis, cujus latus sit distantia illa perexigua, & Index ternario minor quam Index potestatis prioris. De corpore exparticulis constante, quarum vires attractivæ decrescunt in ratione potestatis triplicatæ distantiarum, assertio non valet, propterea quod, in hoc casu, attractio partis illius ulterioris corporis infiniti in Corollario secundo, semper est infinite major quam attractio partis citerioris.
Scholium.
Si corpus aliquod perpendiculariter versus planum datum trahatur, & ex data lege attractionis quæratur motus corporis: Solvetur Problema quærendo (per Prop. XXVII.) motum corporis recta descendentis ad hoc planum, & (per Legum Corol. 2.) componendo motum istum cum uniformi motu, secundum lineas eidem plano parallelas facto. Et contra, si quæratur Lex attractionis in planum secundum lineas perpendiculares factæ, ea conditione ut corpus attractum in data quacunque curva linea moveatur, solvetur Problema operando ad exemplum Problematis tertii.
Operationes autem contrahi solent resolvendo ordinatim applicatas in series convergentes. Ut si ad basem A in angulo quovis dato ordinatim applicetur longitudo B, quæ sit ut basis dignitas quælibet ; & quæratur vis qua corpus, secundum positionem ordinatim applicatæ, vel in basem attractum vel a basi fugatum, moveri possit in curva linea quam ordinatim applicata termino suo superiore semper attingit; Suppono basem augeri parte quam minima O, & ordinatim applicatam resolvo in Seriem infinitam atque hujus termino in quo O duarum est dimensionum, id est termino vim proportionalem esse suppono. Est igitur vis quæsita ut , vel quod perinde est, ut . Ut si ordinatim applicata Parabolam attingat, existente : fiet vis ut data , adeoque dabitur. Data igitur vi corpus movebitur in Parabola, quemadmodum Galilæus demonstravit. Quod si ordinatim applicata Hyperbolam attingat, existente ; feit vis ut seu : adeoque vi, quæ sit reciproce ut cubus ordinatim applicatæ, corpus movebitur in Hyperbola. Sed missis hujusmodi Propositionibus, pergo ad alias quasdam de motu, quas nondum attigi.
SECT. XIV.
De motu corporum minimorum, quæ viribus centripetis ad singulas magni alicujus corporis partes tendentibus agitantur.
Prop. XCIV. Theor. XLVIII.
Si media duo similaria, spatio planis parallelis utrinque terminato, distinguantur ab invicem, & corpus in transitu per hoc spatium attrahatur vel impellatur perpendiculariter versus medium alterutrum, neque ulla alia vi agitetur vel impediatur; Sit autem attractio, in æqualibus ab utroque plano distantiis ad eandem ipsius partem captis, ubique eadem: dico quod sinus incidentiæ in planum alterutrum erit ad sinum emergentiæ ex plano altero in ratione data.
Cas. 1. Sunto Aa, Bb plana duo parallela. Incidat corpus in planum prius Aa secundam 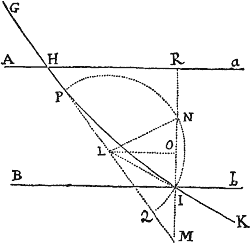 lineam GH, ac toto suo per spatium intermedium transitu attrahatur vel impellatur versus medium incidentiæ, eaque actione describat lineam curvam HI, & emergat secundum lineam IK. Ad planum emergentiæ Bb erigatur perpendiculum IM, occurrens tum lineæ incidentiæ GH productæ in M, tum plano incidentiæ Aa in R; & linea emergentiæ KI producta occurrat HM in L. Centro L intervallo LI describatur circulus, secans tam HM in P & Q, quam MI productam in N; & primo si attractio vel impulsus ponatur uniformis, erit (ex demonstatis Galilæi) curva HI Parabola, cujus hæc est proprietas, ut rectangulum sub dato latere recto & linea IM æquale sit HM quadrato; sed & linea HM bisecabitur in L. Unde si ad MI demittatur
lineam GH, ac toto suo per spatium intermedium transitu attrahatur vel impellatur versus medium incidentiæ, eaque actione describat lineam curvam HI, & emergat secundum lineam IK. Ad planum emergentiæ Bb erigatur perpendiculum IM, occurrens tum lineæ incidentiæ GH productæ in M, tum plano incidentiæ Aa in R; & linea emergentiæ KI producta occurrat HM in L. Centro L intervallo LI describatur circulus, secans tam HM in P & Q, quam MI productam in N; & primo si attractio vel impulsus ponatur uniformis, erit (ex demonstatis Galilæi) curva HI Parabola, cujus hæc est proprietas, ut rectangulum sub dato latere recto & linea IM æquale sit HM quadrato; sed & linea HM bisecabitur in L. Unde si ad MI demittatur 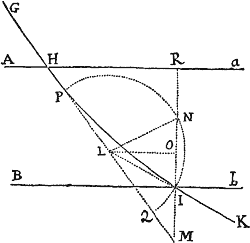 perpendiculum LO, æquales erunt MO, OR; & additis æqualibus IO, ON, fient totæ æquales MN, IR. Proinde cum IR detur, datur etiam MN, estque rectangulum NMI ad rectangulum sub latere recto & IM, hoc est, ad HMq., in data ratione. Sed rectangulum NMI æquale est rectangulo PMQ, id est, differentiæ quadratorum MLq. & PLq. seu LIq.; & HMq. datam rationem habet ad sui ipsius quartam partem LMq.: ergo datur ratio MLq.−LIq. ad MLq., & divisim, ratio LIq. ad MLq., & ratio dimidiata LI ad ML. Sed in omni triangulo LMI, sinus angulorum sunt proportionales lateribus oppositis. Ergo datur ratio sinus anguli incidentiæ LMR ad sinum anguli emergentiæ LIR. Q.E.D.
perpendiculum LO, æquales erunt MO, OR; & additis æqualibus IO, ON, fient totæ æquales MN, IR. Proinde cum IR detur, datur etiam MN, estque rectangulum NMI ad rectangulum sub latere recto & IM, hoc est, ad HMq., in data ratione. Sed rectangulum NMI æquale est rectangulo PMQ, id est, differentiæ quadratorum MLq. & PLq. seu LIq.; & HMq. datam rationem habet ad sui ipsius quartam partem LMq.: ergo datur ratio MLq.−LIq. ad MLq., & divisim, ratio LIq. ad MLq., & ratio dimidiata LI ad ML. Sed in omni triangulo LMI, sinus angulorum sunt proportionales lateribus oppositis. Ergo datur ratio sinus anguli incidentiæ LMR ad sinum anguli emergentiæ LIR. Q.E.D.
Cas. 2. Transeat jam corpus successive per spatia plura parallelis planis terminata, AabB, BbcC &c. agitetur vi quæ sit in singulis separatim uniformis, at in diversis diversa; & per jam demonstrata, sinus incidentiæ in planum primum Aa erit ad sinum emergentiæ ex plano secundo Bb, in data ratione; & hic sinus, qui est sinus incidentiæ in planum secundum Bb, erit ad sinum emergentiæ ex plano tertio Cc, in data ratione; & hic sinus ad sinum emergentiæ ex plano quarto Dd, in data ratione; & sic in infinitum: & ex æquo sinus incidentiæ in planum primum ad sinum emergentiæ ex plano ultimo in data ratione. Minuatur jam planorum intervalla 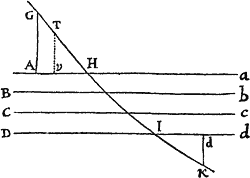 & augeatur numerus in infinitum, eo ut attractionis vel impulsus actio secundum legem quamcunque assignatam continua reddatur; & ratio sinus incidentiæ in planum primum ad sinum emergentiæ ex plano ultimo, semper data existens, etiamnum dabitur. Q.E.D.
& augeatur numerus in infinitum, eo ut attractionis vel impulsus actio secundum legem quamcunque assignatam continua reddatur; & ratio sinus incidentiæ in planum primum ad sinum emergentiæ ex plano ultimo, semper data existens, etiamnum dabitur. Q.E.D.
Prop. XCV. Theor. XLIX.
Iisdem positis; dico quod velocitas corporis ante incidentiam est ad ejus velocitatem post emergentiam, ut sinus emergentiæ ad sinum incidentiæ.
Capiantur AH, Id æquales, & erigantur perpendicula AG, dK occurrentia lineis incidentiæ & emergentiæ GH, IK, in G & K. In GH capiatur TH æqualis IK, & ad planum Aa demittatur normaliter Tv. Et per Legum Corol. 2. distinguatur motus corporis in duos, unum planis Aa, Bb, Cc &c. perpendicularem, alterum iisdem parallelum. Vis attractionis vel impulsus agendo secundum lineas perpendiculares nil mutat motum secundum parallelas, & propterea corpus hoc motu conficiet æqualibus temporibus æqualia illa secundum parallelas intervalla, quæ sunt inter lineam AG & punctum H, interque punctum I & lineam dK; hoc est, æqualibus temporibus describet lineas GH, IK. Proinde velocitas ante incidentiam est ad velocitatem post emergentiam, ut GH ad IK vel TH, id est, ut AH vel Id ad vH, hoc est (respectu radii TH vel IK) ut sinus emergentiæ ad sinum incidentiæ. Q.E.D.
Prop. XCVI. Theor. L.
Iisdem positis & quod motus ante incidentiam velocior sit quam postea: dico quod corpus, inclinando lineam incidentiæ, reflectetur tandem, & angulus reflexionis fiet æqualis angulo incidentiæ.
Nam concipe corpus inter plana parallela Aa, Bb, Cc &c. describere arcus Parabolicos, ut supra; sintque arcus illi HP, PQ, QR, &c. Et sit ea lineæ incidentiæ GH obliquitas ad planum primum Aa, ut sinus incidentiæ sit ad radium circuli, cujus est sinus, in ea ratione quam habet idem sinus incidentiæ ad sinum emergentiæ ex plano Dd, in spatium DdeE: & ob sinum emergentiæ jam factum æqualem radio, angulus emergentiæ erit rectus, adeoque linea emergentiæ 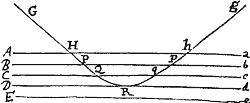 coincidet cum plano Dd. Perveniat corpus ad hoc planum in puncto R; & quoniam linea emergentiæ coincidit cum eodem plano, perspicuum est quod corpus non potest ultra pergere versus planum Ee. Sed nec potest idem pergere in linea emergentiæ Rd, propterea quod perpetuo attrahitur vel impellitur versus medium incidentiæ. Revertetur itaque inter plana Cc, Dd describendo arcum Parabolæ QRq, cujus vertex principalis (juxta demonstrata Galilæi) est in R; secabit planum Cc in eodem angulo in q, ac prius in Q; dein pergendo in arcubus parabolicis qp, ph &c. arcubus prioribus QP, PH similibus & æqualibus, secabit reliqua plana in iisdem angulis in p, h &c. ac prius in P, H &c. emergetque tandem eadem obliquitate in h, qua incidit in H. Concipe jam plaorum Aa, Bb, Cc, Dd, Ee intervalla in infinitum minui & numerum augeri, eo ut actio attractionis vel impulsus secundum legem quamcunque assignatam continua reddatur; & angulus emergentiæ semper angulo incidentiæ æqualis existens, eidem etiamnum manebit æqualis. Q.E.D.
coincidet cum plano Dd. Perveniat corpus ad hoc planum in puncto R; & quoniam linea emergentiæ coincidit cum eodem plano, perspicuum est quod corpus non potest ultra pergere versus planum Ee. Sed nec potest idem pergere in linea emergentiæ Rd, propterea quod perpetuo attrahitur vel impellitur versus medium incidentiæ. Revertetur itaque inter plana Cc, Dd describendo arcum Parabolæ QRq, cujus vertex principalis (juxta demonstrata Galilæi) est in R; secabit planum Cc in eodem angulo in q, ac prius in Q; dein pergendo in arcubus parabolicis qp, ph &c. arcubus prioribus QP, PH similibus & æqualibus, secabit reliqua plana in iisdem angulis in p, h &c. ac prius in P, H &c. emergetque tandem eadem obliquitate in h, qua incidit in H. Concipe jam plaorum Aa, Bb, Cc, Dd, Ee intervalla in infinitum minui & numerum augeri, eo ut actio attractionis vel impulsus secundum legem quamcunque assignatam continua reddatur; & angulus emergentiæ semper angulo incidentiæ æqualis existens, eidem etiamnum manebit æqualis. Q.E.D.
Scholium.
Harum attractionum haud multum dissimiles sunt Lucis reflexiones & refractiones, factæ secundum datam Secantium rationem, ut invenit Snellius, & per consequens secundum datam Sinuum rationem, ut exposuit Cartesius. Namque Lucem successive propagari & spatio quasi decem minutorum primorum a Sole ad Terram venire, jam constat per Phænomena Satellitum Iovis, Observationibus diversorum Astronomorum confirmata. Radii autem in aere existentes (ubi dudum Grimaldus, luce per foramen in tenebrosum cubiculum admissa, invenit, & ipse quoque expertus sum) in transitu suo prope corporum vel opacorum vel perspicuorum angulos (quales sunt nummorum 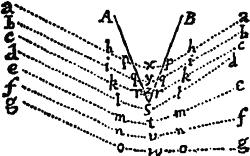 ex auro, argento & ære cusorum termini rectanguli circulares, & cultrorum, lapidum aut fractorum vitrorum acies) incurvantur circum corpora, quasi attracti in eadem; & ex his radiis, qui in transitu illo propius accedunt ad corpora incurvantur magis, quasi magis attracti, ut ipse etiam diligenter observavi. In figura designat s aciem cultri vel cunei cujusvis AsB; & gowog, fnvnf, emtme, dlsld sunt radii, arcubus owo, nvn, mtm, lsl versus cultrum incurvati; idque magis vel minus pro distantia eorum a cultro. Cum autem talis incurvatio radiorum fiat in aere extra cultrum, debebunt etiam radii, qui incidunt in cultrum, prius incurvari in aere quam cultrum attingunt. Et par est ratio incidentium in vitrum. Fit igitur refractio, non in puncto incidentiæ, sed paulatim per continuam incurvationem radiorum, factam partim in aere antequam attingunt vitrum, partim (ni fallor) in vitro, postquam illud ingressi sunt: uti in radiis ckzkc, biyib, ahxha incidentibus ad r, q, p, & inter k & z,
ex auro, argento & ære cusorum termini rectanguli circulares, & cultrorum, lapidum aut fractorum vitrorum acies) incurvantur circum corpora, quasi attracti in eadem; & ex his radiis, qui in transitu illo propius accedunt ad corpora incurvantur magis, quasi magis attracti, ut ipse etiam diligenter observavi. In figura designat s aciem cultri vel cunei cujusvis AsB; & gowog, fnvnf, emtme, dlsld sunt radii, arcubus owo, nvn, mtm, lsl versus cultrum incurvati; idque magis vel minus pro distantia eorum a cultro. Cum autem talis incurvatio radiorum fiat in aere extra cultrum, debebunt etiam radii, qui incidunt in cultrum, prius incurvari in aere quam cultrum attingunt. Et par est ratio incidentium in vitrum. Fit igitur refractio, non in puncto incidentiæ, sed paulatim per continuam incurvationem radiorum, factam partim in aere antequam attingunt vitrum, partim (ni fallor) in vitro, postquam illud ingressi sunt: uti in radiis ckzkc, biyib, ahxha incidentibus ad r, q, p, & inter k & z, 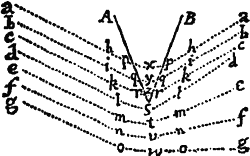 i & y, h & x incurvatis, delineatum est. Igitur ob analogiam quæ est inter propagationem radiorum lucis & progressum corporum, visum est Propositiones sequentes in usus opticos subjungere; interea de natura radiorum (utrum sint corpora necne) nihil omnino disputans, sed trajectorias corporum trajectoriis radiorum persimiles solummodo determinans.
i & y, h & x incurvatis, delineatum est. Igitur ob analogiam quæ est inter propagationem radiorum lucis & progressum corporum, visum est Propositiones sequentes in usus opticos subjungere; interea de natura radiorum (utrum sint corpora necne) nihil omnino disputans, sed trajectorias corporum trajectoriis radiorum persimiles solummodo determinans.
Prop. XCVII. Prob. XLVII.
Posito quod sinus incidentiæ in superficiem aliquam sit ad sinum emergentiæ in data ratione, quodque incurvatio viæ corporum juxta superficiem illam fiat in spatio brevissimo, quod ut punctum considerari possit; determinare superficiem quæ corpuscula omnia de loco dato successive manantia convergere faciat ad alium locum datum.
Sit A locus a quo corpuscula divergunt; B locus in quem convergere debent; CDE curva linea quæ circa axem AB revoluta describat superficiem quæsitam; D, E curvæ illius puncta duo quævis; & EF, EG perpendicula in corporis vias AD, DB demissa. Accedat punctum D ad punctum E; & lineæ DF qua AD augetur, ad lineam DG qua DB diminuitur, ratio ultima erit eadem quæ sinus incidentiæ ad sinum emergentiæ. Datur ergo ratio incrementi lineæ AD ad decrementum lineæ DB; & propterea si in axe AB sumatur ubivis punctum C, per quod curva CDE transire debet, & capiatur ipsius AC incrementum CM, ad ipsius BC decrementum CN in data ratione; centrisque A, B, & intervallis AM, BN describantur circuli duo se mutuo secantes in D: punctum illud D tanget curvam quæsitam CDE, eandemque ubivis tangendo determinabit. Q.E.I.
Corol. 1. Faciendo autem ut punctum A vel B nunc abeat in infinitum, nunc migret ad 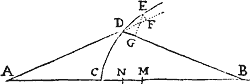 alteras partes puncti C, habebuntur figuræ illæ omnes quas Cartesius in Optica & Geometria ad refractiones exposuit. Quarum inventionem cum Cartesius maximi fecerit & studiose celaverit, visum fuit hic propositione exponere.
alteras partes puncti C, habebuntur figuræ illæ omnes quas Cartesius in Optica & Geometria ad refractiones exposuit. Quarum inventionem cum Cartesius maximi fecerit & studiose celaverit, visum fuit hic propositione exponere.
Corol. 2. Si corpus in superficiem quamvis CD, secundum lineam rectam AD lege quavis ductam incidens, emergat secundum aliam quamvis rectam 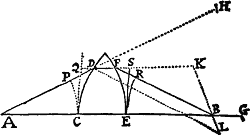 DK, & a puncto C duci intelligantur lineæ curvæ CP, CQ ipsis AD, DK semper perpendiculares: erunt incrementa linearum PD, QD, atque adeo lineæ ipsæ PD, QD, incrementis istis genitæ, ut sinus incidentiæ & emergentiæ ad invicem: & contra.
DK, & a puncto C duci intelligantur lineæ curvæ CP, CQ ipsis AD, DK semper perpendiculares: erunt incrementa linearum PD, QD, atque adeo lineæ ipsæ PD, QD, incrementis istis genitæ, ut sinus incidentiæ & emergentiæ ad invicem: & contra.
Prop. XCVIII. Prob. XLVIII.
Iisdem positis, & circa axem AB descripta superficie quacunque attractiva CD, regulari vel irregulari, per quam corpora de loco dato A exeuntia transire debent: invenire superficiem secundam attractivam EF, quæ corpora illa ad locum datum B convergere faciat.
Juncta AB secet superficiem primam in C & secundam in E, puncto D utcunque assumpto. Et posito sinu incidentiæ in superficiem primam ad sinum emergentiæ ex eadem, & sinu emergentiæ e superficie secunda ad sinum incidentiæ in eandem, ut quantitas aliqua data M ad aliam datam N; produc tum AB ad G ut sit BG ad CE ut M−N ad N, tum AD ad H ut sit AH æqualis AG, tum etiam DF ad K ut sit DK ad DH ut N ad M. Junge KB, & centro D intervallo DH describe circulum occurrentem KB productæ in L, ipsique DL parallelam age BF: & punctum F tanget lineam EF, quæ circa axem AB revoluta describet superficiem quæsitam. Q.E.F.
Nam concipe lineas CP, CQ ipsis AD, DF respective, & lineas ER, ES ipsis FB, FD ubique perpendiculares esse, adeoque QS ipsi CE semper æqualem; & erit (per Corol. 2. Prop. XCVII.) PD ad QD ut 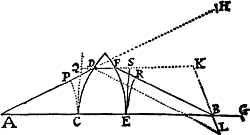 M ad N, adeoque ut DL ad DK vel FB ad FK; & divisim ut DL−FB seu PH−PD−FB ad FD seu FQ−QD; & composite ut HP−FB ad FQ, id est (ob æquales HP & CG, QS & CE) CE+BG−FR ad CE−FS. Verum (ob proportionales BG ad CE & M−N ad N) est etiam CE+BG ad CE ut M ad N: adeoque divisim FR ad FS ut M ad N, & propterea per Corol. 2. Prop. XCVII. superficies EF cogit corpus in se secundum lineam DF incidens pergere in linea FR, ad locum B. Q.E.D.
M ad N, adeoque ut DL ad DK vel FB ad FK; & divisim ut DL−FB seu PH−PD−FB ad FD seu FQ−QD; & composite ut HP−FB ad FQ, id est (ob æquales HP & CG, QS & CE) CE+BG−FR ad CE−FS. Verum (ob proportionales BG ad CE & M−N ad N) est etiam CE+BG ad CE ut M ad N: adeoque divisim FR ad FS ut M ad N, & propterea per Corol. 2. Prop. XCVII. superficies EF cogit corpus in se secundum lineam DF incidens pergere in linea FR, ad locum B. Q.E.D.
Scholium.
Eadem methodo pergere liceret ad superficies tres vel plures. Ad usus autem Opticos maxime accommodatæ sunt figuræ Sphæricæ. Si Perspicillorum vitra Objectiva ex vitris duobus Sphærice figuratis & Aquam inter se claudentibus conflentur, fieri potest ut a refractionibus aquæ errores refractionum, quæ fiunt in vitrorum superficiebus extremis, satis accurate corrigantur. Talia autem vitra Objectiva vitris Ellipticis & Hyperbolicis præferenda sunt, non solum quod facilius & accuratius formari possint, sed etiam quod penicillos radiorum extra axem vitri sitos accuratius refringant. Verum tamen diversa diversorum radiorum refrangibilitas impedimento est, quo minus Optica per figuras vel Sphæricas vel alias quascunque perfici possit. Nisi corrigi possint errores illinc oriundi, labor omnis in cæteris corrigendis imperite collocabitur.
