A Course of Lectures in Natural and Experimental Philosophy, Geography and Astronomy
A
COURSE of LECTURES
IN
NATURAL and EXPERIMENTAL
PHILOSOPHY,
GEOGRAPHY and ASTRONOMY:
IN WHICH THE
Properties, Affections, and Phænomena
of NATURAL BODIES, hitherto discover'd,
Are exhibited and explain'd on the
Principles of the Newtonian Philosophy,
Under the following HEADS, viz.
PHYSICS; or the Doctrine of Matter, and its essential Properties.
MECHANICS; of the Doctrine of Motion, and all Kinds of Forces and Machines.
HYDROSTATICS; or the Nature and Laws of Fluids explained.
HYDRAULICS; or the Theory of the Motion of Fluids, and of all Kinds of Water-Engines.
PNEUMATICS; or the Nature and various Properties of the Air and Atmosphere.
PHONICS; or the Theory of the Winds, Sounds, Musical Strings, Notes, &c.
LIGHT and COLOURS explain'd, according to the Newtonian Theory.
OPTICS; or the Science of Vision, and Theory of all Kinds of Optical Glasses and Instruments.
ASTRONOMY; or the Solar System of the Planets and Comets, and Use of the Celestial Globe, explain'd.
GEOGRAPHY; or the Theory of the Earth, and Use of the Terrestrial Globe, explain'd.
The Whole Confirmed by Experiments, and Illustrated with Copper-Plates.
To which is added,
An APPENDIX, explaining all the Characters, Phrases, and difficult Words, which occur in
these Lectures, and other Treatises of this Kind.
By BENJAMIN MARTIN.
Quae toties animos veterum torsire Sephorum,
Quaeque Scholas frustra rauco certaminie vexant,
Olvia conspicimus, nubem pellente Mathesi.
Halley in Newtoni Princip.
READING
Printed and Sold by J. Newbery and C. Micklewright, in the Market-Place: Also by Mess. Ware, Birt, Astley, Austen, Robinson, Dodsley, and Needham, Booksellers in London; Mr. Fletcher in Oxford; Mr. Thurlbourn in Cambridg; Mess. Ward and Chandler, at York and Scarborough; Mr. Collins in Salisbury; Mr. Frederick at Bath; Mr. Craighton in Ipswich; and Mr. Wimpley in Newbury. MDCCXLIII.
to the most
Conspicuous and Illustrious YOUTH,
THE
Earl of MARCH,
ELDEST SON of the
Duke and Duchess of Richmond,
THIS
COURSE of LECTURES
IN
Natural and Experimental PHILOSOPHY
Is most humbly Addressed an Inscribed
By his LORDSHIP's
Most Obedient and
Most Devoted Humble Servant,
Benjamin Martin.
PREFACE.
THE Reason of my printing these Lectures is, that they might be in the Hands of my subscribers, to peruse not only while they attend my Lectures, but after the Course is finished, to retain and fix those fleeting Ideas which they acquire form a transient View of such a Multiplicity of Subjects and Experiments. And, indeed, it is by this means only that a Course of Experimental Philosophy can be made of any substantial and lasting Use to the Subscribers; who otherwise must find it prove little more than a sublime and rational Amusement, for the instant Hours.
My secondary View was, once more to serve the Publick, by presenting them with a Course of Lectures in Natural and Experimental Philosophy compleat, so as to form a genera Idea or Plan of the Science; which, it is hoped, will be so much the more acceptable, as it contains an account and Description of many new Instruments and Experiments, and several great Points of the Science explain'd, which are no where else to be found in a Course of Lectures.
Again; another thing, which I had a principal View to, was my Character or Reputation as an illustrator of Experimental Philosophy; which I thought myself the more obliged to have regard to, inasmuch as there are many ignorant and empirical Pretenders gone out, who obtrude themselves and a spurious Apparatus on the good-natur'd and generous Part of Mankind, who are not apt to suspect or think ill of a Person, till (too late they find) they have been decoy'd and deceiv'd by him; and then they are prejudiced against and reject all Proposals of this Kind for ever after. Thus is the noble Science brought into Contempt and Disrepute, by the Ignorance and Effrontery of a Set of Men, whom either the Res angusta domi, or the Auri sacra fames, will compel to undertake any thing.
In the last place, it was not the least Part of my Design, to render this Course of Lectures plain and easy to be understood by all Capacities in general, and in particular by the Fair Sex. For why should not the Ladies understand and study the Sciences of Humanity, of which Philosophy holds the First Place? Knowledge is now become a fashionable Thing, and Philosophy is the Science a la Mode: Hence, to cultivate this Study, is only to be in Taste, and Politeness is an inseparable Consequence. Wherefore nothing can be more consistent and rational, than that the Ladies should study Philosophy; or more monstrous and stupid, than that Objection which is sometimes made against it, viz. That the Gentlemen will not like them so well for it. This is a gross Reflection on the good Sense of Gentlemen, and tends to deprive the Ladies of these Qualities which would principally recommend them as their valuable Esteem and Choice.
Nothing can be more shocking than to hear some Men vilify this Noble Science by asking, Of what Use is Philosophy? What shall we get by it? What shall we be the better for it? and such-like derogatory and absurd Queries. If they think, as they are sometimes pleased to say, That Philosophy is a Thing out of their Way, it would much become them not to pretend to Humanity, or any Degree of Rationality, which must be extremely absurd and ridiculous; and I shall take the Liberty to make them a particular Class or Species of Beings, under the Title of Hominiform Animals, or a Species sui Generis.
But, without designing a Panegyric on Philosophy, I will venture to assert, that there is no Art, Profession, or Business of Life, wherein an intelligent Artist will not find the greatest Service and most beneficent Effects redound from this Science. Does not every one know, that Religion is founded wholly in Philosophy, or a true Knowledge of Nature? Is is not from thence that we have the first and truest Notions of the Divine and Adorable Creator of all Things, and the most direct and cogent Arguments for his Existence and Perfections? In short, 'tis a Contradiction to call any Man a Divine or Theologist, who is ont a good Philosopher.
Again; in regard of Chemistry, Pharmacy, and Medicine, no Man of common Modesty can pretend to the least Merit, Character, or Judgement in these Arts, who does not understand the Power and Agency of the corpuscular Parts of Matter, and the different Effects arising from the various Mixtures and Associations of the original Particles of Matter in heterogeneous Bodies; the various Hydrostatic and Hydraulic Laws of Fluids; the Parts and Structure of an Animal Body; the Animal Oeconomy, and the Influences of the Sun and Moon upon it: The Principles of which are no where to be found, but in the several Branches of this Science.
As to Opticians, the Theory of their Art wholly depends on Philosophy, or rather, it makes the most delightful Part of the Science itself. No Man therefore must pretend to understand the Nature, Structure, or Effects of a Microscope, a Telescope, or a Pair of common Spectacles, yea, nor even the Nature and Use of his own Eyes, who has not made some considerable Progress in the Study of Philosophy.
<[vi]>In Navigation, Surveying, Dialing, &c. who knows not the Use of the Loadstone, and the Magnetical Needle? And how awkward must an Artist of this Sort appear, who is not acquainted with no other Property of this wonderful Body, but that which makes his Needle point Northwards?
In Gunnery, the Engineer finds the whole Theory of his Art founded in Philosophy, viz. in the Doctrine of Projectiles, and the Motion of heavy Bodies falling freely by the Power of Gravity. From hence alone he can discover that the Path of the Bomb is a Parabola, and what relates to the Impetus, Elevation, Time, and Random of the Shot or Projection.
Astronomy owes all its Principles to Observation and Experiments, and consequently to Philosophy. The general Law, which all the Heavenly Bodies observe, is conformable to the laws of Gravity, or the Doctrine of Central Forces, as I have shewn in its Place. But why should I mention Particulars, when the whole Science makes but a particular Branch of Philosophy?
Even Poetry borrows from this Science those Ideas, Descriptions, and Subjects, which most of all ennoble it, and make it appear inspired and sublime. Hence all our great Poets constantly invoke the Philosophic Muse, (the Dulces Musæ of Virgil) witness Hesiod and Homer, Virgil and Ovid, Milton and Pope; whose Names and Poems nothing can more contribute to eternize, than those fine and lofty Reflections and Strictures of Natural Science, which distinguish their Works from the Production of inferior Genii.
But what needs Prolixity? Is not all Mechanics, and every Mechanic Art or Trade, founded in Philosophy? Can any Man account for the Effects of the Hammer, the Chisel, the Scissars, (those vulgar Machines) not to mention the Lever, the Pulley, the Screw, &c. without some Degree of Philosophy? I affirm he cannot; and further, that those who learn the Practical Part, without knowing any thing of the Theory or Reason of what they do, are to be consider'd in the same View with the loquacious Parrot, and mimic Chimpanzee, rather than human or rational Artists: For it must be with the utmost Impropriety that we call those Creatures rational, who understand not the Reason of Things in general.
And to the End that no Objection may lie against the Study of so valuable and useful a Science, I have added an Appendix, giving an Explication of all difficult Words, Terms, and Characters, which are used and do often occur, not only in the Course of these Lectures, but in all other Books of modern Date, on this Subject. Also a compleat Index is subjoined, referring to the Pages where every Word or important Point is explain'd.
In the last place, Gentlemen will here find a Description and Prints of several new Philosophical Instruments and Experiments no where else to be met with. The Experiments are all number'd or register'd in the Margin, the better to assist the Memory, and to avoid Confusion: And, in short, I have omitted nothing that I know of, which could be done, to make every thing as easy and intelligible as the Nature of the Subject, and the Limits of the Work, would admit.
<[viii]>To conclude, I suppose no Person has so small a Share of Sense, as to imagine, that because we have attempted to assign the Reason of many Things, we do therefore pretend to account for all the Phænomena of Nature: Or, on the other hand, because all Things are not to be understood, we are therefore not concern'd to account for any. 'Tis certainly every Man's natural Duty to learn and teach as much as hea can of the wonderful Works and surprizing Operations of Nature; and to admire the rest, and adore their infinitely wise and powerful Creator; according to the Poet,
— Nam Rerum Parens,
Libanda tantum quæ venit mortalibus,
Nos scire pauca, multa mirari jubet.
LECTURE I.
THE Business of Experimental Philosophy, (the Subject of this Course of Lectures,) is to enquire into and investigate the Reason and Causes of the various Appearances (or Phænomena) of Nature; and to make the Truth or Probability thereof obvious and evident to the Senses, by plain, undeniable, and adequate Experiments, representing the several Parts of the grand Machinery and Agency of Nature.
In our Enquiries into Nature we are to be conducted by those Rules and Maxims which are found to be genuine, and consonant to a just Method of Physical Reasoning; and these Rules of Philosophizing are, by the greatest Master in this Science, (the incomparable Sir Isaac Newton,) reckon'd Four; which I shall give, from his Principia, as follows:
RULE I. More Causes of natural Things are not to be admitted, than are both true and sufficient to explain the Phænomena. For Nature does nothing in vain, but is simple, and delights not in superfluous Causes of Things.
RULE II. And therefore of natural Effects of the same Kind, the same Causes are to be assign'd, as far as it can be done. As of Respiration in Man and Beasts: Of the Descent of Stones in Europe and America: Of Light in a culinary Fire and in the Sun: And in the Reflection of Light in the Earth and in the Planets.
<2>RULE III. The Qualities of natural Bodies which cannot be increased or diminish'd, and agree to all Bodies in which Experiments can be made, are to be reckon'd as the Qualities of all Bodies whatsoever. Thus because Extension, Divisibility, Hardness, Impenetrability, Mobility, the Vis Inertiæ, and Gravity, are found in all Bodies which fall under our Cognizance or Inspection, we may justly conclude they belong to all Bodies whatsoever; and are therefore to be esteemed the original and universal Properties of all natural Bodies.
RULE IV. In Experimental Philosophy, Propositions collected from the Phænomena by Induction, are to be deem'd (notwithstanding contrary Hypotheses) either exactly or very nearly true, till other Phænomena occur by which they may be render'd either more accurate, or liable to Exception. This ought to be done, lest Arguments of Induction should be dstroy'd by Hypotheses.
If according to these Rules we take a Survey of the visible world, and strictly examine the Nature of particular Bodies, we I shall find that they all consist of one and the same Sort of Matter or Substance; and that all the Diversity or Difference we observe among them arises only from the various Modifications and different Connection or Adhesion of the same primigenial Particles of Matter.
Matter, thus variously modified and configurated, constitutes an infinite variety of Bodies, all which are found to have the following common Properties, viz.
EXTENSION, or that by which it possesses or takes up some Part of universal Space, which Space is call'd the Place of that Body. For all Bodies are extended either (1.) into Length only, and then it is called a Line; or (2.) into Length and Breadth, which is call'd a Superficies; or (3.) into Length, Breadth, and Depth, which then is call'd a Solid. These are the three Dimensions, according to the Quantity of which the Magnitude or Bulks of Bodies are estimated.
SOLIDITY, sometimes called the Impenetrability of Matter, is that Property by which a Body excludes all others from the Place which itself possesseth; for it would be absurd to suppose two Bodies could possess one and the same Place at the fame Time. From this Definition it follows, that the soft Bodies are equally solid with the hardest.
DIVISIBILITY is that Property by which the Particles of Matter in all Bodies are capable of a Separation or Disunion from each other. Hence the Resoluation or Dissolution of Bodies into their constituent Corpuscles, as in many Operations of Chemistry. How far this may actually obtain in Nature is not easy to say: But that Matter is infinitely divisible in a mathematical Consideration, is demonstrable various Ways.
MOBILITY is that Property which all Bodies have, of being moveable or capable of changing their Situations or Places. This Property of Matter is evident to all our Senses; and to deny it would he an Absurdity too flagrant for any but a Cartesian Philosopher.
The VIS INERTIAÆ, (as Sir Isaac called it) or the Inactivity of Matter, is that Property of it by which it endeavours to continue in its State either of Motion or Rest, or by which it resists the Actions and Impressions of all other Bodies which tend to generate or destroy Motion therein.
ATTRACTION is a Property that we find all Matter endued with in a greater or a lesser Degree: By this Property the Particles of Matter attract each other by a Power which causes them mutually to accede to, or approach each other. This Tendency of one Body to another is commonly called Gravitation, with respect to the act; but in regard of the Power, it is called the Gravity or Weight of Bodies.
<4>REPULSION seems to be a Property belonging to the small Particles of Matter universally; for they do not more evidently attract in some Circumstances, than they repell each other in others, as will be evident by Experiments, hereafter to be exhibited. nasa are the general Properties of Matter, which we must regard in our Explications of the various Phænomena of Nature, in the Sense we have defined them. These are the several Data, or fundamental Principles on which the Science of Philosophy depends, and which will each of them afford an ample Field both in the speculative and Practical Part. we shall (for the sake of good Method) begin with the Attraction of Bodies, consider its several Species, and prove their Existence and the Properties of each by Experiments.
The Power of Attraction, or Gravity its Effect, we presume not to define, or say what it is, but only that it is, or does exist, and the Laws of its Action we shall endeavour to assign by what may be discover'd by Reason and Experiment. To this End we must consider, that any Kind of Power or Virtue, proceeding or propagated from a Body in Right Lines every way as from a Center, must decrease in its Strength or Energy as the Squares of the Distances from the Body increase; [Image 1] For for 'tis evident, the Force will be every where as the Number of Particles issuing from the central Body on a given Space, which Number of Particles will decrease as the Squares of the Distances increase. Thus the Number of Particles which at any one Distance AB, from a Point in the Body at A, falls on a Square Inch BEFG, will be sour times as great as the Number which falls on a Square Inch CHIK at twice that Distance AC; and nine times as great as the Number which falls on the said Square Inch DLMN at three times that Distance AD; and so on, as is evident from the Diagram.
Hence, since we have no Reason to doubt but that all Kinds of Attraction consist in fine imperceptible Particles or invisible Effluvia, which proceed from every Point in the Surface of the attracting Body, in all right-lined Directions every way, which in their Progress lighting on other Bodies, urge and solicit them towards the superior attracting Body, therefore the Force or Intensity of the attracting Power in general must always decrease as the Squares of the Distances increase.
Hence also we may observe, by the way, that Light and Heat, Odours and Perfumes, which consist of Particles or Effluvia that proceed every way from luminous, heated, and odoriferous Bodies, as from a Centre, have always their Forces abated according to the above Law. The Force of Sounds also decreases in the same Proportion, for Reasons that will be hereafter assign'd.
By virtue of attracting Power, the grand Machinery of the Solar System, and doubtless of all the others in the Universe, is effected, established, and conserved. It is therefore of the greatest Consequence, to be acquainted with the different Species of this universal Power or Agent, and to learn by Experiments the peculiar Nature, Laws, or Manner of Action in each. By the nicest Enquiry and Observations of Naturalists there are discover'd Four different Sorts of Attraction, viz.
I. The Attraction of Cohesion, which is peculiar to the Corpuscles or primigenial Particles of Matter, of which larger Bodies are composed, by the Accretion and firm Adhesion of those Particles, arising from their strong attractive Power.
II. The Attraction of Electricity, which is peculiar to some Kinds of Bodies, as Glass, Amber, Sealing-wax, &c. which are therefore call'd Electrical.
III. The Attraction of Magnetism, or of the Loadstone, which is peculiar to, and mutual between the Loadstone and Iron.
IV. The Attraction of Gravitation, which is observable only in the larger Compositions and Systems of Matter; as in the Earth and Moon, and the Sun and Planetary Bodies which compose the Solar System. Of each of these Species of Attraction in Order; and first,
Of the Attraction of Cohesion: The Laws and Properties of this Attraction are the following. (1.) It is very discernible and most powerful in Corpuscles, or the smallest Particles of Matter. (2.) It is mutually exerted between those Particles; or they mutually attract, and are attracted by each other. (3.) The sphere of Attraction, or Extent of this Power, is greater in some Particles of Matter than in others, but very small at the utmost: For (4.) This Power is insensible in solid Bodies in the least sensible Distance, acting as it were only on Contact; and therefore, (5.) It must be nearly proportional to the Quantity of contiguous Surfaces; or the Parts of Bodies cohere most strongly, whose touching Surfaces are largest. 6. This Power is supposed to decrease much faster than the Squares of the Distances increase; but nothing certain can be determined in this respect. (7.) Where the Sphere of Attraction ends, there a Repelling Power begins, by which the Particles, instead of attracting, repel and fly from each other. (8.) By this Power the small Portions or Drops of a Fluid conform themselves to a spherical Figure.
The first and second of these Properties are made manifest by various Experiments; as the sudden Union of two contiguous Drops of Mercury, water, &c.. The strong Adhesion of two Leaden Balls, which touch by polish'd Surfaces; as also of Glass Planes, and Crystal Buttons: The Ascent of water between Glass Planes, and in Capillary Tubes; The rising of water by the Sides of a Glass vessel, and into Tubes of Band, Ashes, Sugar, Sponge, and all porous Substances.
The third of these Properties is evident by the Experiments of Water rising above the common Level, and Mercury's sinking below it, in Capillary Tubes; By the sticking rs or adhering of water to common Substances, which by Mercury are left dry.
<7>The fourth and fifth Properties are evinced by the Experiments of the different Heights to which Fluids ascend between Glass Planes unequally inclined, and in Capillary Tubes of different Bores: Also, by the accelerated Motion of a Drop of Oil between two inclined Planes: And likewise by the Hyperbolical Curve form'd by the Superficies of a Fluid ascending between Glass Planes touching each other on one Side.
The sixth Property is not to be determined by any Experimental Proof. The seventh seems evident between fat and oily Particles of Matter, and those of an aqueous Nature: But is most manifest from the Elastic Property of the Air, whose Particles compress'd together restore themselves by this repellent Power to their first State: Also by the Ascent of Steam or Vapour from humid or fluid Bodies: And lastly, by the following Experiment, which demonstrates also,
The eighth Property of this Attraction, viz. Drops of water falling on Dust; by Drops of Dew gathering on the Tops of Grass: and lastly, by Quicksilver divided into small Portions, which always form themselves into perfect Spherules or Globules.
From this Account of the Attraction of Cohesion we learn a rational Solution of several very curious and surprising Phænomena of Nature: As why the Parts of Bodies adhere and stick so firmly together; why some are hard, others soft; some fix'd, others fluid; some elastic, others void of any elastic Quality; which all arise from the different Figure of the Particles, and the greater or lesser Degree of Attraction consequent thereupon. Hence the Reason why Flies walk on the Surface of the water, and wet not their Feet. On this Principle we account for the Manner how Plants imbibe the nutritive Juices or Moisture of the Earth by the Fibres of the Roots; Also for the Rise of the Sap in Vegetables, and for the whole Oeconomy of vegetation in general. Hence the Rationale of the various Secretions of Fluids by the Glands of an Animal Body, and their wonderful Circulation through the fine Capillary vessels. Hence also the Reason of Soldering and Gilding of Metals; also of Melting or Fusion by Heat. Hence also the Exhalation of vapours by the Heat of the Sun or Fire; the Aggregation of aqueous Particles in the Air, forming the Drops of Rain. We hence see the Reason of Distillation, Filtration, Dissolution, Digestion, Sublimation, Precipitation, Crystallization, and all the other Operations of Chemistry and Pharmacy, which are no otherways to be accounted for. Lastly, we find Sir Isaac Newton (at the latter End of his Optics gives a beautiful and clear solution to those wondrous Phænomena of subterranean Accensions and Explosions; of Volcano's and Earthquakes; of Hot Springs, Damps, and suffocating Exhalations in Mines, &c. on the Principles of this Sort of Attraction and Repulsion.
The Second Species of Attraction is that of Electrical Bodies, as Glass, Amber, Sealing-Wax, Jet, &c. the principal Properties of which are as follow. (1.) Those Bodies attract others which are very light, as Feathers, Hairs, Leaf-Brass, &c. (2.) The Sphere or Extent of this attracting Power is at the Distance of several Feet but; (3.) It varies with the State of the weather, being greatest in hot and dry Weather, but weaker in warm and moist. (4.) It may be communicated to a great Distance, viz. seven or eight hundred yards, by the Intervention of a proper Body, as Hempen Strings, &c. (5.) This virtue is excited by Attrition, or hard Rubbing by the Hand or with a Piece of Cloth, but will not be produced by the Warmth of Fire. (6.) It penetrates or pervades the pores of Glass; and, (7.) It may be communicated to other Bodies, so as to render them electrical. (8.) If the Sphere of Attraction be interrupted on any Part, it destroys the Efficacy of the whole. (9.) By this virtue Bodies are not only attracted, but also repelled alternately to a very sensible Distance, and with a surprising velocity. (10.) The Body once repell'd from the Tube, will not be again attracted by it, till it has first touch'd some other Body. (11.) Bodies attracted, and sticking to the Tube, will be then attracted by other Bodies not electrical as the Finger, &c. (12.) This virtue will exert itself in Vacuo, as well as in open Air. (13.) It appears lucid, and sparkles like Fire, in a dark Room. (14.) It is also sensible to the Ear by a crackling Noise, like a green Leaf in the Fire.
The Third Species of Attraction is that of the Magnet, or Loadstone; the primary Properties whereof are the following. (1.) Every Loadstone has two Points call'd Poles, which emit the Magnetic virtue. (2.) One of those Poles attracts, the other repels Iron, but no other Body. (3.) This virtue is communicated to Iron very copiously by the Touch, which renders it strongly Magnetic. (4.) A Piece of Iron so touch'd by the Loadstone, and nicely suspended on a sharp Point, will be determined to settle itself in a Direction nearly North and South. (5.) The End of the Needle touch'd by the South Pole of the Stone will point Northwards; and the contrary. (6.) Needles touch'd by the Stone will dip below the Horizon, or be directed on the touch'd Part to a Point within the Earth's Surface. This is call'd the Dipping Needle. (7.) This virtue is also to be communicated to Iron, by a strong Attrition all one way; whence Files, Drills, &c.. are always found to be Magnetical. (8.) Iron Rods or Bars acquire a Magnetic Virtue by standing long in one Position. (9.) Fire as totally destroys this Virtue by making the Stone or Iron red hot. (10.) This Power is exerted sensibly to the Distance of several Feet. (11.) It is sensibly continued through the substance of several contiguous Bodies or Pieces of Iron, as Keys, &c. (12.) It pervades the Pores of the hardest Bodies; and (13.) equally attracts the Iron in Vacuo, as in open Air.
These, and many others, are the Properties of a Body, not more wonderful than useful to Mankind.
LECTURE II.
THE Fourth and last Species of Attraction is that of Gravitation, which is evident only between large Bodies, as the Earth and Moon, and the Sun and its Planetary Attendants. The Laws of this Attraction are as follows, viz.. (1.) It is common to all Bodies, and mutual between them. (2.) It is proportional to the Quantity of Matter in Bodies. (3.) It is exerted every way from the Centre of the attracting Body in Right-lined Directions.(4.) It decreases as the Squares of the Distances increase. [Image 2] That is, if a Body at A, on the Earth's Surface, distant one Semidiameter from the Centre C, weighs 3600 Pounds, it will at the Distance of 2, 3, 4, 5, 6, Semidiameters weigh 900, 400, 225, 145, 100 Pounds which Numbers decrease as the Squares of the Distances 4, 9, 16, 25, 36, increase.
Hence we learn that all Bodies have Weight, or are heavy; and that there is no such Thing as absolute Levity in Natures And by the second Law, the weight of all Bodies is proportional to the Quantity of Matter they contain; and hence, since Bodies of equal Bulks are sound to have unequal Quantities of Matter, it evidently follows, that a Vacuum, or Space void of Matter, must necessarily exist, and that an absolute Plenum is a Doctrine unphilosophical, and equally false and absurd.
Also, from the third Law it follows, that all Bodies descending freely by their Gravity, tend towards the Earth in Right Lines perpendicular to its Surface; and with equal velocities, (abating for the Resistance of the Air) as will be evident by the second Law above, and what will immediately follow in Mechanics.
Again: Since the Attraction is always directly as the Quantity of Matter, and inversely as the Square of the Distance, it follows, that were the internal Parts of the Earth a perfect void, or hollow Concavity, a Body placed any where therein would be absolutely light, or void of Gravity; but supposing the Earth a solid Body throughout, the Gravity from the Surface to the Centre will decrease with the Distance, or it will be directly proportional to the Distance from the Centre.
Having premised the necessary Præcognita to the Science of Mechanics, which entirely depends on the Principle of Gravitation, we come immediately to consider the Object thereof, viz. The Nature, Kinds, and various Affections of Motion, and moving Bodies; and the Structure and Mechanism of all kind of Machines, commonly call'd Mechanical Powers, whether Simple or Compound.
MOTION is the continual and successive Change of Space, and is either Absolute or Relative. Absolute Motion is the Change of Absolute Space or Place of Bodies, as the Flight of a Bird, the Motion of a Projectile, &c. But Relative Motion is the Change of Relative Space, or that which has Reference to some other Bodies: As of two ships under Sail, the Difference of their velocities is the relative Motion of the Ship sailing fastest; and is that alone which is discernible by us. The same is to be understood of absolute and relative Rest.
Again; Motion is either Equable or Accelerated. Equable Motion is that by which a Body passes over equal Spaces in equal Times. Accelerated Motion is that which is continually augmented or increased; as Retarded Motion is that which continually decreases: And if the Increase or Decrease of Motion be equal in equal Times, the Motion is then said to be equably accelerated or retarded.
The Celerity or Velocity of Motion is that Affection by which a Body passes over a given Space in a given Time, or what we commonly call the Swiftness or Slowness of Motion.
The Momentum or Quantity of Motion is all that Power or Force which a moving Body has to affect or strike any Obstacle or Impediment which opposes its Motion, and is equal to that impressed Force by which the Body is compell'd to change its Place.
Since the Force of a Body is greater or lesser as the Quantity of Matter is so, when the velocity of its Motion is the same; also since the said Force in the same Body is proportional to its velocity: Therefore it follows, that the Momentum or Force of Bodies in Motion is in the compound Ratio of their Quantities of Matter and their velocities conjointly. [Image 3] Thus if one Body strike an Obstacle X, with 3 Parts of Matter and 9 Degrees of Celerity; and another Body strike it with 5 Parts of Matter, and 7 Degrees of Celerity; the Momenta of the respective Strokes will be as 27 to 35.
The general Laws of Motion, which all Bodies observe, are the three following, viz.
LAW I. Every Body will continue in its State of Rest, or moving uniformly in a Right Line, except so far as it is compell'd to change that State by Forces impress'd.
LAW II. The Change of Motion is always proportional to the moving Force impress'd, and is always made according to the Right Line in which that Force is impress'd.
LAW III. Re-action is always equal and contrary to Action; or the Actions of two Bodies upon each other are always equal, and in contrary Directions: That is, by Action and Re-action equal Change of Motion are produced in Bodies acting upon each other; and these Changes are impress'd towards contrary Parts.
The first of these Laws is founded on the Vis Inertiæ of Matter, whereby it is indifferently disposed to persevere in its State of Motion or Rest. 'Tis not more evident that Matter at Rest requires an extrinsic Power to give it Motion, than that when in Motion, the Force of some other Body resisting it is necessary to bring it to a State of Rest. For want of such Resistance we see the Planets and Comets long conserve their Motions undiminish'd; while moving Bowls, and Wheels, are gradually reduced to a State of Rest, by the Friction or Rubbing of the Parts on which they move, against contiguous resisting Bodies; as will be evident by the Experiment of the Axis in Peritrochio, moving first on fix'd Boxes, and afterwards on Friction-Wheels.
From this Law, and what will be farther demonstrated hereafter, it follows, that no perpetual Motion can be effected, at least by any human Power, with Bodies in a resisting Medium.
By the second Law we are instructed how to estimate the Sum of the Motions of Bodies moving the same or contrary Ways, when they directly strike, or impinge on each other. Also we hence learn the Composition and Resolution of Motion arising from Forces impress'd in oblique Directions; a Doctrine of the utmost Use in Philosophy, and the Foundation of all Mechanics. To illustrate this: Let the Body B [Image 4] be impels'd by the Body in the Direction bc, with a Force that would, in a given Time, cause it to move from b to c the same Instant, let another Body strike it in the Direction bd, with a Force that will carry it from b to d in the same Time, then Compleat the Parallelogram bced, and draw the Diagonal be, that will represent the Direction and Distance through which the Body will move in the same Time by both the Forces conjointly.
The third general Law is founded on Reason and Experience: We know from the Nature of Attraction or Gravity, that if a Stone fall towards the Earth, the Quantity of Motion both in the Earth and Stone is the same. That the Iron attracts the Loadstone with an equal Power of Magnetism, is evident by Experiment. That ACtion and Re-action are equal between impinging Bodies, or that the same Quantity of Motion that is generated in one Body is destroy'd in the other by the Stroke, whether the Bodies be elastic or non-elastic, will also be made apparent to the Senses by Experiment. Whence also it will appear, that the Action or Effect of elstic Bodies is twice as great, as that of Bodies void of Elasticity.
From this Law we have a Solution of divers Phænomena otherwise not to be accounted for: As, why soft and unelastic Bodies retain the Impressions of others, while hard and elastic Bodies rebound with equal Force, and under equal Angles. Hence, the Reason of Rowing with Oars, and the Swimming of Fishes in water, also, the Flying of Birds in Air; the Recoiling of Guns; the retro-vertiginous Motion of the Æoliphile; the Hydrostatic Paradox; and many other Things hereafter occasionally mention'd, are accountable for on this and no other Principle.
We proceed next to consider the Nature of Motion Belonging to Bodies which descend freely by the Force of Gravity in Vacuo, or an unresisting Medium: And this Kind of Motion we shall find affected with the following Properties, viz. (1.) That it is equably accelerated. (2.) That its velocity is always proportional to the Time of the Fall. (3.) That the Spaces pass'd through are as the Squares of the Times or velocities. And therefore, (4.) That the velocity, and consequently the Momentum, which is proportional thereto, is as the Square Root of the Space descended through. (5.) That the space pass'd through the first Second is very nearly 16 Feet. (6.) That a Body will pass over twice the Space in an horizontal Direction, with the last acquired velocity of the descending Body, in the same Time.
[Image 5]Hence it follows, that if one Leg AB of a right-angled Triangle represent the Time of the Fall, and the other Leg BC the velocity acquired at the End of the Fall; then will the Area ABC of the Triangle represent the Space pass'd through. And hence the Spaces descended through at the End of every Second, will be as the Square Numbers 1. 4. 9. 16. 25. 36. &c. and therefore the Spaces pass'd through in each Second separately will be as the odd Numbers 1. 3. 5. 7. 8. 11. 13. 15. &c. as in the Figure.
The next Sort of Motion is that of Bodies descending on inclined Planes, and curved Surfaces, which we find distinguish'd with the following Properties. (1.) The Motion on the inclined Planes is equably accelerated, as arising from Gravity. [Image 6] (2.) The Force of Gravity Compelling a Body, as A, to descend on an inclined Plane BD, is to the absolute Force of Gravity as the Height of the Plane BC to its Length BD. (3.) The Spaces descended are as the Squares of the Times. (4.) The Times in which different Planes, BD, BH, of the same Altitude BC are pass'd over, are as their Lengths respectively. (5.) The Velocities acquired by descending through such Planes at the lowest Points, D, H, are all equal. (6.) Therefore if a Body descends from the same Height through several contiguous Planes, ever so different in Number or Situation, it will always acquire the same Velocity in the lowest point. [Image 7](7.) The Times or Velocities of Bodies descending through Planes similarly situated, or alike inclined to the Horizon, as DB, EC, will be as the Square Roots of their Lengths, DB, EC.
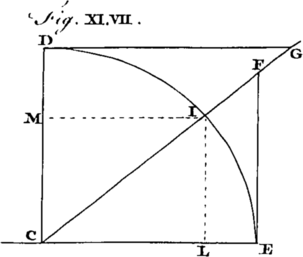
From these Properties of Bodies descending on Inclined Planes, we deduce the following Corollaries, viz. [Image 8] (1.) That the Times in which a Body descends through the Diameter BC, or any Chord BE of a Circle, are equal. Hence, (2.) All the Chords of a Circle are described in equal Times. (3.) The velocities acquired in descending through any Arch of a Circle EC, in the lowest Point C, is equal to that which would be acquired in passing through the same perpendicular Height BC. [Image 9] (4.) The velocities acquired in descending through the Chords IC, EC, of a Circle are, at the lowest Point C, as the Lengths of those Chords. (5.) The Times of Descent through Chords of similar Arches, DB, EC, are as the Square Roots of the Semidiameters AB, AC, of the respective Circles.
From these properties, and their Corollaries, the Doctrine of Pendulums is derived. [Image 10]A Pendulum is any Body B, suspended upon, and moveable about a Point A, as a Centre. The Nature of a Pendulum consists in the following Particulars. (1.) The Times of the vibrations of a pendulum in very small Arches are all equal. (2.) The velocity of the Bob in the lowest point will be nearly as the Length of the Chord of the Arch which it describes in the Descent. (3.) The Times of vibration in different Pendulums, AB, AC, are as the Square Roots of their Lengths. (4.) Hence the Lengths of Pendulums AB, AC, are as the Squares of the Times of their vibrations. (5.) The Time of one vibration is to the Time of Descent through half the Length of the Pendulum, as the Circumference of a Circle to its Diameter. (6.) Whence the Length of a Pendulum vibrating Seconds will be found 39 Inches nearly; and of an Half-Second Pendulum 9,8 Inches. (7.) [Image 11] An uniform homogeneous Body BG, as a Rod, Staff, &c. which is one third Part longer than a Pendulum AD, will vibrate in the same Time with it. (8.) This Centre of Oscillation in the Rod, is also the Centre of Percussion, or that Point in which the Force of the Stroke is the greatest possible.
From these Properties of the Pendulum we may discern its Use as an universal Chronometer, or Regulator of Time, as it is used in Clocks and such-like Machines. By this Instrument also we can measure the Distance of a Ship, by measuring the Interval of Time between the Fire and the Sound of the Gun; also the Distance of a Cloud, by numbering the Seconds or Half-Seconds between the Lightning and Thunder. Thus, suppose between the Lightning and Thunder we number 10 Seconds; then, because Sound passes through 1142 Feet in one Second, we have the Distance of the Cloud equal to 11420 Feet. Again; the Height of any Room, or other Object may be measured by a Pendulum vibrating from the Top thereof. Thus, suppose a Pendulum from the Height of a Room vibrates three times in one Second; then say, As is to the Square of 3, viz. 9, so is 39,2 to 352,8 Feet, the Height required. Lastly, by the Pendulum we discover the different Force of Gravity on diverse Parts of the Earth's Surface, and thence the true Figure of the Earth.
The greatest Inconvenience attending this most useful Instrument is, that it is constantly liable to an Alteration of its Length from the Effects of Heat and Cold, which very sensibly expand and contract all Metalline Bodies, as will be very evident by the Pyrometer.
When Pendulums were first applied to Clocks, they were made very short; and the Arches of the Circle described being large, the Times of vibration through different Arches could not, in that Case, be equal; to effect which, the Pendulum was contrived to vibrate in the Arch of a Cycloid, the Property of which Curve is, that a Body will descend from any Part thereof to the lowest Point in the same Time, and sooner than by any other way.
[Image 12] The Motion of Projectiles comes next to be consider'd. A Projectile is any Body A, thrown or projected in an upright, oblique, or horizontal Direction; as, a Stone from the Hand, an Arrow from the Bow, or a Ball or Bomb from a Cannon or Piece of Ordnance. The Force with which the Body is projected is call'd the Impetus, and the Distance to which it is thrown is call'd the Horizontal Random or Amplitude of the Projection.
Every Projectile is acted upon by two Forces or Powers, viz. the Impetus of the projectile Force, and that of Gravity. By the first, the Body passes over equal Spaces, AG, AH, AI, &c. in equal TImes; and by the second, it descends through Spaces AG, AH, AI, &c. which are as the Squares of the Times; and therefore by these two Forces compounded the Body will describe, not a Right Line, but a Curve AQ and of that Sort which we call a Parabola; and this will be the Case in all Directions but that in the Perpendicular, when the Path of the Projectile will be (to Appearance) a Right Line. [Image 13] The greater the Angle of Elevation KAM of the Cannon is, the greater will by the Height DB to which the projected Body will arise. Also, the greater will be the Distance or Amplitude of the Projection, till the said Angle becomes equal to 45 Degrees KAO; upon which Elevation the Random will be the greatest possible, and equal to twice the Altitude AG of the perpendicular Projection. On any Elevation AM or AM, equally above or below 45 Degrees, as on 40 and 50, 30 and 60, 20 and 70 Degrees, the Random AC will be the same; which Case an Engineer frequently finds of very great Use.
If the Object be situated above the Horizon, then in order to strike it, let a Piece of Looking-glass be fix'd to the Cannon perpendicular to its Axis; and holding a Plumb-Line over the Glass directly under the Eye, the Cannon is to be elevated till the Object appears exactly under the Plummet, and there fix'd, if then it be discharged, it will strike the Object as required.
From what has been said, we may easily understand how a Body projected upright from the Earth's Surface does really describe a Parabola, though to Appearance it ascends and descends in a Right Line. For it is urged by two Forces, viz. the Projectile upwards, and the Force arising from the Motion of the Earth about its Axis from West to East in which Case it must necessarily describe a Parabola, as will be evident from Experiment.
I shall in the last Place consider the Nature of Circular Motion and Central Forces. [Image 14] If a Body be suspended at the End of a String AC, moveable about a Point or Pin C as a Centre, and in that Position it receive an Impulse or Blow in an horizontal Direction, it will be thereby compell'd to describe a Circle about the central Pin: While the circular Motion continues, the Body will have a continual Endeavour to recede or fly off from the Centre, which is call'd its Centrifugal Force, and arises from the horizontal Impetus; with this Force it acts upon the fix'd Centre Pin, and that, by its Renitency or Immobility, re-acts with an equal Force on the Body by means of the String, and solicits it towards the Centre of Motion, whence it is call'd the Centripetal Force and when we speak of either, or both of them indefinitely, they are call'd the Central Forces of the revolving Body.
It is of the last Importance to understand the Nature of this Kind of Motion, since by it all the Machinery of the Planetary System is perform'd, as will be easy to understand, if, for the revolving Body, we substitute a Planet, for the Centre, we place the Sun, for the Centripetal Force, or String, its Power of Attraction; and for the Projectile Force, the Almighty Power of God in the first Creation of Things.
The Theory of this Species of Motion is comprised in the following Propositions, viz. (1.) The projectile Force AH is infinitely greater than the centrifugal Force HE. (2.) The central Force is proportional to the Quantity of Matter in the revolving Body A, all other Things being equal. (3.) If two equal Bodies A, B, describe unequal Circles AM, AN, in equal Times, the central Forces will be as the Distances AC, BC, from the Centre C. (4.) If equal Bodies describe unequal Circles with equal Celerities, the central Forces will be inversely as the Distances. (5.) If equal Bodies describe equal Circles, the Central Forces will be as the Squares of the Celerities. (6.) If equal Bodies describing unequal Circles have their central Forces equal, their Periodical Times will be as the Square Roots of the Distances. (7.) If equal Bodies describe unequal Circles with equal Celerities, the Periodical Times will be as the Distances directly. (8.) Therefore the Squares of the Periodical Times are proportional to the Cubes of the Distances, when neither the Periodical Times nor the Celerities are given. And in that Case, (9.) The central Forces are as Squares of the Distances inversely.
These are the Theorems of circular motions, the two last of which are found by Astronomers to be strictly observed by every Body of the Planetary and Cometary system. for Example: The Periodical Time of Venus is 225 Days, and that of the Earth 365; the Squares of which Numbers are 50626 and 133225: Again, the Distance of Venus from the Sun is to that of the Earth as 72 to 100; the Cubes of which Numbers are 373248 and 1000000; but 50625 : 133225 :: 373248 : 1000000; that is, the Squares of the Periodical Times are as the Cubes of their Distances, very nearly. From hence also it will easily appear, that Bodies under the Equator have the greatest centrifugal Force, which there acts in direct Opposition to Gravity, and diminishes towards the Poles, with the Squares of the Distances from the Earth's Axis. Hence also it is evident, that if ever the Earth was in a fluid State, and at the same Time moving about its Axis, it must necessarily put on the Figure, not of a perfect Sphere or Globe, but of an oblate Spheroid, flatted towards both the Poles as will be manifestly shewn by Experiment.
LECTURE III.
HAVING considered the Nature of every Kind of Motion, with the Properties of each, we should have come immediately to consider the Mechanical Powers or Machines, but that something still remains to be premised thereto, relating to the Centres of Magnitude, of Motion, and of Gravity in Bodies.
Thee Centre of Magnitude is that Point which is equally distant from all the external Parts of the Body: And in Bodies that are uniform and homogeneal, it is the same with
The Centre of Motion, which is that Point which remains at Rest, while all the other Parts of the Body move about it: And this is again the same in uniform Bodies, of the same Matter throughout, as
<22>The Centre of Gravity, which is that Point about which all the Parts of a Body do in any Situation exactly balance each other.
This Centre of Gravity in Bodies is of the greatest Consequence to be well understood, as being the sole Principal of all Mechanical Motions. The particular Properties hereof are as follow. (1.) If a Body be suspended by this Point, as the Centre of Motion, it will remain at Rest in any Position indifferently. (2.) If a Body be suspended in any other Point, it can rest only in two Positions, viz. when the said Centre of Gravity is exactly above or below the Point of Suspension. (3.) When the Centre of Gravity is supported, the whole Body is kept from falling. (4.) Because this Point has a constant Endeavour to descend to the Centre of the Earth therefore; (5.) when this Point is at Liberty to descend, the whole Body must also descend or fall, either by sliding, rolling, or tumbling down. (6.) The Center of Gravity in regular, uniform, and homogeneal Bodies, as Squares, Circles, Spheres, &c. is the middle Point in a Line connecting any two opposite Points or Angles. (7.) In a Triangle it is in a Line drawn from any Angle bisecting the opposite Side, one Third of the Length distant from that Side or Base. (8.) It is also one Third of the Side distant from the Base of an hollow Cone. (9.) But in a solid Cone it is one Fourth of the Side distant from the Base. (10.) In the Human Body, the Centre of Gravity is situated in that Part which is call'd the Pelvis, or in the Middle between the Hips.
Hence the Solution of several very curious Phænomena will be evident with the least Attention; as why some Bodies stand more firmly on their Bases than others; why some stand firmly in an inclined Position; why some Bodies fall in one manner, some in another; why some may seem to rise, while the Centre of Gravity really descends, as the rolling Cone, and Cylinder. Hence the Form of that particular Bucket which descends empty with the Mouth downwards, but is drawn up full with the Mouth upwards. Hence also it appears that a waggon loaded with heavy Matter, as Iron, Stone, &c. will go safely on the Side of a Hill or rising Ground, where a Load of Hay or Corn would be overturn'd. Again, we hence see the Reason why no Man, standing still, can move or stir, without first moving the Centre of Gravity out of its Place; also, why we stand firmly, while the Center of Gravity falls between, or on the Base Line of the Feet; and how necessarily we fall, when the Centre of Gravity falls on one Side or other of the same: With many other Particulars, which naturally result from this Principle.
If two or more Bodies in Motion be connected together, as Chain-Shot, &c. or any how depend on each other, they will have a Common Centre of Gravity, which will be a Point in the Line joining the Centres, so situated, that its Distance from the said Centres will be reciprocally as the Quantity of Matter in each Body.
Whence, since the Earth and Moon are to each other as about 40 to 1, and the Distance of the Moon 60 Semidiameters of the Earth, the Distance of the common Centre of Gravity of the Earth and Moon will be found about 1840 Miles from the Earth's Surface, and it is this common Centre of Gravity that describes the Annual Orbit about the Sun, and not the Earth itself, as is commonly said and thought.
In like manner there is a common Centre of Gravity of the Sun and all the Planets which circulate about him; and were they all placed in a Right Line on one side the Sun, then would the common Centre of Gravity of the whole System be distant from the Sun's Surface eight Tenths of his Semidiameter: And it is about this common Centre of Gravity, and not about the Sun, that not only all the Planets, but even the Sun itself, do constantly move.
The Common Centre of Gravity of any Number of Bodies being supported, none of those Bodies can fall; which is the Reason of many very surprising Appearances in Nature, as that Common Experiment of suspending a Bucket of water at the End of a Stick off the Table without falling; the Toy of the Man a sawing, &c.
We have now premised every thing necessary for understanding the Nature of those Instruments which are commonly call'd Mechanical Powers or Machines: They are Six in Number, as follow, viz. The Lever, the Pulley, the Wheel and Axle, the Inclined Plane, the Wedge, and the Screw. They are call'd Mechanical Powers, because they increase our Power of moving or raising heavy Bodies, which are often unmanageable by any natural human Strength, not thus assisted; and of two or more of these all other compound Instruments and Machines are Contrived and composed.
I. A LEVER is any inflexible Line, Rod, or Beam, moveable about or upon a fix'd Point, (call'd the Prop or Fulcrum) upon one End of which is the weight to be raised, at the other End is the Power applied to raise it, as the Hand, &c. Since (as we have before proved) the Momentums of the Weight, and Power, as are the Quantities of Matter in each multiplied by their respective Celerities; and the Celerities are as the Distances from the Centre of Motion, and also as the Spaces pass'd through in a perpendicular Direction in the same Time; it must follow, that there will be an Equilibrium between the Weight and Power, when they are to each other reciprocally as the Distances from the Center, or as the Celerities of the Motions, or as the perpendicular Ascent and Descent in the same Time; and this universally in all Mechanical Powers whatsoever, which is therefore the fundamental Principle of all Mechanics.
[Image 15] To illustrate this, let AB be a Lever supposed without weight, and F its Fulcrum or Prop; let W be a weight suspended from the End A, and the Power applied to the other End B. Then let the Lever be moved into the Situation CD, 'tis evident the Velocities of the Points A and B will be as the Arches AC and BD described in the same Time: Also the perpendicular Distances, through which the weight and Power move in the same Time, are CE and GD, which are as the Arches AC and BD; and these are as the Radii CF and DF, which are equal to AF and BF. Therefore in order to produce an Equilibrium, it must be , or , or : Consequently, P : W :: AC : BD :: CE : DG :: AF : BF. Note, that in estimating the Effects of Machines, we regard only the Distances of the Power or weight which are perpendicular to the Lines of Direction in which those Powers act, as FB, or FM, which are perpendicular to the Directions PB and LM.
The Lever is of Five Kinds: (1.) The common Sort, where the Prop is between the weight and the Power, but nearest the former. (2.) When the Prop is at one End, the Power applied at the other, and the weight between both. (3.) When the Prop is at one End, the Weight at the other, and the Power applied between both. (3.) The bended Lever, which differs only in Form from the first Sort. (4.) when the Prop is placed at an equal Distance between the Weight and the Power, and this is commonly call'd
The Balance, whose Use is, with a Pair of Scales, to bring one Body to an equal weight with another that is a Standard. The Proportional Balance is without Scales, and is used for discovering or assigning any Proportion of Weight in Bodies. The False Balance makes Bodies of unequal Quantities of Matter appear to have equal Weight. Lastly, the Statera, or Roman Balance, commonly call'd the Steelyard, is a most useful Kind of universal Balance, the Structure and Use whereof will be easy to understand from the above Principles.
II. The PULLEY is an Instrument well known; if single, it is reduced to the Lever of the fifth Sort, or Balance, and so affords no Advantage in raising Weights. If two or more be combined together in the common Way, Then the Power is to the Weight as Unity to the Number of Ropes which go to the Pulleys of the lower Box. But there are different ways of applying Pulleys, whose Advantage or Power will be obvious from the Structure of the several Sorts of Tackles, and the Experiments with them.
III. The WHEEL and AXLE (commonly Call'd the Axis in Peritochio) is the third Mechanical Power. We easily see by its Make, it is reducible to a Lever of the first Sort; and that therefore the Power is to the Weight, as the Diameter of the Axle to the Diameter of the Wheel, in an Equilibrium in this Machine.
IV. The INCLINED PLANE is the fourth Mechanical Power, and from a due Consideration of it, it will appear, that, for an Equilibrium, the Power must be to the Weight, as the Height of the Plane to the Length.
V. The WEDGE is only a double Inclined Plane, intended to separate the Parts of Wood, &c. which strongly cohere together; whence, in the common Form of it, the Power will be to the Resistance to be overcome, as half the Thickness of the Wedge to the Length thereof.
<27>VI. The SCREW is the last mention'd Mechanical Power, whose Use is both for Pressure and raising of Weights, but chiefly the former. The Power is to the Weight, as the Velocity of the Weight to the Velocity of the Power, that is, as the Distance between two Threads of the Screw to the Circumference of a Circle described by the Power.
We have here consider'd the Action or Effect of each of these Machines, as they would answer to the Strictness of the Mathematical Theory, were there no such thing as Friction or rubbing of Parts which move upon each other, by which means one Third Part of the Effect of the Machine is, at a Medium, destroy'd, as will be evident by an Experiment of the Inclined Plane. And farther, concerning Friction we are to observe, that it is not proportional to the Quantity of Surface, but to the Weight of the incumbent Part; as we shall also shew by Experiment.
As to Compound Engines and Machines, they are as numerous, as they are various in their Structure; concerning all which we may observe in general, that they consist of one, two, or more of the Simple Powers combined together; that in most of them the Axis in Peritrochio, the Lever, and the Screw are the constituent Parts; that in all, a certain Power is applied to produce an Effect of much greater Moment; and that, in the last Place, it is known, that the greatest Effect or Perfection of the Machine is then, when it is set to work with four Ninths of that Charge which is equivalent to the Power, or will but just keep the Machine in Equilibrio.
The Common JACK is a compound Engine, where the Weight is the Power applied, the Friction of the Parts, and the Weight with the Spit is charged, is the Force to be overcome; and a steady, uniform Motion, by means of the Fly, is the End or Intention of the Machine.
<28>In CLOCKS, WATCHES, &c. the Power is the weight or Spring; the Force to be overcome is the friction of the numerous parts, which are chiefly a Combination of Wheels and Axes, whose Use is to divide a large portion of Time, as a Day or an Hour, into very minute equal Parts, as Minutes, Seconds, &c. and to point out those Divisions by an equable Motion of a proper Hand or Index round a graduated Circle.
In the ORRERY and COMETARIUM, the whole Machinery is a Compages of Wheels of various Sizes, suitably contrived and adapted to produce circular and elliptical Motions of Bodies representing the Planets and Comets, in such Periods of Time as are exactly proportional and correspondent to the respective Motions of the Heavenly Bodies which they represent; also their several phases, Positions of the Orbits, and other Affections, so as to be a perfect Microcosm, or Solar System in Miniature.
In WATER-MILLS, the Momentum of the falling water is the Power; the Force to be overcome is the great Attrition of the two Stones in grinding the Corn, &c. which is effected wholly by a Complication of wheels and Axles. A Query may here be put, why, since the Power constantly acts upon the wheel, the Motion of the wheel should be equable, and not accelerated? The Answer is, The Increments of velocity keep rising, till the Momentum of the wheel bears a certain Ratio to the Resistance of the Machine after which they are all destroy'd as fast as they arise, and the wheel goes on with an uniform Motion.
In WIND-MILLS the Mechanism is the same, only the Vanes or Sails are to be consider'd as a Wheel on the Axle, actuated by the Power of the wind. In this Machine we have only to consider the Position of the Sails, and the Power of the Wind. As to the former, if the Sails stand right the wind, it cannot affect them at all; if they stand direct to the wind, the Mill will be blown down, at least, the Sails could have no Power to move round; they must therefore be placed oblique to the wind, and that under an Angle of 54 Degrees and 44 Minutes, for the greatest Advantage.
As for the Power of the Wind on the Sail, it is always as the Direction of the wind, and the Number of Particles which strike on the Area of the Sail in a given Time; both which are as the Sine of the Angle of Inclination; and therefore on Windmill Sails, the Force of the Wind increases or decreases with the Squares of the Sine of the Angle of Incidence.
Hence, in respect to the Sails of a Ship, since the Force of a direct Wind is to that of a wind blowing obliquely, as the Square of the Radius to the Square of the Sine of the Angle of Incidence, it will follow, that two equal Sails set oblique to the Wind are more advantageous than one set directly before it; provided the Angle of Obliquity or Inclination exceeds 45 Degrees.
It is to be observed, that in order to turn a Ship about in the least Time, or with the greatest Celerity possible, the Rudder ought to make an Angle with the Stern of 54 Degrees, 44 Minutes: And also, that this is the Angle which the Gates of a Lock or a Sluice upon a River ought to make with the Sides of the River, in order to resist the water with the greatest possible Force.
I shall conclude this Lecture with a few words concerning Wheel-Carriages, the whole Doctrine whereof (as it stands on a Mathematical Theory) may be reduced to the following Particulars, viz. (1.) Wheel-Carriages meet with less Resistance than any other. (2.) The larger the wheels, the easier is the Draught of the Carriage. (3.) A Carriage upon four large wheels, of equal Size, is drawn with less Force than with two of those wheels, and two of a lesser Size. (4.) If the Load be laid on the Axle of the larger Wheels, it will be drawn with less Force than if laid on the Axis of the lesser Wheels, contrary to the common Notion of loading Carriages before. (5.) The Carriage goes with much less Force on Frinction-Wheels, than in the common way; all which will be confirmed by Experiments.
LECTURE IV.
HYDROSTATICS.
HYDROSTATICS is that Part of Philosophy which treats of the Nature, Gravity, and Pressure of Fluids. A Fluid is a Substance whose Particles yield to the least partial Pressure, or Force impress'd. And hence 'tis reasonable to infer, that those Particles must be exceeding small, smooth, round, and ponderous Bodies and observe all the Laws of Motion and mutual Action in common with those of all other Matter. The following are the Laws and Properties of fluid Bodies.
I. All Fluids are incompressible, except Air; or, they cannot by any Force be compress'd into a less Space than what they naturally possess; as is proved by the Florentine Experiment of filling a Globe of Gold with water, which when press'd with a great Force, causes the Water to transude or issue through the Pores of the massy Gold, in Form of Dew, all over its Surface.
II. Air is the only compressible Fluid in Nature; for by an equal Force or Pressure over all its surface it may be reduced within less Dimensions; which is owing to its Elasticity, of which we shall treat in Pneumatics.
III. All Fluids gravitate, or weigh, in proportion to their Quantity of Matter; and that not only in the Air, or in Vacuo, but in proprio Loco; or, a Fluid weighs the same communicating with a Quantity of that Fluid, as in Vacuo; which all Philosophers (till very lately) have denied.
IV. From the Gravity of Fluids arises their Pressure, which is always proportional thereto; and since we may suppose all the Particles of a Fluid to have equal Bulk and weight, the Gravity of the Fluid, and consequently its Pressure, will be always proportional to the Altitude or Depth thereof. Whence the Weight and Pressure of Fluids on the Bottoms of Vessels, &c. must be equal.
V. The Pressure of Fluids upwards is equal to the Pressure downwards, at any given Depth. [Image 16] To illustrate this, and the foregoing Proposition, let ABCD be a vessel of water, whole Altitude EF suppose to consist of a Column of 10 aqueous Particles: Then, 'tis evident, the first or uppermost Particle 1 can affect the next Particle 2 only by its weight or Pressure, which therefore is as 1; and since that Particle 2 is immoveable, and Action and Re-action equal and contrary, the said Particle 2 will re-act upwards upon the Particle with a Force which is as 1. In the same manner the Particle 2 acts on the Particle 3 by Pressure downwards, with a Degrees of Force, arising from its own weight and that of the Particle above it; and accordingly it is press'd upwards with an equal Force by the Re-action of the Particle 3: And so of all the rest. Wherefore the Propositions are manifest.
VI. The Pressure is upon all Particles of the Fluid at the same Depth equal in every Part; or, the Particles of a Fluid, at the same Depth, press each other every way, and in all Directions, equally. For if any Particle were press'd more on one Part than another, it must give way, or yield, till the Pressure became every way equal, otherwise an incessant intestine Motion of the Particles would ensue, which is absurd, and contrary to Experience.
VII. From the mutual Pressure and equal Action of the particles it follows, that the Surface of a Fluid must be perfectly smooth and even; for should any Part stand higher than the rest by any Force, as Attraction, it would immediately subside to a Level with the other Part by the Force of its own Gravity, when that Force is removed.
VIII. The Figure of the Surface of all fluids is spherical or convex; for all the Particles equally gravitating towards the Center of the Earth, will take their places from it at equal Distances at the Surface, and so form a Part of the Superficies of a Sphere, equal to the Bulk of the Earth.
IX. Since Fluids press equally every way, the Pressure of each particle against the Side of a vessel will be proportional to its Altitude; [Image 17] and consequently the Pressures of the Particles 1, 3, 4, &c. of a perpendicular Column against the Side BC will be as a Series of Numbers in Arithmetical progression, whose first Term is 0; therefore the Sum of all the Pressures is equal to the Number of Pressures multiplied by half the greatest Pressure: But the Number of Pressures is as the Number of particles, or Altitude of the Fluid BC, also the greatest Pressure is as the same Altitudes: Wherefore the total Pressure against the Side of a Vessel is as the Square of the Altitude of the Fluid.
X. Hence if the vessel AC be of a Cubical form, the Pressure against a Side BC is half that upon the Bottom CD; and consequently, the total Pressure against the Sides and Bottom is equal to three times the Weight of the Fluid on the Bottom of such a Vessel.
<33>[Image 18] XI. The Weight, Pressure, or Effect of a Fluid upon the Bottom DE of any Vessel ACDEF, is proportional to the Altitude AE only, and not to the Quantity of the Fluid in the Vessel: For every Column of Particles GH, which preses downwards on the Side of the vessel EF, has its Force destroy'd by the equal Re-action of the subjacent Particle H in the Side, and so cannot at all affect the Bottom of the vessel. Again; the Pressure of any Column of Particles LM upwards, against the Side of a vessel CD, is equally re-acted by the Particle of the Vessel over it, and so its Force or Pressure on the Bottom must be the same as that of another Column of Particles AB of equal Altitude with the Fluid: Whence the Proposition is evident.
XII. Hence a very small Quantity of a Fluid, as APRS, may be made to counter-balance or be equivalent to the Weight or Force of any given Quantity TKGV, how great soever; as will be manifest from Experiment.
XIII. When any Body is immersed in a Fluid, it loses just so much of its Weight as is equal to the Weight of an equal Bulk of the Fluid; but the Weight lost by the Body is gain'd by the Fluid, which will be so much heavier than before; as will appear from Experiments.
[Image 19] XIV. If any Body E could be found without Weight, it would, if placed on the Surface of a Fluid AB, float thereon without any Part immersed therein; for being devoid of Gravity, it could have no Force to displace any Particles of the Fluid, and sink therein.
XV. If any heavy Body F, lighter than an equal Bulk of the Fluid, be placed on its Surface, it will sink or descend therein, till it has removed or displaced so much of the Fluid whose Weight is equal to that of the Body: For then the Pressure upwards and downwards on the under Surface of the Body is equal; and consequently the Body will be there quiescent, or in Equilirbio with the fluid. Hence the whole Solid is to the immersed Part, as the specific Gravity of the Fluid to that of the Solid.
XVI. If a Solid, as G, equal in Weight to an equal Bulk of the Fluid, be immersed therein, it will take any Situation indifferently in any Part of the Fluid, as at G, H, I, without any Tendency to ascend or descend therein: For being totally immersed, it must remove a Parcel of the Fluid of equal Bulk and Weight, and consequently the Pressure upwards is equal to the Tendency downwards on the lower Surface every where; and therefore it can have no Power to sink: Also the Pressure downwards must be equal to the Pressure upwards on the upper Surface, whence it can have no Tendency to rise or swim; it will therefore remain at Rest in any Position, G, H, I, wheresoever in the Fluid.
XVII. Lastly, If a Body K or L, heavier than an equal Bulk of the Fluid, be immersed therein, it will descend yb the Excess of its Gravity above that of the Fluid: For, when immersed, it will be resisted by the Force of an equal Bulk of the Fluid, which therefore will destroy just so much of the Gravity of the Solid, and consequently, the Residue or Excess of Gravity in the Solid is that alone by which it must descend.
From what has been premised of the Nature of Fluids, it will be easy to understand, that the lightest Body P may be depress'd in the heaviest Fluid, by any Contrivance to keep the said Fluid from pressing on the under Surface of the light Body, by which means only light Bodies are made to swim. Thus Cork or Wood will abide at the Bottom of a vessel filled with Quicksilver.
Again: On the other hand, the heaviest Body M may be made to swim in the lightest Fluid, by keeping the said Fluid from pressing on its upper Surface, by means of the Tube NO: For when by this means it is immersed so deep as to keep off an equal weight of the Fluid, the Pressure then of the Fluid acting upon its under Surface upwards will be equal to the weight of the Solid tending downwards; and therefore if the Solid be sunk ever so little deeper, it must swim by the superior Force or Pressure of the Fluid upwards.
Hence also the Reason of trying the different Gravity, Density, or Strength (as it is commonly call'd) of divers Fluids or spirituous Liquors by the Hydrometer or Water-Poise: For, since the stronger any Fluid is, the greater will be its Resistance to any Solid immersed, 'tis evident the Hydrometer cannot sink so far into the heavy or strong Fluids, as into those which are lighter or weaker. The several Degrees of Strength, therefore, are easily shewn by the graduated Neck of this Instrument.
The Hydrostatic-Balance is also an Instrument invented on the same Principle. [Image 20] By it we have a most useful and ready Method of finding the various comparative or specific Gravities of Fluids and solid Bodies, to the last Degree of Accuracy; especially in the New Structure and Method of using it, as represented in Plate III. Fig. XVIII.[Image 21]
The specific Gravity of Fluids is readily determin'd by weighing one and the same solid Body in them severally; for since we suppose the Balance in Equilibrio with the Body suspended in the Air, the Equilibrium will be destroy'd when the Solid is immersed in the Fluid, and must be then restored by weights put into that Scale to which the Body is appended. These weights will severally express the Gravities of an equal Bulk of the respective Fluids; and consequently, they may thus be Compared with each other, or all of them with the Gravity of common Water, as usual, and disposed in a proper Table; making that of water 1,000.
<36>In the same manner, if divers Solids are first weigh'd in Air, and then afterwards immersed in the same Fluid, as water, for Instance, the Equilibrium will be destroy'd, which will be restored, as before, by putting in so much weight as is equal to the weight of the same Bulk of Water: The Gravity, therefore, of every Solid is thus compared with water, and consequently with each other, as in the following Table.
The Application of Hydrostatics to the several Uses of Life will be evident from the following Instances, having first premised, that a Cubic Foot of common Water weighs very exactly 1000 Ounces Averdupois, or 62 Pounds and a half; which may be reduced to Troy weight, by considering, that the Averd. Pound is to the Troy Pound as 17 to 14, and the Averd. Ounce to the Troy Ounce as 51 to 56.
Hence, to find the Quantity of Pressure against the Sluice or Bank that pens the Water, we have this Rule: Multiply the Area of the Sluice under Water by the Depth of the Center of Gravity in Feet, and that Product again by 62; the Product will be the Number of Pounds required. Exaple: Admit the Length of the sluice be 20 Feet, the Depth of Water 5; then will the Area under water be 100 Square Feet, which multiplied by 2, the Depth of the Center of Gravity, gives 250 Cubic Feet which again multiplied by 62, gives 15625 lb. equal to 7 Tons nearly.
Again: Since the Weight of Bodies is always as the specific Gravity in equal Bulks, it follows, that the Numbers in the following Table do also express the Number of Averdupois Ounces contain'd in a Cubic foot of each respective Sort of Matter therein mention'd. Therefore, if the Magnitude of any Body be multiplied by the specific Gravity, the Product will be its absolute Weight. Thus, suppose I would know what Weight of Lead will cover a Church whose Area is 30000 Feet, and the Thichness of the Lead of a Foot: Then per Rule, Ounces, or Tons; the Weight required. Another useful Problem is, to find the Magnitude of any Thing, when the Weight is known; which is done, by dividing the Weight by the specific Gravity in the Table, the Quotient is the Magnitude sought. For Instance, what is the Magnitude of several Fragments of Coral whose Weight is 7 Ounces? Divide 7 by the specific Gravity 2690, the Quotient is of a cubic Foot; then Cubic Inches, very nearly, the Magnitude required.
Also, by knowing the Magnitude and Weight, we can find the specific Gravity, by dividing the Weight by the Magnitude in Cubic Geet. Thus suppose a Piece of Marble contain 4 Cubic Feet, and weighs 603 lb. or 10800 Ounces; then , the specific Gravity required, as per Table.
Having given the specific Gravity of Gold to Silver as 19 to 11, and suppose any Compound thereof, as King Heiro's Crown, whose specific Gravity is 16; to determine the Proportion and Weight of the Gold and Silver employ'd in making it, say, As the Difference of the specific Gravities of the Compound and the lighter Ingredient, viz. 5, is to the Difference of the specific Gravities of the heavier Ingredient and the Compound, viz. 3, so is the Bulk of Gold to that of Silver made use of. That is, if the whole Crown were divided into 8 Parts, the Gold would consist of 5, and the Silver of 3: Then the Magnitudes 5 and 3, multiplied by the specific Gravities 19 and 11 severally, will give the Numbers 95 and 33, which express the Proportion of the Weight of the Gold to that of the Silver.
Since Bodies of different specific Gravities, equiponderating each other in Air, upon being immersed into Water, will have the Equilibrium immediately destroy'd by the greater Resistance of the Fluid, and consequently the greater Loss of Weight in the lightest and most bulky Body; therefore it follows, that in buying Gold, which is heavier than Brass, we should chuse the lightest Air, i.e. when the Mercury in the Barometer stands lowest; but in buying Precious Stones, Pearls, &c. which are lighter than Brass, the best Time to do it in is when the Air is heaviest and most buoyant, viz. when the Quicksilver stands highest in the Barometer: But in selling Gold or Jewels, the contrary Rules are to be observed in regard to the Gravity of the Air.
Once more: Since the Goodness of Mineral Water, Druges, Metals, precious Stones, &c. is best shewn by their specific Gravity, it will at once appear of what vast Importance the Hydrostatic Balance is, and how absolutely necessary in the Hands of every judicious Dealer in any such kind of Commodities.
I have thought it expedient the Reader should be acquainted with the Form and Manner of using so curious and valuable an Instrument, as here improved and represented in Fig. XVIII. [Image 22] The Parts of which are AB, the Foot on which it stands; CD, a Pillar supporting a moveable Brass Plate EF, fasten'd thereto by the Screw in the Knob e. In the End of this Plate is fix'd an upright Piece IK, supporting another Plate GH, which slides backwards and forwards thereon, and is moveable every way about it. In the End of this Plate, at H, is fix'd (by a Nut beneath) a Wire LM, tap'd with a fine Thread from one End to the other; upon this moves the Swan-Neck Slip of Brass NO, to which a very exact Balance is hung at the Point N; to one of whose Scales P is appended the heavy Body R, by a fine Horse-hair or Piece of Silk S: The weight of the said Body in the Air is express'd by the Weights put into the Scale Q to make an Equilibrium therewith, which being destroy'd by immersing the Solid in the Fluid TV, contain'd in the Glass WV, is again restored by weights put into the Scale P. So that the Weights in the scale Q compared with those in the Scale P, shew at once the specific Gravity of the Solid R to that of the Fluid TV.
By this means a Table of Specific Gravities for all Sorts of Solids and Fluids may be composed, in a manner of the Specimen following:
| Fine Gold, | 19,640 |
| Standard Gold, | 18,888 |
| Mercury, | 14,000 |
| Lead, | 11,325 |
| Fine Silver, | 11,091 |
| Standard ditto, | 10,535 |
| Copper, | 9,000 |
| Brass, | 8,000 |
| Iron, | 7,645 |
| Tin, | 7,320 |
| Diamond, | 3,400 |
| Glass, | 3,150 |
| Marble, | 2,700 |
| Coral, | 2,690 |
| Stone, | 2,500 |
| Bone, | 2,000 |
| Ivory, | 1,825 |
| Oil of Vitriol, | 1,700 |
| Milk, | 1,030 |
| Common Water, | 1,000 |
| Firr, | 0,550 |
| Cork, | 0,240 |
LECTURE V.
HYDRAULICS.
BY HYDRAULICS we are to understand the Science of the Motion of Fluids, and the Construction of all Kinds of Instruments and Machines relating thereto; also the Nature of Springs, the Theory of the Tides, &c. are usually explain'd under this Head.
The Motion of Fluids viz. their Descent or Rise below or above the common Surface or Level of the Source or Fountain is caused either (1.) By the Natural Gravity or Pressure of the Fluid contain'd in the Reservoir or Fountain; or (2.) By the Pressure or weight of the Air on the Surface of the Fluid in the Reservoir, when it is at the same time either taken off, or diminished, on some Part in Aqueducts, or Pipes of Conduit. (3.) By the Spring or elastic Power of compressed or condensed Air, as in the common Water-Engine. (4.) By the Force or Pressure of Pistons, as in all Kinds of forcing Pumps, &c. (5.) By the Power of Attraction, as in the Case of Tides, &c. Of all which in Order.
I. The most natural Notion of Fluids is that arising ips. hom the Force of their own Gravity, by which those Parts which stand highest press upon others below them, till by that means they rise to the same horizontal Level. [Image 23] Thus Water in a Fountain ABCD by its Pressure raises that in the Aqueduct FGH to the same Height IKLM, in every Direction or Position of the Duct GH or GN; unless the Orifice of the said Duct be below that Level, in which Case the Water will continually flow from the same. The Reason hereof is evident from the Principles of Hydrostatics, where it was shewn, that the Pressure of Fluids was in proportion to the Altitude only, and not according to the Quantity thereof; and therefore the Effect or Rise of the Fluid in the Duct must be equal thereto. Or thus; The Velocity of the Fluid in the Duct at L, is to that in the Fountain at IK, as the Quantity of the Fluid in the Fountain is to that in the Duct; whence (from the Principles of Mechanics) the Momentum of the Fluid in each will be equal, and consequently an Equilibrium will ensue at equal Altitudes K and L in both.
Hence we have Conduits often supplied with water from Springs which lie above them; and Cocks to supply the Inhabitants of a Town with water by Pipes of Conduit proceeding from a Reservoir in a Situation above the highest Part of the Town.
Hence also the Descent of Water in Rivers, Streams, and Canals, from Springs and Sources above the common Surface of the Earth and the Breaking out of Springs at the Bottoms and on the Side of Hills, from Cisterns and Reservoirs in the internal Parts above them, which receive their waters from Rain, Dew, consed Vapours, melted Snow, &c. distilling or percolated through the Pores or Crevices and Chasms of the upper Part of the Earth.
By the Pressure of the Fluid it may easily be convey'd over Vallies and Hills by bended Pipes or Syphons, from Ponds or Reservoirs in a higher Situation; which the Ancients being ignorant of, were at vast Pains and Expence very often to effect. Hence the running of Water through the bended Syphon accounts for the odd Phænomena of intermitting and reciprocating Springs;, and also in that Instrument call'd the Tantalus-Cup; as will be evident from Experiment. The Rise of Water in Wells also is owing to the Weight of that in the subterranean Cisterns from whence they are supplied by proper Canals or Springs.
From the Pressure of the superior Fluid we have the Invention of a Natural Fountain, which playing from small Orifice of an Adjutage at the Bottom, will spout very beautifully nearly to the Height of the water from the Fountain; but it cannot quite reach that Altitude, by reason of the Air's Resistance.
From this Pressure of Fluids, as the Cause, we can estimate the various Momenta or Forces of several Jets spouting through the Sides or Bottoms of vessels at different Depths below the Surface: For the Momenta of Fluids, as well as solid Bodies, is compounded of the Quantity of Matter and Velocity; but in spouting Fluids, the Quantity of the Fluid issuing through the same Hole in the same Time is always as the Celerity of its Motion, as is easy to conceive: Whence the Momenta of spouting Fluids are proportional to the Square of the Velocities, or Quantities of Matter issuing out in a given Time: But since the Momenta are the Effect of Pressure, it is evident, the Velocity, or Quantity of spouting Fluids is ever proportional to the Square Root of the Pressure or Altitude of the Fluid.
<42>From hence it appears, that the Velocity of a Fluid spouting at any Depth below the Surface, is equal to the Velocity a heavy Body would acquire by falling from the same Height; because that Velocity, as was observed, is always as the Square Root of the Space descended through. [Image 24] If therefore on the Altitude of the Fluid AK, as a Diameter, we describe the Semicircle AFK; and from any Point therein, as I, we draw the Perpendicular IH, that shall be proportional to the Distance to which the Fluid will spout from an Adjutage at H: For the Velocity will be as the Square Root of AH, and the Time as the Square Root of HK, whence the Product of these two will express both the Space pass'd over by the projected Body, and also the Line HI, as is well known to Geometers.
Hence it follows, that a Fluid will spout from a Hole or Adjutage D in the Center of the Semicircle, or middle Point of the Altitude AK, to the greatest Horizontal Distance KM possible; because the Perpendicular FD is the greatest that can be drawn to the Diameter AK. Also 'tis evident, that from two Holes B and H, equally distant above and below the middle Altitude D, the Jets of Water will be made to the same horizontal Distance KN; because the Perpendiculars to these two Points, viz. CB and IH, are equal.
Moreover, the horizontal Distance KM, to which the water spouts from the Center, is equal to the Diameter or Altitude AK, or twice DF. For since the velocity of the Jet at O is equal to that acquired by falling thro' the Height AD, or DK, it will, as being uniform, carry the Fluid in an horizontal Direction over twice the Space DK or DF in the same Time: And therefore, since the Distances of Jets from D and B are as DF to BC, and the Distance of the Jet from D is equal to twice DF, the Distance of the Jet from B will be also equal to twice BC, or KN = 2BC.
<43>I shall only observe farther in regard to spouting water, that the Jet will go farther through the bare Hole in the vessel at P, Q or R, than through the Adjutage PB inserted in those Holes, and farther still in proportion as the Adjutage is shorter and the Bore larger. On the contrary, if a Pipe be inserted perpendicularly into the Bottom of a vessel, it will discharge itself sooner thro' it, than thro' the bare Hole; and still quicker as the Pipe is longer and larger.
II. The second Cause of the Rise or Motion of Fluids is the Pressure of the Air on the Surface of that in the Fountain or Reservoir. Thus if a Syphon or Crane be immersed with the shorter Leg in water, and the Air suck'd out of the Instrument, the Fluid will ascend into the vacuous Space by the Pressure of the Air on the water in the vessel, and fill the whole Cavity of the Tube; and because there is a greater Column or Body of water in the longest Leg, it will preponderate and descend through it and thus keep flowing out, till the vessel is exhausted to the Orifice of the shorter Leg.
The Effect of the Common Pump is from the same Principle: For the Bucket or Sucker, raising a Column of Water above it in the Barrel, makes a vacuous Space, or greatly attenuates the Air in the Barrel and Pipe below it; whence the Water must necessarily rise in the Pipe, by the superior Pressure of the Air on the Surface of that in the well. The Water ascending in the Pipe, passes through the valve in the Bottom of the Barrel, which shutting upon the Depression of the sucker, the Water is thereby Forced through the valve of the Sucker into the Cistern of the Pump, and discharged through the Spout. All which is clearly shewn by the Model of a Pump in Glass.
III. IV. But the most considerable of all Water-Engines is that call'd Newsham's Fire-Engine, from the great Improvements which Mr. Newsham made in it; the Nature and Effect of which will be easily understood from a perpendicular Section of a Model, [Image 25] with some variation which I have made in the Structure thereof. The Motion of the Water in this Engine is effected by the Pressure of the Atmosphere, by the Force of Pistons, and by the Spring of condensed Air, in the following Manner, viz.. when the Piston R is raised, a Vacuum would be made in the Barrel TV, did not the Water follow it from the inferior Canal EM (through the valve which rises through the Glass Tube EF immersed in the Water of a vessel by the Pressure of the Atmosphere on the Surface thereof. The Water of the Barrel TV, by the Depression of the Piston R is Forced through the superior Canal ON, to enter by the Valve I into the Air-Vessel abcd; and the like being done alternately by the other Barrel WX, and its Piston S, the Air-vessel is by this means continually filling with Water, which greatly compresses the Air above the Surface of the Water in the Vessel, and thereby proportionably augments its Spring, which at length is so far increased, as to react with great Force on the Surface Y of the subjacent Water, which ascending through the small Tube ef to the Stop-Cock eg, is there, upon turning the Cock, suffered to pass through a Pipe h, fixed to a Ball and Socket, from the Orifice of which it issues with a great Velocity, to a very great Height or Distance, in a small continued Stream, directed every way, or to any particular Place, by means of the Ball and Socket.
There is another Sort of Fire-Engine, which works by Fire, in the following Manner. [Image 26] ABC is a Copper-Vessel, partly fill'd with Water to DE, which being set over a Eire, and made to boil, will fill the upper Part DBE with a vastly elastic Vapour, the sufficient Strength whereof is known by its forcing open a snifting Valve at e: This heated elastic Steam is, by turning a Cock at F, let into the Barrel abcd, where by its elastic Force it raises the Piston G, which drives the Air above it through a proper Clack at the Top. After this, that the Piston may by its Weight descend, a little cold Water from the Fountain fghi, is let in at the Bottom by turning a Cock at k, which, in Form of a Jet, condenses the hot Steam in the Barrel into 13000 times less Space than before it took up, which makes a sufficient Vacuum for the Piston to descend in. The Piston G, and Lever HI, being thus put into Motion, do accordingly raise and depress the Piston K in the Barrel of the Forcing Pump LM on the other Side, which, by the Pipe N, draws the Water from the Depth W, and Forces it to rise and spout through the Tube O, continued to any Height at pleasure. This Engine is used to draw the Water from Coal-Pits and other Mines. Besides these, there are various other Water-Engines of a more complex Structure; but as they all act on the same Principles with these two described, 'tis needless to say any thing of them here.
The above-mention'd prodigious Rarefaction of a small Quantity of Water will be made very sensible by the Æolipile, whose Nature and Use in the Production of a continual and most powerful Blast of Steam, or vapourous Wind, is a Phænomenon equally curious and surprising, as will appear from the Experiment.
V. The last Cause of the Motion of Fluids which I mention'd was that of Attraction. We have already seen how by this means any Fluid will ascend above the common Surface in Capillary Tubes, &c. I shall only take notice here, that the Capillary Syphon, which, by the sole Power of Attraction, will exhaust a vessel of its contain'd Fluid, is a Curiosity which few have seen, and none can sufficiently admire.
But the most notable and obvious Motion of Fluids arising from Attraction, is that of thc Tides; the Waters of the immense Ocean, forgetful, as it were, of their natural Quietus, incessantly move, and roll in swelling Tides obsequious to the sovereign Power of the Moon, and weaker Influence of the Sun.
To illustrate this, [Image 27] let NESQ represent the Earth, covered over with Water ABDF; NS the Axis of the Earth, EQ the Equator, TR the Tropic of Cancer, tr the Tropic of Capricorn, M the Moon in her Orbit, S the Sun in his. Now since all Bodies are endued with an attracting Virtue, the Moon will attract all the Water in the nearest Hemisphere FAB, with Degrees of Force which are inversely as the Squares of the Distances from all Parts; and therefore with the strongest Force where the Distance is least, viz. in the Point A directly under her; and this Attraction being in this Hemisphere contrary to that of the Earth, the Water in all Parts from B and F towards A will have their Gravity gradually decreasing, and be lightest of all at the Part A; and consequently must there stand higher than at the Point F, where they are more attracted by the Earth, and so heavier, as is evident from the Laws of Hydrostatics.
Again: in the other Hemisphere FDB, the Attraction of the Moon conspires with that of the Earth but decreasing as the Squares of the Distances increase, the joint Force of Attraction will every where decrease from and toward D, the Point opposite to the Moon; where, again, the Waters will be lightest, and therefore stand highest to preserve the Equilibrium. Whence it appears, that by this Sum and Difference of the Moon's and Earth's Attraction, there will necessarily ensue a Protuberance or Swelling of the Waters, which we call Tides of Flood, in the two Points A and B directly under the Moon. Also in the two Points F and B, as the Waters are there most attracted, so they will be heaviest, and consequently rise to the least Height from the Earth's Surface, whence they are called Tides of Ebb, or the Ebbing of the Water.
<47>If to the Power of the Moon we add that of the Sun, we shall have the Tides considerably augmented at the Conjunction in S, or Opposition in H, that is, at the New and Full Moons, which are call'd the Spring Tides; as those which happen when the Sun is at O or P are call'd Neap Tides, the Waters A at D and being then lowest, because the Attraction of the Moon is then in some measure counter-acted by that of the Sun. The Power of the Moon to disturb the Waters is to that of the Bun as 51 to 10 very nearly: whence the Power producing the Spring Tides is that which causes the Neap Tides, as the Sum of those Numbers to their Difference, or as 61 to 41, that is, as 3 to 2.
If the New or Full Moon happen in the Equinoctial, the Tides will be the greatest possible, because there the Gravity of the Waters is more than at any other Place diminish'd by the centrifugal Force of the diurnal Rotation: Consequently, all the Causes there conspire to render the Waters lighter, or raise them highest in Tides; especially if the Moon be then nearest the Earth, and the Earth nearest the Sun, as in December it is.
It is farther to be observed, That of the two Tides of Flood at A and D, that at A is greatest to any Place in Northern Latitudes, when the Moon is in Northern Signs, and above the Horizon; for the Point is then nearer the Zenith of the Place G, than the opposite Point is to the same Place at twelve Hours afterwards; and consequently, the Height of the Tide TG is greater than that of the opposite Tide Rg. The contrary happens when the Moon is in Southern Signs.
That there are two Tides of Flood, and two of Ebb, succeeding each other alternately at the Interval of six Hours, is obvious from the Figure. That they happen later each Day near an Hour, is owing to their exact Correspondence to the Motion of the Moon, which daily culminates so much later. That they happen not when the Moon is in the Meridian, but about three Hours after, is owing to the Force of the Moon being then greater than when in the Meridian of any Place; as the Heat of the Day is greater at Three o'Clock than at Twelve; and the Heat of the Summer is greater in August, than at the 10th of June. Lastly, that the greatest Spring Tides happen not at the 10th of March, and 12th of September, but in February and October, is because the Sun being nearest the Earth in December, his Influence is then strongest, and so must quicken the Time of the greatest Vernal Tides; and being weakest in June, the Time of the Autumnal Tides will necessarily be retarded.
Such are the Phænomena of the Tides, according to a general Theory, and are found to be verified in those Parts of the Earth's Surface which are wholly cover'd with Water, as the Theory requires; I mean, the vast Atlantic and Western Oceans.
LECTURE VI.
PNEUMATICS.
THAT Part of Natural Philosophy which treats of the Nature, Properties, and Effects of the Atmosphere, or Body of Air encompassing the Earth, is call'd PNEUMATICS, from the Greek word for Wind or Breath.
The Air is generally esteemed a Fluid, yet differs from the general Nature of Fluids in two Particulars, viz. (1.) In that it is compressible, which Property no other Fluid has and (2.) It cannot be congeal'd, or any how fixed, as all other Fluids may. It must therefore be esteem'd a Fluid sui generis, if it can with Propriety be call'd a Fluid at all.
<49>That the Air was created at first with the Earth itself, is not to be doubted; and that ever since there has been a constant Generation of Particles of Air by the mutual Action of Bodies upon each other, as in Fermentation, and all Kinds of natural and artificial Chemistry, Sir Isaac Newton thinks very reasonable to suppose; and Mr. Boyle has given numerous Experiments relating to the Production of artificial or factitious Air.
That the Air is a heavy or ponderous Body, must follow from the Nature of the Matter of which it doth consist and since those Particles arise from Bodies of every Kind in or upon the Earth, 'tis evident the constituent Parts of Air are of a most heterogeneous Nature, and infinitely various in their specific Gravities: Whence also it will follow, that as the Matter which composes the Body of Air, or Atmosphere, is always variable, so will its Weight or Gravity be likewise; as we constantly experience by the Barometer, of various Kinds and Structure.
Since the Particles of Air are such as being separated from Bodies beyond the Sphere of corpuscular Attraction, are strongly repell'd from those Bodies; which Repellency being mutual between the Particles, they do by this means constantly repel each other, and therefore they must observe a mutual Distance equal to the Diameter of the Sphere of this their repulsive Power: If therefore those aerial Particles should be obliged by any impress'd Force to approach nearer to each other than the said Distance, the repulsive Power will re-act or resist the said Force with an equal Momentum and thus cause what we call Renitency, Elasticity, or Spring of the Air; which is so sensible by the common Experiment of a blown Bladder, and many others on the Air-Pump.
By reason of the Spring of the Air, its Density must be always different in different Altitudes from the Earth's Surface; for the lower Parts of the Air, being pressed by the Weight of the superior Parts, will be made to accede nearer to each other, and the more so as the Weight of the incumbent Air is greater; and hence we see the Density of the Air is greatest at the Earth's Surface; and decreases upwards in geometrical Proportion to the Altitudes taken in artithmetical Progression. Now it is found that the Air is four Times more rare at the Height of seven Miles than at the Earth's Surface; and therefore at the Altitudes of 7. 14. 21. 28. 35. 42. 49. the Rarity of the Air will be 4. 16. 64. 256. 1204 {sic}. 4096. 16384.
If the Air were of an equal Density throughout, the Height of the Atmosphere might be determined; for by Experiment we find the Length of a Column of Air 72 Feet high is equal in Weight to one Inch of Water of the same Base: Hence the Density of Air is to that of Water as 1 to 864. It is also found by Experiment, that the Weight of a Column of Air the Height of the Atmosphere will be equal to the Weight of a Column of Water of the same Base, and 32 Feet, or 384 Inches high: Wherefore 864 multiplied by 384 will produce 331776 Inches, or a little above 5 miles, for the Height of the Atmosphere, were the Density every where the same as at the Earth.
But since the Density of the Air decreases with the Pressure, it will be more rarefied and expanded the higher we go; and by this means the Altitude of the Atmosphere becomes indefinite, and terminates in pure Æther. But though we cannot assign the real Altitude of the Atmosphere, it is certain from Observation and Experiment, that 45 or 50 miles is the utmost Height where the Density is sufficient to refract a Ray of Light; and therefore that may be esteem'd the Altitude of the Air to the least sensible Degree of Density.
Since the Gravity of the Air is so various, that at one time it will sustain a Pillar of mercury 31 Inches high, when at another it will raise it but to the Height of 28 Inches, in the Barometer; it follows, that we may take 29 Inches of Mercury for the mean Altitude, and consequently its Weight for the mean Weight of a Pillar of Air of the same Base. But a Column of Mercury whose Base is one Square Inch, and Altitude 29, weighs about 17lb. which is equal to the Pressure of Air on every Square Inch; and therefore upon every Square Foot it will be 2520lb.; and allowing 14 Square Feet for the Surface of the Body of a middle-sized Man, it must sustain a Pressure of 36540 Pounds, or 16 Tons, when the Air is at a mean Gravity. This prodigious Force would crush us within the Compass of a Pepper-Corn, were it not that it is equal on every Part, and counter-balanced by the equal Re-action of the Spring of the Air within us.
The Weight of the Air is proved by a great variety of curious Experiments, the principal of which here follow. (1.) By actually weighing it in a nice Balance; where we shall see that one Gallon of Air will weigh a Dram very nearly. (2.) By filling a Glass Tube with Mercury, and inverting it in a Bason of the same Fluid, where it will appear that a Column will be supported in the Tube by the sole Weight or Pressure of the Air, to upwards the Height of 28 Inches. (3.) By taking the Air off from the Surface of the Quicksilver in the Gage of the Air-Pump, which then immediately rises by the Pressure of the external Air. (4.) By exhausting a Receiver placed over the Hole of the Brass Plate on the Pump, which will then be kept fast on by the Pressure of the incumbent Air. Or, (5.) more demonstratively by exhausting a small Receiver under one larger, and letting in the Air at once upon it; which will then be fasten'd to the Plate, as before, though not placed over the Hole. (6.) By placing the Hand on the open Receiver, and exhausting, the Weight of the Air on the Hand will be extremely sensible. (7.) By placing a plain Piece of Glass on the said open Receiver, which, when the Air is a little exhausted, will be broke into Pieces by the Weight of the Air. (8.) A Bladder tied over the same Glass will be broke in the same manner. (9.) The Air exhausted from a thin Bottle under a Receiver, and then suddenly let in, will, by its Weight, instantly reduce it to very small Pieces. (10.) Bottle broke by the same means another way. (11.) By putting a Piece of wood under Quicksilver in the Receiver, and then exhausting the Air, and letting it in again, it will by its Weight Force the Quicksilver into the Pores of the wood, and very sensibly increase its Weight. (12.) The exhausted Brass Hemispheres prove not only the prodigious Weight of the Air, but also the Quantity thereof very exactly. (13.) By exhausting Glass Bubbles swimming in Water, and letting the Air in again, it will Force the Water into the Bubbles, and make them sink. (14.) The Syringe with its Weight descending in Vacuo, and ascending again upon the Admission of Air, does very prettily prove the Pressure of the Air, and the Rationale of Syringes in general.
That Water rises in Pumps, Syphons, and all Kinds of Water-Engines, by the Pressure of the Air only, is made evident by taking off the said Pressure (in the exhausted Receiver) from a Bason of Mercury, which then will not rise in the Pipe of the Syringe on drawing up the Piston, as it will in the open Air.
The Spring of the Air is demonstrable by various Experiments: As, (1.) By the great Expansion of a small Quantity of Air in an emptied Bladder, when the Air is taken off from the external Parts in the Receiver. (2.) By the Extrusion of a Fluid out of a Glass Bubble, by the Expansion of the Bubble of Air contain'd therein. (3.) By the Expulsion of the White and Yolk of an Egg through a small Hole in the little End, by the Expansion of the Air contained in the great End; and also, (4.) By raising up the Skin of the Egg (after the Yolk is taken away, and one half of the Shell) by the Expansion of the said included Bubble of Air, so as almost to fill the Half-Shell. (5.) Glass Bubbles and Images fill'd with Water, so as to make them just sink in Water, will, upon exhausting the Air from the Surface, rise to the Top of the vessel. (6.) Also a Bladder fill'd with Air, and just made to sink with a Weight, will, upon Exhaustion, soon rise by the Expansion of the contain'd Air. (7.) The Spring of the Air will shew itself also by raising heavy Weights laid on a Bladder, half fill'd with Air, in a proper vessel under the Receiver. (8.) Beer, Cyder, Water, and porous Bodies, do emit great Quantities of Air under the exhausted Receiver. (9.) Fishes are made so light or buoyant by increasing the Spring of the Air in their Bladders, upon Exhaustion, that they rise to the Top of the Water, and cannot again descend to the Bottom. (10.) Shrivel'.d Apples are made to look fair and smooth by the Spring of the contain'd Air filling out the Wrinkles. (11.) The Spring of the Air in a Square Bottle, cemented close, will immediately burst it in pieces, upon exhausting the incumbent Air. (12.) But that curious Experiment which shews the Force of the Spring of the Air to be equal to its Weight or Pressure, is by raising the Mercury, by the Expansion of a small Quantity of confined Air, to the same Height in an exhausted Tube above the Pump, as that which it is raised to in the Mercurial Gage by the Pressure of the Atmosphere below it.
<54>The great Action of animal Life, viz. Breathing, by Inspirationand Expirationof Air, is owing to the Pressure and Spring of the Air conjointly, as is evident by the Contraction and Expansion of a Bladder in a Bottle, under the Exhausted Receiver.
Hence the Quantity of Air for Respiration and animal Life in most Sorts of Creatures, which die very soon in the exhausted Receiver: Though some Animals will not be kill'd in this manner; as Flies, Frogs, Toads, some sort of Fishes, &c.
That Air passing through the Fire, and heated Brass Tube, is unfit for animal Respiration, is shewn by the sudden Death of any Animal put into a Receiver fill'd therewith. Also Candles and living Coals, put into this adust Air, immediately go out. Hence the noxious and pestilential Qualities of Damps and suffocating Exhalations, so frequent and fatally experienced in Mines, and other subterranean Places.
That Air in its natural State is necessary for Fire and Flame, is obvious from the sudden Extinction of a Candle, a live Coal, &c. in the exhausted Receiver. Also Gunpowder fired therein will not take Flame, or be explosive, but melt and die away.
That the different velocities with which heavy and light Bodies descend in the Air, is owing to the Air's Resistance only, is manifest from the equal velocity or Swiftness with which all Bodies descend in the exhausted Receiver, as is shewn in the Example of a Guinea and a Feather.
Air is likewise necessary for the Existence and Propagation of Sounds; for a Bell placed under the Receiver, and rung, will not be heard when the Air is drawn out; but in condensed Air, the Sound will be augmented in proportion to the Condensation.
<55>That Fermentation, Putrefaction, &c. depend on the Air, and are promoted by it, is shewn by preserving Fruit in their natural Bloom and Perfection through the winter in exhausted Glass.
The Use of the Diving-Bell depends on the Pressure and Spring of the Air: For since the Space which Air takes up is reciprocally as the Power compressing it, 'tis evident that at the Depth of 33 Feet of Water, where the Pressure of the Atmosphere is doubled, the Bell will be half fill'd with Water; at the Depth of 66 Feet it will be two Thirds fill'd; at the Depth of 99 Feet it will be three Fourths fill'd; and so on. Whence appears the Necessity of having the vessel in the Form of a Bell, that the perpendicular- Height of the Water may be as little as possible. Hence also we see how necessary it is to have a very gentle Descent of the Bell, that the Divers may have Time to admit the Air, so greatly condensed, by proper Degrees, lest it should burst the fine vessels of their Bodies,and kill them: Together with several other Particulars relating to the Nature and manner of using this Machine, which will be fully explain'd by Experiment.
The Weight, or Spring of the Air, or both, are most evidently concern'd in that Chirurgical Operation we call Cupping; when a Vacuum is made by a Syringe in the Cupping-Glass applied to any Part, the Spring of the Air in the Flesh under the Glass does strongly act, and by that means causes the Flesh to distend and swell into the Glass, while the Pressure of the Air on the Pairs without the Glass accelerates the Motion of the Blood and Fluids, towards the Part where it is diminish'd or taken off by the Glass.
Since we know that Heat augments the repellent Power in the Particles of a Fluid, and by that means increases its Elasticity, and thereby causes it to expand itself into a larger Space; and that Cold has a quite contrary Effect; we learn the Use of the Thermometer in indicating the various Degrees of Heat and Cold in the Air, by the different Altitudes of the Spirit of Wine in that Instrument.
The Moisture and Dryness of the Air are shewn by the Hygrometer, which is made several ways, but that with a Cord is most common and useful; for that by shrinking with Moisture will turn an Index one way, and extending with Dryness will turn it the contrary way, over the graduated Limb of a Circle.
I shall finish this Lecture with giving you an Account of the Structure and Use of the common Air-Pump, and of one of a new Invention of my own. The Common or large Air-Pump is represented in Fig. XXIV.[Image 28] where aa, aa, are the two Brass Barrels, in which the Pistons cc, cc, move by Chains fasten'd to each of them, and to a Wheel moving on the Axles f, when the Engine is put into Motion by the Winch bb. gg, gg, are two Pillars or Pieces of Wood supporting the Frame of the Pump-Wheel, which is screw'd upon them by Nuts under the little Pieces of wood e, ee. The Tube or Pipe marl'd hh is call'd the Swan-Neck, made of Brass: By this the Air passes from under the Receiver oo, through a small Hole k in the Middle of the Brass Plate iii on the Top of the Pump, to a Brass Piece in the Box dd, which being perforated length-ways to the Middle Point under each Barrel, does there, through a small Hole, by a Bladder-Valve, transmit the Air from the Receiver into each Barrel to be pump'd out by passing through the Hole in the descending Piston. These Holes in the Pistons and Bottoms of the Barrels are cover'd with valves, to prevent the Return of the Air into the Receiver. lll is the Mercurial Gage, or common Barometer, immersed in a Bason of Mercury mm fix'd in the Bottom of the frame, and at top communicates with the Receiver, which therefore shews how much the Receiver is exhausted by the Rising of the Mercury in the Tube, by a graduated Scale affixed thereto. The Stop-cock nn, also, communicates with the Receiver, and consequently with the Swan-Neck and Mercurial Tube: Its Use is, by turning the Cock, to re-admit the Air, when there is Occasion. The Receiver is ground true on the Bottom, and is fix'd on thc Pump at first by means of wetted Leathers, to exclude the Air, instead of Cement formerly used for that purpose.
But with how much more Conveniency, and less Expence, Pneumatical Experiments of all Rinds may be perform'd, by a new, elegant, and portable Air-Pump, which I have lately contrived and made, will be easy to apprehend from a bare view of the Figure thereof: [Image 29] In which AB is the Head or Part containing the Wheel, which alternately raises and depresses the Pistons CD in the Barrels EF, which are strongly press'd down by the said Part AB, supported on the two Pillars GH, fix'd into the Bed or Bottom of the Machine IKL. On this Bottom stands the Receiver MN on a large smooth Brass Plate, in the Middle whereof is a Hole, by which the Air passes out of the Receiver into a small Tube on the under Part of the Frame, and goes to the Piece O, which communicates with the perforated Brass Piece on which the Barrels stand, and from which they receive the Air to be exhausted. On the middle Part of this Brass Piece is a Perforation, over which is placed a small Receiver PQ, and under it a Bason of Mercury R, in which a small Tube RS (hermetically sealed at one End, and fill'd with Quicksilver) is inverted; and therefore as the small Receiver PQ is exhausted, (at the same time with the large one MN) the Approach of the Vacuum will be shewn by the Descent of the Quicksilver in the Tube RS. By the Stop-cock T the Air is again let into the Receiver.
Note, This {sic} Air-Pump, with a Receiver large enough for any Use, may be together included in a Box 12 Inches wide, 14 high, and 14 in Length; which cannot be said of any other Form yet invented. Nor can I at present see or think of any farther Improvement this Engine is capable of; unless it be, that in this form a Pump might easily be made to exhaust 6, 8, or 10 Receivers at once; which Hint may be well worth the Notice of Gentlemen of Spirit, Taste, and Fortune.
LECTURE VII.
The Doctrine of WINDS and SOUNDS.
IN this Lecture I shall consider the Nature of Wind and Sound in general; and of the vibrations of Musical Strings and Sonorous Bodies, with regard to the Science of MUSIC. WIND is a Stream or Current of Air: As the Air is a Fluid, its natural State is that of Rest, which it endeavours always to keep or retrieve by an universal Equilibrium of all its Parts. When, therefore, this natural Equilibrium of the Atmosphere happens by any means to be destroy'd in any Part, there necessarily follows a Motion of all the circumjacent Air towards that Part, to restore it; and this Motion of the Air is all we call Wind.
Hence, with respect to that Place where the Equilibrium of the Air is disturb'd, we see the Wind may blow from every Point of the Compass at the same time; and those who live Northwards of that point have a North Wind; those who live Southwards, a South Wind; and so of the rest: But those who live on the Spot, where all these winds meet and interfere, are oppress'd with turbulent and boisterous weather, whirlwinds and Hurricanes; with Rain, Tempests, Lightning, Thunder, &c. For sulphureous Exhalations from the South, Torrents of Nitre from the North, and acqueous Vapours from every Part, are there confusedly huddled and violently blended together; and rarely fail to produce the Phænomena abovemention'd.
As the Motion of the Air has a greater or lesser Belocity, the Wind is stronger or weaker, and it is found from Observation, that the Velocity of the Wind is various, from the rate of 1 to 50 or 60 Miles per Hour.
Many are the particular Causes which produce wind by interrupting the Equipoise of the Atmosphere; but the most general Causes are two, viz. Heat, which, by rarefying the Air, makes it lighter in some Places than it is in others, and Cold, which, by condensing it, makes it heavier. Hence it is, that in all Parts over the Torrid Zone, the Air being more rarefied by a greater Quantity of the Solar Rays, is much lighter than in the other Parts of the Atmosphere, and most of all over the Equatorial Parts of the Earth. And since the Parts at the Equator are most rarefied which are near the Sun; and those Parts are, by the Earth's diurnal Rotation Eastward, continually shifting to the West; it follows, that the Parts of the Air which lie on the West Side of the Point of greatest Rarefaction, and, by flowing towards it, meet it, have less Motion than those Parts on the East of the said Point, which follow it; and therefore the Motion of the Eastern Air would prevail against that of the Western Air, and so generate a continual East Wind, if this were all the Effect of that Rarefaction. But we are to consider, that as all the Parts of the Atmosphere are so greatly rarefied over the Equator, and all about the Poles greatly condensed by extreme Cold, this heavier Air from either Pole is constantly flowing towards the Equator, to restore the Balance destroy'd by the Rarefaction and Levity of the Air over those Regions: Hence, in this respect alone, a constant North and South Wind would be generated.
Now it is easy to understand, that by a Composition of these two Directions of the Air from the East and North, a North-East Wind will be generated in the Northern Hemisphere, and a constant South-East Wind in the Southern Hemisphere, to a certain Distance on each Side the Equator, all round the Earth. And this Case we find to be verified in the General Trade Winds, which constantly blow from the North-East and South-East, to about 30 Degrees on each Side the Equator, where those Parts are over the open Ocean, and not affected with the Reflection of the Sun-Beams from the heated Surface of the Land; for in this Case the wind will always set in upon the Land, as on the Coast of Guinea, and other Parts of the Torrid Zone, we know it does; which also may be shewn by Experiment.
Thus much may suffice for a general Account of the Nature and Origin of Winds: We proceed now to the Doctrine of Sounds. We know by the Experiment of the Bell in the exhausted Receiver, that Sound has a necessary Dependance on the Air; and if we reflect on the Nature of the Particles of a sonorous Body and those of Air, we shall find that Sound is nothing but the Propagation of the Tremors and Vibrations of the former impress'd on the latter, to the Tympanum or Drum of the Ear, by whose Action they are communicated to the Air in the internal Cavities of the Ear, where the Auditory Nerve receives the Impression, and excites the Sensation in the Common Sensory in the Brain.
For the Parts of a sonorous Body, being put into Motion by Percussion, do vibrate forwards and backwards through very small Spaces, by their elastic Quality. In this Action, they affect the Particles of Air contiguous to them, and compel them upon the first Impulse to move forwards also; and these propel the next, and so on, to a very considerable Distance, according to the Intensity of the percussive Force. By this means the Particles of Air are compress'd nearer together, than in their natural State.
But when the Particles of the sonorous Body make the second Part of the vibration, by returning back again, the Particles of Air also, by their repulsive Power, repel each other towards their proper Places, and thus again expand themselves.
Now since Motion once generated in elastic Bodies continues some time before it can be destroy'd by the Resistance and Counteraction of contiguous Bodies, it follows, that the Particles of the sonorous Body, and consequently those of the adjacent Air, have, for some time, a reciprocal vibratory Motion, by going forwards and backwards through very small Spaces in an indefinitely small Particle of Time; which Motion gradually decreases, till it be totally destroy'd. This may in a good measure be made easy to be understood by an Experiment of a vibrating and spiral Wire.
From the Nature of a Fluid, whatever Motion is generated in any one Particle, it is by that Particle communicated equally to all around it, as from a Center consequently the Tremors of the sounding Body will be propagated all around from the Point of percussion, as a Center, in concentric hollow Superficies or Shells of Air, which are not improperly call'd aerial Pulses, or Waves of Air: Analogous to which are the circular waves generated on the Surface of Water all around the Point where any Impression is made, in any Manner or Direction whatsoever. These Pulses or waves of Air are affected with the following Properties, viz.
I. They are propagated all around, in a spherical undulatory Manner (as I said but now;) and that not only from the tremulous Body, but from the Holes in any Obstacles they meet with: Whence it comes to pass, that one and the same Sound may be heard by several Persons, in any different Situations with respect to the sounding Body, if not at too great a Distance.
II. The Density of these aerial Pulses decreases, as the Squares of the Distances from the sounding Body increase: For since the Force or Motion in each Shell is the same, it must decrease as the Number of Particles increases in each Shell: But this Number of Particles is as the Superficies of the Shell, which is as the Squares of the Diameter or Semidiameter of the Sphere, that is, as the Distance from the sounding Body. Hence the Distinction of Sounds into loud and low, strong and weak, according as we are nearer to, or farther from, the sounding Body. The utmost Limits of audible Sounds are about 180 or 200 Miles.
III. All the Pulses, whether denser or rarer, move with equal Velocities: This Sir Isaac Newton has demonstrated a priori, and also that this velocity is at the rate of 1142 Feet in one Second of Time, which most exactly agrees with the repeated and most accurate Experiments of the late Reverend Mr Derham. The Velocity of Sound is therefore near thirteen times as great as that of the strongest Wind: And since it must necessarily increase with the Air's Elasticity, it will be greatest in Summer when the Air is most heated, and vice versa in winter: Also, as the Motion of the Wind conspires with, or is contrary to that of Sound, the velocity of Sound will be in some small Degree augmented or diminished thereby, though not discernible in Experiments.
IV. The Interval or Distance of the Pulses from each other is the same among all that are excited by the same Stroke: For since each Pulse is caused by a single Vibration of the sounding Body, and since they all move with equal and uniform velocities, 'tis plain they must succeed each other at Intervals proportion'd to the Times of the vibrations: But the Times of the Vibrations of the same Body are all equal; consequently, the Intervals of the Pulses will be so too.
V. The aerial Pulses are propagated together in great Numbers from different Bodies without Disturbance or Confusion; as is evident from Concerts of Musical Instruments, where divers Sounds, of different Intervals and various Coincidences, strike the Ear at once, yet with Distinctness and agreeable Consonance.
<63>VI. The Particles of Air, and consequently the Pulses, striking against an Obstacle, will be reflected back under an Angle equal to that of Incidence; in the same manner as will be shewn in regard to the Rays of Light. Hence a Repetition of the Sound, heard by the direct Pulses, will be made by those which are reflected; which is what we call an Echo.
The Locus, or audible Place of Sound, will be there where the Particles of Air first begin to diffuse themselves in Form of waves. Thus a Person speaking in one End of a Tube, or Trumpet, will be heard as speaking from the other. And as in the Case of Light, we see the Image of an Object always in the Direction of the reflected Ray; so in Echoes, we hear a Person speak at the Place from whence the reflected wave comes to the Ear.
Because the Sound is stronger in proportion as the Air is denser, it must follow, that the voice passing through a Tube or Trumpet must be greatly augmented by the constant Reflection and Agitation of the Air through the Length of the Tube, by which it is condensed, and its Action on the external Air greatly increased at its Exit from the Tube; which from hence is call'd the Stenorophonic Tube, or Speaking-Trumpet.
For the same Reason, those Funnel-like Instruments, which gather the larger and more languid waves of Air, do greatly condense them, and heighten their Power and Action on the Drum of the Ear; by which means, voices and Sounds are render'd strong, loud, and audible, which were not so before to a deafen'd Ear; and hence these Instruments come to be call'd Otacoustics.
I shall only observe, in regard of those Instruments which magnify Sounds, and assist the Hearing, that the longer they are, the greater is their Effect; and that of all the Forms or Shapes, none is so good as that derived from the Revolution of the Logarithmic Curve about its Axis.
From the fourth Property of the aerial Pulses we have the Origin of the various Degrees of what we call the Note, Tone or Tune of Sounds, in regard of which they are distinguish'd into low and high, or grave and acute, by Musicians call'd Flats and Sharps. Now the Tone of a Sound depends on the Time or Duration of the Stroke made on the Drum of the Ear, by a wave or Pulse of Air, for as that is longer or shorter, the Tone will be more grave or acute: And since all the pulses move equally swift, the Duration of a Stroke will be proportional to the Interval between two successive pulses; and consequently, a Sound is more or less Grave or Acute in proportion to the Length of that Interval.
Hence it follows, that all the Sounds from the loudest to the lowest, which are excited by the vibrations of the same Body, are of one Tone. It likewise follows, that all those Bodies whose Parts perform their vibrations in the same or equal Times, have the same Tone: Also, those Bodies which vibrate slowerst, have the gravest or deepest Tone; as those which vibrate quickest, have the sharpest or shrillest Tone.
The Times of the vibrations of Musical Strings, and consequently the Tones, vary in respect of the Length, the Magnitude, and the Tension of those Strings. For if two Strings AB, CD, are of the same Magnitude, and stretch'd by equal Weights E, F, have their Lengths as 2 to 1, the Times of their vibrations will be in the same Ratio. Hence the Number of Vibrations of the two Strings AB, CD, perform'd in the same Time, will be inversely as their Lengths; or CD will make two vibrations, while AB performs one. The vibrations of two such Strings will therefore co-incide at every second of the lesser.
<65>Again: If two Strings AB, CD, have their Diameters as 2 to 1, and are of equal Length, and tended by equal Weights E, F; the Times of the Vibrations will be as their Diameters, viz. as 2 to 1; and so the Vibrations in a given Time, and the Co-incidences, as before.
Lastly: If the Diameters and Lengths of the strings be equal, the Times of the Vibrations will be inversely as the Square Roots of the Weights which stretch them. If the Weights E and F be as 1 to 4 (the Square Root of which are 1 and 2) then the Times of vibration in AB and CD will be as 2 to 1. Hence in constructing string'd Instruments, as Spinets, Harpischords, &c. a skilful Artist will compound these proportions of the Length, Diameter, and Tension of the Strings to very great Advantage.
In Wind-Instruments, as the Flute, Organ, &c. where the Sound is made by the Vibration of a Column of Air contain'd in the Tube, the Time of vibration or Tone of the Instrument will also vary with the Length and Diameter of the said Column of Air, and Force of the Voice, which compresses it; as will be easy to observe from Experiments.
If one Body be made to sound with another, their vibrations will Co-incide after a certain Interval; and the shorter the Interval of the Co-incidence, the more agreeable is the Effect or Consonance to the Ear; consequently, those which are most frequent produce the most perfect Consonance or Concord, as it is commonly call'd. when the Times of Vibration, therefore, are equal, the Concord is most perfect and more agreeable than any other, and this is call'd Unison.
If the Times of vibration are as 1 to 2, the Co-incidence will be at every second vibration of the quickest, and so this is the next perfect Concord, and is what we commonly call a Diapason or Octave.
<66>If the Times of the Vibration be as a 2 to 3, the Co-incidence will be at every third Vibration of the quickest; which therefore is in the next Degree of Perfection, and this is call'd a Diapente, or Fifth. If the Times of Vibration are as 3 to 4, the Co-incidence will be at every 4th of the lesser and this is call'd the Diatessaron or Fourth. But this, and the next which follow in order, are not so agreeable and pleasant to the judicious Ear, and are therefore call'd Imperfect Concords. Nor are there above seven Notes in all the infinite variety of Tones, which can merit a Place in Musical Compositions, and they are exhibited in Fig. XXIX.[Image 30] which represents the Strings in an Octave of a Harpsichord, with the Semitones or Half-Notes, call'd Flats and Sharps, by which the Natural Notes are made half a Note lower or higher, as the Air of the Song or Musick requires. And this is call'd the Diatonic Scale of Music.
In this Scale, the seven natural Notes are mark'd on the Keys by the seven Letters C, D, E, F, G, A, B. The first of which is call'd the Fundamental or Key; the rest in Order are the Second Greater, the Third Greater, the Fourth Greater, the Fifth, the Sixth Greater, the Seventh Greater, and then the Eighth, which begins the next Octave. Between these are interposed the five Semitones, viz. the Second Lesser, the Third Lesser, the Fourth Greater, the Sixth Lesser, the Seventh Lesser. These several Tones and Semitones have the Lengths of the Strings adjusted from the Division of the Monochord, or Line divided into 100 or 1000 equal parts, as is very easy to apprehend from the Figure.
The Number of those Divisions are also shewn for each String, by the first Series of Numbers on the Strings; the next Series shew the Proportion of the Length of each String to that of the Key, or Monochord, and consequently the Number of vibrations of the fundamental and each String respectively, perform'd in the same Time.
<67>Of these twelve Intervals or Ratios of Musical Sounds, the Octaves and Fifths are perfect Concords; the third Greater, third Lesser, the Greater and Lesser Sixth are imperfect Concords; the Greater Fourth, the two Seconds, and two Sevenths are Discords, the Fourth is in its own Nature a perfect Concord, but lying between the Third and Fifth, it cannot be used as such, but when join'd with the Sixth, to which it stands in the Relation of a Third. All Melody and Harmony are compos'd of these twelve Notes; for the Octaves above or below are but the Replications of the same Sounds in a higher or lower Tone. Melody is the agreeable Succession of several Musical Sounds in any single Piece of Music; as Harmony is the Effect of several of those Pieces or Parts of Music play'd together.
Harmonical Proportion is that which is between those Numbers which assign the Lengths of Musical Intervals, or the Lengths of Strings sounding Musical Notes, and of three Numbers it is, when the First is to the Third, as the Difference between the First and Second is to the Difference between the Second and Third; As the Numbers 3, 4, 6. Thus if the Lengths of Strings be as these Numbers, they will sound an Octave, 3 to 6; a Fifth, 2 to 3; and a Fourth, 3 to 4.
Again: Harmonical Proportion between four Numbers is, when the First is to the Fourth as the Difference between the First and Second is to the Difference between the Third and Fourth, as in the Numbers 5, 6, 8, 10: For Strings of such Lengths will sound an Octave, 5 to 10; a Sixth Greater, 6 to 10; a Third Greater, 8 to 10; a Third Lesser, 5 to 6; a Sixth Lesser, 5 to 8; a Fourth, 6 to 8.
It may be here observed, that a Series of Numbers in Harmonical Proportion Are reciprocally as another Series in Arithmetical Progression,
| As | { | Harmon. | 10 | : | 12 | : | 15 | : | 20 | : | 30 | : | 60 | : |
| { | Arithmet. | 6 | : | 5 | : | 4 | : | 3 | : | 2 | : | 1 | : |
for here 10 : 12 :: 5 : 6; and 12 : 15 :: 4 : 5; and so of all the rest. Whence those Series have an obvious Relation to, and Dependence on, each other; which in some Problems of speculative Philosophy will be very useful to know.
[Image 31] If the three Lines AD, BG, CH, be taken in Musical Proportion, or as the Numbers 6, 4, 3; and in the Line AD we take AE equal to BG, AF equal to CH, then will the Line AD be divided in Harmonical Proportion, in the Points A, F, E, D; viz. AD : AF :: DE : EF. And in this manner is the Axis of a Convex and Concave Mirror divided by the Object, the Image, the Vertex of the Mirror, and the Center, as may be easily shewn by Experiment.
Also the Limits of the Colours of Light, as separated by the Prism, fall upon the seven Musical Divisions of the Monochord; as will be farther taken notice of, and exemplified in the next Lecture.
I shall conclude this with taking notice of one singular Property of a Musical Chord, viz. that it will be put into a vibratory Motion by the Pulses of the Air proceeding from the vibrations of another very near it, and in Concord with it: If the vibrating String be Unison with it, the other will tremble through its whole Length; if an Octave, it will vibrate by the Half-Lengths only, if the String which communicates the Motion be a Double-Octave above, or one Fourth of the Length of the other, the Motion will be still correspondent in that other String, for it will vibrate only by the Fourths of its Length from one End to the other. [Image 32] Thus if AB be a String four Feet long, and CD another of one Foot; if the latter be struck with a Quill, the vibrations will be communicated to the former in such a manner that it will vibrate only by a Foot-Length at the same time through the whole String; which will be evident by the small Pieces of Paper b, d, f, h hung upon the Middle of every Foot-Length, suddenly leaping off; while the other Pieces a, c, e, g, i, remain unmoved upon the String at the End of every Foot, where the Vibrations severally begin and end, and consequently where the Line has no Motion at all.
LECTURE VIII.
Of LIGHT and COLOURS.
THAT Light is not a mere Quality of some Bodies, but is itself a real Body, or distinct Species of Matter, and endued with all the natural Properties thereof, will, I presume, be sufficiently manifest from the following Experiments relating thereto. We shall therefore, at present, take it for granted, that Light consists of inconceivably small Particles of Matter of different Magnitudes, which are emitted or reflected from every Point in the Surface of a luminous Body in right Lines, and in all Directions, with an unparallel'd Velocity, and whose Power or Intensity decreases as the Squares of the Distances increase.
That the Particles of Light, refracted through the Humours of the Eye to the Retina, or fine Expansion of the Optic Nerve over all the interior hinder Part of the Eye; and there, by painting the images of external Objects, become the immediate Means of Sight, will be fully shewn in the next Lecture.
We shall now consider Light under the various Characters and Qualities of a Natural Body, and point out those remarkable Affections and Properties so peculiar to itself, and the Causes of so many very curious and extraordinary Phænomena in Nature.
<70>That the Particles of Light are inconceivably small, is evident from hence, that the greatest Quantity of Light, in the State of greatest Density, or Flame, is found to have scarce any sensible Gravity or Weight, which, we have shewn, is always proportional to the Quantity of Matter in all Bodies: Also, because those Particles pervade the Pores of all transparent Bodies, however hard or heavy, as Glass and Adamant. But we know it more especially from hence, that the Stroke we receive by a Particle of Light has no sensible Force or Momentum, which, on account of its prodigious velocity, would be very great, and insufferable, were it of any assignable or considerable Magnitude.
Yet small as they are, we find the Rays consist of different Sorts of Particles in Light emitted from all Bodies; and that this Difference of the Rays of Light arises from the different Magnitude of the Particles, seems most evident from the different Directions the several sorts of Rays move in, after they have pass'd through a Body of Glass, Water, &c. of some special Figure, as that of a Prism especially.
That the Particles of Light are emitted from every Point in the Surface of a Body, is evident from hence, that any given Point in that surface is visible to the Eye in any Situation, from whence a Right Line can be drawn from the Eye to that Point; which could not be, if the Light were not propagated from that Point in all Directions.
That they proceed from the Body in Right Lines, is clearly seen by Experiments on the Sun-Beams, Candle-Light, &c. in a darken'd Room; also from the Shadows which Bodies of every Figure cast, being such as would be determined by Right Lines drawn from the luminous Point touching the Extremities of those Bodies.
The Velocity of the Rays of Light surpasses that of all other Bodies we know of By observing the Times of the Eclipses of Jupiter's Satellites when the Earth is nearest, and again when it is farthest distant from that Planet, we shall find, that in the former Case those Eclipses happen too soon, and in the latter too late, by the Space of about seven Minutes; which shews, that in that Time the Light passes over the Semidiameter of the Earth's Orbit, which is about 82000000 Miles, which is at the rate of 200000 Miles in a Second of Time, and which is therefore nearly 800000 times greater than the velocity of Sound.
Again: Since Light is propagated in Right Lines, its Power or Intensity will decrease as the Squares of the Distances increase; and therefore the Light and Heat of the Sun at the Distances of the Six Planets, Mercury, Venus, Earth, Mars, Jupiter, and Saturn, will be nearly as 700, 200, 100, 43, 3, 1. supposing their Distances as the Numbers 4, 7, 10, 15, 52, 95.
From the stupendous velocity of luminous Particles arise their prodigious Effects in regard of Heat, Flame, Burning, Melting, &c. Thus when they are considerably dense, they act very forcibly on the Parts of an animal Body, and raise the Sensation of Heat, by the great intestine Motion which they produce in every Part. Hence all other Bodies are hotter or colder, as they contain a greater or lesser Quantity of ignitious Particles, and so have a greater or lesser Degree of intestine Motion of the Parts.
If these lucific Particles are sufficiently imbibed or generated in any opake Body, they cause it to shine, or glow, or become red-hot, and by their prodigious Activity will in time disunite, dissolve, and destroy its natural Texture, and thus change its Form, and reduce it to another Species of Matter; even the Asbestos not excepted.
If the ignific Particles of Light are sufficiently condensed, as the Rays of the Sun by a Lens or Burning-Glass, they become ardent, and burn with an Intensity proportional to the Density of the Rays in the Focus, or Burning-Point of the Glass; which Burning Spot, or circular Space, is always as the Area of the Burning-Glass directly, and the Square of the Focal Distance inversely. Thus, suppose the Surface or Area of one Glass contain'd 12 Square inches, and its Focal Distance were 9 Inches; and the Area of another Glass were 9 Square Inches, and its Focal Distance 4 Inches; then the Effects or Intensity of Burning would be as to , or as to ,viz. as 197 to 576.
When Rays of Light fall on the Surface of an opake Body, part thereof are reflected to the Eye, which render it visible, the other part is transmitted, and variously reflected through the pores of the Body, till it becomes totally suffocated and lost therein; and since none of those Rays come from the interior parts to the Eye, we can see nothing of the internal Substance of such a Body, which therefore is said to be opake.
But when Rays of Light fall on transparent Bodies, part is reflected at the first Surface, and part is transmitted into the Body, which is refracted in Right Lines to the second or lower Surface, where it is again partly reflected and in part refracted into the Air, and coming to the Eye, renders the internal parts of those Bodies visible, which for that Reason are said to be diaphanous or transparent.
[Image 33] When a Ray of Light HC falls on any plain, convex, or concave Surface, as AB, DE, FG, in the point C, the Angle HCK, made by the incident Ray and the perpendicular KC, is always equal to the Angle KCI, made by the said perpendicular and the reflected Ray CI: Or the Angle of Incidence is equal to the Angle of Reflection in every Inclination of the Ray of Light. This is evidently shewn by Experiment; and it is very well worth our Observation, that in this Case only, the said Ray takes the shortest Way possible from any point H, to any other Point I, if it must, in its Passage, touch any of those Surfaces.
The Rays of Light reflected from the first Surface of a Glass are more copious than those reflected from the second Surface, as is evident from hence, that the Image form'd in the first Case is more bright and splendid than that of the latter, and if the second Surface be contiguous to any transparent Medium, as Air, Water, &c. the Rays will be reflected from thence in greater Plenty, as the Medium is more rare, whence the Image by Reflection from the second Surface is brighter when that Surface is contiguous to Air, than when it touches Water; and most bright when it is contiguous to a Vaccum.
If the second Surface of Glass be cover'd with an opake Body impervious to the Rays of Light, they will then be reflected in much greater abundance from the second than from the first Surface, and the Image will be proportionally more bright than that form'd by Reflection from the first Surface, which is the Case of all Glasses foliated or quicksilver'd. Whence it appears, that the Light reflected from the first Surface bears a very small proportion to that which is transmitted into the Substance of the Glass.
[Image 34] When a Ray of Light, as HC, passes out of Air into a denser Medium, as ABFO, it will be strongly attracted by the Particles of the Surface of the Medium AB, a little way on each Side; the Consequence whereof is, that its Motion will be accelerated at the Entrance of the Medium, and its Direction somewhat alter'd, for since the Attraction of the Medium is perpendicular to its Surface, it will deflect or bend the Ray out of its first Direction HF, into a new one CE, (through the Medium) which lies nearer to the perpendicular KD, drawn through the Point of Incidence C: And this is call'd the Refraction of a Ray of Light; HCK is the Angle of Incidence, and DCE the Angle of Refraction.
If on the Point C be described a Circle DHKG, and from the points and (where the Circle cuts the incident and refracted Ray) be drawn the Lines HL, GI, at right Angles to the Perpendicular KD, they will be the Sines of the Angles of Incidence and Refraction. And it is several ways demonstrable, that in every Inclination of the Ray of Light to the Surface of the Medium AB, those two Sines HL and GI will always have one certain or constant Ratio or proportion to each other: And that HL : GI :: 4 : 3, if the Refraction be out of Air into Water, but HL : GI :: 17 : 11, or 3 : 2 nearly, if out of Air into Glass; and and {sic} in general, the denser the Medium, the greater its refractive Power, or Disproportion of the Sines; all which Particulars will be very evident by Experiments.
If a Ray of Light, as EC, pass out of a denser Medium into a rarer, as a Water or Glass into Air, it will, upon entering the rarer Medium at C, be refracted from its first Direction EN into a new one CH, which will be farther off from the perpendicular KCD; and in this Case, IG will be the Sine of the Angle of incidence, and HL that of the Angle of Refraction; and all other particulars just the reverse of what they were before under the same Names.
Hence it follows, that if any Object be placed at E, and cover'd with Water to the Height CD, it will be seen by an Eye placed any where above the Surface AB, in a Situation lower than would be otherwise possible, and thus Objects which are invisible may be render'd visible by the Interposition of a denser Medium, as is well known by a common Experiment. On this account it is that we see the Sun, and other Luminaries, while they are yet below the Horizon, in a Morning before they rise, and in the Evening after they are set, by the Refraction of the Atmosphere. Hence also the Difference in the Diameters of the Horizontal Sun and Moon, and their Elliptic Figure, by the greater Refraction of the Rays coming from the lower Limb.
Again; it follows, that if an Object be view'd which is part in one Medium and part in another, as a Staff represented by NE, it will not appear strait, but crooked; for if the Eye be in the rarer Medium, the Part of the Staff in the denser, CE, will be refracted into the Line CF, and the whole Staff will appear in the crooked Form NCF.
Hence also all Objects in a denser Medium appear raised or elevated above their real Situations: Thus the Part of the Staff CE is raised into the Situation CF; and the Bottoms of all vessels, if cover'd with Water, appear raised, or higher by a fourth Part of the Depth of the Water, than what they really are.
The Sun's Rays, as I have said, are not homogeneous, but of different Kinds; and each Sort has a different Degree of Refrangibility; that is, in passing through a dense Medium, they are differently disposed to be refracted, being bent or turn'd out of their first Course to different Distances from the Perpendicular: And these several Sorts of Rays have each a peculiar Colour, viz. those which are least refrangible are Red; the second Sort, Orange, the third Sort, Yellow; the fourth Sort, Green; the fifth Sort, Blue, the sixth Sort, Indigo; and the seventh Sort, Violet, which are most refrangible, or refracted to the greatest Distance from the perpendicular.
To illustrate this Matter, [Image 35] let GF represent a Parcel of the Solar Rays entering through the Hole H of a Window-Shutter, into a darken'd Room and there let them fall on the Prism ABC, in the Point F: In passing through the Prism they will be severally refracted in a different Degree, and thus separated from each other, so that at their Exit on the other Side at E, they will proceed at different Distances from the Perpendicular EP to the other Side of the Room, where they will make a long and various-colour'd Image of the Sun XY, which is, perhaps, one of the most surprizing and agreeable Spectacles of Nature.
The several Sorts of Rays, after they are refracted, appear in their own proper Colours in Order as follows, viz. Those which are least refracted, or fall nearest the Perpendicular PE are Red, and make the red Part of the Spectrum at R; the next are the Orange at O, the Yellow at Y, the Green at G, the Blue at B, the Indigo at I, and the Violet at V: And these Seven are all the original simple Colours in Nature; and of which, by various Mixtures, all others are compounded, in the common Refractions and Reflections from natural Bodies.
Since a Lens does, in the manner of a Prism, more or less separate the Rays of Light passing through it, it follows, that all the several Sorts of Rays will have their proper Focus's, or be convened to so many different Points in the Axis of the Lens, and not all to one Point only, as is necessary for a perfect and uniform Representation of the Image of any Object: For the Red Rays proceeding from the Object will be converged to a Focus at a greater Distance from the Lens, than the Indigo or violet Rays; and so the image will be colour'd and confused in every Point between those Extremes, except just in the middle Point, where the several Sorts of Rays all intersect each other, and exhibit the image tolerably distinct and colourless. To this different Refrangibility of the Rays is owing the Imperfection of the common refracting Telescope, as will be but too easy to experiment.
Hence also Objects of any of the simple Colours, though contiguous to each other, yet, if view'd through a Prism, appear separated, and at a distance from one another: And those Objects will have their images form'd by a Lens at very different Distances in its Axis, especially in Experiments of the deepest Red, and Violet, or Blue Colours; as a Card painted half with Carmine, and half with Ultramarine, made deeper with a little Indigo.
Sir Isaac Newton found, by a very curious and convincing Experiment, that the Rays of Light were as variously reflexible as refrangible; and that those which were most or least refrangible were also most or least reflexible: And farther, that Rays of Light were not reflected by impinging on the solid Parts or Corpuscles of Bodies, and rebounding from thence like a Tennis-Ball, but from some other Principle depending on the Size of the Particles of Light, and the Thickness or Density of the Particles of the Body reflecting it, which are all of them, in the most opake Bodies, transparent in themselves, as is easy to be shewn in the thin Lamellæ or Plates, of which an Oyster-Shell doth consist.
It will be thought very strange to assert, that a rare Medium is more impervious to the Rays of Light than a denser one; and yet nothing is more certain, or easier proved by Experiment: For Example, a Beam of Light is much more copiously reflected from the second Surface of a Piece of Glass when contiguous to the Air, than when it touches Water, and still more, if contiguous to Water, than when it is contiguous to Glass; in which Case the Rays are totally transmitted.
Hence, wonderful as it may seem, 'tis necessary, in order that a Body may be transparent, that its Substance should be very dense, and its Pores very small and that Opacity results chiefly from the Largeness of the Pores of a Body, occasion'd by its Particles touching in but very few Points: Because, if the Pores of such a Body be fill'd with a Substance nearly of the same Density, it becomes in, some Degree transparent, as Paper wetted with Water or Oil: And on the contrary, Water blown up into small Bubbles has its Density diminished, and its Porosity increased, and thus becomes opake.
If the Object-Glass of a large Telescope be laid with its convex Surface on a plain Glass, the Light falling on the thin Portion or Plate of Air contain'd between the Glasses will be, at several Distances from the Center, alternately transmitted and reflected. In the Center of the Lens, where it touches the Glass, it will be transmitted, and so cause a dark Spot to appear: At a small Distance from thence, all around, the Light will be reflected in various-colour'd Rings: In the next Distance it will be transmitted, and in the next to that reflected; and so on alternately to a considerable Distance from the central Spot. If we take the Distances as the Numbers 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, &c. then at the Distances 0, 2, 4, 6, 8, 10, &c. the Light will be transmitted; and at the Distances 1, 3, 5, 7, 9, &c. it will be reflected in colour'd Rings: And this alternate Disposition of Light to be reflected and refracted, Sir Isaac calls the Fits of easy Reflection, and Fits of easy Transmission.
As Light, falling upon this thin Plate of Air between the Glasses, variously disposed to be reflected or transmitted, according to the several Degrees of Thickness; so when it falls on the Surface of natural Bodies, it is as variously reflected from the pores of Air of different Thicknesses in those Bodies, and according to the different Texture of Bodies, and Magnitude of the Particles of Light, it will be either transmitted wholly, or in part; and that which is reflected will be of all one Sort of Rays, or of several Sorts promiscuously and unequally, or of all Sorts equally. Whence it will follow, (1.) If the Light be wholly transmitted, the Body will appear Black, which is the Absence of all colour'd Light. (2.) If the Light reflected from Bodies be all of one Sort, that Body will appear all of one Colour, which will be most simple and intensely deep. (3.) If the Rays are promiscuously reflected, but one Sort more than the rest, the Body will appear of the Colour proper to that Sort of Ray, but it will be not so pure and strong as before. (4.) If three or sour Sorts of Rays are promiscuously reflected more than the rest, the Colour of the Body will be a Mix'd or Compound, inclining to the Tint of the most predominant Colour. (5.) When all Sorts of Rays are equally reflected from Bodies, those Bodies appear White, or of the Colour of the Sun's Light. (6.) Where there is no Light at all incident on Bodies, those Bodies can have no Colour, which is a Property of the Rays of Light only.
[Image 36] Let BNFG be a spherical Drop of falling Rain, and AN a Ray of the Sun falling upon it in the Point N, which Ray suppose refracted to F, from thence reflected to G, and there again refracted in the Direction GR to the Eye of a Spectator; and let IG be perpendicular to the Point G: Then will the Beam, by its Refraction at G, be separated into its several Sorts of Rays, which will paint their respective Colours in that Part of the Drop; of which that next the Perpendicular IG will be red, as being least refracted, and the rest in Order above it. Now it is found by Computation, that the greatest Angle SeO, or EOP, (drawing OP parallel to SE) under which the most refrangible Rays can come to the Eye of a Spectator at O, is 40 Deg. 17 Minutes; and that the greatest Angle FOP, [Image 37] under which the least refrangible Rays come to the Eye at O, is 42 Deg. 2 Minutes. And so all the Particles of Water within the Difference of those two Angles EF will exhibit severally the various Colours of the Prism, and constitute the interior Bow in the Cloud.
If the Beam go not out of the Drop at G, but is reflected (a second time) to H, and is there refracted in the Direction HS, making the Angle SYA with the incident Ray AN, it will paint on the Part the several Colours of Light, but in an inverse Order to the former, and more faint, by reason of the Rays lost by t he second Reflection. It has been found also, that the least Angle SGO, or GOP, under which the least refrangible Rays can come to the Eye at O, after two Reflections and two Refractions, is 50 Deg. 57 Minutes, and the least Angle HOP, under which the most refrangible Rays can come to the Eye in this Case, is 54 Deg. 7 Minutes. Whence all the Colours of the exterior Bow will be form'd in the Drops from G to H, which is the Breadth of this Bow, viz. 3 Deg. 10 Minutes; whereas the Breadth of the other, viz. EF, is but 1 Deg. 45 Min. and the Distance between the Bows, viz. FG, is 8 Deg. 55 Min. And such would be the Measures of the Bows, were the Sun but a Point; but since his Body subtends an Angle of half a Degree, it is evident, by so much each Bow will be increased, and their Distance diminish'd. All which will be illustrated by Experiments.
Halo's are form'd by Rays of Light coming to the Eye after two Refractions through Drops of Rain, or spherical Hail-stones, which Light ought to be strongest at the Distance of about 26 Degrees from the Sun or Moon, or somewhat less, if the said Hail-stones be a little flatted, as often they are. These Halo's, if the Hail he duly figur'd, will be colour'd, and must then appear red within by the least refrangible Rays, and blue without by the most refrangible ones.
The reason why there is always a determinate Angle for exhibiting the Bows, or Halo's, is because there is but one particular Point N in all the Part of the Drop between B and L, where the Rays AN can enter, so that alter a second Refraction at F for Halo's, or Reflection at F and G for the Bows, there can enough go out together at G or H, to form a strong and distinct image of the Sun; which Rays, therefore, entering at the point are call'd efficacious Rays, to distinguish them from the rest which are ineffectual.
LECTURE IX, X.
OPTICS.
WE are now arrived to that Part of Natural Philosophy which treats of Vision, and the various Phænomena of visible Objects, by Rays of Light reflected from Mirrors, and transmitted through Lenses, which constitute the Subject of the most delightful Science of Optics.
The principal Things here to be consider'd are, First, the Rays of Light; Secondly, The Glasses by which they are reflected and refracted; Thirdly, the Theorems or Laws relating to the Formation of the Images of Objects thereby; Fourthly, the Nature of Vision, and Structure of the Eye; and Fifthly, the Structure and Use of the principal Optical Instruments.
The Rays of Light are distinguished into three Sorts, viz. Parallel, Converging, and Diverging Rays. Parallel Rays are such as in their Progress keep always an equal Distance from each other, as ABDC; [Image 38] such are as the Sun's Rays, in their natural State, with respect to Sense. Converging Rays are such as in their Progress approach nearer and nearer to each other, all of them tending towards a certain Point F, where they all unite; as the Rays of the Sun collected by a Glass, as CDF. Diverging Rays are those which proceed from a Point, as F, and in their Progress recede from one another towards the Parts GE.
<82>The Point F, where the Rays are collected, is call'd the Focus, or Burning-Point, because there the Sun's Rays, being united within a very small Compass or Circle, are greatly constipated and condensed, by which means their Action or Heat is proportionably increased, and therefore Objects posited in that Point will be greatly heated, burnt, or melted.
Of Glasses there are two Kinds, viz. Mirrours, and Lenses. A Mirror or Speculum is that, which from one polish'd Surface reflects the Rays of Light; and these are either Convex, Concave, or Plane, as will be shewn. A Lens is any transparent or diaphanous Body, as Glass, Ctystal, Water, &c. through which the Rays of Light do freely pass, and is of a proper Form to collect or disperse them. Of these there are several Species, as a Plane Lense, a Plano-Convex, Plano-Concave, Double-Concave, and Meniscus.
I shall now consider the different Properties and Effects of these Glasses in reflecting and refracting the Sun's Light, and forming the Images of Objects: And this all depends (in Reflection of Light) on that fundamental Law, That the Angle of Incidence is equal to the Angle of Reflection.
[Image 39] Let EH be a concave Mirrour, V its Vertex, and C the Center of its Concavity. Let A be a Ray of the Sun's Light incident on the Point E, and draw EC, which will be perpendicular to the Mirrour in the Point E; make the Angle CEF equal to the Angle AEC, then shall EF be the reflected Ray. Thus also HF will be the reflected Ray of the incident one DH, at an equal Distance on the other Side of the Axis BV.
If now the Points E and H be taken very near the Vertex V, we shall have EF, or HF, very nearly equal to FV, but EF = FC; therefore FV = FC = CV. That is, the Focal Distance FV of parallel Rays will be at the Distance of half the Radius CV of the Concavity of the Mirrour, from the Vertex V, in the Axis BV.
After the same manner, a convex Mirrour [Image 40] is shewn to reflect the Rays AE, DH, into EF, HF, as if they came diverging from a Point F in the Axis CV, which is half the Radius CV distant from the vertex V. But since the Rays do not actually come at, or from the Focus f, it is call'd the Imaginary or Virtual Focus.
Parallel Rays falling directly on a plane Speculum are reflected back upon themselves; if they fall obliquely, they are reflected in the same Angle, and parallel as they fell. Hence there is no such thing, properly speaking, as a Focus belonging to a plane Speculum, neither real nor virtual.
The Focus F, or f, of parallel Rays, is call'd the Solar Focus; because in that the Image of the Sus is form'd, and of all Objects very remote. But the Focus of any Object situated near the Mirrour will have its Distance from the vertex more or less than half the Radius: The Rule in all Cases being as follows:
Multiply the Distance of the Object into the Radius of the Mirrour, and divide that Product by the Sum of the Radius and twice the Distance of the Object; the Quotient will be the Focal Distance of a Convex Mirrour.
Again; for a Concave Mirrour, the same Product of the Radius into the Distance of the Object, divided by the Difference of Radius and twice the Distance of the Object, will give the Focal Distance VF or Vf. And here we are to observe, that as twice the Distance of the Object is lesser or greater than the Radius, so the Focus will be positive or negative, that is, behind the Glass or before it.
The Image of every Object is form'd in the Focus proper to its Distance: And since the writers on Optics demonstrate, that the Angles under which the Object OB [Image 41] and its Image IM are seen from the Center or Vertex of the Mirrour C are always equal; it follows, that the Image IM will be always in Proportion to the Object OB, as the Focal Distance VF to the Object's Distance GV.
The Position of the Object will be always erect at a positive Focus, or behind the Speculum; diminished by a convex, and magnified by a concave one. Hence, since a convex has but one, viz. an affirmative Focus; so it can never magnify any Object, howsoever posited before it.
The Position of the Image in a negative Focus, or that before the Glass, will be ever inverted; and if nearer the vertex than the Center C, it will be less; if farther from it, it will be greater than the Object; but in the Center, it will be equal to the Object, and seem to touch it.
The Image form'd by a Plane Speculum is erect, large as the Life; at the same apparent Distance behind the Glass, as the Object is before it; and on the same Side of the Glass with the Object. These Properties render this Sort of Mirrour of most common Use, viz. as a Looking-Glass.
If the Rays pass directly, or nearly so, on a plane Mirrour, and the Object be opake, there will be but one single Image form'd, or at least be visible; and that by the second Surface of the Speculum, and not by the first, through which the Rays do most of them pass.
But if the Object be luminous, and the Rays pass very obliquely on the Speculum, there will be more than one Image form'd, to an Eye placed in a proper Position to view them. The first Image being form'd by the first Surface will not be so bright as the second, which is form'd by the second Surface. The third, fourth, &c. Images are produced by several Reflections of the Rays between the two Surfaces of the Speculum and since some Light is lost by each Reflection, the Images from the second will appear still more faint and obscure, to the eighth, ninth, or tenth, which can scarcely be discerned at all.
We proceed now to Lenses; and here, since all Vision by them is effected by the Refraction of Rays through their Substance, it will be too intricate an Affair to shew the particular Manner how Rays are collected by them to their several Focus's: It must suffice only to say, That parallel Rays are refracted through a plano-convex Lens to a Point or Focus, which is the Diameter of the Sphere of its Convexity distant from it:
That the same Rays are collected by a double and equally convex Lens in a Point which is the Center of the Sphere of its Convexity:
That parallel Rays are refracted through a plano-concave Lens in such a manner, as though they came from a Point distant from it by the Diameter of tis Concavity:
And that the same Rays are refracted through a double and equally concave Lens, in such manner as though they proceeded from a Point which is the Center of the Concavity.
And in case of a double and equally convex Lens, we have this general Rule for finding the Focus of Rays universally, be the Distance of the Object and Radius of Convexity what it will, viz.
Multiply the Distance of the Object by the Radius of Convexity, and divide that Product by the Difference of the said Distance and Radius; the Quotient will be the Distance of the Focus requir'd.
Hence, if the Distance of the Object be greater than the Radius, the Focus will be affirmative, or behind the Lens; and the Image will be inverted, and diminish'd in Proportion of its Distance to the Distance of the Object.
<86>Again; if the Distance of the Object be less than the Radius, the Focus will be negative, or on the same Side of the Lens as the Object, and the Image will be magnified, and in an erect Position.
If the Distance be equal to the Radius, the Focus will be at an infinite Distance; that is, the Rays, after Refraction, will proceed parallel, and will therefore enlighten Bodies at a vast Distance. Hence the Contrivance of the Dark Lanthorn for this Purpose.
Lastly: If the Distance of the Object be equal to twice the Radius, then will the Distance of the Focus and Image be equal to the Distance of the Object; and consequently the image will be equal in Magnitude to the Object, but inverted. Hence the Use of these Lenses to Painters, and Draught-Men in general, who have often Occasion for the Images of Objects as large as the Life, to delineate or draw from.
As to Plano-concaves, they, having no real Focus, form no Images of Objects; so that we shall pass them to proceed to the Structure of the Eye, the Manner of performing vision therein, the several Defects thereof, and how remedied by Glasses; which will be illustrated by the Dissection of a natural Eye, and exemplified by an artificla one.
The Eye is the noble Organ of Sight or Vision: It consists of various Coats and Humours, of which there are Three remarkable, viz. (1.) The Aqueous or Watry Humour, which lies immediately under the Cornea, and makes the Eye globular before. (2.) The Vitreous Humour, which is by much the greatest Quantity, filling the Cavity of the Eye, and giving it the form of a Globe or Sphere. (3.) The Crystalline Humour, situated between the other two, near the Fore-part of the Eye, and is the immediate instrument of Sight; for being of a lenticular Form, it converges the Rays, which pass through the Pupil, to a Focus on the Bottom of the Eye, where the images of external Objects are by that means form'd and represented.
Over all the Bottom of the Eye is spread a very fine and curious Membrane, call'd the Retina, which is an Expansion of the Optic Nerve; upon which the images of Objects being painted and impress'd, they are by that means convey'd to the Common Sensory in the Brain, where the Mind views and contemplates their Ideas; but this in a Manner too mysterious and abstruse for us to understand.
The Crystalline Humour is of such a Convexity, that in a sound State of the Eye its Focus falls precisely on the Retina, and there paints the Objects; and therefore vision is not distinct, unless by Rays which are parallel, or nearly so; for those only will have their Focus at the Bottom of the Eye: Now Rays proceeding from any Point more than 6 Inches distant from the Eye, will, when they enter the Pupil, be very nearly co-incident with parallel Rays, and therefore to a sound Eye distinct vision Cannot be effected at less than 6 or 8 Inches Distance, as is evident to any who tries the Experiment.
Since then there is a certain and determinate Degree of Convexity in the Cornea and Crystalline Humour, for forming the Images of Objects on the Retina, if it happens that the Convexity of those Parts should be more or less than just, the Focus of Rays will fall short of, or beyond the Retina, and in either Case will cause indistinct Vision. The first is the Case of short-sighted or purblind People, the latter of the Aged.
A purblind Person, having the Convexity of the Eye and Crystalline Humour too great, will have the Rays united in a Point before they reach the Bottom of the Eye, and consequently the Images of Objects will be form'd, not upon the Retina, (as they should be) but above it in the Glassy Humour, and therefore will appear indistinct or confused.
<88>This Defect of the Eye is remedied two Ways, viz. (1.) By diminishing the Distance between the Object and the Eye, for by lessening the Distance of the Object, the Distance of the Focus and Image will be increased, till it falls on the Retina, and appears distinct. (2.) By applying a concave Glass to the Eye, for such a Glass makes the Rays pass more diverging to the Eye, in which Case the Distance of the Focus will be also enlarged, and thrown upon the Retina, where distinct vision will ensue.
Hence the Use of Concave Spectacles: And the Myops or purblind Person, who uses them, has the three following peculiarities, viz. (1.) To him Objects appear nearer than they really are, or do appear to a sound Eye. (2.) The Objects appear less bright, or more obscure, to them than to other People, because a lets Quantity of Rays of Light enter the Pupil. (3.) Their Eyes grow better with Age, for whereas the Fault is too great a Convexity of the Eye, the Aqueous Humour, and also the Crystalline, wasting with Age will grow flatter, and therefore more fit to view distant Objects.
The other Defect of the Eyes arises from a quite contrary Cause, viz. the Cornea and Crystalline Humour being too flat, as is generally the Case of an old Eye. This Defect is remedied by Convex Lenses, such as are the common Spectacles, and Reading Glasses. For since the Rays, in these Eyes, go beyond the Bottom of the Eye, before they come to a Focus, or form the Image; a convex Glass will make the Rays fall more converging to the Pupil, and on the Humours, by which means the Focal Distance will be shorten'd, and adjusted to the Retina, where distinct Vision of Objects will then be effected.
By convex Spectacles Objects appear more bright, because they collect a greater Quantity of Rays on the Pupil. And they appear at a greater Distance than they are; for the nearer the Rays approach to parallel ones, the more distant the Point will be to which they tend.
I have already observed, that if the Object be placed nigher to the convex Glass than its Focus, it will appear erect and magnified which makes them of such general Use as Reading Glasses.
If an Object be placed in the Focus of a convex Lens, the Rays which proceed from it, after they have pass'd through the Glass, will proceed parallel, and therefore an Eye placed any where in the Axis will have the most distinct view of the Object possible; and if it be a Lens of a small Focal Distance, then will the Object appear as much larger as it is nearer, than when you view it with the naked Eye. And hence their Use as Single Microscopes: To give an Instance of which, suppose the Focal Distance of a Lens were one Tenth of an Inch, then will the Diameter or Length of an Object appear 60 times larger than to the naked Eye at six Inches Distance: Also the Superficies of an Object will be 3600 times larger; and the whole Magnitude or Bulk will be 216000 times larger than to the naked Eye it will appear at the abovesaid Distance.
Compound Microscopes, especially the common Sort, are constructed with three Glasses, viz. the Object-Lens de, and two Eye-Glasses DE and GH. The Object abc being placed at a little more than the Focal Distance from the Lens de, will have its Image form'd at a greater Distance on the other Side, and proportionably large, as at MN; which large Image is contracted into one ABC somewhat less, by the lower Eye-Glass DE; and this Image is view'd by the Eye through the upper Eye-Glass GH, where it also distinctly views the Micrometer opq, passing over a minute Part of the Image in measuring it. But what is farther necessary in the Theory and Structure of these Microscopes may be found in my Micrographia Nova, together with a large Account of all Kinds of Micrographic Objects, and a Description of the Solar Microscope. Yet, that the Reader may have an Idea of the two new Forms of Microscopes described in that Book, I have here annex'd the Plates, viz. of the Pocket and Universal Microscope respectively.
The Telescope is of two Sorts, viz. Dioptric, or Refracting; or Cata-Dioptric, by Reflection and Refraction conjointly. [Image 42] A refracting Telescope consists of an Object-Glass xz, by which the image fd of an Object OB, at a distance, is form'd in the Focus a of the said Glass, and in an inverted Position. This Image may be view'd by a single Lens ab, placed at its Focal Distance, as is usually done for viewing the heavenly Bodies, because in them we regard not the Position: But for viewing Objects near us, whose Image we would have erect, we must for that purpose add a second Lens pq, at double its Focal Distance from the other, that the Rays which come from ab may cross each other in the Focus O, in order to erect the Image gn, which it will form in its own Focus m, because the Rays come parallel from the first Lens ab. Lastly, a third Lens ic is added, to view that secondary Image gn. These three Lenses, or Eye-Glasses, are usually of the same Size and Focal Length; and the Power of magnifying is always as the Focal Length of the Object-Glass ew divided by the Focal Length of the Eye-Glass lm or he. For instance: Suppose ew = 10 Feet or 120 Inches, and he or lm = 3 Inches; then will the Length of the Object appear to the Eye through such a Telescope 40 times larger than to the naked Eye, and its surface will be magnified 1600 times, and its Bulk or Solidity 64000 times.
If instead of a convex Eye-Glass we should use a concave one of the same Focal Length, it would represent the Object erect, equally magnified, and more distinct and bright; but the Disadvantage of this Glass is, that it admits of but a small Area, or Field of View, and therefore not to be used when we would see much of an Object, or take in a great Scope; but it is used to great Advantage in viewing the Planets and their Satellites, Saturn's Ring, Jupiter's Belts, &. This is call'd the Galilean Telescope, from Galileo, the inventor, and is the first Sort of Telescope ever made.
The Cata-dioptric or Reflecting Telescope is the most noble and useful of all others; the Mechanism whereof is as follows: [Image 43] ABEH is the large Tube or Body of the Instrument, in which BE is a large reflecting Mirrour, with a Hole in the Middle CD. This Mirrour receives the Rays ac, bd, coming from the Object at a distance, and reflects them converging to its Focus e, where they cross each other, and form the inverted Image IM. xy is a small concave Mirrour, whose Focus is at f, at a small Distance from the Image. By this means the Rays coming from the Image are reflected back through the central Hole CD of the large Mirrour, where they fall on the plano-convex Lens WX, and are by it converged to a Focus, and there form a second Image RS, very large and erect, which is view'd by a Meniscus Eye-Glass YZ by the Eye at P, through a very small Hole in the End of the Eye-Piece YCDZ.
If the first Lens WX were taken away, the Image would be form'd somewhat larger at Mg; but the Area, or Scope, would be less, and therefore the view not so pleasant. At TV is placed a circular Piece of Brass, with a Hole of a proper Size to circumscribe the Image, and cut off all superfluous or extraneous Rays, that so the Object may appear as distinct as possible.
As the Image is form'd by Reflection, the Rays of every Sort will be united nearly in one Point, and will therefore admit of an Eye-Glass YZ of a deep Charge, or small Focal Distance; and so the Power of magnifying will be proportionally greater; for it will be in a Proportion compounded of and , if only one Eye-Glass Yz be used. Thus, in Numbers, suppose Qe = 12 Inches, eG = 3,5; Gk = 18, and kt = 1; then will nearly; whence by such a Telescope the Length of an Object will be magnified 50 times, the Surface 2500 times, and the Solidity 125000 times; yet the Telescope not above 20 Inches long; an Effect equal to that of a refracting Telescope 16 Feet in Length.
As to the Camera Obscura, and Magic Lanthorn, they both perform their Effects by a single Lens; the former being only the Object-Glass of a long Telescope applied in a Scioptric Ball to the Hole of a Window-Shutter, in a darken'd Room; which gives a lively Picture of all the Objects which lie before it, in true Perspective, but in an inverted Position, on a white Sheet or Plane held at the Focal Distance of the said Glass: And on the other hand, the Magic Lanthorn is only a large convex Lens, with a short Focal Distance, which by being placed at a proper Distance from small transparent-colour'd Pictures or Figures, forms a large and surprizing Image thereof at a great Distance; in order to which, it is necessary to illuminate them very strongly with the Light of the Candle thrown on them by another very large and very convex Lens.
The Solar Microscope is of the same Kind with Magic Lanthorn; only here the Objects are very small, and strongly enlighten'd by the Sun through a concave Lens; they are also magnified by a small Lens, of a very short Focal Distance, that the images may he thrown large and distinctly on the opposite wall of a darken'd Room: Which, if well perform'd, is one of the most exquisitely curious and most delightfully surprizing Effects that are possible to be produced by any Optical Instrument whatsoever.
LECTURE XI.
The Copernican or Solar System explain'd by the Orrery and Cometarium.
I SHALL in this Lecture endeavour to exhibit to you a just and natural Idea of the mundane or Solar System, that is, the System of the World; consisting of the Sun; the Primary Planets, and their Secondaries, or Moons; the Comets; and the Fixed Stars; according to the Hypothesis of Pythagoras among the Ancients, and revived by Copernicus: Which System is fully proved, and establish'd on the justest Reasoning, and Physical and Geometrical Conclusions, by all our modern Astronomers.
The most celebrated Hypotheses, or Systems of the World, are three, viz. (1.) The Ptolomean, invented by Ptolomy, an antient Egyptian Philosopher, which assigns such Positions and Motions to the heavenly Bodies, as they appear to the Senses to have. (2.) The Tychonic System, or that of the Noble Danish Philosopher, Tycho Brahe. (3.) The Pythagorean, Copernican, or Solar System, above-mention'd. Of all which in Order.
The Ptolomean System supposes the Earth immoveably fix'd in the Center, not of the World only, but of the Universe; and that the Sun, the Moon, the Planets, and Stars, all moved about it from East to West once in twenty-four Hours, in all the Order following, viz. the Moon, Mercury, Venus, the Sun, Mars, Jupiter, Saturn, the Fix'd Stars; and, above all, the Figment of their Primum Mobile, or the Sphere which gave Motion to all the rest. But this was too gross, and absurd, to be received by any learned Philosopher, after the Discoveries by Observations and Instruments which acquaint us with divers Phænomena of the heavenly Bodies, altogether inconsistent with, and, in some Things, exactly contradictory to, such an Hypothesis; as will be shewn by the Arguments adduced to prove the Truth of the Copernican System.
The Tychonic System supposed the Earth in the Center of the World, that is, of the Firmament of Stars, and also of the Orbits of the Sun and Moon, but at the same time it made the Sun the Center of the Planetary Motions, viz. of the Orbits of Mercury, Venus, Mars, Jupiter, and Saturn. Thus the Sun, with all its Planets, was made to revolve about the Earth once a Year, to solve the Phænomena arising from the annual Motion; and the Earth about its Axis from West to East once in 24 Hours, to account for those of the diurnal Motion. But this Hypothesis is so monstrously absurd, and contrary to the great Simplicity of Nature, and in some respects even contradictory to Appearances, that it obtain'd but little Credit, and soon gave way to
The Copernican System of the World, which supposes the Sun to possess the central Part; and that about it revolve the Planets and Comets in different Periods of Time, and at different Distances therefrom, in the Order following, viz.
I. Mercury, at the Distance of about 32 Millions of Miles, revolves about the Sun in the Space of 87 Days, 23 Hours, and 16 Minutes.
II. Venus, at the Distance of 59 Millions of Miles, in 224 Days, 16 Hours, 49 Minutes.
III. The Earth, at the Distance of about 82 Millions of Miles, in 365d. 6h. 9m. or Sydereal Year.
IV. Mars, at the Distance of 123 Millions of Miles, in 686d. 23h. 27m. or 1 Year, 321d. 17h. 18m.
<95>V. Jupiter, at the Distance of 424 Millions of Miles, in 4332 Days, 12h. 20 m. or almost 12 Years.
VI. Saturn, at the Distance of 777 Millions of Miles, in 10759d. 6h. 36m. or nearly 30 Years.
VII. The Comets, in various and vastly eccentric Orbits, revolve about the Sun in different Situations and Periods of Time, as represented in the Scheme of Mr. Whiston's Solar System.
These are all the heavenly Bodies yet known to circulate about the Sun, as the Center of their Motions; and among the Planets, there are three which are found to have their secondary Planets, Satellites, or Moons revolving constantly about them, as the Centers of their Motions, viz.
The Earth, which has only one Moon revolving about it, in 27d. 7h. 43m. at the mean Distance of about 240000 Miles.
Jupiter is observed with a Telescope to have four Satellites, which move about him in the Times and Distances following, viz.
The First in 1d. 18h. 27m. at the Distance of 5 Semidiameters of Jupiter's Body from his Center, as measured with a Micrometer.
The Second in 3d. 13h. 13m. at the Distance of 9 Semidiameters.
The Third in 7d. 3h. 42m. at the Distance of 14 Semidiameters.
The Fourth in 16d. 16h. 32m. at the Distance of 25 Semidiameters.
Saturn has five Moons; and besides them a stupendous Ring surrounding his Body, whose With and Distance from Saturn's Body are equal, and computed at upwards of 20000 Miles. The Periodical Times and Distances of the Saturnian Moons, in Semidiameters of the Ring, are as follow.
The First, or inmost, revolves about Saturn in 1d. 21h. 18m. at the Distance of near 2 Semidiameters of the Ring.
The Second in 2d. 17h. 41m. at the Dist. of 2 Semidiameters
<96>The Third in 4d. 12h. 25m. at the Distance of 3 Semidiameters.
The Fourth in 15d. 22h. 41m. at the Distance of 8 Semidiameters.
The Fifth in 70d. 22h. 4m. at the Distance of 23 Semidiameters.
These are the constituent parts of the Solar System, which is now received and approved as the only true System of the World, for the following Reasons.
I. It is most simple, and agreeable to the Tenor of Nature in all her Actions; for by the two Motions of the Earth all the Phænomena of the Heavens are resolved, which by other Hypotheses are inexplicable without a great Number of other Motions, contrary to philosophical Reasoning by Rule 1.
II. It is more rational to suppose the Earth moves about the Sun, than that the huge Bodies of the Planets, the stupendous Body of the Sun, and the immense Firmament of Stars, should all move round the inconsiderable Body of the Earth every twenty-four Hours.
III. The Earth moving round the Sun is agreeable to that general Harmony, and universal Law, which all other moving Bodies of the System observe, viz. That the Squares of the periodical Times are as the Cubes of the Distances: But if the Sun move about the Earth, that Law is destroy'd, and the general Order and Symmetry of Nature interrupted; since according to that Law the Sun would be so far from revolving about the Earth in 365 Days, that it would require no less than 5196 Years to accomplish one Revolution.
IV. Again: Did the Sun observe the universal Law, and yet revolve in 365 Days, his Distance ought not to be above 310 Semidiameters of the Earth, whereas it is easy to prove it is really above 20000 Semidiameters distant from us.
V. The Sun is the Fountain of Light and Heat, which it irradiates through all the System, and therefore it ought to be placed in the Center, that so all the Planets may at all times have it in an uniform and equable Manner: For,
VI. If the Earth be in the Center, and the Sun and Planets revolve about it, the Planets would then, like the Comets, be scorched with Heat when nearest the Sun, and frozen with Cold in their Aphelia, or greatest Distance; which is not to be supposed.
VII. If the Sun be placed in the Center of the System, we have then the rational Hypothesis of the Planets being all moved about the Sun by the universal Law or Power of Gravity arising from his vast Body, and every thing will answer to the Laws of circular Motion, and central Forces: But otherwise we are wholly in the dark, and know nothing of the Laws and Operations of Nature.
VIII. But happily we are able to give not only Reason, but demonstrative Proofs, that the Sun does possess the Center of the System, and that the Planets move about it at the Distance and in the Order above assign'd: The first of which is, That Mercury and Venus are ever observed to have two Conjunctions with the Sun, but no Opposition; which could not happen, unless the Orbits of those Planets lay within the Orbit of the Earth.
IX. The second is, That Mars, Jupiter, and Saturn, have each their Conjunctions and Oppositions to the Sun, alternate and successively; which could not be, unless their Orbits were exterior to the Orbit of the Earth.
X. In the third Place, The greatest Elongation or Distance of Mercury from the Sun is but about 20 Degrees, and that of Venus but about 47; which answers exactly to their Distances in the System above assign'd: But in the Ptolomean System, they might and would sometimes be seen 180 Degrees from the Sun, viz. in Opposition to him.
XI. Fourthly, In this Disposition of the Planets they will all of them be sometimes much nearer to the Earth than at others; the Consequence of which is, that their Brightness and Splendor, and also their apparent Diameters, will be proportionally greater at one Time than another: And this we observe to he true every Day. Thus the apparent Diameter of Venus, when greatest, is near 66 Minutes, but when least not more than 9 Minutes and a half; of Mars, when greatest, it is 21 Minutes, but when least no more than 2 Minutes and a half; whereas by the Ptolomean Hypothesis they ought always to he equal.
XII. The fifth is, That when the Planets are view'd with a good Telescope they appear with different Phases, or with different parts of their Bodies enlighten'd. Thus Venus is sometimes new, then horned, after that dichotomized, then gibbous, afterwards full; and so increases and decreases her Light, in the same manner as the Moon, and as the Copernican System requires.
XIII. The sixth is, That the Planets, all of them, do sometimes appear direct in Motion, sometimes retrograde, and at other times stationary. Thus Venus, as she passes from her greatest Elongation Westward to her greatest Elongation Eastward, will appear direct in Motion, but retrograde as she passes from the latter to the former; and when the is in those Points of greatest Distance from the Sun, she seems for some time stationary: All which is necessary upon the Copernican Hypothesis, but cannot happen in any other.
XIV. The seventh is, That the Bodies of Mercury and Venus, in their lower Conjunctions with the Sun, are hid behind the Sun's Body; and, in the upper Conjunctions, are seen to pass over the Suns Body or Disk in form of a black round Spot: Which is necessary in the Copernican, but impossible in the Ptolomean System.
XV. The eigth is, That the Times in which these Conjunctions, Oppositions, Stations, and Retrogradations of the Planets happen, are not such as they would be, were the Earth at Rest in its Orbit but precisely such as would happen, were the Earth to move, and all the Planets in the Periods above assign'd them: And therefore this, and no other, can be the true System of the World; and it will stand the eternal Test of future Ages, for, Mighty is the Force of Truth, and shall prevail.
But though the Planets all move round the Sun in Orbits commonly supposed circular, yet are they not exactly so, but elliptical, or in form of an Ellipsis, which Figure is vulgarly call'd an Oval, as ABPD, described about two Centers S, F, call'd the Foci, or Focal Points of the Ellipse. The Point C is the Center; AP the Axis, or longest Diameter; and BD the shortest Diameter: And in one of these Focus's, viz. S, the Sun is placed, about which the Planet moves in the Orbit ABPD.
Hence, when the Planet is in the Point P, it is nearest the Sun, which Point is, for that Reason, call'd the Perihelion: Here, therefore, the Attraction of the Sun is strongest, his Light and Heat greatest, and his apparent Diameter largest, and in this Point the Planet must consequently move with the greatest velocity. But in the Point A, where the Planet is farthest distant from the Sun, (for that Reason call'd the Aphelion) every thing is just the reverse: And in the Points B or D it is in its mean Distance from the Sun.
Now though the Planetary Orbits are really elliptical, yet is the Eccentricity CS, in most of them, so extremely small, as to be almost insensible, and therefore their Motions may be look'd upon as circular, and as such represented in Orreries and Diagrams, without any sensible Error.
The Orrery is, therefore, an adequate Representation of the True Solar System, and gives a just Idea of the Number, Motions, Order, and Positions of the heavenly Bodies: But the Proportion of Magnitude and Distances of the Planets is not to be expected from the Orrery, but by Delineation, as in Mr. Whiston's Solar System; where the several Orbits of the Planets are laid down in their proportional Distances from the Sun, and their Magnitudes comparatively with each other, and with that of the Sun, express'd by the outmost Circle of the Scheme.
The principal Use of the Orrery is to render the Theory of the Earth and the Moon easy and intelligible; and to evidence to our Senses how all those Appearances happen, which depend on the annual or diurnal Rotation of the Earth, and the monthly Revolution of the Moon: As, the Variety of Seasons, the vicissitudes and various Lengths of Days and Nights, the Manner of Solar and Lunar Eclipses, the various Phases of the Moon, &c.
In my Orrery, which is of a peculiar and most elegant Structure, the Earth in its annual Motion passes round by a Circle, on which is engraved the Calendar, and the Ecliptic; and the Plate which carries the Earth about has an Index on the opposite Part from the Earth, to shew the apparent Place of the Sun in the Ecliptic, for every Day of the Year; and one Turn of the winch carries the Earth once round its Axis, and the said Index over the Space of one Day in the Calendar: So that by this means the true Place of the Earth, and the apparent Place of the Sun, also the Place and Phases of the Moon, may be readily shewn for any Day required.
The Orrery-Part, containing the Wheel-Work, is placed within a large and most beautiful Armillary Sphere, which turns about upon its Axis, with a fairly-engraved and silver'd Horizon, which is also moveable every way upon a most elegant Brass Supporter, with four Legs richly wrought; at the Bottom of which is a noble large silver'd Plate, with a Box and Needle, and Compass, with the Names of all the Points finely engraven in words at Length. The Circles of the Sphere are as follow.
The Equinoctial, which divides the Sphere into two Parts, viz. the Northern and the Southern Hemisphere; and is so call'd, because when the Sun comes to pass over it, (as it does twice every Year) the Days and Nights are then equal. This Circle is divided into 360 Degrees, call'd the Right Ascension of the Sun or Stars.
The Ecliptic is that great Circle which represents the apparent annual Path of the Sun through the Heavens. It is divided into 12 equal Parts call'd Signs, consisting of 30 Degrees each; whose Names and Characters are as follows. 1. Aries, the Ram, ♈; 2. Taurus, the Bull, ♉; 3 Gemini, the Twins, ♊, 4. Cancer, the Crab, ♋; 5. Leo, the Lion, ♌; 6. Virgo, the virgin, ♍; 7. Libra, the Scales, ♎; 8. Scorpio, the Scorpion, ♏; 9. Sagittarius, the Bowman, ♐; 10. Capricorn, the horned Goat, ♑; 11. Aquarius, the Waterer, ♒; 12. Pisces, the Fishes, ♓. The Ecliptic intersects the Equinoctial in the Beginning of Aries and Libra, in an Angle of 23 Degrees, 29 Minutes. In this Circle the Longitude of the heavenly Bodies is reckon'd. The Ecliptic is the Middle of
The Zodiac, which is a broad silver'd Zone, encompassing the Sphere to five Degrees on each Side the Ecliptic; so call'd from the figures of the several Animals, or Constellations of the Signs, with which it is adorned and embellish'd. This Zone comprehends within it the Paths or Orbits of all the Planets.
The Meridian is a great Circle passing through the Poles, and cutting the Equinoctial at Right Angles; so call'd, because when the Sun is upon any Meridian, it makes the Meridies, Mid-Day, or Noon, to all Places under it. Of these, there is one call'd
The General Meridian, within which the whole Sphere turns, and upon which are engraven the Degrees of Latitude, beginning and proceeding each way from the Equinoctial to the Poles. To this Circle the Sphere is suspended; and being moveable within the Horizon, the Sphere may be elavated or rectified for the Latitude of any Place.
The Horizon is that broad silver'd Frame, or Circle, which contains the whole Machine, moveable every way within it. It is so call'd because it bounds our Sight in the Heavens, and divides the Sphere into the upper and lower Hemisphere. Upon this Circle are curiously engraven the Ecliptic Signs and the Calendar, for readily finding the Sun's place for any given Day or Time. On this Circle is also reckon'd the Amplitude of the Sun, &c.
The Points where the Ecliptic intersects the Equinoctial are call'd the Equinoctial Points, or Equinoxes, because when the Sun is in them, the Days and Nights are equal. As the Sun is in one of them in the Spring, it is call'd the Vernal Equinox; and in the other at Autumn, it is call'd the Autumnal Equinox.
The Beginning of Cancer and Capricorn are call'd the Solstitial Points, or the Solstices; which is as much as to say, the Stations of the Sun, because when the Sun is in those Points, he seems stationary, or not to move for some Days: The first is the Summer, the other the Winter Solstice.
The Meridians which pass through the Points above-mention'd are call'd the Equinoctial and Solstitial Coloures respectively. They divide the Sphere into four Quarters, in the Middle of the four Seasons of the Year.
The Lesser Circles of the Sphere are the Tropics and Polar Circles; which are all parallel to the Equinoctial, and are two on either Side. The Northern Tropic is that of Cancer; the Southern, that of Capricorn; as passing through the Beginning of those Signs. They are distant from the Equinoctial 23 Degrees, 29 Minutes, and include that Space or Part of the Sphere which is call'd the Torrid Zone on the Terrestrial Globe, because the Sun is at one Time or other perpendicular over every part, and extremely torrifies or heats it.
Within 23 Deg. 29 Min. of each Pole lie the Polar Circles; of which that about the North Pole is call'd the Arctic Circle, because of the Constellation of the Bear in that part; and the other about the South Pole, the Antarctic Circle. They include those spaces which are call'd the Frigid Zones, by reason of the intense Cold which reigns in those Regions the greatest Part of the Year. Those Spaces which lie between the Tropics and Polar Circles, on either Side, are call'd the Temperate Zones, as enjoying a mean or moderate Degree of Heat and Cold.
The Circles above are essential to the Sphere; besides which there is the Quadrant of Altitude, for shewing the Height of any Luminary above the Horizon; and a large and most beautiful Horary Circle and Index, shewing the Time corresponding to the Motion of the Sphere: Also the Solar Label, for fixing the Sun to its proper place in the Ecliptic.
It is easy to conceive, that the Sun will always enlighten one Half of the Earth; and that when the Sun is in the Equinoctial, the Circle which terminates the enlighten'd and darken'd Hemispheres (which is call'd the Circle of Illumination) will pass thro' the Poles of the Earth, and also divide all the Parallels of Latitude into two equal Parts. But since the Earth moves not in the Plane of the Equinoctial, but that of the Ecliptic, the Axis of the Earth will be inclined to that of the Ecliptic in an Angle of 23 Deg. 29 Min.; and therefore the Circle of Illumination will, at all other Times, divide the Parallels of Latitude into two unequal Parts.
Now since any Parallel is the Path or Tract which any Place therein describes in one Revolution of the Earth, or 24 Hours; therefore that Part of the parallel which lies in the enlighten'd Hemisphere will represent the Diurnal Arch, or Length of the Day; and that Part in the Dark Hemisphere will be the Nocturnal Arch, or Length of the Night, in that Parallel of Latitude.
Hence, when the Orrery is put into Motion, the Earth moving with its Axis always parallel to itself, yet always inclined to the Plane of the Ecliptic, will sometimes have the Northern Parts turn'd more directly to the Sun, and most enlighten'd; and at other times the Southern Parts will be so. Hence various Alterations of Heat and Cold, and Length of Days and Nights, will ensue in the Course of the Revolution of the Earth about the Sun, which will constitute all the Variety of Seasons, as will most naturally and evidently be shewn in the Orrery, as follows.
We will first give the Earth Motion in the first point of Libra; the Sun will then appear to enter Aries, and this will be the Vernal Equinox; for now, the Sun being in the Equinoctial, all Parts of the Earth will be equally enlighten'd from Pole to Pole, and all the Parallels of Latitude divided into two equal parts by the Circle of Illumination. Hence the Days and Nights will be equal, and the Sun's Heat is now at a Mean between the greatest and the least: All which Particulars constitute that agreeable Season we call the Spring, the Middle of which is shewn by the Index to be the 11th of March.
As the Earth passes on from West to East, through Libra, Scorpio, and Sagittarius, to the Beginning of Capricorn, the Sun will appear from the Earth to move through the opposite Signs of the Ecliptic, viz. Aries, Taurus, Gemini, to the Beginning of Cancer; during which Time, by the inclined Position of the Earth's Axis, the Northern parts will he gradually turn'd towards the Sun, and the Southern Parts from it; whence the Sun's Rays will fall more and more directly on the former, and pass through at still less Quantity of the Atmosphere; but in the Southern Parts, the reverse. Also in the Northern Parts the Arches of the Parallels in the enlightened Hemisphere will continually increase, and those in the dark one decrease, shewing the constant Increase of the Days, and Decrease of the Nights: All which will be in their greatest Degree when the Sun is arrived to Cancer; and therefore that will be the Middle of that Season we call Summer, in Northern Latitude; but in Southern Latitude every thing will be the reverse, and their Season Winter.
The North Frigid Zone is now wholly enlighten'd, and the pole turn'd towards the Sun as far as possible; but now as the Earth moves on, the North Pole returns, the Diurnal Arches begin gradually to decrease, and the Nocturnal to increase, and of consequence the Sun's Rays fall more and more obliquely, and his Heat proportionally diminishes till the Earth comes to Aries, when the Sun will appear in Libra; and thus produce an Equality of Light and Heat, of Day and Night, to all Parts of the world. This will be the Middle of the Season call'd Autumn, and that Day, the Autumnal Equinox.
But as the Earth goes on through Aries, Taurus, and Gemini, you will see the Sun pass through the opposite Signs of Libra, Scorpio, Sagittarius. The North Pole is now in the dark Hemisphere, and the Frigid Zone is now more and more Obscured therein: All Northern Latitudes continue gradually turning from the Sun, and his Rays pass more and more obliquely on them, and pass through a larger Body of the Atmosphere: The nocturnal Arches continue to increase, and the diurnal to decrease: All which Contribute to make the dismal dreary Season we call Winter; the midst whereof is shewn by the Sun's entering the first Scruple of Capricorn on the 10th of December, as by the Index may be seen.
Lastly: As the Earth journeys on from thence through Cancer, Leo, and Virgo, the Sun appears to pass through Capricorn, Aquarius, and Pisces; and all Things change their Face. The Northern Climes begin to return, and receive more directly the enlivening Beams of the Sun, whose Meridian Height does now each Day increase; the Days now lengthen, and the tedious Nights Contract their respective Arches and every thing conspires to advance the delightful Season of the Spring, the Midst whereof is shewn by the Earth's returning again to that Point, where first we gave it Motion.
All these Appearances of the Seasons, &c. are shewn as well for the Southern Latitudes, where at the same Time they happen in Order just the reverse to what we have now observed for the Northern. Thus, when it is Summer with us, it is Winter with them, and they have their Days shortest when ours are longest, and vice versa. All which is most distinctly seen in the Orrery.
<106>At the same Time the Earth is going round the Sun, the Moon is seen constantly circulating round the Earth once in 29 Days and a half; which Days are number'd on a silver'd Circle, and shewn by an Index moving over them. Thus each Day of the Moon's Age, and the Phasis proper thereto, are shewn for any required Time; and also why we see always one and the same Face of the Moon viz. on account of her turning about her own Axis in the same Time she takes to revolve about the Earth.
Again: By placing a Lamp in the Orrery, and making the Room dark, we see very naturally how the Sun is eclipsed by the New Moon, and the Shadow passing over the Disk of the Earth and also how the Moon, at Full, is eclipsed by passing through the shadow of the Earth. Here also we see the Manner how Mercury and Venus transit the Sun's Face in form of a dark round Spot; and also why they can never appear at a great Distance from the Sun and various other Phænomena, of the like Nature.
The Cometarium is a very curious Machine, which exhibits an Idea of the Motion or Revolution of a Comet about the Sun, and as this Sort of Motion is not perform'd in circular, but very elliptic Orbits, so in this Instrument, a peculiar Contrivance by elliptical Wheels is necessary to effect it which as a great Curiosity will he shewn, together with all Parts of the Machine, in my new Construction thereof. The Comet here represented is that which appear'd in the Year 1682, whose Period is 75 Years and a half, and therefore will again appear in 1758. By this Piece of Machinery is shewn the unequal Motion of a Comet in every Part of its Orbit, the great Velocity with which it moves in the Perihelion Part of its Orbit, and how from thence it moves with a retarded velocity till it arrives at the Aphelion Point, where its Motion is slowest of all and from thence it is seen continually accelerating its Motion towards the Perihelion, in such manner as the Laws of Attraction require. The Comet is represented by a small Brass Ball, carried by a Radius Vector, or Wire, in an elliptic Groove, about the Sun in one of its Foci; and the Years of its Period are shewn by an index moving with an equable Motion over a graduated silver'd Circle: The Whole being a just Representation of the present Theory of those prodigious and wonderful Phænomena of the Planetary System.
LECTURE XII.
The Use of the GLOBES.
IN this Lecture I shall explain the Nature and Use of both the Globes, by giving you a succinct Account of the Nature and Design of each, and a Solution of the principal Problems that are usually perform'd thereby.
Each Globe is suspended in a General Meridian, and moveable (within an Horizon) about its Axis, in the same manner as the Armillary Sphere of the Orrery; and the Circles of that Sphere, already described, are laid on the corresponding Parts of the Surface of each Globe; and are therefore supposed to be known.
The Surface of the Celestial Globe is a Representation of the concave Surface of the Starry Firmament, there being depicted all the Stars of the first and second Magnitude, and the most noted of all the rest that are visible. So that by this Globe we may shew the Face of the Heavens for any required Time, by Day or Night, throughout the Year, in general; or in regard to any particular Body, as the Sun, Moon, Planet, or Fix'd Star.
The Stars are all disposed into Constellations, under the forms of various Animals, whose Names and Figures are printed on the Paper which covers the Globe; which were invented by the ancient Astronomers and Poets, and are still retain'd for the sake of Distinction and better Arrangement of those Luminaries, which would be otherwise too confused and promiscuous for easy Conception, and a regular Method of treating on them.
In order to understand the following Problems, it will be necessary to premise the following Definitions in relation thereto, viz.
I. The Declinationn of the Sun and Stars is their Distance from the Equinoctial in Degrees of the General Meridian, towards either pole, North or South.
II. Right Ascension is that Degree of the Equinoctial reckon'd from the Beginning of Aries, which comes to the Meridian with the Sun or Star.
III. Oblique Ascension is that Degree of the Equinoctial which comes to the Horizon when the Sun or Star is rising: And Oblique Descension is that Point which comes to the Horizon on the West Part, when the Sun or Star is descending or setting in an oblique Sphere.
IV. Ascensional Difference is the Difference between the Right and Oblique Ascension.
V. The Longitude of the Sun or Star is an Arch of the Ecliptic, between the first Point of Aries, and that Point of the Ecliptic to which the Luminary is referr'd by the Meridian passing through it; and is therefore reckon'd in Signs and Degrees of the Ecliptic.
VI. The Lattitude of a Star is its Distance from the Ecliptic towards the North or South Pole.
VII. Amplitude is the Distance at which the Sun or Star rises or sets, from the East or West Point of the Horizon, towards the North or South.
VIII. Azimuth is the Distance between the North Point of the Horizon, and the Point where the Vertical Circle, passing through the Body of the Sun or Star, cuts the Horizon.
IX. The Altitude of the Sun or Star is its Height above the Horizon, measured in the Degrees of the Quadrant of Altitude, or moveable Azimuth Circle.
X. A Star is said to rise or set Cosmically, when it rises or set when the Sun rises.
XI. A Star rises Acronically, if it rises when the Sun sets.
XII. A Star rises Heliacally, when it emerges out of the Sunbeams, and is seen in the Morning before Sun-rising: And it sets Helically, when it is so near the Sun that it cannot be seen.
XIII. A Right Sphere is that whose Polese are in the Horizon and the Equinoctial, and all its Parallels cut the Horizon at Right Angles.
XIV. A Parallel Sphere is that whose Poles co-incide with the Poles of the Horizon, or Zenith and Nadir; and the Equinoctial with the Horizon; and all the Parallels, parallel thereto.
XV. An Oblique Sphere is that, one of whose Poles is above the Horizon, and the other below it; and the Equinoctial and its Parallels obliquely cutting the same.
The Problems on the Celestial Globe are the following.
PROB. I. To rectify the Globe:
Elevate the Pole to the Latitude of the Place, and every thing as directed under PROB. II. of the Terrestrial Globe, which see.
PROB. II. To find the Sun's Place in the Ecliptic:
Find the Day of the Month in the Calendar on the Horizon, and right against it is the Degree of the Ecliptic which the Sun is in for that Day.
PROB. III. To find the Sun's Declination:
Rectify the Globe, bring the Sun's Place in the Ecliptic to the Meridian, and that Degree which it cuts in the Meridian is the Declination required.
PROB. IV. To find the Sun's Right Ascension:
Bring the Sun's Place to the Meridian, and the Degree in which the Meridian cuts the Equinoctial is the Right Ascension required.
PROB. V. To find the Sun's Amplitude:
Bring the Sun's Place to the Horizon, and the Arch of the Horizon between it and the East or West Point is the Amplitude, North or South.
PROB. VI. To find the Sun's Altitude for any given Day and Hour:
Bring the Sun's Place to the Meridian; set the Hour-Index to the upper XII; then turn the Globe till the Index points to the given Hour, where let it stand; then screwing the Quadrant of Altitude in the Zenith, lay it over the Sun's Place, and the Arch contained between it and the Horizon will give the Degrees of Altitude required.
PROB. VII. To find the Sun's Azimuth for any Hour of the Day:
Every thing being done as in the last Problem, the Arch of the Horizon contain'd between the North Point and that where the Quadrant of Altitude cuts its, is the Azimuth East or West, as required.
PROB. VIII. To find the Time when the Sun rises or sets:
Find the Sun's Place for the given Day; bring it to the Meridian, and set the Hour-Hand to XII; then turn the Glove till the Sun's Place touches the East Part of the Horizon, the Index will shew the Hour of its Rising: After that, turn the Globe to the West Part of the Horizon, and the Index will shew the Time of its Setting for the given Day.
PROB. IX. To find the Length of any given Day or Night:
This is easily known by taking the Number of Hours between the Rising and Setting of the Sun for the Length of the Day; and the Residue, to 24, for the Length of the Night.
<111>PROB. X. To find the Hour of the Day, having the Sun's Altitude given:
Bring the Sun's Place to the Meridian, and set the Hour-Hand to XII; then turn the Globe in such manner, that the Sun's Place may move along by the Quadrant of Altitude, (fix'd in the Zenith) till it touches the Degree of the given Altitude; where stop it, and the Index will shew on the Horary Circle the Hour required.
PROB. XI. To find the Place of the Moon or any Planet, for any given Day:
Take Parker's or Weaver's Ephemeris, and against the given Day of the Month you will find the Degree and Minute of the Sign which the Moon or Planet possesses at Noon, under the Title of Geocentric Motions. The Degree thus found, being mark'd in the Ecliptic on the Globe by a small Patch, or otherwise; you may then proceed to find the Declination, Right Ascension, Latitude, Longitude, Altitude, Azimuth, Rising, Southing, Setting, &c. in the same manner as has been shewn for the Sun.
PROB. XII. To explain the Phænomena of the Harvest Moon:
In order to this we need only consider, that when the Sun is in the Beginning of Aries, the Full Moon on that Day must be in the Beginning of Libra: And since when the Sun sets, or Moon rises, on that Day, those Equinoctial Points will be in the Horizon, and the Ecliptic will then be least of all inclined thereto, the Part or Arch which the Moon describes in one Day, viz. 13 Degrees, will take up about an Hour and a Quarter ascending above the Horizon; and therefore so long will be the Time after Sun-set, the next Night, before the Moon will rise. But at the opposite Time of the Year, when the Sun is in the Autumnal, and Full Moon in the Vernal Equinox, the Ecliptic will, when the Sun is setting, have the greatest Inclination to the Horizon; and therefore 13 Degrees will in this Case soon ascend, viz. in about a Quarter of an Hour, and so long after Sun-set will the Moon rise the next Day after Full: Whence, at this Time of the Year, there is much more Moon-Light than in the Spring; and hence this Autumnal full Moon came to be call'd the Harvest Moon, the Hunter's or Shepherd's Moon: All which will clearly be shewn on the Globe.
PROB. XIII. To represent the Face of the Starry Firmament for any given Hour of the Night:
Rectify the Globe; and turn it about, till the Index points to the given Hour, then will all the upper Hemisphere of the Globe represent the visible Half of the Heavens, and all the Stars on the Globe will be in such Situations as exactly correspond to those in the Heavens, which may therefore be easily found, as will be shewn.
PROB. XIV. To find the Hour when any known Star will rise, or come upon the Meridian:
Rectify the Globe, and set the Index to XII; then turn the Globe till the Star comes to the Horizon or Meridian, and the Index will shew the Hour required.
PROB. XV. To find at what Time of the Year any given Star will be on the Meridian at XII at Night:
Bring the Star to the Meridian, and observe what Degree of the Ecliptic is on the North Meridian under the Horizon; then find in the Calendar on the Horizon the Day of the Year against that Degree, and it will be the Day required.
These are the chief Problems on the Celestial Globe: We now proceed to those on the Terrestrial, but shall first premise the following Definitions relating thereto.
I. The Latitude of any Place is its Distance from the Equator towards either Pole; and is reckon'd in Degrees of the General Meridian, beginning at the Equator.
<113>II. Longitude is the Distance between the Meridian of any Place, and the first or standing meridian, reckon'd in the Degrees of the Equator towards the East or west.
III. A Climate is a Space of the Earth's Surface, parallel to the Equator, where the Length of the Day is half an Hour longer in the Parallel which bounds it on the North, than in that which terminates it on the South.
IV. A Zone is also a Division of the Earth's Surface parallel to the Equator, in regard of the different Degrees of Heat and Cold, which we have described in the preceding Lecture.
V. The Antoeci are those inhabitants of the Earth, who live under the same meridian, but on opposite Parallels, and are therefore equally distant from the Equator. Their Noon and Midnight are at the same Time; the Days of one are equal to the Nights of the other; and their Seasons of the Year are contrary.
VI. The Perioeci are those People who live under the same Parallel, but opposite Meridians. The same Pole is elevated and depress'd to both; are equally distant from the Equator, and on the same Side; when Noon to one, it is Midnight to the other; the Length of Days to one is the Complement of Night to the other, and the contrary; and the Seasons of the Year are the same to both, at the same Time.
VII. The Antipodes are those who live Feet to Feet, or under opposite Parallels and Meridians. They are equally distant from the Equator on different Sides; have the contrary Poles equally elevated, the Noon of one is Midnight to the other; the longest Day or Night to one is shortest to the other, and the Seasons of the Year are contrary, &c.
VIII. Also the Inhabitants of the Torrid Zone are call'd Amphiscii, because their Shadows fall on both Sides of them.
IX. Those of the Frigid Zone are called Periscii, because their Shadows fall all around them.
<114>X. And the Inhabitants of the Temperate Zones are call'd Heteroscii, because they cast their Shadows only one way.
XI. A Continent is the largest Division or Space of Land, comprehending divers Countries and Kingdoms, not separated by Water.
XII. An Island is any small Tract of Land surrounded by Water.
XIII. A Peninsula is a Part of Land encompass'd with Water all around, except on one Part, which is call'd
XIV. An Isthmus, being that narrow Neck of Land which joins it to the Continent.
XV. A Promintory is a mountainous Part of Land standing far out in the Sea, whose Fore-part is call'd a Cape, or Head-Land.
XVI. The Ocean is the largest Collection of Waters, which lies between, and environs the Continents.
XVII. The Sea is a smaller Part of the aqueous Surface of the Earth, interceding the Islands, Promontories, &c.
XVIII. A Gulf is a Part of the Sea every where environ'd with Land, except on one small Part call'd
XIX. A Strait, which is that narrow Passage joining it to the adjacent Sea.
XX. A Lake is any large Quantity of stagnant Water entirely surrounded by Land.
The other Parts of Land or Water need no Explanation.
I shall now proceed to the Solution of the most useful Problems on the Terrestrial Globe, first premising that the Latitude of a Place is equal to the Elevation of the Pole at that Place; for if the Arch of the Meridian between the Place and the Pole be added to the Latitude of the Place, it makes 90 Degrees; also if it be added to the Poles Elevation, or Arch between the Pole and Horizon, the Sum is 90 Degrees: Whence the Proposition is evident.
<115>PROB. I. To find the Latitude of any Place:
Bring the given Place to the Brazen Meridian, and observe what Degree it is under, for that is the Latitude required.
PROB. II. To rectify the Globe for any given Place:
Raise the Pole so high above the Horizon, as is equal to the Latitude of the Place; screw the Quadrant of Altitude in the Zenith; find the Sun's Place, and bring it to the Meridian; set the Hour-Hand to the upper XII; and place the Globe North and South by a Needle, then is it a just Representation of the Globe of the Earth, in regard of that Place, for the given Day at Noon.
PROB. III. To find the Longitude of a given Place:
Bring the Place to the Brazen Meridian, and observe the Degree of the Equator under the same, for that expresses the Longitude required.
PROB. IV. To find any Place by the Latitude and Longitude given:
Bring the given Degree of Longitude to the Meridian, and under the given Degree of Latitude you will see the Place required.
PROB. V. To find all those Places which have the same latitude and Longitude with those of any given Place:
Bring the given Place to the Meridian, then all those Places which lie under the Meridian have the same Longitude: Again, turn the Globe round on its Axis, then all those Places, which pass under the same Degree of the Meridian with any given Place, have the same Latitude with it.
PROB. VI. To find all those Places where it is Noon at any given Hour of the Day, in any Place:
Bring the given Place to the Meridian; set the Index to the given Hour; then turn the Globe, till the said Index points to the upper XII; and observe what Places lie under the Brass Meridian, for to them it is Noon at that Time.
<116>PROB. VII. When it is Noon at any one Place, to find what Hour it is ay any other given Place:
Bring the first given Place to the Meridian, and set the Index to the upper XII, then turn the Globe till the other given Place comes to the Meridian, and the Index will point to the Hour required.
PROB. VIII. For any given Hour of the Day in the Place where you are, to find the Hour of the Day in any other Place:
Bring the Place where you are to the Meridian, set the Index to the given Hour; then turn the Globe about, and when the other Place comes to the Meridian, the Index will shew the Hour of the Day there, as required.
PROB. IX. To find the Distance between any two Places on the Globe in English Miles:
Bring one Place to the Meridian, over which fix the Quadrant of Altitude; and then laying it over the other Place, Count the Number of Degrees thereon contain'd between them, which Number multiply by 69 and a hall, (the Number of Miles in one Degree) and the Product is the Number of English Miles required.
PROB. X. To find how any one Place bears from another:
Bring one Place to the Brass Meridian, and lay the quadrant of Altitude over the other, and it will shew on the Horizon the Point of the Compass on which the latter bears from the former.
PROB. XI. To find those Places to which the Sun is vertical in the Torrid Zone, for any given Day:
Find the Sun's Place in the Ecliptic for the given Time, and bring it to the Meridian, and observe what Degree thereof it cuts, then turn the Globe about, and all those Places which pass under that Degree of the Meridian are those required.
<117>PROB. XII. To find what Day of the Year the Sun will be vertical to any given Place in the Torrid Zone:
Bring the given Place to the Meridian, and mark the Degree exactly over it; then turn the Globe round, and observe the two Points of the Ecliptic which pass under that Degree of the Meridian: Lastly, see on the wooden Horizon, on what Days of the Year the Sun is in those Points of the Ecliptic, for those are the Days required.
PROB. XIII. To find those Places in the North Frigid Zone, where the Sun begins to shine constantly without setting, on any given Day between the 10th of March and the 10th of June:
Find the Sun's Place in the Ecliptic for the given Day; bring it to the General Meridian, and observe the Degrees of Declination, then all those Places which are the same Number of Degrees distant from the pole, are the Places required to be found.
PROB. XIV. To find on what Day the Sun begins to shine constantly without setting, on any given Place in the North Frigid Zone, and how long:
Rectify the Globe to the Latitude of the Place, and, turning it about, observe what point of the Ecliptic between Aries and Cancer, and also between Cancer and Libra, co-incides with the North Point of the Horizon; then find, by the Calendar on the Horizon, what Days the Sun will enter those Degrees of the Ecliptic, and they will satisfy the Problem.
PROB. XV. To find the Place over which the Sun is vertical, on any given Day and Hour:
Find the Sun's Place, and bring it to the Meridian, and mark the Degree of Declination for the given Hour; then find those Places which have the Sun in the Meridian at that Moment; and among them, that which passes under the Degree of Declination is the Place desired.
<118>PROB. XVI. To find, for any given Day and Hour, those Places wherein the Sun is then rising, or setting, or on the Meridian: Also those Places which are enlightend, and those which are not:
Find the place to which the Sun is vertical at the given Time, and bring the same to the Meridian, and elevate the Pole to the Latitude of the Place, then all those Places which are in the western Semicircle of the Horizon have the Sun rising, and those in the Eastern Semicircle see it setting; and to those under the Meridian, it is Noon. Lastly, all Places above the Horizon are enlighten'd, and all below it are in Darkness or Night.
PROB. XVII. The Day and Hour of a Solar or Lunar Eclipse being given, to find all those Places in which the same will be visible:
Find the Place to which the Sun is vertical at the given instant, and elevate the Globe to the Latitude of the Place; then in most of those Places above the Horizon will the Sun be visible during his Eclipse and all those Places below the Horizon will see the Moon pass through the Shadow of the Earth in her Eclipse.
PROB. XVII. The Length of a Degree being given, to find the Number of Miles in a great Circle of the Earth, and thence the Diameter of the Earth:
Admit that one Degree contains 69 English Statute Miles; then multiply 360 (the Number of Degrees in a Great Circle) by 69 and the Product will be 25020, the Miles which measure the Circumference of the Earth. If this Number be divided by 3.1416, the Quotient will be 7963 Miles, for the Diameter of the Earth.
PROB. XIX. The Diameter of the Earth being known, to find the Surface in Square Miles, and its Solidity in Cubic Miles:
Admit the Diameter be 7964 Miles; then multiply the Square of the Diameter by 3.1416, and the Product will be 199250205 very near, which are the Square Miles in the Surface of the Earth. Again, multiply the Cube of the Diameter by 0.5236, and the Product 264466789170 will be the Number of Cubic Miles in the whole Globe of the Earth.
PROB. XX. To express the Velocity of the diurnal Motion of the Earth:
Since a Place in the Equator describes a Circle of a 25020 Miles in 24 Hours, 'tis evident the velocity with which it moves is at the rate of 1042 in one Hour, or 17 Miles per Minute. The velocity in any Parallel of Latitude decreases in the Proportion of the Co-Sine of the Latitude to the Radius. Thus, for the Latitude of London, 51 deg. 30 min. say,
| As Radius | 10.000000 |
| To the Co-Sine of Lat. 51 def. 30 min. | 9.794149 |
| So is the Velocity in the Equator, 17 m. | 2.232046 |
| To the Velocity of the City of London, 10 m. | 2.032195 |
That is, the City of London moves about the Axis of the Earth at the Rate of 10 Miles every Minute of Time. But this is far short of the Velocity of the annual Motion about the Sun; for that is at the Rate of 56000 Miles per Hour, or about 940 Miles each Minute, supposing the Diameter of the annual Orbit to be 81 Millions of Miles.
There is a geometrical Method of describing the Superficies of the Celestial and Terrestrial Globe on a Plane; and this is call'd the Projection of the Sphere in Plano: Thus, one Half of the Globe is projected on one Side of the Plane, and the other Half on the other, and if the Plane be that of the Ecliptic or Equinoctial, as in the Case of the Celestial Globe, these Projections are then call'd the Celestial Hemispheres. But with regard to the Terrestrial Globe, they are generally made on the Plane of the General Meridian or Horizon, and then they are commonly call'd Maps of the World: And the several Circles, and Parts of the Surface of one Hemisphere, are so delineated on the said Plane, as they would appear thereon to an Eye placed in the Pole, or middle Point, of the other Hemisphere. Hence it will come to pass, that the Stars and Constellations of the Hemispheres, and the Parts of Land and Water in the Maps, are not represented in their natural and just Distances, and in their due Magnitudes and Forms, as on the Globes themselves: Yet most of the Problems of either Globe are performable on these artificial Projections, by those who understand their Nature and Use. But these Things will be best understood from a View of those Prints, and a Specimen of the Praxis of their Use.
AN
APPENDIX,
CONTAINING AN
EXPLICATION
OF SUCH
Characters, Words, and Phrases,
As are not explain'd in the foregoing LECTURES, and other Treatises of this Kind.
FOR the Sake of such Gentlemen and Ladies as are not mathematically learned, it will be necessary to explain some Characters, Terms, and Words, that occur in the preceding Lectures, and other Books on the like Subject, that nothing may be wanting to facilitate and expedite their Progress in these most important and sublime Studies.
In all Cases where the Use of Numbers is required, it is now customary, instead of the words Addition, Subtraction, Multiplication, Division &c. to use Characters, for the sake of Brevity, to express the same Things. Thus, for Addition we use the Sign +; as 5 + 3, is to be read 5 more 3, or 3 added to 5.
So for Subtraction we use the Sign -; as 5 - 3, is 5 less 3, or 3 substracted from 5.
For Multiplication we use the Sign ×; thus 5 × 3, is 5 multiplied by 3.
And for Division is used the Sign ÷; thus 15 ÷ 3, is 15 divided by 3; but this is not so frequent.
Again, when we would express Equality, we use the Sign =; 5 + 3 = 8, that is, 5 more 3 is equal to 8; and 5 × 3 = 15, is 5 multiplied by 3 is equal to 15.
<122>In stating Proportions we use the sign : for is to, and :: for so is. Thus, instead of saying, As A is to B, so is C to D, we express it thus, A : B :: C : D.
The Square of any Number is the Product of that Number multiplied by itself; thus the Square of 3 is 3 × 3 = 9; and the Cube of a Number is the Product of that Number multiplied by itself twice; thus the Cube of 3 is at 3 × 3 × 3 = 27. Hence the Number 3 is said to be the Square Root of 9, and the Cube Root of 27; and in Characters the Square Root is thus express'd , and the Cube Root thus ; thus , and ; and so of other Numbers or Quantities.
When any Quantity cannot be expressed in whole Numbers without Fractional Parts, 'tis common now to express those broken Parts in Decimal Numbers, which are distinguish'd from the Whole Number by a Point or Comma: Thus 3,5 is 3 and 5 Tenths of another, or 3,5 = 3 = 3; so 3,1416 is 3; that is, if the Diameter of a Globe be one Foot, the Circle which divides it into two equal Parts will be 3,1416, or 3 Feet; that is, it will be 3 Feet, and 1416 of 10000 Parts of another Foot: And so of other Decimal Numbers.
Proportion is the Comparison of Things in respect of Magnitude: [Image 44] Thus we say four Lines, A, B, C, D, are proportional, when A is to B as C is to D in regard of their Length. And in this Case, the Rectangle or Product of the two Extremes is equal to the Rectangle of the two Means, or Middle Lines, viz. A × D = B × C. If here, while the two first Quantities A and B do increase or decrease, the other two C and D do also proportionably increase or decrease, the Proportion is said to be direct. Note, when Quantities multiplied together are expressed by single Letters, we leave out the Mark ×, and instead of A × D, write only AD. But if while two Quantities A, B, do increase or decrease, other two Quantities C, D, should at the same Time proportionably decrease or increase; then the Proportion between those Quantities is said to be inverse or reciprocal. Thus, because as the Squares of the Distances from the Sun increase, the Effects of its Light and Heat decrease, the latter are said to be reciprocally proportional to the former.
When any two Quantities are proportional to other two Quantities singly, the Proportion is said to be simple: Thus the Circumferences of two unequal Circles are in the simple Proportion of their Diameters.
But if two Quantities are in Proportion to each other as the Squares of two other Quantities, the Proportion is said to be duplicate: Thus because the Lengths of Pendulums are to each other as the Squares of the Times of their Vibrations, therefore the former are said to be in the duplicate Proportion of the latter.
In the same manner, if two Quantities are proportional to the Cubes of two other Quantities, the former are said to be in the triplicate Proportion of the latter. Thus spheres or Globes are in the triplicate Proportion of their Diameters, because their Magnitudes are as the Cubes of the Diameters.
When the Squares of any two Quantities are proportional to the Cubes of two others, the Proportion is said to be sesquiplicate: Thus, because the Squares of the Times, in which any two Planets revolve about the Sun, are proportional to the Cubes of their Distances respectively, the former are said to be in sesquiplicate Proportion of the latter.
If two Quantities have the same Proportion as the Square Roots of two other Quantities, then the Proportion is said to be subduplicate: Thus the Times of Vibrations are said to be in the subduplicate Proportion of the Lengths of Pendulums, because they are as the Square Roots of those Lengths.
And subtriplicate Proportion is that of the Cube Roots: Thus the Diameters of Spheres are in the subtriplicate Proportion of the Spheres themselves. For Example: Let two Spheres or Globes be to each other as 8 and 27; now the Cube Roots of these Numbers are 2 and 3, which therefore will represent the Diameters of the Spheres; and thus we say, 2 is to 3 in the subtriplicate Proportion of 8 to 27.
I shall here exhibit the several Kinds of Proportion in one View, thus:
| Simple Proportion | A : B :: C : D | 2 : 3 :: 6 : 9 |
| Duplicate | A : B :: CC : DD | 4 : 9 :: 16 : 36 |
| Triplicate | A : B :: CCC : DDD | 1 : 8 :: 8 : 64 |
| Sesquiplicate | AA : BB :: CCC : DDD, or A : B :: : | |
| Subduplicate | A : B :: : | 2 : 3 :: 4 : 6 |
| Subtriplicate | A : B :: : | 1 : 2 :: 2 : 4 |
I take it for granted that the Reader knows, that if on any Point C, taken in the Right Line AB, a Circle ADEF be described, the Point C is called the Center, and AE the Diameter of that Circle: To which I shall add, that AC, or CE, is call'd the Radius of the Circle, which is the same thing as the Semidiameter;.
If the Circle be divided into four equal Parts, AD=DE=EF=FA, by the two Diameters AE, DF; then each of the Areas ACD, DCE, ECF, FCA, are called Quadrants, or Quarters of the circular Space; and the Parts of the Circle AD, DE, EF, FA, are called Quadrantal Arches, or Quarters of the Circle.
Every Circle, great or small, is supposed to be divided into 360 equal Parts, called Degrees; consequently each Quarter, AD, DE, &c. will contain 90 of those Degrees, as is evidently represented by the large Half-Circle of Fig. XLVI.[Image 45]
If two Lines BC and FC meet in a Point C, the Space FCB included between them is call'd an Angle; and the Measure of that Angle is the Number of Degrees contain'd in an Arch EI of a Circle described on the angular Point C, and included between the said two Lines BC and FC. Thus the Angle in the Figure contains 40 Degrees.
If a Line, as GC, be drawn through the 90th Degree on the Point C, it will make the Angle on one Side GCB equal to the Angle GCA on the other Side, because each is equal to 90 Degrees. Such an Angle is call'd a Right Angle; and the Line GC is then said to be perpendicular to the Line AB.
The Angle FCB, which is less than a Right Angle or 90 Degrees, is call'd an Acute Angle; and the Angle HCB, which is greater than a Right Angle or 90 Degrees, is call'd an Obtuse Angle. Again; the Arch ID is call'd the Complement of the Arch EI to a Quadrant ED, or 90 Degrees; and the Arch AK is call'd the Supplement of the Arch EK to a Semicircle EDA, or 180 Degrees.
If from the Point I be let fall the Perpendicular IL to the Line or Radius EC, then is that Line IL call'd the Sine of the Angle ICE or FCB. In the same manner the Line IM is the Sine of the Complement-Arch ID, or Angle ICD. But instead of Sine-Complement, we say, in short, Co-Sine: Thus we say that IL is the Sine, and IM the Co-Sine, of the Angle ICE. The Angle FCB is the Inclination of the Line FC to the Perpendicular DC: That is, FC is inclined to BC in an Angle of 40 Degrees, and to DC in an Angle of 50 Degrees. Hence IL and IM are call'd the Sines of Inclination respectively.
Hence, when we say, The Force of a direct Stroke is to that of an oblique one as Radius is to the Sine of Inclination, we only mean, that those Quantities are to each other as the Radius IC to the Sine IL, or IM, according as the Inclination is 40 or 50 Degrees. Also, when 'tis said, that the centrifugal Force decreases from the Equator towards the Poles, in Proportion of Radius to the Co-Sines of the Latitude; no more is mean than this, that if the Radius CE represent the said Force in the Equator E, and EI be any given Latitude, then will IM, the Co-Sine of the Latitude, represent the Force in that Latitude: Or, the Force decreases with the Length of the Line IM, as the Point I moves on from E to D.
In several Books we have Tables of Numbers which express the Length of the Sine of every Degree and Minute of the Quadrant, in such equal Parts as the Radius CE or CI contains 100000. And since it is of the greatest Use to know the Proportion of Radius to the Sine of every Degree, I have here subjoin'd a Table thereof, and a Specimen of its Use.
<125>| Deg. | Parts. | |
| Sine of | 1 | 1745 |
| 2 | 3489 | |
| 3 | 5233 | |
| 4 | 6975 | |
| 5 | 8175 | |
| 6 | 10452 | |
| 7 | 12186 | |
| 8 | 13917 | |
| 9 | 15643 | |
| 10 | 17364 | |
| 11 | 19080 | |
| 12 | 20791 | |
| 13 | 22495 | |
| 14 | 24192 | |
| 15 | 25881 | |
| 16 | 27563 | |
| 17 | 29237 | |
| 18 | 30901 | |
| 19 | 32556 | |
| 20 | 34202 | |
| 21 | 35836 | |
| 22 | 37460 | |
| 23 | 39073 | |
| 24 | 40673 | |
| 25 | 42261 | |
| 26 | 43837 | |
| 27 | 45399 | |
| 28 | 46947 | |
| 29 | 48480 | |
| 30 | 50000 | |
| 31 | 51503 | |
| 32 | 52991 | |
| 33 | 54463 | |
| 34 | 55919 | |
| 35 | 57357 | |
| 36 | 58778 | |
| 37 | 60181 | |
| 38 | 61566 | |
| 39 | 62932 | |
| 40 | 64278 | |
| 41 | 65605 | |
| 42 | 66913 | |
| 43 | 68199 | |
| 44 | 69465 | |
| 45 | 70710 | |
| 46 | 71933 | |
| 47 | 73135 | |
| 48 | 74314 | |
| 49 | 75470 | |
| 50 | 76604 | |
| 51 | 77714 | |
| 52 | 78801 | |
| 53 | 79863 | |
| 54 | 80901 | |
| 55 | 81915 | |
| 56 | 82903 | |
| 57 | 83867 | |
| 58 | 84804 | |
| 59 | 85716 | |
| 60 | 86602 | |
| 61 | 87461 | |
| 62 | 88294 | |
| 63 | 89100 | |
| 64 | 89879 | |
| 65 | 90630 | |
| 66 | 91354 | |
| 67 | 92050 | |
| 68 | 92718 | |
| 69 | 93358 | |
| 70 | 93969 | |
| 71 | 94551 | |
| 72 | 95105 | |
| 73 | 95630 | |
| 74 | 96126 | |
| 75 | 96592 | |
| 76 | 97029 | |
| 77 | 97437 | |
| 78 | 97814 | |
| 79 | 98162 | |
| 80 | 98480 | |
| 81 | 98768 | |
| 82 | 99026 | |
| 83 | 99254 | |
| 84 | 99452 | |
| 85 | 99619 | |
| 86 | 99756 | |
| 87 | 99862 | |
| 88 | 99939 | |
| 89 | 99984 | |
| 90 | 100000 |
The Use of this Table will be obvious from two or three Examples. It was observed, (Page 26.) That the Power is to the Weight it sustains on any inclined Plane IC, as the Height of the Plane IL to the Length thereof IC; that is, as the Sine of the Plane's Inclination to the Radius. Suppose the Angle of Inclination ICE = 40 Degrees, then will the Sine IL be equal to 64278, and the Radius CI equal to 100000, which Numbers are as 64 to 100; therefore 100 Pounds will be sustain'd on the Inclined Plane by a Power equal to 64 Pounds nearly.
Again; since EC = 100000 represents the centrifugal Force under the Equator, then will IM = 76604 (the Sine of 50 Degrees, and Co-Sine of 40) be as the said Force in the Latitude of 40 Degrees: Which Numbers are as 1000 to 766; and such is the Proportion of the Forces in those two Places.
In the same manner, if the Radius CD = 100000 express the Force of any direct Stroke, then will the Sine IL = 64278 be expressive of the Force of an oblique Stroke in the Direction FC, every thing else being equal.
Again; since the Force of a direct Stroke is express'd by CD=100000, if it be required to find the Angle of Obliquity, such that the Force of the Stroke shall be but one fourth Part so great, or 25000, look in the Table for the Number nearest to this, and you will perceive it lie between 14 and 15 Degrees, and therefore about 14 Degrees and a half is the Angle required.
In the last Place: It was said, (Page 29.) That the Force of the Wind on the Sail is proportional to the Squares of the Sines of the Angle of Incidence. This may be illustrated by Numbers, thus: If the Sail be turn'd to the same Wind, first under an Angle of 45 Degrees, and then under an Angle of 30 Degrees; the Sine of the first Angle is (by the Table) 70710, and of the latter 50000, the Squares of which are 4999904100 and 2500000000, which Squares are as 50 to 25, or as 2 to 1; and therefore the Power of the Wind is twice as great upon an Angle of 45 Degrees, as upon an Angle of 30.
Because the Square of the Sine of 45 Degrees is 5000000000, twice that squre will be 10000000000, which is equal to the Square of Radius 100000; 'tis evident the Sum of the Squares of the sines of any two Angles above 45 Degrees will be greater than the Square of Radius; and therefore the Force of the Wind upon two oblique Sails, in that Case, will be greater than upon one sail set direct before the Wind.
After the same manner, the Table of Sines may be applied to Calculation in any other Case of like Nature, where the Proportion of Radius and Sine of an Angle is required to be express'd or stated in Numbers. And since each Degree is divided into 60 equal Parts or Minutes, therefore the Sine of any Number of Degrees and Minutes also may be easily found by the foregoing Table, by those who understand the Rule of Proportion.
I shall only further observe here, that as IL is the Sine, [Image 46] and LM the Co-Sine, of the Arch IE; so if on the extreme Point E of the Radius CE we raise a Perpendicular which shall cut the Line CI, continued, in F, then is the said Perpendicular EF call'd the Tangent of the Angle ICE, and the Line FC the Secant of the same Angle. In like manner, the Perpendicular DG is the Tangent of the Angle DCI, and GC the Secant thereof; and therefore DG is the Co-Tangent, and GC the Co-Secant of the Angle ICE. I thought it necessary to acquaint the Reader with these Definitions, because they sometimes occur in Treatises of this Kind.
[Image 1] Fig. I. 
[Image 2] Fig. II. 
[Image 3] Fig. III. 
[Image 4] Fig. IV. 
[Image 5] Fig. V. 
[Image 6] Fig. VI. 
[Image 7] Fig. VII. 
[Image 8] Fig. VI. 
[Image 9] Fig. VII. 
[Image 10] Fig. VIII. 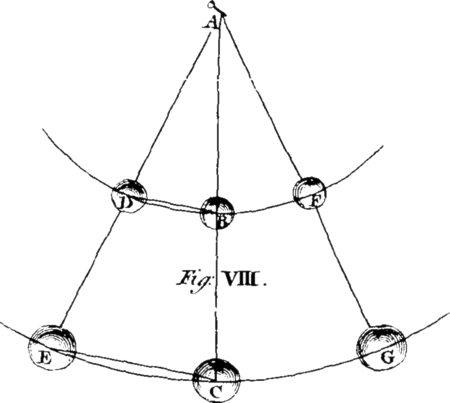
[Image 11] Fig. IX. 
[Image 12] Fig. X, XI. 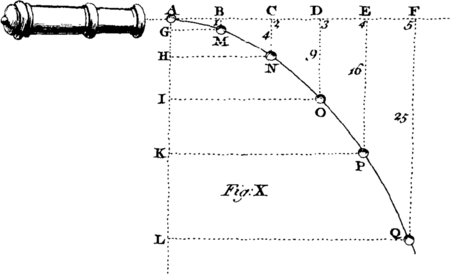

[Image 13] Fig. XII. 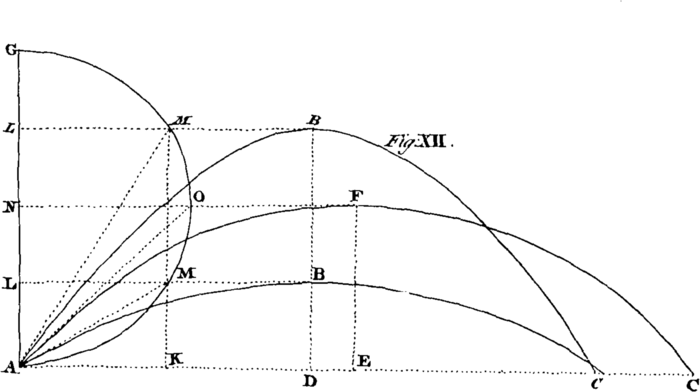
[Image 14] Fig. XIII. 
[Image 15] Fig. XIV. 
[Image 16] Fig. XV. 
[Image 17] Fig. XV. 
[Image 18] Fig. XVI. 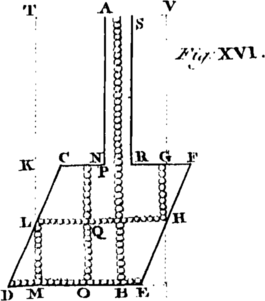
[Image 19] Fig. XVII. 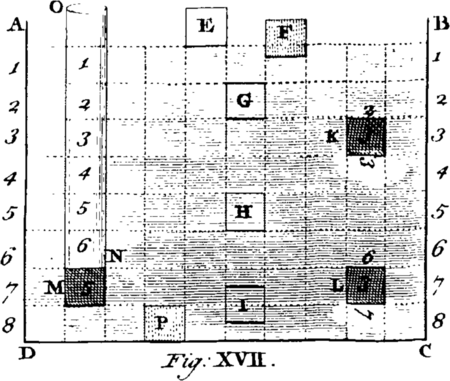
[Image 20] Fig. XVIII. 
[Image 21] Fig. XVIII. 
[Image 22] Fig. XVIII. 
[Image 23] Fig. XIX. 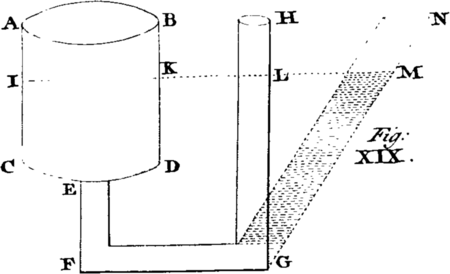
[Image 24] Fig. XX. 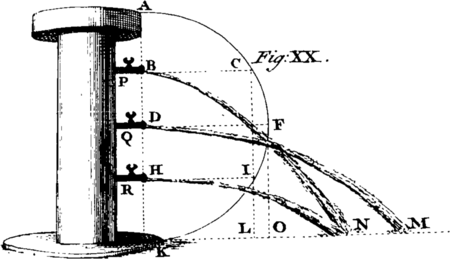
[Image 25] Fig. XXI. 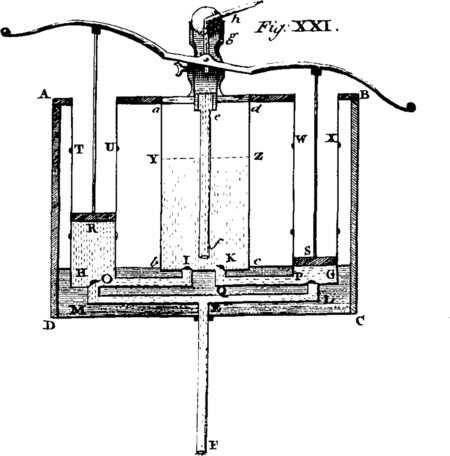
[Image 26] Fig. XXII. 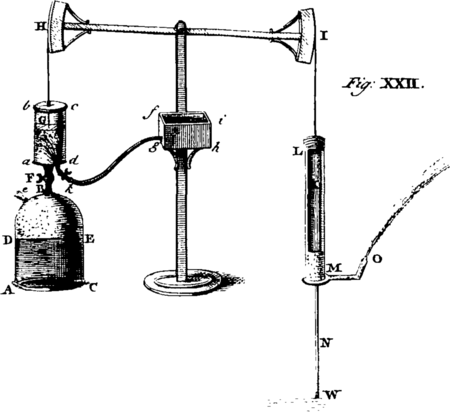
[Image 27] Fig. XXIII. 
[Image 28] Fig. XXIV. 
[Image 29] Fig. XXV. 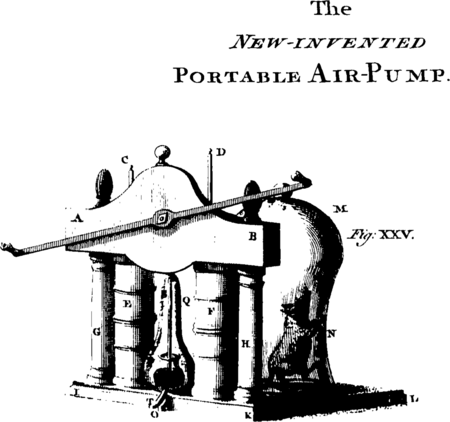
[Image 30] Fig. XXIX. 
[Image 31] Fig. XXX. 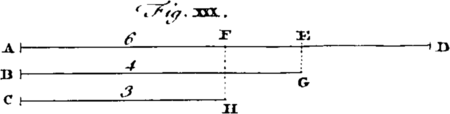
[Image 32] Fi. XXXI. 
[Image 33] F. XXXII. 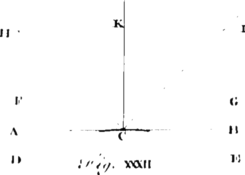
[Image 34] F. XXXIII. 
[Image 35] F. XXXIV. 
[Image 36] F. XXXV. 
[Image 37] Fig. XXXVI. 
[Image 38] Fi. XXXVII. 
[Image 39] F. XXXVIII. 
[Image 40] Fig. XXXIX. 
[Image 41] Fig. XL. 
[Image 42] Fig. XLI. 
[Image 43] Fig. XLII. 
[Image 44] Fig. XLIV. 
[Image 45] Fig. XLVI. 
[Image 46] Fig. XLVII.