Annotations in Commercium Epistolicum

Annotationes in Commercium Epistolicum

Introducti. ad Lectorem pag. 2 l. 7 9 post [fluentium momenta] adde [ad momentum quantitatis uniformiter fluentis applicata.]

Pag 12. l. 22. NB. Pro symbolo $\boxed{\frac{\mathrm{a}\mathrm{a}}{64\mathrm{x}}}$ D. Leibnitius utitur symbolo $\int \frac{\mathrm{a}\mathrm{a}}{64\mathrm{x}}$.

Pag. 15. l. 14. Vt punctum pro linea infin linea infinite brev{is} parva hic punctum vocatur sic superficies latitudinis infinite parvæ hic linea vocatur \dicitur/ & solidum altitudinis infinite parvæ hic \pro/ superficies dicitur \habetur/, ideo ex mente Cavallerij.

Pag. 15. l. 14. Newtonus hic loquitur cum Cavallerio & alijs quo|i| methodis indivisibilium utuntur. Momentum solidi esti solidum infinita parvum id est superficies physica seu crassitudinis infinite parvæ, id{eo} {illeg} et eo sensu superficies hic dicitur. Et Momentum superficiei est superficies infinite parva seu linea lititudinis infinita parvæ et eo sensu linea hic dicitur. Et momentum lineæ est linea infinite parva ideo \et eo sensu/ punctum hic dicitur. Pro crassitudine momenti solidi vel latitudine momenti superficialis Newtonus vel longitudine momenti linearis Newtonus ponit symbl|o|lum o et per hoc symbolum intelligit momentum lineæ unifor{illeg}|m|iter fluentis per quod|am| tempus exponitur. Momenta vero aliarum quantitatum per hoc momentum divisa po ponit pro fluxionibus quantitatum. Et contra; si fluxiones quantitatum per ha{c} symbola quæcun designatur, earum momenta per eadem symbola in momentum o ducta de designabitum|tur| {sic} in h ac methodo; ut fit in sequentibus.

P. 37. l 20. Quod hic Theorema dicitur cujus ope area circulo vel Sectoris ejus dati exacte exprimi potest per seriem quandā numerorum rationalium continue productam in infinitum; in Epistola proxima \sequente/ dicitur Methodus qua arcus quilibet cujus sinus datur Geometrice exhiberi potest per ejusmodi seriem; etiam <236v> nullo ad integræ circumferentiæ dimensionem recursu, Vt adeo necesse non sit Arcus rationem ad circumferentiam nosse. Si ratio arcus ad circumferentiam innotescit habetur circumferentia tota \in serie numerorum rationalium ut hic/ sin minus, habetur arc saltem arcus. [Nam eq eadem methodo qua circumferentia tota innotescit dicit arcum quemlibet ex sinu suo innotescerem.] Est igitur Theorema de quo hic agitur Theo Newtonianum illud quo Arcus quilibet ex sinu suo datur, & cujus Demonstrationem D. Leibnitius postea ab Oldenburgo quæsivit.

P. 45. l. 12. Series de qua aliquaties scripsit dabat arcum ex sinu cognito. Demonstrationem ejus quæsivit ab Oldenburgo per Epistolam sequentem.

P. 61. l. 16. Probandum est. {S}|H|anc seriem anno supendre ab Oldenburgo acceperat.

P. 63. lin. 12|3|. Seriem pro a Newtono communicatam quæ|â| {illeg} Logarithmus prodit ex numero dato, se antea invenisse jam modo prætendebat: jam postulat a Newtono ut methodum Regressuum exponat qua series illa inveniri potest.

P. 63 l 22. Intelligit collectionem Epistolarum Gregorij quam Collinius \per Oldenb. jam modo/ communicaverat.

P. 87. l {illeg}. 17. Methodum tangentium Slusij, \D. Leibnitius/ lectis Newtoni literis 10 Decem 1672 datis et {illeg} una cum Epistolis Gregorij \a Collinio et Oldenburgo/ ad {illeg} {a}|i|psum missis, \jam animo ve{illeg}|rs{a}|t {illeg} et quomodo/ generalem|is| reddere|atu|r et ad omns|a| \genera|i|s/ problematam genera extendatur jam cogitat, sed in methodum Differentialem nondum inc{illeg}|i|dit.

P. 88. l. 15. Slusij methodum tangentium Slusij generalem reddere jam \modo/ didicit et hac ne a Literis Newtoni hoc didicisse <237r> videretur, addit subjungit se \jam/ a multo ho tempore hoc didicisse Barrovius rem tangentium tractavit anno 1670 tractavit per differentias Slusius \anno 1673/ rem tangentium tractavi\erat/t {sic} per differentias Ordinatarū Barrovius idem fecerat generalius anno 1670, Newtonus methodum per differentias fluentium \anno 1669 communicaverat/ ad omnia prop|b|lematū genera extend applicaverat \sese extendentem/ id sine reductione æquati\on/um quantitates fractas & radicales involventium. Leibnitius anno 1677 a Newtono per literas Methodum tangentium Barrovianam amplectitur & a Literis Newtoni admonitus mutatis symbolis a et e in symbola dx|y| et dy|x|, & a Literis Newtoni|o|o admonitus generalem redd{illeg} applicat ad ampliorem reddit applicandos tended|n|do quomodo tangentes ducantur s{illeg} \abs/ reductione frac æquationum quantitates fractas & radicales involventium duci|e||re| possint \didicit/, & p{illeg} methodum eandem ad omnia problematum genera applicuit, & jam primum {illeg} cum amicis lectis scilicet quæ Newtonus de hac Methodo in duabus \tribus/ Epistolis scripserat, Lectis fortean & alijs Newtonianis sub finem Anni 1676 ubi domum per Londinum redibet.

|p. 88. l.| Ex verbis [Hinc nominando in posterum dy differentiam duarum proximarum y &c] pa{illeg}t \colligitur/ D. Leibnitium hoc methodum differentialem ipso tempore methodum differentialem cum amicis scripto communicare cœpisse. Pergit subinde methodum tangentium Barrovij, symbolis mutatis describere, & ostendere quom|d|odo methodus Slusij \quod/ Regula Slusij statim occurrit hanc methodum intelligenti, et quomodo pergendum sit vbi plures \sunt/ literæ indetermit|n|atæ \ut/ & ubi interveniunt il irrationales.

p. 86 94. l. 17. Proposuerat Newtonus æquatione ubi indices potestatum f|s|unt fractiones, ut in hæ|a|c æquatione $20+{\mathrm{x}}^{\frac{3}{7}}-{\mathrm{x}}^{\frac{6}{5}}{\mathrm{y}}^{\frac{2}{3}}-{\mathrm{y}}^{\frac{7}{11}}=0$ vel aut surdæ quantitates ut in hac ${\overline{){\mathrm{x}}^{\sqrt{2}}+{\mathrm{x}}^{\sqrt{7}}}}^{\frac{2}{3}}=\mathrm{y}$. D. Leibnitius hic vicissim proponit æquationes ubi indices potestatum sunt quantitates fluentes. Et |cal|\culum in his/ æquationibꝰ hasce jam Exponentionales|m| \jam/ vocat. Sed usum hujus calculi nondum docuit.

p. 97. p|l|. 21. Post [literis G. G. L. designatus] adde. Descripsit \vero/ methodum tang solam \solammodo methodum/ maximarum & minimarum & methodum eam tangentium, deinde addidit

p. 97. l. 13. Brevi postea . . . . . Aprilis 1668, publicata. Nomina eorum qui circulum quadrarunt quam proxime \quadrarunt/ ut Archimedis Ptolomæi, Vietæ, Metij & Ludolphi a C{em}l{illeg} Coloniensis, D. Leibnitius recenset; ut et nom Cardinalis Cusani, Orontij Finæi Iosephi Scaligeri, Thomæ Gephyrandri, Thomæ Hobbij qui perfectum tetragonismum professu|i|nt sunt, sed scopum minime attigerunt: sed \{e}t/ nomen \et nomen/ Gregorij|u||s| \vero/ qui seriem hanc invenit et nomina \D. Leibnitus \pro{r}sus/ celavit ut/ & Colliniu|j|s & Oldenburgu|i|s a qu{illeg}|i|bus {illeg} \D. Leibnitius hanc/ seriem hanc bis acceperat, seipsum vero primum et unicum seriei \hujus/ inventorem {illeg}atis {c}{illeg} jactavit minime nominantur nomina celantur. Gregorij vero qui seriem hanc invenit & Collinij et Oldenburgi a quibus D. Leibnitius hanc seriem \ea{illeg}em bis/ acceperat, nomin {illeg}|a| celant{illeg}|u|r.

Non multo post, anno scilicet 1684, in ijsdem Actis Leipsicis, pro mense Octobri, Calculi differentialis Elementa primum edidit D. Leibnitius literis G. G. L. designatus sub hoc titulo. Nova methodus pro maximis et minimis item tangentibus quæ nec fractas nec irrationales quantitates moratur, & singulare pro illis calculi genus per G. G. L. Et sub finem addidit: Et hæc sunt quidem initia sunt tantum Geometriæ cujusdam multo sublimioris ad difficillima et pulcherrima quæquæ|e|, etiam mistæ Matheseos problemata pertingentis, quæ sine calculo nostro differentiali, aut SIMILI non temere quisquam pari facilitate tractabit. Per methodum similem hic intellexit Newtonianam, sed quid ab Anglis didicerat minime aperuit.

In Actis Eruditorum pro mense Iunio anni 1686 pag 297, D. Leibnitius scripsit: Malo autem dx et similia adhibere quam literas pro illis, quia istud dx est modificatio quædam ipsius x, &c Intellexit igitur literas in methodo differentiali pro si|y|mbolis dx, dy & similibus usurpari posse.

P: 97. l. 13. Brevi postea . . . . . . . Aprilis 1668 publicata.

✝ In Actis Eruditorum pro mense Octobri \anni 1687,/ pag. 482, dicitu dicitur hanc seriem {tum} jam tum decennio & a{l}|m|plius ab{illeg}nde in|a|binde inventam fuisse (id est anno 1675 ante mensem Octobri) ac demonstrationem ejus partim a Clarissimo Inventore partim ab \ejus/ amicis communicatam esse summis quibusdam Parisinorum ac Londinensium Geometris.

‡ Methodum edidit sub hoc titulo. Nova methodus pro maximis et minimis item tangentibus quæ nec fractas nec irrationales quantitates moratur, & singulare pro illis calculi genus per G. G. L. Et sub finem addidit. Et hæc sunt quidem initia sunt tantum Geometriæ multo sublimioris ad dificillima et pulcherrima quæ, etiam mistæ matheseos problemata pertingentis, quæ sine calculo nostro differentiali, aut SIMILI, non temere quisquam pari facilitate tractabit. Per methodū similem hic intellig|ex|it Newtonianam, sed quid ab Anglis didicerat minime aperuit. In Actis autem Eruditorum pro mense Iunio Anni 1686 pag 297 scripsit: Ma {illeg}|l|o autem dx et similia adhibere quam literas pro illis quia istud dx est modificatio quædam ipsius x, &c. Et his verbis allu d{illeg}|sisse| videtur ad methodum tangentium Barrovij pro cujus qui liter cujus literas a et e mutavit in symbola dy et dx. Methodus igitur ex mente Leibnitij non consistit in usu symbolorum dx dy, sed eadem est sive literæ sive hæc symbola sive literæ sive symbola alia quæcun pro differentijs usurpentur.

E Cæterum \Porro/ D. Leibnitius in Epistola $\frac{7}{17}$ Martij anno 1693 ad Newtonum data, Librum illum per \op{e}/ Analysin non vulgarem ope Analyseos nova compositum fuisse agnovit his verbis Mirifice ampliaveras Geometriam tuis seriebus, sed edito Principiorum opere ostendisti patere tibi etiam quæ Analysi receptæ non subsunt. Conatus sum ego quo notis commodis adhibitis quæ differentias et summas exhibent Geometriam illam quam transcendentem appello, Analysi quodammodo subjicere, nec res male processit.

Eodem anno prodijt Volumen secundum operum Wallisij Et ubi Propositio, prima Libri de Quadratura Curvarum fuse {ex}p exponitur et describitur et ad fluxiones secundas ac tertias alias extenditur. Sed et \methodus extrahendo/ quantitates fluentes ex æquationibus fluxiones \primas secundas tertias quartas alias/ involventibus extrahere docet ostenditur. id & ad æquati & ad fluxiones s Et a|A|nno proximo D. Leibnitius hæc de methodo Newtoni scripsit.|‡|^[1] Reddenda est justitia D. Newtono (cui Geometria Optica et Astronomia multum debent) quod ipse quo {illeg}|a|liquid huic simile proprio marte obtinuit, quemadmodum nos tandem \postea/ didicimus.|✝|^[2] Verum est quod is alijs utitur characteribus: sed qu ipsa char quemadmodum ipsa Characteristica, ut ita dicam, pars magna est artis inventor|t|is|o|nis, credo quod nostra luculentior sit. Et anno tertio D. M. Hospitalius hæc addidit: Debetur autem \etiam/ Newtono justitia, quam \etiam et/ D. Leibnitius ipse \✝/^[3] eidem reddidit: quod uti is etiam aliquid calculo differentiali simile invenit, quemadmodum apparet per librum insignem, Principia Philosophiæ naturalis Principia Mathematica nominatum quem edidit anno 1687 qui pene dixerim totus est de hoc calculo. Sed \☉/ Characte < insertion from f 238r > ☉ characteristica Leibnitij methodum ejus longe faciliorem et expeditiorem reddit, præterquam quod in difficilioribus hæc methodus mirabilia præstat. < text from p 237a(v) resumes >

☉‡ Hæc ex mente Leibnitij. Librum Wallisij D. M. Hospitalius nondum viderat.

Anno 1690 Iab|c|obus Bernoullius \& paulo/ methodum differentialem exercere cœpit

Anno 1690 methodus differentialis apud exteros coli {p} cep exerceri cœpit Iacobo Bernoullio

Ab anno 1690 Methodus differentialis apud exteros celebrari \exerceri/ cœpit, fratri Bernoullijs & Marchione Hospitalio eandem celebrantibus. A Et anno 1695 {illeg} E \Apr 10/ D. Wallisius in epistola A ad Newtonum hæc scripsit. Optarim Vtinam Epistolas tuas prolixas mensibus Iunnio et Octobri Annni {sic} 1676 in lucem ederes. Hoc mihi significatum est ab amicis tuis in Hollandia a Batavia, nempe amicos tuos ibi optare, ut hoc fieret propterea quod inventa tua (de fluxionibus ibi cum applausu celebrantur sub nomine Calculi differentialis Leibnitiani. Hoc mihi significatum est, cum totum hoc {illeg} operum meorum volumen præter partem Præfationis impressum esset, sic, qut|o| factum est ut solum illud hujus rei monitum consulis cum tua |cum| premendo inventa tua donec alij laudem tibi debitam referunt. Conatus sum justitiam \hac {vi{s} r}e/ tibi reddere & penitet me epistolas illas duas non impressisse \e{mis}sisse/ verbatim.

Pag. 3. l. 16. Wallisius indices dignitatum per num{mum}|eros| fract{illeg}ū|os| $\frac{1}{2},\frac{3}{2},\frac{5}{2}$ &c interpolavit, Newtonus indices fractos, surdos, indefinitos & negativos primus in computationes Analyticas introduxit. Leibnitius {illeg} numeros fluentes pro indicibus posuit.

Pag 49. l. 22. Resolutionem Binomij in hujusmodi seriem Anno 1669 Newtono innotuisses patet ex Analysi supra impressa pag. 19. l. 19, 20: inventam vero fuisse anno 1665 dicetur in sequentibus. Eandem D. Leibnitius cum amicis communicavit & celato inventoris nomine.

p. 14. Ad Notam adde: Hic recta AB ut a {illeg} ut uniformiter fluens spectatum, ejus momentum per lineolam infinite parvam quam Newtonus no symbolum quodvis Rectæ AB, BD, {illeg}|C|urva AD et areæ ABKH, ABDA ut fluenti|e|s \hic/ spectantur. Si rectæ AB uniformiter fluentis momentum dicatur o, momenta arearum ABKH et ABDA erunt \areæ infinitæ parvæ/ BK×o et BD×o; id est juxta methodum Cavallerij lineæ \physicæ/ BK et BD qu{illeg}d non geometric{illeg} quoad latitudinem indivisibiles. Hæ lineæ si cum superficiebus conferantur sunt infinite parvæ, & non sunt superficierum momenta nisi quatenus sunt superficies infinitæ|è| parvæ, & seu lineæ latitudinis infinitæ|è| parvæ, id est lineæ in latitudinem infinite parvam o ductæ; ideo siquando lineæ pro momentis arearū ponantur, subintelligendæ sunt lineæ in sensu Cavallerij, id est lineæ in latitudinem infinite d{illeg} parvam ductæ. Et eodem sensu mox dicitur quod unitas quæ pro momento ponitur est line{a} superficies cum de solidis, & linea cum de superficiebus et punctum cum de lineis agitur, id est superficies in {illeg} alitudinem {sic} infinite parvam \o/ ducta, & linea in latitudine infinite parvam o ducta, et punctum in longitudinem infinite parvam o ductum. Nam punctum hocce mox linea infinite parva dicitur, quales|m| \uti/ in methodis indivisibilium pro puncto haberi|e| solet|n|t. Hunc factor{illeg}|e|m indefinite parvum o, Newtonus quando exprimat \ponendo rectangula sub fluxionibus et momentum o pro momentis/ ut fit in calculo sub finem hujus Analyseos, & ubi non exprimet semper \quando subintelli & ubi non exprimit semper/ subintelligit|.| ubi \quoties/ fluxiones pro momentis ponuntur. Fluxiones enim sunt <238r> quantitates finitæ diversi generis a momentis, et pro momentis nunquam ponuntur nisi \quando/ per factorem o (vel expressum vel subintellectum,) vertantur in quantitates infinite parvas ejusdem generis cum fluentibus et earum momentis. Leibnitius autem pro rectangulis sub fluxionibus et momento o, symbolis utitur dz, dy, dx et similibus, pro fluxionibus vera nulla adhibet symbola.

Annotationes in Commercium Epistolicum.

Introductionis ad Lect. pag. 2. l. 19. post [fluentium momenta] adde [ad momentum quantitatis uniformiter fluentis applicata.

Libri pag. 3, l. 16. ✝ Wallisius indices dignitatum per numeros fractos $\frac{1}{2}$ $\frac{3}{2},\frac{5}{2}$ &c interpolavit: Newtonus indices fractos, surd{illeg}|o|s, indefinitos, \&/ negativos primus in computationes Analyticas introduxit: Leibnitius numeros fluentes pro indicibus posuit, nullo cum fructu.

Pag. 12. l. 22. ✝ Pro symbolo $\boxed{\frac{\mathrm{a}\mathrm{a}}{64\mathrm{x}}}$ D. Leibnitius utitur symbolo $\int \frac{\mathrm{a}\mathrm{a}}{64\mathrm{x}}$.

Pag. 14. Ad notam ibi positam adde. Rectæ AB, BD, Curva AD et areæ ABKH & ABDA ut fluentes hic spectantur. Si rectæ AB uniformiter fluentis momentum dicatur o, momenta arearum ABKH et ABDA erunt areæ infinite parvæ BK×o & BD×o, id est, juxta methodum Cavallerij lineæ physicæ BK et BD, non expertes latitudines, sed quoad latitudinem indivisibiles. Hæ uti lineæ non sunt superficierum momenta nisi quatenus sunt superficies infinite parvæ, id est, lineæ in latitudinem latitudinem infinite parvam ductæ o ductæ. Ideo siquando lineæ pro momentis arearum ponantur, subintelligendæ sunt lineæ in sensu Cavallerij, id est lineæ in latitudinem infinite parvam ductæ. Et eodem sensu mox dicitur quod unitas quæ pro momento ponitur est superficies cum de solidis, et linea cum de superficiebus & punctum cum de lineis agitur; id est, superficies in altitudinem infinite parvam o ducta, et linea in latitudinem infinite parvam o ducta, et punctum in longitudinem infinite parvam o ductum Nam statim subjungitur: Nec vereor loqui de punctis unitate in punctis, sive lineis infinite parvis, siquidem proportiones ibi jam contemplantur Geometræ, dum utuntur methodis Indivisibilium. Sunto fluentes z, y, x, v et earum momenta so, ro, qo, po. Fluat z uniformiter et ad \ejus/ momentum so applicentur omnium momenta, & latera $\frac{\mathrm{s}}{\mathrm{s}},\frac{\mathrm{r}}{\mathrm{s}},\frac{\mathrm{q}}{\mathrm{s}},\frac{\mathrm{p}}{\mathrm{s}}$ erunt earum fluxiones respective. Latus autem $\frac{\mathrm{s}}{\mathrm{s}}$ est 1; & inde Newtonus pro fluxione quantitatis uniformiter fluentis ponit unitatem. In hac methodo factor o, ubi Propositiones demonstrandæ sunt, semper exprimitur & supponitur indefinite parvus est|s|e donec calculus per Geometriam Veterum ad finem perducatur, deinde & subinde diminui in infinitum et evanescere. Sed ubi Propositiones d investigandæ sunt, factor o infinite parvus esse supponitur ab initio, & computationes compendij gratia procedunt per approximationes & fluxiones solæ subintellecto factore o pro momentis {illeg}\sc/ribuntur. Vt si fluxiones l, r, q, p pro momentis scribantur, subintelligendum est {illeg}|q|uod pro momentis o, po, qo, ro scribuntur, symbolo \factore/ o, compendij gratia neglecto. Hæc \erat/ methodo|u|s Newtonus usus est Anno 1669 e|u|t ex ijs quæ in hac Analysi pateb sequuntur manifestum erit. Eadem usus est in Tractatu de quadratura Curvarum. Eadem \ut omnium optimam/ us na hodie exercet.

P. 37. l. 20 ^✝ Quod hic Theorema dicitur cujus ope area circuli vel sectoris ejus dati exacte exprimi potest per seriem quandam numerorum rationalium continue productam in infinitum; in Epistola proxime sequente dicitur methodus qua arcus quilibet cujus sinus datur geometrice exhiberi potest per ejusmodi seriem etiam nullo ad integræ circumferentiæ dimensionem recursu, ut adeo <240r> necesse non sit Arcus rationem ad circumferentiam \nosse/. Habe\ba/tur \igitur/ circumferentia tota in sere {sic} numerorum rationalium ex ejus ratione ad arcum aliquem cujus sinus dabatur.

p. 42. Ex Actis Eruditorum anni|o| 1691|85| \pro/ Mense Aprilis O Octobri

pag 482 habentur Editorum verba sequentia.

Author noster adhibendam sibi putavit admirabilem illam proportionē Leibnitianam inter Circulum et quadratum circumscriptum, scilicet ut $\frac{1}{1}-\frac{1}{3}-\frac{1}{5}-\frac{1}{7}-\frac{1}{9}$ &c ad 1, quæ jam decennio & amplius abhinc inventa — Demonstratio autem insignis adeo Theorematis partim a clarissimo Inventore partim ab ejus amicis communica est dudum summis quibusdam P{illeg}|a|risinorum ac Londinensium Geometris, ac magno cum applausu suscepta.

P. 63. l. 22. ✝ Intelligit collectionem epistolarum Leibnitij Gregorij a Collinio factam quam ab Oldenburgo jam modo acceperat.

P. 87. l. 17 ✝ Methodum Tangentium Slusij. D. Leibnitius, lutis|a| Newtoni epistola ad Collinium 10 Decem. 1672 data, jam animo versa{illeg}|t|, & ad omnis generis problemata extendere conatur; sed in methodum differentialem nondum incidit.

P. 88, l. 15. Methodum tangentium Slusij generalem reddere, D. Leibnitius jam modo didicit, & ne a Literis Newtoni hoc didicisse videretur subjungit se jam a multo tempore h{illeg} didicisse.

Hunc factorem o Newtonus, ubi Propositiones demonstrat, semper exprimit, \eundem/ & pro \supponit/ indefinite parvum esse supponit donec calculus \ad finem perducatu{r}/ fi{illeg}ratur, deinde diminui in infinitum et evanescere: A{illeg} \sed/ ubi Propositiones demonstro investigat, factor o infinite parvus esse supponitur ab initio. Priore casu computationes accuratæ sin \& subintelligitur, scripto solum {illeg} fluxionis symbolo./ o sunt, posteriore per appoximationes {sic}, compendij gratia, proced{un}t|ere| {illeg} solent per approximationes

Fluentium vo, xo, yo, zo v x y z z, y, x, v, sunto momenta po, qo, ro, so, ro, qo, po, et Fluat z uniformiter, et per \ad/ momentum ejus po \so/ d{illeg} applicentur omnium p momento|a| et latera $\frac{\mathrm{s}}{\mathrm{s}},\frac{\mathrm{r}}{\mathrm{s}},\frac{\mathrm{q}}{\mathrm{s}},\frac{\mathrm{p}}{\mathrm{s}}$ erunt \earundem/ fluxiones \respective/ Latus autē $\frac{\mathrm{s}}{\mathrm{s}}$ est 1; et inde Newtonus pro fluxione quantitatis uniformiter fluentis unitatem ponit. Factorem o Newtonus semper exprimit & – – – – solent per approximationes, et fluxiones neglecto factore o pro momentis poni. Et in hoc casu ubi \Siquando igitur/ fluxiones 1, r, q, p aut similis, pro momentis ponuntur, hæ pro momentis $1\times \mathrm{o}$, {illeg} $\mathrm{r}\mathrm{o}$, $\mathrm{q}\mathrm{o}$, $\mathrm{p}\mathrm{o}$ scribuntur, subintellecto factore o. Nam fluxiones non sunt partes flux|e|ntium infinita sed \sunt/ velocitates quibus describunt fluunt, non sunt quantitates infinite parvæ sed \sunt/ finitæ; et pro ideo pro infinite parvis fluentium partibus haberi non possunt nisi quatenus per \in/ momentum o ductæ \sunt ut/ in tales partes convert{illeg} \autem/ subintelligantur. Fluxions {sic} autem Newtonus per symbola quæcun designat Pro fluxionibus autem Newtonus ponit symbola quæcun, Leibni Fluxiones autem \duci |sub|intelligantur./ Newtonus \autem Fluxiones/ per symbola quæcun designat: Leibnitius hujus generis symbola non habet.

p. 25. Exemplar hujus Epistolæ anno 1675|6| mense Aprili \Iunio/ a Collinio et Gregor Oldenburgo ad Leibnitium missa fuit. Leibnitius vero seriem \primam Anno 1682/ in Actis Lipsicus Anno 1682 ut suam imprimi curavit celata hac Epistola.

p 28. Mercator Logarithmotechniam MS cum Societatem regia {illeg}|A|nno 1667 mense augusto communicavit. Deinde addidit Quadraturam Hyperbolæ et librum edidit anno 1668 mense Iulio. Postea Gregorij demonstratio Geometrica Quadraturæ hujus eodem anno. Et post aliquot menses, scilicet mense {I}{illeg} Maio vel Iunio anni sequentis missi sunt hi libri ad D. Barrovium Cantabrigiæ. Is mox eosdum cum Newtono communicavit qui statim Analysin suam mutuo dedit & postulant Barrovio concessit ut \cum/ Collinio communicaretur. Ex hisce autem et alijs \quæ olim/ a Newtono cum Barrovio communicata fuerant, patuit illam methodum a Newtono aliquot annis antea excogitatam & modo universali applicatam fuisse.

|p. 48.| Edita fuit Mercatoris Logarithmotechnia mense Augusto vel Septembri Iulio anni 1668, et eodem anno ad finem vergente prodierunt Exercitationes Geometricæ Gregorij, & paucos post menses quam editi sunt hi libri, nempe mense Iunio anni sequentis missi sunt hi libri \C {sic}/ ad D. Barrovium Cantabrigiæ Cantabrigiæ, e{illeg} qui Analysin Newtoni extemplo remisit ex qua et alijs quæ olim ab auctore cum Barrovi{illeg}|o| communicata fuerant pat{e}t|ui|t altam methodum a Newtono aliquot annis [duobus ad minimum] antea excogitatam et modo universali applicatam fuisse, ut supra pag. 28.

p. 38 * Collinius jam ante quadrennium series Newtonianas ante triennium Gregorianas cum amicis \libere/ communicare cœpit. Leibnitius in Anglia diversabatur anno superiore & hujusmodi series nondum communicaverat, nec prius cum amicis com{illeg}|m|unicare cœpit quam ab Anglia discesserat. |Hinc in Galliam profectus {p}{illeg}{te}\scribe/bat se ejusmodi, seriem unam at alteram habere, & anno proximo mense Maio, cum series aliquas ab Oldenburgo accepisset, suas primum ab acceptis {illeg} diversas esse r{illeg}{t}|espon{d}|endebat Tandem vero quas nullas acceperat unam accepta{ra}rum| Subinde cum series aliquas ab Oldenburgo acceperat \distinxit/ eas primum a suis diversas esse fatebatur tandem vero unam Receptarum remisit Oldenburgo ut suam & Anglis ignotam. Nullas autem communicavit nisi quas ab Oldenburgo acceperat.

** Methodum exhibendi arcum cujus sinus datur |D.| Leibnitius ab Oldenburgo postea quæsivit Maij 12 1676, ideo nondum habuit. Sola methodus transmutatoria quam postea communicavit; non dat arcum ex sinu \in serei {sic} numerorum rationalium/, ideo non est methodus de qua hic agitur. [Series \d{efa}s/ forsan habere potuit sed methodum \commun{illeg}{m}/ qua invente sunt nondum habuit.]

p. 41. * Hanc seriem D. Collins initio anni 1671 a Gregorio acceperat ut supra, D. Leibnitius opusculum de eaden cum amicis in Gallia hoc anno communicare cœpit, cœ|e|lata hac epistola.

p. 42 * His verbis Leibnitius series quas ante ante annos aliquot se invenisse professus est, a communicatis diversas fuisse testatur: et unam tamen acceptarum quasi \a se inventam &/ Anglis ignotam, anno proximo Londinum remisit at a se inve Miror quænam fuerint ipsius series quas cum seriebus ab Oldenburgo missis jam comparare non potuit, et quare lucem nunquam viderunt.

✝ Hoc nunquam fecit |D| Leibnitius sed ubi series duas primas {illeg}|p|er Mohrū quendam denuo accepisset, postulavit methodum D. Newtoni perveniendi ad istas series duas series \easdem laudabat ut valde ingeniosas, et eo prætextu postulabat earum demonstrationem/ ad se mitti, quasi \series/ nullas prius ab Oldenburgo \prius/ accepisset. Et hoc pacto Epistolam Oldenburgo|i| oblivioni tradid it|en|da, licentiam obtinuit \tradidit &/ Serierum ab eo acceptarum ultimam sibi vindicandis\vit/ [quasi a nemine acceptam quia longe diversam ab ijs \duabus/ quas ab Oldenburgo acceperat per Georgium Mohr Mohrum acceperat. Certe series hæc Leibnitio ipso teste non est Leibnitiana quia non diversa ab ijs quas ab Oldenburgo acceperat.]

‡ [via quadam sic satis singulari] Leibnitius in Epistola 26 Octob. 1674, dicebat duas |ejus| series suas una et \una et/ eadem methodo inventas esse & hanc methodum {illeg}|j|am vocat viam quandam s{illeg} satis singularem. Sed series ab Oldenburgianis diversas, & viam singularem qua ejusmodi series prodirent nunquam comm{illeg}|un|icavit,|.| Viam quam arcus ex sinu in |serie| \numerorum rationalium sine methodis Newtoni/ prodiret nunquam communicavit, qua\m/vis hac via se in series suas incidisse \primum/ prætendebat anno 1674 sub initio anno superiore prætendebat, & sed anno proximo hanc viam sibi communicari postulabat Docuit tantum seris|e|s ex tangenibus {sic} sectionum conicarum eruere per transmutationem \in alias/ figuras{illeg} eruere m Methodum, inquam, qua series \rationales/ tam ex sinubus quam ex tangentibus sectionum Conicarum prodirent nunquam communicavit.

|Ad p. 70.| Geometræ priores invenerunt hoc Theorema, Quod summa terminorum progressionis Geometricæ in infinitum pergentis est ad terminorum primum & maximum ut hic terminus ad differentiam duorum primorum terminorum primorum. Demonstratur Theorema Arithmetice multiplicando extrema et media. Demonstravit Wallisius Arithetice {sic} dividendo rectangulum sub medijs per extremum ultimum. Vide Wallisij Opus Arithmeticum anno 1675 editum, {illeg}|a|nno 1695 denuo impressum cap. 33. sect 68. Per Divisie|o|nem Wallisij Mercator demonstravit Quadraturam Hyperbolæ a D. Brounker prius inventam. Et Gregorius idem mox demonstravit Geometrice. Sed horum nemo methodum generalem quadrandi Curvas per divisionem invenit. Wall{is} \præter Gregorium./ Mercator hoc \se invenisse/ nunquam professus est. Gregorius hujusmodi methodum licet Vir acutissimus & literis Collinij admonitus vix tandem <243v> invenit. Newtonus invenit per interpolationem serierum initio hujus Epistolæ expositam, et subinde divisionibus et et|x|tractionibus radicum ut notioribus usus est.

$\begin{array}{cc}\text{The fine Gold weighing }{533}^{\mathrm{oz}}.6^{{\mathrm{dw}}^{\mathrm{t}}}.0^{\mathrm{gr}}\text{ at }{4}^{\mathrm{li}}.9^{\mathrm{s}}\phantom{.}{0}^{\mathrm{d}}\text{ per oz comes to}\}& \hfill 2373. 3. 8⁤\frac{1}{2}\\ \text{The making of }735\text{ Medals at }{3}^{\mathrm{s}}\text{ per Medal comes to }& \hfill 110. 5. 0\phantom{⁤\frac{1}{2}}\\ & \hfill 2483. 8. 8⁤\frac{1}{2}\end{array}$

|p. 12| The Nota \Symbolo/ $\boxed{\frac{\mathrm{a}\mathrm{a}}{64\mathrm{x}}}$ \vel etiam hac $▯\frac{\mathrm{a}\mathrm{a}}{64\mathrm{x}}$/ Newtonus aream curvæ \hic/ designat cujus ordinata est $\frac{\mathrm{a}\mathrm{a}}{64\mathrm{x}}$. Leibnitius utitur hac Nota $\int \frac{\mathrm{a}\mathrm{a}}{64\mathrm{x}}$, Newtonus alibi ha{illeg} ▯{illeg} hac $▯\frac{\mathrm{a}\mathrm{a}}{64\mathrm{x}}$ Sic et $▯\frac{\mathrm{a}\mathrm{a}}{\mathrm{a}+\mathrm{x}}$ designat /Newtonus alibi /etiam\\ hac $▯\frac{\mathrm{a}\mathrm{a}}{64\mathrm{x}}$.

|p. 15.| Vbi agitur de arcis infinite par de linea|i|s et unitas ponitur pro puncto momento lineæ uniformiter fluentis seu pro linea \data/ infinite parva \vel puncto physico/, subintelligitur punctum \coefficiens/ nota \infinite parva/ o, sic ut $1\times \mathrm{o}$ lineam illam {illeg}|i|nfinite parvam significet. Et siquando species \aliquæ ut/ v, x, y, z \ponuntur/ pro quantitatibus fluentibus, ponuntur & species aliæ ut p, q, r, s pro earum fluxi{illeg}|o|nibus respective; tunc species op, oq, or, os eorum{illeg} momenta sunt \significant/: quæ momenta per species etiam p q r s designari possunt subintellecta literæ \coefficiente/ o. Et ubi agiter de superficiebus et unitas ponitur pro momento superficiei uniformiter fluentis seu pro et alijs notis \symbolis/ designantur aliarum superficierum momenta subintelligitur quantitates infinite parva o per quam momenta illa [At proprie loquendo p, q, r, s sunt fluxiones et op, oq, or, os momenta. Et sic in alijs quantitatum fluentium {x}, x, y, z.] Et sic si pro fluxionibus aliæ quævis ponuntur symbola \ut $\stackrel{.}{\mathrm{v}}$/ $\stackrel{.}{\mathrm{x}}$ $\stackrel{.}{\mathrm{y}}$ $\stackrel{.}{\mathrm{z}}$, eadem symbola per {illeg} ducta in symbolum o donat{illeg}nt fluxion fluentium momenta] Hujusmodi symbolis \fluxionum per {illeg}|o| multiplicatis/ Newtonus momenta designat ubi Propositiones demonstrare|nd||æ| velit \sunt/, ut mox \fit/ in hoc Tractatu, demonstrando Regulam primam, & in \tractatu de/ Quadratur{illeg}|a| Curvilinea Curvi\iline/arum \figurarum/ demonstrand{illeg}|o| Propositionem primam et {illeg} Sed ubi Propositiones investigat|nd|/æ sunt\ Analytice negligere solet litere symbolum o et eas|d|em \per/ symbola pro fluxionib fluxionum \solarum/ exponere momenta: et contra promiscue pro fluxionibus et \pro/ momentis \pr etiam/ usurpare, promiscue ponendo eadem symbola pro moment fluxionibus et momentis analogis.

p. 19. l 19, 20. Hinc patet resos|l|utionem binomij cujusm|v|is in seriem \infinitam/ generalem Newtono jam tum innotuisse.

D. Leibnitius {illeg} \ab/ anno 1670|1| et deinceps cum D. Oldenburgo commercium philosophicum habuit, et ejus Hypothesin \suam/ Physicam novam Londino \eodem anno Londini/ {illeg} in lucem emisit eodem anno Londini, & Regiæ Societati dicavit, dein anno 1673 ineunte, mense Martio in Galliam navigave transijt.

Vbi unitas ponitur pro momento quantitatis cujusvis uniformit{illeg}|e|r fluentis, sym unitas illa proprie fluxionem uniformem significat & \ut momentum Si/ subintelligitur coefficiens infinite parva o

Si quantitas fluentes \per symbola/ species quæscun, ut v, x, y et z & earum fluxiones, per species \symbola/ alias quascun ut [V X Y et Z vel $\stackrel{.}{\mathrm{y}}$ $\stackrel{.}{\mathrm{x}}$ $\stackrel{.}{\mathrm{y}}$ $\stackrel{.}{\mathrm{z}}$ vel] p, q, r, s, designantur, \Newtonus/ {illeg}|m|omenta fluentium desi designantur per s{illeg} designat \{illeg}r/ possunt \a Newtono in hac methodo/ per symbola fluxionum multiplicata per \ducta in/ quantitatem infinite parvam o uti \per/ op, oq, or, os,. {illeg}|Et| hujusmodi symbolis Newtonus utitur \præsertim/ {illeg} ubi Propositiones {illeg}|d|emonstrandæ sunt, ut mox fit in \fine/ h {illeg}|uj|us Tractatus demonstrando Regulam primam et in Tractatu de Quadratura Figurarum demonstrando Propositionem primam. Sed in investigatione rerum per Analysin \ubi Problemata resolven{d}a sunt/ ubi Problemata resolvenda\te{illeg}/ sunt per Analysin, Newtonus omittit symbolum \omittere licet coefficientem/ enodanda

|o| et ijsdem symbolis per symbola fluxionum designat etiam momenta fluentium, Et unitatem ponit tam pro momento quantitatis uniformiter lfuentis quam pro ejus fluxione] sed ubi Problemata tractantur Analytice, omittere licet coefficientem o, & symbolum fluxionis pro {mo} in symbolis momentorum, & pro momento quantitatis uniformiter fluentis unitatem usurpare ponere.] & symbola sola fluxionum \symbola/ pro momentis ponere, at unitatem pro momento quantitatis uniformiter fluentis usurpare pro momentis usurpare licet sola fluxionum symbola et pro momento quantitatis uniformiter fluentis unitatem ponere, neglecta coefficiente o per quam uti æquatio sub finem operationis dividi deberet. In methodo priore æqu{o} quantitas o \primum/ ut finita prima spectari potest, & \{u}ltimo,/ ubi æquatio inventa est et reducta et per o divisa, {illeg} ut nulla. Et Sic prodibunt rationes fluxiono|u|m ubi quantitas o evanescit. Et hæc est methodus qu{illeg} \analytica/ rationum primarum et ultimarum est perfecte demonstrativa & geometrica. Methodus altera qu{illeg} ubi quantitas {illeg} {illeg} coefficiens o omittitur est magis expeditior sed minus demonstrati halluci{illeg}|n|ationibus magis obnoxia.

Vnde – – – erunt traslationes {sic} directe ut impressiones & inverse ut superfici{es} hoc est directe ut impressiones et inversæ ut superficierum distantiæ ab axe Sunt autem diferentiæ motuum

Translationes autem sunt momenta \differentiæ/ motuum angularium circū axem, ideo momenta \differentiæ/ illæ sunt inverse ut superficierum distantiæ ab axe

pag. 61. {illeg} Hujus Harmoniæ series prima ex secundæ et tertia componitur, secunda \duplicata/ ex hac $\frac{1}{1}-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+\frac{1}{7}-\frac{1}{9}$ conjunctis binis terminis tertia \quadruplicata/ ex hac $\frac{1}{4}$ duplicata $\frac{1}{1}-\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}$ conjunctis binis terminis quarta est series Gregorij et quinta series Brounkeri.

pag. 86. Ad Notas adde. In Regulam quartam \D/ Leibnitius tandem incidit & in Actis Leipsiensibus i|a|nno 1689|93| \pag 295 179/ in lucem edidit, [eandem vocans methodum Tangentium inversam & in qua dicit maximam partem Geometriæ transcendentis contineri]

$1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+\frac{1}{5}=\frac{1}{2}+\frac{1}{2,3}+\frac{1}{3,4}+\frac{1}{4,5}+\frac{1}{5,6}=1$. Vnde $\frac{1}{1}+\frac{1}{3}+\frac{1}{6}+\frac{1}{10}+\frac{1}{15}\mathrm{\&c}=2$. $2-1+1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}$ $1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+\frac{1}{7}-\frac{1}{9}+\frac{1}{9}\mathrm{\&c}=1=\frac{2}{3}+\frac{2}{3,5}+\frac{2}{5,7}+\frac{2}{7,9}\mathrm{\&c}$. Vnde $\frac{1}{3}+\frac{1}{15}\frac{1}{35}+\frac{1}{63}\mathrm{\&}=\frac{1}{2}$ $1-\frac{1}{4}+\frac{1}{4}-\frac{1}{7}+\frac{1}{7}-\frac{1}{10}+\frac{1}{10}-\frac{1}{13}\mathrm{\&}=\frac{3}{4}+\frac{3}{28}+\frac{3}{70}+\frac{3}{130}+\frac{3}{208}=1$. Vnde $\frac{1}{2}+\frac{1}{14}+\frac{1}{35}+\frac{1}{65}+\frac{1}{104}=\frac{2}{3}$ $\frac{2}{2}-\frac{2}{5}+\frac{2}{5}-\frac{2}{8}+\frac{2}{8}-\frac{2}{11}+\frac{2}{11}\mathrm{\&c}=\frac{6}{10}+\frac{6}{40}+\frac{6}{88}+\frac{6}{154}+\mathrm{\&c}$

$\begin{array}{cc}1-\frac{1}{2}+\frac{2}{4}-\frac{1}{2}-\frac{1}{3}-\frac{1}{4}-\frac{1}{5}-\frac{1}{6}\phantom{=\frac{7}{6}}& \phantom{-1-}1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}\phantom{\text{ Or }-2+1+\frac{1}{3}+\frac{1}{6}+\frac{1}{10}+\frac{1}{15}=0\text{.}}\\ \phantom{1}\phantom{-\frac{1}{2}}-\frac{1}{3}+\frac{2}{3}+\frac{2}{4}+\frac{2}{5}+\frac{2}{6}\phantom{-\frac{1}{6}}\phantom{=\frac{7}{6}}& \underline{-1-\frac{1}{2}-\frac{1}{3}-\frac{1}{4}-\frac{1}{5}-\frac{1}{6}}\phantom{\text{ Or }-2+1+\frac{1}{3}+\frac{1}{6}+\frac{1}{10}+\frac{1}{15}=0\text{.}}\\ \underline{\phantom{1}\phantom{-\frac{1}{2}}\phantom{-\frac{1}{3}}-\frac{1}{4}-\frac{1}{5}-\frac{1}{6}-\frac{1}{7}\phantom{-\frac{1}{6}}\phantom{=\frac{7}{6}}}& -\frac{1}{1}+\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+\frac{1}{30}\text{ Or }-2+1+\frac{1}{3}+\frac{1}{6}+\frac{1}{10}+\frac{1}{15}=0\text{.}\\ 1-\frac{1}{2}+\frac{2}{3}-\frac{1}{12}-\frac{1}{30}-\frac{1}{60}-\frac{1}{105}-\mathrm{\&}=\frac{7}{6}& \phantom{-\frac{1}{1}}\phantom{+\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+\frac{1}{30}}\phantom{\text{ Or }-2+1+\frac{1}{3}+\frac{1}{6}+\frac{1}{10}+\frac{1}{15}=0\text{.}}\end{array}$

Series secunda {illeg} fit Conjungendo binos terminos hujus seriei com $1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}\mathrm{\&c}=1$, fit{illeg} {illeg}ū \colligitur/ series secunda $1+\frac{1}{3}+\frac{1}{6}+\frac{1}{10}+\frac{1}{15}\mathrm{\&c}=2$. Et conjungendo ternos terminos hujus seriei $1+\frac{1}{2}$$+\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}=1$ fit \colligitur/ series tertia $-\frac{2}{2}-\frac{2}{3}-\frac{2}{4}-\frac{2}{5}-\frac{2}{6}-\frac{2}{7}-\frac{2}{8}$ {W} $+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+8$ $1+\frac{1}{4}+\frac{1}{10}+\frac{1}{20}+\frac{1}{35}+\frac{1}{56}\mathrm{\&c}=1⁤\frac{1}{2}$.

to the R^t \most/ Hon^ble the Earl of Oxford & Earl Mortimer L^d High Treasurer of great Britain

The humble Petition of \Ms/ Katherine Barton Widdow of Lieut. Col̄l̄ Barton who was lost in y^e late shipwreck in y^e River of Canada \most humbly sheweth/

That yo^r Petitioners {illeg} Husband Lieutenant Collonel Barton having \late/ Husband Lieutenant Col. Barton being los who had served her Maj \in the army/ from the age of nineteen years & was \being/ lost in the late shipwra|e|ck in the late River of Canada & together with his equipage & provisions for the expedition to Canada \Quebeck/ to y^e value of four hundred pounds & \having enjoyed/ his place having of Lieutenant Collonel having cost him seven but half |o|a|n||e| year for w^ch he paid seven hundred pounds, (most part of the said moneys being out of yo^r petitioners fortune) Yo^r Petitioner soon after the said e{illeg}pe shipwack {sic} & having also lost \& leaving yo^r Petitioner w^th three small children, &/ \an/ annuity of 100^li p^r an' in y^e Excheq^r for his life being also lost to his family: Your Petitioner \being left w^th three small children/ soon after the said shipwrack app petitioned her Ma^ty for releif, & your Lord^p being then moved in this me \{illeg}/ behalf of your Petition^r was pleased to give a favourable answer repr{e sa}y \give a very favourable answer importune/ that you would take care of your Petitioner in this matter. Yo^r Petitioner therefore most humbly prays your Lords^p for a speedy releif. in consideration of her great losses

And yo^r Petitioner shall ever pray &c

{illeg}. $\frac{1}{1}.\frac{1}{2}.\frac{1}{3}.\frac{1}{4}$

$\begin{array}{c}\phantom{-1.}-2.-1.0.1.2.34.5.6.\\ \phantom{-1.}\phantom{-}1.\phantom{-}00.136.10.15.21.\\ -1.\phantom{-}0.\phantom{-}00.14.10.20.35.56.\\ \phantom{-1.}\phantom{-}\phantom{0.}\phantom{-}0.0.1.5.15.35.70.126.\\ \phantom{-1.}\phantom{-}\phantom{0.}\phantom{-}\phantom{0.}0.16.21.56.126.252.\end{array}$

$\begin{array}{r}896\\ 7168\\ 14336\end{array}$

Quantitas o \vel/ {illeg}|f|inita \esse/ supponitur \vel infinite parva/ & operationes \omnes peraguntur/ per Geometriam vulga Euclidiam d{illeg}s peragagant{ur} donec ad æquationes pereniantur & æquationes reducantur, dein quantitas o evanesere {sic} fingit & evanescere. Sic metho{illeg}|o|dus quam maxime Geometrica est summe demonstratio{illeg} & finitis computationibus evanescit. Priore casu computationes methodus Gem methodus \dicitur/ rationum primarum et ultimarum, posteriore methodus momentorum, utro methodus fluxionum dicitur.

Quantitas o vel finita esse supponitur vel infinite parva, & finitis computationibus evanescit. Prior casus methodum rationum primarum et {illeg} ultimarum co{st}|n|stituit, postior {sic} methodum momentorum, uter methodum Fluxionum. Methodus prior Geometri{illeg}|c|a est et summe demonstrativa, posterior non et{iam} \espeditior est sed/ principijs nondum demonstratis unititur \unititur &/ expeditij|o|r redditur est

Curvitates per fluxiones secundas & nonnunquam per tertias quartas quintas & superiores determinantur. Newtonus \Scilicet/ easdem sic annis aliquot ante scriptam hanc epistolam sic determinavit. Æquationis cujus termini omnes relationem inter Ordinatam \BC=/y et abscissam \AB/ x definientis, \sint/ termini omnes æquales nihilo. Et ijdem multiplpicati per indices dignitatum {illeg} Abscissæ dicantur $\cdot \mathrm{x}$, multiplicati per indices dignitatum Ordinatæ dicantur $\mathrm{x}\cdot$, pe|m|ultiplicati per indices dignitatum utrius dicantur $\cdot \mathrm{x}\cdot$, et quantit multiplicati \primo/ per indices dignitatum Abscissæ deinde per indices dignitatum earundem unitate diminuta|o|s dicantur $:\mathrm{x}$, et multiplicat \primo/ per indices dignitat{illeg}|u|m Ordinatæ deinde per indices dignitatum earundem {illeg}|u|nitate diminutas dicantur $\mathrm{x}:$. et erit Capia In CB|Or|dinata CB producta capiatur C{D} versus cavitatem Curvæ producta, capiatur 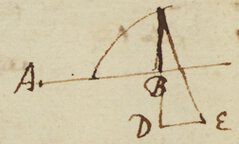$\mathrm{CD}=\frac{\cdot \mathrm{x}\cdot \mathrm{x}\mathrm{x}\cdot {\mathrm{y}}^2+\mathrm{x}\cdot \mathrm{x}\cdot \mathrm{x}\cdot \mathrm{x}\mathrm{x}}{-\cdot \mathrm{x}\cdot \mathrm{x}\mathrm{x}:\mathrm{y}+2\cdot \mathrm{x}\mathrm{x}\cdot .\mathrm{x}.\mathrm{y}-\mathrm{x}\cdot \mathrm{x}\cdot :\mathrm{x}\mathrm{y}}$ et agatur DE Abscissæ parallela & Curva ac CE \ad/ Curvā perpendiculari. Et punctum E ubi hæ actæ rectæ concurrunt erit centrum curvaminis ad punctum linæ hujus Curvæ ad punctum C.

Rem Tangentium jam tum a multo tempore Gregorius & Barrowus lege generalius tractaverant & {illeg} Newtoni id calculo consimili. Sed Newtonus in Epistola \anno 1672 scripta et/ anno superiore \{illeg}/ ad Leibnitium \missa/ scripserat methodum Slusij esse Corollarium tantum methodi longe generalioris & abstrusiora{s} problematum & ad resolvendum alia abstrusiora Problematum genera \se extende{ra}{illeg}/ \citra molestum illum {illeg} \calculum/ abstrusiora Problematum genera tractarentur quæ ex{illeg}d & ad quantitates surdas/; Et in epistolis anno superiore scriptis et ad ipsum \D Leibnitium/ s|m|issis methodum illam plenius descripserat & symbolis partim verbis expressis partim symbolis plenius descripserat: Leibnitius vero ne aliquid a Newton {sic} didicisse videretur scribit se methodum \postquam scripserat se/ {illeg}|N|ewtono assentiri quod \Slusij/ methodus tangentium nondum esset absoluta, & \subjungit/ quod jam a multo tempore rem Tangentium longe generalius tractasset, & mox subinde describit methodum differentialem quasi hanc hanc a multo tempore jam tum didicisset \habuisset/; Et in Epistola |sua| 29 Decem. 1711 \data et mox impressa/ ad D. Hans Sloane missa \& mox impressa/ hoc idem confirmat scribendo se inventum plusquam nonum in annum pressisse, id est se invenisse {illeg} ante mensem Octobrem anni 1675, cum t{illeg}|a|men \{illeg}/ mense Iulio anni 1676 \contra universalitatem methodi Newtoni/ scripserat, cum multa \esse/ us adeo mira esse et implexa ut ne ab æquationibus pendeant ne ex quadraturis qualia sunt (ex multis alijs) Problemata methodi tangentium inversæ. Methodum igitur \per differentias/ quam Fermatius, Slusius Gregorius, Barrowus, Slusius \in maximis & minimis tangentibus & maxi/ coluerant, Newtonus universalem reddiderat, Leibnitus|iu|s novis a{illeg}at symbolis & novo nomine & novis reru{m} \differentiam/ symbolis impositis ad se ra ut suam \& a se olim inventam & Newtonianæ similem ad/ Newton{o}|u||m| mittit, quo effectum est ut suam Newtonus lites aversatus suam tuto edere non posset edere neglite{illeg}itgeret.

Newtonus in tractatu de Analysi qua|e|m Barrovius anno 1669 cum Collinio communicavit, Fluentis quantitates \generis cujuccun/ per areas Curvilinearum, e{illeg} Fluxiones per o|O|rdinatas, tempus per abscissam \tempus per abscissam/ momentum tempore per momentum Abscissæ \momentum temporis per momentum abscissæ {illeg}/ momenta \aliarum fluentium/ per {illeg}|O|rdinatas ductas in momentum Abscissæ & tempus per Abscissam exposuit. Fluxiones vero & mo per symbola quæcun \fluxionem temporis per unitatem/ designavit & \&/ momentum abscissa \temporis/ per literam o, \et/ aream \se{u} fluentium/ per Ordinatam quadrato inclusam. D. Leibnitius per vero tandem anno 1677, Ordinatas designate cœpit per differentias Ordinatarum arearum et areas per summas Ordinatarum temporis per literam o, aream vero designat|v|it per Ordinatam quadrato inclusam et o|O|rdinatam per momentum Areæ applicata ad momentum Ordinatæ Abscissæ \designavit./ Leibnitius vero tandem anno 1677 Ordinatas designare cœpit per differentias aream & areas per summas Ordinatarum: Pro fluxionibus \vero/ symbola nondum adhibet. {Newtonus}

ideo $\mathrm{v}=\boxed{\mathrm{y}}$ flux|e|ns, y fluxio \ejus/ et oy momentum juxta Newtonum D. Leibnitius verò post annos octo calculum suum communicare cœpit, Barrovium in methodo tangentium secutus. & pro ipsius e|a| et {e} symbola dx et dy præterquam quod pro ipsius \sed pro Barrovij symbolis a et e sed pro s{mb}\y/mbolis ejus/ a et e substituit symbola \nova/ dx et dy, & methodum illam \istam illius/ a Newtono admonitus adauxit, {illeg}g{illeg} ac generalem reddidit.

Et fluentis {y}|v| vel $\boxed{\mathrm{y}}$ f{illeg} momentum erit $\mathrm{y}\mathrm{o}$ juxta Newtonū juxta Leibnitius vero pro $\boxed{\mathrm{y}}$ scribit $\int \mathrm{y}$ & pro $\mathrm{y}\mathrm{o}$ post annos octo pro $\boxed{\mathrm{y}}$ \et yo o et yo/ scribere cœpit f $\int \mathrm{y}$ & pro $\mathrm{y}\mathrm{o}$ et dv et dx et dv; pro fluxionibus symbola nondum adhibet. Facem igitur Newtono non prætulit.

Sit|n|t x abscissa, {illeg} fluxio \ejus/, et o momentum ejus, \qua tempus, exponitur, sit {illeg}|e|jus fluxio 1, & momentum o; {illeg} Deinde/ sit et sit y ordinata ordinata et v area Curvæ cujusvis: et fluentis v vel $\boxed{\mathrm{y}}$ fluxio erit y et momentum yo juxta Newtonum. \Analysin illam./ Leibnitius vero post annos octo pro $\boxed{\mathrm{y}}$, o, et $\mathrm{y}\mathrm{o}$ scribere cœpit $\int \mathrm{y}$, dx et dv, [Mutatis Barrovij symbolis a et e in dx et dy|v|] Pro fluxionibus symbola nondum adhibet. Facem igitur Newtono non prætulit <245bis(v)> et hac ratione Analysin \suam/ ibi descriptam generalem reddit.

Causam gravitatis ne Newtonus ne alius quisquam ex phænomenis hactenus deducere potuit. Esse quo vim electricam certissimum est sed ejus causa no ex phænomenis nondum patet.

At the end of M^r Leibnits Letted {sic} dated in April 1676, write Quanquam D. Leibnitius series quas anno superiore a D. Oldenburgo acceperat, se cum suis aliquando collaturum esse promiserat, tame eo nomine series illas a suis diversas esse prodiderat: tamen collatia illa nunquam facta est. Series illæ Leibnitianæ a communicatis diversæ lucem nondum viderunt, de quibus anno 1673 scribere cœperat lucem nondum viderunt. Epistola Oldenburgi qua series alienas acceperat oblivioni tradita est. Et postquam D. Leibnitium|s| annum methodum qu perveniendi ad series illas jam jam anno jam elapso \frustra/ quæsiverat hic meth D. Oldenburgium enixe sollicitat ut \is/ methodum Newtonianam suppeditante |D.| Collinio ad se mitteret. Sed et aliqui e socijs Academiæ scientiarum {illeg}|a|udito quam jam quod D. Gregorius sua jam emortuus esset, hic un{illeg} {illeg} Socijs aliquod|t| Ac socij aliquot Academiæ scientiarum sollicitante D. Leinitio ab Oldenburgio postularunt ut quæ Gregorius cum amicis communicaverat in unum corpus colligerentur et exemplar ejus Lutetiam Parisiorum mitteretur. Extat enim collectio manu D. Collins exaratum cum hoc Titulo

Et collectio illa sic orditur

NB. Hanc Epistolam Leibnitius oblivioni tradidit.

Hinc patet series Leibnitianas (siquas \jam/ invenerat) a communicatis diversas fuisse.

In hac collectione habentur Epistolæ Gregorij scribus refertæ, habetur epistola ejus \ad D. Collins/ data 15 Feb: Anno 167$\frac{0}{1}$, in qua sunt hæ series \habebatur hæc series ut supra/ /fuit hæc series.\ Sit Radius=r Arcus=a, Tangens=t, Secans=s, et erit Et erit $\mathrm{a}=\mathrm{t}-\frac{{\mathrm{t}}^3}{3{\mathrm{r}}^2}+\frac{{\mathrm{t}}^5}{5{\mathrm{r}}^4}-\frac{{\mathrm{t}}^7}{7{\mathrm{r}}^6}+\frac{{\mathrm{t}}^9}{9{\mathrm{r}}^8}$, &c et Leibnitius tamen hanc Erit $\mathrm{t}=\mathrm{a}+\frac{{\mathrm{a}}^3}{3{\mathrm{r}}^2}+\frac{2{\mathrm{a}}^5}{15{\mathrm{r}}^4}+\frac{17{\mathrm{a}}^7}{315{\mathrm{r}}^6}+\frac{62{\mathrm{a}}^9}{2835{\mathrm{r}}^8}$, &c Et $\mathrm{s}=\mathrm{r}+\frac{{\mathrm{a}}^2}{2\mathrm{r}}+\frac{5{\mathrm{a}}^4}{24{\mathrm{r}}^3}+\frac{61{\mathrm{a}}^6}{720{\mathrm{r}}^5}+\frac{277{\mathrm{a}}^8}{8046{\mathrm{r}}^7}$, &c Sit nunc Tangens artificialis=t & secans artificialis=s & integer Quadrans=q, Et erit $\mathrm{s}=\frac{\mathrm{a}}{\mathrm{r}}+\frac{{\mathrm{a}}^4}{12{\mathrm{r}}^3}+\frac{{\mathrm{a}}^6}{45{\mathrm{r}}^5}+\frac{17{\mathrm{a}}^8}{2520{\mathrm{r}}^7}+\frac{62{\mathrm{a}}^{10}}{28350{\mathrm{r}}^9}$, &c Sit $2\mathrm{a}-\mathrm{q}=\mathrm{e}$; et erit $\mathrm{t}=\mathrm{e}+\frac{{\mathrm{e}}^3}{6{\mathrm{r}}^2}+\frac{{\mathrm{e}}^5}{24{\mathrm{r}}^4}+\frac{61{\mathrm{e}}^7}{\phantom{0}}$                           t{illeg} seriem pro sua anno superiore cum amicis communicare cœpit, hoc anno ad D. Oldenburgum ut {illeg} remisit & {illeg} \qui Mathematica non erat noverat/ ut inventum novum |re|misit, & {illeg}in{illeg} Act postea in Actis Le|i|psiensibus \ut suam/ in lucem dedit ne ullibi agnovtit {sic} se eandem anno superiore ab Oldenburgo accepisse & Gregorium eandem a|i|neunte anno 1671 cum D. I. Collins communicasse. Hanc seriem igitur Gregorius methodo Newtoniana prior invenit. In eadem collectione habetur epistola Newtoni ad D. Collins                              data \et superius impressa,/ in qua Newtonus se methodum habere generalem habere dicit ducendi tangentes, quandrandi curvilineas & similia peragendi & methodum exponit exemplo ducendi tangentes: quam methodum Leibnitius differentialem postea vocavit.

Porro cum D Leibnitius in Epistola quam novissima se invent{illeg}|u|m aliquod polire \dicat/ cum Oldenburgo communicandum, \is/ intelligit Opusculum de prædicta Gregorij serie quod anno superiore componere cœpit et cum amicis communicare. Id ex verbis <246v> ejus colligo, cum in Actis Lipsiensibus mense Aprili Anni 168|9|1 in lucem editis ubi hæc leguntur. Iam anno 1675 compositum habebam opusculum Quadraturæ Arithmeticæ ab amicis ab illo tempore lectum, sed quod materia sub manibus c\r/escente limare ad editionem non vacavit postquam aliæ occupationes supervenere [id est postquam ad Electore Hanoveræ in patriam suam revocatus esset & anno 1677 negotijs publicis interesse cœpisset:] præsertim cum nunc prolixius exponere vulgari more quæ Analysis nostra nova paucis exhibet non satis operæ pretium videatur. Interim insignes aliquod|t| quidam Mathematici, quibus veritas primariæ nostræ Propositionis dudum in Actis publicatæ innotuit pro humanitate sua nostri qualiscun inventi candide meminere. Opus\c/ulum igitur his verbis descriptum poliebat, & polire pergebat donec Literis Electoris Hanoveræ in patriam suam revocatus esset ut negotijs publicis interesset, id quod con Et postquam hæ occupationes supervenere id est anno 1677, materia sub manibus crescente {illeg} opusculum \plurius/ limare ad editionem non \amplius/ vacavi|ba|t. præsertim cum tunc prolixius exponere vulgari more quæ Analysis \sua/ nova paucis exhibet non satis operæ pretium videretur. Opusculum igitur illus {sic} prius composuit quam methodum differentialem invenit. Opusculum anno 166 1676 \vulgari more/ limabat, et anno sequente \postea/ methodum suam novam (differentialem scilicet) invenit. Id quod

|NB| Collinius jam ante triennium series Newtonianas \ante biennium Gregorianas/ cum amicis communicare cœpit Leibnitius Londino de|i|scere se quo in hujusmodi seriem a|u|nam at alteram incidisse jactare cœpit, sed hujusmodi seriem \aliquam non prius/ cum amicis non prius communicavit quam ab ab Oldenburgo acceperat ut mox patebit.

Cum |D.| Leibnitius methodum Newtonianam pervendi ad series \anno superiore sibi missas/ Newtonianas frustra quæsiverat, eandem sibi communicare {illeg}b{illeg} postulaverat & Gregoriana omnia Lutetiam mitti: Oldenburgus & Collinius Newtorum {sic} enixe rogarunt ut ipse methodum suam describeret cum Leibnitio communicandam.

|In \Leib/ Epist. 1.| NB Methodum perveniendi ad has series Newton{illeg} Leibnitius|iu||s| {sic} per se invenire non potuit. Eandem postulante Leibnitio Newtonus postulante Leibnitio \Epistola superiore/ communicaverat. Leibnitius jam series \quasdam/ hac methodo inventas sibi arroga{illeg}|t|{illeg} \conatur/ Six et in Actis Lipsientibus Mense Aprili anni 1681 hæc scripb|p|sit. Cæterum ex serib|e|bus infinitis a me alijs Mercatore Newtono Gregorio exhibitis, sequitur . . . . . . . . $\frac{{\mathrm{l}}^5}{1,2,3,5}$ &c. Certe Le

|In Epist. \Newt/ 2| Patuit supra Newtonum anno 1669 \hujusmodi series/ in potestate habuisse adeo methodum|s| fluxionum ipsi ante annum illum innotuit.

|In \L./ Epist. 1.| Hæc methodus \tr/ ejusdem est generis cum /trans{mu}tione{illeg}\ transmutandi \figuras/ curvilineas in alias sibi i{illeg}|p|sis æquales ejusdem est generis cum Barrovianis & Gregorianis. Contingit aliquando figuram simpliciorem prodire sed {illeg} semper Conicæ Sectiones hac methodo semper ad series infinitas reduci possunt per divisiones. Idem \fit/ in Curvis secundi generis punctum duplex habentibus si modo & in curvis tertij generis punctum tri{b}|p|lex habentibus & |in| ijs quarti generis punctum quadruplex habentibus & sic deincips in infinitum \si/ modo punctum illud inveniatur et pro polo habeatur. {illeg} In alijs casibus m|r|es non succedit ido methodus non est generalis. Generaliter obtinet in sectionibus conicis, in alijs Curvis non item.

|In Epist. 1.| Porro \Porro/ Cum hæc methodus Leibnitius hanc methodum vi|u|lgari more \prolixius/ exponat quam Analysis sua nova paucis exhibere potuisset, manifestus|m| est quod Analysis illa nova ipsi nondum intinnotuit{illeg}.

|In Epist \L./ 2.| Cœpit igitur Leibnitius hoc \ipso/ tempore methodum differentialem cum amicis communicare, lectis prius Epistolis quas Newtonus de hac methodo scripserat.

|In Epist 2.| Hæc est Analysis differen æquationes infinitas supra impressa.

|In Epist 2.| Hæc est epistola supra impressa de methodo Slusij.

Erra Corrigenda.

Pag. 2. \lin 22 & 23/ Lege. per hand $1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\frac{1}{6}$ – – – &c, conjungendo singulos – –

P. 8. lin 8, {illeg}|9| {illeg} lege \BD (y) momentum quo/ [curvilinea]

P. 10. l. 3 tia, eorum Momenta

Ib. l. 12. fluentes quantitates,

\P. 14./ \l. 34/ \&/ P. 15. l. 14 data

Pag. 11. lin. 7. $\frac{2}{3}{\mathrm{x}}^{\frac{3}{2}}\mathrm{y}$,

P. 22. l. 6. anno 1675.

P. 31. l 32 \id monitum/ interseruerim. Ib. l. 22. præfatione \Ib. l. 23 editi/

P. 36. l 34 \& p. 37. l. 4, 6, 9, 10/ pro 35, 36, pro x scri{illeg}|b|e $\stackrel{.}{\mathrm{x}}$

P. 37 l. 11 pro xo scribe $\stackrel{.}{\mathrm{x}}\mathrm{o}$. Ib. l. 19 pro arcas scribe areas.

P 47. l. 18. Pro aliam scribe etiam.

P. 53. l. 32. Pro prædicaverat scribe explicaverat.

P. 54. l. 28. lege. 1676, se tum ante annos quin quo quietius –

P. 142. l. 9 pro 1679 scribe 1676.

P. 26. l. 7 lege oblitum jam fuisse. Ib. l. 27. quæ sponte

P 46. l. 30. quæ etiam adhuc

P 19. l 16 In eadem enim Epistola

Pag. 19. l. 16. {illeg}|l|ege i|I|n eadem enim \utique/ epistola. P. 22 l. 6. {illeg}|l|ege anno 1675. P. 26. l. 7 oblitum jam fuisse. Ib. l. 27 quæ sponte. P. 31 l. 22 præfatione. Ib. l. 23 editi. \Ib l. 32 interseruerim/ P. 36. l. 34, 35, 36 & P. 37, l. 4, 6, 9, 10 pro x scribe $\stackrel{.}{\mathrm{x}}$. P. 37. l. 11 pro $\mathrm{x}\mathrm{o}$xo scribe $\stackrel{.}{\mathrm{x}}\mathrm{o}$. Ib. l. 19 areas. P. 46 l. 30 quæ etiam adhuc. P. 47 l. 18 pro aliam scribe etiam. P. 53. l. 32 pro prædicaverat scribe expliccaverat. P. 54. l. 28 lege 1676, se tum ante annos quin quo quietius. P. 142. l. 9 pro 169|7|9 scribe 1676

p. 52. lin 4 pro omnino nullus scribe n{illeg} jus omnino nullum.

p. 3. l. p. 5. l. 11. not exceeding one penny over or under

p. 9 lin. ult penult. We take

p. 10 Kings Clerk. No tale. No uwse of Contollment Roll.

Hæc omnia refutantur supra, pag. \7,/ 8, 9, 10, 12, \24, 25/ 32, 33, 34, 36, 37, 38, 39, 40, \41,/ 52. Methodus fluxionum non consistit in forma symbolorum. Pro fluxionibus ipsarum x, y, z Newtonus quando ponit easdem literas punctis notatas $\stackrel{.}{\mathrm{x}}$, $\stackrel{.}{\mathrm{y}}$, $\stackrel{.}{\mathrm{z}}$, quando ea|s|dem in forma majuscula X, Y, Z, quando liter{a}|{s}|{illeg}{e}s {sic} alias ut p, q, r, quando lineas exponentes ut DE, FG, HI: (p. 37) Et hoc Newtonus in hunc us diem facit uti videre licet in Libro de Quadraturis, ubi fluxiones in Propositione prima denotantur per literas punctatas, in ultima per ordinatas Curvarum, in Introductione per alia symbola dum Methodum explicat illustrat per Exempla. (pag. 37) Omnia Newtoni symbola sunt in suo quæ genere prima (p. 37, 38) Calculo fluxionum utendi Newtonus In Principijs Naturæ Mathematicis Newtonus calculo suo utend fluxionum Analytico utendi nullam \non non/ habuit occasionem f{illeg}requentem. nam liber ille inventus est quidem per Analysit|a|, at scriptus per synthesin more veterum ut oportuit (p. 39       ) At Analysis per tamen per synthesin \illam/ ita elucet ut Marchio Hospitalius agnoverit hunc librum fere totum ex hac Analysi constare (pag. 30      ) Prima vice h{illeg} literæ punctatæ comparuerunt, non in tertio Volumine operum Wallisij quod prodijt anno 1699, sed in secundo volumine operum ejus pro quod prodijt anno 1693, annis duobus antequam fama Calculi differentialis ad aures Wallisij pervenit (p 40, 41) & annis |tribus antequam Marchio Hospitalius Analysin suam infinite parvorum edidit, qua calculus differentialis ubi locorum invalescere cœpit.|. {sic} Vera ratio fluxiones fluxionum capiendi hoc est differentianda differentialia habetur in Propositione prima libri de Quadraturis. Hanc (p. 10, 40) Hanc Propositionem Wallisius cum exemplis in differentijs primis et secundis Wallisius edidit in Tomo secundo Operum suorum (pag 10, 40, 41         Eandem Newtonus demonstravit synthetice in Lem. II Lib. II Princip. (p. Eand 30 Eandem Newtonus posuit in Epistola ad Oldenburgum 24 Octob. 1676 data tanquam fundamentum \hujus/ methodi de quas ante tum ante annos quin scripserat pag 8     ) In eadem Epistola /Propositione\ \Epistola/ Newtonus posuit Methodum suam \(in h{oi} Propositione fundatam)/ quadrandi figuras curvilineas accurate si {illeg}|fi|eri potest (pag

Quam methodum Newtonus habuit anno 1669 (pag 90. lin. 17) ut et omne|i|s aliquot antea testibus Barrovio & Collinio (pag. 103 lin 26, 27, 28, 33.) id est, Anno 1666 aut antea, ut etiam Wallisius de Methodo fluxionum testatum reliquit (pag. 32    )

Newtonus nunquam {mu}{n}quam mutavit literam o in in {sic} literam $\stackrel{.}{\mathrm{x}}$ sed eadem \{illeg}/ usus est in Introductione ad Librum de Quadraturis et adhuc utitur in eodem sensu ac sub intio {sic} (p. 8, 9, 36, 37, 38,

Veram methodum differentiandi differentialia Newtonus habuit anno 1669 p. 7, 11, 12

Ejusdem solutionem Newtonus docuit Anno 1669 in Analy {sic} sua per series, ubi methodum docet regrediendi regressionis ab area solidove contento ad Abscissam, Sp{illeg} vel Ordinatam (pag. 8, {illeg} 9{illeg} 85, 92)

Sed et D. Leibnitius olim agnovit hanc Analysin in Libro Principiorum eluce{illeg}|sc|ere pag. 34, 52

{I} Anno 1669 in Analysi sua per series Newtonus utitur symbolis ov, ox|y|, ox, [

Pro fluxionibus D Leibnitius nulla habet symbola [Pro momentis Newtonus utitur \anno 1669 usu in Analysi sua per series usus est/ symbolis fluxionum ductis in momentum o; vel L Pro ijsdem Leibnitius anno 1677 {illeg}|c|œpit uti symbolis dx, dy, dz. Pro fluentibus Newtonus anno 1669 in Analysi sua ut|s|us est symbolis fluxionum rectangulo inscriptis: pro ijsdem Leibnitius] Leibnitius {illeg}|S|ymbolis momentorum sive differentiarum dx, dy, dz \Leibnitius/ primo uti cœpit anno 1677: Momenta Newtonus denotabat per rectangula sub fluxionibus & momentis|a| o cum Analysin suam scriberet anno 1669 aut ante, Leibnitius symbolis — in quadrato vel rectangulo ad hunc modum $\boxed{\frac{\mathrm{a}\mathrm{a}}{64\mathrm{x}}}$ Omnia <249r> Newtoni symbola sunt in suo quæ genere prima. (p. 37, 38.

Et specimen ejusdem quoad Tangentes ducendas posuit in Epistola ad Oldenburgum ad Collinium 10 Decem. 1672 |(p. 105.)|Et in eadem Epistola addidit Problemata de Curvarum – –

Newtonum accusat quasi Deu qui Deum corpore omni destitutum esse affirmatꝰ, accusat quasi {illeg} sensorium corporeum \& organa/ Deo ja{illeg} tribueret. Gravitatem universalem in argumento Inductionis fundatam negat, nulla in contrarium observatione adducta.

Sed et Sectiones duas primas Libri secundi Principioorum {sic} verbis alijs compo (abs symbolis differentialibus) composuit, & addidit \subjunxit/: Omnia autem respondent nostræ Analysi Infinitorum, hoc est calculo summarum ac differum. (pag. 41, 42, 43.) Noverat ita D. Leibnitius demonstra{ne}s Propositionum in Libro Principiorum calculo differentiali respondere.

{illeg} Keilius hoc notaverat anno {illeg} 1711 (p. 238) Et hoc Newtonus in hunc us diem facit, ut videre licet in

Tabulæ pro Quadrandis figuris anno in Scholio ad Prop. X.libri de Quadraturis \positæ/ {illeg} constructæ erant annis quin \diu ante/ ante {sic} annum 1676, ut ex Ordinatis {illeg}|C|urvarum in Epistolam Newtoni 24 Octob 1{illeg} ad Oldenburgium 24 Octob. 1676 data \data/ positarum\is/ liquet. (pag. 173;) & abs methodo fluxionum & Momentorum construi ne quibant.

Corollarium secundum Propositionis illius decima plenius exponitur in Epistola Newtone|i| ad Collinium Novem. 8. 1676 missa, his verbis. Nulla extat Curva – – – haud tamen adeo generaliter. Et ex his a Hactenus Newtonus. Et ex his \omnibus/ abunde satis liquet Methodum fluxionum et Momentorum quatenus in libris dece Propositionibus decem primis Libri de Quadraturis exponitur Newtono innotuisse anno 1676, aut antea.

Sed \et/ Marchio Hospitalius testis est, \pro Newtono vel potius Iudex,/ qui uti \dixit/ Librum de Principiorum philosophiæ fere totum \esse/ ex hoc calculo con- este s{illeg} ut supra \(p. 30)/, et Leibnitium \in/ Methodum differentialem invenisse incidisse invenien efficiendo ut methodum tangentium Barrovij proceden non hæreret ad radicales \p 26 27, 28/. Newtonus enim \antea/ in Epistolis 10 Decem 1672 & 24 Octob. 1676 Leibnitium admonuit se hoc \antea/ assecutum esse. (p. 26, 27, 28, 30. \105, 166./) Quin et Leibnitius contra seipsum testis est est, p olim agnovit Librum Principiorum ope calculi infinitesimalis compositum fuisse. pag

Miracula vocat quæ admirationem non cient. Loca {illeg}{illeg}|i|bus Deus omni corpore destitutus adest, vocat ejus cerebrum a cerebrum \corporeum/ Spatium et tempus non ad Predicamentum Quantitatis \{illeg}/ sed \id/ Prædicame{n}ta Vbi et Quando refert. Ipse monades indivisibiles negat introducit & tamet|n| atomes negat. Corpuscula poris destituta redet, {illeg} atomos vocat & dari negat. Mundum vult esse absolute perfectum, quia opus Dei: quo nomine pediculi et vermes sunt entia absoluta perfecta. Deum vocat Intelligentiam supramundanam, & spatiam tamen ultra mundum corporum dari negat,

Annotatio

Hæc omnia refutantur supra, pag. 7, 8, 9, 10, \11./ 12, 24, 25, \30, 31./ 32, 33, 34, 36, 37, 38, 39, 40, \41,/ 53, 90 \92, 103/ Methodus fluxionum non consistit in forma symbolorum. Pro fluxionibus ipsarum x, y, z, Newtonus quando ponit easdem literas punctis notatas $\stackrel{.}{\mathrm{x}}$, $\stackrel{.}{\mathrm{y}}$, $\stackrel{.}{\mathrm{z}}$, quando easdem forma majuscula X, Y, Z, quando literas alias ut p, q, r, quando lineas exponentes ut DE, FG, HI (pag. 37.) Et hoc Newtonus in hunc us diem facit, uti videre licet in Libro de Quadraturis, ubi fluxiones in Propositione prima denotantur per literas punctatas, in ultima per ordinatas Curvarum, in Introductione per alia symbola dum Newtonus ibi Methodum explicat illustrat per Exempla (pag. 37.) Omnia Newtoni symbola sunt in suo genere quæ genere prima (pag. 37, 38.) In Principijs Naturæ Mathematicis Newtonus calculo suo fluxionum Analytico Newtonu utendi non habuit frequentem occasionem: Nam Liber ille inventus est quidem per Synthesin Analysit|n|, at scriptus est per synthesin more veterum ut oportuit (pag. 39.) At Analysis tamen per Synthesin illam ita elucet, ut Leibnitius ipse olim agnoverit Newtonum non solum methodo sua tangentes duxisse sed majora multo consecutum, viso demum libro Principiorum, \se/ satis intellexit|s||se| (pag. 52.) Et \alibi/ de sublimi quadam parte methodi qua Newtonus solidum minimæ resistentiæ invenerat, \hæc/ verba haben|t|, Quam methodum ante D. Newtonum et me, nullus quod sciam Geometra habuit, uti ante hunc maximi nominis Geometriam, nemo se habere, PROBAVIT (pag. 34) Et in Epistola ad Newtonum data Hanoveræ 1683 7 Mart. 1693 ita scripsit: Mirifice ampliaveris Geometriam tuis seriebus, sed edito Principiorum opere ostendisti patere tibi quæ Analysi receptæ non subsunt. Conatus sum ego quo notis commodis adhibitis &c. (pag. 30.) De <250v> hoc Libro Principiorum sic locutus est etiam Machio Hospitalius quasi totus fere per hunc Calculum compositus esset. (pag. 30) Literæ punctatæ prima vice comparuerunt, non (ut hic dicitur) in tertio Volumine Operum Wallisij quod prodijt anno 1699, sed in secundo Volumine Operum ejus quod prodijt anno 1693, annis uti duobus anq|t|equam fama calculi diffentialis {sic} ad aures Wallisij pervenit (pag. \10./ 31, 32, 40, 41,) & annis tribus antequam Marchio Hospitalius Analysin suam infinite parvorum edidit, qua calculus differentialis ubi locorum invalescere cœpit. (pag 26      ) Newtonus nunquam mutavit litera o in literam $\stackrel{.}{\mathrm{x}}$ punctatam uno puncto, sed litera illa o usus est in Introductione ad Librum de Quadraturis, & adhuc utitur in eodem \sensu/ ac sub initio \id maximo cum fructu/ (pag. 8, 9, 1|3|6, 37, 38.) Methodus fluxiones capi- Vera methodus fluxiones fluxionum capiendi hoc est differentiandi differentialia habetur in Propositione prima Libri de Quadraturis (p. 10, 40.) {emdi} seu differentiandi differentialia habetur in Propositione prima Libri de Quadraturis; Et Regulam ibi traditam verissimam {illeg} Leibnitius optime noverat esse optime noverat D. Leibnitius {illeg} Eam optime noverat; eadem lu \Idem noverat Iudex ab ipso constitutus:/ eandem cum exemplis in differentijs primis et secundis Wallisius edidit in Tomo secundo Operum suorum pag 392, 393 &c |id| annis \anno 1693 ut supra, annis scilicet/ tribus antequam Regula Leibnitiana|o||rū| differendi differentialia lucem vidit. (pag. 10, 40, 41.) Eandem Regulam Newtonus demonstravit synthetice in Lem. II Lib. II. Princip |(|(p. 30,)|)| & posuit in Epistola ad Oldenburgum 24 Octob. 1676 data tanquam fundamentum hujus methodi de qua tum \ante/ annos quin scripserat (pag. 8) [In eadem Epistola, ut et antea in Epistola ad D Collins 10 Decem 1672 data, Newtonus dixit methodum Tangentium Slusij ex hoc fundamento prompte consequi] Et in Epistola ad Collinium 10 Decem 1672 data, addit Problemata de Curvarum Curvatura seu Geometricarum sive Mechani <251r> carum per eandem methodum solvi. Ex qui|o| manifestum est se jam tum suam Methodum ad secunda ac tertia momenta extendisse: Cum enim Areæ Curvarum considerantur tanquam fluentes, (ut in hac Analysi fieri solet,) ordinatæ exprimunt fluxiones primas; Tangentes autem datæ sunt per fluxiones secundas, & Curvaturæ per tertias (p. 9.) Et anno 1669 in Analysi per series Newtonus ait \dixit;/, {sic} Momentum est superficies, cum de solidis; & Linea cum de superficiebus; & punctum, cum de lineis agitur: \quod/ perinde est ac si dixisset; cum solida considerantur tanquam fluentia, eorum Momenta fluentia sunt superficies sunt, & \horum/ momentorum momenta (vel secunda Momenta) Lineæ sunt; & horum Momen{ta} (sive tertia Momenta) puncta sunt (p. 9, 10) adeo qua ratione momenta prima derivantur a fluentibus, secunda derivantur a primis, tertia a secundis & sic deinceps in infinitum. Et quomodo momenta prima derivantur a fluentibus ostenditur in Analysi per series {illeg} inveniendo Ordinatas ex ares|i|s fluentibus (p. \7,/ 8, 9, 10, \11, 12/ 92   ) In eadem Analysi Newtonus dixit se b curvarum areas & longitudines id modo fiat, beneficio ejusdem Analyseos exacte & Geometrice determinari (pag. 90 \lin 17/) Et methodus hæcce Newtono innotuit annis aliquod|t| antea testibus Barrovio et Collinio (pag. 103. lin. 26, 27, 3|2|8, 33) id est anno 1666 aut antea. Hæc methodus aliquatenus explicatur in Epistola 24 Octob 1676 ad Oldenburgum data, ibi \ibi/ ex Propositione prima Libri de Quadraturis consequi dicitur. (pag 150, 15{illeg}|1|) \sed/ & in Libro illo Propositioni|e|bus quinta et sexta Libri illius plenius explicatur & \hæ Propositiones/ ex Propositionibus quatuor primis Libri de Quad ejusdem consequentur, ideo Methodus fluxionum quatenus in Propositionibus \quin ve{l}/ sex primis Libri de Quadraturis exponitur, Newtono innotuit \Newtono innotuit/ anno 1{illeg}|6|66 aut antea, Newtono innotuit testibus Barrovio et Collinio; ut et teste \etiam/ Wallisio (pag. 32)

(p.      ) Est enim \Et est/ symbolum unicum quo \N./ utitur pro quantitate infinite \in/ indefinite parva,|.| et \Nam/ rectangulum sub {illeg} fluente \hoc symbolo fluxionis/ hoc symbolo o et symbolo fluent|xio|nis (vel expresso vel subintellecto) \& symbolo fluxionis/ pro alijs quantitatibus infinite parvis semper ponit{ur} ponitur. Et symbolum $\stackrel{.}{\mathrm{x}}$ non momentum vel differentiam sed motum fluxionis significat. (pag E|a|t symbolum $\stackrel{.}{\mathrm{x}}$ quantitatem finitam designat (pag. 8, 9, 36, 37, 38.

In y^e year \Anno/ 1689|8| M^r |D. {sic}| Newton \D./ Leibnitius Sectiones duas primas Libri secundi Principiorum \Newtoni/ alijs verbis \alijs/ composuit & \sine symbolis {illeg}itio anni proximi/ in Actis eruditorum edidit sine symbolis suis verbis \{illeg}dis/ apertis sine symbolis edidit & subinde addidit sub finem addidit hæc verba. Multa ex his deduci possent praxi accommodata, sed nobis nunc fundamenta Geometrica jecisse suffecerit in quibus maxima consistebat difficultas. Et fortassis attente consideranti vias quasdam novas satis antea impeditas appæruisse videbimur. Omnia autem respondent nostræ Analysi infinitorum hoc est calculo summarum ac differentiarum (cujus elementa quædam in his Actis dedimus) communibus quoad licuit verbis hic expresso. Hasce omnes vias novas \satis antea impeditas/ Newtonus in Sectionibus illis duobus antea /prius\ \prius/ aperuerat Omnia \Et/ Omnia om autem respondent ejus Analysi per infinitorum, hoc est calculo per fluxiones fluentes & momenta (cujus elementa dedit in Lem. II Lib. II Princip) ut et in Analysi per series) communibus quoad licuit verbis illic expresso.

To S^r Isaac Newton

Nov:^r 5

S^r

Tis with great unwillingess I give y^o this trouble, after y^r very many & great favours y^o have been pleas'd in the most generous manner to grant me I have had the unhappiness of sickness in my family near 2 Months. I shall be very much obliged to y^o, & thankfull for a Guinea; w^ch will at this time be most seasonab{l}{e} I am, S^r, w^th all respect & thankfullness for y^r great kindness,

Y^r most obliged H: Ser^t Iohn Arnold

p. 98, lin penult & p. 120, lin. 7. $1+1+2\sqrt{1+3}$

NB. Hæc omnia refutantur supra p. 9, 10, 12, 32, 33, 34, 36, 37, 38, 39, 40, 52. Newtonus methodum fluxionum docuit & exemplis illustravit \abs literis punctatis/ in Introductione ad librum de Quadraturis, abs literis punctatis ibi etiam usus litera o pro incremento constante ipsius x: & his non obstantibus me veram methodum differentiand differentialia in Propositione prima ejusdem Libri \docuit (p. 10./. {sic} Hanc Propositionem Wallisius e cum exemplis in Propositionibus primis et secundis \& Literis punctatis/ /in Diffentijs {sic} primis & secundis\ Wallisius edidit in Tomo secundo operum suorum anno 1693 annis fere duobus antequā fama methodi differentialis Leibnitianæ ad ejus aures pervenerat \et in eodem secund {sic} Tomo literæ punctatæ lucem viderunt/. Eandem \Prop./ Newtonus demonstravit synthetice in Lem II Lib. II Principiorum Eandem Newtonus posuit in Epistola ad Colliniu Oldenburgium 24 Octob. 1676 \data/ tanquam fundamentum methodi de qua tum ante annos quin scripserat \(pag./. In eadem Epistola Newtonus posuit Methodum \suam/ quadrandi Curvas Figuras curvilineas accurate si fieri potest \hac Propositione fundatam/ (pag       ) quam methodum \is/ habuit anno 1669 (pag. 90. l. 18) ut et annis aliquot antea testibus Barrovio e Collinio (pag. 103   ) id est anno 1666 ut Etiam aut antea, ut etiam Wallisius de methodo fluxionum testatum reliquit. (pag 32   ) Newtonus nunquam mutavit literam o in literam $\stackrel{.}{\mathrm{x}}$ (p. 36, 37).