Enarratio plenior scholii praecedentis
Mens \Enarratio plenior/ Scholij præcedentis.
Brevitate verborum effectum est ut Scholium præcedens a nonnullis perperam expositum fuerit et in disputationes tractum, et propterea rem totam fusius enarrabo.
Analysin per æquationes numero terminorum infinitas a me scriptam Barrovius noster misit ad Collinium mense Iulio anni 1669. Continet autem hic Tractatus Analysin qua Problemata per methodos serierum & fluxionum \momentorum/ conjunctas tractantur. Problemata uti ubi vulgaris Analysis non sufficit, deducuntur ad æquationes per methodum momentorum, quæ et methodus fluxionum dicitur; et æquationes finitæ per methodos in hoc Tractatu descriptas convertuntur (ubi visum est) in series perpetuo convergentes; et Series nonnunquam redeunt in Æquationes finitas; et ubi symbolum aliquod pro serie tota ponitur, Series inter operandum pro symbolo illo nonnunquam substituitur; et ex fluxionibus per Regulas tres initio hujus Tractatus positas eruuntur fluentes; et ex fluentibus vicissim eruuntur fluxiones per easdem Regulas inversas; et methodum ad quantitaties surdas non hærere ostenditur; ut \et Curvas Mechanicas hujus ope Mechanicas ad æquationes reduci,/ et Problemata omnia quæ in Curvis Analyticis tractari solebant, tractari etiam in Curvis Mechanicis per hanc Methodum, et quicquid Analysis vulgaris per æquationes ex finito terminorum numero constantes (quando id sit possibile) perficiat, hanc Methodum per æquationes numero terminorum infinitas semper perficere. Quibus de causis nomen Analyseos huic methodo a me recte impositum fuisse disputatur.
In hoc Tractatu pro fluxione vel Temporis vel quantitatis cujuscun uniformiter fluentis qua tempus exponitur, usurpatur unitas, & pro fluxionibus aliarum quantitatum ponuntur alia quæcun symbola, et pro fluentium momentis (seu particulis momento temporis genitis,) ponuntur rectangula sub fluxionibus & momento dato o. Et siquando symbolum fluxionis pro momento ponitur subintelligitur coefficiens o. Nam fluxio non est momentum sed fluendi velocitas. Fluxio vero rectangulo inclusa fluentem designat. Et symbola pro lubitu variantur cum methodus in forma symbolorum minime consistat. Et specimen calculi exhibetur. sub finem Tractatus.
Collinius autem ex hoc Tractatu Series cum amicis mox communicare cœpit & methodum tanquam generalem celebrare. Et D. Iacobus Gregorius Abredonensis Scotus de his admonitur|s| methodum inveniendi seriem quandam a Collinio ad ipsum missam aliquandiu quæsivit, & sub finem anni 1670 invenit, & mox per Epistolam ad Collinium 15 Feb. 167 datam misit series plures per eandem methodum inventas, & quarum numero erat hæc. \In circulo/ Sit Radius r, Arcus a, et Tangens t, et erit Exemplar autem hujus Epistolæ ad D. Leibnitium missum fuit mense Iunio Anni 1676|, cum ipsa ad illum prius missa fuisset, nempe mense Aprili Anni 1675.|
Interea Gregorius anno 1670, Sept 5, scripsit ad Collinium se ex methodo Tangentium Barrovij \(hoc anno edita)/ et suis methodum generalem invenisse ducendi Tangentes abs calculo; et anno 1672 sub autumno, Slusius scripsit se methodum Tangentium expeditam habere: et subinde Collinius postulavit ut methodum meam communicarem. Qua occasione sequentem Epistolam 10 Decem 1672 ad ipsum scripsi.
Ex anim{a}|o|mgaudeo {sic} D. Barrovij amici nostri reverendi Lectiones Mathematicis exteris adeo placuisse, neque parum me juvat intelligere eos [Slusium et Gregorium] in eandem mecum incidisse ducendi Tangentes methodum. Qualem eam esse conj|i|ciam ex hoc exemplo percipies. 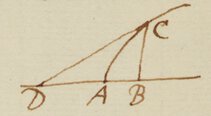 Pone CB applicatam ad AC, et dicatur AB=x et BC y, habitudo inter x et y exprimatur qualibet æquatione, puta , qua ipsa determinetur Curva. Regula ducendi Tangentes|m| hæc est. Multiplicata æquationis terminos per quamlibet Progressionem Arithmeticam juxta dimensiones y, puta , {illeg} ut et juxta dimensiones x, puta . Prius productum erit Numerator & posterius divisum per x Denominator fractionis quæ exprimet longitudinem BD ad cujus extremitatem D ducenda est Tangens CD. Est ergo longitudo . Hoc est unum particulare vel Corollarium potius Methodi generalis quæ extendit se citra molestum ullum calculum, non modo ad ducendum tangentes ad quasvis Curvas sive Geometricas sive Mechanicas vel quomodo cun rectas lineas aliasve Curvas respicientes; verum etiam ad resolvendum alia abstrusiora Problematum genera de Curvitatibus Areis, Longitudinibus, Centris gravitatis Curvarum &c. Neque (quemadmodum Huddenij methodus de Maximis et Minimis) ad solas restringitur æquationes illas quæ quantitatibus surdis sunt immunes. Hanc methodum intertexui {illi} alteri isti quæ|a| æquatione|u|m exegesin instituo reducendo eas ad series infinitas. Memini me ex occasione aliquando narrasse D. Barrovio, edendis suis Lectionibus occupato, instructum me esse hujusmodi methodo Tangentes ducendi: sed nescio quo diverticulo ab ea ipsi describenda fuerim avocatus. Slusij methodum Tangentes ducendi, brevi publice prodituram confido. Quamprimum advenerit, exemplar ejus ad me transmittere ne grave ducas.
Pone CB applicatam ad AC, et dicatur AB=x et BC y, habitudo inter x et y exprimatur qualibet æquatione, puta , qua ipsa determinetur Curva. Regula ducendi Tangentes|m| hæc est. Multiplicata æquationis terminos per quamlibet Progressionem Arithmeticam juxta dimensiones y, puta , {illeg} ut et juxta dimensiones x, puta . Prius productum erit Numerator & posterius divisum per x Denominator fractionis quæ exprimet longitudinem BD ad cujus extremitatem D ducenda est Tangens CD. Est ergo longitudo . Hoc est unum particulare vel Corollarium potius Methodi generalis quæ extendit se citra molestum ullum calculum, non modo ad ducendum tangentes ad quasvis Curvas sive Geometricas sive Mechanicas vel quomodo cun rectas lineas aliasve Curvas respicientes; verum etiam ad resolvendum alia abstrusiora Problematum genera de Curvitatibus Areis, Longitudinibus, Centris gravitatis Curvarum &c. Neque (quemadmodum Huddenij methodus de Maximis et Minimis) ad solas restringitur æquationes illas quæ quantitatibus surdis sunt immunes. Hanc methodum intertexui {illi} alteri isti quæ|a| æquatione|u|m exegesin instituo reducendo eas ad series infinitas. Memini me ex occasione aliquando narrasse D. Barrovio, edendis suis Lectionibus occupato, instructum me esse hujusmodi methodo Tangentes ducendi: sed nescio quo diverticulo ab ea ipsi describenda fuerim avocatus. Slusij methodum Tangentes ducendi, brevi publice prodituram confido. Quamprimum advenerit, exemplar ejus ad me transmittere ne grave ducas.
Missum est autem exemplar hujus Epistolæ ab Oldenburgo ad Slusium 29 Ian. 167, et a Collinio ad Tschurnhausium mense Maio 1675, et ad Leibnitiuim mense Iunio 1676. Et eodem mense Iunio missum est etiam exemplar Epistolæ jam dictæ Gregorij ad Leibnitium. Et ex his Epistolis innotescere potuit quod hæcce Tangentium methodus \{illeg}/ et Corollarium esset Methodi generalis de qua hic locutus sum, et consequentur etiam ex methodi|o| Tangentium Barrovij.
Ineunte anno 1673 D. Leibnitius Londinum venit. Et cum Pellio nostro de rebus Arithmeticis sermones habuit in Geometria sublimiore nondum instructus. At a Pellio \(quis Collinium noverat?)/ de serie Mercatoris &c admonitus, Logarithmotechniam ejus emit & secum Lutetiam tulit. Scripsit vero ad Oldenburgum de numeris is ad mensem Iunium hujus anni, dein siluit per annum integrum & interea Geometriam sublimiorem Hugenio magistro didicit, et anni 1674 mense Iulio silentium abrumpens, de Seriebus ad Oldenburgum scribere cœpit, dicendo se Theorema invenisse cujus ope area circuli vel sectoris ejus dati exacte exprimi posset per seriem numerorum rationalium continue productam in infinitum. Et mense Octobri ejusdem anni exposuit quale esset hoc Theorem a cujus ope area sectoris dati per seriem exprimi posset, dicendo, quod seriem invenisset pro circumferentia tota, et quod eadem methodo etiam arcus cujuslibet cujus sinus daretur, geometrice exhiberi per ejusmodi seriem valor posset nullo ad integræ circumferentiæ dimensionem recursu; ut adeo non necesse esset arcus rationem ad circumferentiam nosse. Theorema igitur ex dato sinu dabat vel sectorem vel arcum; et si ratio arcus ad circumferentiam totam nosceretur dabat etiam circumferentiam totam.
Anno 1675, Apr. 15, D. Oldenburgus suggerente Collinio seriem meam pro inveniendo arcu ex sinu dato, ut et Gregorianam pro inveniendo arcu ex tangenti data, et harum inversas, alias nonnullas ad D. Leibnitium misit, et D. Leibnitius Literis 20 Maij 1675 datis rescripsit in hæc verba: Literas tuas multa fruge Algebraica refertas accepi, pro quibus tibi et doctissimo Collinio gratias ago. Cum nunc præter ordinarias curas mechanicis imprimis negotijs distrahar, non potui examinare series quas misistis ac cum meis comparare. Vbi fecero perscribam tibi sententiam meam, nam aliquot jam anni sunt quod inveni meas via quadam sic satis singulari. De seriebus igitur locutus est quæ a missis diversæ erant & quas habuit ubi primum venit ab Anglia in Galliam.
Eodem anno D. Leibnitius compositum habebat opusculum Quadraturæ Arithemetica \(sc. per seriem jam dictam Gregorij)/ ab amicis ab illo tempore lectum, se{t}|d| quod materia sub manibus crescente limare ad editionem non vacavit postquam aliæ occupationes supervenere, præsertim cum tandem prolixius exponere vulgari more quæ Analysis ejus nova paucis exhibet, non satis opere pretium videbatur; [ut ipse scripsit in Actis Eruditorum anni 1691 pro mense Aprili, pag 178.]
Anno 1676 tempore vero|n|o audita Gregorij morte D. Leibnitius postulavit ab Oldenburgo ut quæ Gregorius cum amicis communicaverat in unum corpus colligerentur & ad se mitterentur. Et Collinius subinde Excerpta Epistolarum Gregorij collegit, & missa est Collectio Lutetiam mense Iunio hujus anni ut a D. Leibnitio legeretur & subinde redderetur Oldenburgo. Ex extat Collectio in Archivis R. Societatis manu Collinij scripta, et inter alia continet Epistolas Gregorij ad Collinium 5 Sept. 1670, et 15 Feb. 167 datas, ut et meam ad Collinium 10 Decem. 1672 datam.
Eodem anno, Maij 12, D. Leibnitius scripsit ad Oldenburgum sequentem Epistolam. Cum Georgius Mohr Danus, in Geometria et Analysi versatissimus nobis attulerit communicatam sibi a doctissimo Collinio vestro expressionem relationis inter arcum et sinum per infinitas series sequentes: Posito sinu x, arcu z, radio 1, Hæc, inquam, cum nobis attulerit ille, quæ mihi valde ingeniosa videntur, et posterior imprimis series elegantiam quandam singularem habeat; ideo rem gratam mihi feceris, Vir clarissime, si demonstrationem transmiseris. Habebis vicissim mea ab his longe diversa circa hanc rem meditata de quibus jam aliquod|t| abhinc annis ad te perscripsisse credo, demonstratione tamen non addita quam nunc polio. Oro ut Cl. Collinio multam a me salutem dicas. Is facile tibi materiam sus|p|peditabit satisfaciendi disederio meo.
Hac occasione sollicitantibus Oldenburgo et Collinio, scripsi Epistolam ad Oldenburgum 13 Iunij proxime sequentis datam, in qua methodum serierum descripsi et addidi, Analysin per easdem ad omnia pene Problemata (si numeralia quædam Diophantæs similia excipiantur) sese extendere; non tamen omnino universalem evadere nisi per ulteriores quasdam methodos eliciendi series infinitas quas non vacabat describere, cum hæ speculationes diu mihi fastidio esse cæpissent adeo ut ab ijsdem tum per quin fere annos abstinuissem. Hæc Analys|is| per series & ulteriores quasdem methodos procedens, illa ipsa est cujus specimen sub titulo Analyseos per æquationes numero terminorum infinitas Barrovius noster anno 1669 ad Collinium misi.
His respondit D. Leibnitius 27 Aug. 1676 in hæc verba. Quod dicere videmini pleras difficultates (exceptis Problematibus Diophantæis) ad series infinitas reduci, id mihi non videtur. Sunt enim multa us adeo mira et implexa ut neque ab æquationibus pendeant neque ex Quadraturis, qualia sunt (ex multis alijs) Problemata mathodi Tangentium inversæ. Et addit se Curvam cujus subtangens datur certa Analysi statim invenisse, sed quicquid in hoc genere desiderari potest nondum consecutum. Nempe si Abscissa crescit in Progressione Arithmetica Ordinata crescet vel decrescet in Progressione Geometrica; ideo si Abscissa sit ut Logarithmus Ordinata erit ut Numerus. Nulla alia Analysis ad inventionem hujus Curvæ requiritur. In eadem Epistola D. Leibnitius misit etiam Quadraturam suam Arithmeticam per hanc seriem &c eandem triennio ante et ultra a se amicis communicatam esse dixit, id est, ubi primum venit ab Anglia in Galliam.
Ipse vero in Epistola 24 Octob. 1676 ad Oldenburgum data et a D. Leibnitio (qui tum Londinum secunda vice venerat) statim lecta, rescripsi quod eo circiter tempore quo Mercatoris Logarithmotechnia prodijt, communicatum fuit per anicum D. Barrow (tunc Matheseos Professorem Cantabrigiensem) cum D. Collinio Compendium quoddam methodi harum serierum, in quo significaveram areas & longitudines Curvarum omnium & solidorum superficies et contenta ex datis Rectis, et vice versa ex his datis Rectas determinari posse; et Methodum ibi indicatam illustraveram diversis seriebus. Hoc Compendium est Analysis illa per Series et momenta et motuum progressus a \Barrovio/ mensi Iulio anni 1669 ad Collinium missa ut supra. Et his admonitus D. Leibnitius Compendium hocce in manu Collinij videre potuit. Is enim Collinium de Commercio Gregorij et meo ad Series maxime spectante consuluit, & partem Literarum nostrarum in ejus manu vidit, et ab Oldenburgo paulo ante postulaverat ut is Demonstrationem mearum serierum a Collinio procuraret et ad se mitteret: quæ Demonstratio extabet in hoc Compendio.
|✝| In eadem Epistola subjunxi quod Collinius subinde non destitit suggerere ut hæc publici juris facerem, et quod ante annos quin [anno scilicet 1671] cum suadentibus amicis concilium cœperam idendi Tractatum de Refractione Lucis et Coloribus, quem tunc in promptu habebam, cœpi de his seriebus iterum cogitare, et Tractatum de ijs etiam conscripsi ut utrum simul ederum. Sed antiquam Tractatum absolvissam lites de coloribus subortæ me quietis amantem a consilio deterruerunt. In eo autem Tractatu fundamentum me aliquatenus posuisse dixi solvendi Problemata quæ ad quadraturas reduci nequeunt, et quomodo methodus Slusiana ducendi Tangentes ex hoc fundamento statim prodiret{illeg} et quod hic non hæretur ad æquationes radicalibus unam vel utram indefinitam quantitatem involventibus utcun affectas sed absque aliqua talium æquationum reductione (quæ opus plerum redderet immensum) Tangens confestim duceretur. Et quod eodem modo se res haberet in quæstionibus de Maximis et Minimis alijs quibusdam. Et fundamentum harum operationum satis obvium esse dixi, sed cum explicationem ejus prosequi non vacaret id celavi hac sententia ænigmatice posita: Data æquatione quotcun fluentes quantitates involvente fluxiones invenire et vice versa. Et hoc fundamento dixi me etiam conatum esse reddere speculationes de Quadratura. Curvarum simpliciores et pervenisse ad Theoremata quædam generalia, et Theorema primum ibi posui et exemplis illustravi. Addidi etiam quod alia haberem Theoremata pro comparatione Figurarum cum Conicis Sectionibus, alijs|| figuris simplicissimis quibuscum possent comparari, meque hujusmodi Theoremata aliqua in Cat{illeg}|al|ogum dudum retulisse; quæ Theoremata vix per transmutationem figurarum quibus Iacobus Gregorius, et alij usi sunt abs ulteriore fundamento [nempe fundamento meo prædicto] inveniri posse putarem. Addidi denique quod inversa de Tangentibus Problemata essent in potestate, alia illis difficiliora ad quæ solvenda usus essem duplici methodo, una concinniori, altera generaliori; & utram literis transpositis consignavi hanc sententiam involventibus: Vna Methodus consistit in extractione fluentis quantitatis ex æquatione simul involvente fluxionem ejus: altera tantum in assumptione seriei pro quantitate qualibet incognita ex quæ cætera commode derivari possunt et in collatione terminorum {illeg} homologorum æquationis resultantis ad eruendos terminos assumptæ seriei. Et methodum ex his omnibus compositam \ibi/ vocabam meam methodum generalem.
His abunde satis patet {a}me anno 1676 & annis minimum quin vel septem prioribus methodum generalem hab\u/isse reducendi Problemata ad æquationes fluxionales & series convergentes, & nomen Analyseos eidem imposuisse; & huic affines fuisse methodos Tangentium Barrovij et Gregorij, propterea quod methodum Tangentium Slusij similiter producerent, sed ab Authoribus in Analysin generalem minime perfectas; et Barrovium Analysin meam ad Collinium ut methodum novam misisse|; et in hac Analysi me exemplo ostendisse quid faciendum sit ubi occurrunt irrationales.|
Lecta hac Epistola D. Leibnitius Londino mox discessit, in Hollandiam navigans, et ubi nunciatum est ipsum tandem Hannoveram pervenissi D. Oldenburgus exemplar ejusdem ad ipsum misit. Hoc fecit Mense Martio anni 1677, et D. Leibnitius Literis {illeg} 21 Iunij 1677 datis respondit in hæc verba. Clarissimi Slusij methodum Tangentium nondum esse absolutam Celeberrimo Newtono assentior. Et jam a multo tempore rem Tangentium \longe/ generalius tractavi, scilicet per differentias Ordinarum. Et subinde descripsit methodum Tangentium Barrovij symbolis mutatis, & ostendit quod Methodus Slusiana statim occurreret hanc meethodum intelligenti, & quomodo irrationales eam nullo morarentur modo; deinde subjunxit: Arbitror quæ celare voluit Newtonus ab his non abludere. Quod addit ex hoc eodem fundamento Quadraturas quo reddi faciliores me in s{t}|e|ntentia hac confirmat. Nimirum semper figuræ illæ sunt quadrabiles quæ sunt ad æquationem Differentialem. Et his verbis agnovit me methodum similem anno 1676 et annis minimum quin præcedentibus habuisse.
Cum vero D. Leibnitius anno 1684 Elementa quædam hujus Analyseos in lucem emitteret et silentio præteriret ea omnia ad hanc methodum spectantia quæ vel ab Oldenburgo acceperat vel in manibus Collinij viderat vel in hac Epistola sua agnoverat: posui Scholium superius ut inde constaret me primum de hac methodo scripsisse, D. Leibnitium eandem tardius intellexisse, Lemma superius ab editis Leibnitianis non fuisse desumptum, et Propositiones difficiliores in hocce Principiorum Libro synethetice demonstratas, vi hujus Analyseos inventas fuisse.
Chartas habeo his omnibus antiquiores, annis scilicet 1665 & 1666 scriptas, in quibus tempora scribendi nonnunquam notantur. Et in Schediasmate 13 Novemb. 1665 conscripto extat Lemma superius verbis sequentibus propositum ac demonstratum.
Novemb. 13, 1665.
Data æquatione mutuam designante relationem duarum vel plurium linearum x, {illeg}y, {illeg}z |&| a duobus vel pluribus corporibus A, B, C \&/ simul descriptarum: invenire relationem velocitatum p, q, r, & quibus corpora lineas illas describunt.
Resolutio.
Ponantur omnes æquationis terminis ex eodem æquationis latere, ut sint æquales nihilo. Et primo multiplicetur terminus quilibet per ductum in numerum dimensionum ipsius x in illo termino. Deinde multiplicetur terminus quilibet per ductum in numerum dimensionum ipsius y in illo termino. Tertio multiplicetur terminus quilibet per ductum in numerum dimensionum ipsius z in illo termino, &c. Et summa omnium productorum æquabitur nihilo. Quæ æquatio exhibebit relationem ipsarum p, q, r ad invicem.
Exempl. 1. Si æquatio sit , Operatio prima per præcendentem Regulam dabit . Secunda dabit . Et horum summa est .
Exempl. 2. Si æquatio sit , operatio prima dabit . Secunda dabit Tertia dabit . Et omnium summa est .
Demonstratio.
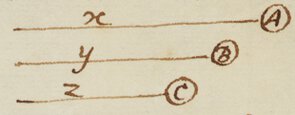 Si corpora duo A et B uniformi cum motu ferantur, unum ab A ad C, E, G successive, alterum temporibus ijsdem a B ad D, F, H, tunc lineæ AC et BD, CE et DF, EG et FH ijsdem temporibus descriptæ, erunt ad invicem ut corporum velocitates p et q. Et quamvis corpora non ferantur uniformi cum motu, tamen lineæ infinite parvæ quas singulis momentis describunt erunt ad invicem ut velocitates corporum easdem describentium. Vt si corpus A cum velocitate p describat lineam in uno temporis momento describat infinite parvam lineam o; corpul|s| B in eodem temporis mometo cum velocitate q describet lineam . Est enim ad o ut q ad p. Vnde si lineæ jam modò descriptæ sint x et y, hæ proximo temporis momento evadent et .
Si corpora duo A et B uniformi cum motu ferantur, unum ab A ad C, E, G successive, alterum temporibus ijsdem a B ad D, F, H, tunc lineæ AC et BD, CE et DF, EG et FH ijsdem temporibus descriptæ, erunt ad invicem ut corporum velocitates p et q. Et quamvis corpora non ferantur uniformi cum motu, tamen lineæ infinite parvæ quas singulis momentis describunt erunt ad invicem ut velocitates corporum easdem describentium. Vt si corpus A cum velocitate p describat lineam in uno temporis momento describat infinite parvam lineam o; corpul|s| B in eodem temporis mometo cum velocitate q describet lineam . Est enim ad o ut q ad p. Vnde si lineæ jam modò descriptæ sint x et y, hæ proximo temporis momento evadent et .
Proinde si æquatio qua linearum x et y relatio ad invicem designatur, sit (verbi gratia) ; hæc equatio proximo temporis momento scribendo pro x et pro y, evadet . Sed ex hypothesi est , eo ablato restat ; et facta divisione per o habetur ; et deletis terminis infinite parvis manet , seu .
Hic observandum venit primo quod termini illi semper evanescunt in quibus o non extat, propterea quod ex hypothesi sunt nihilo æquales; deinde quod in æquatione residue per o divisa termini in quibus o adhuc manet semper evanescunt cum sint infinite parvi: ac deni quod termini residui semper habebunt formam illam quam per præcedentem Regulam habere debeat.
Hæc Regula eodem modo demonstratur ubi tres vel plures habentur quantitates indeterminatæ x, y, z &c.
Hactenus Manuscriptum illud ventus. In alio Manuscripto 16 Maij 1666 composito, methodum solvendi Problemata per motum, complexus sum Propositionibus septem, quarum ultia est Regula jam descripta eliciendi velocitates crescendi vel decrescendi ex æquatione quantitates crescentes vel decrescentes involvente. Et in alio Manuscripto quod mense Octobri ejusdem anni composui, descripsi easdem septem Propositiones, et octavam addidi; septimam vero sequentibus ad auxi.
Si in æquatione quavis occurrat quantitas aliqua vel fracta, vel surda, vel mechanica, (id est quæ Geometrice inveniri non potest sed per aream aliquam curvilineam definitur aut per longitudinem Curvæ alicujus aut solidum contentum figuræ superficiem curvam habentis aut per gravitates eorum &c:) ut inveniatur proportio in qua quantitates indeterminatæ augentur vel diminuuntur, ita procedas. Litera aliqua (qualis ξ) designetur quantitas ill{illeg}|{a}| fracta vel surda vel mechanica et litera alia (qualis π) designetur quantitatis illius motus incrementi vel decrementi seu velocitas qua augetur vel diminuitur. Et facta æquatione inter literam ξ & quantitatem quam significat, quære valorem alterius literæ π, id per Prop. 7 si quantitas illa Geometrica sit vel per alias methodos si sit mechanica. Deinde in æquatione prima pro quantitate per ξ significata substituatur litera illa ξ et per Prop. 7 quæratur æquatio nova involvens incrementorum velocitates. Et in hac nova æquatione pro literis illis ξ et π substitua{tur}|{ntur}| earum valores et habebitur æquatio quam invenire oportuit.
Exempl. 1. Quantitatum x et y quarum relation ad invicem per hanc æquationem designata designatur, quæruntur crescendi velocitates p et q. Primo sit , seu . Et inde per Prop. 7 prodibit , seu . Deinde in æquatione prima pro pro scribatur ξ, et habebitur æquatio & inde per Prop. 7 prodibit æquatio relationem velocitatum p, q, et π definiens, in qua si pro ξ et π scriba\n/tur earum valores, proveniet æquatio quæsita .
Exempl. 2. Si quantitatum x et y relatio ad invicem definiatur per hanc æquationem , et quæratur relatio velocitatum p et q quibus quantitates illæ augentur vel diminuuntur: ponantur , , et ; et velocitates quibus τ, φ, et ξ mutantur, nominentur β, γ & δ respective. Et æquatio prima (per Prop. 7) dabit ; secunda dabit , seu ; Tertia dabit , seu . Deni æquatio est quam invenire oportuit.
Exempl. 3. Curvæ alicujus AC sit Abscissa , et Ordinata rectangula 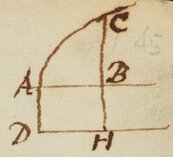 & superficies inclusa ABC dicatur z, et relatio inter x, y et z definiatur per æquationem , et ipsarum motus seu crescendi vel decrescendi velocitates sint p, q et r respective, et quæratur relatio inter p et q. Æquatio (per Prop. 7) dat æquationem novam . Ad ipsius AB terminos A et B erigantur æqualia perpendicula AD et BH et compleatur p{illeg}|a|rallelogrammum ADHB. Et si Abscissa AB augeri concipiatur, superficies duæ ADHB et ACB augebuntur in ratione Ordinatarum BH et BC, id est ita ut p sit ad r ut BH ad BC. Sit et erit \ob/ erit . Quo ipsius r valore in æquationem substituto, prodit æquatio quam invenire oportuit .
& superficies inclusa ABC dicatur z, et relatio inter x, y et z definiatur per æquationem , et ipsarum motus seu crescendi vel decrescendi velocitates sint p, q et r respective, et quæratur relatio inter p et q. Æquatio (per Prop. 7) dat æquationem novam . Ad ipsius AB terminos A et B erigantur æqualia perpendicula AD et BH et compleatur p{illeg}|a|rallelogrammum ADHB. Et si Abscissa AB augeri concipiatur, superficies duæ ADHB et ACB augebuntur in ratione Ordinatarum BH et BC, id est ita ut p sit ad r ut BH ad BC. Sit et erit \ob/ erit . Quo ipsius r valore in æquationem substituto, prodit æquatio quam invenire oportuit .
In octava Propositione docebam vicissim quomodo ex Æquatione velocitates augmentorum vel decrementorum \crescendi vel decrescendi involvente/ quantitates crescentes vel decrescentes deduci possent, id \regrediendo vel/ reducendo Problema ad quadraturam Curvarum et quadrando Curvam per tres illas Regulas quas p etiam postea descripsi in principio Tractatus de Analysi per Æquationes numero terminorum infinitas, ut et per Catalogum Curvarum quæ vel quadrari possunt vel cum Conicis Sectionibus comparari et quarum Ordinatas posui post{illeg}|e|a in Epistola mea ad Oldenburgum 24 Octob 1676 data. Et hæc est methodus a Leibnitio summatoria, a me inversa methodus fluxionum et momentorum dicta.
Hanc methodum annis 1665 et 1666 a me inventam fuisse Barrovius noster per ea tempora Lucasianus Matheseos apud Cantabrigienses Professor, idoneus est testis; et ejus testimonium Collinius noster in Epis{illeg}|o|la sua ad D. Strode 26 Iulij 1672 data sic protulit. Mense septembri 1668 Mercator Logarithmotechniam edidit suam, quæ specimen hujus methodi u|i|n unica tantum figura, nempe quadraturam Hyperbolæ continet. Haud multo postquam prodierat Liber, exemplar ejus Cl. Wallisio Oxonium misi, qui suum de eo judicium in Actis Philosophicis statim fecit, alium Barrovio Cantabrigiam, qui quasdam Newtoni chartas, qui jam Barrovium in Mathematicis Prælectionibus publicis excipit, extemplo remisit: E QVIBVS ET EX ALIIS, QVÆ OLIM AB AVCTORE CVM BARROVIO COMMVNICATA FVERANT, patet illam Methodum a dicto Newton{u}|o| ALIQVOT ANNIS ANTEA EXCOGTATAM et modo unive VNIVERSALI applicatam fuisse: ita ut ejus ope in quavis Figura curvilinea proposita, quæ una vel pluribus proprietatibus definitur, Quadratura vel Area dictæ figuræ accurata si possibile sit, sin minus infinite vero propinqua; Evolutio vel longitudo lineæ Curvæ; Centrum gravitatis figuræ; Solida ejus rotatione genita, et eorum superficies; sine ulla radicum extractione obtineri queant. Hactenus Collinius. Cum vero hæc spectent ad Tractatum de Analysi per series quem Barrovius ad Collinium miserat, & Barrovius hunc Tractatum legerat et intellexerat, et methodus in hoc Tractatu tradita pergat per Series & fluxiones momenta conjunctim, et ejus ope area figuræ accurata si possibile \possibile/ sit sin minus infinite vero propinqua prodire dicatur, et series quarum ope hoc fit inventæ fuerunt per methodum fluxionum ut in Epistola mea 24 Octob. 1676 ad Oldenburgum data traditur: inde discas Analysin in Tractatuo illo expositam quæ ex methodis serierum et momentorum componitur, a me annis aliquot antequam Tractatus ille ad Collinium mitteretur inventam et generalem redditam fuisse.
In Tractatu quem anno 1671 conscripsi, primum docui reductionem quantitatum in series convergentes per divisiones & extractiones radicum tam affectarum quam simplicium. Et his præmissis, methodum fluxionum exposui {illeg}|do|cendo solutionem plurium Problematum, quorum duo prima erant hæc
Prob. 1. Relatione quantitatum fluentium inter se data, fluxionum relationem determinare.
Prob. 2. Exposita æquatione fluxiones quantitatum involvente invenire relationem quantitatum inter se.
Hæc omnia ex veteribus Manuscriptis protuli ut vera Lemmatis hujus origo pateret, et quale esset methodi meæ fundamentum illud quod anno 1676 literis transpositis celavi, sententiam in Scholio præcedente expositam involventibus, id est, sententiam: Data æquatione, quotcun fluentes quantitates involvente, fluxiones invenire, et vice versa.
Si fluxiones pro fluentibus habeantur, operatione repetita prodibunt earum fluxiones, id est fluentium primarum fluxiones secundæ, et sic deinceps in infinitum. Fluxionibus autem secundis et momentis secundis in hisce Principiorum Libris nonnunquam usus sum. In Lib. II Prop. X Exempl. 1 fluxionem secundam Curvaturæ vocavi variationem variationis ejus et in ejusdem Libri Prop. XIV Cas. 3, momentum secundum Areæ vocavi differentiam momentorum ejus. Momentorum secundorum subsidio Demonstrationem illam Propositionis Keplerianæ quæ in Lib. I Prop. XI habetur, inveni anno 1677, et multo ante eorum subsidio inveni Curvaturam Curvarum, de qua uti locutus sum in Epistola mea 10 Decem 1672 ad Collinium data, ut et variationem Curvaturæ de qua egi in Tractatu quem anno 1671 composui et curvaturam maximam vel minimam de qua egi in eodem Tractatu ut et in prædicto Manuscripto quod mensi Octobri anni 1666 composui, in quo etiam literis punctatis nonnunquam usus sum. Sed et considerando momenta prima ut quantitates fluentes inveni solidum resistentiæ minimæ cujus memini in Scholio ad Prop. XXXIV Lib. II.
Computationes per fluentium momenta sæpe contrahuntur resolvendo fluentem uno temporis momento auctam fluendo aut|c|tam in seriem convergentem, ut fit in Scholio ad Prop. XCIII Lib. 1. Nam termini seriei proportionales sunt fluxionibus et momentis, secundus terminus fluxioni primæ et momento primo, tertius fluxioni secundæ et momento secundo, et sic deinceps; et multiplicati respective per terminos hujus seriei , vertuntur in momenta; deinde divisi per terminos hujus &c vertuntur in fluxiones. Et ob hanc methodorum affinitatem eadem conjungi merebantur.
Ad eandem Analysin pertinet etiam artificium ducendi Curvam per puncta quotcun data, et ea ratione interpolandi Series quascun. Nam si, verbi gratia, series aliqua vel fluentium vel fluxionum habeatur, sed fluentes vel fluxiones in intermedijs seriei locis non habeantur: per interpolationem seriei habebuntur eædem in locis quibuscun. Deinde ex lege fluentium sic inventa prodibit lex fluxionum per methodum nostram, et contra. Artificij autem describendi curvam per puncta data memini in epistola prædicta 24 Octobris {illeg} 1676 ad Oldenburgum data.
At hactenus de Analysi qua usus sum in investigatione rerum quas in hisce Principiorum Libris composui.
In Epistola mea 6 Febr. 16 ad |D.| Oldenburgum scripta, & et in Transctionibus Philosophicis pro eodem Mense impressa, scripsi me in{eun}d|t|e anno initio anni 1666 in Theoriam meam {colorum in}{illeg} novam lucis et colorum incidisse. Et in Epistola illam Theoriam eandem ita copiose descripsi uti eandem \et in eandem ibi tam plene/ Et eandem mihi tunc plene immotuisse ex ipsa Epistola constare potest. In Epistola vero 24 Octob 1676 ad Oldenburgū data Vt hæc Philosophia eodem fere tempore cum methodo fluxionum inventa fuit sic etiam utram eodem tempore in lucem edere olim cogitaveram in animum induxeram \& eodem destiti a consilio easdem edend/ S|E|tenim in Epistola mea 24 Octob. 1676 ad Oldenburgum data, non subjunxi ubi dixeram Compendiū meum serierum a D. Barrow ad D. Collins missum fuisse, statim subjunxi: Suborta deinde inter nos Epistolari consuetudine, D. Collinius, Vix in rem Mathematicam promovendam natus, non destitit suggere ut hæc publi juris facerem. Et ante annos quin [1671] cum suadentibus amicis concilium cæperam edendi Tractatum de refractione lucis & coloribus quem tunc in promptu habebat|m|, cœpi de his Seriebus iterum cogitare, & Tractatum de ijs etiam conscripsi ut utrum simul ederem. Sed ex occasione
Mens Scholij præcedentis.
1. Brevitate verborum effectum est ut Scholium præcedens {illeg}l{a} \ad L. perperam/ intellectum fuerit, \perperam expositum fuerit & in disputationes tractum/ et propterea rem totam fusius enarrabo.
2. Anno 1669 mense Iulio Barrovius noster Compendium methodi serierum a me scriptum Analysin per Æquationes numero terminorum infinitas a me scriptam \Barrovius noster/ {illeg} misit ad Collinium, [Et scrinijs Collinij in Ionesij manus \tandem/ incidentibus, Tractatus hisce lucem vidit.] \mense Iulio anni 1669./ Continet autem \hic Tractatus h{illeg}e/ Analysin qua Problemata per methodos serierum & fluxionum conjunctas tractantur. Problemata uti, ubi vulgaris Algebra \Analysis/ non sufficit, deducuntur ad æquationes per methodum fluxionum et momentorum. Et Æquationes finitæ \qundo lubet,/ per methodos in hoc Tractatu descriptas, convertuntur in Series \perpetuo convergentes,/ et Series nonnunquam redeunt in Æquationes finitas; et ubi symbolum aliquod pro serie tota ponitur, Series inter operandum pro symbolo illo nonnunquam su\b/stituitur; et ex fluxionibus simplicibus per Regulas tres pri initio hujus Tractatus positas eruuntur fluentes; & ex fluentibus vicissim \vicissim/ eruuntur fluxiones per \easdem/ Regulam|s| \inversas/ p{rima}; [et h{illeg}c Regularum prima demonstratur per {illeg} methodum fluxionum;] & methodum ad quantitates surdas non hærere ostenditur; & Problemata omnia quæ in Curvis Analyticis tractari solebant, tractari etiam in Curvis Mechanicis per hanc Methodum \dixit |docetur|/; Et quicquid \Analysis/ vulgaris per æquationes ex finito terminorum numero constantes (quando id sit possibile) perficiat, hanc Methodum per æquationes numero terminorum infinitas semper perficere. Quibus de causis nomen Analyseos huic methodo a me \recte/ impositum fuisse d{illeg} contenditur \disputatur./ |disputatur.|
In hoc Tractatu pro fluxione Temporis {sic} 3. In hoc Tractatu pro fluxione \vel/ Temporis vel quantitatis {illeg} cujuscun \uniformiter fluentis/ qua tempus exponitur, usurpatur unitas; & pro fluxionibus aliarum quantitatum ponuntur alia quæcun symbola; & pro fluentium momentis \(seu p{l}|a|rticulis momento temporis genitis)/ ponuntur reg|c|tangula sub fluxionibus & momento ponitur subinteligitur coefficiens o. \Nam fluxio non est momentum sed fluendi velocitas./ Fluxio vero rectangulo inclusa fluentem designat. Et symbola pro lubitu variantur cum methodus in forma symbolorum minime consistat. Et specimen calculi exh{a}|i|betur sub finem Tractatus
< text from f 49r resumes >Pro fluxionibus autem in hoc Tractatu ponuntur symbola quæcun et pro fluentium momentis pr{illeg}|o|nuntur rectangula sub fluxionibus et momento temporis o, & pro fluxione temporis vel quantitatis cujuscun uniformiter fluentis qua tempus exponitur, usurpatur unitas \et siquando symbolum fluxionis pro momento ponitur subintuelligitur coefficiens o./ [tam momenta quantitatum in hoc Tractatu{illeg} vocantur quæ temporis momentis æqualibus {illeg}|g|enerantur & signant|d|o symbolum fluxionis & fluxiones d{illeg} non sunt partes \quantitatum singulis/ momentis genitæ, sed velocitates quibus fluent fluendi quibus fluentis momentis g momenta generantur et fluentes momentis suis augentur.] Et siquando symbolum {illeg} Fluxio vero rectangulo inclusa fluentem desgnat. Et symbola pro lubitu variantur cum methodus in forma symbolorum minime consistat.
\4. Collinius autem/ Ex hoc Tractatu Collinius Series \pro quadraturis figur{illeg}|a|rum/ cum amicis mox communicare cœpit, & methodum \tanquam/ generalem prædicaret \celebrare. Et D. Iacobus/ Gregorius autem de his admonitus methodum inveniendi seriem quandam a Collinio ad ipsum missam \a{illeg} integr{illeg} |aliquandiu|/ quæsivit, et sub finem anni 1670 invenit, & mox per Epistolam ad Collinium 15 Feb. 167 datam, misit series plures \per eandem methodum inventas/ e quarum numero erat hæc. Sit Radius r, Arcus a et Tangens t, et erit {Q} Exemplar autem \autem/ hujus Epistolæ ad |D.| Leibnitium missum fuit mense Iunio Anni 1676
Anno autem 1672 ad finem vergente Collinius scripsit ad me
5 Præ|I|\n/terea Gregorius — — — de methodis Gregorij et Slusij ducendi Tangentes abs calculo et postulavit ut methodum meam communicarem. Qua occasione sequentem Epistolam 10 Decem 1672 ad ipsum scripsi. {illeg}
< insertion from f 49v >|5.| Præ\In/terea Gregorius anno 1670 Sept 5, scripsit ad Collinium se ex methodo Tangentium Barrovij et suis methodum generalem invenisse ducendi Tangentes abs calculo; & anno 1672 sub autumtumno, Slusius scripsit ad Oldenburgum se methodum similem \tangentium expedita ejusmodi/ habere; & subinde Collinius postulavit ut methodum meam communicarem. Qua occasione sequentem Epistolam 10 Decem 1672 ad ipsum scripsi.
< text from f 50r resumes >Ex animo gaudeo D. Barrovij amici nostri reverendi Lectiones Mathematicis exteris adeo placuisse, neque parum me juvat intelligere eos [Slusium et Gregorium] in eandem mecum incidisse ducendi tangentes methodum. Qualem eam esse conjiciam ex hoc exemplo percipies. 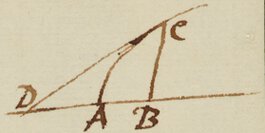 Pone CB applicatam ad AC, et dicatur AB = x & BC y, habitudo inter x et y exprimatur qualibet æquatione, puta , qua ipsa determinetur Curva. Regula ducendi Tangentem hæc est. Multiplicata æquationis terminos per quamlibet progressionem arithmeticam juxta dimensiones y, puta ; ut et juxta dimensiones x, puta . Prius productum erit Numerator et posterius divisum per x Denominator fractionis quæ exprimet longitudinem BD ad cujus extremitatem D ducenda est tangens CD. Est ergo longitudo . Hoc est unum particulare vel Corolarium potius Methodi generalis quæ extendit se, citra molestum ullum calculum, non modo ad ducendum tangentes ad quasvis Curvas sive Geometricas sive Mechanicas vel quomodocun rectas lineas aliasve Curvas respicientes; verum etiam ad resolvendum alias abstrusiora p|P|roblematum genera de Curvitatibus, Areis, Longitudinibus, Centris gravitatis Curvarum &c Neque (quemadmodum Huddenij methodus de Maximis et Minimis) ad solas restringitur ad æquationes illas quæ quantitatibus surdis sunt immunes {illeg}. Hanc methodum intertextui alteri isti, qua æquationum exegesin instituo reducendo eas ad Series infinitas. Memini me ex occasione aliquando narrasse D. Brrovio, edendis suis Lectionibus occupato, instructum me esse hujusmodi methodo Tangentes ducendi: sed nescio quo diverticulo ab ea ipsi describenda fuerim avocatus. Slusij methodum Tangentes ducendi brevi publice prodituram confido. Quamprimum advenerit, exemplar ejus ad me transmittere ne grave ducas
Pone CB applicatam ad AC, et dicatur AB = x & BC y, habitudo inter x et y exprimatur qualibet æquatione, puta , qua ipsa determinetur Curva. Regula ducendi Tangentem hæc est. Multiplicata æquationis terminos per quamlibet progressionem arithmeticam juxta dimensiones y, puta ; ut et juxta dimensiones x, puta . Prius productum erit Numerator et posterius divisum per x Denominator fractionis quæ exprimet longitudinem BD ad cujus extremitatem D ducenda est tangens CD. Est ergo longitudo . Hoc est unum particulare vel Corolarium potius Methodi generalis quæ extendit se, citra molestum ullum calculum, non modo ad ducendum tangentes ad quasvis Curvas sive Geometricas sive Mechanicas vel quomodocun rectas lineas aliasve Curvas respicientes; verum etiam ad resolvendum alias abstrusiora p|P|roblematum genera de Curvitatibus, Areis, Longitudinibus, Centris gravitatis Curvarum &c Neque (quemadmodum Huddenij methodus de Maximis et Minimis) ad solas restringitur ad æquationes illas quæ quantitatibus surdis sunt immunes {illeg}. Hanc methodum intertextui alteri isti, qua æquationum exegesin instituo reducendo eas ad Series infinitas. Memini me ex occasione aliquando narrasse D. Brrovio, edendis suis Lectionibus occupato, instructum me esse hujusmodi methodo Tangentes ducendi: sed nescio quo diverticulo ab ea ipsi describenda fuerim avocatus. Slusij methodum Tangentes ducendi brevi publice prodituram confido. Quamprimum advenerit, exemplar ejus ad me transmittere ne grave ducas
Gregorius uti ad Collinium scripserat 5 Sept. 1670 se ex method{illeg}|i|s tangentium Barrovij & suis, methodum generalem invenisse ducendi Tangentes abs calculo, et postularet Slusius scripseserat Slusius ad Oldenburgum scripserat se methodum similem habere sed neuter methodum suam communicaverat] Missum est aut{illeg}|e|m Exemplar Epistolæ meæ ab Oldenburgo ad Slusium 29 Ian. 167 & a Collinio ad Tschurnhausium mense Maio 1675 et ad Leibnitium mense Iunio 1676. Et eodem mense Iunio missum est Et ex his Epistolis innotescere potuit quod hæcce methodus Tangentium methodus et Corollarium esset methodi generalis de qua hic locutus sum, & consequeretur etiam ex methodo Tangentium Barrovij.
8 Ineunte anno 1673 D. Leibnitius Londinum venit & cum Pellio nostro de rebus Arithmeticis sermones disputavit, in Geometria sublimiori nondum instructus. At a Pellio de serie Mercatoris &c admonitus, Logarithmotechniam ejus \emit &/ secum Lutetiam tulit, & sub finem hujus anni et initium sequentis Geometriam \Scripsit vero ad Oldenburgum de numeris us ad mensem Iunium deinde siluit per annum totum & Geometriam interea Geometriam/ sublimiorem Hugenio magistro didicit, et proxime|i| \anni 1674/ mense Iulio \silentium abrumpit a{illeg}/ de Seriebus ad Oldenburgum scribere cœpit, dicendo se Theorema invenisse cujus ope area Circuli vel Sectoris ejus dati exacte exprimi posset per seriem numerorum rationalium continue productam in infinitum. Et mense Octobri ejusdem anni exposuit quale esset |hoc| Theorema cujus \ope/ area Sectoris dati per seriem exprimi posset, dicendo, quod seriem invenisset pro circumferentia tota et quod eadem methodo etiam arcus cujuslibet cujus series daretur geometrice \exhiberi/ per ejusmodi seriem valos|r| posset nullo ad integræ circumferentiæ dimensionem recursu; ut adeo non necesse esset arcus rationem ad circumferentiam nosse. Theorema igitur ex dato sinu dabat vel sectorem vel arcum, et si ratio arcus ad circumferentiam totam daretur nosceretur dabat etiam circumferentiam totam.
9 Anno 1675 Apr. 15 D. Oldenburgus suggerente Collinio seriem meam pro inveniendo arcu ex sinu dato, ut et Gregorianam pro inveniendo arcu et|x| tangente data & harum inversas alias nonnullas ad D. Leibnitium misit, et D. Leibnitius Literis 20 Maij 1675 datis rescripsit in hæc verba. Literas tuas multa fruge Algebraica refertas accepi, pro quibus tibi et doctissimo Collinio gratias ago. Cum nunc præter ordinarias curas mechanicis imprimis negotijs distrahar, non potui examinare series quas misistis, ac cum meis comparare. Vbi fecero, perscribam tibi sententiam meam, nam aliquot jam anni sunt quod inveni meas via quadam sic satis singulari. |De seriebus igitur locutus est quas habuit [ante mense M{illeg}um anni 1673] ubi primum ab Anglia venit in Galliam.|
10 Eodem anno D. Leibnitius compositet & cum amicis communicavit opusculum quadraturæ Arithmeticæ, ut ipse \scripsit/ in Actis Eruditorum anni 1691 pro mense Aprili pag. 178. Hæc erat Quadratura \Circuli/ per seriem pro {illeg} inveniendo arcu ex tangente data
< insertion from f 51v >10 Eodem anno D. Leibnitius compositum habebat opusculum Quadraturæ Arithmeticæ ab amicis ab{illeg} {sic} illo tempore lectum, sed quod materia sub manibus crescente, limare ad editionem non vacavit postquam aliæ occupationes supervenere præsertim cum postea \tandem/ prolixius exponere vulgari more quæ Analysis ejus nova paucis exlibet, non satis opere pretium videba\re/tur; ut ipse scripsit in Actis Eruditorum anni 1691 pro mense Aprili, pag. 178. Hæc erat Quadratura circuli per seriem pro inveniendo arcu ex Tangente data.
< text from f 51r resumes >10|1| Anno 1676 tep|m|pore verno audita Gregorij morte D. Leibnitius postulavit ab Oldenburgo ut quæ Gregorius cum amicis communicaverat in unum corpus colligerentur & ad se mitterentur. Et Collinius subinde Excerpta Epistolarum Gregorij collegit, et missa est Collectio Lutetiam mense Iunio hujus anni ut a D. Leibnitio legeretur & subinde redderetur Oldenburgo. Et extat Collectio in Archivis R. Societatis m̄{illeg}|a|nu {sic} Collinij scripta, et inter alia, continet Epistolas Gregorij \ad Collinium/ 5 Sept. 1670, et 15 Feb. 167 datas, ut et meam ad Collinium 10 Decem 1672 datam.
12 Eodem ann{illeg}|o|, Maij 12, D. Leibnitius scripsit ad Oldenburgum sequentem Epistolam. Cum Georgius Mohr Danus, in Geometria et Analysi versatissimus nobis attulerit communicatam sibi a Doctissimo Collinio vestro expressionem relationis inter Arcum et Sinum per infinitas Series sequentes: Posito Sinu x, Arcu z, Radio 1, Hæc, inquam, cum nobis attulerit ille, quæ mihi valde ingeniosa videntur, et p{illeg}|os|terior imprimis series elegantiam quandam singularem habeat; ideo rem gratam mihi feceris, Vir clarissime, si demonstrationem transmiseris. Habebis vicissim mea ab his longe diversa circa hanc rem meditata de quibus jam aliquot abhinc annis ad te perscripsisse credo, demonstratione tamen non addita quam nunc polio. Oro ut {illeg} Cl. Collinio multam a me salutem dicas. Is facile tibi materiam suppeditabit satisfaciendi disederio meo.
13 Hac occasione sollicitantibus Oldenburgo et Collinio, |scripsi| Epistolam ad Oldenburgum 13 Iunij proxime sequentis datam in qua methodum serierum descripsi et addidi Analysin per easdem ad omnia pene Problemata (si numeralia quædam Diophantæs similia excipiantur) sese extendere; non tamen omnino universalem evadere nisi per ulteriores quasdam methodos eliciendi series infinitas quas non vacabat describere, cum hæ speculationes diu mihi fastidio esse cœpissent, adeo ut ab ijsdem tum per quin fere annos abstinuissem. Hæc Analysis per Series et ulteriores methodos illa \ipsa/ est cujus specimen sub titulo Analyseos per series æquationes numero terminorum infinitas anno 166 Barrovius noster anno 1669 ad Collinium misit. Ionesius nuper \tandem/ edidit
14 His respondit D. Leibnitius 27 Aug. 1676 in hæc verba: Quod dicere videmini pleras difficultates (exceptis Problematibus Diophantæis) ad series infinitas reduci id mihi non videtur. Sunt enim multa us adeo mira et implexa ut neque ab æquationibus pendeant neque ex Quadraturis, qualia sunt (ex multis alijs) Problemata methodi Tangentium inversæ. ✝ ✝ Et addit se Curvam cujus subtangens \datur/ certa Analysi statim invenisse, sed quicquid in hoc genere desiderari potest nondum consecutum. Nempe si Abscissa crescit in Progressione Arithmetica, Ordinata crescet vel decrescet in Progressione Geometrica; ideo si Abscissa sit ut Logarithmus, Ordinata erit ut Numerus. Nulla alia Analysis ad inventionem hujus Curvæ requiritur. In eadem Epistola D. Leibnitius misit etiam Quadraturam suam Arithmeticam per hanc Seriem In eadem epistola misit etiam Quadraturam suam Arithmeticam per hanc seriem &c eandem Triennio ante et amplius ultra a se \amicis/ communicatam \amicis/ e|fui|sse dixit, id est, ubi primum venit ab Anglia in Galliam.
15 Ipse vero in Epistola ad Oldenburgum 24 Octob. 1676 ad Oldenburgum data et a D. Leibnitio (qui tunc Londinum secunda vice venerat) statim lecta, rescripsi quod eo circiter tempore quo Mercatoris Logarithmotechnia {illeg}|p|rodijt, communicatum {illeg} fuit per amicum D. Barrow (tunc Matheseos Professorem Cantab.) cum |D.| Collinio compendium quoddam \methodi/ harum serierum in quo significaveram areas & longitudines Curvarum omnium & solidorum superficies et contenta, ex datis Rectis; et vice versa ex his datis Rectas determinari posse: et Methodum ibi indicatam illustraveram diversis seriebus. Hoc Compendium est Analysis illa per series \&/ motuum progressus et momenta quam Ionesius edidit. Et his admonitus D. Leibnitius Compendium hocce in manu Collinij videre potuit. Is enim Collinium de commercio Gregorij et meo consuluit & partem Literarum nostrarum in ejus manu vidit, & ab Oldenburgo paulo ante postulaverat ut is Demonstrationem mearum serierum a Collinio procuraret et ad se mitteret: quæ Demonstratio extabat in hoc Compendio.
<53r>|1{illeg}|6|| In eadem Epistola subjunxi quod Collinius noster subinde non destitit suggere{illeg}|re| ut hæc publici juris facerem, et quod ante annos quinque [anno scilicet 1671] cum suadentibus amicis concilium cœperam edende Tractatum de Refractione lucis et Coloribus, quem tunc in promptu habebam, cœpi de his seriebus iterum cogitare & Tractatum de ijs etiam conscripsi ut utrum simul ederem. Sed \antequam Tractatum absolvissem/ lites de coloribus paulo post subortæ me quietis amantem a consilio deterruerunt. In eo autem Tractatu fundamentum me \aliquatenus/ posuisse dixi solvendi Problemata quæ ad Quadraturas reduci nequirent nequeunt, et quomodo methodus Slusiana ducendi Tangentes ex hoc fundamento statim prodiret, et quod hic non hæretur ad æquationes Radicalibus unam vel utram indefinitam quantitatem involventibus utcun affectas sed abs aliqua talium æquationum reductione (quæ opus plerum redderet immensum) Tangens confestim duc{illeg}|ere|tur. Et quod eodem modo se res haberet in quæstionibus de Maximis et Minimis alijs quibusdam. Et fundamentum harum operationum satis obvium esse dixi, sed cum explicationem ejus prosequi non vacaret id celavi hac sententia ænigmatice posita: Data æquatione quotcun fluentes quantitates involvente fluxiones invenire; & vice versa. Et hoc fundamento dixi me etiam conatum esse reddere speculationes de Quadratura Curvarum simpliciores, et pervenisse ad Theoremata quædam generalia et Theorema primum ibi posui et exemplis illustravi. Addidi etiam quod alia haberem Theoremata vix pro comparatione Figurarum cum Conicis Sectionibus, alijsve figuris simplicissimis quibuscum possent comparari, me hujusmodi Theoremata \aliqua/ in Catalogum dudum retulisse; quæ Theoremata vix per transmutationem figurarum quibus Iacobus Gregorius et alij usi sunt, abs ulteriore fundamento [nempe fundamento meo prædicto] inveniri posse putarem. Addidi denique quod ubi dixi omnia pene Problemata solubilia existere, volui de ijs præsertim intelligi circa quæ Mathematici se hactenus occuparunt vel {sane} nimium dixisse {vid}{illeg}r \quod/ inversa de Tangentibus Problemata sunt {sic} \essent/ in potestate, alia illis difficiliora ad quæ solvenda usus sum {sic} \essem/ duplici Methodo una concinniori altera generaliori; & utram literis transpositis consignavi hanc sententiam involventibus: Vna Methodus consistit in extractione fluentis quantitatis ex æquatione simul involvente fluxionem ejus: altera tantum in assumptione Seriei pro quantitate qualibet incognita ex qua cætera commode derivari possunt et in collatione terminorum homologorum æquationis resultantis ad eruendos terminos assumptæ seriei. |Et methodum ex his omnibus compositam vocabam meam methodum generalem.|
< insertion from f 53v >17 His abunde satis patet me anno 1676 & annis minimum quin vel septem prioribus methodum generalem habuisse reducendi Problemata ad æquationes fluxionales & series convergentes, \& regrediendi a fluxionibus ad fluentes/ & nomen Analyseos eidem imposuisse; & huic affines fuisse methodos Tangentium Gregorij et Barrovij propterea quod methodum Tangentium Slusij similiter producerent, sed ab Authoribus in Analysin generalem minime perfectas; & Barrovium Analysin meam ad Collinium ut methodum novam mississe.
Lecta hac Epistola D. Leibnitius Londino ex discessit
< text from f 53r resumes >{illeg} |17| His patet abunde satis patet me anno 1676 & annis \minimum/ quin vel septem prioribus fluxionales, et ex hujusmodi æquationibus tam affectis quam simplicibus eliciendi quantitates fluentes, et in hac methodo quando series assumere pro quantitatibus ignotis, & assumptas terminorum coefficientes et indices dignitatum ex conditionibus Problematum determinare, et fluxiones et momenta inter ex fluentibus et vicissim fluentes ex fluxionibus & momentis inter computandum deducere, et hunc in finem me Theoremata plura pro Quadratura figurarum et inventione fluentium per hanc methodum concinnasse, et propter generalem usum hujus methodi in solutione resolutione Prolbmeatum me nomen Analyseos eidem (ab anno saltem 1669) imposuisse, et huic affines fuisse methodos Tangentium Gregorij et Barrovij propterea quod methodum Tangentium Slusij similiter producerent, sed ab autoribus in Analysin generalem minime perfectas, & Barrovium Analysin meam ad Collinium ut methodum novem \cum laude/ misisse.]
17|8| |18| His lectis D. Leibnitius Londino mox discessit, in Hollandiam navigans, et ubi nunciatum est ipsum \tandem/ Hanoveram pervenisse D. Oldenburgus exemplar hujus Epistolæ \ejusdem/ ad ipsum misit. Hoc fecit mense Martio anni 1677 & D. Leibnitius Literis 21 Iunij 1677 datis respondit in hæc verba. Clarissimi Slusij methodum Tangentium nondum esse absolutam Celeberrimo Newtono assentior Et jam a multo tempore rem Tangentium longe generalius tractavi scilicet per differentias Ordinatarum. Et subinde descripsit Methodum Tangentium Barrovij \symbolis mutatis/ & ostendit quod Methodus Slusiana statim occurreret hanc methodum intelligenti, & quomodo irrationales eam nullo morarentur modo; deinde subju\n/xit: Arbitror quæ celare voluit Newtonus de Tangentibus ducendis ab his non abludere. Quod addit, ex hoc eodem fundamento quadraturas quo reddi faciliores me in sententia hac confirmat. Nimirum semper figuræ illæ sunt quadrabiles quæ sunt ad æquationem differentiaalem {sic}. Et his verbis agnovit me methodum similem anno 1676 et annis minimum quin præcedentibus habuisse.
1{illeg}|9| {C}um vero D. Leibnitius anno 1684 elementa \quædam/ hujus Analyseos in lucem emitteret & silentio præteriret ea omnia quæ ad hanc methodum spectantia quæ vel ab Oldenburgo acceperat vel in manibus Collinij viderat, vel in hac epistola sua agnoverat: posui Scholium superius ut inde constaret me primum de hac methodo scripsisse, D. Leibnitium eandem tardius intellexisse, {et} Lemma superius ab editis Leibnitianis non fuisse desumptum, et me propria Analysi /Propositiones \difficiliores/ in hocce \Principiorum/ Libro synethetice demonstratas invenisse |vi| hujus Analyseos inventas fuisse.\
{illeg} |20| Chartas habeo his omnibus antiquiores, in quibus annis scilicet 1665 et 1666 scriptas, in quibus tempora scribendi notantur nonnunquam notantur et in Schediasmate 13 Novem. 1665 conscripto, extat hoc \hoc/ Lemma ut sequitur \illud verbis sequentibus/ propositum ac demonstratum.
Novem 13 1665.
Data æquatione mutuam designante relationem duarum vel plurium linearum x, y, z \ad invicem/ a duobus vel pluribus corporibus A, B, C simul descriptarum: invenire relationem velocitatum p, q, r, quibus corpora lineas illas describunt.
Resolutio.
Ponantur omnes æquationis termini ex eodem æquationis latere ut sint æquales nihilo. Et primo multiplicetur terminus quilibet per ductum in numerum dimensionum ipsius x in illo termino. Deinde multiplicetur terminus quilibet per ductum in numerum dimensionum ipsius y in illo termino. Tertio multiplicetur terminus quilibet per ductum in numerum dimensionum ipsius z in illo termino, &c. Et summa omnium productorum æquabitur nihilo. Quæ æquatio exhibebit relationem ipsarum p, q, r ad invicem.
<55r>Exempl. 1. Si æquatio sit Operatio prima per præcendentem Regulam dabit Secunda dabit . Et horum summa est .
Exempl. 2. Si æquatio sit , Operatio prima dabit {2zxr} . Secunda dabit . Tertia dabit . Et omnium summa est .
Demonstratio.
 Si corpora duo A et B uniformi cum motu ferantur, unum ab A ad C, E, G, alterum a B ad D, F, H temporibus isdem, tunc lineæ AC et BD, CE et DF, EG et FH ijsdem temporibus descriptæ, erunt ad invicem ut corporum velocitates p et q. Et quamvis corpora non ferantur uniformi cum motu, tamen lineæ infinitæ parvæ quas singulis momentis describunt, erunt ad invicem ut velo{illeg}|c|itates corporum easdem describentium. Vt si corpus A cum velocitate p in uno temporis momento describat infinite parvam lineam o: corpus B in eodem temporis momento cum velocitate q describet lineam Est enim ad o ut q ad p. Vnde si lineæ jam descriptæ sint x et y, hæ proximo temporis momento evadent & .
Si corpora duo A et B uniformi cum motu ferantur, unum ab A ad C, E, G, alterum a B ad D, F, H temporibus isdem, tunc lineæ AC et BD, CE et DF, EG et FH ijsdem temporibus descriptæ, erunt ad invicem ut corporum velocitates p et q. Et quamvis corpora non ferantur uniformi cum motu, tamen lineæ infinitæ parvæ quas singulis momentis describunt, erunt ad invicem ut velo{illeg}|c|itates corporum easdem describentium. Vt si corpus A cum velocitate p in uno temporis momento describat infinite parvam lineam o: corpus B in eodem temporis momento cum velocitate q describet lineam Est enim ad o ut q ad p. Vnde si lineæ jam descriptæ sint x et y, hæ proximo temporis momento evadent & .
Proinde si æquatio qua linearum x et y relatio ad invicem designatur, sit (verbi gratia) , hæc equatio proximo temporis momento scribendo pro x et pro y evadet . Sed ex hypothesi est , eo ablato restat ; et facta divisione per o habetur ; et deletis terminis infinite parvis, manet seu .
Hic observandum venit primo quod termini illi semper evanescunt in quibus o non extat, propterea quod ex hypothesi sunt nihilo æquales; deinde quod in æquatione residue per o divisa termini in quibus o adhuc manet semper evanescunt cum sint infinite parvi; ac deni quod termini residui semper habebunt formam illam quam per præcedentem Regulam habere debent.
Hæc Regula eodem modo demonstratur ubi tres vel plures habentur quantitates indeterminatæ x, y, z &c
|22| At hæc ex veteri Manuscripto descripsi ut vera Lemmatis hujus origo \& verus Scholij sensus/ pateret, & quomodo ex æquationibus fluentes involventibus derivabant fluxiones \antequam Scholium in hoc Lemma Scripsi/ ab initio at adeo quænam \ab initio/ fluxiones pro fluentibus habeantur, operatione repetita prohabe\di/buntur earum fluxiones, id est, fluentium primarum fluxiones secudæ, et sic deinceps in infinitum.
Æquationum termini fracti et \fracti et/ surdi pro fluentibus habendi sunt, et perinde tractandi substituendo symbola pro ipsis et \vicissim/ ipsorum fluxiones pro fluxioni|bu|symbol{illeg} symbolorum. Nam quantitates surdas methodum meam non moravi constat ex epistolis meas \prædictis/ 10 Decem 1672 & 24 Octob 1676 datis, ut et ex Analysi mea a Ionesio edita. pag. 14.
< insertion from f 55v >|1{illeg}|22|| \Hactenus Manuscriptum illud ventus./ Atque hæc \seinde/ ex veteri Manuscripto \Ex Inde vero. hæc/ descripsi ut vera Lemmatis hujus origo pateret, et quale esset methodi meæ fundamentum illud quod anno 1676 literis transpositis celavi sententiam involventibus in Scholio præcedente expositam; nempe \id est sententiam/: Data æquatione quotcun fluentes quantitates involvente, fluxiones invenire; et vice versa.
|22|3|| In Epistolis meis 10 Decem 1672 & 24 Octob 1676 datis, dixi
< text from f 56r resumes >|②| |23|4|| Si fluxiones pro fluentibus habeantur; operatione repetita prodibunt earum fluxiones, id est fluentium primarum fluxiones secundæ, et sic deinceps in infinitum. Fluxion{illeg}|i||bus| autem secunda|i||s| et momenta|is| secunda|is| in h{illeg}|isce| Principiorum Libr{e}|i|s nonnunquam usus sum \ut videre licet in Lib. 11, Prop. XIV cas. 3./ {illeg} Eorum subsidib inveni \tum/ demonstrationem Propositionis undecimæ Libri primi Anno 1677, tut|m| {illeg} Curvaturam Curvarum multo ante; de qua uti locutus sum in Epistola mea 10 Decem. 1672 ad Collinium data {illeg}. |Sed| Et in Schediasmate quadam vetustiore in{illeg} hujus Proble{illeg}o et altero vetustiore \chartis vetustioribus/, determin\an/do Linearum Curvaturam, nunc literis punctatis nunc alijs symbolis usus sum.
|③| |24|5|| Operationes \Computationes/ per fluentium momenta sæpe contrahuntur resolvendo fluentem momento uno \uno temporis momento/ auctam, in seriem convergentem, \ut fit in Scholio ad Prop. XCIII Lib. 1./ Nam termini seriei proportionales {illeg}sunt momen fluxionibus et momentis, secundus terminus fluxioni primæ et momento primo, tertius fluxioni secundæ et momento secundo, & sic deinceps; & multiplicati \respective/ per terminos hujus seriei vertuntur in momenta, Et ob hanc affinitatem et harmoniam ex his methodis conjunctis Analysin unam generalem ab {uti} initio conflavi. \deinde divisi per terminos hujus vertuntur &c vertuntur in fluxiones./ deinde divisi per terminos hujus vertuntur &c vertuntur in fluxiones. Et ob hanc methodorum affinitatem et harmoniam, \eadem conjunxi et/ ex untra Analysin unam generalem ab initio convlavi \ut supra/.
|①| |22|3|| In Epistolis meis \Nam methodum serierum a me proxime ante Pestem anno 1665 Londini gra{illeg}|ss|antem a me inventā [lb]fuisse dixi in epistola mea præd \{illeg} ex superioribus constare potest/ 10 Decem. 1672 & \24 Octob 1676/ data./ 24 Octob. 1676 & 10 Decem 1672 datis, dixi quantitates surdas methodum meam non morari, et hanc rem exemplo explicui in Analysi mea \prædicta/ a Ionesio edita [pag. 14:] Substitatur uti in æquatione pro quantitate radicali symbolum quodvis, tractetur symbolum ut quantitas fluens, & completo opere pro symblo ut ejus fluxione scribatur quantitas radicalis et ejus fluxio.
|4| Ad eandem {illeg} Analysin pertinet etiam artificium ducendi Curvam Analyticam per puncta quotcun \data/ et ea leg ratione interpolandi series quascun. Nam si series fluxionum \verbi gratia, series \vel/ fluentium vel fluxionum/ habeatur, sed fluentes \vel fluxiones/ in intermedijs non habea\n/tur: per interpolationem seriei habebuntur \eædem/ in locis quibuscun. ✝ ✝ Et per \Deinde ex/ legem fluentium sic inventam prodibit lex fluxionum per methodum nostram, et contra. Hujus autem artificij interpolandi series \Artificij autem describendi curvam per puncta data/ memini in Epistola prædicta 24 Octobris 1676 data. Et hujus artificij memini in Epistola \prædicta/ 24 Octobris data. 1676 data.
