Rough drafts of the Leibniz Scholium in the 2nd Edition of the Principia, and proposed additions to it

When two {illeg} spherical bodies strike upon one another, not directly as in the foregoing experiment of Pendulums, but in any obliquity: to find the force of their shock & the motion w^ch they will have afterward, we must first find the plane in they touch one another \right line w^ch passes through their centers/ at the moment of the shock, & then distinguish the motion of each body into two, the one perpendicular to that plane \line/ the other parallel to it. The parallel \perpendicular/ motions will remain unaltered by the shock, the perpendicular \parallel/ will receive the same alteration \by the shock/ as if the bodies had rem{illeg} met directly with those motions alone. As for instance

B. Scholium

In literis quæ mihi cum Geometra peritissimo G. G. Leibnitio annis abhinc decem intercedebant, cum significarem me compotem esse methodi determinandi maximas et minimas, ducendi tangentes, quadrandi figuras curvilineas & similia peragendi quæ in terminis surdis æque ac in rationalibus procederet, et methodum exemplis illustrarem & \sed/ fundamentum ejus literis transpositis hanc sententiam involventalibus [Data æquatione quotcun fluentes quantitates involvente, fluxiones invenire, et vice versa] ^[1]celarem: rescripsit v|V|ir Clarissimus anno proximo, se quo in ejusmodi methodum incidisse, & methodum suam communicavit a mea vix abludentem præterquam in verborum & notarum formulis. ^[2]Vtrius fundamentum continetur in hoc Lemmate.

✝ In eadem Epistola subjunxi — — — a consilio detenuerunt simul ederem. Sed antequam Tractatum illum absolvissem, Epistolá ad te missa qua breviter explicui conceptus meos de natura lucis, lites de coloribus \{illeg} on/ subortæ sunt, quæ me quietis amantem a consilio detenuerunt. Epistola illa data fuit 6 Febr. 16$\frac{71}{72}$ & in Transactionibus Philosophicis eodem mense impressa. Et in eadem scripsi me initio anni 1666 in Theoriā novem \illam/ lucis et colorum incidisse. Inveni igitur hanc Theoriam eodem fere tempore cum methodo fluxionum, utram simul edere constitueram, & ab itrius editione simul destiti quietis gratia. Tandem vere anno 1704

In Tractatu eadem Epistola 24 Octob. 1676 ad Oldenburgum scripta, dixi me in Tractatu illo fundamentum aliquatenus posuisse solvendi Problemata

In my Analysis per series \æquat. communicated by D^r B. to M^r C. in Iuly 1669/ n. L. inf. I said that my methods \of series /by series\/ gave the areas of curvilinear figures exactly & {generat} if it might be done & M^r Collins \M^r Collins in his Letter to M^r Strode dated 26 Iuly 16{illeg}|7|2 afterward the same thing/ & thence it appears that \when I wrote that Analysis/ I had the Me the Method of fluxions so far at least as it is conteined in the first six Propositions of the Book of Quadratures. In that Analysis \Tract/ I represented time by a line {illeg}|i|ncreasing uniformly & a mom^t of time by a particle of the line generated by \in/ a moment \of time/ & thence called the particle of the a moment of the line, & the particles of all other quantite|i|es generated in the same moment of time I called the moments of those quantities, & the fact under the \{re} rectangular/ Ordinate & the Or I & a moment of the Abscissa I called considered as the moment of the Curvilinear area generated described by that Ordinate \while it/ movin|es|g uniformly upon the Abscissa. \And from the fluxion of time came the names of fluents/ And by con\& fluxions. And by con/sidering how to deduce the moments from quantities & quantities from moments I squared Curves & \deduced the areas of figures/ from their areas deduced their Ordinates & their Ordinates from their areas: w^ch is the same thing with deducing fluxions from fluents & fluents from fluxions. |And in the end of the book I applied t deonstrated the first Rule by this calculus. the first of the three Rules set down in the beginning thereof.| And by applying this method not only to finite equations but also to converging Series considered as an Equations consisting of an infinite number terms I gave to this Tract the name of Analysis per S{illeg}s \æquationes/ numero terminorum infinitas. And in my Letter of 13 Iune 1676 I said with relation to of this Analysis: Ex his videre est quantum fines Analyseos per hujusmodi series infinitas æquationes ampliantur: Quippe quæ earum beneficio, ad omnia pene dixerim problemata (si numeralia Diophanti et similia excipias) sese extendit. [Non tamen omnino universalis evadit nisi per ulteriores quasdam methodos eliciendi series infin] And M^r Leibnitz in his Answer dated 27 Aug. 1676, replied Quod dicere videmini pleras Difficultates (exceptis Problematibus Diophantæis) ad Series infinitas reduci; id mihi non videtur. Sunt enim multa us adeo mira et implexa ut ne ab æquationibus pendeant ne ex quadraturis: Qualia sunt (ex multis alijs) Problemata mathodi tangentium inversæ. In the same Letter he placed the perfection of Analysis in another meth not in the Differential Method but in another Method composed of Analytical Tables of Tangents & the Combinatory Art. Nihil est, said he, quod norim . . . . . . cogitationum humarum. This was the top of his skill at that time.

M^r Collins in his Letter to M^r Strode dated 26 Iuly 1672 gave this account of the{illeg} Method. Mense Septembri 1668 — — — — — haud integrum ducit. It appeared \therefore/ to M^r Collins by the testimony of D^r Barrow upon \from/ \grounded upon/ papers which I had communicated to him from time to time that I had the method conteined in the Analysis per Æquationes numero terminorum infinitas that I had this Method some years before the D^r sent that Tract to M^r Collins. And this |is| sufficient to justify w^t I said in the Introduction to the Book of Quadratures.

M^r Iames Gregory \after a years study/ found the Method of Series proprio Marte but did not claim it because he knew that he was not the first invenentor

Nothing has been said to prove that M^r Leibnitz had the method before he came to London the second time. Then he met with D^r Barrows Lectures, & the Marquess de l'Hospital has said that where the D^r left off M^r Leibnitz proceeded, & that the improvement w^ch D|M|^r {B}|L|eibniz <21r> made to the Doctors Methods consisted in shewing how to exclude fractions & surds radicals. But the Marquess did not know that by my Letter of 24 Octob. 1676 & a copy of my Letter of 10 Decem 1672 he had notice of this improvement & that it related to a very general method. He might afterwards find them proprio Marte but by that notice knew that I had them before him. For in his Letter of 21 Iune 1677 wherein he first began to communicate his method he acknowledged that I knew the improvement before him when I wrote my Letter of 24 Octob. 1676.

D^r Barrow then read his Lectures about the generation of figures by motion & that \might/ put me upon taking these things into consideration. In the beginning of the year 1666 I found \also/ the Theory of colours. In the year 1671 I was preparing to publish th{en}|is| \Theory with the methods of Series & fluxions/, but for a reason given \mentioned/ in my Letter of 24 Octob. 1676 I desisted till the year 1704 & then printed both together the Tracts of Colours & Quadratures together.

{I} \That Tract c{illeg}/ was therefore \written/ not only \upon/ a method of \finding/ Series, but \upon/ a general method of Analysi{t}|c| \by/ applying the method of moments to Equations both finite & infinite & to

{illeg} In the beginning of the year 1665, uppon \winter between the years 1664 & 1665 I had the method of Tang^ts/ by considering of how to interpose some Series of D^r Wallis. I found the Rule for \of Hudden Gregory & {Slu}sius & by considering how \Slusius/ & a method of finding the {illeg}|qu|antity of crookedness of curve lines att any given point. {to} And by considering/ set down in my Letter of 13 Iune 1676 for squar reducing any power or dignity of any Binomium into an approximating series, & in the falling Spring, before the Plague, w^ch invaded us that summer, forced me from Cambridge, I found how to do the same thing by \continual/ division & extraction of roots, as I mentioned in my Letter of 24 Octob. 1676 & in the following autum when I was absent from the university I found the direct method of fluxions \either & soon after I extended the Method to the extraction of affected roots out of equations/.

In the beginning of the year 1665 I had the method of tang^ts of G|H|uddon Gregory & Slusius, & soon after I found about the same time or soon after I found the direct method of first fluxions & |I| set it down with examples & a demonstration in a paper dated 13 Novem. 1665.

In the winter between the years 1664 & 1665 I had a method of Tangets like that of Hudden Gregory & Slusius & a method of finding the crokedness of Curves at any given point, & by considering how to interpole certain series of D^r Wallis I found the Rule set down in my Letter of 13 Iune 1676 for reducing any power or dignity of any Binomium into an approximating Series, & in the following Spring, before the Plague, w^ch invaded us that summer, forced me from Cambridge, I found how to do the same thing by continual division & extraction of roots, as I mentioned in my Letter of 24 Octob. 1676. And soon after I extended the Method to the extraction of the roots of affected Equations in species. [And in a paper dated 13 Novem 1665 I find the direct Method of first fluxions set down with examples & a Demonstration] And from all this learnt how to deduce the Ordinates or Abscissas of Curvilinear figures from their Areas or Ac{illeg}s given, as well as the Areas & Arcs from the Abscissas & Ordinates. Thus far I proceeded before the plague frorced me from Cambridge. And in a paper dated 13 Nov. 1665 I find the direct Method of first fluxions set down with examples & a Demonstration.

|A| Scholium.

In litt Literis

Scholium.

In literis quæ mihi cum Geometra peritissimo G. G. Leibnitio anno 1676 intercedebant, cum significarem me compotem esse methodi Analyticæ determinandi Maximas & Minimas, ducendi tangentes, quadrandi Figuras curvilineas, conferendi easdem inter se, & similia peragendi, quæ in terminis surdis æque ac in rationalibus procederet, & Tractatus duos de eadem \similibus |hujusmodi| rebus/ scripsisse alterum anno 1671, \①/ alterum autē {illeg} quem Barrovius noster anno 1669 {and} Collinium misi{illeg}, cum literis transpositis hanc sententiam involventibus [Data æquatione quotcun fluentes quantitates involvente, Fluxiones invenire, et vice versa] fundamentum hujus methodi celarem, specimen vero eusdem \in Curvis quadrandis/ subjungerem & exemplis illustrarem; et cum vir clarissimus \sub. finem mensis Octobris/ in reditu suo e Gallio per Angliam in Germaniam epistolas meas in manu Collinij insuper consuluisset: incidit is in metho\finito itinere in metho finito itinere anno proximo anno proximo in metho paulo post in metho finito itinere in metho/dum similem sub diversis verborum et notarum formulis, Methodi utrius fundamentum continetur in hoc Lemmate. et mense Iunio \anno 1677, sequente/ specimen ejusdem ad me misit. Methodi utrius fundamentum continetur in hoc Lemmate. Collinius Epistolam 10 Decem. 1672 datam a me accepisset in quo methodum hanc descripsissem\eram/ et exemplo Tangentium \more Slusiano/ ducendarum illustrssum\veram/, & hujus Epistolæ exemplar mense Iunio anni 1676 in Galliam ad D. Leibnitium misisset; & Vir Clarissimus sub finem mensis Octobris, in reditu suo & Gallia per Angliam in Germaniam, epistolas meas in manu Collinij insuper consuluisset: incidit is finito itinere \tandem/ in methodum similem sub diversis verborum et notarum formulis, et mense Iunio sequente specimen \ejusdem/ in Tangentibus more Slusiano ducendis ad me misit, {&} \& subjunxit se credere/ eandem a methodo mea \methodum suam a meam a sua/ non abludere \se credere/ subjunxit præsertim cum quadraturæ curvarum \per/ utrā method{a}|u|m faciliores redd\er/entur. Methodi \vero/ utrius fundamentum continetur in hoc Lemmate.

et Tractatum duos de hujusmodi rebus scripsisse alterum quem Barrovius, anno 1669 ad Collinium misit qui jam extat |& methodum sea{illeg} serierum ab momentorum {troc}tat|, & alterum anno 1671 in \qua/ hanc methodum fusius exposueram; cum literis transpositis hanc

et Tractatus duas de hujusmodi scripsisse, alterum quem Barrovius anno 167|6|9 ad Collinium misit, & alterum anno 1671 in quo hanc methodum plures \fusius/ exposuerat|m|; cum literis transpositis fundamentum hujus methodi literis transpositis hanc sententiam involventib [Data — — et vice versa] celarem, specimen vero \ejusdem/ in Curvis quadrandis subjungerem & exemplis illustrarem; et cum Collinius Epistolam 10 Decem 1672 datam a me accepisset,

In uti momenta mea \quantitatum/ differentias vocavit & quantitates ipsas summas momentorum, & literis d et s præfixis \differentias & summas/ notavit, & pro fluxionibus nulla habuit symbola: ego vero

plenius exponitur in Tractatu

Scholium

Analysin meam per series et momenta. Barrovius noster anno 1669 ad Collinium misit. & Easdem methodos \annis 1665 et 1666 inventas/ in alio Tractatu plenius explicim{illeg} anno 1671; et in Epistola 10 Decem 1672 ad Collinium data [methodum meam generalem in \hoc/ Tractatu isto descriptam \hocce/ explicatam verbis generalibus descripsi & exemplo d{illeg} Tangentium more Slusiano ducendarum illustravi dixi eandem ad quantitates surdas non hærere. Collinius vero exemplar hujus Epistolæ mense Iunio anni 1676 ad D. Leibnitium hinc in Gallia agentem misit.] In literis vero \insuper/ quæ mihi cum D. Leibnitio eodem anno \1676/, intercedebant, cum sig \Tractatibus prædictis verba/ \facerem & sig/nificarem me compotem esse methodi Analyticæ determinandi maximas & minimas, ducendi Tangentes, quadrandi figuras curvilineas, conferendi easdem inter se, et similia peragendi quæ in terminis surdis æque ac in rationalibus procederet, ,|[|& Tractatum prædictorum etiam miminisse{illeg}m], & literis transpositis hanc sententiam involventibus [Data æquatione quotcun quantitates involvente, fluxiones invenire, et vice versa] fundamentum hujus methodi celarem, specimen vero ejusdem in curvis \curvilineis/ quadrandis subjungerem et exemplis illustrarem, et Vir clarissimus \eadem anno/ in reditu suo \e Gallia/ per Angliam in Germaniam, sub finem mensis Octobris Epistolas meas in manu Collinij consuluisset \consuleret/: incidit is \non {mu}lo post/ in methodum similem sub diversis verborum et notarum formulis, et mense Iunio sequente specimen ejusdem in Tangentibus more Slusiano ducendis ad me misit; & subjunxit se credere methodum meam a sua non abludere, præsertim cum quadraturæ curvarum per utram methodum \methodum/ faciliores redderentur. Methodi vero utriusque fundamentum continetur in hoc Lemmate.

methodum momentorum exemplo tangentium more Slusiano ducendarum illustravi dixi eandem dixisse eandem /ipsam\ ad Quæstiones de areis areis tangentibus {illeg}s curvitatibus, areis, longitudinibus, centris gravitatum Curvarum & Curvilinearum &c se extendere, et esse general{e}m et ad \ad/ quantitatis surdas non hærere. Et Collinius exemplar

— ad Collinium data inter per methodum generalem quam methodo serierum \[in Tractatu novissimo]/ intertexui, intellexi methodum momentorum, in Tractatu eam verbis generalibus \ibi/ descripsi, et exemplo Tangentium more Slusiano ducendarum illusstravi, dixi eandem ad quantitates surdas non hærere.

— ad Collinium data, ha{illeg} methodum serierum quam in hoc tractatu methodum momentorum [quam in \his/ {illeg} Tractatibus novissimo intertexi methodo serierū intertexa{illeg}\{u}{illeg}m/,] vocavi methodum generalem [eam \ad Curvarum/ eam ve{ra} ad \curvarum/ Tangentes Areas, Curvitates, longitudines, centra gravitis, {illeg} & similia esse extende s|t|em] & exemplo Tangentium more Slusiano ducendarum illustravi, dixi eandem ad quantitates surdas non hærere. Et Collinius vero exemplar hujus epistolæ mense Iunio anni 1676 ad D. Leibnitium misit tunc in Gallia agentem misit.

In literis insuper quæ mihi cum D. Leibnitio anno 1676 intercedebant;

Scholium

Analyseos|in| meam \Tractatum quendam meum/ per series et momenta \a me scriptam/ Barrovius noster anno 1669 ad Collinium misit. Ean|s|dem m|M|ethodos \ibi expositos/ an alio Tractatu plenius explicui anno 1671 {illeg} E{illeg} \{illeg}nd{e}/ in Epistola 10 Decem. 1672 ad Collinium data, methodum momentorum vocavi generalem et exemplo tangentium more Slusiano ducendarum illustravi, dixi eandem |etiam ad quæstiones de curvitatibus, areis, longitudinibus, centris gravitatum Curvarum & Curvilinearum &c sese extendere et esse generalem &| ad quantitates surdas non hærere; et Collinius exemplar hujus epistolæ mense Iunio anni 1676 ad D. Leibnitium tunc in Gallia agentem misit.

In literis insuper quæ mihi cum D. Leibnitio anno 1676 intercedebant, cum verba facerem de Tractatibus prædictis, & Significarem me compotem esse methodi Analyticæ determinandi maximas et minimas, ducendi tangentes, quadrandi figuras curvilineas, conferendi easdem inter se, et similia peragendi quæ in terminis surdis æque ac in rationali{illeg}|b|us procederet; & literis transpositis hanc sententiam involventibus [Data æquatione quotcun fluentes quantitates involventes fluentes quantitates fluxiones invenire, et vice versa] fundamentum hujus methodi celarem, specimen \vero/ ejusdem in curvilineis quadrandis subjungerem & exemplis illustrarem; et Vir celeberrimus eodem anno in reditu suo e Gallia per Angliam in Germaniam, sub finem mensis Octobris, epistolas meas in man{y}|u| Collinij \etiam/ consuluiss\er/et: incidit is non multo post in methodum similem \eandem momentorum/ sub diversis verborum et notarum formulis, et mense Iunio sequente specimen ejusdem in Tangentibus more Slusiano ducendis ad me misit, & subjunxit se credere methodum meam a sua non abludere, præsertim cum quadraturæ curvarum per utram methodum faciliores redderentur. Methodi vera unius /hujus\ fundamentum continetur in hoc Lemmate, et plen hæc methodus

In writing the Book of Principles I made very much use of the following Book of Quadratures & therefore have subjoyned it. This Book is founded upon the method of fluxions, & in the Introduction \to it/ I said that I found the method of fluxions gradually in the years 1665 & 1666, & it may be expected this has be{en} called in question. The accusatio But the accusation is not yet proved as it ought to have been, nor hath any answer been given to the collection of ancient Letters & Papers published by order of the R. Society under the title of Commercim Epistolicum for setting this matter in a fair light. But instead of doing this the accusers have been at work to set up judeges if theie are freeing themselves from calumny \Of the contrary/, the Accusers have been endeavouring to avoid answering it by telling us that we shall not have the pleasure to see them answer & that to answer it would require a book as big as the Commercium, & by appealing to Iudges of their own setting up, & by proposing Problems to be solved challenging \challing {sic} the English Mathematicians/ to solve their Problems, & by framing many new accusasions for ma \to make a squabble/ & writing Letters to \Ladies & other/ persons unacquainted with these matters & to Ladies {illeg} for making an interest] Ho\w/ever, upon publishing this Book anew, {illeg}|it| may be expected that I say some thing in justifation {sic} of what I said in the Preface of the former edition.

Vpon notice from M^r Iohn Collins in December 1672 that M^r Iames Gregory had impr

The Logarithmotechnia {illeg}|of| M^r Mercator was published in septemb \Autumn/ 1668 & a few months after D^r {illeg} M^r Collins D^r Barrow received a copy thereof from M^r Collins & sent back to M^r Collins a small Tract of mine in M.S. entituled Analysis per series numero terminorum infinitas in w^ch I affe were these words concerning the joint method of series & fluxions: Deni ad Analyticam merito pertinere censeatur cujus beneficio curvarum areæ & longitudines &c (id modo fiat {sic} \ID MODO FIAT/) exacte et Geometrice determinentur: sed ista narrandi non est locus. And by the testimony of M^r Collins D^r Barrow & M^r Collins I had this Method some years before the Logarithmotechnia came abroad: Fo{illeg}|r| M^r Collins in a Letter to M^r Strode dated 26 Iuly 1672 & published by order of the R. S. wrote thus Mense Septembri 1668, Mercator Logarithmotechniam edidit suam, quæ specimen hujus methodi (i.e. Serierum) in unica tantum figura, nempe quadraturam Hyperbolæ, continet. Haud multo postquam in publicum prodierat liber, exemplar ejus — Barrovio Cantabrigiam misi, qui quasdam Newtoni chartas — extemplo remisit: e quibus et ALIIS, quæ OLIM ab Auctore cum Barrovio communicata fuerant, patet illam methodum a dicto Newtono aliquot annis antea excogitatam fuisse et modo universali applicatam fuisse: ita ut ejus ope in quavis Figura Curvilinea proposita, quæ una vel pluribus figuris \proprietatibus/ definitur, Quadratura vel Area dictæ Figuræ, accurata si possibile sit ACCVRATA SI POSSIBILE SIT, sin minus infinite \vero/ propinqua, Evolutio vel longitudo lineæ curvæ, centrum gravitatis figuræ, Solida ejus rotatione genita, et eorum superficies,sine ulla radicum extractione, obtineri queant. How this is done I explained in a larger Tract written by me A.C. 1671 {illeg}|a|s I mentioned in a letter to M^r Oldenburg dated 24 Octob 1676 & p {illeg}|ub|lished by D^r Wallis. In {illeg} And in that Letter I set down the foundation of the method in these words Data Æquatione quotcun fluentes quantitates involvente fluxiones invenire et vice versa, & then added y^t upon this foundation I had endeavoured to make advance the Theory of Quadratures & obteined some general Theorems for that purpose, & there set down the first of those Theorems & illustrated it with examamples {sic}. This is a Theoreme for squaring Curves whose Ordinates are Binomial & I added that I had other Theorems Rules for Trinomials & some others And figures. {illeg}|An|d this is the Method for squaring of figures by series w^ch break of & become finite \equations/ when the Curve admits of an exact |& Ge{o}metric| quadrature. Now to do this requires the knowledge of the method of fluxions so far as it is described in the first five or six Propositions, of the <24v> following book of Quadratures. And therefore by the testimony of D^r Barrow & M^r Collins, I knew thus much of the method some years before the Logarithmotechnia came abroad & by consequence in the year 1666. And this may suffice to justify what I said in the Preface of this book.

M^r Iames Gregory in a Letter to D^r Barrow M^r Collins dated 5 Sept 1670, wrote that by comparing D^r Barrows methods of drawing Tangents with his own he had found a method of drawing Tangents to all Curves without calculation. And upon notice of thereof & that M^r Slusius had such another method w^ch he intended to communicate to M^r Oldenburg I wrote the to M^r Collins the following Letter dated 10 Decem 1672. Ex animo gaudeo — — — — reducendo eas ad series infinitas. In this Letter you have — — — — in the third volume of his works. For in the

For from the Tract w^ch I wrote in the year 1671, I extracted in the year 1676 the following Book of Quadratures & in my afores^d Letter of Octob 24 1676 I set down the first Proposition thereof verbatim, & copied without any alteration the two Tables set down in the Scholium upon the tenth Proposition. And in my Letter to M^r Collins dated 8 Novem. 1676 & published by M^r Iones, I had relation to the tenth Proposition of this Book in saying: Nulla extat Curva — — — — was known to me in the year 1676 when I wrote this Letter.

[In a letter dated 12 May 1676 M^r Leibnitz wrote thus to M^r Oldenburg. Cum Georgius Mohr Danus — — — — desiderio meo. M^r Leibnitz therefore knew that M^r L Collins had the Demonstration of thi of this \two/ series that is the & desired a copy of it, that is \a copy/ of the Analysis per series numero terminorum infinitas. For M^r Collins had no other demonstration of those two Series. And thereupon I wrote But M^r Collins & M^r Oldenburg desired \{illeg}/ that I would send hi{illeg} chose rather to write to me to send him what he wanted, & thereupon I wrote my to M^r Oldenburg my Letter of 13 Iune 1676 & M^r Oldenburg sent to him 26 Iune 1676 sent to a copy of it to M^r Leibnitz together with \c/ copies a copy of my Letter of 2|1|0 abovementioned dated 10 Decem 1672, & copies o extracts of many of Gregories Letters amongst w^ch were his \two/ Letters abovementioned dated 5 Sept 1670 & {illeg} another Letter dated 15 Feb. 167$\frac{0}{1}$ in w^ch < insertion from f 24v > in w^ch {sic} M^r Gregory was sent to M^r C <25r> ol there < text from f 24v resumes > the series $\mathrm{a}=\mathrm{t}-\frac{{\mathrm{t}}^3}{3{\mathrm{r}}^2}+\frac{5^5}{5{\mathrm{r}}^4}-\frac{{\mathrm{t}}^7}{7{\mathrm{r}}^5}+\frac{{\mathrm{t}}^9}{9{\mathrm{r}}^7}-\mathrm{\&c}$, where r denoting the radius, t the Tang^t, & a the Arc of a circle. And the same series was sent to M^r Leibnitz \b{illeg} {sic}/ the year before by M^r Oldenburg from M^r Collins in a letter dated 15 Apr. 1675. And M^r Leibnits in answer to all that had been sent him sent back hi a Letter dated 27 Aug. 1676]

In the year 1691 this Book in MS was in the hands of D^r Halley & M^r Raphson as the ones has \left/ attested in print & the other still attests. And hte next year \D^r Wallis/ in the second Volume of his works published \he printed/ the first Proposition of the|i|s Book \illustrated/ with examples in \finding/ first & second Differences \fluxions/ And this is {illeg}|a|t the request of D^r Wallis that I would explain how I found the Theoremes set down in my Letter of 24. Octob. 1676 for squaring Curvilineas w^ch — — — — — — & is still the shortest the clearest & the best. In the beginning of the year 1695 the March 1695 D^r Wallis upon notice \notice from Holland/ that the the Method of fluxions was celebrated in Holland \there/ by the name of the Differential Method of Fluxions M^r Leibnitz, inserted into the Preface of the first Volume of his works {illeg} (w^ch came abroad after the second Volume) the following Preface Paragraph. Quæ in secundo {illeg} Volumine habentur — — — — ab ipso excogitatam. And soo as soon as the Volume was printed off gave me notice of what he had wrote to me the following Letter. dated Apr. 10^th. 1695.

And the next year the Editor of the Acta Eruditorum \in/ gave|ing| an Account of this Volume cited some words out of this Paragraph & D^r Wallis in a Letter dated 1 Decem. 1696 gave notice to M^r Leibnitz of the same Paragraph \in the Leters w^ch ensued between him & D^r W/. And \yet/ neither the Editor of the Acta nor M^r Leibnitz denyed what D^r Wallis had affirmed. On the contrary M^r Leibnitz in a letter to me dated the Marquess {illeg} de L'Hospital {illeg} in the Preface to his book de Infinite parvis published this year of allowed that the Book of Principles published this year was almost wholy of the Differential calculus, & M^r Leibnitz himself three years before in a letter to me dated {illeg} $\frac{7}{17}$ March 1693 acknowledged the same thing (the Original of w^ch is in the Archives of the R. S.) acknowledged the same thing in these words Quantum tibi Scientiam rerum Mathematicarum totius Naturæ debere arbiter, occasione data etiam publice professus sum professus. Mirifice ampliaveras Geometriam tuis seriebus, sed edito Principiorum opere ostendisti patere Tibi, etiam quæ Analysi receptæ non subsunt. Conatus sum ego quo Notis commodis adhibitis quæ differentias & summas exhibent, Geometriam illam quam Transcendentem appello Analysi quodammodo subjicere nec res male processit. Here he gives me the Preference. And in the Acta Eruditorum for May 1700, he acknowledged that I had the was the first who had manifested by a specimen made publick that |I| had the method of maxima & minima in infinitesimals or moments, meaning {illeg} {illeg} \the specimen in/ the Scholium upon the 34^th Proposition of the Book of Math. Principles. And this method I could not have without the Method of Fluxions. And \in general/ this Book of Principles is the first specimen made publick of applying this|e| Method \of Fluxions & Moments/ to the difficulter Problems. And M^r Leibnitz in the Acta Eruditorum for       1684 affirmed that such Problems were not to be solved Without the differential method or another like it, meaning the method of fluxions. For when he wrote h{illeg} to M^r Oldenburg his Letter of 21 Iune 1677 wherein he was \first/ began to make known \write of/ the Differential method, & shewed how it might be deduced it from the method of Tangents of D^r Barrow, he {illeg}|a|knowledged that I had such another method. Clarissimi Slusij (saith he) Methodum Tangentium nondum esse absolutam Celeberrimo Newtono assentior. And after he had shewn how to deduce the method of Slusiu Tangents of Slusius from that of D^r Barrow \(as Gregory had done before)/ & how to make this method proceed without taking away surds, he added: Arbitror quæ celare voluit Newtonus de Tangentibus ducendis ab his non abludere. Quod addit, ex hoc edem fundamento quadraturas quo reddi faciliores, me in sententia hac confirmat. He knew therefore in those days by my Letters that I had a method like the Differential, & by the same Letters he was told that I {illeg} in the year 1671 I wrote a Tract upon this method & the Method of Fluxions \Series/ together.

If it

In the second Let|m|ma of the second Book of Principles I wrote a Tract upon demonstrated the Elements of the Method of fluxions synethetically. And because M^r Leibnitz had published those Elements in another form two years before, without acknowledging the correspondence w^ch had been between us \eight years/ before, I added a Scholium not to give away that Lemma but to put M^r Leibnitz in mind of making a publick acknowledgm^t of that correspondence.

In composing these Books I was much assisted by the Book of Quadratures. At the request of D^r Wallis I sent to him the first & second Proposition of this Book of Q \Aug/ in the year 1692 \Aug. 27/, & he printed it in the second Volume of his works before the end of the year & the Book came abroad in Spring 1693. & \{illeg}/ this was the first time that any rule {illeg} for finding second third & fourth fluxions was published, & \so/ the Rule is the best. This \is/ a proof that the Book of Quadratures was then in Manuscript. And This Book D^r Halley & M^r Ralpson borrowed \it/ of me \saw it in my hands at Cambridge/ in summer 16961 & carried it with them to London as M^r Ralphson has left attested in print, & D^r Halley a living evidence still attests. And therefore it was in MS in y^e year 1691, & continued in MS f{illeg}|th|irteen years at the least before it was published. In my Letter of 24 Octob 1676 I cited many things out of it, Particulary I cited \(in an Enigma)/ the very words of the first Proposition Data æquatione fluentes quotcun quantitates involvent{o}|e| invenire fluxiones, [putting them into an Ænigma] I mentioned also the substance of the fift & sixt Propositions & gave a s{illeg}|o|lution of the fift w^th some examples. These two are the inverse of the third & fourth \Propositions/ & \these two are exampels of the second &/ all of them are deduced from the first & second, & therefore I was in those days no stranger to the first six Propositions of this Book.

In the same Letter of 24 Octob. 1676, I set wrote \thus./ Seriei a D. Leibnitio pro Quadratura Conicarum Sectionum propositæ, affinia sunt Theoremata quædam quæ pro comparatione Conicarum Sectionum Curvarum cum Conicis sectionibus in Catalogum dudum retuli. The series for squaring the Conic sections M^r Leibnitz received \had twice/ from M^r Oldenburg. |The| Theorems for comparing other {illeg} Curves with the Conic Sections, I reduced into a Catalogue in th{illeg}|e| Tract above mentioned w^ch I wrote in the year 1671, & thenc I copied it into the Book of Quadratures & the Ordinates of the \Curves in the/ more intricate {illeg} part of the Table I set down in the said Letter in the very same order & in the very same letters & symbols in w^ch you will \now/ find them in \the scholium upon the 10^th Proposition of/ the Book of Quadratures. And therefore that Table was composed before I wrote that Letter; & the 7^th 8^th 9^th 10^th Propo\si/tions upon w^ch it depends were then known to me.

Between the years 1671 & 1676 I medled not w^th these studies being tyred with them before: but in the year 1676 I extracted the Book of Quadratures from the Tract w^ch I wrote in year 1671 & from other older papers. And \soon/ after I had finished it & I wrote to M^r Collins {illeg}|a| Letter dated Novem. 8. 1676 in which a part of which was in the following words \is here set down/. Nulla extat Curva cujus Æquatio ex tribus constat terminis, in qua, licet quantitates incognitæ se mutuo afficiant, vel Indices dignitatum sint surdæ quantitates (v. g. $\mathrm{a}{\mathrm{x}}^{\mathrm{\lambda }}+\mathrm{b}{\mathrm{x}}^{\mathrm{\mu }}{\mathrm{y}}^{\mathrm{\sigma }}+\mathrm{c}{\mathrm{y}}^{\mathrm{\tau }}=0$, x designat basin, y Ordinatam, λ, μ, σ, τ Indices dignitatum ipsius x et y, & a, b, c quantitates cognitas una cum signis suis + vel −) nulla inquam hujusmodi est Curva, de qua, an quadrari possit necne, vel quænam sint figuræ simplicissimæ quibusquam comparari possit, sive sint Conicæ Sectiones sive aliæ magis complicatæ, intra horæ octantem respondere non possim. Deinde methodo directa & brevi, imo methodorum omnium generalium brevissima, eas modo comparari possint, comparo. To do all this is the inverse \method/ of fluxions so far as that method is carried on in the Book of Quadratures. And by the help of this method I composed the Book of Principles, & therefore in this Edition have added the Book of Quadratures to the end of it.

[I made use also of the method of maxima & minima in Infinitesimals & by the confession of M^r Leibnitz was the first who shewed by a specimen made publick that I had this method. I made use also of the method by me called the differential Method, & for that reason have ann\ex/ed {illeg} the|i|s Method to the Book of Quadratures. In my Letter of Octob. 24 1676 I said that the Tract w^ch I was writing in the year 1671 I never finished, & that that part of it was wanting in w^ch I intended to teach the manner of resolving <26v> Problems w^ch cannot be reduced to Quadratures. But what I \then/ intended to write is now gone out of my mind through long disuse of these methods]

In the Introduction to the Book of Quadratures {w^ch} I wrote I said that I invented the Method of fluxions in the yea gradually in the years 1665 & 1666. & D^r Wallis (who received from M^r Oldenburg copies of my Letters in the year 1676 & corresponded \also/ w^th M^r Collins in those days & was very inquisitive in things of this nature, wrote \affirmed |published| the same things six years before me nine years before me/ in the Introduction to the first Volume of his works w^ch came abroade in the year April 1695. the following Paragraph \His words are/. Quæ in secundo Volumine [ante biennium edito] habentur, in Præfatione eidem præfixa dicitur. Vbi (inter alia) habetur Newtoni Methodus de Fluxionibus (ut ille loquitur) consimilis naturæ \cum Leibnitij/ (ut hic loquitur) Calculo Differentiali, (quod qui utram methodum contulerit, satis animadvertat, utut sub loquendi formulis diversis) quam ego descripsi (Algebræ cap. {illeg} 91 &c præsertim cap. 95) ex binis Newtoni Literis (aut earum alteris) Iunij 13 & Octob. 24 1676 ad Oldenburgum datis, cum Leibnitio tum communicandis (ijsdem fere verbis, saltem leviter mutatis, quæ in illis literis habentur) ubi methodum hanc exponit Leibnitio exponit, tum ante decem annos nedum plures, ab ipso excogitatam.

In the year \Iuly/ 1669 D^r Barrow sent to M^r Collins a small Tract written by me under the Title of Analysis per series numero terminorum infinitas. This title implies that the scope of the Book was not only to reduce finite quantites into converging series but also by the help of those series as well as \to apply/ æquations involving such series to resolve as well as by finite æquations to the resolution of Problems {illeg}|b|y means of the Analysis there proposed And in this Analysis I considered quantities as generated by motion & their parts generated in moments of time I call their moments, & shew how to compute the moments of quantities lines, superficies, & solids & to find as many Curves as I please whose areas w^ch may be squared w^ch is (in substance) the first & second Propositions of the Book of Quadratures. {illeg}And after I had shewed how to find the Ordinate Areas & Lengths of Mechanical lines, I add describe the universality of this method in these words. Nec quicquam hujusmodi scio ad quod hæc methodus, id varijs modis sese non extendit. Imo tangentes — — — — sed ista narrandi non est locus. These last words relate to the method described in the fift & sixt Book of Propositions of the book of Quadratures. And therefore the pro{illeg} Methods conteined in the first six Propositions of this book were then known to me. For the fift & sixt Propositions are the inverse of the third & fourth. [The first Rule in the Analysis per Series is this. Figuræ cujusvis curvilineæ Abscissa \AB/ sit x, & Ordinata \BD/ sit y, & sint a, b, c & quantitates datæ, & m, n num{illeg}|{b}|ri integri, et si sit $\mathrm{a}{\mathrm{x}}^{\frac{\mathrm{m}}{\mathrm{n}}}=\mathrm{y}$, erit $\frac{\mathrm{a}\mathrm{x}}{\mathrm{m}+\mathrm{n}}{\mathrm{x}}^{\frac{\mathrm{m}+\mathrm{n}}{\mathrm{n}}}=\mathrm{are\ae \; Curviline\ae \; ADB}$. Et vicissim si Area sit a{illeg} erit $\mathrm{m}+\mathrm{n}\mathrm{n}\mathrm{x}$ $\mathrm{b}{\mathrm{x}}^{\frac{\mathrm{m}}{\mathrm{n}}}$, o|O|rdinata erit $\frac{\mathrm{m}\mathrm{b}}{\mathrm{n}}{\mathrm{x}}^{\frac{\mathrm{m}-\mathrm{n}}{\mathrm{n}}}$. which is the first] And] In the beginning of this Tract I call this Method methodū generalem olim a me quam olim excogitaveram. This Tract is the Compendium \methodi/ serierum w^ch mentioned in my Letter of {illeg}|O|ctob. 24. 1719, where I say that it was communicated by D^r Barrow to M^r Collins at that time when M^r Mercators Logarithmotechnia came abroad. And M^r Collins in his Letter to M^r Tho. Strode dated 26 Iuly 1672 has testified that by this & other Papers communicated before to D^r Barrow it appeared that I had invented this method & applied it generally some years before he sent it to M^r Collins.

In my Letter of 24 Octob. 1676 at the request of M^r Leibnitz I descri < insertion from the left margin > be < text from f 26v resumes > how I fel found out the method of converging series a little before the plague w^ch raged in London in the year 16 9|6|5, & particularly the how I then invented the {illeg} reduction of any power of any Binomial into such a Series by the Rule set down in teh beginning of my Letter of 13 Iune 1676. Let ${\overline{)\mathrm{x}+\mathrm{o}}}^{\mathrm{n}}$ be any line dignity of any binomial $\mathrm{x}+\mathrm{o}$ & by this Rule ${\overline{)\mathrm{x}+\mathrm{o}}}^{\mathrm{m}}$ will be equal to ${\mathrm{x}}^{\mathrm{n}}+\mathrm{o}\mathrm{o}{\mathrm{x}}^{\mathrm{n}-1}+\frac{\mathrm{n}\mathrm{n}-\mathrm{m}}{2}\mathrm{o}\mathrm{o}{\mathrm{x}}^{\mathrm{n}-2}+\mathrm{\&c}$. And here if x be an increasing quantity \of fluents/ & o its moment, then $\mathrm{n}\mathrm{o}{\mathrm{x}}^{\mathrm{n}-1}$ will be the first moment of the fluent ${\mathrm{x}}^{\mathrm{n}}$. And this Theoreme quickly gave me the first Proposition of the Book of Quadratures & the inverse thereof gave me the two first Rules in the Analysis per æquationes numero terminorum infinitas. And this Relation between the Methods of Series & moments made me joyne them together as two branches of a \one/ very <27r> general method. And all this I hope may suffice to justify me in saying \in the Introduction to the Book of Q./ that I found the method of fluxions gradually in the years 1665 & 1666.

In writing the Book of Principles I made very much use of the following Book of Quadratures, & therefore have subjoyned it. And because my saying in the Introduction, that I found the Method of fluxions gradually in the years 1665 & 166 {sic} has been called in question, it will not be amiss to explain that matter justify what I said

In December 1672 Upon notice from M^r Collins \in Decemb. 1672/ that M^r Iames Gregory had improved the method of Tangents of D^r Barrow so as to {illeg} draw tangents without calculation & that M^r Slusius had such another method w^ch he intended to communicate to M^r Oldenburg, I wrote the following. Letter to M^r Collins dated 10 Decem 1672. "Ex animo gaudeo D. Barrovij, amici nostri reverendi lectiones Mathematicas exteris adeo placuisse, neque parum me juvat intelligere eos [Slusium & Gregorium] in eandem mecum incidisse ducendi Tangentes Methodum. Qualem eam esse conjiciam, ex hoc exemplo percipies. Pone CB applicatam ad AB in quovis angulo dato, terminari ad quamvis Curvarum AC; et dicatur AB x & BC y, habitudo inter x et y exprimatur qualibet æquatione, puta ${\mathrm{x}}^3-2\mathrm{x}\mathrm{x}\mathrm{y}+\mathrm{b}\mathrm{x}\mathrm{x}-\mathrm{b}\mathrm{b}\mathrm{x}+\mathrm{b}\mathrm{y}\mathrm{y}-{\mathrm{y}}^3=0$, qua ipsa determinatur Curva. Regula ducendi Tangentem hæc est: Multiplica æquationis terminos per quamlibet progressionem arithmeticam juxta dimensiones y, puta $\begin{array}{c}{\mathrm{x}}^3-2\mathrm{x}\mathrm{x}\mathrm{y}+\mathrm{b}\mathrm{x}\mathrm{x}-\mathrm{b}\mathrm{b}\mathrm{x}+\mathrm{b}\mathrm{y}\mathrm{y}-{\mathrm{y}}^3\\ 010023\end{array}$; ut et juxta dimensiones x, puta ${\mathrm{x}}^3-2\mathrm{x}\mathrm{x}\mathrm{y}+\mathrm{b}\mathrm{x}\mathrm{x}-\mathrm{b}\mathrm{b}\mathrm{x}+\mathrm{b}\mathrm{y}\mathrm{y}-{\mathrm{y}}^3=0$, qua ipsa determinatur Curva. Regula ducendi Tangentem hæc est: Multiplica æquationis terminos per quamlibet progressionem arithmeticam juxta dimensiones y, puta $\begin{array}{c}{\mathrm{x}}^3-2\mathrm{x}\mathrm{x}\mathrm{y}+\mathrm{b}\mathrm{x}\mathrm{x}-\mathrm{b}\mathrm{b}\mathrm{x}+\mathrm{b}\mathrm{y}\mathrm{y}-{\mathrm{y}}^3\\ 322100\end{array}$ Prius productum erit Numerator, & posterius Denominator divisum, per x Denominator Fractionis quæ exprimet longitudinem BD æd cujus extremitatem D ducenda est Tangens CD. Est ergo longitudo $\mathrm{BD}=\frac{\mathrm{-2}\mathrm{x}\mathrm{x}\mathrm{y}+2\mathrm{b}\mathrm{y}\mathrm{y}-3{\mathrm{y}}^3}{3\mathrm{x}\mathrm{x}-4\mathrm{x}\mathrm{y}+2\mathrm{b}\mathrm{x}-\mathrm{b}\mathrm{b}}$. Hoc est unum particulare vel corollarium potius Methodi generalis quæ extendit se, citra molestum ullum calculum, non ad ducendum Tangentes ad quasvis Curvas, sive Geometricas, sive Mechanicas, vel quomodocun rectas lineas aliasve Curvas respicientes; verum etiam ad resolvendum alia abstrusiora Problematum genera de Curvitatibus, a|A|reis, Longitudinibus, centris gravitatis Curvarum &c. Neque (quemadmodum Huddenij methodus de Maximis et Minimis) ad solas restringitur æquationes illas quæ quantitatibus surdis sunt immunes. Hanc methodum intertexui alteri {sibi} isti, qua Æquationum Exegesin instituo reducendo eas ad Series infinitas. &c. In this Letter you have an example of the Method of Fluxions in drawing of Tangents & a description of the large extent of it in this & other more difficult Problems \without stopping at surds/; & the last words of the Letter relate to a Tract w^ch I wrote the year before & in which the method here described as interwoven with another Method wherein æquations are reduced to converging series, both w^ch methods together constitutde the general Method described in my Letters 14 \to M Oldenburg dated/ 13 Iune & 24 Octob. 1676 & |which Letters {pub}{illeg} were published by D^r Wallis in the third volume of his works|.

For in the year 1671 I wrote a Tract concerning the method of converging series & Fluxions joyntly but did not finish it, that part of it being wanting in w^ch I intended to explain the manner of solving such {illeg} problems as can{illeg}not be reduced to quadratures, as I mentioned in my Letters of 24 Octob. 1676 {illeg} aforesaid. And from this Tract I extracted in the year 1676 the following Book of Quadratures & therein copied from the former Tract without any alteration \{all} all/ the \two/ Tables set down in the \Scholium upon the/ tenth Proposition, \the one/ for squaring some Curves & \the other for/ comparing others with the Conick Sections. |And| In my Letter to M^r Collins dated 8 Novem. 1676 & published by M^r Iones, I had relation to \the 9^th & 10^th Propositions of/ this Book in saying: Nulla extat Curva cujus Æquatio ex tribus constat terminis, in qua, licet quantitates incognitæ se mutuo afficiant, vel indices dignitatum sint surdæ quantitates (v. g. $\mathrm{a}{\mathrm{x}}^{\mathrm{\lambda }}+\mathrm{b}{\mathrm{x}}^{\mathrm{\mu }}{\mathrm{y}}^{\mathrm{\sigma }}+\mathrm{c}{\mathrm{y}}^{\mathrm{\tau }}=0$, x designat Basin, y Ordinatam & λ, μ, σ, τ indices dignitatum ipsius x & y & a, b, c quantitates {illeg} cognitas una cum signis suis + vel −) nulla inquam hujusmodi est Curva de qua an quadrari possit, necne, vel quænam sint Figuræ simplicissimæ quibuscum comparari possit, sive sint Conicæ Sectiones sive aliæ magis complicatæ, intra horæ octantem respondere non possim. Deinde methodo directa et brevi, imo methodorum omnium brevissima generalium brevissima [de qua vide Coroll. 2 Prop. 10 Libri sequentis] eas, \modo/ comparare|i| possint, comparo. Affirmatio quidem videri potest temeraria, propterea quod perdifficile sit dictu an Figura quadrari vel cum alia comparari possit, necne; mihi autem manifestum est, ex eo unde deduxi, quanquan id alijs demon <28v> strare in me suscripere nollem. Eodem methodus Æquationes quatuor terminoru{m} alias complectitur, haud tamen adeo generaliter. All this relates to the method of squaring figures set down in the Book of Quadratures, & chiefly to the tenth Proposition of that Book: & the methodus directa & brevis {illeg} compendi f{illeg} mentioned in this Letter, by w^ch I compare such \trinomial/ figures as may be compared is that described \mentioned/ in Corol 2 Prop. 10; & this Proposition with its Corollaries is deduced from the 5^t 6^th 7^th 8^th & 9^th Propositions of this Book & these are deduced from the first 1^st 2^d 3^d & 4^th Propositions of the same Book: & therefore \the/ method of Quadratures so far as it is conteined in the ten first Propositions of this Book was known to me \in the year 1676/ when I wrote this Letter.

This Book I made use of in the year 1679 when I found the demonstration of Keplers Proposition that the Planets moved in Ellipses, & again in the year 1684, 1685 & 1686 when I wrote the Book of Mathematical Principles of Philosophy \I made much use of it & for that reason I have now subjoyned it to that Book/ In the year 1691 it was in the hands of M^r Ralpson & D^r Halley as the one of them attested in print before his death & the other still attests. And in the year 1692 at the request of D^r Wallis [I sent to him in a Letter dated            the first Proposition of the Book illustrated with examples in \finding first &/ second fluxions & {illeg} it was printed in the second Volume of his works before the end of the year, & the volume came abroad in Spring following \\the/ April 1693/. And this was the first time that any Rule was published for finding second third fourth & other fluxions or differences] that I would explain how I found the Theorems set down in my Letter of 24 Octob 1676 for squaring of Curves by series w^ch break off & become finite equations when the Curves can be squared by finite equations, I sent to him in a Letter dated Aug 27 the fift Proposition of the Book of Quadratures as a more general Theoreme w^ch comprehended the Theorems set down in Letter of mentioned by him & he{illeg} at the same time I sent to him also the first Proposition of this book illustrated with examples in \sending/ first & second fluxions. And these two Propositions were printed \befor the end of the year/ in in {sic} the second Volume of his works pag. 391, 392, 393 & this \which/ Volume came abroad in August 1693. And this was the first time that any Rule was published for finding second third & fourth & other fluxions or differences & is still \the shortest the clearest &/ the {illeg} best. But the Book of Quadratures continued in w^ch I affirmed that I found the Method of fluxions gradually in the years 1665 & 1666. For I thought that I might safely write this because D^r Wallis, in the Preface to the first Volume of his works \w^ch came out after the second & was/ published in Spring \April/ 1695, had said without ever being contradicted, inserted the following Paragraph. Quæ in secundo Volumine habentur in Præfatione eidem præfixa dicitur. Vbi (inter alia) habetur Newtoni Methodus de Fluxionibus (ut {illeg}|il|le loquitur) consimilis naturæ ad {illeg} cum Leibnitij (ut hic loquitur) c|C|alculo Differentiali, (quod qui utram contulerit methodum contulerit, satis animadvertat, utut sub loquendi formulis diversis,) quam ego descripsi (Algebræ cap. 91 &c præsertim cap. 95) ex binis Newtoni literis (aut earum alteris) Iunij 13 & Octob. 24, 1676 ad Oldenburgum datis, cum Leibnitio tum communicandis (ijsdem fere verbis, saltem leviter mutatis, quæ in illis literis habentur;) ubi methodum hanc Leibnitij|o| exponit tum ante decem annos, nedum plures, ab ipso excogitatam.

At the request of M^r Leibnitz I described in my {illeg} said Letter of 24 Oct 1676, how, before the g plague w^ch raged in London in the years 1665 & 1666, by interpoling the series of D^r Wallis, I found the method of converging series together with the Rule for resolving the dignities of Binomials into such series. I there I mentioned also that upon the publication of Mercator's Logarithmotechnia D^r Barrow sent abroad to M^r Collins a Compendium of these series. A copy of this Compendium was in the handwriting of M^r Collins was found \by M^r Iones/ in the Archive of M^r Collins in the handwr & published after it had been collated w^th the original in my custody w^ch M^r Iones borrowed of me for that purpose. The litle thereof was Analysis per Series numero terminorum infinitas. And in this Tract the method of series is interwoven with that of fluxions. For after I had found the method of Series it quickly led me into the method of fluxions, & their affinity made me write of them both together as composing one general method \of Analysis./ In this Tract I affirmed that the|i|s method extende|s|d to all Problemes & that ejus beneficio <29r> Curvarum areæ et longitudines &c (id modo fiat) exacte et Geometrice determinantur. Which I could not have said without understanding at that time so much of the method as is conteined in the first five or six Propositions of the Book of Quadratures.

And by the testimony of D^r Barrow & M^r Collins I understood thus much of the method some years before the \Mercators/ Logarithmotechnia came abroad For M^r Collins in a Letter to M^r Strode dated 26 Iuly 1672 & published by order of the R. Society, wrote thus. Mense Septembri 1668 Mercator Logarithmotechniam edidit suam, quæ specimen hujus methodi (i.e. serierum infinitarum) in unica tantum figura, nempe Quadraturam Hyperbolæ continet Haud multo postquam in publicum prodierat Liber, exemplar ejus Cl. Wallisio Oxonium misi, qui suum de eo judicium in Actis p|P|hilosophicis statim fecit; alium Barrovio Cantabrigiam, qui quasdam Newtoni chartas extemplo remisit: e quibus et ALIIS, quæ OLIM ab Auctore cum Barrovio communicata fuerant, patet illam methodum a dicto Newtona ALIQVOT ANNIS ANTEA excogitatam & modo universali applicatam fuisse: ita ut ejus ope in quavis Figura Curvilinea proposita quæ una vel pluribus proprietatibus definitur Quadratura vel Area dictæ figuræ, ACCVRATA SI POSSIBILE sit|SIT|, sin minus infinite vero propinqua, Evolutio vel Longitudo Curvæ lineæ curvæ, Centrum gravitatis Figuræ; solida ejus rotatione genita, & eorum superficies; sine ulla radicum extractione, obtineri queant. /

And all this may suffice to justify what I said \my saying/ in the Introduction to the Book of Quadratures, that I found this Method gradually in the years 1665 & 1666. |However, the Method is capable of improvements, & the improvements are theirs who make them.|

\Now because/ By the help of this Book of Quadratures \& fluxions/ I found \between the end of the years 1679|8| & 168{7}/ Keplers the demonstration of Keplers Proposition concerning the motion of the Planets in Ellipses, & {illeg} \Method/ I wrote the Book of Principles & \I have/ therefore have \now/ subjoyned thi|e|s book of Quadratures to the end of it. And because the methods \of/ series & fluxions are nearly related to one another & were invented in the same year \(the year 1665)/, & were enjoyned by me in the Tracts w^ch I wrote above 49 years ago \in those days/, & jointly ma{illeg} compose one very general method of Analysis I have here added \to the end of this book/ out of my Letters formerly published, some Propositions for resolving\ducing/ quantities into series, & for resolving Problems by the help of such series quamproxime both methods together. For tho the resolus|t|ion of Problems by the {illeg} into series by continual approximation be not Geometrical, yet it is allowed in Arithmetick, & by consequence \also/ in Algebra; as is manifest by continual approximations in decimal numbers & \by/ perpetual divisions & extractions of square & cube roots & the roots of affected æquations, \allowed in Arithmetick/ & |it| may sometimes lead to \of Problems/ by finite equations

\Now since/ By the help of this Method I wrote the Book of Principles & \I have/ therefore have subjoyned the book of Quadratures to the end of it. And for{illeg} the same reason I have subjoyned also the {illeg} Differential Method. And because many Propositions \the solution of/ several Problems require the Quadrature of figures proposed \in the Book of Principles/ to be solved concessis Figurarum Quadraturis I have added to the end of the Book of Quadratures some Propositions \taken from my Letters already published/ for reducing quantities into converging series \& thereby squaring the figures/. {to} For Quadratures by such series have the same place in Arithmetick & Algebra with operations in decimal numbers|.| & the extractions of roots {illeg}

In the Analysis per series abovementioned were several series for \instances of/ squaring the c|C|ircle & Conic Sections & finding the Arc whose sine was given & the sine of any given arc & other Figures & of finding the lengths of Curve lines, & on the contrary of finding the Abscissas & Ordinates of Figures whose Areas {illeg}|o|r lengths of the Curve lines are given & M^r Collins was very free in communicating \to Mathematicians/ the series there set down. M^r Leibnitz was in London in the begining of y^e year 1673 & conversed w^th D^r Pell &c \above numeral series/ & carried with him to Paris Mercator's Logarithmotechnia but did not yet understand the higher Geometry. The next year he studied this Geometry & in a \two/ Letters dated 15 Iuly & 26 Octob. he wrote to M^r Oldenburg that he had found the circumference of a circle in {rationa} \a/ series of rational numbers, & that by the same method, the any arch of a circle \whose sine was known/ might be known exhibited in a like series whose without knowing its proportion to the whole circumference. Which is as much as to say that that he had found a series \a series of rational numbers expressing/ the length of any arch of a circle whose sine was given, w^ch gave the whole circumference if the \its/ proportion to the Arch was known, or \else/ at least it gave the arch. The next year M^r Oldenburg in a Letter dated 15 Apr. 1675 sent to M^r Leibnitz <29v> these two series w^ch M^r Collins had received from me Posita pro Radio Vnitate, dato x pro sinu, ad inveniendum z Arcum Series est hæc est: $\mathrm{z}=\mathrm{x}+\frac{1}{6}{\mathrm{x}}^3+\frac{3}{40}{\mathrm{x}}^5+\frac{5}{112}{\mathrm{x}}^7+\frac{35}{1152}{\mathrm{x}}^9$ &c et ad invenien si dederis z pro sinu arcu ad inveniendum x sinum series hæc est; $\mathrm{x}=\mathrm{z}-\frac{1}{6}{\mathrm{z}}^3+\frac{1}{120}{\mathrm{z}}^5-\frac{1}{5040}{\mathrm{z}}^7+\frac{1}{362880}{\mathrm{z}}^9-\mathrm{\&c}$ And these two w^ch M^r Collins had received from M^r Newton Iames Gregory. Pone $\mathrm{formula}=\mathrm{r}$, Arcum a, Tangentem t; erit $\mathrm{t}=\mathrm{a}+\frac{{\mathrm{a}}^3}{3{\mathrm{r}}^2}+\frac{2{\mathrm{a}}^5}{15{\mathrm{r}}^4}+\frac{17{\mathrm{a}}^7}{315{\mathrm{r}}^6}+\frac{62{\mathrm{a}}^9}{2835{\mathrm{r}}^8}+\mathrm{\&c}$. Et conversim ex Tangente invenire Arcum ejus $\mathrm{a}=\mathrm{t}-\frac{{\mathrm{t}}^3}{3{\mathrm{r}}^2}+\frac{{\mathrm{t}}^5}{5{\mathrm{r}}^4}-\frac{{\mathrm{t}}^7}{7{\mathrm{r}}^6}+\frac{{\mathrm{t}}^9}{9{\mathrm{r}}^8}-\mathrm{\&c}$. And M^r Leibnitz acknowledged the receipt of these series by a Letter dated May 20^th 1675. Literas tuas multa fruge Algebraica refertas accepi, pro quibus tibi & doctissimo Collinio gratias ago. Cum nunc præter ordinarias Curas Mechanica|i|s imprimis negotijs distrahar, non potui examinare series quas misistis ac cum meis comparare. Vbi fuero perscribam tibi sententiam meam: nam aliquod|t| jam anni sunt quod inveni meas. The next year M^r Oldenburg \Leibnitz/ wrote the following Letter to M^r Oldenburg dated 12 May 1676. Cum Georgius Mohr Danus in Geometria et Analysi versatissimas, nobis attulerit communicatam sibi a Doctissimo Collinio vestro expressionem relationis inter Arcum et Sinum per infinitas series sequentes: Posito sinu x, arcu z, Radio 1. erit $\mathrm{z}=\mathrm{x}+\frac{1}{6}{\mathrm{x}}^3+\frac{3}{40}{\mathrm{x}}^5+\frac{5}{112}{\mathrm{x}}^7+\frac{35}{1152}{\mathrm{x}}^9+\mathrm{\&c}$ et $\mathrm{x}=\mathrm{z}-\frac{1}{6}{\mathrm{z}}^3+\frac{1}{120}{\mathrm{z}}^5-\frac{1}{5040}{\mathrm{z}}^7+\frac{1}{362880}{\mathrm{z}}^9-\mathrm{\&c}$. Hæc inquam Cum nobis attulerit ille, quæ mihi valde ingeniosa videntur, et posterior imprimis series elegantiam singularem habeat, ideo rem gratā mihi feceris, Vir clarissime, si Demonstrationem transmiseris. Habebis vicissim mea ab his longe diversa circa hanc rem meditata, de quibus jam a{n}te aliquot abhinc annis ad te perscripsisse credo, demonstratione tamen non addita quam nunc polio. Oro ut Cl. Collilnio multam a me Salutem dicas: is facile materiam suppeditabit satisfaciendi desiderio meo. By the d|D|emonstration of these series M^r Leibnitz meant the Method of finding them {illeg} by Analysis & since he sent M^r Oldenburg to M^r Collins for the same he meant \had heard of/ the Analysis per series numero terminorum infinitas, & wanted it. But M^r Collins being unwilling to let him have a copy of it he & M^r Oldenburg joyned in desiring that I would send him the Demonstration & thereupon I wrote to M^r Oldenburg my \the following/ letter of dated {illeg} 13 Iune 1676 to be communicated to M^r Leibnitz. And M^r Leibnitz sent back by way of recompence the series of M^r Gregory above mentioned, viz^t $\mathrm{arc}=\mathrm{t}-\frac{{\mathrm{t}}^3}{3}+\frac{5^5}{5}-\frac{{\mathrm{t}}^7}{7}+\frac{{\mathrm{t}}^9}{9}-\mathrm{\&c}$ & five years after published it in the Acta Eruditorum without taking as his own without taking any notice of the correspondence between him & M^r Oldenburgh by w^ch he had received it from London.

And all this may suffice to justify my saying that in the Introduction to the following Book of Quadratures, that I found the method gradually in the years 1665 & 1666 However, the method is capable of improvements & the improvements & theirs who make them.

|C| In the end of the Scholium in Princip. Philos. pag. 227 after the words Vtrius fundamentum continetur in hoc Lemmate, add

Sunto quantitates datæ a, b, c; fluentes x, y, z; fluxiones p, q, r; & momenta op, oq, or: et proponatur æquatio quævis ${\mathrm{x}}^3-2\mathrm{x}\mathrm{x}\mathrm{y}+\mathrm{b}\mathrm{x}\mathrm{x}-\mathrm{b}\mathrm{b}\mathrm{x}+\mathrm{b}\mathrm{y}\mathrm{y}-{\mathrm{y}}^3+\mathrm{c}\mathrm{z}\mathrm{z}=0$. Et per hoc Lemma, Si sola fluat x, erit fluxio totius $3\mathrm{x}\mathrm{x}\mathrm{o}\mathrm{p}-4\mathrm{x}\mathrm{o}\mathrm{p}\mathrm{y}+2\mathrm{b}\mathrm{x}\mathrm{o}\mathrm{p}-\mathrm{b}\mathrm{b}\mathrm{o}\mathrm{p}$; si sola fluat y, erit fluxio totius $\mathrm{-2}\mathrm{x}\mathrm{x}\mathrm{o}\mathrm{q}+2\mathrm{b}\mathrm{y}\mathrm{o}\mathrm{q}-3\mathrm{y}\mathrm{y}\mathrm{o}\mathrm{q}$; si sola fluat z, erit fluxio totius $2\mathrm{c}\mathrm{z}\mathrm{o}\mathrm{r}$; si fluant omnes, erit fluxio totius $3\mathrm{x}\mathrm{x}\mathrm{o}\mathrm{p}-4\mathrm{x}\mathrm{o}\mathrm{p}\mathrm{y}-2\mathrm{b}\mathrm{o}\mathrm{x}\mathrm{p}-\mathrm{b}\mathrm{b}\mathrm{o}\mathrm{p}-2\mathrm{x}\mathrm{x}\mathrm{o}\mathrm{q}+2\mathrm{b}\mathrm{y}\mathrm{o}\mathrm{q}-3\mathrm{y}\mathrm{y}\mathrm{o}\mathrm{q}+2\mathrm{c}\mathrm{z}\mathrm{o}\mathrm{r}$. Et quoniam totum semper æquale est nihilo, erit fluxio totius æqualis nihilo. Dividatur totum per momentum o, et prodibit æquatio quæ ex fluentibus dat fluxiones, viz^t $3\mathrm{x}\mathrm{x}\mathrm{p}-4\mathrm{x}\mathrm{p}\mathrm{y}+2\mathrm{b}\mathrm{x}\mathrm{p}-\mathrm{b}\mathrm{b}\mathrm{p}-2\mathrm{x}\mathrm{x}\mathrm{q}+2\mathrm{b}\mathrm{y}\mathrm{q}-3\mathrm{y}\mathrm{y}\mathrm{q}+2\mathrm{c}\mathrm{z}\mathrm{r}=0$. Exhibet igitur hoc Scholium \Lemma/ solutionem Propositionis præfatæ, Data æquatione fluentes quotcun quantitates involvente in {illeg}ti{illeg} & fluxiones invenire.  < insertion from f 30v >  Dixi vero in Epistola mea 24 Octob. 1676 ad Oldenburgium missa ut cum {illeg} Leibnitio communicaretur \quo mediante commerci{um} tunc habui cum D. Leibnitio/, quod hæc Propositio fundamentum esset methodi d generalis de qua scripse\ram/ anno 1671. < text from f 30r resumes > < insertion from f 30v > Et hanc Propositionem esse fundamentum methodi generalis de qua scripseram anno 1671 dixi in Litteris prædictis < text from f 30r resumes > |Et hanc Propositionem esse fundamentum methodi generalis de qua scripseram anno 1671 de|i|xi in Literis præfatis, anno 1671.|

In Epistola mea 24 Octob 1674|6| ad Oldenburgium missa & cum D. Leibnitio communicata, posui hanc Epistolam Propositionem ut fundamentum methodi de qua scripseram anno 1671. Et hæc methodus facile colligitur etiam ex Epistola quam ad Collinium 10 Decem 1672 scripsi, et cujus exemplar ad D. Leibnitium miss{illeg}|{a}||m| fuit anno 1676. 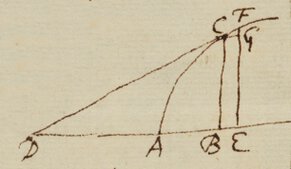Sit ACF linea quævis Curva, AB ejus Abscissa, & BE momentum AB|b|scissæ, et sint BC, EF Ordinatæ duæ ad Curvam in C et F terminatæ, CF momentum Curvæ, & FG momentum Abscissæ {illeg} existentæ BCGE parallelogrammo. Agatur chorda CF et producatur eadem donec Abscissæ occurrat in D: et \similia/ erunt triangula CGF, DBC. Et ubi momentum CF diminuitur in infinitum, recta CD cur\v/am tanget in C. Hoc omnibus notum est. Iam dicatur AB x, & BC y, et sint earum fluxiones p et q, & habitudo inter x & y exprimatur per qualibet æquatione puta ${\mathrm{x}}^3-2\mathrm{x}\mathrm{x}\mathrm{y}+\mathrm{b}\mathrm{x}\mathrm{x}-\mathrm{b}\mathrm{b}\mathrm{x}+\mathrm{b}\mathrm{y}\mathrm{y}-{\mathrm{y}}^3=0$. Et per Epistolam illam Regula ducendi Tangentem hæc erit. Multipliæ æquations|e|s terminos per quamlibet progressionem Arithmeticam juxta dimensiones y, puta $\begin{array}{c}{\mathrm{x}}^3-2\mathrm{x}\mathrm{x}\mathrm{y}+6\mathrm{x}\mathrm{x}-\mathrm{b}\mathrm{b}\mathrm{x}+\mathrm{b}\mathrm{y}\mathrm{y}-{\mathrm{y}}^3=0\\ 010023\end{array}$. ut et juxta dimensiones x, puta $\begin{array}{c}{\mathrm{x}}^3-2\mathrm{x}\mathrm{x}\mathrm{y}+\mathrm{b}\mathrm{x}\mathrm{x}-\mathrm{b}\mathrm{b}\mathrm{x}+\mathrm{b}\mathrm{y}\mathrm{y}-{\mathrm{y}}^3\\ 322100\end{array}$. Prius productum erit Numerator & posterius divisum per x denominator fractionis quæ exprimet longitudinem BD ad cujus extremitatem D. ducenda est Tangens. Ducet {illeg}|ur| est autem BD ad eandem p{illeg}{t}|{lag}|am cum Abscissa AB ubi valor ejus affirmativus et|s|t et ad contrarias|m| partes ubi negativus. Est ergo, per Regulam in hac Epistola positam; Vt summa omnium terminorum multiplicatorum per indices dignitatum x ac divisorum per x ad summam omnium multiplicatorum per indices dignitatum y ac divisorum per y, ita \ut/ est y ad ad — BD, et ita est FG ad — CG seu o{illeg}|q| ad — ox|p|. Ducantur extrema et media in |invicem &| Æquatio \factorum/ per o divid|s|a evadet $3\mathrm{x}\mathrm{x}\mathrm{p}-4\mathrm{x}\mathrm{p}\mathrm{y}+2\mathrm{b}\mathrm{x}\mathrm{p}-\mathrm{b}\mathrm{b}\mathrm{p}=2\mathrm{x}\mathrm{x}\mathrm{q}-2\mathrm{b}\mathrm{y}\mathrm{q}+3\mathrm{y}\mathrm{y}\mathrm{q}$, seu $3\mathrm{x}\mathrm{x}\mathrm{p}-4\mathrm{x}\mathrm{p}\mathrm{y}+2\mathrm{b}\mathrm{x}\mathrm{p}-\mathrm{b}\mathrm{b}\mathrm{p}-2\mathrm{x}\mathrm{x}\mathrm{q}+2\mathrm{b}\mathrm{y}\mathrm{q}-3\mathrm{y}\mathrm{y}\mathrm{q}=0$. Hæc equatio producetur \etiam/ per Lemma ubi duce tantum sunt æquationes fluentes quantitates. Vbi vero sunt plures, eadem operatio applicari debet ad omnes. Et sic habebitur æquatio fluxiones involvens. Et in hac operatione fundatur methodus generalis, uti dixi in edem {sic} Epistola, quæ extendit se citra <31r> molestum ullum calculum non modo ad ducendum Tangentes ad quasvis Curvas sive Geometricas sive mechanicas vel quomodocun rectas lineas aliasve Curvas respicientes; verum etiam ad resolvendum alia abstrusiora Problematum genera de Curvitatibus, Areis, Longitudinibus, centris gravitatis Curvarum &c. Ne quemadmodum Huddenij methodus de Maximis et Minimis) ad solas restringitur æquationes illas, quæ sunt quantitatibus surdis sunt immunes. Hanc methodum intertexui alteri isti quæ Æquationum Exegesin instituo, reducendo eas ad series infinitas: sc. in Tractatu illo quem scripsi anno 1671.

Et hæc Quæstio est: {u}|V|trum D. Leibnitius sit inventor & methodi, & pro differentijs igitur Leibnitianis Newtonus adhibet semper [ex quo methodo intellex\{er}/it \usus est hac methodo/] adhibuit fluxiones, quemadmodum Honoratus Fab{illeg} Fabrius motuum progressus Carallerianæ methodo substituit.

Gregorius ad Collinium scripsit 5 Sept. 1670 se ex Barrovij methodis tangentes ducendi dum quibusdam & suis \& suis invenisse/ Methodum generalem & Geometri\ic/am tangentes ducendi cum quibusdā ad omnes Curvas sine calculo. Newtonus ad eundem c|C|ollinium scripsit in hæc {illeg} 10 Decem 1672 in hæc verba Ex animo gaudeo D. Barrovij nostri reverendi Lectiones Mathematicas exteris adeo placuisse, ne parum me juvat — — — reducendo eas ad quanti series infinitas. Et harum duarum literarum exemplaria ad Leibnitium missa sunt \ab Oldenburgo/ inter excerpta ex Epistolis Gregorij 26 Iunji 1676. Et Leibnitius mense novembri proximo Lectiones Barrovij secum {illeg}tulit in Germaniam.

Sunto jam i{illeg}|p||s|arum x et y fluxiones pet q & momenta op et oq et in AB producta capiatur $\mathrm{BE}=\mathrm{o}\mathrm{p}$, erigatur ordinata EF parallela BC & occurrens Curvæ in F et compleatur parallelogrammum BCGE et erit $\mathrm{FG}=\mathrm{o}\mathrm{q}$, et ex methodo tangentium Barrovij erit $\mathrm{FG}.\mathrm{CG}\colon\colon \mathrm{CB}.\mathrm{BD}$, seu BD{illeg}. CB∷CG.FG∷op. oq∷p.q. adeo BC|D|{illeg}$\frac{\mathrm{p}}{\mathrm{q}}$ B= $\frac{\mathrm{-p}\mathrm{y}}{\mathrm{q}}=\mathrm{BD}=\frac{\mathrm{-2}\mathrm{x}\mathrm{x}\mathrm{y}+2\mathrm{b}\mathrm{y}\mathrm{y}-3{\mathrm{y}}^3}{3\mathrm{x}\mathrm{x}-4\mathrm{x}\mathrm{y}+2\mathrm{b}\mathrm{x}-\mathrm{b}\mathrm{b}}$. Et facta reductione \fit evadit prodit/ $2\mathrm{x}\mathrm{x}\mathrm{q}+2\mathrm{b}\mathrm{y}\mathrm{q}-3\mathrm{y}\mathrm{y}\mathrm{q}-$ habetur $3\mathrm{p}\mathrm{x}\mathrm{x}-4\mathrm{p}\mathrm{x}\mathrm{y}+2\mathrm{b}\mathrm{b}\mathrm{x}-2\mathrm{p}\mathrm{b}\mathrm{b}+2\mathrm{x}\mathrm{x}\mathrm{q}-2\mathrm{b}\mathrm{y}\mathrm{q}-3\mathrm{y}\mathrm{y}\mathrm{q}=0$. Vnder prodit hujusmodi Regula si detur æquatio fluentes quocum \duas/ quantitates \x et y/ involvet|s|e, invenientur æquatio fluxiones involvens p et q involvens multiplicando terminos omnes|m| per æquationes \data/ terminum per indicem dignitatis quantitatis cujus fluentis quam in volvit et in singulis multiplicationibus mutando dignitatis latus in fluxionem suam. & ponendo Nam factorum omnium aggregatum sub proprijs signis erit æquatio nova. Et si plures sint fluentes, eadem operatio instituenda est in singulis. [Hæc est Pro{illeg}|p|ositio prima libri \Newtoni/ de Quadraturis. Hanc Propositionem Newtonus posuit in Epistola 24 Octob 1676.] Et hæc Regula totum illud omne comprehendit quod Leibnitius anno 1677 {a} de methodo differentiali ad Newtonum remisit /rescripsit\ \est Propositio primæ Libri de quadraturis./

In Hæc Regula habetur Algorithmus hujus methodi. Hanc Regulam \eam{}/ Wallisius in lucem edidit anno {illeg}170 1693 in secundo Volumine operum ejus pag 392. in lucem edidit, anno 1693 a Newtono acceptam a Aug 27 anno 1692 a Newtono acceptam Aug. 27 anno 1692 \cum exemplis in fluxionibus primis et secundis inveniendis./ Est Regula antiquissima quæ lucem vidit pro differentialibus differentiandis. Eandem \ut {illeg}{dam}extum methodi fluxionum/ Newtonus posuit in Epistola sua 24 Octob 1676 ad Oldenburgum pro Leibnitio datam Eandem Newtonus \eandem/ demonstravit Synthetice in secundo Lemmamate {sic} Libri Principiorum anno 1686 et prop cum Propositionem \prius/ posuisset in Epistola sua ad 24 Octob. 1676, ad Oldenburgum pro Leibnitio missa, et \ibi/ significasset eandem esse fundamentum methodi de qua scripserat \tum/ ante annos quin id est anno 1671. Demonstratur vero in Lemmate illo in hunc modum.

 < insertion from f 31r >  Sunto quantitates datæ A, B, C a, b, c, fluentes x, y, z fluxiones p, q, r momenta op, oq, or, & proponatur æquatio quævis — — — — — — — exhibet igitur hoc Lemma solutionem Propositionis data æquatione fluentes quotcun quantitates involvente invenire fluxiones. Et hanc Propositionem esse fundamentum methodi generalis de qua{illeg} scripserat anno 1671 dixit Newtonus in Epistola literis prædictis.

Propositionem quintam — < text from f 31v resumes > Propositionem quintam libri de Quadraturis, Wallisius edidit anno 1693 in secundo operum suorum Volumine pag. 391. Hac Propositione quadrantur Figuræ curvilil|n|e accurate & Geometrice {illeg} si fieri potest. Partem hujus Propositionis Newtonus posuit in Epistola 24 Octob 1676 ad Oldenburgum scripta. In Analysi sua per series dixit quod Analysen illius beneficio Curvarum areæ & longitudie, &c (id modo fiat) exacte & Geometrice determinetur: ideo quinta illa Propositio tunc ipsi innotuit. |Hanc Analysen Leibnitio{s} videre potuit in secundo suo in Angliam itinere ubi Collinius ips. monstravit plures Newtoni Gregorij & aliorum Literas quæ circa series præcipue versæbantur. Collinius in Epistola sua| Collinius in Epistola {sic} ad Thomam Strode 26 Iuly 1672 data Scripsit in hæc verba: Mense Septembri 1668 Mercator Logarithmotechniam edidit suam — Haud multo postquam in publicum prodierat liber exemplar ejus Cl. Wallisio Oxonium misi — alium Barrovio Cantabrigiam, qui quasdam Newtoni chartas [sc. Analysin per series] extemplo remisit: e quibus et EX ALIIS quæ OLIM {q} ab auctore communicata fuerant, patet illam Methodum a dicto Newtono aliquot \annis/ antea excogitatam & mod[id est antequam prodiret Logarithmotechnia] illa] excogitatam & modo universali applicatam fuisse: ita ut ejus ope in quavis Fa|i|gura Curvilinea proposita quæ una vel pluribus Proprietatibus definitur, Quadratura vel Area: dictæ figuræ ACCVRATA SI POSSIBILE SIT, sin minus infinite vero propinqua &c — obtineri queat: id est accurata si series abrumpitur, sin minus infinite vero propinqua. Testibus igitur Barrovio et Collinio Newtonus methodum habuit aliquot annis antea quam prodiret Logarithmotechnia illa \adeo/ quadrandi Curvilineas \anno 167|6|6 aut antea, methodum habuit/ per series accurate si series abrumpitur et finita evadit; sin minus infinite vero propinqua. Et ha|o|c {illeg}|f|it per Propositio|nem| illa|m| quintam. Hæc autem Propositio pendet a quatuor prioribus: et propterea Method {u}|i|{s} serierum et \{illeg}/ fluxionum quatenus continea\n/tur in Propositionibus quin primis libri de Quadratura Curvilinearum Newtono innotu{illeg}ere anno 1666 aut antea testibus Barrovio et Collinio; ut et teste etiam Wallisio, qui in Præfatione ad L{illeg} Volumen primū operum suorum ubi scripsit \quod/ Newtonus \in/ literis suis 13 Iunij & 24 Octob. 1676 \datis/ methodum hanc [fluxionum vel differentiar{illeg}|lem|] {illeg}|L|eibnitio exponit tum ante decem annos nedum plures Leib ab ipso excogitatam, i. e. anno 1666 aut antea. < insertion from f 31r > plures ab ipsa excogitam; id est anno 1666 aut antea. Hoc Leinitius et Menkenius legerunt & per ea tempora non negarunt, ut ex Actis Eruditorum & Epistolis a Wallisio editis patet. Paulo post D. Nicolas F{illeg}lio Fatio in Tractatu cui tituli de investigatione solidi minimæ resistentiæ in quod minima fiat resistentia, scripsit se anno 1687 in Calculum differentiali similem incidisse, Newtonum tamen primum ac pluribus annis vetustissimum hujus Calculi inventorem ipsa rerum evidentia se coactum agnoscere, visis scilicet Newtoni manuscriptis codicibus. Et Le {p}|b|neitius in Actis Eruditorum respondendo Ad nondum cœpit hoc negare, sed conatus est tantum se defendere quasi anno 1684 cum elementa calculi sui edidit, ne constabat quidem ipsi aliud de Inventis Newtoni in hoc genere quam quod ipse in hoc genere olim significaverat in literis, posse se Tangentes ducere invenire abs non sublatis irrationalibus: quod Hæ quod Hugenius quo se posse ipsi significavit postea etsi cæterorum istius calculi adhuc expers; & \ipsum/ Fatium agressus est proponendo Problema{illeg} solvendum. Tandem anno 1703 Wallisius mortuus est et anno prox subinde Leibnitius audacior esse cœpit. Nam \cum/ libri Newtoni de coloribus & \de numero c|C|urvarum secondi generis/ d{illeg}|e| quadratura Figurarū anno proximo proximo prodierent & \{illeg} Newtonus/ initio anni sequentis \s{illeg}/ Leibnitij|o| qui synopses librorum mathematicorum ad Mankenium mittere salebat, Newtonus in Actis Eruditorum pro Ianuario anni 1705 accusatus est quasi Leib accusari cæpit quasi Methodum a Leinitio habuisset stylo Leibnitiano stylo Leibnitij qui synopses librorum mathematicorum ad Menkenium mittere solebat. accusari cæpit quasi Methodum a Leibnitij {illeg} suffurasset a Leibnitio habuisset \dedicisset/. Nam Leibnitium enim inventore vocant deinde addant Pro differentijs {illeg} \Ejus/ Elementa, inquiunt, ab I INVENTORE D. G. G|L|eibnitio in his Actis sunt tradita, varijs usus tum ab ipso tum a fr D. D. Fratribus Bernoullijs tum & D. Marchione Hospitalio — sunt ostensi. Pro differentijs igitur Leibnitianis D. Newtonus adhibet semper [ex quo \usus est {hu}c/ methodo{illeg}] coluit \didi{s}it/] adhibuit fluxiones — quemadmodum & Honoratus Fabrius in sua Synopsi Geometrica, motuum progressus Cavalleri{illeg}|a|næ methodo substituit

Quæstio \est/ igitur est utrum Newtonus hanc methodum habuit \didicita/ a Leibnitio. Ad hanc Qu Quæstionem dirimandam editam \sunt anno 1712/ est {illeg} ex antiquis monumentis Commercium Epistolicum 1712 & R \L{illeg} & ineunte anno 1615/ Recensio ejus|dem| Libri. anno \{illeg}/ 1795. {illeg} Anglice {illeg} Hæc Recensio edita fuit Anglicæ in Actis Philosophicis \R. Societatis/, et jam latine versa præponitur Commercio & ad veritatem stabiliendam Commercium citatur Commercio opposuit. Et hæc < text from f 31v resumes > et his præmissis, et quod pro symbolis $\boxed{\frac{\mathrm{a}\mathrm{a}}{64\mathrm{x}}}$ & oυ, {illeg}y \vel oy/ quibus Newtonus utitur in Analysi per series Leibnitius utatur symbolis $\int \frac{\mathrm{a}\mathrm{a}}{64\mathrm{x}}$ & d{illeg} dz, & Analysin illam videre potuit <31r> in secundo suo in Angliam itinere ubi Collinius ipsi monstravit pl{illeg}|u|res Newtoni Gregorij & aliorum Literas quæ circa Series præcipue versabantur: his inquam præmissis, legatur jam Commercium Epistolicum.

Scholium

In literis quæ mihi cum Geometra peritissimo G. G. Leibnitio {illeg}s abhinc decem in anno 1676 intercedebant, cum significarem me compotem esse methodi determinandi Maximas et Minimas, ducendi Tangentes, quadrandi Figuras curvilineas, conferendi easdem cum Sectionibus conicis, \se mutuo/ & similia peragendi quæ in terminis surdis æque ac in rationalibus procederet, & Tractatum de eadem anno 1671 scripsisse, \ut et Tractatum alium quem Barrovius noster anno 1669 ad Collinium/ at literis transpositis hanc sententiam involventibus [Data æquatione quotcun Fluentes quantitates involvente, Fluxiones invenire, et vice versa] eandem celarem: rescripsit Vir Clarissimus mense Iunio anni proximi \1677/ se quo in ejusmodi methodum incidisse; & methodum suam communicavit a mea vix abludent {o}|e|m præterquam in verborum & notarum formulis & Idea generationis quantitatum. Mense Iunio anni 1676 Collin Exta{n} \Incidi paulætim in hanc methodum, annis 167|6|6 & 1667|6|7 Et extant ejusdem/ specimina quædam hujus methodi in Analysi mea per Series quam Barrovius mense Iunio anni 16{illeg}|6|9 ad Collinium misit: Et in mense Iunio anni 1676 Collinius exemplar epistolæ meæ \ut et in Epistola quam/ de hac methodo 10 Decem. 1672 ad ipsum datæ \Collinium misi, et cujus exemplar Collinius mense Iunio anni 1676, {illeg}/ una cum exemplaribus epistolarum plurium Ia. Gregory, \epistolarum/ {illeg} D. Leibnitium in Gallia tunc agentem misit. Et Mense \a{u}tem/ Octobri ejusdem \anni/ ad finem vergente, D. Leibnitius E Gallia in Angliam veniens, ✝ < insertion from f 32r > ✝ vidit Epistolam meam Octob. 24 ad Oldenburgum datam ubi iterum admonitus {illeg} de hac methodo, \locutis sum de {sic}/ de Analysi per series, \ad Collinium missa/ {illeg} de Tractatu quem anno 1671 conscripsi, & \ac/ de methodo \{illeg} qua/ maxima{r}|s|um et minima{r}|s|um, de quadratura figurarum primam exh \et areas curvarum inveniro: Et/ \ubi/ Theorema \etiam/ posui quadrandi figuras ex methodo hac methodo de{illeg} inventem et exemplis illustratam\vi/ Quinetiam \D. Leibnitius/ epistolas autographas et Gregorij et meas in manu Collinij de {illeg} consuluit. Et subinde in Germaniam rediens ut negotijs <32v> publicis interesset, incidit in hanc methodum < text from f 32r resumes > epistolas autographas et Gregorij et meas in manu Collinij consulavis|t|. Et subinde in Germaniam rediens ut negotijs publicis interesset, \in Germaniam rediens/ incidit {illeg} \{illeg}/ in hanc methodum \anno 1677/; et mense Iunio \ejusdem/ anni 1677 specimen ejus ad me misit, ut supra. Ejusmodi \Hujus/ vero \methodi/ fundamentum continetur in hoc Lemmate.

et vice versa] eandem Propositionem principalem \{hujus{illeg}ujus} \fundamentalem |fundamentum| hujus/ methodi hujus/ celarem], specimen vero s{illeg} methodi hujus \ejusdem/ subjungerem et exemplis illustravem; res{illeg} cum vir clarissimus episto in reditu suo e Gallia per Angliam in Germaniam, epistolas in manu |{et}| meas \et {illeg}/ in manu Collinij \insuper etiam/ consuluisset: incidit is in methodum similem sub diversis verborum et notarum formulis. Methodi utrius fundamentum continetur in hoc Lemmate.

Et cum Collinius noster \exemplar/ Epistola|æ|m mea|æ|m 10 Decem. 1672 ad ipsum datæ exemplar mense Iunio anni 16{illeg} in qua methodum hanc descripsissem & ex {illeg} exemplar mense Iunio at Leibnitium misisset

Et cum Collinius Epistolam 10 Decem 1672 datam a me accepisset in qua methodum hanc descripsissem & exemplo Tangentium ducendarum illustrassem, et hujus Epistola exemplar mense Iunio anni {illeg} 1676 in Galliam ad D. Leibnitium misisset; & vir clarissimus sub finem mensis Octobris in reditu suo e Gallia per Angliam {Et} in Germaniam Epistolas meas in manu Collinij insuper consuluisset: incidit is finito itinere, in methodum similem sub diversis verborum et notarum formulis, et mense Iunio sequente specimen ejusdem \in Tangentibus ducendis/ ad me misit, \eandem a methodo mea non abludere subjunxit./ Methodi utrius fundamentum continetur in hoc Lemmate.

^[3]ad Spatium quod corpus in Medid non resistente e queste cadendo eodem tempore describere potest, ut arearum prædictarum differentia ad $\frac{\mathrm{BD}\times {\mathrm{V}}^2}{\mathrm{AB}}$.

In epistola quadam ad D. I. Collinium nostratem {21} \10/ Decem. 1672 data, cum descripsissem metho{illeg}|du|m tangentium quam conjicebam \suspicabar/ eandem esse cum methodo Slusij tum nondum p{illeg} communicata; subjunxi: Hoc est unum particulare, vel corollarium potius Methodi generalis, quæ extendit se, citra molestum ullum calculum, non modo ad ducendum tangentes ad quasvis Curvas sive Geometricas verum etiam ad resolvendum alia abstrusiora problematum genera de curvitatibis|us|, Areis, longitudinibus, centris gravitatis {illeg} curvarum &c. Neque (quemadmodum Huddenij methodus de Maximis et Minimis) ad solas restringitur æquationes illas quæ quantitatibus surdis sunt immunes. Hanc methodum interte{r}texui alteri isti, qua æquationum exegesin instituo, reducendo eas ad series infinitas,. scilicet in tractatum quem tunc ante annum (nempe A.C. 1671) \Hactenus Epistola Et Hæc ultima verba spectant ad Tractatum quem anno 1671 id est/ de his rebus scripseram. Methodi \vero/ hujus \generalis/ fundamentum continetur in Lemmate præcedente. per quod uti resolvitur \pars prior/ cujus problematis, Data æquatione fluentes quotcun quantitates involvente, invenire fluxiones; & vice versa.

Nam \Coroll./ Quare si longitudo \dicatur/ quæ oritur applicando aream DET ad BD et cujus momentum erat m; \lineam BD dicatur M/ Et si longitudo alia V sumatur in ea ratione ad \longit./ M quam habet linea DA ad lineam DE [et cujus momentum propterea erit $\frac{\mathrm{DA}}{\mathrm{DE}}\times \mathrm{m}$] Spatium quod corpus — — — illarum differentia ad $\frac{\mathrm{BD}\times {\mathrm{V}}^2}{\mathrm{AB}}$, ideo ex dato tempore datur. Nam spatium in Medio non resistente est in duplicata ratione temporis sive ut ${\mathrm{V}}^2$, et ob datas BD et AB, ut $\frac{\mathrm{BD}\times {\mathrm{V}}^2}{\mathrm{AB}}$. Hæc area æqualis est areæ $\frac{{\mathrm{DA}}^{\mathrm{q}}\times \mathrm{BD}\times {\mathrm{M}}^2}{{\mathrm{DE}}^{\mathrm{q}}\times \mathrm{AB}}$ et ipsius M momentum erat est m et Augeatur M momento suo m {cl} \et ipsius M momentum est m {illeg} et propterea/ hujus areæ momentū coad et|s|t $\frac{{\mathrm{DA}}^{\mathrm{q}}\times \mathrm{BD}\times {}^2\mathrm{M}\mathrm{m}}{{\mathrm{DE}}^{\mathrm{q}}\times \mathrm{AB}}$. Et hoc momentum est ad momentum differentiæ arearum DET et AbNK viz^t ad $\frac{\mathrm{AP}\times \mathrm{BD}\times \mathrm{m}}{\mathrm{AB}}$ ut ${\mathrm{DA}}^{\mathrm{q}}\times \mathrm{BD}\times \mathrm{M}{\mathrm{DE}}^{\mathrm{q}}$ ad $\frac{1}{2}\mathrm{AP}\times \mathrm{BD}$ sive ut $\frac{{\mathrm{DA}}^{\mathrm{q}}}{{\mathrm{DE}}^{\mathrm{q}}}$ in DET ad DAP adeo ubi areæ DET et DAP quam minimæ sunt, in ratione æqualitatis. Æqualis est igitur area quam minima $\frac{\mathrm{BD}\times {\mathrm{V}}^2}{\mathrm{AB}}$ differetiæ quam minimæ arearum DET & Ab AbNK. Vnde cum spatia in Medio utro <33v> ut $\frac{{\mathrm{DA}}^{\mathrm{q}}\times \mathrm{BD}\times 2\mathrm{M}\times \mathrm{m}}{{\mathrm{DE}}^{\mathrm{q}}\times \mathrm{AB}}+\frac{{\mathrm{DA}}^{\mathrm{q}}\times \mathrm{BD}\times \mathrm{m}\mathrm{m}}{{\mathrm{DE}}^{\mathrm{q}}\times \mathrm{AB}}$ ad $\frac{\mathrm{AP}\times \mathrm{BD}\times \mathrm{m}}{\mathrm{AB}}$ hoc est ut $\frac{{\mathrm{DA}}^{\mathrm{q}}\times \mathrm{BD}\times 2\mathrm{M}+\mathrm{m}}{{\mathrm{BE}}^{\mathrm{q}}}$ ad AP, BD. sive ut $\frac{{\mathrm{DA}}^{\mathrm{q}}}{{\mathrm{DE}}^{\mathrm{q}}}$ in ${}^2\mathrm{DET}+\mathrm{DTV}$ ad $2\mathrm{DAP}$; adeq|o| ubi areæ DET, DAP quam minimæ sunt, et area DET eva{illeg}|nes|cit, in ratione æqualitatis. [Æqualis est igitur area quam minima] seu $\frac{{\mathrm{DA}}^{\mathrm{q}}}{{\mathrm{DE}}^{\mathrm{q}}}$ {illeg} in $\mathrm{DTV}=2\mathrm{DAP}$

$\mathrm{U}=\frac{2\mathrm{DET}\times \mathrm{DA}}{\mathrm{BD}\times \mathrm{DE}}$. $\frac{\mathrm{BD},\mathrm{V}\mathrm{V}}{4\mathrm{AB}}=\frac{\mathrm{DET}\times \mathrm{DET}\times {\mathrm{DA}}^{\mathrm{q}}\times \mathrm{BD}}{\mathrm{AB}\times {\mathrm{DE}}^{\mathrm{q}}\times {\mathrm{BD}}^{\mathrm{q}}}=\frac{{\mathrm{DET}}^{\mathrm{q}}\times {\mathrm{DA}}^{\mathrm{q}}}{\mathrm{AB},{\mathrm{DE}}^{\mathrm{q}}\times \mathrm{BD}}=\frac{\mathrm{DET}\times \mathrm{DET}\times {\mathrm{DA}}^{\mathrm{q}}}{\mathrm{AB}\times {\mathrm{DB}}^{\mathrm{cub}}}=\frac{\mathrm{BD}\times \mathrm{V}\mathrm{V}}{4\mathrm{AB}}$. $\mathrm{M}=\frac{\mathrm{DET}}{\mathrm{BD}}$. $\frac{\mathrm{BD}\times \mathrm{V}\mathrm{V}}{4\mathrm{AB}}=\frac{\mathrm{M}\mathrm{M}\times {\mathrm{DA}}^{\mathrm{q}}}{\mathrm{AB}\times \mathrm{BD}}$.

$\mathrm{V}=\frac{2\mathrm{DA}\times \mathrm{M}}{\mathrm{DE}}$. $\frac{\mathrm{BD},\mathrm{V}\mathrm{V}}{4\mathrm{AB}}=\frac{4{\mathrm{DA}}^{\mathrm{q}}\times {\mathrm{M}}^{\mathrm{q}}\times \mathrm{BD}}{4\mathrm{AB},{\mathrm{DE}}^{\mathrm{q}}}=\frac{{\mathrm{DA}}^{\mathrm{q}}\times {\mathrm{M}}^{\mathrm{q}}\times \mathrm{BD}}{\mathrm{AB}\times {\mathrm{DE}}^{\mathrm{q}}}$

Momentum ${\mathrm{M}}^{\mathrm{q}}=2\mathrm{DEV}\times \mathrm{DVT}+\mathrm{DVT}\mathrm{q}=\frac{2\mathrm{DET}\times \mathrm{DVT}}{{\mathrm{D}}^{\mathrm{q}}}+\frac{{\mathrm{DVT}}^{\mathrm{q}}}{{\mathrm{BD}}^{\mathrm{q}}}=\frac{2\mathrm{DET}\times \mathrm{DVT}}{{\mathrm{BD}}^{\mathrm{q}}}+\frac{{\mathrm{DVT}}^{\mathrm{q}}}{{\mathrm{BD}}^{\mathrm{q}}}=\frac{2\mathrm{DET}\times \mathrm{BD}\times \mathrm{m}}{{\mathrm{BD}}^{\mathrm{q}}}+\frac{{\mathrm{BD}}^{\mathrm{q}}\times {\mathrm{m}}^{\mathrm{q}}}{{\mathrm{BD}}^{\mathrm{q}}}$. $\mathrm{m}=\frac{1}{2}\mathrm{TV}$. $\mathrm{M}=\frac{\mathrm{DET}}{\mathrm{BD}}=\frac{\mathrm{DE}\times \frac{1}{2}\mathrm{ET}}{\mathrm{DE}}=\frac{1}{2}\mathrm{VT}$. $\mathrm{ET}=\mathrm{x}+\mathrm{o}$. ${\mathrm{ET}}^{\mathrm{q}}=\mathrm{x}\mathrm{x}+2\mathrm{o}\mathrm{x}$

lin 1. sive huic æqualis $\frac{{\mathrm{DA}}^{\mathrm{q}}\times \mathrm{BD}\times {\mathrm{M}}^2}{{\mathrm{DE}}^{\mathrm{q}}\times \mathrm{AB}\times \mathrm{BD}}$ et ad momentum differentiæ arearum DET et AβNK ut $\frac{{\mathrm{DA}}^{\mathrm{q}}\times \mathrm{M}\times \mathrm{m}}{{\mathrm{DE}}^{\mathrm{q}}\times \mathrm{AB}}$ ad $\mathrm{AP}\times \mathrm{BD}\times \mathrm{m}\mathrm{AB}$, hoc est ut $\frac{{\mathrm{DA}}^{\mathrm{q}}\times \mathrm{BD}\times \mathrm{M}}{{\mathrm{DE}}^{\mathrm{q}}}$ ad $\frac{\mathrm{AP}\times \mathrm{BD}}{2\mathrm{AB}}$, sive ut $\frac{{\mathrm{DA}}^{\mathrm{q}}\times \mathrm{DET}}{{\mathrm{DE}}^{\mathrm{q}}}$ ad $\mathrm{DAP}\times {\mathrm{BD}}^{\mathrm{q}}=\mathrm{BD}\times 2\mathrm{DAP}$ sive ut $\frac{{\mathrm{DA}}^{\mathrm{q}}}{{\mathrm{BD}}^{\mathrm{q}}}\mathrm{DET}$ ad DAP.

P. 252. lin. 1. sive huic æqualis $\frac{{\mathrm{DA}}^{\mathrm{q}}\times \mathrm{BD}\times {\mathrm{M}}^2}{{\mathrm{DE}}^{\mathrm{q}}\times \mathrm{AB}}$, ad est ad Momentum differentiæ arearum DET et AβNK, ut $\frac{{\mathrm{DA}}^{\mathrm{q}}\times \mathrm{BD}\times \mathrm{M}\times \mathrm{m}}{{\mathrm{DE}}^{\mathrm{q}}\times \mathrm{AB}}$ ad $\mathrm{AP}\times \mathrm{BD}\times \mathrm{m}\mathrm{AB}$, hoc est, ut $\frac{{\mathrm{DA}}^{\mathrm{q}}\times \mathrm{BD}\times \mathrm{M}}{{\mathrm{DE}}^{\mathrm{q}}}$ ad $\mathrm{AP}\times \mathrm{BD}$, sive ut $\frac{{\mathrm{DA}}^{\mathrm{q}}}{{\mathrm{DE}}^{\mathrm{q}}}$ in DET ad $2\mathrm{DAP}$

$\frac{{\mathrm{DA}}^{\mathrm{q}}{\mathrm{M}}^2}{\mathrm{AB},\mathrm{BD}}\begin{array}{l}={\mathrm{DA}}^{\mathrm{q}}\times {\mathrm{M}}^2+2\mathrm{M}\mathrm{o}+\mathrm{o}\mathrm{o}\\ ={\mathrm{BA}}^{\mathrm{q}}\times {\mathrm{M}}^2+\mathrm{M}\times \mathrm{m}\end{array}$. $\mathrm{o}=\frac{1}{2}\mathrm{VT}=\frac{\mathrm{DTV}}{2\mathrm{BD}}$

$\frac{\mathrm{DET}}{\mathrm{DB}}=\mathrm{M}$. $\frac{\mathrm{DET}\times \mathrm{DET}}{{\mathrm{DB}}^{\mathrm{q}}}=\mathrm{MM}$.

Ejus $\mathrm{M\; momentum}=\frac{\mathrm{DVT}}{\mathrm{DB}}=\mathrm{m}$

Corol. Quare si longitudo aliqua V sumatur in ea ratione ad longitudinem M quæ oritur applicando aream DET ad BD quam habet linea DA ad lineam DE: spatium quod corpus ascensu vel descensu tota in Medio resistente describit erit ad spatium quod in Medio non resistente describit eodem tempore describere posset, ut arearum illarum differentia ad $\frac{\mathrm{BD}\times \mathrm{V}\mathrm{V}}{\mathrm{AB}}$ ideo ex dato tempore datur. Nam spatium in Medio non resistente est in duplicata ratione temporis sive ut $\mathrm{V}\mathrm{V}$, et ob datas BD et AB ut $\frac{\mathrm{BD}\times {\mathrm{V}}^{\mathrm{q}}}{\mathrm{AB}}$. Momentum hujus areæ, sive \areæ/ huic æqualis $\frac{{\mathrm{DA}}^{\mathrm{q}}\times \mathrm{BD}\times {\mathrm{M}}^2}{{\mathrm{DE}}^{\mathrm{q}}\times \mathrm{AB}}$ est ad momentum d

Scholium.

Analysin per series et momenta a me scriptam, Barrovius noster anno 1669 ad Collinium misit. Methodos ibi expositas in alio Tractatu plenius explicui anno 1671, I{illeg} sed \hos Tractatus/ in lucem edere distuli quietis gratia \et ex hoc Tractatu Tractatum de quadratura Curvilinearum anno 1676 extraxi. \deinde |Interea|/ Et/ In Epistola 10 Decem. 1672 ad Collinium data, methodum momentorum Exemplo tangentium more Slusiano ducendarum illustravi, dixi eandem etiam ad quæstiones de curvitatibus & longitut{illeg}|di|nibus Curvarum & areis ac centris gravitatis Curvilinearum &c sese extendere, & esse generalem et ad quantitates surdas non hærere, et Collinius exemplar hujus |&| methodo serierum in scriptis meis intertextam esse: et Collinius exemplar hujus Epistolæ mense Iunio anni 1676 ad D. Leibnitium tunc in Gallia agentem misit.

In Literis insuper quæ mihi cum D. Leibnitio anno 1676 intercedebant, cum verba facerem de {scr}iptio {illeg} Tractatibus prædictis, & significarem me compotem esse methodi. Analyticæ determinandi maximas et minimas, ducendi tangentes, quadrandi figuras curvilineas, conferendi easdem inter se, et similia peragendi quæ in terminis surdis æque ac in rationalibus procederet; et literis transpositis hanc sententiam involventibus [Data æquatione quotcun fluentes quantitates involvente, fluxiones invenire, et vice versa] fundamentum hujus methodi celelarem {sic}, specimen vero ejusdem in curvilineis \per seriem/ quadrandis subjungerem et exemplis illustrarem; \☉/ < insertion from the bottom of the page > — et exemplis illustrarem, ☉ \sed/ in lucem vero {illeg}ere \mea |me|/ quietis gratia \hæc/ non edere dicerem; et cum Vir clarissimus eodem anno < text from f 34r resumes > et Vir clarissimus eodem anno in reditu suo e Gallia per Angliam in Germaniam, sub finem mensis Octobris, epistolas meas in manu Collinij consuluisset etiam consuleret: incidit is paulo post non multo post in methodum momentorum sub diversis verborum et notarum formulis, et mense Iunio sequente specimen ejusdem in Tangentibus more Slusiano ducendis \id non obstantibus irrationalibus,/ ad me misit, et subjunxit se credere methodum suor meam a sua non abludere, præsertim cum quadraturæ perutram methodum \meam/ faciliores redderentur. Methodi hujus fundamentum continetur in hoc Lemmate, & in Tractatu de Quadratura curvilinearum plenius \fusius/ exponitur.

Schol.

Per momenta quantitatitatum hic intelligo \earu/ particulas earum mo{mento} temporis genitas. Hæ particulæ non sunt minima indivisibiles, {illeg} sed sunt d{illeg}ibiles \in/ infinitum; non sunt quantitates minimimæ sed sunt indefinite parvæ et \vel {ve}dem {illeg}/ æqu{a}{illeg}|libus| temporis momentis genitæ. Et considerando tempus ut fluxu continuo et æqua{li}li genitum, & alias quantitates ut fluxibus qui|b|\us/cun genitas, seu æquabilibus|is| seu inæquabili\bus/ genitas; expono tempus per quantitatem quancun uniformiter fluentem, uti per lineam {illeg} ve{lx} \lineam v/ & ejus fluxium vel fluxionem per unitate{m}, et ejus momentum per literam {illeg} alias quantitates fluentes (seu indeterminats|o|s) per alias symbola y, denoto per alia symbola, ut x, y, z: et

Schol.

Per momenta quantitatum hic intelligo earum \incrementa momentanea seu/ particulas momento tem- {sic} to {sic} temporis genitas; eas indefinite parvas & in{illeg} infinitum divisibiles. Et expo|desig|nando fluxionem temporis per unitatem & fluxionis aliarum quantitum \ut x y z/ per \x, y, z vel etiam per/ alia symbola uti p, q, r: denoto harum momenta per {illeg} momentum temporis per $1\times \mathrm{o}$ seu {illeg}|o| et fluxiones \momenta/ aliarum quantitatum per po, qo, ro, $\stackrel{.}{\mathrm{x}}\mathrm{o}$, $\stackrel{.}{\mathrm{y}}\mathrm{o}$, $\stackrel{..}{\mathrm{z}}\mathrm{o}$ &c vel po, qo, ro. Et habita quantitatis fluxione pqr ut $\stackrel{.}{\mathrm{x}}$ ut p, q vel r {illeg} quantitate fluentem, \quando/ designo vel \quando/ per eadem symbola vel in impo{illeg}|n|endo lineolam ut in in hunc modum $\mathrm{p}\prime$, $\mathrm{q}\prime$, $\mathrm{r}\prime$ vel \præfigendo aut/ circumscribendo rectangulum ut in his $▯\mathrm{p}$ $▯\mathrm{q}$ $▯\mathrm{r}$ \& his/ vel $\overline{)\mathrm{p}}$, $\overline{)\mathrm{q}}$. Et hujusmodi symbolis \adhibitis/ Analysin instituo in fluentibus et eorum fluxionibus & momentis adhibendo unicam tantum quantitatem indefinite parvam o. Sed hujusmodi Analysin docere non est hujus loci.

|Pag. 226.| In literis quæ mihi cum Geometra peritissimo G. G. Leibnitio annis abhinc decem \Anno 1676/ intercedebant, [viz^t anno 1676,] cum significarem me compotem esse methodi determinandi Maximas & Minimas, ducendi Tangentes, quadrandi figuras curvilineas \conferendi easdem cum Sectionibus Conicis/ & similia peragendi, quæ in terminis surdis æque ac \in/ rationalibus procederet, & Tractatum de eadem anno 1671 scripsisse; & {sic} \at/ literis transpositis hanc sententiam involventibus [Data æquatione — — — — et vice versa] eandem celarem: rescripsit vir clarissimus mense Iunio anni proximi, se quo — — — Lemmate \quantiatum/. [Extant specimina quædam hujus methodi in Analysi mea per Series, a Barovio ad Collinium anno 1669 a Barrovio nostro ad Collinium mi|s|sit|a| Eandem D. Lei] Incidit is in hanc methodum post reditunt \postquam redijt/ {illeg} {æ} Gallia per Angliam in Germaniam \i {sic} uti {illeg} negoti{illeg}|js| publicas interesset,/ id est anno 1677. Vtrius {illeg} methodi fundamentum continetur in hoc Lemmate.] Incidit autem is in hanc methodum post mensem junium anni 1676 quo Exemplar Epistolæ meæ \de hac methodo ad Collinium/ 10 Decem 1672 {illeg} datæ acceperat a Collinio acceperat & specimen hujus methodi a Collinio acceperat & postquam e Gallia per Londinum Angliam in Germaniam redijt ut publicis negotijs interesset; id est anno 1677.] Incidit autem \is/ in hanc methodum post Menseum Iuni{illeg} anni 1676 {illeg} Collinius exemplar Epistolæ meæ de hac hac methodo 10 Decem 1672 \una cum exemplaribus epistolari{a} pl. G. D. Leibnitium/ ipsum misit in Gallia agen{illeg} agentem misit, et postquam e Gallia per Londinu Galliam in Germa \&/ Mense \an{illeg}g{illeg}/ Octobri. ejusdem anni \D Leibnitius/ e Gallia {illeg}|{m}| in Angliam venit & veniens Collinium de commerc{io} suo \Epistolas Gregorij et meas in hanc Collinij consuluit/ consuluit {sic}, & subinde in Germ{illeg}|a|niam rediens ut negotijs publicis interessent, incidit in hanc methodum: Ejus fundamentum continetur in hoc Lemmate. Mense Iunio anni 1676 Collinius exemplar Epistolæ meæ de hac methodo 10 Decem. 1672 ad ipsum datæ, una cum exemplaribus Epistolarum plurium Iacobi Gregorij ad D. Leibnitium in Gallia agentem misit. Mense Octobri ejusdem anni \ad finem vergente/ D. Leibnitius {illeg} E Gallia in Angliam veniens, epistolas autographas et Gregorij et meas in manu {illeg} Collinij consuluit. \inter alias {vidit} epistolam meam 13 Iunij 1676/ ☉ < insertion from lower down f 35r > ☉ Vidit etiam Epistolam meam 1|2|{9} Iune 16 24 Octob. 1676 ad Oldenburgum datam. Et subinde in Germaniam rediens \ut negotijs publicis interesset,/ & incidit in hanc methodum, et mense Iunio {anni} < text from higher up f 35r resumes > & subinde in Germaniam rediens ut negotijs publicis interesset, \incidit/ in hanc methodum: ‡ < insertion from lower down f 35r > ‡ Et mense Iunio anni 1677 specimen ejus ad me misit. Ejus vero fundamentum continetur in hoc Lemmate. < text from higher up f 35r resumes > {illeg}i \Ejus vero/ fundamentum continetur in hoc Lemmate.

Phænomenon VII.

Planetæ circum axes suos uniformi cum motu Iupiter revolvuntur respectu fixarum: Iupiter horis 9. |& min primis| 56′ Mars horis 24.40′ Venus horis 23, Sol diebus 26|5|\$\frac{1}{2}$/ circiter Luna diebus 27. horis {illeg} |7.| minutis primis 43′; & secundis et Terra horis 23 {illeg} minuts|i|s primis 56′

Revolutiones Iovis, Martis, Veneris & Solis per revolutione{m}|s| macularum in eorum corporibus observatæ fuerunt. Maculæ Solis non sunt permanentes. Raro Post mensem unum aut altera evanescere solent, ideo tempus revolutionis corporis ejus nondum satis accurate definiri potuit. Redeunt ad eundem situm \cor{illeg}{bq} solis |in disco Solis|/ Spatio dierum 27$\frac{1}{2}$ vel 28 circiter respectu Terræ et inde colligitur quod respectu fixarum redeunt ad eundem situm diebus 25$\frac{1}{2}$ ve{illeg} 26 circiter. Luna eandem faciem in Terram Eadem Lunæ facies {illeg} Terram semper vertitur \respicit/; [sed cum motu quodam Libratorio ideo respectu fixarum \Luna/ revolvitur circa axem suum semel in mense s{quodie}{illeg} periodico. Eadem vero facies \ejus/ in Terram vertitur \semper respicit/ non accurate sed {illeg} \cum/ motu quodam libratorio tam in Longitudinem quàm in Latitudinem. Librando in Longitudinem faciem eandem semper vertita in {illeg} umbilicum superiorem, Orbis sui \{qu}amproxime{ndi} ex observationibus Hevelianis ol{i}m {di}{illeg} ex observationibus Hevelianis {olim} \d{illeg}{di}ce//, ideo revolutio ejus respectu facerum uniformis est quoad motum in longitudinem. Librando in Latitudinem faciem ejus vertit in boream in Latituduine boreali & in as|u|strum in Latitudine australi {illeg} ex observationibus Hevelianis etiam di id in angulo latitudinem æquante {illeg} (uti ex observationibus Hevelianis etiam didic{i} \uti ex Observationibus Hevelianis etiam {con}stat./) [ideo axis aream quem revolvitur {illeg} plano Eclipticæ perpendicularis est quamproxime. Hæc omnia, quæ ex observationibus Hevelianis olim {illeg}d{illeg} \quæ ex observationibus Hevelianis olim dididi, {illeg}dem {illeg}a me accepta/ D. Mercator in Astronomia \sua initio anni 1676 edita plenius exposuit a me {illeg}/ plenius exposuit, eadem {illeg}nt Phænomenis {illeg}sentire D Cassinus agrovit. [Maculæ in corporibus Saturni et Mercurij nondum observatæ sum{illeg}] Simili motu Satelles extimus Saturnius circa axem suum revolvi videtur, eadem sui facie Saturnum perpetuo respiciens. Nam circa Saturnum revolvendo, quoties ad orbis sui partem orientalem venit \accedit/ ægerrime videtur & plerum videri cessat: id quod evenire videtur \potest/ per maculas quasdam in ea corporis sui parte quæ Terræ tunc advertitur, \{illeg}t{illeg}s/ Simili etiam motu Satelles extimus Ioviales \circa axem suum/ revolvi videtur, propterea |quod| maculam habeat \in p/ in parte corporis Iovi aversa: \maculam habeat, qua tanquam/ [Maculæ in corporibus Saturni et Mercurij & re nondum observantur] quæ macula \tanquam/ in corpore Iovis apparit quoties \cernitur ubi/ Satelles inter Iovem & oculos nostros transit.

Hæc omnia a me anno 1675 accepta D. Mercator in Astronomia sua plurias ex initio anni sequentis \edita/ plenius exposuit

— — id in angulo latid|t|udinem æquante nisi quatenus hic angulus nunc augetur nunc diminuitur aliquantulum per inclinationem axis Lunæ ad planum Eclipticæ Hæ{illeg}c omnia \Librationis rationem/ a me acceptare|{m}|, D. Mercator in Astronomia sua initio anni 1676 edita plenius exposuit. Simili moto Satelles extimus Saturnius circa axem suum revolvi videtur, eadem sui facie — — —

In Analysi mea per series, quam Barrovius mense Iunio anni 165|6|9 ad Collinium misit, extant methodi hujus specimina quadam, tum ante annos aliquot inventæ Mense Iunio anni 1676 Collinius

Pag. 226.

Scholium.

Analysin per series et momenta a me scriptam, Barrovius noster anno 1669 ad Collinium misit. Methodos ibi expositos an alio Tractatu plenius explicui anno 1671, ex hoc Tractatu {illeg} inde Tractatum de Quadratura Curvilinearum anno 1676 extraxi. Interea In Epistola 10 Decem 1672 ad Collinium data, methodum momentorum exemplo tangentium more Slusiano ducendarum illustravi, dixi eandem etiam ad quæstiones de curvitatibus et longitudinibus Curvarum & \ac de{illeg}/ areis & centris gravitatis Curvilinearum &c sese extendere, & esse generalem, et ad quantitates surdas non hærere, & methodo serierum in scriptis meis intertextam esse: et Collinius exemplar hujus Epistolæ mense Iunio anni 1676 ad D. Leibnitium tunc in Gallia agentem misit.

In literis insuper quæ mihi cum D. Leibnitio anno 1676 intercedebant, cum verba facerem de Tractatibus prædictis & significarem me compotem esse methodi Analyticæ determinandi maximas et minimas, ducendi tangentes, quadrandi figuras curvilineas, conferendi easdem inter se, et similia peragendi quæ in terminis surdis æque ac in rationalibus procederet; & literis transpositis hanc sententiam involventibus [Data æquatione quotcun fluentes quantitates involvente, fluxiones invenire, et vice versa] fundamentum hujus methodi celarem, specimen vero ejusdem in curvilineis per seriem quadrandis subjungerem et exemplis illustrarem, sed in lucem me quietis gratia hæc \in lucem/ non edere dicerem; et cum Vir clarissimus \D. Leibnitius/ eodem anno in reditu suo {illeg}E Gallia per Angliam in Germaniam, sub finem mensis Octobris, epistolas meas \Commertium meum/ in manu Collinij etiam consuleret: incidit is non multo post in methodum momentorum sub diversis verborum et notarum formulis, et mense Iunio \{anni}/ sequente|i|s seq specimen ejusdem in Tangentibus more Slusiano ducendis id obstantibus irrationaibus ad me misit, et subjunxit \methodum suam ad irrationales non hærere &/ se credere methodum meam a sua non abludere, præsertim cum quadraturæ per methodum {meum} \utram/ faciliores redderentur. Methodi hujus fundamentum continetur in hæ Lemmate, et in Tractatu \prædictæ/ de Quadraturis curvilinearum \Tractatu/ fusius exponitur. Fluxiones uti sunt velocitates quibus fluentium momenta generantur, et momenta a D. Leibnitio vocantur differentiæ: et inde Methodus fluentium et Methodus fluxionum & Methodus momentorum & Methodus differentialis {illeg}dem \{&} eandem methodum/ significaret Methodus hujus \meæ autem/ fundame|tur|ntum continetur in hoc Lemmate, et in prædicto de Quadraturis Tractatum fusius exponitur eandem methodum significare possunt. Methodi hujus fundamentum continetur in Lemmate præcedente, et in prædicto de Quadraturis Tractatu fusius exponitur.

Sept. Octob 5. 1722. Apog ☽ in ♎|♌| 23$\frac{1}{2}$. ☉ in ♎ 23. ☽ in ♐|♑| 16. $\overline{)\begin{array}{r}1722.\\ 574\phantom{.}\end{array}}$ 1656. 3907. 2251. 563.