Letter to Charles Montagu describing the solution to the mathematical problems proposed by John Bernoulli

<61ar>

Ian. 30. 169$\frac{\text{6}}{\text{7}}$.

< insertion from the top of f 61ar >

3. Epistola, præhonorabili viro D. Carolo Mountague Armig. Scaccarij Cancellario & S. R. Præsidi, \inscripta/ qua solvuntur duo problemata Mathematica a Johanne Bernoullo Mathematico celeberrimo proposita.

Ian. 30. 169$\frac{\text{6}}{\text{7}}$.

< text from f 61ar resumes >

Accepi, Vir Amplissime, ex Gallia hesterno die duo Problematum a Joanne Bernoullo Mathematicorum acutissimo propositorum exemplaria Groningæ edita in hæc verba.

Acutissimis qui toto Orbe florent Mathematicis
S. P. D.
Ioannes Bernoulli Math. P. P.

Cum compertum habeamus &c ........ eruendam relinquimus.

Dabam Groningæ ipsis Cal. Ian. 1697.

Hactenus Bernoullus: Problematum verò solutiones {illeg} {illeg} {illeg}sunt hujusmodi

Probl. I.

Investiganda est curva Linea ADB in 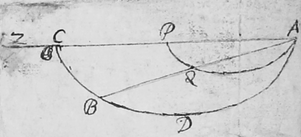qua grave a dato quovis puncto A ad datum quodvis punctum B vi gravitatis suæ citissimè descendet.

Solutio.

A dato puncto A ducatur recta infinita APCZ horizonti parallela et super eadem recta describatur tum Cyclois quæcunqꝫ AQP rectæ AB (ductæ et si opus est productæ) occurrens in puncto Q, tum Cyclois alia ADC cujus basis et altitudo sit ad prioris basem et altitudinem respectivè ut AB ad AQ. Et hæc Cyclois novissima transibit per punctum B et erit Curva illa linea in qua grave a puncto A ad punctum vi gravitatis suæ citissime perveniet. Q.E.I.

^[1]Prob. II{.}

Problema alterum, si recte intellexi, (nam quæ in Actis Lips. ab Auctore citantur ad id spectantia, nondum vidi,) sic proponi potest. Quæritur Curva KIL ea lege ut si recta PKL a 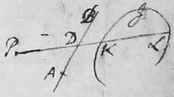dato quodam puncto P, ceu Polo, utcunqꝫ ducatur, et eidem Cur{illeg}|v|æ in punctis duobus K et L occurrat, potestates duorum ejus segmentorum PK et PL a dato illo puncto P ad occursus illos ductorum, si sint æque altæ (id est \vel/ quadrata, vel cubi vel quadrato-quadra{ta} &c) datam summam ${\mathrm{PK}}^q+{\mathrm{PL}}^q$ vel ${\mathrm{PK}}^{cub}+{\mathrm{PL}}^{cub}$ &c (in omni rectæ illius positione) conficiant.

<61av>

Solutio.

Per datum quodvis punctum A ducatur recta quævis infinita positione data ADB rectæ mobili PKL occurrens in D, et nominentur AD x et PK vel PL y, sintqꝫ Q et R quantitates ex quantitatibus quibuscunqꝫ dat{is} et quantitate x quomodocunqꝫ constantes et relatio inter x et y definiatur per hanc æquationem $\mathrm{y}\mathrm{y}+\mathrm{Q}\mathrm{y}+\mathrm{R}=0$. Et si R sit quantitas data, Rectangulum sub segmentis PK et PL dabitur. Si Q sit quantitas data {illeg} summa segmentorum illorum (sub signis propri{js} conjunctorum) dabitur. Si $\mathrm{Q}\mathrm{Q}-2\mathrm{R}$ datur, summa quadratorum $\left({\mathrm{PK}}^q+{\mathrm{PL}}^q\right)$ dabitur. Si ${\mathrm{Q}}^3-3\mathrm{Q}\mathrm{R}$ data sit quantitas, summa cuborum $\left({\mathrm{PK}}^{cub}+{\mathrm{PL}}^{cub}\right)$ dabitur. Si ${\mathrm{Q}}^4-4\mathrm{Q}\mathrm{Q}\mathrm{R}+2\mathrm{R}\mathrm{R}$ data sit quantitas summa quadrato-quadratorum $\left({\mathrm{PK}}^{qq}+{\mathrm{PL}}^{qq}\right)$ dabitur. Et sic deinceps in infinitum. Efficiatur itaqꝫ ut R, Q, $\mathrm{Q}\mathrm{Q}-2\mathrm{R}$, ${\mathrm{Q}}^3-3\mathrm{Q}\mathrm{R}$ &c datæ sint quantitates & Problema solvetur. Q.E.F.

Ad eundem modum Curvæ inveniri possunt quæ tria \vel plura/ abscindent segmenta simile{illeg}|s|{illeg} proprietates habentia. Sit æquatio ${\mathrm{y}}^3+\mathrm{Q}\mathrm{y}\mathrm{y}+\mathrm{R}\mathrm{y}+\mathrm{S}=0$ ubi Q, R et S quantitates significant ex quantitatibus quibuscunqꝫ datis et quantitate x utcunqꝫ constantes; et Curva abscindet segmenta tria. Et si S data sit quantitas contentum solidum illorum trium dabitur [Si Q sit quantitas data, summa trium illorum dabitur]. Si $\mathrm{Q}\mathrm{Q}-2\mathrm{R}$ sit data quantitas, summa quadratorum ex tribus illis dabitur.

<61br> < insertion from the top of f 61br >

A Solution of
Bernoulli's Problemes.
Publ^d in Ph: Tr.
V. L. Abr. V 1. p. 551.

< text from f 61br resumes > < insertion from lower down f 61br >

Newton

< text from higher up f 61br resumes > < insertion from lower down f 61br >

B. 2. 53.

< text from higher up f 61br resumes > < insertion from lower down f 61br >

N P

< text from higher up f 61br resumes > <61bv> < insertion from the right margin of f 61bv >

For the R^t Hon^ble Cha: Montagu {Esq.}
Chancellour of the Exchequer

< text from f 61bv resumes > < insertion from the bottom of f 61bv >

Read Febr: 24: 1696.
Phil. Trans: 224.

< text from f 61bv resumes >