Draft of the 'Discourse Concerning Light and Colors'

<501r>

S^r

I suppose you understand that all transparent substances (as Glass water, Air &c) when made very {illeg}|th|in by being blown into bubbles or otherwise formed into plates, doe exhibit various colours according to their various thinnesse, although at a greater thicknesse they appeare very cleare & colourlesse. In my former discourse about y^e constitution of light, I ommited these colours, because they seemed of a more difficult consideration, & were not necessary for establishment of the Doctrine w^ch I propounded. But because they may conduce to further discoveries for completing that Theory, especially as to y^e constitution of y^e parts of naturall bodies on w^ch their colours or transparency depend, I have now sent you an account of them. To render this discourse short & distinct, I have first described the principall of my Observations, & then considered & made use of them. The Observations are these:

Obs: 1. Compressing two Prisms hard together that their sides (w^ch \by chance/ were a \very/ little convex) might somewhere touch one another, I found the place in w^ch they touched to become absolutely transparent as if they had there been one continued piece of Glasse. For when y^e light fell so obliquely on y^e Air w^ch in other places was between them, as to be all reflected; \it {illeg}|see|med/ in that place of contact it was \to be/ wholly transmitted: in so much that when looked upon it appeared like a black or dark spot by reason y^t no \little or no sensible/ light was reflected from thence as from other places; & when looked through it seemed (as it were,) a hole in that Air what|ich| was formed into a thin plate by being compressed between y^e glasses. And through this hole Objects that were beyond might be seen distinctly w^ch could not at all be seen through other parts of y^e glasses where the Air was interjacent. Although y^e glasses were a little convex yet this transparent spot was of a considerable breadth, w^ch breadth seemed principally to proceed from the yeilding inwards of the glasses by parts of the glasses by reason of their mutuall pressure For by pressing them very hard together it would become much broader then otherwise.

Obs: 2. When the plate of Air, by turning the Prisms about their common Axis became so little inclined by y^e incident rays, that some of them began to be transmitted, there arose in it many slender arcs of colours w^ch at first were shaped almost like a Conchoid as you see them here delineated. And by continuing the motion of the Prisms, these arcs increased & bended more & more about the said transparent spot, till they were comple{illeg}|t|ed into circles or {illeg}|ri|ngs incompassing it, & afterwards continual{illeg}|l|y <501v> grew more & more contracted.

These parcs at their first appearance were of a violet & blew colour, & between them were white arcs of circles w^ch {illeg}|p|resently \(by continuing y^e motion of y^e Prisms)/ became {illeg}|a| little tinged in their inward limbs with red & yellow, & to their outward limbs y^e blew was adjacent. So y^t the order of these colours from the centrall \dark/ spot, was at that time White, Blew, v|V|iolet; b|B|{illeg}|l|a{illeg}|c|k {illeg}; Red, Orange, Yellow, White, Blew, Violet; &c. But the Yellow & Red were much fainter then y^e b|B|lew & v|V|iolet.

The motion of the Prisms about their Axis being continued these colours contracted more & more, shrinking towards the whitenesse on either side of it untill they totally vanished into it. And then the circles in those parts appeared black & white withou{illeg}|t| any other colours intermixed. But by further inclining \moving/ y^e Prisms \about/, the colours again emerged out of the whitenesse, the violet & blew at its ––– inward limb, & at its outward limb the red & yellow. So that now their order from the centrall spot was White, Yellow, Red; Black; Violet, Blew, White, Yellow, Red, &c. contrary to what it was before.

Obs: 3 When the rings or some parts of them {illeg}|a|ppear{illeg}|e|d onlly black & white, they were very distinct & well defined, & the blacknesse seemed as intense as that of y^e centrall spot. Also in y^e vicine places \borders of y^e rings/ where y^e colours began to emerge out of y^e whitenesse, they were pretty distinct, w^ch made them visible to a very great multitude. I have sometimes numbered above thirty successions (recconing every black & white ring for one succession,) & seen more of them w^ch by reason of their smallnesse I could not number. But in other positions of y^e Prisms at w^ch the rings appeared of many colours, I could not distinguish above 8 or {illeg}|9| of them, & the exteriour of those too were r|v|ery confused & dilute.

In these two Observations to see the colour|rings| distinct, & without an{illeg}|y| other colour but black & white, I found it very necessary that I \to/ hold my eye at a good distance from them. For by approaching nearer, although in the same inclination of my eye \to y^e plane of y^e rings/, yet there emerged a blewish colour out of y^e white, w^ch by dilating it selfe more & more into the black rendered the circles lesse distinct, & left y^e white a little tinged with red & yellow. I found also that by looking through a slit or oblong hole w^ch was narrower then the pupill of my eye & held close to it parallel to the Prisms, I could see the circles much distincter & visible to a far greater number then otherwise.

Obs: 4. To observe more nicely the order of the colours w^ch arose out of the white circles as y^e rays became lesse & lesse inclined to the plate of Air; I took t{illeg}|w|o object glasses the one a plano-convex for a fourteen foot Telescope, & the other a large double convex for one of about fifty foot, & upon this laying the other with its plane side downwards, I pressed them slowly together to make the colours succes <502r> sively emerge in{illeg} the middle of the circles & then slowly lifted the upper glasse from y^e lower to make them successively vanish again in the same place, where being of a considerable breadth, I could more easily discerne them. And by this means I observed their succession & quantity to be as followeth.

Next to y^e pellucid centrall spot made by the contact of the glasses, succed|e|ded Violet, Blew, White, Yellow, & Red. The violet & Blew were|as| so very little in quantity that I could not discerne {them} \it/ in the circles made by the Prisme|s|, \nor could I well distinguish any violet in it,/, but y^e Yellow & Red were pretty copious & seemed about as much in {illeg}|ex|tent as the white, & foure or five times more then the Blew & Violet. The next circuit or order of colours immediately incompassing these was v|V|iolet Blew, g|G|reen, Yellow, & Red. And these were all of them copious & vivid excepting the green w^ch was very little in quantity & seemed much more faint & dilute then y^e other colours. Of y^e other four the Violet was least & the blew lesse then y^e yellow or red. The third circuit or order was also Purple, Blew, Green, Yellow, & Red in w^ch the purple seemed {a little} more reddish then the Violet in the former circuit, & y^e Green was much more conspicuous, being as brisque & lively copious as any of y^e other colours a|e|xcept the Yellow, but the Red began to be a little faded inclining very much to purple. After these succeeded \in y^e fourth circuit/ Green & Red. The g|G|reen was very copious & lively, inclining on one side to blew & on y^e other to yellow. But in this 4^th circuit there was neither violet blew nor yellow, & the Red was very imperfect & dirty. Also the succeeding colours became more & more imperfect & dilute till after three or four more revolutions they ended in perfect whitenesse.

Obs: 5. To determin the intervall of the glasses or thicknesse of the interjacent Air by w^ch each colour was produced, I measured the diameters of y^e first six rings at the most lucid par{illeg}|t| of their Orbits, & squaring them I found their s{illeg}|qu|ares to be in Arithmeticall progression of y^e odd numbers 1, 3, 5, 7, 9, 11. And therefore since one of the glasses was plane & the other sphericall, their intervalls at those rings must be in the same progression. I measured also the diameters of the dark or faint {illeg}|r|ings between the more lucid colours & found their squares to be in Arithmeticall progression of the eaven numbers 2, 4, 6, 8, 10, 12. And it being very nice & difficult to ta{illeg}|k|e these measures exactly I repeated them divers times {illeg}|a|t divers parts of the glasses, that by their agreement I might be confirmed in them. And the same Method I used in determining some others of the following Observations.

Obs: 6. The diameter of the sixt ring at the most luci{illeg}|d| part of its orbit was $\frac{58}{100}$ parts of an inch, & the diameter of the Sphere <502v> on w^ch the double convex object glass was ground was 102 foot, as I found by measuring it; & consequently the thicknesse of the Air, or Aereall intervall of the glasses at that ring was $\frac{1}{14554}$ \of an inch/. For as the diameter of the said sphere (102 foot or 1224 inches) is to y^e \semi/diameter of the ring $\frac{29}{100}$ so very nearely is that \semi-/diameter to $\frac{1}{14554}$ y^e said distance \intervall/ of the glasses. Now by the preceedent Observation the eleventh part of this distance \intervall/ ($\frac{1}{160094}$) is the thicknesse of the Air at that interval part of the first ring where the \most lucid of the colours the citrine/ Yellow would be most most vivid were it nor mixed with other colours in the white \of this ring/, & this doubled gives the difference of their intervalls its thicknesses at the \citrine/ Yellow in all the other rings. viz $\frac{1}{80047}$ or to use a round number, the eighty thousandth part of an inch.

Obs: 7. These dimensions were taken when my eye was placed perpendicularly over the glasses in or neare the axis of the r|R|ings But when I viewed them obliquely they became bigger, continually swelling as I removed my eye further from their Axis. And partly by measuring the diameter of the same circle at severall obliquities of my eye, partly by other meanes, as also by making use of the two Prisms for very great obliquities, I found its diameter, & consequently the thicknesse of y^e Air at its perimeter in all those obliquities to be very nearly in the proportions expressed in this Table

In the two first Collumns are expressed the obliquities of the \incident & emergent/ rays to the Plate of Air, that is their angles of incidence & refraction. In the third Collumn y^e diameter of any coloured Ring at those obliquities is exprest in parts of w^ch {illeg}|t|en constitute th {illeg}|a|t diameter when the rays are perpendicular. And in the 4^th Collumn the thicknesse of the Air at y^e circumference of that Ring is exprest in parts of w^ch also 10 constitute that thicknesse when the rays are perpendicular.

<503r>

Obs: 8. The dark spot in the middle of the Rings increased also by y^e obliquation of the eye; although almost insensibly. But if instead of the Object-glasses the Prisms were made use of, its increase was more manifest when viewed so obliquely y^t no colours appeared about it. It was least when the rays were incident most obliquely on y^e interjacent Air, & \as y^e obliquity decreased it/ increased more & more untill y^e coloured rings appeared, & then decreased again, but not so much as it increased before. And hence it is evident that the transparency was not onely at y^e absolute contact of y^e glasses but also where they had some little intervall. I have sometimes \observed/ y^e diameter of that spot to be between half & two fift parts of the diameter of the exterior circumference of the Red in the first circuit or revolution of colours when viewed almost perpendicularly; whereas when viewed obliquely it hath wholly vanished & become opake & white like y^e other parts of y^e glasse. Whence it may be collected y^t the glasses did then scarce{illeg}|l|y or not at all touch one another, & that their intervall at the perimeter of that spot when viewed perpendicularly was about a 5^t or a 6^t part of their intervall at the circumference of the said Red

Obs: 9. By looking through the two contiguous Object-glasses, I found that the interjacent Air exhibited Rings of colours as well by transmitting light as by reflecting it. The centrall spot was now white, & from it the order of the colours were Yellow|ish| Red; Black; Violet, Blew, White, Yellow, Red; Violet, Blew, Green, Yellow, Red, &c But these colours were very faint & dilute unlesse when the light was trajected very obliquely through the glasses. For by that meanes they became pretty vivid. Onely the first Yellowish Red, like y^e Violet & blew in the 4^th Observation was so little & faint as scarcely to be discerned. Compareing the coloured Rings made by reflexion, w^th these made by transmission of the light; I found that White was opposite to Black, Red to Blew, Yellow to Violet, & Green to a compound of Red & Violet. That is, those parts of the glasse were black when looked at through w^ch when looked upon appeared white, & on y^e contrary. And so those w^ch in one case exhibited blew did in the other case exhibit Red. And the like of the other colours.

Obs: 10. Wetting the Object glasses a little at their edges, the water crept in slowly between them, & the circles thereby became lesse & the colours more faint: in so much that as y^e water crept along one half of them at w^ch it first arrived would appeare broken of from y^e other half & contracted into a lesse Room. By measuring them I found the proportion of their diameters to the diameters of the like circles made by Air to be about seven to eight, & consequently the intervalls of the glasses at like circles caused by these two Mediums \water & air/ are as about three to four. Perhaps it may {be} <503v> a generall Rule that if any other Medium more or lesses dense yⁿ water be compressed between the glasses, their intervall at the Rings caused thereby will be to their intervall caused by the interjacent Air, as the sines are w^ch measure the refraction made out of that Medium into Air

Obs: 11. When the water was between the glasses if I pressed the upper glasse variously at its edges to make the Rings move nimbly from one place to another, a little bright spot would –––– immediately follow the center of them, w^ch upon creeping in of the ambient water into that place would presently vanish. It's appearance was such as interjacent Air would have caused, & it exhibited the same colours. But it was not Air, {illeg}|for| where any aereall bubbles were in the water they would not vanish. The reflexion must rather have been caused by a subtiler Medium w^ch could recede through the Glasse at y^e creeping in of the water.

Obs: 12. These Observations were made in the open Air. But further to examin the effects of coloured light falling on y^e Glasses, I darkened the Room & viewed them by reflexion of the colours of a Prism cast on a sheet of white paper \my eye being so placed y^t I could see y^e coloured paper by reflexion in y^e glasses as in a looking glass./. And by this meanes the Rings became distincter & visible to a far greater number then in the open Air. I have sometimes seen more then 20 of them, whereas in y^e open Air I could not discerne above 8 or 9.

Obs: 13. Appointing an Assistant to move the Prism to & fro about its Axis, tha{illeg}|t| all its|the| colours might successively fall on the|at| {illeg} p{illeg}|l|a{illeg}|rt| of the paper \w^ch I saw by reflexion from that part of the glasses where y^e circles appeared/ & be \so y^t all y^e colours might be successively/ reflected from the circles to my eye whilst I held it immoveable; I found the circles w^ch the Red light made to be manifestly biger then those w^ch were made by the Blew & Violet. And it was very pleasant to see them gradually swell or contract accordingly as the colour of the light was change{illeg}|d|. The interval of y^e Glasses at any of the rings when the{illeg}|y| were made by the utmost red light was to their intervall \at y^e same Ring/ when made by the utmost {illeg}|V|iolet, greater then 3 to 2 & lesse then 13 to 8. By the most of my Observations it was as 9 to 14 \to 9/. And this proportion seemed \very nearely/ the same in all obliquities of my eye; unlesse when two Prisms were made use of instead of the Object-glasses. For then at a certain great \great/ obliquity \of y^e rays to y^e plate of air between y^e Prisms/ |of my eye| the Rings made by the severall colours seemed equall, & at a greater \greater/ obliquity those made by the Violet would be greater then the same Rings made by the Red.

Obs 14. \While the Prism was turned about uniformly \its axis/ w^th an eaven motion/ The Contraction or dilatation of a Ring made by all the severall colours of the Prism successively reflected from the Object-Glasses, was swiftest in the Red, slowest in y^e Violet, & in intermediate colours it had intermediate degrees of celerity. Comparing the extent \or breadth of y^e \rings/ or variation of {illeg} the Air's thickness/ w^ch each colour obteined \or moved V{illeg}/ \{illeg} moved through over & took up/ by this contraction or dilatation <504r> I found that the Blew was sensibly more extended then the Violet, y^e Yellow then y^e Blew, & the Red then the Yellow. And to make a juster estimation of their proportions I observed that y^e extent \or breadth/ of the Red \squared that is the variation of y^e \thickness of the/ air where all the \red by/ contraction & dilatation {illeg} appeared/ was almost double to that of the Violet, & that y^e light was of a middle colour between Blew \Yellow/ & Green at that intervall of the Glasses w^ch was an Arithmeticall mean between the two extreames \intervalls which|ere| reflected the whole {illeg} of y^e colours began & ended/: contrary to what happens in the colours made by the refraction of a Prism, where the Red is most contracted, the Violet most expanded, & in y^e midd|s|t of them \all the colours/ is the confine of Green & Blew.

Obs: 15. These Rings were not of various colours like those in the open Air but appeared all over of that Prismatique colour onely w^th w^ch they were illuminated. And by projecting the Prismatique colours immediately upon y^e glasses, I found y^t the light w^ch fell on y^e dark spaces w^ch were between the coloured Rings, was transmitted through y^e Glasses w^thout any variation of colour. For on a white paper placed behind, it would paint Rings of the same colour w^th those w^ch were reflected, & of the bignesse of their intermediate spaces. And from hence the origine of these Rings is manifest, namely that y^e aereall intervall of the glasses, according to its various thicknesse, is disposed in some places to reflect, & in others to transmit the light of any colour, & in the same place to reflect one colour where it transmits another.

Obs: 16. The squares of the diameters of these Rings made by any Prismatique colour were in Arithmeticall Progression as in y^e 5^t Observation. And y^e diameter of y^e sixt circle when made by y^e \citrine/ Yellow & viewed almost perpendicularly, was about $\frac{58}{100}$ parts of an inch, agreable to y^e 6^t Observation.

The precedent o|O|bservations were made w^th a rarer thin Medium terminated by a denser, such as was Air or water ––– comprest between two Glasses. In those that follow are set down the appearances of a denser Medium thin'd within a rarer, such as are p|P|lates of Moscovy Glasse, Bubbles of Water, & some other thin substances terminated as all sides w^th Air

Obs: 17. If a {illeg}|B|ubble be blown w^th water, first made tenacious by dissolving a little soape in it, tis a common observation that after a while it will appeare tinged w^th a great variety of colours. To defend these bubbles from being agitated w^th by the externall Air |(|whereby their colours are irregularly moved one among another, so y^t no accurate observation can be made of them,|)| as soon as I had blown any of them I covered it with a cleare glasse, & by that meanes its colours emerged in a very regular order like so many concentrick rings incompassing the top of the b|B|ubble. And <504v> as y^e bubble grew thinner by the continuall subsiding of y^e water these rings dilated slowly & overspread the whole bubble descending in order to y^e bottom of it where they vanished successively. In the meane while after all the colours were emerged at the top, there grew in the center of the Rings a small round black spot like that in the first Observation w^ch continually dilated it selfe till it became sometimes more then $\frac{1}{2}$ or $\frac{3}{4}$ of an inch in breadth before the Bubble br{illeg}|a|ke. At first I thought there had been no light reflected from the water in that place, but observing it more curiously I saw within it severall smaller round spots w^ch appeared much blacker & darker then the rest, whereby I knew that there was some reflexion of at the other places w^ch were not so dark as that|ose| spots. And by further tryall I found y^t I could see the images of some things (as of a candle or the Sun) very faintly reflected not onely from the great black spot but also from the little darker spots w^ch were within it.

Besides the afforesaid coloured Rings there would often appeare small spots of colours ascending & descending up & down y^e sides of the Bubble, by reason of some inequalities in the subsiding of the water. And sometimes small black spots generated at the sides of would ascend up to y^e larger black spot at y^e top of the Bubble & unite with it.

Obs: 18. Because the colours of these Bubbles were more extended & lively then those of Air thind between t{o}|w|o Glasses, & so more easy to be distinguished: I shall here give you a further description of there|ir| order as they were observed in viewing them by reflexion of y^e Skies when of a white colour, whilst a black substance was placed behind the bubble. And they were these; Red, Blew; Red, Blew; Red, Blew; Red, Green; Red, Yellow, Green, Blew, Purple; Red, Yellow, Green, Blew, Violet; Red, Yellow, White, Blew, Black.

The three first successions of Red & Blew were very dilute & dirty, especially the first where the Red seemed in a manner to be white Amo\n/gst these there was scarcely any other colour sensible, onely the Blews (& principally the second \blew/) inclined a little to Green.

The fourth Red was also dilute & dirty but not so much as y^e former three; After that succeeded little or no Yellow, but a copious Green w^ch at first was inclined a little to yellow, & then became a pretty brisque & good Willow g|G|reen, & afterwards changed to a blewish colour; but there succeeded neither Blew nor violet.

The fift Red at first was \inclined/ very much inclined to purple & afterwards became more bright & brisque but yet not very pure. This was succeeded with a very bright & intense Yellow, w^ch was but little in quantity, & soon changed to Green: But that Green was {copious} & something more pure deep & lively then the former Green. After <505r> that followed an excellent Blew of a bright Sky colour, & then a Purple w^ch was lesse in quantity then the Blew & much inclined to Red.

The sixt Red was at first of a very faire & lively Scarlet, & soon after of a brighter colour being {illeg}|v|ery pure & brisque & the best of all the Reds. Then after a lively Orange followed an intense bright & copious Yellow, which was also the best of all the Yellows; & this changed fir{illeg}|s|t to a Greenish Yellow, & then to a Greenish Blew; but the Green between the Yellow & Blew was very little & dilute, seeming rather a Greenish White then a Green. The Blew w^ch succeeded became very good & of a fair Bright Sky colour, but yet something inferior to the former Blew, And the Violet was intense & deepe w^th little or no rednesse in it And lesse in quantity then y^e Blew

In the last Red appeared a tincture of Scarlet next the Red Violet, w^ch soon changed to a brighter colour inclining to an Oran Orange; And y^e Yellow w^ch followed was at first pretty good & lively but afterwards it grew more & more dilute untill by degrees it ended in perfect whitenesse. And this whitenesse, if the water was very tenacious & well tempered, would slowly spread & dilate it selfe over the greatest part of the bubble, continually growing paler at the top, where {illeg}|at| length it would crack in many places, & those cracks as they dilated would appeare of a pretty good, but yet obscure & dark sky colour; the white between the {illeg}|B|lew spots diminishing, untill it resembled the threds of an irregular net=work, & soon after vanished & let|f|t all the upper part of the Bubble of the said dark Blew colour. And this colour after the afforesaid manner dilated it self downwards untill sometimes it hath overspread the whole Bubble. In the me{illeg}|a|ne|-|while at the top, w^ch was of a darker Blew then the bottom & appeared also full of many round blew spots something darker then the rest, there would emerge one or more very black spots & w^th those other spots of an intenser blacknesse, w^ch I mentioned in y^e former Observation; &|A|nd these continually dilated themselves untill the Bubble brake.

If the water was not very tenacious the Black spots would break forth in the white without any sensible intervention of the blew. And sometimes they would brek|a|k forth within the precedent Yellow, or Red, or perhaps within the Blew of y^e second order before the intermediate colours had time to display themselves.

By this description you may perceive how great an affinity these colours have w^th those \of Air/ described in the 4^th Observation, although set down in a contrary order by reason that they begin to appeare when the Bubble is the thickest, & are most conveniently recconed from the lowest & thickest part of the Bubble upwards.

Obs: 19. Viewing at severall oblique positions of my eye the Bubbles Rings of colours emerging on y^e top of the Bubble, I found that they <505v> were sensibly dilated by {illeg}|in|creasing the obliquity, but yet not so much by far as those made by thinned Air in the 7^th Observation. For there they distended \were dilated/ so much as, when viewed most obliquely, to arrive at a part of the Plate more t{illeg}|h|en {illeg}|tw|elve times thicker then that where they appeared when viewed perpendicularly, whereas in this case the thicknesse of the water at w^ch they arrived when viewed most obliquely, was to that thicknesse w^ch exhibited them by perpendicular rays something lesse then 8 to 5. By the best of my o|O|bservations it was between 15 & $15\frac{1}{2}$ to 10; an increase about 24 times lesse then in in the other case.

Sometimes the Bubble would become of an uniform thicknesse all over except at y^e top of it neare the black spot, as I knew because it would exhibit the same appeareance of colours in all ––– positions of the eye: And then the colours w^ch were seen at its apparent circumference by the obliquest rays would be different from those that were seen in other places by rays lesse oblique to it. And divers Spectators might see y^e same part of it differing colours by viewing it at very differing obliquities. Now observing how much the colours at the same place of the Bubble or at divers places of eq{illeg}|u|all thicknesse were varied by the severall obliquities of the rays; by assistance of the 4^th 14^th 16^th & 18^th Observations, as they are hereafter explained, I collected the thicknesse of the water requisite to exhibit any one & the same colour at severall obliquities to be very nearely in the proportion expressed in this Table.

In the first two Collumns are expressed y^e obliquities of the rays to the superficies of y^e water, that is their angles of incidence & refraction. Where I suppose that y^e sines w^ch measure them are in round numbers as 3 to 4, though probably the dissolution of soape in the water may a little alter its refractive virtue. In the third collumn the thicknesses of y^e Bubble at w^ch any one colour is exhibited in those severall obliquities, is exprest an parts of which ten constitute that thicknesse when the rays are perpendicular.

I have sometimes observed of the colours w^ch arise out of on polished Steel when heating it, or on Belmstall \& some other Metalline substances/ when melted & poured on the ground <506r> where it may cook in the open Air, that they have, like these of water-bubbles, been a little changed by viewing them at divers obliquities, & particulary that a deep blew of violet when viewed very obliquely hath been changed to a deep Red. But y^e changes of these colours are not so \great &/ sensible as of those made by water. For the Scoria or vitrified part of y^e Metall w^ch most Metalls when m|h|eated or melted \do/ continually protrude to their surface where \& which/ by covering them \metalls/ in forme of a thin glassy skin, {illeg} causes these colours, is much denser then water; and I find y^t y^e change made by the obliquation of the eye is least in colours of y^e densest thin substances.

Obs: 20. As in the 9^th Observation so here the Bubble by transmitted light appeared of a contrary colour to that w^ch it exhited by reflexion. Thus when the Bubble being looked on by the light of the clouds reflected from it, seemed Yellow or Red at its apparent circumference, if y^e clouds at y^e same time were or very suddenly \immediately after/ were viewed through it, the colour at its circumference would be blew or Purple or Blew. And on the contrary when by reflected light it appeared Blew, it would appeare Red by transmitted light.

Obs: 21. By wetting \very thin/ Plates of Moscovy-glasse whose thinnesse made the like colours appeare, the colours became more faint; especially by wetting y^e Plates on that side opposite to y^e eye; but I could not perceive any variation of their species. So y^t \then/ the thicknesse of a plate requisite to produce any colour depends onely on y^e density of the Plate & not \on that/ of y^e ambient Medium. And hence by the 10^th & 16^th Observations may be known the thicknesse of \which/ Bubbles of Water or \{thin}/ plates of Moscovy-glasse, or of other substances, w^ch they have at any colour produced by them.

Obs: 22. A thin transparent body w^ch is denser then its ambient Medium, exhibits more brisque & vivid colours then that w^ch is \so much/ rarer; as I have particularly observed in Air & Glasse. For blowing Glasse very thin at a Lamp Furnace, those plates incompassed with Air did exhibit colours much more then \vivid/ then those of Air made thin between two glasses.

Obs: 23. Comparing the quantity of light reflected from the severall Rings, I found it {illeg}|w|as most copious from the first or inmost, & in the exterior Rings became gradually lesse & lesse. Also the whitenesse of the first Ring was stronger then that reflected from those parts of the thinned Medium w^ch were without the Rings; as I could manifestly perceive by viewing at {the} \a/ distance the Rings made by the two Object glasses; Or by compareing two bubbles of water blown at distant times in the first of w^ch the whitenesse appeared w^ch succeded \all/ the colours, & \in the other/ the whitenesse w^ch preceded them in y^e other \all/ .

Obs: 24. When the two Object-Glasses were layd upon one another so as to make the Rings of Colours appeare, though with my naked eye I <506v> could not discerne above 8 or 9 of th{illeg}|os|e rings yet by viewing them through a Prism I have seen a far greater {illeg} \multitude/, ins{illeg}|o|much that I could sometimes number more then fourty besides many others that were so very small & close together that I could not {illeg}|k|eep my eye so steddy on them severally as to number them. But by their extent I have sometimes estimated them to be more then a hundred. And I beleive y^e experiment may be improved to y^e discovery of far greater numbers. For they seem to be really unlimited, though visible onely so far as they can be separated by the refraction, as I shall hereafter explaine.

But it was but one side of these rings, namely that {illeg}|to|wards w^ch the refraction was made, w^ch by that refraction was rendered distinct, & the other side became more confused then to \when viewed by/ y^e naked eye, insomuch that I there I could not discerne above one or two, & sometimes none of those rings, of w^ch I could discerne 8 or 9 w^th my naked |eye.| And their segments or arcs w^ch on the other side ––– appeared so numerous, \did not/ for the most part exceeded not \ed not/ the third part of a circle. If the refraction was very great or the Prisms very distant from the Object-glasses, the middle part of those arcs f|b|eca{illeg}|m|e also confused so as to disappeare & constitute an eaven whitenesse, whilst on either side the|ir| ends of those arcs, as also the whole arcs furthest from the center became distincter then before, appearing in y^e forme you see them here designed.

The arcs when they seemed distinctest were onely white & black successively without any other colours intermixed. But in other places there appeared colours {illeg}|w|hose order was inverted by the refraction in such manner that if I first held the Prism very neare the Object-Glasses & then gradually removed it further of towards my eye, the colours of y^e 2^d 3^d 4^th & following Rings shrunk towards the white that emerged between them, untill they wholly vanished into it at the middle of the arcs, & afterwards emerged again in a contrary order. But at the ends of the arcs they retained their order unchanged.

I have sometimes so layd one Object-glasse upon |t|an|he| other that to the naked eye they have all over seemed uniformly white w^thout the least appearance of any of y^e coloured rings; & yet by viewing them through a Prism great multitudes of those rings have discovered themselves. And in like manner Plates of Moscovy-Glasse & bubbles of Glasse blown at a Lamp-Furnace w^ch were not so thin as to exhibit any colours to y^e naked eye, have through y^e Prism exhibited a great variety of them ranged \irregularly/ up & down in the form of waves. And so bubbles of water before they began to exhibit their colours to y^e naked eye of a by stander have appeared through a Prism, girded about with many parallel & horizontal Rings; to produce w^ch effect, it was necessary to hold the Prism parallel or very nearely parallel to y^e Horizon, & to dispose it so that the rays might be refracted upwards.

The second Part
Remarks upon y^e foregoing Observations.

Having given my Observations of these colours, before I make use of them to unfold the causes of the colours of naturall bodies, it is convenient that by the simplest of them, \such as are the 2^d, 3^d, 4^th, 9^th, 12^th, 18^th 20^th & 24^th,/ I first explaine the more compounded|.| , such as are y^e 2^d, 3^d, 4^th, 9^th, 12^t, 18^th, 20^th & 24^th. And first to show how the colours in the 4^th & 18^th Observations are produced, let there be taken in any right line the lengths YZ, YA, & YH in proportion as 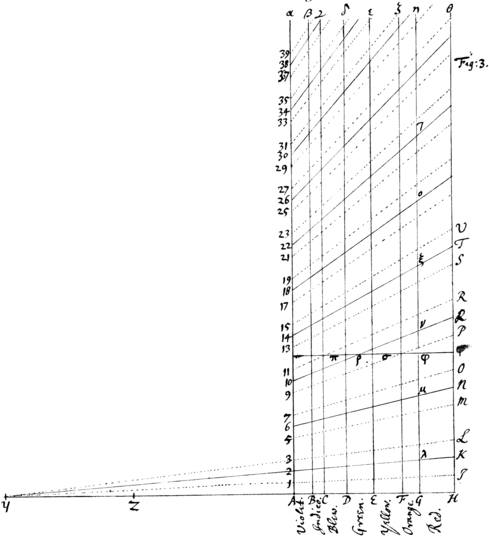4, 9, & 14 | 2 5 & 8 & between ZA & ZH eleven meane proportionalls, of w^ch let ZB be the second, ZC the third, ZD the fift, ZE the seventh, & ZF the ninth, & ZG the tenth. And at the points A, B, C, D, E, F, G, H let perpendiculars \Aα, Bβ &c/ be erected, by whose intervalls the extent of the severall colours set underneath against them, is to be represented. Then divide the line Aα in such proportion as the numbers {illeg}|1|, {illeg}|2|, 3; 5, 6, 7; 9, 10, 11; &c. set at y^e points of division denote. And through those divisions from Y draw lines 1I, 2K, 3L; 5M, 6N, 7O; &c

Now if A2 be supposed to represent the thicknesse of any thin transparent body at which the outmost Violet is most copiously reflected in the first Ring or series of colours, then by the 13^th Observation HK will represent its thicknesse at w^ch the outmost Red is most copiously reflected in the same series. Also by the 5^t & 16 Observations A6 & HN will denote the thicknesses at w^ch those extreme colours are most copiously –––– reflected in the second series, \& A10. HQ the thicknesses at w^ch they are most copiously reflected in y^e third series/ & so on. And the thicknesse at which any of the intermediate colours are reflected most copiously, will \according to y^e 14 Observation/ be defined by \the distance of the line AH from/ the intermediate parts of the lines 2K, 6N, \10Q, {illeg}/ &c against w^ch the names of those colours are written below.

But further to define the latitude of these colours in each Ring or series, let A{2} designe the least thicknesse & A3 the greatest thicknesse at w^ch the extreame Pu|V|iolet in the first series is reflected & let HI & HL designe the like limits for the extreame Red, & let <507v> the intermediate colours be limited by the intermediate parts of the lines 1I & 3L {illeg} {illeg}|a|gainst w^ch the names of those colours are written. And in the second series let those limits be the lines 5M & 7O; & so on: But yet w^th this caution that the reflexions be supposed strongest at the intermediate spaces 2K, 6N, 10{illeg}|Q| &c & \from thence/ to dec{illeg}|r|ease gradually towards these limits 1I, 3L; 5M, 7O; &c on either side; where you must not conceive them to be precisely limited but to decay indefinitely. And whereas I have assigned the same latitude to every series, I did it because although the colours in the first series seem to be a little broader then the rest by reason of a stronger reflexion there, yet that inequality is so insensible as scarcely to be determined by observation.

Now according to this O|D|escription conceiving that the rays in w^ch severall colours inhere are by turnes reflected at the spaces iIL3, 5MO7, 9PR11 &c:, & transmitted at y^e spaces AHI1, 3LM5, 7OP9 &c: it is easy to know what colour must in the open Air be exhibited at any thicknesse of a transparent thin body \Body/. For if a Ruler be applyed parallel to AH at that distance from it by w^ch the thicknesse of the Body is represented, the alternate spaces 1IL3, 5MO7 &c w^ch it crosseth will denote the reflected originall colours of which the colour exhibited in the open Air is compounded. Thus if the constitution of the Green in the third series of colours be desired; apply the Ruler as you see at πρσ, φ, And by its passing through some of the Blew at π, & yellow at σ, as well as through the green at ρ, you mad|y| conclude that the green exhibited at that thicknesse of the Body is principally constituted of originall green, but not without a mixture of some b|B|lew & Yellow.

By this meanes you may know how the colours from the center of the Rings outwards ought to succede in order as they were described in y^e 4^th & 18^th Observations. For if you move the Ruler gradually from AH through all distances, having past over the first space w^ch denotes little or no reflexion to be made by thinnest substances, it will first arrive at 1 the Violet, & then very quickly at the blew & Green w^ch together w^th y^t Violet compound blew, & then at y^e Yellow & Red by whose further addition that Blew is converted into whitenesse, w^ch|h|ich whitenesse continues during the transit \of the edge of the ruler/ from {illeg}|I| to 3, & after that by the successive deficience of its component colours turnes first to compound Yellow & then to Red, & last of all the Red ceaseth at L. Then begin the colours of the second series, w^ch succeed in order \during the transit of the edge of the ruler from 5 & O/ between 5 & O, & are more lively then before because more expanded & severed. And for the same reason instead of the former white there intercedes between y^e blew & Yellow a mixture of Orange, Yellow, Green, Blew & Indico, all w^ch together ought to exhibit a dilute & imperfect Green. So the colours of <508r> the third series all succeed in order; first the Violet w^ch a little interferes with the Red of the second order & is thereby inclined to a reddish Purple; then the Blew & Green w^ch are lesse mixed with other colours & consequently more lively then before, especially the Green: Then follows the Yellow some of which towards the Green is distinct & good, but that part of it towards the succeding Red, as also that {illeg}|R|ed is mixed w^th the v|V|iolet & Blew of the fourth series, whereby various degrees of Red very much inclining to Purple are compou{illeg}|n|ded. This Violet & Blew w^ch should succeed this Red being mixed with & hidden in it, there succeeds a Green, And this at first is much inclined to Blew, but soon becomes a good Green, the onely unmixt & lively colour in this fourth series. For as it verges towards the Yellow it begins to interfere w^th the colours of the fift series, by whose mixture the succeeding Yellow & Red are very much diluted & made dirty, especially the Yellow w^ch being the weaker colour is scarce able to shew it selfe. After this the severall series interfere more & more & their colours become more & more intermixed, till after thre or four more revolutions (i{illeg}|n| w^ch y^e Red & Blew ––– predominate by turnes) all sorts of colours are in all places pretty equally blended & compound an eaven whitenesse.

And since by the 15^th Observation the rays indued w^th one collour are transmitted where those of another colour are reflected, the reason of the colours made by the transmitted light in the 9^th & 20^th Observations is also from hence evident.

If not onely the order & species of these colours, be desired but all|s|o the precise thicknesse of the Plate or thin Body at w^ch they are exhibited, be de{illeg}|si|red in parts of an inch, that may be also performed \obteined/ by assistance of the 6^t or 16^th Observation. For according to those Observations the thicknesse of the thinned Air w^ch between two Glasses exhibited the \most luminous part of the sixt ring/ Orange or Bright Red of the sixt order, was $\frac{1}{14554}$ parts of an inch. Now suppose this thicknesse be represented by G7 & the eleventh part of it Gλ will be about $\frac{1}{160000}$ of an inch. And so Gμ, Gν, Gξ, Gο will be $\frac{3}{160000}$, $\frac{5}{160000}$, $\frac{7}{160000}$, & $\frac{9}{160000}$. And this being known it is easy to determin what thicknesse of Air is represented by Gφ or {illeg} \by/ any other distance of the Ruler from AH.

But further since by the 10^th Observation the thicknesse of Air is|was| to the thicknesse of water w^ch between the same Glasses exhibited the same colour, as 4 to 3; & by the 21^th Observation y^e colours of thin Bodies are not varied by varying the ambient Medium;|:| the thicknesse of a Bubble of water exhibiting any colour will be $\frac{3}{4}$ of the thicknesse of Air produceing the same colour. And so according to the same 10^th & 21^th Observations the thicknesse of a Plate of Glasse whose refraction is measured by the proportion of the sines <508v> 31 to 20 may be $\frac{21}{31}$ of the thicknesse of Air produceing the same colours. And the like of other Mediums. On these grounds I have composed the following Table wherein the thicknesse of Air, water, & glasse at w^ch {illeg}|eac|h colour is most intense & specific, is express{illeg}|ed|{illeg} in parts of an inch divided into ten hundred thousand parts equall parts.

Thethicknesseof In \particles of/ pellucid bodies lesse thenAir ––WaterGlasse In those ofBlack2$1\frac{1}{2}$$1\frac{1}{4}$, or lesse. The Colours
Of the
1^st orderBlew$2\frac{2}{3}$2$1\frac{3}{4}$. White$5\frac{1}{3}$4$3\frac{1}{2}$. Yellow865{illeg}$\frac{1}{6}$ Orange9$6\frac{3}{4}$$5\frac{4}{5}$. Red.10$7\frac{1}{2}$$6\frac{1}{2}$. Violet129$7\frac{3}{4}$. Indico$13\frac{1}{4}${illeg}|9|$\frac{11}{12}$$8\frac{1}{2}$. Blew$14\frac{3}{4}$11$9\frac{1}{2}$. Of the
2^d OrderGreen1612$10\frac{1}{3}$. Yellow$17\frac{1}{2}$$13\frac{1}{8}$$11\frac{1}{3}$. Orange$19\frac{1}{4}$$14\frac{1}{2}$$12\frac{2}{5}$. Bright Red201513. Scarlet$21\frac{1}{4}$16$13\frac{2}{3}$. Purple23$17\frac{1}{4}$14{illeg}$\frac{5}{6}$ Indico2418$15\frac{1}{2}$. Blew$25\frac{1}{5}$19$16\frac{1}{4}$. Of the
3^d orderGreen$27\frac{1}{5}$$20\frac{2}{5}$$17\frac{1}{2}$. Yellow$29\frac{1}{2}$2219. Red31$23\frac{1}{4}$20. Blewish Red$33\frac{1}{2}$25$21\frac{2}{5}$. Blewish Green3627$23\frac{1}{4}$. {Yellow} Green$37\frac{2}{3}$$28\frac{1}{4}$$24\frac{1}{3}$. 4^th OrderYellowish Green$39\frac{1}{3}$$29\frac{1}{2}$$25\frac{1}{3}$. Red4433$28\frac{1}{3}$. 5^t OrderGreenish Blew$50\frac{2}{3}$38$32\frac{2}{3}$. Red$57\frac{1}{3}$4337. 6^t OrderGreenish Blew6448$41\frac{1}{3}$. Red$70\frac{2}{3}$53$45\frac{2}{3}$. 7^th Order.Grenish Blew$77\frac{1}{3}$5850. Red or white8463$54\frac{1}{2}$.

Now if this Table be compared with the 3^d Scheme ^[1] you will there see the constitution of each colour as to its ingredients or the originall colours of w^ch it is compounded, & thence be enabled to judg of its intensenesse or imperfection, w^ch may suffice in explication of the {illeg}|4|^th & 18^th {illeg}\Obser/{illeg}|va|tions, unlesse it be further desired to delineate the manner how the colours appeare {illeg} when y^e two Object-glasses are layd upon one another. To doe w^ch let there be described a large {illeg}|A|rc of a circles & a <509r> streight line w^ch may touch that Arc, & parallel to that Tangent severall occult lines at such distances from it as the numbers set against the severall colours in y^e T{illeg}|a|ble denote. For the Arc & its Tangent will represent colours the superficies of the glasses terminating y^e interjacent Air, & the places where the occult lines cut the Arc will show at what distances from y^e \center or/ point of contact each colour is reflected.

There are also other uses of this Table: For by its assistance y^e Thicknesse of the Bubble in y^e 19^th Observation was determined by the colours w^ch it exhibited. And so y^e bignesse of y^e parts of naturall bodies may be conjectured {illeg}|a|t by their colours, as shall be hereafter shown. Also if two or more very thin Plates be layd one upon another so as to compose one Plate equalling them all in thicknesse, the resulting colour may be hereby determined. For instance, M^r Hook in his Micrographia observes that a faint yellow Plate of Moscovy-Glasse layd upon a blew one constituted a very deep purple. The Yellow of y^e first order is a faint one, & the thicknesse of the Plate exhibiting it, according to y^e Table, is $5\frac{1}{6}$ to w^ch add $9\frac{2}{3}$ the thicknesse exhibiting Blew of y^e second order, & y^e summe will be $14\frac{5}{6}$, w^ch |is| most nearely approaches $14\frac{4}{5}$ the thicknesse exhibiting y^e Purple of y^e third order.

To explain in y^e next place the circumstances of the 2^d & 3^d Observations, that is, how the colours \rings of colours may/, (by turning y^e Prisms about their common Axis y^e contrary way to that expressed in those Observations,|)| may be converted into white & black Rings, & afterwards into \rings of/ colours again \the colours of each ring lying now/ in an inverted order: it must be remembered that those \rings of/ colours are dilated by the obliquation of the rays to y^e Air w^ch intercedes y^e Glasses, & that according to y^e Table in the 7^th Observation their dilatation or recession from their common center \increase of their diameter/ is most manifest & speedy when they are obliquest. Now the rays of Yellow being more refracted by the first superficies of the \said/ Air w^ch intercedes the then those of red are thereby made more oblique to y^e second superficies at w^ch they are reflected to prop{illeg}|du|ce the coloured Rings, & consequently the \circle of/ Yellow \circle/ in each Ring will be more dilated then y^e Red; & y^e excesse of its dilatation will be so much the greater by how much the greater is the obliquity of the rays, untill at last it become of equall extent with the Red of the same Ring. And for the same reason the Green blew & violet will be also so much dilated by the still greater obliquity of their rays as to become all very nearely of equall extent with the Red, that is, equally distant from the center of the Rings. And then all the colours of the same series \ring/ must be coincident, & by their mixture exhibit a white Ring. And these white Rings must have black or dark Rings between them because they doe not spread & interfere with one another as before. <509v> And for that reason also they must become distincter & visible to far greater numbers. But yet y^e Violet being obliquest will be something more dilated in proportion \to its extent/ then the other colours, & so very apt to appeare at the exterior verges of the white.

Afterwards by a greater obliquity of the rays, the Violet & Blew become sensibly more dilated then y^e Red & Yellow & so being further removed from y^e center of the Rings, the colours must emerge out of the white in an order contrary to y^t w^ch they had before, the Violet & Blew at the exterior limbs \of each ring/, & y^e Red & Yellow at y^e interio{illeg}|r|r. And the Violet by reason of the greatest obliquity of its rays being in proportion most of all expanded will soonest appeare at y^e exterior limb of each white Ring & become more cons{illeg}|p|icuous then the rest. And the severall series \of rings/ of colours \belonging to the several rings will/ by their unfolding & spreading will begin again to interfere, & thereby render the Rings lesse distinct, & not visible to so great numbers.

If instead of the Prisms the Object-Glasses be made use of; the Rings w^ch they exhibit become not white & distinct by the obliquity of the eye by reason that the rays in their passage through that Air w^ch ind|t|ercedes y^e Glasses are very nearely parallel to themselves when \{illeg} those lines in w^ch they were first/ incident on the Glasses, & consequently those \the rays/ indued with severall colours are not inclined one more then another to that Air, as it happens in the Prisms.

There is yet another circumstance of these experiments to be considered, & that is why the black & white Rings w^ch when viewed at distance appeare distinct, should not onely become confused by viewing them neare at hand, but also yeild a v|V|iolet colour at both the edges of every white Ring. And the reason is that y^e rays w^ch enter the eye at severall parts of y^e pupill, have severall obliquities to y^e g|G|lasses, & those w^ch are most oblique, if considered apart, would represent the {illeg} \Rings/ bigger then those w^ch are the least oblique. Whence the breadth of the perimeter of every white {illeg} \white/ Ring is expanded outwards by the obliquest rays, & inwards by the least oblique. And this expansion is so much the greater by how much the greater is the difference of the obliquity; that is, by how much the Pupill is wider, or the Eye nearer to the Glasses. And the breadth of the Violet must be most expanded, because the rays apt to excite a sensation of that colour are most oblique to the second or further superficies of the thind Air at w^ch they are reflected, & have also the greatest variation of obliquity, w^ch makes that colour soonest emerge out of the edges of the white. And the breadth of every Ring is thus augmented, the dark intervalls must be diminished untill the neighbouring Rings become continuous, the & are blended, the exterior first, & then those nearer center, so that they can no longer be distinguished apart but seem to constitute an eaven & uniform whitenesse.

<510r>

Amongst all the Observations there is none accompanied with so add circumstances as the 24^th. Of those |y^e| principall are that in thin Plates of w^ch to y^e naked eye seem of an eaven & uniforme trans-\parent/ whitenesse \without any terminations of shadows,/ the refraction of a Prism should make the Rings of colours appeare, whereas it usually makes Objects appeare coloured onely there where they are terminated with shaddows or have parts unequally luminous; & that it should make those Rings exceedingly distinct & white, although it usually renders Objects confused & coloured. The cause of these things you will understand by considering that all the Rings of colours are actually \really/ in the Plate when viewed with the naked eye, although by reason of the great breadth of their circumferences they so much interfere & are blended together that they constitute seem to constitute an eaven whitenesse. But when the rays passe through the Prism to the eye the orbits of the severall colours in every Ring are refracted some more then others according to their degrees of refrangibility: by w^ch meanes the colours on one side of the Ring \(that is on one side of its center)/ become more unfolded & dilated & \those/ on the other side more complicated and contracted. And where by a due refraction they are so much contracted y^t the severall Rings become narrower then to interfere with one another, they must appeare distinct & also white if the constituent colours be so much contracted as to be wholly coincident. But on the other side where \the orbit of/ every Ring is made broader by the further unfolding of its colours, it must interfere more with other Rings then before & so become lesse distinct.

To explaine this a little further suppose the concentrik circles AZ|V| & BZ|X| represent the red & Violet of any order w^ch together w^th the intermediate colours constitute any one of these Rings. Now these being viewed through a Prism the violet circle BC|X| will by a greater refraction be further translated from its place then the Red AZ|V| & so approach nearer to it on that side towards w^ch the refractions are made. For instance, if the Red be translated to a{illeg}v the v|V|iolet may be translated to bx so as to approach nearer to it at x then before, & if y^e Red be further translated to a{illeg}V the v|V|iolet may be so much further translated to bX as to convene with it at {illeg}X, & if the Red be yet further translated to {illeg} \αγ/ the Violet may be still so much further translated to β{illeg}|ξ| as to passe beyond it at {illeg}|ξ| & convene with it at e & f. And this being understood not onely of the Red & Violet but of all the other intermediate colours, & also of every revolution of those colours, you will easily perceive how those of the sam{illeg}|e| revolution or <510v> order by their nearenesse at cd \xv/ & {illeg} \& {sic} γξ/, & their coincidence at cd \XV/, e, & f ought to constitute pretty distinct arcs of circles, especially at cd \XV/ or at e &f, & that they will appeare severall at cd \xv/ ,|&| at cd \XV/ exhibit whitenesse by their coincidence & again appeare severall at {illeg} \γξ/, but yet in a contrary order to that which they had before & still retaine beyond e & f. But on the other side at ab, ab, or αβ these colours must become much more confused by being dilated & spread so as to interfere with those of the other orders. And the same confusion will happen at {illeg} \γξ/ between e & f if the refraction be very great, or the Prism very distant from the Object-Glasses: in w^ch case no parts of the Ring will be seen save onely two little a|A|rcs at e & f whose distance from one another will be augmented by removing the Prism still further from the Object-Glasses. And these little Arcs must be distinctest & whitest at their Middle, & at their ends where they begin to grow confused they must be coloured. And the colours at one end of every Arc must be in a contrary order to those at the other end, by reason that they crosse in the intermediate white. Namely their ends w^ch verge towards {illeg} \γξ/ will be red & yellow on that side next the center, & blew & violet on the other side. But their other ends w^ch verge from {illeg} \γξ/ will on the contrary be blew & violet on that side towards the center & on the other side red & yellow.

For confirmation of all this I need alledg no more than that it is Mathematically demonstrable from my former Principles. But yet I shall add that thay which please to take the paines, may by the Testimony of their senses be assured that these explications are not Hypotheticall but infalibly true & genuine |Now as all these things follow from y^e properties of light of a mathematical way of reasoning so the truth of them may be manifested by experiments.| For in a dark Room by viewing these Rings through a Prism by reflexion of the severall Prismatique colour w^ch an Ast|s|istant causes to move to & fro upon a wall or paper from whence they are reflected, whilst the spectators eye, the Prism and the Object glasses (as in the 12|3|^th Observation) are placed steddy: the position of the circles made successively by the severall colours will be found such in respect of one another as I have described at \in the figures/ abx{illeg}v, or abX{illeg}V, or αβ{illeg}|ξγ|. And by the same method y^e truth of y^e explications of other Observations is {as} \may/ be examined.

By what hath been said, the like Phænomena of water b|B|ubbles \of water/ & thin Plates of Glasse may be understood. But in small fragments of those Plates, there is this further observable, that {if} \when/ lying flat upon a Table be \are/ turned about their centers whilst they are viewed through a Prism \they will in some postures exhibit waves of various colours &/: {the} {illeg} some of them \{will}/ \do/ exhibit \these/ waves in one or two {illeg} onely; but the most of them do \do/ in all positions exhibit {illeg} {illeg} & that for \{illeg} thin {illeg}/ the most part appeare {illeg} almost all {illeg} <511r> the Glasse \plates/. The reason is that the superficies of such Plates are not eaven but have many cavities & swellings w^ch how shallow soever do a little vary the thicknesse of the Plate: {illeg} \For {illeg} at/ the severall sides of those cavities \for the reasons newly described/ there {illeg}|ought|{illeg} to be produced waves in severall postures of the Prism. Now though it be but some very small & narrow parts of the Glasse by which these waves for y^e most part are caused, yet they may seem to extend themselves over the whole Glasse, because from the narrowest of those parts there are colours of severall orders \that is of rings several rings/ confusedly reflected, w^ch by refraction of the Prism are unfolded & \separated &/ \according to their degrees of refraction,/ dispersed to severall places so as to constitute so many sev{illeg}|e|rall waves as there were divers orders of the colours prom{illeg}|i|scuously reflected from that part of the Glasse.

These are the principall Phænomena of thin Plates or Bubbles whose explications depend on those properties of light t|w|hat|ich| I have heretofore di|e|livered. And these you see do necessarily follow from them & agree{illeg} with them even to their very least circumstances; & not onely so, but do very much tend to their proof. Thus by the 24^th Observation it appeares that the rays of severall colours made as well by thin Plates or Bubbles as by the refractions of a Prism have severall degrees of refrangibility whereby those of each order w^ch at their reflexion from the Plate or Bubble are intermixed with those of the other ort|d|ers, are separated from them by refraction, & associated together so as to become visible by themselves like {illeg}|A|rcs of Circles. For if the rays were all alike refrangible, tis impossible that the whitenesse w^ch to the naked sense appeares uniforme should \by refraction/ have its parts transposed & ranged into those black & white Arcs.

It appeares also that the unequall refractions of difform rays proceed not from any contingent irregularity|ies|: Such as are Veines an uneaven polish, or fortuitous position of the po{illeg}|r|es of Glasse; unequall \& casual/ motions in the Air or Æther; \the/ spreading, breaking, or dividing the same ray into many diverging parts; or the like. For admitting any such irregularities, it would be impossible for refractions to render those Rings so very distinct & well defined as they doe in the 24^th Observation. It is necessary therefore that every ray have its proper & constant degree of refrangibility connate with it, according {illeg}|t|o w^ch its refraction is ever justly & regularly performed; & that severall rays have severall of those degrees.

And what is said of their r|R|efrangibility may be also understood of their r|R|eflec|x|tibility; that is of their dispositions to be reflected <511v> some at a greater & others at a lesse thicknessesse of thin Plates or Bubbles namely that those dispositions are also connate with the rays & immutable; as may appeare by the 13^th 14^th & 15^th Observations compared with the 4^th &18^th.

By the precedent Observations it appeares also that whitenesse is a dissimilar mixture of all colours, & that light ia a mixture of rays indued with all those colours. For considering the multitude of the Rings of colours in the 3^d, 12^t, & 24^th Observations, it is manifest that although in the 4^th & 18^th Observations there appeare no more then 8 or 9 of those Rings, yet there are really a far greater number w^ch so much interfere with one & mingle wi{illeg}|t|h one another as after those 8 or 9 revolutions to dilute one another wholly & constitute {illeg}|a|n eaven & uni sensibly uniforme whitenesse. And consequently that whitenesse must be allowed a mixture of all colours, & the light w^ch conveys it to the eye must be a mixture of th rays indued with all those colours. This I beleive hath seemed the most Paradoxicall of all my assertions, & met with the most universall & obstinate Prejudice;|.| b|B|ut to me it appeares as infallibly true & certaine, as it can seem extravagant to others. For hitherto I never tryed any way to mix all colours by which I could not in some degree or other produce whitenesse, & yet I have made as many tryalls as I could excogitate ways of mixing colours; of w^ch I may take occasion to discourse hereafter.

But further by the 24^th Observation it appeares that there is a constant relation between c|C|olours & r|R|efrangibility, the most refrangible rays being Violet, the least refrangible Red, & those of intermediate colours having proportionally intermediate degrees of refrangibility. And by the 13^th, 14^th, & 15^th Observations compared w^th the 4^th {illeg}|or| 18^th, there appeares to be the same constant relation between c|C|olour & r|R|eflect|x|ibility, the Violet being {illeg} on equall termes \in like circumstances/ reflected at least thicknesses of any thin Plate or Bubble, y^e Red at greatest thicknesses, & the intermediate colours at intermediate thicknesses. Whence it follows that the colorifique dispositions of rays are also connate with them & immutable, & by consequence that all the productions & appearances of colours in the world are derived not from any Physicall change caused in light by refraction or reflexion, but onely from the various mixtures or separations of rays by vertue of their different r|R|efrangibility or Reflex{illeg}ibility. And in this respect it is that the Science of colours becomes a Speculation |as truly Mathematical as any other part of Optiques.| more proper for Mathematicians then naturalists. & deserves rather to be esteemed Mathematicall then Physicall, as I told you in my former letter, & may hereafter explane more fully.

The third p|P|art
Conclusions drawn from y^e foregoing Observations.

I am now come to the \another/ last part of thi{illeg}|s| desi{illeg}|g|ne w^ch is to consider how the Phænomena{illeg} of thin transparent Plates stand related to those of all other naturall bodies. Of these bodies I have already told you that they appeare of divers colours accordingly as they are \originally/ disposed to reflect \the rays indued with/ those colours most copiously the rays \originally disposed/ indued with those colours. But their constitutions whereby they reflect some rays more copiously then others remaines {illeg}|t|o be inquired after. And \discovered, &/ these I shall endeavour \to manifest/ in the following Propositions.

Prop: 1. Those superficies \of transparent bodies/ reflect the greatest quantity of light w^ch have the greatest refracting power; that is, w^ch \intercede Mediums that/ differ most in their refractive densities: And in the confines of equally dense |refracting Mediums there is no {illeg} reflexion.|

The Analogy between reflexion & refraction will appeare by considering that when light passeth obliquely out of one Medium into another which refracts from the Perpendicular, the greater is the difference of their \refractive/ density the lesse obliquity is requisite to cause a totall reflexion|.| ; because \For/ as the sines are w^ch measure the refraction, so is the sine of incidence at w^ch the totall reflexion begins; to y^e Radius of y^e Circle, & consequently that incidence is least whe{illeg}|r|e there is the greatest difference of the sines. Thus in the passing of light out of water into Air where the refraction is measured by the ratio of the sines 3 to 4 the totall reflexion begins when the angle of incidence is about 48^degr 35^min. In passing out of Glasse into Air where the refraction is measured by the ratio of y^e sines 20 to 31 the totall reflexion begins when the angle of incidence is 40^degr 10^min. And so in passing out of the Chr|i|stall or more strongly refracting Mediums into Air, there is still a lesse obliquity requisite to cause a totall reflexion. Superficies therefore w^ch refract most do soonest reflect all the light, which is incident on them, & so must be allowed most strongly reflec|x|tive.

But the truth of this Proposition will fu{illeg}|rth|er appeare by observing that in the superficies interceding any two of these \transparent/ Mediums |(|\such as are/ Air, Water, or \any/ other liquors, \oyle/ Common Glasse, Chri|y|stall, & Metalline Glasses \Island glass, {illeg}|w|hite transparent Arsnick, Diamonds &c/,) the reflexion is stronger or weaker accordingly as the superficies hath a greater or lesse refracting power. Thus when other Mediums are contiguous to Air; the reflexion is stronger in the superficies of Glasse then of Water, still stronger in the superficies of Chri|y|stall & strongest in the superficies of Metalline Glasse. So in the confine of Water & common Glasse the |For I|i|n the confine of Air & common glass y^e reflexion is stronger then in the confine of air & water & still stronger in the confine of a|A|ir & c|C|rystal & stronger in the confine of Air & a Diamond. {illeg} {illeg}|I|f any of these solids be immer & such like transparent solids be immerged in water or oyle or \in/ spirit of wine or {illeg}|s|pirit of Turpentine its {beco} reflexion becomes much weaker then before, & still weaker if they be immer| <512v> ged in that denser {illeg} |y^e| heavy liquor of {illeg}well{illeg} rectified oyle of {illeg} Vitriol w^ch \differs less from them in density/ If water be distinguished into {illeg} two parts by any imaginary surface; the refle reflexion is very weake, but yet stronger then in the confine of water & oyle or almost any other two liquors, & still stronger in the confine of water & Chri|y|stall or Metalline Glasse: accordingly as those Mediums differ more or lesse in density. So | {illeg} /reflexion\ in that|e| confine of those two parts is none at all: in the confine of water & ice tis very little, in that of water & oyle tis something greater, in that of water & glass still greater & in that of water & crystal or other denser substances still greater, accordingly as those {illeg} mediums differ more or less in density. {illeg}|H|ence| in the confine of common Glasse & Chri|y|stall there ought to be /a\ weake reflexion & a stronger reflexion in the confine of common & Metalline Glasse \tho I have not yet tried this:/ But in the confine of two Glasses of equall density, there is not any sensible reflex{illeg}|iō| as was shown in y^e 1^st Observation. And the same may be understood of the superficies interceding two chri|y|stalls or li{illeg}|quo|rs or any other substances in w^ch no refraction is caused. Whence it comes to passe that \So then the reason why/ uniforme \pellucid/ Mediums \(such as water glass or crystal)/ have no sensible reflexion but in their externall superficies where they are adjacent to other Mediums of a different density, is because \all/ their contiguous parts have /one & the same degree of density\{illeg}.

Prop 2. The least parts of \almost all/ naturall bodies are in some measure transparent. And the opacity of those bodies ariseth from the multitude of reflexions caused in their internall \transparent/ parts.

That this is so \has been observed by others &/ will e{illeg}|a|sily be granted by them that have been conversant with Microscopes. And it may also be tryed by applying any substance to a hole through w^ch some light is immitted into a dark Room. For how opake soever that substance may seem in the open Air, it will by that meanes appeare very manifestly transparent if it be of a sufficient thinnesse. Only \white/ Metalline Bodies must be exce{illeg}pted w^ch by reason of their excessive density seem to reflect almost all the light incident on their first superficies, |unless by solution in menstruums they be reduced into very small particles, & then they become transparent.|

Prop: 3. Between the parts of opake or coloured bodies are many interstices \spaces, either empty or/ replenished with Mediums of other densities: as water between the tinging corpuscles wherewith any liquor is impregnated; Air between the aqueous globules that constitute Clouds or mi{illeg}|sts| \mists/; & for y^e most part spaces voyd of both Air & Water but yet perhaps replenished w^th some Subtiler Medium \in some measure not wholy void of all substance./ between the parts of naturall \hard/ bodies.

The truth of this is evinced by the two precedent Propositions For by the second Proposition there are many reflexions from \made by/ the internall parts of Bodies, w^ch, by the 1^st Proposition would not happen if the parts of those bodies were cōtinued without any such interstices between them, because reflexions are caused onely in superficies w^ch intercede Mediums of a differing density. \by Prop 1/ But further that this discontinuity of parts is the principall cause of the opacity of Bodies will appeare by considering that {illeg} opake{illeg} substances become transparent by filling their pores with any <513r> substance of equall or almost equall density with their parts. Thus Paper dipped in water or oyle, the Oculus Mundi stone steeped in water, Linnen cloth oyled or varnished, {illeg} & many other substances soaked in such Liquors as will intimately pervade their little pores become by that meanes more transparent then otherwise. So on the contrary the most transparent substances may by \evacuating their pores or/ separating their parts be rendered sufficiently opake, as \salts or wet paper or the Oculus mundi stone by being dried, horn by being scraped,/ Glasse by being reduced to pouder or otherwise flawed, \turpentine by being stirred about with water till they more imperfectly/ {illeg} & water by being formed into many small bubbles either alone in the forme of froth, or by shaking it together \either/ with Oyle of Turpentine or \w^th/ some \w^th/ other convenient Liquor w^th w^ch it will not {illeg} \perfectly/ incorporate|.| & Horne by being scraped.

|And| To the increase of the opacity of these bodies it conduces something that by the 23^rd Observation the reflexions of very thin transparent substances are considerably stronger then those made by the same substances of a greater thicknesse. |[|And to the reflexion of solid bodies it may further add, that the interstices of their parts are voyd of Air. For that for the most part they are so is reasonable to beleive considering the ineptitude w^ch Air hath to pervade small cavities as appeares by the ascension of water in slender glasse pipes, paper, cloth & other such like substances whose pores are found too small to be replenished w^th Air, & yet large enough to admit water; & by the difficulty wherewith Air pervades the pores of a Bladder through w^ch water finds ready passage. And according to y^e 11^th Observation the cavities thus voyd of Air will cause the same kind of effects as to reflexion w^ch those do that are replenished with it, but yet something more manifestly because the Medium in relation to refractions is rarest when most empty of Air as M^r Hook hath proved in his Micrographia. In w^ch Book he hath also largely discoursed of this & the precedent Proposition, & delivered many other very excellent things concerning the colours of thin Plates & other naturall Bodies w^ch I have not scrupled to make use of so far as they were for my purpose.]

Prop: 4. The parts of bodies & their interstices must not be lesse then of some definite bignesse to render them opake & coloured. For the opakest bodies of their parts be subtily divided (as Metall{s} by being dissolved in Acid Menstruums, &c) become perfectly transparent. And you may also remember that in the 8^th Observation there was no \sensible/ reflexion at the superficies of the Object-glasses where they were very neare one another though they did not absolutely touch. And in the 17^th Observation the reflexion of the Water-bubble <513v> where it became thin\n/est, was almost insensible so as to cause the apparitions of very black spots to appear on y^e top of the bubble by the want of reflected light.

On these grounds I conceive it is that water, salte, glasse, stones & such like substances are transparent. For upon divers Considerations they seem to be as porous \full of pores or {illeg} interstices between their parts/ as other bodies \are/, but yet their parts \& parts/ \& interstices to be/ too smal{illeg}|l| to cause any opacity reflexions in their common surfaces.

Prop: 5. The transparent parts of bodies according to their severall sizes must reflect rays of one colour & transmit those of another, on the same grounds that thin Plates or Bubbles doe reflect or transmit those rays. And this I take to be the ground of all their colours.

For if a \thind or/ plated Body w^ch being of an e{illeg}|a|ven thicknesse appeares all over of one uniforme colour should be \slit into threds or/ broken into fragments of the same thicknesse with the Plate,. I see no reason why a heap of those \threds or/ fragments should not constitute a \masse or/ pouder of y^e same colour w^ch the Plate exhibited before it was broken. And the parts of all naturall bodies being like so –– many fragments of a Plate must on the same grounds exhibit the same colours.

Now that they doe so will further appeare by the affinity of their Properties. As that the infusion of Nephritic Wood \Lignum Nep{illeg}|hriti|cum/ & many other substances reflect one colour & transmit another like thin bodies in the 19^th & 20^th Observations. That the colours of Silks, Cloths, & other substances w^ch water or Oyle can intimately penetrate become more faint & obscure by being im̄erged in those liquors, & recover their vigor again by being dryed much after the manner declared of thin Bodies in the 10^th & 21^th Observations. And that some of those coloured pouders w^ch Painters use may have their colours a little changed by being very elaborately & finely ground. Where I see not what can be justly pretended for those changes besides the breaking of their parts into lesse parts by that contrition after the same manner that the colour of a \thin/ Plate is changed by varying its thicknesse. For which reason also it is that y^e many \coloured/ Flowers \of Plants & vegetables/ by being bruised \usually/ become more transparent then before, or at least in some degree or other change their colours. Nor is it much lesse to my purpose that by mixing divers liquors very odd & remarqueable productions & changes of colours may be effected, of w^ch no cause can be more obvious & naturall \rationall/ then <514r> y^t the saline corpuscles of one liquor do variously act upon or unite with the tinging corpl|u|scles of another, so as to make them swell or shrink (whereby not onely their bulk but their density also may be changed,) or to divide them into smaller corpuscles, or make many of them associate into one cluster. For we see how apt those saline Menstruums are to penetrate & dissolve substances to w^ch they are applyed & some of them to precipitate what others dissolve. In like manner if we consider the various Phænomema of the Atmosphære, we may observe that when vapors are first raised, they hinder not the transparency of the Air, being divided into parts too small to cause any reflexion in their superficies. But when in order to compose drops of rain they begin to coalesce & constitute globules of all intermediate sizes, those globules when they become of a convenient size to reflect some colours & transmit others, may constitute clouds of various colours according to their sizes. And I see not what can be rationally conceived in in so transparent a substance as water for the production of these colours besides the various sizes of its \fluid & globular/ parcells, |[|w^ch seem to affect a globular figure most; but yet \perhaps/ not without some irregularity instability in the{illeg} figure smallest of them by reason that those are most easily agitated by heat or any trembling motions in y^e Air.|]|

Prop: 6. The parts of Bodies on w^ch their colours depend are denser then the Medium w^ch pervades their interstices.

This will appeare by considering that the colour of a Body depends not onely on the rays w^ch are incident perpendicularly on its parts, but on those also w^ch are incident at all other angles. |And| that according to y^e 7^th Observation a very little variation of obliquity will change y^e reflected colour where the thin body or small particle is rarer then the ambient Medium, insomuch that such a small particle will at diversly oblique incidences reflect all sorts of colours in so great a variety that the colour resulting from them all confusedly reflected from a heap of such particles must rat{illeg}|he|r be a white or dirty grey then any other colour, or at lea|be|st it must be {some} but a very imperfect & dirty co{illeg}|lou|r. Whereas if the thin Body or small particle be much denser then the ambient Medium, the colours according to the 19^th Observation are so little changed of the variation of obliquity, that the rays w^ch are reflected least obliquely may predominate over the rest so much as to cause a heap of such particles to appear very intensely of their colour. It condu{illeg}|ce|s also something to \the confirmation of/ this Proposition that according <514v> to the 22^th Observation, the colours {illeg}|ex|hibited by the denser thin body within the rarer are more bris then those exhibited by therrarer {sic} within the denser.

Prop: 7. The bignesse of the component parts of Naturall Bodies may be conjectured by their colours.

For since the parts of these bodies by Prop: 5 doe most probably exhibit the same colours with a Plate of equall thicknesse, provided they have the same refractive density; & since their parts seem for y^e most part to have much the same density with water or glasse, as by many circumstances is obvious to collect: to determin the sizes of those parts you need onely have recourse to the precedent Tables in w^ch the thicknesse of Water or Glasse exhibiting any colour is expressed. Thus if it be desired to know the diameter of a corpuscle w^ch being of equall density with glasse shall reflect Green of the third order; the number $17\frac{1}{2}$ shows it to be about $\frac{17\frac{1}{2}}{1000000}$ parts of an inch.

The greatest difficulty is here to know of what order the colour of any Body is. And for this end we must h{illeg}|a|ve recourse to the 4^th & 18^th Observations from whence may be collected these particulars

Scarlets & other Reds, Oranges & Yellows if they be pure & intense are most probably of the second Order. Those of the first & third order {illeg}|a|l{illeg}|s|o may be pretty good, onely the \yellow of the first order is faint & the/ Orange & Red of the third order hath|ve| too|a| great a mixture of Violet & Blew.

There may be good \{illeg}/Greens of the fourth order but the purest are of the third. And of this order the Green of all Vegetables seemes to be, partly by reason of the intensenesse of their colours, & partly because when they wither some of them turne to a greenish Yellow, & others to a more perfect Yellow or Orange or perhaps to Red, pa{illeg}|ss|ing first through all the affore said intermediate colours. Which changes seem to be effected by the exhaling of the moisture w^ch may leave the tinging corpuscles more dense, & something aumented by the accretion of the oyly & earthy part of that moisture. Now the Green without doubt is of the same order with those colours into w^ch it changeth because the changes are graduall, & those colours though usually not very pure \full/ yet for the most part are \often/ too pure \full/ & lively to be of the fourth order.

Blews & Purples may be either of the second or third order But the best are of the third. Thus the colour of violets seems to be of that order becaus their Syrup by acid liquors turnes red <515r> and by urinous & alcalizate turne green. For since it is of the nature of acids to dissolve or attenuate, & of Alcalies to to precipitate or incrassate, if the purple colour of y^e Syrup was of the second order, as acid liquor by attenuating its tinging corpuscles would change it to a red of the first order, & an Alcaly by incrassating them would change it to a green of the second order; w^ch red & Green, especially the Green, seem too imperfect to be the colours produced by these changes. But if the said purple be supposed of the third order, its change to red of the second & green of the third may without any inconvenience be allowed

If there be found any body of a deeper & lesse reddish purple then that of Violets its colour most probably is of the second order. But yet there being no body commonly known whose colour is constantly more deep then theirs, I have made use of their name to denote the deepest & least reddish Purples, such as manifestly transcen{illeg}|t| their colour in purity.

The Blew of the first Order though very faint & little may possibly be the colour of some substances. And particularly the Azure colour of the skys seems to be of this order. For all vapors when they begin to condense & coalesce into small parcells become first of that bignesse whereby such an Azure must be reflected before they can constitute clouds of other colours. And so this being the first colour w^ch vapors begin to reflect, it ought to be the colour of the finest & most transparent Skys in w^ch vapors are not arrived to that gross|n|esse requisite to reflect other colours as we find it is by experience.

Whitenesse if it be intense is either \the most intense & luminous is/ that in the first order of colours. of w^ch sort perhaps is the colour of white Lead \For of this sort I take the colour of white metals to be/; or else it is a mixture of those succeeding the third or fourth order, such as is the colour of paper linnen, & most white substances. If corpuscles of various sizes exhibiting the colours of the second & third order be mixed, they should rather constitute an imperfect whitenesse or Grey of w^ch I have already spoken. But yet it seems not impossible for them to exhibit an intense whitenesse if they be disposed to transmit all the light w^ch they reflect not, & do not retain & stifle some \much/ of it For thus I told you that Froth at a distance hath appeared \very/ white & yet neare at hand the severall Bubbles of w^ch it was constituted were seen tinged all over with rings of colours of the four or five first orders.

Lastly for the production of Black the corpuscles must be lesse then any of those w^ch exhibit colours. For at all greater sizes there is too much light reflected to constitute this colour. But if they be <515v> supposed a little lesse then is requisite to reflect the \white & very faint/ blew of the first order they will according to the 4^th, 8^th, 17^th, & 18^th Observations reflect so very little light as to appeare intensely blac{illeg}|k|, & yet may perhaps varioub|l|ly refract it to & fro with in themselves so long untill it happen to be stifled & lost, {illeg}|b|y w^ch means they will appear black in all positions of the eye without any transparency. And from hence may be understood why Fire & the more subtile dissolver Putrefaction turne substances to black; why small quantities of black substances impart their colour very freely & intensely to \other/ substances to w^ch they are applied; ^x why Glasse ground very elaborately with sand on a Copper plate till it be well polished makes the sand together with what is worne of from the glasse & Copper become very black; why black substances do soonest of all others become hot \in y^e sun's light/ & {illeg} {for} burne, (w^ch effect may proceed partly from y^e multitude of refractions in a little room, & partly from the easy commotion of so very small corpuscles;) & why blacks are usually a little inclined to a blewish colour. For that they are so may be seen by illuminating white paper by reflexion \light reflected/ from black substances, w^ch \For the paper/ will usually appeare of a blewish white. And the reason is that Black borders on the obscure Blew described in of y^e first order. \{illeg}/ described in the 18^th Observation, the {larger} \& therefore the/ corpuscles of black substances {illeg} are most apt to reflect that colour \reflects more rays of that colour then of any other./

In these descriptions I have been the more particular because I hope \it is not imposible but/ that Microscopes will \may/ at length be improved to the discovery of the corpuscles /particles\ of Bodies on w^ch their colours depend \if they are not already in some measure arrived to that degree of perfection/. For if those Instruments \are or/ can be so far improved as with sufficient distinctnesse to represent Objects five or six times hundred times bigger then at a foot distance they appear to o^r naked eyes, I should hope that we might be ap|b|le to discover some of the greatest of those corpuscles. And by one that would magnify thre or four thousand times perhaps they might all be discovered but those which produce blacknesse. In the meane while I see nothing materiall that \in this discourse that/ rationally \may/ be doubted of excepting this p|P|osition, That transparent corpuscles of the same thicknesse & density with a Plate, do exhibit the same colour. And this I would have understood not without some latitude, as well because those corpuscles may be of irregular figures, & many rays must be obliquely incident \on them/, & so have a shorter way through them then the length of their diameters, as because the straitnesse of the Medium pent in on all sides w^ch in such corpuscles may a little after its motions or other qualities on w^ch the reflexion depends. But yet I cannot much suspect the last because I have observed of some small Plates of Moscovy-Glasse w^ch were of an e{illeg}|a|ven thicknesse, that through a Microscope they have appeared of the same colour at their edges & corners where the included <516r> Medium was terminated, w^ch they appeared of in other places. However it will add much to o^r satisfaction if those corpuscles can be discovered with Microscopes, w^ch if we shall at length attain to I feare it will be the utmost improvement of this Sense. For it seems impossible to see the more secret & noble works of Nature within those corpuscles by reason of their transparency.

This may suffice concerning the constitution of naturall bodies on w^ch their colours depend. But for further understanding the nature of reflexions I shall add these two following Propositions.

Prop: 8. The cause of Reflexion is not the impinging of Light on the solid par or impervious parts of bodies, as is commonly supposed. beleived.

This will appear by the following Considerations. First that in the passage of light out of Glasse into Air there \is a/ reflexion is as strong or stronger then \as/ in its passage out of a|A|ir into Glasse \or rather a little stronger/ & by many degrees stronger then {illeg} \stronger then/ in its passage out of Glass into w|W|ater. {illeg}|An|d it seems not probable that Air should have more reflecting parts then water of Glass. But if that should possibly be supposed \yet/ it will availe nothing: for the reflexion is as strong or stronger th|w|hen the Air is drawn away from the Glass, (suppose in y^e Air-Pump invented by M^r Boyle,|)| as when it is adjacent to it. Secondly if light in its passage out of Glass into Air be incident more obliquely then at an angle of 40 or 41 degrees it is wholly reflected, if lesse obliquely it is in great measure transmitted. Now it is not to be imagined that light at one degree of obliquity should meet with pores enew in the Air to transmit the greater part of it, & at another degree of obliquity \should/ meet with nothing but parts to reflect it wholly: especially considering that in its passage out of Air into Glass, how oblique soever be its incidence, it finds pores enew in the Glass to transmit the greatest part of it. If any man suppose that it is not reflected by the Air but by the outmost superficiall parts of the Glasse, there is still the same difficulty: besides that such a supposition is unintelligible, & will also appear to be false by applying water behind some part of y^e Glasse instead of Air. For so in a convenient obliquity of the rays suppose of 45 or 46 degrees at w^ch they are all reflected where the Air is adjacent to the Glass, they shall be in great measure transmitted where the water is adjacent to it: w^ch argues that their reflexion \{illeg}/ or transmission depends on the constitution of the Air & water \behind the glass & not on their parts striking \of y^e rays/ upon the parts of the glass/. Thirdly if the colours made by a Prism placed at the entrance of a beam of light into a darkened Room be successively cast on a second Prism placed at a great distance from the former, in such manner that they are all alike incident upon it the second Prism may be so inclined <516v> to the incident rays that those w^ch are of a {illeg}|b|lew colour shall be all reflected by it, & yet those of a red colour pretty copioul|s|ly transmitted. Now if the reflexion be caused by the parts of Air or Glass I would ask why at the same obliquity of incidence the b|B|lew should wholly impinge on those parts so as to be all reflected, & yet the red find pores enew to be in great measure transmitted Fourthly where two Glasses touch one another there is no sensible reflexion as was declared in the 1^st Observation; & yet I see no reason why the rays shoud {sic} no{illeg}|t| impinge on the parts of Glass when contiguous to another Glasse as much as when contiguous to Air. Fiftly when the top of a water-Bubble (in the 17^th Observation) by the continuall subsiding & exhaleing of the water grew very thin there was such a little & almost insensible quanti{illeg}|t|y of light reflected from it that it appeared intensely black, whereas round about that black spot where the water was thicker the reflexion was so strong as to make the water seem very white. Nor is it onely at the least thicknesse of thin Plates or Bubbles that there is no manifest reflexion but at many other thicknesses continually greater & greater. For in the 15^th Observation the rays of the same colour were by turnes transmitted at one thicknesse & reflected at another thicknesse for an indeterminate number of successions. And yet in the superficies of the thinned Body where it is of any one thicknesse there are as many parts for the rays to impinge on, as where it is of any other thicknesse. Lastly \Lastly/ if reflexion were caused by the parts of reflecting bodies it would be impossible for thin Plates or Bubbles at the same place to reflect the rays of one colour & transmit those of another as they do according to the 13 & 15 Observations. For it is not to be imagined that at one place the rays w^ch for instance exhibit a blew colour should have the fortune to dash upon the parts & those w^ch exhibit a Red to hit upon the pores of t{illeg}|h|e Body; & then at another place where the body is either a little thicker or a little thinner, that on the contrary the b|B|lew should {illeg}hit upon its pores & the Red upon its parts. |Lastly were y^e rays of light reflected by impinging on the solid parts of bodies, their reflexions from polished bodies could not be so regular as they are. For ✝|

Prop. 9. Tis most probb|a|ble that the rays w^ch impinge on the solid parts of any body, are not reflected but shifted & lost in th{illeg}|e|{illeg} body.

This is consentaneous to the precedent Proposition & will further appear by considering that if all the rays should be reflected which impinge on the internall parts of clear water or c{illeg}rystall, those substances should rather have a cloudy \colour/ then so very clear <517r> transparency. And further there would be no Principle of the obsc obscurity or blacknesse w^ch some bodies have in all positions of the eye. For to produce this effect |For if \all or almost all/ the light after in{illeg}|c|ident on those bodies did after many reflexions \& refractions/ come out again it would make those bodies as lucid as other bodies are {illeg} \are/, & therefore to make them look black| it is necessary that many rays be retained |stopt| \retained/ & lost in {illeg} the |them| body|ies|, & it seems not probable that any rays can be retained \{illeg}/ stopt & retained \stifled/ in it|them| w^ch do not impinge on its \their/ parts

If you now ask how rays are reflected without impinging on the parts of a body, & how those w^ch impinge on its parts may be stopped & stifled, it requires an Hypothesis to explaine it by|.| , the description of w^ch is besides my designe. And so th{illeg}|e| manner how severall rays are unequally refrangible & reflec|x|tible, & \originally/ indued with severall \p{illeg}|o|wers of striking y^e sense w^th several/ colours remaines to be explained Hypothetically: But I shall content my self with haveing she|o|wn that de facto the rays of light are \really/ indued with those properties. And the inventing of such an Hypothesis is no part of my designe I undertoo>t|k| only to discover y^e properties of light so far I as I could derive them from experiments; & therefore content my self w^th having shewn that y^e rays of light are endued w^th such properties \the prop{illeg}/ those properties.