Draft of the 'Hypothesis Concerning Light and Colors'

<475r>

S^r

I have sent you y^e papers I mentioned, by Iohn Stiles. Vpon reviewing them I find somethings {sic} so obscure as to need a further explication by figures, & some other things I guess will not be new to to you though almost all was new to me when I wrote them: but {illeg}|{as}| they are I hope you will accept of them though not worth y^e ample thanks you sent. I remember in some discourse w^th M^r Hook I happend to say that I thought light was reflected not by y^e parts of glass water air or other sensible bodies, but by that same superficies of y^e æthereal Mediums w^ch refracts \it/ y^e rays y^t happen to break through it, y^e rays finding some difficulty to break through it in passing out of denser æther into rarer & a greater difficulty in passing out of y^e rarer into y^e denser, & so being either reflected or refracted by y^e superficies as y^e circumstances they happen{d} to be in at their incidence ma{illeg}|k|e 'em \unable or/ able to break through it. And for confirmation of this I added \said further/ tha{illeg}|t| I thought {illeg}|th|e refract|flex|ion of y^e light at its tending out of glass into air would not be diminisht or weakend at its passing by drawing away y^e air in M^r Boyles an air Pump as it ought to be if they were y^e parts of y^e air y^t reflected {illeg}|it||:| But|And| \added/ that I had not tryed this experiment; {illeg} \but/ thought he was not unacquainted w^th notions of this kind. To w^ch he replied that y^e notion was new & y^t he would y^e first opportunity try y^e experiment I propounded. But upon reviewing y^e papers I send you, I find|ound| it there set down for tryed; w^ch mad|k|e|s| me recollect that some years ago I had occasionally observed in an Air Pump here at Christs College y^t I could not perceive y^e reflexion {illeg}|of| y^e inside of y^e glass diminished by drawing out y^e air. {illeg}|This| I thought fit to mention least my former forgetfulness should seem to make me \seem to have/ set down for certain what I had not \never/ tryed.

S^r I had formerly determined \purposed/ never to write any Hypothesis of \light &/ colours, fearing it might be a means to ingage me in vain disputes: but I hope I need not fear y^t if it proceed no further then to y^e ears of y^e Society. Considering therefore that such an Hypothesis will much illustrate y^e papers I send {illeg} you; I shall not longer scruple to describe one so far as it may be done in this cursory letter: not concerning my self whether it \shall/ be thought probable or improbable so it do but render y^e papers I send you more intellegible

<475v>

First then I suppose \in this Hypothesis it is to be supposed/ y^t there is an æthereal Medium much of y^e same constitution w^th air but only \far/ more rare more subtile & more strongly elastic|: And of y^e existence of this Medium y^e motion of a pendulum in M^r Boyles a glass exhasted of air almost as quickly as in y^e open air is no inconsiderable arguments.|

.2. I suppose this æther a vibrating m|M|edium like air, only y^e vibrations far more swift & minute; those of air made by a man's ordinary voice succeeding one another at a foot distance mo more then a foot distance, but those of æther at a less distance then y^e hundred thousandth part of an inch. And as in air y^e vibrations are some larger then others, {illeg} but yet all equally swift (for in a ring of bells y^e sound of every tone is heard at 3 or 4 miles distance, in y^e same order y^t y^e bells are stroke:) so I suppose y^e æthereal {illeg}|v|ibrations differ in bignes but not in swiftness.

3 As y^e air can pervade y^e bores of small glass pipes but yet not so easily as if they were wider, & therefore stands at greater |de|gree of rarity then in y^e free aereal spaces, & at so much a greater degree of rarity as y^e pipe is smaller, as is known by y^e rising of water in such pipes\to a much greater heigh {sic} then y^e surface of y^e stagnating water into w^ch they are dipt/: so I suppose æther, though it pervades the pores of crystal, glass, water {illeg}|&| other natural bodies, yet it stands at a greater degree of rarity in those pores then in the free æthereal spaces & at so much a greater degree of rarity as y^e pores of y^e body are smaller. And this I take to |Whence it may be y^t  for instance though a lighter body yet having subtiler ꝑts & consequently smaller pores then water is the more strongly refracting liquor.| /This also may\ be y^e principall cause of y^e cohesion of y^e parts of solids & {illeg}|fl|uids, & of y^e standing of y^e ☿ in y^e Torricellian experiment at a much greater height then 29 inches: For y^e denser æther w^ch surrounds these bodies must croud & press their parts together much after y^e same manner y^t y^t|^e| air surrounding two marbles presses them together if there be little or no air between them.

4 I suppose light is neither this æther not its \vibrating/ motion, but something of a different kind propagated from lucid bodies, whether it {illeg} be |an aggregate of peripatetic qualities or of unimagi{illeg}|b|ly {sic} small {illeg}|&| swift corpuscles {illeg} from {illeg}|lumi|nous bodies at g^t distances from one another. or any other corporeal emanation, or some motion of the æther of a differing kind from its vibrations it|f| any such can be imagind proper for this purpose, or an impuls or motion of some other medium dispersed through y^e æther For y^e air, vapors – For y^e air, vapours {sic}, exhalations electric & magnetic effluvia are all instances that there may be other various mediums diffused through y^e æther. {sic}| a corporeal emanation or an impuls o{illeg}|r| motion of some \other/ medium dispersed through æther like y^e magnetic or electric effluvia, or some motion of y^e æther of a differing kind from its vibrations if any such can be imagin'd \proper for this purpose/, or a peripatetic quality. To avoyd dispute \& make this Hyposesis {sic} general/ let every man here take his fancy. Only whatever it|light| be I would suppose it consists of successive rays differing from one another in some accidental \contingent/ circumstances, as b{illeg}|ig|nes form or vigour; like as y^e sands on y^e shore y^e waves of y^e sea \the faces of men/ & all other natural things of y^e same kind differ, it being almost impossible for any sort of things to be \found/ w^thout some contingent variety. And further I would suppose it divers from |y^e| æthereal vibrations becaus

[5 As there is a certain tenacity in y^e superficies of water more then in y^e inwards parts of either water or air so that dust or even y^e filings of a meta{illeg}|l| w^ch readily fall in either water or air will swim upon if thrown upon their common superficies: so I suppose there is a greater tenacity in y^e common superficies of a rarer & denser æther then in other places, so that y^e rays of light find some difficulty in passing through y^t superficies & are reflected or refracted or reflected accordingly as they can or cannot overcome that|e| difficulty. Yet this superficies I superficies I suppose to be not a mathematical one like y^t of water, but of some breadth, the æther{illeg} therein being of all intermediate degrees of rarity between y^e rarer & denser Mediums.

6 When y^e rays impinge upon this superficies {illeg}|I| suppose they cause vibrations in it as stones thrown into water do in its surface, & that these vibrations are propagated every way into both y^e rarer & denser Mediums as y^e vibrations of air w^ch cause sound, are from a stroke but yet continue strongest where they began, & alternately contract & dilate y^e æther in that physical superficies: ♀ w^ch superficies being thus continually agitated by vibration & the æther therein continually expanded & comprest by turns; if a ray of <476r> light impinge upon it while it is \much/ comprest, I suppose it is then too dense & {illeg}|stiffe| to let y^e ray pass through {illeg} & so it reflects it, but at|the| otherays that impinge on it at other times, go through & are refracted.

To explain this a little further you may consider how fluids when formed into thin shells or plates grow much more tenacious & tough then otherwise. Thus things \w^ch readily fall upon \in/ water if/ let fall upon a bubble of water \they/ do not so easily break through it as through y^e superficies of stagnating water , but are apt to {illeg}|sl|ide down by y^e sides of it if they be not too bigg & heavy. So if two well polished convex glasses grownd on \very/ large sh|p|heres be laid one upon another, the air between them easily recedes till they almost touch but then begins to resist so much that y^e weight of y^e upper glasse is too little to {illeg}|bri|ng together so as to make y^e black spot mentioned in these papers appeare in y^e middl|st| of y^e rings of colours; & if y^e glasses be plain though no broader then a two pence, a man w^th his whole strength is not able to press all y^e air out from between them so as to make 'em fully touch. You may observe also that Insects will walk upon water w^thout wetting their feet, y^e thin skin or shell between their feet & y^e water bearing them up & so motes falling upon water will often lye long upon it w^thout being wetted. And in like manner I suppose a ray in passing out of denser æther into rarer, when there remains between y^e ray of y^e rarer æther so little distance{illeg} to be part th\r/ough that y^e denser æther between them may be compared to a thin skin or shell, it finds much \some/ difficulty to get through this skin: & this skin bein the æther where this skin is being alternately expanded & comprest by y^e continuall \{illeg}/ vibrations wherewith 'tis continually agitated, the skin is {illeg} sometimes weak{illeg}|n|ed by y^e expansion sometimes strengthend & stifned by y^e compression & accordingly reflects or transmits \or reflects/ y^e ray.

When a ray finds the refracting superficies so much condensed that it cannot get through, so soon as the ray has spent its force upon y^e superficies in endeavouring to pierce it, y^e superficies by its elasticity returns back upon y^e ray as a racket upon a tennis ball, all y^e force it received & so reflects it at an angle equal to that of incidence. But if y^e superficies at y^e arrival of y^e ray be in a state of {illeg}|e|xpansion, or not so much condensed but y^t y^e ray can pierce it, then I suppose upon y^e rays departing into y^e next Medium the \superficies/ acts upon y^e {illeg} it & puts in adds more or less celerity to it according to y^e rarity of th{illeg}|a|t Medium; for the rarer y^e medium is w^ch y^e ray enters, y^e more easily does y^e ray yeild to y^e action of y^e superficies. To use a gross similitude y{illeg}|o|u{illeg} may conceive y^e action of y^e superficies upon y^e departing ray, to be something like that of a man's fingers darting a plumb-stone or other slippery body from between them by compressing it; for |]| {illeg}|W|hen a ray \therefore/ moves through æther of uneaven density, I suppose it may be \is/ most prest, {illeg} urged \or otherwise acted upon by the æther/ by y^e on that side towards y^e denser æther & {illeg} receives a continual impuls\or ply/ from that side \to recede/ towards y^e rarer, & {illeg} be \so is/ accelerated if it move that way or {is} retarded if y^e contrary. On this ground if a ray move obliquely through such an un\eavenly dense/ medium (that is obli{illeg}|q|uely to those imaginary superficies w^ch run through y^e \equally dens/ parts of y^{illeg}|^e| medium of equal density \& may be called y^e refracting superficies/,) it must be incurved, as {illeg} M^r Hook has \it is/ found it {sic} to be by observation \in water when lower parts were gradually made more salt & so more dense then y^e upper/ ^[1]. And this I take to /may\ be y^e gro{illeg}|u|nd of all refraction & reflexion: for \as the rarer air w^th a small glas pipe & y^e denser air w^thout are not disterminated by a mathematical superficies but the air between at y^e orifice of y^e pipe runs through all intermediate degrees of density so/ I suppose y^e refracting superficies of æther between unequally dense Mediums to be not a mathematical one but of some breadth y^e æther therein being of all intermediate degrees of rarity between y^e rarer & denser æthereal mediums, & y^t refraction I conceive to proceed from the continual incurvation of y^e ray all y^e while it is passing this physical superficies. Now if y^e motion of y^e ray be supposed in this passage to be incurved or diminished in a certain proportion according to y^e difference of y^e densities of y^e æthereal mediums, & y^e addition or detraction of y^e motion be reccond in y^e perpendicular frō y^e refracting superficies, the sines <476v> of incidence & refraction will be proportional according |to| w^t Cartes has demonstrated.

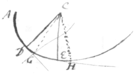
If|The| ray therefore in passing out of y^e rarer medium into y^e denser inclines \continually/ more & more towards y^e refracting superficies & if y^e differing densities of y^e mediums be not so great nor y^e incidence of y^e ray so obli{illeg}|| {illeg} {but that it} as to make it ∥ \to y^t superficies/ before it gets through, then it goes through & is refracted keeps its last inclination & is refracted, but if through y^e aforesaid causes y^e ray become ∥ to that superficies {illeg}|b|ef{illeg}|o|re it can get through, then it \must/ turns back & is|be| reflected. Thus for instance it may be observed that in a \triangular/ glas prism \OEF/ that {illeg}|y|^e rays \AN/ that tend out of |y^e refr. sup| glass into air, \do/ by inclining y^e|ⁿ| refracting superficies more & more to them, emerge more & more obliquely \as at NL/ till they be infinitely oblique y^t is in a manner ∥ to y^e refracting {illeg}|s|uꝑficis {sic} w^ch happens when y^e angle of incidence is about 60 \or 61/ gr. & then if y^e refracting superficies \they/ be a little more inclined y^e rays \they/ become all reflected, \as at Aνλ/ becoming I {illeg}|sup|pose ∥ to y^e superficies before they can get thro\u/gh it. For instance let ABCD represent y^e rarer Medium, EFHG y^e denser CDFE y^e space refracting physical superficies {illeg} space between them in|or| w^ch refracting physicall superficies in w^ch y^e æther is of all intermediate degrees of density from y^e rarest æther at CD to y^e densest at EF. AIKL a ray, AIN it {sic} incident part IK \MN/ its incurvation by y^e refracting superficies, & K|N|L its emergent part. Now if the ray AM become so much incurved as to become at its emergence K|N|, as neare\ly/ as may be ∥ to y^e refrac CD \or EF/, its plain y^t if y^t ray had been incident a little more obliquely \as is represented at Aμ/ it must have become parallel to CD before it had arrived at EF & so could never have got to \y^e outside of the refracting superficies/ EF but must have turnd back & been reflected as it is represented at Aμνλ. And y^e like would have happend if y^e density of y^e æther had further increased from EF to PQ so y^t PQHG might be a denser medium then EFHG was su{illeg}|ppo|sed, for then y^e ray in passing from m to n being so much incurved as \at n/ to become ∥ to CD or P{illeg}|Q|, its impossible it should ever get nearer to PQ but must at N begin by further incurvation to turn back & so be reflected. *○

This may be y^e cause \& manner/ of relexion when light passes out of \tend from/ y^e rarer into \toward/ y^e denser æther, but \to know/ how it should be reflected when it tends out of \from/ y^e denser into y^e rarer is more di{illeg}|ffic|ult to say; yet thus I explain it thus you are to consider how fluids neare their superficies are less pliant & yeilding then in their \more/ inward parts, & if formed into a thin plate or shel they become \much/ more stif & tenacious then otherwise. Thus things let fall –––– And {illeg}|s|o apply {æ} I suppose æther in y^e confine of two mediums is less pliant & yeilding then in other places {illeg}|&| |so| much y^e less pliant by how much y^e mediums differ more in density: so that if a ray in passing {illeg} through this {illeg} {cuticle} & so great difficulty where y^e mediums are of very differing density as to be reflected by incurvation \after y^e manner described above/: y^e parts of y^e æther on that side where they are less pliant & yeilding acting upon y^e ray much after y^e manner that thay would do were they \there/ denser on that side \there/ then on y^e other \side/ [whence if y^e superficies be not so unpliant but that y^e ray can get through it, \yet/ the ray must first becom bent from y^e perpendicular {illeg} incurved till it get to y^e most unpliant part of y^e superficies & |{illeg}| in moving further through y^e less \more/ pliant parts be unbent again & bent y^e contrary way by y^e greater density of y^e Medium y^e ray is moving out of.] And this I suppose {may} be y^e cause of the reflexion of Quicksilver & other metalline bodies. It must concur to increase y^e reflective virtue of y^e superficies when rays tend out of y^e dense /rarer\ into y^e denser. And in that case therefore therefore {sic} y^e reflex \y^e reflexion/ having a double cause <477r> \much/; after the same manner as if all the glass between B & D were broken off at B the obtuse angle of the Diamond cut.

Exempl. 2. In machinis mobilibus.

$\mathrm{Ca}\cdot \mathrm{ab}\colon\colon \mathrm{Cd}\cdot \mathrm{dg}=\frac{\mathrm{ab},\mathrm{Cd}}{\mathrm{Ca}}$. $\mathrm{AF}\cdot \mathrm{CF}\colon\colon \mathrm{Ab}\cdot \mathrm{ba}=\frac{\mathrm{CFAb}}{\mathrm{AF}}$. $\mathrm{Ca}\cdot \mathrm{ab}\colon\colon \mathrm{Cd}\cdot \mathrm{dg}=\frac{\mathrm{CF},\mathrm{Ab},\mathrm{Cd}}{\mathrm{Ca},\mathrm{AF}}$. $\mathrm{Ce}\cdot \mathrm{eD}\colon\colon \mathrm{dg}\cdot \mathrm{gD}=\frac{\mathrm{eD},\mathrm{CF},\mathrm{Ab},\mathrm{Cd}}{\mathrm{Ce},\mathrm{Ca},\mathrm{AF}}$. $\mathrm{Ab}\cdot \mathrm{Dg}\colon\colon \mathrm{Ce},\mathrm{CAa},\mathrm{AF}\cdot \mathrm{De},\mathrm{CF},\mathrm{Cd}$. $\ddot{\mathrm{CA}}\cdot \ddot{\mathrm{CD}}\colon\colon \mathrm{Ce},\mathrm{CA},\mathrm{AF}\cdot \mathrm{De},\mathrm{CF},\mathrm{CD}$. $\ddot{\mathrm{FA}}\cdot \ddot{\mathrm{CA}}\colon\colon \mathrm{CA}\cdot \mathrm{AF}$. $\ddot{\mathrm{FA}}¨\ddot{\mathrm{CD}}\colon\colon \mathrm{Ce},\mathrm{CAq}\cdot \mathrm{De},\mathrm{CF},\mathrm{CD}$. $\ddot{\mathrm{CA}}\cdot \ddot{\mathrm{CD}}\colon\colon \frac{\mathrm{CA},\mathrm{AF}}{\mathrm{CF}}=\mathrm{AH}$. $\frac{\mathrm{De},\mathrm{CD}}{\mathrm{Ce}}=\mathrm{DK}$. $\mathrm{DF}\cdot \mathrm{CF}\colon\colon \mathrm{◻EDG}◻\mathrm{ECG}$. ◻ECG ut $\frac{\mathrm{CF}}{\mathrm{DF}}\mathrm{◻EDG}$. ∠ECG ut $\frac{\mathrm{◻\; ECG}}{\mathrm{ECq}}$ ∠ECG ut $\frac{\mathrm{CF}\times \mathrm{◻EDG.}}{\mathrm{DF},\mathrm{ECq}}=\frac{\mathrm{◻EDG}}{\mathrm{ED},\mathrm{EC}}=\frac{\mathrm{◻EDG}}{\mathrm{EKq}-\mathrm{KDq}}$. ∠ECG×EKq−KDq ut ◻EDG.

Let AB, CD represent y^e ∥ planes of a lookinglass

BD the plane of the Diamond cut making at B a very obtuse angle with y^e plane AB. And let all the light between y^e rays {illeg}^{[Editorial Note 1]} FBM pass perpendicularly through the parallel planes of the glass & fall upon y^e paper between I {illeg} & M & all the light between y^e rays GO et HD be refracted by the plane oblique plane of y^e diamond cut {illeg} BD & fall upon the paper between K & L: and the light w^ch passes perpendicularly thorough the ∥ planes of y^e glass & falls upon the paper between I and M will be bordered with three or more fringes of colours at M If Plates of Looking glass sloopt off {illeg} \neare/ the edges with a diamond cut {illeg} {&} the {illeg} be held in the same beam of light, the light w^ch passes through the parallel planes of the glass, \& is bounded at within/ [& falls upon {illeg} white paper at some distance from the glass] will be bordered with three {illeg} fringes \bordered at the diamond cut {illeg}/ with the like fringes of colours {illeg} although it be bounded only by the diamond cut if {illeg}

Obs. 1. And hence I \seem to / gather that y^e rays in passing by the sides of y^e hair \at a \little/ distance/ are bent & those are most bent w^ch pass by {illeg} paribus) w^ch pass by the hair at y^e leats distance. Let H represent y^e 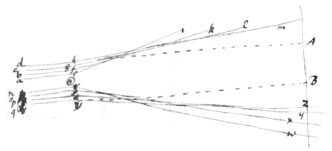hair, aei, bfk, cgl, dhm four rays passing by the hair at several distances & {illeg}|b|ent in e|,| f, g, h & falling let them fall on y^e paper beyond y^e hair at i, k, l, m. And let nrw, osx, pty, qvz represent four other rays passing by the hair on y^e other side & bent in r, s, t, v & let them fall on y^e paper at w, x, y, z. And let mz be y^e shadow of the hair cast upon the paper. [ By this bending of the rays the shadow will become broader then it would be if they were not bent, [&] Produce the outmost rays dh & qu \in right lines/ to A & B & the if those rays were not bent the hai in passing by the hair the breadth of y^e shadow of y^e hair \upon y^e paper/ would not be greater then AB whereas by experrience its found considerably greater.] And if the rays w^ch pass by the hair at the least distance be most bent \as is represented in the figure/ the {illeg} shadow will be broadest in proportion to y^e distance of y^e paper from y^e hair when the paper is nearest \to/ the hair, But as is found true by experience. But if y^e outmost rays dh & qu were \be/ not bent, produce them in right lines & let them fall on y^e paper at A, B & {illeg} will be the breadth of the shadow will be AB w^ch is less then it is found by experience {illeg} if these rays are therefore bent tho not so much <477v> as y^e rays w^ch pass by the hair at a less distance.

So then the dark lines above mentioned w^ch run be|a|long between the first and second fascias of either knife fringes of y^e shadows of either knife & meet in the middle of y^e light w^ch passes between the knives at y^e distance of a fift part of an inch from the concourse of y^e edges of y^e knives, are in the{illeg} passage betwe of y^e light between the knives distant from y^e edges of the knives the 320^th part of an inch or there abouts.

At another time when the two knives were distant eight feet & five inches from the little hole in the window made with a small pin \as above/, the dark line {illeg} or shadow {illeg} the point i where the dark line {illeg}is & xip meet & cross one another between the first fringes of y^e shadows of either the two knives, fell upon a paper \placed/ at the following distances from y^e knives when made at the distances between the edges of the knives were also as follows.

And hence I gather that the light w^ch pass makes the fringes w^th y^e shadows between them passes by the edges of the knives at a less distance \upon the paper/ is not the same light at all distances of y^e paper from y^e knives, but when y^e paper is held neare y^e knives y^e fringes are made by light w^ch passes by the edges of y^e knives at a less distance & is more bent then when the paper is held at a greater distance.

When I made these Observations I designed to repeat \most of/ them with more care & exacti|n|ess & to make some others \new ones/ for determining the manner how the rays of light are bent in their passage{illeg} by bodies for making these {fa} fringes \of colours/ w^th y^e dark lines between them:{But} \but/ I was then interrupted & cannot now think of taking these things into further consideration. And since I have have not finished this part of my designe &|I| shall conclude with proposing \{illeg} only/ some Quæres in or{illeg}|d|er to a further search to be made by others in these matters by others. [who may take these things into consideration]

Quære 1. Do not Bodies act upon light at a distance & by their action bend its rays & is not this action strongest at y^e least distance.

\☉ 1B. Are not &c/ < insertion from f 478r > ☉ 1B. Are not the rays of light in passing by the edges \& sides/ of bodies bent \several times/ backwards & forwards with a motion like that of an Eele.

< text from f 477v resumes >

2 Are not the rays more or less flexible accordingly as they are more or less refrangible, & are they with \Do not the rays w^ch differ in refrangibility differ also in {illeg}flexibility/\& are they not/ by their different inflexions made at equall distances from y^e bodies \are they not/ separated from one another so as {by} after separation to make the \colours in the/ three fringes of colours above described. |And after what manner are they inflected to make those fringes.|

3 Do not the rays of light w^ch fall upon bodies \& are reflected or refracted/ begin to bend before they arive at y^e bodies, & are they not reflected refracted & inflected by one & y^e same Principle acting variously in various circumstances.

4 Do not light & bodies act mutually upon one another, that is to say bodies upon light in emitting reflecting refracting & inflecting it, & light make <478r> ally upon bodies for heating them & pulling their parts into a vibrating motion wherein heat consists. |And do not black bodies conceive heat more easily from light then those ‡| < insertion from lower down f 478r > ‡ {Ad} 4. {illeg} {Ad} Do not black bodies conceive heat more easily \from light/ then those of other colours \do/ by reason that y^e light falling on them is not reflected back but enters y^e bodies & is often reflected & refracted within them before it is shifted & lost. And is not the greatness \or vigour/ of the action between light & sulphureous bodies observed above one reason why sulphureous bodies conceive heat & burn \take fire/ more readily & \burn/ more vehemently then other bodies do?

< text from higher up f 478r resumes >

5 Do not all \fixt/ bodies when heated beyond a certain degree emit light by the vibrating motion of their parts.

6 Is not fire a body heated so hot as to emit light copiously. For what else is a red hot iron \or a red hot stone/ then fire & what {illeg}|el|se is a burning coale then red hot wood [whose heat is preserved by the actions of an acid spirit in the air \acting upon &/ dissolving the wood.

7 Is not the flame a vapour \fume/ or exhalation heated \red hot that is/ so hot as to shine For {illeg} bodies do not \do not/ flame w^ch do not emit a \copious/ fume.

8 Are not the sun & fixt stars {illeg}|g|reat earths vehemently hot whose heat is conserved by the mutuall action & reaction between them & the light w^ch they emit & whose parts are kept from fuming away by the vast weight of the Atmospheres incumbent upon them.

9 Do not the rays of light in falling upon the Tunica retina bottom of the eye, excite vibrations in y^e Tunica retina w^ch vibrations being propagated along the \solid/ fibres of y^e Optick Nerves into the brain cause the sense of seeing. And are not the{illeg} vibrations made by several sorts of rays |*| < insertion from lower down f 478r > * For since dense bodies conserve their heat a long time & the densest bodies conserve their heat the longest, the vibrations of their parts are of a lasting nature & therefore may be propagated along \solid/ fibres of uniform dense matter to a great distance for conveying into the brain the impressions made upon all the Organs of sense. For that motion w^ch can continue long in {illeg} & y^e same part of a body can be propagated a long way from one part to another supposing the body homogeneal so that y^e motion may not be reflected refracted & interrupted or disordered by the any uneavenness of the body. < text from higher up f 478r resumes > 10 Do \And/ not several sorts of rays make vibrations of several bignesses, {illeg} w^ch according to their big several bignesses {illeg} excite sensations of several colours much after the manner that {several} the vibrations of y^e air according to their several bignesses exite sensation of several sounds? And \particularly/ do not the most refrangible rays excite the shortest vibrations for making a sensation of deep violet, the least refrangible the largest for making a sensation of deep red{illeg} & the \several/ intermediate \sorts of/ rays vibrations of \several/ intermediate bignesses to make sensations of \the several/ intermediate colours?

|1|1{illeg} May not the harmony & discord of colours arise from the proportions of the vibrations as the like \propagated \through the optic nerves/ into the brain/ \{and}{illeg}/ \as/ the harmony & discord of sounds \arises from the proportions of y^e vibrations of y^e air/. |For some colours are agreable as th{illeg}|o|se colours of gold & Indigo & others disagree.|

{illeg}1|2| May {illeg} Are not the species of objects seen w^th both eyes united when the Optick nerves meet before they come into the brain: {For} the fibres on the right side of both Nerves uniting there & \after unison/ going thence into y^e brain \in the nerve w^ch is/ on the right side of the head & the fibres on the left side of both nerves uniting in the same place & after union going \into the brain in the nerve w^ch is/ on y^e left side of the head into y^e brain & these two nerves meeting again in the brain in such a manner thet their fibres make but one intire species half of w^ch is on y^e right side of y^e sensorium & comes from y^e right side of both eyes & the other half of w^ch on y^e left side of y^e sensorium comes from the left side of both eyes? For the optic nerves of such animals as look the same way with both eyes (as of Men, Doggs, Sheep, Oxen) meet before they go into the brain, but the Optic nerves of such animals as do not look the same way w^th both eyes (as of Fishes & the Chameleon) do \not/ meet if I am rightly informed.

7B.Is not the

7B. Is not the greatness of the action between light & sulphureous bodies observed above, one reason why sulphureous bodies conceive heat & burn more readily \& more vehemently/ then other bodies do.

<478v>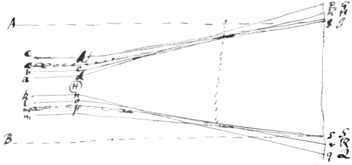

Obs.1. | Let \X{illeg} represent \one end of/ the Hair, cut cross the/ adg, beh, cfi represent three rays passing by one side of y^e hair a{illeg}|t| {illeg}|s|everal distances, & let {illeg} d e & f kng, lor, mps three other rays passing by the hair at other side of y^e hair at y^e like distances; d|,| e|,| f & n, o, p the places where these">these hairs \rays/ are bent in their passage by the hair; g|,| h|,| i, q|,| r|,| s the places where these rays fall on paper {illeg}si the breadth of the shadow where these rays of y^e hair cast on the paper And if the rays w^ch pass by the hair at the least distances be most bent as represented in y^e figure By the bending of y^e rays the shadow becomes broader then it would otherwise be & if the rays which pass by the hair at the least distance be most bent the rays will as is represented in the figure the \breadth of the/ shadow will be broadest \increase most/ in proportion to y^e distance of y^e paper from y^e hair when the paper is nearest to y^e hair as is found by experien{s}|c|e {illeg} |&| Ai |&| Bs two rays passing to y^e p{illeg}|oi|nts i & s \{illeg}/ w{illeg}|it|hout bending when the paper {& not} hair is taken away. {illeg}|And| {illeg}|it| is manifest that since all the light between the lines Ai & Bs is bent & turned asid in passing by the hair & turned aside from y^e shadow: for if any rays \part of this light/ were not bent they \it/ would fall on the paper within the space \shadow/ si & destroy th \there/ illuminate it & take away that part of the shadow where it falls w^ch is contrary to experience. Bodies therefore act upon the light at a gre considerable distance in its {illeg}|p|assing by them; {illeg} but the action is strongest on the rays w^ch pass by at y^e lee|a|st distances & grows weaker & weaker as light the rays on w^ch they {illeg} at \accordingly as the rays/ pass by them at {illeg} distances greater & greater, as is represented in the scheme For thence it comes to pass that the shadow of the hair \is much broader/ is much broader in proportion to y^e distance of the paper from the hair \is much broader when/ when y^e paper is at a dis neare the hair then when it is at a great distance from it. {illeg}

Ad Obs. 6. And hence the light of y^e in w^ch is least bent & goes to the inward ends of the streams passes by the edges of the knives at y^e greatest distance, & this distance \when the shadow begins to appear between the streams is {sic}/ is about y^e eight hundredth part of an inch. And {illeg} the light w^ch passes by the edges of y^e knives at a distance \distances still/ less & less distances is more {illeg}|&| more bent & goes to those parts of y^e streams which are further & further from the{illeg} direct light, [because as the knives approach one another till they touch, the light at y^e inward ends of the streams vanishes more and more untill the who & the streams grow shorter & shorter at those ends untill they \wholy/ disappear.]

Ad Obs. 7. And hence the light of the first fringe passed by the edge of y^e knife at a distance greater then the eight hundreth part of an inch & the light of y^e second \fringe/ passed by the edge of the knife at a greater distance then y^e light of y^e first fringe did, & that of y^e third at a greater distance <479r> Could all \the phænomena of/ nature be \[evidently]/ deduced from \only/ thre or four general suppositions there might be great reason to allow the the reasonables of \{admit} of/ \allow the truth of/ those suppositions {illeg} \to be true:/ but if you where those for \for explaining/ every new Phænomena you make a new Hypothesis if you suppose y^t y^e particles of water \Air/ are of such a figure \size & frame/, those of water of such another figure \those of Vinegre of {illeg} some \such/ another figure/, those of sea salt of such another figure, those of nitre of such another, those of {illeg} Vinegre Vitriol of such another, those of Quicksilver of such another, those of fire of flame of such another, those of Magnetick effluvia of such another, If you suppose that y^erays of light consists in such a motion pression or force, those & that those of several colours differ from one its \various/ colours are made by such |&| such variations of \the/ motion & so of other things: your Philosophy will systeme of Philosophy wi Philosophy will be nothing else then a systeme of a great number of uncertain Hypotheses. And what certainty can there be in a Philosophy w^ch consists in as many Hypotheses as there are Phænomena & & explications of Phæ nomena to be explained. What ever To {do} {illeg} To explain all nature is too difficult a task for any one man or even for any one age. Tis much better to do a little with certainty then to & leave the rest for others that come after, then to explain all things by conjecture & leave without making sure of any thing. And there is no \other/ way of doing any thing with certainty then by drawing conclusio {illeg} drawing conclusions from experiments & phænomena untill you come at such general Principles as are & then from those Principles giving an account of Nature. This is y^e only Whatever is certain in Philosophy is owing to this method & nothing can be done without it. I will instance in some particulars.

One princ{illeg}|ipl|e in Philosophy is y^e being of a God or spirit infinite e{illeg}|te|rnal omniscient, omnipotent, & the best argument for such a being is the frame of nature & chiefly the contrivance of y^e bodies of living creatures. All the great land animals have two eyes, \in the forehead/ a nose between \them/ a mouth under the nose, two ears on y^e sides of y^e head, two arms \or t/ or two fore leggs or two wings on the sholders ,|&| two leggs behind & this symmetry \in y^e several species/ could not proceed \For/ from chance /there being an equal chance for one eye or for three or four eyes as for two, & so of the other members\ Nothing is For Nothing is more curious & difficult then y^e frame of y^e eyes for seeing the \&/ of the ears for hearing of wings for flying & & yet not an animal th {a s a} species no sort of creatures ha{illeg}|s| these members witho to no purpose. What more difficult then to fly? & ye had flying creatures their wings by chance? or has any creature wings without being able to fly? & yet was it by chance y^t all creatures can fly w^ch have wings? Certainly he that framed y^e eyes of all creatures understood the nature of light & vision he that framed their ears understood y^e nature of sounds & hearing, he y^t framed their noses understood y^e nature of odours & smelling, he that framed the wings of flying creatures & y^e fins of fishes understood the {illeg} force of air & water & what members were requ{illeg}|i|sit{illeg}|e| to enable creatures to fly & swim: & therefore y^e first formation of every species of creatures must be ascribed to an intelligent being such a being as we call God These & such like considerations are the most convincing arguments for such a being & have convinced mankind in all ages that y^e world & all y^e species of things therein {illeg} were originally framed by hi{illeg}|s| power & wisdom. And to lay aside this argum^t is {very} unphilosophical.

Another Principle is that matter is impenitrable by other matter. This is usually looked upon as a maxim known to us by y^e light of nature, altho we {know} nothing of bodies but by sense. We find by dayly experience that bodies resist one another as often as they come together & cannot by any force be made <479v> to penetrate one anothers dimensions. And this holding true w^thout exception in all bodies here below in w^ch we can come to make observations we conclude it to be the {illeg} \property of/ all bodies whatsoever. And such observations occurring every day to every man this property of bodies is acknowledged by all {mankin} men without any dispute & looked upon as an Axiom.

A third property of bodies \principle is {sic}/ is that all the great bodies in y^e Vniverse have a tendency towards one another proportional to y^e quantity of matter conteined in them & that this tendency in rec{illeg}|e|ding from the body{illeg} decreases & is reciprocally proportional to y^e square of y^e distance from y^e body: |[And all small bodies have the like tendency towards the great {illeg} ones & this tendenc This tendency \towards y^e earth/ we find in all bodies here below & call it gravity]| {This} \Such a/ tendency \towards the earth/ we find in all bodies here below & call it gravity. \& by experiments of the Pendulum & of falling bodies we find it \exactly/ proportional to the quantity of matter in the several bodies/ We find it also in the Moon, the force w^ch keeps her in her Orb being exactly /reciprocally\ equal to y^e force of gravity.\& recipro/ The like tendency towards y^e sun we find in all the Planets who are thereby kept \proportiall {sic} to y^e square of her distance from y^e earth/ Iupiter we find in y^e|his| four satellites {illeg} \proportial/ which are thereby kept in their Orbs about him & this tendency by comparing the Orbs & Revolutions of y^e Satellites together is proportional to the matter in the Satellites \reciprocally as their squares of their distances from Iupiter/. The like tendency \to Saturn/ we find in this Sa five Satellites, proportional \directly/ to their matter \& {illeg} in reciprocally to the {squares} of their distances/. {illeg}|An|d all the Planets {illeg} \both primary & secondary &/ appear to have & some so many c|C|omets as have been \well/ observed appear to have y^e same tendency towards the Sun \directly/ proportional \directly/ to the{illeg} matter in each of them \& reciprocally to their distances from the sun/. And by y^e rest or very small motion \of the Aphelia of the {sic}/ the Planets it appears by {illeg} that this tendency of all the Planets towards \Iupiter Saturn &/ y^e Sun & of the Moon towards y^e earth {illeg} decreases in receding

^{[Editorial Note 2]}

$\frac{\mathrm{ADq},\mathrm{CFq}}{\mathrm{EFq}}=\mathrm{CDq}+\frac{\mathrm{MCq}}{\mathrm{NGq}}\mathrm{CGq}$. $\frac{\mathrm{CFq}+\mathrm{EFq}}{\mathrm{EFq}}\mathrm{ADq}=\mathrm{MCq}\times \frac{\mathrm{NGq}+\mathrm{CGq}}{\mathrm{NGq}}$. $\frac{\mathrm{ACq},\mathrm{ADq}}{\mathrm{EFq}}=\frac{\mathrm{ACq}\times \mathrm{MCq}}{\mathrm{NGq}}$.

A fourth Principle is that all sensible bodies are aggregated of particles laid together w^th many interstices or pores between them For water soaks into y^e pores of all animal & vegetable substances \& some minerals/ & quicksilver into y^e pores of Metall \& acid liquors into y^e pores of all minerals & metals in dissolving them,/ & light passes through y^e pores of \aire,/ water oyles gla \salt {spars}/ sand glass crystal \gemms {illeg}/ & all \other/ pellucid substances & through the particles of \all/ metals \salts {illeg} & minerals/ dissolved in pellucid menstruums \or vitrified/ & through thin pieces of wood, flesh, bone horn stone & vitrified earth. {As} to the former Principle is As by the former \third/ Principle we gave an account \heretofore/ of y^e motions of {all} the Planets & of y^e flux & reflux of y^e sea, so by this Principle we shall give an acct in y^e following treatise give an acct of y^e permanent colours of natural bodies, nothing further being requisite for y^e production of those colours then that y^e coloured bodies abound with pellud|c|id particles of a certain size & density. {illeg} This is to be understood of the largest particles or particles of y^e last composition. For as bodies are composed of these larger particles with larger pores between them so it is to be conceived that these \larger/ particles are composed of smaller particles with smaller pores between them. {illeg}|A|nd when water dissolves salts & \{illeg}/ acid menstruums \or quicksilver/ dissolves metals it is to be conceived that y^e liquor enters only the larger pores & separates only y^e larger particles of y^e salt or metal from one another without soaking into y^e smaller particles

<480r> ^{[Editorial Note 3]}

$\mathrm{Db}\cdot \mathrm{BD}\colon\colon \mathrm{Mb}\cdot \mathrm{MP}$. $\mathrm{BD}\cdot \mathrm{CE}\colon\colon \mathrm{PB}\cdot \mathrm{PC}$. $\mathrm{CE}\cdot \mathrm{Ec}\colon\colon \mathrm{PN}\cdot \mathrm{Nc}$ | $\mathrm{Db}\cdot \mathrm{Ec}\colon\colon \mathrm{MB},\mathrm{BP},\mathrm{PN}\cdot \mathrm{MP},\mathrm{PC},\mathrm{NC}$. $\colon\colon \frac{\mathrm{MB},\mathrm{BP}}{\mathrm{MP}}\cdot \frac{\mathrm{NC}\times \mathrm{PC}}{\mathrm{PN}}\colon\colon \frac{\mathrm{MB},\mathrm{PB}}{\mathrm{PM}}\cdot \frac{\mathrm{NC},\mathrm{PC}}{\mathrm{PN}}$. // $\mathrm{CE}\cdot \mathrm{Cc}\colon\colon \mathrm{PN}\cdot \mathrm{Pc}$. / $\mathrm{Db}\cdot \mathrm{Cc}\colon\colon \mathrm{MB},\mathrm{PB},\mathrm{PN}\cdot \mathrm{MP},\mathrm{PCq}$, $\frac{\mathrm{MB},\mathrm{PB}}{\mathrm{MP}}\cdot \frac{\mathrm{PCq}}{\mathrm{PN}}$. / $\mathrm{Db}\cdot \mathrm{Ec}\cdot \mathrm{Cc}\cdot \mathrm{Bb}\colon\colon \frac{\mathrm{MB},\mathrm{PB}}{\mathrm{PM}}\cdot \frac{\mathrm{NC},\mathrm{PC}}{\mathrm{PN}}\cdot \frac{\mathrm{PCq}}{\mathrm{PN}}\cdot \frac{\mathrm{PBq}}{\mathrm{PM}}$

Between the sines of incidence & refraction counted from y^e sine of incidence when the refraction is made of of out of the the {illeg}|P|late of any substance into y^e surrounding Medium of any other substance, that is out of in this case out of Glass into Air. Now if the thickness of the g|G|lass be increased by degrees so as to bear to its first thickness (vizt that of an {illeg} a quarter of an inch) the proportions of 34386 to 34385, 34384, 34383, 34382 &c, the secants analogous to these \& the first thickness be divided into 100000000 equal parts the increased/ thicknesses will be 100002908, 100005816, 100007|8|725, 1000011633 &c and the Angles of w^ch these {incumber} thicknesses are secants will be 26' 13'', 37' 5'', 45' 6'', 52' 26'' \the radius being 100000000,/ {illeg}|and| the sines of these Angles are 762, 1079, 1321, 1525 and the proportional sines of refraction 1172, 1659, {illeg} 2031, 2345 the Radius being 100000. For

<480v>

As {illeg} Mathematicians have two Methods of doing things w^ch they call c|C|omposition and {illeg}|R|esolution & in all difficulties have recourse t{illeg}|o| their method of resolution \before they compound/ so in explaining the Phænomena of nature the like methods are to be used & he that expects success must resolve before he compounds. For the explications of Phænomena are Problems much harder then those in abstractio Mathematicks. The method of Resolution consists in trying experiments & considering all the Phænomena of nature from whence any thing can {illeg} \of nature/ relating to the subject in hand \& drawing conclusions from them/ & examining the truth of those conclusions by new experiments & so proceeding drawing new conclusions (if it may be) from those experiments & so proceeding {illeg}|a|lternately from experiments to conclusions & from conclusions to experiments untill you have come to the general properties of things, And when you [& by experiments & phænomena have established the truth of those properties] Then assuming those properties as Principles of Philosophy you may proceed from by them explain the causes of such Phænomena as depend upon them & follow from them: w^ch is the method of Composition. But, if you w^thout deriving the properties of things from Phænomena you explain feign Hypotheses & {illeg} think by them to explain all nature you may make a plausible systeme of Philosophy for getting your self a name, but your systeme being will be little better then a Philosophical Romance \{illeg}/ \Romance/. ‡ To explain all nature is too difficult a task for any one man or \even for/ any one age. Tis much better to do a little with certainty then to seem to no & leave the rest for others that come after you then to then to explain all things \by conjecture/ without making sure of any thing.

Thus in Mathematical Principles of Philosophy I fi{illeg}|rs|t shewed \from Phænomena/ that the all bodies endeavoured by a certain force proportional to their matter to approach ane another, that this force in receding from y^e body grows less & less in reciprocal proportion to y^e square of the distance from it & that it was \is/ equal to gravity & therefore was \is/ one & the same force with gravity. Then using this force as a Principle of gravity I shewed how \Philosophy/ I derived from it all the Phænomena of nature motions of the heavenly bodies & the flux & reflux of y^e sea, shewing by mathematical demonstrations that this force alone was sufficient to produce all those Phænomena, & deriving from it (a priori) some \new/ motions w^ch Astronomers had not then observed but since appeare to be true, as that Saturn & Iupiter draw one another, that y^e Variation of y^e Moon is bigger in winter then in supp|m|mer, that there is an equation of y^e Moons meane motion amounting to almost 5 minutes {.} w^ch depends upon the position of her {Aphelium} Apoge of y^e Sun.

<481v>

Seign^r Rizzetti in the beginning of his paper writes thus. Newtonus cum lumini Solis in refraction objecisset Prisma triangulare, agravit spectrum Solis magis produce quam par lex vulgata refractionis postulasset: ideo lumen solis dispergi in refractione dispergi, ita ut unicus simplex radius in plures discindatur. Vnde apinatus est, id ipsum fore si lumen

But Newton affirms no such thing. He affirms \represents/ that every ray emitted from the Sun or other lucid body, continues one & the same without any dispersion or splitting \by refraction/ or change in repect of refrangibility or colour. For in his first Definition, he calls the Rays of light its least parts, whether successive in the same lines or contemporary in several lines. And in his second Proposition he brings his 5^t, 6^t, 7^th, 8^th, 9^th & 10^th Experiments to prove that that one & the same ray is not split by refraction disturbed shattered, dilated split or spread into many rays. And his first Proposition is that homogeneal light is refracted regularly without any dilatation splitting or shattering of the Rays.

He saith further that if \the breadth of the of/ the image of a lucid point cast upon the bottom of the eye were about the 55^th part{illeg} of the bread of the pupill of the eye the hair of a mans head could not appear so distinct as it really doth; & then he adds. Cum dixerim in visione capilli locum minima esse aberratio ni Newtonianæ quia minime cernitur, adversus hujusmodi argumentum rationabilior mihi videretur objectio ducta a Propositione VII Autoris: nimirum adeo extenuari lumen aberrans in distantia a suo centro, Iut (loquar Newtoni verbis) non sit sensibile nisi in eodem centro aut prope illud. Vt objectioni respondeam, divisa semidiametro luminis aberrantis in undecim partes equales; ejus densitas juxta Newtonianam sententiam, decresit in talam Arithmeticam \proportionem,/ ut cum expressa sit in prima parte a numero 21, exprimatur in secunda a numero 19, & sic deinceps, adeo ut in parte ultima exteriori exprimatur per unitatem. And yet M^r Newton affirms no such Arithmetical proportion. His Rule is that the density of the light at any distance from the center a|i|s as {illeg} \the/ distance from the of that point from the circumference applied to its distance from the center. Let the semidiameter of the erring light be divided into eleven equal pa\r/ts, & the density of the light in the midle of the part next the center will be to its density in the middle of the part next the circumference not as 22|1| to 1 but as $\frac{10\frac{1}{2}}{\frac{1}{2}}$ to $\frac{\frac{1}{2}}{10\frac{1}{2}}$ or as {illeg} 441 to 1

He saith further. Vidit sapientissimus Anglus speciem solarem magis in longum porrectam quam lex vulgaris refractionis postulasset cum illam cerneret diversicolorem, scilicet rubram, mox flavam, deinde viridem, postea cæruleam, & tandem supra violaceam, hoc experimento fretus suum confecit systema luminis at colorum. Omnia experimenta, quibus illud innixum est, renovare curari, & ea (prologu{illeg} id licet?) partim falsa, & omnia reliqua inveni propter omissionem ––– aliquam alicujus circumstantiæ æquivoca ac minime concludentia. Vt unicum [experimentum] allendas obsecro. Then he describes the experiment \of the red & blue colours/ above recited with & tried before the {illeg} Royal Society with success & of the red & blue colours as of the chart painted with red & blue colours of painting a chart w^th red & blue colours & casting the species thereof through a Lens upon which paper \as is described above/ {and denies} as is described above which was lately shewed to the R. S. as is with success as is described above & denies the success. If it did not succeed with him it was because he did not know perfectly well as is desc\r/ibed above. He should have told the world that Newton ground founded his Theory of light & colours upon the experiment w^ch for its \demonstrative/ evidence he calls experimentum crucis. This experiment he could not deny because it hath been tried again & again with full success both in France & in Italy with fo as well as in England: & therefore he passes it by in silence & denies the conclusion drawn from it, & contrary to the <481r> Rules of Logic disputes against the conclusion without taking note of the Premisses.

<482v>

Pag. 2. L. 38 \& p. 6 l 16 Theoriam meam non intelligit/ Radius unus simplex non dispergitur in plures.

Pag. 2. lin. 15. Vult observationem posse corrigi.

Ib. l. 16. {illeg} Telescopia \m{illeg}|a|gis/ {illeg} perficientur per reflexionem et p. 10. l. 13.

P. 4. l. 21. Ergo Newtonus Objectionem prævidit.

P 5. l. 12. Imo ducenties densius et amplius, sed Riz\z/ellus Objectionem \calculum/ ignorat. Sed et Millies densius intra dimid|ti|am c|l|atitudinem capillæ & decies millies densius intra septiman partem latitudines capillæ &c.

P. 6. l. 14. Falsum est.

P. 7. l 6 Hinc patet authorem stuidio partium sesibere.

Ib. l. 8 Verum est experimentum, sed Rizellus calculum ignorat \nescit vere tentare/.

P. 6. l. 1 Lux dispergitur quidem transiens per Prisma et non dispergitur transiens per Lentem! Ita Riz\z/e{illeg}|ll|us, qui et promittit {illeg} se hoc in libro edendo ostensurum esse.

Titus MS^ti est: Christino Martinella P{illeg}|a|tricio Veneto Iohannes Rizzellus S. D.

The Objector doth not unders{illeg}|ta|nd the Theory against which he is writing. For he supposes that \I make/ one single principal ray \to be/ by refraction dispersed & spread into many. Pag. 2. lin. 3, 8 & pag. 6 lin \16/

2 His Emanuensis knows not how to try the Experiments For the experiment w^ch he denyes the success of (pag. 7. lin. 8) doth succeed if tried with intense colours & with a Lens well made, free from veins & of a sufficient breadth.

3 If he had reasoned right he would have found the light upon y^e hair not only twenty times denser but above 200 times denser then at the extremity pag. 5 lin. 12{illeg}.

4 Whence is it that Telescopes by reflexion out do those by refraction, For y^e Telescope by reflexion made by M^r Hadley which is but five feet & a quarter long discovered the four innermost satellites of ♃ when the Moon was up & by reason of the Moonshine the Telescope of Hugenius w^ch is 124 feet long \& a very good one/ discovered only three of them. See {illeg}|P|ag. 2 lin 16 & pag. 10. lin. 13.

5 The Objector denies the c|C|onclusion without shewing the flaw of the Premisses, & brings an {illeg} objection against it. pag. 4. l. 21. Which way of proceeding being once allowed brings every thing to a squabble. & puts an end to experimental Philosophy & even to Mathematicks it self. And the objection is old & sufficiently answered by M^r N. in Prop. VII lib. 1. Optices, if M^r Rizzell had understood the answer. He should either have showed the flaw in the Premisses, or have granted the Conclusion & enquired how, notwithstanding it, {illeg}|v|ision can be so distinct as it is.

6 He tells us that light is dispersed in passing through a Prism but not in passing through a Lens, & that he hath written a book to prove this (pag. 6. lin. 1, 3 & pag. 10 l. 2 & pag. 1. lin. 6, 11) & whereas M^r Newton had shewn how to mend Object Glasses by putting water between two Glasses he proposes to use instead of water a denser Medium then glass. His Paper is a banter like that of Gorden.