Axiomata Sive Leges Motus (1713)
AXIOMATA,
SIVE
LEGES MOTUS
LEX I.
Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in directum, nisi quatenus a viribus impressis cogitur statum illum mutare.
PRojectilia perseverant in motibus suis, nisi quatenus a resistentia aeris retardantur, & vi gravitatis impelluntur deorsum. Trochus, cujus partes cohærendo perpetuo retrahunt sese a motibus rectilineis, non cessat rotari, nisi quatenus ab aere retardatur. Majora autem Planetarum & Cometarum corpora motus suos & progressivos & circulares in spatiis minus resistentibus factos conservant diutius.
LEX II.
Mutationem motus proportionalem esse vi motrici impressæ, & fieri secundum lineam rectam qua vis illa imprimitur.
Si vis aliqua motum quemvis generet; dupla duplum, tripla triplum generabit, sive simul & semel, sive gradatim & successive impressa fuerit. Et hic motus (quoniam in eandem semper plagam cum vi generatrice determinatur) si corpus antea movebatur, motui ejus vel conspiranti additur, vel contrario subducitur, vel obliquo oblique adjicitur, & cum eo secundum utriusque determinationem componitur.
<13>LEX III.
Actioni contrariam semper & æqualem esse reactionem: sive corporum duorum actiones in se mutuo semper esse æquales & in partes contrarias dirigi.
Quicquid premit vel trahit alterum, tantundem ab eo premitur vel trahitur. Si quis lapidem digito premit, premitur & hujus digitus a lapide. Si equus lapidem funi alligatum trahit, retrahetur etiam & equus (ut ita dicam) æqualiter in lapidem: nam funis utrinq; distentus eodem relaxandi se conatu urgebit equum versus lapidem, ac lapidem versus equum; tantumque impediet progressum unius quantum promovet progressum alterius. Si corpus aliquod in corpus aliud impingens, motum ejus vi sua quomodocunque mutaverit, idem quoque vicissim in motu proprio eandem mutationem in partem contrariam vi alterius (ob æqualitatem pressionis mutuæ) subibit. His actionibus æquales fiunt mutationes, non velocitatum, sed motuum; scilicet in corporibus non aliunde impeditis. Mutationes enim velocitatum, in contrarias itidem partes factæ, quia motus æqualiter mutantur, sunt corporibus reciproce proportionales. Obtinet etiam hæc Lex in Attractionibus, ut in Scholio proximo probabitur.
COROLLARIUM I.
Corpus viribus conjunctis diagonalem parallelogrammi eodem tempore describere, quo latera separatis.
Si corpus dato tempore, vi sola 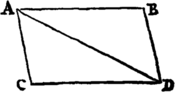 M in loco A impressa, ferretur uniformi cum motu ab A ad B; & vi sola N in eodem loco impressa, ferretur ab A ad C: compleatur parallelogrammum ABDC, & vi utraque feretur id eodem tempore in diagonali ab A ad D. Nam quoniam vis N agit secundum lineam AC ipsi BD parallelam, hæc vis per Legem II nihil mutabit velocitatem accedendi ad lineam illam BD a vi altera genitam. Accedet igitur corpus eodem tempore ad lineam BD; sive vis N imprimatur, sive non; atque adeo in fine illius temporis reperietur alicubi in linea illa BD. Eodem argumento in fine temporis ejusdem reperietur alicubi in linea CD, & idcirco in utriusque lineae concursu D reperiri necesse est. Perget autem motu rectilineo ab A ad D per Legem I.
M in loco A impressa, ferretur uniformi cum motu ab A ad B; & vi sola N in eodem loco impressa, ferretur ab A ad C: compleatur parallelogrammum ABDC, & vi utraque feretur id eodem tempore in diagonali ab A ad D. Nam quoniam vis N agit secundum lineam AC ipsi BD parallelam, hæc vis per Legem II nihil mutabit velocitatem accedendi ad lineam illam BD a vi altera genitam. Accedet igitur corpus eodem tempore ad lineam BD; sive vis N imprimatur, sive non; atque adeo in fine illius temporis reperietur alicubi in linea illa BD. Eodem argumento in fine temporis ejusdem reperietur alicubi in linea CD, & idcirco in utriusque lineae concursu D reperiri necesse est. Perget autem motu rectilineo ab A ad D per Legem I.
COROLLARIUM II.
Et hinc patet compositio vis directæ AD ex viribus quibusvis obliquis AB & BD, & vicissim resolutio vis cujusvis directæ AD in obliquas quascunque AB & BD. Quæ quidem compositio & resolutio abunde confirmatur ex Mechanica.
Ut si de rotæ alicujus centro O exeuntes radii inæquales OM, ON filis MA, NP sustineant pondera A & P, & quærantur vires ponderum ad movendam rotam: Per centrum O agatur recta KOL filis perpendiculariter occurrens in K & L, centroque O & intervallorum OK, OL majore OL 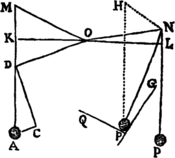 describatur circulus occurrens filo MA in D: & actae rectae OD parallela sit AC, & perpendicularis DC. Quoniam nihil refert, utrum filorum puncta K, L, D affixa sint vel non affixa ad planum rotæ; pondera idem valebunt, ac si suspenderentur a punctis K & L vel D & L. Ponderis autem A exponatur vis tota per lineam AD, & hæc resolvetur in vires AC, CD, quarum AC trahendo radium OD directe a centro nihil valet ad movendam rotam; vis autem altera DC, trahendo radium DO perpendiculariter, idem valet ac si perpendiculariter traheret radium OL ipsi OD æqualem; hoc est idem atq; pondus P, si modo pondus illud sit ad pondus A ut vis DC ad vim DA, id est (ob similia triangula ADC, DOK,) ut OK ad OD seu OL. Pondera igitur A & P, quæ sunt reciproce ut radii in directum positi OK & OL, idem pollebunt, & sic consistent in æquilibrio: quæ est proprietas notissima Libræ, Vectis & Axis in Peritrochio. Sin pondus alterutrum sit majus quam in hac ratione, erit vis ejus ad movendam rotam tanto major.
describatur circulus occurrens filo MA in D: & actae rectae OD parallela sit AC, & perpendicularis DC. Quoniam nihil refert, utrum filorum puncta K, L, D affixa sint vel non affixa ad planum rotæ; pondera idem valebunt, ac si suspenderentur a punctis K & L vel D & L. Ponderis autem A exponatur vis tota per lineam AD, & hæc resolvetur in vires AC, CD, quarum AC trahendo radium OD directe a centro nihil valet ad movendam rotam; vis autem altera DC, trahendo radium DO perpendiculariter, idem valet ac si perpendiculariter traheret radium OL ipsi OD æqualem; hoc est idem atq; pondus P, si modo pondus illud sit ad pondus A ut vis DC ad vim DA, id est (ob similia triangula ADC, DOK,) ut OK ad OD seu OL. Pondera igitur A & P, quæ sunt reciproce ut radii in directum positi OK & OL, idem pollebunt, & sic consistent in æquilibrio: quæ est proprietas notissima Libræ, Vectis & Axis in Peritrochio. Sin pondus alterutrum sit majus quam in hac ratione, erit vis ejus ad movendam rotam tanto major.
Quod si pondus p ponderi P æquale partim suspendatur filo Np, partim incumbat plano obliquo pG: agantur pH, NH, prior horizonti, posterior plano pG perpendicularis; & si vis ponderis p deorsum tendens, exponatur per lineam pH, resolvi potest hæc in vires pN, HN. Si filo pN perpendiculare esset planum aliquod pQ secans planum alterum pG in linea ad horizentem parallela; & pondus p his planis pQ, pG solummodo incumberet; urgeret illud hæc plana viribus pN, HN perpendiculariter, nimirum planum pQ vi pN & planum pG vi HN. Ideoque si tollatur planum pQ ut pondus tendat silum; quoniam silum sustinendo pondus jam vicem præstat plani sublati, tendetur illud eadem vi pN, qua planum antea urgebatur. Unde tensio fili hujus obliqui erit ad tensionem fili alterius perpendicularis PN, ut pN ad pH. Ideoq; si pondus p sit ad pondus A in ratione quæ componitur ex ratione reciproca minimarum distantiarum filorum suorum pN, AM a centro rotæ, & ratione directa pH ad pN; pondera idem valebunt ad rotam movendam, atq; adeo se mutuo sustinebunt, ut quilibet experiri potest.
Pondus autem p, planis illis duobus obliquis incumbens, rationem habet cunei inter corporis fissi facies internas: & inde vires cunei & mallei innotescunt: utpote cum vis qua pondus p urget planum pQ sit ad vim, qua idem vel gravitate sua vel ictu mallei impellitur secundum lineam pH in plano, ut pN ad pH; atque ad vim, qua urget planum alterum pG, ut pN ad NH. Sed & vis Cochleæ per similem virium divisionem colligitur; quippe quæ cuneus est a vecte impulsus. Usus igitur Corollarii hujus latissime patet, & late patendo veritatem ejus evincit; cum pendeat ex jam dictis Mechanica tota ab Auctoribus diversimode demonstrata. Ex hisce enim facile derivantur vires Machinarum, quæ ex Rotis, Tympanis, Trochleis, Vectibus, nervis tensis & ponderibus directe vel oblique ascendentibus, cæterisque potentiis Mechanicis componi solent, ut & vires Tendinum ad animalium ossa movenda.
COROLLARIUM III.
Quantitas motus quæ colligitur capiendo summam motuum factorum ad eandem partem, & differentiam factorum ad contrarias, non mutatur ab actione corporum inter se.
Etenim actio eique contraria reactio æquales sunt per Legem III, adeoque per legem II æquales in motibus efficiunt mutationes versus contrarias partes. Ergo si motus fiunt ad eandem partem; quicquid additur motui corporis fugientis, subducetur motui corporis insequentis sic, ut summa maneat eadem quæ prius. Sin corpora obviam eant; æqualis erit subductio de motu utriusque, adeoque differentia motuum factorum in contrarias partes manebit eadem.
Ut si corpus sphæricum A sit triplo majus corpore sphærico B, habeatque duas velocitatis partes; & B sequatur in eadem recta cum velocitatis partibus decem, adeoque motus ipsius A sit ad motum ipsius B ut sex ad decem: ponantur motus illis esse partium sex & decem, & summa erit partium sexdecim. In corporum igitur concursu, si corpus A lucretur motus partes tres vel quatuor vel quinque, corpus B amittet partes totidem, adeoque perget corpus A post reflexionem cum partibus novem vel decem vel undecim, & B cum partibus septem vel sex vel quinque, existente semper summa partium sexdecim ut prius. Sin corpus A lucretur partes novem vel decem vel undecim vel duodecim, adeoque progrediatur post concursum cum partibus quindecim vel sexdecim vel septendecim vel octodecim; corpus B amittendo tot partes quot A lucratur, vel cum una parte progredietur amissis partibus novem, vel quiescet amisso motu suo progressivo partium decem, vel cum una parte regredietur amisso motu suo & (ut ita dicam) una parte amplius, vel regredietur cum partibus duabus ob detractum motum progressivum partium duodecim. Atque ita summæ motuum conspirantium vel , & differentiæ contrariorum & semper erunt partium sexdecim, ut ante concursum & reflexionem. Cognitis autem motibus quibuscum corpora post reflexionem pergent, invenietur cujusque velocitas, ponendo eam esse ad velocitatem ante reflexionem, ut motus post est ad motum ante. Ut in casu ultimo, ubi corporis A motus erat partium sex ante reflexionem & partium octodecim postea, & velocitas partium duarum ante reflexionem; invenietur ejus velocitas partium sex post reflexionem, dicendo, ut motus partes sex ante reflexionem ad motus partes octodecim postea, ita velocitatis partes duæ ante reflexionem ad velocitatis partes sex postea.
Quod si corpora vel non Sphærica vel diversis in rectis moventia incidant in se mutuo oblique, & requirantur eorum motus post reflexionem; cognoscendus est situs plani a quo corpora concurrentia tanguntur in puncto concursus: dein corporis utriusque motus (per Corol. II.) distinguendus est in duos, unum huic plano perpendicularem, alterum eidem parallelum: motus autem paralleli, propterea quod corpora agant in se invicem secundum lineam huic plano perpendicularem, retinendi sunt iidem post reflexionem atque antea; & motibus perpendicularibus mutationes æquales in partes contrarias tribuendæ sunt sic, ut summa conspirantium & differentia contrariorum maneat eadem quæ prius. Ex hujusmodi reflexionibus oriri etiam solent motus circulares corporum circa centra propria. Sed hos casus in sequentibus non considero, & nimis longum esset omnia huc spectantia demonstrare.
<17>COROLLARIUM IV.
Commune gravitatis Centrum, corporum duorum vel plurium, ab actionibus corporum inter se non mutat statum suum vel motus vel quietis; & propterea corporum omnium in se mutuo agentium (exclusis actionibus & impedimentis externis) commune Centrum gravitatis vel quiescit vel movetur uniformiter in directum.
Nam si puncta duo progrediantur uniformi cum motu in lineis rectis, & distantia eorum dividatur in ratione data, punctum dividens vel quiescet vel progredietur uniformiter in linea recta. Hoc postea in Lemmate XXIII demonstratur, si punctorum motus fiant in eadem plano; & eadem ratione demonstrari potest, si motus illi non fiant in eodem plano. Ergo si corpora quotcunque moventur uniformiter in lineis rectis, commune centrum gravitatis duorum quorumvis vel quiescit vel progreditur uniformiter in linea recta; propterea quod linea, horum corporum centra in rectis uniformiter progredientia jungens, dividitur ab hoc centro communi in ratione data. Similiter & commune centrum horum duorum & tertii cujusvis vel quiescit vel progreditur uniformiter in linea recta; propterea quod ab eo dividitur distantia centri communis corporum duorum & centri corporis tertii in data ratione. Eodem modo & commune centrum horum trium & quarti cujusvis vel quiescit vel progreditur uniformiter in linea recta; propterea quod ab eo dividitur distantia inter centrum commune trium & centrum quarti in data ratione, & sic in infinitum. Igitur in systemate corporum quæ actionibus in se invicem, alijsque omnibus in se extrinsecus impressis omnino vacant, adeoque moventur singula uniformiter in rectis singulis, commune omnium centrum gravitatis vel quiescit vel movetur uniformiter in directum.
Porro in systemate duorum corporum in se invicem agentium, cum distantiæ centrorum utriusque a communi gravitatis centro sint reciproce ut corpora; erunt motus relativi corporum eorundem, vel accedendi ad centrum illud vel ab eodem recedendi, æquales inter se. Proinde centrum illud a motuum æqualibus mutationibus in partes contrarias factis, atque adeo ab actionibus horum corporum inter se, nec promovetur nec retardatur nec mutationem patitur in statu suo quoad motum vel quietem. In systemate autem corporum plurium, quoniam duorum quorumvis in se mutuo agentium commune gravitatis centrum ob actionem illam nullatenus mutat statum suum; & reliquorum, quibuscum actio illa non intercedit, commune gravitatis centrum nihil inde patitur; distantia autem horum duorum centrorum dividitur a communi corporum omnium centro in partes summis totalibus corporum quorum sunt centra reciproce proportionales; adeoque centris illis duobus statum suum movendi vel quiescendi servantibus, commune omnium centrum servat etiam statum suum: manifestum est quod commune illud omnium centrum ob actiones binorum corporum inter se nunquam mutat statum suum quoad motum & quietem. In tali autem systemate actiones omnes corporum inter se, vel inter bina sunt corpora, vel ab actionibus inter bina compositæ; & propterea communi omnium centro mutationem in statu motus ejus vel quietis nunquam inducunt. Quare cum centrum illud ubi corpora non agunt in se invicem, vel quiescit, vel in recta aliqua progreditur uniformiter; perget idem, non obstantibus corporum actionibus inter se, vel semper quiescere, vel semper progredi uniformiter in directum; nisi a viribus in systema extrinsecus impressis deturbetur de hoc statu. Est igitur systematis corporum plurium Lex eadem quæ corporis solitarii, quoad perseverantiam in statu motus vel quietis. Motus enim progressivus seu corporis solitarii seu systematis corporum ex motu centri gravitatis æstimari semper debet.
COROLLARIUM V.
Corporum dato spatio inclusorum iidem sunt motus inter se, sive spatium illud quiescat, sive moveatur idem uniformiter in directum absque motu circulari.
Nam differentiæ motuum tendentium ad eandem partem, & summæ tendentium ad contrarias, ea dem sunt sub initio in utroq; casu (ex hypothesi) & ex his summis vel differentiis oriuntur congressus & impetus quibus corpora se mutuo feriunt. Ergo per Legem II æquales erunt congressuum effectus in utroq; casu; & propterea manebunt motus inter se in uno casu æquales motibus inter se in altero. Idem comprobatur experimento luculento. Motus omnes eodem modo se habent in Navi, sive ea quiescat, sive moveatur uniformiter in directum.
COROLLARIUM VI.
Si corpora moveatur quomodocunq; inter se, & a viribus acceleratricibus æqualibus secundum lineas parallelas urgeantur; pergent omnia eodem modo moveri inter se, ac si viribus illis non essent incitata.
Nam vires illæ æqualiter (pro quantitatibus movendorum corporum) & secundum lineas parallelas agendo, corpora omnia æqualiter (quoad velocitatem) movebunt per Legem II.) adeoque nunquam mutabunt positiones & motus eorum inter se.
Scholium
Hactenus principia tradidi a Mathematicis recepta & experientia multiplici confirmata. Per Leges duas primas & Corollaria duo prima Galilæus invenit descensum Gravium esse in duplicata ratione temporis, & motum projectilium fieri in Parabola; conspirante experientia, nisi quatenus motus illi per aeris resistentiam aliquantulum retardantur. Ab iisdem Legibus & Corollariis pendent demonstrata de temporibus oscillantium Pendulorum, suffragante Horologiorum experientia quotidiana. Ex his iisdem & Lege tertia Christophorus Wrennus Eques Auratus, Iohannes Wallisius S.T.D. & D. Christianus Hugenius, hujus ætatis Geometrarum facile principes, regulas congressuum & reflexionum duorum corporum seorsim invenerunt, & eodem fere tempore cum Societate Regia communicarunt, inter se (quoad has leges) omnino conspirantes: & primus quidem Wallisius, deinde Wrennus & Hugenius inventum prodiderunt. Sed & veritas comprobata est a Wrenno coram Regia Societate per experimentum Pendulorum: quod etiam Clarissimus Mariottus libro integro exponere mox dignatus est. Verum, ut hoc experimentum cum Theoriis ad amussim congruat, habenda est ratio tum resistentiæ aeris, tum etiam vis Elasticæ concurrentium corporum. Pendeant corpora A, B filis parallelis & æqualibus AC, BD, a centris C, D. His centris & intervallis describantur semicirculi EAF, GBH radiis CA, DB bisecti. Trahatur corpus A ad arcus EAF punctum quodvis R, & (subducto corpore B) demittatur inde, redeatque post unam oscillationem ad punctum V. Est RV retardatio 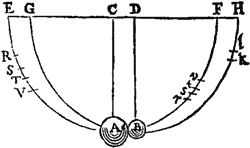 ex resistentia aeris. Hujus RV fiat ST pars quarta sita in medio, ita scilicet ut RS & TV æquentur, sitque RS ad ST ut 3 ad 2. Et ista ST exhibebit retardationem in descensu ab S ad A quam proxime. Restituatur corpus B in locum suum. Cadat corpus A de puncto S, & velocitas ejus in loco reflexionis A, absque errore sensibili, tanta erit ac si in vacuo cecidisset de loco T. Exponatur igitur hæc velocitas per chordam arcus TA. Nam velocitatem Penduli in puncto insimo esse ut chordam arcus quem cadendo descripsit, Propositio est est Geometris notissima. Post reflexionem perveniat corpus A ad locum s, & corpus B ad locum k. Tollatur corpus B & inveniatur locus v; a quo si corpus A demittatur & post unam oscillationem redeat ad locum r, sit st pars quarta ipsius rv sita in medio, ita videlicet ut rs & tu æquentur; & per chordam arcus tA exponatur velocitas quam corpus A proxime post reflexionem habuit in loco A. Namt erit locus ille verus & correctus, ad quem corpus A, sublata aeris resistentia, ascendere debuisset. Simili methodo corrigendus erit locus k, ad quem corpus B ascendit, & inveniendus locus l, ad quem corpus illud ascendere debuisset in vacuo. Hoc pacto experiri licet omnia perinde ac si in vacuo constituti essemus. Tandem ducendum erit corpus A in chordam arcus TA (quæ velocitatem ejus exhibet) ut habeatur motus ejus in loco A proxime ante reflexionem; deinde in chordam arcus tA, ut habeatur motus ejus in loco A proxime post reflexionem. Et sic corpus B ducendum erit in chordam arcus Bl, ut habeatur motus ejus proxime post reflexionem. Et simili methodo, ubi corpora duo simul demittuntur de locis diversis, inveniendi sunt motus utriusq; tam ante, quam post reflexionem; & tum demum conferendi sunt motus inter se & colligendi effectus reflexionis. Hoc modo in Pendulis pedum decem rem tentando, idque in corporibus tam inæqualibus quam æqualibus, & faciendo ut corpora de intervallis amplissimis, puta pedum octo duodecim vel sexdecim, concurrerent; reperi semper sine errore trium digitorum in mensuris, ubi corpora sibi mutuo directe occurrebant, quod æquales erant mutationes motuum corporibus in partes contrarias illatæ, atque adeo quod actio & reactio semper
ex resistentia aeris. Hujus RV fiat ST pars quarta sita in medio, ita scilicet ut RS & TV æquentur, sitque RS ad ST ut 3 ad 2. Et ista ST exhibebit retardationem in descensu ab S ad A quam proxime. Restituatur corpus B in locum suum. Cadat corpus A de puncto S, & velocitas ejus in loco reflexionis A, absque errore sensibili, tanta erit ac si in vacuo cecidisset de loco T. Exponatur igitur hæc velocitas per chordam arcus TA. Nam velocitatem Penduli in puncto insimo esse ut chordam arcus quem cadendo descripsit, Propositio est est Geometris notissima. Post reflexionem perveniat corpus A ad locum s, & corpus B ad locum k. Tollatur corpus B & inveniatur locus v; a quo si corpus A demittatur & post unam oscillationem redeat ad locum r, sit st pars quarta ipsius rv sita in medio, ita videlicet ut rs & tu æquentur; & per chordam arcus tA exponatur velocitas quam corpus A proxime post reflexionem habuit in loco A. Namt erit locus ille verus & correctus, ad quem corpus A, sublata aeris resistentia, ascendere debuisset. Simili methodo corrigendus erit locus k, ad quem corpus B ascendit, & inveniendus locus l, ad quem corpus illud ascendere debuisset in vacuo. Hoc pacto experiri licet omnia perinde ac si in vacuo constituti essemus. Tandem ducendum erit corpus A in chordam arcus TA (quæ velocitatem ejus exhibet) ut habeatur motus ejus in loco A proxime ante reflexionem; deinde in chordam arcus tA, ut habeatur motus ejus in loco A proxime post reflexionem. Et sic corpus B ducendum erit in chordam arcus Bl, ut habeatur motus ejus proxime post reflexionem. Et simili methodo, ubi corpora duo simul demittuntur de locis diversis, inveniendi sunt motus utriusq; tam ante, quam post reflexionem; & tum demum conferendi sunt motus inter se & colligendi effectus reflexionis. Hoc modo in Pendulis pedum decem rem tentando, idque in corporibus tam inæqualibus quam æqualibus, & faciendo ut corpora de intervallis amplissimis, puta pedum octo duodecim vel sexdecim, concurrerent; reperi semper sine errore trium digitorum in mensuris, ubi corpora sibi mutuo directe occurrebant, quod æquales erant mutationes motuum corporibus in partes contrarias illatæ, atque adeo quod actio & reactio semper 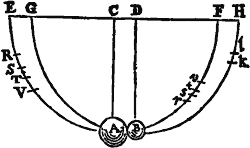 erant æquales. Ut si corpus A incidebat in corpus B cum novem partibus motus, & amissis septem partibus pergebat post reflexionem cum duabus; corpus B resiliebat cum partibus istis septem. Si corpora obviam ibant A cum duodecim partibus & B cum sex, & redibat A cum duabus; redibat B cum octo, facta detractione partium quatuordecim utrinque. De motu ipsius A subducantur partes duodecim & restabit nihil: subducantur aliæ partes duæ, & fiet motus duarum partium in plagam contrariam: & sic de motu corporis B partium sex subducendo partes quatuordecim, fiunt partes octo in plagam contrariam. Quod si corpora ibant ad eandam plagam, A velocius cum partibus quatuordecim, & B tardius cum partibus quinq; & post reflexionem pergebat A cum quinq; partibus; pergebat B cum quatuordecim, facta translatione partium novem de A in B. Et sic in reliquis. A congressu & collisione corporum nunquam mutabatur quantitas motus quæ ex summa motuum conspirantium & differentia contrariorum colligebatur. Nam errorem digiti unius & alterius in mensuris tribuerim difficultati peragendi singula satis accurate. Difficile erat, tum pendula simul demittere sic, ut corpora in se mutuo impingerent in loco infimo AB; tum loca s, k notare ad quæ corpora ascendebant post concursum. Sed & in ipsis pilis inæqualis partium densitas, & textura aliis de causis irregularis, errores inducebant.
erant æquales. Ut si corpus A incidebat in corpus B cum novem partibus motus, & amissis septem partibus pergebat post reflexionem cum duabus; corpus B resiliebat cum partibus istis septem. Si corpora obviam ibant A cum duodecim partibus & B cum sex, & redibat A cum duabus; redibat B cum octo, facta detractione partium quatuordecim utrinque. De motu ipsius A subducantur partes duodecim & restabit nihil: subducantur aliæ partes duæ, & fiet motus duarum partium in plagam contrariam: & sic de motu corporis B partium sex subducendo partes quatuordecim, fiunt partes octo in plagam contrariam. Quod si corpora ibant ad eandam plagam, A velocius cum partibus quatuordecim, & B tardius cum partibus quinq; & post reflexionem pergebat A cum quinq; partibus; pergebat B cum quatuordecim, facta translatione partium novem de A in B. Et sic in reliquis. A congressu & collisione corporum nunquam mutabatur quantitas motus quæ ex summa motuum conspirantium & differentia contrariorum colligebatur. Nam errorem digiti unius & alterius in mensuris tribuerim difficultati peragendi singula satis accurate. Difficile erat, tum pendula simul demittere sic, ut corpora in se mutuo impingerent in loco infimo AB; tum loca s, k notare ad quæ corpora ascendebant post concursum. Sed & in ipsis pilis inæqualis partium densitas, & textura aliis de causis irregularis, errores inducebant.
Porro nequis objiciat Regulam, ad quam probandam inventum est hoc experimentum, præsupponere corpora vel absolute dura esse, vel saltem perfecte elastica, cujusmodi nulla reperiuntur in compositionibus naturalibus; addo quod Experimenta jam descripta succedunt in corporibus mollibus æque ac in duris, nimirum a conditione duritiei neutiquam pendentia. Nam si Regula illa in corporibus non perfecte duris tentanda est, debebit solummodo reflexio minui in certa proportione pro quantitate vis Elasticæ. In Theoria Wrenni & Hugenii corpora absolute dura redeunt ab invicem cum velocitate congressus. Certius id affirmabitur de perfecte Elasticis. In imperfecte Elasticis velocitas reditus minuenda est simul cum vi Elastica; propterea quod vis illa, (nisi ubi partes corporum ex congressu læduntur, vel extensionem aliqualem quasi sub malleo patiuntur,) certa ac determinata sit (quantum sentio) faciatque corpora redire ab invicem cum velocitate relativa, quæ sit ad relativam velocitatem concursus in data ratione. Id in pilis ex lana arcte conglomerata & fortiter constricta sic tentavi. Primum demittendo Pendula & mensurando reflexionem, inveni quantitatem vis Elasticæ; deinde per hanc vim determinavi reflexiones in aliis casibus concursuum, & respondebant Experimenta. Redibant semper pilæ ab invicem cum velocitate relativa, quæ esset ad velocitatem relativam concursus ut 5 ad 9 circiter. Eadem fere cum velocitate redibant pilæ ex chalybe: aliæ ex subere cum paulo minore: in vitreis autem proportio erat 15 ad 16 circiter. Atque hoc pacto Lex tertia quoad ictus & reflexiones per Theoriam comprobata est, quæ cum experientia plane congruit.
<22>In attractionibus rem sic breviter ostendo. Corporibus duobus quibusvis A, B se mutuo trahentibus, concipe obstaculum quodvis interponi quo congressus eorum impediatur. Si corpus alterutrum A magis trahitur versus corpus alterum B, quam illud alterum B in prius A, obstaculum magis urgebitur pressione corporis A quam pressione corporis B; proindeque non manebit in æquilibrio. Prævalebit pressio fortior, facietque systema corporum duorum & obstaculi moveri in directum in partes versus B, motuque in spatiis liberis semper accelerato abire in infinitum. Qoud est absurdum & Legi primæ contrarium. Nam per Legem primam debebit systema perseverare in statu suo quiescendi vel movendi uniformiter in directum, proindeque corpora æqualiter urgebunt obstaculum, & idcirco æqualiter trahentur in invicem. Tentavi hoc in Magnete & ferro. Si hæc in vasculis propriis sese contingentibus seorsim posita, in aqua stagnante juxta fluitent; neutrum propellet alterum, sed æqualitate attractionis utrinq; sustinebunt conatus in se mutuos, ac tandem in æquilibrio constituta quiescent.
Sic etiam gravitas inter Terram & ejus partes, mutua est. Secetur Terra FI plano quovis EG in partes duas EGF & EGI: & æqualia erunt harum pondera in se mutuo.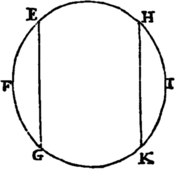 Nam si plano alio HK quod priori EG parallelum sit, pars major EGI secetur in partes duas EGKH & HKI, quarum HKI æqualis sit parti prius abscissæ EFG: manifestum est quod pars media EGKH pondere proprio in neutram partium extremarum propendebit, sed inter utramque in æquilibrio, ut ita dicam, suspendetur, & quiescet. Pars autem extrema HKI toto suo pondere incumbet in partem mediam, & urgebit illam in partem alteram extremam EGF; ideoque vis qua partium HKI & EGKH summa EGI tendit versus partem tertiam EGF, æqualis est ponderi partis HKI, id est ponderi partis tertiæ EGF. Et propterea pondera partium duarum EGI, EGF in se mutuo sunt æqualia, uti volui ostendere. Et nisi pondera illa æqualia essent, Terra tota in libero æthere fluitans ponderi majori cederet, & ab eo fugiendo abiret in infinitum.
Nam si plano alio HK quod priori EG parallelum sit, pars major EGI secetur in partes duas EGKH & HKI, quarum HKI æqualis sit parti prius abscissæ EFG: manifestum est quod pars media EGKH pondere proprio in neutram partium extremarum propendebit, sed inter utramque in æquilibrio, ut ita dicam, suspendetur, & quiescet. Pars autem extrema HKI toto suo pondere incumbet in partem mediam, & urgebit illam in partem alteram extremam EGF; ideoque vis qua partium HKI & EGKH summa EGI tendit versus partem tertiam EGF, æqualis est ponderi partis HKI, id est ponderi partis tertiæ EGF. Et propterea pondera partium duarum EGI, EGF in se mutuo sunt æqualia, uti volui ostendere. Et nisi pondera illa æqualia essent, Terra tota in libero æthere fluitans ponderi majori cederet, & ab eo fugiendo abiret in infinitum.
Ut corpora in concursu & reflexione idem pollent, quorum velocitates sunt reciproce ut vires insitæ: sic in movendis Instrumentis Mechanicis agentia idem pollent & conatibus contrariis se mutuo sustinent, quorum velocitates secundum determinationem virium æstimatae, sunt reciproce ut vires. Sic pondera æquipollent ad movenda brachia Libræ, quæ oscillante Libra sunt reciproce ut eorum velocitates sursum & deorsum: hoc est, pondera, si recta ascendunt & descendunt, æquipollent, quæ sunt reciproce ut punctorum a quibus suspenduntur distantiæ ab axe Libræ; sin planis obliquis aliisve admotis obstaculis impedita ascendunt vel descendunt oblique, æquipollent quæ sunt reciproce ut ascensus & descensus, quatenus facti secundum perpendiculum: id adeo ob determinationem gravitatis deorsum. Similiter in Trochlea seu Polyspasto vis manus funem directe trahentis, quæ sit ad pondus vel directe vel oblique ascendens ut velocitas ascensus perpendicularis ad velocitatem manus funem trahentis, sustinebit pondus. In horologiis & similibus instrumentis, quæ ex rotulis commissis constructa sunt, vires contrariæ ad motum rotularum promovendum & impediendum, si sunt reciproce ut velocitates partium rotularum in quas imprimuntur, sustinebunt se mutuo. Vis Cochleæ ad premendum corpus est ad vim manus manubrium circumagentis, ut circularis velocitas manubrii ea in parte ubi a manu urgetur, ad velocitatem progressivam cochleæ versus corpus pressum. Vires quibus Cuneus urget partes duas ligni fissi sunt est ad vim mallei in cuneum, ut progressus cunei secundum determinationem vis a malleo in ipsum impressæ, ad velocitatem qua partes ligni cedunt cuneo, secundum lineas faciebus cunei perpendiculares. Et par est ratio Machinarum omnium.
Harum efficacia & usus in eo solo consistit, ut diminuendo velocitatem augeamus vim, & contra: Unde solvitur in omni aptorum instrumentorum genere Problema, Datum pondus data vi movendi, aliamve datam resistentiam vi data superandi. Nam si Machinæ ita formentur, ut velocitates Agentis & Resistentis sint reciproce ut vires; Agens resistentiam sustinebit: & majori cum velocitatum disparitate eandem vincet. Certe si tanta sit velocitatum disparitas, ut vincatur etiam resistentia omnis, quæ tam ex contiguorum & inter se labentium corporum attritione, quam ex continuorum & ab invicem separandorum cohæsione & elevandorum ponderibus oriri solet; superata omni ea resistentia, vis redundans accelerationem motus sibi proportionalem, partim in partibus Machinæ, partim in corpore resistente producet. Ceterum Mechanicam tractare non est hujus instituti. Hisce volui tantum ostendere, quam late pateat, quamque certa sit Lex tertia motus. Nam si æstimetur Agentis actio ex ejus vi & velocitate conjunctim; & similiter Resistentis reactio æstimetur conjunctim ex ejus partium singularum velocitatibus & viribus resistendi ab earum attritione, cohæsione, pondere, & acceleratione oriundis; erunt actio & reactio, in omni instrumentorum usu, sibi invicem semper æquales. Et quatenus actio propagatur per instrumentum & ultimo imprimitur in corpus omne resistens, ejus ultima determinatio determinationi reactionis semper erit contraria.
