Catalogue Entry: NATP00221
Newton's Waste Book (Part 2)
[1] 
[2] 
[3] 
[4] 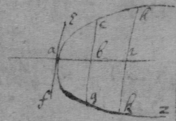
[5] 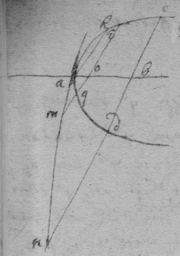
[6] 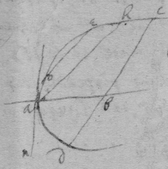
[7] 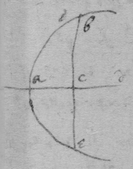
[8] 
[9] October 1664
[10] 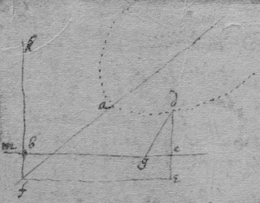
[11] 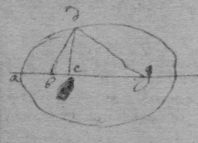
[12] 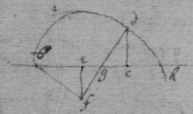
[13] 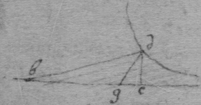
[14] 
[15] 
[16] 
[17] 
[18] 
[19] 
[20] 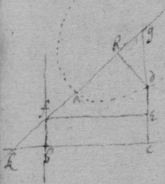
[21] 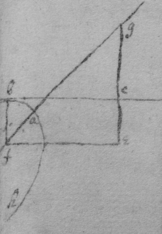
[22] For the first equation of the first sort
[23] For the 2d
[24] For the 3d
[25] For the 4th
[26] For the 5t
[27] For the 6t &c
[28] For the first Equation of the seacond Sort
[29] For the seacond
[30] For the 3d.
[31] 
[32] 
[33] November 1664
[34] 
[36] 
[37] 
[38] 
[39] November 1664
[40] A
[41] 
[42] 
[43] 
[44] 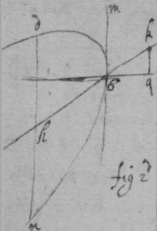
[45] 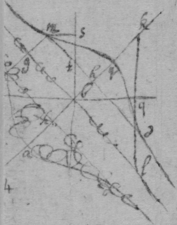
[46] 
[47] 
[48] 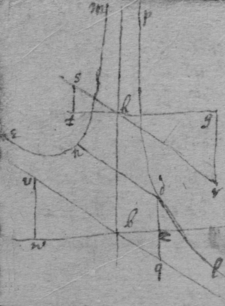
[49] B
[50] 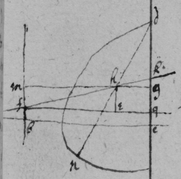
[51] This line is a streight one the equation being divisible by
[52] Endeavor not to find the quantity d in these cases, but suppose it given[Editorial Note 1]
[Editorial Note 1] There is a line connecting the end of this note to the following one
[53] Or else C ☞
[54] December
[55] 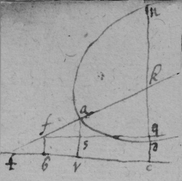
[56] 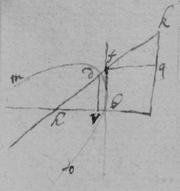
[57] 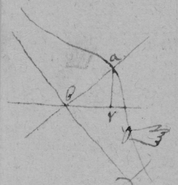
[58] ☞
[59] 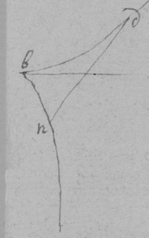
[60] 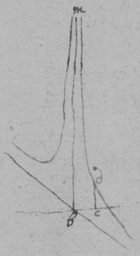
[61] 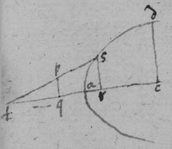
[62] F
[63] 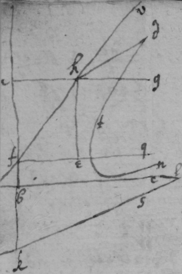
[64] G
[65] 
[66] December 1664
[67] 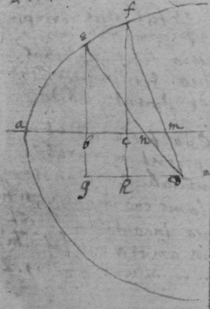
[68] 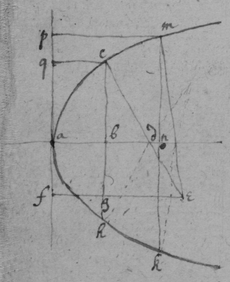
[69] Theorema
[70] 
[71] December 1664.
[72] 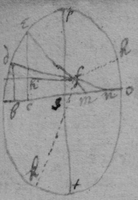
[73] 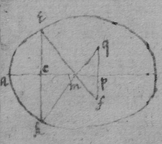
[74] 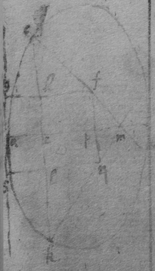
[75] 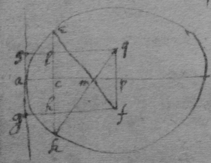
[76] 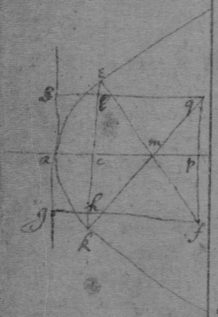
[77] 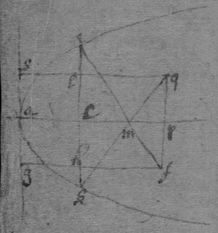
[78] 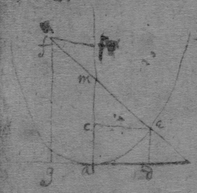
[79] 
[80] 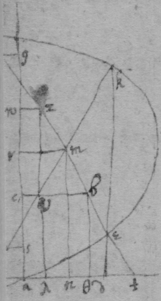
[81] 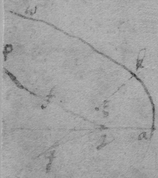
[82] 
[83] Feb 1664
[84] 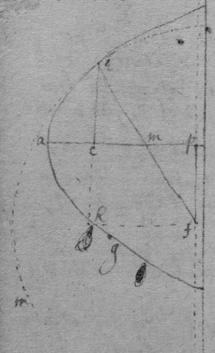
[85] 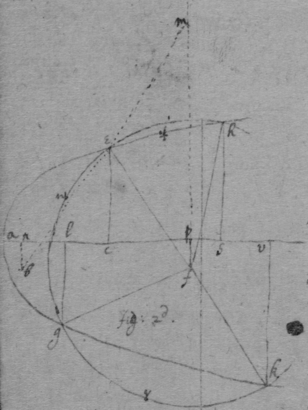
[86] Another way.
[87] 
[88] December 1664
[89] 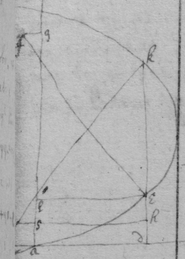
[90] 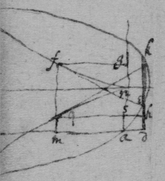
[91] 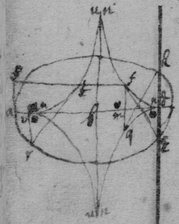
[92] 
[93] 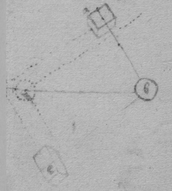
[94] Of compound force.
[95] 
[96] 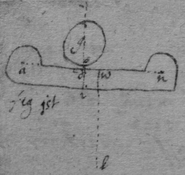
[97] 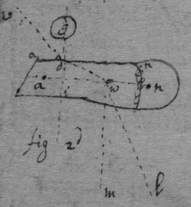
[98] 
[99] 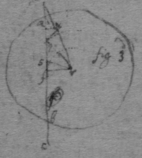
[100] 
[101] May 20th 1665
[102] 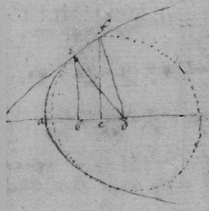
[103] Observation 1st
[104] Observacion 2d
[105] An universall theorem for tangents to crooked lines, when .
[106] See Des Cartes his Geometry. booke 2d, pag 42, 46, 47. Or thus, { }. And .
[107] 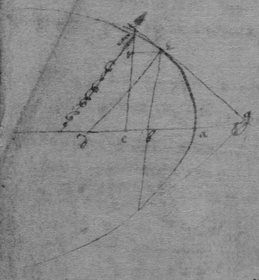
[108] An universall theorem for drawing tangents to crooked lines when x & y intersect at any determined angle
[109] 
[110] A=
[111] 
[Editorial Note 2] The rest of the page is damaged.