References to the original letters contained, or intended to be contained, in the Commercium Epistolicum
Epistola D. Leibnitij ad D. Newtonum 17 Mar. 1693 st. n. data cujus Autographum in Archivis Societatis Regiæ asservatur
Ex Præfatione D. Wallisij in Operum suorum Volumina duo prima Oxonij ineunte anno 1695 scripta.
Ex Epistola D. Wallisij ad D. Newtonum, Oxonij, Apr. 10, 1695, script{a} et in Archivis Regiæ Societatis asservata.
Ex Actis Eruditorum pro mense Iunio Anni 1696 pag. 257 Calculo quoque differentiali Leibnitij affinem esse methodum fluxionum Newtoni - - - - - - - - - - non æque noscebantur
Ex Epistola D. Wallisij ad D. Leibnitium Oxonij Decem. 1. 1696 scripta et in tertio Volumine Operum Wallisij edita. p. 654.
Neque Calculi Differentialis – – – interseruerim.
NB Wallisius Epistolas Newtoni olim acceperat ab Oldenburgo, eas Leibnitij accepit tandem e scrinijs Collinij. In Actis eruditorum verba Wallisij [nequis causetur de Calculo Differentiali nihil a me dictum fuisse] recitantur ideoque Editores Wallisium legerant; Newtonum tamen anno 1676 methodum suam Leibnitio exposuisse, tum ante annos decem nedum plures ab ipso excogitatam, non negant Contendunt tantum quod Newtonus publice et privatim agnovit Leibnitium tum cum inter ipsos, intercedente Oldenburgo, commercium intercederet, methodum habuisse. Et Newtonus quidem Leibnitium quæ in Epistola sua 21 Iunij 1677 data posuit tunc habuisse, nunquam negavit; quid amplius per ea tempora habuerit, minime novit. Scholium vero ad Lemma secundum libri secundi Principiorum posuit, ut Lemma illud in quo methodus fluxionum fundatur, ante annum 1676 sibi cognitum fuisse assereret
Apographum Schediasmatis
Ex Tractatu parvo sub finem anni 1666 conscripto.
Ex Analysi per æquationes numero terminorum infinitas anno 1669 a Barrovi ad Collinium missa.
Ex Tractatu de methodis serierum et fluxionum anno 1671 composito. Fluentes designabo finalibus literis v, x, y, z et celeritates quibus singulæ a motu generante fluunt et augentur designabo literis l, m, n, r respective.
Prob. 1. Relatione quantitatum fluentium inter se data, fluxionum relationem determinare.
Solutio. Equationem qua data relatio exprimitur dispona secundum dimensionis alicuius fluentis quantitatis puta x, ac terminos ejus multiplica per quamlibet Arithmeticam Progressionem ac deinde per . Et hoc opus in qualibet fluente quantitate seorsim institue. Dein omnium factorum summam pone nihilo æqualem et habebis æquationem desideratam.
Prob. 2. Exposita æquatione fluxiones quantitatum involvente invenire relationem quantitatum inter se.
Ex Epistola Newtoni 10 Decem. 1672 ad Collinium missa
Ex Epistola Newtoni 13 Iunij 1676 ad Oldenburgum missa
Ex Epistola Leibnitij 27 Aug 1676 ad Oldenburgum missa
Ex Epistola Newtoni 24 Octob 1676 ad Oldenburgum missa
Ex Epistola Leibnitij 21 Iunij 1677 ad Oldenburgum missa
Ex Schediasmate Leibnitij in Actis Eruditorum pro mense Octobri 1684 edita Et hæc quidem initia sunt – – – pari facilitate tractabit.
Lem. II Lib. II Principiorum Newtoni.
NB. Cum D Leibnitius in Actis Eruditorum, ubi edidit Elementa methodi differentialis, Commercium quod annis 1676 & 1677 cum Newtono mediante Oldenburgo habuerat, silentio præteriret, Newtonus ne Lemma hocce non suum esse videretur, huic Lemmate Scholium sequens subjunxit.
Scholium
Epistola D. Leibnitij ad D. Newtonum 17 Mar 1693 st. n data, cujus Autographum in Archivis Societatis Regiæ asservatur.
Ex Præfatione Wallisij in operum suorum Volumina duo prima
Extracts of Letters found in the custody of the R. Society & among the papers of Mr Iohn Collins, relating to the Collection of Mathematical Letters published by Dr Wallis in the third volume of his works.
– 1 Out of a Letter of Mr Isaac Barrow to Mr Collins dated at Cambridge the 20th of Iuly 1669, & extant in the original hand-writing of the author.
A friend . . . . . . . by the next.
– 2 Out of a Letter of Mr Barrow to Mr Collins dated the 31th of Iuly 1669 & extant in the hand-writing of the author.
I send . . . . . . . . : your desire:
– 3 Out of a Letter of Mr Barrow to Mr Collins dated the 20th of August 1669 & extant in the hand-writing of the Author.
I am glad . . . . . . . Lord Brounker.
– 4 Out of a Copy written in the hand of Mr Collins, found amongst his papers & collated with a MS borrowed of Sir Is. Newton supposed to be the original, the Analysis per æquationes infinitas hath been printed.
– 5 Out of a Paper written in the hand of Mr Collins & directed to Mr Oldenburgh to be communicated to Mr Slusius in the year 1669.
Dr Barrow hath communicated an universal Analytical method imparted to him by Mr Isaac Newton his Collegiate for the mensuration of the Areas of all such Curves & their Perimeters . . . . . . . . . . . . . . . . non opus est quicquam de ijs adjungere.
– 6 Out of a Letter of Mr Collins to Mr Iames Gregory dated the 25th of November 1669, a coyp of which is extant in the hand writing of Mr Collins.
Mr Barrow hath . . . . . . . . . . . . . in the Hyperbola.
– 7 Out of a Letter of Mr Iames Gregory to Mr Collins dated at St Andrews the 20th of April 1670, & extant in the original hand of the author.
I cannot understand the series ye sent me of the circle, vizt . If this be the original, I take it to be no series.
– 8 Out of an original Letter of Mr Iames Gregory to Mr Collins dated at St Andrews the 5t of September 1670
I have read over Mr Barrow's . . . . . . . . . . . . not above twelve Propositions.
<270r>9 – Out of an original Letter of Mr Iames Gregory to Mr Collins dated at St Andrews the 19th of December 1670.
In my last to you I had not taken notice . . . . . . . . . . . . but perchance ye know more of them then my self.
10 – Out of a Letter of Mr Collins to Mr Iames Gregory dated the 24th of December 1670, a copy of which is extant in the hand writing of Mr Collins
When Mr Davy . . . . . . . . . . . as also the finding of the Area.
11 – Out of an original Letter of Mr Iames Gregory to Mr Collins dated at St Andrews the 15th of February 1671.
As for Mr Newtons universal method, I imagin I have some knowledge of it both as to geometrick & mechanick curves. However I thank you for the series ye sent me & send you these following in requital. Sit radius r arcus a, tangens t, secans s erit eritque , et . . . . . . . . . . . . . . . . . for I am little concerned if they be published under any others name or not.
12 – Out of a Letter of Mr Collins to Mr Bertet at Paris, dated the 21th of February 1670, a copy of the Letter being extant in the hand writing of Mr Collins.
To compose . . . . . . . . . . faln into the same method
– 13 – Out of a Letter of Mr Collins sent into Italy to Borellius (the author of the Book de motionibus naturalibus a gravitate pendentibus) dated in December 1671, a copy of which is extant in the hand writing of Mr Collins.
Kinckhuysen's Introduction . . . . . . . . inserting the series.
– 14 Out of a Letter of Mr Collins to Mr Vernon at Paris dated the 26th of December 1671, a copy of which is extant in the hand writing of Mr Collins.
Dr Barrow tells me . . . . . . . deductions can be the same.
– 15 Out of a Letter of Mr Collins to Mr Strode dated the 26th day of Iuly 1672 a copy of which is extant in the handwriting of Mr Collins
As to curvilinear . . . . . . . . the first inventor thereof.
– 16 Out of a Letter of Mr Collins to Mr Newton dated the 30th of Iuly 1672 a copy of which is extant in the hand writing of Mr Collins
In preparing . . . . . . . . . . . . . he may be intent.
– 17 Out of a Letter of Mr Newton to Mr Collins dated the 10th of December 1672 found amongst the papers of Mr Collins in the original handwriting of the author, with a copy in the hand-writing of Mr Collins.
I am heartily glad . . . . . . . . . . . from describing it to him
I suppose Slusius his method of Tangents will shortly appear abroad. When it comes over I'l{l} beg of you the trouble of transmitting a copy to me
<268r>– 18 A Letter of Mr Slusius to Mr Oldenburgh dated at Leige the 17th of Ianuary 1673, & entred in the Books of the R. Society Num. 6 pag 11 was printed in the Transactions Num 90, & conteins his method of drawing Tangents.
– 19 Out of a Letter of Mr Oldenburgh to Mr Slusius dated the 29th of Ianuary 1673 in answer to the preceding Letter of Ian 17, & copied in the books of the R. Society Num 6 pag. 27
Statui Deo dante . . . . . . . . . . ut cum novissimis tuis comparare possis.
– 20 A Letter of Mr Slusius to Mr Oldenburgh dated at Leige the 3d of May 1673 & entred in the books of the R. Society Num. 6, pag. 111 was printed in the Transactions Num 95 & conteins the foundation of his method.
– 21 A Letter of Mr Collins to Mr Newton dated 18th Iune 1673 was printed by Dr Wallis.
– 22 Out of a Letter of Mr Oldenburgh to Mr Slusius dated the 10th of Iuly 1673 & entred in the books of the R. Society. Num. 6. p. 196.
Ex tibi, Vir illustrissime, impressum modum tuum demonstrandi Methodum tuam ducendi Tangentes . . . . . . . . a te acceptum iri confida
– 23 Out of a Letter of Mr Leibnitz to Mr Oldenburgh dated at London the 3d of February 167, extant in the hand-writing of the Author & entred in the Letter-books of the R. Society N. 6, pag 34
Cum heri apud illustrissimum Boylium incidissem in clarissimum Pellium . . . . . . . . . . . . . . aut Triangulo-triangulares &c.
There are five other Letters of Mr Leibnitz to Mr Oldenburgh dated in the year 1673, the first of them at London the of Febr. the rest at Paris the 30 of March the of April, the of May, & the 8th of Iune, all of them in the hand writing of the Author, & the first & three last entred in the books of the R. Society Num. 6, pag. 34, 101, & 137.
Two other Letters of Mr Leibnitz to Mr Oldenburgh dated at Paris the 15th of Iuly 1674, & the 16 of October 1674, entred in the books of the R. Society, Num 7 pag 93 & 110, have been printed by Dr Wallis.
24 – Out of a Letter of Mr Oldenburgh to Mr Leibnitz dated the 8th of December 1674, extant in the hand of the author, entred in the books of the R. Society Num. 7 p. 119, & written in answer to Mr Leibnitz Letter of Octob 16 1674
Quod de profectu in curvilinearum dimensione memoras . . . . . . . . . . . . . de eo quidem tibi gratulor.
<269r>25 – Out of a Letter of Mr Leibnitz to Mr Oldenburgh dated at Paris the 30th of March 1675, extant in the hand of the author entred in the Books of the R. Society Num 7 p 213, & written in answer to Mr Oldenburghs Letter of Decemb. 8, 1674.
Scribis Cl. Newtonum vestrum habere methodum exhibendi quadraturas omnes . . . . . . . . . . . dignam. Addis tale quid Gregorio innotuisse.
26 – Out of a Letter of Mr Oldenburgh to Mr Leibnitz dated the 15th of April 1675, & entred in the books of the R. Society N. 7, p. 216, & writ in answer to Mr Leibnitz's Letter of the 30th of March. It was first writ in English by Mr Collins & is extant in his hand writing, being dated Apr. 10 & sent to Mr Oldenburgh to be translated into Latin & sent to Mr Leibnitz
Dn. Collinus, præmissa salute, quæ sequuntur remittit. Rimò Cl. Gregorium in postrema sua ad Illustrem Hugenium responsione seriem suppeditasse ad semicircumferentiam circuli inveniendam, quæ talis. Pone radium . . . . . . . . . . . . . . . . inventionem orbi mathematico patefaciat.
27 – Out of a Letter of Mr Leibnitz to Mr Oldenburgh dated at Paris the 20th of May 1675 extant in the handwriting of the author entred in the books of the R. Society Num 7 p 235 & written in answer to that of Mr Oldenburgh of the 15th of April 1675.
28 – Out of a Paper written in the hand of Mr Collins & found amongst his papers & corrected in some places in the hand of Mr Oldenburgh in Order to be translated into Latin & sent to Mr Tschurnhause, whose answer was received by Mr Oldenburgh the 8th of Iune 1675 & entituled Responsum ad scriptum D. Collinij de Cartesij inventis.
Des Cartes was accused of arrogance, as asserting that of all ways . . . . . . . . . of the 10th of December 1672.
[Read here the Letter above]
29 – Out of a Letter of Mr Oldenburgh to Mr Leibnitz dated the 24th of Iune 1675 & entred in the Books of the R. Society N 7 p 243 being in answer to the Letter of Mr Leibnitz dated the 20th of May preceding.
Dominus Newtonus beneficio Logarithmorum . . . . . . . . potestas pura radicis quæsitæ
30 – A Letter of Mr Leibnitz to Mr Oldenburgh dated at Paris the 12th of Iuly 1675, extant in the hand writing of the author, entred in the books of the R. Society N. 7 p 149 & written in answer to Mr Oldenburghs Letter of the 24th of Iune, hath been printed by Dr Wallis. In this Letter Parius is corruptly written for Darius.
<267r>
31 — Out of a Letter of Mr Oldenburgh to Mr Leibnitz dated the 30th of September 1675, a copy of which is extant in the hand of Mr Oldenburgh, & which was entred in the books of the R. Society N. 7 p 159 & was written in answer to the former.
Scriptum quoddam Belga quidam Georgius Mohr vocatus . . . . . . . . . . . . . . . . . . . . . Collinius ipsi communicavit.
32 – A Letter of Mr Leibnits to Mr Oldenburgh dated at Paris the 28th of December 1675 extant in the handwriting of the author & entred in the books of the R. Society Num. 7 p. 189, hath been printed by Dr Wallis.
33 – Out of a Letter of Mr Leibnitz to Mr Oldenburgh dated at Paris the 12th of May 1676 & found amongst the papers of the R. Society in the original hand of the author, with Notes on the backside in the hand of Mr Oldenburgh.
Cum Georgius Mohr Danus . . . . . . . . . . . . . . . . . satisfaciendi desiderio meo.
34 – Out of a Letter of Mr Collins to Mr Oldenburgh to be sent to Mr Leibnitz at Paris; a Copy of which dated the 14th day of Iune 1676 was found amongst the papers of Mr Collins & in his handwriting.
In answer to Mr Leibnitz Letter of the 12th of May . . . . . . . . . . . . . . . . . was but as dawning to noon day.
35 – Out of a Letter of Mr Collins to Mr David Gregory the brother of Mr Iames Gregory newly deceased, dated the 11th of August 1676, a copy of which is extant in the handwriting of Mr Collins.
I have drawn up an account of the Letter commerce . . . . . . . . . . . . . . . as himself acknowledgeth in his Letter of the 19th of December 1670.
– Vpon the receipt of the Letter of Mr Leibnitz dated the 12th of May, Mr Oldenburgh & Mr Collins sollicited Mr Newton for an account of his method of infinite series: which occasioned his two Letters dated 13 Iune & 24 October 1676, with Mr Leibnitz answers the first at Paris the th of August 1676, the second at Hanover the 21th of Iune 1677, & a supplement to the second answer dated also at Hanover the 12th of Iuly 1677 & a Letter of Mr Collins to Mr Newton dated the 5t of March 167, all printed by Dr Wallis.
<266r>36. – Out of a Letter of Mr Tschurnhause dated at Paris 1 Sept. 1676, a copy of which is extant in the hand-writing of Mr Collins.
Expectabam cum desiderio Responsum . . . . . . . . . . . . operam navabunt.
1 Out of a Letter of Mr Leibnitz to Mr Oldenburgh dated at London 3d Feb 167 & extant in the hand of the author & entred in the Letter books of the R. Society. N 6 pag 3. It concerens the differential method ascribed by Dr Pell to Mouton.
2 Out of a Letter of Mr Leibnitz to Mr Oldenburgh dated at London Feb 1673 & extant in the hand of the author & entred in the Letter book of the R. Society Num. 6. pag 34. Desires to be a Fellow of the R. Society.
3 Out of a Letter of Mr Leibnitz to Mr Oldenburgh dated at Paris March 30th 1675 & extant in the hand of the author,
4 Out of a Letter of Mr Leibnitz to Mr Oldenburgh dated at Paris Apr. 1673 & extant in the hand of the author & copied in the books of the R. Society Num 6. p. 101. Subtilissimo Collinio tam præclara communicanti obligatum me profiteor
5 Out of a Letter of Mr Leibnitz to Mr Oldenburgh dated at Paris May 1673 & extant in the hand of the author & entred in the books of the R Society N 6
6 Out of a Letter of Mr Leibnitz to Mr Oldenburgh dated at Paris 1 Iune 167 returning thanks for his being elected fellow of the R Society. It is entred in the books of the Society N 6 p 137.
NB. Mr Leibnitz was proposed to the R Society & elected
7 A Letter of Mr Leibnits to Mr Oldenburgh dated at Paris 15th 1674, extant in the hand of the Author & entred in the books of the R Society N 7 p 93. was printed by Dr Wallis in the 3d Volume of his works
8 And another Letter of Mr Leibnits to Mr Oldenburgh dated at Paris Octob 1674, & entred in the books of the R. Society N 7 p 110, & were printed by Dr Wallis in the 3d volume of his works.
9 Out of a Letter of Mr Oldenburgh to Mr Leibnitz dated 8th of December 1674 extant in the hand of the author & entred in the books of the R. Society Num 7 p. 119. It conteins an answer to Mr Leibnitz Letter of Octob 16 1674.
10 Out of a Letter of Mr Leibnitz to Mr Oldenburg dated at Paris 30th March 1675, extant in the hand of the author & entred in the books of the R Society Num 7 p. 213, & written in answer to Mr Oldenburghs Letter of 8th Decemb. 1674.
11 Out of a Letter of Mr Oldenburgh to Mr Leibnits dated 15th April 1675 extant in the hand of Mr Collins in English & entred in L. Latin in the books of the R Society N. 7, p. 216. It was writ in answer to Mr Leibnitz's Letter of 30 March 1675, the English copy being dated 10th April & the Latin 15th Apr.
12 Out of a Letter of Mr Leibnitz to Mr Oldenburgh dated at Paris 20th May 1675, extant in the hand of the author entred in the books of the R. Society Num 7 p. 235, & written in answer to the of Mr Oldenburgh of 15 Apr. 1675.
13 Out of a Letter of Mr Oldenburg to Mr Leibnitz dated 24 Iune 1675, & entred in the books of the R. Society N. 7 p. 243. being in answer to the former.
<271v>14 Out of a Letter of Mr Leibnitz to Mr Oldenburgh dated [at Paris] 12 Iuly 1675, extant in the original hand, entred in the Books of the R Society N 7 p 149 printed by Dr Wallis & written in answer to Mr Oldenbergs Letter of 24 Iune. In this Letter Parius is corruptly written for Darius.
15 Out of a Letter of Mr Oldenburgh to Mr Leibnits 30 Sept 1675 extant in the hand of Mr Oldenburgh & entred in the books of the R Society Num 7 p 159. It was writ in answer to the former. Mr Tschurnhause was then newly gone from London to Paris having received of Mr Collins at London one of Gregories series for the circle.
16 Out of a Paper written in the hand of Mr Collins & found amongst his papers & corrected in some places in the hand of Mr Oldenburgh in Order to be copied & sent to Mr Tschurnhaus.
NB The answer of Mr Tschurnhau to this paper was received by Mr Oldenburgh the 8th of Iune 1675 & entituled Responsum ad scriptum Domini Collinij de Cartesij inventis.
17 Out of a Letter of Mr Leibnitz to Mr Oldenbergh dated at Paris 28 Decemb 1675, extant in the hand of the author, entred in the books of the Society Num 7 p 189 & printed by Dr Wallis.
18 Out of a Letter of Mr Leibnitz to Mr Oldenberg dated at Paris 12 May 1676 found amongst the papers of the R. Society in the original hand of Mr Leibnitz with notes on the back side in the hand of Mr Oldenburgh, for returning an answer. This Letter occasioned the Letters of Mr Newton.
19 Out of a Letter of Mr Collins to Mr Oldenberg to be sent to Mr Leibnitz in answer to his Letter of the 12th of May. A copy of this was found amongst the papers of Mr Collins & in his hand, & dated 14th Iune 1676
20 Out of Mr Newtons Letter of Iune 13 1676.
21 Out of the Answer of Mr Leibnitz dated at Paris Aug. 1676
22 Out of a Letter of Mr Tschurnhause dated at Paris 1 Sept 1676 N.S
23 Out of {a} Letter of Mr Collins to Mr Newton dated 31 Aug. 1676 O.S.
24 Out of Mr Collins Letter to Mr Newton dated 9 Sept 1676.
25 Out of Mr Newtons Answer to Mr Leibnitz dated Octob 24. 1676.
26 Out of Mr Leibnitz Letter to Mr Oldenberg dated at Amsterdam Novemb 1676. Printed by Dr Wallis in a Letter of Mr Collins dated 5 March 167.
27 Out of a Letter of Mr Leibnitz to Mr Oldenberg dated from Hannover 28 Ian 1677. Extant in the Original
29 Out of an Original Letter of Mr Leibnitz to Mr Oldenb. dated from Hannover March 1677.
30 Out of an original Letter of Mr Leibnitz to Mr Oldenburgh dated from Hannover 30 May 1677.
28 Out of a Letter of Mr Collins to Dr Wallis dated the 14th of February 167 a copy of which is extant in the hand writing of Mr Collins.
Out of a Letter of Mr Collins to Mr Newton dated 5 March 167 & published by Dr Wallis. Aderat hic . . . . . . prope diem missurum. P.S. Exemplar Epistol{a} . . . . . . laturus est.
1 Out of a Letter of Dr Barrow to Mr Collins dated the 20th of Iuly 1669 & extant in the original hand of the author.
2 Out of a Letter of Dr Barrow to Mr Collins dated the 31th of Iuly 1669 & extant in the original hand.
3 Out of a Letter of Dr Barrow to Mr Collins dated the 20th of August & extant in the original hand.
7 Out of an original Letter of Mr Iames Gregory to Mr Collins dated at St Andrews the 20th of April 1670 & extant in the original hand of Mr Gregory.
8 Out of a original Letter of Mr Iames Gregory to Mr Collins dated at St Andrews the 19th of December & extant in the original hand
10 Out of an original Letter of Mr Iames Gregory to Mr Collins dated at St Andrews the 15th of February 1671
5 Out of an Letter of Mr Collins to Mr Iames Gregory dated the 25t of November 1669 a copy of which is extant in the hand writing of Mr Collins.
6 Out of a{n} original Letter of Mr Iames Gregory to Mr Collins dated the 5t of September 1670
9 Out of a Letter of Mr Collins to Mr Iames Gregory dated the 24th of December 1670, a copy of which is extant in the hand writing of Mr Collins.
11 Out of a Letter of Mr Collins to Mr Bertet dated the 21th of Feb. 1670 Mr Bertet being then at Paris & a copy of the Letter being extant in the hand writing of Mr Collins.
12 Out of a Letter of Mr Collins sent into Italy to Borellius (the author of the book de motionibus naturalibus a gravitate pendentibus) dated in December 1671, a copy of which is extant in the hand writing of Mr Collins.
13 Out of a Letter of Mr Collins to Mr Vernon dated the 26th of December 1671 Mr Vernon being then at Paris. A copy of the Letter is extant in the hand writing of Mr Collins.
14 Out of a Letter of Mr Collins to Mr Strode dated the 26th of Iuly 1672, a copy of which is extant in the hand writing of Mr Collins.
15 Out of a Letter of Mr Collins to Mr Newton dated the 30th of Iuly 1672 a copy of which is extant in the hand of Mr Collins
16 Out of a Letter of Mr Newton to Mr Collins dated the 10th of December 1672 found amongst the papers of Mr Collins in the original hand writing of the Author with a copy in the hand writing of Mr Collins.
18 Out of a Letter of Mr Oldenburgh to Monsr Fr. Slusius dated the 29th of Ianuary 1673 in answer to the Letter dated the 17th of Ian 167. This Letter is copied in the Letterbook of the R. Society N. 6. p. 27.
20 Out of a Letter of Mr Oldenburgh to Mr Slusius dated the 10th of Iuly 1673 extant in the books of the R. Society. N 6 p 196.
17 A Letter of Mr Slusius to Mr Old. dated at Leige 17th Ian 1673 extant in the books of the Society N 6. p. 11 & printed in the Transactions, Num 90 conteins his method of drawing Tangents.
19 Out of a Letter of Mr Slusius to Mr Oldenb. dated at Leige 3d May 1673 extant in the books of the Society. Num 6. pag 111, & printed in the Transaction Num 95 p 6059, nisi quod Newtoni nomen subticetur
Out of a Letter of Mr Collins to Mr David Gregory the brother of Mr Iames Gregory newly deceased dated 11th August 1676, a copy of which is extant in the hand of Mr Collins.
4 Out of a Copy written in the hand of Mr Collins & found amongst his papers & collated with the original MS borrowed of Mr Newton by Mr Iones the Analysis per æquationes infinitas has been published by the said Mr Iones.
And the Tract here mentioned conteining the general method for finding such series, is that which Mr Newton spake of in his Letter of Octob 24 1675 as written five years before
There are five other Letters of Mr Leibnitz to Mr Oldenburgh in the year 1673 dated the first at London Feb. the rest at Paris 30 March 30, Apr , May & Iune 1st all of them (except the last) in the hand writing of the author & the first & the last entred in the Letter books of the Society Num 6 pag 34, 101, 137
1. Out of a Letter of Mr Isaac Barrow to Mr Collins dated at Cambridge the 20th of Iuly 1669 & extant in the original hand of the Author.
2. Out of a Letter of Mr Barrow to Mr Collins dated the 31th of Iuly 1669 & extant in the hand-writing of the Author.
3. Out of a Letter of Mr Barrow to Mr Collins dated the 20th of August 1669 & extant in the hand-writing of the Author.
4. Out of a Copy written in the hand of Mr Collins & found amongst his papers & collated with a MS borrowed of Sir Is. Newton by Mr Iones & supposed to be the original, the Analysis per æquationes infinitas hath been printed.
6 Out of a Letter of Mr Collins to Mr Iames Gregory dated the 25th of November 1669, a copy of which is extant in the hand writing of Mr Collins.
8 Out of an original Letter of Mr Iames Gregory to Mr Collins dated at St Andrews the 5th of September 1670.
7 Out of an original Letter of Mr Iames Gregory to Mr Collins dated at St Andrews the 20th of April 1670
9 Out of an original Letter of Mr Iames Gregory to Mr Collins dated at St Andrews the 19th of December 1670
10 Out of a Letter of Mr Collins to Mr Iames Gregory dated the 24th of December 1670 a copy of which is extant in the hand writing of Mr Collins
11 Out of an original Letter of Mr Iames Gregory to Mr Collins dated at St Andrews the 15th of February 1671.
5 Out of a Paper written in the hand of Mr Collins & directed to Mr Oldenburgh to be communicated to Mr Slusius in the year 1669 before
12 Out of a Letter of Mr Collins to Mr Bertet at Paris dated the 21th of Feb 1670, a copy of the Letter being extant in the hand writing of Mr Collins.
13 Out of a Letter of Mr Collins sent into Italy to Borellius (the author of the Book de motionibus naturalibus a gravitate pendentibus) dated in December 1671, a copy of which is extant in the hand writing of Mr Collins.
14 Out of a Letter of Mr Collins to Mr Vernon at Paris dated the 26th of December 1671, a copy of which is extant in the hand writing of Mr Collins.
15 Out of a Letter of Mr Collins to Mr Strode dated the 26th day of Iuly 1672, a copy of which is extant in the hand writing of Mr Collins.
16 Out of a Letter of Mr Collins to Mr Newton dated the 30th of Iuly 1672, a copy of which is extant in the hand writing of Mr Collins
17 Out of a Letter of Mr Newton to Mr Collins dated the 10th of December 1672 found amongst the papers of Mr Collins in the original hand writing of the author, with a copy in the hand writing of Mr Collins.
18 A Letter of Mr Slusius to Mr Oldenburgh dated at Leige 17th Ian 1673, entred in the books of the R. Society Num. 6 pag. 11, conteins his method of drawing Tangents & was printed in the Transactions Num. 90. It conteins his method of drawing Tangents
19 Out of a Letter of Mr Oldenburgh to Monsr Slusius dated the 29th of Ianuary 1673 in answer to the preceding Letter of Ian 17 & copied in the Books of the R. Society Num. 6, pag. 27.
<274r>20 A Letter of Mr Slusius to Mr Oldenberg dated at Leige the 3d May 1673, entred in the books of the R. Society. Num 6 pag 111 , conteining the Demonstration of his method was printed in the Transactions Num 95 p 6059.
21 A Letter of Mr Collins to Mr Newton dated 18 Iune 1673 was printed by Dr Wallis.
22 Out of a Letter of Mr Oldenburgh to Mr Slusius dated the 10th of Iuly 1673, & entred in the books of the R. Society. Num 6. p 196.
24 Out of a Letter of Mr Collins to Mr David Gregory the brother of Mr Iames Gregory newly deceased, dated 11th August 1676, a copy of which is extant in the hand of Mr Collins.
23 Out of a paper written in the hand of Mr Collins & corrected in some places in the hand of Mr Oldenburgh in order to be copied & sent to Mr Tschunhaus
A Letter of Mr Leibnitz to Mr Oldenburgh dated at Paris the 28th of December 1675 extant in the handwriting of the author & entred in the books of the R. Society Num 7 p 189, hath been printed by Dr Wallis.
Out of a Letter of Mr Leibnitz to Mr Oldenbergh dated at Paris the 12th of May 1676 & found amongst the papers of the R. Society in the original hand of Mr Leibnitz with notes on the back side in the hand of Mr Oldenburgh
Cum Georgius Mohr Danus . . . . . . . . . . satisfaciendi desiderio meo.
Vpon the receipt of this Letter Mr Oldenburgh & Mr Collins sollicited Mr Newton . . . . . . . . . . . . . all printed by Dr Wallis.
Out of a Letter of Mr Collins to Mr Oldenberg to be sent to Mr Leibnitz in answer to his Letter of the 12th of May. A copy of this Letter was found amongst the papers of Mr Collins & in his hand-writing & was dated the 14th of Iune 1676
In answer to Mr Leibnitz Letter of the 12th of May . . . . . . . . . . . . . . was but as dawning to noon day.
② Out of a Letter of Mr Collins to Mr David Gregory the brother of Mr Iames Gregory newly deceased, dated 11th of August 1676, a copy of which is extant in the hand writing of Mr Collins.
I have drawn up an account of the Letter commerce . . . . . . . . . . . . as himself acknowledgeth in his Letter of 19th December 1670.
① Out of a Letter of Mr Tschunhause dated at Paris 1 Sept. 1676, a copy of which is extant in the hand writing of Mr Collins
Expectabam cum desiderio Responsum . . . . . . . . . . . . . . operam navabunt.
③ A Letter of Mr Leibnitz to Mr Oldenburgh dated at Hanover the 12th of Iuly 1677 & extant in the hand-writing of the Author, hath been printed by Dr Wallis.
①
'Out of a Letter of Mr Collins to Mr Iames Gregory dated the 25 of November 1669
Mr Barrow hath resigned his Lecturers place to one Mr Newton of Cambridge whom he mentioneth in his Optick Præface as a very ingenious person, one who hath (before Mr Mercators Logarithmotechnia was extant) invented the same method & applied it generally to all Curves & divers ways to the circle whereof either for the whole or the parts it more readily rendreth the Area then it doth in the Hyperbola.
③ 'Out of a Letter of Mr Collins to Mr Strode dated the 26 of Iuly 1672
As to Curvilinear & solid Geometry that this should at last generally fall under a calculus Analyticus s News to the World, the Æquations being series consisting of an infinite number of terms (whereof few are sufficient for use) derived from the known properties of Curves. As to the Author & Excellency of this method take this narrative.
In September 1668 Mr Mercator published his Logarithmotechnia containing a specimen of this Method in one only figure, to wit in the quadrature of the Hyperbola. Not long after forthwith gave his sense of it in the Transactions. Another of them I sent to Dr Barrow at Cambridge who forthwith sent me up some Papers of Mr Newton who is since become Dr Barrows successor in the Mathematical Lecture there, by which & former communications made thereof by the Author to the Doctor, it appears that the said method was invented some years before by the said Mr Newton & generally applied. So that thereby in any Curvilinear figure proposed that is determined by one or more common properties, by the said Method may be obtained the quadrature or Area of the said figure accurately when it is quadraturæ capax, but always infinitely neare, the evolution or length of the curved line, the center of gravity of the figure, its round solids made by rotation & their surfaces & all performed without any extractions of roots.
Both Mr Newton & Mr Gregory intend to write of this method in Latin, but Mr Gregory will not anticipate Mr Newton the first inventor thereof.
④ 'Out of Mr Newtons Letter of the 10th of December 1672
Mr Newton in his letter of December 10th 1672 takes notice that he was informed by Mr Collins that Slusius & Mr Gregory were fallen into new methods of drawing Tangents & that Dr Barrows Lectures were of high esteem amongst the learned & in answer thereto saith thus I am heartily glad at the acceptance our Reverend friend Dr Barrows Lectures find with foreign Mathematicians, & it pleased me not a little to understand that they [Slusius & Gregory] are fallen into the same method of drawing Tangents with me. What I ghesse their method to be you will apprehend by this example. Suppose CB applied to AB in any given angle be 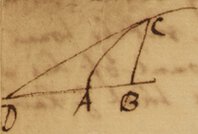 terminated at any curve line AC. Putting , & let the relation between x & y be expressed by any Æquation as whereby the Curve is determined. To draw the tangent CD the rule is this.
terminated at any curve line AC. Putting , & let the relation between x & y be expressed by any Æquation as whereby the Curve is determined. To draw the tangent CD the rule is this.
Multiply the termes of the Æquation by any Arithmetical Progression according to the dimensions of x & y; suppose thus.
The first product shall be the Numerator, & the last divided by x the Denominator of a fraction which expresseth the length of BD to whose end D the tangent CD must be drawn. The length BD therefore is .
This Sir is one particular or another a Corollary of a general method which extends it self without any troublesome calculation not only to the drawing Tangents to all curve Lines whether Geometric or Mechanic or however related to streight Lines or to other curve Lines, but also to the resolving other abstruser kinds of Problems about the crookedness, Areas, Lengths, centers of gravity of Curves &c. Nor is it (as Huddens method de maximis et minimis, & consequently Slusius's new method of tangents as I presume) limited to æquations which are free from surd quantities. This method I have interwoven with that other of working in æquations by reducing them to infinite Series. I remember I once occasionally told Dr Barrow when he was about to publish his Lectures that I had such a method of drawing Tangents, but some divertisment or other hindred me from describing it to him.
‡ ‡ 'A copy of this Letter was sent to Mr Tschurnhause A.C. 1674 or 1675 & another copy to the Royal Academy at Paris A.C. 1676, as will appear by the two next extracts.
< text from f 278r resumes >'Out of a Letter of Mr Collins to Mr David Gregory the brother of Mr Iames Gregory newly deceased, dated 11 Aug. 1676.
I have drawn up an account of the Letter commerce, & of all that was mathematical, that I at any time received from your brother either in writing or discourse, with an intent to impart the same to the Royal Society whereof he was a member, where any friend of his may peruse the same or have it transcribed upon paying for the Duplicate which will be half a quire of paper or more, whereof without omitting any thing material that was not controversial with Hugenius &c I can safely touch the altar. The French being desirous to have an account of his attainments & Remains, you will see by what follows that I have endeavoured the same.
'And at the end of the Letter was added.
The Learned of the Royal Academy at Paris hearing of Mr Gregories death & being desirous to know what remains he left & to have an account of the doctrine of infinite Series, invented here, the following account was transmitted to them, & since to Mr David Gregory the surviving brother of the deceased.
1. As to the doctrine of infinite series, that Mercator in his Logarithmotechnia was the first person that published any thing of it to the world, applying it only to the Quadrature of the Hyperbola & the making of Logarithms without extraction of roots, the which doctrine of his was illustrated by Dr Wallis in the Transactions of the Royal Society, & afterwards commented on & advanced by Mr Gregory in his Exercitationes Geometricæ in 1668.
2. The said Books being some few months after they were published sent to Mr Barrow at Cambridge, in return he gave answer that the said doctrine of infinite series was invented by Mr Isaac Newton above two years before & generally applied to all figures; with which answer a Manuscript of Mr Newtonwhichs pains was transmitted to Collins & communicated to the Lord Brouncker President of the Royal Society & afterwards when Mr Barrow left his place as Mathematick Professor he recommended Mr Newton to it who read Lectures on the said Doctrine which were put into the publick Library at Cambridge.
3 Collins by means of Dr Barrow grew acquainted with Mr Newton & kept a correspondence with him: from whom Collins receiving a Letter of 10 December 1672 about drawing Tangents to Geometric Curves out of the Equation that expresseth the relation of the Ordinates to the Base subjoyns [it] in these words.
4 A blank space was here left in the MS for the words of the Letter.
5 Collins in divers of his Letters to Mr Gregory in the year 1669 acquainted him with Mr Newtons success in the said doctrine. To which Mr Gregory replied that himself had many series for the circle & desired earnestly to have some of Mr Newton's sent to him to compare with his own. And Mr Collins accordingly sent him some; which Mr Gregory finding to be wholy different from his & much more easy & proper for calculation, did about December 1670, after much search, fall into Mr Newton's method, as himself acknowledgeth in his Letter of 19th December 1670.
<279r>Out of a Mr Iames Gregories Letter of the 19th of December 1670
9– In my last to you, I had not taken notice that Mr Newtons series for the Zones of a circle (which ye sent me a long time ago,) together with an infinite number of series of the like nature may be a consectarie to that which I sent you concerning logarithms, viz Dato logarithmo invenire ejus numerum, vel radicem potestatis cujuscunque puræ in infinitam seriem permutare. I admire much my own dulness that in such a considerable time, I had not taken notice of this, nevertheless that I had taken much pains to find out that series. But the truth is, I thought always (if so be it were a series) that I might fall upon it by some combination of my serieses for the circle, seing I had such infinite numbers of them; not so much as once desiring any other method. Your series a little produced is . Iisdem etiam positis, erit arcus (cujus sinus B) . I could give you several other serieses of this nature, but perchance ye know more of them then my self.
This is in another place
– 11 Out of Mr Gregories Letter of 15th Feb. 1671.
Since my last to you I have received three of yours, one dated Decem. 15th another Decem. 24th, the third Ianuary 21th. As for Mr Newton his universal method I imagin I have some knowledg of it both as to Geometrick & Mechanick Curves. However I thank you for the series ye sent me & send you these following in requital Sit radius=r, arcus=a, tangens=t, secans=s, et erit , eritque , et . Sit nunc tangens artificialis=t, et secans artificialis=s & integer quadrans=q, erit . Sit nunc secans artificialis , sitque s+l secans artificialis ad libitum, erit ejus arcus ; eritque . Ye shall here take notice that the radius artificalis , & that when ye find , or the artificial secant of 45gr be greater then the given secant, to alter the signes & go on in the work according to the ordinary precepts of Algebra. Sit ellipsis cujus unus semiaxis=r, alter=c. Ex quolibet Curvæ Ellipticæ puncto demittatur in semiaxem r recta perpendicularis=a. Erit area Elliptica perpendiculari a adjacens Si determinetur Ellipseos species, series hæc simplicior evadet. Vt si , foret curva prædicta Reliquis vero manentibus si curva prædicta esset Hyperbola, prædicta quoque series ei inserviret, si omnium terminorum partes affirmentur, & negentur totus terminus tertius, totus quintus, septimus &c in locus imparibus. I thank you heartily for your good advice as to the publication of my notions & for your civil profer. I would be very sorry to put you to so much trouble. I have no inclination to publish any thing save only to reprint my quadrature of the circle, & to add some little trifles to it. As to my method for finding the roots of all equations; one series gives only one root, but for every root there may be infinite numbers of serieses. There is some industry required to enter the series & know what root it relateth to: but it is like I may entertain you at more length with this matter hereafter. Ye need not be so close handed of any thing I send you. Ye may communicate them to whom ye will, for I am little concerned if they be published under any anothers name or not.
<281r>⑧ Out of a Letter of Mr Collins to Mr Oldenberg to be communicated to Mr Leibnitz dated Apr. 10th 1675
In answer to the desire of Mr Leibnitz I here impart what I observe first to be in print. Mr Gregory in his last answer to Hygens hath given a Series for finding the Semi-circumference of a circle, and it is this. Put the Radius = r, half the side of a square inscribe in a circle = d & the difference between the Radius & the side of the square = e. Then is the circumference equal to in infinitum. Which series may be so produced that it differs from the semicircle less then any quantity assignable.
This he published after Mr Mercators Logarithmotechnia was extant, which as soon as it came forth, I sent to Dr Barrow & he observing an infinite series therein used for the making of the Logarithms writ back that the said method had been sometime before found out by his successor Mr Neton & generally applied to all Curves & their portions, as well Geometrical as Mechanical & sent up some specimina thereof
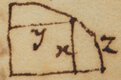 Putting the Radius unit, if you give x the sine, to find z the arch, the series is in infinitum. And extracting the root of this Equation in species, if you give z the arch to find x the sine the series is And these Series are easily continued ad infinitum. By the first out of the sine of 30deg. Van Coullens numbers are easily raised.
Putting the Radius unit, if you give x the sine, to find z the arch, the series is in infinitum. And extracting the root of this Equation in species, if you give z the arch to find x the sine the series is And these Series are easily continued ad infinitum. By the first out of the sine of 30deg. Van Coullens numbers are easily raised.
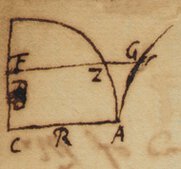 In like manner if you put the Radius R, & B the sine of an arch, the zone between the Diameter & a Chord parallel thereto is
In like manner if you put the Radius R, & B the sine of an arch, the zone between the Diameter & a Chord parallel thereto is
And the same series changing the sines of the second fourth & sixt terms &c serves to give the Area of the zone of the equilateral Hyperbola, vizt
Again
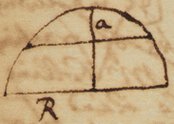 If you give the Radius R & the versed sine, or sagitta a & would find the Area of the segment cutt off by the chord line: for and the segment. And the intire Arch These two Series are Mr Gregories since he fell into this method, which was some years after he heard Mr Newton had generally applied the same. Since which he hath sent up the like for attaining the natural tangents out of their arch, & the converse.
If you give the Radius R & the versed sine, or sagitta a & would find the Area of the segment cutt off by the chord line: for and the segment. And the intire Arch These two Series are Mr Gregories since he fell into this method, which was some years after he heard Mr Newton had generally applied the same. Since which he hath sent up the like for attaining the natural tangents out of their arch, & the converse.
For example, put the Radius = R the arch = a & the Tangent T, then is
And conversly out of the tangent to find the arch thereto
And now you see this done you may easily beleive that by the same method you may as easily out of the arch find the Logarithm sine or tangent without finding the natural. You may also beleive that this method is applied to the streightning or rectification of all kinds of curve lines, as particularly to the Linea quadratrix & to the finding the area of that figure, which hath not been performed before by any method whatsoever. With some further toyle in the calculation it is applied to the finding the areas of the surfaces of inclined round solids, as also to the finding the solidities of the second segments of round solids. For instance, if a Conoid were cut by a plane passing through the Base thereof, this may be called the first segment, & if this portion be cut again by a plane erect to the former cutting plane, the portion so cut is hereby intended to be a segment.
It is also applied to the finding the roots of pure powers or high affected equations, so that out of any number without aid of Logarithms you may raise any power per saltum, & out of any power tho never so high find the root thereof or any mean assigned between it & Vnit. Mr Gregory hath with much labour prepared infinite Series to be generally fitted to the respective adfected Potestates of any Equation proposed, so that an Algebraist being furnished with his stock, will quickly fit a series for the finding of any one of the roots of any equation proposed after it be known on which side of which Limit the root falls. But this he hath not yet communicated, nor [been] pressed to do it, he willingly leaving it to Mr Newton to make the first discovery of this new method of infinite Series to the world.
The next year (May 12th) Mr Leibnitz wrote back an Answer to this Letter, & Mr Collins having signified that the series of Mr Newton were easily continued, he desired in this Answer to know how they were continued, & signified that he had contemplations also on the same argument & had found a method of reducing any quantities into the like series. Whereupon both Mr Oldenberg, & Mr Collins wrote pressing Letters to Mr Newton to communicate his method at large in writing to be made publick least he should be prevented by Mr Leibnitz. And Mr Collins wrote the following Letter to Mr Oldenberg to be sent to Mr Leibnits
⑨. Iune 14 1676
Mr Oldenburgh
Sir
In answer to Mr Leibnits Letter of the 12 of May be pleased to return that as to the first Series the Coefficients whereof are , they are thus made , & , and , and , and , and so ad infinitum; so that he may conceive this series not to fall short in its elegancy to the converse which he the rather commends. His contemplations on the same argument being on other foundations, will be very acceptable to us, & [we] wish they may exceed our beleif as to the excellency of this method, which is so extensive as to sweep away all difficulties, so that I apprehend Mr Gregory &c to be of opinion that all that was known before it was but as dawning to noon day. &c.
At the same time that Mr Collins wrote this Letter, Mr Newton sent another to Mr Oldenburg dated Iune 13th in answe{r} to the Letter above mentioned of him & Mr Collins. And in this Letter he described his method of infinite series giving many les examples thereof. Mr Leibnits was directed to communicate the same to Mr Tschurnhause, & about the tenth of September Mr Newton received their answers directed to Mr Oldenburgh & the answer of Mr Tschurnhause began in this manner
Parisijs Primo Septembris 1676.
Nobilissime Vir
Expectabam cum desiderio Responsum cum aliquot abhinc mensibus ad te literas meas transmiseram. Sed nec ex modo datis colligere licet has receptas fuisse. Interim admodum oblectatus fui hisce conspectis quæ ad D. Leibnitium exaratæ, maximeque me tibi devinxisti quod me participem volueris facere tam ingeniosarum inventionum et promotionis Geometriæ tam pulchræ quam utilis statim cursim eas pervolvi ut viderem num forte inter hasce series infinitas existeret ea qua ingeniosissimus D. Leibnitius Circulum, imo quamvis Sectionem Conicam (Centro in finita distantia gaudentem) quadravit, tali ratione ut mihi persuadeam simpliciorem viam nec quoad linearem Constructionem nec numeralem expressionem nunquam visum iri; quique hisce porro insistens generalem adiuvenit methodum figuram quamvis datam in talem rationalem transmutandi, quæ per solum Inventum (admodum præstans meo judicio) D. Mercatoris ad seriem infinitam posset, reduci. Sed hac de matera cum ipse non ita pridem mentem suam declaravit non opus [est] ut prolixior sim. Verum ut ad specimina perquam ingeniosa Newtoni revertar, hæc non potuere non mihi placere tam ob utilitatem qua se tam tale ad quarumvis quantitatum dimensiones ac alia difficilia enodanda in Mathematicis extendunt, quam ob deductionem harum a fundamentis non minus generalibus quam ingeniose derivatam. Non obstante quod existimem ad quantitatem quamvis ad infinitam seriem æquipollentem reducendi, fundamenta adhuc dari et simpliciora et universaliora &c.
Mr Leibnitz in his Answer dated described his method of transmutations for reducing all quantities into infinite series
After the arrival of these Letters Mr Leibnitz came to London for a week in October & returned back before the receipt of Mr Newton's next Letter which was dated 24th Octob. 1676, & received not this Letter till the spring following. In this Letter Mr Newton mentioned the Tract communicated by Dr Barrow to Mr Collins & lately published by Mr Iones & another larger tract written about the year 1671 on the method of infinite series & the method of fluxions together. & represented that the method of fluxions was the same with that of Slusius for drawing of tangents but much more general, not stopping at fractions or surds & extending to abstruser Problems, & of this method he gave some examples, but concealed the name of fluxions. And this gave occasion to Mr Leibnits in his Letter of
to signify that he had also such a method & to describe the same. This was the first discovery of the Differential method made by Mr Leibnitz to us in England. The two Letters of Mr Newton with the Answers of Mr Leibnitz were published by Dr Wallis in the third volume of his works.
As Mr Leibnitz in the year 1682 published the Series of Gregory for the circle without mentioning that he had received it from Mr Oldenburg in the year 1675 & again in the year 1676; & that in the year 1676 he had received it again in a copy of Gregories Letter dated 15 Feb 1671: so in the year 1684 he published the elements of his Calculus differentialis without mentioning the letters which had passed between him & me in the years 1676 & 1677 about this method. Which omission put me upon writing the Scholium upon the second Lemma of the second book of the Principia Philosophiæ Mathematica for asserting that Lemma to my self. Mr Leibnitz in the year 1684 published only the Elements of the Calculus Differentialis & applied them to – – – –
Out of the Account given of Dr Wallis's works in the Acta eruditorum for Iune 1696 pag 257, 258.
Cæterum ipse Newtonus non minus candore quam præclaris in rem mathematicam meritis insignis, publice et privatim agnovit, Leibnitium tum cum (interveniente celeberrimo viro Henrico Oldenburgio . . . reciprocum.
NB Nunquam agnovi D. Leibnitium ante annum 1676 nedum anno 1676 calculum suum differentialem habuisse. Nihil unquam agnovi de impentione hujus calcul{i} ante annum 1677: cum interea semper assererem me anno 1676 de Methodo fluxionum ad D. Leinitium scripsisse; quamvis rem non tanti esse crederem ut de ea contenderem, neque de hac re jam scripsissem nisi accusatus. Seriem pro arcu inveniendo ex Tangente assumpta Gregorianam esse et anno 1675 ab Oldenburgo ad Leibnitium missam per ea tempora minims noveram. Leibnitium vero pro seriebus methodum generalem per ea tempora habuisse nunquam agnovi. Methodus per transmutationem figurarum non est methodus generalis serierum nedum methodus serierum proprie dicta, sed præpartio tantum qua series per divisionem nonnunquam obtineri queant quæ melius per extractionem radicum prodeunt.
NB I never allowed that Mr Leibnitz had the Differential Method before the year 1677, nor in those days knew more of it then what he described that year in his Letter of 13 Iune 13: [& I always represented that in the year 1676 I wrote to him about the method of fluxions. nor accounted the method of Transmutations [which he sent me in his Letter of 27 Aug. 1676, ] a general method for Series, nor knew that the series which he then sent to me was sent to him the year before by Mr Oldenburg & invented in the beginning of the year 1671 by Mr Iames Gregory. The Editors complain Dr Wallis forbad saying so little of the Differential Method while he said so much of the method of fluxions, & yet excuse him because perhaps he might not know all this. And indeed the Doctor had received from Mr Old. in the year 1676 copies my two Letters dated that year in Iune & Octob. but had not yet seen the Letter of Mr Leibnitz dated 27 Iune 1677 wherin{g} the differential method was described.
Part of a Letter of Dr Wallis &c
Neque Calculi – – – – inseruerim
Part of a Letter of Mr Leibnitz to the Editors of the Acta Eruditorum published in these Acta for Iune 1697 pag. 254.
Dn Iohannes Wallisius, Vir magnis in Geometriam meritis celeberrimus – – – – si non omnia sit sciscitatus.
NB. Several Letters passed afterwards between Mr Leibnitz & the Doctor & in a friendly manner. And in all this neither the Editors nor Mr Leibnitz himself found fault with the Doctor for saying that in my two Letters writ in the year 1676 I had explained to Mr Leibnitz the Method found by me ten years before that time or above, nor contradicted it
Part of the book of Mr Nicolas Fatio de Duillier intituled Investigatio Geometrica solidi rotundi in quod minima fiat resistentia & published in the year 1699
Quæret forsan Cl. Leibnitius, unde mihi cognitus sit iste Calculus quo utor Ejus equidem fundamenta universa – – – – – – – quæ ipse evolvi, instrumenta.
NB The method of converging series by division & extraction of roots was found by me in the beginning of the year 1665 & the Theoreme for reducing the dignities & roots of Binomials into series, set down in my Letter of 13 Iune 1676, I found at the sme time. Dr Barrow soon after save notice of this to Mr Collins. My Lord Brounker in the beginning of the year 1668 published the squaring of the Hyperbola by this series . Mr Mercator {a} few months after published the invention of the same series by a division of Dr Wallis, but went no further. Mr Collins in the y ear 1669 gave notice of my Method to Mr Iames Gregory who after a years study found it out & sent back many series to Mr Collins in a Letter dated 15 Feb. 167. Mr Collins communicated these & mine freely to his friends both at home & abroad. Mr Leibnitz in the year 1673 carried Mercators series with him into France but was not yet acquainted with the higher Geometry. In the year 1674 he pretended to have found a series for the arc whose sine was given. The next year Mr Oldenburg sent to him the Series of Gregory for the Arc whose tangent was given. The third year in Iune Mr Oldenburg sent to him a copy of the Letter of Gregory dated 15 Feb. 1671 wherein this series, & the same year in August Mr Leibnitz sent back his method of Transmutations with that Series to Mr Oldenburg to be communicated to me as a recompense for my method of series. & in the year 1682 printed it in the Acta Lips. without letting us know that he had received it twice from England; & soon after claimed my method of arbitrary Series, a method which he might find out by himself but not so early. And is the history of the method of Series. Mr Bernoulli observes that these series are for Determining such quantities as transcend vurgar equations & therefore are by Mr Leibnitz called transcendent, & Mr Leibnitz himself boasts that he has reduced transcendent quantities to æquations by the Differential method: The name of transcendent is new but the methods of reducing them to equations are fifty years old. And because they are the subject both of the Method of series & of that of fluxions therefore I began about fifty years ago to joyne those two methods & make but one general Analysis of them both, putting
And if you read the latter part of the Letter of Mr Leibnitz dated 28 May 1697 you will find that Mr Leibnitz claimed the improvements to himself & therefore left the first invention to me. For he claimed the expression of transcendent quantities & of Mechanical Curves by equations & then added Primus autem, ni fallor etiam Exponentiales æquationes introduxi. And thus Mr Leibnitz & the Doctor were agreed to allow me the first invention so far as the methods agreed & that the improvements made by Mr Leibnitz should be his; as the improvements made by Cartes to the Method of Vieta, belonged to Cartes. For my part
P.S.
When the Committe of the Royall Society published the Commercium Epistolicum, the Letters & Papers in my custody were not produced. Among them were the following Letter of Mr Leibnitz dated 7 Mar 1693 & a Letter of Dr Wallis dated Apr. 18. 1695 both which upon a fresh occasion were two years ago produced, examined & left in the Archives of the Royal Society. The first shews what was his opinion of this matter before he knew my symbols or any thing more of the Method of fluxions then what he learnt from my Letters & Papers writ in or before the year 1676 or from the Principia Philosophiæ Mathematica, the second (compared with the Preface to the Doctors works) shews what opinion the English Mathematicians had of these things when the differential method began first to be celebrated in Holland as invented by Mr Leibnitz. The first of th{e}se two Letters & part of the second are hereunto annexed.
Illustri Viro ISAACO NEWTONO Godefridus Gulielmus Leibnitius S.P.D.
Quantum tibi scientiam rerum Mathematicarum – – – – – – Vale. Dabam Hannoveræ Martij 1693.
1. Part of a Letter of Dr Wallis to Mr Isaac Newton dated from Oxford Apr. 10. 1695
I wish you would print the two large Letters of Iune & October 1676. I had intimation from Holland as desired there by your friends that somewhat of that kind were done, because your notions of fluxions pass there with great applause by the name of Leibnitz's Calculus differentialis. I had this intimation when all but part of the Preface to this Volume was printed off: so that I could only insert (while the Press stayd) that short intimation thereof which you there find. You are not so kind to your reputation (& that of the Nation) as you might be when you let things of worth lye by you so long till others carry away the reputation which is due to you. I have endeavoured to do you justice in that point; & am now sorry that I did not print those two Letters verbatim.
3. Part of a Letter of Dr. Wallis to Mr Leibnitz dated from Oxford Decem. 1. 1696 & published in the third Volume of the Doctors works. pag. 653, 654.
Neque Calculi Differentialis vel nomen audivisse me memini, nisi postquam utrumque Volumen absolverant operæ, eratque Præfationis (præ figendæ) postremum folium sub Prælo, ejusque typos jam posuerant typothetæ. Quippe tum me monuit amicus quidam (harum rerum gnarus) qui peregre fuerat, tum talem methodum in Belgio prædicari, tum illam cum Newtoni methodo Fluxionum quasi coincidere. Quod fecit ut (transmotis typis jam positis) id monitum inseruerim.
2. Part of the Præface to the two first Volumes of Dr Wallis's Works published at Oxford in April 1695.
<284r>NB. The complaint of the Editors of the Acta Eruditorum against Dr Wallis was that the said so much of the Method of fluxions & so little of the Differential Method. But they excuse him because perhaps he might know but little of that Method. And indeed he had received copies of My Letters of Iune & October 1676 from Mr Oldenburg but had not yet seen the Letter of 27 Iune 1677 wherein Mr Leibnitz began first to describe his method. The Doctor in his Letter to Mr Leibnitz approves of this excuse & Mr Leibnitz sends the Doctors approbation to the Editors of the Acta. But neither the Editors nor Mr Leibnitz himself complained of the Doctor for saying that in my Letters of Iune & October 1676 I explained to Mr Leibnitz the Method of fluxions found by me ten years before those days or above, nor contradicted the Doctor therein.
NB. In All this the Editors of the Acta Eruditorum that Dr Wallis in his works had said so much of the Method of fluxions & nothing of the Differential M. & in his Preface had but just mentioned it & represented it the same method with that of fluxions. And indeed the Doctor in the year 1676 had received from Mr Oldenburg copies of my two Letters of Iune & October whereby h{e} had notice of the method of Fl. but had not yet seen the Letter of Mr Leibnitz dated 27 Iune 1677, nor heard of the Differential method till the last sheet of his Preface was in the Press. But neither the Editors nor Mr Leibnitz himself complained of the Doctor for saying that in my Letters of Iune & October 1676 I had explained to Mr Leibnitz the Method of Fluxions found by me ten years before those days or above. On the contrary in answer to his saying that the Differential method was the same with that of Fluxions excepting the different forms of Speaking, Mr Leibnitz replied that as the Analysis of Vieta & Cartes agreed in the main but had some differences so mine & his might differ in some things. He did not claim the whole, nor deny the antiquity of mine, but only contended that there were some differences. And whether his meaning was that I had improved his method or that he had improved mine let the Reader judge. For my part I do not know that I have improved this method since the year 1672, but on the contrary I have been forgetting it ever since since the writing of the Principia Philosophiæ & should not have meddled with this dispute had it not been for wiping off the odious reflexion cast upon me in point of probity & candor
NB In these Extracts, Dr Wallis represented in his Preface that the two Methods were the same exceps in forms of speaking & that in my Letters of Iune & October 1676 I had explained to Mr Leibnitz this method found by me ten years before or above & that he inserted this admonition nequis causetur de calculo differentiali nihil ab ipso dictum esse. The Editors of the Acta Eruditorum reciting these last words complained that the Doctor had said that in the year 1676 I explained to Mr Leibnitz the method of fluxions found by me ten years before those days or above. This was not denyed by them . But whereas the Doctor had said that the Differential Method was the same with mine except in forms of words Mr Leibnitz replied that the Methods indeed were of the same kind & therefore he called them by the common name of the infinitesimal method; but yet as the Analysis of Vieta & that of Cartes are called by the common name of Analysis speciosa & yet differ in some things, so perhaps my method & his may differ in some things. For my part I had fluxional Equations & knew how to apply them to such Curves as Cartes Calls mechanical & to resolve them vnto converging Series fifty years ago I d. I do not know that I have improved this method since the year 1671, but on the contrary I have been forgetting it ever since I wrote the Principia Philosophiaæ mathematica, & have been very unwillingly drawn into this dispute.
Out of the Account given of the Works of Dr Wallis in the Acta Eruditorum for Iune 1696 pag. 257, 258.
Cæterum ipse Newtonus non minus candore quam præclaris in rem Mathematicam meritis insignis, publice & privatim agnovit, Leibnitzium tum cum (interveniente celeberrimo Viro Henrico Oldenburgio Bremensi Societatis Regiæ Anglicanæ tunc Secretario) inter ipsos (ejusdem jam tum Societatis Socios) commercium intercederet, id est jam fere ante annos viginti et amplius calculum suum differentialem seriesque infinitas & pro ijs quoque methodos generales habuisse; quod Wallisius, in Præfatione Operum factæ inter eos communicationis mentionem faciens, præterijt, quoniam de eo fortasse non satis ipsi constabat. Cæterum differentiarum consideratio Leibnitziana, cujus mentionem facit Wallisius (ne quis scilicet, ut ipse ait, causaretur de calculo differentiali nihil ab ipso dictum fuisse) meditationes aperuit, quæ aliunde non æque nascebantur. Est enim differentia Analyticum quiddam & calculi capax, & quod rei caput est, summæ reciprocum.
NB. In my Letters of 13 Iune & 24 October 1676 I affirmed that I had the method of fluxions some years before that time, but never allowed that Mr Leibnitz had the Differential Method before the year 1677, nor in those days did I know more of it then what he represented that year in his Letter of 13 Iune, nor did I allow the method of Transmutations to be a general method of series, nor do now look upon it to be a method of Series or any thing more then a particular method of Transmutations like those of Gregory & Barrow, nor did I then know that the series which he then sent to me was sent to him by Mr Oldenburg the year before & invented by Mr Iames Gregory in the year 1671.
Part of a Letter of Dr Wallis to Mr Leibnitz dated from Oxford Decem. 1. 1696, & published in the Doctor's Works. Vol. 3. pag. 653, 654.
Neque calculi Differentialis vel nomen audivisse memini, nisi postquam utrumque Volumen absolverant operæ, eratque Præfationis (præfigendæ) postremum folium sub Prelo ejusque typos jam posuerant typothetæ. Quippe tum me monuit amicus quidam (harum rerum gnarus) qui peregre fuerat, tum talem methodum in Belgio prædicari, tum illam cum Newtoni methodo fluxionum quasi coincidere Quod fecit ut (transmotis typis jam positis) id monitum inseruerim. ✝ Sed ✝ Sed et ante monueram, Algebræ Prop. 95 pag. 389 (quod solum potui) Leibnitium & Tschurnhausium talia meditatos; sed quæ ego non videram. (Nudum vidi.) Et sicubi forte viderim literas G.G.L. nesciebam quem illæ virum indicabant. Extant credo plura in Actis Lipsicis, sed quæ ego non vidi Vti nec credo vidisti Brunkeri quadraturam Hyperbolæ, quæ extat in Transactionibus Londinensibus. Mihique condonari potest h ac ætate (qui annum Octagesimum superavi) si non omnia sciscitarer. Noveram quidem jamdudum (et indicavi) de rebus hujusmodi nonnulla Te meditatum esse Tibique cum Newtono (mediante Oldenburgio) intercessisse Literas quasdam tuas sed quas Ego non vidi, nec scio quales fuerint: eratque Oldenburgius diu mortuus, ut non potuerim ab illo sciscitari. Rogabam quidem per literas Newtonum nostrum, ut si eas penes se haberet earum mihi copiam faceret literarum; sed retulit ille se non habere. (Et quidem perijsse credo flammis inopinato correptas, cum plurimis Newtoni scriptis, meliori luce dignis: et nisi per me stetisset, perijssent etiam Newtoni literæ.) Eoque animo rogabam ut tuas illas cum Newtoni literis junctim ederem. Idque etiamnum, si ferat occasio, facturus forte sum, modo mihi dignaberis earum copiam facere.
NB. At the bottom of the page Dr Wallis made this Note. Obtinui tandem ex Schediasmatis Collinij. Copies of my two Letters he had received twenty years before from Mr Oldenburgh himself, as he mentioned in the second Volume of his works, pag. 368, & thence he learnt what he said of those two Letters in his Preface.
Part of a Letter of Mr Leibnitz to the Editors of the Acta Eruditorum, published in these Acta for Iune 1697. pag. 254.
Dn. Ioh. Wallisius, Vir magnis in Geometriam meritis celeberrimus, occasione quarundam suarum ad me literarum, significavit nonnulla, circa recensionem operum suorum Actis Iunij superioris anni insertam monenda, occurrisse. Nempe in ea videri oblique insinuari, quasi nostrorum inventorum parcius meminerit; quæ autem viderit candide retulisse. Calculi autem differentialis ne nomen quidem audivisse antequam absoluto utroque Volumine operum, pro ultimo præfigendæ Præfationis folio jam typos posuissent typothetæ. Ac tum demum ab amico qui peregre fuerat, mentionem ejus apud se factam & typis transmotis a se inser{t}am, sibi autem hac ætate, cum annum octagesimum superaverit, condonavi posse, si non omnia sit sciscitatus.
Part of a Letter of Mr Leibnitz to Dr Wallis 29 Mar. 1697. st. n
— Novo calculi genere effeci ut etiam Algebram transcendentia Analysi subjicientur, et Curvas quas Cartesius a Geometria male excluserat, suis quibusdam æquationibus explicare docui. — De te — De te autem queri nunquam mihi in mentem venit; quem facile apparet nostra, in Actis Lipsicis, prodita, non satis Quæ inter Oldenburgum et me commutatæ sunt Literæ, quibus aliqua accesserant a Domino Newtono, excellentis ingenij Viro, varijs meis itineribus & negotijs ab hoc studiorum genere plane diversis, vel periere, ut alia multa, vel jacent in mole chartarum aliquando excutienda digerendaque, ubi a necessarijs occupationibus vacatio erit; quam mihi tam subito, quam vellem, promittere non possum.
Part of a Letter of Dr Wallis to Mr Leibnitz Apr. 1697
Veniam interim exorare debeo si locorum distantia fecerit ut eruditissima tua scripta & inventa minus ego sciverim aut intellexerim quam vellem; et quidem quis sit ille tuus Calculus Differentialis non satis mihi comportum sit; nisi quod mihi nuper nunciatum est, eum cum Newtoni Doctrina Fluxionum quasi coincidere.
Part of a Letter of Mr Leibnitz to Dr Wallis 28 May. 1697
Methodum Fluxionum profundissimi Newtoni, cognatam esse methodum meæ Differentiali, non tantum animadverti postquam opus ejus et tuum prodijt; sed etiam professus sum in Actis Eruditorum, et alias quoque monui. Id enim candori meo convenire judicavi non minus quam ipsius merito. Itaque communi nomine designare soleo Analyseos Infinitesimalis, quæ latius quam Tetragonistica patet. Interim. quemadmodum et Vietæ et Cartesiana methodus Analyseos speciosæ nommine venit; discrimina tamen nonnulla supersunt; ita fortasse et Newtoniana et Mea differunt in nonnullis. Mihi consideratio differentiarum et summarum in seriebus numerorum primam lucem affuderat cum animadverterem Differentias Tangentibus et Summas Quadraturis respondere.
NB. For understanding the last words, they may be compared with the beginning of his Letter of 27 Aug. 1677, where he writes thus
Part of a Letter of Dr Wallis to Mr Leibnitz Iuly 30 1697.
Optaverim item ut tibi vacet tuum Calculum Differentialem & Newtono suum fluxionum methodum, justo ordine exponere; ut quid sit utrique commune, & quid intersit discriminis, & utramque distinctius, intelligamus.
NB. In these Extracts, Dr Wallis represented that the two Methods were the same except in forms of speaking & that in my Letters of Iune & October 1676 I explained to Mr Leibnitz this Method found by me ten years before or above & that he inserted this admonition nequis causetur de calculo differentiali nihil ab ipso dictum esse. The Editors of the Acta Eruditorum reciting these last words complained that the Doctor had said so little of the Differential method; but neither they nor Mr Leibnitz himself complained that the Doctor had said that in the year 1676 I explained to Mr Leibnitz this method found by me ten years before that year or above. Mr Leibnitz only put a further difference between the methods then the Doctor did, saying that they were indeed of the same kind, & therefore he called them both the infinitesimal method: but yet as the Analysis of Vieta & that of Cartes are called by the common name of Analysis speciosa & yet differ in some things; so perhaps my method & his may differ in some things. By this its manifest that he did not yet begin to claim the whole. And its as manifest that the Doctor claimed for me not the differences but the common method, & was not contradicted in his claim. For my part I had fluxional Equations fifty years ago and then knew how to apply them to such Curves as Cartes calls Mechanical & to almost all sorts of Problems & to resolve them into converging Series, & have neglected & been forgetting this method ever since I wrote the Principia Philosophiaæ Mathematica, & am now so very we are of these things that I should never have resumed the consideration thereof had it not been to wipe of aspersions
⑤Out of a Manuscript written in the hand of Mr Collins & corrected in some places in the hand of Mr Oldenburge in order to be to be copied & & sent to Mr Tschurnhause sometime before Iune 1675 to diswade him from ascribing too much to Des Cartes.
NB. Des Cartes was likewise accused of Arrogance as asserting that of all ways & methods possible he had fallen on the best. How true soever the relation is I know not but tis certain the method of tangents hath been since much advanced by Mr Newton & Mr Gregory. Thus saith Mr Newton in his Letter of 10 December 1672. [Here was a large blank in the MS for entring the words of the Letter & a reference to another page where the Letter was entred, & after the blank the MS thus proceeds.]
N. Mr Newton hath invented a new method of infinite series by which he performs these things. 1 Streightens all Curves. 2 Squares all curvilinear figures. 3 Finds their centers of gravity, round solids, the surfaces of those round solids whether upright or inclined. 4 The second segments of such solids. 5 Applies those series for finding the roots of all Equations. And for all this, being the main things wanting in Geometry the World is no more beholden to Des Cartes then to Plato. He in pag 39 saith that Ratio quæ inter rectas & curvas existit non cognita est, nec etiam ab hominibus ut arbitror cognosci queat. But by his good favour Dr Barrow hath given a ratio between infinite. And before him Mr William Neile the first of mortals streigned the quadratick Parabolick Line on supposition of the quadrature of the Hyperbola. And Sir Christopher Wren streighned the Cycloidical line on supposition of the Quadrature of the circle. And Mr Newton in the Circle hath performed this. If any sine chord tangent secant or versed sine be given he hath fitted series for finding the length of the arch, which are derived from the touch line of a circle & Cavaleirs method of indivisibles. Yea & giving the arch he finds the converse of the Logarithm Sine Tangent or Secant thereto without finding the natural. And this converse work for the natural Adscripts or Inscripts ariseth from Vietas general method of extracting the roots of adfected Æquations not in numbers but in species: a Doctrine that will be difficult to those that understand it not. And to ascribe this to DesCartes were very injurious to others; Du{L}aurens acknowledging in his Præface that to apply Algebra to those parts of Mathematicks there had been no medium yet found.
⑥The answer of Mr Tschurnhause to this paper is entred in the same MS in the hand of Mr Collins with a note that it was received the 8th of Iune 1675. For when Mr Oldenburg received papers of moment he used to write upon them the day of his receiving them. The title to this Answer is Responsum ad scriptum Dn. Collinij de Cartesij inventis. And the answer of Mr Tschurnhause to the four Articles above recited is in these words
NB. Hic rursum nonnulla circa superius a me dicta confirmantur et fateor egregium esse illud Inventum Newtoni et ejusmodi promotionem Geometriæ qualem primo loco superius tradidi [i.e. facilem], proindeque nihil contrarium sententiæ meæ afferri. Esse vero eam ejusmodi promotionem qua nempe speciali ex generali methodo Geometriæ Cartesianæ eliciuntur, ipse Objectionum author affirmat dum ait, Hanc si non solvisset forte infecta mansisset. Vnde inferri jure potest nec Dn Newtonum forte egregium illud inventum exinde nobis exhibere potuisse, proindeque constare quantum Cartesio nostro debeamus.
Ad M. Si intelligatur hic per præstantiam alicujus rei præ alia ad quam detegendam plus virium ingenij est opus, loquamurque solum de Methodo quam ex Calculo indagare nobis licet circa curvas Geometricas (qua de re solum locutus est Cartesius) probare possem, ejus methodum esse præstantissimam omnium, imo universalissimam ex qua infinitæ aliæ regulæ poterunt facillime deduci.
Ad N. Ante jam concessi hanc esse promotionem Geometriæ Cartesianæ. Interim candide fassus est Heuratius se eo non pervenisse nisi instructus Cartesij Principijs fuisset, quibus adjutus, omnium Curvarum Geometricarum in rectas transmutationem generalem quoque tradidit. Verum cætera quæ hic habentur, fateor si hæc inventa fuerint mathematice esse sane promotionem quam optarem. Alias quæ absolute mathematice possunt inveniri circa dimensionem ea poterunt omnia expedite methodo Cartesij explicari. Nec veritati quicquam derogat quod Du Laurens hæc ignoraverit.
Ad D. Quoad inventa Gregorij fateor a tanto Viro non nisi præclara esse expectanda. Et sane si hæ quæ referuntur inveniri possint Mathematice, lubens concedam promotionem Geometriæ factam esse eo sensu quo eam secundo loco accepi [i.e. particulariter] Sed hæc mihi ignota sunt, nec nisi de ijs locutus [sum] quæ publice extant.
⑦ Out of a Letter of Mr Iames Gregory to Mr Collins dated 20 Aug 1675
I can leave but little charity for any person that so overvalues Des Cartes method as to think all since discovered to be but its Consectaries.
B As to Cartes's Probleme of 3, 4, 5, 6, 7 or more lines out of Pappus & his describing the nature of a Locus, it is the best thing in his works, worthy the Author. And perchance if he had not solved it, it had remained hitherto undone. But since him (tho not yet extant) Mr Newton hath solved the said Probleme with much more ease & variety; namely by five points in an Ellipsis or Hyperbola & four in a Parabola he describes the figure by aid of two moveable angles. Whilst one pair of leggs move in a right line the other intersect in a Conic section: Without which aid the actual description of those Sections in constructions for æquations would be unpleasing.
D As to his curves in pag 20 for finding of mean proportionals they are estemed of little use, forasmuch as there may be a Logarithmic Curve, or a Spiral line made by aid of a rank of lines in continual proportion standing at equal parallel distances or issuing at equal angles from the same pole point, by help of either of which ungraduated lines, any number of means may be found between any two extremes given. But if it be the Spiral, then the help of a Sector or moveable Angle is required, which may have lines graduated upon it to divide an angle in ratione data. — From the nature of this Spiral Mr Gregory hath derived an infinite series for finding in numbers any one, upon demand, of the means that shall be required between any two extreme numbers given, being herein more fertile then any thing that can be pretended to be derived from Des Cartes's doctrine.
Extracts of the MS Papers of Mr Iohn Collins concerning some late improvements of Algebra
Dr Wallis having published in the third Volume of his works several Letters between himself Mr Oldenburg Mr Collins Mr Leibnitz & Mr Newton, & some others letters relating to that Collection being found among the papers of Mr I. Collins, it has been thought to make them publick.
Extracts of Letters found among the papers of Mr Iohn Collins relating to the collection of mathematical Letters published by Dr Wallis in the third volume of his works.
<289v>② Out of a Letter of Mr Iames Gregory to Mr Collins date the 5th of September 1670.[1]
I have read over Mr Barrow's Geometrical Lectures with much pleasure & attention wherein I find him to have infinitely transcended all that ever writ before him. I have discovered from his method of drawing Tangents together with some of my own a General Geometrical method without calculation, of drawing tangents to all Curves comprehending not only Mr Barrows particular methods but also his general Analytical method in the end of the 10th Lecture. My method contains not above 12 Propositions.
N. 6. pag 35.[2]
A Letter of Mr Leibnitz to Mr Oldenb. dated at London 3d Feb 167 concerning Moutons differential method in which Mr Leibnitz had made progress, & for clearing himself from plagiary
Another Letter of Mr Leibnitz to Mr O. dated at London Feb 1673 desiring to be a member of the Society. N. 6. pag. 34.
Another of April 1673 from Paris, concerning the summs of fractions whose denominators are figurate numbers. In this Letter he saith: Subtilissimo Collinio tam præclara communicanti obligatum me profiteor. N 6 p. 101
Another from Paris May 1673.
Another from Paris 1 Iune 1673 returning thanks for electing him felllow of the R. S. N 6. p 137
Oldenberg to Slusius 10 Feb 167 reciting Mr Newtons Letter N 6 p 1
Another of Leibnitz to Oldenburg[3] dated at Paris Iul. 15. 1674 concerning his arithmetical instrument & the squaring a portion of the Cycloid. Impress. a Wallisio. N 7 p 93.
N 7 p 110[4] Another of Leibnitz to Oldenberg of Oct 1674 from Paris, published by Wallis. Etsi enim Illi Brunkerus & Wallisius dederint numeros rationales magis magisque approprinquantes: Nemo tamen dedit progressionem numerorum rationalium cujus in infinitum continuatæ summa sit exacte æquatis circulo. Id vero mihi tandem fœliciter successit Inveni enim Seriem numerorum valde simplicium cujus summa exacte æquatur circumferentiæ circuli posito diametrum esse unitatem. [Impress a Walis.]
Another of Leibnitz to Oldenburgh[5] 12 Iuly 1675 in the Original in which Parisius [M. Darius is twice mentioned. Printed by Wallis without a date. Impress. N. 7. p. 149.
N. 7. p. 189.[6] Another of Leibnitz to Oldenburg 28 Decemb 1674 [or 75 as tis printed] from Paris He was then taking a short journey from Paris. Printed (I think) by Wallis
N. 7. pag 213.[7] Another of Leibnitz to Oldenburg 30 March 1675 from Paris. In this he writes. Scribis Iacobum Gregorium vestrum nescio quid demonstraturum se minari quod Tu meæ de quadratura circuli Arithmetico demonstrationi adversum putas . Sed Gregorius hoc tantum demonstrare pollicitus est, rationem diametri ad circumferentiam nulla æquatione sive relatione analytica exacte exprimi posse, quod mihi non est adversum qui seriem infinitam sed numerorum rationalium, eamque valde simplicem affero, cujus summa exacte æquali circulo, posito diametrum esse unitatem. &c. Scribis Cl. Newtonum vestrum habere methodum exhibendi quadraturas omnes, omniumque curvarum superficium et solidorum ex revolutione genitorum dimensiones & centrorum gravitatis inventiones, per appropinquationes scilicet, ita enim interpretor. Quæ methodus si est universali et commoda, meretur æstimari, nec dubito fore ingeniosissimo Authorè dignam. Addis tale quid Gregorio innotuisse &c
Mr Oldenbergs Answer to Mr Leibnitz 15 April 1675.[8] In this Letter are set down several series of Mr Newton & Mr Gregory & the general extent of Mr Newtons method is described, as also the description of Curves by two angles. N 7 p. 216.
N. 7. p. 235. Another of Mr Leibnitz to Mr Oldenberg 20 May 1675[9] from Paris
Oldenberg to Leibnitz 8 Decem 1674[10] in answer to Leibnitz of Octob. 16, 1674. – Quod de profectu in curvilearum dimensione memoras bene se habet, sed ignorare te nolim Curvarum dimetiendarum rationem & methodum a laudato Gregorio nec non ab Isaaco Newtono ad Curvas quaslibet tum Mechanicas tum Geometricas quin et Circulum se extendere, ita scilicet ut si in aliqua Curva Ordinatam dederis, istius methodi beneficio possis lineæ Curvæ longitudinem, aream figuræ, ejusdem centrum gravitatis; solidum rotundum ejusque superficiem sive erectam sive inclinatam, solidique rotundi segmenta secunda horumque omnium conversa invenire; quin et, dato quolibet arcu in quadrato Logarithmicum sinum tangentem vel secantem non cognito naturali, & conversum computare. Quod vero ais neminem hactenus dedisse progressionem numerorum rationalium, cujus in infinitum continuatæ summa sit exacte æqualis circulo, id vero Tibi tandem fœliciter successisse; de eo quidem tibi gratulor &c. N 7 p. 119.
Oldenburgh to Leibnitz 30th Sept. 1675.[11] Tschunhause then newly gone to Leibnitz at Paris, having received at London one of Gregories Series for the circle. N 7 p 159.
Oldenberg to Leibnitz 24 Iun 1675 [N 7 p. 243][12] conteining several things in relation to Cardans rules called the cubicus malleus of Cartes & Daries considerations thereon: in answer to which was the letter above mentioned without a Date (printed by wallis) in which Davy is called Parius.
Letters in the hand of Mr Leibnitz. 3 Feb. 170. March {3}0 1675 from Paris, Hannover 30 May 1677, March 1677, Iuly 1677, 21. 20 May 1675. 28 Ianuar 1677 from Hanover. 28 Decemb 1675 12 Iuly 1675, Franckford 29 Apr. 1671. Mente Septemb 1670, 15 Iuly 1674, Feb. 1673. 8 Iune 1673 Gratias reddit Societati Regia de electione sua. May 1673 from Paris. Apr 1673. 16 Octob. 1674.
22 – Out of a Letter of Mr Oldenburg to Monsr. Renatus Fran. Slusius dated the 10th. Iuly 1673.
Ex tibi, Vir illustrissime, impressum modum tuum demonstrandi Methodum tuam ducendi Tangentis ad quaslibet curvas, quemadmodum postremis tuis litoris cum mihi communicaveras: subticui viri nomen, offensionis coitandi causâ; Scripsit mihi Dn. Newtonus in hac Sententia Cum "Ex priori tua Epistola subdubitabam, existemaretne celeberrimus Slusius per ea, quæ ipsi de me Scripseras, me mihi tribuere methodum ipsius ducendi Tangentes; donec intelligerem a Dno. Collinio, Te ipsi significasse, eam, ex opinione tuâ, Serius hic inventam fuisse. Mihi quippe videtur, eam Dno. Slusio perspectam fuisse aliquot annis priusquam ederet Mesolabium suum, proindeque antequam Ego eum intelligerem. At si res secus se haberet, cum tamen cum primus communicaverit amicis Suis & Literato Orbi, Iure merito ipsi Lebitur. Quoad Methodus illas, eædem sunt, quanquam crediderim, ex principiis diversis derivatæ. Nescio tamen, num ipsius principia eam largiantur adeo generalem, ac mea; quæ ad æquationes terminis Surdis affectis se extendunt, absque eorum ad aliam formam reductione. Hæc ille, quæ in bonum partem a te acceptum iri confido.
– 5 Out of a paper written in the hand of Mr Collins & directed to Mr Oldenburgh to be communicated to Mr Slusius in the later end of summer 1669, when Mr Barrows optical Lectures were above half printed.
Mr Barrow hath communicated an universal Analytical method imparted to him by Mr Isaac Newton his Collegiate for the mensuration of the Areas of all such Curves & their Perimeters wherein the Ordinates have one common habitude to the Base line, & this is no other then the Method particularly applied by Mercator for the finding of the Area of the Hyperbola rendred universal. The Author thus begins
De Analysi per Æquationes numero terminorum infinitas.
Methodum generalem quam de Curvarum quantitate per infinitam terminorum seriem mensuranda olim excogitaveram &c. And having shewed thereby the quadrature of many Curves, he then comes to the Circle & by turning the or into an infinite series, sheweth that there may be divers such Series applied to the Circle so that giving any two of these Data, the Radius Sine Arch & Area of the segment, either of the rest may be found infinitely true upon demand, a thing much coveted by all former writers. He hath likewise thereby incredibly faciliated the finding the root of any Æquation & of mean Proportionalls & gives a Series for finding the length of an Elliptick Line. He likewise to shew that his method extends to Mechanick Curves & their Tangents, squares the Cycloid & its portions & finds the Area of the Quadratick Curve & its Perimeter; & as a conclusion thereto saith thus. Nec quicquam hujusmodi scio ad quod hæc methodus varijs modis sese non extendit, imo tangentes ad curvas mechanicas (siquando id non alias fiat) hujus ope ducantur, et quicquid vulgaris Analysis per æquationes ex finito terminorum numero constantes (quando id sit possibile) perficit hæc per Æquationes infinitas semper perficit. Et hæc de areis Curvarum investigandis dicta sufficiant. Imo cum Problemata de Curvarum longitudine, de quantitate et superficie solida, deque centro gravitatis, omnia possunt eò tandem reduci ut quæratur quantitas Superficiei planæ linea Curva terminatæ, non opus est quicquam de ijs adjungere.
Out of a Letter of Mr Oldenberg to Mr Leibnitz dated 12 Iuly 1677 a copy of which is extant in the hand of the Author
Scripsi ad Te die 2 Maij novissimi & literis meis inserui prolixæ satis Epistolæ Clarissimi Newtoni ad me datæ apographum, fasciculumque hunc Dno Sch{o}otero commisi &c.
Out of a Letter of Mr Leibnitz to Mr Oldenberg dated at Hanover Iuly 1677, & printed Dr Wallis.
Nuperas meas credo acceperis; nunc istas mature submito . . . .
7 – Out of Gregories Letter of 20 Apr. 1670. I cannot understand the series yee sent me of the circle vizt &c If this be the original I take it to be no series.
9 – Out of Gregories Letter of 19th December 1670. In my last to you I had not taken notice that Mr Newtons series for the zones of a circle (which ye sent me a long time ago) together with an infinite number of series of the like nature may be a consectary to that which I sent you concerning Logarithms; vizt Dato Logarithmo invenire ejus numerum, vel radicem potestatis cujuscunque puræ in infinitam seriem permutare. I admire much my own dulness, that in such a considerable time I had not taken notice of this; nevertheless that I had taken much pains to find out that series. But the truth is, I thought always (if so be it were a series) that I might fall upon it by some combination of my serieses for the circle, seing I had such infinite numbers of them, not so much as once desiring any other method. Your series a little produced is . Eisdem etiam positis erit arcus (cujus sinus B). I could give you several other serieses of this nature, but perchance ye know more of them then my self.
– 27 Out of Leibnits Letter to Oldenberg 20th May 1675. Literas tuas multa fruge Algebraica refertas accepi, pro quibus Tibi et doctissimmo Collinio gratias ago. Cum nunc præter ordinarias curas mechanicis imprimis negotijs distrahar, non potui examinare series quas misistis, ac cum meis comparare. Vbi fecero præscribam Tibi sententiam meam. Nam aliquot jam anni sunt quod inveni meas via quadam sic satis singulari. Collinium ipsum magni facio quoniam omnes puræ Matheseos partes ab ipso egregie cultas video. Multa habeo destinata a quibus me deterrent calculi tantùm, qui nec suscipi facile ab homine occupato, nec alteri nisi doctissimo ac sincerissimo tutò credi possunt
29 – Out of a Letter of Mr Oldenburgh to Mr Leibnitz 24 Iune 1675. Dominus Newtonus beneficio Logarithmorum graduatorum in scalis παραλλελως locandis ad distantias æquales, vel circulorum concentricorum eo modo graduatorum adminiculo invenit radices æquationum. Tres Regulæ rem conficiunt pro cubicis quatuor pro biquadraticis. In harum dispositione respectivæ coefficientes omnes jacent in eadem linea recta a cujus puncto tam remoto a prima Regula ac scalæ graduatæ sunt ab invicem linea recta ijs super-extenditur una cum præscriptis confirmibus genio æquationis, quâ in regularum unâ datur potestas pura radicis quæsitæ.
{spe}ciatim alicujus arcus circuli rectificationem impartiri tibi poterit laudatus Tschurnhausius methodum a Gregorio nostro inventam, quam cum apud nos esset Collinius ipsi communicavit.
26 – Out of a Letter of Mr Oldenburgh to Mr Leibnitz dated 15 April 1675.
Dn. Collinius, præmissa salute, qua sequuntur remittit. Primò Cl. Gregorium in postrema sua ad Illustrem Hugenium responsione seriem suppeditasse ad semicumferentiam circuli inveniendam quæ totis.
Pone radium=r, dimidium latus quadrati inscripti circulo=d et differentiam inter radium et latus quadrati=e. Semicircumferentia æqualis est in infinitum: quæ series adeo produci potest ut a semicircumferentia minus differat quam ulla quantitas assignabilis.
Editum hoc fuit a Dno Gregorio postquam Dni Mercatoris Logarithmotechnia jam extabat, quæ quam primum viderat lucem, ad Dominum Barrovium a me fuit transmissa, qui observato in ea infinitæ seriei usu ad Logarithmos construendos rescribebat methodum illam jam aliquamdiu excogitatam fuisse a successore suos Newtono, omnibusque curvis, earumque portionibus geometricis æque ac mechanicis universim applicatam, cujus rei specimina quædam subjecit, vizt
Posita pro Radio unitate, datoque x pro sinu, ad inveniendum z arcum  series hæc est in infinitum. Et extracta radice hujus æquationis methodo symbolica, si dederis z pro arcu ad inveniendum x sinum series hæc est . Atque hæc series facile continuatur in infinitum. Prioris beneficio ex sinu 30 graduum Ceulenij numeri facile struuntur.
series hæc est in infinitum. Et extracta radice hujus æquationis methodo symbolica, si dederis z pro arcu ad inveniendum x sinum series hæc est . Atque hæc series facile continuatur in infinitum. Prioris beneficio ex sinu 30 graduum Ceulenij numeri facile struuntur.
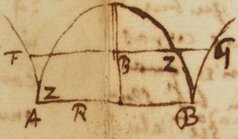 Consimiliter si ponas radium R, et B sinum arcus: zona inter diametrum et chordam illi parallelam est . Atque eadem series mutatis signis termini secundi quarti et sexti &c inservit assignandæ areæ zonæ æquilateris Hyperbolæ, vizt
Consimiliter si ponas radium R, et B sinum arcus: zona inter diametrum et chordam illi parallelam est . Atque eadem series mutatis signis termini secundi quarti et sexti &c inservit assignandæ areæ zonæ æquilateris Hyperbolæ, vizt
Rursum, Dato Radio R, et sinu verso sive sagitta a, ad inveniendam aream segmenti resecti a chorda pone pro et segmentum . Et arcus integer . Duæ hæ series Dno Gregorio debentur, quas exhibuit ex eo tempore quo usus est hac methodo, quod ab ipso aliquot post annos factum, postquam scilicet intellexerat Dnum Newtonum generatim eam applicasse. Exinde quoque ad nos misit series consimiles ad Tangentes naturales ex earundem Arcu et conversim obtinendum. E.g. Pone Radium, Arcum, et Tangentem=T; erit . Et conversim ex Tangente invenire Arcum ejus .
Atque hoc factum cum vides, facile credideris, posse eadem methodo æque facile ex Arcu invenire sinum vel tangentum Logarithmicum absque inventione naturalis, et conversim. Pronum quoque tibi fuerit credere methodum hanc applicari posse ad rectificationem quarumlibet curvarum, particulatim vero ad lineam quadratricam, et ad inveniendam aream illius figuræ: id quod antehac nulla demum cum methodo fuit præstitum. Atque ulteriori calculationis labore extendi potest ad inveniendas areas superficierum in rotundis solidis inclinatibus, nec non ad inveniendas soliditates secundorum segmentorum in solidis rotundis. E.G. si Conoides aliqua secetur a plano transeunte per Basim ejus poterit id vocari segmentum ejus primum; et si hæc portio iterum secetur a plano recto ad planum, prius secans, portio eum in modum secta hoc ipso intendetur ut sit segmentum [secundum.]
Porro methodus eadem applicatur inveniendis radicibus purarum potestatum, valdeque affectarum æquationum, ita ut ex quolibet numero absque logarithmorum ope, excitare possis quamlibet potestatem per saltum, et ex quavis potestate, ut ut affecta invenire radicem ejus, vel quodvis medium illud inter et unitatem assignatum. Dnus Gregorius magno labore paravit seriem infinitam generatim respectivis potestatibus affectis cujuslibet æquationis propositæ adaptandam, ita ut quivis Algebræ cultor, plenu ipsius instructus, mox aptare possit seriem aliquam ad inveniendam quamlibet radicem cujusvis æquationis propositæ, postquam innotuit ad quod latus noli limitis radix ceciderit. Verum id hactenus nobis non communicavit, uti nec nos illum ad id faciendum sollicitavimus, imprimis cum ipse lubens permittat Newtono ut ille primus novæ hujus methodi de infinita serie inventionem orbi mathematico patefaciat.
in another place
At the end of Mr Leibnits letter to Mr Oldenburg dated 1675 write. NB. Quanquam D. Leibnitius series quas ab Oldenburgio anno superiore acceperat a suis diversas esse hic concedat easque cum suis se aliquando collaturum pomittat: tamen epistolo Oldenburgi oblivioni tradita est & Leibnitius Opusculum de serie Gregorij pro arcu circuli ex tangente inveniendo ut sua & {j}am compositum cum amicis in Gallia communicare cœpit, cœlato primi inventoris nomine qui eandem ineunte anno 1671 cum Collinio (ut supra) communicaverat. Id liquet ex verbis Leibnitij in Actis Lipsiensibus mense Aprili anni 1681 in lucem editis, ubi hæc leguntur. Iam anno 1675 composituum habebam Opusculum Quadraturæ Arithmeticæ ab amicis ab illo tempore lectum, sed quod materia sub manibus crescente limabre ad editionem non vacavit, postquam aliæ occupationes supervenere: præsertim cum nunc prolixius exponere vulgari more, quæ Analysis nostra nova paucis exhibet non satis pretium operæ videatur: Interim insignes quidam Mathematici, quibus veritas primariæ nostræ propositionis dudum in his Actis publicatæ innotuit, pro humanitate sua nostri qualiscunque inventi candide meminire Ex his verbis manifestum est etiam quod Leibnitius Analysin {s}uam novam, id est methodum differentialem, nondum invenerate.
At the end of the next Letter of Mr Leibnitz in which he desires to know how the two series were found out which Mr Moore brought him from London add this note.
NB. Ex hac Epistola manifestum est quod modus perveniendi ad has series Leibnitio nondum invenerat licet annus jam elapsus esset ex quo series octo a D. Oldenburgo acceperat. Audito igitur quod D. Gregorius jam emortuus esset postulavit a D. Oldenburgo ut quæ Gregorius cum amicis communicaverat in unum corpus colligerentur et exemplar ejus Lutetiam Parisiorum mitteretur. Extat enim collectio manu D. I. Collins exaratum cum hoc Titulo & sic Orditur
Et notandum est quod in hac Collectione habetur Epistolam Newtoni ad D. I. Collins data habetur in qua methodum generalem se habere dicit ducendi tangentes, quadrandi Curvilineas & alia peragendi & methodum exponit exemplo ducendi Tangentes. Hæc est methodus fluxionum quam Leibnitius postea Differentialem vocavit. Et quamvis Leibnitius series bene multas a D. Oldenburgo jam acceperat, et methodum perveniendi ad has series nondum investigare potuerat, tamen accepta Newtoni epistola sequente in qua Methodus a Leibnitio tantopere desiderata explicatur, Leibnitius tam in Epistola qua Newtono respondet quam in Actis Lipsiensibus tam sibi quam Newtono et Gregorio serierum illarum inventionem tribuere cœpit.
Ad An. 1675. NB. Hanc Epistolam Leibnitius oblivioni tradidit.
After the Epistoles add.
Newtonus anno 1684 Propositiones suas principales de motibus corporum cœlestium in Orbibus Ellipticis cum R. S. communicavit, annoque 1686 Principa sua Philosophiæ mathematica ad Societatem illam misit. Wallisius Curvam inde desumptam & a se mi{ss} jam quam projectilia in medio resistente ubi resistentia est ut velocitas describunt, calculo suo examinavit & calculum ejus D. Oldenburgus eodem anno in Actis Philosophis publicavit. Proximo anno prodijt Newtoni liber. Anno sequente synopsis ejus in Actis Lipsiensibus prodijt, [in qua Newtonus de resistentijs corporum in medio raro et Elastico et per eas inveniendis figuris ad continuandos motus in Medijs resistentibus aptioribus scripsisse dicitur]. Deinde Leibnitius anno 1689 lecta illa synopsi dicit Newtonianum opus ipsum excitasse ut schediasma de Resistentia Medij et Motu projectorum gravium in Medio resistente & meditationes de causa physica motuum cœlestium in publicum p{ro}ferret. Anno 1690 prodijt Liber Hugenij de Lumine & Gravitate & anno proximo mense Aprili Leibnitius in Actis Lipsiensibus ita scribit Postquam meditationes quasdam de Medij resistentia in his Actis publicavi venere in manus meas quæ Viri in Mathematica Naturæ cognitione præcellentissimi Hugenius & Newtonus in novissimus operibus de eodem argumento sunt commentati. Sed opus Newtoni prius consulere debuisset ne et huic injuriosus esset aliena inventa sibi arrogando et Lectori molestus jam vulgata repetendo, et præterea opusculum Wallisij in Actis Philosophis editis silentio præteriri non debuissit. Vtrum Leibnitius antiqua inventa an cogitata nova et indigesta festinante et fortean errange calamo in lucem dedit non est hujus loci expendere.
Out of a Letter of Mr Oldenburgh to Mr Leibnitz 30 Sept 1675. – 31 Scriptum quoddam Belgicum, Belga quidam Georgius Moor vocatus, Algebræ et Mechanices probe peritus apud Collinium nostrum reliquit, qui apographum ejus, quale hic insertum vides, impertire tibi voluit — — Tschurnhausius nuper Parisios hinc profectus est et Te sine dubio jam Salutavit. — Scire cupis an dare nostrates geometrice possint dimensionem curvæ Ellipseos aut Hyperbolæ, ex data circuli aut Hyperbolæ quadratura. Ait Collinius hos id præstare non posse Geometrica præcisione, sed dare eos posse ejusmodi approximationes quæ quacumque quantitate data minus a scopo aberrabunt. Et speciatim quod attinet alicujus arcûs circuli rectificationem, impartiri tibi poterit laudatus Tschurnhausius methodum a Gregorio nostro inventam, quam cum apud nos esset Collinius ipsi communicavit.
5] 7 Ex Præfatione in Analysin infinite parvorum a Marchesio Hospitalio anno 1696 in lucem editam.
Paulo post editam a Cartesio methodum tangentium, D. Fermatius methodum invenit quam Cartesius tandem propria ut plurimum simpliciorem esse agnovit. Attamen hæc non tam simplex fuit quam D. Barrovius illam postea reddidit considerando distinctius naturam polygonorum quæ naturaliter triangulum quoddam parum offert factum ex particula curvæ comprehensa inter duas ordinatas infinite propinquas, ex harum differentia, & ex illa duarum abscissarum correspondentium Abscissarum. Et hoc triangulum simile est illi quod formatur ex tangente Ordinata et Subtangente: sic, ut per unam simplicem analogiam hæc posterior methodus totum peragat calculum quem ea Cartesij, et quem methodus hæc ipsa prius postulabat.
D. Barrovius hic non substitit. Invenit etiam speciem calculi qui huic methodo conveniret. Sed hoc deerat in his methodis, fractiones scilicet et signa omnia radicalia computis excludere
Ob defectum hujus calculi supervenit ille celeberrimi Leibnitij: et peritissimus hicce Geometra cœpit ubi Barrovius et alij desierunt.
Et paulo post.
Insuper debetur D. Newtono justicia, quam et ipse D. Leibnitius illi reddidit: Quod utique ipse etiam aliquid invenit Calculo Differentiali simile, quemadmodum apparet per librum insignum Principiorum mathematicorum Philosophiæ naturalis anno 1687 editum, qui fere totus constat ex hoc calculo. Sed Characteristica Leibnitij methodum ejus faciliorem et magis expeditum reddit, præterquam quod hæc mirabile est subsidium in plurimis quæ occurrunt.
7] 6 E Schediasmate D. Leibnitij, de differentia inter Analysin vulgarem et transcendentalem, in Diario doctorum 23 Augusti 1694 impresso[13]
Reddenda est hæc justitia D. Newtono (cui Geometria Optica et Astronomia plurimum debent) quod is proprio marte aliquid huic simile habuit, uti postea cognovi. Verum est quod is alijs utitur characteribus: sed quemadmodum ipsa characteristica, ut ita dicam, est magna pars artis inveniendi, credo quod nostra introitum magis patentem affert.
3]4 Ex D. Barrovij Lect. 10, anno 1670 in lucem emissa.[14]
Methodus nostra ex Calculo tangentes reperiendi, hæc est. 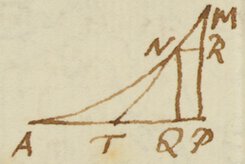 Sint AP, PM positione datæ rectæ lineæ (quarum PM propositam curvam sec{a}t in M) et MT curvam tangere ponatur ad M, rectam AP secare ad T. Vt ipsius jam rectæ PT quantitatem exquiram, curvæ arcum indefinite parvum statuo; tum duco rectas NQ ad MP et NR ad AP parallelas; nomino MP=m, PT=t, MR=a, NR=e, reliquasque rectas ex speciali Curvæ natura determinatas, utiles proposito, nominibus designo; ipsas autem MR, NR (et mediantibus illis ipsas MP, (PT) per æquationem e calculo deprehensam inter se comparo, regulas interim has observans.
Sint AP, PM positione datæ rectæ lineæ (quarum PM propositam curvam sec{a}t in M) et MT curvam tangere ponatur ad M, rectam AP secare ad T. Vt ipsius jam rectæ PT quantitatem exquiram, curvæ arcum indefinite parvum statuo; tum duco rectas NQ ad MP et NR ad AP parallelas; nomino MP=m, PT=t, MR=a, NR=e, reliquasque rectas ex speciali Curvæ natura determinatas, utiles proposito, nominibus designo; ipsas autem MR, NR (et mediantibus illis ipsas MP, (PT) per æquationem e calculo deprehensam inter se comparo, regulas interim has observans.
1 Inter computandum omnes abjicio terminos, literis constantes in quibus ipsarum a vel e potestas habetur, vel in quibus ipsæ ducuntur in se. Etenim isti termini nihil valebunt.
2 Post æquationem constitutam omnes abjicio terminos literis constantes quantitates notas seu determinatas designantibus, aut in quibus non habetur a vel e. Etenim illi termini semper, ad unam æquationis partem adducti, nihilum adæquabunt.
6]3 p. 98. Ex Epistola D. Leibnitij Hanoveræ ad D. Newtonum Martij 1693 data, cujus jam extat Autographum in Scrinijs Societatis Regiæ.
Quantum tibi scientiam rerum mathematicarum totiusque Naturæ debere arbitrer, occasione data etiam publice sum professus Mirifice ampliaveras Geometriam tuis seriebus, sed edito Principiorum opere ostendisti patere etiam quæ Analysi receptæ non subsunt. Conatus sum Ego quoque, notis commodis ahibitis quæ differentias et summas exhibent, Geometriam illam quam transcendentem appello, Analysi quodammodo subjicere, nec res male processit. Sed a Te adhuc magni aliquod expecto ad summam manum imponendam, tum ut Problemata quæ ex data tangentium proprietate quærunt lineas, reducantur optime ad quadraturas; tum ut quadraturæ ipsæ (quod valde vellem) reducantur ad curvarum rectificationes, ubique superficiem aut corporum dimensionibus simpliciores
Sed super omnia optem ut Geometricis absolutis, naturam uti cœpisti, mathematice tractare pergas, in quo genere certe est quod invenisti Ellipses Keplerianas prodire, si tantummodo attraction sive gravitatio et trajectio in Planeta concipiantur Tametsi enim eò inclinem, ut credam hæc omnia fluidi ambientis motu sive effici sive regi, analogia gravitatis et magnetismi apud nos, nihil tamen ea res dignitati et veritati inventi tui detraxerit. &c
8] Ex Epistola D. Wallisij Oxonij ad D. Newtonum Apr. 10 1695 data, cujus jam extat Autographum in Scrinijs Societatis Regiæ.
I wish you would print the two large letters of Iune & August 1676. I had intimation from Holland as desired there by your friends, that somewhat of that kind were done, because your notions of fluxions pass there with great applause by the name of Leibnitz's Calculus differentialis. I had this intimation when all but part of the Preface to this Volume was printed off; so that I could only insert (while the Press stayd) that short intimation thereof which you there find. You are not so kind to your reputation (& that of the Nation) as you might be, when you let things of worth lye by you so long till others carry away the reputation which is due to you. I have endeavoured to do you justice in that point; & am now sorry that I did not print those two Letters verbatim.
9] Ex Præfatione in Volumine duo prima Operum D. Wallisij mense Martio anni 1695 impressa.
Quæ in secundo Volumine habentur, in Præfatione eidem præfixa dicitur. Vbi (inter alia) habetur Newtoni methodus de fluxionibus (ut ille loquitur,) consimilis naturæ cum Leibnitij (ut hic loquitur) calculo differentiali (quod qui utramque methodum contulerit, satis animadvertat, utut sub loquendi formulis diversis) quam ego descripsi (Algebræ cap. 91 &c præsertim cap. 95) ex binis Newtoni Literis (aut earum alteris Iunij 13 & Augusti 24 1676, ad Oldenburgum datis cum Leibnitio tum communicandis (ijsdem fere verbis saltem leviter mutatis quæ in illis literis habentur) ubi methodum hanc Leibnitio exponit tum ante decem annos nedum plures ab ipso excogitatam. Quod moneo nequis causetur de hoc calculo differentiali nihil a nobis dictum esse.
10] p. 108 Ex Introductione ad Tractatum Newtoni de Quadratura curvarum, anno 1704 in lucem editum.
Quantitates Mathematicas non ut ex partibus quam minimis constantes sed ut motu continuo descriptas hic consideto Lineæ describuntur ac describendo generantur non per oppositionem partium sed per motum continuum punctorum, superficies per motum linearum, solida per motum superficierum anguli per rotationem laterum, tempora per fluxum continuum, & sic in cæteris. Hæ Geneses in rerum natura locum vere habent, & in motu corporum quotidie cernuntur. Et ad hunc modum Veteres ducendo rectas mobiles in longitudinem rectarum immobilium genesin docuerunt rectangulorum.
Considerando igitur quod quantitates æqualibus temporibus crescentes & crescendo genitæ, pro velocitate majori vel minori qua crescunt ac generantur, evadunt majores vel minores; methodum quærebam determinandi quantitates ex velocitatibus motuum vel incrementorum quibus generantur. Et has motuum vel incrementorum velocitates nominando fluxiones & quantitates genitas nominando fluentes, incidi paulatim annis 1665 & 1666 in methodum fluxionum qua hic usus sum in quadratura Curvarum.
1] Pag. 97 lin 20, post verba – literis G. G. L. designatus, adde, idque sub hoc titulo. Nova methodus pro maximis et minimis itemque tangentibus quæ nec fractas nec irrationales quantitates movatur, et singulare pro illis calculi genus, per G. G. L. Sub finem autem hujus schediasmatis subjungit. Et hæc quidem initia sunt tantum Geometriæ cujusdam sublimioris ad difficillima et pulcherrima quæque etiam mistæ Matheseos problemata pertingentis, quæ sine calculo nostro differentiali, AVT SIMILI, non temere quisquam pari facilitate tractabit.
Anno autem 1683 ad finem vergente D. Newtonus &c – – nondum vidisset
2] Ex Schediasmate D. Leibnitij in Actis Eruditorum pro mense Iunio anni 1686 impressis pag 297 , 298 & 299.
Malo dx et similia adhibere quam literas pro illis, quia istud dx est modificatio quædam ipsius x, & ita ope ejus fit, ut sola quando id fieri opus est litera x cum suis scilicet potestatibus et differentialibus calculum ingrediatur et relationes transcendentes inter x et aliud exprimantur. — — quicquid in hoc genere ipse antea fueram admiratus.
a Notationem suam cum Barroviana confert. b b D. Leibnitius Anno 1671, ubi Theoriam motus abstracti edidit, Wallisij opera nondum | minime viderat. Anno 1673 ineunte, versabatur in theorijs numerorum, ut ex epistola ejus ad Oldenburgum 3 Feb. 1673 data apparet. Anno 1674 calculum Algebraicum Geometricis adjecit. Anno 1675 quadraturam suam Arithmeticam invenit, ac more vulgari compositam cum amicis communicare cœpit. Anno 1677 incidit in Analysin differentialem.
pag. 108 lin 11, scribe. Dein libri alterius in quo scripserat se methodum fluxionum annis 1665 & 1666 invenisse , Synopsin sequentem (si Synopsis dici mercatur) eodem stylo subjunxerunt.
Et eadem pagina lin 1 scribe. Tandem ubi D. Wallisius mortuus esset et prodiere Newtoni Libri de Numero Curvarum secundi generis.
<19:iv(r)>3 Pro a ipsam ex (vel MP.) pro e ipsam t (vel PT) substituo Hinc demum ipsius PT quantitas dignoscetur.
4]5 E Specimine calculi differentialis Iacobi Bernoulli in Actis Eruditorum pro Mense Ianuario anni 1691 pag. 13 edito.
Quo calculum Barrovianum quem decennio ante [editam a D. Leibnitio methodum differentialem] in Lectionibus suis Geometricis adumbravit Acutor, cujusque specimina sunt tota illa Propositionum inibi contentarum farrago) intellexerit, alterum a Dn L. inventum ignorare vix poterit, utpote qui in priori illo fundatus est, & nisi forte in differentialium notatione, et operationis aliquo compendio ab eo non differt.
13] Scholium Lemmatis secundi Libri secundi Principiorum Philosophiæ anno 1686 ante mensem Maium scriptum
Postquam Newtonus Elementa methodi Fluxionum in hoc Lemmate Geometrice demonstrasset, is addibit hoc Scholium.
In literis quæ mihi cum Geometra peritissimo G. G. Leibnitio annis abhuic decem intercedebant, cum significarem me compotem esse methodi determinandi Maximas et Minimas, ducendi Tangentes, et similia peragendi quæ in terminis surdis æque ac in rationalibus procederet, & literis transpositis hanc sententiam involventibus [Data æquatione quotcunque fluentes quantitates involves fluxiones invenire, & vice versa] eandem celarem: rescripsit vir clarissimus se quoque in ejusmodi methodum incidisse, et methodum suam communicavit a mea vix abludentem præterquam in verborum et notarum formulis Utriusque fundamentum continetur in hoc Lemmate.
<19:iv(v)>Notæ
1] Conferantur hæc cum Epistola Newtoni 10 Decem 1672 scripta et anno 1676 cum D. Leibnitio communicata.
1B] Scripsit Newtonus 24 Octob. 1676, rescripsit Leibnitius 21 Iunij 1677, acceptis prius Newtoni literis 10 Decem 1672, 13 Iun. et 24 Octob 1676 scriptis
2] Annon hic allusum sit ad litteras a et e pro quibus D. Leibnitius symbola dy ac dx adhibuit.
5]
9] Quod Wallisius jam dixerit Newtonum anno 1676 aut antea methodum fluxionum invenisse, Leibnitius minime conquestus est. At mortuo Wallisio cœpit se methodum hanc omnium primum invenisse contendere
3]4. Cum hac methodo conferatur methodus tangentium D. Leibnitij in Epistola ad Oldenburgum 21 Iun. 1677 data & superius impressa p. 88 & 89.
4]5. Operationis compendium Newtonus in Epistolis 10 Decem 1672, & 24 Octob. 1676 scriptis dictitavit, nempe progrediendo absque reductione æquationum quæ radicales involvunt.
5]7
Hoc defuisse et se supplevisse, Newtonus in prædictis Epistolis submonuit.
6]3 Analysin fluxionum Newtonum in componendo Principiorum opere adhibuisse D. Leibnitius fatetur.
9 Hæc ultima verba recitantur in Actis Lipsicis mense Iunio anni 1696 pag. 57, idque ni fallor ab ipso Leibnitio: nec tamen querela ulla tunc subdota fuit de eo quod Wallisius hic scripserat Newtonum anno 1666 aut antea methodum fluxionum invenisse. Imo methodum D. Leibnitius Newtono tunc concedebat; se vero nonnulla addidisse contendebat. Verba ejus in Epistola ad Wallisium 28 Maij 1697 data, hujusmodi sunt. Quemadmodum et Vietæa et Cartesiana methodus Analyseos speciosæ nomine venit discrimina tamen nonnulla supersunt: ita fortasse & Newtoniana et Mea differunt in nonnullis.
<19:v(r)>p. 39. lin penult. scribe tenuisque gloria et nullum jus. Primi inventoris jus est totum donec alter invenerit, quo casu, aufferre jus primi Inventoris & inter ipsum & Inventorem novum dividere, injustum esset.
tituli vel juris nihil est nisi quod a primis Inventoribus aufert
Appendix.
When the Committee of the R. S. collected the Letters in the Commercium Epistolicum Mr Newton forbore to give them some Letters which he had in his custody least he should seem to make himself a witness in his own cause. But in the year 1714 Mr Leibnitz in a Letter to Mr Chamberlain dated 25 Aug. wrote thus. Quoniam probabile est literas aliquas ad ipsum spectantes inter eas Oldenburgij & Collinij superessæ quæ nondum publicatæ essent, optarem ut Societas regia juberet easdem ad me mitti Nam quando Hannoveram rediero, in lucem etiam edere possim Commercium Epistolicum quod Historiæ Literariæ inserviet. Et in animo habeo non minus eas edere quæ contra me allegari possunt quam quæ pro me faciunt; et judicium de ijsdem relinquam Lectoribus. His coram Societate lectis, Newtonus monuit Consessum a Societate constitutum hic accusari. Epistolas originales servandas esse, seipsum et Leib non esse idoneos qui Commercium edant cum testes esse non possint in propria causa, tantum abfuisse ut ipse Commercium ederet, ut Literas antiquas quas penes se haberet, minime communicaret Concessu: et in ejus rei testimonium literas duas produxit unam Leibnitij ipsius alteram Wallisij
missis agrorum somnijs, Commercium Epistolicum quod Leibnitius & ejus amici absque responso eludere et oblivioni dare conati sunt, in lucem revocari debet et Quæstio tota ad Epistolas antiquas referri.
Quod ad fratres duos Iacobum & Iohannem Bernoullios spectat hæc accipe. Iacobus specimina quædam facilia methodi differentialis dedit annis 1690 & 1691 in Actis Eruditorum et mense Maio anni 1690 Problema funiculare proposuit sed nondum potuit resolvere Leibnitius idem resolvit mense Iulio subsequente & Iohannes tandem mense Decembri ejusdem anni. Et ab eo tempore fratres duo in hac methodo proprijs studijs multum profecerunt, annoque 1692 Leibnitius in Actis eruditorum pro mense Septembri pag. 445 de ijsdem sic scripsit Quod D. Ia. Bernoulli innuit se Fratremque in calculo meo plurimumque profecisse, id agnosco gratulorque non illis magis quam mihi. Valde autem nosce velim an ultra metas illas sint proveati ad quas ego perveni. Seorsim igitur profecerunt Bernoullij duo, & annis tribus sequentibus Ioannes cum Marchione Hospitalio plurima communicavit.
Interea Newtonus ope libri de Quadratura Curvarum scripsit Principia sua Philosophiæ Mathematica & in Lemmate secundo Libri secundi demonstravit solutionem Propositionis Primæ Libri illius de Quadraturis Et Ralphsonus & Halleius tempore æstivo anni 1691 librum illum MS, manibus suis triverunt Cantabrigiæ, ut Ralphsonus testatum reliquit. Et anno proximo Newtonus literis ad Wallisium datis Aug. 27 & Sept. 17, misit ei Propositionem primam et quintam Libri ejusdem, et Wallisius easdem edidit anno 1693 in secundo Operum Volumine pag. 391, 392 & 393. Sic literæ punctis notatæ, & Algorithmus methodi Newtoni, & Regula differentiandi differentialia lucem viderunt et Regula illa verissima est. Post biennium fama methodi differentialis in Hollandia celæbratæ ad Wallisij aures pervenit Et anno terio (1696) Marchio Hospitalius Librum suum de infinite parvis edidit. Et ab eo tempore Methodus differentiandi differentialia alijs alijs familiaris esse cœpit. Hospitalius methodum directam differentialem tractavit. Methodus inversa nondum perfecta est, et Bernoullio reliquuntur quæ de hac re ante cæptam hanc Controversiam non sunt edita
p. 42. l. 28. pro itidem ut Slusianam scribe
p. 33 l. 20 pro fidem faciat scribe probet
p. 39 l. antepenult.
p. 40. l. 30. recensent Editores stylo Leibnitiano [hoc est ipse Leibnitius]
p. 41 l. 20, 34.
p. 26 l. 2. Stylo Leibnitiano [hoc est ipse Leibn.
p. 27 l. 17 Adde in margine. De hoc Tractatu Ralpsonus in Historia sua fluxionum cap. 1, sic scripsit Newtonus anno 1704 parvum edidit Tractatum quem circa annum 1676 ex Tractatu antiquiore extraxit, quemque doctus Halleius et ego circa annum 1691 Cantabrigiæ in manibus nostris habuimus. Et Halleius se & Ralphsonum eo anno Cantabrigiæ Tractatum hunc in manibus suis habuisse adhuc testatur.
p. 28 l. 27. huc
p. 32 l 5 fluxionum inveniendarum.
p. 14 l. 22. In margine scribe. Anno 1715 NB Cum hæc Recensio scribebatur non agnoverat, sed anno subsequente in Epistola ad Cometissam de Kilmansegg agnovit se ab Oldenburgo accepisse [des essais] serierum specimina.
p. 20 l. 26. eodem mense vel Novembri sequente Or in fine mensis illius vel initio sequentis
