The Second Book of Opticks. Part III (1718)
THE
SECOND BOOK
OF
OPTICKS.
PART III.
Of the permanent Colours of natural Bodies, and the Analogy between them and the Colours of thin transparent Plates.
I AM now come to another part of this Design, which is to consider how the Phænomena of thin transparent Plates stand related to those of all other natural Bodies. Of these Bodies I have already told you that they appear of divers Colours, accordingly as they are disposed to reflect most copiously the Rays originally endued with those Colours. But their Constitutions, whereby they reflect some Rays more copiously than others, remain to be discover'd, and these I shall endeavour to manifest in the following Propositions.
Prop. I.
Those Superficies of transparent Bodies reflect the greatest quantity of Light, which have the greatest refracting Power; that is, which intercede Mediums that differ most in their refractive Densities. And in the Confines of equally refracting Mediums there is no Reflexion.
THE Analogy between Reflexion and Refraction will appear by considering, that when Light passeth obliquely out of one Medium into another which refracts from the perpendicular, the greater is the difference of their refractive Density, the less Obliquity of Incidence is requisite to cause a total Reflexion. For as the Sines are which measure the Refraction, so is the Sine of Incidence at which the total Reflexion begins, to the Radius of the Circle, and consequently that Angle of Incidence is least where there is the greatest difference of the Sines. Thus in the passing of Light out of Water into Air, where the Refraction is measured by the Ratio of the Sines 3 to 4, the total Reflexion begins when the Angle of Incidence is about 48 Degrees 35 Minutes. In passing out of Glass into Air, where the Refraction is measured by the Ratio of the Sines 20 to 31, the total Reflexion begins when the Angle of Incidence is 40 Degrees 10 Minutes; and so in passing out of Crystal, or more strongly refracting Mediums into Air, there is still a less Obliquity requisite to cause a total reflexion. Superficies therefore which refract most do soonest reflect all the Light which is incident on them, and so must be allowed most strongly reflexive.
But the truth of this Proposition will farther appear by observing, that in the Superficies interceding two transparent Mediums, (such as are Air, Water, Oil, common Glass, Crystal, metalline Glasses, Island Glasses, white transparent Arsenick, Diamonds, &c.) the Reflexion is stronger or weaker accordingly, as the Superficies hath a greater or less refracting Power. For in the Confine of Air and Sal-gem 'tis stronger than in the Confine of Air and Water, and still stronger in the Confine of Air and common Glass or Crystal, and stronger in the Confine of Air and a Diamond. If any of these, and such like transparent Solids, be immerged in Water, its Reflexion becomes much weaker than before, and still weaker if they be immerged in the more strongly refracting Liquors of well rectified Oil of Vitriol or Spirit of Turpentine. If Water be distinguish'd into two parts, by any imaginary Surface, the Reflexion in the Confine of those two parts is none at all. In the Confine of Water and Ice 'tis very little, in that of Water and Oil 'tis something greater, in that of Water and Sal-gem still greater, and in that of Water and Glass, or Crystal, or other denser Substances still greater, accordingly as those Mediums differ more or less in their refracting Powers. Hence in the Confine of common Glass and Crystal, there ought to be a weak Reflexion, and a stronger Reflexion in the Confine of common and metalline Glass, though I have not yet tried this. But, in the Confine of two Glasses of equal density, there is not any sensible Reflexion, as was shewn in the first Observation. And the same may be understood of the Superficies interceding two Crystals, or two Liquors, or any other Substances in which no Refraction is caused. So then the reason why uniform pellucid Mediums, (such as Water, Glass, or Crystal) have no sensible Reflexion but in their external Superficies, where they are adjacent to other Mediums of a different density, is because all their contiguous parts have one and the same degree of density.
Prop. II.
The least parts of almost all natural Bodies are in some measure transparent: And the Opacity of those Bodies ariseth from the multitude of Reflexions caused in their internal Parts.
THAT this is so has been observed by others, and will easily be granted by them that have been conversant with Microscopes. And it may be also tried by applying any substance to a hole through which some Light is immitted into a dark Room. For how opake soever that Substance may seem in the open Air, it will by that means appear very manifestly transparent, if it be of a sufficient thinness. Only white metalline Bodies must be excepted, which by reason of their excessive density seem to reflect almost all the Light incident on their first Superficies, unless by solution in Menstruums they be reduced into very small Particles, and then they become transparent.
Prop. III.
Between the parts of opake and colour'd Bodies are many Spaces, either empty or replenish'd, with Mediums of other Densities; as Water between the tinging Corpuscles wherewith any Liquor is impregnated, Air between the aqueous Globules that constitute Clouds or Mists; and for the most part Spaces void of both Air and Water, but yet perhaps not wholly void of all Substance, between the parts of hard Bodies.
THE truth of this is evinced by the two precedent Propositions: For by the second Proposition there are many Reflexions made by the internal parts of Bodies, which, by the first Proposition, would not happen if the parts of those Bodies were continued without any such Interstices between them, because Reflexions are caused only in Superficies, which intercede Mediums of a differing density by Prop. 1.
<224>But farther, that this discontinuity of parts is the principal Cause of the opacity of Bodies, will appear by considering, that opake Substances become transparent by filling their Pores with any Substance of equal or almost equal density with their parts. Thus Paper dipped in Water or Oil, the Oculus Mundi Stone steep'd in Water, Linnen Cloth oiled or varnish'd, and many other Substances soaked in such Liquors as will intimately pervade their little Pores, become by that means more transparent than otherwise; so, on the contrary, the most transparent Substances may by evacuating their Pores, or separating their parts, be render'd sufficiently opake, as Salts or wet Paper, or the Oculus Mundi Stone by being dried, Horn by being scraped, Glass by being reduced to Powder, or otherwise flawed, Turpentine by being stirred about with Water till they mix imperfectly, and Water by being form'd into many small Bubbles, either alone in the form of Froth, or by shaking it together with Oil of Turpentine, or Oil Olive, or with some other convenient Liquor, with which it will not perfectly incorporate. And to the increase of the opacity of these Bodies it conduces something, that by the 23d Observation the Reflexions of very thin transparent Substances are considerably stronger than those made by the same Substances of a greater thickness.
<225>Prop. IV.
The parts of Bodies and their Interstices must not be less than of some definite bigness, to render them opake and colour'd.
FOR the opakest Bodies, if their parts be subtilly divided, (as Metals by being dissolved in acid Menstruums, &c.) become perfectly transparent. And you may also remember, that in the eighth Observation there was no sensible reflexion at the Superficies of the Object-glasses where they were very near one another, though they did not absolutely touch. And in the 17th Observation the Reflexion of the Water-bubble where it became thinnest was almost insensible, so as to cause very black Spots to appear on the top of the Bubble by the want of reflected Light.
On these grounds I perceive it is that Water, Salt, Glass, Stones, and such like Substances, are transparent. For, upon divers Considerations, they seem to be as full of Pores or Interstices between their parts as other Bodies are, but yet their Parts and Interstices to be too small to cause Reflexions in their common Surfaces.
<226>Prop. V.
The transparent parts of Bodies according to their several sizes reflect Rays of one Colour, and transmit those of another, on the same grounds that thin Plates or Bubbles do reflect or transmit those Rays. And this I take to be the ground of all their Colours.
FOR if a thinn'd or plated Body, which being of an even thickness, appears all over of one uniform Colour, should be slit into Threads, or broken into Fragments, of the same thickness with the Plate; I see no reason why every Thread or Fragment should not keep its Colour, and by consequence why a heap of those Threads or Fragments should not constitute a Mass or Powder of the same Colour, which the Plate exhibited before it was broken. And the parts of all natural Bodies being like so many Fragments of a Plate, must on the same grounds exhibit the same Colours.
Now, that they do so, will appear by the affinity of their Properties. The finely colour'd Feathers of some Birds, and particularly those of Peacocks Tails, do in the very same part of the Feather appear of several Colours in several Positions of the Eye, after the very same manner that thin Plates were found to do in the 7th and 19th Observations, and therefore their Colours arise from the thinness of the transparent parts of the Feathers; that is, from the slenderness of the very fine Hairs, or Capillamenta, which grow out of the sides of the grosser lateral Branches or Fibres of those Feathers. And to the same purpose it is, that the Webs of some Spiders by being spun very fine have appeared colour'd, as some have observ'd, and that the colour'd Fibres of some Silks by varying the Position of the Eye do vary their Colour. Also the Colours of Silks, Cloths, and other Substances, which Water or Oil can intimately penetrate, become more faint and obscure by being immerged in those Liquors, and recover their Vigor again by being dried, much after the manner declared of thin Bodies in the 10th and 21St Observations. Leaf Gold, some sorts of painted Glass, the Infusion of Lignunm Nephriticum, and some other Substances reflect one Colour, and transmit another, like thin Bodies in the 9th and 20th Observations. And some of those colour'd Powders which Painters use, may have their Colours a little changed, by being very elaborately and finely ground. Where I see not what can be justly pretended for those changes, besides the breaking of their parts into less parts by that contrition after the same manner that the Colour of a thin Plate is changed by varying its thickness. For which reason also it is that the colour'd Flowers of Plants and Vegetables by being bruised usually become more transparent than before, or at least in some degree or other change their Colours. Nor is it much less to my purpose, that by mixing divers Liquors very odd and remarkable Productions and Changes of Colours may be effected, of which no cause can be more obvious and rational than the saline Corpuscles of one Liquor do variously act upon or unite with the tinging Corpuscles of another, so as to make them swell, or shrink (whereby not only their bulk but their density also may be changed) or to divide them into smaller Corpuscles, (whereby a colour'd Liquor may become transparent) or to make many of them associate into one cluster, whereby two transparent Liquors may compose a colour'd one. For we see how apt those saline Menstruums are to penetrate and dissolve Substances to which they are applied, and some of them to precipitate what others dissolve. In like manner, if we consider the various Phænomena of the Atmosphere, we may observe, that when Vapours are first raised, they hinder not the transparency of the Air, being divided into parts too small to cause any Reflexion in their Superficies. But when in order to compose Drops of Rain they begin to coalesce and constitute Globules of all intermediate sizes, those Globules when they become of convenient size to reflect some Colours and transmit others, may constitute Clouds of various Colours according to their sizes. And I see not what can be rationally conceived in so transparent a Substance as Water for the production of these Colours, besides the various sizes of its fluid and globular Parcels.
<229>Prop. VI.
The parts of Bodies on which their Colours depend, are denser than the Medium, which pervades their Interstices.
THIS will appear by considering, that the Colour of a Body depends not only on the Rays which are incident perpendicularly on its parts, but on those also which are incident at all other Angles. And that according to the 7th Observation, a very little variation of obliquity will change the reflected Colour where the thin Body or small Particle is rarer than the ambient Medium, insomuch that such a small Particle will at diversly oblique Incidences reflect all sorts of Colours, in so great a variety that the Colour resulting from them all, confusedly reflected from a heap of such Particles, must rather be a white or grey than any other Colour, or at best it must be but a very imperfect and dirty Colour. Whereas if the thin Body or small Particle be much denser than the ambient Medium, the Colours according to the 19th Observation are so little changed by the variation of obliquity, that the Rays which are reflected least obliquely may predominate over the rest so much as to cause a heap of such Particles to appear very intensely of their Colour.
It conduces also something to the confirmation of this Proposition, that, according to the 22d Observation, the Colours exhibited by the denser thin Body within the rarer, are more brisk than those exhibited by the rarer within the denser.
Prop. VII.
The bigness of the component parts of natural Bodies may be conjectured by their Colours.
FOR since the parts of these Bodies by Prop. 5. do most probably exhibit the same Colours with a Plate of equal thickness, provided they have the same refractive density; and since their parts seem for the most part to have much the same density with Water or Glass, as by many circumstances is obvious to collect; to determine the sizes of those parts you need only have recourse to the precedent Tables, in which the thickness of Water or Glass exhibiting any Colour is expressed. Thus if it be desired to know the diameter of a Corpuscle, which being of equal density with Glass shall reflect green of the third Order; the Number shews it to be parts of an Inch.
The greatest difficulty is here to know of what Order the Colour of any Body is. And for this end we must have recourse to the 4th and 18th Observations, from whence may be collected these particulars.
Scarlets, and other reds, oranges and yellows, if they be pure and intense are most probably of the second order. Those of the first and third order also may be pretty good, only the yellow of the first order is faint, and the orange and red of the third order have a great mixture of violet and blue.
There may be good greens of the fourth order, but the purest are of the third. And of this order the green of all Vegetables seem to be, partly by reason of the intenseness of their Colours, and partly because when they wither some of them turn to a greenish yellow, and others to a more perfect yellow or orange, or perhaps to red, passing first through all the aforesaid intermediate Colours. Which Changes seem to be effected by the exhaling of the moisture which may leave the tinging Corpuscles more dense, and something augmented by the accretion of the oily and earthy part of that moisture. Now the green without doubt is of the same order with those Colours into which it changeth, because the Changes are gradual, and those Colours, though usually not very full, yet are often too full and lively to be of the fourth order.
Blues and purples may be either of the second or third order, but the best are of the third. Thus the Colour of violets seems to be of that order, because their Syrup by acid Liquors turns red, and by urinous and alcalizate turns green. For since it is of the nature of Acids to dissolve or attenuate, and of Alcalies to precipitate or incrassate, if the purple Colour of the Syrup was of the second Order, an acid Liquor by attenuating its tinging Corpuscles would change it to a red of the first order, and an Alcali by incrassating them would change it to a green of the second order; which red and green, especially the green, seem too imperfect to be the Colours produced by these Changes. But if the said purple be supposed of the third order, its Change to red of the second, and green of the third, may without any inconvenience be allow'd.
If there be found any Body of a deeper and less reddish purple than that of the violets, its Colour most probably is of the second order. But yet there being no Body commonly known whose Colour is constantly more deep than theirs, I have made use of their name to denote the deepest and least reddish purples, such as manifestly transcend their Colour in purity.
The blue of the first order, though very faint and little, may possibly be the Colour of some Substances; and particularly the azure Colour of the Skies seems to be of this order. For all Vapours when they begin to condense and coalesce into small parcels, become first of that bigness whereby such an Azure must be reflected before they can constitute Clouds of other Colours. And so this being the first Colour which Vapours begin to reflect, it ought to be the Colour of the finest and most transparent Skies in which Vapours are not arrived to that grossness requisite to reflect other Colours, as we find it is by experience.
Whiteness, if most intense and luminous, is that of the first order, if less strong and luminous a mixture of the Colours of several orders. Of this last kind is the whiteness of Froth, Paper, Linen, and most white Substances; of the former I reckon that of white Metals to be. For whilst the densest of Metals, Gold, if foliated, is transparent, and all Metals become transparent if dissolved in Menstruums or vitrified, the opacity of white Metals ariseth not from their density alone. They being less dense than Gold would be more transparent than it, did not some other Cause concur with their density to make them opake. And this cause I take to be such a bigness of their Particles as fits them to reflect the white of the first order. For if they be of other thicknesses they may reflect other Colours, as is manifest by the Colours which appear upon hot Steel in tempering it, and sometimes upon the Surface of melted Metals in the Skin or Scoria which arises upon them in their cooling. And as the white of the first order is the strongest which can be made by Plates of transparent Substances, so it ought to be stronger in the denser Substances of Metals than in the rarer of Air, Water and Glass. Nor do I see but that metallic Substances of such a thickness as may fit them to reflect the white of the first order, may, by reason of their great density (according to the tenour of the first of these Propositions) reflect all the Light incident upon them, and so be as opake and splendent as it's possible for any Body to be. Gold, or Copper mix'd with less than half their weight of Silver, or Tin, or Regulus of Antimony, in fusion, or amalgamed with a very little Mercury, become white; which shews both that the Particles of white Metals have much more Superficies, and so are smaller, than those of Gold and Copper, and also that they are so opake as not to suffer the Particles of Gold or Copper to shine through them. Now it is scarce to be doubted, but that the Colours of Gold and Copper are of the second and third order, and therefore the Particles of white Metals cannot be much bigger than is requisite to make them reflect the white of the first order. The Volatility of Mercury argues that they are not much bigger, nor may they be much less, lest they lose their opacity, and become either transparent as they do when attenuated by vitrification, or by Solution in Menstruums, or black as they do when ground smaller, by rubbing Silver, or Tin, or Lead, upon other Substances to draw black Lines. The first and only Colour which white Metals take by grinding their Particles smaller, is black, and therefore their white ought to be that which borders upon the black Spot in the Center of the Rings of Colours, that is, the white of the first order. But if you would hence gather the bigness of metallic Particles, you must allow for their density. For were Mercury transparent, its density is such that the Sine of Incidence upon it (by my computation) would be to the Sine of its Refraction, as 71 to 20, or 7 to 2. And therefore the thickness of its Particles, that they may exhibit the same Colours with those of Bubbles of Water, ought to be less than the thickness of the Skin of those Bubbles in the proportion of 2 to 7. Whence it's possible that the Particles of Mercury may be as little as the Particles of some transparent and volatile Fluids, and yet reflect the white of the first order.
Lastly, for the production of black, the Corpuscles must be less than any of those which exhibit Colours. For at all greater sizes there is too much Light reflected to constitute this Colour. But if they be supposed a little less than is requisite to reflect the white and very faint blue of the first order, they will, according to the 4th, 8th, 17th and 18th Observations, reflect so very little Light as to appear intensely black, and yet may perhaps variously refract it to and fro within themselves so long, until it happen to be stifled and lost, by which means they will appear black in all positions of the Eye without any transparency. And from hence may be understood why Fire, and the more subtile dissolver Putrefaction, by dividing the Particles of Substances, turn them to black, why small quantities of black Substances impart their Colour very freely and intensely to other Substances to which they are applied; the minute particles of these, by reason of their very great number, easily overspreading the gross Particles of others; why Glass ground very elaborately with Sand on a Copper Plate, 'till it be well polish'd, makes the Sand, together with what is worn off from the Glass and Copper, become very black: why black Substances do soonest of all others become hot in the Sun's Light and burn, (which Effect may proceed partly from the multitude of Refractions in a little room, and partly from the easy Commotion of so very small Corpuscles;) and why blacks are usually a little inclined to a bluish Colour. For that they are so may be seen by illuminating white Paper by Light reflected from black Substances. For the Paper will usually appear of a bluish white; and the reason is, that black Borders on the obscure blue of the first order described in the 18th Observation, and therefore reflects more Rays of that Colour than of any other.
In these Descriptions I have been the more particular, because it is not impossible but that Miscroscopes may at length be improved to the discovery of the Particles of Bodies on which their Colours depend, if they are not already in some measure arrived to that degree of perfection. For if those Instruments are or can be so far improved as with sufficient distinctness to represent Objects five or six hundred times bigger than at a Foot distance they appear to our naked Eyes, I should hope that we might be able to discover some of the greatest of those Corpuscles. And by one that would magnify three or four thousand times perhaps they might all be discover'd, but those which produce blackness. In the mean while I see nothing material in this Discourse that may rationally be doubted of, excepting this Position. That transparent Corpuscles of the same thickness and density with a Plate, do exhibit the same Colour. And this I would have understood not without some Latitude, as well because those Corpuscles may be of irregular Figures, and many Rays must be obliquely incident on them, and so have a shorter way through them than the length of their Diameters, as because the straitness of the Medium pent in on all sides within such Corpuscles may a little alter its Motions or other qualities on which the Reflexion depends. But yet I cannot much suspect the last, because I have observed of some small Plates of Muscovy Glass which were of an even thickness, that through a Microscope they have appeared of the same Colour at their edges and corners where the included Medium was terminated, which they appeared of in other places. However it will add much to our Satisfaction, if those Corpuscles can be discover'd with Microscopes; which if we shall at length attain to, I fear it will be the utmost improvement of this Sense. For it seems impossible to see the more secret and noble Works of Nature within the Corpuscles by reason of their transparency.
Prop. VIII.
The Cause of Reflexion is not the impinging of Light on the solid or impervious parts of Bodies, as is commonly believed.
THIS will appear by the following Considerations. First, That in the passage of Light out of Glass into Air there is a Reflexion as strong as in its passage out of Air into Glass, or rather a little stronger, and by many degrees stronger than in its passage out of Glass into Water. And it seems not probable that Air should have more strongly reflecting parts than Water or Glass. But if that should possibly be supposed, yet it will avail nothing; for the Reflexion is as strong or stronger when the Air is drawn away from the Glass, (suppose in the Air-Pump invented by Otto Gueric, and improved and made useful by Mr. Boyle) as when it is adjacent to it. Secondly, If Light in its passage out of Glass into Air be incident more obliquely than at an Angle of 40 or 41 Degrees it is wholly reflected, if less obliquely it is in great measure transmitted. Now it is not to be imagined that Light at one degree of obliquity should meet with Pores enough in the Air to transmit the greater part of it, and at another degree of obliquity should meet with nothing but parts to reflect it wholly, especially considering that in its passage out of Air into Glass, how oblique soever be its Incidence, it finds Pores enough in the Glass to transmit a great part of it. If any Man suppose that it is not reflected by the Air, but by the outmost superficial parts of the Glass, there is still the same difficulty: Besides, that such a Supposition is unintelligible, and will also appear to be false by applying Water behind some part of the Glass instead of Air. For so in a convenient obliquity of the Rays, suppose of 45 or 46 Degrees, at which they are all reflected where the Air is adjacent to the Glass, they shall be in great measure transmitted where the Water is adjacent to it; which argues, that their Reflexion or Transmission depends on the constitution of the Air and Water behind the Glass, and not on the striking of the Rays upon the parts of the Glass. Thirdly, If the Colours made by a Prism placed at the entrance of a Beam of Light into a darken'd Room be successively cast on a second Prism placed at a greater distance from the former, in such manner that they are all alike incident upon it, the second Prism may be so inclined to the incident Rays, that those which are of a blue Colour shall be all reflected by it, and yet those of a red Colour pretty copiously transmitted. Now if the Reflexion be caused by the parts of Air or Glass, I would ask, why at the same Obliquity of Incidence the blue should wholly impinge on those parts so as to be all reflected, and yet the red find Pores enough to be in a great measure transmitted. Fourthly, Where two Glasses touch one another, there is no sensible Reflexion as was declared in the first Observation; and yet I see no reason why the Rays should not impinge on the parts of Glass as much when contiguous to other Glass as when contiguous to Air. Fifthly, When the top of a Water-Bubble (in the 17th Observation) by the continual subsiding and exhaling of the Water grew very thin, there was such a little and almost insensible quantity of Light reflected from it, that it appeared intensely black; whereas round about that black Spot, where the Water was thicker, the Reflexion was so strong as to make the Water seem very white. Nor is it only at the least thickness of thin Plates or Bubbles, that there is no manifest Reflexion, but at many other thicknesses continually greater and greater. For in the 15th Observation the Rays of the same Colour were by turns transmitted at one thickness, and reflected at another thickness, for an indeterminate number of Successions. And yet in the Superficies of the thinned Body, where it is of any one thickness, there are as many parts for the Rays to impinge on, as where it is of any other thickness. Sixthly, If Reflexion were caused by the parts of reflecting Bodies, it would be impossible for thin Plates or Bubbles at one and the same place to reflect the Rays of one Colour and transmit those of another, as they do according to the 13th and 15th Observations. For it is not to be imagined that at one place the Rays which for instance exhibit a blue Colour, should have the fortune to dash upon the parts, and those which exhibit a red to hit upon the Pores of the Body; and then at another place, where the Body is either a little thicker, or a little thinner, that on the contrary the blue should hit upon its pores, and the red upon its parts. Lastly, were the Rays of Light reflected by impinging on the solid parts of Bodies, their Reflexions from polish'd Bodies could not be so regular as they are. For in polishing Glass with Sand, Putty or Tripoly, it is not to be imagined that those Substances can by grating and fretting the Glass bring all its least Particles to an accurate Polish; so that all their Surfaces shall be truly plain or truly spherical, and look all the same way, so as together to compose one even Surface. The smaller the Particles of those Substances are, the smaller will be the Scratches by which they continually fret and wear away the Glass until it be polish'd, but be they never so small they can wear away the Glass no otherwise than by grating and scratching it, and breaking the Protuberances, and therefore polish it no otherwise than by bringing its roughness to a very fine Grain, so that the Scratches and Frettings of the Surface become too small to be visible. And therefore if Light were reflected by impinging upon the solid parts of the Glass, it would be scatter'd as much by the most polish'd Glass as by the roughest. So then it remains a Problem, how Glass polish'd by fretting Substances can reflect Light so regularly as it does. And this Problem is scarce otherwise to be solved than by saying, that the Reflexion of a Ray is effected, not by a single point of the reflecting Body, but by some power of the Body which is evenly diffused all over its Surface, and by which it acts upon the Ray without immediate Contact. For that the parts of Bodies do act upon Light at a distance shall be shewn hereafter.
Now if Light be reflected not by impinging on the solid parts of Bodies, but by some other principle; it's probable that as many of its Rays as impinge on the solid parts of Bodies are not reflected but stifled and lost in the Bodies. For otherwise we must allow two sorts of Reflexions. Should all the Rays be reflected which impinge on the internal parts of clear Water or Crystal, those Substances would rather have a cloudy Colour than a clear Transparency. To make Bodies look black, it's necessary that many Rays be stopp'd, retained and lost in them, and it seems not probable that any Rays can be stopp'd and stifled in them which do not impinge on their parts.
<242>And hence we may understand that Bodies are much more rare and porous than is commonly believed. Water is nineteen times lighter, and by consequence nineteen times rarer than Gold, and Gold is so rare as very readily and without the least opposition to transmit the magnetick Effluvia, and easily to admit Quicksilver into its Pores, and to let Water pass through it. For a concave Sphere of Gold filled with Water, and soder'd up, has upon pressing the Sphere with great force, let the Water squeeze through it, and stand all over its outside in multitudes of small Drops, like Dew, without bursting or cracking the Body of the Gold as I have been inform'd by an Eye witness. From all which we may conclude, that Gold has more Pores than solid parts, and by consequence that Water has above forty times more Pores than Parts. And he that shall find out an Hypothesis, by which Water may be so rare, and yet not be capable of compression by force, may doubtless by the same Hypothesis make Gold and Water, and all other Bodies as much rarer as he pleases; so that Light may find a ready passage through transparent Substances.
The Magnet acts upon Iron through all dense Bodies not magnetick nor red hot, without any diminution of its virtue; as for instance, through Gold, Silver, Lead, Glass, Water. The gravitating Power of the Sun is transmitted through the vast Bodies of the Planets without any diminution, so as to act upon all their parts to their very centers with the same Force and according to the same Laws as if the part upon which it acts were not surrounded with the Body of the Planet. The Rays of Light whether they be very small Bodies projected, or only Motion or Force propagated, are moved in right Lines; and whenever a Ray of Light is by any Obstacle turned out of its rectilinear way, it will never return into the same rectilinear way, unless perhaps by very great accident. And yet Light is transmitted through pellucid solid Bodies in right Lines to very great distances. How Bodies can have a sufficient quantity of Pores for producing these Effects is very difficult to conceive, but perhaps not altogether impossible. For the Colours of Bodies arise from the Magnitudes of the Particles which reflect them, as was explained above. Now if we conceive these Particles of Bodies to be so disposed amongst themselves, that the Intervals or empty Spaces between them may be equal in magnitude to them all; and that these Particles may be composed of other Particles much smaller, which have as much empty Space between them as equals all the Magnitudes of these smaller Particles: And that in like manner these smaller Particles are again composed of others much smaller, all which together are equal to all the Pores or empty Spaces between them; and so on perpetually till you come to solid Particles, such as have no Pores or empty Spaces within them: And if in any gross Body there be, for instance, three such degrees of Particles, the least of which are solid; this Body will have seven times more Pores than solid Parts. But if there be four such degrees of Particles, the least of which are solid, the Body will have fifteen times more Pores than solid Parts. If there be five degrees, the Body will have one and thirty times more Pores than solid Parts. If six degrees, the Body will have sixty and three times more Pores than solid Parts. And so on perpetually. And there are other ways of conceiving how Bodies may be exceeding porous. But what is really their inward Frame is not yet known to us.
Prop. IX.
Bodies reflect and refract Light by one and the same power variously exercised in various Circumstances.
THIS appears by several Considerations. First, Because when Light goes out of Glass into Air, as obliquely as it can possibly do. If its Incidence be made still more oblique, it becomes totally reflected. For the power of the Glass after it has refracted the Light as obliquely as is possible if the Incidence be still made more oblique, becomes too strong to let any of its Rays go through, and by consequence causes total Reflexions. Secondly, Because Light is alternately reflected and transmitted by thin Plates of Glass for many Successions accordingly as the thickness of the Plate increases in an arithmetical Progression. For here the thickness of the Glass determines whether that Power by which Glass acts upon Light shall cause it to be reflected, or suffer it to be transmitted. And, Thirdly, because those Surfaces of transparent Bodies which have the greatest refracting Power, reflect the greatest quantity of Light, as was shew'd in the first Proposition.
Prop. X.
If Light be swifter in Bodies than in Vacuo in the proportion of the Sines which measure the Refraction of the Bodies, the Forces of the Bodies to reflect and refract Light, are very nearly proportional to the densities of the same Bodies, excepting that unctuous and sulphureous Bodies refract more than others of this same density.
LET AB represent the refracting plane Surface of any Body, and IC a Ray incident very obliquely upon the Body in C, so that the 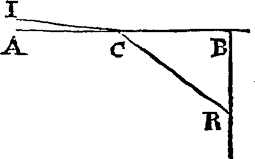 Angle ACI may be infinitely little, and let CR be the refracted Ray. From a given Point B perpendicular to the refracting Surface erect BR meeting with the refracted Ray CR in R, and if CR represent the Motion of the refracted Ray, and this Motion be distinguish'd into two Motions CB and BR, whereof CB is parallel to the refracting Plane, and BR perpendicular to it: CB shall represent the Motion of the incident Ray, and BR the Motion generated by the Refraction, as Opticians have of late explain'd.
Angle ACI may be infinitely little, and let CR be the refracted Ray. From a given Point B perpendicular to the refracting Surface erect BR meeting with the refracted Ray CR in R, and if CR represent the Motion of the refracted Ray, and this Motion be distinguish'd into two Motions CB and BR, whereof CB is parallel to the refracting Plane, and BR perpendicular to it: CB shall represent the Motion of the incident Ray, and BR the Motion generated by the Refraction, as Opticians have of late explain'd.
Now if any Body or thing, in moving through any Space of a given breadth terminated on both sides by two parallel Planes, be urged forward in all parts of that Space by Forces tending directly forwards towards the last Plane, and before its Incidence on the first Plane, had no Motion towards it, or but an infinitely little one; and if the Forces in all parts of that Space, between the Planes be at equal distances from the Planes equal to one another, but at several distances be bigger or less in any given Proportion, the Motion generated by the Forces in the whole passage of the Body or thing through that Space shall be in a subduplicate Proportion of the Forces, as Mathematicians will easily understand. And therefore if the Space of activity of the refracting Superficies of the Body be consider'd as such a Space, the Motion of the Ray generated by the refracting Force of the Body, during its passage through that Space, that is the Motion BR, must be in subduplicate Proportion of that refracting Force. I say therefore that the Square of the Line BR, and by consequence the refracting Force of the Body is very nearly as the density of the same Body. For this will appear by the following Table, wherein the Proportion of the Sines which measure the Refractions of several Bodies, the Square of BR supposing CB an unite, the Densities of the Bodies estimated by their Specifick gravities, and their refractive Power in respect of their densities are set down in several Columns.
| The refracting Bodies. | The Proportion of the Sines of Incidence and Refraction of yellow Light. | The Square of BR, to which the refracting force of the Body is proportionate | The density and specifick gravity of the Body. | The refractive Power of the Body in respect of its density. |
| A Pseudo-Topazius, being a natural, pellucid, britt{l}e, hairy Stone, of a yellow Colour | 23 to 14 | 1'699 | 4'27 | 3979 |
| Air. | 3201 to 3200 | 0'000625 | 0'0012 | 5208 |
| Glass of Antimony. | 17 to 9 | 2'568 | 5'28 | 4864 |
| A Selenitis. | 61 to 41 | 1'213 | 2'252 | 5386 |
| Glass vulgar. | 31 to 20 | 1'4025 | 2'58 | 5436 |
| Crystal of the Rock. | 25 to 16 | 1'445 | 2'65 | 5450 |
| Island Crystal. | 5 to 3 | 1'778 | 2'72 | 6536 |
| Sal Gemmæ. | 17 to 11 | 1'388 | 2'143 | 6477 |
| Alume. | 35 to 24 | 1'1267 | 1'714 | 6570 |
| Borax. | 22 to 15 | 1'1511 | 1'714 | 6716 |
| Niter. | 32 to 21 | 1'345 | 1'9 | 7079 |
| Dantzick Vitriol. | 303 to 200 | 1'295 | 1'715 | 7551 |
| Oil of Vitriol. | 10 to 7 | 1'041 | 1'7 | 6124 |
| Rain Water. | 529 to 396 | 0'7845 | 1' | 7845 |
| Gum Arabick. | 31 to 21 | 1'179 | 1'375 | 8574 |
| Spirit of Wine well rectified. | 100 to 73 | 0'8765 | 0'866 | 10121 |
| Camphire. | 3 to 2 | 1'25 | 0'996 | 12551 |
| Oil Olive. | 22 to 15 | 1'1511 | 0'913 | 12607 |
| Linseed Oil. | 40 to 27 | 1'1948 | 0'932 | 12819 |
| Spirit of Turpentine. | 25 to 17 | 1'1626 | 0'874 | 13222 |
| Ambar. | 14 to 9 | 1'42 | 1'04 | 13654 |
| A Diamond. | 100 to 41 | 4'949 | 3'4 | 14556 |
The Refraction of the Air in this Table is determin'd by that of the Atmosphere observed by Astronomers. For if Light pass through many refracting Substances or Mediums gradually denser and denser, and terminated with parallel Surfaces, the sum of all the Refractions will be equal to the single Refraction which it would have suffer'd in passing immediately out of the first Medium into the last. And this holds true, though the number of the refracting Substances be increased to infinity, and the distances from one another as much decreased, so that the Light may be refracted in every point of its Passage, and by continual Refractions bent into a curve Line. And therefore the whole Refraction of Light in passing through the Atmosphere from the highest and rarest part thereof down to the lowest and densest part, must be equal to the Refraction which it would suffer in passing at like obliquity out of a Vacuum immediately into Air of equal density with that in the lowest part of the Atmosphere.
Now, although a Pseudo-Topaz, a Selenitis, Rock Crystal, Island Crystal, Vulgar Glass (that is, Sand melted together) and Glass of Antimony, which are terrestrial stony alcalizate Concretes, and Air which probably arises from such Substances by Fermentation, be Substances very differing from one another in density, yet by this Table, they have their refractive Powers almost in the same proportion to one another as their densities are, excepting that the Refraction of that strange Substance Island Crystal is a little bigger than the rest. And particularly Air, which is 3500 times rarer than the Pseudo-Topaz, and 4400 times rarer than Glass of Antimony, and 2000 times rarer than the Selenitis, Glass vulgar, or Crystal of the Rock, has notwithstanding its rarity the same refractive Power in respect of its density which those very dense Substances have in respect of theirs, excepting so far as those differ from one another.
Again, the Refraction of Camphire, Oil Olive, Linseed Oil, Spirit of Turpentine and Ambar, which are fat sulphureous unctuous Bodies, and a Diamond, which probably is an unctuous Substance coagulated, have their refractive Powers in proportion to one another as their densities without any considerable variation. But the refractive Powers of these unctuous Substances are two or three times greater in respect of their densities than the refractive Powers of the former Substances in respect of theirs.
Water has a refractive Power in a middle degree between those two sorts of Substances, and probably is of a middle nature. For out of it grow all vegetable and animal Substances, which consist as well of sulphureous fat and inflamable parts, as of earthy lean and alcalizate ones.
Salts and Vitriols have refractive Powers in a middle degree between those of earthy Substances and Water, and accordingly are composed of those two sorts of Substances. For by distillation and rectification of their Spirits a great part of them goes into Water, and a great part remains behind in the form of a dry fix'd Earth capable of vitrification.
<250>Spirit of Wine has a refractive Power in a middle degree between those of Water and oily Substances, and accordingly seems to be composed of both, united by Fermentation; the Water, by means of some saline Spirits with which 'tis impregnated, dissolving the Oil, and volatizing it by the action. For Spirit of Wine is inflamable by means of its oily parts, and being distilled often from Salt of Tartar, grows by every distillation more and more aqueous and phlegmatick. And Chymists observe, that Vegetables (as Lavender, Rue, Marjoram, &c.) distilled per se, before fermentation yield Oils without any burning Spirits, but after fermentation yield ardent Spirits without Oils: Which shews, that their Oil is by fermentation converted into Spirit. They find also, that if Oils be poured in a small quantity upon fermentating Vegetables, they distil over after fermentation in the form of Spirits.
So then, by the foregoing Table, all Bodies seem to have their refractive Powers proportional to their densities, (or very nearly;) excepting so far as they partake more or less of sulphureous oily Particles, and thereby have their refractive Power made greater or less. Whence it seems rational to attribute the refractive Power of all Bodies chiefly, if not wholly, to the sulphureous parts with which they abound. For it's probable that all Bodies abound more or less with Sulphurs. And as Light congregated by a Burning-glass acts most upon sulphureous Bodies, to turn them into Fire and Flame ; so, since all action is mutual, Sulphurs ought to act most upon Light. For that the action between Light and Bodies is mutual, may appear from this Consideration; That the densest Bodies which refract and reflect Light most strongly grow hottest in the Summer Sun, by the action of the refracted or reflected Light.
I have hitherto explain'd the Power of Bodies to reflect and refract, and shew'd, that thin transparent Plates, Fibres and Particles do, according to their several thicknesses and densities, reflect several sorts of Rays, and thereby appear of several Colours, and by consequence that nothing more is requisite for producing all the Colours of natural Bodies than the several sizes and densities of their transparent Particles. But whence it is that these Plates, Fibres and particles do, according to their several thicknesses and densities, reflect several sorts of Rays, I have not yet explain'd. To give some insight into this'matter, and make way for understanding the next part of this Book, I shall conclude this part with a few more Propositions. Those which preceded respect the nature of Bodies, these the nature of Light: For both must be understood before the reason of their actions upon one another can be known. And because the last Proposition depended upon the velocity of Light, I will begin with a Proposition of that kind.
<252>Prop. XI.
Light is propagated from luminous Bodies in time, and spends about seven or eight Minutes of an Hour in passing from the Sun to the Earth.
THIS was observed first by Roemer, and then by others, by means of the Eclipses of the Satellites of Jupiter. For these Eclipses, when the Earth is between the Sun and Jupiter, happen about seven or eight Minutes sooner than they ought to do by the Tables, and when the Earth is beyond the Sun they happen about seven or eight Minutes later than they ought to do; the reason being, that the Light of the Satellites has farther to go in the latter case than in the former by the Diameter of the Earth's Orbit. Some inequalities of time may arise from the Excentricities of the Orbs of the Satellites; but those cannot answer in all the Satellites, and at all times to the position and distance of the Earth from the Sun. The mean motions of Jupiter's Satellites is also swifter in his descent from his Aphelium to his Perihelium, than in his ascent in the other half of his Orb: But this inequality has no respect to the position of the Earth, and in the three interior Satellites is insensible, as I find by computation from the Theory of their gravity.
<253>Prop. XII.
Every Ray of Light in its passage through any refracting Surface is put into a certain transient Constitution or State, which in the progress of the Ray returns at equal Intervals, and disposes the Ray at every return to be easily transmitted through the next refracting Surface, and between the returns to be easily reflected by it.
THIS is manifest by the 5th, 9th, 12th, and 15th Observations. For by those Observations it appears, that one and the same sort of Rays at equal Angles of Incidence on any thin transparent Plate, is alternately reflected and transmitted for many Successions accordingly as the thickness of the Plate increases in arithmetical Progression of the Numbers, 0, 1, 2, 3, 4, 5, 6, 7, 8, &c. so that if the first Reflexion (that which makes the first or innermost of the Rings of Colours there described) be made at the thickness 1, the Rays shall be transmitted at the thicknesses 0, 2, 4, 6, 8, 10, 12, &c. and thereby make the central Spot and Rings of Light, which appear by transmission, and be reflected at the thickness 1, 3, 5, 7, 9, 11, &c. and thereby make the Rings which appear by Reflexion. And this alternate Reflexion and Transmission, as I gather by the 24th Observation, continues for above an hundred vicissitudes, and by the Observations in the next part of this Book, for many thousands, being propagated from one Surface of a Glass Plate to the other, though the thickness of the Plate be a quarter of an Inch or above: So that this alternation seems to be propagated from every refracting Surface to all distances without end or limitation.
This alternate Reflexion and Refraction depends on both the Surfaces of every thin Plate, because it depends on their distance. By the 21st Observation, if either Surface of a thin Plate of Muscovy Glass be wetted, the Colours caused by the alternate Reflexion and Refraction grow faint, and therefore it depends on them both.
It is therefore perform'd at the second Surface; for if it were perform'd at the first, before the Rays arrive at the second, it would not depend on the second.
It is also influenced by some action or disposition, propagated from the first to the second, because otherwise at the second it would not depend on the first. And this action or disposition, in its propagation, intermits and returns by equal Intervals, because in all its progress it inclines the Ray at one distance from the first Surface to be reflected by the second, at another to be transmitted by it, and that by equal Intervals for innumerable vicissitudes. And because the Ray is disposed to Reflexion at the distances 1, 3, 5, 7, 9, &c. and to Transmission at the distances 0, 2, 4, 6, 8, 10, &c. (for its transmission through the first Surface, is at the distance 0, and it is transmitted through both together, if their distance be infinitely little or much less than 1) the disposition to be transmitted at the distances 2, 4, 6, 8, 10, &c. is to be accounted a return of the same disposition which the Ray first had at the distance 0, that is at its transmission through the first refracting Surface. All which is the thing I would prove.
What kind of action or disposition this is; Whether it consists in a circulating or a vibrating motion of the Ray, or of the Medium, or something else, I do not here enquire. Those that are averse from assenting to any new Discoveries, but such as they can explain by an Hypothesis, may for the present suppose, that as Stones by falling upon Water put the Water into an undulating Motion, and all Bodies by percussion excite vibrations in the Air; so the Rays of Light, by impinging on any refracting or reflecting Surface, excite vibrations in the refracting or reflecting Medium or Substance, and by exciting them agitate the solid parts of the refracting or reflecting Body, and by agitating them cause the Body to grow warm or hot; that the vibrations thus excited are propagated in the refracting or reflecting Medium or Substance, much after the manner that vibrations are propagated in the Air for causing Sound, and move faster than the Rays so as to overtake them; and that when any Ray is in that part of the vibration which conspires with its Motion, it easily breaks through a refracting Surface, but when it is in the contrary part of the vibration which impedes its Motion, it is easily reflected; and, by consequence, that every Ray is successively disposed to be easily reflected, or easily transmitted, by every vibration which overtakes it. But whether this Hypothesis be true or false I do not here consider. I content my self with the bare Discovery, that the Rays of Light are by some cause or other alternately disposed to be reflected or refracted for many vicissitudes.
DEFINITION.
The returns of the disposition of any Ray to be reflected I will call its Fits of easy Reflexion, and those of its disposition to be transmitted its Fits of easy Transmission, and the space it passes between every return and the next return, the Interval of its Fits.
Prop. XIII.
The reason why the Surfaces of all thick transparent Bodies reflect part of the Light incident on them, and refract the rest, is, that some Rays at their Incidence are in Fits of easy Reflexion, and others in Fits of easy Transmission.
THIS may be gather'd from the 24th Observation, where the Light reflected by thin Plates of Air and Glass, which to the naked Eye appear'd evenly white all over the Plate, did through a Prism appear waved with many Successions of Light and Darkness made by alternate Fits of easy Reflexion and easy Transmission, the Prism severing and distinguishing the Waves of which the white reflected Light was composed, as was explain'd above.
<257>And hence Light is in Fits of easy Reflexion and easy Transmission, before its Incidence on transparent Bodies. And probably it is put into such Fits at its first emission from luminous Bodies, and continues in them during all its progress. For these Fits are of a lasting nature, as will appear by the next part of this Book.
In this Proposition I suppose the transparent Bodies to be thick, because if the thickness of the Body be much less than the Interval of the Fits of easy Reflexion and Transmission of the Rays, the Body loseth its reflecting power. For if the Rays, which at their entering into the Body are put into Fits of easy Transmission, arrive at the farthest Surface of the Body before they be out of those Fits they must be transmitted. And this is the reason why Bubbles of Water lose their reflecting power when they grow very thin, and why all opake Bodies when reduced into very small parts become transparent.
Prop. XIV.
Those Surfaces of transparent Bodies, which if the Ray be in a Fit of Refraction do refract it most strongly, if the Ray be in a Fit of Reflexion do reflect it most easily.
FOR we shewed above in Prop. 8. that the cause of Reflexion is not the impin{g}ing of Light on the solid impervious parts of Bodies, but some other Power by which those solid parts act on Light at a distance. We shewed also in Prop. 9. that Bodies reflect and refract Light by one and the same Power variously exercised in various circumstances, and in Prop. 1. that the most strongly refracting Surfaces reflect the most Light: All which compared together evince and ratify both this and the last Proposition.
Prop. XV.
In any one and the same sort of Rays, emerging in any Angle out Of any refracting Surface into one and the same Medium, the Interval of the following Fits of easy Reflexion and Transmission are either accurately or very nearly, as the Rectangle of the Secant of the Angle of Refraction, and of the Secant of another Angle, whose Sine is the first of 106 arithmetical mean Proportionals, between the Sines of Incidence and Refraction counted from the Sine of Refraction.
THIS is manifest by the 7th and 19th Observations.
<259>Prop. XVI.
In several sorts of Rays emerging in equal Angles out of any refracting Surface into the same Medium, the Intervals of the following Fits of easy Reflexion and easy Transmission are either accurately, or very nearly, as the Cube-Roots of the Squares of the lengths of a Chord, which found the Notes in an Eight, sol, la, fa, sol, la, mi, fa, sol, with all their imtermediate degrees answering to the Colours of those Rays, according to the Analogy described in the seventh Experiment of the second Part of the first Book.
THIS is manifest by the 13th and 14th Observations.
Prop. XVII.
If Rays of any sort pass perpendicularly into several Mediums, the Intervals of the Fits of easy Reflexion and Transmission in any one Medium, are to those Intervals in an other as the Sine of Incidence to the Sine of Refraction, when the Rays pass out of the first of those two Mediums into the second.
T HIS is manifest by the 10th Observation.
<260>Prop. XVIII.
If the Rays which paint the Colour in the Confine of yellow and orange pass perpendicularly out of any Medium into Air, the Intervals of their Fits of easy Reflexion are the th part of an Inch. And of the same length are the Intervals of their Fits of easy Transmission.
THIS is manifest by the 6th Observation.
From these Propositions it is easy to collect the Intervals of the Fits of easy Reflexion and easy Transmission of any sort of Rays refracted in any angle into any Medium, and thence to know, whether the Rays shall be reflected or transmitted at their subsequent Incidence upon any other pellucid Medium. Which thing being useful for understanding, the next part of this Book was here to be set down. And for the same reason I add the two following Propositions.
<261>Prop. XIX.
If any sort of Rays falling on the polite Surface of any pellucid Medium be reflected back, the Fits of easy Reflexion which they have at the point of Reflexion, shall still continue to return, and the returns shall be at distances from the point of Reflexion in the arithmetical progression of the Numbers 2, 4, 6, 8, 10, 12, &c. and between these Fits the Rays shall be in Fits of easy Transmission.
FOR since the Fits of easy Reflexion and easy Transmission are of a returning nature, there is no reason why these Fits, which continued till the Ray arrived at the reflecting Medium, and there inclined the Ray to Reflexion, should there cease. And if the Ray at the point of Reflexion was in a Fit of easy Reflexion, the progression of the distances of these Fits from that point must begin from 0, and so be of the Numbers 0, 2, 4, 6, 8, &c. And therefore the progression of the distances of the intermediate Fits of easy Transmission reckon'd from the same point, must be in the progression of the odd Numbers 1, 3, 5, 7, 9, &c. contrary to what happens when the fits are propagated from points of Refraction.
<262>Prop. XX.
The Intervals of the Fits of easy Reflexion and easy Transmission, propagated from points of Reflexion into any Medium, are equal to the Intervals of the like Fits which the same Rays would have, if refracted into the same Medium in Angles of Refraction equal to their Anales of Reflexion.
FOR when Light is reflected by the second Surface of thin Plates, it goes out afterwards freely at the first Surface to make the Rings of Colours which appear by Reflexion, and by the freedom of its egress, makes the Colours of these Rings more vivid and strong than those which appear on the other side of the Plates by the transmitted Light. The reflected Rays are therefore in Fits of easy Transmission at their egress; which would not always happen, if the Intervals of the Fits within the Plate after Reflexion were not equal both in length and number to their Intervals before it. And this confirms also the Proportions set down in the former Proposition. For if the Rays both in going in and out at the first Surface be in Fits of easy Transmission, and the Intervals and Numbers of those Fits between the first and second Surface, before and after Reflexion, be equal; the distances of the Fits of easy Transmission from either Surface, must be in the same progression after Reflexion as before; that is, from the first Surface which transmitted them, in the progression of the even Numbers 0, 2, 4, 6, 8, &c. and from the second which reflected them, in that of the odd Numbers 1, 3, 5, 7, &c. But these two Propositions will become much more evident by the Observations in the following part of this Book.
