A particular Answer of Mr. Isaak Newton to Mr. Linus his Letter
A particular Answer of Mr. Isaak Newton to Mr. Linus his Letter, printed in Numb. 121. p. 499. about an Experiment relating to the New Doctrine of Light and Colours: This Answer sent from Cambridge in a Letter to the Publisher Febr. 29. 167.
Sir,
BY reading Mr. Linus's Letter when you shew'd it to me at London, I retained only a general remembrance, that Mr. Linus deny'd what I affirmed, and so could lately say nothing in particular to it; but having the opportunity to read it again in Numb. 121. of the Transactions, I perceive he would perswade you, that the information you gave him about the Experiment is as inconsistent with my printed Letters as with experience; and therefore, lest any who have not read those Letters should take my silence in this point for an acknowledgment, I thought it not amiss, to send you something in answer to this also.
<557>He tells you that, Whereas you assure him, First, that the Experiment was made in clear days; secondly, that the Prism was placed close to the hole, so that the light had no room to diverge; and thirdly, that the Image was not parallel but transverse to the axis of the Prism: If these Assertions be compared with my Relation of the Experiment in the Phil. Transaction N. 80. p. 3076. it will evidently appear, they cannot be admitted as being directly contary to what is there delivered. His reasons are these:
First, that I said, the ends of the long Image seemed semicircular, which, saies he, never happens in any of the three cases above said. But this is not to set me at odds with my self, but with the experiment; for it is there described to happen in them all; and I still say, it doth happen in them. Let others try the Experiment, and judge.
Further he saies, that the Prism is placed at a distance from the hole in the Scheme of the Experiment in N. 84. p 4091. But, what if it were so there? For, that is the Scheme of a demonstration, not of the experiment, and would have served for the demonstration, had the distance been put twenty times greater than it is. In the Schemes of the Experiment N. 80. p. 3086, and N. 82. p. 5016 it is represented close, and close enough in the Scheme, N. 83. p. 4061: But Mr. Linus though fit to wink at these, and pitch upon the Schemeof a Demonstration, and such a Scheme too as hath no hole at all represented in it. For the Scheme ✝[1] Numb. 84. p. 491 is this; 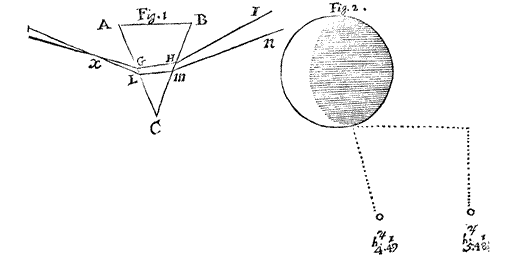 in which the rays are not so far distant from one another at GL, but that the hole, had I exprest it, might have been put there, and yet have comprehended them. But if we should put the hole at x, their decussation; yet will it not be any thing to his purpose; the distance xG or xL being but about half the breadth of a side of the Prism ( AC) which I conceive is not the twentieth part of the distance requisite in his conjecture.
in which the rays are not so far distant from one another at GL, but that the hole, had I exprest it, might have been put there, and yet have comprehended them. But if we should put the hole at x, their decussation; yet will it not be any thing to his purpose; the distance xG or xL being but about half the breadth of a side of the Prism ( AC) which I conceive is not the twentieth part of the distance requisite in his conjecture.
3. He says, that more might be said out of my relation to shew, that the Image was not transvers, for if it had been transvers, I could not have been surprized (as I said I was) to see the length thereof so much exceed the breadth, it being a thing so obvious & easie to be explicated by the ordinary rules of Refraction. But on the contrary, it may rather be said, that if the Image had been parallel, I could not have been surprized to see the length thereof so much exceed the breadth, it being a thing so extreamly obvious as not to need any explication. For who that had but common sense, and saw the whole Prism or a good part of it illuminated, could not expect the light should have the same long figure upon the wall that it had when it came out of the Prism? Mr. Linus therefore, while he would strengthen his argument by representing me well skilled in Opticks, does but overthrow it. But whereas he sayes, I could not have been surprized at the length, had the Image been parallel, it being a thing so obvious and easy to be explicated by the ordinary rules of refraction: Let any Man take the Experiment intire as I have there delivered it, that is, with this condition, that the refractions on both sides of the Prism were equal, and try if he can reconcile it with the ordinary rules of refraction. On the contrary, he may find the impossibility of such a reconciliation, demonstrated in my Answer to P. Pardies N. 84, p. 4091.
In the last place, he objects, that my saying in N. 80, p. 3077, that the incident refractions were in the Experiment equal to the emergent, proves again, that the long Image was parallel. And yet that very saying is a sufficient argument, that I meant to the contrary, because it becomes wholly impertinent, if apply'd to a parallel image; but in the other case is a very necessary circmstance. What is added therefore of P. Pardies, might have been spared, especially since that Learned Person understood my discourse to be meant of a transvers Image, and acquiesced in my Answers.
This in Answer to Mr. Linus's Letter: And now to take away the like suspicions from his Friends, if my declaration of my meaning satisfie not, I shall note some further passages in my Letters, whereby they may see, how I was to be understood from the beginning, as to the aforesaid three circumstances.
For the Day; I express every where that the Experiment was tried in the Sun's light, and in N. 80. p. 3077, that the breadth of the Image by measure answered to the Sun's diameter: But because it is pretended, I was imposed upon, I would ask, what the Experiment as it is advanced to that which I called the Experimen- tum Crucis, can have to do with a cloudy day? For, if the Experimentum Crucis (which is that which I depend on) can have nothing to do with a cloudy day, then it is to no purpose to talk of a cloudy day in the first Experiment, which does but lead on to that. But if this satisfie not, let the Transactions N. 83. p. 4060, be consulted: For. there I tell you, how by applying a Lens to the Prism, the streight edges of the oblong Image became distincter than they would have been without the Lens: a circumstance which cannot happen in Mr. Linus's case of a bright cloud.
For the Position of the Prism; I tell you N. 80. p. 3076, that it was placed at the Sun's entrance into the Chamber, and in p. 3085. I bad to make a hole in the shut, and there place the Prism, and in the next page I say again, that the Prism ABC is to be set close by the hole F of the window EG; and accordingly represent it close in the Figure. Also in pag. 3077 I tell you, that the distance of the Image from the hole or prism was 22 foot; which is as much as to say, that the Prism (suppose that side of it next the hole) was as far from the Image as the hole it self was, and consequently that the Prism and Hole were contiguous. Also in p. 3078, where instead of the Window shut I made use of a hole in a loose board, I tell you expressly, that I placed the board close behind the Prism. All these passages are in my very first Letter about Colours; and who therefore would imagine, that any one that had read that Letter should so much as suspect, that I placed the Prism, I say not at so great a distance as Mr. Linus supposes, but at any distance worth considering?
Lastly, for the Position of the Image, it is represented transvers to the axis of the Prism in the figures N. 80. p. 3086. N. 83. p. 4061, and N. 85. p. 5016. And in N. 88. p. 5093, where I made use of two cross Prisms, I tell you expresly, that the Image was cross to both of them at an angle of 45 degrees. The calculations also N. 80. p. 3077. are not to be understood without supposing the Image cross. Nor are my notions about different Refrangibility otherwise intelligible: For in Mr. Linus's supposition, the rays that go to the two ends of the Image, are equally refracted. So the colours, the red, according to my description, falls at one end of the Image, and the blew at the other; which cannot happen but in a tranvers Image. The same position is also demonstrable from what I said in N. 80. p. 3076, about turning the long Image into a round one, by the contrary refraction of a second Prism, further explained in Num. 83. p. 4061. For this is not to be done in Mr. Linus surmise of a parallel Image, and therefore had Mr. Linus considered it, he could never have run into that surmise.
This I suppose is enough to manifest the three particulars; any one of which being evidenced, is sufficient to tak away the scruple. And therefore Mr. Linus Friends need not fear but that the further directions I sent them lately for trying the Experiment are the same with those I have follow'd from the beginning; nor trouble themselves about any thing but to try the Experiment right. But yet, because Mr. Gascoin has been pleased to insinuate his suspicion that I do differ from himself in those directions, I shall not scruple here to reduce them to particulars, and shew where each particular is to be found.
1. Then, he is to get a Prism with an angle about 60 or 65 degrees, N. 80. p. 3077, and p. 3086. If the angle be about 63 degrees, as that was which I made use of N. 80. p. 3077, he will find all things succeed exactly as I described them there. But if it be bigger or less, as 30, 40, 50, or 70 degrees, the Refraction will be accordingly bigger or less, and consequently the Image longer or shorter. If his Prism be pretty nearly equilateral (such as I suppose are usually sold in other places as well as in England) he may make use of the biggest angle. But he must be sure to place the Prism so, that the Refraction be made by the two planes which comprehend this angle. I could almost suspect, by considering some circumstances in Mr. Linus's Letter, that his error was in this point, he expecting the Image should become as long by a little refraction as by a great one; which yet being too gross an error to be expected of any Optician, I say nothing of it, but only hint this to Mr. Gascoin, that he may examine all things.
2. Having such a Prism, he must place it so, that its Axis be perpendicular to the rays N. 84, p. 4091, lin. 18, 19. A little error in this point makes no sensible variation of the effect.
3. The Prism must be so placed, that the Refractions on both sides be equal N. 80, p. 3077: which how it was to be readily done by turning it about its Axis, and staying it when you see the Image rest between too contrary motions, as I explained in my late Descriptions, so I hinted before N. 80. p. 3077, lin. 34, 35, 36. If there should be a little error in this point also, it can do no hurt.
<561>4. The Diameter of the hole I put of an inch N. 80, p. 3077, and placed the Prism close to it, even so close as to be contiguous, N. 80, p. 3077, lin. 4, 5. But yet there needs no curiosity in these circumstances. The hole may be of any other bigness, and the Prism at a distance from the hole, provided things be so ordered, that the light appear of a round form, if intercepted perpendicularly at its coming out of the Prism. Nor needs there any curiosity in the day. The clearer it is the better; but if it be a little bit cloudy, that cannot much prejudice the Experiment, so the Sun do but shine distinctly through the cloud.
These things being thus ordered, if the refracted light fall perpendicularly on a wall or paper at 20 foot or more from the Prism, it will appear in an oblong form, cross to the axis of the Prism, red at one end, and violet at the other; the length five times the breadth (more or less according to the quantity of the refraction,) the sides, streight lines, parallel to one another, and the ends confused, but yet seeming semi-circular.
I hope therefore, Mr. Linus's Friends will not entertain themselves any further about incongruous surmises, but try the Experiment as Mr. Gascoin has promised. And then, since Mr. Gascoin tells you, That the Experiment being of it self extraordinary and surprizing, and besides ushering in new Principles into Opticks, quite contrary to the common and received, it will be hard to perswade it as a truth, till it be made so visible to all as it were a shame to deny it: if he esteem it so extraordinary, he may have the priviledg of making it so visible to all, that it will be a shame to deny it. For, I dare say, after his testimony no body else will scruple it. And I make no question but he will hit of it, it being so plain and easy, that I am very much at a loss to imagine what way Mr. Linus took to miss.
Dat. Cambridge Feb. 29 167.
[1] ✝ See Fig. 1.
