Letter to Edmund Halley on work on ellipses and the descent of falling bodies
July 14. 16{illeg}|8|6.
Sr
I have considered yor proposal about wooden cuts & beleive it will be much convenienter for ye Reader & may be sufficiently handsome but I leave it to your determination. If you go this way, then I desire you would divide ye first figure into these two. 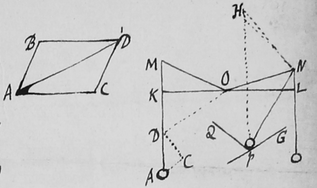 I crouded ym into one to save ye trouble of altering ye numbers in ye schemes you have. I am very sensible of ye great kindness of ye Gentlemen of your Society to me, far beyond wt I could ever expect or deserve & know how to distinguish between their favour & anothers humour. Now I understand he was in some respects misrepresented to me I wish I had spared ye Postscript in my last. This is true, that his Letters occasioned my finding the method of determining Figures, wch when I had tried in ye Ellipsis, I threw the calculation by being upon other studies & so it rested for about 5 yeares till upon your request I sought for yt paper, & not finding it did it again & reduced it into ye Propositions shewed you by Mr Paget: but for ye duplicate proportion I can affirm yt I gathered it from Keplers Theorem about 20 yeares ago. And so Sr Christopher Wren's examining ye Ellipsis over agt ye Focus shews yt he knew it many yeares ago before he left of his enquiry after ye figure by an imprest motion & a descent compounded together. There was another thing in Mr Hooks letters wch he will think I had from him. He told me yt my proposed expt about ye descent of falling bodies was not ye only way to prove ye motion ofye earth & so added ye expt of yor Pendulum Clock at St Helle{na} as an argumt of gravities being lessened at ye equator by ye diurnal moti{on.} The expt was new to me but not ye notion. For in yt very paper wch I told you was writ some time above 15 yeares ago & to ye best of my memory was writ 18 or 19 years ago, I calculated ye force of ascent at ye Equator arising from ye earth's diurnal motion in order to know what would be ye diminution \of gravity/ thereby. But yet to do this business right is a thing of far greater difficulty then I was aware of. A third thing there was in his letters, wch was new to me & I shall acknowledge it if I make use of it. 'Twas ye deflexion of falling f|b|odies to ye south east in or Latitude. And now having sincerely told you ye case between Mr Hook & me I hope I shall be free for ye future from ye prejudice of his Letters. I have considered how best to compose ye present dispute & I think it may be done by ye inclosed Scholium to ye fourth Proposition. In {illeg} turning over some old papers I met with another demonstration of that Proposition, wch I have added at ye end of this Scholium. Which is all at present from
I crouded ym into one to save ye trouble of altering ye numbers in ye schemes you have. I am very sensible of ye great kindness of ye Gentlemen of your Society to me, far beyond wt I could ever expect or deserve & know how to distinguish between their favour & anothers humour. Now I understand he was in some respects misrepresented to me I wish I had spared ye Postscript in my last. This is true, that his Letters occasioned my finding the method of determining Figures, wch when I had tried in ye Ellipsis, I threw the calculation by being upon other studies & so it rested for about 5 yeares till upon your request I sought for yt paper, & not finding it did it again & reduced it into ye Propositions shewed you by Mr Paget: but for ye duplicate proportion I can affirm yt I gathered it from Keplers Theorem about 20 yeares ago. And so Sr Christopher Wren's examining ye Ellipsis over agt ye Focus shews yt he knew it many yeares ago before he left of his enquiry after ye figure by an imprest motion & a descent compounded together. There was another thing in Mr Hooks letters wch he will think I had from him. He told me yt my proposed expt about ye descent of falling bodies was not ye only way to prove ye motion ofye earth & so added ye expt of yor Pendulum Clock at St Helle{na} as an argumt of gravities being lessened at ye equator by ye diurnal moti{on.} The expt was new to me but not ye notion. For in yt very paper wch I told you was writ some time above 15 yeares ago & to ye best of my memory was writ 18 or 19 years ago, I calculated ye force of ascent at ye Equator arising from ye earth's diurnal motion in order to know what would be ye diminution \of gravity/ thereby. But yet to do this business right is a thing of far greater difficulty then I was aware of. A third thing there was in his letters, wch was new to me & I shall acknowledge it if I make use of it. 'Twas ye deflexion of falling f|b|odies to ye south east in or Latitude. And now having sincerely told you ye case between Mr Hook & me I hope I shall be free for ye future from ye prejudice of his Letters. I have considered how best to compose ye present dispute & I think it may be done by ye inclosed Scholium to ye fourth Proposition. In {illeg} turning over some old papers I met with another demonstration of that Proposition, wch I have added at ye end of this Scholium. Which is all at present from
Yor affectionate Friend & humble Servant
Is. Newton.
<56v> < insertion from the left of f 56v > < text from f 56v resumes > < insertion from the right of f 56v >Lres from Mr Newton
Aug. 20. July. 14. Octob. 18
