Copy of an extract from Newton to John Collins, dated 10 December 1672
Extract of Mr Newtons Letter
to M. Collins. Dec. 10. 1672.
I am heartily glad at ye acceptance, wch D. Barrow's Lectures finds wth forrein Mathematicians; and it pleas'd me not a little to undstand yt they are falne into ye same method of drawg Tangents wth me. What I guess their method to be, you will apprehend by this example;
Suppose CB applied to AB in any given angle be terminated at any Curve line AC, and calling AB x and BC y, let the relaon betw{illeg}t ye between x and y be exprest by any æquaon; as , whereby the Curve is determin'd. To draw the Tangent CD, ye Rule is this. Multiply ye termes of ye æquation by any Arithmetical progression accordg to ye dimensions of y, suppose thus ; also accordg to ye dimensions of x sup\po/se thus . The first product shall be ye Numerator, and ye last divided by x ye Denominator of a fraction wch expresses ye length of BD, to whose end D ye tangent CD must be drawn. The length BC therefore is .
This is one particular, or rather a Corollary of a general Method wch extends itself, wthout any troublesome calculaon, not only to ye drawing tangents to all Curve lines, whether Geometric, or Mechanic, or however related to streight lines or to other Curve lines, but also to ye resolvg other abstruser kinds of problems abou{illeg}|t| ye crookedness, areas, lengths, centers of gravity of curves &c. Nor is it (as Huddens method de maximis et minimis, and conseqntly Slusius his new method of Tangents, as I presume,) limited to æquaons wch are free from surd quantities. This method I have interwoven wth yt other of working in æquaons by reducing ym to infinit series. I rememb, I once occasionally told Dr Barrow, when he was about to publish his Lectures, yt I had such a method of drawg Tangents, but some divertisemt or other hinder'd me from describg it to him.
Of resolvg by Cardans rules Æquaons yt have 3 possible roots, there may be examples fram'd at pleasure; but unless Brasser show a direct method of performing it, wch Ferguson dos not, it will not be allow'd scientific. How it is to be done directly, I may possibly show upon occaon.
<43r>Ex ead. {epta} Newtoni ad Colliniu
d. 10. Dec. 1672.
Mr Gregory is pleased to consider further ye most advantageous construction of Cata-dioptrical Telescopes. And as his dessein in his Opt. promota excels yt of M. Cassegrain (though they differ so slightly, yt I thought it not worth ye while to take notice of ye difference,) ye advantage being, yt ye litle {sic} concave Ellipsis coms {sic} nearer to a Spherical figure, than ye c|C|onvex Hypbola; so I conceive his present proposall excells ym both, of making yt speculu plane. And this I conjecture is ye way, wch Signr Salvetti, one of ye G. Dukes Musicians, mention'd in ye last Transactions, intends to make Expt of, excepting yt instead of the Convex Ey-glas glass he may probably substitut a Concave one to erect ye object. But yet I cannot think it ye best, it being liable to the first, 3d and last of those difficulties, I urg'd agst M. Cassegrain, and in my Judgemt not wholly capable of ye advantages, wch M. Gregory propounds. The first disadvantage was, that more light is lost in direct than oblique ref{illeg}|le|ctions. I am convinc'd by several ObservaonsObservations, yt reflexion is not made by ye solid parts of a body, (as is commonly presum'd,) but by ye confine of ye two mediums, whereof one is wthin, and ye other wthout ye body. And as stones are reflected by water, when thrown obliquely, wch force their way into it when thrown directly downwards; so ye rays of Light (whether Corporeal like stones, or not,) are most easily and copiously reflected when incident most obliquely. This you may observe in ye passage of Light out of Glass into Air, wch is reflected more and more copiously, as ye obliquity is increas'd, untill beyond a certain degree of obliquity it be wholly reflected. Also in ye reflexion of Light by an imperfectly polish't plate of Brass or Silver or any other metall, you may observe yt ye Images of objects, wch by direct reflexion appear dull and confus'd, appear by very oblique reflexion pretty distinct and vigorous. This advantage of oblique reflexion would be inconsiderable, if metall reflected almost all ye light directly incident on it, but so far as I can observe, there is at least a 3d part, if not ye better half, of ye light lost and stifled in ye metal at every reflexion; and it is of some estimaon if a 3d or 4th part of yt can be redeem'd by setting ye flat speculu obliquely. As for Mr Gregory's insinuaon, yt direct rays have ye advantage of oblique, because a direct ball is reflected more regularly from a rough wall, than an oblique one; if he please to consider, how different are the causes and circu{illeg}|m|stances of those reflexions, possibly upon second thoughts he may apprehend, why ye contrary ought to happen in Light, at least ye Experimt of the rudely polish't plate of metall may persuade him.
The next dis-advantage arising from ye di{illeg}|s|tance of ye litle speculu from ye Ey-glass, being allow'd, I pass to ye last, wch is to this effect; That; if to diminish ye magnifying virtue of ye instrumt the litle speculu be made of a larger sphere, (as it is in M. Gregory's dessein, a plane being equivalent to a sphere whose center is indefinitly distant,) yt would cause too many of ye best rays to be intercepted. And tho in his designe scarce a forth part of ye whole light be intercepted, yet those rays seem to me of more value than twice their number next ye circumference of the; Tube, because they principally conduce to distinct vision. Their loss will be judged considerable by those, yt have thought ye loss of scarce the 40th part of the Light in my way worthy of being objected by reason yt they were ye best of ye rays.
There are yet other Consideraons, by wch Mr Gregory's Tube may perhaps be thought less advantagious, as, yt unles ye speculu F be made so broad as to intercept more than a quarter, or perhaps than a third part of the whole Light, it will be difficult to enlarge the aperture as is requisite for viewing dull and obscure objects. That ye Ey-glas, if placed at ye bottom, will scarcely be well defended from ye unusefull glaring light wch in ye day-time comes from objects on all sides ye flat speculu, at least not so well as by setting it at ye side: And yt an Artificer can \scarcely/ polish ye great Concave so truly when perforated in ye midle; for ye metal near yt hole will be apt to weare away too fast, as it doth near ye exterior limb. And tho ye hole may be made after 'tis polish't, yet if ye figure happen to be less true, or if afterwards ye metal chance to tarnish, it must be polish't again.
As for the Advantages propounded by M. Gregory, I see not, why ye first {illeg} should be reckon'd for one, viz. That ye distance EF grows almost ye one half less, and therefore ye Errors of ye Concave CD are also diminish't upon ye plane F by one half. For, how much those Errors of ye Concave CD are increas'd or diminish'd is to be estimated by ye prevarication of ye rays not at ye plane F, but at ye focus of yt concave CD. And there ye Errors in both cases will be alike, provided ye speculu F be accurately plane; but if there be any irregularities in ye figure of yt Speculu F, they will cause Errors so much greater in one case than in ye other, as yt speculu is remoter from ye Ey-glass; wch in large Telescopes may be more than 15 or 20 times.
The other Advantage, viz. That his Tube will be litle more than half ye length of mine, I should allow to be very considerable, i{f} {I} thought, yt wth equall art in ye mechanisme it could be made to doe ye same effect. The greatest difficulty is in forming ye great Concave, wch when once well done, perhaps it may be thought most advantagious, to make ye best use of it wth a longer Tube.
The suppos'd Advantage of Telescopes wth Convex or Concave speculums i{illeg}|n| that they may have any desirable charge by altering ye distances of the Ey-glass and specula, agrees more conveniontly dessein of ye Instrumt if yt speculu be made use of, wch I described in a letter to M. Oldenburg in answer to M. Auzouts Considerations on these Instrum'ts, wch possibly you may have seen. For instance, to double ye charge, ye Ey-glass in ye other way must be drawn out almost as far behind ye great concave as ye litle speculu is before it, whereby ye length of ye Tube will be almost doubled; whereas in my way it need be drawn out no f{illeg}|a|rther from ye side of ye Tube than a quarter of ye Tube's diameter. The charge may be also conveniently varied by having 2 or 3 Ey-glasses of severall depths set in a girdle; any of wch may be adjusted to ye metal F, by sliding yt girdle about ye Tube or by sliding ye ring wthin ye Tube, to wch yt metal F is fastned.
That Telescopes by Convex or concave speculums should be overcharg'd is not necessary; but yet it is not avoidable wthout running upon one of ye other two inconveniences, described in the 7th particular of my consideraons on M. Cassegrains Tube, as I there intimated.
To diminish some of the aforesd disadvantages, there may be still new variaons or additions to these designes. As, for instance, by using two Ey-glasses. Suppos{illeg}|e|{illeg} CD represent ye great Concave, F ye litle Speculu, E ye Ey-glas and G another double 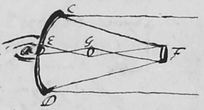 Convex-glas between E and F between E and F, {sic} on both sides of wch ye rays crosse. This way of redoubling ye these Tubes seems not inferior to ye rest: for, thus ye object appears erect, ye speculu F intercepts less light, and ye charge may be varied at pleasure, only by changing ye positions of G and F. But yet this is not wthout its imperfections, and particularly (besides those common wth ye other designs,) ye glass G will intercept many of ye best rays in their passage from ye Concave CD to ye litle speculu F, unless it be made less than is consistent wth some other conveniences. And by ye iterated decussations of ye rays, objects will be rendred less distinct, as i{illeg}|s| manifest in Dioptric Telescopes, where 2 or 3 Ey-glasses are applyed to erect ye object.
Convex-glas between E and F between E and F, {sic} on both sides of wch ye rays crosse. This way of redoubling ye these Tubes seems not inferior to ye rest: for, thus ye object appears erect, ye speculu F intercepts less light, and ye charge may be varied at pleasure, only by changing ye positions of G and F. But yet this is not wthout its imperfections, and particularly (besides those common wth ye other designs,) ye glass G will intercept many of ye best rays in their passage from ye Concave CD to ye litle speculu F, unless it be made less than is consistent wth some other conveniences. And by ye iterated decussations of ye rays, objects will be rendred less distinct, as i{illeg}|s| manifest in Dioptric Telescopes, where 2 or 3 Ey-glasses are applyed to erect ye object.
As to ye attempt in wch Mr Reeves was imployed, I presum'd, it had been done wth much more accuratness than Mr Gregory now signifyes, because Mr Hook, who you know is a curious and accurate Expimenter, affirms in his consideraons on my letter to M. Oldenburg concerning refractions & colors, pu publish't in ye Transactions No 80, yt he made several Expts wth yt Instrument. And though he lays ye blame on M. Reeve's Encheiria, yet he says not, yt he blam'd him yn; when the Expt was made. His words are these;
"I have made many tryals both for Telescopes and Microscopes by reflexion, wch I have mention'd in my Micrography, but deserted it as to Telescopes, when I considered, yt yn focus of a spherical Concave is not a point but a line, and yt yn rays are lesse true reflected to a point by a Concave, than refracted by a Convex; wch made me seek yt by refraction, wch I found could not be expected by reflexion. Nor indeed could I find any effect of it by one of six foot radius wch about 7 or {8} years since Mr Reeve made for M. Gregory, wth wch I made severall tryals; but it now appears, yt it was for want of a good encheiria; from wch cause many good Expts have been lost. Both wch consideraons discourag'd me from attempting further yt way, especially since I found ye Parabola much more difficult to describe, than the Hypbola or Ellipsis.{"}
From hence I might well infer yt ye want of a good Encheiria appear'd not till now: And yt Mr Hook was discouraged from attempting further yt way only by these 2 or 3 consideraons; That a Convex (as he presumes) refracts more truly, th{illeg}|a|n a concave reflects; yt he found no effect by one of 6 foot radius, wch till now he attributed to some other cause then ye want of a good encheiria, namly to ye supposedly less true reflexion of a spherical concave; and yt he apprehended a greater difficulty of describing a parabola than an Hyperbola or Ellipsis. Nor could I well interpr{illeg}|et| ye cause, from wch many good Expts have been lost, to have been other than ye want of a good Encheiria, wch till afterwards appears not to have been wanting. I contend not, yt this was M. Hooks meaning, but only yt his words seem'd to import thus much: wch gave me occasion to think, there was no diligence wanting in making that Expt, especially since he expresseth, yt he made severall tr{illeg}|y|als wth it.
< insertion from the left margin of f 42v >Newton? Sept. 23. 72.
< text from f 42v resumes >And yt you may not think I strain'd Mr Gregorys sense, where he spake of Hyperbolic and Elliptic Glasses and Speculums attempted in vain; I would aske, to what end those Speculums were attempted in va if not to compose optic Instrumts; wch is all I would inferr from those words. For, yt these Instrumts, if at all attempted, were attempted in vain, is evident by ye want of success.
This, Sr, I have said, not yt I desire to discourage ye tryall of any practicable way, or to contend wth Mr Gregory about so slender a difference. For, I doubt not but when he wrote his Optica promota, he could have described more fashions than one of these Telescopes and perhaps have run through all ye possible cases of ym, if he had thought it worth his pains. Because M. Cassegrain propounded his suppos'd Invention pompously, as if ye main busines was in ye contrivance of these Instrumts, I thought fit to signify, yt yt was none of his contrivance, nor so advantageous as he imagin'd. And I have now sent you these further Consideraons on M. Gregory's {illeg}|A|nswer, only to let you see, yt I chose ye most easy and practicable way to make ye first Tryals. Others may try other ways. Nor doe I think it material, wch way these Instrumts are perfected, so they be perfected.
