Method of Curves and Infinite Series, and application to the Geometry of Curves (Part 1)

<3>

divisoris termino hoc modo $\left.\mathrm{x}+\mathrm{b}\right)\mathrm{a}\mathrm{a}\left(\text{prodibit}\frac{\mathrm{a}\mathrm{a}}{\mathrm{x}}-\frac{\mathrm{a}\mathrm{a}\mathrm{b}}{\mathrm{x}\mathrm{x}}\right.$$+\frac{\mathrm{a}\mathrm{a}\mathrm{b}\mathrm{b}}{{\mathrm{x}}^3}-\frac{\mathrm{a}\mathrm{a}{\mathrm{b}}^3}{{\mathrm{x}}^4}\text{\&c}$.

Ad eundem modum fractio $\frac{1}{1+\mathrm{x}\mathrm{x}}$ reducitur ad $1-\mathrm{x}\mathrm{x}+$${\mathrm{x}}^4-{\mathrm{x}}^6+{\mathrm{x}}^8\text{\&c}$ vel ad ${\mathrm{x}}^{-2}-{\mathrm{x}}^{-4}+{\mathrm{x}}^{-6}-{\mathrm{x}}^{-8}\text{\&c}$

Et fractio $\frac{2{\mathrm{x}}^{\frac{1}{2}}-{\mathrm{x}}^{\frac{3}{2}}}{1+{\mathrm{x}}^{\frac{1}{2}}-3\mathrm{x}}$ ad $2{\mathrm{x}}^{\frac{1}{2}}-2\mathrm{x}+7{\mathrm{x}}^{\frac{3}{2}}-13{\mathrm{x}}^2+34{\mathrm{x}}^{\frac{5}{2}}\text{\&c}$

Ubi obiter notandum est quòd usurpo ${\mathrm{x}}^{-1}$, ${\mathrm{x}}^{-2}$, ${\mathrm{x}}^{-3}$, ${\mathrm{x}}^{-4}$, &c: pro $\frac{1}{\mathrm{x}}$, $\frac{1}{\mathrm{x}\mathrm{x}}$, $\frac{1}{{\mathrm{x}}^3}$, $\frac{1}{{\mathrm{x}}^4}$; & ${\mathrm{x}}^{\frac{1}{2}}$, ${\mathrm{x}}^{\frac{3}{2}}$, ${\mathrm{x}}^{\frac{5}{2}}$, ${\mathrm{x}}^{\frac{1}{3}}$, ${\mathrm{x}}^{\frac{2}{3}}$, &c: pro $\sqrt{}\mathrm{x}$, $\sqrt{}{\mathrm{x}}^3$, $\sqrt{}{\mathrm{x}}^5$, $\sqrt{}c:\mathrm{x}$, $\sqrt{}c:\mathrm{x}\mathrm{x}$; & ${\mathrm{x}}^{-\frac{1}{2}}$, ${\mathrm{x}}^{-\frac{2}{3}}$, ${\mathrm{x}}^{-\frac{1}{4}}$, &c pro $\frac{1}{\sqrt{}\mathrm{x}}$, $\frac{1}{\sqrt{}c:\mathrm{x}\mathrm{x}}$, $\frac{1}{\sqrt{}4:\mathrm{x}}$. Idqꝫ ob analogiam rei, quæ deprehendi potest {illeg}|ex| hujusmodi \geometricis/ progressionibus ${\mathrm{x}}^3$, ${\mathrm{x}}^{\frac{5}{2}}$, $\mathrm{x}\mathrm{x}$, ${\mathrm{x}}^{\frac{3}{2}}$, x, ${\mathrm{x}}^{\frac{1}{2}}$, ${\mathrm{x}}^0$ (sive 1,) ${\mathrm{x}}^{-\frac{1}{2}}$, ${\mathrm{x}}^{-1}$, ${\mathrm{x}}^{-\frac{3}{2}}$, ${\mathrm{x}}^{-2}$ &c

Sic vice Ad hunc modum pro $\frac{\mathrm{a}\mathrm{a}}{\mathrm{x}}-\frac{\mathrm{a}\mathrm{a}\mathrm{b}}{\mathrm{x}\mathrm{x}}+\frac{\mathrm{a}\mathrm{a}\mathrm{b}\mathrm{b}}{{\mathrm{x}}^3}\text{\&c}$ scribi potest $\mathrm{a}\mathrm{a}{\mathrm{x}}^{-1}-\mathrm{a}\mathrm{a}\mathrm{b}{\mathrm{x}}^{-2}+\mathrm{a}\mathrm{a}\mathrm{b}\mathrm{b}{\mathrm{x}}^{-3}\text{\&c}$. Et sic vice $\sqrt{}\stackrel{\_}{\mathrm{a}\mathrm{a}-\mathrm{x}\mathrm{x}}$ scribi potest ${\stackrel{\_}{\mathrm{a}\mathrm{a}-\mathrm{x}\mathrm{x}}}^{\frac{1}{2}}$; et ${\stackrel{\_}{\mathrm{a}\mathrm{a}-\mathrm{x}\mathrm{x}}}^2$ vice quadrati ex $\mathrm{a}\mathrm{a}-\mathrm{x}\mathrm{x}$; et ${\left.\frac{\mathrm{a}\mathrm{b}\mathrm{b}-{\mathrm{y}}^3}{\mathrm{b}\mathrm{y}+\mathrm{y}\mathrm{y}}\right|}^{\frac{1}{3}}$ vice $\sqrt{}c:\frac{\mathrm{a}\mathrm{b}\mathrm{b}-{\mathrm{y}}^3}{\mathrm{b}\mathrm{y}+\mathrm{y}\mathrm{y}}$. Et sic in alijs. Unde meritò potestates distingui possunt in affermativas et negativas, integras, et fractas.

Exempla \reductionum/ per extractionem radicum.

Proposito $\mathrm{a}\mathrm{a}+\mathrm{x}\mathrm{x}$, radicem ejus ut sequitur extrah{illeg}|e|s,
$$\begin{array}{l}\begin{array}{c}\mathrm{a}\mathrm{a}+\mathrm{x}\mathrm{x}\left(\mathrm{a}+\frac{\mathrm{x}\mathrm{x}}{2\mathrm{a}}-\frac{{\mathrm{x}}^4}{8{\mathrm{a}}^3}+\frac{{\mathrm{x}}^6}{16{\mathrm{a}}^5}-\frac{5{\mathrm{x}}^8}{128{\mathrm{a}}^7}+\frac{7{\mathrm{x}}^{10}}{256{\mathrm{a}}^9}-\frac{21{\mathrm{x}}^{12}}{1024{\mathrm{a}}^{11}}\text{\&c}\right.\end{array}\\ \begin{array}{l}\underset{\_}{\mathrm{a}\mathrm{a}}\\ \phantom{0}0+\mathrm{x}\mathrm{x}\\ \phantom{0}\phantom{0}\phantom{+}\underset{\_}{\mathrm{x}\mathrm{x}+\frac{{\mathrm{x}}^4}{4\mathrm{a}\mathrm{a}}}\\ \phantom{0}\phantom{0}\phantom{+}\phantom{\mathrm{x}\mathrm{x}}-\frac{{\mathrm{x}}^4}{4\mathrm{a}\mathrm{a}}\\ \phantom{0}\phantom{0}\phantom{+}\phantom{\mathrm{x}\mathrm{x}}-\underset{\_}{\frac{{\mathrm{x}}^4}{4\mathrm{a}\mathrm{a}}-\frac{{\mathrm{x}}^6}{8{\mathrm{a}}^4}+\frac{{\mathrm{x}}^8}{64{\mathrm{a}}^6}}\\ \phantom{0}\phantom{0}\phantom{+}\phantom{\mathrm{x}\mathrm{x}}\phantom{-}\phantom{\frac{{\mathrm{x}}^4}{4\mathrm{a}\mathrm{a}}}+\frac{{\mathrm{x}}^6}{8{\mathrm{a}}^4}-\frac{{\mathrm{x}}^8}{64{\mathrm{a}}^6}\\ \phantom{0}\phantom{0}\phantom{+}\phantom{\mathrm{x}\mathrm{x}}\phantom{-}\phantom{\frac{{\mathrm{x}}^4}{4\mathrm{a}\mathrm{a}}}\phantom{+}\underset{\_}{\frac{{\mathrm{x}}^6}{8{\mathrm{a}}^4}+\frac{{\mathrm{x}}^8}{16{\mathrm{a}}^6}-\frac{{\mathrm{x}}^{10}}{\phantom{0}64{\mathrm{a}}^8}+\frac{{\mathrm{x}}^{12}}{256{\mathrm{a}}^{10}}}\\ \phantom{0}\phantom{0}\phantom{+}\phantom{\mathrm{x}\mathrm{x}}\phantom{-}\phantom{\frac{{\mathrm{x}}^4}{4\mathrm{a}\mathrm{a}}}\phantom{+}\phantom{\frac{{\mathrm{x}}^6}{8{\mathrm{a}}^4}}-\frac{5{\mathrm{x}}^8}{64{\mathrm{a}}^6}+\frac{{\mathrm{x}}^{10}}{\phantom{0}64{\mathrm{a}}^8}-\frac{{\mathrm{x}}^{12}}{256{\mathrm{a}}^{10}}& \text{\&c}\\ \phantom{0}\phantom{0}\phantom{+}\phantom{\mathrm{x}\mathrm{x}}\phantom{-}\phantom{\frac{{\mathrm{x}}^4}{4\mathrm{a}\mathrm{a}}}\phantom{+}\phantom{\frac{{\mathrm{x}}^6}{8{\mathrm{a}}^4}}-\underset{\_}{\frac{5{\mathrm{x}}^8}{64{\mathrm{a}}^6}-\frac{5{\mathrm{x}}^8}{128{\mathrm{a}}^8}+\frac{5{\mathrm{x}}^{12}}{512{\mathrm{a}}^{10}}}\\ \phantom{0}\phantom{0}\phantom{+}\phantom{\mathrm{x}\mathrm{x}}\phantom{-}\phantom{\frac{{\mathrm{x}}^4}{4\mathrm{a}\mathrm{a}}}\phantom{+}\phantom{\frac{{\mathrm{x}}^6}{8{\mathrm{a}}^4}}\phantom{-}\phantom{\frac{5{\mathrm{x}}^8}{64{\mathrm{a}}^6}}\phantom{-}\frac{7{\mathrm{x}}^{10}}{128{\mathrm{a}}^8}-\frac{7{\mathrm{x}}^{12}}{512{\mathrm{a}}^{10}}\\ \phantom{0}\phantom{0}\phantom{+}\phantom{\mathrm{x}\mathrm{x}}\phantom{-}\phantom{\frac{{\mathrm{x}}^4}{4\mathrm{a}\mathrm{a}}}\phantom{+}\phantom{\frac{{\mathrm{x}}^6}{8{\mathrm{a}}^4}}\phantom{-}\phantom{\frac{5{\mathrm{x}}^8}{64{\mathrm{a}}^6}}\phantom{-}\underset{\_}{\frac{7{\mathrm{x}}^{10}}{128{\mathrm{a}}^8}+\frac{7{\mathrm{x}}^{12}}{512{\mathrm{a}}^{10}}}\\ \phantom{0}\phantom{0}\phantom{+}\phantom{\mathrm{x}\mathrm{x}}\phantom{-}\phantom{\frac{{\mathrm{x}}^4}{4\mathrm{a}\mathrm{a}}}\phantom{+}\phantom{\frac{{\mathrm{x}}^6}{8{\mathrm{a}}^4}}\phantom{-}\phantom{\frac{5{\mathrm{x}}^8}{64{\mathrm{a}}^6}}\phantom{-}\phantom{\frac{7{\mathrm{x}}^{10}}{128{\mathrm{a}}^8}}-\frac{21{\mathrm{x}}^{12}}{512{\mathrm{a}}^{10}}\end{array}\end{array}$$ <4> et prodit $\mathrm{a}+\frac{\mathrm{x}\mathrm{x}}{2\mathrm{a}}-\frac{{\mathrm{x}}^4}{8{\mathrm{a}}^3}\text{\&c}$. Ubi notandum venit quòd circa finem operis eos omnes terminos negligo quorum dimensiones trascenderent dimensiones ultimi termini ad quem cupio quotientem solummodò produci, puta $\frac{{\mathrm{x}}^{12}}{{\mathrm{a}}^{11}}$. Potest etiam ordo terminorum inverti ad hunc modum $\mathrm{x}\mathrm{x}+\mathrm{a}\mathrm{a}$, et radix est $\mathrm{x}+\frac{\mathrm{a}\mathrm{a}}{2\mathrm{x}}-\frac{{\mathrm{a}}^4}{8{\mathrm{x}}^3}+\frac{{\mathrm{a}}^6}{16{\mathrm{x}}^5}\text{\&c}$.

Sic ex $\mathrm{a}\mathrm{a}-\mathrm{x}\mathrm{x}$ radix est $\mathrm{a}-\frac{\mathrm{x}\mathrm{x}}{2\mathrm{a}}-\frac{{\mathrm{x}}^4}{8{\mathrm{a}}^3}-\frac{{\mathrm{x}}^6}{16{\mathrm{a}}^5}\text{\&c}$

Et ex $\mathrm{x}-\mathrm{x}\mathrm{x}$ est ${\mathrm{x}}^{\frac{1}{2}}-\frac{1}{2}{\mathrm{x}}^{\frac{3}{2}}-\frac{1}{8}{\mathrm{x}}^{\frac{5}{2}}-\frac{1}{16}{\mathrm{x}}^{\frac{7}{2}}\text{\&c}$

* |* et ex $\mathrm{a}\mathrm{a}+\mathrm{b}\mathrm{x}-\mathrm{x}\mathrm{x}$ est $\mathrm{a}+\frac{\mathrm{b}\mathrm{x}}{2\mathrm{a}}-\frac{\mathrm{x}\mathrm{x}}{2\mathrm{a}}-\frac{\mathrm{b}\mathrm{b}\mathrm{x}\mathrm{x}}{8{\mathrm{a}}^3}\text{\&c}$|

Et ex $\frac{1+\mathrm{a}\mathrm{x}\mathrm{x}}{1-\mathrm{b}\mathrm{x}\mathrm{x}}$ est $\frac{1+\frac{1}{2}\mathrm{a}{\mathrm{x}}^2-\frac{1}{8}\mathrm{a}\mathrm{a}{\mathrm{x}}^4+\frac{1}{16}{\mathrm{a}}^3{\mathrm{x}}^6}{1-\frac{1}{2}\mathrm{b}\mathrm{x}\mathrm{x}-\frac{1}{8}\mathrm{b}\mathrm{b}{\mathrm{x}}^4-\frac{1}{16}{\mathrm{b}}^3{\mathrm{x}}^6}\text{\&c}$. {illeg} \{illeg}/ factâqꝫ \in super/ divisione, {illeg}|fit| {illeg} $\begin{array}{cccccccccccc}{1}^{\phantom{0}}& & \begin{array}{r}+\frac{1}{2}\mathrm{b}\\ +\frac{1}{2}\mathrm{a}\end{array}& {\mathrm{x}}^2& & \begin{array}{r}+\frac{3}{8}\mathrm{b}\mathrm{b}\\ +\frac{1}{4}\mathrm{a}\mathrm{b}\\ -\frac{1}{8}\mathrm{a}\mathrm{a}\end{array}& {\mathrm{x}}^4& & \begin{array}{r}+\frac{5}{16}{\mathrm{b}}^3\\ +\frac{3}{16}\mathrm{a}\mathrm{b}\mathrm{b}\\ -\frac{1}{16}\mathrm{a}\mathrm{a}\mathrm{b}\\ +\frac{1}{16}{\mathrm{a}}^3\end{array}& {\mathrm{x}}^6& & \text{\&c}\end{array}$

Operationes verò per debitam æquationis præparatione non rarò abbreviari possunt; {illeg}|U|t in allato exemplo {illeg} |ad extrahendam| {illeg} $\sqrt{}\frac{1+\mathrm{a}\mathrm{x}\mathrm{x}}{1-\mathrm{b}\mathrm{x}\mathrm{x}}$, si non eadem fuisset numeratoris ac denominatoris forma, utrumqꝫ multiplicassem per $\sqrt{}\stackrel{\_}{1-\mathrm{b}\mathrm{x}\mathrm{x}}$ & sic prodijsset $\frac{\sqrt{}:1\begin{array}{c}+\mathrm{a}\\ -\mathrm{b}\end{array}\mathrm{x}\mathrm{x}-\mathrm{a}\mathrm{b}{\mathrm{x}}^4:}{1-\mathrm{b}\mathrm{x}\mathrm{x}}$, et reliquum opus perficeretur extrahendo radicem numeratoris tantùm ac dividendo per denominatorem.

Ex hisce credo manifestum es{illeg}|t| quo pacto radices aliæ possunt ex{illeg}|t|rahi et quælibet compositæ quantitates (quibuscunqꝫ radicibus vel denominatoribus perplexæ, ut hic videre est ${\mathrm{x}}^3+\frac{\sqrt{}\stackrel{\_}{\mathrm{x}-\sqrt{}\stackrel{\_}{1-\mathrm{x}\mathrm{x}}}}{\sqrt{}3:\mathrm{a}\mathrm{x}\mathrm{x}+{\mathrm{x}}^3}-\frac{\sqrt{}5:\stackrel{\_}{{\mathrm{x}}^3+2{\mathrm{x}}^5-{\mathrm{x}}^{\frac{3}{2}}}}{\sqrt{}3:\stackrel{\_}{\mathrm{x}+\mathrm{x}\mathrm{x}}-\sqrt{}\stackrel{\_}{2\mathrm{x}-{\mathrm{x}}^{\frac{2}{3}}}}$.) in series infinitas simplicium terminorum reduci.

De {illeg}|A|ffectarum æquationum reductione.

Propositis verò affectis æquationibus, modus quo radices earum ad hujusmodi series reduci possint obnixiùs explicari debet idqꝫ cùm earum doctrina quam hactenus in numeris exposuerunt Mathematici, per ambages (superfluis etiam operationibus adhibitis) obscurè trada{illeg}tur, ut in specimen <5> operis in speciebus non debeat adhiberi. Imprimis itaqꝫ numerosam affectarum æquation{illeg}|um| resolutionem compendiosè tradam, dein spe{illeg}|ci|osam similiter explicabo.

Proponatur æquatio ${\mathrm{y}}^3-2\mathrm{y}-5=0$ resolvenda, Et sit 2 numerus utcunqꝫ inventus qui minùs quàm decimâ sui parte differt a radice quæsitâ. Tum pono $2+\mathrm{p}=\mathrm{y}$, et \pro y/ substituo hunc sibi valorem \$2+\mathrm{p}$/ in æquationem, et inde nova prodit ${\mathrm{p}}^3+6\mathrm{p}\mathrm{p}+10\mathrm{p}-1=0$. cujus radix p exquirenda est ut quotienti addatur. Nempe (neglectis ${\mathrm{p}}^3+6\mathrm{p}\mathrm{p}$ ob parvitatem) $10\mathrm{p}-1$$=0$ sive $\mathrm{p}=\mathrm{0,1}$ prope \ad/ veritatem {illeg} est \proxime accedit/. Scribo itáqꝫ 0,1 in quotiente & suppono $\mathrm{0,1}+\mathrm{q}=\mathrm{p}$, et hunc ejus fictitiu valorem ut ante substituo, et prodit ${\mathrm{q}}^3+\mathrm{6,3}\mathrm{q}\mathrm{q}+\mathrm{11,23}\mathrm{q}+\mathrm{0,061}=0$. Et cùm $\mathrm{11,23}\mathrm{q}+\mathrm{0,061}$ ad \$=0$/ veritatem prope accedi|a||t| \appropinque{illeg}|t|{illeg}/ sive ferè sit $\mathrm{q}=-\mathrm{0,0054}$ (dividendo nempe \$\mathrm{0,061}$ per $\mathrm{11,23}$/ donec tot eliciantur figuræ quot loca primis figuris hujus et principalis quoti{illeg}|e|ntis exclusivè intercedunt, quemadmodum hic duo sunt inter 2, & 0,005) scribo $-\mathrm{0,0054}$ in inferiori parte quotientis siquidem negativa sit, et supponens $-\mathrm{0,0054}+\mathrm{r}=\mathrm{q}$, hunc ut priùs substituo. Et sic operationem ad placitum produco, pro more subjecti diagrammatis.

$$\begin{array}{l}\begin{array}{rr}\phantom{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_}& \phantom{\_}\\ & \begin{array}{r}\left(\begin{array}{cc}+& \mathrm{2,10000000}\\ -& \mathrm{0,00544852}\end{array}\right.\\ \begin{array}{cc}+& \mathrm{2,09455148}\end{array}\end{array}\hfill \end{array}\\ \begin{array}{rr}\phantom{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_}& \phantom{\_}\\ \begin{array}{rr}2+\mathrm{p}=\mathrm{y}\text{.}\phantom{\mathrm{0,0000000}}& \phantom{+}{\mathrm{y}}^3\\ & -2\mathrm{y}\\ & -5\end{array}& \begin{array}{llllllll}+& 8& +& 12\mathrm{p}& +& 6\mathrm{p}\mathrm{p}& +& {\mathrm{p}}^3\\ -& 4& -& \phantom{0}2\mathrm{p}\\ -& 5\end{array}\hfill \\ \begin{array}{c}\\ \phantom{{\mathrm{p}}^3}\text{Summa}\phantom{{\mathrm{p}}^3}\end{array}& \begin{array}{l}\\ -& 1& +& 10\mathrm{p}& +& 6\mathrm{p}\mathrm{p}& +& {\mathrm{p}}^3\end{array}\hfill \end{array}\\ \begin{array}{rr}\phantom{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_}& \phantom{\_}\\ \begin{array}{rr}\mathrm{0,1}+\mathrm{q}=\mathrm{p}\text{.}\phantom{0000000}& +{\mathrm{p}}^3\\ & +6\mathrm{p}\mathrm{p}\\ & +10\mathrm{p}\\ & -1\end{array}& \begin{array}{llllllll}+& \mathrm{0,001}& +& \phantom{0}\mathrm{0,03}\mathrm{q}& +& \mathrm{0,3}\mathrm{q}\mathrm{q}& +& {\mathrm{q}}^3\\ +& \mathrm{0,06}\phantom{1}& +& \phantom{0}\mathrm{1,2}\phantom{0\mathrm{q}}& +& \mathrm{6,}\phantom{3\mathrm{q}\mathrm{q}}\\ +& 1\phantom{\mathrm{,001}}& +& \mathrm{10,}\phantom{0\mathrm{q}}\\ -& 1\end{array}\hfill \\ \begin{array}{c}\\ \phantom{{\mathrm{q}}^3}\text{Summa}\phantom{{\mathrm{q}}^3}\end{array}& \begin{array}{r}\\ \phantom{+}& \mathrm{0,061}& +& \mathrm{11,23}\mathrm{q}& +& \mathrm{6,3}\mathrm{q}\mathrm{q}& +& {\mathrm{q}}^3\end{array}\hfill \end{array}\\ \begin{array}{rr}\phantom{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_}& \phantom{\_}\\ \begin{array}{rr}\begin{array}{c}-\mathrm{0,0054}+\mathrm{r}=\mathrm{q}\text{.}\phantom{00000}\end{array}& \phantom{\stackrel{.}{0}}+{\mathrm{q}}^3\\ & \phantom{\stackrel{.}{0}}+\mathrm{6,3}\mathrm{q}\mathrm{q}\\ & +\mathrm{11,23}\mathrm{q}\\ & +\mathrm{0,061}\end{array}& \begin{array}{lllllllll}-& \mathrm{0,0000001}\stackrel{.}{5}\stackrel{.}{7}\stackrel{.}{4}\stackrel{.}{6}\stackrel{.}{4}& +& \phantom{0}\mathrm{0,000}\stackrel{.}{0}\stackrel{.}{8}\stackrel{.}{7}\stackrel{.}{4}\stackrel{.}{8}\mathrm{r}& -& \stackrel{.}{0},\stackrel{.}{0}\stackrel{.}{1}\stackrel{.}{6}\stackrel{.}{2}\mathrm{r}\mathrm{r}& +& \stackrel{.}{1}{\mathrm{r}}^3& \phantom{{\mathrm{q}}^3}\\ +& \mathrm{0,0001837}\stackrel{.}{0}\stackrel{.}{8}& -& \phantom{0}\mathrm{0,068}\stackrel{.}{0}\stackrel{.}{4}& +& \stackrel{.}{6},\stackrel{.}{3}& \phantom{{\mathrm{q}}^3}\\ -& \mathrm{0,060642}\phantom{0}& +& \mathrm{11,23}& \phantom{\mathrm{q}}\\ +& \mathrm{0,061}\end{array}\hfill \\ \begin{array}{c}\\ \phantom{{\mathrm{q}}^3}\text{Summa}\phantom{{\mathrm{q}}^3}\end{array}& \begin{array}{r}\\ +& \mathrm{0,0005416}\phantom{\stackrel{.}{0}\stackrel{.}{0}\stackrel{.}{0}\stackrel{.}{0}\stackrel{.}{0}}& +& \mathrm{11,162}\mathrm{r}& \phantom{0000000000000000000}\end{array}\hfill \end{array}\\ \begin{array}{rr}\phantom{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_}& \phantom{\_}\\ \hfill \begin{array}{c}-\mathrm{0,00004852}+\mathrm{s}=\mathrm{r}\text{.}\end{array}\hfill & \phantom{0}\\ \phantom{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_}& \phantom{\_}\end{array}\end{array}$$

<6>

{illeg}|O|pus verò sub fine (præsertim in æquationibus plurium dimensionum) hac methodo multùm abbreviabitur. Determinato quousqꝫ velis radicem extrahi, tot loca post prima figuram coefficientis penultimi termini æquationum in dextra parte diagrammatis resultantium {illeg} ad{illeg}|n|umera, quot supersunt loca in quotiente complenda, et subsequentes decimales neglige. In ultimo verò termino decimales post tot plura loca neglige quot in quot in quotiente complentur loca decimalia. Inqꝫ antepenultimo termino neglige omnes post tota pauciora loca. Et sic deinceps, Arithmeticè progrediendo per intervallu istud locorum, s{illeg}ive quod perinde est, tot figuras passim elidendo quot in penultimo termino, modò depressissima earum loca sint in Arithmeticâ progressione juxta seriem terminorum, aut circulis compleri subintelligantur ubi res aliter eveniat. Sic in exemplo jam posito, si cupiam ut quotiens ad octavum tantùm decimalem locum compleatur; inter substituendum $\mathrm{0,0054}+\mathrm{r}$ pro q, u{illeg}|b|i quatuor loca decimalia in quotiente complentur ac totidem supersunt complenda, potui figuras \in inferioribus {illeg}|q|uinqꝫ locis/ omisisse quas eapropter lineolâ transversim notavi; imò primum terminum ${\mathrm{r}}^3$, etsi coefficiente habui 99999 habuisset, potui tamen penitus omi{illeg}|sis|se. Expunctis itaqꝫ figuris istis, pro subsequente operatione prodit summa $\mathrm{0,0005416}+\mathrm{11,162}\mathrm{r}$, quæ per divisione ad usqꝫ præscriptum terminum peractam dat $-\mathrm{0,00004852}$ pro r, quod quotientem ad optatam periodum complet.

Deniqꝫ negativam partem quotientis ab affirmativâ subduco, et oritur 2,09455148 quotiens absoluta.

Præterea notandum est quòd sub initio operis si dubitarem an {illeg} $\mathrm{0,1}=\mathrm{p}$ ad veritatem satis accederet, vi{illeg}|c|e $10\mathrm{p}-1=0$ finxissem $6\mathrm{p}\mathrm{p}+10\mathrm{p}-1=0$, et ejus radicis nihilo propioris primam figuram in quotiente scripsissem. Et hoc modo secundam vel etiam tertiam quotientis figuram explorare convenit ubi in æquatione secundaria circa quam <7> versaris, quadratum coefficientis penultimi termini non sit decies {illeg}|m|ajor quàm factus ex ultimo termino ducto in coefficientem termini antepenultimi. Quinimò laborem plerumqꝫ minues, præsertim in æquationibus plurimarum dimensionum, si figuras omnes quotienti addendas hoc modo (id est extrahendo minorem radicum ex tribus ultimis terminis æquation{illeg}|is| novissimè resultantis ejus secundariæ) quæras. Sic enim figur{illeg}|a|s duplo plures in quotiente quâlibet vice lucraberis.

His in numeris sic ostensis, consimiles operationes in speciebus explicandæ restant, de quibus juvabit \convenit/ sequentia prænoscere. 1 Quod e speciebus radicem definientibus \coefficientibus/ aliqua{illeg} præ reliquis (si sint plures) insignio|e||nda| \sit/, {illeg} \ea/ nempe quæ{illeg} s{illeg}o aut m{illeg}s possum fingere \{illeg}|e|st, aut fingi potest esse/ esse omnium longè minimam vel maximam \vel datæ quantitati vicinissima; sive indefinitè parvam vel magnam datæ{illeg} quantitati vicinam./. Cujus rei causa est, ut {illeg} dimensionum ob ejus dimensiones in numeratoribus vel denominatoribus terminorum quotientis perpetim auctas, illi termini continuò minores et inde quotiens radici propinquior evadat, sicut ante de specie x in exemplis reductionum per divisionem et extractionem radicum manifestum est|s||e| \potest/. Pro isthâc verò specie in sequentibus ut {illeg}|p|lurimùm usurpabo {illeg} etiam x vel z, quemadmodum ety, p, q, r, s &c pro specie radicali extrahenda.

2 Siquando fractiones {illeg}|int|ricatæ \complexæ/ vel surdæ quantitates in æquatione propositâ vel post in operatione occurrant, tolli debent per \me/m|th|odos Analystis satis notas. Quemadmodum si habeatur ${\mathrm{y}}^3+\frac{\mathrm{b}\mathrm{b}}{\mathrm{b}-\mathrm{x}}\mathrm{y}\mathrm{y}-{\mathrm{x}}^3=0$, multiplico per $\mathrm{b}-\mathrm{x}$ et {illeg} \ex facto{illeg}/ $\mathrm{b}{\mathrm{y}}^3-\mathrm{x}{\mathrm{y}}^3+\mathrm{b}\mathrm{b}\mathrm{y}\mathrm{y}-\mathrm{b}{\mathrm{x}}^3+{\mathrm{x}}^4=0$ resolvo \valorem y elicio./ Vel possum fingere $\mathrm{y}\times \stackrel{\_}{\mathrm{b}-\mathrm{x}}=\mathrm{v}$, et sic scribendo $\frac{\mathrm{v}}{\mathrm{b}-\mathrm{x}}$ pro y, orietur ${\mathrm{v}}^3+\mathrm{b}\mathrm{b}\mathrm{y}\mathrm{y}-\mathrm{b}\mathrm{b}{\mathrm{x}}^3+2\mathrm{b}{\mathrm{x}}^4-{\mathrm{x}}^5=0$ dein extractâ radice v, divido quotientem per $\mathrm{b}-\mathrm{x}$ ut obtineatur valor y. Item si proponatur {illeg} |${\mathrm{y}}^3-\mathrm{x}{\mathrm{y}}^{\frac{1}{2}}+{\mathrm{x}}^{\frac{4}{3}}$|{illeg}$=0$ fingo {illeg} ${\mathrm{y}}^{\frac{1}{2}}=\mathrm{v}$, et ${\mathrm{x}}^{\frac{1}{3}}=\mathrm{z}$, et sic scribendo $\mathrm{v}\mathrm{v}$ pro y et ${\mathrm{z}}^3$ pro x, oritur {illeg} |${\mathrm{v}}^6-{\mathrm{z}}^3\mathrm{v}+\mathrm{z}$| {illeg}; qua \æquatione/ resolutâ restituo y et x. Scilicet radix invenietur $\mathrm{v}=\mathrm{z}+{\mathrm{z}}^3+6{\mathrm{z}}^5\text{\&c}$, et restitutis y et x orietur <8> ${\mathrm{y}}^{\frac{1}{2}}={\mathrm{x}}^{\frac{1}{3}}+\mathrm{x}+6{\mathrm{x}}^{\frac{5}{3}}\text{\&c}$; {illeg} e{illeg}|t| quadrando, $\mathrm{y}={\mathrm{x}}^{\frac{2}{3}}+2{\mathrm{x}}^{\frac{4}{3}}+13\mathrm{x}\mathrm{x}\text{\&c}$. Ad eundem modum siquæ sint negativæ ips{illeg}|o|ru $\mathrm{x}$ et $\mathrm{y}$, facio nullas esse \tollo/ multiplicando per easdem $\mathrm{x}$ et $\mathrm{y}$ Sic habito ${\mathrm{x}}^3+3\mathrm{x}\mathrm{x}{\mathrm{y}}^{-1}-2{\mathrm{x}}^{-1}-16{\mathrm{y}}^{-3}=0$, multiplico per x et ${\mathrm{y}}^3$, oriturqꝫ ${\mathrm{x}}^4{\mathrm{y}}^3+3{\mathrm{x}}^3\mathrm{y}\mathrm{y}-2{\mathrm{y}}^3-16=0$. Et habito $\mathrm{x}=\frac{\mathrm{a}\mathrm{a}}{\mathrm{y}}-\frac{2{\mathrm{a}}^3}{\mathrm{y}\mathrm{y}}+\frac{3{\mathrm{a}}^4}{{\mathrm{y}}^3}$ duco in ${\mathrm{y}}^3$ et oritur $\mathrm{x}{\mathrm{y}}^3=\mathrm{y}\mathrm{y}-2\mathrm{y}+3$. Et sic de cæteris.

3 Æquatione sic præparatâ, ob|p|us ab inventione primi termini quotientis initium sumit, de quâ ut et consimili subsequentium terminorum inventione hæc esto regula generalis cùm species indefinita \(x vel z)/ parva esse fingitur, * |* ad quem casum cæteri duo \casus/ sunt reducibiles|. E terminis in qu{illeg}|i|bus species radicalis (y, p, q vel r &c) non reperitur selige depressissimum respectu dimensionum indefinitæ speciei ({illeg}|x| vel z &c) dein alium terminum in quo sit illa species radicalis selige, talem {illeg}|n|empe ut progressio dimensionum utriusqꝫ præfatæ speciei a termi{illeg}|n|o priùs assumpto ad hunc terminum continuata, quàm maximè potest descendat vel minimè ascendat. Et siqui sint alij termini quorum dimensiones cum hâc progressione ad arbitrium continuatâ conveniant, eos etiam selige. Deniqꝫ ex his selectis terminis tanquam nihilo æqualibus quære \primum terminum/ valore{illeg}|m| dictæ speciei radicalis et quotienti appone {illeg}, \vel {illeg} primum terminum ejus/ et quotienti appone.

Cæterùm ut hæc regula magis elucescat, placuit insuper ope sequentis diagrammatis exponere. Descripto angulo recto BAC, latera ejus BA, AC di{illeg}|v|ido in partes æquales, et inde normales erigo distribuentes angulare spatium in æqualia quadrata vel parallelogramma, quæ conci{illeg}|p|io denominata esse a dimensionibus specierum x et y, {illeg} \pro ut/ vides in fig 1 inscriptas. Deinde cùm æquatio aliqua proponitur, parallelogramma singulis ejus terminis 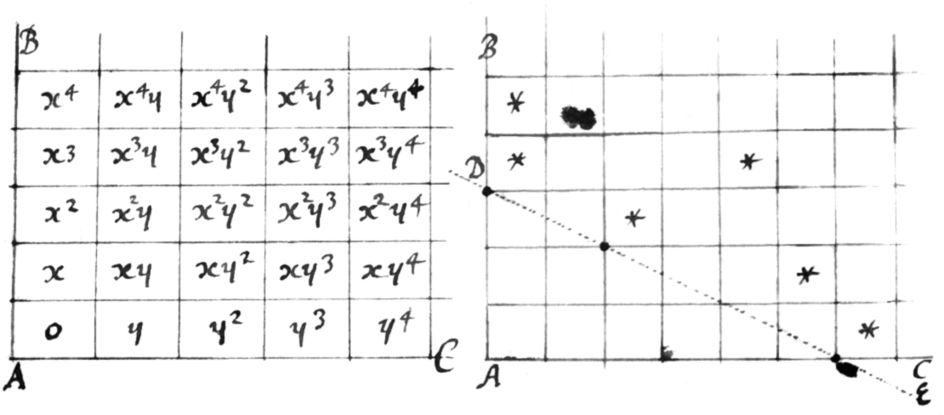correspondentia insignio notâ aliquâ et Regulâ ad duo vel forte plura ex insignitis parallelogrammis applicatâ, quoru unum sit humillimum in columnâ sinistra juxta AB, et alia \ad regulam/ dextrorsum sita, cæteraqꝫ omnia non contingentia <9> regulam supra eam jaceant: seligo terminos æquationis per parallelogramma contingentia regulam designatos et inde quæro quantitatem quotienti addendam.

Sic ad extrahendam radicem y ex ${\mathrm{y}}^6-5\mathrm{x}{\mathrm{y}}^5+\frac{{\mathrm{x}}^3}{\mathrm{a}}{\mathrm{y}}^4-$$7\mathrm{a}\mathrm{a}\mathrm{x}\mathrm{x}\mathrm{y}\mathrm{y}+6{\mathrm{a}}^3{\mathrm{x}}^3+\mathrm{b}\mathrm{b}{\mathrm{x}}^4=0$; parallelogramma hujus terminis respondend|t|ia signo nota aliqua ∗ ut vides in schem. 2. Dein applico regulam DE ad inferiorem e locis \signatis/ in sinistra columna, eámqꝫ ab inferioribus dextrorsum ad superiora dextrorsum gyrare facio donec alium similiter vel fortè plura e reliquis signatis locis quam primum attinget \cœperit attingere/, videóqꝫ loca sic attracta esse ${\mathrm{x}}^3$, ${\mathrm{x}}^2{\mathrm{y}}^2$, & ${\mathrm{y}}^6$. E terminis itáqꝫ ${\mathrm{y}}^6-7\mathrm{a}\mathrm{a}\mathrm{x}\mathrm{x}\mathrm{y}\mathrm{y}+6{\mathrm{a}}^3{\mathrm{x}}^3$ tanquam nihilo æqualibus (et insuper si placet reductis ad ${\mathrm{v}}^6-7\mathrm{v}\mathrm{v}+6=0$ ponendo $\mathrm{y}\times \sqrt{}\mathrm{a}\mathrm{x}$) quæro valorem y, et invenio quadruplicem $+\sqrt{}\mathrm{a}\mathrm{x}$, $-\sqrt{}\mathrm{a}\mathrm{x}$, $+\sqrt{}2\mathrm{a}\mathrm{x}$ & $-\sqrt{}2\mathrm{a}\mathrm{x}$, quorum quemlibet pro initio quotientis accip{illeg}|er|e \liceat/ prout e radicibus quampiam extrahere decre{illeg}|tu|m est

Sic ex ${\mathrm{y}}^5-\mathrm{b}\mathrm{y}\mathrm{y}+9\mathrm{b}\mathrm{x}\mathrm{x}-{\mathrm{x}}^3=0$ seligo $-\mathrm{b}\mathrm{y}\mathrm{y}+9\mathrm{b}\mathrm{x}\mathrm{x}$, et inde obtineo $+3\mathrm{x}$ pro initiali termino quotientis

Et ex ${\mathrm{y}}^3+\mathrm{a}\mathrm{x}\mathrm{y}+\mathrm{a}\mathrm{a}\mathrm{y}-{\mathrm{x}}^3-2{\mathrm{a}}^3=0$ seligo ${\mathrm{y}}^3+\mathrm{a}\mathrm{a}\mathrm{y}-2{\mathrm{a}}^3$, et radicem ejus $+\mathrm{a}$ scribo in quotiente.

Et ex $\mathrm{x}\mathrm{x}{\mathrm{y}}^5-3{\mathrm{c}}^4\mathrm{x}\mathrm{y}\mathrm{y}-{\mathrm{c}}^5\mathrm{x}\mathrm{x}+{\mathrm{c}}^7=0$ seligo $\mathrm{x}\mathrm{x}{\mathrm{y}}^5+{\mathrm{c}}^7$, quod exhibet $\sqrt{}5:\frac{{\mathrm{c}}^7}{\mathrm{x}\mathrm{x}}$ pro initio quotientis. Et sic de cæteris.

Cæterùm invento hoc termino, si \is/ contingat esse negativæ potestatis, æquationem per eandem potestatem indefinitæ speciei potestatem deprimo, \eo ut/ non opus sit inter solvendum deprimere, et \insuper/ ut regula de superfluis termin{illeg}|i|s elidendis \mox tradenda/ aptè possit adhiberi. Sic proposito $8{\mathrm{z}}^6{\mathrm{y}}^3+\mathrm{a}{\mathrm{z}}^6\mathrm{y}\mathrm{y}-27{\mathrm{a}}^9=0$, cujus quotiens exordiri debet a $\frac{3{\mathrm{a}}^3}{2\mathrm{z}\mathrm{z}}$, deprimo per $\mathrm{z}\mathrm{z}$, ut fiat $8{\mathrm{z}}^4{\mathrm{y}}^3+\mathrm{a}{\mathrm{z}}^4\mathrm{y}\mathrm{y}-27{\mathrm{a}}^9{\mathrm{z}}^{-2}=0$, antequam solutionem {illeg}|i|neo.

Subsequentes q{illeg}|uo|tientum termini eâdem methodo ex æquationibus secundarijs inter operandum prodeuntibus eruuntur, sed \ut plurimum/ leviori tamen curâ. Res enim peragi solet dividendo depressi\ssi/mum e terminis cum indefinit{illeg}|è| \parva/ specie (x, $\mathrm{x}\mathrm{x}$, ${\mathrm{x}}^3$ &c) absqꝫ specie radicali (p, q, r &c) affectis, per quantitatem quâcum species illa radicalis unius tantùm dimensionis abqꝫ alterâ indefinitâ specie afficitur, et exitum scribendo in quotiente. Sic in exemplo sequente termini quotientis $\frac{\mathrm{x}}{4}$, $\frac{\mathrm{x}\mathrm{x}}{64\mathrm{a}}$, {illeg} $\frac{131{\mathrm{x}}^3}{512\mathrm{a}\mathrm{a}}$ &c eliciuntur dividendo $\mathrm{a}\mathrm{a}\mathrm{x}$, $\frac{1}{16}\mathrm{a}\mathrm{x}\mathrm{x}${,} $\frac{131}{128}{\mathrm{x}}^3$ &c per $4\mathrm{a}\mathrm{a}$.

Cæterùm

<10>

His praemissis restat ut praxis|n| resolutionis exhibe{illeg}|a|m. Sit itáqꝫ ${\mathrm{y}}^3+\mathrm{a}\mathrm{a}\mathrm{y}+\mathrm{a}\mathrm{x}\mathrm{y}-2{\mathrm{a}}^3-{\mathrm{x}}^3=0$ æquatio resolvenda, et ex ejus terminis ${\mathrm{y}}^3+\mathrm{a}\mathrm{a}\mathrm{y}-2{\mathrm{a}}^3=0$ \æquatione fictitiâ,/ juxta tertium e præmissis elicio $\mathrm{y}-\mathrm{a}=0$, & scribo {illeg} $+\mathrm{a}$ in quotiente. Deinde cùm $+\mathrm{a}$ non accurate valet|a|t y, pono $\mathrm{a}+\mathrm{p}=\mathrm{y}$, et pro y substit{illeg} in terminis æquationis \in/ margine {illeg} scriptis substituo $\mathrm{a}+\mathrm{p}$, terminosqꝫ resultantes (${\mathrm{p}}^3+3\mathrm{a}\mathrm{p}\mathrm{p}+\mathrm{a}\mathrm{x}\mathrm{p}$ &c) {illeg}rursum {illeg} scribo in margin{illeg}|e|, ex quibus iterum juxta tertium e præmissis excerpo terminos $+4\mathrm{a}\mathrm{a}\mathrm{p}+\mathrm{a}\mathrm{a}\mathrm{x}=0$ pro æquatione fictitiâ, quæ cùm {illeg}exhibet|a|t {illeg} $\mathrm{p}=-\frac{1}{4}\mathrm{x}$, scribo $-\frac{1}{4}\mathrm{x}$ in quotiente. Præterea cùm $-\frac{1}{4}\mathrm{x}$ non accurate valet|a|t p, pono $-\frac{1}{4}\mathrm{x}+\mathrm{q}$$=\mathrm{p}$, & pro p in terminis margi{illeg}|n|a\libus/ adscriptis substituo $-\frac{1}{4}\mathrm{x}+\mathrm{q}$, terminosqꝫ resultantes ({illeg} ${\mathrm{q}}^3-\frac{3}{4}\mathrm{x}\mathrm{q}\mathrm{q}+$$3\mathrm{a}\mathrm{q}\mathrm{q}$ &c) iterum {illeg} scribo \in/ margine, ex quibus {illeg}|d|e{illeg}|n|u{illeg}|ò| juxta regulam præfatam seligo terminos $4\mathrm{a}\mathrm{a}\mathrm{q}-\frac{1}{16}\mathrm{a}\mathrm{x}\mathrm{x}=0$ pro æquatione fictitiâ quae cùm {illeg} exhibet|a|t {illeg} $\mathrm{q}=\frac{\mathrm{x}\mathrm{x}}{\mathrm{6a}\mathrm{a}}$ scribo $+\frac{\mathrm{x}\mathrm{x}}{64\mathrm{a}}$ in quotiente. Porrò cùm $\frac{\mathrm{x}\mathrm{x}}{64\mathrm{a}}$ non accuratè valet|a|t q, pono $\frac{\mathrm{x}\mathrm{x}}{64\mathrm{a}}+\mathrm{r}=\mathrm{q}$ & pro q in terminis marginalibus adscriptis substituo $\frac{\mathrm{x}\mathrm{x}}{64\mathrm{a}}+\mathrm{r}$, & sic opus ad placitum produco prout indicat subjectum diagramma.

$$\begin{array}{l}\begin{array}{rr}\phantom{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_}& \phantom{\_}\\ & \left(\mathrm{a}-\frac{\mathrm{x}}{4}+\frac{\mathrm{x}\mathrm{x}}{64\mathrm{a}}+\frac{131{\mathrm{x}}^3}{512\mathrm{a}\mathrm{a}}+\frac{509{\mathrm{x}}^4}{16384{\mathrm{a}}^3}\text{\&c}\right.\hfill \end{array}\\ \begin{array}{rr}\phantom{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_}& \phantom{\_}\\ \begin{array}{rr}+\mathrm{a}+\mathrm{p}=\mathrm{y}\text{.}\phantom{000000000}& +{\mathrm{y}}^3\\ & +\mathrm{a}\mathrm{x}\mathrm{y}\\ \phantom{{\mathrm{p}}^0}& +\mathrm{a}\mathrm{a}\mathrm{y}\\ & -{\mathrm{x}}^3\\ & -2{\mathrm{a}}^3\end{array}& \begin{array}{llllllll}+& {\mathrm{a}}^3& +& 3\mathrm{a}\mathrm{a}\mathrm{p}& +& 3\mathrm{a}\mathrm{p}\mathrm{p}& +& {\mathrm{p}}^3\\ +& \mathrm{a}\mathrm{a}\mathrm{x}& +& \mathrm{a}\mathrm{x}\mathrm{p}\\ +& {\mathrm{a}}^3& +& \mathrm{a}\mathrm{a}\mathrm{p}\\ -& {\mathrm{x}}^3\\ -& 2{\mathrm{a}}^3\end{array}\hfill \end{array}\\ \begin{array}{rr}\phantom{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_}& \phantom{\_}\\ \begin{array}{rr}-\frac{1}{4}\mathrm{x}+\mathrm{q}=\mathrm{p}\text{.}\phantom{0000000}& \phantom{\frac{0}{0}}+{\mathrm{p}}^3\\ & \phantom{\frac{0}{0}}+3\mathrm{a}{\mathrm{p}}^2\\ & \phantom{\frac{0}{0}}+\mathrm{a}\mathrm{x}\mathrm{p}\\ & +4\mathrm{a}\mathrm{a}\mathrm{p}\\ & +\mathrm{a}\mathrm{a}\mathrm{x}\\ & -{\mathrm{x}}^3\end{array}& \begin{array}{lllllllll}-& \frac{1}{64}{\mathrm{x}}^3& +& \frac{3}{16}\mathrm{x}\mathrm{x}\mathrm{q}& \ast & -& \frac{3}{4}\mathrm{x}\mathrm{q}\mathrm{q}& +& {\mathrm{q}}^3\\ +& \frac{3}{16}\mathrm{a}\mathrm{x}\mathrm{x}& -& \frac{3}{2}\mathrm{a}\mathrm{x}\mathrm{q}& & +& 3\mathrm{a}\mathrm{q}\mathrm{q}\\ -& \frac{1}{4}\mathrm{a}\mathrm{x}\mathrm{x}& +& \mathrm{a}\mathrm{x}\mathrm{q}\\ -& \mathrm{a}\mathrm{a}\mathrm{x}& +& 4\mathrm{a}\mathrm{a}\mathrm{q}\\ +& \mathrm{a}\mathrm{a}\mathrm{x}\\ -& {\mathrm{x}}^3\end{array}\hfill \end{array}\\ \begin{array}{rr}\phantom{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_}& \phantom{\_}\\ \begin{array}{rr}+\frac{\mathrm{x}\mathrm{x}}{64\mathrm{a}}\mathrm{x}+\mathrm{r}=\mathrm{q}\text{.}\phantom{0000}& \phantom{\frac{0}{0}}+{\mathrm{q}}^3\\ & -\frac{3}{4}\mathrm{x}\mathrm{q}\mathrm{q}\\ & \phantom{\frac{{\mathrm{x}}^0}{0}}+3\mathrm{a}\mathrm{q}\mathrm{q}\\ & \phantom{\frac{{\mathrm{x}}^0}{0}}+\frac{3}{16}\mathrm{x}\mathrm{x}\mathrm{q}\\ & -\frac{1}{2}\mathrm{a}\mathrm{x}\mathrm{q}\\ & \phantom{\frac{0}{0}}+4\mathrm{a}\mathrm{a}\mathrm{q}\\ & -\frac{65}{64}{\mathrm{x}}^3\\ & -\frac{1}{16}\mathrm{a}\mathrm{x}\mathrm{x}\end{array}& \begin{array}{ll}\ast & \phantom{\frac{0}{0}}\\ \ast & \phantom{\frac{0}{0}}\\ +& \frac{3{\mathrm{x}}^4}{4096\mathrm{a}}& \ast & +& \frac{3}{32}\mathrm{x}\mathrm{x}\mathrm{r}& +& 3\mathrm{a}\mathrm{r}\mathrm{r}\\ +& \frac{3{\mathrm{x}}^4}{1024\mathrm{a}}& \ast & +& \frac{3}{16}\mathrm{x}\mathrm{x}\mathrm{r}\\ -& \frac{1}{128}{\mathrm{x}}^3& & -& \frac{1}{2}\mathrm{a}\mathrm{x}\mathrm{r}\\ +& \frac{1}{16}\mathrm{a}\mathrm{x}\mathrm{x}& & +& 4\mathrm{a}\mathrm{a}\mathrm{r}\\ -& \frac{65}{64}{\mathrm{x}}^3& \\ -& \frac{1}{16}\mathrm{a}\mathrm{x}\mathrm{x}& \end{array}\hfill \end{array}\\ \begin{array}{c}\phantom{\_}\\ \left.+4\mathrm{a}\mathrm{a}-\frac{1}{2}\mathrm{a}\mathrm{x}\right)+\frac{131}{128}{\mathrm{x}}^3-\frac{15{\mathrm{x}}^4}{4096\mathrm{a}}\left(+\frac{131{\mathrm{x}}^3}{512\mathrm{a}\mathrm{a}}+\frac{509{\mathrm{x}}^4}{16384{\mathrm{a}}^3}\right.\text{.}\\ \phantom{\_}\end{array}\end{array}$$

<11>

Quod si Quotientem ad certam usqꝫ periodum continuari \produci/ cupi{illeg}|am|, ut x nempe in ultimo ejus termino ultra datum dimensionum numerum non ascendat; inter substituendum, terminos istas \inter substituendum/ semper omitto quos nulli deinceps usui fore prævide{illeg}|am|. Cujus rei regula esto, quòd post primum terminum ex qualibet quantitate sibi in margine collaterali resultantem non addan\tur/ plures dextrorsum, quàm istius primò resultantis termini dimensio a periodica \sive maximâ/ dimensione quotientis distat unitatibus \deficit gradibus/. Ut in hoc exemplo si cupiam ut quotiens (sive x in quotiente) ad quatuor tantùm dimensiones ascendat, omitto omnes terminos post ${\mathrm{x}}^4$, & post ${\mathrm{x}}^3$ pono unicum tantùm. Terminos itaqꝫ post notam ∗ delendos esse concipe: Et opere sic continuato donec ultimò ad terminos $\left(\frac{15{\mathrm{x}}^4}{4096\mathrm{a}}-\frac{131}{128}{\mathrm{x}}^3+4\mathrm{a}\mathrm{a}\mathrm{r}-\frac{1}{2}\mathrm{a}\mathrm{x}\mathrm{r}\right)$ deveniatur in quibus (p, q, r vel s &c) residuum radicis extrahendæ sit uni|c|æ tantùm dimensionis; tot terminos $\left(+\frac{131{\mathrm{x}}^3}{512\mathrm{a}\mathrm{a}}+\frac{509{\mathrm{x}}^4}{16384{\mathrm{a}}^3}\right)$ per divisionem elicio|e|s, quot ad complendum quotientem deesse videbis. Atqꝫ ita tandem obtinebitur $\mathrm{y}=\mathrm{a}-\frac{1}{4}\mathrm{x}+\frac{\mathrm{x}\mathrm{x}}{64\mathrm{a}}+\frac{131{\mathrm{x}}^3}{512{\mathrm{a}}^2}+\frac{509{\mathrm{x}}^4}{16384{\mathrm{a}}^3}$.

Plenioris illustrationis gratia dedi aliud exemplum resolvendi|o| $\frac{1}{5}{\mathrm{y}}^5-\frac{1}{4}{\mathrm{y}}^4+\frac{1}{3}{\mathrm{y}}^3-\frac{1}{2}\mathrm{y}\mathrm{y}+\mathrm{y}-\mathrm{z}=0$ \{illeg}/, {illeg}|u|bi proponitur inventio quotientis ad quintam tantùm dimensionem, {illeg}|te|rminiqꝫ superflui post notam (&c) negliguntur.

$$\begin{array}{l}\begin{array}{rr}\phantom{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_}& \phantom{\_}\\ & \left(\mathrm{z}+\frac{1}{2}\mathrm{z}\mathrm{z}+\frac{1}{6}{\mathrm{z}}^3+\frac{1}{24}{\mathrm{z}}^4+\frac{1}{120}{\mathrm{z}}^5\text{\&c}\right.\hfill \end{array}\\ \begin{array}{rr}\phantom{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_}& \phantom{\_}\\ \begin{array}{rr}\mathrm{z}+\mathrm{p}=\mathrm{y}\phantom{0000000000}& +\frac{1}{5}{\mathrm{y}}^5\\ & -\frac{1}{4}{\mathrm{y}}^4\\ & +\frac{1}{3}{\mathrm{y}}^3\\ & -\frac{1}{2}{\mathrm{y}}^2\\ & +\mathrm{y}\\ & -\mathrm{z}\end{array}& \begin{array}{llll}+& \frac{1}{5}{\mathrm{z}}^5& & \text{\&c}\\ -& \frac{1}{4}{\mathrm{z}}^4& -& {\mathrm{z}}^3\mathrm{p}& & \text{\&c}\\ +& \frac{1}{3}{\mathrm{z}}^3& +& {\mathrm{z}}^2\mathrm{p}& +& \mathrm{z}\mathrm{p}\mathrm{p}& \phantom{+}& \text{\&c}\\ -& \frac{1}{2}{\mathrm{z}}^2& -& \mathrm{z}\mathrm{p}& -& \frac{1}{2}\mathrm{p}\mathrm{p}\\ +& \mathrm{z}& +& \mathrm{p}\\ -& \mathrm{z}\end{array}\hfill \end{array}\\ \begin{array}{rr}\phantom{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_}& \phantom{\_}\\ \begin{array}{rr}+\frac{1}{2}\mathrm{z}\mathrm{z}+\mathrm{q}=\mathrm{p}\text{.}\phantom{00000000}& +\mathrm{z}{\mathrm{p}}^2\\ & -\frac{1}{2}{\mathrm{p}}^2\\ & \phantom{\frac{0}{0}}-{\mathrm{z}}^3\mathrm{p}\\ & \phantom{\frac{0}{0}}+{\mathrm{z}}^2\mathrm{p}\\ & \phantom{\frac{0}{0}}-\mathrm{z}\mathrm{p}\\ & \phantom{\frac{0}{0}}+\mathrm{p}\\ & +\frac{1}{5}{\mathrm{z}}^5\\ & -\frac{1}{4}{\mathrm{z}}^4\\ & +\frac{1}{3}{\mathrm{z}}^3\\ & -\frac{1}{2}{\mathrm{z}}^2\end{array}& \begin{array}{llll}+& \frac{1}{4}{\mathrm{z}}^5& & \text{\&c}\\ -& \frac{1}{8}{\mathrm{z}}^4& -& \frac{1}{2}{\mathrm{z}}^2\mathrm{q}& \phantom{+}& \text{\&c}\\ -& \frac{1}{2}{\mathrm{z}}^5& & \text{\&c}\\ +& \frac{1}{2}{\mathrm{z}}^4& +& {\mathrm{z}}^2\mathrm{q}\\ -& \frac{1}{2}{\mathrm{z}}^3& -& \mathrm{z}\mathrm{q}\\ +& \frac{1}{2}{\mathrm{z}}^2& +& \mathrm{q}\\ +& \frac{1}{5}{\mathrm{z}}^5\\ -& \frac{1}{4}{\mathrm{z}}^4\\ +& \frac{1}{3}{\mathrm{z}}^3\\ -& \frac{1}{2}{\mathrm{z}}^2\end{array}\hfill \end{array}\\ \begin{array}{c}\phantom{\_}\\ \left.1-\mathrm{z}+\frac{1}{2}\mathrm{z}\mathrm{z}\right)+\frac{1}{6}{\mathrm{z}}^3-\frac{1}{8}{\mathrm{z}}^4+\frac{1}{20}{\mathrm{z}}^5\left(+\frac{1}{6}{\mathrm{z}}^3+\frac{1}{24}{\mathrm{z}}^4+\frac{1}{120}{\mathrm{z}}^5\right.\text{.}\\ \phantom{\_}\end{array}\end{array}$$

Atqꝫ ita si cupiam æquationem $\frac{63{\mathrm{y}}^{11}}{2816}+\frac{35}{1152}{\mathrm{y}}^9+\frac{5}{112}{\mathrm{y}}^7+$ <12> $\frac{3}{40}{\mathrm{y}}^5+\frac{1}{6}{\mathrm{y}}^3+\mathrm{y}-\mathrm{z}=0$ ad usqꝫ nonam tantùm dimensione quotientis resolvi, ante opus initum {illeg} negligo terminum $\frac{63}{2816}{\mathrm{y}}^{11}$, deinde inter operandum negligo etiam omnes term{illeg}|i|nos post ${\mathrm{z}}^9$, post ${\mathrm{z}}^7$ pono unicum, ac duos tantum post ${\mathrm{z}}^5$, eò quòd percipio quotientem ubiqꝫ per gradus binarum {unitatum} (hoc modo z, ${\mathrm{z}}^3$, ${\mathrm{z}}^5$, &c) \debere/ ascendere. Tandemqꝫ prodit /$\mathrm{y}=\mathrm{z}-\frac{1}{6}{\mathrm{z}}^3+\frac{1}{120}{\mathrm{z}}^5-\frac{1}{5040}{\mathrm{z}}^7+\frac{1}{362880}{\mathrm{z}}^9$ {illeg}\

Et hinc pad|t|et {illeg} artificium quo æquationes in infinitum affectæ, vel utcunqꝫ {illeg} multis {illeg} numeróve infinitis terminis constantes possunt solvi. Scili{illeg}|c|et omnes termini ante opus initum debent negligi in quibus dimensio speciei indefinita|è| parvæ non affectæ cum {illeg}|r|adicali specie transcendit maximam desideratamdimensionem in quotiente \desideratam/ vel ex quibus, (substituendo \pro {illeg}|r|adicali specie {illeg}/ primum terminum quotientis ope tessellatæ tabulæ inventum), non nisi ejusmodi transcendentes termini possunt emergere. Sic in exemplo novissimo terminos omnes supra ${\mathrm{y}}^9$, {illeg}|q|uamvis infinitè progrederentur, omiss|i|ssem. Et sic in hâc æquatione
$0=\left\{\begin{array}{rrrrrrrrrrrr}-& 8& \hfill +\hfill & \mathrm{z}\mathrm{z}& -& 4{\mathrm{z}}^4& +& 9{\mathrm{z}}^6& -& 16{\mathrm{z}}^8& \phantom{+}& \text{\&c}\\ +& \mathrm{y}& in& \mathrm{z}\mathrm{z}& -& 2{\mathrm{z}}^4& +& 3{\mathrm{z}}^6& -& 4{\mathrm{z}}^8& \phantom{+}& \text{\&c}\\ -& \mathrm{y}\mathrm{y}& in& \mathrm{z}\mathrm{z}& -& {\mathrm{z}}^4& +& {\mathrm{z}}^6& -& {\mathrm{z}}^8& \phantom{+}& \text{\&c}\\ +& {\mathrm{y}}^3& in& \mathrm{z}\mathrm{z}& -& \frac{1}{2}{\mathrm{z}}^4& +& \frac{1}{3}{\mathrm{z}}^6& -& \frac{1}{4}{\mathrm{z}}^8& \phantom{+}& \text{\&c}\end{array}\right.$
ut radix cubica ad quatuor tantùm dimensiones ipsius z extrahatur, mitto omnes in infinitum terminos post $+{\mathrm{y}}^{3}in\mathrm{z}\mathrm{z}-\frac{1}{2}{\mathrm{z}}^4+\frac{1}{3}{\mathrm{z}}^6$, et post $-\mathrm{y}\mathrm{y}in\mathrm{z}\mathrm{z}-{\mathrm{z}}^4+{\mathrm{z}}^6$ et post $+\mathrm{y}in\mathrm{z}\mathrm{z}-2{\mathrm{z}}^4$, et post $-8+\mathrm{z}\mathrm{z}-4{\mathrm{z}}^4$. Et hanc tantù \æquationem/ $\frac{1}{3}{\mathrm{z}}^6{\mathrm{y}}^3-\frac{1}{2}{\mathrm{z}}^4{\mathrm{y}}^3+\mathrm{z}\mathrm{z}{\mathrm{y}}^3-{\mathrm{z}}^6\mathrm{y}\mathrm{y}+{\mathrm{z}}^4\mathrm{y}\mathrm{y}-2{\mathrm{z}}^4\mathrm{y}+\mathrm{z}\mathrm{z}\mathrm{y}-4{\mathrm{z}}^4$$+\mathrm{z}\mathrm{z}-8=0$ resolvendam sumo, siquidem $2{\mathrm{z}}^{-\frac{2}{3}}$ (primus nempe quotientis terminus,) pro y in reliquâ æquatione per |${\mathrm{z}}^{\frac{2}{3}}$| substitutus, dat plures ubiqꝫ quàm quatuor dimensiones{.}

Quæ de altioribus æquationibus dixi, ad quadraticas etiam applicari possunt. Quemadmodum si hujus
$0=\left\{\begin{array}{cc}\phantom{+}\mathrm{y}\mathrm{y}& \text{.}\\ -\mathrm{y}& in& \mathrm{a}& +& \mathrm{x}& +& \frac{\mathrm{x}\mathrm{x}}{\mathrm{a}}& +& \frac{{\mathrm{x}}^3}{\mathrm{a}\mathrm{a}}& +& \frac{{\mathrm{x}}^4}{{\mathrm{a}}^3}& \phantom{+}& \text{\&c}\\ +\frac{{\mathrm{x}}^4}{4\mathrm{a}\mathrm{a}}& \text{.}\end{array}\right.$
radicem ad usqꝫ periodum ${\mathrm{x}}^6$ desiderem, mitto terminos in infinitum post $-\mathrm{y}in\mathrm{a}+\mathrm{x}+\frac{\mathrm{x}\mathrm{x}}{\mathrm{a}}$ et isthanc tantùm <13> $\mathrm{y}\mathrm{y}-\mathrm{a}\mathrm{y}-\mathrm{x}\mathrm{y}+\frac{\mathrm{x}\mathrm{x}}{\mathrm{a}}\mathrm{y}+\frac{{\mathrm{x}}^4}{4\mathrm{a}\mathrm{a}}=0$, sive id fiat hâc lege $\mathrm{y}=\frac{1}{2}\mathrm{a}+\frac{1}{2}\mathrm{x}+\frac{\mathrm{x}\mathrm{x}}{2\mathrm{a}}-\sqrt{}\stackrel{\_}{\frac{1}{4}\mathrm{a}\mathrm{a}+\frac{1}{2}\mathrm{a}\mathrm{x}+\frac{3}{4}\mathrm{x}\mathrm{x}+\frac{{\mathrm{x}}^3}{2\mathrm{a}}}$, ut solet, sive expeditiùs per methodum de affectis æquationibus jam traditam, resolvo; et exit $\mathrm{y}=\frac{{\mathrm{x}}^4}{4{\mathrm{a}}^3}-\frac{{\mathrm{x}}^5}{4{\mathrm{a}}^4}\ast$, ultimo desiderato termino existente nullo.

Postquam verò radices ad convenientem periodum extractæ sunt, poss{illeg}s plerumqꝫ \possunt aliquando/, ex analogiâ seriei observatâ, ad placitum produci{illeg}. Sic hanc $\mathrm{z}+\frac{1}{2}\mathrm{z}\mathrm{z}+\frac{1}{6}{\mathrm{z}}^3+\frac{1}{24}{\mathrm{z}}^4+\frac{1}{120}{\mathrm{z}}^5\text{\&c}$ (radicem æquationis infinitæ $\mathrm{x}=\mathrm{y}+\frac{1}{2}\mathrm{y}\mathrm{y}+\frac{1}{3}{\mathrm{y}}^3\text{\&c}$) perpetuò produces dividendo ultimum terminum per hos ordine numeros $2,3,4,5,6,7$ &c. Et hanc $\mathrm{z}-\frac{1}{6}{\mathrm{z}}^3+\frac{1}{120}{\mathrm{z}}^5-\frac{1}{5040}{\mathrm{z}}^7$$+\frac{1}{362880}{\mathrm{z}}^9\text{\&c}$ dividendo per hos $2\times 3,4\times 5,6\times 7,8\times 9$ &c [Et hanc $\mathrm{a}+\frac{\mathrm{x}\mathrm{x}}{2\mathrm{a}}-\frac{{\mathrm{x}}^4}{8{\mathrm{a}}^3}+\frac{{\mathrm{x}}^6}{16{\mathrm{a}}^5}-\frac{5{\mathrm{x}}^8}{128{\mathrm{a}}^7}\text{\&c}$ multiplicando per hos $\frac{1}{\hfill 2}.\frac{-1}{\hfill 4}.\frac{-3}{\hfill 6}.\frac{-5}{\hfill 8}.\frac{-7}{\hfill 10}$ &c.] Et sic in alijs.

Cæterùm in in{illeg}|v|entione primi termini quotientis et nonnunquam secundi tertijve difficultat|s|is etiamnum enodanda superest. Potest enim valor ejus secundum præcedentia quæsitus esse surda sive inextricabilis radix æquationis multipliciter affectæ. Quod cùm accidit, modò non sit insuper impossibilis, illum literâ aliquâ designabis, dein operabere tanquam si {illeg}cognitum haberes. Quemadmodu in exemplo ${\mathrm{y}}^3+\mathrm{a}\mathrm{x}\mathrm{y}+\mathrm{a}\mathrm{a}\mathrm{y}-{\mathrm{x}}^3-2{\mathrm{a}}^3=0$, si radix hujus ${\mathrm{y}}^3+\mathrm{a}\mathrm{a}\mathrm{y}-2{\mathrm{a}}^3=0$ fuisset surda vel ignota finxissem quamlibet $\left(\mathrm{b}\right)$, pro ea ponendam esse, et resolutionem \(puta ad tertiam dimensionem )|q|uotientis)/ ut sequitur perfecissem.

$$\begin{array}{l}\begin{array}{rr}\phantom{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_}& \phantom{\_}\\ & \left(\mathrm{b}-\frac{\mathrm{a}\mathrm{b}\mathrm{x}}{\mathrm{c}\mathrm{c}}+\frac{{\mathrm{a}}^4\mathrm{b}\mathrm{x}\mathrm{x}}{{\mathrm{c}}^6}+\frac{{\mathrm{x}}^3}{\mathrm{c}\mathrm{c}}+\frac{{\mathrm{a}}^4{\mathrm{b}}^3{\mathrm{x}}^3}{{\mathrm{c}}^8}-\frac{{\mathrm{a}}^5\mathrm{b}{\mathrm{x}}^3}{{\mathrm{c}}^8}+\frac{6{\mathrm{a}}^5{\mathrm{b}}^3{\mathrm{x}}^3}{{\mathrm{c}}^{10}}\text{.}\right.\hfill \end{array}\\ \begin{array}{rr}\phantom{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_}& \phantom{\_}\\ \begin{array}{rr}\mathrm{b}+\mathrm{p}=\mathrm{y}\text{.}\phantom{0000000}& \phantom{{\mathrm{b}}^0}+{\mathrm{y}}^3\\ & \phantom{\mathrm{b}}+\mathrm{a}\mathrm{x}\mathrm{y}\\ & \phantom{\mathrm{b}}+\mathrm{a}\mathrm{a}\mathrm{y}\\ & -{\mathrm{x}}^3\\ & -2{\mathrm{a}}^3\end{array}& \begin{array}{llllllll}+& {\mathrm{b}}^3& +& 3\mathrm{b}\mathrm{b}\mathrm{p}& +& 3\mathrm{b}\mathrm{p}\mathrm{p}& +& {\mathrm{p}}^3\\ +& \mathrm{a}\mathrm{b}\mathrm{x}& +& \mathrm{a}\mathrm{x}\mathrm{p}\\ +& \mathrm{a}\mathrm{a}\mathrm{b}& +& \mathrm{a}\mathrm{a}\mathrm{p}\\ -& {\mathrm{x}}^3\\ -& 2{\mathrm{a}}^3\end{array}\hfill \end{array}\\ \begin{array}{rr}\phantom{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_}& \phantom{\_}\\ \begin{array}{rr}\phantom{\frac{{\mathrm{b}}^0}{{\mathrm{c}}^0}}\frac{-\mathrm{a}\mathrm{b}\mathrm{x}}{\mathrm{c}\mathrm{c}}+\mathrm{q}=\mathrm{p}\text{.}\phantom{00000}& +{\mathrm{p}}^3\\ & \phantom{\frac{{\mathrm{b}}^0}{{\mathrm{c}}^0}}+3\mathrm{b}\mathrm{p}\mathrm{p}\\ & \phantom{\frac{\mathrm{b}}{\mathrm{c}}}+\mathrm{a}\mathrm{x}\mathrm{p}\\ & \phantom{\mathrm{b}}+\mathrm{c}\mathrm{c}\mathrm{p}\\ & -{\mathrm{x}}^3\\ & +\mathrm{a}\mathrm{b}\mathrm{x}\end{array}& \begin{array}{llll}-& \frac{{\mathrm{a}}^3{\mathrm{b}}^3{\mathrm{x}}^3}{{\mathrm{c}}^6}& \phantom{+}& \text{\&c}\\ +& \frac{3\mathrm{a}\mathrm{a}{\mathrm{b}}^3\mathrm{x}\mathrm{x}}{{\mathrm{c}}^4}& -& \frac{6\mathrm{a}\mathrm{b}\mathrm{b}\mathrm{x}}{\mathrm{c}\mathrm{c}}\mathrm{q}& \phantom{+}& \text{\&c}\\ -& \frac{\mathrm{a}\mathrm{a}\mathrm{b}\mathrm{x}\mathrm{x}}{\mathrm{c}\mathrm{c}}& +& \mathrm{a}\mathrm{x}\mathrm{q}\\ -& \mathrm{a}\mathrm{b}\mathrm{x}& +& \mathrm{c}\mathrm{c}\mathrm{q}\\ -& {\mathrm{x}}^3\\ +& \mathrm{a}\mathrm{b}\mathrm{x}\end{array}\hfill \end{array}\\ \begin{array}{c}\phantom{\_}\\ \left.\mathrm{c}\mathrm{c}+\mathrm{a}\mathrm{x}-\frac{6\mathrm{a}\mathrm{b}\mathrm{b}\mathrm{x}}{\mathrm{c}\mathrm{c}}\mathrm{z}\mathrm{z}\right)\frac{{\mathrm{a}}^4\mathrm{b}\mathrm{x}\mathrm{x}}{{\mathrm{c}}^4}+{\mathrm{x}}^3+\frac{{\mathrm{a}}^3{\mathrm{b}}^3{\mathrm{x}}^3}{{\mathrm{c}}^6}\left(\frac{{\mathrm{a}}^4\mathrm{b}\mathrm{x}\mathrm{x}}{{\mathrm{c}}^6}+\frac{{\mathrm{x}}^3}{\mathrm{c}\mathrm{c}}+\frac{{\mathrm{a}}^3{\mathrm{b}}^3{\mathrm{x}}^3}{{\mathrm{c}}^8}\text{\&c}\right.\\ \phantom{\_}\end{array}\end{array}$$

<14>

Scribens b in quotiente suppono $\mathrm{b}+\mathrm{p}=\mathrm{y}$ & pro y substituo ut vides: unde prodit ${\mathrm{p}}^3+3\mathrm{b}\mathrm{p}\mathrm{p}$ &c, rejectis terminis ${\mathrm{b}}^3+\mathrm{a}\mathrm{a}\mathrm{b}$$-2{\mathrm{a}}^3$, qui nihilo sunt æquales propterea quod b supponitur radix hujus ${\mathrm{y}}^3+\mathrm{a}\mathrm{a}\mathrm{y}-2{\mathrm{a}}^3=0$. Deinde termini $3\mathrm{b}\mathrm{b}\mathrm{p}+\mathrm{a}\mathrm{a}\mathrm{p}$$+\mathrm{a}\mathrm{b}\mathrm{x}$ dant $\frac{-\mathrm{a}\mathrm{b}\mathrm{x}}{3\mathrm{b}\mathrm{b}+\mathrm{a}\mathrm{a}}$, quotienti apponendum & $\frac{-\mathrm{a}\mathrm{b}\mathrm{x}}{3\mathrm{b}\mathrm{b}+\mathrm{a}\mathrm{a}}+\mathrm{q}$ substituendum pro p. Brevitatis autem gratiâ scribo $\mathrm{c}\mathrm{c}$ pro $3\mathrm{b}\mathrm{b}+\mathrm{a}\mathrm{a}$, cavendo tamen ut $3\mathrm{b}\mathrm{b}+\mathrm{a}\mathrm{a}$ restituatur ubi terminos sic abbreviari posse percipiam. Completo opere assumo numerum aliquem pro a, et hanc ${\mathrm{y}}^3+\mathrm{a}\mathrm{a}\mathrm{y}$$-2{\mathrm{a}}^3=0$ (sicut de numerali æquatione ostensum supra) resolvo, et quamvis \quamlibet/ ejus radicem (modo tres haberet) pro b substituo. Vel potiùs hujusmodi æquationes a speciebus, ut possum, libero, præsertim ab indefinitâ; idqꝫ pro morequem volui innuere pag 9 lin 14: et pro cæteris tantùm (siquæ supersint indelebiles) pono numeros. Sic ${\mathrm{y}}^3+\mathrm{a}\mathrm{a}\mathrm{y}-2{\mathrm{a}}^3=0$ liberabitur ab a dividendo radicem per a, fietqꝫ ${\mathrm{y}}^3+\mathrm{y}-2=0$, cujus {illeg}|i|nventa radix ducta in a substitui debet pro b.

Hactenus indefinitam speciem suposui parvam esse. Quod si datæ quantitati vicina supponatur, pro indefinitè parvâ differentiâ pono speciem aliquam, et hâc substitutâ, solvo ut ante. Quemadmodum in $\frac{1}{5}{\mathrm{y}}^5-\frac{1}{4}{\mathrm{y}}^4+\frac{1}{3}{\mathrm{y}}^3-\frac{1}{2}{\mathrm{y}}^2$$+\mathrm{y}-\mathrm{a}-\mathrm{x}=0$, cognito vel ficto x esse ejusdem prope quantitatis ac a, pono z differentiam ex \inter ea/, & scribendo $\mathrm{a}+\mathrm{z}$, {illeg} {illeg} |vel $\mathrm{a}-\mathrm{z}$| pro x, orietur $\frac{1}{5}{\mathrm{y}}^5-\frac{1}{4}{\mathrm{y}}^4+\frac{1}{3}{\mathrm{y}}^3-\frac{1}{2}{\mathrm{y}}^2+\mathrm{y}-\; vel\; +\mathrm{z}=0$ solvendum ut in præcedentibus.

Si verò species illa \supponatur/ indefinitè magna, pro reciproco ejus indefinitè parvo pono speciem \aliquam/, et hâc substitutâ, solvo ut ante. Sic in {illeg} ${\mathrm{y}}^3+{\mathrm{y}}^2+\mathrm{y}=0$, cognito vel ficto z esse valde magnum, pro reciprocè parvo $\frac{1}{\mathrm{z}}$ pono x, et substituto $\frac{1}{\mathrm{x}}$ pro z {illeg}|o|rietur $\frac{1}{5}{\mathrm{y}}^5$$-\frac{1}{4}{\mathrm{y}}^4+\frac{1}{3}{\mathrm{y}}^3-\frac{1}{2}\mathrm{y}\mathrm{y}+\mathrm{y}-\frac{1}{\mathrm{x}}=0$ sive {illeg} {illeg}$=0$, cujus radix secundum præcedentia extrahitur fitqꝫ $\sqrt{}5:\frac{5}{\mathrm{x}}+\frac{1}{4}-\frac{1}{8}\sqrt{}5:\mathrm{x}-\frac{1}{12}\sqrt{}5:5\mathrm{x}\text{\&c}$.

Sin autem species ilia supponatur indefinite magna, pro reciproco ejus indefinitè parvo pono speciem aliquam, quâ substitutâ solvo ut ante. Sic habito ${\mathrm{y}}^3+{\mathrm{y}}^2+\mathrm{y}-{\mathrm{x}}^3=0$ ubi x cognoscitur vel fingitur esse valde magnum, <15> pro reciprocè parvo $\frac{1}{\mathrm{x}}$ pono z, et substituto $\frac{1}{\mathrm{z}}$ pro x, orietur ${\mathrm{y}}^3+\mathrm{y}\mathrm{y}+\mathrm{y}-\frac{1}{{\mathrm{z}}^3}=0$, cujus radix est $\frac{1}{\mathrm{z}}-\frac{1}{3}-\frac{2}{9}\mathrm{z}+\frac{7}{81}\mathrm{z}\mathrm{z}+\frac{5}{81}{\mathrm{z}}^3\text{\&c.}$ {illeg} et x si plat|c|et restituto fit $\mathrm{y}=\mathrm{x}-\frac{1}{3}-\frac{2}{9\mathrm{x}}+\frac{7}{81\mathrm{x}\mathrm{x}}+\frac{5}{81{\mathrm{x}}^3}\text{\&c}${.}

Siquando ex aliquâ harum trium suppositionum res non {illeg}omninò aut non commodè succedat, ad aliam recurri potest. Quemadmodum \Sic/ in ${\mathrm{y}}^4-\mathrm{x}\mathrm{x}\mathrm{y}\mathrm{y}+\mathrm{x}\mathrm{y}\mathrm{y}+2\mathrm{y}\mathrm{y}-2\mathrm{y}+1=0$ {illeg} \cùm/ primus terminus obtineri debet|a|t \deberet/ fingendo ${\mathrm{y}}^4+2\mathrm{y}\mathrm{y}-2\mathrm{y}+1=0$, quæ tamen nullam admittit possibilem radicem, Tento {illeg}qꝫ quid fiet aliter: quemadmodum si fingam x parùm differre a $+2$ sive \esse/ $2+\mathrm{z}=\mathrm{x}$, substituendo \$2+\mathrm{z}$ vice x/ prodibit ${\mathrm{y}}^4-\mathrm{z}\mathrm{z}\mathrm{y}\mathrm{y}-2\mathrm{z}\mathrm{y}\mathrm{y}$$-2\mathrm{y}+1=0$, et quotiens exordietur ab $+1$. Vel si fingam x indefinitè magnam esse, sive $\frac{1}{\mathrm{x}}=\mathrm{z}$, obtinebitur ${\mathrm{y}}^4-$$\frac{\mathrm{y}\mathrm{y}}{\mathrm{z}\mathrm{z}}+\frac{\mathrm{y}\mathrm{y}}{\mathrm{z}}+2\mathrm{y}\mathrm{y}-2\mathrm{y}+1=0$, & $+\mathrm{z}$ pro initio quotientis. Et hac ratione secundum varias Hypotheses procedendo, licebit varijs modis extrahere ac designare radices.

Quod si cupias explorare quot modis id potest fieri, tentabis quænam quantitates pro indefinitâ specie in æquationem propositam substitutæ, efficient divisibilem per y + vel − aliquâ quantitate vel per y solum. Id quod verbi gratia in æquatione ${\mathrm{y}}^3+\mathrm{a}\mathrm{x}\mathrm{y}+\mathrm{a}\mathrm{a}\mathrm{y}-{\mathrm{x}}^3-2{\mathrm{a}}^3=0$ eveniet substituendo $+\mathrm{a}$, vel $-\mathrm{a}$, vel $-2\mathrm{a}$, vel $\sqrt{}c:-2{\mathrm{a}}^3$, &c \pro y/. Atqꝫ ad{illeg} \ita/ possis commodè supponere quantitatem x parùm ab $+\mathrm{a}$, vel $-\mathrm{a}$, vel $-2\mathrm{a}$, vel $\sqrt{}c:-2{\mathrm{a}}^3$ differre, et \inde/ radicem propositæ æquationis tot modis extrahere. Imò et fortasse tot alijs mo{illeg}|d|is fingendo differentias istas esse indefinitè magnas. Quinetiam si aliam atqꝫ aliam e speciebus radice definientibus pro indefinitâ adhibeas, possis alijs adhuc fortassè modis propositum consequi; et etiamnum alijs substituendo valores quâcunqꝫ ratione fictos et (quales sunt $\mathrm{a}\mathrm{z}+\mathrm{b}\mathrm{z}\mathrm{z}$, $\frac{\mathrm{a}}{\mathrm{b}+\mathrm{z}}$, $\frac{\mathrm{a}+\mathrm{c}\mathrm{z}}{\mathrm{b}+\mathrm{z}}$ &c) pro indefinitâ specie & in æquatione resultante operando sicut in præcedentibus.

Cæterùm ut conclusionum veritas constet, quotientes nempe sic extractos, dum producuntur, ita propiùs ad radicem accedere, ut minùs tandem quâvis datâ quantitate differant, adeóqꝫ in infinitum productos non omninò differre: perpende <16> \quod/ quantitates in sinistrâ columnâ dextræ partis diagrammatum, quòd sint ultimi termini æquationum quarum p, q, r, s, &c existunt radices et inde quòd ipsis evanescentibus, illæ p, q, r, s, id est differentiæ \inter/ quotient{illeg}|e| {illeg}|&| quæsita radice, simul evanescunt. Adeóqꝫ quotiens tunc non differt a radice. Quamobrem sub initio operis si terminos in dictâ columnâ sese omnes destruere videas, conclude quotientem eatinus extractam, esse justam radicem. Sin aliter, videbis tamen terminos in quibus {illeg} est indefinite parva species est pauciorum dimensionum, id est longè maximos, e columna ista perpetuò tolli, ut tandem non restent nisi datâ quâvis quantitate minores, et proinde non majores nihilo cùm opus infinitè producitur. Quare quoti{illeg}ens infinitè extracta fiet etiam justa radix.

[Etsi deniqꝫ species, quam|s| hactenus perspicuitatis gra supposui indefinitè parva{illeg}|s|{illeg} esse, quantumvis magnæ supponàtur, \tamen veræ erunt/ quotientu|es|m, ut ut minùs citò ad justam radicem converge|a|ntium veritas tamen \ad ve/ \quemadmodum/ ex analogiâ rei consta|e|bit. Sed hic radicum termini, maximæqꝫ et minimæ quantitates spectandæ veniunt: Nam infinitarum cum finitis asquationibus communia sunt hujusmodi symptomata {illeg}. Radi{illeg}|x| autem in his maxima fit vel minima quando maxima vel minima est differentia summæ affirmativorum terminorum a summâ negativorum, ac terminatur cùm indefinita parva quantitas \(quam {illeg}|ideò| parvam esse non immeritò finxi)/ non potest major sumi quam quin magnitudo radicis in infinitum prosiliet, ho{illeg}|c| est fiet impossibilis. Verbi gratiâ posito ACD semicirculo super diametro AD descripto, et BC ordinatim applicatâ: Dic $\mathrm{AB}=\mathrm{x}$ {illeg} \$\mathrm{BC}=\mathrm{y}$/ $\mathrm{AD}=\mathrm{a}$ et {illeg} erit 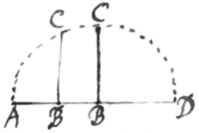$\mathrm{y}=\left(\sqrt{}\stackrel{\_}{\mathrm{a}\mathrm{x}-\mathrm{x}\mathrm{x}}=\right)\sqrt{}\mathrm{a}\mathrm{x}-\frac{\mathrm{x}}{2\mathrm{a}}\sqrt{}\mathrm{a}\mathrm{x}-\frac{\mathrm{x}\mathrm{x}}{8\mathrm{a}\mathrm{a}}\sqrt{}\mathrm{a}\mathrm{x}$ $-\frac{{\mathrm{x}}^3}{16{\mathrm{a}}^3}\sqrt{}\mathrm{a}\mathrm{x}\text{\&c}$. Fitqꝫ \ergo/ BC sive y maxima cum $\sqrt{}\mathrm{a}\mathrm{x}$ maximè superat omnes $\frac{\mathrm{x}}{2\mathrm{a}}\sqrt{}\mathrm{a}\mathrm{x}+\frac{\mathrm{x}\mathrm{x}}{8\mathrm{a}\mathrm{a}}\sqrt{}\mathrm{a}\mathrm{x}+\frac{{\mathrm{x}}^3}{16{\mathrm{a}}^3}\sqrt{}\mathrm{a}\mathrm{x}\text{\&c}$, id est cùm sit $\mathrm{x}=\frac{1}{2}\mathrm{a}$: terminabitur autem cùm sit $\mathrm{x}=\mathrm{a}$ s|q|uia si sumas {sic} $\mathrm{x}\stackrel{\_}{\underset{\_}{|\phantom{\_}}\phantom{\_}}\mathrm{a}$, summa omnium terminorum $-\frac{\mathrm{x}}{2\mathrm{a}}\sqrt{}\mathrm{a}\mathrm{x}-\frac{\mathrm{x}\mathrm{x}}{8\mathrm{a}\mathrm{a}}\sqrt{}\mathrm{a}\mathrm{x}-\frac{{\mathrm{x}}^3}{16{\mathrm{a}}^3}\sqrt{}\mathrm{a}\mathrm{x}\text{\&c}$ erit infinita. Est et alius ter{illeg}|m|inus cùm ponitur $\mathrm{x}=0$, propter impossibilitatem radicalis $\sqrt{}-\mathrm{a}\mathrm{x}$; {illeg}|Q|uibus terminis correspondent semicirculi limites A et D.] Et hic differentia inter in finitas

<17>

Hactenus de modis computandi quorum poshac {sic} frequens erit usus: Jam restat ut in illustrationem hujus Artis \Analyticæ/ tradam aliquot Problematum specimina qualia præsertim natura curvarum ministrabit. Sed imprimis observandum venit quod hujusmodi difficultates possunt omnes ad hæc duo tantùm problemata reduci quæ circa spatium motu locali utcunqꝫ accelerato vel retardato descriptum proponere licebit.

1. Spatij longitudine continuò (sive ad omne τα νυν \tempus/) data, celeritatem motûs ad tempus propositum invenire.

2. Celeritate motûs continuò datâ longitudinem spatij \2/ {illeg}descripti \1/ ad tempus propositum invenire.

Sic in æquatione $\mathrm{x}\mathrm{x}=\mathrm{y}$ si y designat spatij longitudinem ad quodlibet tempus quod aliud spatium x uniformi celeritate in crescendo mensurat et exhibet descriptam: tunc $2\mathrm{m}\mathrm{x}$ designabit celeritatem qua spatium y ad idem temporis momentum describi pergit; et contra. Et hinc est quod in sequentibus considero|e|m quantitates quasi generatæ essent per incrementum continuum ad modum spatij quod mobile percurrendo describit{.}

Cùm autem temporis nullam habe|a|mus æstimationem nisi quatenus, \id/ per æquabilem motum localem exponitur et mensuratur, et præterea cùm quantitates ejusdem tantùm generis inter se conferri possint et earum incrementi et decrementi celeritates inter se, \eapropter ad tempus formaliter spectatum in sequentibus haud respiciam, sed e propositis quantitatibus quæ sunt ejusdem generis aliquam/ quantitatum aliquam {sic} æquabili fluxione ad generatam augeri debemus fingere|am| quæ cui cæteræ tant|q|uam tempori referantur, adeoqꝫ cui nomen temporis analogie|c|è tribui mereatur. Siquando itaqꝫ vocabulum temporis in sequentibus occurrat (quemadmodum perspicuitatis et distinctionis gratia nonn{illeg}|u|{illeg}|quàm| intertexui) eo nomine non tempus formaliter spectatum subintelligi debet sed illa alia quantitas cujus æquabili incremento sive fluxione tempus exponitur et mensuratur.

Quantitates autem quas ut {illeg}|se|nsim crescentes indefinitè considero, quo distinguam ab alijs quantitatibus quæ in æquationibus quibuscunqꝫ pro determinatis et cognitis habendæ sunt ac <18> initialibus literis a, b, c, &c designantur, posthac denominabo fluentes, ac designabo finalibus literis v, x, y, et z. Et celeritates {illeg} quibus singulæ \a motu generante/ fluunt et augentur (quas possim fluxiones vel simpliciter celeritates vocita{illeg}|r|e) designabo literis l, m, n et r. Nemp{e} pro celeritate quantitatis v ponam l et sic pro celeritatibus aliarum quantitatum x, y, et z ponam m, n, et r respectivè. His præmissis, e vestigio rem aggredior, imprimis duorum jam modo propositoru problematum solutionem exhibiturus.

Prob: 1.
Relatione quantitatum fluentium inter se datâ, fluxionum relationem determinare.
Solutio.

Æquationem qua data relatio exprimitur dispone secundum dimensiones alicujus fluentis quantitatis puta x, ac terminos ejus multiplica per quamlibet Arithmeticam progressionem ac deinde per $\frac{\mathrm{m}}{\mathrm{x}}$. Et hoc opus in qualibet fluenti quantitate seorsim institue. Dein omnium factorum summam pone nihilo æqualem, et habes æquationem desideratam.

Exemp: 1. Si quantitatum x et y relatio sit ${\mathrm{x}}^3-\mathrm{a}\mathrm{x}\mathrm{x}+\mathrm{a}\mathrm{x}\mathrm{y}-{\mathrm{y}}^3$$=0$, terminos primò secundum x ad|c| deinde secund{illeg}|u|m y dispositos multiplico ad hunc modum.
$$\begin{array}{cc}\begin{array}{cccccccccc}\text{Mult:}& {\mathrm{x}}^3& -& \mathrm{a}\mathrm{x}\mathrm{x}& +& \mathrm{a}\mathrm{x}\mathrm{y}& -& {\mathrm{y}}^3& \text{.}& \phantom{\begin{array}{cc}-& 0\\ +& {\mathrm{x}}^0\end{array}\text{.}}\\ \text{per}& \frac{3\mathrm{m}}{\mathrm{x}}\text{.}& & \frac{2\mathrm{m}}{\mathrm{x}}\text{.}& & \frac{\mathrm{m}}{\mathrm{x}}\text{.}& & 0& \text{.}\\ \text{fit}& 3\mathrm{m}\mathrm{x}\mathrm{x}& -& 2\mathrm{m}\mathrm{a}\mathrm{x}& +& \mathrm{m}\mathrm{a}\mathrm{y}\text{.}& & \ast & \text{.}\end{array}& \begin{array}{cccccccc}\phantom{\begin{array}{cc}-& 0\\ +& {\mathrm{x}}^0\end{array}\text{.}}& \text{Mult}& -& {\mathrm{y}}^3& +& \mathrm{a}\mathrm{x}\mathrm{y}& \begin{array}{cc}-& \mathrm{a}\mathrm{x}\mathrm{x}\\ +& {\mathrm{x}}^3\end{array}& \text{.}\\ & \text{per}& & \frac{3\mathrm{n}}{\mathrm{y}}\text{.}& & \frac{\mathrm{n}}{\mathrm{y}}\text{.}& \begin{array}{cc}\phantom{+}& 0\end{array}& \text{.}\\ & \text{fit}& -& 3\mathrm{n}\mathrm{y}\mathrm{y}& +& \mathrm{a}\mathrm{n}\mathrm{x}\text{.}& \begin{array}{cc}\phantom{+}& \ast \end{array}& \text{.}\end{array}\end{array}$$
Et factorum summa est $3\mathrm{m}\mathrm{x}\mathrm{x}-2\mathrm{a}\mathrm{m}\mathrm{x}+\mathrm{a}\mathrm{m}\mathrm{y}-3\mathrm{n}\mathrm{y}\mathrm{y}+\mathrm{a}\mathrm{n}\mathrm{x}=0\text{.}$ æquatio quæ dat relationem inter fluxiones m et n. Nempe si assumas x ad arbitrium, æquatio ${\mathrm{x}}^3-\mathrm{a}\mathrm{x}\mathrm{x}+\mathrm{a}\mathrm{x}\mathrm{y}-{\mathrm{y}}^3=0$ dabit y. Quibus determinatis erit $\mathrm{m}.\mathrm{n}\colon\colon 3\mathrm{y}\mathrm{y}-\mathrm{a}\mathrm{x}.3\mathrm{x}\mathrm{x}-2\mathrm{a}\mathrm{x}+\mathrm{a}\mathrm{y}$.

Exempl 2. Si quantitatum x, y, et z relatio sit $2{\mathrm{y}}^3+\mathrm{x}\mathrm{x}\mathrm{y}-2\mathrm{c}\mathrm{y}\mathrm{z}+3\mathrm{y}\mathrm{z}\mathrm{z}-{\mathrm{z}}^3=0$,
$$\begin{array}{ccc}\begin{array}{cccccc}\text{Mult}& 2{\mathrm{y}}^3& \begin{array}{ll}+& \mathrm{x}\mathrm{x}\\ -& 2\mathrm{c}\mathrm{z}\\ +& 3\mathrm{z}\mathrm{z}\end{array}\mathrm{y}& -& {\mathrm{z}}^3& \text{.}\\ \text{per}& \frac{2\mathrm{n}}{\mathrm{y}}\text{.}& 0\text{.}& -& \frac{\mathrm{n}}{\mathrm{y}}& \text{.}\\ \text{fit}& 4\mathrm{n}\mathrm{y}\mathrm{y}& \ast & +& \frac{\mathrm{n}{\mathrm{z}}^3}{\mathrm{y}}& \text{.}& \phantom{\frac{0^0}{0}}\end{array}& \begin{array}{ccccc}& \text{Mult}& \mathrm{x}\mathrm{y}\mathrm{y}& \begin{array}{ll}+& 2{\mathrm{y}}^3\\ -& 2\mathrm{c}\mathrm{y}\mathrm{z}\\ +& 3\mathrm{y}\mathrm{z}\mathrm{z}\\ -& {\mathrm{z}}^3\end{array}& \text{.}\\ & \text{per}& \frac{2\mathrm{m}}{\mathrm{x}}\text{.}& 0& \text{.}& \phantom{\frac{0^0}{0}}\\ \phantom{\frac{0^0}{0}}& \text{fit}& 2\mathrm{m}\mathrm{x}\mathrm{y}& \ast & \text{.}& \phantom{\frac{0^0}{0}}\end{array}& \begin{array}{cccccccccc}& \text{Mult}& -& {\mathrm{z}}^3& +& 3\mathrm{y}\mathrm{z}\mathrm{z}& -& 2\mathrm{c}\mathrm{y}\mathrm{z}& \begin{array}{ll}+& \mathrm{x}\mathrm{x}\mathrm{y}\\ +& 2{\mathrm{y}}^3\end{array}& \text{.}\\ & \text{per}& & \frac{3\mathrm{r}}{\mathrm{z}}\text{.}& & \frac{2\mathrm{r}}{\mathrm{z}}\text{.}& & \frac{\mathrm{r}}{\mathrm{z}}\text{.}& 0& \text{.}\\ \phantom{\frac{0^0}{0}}& \text{fit}& -& 3\mathrm{r}\mathrm{z}\mathrm{z}& +& 6\mathrm{r}\mathrm{y}\mathrm{z}& -& 2\mathrm{c}\mathrm{r}\mathrm{y}& \ast & \text{.}\end{array}\end{array}$$
Qu{illeg}|a|re fluendi celeritatum m n et r relatio est $4\mathrm{n}\mathrm{y}\mathrm{y}+\frac{\mathrm{n}{\mathrm{z}}^3}{\mathrm{y}}+2\mathrm{m}\mathrm{x}\mathrm{y}$$-3\mathrm{r}\mathrm{z}\mathrm{z}+6\mathrm{r}\mathrm{y}\mathrm{z}-2\mathrm{c}\mathrm{r}\mathrm{y}=0$.

Cæterùm cùm tres s{illeg}|i|nt hic fluentes quantitates x, y, et z deberet alia insuper æquatio dari qua relatio inter ipsas ut et inter earum fluxiones penitiùs determinetur. Quemadmodum si ponitur esse $\mathrm{x}+\mathrm{y}-\mathrm{z}=0\text{.}$ exinde fluxionum alia relatio juxta Regulam erit $\mathrm{m}+\mathrm{n}-\mathrm{r}=0\text{.}$ Confer <19> jam hasce cum præcedentibus æquationibus, eliminando quamlibet e tribus quantitatibus et quo|a|d\m/libet \etiam/ e tribus earum momentis \fluxionibus/, et reliquorum relationes penitiùs determinatas obtinebis.

Siquando in æquatione propositâ insint fractiones intricatæ \complexæ/ aut surdæ quantitates, pro singulis pono totidem literas, easqꝫ fingens designare quantitates mutabiles \fluentes/, operor ut ante. Dein supprimo \et extermino/ literas ascriptitias, ut hi{illeg}|c| videre est{.}

Exempl: 3. Si quantitatum x et y relatio sit $\mathrm{y}\mathrm{y}-\mathrm{a}\mathrm{a}-\mathrm{x}\sqrt{}\stackrel{\_}{\mathrm{a}\mathrm{a}-\mathrm{x}\mathrm{x}}$: pro $\mathrm{x}\sqrt{}\stackrel{\_}{\mathrm{a}\mathrm{a}-\mathrm{x}\mathrm{x}}$ {illeg} scribo z et inde habeo duas æquationes $\mathrm{y}\mathrm{y}-\mathrm{a}\mathrm{a}-\mathrm{z}=0$, et $\mathrm{a}\mathrm{a}\mathrm{x}\mathrm{x}-{\mathrm{x}}^4-\mathrm{z}\mathrm{z}=0$ quarum prior {illeg}|u|t ante dabit $2\mathrm{n}\mathrm{y}-\mathrm{r}=0$ pro relatione momentorum \fluxionum celeritatum/ n et r, et posterior dabit $2\mathrm{a}\mathrm{a}\mathrm{m}\mathrm{x}-4\mathrm{m}{\mathrm{x}}^3-2\mathrm{r}\mathrm{z}=0$ sive $\frac{\mathrm{a}\mathrm{a}\mathrm{m}\mathrm{x}-2\mathrm{m}{\mathrm{x}}^3}{\mathrm{z}}=\mathrm{r}$ pro relatione momentorum \celeritatum/ m et r. Jam r suppresso fiet $2\mathrm{n}\mathrm{y}\frac{-\mathrm{a}\mathrm{a}\mathrm{m}\mathrm{x}+2\mathrm{m}{\mathrm{x}}^3}{\mathrm{z}}=0$, & \{illeg}|d|ein/ restituto $\mathrm{x}\sqrt{}\stackrel{\_}{\mathrm{a}\mathrm{a}-\mathrm{x}\mathrm{x}}$ pro z habebitur $2\mathrm{n}\mathrm{y}\frac{-\mathrm{a}\mathrm{a}\mathrm{m}+2\mathrm{m}\mathrm{x}\mathrm{x}}{\sqrt{}\stackrel{\_}{\mathrm{a}\mathrm{a}-\mathrm{x}\mathrm{x}}}=0$ relatio inter m et n quæ quærebatur.

Exempl: 4. Si ${\mathrm{x}}^3-\mathrm{a}\mathrm{y}\mathrm{y}+\frac{\mathrm{b}{\mathrm{y}}^3}{\mathrm{a}+\mathrm{y}}-\mathrm{x}\mathrm{x}\sqrt{}\stackrel{\_}{\mathrm{a}\mathrm{y}+\mathrm{x}\mathrm{x}}=0$ designat relationem inter x et y: pono z pro $\frac{\mathrm{b}{\mathrm{y}}^3}{\mathrm{a}+\mathrm{y}}$, et v pro $\mathrm{x}\mathrm{x}\sqrt{}\stackrel{\_}{\mathrm{a}\mathrm{y}+\mathrm{x}\mathrm{x}}$ et inde nactus sum tres æquationes ${\mathrm{x}}^3-\mathrm{a}\mathrm{y}\mathrm{y}+\mathrm{z}-\mathrm{v}=0$, $\mathrm{a}\mathrm{z}+\mathrm{y}\mathrm{z}-\mathrm{b}{\mathrm{y}}^3=0$, & $\mathrm{a}{\mathrm{x}}^4\mathrm{y}+{\mathrm{x}}^6-\mathrm{v}\mathrm{v}=0$. Prima dat $3\mathrm{m}\mathrm{x}\mathrm{x}-2\mathrm{a}\mathrm{n}\mathrm{y}+\mathrm{r}-\mathrm{l}=0$, secunda dat $\mathrm{a}\mathrm{r}+\mathrm{r}\mathrm{y}$$+\mathrm{n}\mathrm{z}-3\mathrm{b}\mathrm{n}\mathrm{y}\mathrm{y}=0$, et tertia dat $4\mathrm{a}\mathrm{m}{\mathrm{x}}^3\mathrm{y}+6\mathrm{m}{\mathrm{x}}^5+\mathrm{a}\mathrm{n}{\mathrm{x}}^4-2\mathrm{l}\mathrm{v}=0$ pro relationibus momentorum \celeritatum/ l, m, n et r. Ipsorum verò r et l valores per secundam ac tertiam inventos (nempe $\frac{3\mathrm{b}\mathrm{n}\mathrm{y}\mathrm{y}-\mathrm{n}\mathrm{z}}{\mathrm{a}+\mathrm{y}}$ pro r, et $\frac{4\mathrm{a}\mathrm{m}{\mathrm{x}}^3\mathrm{y}+6\mathrm{m}{\mathrm{x}}^5+\mathrm{a}\mathrm{n}{\mathrm{x}}^4}{2\mathrm{v}}$ pro l) substituo in primam et oritur $3\mathrm{m}\mathrm{x}\mathrm{x}-2\mathrm{a}\mathrm{n}\mathrm{y}\frac{3\mathrm{b}\mathrm{n}\mathrm{y}\mathrm{y}-\mathrm{n}\mathrm{z}}{\mathrm{a}+\mathrm{y}}$$\frac{-4\mathrm{a}\mathrm{m}{\mathrm{x}}^3\mathrm{y}-6\mathrm{m}{\mathrm{x}}^5-\mathrm{a}\mathrm{n}{\mathrm{x}}^4}{2\mathrm{v}}=0$. Et vice z et v restitutis valoribus $\frac{\mathrm{b}{\mathrm{y}}^3}{\mathrm{a}+\mathrm{y}}$ et $\mathrm{x}\mathrm{x}\sqrt{}\stackrel{\_}{\mathrm{a}\mathrm{y}+\mathrm{x}\mathrm{x}}$, prodit æquatio quæsita $3\mathrm{m}\mathrm{x}\mathrm{x}-2\mathrm{a}\mathrm{n}\mathrm{y}\frac{3\mathrm{a}\mathrm{b}\mathrm{n}\mathrm{y}\mathrm{y}+2\mathrm{b}\mathrm{n}{\mathrm{y}}^3}{\mathrm{a}\mathrm{a}+2\mathrm{a}\mathrm{y}+\mathrm{y}\mathrm{y}}\frac{-4\mathrm{a}\mathrm{m}\mathrm{x}\mathrm{y}-6\mathrm{m}{\mathrm{x}}^3-\mathrm{a}\mathrm{n}\mathrm{x}\mathrm{x}}{2\sqrt{}\stackrel{\_}{\mathrm{a}\mathrm{y}+\mathrm{x}\mathrm{x}}}=0$ quâ relatio momentorum \celeritatum/ m et n designatur.

Quo pacto in ali{illeg}|j|s casibus operandum est, quemadmodu cùm in æquatione propositâ reperiuntur surdi denominatores, radicales cubicæ, radicales intra radicales ut $\sqrt{}\stackrel{\_}{\mathrm{a}\mathrm{x}+\sqrt{}\stackrel{\_}{\mathrm{a}\mathrm{a}-\mathrm{x}\mathrm{x}}}$ <20> aut alij ejusmodi perplexi termini, ex his credo manifestum esse. Quinimò si in æquatione quantitates invol{illeg}|van|tur quæ nullâ ratione geometricâ determinari et exprimi possunt, quales sunt areæ vel longitudines curvarum: tamen relationes momentorum \fluxionum/ haud secus investigantur, prout in exemplo sequente manif constabit.

Præparatio in Exemplum 5.

Exempl: 5. Pone BD ordinatam esse 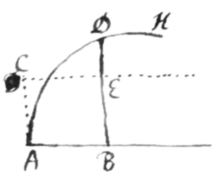in angulo recto ad AB et quod ADH sit curva quæ per relationem inter AB et BD æquatione qualibet exhibitam definitur. AB verò dica{illeg}|tur| {illeg} x et curvæ area ADB ad unitatem applicata dicatur {illeg} z{.} Dein erige perpendiculum AC =|æ|q{illeg}|u|ale unitati et per C {illeg} duc CE parallelam AB et occurrentem BD in E, et concipiendo has duas superficies ADB et ACEB genitas esse per motum rectæ BED, manifestum erit quòd earum momenta \fluxiones/ (hoc est momenta \fluxiones/ quantitatum $1\times \mathrm{z}$ et $1\times \mathrm{x}$, sive quantitatum z et x) sunt inter se ut BD & BE lineæ generantes. Est ergo $\mathrm{r}.\mathrm{m}\colon\colon \mathrm{BD}.\mathrm{BE}$ sive 1, adeóqꝫ $\mathrm{r}=\mathrm{m}\times \mathrm{BD}$. Et hinc fit quod z in æquatione quâlibet designante relationem inter x et aliam quamvis mutabilem \fluentem/ quantitatem y involvi potest, et tamen momentorum \fluxionorum/ m et n relatio nihil minùs inveni{illeg}ri.

Exemplum 5. Quemadmodum si proponitur $\mathrm{z}\mathrm{z}+\mathrm{a}\mathrm{x}\mathrm{z}-$${\mathrm{y}}^4=0$ pro designanda relatione inter x et y, ut et $\sqrt{}\stackrel{\_}{\mathrm{a}\mathrm{x}-\mathrm{x}\mathrm{x}}=\mathrm{BD}$ pro curvâ determinandâ, quæ proin erit circulus: æquatio $\mathrm{z}\mathrm{z}+\mathrm{a}\mathrm{x}\mathrm{z}-{\mathrm{y}}^4=0$ sicut in præcedentibus dabit $2\mathrm{r}\mathrm{z}+\mathrm{a}\mathrm{r}\mathrm{x}+\mathrm{a}\mathrm{m}\mathrm{z}-4\mathrm{n}{\mathrm{y}}^3=0$, pro determinanda relatione momentorum \celeritatum/ m, n, et r. Et præterea cùm sit $\mathrm{r}=\mathrm{m}\times \mathrm{BD}$ sive $\mathrm{m}\sqrt{}\stackrel{\_}{\mathrm{a}\mathrm{x}-\mathrm{x}\mathrm{x}}$, pro eo substitue hunc valore, et orietur $\stackrel{\_}{2\mathrm{m}\mathrm{z}+\mathrm{a}\mathrm{m}\mathrm{x}}\sqrt{}\stackrel{\_}{\mathrm{a}\mathrm{x}-\mathrm{x}\mathrm{x}}+\mathrm{a}\mathrm{m}\mathrm{z}-4\mathrm{n}{\mathrm{y}}^3=0$ æquatio definiens relationem momentorum \celeritatum/ m et n.

Demonstratio.

Fluentium quantitatum momenta (i.e. earum partes indefinitè parvæ quarum additamento per singula temporis indefinita parva spatia augentur,) adeoqꝫ sunt ut fluendi celeritates. Quare si cujusvis ut x momentum per momentum per factum ex {illeg}cel ejus celeritate m et indefinitè parva quantitate o desi{illeg} (i.e. per $\mathrm{m}\mathrm{o}$) designetur, cæterorum v, y, z momenta per $\mathrm{l}\mathrm{o}$, $\mathrm{n}\mathrm{o}$, $\mathrm{r}\mathrm{o}$ designabuntur, siquidem $\mathrm{l}\mathrm{o}$, $\mathrm{m}\mathrm{o}$, $\mathrm{n}\mathrm{o}$, et $\mathrm{r}\mathrm{o}$ sunt <21> inter se ut l, m, n, et r.

Demonstratio

Jam \cùm/ quantitatum fluentium (ut x et y) momenta (ut $\mathrm{m}\mathrm{o}$ et $\mathrm{n}\mathrm{o}$) {illeg} sint additamenta infinitè parva quibus illæ quantitates per singula temporis infinite parva intervalla augentur, sequitur quod quantitates illæ x & y post quodlibet infinite parvum temporis intervallum futuræ sunt $\mathrm{x}+\mathrm{m}\mathrm{o}$ et $\mathrm{y}+\mathrm{n}\mathrm{o}$. e|E|t inde æquatio quæ relationem quantitatum fluentium ad omne tempus indifferenter designat, æque designabit relationem inter $\mathrm{x}+\mathrm{m}\mathrm{o}$ et $\mathrm{y}+\mathrm{n}\mathrm{o}$, ac inter x et y: adeò ut $\mathrm{x}+\mathrm{m}\mathrm{o}$ et $\mathrm{y}+\mathrm{n}\mathrm{o}$ pro quantitatibus istis vice x et y in dictam æquationem substitui poss{illeg}|i|nt.

Detur itaqꝫ quælibet æquatio ${\mathrm{x}}^3-\mathrm{a}\mathrm{x}\mathrm{x}+\mathrm{a}\mathrm{x}\mathrm{y}-{\mathrm{y}}^3=0$, et substitue $\mathrm{x}+\mathrm{m}\mathrm{o}$ pro x et $\mathrm{y}+\mathrm{n}\mathrm{o}$ pro y, et emerget
$\left.\begin{array}{l}\phantom{+}{\mathrm{x}}^3+3\mathrm{m}\mathrm{o}\mathrm{x}\mathrm{x}+3\mathrm{m}\mathrm{m}\mathrm{o}\mathrm{o}\mathrm{x}+{\mathrm{m}}^3{\mathrm{o}}^3\\ -\mathrm{a}\mathrm{x}\mathrm{x}-2\mathrm{a}\mathrm{m}\mathrm{o}\mathrm{x}-\mathrm{a}\mathrm{m}\mathrm{m}\mathrm{o}\mathrm{o}\phantom{0^0}\\ +\mathrm{a}\mathrm{x}\mathrm{y}+\mathrm{a}\mathrm{m}\mathrm{o}\mathrm{y}+\mathrm{a}\mathrm{n}\mathrm{o}\mathrm{x}+\mathrm{a}\mathrm{m}\mathrm{n}\mathrm{o}\mathrm{o}\phantom{0^0}\\ -{\mathrm{y}}^3-3\mathrm{n}\mathrm{o}\mathrm{y}\mathrm{y}-3\mathrm{n}\mathrm{n}\mathrm{o}\mathrm{o}\mathrm{y}-{\mathrm{n}}^3{\mathrm{o}}^3\end{array}\right\}=0$
Jam ex Hypothesi sunt ${\mathrm{x}}^3-\mathrm{a}\mathrm{x}\mathrm{x}+\mathrm{a}\mathrm{x}\mathrm{y}-{\mathrm{y}}^3=0$, quibus deletis et reliquis terminis per o divisis restabunt $3\mathrm{m}\mathrm{x}\mathrm{x}+3\mathrm{m}\mathrm{m}\mathrm{o}\mathrm{x}+{\mathrm{m}}^3\mathrm{o}\mathrm{o}$$-2\mathrm{a}\mathrm{m}\mathrm{x}-\mathrm{a}\mathrm{m}\mathrm{m}\mathrm{o}+\mathrm{a}\mathrm{m}\mathrm{y}+\mathrm{a}\mathrm{n}\mathrm{x}+\mathrm{a}\mathrm{m}\mathrm{n}\mathrm{o}-3\mathrm{n}\mathrm{y}\mathrm{y}-3\mathrm{n}\mathrm{n}\mathrm{o}\mathrm{y}-{\mathrm{n}}^3\mathrm{o}\mathrm{o}=0${.} Et insuper cùm o {illeg}|s|upponitur esse infinitè parvum, eo ut momenta quantitatum designare possit, termini per illud multiplicati respectu cæterorum nihil valebunt. Rejicio itaqꝫ, et restat $3\mathrm{m}\mathrm{x}\mathrm{x}-2\mathrm{a}\mathrm{m}\mathrm{x}$$+\mathrm{a}\mathrm{m}\mathrm{y}+\mathrm{a}\mathrm{n}\mathrm{x}-3\mathrm{n}\mathrm{y}\mathrm{y}=0$, ut supra in Exempl: 1.

Hinc observare est primò quòd termini non multiplicati per o semper evanesc{illeg}|e|nt, {illeg} ut et illi multiplicati per o plusquam unius dimensionis: et quòd reliquo\ru/ termino\rum/ per o divisi|o|rum ea semper erit forma quam juxta præcedentia debent habere Regulam habere debent. Id quod volui ostendere.

Ex hoc monstrato cætera quæ {illeg}|R|egula involvit facilè consequentur; quemadmodum quòd in æquatione propositâ plures fluentes quantitates involvi possunt, et quòd termini non modò per numerum d{illeg}|i|mensionum {illeg} quantitatum fluentium sed per quaslibet alias Arithmeticas progressiones multiplicari possunt dummodò {illeg} in operatione juxta quamlibet fluentem quantitatem sit eadem terminorum differentia, et progressio secundum eundem cujusqꝫ dimensionum ordinem disponatur. Et his concessis quæ præterea in exemplis 3, 4, et 5 docentur, per se manifesta sunt.

<22>

Prob 2

Exposita quantitate fluent{illeg}|e| ad cujus momenta relatio momentorum alterius alicujus fluentis quantitatis datur, quantitatum relationum inter se relationem invenire.

Rationis momentorum {illeg} quæsitæ quantitatis ad momenta quantitatis exposit{illeg}|æ| valorem multiplica per expositam quantitatem (si liber sit ab assymmetria et non afficitur denominator|e| {illeg} \aliquo/ plurium dimensionum terminorumy) multiplica per expositam quantitatem, dein termin{illeg}|um| \unumquemqꝫ/ sigillatim divide per \proprium/ numerum dimensionum \ejusdem/ quantitatis; et quod oritur valebit qu{illeg}|anti|tate quæsitâ.

Quemadmodum {illeg} si exponatur x, et y quæratur: Rationis $\frac{\mathrm{n}}{\mathrm{m}}$ valorem in datâ quâlibet æquatione, exhibitum duc{illeg} in x, et unumquemqꝫ te{illeg}|r|minum divide per numerum dimensionum ejus. Dein pone $=\mathrm{y}$.

Exemplum 1. Si detur $\frac{\mathrm{n}}{\mathrm{m}}=\frac{\mathrm{x}}{\mathrm{a}}$, duco $\frac{\mathrm{x}}{\mathrm{a}}$ et fit $\frac{\mathrm{x}\mathrm{x}}{\mathrm{a}}$, ubi cùm x sit duarum dimensionum divido per 2 et fit $\frac{\mathrm{x}\mathrm{x}}{2\mathrm{a}}$ quod pono æquale y.

<23>

Prob 2
Exposita æquatione fluxiones quantitatum
involvente, invenire relationem quantitatum
inter se.

Solutio particularis.

Cum hoc Problema \sit/ præcedentis contraria|e|turversum, contrario modo solvi debet: Utpote terminos per m multiplicatos disponendo secundum dimensiones ipsius x, dividendoqꝫ per $\frac{\mathrm{m}}{\mathrm{x}}$ ac deinde per numerum dimensionum aut fortasse per aliam arithmeticam progressionem, Atqꝫ idem opus in terminis per l, n, vel r multiplicatis instituendo, Et resultantium summam, rejectis terminis redundantibus, ponendo æqualem nihil{illeg}|o|.

Exempl. Sic expositâ æquatione $3\mathrm{m}\mathrm{x}\mathrm{x}-2\mathrm{a}\mathrm{m}\mathrm{x}+$$\mathrm{a}\mathrm{m}\mathrm{y}-3\mathrm{n}\mathrm{y}\mathrm{y}+\mathrm{a}\mathrm{n}\mathrm{x}=0$; Operor ad hunc modum,
$$\begin{array}{cc}\begin{array}{ccccccc}\text{Divido}& 3\mathrm{m}\mathrm{x}\mathrm{x}& -& 2\mathrm{a}\mathrm{m}\mathrm{x}& +& \mathrm{a}\mathrm{m}\mathrm{y}& \phantom{0}\\ \text{per}\frac{\mathrm{m}}{\mathrm{x}}\text{, \& fit}& 3{\mathrm{x}}^3& -& 2\mathrm{a}\mathrm{x}\mathrm{x}& +& \mathrm{a}\mathrm{x}\mathrm{y}\\ \text{Dein divido per}& 3\text{.}& & 2\text{.}& & 1\text{.}\\ \text{et fit}& {\mathrm{x}}^3& -& \mathrm{a}\mathrm{x}\mathrm{x}& +& \mathrm{a}\mathrm{x}\mathrm{y}\end{array}& \begin{array}{cccccc}\phantom{0}& \text{Div:}& -& 3\mathrm{n}\mathrm{y}\mathrm{y}& +& \mathrm{a}\mathrm{n}\mathrm{x}\\ & \text{per}\frac{\mathrm{n}}{\mathrm{y}}\text{, fit}& -& 3{\mathrm{y}}^3& +& \mathrm{a}\mathrm{x}\mathrm{y}\\ & \text{Div: per}& & 3\text{.}& & 1\text{.}\\ & \text{fit}& -& {\mathrm{y}}^3& +& \mathrm{a}\mathrm{x}\mathrm{y}& \text{.}\end{array}\end{array}$$

Et summa ${\mathrm{x}}^3-\mathrm{a}\mathrm{x}\mathrm{x}+\mathrm{a}\mathrm{x}\mathrm{y}-{\mathrm{y}}^3=0$ erit relatio desiderata quantitatum x et y. Ubi observandum venit quod etsi terminus $\mathrm{a}\mathrm{x}\mathrm{y}$ bis resultavit, tamen non pono bis in hac summâ ${\mathrm{x}}^3-\mathrm{a}\mathrm{x}\mathrm{x}+\mathrm{a}\mathrm{x}\mathrm{y}-{\mathrm{y}}^3$ sed redundantem terminum negligo rejicio. Et sic ubicunqꝫ terminus aliquis bis \resultat/ (aut sæpius si de pluribus fluentibus quantitatibus agitur,) semel tantùm in summâ terminorum scribo{.}

Sunt et aliæ circumstantiæ quas Artificis ingenio pro re nata observandas esse remitto; nam supervacaneum esset his multa verba impendere, siquidem Problema non semper potest hoc artificio solvi. Addo tamen quod postquam Artifex relationem fluentium quantitatum hac methodo adeptus est, si juxta Prob:{illeg} 1 {illeg} potest regredi ad expositam æquationem fluxiones involventem, rectè operatus est; sin secùs, vitiosè. Sic in exemp{illeg}|l|o proposito, ubi æquationem ${\mathrm{x}}^3-\mathrm{a}\mathrm{x}\mathrm{x}+\mathrm{a}\mathrm{x}\mathrm{y}-{\mathrm{y}}^3=0$ adeptus sum, si relatio inter m et x jux ope primi Problematis <24> vicissim exquir{illeg} inde requiratur, obtinebitur æquatio exposita $3\mathrm{m}\mathrm{x}\mathrm{x}-2\mathrm{a}\mathrm{m}\mathrm{x}+\mathrm{a}\mathrm{m}\mathrm{y}-3\mathrm{n}\mathrm{y}\mathrm{y}+\mathrm{a}\mathrm{n}\mathrm{x}=0$. Unde constat æquationem ${\mathrm{x}}^3-\mathrm{a}\mathrm{x}\mathrm{x}+\mathrm{a}\mathrm{x}\mathrm{y}-{\mathrm{y}}^3=0$ rectè inventam fuisse. At si æquatio $\mathrm{m}-\mathrm{m}\mathrm{y}+\mathrm{n}\mathrm{a}=0$ exponeretur, et inde præscripta methodo elicerem $\frac{1}{2}\mathrm{x}\mathrm{x}-\mathrm{x}\mathrm{y}+\mathrm{a}\mathrm{y}=0$, pro relatione inter x et y, vitiosa foret operatio siquidem exinde per Prob 1 vicissim produceretur $\mathrm{m}\mathrm{x}-\mathrm{m}\mathrm{y}-\mathrm{n}\mathrm{x}+\mathrm{n}\mathrm{a}=0$, quæ differt ab æquatione primo exposita{.}

Hæc itaqꝫ perfunctoriè no{illeg}|t|ata prætermittens, solutionem generalem aggredior.

Præparatio in generalem solutionem.

Et in hunc finem convenit ut exposita æquatio ad talem formam semper reducatur ut ex una parte habeatur rati{illeg}|o| fluxionum ut $\frac{\mathrm{n}}{\mathrm{m}}$ (vel $\frac{\mathrm{m}}{\mathrm{n}}$ aut $\frac{\mathrm{r}}{\mathrm{m}}$ &c prout fluxiones alijs atqꝫ alijs symbolis exprimuntur,) et ex altera parte valor ejus rationis simplicibus terminis Algebraicis designatus. Sicut hic videre est $\frac{\mathrm{n}}{\mathrm{m}}=2+2\mathrm{x}-\mathrm{y}$.

Quamobrem cum in illo valore terminus aliquis a compositis|a| quantitate denomin{illeg}|e|tur, vel sit radicalis vel si $\frac{\mathrm{n}}{\mathrm{m}}$ ratio illa $\frac{\mathrm{n}}{\mathrm{m}}$ sit aff æquationis radix affecta, æquatio semper debet ad præscriptam formam reduci, idqꝫ vel dividendo per compositum denominatorem, vel extrahend{illeg}|o|{illeg} radicem, vel affectam æquationem resolvendo, prout in superioribus ostensum est.

Quemadmodum si exponitur $\mathrm{n}\mathrm{a}-\mathrm{n}\mathrm{x}-\mathrm{m}\mathrm{a}+\mathrm{m}\mathrm{x}-\mathrm{m}\mathrm{y}=0$. Sive (facta reductione) $\frac{\mathrm{n}}{\mathrm{m}}=1+\frac{\mathrm{y}}{\mathrm{a}-\mathrm{x}}$. Terminum $\frac{\mathrm{y}}{\mathrm{a}-\mathrm{x}}$ a composita quantitate $\mathrm{a}-\mathrm{x}$ denominatum reduco ad infinitam seriem simplicium terminorum $\frac{\mathrm{y}}{\mathrm{a}}+\frac{\mathrm{x}\mathrm{y}}{\mathrm{a}\mathrm{a}}+\frac{\mathrm{x}\mathrm{x}\mathrm{y}}{{\mathrm{a}}^3}+\frac{{\mathrm{x}}^3\mathrm{y}}{{\mathrm{a}}^4}\text{\&c}$ dividendo numeratorem y per denominatorem $\mathrm{a}-\mathrm{x}$. Et sic obtineo $\frac{\mathrm{n}}{\mathrm{m}}=1+\frac{\mathrm{y}}{\mathrm{a}}+\frac{\mathrm{x}\mathrm{y}}{\mathrm{a}\mathrm{a}}+\frac{\mathrm{x}\mathrm{x}\mathrm{y}}{{\mathrm{a}}^3}+\frac{{\mathrm{x}}^3\mathrm{y}}{{\mathrm{a}}^4}\text{\&c}$ cujus ope{illeg} relatio inter x et y determinanda est.

Sic exposito $\mathrm{n}\mathrm{n}=\mathrm{m}\mathrm{n}+\mathrm{m}\mathrm{m}\mathrm{x}\mathrm{x}$. Sive $\frac{\mathrm{n}\mathrm{n}}{\mathrm{m}\mathrm{m}}=\frac{\mathrm{n}}{\mathrm{m}}+\mathrm{x}\mathrm{x}$, et ulteriori reductione, $\frac{\mathrm{n}}{\mathrm{m}}=\frac{1}{2}\pm \sqrt{}\stackrel{\_}{\frac{1}{4}+\mathrm{x}\mathrm{x}}$: Radicem quadratica e terminis $\frac{1}{4}+\mathrm{x}\mathrm{x}$ extraho, & obtineo infinitam seriem $\frac{1}{2}+$$\mathrm{x}\mathrm{x}-{\mathrm{x}}^4+2{\mathrm{x}}^6-5{\mathrm{x}}^8+14{\mathrm{x}}^{10}\text{\&c}$ quam pro $\sqrt{}\frac{1}{4}+\mathrm{x}\mathrm{x}$ subti

<25>

Præparatio in generalem solutionem.

Et imprimis observandum est quod in exposita æquatione symbola Fluxionum (cum sint quantitates diversi generis a quantitatibus quarum sunt fluxiones) in singulis terminis debent ad æque-multas dimensiones ascendere. Et ubi res aliter se habet, alia alicujus fluentis quantitatis fluxio subintellegi debet esse unitas per quam termini {illeg}|d|epressiores t{illeg}|o|ties multiplicantur ut in omnibus symbola fluxionum ad eundem dimensionum gradum ascendant. Quemadmodum si exponitur æquatio $\mathrm{m}+\mathrm{m}\mathrm{n}\mathrm{x}-\mathrm{a}\mathrm{x}\mathrm{x}=0$, tertiæ alicujus fluentis quantitatis ut z fluxio r subintelligi debet esse unitas per quam primus terminus semel m semel et ultimus $\mathrm{a}\mathrm{x}\mathrm{x}$ bis multiplicetur ut fluxiones inibi ad æque-multas dimensiones ac in secundo termino $\mathrm{m}\mathrm{n}\mathrm{x}$ ascendant quasi exposita æquatio ex hac $\mathrm{m}\mathrm{r}+$$\mathrm{m}\mathrm{n}\mathrm{x}-\mathrm{r}\mathrm{r}\mathrm{x}\mathrm{x}=0$ derivata fuisset ponendo $\mathrm{r}=1$. Et sic in æquatione $\mathrm{n}\mathrm{x}=\mathrm{y}\mathrm{y}$ debes imaginari m esse unitatem per quam terminus $\mathrm{y}\mathrm{y}$ multiplicatur.

Æquationes autem in quibus duæ tantum sunt fluentes quantitates quæ ad æquè multas dimensiones passim ascendunt, semper possunt ad talem formam reduci ut ex una parte habeatur ratio fluxionum (velut $\frac{\mathrm{n}}{\mathrm{m}}$ vel $\frac{\mathrm{m}}{\mathrm{n}}$ vel $\frac{\mathrm{r}}{\mathrm{m}}$ &c ) prout et ex altera parte valor ejus rationis simplicibus terminis Algebraicis designatus; sicut hic videre est $\frac{\mathrm{n}}{\mathrm{m}}=2+2\mathrm{x}-\mathrm{y}$. Et ubi æquationibus præcedens particularis solutio non satisfacit, requiritur ut ad hanc formam reducas.

Quamobrem cum in illius rationis valore terminus aliquis a composita quantitate denominetur vel sit radicalis vel si ratio illa sit æquationis radix affecta: reductio vel per divisionem, vel extractionem radicis, {illeg}|v|el æquationis affectæ resolutionem institui debet, prout in se|u|perioribus ostensum est.

Quemadmodum si exponitur $\mathrm{n}\mathrm{a}-\mathrm{n}\mathrm{x}-\mathrm{m}\mathrm{a}+\mathrm{m}\mathrm{x}-\mathrm{m}\mathrm{y}=0$. Hæc imprimis reductione \vel/ fit $\frac{\mathrm{n}}{\mathrm{m}}=1+\frac{\mathrm{y}}{\mathrm{a}-\mathrm{x}}$, {illeg}|ve|l $\frac{\mathrm{m}}{\mathrm{n}}=\frac{\mathrm{a}-\mathrm{x}}{\mathrm{a}-\mathrm{x}+\mathrm{y}}$. Et in priori casu si terminum $\frac{\mathrm{y}}{\mathrm{a}-\mathrm{x}}$ a composita quantitate $\mathrm{a}-\mathrm{x}$ denominatum reduco ad infinitam seriem dividendo simplicium terminorum dividendo $\frac{\mathrm{y}}{\mathrm{a}}+\frac{\mathrm{x}\mathrm{y}}{\mathrm{a}\mathrm{a}}+\frac{\mathrm{x}\mathrm{x}\mathrm{y}}{{\mathrm{a}}^3}+\frac{{\mathrm{x}}^3\mathrm{y}}{{\mathrm{a}}^4}\text{\&c}$ dividendo numeratorem y per denominatorem $\mathrm{a}-\mathrm{x}$, obtinebo $\frac{\mathrm{n}}{\mathrm{m}}=1+\frac{\mathrm{y}}{\mathrm{a}}+\frac{\mathrm{x}\mathrm{y}}{\mathrm{a}\mathrm{a}}+\frac{\mathrm{x}\mathrm{x}\mathrm{y}}{{\mathrm{a}}^3}+\frac{{\mathrm{x}}^3\mathrm{y}}{{\mathrm{a}}^4}\text{\&c}$ cujus ope relatio inter x et y determinanda est.

Sic exposita $\mathrm{n}\mathrm{n}=\mathrm{m}\mathrm{n}+\mathrm{m}\mathrm{m}\mathrm{x}\mathrm{x}$, sive $\frac{\mathrm{n}\mathrm{n}}{\mathrm{m}\mathrm{m}}=\frac{\mathrm{n}}{\mathrm{m}}+\mathrm{x}\mathrm{x}$, et ulteriori reductione $\frac{\mathrm{n}}{\mathrm{m}}=\frac{1}{2}\pm \sqrt{}\stackrel{\_}{\frac{1}{4}+\mathrm{x}\mathrm{x}}$: Radicem quadraticam e terminis $\frac{1}{4}+\mathrm{x}\mathrm{x}$ extraho et obtineo infinitam seriem $\frac{1}{2}+\mathrm{x}\mathrm{x}-{\mathrm{x}}^4+2{\mathrm{x}}^6-5{\mathrm{x}}^8+14{\mathrm{x}}^{10}\text{\&c}$ <26> quam pro $\sqrt{}\stackrel{\_}{\frac{1}{4}+\mathrm{x}\mathrm{x}}$ substituendo prodit $\frac{\mathrm{n}}{\mathrm{m}}=1+\mathrm{x}\mathrm{x}-{\mathrm{x}}^4+2{\mathrm{x}}^6-5{\mathrm{x}}^8\text{\&c}$. Vel $\frac{\mathrm{n}}{\mathrm{m}}=-\mathrm{x}\mathrm{x}+{\mathrm{x}}^4-2{\mathrm{x}}^6+5{\mathrm{x}}^8\text{\&c}$, prout $\sqrt{}\stackrel{\_}{\frac{1}{4}+\mathrm{x}\mathrm{x}}$ additur vel subducitur a $\frac{1}{2}$.

Atqꝫ ita si exponitur ${\mathrm{n}}^3+\mathrm{a}\mathrm{x}\mathrm{m}\mathrm{m}\mathrm{n}+\mathrm{a}\mathrm{a}\mathrm{m}\mathrm{m}\mathrm{n}-{\mathrm{m}}^3-2{\mathrm{m}}^3{\mathrm{a}}^3=0\text{.}$ sive $\frac{{\mathrm{n}}^3}{{\mathrm{m}}^3}+\mathrm{a}\mathrm{x}\frac{\mathrm{n}}{\mathrm{m}}+\mathrm{a}\mathrm{a}\frac{\mathrm{n}}{\mathrm{m}}-{\mathrm{x}}^3-2{\mathrm{a}}^3=0$, extraho radicem cubicè affectam et prodit $\frac{\mathrm{n}}{\mathrm{m}}=\mathrm{a}-\frac{\mathrm{x}}{4}+\frac{\mathrm{x}\mathrm{x}}{64\mathrm{a}}+\frac{131{\mathrm{x}}^3}{512\mathrm{a}\mathrm{a}}+\frac{509{\mathrm{x}}^4}{16384{\mathrm{a}}^3}\text{\&c}$ prout videre est ad pag 10.

Cæterum hic observandum venit quod terminos solummodò pro compositis habeo qui ex parte fluentium quantitatum componuntur. Terminos ubi nulla est nisi ex parte datarum quantitatum \compositio/ pro simplicibus habeo, siquidem ad simplices reduci possunt fingendo æquales esse alijs datis. Sic quantitates $\frac{\mathrm{a}\mathrm{x}+\mathrm{b}\mathrm{x}}{\mathrm{c}}$, $\frac{\mathrm{x}}{\mathrm{a}+\mathrm{b}}$, $\frac{\mathrm{b}\mathrm{c}\mathrm{c}}{\mathrm{a}\mathrm{x}+\mathrm{b}\mathrm{x}}$, $\frac{{\mathrm{b}}^4}{\mathrm{a}\mathrm{x}\mathrm{x}+\mathrm{b}\mathrm{x}\mathrm{x}}$, $\sqrt{}\stackrel{\_}{\mathrm{a}\mathrm{x}+\mathrm{b}\mathrm{x}}$ &c pro simplicibus habeo siquidem ad simplices $\frac{\mathrm{e}\mathrm{x}}{\mathrm{c}}$, $\frac{\mathrm{x}}{\mathrm{e}}$, $\frac{\mathrm{b}\mathrm{c}\mathrm{c}}{\mathrm{e}\mathrm{x}}$, $\frac{{\mathrm{b}}^4}{\mathrm{e}\mathrm{x}\mathrm{x}}$, $\sqrt{}\mathrm{e}\mathrm{x}$ {illeg} sive ${\mathrm{e}}^{\frac{1}{2}}{\mathrm{x}}^{\frac{1}{2}}$ &c reduci possunt fingendo esse $\mathrm{a}+\mathrm{b}=\mathrm{e}$.

Præterea quo fluentes quantitates a se invicem clarius distinguantur, Fluxionem quæ in Numeratore Rationis disponitur, sive Antecedentem Rationis haud impropriè {illeg}|R|elatam Quantitatem nominare possum, et alteram ad quam reftur {sic}, Correlatam; {illeg}|u|t {illeg}|e|t {illeg} fluentes Quantitates ijsdem respectivè nominibus insignire possunt. Et quo sequentia promptiùs intelligantur, possis imaginari Correltam {sic} Quantitatem esse Tempus vel potiùs aliam quamvis æquabiliter fluentem quantitatem qua Tempus exponitur et mensuratur, et alteram sive Relatam Quantitatem esse spatium quod mobi{illeg}|l|e utcunqꝫ acceleratum vel retardatum in illo tempore transigit. Et quod Problematis intensio est ut e celeritate motûs ad omne tempus datâ spatium in toto tempore transactum determinetur.

Cæterùm æquationes respectu hujus Problematis in tres ordines distingui convenit. 1 In quibus duæ quantitatum fluxiones et alterutra tantùm fluens quantitas involvuntur. 2 In quibus duæ involvuntur fluentes quantitates unà cum earum fluxionibus. 3 Quæ plures duabus quantitatum fluxionibus complectuntur. Et his præmissis, Problematis confectionem secundum hosce tres casus aggrediar.

Solutionis Cas: 1.

Fluentem quantitatem, quam unicè æquatio complectitur suppone Correlatam esse, et æquatione perinde dispositâ, (hoc est faciendo ut ex una parte habeatur fluxionis alterius ad hujus fluxionem R{illeg}atio, et valor ejus i{illeg}|n| simplicibus terminis ex altera) Multiplica valorem r|R|ationis Fluxionum per Correlatam Quantitatem, dein singulos ejus terminos {illeg}|d|ivide per numerum dimensionum quibus illa q|Q|uantitas inibi afficitur, et quod oritur valebit altera Fluenti Quantitate.

Sic habit {illeg} expositâ $\mathrm{n}\mathrm{n}=\mathrm{m}\mathrm{n}+\mathrm{m}\mathrm{m}\mathrm{x}\mathrm{x}$, et æquatio suppono x esse fluentem Q Correlatam Quantitatem, et æquatione perinde reduc{illeg}|t|â habebitur $\frac{\mathrm{n}}{\mathrm{m}}=1+\mathrm{x}\mathrm{x}-{\mathrm{x}}^4+2{\mathrm{x}}^6\text{\&c}$. Jam duco valorem $\frac{\mathrm{n}}{\mathrm{m}}$ in x et oritur $\mathrm{x}+{\mathrm{x}}^3-{\mathrm{x}}^5+2{\mathrm{x}}^7\text{\&c}$ quos terminos sigillatim per numerum dimensionum divido et exitum $\mathrm{x}+\frac{1}{3}{\mathrm{x}}^3-\frac{1}{5}{\mathrm{x}}^5+\frac{2}{7}{\mathrm{x}}^7\text{\&c}$ pono $=\mathrm{y}$. Et isthac æquatione desiderata relatio inter x et y determinatur.

Sic habitâ $\frac{\mathrm{n}}{\mathrm{m}}=\mathrm{a}-\frac{\mathrm{x}}{4}+\frac{\mathrm{x}\mathrm{x}}{64\mathrm{a}}+\frac{131{\mathrm{x}}^3}{512\mathrm{a}\mathrm{a}}\text{\&c}$, prodibit $\mathrm{y}=\mathrm{a}\mathrm{x}-\frac{\mathrm{x}\mathrm{x}}{8}+\frac{{\mathrm{x}}^3}{192\mathrm{a}}+\frac{131{\mathrm{x}}^4}{2048\mathrm{a}\mathrm{a}}$ pro determinanda relatione inter x et y.

<27>

Et sic æquatio $\frac{\mathrm{n}}{\mathrm{m}}=\frac{1}{{\mathrm{x}}^3}-\frac{1}{\mathrm{x}\mathrm{x}}+\frac{\mathrm{a}}{{\mathrm{x}}^{\frac{1}{2}}}-{\mathrm{x}}^{\frac{1}{2}}+{\mathrm{x}}^{\frac{3}{2}}$ dat $\mathrm{y}=-\frac{1}{2\mathrm{x}\mathrm{x}}$$+\frac{1}{\mathrm{x}}+2\mathrm{a}{\mathrm{x}}^{\frac{1}{2}}-\frac{2}{3}{\mathrm{x}}^{\frac{3}{2}}+\frac{2}{5}{\mathrm{x}}^{\frac{5}{2}}$. n|N|am valorem $\frac{\mathrm{n}}{\mathrm{m}}$ duc in x, et fit $\frac{1}{\mathrm{x}\mathrm{x}}-\frac{1}{\mathrm{x}}+\mathrm{a}{\mathrm{x}}^{\frac{1}{2}}-{\mathrm{x}}^{\frac{3}{2}}+{\mathrm{x}}^{\frac{5}{2}}$, sive ${\mathrm{x}}^{-2}-{\mathrm{x}}^{-1}+\mathrm{a}{\mathrm{x}}^{\frac{1}{2}}-{\mathrm{x}}^{\frac{3}{2}}+{\mathrm{x}}^{\frac{5}{2}}$ Quibus terminis per numerum dimensionum divisis emergit valor assignatus y.

Ad eundem modum æquatio bb $\frac{\mathrm{m}}{\mathrm{n}}=\frac{2\mathrm{b}\mathrm{b}\mathrm{c}}{\sqrt{}\mathrm{a}{\mathrm{y}}^3}+\frac{3\mathrm{y}\mathrm{y}}{\mathrm{a}+\mathrm{b}}+$$\sqrt{}\stackrel{\_}{\mathrm{b}\mathrm{y}+\mathrm{c}\mathrm{y}}$ dat $\mathrm{x}=-\frac{4\mathrm{b}\mathrm{b}\mathrm{c}}{\sqrt{}\mathrm{a}\mathrm{y}}+\frac{{\mathrm{y}}^3}{\mathrm{a}+\mathrm{b}}+\frac{2}{3}\sqrt{}\stackrel{\_}{\mathrm{b}{\mathrm{y}}^3+\mathrm{c}{\mathrm{y}}^3}$. Nam valore $\frac{\mathrm{m}}{\mathrm{n}}$ ducto in y, oritur $\frac{2\mathrm{b}\mathrm{b}\mathrm{c}}{\sqrt{}\mathrm{a}\mathrm{y}}+\frac{3{\mathrm{y}}^3}{\mathrm{a}+\mathrm{b}}+\sqrt{}\stackrel{\_}{\mathrm{b}{\mathrm{y}}^3+\mathrm{c}{\mathrm{y}}^3}$ sive $2\mathrm{b}\mathrm{b}\mathrm{c}{\mathrm{a}}^{\frac{1}{2}}{\mathrm{y}}^{\frac{1}{2}}+\frac{3}{\mathrm{a}+\mathrm{b}}{\mathrm{y}}^3+\sqrt{}\stackrel{\_}{\mathrm{b}+\mathrm{c}}\times {\mathrm{y}}^{\frac{3}{2}}$. Et inde prodit valor x, dividendo per numerum dimensionum cujusqꝫ termini.

Atqꝫ ita $\frac{\mathrm{n}}{\mathrm{r}}={\mathrm{z}}^{\frac{2}{3}}$ dat $\mathrm{y}=\frac{3}{5}{\mathrm{z}}^{\frac{5}{3}}$. Et $\frac{\mathrm{n}}{\mathrm{m}}=\frac{\mathrm{a}\mathrm{b}}{\mathrm{c}{\mathrm{x}}^{\frac{1}{3}}}$ dat $\mathrm{y}=\frac{3\mathrm{a}\mathrm{b}{\mathrm{x}}^{\frac{2}{3}}}{2\mathrm{c}}$. At æquatio $\frac{\mathrm{n}}{\mathrm{m}}=\frac{\mathrm{a}}{\mathrm{x}}$ dat $\mathrm{y}=\frac{\mathrm{a}}{0}$. Nam $\frac{\mathrm{a}}{\mathrm{x}}$ ductum in x fit a, quo per numerum dimensionum (qui nullus est) diviso prodit $\frac{\mathrm{a}}{0}$ quantias {sic} infinita pro valore y{.}

Quamobrem siquando consimilis terminus (cujus denominator involvit {illeg} \Correlatam Quantitatem/ unius tantùm dimensionis) in valore $\frac{\mathrm{n}}{\mathrm{m}}$ reperiatur, quantitas x \debet/ auger {illeg} vel minui per datam quamvis \pro Correlatam Quantitatem/ quantitatem. Veluti substituendo z + vel − quavis data quantitate s pro x, ut et ejus fluxionis symbolo r pro {illeg} pro {illeg} substitue summam vel differentiam inter eandem \quantitatem/ {illeg} et aliam quamvis datam quantitatem pro arbitrio assumptam. Nam quantitatum $\mathrm{x}$ et $\mathrm{y}$ \fluentium/ juxta prodeuntem æquationem eadem erit inter se fluendi r{illeg}|ela|tio ac juxta æquationem primò expositam; et infinita quantitas {illeg} \{illeg}|R|elata/ hoc pacto parte infinitâ diminuetur et evadet finita, sed terminis /tamen numero infinitis constans.\

Æquatione itaqꝫ $\frac{\mathrm{n}}{\mathrm{m}}=\frac{\mathrm{a}}{\mathrm{m}}$ expositâ, si pro x scribam {illeg} $\mathrm{b}+\mathrm{x}$, quantitatem b pro lubitu assumptâ\ens/; prodibit $\frac{\mathrm{n}}{\mathrm{m}}=\frac{\mathrm{a}}{\mathrm{b}+\mathrm{x}}$; factâqꝫ divisione, $\frac{\mathrm{n}}{\mathrm{m}}=\frac{\mathrm{a}}{\mathrm{b}}-\frac{\mathrm{a}\mathrm{x}}{\mathrm{b}\mathrm{b}}+\frac{\mathrm{a}\mathrm{x}\mathrm{x}}{{\mathrm{b}}^3}-\frac{\mathrm{a}{\mathrm{x}}^4}{{\mathrm{b}}^4}\text{\&c}$. Et inde Regula ut in superioribus dabit $\mathrm{y}=\frac{\mathrm{a}\mathrm{x}}{\mathrm{b}}-\frac{\mathrm{a}\mathrm{x}\mathrm{x}}{2\mathrm{b}\mathrm{b}}+\frac{\mathrm{a}{\mathrm{x}}^3}{3{\mathrm{b}}^3}-\frac{\mathrm{a}{\mathrm{x}}^4}{4{\mathrm{b}}^4}\text{\&c}$ /relationem inter x et y\.

Sic etiam habitâ æquatione $\frac{\mathrm{n}}{\mathrm{m}}=\frac{2}{\mathrm{m}}+3-\mathrm{x}\mathrm{x}$, si (propter terminum $\frac{2}{\mathrm{x}}$) scribam $1+\mathrm{x}$ pro x, emerget $\frac{\mathrm{n}}{\mathrm{m}}=\frac{2}{1+\mathrm{x}}+2-2\mathrm{x}-\mathrm{x}\mathrm{x}$ terminoqꝫ $\frac{2}{1+\mathrm{x}}$ in infinitam seriem $2-2\mathrm{x}+2\mathrm{x}\mathrm{x}-2{\mathrm{x}}^3+2{\mathrm{x}}^4\text{\&c}$ <28> reda|u|cto erit $\frac{\mathrm{n}}{\mathrm{m}}=4-4\mathrm{x}+\mathrm{x}\mathrm{x}-2{\mathrm{x}}^3+2{\mathrm{x}}^4\text{\&c}$. Adeoqꝫ juxta Regulam obtinebitur $\mathrm{y}=4\mathrm{x}-2\mathrm{x}\mathrm{x}+\frac{1}{3}{\mathrm{x}}^3-\frac{1}{2}{\mathrm{x}}^4+\frac{2}{5}{\mathrm{x}}^5\text{\&c}$ relatio inter x et y.

Atqꝫ ita si propononitur $\frac{\mathrm{n}}{\mathrm{m}}={\mathrm{x}}^{-\frac{1}{2}}+{\mathrm{x}}^{-1}-{\mathrm{x}}^{\frac{1}{2}}$ Quia terminum ${\mathrm{x}}^{-1}$ (sive $\frac{1}{\mathrm{x}}$) inesse video, transmuto x: quemadmodum pro eo substituendo $1-\mathrm{x}$, et oritur $\frac{\mathrm{n}}{\mathrm{m}}=\frac{1}{\sqrt{}\stackrel{\_}{1-\mathrm{x}}}+$$\frac{1}{1-\mathrm{x}}-\sqrt{}\stackrel{\_}{1-\mathrm{x}}$. Terminus autem $\frac{1}{1-\mathrm{x}}$ valet $1+\mathrm{x}+\mathrm{x}\mathrm{x}$$+{\mathrm{x}}^3\text{\&c}$; Et $\sqrt{}\stackrel{\_}{1-\mathrm{x}}$ valet $1-\frac{1}{2}\mathrm{x}-\frac{\mathrm{x}\mathrm{x}}{8}-\frac{{\mathrm{x}}^3}{16}\text{\&c}$. adeoqꝫ $\frac{1}{\sqrt{}\stackrel{\_}{1-\mathrm{x}}}$ sive $\frac{1}{1-\frac{1}{2}\mathrm{x}-\frac{1}{8}\mathrm{x}\mathrm{x}-\frac{1}{16}{\mathrm{x}}^3\text{\&c}}$ valet $1+\frac{1}{2}\mathrm{x}+\frac{3}{8}\mathrm{x}\mathrm{x}+\frac{5}{8}{\mathrm{x}}^3\text{\&c}$. Quamobrem (valoribus hisce substitutis) e{illeg}|r|i{illeg}|t| $\frac{\mathrm{n}}{\mathrm{m}}=1+2\mathrm{x}+\frac{3}{2}\mathrm{x}\mathrm{x}+\frac{27}{16}{\mathrm{x}}^3\text{\&c}$ Et inde per regulam fit $\mathrm{y}=\mathrm{x}+\mathrm{x}\mathrm{x}+\frac{1}{2}{\mathrm{x}}^3+\frac{27}{64}{\mathrm{x}}^4\text{\&c}$. Et sic in alijs.

Hujusmodi etiam transmutatione fluentis quan{illeg}|t|itatis æquati{illeg}|o| in alijs casibus nonnunquam commode reduci poterit. Quemadmodum si exponitur $\frac{\mathrm{n}}{\mathrm{m}}=\frac{\mathrm{c}\mathrm{c}\mathrm{x}}{{\mathrm{c}}^3-3\mathrm{c}\mathrm{c}\mathrm{x}+3\mathrm{c}\mathrm{x}\mathrm{x}-{\mathrm{x}}^3}$ pro {illeg} x scribo $\mathrm{c}-\mathrm{x}$ et obtineo $\frac{\mathrm{n}}{\mathrm{m}}=\frac{{\mathrm{c}}^3-\mathrm{c}\mathrm{c}\mathrm{x}}{{\mathrm{x}}^3}$ sive $=\frac{{\mathrm{c}}^3}{{\mathrm{x}}^3}-\frac{\mathrm{c}\mathrm{c}}{\mathrm{x}\mathrm{x}}$ et inde per Reg: $\mathrm{y}=-\frac{{\mathrm{c}}^3}{2\mathrm{x}\mathrm{x}}+\frac{\mathrm{c}\mathrm{c}}{\mathrm{x}}$. At harum transmutationum usus in sequentibus magis elucescet.

In Casu 2 Præparatio.

Hæc itaqꝫ de æquationibus involventibus unica{illeg}|m| tantum fluentem quantitatem. Cum verò utraqꝫ in {sic} exposita æquatione involvitur, {illeg}|æ|quatio imprimis ad præscriptam formam redigenda est, e{illeg}|f|ficiendo scilicet ut ex una tantum parte habeatur Fluxionum ratio æqualis aggregato simplicium terminorum ex alterâ. Quemadmodum si exponitur {illeg} $\mathrm{n}\mathrm{a}-\mathrm{n}\mathrm{x}-\mathrm{m}\mathrm{a}+\mathrm{m}\mathrm{x}-\mathrm{m}\mathrm{y}=0$ eadem per debitam reductionem vel fiet $\frac{\mathrm{m}}{\mathrm{n}}=\frac{\mathrm{a}-\mathrm{x}}{\mathrm{a}-\mathrm{x}+\mathrm{y}}$, vel $\frac{\mathrm{n}}{\mathrm{m}}=1+\frac{\mathrm{y}}{\mathrm{a}-\mathrm{x}}$. Et in posteriori casu si $\frac{\mathrm{y}}{\mathrm{a}-\mathrm{x}}$ ad infinitam seriem simplicium terminorum reducatur, emerget $\frac{\mathrm{n}}{\mathrm{m}}=1+\frac{\mathrm{y}}{\mathrm{a}}+\frac{\mathrm{x}\mathrm{y}}{\mathrm{a}\mathrm{a}}$$+\frac{\mathrm{x}\mathrm{x}\mathrm{y}}{{\mathrm{a}}^3}+\frac{{\mathrm{x}}^3\mathrm{y}}{{\mathrm{a}}^4}\text{\&c}$ Cujus ope relatio inter x et y determinanda restat. Haud secus ad exemplar eorum quæ in priori casu tradita sunt possis vel radicales vel utcunqꝫ affectas <29> æquationes (siquando opus est) reducere.

{illeg}|Et|{illeg} præterea siquæ sunt {illeg}in æquationibus sic reductis fractiones quæ denominantur a fluenti{illeg} quantitate{illeg}, a denominatoribus istis liberari debent per transmutationem |ejus| fluentis quantitatis paulo ante commemoratam. Sic exposita æquatione $\mathrm{n}\mathrm{a}\mathrm{x}-\mathrm{m}\mathrm{x}\mathrm{y}-\mathrm{m}\mathrm{a}\mathrm{a}=0$ sive $\frac{\mathrm{n}}{\mathrm{m}}=\frac{\mathrm{y}}{\mathrm{a}}+\frac{\mathrm{a}}{\mathrm{x}}\text{.}$ \propter terminum $\frac{\mathrm{a}}{\mathrm{x}}$/ assumo b ad arbitrium et pro x vel scribo $\mathrm{b}+\mathrm{x}$ {illeg}, {illeg} vel $\mathrm{b}-\mathrm{x}$ vel $\mathrm{x}-\mathrm{b}$. Quemadmodum si scribam $\mathrm{b}+\mathrm{x}$ fiet $\frac{\mathrm{n}}{\mathrm{m}}=\frac{\mathrm{y}}{\mathrm{a}}+\frac{\mathrm{a}}{\mathrm{b}+\mathrm{x}}$. Adeóqꝫ termino $\frac{\mathrm{a}}{\mathrm{b}+\mathrm{x}}$, in infinitam seriem per divisionem redacto erit $\frac{\mathrm{n}}{\mathrm{m}}=\frac{\mathrm{y}}{\mathrm{a}}+\frac{\mathrm{a}}{\mathrm{b}}-\frac{\mathrm{a}\mathrm{x}}{\mathrm{b}\mathrm{b}}+\frac{\mathrm{a}\mathrm{x}\mathrm{x}}{{\mathrm{b}}^3}-\frac{\mathrm{a}{\mathrm{x}}^3}{{\mathrm{b}}^4}\text{\&c}${.}

Et ad eundem modum exposita æquatione $\frac{\mathrm{n}}{\mathrm{m}}=3\mathrm{y}-2\mathrm{x}$$+\frac{\mathrm{x}}{\mathrm{y}}-\frac{2\mathrm{y}}{\mathrm{x}\mathrm{x}}$; si (propter terminos $\frac{\mathrm{x}}{\mathrm{y}}$ & $\frac{2\mathrm{y}}{\mathrm{x}\mathrm{x}}$) scribam $1-\mathrm{y}$ pro y et $1-\mathrm{x}$ pro x, orietur $\frac{\mathrm{n}}{\mathrm{m}}=1-3\mathrm{y}+2\mathrm{x}+\frac{1-\mathrm{x}}{1-\mathrm{y}}$$+\frac{2\mathrm{y}-2}{1-2\mathrm{x}+\mathrm{x}\mathrm{x}}$. Terminus autem $\frac{1-\mathrm{x}}{1-\mathrm{y}}$ per infinitam divisionem dat $2\mathrm{y}-2+4\mathrm{x}\mathrm{y}-4\mathrm{x}+6\mathrm{x}\mathrm{x}\mathrm{y}-6\mathrm{x}\mathrm{x}+8{\mathrm{x}}^3\mathrm{y}-8{\mathrm{x}}^3+10{\mathrm{x}}^4\mathrm{y}-10{\mathrm{x}}^4\text{\&c}$ Quare est $\frac{\mathrm{m}}{\mathrm{n}}=-3\mathrm{x}+3\mathrm{x}\mathrm{y}+\mathrm{y}\mathrm{y}-\mathrm{x}\mathrm{y}\mathrm{y}+{\mathrm{y}}^3-\mathrm{y}{\mathrm{y}}^3\text{\&c}+6\mathrm{x}\mathrm{x}\mathrm{y}$$-6\mathrm{x}\mathrm{x}+8{\mathrm{x}}^3\mathrm{y}-8{\mathrm{x}}^3+10{\mathrm{x}}^4\mathrm{y}-10{\mathrm{x}}^4\text{\&c}$.

Regula.

Æquatione cùm opus est sic præparata: terminos ordina juxta dimensiones fluentium quantitatum ponendo imprimis non affectos Relata Quantitate, deinde affectos minima ejus dimensione, &c {sic} sic deinceps. Terminos etiam in his singulis classibus juxta dimensiones alterius Correlatæ quantitatis pariter dispone, eosqꝫ in prima classe (i.e. quos Relata Quantitas non afficit) scriba in serie collaterali dextrorsum pergente, et cæteros in seriebus descendentibus in s{illeg}|i|nistra col{illeg}lumnâ prout indicant subsequentia Diagrammata. Opere sic instituto Primum sive depressissimum e terminis in prima classe duc{illeg} in c|C|orrelatam q|Q|uantitatem dividéqꝫ per numerum <30> dimensionum, et in Quotiente, (pro initiali termino valoris r|R|elatæ Quantitatis ,|r|e{illeg}|p|one. Hunc deinde in æquationis terminos \in sinistrâ columnâ dispositos/ pro r|R|elatâ q|Q|uantitate substitue, et e terminis proximè depressissimis secundum Quotientis terminum eadem ratione quâ primum elicies. Et eâdem operatione sæpiùs repetitâ Quotientem ad arbitrium producere possis. Se{illeg}|d| res exemplo clariùs patebit{.}

Ex: 1. Exponatur æquatio $\frac{\mathrm{n}}{\mathrm{m}}=1-3\mathrm{x}+\mathrm{y}+\mathrm{x}\mathrm{x}+\mathrm{x}\mathrm{y}$ cujus
$\begin{array}{c}\begin{array}{ccccccc}\phantom{0}& +& 1& -& 3\mathrm{x}& +& \mathrm{x}\mathrm{x}\\ +\mathrm{y}& \phantom{+}& \ast & +& \mathrm{x}& -& \mathrm{x}\mathrm{x}& +& \frac{1}{3}{\mathrm{x}}^3& -& \frac{1}{6}{\mathrm{x}}^4& +& \frac{1}{30}{\mathrm{x}}^5& \phantom{0}& \phantom{0}\\ +\mathrm{x}\mathrm{y}& \phantom{+}& \ast & & \ast & +& \mathrm{x}\mathrm{x}& -& {\mathrm{x}}^3& -& \frac{1}{3}{\mathrm{x}}^4& -& \frac{1}{6}{\mathrm{x}}^5& +& \frac{1}{30}{\mathrm{x}}^6\\ \text{Summa}& \phantom{+}& 1& -& 2\mathrm{x}& +& \mathrm{x}\mathrm{x}& -& \frac{2}{3}{\mathrm{x}}^3& +& \frac{1}{6}{\mathrm{x}}^4& +& \frac{4}{30}{\mathrm{x}}^5& \phantom{0}& \phantom{0}\end{array}\\ \begin{array}{c}\phantom{0}\\ \mathrm{y}& =& \mathrm{x}-\mathrm{x}\mathrm{x}+\frac{1}{3}{\mathrm{x}}^3-\frac{1}{6}{\mathrm{x}}^4+\frac{1}{30}{\mathrm{x}}^5+\frac{1}{45}{\mathrm{x}}^6\text{\&c}\end{array}\end{array}$
terminos $1-3\mathrm{x}$$+\mathrm{x}\mathrm{x}$ non affectos Relata quantitate y vides in suprema serie collateraliter dispositos, cæterosqꝫ y et $\mathrm{x}\mathrm{y}$ in sinistrâ columnâ. Et imprimis terminum initialem 1 duco in Correlatam quantitate{illeg}|m| x fitqꝫ x, quem per numerum dimensionum 1 divisum repono in subscripta Quotiente. Dein hoc termino pro y in marginalibus substituto, vice $+\mathrm{y}$ et $+\mathrm{x}\mathrm{y}$ \substituto,/ obtineo $+\mathrm{x}$ et $+\mathrm{x}\mathrm{x}$, quos e regione dextrorsum scribens, ex omnibus excerpo depressimos {sic} terminos $-3\mathrm{x}$ & {illeg} $+\mathrm{x}$ quorum aggregatum $-2\mathrm{x}$ ductum in x fit $-2\mathrm{x}\mathrm{x}$, et per d numerum dimensionum 2 divisum dat $-\mathrm{x}\mathrm{x}$ pro secundo termino valoris y in Quotiente. Hoc proinde termino ad complendum valorem y in marginalibus $+\mathrm{y}$ et $+\mathrm{x}\mathrm{y}$ adscito, oriuntur præterea $-\mathrm{x}\mathrm{x}$ et $-{\mathrm{x}}^3$ prioribus terminis priùs oriundis $+\mathrm{x}$ et $+\mathrm{x}\mathrm{x}$ adnectend{illeg}|i|. Quo facto iterum terminos proximè depressissimos $+\mathrm{x}\mathrm{x}$, $-\mathrm{x}\mathrm{x}$, et $+\mathrm{x}\mathrm{x}$ in unam summa $\mathrm{x}\mathrm{x}$ colligo et inde ut priùs tertium terminum $\frac{1}{3}{\mathrm{x}}^3$ in valore y reponendum elicio. Iterumqꝫ $\frac{1}{3}\mathrm{x}$ <31> in valore y reponendum elicia {illeg} marginalium terminorum valores adscito, e proxime depressissimis $\frac{1}{3}{\mathrm{x}}^3$ et $-{\mathrm{x}}^3$ in unum aggregatis elicio $-\frac{1}{6}{\mathrm{x}}^4$ quartum terminum valoris y. Et sic in infinitum.

|Ex: 2.| Ad eundem modum si relationem inter x et y, habita æquatione $\frac{\mathrm{n}}{\mathrm{m}}=1+\frac{\mathrm{y}}{\mathrm{a}}+\frac{\mathrm{x}\mathrm{y}}{\mathrm{a}\mathrm{a}}+\frac{\mathrm{x}\mathrm{x}\mathrm{y}}{{\mathrm{a}}^3}+\frac{{\mathrm{x}}^3\mathrm{y}}{{\mathrm{a}}^4}\text{\&c}$ cujus terminorum series infinite progredi subintelligitur, determinare oportet. Operationem ex adjuncto diagrammate credo satis manifestam esse.
$\begin{array}{c}\begin{array}{cc}\phantom{0}& +1\\ +\frac{\mathrm{y}}{\mathrm{a}}& \ast & +& \frac{\mathrm{x}}{\mathrm{a}}& +& \frac{\mathrm{x}\mathrm{x}}{2\mathrm{a}\mathrm{a}}& +& \frac{{\mathrm{x}}^3}{2{\mathrm{a}}^3}& +& \frac{{\mathrm{x}}^4}{2{\mathrm{a}}^4}& +& \frac{{\mathrm{x}}^5}{2{\mathrm{a}}^5}& \text{\&c}\\ +\frac{\mathrm{x}\mathrm{y}}{\mathrm{a}\mathrm{a}}& \ast & \phantom{+}& \ast & +& \frac{\mathrm{x}\mathrm{x}}{\mathrm{a}\mathrm{a}}& +& \frac{{\mathrm{x}}^3}{2{\mathrm{a}}^3}& +& \frac{{\mathrm{x}}^4}{2{\mathrm{a}}^4}& +& \frac{{\mathrm{x}}^5}{2{\mathrm{a}}^5}& \text{\&c}\\ +\frac{\mathrm{x}\mathrm{x}\mathrm{y}}{{\mathrm{a}}^3}& \ast & \phantom{+}& \ast & \phantom{+}& \ast & +& \frac{{\mathrm{x}}^3}{{\mathrm{a}}^3}& +& \frac{{\mathrm{x}}^4}{2{\mathrm{a}}^4}& +& \frac{{\mathrm{x}}^5}{2{\mathrm{a}}^5}& \text{\&c}\\ +\frac{{\mathrm{x}}^3\mathrm{y}}{{\mathrm{a}}^4}& \ast & \phantom{+}& \ast & \phantom{+}& \ast & \phantom{+}& \ast & +& \frac{{\mathrm{x}}^4}{{\mathrm{a}}^4}& +& \frac{{\mathrm{x}}^5}{2{\mathrm{a}}^5}& \text{\&c}\\ +\frac{{\mathrm{x}}^4\mathrm{y}}{{\mathrm{a}}^5}& \ast & \phantom{+}& \ast & \phantom{+}& \ast & \phantom{+}& \ast & \phantom{+}& \ast & +& \frac{{\mathrm{x}}^5}{{\mathrm{a}}^5}& \text{\&c}\\ \text{Summa}& 1& +& \frac{\mathrm{x}}{\mathrm{a}}& +& \frac{3\mathrm{x}\mathrm{x}}{2\mathrm{a}\mathrm{a}}& +& \frac{2{\mathrm{x}}^3}{{\mathrm{a}}^3}& +& \frac{5{\mathrm{x}}^4}{{\mathrm{a}}^4}& +& \frac{3{\mathrm{x}}^5}{{\mathrm{a}}^5}& \phantom{\text{\&c}}\end{array}\\ \begin{array}{c}\phantom{0}\\ \mathrm{y}& =& \mathrm{x}+\frac{\mathrm{x}\mathrm{x}}{2\mathrm{a}}+\frac{{\mathrm{x}}^3}{2\mathrm{a}\mathrm{a}}+\frac{{\mathrm{x}}^4}{2{\mathrm{a}}^3}+\frac{{\mathrm{x}}^5}{2{\mathrm{a}}^4}+\frac{{\mathrm{x}}^6}{2{\mathrm{a}}^5}\text{\&c}\end{array}\end{array}$
Pono 1 in capite reliquosqꝫ terminos in sinistra columna. Reliquamqꝫ \Et/ opus deinde prosequor pro more adjuncti diagrammatis. Ubi propositum est mihi elicere valorem y ad usqꝫ sex dimensiones x, et eâ de causâ terminos omnes quos proposito nihil conducere prævideo, inter operandun missos facio, sicut innuit nota &c quam seriebus intercisis adnexui.

Ex: 3. Pari methodo si proponitur æquatio $\mathrm{n}=-3\mathrm{x}+$$3\mathrm{x}\mathrm{y}+\mathrm{y}\mathrm{y}-\mathrm{x}\mathrm{y}\mathrm{y}+{\mathrm{y}}^3-\mathrm{x}{\mathrm{y}}^3+{\mathrm{y}}^4-\mathrm{x}{\mathrm{y}}^4\text{\&c}+6\mathrm{x}\mathrm{x}\mathrm{y}-6\mathrm{x}\mathrm{x}$$+8{\mathrm{x}}^3\mathrm{y}-8{\mathrm{x}}^3+10{\mathrm{x}}^4\mathrm{y}-10{\mathrm{x}}^4+12{\mathrm{x}}^5\mathrm{y}-12{\mathrm{x}}^5\text{\&c}$. Et valorem y ad usqꝫ septem dimensiones x eruere institutum est, terminos, ut in adjuncto diagrammate, in ordinem redigo et operor sicut in præcedentibus hoc tantùm excepto quod cùm hic in sinistrâ columnâ y non tantùm unius dimensionis sed etiam duarum ac trium dimensionum existit (vel \etiam/ plurium prout valorem y ultra gradum <32> ${\mathrm{x}}^7$ extrahere statuam) subjicio quadratum et cubum valoris
$\begin{array}{c}\begin{array}{cccccccccccccc}\phantom{00000000}& -& 3\mathrm{x}& -& 6\mathrm{x}\mathrm{x}& -& 8{\mathrm{x}}^3& -& 10{\mathrm{x}}^4& -& 12{\mathrm{x}}^5& -& 14{\mathrm{x}}^6& \text{\&c}\\ +3\mathrm{x}\mathrm{y}& \phantom{+}& \ast & \phantom{+}& \ast & -& \frac{9}{2}{\mathrm{x}}^3& -& 6{\mathrm{x}}^4& -& \frac{75}{8}{\mathrm{x}}^5& -& \frac{273}{20}{\mathrm{x}}^6& \text{\&c}\\ +6\mathrm{x}\mathrm{x}\mathrm{y}& \phantom{+}& \ast & \phantom{+}& \ast & \phantom{+}& \ast & -& 9{\mathrm{x}}^4& -& 12{\mathrm{x}}^5& -& \frac{75}{4}{\mathrm{x}}^6& \text{\&c}\\ +8{\mathrm{x}}^3\mathrm{y}& \phantom{+}& \ast & \phantom{+}& \ast & \phantom{+}& \ast & \phantom{+}& \ast & -& 12{\mathrm{x}}^5& -& 16{\mathrm{x}}^6& \text{\&c}\\ +10{\mathrm{x}}^4\mathrm{y}& \phantom{+}& \ast & \phantom{+}& \ast & \phantom{+}& \ast & \phantom{+}& \ast & \phantom{+}& \ast & -& 15{\mathrm{x}}^6& \text{\&c}\\ \underset{\_}{\phantom{000}\text{\&c}\phantom{000}}& \phantom{0}& \phantom{0}& \phantom{0}& \phantom{0}& \phantom{0}& \phantom{0}& \phantom{0}& \phantom{0}& \phantom{0}\\ +\mathrm{y}\mathrm{y}& \phantom{+}& \ast & \phantom{+}& \ast & \phantom{+}& \ast & +& \frac{9}{4}{\mathrm{x}}^4& +& 6{\mathrm{x}}^5& +& \frac{107}{8}{\mathrm{x}}^6& \text{\&c}\\ -\mathrm{x}\mathrm{y}\mathrm{y}& \phantom{+}& \ast & \phantom{+}& \ast & \phantom{+}& \ast & \phantom{+}& \ast & -& \frac{9}{4}{\mathrm{x}}^5& -& 6{\mathrm{x}}^6& \text{\&c}\\ +{\mathrm{y}}^3& \phantom{+}& \ast & \phantom{+}& \ast & \phantom{+}& \ast & \phantom{+}& \ast & \phantom{+}& \ast & -& \frac{27}{8}{\mathrm{x}}^6& \text{\&c}\\ \text{\&c}& \phantom{0}& \phantom{0}& \phantom{0}& \phantom{0}& \phantom{0}& \phantom{0}& \phantom{0}& \phantom{0}\\ \text{Summa}& -& 3\mathrm{x}& -& 6\mathrm{x}\mathrm{x}& -& \frac{25}{2}{\mathrm{x}}^3& -& \frac{91}{4}{\mathrm{x}}^4& -& \frac{333}{8}{\mathrm{x}}^5& -& \frac{302}{5}{\mathrm{x}}^6& \phantom{0}\end{array}\\ \begin{array}{c}\phantom{0}\\ \mathrm{y}& =& -\frac{3}{2}\mathrm{x}\mathrm{x}-2{\mathrm{x}}^3-\frac{25}{8}{\mathrm{x}}^4-\frac{91}{20}{\mathrm{x}}^5-\frac{111}{16}{\mathrm{x}}^6-\frac{302}{35}{\mathrm{x}}^7\text{\&c}\\ \mathrm{y}\mathrm{y}& =& +\frac{9}{4}{\mathrm{x}}^4+6{\mathrm{x}}^5-\frac{111}{16}{\mathrm{x}}^6+\frac{107}{8}{\mathrm{x}}^6\text{\&c}\hfill \\ {\mathrm{y}}^3& =& -\frac{27}{8}{\mathrm{x}}^6\text{\&c}\hfill \end{array}\end{array}$
y eatinus gradatim productu, ut cùm in valoribus marginaliu terminoru dextrorsum gradibus inscribuntur, termini tot dimensionum emergant quot ad sequentem operationem requiri percipio. Et hac methodo prodit tandem $\mathrm{y}=-\frac{3}{2}\mathrm{x}\mathrm{x}-6{\mathrm{x}}^3-\frac{25}{8}{\mathrm{x}}^4\text{\&c}$ æquatio desiderata. |Qui valor cùm sit negativus, patet alterum e quantitatibus x et y decrescere dum altera increscit * |* Atqꝫ idem pariter concludi debet cum fluxionum diversa sunt altera affirmativa est et altera negativa.||

|Ex: 4.| Haud secus cùm \Relata/ quantitas indefinitè quæsita fractis dimensionibus afficitur \possis/ valorem ejus extrahere. {illeg} Veluti si proponitur $\frac{\mathrm{m}}{\mathrm{n}}=\frac{1}{2}\mathrm{y}-4\mathrm{y}\mathrm{y}+2\mathrm{y}{\mathrm{x}}^{\frac{1}{2}}-\frac{4}{5}\mathrm{x}\mathrm{x}$$+\frac{7}{4}{\mathrm{y}}^{\frac{5}{2}}+2{\mathrm{y}}^3$, ubi x in termino $2\mathrm{y}{\mathrm{x}}^{\frac{1}{2}}$ (sive $2\mathrm{y}\sqrt{}\mathrm{x}$ fracta
$\begin{array}{c}\begin{array}{ccccccccccccccc}\phantom{0}& +& \frac{1}{2}\mathrm{y}& ·& -& 4\mathrm{y}\mathrm{y}& +& 7{\mathrm{y}}^{\frac{5}{2}}& +& 2{\mathrm{y}}^3& \phantom{0}& ·& \phantom{0}& ·& \phantom{0}\\ 2\mathrm{y}{\mathrm{x}}^{\frac{1}{2}}& \phantom{+}& ·& ·& +& \mathrm{y}\mathrm{y}& \phantom{+}& ·& -& 2{\mathrm{y}}^3& +& 4{\mathrm{y}}^{\frac{7}{2}}& -& 2{\mathrm{y}}^4& \text{\&c}\\ -\frac{4}{5}\mathrm{x}\mathrm{x}& \phantom{+}& ·& ·& \phantom{+}& ·& \phantom{+}& ·& \phantom{+}& ·& \phantom{+}& ·& -& \frac{1}{20}{\mathrm{y}}^4& \text{\&c}\\ \text{Summa}& +& \frac{1}{2}\mathrm{y}& ·& -& 3\mathrm{y}\mathrm{y}& +& 7{\mathrm{y}}^{\frac{5}{2}}& \phantom{0}& ·& +& 4{\mathrm{y}}^{\frac{7}{2}}& +& \frac{41}{20}{\mathrm{y}}^4& \phantom{0}\end{array}\\ \begin{array}{c}\phantom{0}\\ \mathrm{x}& =& +\frac{1}{4}\mathrm{y}\mathrm{y}·-{\mathrm{y}}^3+2{\mathrm{y}}^{\frac{7}{2}}·+\frac{8}{9}{\mathrm{x}}^{\frac{9}{2}}-\frac{41}{100}{\mathrm{y}}^5\text{\&c}\\ {\mathrm{x}}^{\frac{1}{2}}& =& +\frac{1}{2}\mathrm{y}-\mathrm{y}\mathrm{y}+2{\mathrm{y}}^{\frac{5}{2}}-{\mathrm{y}}^3\text{\&c}\hfill \\ \mathrm{x}\mathrm{x}& =& \frac{1}{16}{\mathrm{y}}^4\text{\&c}\hfill \end{array}\end{array}$
dimensione $\frac{1}{2}$ afficitur: Ejus ${\mathrm{x}}^{\frac{1}{2}}$ valorem e valore x paulatim elicio (extrahendo nempe radicem quadraticam) sicut in inferiori parte diagrammatis videre est; eò ut in maginalis {sic} termini vale $2\mathrm{y}{\mathrm{x}}^{\frac{1}{2}}$ <33> valorem gradatim adap transferri \et inseri/ possit. Et sic tandem adipiscor æquationem $\mathrm{x}=\frac{1}{4}\mathrm{y}\mathrm{y}-{\mathrm{y}}^3+2{\mathrm{y}}^{\frac{7}{2}}+\frac{8}{9}{\mathrm{y}}^{\frac{9}{2}}-\frac{41}{100}{\mathrm{y}}^5\text{\&c}$ qua x \respectu y/ indefinitè determinatur.

Et sic in alijs quibuscunqꝫ casibus operari licet.

Cæterùm di{illeg}|x|i hasce solutiones infinitis modis præstari posse. Et hoc fiet si non tantùm initialem quantitatem supremæ seriei sed et aliam quamvis datam quantitatem pro primo termino Quotientis ad arbitrium assumas, ad ac deinde opereris ut in æquantibus præcedentibus. Sic in primo præcedentium exemplorum si pro primo termino
$\begin{array}{c}\begin{array}{ccccccc}\phantom{0}& +& 1& -& 3\mathrm{x}& +& \mathrm{x}\mathrm{x}\\ +\mathrm{y}& +& 1& +& 2\mathrm{x}& \phantom{+}& ·& +& {\mathrm{x}}^3& +& \frac{1}{4}{\mathrm{x}}^4& \text{\&c}\\ +\mathrm{x}\mathrm{y}& \phantom{+}& ·& +& \mathrm{x}& +& 2\mathrm{x}\mathrm{x}& \phantom{+}& ·& +& {\mathrm{x}}^4& \text{\&c}\\ \text{Summa}& +& 2& \phantom{+}& ·& +& 3\mathrm{x}\mathrm{x}& +& {\mathrm{x}}^3& +& \frac{5}{4}{\mathrm{x}}^4& \phantom{0}\end{array}\\ \begin{array}{c}\phantom{0}\\ \mathrm{y}& =& 1+2\mathrm{x}·+{\mathrm{x}}^3+\frac{1}{4}{\mathrm{x}}^4+\frac{1}{4}{\mathrm{x}}^5\text{\&c}\end{array}\end{array}$
valoris y assumas 1, et pro y in terminis marginalibus ($+\mathrm{y}$ & $+\mathrm{x}\mathrm{y}$) substituas, reliquamqꝫ operationem (cujus specimen adjunxi) sicu{illeg}|t| in præcedentibus prosequaris, ipsius y alius exurget valor $1+2\mathrm{x}+{\mathrm{x}}^3+\frac{1}{4}{\mathrm{x}}^4\text{\&c}$. Et sic alius atqꝫ alius exurget assumendo 2, 3, vel alium quemvis numerum pro primo ejus termino. Vel si symbolum aliquod, ut a, pro illo termino indefinitè designando usurpes,
$\begin{array}{c}\begin{array}{cccc}\phantom{0000000}& +1& -3\mathrm{x}& +\mathrm{x}\mathrm{x}\\ \hfill +\mathrm{y}\hfill & +\mathrm{a}& \begin{array}{l}+\mathrm{x}\phantom{\frac{0}{0}}\\ +\mathrm{a}\mathrm{x}\phantom{\frac{0}{0}}\end{array}& \begin{array}{l}-\mathrm{x}\mathrm{x}\phantom{\frac{0}{0}}\\ +\mathrm{a}\mathrm{x}\mathrm{x}\phantom{\frac{0}{0}}\end{array}& \begin{array}{l}+\frac{1}{2}{\mathrm{x}}^3\\ +\frac{2}{3}\mathrm{a}{\mathrm{x}}^3\end{array}& \text{\&c.}\\ \phantom{0}& \phantom{0}& \phantom{0}\\ \hfill +\mathrm{x}\mathrm{y}\hfill & \hfill ·\hfill & \begin{array}{l}+\mathrm{a}\mathrm{x}\end{array}& \begin{array}{l}+\mathrm{x}\mathrm{x}\phantom{0^0}\\ +\mathrm{a}\mathrm{x}\mathrm{x}\phantom{0^0}\end{array}& \begin{array}{l}-{\mathrm{x}}^3\\ +\mathrm{a}{\mathrm{x}}^3\end{array}& \text{\&c.}\\ \text{Summe}& \begin{array}{l}+1\phantom{\frac{0}{0}}\\ +\mathrm{a}\phantom{\frac{0}{0}}\end{array}& \begin{array}{l}-2\mathrm{x}\phantom{\frac{0}{0}}\\ +2\mathrm{a}\mathrm{x}\phantom{\frac{0}{0}}\end{array}& \begin{array}{l}+\mathrm{x}\mathrm{x}\phantom{\frac{0}{0}}\\ +2\mathrm{a}\mathrm{x}\mathrm{x}\phantom{\frac{0}{0}}\end{array}& \begin{array}{l}-\frac{2}{3}{\mathrm{x}}^3\\ +\frac{5}{3}\mathrm{a}{\mathrm{x}}^3\end{array}& \phantom{0}\end{array}\\ \begin{array}{c}\phantom{0}\\ \mathrm{y}& =& \mathrm{a}& \begin{array}{l}+\mathrm{x}\phantom{\frac{0}{0}}\\ +\mathrm{a}\mathrm{x}\phantom{\frac{0}{0}}\end{array}& \begin{array}{l}-\mathrm{x}\mathrm{x}\phantom{\frac{0}{0}}\\ +\mathrm{a}\mathrm{x}\mathrm{x}\phantom{\frac{0}{0}}\end{array}& \begin{array}{l}+\frac{1}{3}{\mathrm{x}}^3\\ +\frac{2}{3}\mathrm{a}{\mathrm{x}}^3\end{array}& \begin{array}{l}-\frac{1}{6}{\mathrm{x}}^4\\ +\frac{5}{12}\mathrm{a}{\mathrm{x}}^4\end{array}& \text{\&c.}\end{array}\end{array}$
eadem operandi method{illeg}|o| (quam hic etiam designatam habes) elicies tandem $\mathrm{y}=\mathrm{a}+\mathrm{x}+\mathrm{a}\mathrm{x}$$-\mathrm{x}\mathrm{x}+\mathrm{a}\mathrm{x}\mathrm{x}+\frac{1}{3}{\mathrm{x}}^3+\frac{2}{3}\mathrm{a}{\mathrm{x}}^3\text{\&c}$. Qua inventa possis pro a arbitrio substiture {sic} 1, vel 2, vel 0, {illeg} $\frac{1}{2}$, {illeg}|aut| quem vi{illeg}|s| numerum, et sic relationem inter x et y modis infinitis obtinere.

Et nota quod ubi quantitas elicienda afficitur fracta dimensione (ut in præcedentium exemplorum quart{illeg}|ó| vides) convenit plerumqꝫ unitatem (vel alium quemvis aptum <34> numerum{)} pro primo ejus termino adhibere; immò hoc necesse est ubi radix (ad fractæ illius dimensionis valorem obtinendum) propter negativum signum nequit alias ex{illeg}|t|rahi, ut et ubi nulli sunt termini in prima sive capitali classe reponendi, ex quibut|s| {illeg} initialis ille terminus eliciatur.

Sic tandem {illeg} hoc molestissimum et omnium difficillimum Problema, ubi duæ tantùm fluenti{illeg}|es| quantitat{illeg}|es| una cum earum fluxionibus in æquatione compl|r|eh\en/duntur, absolvi. Sed præter generalem methodum qua omnes difficultates complexus sum sunt aliæ plerumqꝫ contractiores qu{illeg}|i|bus opus aliquando sublevari possit, et quarum aliqua specimina ex abundanti perstringere forte non erit ingratum.

1. Siquando itaqꝫ quantitas elicienda sit alicubi negatæ {sic} dimensionis non est absolutè necessarium ut æquatio propterea ad aliam formam reducatur. Sic enim expositâ æquatione {illeg} $\mathrm{n}=\frac{1}{\mathrm{y}}-\mathrm{x}\mathrm{x}$ ubi y est unis|u|s negatæ {sic} dimensionis, possim equidem ad aliam formam reducere, {illeg} \veluti/ scribendo $1+\mathrm{y}$ pro y {illeg}, sed expeditior erit resolutio quam in
$\begin{array}{c}\begin{array}{cccccc}\phantom{0}& ·& \phantom{+}& ·& -& \mathrm{x}\mathrm{x}\hfill \\ \frac{1}{\mathrm{y}}& 1& -& \mathrm{x}& +& \frac{3}{2}\mathrm{x}\mathrm{x}& \text{\&c}\\ \text{Summa}& 1& -& \mathrm{x}& +& \frac{1}{2}\mathrm{x}\mathrm{x}& \phantom{\text{\&c}}\end{array}\\ \begin{array}{c}\phantom{0}\\ \mathrm{y}& =& 1+\mathrm{x}+\frac{1}{2}{\mathrm{x}}^2+\frac{1}{6}{\mathrm{x}}^3\text{\&c}\\ \frac{1}{\mathrm{y}}& =& 1-\mathrm{x}+\frac{3}{2}\mathrm{x}\mathrm{x}\text{\&c}\hfill \end{array}\end{array}$
annexo diagrammate designatam habes, ubi assumpto 1 pro initio valoris y cæteros ejus terminos ut in præcedend|t|ibus extraho, et interea valorem $\frac{1}{\mathrm{y}}$ exinde per divisionem paulatim institutam elicio et insero in valorem marginalis termini.

<35>

2. Neqꝫ \semper/ opus est ut alterius fluentis quantitatis dimensiones sint passim affirmativæ. Nam ex æquatione $\mathrm{n}=3+2\mathrm{y}-\frac{\mathrm{y}\mathrm{y}}{\mathrm{x}}$, absqꝫ termini $\frac{\mathrm{y}\mathrm{y}}{\mathrm{x}}$ reductione præscriptâ emerget $\mathrm{y}=3\mathrm{x}-\frac{3}{2}\mathrm{x}\mathrm{x}-4{\mathrm{x}}^3\text{\&c}$. Et ex $\mathrm{n}=\mathrm{y}+\frac{1}{\mathrm{x}}-\frac{1}{\mathrm{x}\mathrm{x}}$ (opere ad modum annexi speciminis instito {sic}) emerget $\mathrm{y}=\frac{1}{\mathrm{x}}$.
$\begin{array}{c}\begin{array}{ccccc}\phantom{0}& -& \frac{1}{\mathrm{x}\mathrm{x}}& +& \frac{1}{\mathrm{x}}\\ -\mathrm{y}& \phantom{+}& ·& -& \frac{1}{\mathrm{x}}\\ \text{Summa}& -& \frac{1}{\mathrm{x}\mathrm{x}}& \phantom{+}& 0\end{array}\\ \begin{array}{c}\phantom{0}\\ \mathrm{y}& =& \frac{1}{\mathrm{x}}\end{array}\end{array}$
{illeg}|Ub|i \obiter/ nota quod inter modos infinitos quibus quælibet æquatio resolvi potest sæpe numero contingit aliquos esse quibus \ad/ finitum valorem quantitatis elicient|d|æ sicut in allato specimine finiuntur, et quod|s| haud difficile{illeg} est invenire si pro primo valoris termino symbolum aliquod assumatur. Et resolutione peractâ consulatur de symboli illius quantitate qua valor elicitus evadat finitus.

Porro si æquatio valor y ex æquatione $\mathrm{n}=\frac{\mathrm{y}}{2\mathrm{x}}$$+1-2\mathrm{x}+\frac{1}{2}\mathrm{x}\mathrm{x}$ eliciendus si{illeg}|t|, id sine aliqua reductione termini $\frac{\mathrm{y}}{2\mathrm{x}}$ non incommodè fiet fingendo (pro more Analytico) datum esse quod quæritur. Utpote pro primo termino valoris ejus effingo $2\mathrm{e}\mathrm{x}$ assumendo $2\mathrm{e}$ pro
$\begin{array}{c}\begin{array}{cccc}\phantom{0000000}& 1& -2\mathrm{x}& +\frac{1}{2}\mathrm{x}\mathrm{x}\\ \hfill \frac{\mathrm{y}}{2\mathrm{x}}\hfill & \mathrm{e}& +\mathrm{f}\mathrm{x}& +\mathrm{g}\mathrm{x}\mathrm{x}& +\mathrm{h}{\mathrm{x}}^3\\ \text{Summa}& \begin{array}{l}+1\phantom{\frac{0}{0}}\\ +\mathrm{e}\phantom{\frac{0}{0}}\end{array}& \begin{array}{l}-2\mathrm{x}\phantom{\frac{0}{0}}\\ +\mathrm{f}\mathrm{x}\phantom{\frac{0}{0}}\end{array}& \begin{array}{l}+\frac{1}{2}\mathrm{x}\mathrm{x}\phantom{\frac{0}{0}}\\ +\mathrm{g}\mathrm{x}\mathrm{x}\phantom{\frac{0}{0}}\end{array}& \begin{array}{l}+\mathrm{h}{\mathrm{x}}^3\\ \phantom{\frac{0}{0}}\end{array}\end{array}\\ \begin{array}{c}\phantom{0}\\ \text{Hypotheticè}& \mathrm{y}& =& 2\mathrm{e}\mathrm{x}& +2\mathrm{f}\mathrm{x}\mathrm{x}& +2\mathrm{g}{\mathrm{x}}^3& +2\mathrm{h}{\mathrm{x}}^4\\ \phantom{0}& \phantom{0}& \phantom{0}& =& =& =& =\\ \text{Consequenter}& \mathrm{y}& =& \begin{array}{l}+\mathrm{x}\phantom{\frac{0}{0}}\\ +\mathrm{e}\mathrm{x}\phantom{\frac{0}{0}}\end{array}& \begin{array}{l}-\mathrm{x}\mathrm{x}\phantom{\frac{0}{0}}\\ +\frac{1}{2}\mathrm{f}\mathrm{x}\mathrm{x}\phantom{\frac{0}{0}}\end{array}& \begin{array}{l}+\frac{1}{6}{\mathrm{x}}^3\\ +\frac{1}{3}\mathrm{g}{\mathrm{x}}^3\end{array}& \begin{array}{l}+\frac{1}{4}\mathrm{h}{\mathrm{x}}^4\end{array}\\ \text{Revera}& \mathrm{y}& =& 2\mathrm{x}& -\frac{4}{3}\mathrm{x}\mathrm{x}\hfill & +\frac{1}{5}{\mathrm{x}}^3\hfill \end{array}\end{array}$
numerali coefficiente quæ nondum innotescit. Et hunc $2\mathrm{e}\mathrm{x}$ pro y in termino marginali \$\frac{\mathrm{y}}{2\mathrm{X}}$/ substituens prodit e quem scribo ad dextram et summa{illeg} $1+\mathrm{e}$ dabit $\mathrm{x}+\mathrm{e}\mathrm{x}$ pro
eodem primo termino valoris y quem prius designaveram <36> termino $2\mathrm{e}\mathrm{x}$. Pono itaqꝫ $2\mathrm{e}\mathrm{x}=\mathrm{x}+\mathrm{e}\mathrm{x}$ et inde elicio $\mathrm{e}=1$. Adeoqꝫ primus valoris y {illeg} primus terminus ($2\mathrm{e}\mathrm{x}$) est $2\mathrm{x}$. Et sic p{illeg} Ad eundem modum pro secundo termino designando effictum $2\mathrm{f}{\mathrm{x}}^2$ usurpo et inde tandem eruo {illeg} $-\frac{2}{3}$ pro valore f, adeoqꝫ $-\frac{4}{3}\mathrm{x}\mathrm{x}$ pro secundo termino. Et sic effictus {illeg} g {illeg} in tertio termino valebit $\frac{1}{10}$ {illeg}, at h in quarto valebit 0, et proinde cum nullos præterea terminos superesse video, concludo opus finitum esse et y valere $2\mathrm{x}-\frac{4}{3}\mathrm{x}\mathrm{x}$$+\frac{1}{5}{\mathrm{x}}^3$ præcisè. |Ad eundem ferè modum si esset $\mathrm{n}=\frac{3\mathrm{y}}{4\mathrm{x}}$, effinge $\mathrm{y}=\mathrm{e}{\mathrm{x}}^{\mathrm{s}}$ ubi e ignotum coefficientem et s numerum dimensionum similiter ignotum denotet. Et ** |** Et {sic} $\mathrm{e}{\mathrm{x}}^{\mathrm{s}}$ pro y substituto, prodibit $\mathrm{n}=\frac{3\mathrm{e}{\mathrm{x}}^{\mathrm{s}-1}}{4}$. et inde rursus $\mathrm{y}=\frac{3\mathrm{e}{\mathrm{x}}^{\mathrm{s}}}{4\mathrm{s}}$. Conferantur jam valores y, et videbis esse $\frac{3\mathrm{e}}{4\mathrm{s}}=\mathrm{e}$, adeòqꝫ $\mathrm{s}=\frac{3}{4}$, et e indefinitum. Quare assumpto utcunqꝫ e, erit $\mathrm{y}=\mathrm{e}{\mathrm{x}}^{\frac{3}{4}}$.||.

4. Adhæc nonnunquam opus ab altissima dimensione æquabilis quantitatis inch\o/ari potest et ad depressiores continuo pergere. Veluti si detur $\mathrm{n}=\frac{\mathrm{y}}{\mathrm{x}\mathrm{x}}+\frac{1}{\mathrm{x}\mathrm{x}}+3$$+2\mathrm{x}-\frac{4}{\mathrm{x}}$, & ab altissimo termino $2\mathrm{x}$ opus inchoetur
$\begin{array}{c}\begin{array}{cccccccccc}\phantom{0}& +& 2\mathrm{x}& +& 3& -& \frac{4}{\mathrm{x}}& +& \frac{1}{\mathrm{x}\mathrm{x}}& \text{.}\\ +\frac{\mathrm{y}}{\mathrm{x}\mathrm{x}}& \phantom{+}& ·& +& 1& +& \frac{4}{\mathrm{x}}& \phantom{+}& ·& -& \frac{1}{{\mathrm{x}}^3}& +& \frac{1}{2{\mathrm{x}}^4}& \text{\&c}\\ \text{Summa}& -& 2\mathrm{x}& +& 4& \phantom{+}& ·& +& \frac{1}{\mathrm{x}\mathrm{x}}& -& \frac{1}{{\mathrm{x}}^3}& +& \frac{1}{2{\mathrm{x}}^4}\end{array}\\ \begin{array}{c}\phantom{0}\\ \mathrm{y}& =& \mathrm{x}\mathrm{x}+4\mathrm{x}·-\frac{1}{\mathrm{x}}+\frac{1}{2\mathrm{x}\mathrm{x}}-\frac{1}{6{\mathrm{x}}^3}\text{\&c}\end{array}\end{array}$
disponendo capitalem seriem in ordine præcedentibus contrario, emerget tandem $\mathrm{y}=\mathrm{x}\mathrm{x}+4\mathrm{x}-\frac{1}{\mathrm{x}}\text{\&c}$ prout in appositâ operandi forma videre est. Et hic in tran{illeg}|situ| notari potest quod inter operandum potuit inter terminos $4\mathrm{x}$ et $-\frac{1}{\mathrm{x}}$ pro intermedio deficienti termino quælibet data quantitas inseri et sic valor y modis infinitis extrahi.

5. Siquæ præterea s{illeg}|i|nt fractæ dimensionum Relatæ Quantitatis indices, ad integras reduci possunt fingendo Quantitatem illam sua fracta dimensione affectam esse alij cuilibet tertiæ fluenti quantitati æqualem, et substituendo tum illam quantitatem tum fluxionem ejus ab ilia fi{illeg}|c|tâ æquatione oriundam pro Relata Quantitate et ejus fluxione. Quemadmodum si exponitur <37> æquatio $\mathrm{n}=3\mathrm{x}{\mathrm{y}}^{\frac{2}{3}}+\mathrm{y}$, ubi Relata Quantitas fractâ dimensionis indice $\frac{2}{3}$ afficitur, assumpta ad arbitrium fluenti quantitate z fingo esse ${\mathrm{y}}^{\frac{1}{3}}=\mathrm{z}$ sive $\mathrm{y}={\mathrm{z}}^3$ et fluxio
num relatio juxta Reg Prob: 1. erit $\mathrm{n}=3\mathrm{r}\mathrm{z}\mathrm{z}$. Quare substituto $3\mathrm{r}\mathrm{z}\mathrm{z}$ pro n ut et ${\mathrm{z}}^3$ pro y ac $\mathrm{z}\mathrm{z}$ pro ${\mathrm{y}}^{\frac{2}{3}}$, emerget $3\mathrm{r}\mathrm{z}\mathrm{z}=3\mathrm{x}\mathrm{z}\mathrm{z}+{\mathrm{z}}^3$ sive $\mathrm{r}=\mathrm{x}+\frac{1}{3}\mathrm{z}$. Ubi z supplet vices Relatæ quantitatis. Postquam vel vel|r|o valor z \eo nomine/ eruitur utpote $\mathrm{z}=\frac{1}{2}\mathrm{x}\mathrm{x}+\frac{1}{18}{\mathrm{x}}^3+\frac{1}{216}{\mathrm{x}}^4+\frac{1}{3240}{\mathrm{x}}^5\text{\&c}$, {illeg} pro z restitue ${\mathrm{y}}^{\frac{1}{3}}$ et habebis desideratam relationem inter x et y nempe ${\mathrm{y}}^{\frac{1}{3}}=\frac{1}{2}\mathrm{x}\mathrm{x}+\frac{1}{18}{\mathrm{x}}^3+\frac{1}{216}{\mathrm{x}}^4\text{\&c}$, et cubis partium utrobiqꝫ positis erit $\mathrm{y}=\frac{1}{8}{\mathrm{x}}^6+\frac{1}{24}{\mathrm{x}}^7+\frac{1}{288}{\mathrm{x}}^8\text{\&c}$. Pari ratione si detur $\mathrm{n}=\sqrt{}4\mathrm{y}+\sqrt{}\mathrm{x}\mathrm{y}$, s{illeg}|i|ve $=2{\mathrm{y}}^{\frac{1}{2}}+{\mathrm{x}}^{\frac{1}{2}}{\mathrm{y}}^{\frac{1}{2}}\text{.}$ fingo $\mathrm{z}={\mathrm{y}}^{\frac{1}{2}}$ sive $\mathrm{z}\mathrm{z}=\mathrm{y}$, et inde per Prob 1 elicio $2\mathrm{r}\mathrm{z}=\mathrm{n}$ et consequenter est $2\mathrm{r}\mathrm{z}=2\mathrm{z}+{\mathrm{x}}^{\frac{1}{2}}\mathrm{z}$ sive $\mathrm{r}=1+\frac{1}{2}{\mathrm{x}}^{\frac{1}{2}}$. Adeoqꝫ per casum priorem hujus est $\mathrm{z}\left({\mathrm{y}}^{\frac{1}{2}}\right)=\mathrm{x}+\frac{1}{3}{\mathrm{x}}^{\frac{3}{2}}$ vel {illeg} e{illeg}|t| partibus quadratis $\mathrm{y}=\mathrm{x}\mathrm{x}+\frac{2}{3}{\mathrm{x}}^{\frac{5}{2}}+\frac{1}{9}{\mathrm{x}}^3$. Sin valorem y modis infinitis desideres fac $\mathrm{z}=\mathrm{c}+\mathrm{x}+\frac{1}{3}{\mathrm{x}}^{\frac{3}{2}}$ assumpto utcunqꝫ initiali termino c, et erit $\mathrm{y}\left(\mathrm{z}\mathrm{z}\right)=\mathrm{c}\mathrm{c}+2\mathrm{c}\mathrm{x}+\frac{2}{3}\mathrm{c}{\mathrm{x}}^{\frac{3}{2}}+\mathrm{x}\mathrm{x}$$+\frac{2}{3}{\mathrm{x}}^{\frac{5}{2}}+\frac{1}{9}{\mathrm{x}}^3$.

Ast haec nimis officiose tractare videor siquidem rarissime usui esse possunt. Quamobrem de resolutione |Ast haec nimis officiose tractare videor siquidem rarissime usui esse possunt.|

|Casus 3.|

Problematis ubi tres vel plures quantitatum flux{illeg}iones æquatio complectitur haud operæ pretium \Resolutio brevi absolvitur/ erit aliquid disserere; sed dicam tamen brevitur quod \Scilicet/ inter duas quaslibet istarum quantitatum relatio (ubi ex statu Probl{illeg} Quæstionis non determinatur) quælibet effingi debet, et earum fluxionum exinde quæri, eo ut alterutra unà cum ejus fluxione ex æquatione expositâ exterminari possit. Quâ de causâ, si trium insunt in æquati quantitatum fluxiones unica effingenda est æquatio ac duæ si insunt quatuor, et sic porro, ut exposita <38> æquatio in aliam tandem æquationem transformetur cui non insint plures duabus; Et hæ|â|c deinde ut supra resol{illeg}|u|tâ{illeg}, qu{illeg} reliquarum fluentium quantitatum obtinentur relationes \eruentur/. Sic æquatione $2\mathrm{m}-\mathrm{r}+\mathrm{n}\mathrm{x}=0$ exposita; quo {illeg} quantitatum x y et z (quarum fluxiones m n et r æquatio complectitur) relationes \inter se/ obtineam, relationem inter duas quaslibet ut x et y pro lubitu effingo puta quod sit $\mathrm{x}=\mathrm{y}$, vel $2\mathrm{y}=\mathrm{a}+\mathrm{z}$, vel $\mathrm{x}=\mathrm{y}\mathrm{y}$ &c{.} Sit autem $\mathrm{x}=\mathrm{y}\mathrm{y}$ et inde erit $\mathrm{m}=2\mathrm{n}\mathrm{y}$, Quare scriptis $2\mathrm{n}\mathrm{y}$ pro m et $\mathrm{y}\mathrm{y}$ pro x, exposita æquatio transform\ab/itur in $4\mathrm{n}\mathrm{y}-\mathrm{r}+\mathrm{n}\mathrm{y}\mathrm{y}=0$. Ubi si x vicissim pro $\mathrm{y}\mathrm{y}$ scribatur prodibit etiam Et inde relatio inter y et z emerget $2\mathrm{y}\mathrm{y}+\frac{1}{3}{\mathrm{y}}^3=\mathrm{z}$. Ubi si x pro $\mathrm{y}\mathrm{y}$ et ${\mathrm{x}}^{\frac{3}{2}}$ pro ${\mathrm{y}}^3$ vicissim scribatur prodibit etiam $2\mathrm{x}+$$\frac{1}{3}{\mathrm{x}}^{\frac{3}{2}}=\mathrm{z}$. Adeóqꝫ inter x, y et modos infinitos quibus x, y et z ad invicem referuntur uni{illeg}us his aequationibus $\mathrm{x}=\mathrm{y}\mathrm{y}\text{.}$ $2\mathrm{y}\mathrm{y}+\frac{1}{3}{\mathrm{y}}^3=\mathrm{z}$ et $2\mathrm{x}+\frac{1}{3}{\mathrm{x}}^{\frac{3}{2}}=\mathrm{z}$ designatus investigatur.

Demonstratio.

Jam {deniqꝫ harum} \Problema tandem cofecimus sed/ demonstratio superest. Et in tanta rerum copiâ ne per nimias ambages e proprijs fundamentis Syntheticè derivetur, sufficiat per Analysin sic breviter indicare. Scilicet æquatione quâlibet expositâ, postquam opus ad finem perduxeris experiri est quod ex elicita æqu\a/tione exposita vicissim (per Prob 1) eruetur. Et proinde quantitatum relatio in elicita æquatione exigit relationem fluxionum in exposita, et contra: sicut ostendendum erat. Sic æquatione $\mathrm{n}=\mathrm{x}$ expositâ elicietur $\mathrm{y}=\frac{1}{2}\mathrm{x}\mathrm{x}$ et \inde/ vicissim (per prob 1) {illeg} $\mathrm{n}=\mathrm{m}\mathrm{x}$ sive $=\mathrm{x}$ quandoquidem m supponitur esse 1. ^[1]Et sic ex $\mathrm{n}=1-3\mathrm{x}+\mathrm{y}+\mathrm{x}\mathrm{x}+\mathrm{x}\mathrm{y}$ provenit $\mathrm{y}=\mathrm{x}-\mathrm{x}\mathrm{x}+\frac{1}{3}{\mathrm{x}}^3-\frac{1}{6}{\mathrm{x}}^4+\frac{1}{30}{\mathrm{x}}^5-\frac{1}{45}{\mathrm{x}}^6\text{\&c}$ et inde vicissim per Prob 1, et $\mathrm{n}=1-2\mathrm{x}+{\mathrm{x}}^2-\frac{2}{3}{\mathrm{x}}^3+\frac{1}{6}{\mathrm{x}}^4-\frac{2}{15}{\mathrm{x}}^5\text{\&c}$ Qui <39> duo valores ipsius n conveniunt, ut patet substituendo $\mathrm{x}-\mathrm{x}\mathrm{x}$$+\frac{1}{3}{\mathrm{x}}^3-\frac{1}{6}{\mathrm{x}}^4+\frac{1}{30}{\mathrm{x}}^5\text{\&c}$ pro y in priori.

Cæterùm in æquationum reductione adhibui operationem de qua præterea rationem reddere oportet: {illeg}|E|stqꝫ transmutatio fluentis quantitatis per connexionem cum quantitate data. Sunto AE et ae 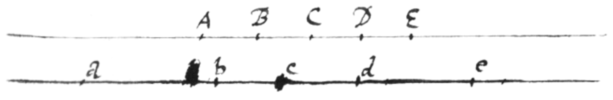linæ utrinqꝫ infinitæ per quas mobilia duo e longinquo trajiciantur simul{illeg} attingentia locos A et a, B et b, C et c, D et d &c; et sit B punctum a cujus et rei mobilis distantiâ in AE motus æstimetur ita ut $-\mathrm{BA}$, {illeg} {illeg} BC, BD, BE successive sint fluentes quantitates quando mobile sit in locis A, C, D, E. Sitqꝫ b consimile punctum in altera linea: et erunt $-\mathrm{BA}$ ac $-\mathrm{ba}$ contemporaneæ fluentes quantitates, ut et BC ac bc, BD ac bd, BE ac be &c. Quod si vice punctorum B et b substituantur A et c ad quæ tanquam quiescentia motus referantur, tunc 0 & $-\mathrm{ca}$, AB et $-\mathrm{cb}$, AC et 0, AD et cd, AE et ce &c erunt contemporaneæ fluentes quantitates. Mutantur itaqꝫ fluentes quantitates additione et substractione datarum AB et be, sed non mutantur quoad motûs celeritatem et fluxionis mutuum respectum: nam ejusdem longitudinis sunt partes contemporaneæ AB et ab, BC et bc, CD et cd, DE e{illeg}|t| de in utroqꝫ casu. {illeg}|E|t sic in æquationibus quibus hæ quanti{illeg}|t|ates designantur partes contemporaneæ quantitatum non ideo mutantur quod earum absoluta longitudo datâ aliquâ augeatur vel minuatur. Unde constat Propositum: Nam Problematis hujus scopus propriè non alius est quam contemporaneas partes sive absolutat|r|um quantitatum (v, x, y, aut z) contemporaneas differentias data fluendi ratione descriptas determinare. Et perinde est cujusnam sint absolutæ longitudinis quantitates illæ dummodo contemporaneæ sive correspondentes earum differentiæ cum exposita <40> fluxionum relatione conveniat|n|t.

Potest et hujus rei ratio sic Algebraicè reddi. Proponatur $\mathrm{n}=\mathrm{m}\mathrm{x}\mathrm{y}$, et finge $\mathrm{x}=1+\mathrm{z}$, eritqꝫ (per Prob 1) $\mathrm{n}=\mathrm{r}$. Adeoqꝫ pro $\mathrm{n}=\mathrm{m}\mathrm{x}\mathrm{y}$ scribi potest $\mathrm{r}=\mathrm{m}\mathrm{y}+\mathrm{m}\mathrm{z}\mathrm{y}$. Jam cum sit $\mathrm{n}=\mathrm{r}$, patet quantitates x et z etsi non sint ejusdem longitudinis, pariter tamen fluere respectu ipsius y, et pares habere partes contemporaneas. Quid itaqꝫ si ijsdem symbolis denotem quæ fluendi ratione conveniunt et vice ad contt|e|mporaneas differentias determinandas vice $\mathrm{n}=\mathrm{m}\mathrm{x}\mathrm{y}$ usurpem $\mathrm{n}=\mathrm{m}\mathrm{y}+\mathrm{m}\mathrm{x}\mathrm{y}$.

Jam deniqꝫ quo pacto partes contemporaneæ ex ex æquatione quantitates involvente inveniri possint per se manifestum est. E.G. Sit $\mathrm{y}=\frac{1}{\mathrm{x}}+\mathrm{x}$ æquatio. Et posito \cum sit/ $\mathrm{x}=2$ erit $\mathrm{y}=2\frac{1}{2}$, dein posito cum verò sit $\mathrm{x}=3$ erit $\mathrm{y}=3\frac{1}{3}$. Ergo dum x fluit a 2 ad 3 y fluet a $2\frac{1}{2}$ ad $3\frac{1}{3}$. Adeoqꝫ partes in hoc tempore transactæ sunt $\left(3-2\right)1$ et $\left(3\frac{1}{3}-2\frac{1}{2}\right)\frac{5}{6}$. Atqꝫ ita cum x sit \0 erit y infinit {sic} et cum x sit $-1$ / erit $\mathrm{y}=-2$. Ergo dum x fluit a $-1$ ad $+3$ y fluet ab $-2$ per infinitatem ad $+3\frac{1}{3}$. Et x in hoc tempore {illeg} Hoc est Adeoqꝫ partes contemporanæ sunt 4 et infinitum spatium.

Jactis hisce sequentium fundamentis, ad Problemata magis particularia jam transeo.

<41>

Prob 3.
Determinare maximas et minimas.

Quantitas ubi maxima est vel minima, in illo momento nec profluit nec refluit. n|N|am si profluit, sequitur \id arguit/ minorem fuisse et statim majorem fore quam jam est; et contra si refluit. Quamobrem fluxionem ejus per Prob: {illeg}|1| quære et pone nullam esse.

Exemp 1. Si maxima quantitas x in æquatione ${\mathrm{x}}^3-\mathrm{a}\mathrm{x}\mathrm{x}+\mathrm{a}\mathrm{x}\mathrm{y}-{\mathrm{y}}^3=0$ desideretur. ^[2]Quantitatum x et y fluxiones quære et prodibit $3\mathrm{m}\mathrm{x}\mathrm{x}-2\mathrm{a}\mathrm{m}\mathrm{x}+\mathrm{a}\mathrm{m}\mathrm{y}-3\mathrm{n}\mathrm{y}\mathrm{y}$$+\mathrm{a}\mathrm{n}\mathrm{x}=0$. Positóqꝫ $\mathrm{m}=0$ restabit $-3\mathrm{n}\mathrm{y}\mathrm{y}+\mathrm{a}\mathrm{n}\mathrm{x}=0$ sive {illeg} $3\mathrm{y}\mathrm{y}=\mathrm{a}\mathrm{x}$. Cujus ope possis alterutram x vel y in æquatione primariâ exterminare, et per æquationem {resu{illeg}|l|tantem}{restantem} determinare alteram, et utramqꝫ deinde per $3\mathrm{y}\mathrm{y}+\mathrm{a}\mathrm{x}=0$ {sic}.

Perinde est hæc operatio ac si multiplicasses terminos propositæ æquationis per numerum dimensionum alterius fluentis quantitatis y. Unde prodit Huddeniana notissima Regula quod ad obtinendum maximam {illeg} aut minimam Relatam Quantitatem Æquatio juxta dimensiones Correlatæ q|Q|uantitatis disponi debet et per quamlibet Arithmeticam progressionem multiplicari. Ast cùm neqꝫ hæc regula ad æquationes surdis quantitatibus affectas neqꝫ ulla alia hactenus quod sciam evulgata se extendit absqꝫ prævia reductione se extendi|a|t: ejus rei accipe sequens exemplum.

^[3]Ex: 2. Si maxima quantitas y in æquatione ${\mathrm{x}}^3-\mathrm{a}\mathrm{y}\mathrm{y}+\frac{\mathrm{b}{\mathrm{y}}^3}{\mathrm{a}+\mathrm{y}}-\mathrm{x}\mathrm{x}\sqrt{}\stackrel{\_}{\mathrm{a}\mathrm{y}+\mathrm{x}\mathrm{x}}=0$ determinanda est; ipsarum x et y fluxiones \quære/ et emerget $3\mathrm{m}\mathrm{x}\mathrm{x}-2\mathrm{a}\mathrm{n}\mathrm{y}\frac{+3\mathrm{a}\mathrm{b}\mathrm{n}\mathrm{y}\mathrm{y}+2\mathrm{b}\mathrm{n}{\mathrm{y}}^3}{\mathrm{a}\mathrm{a}+2\mathrm{a}\mathrm{y}+\mathrm{y}\mathrm{y}}$$\frac{-4\mathrm{a}\mathrm{m}\mathrm{x}\mathrm{y}-6\mathrm{m}{\mathrm{x}}^3-\mathrm{a}\mathrm{n}\mathrm{x}\mathrm{x}}{2\sqrt{}\stackrel{\_}{\mathrm{a}\mathrm{y}+\mathrm{x}\mathrm{x}}}=0$. Et cum ex hypothesi sit $\mathrm{n}=0$ neglige terminos in n ductos (id quod inter operant|d|um ad minuendum laborem antea fieri potuit) cæterosqꝫ per $\mathrm{m}\mathrm{x}$ <42> divide et restabit $3\mathrm{x}\frac{-2\mathrm{a}\mathrm{y}-3\mathrm{x}\mathrm{x}}{\sqrt{}\stackrel{\_}{\mathrm{a}\mathrm{y}+\mathrm{x}\mathrm{x}}}=0$, factaqꝫ reductione exurget $4\mathrm{a}\mathrm{y}+3\mathrm{x}\mathrm{x}=0$. Cujus ope possis utramvis quantitatem x vel y ex æquatione primò proposita exterminare ac deinde ex æquatione resultante (quæ cubica erit) valorem alterius elicere.

Ex hoc problemate sequentium resolu{illeg}|t|io petenda est. cujusmodi Problematis hujus beneficio sequentia resolvenda sunt, unà et alia permulta facilius excogitari
cum ejusmodi permultis alijs quæ ut plurimùm facilius excogitari possunt quam (propter computandi molestiam) resolvi.

In dato Triangulo aut Segmento cujusvis c|C|urvæ, maximum rectangulum inscribere.

Maximam vel minimam rectarum ducere quæ inter datum punctum et curvam positione datam interjacent. Sive, A dato puncto ad Curvam ducere perpendiculum.

Maximam vel minimam rectarum ducere quæ per datum punctum transeuntes interjacent alijs duabus sive rectis sive curvis linei{illeg}s.

A puncto intra Parabolam dato rectam ducere quæ Parabolam omnium obliquissimè secabit. Et idem in alijs curvis facere.

Curvarum \vertices/ maximam|s| a{illeg}|u|t minimam|s| latitudines \vertices puncta in quibus partes circumactæ se decussant/ determinare.

Curvarum puncta invenire ubi maxime aut minimè curvantur.

Invenire minimum angulorum in quibus rectæ ad diametros {illeg}|s|uas in data Ellipsi ordinatim applicantur.

Ellipsium per data quatuor puncta transeuntium vel minimam definire vel \eam/ quæ ad formam circularem maximè accedit.

Amplitudinem sphæricæ superficiei determinare quam lux e longinquo fluens postquam ab anteriori hemisphærio refracta fuit illustrat in posteriori.

Et hujusmodi alia permulta facilis|ù|s excogitari possunt quàm (propter computandi molestiam \fastidium/) resolvi.

<43>

Prob 4.
Curvarum Tangentes ducere.
Modus 1.

Tangentes pro varijs relationibus curvarum ad rectas, variè ducuntur. ^[4]Et imprimis esto BD recta in dato angulo ad aliam rectam AB tanquam basin ordinata et ad curvam ED terminata. Et moveatur hæc ordinata per indefinitè parvum spatium ad locum bd, ita ut momento 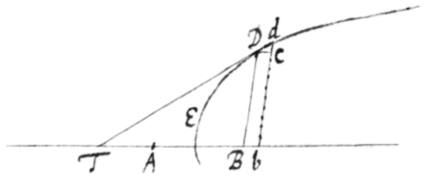{illeg} cd augeatur dum AB augetur momento Bb, cui Dc æqualis{illeg} est. Jam producatur Dd donec cum AB in T conveniat et hæc tanget curvam in D vel d, Eruntqꝫ triangula dcD, DBT similia. Adeóqꝫ $\mathrm{TB}.\mathrm{BD}\colon\colon \mathrm{Dc}.\mathrm{cd}$.

Cùm itaqꝫ relatio BD ad AB in æquatione qualibet pro curvâ determinandâ exponitur; quære relationem fluxionum \per Prob 1/, et cape TB ad BD in ratione fluxionis AB ad fluxionem BD, ac TD tanget curvam in D.

Exemp 1. Nominata AB x et BD y esto earum relatio ${\mathrm{x}}^3-\mathrm{a}\mathrm{x}\mathrm{x}+\mathrm{a}\mathrm{x}\mathrm{y}-{\mathrm{y}}^3=0$. Et fluxionum relatio erit $3\mathrm{m}\mathrm{x}\mathrm{x}-2\mathrm{a}\mathrm{m}\mathrm{x}+\mathrm{a}\mathrm{m}\mathrm{y}-3\mathrm{n}\mathrm{y}\mathrm{y}+\mathrm{a}\mathrm{n}\mathrm{x}=0$. Adeoqꝫ $\mathrm{n}.\mathrm{m}\colon\colon 3\mathrm{x}\mathrm{x}-2\mathrm{a}\mathrm{x}+\mathrm{a}\mathrm{y}.3\mathrm{y}\mathrm{y}-\mathrm{a}\mathrm{x}\colon\colon \mathrm{BD}\left(\mathrm{y}\right).\mathrm{BT}$. Est ergo $\mathrm{BT}=\frac{3{\mathrm{y}}^3-\mathrm{a}\mathrm{x}\mathrm{y}}{3\mathrm{x}\mathrm{x}-2\mathrm{a}\mathrm{x}+\mathrm{a}\mathrm{y}}$. Quamobrem data vel assumpta utcunqꝫ longitudine AB per x, et inde per expositam Dato itaqꝫ puncto D, et inde x et y \DB et AB sive y et x;/ dabitur longitudo BT {illeg}|q|ua tangens TD determinatur.

Potest autem hæc operandi methodus sic {illeg}\con/cinnari. Æquationis expositæ terminos \fac esse nihilo aequales; deinde/ per proprium numerum dimensionum ordinatæ quantitatis multiplica, et exitum colloca in numeratore; Dein terminos ejusdem æquationis per proprium numerum dimensionum Basis multiplica et exitum per Basin divisum colloca in denominatore valoris BT. Et illam BT cape \ad partes/ adversus A si valor ejus sit affirmativus, aut versus A si sit negativus.

Sic æquatio $\begin{array}{cccccccc}0.& & 0.& & 1.& & 3.& \\ {\mathrm{x}}^3& -& \mathrm{a}\mathrm{x}\mathrm{x}& +& \mathrm{a}\mathrm{x}\mathrm{y}& -& {\mathrm{y}}^3& =& 0\\ 3.& & 2.& & 1.& & 0.& \end{array}$ per superiores <44> numeros multiplicata dat $\mathrm{a}\mathrm{x}\mathrm{y}-3{\mathrm{y}}^3$ pro numeratore, et per inferiores multiplicata dat ac divisa per x dat $3\mathrm{x}\mathrm{x}-2\mathrm{a}\mathrm{x}+\mathrm{a}\mathrm{y}$ pro denominatore valoris BT.

^[5]Sic æquatio ${\mathrm{y}}^3-\mathrm{b}\mathrm{y}\mathrm{y}-\mathrm{c}\mathrm{d}\mathrm{y}+\mathrm{b}\mathrm{c}\mathrm{d}+\mathrm{d}\mathrm{x}\mathrm{y}=0$ (quæ designat Parabolam secundi generis cujus beneficio Des-Cartes construxit æquationes 6 dimensionum) primâ fronte dat $\frac{3{\mathrm{y}}^3-2\mathrm{b}\mathrm{y}\mathrm{y}-\mathrm{c}\mathrm{d}\mathrm{y}+\mathrm{d}\mathrm{x}\mathrm{y}}{\mathrm{d}\mathrm{y}}$, sive $\frac{3\mathrm{y}\mathrm{y}}{\mathrm{d}}-\frac{2\mathrm{b}\mathrm{y}}{\mathrm{d}}-\mathrm{c}+\mathrm{x}=\mathrm{BT}$.

Et sic $\mathrm{a}\mathrm{a}-\frac{\mathrm{r}}{\mathrm{q}}\mathrm{x}\mathrm{x}-\mathrm{y}\mathrm{y}=0$ (quæ designat Ellipsin cujus centrum A) dat $\frac{-2\mathrm{y}\mathrm{y}}{-2\frac{\mathrm{r}}{\mathrm{q}}\mathrm{x}}$ sive $\frac{\mathrm{q}\mathrm{y}\mathrm{y}}{\mathrm{r}\mathrm{x}}=\mathrm{BT}$. Et sic in alijs.

Et nota quod nihil interest cujusnam quantitatis sit angulus ordinationis ABD.

Ast hæc Regula se ad æquationes surdis quantitatibus affectas \Curvasqꝫ Mechanicas/ non extendit. In istis casibus ad fundamentalem methodum recurrendum est.

^[6]Exempl: 2. Esto ${\mathrm{x}}^3-\mathrm{a}\mathrm{y}\mathrm{y}+\frac{\mathrm{b}{\mathrm{y}}^3}{\mathrm{a}+\mathrm{y}}-\mathrm{x}\mathrm{x}\sqrt{}\stackrel{\_}{\mathrm{a}\mathrm{y}+\mathrm{x}\mathrm{x}}=0$ æquatio designans relationem inter AB et BD, et per Prob 1 relatio fluxionum erit $3\mathrm{m}\mathrm{x}\mathrm{x}-2\mathrm{a}\mathrm{n}\mathrm{y}+$$\frac{3\mathrm{a}\mathrm{b}\mathrm{n}\mathrm{y}\mathrm{y}+2\mathrm{b}\mathrm{n}{\mathrm{y}}^3}{\mathrm{a}\mathrm{a}+2\mathrm{a}\mathrm{y}+\mathrm{y}\mathrm{y}}\frac{-4\mathrm{a}\mathrm{m}\mathrm{x}\mathrm{y}-6\mathrm{m}{\mathrm{x}}^3-\mathrm{a}\mathrm{n}\mathrm{x}\mathrm{x}}{2\sqrt{}\stackrel{\_}{\mathrm{a}\mathrm{y}+\mathrm{x}\mathrm{x}}}=0$. Atqꝫ adeò est $3\mathrm{x}\mathrm{x}\frac{-4\mathrm{a}\mathrm{x}\mathrm{y}-6{\mathrm{x}}^3}{2\sqrt{}\stackrel{\_}{\mathrm{a}\mathrm{y}+\mathrm{x}\mathrm{x}}}.2\mathrm{a}\mathrm{y}\frac{+3\mathrm{a}\mathrm{b}\mathrm{y}\mathrm{y}+2\mathrm{b}{\mathrm{y}}^3}{\mathrm{a}\mathrm{a}+2\mathrm{a}\mathrm{y}+\mathrm{y}\mathrm{y}}\frac{-\mathrm{a}\mathrm{x}\mathrm{x}}{2\sqrt{}\stackrel{\_}{\mathrm{a}\mathrm{y}+\mathrm{x}\mathrm{x}}}\left(\colon\colon \mathrm{n}.\mathrm{m}\right)$$\colon\colon \mathrm{BD}.\mathrm{BT}$.

Exempl. 3. Sit ED prima Conchoïdes Nichomedea {Vetera} Polo G, Asymptoto AT 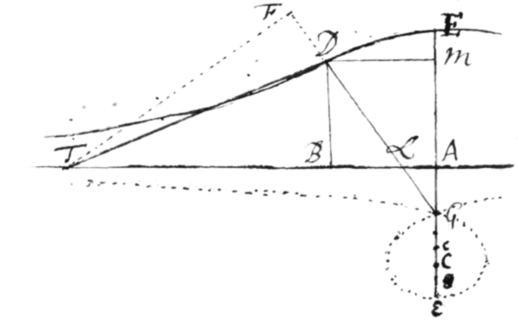et intervallo LD descripta. Sitqꝫ $\mathrm{GA}=\mathrm{b}$, $\mathrm{LD}=\mathrm{c}$, $\mathrm{AB}=\mathrm{x}$ et $\mathrm{BD}=\mathrm{y}$. Et propter similia triangula DBL et BMG {sic} erit $\begin{array}{ccccccc}\mathrm{LB}& .& \mathrm{BD}& \colon\colon & \mathrm{DM}& .& \mathrm{MG}\\ \sqrt{}\stackrel{\_}{\mathrm{c}\mathrm{c}-\mathrm{y}\mathrm{y}}& & \mathrm{y}& & \mathrm{x}& & \mathrm{b}+\mathrm{y}\end{array}$. Adeoqꝫ $\stackrel{\_}{\mathrm{b}+\mathrm{y}}in\sqrt{}\stackrel{\_}{\mathrm{c}\mathrm{c}-\mathrm{y}\mathrm{y}}=\mathrm{y}\mathrm{x}$. Nactus hanc æquationem fingo $\sqrt{}\stackrel{\_}{\mathrm{c}\mathrm{c}-\mathrm{y}\mathrm{y}}=\mathrm{z}$ et sic duas æquationes {illeg} <45> $\mathrm{b}\mathrm{z}+\mathrm{y}\mathrm{z}=\mathrm{y}\mathrm{x}$ et $\mathrm{z}\mathrm{z}=\mathrm{c}\mathrm{c}-\mathrm{y}\mathrm{y}$ habeo. Quarum ope velocitates qua fluxiones quantitatum x, y, et z (Per Prob 1) quæro et e prima prodit $\mathrm{b}\mathrm{r}+\mathrm{y}\mathrm{r}+\mathrm{n}\mathrm{z}=\mathrm{n}\mathrm{x}+\mathrm{m}\mathrm{y}$, ac e secunda $2\mathrm{r}\mathrm{z}=-2\mathrm{n}\mathrm{y}$, |sive $\mathrm{r}\mathrm{z}+\mathrm{n}\mathrm{y}=0$.| E quibus exterminato r, oritur $-\frac{\mathrm{b}\mathrm{n}\mathrm{y}}{\mathrm{z}}-\frac{\mathrm{n}\mathrm{y}\mathrm{y}}{\mathrm{z}}+\mathrm{n}\mathrm{z}=\mathrm{n}\mathrm{x}+\mathrm{m}\mathrm{y}$. Quâ resolutâ fit $\mathrm{y}.\mathrm{z}-\frac{\mathrm{b}\mathrm{y}}{\mathrm{z}}-\frac{\mathrm{y}\mathrm{y}}{\mathrm{z}}-\mathrm{x}\left(\colon\colon \mathrm{n}.\mathrm{m}\right)\colon\colon \mathrm{BD}.\mathrm{BT}$. Cùm ergo BD sit $=\mathrm{y}$, erit $\mathrm{BT}=\mathrm{z}-\mathrm{x}\frac{-\mathrm{b}\mathrm{y}-\mathrm{y}\mathrm{y}}{\mathrm{z}}$. Hoc est $-\mathrm{BT}=\mathrm{AL}+\frac{\mathrm{BD}\times \mathrm{GM}}{\mathrm{BL}}$. Ubi signum − ipsi BT præfixum denotat punctum T ad partes adversus A capiendum esse.

Schol:{} Et hinc obiter {determinatio} \inventio/ puncti disterminantis concavam et convexam partem Conchoidis prodit. Nempe cùm AT sit omnium minima, erit D ejusmodi punctum. Esto itaqꝫ $\mathrm{AT}=\mathrm{v}$, et cùm sit $\mathrm{BT}=-\mathrm{z}+\mathrm{x}\frac{+\mathrm{b}\mathrm{y}+\mathrm{y}\mathrm{y}}{\mathrm{z}}$ erit $\mathrm{v}=-\mathrm{z}+2\mathrm{x}\frac{+\mathrm{b}\mathrm{y}+\mathrm{y}\mathrm{y}}{\mathrm{z}}$. Ubi ad opus abbreviandum pro x substitue $\frac{\mathrm{b}\mathrm{z}+\mathrm{y}\mathrm{z}}{\mathrm{y}}$ valorem e superioribus erutum et fiet $\frac{2\mathrm{b}\mathrm{z}}{\mathrm{y}}+\mathrm{z}\frac{+\mathrm{b}\mathrm{y}+\mathrm{y}\mathrm{y}}{\mathrm{z}}=\mathrm{v}$. Unde per Prob 1 fluxionibus l, n, et r quæsitis, et per Prob 3 supposita $\mathrm{l}=0$, emerget $\frac{2\mathrm{b}\mathrm{r}}{\mathrm{y}}-\frac{2\mathrm{b}\mathrm{n}\mathrm{z}}{\mathrm{y}\mathrm{y}}+\mathrm{r}+\frac{\mathrm{b}\mathrm{n}+2\mathrm{y}\mathrm{n}}{\mathrm{z}}\frac{-\mathrm{b}\mathrm{r}\mathrm{y}-\mathrm{r}\mathrm{y}\mathrm{y}}{\mathrm{z}\mathrm{z}}=\left(\mathrm{l}=\right)0$. In hâc deniqꝫ substitue $\frac{-\mathrm{n}\mathrm{y}}{\mathrm{z}}$ pro r et $\mathrm{c}\mathrm{c}-\mathrm{y}\mathrm{y}$ pro $\mathrm{z}\mathrm{z}$ (valores r et $\mathrm{z}\mathrm{z}$ e superioribus petendos) et facta reductione obtinebitur ${\mathrm{y}}^3+3\mathrm{b}\mathrm{y}\mathrm{y}-2\mathrm{b}\mathrm{c}\mathrm{c}=0$. Cujus æquationis constructione dd|a|bitur y sive AM; et per M acta MD ipsi AB parallela ind|c|idet in punctum flexùs contrarij D. ***

< insertion from p 53 >

***^[7]

Præterea si curva Mechanica est cujus tangentem ducere oportet, quantitatum fluxiones ut in exemplo 5 Prob 1 quærendæ sunt, cæteráqꝫ ut in præcedentibus peragenda.

Exempl 4. Sunto AC et AD duæ curvæ quibus recta BCD ad Basin AB in dato angulo applicata occurrit in C et D 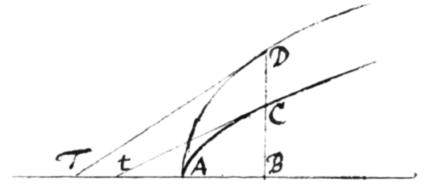et appelletur $\mathrm{AB}=\mathrm{x}$, $\mathrm{BD}=\mathrm{y}$, et $\frac{\mathrm{area\; ACB}}{1}=\mathrm{z}$; et per Prob: 1, Præparat: ad Exempl 5, erit $\mathrm{r}=\mathrm{m}\times \mathrm{BC}$.

Jam sit AC circulus aut curva quævis nota et ad alteram curvam AD definiendam exponatur quævis æquatio cui z intexta est veluti $\mathrm{z}\mathrm{z}+\mathrm{a}\mathrm{x}\mathrm{z}={\mathrm{y}}^4$. Et per Prob 1 erit $2\mathrm{r}\mathrm{z}+\mathrm{a}\mathrm{x}\mathrm{r}+\mathrm{a}\mathrm{m}\mathrm{z}=4\mathrm{n}{\mathrm{y}}^3$. Et scripto $\mathrm{m}\times \mathrm{BC}$ pro r, fiet $2\mathrm{m}\mathrm{z}\times \mathrm{BC}+\mathrm{a}\mathrm{m}\mathrm{x}\times \mathrm{BC}+\mathrm{a}\mathrm{m}\mathrm{z}=4\mathrm{n}{\mathrm{y}}^3$. Adeoqꝫ $2\mathrm{z}\times \mathrm{BC}+\mathrm{a}\mathrm{x}\times \mathrm{BC}+\mathrm{a}\mathrm{z}.4{\mathrm{y}}^3\left(\colon\colon \mathrm{n}.\mathrm{m}\right)\colon\colon \mathrm{BD}.\mathrm{BT}$. Quamobrem si ex natura curvæ AC detur ordinata BC et area ACB sive z, dabitur punctum T per quod tangens DT transibit.

Ad eundem modum si $3\mathrm{z}=2\mathrm{y}$ sit æquatio ad curvam AD, erit $3\mathrm{r}\left(3\mathrm{m}\times \mathrm{BC}\right)=2\mathrm{n}$. Adeoqꝫ $3\mathrm{BC}.2\left(\colon\colon \mathrm{n}.\mathrm{m}\right)\colon\colon \mathrm{BD}.\mathrm{BT}$. Et sic in alijs.

Exempl: 5. Sit $\mathrm{AB}=\mathrm{x}$, $\mathrm{BD}=\mathrm{y}$ ut ante, et Curvæ cujusvis AC longitudo sit z; ductâqꝫ ad eam tangente Ct, erit $\mathrm{Bt}.\mathrm{Ct}\colon\colon \mathrm{m}.\mathrm{r}$, sive $\mathrm{r}=\frac{\mathrm{m}\times \mathrm{Ct}}{\mathrm{Bt}}$.

Jam ad aliam curvam AD cujus tangens ducenda est, detur quælibet æquatio in qua z involvitur, puta si $\mathrm{z}=\mathrm{y}$, erit $\mathrm{r}=\mathrm{n}$. Adeoqꝫ $\mathrm{Bt}.\mathrm{Ct}\left(\colon\colon \mathrm{n}.\mathrm{m}\right)$$\colon\colon \mathrm{BD}.\mathrm{BT}$. Invento autem T age DT tangentem.

Sic posito $\mathrm{x}\mathrm{z}=\mathrm{y}\mathrm{y}$ erit $\mathrm{m}\mathrm{z}+\mathrm{r}\mathrm{x}=2\mathrm{n}\mathrm{y}$, et pro r scripto $\frac{\mathrm{m}\times \mathrm{Ct}}{\mathrm{Bt}}$, emerget $\mathrm{m}\mathrm{z}+\frac{\mathrm{m}\mathrm{x}\times \mathrm{Ct}}{\mathrm{Bt}}=2\mathrm{n}\mathrm{y}$. Quare est $\mathrm{z}+\frac{\mathrm{x}\times \mathrm{Ct}}{\mathrm{Bt}}.2\mathrm{y}\colon\colon \mathrm{BD}.\mathrm{DT}$.

Exempl: 6. Sit AC circulus aut alia quævis nota curva quam tangat Ct, et sit AD alia curva cujus tangentem DT ducere oportet, et quæ definitur assumendo $\mathrm{AB}=\text{arcui}\mathrm{AC}$, et (CE, ac BD in dato angulo ad AB ordinatis) referendo BD ad CE vel AE in æquatione aliqua. Dic ergo AB vel $\mathrm{AC}=\mathrm{x}$, $\mathrm{BD}=\mathrm{y}$, $\mathrm{AE}=\mathrm{z}$, et $\mathrm{CE}=\mathrm{v}$, et patet l, m, et r 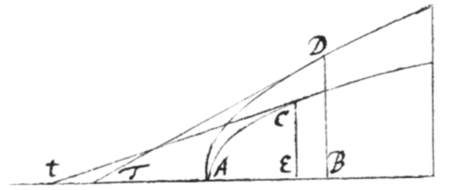fluxiones ipsarum CE, AC, et AE esse inter se ut sunt CE, Ct et Et, Adeoqꝫ $\mathrm{m}\times \frac{\mathrm{CE}}{\mathrm{Ct}}=\mathrm{l}$, et $\frac{\mathrm{m}\times \mathrm{Et}}{\mathrm{Ct}}=\mathrm{r}$.

Detur jam quælibet æquatio ad definiendam Curvam AD, veluti $\mathrm{y}=\mathrm{z}$, et erit $\mathrm{n}=\mathrm{r}$, Adeoqꝫ $\mathrm{Et}.\mathrm{Ct}\left(\colon\colon \mathrm{n}.\mathrm{m}\right)\colon\colon \mathrm{BD}.\mathrm{BT}$.

Vel detur $\mathrm{y}=\mathrm{z}+\mathrm{v}-\mathrm{x}$, et erit $\mathrm{n}=\left(\mathrm{l}+\mathrm{r}-\mathrm{m}=\right)\frac{\mathrm{m}\times \mathrm{CE}+\mathrm{Et}-\mathrm{Ct}}{\mathrm{Ct}}$. Adeoqꝫ $\mathrm{CE}+\mathrm{Et}-\mathrm{Ct}.\mathrm{Ct}\left(\colon\colon \mathrm{n}.\mathrm{m}\right)\colon\colon \mathrm{BD}.\mathrm{BT}$.

Vel deniqꝫ detur $\mathrm{a}\mathrm{y}\mathrm{y}={\mathrm{v}}^3$, et erit $2\mathrm{a}\mathrm{n}\mathrm{y}=\left(3\mathrm{l}\mathrm{v}\mathrm{v}=\right)\frac{3\mathrm{m}\mathrm{v}\mathrm{v}\times \mathrm{CE}}{\mathrm{Ct}}$. Adeoqꝫ $3\mathrm{v}\mathrm{v}\times \mathrm{CE}.2\mathrm{a}\mathrm{y}\times \mathrm{Ct}\colon\colon \mathrm{BD}.\mathrm{BT}$.

Exempl 7. Sit FC circulus quem tangat Ct {sic}, sitqꝫ FD Curva quæ definitur assumendo quamvis relationem applicatæ DB ad FC arcum quem DA ad centrum ducta intercipit. Et demissa CE in circulo <54> applicata dic AC vel 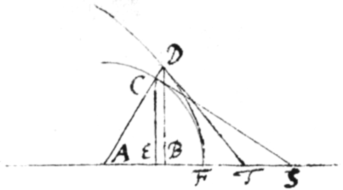$\mathrm{AF}=1$, $\mathrm{AB}=\mathrm{x}$, $\mathrm{BD}=\mathrm{y}$, $\mathrm{AE}=\mathrm{z}$, $\mathrm{CE}=\mathrm{v}$, $\mathrm{CF}=\mathrm{t}$ et ipsius t fluxionem k, et erit $\mathrm{k}\mathrm{x}\left(=\frac{\mathrm{k}\times \mathrm{CE}}{\mathrm{CS}}\right)=\mathrm{l}$ {sic}, et $-\mathrm{k}\mathrm{v}\left(=\frac{\mathrm{k}\times -\mathrm{ES}}{\mathrm{CS}}\right)=\mathrm{r}$. Ubi pono r negativè, quòd AE diminuitur dum EC augetur. Est insuper $\mathrm{AE}.\mathrm{EC}\colon\colon \mathrm{AB}.\mathrm{BD}$, adeoqꝫ $\mathrm{z}\mathrm{y}=\mathrm{v}\mathrm{x}$ et inde per Prob: 1, $\mathrm{r}\mathrm{y}+\mathrm{n}\mathrm{z}=\mathrm{l}\mathrm{x}+\mathrm{m}\mathrm{v}$. Et hi|æ|c, exterminatis l, r, et v, fit \faciunt/ $\mathrm{n}\mathrm{x}$$-\mathrm{k}\mathrm{y}\mathrm{y}-\mathrm{k}\mathrm{x}\mathrm{x}=\mathrm{m}\mathrm{y}$.

Definiatur jam curva DF æquatione quavis unde \a qua/ valor k hic substituendus deduci possit: puta sit $\mathrm{t}=\mathrm{y}$ \(æquatio ad primam Quadratricem,)/ et per Prob: 1 erit $\mathrm{k}=\mathrm{n}$. Adeoqꝫ $\mathrm{n}\mathrm{x}-\mathrm{n}\mathrm{y}\mathrm{y}-\mathrm{n}\mathrm{x}\mathrm{x}=\mathrm{m}\mathrm{y}$. Unde {illeg} $\mathrm{y}.\mathrm{x}\mathrm{x}+\mathrm{y}\mathrm{y}-\mathrm{x}$$\left(\colon\colon \mathrm{n}.-\mathrm{m}\right)\colon\colon \mathrm{DB}\left(\mathrm{y}\right).\mathrm{BT}$. {illeg} Quare $\mathrm{BT}=\mathrm{x}\mathrm{x}+\mathrm{y}\mathrm{y}-\mathrm{x}$. Et $\mathrm{AT}=$$\mathrm{x}\mathrm{x}+\mathrm{y}\mathrm{y}=\frac{{\mathrm{AD}}^q}{\mathrm{AF}}$.

Ad eundem modum si sit $\mathrm{t}\mathrm{t}=\mathrm{b}\mathrm{y}$, proveniet $2\mathrm{k}\mathrm{t}=\mathrm{b}\mathrm{n}$, et inde $\mathrm{AT}=\frac{\mathrm{b}\times {\mathrm{AD}}^q}{\mathrm{z}\mathrm{t}\times \mathrm{AF}}$. Et sic in alijs.

Exempl 8. Quod si AD sumatur æqualis 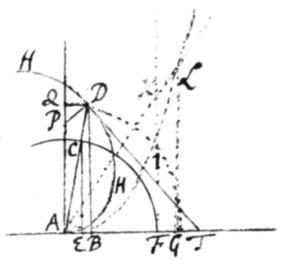arcui FC, existente ADH spirali Archimedea, tum stantibus jàm positis linearum nominibus, est (propter ang: ABD rect:) $\mathrm{x}\mathrm{x}+\mathrm{y}\mathrm{y}=\mathrm{t}\mathrm{t}$. Et inde per Prob: 1 $\mathrm{m}\mathrm{x}+\mathrm{n}\mathrm{y}=\mathrm{k}\mathrm{t}$. Est etiam $\mathrm{AD}.\mathrm{AC}\colon\colon \mathrm{DB}.\mathrm{CE}$, adeoqꝫ $\mathrm{t}\mathrm{v}=\mathrm{y}$ et inde per Prob 1 $\mathrm{k}\mathrm{v}+\mathrm{t}\mathrm{l}=\mathrm{n}$. Deniqꝫ est fluxio arcus FC ad fluxionem rectæ CE ut AC ad AE sive ut AD ad AB hoc est $\mathrm{k}.\mathrm{l}\colon\colon \mathrm{t}.\mathrm{x}$, et inde $\mathrm{k}\mathrm{x}=\mathrm{t}\mathrm{l}$. {illeg} Confer jam inventas æquationes et videbis esse $\mathrm{k}\mathrm{v}+\mathrm{k}\mathrm{x}=\mathrm{n}$, et \inde/ $\mathrm{m}\mathrm{x}+\mathrm{n}\mathrm{y}\left(=\mathrm{k}\mathrm{t}\right)=\frac{\mathrm{n}\mathrm{t}}{\mathrm{v}+\mathrm{x}}$. Atqꝫ adeo (completo parallelogrammo ABDQ) si fiat $\mathrm{QD}.\mathrm{QP}$$\left(\colon\colon \mathrm{BD}.\mathrm{BT}\colon\colon \mathrm{n}.-\mathrm{m}\right)\colon\colon \mathrm{x}.\mathrm{y}-\frac{\mathrm{t}}{\mathrm{v}+\mathrm{x}}$, hoc est si capiatur $\mathrm{AP}=\frac{\mathrm{t}}{\mathrm{v}+\mathrm{x}}$, erit PD ad spiralem perpendicularis.

Ex his opinor satis manifestum est quo pacto curvarum omnium tangentes ducendæ sunt. Attamen ut facillima et simplicissima methodus pro singulis curvis adhibeatur, non abs re erit si præterea confectionem Problematis ubi curvæ alijs quibuscunqꝫ modis ad rectas referuntur ostendero, ut \e pluribus Methodis/ facillima et simplicissima methodus semper possit adhiberi.

< text from p 45 resumes >

^[8]Cæterùm ad Tangentium doctrinam {illeg} revertamur earum determinatione jam aggressi cum curvæ alijs modis ad rectas referuntur. \Mod: 2./ Sit itaqꝫ D punctum in curva a quo subtensa DG ducitur ad datum punctum G ac DB in dato quovis angulo ordinatur ad Basin AB. 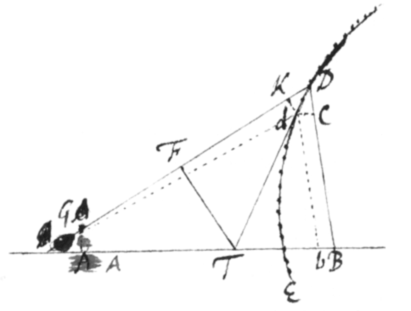Punctum verò D per infinitè parvum intervallum Dd in curva fluat, inqꝫ GD sumatur GK æqualis Gd et compleatur parallelogrammum dbBC. Et erunt {illeg} DK ac DC contemporanea momenta ipsarum GD et BD quibus nempe diminuuntur dum D transfertur ad d. Jam <46> Dd rectà producatur donec cum AB conveniat in T et ab isto T ad subtensam GD demittatur perpendiculum TF et erunt Trapezia DCdK ac DBTK {sic} similia adeoqꝫ $\mathrm{DB}.\mathrm{DF}\colon\colon \mathrm{DC}.\mathrm{DK}$.

Cùm itaqꝫ relatio BD ad GD in æquatione qualibet, pro curva definienda exponitur, quære relationem fluxionum et cape FD ad DB in ratione fluxionis GD ad fluxionem BD. Dein ab F erige perpendiculum FT quod cum AB concurrat in T et acta TD curvam tanget in D. Cape autem DF versus G si sit affirmativa; sin secus, cape ad contrarias partes{.}

Exempl 1. Dic $\mathrm{GD}=\mathrm{x}$ et $\mathrm{BD}=\mathrm{y}$ et esto earum relatio ${\mathrm{x}}^3-\mathrm{a}\mathrm{x}\mathrm{x}+\mathrm{a}\mathrm{x}\mathrm{y}-{\mathrm{y}}^3=0$ Eritqꝫ fluxionum relatio ${\mathrm{x}}^3-\mathrm{a}\mathrm{x}\mathrm{x}$ $3\mathrm{m}\mathrm{x}\mathrm{x}-2\mathrm{a}\mathrm{m}\mathrm{x}+\mathrm{a}\mathrm{m}\mathrm{y}+\mathrm{a}\mathrm{x}\mathrm{n}-3\mathrm{n}\mathrm{y}\mathrm{y}=0$. Atqꝫ adeò $3\mathrm{x}\mathrm{x}-2\mathrm{a}\mathrm{x}$$+\mathrm{a}\mathrm{y}.3\mathrm{y}\mathrm{y}-\mathrm{a}\mathrm{x}\left(\colon\colon \mathrm{m}.\mathrm{n}\right)\colon\colon \mathrm{DB}\left(\mathrm{y}\right).\mathrm{DF}$. Et hinc dato quolibet in curva puncto D Est ergo $\mathrm{DF}=\frac{3{\mathrm{y}}^3-\mathrm{a}\mathrm{x}\mathrm{y}}{3\mathrm{x}\mathrm{x}-2\mathrm{a}\mathrm{x}+\mathrm{a}\mathrm{y}}$. Adeoqꝫ dato quolibet in curva puncto D, et inde BD et GD sive y et x; dabit hinc dabitur punctum F: Unde si normalem FT erigas; ad ejus concursum cum basi AB ducta DT curvam tanget.

Et hinc patet Regulam perinde ac in priori casu concinnari posse. Scilicet æqu\a/tionis expositæ terminos \omnes ad easdem partes dispone et/ sigillatim per terminos dimensiones ordinatæ y multiplica et exitum colloca in Numeratore. Dein terminos ejus sigillatim per dimensiones subtensæ x multiplica, et exitum per subtensam illam x divisum colloca in Denominatore valoris DF. Illamqꝫ DF cape ad partes contra G si sit affirmativa, sin secus, cape ad easdem partes. |Et nota quod nihil intersit quanto intervallo punctum G distat a Basi AB, si {illeg}|fortè| distat, neqꝫ quinam sit angulus ordinationis ABD.|

Sic æquatio superior ${\mathrm{x}}^3-\mathrm{a}\mathrm{x}\mathrm{x}+\mathrm{a}\mathrm{x}\mathrm{y}-{\mathrm{y}}^3=0$ prima fronte dat $\mathrm{a}\mathrm{x}\mathrm{y}-3{\mathrm{y}}^3$ pro numeratore et $3\mathrm{x}\mathrm{x}-2\mathrm{a}\mathrm{x}+\mathrm{a}\mathrm{y}$ pro Denominatore valoris DF.

Sic etiam $\mathrm{a}+\frac{\mathrm{b}}{\mathrm{a}}\mathrm{x}-\mathrm{y}=0$, (quæ æquatio est ad Conicam sectionem) \dat/ $-\mathrm{y}$ pro numeratore et $\frac{\mathrm{b}}{\mathrm{a}}$ pro denominatore valoris DF quæ ideo erit $=\frac{-\mathrm{a}\mathrm{y}}{\mathrm{b}}$.

Et sic in Conchoide, (ubi res si expeditiùs obsolvitur quàm <47> ante) posito $\mathrm{GA}=\mathrm{b}$, $\mathrm{LD}=\mathrm{c}$, $\mathrm{GD}=\mathrm{x}$, et $\mathrm{BD}=\mathrm{y}$, erit $\begin{array}{ccccccc}\mathrm{BD}& .& \mathrm{DL}& \colon\colon & \mathrm{GA}& .& \mathrm{GL}\\ \mathrm{y}& & \mathrm{c}& & \mathrm{b}& & \mathrm{x}-\mathrm{c}\end{array}$.^[9] Adeoqꝫ $\mathrm{x}\mathrm{y}-\mathrm{c}\mathrm{y}=\mathrm{c}\mathrm{b}$, sive $\mathrm{x}\mathrm{y}-\mathrm{c}\mathrm{y}-\mathrm{c}\mathrm{b}=0$ Quæ æquatio juxta Regulam dat $\frac{\mathrm{x}\mathrm{y}-\mathrm{c}\mathrm{y}}{\mathrm{y}}$ hoc est $\mathrm{x}-\mathrm{c}=$DF. Produc ergo GD ad F ut sit $\mathrm{DF}=\mathrm{LG}$, et ab|d| F erige normalem FT occurrentem {illeg} Asymptoto AB in T, et acta DT Conchoidem tanget.

Siquando compositæ quantitates in æquatione reperiantur ad methodum generalem recurrendum est, nisi ubi malueris æquationem reducere.

Exe{illeg}|m|pl. 2. Si detur æquatio {illeg} $\stackrel{\_}{\mathrm{b}+\mathrm{x}}\sqrt{}\stackrel{\_}{\mathrm{c}\mathrm{c}-\mathrm{y}\mathrm{y}}=\mathrm{y}\mathrm{x}$ pro relatione inter GD et BD determinanda, fluxionum relationem juxta Prob 1 quære. Utpote ficto $\sqrt{}\stackrel{\_}{\mathrm{c}\mathrm{c}-\mathrm{y}\mathrm{y}}=\mathrm{z}$, æquationes $\mathrm{b}\mathrm{z}+\mathrm{y}\mathrm{z}=\mathrm{y}\mathrm{x}$ et $\mathrm{c}\mathrm{c}-\mathrm{y}\mathrm{y}=\mathrm{z}\mathrm{z}$ habebis, et inde fluxionum \m n et r/ relationes $\mathrm{b}\mathrm{r}+\mathrm{y}\mathrm{r}+\mathrm{n}\mathrm{z}=\mathrm{n}\mathrm{x}+\mathrm{y}\mathrm{m}$, et $-2\mathrm{n}\mathrm{y}=2\mathrm{r}\mathrm{z}$. Et exterminatis r et z orietur $\mathrm{n}\sqrt{}\stackrel{\_}{\mathrm{c}\mathrm{c}-\mathrm{y}\mathrm{y}}\frac{-\mathrm{b}\mathrm{n}\mathrm{y}-\mathrm{n}\mathrm{y}\mathrm{y}}{\sqrt{}\stackrel{\_}{\mathrm{c}\mathrm{c}-\mathrm{y}\mathrm{y}}}-\mathrm{n}\mathrm{x}=\mathrm{m}\mathrm{y}$. Est ergo $\mathrm{y}.\sqrt{}\stackrel{\_}{\mathrm{c}\mathrm{c}-\mathrm{y}\mathrm{y}}\frac{-\mathrm{b}\mathrm{y}-\mathrm{y}\mathrm{y}}{\sqrt{}\stackrel{\_}{\mathrm{c}\mathrm{c}-\mathrm{y}\mathrm{y}}}-\mathrm{n}\mathrm{x}\left(\colon\colon \mathrm{n}.\mathrm{m}\right)\colon\colon \mathrm{BD}\left(\mathrm{y}\right).\mathrm{DF}$.

^[10]|Mod: 3.| Præterea si Curva ad duas subtensas AD et BD referatur quæ a datis punctis A ac B {illeg}ductæ ad Curvam terminantur conveniunt: \concipe/ punctum illud D per infinitè parvum spatium Dd in curva profluere 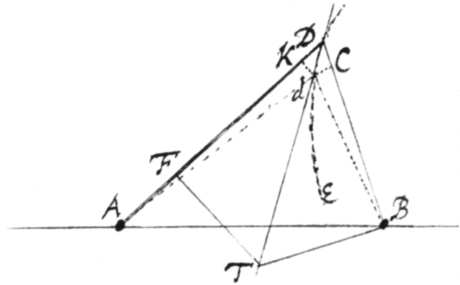et in AD et BD cape $\mathrm{AK}=\mathrm{Ad}$ et $\mathrm{BC}=\mathrm{Bd}$ et erunt KD et CD contemporanea momenta linearum AD et BD. Cape jam DF ad BD in ratione momenti DK ad momentum DC (i.e. in ratione fluxionis Li{illeg}|ne|æ AD ad Fluxionem lineæ BD,) et Lineam erige perpendicula BT, FT concurrentia in T eruntqꝫ trapezia DTFB ac DKdC similia, et proinde diagonalis DT curvam tanget.

Per æquationem itaqꝫ qua relatio inter AD et BD definitur, quære relationem fluxionum ope{illeg} Prob 1, et cape <48> FD ad BD in eadem ratione{.}

Exempl. Posito $\mathrm{AD}=\mathrm{x}$ et $\mathrm{BD}=\mathrm{y}$ sit earum relatio $\mathrm{a}+\frac{\mathrm{e}\mathrm{x}}{\mathrm{d}}-\mathrm{y}=0$ (quæ æquatio est ad Ellipses secundi generis quarum proprietates ad Lucem refringendam Des-Cartes in {illeg}|L|ib 2 Geometriæ docuit) et fluxionum relatio erit $\frac{\mathrm{e}\mathrm{m}}{\mathrm{d}}-\mathrm{n}=0$. Est itaqꝫ {illeg} $\mathrm{e}.\mathrm{d}\left(\colon\colon \mathrm{n}.\mathrm{m}\right)\colon\colon \mathrm{BD}.\mathrm{DF}$. {illeg}

Et pari ratione si 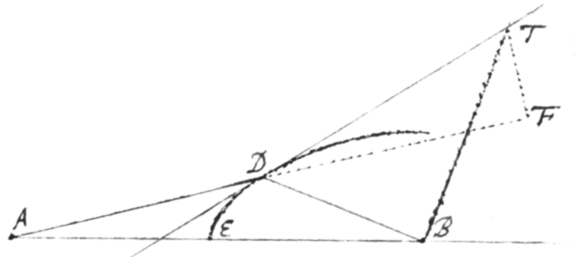$\mathrm{a}-\frac{\mathrm{e}\mathrm{x}}{\mathrm{d}}-\mathrm{y}=0$, erit $\mathrm{e}.-\mathrm{d}\colon\colon \mathrm{BD}.\mathrm{DF}$. In priori casu cape DF versus A, et in poster ad contrarias partes in posteriori.

Coroll: 1. Hinc si $\mathrm{d}=\mathrm{e}$ (quo casu curva evadit conica sectio) erit $\mathrm{DF}=\mathrm{DB}$. et inde triangula DFT, DBT æqualia, angulusqꝫ FDB a tangente bisecabitur.

Coroll 2. Hinc etiam quæ Des-Cartes haud absqꝫ circuitu de his curvis circa refractiones haud absqꝫ circuitu demonstravit, per se manifesta sunt: siquidem DF ac DB (quæ sunt in data ratione d ad e) respectu sinus totius DT su|i|nt sinus angulorum {illeg} et {illeg} DTF ac DTB. id est incidentiæ radij AD in superficiem curvæ, et reflectionis vel refractionis ejus DB. Estqꝫ par ratio de refractionibus Conicarum Sectionum si modo punctorum A vel B alterutrum {illeg} infinitè dista{illeg}|r|e concipiatur.

Perfacile est hanc regulam pro more præcedentium concinnare et pluribus exemplis donare.|.| et ad harum Quinimò ubi curvæ alijs quibuscunqꝫ modis ad rectas referuntur, et ad præcedentes formas haud commodè reduci possunt; perfacile est alias Regulas ad harum exemplar pro re nata excogitare.

^[11]|Mod 4| Quemadmodum si rectæ BD circa datum punctum B volventis punctum D sit ad Curvam aliquam, et C \sit/ intersectio \ejus/ cum rectâ AC positione datâ; habeaturqꝫ relatio inter BC et BD quacunqꝫ æquatione designata; Age BF parallelam AC, eiqꝫ occurrat DF normalis ad <49> BF {sic}. Et ad DF itidem erige 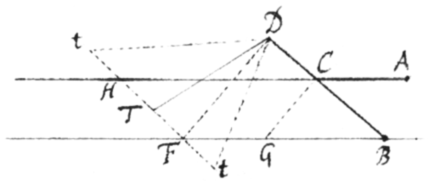normalem FT, et cape in ratione ad BC quam habet fluxio ipsius BD ad fluxionem ipsius BC: Actáqꝫ DT curvam tanget.

^[12]|Mod 5| Sin, dato puncto A, æquatio relationem inter AC et BD designat, duc CG parallelam DF, et cape FT in ratione ad BG quam habet fluxio BD ad fluxionem AC.

^[13]|Mod 6| Vel deniqꝫ si æquatio relationem inter AC et CD definit: conveniant AC et FT in H, et cape HT in ratione ad BG quam habet fluxio CD ad fluxionem AC. Et sic in alijs.

^[14]|Mod 7|. Præterea cum \Haud secus absolvitur Problema ubi/ curvæ non ad rectas sed ad alias curvas referuntur \lineas/ (uti solent Mechanicæ) possis \uti solent/ tangentes nihil secans ducere \referuntur/. Sit BG circuli periferia in cujus semidiametro AG, dum circa centrum A convolvitur, moveatur utcunqꝫ punctum D et spiralem ADE describat. Et concipe Dd et partem curvæ infinitè parvam per quam D fluit, et in AD cape $\mathrm{AC}=\mathrm{Ad}$ et erunt CD ac Gg contemporanea momenta rectæ AD et {illeg} arcus periferiæ BG. Duc ergo At parallelam CD, id est perpendicularem AD, et cum ea tangens DT convenit|a|t in T, eritqꝫ $\mathrm{cd}.\mathrm{CD}\colon\colon \mathrm{AD}.\mathrm{A}$ $\mathrm{CD}.\mathrm{Cd}\colon\colon \mathrm{AD}.\mathrm{AT}$. Sit insuper Gt parallela tangenti, et erit {illeg} $\mathrm{Cd}.\mathrm{Gg}\left(\colon\colon \mathrm{Ad}\text{vel}\mathrm{AD}.\mathrm{AG}\right)\colon\colon \mathrm{AT}.\mathrm{At}$.

Quare obrem exposita quacunqꝫ æquatione quâ relatio inter AD et BG \BG ad AD/ definitur, quære r{illeg}ationem {sic} fluxionum per Prob 1, et cape At {illeg}|i|n illa ratione ad AD. Eritqꝫ Gt tangent et ipsi Gt parallelam age DT quaæ curvam tanget eritꝫ Gt tangenti parallela.

Exempl 1. Dictis $\mathrm{BG}=\mathrm{x}$ et $\mathrm{AD}=\mathrm{y}$, sit earum relatio ${\mathrm{x}}^3-\mathrm{a}\mathrm{x}\mathrm{x}+\mathrm{a}\mathrm{x}\mathrm{y}-{\mathrm{y}}^3=0$ et ope Prob 1 emerget $3\mathrm{x}\mathrm{x}-2\mathrm{a}\mathrm{x}$$+\mathrm{a}\mathrm{y}.3\mathrm{y}\mathrm{y}-\mathrm{a}\mathrm{x}\left(\colon\colon \mathrm{n}.\mathrm{m}\right)\colon\colon \mathrm{AD}.\mathrm{At}\colon\colon \mathrm{AP}.\mathrm{AG}${.} Puncto t sic invento duc <50> Gt eiqꝫ parallelam DT, et illa Curvam tanget.

Exempl 2. Si sit $\frac{\mathrm{a}\mathrm{x}}{\mathrm{b}}=\mathrm{y}$ (quæ æquatio est ad Spiralem Archimedeam) erit $\frac{\mathrm{a}\mathrm{m}}{\mathrm{b}}=\mathrm{n}$. Adeoqꝫ $\mathrm{a}.\mathrm{b}\left(\colon\colon \mathrm{n}.\mathrm{m}\right)\colon\colon \mathrm{AD}.\mathrm{At}$. |Unde obiter si TA producatur ad P ut sit $\mathrm{AP}.\mathrm{AB}\colon\colon \mathrm{a}.\mathrm{b}$, PD ad curvam recta erit.|

Exempl 3. Si $\mathrm{x}\mathrm{x}=\mathrm{b}\mathrm{y}$, erit $2\mathrm{m}\mathrm{x}=\mathrm{b}\mathrm{n}$. Adeoqꝫ $2\mathrm{x}.\mathrm{b}\colon\colon \mathrm{AD}.\mathrm{At}$. Et sic tangentes ad quibascunqꝫ spirali|e|bus nullo negotio determina{illeg}ri possunt.

^[15]|Mod 8|. Ad hæc si curva sit ejusmodi ut per centrum A ductâ utcunqꝫ AGD quæ circulo 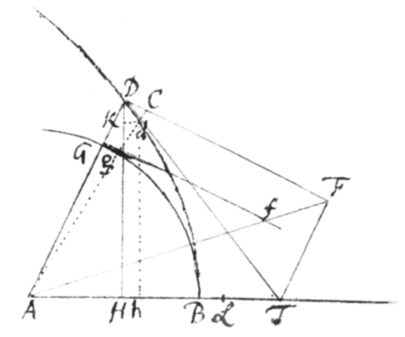in G, curvæqꝫ in D occurrat, relatio inter arcum BG et rectam DH quæ in dato angulo ad Basin AB ordinat{illeg}|a| est, æquatione quavis definiatur: Concipe punctum D per infinitè parvum intervallum ad d in curva moveri et completo parallelogrammo {illeg} dhHK productâqꝫ Ad ad C ut sit $\mathrm{AC}=\mathrm{AD}$; erunt Gg arcûs BG et DK ordinatæ DH contemporanea momenta. Produc jam Dd rectà ad T ubi cum AB conveniat et demitte TF in DC perpendicularem, eruntqꝫ trapezia DKdc, DHTF similia; At{illeg} atqꝫ adeo $\mathrm{DK}.\mathrm{DC}\colon\colon \mathrm{DH}.\mathrm{DF}$. Et præterea si Gf ad AG normalis erigatur quæ cum AF concurrat in {illeg} f propter parallelas DF, Gf erit $\mathrm{DC}.\mathrm{Gg}\colon\colon \mathrm{DF}.\mathrm{Gf}$. Quamobrem ex æquo est $\mathrm{DK}.\mathrm{Gg}\colon\colon \mathrm{DH}.\mathrm{Gf}$, hoc est, ut momenta sive fluxiones linearum DH et BG.

Per æquationem itaqꝫ quâ relatio BG ad DH definitur quære rationem fluxionum \per Prob. 1/ et in ea ratione cape Gf (tangentem circuli BG) ad DH ordinatur DH. Age DF parallelam Gf quæ cum Af producta conveniat in F Et ad F erige normalem FT occurrentem AB in T et acta DT Qu{illeg}|adr|atrice tanget.

Exempl 1. Nominatis $\mathrm{BG}=\mathrm{x}$, ac $\mathrm{DH}=\mathrm{y}$, esto $\mathrm{x}\mathrm{x}=\mathrm{b}\mathrm{y}$ et (per Prob. 1) erit $2\mathrm{m}\mathrm{x}=\mathrm{b}\mathrm{n}$. Adeoqꝫ $2\mathrm{x}.\mathrm{b}\left(\colon\colon \mathrm{n}.\mathrm{m}\right)\colon\colon \mathrm{DH}.\mathrm{Gf}$. Et invento f, cætera ut præscriptum est determinabis.

<51>

Cæterum hæc Regula forte sic elegantior evadet. Cape AL Fac est {illeg} Cape {illeg} Fac $\mathrm{m}.\mathrm{n}\colon\colon \mathrm{AB}.\mathrm{AL}$. Dein $\mathrm{AL}.\mathrm{AD}\colon\colon$$\mathrm{AD}.\mathrm{AT}$ et DT curvam tanget. Nam propter æqualia triangula AFD, ATD, est $\mathrm{AD}\times \mathrm{DF}=\mathrm{AT}\times \mathrm{DH}$. Adeoqꝫ $\mathrm{AT}.\mathrm{AD}\left(\colon\colon \mathrm{DF}.\mathrm{DH}\text{, sive}\frac{\mathrm{n}}{\mathrm{m}}\mathrm{Gf}\right)\colon\colon \mathrm{AD}.\frac{\mathrm{n}}{\mathrm{m}}\mathrm{AG}\text{, sive}\mathrm{AL}$.

Exempl 2. Esto $\mathrm{x}=\mathrm{y}$ (quæ æquatio est ad simplicem \veterum/ Quadratricem) et erit $\mathrm{m}=\mathrm{n}$. Adeoqꝫ $\mathrm{AB}.\mathrm{AD}\colon\colon \mathrm{AD}.\mathrm{AT}$.

Exempl 3. Esto $\mathrm{a}\mathrm{x}\mathrm{x}={\mathrm{y}}^3$, et erit $2\mathrm{a}\mathrm{m}\mathrm{x}=3\mathrm{n}\mathrm{y}\mathrm{y}$. Fac ergo {illeg} $3\mathrm{y}\mathrm{y}.2\mathrm{a}\mathrm{x}\left(\colon\colon \mathrm{m}.\mathrm{n}\right)\colon\colon \mathrm{AB}.\mathrm{AL}$. Dein $\mathrm{AL}.\mathrm{AD}\colon\colon \mathrm{AD}.\mathrm{AT}$.

Et sic tangentes ad alias utcunqꝫ compositas Quadratrices possis expeditè determinare; et hujusmodi Regulas pro alijs quibuscunqꝫ Mechanicarum Curvarum generibus excogitare.

Siquando in æquationibus Mechanicæ quantitates involvantur earum fluxiones ut in exemplo 5 Prob 1 quærere oportet cæteraqꝫ ut supra peragere{.}.

^[16]Exempl 1. Rectâ BCD in dato angulo ad basin AB ordinatâ, {illeg} dic $\mathrm{AB}=\mathrm{x}$, $\mathrm{BD}=\mathrm{y}$, & aream $\frac{\mathrm{ACB}}{1}=\mathrm{z}$, et sit $\sqrt{}\stackrel{\_}{\mathrm{a}\mathrm{x}-\mathrm{x}\mathrm{x}}$$=\mathrm{BC}$ æquatio ad curvam AC et $\mathrm{z}\mathrm{z}+\mathrm{a}\mathrm{x}\mathrm{z}-{\mathrm{y}}^4=0$ æquatio ad alteram curvam cujus tangens ducenda est: et per Prob 1 exempl 5 relatio fluxionum m et n erit $\stackrel{\_}{2\mathrm{m}\mathrm{z}+\mathrm{a}\mathrm{m}\mathrm{x}}\sqrt{}\stackrel{\_}{\mathrm{a}\mathrm{x}-\mathrm{x}\mathrm{x}}$$+\mathrm{a}\mathrm{m}\mathrm{z}-4\mathrm{n}{\mathrm{y}}^3=0$. Fac itaqꝫ $\stackrel{\_}{2\mathrm{z}+\mathrm{a}\mathrm{x}}\sqrt{}\stackrel{\_}{\mathrm{a}\mathrm{x}-\mathrm{x}\mathrm{x}}+\mathrm{a}\mathrm{z}.4{\mathrm{y}}^3$$\left(\colon\colon \mathrm{n}.\mathrm{m}\right)\colon\colon \mathrm{BD}.\mathrm{BT}$, et {illeg} juxta casu 1, et age tangentem DT.

< insertion from p 52 >

Exempl 1. Sunto AC et AD duæ curvæ quibus \re{illeg}|c|ta/ BCD ad Basin AB in dato angulo ordinata occurrit in C et D. Et appelletur $\mathrm{AB}=\mathrm{x}$, $\mathrm{BD}=\mathrm{y}$, et $\frac{\text{area}\mathrm{ACB}}{1}=\mathrm{z}$ et per Prob 1 Præparat: ad Exemp: 5 erit $\mathrm{r}=\mathrm{m}\times \mathrm{BC}$.

Jam sit AC circulus aut curva quævis nota et ad alteram curvam AD definiendam exponatur quævis æquatio cui z {illeg} intexta est: veluti $\mathrm{z}\mathrm{z}+\mathrm{a}\mathrm{x}\mathrm{z}={\mathrm{y}}^4$. Et per Prob 1 erit $2\mathrm{r}\mathrm{z}${illeg}$+\mathrm{a}\mathrm{x}\mathrm{r}+\mathrm{a}\mathrm{m}\mathrm{z}=4\mathrm{n}{\mathrm{y}}^3$. Et inscripto $\mathrm{m}\times \mathrm{BC}$ pro r, fiet {illeg} $2\mathrm{m}\mathrm{z}\times \mathrm{BC}+\mathrm{a}\mathrm{m}\mathrm{x}\times \mathrm{BC}$$+\mathrm{a}\mathrm{m}\mathrm{z}=4\mathrm{n}{\mathrm{y}}^3$, Adeoqꝫ $2\mathrm{z}\times \mathrm{BC}+\mathrm{a}\mathrm{x}\times \mathrm{BC}+\mathrm{a}\mathrm{z}.4{\mathrm{y}}^3\left(\colon\colon \mathrm{n}.\mathrm{m}\right)$$\colon\colon \mathrm{BD}.\mathrm{BT}$ sicut in primo præcedentium casuum. Quamobrem si ex natura cur{illeg}|v|æ AC detur ordinata BC et area ACB sive z dabitur punctum T per quod tangens DT transibit.

Ad eundem modum si $3\mathrm{z}=2\mathrm{y}$ sit æquatio ad curvam AD, erit $3\mathrm{r}${illeg}$\left(3\mathrm{m}\times \mathrm{BC}\right)=2\mathrm{n}$. Adeoqꝫ $3\mathrm{BC}.2$$\left(\colon\colon \mathrm{n}.\mathrm{m}\right)\colon\colon \mathrm{BD}.\mathrm{BT}$. Et sic in alijs.

< text from p 51 resumes >

Exempl: 2. Sit $\mathrm{AB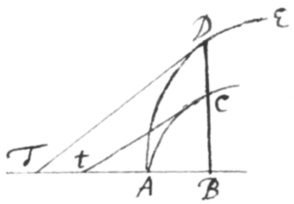}=\mathrm{x}$, $\mathrm{BD}=\mathrm{y}$ (ut ante) et curvæ \cujusvis/ AC longitudo $=\mathrm{z}$, angulusqꝫ ABD rectus. Sit etiam $\sqrt{}\stackrel{\_}{\mathrm{a}\mathrm{x}+\mathrm{x}\mathrm{x}}=\mathrm{BC}$ æquatio ad curvam AC (quæ proinde erit Hyperbola) sit etia $\mathrm{z}=\mathrm{y}$ æquatio ad curvam ADE cujus tangentem {illeg} ducere oportet. Jam quo relatio inter m et n determinetur video imprimis (propter $\mathrm{z}=\mathrm{y}$) esse {illeg} $\mathrm{r}=\mathrm{n}$. Dein ad Hyperbolam \curvam AC/ ductâ tangente Ct erit|sse| $\mathrm{r}.\mathrm{m}\colon\colon \mathrm{Ct}.\mathrm{Bt}$. Sit autem $\mathrm{Bt}=\frac{2\mathrm{a}\mathrm{x}+2\mathrm{x}\mathrm{x}}{\mathrm{a}+2\mathrm{x}}$ cujus quadrato adde ${\mathrm{Bt}}^q$ et fiet ${\mathrm{Ct}}^q=\frac{{\mathrm{a}}^3\mathrm{x}+9\mathrm{a}\mathrm{a}\mathrm{x}\mathrm{x}+16\mathrm{a}{\mathrm{x}}^3+8{\mathrm{x}}^4}{\mathrm{a}\mathrm{a}+4\mathrm{a}\mathrm{x}+4\mathrm{x}\mathrm{x}}$ curvæ cujusvis AC longitudo sit z, ductaqꝫ ad eam tangente Ct erit $\mathrm{Bt}.\mathrm{Ct}\colon\colon \mathrm{m}.\mathrm{r}$ sive $\mathrm{r}=\frac{\mathrm{m}\times \mathrm{Ct}}{\mathrm{Bt}}$.

Jam ad aliam curvam AD cujus tangens ducenda est detur <52> quælibet æquatio in qua z involvitur, puta si $\mathrm{z}=\mathrm{y}$ $\mathrm{r}=\mathrm{n}$ Adeoqꝫ $\mathrm{Ct}.\mathrm{Bt}\left(\colon\colon \mathrm{n}.\mathrm{m}\right)\colon\colon \mathrm{BD}.\mathrm{BT}$, ut in primo casu. Invento autem T age tangentem DT.

Vel Sic \posito/ $\mathrm{x}\mathrm{z}=\mathrm{y}\mathrm{y}$, erit $\mathrm{m}\mathrm{z}+\mathrm{r}\mathrm{x}=2\mathrm{n}\mathrm{y}$, et pro r scripto $\frac{\mathrm{m}\times \mathrm{Ct}}{\mathrm{Bt}}$ emerget $\mathrm{m}\mathrm{z}+\frac{\mathrm{m}\mathrm{x}\times \mathrm{Ct}}{\mathrm{Bt}}=2\mathrm{n}\mathrm{y}$ Quare $\mathrm{z}+\frac{\mathrm{x}\times \mathrm{Ct}}{\mathrm{Bt}}.2\mathrm{y}${$\colon\colon$}$\mathrm{BD}.\mathrm{DT}$.

Exempl 3{.} Sic AC circulus aut alia quævis \nota/ curva quam tangat Ct, et sit AD alia curva cujus tangentem DT ducere oportet, et quæ definitur assumendo $\mathrm{AB}=$ arcui AC, et (CE, BD in dato angulo ad AB ordinatis) referendo BD ad CE vel AE in æquatione aliqua. Dic ergo AB, vel $\mathrm{AC}=\mathrm{x}$. $\mathrm{BD}=\mathrm{y}$. $\mathrm{AE}=\mathrm{z}$ et $\mathrm{CE}=\mathrm{v}$, et patet l, m, et r (fluxiones ipsarum v, x {illeg} CE, AC, et AE) esse inter se ut sunt CE, Ct et Et. Adeóqꝫ 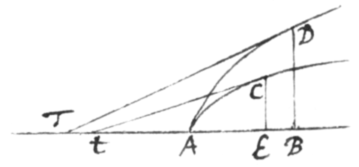$\frac{\mathrm{m}\times \mathrm{CE}}{\mathrm{Ct}}=\mathrm{l}$, et $\frac{\mathrm{m}\times \mathrm{Et}}{\mathrm{Ct}}=\mathrm{r}$.

Detur jam quælibet æquatio ad curvam AD deter{illeg}|m|inandam veluti $\mathrm{y}=\mathrm{z}$ et erit $\mathrm{n}=\mathrm{r}=\frac{\mathrm{m}\times \mathrm{Et}}{\mathrm{Ct}}$. Adeoqꝫ $\mathrm{Et}.\mathrm{Ct}\left(\colon\colon \mathrm{n}.\mathrm{m}\right)\colon\colon \mathrm{BD}.\mathrm{BT}$.

< insertion from the left margin of p 52 >

Vel detur $\mathrm{y}=\mathrm{v}-\mathrm{z}+\mathrm{x}$, et erit $\mathrm{n}=\left(\mathrm{l}-\mathrm{r}+\mathrm{m}=\right)\frac{\mathrm{m}\times \mathrm{CE}+\mathrm{Et}+\mathrm{Ct}}{\mathrm{Ct}}$. Adeoqꝫ $\mathrm{CE}+\mathrm{Et}+\mathrm{Ct}$$.\mathrm{Ct}\left(\colon\colon \mathrm{n}.\mathrm{m}\right)\colon\colon \mathrm{BD}.\mathrm{BT}$.

{illeg}|V|el deniqꝫ detur $\mathrm{a}\mathrm{y}\mathrm{y}={\mathrm{v}}^3$ e{illeg}|t| erit $2\mathrm{a}\mathrm{n}\mathrm{y}=\left(3\mathrm{l}\mathrm{v}\mathrm{v}\right)\frac{3\mathrm{m}\mathrm{v}\mathrm{v}\times \mathrm{CE}}{\mathrm{Ct}}$. Adeoqꝫ $3\mathrm{v}\mathrm{v}\times \mathrm{CE}.2\mathrm{a}\mathrm{y}\times \mathrm{Ct}\colon\colon \mathrm{BD}.\mathrm{BT}$.

Quemadmodum in primo præcedentium octo casuum his exemplis illustrato sic etiam in quovis alio hujusmodi æquationibus adhibitis tangentes duci possunt{.}

Et hæc in hujus explicationem hujus methodi generalis qua curvarum om{illeg}|n|ium tangentes absqꝫ solitâ calculi molestiâ prompte et concinnè determinantur, adduxisse sufficiat.

< text from p 52 resumes > <55>

Cæterum hæc Regula forte sic elegantior evadet, Fac $\mathrm{m}.\mathrm{n}\colon\colon \mathrm{AB}.\mathrm{AL}$. Dein $\mathrm{AL}.\mathrm{AD}\colon\colon \mathrm{AD}.\mathrm{AT}$, et DT curvam tanget. Nam propter æqualia triangula AFD, ATD, est $\mathrm{AD}\times \mathrm{DF}=\mathrm{AT}\times \mathrm{DH}$. Adeoqꝫ $\mathrm{AT}.\mathrm{AD}\left(\colon\colon \mathrm{DF}.\mathrm{DH}\text{, sive}\frac{\mathrm{n}}{\mathrm{m}}\mathrm{Gf}\right)$$\colon\colon \mathrm{AD}.\frac{\mathrm{n}}{\mathrm{m}}\mathrm{AG}\text{, sive}\mathrm{AL}$.

Exempl 2. Esto $\mathrm{x}=\mathrm{y}$ (quæ æquatio est ad Veteru Quadratricem per Prob 1 erit $\mathrm{m}=\mathrm{n}$. Adeoqꝫ $\mathrm{AB}.\mathrm{AD}\colon\colon \mathrm{AD}.\mathrm{AT}$.

Exempl 3. Esto $\mathrm{a}\mathrm{x}\mathrm{x}={\mathrm{y}}^3$ et erit $2\mathrm{a}\mathrm{m}\mathrm{x}=3\mathrm{n}\mathrm{y}\mathrm{y}$. Fac ergo $3\mathrm{y}\mathrm{y}.2\mathrm{a}\mathrm{x}\left(\colon\colon \mathrm{m}.\mathrm{n}\right)\colon\colon \mathrm{AB}.\mathrm{AL}$. Dein $\mathrm{AL}.\mathrm{AD}\colon\colon \mathrm{AD}.\mathrm{AT}$.

Atqꝫ ita tangentes \aliarum/ Quadratricum utcunqꝫ compositarum possis expeditè determinare.

Mod. 9. Si deniqꝫ ABF sit curva quævis data quam tangat recta recta Bt, et rectæ BC in dato 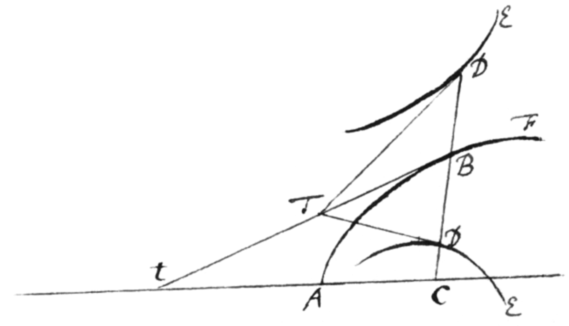angulo ad basin AC applicatæ pars BD inter hanc et aliam curvam DE intercepta relationem at|d| curvæ portionem AB in æquatione quacunqꝫ definitam habeat: alterius curvæ tangentem DT duces capiendo in hujus tangente, BT in ea relatione ad BD, quam habet fluxio curvæ AB ad fluxionem rectæ BD.

Exempl 1. Dictis $\mathrm{AB}=\mathrm{x}$ et $\mathrm{BD}=\mathrm{y}$, esto $\mathrm{a}\mathrm{x}=\mathrm{y}\mathrm{y}$ et per{illeg} Prob: 1, erit $\mathrm{a}\mathrm{m}=2\mathrm{n}\mathrm{y}$, adeoqꝫ $\mathrm{a}.2\mathrm{y}\left(\colon\colon \mathrm{n}.\mathrm{m}\right)\colon\colon \mathrm{BD}.\mathrm{BT}$.

Exempl 2. Sit $\frac{\mathrm{a}}{\mathrm{b}}\mathrm{x}=\mathrm{y}$ (æquatio ad Trochoidem si modò ABF sit circulus) et erit $\frac{\mathrm{a}}{\mathrm{b}}\mathrm{m}=\mathrm{n}$. Adeoqꝫ $\mathrm{a}.\mathrm{b}\colon\colon \mathrm{BD}.\mathrm{BT}$.

Et nihilo difficiliùs tangentes, ubi ipsius BD ad AC vel ad BC relatio in æquatione quavis exp{illeg}|r|imitur, vel ubi curvæ alijs quibuscunqꝫ modis ad rectas aliasve curvas refe{illeg}|r|untur, possis ducere.

Sunt etiam alia non pauca Problemata quorum solutiones ex hisce s{illeg}turiunt \fluunt/. Cujusmodi sunt; 1{.} Invenire punctum Curvæ ubi tangens est ad Basin (vel quamvis positione datam rec{illeg}|t|am) parallela vel perpendicularis vel in alio quovis angulo inclinata.

2{.} Invenire punctum ubi tangens maxime minimève ad Basin {illeg} aut aliam positione datam rectam inclinatur. Hoc est invenire <56> confinium flexûs contrarij. Hujus autem specimen in Conchoide jam ante exhibui{.}

3. A dato quovis extra curvæ perimetrum puncto rectam ducere quæ cum curva \perimetro/ aut angulum contactûs aut rectum angulum, aut alium quemvis datum conficiet. Hoc est rectas tangentes vel perpendiculares rectas vel \aliter/ ad curvam in datis >inclinatas rectas \a dato quovis puncto/ ducere{.}

4{.} A dato quovis intra Parabolam puncto rectam ducere quæ maximum minimumve quem potest angulum cum perimetro ejus conficiet. Et idem de alijs curvis intellige.

5. Rectam ducere quæ duas positione datas curvas, vel eandem curvam (si modò potest) in duobus punctis tangat.

6. Curvam quamvis sub datis conditionibus ducere quæ aliam positione datam curvam in dato puncto tanget.

7{.} Luce in \quamlibet/ curvam superficiem incidente, cujusvis radij fractionem determinare.

Horum et similium Problematum confectiones, ubi non obstat computandi tædium, non sunt ita difficiles ut {illeg} ijs explicandis immorari opus sit. Et Geometris, credo, magis gratum erit sic tantùm recensuisse.