Draft of the 'Discourse concerning Light and Colors'
SR
I suppose you understand yt all transparent substances (as Glasse, water, Air &c) when made very thinne by being blown into bubbles or otherwise formed into plates, doe exhibite various colours according to their various thinnesse, although at a greater thicknesse they appear very clear & colourlesse. In my former discourse about ye constitution of light, I omitted those colours, because they seemed of a more difficult consideration, & were not necessary for stablishmt of ye Doctrine which I propounded. But because they may conduce to further discoveries for completing that Theory, especially as to ye constitution of ye parts of naturall bodies on wch their colours or transparency depend, I have now sent you an account of them. To render this discourse short & distinct, I have first described ye principall of my observations & then considered & made use of them. The Observations are these.
Obs: 1. Compressing two Prisms hard together that their sides (wch \by chance/ were a \very/ little convex) might somwhere touch one another, I found ye place in wch they touched to become *[1] absolutely transparent, as if they had been there one continued peice of Glasse. for when ye light fell so obliquely on ye Air, which in other places places was between them, as to be all reflected; in that place of contact it was \seemed/ wholy transmitted: in so much that when looked upon it apeared like a black or dark spot by reason yt no \sensible/ light was reflected frō thence as frō other places; & when looked through it seemed as it were, a hole in ye|t| Air that was formed into a thinner plate by being compressed between ye|t| glasses. And through this hole objects that were beyond might be seen distinctly wch could not at all be seen through other parts of ye g|G|lasses, where ye Air was interjacent. Although ye glasses were a little conve{illeg}|x| yet this transparent spot {illeg}|w|as {illeg} considerable bre\a/dth, wch bre|ea|dth seemed principally {illeg} proceed frō ye yeilding inwards of ye parts of ye glasses {illeg} {reason} of their mutual pressure. For by pressing them {illeg} hard together it would become much broader then other. Obs: 2. When ye plate of Air, by turning the Prisms about their com̄on Axis became so little inclined to ye incident rays, that some of ym began to be transmitted; there arose in it many slender Arc{illeg}|s| of coloures wch at 
first were shaped almost like the conchoid as you see them here delineated. And by {ye} continuing the motion of ye Prisms, those Arcs increased & b{illeg}|{e}|nded more & more about ye said transparent spot, till they were completed into circles or rings incompassing it, & afterwards continually grew more & more contracted.
These Arcs at their first appe|a|re|a|nce were of a b|v|iol|e|t & blew colour, & between them were white Arcs of circles {illeg}|w|ch presently became a little tinged in their inward limbs wth red & yellow, & to their outward limbs ye blew was adjacent. So yt ye order of those colours frō ye Centrall dark spot, was at that time white, Blew, Violet; {Darknesse} \Black/; Red, Orang, yellow, White Blew, Violet, &c. But the yellow & Red were much fainter then ye Blew & Violet.
The motion of ye Prisms about their Axis being continued those colours contracted more & more, shrinking towards ye whitenesse on either side of it, |un|till they totally v{illeg}|a|nished into it. And then ye circles in those parts appeared black & white wthout any other colours intermixed. But by further m{illeg} \moving/ ye Prisms \about/, the colours again emerged out of ye whitenesse, the Violet & blew at its inward limb, & at its outward limb the red & yellow. So that now their order frō ye centrall spot was white, Yellow, Red, Black, Violet, Blew y|w|hite, yellow, Red, &c. contrary to what it was before.
Obs: 3. When the rings {at} some parts of them appeared only black & white, they were very distinct & wel-defined & the blackness{illeg}|e| seemed as intense as that of ye Centrall Spot. Also in ye {illeg} places \Borders of these rings/ where ye colours began to emerge out of ye whitenesse, they were pretty distinct, {illeg}|w|ch made them visible to a very great multitude. I have sometimes numbered abo{illeg}|ve| thirty successions (recconing every black & white ring for one succes{illeg}|s|ion) & seen more of them wch by reason of their smalnesse I could not number. But in other Positions of ye Prisms at wch ye {illeg} appeared of many colours, I could not distinguish above {illeg} of them, & ye exteriour of those too were {illeg} {illeg} dilute.
In these two Observations to see ye Colours \ring{s}/ {illeg} any other colour but black & white, I found {illeg} that I held my eye at a good distance frō them. For by approaching nearer, although in ye same inclination of my eye, yet th{illeg}|e|re {illeg}ged a ble{illeg}|w|ish colour out {illeg}|o|f ye white, which by de|i|lating it selfe more & more into the black rendered ye circles lesse distinct & left yt|e| {illeg}|w|hite a little tinged wth red & yellow. I found also yt by looking through a slit or oblong hole wch was narrower then the pupill of my eye & held close to it p{illeg}|a|ralell to ye Prisms, I could see ye circles much distincter & visible to a far greater number then otherwise.
Obs: 4. To observe more nicely the order of the colours wch arose out of ye white circles as ye rays became lesse & lesse inl{illeg}|cl|ined to ye plate of Air; I took two Objectglasses the one of a plano-conve{illeg}|x| for a fourteen foot Telescope, & ye other a large double convex for one of fifty foot, & upon this laying ye other wth its plane side downwards, I pressed ym slowly together to make the colours successively emerge in ye middle of ye Circles & yn slowly lifted the upper glasse frō y{illeg}|e| lower to make them successively vanish again in ye same place, {illeg}|w|here being of a considerable bredth, I could more easily discern them. And by this meanes I observed their succession & quantity to be as followeth.
Next to ye pellucid centrall pot made by y{illeg}|e| contact of ye glasses succeeded Violet, Blew, White, Yellow, & Red. The Violet & blew were soe very little in quantity that I could not discerne them in ye circles made by ye Prisms, but ye yellow & Red were pretty copious, & seemed about as much in extent as the white, & 4 or 5 times more then ye blew & Violet. The next circuit or order o{illeg}|f| colours imediately incompassing these was Violet, Blew, Green, yellow, & Red. And these were all of them copious & vivid excepting ye green wch was very little in quantity & seemed much more faint & dilute then ye other colours. Of ye other four the Violet was least & ye blew lesse then ye yellow or Red. The third circuit or order was also Purple, Blew, Green, yellow, & Red, in which the Purple seemed more redish then ye Violet in ye former circuit, & ye green was much more conspicuous, being as bris & copious as any of ye other colo{illeg}|u|rs except ye yellow, but ye Red began to be a little faded inclining very much to purple. After these succeded {Green} & Red. The Green was very copio{illeg}|u|s & lively inclining on ye {illeg} side to blew & ye other to ye|ye|llow. But in this \4th/ circuit {illeg} was neither Violet, blew, nor yellow & ye red was very imꝑfect & dirty. Also the succeeding colours b{illeg}|e|came more & more imꝑfect & dilute after three or four more revo Revolutions they ended in ꝑfect whitenesse.
Obs: 5. To determine the intervall of ye glasses, or thicknesse of ye interjacent Air by which each colour was produced, I measured ye diameters of ye first six rings at ye most lucid part of their Orbits & squaring them I found their Squares to be in Ar{illeg}|i|thmeti{illeg}|ca|ll progression of ye odd numbers 1, 3, 5, 7, 9, 11. And since one of ye glasses was plane & ye other Sphericall their intervalls at those rings must be in|of| ye same proportion|gression|. I measured also the diameters of ye dark or faint rings between the more lucid colours & found their squares to be in Arithmeticall progression of ye eaven numbers 2, 4, 6, 8, 10, 12. And it being very nice & difficult to take those measures exactly I repeated them diverse times at divers parts of ye glasses, that by their agreement I might be confirmed in them. And the same Method I used in determining some others of ye following observations.
Obs: 6. The diameter of ye first ring at ye most lucid part of its orbit was parts of an inch & ye diameter of ye Sphere on which ye double convex object glasse was ground was 102 foot, as I found by measuring it; & consequently ye thicknesse of ye Air, or {illeg}|Ae|reall intervall of ye glasses at yt ring was \of an inch/. For as ye diameter of ye said sphere (1{illeg}|0|2 foot or 1224 inches) is to ye semi diameter of ye ring so very nearly is yt semi diameter to ye said distance of ye glasses. Now by ye precedent observations ye eleventh part of this distance () is ye thicknesse of ye Air at yt part of ye first ring where ye yellow would be most vivid {illeg}|w|ere it not mixed wth other colours in ye {illeg}|w|hite, & this doubled gives ye difference of its thicknesses at ye yellow in all ye other rings. viz or to use a round number ye eighty thousandth part of an inch.
Obs: 7. Those dimensions {illeg}|w|ere taken when my ey{illeg}|e| was placed perpendicularly over ye glasses in or near ye Axis of ye {illeg}|R|ings, but when I viewed ym -->oblily they became bigger continually swelling as I removed my eye further frō their Axis. And partly by measuring ye diameter of ye same Circle at severall obliquities of my eye, partly {illeg} as also by making use of ye two Prisms for{illeg} {illeg}tios, I found its diameter, & consequently ye thicknesse {illeg} at its Perimeter in all those obliquities to be {illeg} Proportions expressed in this Table.
<551r>In the two first Columns are expressed the obliquities of ye rayes to ye p|P|late of Air, that is their angles of inciden{illeg} & refraction. In the third Column ye diameter, of any coloured Ring in those obliquities, is exprest in parts of wch ten constitute that diameter when the rayes are perpendicular. And in ye fourth Column the thicknesse of ye Air at ye Circūference of that Ring is exprest in parts of which also 10 constitute that thicknesse when ye rayes are perpendicular.
Obs. 8. The dark Spot in ye middle of ye Ring{illeg}s increased also by ye obliquation of ye eye although almost in sensibly But |if| in stead of ye Object-glasses ye Prisms were made use of, its in{illeg}|c|rease was more manifest when viewed soe obliquely yt no colours appea{illeg}|r|ed about it. It was least when the rays were in{illeg}|c|ident most obliq{illeg}|u|ely on ye interjacent Air & increased more & more untill ye coloured rings appeared, & then decreased again but not soe much as it increased before. And hence {it} is evident yt ye transparency was not only at ye absolute contac{illeg} of ye glasses but also where they had some little intervall. I have sometimes \observed/ the diameter of yt spot to be between halfe & two fift parts of ye diameter of ye exterior circumference of the Red in ye first circuit or {illeg}|r|evolution of colours when viewed almost perpendicularly, wheras when viewed oblily it hath wholy vanish'd & become opake & white like ye other parts of ye glasse. Whence it may be collected that the glasses did then scearcly {sic} or not at all touch one another, & that their intervall at ye perimeter of that Spot when viewed perpendi{cu}larly was about a 5{illeg}th or 6th part of their intervall at ye circumference of ye said {illeg}|R|ed.
Obs: 9. By looking through ye two contiguous o|)|bject-glasses, I {illeg}ye interjacent Air exhibited Rings of colours as well {illeg} by reflecting it. The centrall Spot was now white, & frō it ye order of ye colours were yellowish Red, Black, Violet, Blew, white, yellow, Red; Violet Blew, Green, yellow, Red &c. But these colours \were/ very faint & dilute unlesse when the light was trajected very obliquely through ye glasses, For by that means they became pretty vivid. Onely ye first yellowish-Red, like ye blew in ye 4th Observation was soe little & faint as scearcely, to be discerned: comparing ye coloured Rings made by reflexion, wth those made by transmission of ye light I found yt white was opposite to black, Red to blew, y{illeg}|e|llow to Violet & green to a compound of Red & Violet. That is, those parts of ye glasse were black when looked through, wch when looked upon appeared white & on ye contrary. And so those wch in one case exhibited blew, did in ye other case exbite {sic} Red. And the like of ye other colours.
Obs: 10. Wetting the object-glasses a little at their edges the water crept in slowly between ym & ye circles thereby became lesse & ye colours more faint: in so mu{illeg}|c|h that as ye water crept along, one halfe of them at wch it first arrived would appear broken off frō ye other halfe & contracted into a lesse r|R|oom. {illeg}|B|y measuring them I found the proportion of their diameters to ye diameters of ye like circles made by Air to be about seaven {sic} to eight, & consequently ye intervalls or the glasses at like circles caused by those two mediums \water & Air/ are as about three to four. {illeg}|P|erhaps it may be a generall {illeg}|R|ule that if any other medium more or lesse dense then water be compressed between ye glasses, their intervall at the Rings caused thereby will be to their intervall caused by interjacent Air, as the sines are wch measure the refraction made out of th{illeg}|a|t Medium into Air.
Obs: 11. When the water was between the glasses If I pressed the upper glasse variously at its edges to make ye Rings move nimbly from one place to another, a little bright Spot would immediately follow ye center of them, wch upon creeping in of the ambient water into that place would presently vanish; Its appearance was such as interjacent Air would have caused & it exhibited the same colours. But it was not Air for where any aereall bubbles were in ye water they would not vanish. The reflexion must rather have been caused by a {sensible} {illeg} wch could recede through the glasse at {illeg} Water
Obs: 12 These observations were made in {illeg}ther to examine ye effects of coloured light {illeg} {illeg} darkned ye Room & viewed ym by reflec|x|t{ein} {illeg} cast on a sheet of white paper. And by this {illeg} {illeg} & visible to a {far} another number {illeg} I have sometimes seen more then 20 of them, wheras in ye open Air I cou{illeg}|ld| not discerne above 8 or 9.
Obs: 13. Appointing {illeg}|a|n Assistant to move the Prism to & frō about its Axis, that all its colours might suc{illeg}|c|essively fall on ye same place of ye paper & be re{illeg}|f|lected from ye circles to my eye whilst I held it immoveable; I found the circles which ye red light {illeg}|m|ade to be manifestly bigger then those which were made by ye Blew & Violet. And it was very pleasant to s{illeg}|e|e them gradually swell or contract accordingly as ye colour of ye light was changed. The intervall of ye Glasses at any of ye Rings when they were made by ye utmost red light was to their intervall at ye same Ring when made by ye utmost Violet, greater then 3 to 2 & lesse then 13 to 8. By the most of my Observations it was as 9 to 14. And this proportion seemed very nearly the same in all obliquities of my eye; unlesse when two Prisms were made use of instead of ye y|O|bject-glasses. For then at a certain great obliquity the Rings made by ye severall colours seemed equall, & at a gr{illeg}|e|ate{illeg}|r| obliquity those made by ye Violet would be greater then ye same Rings made by ye Red.
Obs: 14. \While the Prism was turned about uniformly,/ The contraction or dilatation of a Ring made by all ye severall colours of ye Prism successively reflected frō ye Object glasses, was swiftest in ye Red, slowest in ye Violet & in intermediate colours it had intermediate degrees of celerity. comparing the extent wch each colour obteined by this contr{illeg}|a|ction or dilatation I found that the blew was sensibly more extended then the v|V|iolet, the yellow then ye Blew, & the Red then the yellow. And to make a juster estimation of their proportions I observed that the extent of ye Red was almost double to that of ye Violet, & that ye light was {illeg} of a middle colour between yellow & Green at that intervall of ye Glasses, wch was an Arithmeticall mean between ye two extreames: contrary to what happens in the colours made by the refraction of a Prism, where the r|R|ed is most contracted, the Violet most expanded, & in ye midst of them is ye confine of Green & {illeg}|B|lew.
Obs: 15. These Rings were not of various colours like those in ye open Air but appeared all over of that Prismati colours only wth wch they were illuminated. And by projecting the Prismati colours im̄ediately upon ye glasses I found that the light {illeg} fell on ye dark Spaces wch were between the coloured Rings {illeg} as transmitted through the Glasses wthout any variation of colou{illeg} {illeg} on a white paper placed behind, it would paint Rings of ye {illeg} colour wth those which were reflected & of the bignesse. And frō hence ye origine of those Rings is manifest, namely that ye Aereall intervall of the glasses, ac{illeg}|c|ording to its {illeg}|v|arious thicknesse, is disposed in some places, to reflect, & in others to transmitt ye light of any colour, & in ye same place to reflect one colour where it transmitts another.
Obs: 16. The squares of the diameters of these Rings made by any Prismati colour were in Arithmeticall progression as in ye 5t Observation. And the diameter of ye 6t circle when made by ye yellow & viewed almost perpendicularly was about parts of an inch, agreeable to ye 6t Observation.
The precedent Observations {illeg}|w|ere made wth a rarer thin Medium terminated by a denser, such as was Air or water compressed betwixt two Glasses. In those that follow are set down the appearances of a denser medium thin'd wthin a rarer, such as are plates of Moscovy-glasse, Bubbles of water, & some others {sic} {illeg}|t|hin substances terminated on all sides wth Air.
Obs: 17. If a Bubble be blown wth water, first made tenacious by dissolving a little soap in it tis a com̄on observation that after a while it will appear tinged wth a great variety of colours. To de{illeg}|f|end these Bubbles frō being agitated by the externall Air (wherby their colours are irregularly moved one among another, so yt no acurate observation can be made of them,) as soon as I had blown any of them I covered it wth a clear glasse, & by that means its colours emerged in a very regular order like soe many concentrick Rings incompassing the top of the Bubbles And as ye Bubble grew thinner by ye continuall subsiding of ye water these Rings dilated slowly & overspread the whole Bubble descending in order to ye bottom of it where they vanished successively. In the mean time while after all th{illeg}|e| colours were emerged at y{illeg}|e| top, there grew in ye center of ye Rings a small round black Spot, like that in ye first observation, wch continually dilated it selfe till it became sometimes mo{illeg}|r|e then or of an inch in breadth before the Bubble br{illeg}|o|ak. At first I thought there had been noe light reflected frō ye water in that place, but observing it more curiously I saw wthin it severall smaller ro{illeg}|u|nd spots wch appeared much blacker & darker then ye rest, whereby I know that there was some reflection at the other places wch were not soe dark as those Spots. And by further tryall I found that I could see the images of {illeg} of a candle or ye Sun) very faintly reflected {illeg} great black spot but also frō the little {illeg} wthin it.
Besides the aforesaid coloured Rings {illeg} {illeg} pear small Spots of colours ascending {illeg} {illeg} ye sides of the Bubble {illeg} subsiding of the water. And sometimes small black Spots generated at ye sides would ascend up to ye larger black Spot at ye top of the Bubble & unite wth it.
Obs: 18. Because the colours of these Bubbles were more extended & l{illeg}|i|vely then those of Air thin'd between two Glasses, & so more easie to be distinguished. I shall now give you a further description of their order as they were observed in viewing them by reflexion of the skies when of a white colour whilst a black substance was placed behind them Bubble. And they were these; Red, Blew; Red, Blew; Red, Blew; Red, Green; Red, yellow, Green, Blew, Purple; Red, yellow Green, Blew, Violet; Red, yellow, white, Blew, Black.
The three first successions of Red & Blew were very dilute & dirty, specially the first where the Red seemed in a manner to be white; Amongst those there was scarcely any other colour sensible, in|one|ly ye Blewes (& principally the second,) inclined a little to Green.
The fourth Red was also dilute & dirty but not so much as ye former three; after that succeeded little or no yellow, but a copious green wch at first was inclined a little to yellow, & then became a pretty bris and good willow Green, & afterwards changed to a blewish colour; but there succeeded neither Blew nor Violet.
The fift Red at first was {illeg}|v|ery much inclined to purple & afterwards became more bright & brisk but yet not very pure. This was succeeded wth a very bright & intense yellow, wch was but little in quantity, & soon changed to Green: But that Green was copious & something more pure, deep & lively then the former Green. After that followed an excellent Blew, of a bright sky colour, & then a purpl{illeg}|e| wch was lesse in quantity then the Blew & much inclined to Red.
S|T|he sixt Red was at first of a very fair & lively scarlet, & soon after of a brighter colour being very pure & brisk & the best of all the Reds. Then {illeg}|a|fter a {illeg}|liv|ely Orange followed an intense bright & copious yellow, which was also ye best of all ye yellows; & this changed first to a greenish yellow, &then to a greenish Blew; But ye green between the yellow & blew was very little & dilute, seeming rather a greenish white then a green. The blew wch succeeded became very {illeg} & of a fair bright sky colour, but yet something {inferior} to ye former Blew, And the Violet was intense & {illeg} wch little or no rednesse i{illeg}|n| it, And lesse in quantity {illeg} the Blew.
<553v>In the last Red appeared a tincture of Scarlet next the Violet, wch soon changed to a brighter colour inclining to an Orange; And ye yellow wch followed was at first pretty good & lively, but afterwards it grew more & more dilute untill by degrees it ended in ꝑfect whitenesse. And this whitenesse if the water was very tenacious & well tempered; would slowly Spread & dilate it selfe over ye greatest part of the Bubble, continually growing paler at ye top, where at length it would crack in many places, & those cracks as they dilated would appear of a pretty good, but yet obscure & dark sky colour; the white between the blew Spots diminishing untill it resembled the threds of an irregular nett-work & soon after vanished & l{illeg}|e|ft all ye upper part of ye Bubble of ye said dark blew colour. And this colour after the aforesaid manner dilated it selfe downwards untill sometimes it hath overspread the whole Bubble. In the mean while at ye top wch was of a darker Blew then the bottom & appeared also of many round blew Spots something darker then the rest, there would emerge one or more very dark \black/ Spots & wthin those other Spots of an intenser blacknesse, wch I mentioned in ye former observation And these continually dilated them selves untill ye Bubble broak.
If the water was not very tenacious the Black spots would break forth in the white wthout any sensible intervention of the blew: And sometimes they would break forth wthin ye precedent yellow, or Red, or perhaps wthin the Blew of ye second order before the intermediate colours had time to display themselves.
By this description you may perceive how great an affinity these colours have wth those of Air described in ye 4th Observation although set down in a contrary order by reason that they begin to appear when the Bubble is thickest, & are most conveniently reckoned from the lowest & thickest part of the Bubble upwards.
Obs: 19. Viewing at severall oblique positions of my eye the Rings of colours emergin{illeg}|g| on ye top of the Bubble; I found that they were sensibly dilated by increasing the obliquity but yet not so much by far as those made by thin'd Air in ye 7th Observation. For there they distended {illeg} viewed most oblily to arrive at a part {illeg} {illeg}12 times thicker then that where they {illeg} {illeg} perpendicularly, whereas in this case the {illeg} at wch they arriv'd when {illeg}|v|iewed most oblily {illeg} which exhibited ym by perpendicular Rayes {illeg} {illeg} By the best of my Observations it was between 15 and 15 to 10; an increase about 24 times lesse then in the other case.
Sometimes the Bubble would become of an uniform thicknesse all over except at ye top of it near ye black Spot; as I knew because it \would/ exhibit ye same appe{illeg}|a|rance of colours in all positions of ye eye: And then the colours wch were seen at its apparent circumference by ye obliquest rays would be different frō those yt were seen in other places by rayes lesse oblique to it. And divers spectators might see ye same part of it of differing colours by viewing it at very differing obliquities. Now observing how much ye colours at ye same place of ye Bubble or at divers places of equall thicknesse were varied by ye severall obliquities of ye rayes; by assistance of ye 4th, 14th, 16th & 18th observations as they are hereafter explained, I collected the thicknesse of ye water requisite to exhibit any one {or} ye same colour as severall obliquities to be very nearly |in| ye proportion expressed in this Table.
In the two first columns are expe|r|essed ye obliquities of ye rayes to ye superficies of ye water, that is their angles of incidence & refraction. Where I suppose that ye sines wch measure them are in round numbers as three to four, though probably ye dissolution of soape in ye water may a little alter its refractive Virtue. In the third column the thicknesses of ye Bubble at wch any one colours is exhibited in those severall obliquities, is exprest in parts of which {ten} constitute that thicknesse when the rays are perpendicular.
I have sometimes observed of the colours wch arise on polished steel by heating it, or on Bell-metall & some other me{illeg} substances when melted & poured on the ground where {illeg} {cool} in ye open Air, that they have like those of water-bubbles, been a little changed by viewing them at divers obliquities, & particularly that a deep Blew or Violet when viewed very oblily hath been changed to a deep Red. But ye Changes of these colours are not so sensible as of those made by water For the coria or vitrified part of ye metall wch most metalls when heated or melted continually protrude to their surface where by covering them in form of a thin glassy skin it causes these colours, is much denser then water; and I find that ye change made by the obliquation of ye eye is least in colours of ye densest thin substances.
Obs: 20. As in the 9th Observation so here the Bubble by transmitted light appeared of a contrary colour t{illeg}|o| that wch it exhibited by reflexion. Thus when the Bubble being looked on by ye light of ye clouds reflected frō it, seemed Red at its apparent circumference, if the clouds at ye same time or very suddenly were viewed through it, the colour at its circumference would be blew. And on the contrary when by reflected light it appeared blew, it would appear Red by transmitted light.
Obs: 21. By wetting Plates of Muscovy-glasse whose thinnesse made the like colours appear, the colours became more faint, especially by wetting ye Plates on that side opposite to ye eye; but I could not perceive {illeg}|a|ny variation of their Species. So that ye thicknesse of a Plate requisite to produce any colour depends only on the density of ye Plate & not of ye ambient medium. And hence by ye 10th & 16th observations may be known the thicknesse of Bubbles of water or Plates of Moscovy-glasse, or of any other substances wch they have at any colour produced by them.
Obs: 22. A thin transparent body wch is denser then its ambient medium, exhibits more brisk & vivid colours then that wch is so much rarer; as I have particularly observ{illeg}|e|d in Air & Glasse. For blowing glasse very thin at a lamp furnace, those Plates encompassed wth Air did exhibit colours much more vivid then those of Air made thin between two glasses.
Obs: 23. Comparing the quantity of light reflected frō the severall Rings, I found it was most copious from the first or inmost, & in ye exterior Rings be{illeg}|c|ame gradually lesse & lesse. Also the whitenesse of the first {Ring was}stronger then {illeg}|th|at reflected frō those parts of the {illeg} were wthout ye Rings; as I could manifest{illeg} {illeg} at distance ye Rings made by the two {colours} {illeg} comparing two Bubbles of water blown {illeg} the first of wch the whitenesse appeared {illeg} lours, & the whitenesse wch preceded {illeg}
<555r>Obs: 24. When the two object glasses were layd upon one another so as to make the Ringes of colours appear, though wth my naked eye I could not discern above 8 or 9 of those Ringes yet by viewing them through a Prism I have seen a far greater multitude, in so much that I could number more then fourty, besides m{illeg}|a|ny others that were so very small & close together that I could not keep my eye so steddy on them severally as to number them. But by their extent I have sometimes estimated them to be more then a hundred. And I beleive ye experiment may be improved to the discovery of far greater numbers. For they seem to be really unlimited, thro|o|ugh visible onely so far as they {illeg}|can| be separated by ye refraction, as I shall hereafter explain.
But it was but one side of the Rings, namely that tow{illeg}|a|rds wch ye refraction was made , wch by that refraction {illeg}|w|as rendered distinct, & ye other side became more confused then to ye naked eye, In so much yt there I could not discerne above one or two, & sometimes none of those Rings, of wch I could discern 8 or 9 wth my naked eye. And their segments or arcs wch on the other side appeared so numerous, for ye most p{illeg}|a|rt exceeded not ye third part of a circle. If the refraction was very great or ye Prisms very distant from ye Object-glasses, the middle part of those arcs became also conf{illeg}|u|sed so as to disappear & constitute a{illeg}|n| even whitenenesse, whilst on either side their ends, as also the whole arcs furthes{illeg}|t| from ye center became distincter 
then before, appearing in the form you see them here designed.
The arcs where they seemed distinctest were only white & black successively wthout any other colours intermixed. {illeg}|B|ut in other places the{illeg}re appeared colours whose order was inverted by ye refraction in such manner that if I first held the Prism very near the Object glasses & then gradually removed it farther of towards my eye, the colours of ye 2d, 3d, 4th & following Rings shrunk towards ye {illeg}|w|hite that emerged between ym untill they wholy vanished into it at ye middle of ye Arcs, & afterwards {illeg}|e|merged again in a contrary order. But at ye ends of the arcs they retained their order unchanged.
I have sometimes so layd {illeg} \one/ Object-glasse upon the other that to the naked eye they have all over seemed uniformly white wthout the least appearance of any of ye coloured Rings; & yet by view{illeg}|i|ng them through a Prism great multitudes of those Rings have Discover{illeg}|e|d themselves. And in like manner Plates of Moscovy-glasse & bubbles of glasse blown at a lamp-furnace which were not soe thin as to exhibit any colours to ye naked eye, have through the Prism exhibited a great variety of them ranged irregularly up & down in the form of w|W|aves. And so bubbles of water before they beg{illeg}|a|n to exhibit their colours to the naked eye of a by stander have appeared through a Prism, girded about wth many parallell & horizontal Rings: to produce wch effect, it was necessary to hold |ye| Prism parallel or very nearly par{illeg}|a|llel to ye Horizon, & to dispose it so that the rayes mig{illeg}|ht| be refracted upwards.
Having given my Observations of these colours before I m{illeg}|a|ke use of them to unfold ye causes of |ye| colours of naturall bodies, it is convenient that by ye simplest of them, I first e{illeg}|x|plain the more compounded, such as are ye 2d, 3d, 4th, 5|9|th, 12th, 18th, 20th, & 24th.
And first to show how ye colours in ye 4th & 1{illeg}|8|th Observations are produced, let there be taken in any right line ye lengths YZ, YA, & YH in proportion as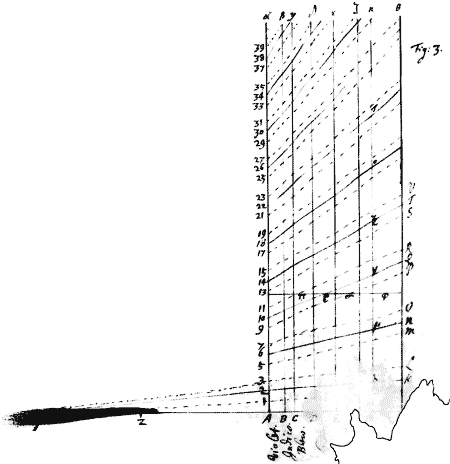 
4, 9, & 14 & between ZA & ZH eleven mean proportionalls, of wch let ZB be ye secon{illeg}|d|, ZC the third, ZD the fift, ZE ye seventh, ZF ye ninth, & ZG the tenth. And at the points A, B, C, D, E, F, G, H, let perpendiculars Aα, Bβ, &c. be erected, by whose intervalls, the extent of the severall colours set underneath agt ym, is to be represented. Then divide the line Aα in such proportion as the numbers 1, 2, 3; 5, 6, 7; 9, 10, 11; &c. set at the point of division denote. And through those divisions from Y draw lines 1J, 2K, 3L; 5M, 6N, 7O; &c
Now if A2 be supposed to represent the thicknesse of any thin transparent body at which the utmost violet is most copiously reflected in ye first Ring or series of colours, then by the 13th Observa{illeg} {illeg} sent its thicknesse at wch the utmost Red {illeg} in the same series. Also by the 5t & 16th Observations {illeg} HN will denote the thicknesses at wch those extream colours are most copiously reflected reflected in ye second series, & so on. And the thicknesse \at which/ any of the intermediate colours are reflected most copiously \will/ according to ye 14th Observation, be defined by the intermediate parts of the lines 2K, 6N, &c agt which the names of those colours are written belo{illeg}|w|.
But fa|u|rther to define the latitude of these colours in each Ring or series let A1 design the least thicknesse & A3 the greatest thicknesse at wch the extream {illeg}|V|iolet in the first series is reflected, & let HJ & HL design the like limits for the {illeg}|e|xtream Red, & the intermediate colours be limited by the intermediate parts of ye lines 1J & 3L; against wch the names of those colours are written. And in the second series let those limits of the lines 5M & 7O; & so on: But yet wth this caution that the reflexions be supposed strongest at the intermediate spaces 2K, 6N, 10R &c & to decrease gradually towards these limits 1J,3L; 5M, 7O; &c on either side, where you must not conceive ym to be precisely limited but to decay indefinitely. And wheras I have design|assig|ned the same latitude to every series, I did it beca{illeg}|u|se although the colours in ye first series seem to be a little broader then ye rest by reason of a stronger reflexion there, yet that inequ{illeg}|a|lity is so insensible as scarcely to d|b|e determined by observation.
Now according to this Description conceiving that the rayes in yt severall colours in here are by turnes reflected at the spaces 1J, L3, 5MO7, 9PR11, &c; & transmitted at the Spaces AHJ1, 3LM5, 7OP9 &c; it is easi{illeg}|e| to know what colour must in the open Air be exhibited at any thicknesse of a transparent thin b|B|ody. For if a Ruler be {illeg}|a|ppl{illeg}|y|ed parallel to AH, at that distance frō it by which the distance thicknesse of ye b|B|ody is represented, the alternate spaces 1JL3, 5MO7 &c. {illeg}|w|hich it crosseth will denote ye reflected originall colours of which the colo{illeg}|u|r exhibited in the open Air is compounded: Thus if the constitution of |ye| Green in the third series of colours be desired; apply the Ruler as you see at π, {illeg}|ρ| σ, φ, And by its passing through some of{f} the Blew at π, & yellow at σ, as well as through ye green ρ, you may conclude that green exhibited at that thicknesse of ye body is principally constituted of originall {illeg} green, but not wthout a mixture of some blew & yellow.
By this meanes you may know how ye colours frō the water of the Rings outwards ought to succeed in order as they were described in the fourth & 18th observations. For if you move the Ruler gradually frō AH through all distances, having past over the first space wch denotes litth|l|e or no reflexion to be made by thinnest substances, it will first arrive at {illeg} ye Violet & then very quickly at t{illeg}|h|e {illeg}|B|lew & green wch together wth that Violet compound Blew, & then at ye yellow & Red by {illeg}|w|hose further addition that Blew is converted into whitenesse, which whitenesse continues during the transit frō J to 3, & after that by ye successive deficience of its component colours turnes first to compound yellow & then to Red, & last of all the {illeg}|R|ed ceaseth at L. Then begin the colours of ye second series, wch succeed in order between 5 & O, & are more liv{illeg}|e|ly then before because more expanded & severed And for the same reason instead of ye former white {there} intercedes between ye blew & yellow a mixture of Orange, Yellow, Green, Blew & Indico, all wch together ought to exhibit a dilute & imperfect Green. So the colours of the third series all succeed in order; first the Violet wch a little interferes wth the Red of ye second order & is thereby inclined to a reddish Purple; then the|e|y blew & green wt|c|h are lesse mixed wth other colours & consequently more lively then before; especially the Green: Then followes ye yellow some of wch towards ye Green is distinct & good, but that part of it towards ye succeeding Red, as also that Red is mixed wth the Violet & Blew of the fourth series whereb{illeg}|y| various degrees of Red very much inclining to Purple are compounded. The Violet & Blew wch should succeed this Red being mixed wth & hidden in it, there succeeds a Green, a|A|nd this at first is much inclined to blew, but soon becomes a good Green, the only unmixt & lively colour in this fourth series. For as it verges to{illeg}|w|ards ye yellow its begins to interfere wth ye colours of ye fift series, by whose mixture ye succeeding yellow & Red are very much diluted & made dirty, especially the yellow wch being the weaker colour is scarce able to show it selfe. After this the severall se{illeg}|r|ies interfere more & more & their colours become more & more intermixed t{illeg}|i|ll after three or four more revolutions (in wch ye Red & blew predominate by turnes) all so{illeg}|r|ts of colours {illeg}|a|re in all places pretty equally blended & compound one eaven whitenesse.
And since by ye 15th Observation the rayes indued with one colour are transmitted where those of another clolour {illeg} reason of ye colours made by ye transmitted {illeg} {illeg} Observations is also frō hence evident.
If not only ye order & Species of {these} {illeg} the precise thicknesse of ye Plate of thin{illeg} {illeg} are exhibited, be defined in parts of an {illeg} performed by performed by assistance of ye 6t or 6th {illeg} For according to those observations the thicknesse of ye thin Air wch between two glasses exhibited the Orange as bright red of ye 6th order was parts of an inch. Now suppose this thicknesse to be represented by Gτ & ye eleventh part of it Gλ as will be about of an inch. And so Gμ, Gν, Gζ, Gο, will be , , , & . And this being known it is easie to determine what thicknesse of Air is represented by Gφ or any other distance of ye Ruler frō AH.
But further since by ye 10th observation the thicknesse of Air was to the thicknesse of {illeg}|w|ater wch between the same glasses exhibited the same colour, as 4 to 3; & by ye 21th observation ye colours of thin Bodies are not varied by varying ye ambient Medium; the thicknesse of a Bubble of {illeg}|w|ater exhibiting any colour will be of the thicknesse of Air producing the same colour. And so according to the same 10th &. 21th Observations the thicknesse of a Plate of glasse whose refraction is measured by the proportion of ye series sines 31 to 20 may be of the thicknesse of Air producing the same colours. And the like of other Mediums. On these grounds I have composed the following Table wherin the thicknesse of Air, water, & glasse at wch each colour is most intense & specifi{illeg}|c|, is expressed in parts of an inch divided into ten hundred thousand equall parts.
| The thicknesse of | ||||
| Air | water | Glasse | ||
| _______________________________________________________________ | ||||
| Black | 2 | 1 | {illeg}|1|, or lesse | |
| The colours | Blew | 2 | 2 | 1. |
| of ye{illeg}|f|irst | white | 5 | {illeg}|4| | 3. |
| order | Yellow | 8 | 6 | 5. |
| Orange | 9 | 6 | 5. | |
| Red. | 10 | 7 | 6 | |
| _______________________________________________________________ | ||||
| Violet | 12 | 9 | 7. | |
| Indico | 13 | 9 | 8. | |
| Of the | Ble{illeg}|w| | 14 | 11 | 9. |
| second | Green | 16 | 12 | 10. |
| order | Yellow | 17 | 13 | 11. |
| Orange | 19 | 14 | 12. | |
| Bright Red | 20 | 15 | 13. | |
| Scarlet | 21 | 16 | 13. | |
| _______________________________________________________________ | ||||
| Purple | 23 | 17 | . | |
| Indico | 24 | 18 | 15. | |
| Of the | Blew | 25 | 19 | 16. |
| third order | Green | 27 | 20 | 17. |
| Yellow | 29 | 22 | 19. | |
| Red | 31 | 23 | 20. | |
| Blewish Red | 33 | 25 | 21. | |
| _______________________________________________________________ | ||||
| _______________________________________________________________ | ||||
| Blewish Green | 36 | 27 | 23. | |
| 4th o|O|rder | Green | 37 | 28 | 24. |
| Yellowish green | 39 | 29 | 25. | |
| Red. | 44 | 33 | 28. | |
| _______________________________________________________________ | ||||
| 5t Order | Greenish blew | 38 | 32. | |
| Red | 57 | 43 | 37. | |
| _______________________________________________________________ | ||||
| 6t Order | Greenish blew | 64 | 48 | 41. |
| Red | 53 | 45. | ||
| _______________________________________________________________ | ||||
| 7th Order | Greenish blew | 77 | 58 | 50. |
| Red or white | 84 | 63 | 54. | |
| _______________________________________________________________ | ||||
Now if this Table be compared wth the third Scheme you will there see the constitution of each colour as to its ingredients or the originall colours of wch it is compounded, & thence be enabled to judge of its intensenesse or imperfection; wch may suffice i{illeg}|n| explication of ye fourth & 18th {illeg} \Observations/ unlesse it be further desired to delineate the manner how the colours appear when the two Object-glasses are layd upon one another. To doe wch let there be described a large Arc of a Circle, & a streight lines wch may touch that Arc, & parallel to that Tangent severall occult lines at such distances frō it as the numbers set agt ye severall colours in ye Table denote. For ye Arc & its Tangent will represent the suꝑficies of ye glasses terminating ye interjacent Air, & the places where the occult lines cut the Arc will show at what distances frō the \center or/ point of contact each colour is reflected.
There a{illeg}|re| also other uses of this Table: For bi|y| its assistance ye thicknesse of ye Bubble in ye 19th Observation was determined by ye colours wch it exhibited. And so ye bignesse of ye parts of naturall bodies may be conjectured at by their colours, as shall be hereafter shown. Also if two or more very thin Plates be layd one upon another so as to compose one Plate equalling them all in thicknesse, the resulting colour may be hereby d{illeg}|e|termined. For instance, Mr Hook in his Moscovy Micrographia observes that a faint yellow plate of Moscovy glasse layd upon a blew one constituted a very deep purple. The yellow of ye first order is a faint one, & the thicknesse of ye plate exhibiting it according to the Table, is 5 to wch add 9 {the thicknesse} exhibiting Blew of ye second order, & ye summe {illeg} nearly approaching 14 the thicknesse {illeg} {illeg} the third order.
To explain in the next place the {illeg} 2d & 3d Observ{illeg}|a|tions, that is, how ys colours {illeg} Prisms about their com̄on Axis ye {illeg} that expressed in those Observations) may be converted into white & black Rings, & afterwards into colours ag{illeg}|a|in in an inverted order: it must be remembred that those colours are dilated by ye obliquation of ye rayes to ye Air wch intercedes ye Glasses, & that according to ye Table in ye 7th Observation their dilatation or recession frō their com̄on center is most manifest & speedy when they are obliquest. Now ye rays of yellow being more refracted by ye first suꝑficies of|at| the said Air then those of Red, are therby made more obli to the second suꝑficies at wch they are reflected to produce the coloured Rings, & consequently ye yellow in each Ring will be more dilated then the R{illeg}|e|d; & the excesse of its dilatation will be so much the greater by how much ye greater is ye obliquity of ye rayes, untill at last it become of equall extent wth ye Red of ye same Ring. And for ye same reason the Green, blew & Violet will be also so much dilated by ye still greater obliquity of their rayes as to become all very nearly of equall extent wth ye Red, that is, equally distant frō ye center of the Rings. And then all ye colours of ye same series must be coincident, & by their mixture exhibit a White Ring. And these White Rings must have black or dark Rings between them because they doe not spread & interfere {illeg}|w|th {illeg}|o|ne another as before. And for that reason also they must become distincter & visible to far greater numbers. But yet ye Violet being obliquest will be something more dilated in proportio{illeg}|n| then the other colours, & so {illeg}|v|ery apt to appear at ye exterior verges of ye white.
Afterwards by a greater obliquity of |ye| rays, the Violet & Blew become sensibly more dilated then ye Red & y|Y|ellow, & so being further removed frō ye center of ye Rings, the colours must emerge out of ye white in an order contrary to yt which they had before, ye Violet & Blew at ye exterior limbs, & ye Red & yellow at ye interior. And ye Viol{illeg}|e|t by reason of ye greatest obliquity of its rayes being in proportion most of all expanded will soonest appear at ye exterior limb of each White Ring & become more conspicuous then the rest. And ye severall series of colours by their unfolding & spreading will begin again to interfere, & thereby render the Rings lesse distinct & not visible to soe great numbers.
If instead of ye Prisms the objectglasses be made use of the Rings whic{illeg}|h| they exhibit become not white & distinct {by ye} obliquity of ye eye, by reason yt ye rayes in thei{illeg}|r| p|P|assage through that Air wch intercedes|d| ye glasses are very nearly pa{illeg}|r|allel to themselves when first incident on the glasses, & consequently those indued wth severall colours are not inclined one m{illeg}|o|re then another to that Air as it happens in the Prisms.
There is yet another circumstance of these experiments to be consider{illeg}|e|d, & that is why the black & white Rings wch when viewed at distance appear distinct, should not only becom confused by viewing them near at hand, but also yeild a Violet colour at both ye edges of every white Ring. And ye reason is that ye rayes wch enter ye eye at severall parts of ye Pupill have severall obliquities to ye glasses, & those wch are most obli, if considered apart, would represent the Rings bigger then those wch are ye least oblique. When{illeg}|ce| ye breadth of the Perimeter of every white Ring is expanded outwards by ye obliquest rays & inwards by ye least oblique. And this expansion is so much the greater by how much the {illeg}|{illeg}| \greater/ is ye difference of ye obliquity that is, by how much the Pupill is {illeg}|w|ider, or ye eye nearer to ye Glasses. And the breadth of the Violet must be most expanded, because the rayes apt to excite a sensation of that colour are most oblique to ye second or further suꝑficies of the thin'd Air at wch they are reflected, & have also ye greatest variation of obliquity, wch makes that colour soonest emerge out of ye edges of ye white. And as the breadth of every Ring is thus augmented, the dark intervalls must be diminished, untill the neighbouring Rings become continuous, & are blended, the exterior first, & then those nearer the center, so that they can no longer be distinguished apart but seem to co{illeg}|n|stitute an eaven & uniform whitenesse.
Amongst all ye Observations theire is none accompanied wth so odd circūstances as ye 24th. Of those |ye| Principall are that in thin Plates wch to the naked eye seem of an eaven & uniform transparent whitenesse the refraction of a Prism should make the Rings of colo{illeg}|u|rs appear; wheras it usually makes Objects appear coloured onely where they are terminated {illeg}|w|th shadows, or have parts unequally luminous, & that it should make those Rings exceedingly distinct & white although it usually renders objects confused & coloured. The cause of these things you will understand, by considering that all the Rings of colours are actually \really/ in the Plate when viewed wth the {illeg} although by reason of the great breadth of {illeg} {illeg}rency they so much interfere & are blended {illeg} they seem to constitute an eaven whitenesse {illeg} rayes passe through the Prism to the eye {illeg} severall colours {illeg}|i|n {illeg}|e|very Ring are {illeg} then others according to their degree of refrangibility wch meanes the colours one one side of the Ring become more unfolded & dilated & on the other side more complicated & contracted. And where by a due refraction they are so much contracted that the severall Rings become narrower then to interfere wth one another, they must appear distinct & also white if the constituent colors be so much c{illeg}|o|ntracted as to be wholy coincident. But on the other side where every Ring is made broader by the further unfolding of its colours, it must interfere more wth other Rings then before & so become lesse distinct
To explain this a little further, suppose the concentrick circles AB and CD represent the red & Violet of any order wch together wth the intermediate colours constitute any one of these Rings. Now these being viewed through a Prism the Violet circle BC will by a greater refraction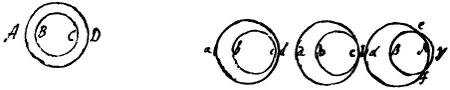 
be further translated from its place then the Red AD & so approach nearer to it on t{illeg}|h|at side towards wch the refractions are made. For instance, if the Red be translated to ad the Violet may be translated to bc so as to approach nearer to it at c then before, & if the Red be further translated to ad the Violet may be {still} so much further translated to {illeg} bc as to convene wth it at c, & if the Red be yet further translated to αδ, the Violet may be still so much further translated to βγ as to pass beyond {illeg}|i|t at γ & convene wth it at e & f. And this being understood not only of the Red & Violet but of all the other intermediate colours, & also of ev{illeg}|e|ry revolution of t{illeg}|h|ose colours, you will easily perceive how these of the same revolution or order by their nearnesse {at} cd & δγ & their coincidence at cd, e, & f ought to constitute pretty distinct arcs of circles, especially at cd or at e & f {&} that they will appear s{illeg}|e|verall at at {sic} cd, at cd exhibit whitenesse by their coincidence, & again appear severall at δγ, but yet in a contrary order to that which they had before & still retain beyond e and f. But on the other side at ab, ab, {illeg} αβ these colours must become much more confused by being dilated & spread soe as to interfere wth those of other orders. And the same confusion will happen at δγ between e & f if the refraction be very great, or the Prism very distant from the Object-Glasses. And these little Arcs must be distinctest & whitest at their middle, & at their ends, where in which case no parts of the Ring will b{illeg}|e| seen save only two little Arcs at e & f whose distance from one another will be augmented by removing the Prism still further from the Object-Glasses. And these little Arcs must be distinctest & whitest at their middle, & at their ends where they begin to grow confused, they must be coloured. And the colours at one end of every Arc must be in a contrary order the those at ye other end, by reason that they crosse in the intermediate wh{illeg}|i|te. Namely their ends wch verge towards δγ will be red & yellow on that side next ye center & blew & Violet on the other side. But their other ends which verge from δγ will on ye contrary be blew & Violet on that side towards the center & on the other side red & yellow.
For confirmation of all this I need alledge no more yn that it is mathematically demonstrable from my former Principles. But yet I shall add that they which please to take the pains, may by the Testimony of their senses be assured that these explications are not Hypotheticall but infallibly true & genuine. For in a dark Room by viewing these Rings through a Prism by reflextion of the severall Prismati colours wch an Assistant causes to move to & fro upon a wall or paper from whence they are reflected, whilst the spectators eye, the Prism & Object-glasses (as in the 13 observation) are placed steddy: the position of ye circles made successively by the severall colours will be found such in respect of one another as I have described at abcd, or abcd or αβγδ. And by the same Method, the truth of ye {explications} {of}the other Observations, is to be examined.
By what hath been said, the the like {illeg} Bubbles & thin Plates of Glasse may be {illeg} small fragments of those Plates there is {illeg} servable, that if they lying flatt {illeg} be turned about their centers whilst they are viewed through a Prism: some of them exhibit waves in one or two positions only, but the most of them do in all positions exhibit those waves & that for ye most part appearing, almost all over the Glasse. The reason is that ye suꝑficies of such Pl{illeg}|a|tes are not eaven but \have/ many ca{illeg}|v|ities & swellings wch how shallow soever do a little vary the thicknesse of the Plate: And by the severall sides os|f| those cavities there must be produ{illeg}|ce|d waves in severall postures of ye Prism. Now though it be but some very small and narrow parts of ye Glasse by which these waves for the most part are caused yet they may seem to extend themselves ov{illeg}|e|r the whole Glasse, because from the narrowest of those parts there are colours of severall orders confusedly reflected wch by refraction of the Prism are {illeg}|u|nfolded & dispersed to severall places so as to constitute so many severall waves {illeg}|a|s there were divers orders of ye colours promiscuously reflected from that part of th{illeg}|e| Glasse.
These are the Principall Phænomena of thin Plates or Bubbles whose explications depend on the Properties of light that I have heretofore delivered: And these you see doe neccessarily follow from them & agree wth them even to their {illeg}|v|ery least circumstances; & not on{illeg}|e|ly so, but doe very much tend to their proof. Thus by the 24th Observation it appears that the rayes of severall colours made as well by thin Plates or Bubbles as by ye refractions of a Prism have severall degrees of refrangibility, whereby those of each order which at their reflexion from the Plate or Bubble are intermixed wth those of other orders, are {illeg}|s|eperated from them by refraction, & associated together so as to become visible by themselves like Arcs of c|C|ircles. For if the rayes were all alike refrangible, 'tis impossible that the whitenesse which to the naked sense appears uniform should by refraction have its parts transposed & ranged into those black & white Arcs.
It appears also that the unequall refractions {difform} rayes proceed not from any contingent irregularities. Such as are V{illeg}|{illeg}|, an uneaven polish, or for fortuitous position of the pores of the Glasse; unequall motions in ye Air or Æther{.} spreading, breaking or dividing the same ray into many diverging parts; or ye like. For admitting any such irregularities, it would be impossible for refractions to render those Rings so very distinct & well defined, as they doe in the 24th o|O|bservation. It is necessary therefore that every ray have its proper & constant degree of refrangibility connate wth it, according to wch its refraction is ever justly & regularly {illeg}|p|erformed; & that severall rayes have severall of those degrees.
And what is said of their r|R|efrangibility may be also understood of their Reflex{illeg}ibility, that is of their dispositions to be reflected some at a greater & others at a lesse thicknesse of thin Plates or Bubbles, namely yt those dispositions are also connate wth the rayes & im̄utable{,} as may appear by the 13th 14th & 15th Observations compared wth the 4th & 18th.
By the precedent Observations it appears also that whitenesse is a dissimilar mixture of all colours, & that light is a mixture of rayes endewed wth all \those/ colours. For considering the multitude of |ye| Rings of colours in ye 3d, 12t, & 24th Observations, it is manifest t{illeg}|ha|t although in the 4th & 18th Observations there appear noe more than 8 or 9 of those Rings, yet there are really a far greater number wch soe much interfere & mingle wth on {sic} another as after those 8 or 9 revolutions to dilute one another wholy & constitute an eaven & sensibly uniforme whitenesse. And consequently that whitenesse must be allowed a mixture of all colours, & the light which conveys it to the eye must be a mixture of rayes endewed wth all those colours.This I beleive hath seemed the most paradoxical of all my assertions, & met with the most universall & obstinate prejudice; But to me it appears as infallibly true & certain, as it can seem extravagent to others. For hitherto I never tried any way to {sic}to mix all colours by which I could not in some degree or other produce whitenesse & yet I have made as {many} trialls as I could excogitate ways of mixing colours {illeg} which I may take occasion to discourse {illeg}
But further by the 24th Observation it {illeg} is a constant relation between colours & {illeg} refrangible rayes being Violet, the least {illeg} of intermediate colours having proportionally {illeg} refrangibility. And by the 13th, 14th, & 15th Observations compared wth the 4th or 18th, there appears to be ye same constant relation bet{illeg}|w|een colour & reflextibility, the Violet being on equall termes reflected at least thicknesse of any thin {illeg}|P|late or Bubble, ye r|R|ed at greatest thicknesse, & the intermedi{illeg}|a|te colours at intermediate thicknesses. Whence a|i|t followes that ye colorifi dispositions of rayes are also connate wth them & im̄utable, & by consequence that all ye productions & appearances of colours in the world are derived not from any Physicall change caused {illeg}|i|n {illeg}|l|ight by refraction or reflexion but only from ye various mixtures or seperations of rayes by virtue of their different {illeg}|R|efrangibility or Reflextibility. And in this respect it is that ye science of colours becomes a speculation more proper for Mathematicians then naturalists, & deserves rather to be esteemed Mathematicall then Physicall, as I told you in my former letter, & may hereafter explain more fully.
I am now come to ye last part of this design wch is to consider how ye Phænomena of thin transparent Plates stand related to those of all other naturall bodies. Of these bodies I have already told you that they appear of divers colours accordingly as they are disposed to reflect most copious by the rayes endewed wth those colours. But their constitutions wherby they reflect some more rayes more copiously then others, remaines to be enquired after. And this I shall endeavour in the following Propositions.
Prop.1. Those superficies reflect ye greatest quantity of light wch have ye greatest refracting power, that is, which intercede mediums that differ most in their refracting densities. And in the confines of equally dense mediums there is noe reflexton.
The analogy bet{illeg}|w|een reflexion & refraction will appear by considering that when light passeth oblily out of one Medium into another which refracts from the perpendicular, the greater is the difference of their density ye lesse obliquity is requisite to cause a totall reflexion; because as the sines are which measure the refraction, so is ye sine of incidence at which the totall {illeg}|reflex|ion begins, to ye radius {of} ye circle, & consequently that incidence is least where there is the greatest difference o{illeg}|f| the sines. Thus in ye passing of light out of water into Air where the refraction is measured by the ratio of the sines 3 to 4 the totall reflexion begins when the angle of incidence is sbout 48degr 35min. In passing out of Glasse into Air where the refraction is measured by the ratio of ye sines 20 to 31 the totall reflexion {illeg}|b|egins when ye angle of incidence is {illeg}|4|0degr. 10min. And so i{illeg}|n| passing out of Chri|y|stall or more strongly refracting Mediums into Air, there is still a lesse obliquity requisite to cause a totall reflexion. Superficies therfore wch refract most do soonest reflect all the light which is incident on them, & so must be allowed most strongly reflective.
But the truth of this Proposition will further appear by observing that in ye superficies interceding any two of those Mediums, Air of water or other liquors, com̄on Glasse, Chrystall, & Metalline Glasses, the reflexion is stronger or weaker accordingly as ye superficies hath a greater or lesse refracting power. Th{illeg}|u|s when other Mediums are contiguous to Air; the reflexion is stronger in the suꝑficies of Glasse then of water; still stronger in ye superficies of Chrystall, & strongest in ye superficies of metalline Glasse. So in ye confine of water & com̄on Glasse the reflexion is very weak, b{illeg}|u|t yet stronger then in ye confine of water & oyle or almost any other two liquors, & still stronger in the confine of water & Chrystall or Metalline Glasse: accordingly as those Mediums differ more or lesse in density. So in ye confine of com̄on Glasse & Chrystall there is a weak reflexion & a stronger reflexion in the confine of com̄on & mealline Glasse. But in ye confine of two Glasses of equall density, there is not any sensible reflexion as was shown in ye 1st Observation. And ye same may be understood of ye superficies \of/ two Chrystalls or liquors or any other substances in which no refl|r|action is caused. Whence it comes to passe that uniform Mediums have no sensible reflexion but in their externall superficies where they are adjacent to other Mediums of a different densi{ity.}
Prop: 2. {illeg}|T|he least parts of naturall bodies {are} in {some}measure transparent; And the opacity of those {illeg} the multitude of ref{illeg}|lexions| caused caused in their {illeg}
That this is so wil{illeg}|l| easily be granted {illeg} been conversant wth Microscopes. And it may be also tried by applying any substance to a hole through which some light is immitted into a dark room For how opake sooner that substance may b|s|eem in ye open Air, it will by that means appear very manifestly transparent if it be of a sufficient thinnesse. Onely metalline bodies must be exempted wch by reason of their excessive density seem to reflect almost all the light incident on their first superficies.
Prop: 3: Between the parts of opake or coloured bodies are many interstices replenished wth mediums of other densities: as water between the tinging corpuscles wherwth any liquor is impregnated; Air between the aqueous globu{illeg}|les| that constitute Clouds or mists; & for the most part spaces {illeg}|v|oid of both Air & water; but yet perhaps replenished wth some subtiler Medium between the parts of hard bodies.
The truth of this is evinced by the two precedent Propositions, For by ye second Proposition there are many reflexions from ye internall parts of bodies, wch by the 1st Proposition would not happen if the parts of those bodies were continu{illeg}|e|d wthout any such interstices between them, because reflexions are caused only in superficies wch intercede Mediums of a differing density.
But further that this discontinuity of parts is the Principall cause of the opacity of bodies will appear by considering that opake substances become transparent by filling their pores wth any subs{illeg}|ta|nce of equall or almost equall density wth their parts. Thus paper dipped in water or oyle, the oculus mundi stone steeped in water, linnen cloth oyl'd or varnished, & many other substances soaked in such liquors as will intimately pervade their little pores become by that means more transparent then otherwise. So on the contrary the most transparent substances may by seperating their parts become rendered sufficiently opake, as Glasse by being reduced to powder or otherwise flawed, water by being formed into many small bubbles either alone in the form of froth, or by shaking it together wth oyle of Turpentine or some other convenient liquor wth wch it will not incorporate, & Horn by being scraped.
<562v>To the increase of of the opacity of these bodies it conduces something that by ye 23d Observation the reflexions of very thin transparent substances are considerably stronger then those made by ye same substances are considerably of a greater thicknesse. And to the reflexion of solid bodies it may further add, that the interstices of their parts are void of Air. For that for ye most part they ar{illeg}|e| so is reasonable to beleive considering ye ineptitude wch Air hath to pervade small cavities as appears by ye ascention of water in slender glasse pipes, paper, cloth & other such like substances whose pores are found too small to be replenished wth Air, & yet large enough to admit water; & by ye difficulty wherewth Air pervades ye pores of a Bladder through wch water finds ready passage. And according to ye 11th Observation the cavities this|u|s void of Air will cause the same kind of effects as to reflexion wch those doe yt are replenished wth it, but yet something more manifestly because the Medium in relation to refractions is rarest when most empty of Air as Mr Hook hath proved in his Micrographia. In wch Book he \hath/ also largely discoursed of this & precedent Proposition, & declined many other very excellent thing{illeg}|s| concerning ye colours of thin Plates & other naturall bodies wch I have not scrupled to make use of so far as they were for my purpose.
Prop: 4. The parts of bodies & their interstices must not be lesse then of some definite bignesse \thickness/ to render ym opake & coloured. For ye opakest bodies if their parts be subtily divided (as Metalls by being dissolved in acid Menstruums, &c) become perfectly transparent. And you may also remember that in ye 8th Observation there was no reflexion at ye superficies of ye Object-glasses where they were very near one another though they did not {abso}lutely touch. And in ye 17th Observation {illeg} {illeg} the water-bubble where it became thin {illeg} insensible so as to cause the apparitions {illeg} spots.
<563r>On these grounds I conceive it is that wa{illeg}|t|er, salt, glasse, stones & such like substances are transparent For upon divers considerations they seem to be as porous as ot{illeg}|h|er bodies, but yet their pores & parts too small to cause any opacity.
Prop: 5. The transparent parts of bodies according to their severall sizes must reflect rayes of one colour, & transmitt those of another, on the same grounds that thinne plates o{illeg}|r| Bubbles doe reflect or transmitt those rayes. And this I take to be ye ground of all their colours.
For If if a thin'd or plated body wch being of an eaven thicknesse appeares all over of {one} uniform colour should be broken into fragments of ye same thicknesse wth the plate, I see noe reason why a heap of those fragments should not constitute {illeg}|a| powder of ye same colour wch ye Plates exhibited before it was broken. And the parts of all naturall bodies being like soe many fragments of a Plate must on ye same grounds exhibit the same colours.
Now that they doe soe will further appear by ye affinity of their properties. A{illeg}|s| that ye infusion of Nephritic wood & many other substances reflect one colour & transmitt another like thin bodies in ye 9th & 20th Observations. That ye colours of silks, cloths, & other substances wch water or oyle can intimately penetrate become more faint & obscure by being im̄merged in those liquors, & recover their vigor again by being dryed much after the manner {illeg}|de|clared of thin bodies in ye 10th & 21 Observations. And that some of those coloured powders wch {illeg}|P|ainters use may have their colours a little changed by being {illeg}|v|er{illeg}|y| elaborately & finely ground. Where I see not what can be justly pretended for those changes besides the bre{illeg}|a|king of their parts into lesse parts by that contrition after ye same manner that ye colour of a Plate is changed by varying its thicknesse. For which reason also it is that many flowers by being bruised become more transparent then before; or at least in some degree or another change their colours. Nor is it much lesse to my purpose that by mixing divers liquors very odd & remarkable productions & changes of colours may be effe{illeg}|c|ted, of wch no cause can be more obvious & naturall than that the saline corpuscles of one liquor do variously act upon or unite wth the tinging corpuscles of another, so as to make them swell or shrink (whereby not only their bulk but their density also may be changed) or to divide them into smaller corpuscles, or make many of them associate into one cluster; For wee see how apt those saline {illeg}|M|enstruums are to penetrate & dissolve substances to wch they are applyed & some of them to precipitate what others dissolve. In like manner if wee consider the various Phæ nomena of the Atmosh|p|here, wee may observe that when vapours are first raised, they hinder not ye transparency of the Air, being divided into parts too small to cause any reflect|x|ion in their superficies. But when in order to compose drops of rain they begin to coalesce & constitute globules of all intermediate sizes, those globules when they become of a convenient size to reflect some colours & transmitt others, may constitute clouds of various cl|o|lours acording to their sizes. And I see not what can be rationally conceived in so transparent a substance as water for the production of these colours besides the various sizes of these its parcells, wch seem to affect a globular figure most; but yet \perhaps/ not wthout some instability in ye smallest of them by reason t{illeg}|h|at those are most easily agitated by heat or any trembling motio{illeg}|n|s in ye Air.
Prop: 6. Then parts of Bodies on which their colours depend are denser then ye medium wch pervades the interstices.
This will appear by considering t{illeg}|h|at ye colour {illeg} body depends not only on ye rayes wch are {illeg}pendicularly on its parts, but on those {also} {illeg}dent at all other angles. And that {illeg} 7th Observation a very little variation of obliquity will change ye reflected colour where the thinne body or small particle is rarer then ye ambient Medium, in so much that such a small particle will at diversly oblique incidences reflect all sorts of colours in so great a variety that the colour resulting from them all confusedly reflected from a heap of such particles must rather be a white or grey then any other colour, or at best it must be but a very imperfect & dirty colour. Wher|e|as if the thin Body or small particle be much denser then the ambient Medium, the colours according to the 19th Observation are so little changed by the variation of obliquity, that the rayes which are reflected least oblily, may predominate over the rest so much as to cau{illeg}|s|e a heap of such particles to appear very intensly of their colour.
It conduces also something to this Proposition that according to 22th Observation, the colours exhibited by the denser thin body wthin ye rarer are more bris then those exhibited by the rarer wthin ye denser.
Prop: 7th. The bignesse of ye component parts of naturall bodies may be conjectured by their colours.
For since ye parts of those bodies by p|P|rop: 5 doe most probably exhibit the same colours wth a plate of equall thicknesse, provided they have ye same refractive density; & since their parts seem for ye most part to have much ye same density wth water or glasse, as by many circumstances is obvious to collect: to determine ye sizes of those parts you need only have recourse to ye precedent Tables in which ye thicknesse of water or Glasse exhibiting any colour is expressed. Thus if it b{illeg}|e| desired to {illeg} ye diameter of a corpuscle which being of equall density wth glasse, shall reflect Green of ye third order; the number showes it to be about parts of an inch. The greatest difficulty is here to know of what order the colour of any body is. And for this end wee must have recourse to ye 4th & 18th Observations from whence may be collected these perticulars.
Scarlets & other Reds, Oreanges & yellowes if they be pure & intense are most probably of ye second order. Those of ye first & third order also may be pretty good, only ye Orange & Red of the third order have too great a mixture of Violet & Blew.
There may be good Greens of ye fourth order but the purest are of the third. And of this order ye G{illeg}|re|en of all Vegetables seems to be, partly by reason of ye intensnesse of their colours, & partly because when they wither some of them turn to a greenish yellow, & others to a more ꝑfect yellow or Orange or perhaps to Red, passing first through all ye aforesaid intermediate colours. which changes seem to be effected by the exhaling of the moisture wch may leave the tinging corpuscles more de{illeg}|n|se, & something augmented by ye accretion of y{illeg}|e| oyle|y| & earthy part of that moisture. Now ye Green wthout doubt is of ye same order wth those colours into wch it changeth because the changes are graduall & those colours though usually not very pure yet for ye most part are too pure & lively to be of ye fourth order.
Blewes & Purples may be either of ye second or third order. But ye best are of the third. Thus ye colour of Violets seems to be of that order, because their syrrup by acid liquors turnes red and by urinous & alcalizate turn green. For since it is of ye nature of acids to dissolve or attenuate, & of Alcalies to precipitate or incrassate, if the purple colour of ye syrrup was of ye second order, an acid liquor by attenuating its tinging corpuscles would change it to {illeg} Red of ye first order, & an Alcaly by {incrassate} them would change it to a green of ye second {illeg} red & Green, especially ye Green, seem {illeg} be ye colours produced by these {changes} {illeg} But if the said purple be supposed of the third order its change to red of ye second & green of the third may wthout any inconvenience be allowed.
If there be found any body of a deeper & lesse reddish purple then that of Violets its colour most probably, is of ye second order. But yet there being no body com̄only known whose colour is constantly more deep then theirs, I have made use of their na name to denote the deepest & least reddish Purples, such as manifestly transcend their colour in purity.
The Blew of ye first Order though very faint & little, may possibly be ye colour of some substances. And perticularly ye Azure colour of ye skys seems to be of this order. For all vapors when they begin to condense & coalesce into small parcells, become first of that bignesse whereby such an Azure must be reflected before they can constitute clouds of other colours. And so the|i|s being the first colour which vapors begin to reflect, it ought to be ye colour of ye finest & most transparent skys in wch vapors are not arrived to that grossnesse requisite to reflect other colours as we find it |is| by experience.
Whitenesse if it be intense is either that in ye first order of colours, of wch sort perhaps is ye colour of white lead; or else it is a mixture of those succeeding the third or fourth order, such as is ye colour of paper, linnen, & most white substances. If corpuscles of various sizes exhibiting the colours of ye second {illeg}|&| third order be mixed, they should rather constitute an imperfect whitenesse or Grey of wt|c|h I have already spoken. But yet it seems not impossible for them to exhibit an intense whitenesse {if} they be disposed to transmitt all ye light wch they reflect not, & do not retain & stifle much of it. For thus I told you that {illeg}|f|roth at a distance hath appeared very white & yet near at hand ye severall Bubbles of wch it was constituted were seen tinged all over wth Rin{illeg}|g|s of colours of ye four or five first orders.
<565v>Lastly for ye production of Black the corpuscles must be lesse then any of those which exhibit colours. For at all greater sizes there is too much light reflected to constitute this colour. But if they be supposed a little lesse then is requisite to reflect the blew of the fi{illeg}|r|st order they will according to the 4th , 8th, 17th, & 18th Observations reflect so very little light as to appear intensely black, & yet may perhaps variously reflect refract it to & fro wthin themselves so long \un/till it happen to be stifled & lost, B|b|y which meanes they will appear black in all positions of the eye wthout any transparency. And from hence may be understood why Fire & the more subtile dissolver Putrefaction turne substan{illeg}|c|es to black; why small quantities of black substances impart their colour very freely & intensely to other substances to wch they are applied;* why Glasse ground very elaborately wth sand together wth what is worn of from the glasse & Copper become very black; why black substances doe on a Copper plate till it be well polished makes ye sand together wth what is worne off from the Glasse, & copper become very black; why black substances do soonest of all others become hot & burne, wch effect may proceed partly from ye multitude of {illeg}|r|efractions in a little room, & partly from ye very easie com̄otion of so very small corpuscles; & why blacks are usually a little inclined to a blewish colour. For that they are so may be seen by illuminating white paper by reflextion from black substances, which will usu{illeg}|a|lly appear of a blewish white. And the reason is that black bodies on ye obscure blew of ye first order, {illeg}|as| described in ye 18th Observation, whence the corpuscles of black substances are most apt to reflect that colour.
In these descriptions I have been the more {popu}lar because I hope \its not impossible but/ that Microscopes will \may/ {illeg} be improved to the discovery of corpuscles {illeg} wch their colours depend. For if those {illeg} be so far improved as wth sufficient {illeg} represent objects five or six hundred {illeg} then at a foot distance they appear to or naked eyes I should hope that wee might be able to discover some of the greatest of those corpuscles. And by one that would magnifie three or four thousand times perhaps they might all be discovered but those which produce blacknesse. In the mean while I see nothing material that rationally can be doubted of excepting this Position, {sic}. {illeg}|T|hat transparent corpuscles of the same thicknesse & density with a Plate, do exhibit the same colour. And this I would have understood not wthout some latitude, as well because those corpuscles may be of irregular figures, & many rayes must be oblily incident, & so have a shorter way through them then ye length of their diameter, as because the straitnesse of ye Medium pent in on all sides may a little alter its motions or other qualities on wch the reflexion depends. But yet I cannot much suspect the last because I have observed of some small plates of Moscovy-Glasse wch were of an eaven thicknesse, that through a Microsp|c|ope they have appeared of ye same colour at their edges & corners where included the Medium was terminated, wch they appeared of in other places. However it {will}|would| add much to or satisfaction if those corpuscles can be discovered wth Microscopes, wch if wee shall at length \ever/ attain to I fear it {illeg}|w|ill be ye ut{illeg}|m|ost improvement of this sense. For it seems impossible to see ye more secret & noble works of Nature wthin those corpuscles by reason of their transparency.
This may suffice concerning the constitution of naturall bodies on which their colours depend. But for further understanding the nature of reflexions I s{illeg}|h|all add these t{illeg}|w|o following Propositions.
Prop: 8. The cause of r|R|eflexion is not ye impinging of light on ye solid & impervious parts of bodies, as is com̄only supposed.
This will appear by the following considera{illeg}|t|ion First that in ye passage of li{illeg}|g|ht out of glasse into Air their|re| is a reflexion as strong or stronger then in its passage out of Air into Glasse & by many degrees stronger then in its passage out of Glasse into water. And it seems not probable that Air should have more reflecting parts then water or Glasse. But if t{illeg}|h|at should possibly be supposed it will availe nothing: for the reflexion is as strong \if/ not . \perhaps/ stronger when the Air is drawn away from the Glasse, (suppose in the Air-Pump invented by Mr Boyle) as when it is adjacent to it. Secondly, if light in its passage out of Glasse into Air be incident more oblily then at an angle of 40 or 41 degrees it is wholly reflected, if lesse obliquely it is in great measure transmitted. Now it is not to be imagined that light at one degree of obliquity should |meet| wth pores enough in the Air to transmitt the greater pt of it, & at another degree of obliquity meet wth nothing but parts to reflect it wholly: especially considering that in its passage out of Air into Glasse, how oblique soever be its incidence it finds pores enough in the Glass to transmitt ye greatest part of it; If any man suppose that it is not reflected by the Air but by ye utmost superficiall parts of ye Glasse, there is still the same difficulty: besides that such a supposition is unintelligible, & will also appear to be false by applying water behind some part of ye Glasse instead of Air. For so in a convenient obliquity of ye rayes suppose of 45 or 46 degrees at wch they are all reflected where the Air is adjacent to ye Glasse, they shall be in great measure transmitted where the water is adjacent to it: wch argues that their reflexion or {trans}mission depends on ye constitution of ye Air & water. \hind the glass, & not on the parts of ye glass/ Thirdly if ye colours made by a Prism placed at ye {illeg} of a beam of light into a darkned Room {illeg} cast on a second Prism placed at a {illeg} the former, in such manner that they {illeg} incident upon it: the second Prism {illeg} to the incident rayes that those wch are of a blew colour shall be all reflected by it, & yet those of a red colour pretty copiously transmitted. Now if the reflexion be caused by the parts of Air or Glasse I would ask why at ye same obliquity of incidence the blew should wholly impinge on those parts so as to be all reflected & yet the red find pores enough to be in great measure transmitted. Fourthly where two Glasses touch one another there is no sensible reflexion as was declared in the 1st Observation; & yet I see no reason why the rayes should not impinge on the parts of Glasse when contiguous to one another Glasse as much as when contiguous to Air. Firstly when the top of a water-Bubble (in ye 17th Observation) by the continuall subsiding & exhaling of the water grew very thin there was such a little & almost insensible quantity of light reflected from it that it appeared intensly black, wheras round about that black spot where the water was thicker the reflexion was soe strong as to make ye water seem very white. Nor is it onely at the least thicknesse of thin Plates or Bubbles that there is no manifest refl{illeg}|exi|on but at many other thicknesses continually greater & greater. For in ye 15th Observation the rayes of ye same colour were by turnes transmitted at one thicknesse & reflected at another thicknesse for {illeg}|a|n indeterminate number of successions. And yet in ye suꝑficies of the thin'd body where it is of any one thicknesse there are as many parts for the rayes to impinge on, as where it is of any other thicknesse. Lastly if reflexion were caused by the parts of reflecting bodies it would be impossible for thin Plates or Bubbles at ye same place to reflect the rayes of one colour & transmitt those of another as they do according to the 13 & 15 Observations. For it is not to be īmagined that at one place the rayes which for instance exhibit a blew colour should have the fortune to dash upon the parts & those wch e{illeg}|x|hibit a Red to let upon the Pores of the body; & then at another place {soe} the Body is either a little thicker, or a little thinner {illeg} that on ye contrary the Blew should hit upon its pores & the Red upon its parts.
Prop: 9. 'Tis most probable yt ye rayes wch impinge on ye solid parts of any body, are not reflected but shifted & lost in that body.
This is consentane{illeg}|ou|s to ye Precedent Proposition & will further appear by considering that if all the rayes should be reflected which impinge on ye internall parts of clear water or Chrystall, those substances should rather have a cloudy then so very clear transparency. And further there would be no Principle of the ob obscurity or blacknesse wch some bodies have in all positions of ye eye. For to produce this effect it is necessary that many rayes be retained & lost in ye body & it seems not probable that any rayes can be stopt & retained in it wch do \not/ impinge on its parts.
If you now ask how rayes are reflected wthout impinging on ye parts of a body, & how those wch impinge on its parts may be stopped & shifted, it requires an Hypothesis to explain it by, the description of wch is besides my design. And so ye manner how severall rayes are unequally refrangible & reflec|x|tible & originally indued wth severall colours remains to be explained Hypothetically. But I shall content my selfe in having shown that de facto the rayes rayes of light are ind{illeg}|ue|d wth those properties.
[1] *Note that there is some little light reflected from ye \those/ parts of this black spot where ye glasses by reason of their convexity & some little uneavenness of their surfaces do not come to absolute contact. For by viewing ye sun by reflexion from this spot, not only ye verges of it became lucid, but divers lucid veins & specks appeared into ye midst of ye thickness. But {yet} some parts of ye spot seemed still {as} black as before {illeg} I {take} {illeg}.
