'De motu corporum in gyrum'

<55r>

De motu corporum in gyrum.

Def. 1. Vim centripetam appello qua corpus impellitur vel attrahitur versus aliquod punctum quod ut centrum spectatur.

Def 2 Et vim corporis seu corpori insitam qua id conatur perseverare in motu suo secundum lineam rectam.

Hypoth 1 Corpora nec medio impediri nec alijs causis externis qua{illeg} minus viribus {insitæ} et centripetæ exquisitæ {cedant} |Resistentiam esse ut corporis celeritas et medij densitas conjunctim in proximis novem propositionibus nullam esse, in sequentibus esse ut corporis celeritas et medij densitas conjunctim.|

Hypoth 2. Corpus omne sola vi insita uniformiter secundum rectam lineam in infinitum progredi nisi aliquid extrinsecus impeda|i|at.

/Hypoth. 1. Resistentiam in proximis novem propositionibus nullam esse in sequentibus esse ut corporis celeritas et medij densitas conjunctim.\

|Def 3 Et resistentiam quæ est medij \regulariter/ impedientis.|

|Hyp. 3. Corpus minibus in dato tempore viribus conjunctis eo ferri quo viribus divisis in temporibus æqualibus successivè. Hyp 4|

Theorema 1. Gyrantia omnia radijs ad centrum ductis areas temporibus proportionales describere.

Dividatur tempus in partes æquales, et 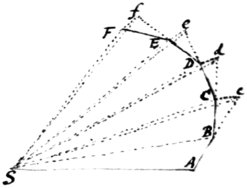prima temporis parte describat corpus vi insita rectam AB. Idem secunda temporis parte si nil impediret^a[1] rectà pergeret ad {C} c describens lineam Bc æqualem ipsi AB adeo ut radijs AS, BS, cS ad centrum actis confectæ forent æquales areæ ASB, BSc. Verum ubi corpus venit ad B agat vis centripeta impulsu unico sed magno, faciat corpus {illeg} a recta Bc deflectere et pergere in recta BC. Ipsi BS parallela agatur cC occurrens BC in C et completa secunda temporis parte ^b[2] corpus reperietur in C. Iunge SC et triangulum SBC ob parallelas SB, Cc æquale erit triangulo SBc atqu adeo etiam triangulo SC|A|B. Simili argumento si vis centripeta successivè agat in C, D, E &c, faciens corpus singulis temporis momentis singulas describere rectas CD, DE, EF &c triangulum SBCD triangulo SBC et SDE ipsi SCD et SEF ipsi SDE æquale erit. Æqualibus igitur te{illeg}\mp/oribus æquales areæ describuntur. Sunto jam hæc triangula numero infinita et infinitè parva, sic, ut singulis temporis momentis singula respondeant triangula, agente vi centripeta sine intermissione, & constabit proposit{illeg}|io|.

Theorem. 2. Corporibus in circumferentijs circulorum uniformiter gyrantibus vires centripetas esse ut \celeritatum sive/ arcuum simul descriptorum quadrata applicata ad radios circulorum.

Corpora B, b in circumferentijs 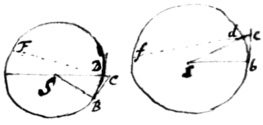circulorum BD, bd gyrantia simul describant arcus BD, bd. Sola vi insita describerent tangentes BC, bc his arcubus æquales. Vires centripetæ sunt quæ perpetuò retrahunt corpora de tangentibus ad circumferentias, atq adeo hæ sunt ad invicem ut spatia ipsis superata CD, cd, id est productis CD, cd ad F et f ut $\frac{{\mathrm{BC}}^{\mathrm{quad}}}{\mathrm{CF}}$ ad $\frac{{\mathrm{bc}}^{\mathrm{quad}}}{\mathrm{cf}}$ sive ut $\frac{{\mathrm{BD}}^{\mathrm{quad.}}}{\frac{1}{2}\mathrm{CF}}$ ad $\frac{{\mathrm{bd}}^{\mathrm{quad.}}}{\frac{1}{2}\mathrm{cf}}$. Loquor de spatijs BD, bd minutissimi{s} inq infinitum diminuendis sic ut pro $\frac{1}{2}\mathrm{CF}$, $\frac{1}{2}\mathrm{cf}$ scribere liceat {AB,Cd} \circulorum radios/ SB, sb. Quo facto constat Propositio.

<56r>

Cor 1. Hinc vires centripetæ sunt ut celeritatum quadrata applicata ad radios circulorum

Cor 2 Et reciprocè ut quadrata temporum periodicorum applicata ad radios.

Cor 3 Vnde si quadrata temporum periodicorum sunt ut radij circulorum vires centripetæ sunt æquales. Et vice versa

Cor 4 Si quadrata temporum \periodicorum/ sunt ut quadrata radiorum vires centripetæ sunt reciprocè ut radij. Et vice versa

Cor 5 Si quadrata temporum \periodicorum/ sunt ut cubi radiorum vires centripetæ sunt reciprocè ut quadrata radiorum. Et sic deinceps vice versa.

Schol. Casus Corollarij quinti obtinet in corporibus cœlestibus. Quadrata temporum periodicorum sunt ut cubi distantiarum a communi centro circum quod volvuntur. Id obtinere in Planetis majoribus circa Solem gyrantibus in minoribus circa Iovem et Saturnum jam statuunt Astronomi. V{illeg}

Theor. 3. Si corpus P circa centrum S gyrando, describat lineam quamvis curvam APQ, et si tangat recta 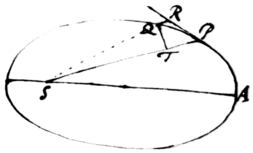PR curvam illam in puncto quovis P et ad tangentem ab alio quovis curvæ puncto Q agatur QR distantiæ SP parallela ac demittatur QT perpendicularis ad distantiam SP: dico quod punctis vis centripeta sit reciprocè ut solidum $\frac{{\mathrm{SP}}^{\mathrm{quad.}}\times {\mathrm{QT}}^{\mathrm{quad.}}}{\mathrm{QR}}$, si modò solidi illius ea semper sumatur quantitas quæ ultimò fit ubi coeunt puncta P et Q.

Namq in figura indefinitè parva QRPT lineola QR dato tempore est ut vis centripeta et data vi ut^a[3] quadratum temporis atq adeo neutro dato ut quadratum t vis centripeta et quadratum temporis conjunctim, id est ut vis centripeta semel et area SQP tempori proportiol|n|alis (seu \vel/ duplum ejus $\mathrm{SP}\times \mathrm{QT}$) bis. Applicetur hujus proportionalitatis pars utraq ad lineolam QR et fiet unitas ut vis centripeta et $\frac{{\mathrm{SP}}^{\mathrm{q}}\times {\mathrm{QT}}^{\mathrm{q}}}{\mathrm{QR}}$ conjunctim, hoc est vis centripeta ut reciprocè ut $\frac{{\mathrm{SP}}^{\mathrm{q}}\times {\mathrm{QT}}^{\mathrm{q}}}{\mathrm{QR}}$. Q. E. D.

Corol. Hinc si detur figura quævis et in ea punctum ad quod vis centripeta dirigitur, inveniri potest lex vis centripetæ quæ corpus in figuræ illius perimetro gyrare faciat. Nimirum computandum est solidum $\frac{{\mathrm{SP}}^{\mathrm{q}}\times {\mathrm{QT}}^{\mathrm{q}}}{\mathrm{QR}}$ huic vi reciprocè proportionale. Ejus rei dabimus exempla in problematis sequentibus.

Prob. 1. Gyrat corpus in circumferentia circuli requiritur lex gravitatis \vis centripetæ/ tendentis ad punctū aliquod in circumferentia.

Esto circuli circumferentia SQPA, centrum gravitatis \vis centripetæ/ S, corpus in circumferentia latum P, locus proximus in quem movebitur Q. Ad SA \diametrum/ et SP demitte perpendicula PK QT et per Q ipsi SP agatur parallelam aga|e|tur LR occurrentem circulo in L et tangenti PR in R, \et coeant TQ, PR in Z. Ob similitudinem triangulorum ZQR, ZTP, SPA/. Erit RP^q (hoc est QRL) ad QT^q ut SA^q. Ergo $\frac{\mathrm{QRL}\times {\mathrm{SP}}^{\mathrm{q}}}{{\mathrm{SA}}^{\mathrm{q}}}={\mathrm{QT}}^{\mathrm{q}}$. Ducantur hæc æqualia in $\frac{{\mathrm{SP}}^{\mathrm{q}}}{\mathrm{QR}}$ et punctis P et Q coeuntibus scribatur SP pro RL. Sic fiet $\frac{{\mathrm{SP}}^{\mathrm{qc}}}{{\mathrm{SA}}^{\mathrm{q}}}=\frac{{\mathrm{QT}}^{\mathrm{q}}\times {\mathrm{SP}}^{\mathrm{q}}}{\mathrm{QR}}$. Ergo gravitas \vis centripeta/ reciproce est ut $\frac{{\mathrm{SP}}^{\mathrm{qc}}}{{\mathrm{SA}}^{\mathrm{q}}}$, id est (ob datum SA^q) ut quadraton cubus distantiæ SP. Quod erat inveniendum.

Schol. Cæterum in hoc {casu} et similibus concipiendum est quod <57r> postquam corpus pervenit ad centrum S, id non amplius redibit in orbem sed abibit in tangente. In spirali quæ secat radios omnes in dato angulo vis centripeta tendens ad Spiralis principium est in ratione triplicata distantiæ reciprocè, sed in principio illo recta nulla positione determinata spiralem tangit.

Prob 2. Gyrat corpus in Ellipsi veterum: requisitur lex gravitati vis centripetæ tendentis ad centrum Ellipseos.

Sunto CA, CB semi–axes Ellipseos, GP, DK 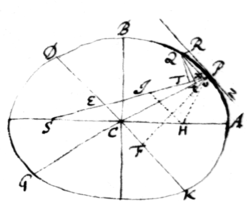diametri conjugatæ, PF, Qt perpendicula ad diametros QV ordinatim applicata ad diametrum GP et QVPR parallelogrammum. ^[4] His constructis erit \(ex Conicis)/ PVG ad QV^q ut PC^q ad CD^q et QV^q ad QT|t|^q ut PC^q ad PF^q et conjunctis rationibus PVG ad QT|t|^q ut PC^q ad CD^q et PC^q ad PF^q, id est VG ad $\frac{{\mathrm{Qt}}^{\mathrm{q}}}{\mathrm{PV}}$ ut PC^q ad $\frac{{\mathrm{CD}}^{\mathrm{q}}\times {\mathrm{PF}}^{\mathrm{q}}}{{\mathrm{PC}}^{\mathrm{q}}}$. Scribe QR pro PV ^a[5]et $\mathrm{BC}\times \mathrm{CA}$ pro $\mathrm{CD}\times \mathrm{PF}$, nec non (punctis P et Q coeuntibus) 2PC pro VG et ductis extremis et medijs in se mutuò, fiet $\frac{{\mathrm{Qt}}^{\mathrm{q}}\times {\mathrm{PC}}^{\mathrm{q}}}{\mathrm{QR}}=\frac{{\mathrm{2BC}}^{\mathrm{q}}\times {\mathrm{CA}}^{\mathrm{q}}}{\mathrm{PC}}$. Est ergo vis centripeta reciprocè ut $\frac{{\mathrm{2BC}}^{\mathrm{q}}\times {\mathrm{CA}}^{\mathrm{q}}}{\mathrm{PC}}$ id est (ob datum ${\mathrm{2BC}}^{\mathrm{q}}\times {\mathrm{CA}}^{\mathrm{q}}$) ut $\frac{1}{\mathrm{PC}}$, hoc est directè, ut distantia PC {illeg} Q. E. I.

Prob. 3. Gyrat corpus in ellipsi: requiritur lex gravitatis \vis centripetæ/ tendentis ad umbilicum Ellipseos.

Esto Ellipseos superioris umbilicus S. Agatur SP secans Ellipseos diametrum DK in E. Patet EP æqualem esse semi–axi majori AC eò, quod actâ ab altero Ellipseos umbilico H linea HI ipsi EC parallela, ob æquales CS, CH æquentur ES, EI, adeo ut EP semisumma sit ipsarum PS, PI id est \(ob parallelas HI, PR & æquales angulos æquales IPR, HPZ)/ ipsarum PS, PH quæ conjunctim axem totum 2AC adæquant. A{illeg}|d| SP demittatur perpendicularis QT. Et Ellipseos latere recto principali (seu $\frac{{\mathrm{2BC}}^{\mathrm{q}}}{\mathrm{AC}}$) dicto L, erit $\mathrm{L}\times \mathrm{QR}$ ad $\mathrm{L}\times \mathrm{PV}$ ut QR ad PV id est ut PE (seu AC) ad PC. et $\mathrm{L}\times \mathrm{PV}$ ad GVP ut L ad GV et GVP ad QV^q ut CP^q ad CD^q et QV^q ad QX^q puta ut M ad N et QX^q ad QT^q ut EP^q ad PF^q id est ut CA^q ad PF^q sive ^a[6] ut CD^q ad CB^q. et conjunctis his omnibus rationibus, $\mathrm{L}\times \mathrm{QR}$ ad QT^q ut AC ad $\mathrm{PC}+\mathrm{L}$ ad $\mathrm{GV}+{\mathrm{CP}}^{\mathrm{q}}$ ad ${\mathrm{CD}}^{\mathrm{q}}+\mathrm{M}$ ad $\mathrm{N}+{\mathrm{CD}}^{\mathrm{q}}$ ad CB^q, id est ut $\mathrm{AC}\times \mathrm{L}$ (seu ${\mathrm{2BC}}^{\mathrm{q}}$) ad $\mathrm{PC}\times \mathrm{GV}+{\mathrm{CP}}^{\mathrm{q}}$ ad ${\mathrm{CB}}^{\mathrm{q}}$ $+\mathrm{M}$ ad N, sive ut 2PC ad $\mathrm{GV}+\mathrm{M}$ ad N. Sed punctis Q et P coeuntibus rationes 2PC ad GV et M ad N fiunt æqualitatis: Ergo et ex his composita ratio $\mathrm{L}\times \mathrm{QR}$ ad QT^q. Ducatur pars utra in $\frac{{\mathrm{SP}}^{\mathrm{q}}}{\mathrm{QR}}$ et fiet $\mathrm{L}\times {\mathrm{SP}}^{\mathrm{q}}=\frac{{\mathrm{SP}}^{\mathrm{q}}\times {\mathrm{QT}}^{\mathrm{q}}}{\mathrm{QR}}$. Ergo gravitas \vis centripeta/ reciprocè est ut $\mathrm{L}\times {\mathrm{SP}}^{\mathrm{q}}$ id est in ratione duplicata distantiæ SP. Q. E. I.

Cor Punctis P et Q coeu

Schol. Gyrant ergo Planetæ majores in ellipsibus habentibus umbilicum in centro solis, et radijs ad Solem ductis describunt areas temporibus proportionales, omninò ut supposuit Keplerus. Et harum Ellipseon latera recta sunt $\frac{{\mathrm{QT}}^{\mathrm{q}}}{\mathrm{QR}}$, existentibus figuris QTPR punctis P et Q spatio quàm minimo et quasi infinitè parvo distantibus.

<58r>

Theorem. 4 Posito quod vis centripeta sit reciprocè proportionalis quadrato distantiæ a centro, quadrata temporum periodicorum in Ellipsibus sunt ut cubi transversorum axium.

Sunto Ellipseos umbilici S, H centrum C, 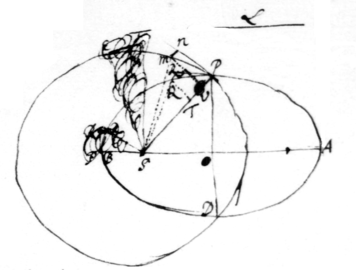axis transversus {illeg}AB, tangens ad verticem PR axis alter R|P|D latus rectum L, umbilicus alteruter S. Centro S radio intervallo SP describatur circulus PMD. Et eodem tempore describant corpora duo gyrantia arcum \Ellipticum/ PQ et \circulorem/ PM, vi centripeta ad umbilicum S tendente. Ipsis P Ellipsis et circulum tangant PR, PN in puncto P. Ipsi PS agantur parallelæ QR, MN tangentibus occurrentes in R et N. Sint autem figuræ PQR, TV{illeg} \PMN/ indefinitè parvæ sic ut (per schol. Theorem Prob. 3) fiat $\mathrm{L}\times \mathrm{QR}={\mathrm{QT}}^{\mathrm{q}}$ et $\mathrm{2SP}\times \mathrm{MN}={\mathrm{MV}}^{\mathrm{q}}$. Ob communem a centro S distantiam SP et inde æquales vires centripetas sunt MN et QR æquales. Ergo QT^q ad MV^q est ut L ad 2{illeg}SP, et QT ad MV ut medium proportionale inter L et 2SP seu PD ad 2SP. Hoc est area SPQ ad aream SPM ut area tota Ellipseos ad aream totam circuli. Sed partes arearum singulis momentis genitæ sunt ut areæ SPQ et SPM at adeo ut areæ totæ et proinde per numerum momentorum multiplicatæ simul evadent totis æquales. Revolutiones igitur eodem tempore in ellipsibus perficiuntur ac in circulis quorum diametri sunt axibus transversis Ellipseon æquales. Sed (per Prop \Cor. 5/ Theor 2) quadrata temporum periodicorum in circulis sunt ut cubi diametrorum. Ergo et in Ellipsibus. Q. E. D.

Schol. Hinc in Systemate cœlesti ex temporibus periodicis Planetarum innotescunt proportiones transversorum axium Orbitarum. Axem unum licebit assumere. Inde dabuntur cæteri. Datis autem axibus determinabuntur Orbitæ in hunc modum. Sit S locus Solis seu Ellipseos umbilicus 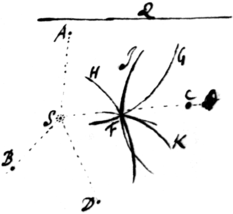unus A, B, C, D loca Planetæ observatione inventa et Q axis transversus Ellipseos. Centro A radio $\mathrm{Q}—\mathrm{AS}$ describatur circulus FG et erit ellipseos umbilicus alter in in {sic} hujus circumferentia. Centris B, C, D, &c intervallis $\mathrm{Q}—\mathrm{BS}$, $\mathrm{Q}—\mathrm{CS}$, $\mathrm{Q}—\mathrm{DS}$ &c describantur itidem alij quotcun circuli & erit umbilicus ille alter in omnium circumferentijs at adeo in omniū intersectione communi F. Si intersectiones omnes non coincidunt, sumendum erit punctum medium pro umbilico. Praxis hujus commoditas est quod ad unam conclusionem eliciendam adhiberi possint et inter se \expeditè/ comparari observationes quamplurimæ. Planetæ autem loca singula A, B, C, D &c ex binis observationibus, cognito Telluris orbe magno invenire docuit Halleus. Si orbis illa magnus nondum satis exactè determinatus habetur, ex eo propè cognito, determinabitur orbita Planetæ alicujus puta Mart{e}|i|s propius. Deinde ex orbita Martis <59r> Planetæ per eandem methodum determinabitur orbita telluris adhuc propius: Tum ex orbita Telluris determinabitur orbita Planetæ multò exactiùs quam priùs: Et sic per vices donec circulorum intersectiones in f umbilico orbitæ utrius exactè satis conveniant.

Hac methodo determinare licet orbitas Telluris, Martis, Iovis et Saturni, Orbitas autem Veneris et Mercurij sic. Observationibus in maxima Planetarum a Sole digressione factis, habentur Orbitarum tangentes. Ad ejusmodis tangentem KL demittatur a Sole perpendiculum SL centro L et intervallo dim{ij}|i|dij axis Ellipseos describatur circulus KM. Erit centrum Ellipseos in hujus circumferentia, adeo descriptis hujusmodi pluribus circulis reperietur in omnium intersectione. T{illeg}m, {sic} c|C|ognitis \tandem/ orbitarum dimensionibus, longitudines horum Planetarum \postmodum/ exactiùs ex transitu \suo/ per discum Solis determinabuntur.

Prob 4 Posito quod vis centripeta sit reciprocè proportionalis quadrato distantiæ a centro, et cognita vis illius quantitate; requisitur Ellipsis quam corpus describet de loco dato cum data celeritate secundum datam rectam emissum.

Vis centripeta tendens ad punctum S ea sit quæ corpus ω in circulo πχ centro S intervallo quovis \Sω/ descripto gyrare faciat. De loco P secundum lineam PR 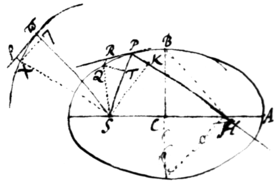emittatur corpus P ea celeritate quæ sit ad celeritatem uniformen corporis ω ut recta quævis PR ad rectam quamvis ωρ et mox inde cogente vi centripeta deflectat in Ellipsin PQ. Hanc igitur recta PR tanget in P. Tangat itidem recta πρ circulum in ω sit {illeg} PR ad ωρ ut prima celeritas corporis emissi P ad uniformem celeritatem corporis ω. Ipsis SP et Sω parallelæ agantur RQ et ρχ hæc circulo in χ illa Ellipsi in Q occurrens, et a Q et χ ad SP et ρω demittantur perpendicula QT et χτ. Est RQ ad ρχ ut vis centripeta in P ad vim centripetam in ω id est ut Sω^quad. ad SP^quad., adeo datur illa ratio. Datur etiam ratio QT ad RP et ratio RP ad ρω seu χτ et inde composita ratio QT ad χτ. De \hac/ ratione {illeg} duplicata auferatúr {sic} ratio data QR ad χρ et dabitur ratio manebit data ratio $\frac{{\mathrm{QT}}^{\mathrm{q}}}{\mathrm{QR}}$ ad $\frac{{\mathrm{\chi \tau }}^{\mathrm{q}}}{\mathrm{\chi \rho }}$, id est (per Schol. Prob. 3) ratio lateris recti \{El}/ ad latus transversum Ellipseos ad diametrum circuli. Datur {adeo} d|D|atur \igitur/ r|l|atus rectum Ellipseos. Sit istud L. Datur præterea Ellipseos umbilicus S. Anguli RPS complementū ad duos rectos fiat angulus RPH et dabitur positione linea PH in qua umbilicus alter H locatur. Demisso ad PH perpendiculo SK \et erecto semiaxe minore BC/ est ${\mathrm{SP}}^{\mathrm{q}}—2\mathrm{KPH}+{\mathrm{PH}}^{\mathrm{q}}={\mathrm{SH}}^{\mathrm{q}}=4{\mathrm{BH}}^{\mathrm{q}}-4{\mathrm{BC}}^{\mathrm{q}}={\overline{\mathrm{SP}+\mathrm{PH}}}^{\mathrm{quad.}}-\mathrm{L}\times \overline{\mathrm{SP}+\mathrm{PH}}={\mathrm{SP}}^{\mathrm{q}}+2\mathrm{SPH}+{\mathrm{PH}}^{\mathrm{q}}-\mathrm{L}\times \overline{\mathrm{SP}+\mathrm{PH}}$. Addantur utrobi $2\mathrm{KPH}+\mathrm{L}\times \mathrm{SP}+\mathrm{PH}-{\mathrm{SP}}^{\mathrm{q}}-{\mathrm{PH}}^{\mathrm{q}}$ et fiet $\mathrm{L}\times \overline{\mathrm{SP}+\mathrm{PH}}=2\mathrm{SPH}+2\mathrm{KPH}$, seu $\mathrm{SP}+\mathrm{PH}$ ad PH <60r> ut $2\mathrm{SP}+2\mathrm{KP}$ ad L. Vnde datur ub|m|bilicus alter H. Datis autem umbilicis una cum axe transverso $\mathrm{SP}+\mathrm{PH}$, datur Ellipsis. Q. {illeg} E.I.

Hæc ita se habent ubi figura Ellipsis est. Fieri enim potest ut corpus moveat in Parabola vel Hyperbola. Nimirum si tanta est corporis celeritas ut sit L latus rectum L æquale $2\mathrm{SP}+2\mathrm{KP}$, Figura erit Parabola umbilicum habens in puncto S et diametros omnes parallelas lineæ PH. Sin corpus majori adhuc celeritate emittitur movebi{illeg}|t|ur id in Hyperbola habente umbilicum unum in puncto S alterum in puncto H sumpto ad contrarias partes puncti P et axem transversum æqualem differentiæ {inter} linea{m}|r|ū PS et P{illeg}H.

Schol. Iam verò beneficio hujus Problematis soluti, Pla\Co/n|m|etarum orbitas definire concessum est, et inde revolutionum tempora, et ex orbitarum magnitudine, excentricitate, Aphelijs, inclinationibus ad planum Eclipticæ et nodis inter se collatis cognoscere an idem Cometa ad nos sæpius redeat. Nimirum ex quator observationibus locorum Cometæ, juxta Hypothesin quod Cometa movetur uniformiter in linea recta, determinanda est ejus via rectilinea. Sit ea APBD, sint A, P, B, D loca cometæ \in via illa/ temporibus observationum, et S locus solis. Ea celeritate qua Cometa uniformiter percurrit 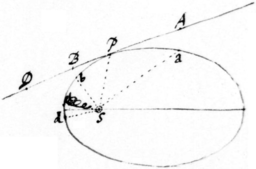rectam AD finge ipsum emitti de locorum suorum aliquo P et vi centripeta mox correptum deflectere in Ellipsi a recto tramite in Ellipsin et abire in Ellipsi Pbda. Hæc Ellipsis determinanda est ut in superiore Problemate. In ea sunto a, P, b, d loca c|C|ometæ temporibus observationum. Cognoscantur horum locorum \e terræ/ longitudines et latitudines. Quanto majores vel minores sunt his longitudines et latitudines observatæ tantò majores vel minores observatis sumantur longitudines et latitudines novæ. Ex his novis inveniatur denuò via rectilinea cometæ et inde via Elliptica ut priùs. Et loca quatuor nova in via Elliptica prioribus erroribus aucta vel diminuta jam congruent cum observationibus exactè satis. Aut si fortè errores etiamnum sensibiles manserint potest opus totum repeti. Et nè computa Astronomos molestè habeant suffecerit hæc omnia per praxin Geometricam \descriptionem linearum/ determinare.

Sed areas aSP, PSb, bSd temporibus proportionales assignare difficile est. Super Ellipseos 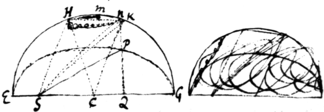axe majore EG describatur semicirculus EHG. Sumatur angulus ECH tempori proportionalis. Agatur SH ei parallela CK circulo occurrens in K. Iungatur HK et circuli segmento <61r> HKM (per tabulam segmentorum vel secus) æquale fiat triangulum SKN. Ad EG demitte perpendiculum NQ, et in eo cape PQ ad NQ ut Ellipseos axis minor ad axem majorem et erit punctum P in Ellipsi at acta recta SP abscindetur area Ellipseos EPS tempori proportionalis. Nam area HSNM triangulo SNK aucta et huic æquali segmento HKM diminuta fit triangulo HSK id est triangulo HSC æquale. Hæc æqualia adde areæ ESH, fient areæ æquales EHNS et EHC. Cùm igitur Sector EHC tempori proportionalis sit et area EPS areæ EHNS, erit etiam area EP tempori proportionalis.

Prob. 5. Posito quod gravitas \vis centripeta/ sit reciprocè proportionalis dis quadrato distantiæ a centro \terræ/, spatia definire quæ gravia \corpus recta/ cadendo datis temporibus describunt|it|.

Si grave \corpus/ non cadit perpendiculariter describet id Ellipsin puta APB cujus umbilicus inferior puta S congruet cum centro terræ. Id ex jam demonstratis constat. Super 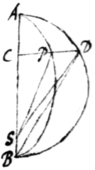ellipseos axe majore AB describatur semicirculus ADB et per grave \corpus/ decidens cadet transeat \recta DPC/ perpendicularis ad axem, actis DS, PS, erit area ASD areæ ASP at adeò etiam tempori proportionalis. Manente axe AB minuatur perpetuò latitudo Ellipseos, et semper manebit area AS{P}|D| tempori proportionalis. Minuatur axes \latitudo/ illa in infinitum et Orbita APB jam coincidente cum axe AB et umbilico S cum axis termino B descendet grave \corpus/ in recta AC et area ABD evadet tempori proportionalis. Definietur ita spatium AC quod grave \corpus/ de loco A perpendiculariter cadendo tempore dato describit si modò tempori proportionalis capiatur area ABD et a puncto D ad rectam AB demittatur perpendicularis DC. Q. E. F.

Schol. Pr{o}|i|ore Problemate definiuntur motus \gravium/ projectilium, \in aere nostro/ hacce motus gravium perpendiculariter cadentium posites \ex Hypothesi/ quod gravitas reciprocè porportionalis sit quadrato distantiæ a centro terræ quod medium \aeris/ nihil resistat. Sequentibus consideratur resistentia medij similaris et gravitas uniformis consideratur. Nam \primùm abs gravitate dein cum gravitate/ \Nam gravitas est species una/ vis centripetæ|.| species una est gravitas.

Prob. 6 Corporis sola vi insita per medium similare \resistens/ delati motum definire.

Asymptotis rectangulis ADC, CH describatur 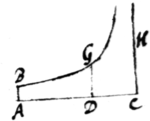Hyperbola {illeg} secans perpendicula AB, DG in B, G. Exponatur tum corporis celeritas tum resistentia medij ipso motus initio per lineam {datam} quamvis datam AC elapso tempore aliquo per lineam DC et tempus exponi potest per aream ABGD at spatium eo tempore descriptum per: {sic} lineam AD. Nam celeritati proportionalis est resistentia medij et resistentiæ proportionale est decrementum celeritatis, hoc est, si tempus in partes æquales dividatur, celeritates ipsarum initijs sunt differentijs suis proportionales. Decrescit ergo celeritas in ^a[7] proportione Geometrica dum tempus crescit in Arithmetica. Sed tale est decrementum lineæ DC et incrementum areæ ABGD, ut notum est. Ergo tempus per aream et celeritas per lineam illam rectè exponitur. Q. E. D. Porrò celeritati at adeo decremento celeritatis proportionale est incrementum spatij descripti sed et decremento lineæ DC proportionale est incrementum lineæ AD. Ergo incrementum spatij per incrementum lineæ AD, at adeo spatium ipsum per <62r> lineam illam rectè exponitur. Q. E. D.

Prob 7. Posita uniformi vi centripeta, motum corporis in medio similari rectà ascendentis ac descendentis exponere \definire/.

Corpore ascendente exponatur vis centripeta 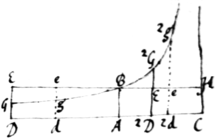per datum quodvis rectangulum BC et resistentia medij initio {illeg} ascensus per rectangulum BD sumptum ad contrarias partes. Asymptotis rectangulis AC, CH, secans per punctum B describatur Hyperbola secans perpendicula DE, de in G, g et corpus ascendendo tempore DGgd describet spatium EGge, tempore DGBA spatium ascensus totius EGB, tempore AB²G²D spatium descensus BE²G at tempore 2D²G²g²d spatium descensus 2GEe²g: Et celeritas corporis resistentiæ medij proportionalis, erit in horum temporum periodis B\A/DE B\A/de, nihil B\A/²DE B\A/²de, at maxima celeritas quàm corpus descendendo potest acquirere erit BC. \B/ ABED, ABed, nulla, ABE²D, ABe²d; at maxima celeritas quam corpus descendendo potest acquirere erit BC.

Resolvatur enim parallelogrammum \rectangulum/ AH 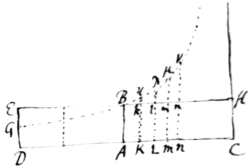in rectangula innum \innumera/ Ak, Kl, Lm, Mn &c quæ sint ut incrementa celeritatum æqualibus totidem temporibus facta et erunt Ak, Al, Am, An &c ut celeritates totæ at adeo ^a[8] ut resistentiæ medij in fine singulorum temporum æqualium. Fiat AC ad {illeg} AK, vel ABHC ad ABkK ut vis centripeta ad resistentiam in fine temporis primi et erunt ABHC, KkHC, LlHC, NnHC &c ut vires absolutæ quibus corpus urgetur at adeo ut incrementa celeritatum, id est ut rectangula Ak, Kl, Lm, Mn &c & ^b[9]proinde in progressione geometrica. Quare si {illeg} rectæ Kk, Ll, Mm, Nn productæ occurrant Hyperbolæ in κ, λ, μ, ν |&c| erunt areæ ABκK,KκλL, LλμM, MμνN &c æquales, adeo tum temporibus æqualibus tum viribus centripetis \semper/ æqualibus analogæ. Subducantur rectangula Ak, Kl, L{illeg}m, Mn &c viribus absolutis {illeg} analoga et relinquentur areæ Bkκ, kκλl, lλμm, mμνn &c resistentijs medij in fine singulorum temporum, hoc est celeritatibus at adeo descriptis spatijs analogæ. Sumantur analogarum summæ et erunt areæ Bkκ, Blλ, Bmμ, Bnν &c spatijs totis descriptis analogæ, nec non areæ ABκK, ABλL, ABμM, ABνN &c temporibus. Q. E. D. Corpus igitur inter descendendum tempore quovis ABλL describit spatium Blλ et tempore Lλμ {sic}M|N| spatium λlνN λlnν Q. E. D. Et similis est demonstratio motus expositi in ascensu. Q. E. D.

Schol. Beneficio duorum novissimorum problematum innotescunt motus projectilium in aëre nostro, ex hypothesi quod aer iste similaris sit quod gravitas uniformiter & secundum lineas parallelas agat. Nam si motus omnis obliquus corporis projecti distinguatur in duos, unum ascensus vel descensus alterum progressus horizontalis: motus posterior determinabitur per Problema sextum, prior per septimum ut fit in hoc diagrammate.

Ex loco quovis D ejaculetur corpus secundum lineam quamvis rectam DP, sit \& per/ longitudinem DP exponatur celeritas {per} corporis \ejusdem/ celeritas sub initio motus. A puncto P ad lineam horizontalem DC <62*r> demittatur perpendiculum PC|,|. {sic} Ad \ut et {ad}/ DP erigatur 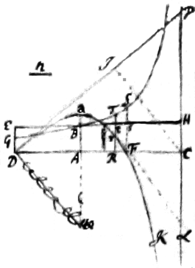perpendiculum {illeg} \Cg, ad/ quod sit {illeg} DA ut est resistentia medij ipso motus initio ad vim gravitatis. Erigatur perpendiculum AB cujusvis longitudinis et completis parallelogrammis DABE, CABH, per punctum B asymptotis DC CP describatur Hyperbola secans DE in G. Capiatur {illeg} linea N ad EG ut est DC ad CP et ad rectæ DC punctum quodvis R erecto perpendiculo RtT quod occurrat Hyperbolæ in T et rectæ EH in t, in eo cape $\mathrm{Rr}=\frac{\mathrm{DRtE}-\mathrm{DRTBG}}{\mathrm{N}}$ et projectile tempore DRTBG perveniet ad punctum r, describens curvam lineam DarFK quam punctum r semper tangit, perveniens autem ad maximam altitudinem a in {illeg} in perpendiculo AB, deinde incidens in lineam horizontalem DC ad F ubi areæ DFsE, DFSBG æquantur et postea semper appropinquans Asymptoton P{illeg}CL. Est celeritas \ejus/ in puncto quovis r ut curvæ tangens rL.

Si proportio resistentiæ aeris ad vim gravitatis nondum innotescit: cognoscantur (ex observatione aliqua) anguli ADP, AFr in quibus curva DarFK secat lineam horizontalem DC. Super DF constituatur rectangulum DFsE altitudinis cujusvis, ac describatur Hyperbola rectangula ea lege ut ejus una Asymptotos sit DF, ut areæ DFsE, DFSBG æquentur et ut sS sit ad EG sicut tangens anguli AFr ad tangentem anguli ADP. Ab hujus Hyperbolæ centro C ad rectam DP demitte perpendiculum cI ut et a puncto B ubi ea secat rectam Es, ad rectam DC perpendiculum BA, et habebitur proportio quæsita DA ad CI, quæ est resistentiæ medij ipso motus initio ad {illeg}in gravitatem projectilis. \Quæ omnia ex prædemonstratis facilè eruuntur/. Sunt et alij modi inveniendi resistentiam aeris quos lubens prætereo. Postquam autem inventa h est hæc resistentia in uno casu, capienda est ea in alijs quibusvis ut corporis celeritas et superficies sphærica conjunctim, (Nam projectile sphæricum esse passim suppono;) vis autem gravitatis innotescit ex pondere. Sic habebitur semper proportio resistentiæ ad gravitatem seu lineæ DA ad lineam CI. Hac proportione \et angulo ADP/ determinatur specie figura DarFKLP: et capiendo longitudinem DP proportionalem celeritati projectilis in loco D determinatur eadem magnitudine sic {illeg} ut altitudo Aa al maximæ altitudini projectilis et longitudo DF longitudini inter horizontali inter ascensum et casum projectilis semper sit proportionalis, at adeò ex longitudine DF in agro semel {emen} mensurata semper determinet tum {illeg} agro tum longitudinem illam \DF/ tum alias omnes dimensiones figuræ Da|r|FK quam projectile describit in agro. Sed in colligendis hisce dimensionibus usurpandi sunt logarithmi pro area Hyperbolica DRTBG.

Eadem ratione determinantur etiam motus corporum gravitate vel levitate & vi quacun simul et semel impressa moventium in aqua