The First Book of Opticks. Part I (1704)
The FIRST BOOK
OF
OPTICKS.
PART I.
MY Design in this Book is not to explain the Properties of Light by Hypotheses, but to propose and prove them by Reason and Experiments: In order to which, I shall premise the following Definitions and Axioms.
DEFINITIONS.
DEFIN. I.
BY the Rays of Light I understand its least Parts, and those as well Successive in the same Lines as Contemporary in several Lines. For it is manifest that Light consists of parts both Successive and Contemporary; because in the same place you may stop that which comes one moment, and let pass that which comes presently after; and in the same time you may stop it in any one place, and let it pass in any other. For that part of Light which is stopt cannot be the same with that which is let pass. The least Light or part of Light, which may be stopt alone without the rest of the Light, or propagated alone, or do or suffer any thing alone, which the rest of the Light doth not or suffers not, I call a Ray of Light.
DEFIN. II.
Refrangibility of the Rays of Light, is their Disposition to be refracted or turned out of their Way in passing out of one transparent Body or Medium into another. And a greater or less Refrangibility of Rays, is their Disposition to be turned more or less out of their Way in like Incidences on the same Medium. Mathematicians usually consider the Rays of Light to be Lines reaching from the luminous Body to the Body to be illuminated, and the refraction of those Rays to be the bending or breaking of those lines in their passing out of one Medium into another. And thus may Rays and Refractions be considered, if Light is propagated in an instant. But by an Argument taken from the Æquations of the times of the Eclipses of Jupiter's Satellites it seems that Light is propagated in time, spending in its passage from the Sum to us about seven Minutes of time: And therefore I have chosen to define Rays and Refractions in such general terms as may agree to Light in both cases.
DEFIN. III.
Reflexibility of Rays, is their Disposition to be reflected or turned back into the same Medium from any other Medium upon whose Surface they fall. And Rays are more or less reflexible, which are returned back more or less easily. As if Light pass out of Glass into Air, and by being inclined more and more to the common Surface of the Glass and Air, begins at length to be totally reflected by that Surface; those sorts of Rays which at like Incidences are reflected most copiously, or by inclining the Rays begin soonest to be totally reflected, are most reflexible.
<3>DEFIN. IV.
The Angle of Incidence, is that Angle, which the Line described by the incident Ray contains with the Perpendicular to the reflecting or refracting Surface at the Point of Incidence.
DEFIN. V.
The Angle of Reflection or Refraction, is the Angle which the Line described by the reflected or refracted Ray containeth with the Perpendicular to the reflecting or refracting Surface at the Point of Incidence.
DEFIN. VI.
The Sines of Incidence, Reflexion, and Refraction, are the Sines of the Angles of Incidence, Reflexion, and Refraction.
DEFIN. VII.
The Light whose Rays are all alike Refrangible, I call Simple, Homogeneal and Similar; and that whose Rays are some more Refrangible than others, I call Compound, Heterogenal and Dissimilar. The former Light I call Homogeneal, not because I would affirm it so in all respects; but because the Rays which agree in Refrangibility, agree at least in all those their other Properties. Which I consider in the following Discourse.
DEFIN. VIII.
The Colours of Homogeneal Lights, I call Primary, Homogeneal and Simple; and those of Heterogeneal Lights, Heterogeneal and Compound. For these are always compounded of the colours of Homogeneal Lights; as will appear in the following Discourse.
<4>AXIOMS.
AX. I.
THE Angles of Incidence, Reflexion, and Refraction, lye in one and the same Plane.
AX. II.
The Angle of Reflexion is equal to the Angle of Incidence.
AX. III.
If the Refracted Ray be returned directly back to the Point of Incidence, it shall be refracted into the Line before described by the incident Ray.
AX. IV.
Refraction out of the rarer Medium into the denser, is made towards the Perpendicular, that is, so that the Angle of Refraction be less than the Angle of Incidence.
AX. V.
The Sine of Incidence, is either accurately or very nearly in a given Ratio to the Sine of Refraction.
Whence if that Proportion be known in any one Inclination of the incident Ray, 'tis known in all the Inclinations, and thereby the Refraction in all cases of Incidence on the same refracting Body may be determined. Thus if the Refraction be made out of Air into Water, the Sine of Incidence of the red Light is to the Sine of its Refraction as 4 to 3. If out of Air into Glass, the Sines are as 17 to 11. In Light of other Colours the Sines have other Proportions: but the difference is so little that it need seldom be consdered.
Suppose therefore, that RS represents the Surface of stagnating Water,[Image 1] and that C is the point of Incidence in which any Ray coming in the Air from A in the Line AC is reflected or refracted, and I would know whither this Ray shall go after Reflexion or Refraction: I erect upon the Surface of the Water from the point of Incidence the Perpendicular CP and produce it downwards to Q, and conclude by the first Axiom, that the Ray after Reflexion and Refraction, shall be found somewhere in the Plane of the Angle of Incidence ACP produced. I let fall therefore upon the Perpendicular CP the Sine of Incidence AD, and if the reflected Ray be desired, I produce AD to B so that DB be equal to AD, and draw CB. For this Line CB shall be the reflected Ray; the Angle of Reflexion BCP and its Sine BD being equal to the Angle and Sine of Incidence, as they ought to be by the second Axiom. But if the refracted Ray be desired, I produce AD to H, so that DH may be to AD as the Sine of Refraction to the Sine of Incidence, that is as 3 to 4; and about the Center C and in the Plane ACP with the Radius CA describing a Circle ABE I draw Parallel to the Perpendicular CPQ, the Line HE cutting the circumference in E, and joining CE, this Line CE shall be the Line of the refracted Ray. For if EF be let fall perpendicularly on the Line PQ, this Line EF shall be the Sine of Refraction of the Ray CE, the Angle of Refraction being ECQ; and this Sine EF is equal to DH, and consequently in Proportion to the Sine of Incidence AD as 3 to 4.
<6>In like manner, if there be a Prism of Glass (that is a Glass bounded with two Equal and Parallel Triangular ends, and three plain and well polished Sides, which meet in three Parallel Lines running from the three Angles of one end to the three Angles of the other end) and if the Refraction of the Light in passing cross this Prism be desired:[Image 2] Let ACB represent a Plane cutting this Prism transversly to its three Parallel lines or edges there where the Light passeth through it, and let dE be the Ray incident upon the first side of the Prism AC where the Light goes into the Glass; and by putting the Proportion of the Sine of Incidence to the Sine of Refraction as 17 to 11 find EF the first refracted Ray. Then taking this Ray for the Incident Ray upon the second side of the Glass BC where the Light goes out, find the next refracted Ray FG by putting the Proportion of the Sine of Incidence to the Sine of Refraction as 11 to 17. For if the Sine of Incidence out of Air into Glass be to the Sine of Refraction as 17 to 11, the Sine of Incidence out of Glass into Air must on the contrary be to the Sine of Refraction as 11 to 17, by the third Axiom.
Much after the same manner, if ACBD represent a Glass spherically convex on both sides (usually called a Lens, such as is a Burning-glass, or Spectacle-glass, or an Object-glass of a Telescope)[Image 3] and it be required to know how Light falling upon it from any lucid point Q shall be refracted, let QM represent a Ray falling upon any point M of its first spherical Surface ACB, and by erecting a Perpendicular to the Glass at the point M, find the first refracted Ray MN by the Proportion of the Sines 17 to 11. Let that Ray in going out of the Glass be incident upon N, and then find the second refracted Ray Nq by the Proportion of the Sines 11 to 17. And after the same manner may the Refraction be found when the Lens is Convex on one side and Plane or Concave on the other, or Concave on both sides.
AX. VI.
Homogeneal Rays which flow from several Points of any Object, and fall almost Perpendicularly on any reflecting or refracting Plane or spherical Surface, shall afterwards diverge from so many other Points, or be parallel to so many other Lines, or converge to so many other Points, either accurately or without any sensible Error. And the same thing will happen, if the Rays be reflected or refracted successively by two or three or more Plane or spherical Surfaces.
The Point from which Rays diverge or to which they converge may be called their Focus. And the Focus of the incident Rays being given, that of the reflected or refracted ones may be found by finding the Refraction of any two Rays, as above; or more readily thus.
Cas. 1. Let ACB be a reflecting or refracting Plane,[Image 4] and Q the Focus of the incident Rays, and QqC a perpendicular to that Plane. And if this perpendicular be produced to q, so that qC be equal to QC, the point q shall be the Focus Of the reflected Rays. Or if qC be taken on the same side of the Plane with QC and in Proportion to QC as the Sine of Incidence to the Sine of Refraction, the point q shall be the Focus of the refracted Rays.
Cas. 2. Let ACB be the reflecting Surface of any Sphere whose Center is E.[Image 5] Bisect any Radius thereof (suppose EC) in T, and if in that Radius on the same side the point T you take the Points Q and q, so that TQ, TE, and Tq be continual Proportionals, and the point Q be the Focus of the incident Rays, the point q shall be the Focus of the reflected ones.
Cas. 3. Let ACB be the refracting Surface of any Sphere whose Center is E.[Image 6] In any Radius thereof EC produced both ways take ET and Ct severally in such Proportion to that Radius as the lesser of the Sines of Incidence and Refraction hath to the difference of those Sines. And then if in the same Line you find any two Points Q and q, so that TQ be to ET as Et to tq, taking tq the contrary way from t which TQ lieth from T, and if the Point Q be the Focus of any incident Rays, the Point q shall be the Focus of the refracted ones.
And by the same means the Focus of the Rays after two or more Reflexions or Refractions may be found.
Cas. 4. Let ACBD be any refracting Lens,[Image 7] spherically Convex or Concave or Plane on either side, and let CD be its Axis (that is the Line which cuts both its Surfaces perpendicularly, and passes through the Centers of the Spheres,) and in this Axis let F and f be the Foci of the refracted Rays found as above, when the incident Rays on both sides the Lens are parallel to the same Axis; and upon the Diameter Ff bisected in E, describe a Circle. Suppose now that any Point Q be the Focus of any incident Rays. Draw QE cutting the said Circle in T and t, and therein take tq in such proportion to tE as tE or TE hath to TQ. Let tq lye the contrary way from t which TQ doth from T, and q shall be the Focus of the refracted Rays without any sensible Error, provided the Point Q be not so remote from the Axis, nor the Lens so broad as to make any of the Rays fall too obliquely on the refracting Surfaces.
And by the like Operations may the reflecting or refracting Surfaces be found when the two Foci are given, and thereby a Lens be formed, which shall make the Rays flow towards or from what place you please.
So then the Meaning of this Axiom is, that if Rays fall upon any Plane or Spherical Surface or Lens, and before their Incidence flow from or towards any Point Q, they shall after Reflexion or Refraction flow from or towards the Point q found by the foregoing Rules. And if the incident Rays flow from or towards several points Q, the reflected or refracted Rays shall flow from or towards so many other Points q found by the same Rules. Whether the reflected and refracted Rays flow from or towards the Point q is easily known by the situation of that Point. For if that Point be on the same side of the reflecting or refracting Surface or Lens with the Point Q, and the incident Rays flow from the Point Q, the reflected flow towards the Point q and the refracted from it; and if the incident Rays flow towards Q, the reflected flow from q, and the refracted towards it. And the contrary happens when q is on the other side of that Surface.
AX. VII.
Wherever the Rays which come from all the Points of any Object meet again in so many Points after they have been made to converge by Reflexion or Refraction, there they will make a Picture of the Object upon any white Body on which they fall.
So if PR represent any Object without Doors,[Image 8] and AB be a Lens placed at a hole in the Window-shut of a dark Chamber, whereby the Rays that come from any Point Q of that Object are made to converge and meet again in the Point q; and if a Sheet of white Paper be held at q for the Light there to fall upon it: the Picture of that Object PR will appear upon the Paper in its proper shape and Colours. For as the Light which comes from the Point Q goes to the Point q, so the Light which comes from other Points P and R of the Object, will go to so many other correspondent Points p and r (as is manifest by the sixth Axiom;) so that every Point of the Object shall illuminate a correspondent Point of the Picture, and thereby make a Picture like the Object in Shape and Colour, this only excepted that the Picture shall be inverted. And this is the reason of that vulgar Experiment of casting the Species of Objects from abroad upon a Wall or Sheet of white Paper in a dark Room.
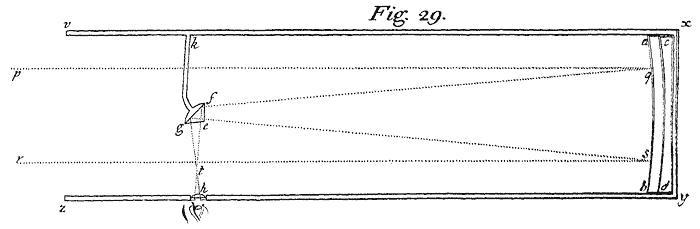
In like manner when a Man views any Object PQR,[Image 9] the Light which comes from the several Points of the Object is so refracted by the transparent skins and humours of the Eye, (that is by the outward coat EFG called the Tunica Cornea, and by the crystalline humour AB which is beyond the Pupil mk) as to converge and meet again in so many Points in the bottom of the Eye, and there to paint the Picture of the Object upon that skin (called the Tunica Retina) with which the bottom of the Eye is covered. For Anatomists when they have taken off from the bottom of the Eye that outward and most thick Coat called the Dura Mater, can then see through the thinner Coats the Pictures of Objects lively painted thereon. And these Pictures propagated by Motion along the Fibres of the Optick Nerves into the Brain, are the cause of Vision. For accordingly as these Pictures are perfect or imperfect, the Object is seen perfectly or imperfectly. If the Eye be tinged with any colour (as in the Disease of the Jaundice) so as to tinge the Pictures in the bottom of the Eye with that Colour, then all Objects appear tinged with the same Colour. If the Humours of the Eye by old Age decay, so as by shrinking to make the Cornea and Coat of the Crystalline Humour grow flatter than before, the Light will not be refracted enough, and for want of a sufficient Refraction will not converge to the bottom of the Eye but to some place beyond it, and by consequence paint in the bottom of the Eye a confused Picture, and according to the indistinctness of this Picture the Object will appear confused. This is the reason of the decay of sight in old Men, and shews why their Sight is mended by Spectacles. For those Convex-glasses supply the defect of plumpness in the Eye, and by encreasing the Refraction make the Rays converge sooner, so as to convene distinctly at the bottom of the Eye if the Glass have a due degree of convexity. And the contrary happens in short-sighted Men whose Eyes are too plump. For the Refraction being now too great, the Rays converge and convene in the Eyes before they come at the bottom; and therefore the Picture made in the bottom and the Vision caused thereby will not be distinct, unless the Object be brought so near the Eye as that the place where the converging Rays convene may be removed to the bottom, or that the plumpness of the Eye be taken off and the Refractions diminished by a Concave-glass of a due degree of Concavity, or lastly that by Age the Eye grow flatter till it come to a due Figure: For short-sighted Men see remote Objects best in Old Age, and therefore they are accounted to have the most lasting Eyes.
AX. VIII.
An Object seen by Reflexion or Refraction, appears in that place from whence the Rays after their last Reflexion or Refraction diverge in falling on the Spectator's Eye.
If the Object A be seen by Reflexion of a Looking-glass m n,[Image 10] it shall appear, not in its proper place A, but behind the Glass at a, from whence any Rays AB, AC, AD, which flow from one and the same Point of the Object, do after their Reflexion made in the Points B, C, D, diverge in going from the Glass to E, F, G, where they are incident on the Spectator's Eyes. For these Rays do make the same Picture in the bottom of the Eyes as if they had come from the Object really placed at a without the interposition of the Looking-glass; and all Vision is made according to the place and shape of that Picture.
In like manner the Object D seen through a Prism appears not in its proper place D,[Image 11] but is thence translated to some other place d situated in the last refracted Ray FG drawn backward from F to d.
And so the Object Q seen through the Lens AB, appears at the place q from whence the Rays diverge in passing from the Lens to the Eye.[Image 12] Now it is to be noted, that the Image of the Object at q is so much bigger or lesser than the Object it self at Q, as the distance of the Image at q from the Lens AB is bigger or less than the distance of the Object at Q from the same Lens. And if the Object be seen through two or more such Convex or Concave-glasses, every Glass shall make a new Image, and the Object shall appear in the place of the bigness of the last Image. Which consideration unfolds the Theory of Microscopes and Telescopes. For that Theory consists in almost nothing else than the describing such Glasses as shall make the last Image of any Object as distinct and large and luminous as it can conveniently be made.
I have now given in Axioms and their Explications the summ of what hath hitherto been treated of in Opticks. For what hath been generally agreed on I content myself to assume under the notion of Principles, in order to what I have further to write. And this may suffice for an Introduction to Readers of quick Wit and good Understanding not yet versed in Opticks: Although those who are already acquainted with this Science, and have handled Glasses, will more readily apprehend what followeth.
PROPOSITIONS.
PROP. I. Theor. I.
LIGHTS which differ in Colour, differ also in Degrees of Refrangibility.
The Proof by Experiments.
Exper. 1 . I took a black oblong stiff Paper terminated by Parallel Sides, and with a Perpendicular right Line drawn cross from one Side to the other, distinguished it into two equal Parts. One of these parts I painted with a red colour and the other with a blew. The Paper was very black, and the Colours intense and thickly laid on, that the Phænomenon might be more conspicuous. This Paper I viewed through a Prism of solid Glass, whose two Sides through which the Light passed to the Eye were plane and well polished, and contained an Angle of about Sixty Degrees: which Angle I call the refracting Angle of the Prism. And whilst I viewed it, I held it before a Window in such manner that the Sides of the Paper were parallel to the Prism, and both those Sides and the Prism were parallel to the Horizon, and the cross Line perpendicular to it; and that the Light which fell from the Window upon the Paper made an Angle with the Paper, equal to that Angle which was made with the same Paper by the Light reflected from it to the Eye. Beyond the Prism was the Wall of the Chamber under the Window covered over with black Cloth, and the Cloth was involved in Darkness that no Light might be reflected from thence, which in passing by the Edges of the Paper to the Eye, might mingle it self with the Light of the Paper and obscure the Phænomenon thereof. These things being thus ordered, I found that if the refracting Angle of the Prism be turned upwards, so that the Paper may seem to be lifted upwards by the Refraction, its blew half will be lifted higher by the Refraction than its red half. But if the refracting Angle of the Prism be turned downward, so that the Paper may seem to be carried lower by the Refraction, its blew half will be carried something lower thereby than its red half. Wherefore in both cases the Light which comes from the blew half of the Paper through the Prism to the Eye, does in like Circumstances suffer a greater Refraction than the Light which comes from the red half, and by consequence is more refrangible.
Illustration. In the Eleventh Figure,[Image 13] MN represents the Window,and DE the Paper terminated with parallel Sides DJ and HE, and by the transverse Line FG distinguished into two halfs, the one DG of an intensely blew Colour, the other FE of an intensely red. And BACcab represents the Prism whose refracting Planes ABba and ACca meet in the edge of the refracting Angle Aa. This edge Aa being upward, is parallel both to the Horizon and to the parallel edges of the Paper DJ and HE. And de represents the Image of the Paper seen by Refraction upwards in such manner that the blew half DG is carried higher to dg than the red half FE is to fe, and therefore suffers a greater Refraction. If the edge of the refracting Angle be turned downward, the Image of the Paper will be refracted downward suppose to δε, and the blew half will be refracted lower to δγ than the red half is to φε.
Exper. 2. About the aforesaid Paper, whose two halfs were painted over with red and blew, and which was stiff like thin Pastboard, I lapped several times a slender thred of very black Silk, in such manner that the several parts of the thred might appear upon the Colours like so many black Lines drawn over them, or like long and slender dark Shadows cast upon them. I might have drawn black Lines with a Pen, but the threds were smaller and better defined. This Paper thus coloured and lined I set against a Wall perpendicularly to the Horizon, so that one of the Colours might stand to the right hand and the other to the left. Close before the Paper at the confine of the Colours below I placed a Candle to illuminate the Paper strongly: For the Experiment was tried in the Night. The Flame of the Candle reached up to the lower edge of the Paper, or a very little higher. Then at the distance of Six Feet and one or two Inches from the Paper upon the Floor I erected a glass Lens four Inches and a quarter broad, which might collect the Rays coming from the several Points of the Paper, and make them converge towards so many other Points at the same distance of six Feet and one or two Inches on the other side of the Lens, and so form the Image of the coloured Paper upon a white Paper placed there; after the same manner that a Lens at a hole in a Window casts the Images of Objects abroad upon a Sheet of white Paper in a dark Room. The aforesaid white Paper, erected perpendicular to the Horizon and to the Rays which fell upon it from the Lens, I moved sometimes towards the Lens, sometimes from it, to find the places where the Images of the blew and red parts of the coloured Paper appeared most distinct. Those places I easily knew by the Images of the black Lines which I had made by winding the Silk about the Paper. For the Images of those fine and slender Lines (which by reason of their blackness were like Shadows on the Colours) were confused and scarce visible, unless when the Colours on either side of each Line were terminated most distinctly. Noting therefore, as diligently as I could, the places where the Images of the red and blew halfs of the coloured Paper appeared most distinct, I found that where the red half of the Paper appeared distinct, the blew half appeared confused, so that the black Lines drawn upon it could scarce be seen; and on the contrary where the blew half appeared most distinct, the red half appeared confused, so that the black Lines upon it were scarce visible. And between the two places where these Images appeared distinct there was the distance of an Inch and a half: the distance of the white Paper from the Lens, when the Image of thered half of the coloured Paper appeared most distinct, being greater by an Inch and an half than the distance of the same white Paper from the Lens when the Image of the blew half appeared most distinct. In like Incidences therefore of the blew and red upon the Lens, the blew was refracted more by the Lens than the red, so as to converge sooner by an Inch and a half, and therefore is more refrangible.
Illustration. In the Twelfth Figure,[Image 14] DE signifies the coloured Paper, DG theb lew half, FE the red half, MN the Lens, HJ the white Paper in that place where the red half with its black Lines appeared distinct, and hi the same Paper in that place where the blew half appeared distinct. The place hi was nearer to the Lens MN than the Place HJ by an Inch and an half.
<17>Scholium. The same things succeed notwithstanding that some of the Circumstances be varied: as in the first Experiment when the Prism and Paper are any ways inclined to the Horizon, and in both when coloured Lines are drawn upon very black Paper. But in the Description of these Experiments, I have set down such Circumstances by which either the Phænomenon might be rendred more conspicuous, or a Novice might more easily try them, or by which I did try them only. The same thing I have often done in the following Experiments: Concerning all which this one Admonition may suffice. Now from these Experiments it follows not that all the Light of the blew is more Refrangible than all the Light of the red ; For both Lights are mixed of Rays differently Refrangible, So that in the red there are some Rays not less refrangible than those of the blew, and in the blew there are some Rays not more Refrangible than those of the red; But these Rays in proportion to the whole Light are but few, and serve to diminish the Event of the Experiment, but are not able to destroy it. For if the red and blew Colours were more dilute and weak, the distance of the Images would be less than an Inch and a half; and if they were more intense and full, that distance would be greater, as will appear hereafter. These Experiments may suffice for the Colours of Natural Bodies. For in the Colours made by the Refraction of Prisms this Proposition will appear by the Experiments which are now to follow in the next Proposition.
<18>PROP. II. Theor. II.
The Light of the Sun consists of Rays differently Refrangible.
The Proof by Experiments.
Exper. 3. IN a very dark Chamber at a round hole about one third part of an Inch broad made in the Shut of a Window I placed a Glass Prism, whereby the beam of the Sun's Light which came in at that hole might be refracted upwards toward the opposite Wall of the Chamber, and there form a coloured Image of the Sun. The Axis of the Prism (that is the Line passing through the middle of the Prism from one end of it to the other end parallel to the edge of the Refracting Angle) was in this and the following Experiments perpendicular to the incident Rays. About this Axis I turned the Prism slowly, and saw the refracted Light on the Wall or coloured Image of the Sun first to descend and then to ascend. Between the Descent and Ascent when the Image seemed Stationary, I stopt the Prism, and fixt it in that posture, that it should be moved no more. For in that posture the Refractions of the Light at the two sides of the Refracting Angle, that is at the entrance of the Rays into the Prism and at their going out of it, were equal to one another. So also in other Experiments as often as I would have the Refractions on both sides the Prism to be equal to one another, I noted the place where the Image of the Sun formed by the refracted Light stood still between its two contrary Motions, in the common Period of its progress and regress; and when the Image fell upon that place, I made fast the Prism. And in this Posture, as the most convenient,it is to be understood that all the Prisms are placed in the following Experiments, unless where some other posture is described. The Prism therefore being placed in this posture, I let the refracted Light fall perpendicularly upon a Sheet of white Paper at the opposite Wall of the Chamber, and observed the Figure and Dimensions of the Solar Image formed on the Paper by that Light. This Image was Oblong and not Oval, but terminated with two Rectilinear and Parallel Sides, and two Semicircular Ends. On its Sides it was bounded pretty distinctly, but on its Ends very confusedly and indistinctly, the Light there decaying and vanishing by degrees. The breadth of this Image answered to the Sun's Diameter, and was about two Inches and the eighth part of an Inch, including the Penumbra. For the Image was eighteen Feet and an half distant from the Prism, and at this distance that breadth if diminished by the Diameter of the hole in the Window-shut, that is by a quarter of an Inch, subtended an Angle at the Prism of about half a Degree, which is the Sun's apparent Diameter. But the Length of the Image was about ten Inches and a quarter, and the length of the Rectilinear Sides about eight Inches; and the refracting Angle of the Prism whereby so great a length was made, was 64 degr. With a less Angle the length of the Image was less, the breadth remaining the same. If the Prism was turned about its Axis that way which made the Rays emerge more obliquely out of the second refracting Surface of the Prism, the Image soon became an Inch or two longer, or more; and if the Prism was turned about the contrary way, so as to make the Rays fall more obliquely on the first refracting Surface, the Image soon became an Inch or two shorter. And therefore in trying this Experiment, I was as curious as I could be in placing the Prism by the above-mentioned Rule exactly in such a posture that the Refractions of the Rays at their emergence out of the Prism might be equal to that at their incidence on it. This Prism had some Veins running along within the Glass from one end to the other, which scattered some of the Sun's Light irregularly, but had no sensible effect in increasing the length of the coloured Spectrum. For I tried the same Experiment with other Prisms with the same Success. And particularly with a Prism which seemed free from such Veins, and whose refracting Angle was Degrees, I found the length of the Image or 10 Inches at the distance of Feet from the Prism, the breadth of the hole in the Window-shut being of an Inch as before. And because it is easie to commit a mistake in placing the Prism in its due posture, I repeated the Experiment four or five times, and always found the length of the Image that which is set down above. With another Prism of clearer Glass and better Pollish, which seemed free from Veins, and whose refracting Angle was Degrees, the length of this Image at the same distance of Feet was also about 10 Inches, or . Beyond these Measures for about or of an Inch at either end of the Spectrum the Light of the Clouds seemed to be a little tinged with red and violet, but so very faintly that I suspected that tincture might either wholly or in great measure arise from some Rays of the Spectrum scattered irregularly by some inequalities in the Substance and Polish of the Glass, and therefore I did not include it in these Measures. Now the different Magnitude of the hole in the Window-shut, and different thickness of the Prism where the Rays passed through it, and different inclinations of the Prism to the Horizon, made no sensible changes in the length of the Image. Neither did the different matter of the Prisms make any : for in a Vessel made of polished Plates of Glass cemented together in the shape of a Prism and filled with Water, there is the like Success of the Experiment according to the quantity of the Refraction. It is further to be observed, that the Rays went on in right Lines from the Prism to the Image, and therefore at their very going out of the Prism had all that Inclination to one another from which the length of the Image proceeded, that is the Inclination of more than two Degrees and an half. And yet according to the Laws of Opticks vulgarly received, they could not possibly be so much inclined to one another. For let EG represent the Window-shut[Image 15], F the hole made therein through which a beam of the Sun's Light was transmitted into the darkened Chamber, and ABC a Triangular Imaginary Plane whereby the Prism is feigned to be cut transversely through the middle of the Light. Or if you please, let ABC represent the Prism it self, looking directly towards the Spectator's Eye with its nearer end : And let XY be the Sun, MN the Paper upon which the Solar Image or Spectrum is cast, and PT the Image it self whose sides towards V and W are Rectilinear and Parallel, and ends towards P and T Semicircular. YKHP and XLJT are two Rays, the first of which comes from the lower part of the Sun to the higher part of the Image, and is refracted in the Prism at K and H, and the latter comes from the higher part of the Sun to the lower part of the Image, and is refracted at L and J. Since the Refractions on both sides the Prism are equal to one another, that is the Refraction at K equal to the Refraction at J, and the Refraction at L equal to the Refraction at H, so that the Refractions of the incident Rays at K and L taken together are equal to the Refractions of the emergent Rays at H and J taken together : it follows by adding equal things to equal things, that the Refractions at K and H taken together, are equal to the Refractions at J and L taken together, and therefore the two Rays being equally refracted have the same Inclination to one another after Refraction which they had before, that is the Inclination of half a Degree answering to the Sun's Diameter. For so great was the inclination of the Rays to one another before Refraction. So then, the length of the Image PT would by the Rules of Vulgar Opticks subtend an Angle of half a Degree at the Prism, and by consequence be equal to the breadth vw; and therefore the Image would be round. Thus it would be were the two Rays XLJT and YKHP and all the rest which form the Image PwTv, alike refrangible. And therefore seeing by Experience it is found that the Image is not round but about five times longer than broad, the Rays which going to the upper end P of the Image suffer the greatest Refraction, must be more Refrangible than those which go to the lower end T, unless the inequality of Refraction be casual.
This Image or Spectrum PT was coloured, being red at its least refracted end T, and violet at its most refracted end P, and yellow green and blew in the intermediate spaces. Which agrees with the first Proposition, that Lights which differ in Colour do also differ in Refrangibility. The length of the Image in the foregoing Experiments I measured from the faintest and outmost red at one end, to the faintest and outmost blew at the other end.
Exper. 4. In the Sun's beam which was propagated into the Room through the hole in the Window-shut, at the distance of some Feet from the hole, I held the Prism in such a posture that its Axis might be perpendicular to that beam. Then I looked through the Prism upon the hole, and turning the Prism to and fro about its Axis to make the Image of the hole ascend and descend, when between its two contrary Motions it seemed stationary, I stopt the Prism that the Refractions of both sides of the refracting Angle might be equal to each other as in the former Experiment. In this situation of the Prism viewing through it the said hole, I observed the length of its refracted Image to be many times greater than its breadth, and that the most refracted part thereof appeared violet, the least refracted red, the middle parts blew green and yellow in order. The same thing happened when I removed the Prism out of the Sun's Light, and looked through it upon the hole shining by the Light of the Clouds beyond it. And yet if the Refraction were done regularly according to one certain Proportion of the Sines of Incidence and Refraction as is vulgarly supposed, the refracted Image ought to have appeared round.
So then, by these two Experiments it appears that in equal Incidences there is a considerable inequality of Refractions : But whence this inequality arises, whether it be that some of the incident Rays are refracted more and others less, constantly or by chance, or that one and the same Ray is by Refraction disturbed, shattered, dilated, and as it were split and spread into many diverging Rays, as Grimaldo supposes, does not yet appear by these Experiments, but will appear by those that follow.
Exper. 5. Considering therefore, that if in the third Experiment the Image of the Sun should be drawn out into an oblong form, either by a Dilatation of every Ray, or by any other casual inequality of the Refractions, the same oblong Image would by a second Refraction made sideways be drawn out as much in breadth by the like Dilatation of the Rays or other casual inequality of the Refractions sideways, I tried what would be the Effects of such a second Refraction. For this end I ordered all things as in the third Experiment, and then placed a second Prism immediately after the first in a cross Position to it, that it might again refract the beam of the Sun's Light which came to it through the first Prism. In the first Prism this beam was refracted upwards, and in the second sideways. And I found that by the Refraction of the second Prism the breadth of the Image was not increased, but its superior part which in the first Prism suffered the greater Refraction and appeared violet and blew, did again in the second Prism suffer a greater Refraction than its inferior part, which appeared red and yellow , and this without any Dilatation of the Image in breadth.
Illustration. Let S represent the Sun,[Image 16] F the hole in the Window, ABC the first Prism, DH the second Prism, Y the round Image of the Sun made by a direct beam of Light when the Prisms are taken away, PT the oblong Image of the Sun made by that beam passing through the first Prism alone when the second Prism is taken away, and pt the Image made by the cross Refractions of both Prisms together. Now if the Rays which tend towards the several Points of the round Image Y were dilated and spread by the Refraction of the first Prism, so that they should not any longer go in single Lines to single Points, but that every Ray being split, shattered, and changed from a Linear Ray to a Superficies of Rays diverging from the Point of Refraction, and lying in the Plane of the Angles of Incidence and Refraction, they should go in those Planes to so many Lines reaching almost from one end of the Image PT to the other, and if that Image should thence become oblong : those Rays and their several parts tending towards the several Points of the Image PT ought to be again dilated and spread Sideways by the transverse Refraction of the second Prism, so as to compose a foursquare Image, such as is represented at ττ. For the better understanding of which, let the Image PT be distinguished into five equal parts PQK, KQRL, LRSM, MSVN, NVT. And by the same irregularity that the Orbicular Light Y is by the Refraction of the first Prism dilated and drawn out into a long Image PT, the Light PQK which takes up a space of the same length and breadth with the Light Y ought to be by the Refraction of the second Prism dilated and drawn out into the long Image πqkp, and the Light KQRL into the long Image kqrl, and the Lights LRSM, MSVN, NVT, into so many other long Images lrsm, msvn, nvtτ; and all these long Images would compose the foursquare Image πτ. Thus it ought to be were every Ray dilated by Refraction, and spread into a triangular Superficies of Rays diverging from the Point of Refraction. For the second Refraction would spread the Rays one way as much as the first doth another, and so dilate the Image in breadth as much as the first doth in length. Amd the same thing ought to happen, were some Rays casually refracted more than others. But the Event is otherwise. The Image PT was not made broader by the Refraction of the second Prism, but only became oblique, as 'tis represented at pt, its upper end P being by the Refraction translated to a greater distance than its lower end T. So then the Light which went towards the upper end P of the Image, was (at equal Incidences) more refracted in the second Prism than the Light which tended towards the lower end T, that is the blew and violet, than the red and yellow; and therefore was more refrangible. The same Light was by the Refraction of the first Prism translated further from the place Y to which it tended before Refraction; and therefore suffered as well in the first Prism as in the second a greater Refraction than the rest of the Light, and by consequence was more Refrangible than the rest, even before its incidence on the first Prism.
Sometimes I placed a third Prism after the second, and sometimes also a fourth after the third, by all which the Image might be often refracted sideways: but the Rays which were more refracted than the rest in the first Prism were also more refracted in all the rest, and that without any Dilatation of the Image sideways: and therefore those Rays for their constancy of a greater Refraction are deservedly reputed more Refrangible.
But that the meaning of this Experiment may more clearly appear,[Image 17] it is to be considered that the Rays which are equally Refrangible do fall upon a circle answering to the Sun's Disque. For this was proved in the third Experiment. By a circle I understand not here a perfect Geometrical Circle, but any Orbicular Figure whose length is equal to its breadth, and which, as to sense, may seem circular. Let therefore AG represent the circle which all the most Refrangible Rays propagated from the whole Disque of the Sun, would illuminate and paint upon the opposite Wall if they were alone; EL the circle which all the least Refrangible Rays would in like manner illuminate and paint if they were alone; BH, CJ, DK, the circles which so many intermediate sorts of Rays would successively paint upon the Wall, if they were singly propagated from the Sun in successive Order, the rest being always intercepted; And conceive that there are other intermediate Circles without number which innumerable other intermediate sorts of Rays would successively paint upon the Wall if the Sun should successively {emit every} sort apart. And seeing the Sun emits all these sorts at once, they must all together illuminate and paint innumerable equal circles, of all which, being according to their degrees of Refrangibility placed in order in a continual series, that oblong Spectrum PT is composed which I described in the third Experiment. Now if the Sun's circular Image Y which is made by an unrefracted beam of Light was by any dilation of the single Rays, or by any other irregularity in the Refraction of the first Prism, converted into the Oblong Spectrum, PT: then ought every Circle AG, BH, CJ, &c. in that Spectrum, by the cross Refraction of the second Prism again dilating or otherwise scattering the Rays as before, to be in like manner drawn out and transformed into an Oblong Figure, and thereby the breadth of the Image PT would be now as much augmented as the length of the Image Y was before by the Refraction of the first Prism; and thus by the Refractions of both Prisms together would be formed a foursquare Figure pπtτ as I described above. Wherefore since the breadth of the Spectrum PT is not increased by the Refraction sideways, it is certain that the Rays are not split or dilated, or otherways irregularly scattered by that Refraction, but that every circle is by a regular and uniform Refraction translated entire into another place, as the circle AG by the greatest Refraction into the place ag, the circle BH by a less Refraction into the place bh, the circle CJ by a Refraction still less into the place ci, and so of the rest; by which means a new Spectrum pt inclined to the former PT is in like manner composed of circles lying in a right Line; and these circles must be of the same bigness with the former, because the breadths of all the Spectrums Y, PT and pt at equal distances from the Prisms are equal.
<28>I considered further that by the breadth of the hole F through which the Light enters into the Dark Chamber, there is a Penumbra made in the circuit of the Spectrum Y, and that Penumbra remains in the rectilinear Sides of the Spectrums PT and pt. I placed therefore at that hole a Lens or Object-glass of a Telescope which might cast the Image of the Sun distinctly on Y without any Penumbra at all, and found that the Penumbra of the Rectilinear Sides of the oblong Spectrums PT and pt was also thereby taken away, so that those Sides appeared as distinctly defined as did the Circumference of the first Image Y. Thus it happens if the Glass of the Prisms be free from veins, atd their sides be accurately plane and well polished without those numberless waves or curles which usually arise from Sand-holes a little smoothed in polishing with Putty. If the Glass be only well polished and free from veins and the Sides not accurately plane but a little Convex or Concave, as it frequently happens; yet may the three Spectrums Y, PT and pt want Penumbras, but not in equal distances from the Prisms. Now from this want of Penumbras, I knew more certainly that every one of the circles was refracted according to some most regular, uniform, and constant Law. For if there were any irregularity in the Refraction, the right Lines AE and GL which all the circles in the Spectrum PT do touch, could not by that Refraction be translated into the Lines ae and gl as distinct and straight as they were before, but there would arise in those translated Lines some Penumbra or crookedness or undulation, or other sensible Perturbation contrary to what is found by Experience. Whatsoever Penumbra or Perturbation should be made in the circles by the cross Refraction of the second Prism, all that Penumbra or Perturbation would be conspicuous in the right Lines ae and gl which touch those circles. And therefore since there is no such Penumbra or Perturbation in those right Lines there must be none in the circles. Since the distance between those Tangents or breadth of the Spectrum is not increased by the Refractions, the Diameters of the circles are not increased thereby. Since those Tangents continue to be right Lines, every circle which in the first Prism is more or less refracted, is exactly in the same Proportion more or less refracted in the second. And seeing all these things continue to succeed after the same manner when the Rays are again in a third Prism, and again in a fourth refracted Sideways, it is evident that the Rays of one and the same circle as to their degree of Refrangibility continue always Uniform and Homogeneal to one another, and that those of several circles do differ in degree of Refrangibility, and that in some certain and constant Proportion. Which is the thing I was to prove.
There is yet another Circumstance or two of this Experiment by which it becomes still more plain and convincing.[Image 18] Let the second Prism DH be placed not immediately after the first, but at some distance from it; Suppose in the mid-way between it and the Wall on which the oblong Spectrum PT is cast, so that the Light from the first Prism may fall upon it in the form of an oblong Spectrum pπtτ Parallel to this second Prism, and be refracted Sideways to form the oblong Spectrum pt upon the Wall. And you will find as before, that this Spectrum pt is inclined to that Spectrum PT, which the first Prism forms alone without the second; the blew ends P and p being further distant from one another than the red ones T and t, and by consequence that the Rays which go to the blew end π of the Image πτ and which therefore suffer the greatest Refraction in the first Prism, are again in the second Prism more refracted than the rest.
<30>The same thing I try'd also by letting the Sun's Light into a dark Room through two little round holes F and φ made in the Window,[Image 19] and with two Parallel Prisms ABC and αβγ placed at those holes (one at each) refracting those two beams of Light to the opposite Wall of the Chamber, in such manner that the two colour'd Images PT and mn which they there painted were joyned end to end and lay in one straight Line, the red end T of the one touching the blew end m of the other. For if these two refracted beams were again by a third Prism DH placed cross to the two first, refracted Sideways, and the Spectrums thereby translated to some other part of the Wall of the Chamber, suppose the Spectrum PT to pt and the Spectrum MN to mn, these translated Spectrums pt and mn would not lie in one straight Line with their ends contiguous as before, but be broken off from one another and become Parallel, the blew end of the Image mn being by a greater Refraction translated farther from its former place MT, than the red end t of the other Image pt from the same place MT which puts the Proposition past dispute. And this happens whether the third Prism DH be placed immediately after the two first or at a great distance from them, so that the Light refracted in the two first Prisms be either white and circular, or coloured and oblong when it falls on the third.
Exper. 6. In the middle of two thin Boards I made round holes a third part of an Inch in Diameter, and in the Window-shut a much broader hole, being made to let into my darkned Chamber a large beam of the Sun's Light; I placed a Prism behind the Shut in that beam to refract it towards the opposite Wall, and close behind the Prism I fixed one of the Boards, in such manner that the middle of the refracted Light might {pass} through the hole made in it, and the rest be intercepted by the Board. Then at the distance of about twelve Feet from the first Board I fixed the other Board, in such manner that the middle of the refracted Light which came through the hole in the first Board and fell upon the opposite Wall might pass through the hole in this other Board, and the rest being intercepted by the Board might paint upon it the coloured Spectrum of the Sun. And close behind this Board I fixed another Prism to refract the Light which came through the hole. Then I returned speedily to the first Prism, and by turning it slowly to and fro about its Axis, I caused the Image which fell upon the second Board to move up and down upon that Board, that all its parts might successively pass through the hole in that Board and fall upon the Prism behind it. And in the mean time, I noted the places on the opposite Wall to which that Light after its Refraction in the second Prism did pass; and by the difference of the places I found that the Light which being most refracted in the first Prism did go to the blew end of the Image, was again more refracted in the second Prism than the Light which went to the red end of that Image, which proves as well the first Proposition as the second. And this happened whether the Axis of the two Prisms were parallel, or inclined to one another and to the Horizon in any given Angles.
Illustration.[Image 20] Let F be the wide hole in the Window-shut, through which the Sun shines upon the first Prism ABC, and let the refracted Light fall upon the middle of the Board DE, and the middle part of that Light upon the hole G made in the middle part of that Board. Let this trajected part of that Light fall again upon the middle of the second Board de, and there paint such an oblong coloured Image of the Sun as was described in the third Experiment. By turning the Prism ABC slowly to and fro about its Axis this Image will be made to move up and down the Board de, and by this means all its parts from one end to the other may be made to pass successively through the hole g which is made in the middle of that Board. In the mean while another Prism abc is to be fixed next after that hole g to refract the trajected Light a second time. And these things being thus ordered, I marked the places M and N of the opposite Wall upon which the refracted Light fell, and found that whilst the two Boards and second Prism remained unmoved, those places by turning the first Prism about its Axis were changed perpetually. For when the lower part of the Light which fell upon the second Board de was cast through the hole g it went to a lower place M on the Wall, and when the higher part of that Light was cast thrbugh the same hole g, it went to a higher place N on the Wall, and when any intermediate part of the Light was cast through that hole it went to some place on the Wall between M and N. The unchanged Position of the holes in the Boards, made the Incidence of the Rays upon the second Prism to be the same in all cases. And yet in that common Incidence some of the Rays were more refracted and others less. And those were more refracted in this Prism which by a greater Refraction in the first Prism were more turned out of the way, and therefore for their constancy of being more refracted are deservedly called more Refrangible.
Exper. 7. At two holes made near one another in my Window-shut I placed two Prisms, one at each, which might cast upon the opposite Wall (after the manner of the third Experiment) two oblong coloured Images of the Sun. And at a little distance from the Wall I placed a long slender Paper with straight and parallel edges, and ordered the Prisms and Paper so, that the red Colour of one Image might fall directly upon one half of the Paper, and the violet colour of the other Image upon the other half of the same Paper; so that the Paper appeared of two Colours, red and violet, much after the manner of the painted Paper in the first and second Experiments. Then with a black Cloth I covered the Wall behind the Paper, that no Light might be reflected from it to disturb the Experiment, and viewing the Paper through a third Prism held parallel to it, I saw that half of it which was illuminated by the violet-Light to be divided from the other half by a greater Refraction, especially when I went a good way off from the Paper. For when I viewed it too near at hand, the two halfs of the Paper did not appear fully divided from one another, but seemed contiguous at one of their Angles like the painted Paper in the first Experiment. Which also happened when the Paper was too broad.
Sometimes instead of the Paper I used a white Thred, and this appeared through the Prism divided into two Parallel Threds as is represented in the 19th Figure,[Image 21] where DG denotes the Thred illuminated with violet Light from D to E and with red Light from F to G, and de fg are the parts of the Thred seen by Refraction. If one half of the Thred be constantly illuminated with red, and the other half be illuminated with all the Colours successively, (which may be done by causing one of the Prisms to be turned about its Axis whilst the other remains unmoved) this other half in viewing the Thred through the Prism, will appear in a continued right Line with the first half when illuminated with red, and begin to be a little divided from it when illuminated with Orange, and remove further from it when illuminated with Yellow, and still further when with Green, and further when with Blew, and go yet further off when illuminated with Indigo, and furthest when with deep Violet. Which plainly shews, that the Lights of several Colours are more and more Refrangible one than another, in this order of their Colours, Red, Orange, Yellow, Green, Blew, Indigo, deep Violet; and so proves as well the first Proposition as the second.
I caused also the coloured Spectrums PT and MN made in a dark Chamber by the Refractions of two Prisms to lye in a right Line end to end,[Image 22] as was described above in the fifth Experiment, and viewing them through a third Prism held Parallel to their Length, they appeared no longer in a right Line, but became broken from one another, as they are represented at pt and mn, the violet end m of the Spectrum mn being by a greater Refraction translated further from its former Place MT than the red end t of the other Spectrum pt.
I further caused those two Spectrums PT and MN to become co-incident in an inverted order of their Colours,[Image 23] the red end of each falling on the violet end of the other, as they are represented in the oblong Figure PTMN; and then viewing them through a Prism DH held Parallel to their length, they appeared not co-incident as when viewed with the naked Eye, but in the form of two distinct Spectrums pt and mn crossing one another in the middle after the manner of the letter X. Which shews that the red of the one Spectrum and violet of the other, which were co-incident at PN and MT, being parted from one another by a greater Refraction of the violet to p and m than of the red to n and t, do differ in degrees of Refrangibility.
I illuminated also a little circular piece of white Paper all over with the Lights of both Prisms intermixed, and when it was illuminated with the red of one Spectrum and deep violet of the other, so as by the mixture of those Colours to appear all over purple, I viewed the Paper, first at a less distance, and then at a greater, through a third Prism; and as I went from the Paper, the refracted Image thereof became more and more divided by the unequal Refraction of the two mixed Colours, and at length parted into two distinct Images, a red one and a violet one, whereof the violet was furthest from the Paper, and therefore suffered the greatest Refraction. And when that Prism at the Window which cast the violet on the Paper was taken away, the violet Image disappeared; but when the other Prism was taken away the red vanished: which shews that these two Images were nothing else than the Lights of the two Prisms which had been intermixed on the purple Paper, but were parted again by their unequal Refractions made in the third Prism through which the Paper was viewed. This also was observable that if one of the Prisms at the Window, suppose that which cast the violet on the Paper, was turned about its Axis to make all the Colours in this order, Violet, Indigo, Blew, Green, Yellow, Orange, Red, fall successively on the Paper from that Prism, the violet Image changed Colour accordingly, and in changing Colour came nearer and nearer to the red one, until when it was also red they both became fully co-incident.
I placed also two Paper circles very near one another, the one in the red Light of one Prism, and the other in the violet Light of the other. The circles were each of them an Inch in diameter, and behind them the Wall was dark that the Experiment might not be disturbed by any Light coming from thence. These circles thus illuminated, I viewed through a Prism so held that the Refraction might be made towards the red circle, and as I went from them they came nearer and nearer together, and at length became co-incident; and afterwards when I went still further off, they parted again in a contrary order, the violet by a greater Refraction being carried beyond the red.
Exper. 8. In Summer when the Sun's Light uses to be strongest, I placed a Prism at the hole of the Window-shut, as in the third Experiment, yet so that its Axis might be Parallel to the Axis of the World, and at the opposite Wall in the Sun's refracted Light, I placed an open Book. Then going Six Feet and tvvo Inches from the Book, I placed there the abovementioned Lens, by vvhich the Light reflected from the Book might be made to converge and meet again at the distance of six Feet and tvvo Inches behind the Lens, and there paint the Species of the Book upon a sheet of vvhite Paper much after the manner of the second Experiment. The Book and Lens being made fast, I noted the place vvhere the Paper vvas, vvhen the Letters of the Book, illuminated by the fullest red Light of the solar Image falling upon it, did cast their Species on that Paper most distinctly; And then I stay'd till by the Motion of the Sun and consequent Motion of his Image on the Book, all the Colours from that red to the middle of the blew pass'd over those Letters; and when those Letters were illuminated by that blew, I noted again the place of the Paper when they cast their Species most distinctly upon it: And I found that this last place of the Paper was nearer to the Lens than its former place by about two Inches and an half, or two and three quarters. So much sooner therefore did the Light in the violet end of the Image by a greater Refraction converge and meet, than the Light in the red end. But in trying this the Chamber was as dark as I could make it. For if these Colours be diluted and weakned by the mixture of any adventitious Light, the distance between the places of the Paper will not be so great. This distance in the second Experiment where the Colours of natural Bodies were made use of, was but an Inch and an half, by reason of the imperfection of those Colours. Here in the Colours of the Prism, which are manifestly more full, intense, and lively than those of natural Bodies, the distance is two Inches and three quarters. And were the Colours still more full, I question not but that the distance would be considerably greater. For the coloured Light of the Prism, by the interfering of the Circles described in the 11th Figure of the fifth Experiment, and also by the Light of the very bright Clouds next the Sun's Body intermixing with these Colours, and by the Light scattered by the inequalities in the polish of the Prism, was so very much compounded, that the Species which those faint and dark Colours, the Indigo and Violet, cast upon the Paper were not distinct enough to be well observed.
Exper. 9. A Prism, whose two Angles at its Base were equal to one another and half right ones, and the third a right one, I placed in a beam of the Sun's Light let into a dark Chamber through a hole in the Window-shut as in the third Experiment. And turning the Prism slowly about its Axis until all the Light which went through one of its Angles and was refracted by it began to be reflected by its Base, at which till then it went out of the Glass, I observed that those Rays which had suffered the greatest Refraction were sooner reflected than the rest. I conceived therefore that those Rays of the reflected Light, which were most Refrangible, did first of all by a total Reflexion become more copious in that Light than the rest, and that afterwards the rest also, by a total Reflexion, became as copious as these. To try this, I made the reflected Light pass through another Prism, and being refracted by it to fall afterwards upon a sheet of white Paper placed at some distance behind it, and there by that Refraction to paint the usual Colours of the Prism. And then causing the first Prism to be turned about its Axis as above, I observed that when those Rays which in this Prism had suffered the greatest Refraction and appeared of a blew and violet Colour began to be totally reflected, the blew and violet Light on the Paper which was most refracted in the second Prism received a sensible increase above that of the red and yellow, which was least refracted; and afterwards when the rest of the Light which was green, yellow and red began to be totally reflected in the first Prism, the Light of those Colours on the Paper received as great an increase as the violet and blew had done before. Whence 'tis manifest, that the beam of Light reflected by the Base of the Prism, being augmented first by the more Refrangible Rays and afterwards by the less Refrangible ones, is compounded of Rays differently Refrangible. And that all such reflected Light is of the same Nature with the Sun's Light, before its Incidence on the Base of the Prism, no Man ever doubted: it being generally allowed, that Light by such Reflexions suffers no Alteration in its Modifications and Properties. I do not here take notice of any Refractions made in the Sides of the first Prism, because the Light enters it perpendicularly at the first Side, and goes out perpendicularly at the second Side, and therefore suffers none. So then, the Sun's incident Light being of the same temper and constitution with his emergent Light, and the last being compounded of Rays differently Refrangible, the first must be in like manner compounded.
Illustration. In the 21th Figure,[Image 24] ABC is the first Prism, BC its Base, B and C its equal Angles at the Base, each of 45 degrees, A its Rectangular Vertex, FM a beam of the Sun's Light let into a dark Room through a hole F one third part of an Inch broad, M its Incidence on the Base of the Prism, MG a less refracted Ray, MH a more refracted Ray, MN the beam of Light reflected from the Base, VXY the second Prism by which this beam in passing through it is refracted, Nt the less refracted Light of this beam, and Np the more refracted part thereof. When the first Prism ABC is turned about its Axis according to the order of the Letters ABC, the Rays MH emerge more and more obliquely out of that Prism, and at length after their most oblique Emergence are reflected towards N, and going on to p do increase the number of the Rays Np. Aftervvards by continuing the motion of the first Prism, the Rays MG are also reflected to N and increase the number of the Rays Nt. And therefore the Light MN admits into its Composition, first the more Refrangible Rays, and then the less Refrangible Rays, and yet after this Composition is of the same Nature vvith the Sun's immediate Light FM, the Reflexion of the specular Base BC causing no Alteration therein.
Exper. 10. Two Prisms, which were alike in shape, I tied so together, that their Axes and opposite Sides being Parallel, they composed a Parallelopiped. And, the Sun shining into my dark Chamber through a little hole in the Window-shut, I placed that Parallelopiped in his beam at some distance from the hole, in such a posture that the Axes of the Prisms might be perpendicular to the incident Rays, and that those Rays being incident upon the first Side of one Prism, might go on through the two contiguous Sides of both Prisms, and emerge out of the last Side of the second Prism. This Side being Parallel to the first Side of the first Prism, caused the emerging Light to be Parallel to the incident. Then, beyond these two Prisms I placed a third, which might refract that emergent Light, and by that Refraction cast the usual Colours of the Prism upon the opposite Wall, or upon a sheet of white Paper held at a convenient distance behind the Prism for that refracted Light to fall upon it. After this I turned the Parallelopiped about its Axis, and found that when the contiguous Sides of the two Prisms became so oblique to the incident Rays that those Rays began all of them to be reflected, those Rays which in the third Prism had suffered the greatest Refraction and painted the Paper with violet and blew, were first of all by a total Reflexion taken out of the transmitted Light, the rest remaining and on the Paper painting their Colours of Green, Yellow, Orange, and Red as before; and afterwards by continuing the motion of the two Prisms, the rest of the Rays also by a total Reflexion vanished in order, according to their degrees of Refrangibility. The Light therefore which emerged out of the two Prisms is compounded of Rays differently Refrangible, seeing the more Refrangible Rays may be taken out of it while the less Refrangible remain. But this Light being trajected only through the Parallel Superficies of the two Prisms, if it suffered any change by the Refraction of one Superficies it lost that impression by the contrary Refraction of the other Superficies, and so being restored to its pristine constitution became of the same nature and condition as at first before its Incidence on those Prisms; and therefore, before its Incidence, was as much compounded of Rays differently Refrangible as afterwards.
Illustration. In the 22th Figure[Image 25] ABC and BCD are the two Prisms tied together in the form of a Parallelopiped, their Sides BC and CB being contiguous, and their Sides AB and CD Parallel. And HJK is the third Prism, by which the Sun's Light propagated through the hole F into the dark Chamber, and there passing through those sides of the Prisms AB, BC, CB and CD, is refracted at O to the white Paper PT, falling there partly upon P by a greater Refraction, partly upon T by a less Refraction, and partly upon R and other intermediate places by intermediate Refractions. By turning the Parallelopiped ACBD about its Axis, according to the order of the Letters A, C, D, B, at length when the contiguous Planes BC and CB become sufficiently oblique to the Rays FM, which are incident upon them at M, there will vanish totally out of the refracted Light OPT, first of all the most refracted Rays OP, (the rest OR and OT remaining as before) then the Rays OR and other intermediate ones, and lastly, the least refracted Rays OT. For when the Plane BC becomes sufficiently oblique to the Rays incident upon it, those Rays will begin to be totally reflected by it towards N; and first the most Refrangible Rays will be totally reflected (as was explained in the preceding experiment) and by consequence must first disappear at P, and afterwards the rest as they are in order totally reflected to N, they must disappear in the same order at R and T. So then the Rays which at O suffer the greatest Refraction, may be taken out of the Light MO whilst the rest of the Rays remain in it, and therefore that Light MO is Compounded of Rays differently Refrangible. And because the Planes AB and CD are parallel, and therefore by equal and contrary Refractions destroy one anothers Effects, the incident Light FM must be of the same kind and nature with the emergent Light MO, and therefore doth also consist of Rays differently Refrangible. These two Lights FM and MO, before the most refrangible Rays are separated out of the emergent Light MO agree in Colour, and in all other properties so far as my observation reaches, and therefore are deservedly reputed of the same Nature and Constitution, and by consequence the one is compounded as well as the other. But after the most Refrangible Rays begin to be totally reflected, and thereby separated out of the emergent Light MO, that Light changes its Colour from white to a dilute and faint yellow, a pretty good orange, a very full red successively and then totally vanishes. For after the most Refrangible Rays which paint the Paper at P with a Purple Colour, are by a total reflexion taken out of the Beam of Light MO, the rest of the Colours which appear on the Paper at R and T being mixed in the Light MO compound there a faint yellow, and after the blue and part of the green which appear on the Paper between P and R are taken away, the rest which appear between R and T (that is the Yellow, Orange, Red and a little Green) being mixed in the beam MO compound there an Orange; and when all the Rays are by reflexion taken out of the Beam MO, except the least Refrangible, which at T appear of a full Red, their Colour is the same in that Beam MO as afterwards at T, the Refraction of the Prism HJK serving only to separate the differently Refrangible Rays, without making any alteration in their Colours, as shall be more fully proved hereafter. All which confirms as well the first Proposition as the second.
Scholium. If this Experiment and the former be conjoyned and made one,[Image 26] by applying a fourth Prism VXY to refract the reflected Beam MN towards tp, the conclusion will be clearer. For then the Light Np which in the 4th Prism is more refracted, will become fuller and stronger when the Light OP, which in the third Prism HJK is more refracted, vanishes at P; and afterwards when the less refracted Light OT vanishes at T, the less refracted Light Nt will become encreased whilst the more refracted Light at p receives no further encrease. And as the trajected Beam MO in vanishing is always of such a Colour as ought to result from the mixture of the Colours which fall upon the Paper PT, so is the reflected Beam MN always of such a Colour as ought to result from the mixture of the Colours which fall upon the Paper pt. For when the most refrangible Rays are by a total Reflexion taken out of the Beam MO, and leave that Beam of an Orange Colour, the excess of those Rays in the reflected Light, does not only make the Violet, Indigo and Blue at p more full, but also makes the Beam MN change from the yellowish Colour of the Sun's Light, to a pale white inclining to blue, and afterward recover its yellowish Colour again, so soon as all the rest of the transmitted light MOT is reflected.
Now seeing that in all this variety of Experiments, whether the trial be made in Light reflected, and that either from natural Bodies, as in the first and second Experiment, or Specular, as in the Ninth; or in Light refracted, and that either before the unequally refracted Rays are by diverging separated from one another, and losing their whiteness which they have altogether, appear severally of several Colours, as in the fifth Experiment; or after they are separated from one another, and appear Coloured as in the sixth, seventh, and eighth Experiments; or in Light trajected through Parallel superficies, destroying each others Effects, as in the 10th Experiment; there are always found Rays, which at equal Incidences on the same Medium suffer unequal Refractions, and that without any splitting or dilating of single Rays, or contingence in the inequality of the Refractions, as is proved in the fifth and sixth Experiments; and seeing the Rays which differ in Refrangibility may be parted and sorted from one another, and that either by Refraction as in the third Experiment, or by Reflexion as in the tenth, and then the several sorts apart at equal Incidences suffer unequal Refractions, and those sorts are more refracted than others after separation, which were more refracted before it, as in the sixth and following Experiments, and if the Sun's Light be trajected through three or more cross Prisms successively, those Rays which in the first Prism are refracted more than others are in all the following Prisms refracted more then others in the same rate and proportion, as appears by the fifth Experiment; it's manifest that the Sun's Light is an Heterogeneous mixture of Rays, some of which are constantly more refrangible then others, as was proposed.
PROP. III. Theor. III.
The Sun's Light consists of Rays differing in Reflexibility, and those Rays are more Reflexible than others which are more Refrangible.
THIS is manifest by the ninth and tenth Experiments: For in the ninth Experiment, by turning the Prism about its Axis, until the Rays within it which in going out into the Air were refracted by its Base, became so oblique to that Base, as to begin to be totally reflected thereby; those Rays became first of all totally reflected which before at equal Incidences with the rest had suffered the greatest Refraction. And the same thing happens in the Reflexion made by the common Base of the two Prisms in the tenth Experiment.
<45>PROP. IV. Prob. I.
To separate from one another the Heterogeneous Rays of compound Light.
THE Heterogeneous Rays are in some measure separated from one another by the Refraction of the Prism in the third Experiment, and in the fifth Experiment by taking away the Penumbra from the Rectilinear sides of the Coloured Image, that separation in those very Rectilinear sides or straight edges of the Image becomes perfect. But in all places between those rectilinear edges, those innumerable Circles there described, which are severally illuminated by Homogeneal Rays, by interfering with one another, and being every where commixt, do render the Light sufficiently Compound. But if these Circles, whilst their Centers keep their distances and positions, could be made less in Diameter, their interfering one with another and by consequence the mixture of the Heterogeneous Rays would be proportionally diminished. In the 23th {sic} Figure[Image 27] let AG, BH, CJ, DK, EL, FM be the Circles which so many sorts of Rays flowing from the same Disque of the Sun, do in the third Experiment illuminate; of all which and innumerable other intermediate ones lying in a continual Series between the two Rectilinear and Parallel edges of the Sun's oblong Image PT, that Image is composed as was explained in the fifth Experiment. And let ag, bh, ci, dk, el, fm be so many less Circles lying in a like continual Series between two Parallel right Lines af and gm with the same distances between their Centers, and illuminated by the same sorts of Rays, that is the Circle ag with the same sort by which the corresponding Circle AG was illuminated, and the Circle bh with the same sort by which the corresponding Circle BH was illuminated, and the rest of the Circles ci, dk, el, fm respectively, with the same sorts of Rays by which the several corresponding Circles CJ, DK, EL, FM were illuminated. In the Figure PT composed of the greater Circles, three of those Circles AG, BH, CJ, are so expanded into one another, that the three sorts of Rays by which those Circles are illuminated, together with other innumerable sorts of intermediate Rays, are mixed at QR in the middle of the Circle BH. And the like mixture happens throughout almost the whole length of the Figure PT. But in the Figure pt composed of the less Circles, the three less Circles ag, bh, ci, which answer to those three greater, do not extend into one another; nor are there any where mingled so much as any two of the three sorts of Rays by which those Circles are illuminated, and which in the Figure PT are all of them intermingled at BH.
Now he that shall thus consider it, will easily understand that the mixture is diminished in the same Proportion with the Diameters of the Circles. If the Diameters of the Circles whilst their Centers remain the same, be made three times less than before, the mixture will be also three times less; if ten times less, the mixture will be ten times less, and so of other Proportions. That is, the mixture of the Rays in the greater Figure PT will be to their mixture in the less pt, as the Latitude of the greater Figure is to the Latitude of the less. For the Latitudes of these Figures are equal to the Diameters of their Circles. And hence it easily follows, that the mixture of the Rays in the refracted Spectrum pt is to the mixture of the Rays in the direct and immediate Light of the Sun, as the breadth of that Spectrum is to the difference between the length and breadth of the same Spectrum.
<47>So then, if we would diminish the mixture of the Rays, we are to diminish the Diameters of the Circles. Now these would be diminished if the Sun's Diameter to which they answer could be made less than it is, or (which comes to the same purpose) if without Doors, at a great distance from the Prism towards the Sun, some opake Body were placed, with a round hole in the middle of it, to intercept all the Sun's Light, excepting so much as coming from the middle of his Body could pass through that hole to the Prism. For so the Circles AG, BH and the rest, would not any longer answer to the whole Disque of the Sun, but only to that part of it which could be seen from the Prism through that hole, that it is to the apparent magnitude of that hole viewed from the Prism. But that these Circles may answer more distinctly to that hole a Lens is to be placed by the Prism to cast the Image of the hole, (that is, every one of the Circles AG, BH, &c.) distinctly upon the Paper at PT, after such a manner as by a Lens placed at a Window the Species of Objects abroad are cast distinctly upon a Paper within the Room, and the Rectilinear Sides of the oblong solar Image in the fifth Experiment became distinct without any Penumbra. If this be done it will not be necessary to place that hole very far off, no not beyond the Window. And therefore instead of that hole, I used the hole in the Window-shut as follows.
Exper. 11. In the Sun's Light let into my darkned Chamber through a small round hole in my Window-shut, at about 10 or 12 Feet from the Window, I placed a Lens, by which the Image of the hole might be distinctly cast upon a Sheet of white Paper, placed at the distance of six, eight, ten or twelve Feet from the Lens. For according to the difference of the Lenses I used various distances, which I think not worth the while to describe. Then immediately after the Lens I placed a Prism, by which the trajected Light might be refracted either upwards or sideways, and thereby the round Image which the Lens alone did cast upon the Paper might be drawn out into a long one with Parallel Sides, as in the third Experiment. This oblong Image I let fall upon another Paper at about the same distance from the Prism as before, moving the Paper either towards the Prism or from it, until I found the just distance where the Rectilinear Sides of the Image became most distinct. For in this case the circular Images of the hole which compose that Image after the same manner that the Circles ag, bh, ci, &c. do the Figure pt,[Image 28] were terminated most distinctly without any Penumbra, and therefore extended into one another the least that they could, and by consequence the mixture of the Heterogeneous Rays was now the least of all. By this means I used to form an oblong Image[Image 29] (such as is pt) of circular Images of the hole (such as are ag, bh, ci, &c.) and by using a greater or less hole in the Window-shut, I made the circular Images ag, bh, ci, &c. of which it was formed, to become greater or less at pleasure, and thereby the mixture of the Rays in the Image pt to be as much or as little as I desired.
Illustration. In the 24th Figure,[Image 30] F represents the circular hole in the Window-shut, MN the Lens whereby the Image or Species of that hole is cast distinctly upon a Paper at J, ABC the Prism whereby the Rays are at their emerging out of the Lens refracted from J towards another Paper at pt, and the round Image at J is turned into an oblong Image pt falling on that other Paper. This Image pt consists of Circles placed one after another in a Rectilinear order, as was sufficiently explained in the fifth Experiment; and these Circles are equal to the Circle I, and consequently answer in magnitude to the hole F; and therefore by diminishing that hole they may be at pleasure diminished, whil'st their Centers remain in their places. By this means I made the breadth of the Image pt to be forty times, and sometimes sixty or seventy times less than its length. As for instance, if the breadth of the hole F be of an Inch, and MF the distance of the Lens from the hole be 12 Feet; and if pB or pM the distance of the Image pt from the Prism or Lens be 10 Feet, and the refracting Angle of the Prism be 62 Degrees, the breadth of the Image pt will be of an Inch and the length about six Inches, and therefore the length to the breadth as 72 to 1, and by consequence the Light of this Image 71 times less compound than the Sun's direct Light. And Light thus far Simple and Homogeneal, is sufficient for trying all the Experiments in this Book about simple Light. For the composition of Heterogeneal Rays is in this Light so little that it is scarce to be discovered and perceived by sense, except perhaps in the Indigo and Violet; for these being dark Colours, do easily suffer a sensible allay by that little scattering Light which uses to be refracted irregularly by the inequalities of the Prism.
Yet instead of the circular hole F, 'tis better to substitute an oblong hole shaped like a long Parallelogram with its length Parallel to the Prism ABC. For if this hole be an Inch or two long, and but a tenth or twentieth part of an Inch broad, or narrower: the Light of the Image pt will be as simple as before or simpler, and the Image will become much broader, and therefore more fit to have Experiments tried in its Light than before.
Instead of this Parallelogram-hole may be substituted a Triangular one of equal Sides, whose Base for instance is about the tenth part of an Inch, and its height an Inch or more. For by this means, if the Axis of the Prism be Parallel to the Perpendicular of the Triangle, the Image pt will now be formed of Equicrural Triangles ag, bh, ci, dk, el, fm, &c.[Image 31] and innumerable other intermediate ones answering to the Triangular hole in shape and bigness, and lying one after another in a continual Series between two Parallel Lines af and gm. These Triangles are a little intermingled at their Bases but not at their Vertices, and therefore the Light on the brighter side af of the Image where the Bases of the Triangles are is a little compounded, but on the darker side gm is altogether uncompounded, and in all places between the sides the Composition is Proportional to the distances of the places from that obscurer side gm. And having a Spectrum pt of such a Composition, we may try Experiments either in its stronger and less simple Light near the side af, or in its weaker and simpler Light near the other side lm, as it shall seem most convenient.
But in making Experiments of this kind the Chamber ought to be made as dark as can be, lest any foreign Light mingle it self with the Light of the Spectrum pt, and render it compound; especially if we would try Experiments in the more simple Light next the side gm of the Spectrum; which being fainter, will have a less Proportion to the forreign Light; and so by the mixture of that Light be more troubled and made more compound. The Lens also ought to be good, such as may serve for Optical Uses, and the Prism ought to have a large Angle, suppose of 70 Degrees, and to be well wrought, being made of Glass free from Bubbles and Veins, with its sides not a little Convex or Concave as usually happens but truly plane, and its pollish elaborate, as in working Optickglasses, and not such as is usually wrought with Putty, whereby the edges of the Sand-holes being worn away, there are left all over the Glass a numberless company of very little Convex polite risings like Waves. The edges also of the Prism and Lens so far as they may make any irregular Refraction, must be covered with a black Paper glewed on. And all the Light of the Sun's beam let into the Chamber which is useless and unprofitable to the Experiment, ought to be intercepted with black Paper or other black Obstacles. For otherwise the useless Light being reflected every way in the Chamber, will mix with the oblong Spectrum and help to disturb it. In trying these things so much diligence is not altogether necessary, but it will promote the success of the Experiments, and by a very scrupulous Examiner of things deserves to be applied. It's difficult to get Glass Prisms fit for this purpose, and therefore I used sometimes Prismatick Vessels made with pieces of broken Looking-glasses, and filled with rain Water. And to increase the Refraction, I sometimes impregnated the Water strongly with Saccharum Saturni.
PROP. V. Theor. IV.
Homogeneal Light is refracted regularly without any Dilatation splitting or shattering of the Rays, and the confused Vision of Objects seen through Refracting Bodies by Heterogeneal Light arises from the different Refrangibility of several sorts of Rays.
THE first Part of this Proposition has been already sufficiently proved in the fifth Experiment, and will further appear by the Experiments which follow.
<52>Exper. 12. In the middle of a black Paper I made a round hole about a fifth or sixth part of an Inch in diameter. Upon this Paper I caused the Spectrum of Homogeneal Light described in the former Proposition, so to fall, that some part of the Light might pass through the hole of the Paper. This transmitted part of the Light I refracted with a Prism placed behind the Paper, and letting this refracted Light fall perpendicularly upon a white Paper two or three Feet distant from the Prism, I found that the Spectrum formed on the Paper by this Light was not oblong, as when 'tis made (in the third Experiment) by Refracting the Sun's compound Light, but was (so far as I could judge by my Eye) perfectly circular, the length being no greater than the breadth. Which shews that this Light is refracted regularly without any Dilatation of the Rays.
Exper. 13 In the Homogeneal Light I placed a Paper Circle of an Inch in Diameter, and in the Sun's unrefracted Heterogeneal white Light I placed another Paper Circle of the same bigness. And going from the Papers to the distance of some Feet, I viewed both Circles through a Prism. The Circle illuminated by the Sun's Heterogeneal Light appeared very oblong as in the fourth Experiment, the length being many times greater than the breadth: but the other Circle illuminated with Homogeneal Light appeared Circular and distinctly defined as when 'tis viewed with the naked Eye. Which proves the whole Proposition.
Exper. 14. In the Homogeneal Light I placed Flies and such like Minute Objects, and viewing them through a Prism, I saw their Parts as distinctly defined as if I had viewed them with the naked Eye. The same Objects placed in the Sun's unrefracted Heterogeneal Light which was white I viewed also through a Prism, and saw them most confusedly defined, so that I could not distinguish their smaller parts from one another. I placed also the Letters of a small Print one while in the Homogeneal Light and then in the Heterogeneal, and viewing them through a Prism, they appeared in the latter case so confused and indistinct that I could not read them; but in the former they appeared so distinct that I could read readily, and thought I saw them as distinct as when I viewed them with my naked Eye. In both cases I viewed the same Objects through the same Prism at the same distance from me and in the same Situation. There was no difference but in the Light by which the Objects were illuminated, and which in one case was Simple and in the other Compound, and therefore the distinct Vision in the former case and confused in the latter could arise from nothing else than from that difference of the Lights. Which proves the whole Proposition.
And in these three Experiments it is further very remarkable, that the Colour of Homogeneal Light was never changed by the Refraction.
PROP. VI. Theor. V.
The Sine of Incidence of every Ray considered apart, is to its Sine of Refraction in a given Ratio.
THAT every Ray considered apart is constant to it self in some degree of Refrangibility, is sufficiently manifest out of what has been said. Those Rays which in the first Refraction are at equal Incidences most refracted, are also in the following Refractions at equal Incidences most refracted; and so of the least Refrangible, and the rest which have any mean degree of Refrangibility, as is manifest by the 5th, 6th, 7th, 8th, and 9th Experiments. And those which the first time at like Incidences are equally refracted, are again at like Incidences equally and uniformly refracted, and that whether they be refracted before they be separated from one another as in the 5th Experiment, or whether they be refracted apart, as in the 12th, 13th and 14th Experiments. The Refraction therefore of every Ray apart is regular, and what Rule that Refraction observes we are now to shew.
The late Writers in Opticks teach, that the Sines of Incidence are in a given Proportion to the Sines of Refraction, as was explained in the 5th Axiom; and some by Instruments fitted for measuring of Refractions, or otherwise experimentally examining this Proportion, do acquaint us that they have found it accurate. But whilst they, not understanding the different Refrangibility of several Rays, conceived them all to be refracted according to one and the same Proportion, 'tis to be presumed that they adapted their Measures only to the middle of the refracted Light; so that from their measures we may conclude only that the Rays which have a mean degree of Refrangibility, that is those which when separated from the rest appear green, are refracted according to a given Proportion of their Sines. Amd therefore we are now to shew that the like given Proportions obtain in all the rest. That it should be so is very reasonable, Nature being ever conformable to her self; but an experimental Proof is desired. And such a Proof will be had if we can shew that the Sines of Refraction of Rays differently Refrangible are one to another in a given Proportion when their Sines of Incidence are equal. For if the Sines of Refraction of all the Rays are in given Proportions to the Sine of Refraction of a Ray which has a mean degree of Refrangibility, and this Sine is in a given Proportion to the equal Sines of Incidence, those other Sines of Refraction will also be in given Proportions to the equal Sines of Incidence. Now when the Sines of Incidence are equal, it will appear by the following Experiment that the Sines of Refraction are in a given Proportion to one another.
Exper. 15. The Sun shining into a dark Chamber through a little round hole in the Window-shut, let S represent his round white Image painted on the opposite Wall by his direct Light, PT his oblong coloured Image made by refracting that Light with a Prism placed at the Window;[Image 32] and pt, or 2p2t, 3p 3t, his oblong coloured Image made by refracting again the same Light sideways with a second Prism placed immediately after the first in a cross position to it, as was explained in the fifth Experiment; that is to say, pt when the Refraction of the second Prism is small, 2p 2t when its Refraction is greater, and 3p 3t when it is greatest. For such will be the diversity of the Refractions if the refracting Angle of the second Prism be of various Magnitudes; suppose of fifteen or twenty degrees to make the Image pt, of thirty or forty to make the Image 2p 2t, and of sixty to make the Image 3p 3t. But for want of solid Glass Prisms with Angles of convenient bignesses, there may be Vessels made of polished Plates of Glass cemented together in the form of Prisms and filled with Water. These things being thus ordered, I observed that all the solar Images or coloured Spectrums PT, pt, 2p 2t, 3p 3t did very nearly converge to the place S on which the direct Light of the Sun fell and painted his white round Image when the Prisms were taken away. The Axis of the Spectrum PT, that is the Line drawn through the middle of it Parallel to its Rectilinear Sides, did when produced pass exactly through the middle of that white round Image S. And when the Refraction of the second Prism was equal to the Refraction of the first, the refracting Angles of them both being about 60 Degrees, the Axis of the Spectrum 3p 3t made by that Refraction, did when produced pass also through the middle of the same white round Image S. But when the Refraction of the second Prism was less than that of the first, the produced Axes of the Spectrums tp or 2t 2p made by that Refraction did cut the produced Axis of the Spectrum TP in the Points m and n, a little beyond the Center of that white round Image S. Whence the Proportion of the Line 3tT to the Line 3pP was a little greater than the Proportion of 2tT or 2pP, and this Proportion a little greater than that of tT to pP. Now when the Light of the Spectrum PT falls perpendicularly upon the Wall, those Lines 3tT, 3pP, and 2tT, 2pP and tT, pP, are the Tangents of the Refractions; and therefore by this Experiment the Proportions of the Tangents of the Refractions are obtained, from whence the Proportions of the Sines being derived, they come out equal, so far as by viewing the Spectrums and using some Mathematical Reasoning I could estimate. For I did not make an Accurate Computation. So then the Proposition holds true in every Ray apart, so far as appears by Experiment. And that it is accurately true may be demonstrated upon this Supposition, That Bodies refract Light by acting upon its Rays in Lines Perpendicular to their Surfaces. But in order to this Demonstration, I must distinguish the Motion of every Ray into two Motions, the one Perpendicular to the refracting Surface, the other Parallel to it, and concerning the Perpendicular Motion lay down the following Proposition.
<57>If any Motion or moving thing whatsoever be incident with any velocity on any broad and thin Space terminated on both sides by two parallel Planes, and in its passage through that space be urged perpendicularly towards the further Plane by any force which at given distances from the Plane is of given quantities; the perpendicular Velocity of that Motion or Thing, at its emerging out of that space, shall be always equal to the Square Root of the summ of the Square of the perpendicular Velocity of that Motion or Thing at its Incidence on that space; and of the Square of the perpendicular Velocity which that Motion or Thing would have at its Emergence, if at its Incidence its perpendicular Velocity was infinitely little.
And the same Proposition holds true of any Motion or Thing perpendicularly retarded in its passage through that space, if instead of the Summ of the two Squares you take their difference. The Demonstration Mathematicians will easily find out, and therefore I shall not trouble the Reader with it.
Suppose now that a Ray coming most obliquely in the Line MC be refracted at C by the Plane RS into the Line CN,[Image 33] and if it be required to find the Line CE into which any other Ray AC shall be refracted; let MC, AD, be the Sines of incidence of the two Rays, and NG, EF, their Sines of Refraction, and let the equal Motions of the incident Rays be represented by the equal Lines MC and AC, and the Motion MC being considered as parallel to the refracting Plane, let the other Motion AC be distinguished into two Motions AD and DC, one of which AD is parallel, and the other DC perpendicular to the refracting Surface. In like manner, let the Motions of the emerging Rays be distinguish'd into two, whereof the perpendicular ones are and . And if the force of the refracting Plane begins to act upon the Rays either in that Plane or at a certain distance from it on the one side, and ends at a certain distance from it on the other side, and in all places between those two Limits acts upon the Rays in Lines perpendicular to that refracting Plane, and the Actions upon the Rays at equal distances from the refracting Plane be equal, and at unequal ones either equal or unequal according to any rate whatever; that motion of the Ray which is Parallel to the refracting Plane will suffer no alteration by that force; and that motion which is perpendicular to it will be altered according to the rule of the foregoing Proposition. If therefore for the perpendicular Velocity of the emerging Ray CN you write as above, then the perpendicular Velocity of any other emerging Ray CE which was , will be equal to the square Root of . And by squaring these equals, and adding to them the Equals ADq and MCq---CDq, and dividing the Summs by the Equals CFq + EFq and CGq + NGq, you will have equal to . Whence AD, the Sine of Incidence, is to EF the Sine of Refraction, as MC to NG, that is, in a given ratio. And this Demonstration being general, without determining what Light is, or by what kind of force it is refracted, or assuming any thing further than that the refracting Body acts upon the Rays in Lines perpendicular to its Surface; I take it to be a very convincing Argument of the full Truth of this Proposition.
<59>So then, if the ratio of the Sines of Incidence and Refraction of any sort of Rays be found in any one Case, 'tis given in all Cases; and this may be readily found by the Method in the following Proposition.
PROP. VII. Theor. VI.
The Perfection of Telescopes is impeded by the different Refrangibility of the Rays of Light.
THE imperfection of Telescopes is vulgarly attributed to the spherical Figures of the Glasses, and therefore Mathematicians have propounded to Figure them by the Conical Sections. To shew that they are mistaken, I have inserted this Proposition; the truth of which will appear by the measures of the Refractions of the several sorts of Rays; and these measures I thus determine.
In the third Experiment of the first Book, where the refracting Angle of the Prism was degrees, the half of that Angle 31 deg. 15 min. is the Angle of Incidence of the Rays at their going out of the Glass into the Air; and the Sine of this Angle is 5188, the Radius being 10000. When the Axis of this Prism was parallel to the Horizon, and the Refraction of the Rays at their Incidence on this Prism equal to that at their Emergence out of it, I observed with a Quadrant the Angle which the mean refrangible Rays (that is, those which went to the middle of the Sun's coloured Image) made with the Horizon and by this Angle and the Sun's altitude observed at the same time, I found the Angle which the emergent Rays contained with the incident to be 44 deg. and 40 min. and the half of this Angle added to the Angle of Incidence 31 deg. 15 min. makes the Angle of Refraction, which is therefore 53 deg. 35 min. and its Sine 8047. These are the Sines of Incidence and Refraction of the mean refrangible Rays, and their proportion in round numbers is 20 to 31. This Glass was of a Colour inclining to green. The last of the Prisms mentioned in the third Experiment was of clear white Glass. Its refracting Angle degrees. The Angle which the emergent Rays contained, with the incident 45 deg. 50 min. The Sine of half the first Angle 5262. The Sine of half the Summ of the Angles 8157. And their proportion in round numbers 20 to 31 as before.
From the Length of the Image, which was about or 10 Inches, subduct its Breadth, which was Inches, and the Remainder Inches would be the length of the Image were the Sun but a point, and therefore subtends the Angle which the most and least refrangible Rays, when incident on the Prism in the same Lines, do contain with one another after their Emergence. Whence this Angle is 2 deg. 0′. 7″. For the distance between the Image and the Prism where this Angle is made, was Feet, and at that distance the Chord Inches subtends an Angle of 2 deg. 0′ 7″. Now half this Angle is the Angle which these emergent Rays contain with the emergent mean refrangible Rays, and a quarter thereof, that is 30′. 2″. may be accounted the Angle which they would contain with the same emergent mean refrangible Rays, were they co-incident to them within the Glass and suffered no other Refraction then that at their Emergence. For if two equal Refractions, the one at the incidence of the Rays on the Prism, the other at their Emergence, make half the Angle 2 deg. 0′. 7″. then one of those Refractions will make about a quarter of that Angle, and this quarter added to and subducted from the Angle of Refraction of the mean refrangible Rays, which was 53 deg. 35′, gives the Angles of Refraction of the most and least refrangible Rays 54 deg. 5′ 2″, and 53 deg. 4′ 58″, whose Sines are 8099 and 7995, the common Angle of Incidence being 31 deg. 15′ and its Sine 5188; and these Sines in the least round numbers are in proportion to one another as 78 and 77 to 50.
Now if you subduct the common Sine of Incidence 50 from the Sines of Refraction 77 and 78, the remainders 27 and 28 shew that in small Refractions the Refraction of the least refrangible Rays is to the Refraction of the most refrangible ones as 27 to 28 very nearly, and that the difference of the Refractions of the least refrangible and most refrangible Rays is about the th part of the whole Refraction of the mean refrangible Rays.
Whence they that are skilled in Opticks will easily understand, that the breadth of the least circular space into which Object-Glasses of Telescopes can collect all sorts of Parallel Rays, is about the th part of half the aperture of the Glass, or 55th Part of the whole aperture; and that the Focus of the most refrangible Rays is nearer to the Object-Glass than the Focus of the least refrangible ones, by about the th part of the distance between the Object-Glass and the Focus of the mean refrangible ones.
And if Rays of all sorts, flowing from any one lucid point in the Axis of any convex Lens, be made by the Refraction of the Lens to converge to points not too remote from the Lens, the Focus of the most refrangible Rays shall be nearer to the Lens than the Focus of the least refrangible ones, by a distance which is to the th part of the distance of the Focus of the mean refrangible Rays from the Lens as the distance between that Focus and the lucid point from whence the Rays flow is to the distance between that lucid point and the Lens very nearly.
Now to examine whether the difference between the Refractions which the most refrangible and the least refrangible Rays flowing from the same point suffer in the Object-Glasses of Telescopes and such like Glasses, be so great as is here described, I contrived the following Experiment.
Exper. 16. The Lens which I used in the second and eighth Experiments, being placed six Feet and an Inch distant from any Object, collected the Species of that Object by the mean refrangible Rays at the distance of six Feet and an Inch from the Lens on the other side. And therefore by the foregoing Rule it ought to collect the Species of that Object by the least refrangible Rays at the distance of six Feet and Inches from the Lens, and by the most refrangible ones at the distance of five Feet and Inches from it: So that between the two places where these least and most refrangible Rays collect the Species, there may be the distance of about Inches. For by that Rule, as six Feet and an Inch (the distance of the Lens from the lucid Object) is to twelve Feet and two Inches (the distance of the lucid Object from the Focus of the mean refrangible Rays) that is, as one is to two, so is the th part of six Feet and an Inch (the distance between the Lens and the same Focus) to the distance between the Focus of the most refrangible Rays and the Focus of the least refrangible ones, which is therefore Inches, that is very nearly Inches. Now to know whether this measure was true, I repeated the second and eighth Experiment of this Book with coloured Light, which was less compounded than that I there made use of: For I now separated the heterogeneous Rays from one another by the method I described in the 11th Experiment, so as to make a coloured Spectrum about twelve or fifteen times longer than broad. This Spectrum I cast on a printed book, and placing the above-mentioned Lens at the distance of six Feet and an Inch from this Spectrum to collect the Species of the illuminated Letters at the same distance on the other side, I found that the Species of the Letters illuminated with Blue were nearer to the Lens than those illuminated with deep Red by about three Inches or three and a quarter: but the Species of the Letters illuminated with Indigo and Violet appeared so confused and indistinct, that I could not read them: Whereupon viewing the Prism, I found it was full of Veins running from one end of the Glass to the other; so that the Refraction could not be regular. I took another Prism therefore which was free from Veins, and instead of the Letters I used two or three parallel black Lines a little broader than the strokes of the Letters, and casting the Colours upon these Lines in such manner that the Lines ran along the Colours from one end of the Spectrum to the other, I found that the Focus where the Indigo, or confine of this colour and Violet cast the Species of the black Lines most distinctly, to be about 4 Inches or nearer to the Lens than the Focus where the deepest Red cast the Species of the same black Lines most distinctly. The violet was so faint and dark, that I could not discern the Species of the Lines distinctly by that Colour; and therefore considering that the Prism was made of a dark coloured Glass inclining to Green, I took another Prism of clear white Glass; but the Spectrum of Colours which this Prism made had long white streams of faint Light shooting out from both ends of the Colours, which made me conclude that something was amiss; and viewing the Prism, I found two or three little Bubbles in the Glass which refracted the Light irregulariy. Wherefore I covered that part of the Glass with black Paper, and letting the Light pass through another part of it which was free from such Bubbles, the Spectrum of Colours became free from those irregular Streams of Light, and was now such as I desired. But still I found the Violet so dark and faint, that I could scarce see the Species of the Lines by the Violet, and not at all by the deepest part of it, which was next the end of the Spectrum. I suspected therefore that this faint and dark Colour might be allayed by that scattering Light which was refracted, and reflected irregularly, partly by some very small Bubbles in the Glasses and partly by the inequalities of their Polish: which Light, tho' it was but little, yet it being of a White Colour, might suffice to affect the Sense so strongly as to disturb the Phænomena of that weak and dark Colour the Violet, and therefore I tried, as in the 12th, 13th, 14th Experiments, whether the Light of this Colour did not consist of a sensible mixture of heterogeneous Rays, but found it did not. Nor did the Refractions cause any other sensible Colour than Violet to emerge out of this Light, as they would have done out of White Light, and by consequence out of this Violet Light had it been sensibly compounded with White Light. And therefore I concluded, that the reason why I could not see the Species of the Lines distinctly by this Colour, was only the darkness of this Colour and Thinness of its Light, and its distance from the Axis of the Lens; I divided therefore those Parallel Black Lines into equal Parts, by which I might readily know the distances of the Colours in the Spectrum from one another, and noted the distances of the Lens from the Foci of such Colours as cast the Species of the Lines distinctly, and,then considered whether the difference of those distances bear such proportion to Inches, the greatest difference of the distances which the Foci of the deepest Red and Violet ought to have from the Lens, as the distance of the observed Colours from one another in the Spectrum bear to the like distance of the deepest Red and Violet measured in the rectilinear sides of the Spectrum, that is, to the length of those sides or excess of the length of the Spectrum above its breadth. And my Observations were as follows.
When I observed and compared the deepest sensible Red, and the Colour in the Confine of Green and Blue, which at the rectilinear sides of the Spectrum was distant from it half the length of those sides, the Focus where the Confine of Green and Blue cast the Species of the Lines distinctly on the Paper, was nearer to the Lens than the Focus where the Red cast those Lines distinctly on it by about or Inches. For sometimes the Measures were a little greater, sometimes a little less, but seldom varied from one another above of an Inch. For it was very difficult to define the places of the Foci, without some little Errors. Now if the Colours distant half the length of the Image, (measured at its rectilinear sides) give or difference of the distances of their Foci from the Lens, then the Colours distant the whole length ought to give 5 or Inches difference of those distances.
But here it's to be noted, that I could not see the Red to the full End of the Spectrum, but only to the Center of the Semicircle which bounded that End, or a little farther; and therefore I compared this Red not with that Colour which was exactly in the middle of the Spectrum, or Confine of Green and Blue, but with that which verged a little more to the Blue than to the Green: And as I reckoned the whole length of the Colours not to be the whole length of the Spectrum, but the length of its rectilinear sides, so completing the Semicirlar Ends into Circles, when either of the observed Colours fell within those Circles, I measured the distance of that Colour from the End of the Spectrum, and subducting half this distance from the measured distance of the Colours, I took the remainder for their corrected distance; and in these Observations set down this corrected distance for the difference of the distances from the Lens. For as the length of the rectilinear sides of the Spectrum would be the whole length of all the Colours, were the Circles of which (as we shewed) that Spectrum consists contracted and reduced to Physical Points, so in that Case this corrected distance would be the real distance of the observed Colours.
When therefore I further observed the deepest sensible Red, and that Blue whose corrected distance from it was parts of the length of the rectilinear sides of the Spectrum, the difference of the distances of their Foci from the Lens was about Inches, and as 7 to 12 so is to .
When I observed the deepest sensible Red, and that Indigo whose corrected distance was or of the length of the rectilinear sides of the Spectrum, the difference of the distances of their Foci from the Lens, was about Inches, and as 2 to 3 so is to .
When I observed the deepest sensible Red, and that deep Indigo whose corrected distance from one another was or of the length of the rectilinear sides of the Spectrum, the difference of the distances of their Foci from the Lens was about 4 Inches; and as 3 to 4 so is 4 to .
When I observed the deepest sensible Red, and that part of the Violet next the Indigo whose corrected distance from the Red was or of the length of the rectilinear sides of the Spectrum, the difference of the distances of their Foci from the Lens was about Inches; and as 5 to 6, so is to {}. For sometimes when the Lens was advantagiously placed, so that its Axis respected the Blue, and all things else were well ordered, and the Sun shone clear, and I held my Eye very near to the Paper on which the Lens cast the Species of the Lines, I could see pretty distinctly the Species of those Lines by that part of the Violet which was next the Indigo; and sometimes I could see them by above half the Violet. For in making these Experiments I had observed, that the Species of those Colours only appear distinct which were in or near the Axis of the Lens: So that if the Blue or Indigo were in the Axis, I could see their Species distinctly; and then the Red appeared much less distinct than before. Wherefore I contrived to make the Spectrum of Colours shorter than before, so that both its Ends might be nearer to the Axis of the Lens. And now its length was about Inches and breadth about or of an Inch. Also instead of the black Lines on which the Spectrum was cast, I made one black Line broader than those, that I might see its Species more easily; and this Line I divided by short cross Lines into equal Parts, for measuring the distances of the observed Colours. And now I could sometimes see the Species of this Line with its divisions almost as far as the Centers of the Semicircular Violet End of the Spectrum, and made these further Observations.
When I observed the deepest sensible Red, and that part of the Violet whose corrected distance from it was about Parts of the rectilinear sides of the Spectrum the difference of the distances of the Foci of those Colours from the Lens, was one time , another time , another time {} Inches, and as 8 to 9, so are , , {}, to respectively.
<68>When I observed the deepest sensible Red, and deepest sensible Violet, (the corrected distance of which Colours when all things were ordered to the best advantage, and the Sun shone very clear, was about or parts of the length of the rectilinear sides of the coloured Spectrum) I found the difference of the distances of their Foci from the Lens sometimes sometimes , and for the most part 5 Inches or thereabouts: and as 11 to 12 or 15 to 16, so is five Inches to or Inches.
And by this progression of Experiments I satisfied my self, that had the Light at the very Ends of the Spectrum been strong enough to make the Species of the black Lines appear plainly on the Paper, the Focus of the deepest Violet would have been found nearer to the Lens, than the Focus of the deepest Red, by about Inches at least. And this is a further Evidence, that the Sines of Incidence and Refraction of the several sorts of Rays, hold the same proportion to one another in the smallest Refractions which they do in the greatest.
My progress in making this nice and troublesome Experiment I have set down more at large, that they that shall try it after me may be aware of the Circumspection requisite to make it succeed well. And if they cannot make it succeed so well as I did, they may notwithstanding collect by the Proportion of the distance of the Colours of the Spectrum, to the difference of the distances of their Foci from the Lens, what would be the success in the more distant Colours by a better Trial. And yet if they use a broader Lens than I did, and fix it to a long streight Staff by means of which it may be readily and truly directed to the Colour whose Focus is desired, I question not but the Experiment will succeed better with them than it did with me. For I directed the Axis as nearly as I could to the middle of the Colours, and then the faint Ends of the Spectrum being remote from the Axis, cast their Species less distinctly on the Paper than they would have done had the Axis been successively directed to them.
Now by what has been said, its certain that the Rays which differ in refrangibility do not converge to the same Focus, but if they flow from a lucid point, as far from the Lens on one side as their Foci are on the other, the Focus of the most refrangible Rays shall be nearer to the Lens than that of the least refrangible, by above the fourteenth part of the whole distance: and if they flow from a lucid point, so very remote from the Lens that before their Incidence they may be accounted Parallel, the Focus of the most refrangible Rays shall be nearer to the Lens than the Focus of the least refrangible, by about the 27th or 28th part of their whole distance from it. And the Diameter of the Circle in the middle space between those two Foci which they illuminate when they fall there on any Plane, perpendicular to the Axis (which Circle is the least into which they can all be gathered) is about the 55th part of the Diameter of the aperture of the Glass. So that 'tis a wonder that Telescopes represent Objects so distinct as they do. But were all the Rays of Light equally refrangible, the Error arising only from the Sphericalness of the Figures of Glasses would be many hundred times less. For if the Object-glass of a Telescope be Plano-convex, and the Plane side be turned towards the Object, and the Diameter of the Sphere whereof this Glass is a segment, be called D, and the Semidiameter of the aperture of the Glass be called S, and the Sine of Incidence out of Glass into Air, be to the Sine of Refraction as I to R: the Rays which come Parallel to the Axis of the Glass, shall in the place where the Image of the Object is most distinctly made, be scattered all over a little Circle whose Diameter is very nearly, as I gather by computing the Errors of the Rays by the method of infinite Series, and rejecting the Terms whose quantities are inconsiderable. As for instance, if the Sine of Incidence I, be to the Sine of Refraction R, as 20 to 31, and if D the Diameter of the Sphere to which the Convex side of the Glass is ground, be 100 Feet or 1200 Inches, and S the Semidiameter of the aperture be two Inches, the Diameter of the little Circle, (that is ) will be (or ) parts of an Inch. But the Diameter of the little Circle through which these Rays are scattered by unequal refrangibility, will be about the 55th part of the aperture of the Object-glass, which here is four Inches. And therefore the Error arising from the spherical Figure of the Glass, is to the Error arising from the different Refrangibility of the Rays, as to that is as 1 to 8151: and therefore being in Comparison so very little, deserves not to be considered.
But you will say, if the Errors caused by the different refrangibility be so very great, how comes it to pass that Objects appear through Telescopes so distinct as they do? I answer, 'tis because the erring Rays are not scattered uniformly over all that circular space, but collected infinitely more densely in the Center than in any other part of the Circle, and in the way from the Center to the Circumference grow continually rarer and rarer, so as at the Circumference to become infinitely rare; and by reason of their rarity are not strong enough to be visible, unless in the Center and very near it. Let ADE represent one of those Circles described with the Center C and Semidiameter AC, and let BFG be a smaller Circle concentric to the former,[Image 34] cutting with its Circumference the Diameter AC in B, and bisect AC in N, and by my reckoning the density of the Light in any Place B will be to its density in N, as AB to BC; and the whole Light within the lesser Circle BFG, will be to the whole Light within the greater AED, as the Excess of the Square of AC above the Square of AB, is to the Square of AC. As if BC be the fifth part of AC, the Light will be four times denser in B than in N, and the whole Light within the less Circle, will be to the whole Light within the greater, as nine to twenty five. Whence it's evident that the Light within the less Circle, must strike the sense much more strongly, than that faint and dilated Light round about between it and the Circumference of the greater.
But its further to be noted, that the most luminous of the prismatick Colours are the Yellow and Orange. These affect the Senses more strongly than all the rest together, and next to these in strength are the Red and Green. The Blue compared with these is a faint and dark Colour, and the Indigo and Violet are much darker and fainter, so that these compared with the stronger Colours are little to be regarded. The Images of Objects are therefore to be placed, not in the Focus of the mean refrangible Rays which are in the confine of Green and Blue, but in the Focus of those Rays which are in the middle of the Orange and Yellow; there where the Colour is most luminous and fulgent, that is in the brightest Yellow, that Yellow which inclines more to Orange than to Green. And by the Refraction of these Rays (whose Sines of Incidence and Refraction in Glass are as 17 and 11) the Refraction of Glass and Crystal for optical uses is to be measured. Let us therefore place the Image of the Object in the Focus of these Rays, and all the Yellow and Orange will fall within a Circle, whose Diameter is about the 250th Part of the Diameter of the aperture of the Glass. And if you add the brighter half of the Red, (that half which is next the Orange, and the brighter half of the Green, (that half which is next the Yellow,) about three fifth parts of the Light of these two Colours will fall within the same Circle, and two fifth parts will fall without it round about; and that which falls without will be spread through almost as much more space as that which falls within, and so in the gross be almost three times rarer. Of the other half of the Red and Green, (that is of the deep dark Red and Willow Green) about one quarter will fall within this Circle, and three quarters without, and that which falls without will be spread through about four or five times more space than that which falls within; and so in the gross be rarer, and if compared with the whole Light within it, will be about 25 times rarer than all that taken in the gross; or rather more than 30 or 40 times rarer, because the deep red in the end of the Spectrum of Colours made by a Prism is very thin and rare, and the Willow Green is something rarer than the Orange and Yellow. The Light of these Colours therefore being so very much rarer than that within the Circle, will scarce affect the Sense, especially since the deep Red and Willow Green of this Light, are much darker Colours than the rest. And for the same reason the Blue and Violet being much darker Colours than these, and much more rarified, may be neglected. For the dense and bright Light of the Circle, will obscure the rare and weak Light of these dark Colours round about it, and render fhem almost insensible. The sensible Image of a lucid point is therefore scarce broader than a Circle whose Diameter is the 250th part of the diameter of the aperture of the Object Glass of a good Telescope, or not much broader, if you except a faint and dark misty light round about it, which a Spectator will scarce regard. And therefore in a Telescope whose aperture is four Inches, and length an hundred Feet, it exceeds not 2″ 45", or 3″. And in a Telescope whose aperture is two Inches, and length 20 or 30 Feet, it may be 5″ or 6″ and scarce above. And this Answers well to Experience: For some Astronomers have found the Diameters of the fixt Stars, in Telescopes of between twenty and sixty Feet in length, to be about 4″ or 5″, or at most 6″ in diameter. But if the Eye-Glass be tincted faintly with the smoke of a Lamp or Torch, to obscure the Light of the Star, the fainter Light in the Circumference of the Star ceases to be visible, and the Star (if the Glass be sufficiently soiled with smoke) appears something more like a Mathematical Point. And for the same reason, the enormous part of the Light in the Circumference of every lucid Point ought to be less discernable in shorter Telescopes than in longer, because the shorter transmit less Light to the Eye.
Now if we suppose the sensible Image of a lucid Point, to be even 250 times narrower than the aperture of the Glass: yet were it not for the different refrangibility of the Rays, its breadth in an 100 Foot Telescope whose aperture is 4 Inches would be but parts of an Inch, as is manifest by the foregoing Computation. And therefore in this Case the greatest Errors arising from the spherical Figure of the Glass, would be to the greatest sensible Errors arising from the different refrangibility of the Rays as to at most, that is only as 1 to 1826. And this sufficiently shews that it is not the spherical Figures of Glasses but the different refrangibility of the Rays which hinders the perfection of Telescopes.
There is another Argument by which it may appear that the different refrangibility of Rays, is the true cause of the imperfection of Telescopes. For the Errors of the Rays arising from the spherical Figures of Object-Glasses, are as the Cubes of the apertures of the Object-Glasses; and thence to make Telescopes of various lengths, magnify with equal distinctness, the apertures of the Object-Glasses, and the Charges or magnifying Powers, ought to be as the Cubes of the square Roots of their lengths; which doth not answer to Experience. But the errors of the Rays arising from the different refrangibility, are as the apertures of the Object-Glasses, and thence to make Telescopes of various lengths, magnify with equal distinctness, their apertures and charges ought to be as the square Roots of their lengths; and this answers to experience as is well known. For instance, a Telescope of 64 Feet in length, with an aperture of Inches, magnifies about 120 times, with as much distinctness as one of a Foot in length, with {} of an Inch aperture, magnifies 15 times.
Now were it not for this different refrangibility of Rays, Telescopes might be brought to a greater Perfection than we have yet described, by composing the Object-Glass of two Glasses with Water between them. Let ADFC represent the Object-Glass composed of two Glasses ABED and BEFC,[Image 35] alike convex on the outsides AGD and CHF, and alike concave on the insides BME, BNE, with Water in the concavity BMEN. Let the Sine of Incidence out of Glass into Air be as I to R and out of Water into Air as K to R, and by consequence out of Glass into Water, as I to K: and let the Diameter of the Sphere to which the convex sides AGD and CHF are ground be D, and the Diameter of the Sphere to which the concave sides BME and BNE are ground be to D, as the Cube Root of KK-KI to the Cube Root of RK-RI: and the Refractions on the concave sides of the Glasses, will very much correct the Errors of the Refractions on the convex sides, so far as they arise from the sphericalness of the Figure. And by this means might Telescopes be brought to sufficient perfection, were it not for the different refrangibility of several sorts of Rays. But by reason of this different refrangibility, I do not yet see any other means of improving Telescopes by Refractions alone than that of increasing their lengths, for which end the late contrivance of Hugenius seems well accommodated. For very long Tubes are cumbersome, and scarce to be readily managed, and by reason of their length are very apt to bend, and shake by bending so as to cause a continual trembling in the Objects, whereby it becomes difficult to see them distinctly: whereas by his contrivance the Glasses are readily manageable, and the Object-Glass being fixt upon a strong upright Pole becomes more steddy.
Seeing therefore the improvement of Telescopes of given lengths by Refractions is desperate; I contrived heretofore a Perspective by reflexion, using instead of an Object-Glass a concave Metal. The diameter of the Sphere to which the Metal was ground concave was about 25 English Inches, and by consequence the length of the Instrument about six Inches and a quarter. The Eye-Glass was plano-convex, and the Diameter of the Sphere to which the convex side was ground was about of an Inch, or a little less, and by consequence it magnified between 30 and 40 times. By another way of measuring I found that it magnified about 35 times. The Concave Metal bore an aperture of an Inch and a third part; but the aperture was limited not by an opake Circle, covering the Limb of the Metal round about, but by an opake circle placed between the Eye-Glass and the Eye, and perforated in the middle with a little round hole for the Rays to pass through to the Eye. For this Circle by being placed here, stopt much of the erroneous Light, which otherwise would have disturbed the Vision. By comparing it with a pretty good Perspective of four Feet in length, made with a concave Eye-Glass, I could read at a greater distance with my own Instrument than with the Glass. Yet Objects appeared much darker in it than in the Glass, and that partly because more Light was lost by reflexion in the Metal, then by refraction in the Glass, and partly because my Instrument was overcharged. Had it magnified but 30 or 25 times it would have made the Object appear more brisk and pleasant. Two of these I made about 16 Years ago, and have one of them still by me by which I can prove the truth of what I write. Yet it is not so good as at the first. For the concave has been divers times tarnished and cleared again, by rubbing it with very soft Leather. When I made these, an Artist in London undertook to imitate it; but using another way of polishing them than I did, he fell much short of what I had attained to, as I afterwards understood by discoursing the under-Workman he had imployed. The Polish I used was in this manner. I had two round Copper Plates each six Inches in Diameter, the one convex the other concave, ground very true to one another. On the convex I ground the Object-Metal or concave which was to be polish'd, till it had taken the Figure of the convex and was ready for a Polish. Then I pitched over the convex very thinly, by dropping melted pitch upon it and warming it to keep the pitch soft, whilst I ground it with the concave Copper wetted to make it spread eavenly all over the convex. Thus by working it well I made it as thin as a Groat, and after the convex was cold I ground it again to give it as true a Figure as I could. Then I took Putty which I had made very fine by washing it from all its grosser Particles, and laying a little of this upon the pitch, I ground it upon the Pitch with the concave Copper till it had done making a noise; and then upon the Pitch I ground the Object-Metal with a brisk Motion, for about two or three Minutes of time, leaning hard upon it. Then I put fresh Putty upon the Pitch and ground it again till it had done making a noise, and afterwards ground the Object Metal upon it as before. And this Work I repeated till the Metal was polished, grinding it the last time with all my strength for a good while together, and frequently breathing upon the Pitch to keep it moist without laying on any more fresh Putty. The Object-Metal was two Inches broad and about one third part of an Inch thick, to keep it from bending. I had two of these Metals, and when I had polished them both I tried which was best, and ground the other again to see if I could make it better than that which I kept. And thus by many Trials I learn'd the way of polishing, till I made those two reflecting Perspectives I spake of above. For this Art of polishing will be better learnt by repeated Practice than by my description. Before I ground the Object Metal on the Pitch, I always ground the Putty on it with the concave Copper till it had done making a noise, because if the Particles of the Putty were not by this means made to stick fast in the Pitch, they would by rolling up and down grate and fret the Object Metal and fill it full of little holes.
But because Metal is more difficult to polish than Glass and is afterwards very apt to be spoiled by tarnishing, and reflects not so much Light as Glass quick-silvered over does: I would propound to use instead of the Metal, a Glass ground concave on the foreside, and as much convex on the backside, and quick-silvered over on the convex side. The Glass must be every where of the same thickness exactly. Otherwise it will make Objects look coloured and indistinct. By such a Glass I tried about five or six Years ago to make a reflecting Telescope of four Feet in length to magnify about 150 times, and I satisfied my self that there wants nothing but a good Artist to bring the design to perfection. For the Glass being wrought by one of our London Artists after such a manner as they grind Glasses for Telescopes, tho it seemed as well wrought as the Object Glasses use to be, yet when it was quick-silvered, the reflexion discovered innumerable Inequalities all over the Glass. And by reason of these Inequalities, Objects appeared indistinct in this Instrument. For the Errors of reflected Rays caused by any Inequality of the Glass, are about six times greater than the Errors of refracted Rays caused by the like Inequalities. Yet by this Experiment I satisfied my self that the reflexion on the concave side of the Glass, which I feared would disturb the vision, did no sensible prejudice to it, and by consequence that nothing is wanting to perfect these Telescopes, but good Workmen who can grind and polish Glasses truly spherical. An Object-Glass of a fourteen Foot Telescope, made by one of our London Artificers, I once mended considerably, by grinding it on Pitch with Putty, and leaning very easily on it in the grinding, lest the Putty should scratch it. Whether this way may not do well enough for polishing these reflecting Glasses, I have not yet tried. But he that shall try either this or any other way of polishing which he may think better, may do well to make his Glasses ready for polishing by grinding them without that violence, wherewith our London Workmen press their Glasses in grinding. For by such violent pressure, Glasses are apt to bend a little in the grinding, and such bending will certainly spoil their Figure. To recommend therefore the consideration of these reflecting Glasses, to such Artists as are curious in figuring Glasses, I shall describe this Optical Instrument in the following Proposition.
<79>PROP. VII. Prob. II.
To shorten Telescopes.
LET ABCD represent a Glass spherically concave on the foreside AB,[Image 36] and as much convex on the backside CD, so that it be every where of an equal thickness. Let it not be thicker on one side than on the other, lest it make Objects appear coloured and indistinct, and let it be very truly wrought and quick-silvered over on the backside; and set in the Tube VXYZ which must be very black within. Let EFG represent a Prism of Glass or Crystal placed near the other end of the Tube, in the middle of it, by means of a handle of Brass or Iron FGK, to the end of which made flat it is cemented. Let this Prism be rectangular at E, and let the other two Angles at F and G be accurately equal to each other, and by consequence equal to half right ones, and let the plane sides FE and GE be square, and by consequence the third side FG a rectangular parallelogram, whose length is to its breadth in a subduplicate proportion of two to one. Let it be so placed in the Tube, that the Axis of the Speculum may pass through the middle of the square side EF perpendicularly, and by consequence through the middle of the side FG at an Angle of 45 Degrees, and let the side EF be turned towards the Speculum, and the distance of this Prism from the Speculum be such that the Rays of the Light PQ, RS, &c. which are incident upon the Speculum in Lines parallel to the Axis thereof, may enter the Prism at the side EF, and be reflected by the side FG, and thence go out of it through the side GE, to the Point T which must be the common Focus of the Speculnm ABDC, and of a Plano-convex Eye-Glass H, through which those Rays must pass to the Eye. And let the Rays at their coming out of the Glass pass through a small round hole, or aperture made in a little plate of Lead, Brass, or Silver, wherewith the Glass is to be covered, which hole must be no bigger than is necessary for light enough to pass through. For so it will render the Object distinct, the Plate in which 'tis made intercepting all the erroneous part of the Light which comes from the verges of the Speculum AB. Such an Instrument well made if it be 6 Foot long, (reckoning the length from the Speculum to the Prism, and thence to the Focus T) will bear an aperture of 6 Inches at the Speculum, and magnify between two and three hundred times. But the hole H here limits the aperture with more advantage, than if the aperture was placed at the Speculum. If the Insirument be made longer or shorter, the aperture must be in proportion as the Cube of the square Root of the length, and the magnifying as the aperture. But its convenient that the Speculum be an Inch or two broader than the aperture at the least, and that the Glass of the Speculum be thick, that it bend not in the working. The Prism EFG must be no bigger than is necessary, and its back side FG must not be quick-silvered over. For without quick-silver it will reflect all the Light incident on it from the Speculum.
In this Instrument the Object will be inverted, but may be erected by making the square sides FF and EG of the Prism EFG not plane but spherically convex, that the Rays may cross as well before they come at it as afterwards between it and the Eye-Glass. If it be desired that the Instrument bear a larger aperture, that may be also done by composing the Speculum of two Glasses with Water between them.
[Image 1] Fig. 1. 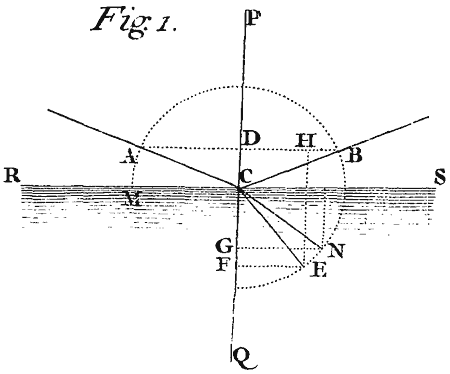
[Image 2] Fig. 2. 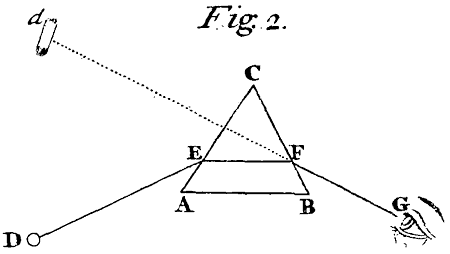
[Image 3] Fig. 3. 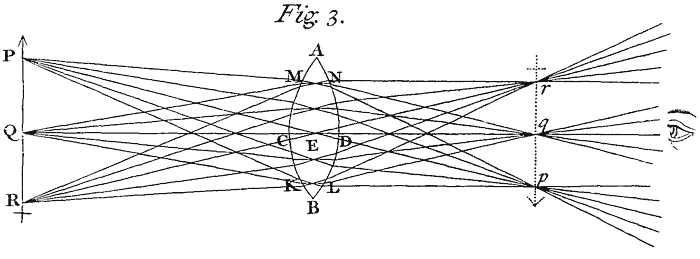
[Image 4] Fig. 4. 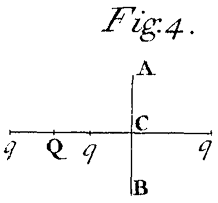
[Image 5] Fig. 5. 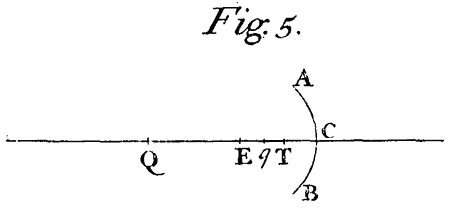
[Image 6] Fig. 6. 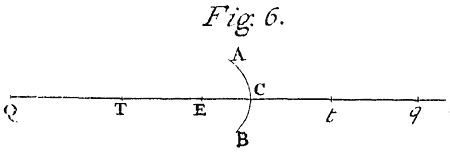
[Image 7] Fig. 7. 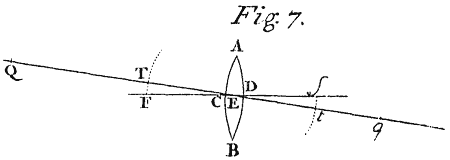
[Image 8] Fig. 3. 
[Image 9] Fig. 8. 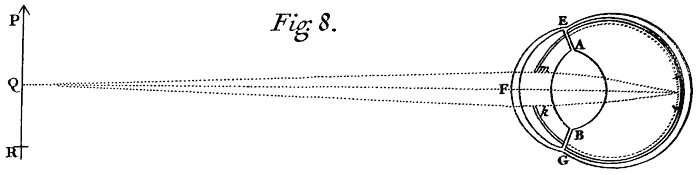
[Image 10] Fig. 9. 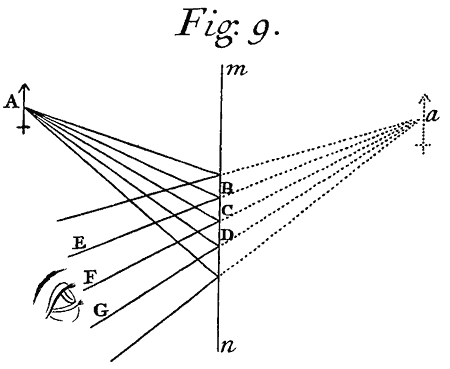
[Image 11] Fig. 2. 
[Image 12] Fig. 10. 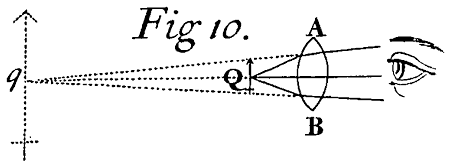
[Image 13] Fig. 11. 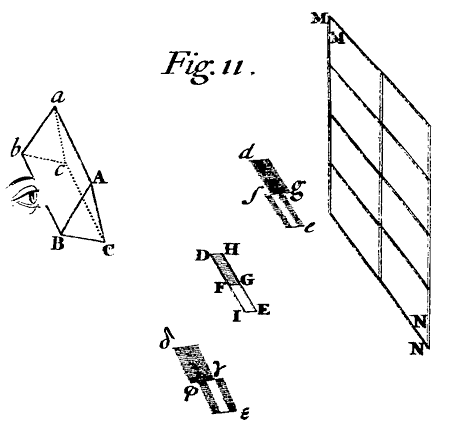
[Image 14] Fig. 12. 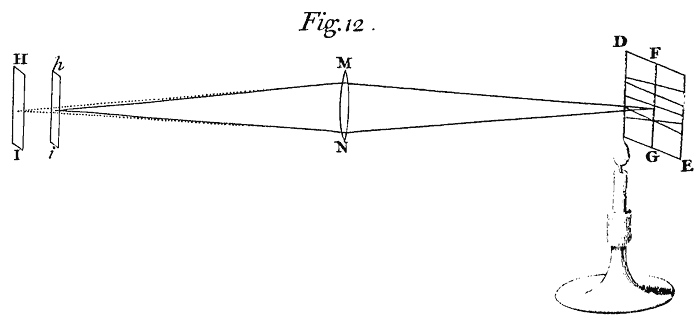
[Image 15] Fig. 13. 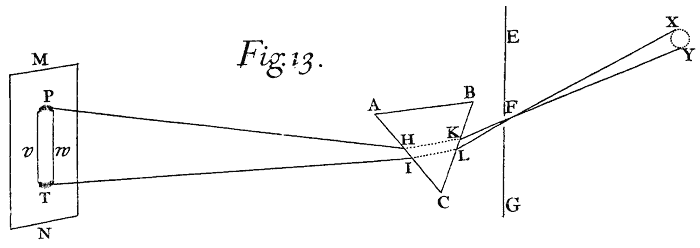
[Image 16] Fig. 14. 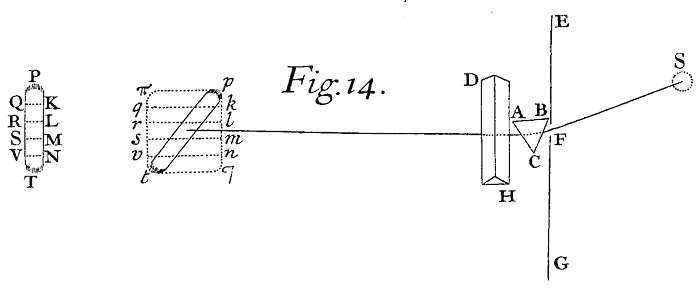
[Image 17] Fig. 15. 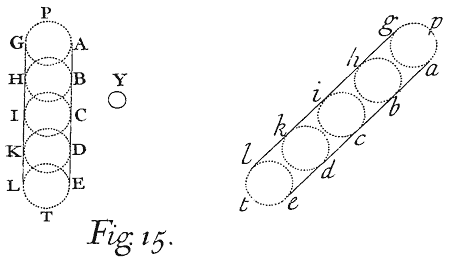
[Image 18] Fig. 16. 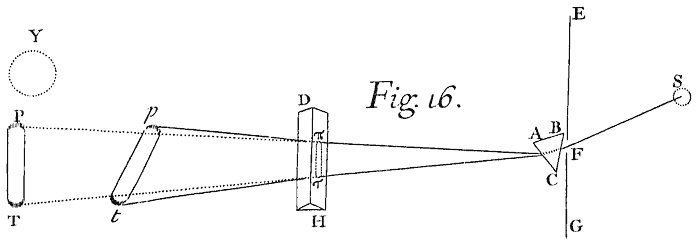
[Image 19] Fig. 17. 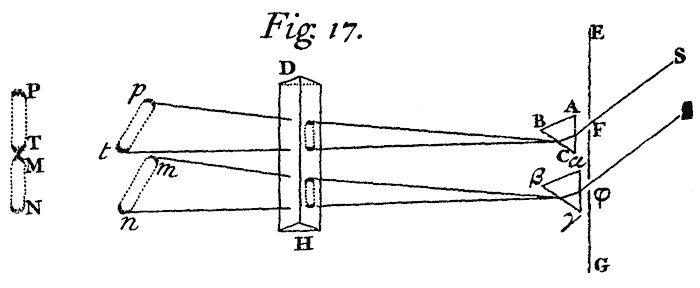
[Image 20] Fig. 18. 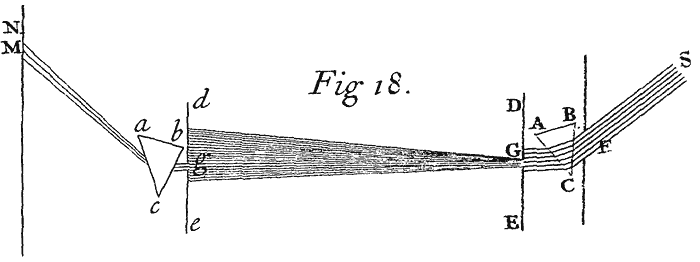
[Image 21] Fig. 19. 
[Image 22] Fig. 17. 
[Image 23] Fig. 20. 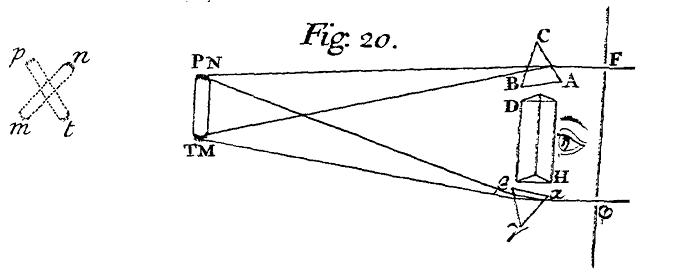
[Image 24] Fig. 21. 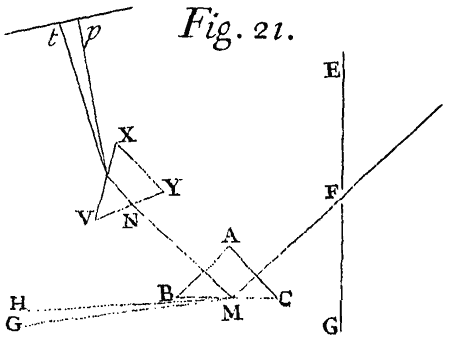
[Image 25] Fig. 22. 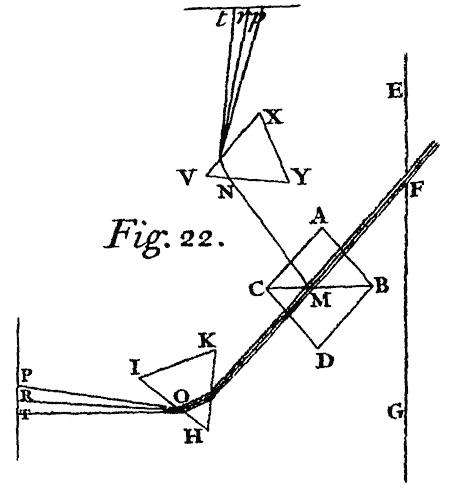
[Image 26] Fig. 22. 
[Image 27] Fig. 23. 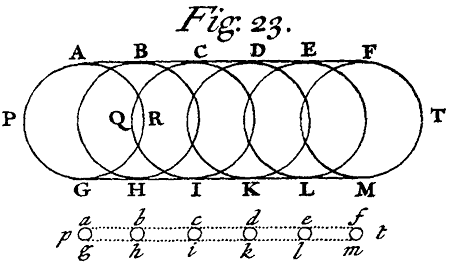
[Image 28] Fig. 23. 
[Image 29] Fig. 23, and 24. 
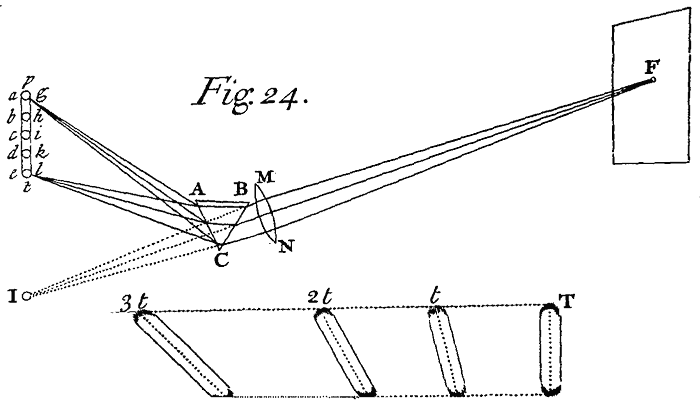
[Image 30] Fig. 24. 
[Image 31] Fig. 25. 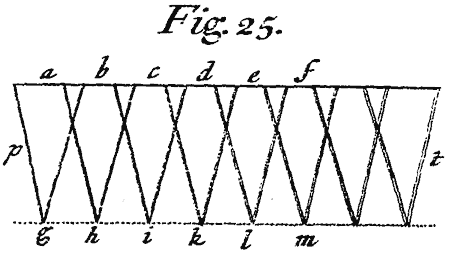
[Image 32] Fig. 26. 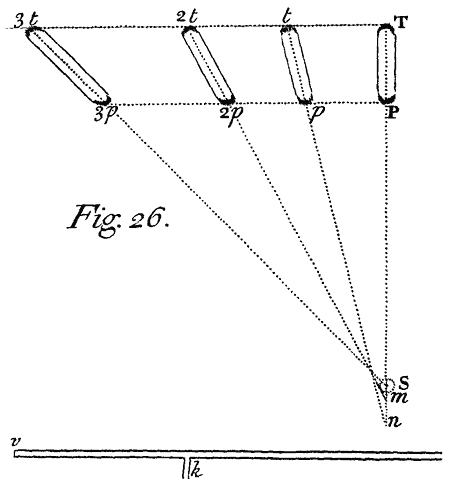
[Image 33] Fig. 1. 
[Image 34] Fig. 27. 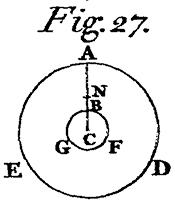
[Image 35] Fig. 28. 
[Image 36] Fig. 29.